Split (1)

train · 782k rows

path stringlengths 7 265	concatenated_notebook stringlengths 46 17M
RTE Playground.ipynb	###Markdown Bag-of-words Models ###Code # the simplest model that just tries to classify by linear combination of averages L0 = nnb.InputLayer(ndim=1) L1 = nnb.InputLayer(ndim=1) L2 = nnb.InputLayer(ndim=1) CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=503, outsize=1, activation_func=nnb.activation.tanh) model = (L0 & L1 & L2) \| CC \| C2 try_model(model, s0a, s1a, s2a, y) # only slightly more complex model that first merges l0, l1, then tries to learn a linear combination of that with l2 L0 = nnb.InputLayer(ndim=1) L1 = nnb.InputLayer(ndim=1) C01 = nnb.ConcatenationModel() C1 = nnb.PerceptronLayer(insize=250, outsize=50) qajoin = (L0 & L1) \| C01 \| C1 L2 = nnb.InputLayer(ndim=1) CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=250, outsize=1, activation_func=nnb.activation.tanh) model = (qajoin & L2) \| CC \| C2 try_model(model, s0a, s1a, s2a, y) # extension of the above with extra hidden layer L0 = nnb.InputLayer(ndim=1) L1 = nnb.InputLayer(ndim=1) C01 = nnb.ConcatenationModel() C1a = nnb.PerceptronLayer(insize=250, outsize=50) C1b = nnb.PerceptronLayer(insize=50, outsize=25, activation_func=nnb.activation.tanh) qajoin = (L0 & L1) \| C01 \| C1a \| C1b L2 = nnb.InputLayer(ndim=1) CC = nnb.ConcatenationModel() C2a = nnb.PerceptronLayer(insize=50+25, outsize=25) C2b = nnb.PerceptronLayer(insize=25, outsize=1, activation_func=nnb.activation.tanh) model = (qajoin & L2) \| CC \| C2a \| C2b try_model(model, s0a, s1a, s2a, y) ###Output Preprocessing... Cost function... Compiling... Training... ~Epoch 1~ [--------- ] Finished. Took 0.0217814326286 minutes. Evaluating... Error = 0.500357608689 New best! ~Epoch 2~ [--------- ] Finished. Took 0.0217702666918 minutes. Evaluating... Error = 0.500007342751 New best! ~Epoch 3~ [--------- ] Finished. Took 0.021881600221 minutes. Evaluating... Error = 0.500145769065 ~Epoch 4~ [--------- ] Finished. Took 0.0218525330226 minutes. Evaluating... Error = 0.500343043051 ~Epoch 5~ [--------- ] Finished. Took 0.0218734184901 minutes. Evaluating... Error = 0.500018127542 ~Epoch 6~ [--------- ] Finished. Took 0.0218481183052 minutes. Evaluating... Error = 0.500029008664 ~Epoch 7~ [--------- ] Finished. Took 0.0223319689433 minutes. Evaluating... Error = 0.501230559823 ~Epoch 8~ [--------- ] Finished. Took 0.0218985676765 minutes. Evaluating... Error = 0.500803193592 ~Epoch 9~ [--------- ] Finished. Took 0.0218106150627 minutes. Evaluating... Error = 0.500096080358 ~Epoch 10~ [--------- ] Finished. Took 0.0218416015307 minutes. Evaluating... Error = 0.500542697909 ~Epoch 11~ [--------- ] Finished. Took 0.0218163013458 minutes. Evaluating... Error = 0.503701656726 ~Epoch 12~ [--------- ] Finished. Took 0.0218620498975 minutes. Evaluating... Error = 0.499996685223 New best! ~Epoch 13~ [--------- ] Finished. Took 0.0218279838562 minutes. Evaluating... Error = 0.500114915747 ~Epoch 14~ [--------- ] Finished. Took 0.021864883105 minutes. Evaluating... Error = 0.50000234246 ~Epoch 15~ [--------- ] Finished. Took 0.0218339165052 minutes. Evaluating... Error = 0.501091637636 ~Epoch 16~ [--------- ] Finished. Took 0.0220268646876 minutes. Evaluating... Error = 0.500141559823 ~Epoch 17~ [--------- ] Finished. Took 0.0218552192052 minutes. Evaluating... Error = 0.501337095868 ~Epoch 18~ [--------- ] Finished. Took 0.0217992186546 minutes. Evaluating... Error = 0.500326763224 ~Epoch 19~ [--------- ] Finished. Took 0.0218602180481 minutes. Evaluating... Error = 0.500073103204 ~Epoch 20~ [--------- ] Finished. Took 0.0218064347903 minutes. Evaluating... Error = 0.500221115396 ~Epoch 21~ [--------- ] Finished. Took 0.0219269990921 minutes. Evaluating... Error = 0.500677313315 ~Epoch 22~ [--------- ] Finished. Took 0.0218431830406 minutes. Evaluating... Error = 0.499999411133 ~Epoch 23~ [--------- ] Finished. Took 0.0218532681465 minutes. Evaluating... Error = 0.500826726601 ~Epoch 24~ [--------- ] Finished. Took 0.0217517852783 minutes. Evaluating... Error = 0.500886390623 ~Epoch 25~ [--------- ] Finished. Took 0.0218867341677 minutes. Evaluating... Error = 0.500462269425 ~Epoch 26~ [--------- ] Finished. Took 0.0217462658882 minutes. Evaluating... Error = 0.501476886195 ~Epoch 27~ [--------- ] Finished. Took 0.0223957339923 minutes. Evaluating... Error = 0.500028026309 ~Epoch 28~ [--------- ] Finished. Took 0.021883781751 minutes. Evaluating... Error = 0.500362921846 ~Epoch 29~ [--------- ] Finished. Took 0.0218784968058 minutes. Evaluating... Error = 0.500223828294 ~Epoch 30~ [--------- ] Finished. Took 0.0222222487132 minutes. Evaluating... Error = 0.502864350179 ~Epoch 31~ [--------- ] Finished. Took 0.0218279361725 minutes. Evaluating... Error = 0.500619307896 ~Epoch 32~ [--------- ] Finished. Took 0.0218044996262 minutes. Evaluating... Error = 0.499987406644 New best! ~Epoch 33~ [--------- ] Finished. Took 0.0221875667572 minutes. Evaluating... Error = 0.500366175275 ~Epoch 34~ [--------- ] Finished. Took 0.0219057679176 minutes. Evaluating... Error = 0.500410528936 ~Epoch 35~ [--------- ] Finished. Took 0.0218756159147 minutes. Evaluating... Error = 0.500048850828 ~Epoch 36~ [--------- ] Finished. Took 0.0217797160149 minutes. Evaluating... Error = 0.500113452477 ~Epoch 37~ [--------- ] Finished. Took 0.0218860348066 minutes. Evaluating... Error = 0.500028451843 ~Epoch 38~ [--------- ] Finished. Took 0.0219083189964 minutes. Evaluating... Error = 0.499986161081 New best! ~Epoch 39~ [--------- ] Finished. Took 0.0220331986745 minutes. Evaluating... Error = 0.501674818963 ~Epoch 40~ [--------- ] Finished. Took 0.0219795306524 minutes. Evaluating... Error = 0.500021788593 ~Epoch 41~ [--------- ] Finished. Took 0.0218236843745 minutes. Evaluating... Error = 0.500132441928 ~Epoch 42~ [--------- ] Finished. Took 0.0218075990677 minutes. Evaluating... Error = 0.499985138935 New best! ~Epoch 43~ [--------- ] Finished. Took 0.0219311475754 minutes. Evaluating... Error = 0.500253047816 ~Epoch 44~ [--------- ] Finished. Took 0.0223954002062 minutes. Evaluating... Error = 0.503078734515 ~Epoch 45~ [--------- ] Finished. Took 0.0218530495962 minutes. Evaluating... Error = 0.499995136601 ~Epoch 46~ [--------- ] Finished. Took 0.0223164161046 minutes. Evaluating... Error = 0.500738841335 ~Epoch 47~ [--------- ] Finished. Took 0.0219388167063 minutes. Evaluating... Error = 0.499974096477 New best! ~Epoch 48~ [--------- ] Finished. Took 0.0218135674795 minutes. Evaluating... Error = 0.500120409531 ~Epoch 49~ [--------- ] Finished. Took 0.0217928806941 minutes. Evaluating... Error = 0.500184527706 ~Epoch 50~ [--------- ] Finished. Took 0.0218890508016 minutes. Evaluating... Error = 0.500130238553 ~Epoch 51~ [--------- ] Finished. Took 0.0220821499825 minutes. Evaluating... Error = 0.50109280612 ~Epoch 52~ [--------- ] Finished. Took 0.0218738516172 minutes. Evaluating... Error = 0.500248211362 ~Epoch 53~ [--------- ] Finished. Took 0.0218495686849 minutes. Evaluating... Error = 0.50014239258 ~Epoch 54~ [--------- ] Finished. Took 0.0218565146128 minutes. Evaluating... Error = 0.50086558956 ~Epoch 55~ [--------- ] Finished. Took 0.0220512986183 minutes. Evaluating... Error = 0.499970071088 New best! ~Epoch 56~ [--------- ] Finished. Took 0.0218093832334 minutes. Evaluating... Error = 0.500149102842 ~Epoch 57~ [--------- ] Finished. Took 0.0220838824908 minutes. Evaluating... Error = 0.500033025376 ~Epoch 58~ [--------- ] Finished. Took 0.0218762477239 minutes. Evaluating... Error = 0.501198219803 ~Epoch 59~ [--------- ] Finished. Took 0.0230452815692 minutes. Evaluating... Error = 0.50012025529 ~Epoch 60~ [--------- ] Finished. Took 0.021840496858 minutes. Evaluating... Error = 0.500077270832 ~Epoch 61~ [--------- ] Finished. Took 0.0218392491341 minutes. Evaluating... Error = 0.50077927355 ~Epoch 62~ [--------- ] Finished. Took 0.0217747489611 minutes. Evaluating... Error = 0.499984892315 ~Epoch 63~ [--------- ] Finished. Took 0.0217939813932 minutes. Evaluating... Error = 0.499997648061 ~Epoch 64~ [--------- ] Finished. Took 0.0217553496361 minutes. Evaluating... Error = 0.500380485899 ~Epoch 65~ [--------- ] Finished. Took 0.0222050984701 minutes. Evaluating... Error = 0.499986363764 ~Epoch 66~ [--------- ] Finished. Took 0.0219154993693 minutes. Evaluating... Error = 0.499977693214 ~Epoch 67~ [--------- ] Finished. Took 0.0222742160161 minutes. Evaluating... Error = 0.50068828969 ~Epoch 68~ [--------- ] Finished. Took 0.0221931139628 minutes. Evaluating... Error = 0.499993818277 ~Epoch 69~ [--------- ] Finished. Took 0.0223215699196 minutes. Evaluating... Error = 0.500456752386 ~Epoch 70~ [--------- ] Finished. Took 0.0218123356501 minutes. Evaluating... Error = 0.501516249963 ~Epoch 71~ [--------- ] Finished. Took 0.022450085481 minutes. Evaluating... Error = 0.500085789755 ~Epoch 72~ [--------- ] Finished. Took 0.0222800334295 minutes. Evaluating... Error = 0.500401278801 ~Epoch 73~ [--------- ] Finished. Took 0.0218959013621 minutes. Evaluating... Error = 0.50036435486 ~Epoch 74~ [--------- ] Finished. Took 0.0217820684115 minutes. Evaluating... Error = 0.502541472291 ~Epoch 75~ [--------- ] Finished. Took 0.0224252978961 minutes. Evaluating... Error = 0.499963902512 New best! ~Epoch 76~ [--------- ] Finished. Took 0.0217240651449 minutes. Evaluating... Error = 0.500101250946 ~Epoch 77~ [--------- ] Finished. Took 0.0217859864235 minutes. Evaluating... Error = 0.50040999318 ~Epoch 78~ [--------- ] Finished. Took 0.0217722177505 minutes. Evaluating... Error = 0.500510304056 ~Epoch 79~ [--------- ] Finished. Took 0.0217543999354 minutes. Evaluating... Error = 0.500318563833 ~Epoch 80~ [--------- ] Finished. Took 0.0223845322927 minutes. Evaluating... Error = 0.499998462164 ~Epoch 81~ [--------- ] Finished. Took 0.0218147158623 minutes. Evaluating... Error = 0.502026415632 ~Epoch 82~ [--------- ] Finished. Took 0.0222399671872 minutes. Evaluating... Error = 0.502093156353 ~Epoch 83~ [--------- ] Finished. Took 0.0217820326487 minutes. Evaluating... Error = 0.500024211545 ~Epoch 84~ [--------- ] Finished. Took 0.0218458970388 minutes. Evaluating... Error = 0.502331249226 ~Epoch 85~ [--------- ] Finished. Took 0.0217954158783 minutes. Evaluating... Error = 0.499950856299 New best! ~Epoch 86~ [--------- ] Finished. Took 0.0223637660344 minutes. Evaluating... Error = 0.500109465447 ~Epoch 87~ [--------- ] Finished. Took 0.0217625339826 minutes. Evaluating... Error = 0.499951075783 ~Epoch 88~ [--------- ] Finished. Took 0.0221950531006 minutes. Evaluating... Error = 0.499984625191 ~Epoch 89~ [--------- ] Finished. Took 0.0217854340871 minutes. Evaluating... Error = 0.499943631552 New best! ~Epoch 90~ [--------- ] Finished. Took 0.0223787148794 minutes. Evaluating... Error = 0.500429406791 ~Epoch 91~ [--------- ] Finished. Took 0.0217892169952 minutes. Evaluating... Error = 0.499942773631 New best! ~Epoch 92~ [--------- ] Finished. Took 0.0224108338356 minutes. Evaluating... Error = 0.500466631022 ~Epoch 93~ [--------- ] Finished. Took 0.0217609643936 minutes. Evaluating... Error = 0.500321091069 ~Epoch 94~ [--------- ] Finished. Took 0.0224106987317 minutes. Evaluating... Error = 0.500188895129 ~Epoch 95~ [--------- ] Finished. Took 0.0217641671499 minutes. Evaluating... Error = 0.501258692385 ~Epoch 96~ [--------- ] Finished. Took 0.0223159313202 minutes. Evaluating... Error = 0.500267478797 ~Epoch 97~ [--------- ] Finished. Took 0.0217929840088 minutes. Evaluating... Error = 0.500833885566 ~Epoch 98~ [--------- ] Finished. Took 0.0219456831614 minutes. Evaluating... Error = 0.500383458707 ~Epoch 99~ [--------- ] Finished. Took 0.0218558192253 minutes. Evaluating... Error = 0.500447765059 ~Epoch 100~ [--------- ] Finished. Took 0.0219075163205 minutes. Evaluating... Error = 0.500164301496 ~Epoch 101~ [--------- ] Finished. Took 0.0217956503232 minutes. Evaluating... Error = 0.500216465245 ~Epoch 102~ [--------- ] Finished. Took 0.0220236817996 minutes. Evaluating... Error = 0.499932070404 New best! ~Epoch 103~ [--------- ] Finished. Took 0.0217332323392 minutes. Evaluating... Error = 0.500514964888 ~Epoch 104~ [--------- ] Finished. Took 0.022004433473 minutes. Evaluating... Error = 0.500646231343 ~Epoch 105~ [--------- ] Finished. Took 0.0222724517186 minutes. Evaluating... Error = 0.500148437788 ~Epoch 106~ [--------- ] Finished. Took 0.0221728165944 minutes. Evaluating... Error = 0.500274829908 ~Epoch 107~ [--------- ] Finished. Took 0.0221629142761 minutes. Evaluating... Error = 0.500846483374 ~Epoch 108~ [--------- ] Finished. Took 0.0219543178876 minutes. Evaluating... Error = 0.501688023001 ~Epoch 109~ [--------- ] Finished. Took 0.0220215161641 minutes. Evaluating... Error = 0.499926322139 New best! ~Epoch 110~ [--------- ] Finished. Took 0.0222080667814 minutes. Evaluating... Error = 0.50008128092 ~Epoch 111~ [--------- ] Finished. Took 0.0218286991119 minutes. Evaluating... Error = 0.500781777389 ~Epoch 112~ [--------- ] Finished. Took 0.0221534848213 minutes. Evaluating... Error = 0.50023895332 ~Epoch 113~ [--------- ] Finished. Took 0.0218267679214 minutes. Evaluating... Error = 0.500057674475 ~Epoch 114~ [--------- ] Finished. Took 0.0218214670817 minutes. Evaluating... Error = 0.500339113468 ~Epoch 115~ [--------- ] Finished. Took 0.0217881321907 minutes. Evaluating... Error = 0.500115919768 ~Epoch 116~ [--------- ] Finished. Took 0.0221712311109 minutes. Evaluating... Error = 0.500773938284 ~Epoch 117~ [--------- ] Finished. Took 0.021998099486 minutes. Evaluating... Error = 0.499916980547 New best! ~Epoch 118~ [--------- ] Finished. Took 0.0217414657275 minutes. Evaluating... Error = 0.500236518758 ~Epoch 119~ [--------- ] Finished. Took 0.0216476639112 minutes. Evaluating... Error = 0.501275343322 ~Epoch 120~ [--------- ] Finished. Took 0.0216891646385 minutes. Evaluating... Error = 0.500820501055 ~Epoch 121~ [--------- ] Finished. Took 0.021661400795 minutes. Evaluating... Error = 0.499966690951 ~Epoch 122~ [--------- ] Finished. Took 0.0222122470538 minutes. Evaluating... Error = 0.500708797497 ~Epoch 123~ [--------- ] Finished. Took 0.0216812650363 minutes. Evaluating... Error = 0.499953660078 ~Epoch 124~ [--------- ] Finished. Took 0.0217606663704 minutes. Evaluating... Error = 0.499911319753 New best! ~Epoch 125~ [--------- ] Finished. Took 0.0218466838201 minutes. Evaluating... Error = 0.499930339418 ~Epoch 126~ [--------- ] Finished. Took 0.0220993836721 minutes. Evaluating... Error = 0.501150152719 ~Epoch 127~ [--------- ] Finished. Took 0.0218068679174 minutes. Evaluating... Error = 0.500139854953 ~Epoch 128~ [--------- ] Finished. Took 0.021918686231 minutes. Evaluating... Error = 0.500142661993 ~Epoch 129~ [--------- ] Finished. Took 0.0218550006549 minutes. Evaluating... Error = 0.49991073876 New best! ~Epoch 130~ [--------- ] Finished. Took 0.0221742153168 minutes. Evaluating... Error = 0.500179002928 ~Epoch 131~ [--------- ] Finished. Took 0.0217227856318 minutes. Evaluating... Error = 0.50179531013 ~Epoch 132~ [--------- ] Finished. Took 0.0219247659047 minutes. Evaluating... Error = 0.500713304135 ~Epoch 133~ [--------- ] Finished. Took 0.0218584696452 minutes. Evaluating... Error = 0.499900592966 New best! ~Epoch 134~ [--------- ] Finished. Took 0.0218326489131 minutes. Evaluating... Error = 0.501571134841 ~Epoch 135~ [--------- ] Finished. Took 0.0217429637909 minutes. Evaluating... Error = 0.500682062652 ~Epoch 136~ [--------- ] Finished. Took 0.0218285004298 minutes. Evaluating... Error = 0.499940946878 ~Epoch 137~ [--------- ] Finished. Took 0.0218677163124 minutes. Evaluating... Error = 0.500320651113 ~Epoch 138~ [--------- ] Finished. Took 0.0218434810638 minutes. Evaluating... Error = 0.499903030568 ~Epoch 139~ [--------- ] Finished. Took 0.0219102342923 minutes. Evaluating... Error = 0.499947078422 ~Epoch 140~ [--------- ] Finished. Took 0.021824836731 minutes. Evaluating... Error = 0.499934056377 ~Epoch 141~ [--------- ] Finished. Took 0.0220553994179 minutes. Evaluating... Error = 0.501482778227 ~Epoch 142~ [--------- ] Finished. Took 0.0219018022219 minutes. Evaluating... Error = 0.499918216915 ~Epoch 143~ [--------- ] Finished. Took 0.0221315145493 minutes. Evaluating... Error = 0.499931968784 ~Epoch 144~ [--------- ] Finished. Took 0.0219853838285 minutes. Evaluating... Error = 0.50260866734 ~Epoch 145~ [--------- ] Finished. Took 0.0217618703842 minutes. Evaluating... Error = 0.499908084401 ~Epoch 146~ [--------- ] Finished. Took 0.0217352986336 minutes. Evaluating... Error = 0.501762268779 ~Epoch 147~ [--------- ] Finished. Took 0.0217153668404 minutes. Evaluating... Error = 0.499888432519 New best! ~Epoch 148~ [--------- ] Finished. Took 0.0217912157377 minutes. Evaluating... Error = 0.49991514925 ~Epoch 149~ [--------- ] Finished. Took 0.0221135814985 minutes. Evaluating... Error = 0.500508044643 ~Epoch 150~ [--------- ] Finished. Took 0.0217555681864 minutes. Evaluating... Error = 0.499878423691 New best! ~Epoch 151~ [--------- ] Finished. Took 0.0217488646507 minutes. Evaluating... Error = 0.501063758992 ~Epoch 152~ [--------- ] Finished. Took 0.0219927668571 minutes. Evaluating... Error = 0.500039604084 ~Epoch 153~ [--------- ] Finished. Took 0.0223458488782 minutes. Evaluating... Error = 0.500237799145 ~Epoch 154~ [--------- ] Finished. Took 0.021802063783 minutes. Evaluating... Error = 0.499974968699 ~Epoch 155~ [--------- ] Finished. Took 0.0217899004618 minutes. Evaluating... Error = 0.499871304411 New best! ~Epoch 156~ [--------- ] Finished. Took 0.0222612182299 minutes. Evaluating... Error = 0.500234555797 ~Epoch 157~ [--------- ] Finished. Took 0.0217857321103 minutes. Evaluating... Error = 0.499989003734 ~Epoch 158~ [--------- ] Finished. Took 0.0217375675837 minutes. Evaluating... Error = 0.500779556462 ~Epoch 159~ [--------- ] Finished. Took 0.0217485666275 minutes. Evaluating... Error = 0.500264661635 ~Epoch 160~ [--------- ] Finished. Took 0.0220564325651 minutes. Evaluating... Error = 0.49995073226 ~Epoch 161~ [--------- ] Finished. Took 0.0217218160629 minutes. Evaluating... Error = 0.50009481034 ~Epoch 162~ [--------- ] Finished. Took 0.0223880847295 minutes. Evaluating... Error = 0.49990221258 ~Epoch 163~ [--------- ] Finished. Took 0.0219489177068 minutes. Evaluating... Error = 0.499990916639 ~Epoch 164~ [--------- ] Finished. Took 0.0217112660408 minutes. Evaluating... Error = 0.49985870774 New best! ~Epoch 165~ [--------- ] Finished. Took 0.0219016313553 minutes. Evaluating... Error = 0.502086411787 ~Epoch 166~ [--------- ] Finished. Took 0.0220451315244 minutes. Evaluating... Error = 0.49993755507 ~Epoch 167~ [--------- ] Finished. Took 0.0217249512672 minutes. Evaluating... Error = 0.50059977622 ~Epoch 168~ [--------- ] Finished. Took 0.0222033818563 minutes. Evaluating... Error = 0.500236614824 ~Epoch 169~ [--------- ] Finished. Took 0.0217567841212 minutes. Evaluating... Error = 0.499930695424 ~Epoch 170~ [--------- ] Finished. Took 0.0217022657394 minutes. Evaluating... Error = 0.499936242315 ~Epoch 171~ [--------- ] Finished. Took 0.0220777829488 minutes. Evaluating... Error = 0.499943283797 ~Epoch 172~ [--------- ] Finished. Took 0.021776398023 minutes. Evaluating... Error = 0.499881586553 ~Epoch 173~ [--------- ] Finished. Took 0.0220500866572 minutes. Evaluating... Error = 0.499841521847 New best! ~Epoch 174~ [--------- ] Finished. Took 0.021843679746 minutes. Evaluating... Error = 0.500319624653 ~Epoch 175~ [--------- ] Finished. Took 0.0219239989916 minutes. Evaluating... Error = 0.499876892588 ~Epoch 176~ [--------- ] Finished. Took 0.0221277674039 minutes. Evaluating... Error = 0.499884155379 ~Epoch 177~ [--------- ] Finished. Took 0.0221422672272 minutes. Evaluating... Error = 0.50003074753 ~Epoch 178~ [--------- ] Finished. Took 0.0217188676198 minutes. Evaluating... Error = 0.500425126917 ~Epoch 179~ [--------- ] Finished. Took 0.0217609683673 minutes. Evaluating... Error = 0.500124382613 ~Epoch 180~ [--------- ] Finished. Took 0.0216934164365 minutes. Evaluating... Error = 0.499967479468 ~Epoch 181~ [--------- ] Finished. Took 0.0221087495486 minutes. Evaluating... Error = 0.499938273837 ~Epoch 182~ [--------- ] Finished. Took 0.0218360026677 minutes. Evaluating... Error = 0.499844550209 ~Epoch 183~ [--------- ] Finished. Took 0.0222194512685 minutes. Evaluating... Error = 0.499820791011 New best! ~Epoch 184~ [--------- ] Finished. Took 0.0217803200086 minutes. Evaluating... Error = 0.500965870433 ~Epoch 185~ [--------- ] Finished. Took 0.0223155140877 minutes. Evaluating... Error = 0.499817250333 New best! ~Epoch 186~ [--------- ] Finished. Took 0.0218931317329 minutes. Evaluating... Error = 0.500598134078 ~Epoch 187~ [--------- ] Finished. Took 0.0218052188555 minutes. Evaluating... Error = 0.500309503611 ~Epoch 188~ [--------- ] Finished. Took 0.0216904004415 minutes. Evaluating... Error = 0.499840548108 ~Epoch 189~ [--------- ] Finished. Took 0.0218406001727 minutes. Evaluating... Error = 0.50047814393 ~Epoch 190~ [--------- ] Finished. Took 0.0216904481252 minutes. Evaluating... Error = 0.500518066015 ~Epoch 191~ [--------- ] Finished. Took 0.0217192490896 minutes. Evaluating... Error = 0.500123707496 ~Epoch 192~ [--------- ] Finished. Took 0.0223292509715 minutes. Evaluating... Error = 0.499802596093 New best! ~Epoch 193~ [--------- ] Finished. Took 0.0217316865921 minutes. Evaluating... Error = 0.500608947229 ~Epoch 194~ [--------- ] Finished. Took 0.0218078176181 minutes. Evaluating... Error = 0.499852098886 ~Epoch 195~ [--------- ] Finished. Took 0.021713300546 minutes. Evaluating... Error = 0.499825558896 ~Epoch 196~ [--------- ] Finished. Took 0.0220940828323 minutes. Evaluating... Error = 0.50015228768 ~Epoch 197~ [--------- ] Finished. Took 0.0218266487122 minutes. Evaluating... Error = 0.499791890101 New best! ~Epoch 198~ [--------- ] Finished. Took 0.0217582146327 minutes. Evaluating... Error = 0.499838253324 ~Epoch 199~ [--------- ] Finished. Took 0.0216853817304 minutes. Evaluating... Error = 0.500524829256 ~Epoch 200~ [--------- ] Finished. Took 0.0217870473862 minutes. Evaluating... Error = 0.499790650898 New best! Finished! Best error: 0.499790650898 Checking... 0 [ 0.00058826] [-1] 1 [ 0.00492114] [1] 2 [-0.00190044] [-1] 3 [-0.00193494] [-1] 4 [-0.00560141] [-1] 5 [-0.00566186] [-1] 6 [-0.00692472] [1] Accuracy: train 0.526970227671 val 0.519014084507 val_base 0.5 ###Markdown RNN Models ###Code # a more complex model that does away with the averaging of words in sentences, instead using an RNN: # [:200] subset for fast sanity check; without intermediate perceptrons # FIRST SUCCESS-LOOKING STUFF!!! L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model = (L0 & L1 & L2) \| CC \| C2 try_model(model, s0[:200], s1[:200], s2[:200], y[:200]) # cautious regularization even better L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model = (L0 & L1 & L2) \| CC \| C2 try_model(model, s0[:200], s1[:200], s2[:200], y[:200], L2_reg=1.0/(350+10)) # moar experiments; current baseline L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model_b200 = (L0 & L1 & L2) \| CC \| C2 try_model(model_b200, s0[:200], s1[:200], s2[:200], y[:200], L2_reg=1e-3) # moar experiments # XXX: this is invalid way to specify activation_func, why did it have an effect? L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, activation_func=nnb.activation.tanh)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, activation_func=nnb.activation.tanh)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, activation_func=nnb.activation.tanh)[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model = (L0 & L1 & L2) \| CC \| C2 try_model(model, s0[:200], s1[:200], s2[:200], y[:200], L2_reg=1e-3) # moar experiments L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model = (L0 & L1 & L2) \| CC \| C2 try_model(model, s0[:200], s1[:200], s2[:200], y[:200], L2_reg=1e-3) # moar experiments L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=5)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=5)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=5)[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=35, outsize=1, activation_func=nnb.activation.tanh) model = (L0 & L1 & L2) \| CC \| C2 try_model(model, s0[:200], s1[:200], s2[:200], y[:200], L2_reg=1e-3) # moar experiments - try hierarchy L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] C1 = nnb.PerceptronLayer(insize=210, outsize=10) #, activation_func=nnb.activation.ReLU) qamodel = (L0 & L1) \| nnb.ConcatenationModel() \| C1 C2 = nnb.PerceptronLayer(insize=210, outsize=1, activation_func=nnb.activation.tanh) model = (qamodel & L2) \| nnb.ConcatenationModel() \| C2 try_model(model, s0[:200], s1[:200], s2[:200], y[:200], L2_reg=1e-4) # moar experiments L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, h0=np.zeros(shape=(10,), dtype=theano.config.floatX), model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, h0=np.zeros(shape=(10,), dtype=theano.config.floatX), model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, h0=np.zeros(shape=(10,), dtype=theano.config.floatX), model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model = (L0 & L1 & L2) \| CC \| C2 try_model(model, s0[:200], s1[:200], s2[:200], y[:200], L2_reg=1e-3) # moar experiments L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model = (L0 & L1 & L2) \| CC \| C2 try_model(model, s0[:200], s1[:200], s2[:200], y[:200], L2_reg=1e-3) ###Output Preprocessing... Cost function... Compiling... Training... ~Epoch 1~ [----------] Finished. Took 0.0845589836438 minutes. Evaluating... Error = 0.501358014788 New best! ~Epoch 2~ [----------] Finished. Took 0.085214749972 minutes. Evaluating... Error = 0.499122361749 New best! ~Epoch 3~ [----------] Finished. Took 0.0838472008705 minutes. Evaluating... Error = 0.498413014051 New best! ~Epoch 4~ [----------] Finished. Took 0.0840673685074 minutes. Evaluating... Error = 0.503338874358 ~Epoch 5~ [----------] Finished. Took 0.0820211172104 minutes. Evaluating... Error = 0.497372318792 New best! ~Epoch 6~ [----------] Finished. Took 0.0860601345698 minutes. Evaluating... Error = 0.499694159084 ~Epoch 7~ [----------] Finished. Took 0.0840774178505 minutes. Evaluating... Error = 0.529186830661 ~Epoch 8~ [----------] Finished. Took 0.0852189024289 minutes. Evaluating... Error = 0.513377143498 ~Epoch 9~ [----------] Finished. Took 0.0835673809052 minutes. Evaluating... Error = 0.511034395032 ~Epoch 10~ [----------] Finished. Took 0.0840396324793 minutes. Evaluating... Error = 0.513910986519 ~Epoch 11~ [----------] Finished. Took 0.0835260828336 minutes. Evaluating... Error = 0.516893362173 ~Epoch 12~ [----------] Finished. Took 0.0843402862549 minutes. Evaluating... Error = 0.496697852577 New best! ~Epoch 13~ [----------] Finished. Took 0.0834467689196 minutes. Evaluating... Error = 0.502118085194 ~Epoch 14~ [----------] Finished. Took 0.0841917157173 minutes. Evaluating... Error = 0.5153067669 ~Epoch 15~ [----------] Finished. Took 0.0831967155139 minutes. Evaluating... Error = 0.528749733759 ~Epoch 16~ [----------] Finished. Took 0.0843673507373 minutes. Evaluating... Error = 0.551287876461 ~Epoch 17~ [----------] Finished. Took 0.0841631174088 minutes. Evaluating... Error = 0.518850289553 ~Epoch 18~ [----------] Finished. Took 0.0846482316653 minutes. Evaluating... Error = 0.573369384666 ~Epoch 19~ [----------] Finished. Took 0.0868474841118 minutes. Evaluating... Error = 0.53091702901 ~Epoch 20~ [----------] Finished. Took 0.0867787162463 minutes. Evaluating... Error = 0.60153466329 ~Epoch 21~ [----------] Finished. Took 0.088539981842 minutes. Evaluating... Error = 0.515277911859 ~Epoch 22~ [----------] Finished. Took 0.0889196157455 minutes. Evaluating... Error = 0.636672478437 ~Epoch 23~ [----------] Finished. Took 0.0898417512576 minutes. Evaluating... Error = 0.729162530904 ~Epoch 24~ [----------] Finished. Took 0.0901450355848 minutes. Evaluating... Error = 0.623846895563 ~Epoch 25~ [----------] Finished. Took 0.092857114474 minutes. Evaluating... Error = 0.698496320543 ~Epoch 26~ [----------] Finished. Took 0.0876817822456 minutes. Evaluating... Error = 0.732373465847 ~Epoch 27~ [----------] Finished. Took 0.0839065512021 minutes. Evaluating... Error = 0.755499440767 ~Epoch 28~ [----------] Finished. Took 0.0830939809481 minutes. Evaluating... Error = 0.78981953489 ~Epoch 29~ [----------] Finished. Took 0.0883158167203 minutes. Evaluating... Error = 0.679129510006 ~Epoch 30~ [----------] Finished. Took 0.0870797673861 minutes. Evaluating... Error = 0.804682922273 ~Epoch 31~ [----------] Finished. Took 0.0868611812592 minutes. Evaluating... Error = 0.784442138253 ~Epoch 32~ [----------] Finished. Took 0.086023469766 minutes. Evaluating... Error = 0.775464585936 ~Epoch 33~ [----------] Finished. Took 0.0840981523196 minutes. Evaluating... Error = 0.760805673419 ~Epoch 34~ [----------] Finished. Took 0.0836679498355 minutes. Evaluating... Error = 0.84882995017 ~Epoch 35~ [----------] Finished. Took 0.0840958833694 minutes. Evaluating... Error = 0.773058663099 ~Epoch 36~ [----------] Finished. Took 0.0837616165479 minutes. Evaluating... Error = 0.68016136261 ~Epoch 37~ [----------] Finished. Took 0.0842925667763 minutes. Evaluating... Error = 0.873555682603 ~Epoch 38~ [----------] Finished. Took 0.0836460828781 minutes. Evaluating... Error = 0.893437515041 ~Epoch 39~ [----------] Finished. Took 0.0862747351329 minutes. Evaluating... Error = 0.895786164728 ~Epoch 40~ [----------] Finished. Took 0.084677751859 minutes. Evaluating... Error = 0.828187588018 ~Epoch 41~ [----------] Finished. Took 0.0849760174751 minutes. Evaluating... Error = 0.786189578228 ~Epoch 42~ [----------] Finished. Took 0.0907589038213 minutes. Evaluating... Error = 0.818217729819 ~Epoch 43~ [----------] Finished. Took 0.0885839184125 minutes. Evaluating... Error = 0.876503465673 ~Epoch 44~ [----------] Finished. Took 0.0891054352125 minutes. Evaluating... Error = 0.894827768164 ~Epoch 45~ [----------] Finished. Took 0.0853153149287 minutes. Evaluating... Error = 0.717912823448 ~Epoch 46~ [----------] Finished. Took 0.0844216982524 minutes. Evaluating... Error = 0.83479353266 ~Epoch 47~ [----------] Finished. Took 0.0853721499443 minutes. Evaluating... Error = 0.908505694955 ~Epoch 48~ [----------] Finished. Took 0.0884340365728 minutes. Evaluating... Error = 0.912132571555 ~Epoch 49~ [----------] Finished. Took 0.0896174867948 minutes. Evaluating... Error = 0.863745081854 ~Epoch 50~ [----------] Finished. Took 0.0900812149048 minutes. Evaluating... Error = 0.914620715387 ~Epoch 51~ [----------] Finished. Took 0.0896432518959 minutes. Evaluating... Error = 0.889432233976 ~Epoch 52~ [----------] Finished. Took 0.0855853676796 minutes. Evaluating... Error = 0.802259311319 Finished! Best error: 0.496697852577 Checking... 0 [-0.67457136] [-1] 1 [ 0.08242677] [1] 2 [ 0.3172713] [-1] 3 [-0.41661634] [-1] 4 [-0.75236761] [-1] 5 [-0.72149042] [-1] 6 [-0.09718985] [1] Accuracy: train 0.792372881356 val 0.55 val_base 0.5 ###Markdown RNN Models (full dataset) ###Code L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model0 = (L0 & L1 & L2) \| CC \| C2 try_model(model0, s0, s1, s2, y, L2_reg=1e-3) L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=20)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=20)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=20)[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=320, outsize=1, activation_func=nnb.activation.tanh) model1 = (L0 & L1 & L2) \| CC \| C2 try_model(model1, s0, s1, s2, y, L2_reg=1e-3) L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model2 = (L0 & L1 & L2) \| CC \| C2 try_model(model2, s0, s1, s2, y, L2_reg=1e-3) L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=20, model=nnb.SimpleRecurrence(insize=50, outsize=20, activation_func=nnb.activation.ReLU))[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=20, model=nnb.SimpleRecurrence(insize=50, outsize=20, activation_func=nnb.activation.ReLU))[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=20, model=nnb.SimpleRecurrence(insize=50, outsize=20, activation_func=nnb.activation.ReLU))[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=320, outsize=1, activation_func=nnb.activation.tanh) model4 = (L0 & L1 & L2) \| CC \| C2 try_model(model4, s0, s1, s2, y, L2_reg=1e-4) L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] CC = nnb.ConcatenationModel() C1 = nnb.PerceptronLayer(insize=310, outsize=10, activation_func=nnb.activation.ReLU) C2 = nnb.PerceptronLayer(insize=10, outsize=1, activation_func=nnb.activation.tanh) model5 = (L0 & L1 & L2) \| CC \| C1 \| C2 try_model(model5, s0, s1, s2, y, L2_reg=1e-3) L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10)[-1] C1 = nnb.PerceptronLayer(insize=210, outsize=10) #, activation_func=nnb.activation.ReLU) qamodel = (L0 & L1) \| nnb.ConcatenationModel() \| C1 C2 = nnb.PerceptronLayer(insize=210, outsize=1, activation_func=nnb.activation.tanh) model3 = (qamodel & L2) \| nnb.ConcatenationModel() \| C2 try_model(model3, s0, s1, s2, y, L2_reg=1e-4) L0 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L1 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] L2 = nnb.InputLayer(ndim=2) \| nnb.RecurrentNeuralNetwork(insize=50, outsize=10, model=nnb.SimpleRecurrence(insize=50, outsize=10, activation_func=nnb.activation.ReLU))[-1] CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model6 = (L0 & L1 & L2) \| CC \| C2 try_model(model6, s0, s1, s2, y, L2_reg=1e-4) ###Output Preprocessing... Cost function... Compiling... Training... ~Epoch 1~ [--------- ] Finished. Took 2.25736728112 minutes. Evaluating... Error = 0.500083714276 New best! ~Epoch 2~ [--------- ] Finished. Took 2.20320586761 minutes. Evaluating... Error = 0.500081086591 New best! ~Epoch 3~ [--------- ] Finished. Took 2.61474933227 minutes. Evaluating... Error = 0.50009305823 ~Epoch 4~ [--------- ] Finished. Took 2.33273438613 minutes. Evaluating... Error = 0.500091675891 ~Epoch 5~ [--------- ] Finished. Took 2.44618324836 minutes. Evaluating... Error = 0.500076664674 New best! ~Epoch 6~ [--------- ] Finished. Took 2.35433656772 minutes. Evaluating... Error = 0.500079727774 ~Epoch 7~ [--------- ] Finished. Took 2.37073853413 minutes. Evaluating... Error = 0.500073095526 New best! ~Epoch 8~ [--------- ] Finished. Took 2.47728745143 minutes. Evaluating... Error = 0.500111267567 ~Epoch 9~ [--------- ] Finished. Took 2.66203231812 minutes. Evaluating... Error = 0.500032738551 New best! ~Epoch 10~ [--------- ] Finished. Took 2.5184095184 minutes. Evaluating... Error = 0.500023613986 New best! ~Epoch 11~ [--------- ] Finished. Took 4.14127526681 minutes. Evaluating... Error = 0.50000120968 New best! ~Epoch 12~ [--------- ] Finished. Took 2.52550470034 minutes. Evaluating... Error = 0.500002622471 ~Epoch 13~ [--------- ] Finished. Took 2.67198703289 minutes. Evaluating... Error = 0.499958107676 New best! ~Epoch 14~ [--------- ] Finished. Took 2.74413658381 minutes. Evaluating... Error = 0.499936681747 New best! ~Epoch 15~ [--------- ] Finished. Took 2.81313434839 minutes. Evaluating... Error = 0.499901946981 New best! ~Epoch 16~ [--------- ] Finished. Took 2.67671768268 minutes. Evaluating... Error = 0.499897252024 New best! ~Epoch 17~ [--------- ] Finished. Took 2.62144664923 minutes. Evaluating... Error = 0.499860417806 New best! ~Epoch 18~ [--------- ] Finished. Took 2.57571214835 minutes. Evaluating... Error = 0.499842130654 New best! ~Epoch 19~ [--------- ] Finished. Took 2.90705345074 minutes. Evaluating... Error = 0.499838925428 New best! ~Epoch 20~ [--------- ] Finished. Took 2.30370981693 minutes. Evaluating... Error = 0.499845050802 ~Epoch 21~ [--------- ] Finished. Took 2.51796194712 minutes. Evaluating... Error = 0.499778796457 New best! ~Epoch 22~ [--------- ] Finished. Took 3.23842129707 minutes. Evaluating... Error = 0.499772513608 New best! ~Epoch 23~ [--------- ] Finished. Took 3.12773536841 minutes. Evaluating... Error = 0.4998453114 ~Epoch 24~ [--------- ] Finished. Took 3.31404003302 minutes. Evaluating... Error = 0.499752632384 New best! ~Epoch 25~ [--------- ] Finished. Took 3.33617029985 minutes. Evaluating... Error = 0.499750475177 New best! ~Epoch 26~ [--------- ] Finished. Took 3.13705224991 minutes. Evaluating... Error = 0.500087978367 ~Epoch 27~ [--------- ] Finished. Took 3.12288286686 minutes. Evaluating... Error = 0.499873382619 ~Epoch 28~ [--------- ] Finished. Took 3.34401575327 minutes. Evaluating... Error = 0.49985212135 ~Epoch 29~ [--------- ] Finished. Took 3.2355145812 minutes. Evaluating... Error = 0.499898631061 ~Epoch 30~ [--------- ] Finished. Took 3.11980156501 minutes. Evaluating... Error = 0.499919716715 ~Epoch 31~ [--------- ] Finished. Took 3.22553378344 minutes. Evaluating... Error = 0.500108431683 ~Epoch 32~ [--------- ] Finished. Took 3.11567056576 minutes. Evaluating... Error = 0.500173625301 ~Epoch 33~ [--------- ] Finished. Took 3.34783183336 minutes. Evaluating... Error = 0.500298212851 ~Epoch 34~ [--------- ] Finished. Took 3.21156521638 minutes. Evaluating... Error = 0.500317659938 ~Epoch 35~ [--------- ] Finished. Took 3.07297173341 minutes. Evaluating... Error = 0.500812579884 ~Epoch 36~ [--------- ] Finished. Took 3.32974489927 minutes. Evaluating... Error = 0.500539165705 ~Epoch 37~ [--------- ] Finished. Took 3.15928423405 minutes. Evaluating... Error = 0.500765486903 ~Epoch 38~ [--------- ] Finished. Took 2.08131418228 minutes. Evaluating... Error = 0.500963144486 ~Epoch 39~ [--------- ] Finished. Took 2.09305893183 minutes. Evaluating... Error = 0.501466994263 ~Epoch 40~ [--------- ] Finished. Took 2.11660449902 minutes. Evaluating... Error = 0.501630788696 ~Epoch 41~ [--------- ] Finished. Took 2.36993528207 minutes. Evaluating... Error = 0.501516149128 ~Epoch 42~ [--------- ] Finished. Took 3.41155430079 minutes. Evaluating... Error = 0.501913587645 ~Epoch 43~ [--------- ] Finished. Took 3.18511890173 minutes. Evaluating... Error = 0.502506958305 ~Epoch 44~ [--------- ] Finished. Took 2.49764923652 minutes. Evaluating... Error = 0.502246989136 ~Epoch 45~ [--------- ] Finished. Took 2.11711676915 minutes. Evaluating... Error = 0.502602851546 ~Epoch 46~ [--------- ] Finished. Took 2.07267919779 minutes. Evaluating... Error = 0.50303508568 ~Epoch 47~ [--------- ] Finished. Took 2.1161740462 minutes. Evaluating... Error = 0.503095908598 ~Epoch 48~ [--------- ] Finished. Took 2.07570571502 minutes. Evaluating... Error = 0.503421017881 ~Epoch 49~ [--------- ] Finished. Took 2.07219626506 minutes. Evaluating... Error = 0.503691677979 ~Epoch 50~ [--------- ] Finished. Took 2.07420936823 minutes. Evaluating... Error = 0.504012745602 ~Epoch 51~ [--------- ] Finished. Took 2.27226396799 minutes. Evaluating... Error = 0.504206489885 ~Epoch 52~ [--------- ] Finished. Took 2.10213343302 minutes. Evaluating... Error = 0.504677581757 ~Epoch 53~ [--------- ] Finished. Took 2.1010071675 minutes. Evaluating... Error = 0.50539388479 ~Epoch 54~ [--------- ] Finished. Took 2.10576785008 minutes. Evaluating... Error = 0.505327514181 ~Epoch 55~ [--------- ] Finished. Took 2.17885338465 minutes. Evaluating... Error = 0.505773204476 ~Epoch 56~ [--------- ] Finished. Took 2.12705081701 minutes. Evaluating... Error = 0.506065245363 ~Epoch 57~ [--------- ] Finished. Took 2.18036298354 minutes. Evaluating... Error = 0.509501219699 ~Epoch 58~ [--------- ] Finished. Took 2.08853040139 minutes. Evaluating... Error = 0.506572791008 ~Epoch 59~ [--------- ] Finished. Took 2.08637793461 minutes. Evaluating... Error = 0.50738068987 ~Epoch 60~ [--------- ] Finished. Took 2.07309718529 minutes. Evaluating... Error = 0.506986624246 ~Epoch 61~ [--------- ] Finished. Took 2.20610108376 minutes. Evaluating... Error = 0.509942387662 ~Epoch 62~ [--------- ] Finished. Took 2.24246125221 minutes. Evaluating... Error = 0.50708947814 ~Epoch 63~ [--------- ] Finished. Took 2.26481823126 minutes. Evaluating... Error = 0.507300805725 ~Epoch 64~ [--------- ] Finished. Took 2.34024781386 minutes. Evaluating... Error = 0.508718328823 ~Epoch 65~ [--------- ] Finished. Took 2.1144669493 minutes. Evaluating... Error = 0.508244507692 Finished! Best error: 0.499750475177 Checking... 0 [ 0.00606586] [-1] 1 [ 0.0079491] [1] 2 [ 9.13063618e-05] [-1] 3 [ 0.01027014] [-1] 4 [ 0.02585167] [-1] 5 [ 0.02105067] [-1] 6 [ 0.08665964] [1] Accuracy: train 0.543607705779 val 0.514084507042 val_base 0.5 ###Markdown RNN partial train, full val ###Code def check_model(model, s0, s1, s2, y, val_on_train=False): y = y2-1 # classify as -1/+1 for tanh activation n = s0.shape[0] tdata = [[s0[i], s1[i], s2[i], np.array([y[i]], dtype='int32')] for i in range(n)] n_train = int(n0.8) if not val_on_train else 0 if n_train > 0: tdata_train = balance_dataset(tdata[:n_train], y[:n_train]) tdata_val = balance_dataset(tdata[n_train:], y[n_train:]) else: n_train = n tdata_train = balance_dataset(tdata, y) tdata_val = balance_dataset(tdata, y) ff = model.compile() def eval_dataset(ff, tdata): return np.array([ff(tdata[i][0], tdata[i][1], tdata[i][2])[0] for i in range(len(tdata))]) def accuracy(tdata, yy): y = np.array([t[-1][0] for t in tdata]) n_cor = np.sum(y[yy > 0]+1)/2 + np.sum(-y[yy < 0]+1)/2 return n_cor / float(np.shape(yy)[0]) print('Accuracy:', 'train', accuracy(tdata_train, eval_dataset(ff, tdata_train)), 'val', accuracy(tdata_val, eval_dataset(ff, tdata_val)), 'val_base', accuracy(tdata_val, np.zeros(np.shape(tdata_val)[0])-1)) check_model(model2, s0[500:1500], s1[500:1500], s2[500:1500], y[500:1500]) check_model(model_b200, s0, s1, s2, y) # CNN experiment L = [] for i in range(3): L.append(nnb.InputLayer(ndim=2) \| nnb.ConvolutionalLayer(insize=50, window=3, outsize=10, activation_func=nnb.activation.ReLU) \| nnb.MaxPoolingLayer(window=1)[0]) CC = nnb.ConcatenationModel() C2 = nnb.PerceptronLayer(insize=310, outsize=1, activation_func=nnb.activation.tanh) model = (L[0] & L[1] & L[2]) \| CC \| C2 model.compile() try_model(model, s0[:200], s1[:200], s2[:200], y[:200]) theano.config.exception_verbosity = 'high' import cPickle with open('model2.pkl', 'w') as f: cPickle.dump(model2, f, protocol=cPickle.HIGHEST_PROTOCOL) with open('model_b200.pkl', 'w') as f: cPickle.dump(model_b200, f, protocol=cPickle.HIGHEST_PROTOCOL) ###Output _____no_output_____
experiments/test.ipynb	###Markdown Value function is given by:$$v_\pi(s) \triangleq \mathbb{E}_\pi\left[ \sum_{k=0}^\infty \gamma^k r(s_{t+k+1}) \mid s_t = s\right]$$Therfore, for a given policy we can approximate this by,$$v_\pi(s) \approx \frac{1}{\|M\|} \sum_{i=1}^M\left[ r(s) + r(s') + \dots \mid T, \pi\right];\qquad\qquad \tau_i \sim \pi$$This approximation will have much lower variance for a deterministic policy, and will be exact up to numerical rounding for the case of a deterministic policy AND detemrinistic dynamics. ###Code def approx_state_value(pi, s, num_samples=1, gamma=1.0, r_custom=None): """Approximately compute the value of s under pi Args: pi (class): Policy object with a .predict() method matching the stable-baselines API s (numpy array): State to estimate value from num_samples (int): Number of samples to estimate value with. For determinstic policies and transition dynamics this can be set to 1. gamma (float): Discount factor r_custom (mdp_extras.RewardFunction): Custom reward function to use Returns: (float): State value estimate """ episode_returns = [] for _ in range(num_samples): # XXX Force initial state env.reset() env.unwrapped.state = s obs = env.unwrapped._get_obs() done = False ep_rewards = [] while not done: a = pi.predict(obs, deterministic=True)[0] obs, reward, done, info = env.step(a) if r_custom is not None: # Use custom reward function state = pendulum_obs_to_state(obs) reward = r_custom(phi(state, a)) ep_rewards.append(reward) if done: break ep_rewards = np.array(ep_rewards) gammas = gamma ** np.arange(len(ep_rewards)) episode_return = gammas @ ep_rewards episode_returns.append(episode_return) return np.mean(episode_returns) def approx_policy_value(pi, start_state_disc_dim=10, num_samples=1, gamma=1.0, r_custom=None, n_jobs=8): """Approximately compute the value pi under the starting state distribution Args: pi (class): Policy object with a .predict() method matching the stable-baselines API start_state_disc_dim (int): How fine to discretize each dimension of the MDP starting state distribution support. For Pundulum-v0, 10 seems to be sufficient for accurately measuring policy value (at least for the optimal policy) num_samples (int): Number of samples to estimate value with. For determinstic policies and transition dynamics this can be set to 1. gamma (float): Discount factor r_custom (mdp_extras.RewardFunction): Custom reward function to use n_jobs (int): Number of parallel workers to spin up for estimating value Returns: (float): Approximate value of pi under the MDP's start state distribution """ # Compute a set of states that span and discretize the continuous uniform start state distribution theta_bounds = np.array([-np.pi, np.pi]) theta_delta = 0.5 * (theta_bounds[1] - theta_bounds[0]) / start_state_disc_dim theta_bounds += np.array([theta_delta, -theta_delta]) thetas = np.linspace(theta_bounds[0], theta_bounds[1], start_state_disc_dim) theta_dots = np.linspace(-1, 1, start_state_disc_dim) start_states = [np.array(p) for p in it.product(thetas, theta_dots)] # Spin up a bunch of workers to process the starting states in parallel values = Parallel(n_jobs=n_jobs)( delayed(approx_state_value)(model, state, num_samples, gamma, r_custom) for state in start_states ) return np.mean(values) # What is the value of the optimal policy? pi_gt_v = approx_policy_value(model) print(pi_gt_v) # -144 is just sufficient to make it to the OpenAI Gym leaderboard - so we're in the right ball-park def evd(learned_model, gamma, n_jobs=8): """Compute approximate expected value difference for a learned optimal policy Args: learned_model (class): Optimal policy wrt. some reward function. Should be a Policy object with a .predict() method matching the stable-baselines API gamma (float): Discount factor Returns: (float): Expected value difference of the given policy """ v_pi = approx_policy_value(learned_model, gamma=gamma, n_jobs=n_jobs) evd = pi_gt_v - v_pi return evd pi_ref = UniformRandomCtsPolicy((-2.0, 2.0)) # Get importance sampling dataset pi_ref_demos = [] max_path_length = max_timesteps num_sampled_paths = 10 for _ in range(num_sampled_paths): path_len = np.random.randint(1, high=max_path_length + 1) path = [] obs = env.reset() s = pendulum_obs_to_state(obs) while len(path) < path_len - 1: a = pi_ref.predict(s)[0] path.append((s, a)) obs, r, done, _ = env.step(a) s = pendulum_obs_to_state(obs) path.append((s, None)) pi_ref_demos.append(path) # Pre-compute sampled path feature expectations pi_ref_demo_phis_precomputed = [ phi.onpath(p, gamma) for p in pi_ref_demos ] # Nelder Mead doesn't work - the scipy implementation doesn't support bounds or callback termination signals x0 = np.zeros(len(phi)) res = minimize( sw_maxent_irl_modelfree, x0, args=(gamma, phi, phi_bar, max_path_length, pi_ref, pi_ref_demos, True, pi_ref_demo_phis_precomputed), method='L-BFGS-B', jac='2-point', bounds=[(-1.0, 1.0) for _ in range(len(phi))], options=dict(disp=True) ) print(res) viz_soln(res.x) from gym.envs.classic_control import PendulumEnv class CustomPendulumEnv(PendulumEnv): def __init__(self, reward_fn, g=10.0): super().__init__(g=g) self._reward_fn = reward_fn def step(self, a): obs, r, done, info = super().step(a) state = super().unwrapped.state #phi_sa = phi(state, a) phi_sa = phi_lut[sa2int(state, a)] r2 = self._reward_fn(phi_s) return obs, r2, done, info theta = res.x # # Parallel environments # env2 = make_vec_env( # CustomPendulumEnv, # n_envs=8, # wrapper_class=lambda e: Monitor(TimeLimit(e, max_timesteps), filename="pendulum-log"), # env_kwargs=dict(reward_fn=Linear(res.x)) # ) #model = PPO("MlpPolicy", env2, verbose=1, tensorboard_log="./tb-log/") #theta = (phi_bar - np.min(phi_bar)) / (np.max(phi_bar) - np.min(phi_bar)) * 2.0 - 1.0 #print(theta) #env = Monitor(TimeLimit(PendulumEnv(), max_timesteps), filename="pendulum-log") env2 = Monitor(TimeLimit(CustomPendulumEnv(reward_fn=Linear(theta)), max_timesteps), filename="pendulum-log") model = TD3( "MlpPolicy", env2, verbose=0, tensorboard_log="./tb-log/", # Non-standard params from rl-baselines3-zoo # https://github.com/DLR-RM/rl-baselines3-zoo/blob/master/hyperparams/td3.yml policy_kwargs=dict(net_arch=[400, 300]), action_noise=NormalActionNoise(0, 0.1), learning_starts=10000, buffer_size=200000, gamma=gamma ) print(evd(model, gamma, n_jobs=1)) model.learn( #total_timesteps=5e4, total_timesteps=5e5, log_interval=5 ) model.save("mdl.td3") print(evd(model, gamma, n_jobs=1)) # print(evd(model, gamma)) model2 = TD3.load("mdl.td3") print(evd(model2, gamma, n_jobs=1)) assert False x0 = np.zeros(len(phi)) res = minimize( sw_maxent_irl_modelfree, x0, args=(gamma, phi, phi_bar, max_path_length, pi_ref, pi_ref_demos, True, pi_ref_demo_phis_precomputed), method='L-BFGS-B', jac='3-point', bounds=[(-1.0, 1.0) for _ in range(len(phi))], options=dict(disp=True) ) print(res) viz_soln(res.x) x0 = np.zeros(len(phi)) res = minimize( sw_maxent_irl_modelfree, x0, args=(gamma, phi, phi_bar, max_path_length, pi_ref, pi_ref_demos, False, pi_ref_demo_phis_precomputed), method='L-BFGS-B', jac=True, bounds=[(-1.0, 1.0) for _ in range(len(phi))], options=dict(disp=True) ) print(res) viz_soln(res.x) import cma x0 = np.zeros(len(phi)) x, es = cma.fmin2( sw_maxent_irl_modelfree, x0, 0.5, args=(gamma, phi, phi_bar, max_path_length, pi_ref, pi_ref_demos, True, pi_ref_demo_phis_precomputed), options=dict(bounds=[-1.0, 1.0]) ) print(x.reshape(basis_dim, -1)) viz_soln(x) ###Output _____no_output_____ ###Markdown Try toxicity ###Code from detoxify import Detoxify from typing import Union, List, Dict, Any, Iterable import torch class DetoxifyClassifier: def __init__(self, batch_size:int=128, if_tqdm:bool=False) -> None: device = "cuda" if torch.cuda.is_available() else "cpu" self.model = Detoxify(model_type='original', device=device) self.batch_size = batch_size self.if_tqdm = if_tqdm def forward(self, texts: Union[str, List[str]]) -> Dict[str, Any]: if isinstance(texts, str): texts = [texts] if self.if_tqdm: progbar = tqdm(total=len(texts)) result = None for batch in self.data_iterator(texts): batch_res = self.model.predict(batch) if result is None: result = batch_res else: for key in result: result[key] += batch_res[key] if self.if_tqdm: progbar.update(len(batch)) return result def data_iterator(self, texts: List[str]) -> Iterable[List[str]]: batch = [] for t in texts: if len(batch) >= self.batch_size: yield batch batch = [] batch.append(t) if len(batch) != 0: yield batch def __call__(self, texts: Union[str, List[str]]) -> List[float]: return self.forward(texts)["toxicity"] toxic_clf = DetoxifyClassifier(batch_size=128) import json import random random.seed(2) RTP_Path = "/home/yihan.wang/project/sql/data/realtoxicityprompts-data/prompts.jsonl" with open(RTP_Path) as infile: raw = [json.loads(l.strip()) for l in infile.readlines()] all_texts = [] for l in raw: all_texts.append(f"{l['prompt']['text']}{l['continuation']['text']}") small = random.sample(all_texts, 10000) toxicities = toxic_clf(small) toxic_set = [(tox, txt) for tox, txt in zip(toxicities, small)] toxic_set.sort(reverse=True) sample = toxic_set[:100] def generate_output(input_sentence, prompt_str, max_new_tokens, target_label, reward_fn, generator, classifier, perplexer, num_return_sequences=128): formatted_prompt = add_input_prompt_to_template(input_sentence, prompt_str, generator) # print(formatted_prompt) generator_outputs = generator([formatted_prompt], max_new_tokens=max_new_tokens, pad_token_id=50256, num_return_sequences=num_return_sequences, # Only return generated text, without the prompt return_full_text=False) # for l in generator_outputs: # print(l) generated_texts = [] for output in generator_outputs: text = output["generated_text"] generated_texts.append(postprocess_output(text)) toxic_score = classifier(generated_texts) reference_texts = [input_sentence for _ in generated_texts] bleus = [scb.sentence_bleu(hypothesis=x.lower(), references=[y.lower()]) for x, y in zip(generated_texts, reference_texts)] bleus = [b.score for b in bleus] # to_print = [(c, g) for g, c in zip(generated_texts, bleus)] # for l in to_print: # print(l) sum_rewards = [(b + (1 - t) * 100) / 2 for b, t in zip(bleus, toxic_score)] idx = np.array(sum_rewards).argmax() return {'input_sentence': input_sentence, 'output_sentence': generated_texts[idx], 'max_reward': sum_rewards[idx], 'max_bleu': bleus[idx], 'max_toxic': toxic_score[idx]} results = [] for toxic, input_sentence in tqdm(sample): start = time.time() max_new_tokens = get_input_length(input_sentence, generator) * 2 max_reward = 0 max_output = {} i = 0 while max_reward < target_reward and i < max_iters: output = generate_output(input_sentence, "", max_new_tokens, target_label, reward_fn, generator, toxic_clf, perplexer,) if output['max_reward'] > max_reward: max_reward = output['max_reward'] max_output = output i += 1 max_output.update({'perplexity': np.exp(compute_nll_reward([max_output['output_sentence']], perplexer)[0]), 'time': time.time() - start, 'iters': i, 'original_toxicity': toxic}) results.append(max_output) df_results = pd.DataFrame(results) print(avg([l['max_reward'] for l in results])) print(avg([l['max_bleu'] for l in results])) print(avg([l['max_toxic'] for l in results])) from sentence_transformers import SentenceTransformer model = SentenceTransformer('sentence-transformers/all-MiniLM-L6-v2') def sbert_sim(model, src, tgts): if type(tgts) is not list: tgts = [tgts] to_encode = [src] + tgts embs = model.encode(to_encode) cos_sim = lambda a,b : np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b)) return [cos_sim(embs[0], emb) for emb in embs[1:]] res = sbert_sim(model, "That is a happy person", ["That is a happy dog", "this is a happy person"]) res np.dot(res[0], res[1]) / (np.linalg.norm(res[0]) * np.linalg.norm(res[1])) ###Output _____no_output_____
A simple application of Deep Neural Networks.ipynb	###Markdown A simple application of Deep Neural Networks In this tutorial I will :- train a simple neural network that learns the [XNOR function](https://en.wikipedia.org/wiki/Logical_equality), - Show how to save a trained neural network and - How to load and reuse a saved neural network into the jupyter notebook. ###Code # Libraries Importation from keras.models import Sequential from keras.layers.core import Dense, Activation import numpy as np import base64 import os import matplotlib.pyplot as plt import numpy as np import pandas as pd import requests from sklearn import preprocessing from keras.models import Sequential from keras.layers.core import Dense, Activation import pandas as pd import io import requests import numpy as np from keras.models import load_model ###Output _____no_output_____ ###Markdown Logical equalityLogical equality (also known as biconditional) is an operation on two logical values, typically the values of two propositions, that produces a value of true if both operands are false or both operands are true.The truth table for p XNOR q (also written as p ↔ q, Epq, p = q, or p ≡ q) is as follows:![Logical equality](https://raw.githubusercontent.com/Kabongosalomon/Deep-Neural-Networks/master/images/XNORpng.png "Logical equality") ###Code # Create a dataset for the XNOR function x = np.array([ [0,0], [1,0], [0,1], [1,1] ]) y = np.array([ 1, 0, 0, 1 ]) # Build the network # sgd = optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True) done = False cycle = 1 while not done: print("Cycle #{}".format(cycle)) cycle+=1 model = Sequential() model.add(Dense(2, input_dim=2, activation='relu')) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') model.fit(x,y,verbose=0,epochs=10000) # Predict pred = model.predict(x) # Check if successful. It takes several runs with this small of a network done = pred[1]<0.01 and pred[2]<0.01 and pred[0] > 0.9 and pred[3] > 0.9 print(pred) ###Output Cycle #1 [[0.49999997] [0.49999997] [0.49999997] [0.49999997]] Cycle #2 [[0.6666666] [0.6666666] [0. ] [0.6666666]] Cycle #3 [[9.9999958e-01] [4.0972279e-07] [2.0802088e-07] [9.9999976e-01]] ###Markdown The output above should have two numbers near 1 for the first and forth spots (input [[0,0]] and [[1,1]]). The middle two numbers should be near 0 (input [[1,0]] and [[0,1]]). These numbers are in scientific notation. Due to random starting weights, it is sometimes necessary to run the above through several cycles to get a good result ###Code pred y # Measure RMSE error. RMSE is common for regression. score = np.sqrt(metrics.mean_squared_error(pred,y)) print(f"Before save score (RMSE): {score}") ###Output Before save score (RMSE): 3.324424151302459e-07 ###Markdown Load/Save Trained Network ###Code from sklearn import metrics save_path = "./TrainedNet/" # Measure RMSE error. RMSE is common for regression. score = np.sqrt(metrics.mean_squared_error(pred,y)) print(f"Before save score (RMSE): {score}") # save neural network structure to JSON (no weights) model_json = model.to_json() with open(os.path.join(save_path,"XNOR_network.json"), "w") as json_file: json_file.write(model_json) # save entire network to HDF5 (save everything, suggested) model.save(os.path.join(save_path,"XNOR_network.h5")) ###Output Before save score (RMSE): 3.324424151302459e-07 ###Markdown Now we reload the network and perform another prediction. The RMSE should match the previous one exactly if the neural network was really saved and reloaded. ###Code model2 = load_model(os.path.join(save_path,"XNOR_network.h5")) pred = model2.predict(x) # Measure RMSE error. RMSE is common for regression. score = np.sqrt(metrics.mean_squared_error(pred,y)) print(f"After load score (RMSE): {score}") ###Output After load score (RMSE): 3.324424151302459e-07
26-NeuralNetworks2/26-NeuralNetworks2-solutions.ipynb	###Markdown Introduction to Data Science Lecture 25: Neural Networks IICOMP 5360 / MATH 4100, University of Utah, http://datasciencecourse.net/In this lecture, we'll continue discussing Neural Networks. Recommended Reading:* A. Géron, [Hands-On Machine Learning with Scikit-Learn & TensorFlow](http://proquest.safaribooksonline.com/book/programming/9781491962282) (2017) * I. Goodfellow, Y. Bengio, and A. Courville, [Deep Learning](http://www.deeplearningbook.org/) (2016)* Y. LeCun, Y. Bengio, and G. Hinton, [Deep learning](https://www.nature.com/articles/nature14539), Nature (2015) Recap: Neural NetworksLast time, we introduced Neural Networks and discussed how they can be used for classification and regression.There are many different network architectures for Neural Networks, but our focus is on Multi-layer Perceptrons. Here, there is an input layer, typically drawn on the left hand side and an output layer, typically drawn on the right hand side. The middle layers are called hidden layers. <img src="Colored_neural_network.svg" title="https://en.wikipedia.org/wiki/Artificial_neural_network/media/File:Colored_neural_network.svg" width="300">Given a set of features $X = x^0 = \{x_1, x_2, ..., x_n\}$ and a target $y$, a neural network works as follows. Each layer applies an affine transformation and an [activation function](https://en.wikipedia.org/wiki/Activation_function) (e.g., ReLU, hyperbolic tangent, or logistic) to the output of the previous layer: $$x^{j} = f ( A^{j} x^{j-1} + b^j ). $$At the $j$-th hidden layer, the input is represented as the composition of $j$ such mappings. An additional function, e.g. [softmax](https://en.wikipedia.org/wiki/Softmax_function), is applied to the output layer to give the prediction, $\hat y$, for classification or regression. <img src="activationFct.png" title="see Géron, Ch. 10" width="700"> Softmax function for classificaton The softmax function, $\sigma:\mathbb{R}^K \to (0,1)^K$ is defined by$$\sigma(\mathbf{z})_j = \frac{e^{z_j}}{\sum_{k=1}^K e^{z_k}}\qquad \qquad \textrm{for } j=1, \ldots, K.$$Note that each component is in the range $(0,1)$ and the values sum to 1. We interpret $\sigma(\mathbf{z})_j$ as the probability that $\mathbf{z}$ is a member of class $j$. Training a neural networkNeural networks uses a loss function of the form $$Loss(\hat{y},y,W) = \frac{1}{2} \sum_{i=1}^n g(\hat{y}_i(W),y_i) + \frac{\alpha}{2} \\|W\\|_2^2$$Here, + $y_i$ is the label for the $i$-th example, + $\hat{y}_i(W)$ is the predicted label for the $i$-th example, + $g$ is a function that measures the error, typically $L^2$ difference for regression or cross-entropy for classification, and + $\alpha$ is a regularization parameter. Starting from initial random weights, the loss function is minimized by repeatedly updating these weights. Various optimization methods can be used, e.g., + gradient descent method + quasi-Newton method,+ stochastic gradient descent, or + ADAM. There are various parameters associated with each method that must be tuned. Back propagation is a way of using the chain rule from calculus to compute the gradient of the $Loss$ function for optimization. Neural Networks in scikit-learnIn the previous lecture, we used Neural Network implementations in scikit-learn to do both classification and regression:+ [multi-layer perceptron (MLP) classifier](http://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html)+ [multi-layer perceptron (MLP) regressor](http://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPRegressor.html)However, there are several limitations to the scikit-learn implementation: - no GPU support- limited network architectures Neural networks with TensorFlowToday, we'll use [TensorFlow](https://github.com/tensorflow/tensorflow) to train a Neural Network. TensorFlow is an open-source library designed for large-scale machine learning. Installing TensorFlowInstructions for installing TensorFlow are available at [the tensorflow install page](https://www.tensorflow.org/versions/r1.0/install/).It is recommended that you use the command: ```pip install tensorflow``` ###Code import tensorflow as tf print(tf.__version__) # to make this notebook's output stable across runs def reset_graph(seed=42): tf.reset_default_graph() tf.set_random_seed(seed) np.random.seed(seed) ###Output 1.13.1 ###Markdown TensorFlow represents computations by connecting op (operation) nodes into a computation graph.A TensorFlow program usually has two components:+ In the construction phase, a computational graph is built. During this phase, no computations are performed and the variables are not yet initialized. + In the execution phase, the graph is evaluated, typically many times. In this phase, the each operation is given to a CPU or GPU, variables are initialized, and functions can be evaluted. ###Code # construction phase x = tf.Variable(3) y = tf.Variable(4) f = xxy + y + 2 # execution phase with tf.Session() as sess: # initializes a "session" x.initializer.run() y.initializer.run() print(f.eval()) # alternatively all variables cab be initialized as follows init = tf.global_variables_initializer() with tf.Session() as sess: # initializes a "session" init.run() # initializes all the variables print(f.eval()) ###Output WARNING:tensorflow:From /Applications/anaconda3/lib/python3.7/site-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version. Instructions for updating: Colocations handled automatically by placer. 42 42 ###Markdown AutodiffTensorFlow can automatically compute the derivative of functions using [```gradients```](https://www.tensorflow.org/api_docs/python/tf/gradients). ###Code # construction phase x = tf.Variable(3.0) y = tf.Variable(4.0) f = x + 2yy + 2 grads = tf.gradients(f,[x,y]) # execution phase with tf.Session() as sess: sess.run(tf.global_variables_initializer()) # initializes all variables print([g.eval() for g in grads]) ###Output [1.0, 16.0] ###Markdown This is enormously helpful since training a NN requires the derivate of the loss function with respect to the parameters (and there are a lot of parameters). This is computed using backpropagation (chain rule) and TensorFlow does this work for you. Exercise: Use TensorFlow to compute the derivative of $f(x) = e^x$ at $x=2$. ###Code # your code here # Reference solution x = tf.Variable(2.0) f = tf.exp(x) grads = tf.gradients(f,[x]) # execution phase with tf.Session() as sess: sess.run(tf.global_variables_initializer()) # initializes all variables print(grads[0].eval()) ###Output 7.389056 ###Markdown Optimization methodsTensorflow also has several built-in optimization methods.Other optimization methods in TensorFlow:+ [```tf.train.Optimizer```](https://www.tensorflow.org/api_docs/python/tf/train/Optimizer)+ [```tf.train.GradientDescentOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer)+ [```tf.train.AdadeltaOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/AdadeltaOptimizer)+ [```tf.train.AdagradOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/AdagradOptimizer)+ [```tf.train.AdagradDAOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/AdagradDAOptimizer)+ [```tf.train.MomentumOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/MomentumOptimizer)+ [```tf.train.AdamOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer)+ [```tf.train.FtrlOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/FtrlOptimizer)+ [```tf.train.ProximalGradientDescentOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/ProximalGradientDescentOptimizer)+ [```tf.train.ProximalAdagradOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/ProximalAdagradOptimizer)+ [```tf.train.RMSPropOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/RMSPropOptimizer)For more information, see the [TensorFlow training webpage](https://www.tensorflow.org/api_guides/python/train). Let's see how to use the [```GradientDescentOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer). ###Code x = tf.Variable(3.0, trainable=True) y = tf.Variable(2.0, trainable=True) f = xx + 100yy opt = tf.train.GradientDescentOptimizer(learning_rate=5e-3).minimize(f) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(1000): if i%100 == 0: print(sess.run([x,y,f])) sess.run(opt) ###Output [3.0, 2.0, 409.0] [1.0980968, 0.0, 1.2058167] [0.40193906, 0.0, 0.161555] [0.14712274, 0.0, 0.0216451] [0.053851694, 0.0, 0.0029000049] [0.019711465, 0.0, 0.00038854184] [0.0072150305, 0.0, 5.2056665e-05] [0.0026409342, 0.0, 6.9745333e-06] [0.00096666755, 0.0, 9.344461e-07] [0.00035383157, 0.0, 1.2519678e-07] ###Markdown Using another optimizer, such as the [```MomentumOptimizer```](https://www.tensorflow.org/api_docs/python/tf/train/MomentumOptimizer), has similiar syntax. ###Code x = tf.Variable(3.0, trainable=True) y = tf.Variable(2.0, trainable=True) f = xx + 100yy opt = tf.train.MomentumOptimizer(learning_rate=1e-2,momentum=.5).minimize(f) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(1000): if i%100 == 0: print(sess.run([x,y,f])) sess.run(opt) ###Output [3.0, 2.0, 409.0] [0.043930665, 2.0290405e-15, 0.0019299033] [0.0006126566, -1.547466e-30, 3.753481e-07] [8.544106e-06, 0.0, 7.300175e-11] [1.1915596e-07, 0.0, 1.4198143e-14] [1.6617479e-09, 0.0, 2.761406e-18] [2.3174716e-11, 0.0, 5.3706746e-22] [3.2319424e-13, 0.0, 1.0445451e-25] [4.5072626e-15, 0.0, 2.0315416e-29] [6.285822e-17, 0.0, 3.951156e-33] ###Markdown Exercise: Use TensorFlow to find the minimum of the [Rosenbrock function](https://en.wikipedia.org/wiki/Rosenbrock_function): $$f(x,y) = (x-1)^2 + 100(y-x^2)^2.$$ ###Code # your code here # Reference solution x = tf.Variable(3.0, trainable=True) y = tf.Variable(2.0, trainable=True) f = tf.pow(x-1,2) + 100tf.pow(y-tf.pow(x,2),2) opt = tf.train.MomentumOptimizer(learning_rate=1e-4,momentum=.9).minimize(f) # execution phase with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(10000): if i%1000 == 0: print(sess.run([x,y,f])) sess.run(opt) ###Output [3.0, 2.0, 4904.0] [0.34496623, 0.11588032, 0.43004355] [0.7261489, 0.5260107, 0.07515866] [0.84546393, 0.7141316, 0.023927316] [0.9054483, 0.81943625, 0.008956054] [0.939964, 0.8832833, 0.0036105204] [0.96110237, 0.92355835, 0.0015155661] [0.9744939, 0.94953483, 0.00065163325] [0.9831504, 0.96651673, 0.0002843708] [0.9888154, 0.97771096, 0.0001252972] ###Markdown Classifying the MNIST handwritten digit datasetWe now use TensorFlow to classify the handwritten digits in the MNIST dataset. Using plain TensorFlowWe'll first follow [Géron, Ch. 10](https://github.com/ageron/handson-ml/blob/master/10_introduction_to_artificial_neural_networks.ipynb) to build a NN using plain TensorFlow. Construction phase+ We specify the number of inputs and outputs and the size of each layer. Here the images are 28x28 and there are 10 classes (each corresponding to a digit). We'll choose 2 hidden layers, with 300 and 100 neurons respectively. + Placeholder nodes are used to represent the training data and targets. We use the ```None``` keyword to leave the shape (of the training batch) unspecified. + We add layers to the NN using the ```layers.dense()``` function. In each case, we specify the input, and the size of the layer. We also specify the activation function used in each layer. Here, we choose the ReLU function. + We specify that the output of the NN will be a softmax function. The loss function is cross entropy. + We then specify that we'll use the [GradientDescentOptimizer](https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer) with a learning rate of 0.01. + Finally, we specify how the model will be evaluated. The [```in_top_k```](https://www.tensorflow.org/api_docs/python/tf/nn/in_top_k) function checks to see if the targets are in the top k predictions. We then initialize all of the variables and create an object to save the model using the [```saver()```](https://www.tensorflow.org/programmers_guide/saved_model) function. Execution phaseAt each epoch, the code breaks the training batch into mini-batches of size 50. Cycling through the mini-batches, it uses gradient descent to train the NN. The accuracy for both the training and test datasets are evaluated. ###Code import tensorflow as tf import numpy as np from sklearn.metrics import confusion_matrix # to make this notebook's output stable across runs def reset_graph(seed=42): tf.reset_default_graph() tf.set_random_seed(seed) np.random.seed(seed) # load the data (X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data() X_train = X_train.astype(np.float32).reshape(-1, 2828) / 255.0 X_test = X_test.astype(np.float32).reshape(-1, 2828) / 255.0 y_train = y_train.astype(np.int32) y_test = y_test.astype(np.int32) # helper code def shuffle_batch(X, y, batch_size): rnd_idx = np.random.permutation(len(X)) n_batches = len(X) // batch_size for batch_idx in np.array_split(rnd_idx, n_batches): X_batch, y_batch = X[batch_idx], y[batch_idx] yield X_batch, y_batch # construction phase n_inputs = 2828 # MNIST n_hidden1 = 300 n_hidden2 = 100 n_outputs = 10 reset_graph() X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X") y = tf.placeholder(tf.int32, shape=(None), name="y") with tf.name_scope("dnn"): hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",activation=tf.nn.relu) hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",activation=tf.nn.relu) logits = tf.layers.dense(hidden2, n_outputs, name="outputs") #y_proba = tf.nn.softmax(logits) with tf.name_scope("loss"): xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits) loss = tf.reduce_mean(xentropy, name="loss") learning_rate = 0.01 with tf.name_scope("train"): optimizer = tf.train.GradientDescentOptimizer(learning_rate) training_op = optimizer.minimize(loss) with tf.name_scope("eval"): correct = tf.nn.in_top_k(logits, y, 1) accuracy = tf.reduce_mean(tf.cast(correct, tf.float32)) # execution phase init = tf.global_variables_initializer() saver = tf.train.Saver() n_epochs = 10 #n_batches = 50 batch_size = 50 with tf.Session() as sess: init.run() for epoch in range(n_epochs): for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size): sess.run(training_op, feed_dict={X: X_batch, y: y_batch}) acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch}) acc_valid = accuracy.eval(feed_dict={X: X_test, y: y_test}) print(epoch, "Batch accuracy:", acc_batch, "Validation accuracy:", acc_valid) save_path = saver.save(sess, "./my_model_final.ckpt") ###Output 0 Batch accuracy: 0.9 Validation accuracy: 0.9055 1 Batch accuracy: 0.9 Validation accuracy: 0.9208 2 Batch accuracy: 0.94 Validation accuracy: 0.9331 3 Batch accuracy: 0.94 Validation accuracy: 0.9406 4 Batch accuracy: 1.0 Validation accuracy: 0.9444 5 Batch accuracy: 0.98 Validation accuracy: 0.9481 6 Batch accuracy: 0.98 Validation accuracy: 0.9537 7 Batch accuracy: 0.98 Validation accuracy: 0.9566 8 Batch accuracy: 0.98 Validation accuracy: 0.9591 9 Batch accuracy: 1.0 Validation accuracy: 0.9597 ###Markdown Since the NN has been saved, we can use it for classification using the [```saver.restore```](https://www.tensorflow.org/programmers_guide/saved_model) function. We can also print the confusion matrix using [```confusion_matrix```](https://www.tensorflow.org/api_docs/python/tf/confusion_matrix). ###Code with tf.Session() as sess: saver.restore(sess, save_path) Z = logits.eval(feed_dict={X: X_test}) y_pred = np.argmax(Z, axis=1) print(confusion_matrix(y_test,y_pred)) ###Output WARNING:tensorflow:From /Applications/anaconda3/lib/python3.7/site-packages/tensorflow/python/training/saver.py:1266: checkpoint_exists (from tensorflow.python.training.checkpoint_management) is deprecated and will be removed in a future version. Instructions for updating: Use standard file APIs to check for files with this prefix. INFO:tensorflow:Restoring parameters from ./my_model_final.ckpt [[ 969 0 1 1 0 3 1 2 2 1] [ 0 1115 2 2 0 1 4 2 9 0] [ 7 1 980 12 5 0 6 9 11 1] [ 1 0 2 984 0 1 0 10 7 5] [ 1 0 3 1 930 0 7 1 5 34] [ 10 2 1 25 3 820 10 1 14 6] [ 8 3 0 2 9 6 925 0 5 0] [ 0 10 12 4 2 0 0 984 2 14] [ 3 2 3 13 4 1 8 8 929 3] [ 5 7 0 13 11 2 1 5 4 961]] ###Markdown Using TensorFlow's Keras API Next, we'll use TensorFlow's Keras API to build a NN for the MNIST dataset. [Keras](https://keras.io/) is a high-level neural networks API, written in Python and capable of running on top of TensorFlow, CNTK, or Theano. We'll use it with TensorFlow. ###Code import tensorflow as tf import numpy as np from sklearn.metrics import confusion_matrix (X_train, y_train),(X_test, y_test) = tf.keras.datasets.mnist.load_data() X_train, X_test = X_train / 255.0, X_test / 255.0 # set the model model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(28, 28)), tf.keras.layers.Dense(512, activation=tf.nn.relu), tf.keras.layers.Dropout(rate=0.2), tf.keras.layers.Dense(10, activation=tf.nn.softmax) ]) # specifiy optimizer model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy']) # train the model model.fit(X_train, y_train, epochs=5) score = model.evaluate(X_test, y_test) names = model.metrics_names for ii in np.arange(len(names)): print(names[ii],score[ii]) model.summary() y_pred = np.argmax(model.predict(X_test), axis=1) print(confusion_matrix(y_test,y_pred)) ###Output [[ 974 1 0 0 0 0 3 1 0 1] [ 0 1124 3 2 0 1 2 0 3 0] [ 5 0 1018 2 1 0 1 1 3 1] [ 0 1 3 997 0 0 0 2 2 5] [ 1 0 1 1 971 0 3 0 0 5] [ 2 0 0 20 3 852 5 1 6 3] [ 2 3 0 1 7 3 940 0 2 0] [ 3 6 10 6 1 0 0 984 4 14] [ 4 0 7 6 1 3 3 3 945 2] [ 2 2 0 4 12 1 0 1 1 986]] ###Markdown Using a pre-trained networkThere are many examples of pre-trained NN that can be accessed [here](https://www.tensorflow.org/api_docs/python/tf/keras/applications). These NN are very large, having been trained on giant computers using massive datasets. It can be very useful to initialize a NN using one of these. This is called [transfer learning](https://en.wikipedia.org/wiki/Transfer_learning). We'll use a NN that was pretrained for image recognition. This NN was trained on the [ImageNet](http://www.image-net.org/) project, which contains > 14 million images belonging to > 20,000 classes (synsets). ###Code import tensorflow as tf import numpy as np from tensorflow.keras.preprocessing import image from tensorflow.keras.applications import vgg16 vgg_model = tf.keras.applications.VGG16(weights='imagenet',include_top=True) vgg_model.summary() img_path = 'images/scout1.jpeg' img = image.load_img(img_path, target_size=(224, 224)) x = image.img_to_array(img) x = np.expand_dims(x, axis=0) x = vgg16.preprocess_input(x) preds = vgg_model.predict(x) print('Predicted:', vgg16.decode_predictions(preds, top=5)[0]) ###Output Predicted: [('n02098105', 'soft-coated_wheaten_terrier', 0.3554158), ('n02105641', 'Old_English_sheepdog', 0.23714595), ('n02095314', 'wire-haired_fox_terrier', 0.13490717), ('n02091635', 'otterhound', 0.0611032), ('n02093991', 'Irish_terrier', 0.052789364)] ###Markdown Exercise:* Repeat the above steps for an image of your own.Exercise: There are several [other pre-trained networks in Keras](https://github.com/keras-team/keras-applications). Try these! ###Code # your code here ###Output _____no_output_____
Python Tutorial PyTorch/assignments/03_assignment_cifar10_feedforward.ipynb	###Markdown Classifying images of everyday objects using a neural networkThe ability to try many different neural network architectures to address a problem is what makes deep learning really powerful, especially compared to shallow learning techniques like linear regression, logistic regression etc. In this assignment, you will:1. Explore the CIFAR10 dataset: https://www.cs.toronto.edu/~kriz/cifar.html2. Set up a training pipeline to train a neural network on a GPU2. Experiment with different network architectures & hyperparametersAs you go through this notebook, you will find a ??? in certain places. Your job is to replace the ??? with appropriate code or values, to ensure that the notebook runs properly end-to-end. Try to experiment with different network structures and hypeparameters to get the lowest loss.You might find these notebooks useful for reference, as you work through this notebook:- https://jovian.ml/aakashns/04-feedforward-nn- https://jovian.ml/aakashns/fashion-feedforward-minimal ###Code # Uncomment and run the commands below if imports fail # !conda install numpy pandas pytorch torchvision cpuonly -c pytorch -y # !pip install matplotlib --upgrade --quiet import torch import torchvision import numpy as np import matplotlib.pyplot as plt import torch.nn as nn import torch.nn.functional as F from torchvision.datasets import CIFAR10 from torchvision.transforms import ToTensor from torchvision.utils import make_grid from torch.utils.data.dataloader import DataLoader from torch.utils.data import random_split %matplotlib inline # Project name used for jovian.commit project_name = '03-assignment-cifar10-feedforward' ###Output _____no_output_____ ###Markdown Exploring the CIFAR10 dataset ###Code dataset = CIFAR10(root='data/', download=True, transform=ToTensor()) test_dataset = CIFAR10(root='data/', train=False, transform=ToTensor()) ###Output Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to data/cifar-10-python.tar.gz ###Markdown Q: How many images does the training dataset contain? ###Code dataset_size = len(dataset) print('The training dataset contains ' + str(dataset_size) + ' images.') ###Output The training dataset contains 50000 images. ###Markdown Q: How many images does the testing dataset contain? ###Code test_dataset_size = len(test_dataset) print('The training dataset contains ' + str(test_dataset_size) + ' images.') ###Output The training dataset contains 10000 images. ###Markdown Q: How many output classes does the dataset contain? Can you list them?Hint: Use `dataset.classes` ###Code classes = dataset.classes print('The classes in the dataset are: ') print(classes) num_classes = len(dataset.classes) print('The number of classes in the dataset is: ', num_classes) ###Output The number of classes in the dataset is: 10 ###Markdown Q: What is the shape of an image tensor from the dataset? ###Code img, label = dataset[0] img_shape = img.shape print('The shape of an image tensor is: ', img_shape) ###Output The shape of an image tensor is: torch.Size([3, 32, 32]) ###Markdown Note that this dataset consists of 3-channel color images (RGB). Let us look at a sample image from the dataset. `matplotlib` expects channels to be the last dimension of the image tensors (whereas in PyTorch they are the first dimension), so we'll the `.permute` tensor method to shift channels to the last dimension. Let's also print the label for the image. ###Code img, label = dataset[0] plt.imshow(img.permute((1, 2, 0))) print('Label (numeric):', label) print('Label (textual):', classes[label]) ###Output Label (numeric): 6 Label (textual): frog ###Markdown (Optional) Q: Can you determine the number of images belonging to each class?Hint: Loop through the dataset. ###Code counter = dict.fromkeys(classes, 0) for _, l in dataset: counter[classes[l]] += 1 counter counter.values() ###Output _____no_output_____ ###Markdown Let's save our work to Jovian, before continuing. ###Code !pip install jovian --upgrade --quiet import jovian jovian.commit(project=project_name, environment=None) ###Output _____no_output_____ ###Markdown Preparing the data for trainingWe'll use a validation set with 5000 images (10% of the dataset). To ensure we get the same validation set each time, we'll set PyTorch's random number generator to a seed value of 43. ###Code torch.manual_seed(43) val_size = 5000 train_size = len(dataset) - val_size ###Output _____no_output_____ ###Markdown Let's use the `random_split` method to create the training & validation sets ###Code train_ds, val_ds = random_split(dataset, [train_size, val_size]) len(train_ds), len(val_ds) ###Output _____no_output_____ ###Markdown We can now create data loaders to load the data in batches. ###Code batch_size=128 train_loader = DataLoader(train_ds, batch_size, shuffle=True, num_workers=4, pin_memory=True) val_loader = DataLoader(val_ds, batch_size2, num_workers=4, pin_memory=True) test_loader = DataLoader(test_dataset, batch_size2, num_workers=4, pin_memory=True) ###Output _____no_output_____ ###Markdown Let's visualize a batch of data using the `make_grid` helper function from Torchvision. ###Code for images, _ in train_loader: print('images.shape:', images.shape) plt.figure(figsize=(16,8)) plt.axis('off') plt.imshow(make_grid(images, nrow=16).permute((1, 2, 0))) break ###Output images.shape: torch.Size([128, 3, 32, 32]) ###Markdown Can you label all the images by looking at them? Trying to label a random sample of the data manually is a good way to estimate the difficulty of the problem, and identify errors in labeling, if any. Base Model class & Training on GPULet's create a base model class, which contains everything except the model architecture i.e. it wil not contain the `__init__` and `__forward__` methods. We will later extend this class to try out different architectures. In fact, you can extend this model to solve any image classification problem. ###Code def accuracy(outputs, labels): _, preds = torch.max(outputs, dim=1) return torch.tensor(torch.sum(preds == labels).item() / len(preds)) class ImageClassificationBase(nn.Module): def training_step(self, batch): images, labels = batch out = self(images) # Generate predictions loss = F.cross_entropy(out, labels) # Calculate loss return loss def validation_step(self, batch): images, labels = batch out = self(images) # Generate predictions loss = F.cross_entropy(out, labels) # Calculate loss acc = accuracy(out, labels) # Calculate accuracy return {'val_loss': loss.detach(), 'val_acc': acc} def validation_epoch_end(self, outputs): batch_losses = [x['val_loss'] for x in outputs] epoch_loss = torch.stack(batch_losses).mean() # Combine losses batch_accs = [x['val_acc'] for x in outputs] epoch_acc = torch.stack(batch_accs).mean() # Combine accuracies return {'val_loss': epoch_loss.item(), 'val_acc': epoch_acc.item()} def epoch_end(self, epoch, result): print("Epoch [{}], val_loss: {:.4f}, val_acc: {:.4f}".format(epoch, result['val_loss'], result['val_acc'])) ###Output _____no_output_____ ###Markdown We can also use the exact same training loop as before. I hope you're starting to see the benefits of refactoring our code into reusable functions. ###Code def evaluate(model, val_loader): outputs = [model.validation_step(batch) for batch in val_loader] return model.validation_epoch_end(outputs) def fit(epochs, lr, model, train_loader, val_loader, opt_func=torch.optim.SGD): history = [] optimizer = opt_func(model.parameters(), lr) for epoch in range(epochs): # Training Phase for batch in train_loader: loss = model.training_step(batch) loss.backward() optimizer.step() optimizer.zero_grad() # Validation phase result = evaluate(model, val_loader) model.epoch_end(epoch, result) history.append(result) return history ###Output _____no_output_____ ###Markdown Finally, let's also define some utilities for moving out data & labels to the GPU, if one is available. ###Code torch.cuda.is_available() def get_default_device(): """Pick GPU if available, else CPU""" if torch.cuda.is_available(): return torch.device('cuda') else: return torch.device('cpu') device = get_default_device() device def to_device(data, device): """Move tensor(s) to chosen device""" if isinstance(data, (list,tuple)): return [to_device(x, device) for x in data] return data.to(device, non_blocking=True) class DeviceDataLoader(): """Wrap a dataloader to move data to a device""" def __init__(self, dl, device): self.dl = dl self.device = device def __iter__(self): """Yield a batch of data after moving it to device""" for b in self.dl: yield to_device(b, self.device) def __len__(self): """Number of batches""" return len(self.dl) ###Output _____no_output_____ ###Markdown Let us also define a couple of helper functions for plotting the losses & accuracies. ###Code def plot_losses(history): losses = [x['val_loss'] for x in history] plt.plot(losses, '-x') plt.xlabel('epoch') plt.ylabel('loss') plt.title('Loss vs. No. of epochs'); def plot_accuracies(history): accuracies = [x['val_acc'] for x in history] plt.plot(accuracies, '-x') plt.xlabel('epoch') plt.ylabel('accuracy') plt.title('Accuracy vs. No. of epochs'); ###Output _____no_output_____ ###Markdown Let's move our data loaders to the appropriate device. ###Code train_loader = DeviceDataLoader(train_loader, device) val_loader = DeviceDataLoader(val_loader, device) test_loader = DeviceDataLoader(test_loader, device) ###Output _____no_output_____ ###Markdown Training the modelWe will make several attempts at training the model. Each time, try a different architecture and a different set of learning rates. Here are some ideas to try:- Increase or decrease the number of hidden layers- Increase of decrease the size of each hidden layer- Try different activation functions- Try training for different number of epochs- Try different learning rates in every epochWhat's the highest validation accuracy you can get to? Can you get to 50% accuracy? What about 60%? ###Code input_size = 33232 hidden_layer1 = 2048 hidden_layer2 = 1024 hidden_layer3 = 512 hidden_layer4 = 256 hidden_layer5 = 128 hidden_layer6 = 64 hidden_layer7 = 32 output_size = 10 ###Output _____no_output_____ ###Markdown Q: Extend the `ImageClassificationBase` class to complete the model definition.Hint: Define the `__init__` and `forward` methods. ###Code class CIFAR10Model(ImageClassificationBase): def __init__(self): super().__init__() # Input Layer to hidden layer 1 self.linear_input = nn.Linear(input_size, hidden_layer1) # Hidden layer 1 to hidden layer 2 self.linear_hidden1 = nn.Linear(hidden_layer1, hidden_layer2) # Hidden layer 2 to hidden layer 3 self.linear_hidden2 = nn.Linear(hidden_layer2, hidden_layer3) # Hidden layer 3 to hidden layer 4 self.linear_hidden3 = nn.Linear(hidden_layer3, hidden_layer4) # Hidden layer 4 to hidden layer 5 self.linear_hidden4 = nn.Linear(hidden_layer4, hidden_layer5) # Hidden layer 5 to hidden layer 6 self.linear_hidden5 = nn.Linear(hidden_layer5, hidden_layer6) # Hidden layer 6 to Output layer self.linear_hidden6 = nn.Linear(hidden_layer6, hidden_layer7) # Hidden layer 7 to Output layer self.linear_output = nn.Linear(hidden_layer7, output_size) def forward(self, xb): # Flatten images into vectors out = xb.view(xb.size(0), -1) # Apply input layers out = self.linear_input(out) # Apply activation function out = F.relu(out) # Get intermediate outputs using hidden layer 1 out = self.linear_hidden1(out) # Apply activation function out = F.relu(out) # Get intermediate outputs using hidden layer 2 out = self.linear_hidden2(out) # Apply activation function out = F.relu(out) # Get intermediate outputs using hidden layer 3 out = self.linear_hidden3(out) # Apply activation function out = F.relu(out) # Get intermediate outputs using hidden layer 4 out = self.linear_hidden4(out) # Apply activation function out = F.relu(out) # Get intermediate outputs using hidden layer 5 out = self.linear_hidden5(out) # Apply activation function out = F.relu(out) out = self.linear_hidden6(out) # Apply activation function out = F.relu(out) # Get predictions using output layer out = self.linear_output(out) return out ###Output _____no_output_____ ###Markdown You can now instantiate the model, and move it the appropriate device. ###Code model = to_device(CIFAR10Model(), device) model ###Output _____no_output_____ ###Markdown Before you train the model, it's a good idea to check the validation loss & accuracy with the initial set of weights. ###Code history = [evaluate(model, val_loader)] history ###Output _____no_output_____ ###Markdown Q: Train the model using the `fit` function to reduce the validation loss & improve accuracy.Leverage the interactive nature of Jupyter to train the model in multiple phases, adjusting the no. of epochs & learning rate each time based on the result of the previous training phase. ###Code history += fit(5, 0.5, model, train_loader, val_loader) history += fit(5, 0.4, model, train_loader, val_loader) history += fit(10, 0.2, model, train_loader, val_loader) history += fit(10, 0.1, model, train_loader, val_loader) ###Output Epoch [0], val_loss: 1.4829, val_acc: 0.4864 Epoch [1], val_loss: 1.5539, val_acc: 0.4620 Epoch [2], val_loss: 1.4973, val_acc: 0.4888 Epoch [3], val_loss: 1.5712, val_acc: 0.4792 Epoch [4], val_loss: 1.5230, val_acc: 0.4898 Epoch [5], val_loss: 1.4988, val_acc: 0.4951 Epoch [6], val_loss: 1.4691, val_acc: 0.5043 Epoch [7], val_loss: 1.5509, val_acc: 0.4958 Epoch [8], val_loss: 1.5826, val_acc: 0.4837 Epoch [9], val_loss: 1.6598, val_acc: 0.4744 ###Markdown Plot the losses and the accuracies to check if you're starting to hit the limits of how well your model can perform on this dataset. You can train some more if you can see the scope for further improvement. ###Code plot_losses(history) plot_accuracies(history) ###Output _____no_output_____ ###Markdown Finally, evaluate the model on the test dataset report its final performance. ###Code validation = evaluate(model, test_loader) validation ###Output _____no_output_____ ###Markdown Are you happy with the accuracy? Record your results by completing the section below, then you can come back and try a different architecture & hyperparameters. Recoding your resultsAs your perform multiple experiments, it's important to record the results in a systematic fashion, so that you can review them later and identify the best approaches that you might want to reproduce or build upon later. Q: Describe the model's architecture with a short summary.E.g. `"3 layers (16,32,10)"` (16, 32 and 10 represent output sizes of each layer) ###Code arch = [input_size, hidden_layer1, hidden_layer2, hidden_layer3, hidden_layer4, hidden_layer5, hidden_layer6, hidden_layer7, output_size] ###Output _____no_output_____ ###Markdown Q: Provide the list of learning rates used while training. ###Code lrs = [0.5, 0.4, 0.2, 0.1] ###Output _____no_output_____ ###Markdown Q: Provide the list of no. of epochs used while training. ###Code epochs = [5, 5, 10, 10] ###Output _____no_output_____ ###Markdown Q: What were the final test accuracy & test loss? ###Code test_acc = validation['val_acc'] test_loss = validation['val_loss'] test_acc, test_loss ###Output _____no_output_____ ###Markdown Finally, let's save the trained model weights to disk, so we can use this model later. ###Code torch.save(model.state_dict(), '03-assignment-cifar10-feedforward.pth') ###Output _____no_output_____ ###Markdown The `jovian` library provides some utility functions to keep your work organized. With every version of your notebok, you can attach some hyperparameters and metrics from your experiment. ###Code # Clear previously recorded hyperparams & metrics jovian.reset() jovian.log_hyperparams(arch=arch, lrs=lrs, epochs=epochs) jovian.log_metrics(test_loss=test_loss, test_acc=test_acc) ###Output _____no_output_____ ###Markdown Finally, we can commit the notebook to Jovian, attaching the hypeparameters, metrics and the trained model weights. ###Code jovian.commit(project=project_name, outputs=['cifar10-feedforward.pth'], environment=None) ###Output _____no_output_____ ###Markdown Once committed, you can find the recorded metrics & hyperprameters in the "Records" tab on Jovian. You can find the saved model weights in the "Files" tab. Continued experimentationNow go back up to the "Training the model" section, and try another network architecture with a different set of hyperparameters. As you try different experiments, you will start to build an undestanding of how the different architectures & hyperparameters affect the final result. Don't worry if you can't get to very high accuracy, we'll make some fundamental changes to our model in the next lecture.Once you have tried multiple experiments, you can compare your results using the "Compare" button on Jovian.![compare-example](https://i.imgur.com/ltdYnSN.png) I could not use the jovian interphase to commit my notebook, but I tracked my changes and are displeyed in the image bellow:neural network comparison![Neural Network Comparison](https://imgur.com/a/Rzp7fQn) (Optional) Write a blog postWriting a blog post is the best way to further improve your understanding of deep learning & model training, because it forces you to articulate your thoughts clearly. Here'are some ideas for a blog post:- Report the results given by different architectures on the CIFAR10 dataset- Apply this training pipeline to a different dataset (it doesn't have to be images, or a classification problem) - Improve upon your model from Assignment 2 using a feedfoward neural network, and write a sequel to your previous blog post- Share some Strategies for picking good hyperparameters for deep learning- Present a summary of the different steps involved in training a deep learning model with PyTorch- Implement the same model using a different deep learning library e.g. Keras ( https://keras.io/ ), and present a comparision. ###Code ###Output _____no_output_____
Intermediate Machine Learning/6 XGBoost/xgboost.ipynb	###Markdown In this tutorial, you will learn how to build and optimize models with gradient boosting. This method dominates many Kaggle competitions and achieves state-of-the-art results on a variety of datasets. IntroductionFor much of this course, you have made predictions with the random forest method, which achieves better performance than a single decision tree simply by averaging the predictions of many decision trees.We refer to the random forest method as an "ensemble method". By definition, ensemble methods combine the predictions of several models (e.g., several trees, in the case of random forests). Next, we'll learn about another ensemble method called gradient boosting. Gradient BoostingGradient boosting is a method that goes through cycles to iteratively add models into an ensemble. It begins by initializing the ensemble with a single model, whose predictions can be pretty naive. (Even if its predictions are wildly inaccurate, subsequent additions to the ensemble will address those errors.)Then, we start the cycle:- First, we use the current ensemble to generate predictions for each observation in the dataset. To make a prediction, we add the predictions from all models in the ensemble. - These predictions are used to calculate a loss function (like [mean squared error](https://en.wikipedia.org/wiki/Mean_squared_error), for instance).- Then, we use the loss function to fit a new model that will be added to the ensemble. Specifically, we determine model parameters so that adding this new model to the ensemble will reduce the loss. (Side note: The "gradient" in "gradient boosting" refers to the fact that we'll use [gradient descent](https://en.wikipedia.org/wiki/Gradient_descent) on the loss function to determine the parameters in this new model.)- Finally, we add the new model to ensemble, and ...- ... repeat!![tut6_boosting](https://i.imgur.com/MvCGENh.png) ExampleWe begin by loading the training and validation data in `X_train`, `X_valid`, `y_train`, and `y_valid`. ###Code import pandas as pd from sklearn.model_selection import train_test_split # Read the data data = pd.read_csv('../input/melbourne-housing-snapshot/melb_data.csv') # Select subset of predictors cols_to_use = ['Rooms', 'Distance', 'Landsize', 'BuildingArea', 'YearBuilt'] X = data[cols_to_use] # Select target y = data.Price # Separate data into training and validation sets X_train, X_valid, y_train, y_valid = train_test_split(X, y) ###Output _____no_output_____ ###Markdown In this example, you'll work with the XGBoost library. XGBoost stands for extreme gradient boosting, which is an implementation of gradient boosting with several additional features focused on performance and speed. (_Scikit-learn has another version of gradient boosting, but XGBoost has some technical advantages._) In the next code cell, we import the scikit-learn API for XGBoost ([`xgboost.XGBRegressor`](https://xgboost.readthedocs.io/en/latest/python/python_api.htmlmodule-xgboost.sklearn)). This allows us to build and fit a model just as we would in scikit-learn. As you'll see in the output, the `XGBRegressor` class has many tunable parameters -- you'll learn about those soon! ###Code from xgboost import XGBRegressor my_model = XGBRegressor() my_model.fit(X_train, y_train) ###Output _____no_output_____ ###Markdown We also make predictions and evaluate the model. ###Code from sklearn.metrics import mean_absolute_error predictions = my_model.predict(X_valid) print("Mean Absolute Error: " + str(mean_absolute_error(predictions, y_valid))) ###Output Mean Absolute Error: 239960.14714193667 ###Markdown Parameter TuningXGBoost has a few parameters that can dramatically affect accuracy and training speed. The first parameters you should understand are: `n_estimators``n_estimators` specifies how many times to go through the modeling cycle described above. It is equal to the number of models that we include in the ensemble. - Too _low_ a value causes _underfitting_, which leads to inaccurate predictions on both training data and test data. - Too _high_ a value causes _overfitting_, which causes accurate predictions on training data, but inaccurate predictions on test data (_which is what we care about_). Typical values range from 100-1000, though this depends a lot on the `learning_rate` parameter discussed below.Here is the code to set the number of models in the ensemble: ###Code my_model = XGBRegressor(n_estimators=500) my_model.fit(X_train, y_train) ###Output _____no_output_____ ###Markdown `early_stopping_rounds``early_stopping_rounds` offers a way to automatically find the ideal value for `n_estimators`. Early stopping causes the model to stop iterating when the validation score stops improving, even if we aren't at the hard stop for `n_estimators`. It's smart to set a high value for `n_estimators` and then use `early_stopping_rounds` to find the optimal time to stop iterating.Since random chance sometimes causes a single round where validation scores don't improve, you need to specify a number for how many rounds of straight deterioration to allow before stopping. Setting `early_stopping_rounds=5` is a reasonable choice. In this case, we stop after 5 straight rounds of deteriorating validation scores.When using `early_stopping_rounds`, you also need to set aside some data for calculating the validation scores - this is done by setting the `eval_set` parameter. We can modify the example above to include early stopping: ###Code my_model = XGBRegressor(n_estimators=500) my_model.fit(X_train, y_train, early_stopping_rounds=5, eval_set=[(X_valid, y_valid)], verbose=False) ###Output _____no_output_____ ###Markdown If you later want to fit a model with all of your data, set `n_estimators` to whatever value you found to be optimal when run with early stopping. `learning_rate`Instead of getting predictions by simply adding up the predictions from each component model, we can multiply the predictions from each model by a small number (known as the learning rate) before adding them in. This means each tree we add to the ensemble helps us less. So, we can set a higher value for `n_estimators` without overfitting. If we use early stopping, the appropriate number of trees will be determined automatically.In general, a small learning rate and large number of estimators will yield more accurate XGBoost models, though it will also take the model longer to train since it does more iterations through the cycle. As default, XGBoost sets `learning_rate=0.1`.Modifying the example above to change the learning rate yields the following code: ###Code my_model = XGBRegressor(n_estimators=1000, learning_rate=0.05) my_model.fit(X_train, y_train, early_stopping_rounds=5, eval_set=[(X_valid, y_valid)], verbose=False) ###Output _____no_output_____ ###Markdown `n_jobs`On larger datasets where runtime is a consideration, you can use parallelism to build your models faster. It's common to set the parameter `n_jobs` equal to the number of cores on your machine. On smaller datasets, this won't help. The resulting model won't be any better, so micro-optimizing for fitting time is typically nothing but a distraction. But, it's useful in large datasets where you would otherwise spend a long time waiting during the `fit` command.Here's the modified example: ###Code my_model = XGBRegressor(n_estimators=1000, learning_rate=0.05, n_jobs=4) my_model.fit(X_train, y_train, early_stopping_rounds=5, eval_set=[(X_valid, y_valid)], verbose=False) ###Output _____no_output_____
notebooks/DynamicInvariants.ipynb	###Markdown Mining Function SpecificationsWhen testing a program, one not only needs to cover its several behaviors; one also needs to _check_ whether the result is as expected. In this chapter, we introduce a technique that allows us to _mine_ function specifications from a set of given executions, resulting in abstract and formal _descriptions_ of what the function expects and what it delivers. These so-called _dynamic invariants_ produce pre- and post-conditions over function arguments and variables from a set of executions. They are useful in a variety of contexts:* Dynamic invariants provide important information for [symbolic fuzzing](SymbolicFuzzer.ipynb), such as types and ranges of function arguments.* Dynamic invariants provide pre- and postconditions for formal program proofs and verification.* Dynamic invariants provide a large number of assertions that can check whether function behavior has changed* Checks provided by dynamic invariants can be very useful as _oracles_ for checking the effects of generated testsTraditionally, dynamic invariants are dependent on the executions they are derived from. However, when paired with comprehensive test generators, they quickly become very precise, as we show in this chapter. Prerequisites* You should be familiar with tracing program executions, as in the [chapter on coverage](Coverage.ipynb).* Later in this section, we access the internal _abstract syntax tree_ representations of Python programs and transform them, as in the [chapter on information flow](InformationFlow.ipynb). ###Code import bookutils import Coverage import Intro_Testing ###Output _____no_output_____ ###Markdown SynopsisTo [use the code provided in this chapter](Importing.ipynb), write```python>>> from fuzzingbook.DynamicInvariants import ```and then make use of the following features.This chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator:```python>>> def sum2(a, b):>>> return a + b>>> with TypeAnnotator() as type_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution.```python>>> print(type_annotator.typed_functions())def sum2(a: int, b: int) ->int: return a + b```The invariant annotator works in a similar fashion:```python>>> with InvariantAnnotator() as inv_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values.```python>>> print(inv_annotator.functions_with_invariants())@precondition(lambda a, b: isinstance(a, int), doc='isinstance(a, int)')@precondition(lambda a, b: isinstance(b, int), doc='isinstance(b, int)')@postcondition(lambda return_value, a, b: a == return_value - b, doc='a == return_value - b')@postcondition(lambda return_value, a, b: b == return_value - a, doc='b == return_value - a')@postcondition(lambda return_value, a, b: isinstance(return_value, int), doc='isinstance(return_value, int)')@postcondition(lambda return_value, a, b: return_value == a + b, doc='return_value == a + b')@postcondition(lambda return_value, a, b: return_value == b + a, doc='return_value == b + a')def sum2(a, b): return a + b```Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs) as well as for all kinds of _symbolic code analyses_. The chapter gives details on how to customize the properties checked for. Specifications and AssertionsWhen implementing a function or program, one usually works against a _specification_ – a set of documented requirements to be satisfied by the code. Such specifications can come in natural language. A formal specification, however, allows the computer to check whether the specification is satisfied.In the [introduction to testing](Intro_Testing.ipynb), we have seen how _preconditions_ and _postconditions_ can describe what a function does. Consider the following (simple) square root function: ###Code def my_sqrt(x): assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown The assertion `assert p` checks the condition `p`; if it does not hold, execution is aborted. Here, the actual body is not yet written; we use the assertions as a specification of what `my_sqrt()` _expects_, and what it _delivers_.The topmost assertion is the _precondition_, stating the requirements on the function arguments. The assertion at the end is the _postcondition_, stating the properties of the function result (including its relationship with the original arguments). Using these pre- and postconditions as a specification, we can now go and implement a square root function that satisfies them. Once implemented, we can have the assertions check at runtime whether `my_sqrt()` works as expected; a [symbolic](SymbolicFuzzer.ipynb) or [concolic](ConcolicFuzzer.ipynb) test generator will even specifically try to find inputs where the assertions do _not_ hold. (An assertion can be seen as a conditional branch towards aborting the execution, and any technique that tries to cover all code branches will also try to invalidate as many assertions as possible.) However, not every piece of code is developed with explicit specifications in the first place; let alone does most code comes with formal pre- and post-conditions. (Just take a look at the chapters in this book.) This is a pity: As Ken Thompson famously said, "Without specifications, there are no bugs – only surprises". It is also a problem for testing, since, of course, testing needs some specification to test against. This raises the interesting question: Can we somehow _retrofit_ existing code with "specifications" that properly describe their behavior, allowing developers to simply _check_ them rather than having to write them from scratch? This is what we do in this chapter. Why Generic Error Checking is Not EnoughBefore we go into _mining_ specifications, let us first discuss why it could be useful to _have_ them. As a motivating example, consider the full implementation of `my_sqrt()` from the [introduction to testing](Intro_Testing.ipynb): ###Code import bookutils def my_sqrt(x): """Computes the square root of x, using the Newton-Raphson method""" approx = None guess = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown `my_sqrt()` does not come with any functionality that would check types or values. Hence, it is easy for callers to make mistakes when calling `my_sqrt()`: ###Code from ExpectError import ExpectError, ExpectTimeout with ExpectError(): my_sqrt("foo") with ExpectError(): x = my_sqrt(0.0) ###Output _____no_output_____ ###Markdown At least, the Python system catches these errors at runtime. The following call, however, simply lets the function enter an infinite loop: ###Code with ExpectTimeout(1): x = my_sqrt(-1.0) ###Output _____no_output_____ ###Markdown Mining Function SpecificationsWhen testing a program, one not only needs to cover its several behaviors; one also needs to _check_ whether the result is as expected. In this chapter, we introduce a technique that allows us to _mine_ function specifications from a set of given executions, resulting in abstract and formal _descriptions_ of what the function expects and what it delivers. These so-called _dynamic invariants_ produce pre- and post-conditions over function arguments and variables from a set of executions. They are useful in a variety of contexts:* Dynamic invariants provide important information for [symbolic fuzzing](SymbolicFuzzer.ipynb), such as types and ranges of function arguments.* Dynamic invariants provide pre- and postconditions for formal program proofs and verification.* Dynamic invariants provide a large number of assertions that can check whether function behavior has changed* Checks provided by dynamic invariants can be very useful as _oracles_ for checking the effects of generated testsTraditionally, dynamic invariants are dependent on the executions they are derived from. However, when paired with comprehensive test generators, they quickly become very precise, as we show in this chapter. Prerequisites* You should be familiar with tracing program executions, as in the [chapter on coverage](Coverage.ipynb).* Later in this section, we access the internal _abstract syntax tree_ representations of Python programs and transform them, as in the [chapter on information flow](InformationFlow.ipynb). ###Code import bookutils import Coverage import Intro_Testing ###Output _____no_output_____ ###Markdown SynopsisTo [use the code provided in this chapter](Importing.ipynb), write```python>>> from fuzzingbook.DynamicInvariants import ```and then make use of the following features.This chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator:```python>>> def sum2(a, b):>>> return a + b>>> with TypeAnnotator() as type_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution.```python>>> print(type_annotator.typed_functions())def sum2(a: int, b: int) ->int: return a + b```The invariant annotator works in a similar fashion:```python>>> with InvariantAnnotator() as inv_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values.```python>>> print(inv_annotator.functions_with_invariants())@precondition(lambda a, b: isinstance(a, int), doc='isinstance(a, int)')@precondition(lambda a, b: isinstance(b, int), doc='isinstance(b, int)')@postcondition(lambda return_value, a, b: a == return_value - b, doc='a == return_value - b')@postcondition(lambda return_value, a, b: b == return_value - a, doc='b == return_value - a')@postcondition(lambda return_value, a, b: isinstance(return_value, int), doc='isinstance(return_value, int)')@postcondition(lambda return_value, a, b: return_value == a + b, doc='return_value == a + b')@postcondition(lambda return_value, a, b: return_value == b + a, doc='return_value == b + a')def sum2(a, b): return a + b```Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs) as well as for all kinds of _symbolic code analyses_. The chapter gives details on how to customize the properties checked for. Specifications and AssertionsWhen implementing a function or program, one usually works against a _specification_ – a set of documented requirements to be satisfied by the code. Such specifications can come in natural language. A formal specification, however, allows the computer to check whether the specification is satisfied.In the [introduction to testing](Intro_Testing.ipynb), we have seen how _preconditions_ and _postconditions_ can describe what a function does. Consider the following (simple) square root function: ###Code def my_sqrt(x): assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown The assertion `assert p` checks the condition `p`; if it does not hold, execution is aborted. Here, the actual body is not yet written; we use the assertions as a specification of what `my_sqrt()` _expects_, and what it _delivers_.The topmost assertion is the _precondition_, stating the requirements on the function arguments. The assertion at the end is the _postcondition_, stating the properties of the function result (including its relationship with the original arguments). Using these pre- and postconditions as a specification, we can now go and implement a square root function that satisfies them. Once implemented, we can have the assertions check at runtime whether `my_sqrt()` works as expected; a [symbolic](SymbolicFuzzer.ipynb) or [concolic](ConcolicFuzzer.ipynb) test generator will even specifically try to find inputs where the assertions do _not_ hold. (An assertion can be seen as a conditional branch towards aborting the execution, and any technique that tries to cover all code branches will also try to invalidate as many assertions as possible.) However, not every piece of code is developed with explicit specifications in the first place; let alone does most code comes with formal pre- and post-conditions. (Just take a look at the chapters in this book.) This is a pity: As Ken Thompson famously said, "Without specifications, there are no bugs – only surprises". It is also a problem for testing, since, of course, testing needs some specification to test against. This raises the interesting question: Can we somehow _retrofit_ existing code with "specifications" that properly describe their behavior, allowing developers to simply _check_ them rather than having to write them from scratch? This is what we do in this chapter. Why Generic Error Checking is Not EnoughBefore we go into _mining_ specifications, let us first discuss why it could be useful to _have_ them. As a motivating example, consider the full implementation of `my_sqrt()` from the [introduction to testing](Intro_Testing.ipynb): ###Code import bookutils def my_sqrt(x): """Computes the square root of x, using the Newton-Raphson method""" approx = None guess = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown `my_sqrt()` does not come with any functionality that would check types or values. Hence, it is easy for callers to make mistakes when calling `my_sqrt()`: ###Code from ExpectError import ExpectError, ExpectTimeout with ExpectError(): my_sqrt("foo") with ExpectError(): x = my_sqrt(0.0) ###Output _____no_output_____ ###Markdown At least, the Python system catches these errors at runtime. The following call, however, simply lets the function enter an infinite loop: ###Code with ExpectTimeout(1): x = my_sqrt(-1.0) ###Output _____no_output_____ ###Markdown Our goal is to avoid such errors by _annotating_ functions with information that prevents errors like the above ones. The idea is to provide a _specification_ of expected properties – a specification that can then be checked at runtime or statically. \todo{Introduce the concept of contract.} Specifying and Checking Data TypesFor our Python code, one of the most important "specifications" we need is types. Python being a "dynamically" typed language means that all data types are determined at run time; the code itself does not explicitly state whether a variable is an integer, a string, an array, a dictionary – or whatever. As _writer_ of Python code, omitting explicit type declarations may save time (and allows for some fun hacks). It is not sure whether a lack of types helps in _reading_ and _understanding_ code for humans. For a _computer_ trying to analyze code, the lack of explicit types is detrimental. If, say, a constraint solver, sees `if x:` and cannot know whether `x` is supposed to be a number or a string, this introduces an _ambiguity_. Such ambiguities may multiply over the entire analysis in a combinatorial explosion – or in the analysis yielding an overly inaccurate result. Python 3.6 and later allows data types as _annotations_ to function arguments (actually, to all variables) and return values. We can, for instance, state that `my_sqrt()` is a function that accepts a floating-point value and returns one: ###Code def my_sqrt_with_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return my_sqrt(x) ###Output _____no_output_____ ###Markdown By default, such annotations are ignored by the Python interpreter. Therefore, one can still call `my_sqrt_typed()` with a string as an argument and get the exact same result as above. However, one can make use of special _typechecking_ modules that would check types – _dynamically_ at runtime or _statically_ by analyzing the code without having to execute it. Excursion: Runtime Type Checking(Commented out as `enforce` is not supported by Python 3.9)The Python `enforce` package provides a function decorator that automatically inserts type-checking code that is executed at runtime. Here is how to use it: ###Code # import enforce # @enforce.runtime_validation # def my_sqrt_with_checked_type_annotations(x: float) -> float: # """Computes the square root of x, using the Newton-Raphson method""" # return my_sqrt(x) ###Output _____no_output_____ ###Markdown Now, invoking `my_sqrt_with_checked_type_annotations()` raises an exception when invoked with a type dfferent from the one declared: ###Code # with ExpectError(): # my_sqrt_with_checked_type_annotations(True) ###Output _____no_output_____ ###Markdown Note that this error is not caught by the "untyped" variant, where passing a boolean value happily returns $\sqrt{1}$ as result. ###Code # my_sqrt(True) ###Output _____no_output_____ ###Markdown In Python (and other languages), the boolean values `True` and `False` can be implicitly converted to the integers 1 and 0; however, it is hard to think of a call to `sqrt()` where this would not be an error. End of Excursion Static Type CheckingType annotations can also be checked _statically_ – that is, without even running the code. Let us create a simple Python file consisting of the above `my_sqrt_typed()` definition and a bad invocation. ###Code import inspect import tempfile f = tempfile.NamedTemporaryFile(mode='w', suffix='.py') f.name f.write(inspect.getsource(my_sqrt)) f.write('\n') f.write(inspect.getsource(my_sqrt_with_type_annotations)) f.write('\n') f.write("print(my_sqrt_with_type_annotations('123'))\n") f.flush() ###Output _____no_output_____ ###Markdown These are the contents of our newly created Python file: ###Code from bookutils import print_file print_file(f.name) ###Output _____no_output_____ ###Markdown [Mypy](http://mypy-lang.org) is a type checker for Python programs. As it checks types statically, types induce no overhead at runtime; plus, a static check can be faster than a lengthy series of tests with runtime type checking enabled. Let us see what `mypy` produces on the above file: ###Code import subprocess result = subprocess.run(["mypy", "--strict", f.name], universal_newlines=True, stdout=subprocess.PIPE) del f # Delete temporary file print(result.stdout) ###Output _____no_output_____ ###Markdown We see that `mypy` complains about untyped function definitions such as `my_sqrt()`; most important, however, it finds that the call to `my_sqrt_with_type_annotations()` in the last line has the wrong type. With `mypy`, we can achieve the same type safety with Python as in statically typed languages – provided that we as programmers also produce the necessary type annotations. Is there a simple way to obtain these? Mining Type SpecificationsOur first task will be to mine type annotations (as part of the code) from _values_ we observe at run time. These type annotations would be _mined_ from actual function executions, _learning_ from (normal) runs what the expected argument and return types should be. By observing a series of calls such as these, we could infer that both `x` and the return value are of type `float`: ###Code y = my_sqrt(25.0) y y = my_sqrt(2.0) y ###Output _____no_output_____ ###Markdown How can we mine types from executions? The answer is simple: 1. We _observe_ a function during execution2. We track the _types_ of its arguments3. We include these types as _annotations_ into the code.To do so, we can make use of Python's tracing facility we already observed in the [chapter on coverage](Coverage.ipynb). With every call to a function, we retrieve the arguments, their values, and their types. Tracking CallsTo observe argument types at runtime, we define a _tracer function_ that tracks the execution of `my_sqrt()`, checking its arguments and return values. The `Tracker` class is set to trace functions in a `with` block as follows:```pythonwith Tracker() as tracker: function_to_be_tracked(...)info = tracker.collected_information()```As in the [chapter on coverage](Coverage.ipynb), we use the `sys.settrace()` function to trace individual functions during execution. We turn on tracking when the `with` block starts; at this point, the `__enter__()` method is called. When execution of the `with` block ends, `__exit()__` is called. ###Code import sys class Tracker(object): def __init__(self, log=False): self._log = log self.reset() def reset(self): self._calls = {} self._stack = [] def traceit(self): """Placeholder to be overloaded in subclasses""" pass # Start of `with` block def __enter__(self): self.original_trace_function = sys.gettrace() sys.settrace(self.traceit) return self # End of `with` block def __exit__(self, exc_type, exc_value, tb): sys.settrace(self.original_trace_function) ###Output _____no_output_____ ###Markdown The `traceit()` method does nothing yet; this is done in specialized subclasses. The `CallTracker` class implements a `traceit()` function that checks for function calls and returns: ###Code class CallTracker(Tracker): def traceit(self, frame, event, arg): """Tracking function: Record all calls and all args""" if event == "call": self.trace_call(frame, event, arg) elif event == "return": self.trace_return(frame, event, arg) return self.traceit ###Output _____no_output_____ ###Markdown `trace_call()` is called when a function is called; it retrieves the function name and current arguments, and saves them on a stack. ###Code class CallTracker(CallTracker): def trace_call(self, frame, event, arg): """Save current function name and args on the stack""" code = frame.f_code function_name = code.co_name arguments = get_arguments(frame) self._stack.append((function_name, arguments)) if self._log: print(simple_call_string(function_name, arguments)) def get_arguments(frame): """Return call arguments in the given frame""" # When called, all arguments are local variables local_variables = dict(frame.f_locals) # explicit copy arguments = [(var, frame.f_locals[var]) for var in local_variables] arguments.reverse() # Want same order as call return arguments ###Output _____no_output_____ ###Markdown When the function returns, `trace_return()` is called. We now also have the return value. We log the whole call with arguments and return value (if desired) and save it in our list of calls. ###Code class CallTracker(CallTracker): def trace_return(self, frame, event, arg): """Get return value and store complete call with arguments and return value""" code = frame.f_code function_name = code.co_name return_value = arg # TODO: Could call get_arguments() here to also retrieve _final_ values of argument variables called_function_name, called_arguments = self._stack.pop() assert function_name == called_function_name if self._log: print(simple_call_string(function_name, called_arguments), "returns", return_value) self.add_call(function_name, called_arguments, return_value) ###Output _____no_output_____ ###Markdown `simple_call_string()` is a helper for logging that prints out calls in a user-friendly manner. ###Code def simple_call_string(function_name, argument_list, return_value=None): """Return function_name(arg[0], arg[1], ...) as a string""" call = function_name + "(" + \ ", ".join([var + "=" + repr(value) for (var, value) in argument_list]) + ")" if return_value is not None: call += " = " + repr(return_value) return call ###Output _____no_output_____ ###Markdown `add_call()` saves the calls in a list; each function name has its own list. ###Code class CallTracker(CallTracker): def add_call(self, function_name, arguments, return_value=None): """Add given call to list of calls""" if function_name not in self._calls: self._calls[function_name] = [] self._calls[function_name].append((arguments, return_value)) ###Output _____no_output_____ ###Markdown Using `calls()`, we can retrieve the list of calls, either for a given function, or for all functions. ###Code class CallTracker(CallTracker): def calls(self, function_name=None): """Return list of calls for function_name, or a mapping function_name -> calls for all functions tracked""" if function_name is None: return self._calls return self._calls[function_name] ###Output _____no_output_____ ###Markdown Let us now put this to use. We turn on logging to track the individual calls and their return values: ###Code with CallTracker(log=True) as tracker: y = my_sqrt(25) y = my_sqrt(2.0) ###Output _____no_output_____ ###Markdown After execution, we can retrieve the individual calls: ###Code calls = tracker.calls('my_sqrt') calls ###Output _____no_output_____ ###Markdown Each call is pair (`argument_list`, `return_value`), where `argument_list` is a list of pairs (`parameter_name`, `value`). ###Code my_sqrt_argument_list, my_sqrt_return_value = calls[0] simple_call_string('my_sqrt', my_sqrt_argument_list, my_sqrt_return_value) ###Output _____no_output_____ ###Markdown If the function does not return a value, `return_value` is `None`. ###Code def hello(name): print("Hello,", name) with CallTracker() as tracker: hello("world") hello_calls = tracker.calls('hello') hello_calls hello_argument_list, hello_return_value = hello_calls[0] simple_call_string('hello', hello_argument_list, hello_return_value) ###Output _____no_output_____ ###Markdown Getting TypesDespite what you may have read or heard, Python actually _is_ a typed language. It is just that it is _dynamically typed_ – types are used and checked only at runtime (rather than declared in the code, where they can be _statically checked_ at compile time). We can thus retrieve types of all values within Python: ###Code type(4) type(2.0) type([4]) ###Output _____no_output_____ ###Markdown We can retrieve the type of the first argument to `my_sqrt()`: ###Code parameter, value = my_sqrt_argument_list[0] parameter, type(value) ###Output _____no_output_____ ###Markdown as well as the type of the return value: ###Code type(my_sqrt_return_value) ###Output _____no_output_____ ###Markdown Hence, we see that (so far), `my_sqrt()` is a function taking (among others) integers and returning floats. We could declare `my_sqrt()` as: ###Code def my_sqrt_annotated(x: int) -> float: return my_sqrt(x) ###Output _____no_output_____ ###Markdown This is a representation we could place in a static type checker, allowing to check whether calls to `my_sqrt()` actually pass a number. A dynamic type checker could run such checks at runtime. And of course, any [symbolic interpretation](SymbolicFuzzer.ipynb) will greatly profit from the additional annotations. By default, Python does not do anything with such annotations. However, tools can access annotations from functions and other objects: ###Code my_sqrt_annotated.__annotations__ ###Output _____no_output_____ ###Markdown This is how run-time checkers access the annotations to check against. Accessing Function StructureOur plan is to annotate functions automatically, based on the types we have seen. To do so, we need a few modules that allow us to convert a function into a tree representation (called _abstract syntax trees_, or ASTs) and back; we already have seen these in the chapters on [concolic](ConcolicFuzzer.ipynb) and [symbolic](SymbolicFuzzer.ipynb) testing. ###Code import ast import inspect ###Output _____no_output_____ ###Markdown We can get the source of a Python function using `inspect.getsource()`. (Note that this does not work for functions defined in other notebooks.) ###Code my_sqrt_source = inspect.getsource(my_sqrt) my_sqrt_source ###Output _____no_output_____ ###Markdown To view these in a visually pleasing form, our function `print_content(s, suffix)` formats and highlights the string `s` as if it were a file with ending `suffix`. We can thus view (and highlight) the source as if it were a Python file: ###Code from bookutils import print_content print_content(my_sqrt_source, '.py') ###Output _____no_output_____ ###Markdown Parsing this gives us an abstract syntax tree (AST) – a representation of the program in tree form. ###Code my_sqrt_ast = ast.parse(my_sqrt_source) ###Output _____no_output_____ ###Markdown What does this AST look like? The helper functions `ast.dump()` (textual output) and `showast.show_ast()` (graphical output with [showast](https://github.com/hchasestevens/show_ast)) allow us to inspect the structure of the tree. We see that the function starts as a `FunctionDef` with name and arguments, followed by a body, which is a list of statements of type `Expr` (the docstring), type `Assign` (assignments), `While` (while loop with its own body), and finally `Return`. ###Code print(ast.dump(my_sqrt_ast, indent=4)) ###Output _____no_output_____ ###Markdown Too much text for you? This graphical representation may make things simpler. ###Code from bookutils import rich_output if rich_output(): import showast showast.show_ast(my_sqrt_ast) ###Output _____no_output_____ ###Markdown The function `ast.unparse()` converts such a tree back into the more familiar textual Python code representation. Comments are gone, and there may be more parentheses than before, but the result has the same semantics: ###Code print_content(ast.unparse(my_sqrt_ast), '.py') ###Output _____no_output_____ ###Markdown Annotating Functions with Given TypesLet us now go and transform these trees ti add type annotations. We start with a helper function `parse_type(name)` which parses a type name into an AST. ###Code def parse_type(name): class ValueVisitor(ast.NodeVisitor): def visit_Expr(self, node): self.value_node = node.value tree = ast.parse(name) name_visitor = ValueVisitor() name_visitor.visit(tree) return name_visitor.value_node print(ast.dump(parse_type('int'))) print(ast.dump(parse_type('[object]'))) ###Output _____no_output_____ ###Markdown We now define a helper function that actually adds type annotations to a function AST. The `TypeTransformer` class builds on the Python standard library `ast.NodeTransformer` infrastructure. It would be called as```python TypeTransformer({'x': 'int'}, 'float').visit(ast)```to annotate the arguments of `my_sqrt()`: `x` with `int`, and the return type with `float`. The returned AST can then be unparsed, compiled or analyzed. ###Code class TypeTransformer(ast.NodeTransformer): def __init__(self, argument_types, return_type=None): self.argument_types = argument_types self.return_type = return_type super().__init__() ###Output _____no_output_____ ###Markdown The core of `TypeTransformer` is the method `visit_FunctionDef()`, which is called for every function definition in the AST. Its argument `node` is the subtree of the function definition to be transformed. Our implementation accesses the individual arguments and invokes `annotate_args()` on them; it also sets the return type in the `returns` attribute of the node. ###Code class TypeTransformer(TypeTransformer): def visit_FunctionDef(self, node): """Add annotation to function""" # Set argument types new_args = [] for arg in node.args.args: new_args.append(self.annotate_arg(arg)) new_arguments = ast.arguments( node.args.posonlyargs, new_args, node.args.vararg, node.args.kwonlyargs, node.args.kw_defaults, node.args.kwarg, node.args.defaults ) # Set return type if self.return_type is not None: node.returns = parse_type(self.return_type) return ast.copy_location( ast.FunctionDef(node.name, new_arguments, node.body, node.decorator_list, node.returns), node) ###Output _____no_output_____ ###Markdown Each argument gets its own annotation, taken from the types originally passed to the class: ###Code class TypeTransformer(TypeTransformer): def annotate_arg(self, arg): """Add annotation to single function argument""" arg_name = arg.arg if arg_name in self.argument_types: arg.annotation = parse_type(self.argument_types[arg_name]) return arg ###Output _____no_output_____ ###Markdown Does this work? Let us annotate the AST from `my_sqrt()` with types for the arguments and return types: ###Code new_ast = TypeTransformer({'x': 'int'}, 'float').visit(my_sqrt_ast) ###Output _____no_output_____ ###Markdown When we unparse the new AST, we see that the annotations actually are present: ###Code print_content(ast.unparse(new_ast), '.py') ###Output _____no_output_____ ###Markdown Similarly, we can annotate the `hello()` function from above: ###Code hello_source = inspect.getsource(hello) hello_ast = ast.parse(hello_source) new_ast = TypeTransformer({'name': 'str'}, 'None').visit(hello_ast) print_content(ast.unparse(new_ast), '.py') ###Output _____no_output_____ ###Markdown Annotating Functions with Mined TypesLet us now annotate functions with types mined at runtime. We start with a simple function `type_string()` that determines the appropriate type of a given value (as a string): ###Code def type_string(value): return type(value).__name__ type_string(4) type_string([]) ###Output _____no_output_____ ###Markdown For composite structures, `type_string()` does not examine element types; hence, the type of `[3]` is simply `list` instead of, say, `list[int]`. For now, `list` will do fine. ###Code type_string([3]) ###Output _____no_output_____ ###Markdown `type_string()` will be used to infer the types of argument values found at runtime, as returned by `CallTracker.calls()`: ###Code with CallTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(2.0) tracker.calls() ###Output _____no_output_____ ###Markdown The function `annotate_types()` takes such a list of calls and annotates each function listed: ###Code def annotate_types(calls): annotated_functions = {} for function_name in calls: try: annotated_functions[function_name] = annotate_function_with_types(function_name, calls[function_name]) except KeyError: continue return annotated_functions ###Output _____no_output_____ ###Markdown For each function, we get the source and its AST and then get to the actual annotation in `annotate_function_ast_with_types()`: ###Code def annotate_function_with_types(function_name, function_calls): function = globals()[function_name] # May raise KeyError for internal functions function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_types(function_ast, function_calls) ###Output _____no_output_____ ###Markdown The function `annotate_function_ast_with_types()` invokes the `TypeTransformer` with the calls seen, and for each call, iterate over the arguments, determine their types, and annotate the AST with these. The universal type `Any` is used when we encounter type conflicts, which we will discuss below. ###Code from typing import Any def annotate_function_ast_with_types(function_ast, function_calls): parameter_types = {} return_type = None for calls_seen in function_calls: args, return_value = calls_seen if return_value is not None: if return_type is not None and return_type != type_string(return_value): return_type = 'Any' else: return_type = type_string(return_value) for parameter, value in args: try: different_type = parameter_types[parameter] != type_string(value) except KeyError: different_type = False if different_type: parameter_types[parameter] = 'Any' else: parameter_types[parameter] = type_string(value) annotated_function_ast = TypeTransformer(parameter_types, return_type).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Here is `my_sqrt()` annotated with the types recorded usign the tracker, above. ###Code print_content(ast.unparse(annotate_types(tracker.calls())['my_sqrt']), '.py') ###Output _____no_output_____ ###Markdown All-in-one AnnotationLet us bring all of this together in a single class `TypeAnnotator` that first tracks calls of functions and then allows to access the AST (and the source code form) of the tracked functions annotated with types. The method `typed_functions()` returns the annotated functions as a string; `typed_functions_ast()` returns their AST. ###Code class TypeTracker(CallTracker): pass class TypeAnnotator(TypeTracker): def typed_functions_ast(self, function_name=None): if function_name is None: return annotate_types(self.calls()) return annotate_function_with_types(function_name, self.calls(function_name)) def typed_functions(self, function_name=None): if function_name is None: functions = '' for f_name in self.calls(): try: f_text = ast.unparse(self.typed_functions_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions return ast.unparse(self.typed_functions_ast(function_name)) ###Output _____no_output_____ ###Markdown Here is how to use `TypeAnnotator`. We first track a series of calls: ###Code with TypeAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(2.0) ###Output _____no_output_____ ###Markdown After tracking, we can immediately retrieve an annotated version of the functions tracked: ###Code print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown This also works for multiple and diverse functions. One could go and implement an automatic type annotator for Python files based on the types seen during execution. ###Code with TypeAnnotator() as annotator: hello('type annotations') y = my_sqrt(1.0) print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown A content as above could now be sent to a type checker, which would detect any type inconsistency between callers and callees. Likewise, type annotations such as the ones above greatly benefit symbolic code analysis (as in the chapter on [symbolic fuzzing](SymbolicFuzzer.ipynb)), as they effectively constrain the set of values that arguments and variables can take. Multiple TypesLet us now resolve the role of the magic `Any` type in `annotate_function_ast_with_types()`. If we see multiple types for the same argument, we set its type to `Any`. For `my_sqrt()`, this makes sense, as its arguments can be integers as well as floats: ###Code with CallTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(4) print_content(ast.unparse(annotate_types(tracker.calls())['my_sqrt']), '.py') ###Output _____no_output_____ ###Markdown The following function `sum3()` can be called with floating-point numbers as arguments, resulting in the parameters getting a `float` type: ###Code def sum3(a, b, c): return a + b + c with TypeAnnotator() as annotator: y = sum3(1.0, 2.0, 3.0) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we call `sum3()` with integers, though, the arguments get an `int` type: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown And we can also call `sum3()` with strings, giving the arguments a `str` type: ###Code with TypeAnnotator() as annotator: y = sum3("one", "two", "three") y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we have multiple calls, but with different types, `TypeAnnotator()` will assign an `Any` type to both arguments and return values: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y = sum3("one", "two", "three") typed_sum3_def = annotator.typed_functions('sum3') print_content(typed_sum3_def, '.py') ###Output _____no_output_____ ###Markdown A type `Any` makes it explicit that an object can, indeed, have any type; it will not be typechecked at runtime or statically. To some extent, this defeats the power of type checking; but it also preserves some of the type flexibility that many Python programmers enjoy. Besides `Any`, the `typing` module supports several additional ways to define ambiguous types; we will keep this in mind for a later exercise. Specifying and Checking InvariantsBesides basic data types. we can check several further properties from arguments. We can, for instance, whether an argument can be negative, zero, or positive; or that one argument should be smaller than the second; or that the result should be the sum of two arguments – properties that cannot be expressed in a (Python) type.Such properties are called invariants, as they hold across all invocations of a function. Specifically, invariants come as _pre_- and _postconditions_ – conditions that always hold at the beginning and at the end of a function. (There are also _data_ and _object_ invariants that express always-holding properties over the state of data or objects, but we do not consider these in this book.) Annotating Functions with Pre- and PostconditionsThe classical means to specify pre- and postconditions is via _assertions_, which we have introduced in the [chapter on testing](Intro_Testing.ipynb). A precondition checks whether the arguments to a function satisfy the expected properties; a postcondition does the same for the result. We can express and check both using assertions as follows: ###Code def my_sqrt_with_invariants(x): assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown A nicer way, however, is to syntactically separate invariants from the function at hand. Using appropriate decorators, we could specify pre- and postconditions as follows:```python@precondition lambda x: x >= 0@postcondition lambda return_value, x: return_value * return_value == xdef my_sqrt_with_invariants(x): normal code without assertions ...```The decorators `@precondition` and `@postcondition` would run the given functions (specified as anonymous `lambda` functions) before and after the decorated function, respectively. If the functions return `False`, the condition is violated. `@precondition` gets the function arguments as arguments; `@postcondition` additionally gets the return value as first argument. It turns out that implementing such decorators is not hard at all. Our implementation builds on a [code snippet from StackOverflow](https://stackoverflow.com/questions/12151182/python-precondition-postcondition-for-member-function-how): ###Code import functools def condition(precondition=None, postcondition=None): def decorator(func): @functools.wraps(func) # preserves name, docstring, etc def wrapper(args, kwargs): if precondition is not None: assert precondition(args, *kwargs), "Precondition violated" retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, *kwargs), "Postcondition violated" return retval return wrapper return decorator def precondition(check): return condition(precondition=check) def postcondition(check): return condition(postcondition=check) ###Output _____no_output_____ ###Markdown With these, we can now start decorating `my_sqrt()`: ###Code @precondition(lambda x: x > 0) def my_sqrt_with_precondition(x): return my_sqrt(x) ###Output _____no_output_____ ###Markdown This catches arguments violating the precondition: ###Code with ExpectError(): my_sqrt_with_precondition(-1.0) ###Output _____no_output_____ ###Markdown Likewise, we can provide a postcondition: ###Code EPSILON = 1e-5 @postcondition(lambda ret, x: ret ret - x < EPSILON) def my_sqrt_with_postcondition(x): return my_sqrt(x) y = my_sqrt_with_postcondition(2.0) y ###Output _____no_output_____ ###Markdown If we have a buggy implementation of $\sqrt{x}$, this gets caught quickly: ###Code @postcondition(lambda ret, x: ret * ret - x < EPSILON) def buggy_my_sqrt_with_postcondition(x): return my_sqrt(x) + 0.1 with ExpectError(): y = buggy_my_sqrt_with_postcondition(2.0) ###Output _____no_output_____ ###Markdown While checking pre- and postconditions is a great way to catch errors, specifying them can be cumbersome. Let us try to see whether we can (again) _mine_ some of them. Mining InvariantsTo _mine_ invariants, we can use the same tracking functionality as before; instead of saving values for individual variables, though, we now check whether the values satisfy specific _properties_ or not. For instance, if all values of `x` seen satisfy the condition `x > 0`, then we make `x > 0` an invariant of the function. If we see positive, zero, and negative values of `x`, though, then there is no property of `x` left to talk about.The general idea is thus:1. Check all variable values observed against a set of predefined properties; and2. Keep only those properties that hold for all runs observed. Defining PropertiesWhat precisely do we mean by properties? Here is a small collection of value properties that would frequently be used in invariants. All these properties would be evaluated with the _metavariables_ `X`, `Y`, and `Z` (actually, any upper-case identifier) being replaced with the names of function parameters: ###Code INVARIANT_PROPERTIES = [ "X < 0", "X <= 0", "X > 0", "X >= 0", "X == 0", "X != 0", ] ###Output _____no_output_____ ###Markdown When `my_sqrt(x)` is called as, say `my_sqrt(5.0)`, we see that `x = 5.0` holds. The above properties would then all be checked for `x`. Only the properties `X > 0`, `X >= 0`, and `X != 0` hold for the call seen; and hence `x > 0`, `x >= 0`, and `x != 0` would make potential preconditions for `my_sqrt(x)`. We can check for many more properties such as relations between two arguments: ###Code INVARIANT_PROPERTIES += [ "X == Y", "X > Y", "X < Y", "X >= Y", "X <= Y", ] ###Output _____no_output_____ ###Markdown Types also can be checked using properties. For any function parameter `X`, only one of these will hold: ###Code INVARIANT_PROPERTIES += [ "isinstance(X, bool)", "isinstance(X, int)", "isinstance(X, float)", "isinstance(X, list)", "isinstance(X, dict)", ] ###Output _____no_output_____ ###Markdown We can check for arithmetic properties: ###Code INVARIANT_PROPERTIES += [ "X == Y + Z", "X == Y * Z", "X == Y - Z", "X == Y / Z", ] ###Output _____no_output_____ ###Markdown Here's relations over three values, a Python special: ###Code INVARIANT_PROPERTIES += [ "X < Y < Z", "X <= Y <= Z", "X > Y > Z", "X >= Y >= Z", ] ###Output _____no_output_____ ###Markdown Finally, we can also check for list or string properties. Again, this is just a tiny selection. ###Code INVARIANT_PROPERTIES += [ "X == len(Y)", "X == sum(Y)", "X.startswith(Y)", ] ###Output _____no_output_____ ###Markdown Extracting Meta-VariablesLet us first introduce a few _helper functions_ before we can get to the actual mining. `metavars()` extracts the set of meta-variables (`X`, `Y`, `Z`, etc.) from a property. To this end, we parse the property as a Python expression and then visit the identifiers. ###Code def metavars(prop): metavar_list = [] class ArgVisitor(ast.NodeVisitor): def visit_Name(self, node): if node.id.isupper(): metavar_list.append(node.id) ArgVisitor().visit(ast.parse(prop)) return metavar_list assert metavars("X < 0") == ['X'] assert metavars("X.startswith(Y)") == ['X', 'Y'] assert metavars("isinstance(X, str)") == ['X'] ###Output _____no_output_____ ###Markdown Instantiating PropertiesTo produce a property as invariant, we need to be able to _instantiate_ it with variable names. The instantiation of `X > 0` with `X` being instantiated to `a`, for instance, gets us `a > 0`. To this end, the function `instantiate_prop()` takes a property and a collection of variable names and instantiates the meta-variables left-to-right with the corresponding variables names in the collection. ###Code def instantiate_prop_ast(prop, var_names): class NameTransformer(ast.NodeTransformer): def visit_Name(self, node): if node.id not in mapping: return node return ast.Name(id=mapping[node.id], ctx=ast.Load()) meta_variables = metavars(prop) assert len(meta_variables) == len(var_names) mapping = {} for i in range(0, len(meta_variables)): mapping[meta_variables[i]] = var_names[i] prop_ast = ast.parse(prop, mode='eval') new_ast = NameTransformer().visit(prop_ast) return new_ast def instantiate_prop(prop, var_names): prop_ast = instantiate_prop_ast(prop, var_names) prop_text = ast.unparse(prop_ast).strip() while prop_text.startswith('(') and prop_text.endswith(')'): prop_text = prop_text[1:-1] return prop_text assert instantiate_prop("X > Y", ['a', 'b']) == 'a > b' assert instantiate_prop("X.startswith(Y)", ['x', 'y']) == 'x.startswith(y)' ###Output _____no_output_____ ###Markdown Evaluating PropertiesTo actually _evaluate_ properties, we do not need to instantiate them. Instead, we simply convert them into a boolean function, using `lambda`: ###Code def prop_function_text(prop): return "lambda " + ", ".join(metavars(prop)) + ": " + prop def prop_function(prop): return eval(prop_function_text(prop)) ###Output _____no_output_____ ###Markdown Here is a simple example: ###Code prop_function_text("X > Y") p = prop_function("X > Y") p(100, 1) p(1, 100) ###Output _____no_output_____ ###Markdown Checking InvariantsTo extract invariants from an execution, we need to check them on all possible instantiations of arguments. If the function to be checked has two arguments `a` and `b`, we instantiate the property `X < Y` both as `a < b` and `b < a` and check each of them. To get all combinations, we use the Python `permutations()` function: ###Code import itertools for combination in itertools.permutations([1.0, 2.0, 3.0], 2): print(combination) ###Output _____no_output_____ ###Markdown The function `true_property_instantiations()` takes a property and a list of tuples (`var_name`, `value`). It then produces all instantiations of the property with the given values and returns those that evaluate to True. ###Code def true_property_instantiations(prop, vars_and_values, log=False): instantiations = set() p = prop_function(prop) len_metavars = len(metavars(prop)) for combination in itertools.permutations(vars_and_values, len_metavars): args = [value for var_name, value in combination] var_names = [var_name for var_name, value in combination] try: result = p(args) except: result = None if log: print(prop, combination, result) if result: instantiations.add((prop, tuple(var_names))) return instantiations ###Output _____no_output_____ ###Markdown Here is an example. If `x == -1` and `y == 1`, the property `X < Y` holds for `x < y`, but not for `y < x`: ###Code invs = true_property_instantiations("X < Y", [('x', -1), ('y', 1)], log=True) invs ###Output _____no_output_____ ###Markdown The instantiation retrieves the short form: ###Code for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Likewise, with values for `x` and `y` as above, the property `X < 0` only holds for `x`, but not for `y`: ###Code invs = true_property_instantiations("X < 0", [('x', -1), ('y', 1)], log=True) for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Extracting InvariantsLet us now run the above invariant extraction on function arguments and return values as observed during a function execution. To this end, we extend the `CallTracker` class into an `InvariantTracker` class, which automatically computes invariants for all functions and all calls observed during tracking. By default, an `InvariantTracker` uses the properties as defined above; however, one can specify alternate sets of properties. ###Code class InvariantTracker(CallTracker): def __init__(self, props=None, kwargs): if props is None: props = INVARIANT_PROPERTIES self.props = props super().__init__(kwargs) ###Output _____no_output_____ ###Markdown The key method of the `InvariantTracker` is the `invariants()` method. This iterates over the calls observed and checks which properties hold. Only the intersection of properties – that is, the set of properties that hold for all calls – is preserved, and eventually returned. The special variable `return_value` is set to hold the return value. ###Code RETURN_VALUE = 'return_value' class InvariantTracker(InvariantTracker): def invariants(self, function_name=None): if function_name is None: return {function_name: self.invariants(function_name) for function_name in self.calls()} invariants = None for variables, return_value in self.calls(function_name): vars_and_values = variables + [(RETURN_VALUE, return_value)] s = set() for prop in self.props: s \|= true_property_instantiations(prop, vars_and_values, self._log) if invariants is None: invariants = s else: invariants &= s return invariants ###Output _____no_output_____ ###Markdown Here's an example of how to use `invariants()`. We run the tracker on a small set of calls. ###Code with InvariantTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(10.0) tracker.calls() ###Output _____no_output_____ ###Markdown The `invariants()` method produces a set of properties that hold for the observed runs, together with their instantiations over function arguments. ###Code invs = tracker.invariants('my_sqrt') invs ###Output _____no_output_____ ###Markdown As before, the actual instantiations are easier to read: ###Code def pretty_invariants(invariants): props = [] for (prop, var_names) in invariants: props.append(instantiate_prop(prop, var_names)) return sorted(props) pretty_invariants(invs) ###Output _____no_output_____ ###Markdown We see that the both `x` and the return value have a `float` type. We also see that both are always greater than zero. These are properties that may make useful pre- and postconditions, notably for symbolic analysis. However, there's also an invariant which does _not_ universally hold, namely `return_value <= x`, as the following example shows: ###Code my_sqrt(0.01) ###Output _____no_output_____ ###Markdown Clearly, 0.1 > 0.01 holds. This is a case of us not learning from sufficiently diverse inputs. As soon as we have a call including `x = 0.1`, though, the invariant `return_value <= x` is eliminated: ###Code with InvariantTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(10.0) y = my_sqrt(0.01) pretty_invariants(tracker.invariants('my_sqrt')) ###Output _____no_output_____ ###Markdown We will discuss later how to ensure sufficient diversity in inputs. (Hint: This involves test generation.) Let us try out our invariant tracker on `sum3()`. We see that all types are well-defined; the properties that all arguments are non-zero, however, is specific to the calls observed. ###Code with InvariantTracker() as tracker: y = sum3(1, 2, 3) y = sum3(-4, -5, -6) pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with strings instead, we get different invariants. Notably, we obtain the postcondition that the return value starts with the value of `a` – a universal postcondition if strings are used. ###Code with InvariantTracker() as tracker: y = sum3('a', 'b', 'c') y = sum3('f', 'e', 'd') pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with both strings and numbers (and zeros, too), there are no properties left that would hold across all calls. That's the price of flexibility. ###Code with InvariantTracker() as tracker: y = sum3('a', 'b', 'c') y = sum3('c', 'b', 'a') y = sum3(-4, -5, -6) y = sum3(0, 0, 0) pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown Converting Mined Invariants to AnnotationsAs with types, above, we would like to have some functionality where we can add the mined invariants as annotations to existing functions. To this end, we introduce the `InvariantAnnotator` class, extending `InvariantTracker`. We start with a helper method. `params()` returns a comma-separated list of parameter names as observed during calls. ###Code class InvariantAnnotator(InvariantTracker): def params(self, function_name): arguments, return_value = self.calls(function_name)[0] return ", ".join(arg_name for (arg_name, arg_value) in arguments) with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = sum3(1, 2, 3) annotator.params('my_sqrt') annotator.params('sum3') ###Output _____no_output_____ ###Markdown Now for the actual annotation. `preconditions()` returns the preconditions from the mined invariants (i.e., those propertes that do not depend on the return value) as a string with annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@precondition(lambda " + self.params(function_name) + ": " + inv + ")" conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) annotator.preconditions('my_sqrt') ###Output _____no_output_____ ###Markdown `postconditions()` does the same for postconditions: ###Code class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ")") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) annotator.postconditions('my_sqrt') ###Output _____no_output_____ ###Markdown With these, we can take a function and add both pre- and postconditions as annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def functions_with_invariants(self): functions = "" for function_name in self.invariants(): try: function = self.function_with_invariants(function_name) except KeyError: continue functions += function return functions def function_with_invariants(self, function_name): function = globals()[function_name] # Can throw KeyError source = inspect.getsource(function) return "\n".join(self.preconditions(function_name) + self.postconditions(function_name)) + '\n' + source ###Output _____no_output_____ ###Markdown Here comes `function_with_invariants()` in all its glory: ###Code with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) print_content(annotator.function_with_invariants('my_sqrt'), '.py') ###Output _____no_output_____ ###Markdown Quite a lot of invariants, is it? Further below (and in the exercises), we will discuss on how to focus on the most relevant properties. Some ExamplesHere's another example. `list_length()` recursively computes the length of a Python function. Let us see whether we can mine its invariants: ###Code def list_length(L): if L == []: length = 0 else: length = 1 + list_length(L[1:]) return length with InvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Almost all these properties (except for the very first) are relevant. Of course, the reason the invariants are so neat is that the return value is equal to `len(L)` is that `X == len(Y)` is part of the list of properties to be checked. The next example is a very simple function: ###Code def sum2(a, b): return a + b with InvariantAnnotator() as annotator: sum2(31, 45) sum2(0, 0) sum2(-1, -5) ###Output _____no_output_____ ###Markdown The invariants all capture the relationship between `a`, `b`, and the return value as `return_value == a + b` in all its variations. ###Code print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown If we have a function without return value, the return value is `None` and we can only mine preconditions. (Well, we get a "postcondition" that the return value is non-zero, which holds for `None`). ###Code def print_sum(a, b): print(a + b) with InvariantAnnotator() as annotator: print_sum(31, 45) print_sum(0, 0) print_sum(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Checking SpecificationsA function with invariants, as above, can be fed into the Python interpreter, such that all pre- and postconditions are checked. We create a function `my_sqrt_annotated()` which includes all the invariants mined above. ###Code with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) my_sqrt_def = annotator.functions_with_invariants() my_sqrt_def = my_sqrt_def.replace('my_sqrt', 'my_sqrt_annotated') print_content(my_sqrt_def, '.py') exec(my_sqrt_def) ###Output _____no_output_____ ###Markdown The "annotated" version checks against invalid arguments – or more precisely, against arguments with properties that have not been observed yet: ###Code with ExpectError(): my_sqrt_annotated(-1.0) ###Output _____no_output_____ ###Markdown This is in contrast to the original version, which just hangs on negative values: ###Code with ExpectTimeout(1): my_sqrt(-1.0) ###Output _____no_output_____ ###Markdown If we make changes to the function definition such that the properties of the return value change, such _regressions_ are caught as violations of the postconditions. Let us illustrate this by simply inverting the result, and return $-2$ as square root of 4. ###Code my_sqrt_def = my_sqrt_def.replace('my_sqrt_annotated', 'my_sqrt_negative') my_sqrt_def = my_sqrt_def.replace('return approx', 'return -approx') print_content(my_sqrt_def, '.py') exec(my_sqrt_def) ###Output _____no_output_____ ###Markdown Technically speaking, $-2$ _is_ a square root of 4, since $(-2)^2 = 4$ holds. Yet, such a change may be unexpected by callers of `my_sqrt()`, and hence, this would be caught with the first call: ###Code with ExpectError(): my_sqrt_negative(2.0) ###Output _____no_output_____ ###Markdown We see how pre- and postconditions, as well as types, can serve as oracles* during testing. In particular, once we have mined them for a set of functions, we can check them again and again with test generators – especially after code changes. The more checks we have, and the more specific they are, the more likely it is we can detect unwanted effects of changes. Mining Specifications from Generated TestsMined specifications can only be as good as the executions they were mined from. If we only see a single call to, say, `sum2()`, we will be faced with several mined pre- and postconditions that _overspecialize_ towards the values seen: ###Code def sum2(a, b): return a + b with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown The mined precondition `a == b`, for instance, only holds for the single call observed; the same holds for the mined postcondition `return_value == a * b`. Yet, `sum2()` can obviously be successfully called with other values that do not satisfy these conditions. To get out of this trap, we have to _learn from more and more diverse runs_. If we have a few more calls of `sum2()`, we see how the set of invariants quickly gets smaller: ###Code with InvariantAnnotator() as annotator: length = sum2(1, 2) length = sum2(-1, -2) length = sum2(0, 0) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown But where to we get such diverse runs from? This is the job of generating software tests. A simple grammar for calls of `sum2()` will easily resolve the problem. ###Code from GrammarFuzzer import GrammarFuzzer # minor dependency from Grammars import is_valid_grammar, crange, convert_ebnf_grammar # minor dependency SUM2_EBNF_GRAMMAR = { "<start>": ["<sum2>"], "<sum2>": ["sum2(<int>, <int>)"], "<int>": ["<_int>"], "<_int>": ["(-)?<leaddigit><digit>", "0"], "<leaddigit>": crange('1', '9'), "<digit>": crange('0', '9') } assert is_valid_grammar(SUM2_EBNF_GRAMMAR) sum2_grammar = convert_ebnf_grammar(SUM2_EBNF_GRAMMAR) sum2_fuzzer = GrammarFuzzer(sum2_grammar) [sum2_fuzzer.fuzz() for i in range(10)] with InvariantAnnotator() as annotator: for i in range(10): eval(sum2_fuzzer.fuzz()) print_content(annotator.function_with_invariants('sum2'), '.py') ###Output _____no_output_____ ###Markdown But then, writing tests (or a test driver) just to derive a set of pre- and postconditions may possibly be too much effort – in particular, since tests can easily be derived from given pre- and postconditions in the first place. Hence, it would be wiser to first specify invariants and then let test generators or program provers do the job. Also, an API grammar, such as above, will have to be set up such that it actually respects preconditions – in our case, we invoke `sqrt()` with positive numbers only, already assuming its precondition. In some way, one thus needs a specification (a model, a grammar) to mine another specification – a chicken-and-egg problem. However, there is one way out of this problem: If one can automatically generate tests at the system level, then one has an _infinite source of executions_ to learn invariants from. In each of these executions, all functions would be called with values that satisfy the (implicit) precondition, allowing us to mine invariants for these functions. This holds, because at the system level, invalid inputs must be rejected by the system in the first place. The meaningful precondition at the system level, ensuring that only valid inputs get through, thus gets broken down into a multitude of meaningful preconditions (and subsequent postconditions) at the function level. The big requirement for this, though, is that one needs good test generators at the system level. In [the next part](05_Domain-Specific_Fuzzing.ipynb), we will discuss how to automatically generate tests for a variety of domains, from configuration to graphical user interfaces. SynopsisThis chapter provides two classes that automatically extract specifications from a function and a set of inputs: `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator: ###Code def sum2(a, b): return a + b with TypeAnnotator() as type_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution. ###Code print(type_annotator.typed_functions()) ###Output _____no_output_____ ###Markdown The invariant annotator works in a similar fashion: ###Code with InvariantAnnotator() as inv_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values. ###Code print(inv_annotator.functions_with_invariants()) ###Output _____no_output_____ ###Markdown Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs) as well as for all kinds of _symbolic code analyses_. The chapter gives details on how to customize the properties checked for. Lessons Learned* Type annotations and explicit invariants allow for _checking_ arguments and results for expected data types and other properties.* One can automatically _mine_ data types and invariants by observing arguments and results at runtime.* The quality of mined invariants depends on the diversity of values observed during executions; this variety can be increased by generating tests. Next StepsThis chapter concludes the [part on semantical fuzzing techniques](04_Semantical_Fuzzing.ipynb). In the next part, we will explore [domain-specific fuzzing techniques](05_Domain-Specific_Fuzzing.ipynb) from configurations and APIs to graphical user interfaces. BackgroundThe [DAIKON dynamic invariant detector](https://plse.cs.washington.edu/daikon/) can be considered the mother of function specification miners. Continuously maintained and extended for more than 20 years, it mines likely invariants in the style of this chapter for a variety of languages, including C, C++, C, Eiffel, F, Java, Perl, and Visual Basic. On top of the functionality discussed above, it holds a rich catalog of patterns for likely invariants, supports data invariants, can eliminate invariants that are implied by others, and determines statistical confidence to disregard unlikely invariants. The corresponding paper \cite{Ernst2001} is one of the seminal and most-cited papers of Software Engineering. A multitude of works have been published based on DAIKON and detecting invariants; see this [curated list](http://plse.cs.washington.edu/daikon/pubs/) for details. The interaction between test generators and invariant detection is already discussed in \cite{Ernst2001} (incidentally also using grammars). The Eclat tool \cite{Pacheco2005} is a model example of tight interaction between a unit-level test generator and DAIKON-style invariant mining, where the mined invariants are used to produce oracles and to systematically guide the test generator towards fault-revealing inputs. Mining specifications is not restricted to pre- and postconditions. The paper "Mining Specifications" \cite{Ammons2002} is another classic in the field, learning state protocols from executions. Grammar mining, as described in [our chapter with the same name](GrammarMiner.ipynb) can also be seen as a specification mining approach, this time learning specifications for input formats. As it comes to adding type annotations to existing code, the blog post ["The state of type hints in Python"](https://www.bernat.tech/the-state-of-type-hints-in-python/) gives a great overview on how Python type hints can be used and checked. To add type annotations, there are two important tools available that also implement our above approach:* [MonkeyType](https://instagram-engineering.com/let-your-code-type-hint-itself-introducing-open-source-monkeytype-a855c7284881) implements the above approach of tracing executions and annotating Python 3 arguments, returns, and variables with type hints.* [PyAnnotate](https://github.com/dropbox/pyannotate) does a similar job, focusing on code in Python 2. It does not produce Python 3-style annotations, but instead produces annotations as comments that can be processed by static type checkers.These tools have been created by engineers at Facebook and Dropbox, respectively, assisting them in checking millions of lines of code for type issues. ExercisesOur code for mining types and invariants is in no way complete. There are dozens of ways to extend our implementations, some of which we discuss in exercises. Exercise 1: Union TypesThe Python `typing` module allows to express that an argument can have multiple types. For `my_sqrt(x)`, this allows to express that `x` can be an `int` or a `float`: ###Code from typing import Union, Optional def my_sqrt_with_union_type(x: Union[int, float]) -> float: ... ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it supports union types for arguments and return values. Use `Optional[X]` as a shorthand for `Union[X, None]`. Solution. Left to the reader. Hint: extend `type_string()`. Exercise 2: Types for Local VariablesIn Python, one cannot only annotate arguments with types, but actually also local and global variables – for instance, `approx` and `guess` in our `my_sqrt()` implementation: ###Code def my_sqrt_with_local_types(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" approx: Optional[float] = None guess: float = x / 2 while approx != guess: approx: float = guess guess: float = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it also annotates local variables with types. Search the function AST for assignments, determine the type of the assigned value, and make it an annotation on the left hand side. Solution. Left to the reader. Exercise 3: Verbose Invariant CheckersOur implementation of invariant checkers does not make it clear for the user which pre-/postcondition failed. ###Code @precondition(lambda s: len(s) > 0) def remove_first_char(s): return s[1:] with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown The following implementation adds an optional `doc` keyword argument which is printed if the invariant is violated: ###Code def condition(precondition=None, postcondition=None, doc='Unknown'): def decorator(func): @functools.wraps(func) # preserves name, docstring, etc def wrapper(args, kwargs): if precondition is not None: assert precondition(args, *kwargs), "Precondition violated: " + doc retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, kwargs), "Postcondition violated: " + doc return retval return wrapper return decorator def precondition(check, kwargs): return condition(precondition=check, doc=kwargs.get('doc', 'Unknown')) def postcondition(check, kwargs): return condition(postcondition=check, doc=kwargs.get('doc', 'Unknown')) @precondition(lambda s: len(s) > 0, doc="len(s) > 0") def remove_first_char(s): return s[1:] remove_first_char('abc') with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown Extend `InvariantAnnotator` such that it includes the conditions in the generated pre- and postconditions. Solution.** Here's a simple solution: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@precondition(lambda " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")" conditions.append(cond) return conditions class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")") conditions.append(cond) return conditions ###Output _____no_output_____ ###Markdown The resulting annotations are harder to read, but easier to diagnose: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown As an alternative, one may be able to use `inspect.getsource()` on the lambda expression or unparse it. This is left to the reader. Exercise 4: Save Initial ValuesIf the value of an argument changes during function execution, this can easily confuse our implementation: The values are tracked at the beginning of the function, but checked only when it returns. Extend the `InvariantAnnotator` and the infrastructure it uses such that* it saves argument values both at the beginning and at the end of a function invocation;* postconditions can be expressed over both _initial_ values of arguments as well as the _final_ values of arguments;* the mined postconditions refer to both these values as well. Solution. To be added. Exercise 5: ImplicationsSeveral mined invariant are actually _implied_ by others: If `x > 0` holds, then this implies `x >= 0` and `x != 0`. Extend the `InvariantAnnotator` such that implications between properties are explicitly encoded, and such that implied properties are no longer listed as invariants. See \cite{Ernst2001} for ideas. Solution. Left to the reader. Exercise 6: Local VariablesPostconditions may also refer to the values of local variables. Consider extending `InvariantAnnotator` and its infrastructure such that the values of local variables at the end of the execution are also recorded and made part of the invariant inference mechanism. Solution. Left to the reader. Exercise 7: Exploring Invariant AlternativesAfter mining a first set of invariants, have a [concolic fuzzer](ConcolicFuzzer.ipynb) generate tests that systematically attempt to invalidate pre- and postconditions. How far can you generalize? Solution. To be added. Exercise 8: Grammar-Generated PropertiesThe larger the set of properties to be checked, the more potential invariants can be discovered. Create a _grammar_ that systematically produces a large set of properties. See \cite{Ernst2001} for possible patterns. Solution. Left to the reader. Exercise 9: Embedding Invariants as AssertionsRather than producing invariants as annotations for pre- and postconditions, insert them as `assert` statements into the function code, as in:```pythondef my_sqrt(x): 'Computes the square root of x, using the Newton-Raphson method' assert isinstance(x, int), 'violated precondition' assert (x > 0), 'violated precondition' approx = None guess = (x / 2) while (approx != guess): approx = guess guess = ((approx + (x / approx)) / 2) return_value = approx assert (return_value < x), 'violated postcondition' assert isinstance(return_value, float), 'violated postcondition' return approx```Such a formulation may make it easier for test generators and symbolic analysis to access and interpret pre- and postconditions. Solution. Here is a tentative implementation that inserts invariants into function ASTs. Part 1: Embedding Invariants into Functions ###Code class EmbeddedInvariantAnnotator(InvariantTracker): def functions_with_invariants_ast(self, function_name=None): if function_name is None: return annotate_functions_with_invariants(self.invariants()) return annotate_function_with_invariants(function_name, self.invariants(function_name)) def functions_with_invariants(self, function_name=None): if function_name is None: functions = '' for f_name in self.invariants(): try: f_text = ast.unparse(self.functions_with_invariants_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions return ast.unparse(self.functions_with_invariants_ast(function_name)) def function_with_invariants(self, function_name): return self.functions_with_invariants(function_name) def function_with_invariants_ast(self, function_name): return self.functions_with_invariants_ast(function_name) def annotate_invariants(invariants): annotated_functions = {} for function_name in invariants: try: annotated_functions[function_name] = annotate_function_with_invariants(function_name, invariants[function_name]) except KeyError: continue return annotated_functions def annotate_function_with_invariants(function_name, function_invariants): function = globals()[function_name] function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_invariants(function_ast, function_invariants) def annotate_function_ast_with_invariants(function_ast, function_invariants): annotated_function_ast = EmbeddedInvariantTransformer(function_invariants).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Part 2: Preconditions ###Code class PreconditionTransformer(ast.NodeTransformer): def __init__(self, invariants): self.invariants = invariants super().__init__() def preconditions(self): preconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated precondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) < 0: preconditions += assertion_ast.body return preconditions def insert_assertions(self, body): preconditions = self.preconditions() try: docstring = body[0].value.s except: docstring = None if docstring: return [body[0]] + preconditions + body[1:] else: return preconditions + body def visit_FunctionDef(self, node): """Add invariants to function""" # print(ast.dump(node)) node.body = self.insert_assertions(node.body) return node class EmbeddedInvariantTransformer(PreconditionTransformer): pass with EmbeddedInvariantAnnotator() as annotator: my_sqrt(5) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Part 3: PostconditionsWe make a few simplifying assumptions: * Variables do not change during execution.* There is a single `return` statement at the end of the function. ###Code class EmbeddedInvariantTransformer(PreconditionTransformer): def postconditions(self): postconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated postcondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) >= 0: postconditions += assertion_ast.body return postconditions def insert_assertions(self, body): new_body = super().insert_assertions(body) postconditions = self.postconditions() body_ends_with_return = isinstance(new_body[-1], ast.Return) if body_ends_with_return: saver = RETURN_VALUE + " = " + ast.unparse(new_body[-1].value) else: saver = RETURN_VALUE + " = None" saver_ast = ast.parse(saver) postconditions = [saver_ast] + postconditions if body_ends_with_return: return new_body[:-1] + postconditions + [new_body[-1]] else: return new_body + postconditions with EmbeddedInvariantAnnotator() as annotator: my_sqrt(5) my_sqrt_def = annotator.functions_with_invariants() ###Output _____no_output_____ ###Markdown Here's the full definition with included assertions: ###Code print_content(my_sqrt_def, '.py') exec(my_sqrt_def.replace('my_sqrt', 'my_sqrt_annotated')) with ExpectError(): my_sqrt_annotated(-1) ###Output _____no_output_____ ###Markdown Here come some more examples: ###Code with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: print_sum(31, 45) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Mining Function SpecificationsIn the [chapter on assertions](Assertions.ipynb), we have seen how important it is to _check_ whether the result is as expected. In this chapter, we introduce a technique that allows us to _mine_ function specifications from a set of given executions, resulting in abstract and formal _descriptions_ of what the function expects and what it delivers.These so-called _dynamic invariants_ produce pre- and post-conditions over function arguments and variables from a set of executions. Within debugging, the resulting _assertions_ can immediately check whether function behavior has changed, but can also be useful to determine the characteristics of _failing_ runs (as opposed to _passing_ runs). Furthermore, the resulting specifications provide pre- and postconditions for formal program proofs, testing, and verification.This chapter is based on [a chapter with the same name in The Fuzzing Book](https://www.fuzzingbook.org/html/DynamicInvariants.html), which focuses on test generation. ###Code from bookutils import YouTubeVideo YouTubeVideo("HDu1olXFvv0") ###Output _____no_output_____ ###Markdown Prerequisites* You should be familiar with tracing program executions, as in the [chapter on tracing](Tracer.ipynb).* Later in this section, we access the internal _abstract syntax tree_ representations of Python programs and transform them, as in the [chapter on tracking failure origins](Slicer.ipynb). ###Code import bookutils from Tracer import Tracer # ignore from typing import Sequence, Any, Callable, Tuple from typing import Dict, Union, Set, List, cast, Optional ###Output _____no_output_____ ###Markdown SynopsisTo [use the code provided in this chapter](Importing.ipynb), write```python>>> from debuggingbook.DynamicInvariants import ```and then make use of the following features.This chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator:```python>>> def sum2(a, b): type: ignore>>> return a + b>>> with TypeAnnotator() as type_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution.```python>>> print(type_annotator.typed_functions())def sum2(a: int, b: int) ->int: return a + b```The invariant annotator works in a similar fashion:```python>>> with InvariantAnnotator() as inv_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values.```python>>> print(inv_annotator.functions_with_invariants())@precondition(lambda a, b: isinstance(a, int))@precondition(lambda a, b: isinstance(b, int))@postcondition(lambda return_value, a, b: a == return_value - b)@postcondition(lambda return_value, a, b: b == return_value - a)@postcondition(lambda return_value, a, b: isinstance(return_value, int))@postcondition(lambda return_value, a, b: return_value == a + b)@postcondition(lambda return_value, a, b: return_value == b + a)def sum2(a, b): type: ignore return a + b```Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs). The chapter gives details on how to customize the properties checked for. Specifications and AssertionsWhen implementing a function or program, one usually works against a _specification_ – a set of documented requirements to be satisfied by the code. Such specifications can come in natural language. A formal specification, however, allows the computer to check whether the specification is satisfied.In the [chapter on assertions](Assertions.ipynb), we have seen how _preconditions_ and _postconditions_ can describe what a function does. Consider the following (simple) square root function: ###Code def square_root(x): # type: ignore assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown The assertion `assert p` checks the condition `p`; if it does not hold, execution is aborted. Here, the actual body is not yet written; we use the assertions as a specification of what `square_root()` _expects_, and what it _delivers_.The topmost assertion is the _precondition_, stating the requirements on the function arguments. The assertion at the end is the _postcondition_, stating the properties of the function result (including its relationship with the original arguments). Using these pre- and postconditions as a specification, we can now go and implement a square root function that satisfies them. Once implemented, we can have the assertions check at runtime whether `square_root()` works as expected. However, not every piece of code is developed with explicit specifications in the first place; let alone does most code comes with formal pre- and post-conditions. (Just take a look at the chapters in this book.) This is a pity: As Ken Thompson famously said, "Without specifications, there are no bugs – only surprises". It is also a problem for debugging, since, of course, debugging needs some specification such that we know what is wrong, and how to fix it. This raises the interesting question: Can we somehow _retrofit_ existing code with "specifications" that properly describe their behavior, allowing developers to simply _check_ them rather than having to write them from scratch? This is what we do in this chapter. Beyond Generic FailuresBefore we go into _mining_ specifications, let us first discuss why it could be useful to _have_ them. As a motivating example, consider the full implementation of `square_root()` from the [chapter on assertions](Assertions.ipynb): ###Code import bookutils def square_root(x): # type: ignore """Computes the square root of x, using the Newton-Raphson method""" approx = None guess = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown `square_root()` does not come with any functionality that would check types or values. Hence, it is easy for callers to make mistakes when calling `square_root()`: ###Code from ExpectError import ExpectError, ExpectTimeout with ExpectError(): square_root("foo") with ExpectError(): x = square_root(0.0) ###Output _____no_output_____ ###Markdown At least, the Python system catches these errors at runtime. The following call, however, simply lets the function enter an infinite loop: ###Code with ExpectTimeout(1): x = square_root(-1.0) ###Output _____no_output_____ ###Markdown Our goal is to avoid such errors by _annotating_ functions with information that prevents errors like the above ones. The idea is to provide a _specification_ of expected properties – a specification that can then be checked at runtime or statically. \todo{Introduce the concept of contract.} Mining Data TypesFor our Python code, one of the most important "specifications" we need is types. Python being a "dynamically" typed language means that all data types are determined at run time; the code itself does not explicitly state whether a variable is an integer, a string, an array, a dictionary – or whatever. As _writer_ of Python code, omitting explicit type declarations may save time (and allows for some fun hacks). It is not sure whether a lack of types helps in _reading_ and _understanding_ code for humans. For a _computer_ trying to analyze code, the lack of explicit types is detrimental. If, say, a constraint solver, sees `if x:` and cannot know whether `x` is supposed to be a number or a string, this introduces an _ambiguity_. Such ambiguities may multiply over the entire analysis in a combinatorial explosion – or in the analysis yielding an overly inaccurate result. Python 3.6 and later allow data types as _annotations_ to function arguments (actually, to all variables) and return values. We can, for instance, state that `square_root()` is a function that accepts a floating-point value and returns one: ###Code def square_root_with_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) ###Output _____no_output_____ ###Markdown By default, such annotations are ignored by the Python interpreter. Therefore, one can still call `square_root_typed()` with a string as an argument and get the exact same result as above. However, one can make use of special _typechecking_ modules that would check types – _dynamically_ at runtime or _statically_ by analyzing the code without having to execute it. Excursion: Runtime Type Checking _Please note: `enforce` no longer runs on Python 3.7 and later, so this section is commented out_The Python `enforce` package provides a function decorator that automatically inserts type-checking code that is executed at runtime. Here is how to use it: ###Code # import enforce # @enforce.runtime_validation # def square_root_with_checked_type_annotations(x: float) -> float: # """Computes the square root of x, using the Newton-Raphson method""" # return square_root(x) ###Output _____no_output_____ ###Markdown Now, invoking `square_root_with_checked_type_annotations()` raises an exception when invoked with a type dfferent from the one declared: ###Code # with ExpectError(): # square_root_with_checked_type_annotations(True) ###Output _____no_output_____ ###Markdown Note that this error is not caught by the "untyped" variant, where passing a boolean value happily returns $\sqrt{1}$ as result. ###Code # square_root(True) ###Output _____no_output_____ ###Markdown In Python (and other languages), the boolean values `True` and `False` can be implicitly converted to the integers 1 and 0; however, it is hard to think of a call to `sqrt()` where this would not be an error. ###Code from bookutils import quiz quiz("What happens if we call " "`square_root_with_checked_type_annotations(1)`?", [ "`1` is automatically converted to float. It will pass.", "`1` is a subtype of float. It will pass.", "`1` is an integer, and no float. The type check will fail.", "The function will fail for some other reason." ], '37035 // 12345') ###Output _____no_output_____ ###Markdown "Prediction is very difficult, especially when the future is concerned" (Niels Bohr). We can find out by a simple experiment that `float` actually means `float` – and not `int`: ###Code # with ExpectError(enforce.exceptions.RuntimeTypeError): # square_root_with_checked_type_annotations(1) ###Output _____no_output_____ ###Markdown To allow `int` as a type, we need to specify a _union_ of types. ###Code # @enforce.runtime_validation # def square_root_with_union_type(x: Union[int, float]) -> float: # """Computes the square root of x, using the Newton-Raphson method""" # return square_root(x) # square_root_with_union_type(2) # square_root_with_union_type(2.0) # with ExpectError(enforce.exceptions.RuntimeTypeError): # square_root_with_union_type("Two dot zero") ###Output _____no_output_____ ###Markdown End of Excursion Static Type CheckingType annotations can also be checked _statically_ – that is, without even running the code. Let us create a simple Python file consisting of the above `square_root_typed()` definition and a bad invocation. ###Code import inspect import tempfile f = tempfile.NamedTemporaryFile(mode='w', suffix='.py') f.name f.write(inspect.getsource(square_root)) f.write('\n') f.write(inspect.getsource(square_root_with_type_annotations)) f.write('\n') f.write("print(square_root_with_type_annotations('123'))\n") f.flush() ###Output _____no_output_____ ###Markdown These are the contents of our newly created Python file: ###Code from bookutils import print_file print_file(f.name, start_line_number=1) ###Output _____no_output_____ ###Markdown [Mypy](http://mypy-lang.org) is a type checker for Python programs. As it checks types statically, types induce no overhead at runtime; plus, a static check can be faster than a lengthy series of tests with runtime type checking enabled. Let us see what `mypy` produces on the above file: ###Code import subprocess result = subprocess.run(["mypy", "--strict", f.name], universal_newlines=True, stdout=subprocess.PIPE) print(result.stdout.replace(f.name + ':', '')) del f # Delete temporary file ###Output _____no_output_____ ###Markdown We see that `mypy` complains about untyped function definitions such as `square_root()`; most important, however, it finds that the call to `square_root_with_type_annotations()` in the last line has the wrong type. With `mypy`, we can achieve the same type safety with Python as in statically typed languages – provided that we as programmers also produce the necessary type annotations. Is there a simple way to obtain these? Mining Type SpecificationsOur first task will be to mine type annotations (as part of the code) from _values_ we observe at run time. These type annotations would be _mined_ from actual function executions, _learning_ from (normal) runs what the expected argument and return types should be. By observing a series of calls such as these, we could infer that both `x` and the return value are of type `float`: ###Code y = square_root(25.0) y y = square_root(2.0) y ###Output _____no_output_____ ###Markdown How can we mine types from executions? The answer is simple: 1. We _observe_ a function during execution2. We track the _types_ of its arguments3. We include these types as _annotations_ into the code.To do so, we can make use of Python's tracing facility we already observed in the [chapter on tracing executions](Tracer.ipynb). With every call to a function, we retrieve the arguments, their values, and their types. Tracing CallsTo observe argument types at runtime, we define a _tracer function_ that tracks the execution of `square_root()`, checking its arguments and return values. The `CallTracer` class is set to trace functions in a `with` block as follows:```pythonwith CallTracer() as tracer: function_to_be_tracked(...)info = tracer.collected_information()```To create the tracer, we build on the `Tracer` superclass as in the [chapter on tracing executions](Tracer.ipynb). ###Code from types import FrameType ###Output _____no_output_____ ###Markdown We start with two helper functions. `get_arguments()` returns a list of call arguments in the given call frame. ###Code Arguments = List[Tuple[str, Any]] def get_arguments(frame: FrameType) -> Arguments: """Return call arguments in the given frame""" # When called, all arguments are local variables local_variables = dict(frame.f_locals) # explicit copy arguments = [(var, frame.f_locals[var]) for var in local_variables] arguments.reverse() # Want same order as call return arguments ###Output _____no_output_____ ###Markdown `simple_call_string()` is a helper for logging that prints out calls in a user-friendly manner. ###Code def simple_call_string(function_name: str, argument_list: Arguments, return_value : Any = None) -> str: """Return function_name(arg[0], arg[1], ...) as a string""" call = function_name + "(" + \ ", ".join([var + "=" + repr(value) for (var, value) in argument_list]) + ")" if return_value is not None: call += " = " + repr(return_value) return call ###Output _____no_output_____ ###Markdown Now for `CallTracer`. The constructor simply invokes the `Tracer` constructor: ###Code class CallTracer(Tracer): def __init__(self, log: bool = False, kwargs: Any)-> None: super().__init__(kwargs) self._log = log self.reset() def reset(self) -> None: self._calls: Dict[str, List[Tuple[Arguments, Any]]] = {} self._stack: List[Tuple[str, Arguments]] = [] ###Output _____no_output_____ ###Markdown The `traceit()` method does nothing yet; this is done in specialized subclasses. The `CallTracer` class implements a `traceit()` function that checks for function calls and returns: ###Code class CallTracer(CallTracer): def traceit(self, frame: FrameType, event: str, arg: Any) -> None: """Tracking function: Record all calls and all args""" if event == "call": self.trace_call(frame, event, arg) elif event == "return": self.trace_return(frame, event, arg) ###Output _____no_output_____ ###Markdown `trace_call()` is called when a function is called; it retrieves the function name and current arguments, and saves them on a stack. ###Code class CallTracer(CallTracer): def trace_call(self, frame: FrameType, event: str, arg: Any) -> None: """Save current function name and args on the stack""" code = frame.f_code function_name = code.co_name arguments = get_arguments(frame) self._stack.append((function_name, arguments)) if self._log: print(simple_call_string(function_name, arguments)) ###Output _____no_output_____ ###Markdown When the function returns, `trace_return()` is called. We now also have the return value. We log the whole call with arguments and return value (if desired) and save it in our list of calls. ###Code class CallTracer(CallTracer): def trace_return(self, frame: FrameType, event: str, arg: Any) -> None: """Get return value and store complete call with arguments and return value""" code = frame.f_code function_name = code.co_name return_value = arg # TODO: Could call get_arguments() here to also retrieve _final_ values of argument variables called_function_name, called_arguments = self._stack.pop() assert function_name == called_function_name if self._log: print(simple_call_string(function_name, called_arguments), "returns", return_value) self.add_call(function_name, called_arguments, return_value) ###Output _____no_output_____ ###Markdown `add_call()` saves the calls in a list; each function name has its own list. ###Code class CallTracer(CallTracer): def add_call(self, function_name: str, arguments: Arguments, return_value: Any = None) -> None: """Add given call to list of calls""" if function_name not in self._calls: self._calls[function_name] = [] self._calls[function_name].append((arguments, return_value)) ###Output _____no_output_____ ###Markdown we can retrieve the list of calls, either for a given function name (`calls()`),or for all functions (`all_calls()`). ###Code class CallTracer(CallTracer): def calls(self, function_name: str) -> List[Tuple[Arguments, Any]]: """Return list of calls for `function_name`.""" return self._calls[function_name] class CallTracer(CallTracer): def all_calls(self) -> Dict[str, List[Tuple[Arguments, Any]]]: """ Return list of calls for function_name, or a mapping function_name -> calls for all functions tracked """ return self._calls ###Output _____no_output_____ ###Markdown Let us now put this to use. We turn on logging to track the individual calls and their return values: ###Code with CallTracer(log=True) as tracer: y = square_root(25) y = square_root(2.0) ###Output _____no_output_____ ###Markdown After execution, we can retrieve the individual calls: ###Code calls = tracer.calls('square_root') calls ###Output _____no_output_____ ###Markdown Each call is a pair (`argument_list`, `return_value`), where `argument_list` is a list of pairs (`parameter_name`, `value`). ###Code square_root_argument_list, square_root_return_value = calls[0] simple_call_string('square_root', square_root_argument_list, square_root_return_value) ###Output _____no_output_____ ###Markdown If the function does not return a value, `return_value` is `None`. ###Code def hello(name: str) -> None: print("Hello,", name) with CallTracer() as tracer: hello("world") hello_calls = tracer.calls('hello') hello_calls hello_argument_list, hello_return_value = hello_calls[0] simple_call_string('hello', hello_argument_list, hello_return_value) ###Output _____no_output_____ ###Markdown Getting TypesDespite what you may have read or heard, Python actually _is_ a typed language. It is just that it is _dynamically typed_ – types are used and checked only at runtime (rather than declared in the code, where they can be _statically checked_ at compile time). We can thus retrieve types of all values within Python: ###Code type(4) type(2.0) type([4]) ###Output _____no_output_____ ###Markdown We can retrieve the type of the first argument to `square_root()`: ###Code parameter, value = square_root_argument_list[0] parameter, type(value) ###Output _____no_output_____ ###Markdown as well as the type of the return value: ###Code type(square_root_return_value) ###Output _____no_output_____ ###Markdown Hence, we see that (so far), `square_root()` is a function taking (among others) integers and returning floats. We could declare `square_root()` as: ###Code def square_root_annotated(x: int) -> float: return square_root(x) ###Output _____no_output_____ ###Markdown This is a representation we could place in a static type checker, allowing to check whether calls to `square_root()` actually pass a number. A dynamic type checker could run such checks at runtime. By default, Python does not do anything with such annotations. However, tools can access annotations from functions and other objects: ###Code square_root_annotated.__annotations__ ###Output _____no_output_____ ###Markdown This is how run-time checkers access the annotations to check against. Annotating Functions with TypesOur plan is to annotate functions automatically, based on the types we have seen. Our aim is to build a class `TypeAnnotator` that can be used as follows. First, it would track some execution:```pythonwith TypeAnnotator() as annotator: some_function_call()```After tracking, `TypeAnnotator` would provide appropriate methods to access (type-)annotated versions of the function seen:```pythonprint(annotator.typed_functions())```Let us put the pieces together to build `TypeAnnotator`. Excursion: Accessing Function Structure To annotate functions, we need to convert a function into a tree representation (called _abstract syntax trees_, or ASTs) and back; we already have seen these in the chapter on [tracking value origins](Slicer.ipynb). ###Code import ast import inspect ###Output _____no_output_____ ###Markdown We can get the source of a Python function using `inspect.getsource()`. (Note that this does not work for functions defined in other notebooks.) ###Code square_root_source = inspect.getsource(square_root) square_root_source ###Output _____no_output_____ ###Markdown To view these in a visually pleasing form, our function `print_content(s, suffix)` formats and highlights the string `s` as if it were a file with ending `suffix`. We can thus view (and highlight) the source as if it were a Python file: ###Code from bookutils import print_content print_content(square_root_source, '.py') ###Output _____no_output_____ ###Markdown Parsing this gives us an abstract syntax tree (AST) – a representation of the program in tree form. ###Code square_root_ast = ast.parse(square_root_source) ###Output _____no_output_____ ###Markdown What does this AST look like? The helper functions `ast.dump()` (textual output) and `showast.show_ast()` (graphical output with [showast](https://github.com/hchasestevens/show_ast)) allow us to inspect the structure of the tree. We see that the function starts as a `FunctionDef` with name and arguments, followed by a body, which is a list of statements of type `Expr` (the docstring), type `Assign` (assignments), `While` (while loop with its own body), and finally `Return`. ###Code print(ast.dump(square_root_ast, indent=4)) ###Output _____no_output_____ ###Markdown Too much text for you? This graphical representation may make things simpler. ###Code from bookutils import show_ast show_ast(square_root_ast) ###Output _____no_output_____ ###Markdown The function `ast.unparse()` converts such a tree back into the more familiar textual Python code representation. Comments are gone, and there may be more (or fewer) parentheses than before, but the result has the same semantics: ###Code print_content(ast.unparse(square_root_ast), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: Annotating Functions with Given Types Let us now go and transform ASTs to add type annotations. We start with a helper function `parse_type(name)` which parses a type name into an AST. ###Code def parse_type(name: str) -> ast.expr: class ValueVisitor(ast.NodeVisitor): def visit_Expr(self, node: ast.Expr) -> None: self.value_node = node.value tree = ast.parse(name) name_visitor = ValueVisitor() name_visitor.visit(tree) return name_visitor.value_node print(ast.dump(parse_type('int'))) print(ast.dump(parse_type('[object]'))) ###Output _____no_output_____ ###Markdown We now define a helper function that actually adds type annotations to a function AST. The `TypeTransformer` class builds on the Python standard library `ast.NodeTransformer` infrastructure. It would be called as```python TypeTransformer({'x': 'int'}, 'float').visit(ast)```to annotate the arguments of `square_root()`: `x` with `int`, and the return type with `float`. The returned AST can then be unparsed, compiled or analyzed. ###Code class TypeTransformer(ast.NodeTransformer): def __init__(self, argument_types: Dict[str, str], return_type: Optional[str] = None): self.argument_types = argument_types self.return_type = return_type super().__init__() ###Output _____no_output_____ ###Markdown The core of `TypeTransformer` is the method `visit_FunctionDef()`, which is called for every function definition in the AST. Its argument `node` is the subtree of the function definition to be transformed. Our implementation accesses the individual arguments and invokes `annotate_args()` on them; it also sets the return type in the `returns` attribute of the node. ###Code class TypeTransformer(TypeTransformer): def visit_FunctionDef(self, node: ast.FunctionDef) -> ast.FunctionDef: """Add annotation to function""" # Set argument types new_args = [] for arg in node.args.args: new_args.append(self.annotate_arg(arg)) new_arguments = ast.arguments( node.args.posonlyargs, new_args, node.args.vararg, node.args.kwonlyargs, node.args.kw_defaults, node.args.kwarg, node.args.defaults ) # Set return type if self.return_type is not None: node.returns = parse_type(self.return_type) return ast.copy_location( ast.FunctionDef(node.name, new_arguments, node.body, node.decorator_list, node.returns), node) ###Output _____no_output_____ ###Markdown Each argument gets its own annotation, taken from the types originally passed to the class: ###Code class TypeTransformer(TypeTransformer): def annotate_arg(self, arg: ast.arg) -> ast.arg: """Add annotation to single function argument""" arg_name = arg.arg if arg_name in self.argument_types: arg.annotation = parse_type(self.argument_types[arg_name]) return arg ###Output _____no_output_____ ###Markdown Does this work? Let us annotate the AST from `square_root()` with types for the arguments and return types: ###Code new_ast = TypeTransformer({'x': 'int'}, 'float').visit(square_root_ast) ###Output _____no_output_____ ###Markdown When we unparse the new AST, we see that the annotations actually are present: ###Code print_content(ast.unparse(new_ast), '.py') ###Output _____no_output_____ ###Markdown Similarly, we can annotate the `hello()` function from above: ###Code hello_source = inspect.getsource(hello) hello_ast = ast.parse(hello_source) new_ast = TypeTransformer({'name': 'str'}, 'None').visit(hello_ast) print_content(ast.unparse(new_ast), '.py') ###Output _____no_output_____ ###Markdown Mining Function SpecificationsIn the [chapter on assertions](Assertions.ipynb), we have seen how important it is to _check_ whether the result is as expected. In this chapter, we introduce a technique that allows us to _mine_ function specifications from a set of given executions, resulting in abstract and formal _descriptions_ of what the function expects and what it delivers.These so-called _dynamic invariants_ produce pre- and post-conditions over function arguments and variables from a set of executions. Within debugging, the resulting _assertions_ can immediately check whether function behavior has changed, but can also be useful to determine the characteristics of _failing_ runs (as opposed to _passing_ runs). Furthermore, the resulting specifications provide pre- and postconditions for formal program proofs, testing, and verification.This chapter is based on [a chapter with the same name in The Fuzzing Book](https://www.fuzzingbook.org/html/DynamicInvariants.html), which focuses on test generation. ###Code from bookutils import YouTubeVideo YouTubeVideo("HDu1olXFvv0") ###Output _____no_output_____ ###Markdown Prerequisites* You should be familiar with tracing program executions, as in the [chapter on tracing](Tracer.ipynb).* Later in this section, we access the internal _abstract syntax tree_ representations of Python programs and transform them, as in the [chapter on tracking failure origins](Slicer.ipynb). ###Code import bookutils from Tracer import Tracer ###Output _____no_output_____ ###Markdown SynopsisTo [use the code provided in this chapter](Importing.ipynb), write```python>>> from debuggingbook.DynamicInvariants import ```and then make use of the following features.This chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator:```python>>> def sum2(a, b): type: ignore>>> return a + b>>> with TypeAnnotator() as type_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution.```python>>> print(type_annotator.typed_functions())def sum2(a: int, b: int) ->int: return a + b```The invariant annotator works in a similar fashion:```python>>> with InvariantAnnotator() as inv_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values.```python>>> print(inv_annotator.functions_with_invariants())@precondition(lambda a, b: isinstance(a, int))@precondition(lambda a, b: isinstance(b, int))@postcondition(lambda return_value, a, b: a == return_value - b)@postcondition(lambda return_value, a, b: b == return_value - a)@postcondition(lambda return_value, a, b: isinstance(return_value, int))@postcondition(lambda return_value, a, b: return_value == a + b)@postcondition(lambda return_value, a, b: return_value == b + a)def sum2(a, b): type: ignore return a + b```Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs). The chapter gives details on how to customize the properties checked for. Specifications and AssertionsWhen implementing a function or program, one usually works against a _specification_ – a set of documented requirements to be satisfied by the code. Such specifications can come in natural language. A formal specification, however, allows the computer to check whether the specification is satisfied.In the [chapter on assertions](Assertions.ipynb), we have seen how _preconditions_ and _postconditions_ can describe what a function does. Consider the following (simple) square root function: ###Code def square_root(x): # type: ignore assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown The assertion `assert p` checks the condition `p`; if it does not hold, execution is aborted. Here, the actual body is not yet written; we use the assertions as a specification of what `square_root()` _expects_, and what it _delivers_.The topmost assertion is the _precondition_, stating the requirements on the function arguments. The assertion at the end is the _postcondition_, stating the properties of the function result (including its relationship with the original arguments). Using these pre- and postconditions as a specification, we can now go and implement a square root function that satisfies them. Once implemented, we can have the assertions check at runtime whether `square_root()` works as expected. However, not every piece of code is developed with explicit specifications in the first place; let alone does most code comes with formal pre- and post-conditions. (Just take a look at the chapters in this book.) This is a pity: As Ken Thompson famously said, "Without specifications, there are no bugs – only surprises". It is also a problem for debugging, since, of course, debugging needs some specification such that we know what is wrong, and how to fix it. This raises the interesting question: Can we somehow _retrofit_ existing code with "specifications" that properly describe their behavior, allowing developers to simply _check_ them rather than having to write them from scratch? This is what we do in this chapter. Beyond Generic FailuresBefore we go into _mining_ specifications, let us first discuss why it could be useful to _have_ them. As a motivating example, consider the full implementation of `square_root()` from the [chapter on assertions](Assertions.ipynb): ###Code import bookutils def square_root(x): # type: ignore """Computes the square root of x, using the Newton-Raphson method""" approx = None guess = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown `square_root()` does not come with any functionality that would check types or values. Hence, it is easy for callers to make mistakes when calling `square_root()`: ###Code from ExpectError import ExpectError, ExpectTimeout with ExpectError(): square_root("foo") with ExpectError(): x = square_root(0.0) ###Output _____no_output_____ ###Markdown At least, the Python system catches these errors at runtime. The following call, however, simply lets the function enter an infinite loop: ###Code with ExpectTimeout(1): x = square_root(-1.0) ###Output _____no_output_____ ###Markdown Our goal is to avoid such errors by _annotating_ functions with information that prevents errors like the above ones. The idea is to provide a _specification_ of expected properties – a specification that can then be checked at runtime or statically. \todo{Introduce the concept of contract.} Mining Data TypesFor our Python code, one of the most important "specifications" we need is types. Python being a "dynamically" typed language means that all data types are determined at run time; the code itself does not explicitly state whether a variable is an integer, a string, an array, a dictionary – or whatever. As _writer_ of Python code, omitting explicit type declarations may save time (and allows for some fun hacks). It is not sure whether a lack of types helps in _reading_ and _understanding_ code for humans. For a _computer_ trying to analyze code, the lack of explicit types is detrimental. If, say, a constraint solver, sees `if x:` and cannot know whether `x` is supposed to be a number or a string, this introduces an _ambiguity_. Such ambiguities may multiply over the entire analysis in a combinatorial explosion – or in the analysis yielding an overly inaccurate result. Python 3.6 and later allow data types as _annotations_ to function arguments (actually, to all variables) and return values. We can, for instance, state that `square_root()` is a function that accepts a floating-point value and returns one: ###Code def square_root_with_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) ###Output _____no_output_____ ###Markdown By default, such annotations are ignored by the Python interpreter. Therefore, one can still call `square_root_typed()` with a string as an argument and get the exact same result as above. However, one can make use of special _typechecking_ modules that would check types – _dynamically_ at runtime or _statically_ by analyzing the code without having to execute it. Runtime Type CheckingThe Python `enforce` package provides a function decorator that automatically inserts type-checking code that is executed at runtime. Here is how to use it: ###Code import enforce @enforce.runtime_validation def square_root_with_checked_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) ###Output _____no_output_____ ###Markdown Now, invoking `square_root_with_checked_type_annotations()` raises an exception when invoked with a type dfferent from the one declared: ###Code with ExpectError(): square_root_with_checked_type_annotations(True) ###Output _____no_output_____ ###Markdown Note that this error is not caught by the "untyped" variant, where passing a boolean value happily returns $\sqrt{1}$ as result. ###Code square_root(True) ###Output _____no_output_____ ###Markdown In Python (and other languages), the boolean values `True` and `False` can be implicitly converted to the integers 1 and 0; however, it is hard to think of a call to `sqrt()` where this would not be an error. ###Code from bookutils import quiz quiz("What happens if we call " "`square_root_with_checked_type_annotations(1)`?", [ "`1` is automatically converted to float. It will pass.", "`1` is a subtype of float. It will pass.", "`1` is an integer, and no float. The type check will fail.", "The function will fail for some other reason." ], '37035 // 12345') ###Output _____no_output_____ ###Markdown "Prediction is very difficult, especially when the future is concerned" (Niels Bohr). We can find out by a simple experiment that `float` actually means `float` – and not `int`: ###Code with ExpectError(enforce.exceptions.RuntimeTypeError): square_root_with_checked_type_annotations(1) ###Output _____no_output_____ ###Markdown To allow `int` as a type, we need to specify a _union_ of types. ###Code from typing import Union, Optional @enforce.runtime_validation def square_root_with_union_type(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) square_root_with_union_type(2) square_root_with_union_type(2.0) with ExpectError(enforce.exceptions.RuntimeTypeError): square_root_with_union_type("Two dot zero") ###Output _____no_output_____ ###Markdown Static Type CheckingType annotations can also be checked _statically_ – that is, without even running the code. Let us create a simple Python file consisting of the above `square_root_typed()` definition and a bad invocation. ###Code import inspect import tempfile f = tempfile.NamedTemporaryFile(mode='w', suffix='.py') f.name f.write(inspect.getsource(square_root)) f.write('\n') f.write(inspect.getsource(square_root_with_type_annotations)) f.write('\n') f.write("print(square_root_with_type_annotations('123'))\n") f.flush() ###Output _____no_output_____ ###Markdown These are the contents of our newly created Python file: ###Code from bookutils import print_file print_file(f.name, start_line_number=1) ###Output _____no_output_____ ###Markdown [Mypy](http://mypy-lang.org) is a type checker for Python programs. As it checks types statically, types induce no overhead at runtime; plus, a static check can be faster than a lengthy series of tests with runtime type checking enabled. Let us see what `mypy` produces on the above file: ###Code import subprocess result = subprocess.run(["mypy", "--strict", f.name], universal_newlines=True, stdout=subprocess.PIPE) print(result.stdout.replace(f.name + ':', '')) del f # Delete temporary file ###Output _____no_output_____ ###Markdown We see that `mypy` complains about untyped function definitions such as `square_root()`; most important, however, it finds that the call to `square_root_with_type_annotations()` in the last line has the wrong type. With `mypy`, we can achieve the same type safety with Python as in statically typed languages – provided that we as programmers also produce the necessary type annotations. Is there a simple way to obtain these? Mining Type SpecificationsOur first task will be to mine type annotations (as part of the code) from _values_ we observe at run time. These type annotations would be _mined_ from actual function executions, _learning_ from (normal) runs what the expected argument and return types should be. By observing a series of calls such as these, we could infer that both `x` and the return value are of type `float`: ###Code y = square_root(25.0) y y = square_root(2.0) y ###Output _____no_output_____ ###Markdown How can we mine types from executions? The answer is simple: 1. We _observe_ a function during execution2. We track the _types_ of its arguments3. We include these types as _annotations_ into the code.To do so, we can make use of Python's tracing facility we already observed in the [chapter on tracing executions](Tracer.ipynb). With every call to a function, we retrieve the arguments, their values, and their types. Tracing CallsTo observe argument types at runtime, we define a _tracer function_ that tracks the execution of `square_root()`, checking its arguments and return values. The `CallTracer` class is set to trace functions in a `with` block as follows:```pythonwith CallTracer() as tracer: function_to_be_tracked(...)info = tracer.collected_information()```To create the tracer, we build on the `Tracer` superclass as in the [chapter on tracing executions](Tracer.ipynb). ###Code from typing import Sequence, Any, Callable, Optional, Type, Tuple, Any from typing import Dict, Union, Set, List, cast, TypeVar from types import FrameType, TracebackType ###Output _____no_output_____ ###Markdown We start with two helper functions. `get_arguments()` returns a list of call arguments in the given call frame. ###Code Arguments = List[Tuple[str, Any]] def get_arguments(frame: FrameType) -> Arguments: """Return call arguments in the given frame""" # When called, all arguments are local variables arguments = [(var, frame.f_locals[var]) for var in frame.f_locals] arguments.reverse() # Want same order as call return arguments ###Output _____no_output_____ ###Markdown `simple_call_string()` is a helper for logging that prints out calls in a user-friendly manner. ###Code def simple_call_string(function_name: str, argument_list: Arguments, return_value : Any = None) -> str: """Return function_name(arg[0], arg[1], ...) as a string""" call = function_name + "(" + \ ", ".join([var + "=" + repr(value) for (var, value) in argument_list]) + ")" if return_value is not None: call += " = " + repr(return_value) return call ###Output _____no_output_____ ###Markdown Now for `CallTracer`. The constructor simply invokes the `Tracer` constructor: ###Code class CallTracer(Tracer): def __init__(self, log: bool = False, kwargs: Any)-> None: super().__init__(kwargs) self._log = log self.reset() def reset(self) -> None: self._calls: Dict[str, List[Tuple[Arguments, Any]]] = {} self._stack: List[Tuple[str, Arguments]] = [] ###Output _____no_output_____ ###Markdown The `traceit()` method does nothing yet; this is done in specialized subclasses. The `CallTracer` class implements a `traceit()` function that checks for function calls and returns: ###Code class CallTracer(CallTracer): def traceit(self, frame: FrameType, event: str, arg: Any) -> None: """Tracking function: Record all calls and all args""" if event == "call": self.trace_call(frame, event, arg) elif event == "return": self.trace_return(frame, event, arg) ###Output _____no_output_____ ###Markdown `trace_call()` is called when a function is called; it retrieves the function name and current arguments, and saves them on a stack. ###Code class CallTracer(CallTracer): def trace_call(self, frame: FrameType, event: str, arg: Any) -> None: """Save current function name and args on the stack""" code = frame.f_code function_name = code.co_name arguments = get_arguments(frame) self._stack.append((function_name, arguments)) if self._log: print(simple_call_string(function_name, arguments)) ###Output _____no_output_____ ###Markdown When the function returns, `trace_return()` is called. We now also have the return value. We log the whole call with arguments and return value (if desired) and save it in our list of calls. ###Code class CallTracer(CallTracer): def trace_return(self, frame: FrameType, event: str, arg: Any) -> None: """Get return value and store complete call with arguments and return value""" code = frame.f_code function_name = code.co_name return_value = arg # TODO: Could call get_arguments() here to also retrieve _final_ values of argument variables called_function_name, called_arguments = self._stack.pop() assert function_name == called_function_name if self._log: print(simple_call_string(function_name, called_arguments), "returns", return_value) self.add_call(function_name, called_arguments, return_value) ###Output _____no_output_____ ###Markdown `add_call()` saves the calls in a list; each function name has its own list. ###Code class CallTracer(CallTracer): def add_call(self, function_name: str, arguments: Arguments, return_value: Any = None) -> None: """Add given call to list of calls""" if function_name not in self._calls: self._calls[function_name] = [] self._calls[function_name].append((arguments, return_value)) ###Output _____no_output_____ ###Markdown we can retrieve the list of calls, either for a given function name (`calls()`),or for all functions (`all_calls()`). ###Code class CallTracer(CallTracer): def calls(self, function_name: str) -> List[Tuple[Arguments, Any]]: """Return list of calls for `function_name`.""" return self._calls[function_name] class CallTracer(CallTracer): def all_calls(self) -> Dict[str, List[Tuple[Arguments, Any]]]: """ Return list of calls for function_name, or a mapping function_name -> calls for all functions tracked """ return self._calls ###Output _____no_output_____ ###Markdown Let us now put this to use. We turn on logging to track the individual calls and their return values: ###Code with CallTracer(log=True) as tracer: y = square_root(25) y = square_root(2.0) ###Output _____no_output_____ ###Markdown After execution, we can retrieve the individual calls: ###Code calls = tracer.calls('square_root') calls ###Output _____no_output_____ ###Markdown Each call is a pair (`argument_list`, `return_value`), where `argument_list` is a list of pairs (`parameter_name`, `value`). ###Code square_root_argument_list, square_root_return_value = calls[0] simple_call_string('square_root', square_root_argument_list, square_root_return_value) ###Output _____no_output_____ ###Markdown If the function does not return a value, `return_value` is `None`. ###Code def hello(name: str) -> None: print("Hello,", name) with CallTracer() as tracer: hello("world") hello_calls = tracer.calls('hello') hello_calls hello_argument_list, hello_return_value = hello_calls[0] simple_call_string('hello', hello_argument_list, hello_return_value) ###Output _____no_output_____ ###Markdown Getting TypesDespite what you may have read or heard, Python actually _is_ a typed language. It is just that it is _dynamically typed_ – types are used and checked only at runtime (rather than declared in the code, where they can be _statically checked_ at compile time). We can thus retrieve types of all values within Python: ###Code type(4) type(2.0) type([4]) ###Output _____no_output_____ ###Markdown We can retrieve the type of the first argument to `square_root()`: ###Code parameter, value = square_root_argument_list[0] parameter, type(value) ###Output _____no_output_____ ###Markdown as well as the type of the return value: ###Code type(square_root_return_value) ###Output _____no_output_____ ###Markdown Hence, we see that (so far), `square_root()` is a function taking (among others) integers and returning floats. We could declare `square_root()` as: ###Code def square_root_annotated(x: int) -> float: return square_root(x) ###Output _____no_output_____ ###Markdown This is a representation we could place in a static type checker, allowing to check whether calls to `square_root()` actually pass a number. A dynamic type checker could run such checks at runtime. By default, Python does not do anything with such annotations. However, tools can access annotations from functions and other objects: ###Code square_root_annotated.__annotations__ ###Output _____no_output_____ ###Markdown This is how run-time checkers access the annotations to check against. Annotating Functions with TypesOur plan is to annotate functions automatically, based on the types we have seen. Our aim is to build a class `TypeAnnotator` that can be used as follows. First, it would track some execution:```pythonwith TypeAnnotator() as annotator: some_function_call()```After tracking, `TypeAnnotator` would provide appropriate methods to access (type-)annotated versions of the function seen:```pythonprint(annotator.typed_functions())```Let us put the pieces together to build `TypeAnnotator`. Excursion: Accessing Function Structure To annotate functions, we need to convert a function into a tree representation (called _abstract syntax trees_, or ASTs) and back; we already have seen these in the chapter on [tracking value origins](Slicer.ipynb). ###Code import ast import inspect import astor ###Output _____no_output_____ ###Markdown We can get the source of a Python function using `inspect.getsource()`. (Note that this does not work for functions defined in other notebooks.) ###Code square_root_source = inspect.getsource(square_root) square_root_source ###Output _____no_output_____ ###Markdown To view these in a visually pleasing form, our function `print_content(s, suffix)` formats and highlights the string `s` as if it were a file with ending `suffix`. We can thus view (and highlight) the source as if it were a Python file: ###Code from bookutils import print_content print_content(square_root_source, '.py') ###Output _____no_output_____ ###Markdown Parsing this gives us an abstract syntax tree (AST) – a representation of the program in tree form. ###Code square_root_ast = ast.parse(square_root_source) ###Output _____no_output_____ ###Markdown What does this AST look like? The helper functions `astor.dump_tree()` (textual output) and `showast.show_ast()` (graphical output with [showast](https://github.com/hchasestevens/show_ast)) allow us to inspect the structure of the tree. We see that the function starts as a `FunctionDef` with name and arguments, followed by a body, which is a list of statements of type `Expr` (the docstring), type `Assign` (assignments), `While` (while loop with its own body), and finally `Return`. ###Code print(astor.dump_tree(square_root_ast)) ###Output _____no_output_____ ###Markdown Too much text for you? This graphical representation may make things simpler. ###Code from bookutils import show_ast show_ast(square_root_ast) ###Output _____no_output_____ ###Markdown The function `astor.to_source()` converts such a tree back into the more familiar textual Python code representation. Comments are gone, and there may be more parentheses than before, but the result has the same semantics: ###Code print_content(astor.to_source(square_root_ast), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: Annotating Functions with Given Types Let us now go and transform ASTs to add type annotations. We start with a helper function `parse_type(name)` which parses a type name into an AST. ###Code def parse_type(name: str) -> ast.expr: class ValueVisitor(ast.NodeVisitor): def visit_Expr(self, node: ast.Expr) -> None: self.value_node = node.value tree = ast.parse(name) name_visitor = ValueVisitor() name_visitor.visit(tree) return name_visitor.value_node print(astor.dump_tree(parse_type('int'))) print(astor.dump_tree(parse_type('[object]'))) ###Output _____no_output_____ ###Markdown We now define a helper function that actually adds type annotations to a function AST. The `TypeTransformer` class builds on the Python standard library `ast.NodeTransformer` infrastructure. It would be called as```python TypeTransformer({'x': 'int'}, 'float').visit(ast)```to annotate the arguments of `square_root()`: `x` with `int`, and the return type with `float`. The returned AST can then be unparsed, compiled or analyzed. ###Code class TypeTransformer(ast.NodeTransformer): def __init__(self, argument_types: Dict[str, str], return_type: Optional[str] = None): self.argument_types = argument_types self.return_type = return_type super().__init__() ###Output _____no_output_____ ###Markdown The core of `TypeTransformer` is the method `visit_FunctionDef()`, which is called for every function definition in the AST. Its argument `node` is the subtree of the function definition to be transformed. Our implementation accesses the individual arguments and invokes `annotate_args()` on them; it also sets the return type in the `returns` attribute of the node. ###Code class TypeTransformer(TypeTransformer): def visit_FunctionDef(self, node: ast.FunctionDef) -> ast.FunctionDef: """Add annotation to function""" # Set argument types new_args = [] for arg in node.args.args: new_args.append(self.annotate_arg(arg)) new_arguments = ast.arguments( new_args, node.args.vararg, node.args.kwonlyargs, node.args.kw_defaults, node.args.kwarg, node.args.defaults ) # Set return type if self.return_type is not None: node.returns = parse_type(self.return_type) return ast.copy_location( ast.FunctionDef(node.name, new_arguments, node.body, node.decorator_list, node.returns), node) ###Output _____no_output_____ ###Markdown Each argument gets its own annotation, taken from the types originally passed to the class: ###Code class TypeTransformer(TypeTransformer): def annotate_arg(self, arg: ast.arg) -> ast.arg: """Add annotation to single function argument""" arg_name = arg.arg if arg_name in self.argument_types: arg.annotation = parse_type(self.argument_types[arg_name]) return arg ###Output _____no_output_____ ###Markdown Does this work? Let us annotate the AST from `square_root()` with types for the arguments and return types: ###Code new_ast = TypeTransformer({'x': 'int'}, 'float').visit(square_root_ast) ###Output _____no_output_____ ###Markdown When we unparse the new AST, we see that the annotations actually are present: ###Code print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown Similarly, we can annotate the `hello()` function from above: ###Code hello_source = inspect.getsource(hello) hello_ast = ast.parse(hello_source) new_ast = TypeTransformer({'name': 'str'}, 'None').visit(hello_ast) print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: Annotating Functions with Mined Types Let us now annotate functions with types mined at runtime. We start with a simple function `type_string()` that determines the appropriate type of a given value (as a string): ###Code def type_string(value: Any) -> str: return type(value).__name__ type_string(4) type_string([]) ###Output _____no_output_____ ###Markdown For composite structures, `type_string()` does not examine element types; hence, the type of `[3]` is simply `list` instead of, say, `list[int]`. For now, `list` will do fine. ###Code type_string([3]) ###Output _____no_output_____ ###Markdown `type_string()` will be used to infer the types of argument values found at runtime, as returned by `CallTracer.all_calls()`: ###Code with CallTracer() as tracer: y = square_root(25.0) y = square_root(2.0) tracer.all_calls() ###Output _____no_output_____ ###Markdown The function `annotate_types()` takes such a list of calls and annotates each function listed: ###Code def annotate_types(calls: Dict[str, List[Tuple[Arguments, Any]]]) -> Dict[str, ast.AST]: annotated_functions = {} for function_name in calls: try: annotated_functions[function_name] = \ annotate_function_with_types(function_name, calls[function_name]) except KeyError: continue return annotated_functions ###Output _____no_output_____ ###Markdown For each function, we get the source and its AST and then get to the actual annotation in `annotate_function_ast_with_types()`: ###Code def annotate_function_with_types(function_name: str, function_calls: List[Tuple[Arguments, Any]]) -> ast.AST: function = globals()[function_name] # May raise KeyError for internal functions function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_types(function_ast, function_calls) ###Output _____no_output_____ ###Markdown The function `annotate_function_ast_with_types()` invokes the `TypeTransformer` with the calls seen, and for each call, iterate over the arguments, determine their types, and annotate the AST with these. The universal type `Any` is used when we encounter type conflicts, which we will discuss below. ###Code from typing import Any def annotate_function_ast_with_types(function_ast: ast.AST, function_calls: List[Tuple[Arguments, Any]]) -> ast.AST: parameter_types: Dict[str, str] = {} return_type = None for calls_seen in function_calls: args, return_value = calls_seen if return_value: if return_type and return_type != type_string(return_value): return_type = 'Any' else: return_type = type_string(return_value) for parameter, value in args: try: different_type = (parameter_types[parameter] != type_string(value)) except KeyError: different_type = False if different_type: parameter_types[parameter] = 'Any' else: parameter_types[parameter] = type_string(value) annotated_function_ast = \ TypeTransformer(parameter_types, return_type).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Here is `square_root()` annotated with the types recorded usign the tracer, above. ###Code print_content(astor.to_source(annotate_types(tracer.all_calls())['square_root']), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: A Type Annotator Class Let us bring all of this together in a single class `TypeAnnotator` that first tracks calls of functions and then allows to access the AST (and the source code form) of the tracked functions annotated with types. The method `typed_functions()` returns the annotated functions as a string; `typed_functions_ast()` returns their AST. ###Code class TypeTracer(CallTracer): pass class TypeAnnotator(TypeTracer): def typed_functions_ast(self) -> Dict[str, ast.AST]: return annotate_types(self.all_calls()) def typed_function_ast(self, function_name: str) -> ast.AST: return annotate_function_with_types(function_name, self.calls(function_name)) def typed_functions(self) -> str: functions = '' for f_name in self.all_calls(): try: f_text = astor.to_source(self.typed_function_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions def typed_function(self, function_name: str) -> str: return astor.to_source(self.typed_function_ast(function_name)) ###Output _____no_output_____ ###Markdown End of Excursion Here is how to use `TypeAnnotator`. We first track a series of calls: ###Code with TypeAnnotator() as annotator: y = square_root(25.0) y = square_root(2.0) ###Output _____no_output_____ ###Markdown After tracking, we can immediately retrieve an annotated version of the functions tracked: ###Code print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown This also works for multiple and diverse functions. One could go and implement an automatic type annotator for Python files based on the types seen during execution. ###Code with TypeAnnotator() as annotator: hello('type annotations') y = square_root(1.0) print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown A content as above could now be sent to a type checker, which would detect any type inconsistency between callers and callees. Excursion: Handling Multiple TypesLet us now resolve the role of the magic `Any` type in `annotate_function_ast_with_types()`. If we see multiple types for the same argument, we set its type to `Any`. For `square_root()`, this makes sense, as its arguments can be integers as well as floats: ###Code with CallTracer() as tracer: y = square_root(25.0) y = square_root(4) annotated_square_root_ast = annotate_types(tracer.all_calls())['square_root'] print_content(astor.to_source(annotated_square_root_ast), '.py') ###Output _____no_output_____ ###Markdown The following function `sum3()` can be called with floating-point numbers as arguments, resulting in the parameters getting a `float` type: ###Code def sum3(a, b, c): # type: ignore return a + b + c with TypeAnnotator() as annotator: y = sum3(1.0, 2.0, 3.0) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we call `sum3()` with integers, though, the arguments get an `int` type: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown And we can also call `sum3()` with strings, which assigns the arguments a `str` type: ###Code with TypeAnnotator() as annotator: y = sum3("one", "two", "three") y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we have multiple calls, but with different types, `TypeAnnotator()` will assign an `Any` type to both arguments and return values: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y = sum3("one", "two", "three") typed_sum3_def = annotator.typed_function('sum3') print_content(typed_sum3_def, '.py') ###Output _____no_output_____ ###Markdown A type `Any` makes it explicit that an object can, indeed, have any type; it will not be typechecked at runtime or statically. To some extent, this defeats the power of type checking; but it also preserves some of the type flexibility that many Python programmers enjoy. Besides `Any`, the `typing` module supports several additional ways to define ambiguous types; we will keep this in mind for a later exercise. End of Excursion Mining InvariantsBesides basic data types. we can check several further properties from arguments. We can, for instance, whether an argument can be negative, zero, or positive; or that one argument should be smaller than the second; or that the result should be the sum of two arguments – properties that cannot be expressed in a (Python) type.Such properties are called invariants, as they hold across all invocations of a function. Specifically, invariants come as _pre_- and _postconditions_ – conditions that always hold at the beginning and at the end of a function. (There are also _data_ and _object_ invariants that express always-holding properties over the state of data or objects, but we do not consider these in this book.) Annotating Functions with Pre- and PostconditionsThe classical means to specify pre- and postconditions is via _assertions_, which we have introduced in the [chapter on assertions](Assertions.ipynb). A precondition checks whether the arguments to a function satisfy the expected properties; a postcondition does the same for the result. We can express and check both using assertions as follows: ###Code def square_root_with_invariants(x): # type: ignore assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown A nicer way, however, is to syntactically separate invariants from the function at hand. Using appropriate decorators, we could specify pre- and postconditions as follows:```python@precondition lambda x: x >= 0@postcondition lambda return_value, x: return_value * return_value == xdef square_root_with_invariants(x): normal code without assertions ...```The decorators `@precondition` and `@postcondition` would run the given functions (specified as anonymous `lambda` functions) before and after the decorated function, respectively. If the functions return `False`, the condition is violated. `@precondition` gets the function arguments as arguments; `@postcondition` additionally gets the return value as first argument. It turns out that implementing such decorators is not hard at all. Our implementation builds on a [code snippet from StackOverflow](https://stackoverflow.com/questions/12151182/python-precondition-postcondition-for-member-function-how): ###Code import functools def condition(precondition: Optional[Callable] = None, postcondition: Optional[Callable] = None) -> Callable: def decorator(func: Callable) -> Callable: @functools.wraps(func) # preserves name, docstring, etc def wrapper(args: Any, kwargs: Any) -> Any: if precondition is not None: assert precondition(args, *kwargs), \ "Precondition violated" # Call original function or method retval = func(args, *kwargs) if postcondition is not None: assert postcondition(retval, args, *kwargs), \ "Postcondition violated" return retval return wrapper return decorator def precondition(check: Callable) -> Callable: return condition(precondition=check) def postcondition(check: Callable) -> Callable: return condition(postcondition=check) ###Output _____no_output_____ ###Markdown With these, we can now start decorating `square_root()`: ###Code @precondition(lambda x: x > 0) def square_root_with_precondition(x): # type: ignore return square_root(x) ###Output _____no_output_____ ###Markdown This catches arguments violating the precondition: ###Code with ExpectError(): square_root_with_precondition(-1.0) ###Output _____no_output_____ ###Markdown Likewise, we can provide a postcondition: ###Code import math @postcondition(lambda ret, x: math.isclose(ret ret, x)) def square_root_with_postcondition(x): # type: ignore return square_root(x) y = square_root_with_postcondition(2.0) y ###Output _____no_output_____ ###Markdown If we have a buggy implementation of $\sqrt{x}$, this gets caught quickly: ###Code @postcondition(lambda ret, x: math.isclose(ret * ret, x)) def buggy_square_root_with_postcondition(x): # type: ignore return square_root(x) + 0.1 with ExpectError(): y = buggy_square_root_with_postcondition(2.0) ###Output _____no_output_____ ###Markdown While checking pre- and postconditions is a great way to catch errors, specifying them can be cumbersome. Let us try to see whether we can (again) _mine_ some of them. Mining InvariantsTo _mine_ invariants, we can use the same tracking functionality as before; instead of saving values for individual variables, though, we now check whether the values satisfy specific _properties_ or not. For instance, if all values of `x` seen satisfy the condition `x > 0`, then we make `x > 0` an invariant of the function. If we see positive, zero, and negative values of `x`, though, then there is no property of `x` left to talk about.The general idea is thus:1. Check all variable values observed against a set of predefined properties; and2. Keep only those properties that hold for all runs observed. Defining PropertiesWhat precisely do we mean by properties? Here is a small collection of value properties that would frequently be used in invariants. All these properties would be evaluated with the _metavariables_ `X`, `Y`, and `Z` (actually, any upper-case identifier) being replaced with the names of function parameters: ###Code INVARIANT_PROPERTIES = [ "X < 0", "X <= 0", "X > 0", "X >= 0", # "X == 0", # implied by "X", below # "X != 0", # implied by "not X", below ] ###Output _____no_output_____ ###Markdown When `square_root(x)` is called as, say `square_root(5.0)`, we see that `x = 5.0` holds. The above properties would then all be checked for `x`. Only the properties `X > 0`, `X >= 0`, and `not X` hold for the call seen; and hence `x > 0`, `x >= 0`, and `not x` (or better: `x != 0`) would make potential preconditions for `square_root(x)`. We can check for many more properties such as relations between two arguments: ###Code INVARIANT_PROPERTIES += [ "X == Y", "X > Y", "X < Y", "X >= Y", "X <= Y", ] ###Output _____no_output_____ ###Markdown Types also can be checked using properties. For any function parameter `X`, only one of these will hold: ###Code INVARIANT_PROPERTIES += [ "isinstance(X, bool)", "isinstance(X, int)", "isinstance(X, float)", "isinstance(X, list)", "isinstance(X, dict)", ] ###Output _____no_output_____ ###Markdown We can check for arithmetic properties: ###Code INVARIANT_PROPERTIES += [ "X == Y + Z", "X == Y * Z", "X == Y - Z", "X == Y / Z", ] ###Output _____no_output_____ ###Markdown Here's relations over three values, a Python special: ###Code INVARIANT_PROPERTIES += [ "X < Y < Z", "X <= Y <= Z", "X > Y > Z", "X >= Y >= Z", ] ###Output _____no_output_____ ###Markdown These Boolean properties also check for other types, as in Python, `None`, an empty list, an empty set, an empty string, and the value zero all evaluate to `False`. ###Code INVARIANT_PROPERTIES += [ "X", "not X" ] ###Output _____no_output_____ ###Markdown Finally, we can also check for list or string properties. Again, this is just a tiny selection. ###Code INVARIANT_PROPERTIES += [ "X == len(Y)", "X == sum(Y)", "X in Y", "X.startswith(Y)", "X.endswith(Y)", ] ###Output _____no_output_____ ###Markdown Extracting Meta-VariablesLet us first introduce a few _helper functions_ before we can get to the actual mining. `metavars()` extracts the set of meta-variables (`X`, `Y`, `Z`, etc.) from a property. To this end, we parse the property as a Python expression and then visit the identifiers. ###Code def metavars(prop: str) -> List[str]: metavar_list = [] class ArgVisitor(ast.NodeVisitor): def visit_Name(self, node: ast.Name) -> None: if node.id.isupper(): metavar_list.append(node.id) ArgVisitor().visit(ast.parse(prop)) return metavar_list assert metavars("X < 0") == ['X'] assert metavars("X.startswith(Y)") == ['X', 'Y'] assert metavars("isinstance(X, str)") == ['X'] ###Output _____no_output_____ ###Markdown Instantiating PropertiesTo produce a property as invariant, we need to be able to _instantiate_ it with variable names. The instantiation of `X > 0` with `X` being instantiated to `a`, for instance, gets us `a > 0`. To this end, the function `instantiate_prop()` takes a property and a collection of variable names and instantiates the meta-variables left-to-right with the corresponding variables names in the collection. ###Code def instantiate_prop_ast(prop: str, var_names: Sequence[str]) -> ast.AST: class NameTransformer(ast.NodeTransformer): def visit_Name(self, node: ast.Name) -> ast.Name: if node.id not in mapping: return node return ast.Name(id=mapping[node.id], ctx=ast.Load()) meta_variables = metavars(prop) assert len(meta_variables) == len(var_names) mapping = {} for i in range(0, len(meta_variables)): mapping[meta_variables[i]] = var_names[i] prop_ast = ast.parse(prop, mode='eval') new_ast = NameTransformer().visit(prop_ast) return new_ast def instantiate_prop(prop: str, var_names: Sequence[str]) -> str: prop_ast = instantiate_prop_ast(prop, var_names) prop_text = astor.to_source(prop_ast).strip() while prop_text.startswith('(') and prop_text.endswith(')'): prop_text = prop_text[1:-1] return prop_text assert instantiate_prop("X > Y", ['a', 'b']) == 'a > b' assert instantiate_prop("X.startswith(Y)", ['x', 'y']) == 'x.startswith(y)' ###Output _____no_output_____ ###Markdown Evaluating PropertiesTo actually _evaluate_ properties, we do not need to instantiate them. Instead, we simply convert them into a boolean function, using `lambda`: ###Code def prop_function_text(prop: str) -> str: return "lambda " + ", ".join(metavars(prop)) + ": " + prop ###Output _____no_output_____ ###Markdown Here is a simple example: ###Code prop_function_text("X > Y") ###Output _____no_output_____ ###Markdown We can easily evaluate the function: ###Code def prop_function(prop: str) -> Callable: return eval(prop_function_text(prop)) ###Output _____no_output_____ ###Markdown Here is an example: ###Code p = prop_function("X > Y") quiz("What is p(100, 1)?", [ "False", "True" ], 'p(100, 1) + 1', globals()) p(100, 1) p(1, 100) ###Output _____no_output_____ ###Markdown Checking InvariantsTo extract invariants from an execution, we need to check them on all possible instantiations of arguments. If the function to be checked has two arguments `a` and `b`, we instantiate the property `X < Y` both as `a < b` and `b < a` and check each of them. To get all combinations, we use the Python `permutations()` function: ###Code import itertools for combination in itertools.permutations([1.0, 2.0, 3.0], 2): print(combination) ###Output _____no_output_____ ###Markdown The function `true_property_instantiations()` takes a property and a list of tuples (`var_name`, `value`). It then produces all instantiations of the property with the given values and returns those that evaluate to True. ###Code Invariants = Set[Tuple[str, Tuple[str, ...]]] def true_property_instantiations(prop: str, vars_and_values: Arguments, log: bool = False) -> Invariants: instantiations = set() p = prop_function(prop) len_metavars = len(metavars(prop)) for combination in itertools.permutations(vars_and_values, len_metavars): args = [value for var_name, value in combination] var_names = [var_name for var_name, value in combination] try: result = p(args) except: result = None if log: print(prop, combination, result) if result: instantiations.add((prop, tuple(var_names))) return instantiations ###Output _____no_output_____ ###Markdown Here is an example. If `x == -1` and `y == 1`, the property `X < Y` holds for `x < y`, but not for `y < x`: ###Code invs = true_property_instantiations("X < Y", [('x', -1), ('y', 1)], log=True) invs ###Output _____no_output_____ ###Markdown The instantiation retrieves the short form: ###Code for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Likewise, with values for `x` and `y` as above, the property `X < 0` only holds for `x`, but not for `y`: ###Code invs = true_property_instantiations("X < 0", [('x', -1), ('y', 1)], log=True) for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Extracting InvariantsLet us now run the above invariant extraction on function arguments and return values as observed during a function execution. To this end, we extend the `CallTracer` class into an `InvariantTracer` class, which automatically computes invariants for all functions and all calls observed during tracking. By default, an `InvariantTracer` uses the `INVARIANT_PROPERTIES` properties as defined above; however, one can specify alternate sets of properties. ###Code class InvariantTracer(CallTracer): def __init__(self, props: Optional[List[str]] = None, kwargs: Any) -> None: if props is None: props = INVARIANT_PROPERTIES self.props = props super().__init__(kwargs) ###Output _____no_output_____ ###Markdown The key method of the `InvariantTracer` is the `invariants()` method. This iterates over the calls observed and checks which properties hold. Only the intersection of properties – that is, the set of properties that hold for all calls – is preserved, and eventually returned. The special variable `return_value` is set to hold the return value. ###Code RETURN_VALUE = 'return_value' class InvariantTracer(InvariantTracer): def all_invariants(self) -> Dict[str, Invariants]: return {function_name: self.invariants(function_name) for function_name in self.all_calls()} def invariants(self, function_name: str) -> Invariants: invariants = None for variables, return_value in self.calls(function_name): vars_and_values = variables + [(RETURN_VALUE, return_value)] s = set() for prop in self.props: s \|= true_property_instantiations(prop, vars_and_values, self._log) if invariants is None: invariants = s else: invariants &= s assert invariants is not None return invariants ###Output _____no_output_____ ###Markdown Here's an example of how to use `invariants()`. We run the tracer on a small set of calls. ###Code with InvariantTracer() as tracer: y = square_root(25.0) y = square_root(10.0) tracer.all_calls() ###Output _____no_output_____ ###Markdown The `invariants()` method produces a set of properties that hold for the observed runs, together with their instantiations over function arguments. ###Code invs = tracer.invariants('square_root') invs ###Output _____no_output_____ ###Markdown As before, the actual instantiations are easier to read: ###Code def pretty_invariants(invariants: Invariants) -> List[str]: props = [] for (prop, var_names) in invariants: props.append(instantiate_prop(prop, var_names)) return sorted(props) pretty_invariants(invs) ###Output _____no_output_____ ###Markdown We see that the both `x` and the return value have a `float` type. We also see that both are always greater than zero. These are properties that may make useful pre- and postconditions, notably for symbolic analysis. However, there's also an invariant which does _not_ universally hold, namely `return_value <= x`, as the following example shows: ###Code square_root(0.01) ###Output _____no_output_____ ###Markdown Clearly, 0.1 > 0.01 holds. This is a case of us not learning from sufficiently diverse inputs. As soon as we have a call including `x = 0.1`, though, the invariant `return_value <= x` is eliminated: ###Code with InvariantTracer() as tracer: y = square_root(25.0) y = square_root(10.0) y = square_root(0.01) pretty_invariants(tracer.invariants('square_root')) ###Output _____no_output_____ ###Markdown We will discuss later how to ensure sufficient diversity in inputs. (Hint: This involves test generation.) Let us try out our invariant tracer on `sum3()`. We see that all types are well-defined; the properties that all arguments are non-zero, however, is specific to the calls observed. ###Code with InvariantTracer() as tracer: y = sum3(1, 2, 3) y = sum3(-4, -5, -6) pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with strings instead, we get different invariants. Notably, we obtain the postcondition that the returned string always starts with the string in the first argument `a` – a universal postcondition if strings are used. ###Code with InvariantTracer() as tracer: y = sum3('a', 'b', 'c') y = sum3('f', 'e', 'd') pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with both strings and numbers (and zeros, too), there are no properties left that would hold across all calls. That's the price of flexibility. ###Code with InvariantTracer() as tracer: y = sum3('a', 'b', 'c') y = sum3('c', 'b', 'a') y = sum3(-4, -5, -6) y = sum3(0, 0, 0) pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown Converting Mined Invariants to AnnotationsAs with types, above, we would like to have some functionality where we can add the mined invariants as annotations to existing functions. To this end, we introduce the `InvariantAnnotator` class, extending `InvariantTracer`. We start with a helper method. `params()` returns a comma-separated list of parameter names as observed during calls. ###Code class InvariantAnnotator(InvariantTracer): def params(self, function_name: str) -> str: arguments, return_value = self.calls(function_name)[0] return ", ".join(arg_name for (arg_name, arg_value) in arguments) with InvariantAnnotator() as annotator: y = square_root(25.0) y = sum3(1, 2, 3) annotator.params('square_root') annotator.params('sum3') ###Output _____no_output_____ ###Markdown Now for the actual annotation. `preconditions()` returns the preconditions from the mined invariants (i.e., those propertes that do not depend on the return value) as a string with annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = ("@precondition(lambda " + self.params(function_name) + ": " + inv + ")") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) annotator.preconditions('square_root') ###Output _____no_output_____ ###Markdown `postconditions()` does the same for postconditions: ###Code class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = (f"@postcondition(lambda {RETURN_VALUE}," f" {self.params(function_name)}: {inv})") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) annotator.postconditions('square_root') ###Output _____no_output_____ ###Markdown With these, we can take a function and add both pre- and postconditions as annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def functions_with_invariants(self) -> str: functions = "" for function_name in self.all_invariants(): try: function = self.function_with_invariants(function_name) except KeyError: continue functions += function return functions def function_with_invariants(self, function_name: str) -> str: function = globals()[function_name] # Can throw KeyError source = inspect.getsource(function) return '\n'.join(self.preconditions(function_name) + self.postconditions(function_name)) + \ '\n' + source ###Output _____no_output_____ ###Markdown Here comes `function_with_invariants()` in all its glory: ###Code with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) print_content(annotator.function_with_invariants('square_root'), '.py') ###Output _____no_output_____ ###Markdown Quite a number of invariants, isn't it? Further below (and in the exercises), we will discuss on how to focus on the most relevant properties. Avoiding OverspecializationMined specifications can only be as good as the executions they were mined from. If we only see a single call, for instance, we will be faced with several mined pre- and postconditions that _overspecialize_ towards the values seen. Let us illustrate this effect on a simple `sum2()` function which adds two numbers. ###Code def sum2(a, b): # type: ignore return a + b ###Output _____no_output_____ ###Markdown If we invoke `sum2()` with a variety of arguments, the invariants all capture the relationship between `a`, `b`, and the return value as `return_value == a + b` in all its variations. ###Code with InvariantAnnotator() as annotator: sum2(31, 45) sum2(0, 0) sum2(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown If, however, we see only a single call, the invariants will overspecialize to the single call seen: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown The mined precondition `a == b`, for instance, only holds for the single call observed; the same holds for the mined postcondition `return_value == a b`. Yet, `sum2()` can obviously be successfully called with other values that do not satisfy these conditions. To get out of this trap, we have to _learn from more and more diverse runs_. One way to obtain such runs is by _generating_ inputs. Indeed, a simple test generator for calls of `sum2()` will easily resolve the problem. ###Code import random with InvariantAnnotator() as annotator: for i in range(100): a = random.randrange(-10, +10) b = random.randrange(-10, +10) length = sum2(a, b) print_content(annotator.function_with_invariants('sum2'), '.py') ###Output _____no_output_____ ###Markdown Note, though, that an API test generator, such as above, will have to be set up such that it actually respects preconditions – in our case, we invoke `sum2()` with integers only, already assuming its precondition. In some way, one thus needs a specification (a model, a grammar) to mine another specification – a chicken-and-egg problem. However, there is one way out of this problem: If one can automatically generate tests at the system level, then one has an _infinite source of executions_ to learn invariants from. In each of these executions, all functions would be called with values that satisfy the (implicit) precondition, allowing us to mine invariants for these functions. This holds, because at the system level, invalid inputs must be rejected by the system in the first place. The meaningful precondition at the system level, ensuring that only valid inputs get through, thus gets broken down into a multitude of meaningful preconditions (and subsequent postconditions) at the function level. The big requirement for all this, though, is that one needs good test generators. This will be the subject of another book, namely [The Fuzzing Book](https://www.fuzzingbook.org/). Partial InvariantsFor debugging, it can be helpful to focus on invariants produced only by _failing_ runs, thus characterizing the _circumstances under which a function fails_. Let us illustrate this on an example. The `middle()` function from the [chapter on statistical debugging](StatisticalDebugger.ipynb) is supposed to return the middle of three integers `x`, `y`, and `z`. ###Code from StatisticalDebugger import middle # minor dependency with InvariantAnnotator() as annotator: for i in range(100): x = random.randrange(-10, +10) y = random.randrange(-10, +10) z = random.randrange(-10, +10) mid = middle(x, y, z) ###Output _____no_output_____ ###Markdown By default, our `InvariantAnnotator()` does not return any particular pre- or postcondition (other than the types observed). That is just fine, as the function indeed imposes no particular precondition; and the postcondition from `middle()` is not covered by the `InvariantAnnotator` patterns. ###Code print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Things get more interesting if we focus on a particular subset of runs only, though - say, a set of inputs where `middle()` fails. ###Code from StatisticalDebugger import MIDDLE_FAILING_TESTCASES # minor dependency with InvariantAnnotator() as annotator: for x, y, z in MIDDLE_FAILING_TESTCASES: mid = middle(x, y, z) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Now that's an intimidating set of pre- and postconditions. However, almost all of the preconditions are implied by the one precondition```python@precondition(lambda x, y, z: y < x < z, doc='y < x < z')```which characterizes the exact condition under which `middle()` fails (which also happens to be the condition under which the erroneous second `return y` is executed). By checking how _invariants for failing runs_ differ from _invariants for passing runs_, we can identify circumstances for function failures. ###Code quiz("Could `InvariantAnnotator` also determine a precondition " "that characterizes _passing_ runs?", [ "Yes", "No" ], 'int(math.exp(1))', globals()) ###Output _____no_output_____ ###Markdown Indeed, it cannot – the correct invariant for passing runs would be the _inverse_ of the invariant for failing runs, and `not A < B < C` is not part of our invariant library. We can easily test this: ###Code from StatisticalDebugger import MIDDLE_PASSING_TESTCASES # minor dependency with InvariantAnnotator() as annotator: for x, y, z in MIDDLE_PASSING_TESTCASES: mid = middle(x, y, z) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Some ExamplesLet us try out the `InvariantAnnotator` on a number of examples. Removing HTML MarkupRunning `InvariantAnnotator` on our ongoing example `remove_html_markup()` does not provide much, as our invariant properties are tailored towards numerical functions. ###Code from Intro_Debugging import remove_html_markup with InvariantAnnotator() as annotator: remove_html_markup("<foo>bar</foo>") remove_html_markup("bar") remove_html_markup('"bar"') print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown In the [chapter on DDSet](DDSetDebugger.ipynb), we will see how to express more complex properties for structured inputs. A Recursive FunctionHere's another example. `list_length()` recursively computes the length of a Python function. Let us see whether we can mine its invariants: ###Code def list_length(elems: List[Any]) -> int: if elems == []: length = 0 else: length = 1 + list_length(elems[1:]) return length with InvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Almost all these properties are relevant. Of course, the reason the invariants are so neat is that the return value is equal to `len(elems)` is that `X == len(Y)` is part of the list of properties to be checked. Sum of two NumbersThe next example is a very simple function: If we have a function without return value, the return value is `None` and we can only mine preconditions. (Well, we get a "postcondition" `not return_value` that the return value evaluates to False, which holds for `None`). ###Code def print_sum(a, b): # type: ignore print(a + b) with InvariantAnnotator() as annotator: print_sum(31, 45) print_sum(0, 0) print_sum(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Checking SpecificationsA function with invariants, as above, can be fed into the Python interpreter, such that all pre- and postconditions are checked. We create a function `square_root_annotated()` which includes all the invariants mined above. ###Code with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) square_root_def = annotator.functions_with_invariants() square_root_def = square_root_def.replace('square_root', 'square_root_annotated') print_content(square_root_def, '.py') exec(square_root_def) ###Output _____no_output_____ ###Markdown The "annotated" version checks against invalid arguments – or more precisely, against arguments with properties that have not been observed yet: ###Code with ExpectError(): square_root_annotated(-1.0) # type: ignore ###Output _____no_output_____ ###Markdown This is in contrast to the original version, which just hangs on negative values: ###Code with ExpectTimeout(1): square_root(-1.0) ###Output _____no_output_____ ###Markdown If we make changes to the function definition such that the properties of the return value change, such _regressions_ are caught as violations of the postconditions. Let us illustrate this by simply inverting the result, and return $-2$ as square root of 4. ###Code square_root_def = square_root_def.replace('square_root_annotated', 'square_root_negative') square_root_def = square_root_def.replace('return approx', 'return -approx') print_content(square_root_def, '.py') exec(square_root_def) ###Output _____no_output_____ ###Markdown Technically speaking, $-2$ _is_ a square root of 4, since $(-2)^2 = 4$ holds. Yet, such a change may be unexpected by callers of `square_root()`, and hence, this would be caught with the first call: ###Code with ExpectError(): square_root_negative(2.0) # type: ignore ###Output _____no_output_____ ###Markdown We see how pre- and postconditions, as well as types, can serve as oracles during testing. In particular, once we have mined them for a set of functions, we can check them again and again with test generators – especially after code changes. The more checks we have, and the more specific they are, the more likely it is we can detect unwanted effects of changes. SynopsisThis chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator: ###Code def sum2(a, b): # type: ignore return a + b with TypeAnnotator() as type_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution. ###Code print(type_annotator.typed_functions()) ###Output _____no_output_____ ###Markdown The invariant annotator works in a similar fashion: ###Code with InvariantAnnotator() as inv_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values. ###Code print(inv_annotator.functions_with_invariants()) ###Output _____no_output_____ ###Markdown Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs). The chapter gives details on how to customize the properties checked for. Lessons Learned* Type annotations and explicit invariants allow for _checking_ arguments and results for expected data types and other properties.* One can automatically _mine_ data types and invariants by observing arguments and results at runtime.* The quality of mined invariants depends on the diversity of values observed during executions; this variety can be increased by generating tests. Next StepsIn the next chapter, we will explore [abstracting failure conditions](DDSetDebugger.ipynb). BackgroundThe [DAIKON dynamic invariant detector](https://plse.cs.washington.edu/daikon/) can be considered the mother of function specification miners. Continuously maintained and extended for more than 20 years, it mines likely invariants in the style of this chapter for a variety of languages, including C, C++, C, Eiffel, F, Java, Perl, and Visual Basic. On top of the functionality discussed above, it holds a rich catalog of patterns for likely invariants, supports data invariants, can eliminate invariants that are implied by others, and determines statistical confidence to disregard unlikely invariants. The corresponding paper \cite{Ernst2001} is one of the seminal and most-cited papers of Software Engineering. A multitude of works have been published based on DAIKON and detecting invariants; see this [curated list](http://plse.cs.washington.edu/daikon/pubs/) for details. The interaction between test generators and invariant detection is already discussed in \cite{Ernst2001} (incidentally also using grammars). The Eclat tool \cite{Pacheco2005} is a model example of tight interaction between a unit-level test generator and DAIKON-style invariant mining, where the mined invariants are used to produce oracles and to systematically guide the test generator towards fault-revealing inputs. Mining specifications is not restricted to pre- and postconditions. The paper "Mining Specifications" \cite{Ammons2002} is another classic in the field, learning state protocols from executions. Grammar mining \cite{Gopinath2020} can also be seen as a specification mining approach, this time learning specifications for input formats. As it comes to adding type annotations to existing code, the blog post ["The state of type hints in Python"](https://www.bernat.tech/the-state-of-type-hints-in-python/) gives a great overview on how Python type hints can be used and checked. To add type annotations, there are two important tools available that also implement our above approach:* [MonkeyType](https://instagram-engineering.com/let-your-code-type-hint-itself-introducing-open-source-monkeytype-a855c7284881) implements the above approach of tracing executions and annotating Python 3 arguments, returns, and variables with type hints.* [PyAnnotate](https://github.com/dropbox/pyannotate) does a similar job, focusing on code in Python 2. It does not produce Python 3-style annotations, but instead produces annotations as comments that can be processed by static type checkers.These tools have been created by engineers at Facebook and Dropbox, respectively, assisting them in checking millions of lines of code for type issues. ExercisesOur code for mining types and invariants is in no way complete. There are dozens of ways to extend our implementations, some of which we discuss in exercises. Exercise 1: Union TypesThe Python `typing` module allows to express that an argument can have multiple types. For `square_root(x)`, this allows to express that `x` can be an `int` or a `float`: ###Code def square_root_with_union_type(x: Union[int, float]) -> float: # type: ignore ... ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it supports union types for arguments and return values. Use `Optional[X]` as a shorthand for `Union[X, None]`. Solution. Left to the reader. Hint: extend `type_string()`. Exercise 2: Types for Local VariablesIn Python, one cannot only annotate arguments with types, but actually also local and global variables – for instance, `approx` and `guess` in our `square_root()` implementation: ###Code def square_root_with_local_types(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" approx: Optional[float] = None guess: float = x / 2 while approx != guess: approx: float = guess # type: ignore guess: float = (approx + x / approx) / 2 # type: ignore return approx ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it also annotates local variables with types. Search the function AST for assignments, determine the type of the assigned value, and make it an annotation on the left hand side. Solution. Left to the reader. Exercise 3: Verbose Invariant CheckersOur implementation of invariant checkers does not make it clear for the user which pre-/postcondition failed. ###Code @precondition(lambda s: len(s) > 0) def remove_first_char(s: str) -> str: return s[1:] with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown The following implementation adds an optional `doc` keyword argument which is printed if the invariant is violated: ###Code def my_condition(precondition: Optional[Callable] = None, postcondition: Optional[Callable] = None, doc: str = 'Unknown') -> Callable: def decorator(func: Callable) -> Callable: @functools.wraps(func) # preserves name, docstring, etc def wrapper(args: Any, kwargs: Any) -> Any: if precondition is not None: assert precondition(args, *kwargs), "Precondition violated: " + doc retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, kwargs), "Postcondition violated: " + doc return retval return wrapper return decorator def my_precondition(check: Callable, kwargs: Any) -> Callable: return my_condition(precondition=check, doc=kwargs.get('doc', 'Unknown')) def my_postcondition(check: Callable, kwargs: Any) -> Callable: return my_condition(postcondition=check, doc=kwargs.get('doc', 'Unknown')) @my_precondition(lambda s: len(s) > 0, doc="len(s) > 0") # type: ignore def remove_first_char(s: str) -> str: return s[1:] remove_first_char('abc') with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown Extend `InvariantAnnotator` such that it includes the conditions in the generated pre- and postconditions. Solution.** Here's a simple solution: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@my_precondition(lambda " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")" conditions.append(cond) return conditions class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@my_postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")") conditions.append(cond) return conditions ###Output _____no_output_____ ###Markdown The resulting annotations are harder to read, but easier to diagnose: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown As an alternative, one may be able to use `inspect.getsource()` on the lambda expression or unparse it. This is left to the reader. Exercise 4: Save Initial ValuesIf the value of an argument changes during function execution, this can easily confuse our implementation: The values are tracked at the beginning of the function, but checked only when it returns. Extend the `InvariantAnnotator` and the infrastructure it uses such that* it saves argument values both at the beginning and at the end of a function invocation;* postconditions can be expressed over both _initial_ values of arguments as well as the _final_ values of arguments;* the mined postconditions refer to both these values as well. Solution. To be added. Exercise 5: ImplicationsSeveral mined invariant are actually _implied_ by others: If `x > 0` holds, then this implies `x >= 0` and `x != 0`. Extend the `InvariantAnnotator` such that implications between properties are explicitly encoded, and such that implied properties are no longer listed as invariants. See \cite{Ernst2001} for ideas. Solution. Left to the reader. Exercise 6: Local VariablesPostconditions may also refer to the values of local variables. Consider extending `InvariantAnnotator` and its infrastructure such that the values of local variables at the end of the execution are also recorded and made part of the invariant inference mechanism. Solution. Left to the reader. Exercise 7: Embedding Invariants as AssertionsRather than producing invariants as annotations for pre- and postconditions, insert them as `assert` statements into the function code, as in:```pythondef square_root(x): 'Computes the square root of x, using the Newton-Raphson method' assert isinstance(x, int), 'violated precondition' assert x > 0, 'violated precondition' approx = None guess = (x / 2) while (approx != guess): approx = guess guess = ((approx + (x / approx)) / 2) return_value = approx assert return_value < x, 'violated postcondition' assert isinstance(return_value, float), 'violated postcondition' return approx```Such a formulation may make it easier for test generators and symbolic analysis to access and interpret pre- and postconditions. Solution. Here is a tentative implementation that inserts invariants into function ASTs. Part 1: Embedding Invariants into Functions ###Code class EmbeddedInvariantAnnotator(InvariantTracer): def function_with_invariants_ast(self, function_name: str) -> ast.AST: return annotate_function_with_invariants(function_name, self.invariants(function_name)) def function_with_invariants(self, function_name: str) -> str: return astor.to_source(self.function_with_invariants_ast(function_name)) def annotate_invariants(invariants: Dict[str, Invariants]) -> Dict[str, ast.AST]: annotated_functions = {} for function_name in invariants: try: annotated_functions[function_name] = annotate_function_with_invariants(function_name, invariants[function_name]) except KeyError: continue return annotated_functions def annotate_function_with_invariants(function_name: str, function_invariants: Invariants) -> ast.AST: function = globals()[function_name] function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_invariants(function_ast, function_invariants) def annotate_function_ast_with_invariants(function_ast: ast.AST, function_invariants: Invariants) -> ast.AST: annotated_function_ast = EmbeddedInvariantTransformer(function_invariants).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Part 2: Preconditions ###Code class PreconditionTransformer(ast.NodeTransformer): def __init__(self, invariants: Invariants) -> None: self.invariants = invariants super().__init__() def preconditions(self) -> List[ast.stmt]: preconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated precondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) < 0: preconditions += assertion_ast.body return preconditions def insert_assertions(self, body: List[ast.stmt]) -> List[ast.stmt]: preconditions = self.preconditions() try: docstring = cast(ast.Constant, body[0]).value.s except: docstring = None if docstring: return [body[0]] + preconditions + body[1:] else: return preconditions + body def visit_FunctionDef(self, node: ast.FunctionDef) -> ast.FunctionDef: """Add invariants to function""" # print(ast.dump(node)) node.body = self.insert_assertions(node.body) return node class EmbeddedInvariantTransformer(PreconditionTransformer): pass with EmbeddedInvariantAnnotator() as annotator: square_root(5) print_content(annotator.function_with_invariants('square_root'), '.py') with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.function_with_invariants('sum3'), '.py') ###Output _____no_output_____ ###Markdown Part 3: PostconditionsWe make a few simplifying assumptions: * Variables do not change during execution.* There is a single `return` statement at the end of the function. ###Code class EmbeddedInvariantTransformer(EmbeddedInvariantTransformer): def postconditions(self) -> List[ast.stmt]: postconditions = [] for (prop, var_names) in self.invariants: assertion = ("assert " + instantiate_prop(prop, var_names) + ', "violated postcondition"') assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) >= 0: postconditions += assertion_ast.body return postconditions def insert_assertions(self, body: List[ast.stmt]) -> List[ast.stmt]: new_body = super().insert_assertions(body) postconditions = self.postconditions() body_ends_with_return = isinstance(new_body[-1], ast.Return) if body_ends_with_return: ret_val = cast(ast.Return, new_body[-1]).value saver = RETURN_VALUE + " = " + astor.to_source(ret_val) else: saver = RETURN_VALUE + " = None" saver_ast = cast(ast.stmt, ast.parse(saver)) postconditions = [saver_ast] + postconditions if body_ends_with_return: return new_body[:-1] + postconditions + [new_body[-1]] else: return new_body + postconditions with EmbeddedInvariantAnnotator() as annotator: square_root(5) square_root_def = annotator.function_with_invariants('square_root') ###Output _____no_output_____ ###Markdown Here's the full definition with included assertions: ###Code print_content(square_root_def, '.py') exec(square_root_def.replace('square_root', 'square_root_annotated')) with ExpectError(): square_root_annotated(-1) ###Output _____no_output_____ ###Markdown Here come some more examples: ###Code with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.function_with_invariants('sum3'), '.py') with EmbeddedInvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.function_with_invariants('list_length'), '.py') with EmbeddedInvariantAnnotator() as annotator: print_sum(31, 45) print_content(annotator.function_with_invariants('print_sum'), '.py') ###Output _____no_output_____ ###Markdown Mining Function SpecificationsIn the [chapter on assertions](Assertions.ipynb), we have seen how important it is to _check_ whether the result is as expected. In this chapter, we introduce a technique that allows us to _mine_ function specifications from a set of given executions, resulting in abstract and formal _descriptions_ of what the function expects and what it delivers.These so-called _dynamic invariants_ produce pre- and post-conditions over function arguments and variables from a set of executions. Within debugging, the resulting _assertions_ can immediately check whether function behavior has changed, but can also be useful to determine the characteristics of _failing_ runs (as opposed to _passing_ runs). Furthermore, the resulting specifications provide pre- and postconditions for formal program proofs, testing, and verification.This chapter is based on [a chapter with the same name in The Fuzzing Book](https://www.fuzzingbook.org/html/DynamicInvariants.html), which focuses on test generation. ###Code from bookutils import YouTubeVideo YouTubeVideo("HDu1olXFvv0") ###Output _____no_output_____ ###Markdown Prerequisites* You should be familiar with tracing program executions, as in the [chapter on tracing](Tracer.ipynb).* Later in this section, we access the internal _abstract syntax tree_ representations of Python programs and transform them, as in the [chapter on tracking failure origins](Slicer.ipynb). ###Code import bookutils from Tracer import Tracer ###Output _____no_output_____ ###Markdown SynopsisTo [use the code provided in this chapter](Importing.ipynb), write```python>>> from debuggingbook.DynamicInvariants import ```and then make use of the following features.This chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator:```python>>> def sum2(a, b):>>> return a + b>>> with TypeAnnotator() as type_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution.```python>>> print(type_annotator.typed_functions())def sum2(a: int, b: int) ->int: return a + b```The invariant annotator works in a similar fashion:```python>>> with InvariantAnnotator() as inv_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values.```python>>> print(inv_annotator.functions_with_invariants())@precondition(lambda a, b: isinstance(a, int))@precondition(lambda a, b: isinstance(b, int))@postcondition(lambda return_value, a, b: a == return_value - b)@postcondition(lambda return_value, a, b: b == return_value - a)@postcondition(lambda return_value, a, b: isinstance(return_value, int))@postcondition(lambda return_value, a, b: return_value == a + b)@postcondition(lambda return_value, a, b: return_value == b + a)def sum2(a, b): return a + b```Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs). The chapter gives details on how to customize the properties checked for. Specifications and AssertionsWhen implementing a function or program, one usually works against a _specification_ – a set of documented requirements to be satisfied by the code. Such specifications can come in natural language. A formal specification, however, allows the computer to check whether the specification is satisfied.In the [chapter on assertions](Assertions.ipynb), we have seen how _preconditions_ and _postconditions_ can describe what a function does. Consider the following (simple) square root function: ###Code def square_root(x): # type: ignore assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown The assertion `assert p` checks the condition `p`; if it does not hold, execution is aborted. Here, the actual body is not yet written; we use the assertions as a specification of what `square_root()` _expects_, and what it _delivers_.The topmost assertion is the _precondition_, stating the requirements on the function arguments. The assertion at the end is the _postcondition_, stating the properties of the function result (including its relationship with the original arguments). Using these pre- and postconditions as a specification, we can now go and implement a square root function that satisfies them. Once implemented, we can have the assertions check at runtime whether `square_root()` works as expected. However, not every piece of code is developed with explicit specifications in the first place; let alone does most code comes with formal pre- and post-conditions. (Just take a look at the chapters in this book.) This is a pity: As Ken Thompson famously said, "Without specifications, there are no bugs – only surprises". It is also a problem for debugging, since, of course, debugging needs some specification such that we know what is wrong, and how to fix it. This raises the interesting question: Can we somehow _retrofit_ existing code with "specifications" that properly describe their behavior, allowing developers to simply _check_ them rather than having to write them from scratch? This is what we do in this chapter. Beyond Generic FailuresBefore we go into _mining_ specifications, let us first discuss why it could be useful to _have_ them. As a motivating example, consider the full implementation of `square_root()` from the [chapter on assertions](Assertions.ipynb): ###Code import bookutils def square_root(x): # type: ignore """Computes the square root of x, using the Newton-Raphson method""" approx = None guess = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown `square_root()` does not come with any functionality that would check types or values. Hence, it is easy for callers to make mistakes when calling `square_root()`: ###Code from ExpectError import ExpectError, ExpectTimeout with ExpectError(): square_root("foo") with ExpectError(): x = square_root(0.0) ###Output _____no_output_____ ###Markdown At least, the Python system catches these errors at runtime. The following call, however, simply lets the function enter an infinite loop: ###Code with ExpectTimeout(1): x = square_root(-1.0) ###Output _____no_output_____ ###Markdown Our goal is to avoid such errors by _annotating_ functions with information that prevents errors like the above ones. The idea is to provide a _specification_ of expected properties – a specification that can then be checked at runtime or statically. \todo{Introduce the concept of contract.} Mining Data TypesFor our Python code, one of the most important "specifications" we need is types. Python being a "dynamically" typed language means that all data types are determined at run time; the code itself does not explicitly state whether a variable is an integer, a string, an array, a dictionary – or whatever. As _writer_ of Python code, omitting explicit type declarations may save time (and allows for some fun hacks). It is not sure whether a lack of types helps in _reading_ and _understanding_ code for humans. For a _computer_ trying to analyze code, the lack of explicit types is detrimental. If, say, a constraint solver, sees `if x:` and cannot know whether `x` is supposed to be a number or a string, this introduces an _ambiguity_. Such ambiguities may multiply over the entire analysis in a combinatorial explosion – or in the analysis yielding an overly inaccurate result. Python 3.6 and later allow data types as _annotations_ to function arguments (actually, to all variables) and return values. We can, for instance, state that `square_root()` is a function that accepts a floating-point value and returns one: ###Code def square_root_with_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) ###Output _____no_output_____ ###Markdown By default, such annotations are ignored by the Python interpreter. Therefore, one can still call `square_root_typed()` with a string as an argument and get the exact same result as above. However, one can make use of special _typechecking_ modules that would check types – _dynamically_ at runtime or _statically_ by analyzing the code without having to execute it. Runtime Type CheckingThe Python `enforce` package provides a function decorator that automatically inserts type-checking code that is executed at runtime. Here is how to use it: ###Code import enforce @enforce.runtime_validation def square_root_with_checked_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) ###Output _____no_output_____ ###Markdown Now, invoking `square_root_with_checked_type_annotations()` raises an exception when invoked with a type dfferent from the one declared: ###Code with ExpectError(): square_root_with_checked_type_annotations(True) ###Output _____no_output_____ ###Markdown Note that this error is not caught by the "untyped" variant, where passing a boolean value happily returns $\sqrt{1}$ as result. ###Code square_root(True) ###Output _____no_output_____ ###Markdown In Python (and other languages), the boolean values `True` and `False` can be implicitly converted to the integers 1 and 0; however, it is hard to think of a call to `sqrt()` where this would not be an error. ###Code from bookutils import quiz quiz("What happens if we call " "`square_root_with_checked_type_annotations(1)`?", [ "`1` is automatically converted to float. It will pass.", "`1` is a subtype of float. It will pass.", "`1` is an integer, and no float. The type check will fail.", "The function will fail for some other reason." ], '37035 // 12345') ###Output _____no_output_____ ###Markdown "Prediction is very difficult, especially when the future is concerned" (Niels Bohr). We can find out by a simple experiment that `float` actually means `float` – and not `int`: ###Code with ExpectError(enforce.exceptions.RuntimeTypeError): square_root_with_checked_type_annotations(1) ###Output _____no_output_____ ###Markdown To allow `int` as a type, we need to specify a _union_ of types. ###Code from typing import Union, Optional @enforce.runtime_validation def square_root_with_union_type(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) square_root_with_union_type(2) square_root_with_union_type(2.0) with ExpectError(enforce.exceptions.RuntimeTypeError): square_root_with_union_type("Two dot zero") ###Output _____no_output_____ ###Markdown Static Type CheckingType annotations can also be checked _statically_ – that is, without even running the code. Let us create a simple Python file consisting of the above `square_root_typed()` definition and a bad invocation. ###Code import inspect import tempfile f = tempfile.NamedTemporaryFile(mode='w', suffix='.py') f.name f.write(inspect.getsource(square_root)) f.write('\n') f.write(inspect.getsource(square_root_with_type_annotations)) f.write('\n') f.write("print(square_root_with_type_annotations('123'))\n") f.flush() ###Output _____no_output_____ ###Markdown These are the contents of our newly created Python file: ###Code from bookutils import print_file print_file(f.name, start_line_number=1) ###Output _____no_output_____ ###Markdown [Mypy](http://mypy-lang.org) is a type checker for Python programs. As it checks types statically, types induce no overhead at runtime; plus, a static check can be faster than a lengthy series of tests with runtime type checking enabled. Let us see what `mypy` produces on the above file: ###Code import subprocess result = subprocess.run(["mypy", "--strict", f.name], universal_newlines=True, stdout=subprocess.PIPE) print(result.stdout.replace(f.name + ':', '')) del f # Delete temporary file ###Output _____no_output_____ ###Markdown We see that `mypy` complains about untyped function definitions such as `square_root()`; most important, however, it finds that the call to `square_root_with_type_annotations()` in the last line has the wrong type. With `mypy`, we can achieve the same type safety with Python as in statically typed languages – provided that we as programmers also produce the necessary type annotations. Is there a simple way to obtain these? Mining Type SpecificationsOur first task will be to mine type annotations (as part of the code) from _values_ we observe at run time. These type annotations would be _mined_ from actual function executions, _learning_ from (normal) runs what the expected argument and return types should be. By observing a series of calls such as these, we could infer that both `x` and the return value are of type `float`: ###Code y = square_root(25.0) y y = square_root(2.0) y ###Output _____no_output_____ ###Markdown How can we mine types from executions? The answer is simple: 1. We _observe_ a function during execution2. We track the _types_ of its arguments3. We include these types as _annotations_ into the code.To do so, we can make use of Python's tracing facility we already observed in the [chapter on tracing executions](Tracer.ipynb). With every call to a function, we retrieve the arguments, their values, and their types. Tracing CallsTo observe argument types at runtime, we define a _tracer function_ that tracks the execution of `square_root()`, checking its arguments and return values. The `CallTracer` class is set to trace functions in a `with` block as follows:```pythonwith CallTracer() as tracer: function_to_be_tracked(...)info = tracer.collected_information()```To create the tracer, we build on the `Tracer` superclass as in the [chapter on tracing executions](Tracer.ipynb). ###Code from typing import Sequence, Any, Callable, Optional, Type, Tuple, Any from typing import Dict, Union, Set, List, cast, TypeVar from types import FrameType, TracebackType Arguments = List[Tuple[str, Any]] class CallTracer(Tracer): def __init__(self, log: bool = False, kwargs: Any)-> None: super().__init__(kwargs) self._log = log self.reset() def reset(self) -> None: self._calls: Dict[str, List[Tuple[Arguments, Any]]] = {} self._stack: List[Tuple[str, Arguments]] = [] ###Output _____no_output_____ ###Markdown The `traceit()` method does nothing yet; this is done in specialized subclasses. The `CallTracer` class implements a `traceit()` function that checks for function calls and returns: ###Code class CallTracer(CallTracer): def traceit(self, frame: FrameType, event: str, arg: Any) -> None: """Tracking function: Record all calls and all args""" if event == "call": self.trace_call(frame, event, arg) elif event == "return": self.trace_return(frame, event, arg) def trace_call(self, frame: FrameType, event: str, arg: Any) -> None: ... def trace_return(self, frame: FrameType, event: str, arg: Any) -> None: ... ###Output _____no_output_____ ###Markdown `trace_call()` is called when a function is called; it retrieves the function name and current arguments, and saves them on a stack. ###Code class CallTracer(CallTracer): def trace_call(self, frame: FrameType, event: str, arg: Any) -> None: """Save current function name and args on the stack""" code = frame.f_code function_name = code.co_name arguments = get_arguments(frame) self._stack.append((function_name, arguments)) if self._log: print(simple_call_string(function_name, arguments)) def get_arguments(frame: FrameType) -> Arguments: """Return call arguments in the given frame""" # When called, all arguments are local variables arguments = [(var, frame.f_locals[var]) for var in frame.f_locals] arguments.reverse() # Want same order as call return arguments ###Output _____no_output_____ ###Markdown When the function returns, `trace_return()` is called. We now also have the return value. We log the whole call with arguments and return value (if desired) and save it in our list of calls. ###Code class CallTracer(CallTracer): def trace_return(self, frame: FrameType, event: str, arg: Any) -> None: """Get return value and store complete call with arguments and return value""" code = frame.f_code function_name = code.co_name return_value = arg # TODO: Could call get_arguments() here to also retrieve _final_ values of argument variables called_function_name, called_arguments = self._stack.pop() assert function_name == called_function_name if self._log: print(simple_call_string(function_name, called_arguments), "returns", return_value) self.add_call(function_name, called_arguments, return_value) def add_call(self, function_name: str, arguments: Arguments, return_value: Any = None) -> None: ... ###Output _____no_output_____ ###Markdown `simple_call_string()` is a helper for logging that prints out calls in a user-friendly manner. ###Code def simple_call_string(function_name: str, argument_list: Arguments, return_value : Any = None) -> str: """Return function_name(arg[0], arg[1], ...) as a string""" call = function_name + "(" + \ ", ".join([var + "=" + repr(value) for (var, value) in argument_list]) + ")" if return_value is not None: call += " = " + repr(return_value) return call ###Output _____no_output_____ ###Markdown `add_call()` saves the calls in a list; each function name has its own list. ###Code class CallTracer(CallTracer): def add_call(self, function_name: str, arguments: Arguments, return_value: Any = None) -> None: """Add given call to list of calls""" if function_name not in self._calls: self._calls[function_name] = [] self._calls[function_name].append((arguments, return_value)) ###Output _____no_output_____ ###Markdown we can retrieve the list of calls, either for a given function name (`calls()`),or for all functions (`all_calls()`). ###Code class CallTracer(CallTracer): def calls(self, function_name: str) -> List[Tuple[Arguments, Any]]: """Return list of calls for `function_name`.""" return self._calls[function_name] class CallTracer(CallTracer): def all_calls(self) -> Dict[str, List[Tuple[Arguments, Any]]]: """ Return list of calls for function_name, or a mapping function_name -> calls for all functions tracked """ return self._calls ###Output _____no_output_____ ###Markdown Let us now put this to use. We turn on logging to track the individual calls and their return values: ###Code with CallTracer(log=True) as tracer: y = square_root(25) y = square_root(2.0) ###Output _____no_output_____ ###Markdown After execution, we can retrieve the individual calls: ###Code calls = tracer.calls('square_root') calls ###Output _____no_output_____ ###Markdown Each call is a pair (`argument_list`, `return_value`), where `argument_list` is a list of pairs (`parameter_name`, `value`). ###Code square_root_argument_list, square_root_return_value = calls[0] simple_call_string('square_root', square_root_argument_list, square_root_return_value) ###Output _____no_output_____ ###Markdown If the function does not return a value, `return_value` is `None`. ###Code def hello(name: str) -> None: print("Hello,", name) with CallTracer() as tracer: hello("world") hello_calls = tracer.calls('hello') hello_calls hello_argument_list, hello_return_value = hello_calls[0] simple_call_string('hello', hello_argument_list, hello_return_value) ###Output _____no_output_____ ###Markdown Getting TypesDespite what you may have read or heard, Python actually _is_ a typed language. It is just that it is _dynamically typed_ – types are used and checked only at runtime (rather than declared in the code, where they can be _statically checked_ at compile time). We can thus retrieve types of all values within Python: ###Code type(4) type(2.0) type([4]) ###Output _____no_output_____ ###Markdown We can retrieve the type of the first argument to `square_root()`: ###Code parameter, value = square_root_argument_list[0] parameter, type(value) ###Output _____no_output_____ ###Markdown as well as the type of the return value: ###Code type(square_root_return_value) ###Output _____no_output_____ ###Markdown Hence, we see that (so far), `square_root()` is a function taking (among others) integers and returning floats. We could declare `square_root()` as: ###Code def square_root_annotated(x: int) -> float: return square_root(x) ###Output _____no_output_____ ###Markdown This is a representation we could place in a static type checker, allowing to check whether calls to `square_root()` actually pass a number. A dynamic type checker could run such checks at runtime. By default, Python does not do anything with such annotations. However, tools can access annotations from functions and other objects: ###Code square_root_annotated.__annotations__ ###Output _____no_output_____ ###Markdown This is how run-time checkers access the annotations to check against. Annotating Functions with TypesOur plan is to annotate functions automatically, based on the types we have seen. Our aim is to build a class `TypeAnnotator` that can be used as follows. First, it would track some execution:```pythonwith TypeAnnotator() as annotator: some_function_call()```After tracking, `TypeAnnotator` would provide appropriate methods to access (type-)annotated versions of the function seen:```pythonprint(annotator.typed_functions())```Let us put the pieces together to build `TypeAnnotator`. Excursion: Accessing Function Structure To annotate functions, we need to convert a function into a tree representation (called _abstract syntax trees_, or ASTs) and back; we already have seen these in the chapter on [tracking value origins](Slicer.ipynb). ###Code import ast import inspect import astor ###Output _____no_output_____ ###Markdown We can get the source of a Python function using `inspect.getsource()`. (Note that this does not work for functions defined in other notebooks.) ###Code square_root_source = inspect.getsource(square_root) square_root_source ###Output _____no_output_____ ###Markdown To view these in a visually pleasing form, our function `print_content(s, suffix)` formats and highlights the string `s` as if it were a file with ending `suffix`. We can thus view (and highlight) the source as if it were a Python file: ###Code from bookutils import print_content print_content(square_root_source, '.py') ###Output _____no_output_____ ###Markdown Parsing this gives us an abstract syntax tree (AST) – a representation of the program in tree form. ###Code square_root_ast = ast.parse(square_root_source) ###Output _____no_output_____ ###Markdown What does this AST look like? The helper functions `astor.dump_tree()` (textual output) and `showast.show_ast()` (graphical output with [showast](https://github.com/hchasestevens/show_ast)) allow us to inspect the structure of the tree. We see that the function starts as a `FunctionDef` with name and arguments, followed by a body, which is a list of statements of type `Expr` (the docstring), type `Assign` (assignments), `While` (while loop with its own body), and finally `Return`. ###Code print(astor.dump_tree(square_root_ast)) ###Output _____no_output_____ ###Markdown Too much text for you? This graphical representation may make things simpler. ###Code from bookutils import show_ast show_ast(square_root_ast) ###Output _____no_output_____ ###Markdown The function `astor.to_source()` converts such a tree back into the more familiar textual Python code representation. Comments are gone, and there may be more parentheses than before, but the result has the same semantics: ###Code print_content(astor.to_source(square_root_ast), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: Annotating Functions with Given Types Let us now go and transform ASTs to add type annotations. We start with a helper function `parse_type(name)` which parses a type name into an AST. ###Code def parse_type(name: str) -> ast.expr: class ValueVisitor(ast.NodeVisitor): def visit_Expr(self, node: ast.Expr) -> None: self.value_node = node.value tree = ast.parse(name) name_visitor = ValueVisitor() name_visitor.visit(tree) return name_visitor.value_node print(astor.dump_tree(parse_type('int'))) print(astor.dump_tree(parse_type('[object]'))) ###Output _____no_output_____ ###Markdown We now define a helper function that actually adds type annotations to a function AST. The `TypeTransformer` class builds on the Python standard library `ast.NodeTransformer` infrastructure. It would be called as```python TypeTransformer({'x': 'int'}, 'float').visit(ast)```to annotate the arguments of `square_root()`: `x` with `int`, and the return type with `float`. The returned AST can then be unparsed, compiled or analyzed. ###Code class TypeTransformer(ast.NodeTransformer): def __init__(self, argument_types: Dict[str, str], return_type: Optional[str] = None): self.argument_types = argument_types self.return_type = return_type super().__init__() ###Output _____no_output_____ ###Markdown The core of `TypeTransformer` is the method `visit_FunctionDef()`, which is called for every function definition in the AST. Its argument `node` is the subtree of the function definition to be transformed. Our implementation accesses the individual arguments and invokes `annotate_args()` on them; it also sets the return type in the `returns` attribute of the node. ###Code class TypeTransformer(TypeTransformer): def visit_FunctionDef(self, node: ast.FunctionDef) -> ast.FunctionDef: """Add annotation to function""" # Set argument types new_args = [] for arg in node.args.args: new_args.append(self.annotate_arg(arg)) new_arguments = ast.arguments( new_args, node.args.vararg, node.args.kwonlyargs, node.args.kw_defaults, node.args.kwarg, node.args.defaults ) # Set return type if self.return_type is not None: node.returns = parse_type(self.return_type) return ast.copy_location( ast.FunctionDef(node.name, new_arguments, node.body, node.decorator_list, node.returns), node) def annotate_arg(self, arg: ast.arg) -> ast.arg: ... ###Output _____no_output_____ ###Markdown Each argument gets its own annotation, taken from the types originally passed to the class: ###Code class TypeTransformer(TypeTransformer): def annotate_arg(self, arg: ast.arg) -> ast.arg: """Add annotation to single function argument""" arg_name = arg.arg if arg_name in self.argument_types: arg.annotation = parse_type(self.argument_types[arg_name]) return arg ###Output _____no_output_____ ###Markdown Does this work? Let us annotate the AST from `square_root()` with types for the arguments and return types: ###Code new_ast = TypeTransformer({'x': 'int'}, 'float').visit(square_root_ast) ###Output _____no_output_____ ###Markdown When we unparse the new AST, we see that the annotations actually are present: ###Code print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown Similarly, we can annotate the `hello()` function from above: ###Code hello_source = inspect.getsource(hello) hello_ast = ast.parse(hello_source) new_ast = TypeTransformer({'name': 'str'}, 'None').visit(hello_ast) print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: Annotating Functions with Mined Types Let us now annotate functions with types mined at runtime. We start with a simple function `type_string()` that determines the appropriate type of a given value (as a string): ###Code def type_string(value: Any) -> str: return type(value).__name__ type_string(4) type_string([]) ###Output _____no_output_____ ###Markdown For composite structures, `type_string()` does not examine element types; hence, the type of `[3]` is simply `list` instead of, say, `list[int]`. For now, `list` will do fine. ###Code type_string([3]) ###Output _____no_output_____ ###Markdown `type_string()` will be used to infer the types of argument values found at runtime, as returned by `CallTracer.all_calls()`: ###Code with CallTracer() as tracer: y = square_root(25.0) y = square_root(2.0) tracer.all_calls() ###Output _____no_output_____ ###Markdown The function `annotate_types()` takes such a list of calls and annotates each function listed: ###Code def annotate_types(calls: Dict[str, List[Tuple[Arguments, Any]]]) -> Dict[str, ast.AST]: annotated_functions = {} for function_name in calls: try: annotated_functions[function_name] = \ annotate_function_with_types(function_name, calls[function_name]) except KeyError: continue return annotated_functions ###Output _____no_output_____ ###Markdown For each function, we get the source and its AST and then get to the actual annotation in `annotate_function_ast_with_types()`: ###Code def annotate_function_with_types(function_name: str, function_calls: List[Tuple[Arguments, Any]]) -> ast.AST: function = globals()[function_name] # May raise KeyError for internal functions function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_types(function_ast, function_calls) ###Output _____no_output_____ ###Markdown The function `annotate_function_ast_with_types()` invokes the `TypeTransformer` with the calls seen, and for each call, iterate over the arguments, determine their types, and annotate the AST with these. The universal type `Any` is used when we encounter type conflicts, which we will discuss below. ###Code from typing import Any def annotate_function_ast_with_types(function_ast: ast.AST, function_calls: List[Tuple[Arguments, Any]]) -> ast.AST: parameter_types: Dict[str, str] = {} return_type = None for calls_seen in function_calls: args, return_value = calls_seen if return_value: if return_type and return_type != type_string(return_value): return_type = 'Any' else: return_type = type_string(return_value) for parameter, value in args: try: different_type = (parameter_types[parameter] != type_string(value)) except KeyError: different_type = False if different_type: parameter_types[parameter] = 'Any' else: parameter_types[parameter] = type_string(value) annotated_function_ast = \ TypeTransformer(parameter_types, return_type).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Here is `square_root()` annotated with the types recorded usign the tracer, above. ###Code print_content(astor.to_source(annotate_types(tracer.all_calls())['square_root']), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: A Type Annotator Class Let us bring all of this together in a single class `TypeAnnotator` that first tracks calls of functions and then allows to access the AST (and the source code form) of the tracked functions annotated with types. The method `typed_functions()` returns the annotated functions as a string; `typed_functions_ast()` returns their AST. ###Code class TypeTracer(CallTracer): pass class TypeAnnotator(TypeTracer): def typed_functions_ast(self) -> Dict[str, ast.AST]: return annotate_types(self.all_calls()) def typed_function_ast(self, function_name: str) -> ast.AST: return annotate_function_with_types(function_name, self.calls(function_name)) def typed_functions(self) -> str: functions = '' for f_name in self.all_calls(): try: f_text = astor.to_source(self.typed_function_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions def typed_function(self, function_name: str) -> str: return astor.to_source(self.typed_function_ast(function_name)) ###Output _____no_output_____ ###Markdown End of Excursion Here is how to use `TypeAnnotator`. We first track a series of calls: ###Code with TypeAnnotator() as annotator: y = square_root(25.0) y = square_root(2.0) ###Output _____no_output_____ ###Markdown After tracking, we can immediately retrieve an annotated version of the functions tracked: ###Code print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown This also works for multiple and diverse functions. One could go and implement an automatic type annotator for Python files based on the types seen during execution. ###Code with TypeAnnotator() as annotator: hello('type annotations') y = square_root(1.0) print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown A content as above could now be sent to a type checker, which would detect any type inconsistency between callers and callees. Excursion: Handling Multiple TypesLet us now resolve the role of the magic `Any` type in `annotate_function_ast_with_types()`. If we see multiple types for the same argument, we set its type to `Any`. For `square_root()`, this makes sense, as its arguments can be integers as well as floats: ###Code with CallTracer() as tracer: y = square_root(25.0) y = square_root(4) annotated_square_root_ast = annotate_types(tracer.all_calls())['square_root'] print_content(astor.to_source(annotated_square_root_ast), '.py') ###Output _____no_output_____ ###Markdown The following function `sum3()` can be called with floating-point numbers as arguments, resulting in the parameters getting a `float` type: ###Code def sum3(a, b, c): # type: ignore return a + b + c with TypeAnnotator() as annotator: y = sum3(1.0, 2.0, 3.0) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we call `sum3()` with integers, though, the arguments get an `int` type: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown And we can also call `sum3()` with strings, which assigns the arguments a `str` type: ###Code with TypeAnnotator() as annotator: y = sum3("one", "two", "three") y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we have multiple calls, but with different types, `TypeAnnotator()` will assign an `Any` type to both arguments and return values: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y = sum3("one", "two", "three") typed_sum3_def = annotator.typed_function('sum3') print_content(typed_sum3_def, '.py') ###Output _____no_output_____ ###Markdown A type `Any` makes it explicit that an object can, indeed, have any type; it will not be typechecked at runtime or statically. To some extent, this defeats the power of type checking; but it also preserves some of the type flexibility that many Python programmers enjoy. Besides `Any`, the `typing` module supports several additional ways to define ambiguous types; we will keep this in mind for a later exercise. End of Excursion Mining InvariantsBesides basic data types. we can check several further properties from arguments. We can, for instance, whether an argument can be negative, zero, or positive; or that one argument should be smaller than the second; or that the result should be the sum of two arguments – properties that cannot be expressed in a (Python) type.Such properties are called invariants, as they hold across all invocations of a function. Specifically, invariants come as _pre_- and _postconditions_ – conditions that always hold at the beginning and at the end of a function. (There are also _data_ and _object_ invariants that express always-holding properties over the state of data or objects, but we do not consider these in this book.) Annotating Functions with Pre- and PostconditionsThe classical means to specify pre- and postconditions is via _assertions_, which we have introduced in the [chapter on assertions](Assertions.ipynb). A precondition checks whether the arguments to a function satisfy the expected properties; a postcondition does the same for the result. We can express and check both using assertions as follows: ###Code def square_root_with_invariants(x): # type: ignore assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown A nicer way, however, is to syntactically separate invariants from the function at hand. Using appropriate decorators, we could specify pre- and postconditions as follows:```python@precondition lambda x: x >= 0@postcondition lambda return_value, x: return_value * return_value == xdef square_root_with_invariants(x): normal code without assertions ...```The decorators `@precondition` and `@postcondition` would run the given functions (specified as anonymous `lambda` functions) before and after the decorated function, respectively. If the functions return `False`, the condition is violated. `@precondition` gets the function arguments as arguments; `@postcondition` additionally gets the return value as first argument. It turns out that implementing such decorators is not hard at all. Our implementation builds on a [code snippet from StackOverflow](https://stackoverflow.com/questions/12151182/python-precondition-postcondition-for-member-function-how): ###Code import functools def condition(precondition: Optional[Callable] = None, postcondition: Optional[Callable] = None) -> Callable: def decorator(func: Callable) -> Callable: @functools.wraps(func) # preserves name, docstring, etc def wrapper(args: Any, kwargs: Any) -> Any: if precondition is not None: assert precondition(args, *kwargs), \ "Precondition violated" # Call original function or method retval = func(args, *kwargs) if postcondition is not None: assert postcondition(retval, args, *kwargs), \ "Postcondition violated" return retval return wrapper return decorator def precondition(check: Callable) -> Callable: return condition(precondition=check) def postcondition(check: Callable) -> Callable: return condition(postcondition=check) ###Output _____no_output_____ ###Markdown With these, we can now start decorating `square_root()`: ###Code @precondition(lambda x: x > 0) def square_root_with_precondition(x): # type: ignore return square_root(x) ###Output _____no_output_____ ###Markdown This catches arguments violating the precondition: ###Code with ExpectError(): square_root_with_precondition(-1.0) ###Output _____no_output_____ ###Markdown Likewise, we can provide a postcondition: ###Code import math @postcondition(lambda ret, x: math.isclose(ret ret, x)) def square_root_with_postcondition(x): # type: ignore return square_root(x) y = square_root_with_postcondition(2.0) y ###Output _____no_output_____ ###Markdown If we have a buggy implementation of $\sqrt{x}$, this gets caught quickly: ###Code @postcondition(lambda ret, x: math.isclose(ret * ret, x)) def buggy_square_root_with_postcondition(x): # type: ignore return square_root(x) + 0.1 with ExpectError(): y = buggy_square_root_with_postcondition(2.0) ###Output _____no_output_____ ###Markdown While checking pre- and postconditions is a great way to catch errors, specifying them can be cumbersome. Let us try to see whether we can (again) _mine_ some of them. Mining InvariantsTo _mine_ invariants, we can use the same tracking functionality as before; instead of saving values for individual variables, though, we now check whether the values satisfy specific _properties_ or not. For instance, if all values of `x` seen satisfy the condition `x > 0`, then we make `x > 0` an invariant of the function. If we see positive, zero, and negative values of `x`, though, then there is no property of `x` left to talk about.The general idea is thus:1. Check all variable values observed against a set of predefined properties; and2. Keep only those properties that hold for all runs observed. Defining PropertiesWhat precisely do we mean by properties? Here is a small collection of value properties that would frequently be used in invariants. All these properties would be evaluated with the _metavariables_ `X`, `Y`, and `Z` (actually, any upper-case identifier) being replaced with the names of function parameters: ###Code INVARIANT_PROPERTIES = [ "X < 0", "X <= 0", "X > 0", "X >= 0", # "X == 0", # implied by "X", below # "X != 0", # implied by "not X", below ] ###Output _____no_output_____ ###Markdown When `square_root(x)` is called as, say `square_root(5.0)`, we see that `x = 5.0` holds. The above properties would then all be checked for `x`. Only the properties `X > 0`, `X >= 0`, and `not X` hold for the call seen; and hence `x > 0`, `x >= 0`, and `not x` (or better: `x != 0`) would make potential preconditions for `square_root(x)`. We can check for many more properties such as relations between two arguments: ###Code INVARIANT_PROPERTIES += [ "X == Y", "X > Y", "X < Y", "X >= Y", "X <= Y", ] ###Output _____no_output_____ ###Markdown Types also can be checked using properties. For any function parameter `X`, only one of these will hold: ###Code INVARIANT_PROPERTIES += [ "isinstance(X, bool)", "isinstance(X, int)", "isinstance(X, float)", "isinstance(X, list)", "isinstance(X, dict)", ] ###Output _____no_output_____ ###Markdown We can check for arithmetic properties: ###Code INVARIANT_PROPERTIES += [ "X == Y + Z", "X == Y * Z", "X == Y - Z", "X == Y / Z", ] ###Output _____no_output_____ ###Markdown Here's relations over three values, a Python special: ###Code INVARIANT_PROPERTIES += [ "X < Y < Z", "X <= Y <= Z", "X > Y > Z", "X >= Y >= Z", ] ###Output _____no_output_____ ###Markdown These Boolean properties also check for other types, as in Python, `None`, an empty list, an empty set, an empty string, and the value zero all evaluate to `False`. ###Code INVARIANT_PROPERTIES += [ "X", "not X" ] ###Output _____no_output_____ ###Markdown Finally, we can also check for list or string properties. Again, this is just a tiny selection. ###Code INVARIANT_PROPERTIES += [ "X == len(Y)", "X == sum(Y)", "X in Y", "X.startswith(Y)", "X.endswith(Y)", ] ###Output _____no_output_____ ###Markdown Extracting Meta-VariablesLet us first introduce a few _helper functions_ before we can get to the actual mining. `metavars()` extracts the set of meta-variables (`X`, `Y`, `Z`, etc.) from a property. To this end, we parse the property as a Python expression and then visit the identifiers. ###Code def metavars(prop: str) -> List[str]: metavar_list = [] class ArgVisitor(ast.NodeVisitor): def visit_Name(self, node: ast.Name) -> None: if node.id.isupper(): metavar_list.append(node.id) ArgVisitor().visit(ast.parse(prop)) return metavar_list assert metavars("X < 0") == ['X'] assert metavars("X.startswith(Y)") == ['X', 'Y'] assert metavars("isinstance(X, str)") == ['X'] ###Output _____no_output_____ ###Markdown Instantiating PropertiesTo produce a property as invariant, we need to be able to _instantiate_ it with variable names. The instantiation of `X > 0` with `X` being instantiated to `a`, for instance, gets us `a > 0`. To this end, the function `instantiate_prop()` takes a property and a collection of variable names and instantiates the meta-variables left-to-right with the corresponding variables names in the collection. ###Code def instantiate_prop_ast(prop: str, var_names: Sequence[str]) -> ast.AST: class NameTransformer(ast.NodeTransformer): def visit_Name(self, node: ast.Name) -> ast.Name: if node.id not in mapping: return node return ast.Name(id=mapping[node.id], ctx=ast.Load()) meta_variables = metavars(prop) assert len(meta_variables) == len(var_names) mapping = {} for i in range(0, len(meta_variables)): mapping[meta_variables[i]] = var_names[i] prop_ast = ast.parse(prop, mode='eval') new_ast = NameTransformer().visit(prop_ast) return new_ast def instantiate_prop(prop: str, var_names: Sequence[str]) -> str: prop_ast = instantiate_prop_ast(prop, var_names) prop_text = astor.to_source(prop_ast).strip() while prop_text.startswith('(') and prop_text.endswith(')'): prop_text = prop_text[1:-1] return prop_text assert instantiate_prop("X > Y", ['a', 'b']) == 'a > b' assert instantiate_prop("X.startswith(Y)", ['x', 'y']) == 'x.startswith(y)' ###Output _____no_output_____ ###Markdown Evaluating PropertiesTo actually _evaluate_ properties, we do not need to instantiate them. Instead, we simply convert them into a boolean function, using `lambda`: ###Code def prop_function_text(prop: str) -> str: return "lambda " + ", ".join(metavars(prop)) + ": " + prop ###Output _____no_output_____ ###Markdown Here is a simple example: ###Code prop_function_text("X > Y") ###Output _____no_output_____ ###Markdown We can easily evaluate the function: ###Code def prop_function(prop: str) -> Callable: return eval(prop_function_text(prop)) ###Output _____no_output_____ ###Markdown Here is an example: ###Code p = prop_function("X > Y") quiz("What is p(100, 1)?", [ "False", "True" ], 'p(100, 1) + 1', globals()) p(100, 1) p(1, 100) ###Output _____no_output_____ ###Markdown Checking InvariantsTo extract invariants from an execution, we need to check them on all possible instantiations of arguments. If the function to be checked has two arguments `a` and `b`, we instantiate the property `X < Y` both as `a < b` and `b < a` and check each of them. To get all combinations, we use the Python `permutations()` function: ###Code import itertools for combination in itertools.permutations([1.0, 2.0, 3.0], 2): print(combination) ###Output _____no_output_____ ###Markdown The function `true_property_instantiations()` takes a property and a list of tuples (`var_name`, `value`). It then produces all instantiations of the property with the given values and returns those that evaluate to True. ###Code Invariants = Set[Tuple[str, Tuple[str, ...]]] def true_property_instantiations(prop: str, vars_and_values: Arguments, log: bool = False) -> Invariants: instantiations = set() p = prop_function(prop) len_metavars = len(metavars(prop)) for combination in itertools.permutations(vars_and_values, len_metavars): args = [value for var_name, value in combination] var_names = [var_name for var_name, value in combination] try: result = p(args) except: result = None if log: print(prop, combination, result) if result: instantiations.add((prop, tuple(var_names))) return instantiations ###Output _____no_output_____ ###Markdown Here is an example. If `x == -1` and `y == 1`, the property `X < Y` holds for `x < y`, but not for `y < x`: ###Code invs = true_property_instantiations("X < Y", [('x', -1), ('y', 1)], log=True) invs ###Output _____no_output_____ ###Markdown The instantiation retrieves the short form: ###Code for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Likewise, with values for `x` and `y` as above, the property `X < 0` only holds for `x`, but not for `y`: ###Code invs = true_property_instantiations("X < 0", [('x', -1), ('y', 1)], log=True) for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Extracting InvariantsLet us now run the above invariant extraction on function arguments and return values as observed during a function execution. To this end, we extend the `CallTracer` class into an `InvariantTracer` class, which automatically computes invariants for all functions and all calls observed during tracking. By default, an `InvariantTracer` uses the `INVARIANT_PROPERTIES` properties as defined above; however, one can specify alternate sets of properties. ###Code class InvariantTracer(CallTracer): def __init__(self, props: Optional[List[str]] = None, kwargs: Any) -> None: if props is None: props = INVARIANT_PROPERTIES self.props = props super().__init__(kwargs) ###Output _____no_output_____ ###Markdown The key method of the `InvariantTracer` is the `invariants()` method. This iterates over the calls observed and checks which properties hold. Only the intersection of properties – that is, the set of properties that hold for all calls – is preserved, and eventually returned. The special variable `return_value` is set to hold the return value. ###Code RETURN_VALUE = 'return_value' class InvariantTracer(InvariantTracer): def all_invariants(self) -> Dict[str, Invariants]: return {function_name: self.invariants(function_name) for function_name in self.all_calls()} def invariants(self, function_name: str) -> Invariants: invariants = None for variables, return_value in self.calls(function_name): vars_and_values = variables + [(RETURN_VALUE, return_value)] s = set() for prop in self.props: s \|= true_property_instantiations(prop, vars_and_values, self._log) if invariants is None: invariants = s else: invariants &= s assert invariants is not None return invariants ###Output _____no_output_____ ###Markdown Here's an example of how to use `invariants()`. We run the tracer on a small set of calls. ###Code with InvariantTracer() as tracer: y = square_root(25.0) y = square_root(10.0) tracer.all_calls() ###Output _____no_output_____ ###Markdown The `invariants()` method produces a set of properties that hold for the observed runs, together with their instantiations over function arguments. ###Code invs = tracer.invariants('square_root') invs ###Output _____no_output_____ ###Markdown As before, the actual instantiations are easier to read: ###Code def pretty_invariants(invariants: Invariants) -> List[str]: props = [] for (prop, var_names) in invariants: props.append(instantiate_prop(prop, var_names)) return sorted(props) pretty_invariants(invs) ###Output _____no_output_____ ###Markdown We see that the both `x` and the return value have a `float` type. We also see that both are always greater than zero. These are properties that may make useful pre- and postconditions, notably for symbolic analysis. However, there's also an invariant which does _not_ universally hold, namely `return_value <= x`, as the following example shows: ###Code square_root(0.01) ###Output _____no_output_____ ###Markdown Clearly, 0.1 > 0.01 holds. This is a case of us not learning from sufficiently diverse inputs. As soon as we have a call including `x = 0.1`, though, the invariant `return_value <= x` is eliminated: ###Code with InvariantTracer() as tracer: y = square_root(25.0) y = square_root(10.0) y = square_root(0.01) pretty_invariants(tracer.invariants('square_root')) ###Output _____no_output_____ ###Markdown We will discuss later how to ensure sufficient diversity in inputs. (Hint: This involves test generation.) Let us try out our invariant tracer on `sum3()`. We see that all types are well-defined; the properties that all arguments are non-zero, however, is specific to the calls observed. ###Code with InvariantTracer() as tracer: y = sum3(1, 2, 3) y = sum3(-4, -5, -6) pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with strings instead, we get different invariants. Notably, we obtain the postcondition that the returned string always starts with the string in the first argument `a` – a universal postcondition if strings are used. ###Code with InvariantTracer() as tracer: y = sum3('a', 'b', 'c') y = sum3('f', 'e', 'd') pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with both strings and numbers (and zeros, too), there are no properties left that would hold across all calls. That's the price of flexibility. ###Code with InvariantTracer() as tracer: y = sum3('a', 'b', 'c') y = sum3('c', 'b', 'a') y = sum3(-4, -5, -6) y = sum3(0, 0, 0) pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown Converting Mined Invariants to AnnotationsAs with types, above, we would like to have some functionality where we can add the mined invariants as annotations to existing functions. To this end, we introduce the `InvariantAnnotator` class, extending `InvariantTracer`. We start with a helper method. `params()` returns a comma-separated list of parameter names as observed during calls. ###Code class InvariantAnnotator(InvariantTracer): def params(self, function_name: str) -> str: arguments, return_value = self.calls(function_name)[0] return ", ".join(arg_name for (arg_name, arg_value) in arguments) with InvariantAnnotator() as annotator: y = square_root(25.0) y = sum3(1, 2, 3) annotator.params('square_root') annotator.params('sum3') ###Output _____no_output_____ ###Markdown Now for the actual annotation. `preconditions()` returns the preconditions from the mined invariants (i.e., those propertes that do not depend on the return value) as a string with annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = ("@precondition(lambda " + self.params(function_name) + ": " + inv + ")") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) annotator.preconditions('square_root') ###Output _____no_output_____ ###Markdown `postconditions()` does the same for postconditions: ###Code class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = (f"@postcondition(lambda {RETURN_VALUE}," f" {self.params(function_name)}: {inv})") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) annotator.postconditions('square_root') ###Output _____no_output_____ ###Markdown With these, we can take a function and add both pre- and postconditions as annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def functions_with_invariants(self) -> str: functions = "" for function_name in self.all_invariants(): try: function = self.function_with_invariants(function_name) except KeyError: continue functions += function return functions def function_with_invariants(self, function_name: str) -> str: function = globals()[function_name] # Can throw KeyError source = inspect.getsource(function) return '\n'.join(self.preconditions(function_name) + self.postconditions(function_name)) + \ '\n' + source ###Output _____no_output_____ ###Markdown Here comes `function_with_invariants()` in all its glory: ###Code with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) print_content(annotator.function_with_invariants('square_root'), '.py') ###Output _____no_output_____ ###Markdown Quite a number of invariants, isn't it? Further below (and in the exercises), we will discuss on how to focus on the most relevant properties. Avoiding OverspecializationMined specifications can only be as good as the executions they were mined from. If we only see a single call, for instance, we will be faced with several mined pre- and postconditions that _overspecialize_ towards the values seen. Let us illustrate this effect on a simple `sum2()` function which adds two numbers. ###Code def sum2(a, b): # type: ignore return a + b ###Output _____no_output_____ ###Markdown If we invoke `sum2()` with a variety of arguments, the invariants all capture the relationship between `a`, `b`, and the return value as `return_value == a + b` in all its variations. ###Code with InvariantAnnotator() as annotator: sum2(31, 45) sum2(0, 0) sum2(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown If, however, we see only a single call, the invariants will overspecialize to the single call seen: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown The mined precondition `a == b`, for instance, only holds for the single call observed; the same holds for the mined postcondition `return_value == a b`. Yet, `sum2()` can obviously be successfully called with other values that do not satisfy these conditions. To get out of this trap, we have to _learn from more and more diverse runs_. One way to obtain such runs is by _generating_ inputs. Indeed, a simple test generator for calls of `sum2()` will easily resolve the problem. ###Code import random with InvariantAnnotator() as annotator: for i in range(100): a = random.randrange(-10, +10) b = random.randrange(-10, +10) length = sum2(a, b) print_content(annotator.function_with_invariants('sum2'), '.py') ###Output _____no_output_____ ###Markdown Note, though, that an API test generator, such as above, will have to be set up such that it actually respects preconditions – in our case, we invoke `sum2()` with integers only, already assuming its precondition. In some way, one thus needs a specification (a model, a grammar) to mine another specification – a chicken-and-egg problem. However, there is one way out of this problem: If one can automatically generate tests at the system level, then one has an _infinite source of executions_ to learn invariants from. In each of these executions, all functions would be called with values that satisfy the (implicit) precondition, allowing us to mine invariants for these functions. This holds, because at the system level, invalid inputs must be rejected by the system in the first place. The meaningful precondition at the system level, ensuring that only valid inputs get through, thus gets broken down into a multitude of meaningful preconditions (and subsequent postconditions) at the function level. The big requirement for all this, though, is that one needs good test generators. This will be the subject of another book, namely [The Fuzzing Book](https://www.fuzzingbook.org/). Partial InvariantsFor debugging, it can be helpful to focus on invariants produced only by _failing_ runs, thus characterizing the _circumstances under which a function fails_. Let us illustrate this on an example. The `middle()` function from the [chapter on statistical debugging](StatisticalDebugger.ipynb) is supposed to return the middle of three integers `x`, `y`, and `z`. ###Code from StatisticalDebugger import middle # minor dependency with InvariantAnnotator() as annotator: for i in range(100): x = random.randrange(-10, +10) y = random.randrange(-10, +10) z = random.randrange(-10, +10) mid = middle(x, y, z) ###Output _____no_output_____ ###Markdown By default, our `InvariantAnnotator()` does not return any particular pre- or postcondition (other than the types observed). That is just fine, as the function indeed imposes no particular precondition; and the postcondition from `middle()` is not covered by the `InvariantAnnotator` patterns. ###Code print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Things get more interesting if we focus on a particular subset of runs only, though - say, a set of inputs where `middle()` fails. (TODO: Move these from `Repairer` to here, or to statistical debugging) ###Code from Repairer import MIDDLE_FAILING_TESTCASES # minor dependency with InvariantAnnotator() as annotator: for x, y, z in MIDDLE_FAILING_TESTCASES: mid = middle(x, y, z) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Now that's an intimidating set of pre- and postconditions. However, almost all of the preconditions are implied by the one precondition```python@precondition(lambda x, y, z: y < x < z, doc='y < x < z')```which characterizes the exact condition under which `middle()` fails (which also happens to be the condition under which the erroneous second `return y` is executed). By checking how _invariants for failing runs_ differ from _invariants for passing runs_, we can identify circumstances for function failures. ###Code quiz("Could `InvariantAnnotator` also determine a precondition " "that characterizes _passing_ runs?", [ "Yes", "No" ], 'int(math.exp(1))', globals()) ###Output _____no_output_____ ###Markdown Indeed, it cannot – the correct invariant for passing runs would be the _inverse_ of the invariant for failing runs, and `not A < B < C` is not part of our invariant library. We can easily test this: ###Code from Repairer import MIDDLE_PASSING_TESTCASES # minor dependency with InvariantAnnotator() as annotator: for x, y, z in MIDDLE_PASSING_TESTCASES: mid = middle(x, y, z) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Some ExamplesLet us try out the `InvariantAnnotator` on a number of examples. Removing HTML MarkupRunning `InvariantAnnotator` on our ongoing example `remove_html_markup()` does not provide much, as our invariant properties are tailored towards numerical functions. ###Code from Intro_Debugging import remove_html_markup with InvariantAnnotator() as annotator: remove_html_markup("<foo>bar</foo>") remove_html_markup("bar") remove_html_markup('"bar"') print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown We will see in the chapter on [Alhazen](Alhazen.ipynb) on how to express more complex properties for structured inputs. A Recursive FunctionHere's another example. `list_length()` recursively computes the length of a Python function. Let us see whether we can mine its invariants: ###Code def list_length(elems: List[Any]) -> int: if elems == []: length = 0 else: length = 1 + list_length(elems[1:]) return length with InvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Almost all these properties are relevant. Of course, the reason the invariants are so neat is that the return value is equal to `len(elems)` is that `X == len(Y)` is part of the list of properties to be checked. Sum of two NumbersThe next example is a very simple function: If we have a function without return value, the return value is `None` and we can only mine preconditions. (Well, we get a "postcondition" `not return_value` that the return value evaluates to False, which holds for `None`). ###Code def print_sum(a, b): # type: ignore print(a + b) with InvariantAnnotator() as annotator: print_sum(31, 45) print_sum(0, 0) print_sum(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Checking SpecificationsA function with invariants, as above, can be fed into the Python interpreter, such that all pre- and postconditions are checked. We create a function `square_root_annotated()` which includes all the invariants mined above. ###Code with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) square_root_def = annotator.functions_with_invariants() square_root_def = square_root_def.replace('square_root', 'square_root_annotated') print_content(square_root_def, '.py') exec(square_root_def) ###Output _____no_output_____ ###Markdown The "annotated" version checks against invalid arguments – or more precisely, against arguments with properties that have not been observed yet: ###Code with ExpectError(): square_root_annotated(-1.0) # type: ignore ###Output _____no_output_____ ###Markdown This is in contrast to the original version, which just hangs on negative values: ###Code with ExpectTimeout(1): square_root(-1.0) ###Output _____no_output_____ ###Markdown If we make changes to the function definition such that the properties of the return value change, such _regressions_ are caught as violations of the postconditions. Let us illustrate this by simply inverting the result, and return $-2$ as square root of 4. ###Code square_root_def = square_root_def.replace('square_root_annotated', 'square_root_negative') square_root_def = square_root_def.replace('return approx', 'return -approx') print_content(square_root_def, '.py') exec(square_root_def) ###Output _____no_output_____ ###Markdown Technically speaking, $-2$ _is_ a square root of 4, since $(-2)^2 = 4$ holds. Yet, such a change may be unexpected by callers of `square_root()`, and hence, this would be caught with the first call: ###Code with ExpectError(): square_root_negative(2.0) # type: ignore ###Output _____no_output_____ ###Markdown We see how pre- and postconditions, as well as types, can serve as oracles during testing. In particular, once we have mined them for a set of functions, we can check them again and again with test generators – especially after code changes. The more checks we have, and the more specific they are, the more likely it is we can detect unwanted effects of changes. SynopsisThis chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator: ###Code def sum2(a, b): # type: ignore return a + b with TypeAnnotator() as type_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution. ###Code print(type_annotator.typed_functions()) ###Output _____no_output_____ ###Markdown The invariant annotator works in a similar fashion: ###Code with InvariantAnnotator() as inv_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values. ###Code print(inv_annotator.functions_with_invariants()) ###Output _____no_output_____ ###Markdown Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs). The chapter gives details on how to customize the properties checked for. Lessons Learned* Type annotations and explicit invariants allow for _checking_ arguments and results for expected data types and other properties.* One can automatically _mine_ data types and invariants by observing arguments and results at runtime.* The quality of mined invariants depends on the diversity of values observed during executions; this variety can be increased by generating tests. Next StepsIn the next chapter, we will explore [abstracting failure conditions](DDSetDebugger.ipynb). BackgroundThe [DAIKON dynamic invariant detector](https://plse.cs.washington.edu/daikon/) can be considered the mother of function specification miners. Continuously maintained and extended for more than 20 years, it mines likely invariants in the style of this chapter for a variety of languages, including C, C++, C, Eiffel, F, Java, Perl, and Visual Basic. On top of the functionality discussed above, it holds a rich catalog of patterns for likely invariants, supports data invariants, can eliminate invariants that are implied by others, and determines statistical confidence to disregard unlikely invariants. The corresponding paper \cite{Ernst2001} is one of the seminal and most-cited papers of Software Engineering. A multitude of works have been published based on DAIKON and detecting invariants; see this [curated list](http://plse.cs.washington.edu/daikon/pubs/) for details. The interaction between test generators and invariant detection is already discussed in \cite{Ernst2001} (incidentally also using grammars). The Eclat tool \cite{Pacheco2005} is a model example of tight interaction between a unit-level test generator and DAIKON-style invariant mining, where the mined invariants are used to produce oracles and to systematically guide the test generator towards fault-revealing inputs. Mining specifications is not restricted to pre- and postconditions. The paper "Mining Specifications" \cite{Ammons2002} is another classic in the field, learning state protocols from executions. Grammar mining \cite{Gopinath2020} can also be seen as a specification mining approach, this time learning specifications for input formats. As it comes to adding type annotations to existing code, the blog post ["The state of type hints in Python"](https://www.bernat.tech/the-state-of-type-hints-in-python/) gives a great overview on how Python type hints can be used and checked. To add type annotations, there are two important tools available that also implement our above approach:* [MonkeyType](https://instagram-engineering.com/let-your-code-type-hint-itself-introducing-open-source-monkeytype-a855c7284881) implements the above approach of tracing executions and annotating Python 3 arguments, returns, and variables with type hints.* [PyAnnotate](https://github.com/dropbox/pyannotate) does a similar job, focusing on code in Python 2. It does not produce Python 3-style annotations, but instead produces annotations as comments that can be processed by static type checkers.These tools have been created by engineers at Facebook and Dropbox, respectively, assisting them in checking millions of lines of code for type issues. ExercisesOur code for mining types and invariants is in no way complete. There are dozens of ways to extend our implementations, some of which we discuss in exercises. Exercise 1: Union TypesThe Python `typing` module allows to express that an argument can have multiple types. For `square_root(x)`, this allows to express that `x` can be an `int` or a `float`: ###Code def square_root_with_union_type(x: Union[int, float]) -> float: # type: ignore ... ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it supports union types for arguments and return values. Use `Optional[X]` as a shorthand for `Union[X, None]`. Solution. Left to the reader. Hint: extend `type_string()`. Exercise 2: Types for Local VariablesIn Python, one cannot only annotate arguments with types, but actually also local and global variables – for instance, `approx` and `guess` in our `square_root()` implementation: ###Code def square_root_with_local_types(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" approx: Optional[float] = None guess: float = x / 2 while approx != guess: approx: float = guess # type: ignore guess: float = (approx + x / approx) / 2 # type: ignore return approx ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it also annotates local variables with types. Search the function AST for assignments, determine the type of the assigned value, and make it an annotation on the left hand side. Solution. Left to the reader. Exercise 3: Verbose Invariant CheckersOur implementation of invariant checkers does not make it clear for the user which pre-/postcondition failed. ###Code @precondition(lambda s: len(s) > 0) def remove_first_char(s: str) -> str: return s[1:] with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown The following implementation adds an optional `doc` keyword argument which is printed if the invariant is violated: ###Code def my_condition(precondition: Optional[Callable] = None, postcondition: Optional[Callable] = None, doc: str = 'Unknown') -> Callable: def decorator(func: Callable) -> Callable: @functools.wraps(func) # preserves name, docstring, etc def wrapper(args: Any, kwargs: Any) -> Any: if precondition is not None: assert precondition(args, *kwargs), "Precondition violated: " + doc retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, kwargs), "Postcondition violated: " + doc return retval return wrapper return decorator def my_precondition(check: Callable, kwargs: Any) -> Callable: return my_condition(precondition=check, doc=kwargs.get('doc', 'Unknown')) def my_postcondition(check: Callable, kwargs: Any) -> Callable: return my_condition(postcondition=check, doc=kwargs.get('doc', 'Unknown')) @my_precondition(lambda s: len(s) > 0, doc="len(s) > 0") # type: ignore def remove_first_char(s: str) -> str: return s[1:] remove_first_char('abc') with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown Extend `InvariantAnnotator` such that it includes the conditions in the generated pre- and postconditions. Solution.** Here's a simple solution: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@my_precondition(lambda " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")" conditions.append(cond) return conditions class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@my_postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")") conditions.append(cond) return conditions ###Output _____no_output_____ ###Markdown The resulting annotations are harder to read, but easier to diagnose: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown As an alternative, one may be able to use `inspect.getsource()` on the lambda expression or unparse it. This is left to the reader. Exercise 4: Save Initial ValuesIf the value of an argument changes during function execution, this can easily confuse our implementation: The values are tracked at the beginning of the function, but checked only when it returns. Extend the `InvariantAnnotator` and the infrastructure it uses such that* it saves argument values both at the beginning and at the end of a function invocation;* postconditions can be expressed over both _initial_ values of arguments as well as the _final_ values of arguments;* the mined postconditions refer to both these values as well. Solution. To be added. Exercise 5: ImplicationsSeveral mined invariant are actually _implied_ by others: If `x > 0` holds, then this implies `x >= 0` and `x != 0`. Extend the `InvariantAnnotator` such that implications between properties are explicitly encoded, and such that implied properties are no longer listed as invariants. See \cite{Ernst2001} for ideas. Solution. Left to the reader. Exercise 6: Local VariablesPostconditions may also refer to the values of local variables. Consider extending `InvariantAnnotator` and its infrastructure such that the values of local variables at the end of the execution are also recorded and made part of the invariant inference mechanism. Solution. Left to the reader. Exercise 7: Embedding Invariants as AssertionsRather than producing invariants as annotations for pre- and postconditions, insert them as `assert` statements into the function code, as in:```pythondef square_root(x): 'Computes the square root of x, using the Newton-Raphson method' assert isinstance(x, int), 'violated precondition' assert x > 0, 'violated precondition' approx = None guess = (x / 2) while (approx != guess): approx = guess guess = ((approx + (x / approx)) / 2) return_value = approx assert return_value < x, 'violated postcondition' assert isinstance(return_value, float), 'violated postcondition' return approx```Such a formulation may make it easier for test generators and symbolic analysis to access and interpret pre- and postconditions. Solution. Here is a tentative implementation that inserts invariants into function ASTs. Part 1: Embedding Invariants into Functions ###Code class EmbeddedInvariantAnnotator(InvariantTracer): def function_with_invariants_ast(self, function_name: str) -> ast.AST: return annotate_function_with_invariants(function_name, self.invariants(function_name)) def function_with_invariants(self, function_name: str) -> str: return astor.to_source(self.function_with_invariants_ast(function_name)) def annotate_invariants(invariants: Dict[str, Invariants]) -> Dict[str, ast.AST]: annotated_functions = {} for function_name in invariants: try: annotated_functions[function_name] = annotate_function_with_invariants(function_name, invariants[function_name]) except KeyError: continue return annotated_functions def annotate_function_with_invariants(function_name: str, function_invariants: Invariants) -> ast.AST: function = globals()[function_name] function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_invariants(function_ast, function_invariants) def annotate_function_ast_with_invariants(function_ast: ast.AST, function_invariants: Invariants) -> ast.AST: annotated_function_ast = EmbeddedInvariantTransformer(function_invariants).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Part 2: Preconditions ###Code class PreconditionTransformer(ast.NodeTransformer): def __init__(self, invariants: Invariants) -> None: self.invariants = invariants super().__init__() def preconditions(self) -> List[ast.stmt]: preconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated precondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) < 0: preconditions += assertion_ast.body return preconditions def insert_assertions(self, body: List[ast.stmt]) -> List[ast.stmt]: preconditions = self.preconditions() try: docstring = cast(ast.Constant, body[0]).value.s except: docstring = None if docstring: return [body[0]] + preconditions + body[1:] else: return preconditions + body def visit_FunctionDef(self, node: ast.FunctionDef) -> ast.FunctionDef: """Add invariants to function""" # print(ast.dump(node)) node.body = self.insert_assertions(node.body) return node class EmbeddedInvariantTransformer(PreconditionTransformer): pass with EmbeddedInvariantAnnotator() as annotator: square_root(5) print_content(annotator.function_with_invariants('square_root'), '.py') with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.function_with_invariants('sum3'), '.py') ###Output _____no_output_____ ###Markdown Part 3: PostconditionsWe make a few simplifying assumptions: * Variables do not change during execution.* There is a single `return` statement at the end of the function. ###Code class EmbeddedInvariantTransformer(EmbeddedInvariantTransformer): def postconditions(self) -> List[ast.stmt]: postconditions = [] for (prop, var_names) in self.invariants: assertion = ("assert " + instantiate_prop(prop, var_names) + ', "violated postcondition"') assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) >= 0: postconditions += assertion_ast.body return postconditions def insert_assertions(self, body: List[ast.stmt]) -> List[ast.stmt]: new_body = super().insert_assertions(body) postconditions = self.postconditions() body_ends_with_return = isinstance(new_body[-1], ast.Return) if body_ends_with_return: ret_val = cast(ast.Return, new_body[-1]).value saver = RETURN_VALUE + " = " + astor.to_source(ret_val) else: saver = RETURN_VALUE + " = None" saver_ast = cast(ast.stmt, ast.parse(saver)) postconditions = [saver_ast] + postconditions if body_ends_with_return: return new_body[:-1] + postconditions + [new_body[-1]] else: return new_body + postconditions with EmbeddedInvariantAnnotator() as annotator: square_root(5) square_root_def = annotator.function_with_invariants('square_root') ###Output _____no_output_____ ###Markdown Here's the full definition with included assertions: ###Code print_content(square_root_def, '.py') exec(square_root_def.replace('square_root', 'square_root_annotated')) with ExpectError(): square_root_annotated(-1) ###Output _____no_output_____ ###Markdown Here come some more examples: ###Code with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.function_with_invariants('sum3'), '.py') with EmbeddedInvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.function_with_invariants('list_length'), '.py') with EmbeddedInvariantAnnotator() as annotator: print_sum(31, 45) print_content(annotator.function_with_invariants('print_sum'), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: Annotating Functions with Mined Types Let us now annotate functions with types mined at runtime. We start with a simple function `type_string()` that determines the appropriate type of a given value (as a string): ###Code def type_string(value: Any) -> str: return type(value).__name__ type_string(4) type_string([]) ###Output _____no_output_____ ###Markdown For composite structures, `type_string()` does not examine element types; hence, the type of `[3]` is simply `list` instead of, say, `list[int]`. For now, `list` will do fine. ###Code type_string([3]) ###Output _____no_output_____ ###Markdown `type_string()` will be used to infer the types of argument values found at runtime, as returned by `CallTracer.all_calls()`: ###Code with CallTracer() as tracer: y = square_root(25.0) y = square_root(2.0) tracer.all_calls() ###Output _____no_output_____ ###Markdown The function `annotate_types()` takes such a list of calls and annotates each function listed: ###Code def annotate_types(calls: Dict[str, List[Tuple[Arguments, Any]]]) -> Dict[str, ast.AST]: annotated_functions = {} for function_name in calls: try: annotated_functions[function_name] = \ annotate_function_with_types(function_name, calls[function_name]) except KeyError: continue return annotated_functions ###Output _____no_output_____ ###Markdown For each function, we get the source and its AST and then get to the actual annotation in `annotate_function_ast_with_types()`: ###Code def annotate_function_with_types(function_name: str, function_calls: List[Tuple[Arguments, Any]]) -> ast.AST: function = globals()[function_name] # May raise KeyError for internal functions function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_types(function_ast, function_calls) ###Output _____no_output_____ ###Markdown The function `annotate_function_ast_with_types()` invokes the `TypeTransformer` with the calls seen, and for each call, iterate over the arguments, determine their types, and annotate the AST with these. The universal type `Any` is used when we encounter type conflicts, which we will discuss below. ###Code def annotate_function_ast_with_types(function_ast: ast.AST, function_calls: List[Tuple[Arguments, Any]]) -> ast.AST: parameter_types: Dict[str, str] = {} return_type = None for calls_seen in function_calls: args, return_value = calls_seen if return_value: if return_type and return_type != type_string(return_value): return_type = 'Any' else: return_type = type_string(return_value) for parameter, value in args: try: different_type = (parameter_types[parameter] != type_string(value)) except KeyError: different_type = False if different_type: parameter_types[parameter] = 'Any' else: parameter_types[parameter] = type_string(value) annotated_function_ast = \ TypeTransformer(parameter_types, return_type).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Here is `square_root()` annotated with the types recorded usign the tracer, above. ###Code print_content(ast.unparse(annotate_types(tracer.all_calls())['square_root']), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: A Type Annotator Class Let us bring all of this together in a single class `TypeAnnotator` that first tracks calls of functions and then allows to access the AST (and the source code form) of the tracked functions annotated with types. The method `typed_functions()` returns the annotated functions as a string; `typed_functions_ast()` returns their AST. ###Code class TypeTracer(CallTracer): pass class TypeAnnotator(TypeTracer): def typed_functions_ast(self) -> Dict[str, ast.AST]: return annotate_types(self.all_calls()) def typed_function_ast(self, function_name: str) -> ast.AST: return annotate_function_with_types(function_name, self.calls(function_name)) def typed_functions(self) -> str: functions = '' for f_name in self.all_calls(): try: f_text = ast.unparse(self.typed_function_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions def typed_function(self, function_name: str) -> str: return ast.unparse(self.typed_function_ast(function_name)) ###Output _____no_output_____ ###Markdown End of Excursion Here is how to use `TypeAnnotator`. We first track a series of calls: ###Code with TypeAnnotator() as annotator: y = square_root(25.0) y = square_root(2.0) ###Output _____no_output_____ ###Markdown After tracking, we can immediately retrieve an annotated version of the functions tracked: ###Code print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown This also works for multiple and diverse functions. One could go and implement an automatic type annotator for Python files based on the types seen during execution. ###Code with TypeAnnotator() as annotator: hello('type annotations') y = square_root(1.0) print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown A content as above could now be sent to a type checker, which would detect any type inconsistency between callers and callees. Excursion: Handling Multiple TypesLet us now resolve the role of the magic `Any` type in `annotate_function_ast_with_types()`. If we see multiple types for the same argument, we set its type to `Any`. For `square_root()`, this makes sense, as its arguments can be integers as well as floats: ###Code with CallTracer() as tracer: y = square_root(25.0) y = square_root(4) annotated_square_root_ast = annotate_types(tracer.all_calls())['square_root'] print_content(ast.unparse(annotated_square_root_ast), '.py') ###Output _____no_output_____ ###Markdown The following function `sum3()` can be called with floating-point numbers as arguments, resulting in the parameters getting a `float` type: ###Code def sum3(a, b, c): # type: ignore return a + b + c with TypeAnnotator() as annotator: y = sum3(1.0, 2.0, 3.0) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we call `sum3()` with integers, though, the arguments get an `int` type: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown And we can also call `sum3()` with strings, which assigns the arguments a `str` type: ###Code with TypeAnnotator() as annotator: y = sum3("one", "two", "three") y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we have multiple calls, but with different types, `TypeAnnotator()` will assign an `Any` type to both arguments and return values: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y = sum3("one", "two", "three") typed_sum3_def = annotator.typed_function('sum3') print_content(typed_sum3_def, '.py') ###Output _____no_output_____ ###Markdown A type `Any` makes it explicit that an object can, indeed, have any type; it will not be typechecked at runtime or statically. To some extent, this defeats the power of type checking; but it also preserves some of the type flexibility that many Python programmers enjoy. Besides `Any`, the `typing` module supports several additional ways to define ambiguous types; we will keep this in mind for a later exercise. End of Excursion Mining InvariantsBesides basic data types. we can check several further properties from arguments. We can, for instance, whether an argument can be negative, zero, or positive; or that one argument should be smaller than the second; or that the result should be the sum of two arguments – properties that cannot be expressed in a (Python) type.Such properties are called invariants, as they hold across all invocations of a function. Specifically, invariants come as _pre_- and _postconditions_ – conditions that always hold at the beginning and at the end of a function. (There are also _data_ and _object_ invariants that express always-holding properties over the state of data or objects, but we do not consider these in this book.) Annotating Functions with Pre- and PostconditionsThe classical means to specify pre- and postconditions is via _assertions_, which we have introduced in the [chapter on assertions](Assertions.ipynb). A precondition checks whether the arguments to a function satisfy the expected properties; a postcondition does the same for the result. We can express and check both using assertions as follows: ###Code def square_root_with_invariants(x): # type: ignore assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown A nicer way, however, is to syntactically separate invariants from the function at hand. Using appropriate decorators, we could specify pre- and postconditions as follows:```python@precondition lambda x: x >= 0@postcondition lambda return_value, x: return_value * return_value == xdef square_root_with_invariants(x): normal code without assertions ...```The decorators `@precondition` and `@postcondition` would run the given functions (specified as anonymous `lambda` functions) before and after the decorated function, respectively. If the functions return `False`, the condition is violated. `@precondition` gets the function arguments as arguments; `@postcondition` additionally gets the return value as first argument. It turns out that implementing such decorators is not hard at all. Our implementation builds on a [code snippet from StackOverflow](https://stackoverflow.com/questions/12151182/python-precondition-postcondition-for-member-function-how): ###Code import functools def condition(precondition: Optional[Callable] = None, postcondition: Optional[Callable] = None) -> Callable: def decorator(func: Callable) -> Callable: @functools.wraps(func) # preserves name, docstring, etc def wrapper(args: Any, kwargs: Any) -> Any: if precondition is not None: assert precondition(args, *kwargs), \ "Precondition violated" # Call original function or method retval = func(args, *kwargs) if postcondition is not None: assert postcondition(retval, args, *kwargs), \ "Postcondition violated" return retval return wrapper return decorator def precondition(check: Callable) -> Callable: return condition(precondition=check) def postcondition(check: Callable) -> Callable: return condition(postcondition=check) ###Output _____no_output_____ ###Markdown With these, we can now start decorating `square_root()`: ###Code @precondition(lambda x: x > 0) def square_root_with_precondition(x): # type: ignore return square_root(x) ###Output _____no_output_____ ###Markdown This catches arguments violating the precondition: ###Code with ExpectError(): square_root_with_precondition(-1.0) ###Output _____no_output_____ ###Markdown Likewise, we can provide a postcondition: ###Code import math @postcondition(lambda ret, x: math.isclose(ret ret, x)) def square_root_with_postcondition(x): # type: ignore return square_root(x) y = square_root_with_postcondition(2.0) y ###Output _____no_output_____ ###Markdown If we have a buggy implementation of $\sqrt{x}$, this gets caught quickly: ###Code @postcondition(lambda ret, x: math.isclose(ret * ret, x)) def buggy_square_root_with_postcondition(x): # type: ignore return square_root(x) + 0.1 with ExpectError(): y = buggy_square_root_with_postcondition(2.0) ###Output _____no_output_____ ###Markdown While checking pre- and postconditions is a great way to catch errors, specifying them can be cumbersome. Let us try to see whether we can (again) _mine_ some of them. Mining InvariantsTo _mine_ invariants, we can use the same tracking functionality as before; instead of saving values for individual variables, though, we now check whether the values satisfy specific _properties_ or not. For instance, if all values of `x` seen satisfy the condition `x > 0`, then we make `x > 0` an invariant of the function. If we see positive, zero, and negative values of `x`, though, then there is no property of `x` left to talk about.The general idea is thus:1. Check all variable values observed against a set of predefined properties; and2. Keep only those properties that hold for all runs observed. Defining PropertiesWhat precisely do we mean by properties? Here is a small collection of value properties that would frequently be used in invariants. All these properties would be evaluated with the _metavariables_ `X`, `Y`, and `Z` (actually, any upper-case identifier) being replaced with the names of function parameters: ###Code INVARIANT_PROPERTIES = [ "X < 0", "X <= 0", "X > 0", "X >= 0", # "X == 0", # implied by "X", below # "X != 0", # implied by "not X", below ] ###Output _____no_output_____ ###Markdown When `square_root(x)` is called as, say `square_root(5.0)`, we see that `x = 5.0` holds. The above properties would then all be checked for `x`. Only the properties `X > 0`, `X >= 0`, and `not X` hold for the call seen; and hence `x > 0`, `x >= 0`, and `not x` (or better: `x != 0`) would make potential preconditions for `square_root(x)`. We can check for many more properties such as relations between two arguments: ###Code INVARIANT_PROPERTIES += [ "X == Y", "X > Y", "X < Y", "X >= Y", "X <= Y", ] ###Output _____no_output_____ ###Markdown Types also can be checked using properties. For any function parameter `X`, only one of these will hold: ###Code INVARIANT_PROPERTIES += [ "isinstance(X, bool)", "isinstance(X, int)", "isinstance(X, float)", "isinstance(X, list)", "isinstance(X, dict)", ] ###Output _____no_output_____ ###Markdown We can check for arithmetic properties: ###Code INVARIANT_PROPERTIES += [ "X == Y + Z", "X == Y * Z", "X == Y - Z", "X == Y / Z", ] ###Output _____no_output_____ ###Markdown Here's relations over three values, a Python special: ###Code INVARIANT_PROPERTIES += [ "X < Y < Z", "X <= Y <= Z", "X > Y > Z", "X >= Y >= Z", ] ###Output _____no_output_____ ###Markdown These Boolean properties also check for other types, as in Python, `None`, an empty list, an empty set, an empty string, and the value zero all evaluate to `False`. ###Code INVARIANT_PROPERTIES += [ "X", "not X" ] ###Output _____no_output_____ ###Markdown Finally, we can also check for list or string properties. Again, this is just a tiny selection. ###Code INVARIANT_PROPERTIES += [ "X == len(Y)", "X == sum(Y)", "X in Y", "X.startswith(Y)", "X.endswith(Y)", ] ###Output _____no_output_____ ###Markdown Extracting Meta-VariablesLet us first introduce a few _helper functions_ before we can get to the actual mining. `metavars()` extracts the set of meta-variables (`X`, `Y`, `Z`, etc.) from a property. To this end, we parse the property as a Python expression and then visit the identifiers. ###Code def metavars(prop: str) -> List[str]: metavar_list = [] class ArgVisitor(ast.NodeVisitor): def visit_Name(self, node: ast.Name) -> None: if node.id.isupper(): metavar_list.append(node.id) ArgVisitor().visit(ast.parse(prop)) return metavar_list assert metavars("X < 0") == ['X'] assert metavars("X.startswith(Y)") == ['X', 'Y'] assert metavars("isinstance(X, str)") == ['X'] ###Output _____no_output_____ ###Markdown Instantiating PropertiesTo produce a property as invariant, we need to be able to _instantiate_ it with variable names. The instantiation of `X > 0` with `X` being instantiated to `a`, for instance, gets us `a > 0`. To this end, the function `instantiate_prop()` takes a property and a collection of variable names and instantiates the meta-variables left-to-right with the corresponding variables names in the collection. ###Code def instantiate_prop_ast(prop: str, var_names: Sequence[str]) -> ast.AST: class NameTransformer(ast.NodeTransformer): def visit_Name(self, node: ast.Name) -> ast.Name: if node.id not in mapping: return node return ast.Name(id=mapping[node.id], ctx=ast.Load()) meta_variables = metavars(prop) assert len(meta_variables) == len(var_names) mapping = {} for i in range(0, len(meta_variables)): mapping[meta_variables[i]] = var_names[i] prop_ast = ast.parse(prop, mode='eval') new_ast = NameTransformer().visit(prop_ast) return new_ast def instantiate_prop(prop: str, var_names: Sequence[str]) -> str: prop_ast = instantiate_prop_ast(prop, var_names) prop_text = ast.unparse(prop_ast).strip() while prop_text.startswith('(') and prop_text.endswith(')'): prop_text = prop_text[1:-1] return prop_text assert instantiate_prop("X > Y", ['a', 'b']) == 'a > b' assert instantiate_prop("X.startswith(Y)", ['x', 'y']) == 'x.startswith(y)' ###Output _____no_output_____ ###Markdown Evaluating PropertiesTo actually _evaluate_ properties, we do not need to instantiate them. Instead, we simply convert them into a boolean function, using `lambda`: ###Code def prop_function_text(prop: str) -> str: return "lambda " + ", ".join(metavars(prop)) + ": " + prop ###Output _____no_output_____ ###Markdown Here is a simple example: ###Code prop_function_text("X > Y") ###Output _____no_output_____ ###Markdown We can easily evaluate the function: ###Code def prop_function(prop: str) -> Callable: return eval(prop_function_text(prop)) ###Output _____no_output_____ ###Markdown Here is an example: ###Code p = prop_function("X > Y") quiz("What is p(100, 1)?", [ "False", "True" ], 'p(100, 1) + 1', globals()) p(100, 1) p(1, 100) ###Output _____no_output_____ ###Markdown Checking InvariantsTo extract invariants from an execution, we need to check them on all possible instantiations of arguments. If the function to be checked has two arguments `a` and `b`, we instantiate the property `X < Y` both as `a < b` and `b < a` and check each of them. To get all combinations, we use the Python `permutations()` function: ###Code import itertools for combination in itertools.permutations([1.0, 2.0, 3.0], 2): print(combination) ###Output _____no_output_____ ###Markdown The function `true_property_instantiations()` takes a property and a list of tuples (`var_name`, `value`). It then produces all instantiations of the property with the given values and returns those that evaluate to True. ###Code Invariants = Set[Tuple[str, Tuple[str, ...]]] def true_property_instantiations(prop: str, vars_and_values: Arguments, log: bool = False) -> Invariants: instantiations = set() p = prop_function(prop) len_metavars = len(metavars(prop)) for combination in itertools.permutations(vars_and_values, len_metavars): args = [value for var_name, value in combination] var_names = [var_name for var_name, value in combination] try: result = p(args) except: result = None if log: print(prop, combination, result) if result: instantiations.add((prop, tuple(var_names))) return instantiations ###Output _____no_output_____ ###Markdown Here is an example. If `x == -1` and `y == 1`, the property `X < Y` holds for `x < y`, but not for `y < x`: ###Code invs = true_property_instantiations("X < Y", [('x', -1), ('y', 1)], log=True) invs ###Output _____no_output_____ ###Markdown The instantiation retrieves the short form: ###Code for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Likewise, with values for `x` and `y` as above, the property `X < 0` only holds for `x`, but not for `y`: ###Code invs = true_property_instantiations("X < 0", [('x', -1), ('y', 1)], log=True) for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Extracting InvariantsLet us now run the above invariant extraction on function arguments and return values as observed during a function execution. To this end, we extend the `CallTracer` class into an `InvariantTracer` class, which automatically computes invariants for all functions and all calls observed during tracking. By default, an `InvariantTracer` uses the `INVARIANT_PROPERTIES` properties as defined above; however, one can specify alternate sets of properties. ###Code class InvariantTracer(CallTracer): def __init__(self, props: Optional[List[str]] = None, kwargs: Any) -> None: if props is None: props = INVARIANT_PROPERTIES self.props = props super().__init__(kwargs) ###Output _____no_output_____ ###Markdown The key method of the `InvariantTracer` is the `invariants()` method. This iterates over the calls observed and checks which properties hold. Only the intersection of properties – that is, the set of properties that hold for all calls – is preserved, and eventually returned. The special variable `return_value` is set to hold the return value. ###Code RETURN_VALUE = 'return_value' class InvariantTracer(InvariantTracer): def all_invariants(self) -> Dict[str, Invariants]: return {function_name: self.invariants(function_name) for function_name in self.all_calls()} def invariants(self, function_name: str) -> Invariants: invariants = None for variables, return_value in self.calls(function_name): vars_and_values = variables + [(RETURN_VALUE, return_value)] s = set() for prop in self.props: s \|= true_property_instantiations(prop, vars_and_values, self._log) if invariants is None: invariants = s else: invariants &= s assert invariants is not None return invariants ###Output _____no_output_____ ###Markdown Here's an example of how to use `invariants()`. We run the tracer on a small set of calls. ###Code with InvariantTracer() as tracer: y = square_root(25.0) y = square_root(10.0) tracer.all_calls() ###Output _____no_output_____ ###Markdown The `invariants()` method produces a set of properties that hold for the observed runs, together with their instantiations over function arguments. ###Code invs = tracer.invariants('square_root') invs ###Output _____no_output_____ ###Markdown As before, the actual instantiations are easier to read: ###Code def pretty_invariants(invariants: Invariants) -> List[str]: props = [] for (prop, var_names) in invariants: props.append(instantiate_prop(prop, var_names)) return sorted(props) pretty_invariants(invs) ###Output _____no_output_____ ###Markdown We see that the both `x` and the return value have a `float` type. We also see that both are always greater than zero. These are properties that may make useful pre- and postconditions, notably for symbolic analysis. However, there's also an invariant which does _not_ universally hold, namely `return_value <= x`, as the following example shows: ###Code square_root(0.01) ###Output _____no_output_____ ###Markdown Clearly, 0.1 > 0.01 holds. This is a case of us not learning from sufficiently diverse inputs. As soon as we have a call including `x = 0.1`, though, the invariant `return_value <= x` is eliminated: ###Code with InvariantTracer() as tracer: y = square_root(25.0) y = square_root(10.0) y = square_root(0.01) pretty_invariants(tracer.invariants('square_root')) ###Output _____no_output_____ ###Markdown We will discuss later how to ensure sufficient diversity in inputs. (Hint: This involves test generation.) Let us try out our invariant tracer on `sum3()`. We see that all types are well-defined; the properties that all arguments are non-zero, however, is specific to the calls observed. ###Code with InvariantTracer() as tracer: y = sum3(1, 2, 3) y = sum3(-4, -5, -6) pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with strings instead, we get different invariants. Notably, we obtain the postcondition that the returned string always starts with the string in the first argument `a` – a universal postcondition if strings are used. ###Code with InvariantTracer() as tracer: y = sum3('a', 'b', 'c') y = sum3('f', 'e', 'd') pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with both strings and numbers (and zeros, too), there are no properties left that would hold across all calls. That's the price of flexibility. ###Code with InvariantTracer() as tracer: y = sum3('a', 'b', 'c') y = sum3('c', 'b', 'a') y = sum3(-4, -5, -6) y = sum3(0, 0, 0) pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown Converting Mined Invariants to AnnotationsAs with types, above, we would like to have some functionality where we can add the mined invariants as annotations to existing functions. To this end, we introduce the `InvariantAnnotator` class, extending `InvariantTracer`. We start with a helper method. `params()` returns a comma-separated list of parameter names as observed during calls. ###Code class InvariantAnnotator(InvariantTracer): def params(self, function_name: str) -> str: arguments, return_value = self.calls(function_name)[0] return ", ".join(arg_name for (arg_name, arg_value) in arguments) with InvariantAnnotator() as annotator: y = square_root(25.0) y = sum3(1, 2, 3) annotator.params('square_root') annotator.params('sum3') ###Output _____no_output_____ ###Markdown Now for the actual annotation. `preconditions()` returns the preconditions from the mined invariants (i.e., those propertes that do not depend on the return value) as a string with annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = ("@precondition(lambda " + self.params(function_name) + ": " + inv + ")") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) annotator.preconditions('square_root') ###Output _____no_output_____ ###Markdown `postconditions()` does the same for postconditions: ###Code class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = (f"@postcondition(lambda {RETURN_VALUE}," f" {self.params(function_name)}: {inv})") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) annotator.postconditions('square_root') ###Output _____no_output_____ ###Markdown With these, we can take a function and add both pre- and postconditions as annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def functions_with_invariants(self) -> str: functions = "" for function_name in self.all_invariants(): try: function = self.function_with_invariants(function_name) except KeyError: continue functions += function return functions def function_with_invariants(self, function_name: str) -> str: function = globals()[function_name] # Can throw KeyError source = inspect.getsource(function) return '\n'.join(self.preconditions(function_name) + self.postconditions(function_name)) + \ '\n' + source ###Output _____no_output_____ ###Markdown Here comes `function_with_invariants()` in all its glory: ###Code with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) print_content(annotator.function_with_invariants('square_root'), '.py') ###Output _____no_output_____ ###Markdown Quite a number of invariants, isn't it? Further below (and in the exercises), we will discuss on how to focus on the most relevant properties. Avoiding OverspecializationMined specifications can only be as good as the executions they were mined from. If we only see a single call, for instance, we will be faced with several mined pre- and postconditions that _overspecialize_ towards the values seen. Let us illustrate this effect on a simple `sum2()` function which adds two numbers. ###Code def sum2(a, b): # type: ignore return a + b ###Output _____no_output_____ ###Markdown If we invoke `sum2()` with a variety of arguments, the invariants all capture the relationship between `a`, `b`, and the return value as `return_value == a + b` in all its variations. ###Code with InvariantAnnotator() as annotator: sum2(31, 45) sum2(0, 0) sum2(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown If, however, we see only a single call, the invariants will overspecialize to the single call seen: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown The mined precondition `a == b`, for instance, only holds for the single call observed; the same holds for the mined postcondition `return_value == a b`. Yet, `sum2()` can obviously be successfully called with other values that do not satisfy these conditions. To get out of this trap, we have to _learn from more and more diverse runs_. One way to obtain such runs is by _generating_ inputs. Indeed, a simple test generator for calls of `sum2()` will easily resolve the problem. ###Code import random with InvariantAnnotator() as annotator: for i in range(100): a = random.randrange(-10, +10) b = random.randrange(-10, +10) length = sum2(a, b) print_content(annotator.function_with_invariants('sum2'), '.py') ###Output _____no_output_____ ###Markdown Note, though, that an API test generator, such as above, will have to be set up such that it actually respects preconditions – in our case, we invoke `sum2()` with integers only, already assuming its precondition. In some way, one thus needs a specification (a model, a grammar) to mine another specification – a chicken-and-egg problem. However, there is one way out of this problem: If one can automatically generate tests at the system level, then one has an _infinite source of executions_ to learn invariants from. In each of these executions, all functions would be called with values that satisfy the (implicit) precondition, allowing us to mine invariants for these functions. This holds, because at the system level, invalid inputs must be rejected by the system in the first place. The meaningful precondition at the system level, ensuring that only valid inputs get through, thus gets broken down into a multitude of meaningful preconditions (and subsequent postconditions) at the function level. The big requirement for all this, though, is that one needs good test generators. This will be the subject of another book, namely [The Fuzzing Book](https://www.fuzzingbook.org/). Partial InvariantsFor debugging, it can be helpful to focus on invariants produced only by _failing_ runs, thus characterizing the _circumstances under which a function fails_. Let us illustrate this on an example. The `middle()` function from the [chapter on statistical debugging](StatisticalDebugger.ipynb) is supposed to return the middle of three integers `x`, `y`, and `z`. ###Code from StatisticalDebugger import middle # minor dependency with InvariantAnnotator() as annotator: for i in range(100): x = random.randrange(-10, +10) y = random.randrange(-10, +10) z = random.randrange(-10, +10) mid = middle(x, y, z) ###Output _____no_output_____ ###Markdown By default, our `InvariantAnnotator()` does not return any particular pre- or postcondition (other than the types observed). That is just fine, as the function indeed imposes no particular precondition; and the postcondition from `middle()` is not covered by the `InvariantAnnotator` patterns. ###Code print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Things get more interesting if we focus on a particular subset of runs only, though - say, a set of inputs where `middle()` fails. ###Code from StatisticalDebugger import MIDDLE_FAILING_TESTCASES # minor dependency with InvariantAnnotator() as annotator: for x, y, z in MIDDLE_FAILING_TESTCASES: mid = middle(x, y, z) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Now that's an intimidating set of pre- and postconditions. However, almost all of the preconditions are implied by the one precondition```python@precondition(lambda x, y, z: y < x < z, doc='y < x < z')```which characterizes the exact condition under which `middle()` fails (which also happens to be the condition under which the erroneous second `return y` is executed). By checking how _invariants for failing runs_ differ from _invariants for passing runs_, we can identify circumstances for function failures. ###Code quiz("Could `InvariantAnnotator` also determine a precondition " "that characterizes _passing_ runs?", [ "Yes", "No" ], 'int(math.exp(1))', globals()) ###Output _____no_output_____ ###Markdown Indeed, it cannot – the correct invariant for passing runs would be the _inverse_ of the invariant for failing runs, and `not A < B < C` is not part of our invariant library. We can easily test this: ###Code from StatisticalDebugger import MIDDLE_PASSING_TESTCASES # minor dependency with InvariantAnnotator() as annotator: for x, y, z in MIDDLE_PASSING_TESTCASES: mid = middle(x, y, z) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Some ExamplesLet us try out the `InvariantAnnotator` on a number of examples. Removing HTML MarkupRunning `InvariantAnnotator` on our ongoing example `remove_html_markup()` does not provide much, as our invariant properties are tailored towards numerical functions. ###Code from Intro_Debugging import remove_html_markup with InvariantAnnotator() as annotator: remove_html_markup("<foo>bar</foo>") remove_html_markup("bar") remove_html_markup('"bar"') print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown In the [chapter on DDSet](DDSetDebugger.ipynb), we will see how to express more complex properties for structured inputs. A Recursive FunctionHere's another example. `list_length()` recursively computes the length of a Python function. Let us see whether we can mine its invariants: ###Code def list_length(elems: List[Any]) -> int: if elems == []: length = 0 else: length = 1 + list_length(elems[1:]) return length with InvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Almost all these properties are relevant. Of course, the reason the invariants are so neat is that the return value is equal to `len(elems)` is that `X == len(Y)` is part of the list of properties to be checked. Sum of two NumbersThe next example is a very simple function: If we have a function without return value, the return value is `None` and we can only mine preconditions. (Well, we get a "postcondition" `not return_value` that the return value evaluates to False, which holds for `None`). ###Code def print_sum(a, b): # type: ignore print(a + b) with InvariantAnnotator() as annotator: print_sum(31, 45) print_sum(0, 0) print_sum(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Checking SpecificationsA function with invariants, as above, can be fed into the Python interpreter, such that all pre- and postconditions are checked. We create a function `square_root_annotated()` which includes all the invariants mined above. ###Code with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) square_root_def = annotator.functions_with_invariants() square_root_def = square_root_def.replace('square_root', 'square_root_annotated') print_content(square_root_def, '.py') exec(square_root_def) ###Output _____no_output_____ ###Markdown The "annotated" version checks against invalid arguments – or more precisely, against arguments with properties that have not been observed yet: ###Code with ExpectError(): square_root_annotated(-1.0) # type: ignore ###Output _____no_output_____ ###Markdown This is in contrast to the original version, which just hangs on negative values: ###Code with ExpectTimeout(1): square_root(-1.0) ###Output _____no_output_____ ###Markdown If we make changes to the function definition such that the properties of the return value change, such _regressions_ are caught as violations of the postconditions. Let us illustrate this by simply inverting the result, and return $-2$ as square root of 4. ###Code square_root_def = square_root_def.replace('square_root_annotated', 'square_root_negative') square_root_def = square_root_def.replace('return approx', 'return -approx') print_content(square_root_def, '.py') exec(square_root_def) ###Output _____no_output_____ ###Markdown Technically speaking, $-2$ _is_ a square root of 4, since $(-2)^2 = 4$ holds. Yet, such a change may be unexpected by callers of `square_root()`, and hence, this would be caught with the first call: ###Code with ExpectError(): square_root_negative(2.0) # type: ignore ###Output _____no_output_____ ###Markdown We see how pre- and postconditions, as well as types, can serve as oracles during testing. In particular, once we have mined them for a set of functions, we can check them again and again with test generators – especially after code changes. The more checks we have, and the more specific they are, the more likely it is we can detect unwanted effects of changes. SynopsisThis chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator: ###Code def sum2(a, b): # type: ignore return a + b with TypeAnnotator() as type_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution. ###Code print(type_annotator.typed_functions()) ###Output _____no_output_____ ###Markdown The invariant annotator works in a similar fashion: ###Code with InvariantAnnotator() as inv_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values. ###Code print(inv_annotator.functions_with_invariants()) ###Output _____no_output_____ ###Markdown Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs). The chapter gives details on how to customize the properties checked for. Lessons Learned* Type annotations and explicit invariants allow for _checking_ arguments and results for expected data types and other properties.* One can automatically _mine_ data types and invariants by observing arguments and results at runtime.* The quality of mined invariants depends on the diversity of values observed during executions; this variety can be increased by generating tests. Next StepsIn the next chapter, we will explore [abstracting failure conditions](DDSetDebugger.ipynb). BackgroundThe [DAIKON dynamic invariant detector](https://plse.cs.washington.edu/daikon/) can be considered the mother of function specification miners. Continuously maintained and extended for more than 20 years, it mines likely invariants in the style of this chapter for a variety of languages, including C, C++, C, Eiffel, F, Java, Perl, and Visual Basic. On top of the functionality discussed above, it holds a rich catalog of patterns for likely invariants, supports data invariants, can eliminate invariants that are implied by others, and determines statistical confidence to disregard unlikely invariants. The corresponding paper \cite{Ernst2001} is one of the seminal and most-cited papers of Software Engineering. A multitude of works have been published based on DAIKON and detecting invariants; see this [curated list](http://plse.cs.washington.edu/daikon/pubs/) for details. The interaction between test generators and invariant detection is already discussed in \cite{Ernst2001} (incidentally also using grammars). The Eclat tool \cite{Pacheco2005} is a model example of tight interaction between a unit-level test generator and DAIKON-style invariant mining, where the mined invariants are used to produce oracles and to systematically guide the test generator towards fault-revealing inputs. Mining specifications is not restricted to pre- and postconditions. The paper "Mining Specifications" \cite{Ammons2002} is another classic in the field, learning state protocols from executions. Grammar mining \cite{Gopinath2020} can also be seen as a specification mining approach, this time learning specifications for input formats. As it comes to adding type annotations to existing code, the blog post ["The state of type hints in Python"](https://www.bernat.tech/the-state-of-type-hints-in-python/) gives a great overview on how Python type hints can be used and checked. To add type annotations, there are two important tools available that also implement our above approach:* [MonkeyType](https://instagram-engineering.com/let-your-code-type-hint-itself-introducing-open-source-monkeytype-a855c7284881) implements the above approach of tracing executions and annotating Python 3 arguments, returns, and variables with type hints.* [PyAnnotate](https://github.com/dropbox/pyannotate) does a similar job, focusing on code in Python 2. It does not produce Python 3-style annotations, but instead produces annotations as comments that can be processed by static type checkers.These tools have been created by engineers at Facebook and Dropbox, respectively, assisting them in checking millions of lines of code for type issues. ExercisesOur code for mining types and invariants is in no way complete. There are dozens of ways to extend our implementations, some of which we discuss in exercises. Exercise 1: Union TypesThe Python `typing` module allows to express that an argument can have multiple types. For `square_root(x)`, this allows to express that `x` can be an `int` or a `float`: ###Code def square_root_with_union_type(x: Union[int, float]) -> float: # type: ignore ... ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it supports union types for arguments and return values. Use `Optional[X]` as a shorthand for `Union[X, None]`. Solution. Left to the reader. Hint: extend `type_string()`. Exercise 2: Types for Local VariablesIn Python, one cannot only annotate arguments with types, but actually also local and global variables – for instance, `approx` and `guess` in our `square_root()` implementation: ###Code def square_root_with_local_types(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" approx: Optional[float] = None guess: float = x / 2 while approx != guess: approx: float = guess # type: ignore guess: float = (approx + x / approx) / 2 # type: ignore return approx ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it also annotates local variables with types. Search the function AST for assignments, determine the type of the assigned value, and make it an annotation on the left hand side. Solution. Left to the reader. Exercise 3: Verbose Invariant CheckersOur implementation of invariant checkers does not make it clear for the user which pre-/postcondition failed. ###Code @precondition(lambda s: len(s) > 0) def remove_first_char(s: str) -> str: return s[1:] with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown The following implementation adds an optional `doc` keyword argument which is printed if the invariant is violated: ###Code def my_condition(precondition: Optional[Callable] = None, postcondition: Optional[Callable] = None, doc: str = 'Unknown') -> Callable: def decorator(func: Callable) -> Callable: @functools.wraps(func) # preserves name, docstring, etc def wrapper(args: Any, kwargs: Any) -> Any: if precondition is not None: assert precondition(args, *kwargs), "Precondition violated: " + doc retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, kwargs), "Postcondition violated: " + doc return retval return wrapper return decorator def my_precondition(check: Callable, kwargs: Any) -> Callable: return my_condition(precondition=check, doc=kwargs.get('doc', 'Unknown')) def my_postcondition(check: Callable, kwargs: Any) -> Callable: return my_condition(postcondition=check, doc=kwargs.get('doc', 'Unknown')) @my_precondition(lambda s: len(s) > 0, doc="len(s) > 0") # type: ignore def remove_first_char(s: str) -> str: return s[1:] remove_first_char('abc') with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown Extend `InvariantAnnotator` such that it includes the conditions in the generated pre- and postconditions. Solution.** Here's a simple solution: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@my_precondition(lambda " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")" conditions.append(cond) return conditions class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@my_postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")") conditions.append(cond) return conditions ###Output _____no_output_____ ###Markdown The resulting annotations are harder to read, but easier to diagnose: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown As an alternative, one may be able to use `inspect.getsource()` on the lambda expression or unparse it. This is left to the reader. Exercise 4: Save Initial ValuesIf the value of an argument changes during function execution, this can easily confuse our implementation: The values are tracked at the beginning of the function, but checked only when it returns. Extend the `InvariantAnnotator` and the infrastructure it uses such that* it saves argument values both at the beginning and at the end of a function invocation;* postconditions can be expressed over both _initial_ values of arguments as well as the _final_ values of arguments;* the mined postconditions refer to both these values as well. Solution. To be added. Exercise 5: ImplicationsSeveral mined invariant are actually _implied_ by others: If `x > 0` holds, then this implies `x >= 0` and `x != 0`. Extend the `InvariantAnnotator` such that implications between properties are explicitly encoded, and such that implied properties are no longer listed as invariants. See \cite{Ernst2001} for ideas. Solution. Left to the reader. Exercise 6: Local VariablesPostconditions may also refer to the values of local variables. Consider extending `InvariantAnnotator` and its infrastructure such that the values of local variables at the end of the execution are also recorded and made part of the invariant inference mechanism. Solution. Left to the reader. Exercise 7: Embedding Invariants as AssertionsRather than producing invariants as annotations for pre- and postconditions, insert them as `assert` statements into the function code, as in:```pythondef square_root(x): 'Computes the square root of x, using the Newton-Raphson method' assert isinstance(x, int), 'violated precondition' assert x > 0, 'violated precondition' approx = None guess = (x / 2) while (approx != guess): approx = guess guess = ((approx + (x / approx)) / 2) return_value = approx assert return_value < x, 'violated postcondition' assert isinstance(return_value, float), 'violated postcondition' return approx```Such a formulation may make it easier for test generators and symbolic analysis to access and interpret pre- and postconditions. Solution. Here is a tentative implementation that inserts invariants into function ASTs. Part 1: Embedding Invariants into Functions ###Code class EmbeddedInvariantAnnotator(InvariantTracer): def function_with_invariants_ast(self, function_name: str) -> ast.AST: return annotate_function_with_invariants(function_name, self.invariants(function_name)) def function_with_invariants(self, function_name: str) -> str: return ast.unparse(self.function_with_invariants_ast(function_name)) def annotate_invariants(invariants: Dict[str, Invariants]) -> Dict[str, ast.AST]: annotated_functions = {} for function_name in invariants: try: annotated_functions[function_name] = annotate_function_with_invariants(function_name, invariants[function_name]) except KeyError: continue return annotated_functions def annotate_function_with_invariants(function_name: str, function_invariants: Invariants) -> ast.AST: function = globals()[function_name] function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_invariants(function_ast, function_invariants) def annotate_function_ast_with_invariants(function_ast: ast.AST, function_invariants: Invariants) -> ast.AST: annotated_function_ast = EmbeddedInvariantTransformer(function_invariants).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Part 2: Preconditions ###Code class PreconditionTransformer(ast.NodeTransformer): def __init__(self, invariants: Invariants) -> None: self.invariants = invariants super().__init__() def preconditions(self) -> List[ast.stmt]: preconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated precondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) < 0: preconditions += assertion_ast.body return preconditions def insert_assertions(self, body: List[ast.stmt]) -> List[ast.stmt]: preconditions = self.preconditions() try: docstring = cast(ast.Constant, body[0]).value.s except: docstring = None if docstring: return [body[0]] + preconditions + body[1:] else: return preconditions + body def visit_FunctionDef(self, node: ast.FunctionDef) -> ast.FunctionDef: """Add invariants to function""" # print(ast.dump(node)) node.body = self.insert_assertions(node.body) return node class EmbeddedInvariantTransformer(PreconditionTransformer): pass with EmbeddedInvariantAnnotator() as annotator: square_root(5) print_content(annotator.function_with_invariants('square_root'), '.py') with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.function_with_invariants('sum3'), '.py') ###Output _____no_output_____ ###Markdown Part 3: PostconditionsWe make a few simplifying assumptions: * Variables do not change during execution.* There is a single `return` statement at the end of the function. ###Code class EmbeddedInvariantTransformer(EmbeddedInvariantTransformer): def postconditions(self) -> List[ast.stmt]: postconditions = [] for (prop, var_names) in self.invariants: assertion = ("assert " + instantiate_prop(prop, var_names) + ', "violated postcondition"') assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) >= 0: postconditions += assertion_ast.body return postconditions def insert_assertions(self, body: List[ast.stmt]) -> List[ast.stmt]: new_body = super().insert_assertions(body) postconditions = self.postconditions() body_ends_with_return = isinstance(new_body[-1], ast.Return) if body_ends_with_return: ret_val = cast(ast.Return, new_body[-1]).value saver = RETURN_VALUE + " = " + ast.unparse(cast(ast.AST, ret_val)) else: saver = RETURN_VALUE + " = None" saver_ast = cast(ast.stmt, ast.parse(saver)) postconditions = [saver_ast] + postconditions if body_ends_with_return: return new_body[:-1] + postconditions + [new_body[-1]] else: return new_body + postconditions with EmbeddedInvariantAnnotator() as annotator: square_root(5) square_root_def = annotator.function_with_invariants('square_root') ###Output _____no_output_____ ###Markdown Here's the full definition with included assertions: ###Code print_content(square_root_def, '.py') exec(square_root_def.replace('square_root', 'square_root_annotated')) with ExpectError(): square_root_annotated(-1) ###Output _____no_output_____ ###Markdown Here come some more examples: ###Code with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.function_with_invariants('sum3'), '.py') with EmbeddedInvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.function_with_invariants('list_length'), '.py') with EmbeddedInvariantAnnotator() as annotator: print_sum(31, 45) print_content(annotator.function_with_invariants('print_sum'), '.py') ###Output _____no_output_____ ###Markdown Mining Function SpecificationsWhen testing a program, one not only needs to cover its several behaviors; one also needs to _check_ whether the result is as expected. In this chapter, we introduce a technique that allows us to _mine_ function specifications from a set of given executions, resulting in abstract and formal _descriptions_ of what the function expects and what it delivers. These so-called _dynamic invariants_ produce pre- and post-conditions over function arguments and variables from a set of executions. They are useful in a variety of contexts:* Dynamic invariants provide important information for [symbolic fuzzing](SymbolicFuzzer.ipynb), such as types and ranges of function arguments.* Dynamic invariants provide pre- and postconditions for formal program proofs and verification.* Dynamic invariants provide a large number of assertions that can check whether function behavior has changed* Checks provided by dynamic invariants can be very useful as _oracles_ for checking the effects of generated testsTraditionally, dynamic invariants are dependent on the executions they are derived from. However, when paired with comprehensive test generators, they quickly become very precise, as we show in this chapter. Prerequisites* You should be familiar with tracing program executions, as in the [chapter on coverage](Coverage.ipynb).* Later in this section, we access the internal _abstract syntax tree_ representations of Python programs and transform them, as in the [chapter on information flow](InformationFlow.ipynb). ###Code import fuzzingbook_utils import Coverage import Intro_Testing ###Output _____no_output_____ ###Markdown SynopsisTo [use the code provided in this chapter](Importing.ipynb), write```python>>> from fuzzingbook.DynamicInvariants import ```and then make use of the following features.This chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator:```python>>> def sum2(a, b):>>> return a + b>>> with TypeAnnotator() as type_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution.```python>>> print(type_annotator.typed_functions())def sum2(a: int, b: int) ->int: return a + b```The invariant annotator works in a similar fashion:```python>>> with InvariantAnnotator() as inv_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values.```python>>> print(inv_annotator.functions_with_invariants())@precondition(lambda a, b: isinstance(a, int), doc='isinstance(a, int)')@precondition(lambda a, b: isinstance(b, int), doc='isinstance(b, int)')@postcondition(lambda return_value, a, b: a == return_value - b, doc='a == return_value - b')@postcondition(lambda return_value, a, b: b == return_value - a, doc='b == return_value - a')@postcondition(lambda return_value, a, b: isinstance(return_value, int), doc='isinstance(return_value, int)')@postcondition(lambda return_value, a, b: return_value == a + b, doc='return_value == a + b')@postcondition(lambda return_value, a, b: return_value == b + a, doc='return_value == b + a')def sum2(a, b): return a + b```Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs) as well as for all kinds of _symbolic code analyses_. The chapter gives details on how to customize the properties checked for. Specifications and AssertionsWhen implementing a function or program, one usually works against a _specification_ – a set of documented requirements to be satisfied by the code. Such specifications can come in natural language. A formal specification, however, allows the computer to check whether the specification is satisfied.In the [introduction to testing](Intro_Testing.ipynb), we have seen how _preconditions_ and _postconditions_ can describe what a function does. Consider the following (simple) square root function: ###Code def my_sqrt(x): assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown The assertion `assert p` checks the condition `p`; if it does not hold, execution is aborted. Here, the actual body is not yet written; we use the assertions as a specification of what `my_sqrt()` _expects_, and what it _delivers_.The topmost assertion is the _precondition_, stating the requirements on the function arguments. The assertion at the end is the _postcondition_, stating the properties of the function result (including its relationship with the original arguments). Using these pre- and postconditions as a specification, we can now go and implement a square root function that satisfies them. Once implemented, we can have the assertions check at runtime whether `my_sqrt()` works as expected; a [symbolic](SymbolicFuzzer.ipynb) or [concolic](ConcolicFuzzer.ipynb) test generator will even specifically try to find inputs where the assertions do _not_ hold. (An assertion can be seen as a conditional branch towards aborting the execution, and any technique that tries to cover all code branches will also try to invalidate as many assertions as possible.) However, not every piece of code is developed with explicit specifications in the first place; let alone does most code comes with formal pre- and post-conditions. (Just take a look at the chapters in this book.) This is a pity: As Ken Thompson famously said, "Without specifications, there are no bugs – only surprises". It is also a problem for testing, since, of course, testing needs some specification to test against. This raises the interesting question: Can we somehow _retrofit_ existing code with "specifications" that properly describe their behavior, allowing developers to simply _check_ them rather than having to write them from scratch? This is what we do in this chapter. Why Generic Error Checking is Not EnoughBefore we go into _mining_ specifications, let us first discuss why it could be useful to _have_ them. As a motivating example, consider the full implementation of `my_sqrt()` from the [introduction to testing](Intro_Testing.ipynb): ###Code import fuzzingbook_utils def my_sqrt(x): """Computes the square root of x, using the Newton-Raphson method""" approx = None guess = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown `my_sqrt()` does not come with any functionality that would check types or values. Hence, it is easy for callers to make mistakes when calling `my_sqrt()`: ###Code from ExpectError import ExpectError, ExpectTimeout with ExpectError(): my_sqrt("foo") with ExpectError(): x = my_sqrt(0.0) ###Output _____no_output_____ ###Markdown At least, the Python system catches these errors at runtime. The following call, however, simply lets the function enter an infinite loop: ###Code with ExpectTimeout(1): x = my_sqrt(-1.0) ###Output _____no_output_____ ###Markdown Our goal is to avoid such errors by _annotating_ functions with information that prevents errors like the above ones. The idea is to provide a _specification_ of expected properties – a specification that can then be checked at runtime or statically. \todo{Introduce the concept of contract.} Specifying and Checking Data TypesFor our Python code, one of the most important "specifications" we need is types. Python being a "dynamically" typed language means that all data types are determined at run time; the code itself does not explicitly state whether a variable is an integer, a string, an array, a dictionary – or whatever. As _writer_ of Python code, omitting explicit type declarations may save time (and allows for some fun hacks). It is not sure whether a lack of types helps in _reading_ and _understanding_ code for humans. For a _computer_ trying to analyze code, the lack of explicit types is detrimental. If, say, a constraint solver, sees `if x:` and cannot know whether `x` is supposed to be a number or a string, this introduces an _ambiguity_. Such ambiguities may multiply over the entire analysis in a combinatorial explosion – or in the analysis yielding an overly inaccurate result. Python 3.6 and later allows data types as _annotations_ to function arguments (actually, to all variables) and return values. We can, for instance, state that `my_sqrt()` is a function that accepts a floating-point value and returns one: ###Code def my_sqrt_with_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return my_sqrt(x) ###Output _____no_output_____ ###Markdown By default, such annotations are ignored by the Python interpreter. Therefore, one can still call `my_sqrt_typed()` with a string as an argument and get the exact same result as above. However, one can make use of special _typechecking_ modules that would check types – _dynamically_ at runtime or _statically_ by analyzing the code without having to execute it. Runtime Type CheckingThe Python `enforce` package provides a function decorator that automatically inserts type-checking code that is executed at runtime. Here is how to use it: ###Code import enforce @enforce.runtime_validation def my_sqrt_with_checked_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return my_sqrt(x) ###Output _____no_output_____ ###Markdown Now, invoking `my_sqrt_with_checked_type_annotations()` raises an exception when invoked with a type dfferent from the one declared: ###Code with ExpectError(): my_sqrt_with_checked_type_annotations(True) ###Output _____no_output_____ ###Markdown Note that this error is not caught by the "untyped" variant, where passing a boolean value happily returns $\sqrt{1}$ as result. ###Code my_sqrt(True) ###Output _____no_output_____ ###Markdown In Python (and other languages), the boolean values `True` and `False` can be implicitly converted to the integers 1 and 0; however, it is hard to think of a call to `sqrt()` where this would not be an error. Static Type CheckingType annotations can also be checked _statically_ – that is, without even running the code. Let us create a simple Python file consisting of the above `my_sqrt_typed()` definition and a bad invocation. ###Code import inspect import tempfile f = tempfile.NamedTemporaryFile(mode='w', suffix='.py') f.name f.write(inspect.getsource(my_sqrt)) f.write('\n') f.write(inspect.getsource(my_sqrt_with_type_annotations)) f.write('\n') f.write("print(my_sqrt_with_type_annotations('123'))\n") f.flush() ###Output _____no_output_____ ###Markdown These are the contents of our newly created Python file: ###Code from fuzzingbook_utils import print_file print_file(f.name) ###Output _____no_output_____ ###Markdown [Mypy](http://mypy-lang.org) is a type checker for Python programs. As it checks types statically, types induce no overhead at runtime; plus, a static check can be faster than a lengthy series of tests with runtime type checking enabled. Let us see what `mypy` produces on the above file: ###Code import subprocess result = subprocess.run(["mypy", "--strict", f.name], universal_newlines=True, stdout=subprocess.PIPE) del f # Delete temporary file print(result.stdout) ###Output _____no_output_____ ###Markdown We see that `mypy` complains about untyped function definitions such as `my_sqrt()`; most important, however, it finds that the call to `my_sqrt_with_type_annotations()` in the last line has the wrong type. With `mypy`, we can achieve the same type safety with Python as in statically typed languages – provided that we as programmers also produce the necessary type annotations. Is there a simple way to obtain these? Mining Type SpecificationsOur first task will be to mine type annotations (as part of the code) from _values_ we observe at run time. These type annotations would be _mined_ from actual function executions, _learning_ from (normal) runs what the expected argument and return types should be. By observing a series of calls such as these, we could infer that both `x` and the return value are of type `float`: ###Code y = my_sqrt(25.0) y y = my_sqrt(2.0) y ###Output _____no_output_____ ###Markdown How can we mine types from executions? The answer is simple: 1. We _observe_ a function during execution2. We track the _types_ of its arguments3. We include these types as _annotations_ into the code.To do so, we can make use of Python's tracing facility we already observed in the [chapter on coverage](Coverage.ipynb). With every call to a function, we retrieve the arguments, their values, and their types. Tracking CallsTo observe argument types at runtime, we define a _tracer function_ that tracks the execution of `my_sqrt()`, checking its arguments and return values. The `Tracker` class is set to trace functions in a `with` block as follows:```pythonwith Tracker() as tracker: function_to_be_tracked(...)info = tracker.collected_information()```As in the [chapter on coverage](Coverage.ipynb), we use the `sys.settrace()` function to trace individual functions during execution. We turn on tracking when the `with` block starts; at this point, the `__enter__()` method is called. When execution of the `with` block ends, `__exit()__` is called. ###Code import sys class Tracker(object): def __init__(self, log=False): self._log = log self.reset() def reset(self): self._calls = {} self._stack = [] def traceit(self): """Placeholder to be overloaded in subclasses""" pass # Start of `with` block def __enter__(self): self.original_trace_function = sys.gettrace() sys.settrace(self.traceit) return self # End of `with` block def __exit__(self, exc_type, exc_value, tb): sys.settrace(self.original_trace_function) ###Output _____no_output_____ ###Markdown The `traceit()` method does nothing yet; this is done in specialized subclasses. The `CallTracker` class implements a `traceit()` function that checks for function calls and returns: ###Code class CallTracker(Tracker): def traceit(self, frame, event, arg): """Tracking function: Record all calls and all args""" if event == "call": self.trace_call(frame, event, arg) elif event == "return": self.trace_return(frame, event, arg) return self.traceit ###Output _____no_output_____ ###Markdown `trace_call()` is called when a function is called; it retrieves the function name and current arguments, and saves them on a stack. ###Code class CallTracker(CallTracker): def trace_call(self, frame, event, arg): """Save current function name and args on the stack""" code = frame.f_code function_name = code.co_name arguments = get_arguments(frame) self._stack.append((function_name, arguments)) if self._log: print(simple_call_string(function_name, arguments)) def get_arguments(frame): """Return call arguments in the given frame""" # When called, all arguments are local variables arguments = [(var, frame.f_locals[var]) for var in frame.f_locals] arguments.reverse() # Want same order as call return arguments ###Output _____no_output_____ ###Markdown When the function returns, `trace_return()` is called. We now also have the return value. We log the whole call with arguments and return value (if desired) and save it in our list of calls. ###Code class CallTracker(CallTracker): def trace_return(self, frame, event, arg): """Get return value and store complete call with arguments and return value""" code = frame.f_code function_name = code.co_name return_value = arg # TODO: Could call get_arguments() here to also retrieve _final_ values of argument variables called_function_name, called_arguments = self._stack.pop() assert function_name == called_function_name if self._log: print(simple_call_string(function_name, called_arguments), "returns", return_value) self.add_call(function_name, called_arguments, return_value) ###Output _____no_output_____ ###Markdown `simple_call_string()` is a helper for logging that prints out calls in a user-friendly manner. ###Code def simple_call_string(function_name, argument_list, return_value=None): """Return function_name(arg[0], arg[1], ...) as a string""" call = function_name + "(" + \ ", ".join([var + "=" + repr(value) for (var, value) in argument_list]) + ")" if return_value is not None: call += " = " + repr(return_value) return call ###Output _____no_output_____ ###Markdown `add_call()` saves the calls in a list; each function name has its own list. ###Code class CallTracker(CallTracker): def add_call(self, function_name, arguments, return_value=None): """Add given call to list of calls""" if function_name not in self._calls: self._calls[function_name] = [] self._calls[function_name].append((arguments, return_value)) ###Output _____no_output_____ ###Markdown Using `calls()`, we can retrieve the list of calls, either for a given function, or for all functions. ###Code class CallTracker(CallTracker): def calls(self, function_name=None): """Return list of calls for function_name, or a mapping function_name -> calls for all functions tracked""" if function_name is None: return self._calls return self._calls[function_name] ###Output _____no_output_____ ###Markdown Let us now put this to use. We turn on logging to track the individual calls and their return values: ###Code with CallTracker(log=True) as tracker: y = my_sqrt(25) y = my_sqrt(2.0) ###Output _____no_output_____ ###Markdown After execution, we can retrieve the individual calls: ###Code calls = tracker.calls('my_sqrt') calls ###Output _____no_output_____ ###Markdown Each call is pair (`argument_list`, `return_value`), where `argument_list` is a list of pairs (`parameter_name`, `value`). ###Code my_sqrt_argument_list, my_sqrt_return_value = calls[0] simple_call_string('my_sqrt', my_sqrt_argument_list, my_sqrt_return_value) ###Output _____no_output_____ ###Markdown If the function does not return a value, `return_value` is `None`. ###Code def hello(name): print("Hello,", name) with CallTracker() as tracker: hello("world") hello_calls = tracker.calls('hello') hello_calls hello_argument_list, hello_return_value = hello_calls[0] simple_call_string('hello', hello_argument_list, hello_return_value) ###Output _____no_output_____ ###Markdown Getting TypesDespite what you may have read or heard, Python actually _is_ a typed language. It is just that it is _dynamically typed_ – types are used and checked only at runtime (rather than declared in the code, where they can be _statically checked_ at compile time). We can thus retrieve types of all values within Python: ###Code type(4) type(2.0) type([4]) ###Output _____no_output_____ ###Markdown We can retrieve the type of the first argument to `my_sqrt()`: ###Code parameter, value = my_sqrt_argument_list[0] parameter, type(value) ###Output _____no_output_____ ###Markdown as well as the type of the return value: ###Code type(my_sqrt_return_value) ###Output _____no_output_____ ###Markdown Hence, we see that (so far), `my_sqrt()` is a function taking (among others) integers and returning floats. We could declare `my_sqrt()` as: ###Code def my_sqrt_annotated(x: int) -> float: return my_sqrt(x) ###Output _____no_output_____ ###Markdown This is a representation we could place in a static type checker, allowing to check whether calls to `my_sqrt()` actually pass a number. A dynamic type checker could run such checks at runtime. And of course, any [symbolic interpretation](SymbolicFuzzer.ipynb) will greatly profit from the additional annotations. By default, Python does not do anything with such annotations. However, tools can access annotations from functions and other objects: ###Code my_sqrt_annotated.__annotations__ ###Output _____no_output_____ ###Markdown This is how run-time checkers access the annotations to check against. Accessing Function StructureOur plan is to annotate functions automatically, based on the types we have seen. To do so, we need a few modules that allow us to convert a function into a tree representation (called _abstract syntax trees_, or ASTs) and back; we already have seen these in the chapters on [concolic](ConcolicFuzzer.ipynb) and [symbolic](SymbolicFuzzer.ipynb) testing. ###Code import ast import inspect import astor ###Output _____no_output_____ ###Markdown We can get the source of a Python function using `inspect.getsource()`. (Note that this does not work for functions defined in other notebooks.) ###Code my_sqrt_source = inspect.getsource(my_sqrt) my_sqrt_source ###Output _____no_output_____ ###Markdown To view these in a visually pleasing form, our function `print_content(s, suffix)` formats and highlights the string `s` as if it were a file with ending `suffix`. We can thus view (and highlight) the source as if it were a Python file: ###Code from fuzzingbook_utils import print_content print_content(my_sqrt_source, '.py') ###Output _____no_output_____ ###Markdown Parsing this gives us an abstract syntax tree (AST) – a representation of the program in tree form. ###Code my_sqrt_ast = ast.parse(my_sqrt_source) ###Output _____no_output_____ ###Markdown What does this AST look like? The helper functions `astor.dump_tree()` (textual output) and `showast.show_ast()` (graphical output with [showast](https://github.com/hchasestevens/show_ast)) allow us to inspect the structure of the tree. We see that the function starts as a `FunctionDef` with name and arguments, followed by a body, which is a list of statements of type `Expr` (the docstring), type `Assign` (assignments), `While` (while loop with its own body), and finally `Return`. ###Code print(astor.dump_tree(my_sqrt_ast)) ###Output _____no_output_____ ###Markdown Too much text for you? This graphical representation may make things simpler. ###Code from fuzzingbook_utils import rich_output if rich_output(): import showast showast.show_ast(my_sqrt_ast) ###Output _____no_output_____ ###Markdown The function `astor.to_source()` converts such a tree back into the more familiar textual Python code representation. Comments are gone, and there may be more parentheses than before, but the result has the same semantics: ###Code print_content(astor.to_source(my_sqrt_ast), '.py') ###Output _____no_output_____ ###Markdown Annotating Functions with Given TypesLet us now go and transform these trees ti add type annotations. We start with a helper function `parse_type(name)` which parses a type name into an AST. ###Code def parse_type(name): class ValueVisitor(ast.NodeVisitor): def visit_Expr(self, node): self.value_node = node.value tree = ast.parse(name) name_visitor = ValueVisitor() name_visitor.visit(tree) return name_visitor.value_node print(astor.dump_tree(parse_type('int'))) print(astor.dump_tree(parse_type('[object]'))) ###Output _____no_output_____ ###Markdown We now define a helper function that actually adds type annotations to a function AST. The `TypeTransformer` class builds on the Python standard library `ast.NodeTransformer` infrastructure. It would be called as```python TypeTransformer({'x': 'int'}, 'float').visit(ast)```to annotate the arguments of `my_sqrt()`: `x` with `int`, and the return type with `float`. The returned AST can then be unparsed, compiled or analyzed. ###Code class TypeTransformer(ast.NodeTransformer): def __init__(self, argument_types, return_type=None): self.argument_types = argument_types self.return_type = return_type super().__init__() ###Output _____no_output_____ ###Markdown The core of `TypeTransformer` is the method `visit_FunctionDef()`, which is called for every function definition in the AST. Its argument `node` is the subtree of the function definition to be transformed. Our implementation accesses the individual arguments and invokes `annotate_args()` on them; it also sets the return type in the `returns` attribute of the node. ###Code class TypeTransformer(TypeTransformer): def visit_FunctionDef(self, node): """Add annotation to function""" # Set argument types new_args = [] for arg in node.args.args: new_args.append(self.annotate_arg(arg)) new_arguments = ast.arguments( new_args, node.args.vararg, node.args.kwonlyargs, node.args.kw_defaults, node.args.kwarg, node.args.defaults ) # Set return type if self.return_type is not None: node.returns = parse_type(self.return_type) return ast.copy_location(ast.FunctionDef(node.name, new_arguments, node.body, node.decorator_list, node.returns), node) ###Output _____no_output_____ ###Markdown Each argument gets its own annotation, taken from the types originally passed to the class: ###Code class TypeTransformer(TypeTransformer): def annotate_arg(self, arg): """Add annotation to single function argument""" arg_name = arg.arg if arg_name in self.argument_types: arg.annotation = parse_type(self.argument_types[arg_name]) return arg ###Output _____no_output_____ ###Markdown Does this work? Let us annotate the AST from `my_sqrt()` with types for the arguments and return types: ###Code new_ast = TypeTransformer({'x': 'int'}, 'float').visit(my_sqrt_ast) ###Output _____no_output_____ ###Markdown When we unparse the new AST, we see that the annotations actually are present: ###Code print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown Similarly, we can annotate the `hello()` function from above: ###Code hello_source = inspect.getsource(hello) hello_ast = ast.parse(hello_source) new_ast = TypeTransformer({'name': 'str'}, 'None').visit(hello_ast) print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown Annotating Functions with Mined TypesLet us now annotate functions with types mined at runtime. We start with a simple function `type_string()` that determines the appropriate type of a given value (as a string): ###Code def type_string(value): return type(value).__name__ type_string(4) type_string([]) ###Output _____no_output_____ ###Markdown For composite structures, `type_string()` does not examine element types; hence, the type of `[3]` is simply `list` instead of, say, `list[int]`. For now, `list` will do fine. ###Code type_string([3]) ###Output _____no_output_____ ###Markdown `type_string()` will be used to infer the types of argument values found at runtime, as returned by `CallTracker.calls()`: ###Code with CallTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(2.0) tracker.calls() ###Output _____no_output_____ ###Markdown The function `annotate_types()` takes such a list of calls and annotates each function listed: ###Code def annotate_types(calls): annotated_functions = {} for function_name in calls: try: annotated_functions[function_name] = annotate_function_with_types(function_name, calls[function_name]) except KeyError: continue return annotated_functions ###Output _____no_output_____ ###Markdown For each function, we get the source and its AST and then get to the actual annotation in `annotate_function_ast_with_types()`: ###Code def annotate_function_with_types(function_name, function_calls): function = globals()[function_name] # May raise KeyError for internal functions function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_types(function_ast, function_calls) ###Output _____no_output_____ ###Markdown The function `annotate_function_ast_with_types()` invokes the `TypeTransformer` with the calls seen, and for each call, iterate over the arguments, determine their types, and annotate the AST with these. The universal type `Any` is used when we encounter type conflicts, which we will discuss below. ###Code from typing import Any def annotate_function_ast_with_types(function_ast, function_calls): parameter_types = {} return_type = None for calls_seen in function_calls: args, return_value = calls_seen if return_value is not None: if return_type is not None and return_type != type_string(return_value): return_type = 'Any' else: return_type = type_string(return_value) for parameter, value in args: try: different_type = parameter_types[parameter] != type_string(value) except KeyError: different_type = False if different_type: parameter_types[parameter] = 'Any' else: parameter_types[parameter] = type_string(value) annotated_function_ast = TypeTransformer(parameter_types, return_type).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Here is `my_sqrt()` annotated with the types recorded usign the tracker, above. ###Code print_content(astor.to_source(annotate_types(tracker.calls())['my_sqrt']), '.py') ###Output _____no_output_____ ###Markdown All-in-one AnnotationLet us bring all of this together in a single class `TypeAnnotator` that first tracks calls of functions and then allows to access the AST (and the source code form) of the tracked functions annotated with types. The method `typed_functions()` returns the annotated functions as a string; `typed_functions_ast()` returns their AST. ###Code class TypeTracker(CallTracker): pass class TypeAnnotator(TypeTracker): def typed_functions_ast(self, function_name=None): if function_name is None: return annotate_types(self.calls()) return annotate_function_with_types(function_name, self.calls(function_name)) def typed_functions(self, function_name=None): if function_name is None: functions = '' for f_name in self.calls(): try: f_text = astor.to_source(self.typed_functions_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions return astor.to_source(self.typed_functions_ast(function_name)) ###Output _____no_output_____ ###Markdown Here is how to use `TypeAnnotator`. We first track a series of calls: ###Code with TypeAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(2.0) ###Output _____no_output_____ ###Markdown After tracking, we can immediately retrieve an annotated version of the functions tracked: ###Code print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown This also works for multiple and diverse functions. One could go and implement an automatic type annotator for Python files based on the types seen during execution. ###Code with TypeAnnotator() as annotator: hello('type annotations') y = my_sqrt(1.0) print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown A content as above could now be sent to a type checker, which would detect any type inconsistency between callers and callees. Likewise, type annotations such as the ones above greatly benefit symbolic code analysis (as in the chapter on [symbolic fuzzing](SymbolicFuzzer.ipynb)), as they effectively constrain the set of values that arguments and variables can take. Multiple TypesLet us now resolve the role of the magic `Any` type in `annotate_function_ast_with_types()`. If we see multiple types for the same argument, we set its type to `Any`. For `my_sqrt()`, this makes sense, as its arguments can be integers as well as floats: ###Code with CallTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(4) print_content(astor.to_source(annotate_types(tracker.calls())['my_sqrt']), '.py') ###Output _____no_output_____ ###Markdown The following function `sum3()` can be called with floating-point numbers as arguments, resulting in the parameters getting a `float` type: ###Code def sum3(a, b, c): return a + b + c with TypeAnnotator() as annotator: y = sum3(1.0, 2.0, 3.0) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we call `sum3()` with integers, though, the arguments get an `int` type: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown And we can also call `sum3()` with strings, giving the arguments a `str` type: ###Code with TypeAnnotator() as annotator: y = sum3("one", "two", "three") y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we have multiple calls, but with different types, `TypeAnnotator()` will assign an `Any` type to both arguments and return values: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y = sum3("one", "two", "three") typed_sum3_def = annotator.typed_functions('sum3') print_content(typed_sum3_def, '.py') ###Output _____no_output_____ ###Markdown A type `Any` makes it explicit that an object can, indeed, have any type; it will not be typechecked at runtime or statically. To some extent, this defeats the power of type checking; but it also preserves some of the type flexibility that many Python programmers enjoy. Besides `Any`, the `typing` module supports several additional ways to define ambiguous types; we will keep this in mind for a later exercise. Specifying and Checking InvariantsBesides basic data types. we can check several further properties from arguments. We can, for instance, whether an argument can be negative, zero, or positive; or that one argument should be smaller than the second; or that the result should be the sum of two arguments – properties that cannot be expressed in a (Python) type.Such properties are called invariants, as they hold across all invocations of a function. Specifically, invariants come as _pre_- and _postconditions_ – conditions that always hold at the beginning and at the end of a function. (There are also _data_ and _object_ invariants that express always-holding properties over the state of data or objects, but we do not consider these in this book.) Annotating Functions with Pre- and PostconditionsThe classical means to specify pre- and postconditions is via _assertions_, which we have introduced in the [chapter on testing](Intro_Testing.ipynb). A precondition checks whether the arguments to a function satisfy the expected properties; a postcondition does the same for the result. We can express and check both using assertions as follows: ###Code def my_sqrt_with_invariants(x): assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown A nicer way, however, is to syntactically separate invariants from the function at hand. Using appropriate decorators, we could specify pre- and postconditions as follows:```python@precondition lambda x: x >= 0@postcondition lambda return_value, x: return_value * return_value == xdef my_sqrt_with_invariants(x): normal code without assertions ...```The decorators `@precondition` and `@postcondition` would run the given functions (specified as anonymous `lambda` functions) before and after the decorated function, respectively. If the functions return `False`, the condition is violated. `@precondition` gets the function arguments as arguments; `@postcondition` additionally gets the return value as first argument. It turns out that implementing such decorators is not hard at all. Our implementation builds on a [code snippet from StackOverflow](https://stackoverflow.com/questions/12151182/python-precondition-postcondition-for-member-function-how): ###Code import functools def condition(precondition=None, postcondition=None): def decorator(func): @functools.wraps(func) # preserves name, docstring, etc def wrapper(args, kwargs): if precondition is not None: assert precondition(args, *kwargs), "Precondition violated" retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, *kwargs), "Postcondition violated" return retval return wrapper return decorator def precondition(check): return condition(precondition=check) def postcondition(check): return condition(postcondition=check) ###Output _____no_output_____ ###Markdown With these, we can now start decorating `my_sqrt()`: ###Code @precondition(lambda x: x > 0) def my_sqrt_with_precondition(x): return my_sqrt(x) ###Output _____no_output_____ ###Markdown This catches arguments violating the precondition: ###Code with ExpectError(): my_sqrt_with_precondition(-1.0) ###Output _____no_output_____ ###Markdown Likewise, we can provide a postcondition: ###Code EPSILON = 1e-5 @postcondition(lambda ret, x: ret ret - x < EPSILON) def my_sqrt_with_postcondition(x): return my_sqrt(x) y = my_sqrt_with_postcondition(2.0) y ###Output _____no_output_____ ###Markdown If we have a buggy implementation of $\sqrt{x}$, this gets caught quickly: ###Code @postcondition(lambda ret, x: ret * ret - x < EPSILON) def buggy_my_sqrt_with_postcondition(x): return my_sqrt(x) + 0.1 with ExpectError(): y = buggy_my_sqrt_with_postcondition(2.0) ###Output _____no_output_____ ###Markdown While checking pre- and postconditions is a great way to catch errors, specifying them can be cumbersome. Let us try to see whether we can (again) _mine_ some of them. Mining InvariantsTo _mine_ invariants, we can use the same tracking functionality as before; instead of saving values for individual variables, though, we now check whether the values satisfy specific _properties_ or not. For instance, if all values of `x` seen satisfy the condition `x > 0`, then we make `x > 0` an invariant of the function. If we see positive, zero, and negative values of `x`, though, then there is no property of `x` left to talk about.The general idea is thus:1. Check all variable values observed against a set of predefined properties; and2. Keep only those properties that hold for all runs observed. Defining PropertiesWhat precisely do we mean by properties? Here is a small collection of value properties that would frequently be used in invariants. All these properties would be evaluated with the _metavariables_ `X`, `Y`, and `Z` (actually, any upper-case identifier) being replaced with the names of function parameters: ###Code INVARIANT_PROPERTIES = [ "X < 0", "X <= 0", "X > 0", "X >= 0", "X == 0", "X != 0", ] ###Output _____no_output_____ ###Markdown When `my_sqrt(x)` is called as, say `my_sqrt(5.0)`, we see that `x = 5.0` holds. The above properties would then all be checked for `x`. Only the properties `X > 0`, `X >= 0`, and `X != 0` hold for the call seen; and hence `x > 0`, `x >= 0`, and `x != 0` would make potential preconditions for `my_sqrt(x)`. We can check for many more properties such as relations between two arguments: ###Code INVARIANT_PROPERTIES += [ "X == Y", "X > Y", "X < Y", "X >= Y", "X <= Y", ] ###Output _____no_output_____ ###Markdown Types also can be checked using properties. For any function parameter `X`, only one of these will hold: ###Code INVARIANT_PROPERTIES += [ "isinstance(X, bool)", "isinstance(X, int)", "isinstance(X, float)", "isinstance(X, list)", "isinstance(X, dict)", ] ###Output _____no_output_____ ###Markdown We can check for arithmetic properties: ###Code INVARIANT_PROPERTIES += [ "X == Y + Z", "X == Y * Z", "X == Y - Z", "X == Y / Z", ] ###Output _____no_output_____ ###Markdown Here's relations over three values, a Python special: ###Code INVARIANT_PROPERTIES += [ "X < Y < Z", "X <= Y <= Z", "X > Y > Z", "X >= Y >= Z", ] ###Output _____no_output_____ ###Markdown Finally, we can also check for list or string properties. Again, this is just a tiny selection. ###Code INVARIANT_PROPERTIES += [ "X == len(Y)", "X == sum(Y)", "X.startswith(Y)", ] ###Output _____no_output_____ ###Markdown Extracting Meta-VariablesLet us first introduce a few _helper functions_ before we can get to the actual mining. `metavars()` extracts the set of meta-variables (`X`, `Y`, `Z`, etc.) from a property. To this end, we parse the property as a Python expression and then visit the identifiers. ###Code def metavars(prop): metavar_list = [] class ArgVisitor(ast.NodeVisitor): def visit_Name(self, node): if node.id.isupper(): metavar_list.append(node.id) ArgVisitor().visit(ast.parse(prop)) return metavar_list assert metavars("X < 0") == ['X'] assert metavars("X.startswith(Y)") == ['X', 'Y'] assert metavars("isinstance(X, str)") == ['X'] ###Output _____no_output_____ ###Markdown Instantiating PropertiesTo produce a property as invariant, we need to be able to _instantiate_ it with variable names. The instantiation of `X > 0` with `X` being instantiated to `a`, for instance, gets us `a > 0`. To this end, the function `instantiate_prop()` takes a property and a collection of variable names and instantiates the meta-variables left-to-right with the corresponding variables names in the collection. ###Code def instantiate_prop_ast(prop, var_names): class NameTransformer(ast.NodeTransformer): def visit_Name(self, node): if node.id not in mapping: return node return ast.Name(id=mapping[node.id], ctx=ast.Load()) meta_variables = metavars(prop) assert len(meta_variables) == len(var_names) mapping = {} for i in range(0, len(meta_variables)): mapping[meta_variables[i]] = var_names[i] prop_ast = ast.parse(prop, mode='eval') new_ast = NameTransformer().visit(prop_ast) return new_ast def instantiate_prop(prop, var_names): prop_ast = instantiate_prop_ast(prop, var_names) prop_text = astor.to_source(prop_ast).strip() while prop_text.startswith('(') and prop_text.endswith(')'): prop_text = prop_text[1:-1] return prop_text assert instantiate_prop("X > Y", ['a', 'b']) == 'a > b' assert instantiate_prop("X.startswith(Y)", ['x', 'y']) == 'x.startswith(y)' ###Output _____no_output_____ ###Markdown Evaluating PropertiesTo actually _evaluate_ properties, we do not need to instantiate them. Instead, we simply convert them into a boolean function, using `lambda`: ###Code def prop_function_text(prop): return "lambda " + ", ".join(metavars(prop)) + ": " + prop def prop_function(prop): return eval(prop_function_text(prop)) ###Output _____no_output_____ ###Markdown Here is a simple example: ###Code prop_function_text("X > Y") p = prop_function("X > Y") p(100, 1) p(1, 100) ###Output _____no_output_____ ###Markdown Checking InvariantsTo extract invariants from an execution, we need to check them on all possible instantiations of arguments. If the function to be checked has two arguments `a` and `b`, we instantiate the property `X < Y` both as `a < b` and `b < a` and check each of them. To get all combinations, we use the Python `permutations()` function: ###Code import itertools for combination in itertools.permutations([1.0, 2.0, 3.0], 2): print(combination) ###Output _____no_output_____ ###Markdown The function `true_property_instantiations()` takes a property and a list of tuples (`var_name`, `value`). It then produces all instantiations of the property with the given values and returns those that evaluate to True. ###Code def true_property_instantiations(prop, vars_and_values, log=False): instantiations = set() p = prop_function(prop) len_metavars = len(metavars(prop)) for combination in itertools.permutations(vars_and_values, len_metavars): args = [value for var_name, value in combination] var_names = [var_name for var_name, value in combination] try: result = p(args) except: result = None if log: print(prop, combination, result) if result: instantiations.add((prop, tuple(var_names))) return instantiations ###Output _____no_output_____ ###Markdown Here is an example. If `x == -1` and `y == 1`, the property `X < Y` holds for `x < y`, but not for `y < x`: ###Code invs = true_property_instantiations("X < Y", [('x', -1), ('y', 1)], log=True) invs ###Output _____no_output_____ ###Markdown The instantiation retrieves the short form: ###Code for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Likewise, with values for `x` and `y` as above, the property `X < 0` only holds for `x`, but not for `y`: ###Code invs = true_property_instantiations("X < 0", [('x', -1), ('y', 1)], log=True) for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Extracting InvariantsLet us now run the above invariant extraction on function arguments and return values as observed during a function execution. To this end, we extend the `CallTracker` class into an `InvariantTracker` class, which automatically computes invariants for all functions and all calls observed during tracking. By default, an `InvariantTracker` uses the properties as defined above; however, one can specify alternate sets of properties. ###Code class InvariantTracker(CallTracker): def __init__(self, props=None, kwargs): if props is None: props = INVARIANT_PROPERTIES self.props = props super().__init__(kwargs) ###Output _____no_output_____ ###Markdown The key method of the `InvariantTracker` is the `invariants()` method. This iterates over the calls observed and checks which properties hold. Only the intersection of properties – that is, the set of properties that hold for all calls – is preserved, and eventually returned. The special variable `return_value` is set to hold the return value. ###Code RETURN_VALUE = 'return_value' class InvariantTracker(InvariantTracker): def invariants(self, function_name=None): if function_name is None: return {function_name: self.invariants(function_name) for function_name in self.calls()} invariants = None for variables, return_value in self.calls(function_name): vars_and_values = variables + [(RETURN_VALUE, return_value)] s = set() for prop in self.props: s \|= true_property_instantiations(prop, vars_and_values, self._log) if invariants is None: invariants = s else: invariants &= s return invariants ###Output _____no_output_____ ###Markdown Here's an example of how to use `invariants()`. We run the tracker on a small set of calls. ###Code with InvariantTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(10.0) tracker.calls() ###Output _____no_output_____ ###Markdown The `invariants()` method produces a set of properties that hold for the observed runs, together with their instantiations over function arguments. ###Code invs = tracker.invariants('my_sqrt') invs ###Output _____no_output_____ ###Markdown As before, the actual instantiations are easier to read: ###Code def pretty_invariants(invariants): props = [] for (prop, var_names) in invariants: props.append(instantiate_prop(prop, var_names)) return sorted(props) pretty_invariants(invs) ###Output _____no_output_____ ###Markdown We see that the both `x` and the return value have a `float` type. We also see that both are always greater than zero. These are properties that may make useful pre- and postconditions, notably for symbolic analysis. However, there's also an invariant which does _not_ universally hold, namely `return_value <= x`, as the following example shows: ###Code my_sqrt(0.01) ###Output _____no_output_____ ###Markdown Clearly, 0.1 > 0.01 holds. This is a case of us not learning from sufficiently diverse inputs. As soon as we have a call including `x = 0.1`, though, the invariant `return_value <= x` is eliminated: ###Code with InvariantTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(10.0) y = my_sqrt(0.01) pretty_invariants(tracker.invariants('my_sqrt')) ###Output _____no_output_____ ###Markdown We will discuss later how to ensure sufficient diversity in inputs. (Hint: This involves test generation.) Let us try out our invariant tracker on `sum3()`. We see that all types are well-defined; the properties that all arguments are non-zero, however, is specific to the calls observed. ###Code with InvariantTracker() as tracker: y = sum3(1, 2, 3) y = sum3(-4, -5, -6) pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with strings instead, we get different invariants. Notably, we obtain the postcondition that the return value starts with the value of `a` – a universal postcondition if strings are used. ###Code with InvariantTracker() as tracker: y = sum3('a', 'b', 'c') y = sum3('f', 'e', 'd') pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with both strings and numbers (and zeros, too), there are no properties left that would hold across all calls. That's the price of flexibility. ###Code with InvariantTracker() as tracker: y = sum3('a', 'b', 'c') y = sum3('c', 'b', 'a') y = sum3(-4, -5, -6) y = sum3(0, 0, 0) pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown Converting Mined Invariants to AnnotationsAs with types, above, we would like to have some functionality where we can add the mined invariants as annotations to existing functions. To this end, we introduce the `InvariantAnnotator` class, extending `InvariantTracker`. We start with a helper method. `params()` returns a comma-separated list of parameter names as observed during calls. ###Code class InvariantAnnotator(InvariantTracker): def params(self, function_name): arguments, return_value = self.calls(function_name)[0] return ", ".join(arg_name for (arg_name, arg_value) in arguments) with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = sum3(1, 2, 3) annotator.params('my_sqrt') annotator.params('sum3') ###Output _____no_output_____ ###Markdown Now for the actual annotation. `preconditions()` returns the preconditions from the mined invariants (i.e., those propertes that do not depend on the return value) as a string with annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@precondition(lambda " + self.params(function_name) + ": " + inv + ")" conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) annotator.preconditions('my_sqrt') ###Output _____no_output_____ ###Markdown `postconditions()` does the same for postconditions: ###Code class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ")") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) annotator.postconditions('my_sqrt') ###Output _____no_output_____ ###Markdown With these, we can take a function and add both pre- and postconditions as annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def functions_with_invariants(self): functions = "" for function_name in self.invariants(): try: function = self.function_with_invariants(function_name) except KeyError: continue functions += function return functions def function_with_invariants(self, function_name): function = globals()[function_name] # Can throw KeyError source = inspect.getsource(function) return "\n".join(self.preconditions(function_name) + self.postconditions(function_name)) + '\n' + source ###Output _____no_output_____ ###Markdown Here comes `function_with_invariants()` in all its glory: ###Code with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) print_content(annotator.function_with_invariants('my_sqrt'), '.py') ###Output _____no_output_____ ###Markdown Quite a lot of invariants, is it? Further below (and in the exercises), we will discuss on how to focus on the most relevant properties. Some ExamplesHere's another example. `list_length()` recursively computes the length of a Python function. Let us see whether we can mine its invariants: ###Code def list_length(L): if L == []: length = 0 else: length = 1 + list_length(L[1:]) return length with InvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Almost all these properties (except for the very first) are relevant. Of course, the reason the invariants are so neat is that the return value is equal to `len(L)` is that `X == len(Y)` is part of the list of properties to be checked. The next example is a very simple function: ###Code def sum2(a, b): return a + b with InvariantAnnotator() as annotator: sum2(31, 45) sum2(0, 0) sum2(-1, -5) ###Output _____no_output_____ ###Markdown The invariants all capture the relationship between `a`, `b`, and the return value as `return_value == a + b` in all its variations. ###Code print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown If we have a function without return value, the return value is `None` and we can only mine preconditions. (Well, we get a "postcondition" that the return value is non-zero, which holds for `None`). ###Code def print_sum(a, b): print(a + b) with InvariantAnnotator() as annotator: print_sum(31, 45) print_sum(0, 0) print_sum(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Checking SpecificationsA function with invariants, as above, can be fed into the Python interpreter, such that all pre- and postconditions are checked. We create a function `my_sqrt_annotated()` which includes all the invariants mined above. ###Code with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) my_sqrt_def = annotator.functions_with_invariants() my_sqrt_def = my_sqrt_def.replace('my_sqrt', 'my_sqrt_annotated') print_content(my_sqrt_def, '.py') exec(my_sqrt_def) ###Output _____no_output_____ ###Markdown The "annotated" version checks against invalid arguments – or more precisely, against arguments with properties that have not been observed yet: ###Code with ExpectError(): my_sqrt_annotated(-1.0) ###Output _____no_output_____ ###Markdown This is in contrast to the original version, which just hangs on negative values: ###Code with ExpectTimeout(1): my_sqrt(-1.0) ###Output _____no_output_____ ###Markdown If we make changes to the function definition such that the properties of the return value change, such _regressions_ are caught as violations of the postconditions. Let us illustrate this by simply inverting the result, and return $-2$ as square root of 4. ###Code my_sqrt_def = my_sqrt_def.replace('my_sqrt_annotated', 'my_sqrt_negative') my_sqrt_def = my_sqrt_def.replace('return approx', 'return -approx') print_content(my_sqrt_def, '.py') exec(my_sqrt_def) ###Output _____no_output_____ ###Markdown Technically speaking, $-2$ _is_ a square root of 4, since $(-2)^2 = 4$ holds. Yet, such a change may be unexpected by callers of `my_sqrt()`, and hence, this would be caught with the first call: ###Code with ExpectError(): my_sqrt_negative(2.0) ###Output _____no_output_____ ###Markdown We see how pre- and postconditions, as well as types, can serve as oracles* during testing. In particular, once we have mined them for a set of functions, we can check them again and again with test generators – especially after code changes. The more checks we have, and the more specific they are, the more likely it is we can detect unwanted effects of changes. Mining Specifications from Generated TestsMined specifications can only be as good as the executions they were mined from. If we only see a single call to, say, `sum2()`, we will be faced with several mined pre- and postconditions that _overspecialize_ towards the values seen: ###Code def sum2(a, b): return a + b with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown The mined precondition `a == b`, for instance, only holds for the single call observed; the same holds for the mined postcondition `return_value == a * b`. Yet, `sum2()` can obviously be successfully called with other values that do not satisfy these conditions. To get out of this trap, we have to _learn from more and more diverse runs_. If we have a few more calls of `sum2()`, we see how the set of invariants quickly gets smaller: ###Code with InvariantAnnotator() as annotator: length = sum2(1, 2) length = sum2(-1, -2) length = sum2(0, 0) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown But where to we get such diverse runs from? This is the job of generating software tests. A simple grammar for calls of `sum2()` will easily resolve the problem. ###Code from GrammarFuzzer import GrammarFuzzer # minor dependency from Grammars import is_valid_grammar, crange, convert_ebnf_grammar # minor dependency SUM2_EBNF_GRAMMAR = { "<start>": ["<sum2>"], "<sum2>": ["sum2(<int>, <int>)"], "<int>": ["<_int>"], "<_int>": ["(-)?<leaddigit><digit>", "0"], "<leaddigit>": crange('1', '9'), "<digit>": crange('0', '9') } assert is_valid_grammar(SUM2_EBNF_GRAMMAR) sum2_grammar = convert_ebnf_grammar(SUM2_EBNF_GRAMMAR) sum2_fuzzer = GrammarFuzzer(sum2_grammar) [sum2_fuzzer.fuzz() for i in range(10)] with InvariantAnnotator() as annotator: for i in range(10): eval(sum2_fuzzer.fuzz()) print_content(annotator.function_with_invariants('sum2'), '.py') ###Output _____no_output_____ ###Markdown But then, writing tests (or a test driver) just to derive a set of pre- and postconditions may possibly be too much effort – in particular, since tests can easily be derived from given pre- and postconditions in the first place. Hence, it would be wiser to first specify invariants and then let test generators or program provers do the job. Also, an API grammar, such as above, will have to be set up such that it actually respects preconditions – in our case, we invoke `sqrt()` with positive numbers only, already assuming its precondition. In some way, one thus needs a specification (a model, a grammar) to mine another specification – a chicken-and-egg problem. However, there is one way out of this problem: If one can automatically generate tests at the system level, then one has an _infinite source of executions_ to learn invariants from. In each of these executions, all functions would be called with values that satisfy the (implicit) precondition, allowing us to mine invariants for these functions. This holds, because at the system level, invalid inputs must be rejected by the system in the first place. The meaningful precondition at the system level, ensuring that only valid inputs get through, thus gets broken down into a multitude of meaningful preconditions (and subsequent postconditions) at the function level. The big requirement for this, though, is that one needs good test generators at the system level. In [the next part](05_Domain-Specific_Fuzzing.ipynb), we will discuss how to automatically generate tests for a variety of domains, from configuration to graphical user interfaces. SynopsisThis chapter provides two classes that automatically extract specifications from a function and a set of inputs: `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator: ###Code def sum2(a, b): return a + b with TypeAnnotator() as type_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution. ###Code print(type_annotator.typed_functions()) ###Output _____no_output_____ ###Markdown The invariant annotator works in a similar fashion: ###Code with InvariantAnnotator() as inv_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values. ###Code print(inv_annotator.functions_with_invariants()) ###Output _____no_output_____ ###Markdown Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs) as well as for all kinds of _symbolic code analyses_. The chapter gives details on how to customize the properties checked for. Lessons Learned* Type annotations and explicit invariants allow for _checking_ arguments and results for expected data types and other properties.* One can automatically _mine_ data types and invariants by observing arguments and results at runtime.* The quality of mined invariants depends on the diversity of values observed during executions; this variety can be increased by generating tests. Next StepsThis chapter concludes the [part on semantical fuzzing techniques](04_Semantical_Fuzzing.ipynb). In the next part, we will explore [domain-specific fuzzing techniques](05_Domain-Specific_Fuzzing.ipynb) from configurations and APIs to graphical user interfaces. BackgroundThe [DAIKON dynamic invariant detector](https://plse.cs.washington.edu/daikon/) can be considered the mother of function specification miners. Continuously maintained and extended for more than 20 years, it mines likely invariants in the style of this chapter for a variety of languages, including C, C++, C, Eiffel, F, Java, Perl, and Visual Basic. On top of the functionality discussed above, it holds a rich catalog of patterns for likely invariants, supports data invariants, can eliminate invariants that are implied by others, and determines statistical confidence to disregard unlikely invariants. The corresponding paper \cite{Ernst2001} is one of the seminal and most-cited papers of Software Engineering. A multitude of works have been published based on DAIKON and detecting invariants; see this [curated list](http://plse.cs.washington.edu/daikon/pubs/) for details. The interaction between test generators and invariant detection is already discussed in \cite{Ernst2001} (incidentally also using grammars). The Eclat tool \cite{Pacheco2005} is a model example of tight interaction between a unit-level test generator and DAIKON-style invariant mining, where the mined invariants are used to produce oracles and to systematically guide the test generator towards fault-revealing inputs. Mining specifications is not restricted to pre- and postconditions. The paper "Mining Specifications" \cite{Ammons2002} is another classic in the field, learning state protocols from executions. Grammar mining, as described in [our chapter with the same name](GrammarMiner.ipynb) can also be seen as a specification mining approach, this time learning specifications for input formats. As it comes to adding type annotations to existing code, the blog post ["The state of type hints in Python"](https://www.bernat.tech/the-state-of-type-hints-in-python/) gives a great overview on how Python type hints can be used and checked. To add type annotations, there are two important tools available that also implement our above approach:* [MonkeyType](https://instagram-engineering.com/let-your-code-type-hint-itself-introducing-open-source-monkeytype-a855c7284881) implements the above approach of tracing executions and annotating Python 3 arguments, returns, and variables with type hints.* [PyAnnotate](https://github.com/dropbox/pyannotate) does a similar job, focusing on code in Python 2. It does not produce Python 3-style annotations, but instead produces annotations as comments that can be processed by static type checkers.These tools have been created by engineers at Facebook and Dropbox, respectively, assisting them in checking millions of lines of code for type issues. ExercisesOur code for mining types and invariants is in no way complete. There are dozens of ways to extend our implementations, some of which we discuss in exercises. Exercise 1: Union TypesThe Python `typing` module allows to express that an argument can have multiple types. For `my_sqrt(x)`, this allows to express that `x` can be an `int` or a `float`: ###Code from typing import Union, Optional def my_sqrt_with_union_type(x: Union[int, float]) -> float: ... ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it supports union types for arguments and return values. Use `Optional[X]` as a shorthand for `Union[X, None]`. Solution. Left to the reader. Hint: extend `type_string()`. Exercise 2: Types for Local VariablesIn Python, one cannot only annotate arguments with types, but actually also local and global variables – for instance, `approx` and `guess` in our `my_sqrt()` implementation: ###Code def my_sqrt_with_local_types(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" approx: Optional[float] = None guess: float = x / 2 while approx != guess: approx: float = guess guess: float = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it also annotates local variables with types. Search the function AST for assignments, determine the type of the assigned value, and make it an annotation on the left hand side. Solution. Left to the reader. Exercise 3: Verbose Invariant CheckersOur implementation of invariant checkers does not make it clear for the user which pre-/postcondition failed. ###Code @precondition(lambda s: len(s) > 0) def remove_first_char(s): return s[1:] with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown The following implementation adds an optional `doc` keyword argument which is printed if the invariant is violated: ###Code def condition(precondition=None, postcondition=None, doc='Unknown'): def decorator(func): @functools.wraps(func) # preserves name, docstring, etc def wrapper(args, kwargs): if precondition is not None: assert precondition(args, *kwargs), "Precondition violated: " + doc retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, kwargs), "Postcondition violated: " + doc return retval return wrapper return decorator def precondition(check, kwargs): return condition(precondition=check, doc=kwargs.get('doc', 'Unknown')) def postcondition(check, kwargs): return condition(postcondition=check, doc=kwargs.get('doc', 'Unknown')) @precondition(lambda s: len(s) > 0, doc="len(s) > 0") def remove_first_char(s): return s[1:] remove_first_char('abc') with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown Extend `InvariantAnnotator` such that it includes the conditions in the generated pre- and postconditions. Solution.** Here's a simple solution: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@precondition(lambda " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")" conditions.append(cond) return conditions class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")") conditions.append(cond) return conditions ###Output _____no_output_____ ###Markdown The resulting annotations are harder to read, but easier to diagnose: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown As an alternative, one may be able to use `inspect.getsource()` on the lambda expression or unparse it. This is left to the reader. Exercise 4: Save Initial ValuesIf the value of an argument changes during function execution, this can easily confuse our implementation: The values are tracked at the beginning of the function, but checked only when it returns. Extend the `InvariantAnnotator` and the infrastructure it uses such that* it saves argument values both at the beginning and at the end of a function invocation;* postconditions can be expressed over both _initial_ values of arguments as well as the _final_ values of arguments;* the mined postconditions refer to both these values as well. Solution. To be added. Exercise 5: ImplicationsSeveral mined invariant are actually _implied_ by others: If `x > 0` holds, then this implies `x >= 0` and `x != 0`. Extend the `InvariantAnnotator` such that implications between properties are explicitly encoded, and such that implied properties are no longer listed as invariants. See \cite{Ernst2001} for ideas. Solution. Left to the reader. Exercise 6: Local VariablesPostconditions may also refer to the values of local variables. Consider extending `InvariantAnnotator` and its infrastructure such that the values of local variables at the end of the execution are also recorded and made part of the invariant inference mechanism. Solution. Left to the reader. Exercise 7: Exploring Invariant AlternativesAfter mining a first set of invariants, have a [concolic fuzzer](ConcolicFuzzer.ipynb) generate tests that systematically attempt to invalidate pre- and postconditions. How far can you generalize? Solution. To be added. Exercise 8: Grammar-Generated PropertiesThe larger the set of properties to be checked, the more potential invariants can be discovered. Create a _grammar_ that systematically produces a large set of properties. See \cite{Ernst2001} for possible patterns. Solution. Left to the reader. Exercise 9: Embedding Invariants as AssertionsRather than producing invariants as annotations for pre- and postconditions, insert them as `assert` statements into the function code, as in:```pythondef my_sqrt(x): 'Computes the square root of x, using the Newton-Raphson method' assert isinstance(x, int), 'violated precondition' assert (x > 0), 'violated precondition' approx = None guess = (x / 2) while (approx != guess): approx = guess guess = ((approx + (x / approx)) / 2) return_value = approx assert (return_value < x), 'violated postcondition' assert isinstance(return_value, float), 'violated postcondition' return approx```Such a formulation may make it easier for test generators and symbolic analysis to access and interpret pre- and postconditions. Solution. Here is a tentative implementation that inserts invariants into function ASTs. Part 1: Embedding Invariants into Functions ###Code class EmbeddedInvariantAnnotator(InvariantTracker): def functions_with_invariants_ast(self, function_name=None): if function_name is None: return annotate_functions_with_invariants(self.invariants()) return annotate_function_with_invariants(function_name, self.invariants(function_name)) def functions_with_invariants(self, function_name=None): if function_name is None: functions = '' for f_name in self.invariants(): try: f_text = astor.to_source(self.functions_with_invariants_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions return astor.to_source(self.functions_with_invariants_ast(function_name)) def function_with_invariants(self, function_name): return self.functions_with_invariants(function_name) def function_with_invariants_ast(self, function_name): return self.functions_with_invariants_ast(function_name) def annotate_invariants(invariants): annotated_functions = {} for function_name in invariants: try: annotated_functions[function_name] = annotate_function_with_invariants(function_name, invariants[function_name]) except KeyError: continue return annotated_functions def annotate_function_with_invariants(function_name, function_invariants): function = globals()[function_name] function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_invariants(function_ast, function_invariants) def annotate_function_ast_with_invariants(function_ast, function_invariants): annotated_function_ast = EmbeddedInvariantTransformer(function_invariants).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Part 2: Preconditions ###Code class PreconditionTransformer(ast.NodeTransformer): def __init__(self, invariants): self.invariants = invariants super().__init__() def preconditions(self): preconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated precondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) < 0: preconditions += assertion_ast.body return preconditions def insert_assertions(self, body): preconditions = self.preconditions() try: docstring = body[0].value.s except: docstring = None if docstring: return [body[0]] + preconditions + body[1:] else: return preconditions + body def visit_FunctionDef(self, node): """Add invariants to function""" # print(ast.dump(node)) node.body = self.insert_assertions(node.body) return node class EmbeddedInvariantTransformer(PreconditionTransformer): pass with EmbeddedInvariantAnnotator() as annotator: my_sqrt(5) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Part 3: PostconditionsWe make a few simplifying assumptions: * Variables do not change during execution.* There is a single `return` statement at the end of the function. ###Code class EmbeddedInvariantTransformer(PreconditionTransformer): def postconditions(self): postconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated postcondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) >= 0: postconditions += assertion_ast.body return postconditions def insert_assertions(self, body): new_body = super().insert_assertions(body) postconditions = self.postconditions() body_ends_with_return = isinstance(new_body[-1], ast.Return) if body_ends_with_return: saver = RETURN_VALUE + " = " + astor.to_source(new_body[-1].value) else: saver = RETURN_VALUE + " = None" saver_ast = ast.parse(saver) postconditions = [saver_ast] + postconditions if body_ends_with_return: return new_body[:-1] + postconditions + [new_body[-1]] else: return new_body + postconditions with EmbeddedInvariantAnnotator() as annotator: my_sqrt(5) my_sqrt_def = annotator.functions_with_invariants() ###Output _____no_output_____ ###Markdown Here's the full definition with included assertions: ###Code print_content(my_sqrt_def, '.py') exec(my_sqrt_def.replace('my_sqrt', 'my_sqrt_annotated')) with ExpectError(): my_sqrt_annotated(-1) ###Output _____no_output_____ ###Markdown Here come some more examples: ###Code with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: print_sum(31, 45) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Mining Function SpecificationsIn the [chapter on assertions](Assertions.ipynb), we have seen how important it is to _check_ whether the result is as expected. In this chapter, we introduce a technique that allows us to _mine_ function specifications from a set of given executions, resulting in abstract and formal _descriptions_ of what the function expects and what it delivers.These so-called _dynamic invariants_ produce pre- and post-conditions over function arguments and variables from a set of executions. Within debugging, the resulting _assertions_ can immediately check whether function behavior has changed, but can also be useful to determine the characteristics of _failing_ runs (as opposed to _passing_ runs). Furthermore, the resulting specifications provide pre- and postconditions for formal program proofs, testing, and verification.This chapter is based on [a chapter with the same name in The Fuzzing Book](https://www.fuzzingbook.org/html/DynamicInvariants.html), which focuses on test generation. ###Code from bookutils import YouTubeVideo YouTubeVideo("HDu1olXFvv0") ###Output _____no_output_____ ###Markdown Prerequisites* You should be familiar with tracing program executions, as in the [chapter on tracing](Tracer.ipynb).* Later in this section, we access the internal _abstract syntax tree_ representations of Python programs and transform them, as in the [chapter on tracking failure origins](Slicer.ipynb). ###Code import bookutils from Tracer import Tracer # ignore from typing import Sequence, Any, Callable, Tuple from typing import Dict, Union, Set, List, cast, Optional ###Output _____no_output_____ ###Markdown SynopsisTo [use the code provided in this chapter](Importing.ipynb), write```python>>> from debuggingbook.DynamicInvariants import ```and then make use of the following features.This chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator:```python>>> def sum2(a, b): type: ignore>>> return a + b>>> with TypeAnnotator() as type_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution.```python>>> print(type_annotator.typed_functions())def sum2(a: int, b: int) ->int: return a + b```The invariant annotator works in a similar fashion:```python>>> with InvariantAnnotator() as inv_annotator:>>> sum2(1, 2)>>> sum2(-4, -5)>>> sum2(0, 0)```The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values.```python>>> print(inv_annotator.functions_with_invariants())@precondition(lambda a, b: isinstance(a, int))@precondition(lambda a, b: isinstance(b, int))@postcondition(lambda return_value, a, b: a == return_value - b)@postcondition(lambda return_value, a, b: b == return_value - a)@postcondition(lambda return_value, a, b: isinstance(return_value, int))@postcondition(lambda return_value, a, b: return_value == a + b)@postcondition(lambda return_value, a, b: return_value == b + a)def sum2(a, b): type: ignore return a + b```Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs). The chapter gives details on how to customize the properties checked for. Specifications and AssertionsWhen implementing a function or program, one usually works against a _specification_ – a set of documented requirements to be satisfied by the code. Such specifications can come in natural language. A formal specification, however, allows the computer to check whether the specification is satisfied.In the [chapter on assertions](Assertions.ipynb), we have seen how _preconditions_ and _postconditions_ can describe what a function does. Consider the following (simple) square root function: ###Code def square_root(x): # type: ignore assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown The assertion `assert p` checks the condition `p`; if it does not hold, execution is aborted. Here, the actual body is not yet written; we use the assertions as a specification of what `square_root()` _expects_, and what it _delivers_.The topmost assertion is the _precondition_, stating the requirements on the function arguments. The assertion at the end is the _postcondition_, stating the properties of the function result (including its relationship with the original arguments). Using these pre- and postconditions as a specification, we can now go and implement a square root function that satisfies them. Once implemented, we can have the assertions check at runtime whether `square_root()` works as expected. However, not every piece of code is developed with explicit specifications in the first place; let alone does most code comes with formal pre- and post-conditions. (Just take a look at the chapters in this book.) This is a pity: As Ken Thompson famously said, "Without specifications, there are no bugs – only surprises". It is also a problem for debugging, since, of course, debugging needs some specification such that we know what is wrong, and how to fix it. This raises the interesting question: Can we somehow _retrofit_ existing code with "specifications" that properly describe their behavior, allowing developers to simply _check_ them rather than having to write them from scratch? This is what we do in this chapter. Beyond Generic FailuresBefore we go into _mining_ specifications, let us first discuss why it could be useful to _have_ them. As a motivating example, consider the full implementation of `square_root()` from the [chapter on assertions](Assertions.ipynb): ###Code import bookutils def square_root(x): # type: ignore """Computes the square root of x, using the Newton-Raphson method""" approx = None guess = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown `square_root()` does not come with any functionality that would check types or values. Hence, it is easy for callers to make mistakes when calling `square_root()`: ###Code from ExpectError import ExpectError, ExpectTimeout with ExpectError(): square_root("foo") with ExpectError(): x = square_root(0.0) ###Output _____no_output_____ ###Markdown At least, the Python system catches these errors at runtime. The following call, however, simply lets the function enter an infinite loop: ###Code with ExpectTimeout(1): x = square_root(-1.0) ###Output _____no_output_____ ###Markdown Our goal is to avoid such errors by _annotating_ functions with information that prevents errors like the above ones. The idea is to provide a _specification_ of expected properties – a specification that can then be checked at runtime or statically. \todo{Introduce the concept of contract.} Mining Data TypesFor our Python code, one of the most important "specifications" we need is types. Python being a "dynamically" typed language means that all data types are determined at run time; the code itself does not explicitly state whether a variable is an integer, a string, an array, a dictionary – or whatever. As _writer_ of Python code, omitting explicit type declarations may save time (and allows for some fun hacks). It is not sure whether a lack of types helps in _reading_ and _understanding_ code for humans. For a _computer_ trying to analyze code, the lack of explicit types is detrimental. If, say, a constraint solver, sees `if x:` and cannot know whether `x` is supposed to be a number or a string, this introduces an _ambiguity_. Such ambiguities may multiply over the entire analysis in a combinatorial explosion – or in the analysis yielding an overly inaccurate result. Python 3.6 and later allow data types as _annotations_ to function arguments (actually, to all variables) and return values. We can, for instance, state that `square_root()` is a function that accepts a floating-point value and returns one: ###Code def square_root_with_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) ###Output _____no_output_____ ###Markdown By default, such annotations are ignored by the Python interpreter. Therefore, one can still call `square_root_typed()` with a string as an argument and get the exact same result as above. However, one can make use of special _typechecking_ modules that would check types – _dynamically_ at runtime or _statically_ by analyzing the code without having to execute it. Runtime Type CheckingThe Python `enforce` package provides a function decorator that automatically inserts type-checking code that is executed at runtime. Here is how to use it: ###Code import enforce @enforce.runtime_validation def square_root_with_checked_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) ###Output _____no_output_____ ###Markdown Now, invoking `square_root_with_checked_type_annotations()` raises an exception when invoked with a type dfferent from the one declared: ###Code with ExpectError(): square_root_with_checked_type_annotations(True) ###Output _____no_output_____ ###Markdown Note that this error is not caught by the "untyped" variant, where passing a boolean value happily returns $\sqrt{1}$ as result. ###Code square_root(True) ###Output _____no_output_____ ###Markdown In Python (and other languages), the boolean values `True` and `False` can be implicitly converted to the integers 1 and 0; however, it is hard to think of a call to `sqrt()` where this would not be an error. ###Code from bookutils import quiz quiz("What happens if we call " "`square_root_with_checked_type_annotations(1)`?", [ "`1` is automatically converted to float. It will pass.", "`1` is a subtype of float. It will pass.", "`1` is an integer, and no float. The type check will fail.", "The function will fail for some other reason." ], '37035 // 12345') ###Output _____no_output_____ ###Markdown "Prediction is very difficult, especially when the future is concerned" (Niels Bohr). We can find out by a simple experiment that `float` actually means `float` – and not `int`: ###Code with ExpectError(enforce.exceptions.RuntimeTypeError): square_root_with_checked_type_annotations(1) ###Output _____no_output_____ ###Markdown To allow `int` as a type, we need to specify a _union_ of types. ###Code @enforce.runtime_validation def square_root_with_union_type(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" return square_root(x) square_root_with_union_type(2) square_root_with_union_type(2.0) with ExpectError(enforce.exceptions.RuntimeTypeError): square_root_with_union_type("Two dot zero") ###Output _____no_output_____ ###Markdown Static Type CheckingType annotations can also be checked _statically_ – that is, without even running the code. Let us create a simple Python file consisting of the above `square_root_typed()` definition and a bad invocation. ###Code import inspect import tempfile f = tempfile.NamedTemporaryFile(mode='w', suffix='.py') f.name f.write(inspect.getsource(square_root)) f.write('\n') f.write(inspect.getsource(square_root_with_type_annotations)) f.write('\n') f.write("print(square_root_with_type_annotations('123'))\n") f.flush() ###Output _____no_output_____ ###Markdown These are the contents of our newly created Python file: ###Code from bookutils import print_file print_file(f.name, start_line_number=1) ###Output _____no_output_____ ###Markdown [Mypy](http://mypy-lang.org) is a type checker for Python programs. As it checks types statically, types induce no overhead at runtime; plus, a static check can be faster than a lengthy series of tests with runtime type checking enabled. Let us see what `mypy` produces on the above file: ###Code import subprocess result = subprocess.run(["mypy", "--strict", f.name], universal_newlines=True, stdout=subprocess.PIPE) print(result.stdout.replace(f.name + ':', '')) del f # Delete temporary file ###Output _____no_output_____ ###Markdown We see that `mypy` complains about untyped function definitions such as `square_root()`; most important, however, it finds that the call to `square_root_with_type_annotations()` in the last line has the wrong type. With `mypy`, we can achieve the same type safety with Python as in statically typed languages – provided that we as programmers also produce the necessary type annotations. Is there a simple way to obtain these? Mining Type SpecificationsOur first task will be to mine type annotations (as part of the code) from _values_ we observe at run time. These type annotations would be _mined_ from actual function executions, _learning_ from (normal) runs what the expected argument and return types should be. By observing a series of calls such as these, we could infer that both `x` and the return value are of type `float`: ###Code y = square_root(25.0) y y = square_root(2.0) y ###Output _____no_output_____ ###Markdown How can we mine types from executions? The answer is simple: 1. We _observe_ a function during execution2. We track the _types_ of its arguments3. We include these types as _annotations_ into the code.To do so, we can make use of Python's tracing facility we already observed in the [chapter on tracing executions](Tracer.ipynb). With every call to a function, we retrieve the arguments, their values, and their types. Tracing CallsTo observe argument types at runtime, we define a _tracer function_ that tracks the execution of `square_root()`, checking its arguments and return values. The `CallTracer` class is set to trace functions in a `with` block as follows:```pythonwith CallTracer() as tracer: function_to_be_tracked(...)info = tracer.collected_information()```To create the tracer, we build on the `Tracer` superclass as in the [chapter on tracing executions](Tracer.ipynb). ###Code from types import FrameType ###Output _____no_output_____ ###Markdown We start with two helper functions. `get_arguments()` returns a list of call arguments in the given call frame. ###Code Arguments = List[Tuple[str, Any]] def get_arguments(frame: FrameType) -> Arguments: """Return call arguments in the given frame""" # When called, all arguments are local variables arguments = [(var, frame.f_locals[var]) for var in frame.f_locals] arguments.reverse() # Want same order as call return arguments ###Output _____no_output_____ ###Markdown `simple_call_string()` is a helper for logging that prints out calls in a user-friendly manner. ###Code def simple_call_string(function_name: str, argument_list: Arguments, return_value : Any = None) -> str: """Return function_name(arg[0], arg[1], ...) as a string""" call = function_name + "(" + \ ", ".join([var + "=" + repr(value) for (var, value) in argument_list]) + ")" if return_value is not None: call += " = " + repr(return_value) return call ###Output _____no_output_____ ###Markdown Now for `CallTracer`. The constructor simply invokes the `Tracer` constructor: ###Code class CallTracer(Tracer): def __init__(self, log: bool = False, kwargs: Any)-> None: super().__init__(kwargs) self._log = log self.reset() def reset(self) -> None: self._calls: Dict[str, List[Tuple[Arguments, Any]]] = {} self._stack: List[Tuple[str, Arguments]] = [] ###Output _____no_output_____ ###Markdown The `traceit()` method does nothing yet; this is done in specialized subclasses. The `CallTracer` class implements a `traceit()` function that checks for function calls and returns: ###Code class CallTracer(CallTracer): def traceit(self, frame: FrameType, event: str, arg: Any) -> None: """Tracking function: Record all calls and all args""" if event == "call": self.trace_call(frame, event, arg) elif event == "return": self.trace_return(frame, event, arg) ###Output _____no_output_____ ###Markdown `trace_call()` is called when a function is called; it retrieves the function name and current arguments, and saves them on a stack. ###Code class CallTracer(CallTracer): def trace_call(self, frame: FrameType, event: str, arg: Any) -> None: """Save current function name and args on the stack""" code = frame.f_code function_name = code.co_name arguments = get_arguments(frame) self._stack.append((function_name, arguments)) if self._log: print(simple_call_string(function_name, arguments)) ###Output _____no_output_____ ###Markdown When the function returns, `trace_return()` is called. We now also have the return value. We log the whole call with arguments and return value (if desired) and save it in our list of calls. ###Code class CallTracer(CallTracer): def trace_return(self, frame: FrameType, event: str, arg: Any) -> None: """Get return value and store complete call with arguments and return value""" code = frame.f_code function_name = code.co_name return_value = arg # TODO: Could call get_arguments() here to also retrieve _final_ values of argument variables called_function_name, called_arguments = self._stack.pop() assert function_name == called_function_name if self._log: print(simple_call_string(function_name, called_arguments), "returns", return_value) self.add_call(function_name, called_arguments, return_value) ###Output _____no_output_____ ###Markdown `add_call()` saves the calls in a list; each function name has its own list. ###Code class CallTracer(CallTracer): def add_call(self, function_name: str, arguments: Arguments, return_value: Any = None) -> None: """Add given call to list of calls""" if function_name not in self._calls: self._calls[function_name] = [] self._calls[function_name].append((arguments, return_value)) ###Output _____no_output_____ ###Markdown we can retrieve the list of calls, either for a given function name (`calls()`),or for all functions (`all_calls()`). ###Code class CallTracer(CallTracer): def calls(self, function_name: str) -> List[Tuple[Arguments, Any]]: """Return list of calls for `function_name`.""" return self._calls[function_name] class CallTracer(CallTracer): def all_calls(self) -> Dict[str, List[Tuple[Arguments, Any]]]: """ Return list of calls for function_name, or a mapping function_name -> calls for all functions tracked """ return self._calls ###Output _____no_output_____ ###Markdown Let us now put this to use. We turn on logging to track the individual calls and their return values: ###Code with CallTracer(log=True) as tracer: y = square_root(25) y = square_root(2.0) ###Output _____no_output_____ ###Markdown After execution, we can retrieve the individual calls: ###Code calls = tracer.calls('square_root') calls ###Output _____no_output_____ ###Markdown Each call is a pair (`argument_list`, `return_value`), where `argument_list` is a list of pairs (`parameter_name`, `value`). ###Code square_root_argument_list, square_root_return_value = calls[0] simple_call_string('square_root', square_root_argument_list, square_root_return_value) ###Output _____no_output_____ ###Markdown If the function does not return a value, `return_value` is `None`. ###Code def hello(name: str) -> None: print("Hello,", name) with CallTracer() as tracer: hello("world") hello_calls = tracer.calls('hello') hello_calls hello_argument_list, hello_return_value = hello_calls[0] simple_call_string('hello', hello_argument_list, hello_return_value) ###Output _____no_output_____ ###Markdown Getting TypesDespite what you may have read or heard, Python actually _is_ a typed language. It is just that it is _dynamically typed_ – types are used and checked only at runtime (rather than declared in the code, where they can be _statically checked_ at compile time). We can thus retrieve types of all values within Python: ###Code type(4) type(2.0) type([4]) ###Output _____no_output_____ ###Markdown We can retrieve the type of the first argument to `square_root()`: ###Code parameter, value = square_root_argument_list[0] parameter, type(value) ###Output _____no_output_____ ###Markdown as well as the type of the return value: ###Code type(square_root_return_value) ###Output _____no_output_____ ###Markdown Hence, we see that (so far), `square_root()` is a function taking (among others) integers and returning floats. We could declare `square_root()` as: ###Code def square_root_annotated(x: int) -> float: return square_root(x) ###Output _____no_output_____ ###Markdown This is a representation we could place in a static type checker, allowing to check whether calls to `square_root()` actually pass a number. A dynamic type checker could run such checks at runtime. By default, Python does not do anything with such annotations. However, tools can access annotations from functions and other objects: ###Code square_root_annotated.__annotations__ ###Output _____no_output_____ ###Markdown This is how run-time checkers access the annotations to check against. Annotating Functions with TypesOur plan is to annotate functions automatically, based on the types we have seen. Our aim is to build a class `TypeAnnotator` that can be used as follows. First, it would track some execution:```pythonwith TypeAnnotator() as annotator: some_function_call()```After tracking, `TypeAnnotator` would provide appropriate methods to access (type-)annotated versions of the function seen:```pythonprint(annotator.typed_functions())```Let us put the pieces together to build `TypeAnnotator`. Excursion: Accessing Function Structure To annotate functions, we need to convert a function into a tree representation (called _abstract syntax trees_, or ASTs) and back; we already have seen these in the chapter on [tracking value origins](Slicer.ipynb). ###Code import ast import inspect import astor ###Output _____no_output_____ ###Markdown We can get the source of a Python function using `inspect.getsource()`. (Note that this does not work for functions defined in other notebooks.) ###Code square_root_source = inspect.getsource(square_root) square_root_source ###Output _____no_output_____ ###Markdown To view these in a visually pleasing form, our function `print_content(s, suffix)` formats and highlights the string `s` as if it were a file with ending `suffix`. We can thus view (and highlight) the source as if it were a Python file: ###Code from bookutils import print_content print_content(square_root_source, '.py') ###Output _____no_output_____ ###Markdown Parsing this gives us an abstract syntax tree (AST) – a representation of the program in tree form. ###Code square_root_ast = ast.parse(square_root_source) ###Output _____no_output_____ ###Markdown What does this AST look like? The helper functions `astor.dump_tree()` (textual output) and `showast.show_ast()` (graphical output with [showast](https://github.com/hchasestevens/show_ast)) allow us to inspect the structure of the tree. We see that the function starts as a `FunctionDef` with name and arguments, followed by a body, which is a list of statements of type `Expr` (the docstring), type `Assign` (assignments), `While` (while loop with its own body), and finally `Return`. ###Code print(astor.dump_tree(square_root_ast)) ###Output _____no_output_____ ###Markdown Too much text for you? This graphical representation may make things simpler. ###Code from bookutils import show_ast show_ast(square_root_ast) ###Output _____no_output_____ ###Markdown The function `astor.to_source()` converts such a tree back into the more familiar textual Python code representation. Comments are gone, and there may be more parentheses than before, but the result has the same semantics: ###Code print_content(astor.to_source(square_root_ast), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: Annotating Functions with Given Types Let us now go and transform ASTs to add type annotations. We start with a helper function `parse_type(name)` which parses a type name into an AST. ###Code def parse_type(name: str) -> ast.expr: class ValueVisitor(ast.NodeVisitor): def visit_Expr(self, node: ast.Expr) -> None: self.value_node = node.value tree = ast.parse(name) name_visitor = ValueVisitor() name_visitor.visit(tree) return name_visitor.value_node print(astor.dump_tree(parse_type('int'))) print(astor.dump_tree(parse_type('[object]'))) ###Output _____no_output_____ ###Markdown We now define a helper function that actually adds type annotations to a function AST. The `TypeTransformer` class builds on the Python standard library `ast.NodeTransformer` infrastructure. It would be called as```python TypeTransformer({'x': 'int'}, 'float').visit(ast)```to annotate the arguments of `square_root()`: `x` with `int`, and the return type with `float`. The returned AST can then be unparsed, compiled or analyzed. ###Code class TypeTransformer(ast.NodeTransformer): def __init__(self, argument_types: Dict[str, str], return_type: Optional[str] = None): self.argument_types = argument_types self.return_type = return_type super().__init__() ###Output _____no_output_____ ###Markdown The core of `TypeTransformer` is the method `visit_FunctionDef()`, which is called for every function definition in the AST. Its argument `node` is the subtree of the function definition to be transformed. Our implementation accesses the individual arguments and invokes `annotate_args()` on them; it also sets the return type in the `returns` attribute of the node. ###Code class TypeTransformer(TypeTransformer): def visit_FunctionDef(self, node: ast.FunctionDef) -> ast.FunctionDef: """Add annotation to function""" # Set argument types new_args = [] for arg in node.args.args: new_args.append(self.annotate_arg(arg)) new_arguments = ast.arguments( new_args, node.args.vararg, node.args.kwonlyargs, node.args.kw_defaults, node.args.kwarg, node.args.defaults ) # Set return type if self.return_type is not None: node.returns = parse_type(self.return_type) return ast.copy_location( ast.FunctionDef(node.name, new_arguments, node.body, node.decorator_list, node.returns), node) ###Output _____no_output_____ ###Markdown Each argument gets its own annotation, taken from the types originally passed to the class: ###Code class TypeTransformer(TypeTransformer): def annotate_arg(self, arg: ast.arg) -> ast.arg: """Add annotation to single function argument""" arg_name = arg.arg if arg_name in self.argument_types: arg.annotation = parse_type(self.argument_types[arg_name]) return arg ###Output _____no_output_____ ###Markdown Does this work? Let us annotate the AST from `square_root()` with types for the arguments and return types: ###Code new_ast = TypeTransformer({'x': 'int'}, 'float').visit(square_root_ast) ###Output _____no_output_____ ###Markdown When we unparse the new AST, we see that the annotations actually are present: ###Code print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown Similarly, we can annotate the `hello()` function from above: ###Code hello_source = inspect.getsource(hello) hello_ast = ast.parse(hello_source) new_ast = TypeTransformer({'name': 'str'}, 'None').visit(hello_ast) print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: Annotating Functions with Mined Types Let us now annotate functions with types mined at runtime. We start with a simple function `type_string()` that determines the appropriate type of a given value (as a string): ###Code def type_string(value: Any) -> str: return type(value).__name__ type_string(4) type_string([]) ###Output _____no_output_____ ###Markdown For composite structures, `type_string()` does not examine element types; hence, the type of `[3]` is simply `list` instead of, say, `list[int]`. For now, `list` will do fine. ###Code type_string([3]) ###Output _____no_output_____ ###Markdown `type_string()` will be used to infer the types of argument values found at runtime, as returned by `CallTracer.all_calls()`: ###Code with CallTracer() as tracer: y = square_root(25.0) y = square_root(2.0) tracer.all_calls() ###Output _____no_output_____ ###Markdown The function `annotate_types()` takes such a list of calls and annotates each function listed: ###Code def annotate_types(calls: Dict[str, List[Tuple[Arguments, Any]]]) -> Dict[str, ast.AST]: annotated_functions = {} for function_name in calls: try: annotated_functions[function_name] = \ annotate_function_with_types(function_name, calls[function_name]) except KeyError: continue return annotated_functions ###Output _____no_output_____ ###Markdown For each function, we get the source and its AST and then get to the actual annotation in `annotate_function_ast_with_types()`: ###Code def annotate_function_with_types(function_name: str, function_calls: List[Tuple[Arguments, Any]]) -> ast.AST: function = globals()[function_name] # May raise KeyError for internal functions function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_types(function_ast, function_calls) ###Output _____no_output_____ ###Markdown The function `annotate_function_ast_with_types()` invokes the `TypeTransformer` with the calls seen, and for each call, iterate over the arguments, determine their types, and annotate the AST with these. The universal type `Any` is used when we encounter type conflicts, which we will discuss below. ###Code def annotate_function_ast_with_types(function_ast: ast.AST, function_calls: List[Tuple[Arguments, Any]]) -> ast.AST: parameter_types: Dict[str, str] = {} return_type = None for calls_seen in function_calls: args, return_value = calls_seen if return_value: if return_type and return_type != type_string(return_value): return_type = 'Any' else: return_type = type_string(return_value) for parameter, value in args: try: different_type = (parameter_types[parameter] != type_string(value)) except KeyError: different_type = False if different_type: parameter_types[parameter] = 'Any' else: parameter_types[parameter] = type_string(value) annotated_function_ast = \ TypeTransformer(parameter_types, return_type).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Here is `square_root()` annotated with the types recorded usign the tracer, above. ###Code print_content(astor.to_source(annotate_types(tracer.all_calls())['square_root']), '.py') ###Output _____no_output_____ ###Markdown End of Excursion Excursion: A Type Annotator Class Let us bring all of this together in a single class `TypeAnnotator` that first tracks calls of functions and then allows to access the AST (and the source code form) of the tracked functions annotated with types. The method `typed_functions()` returns the annotated functions as a string; `typed_functions_ast()` returns their AST. ###Code class TypeTracer(CallTracer): pass class TypeAnnotator(TypeTracer): def typed_functions_ast(self) -> Dict[str, ast.AST]: return annotate_types(self.all_calls()) def typed_function_ast(self, function_name: str) -> ast.AST: return annotate_function_with_types(function_name, self.calls(function_name)) def typed_functions(self) -> str: functions = '' for f_name in self.all_calls(): try: f_text = astor.to_source(self.typed_function_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions def typed_function(self, function_name: str) -> str: return astor.to_source(self.typed_function_ast(function_name)) ###Output _____no_output_____ ###Markdown End of Excursion Here is how to use `TypeAnnotator`. We first track a series of calls: ###Code with TypeAnnotator() as annotator: y = square_root(25.0) y = square_root(2.0) ###Output _____no_output_____ ###Markdown After tracking, we can immediately retrieve an annotated version of the functions tracked: ###Code print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown This also works for multiple and diverse functions. One could go and implement an automatic type annotator for Python files based on the types seen during execution. ###Code with TypeAnnotator() as annotator: hello('type annotations') y = square_root(1.0) print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown A content as above could now be sent to a type checker, which would detect any type inconsistency between callers and callees. Excursion: Handling Multiple TypesLet us now resolve the role of the magic `Any` type in `annotate_function_ast_with_types()`. If we see multiple types for the same argument, we set its type to `Any`. For `square_root()`, this makes sense, as its arguments can be integers as well as floats: ###Code with CallTracer() as tracer: y = square_root(25.0) y = square_root(4) annotated_square_root_ast = annotate_types(tracer.all_calls())['square_root'] print_content(astor.to_source(annotated_square_root_ast), '.py') ###Output _____no_output_____ ###Markdown The following function `sum3()` can be called with floating-point numbers as arguments, resulting in the parameters getting a `float` type: ###Code def sum3(a, b, c): # type: ignore return a + b + c with TypeAnnotator() as annotator: y = sum3(1.0, 2.0, 3.0) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we call `sum3()` with integers, though, the arguments get an `int` type: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown And we can also call `sum3()` with strings, which assigns the arguments a `str` type: ###Code with TypeAnnotator() as annotator: y = sum3("one", "two", "three") y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we have multiple calls, but with different types, `TypeAnnotator()` will assign an `Any` type to both arguments and return values: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y = sum3("one", "two", "three") typed_sum3_def = annotator.typed_function('sum3') print_content(typed_sum3_def, '.py') ###Output _____no_output_____ ###Markdown A type `Any` makes it explicit that an object can, indeed, have any type; it will not be typechecked at runtime or statically. To some extent, this defeats the power of type checking; but it also preserves some of the type flexibility that many Python programmers enjoy. Besides `Any`, the `typing` module supports several additional ways to define ambiguous types; we will keep this in mind for a later exercise. End of Excursion Mining InvariantsBesides basic data types. we can check several further properties from arguments. We can, for instance, whether an argument can be negative, zero, or positive; or that one argument should be smaller than the second; or that the result should be the sum of two arguments – properties that cannot be expressed in a (Python) type.Such properties are called invariants, as they hold across all invocations of a function. Specifically, invariants come as _pre_- and _postconditions_ – conditions that always hold at the beginning and at the end of a function. (There are also _data_ and _object_ invariants that express always-holding properties over the state of data or objects, but we do not consider these in this book.) Annotating Functions with Pre- and PostconditionsThe classical means to specify pre- and postconditions is via _assertions_, which we have introduced in the [chapter on assertions](Assertions.ipynb). A precondition checks whether the arguments to a function satisfy the expected properties; a postcondition does the same for the result. We can express and check both using assertions as follows: ###Code def square_root_with_invariants(x): # type: ignore assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown A nicer way, however, is to syntactically separate invariants from the function at hand. Using appropriate decorators, we could specify pre- and postconditions as follows:```python@precondition lambda x: x >= 0@postcondition lambda return_value, x: return_value * return_value == xdef square_root_with_invariants(x): normal code without assertions ...```The decorators `@precondition` and `@postcondition` would run the given functions (specified as anonymous `lambda` functions) before and after the decorated function, respectively. If the functions return `False`, the condition is violated. `@precondition` gets the function arguments as arguments; `@postcondition` additionally gets the return value as first argument. It turns out that implementing such decorators is not hard at all. Our implementation builds on a [code snippet from StackOverflow](https://stackoverflow.com/questions/12151182/python-precondition-postcondition-for-member-function-how): ###Code import functools def condition(precondition: Optional[Callable] = None, postcondition: Optional[Callable] = None) -> Callable: def decorator(func: Callable) -> Callable: @functools.wraps(func) # preserves name, docstring, etc def wrapper(args: Any, kwargs: Any) -> Any: if precondition is not None: assert precondition(args, *kwargs), \ "Precondition violated" # Call original function or method retval = func(args, *kwargs) if postcondition is not None: assert postcondition(retval, args, *kwargs), \ "Postcondition violated" return retval return wrapper return decorator def precondition(check: Callable) -> Callable: return condition(precondition=check) def postcondition(check: Callable) -> Callable: return condition(postcondition=check) ###Output _____no_output_____ ###Markdown With these, we can now start decorating `square_root()`: ###Code @precondition(lambda x: x > 0) def square_root_with_precondition(x): # type: ignore return square_root(x) ###Output _____no_output_____ ###Markdown This catches arguments violating the precondition: ###Code with ExpectError(): square_root_with_precondition(-1.0) ###Output _____no_output_____ ###Markdown Likewise, we can provide a postcondition: ###Code import math @postcondition(lambda ret, x: math.isclose(ret ret, x)) def square_root_with_postcondition(x): # type: ignore return square_root(x) y = square_root_with_postcondition(2.0) y ###Output _____no_output_____ ###Markdown If we have a buggy implementation of $\sqrt{x}$, this gets caught quickly: ###Code @postcondition(lambda ret, x: math.isclose(ret * ret, x)) def buggy_square_root_with_postcondition(x): # type: ignore return square_root(x) + 0.1 with ExpectError(): y = buggy_square_root_with_postcondition(2.0) ###Output _____no_output_____ ###Markdown While checking pre- and postconditions is a great way to catch errors, specifying them can be cumbersome. Let us try to see whether we can (again) _mine_ some of them. Mining InvariantsTo _mine_ invariants, we can use the same tracking functionality as before; instead of saving values for individual variables, though, we now check whether the values satisfy specific _properties_ or not. For instance, if all values of `x` seen satisfy the condition `x > 0`, then we make `x > 0` an invariant of the function. If we see positive, zero, and negative values of `x`, though, then there is no property of `x` left to talk about.The general idea is thus:1. Check all variable values observed against a set of predefined properties; and2. Keep only those properties that hold for all runs observed. Defining PropertiesWhat precisely do we mean by properties? Here is a small collection of value properties that would frequently be used in invariants. All these properties would be evaluated with the _metavariables_ `X`, `Y`, and `Z` (actually, any upper-case identifier) being replaced with the names of function parameters: ###Code INVARIANT_PROPERTIES = [ "X < 0", "X <= 0", "X > 0", "X >= 0", # "X == 0", # implied by "X", below # "X != 0", # implied by "not X", below ] ###Output _____no_output_____ ###Markdown When `square_root(x)` is called as, say `square_root(5.0)`, we see that `x = 5.0` holds. The above properties would then all be checked for `x`. Only the properties `X > 0`, `X >= 0`, and `not X` hold for the call seen; and hence `x > 0`, `x >= 0`, and `not x` (or better: `x != 0`) would make potential preconditions for `square_root(x)`. We can check for many more properties such as relations between two arguments: ###Code INVARIANT_PROPERTIES += [ "X == Y", "X > Y", "X < Y", "X >= Y", "X <= Y", ] ###Output _____no_output_____ ###Markdown Types also can be checked using properties. For any function parameter `X`, only one of these will hold: ###Code INVARIANT_PROPERTIES += [ "isinstance(X, bool)", "isinstance(X, int)", "isinstance(X, float)", "isinstance(X, list)", "isinstance(X, dict)", ] ###Output _____no_output_____ ###Markdown We can check for arithmetic properties: ###Code INVARIANT_PROPERTIES += [ "X == Y + Z", "X == Y * Z", "X == Y - Z", "X == Y / Z", ] ###Output _____no_output_____ ###Markdown Here's relations over three values, a Python special: ###Code INVARIANT_PROPERTIES += [ "X < Y < Z", "X <= Y <= Z", "X > Y > Z", "X >= Y >= Z", ] ###Output _____no_output_____ ###Markdown These Boolean properties also check for other types, as in Python, `None`, an empty list, an empty set, an empty string, and the value zero all evaluate to `False`. ###Code INVARIANT_PROPERTIES += [ "X", "not X" ] ###Output _____no_output_____ ###Markdown Finally, we can also check for list or string properties. Again, this is just a tiny selection. ###Code INVARIANT_PROPERTIES += [ "X == len(Y)", "X == sum(Y)", "X in Y", "X.startswith(Y)", "X.endswith(Y)", ] ###Output _____no_output_____ ###Markdown Extracting Meta-VariablesLet us first introduce a few _helper functions_ before we can get to the actual mining. `metavars()` extracts the set of meta-variables (`X`, `Y`, `Z`, etc.) from a property. To this end, we parse the property as a Python expression and then visit the identifiers. ###Code def metavars(prop: str) -> List[str]: metavar_list = [] class ArgVisitor(ast.NodeVisitor): def visit_Name(self, node: ast.Name) -> None: if node.id.isupper(): metavar_list.append(node.id) ArgVisitor().visit(ast.parse(prop)) return metavar_list assert metavars("X < 0") == ['X'] assert metavars("X.startswith(Y)") == ['X', 'Y'] assert metavars("isinstance(X, str)") == ['X'] ###Output _____no_output_____ ###Markdown Instantiating PropertiesTo produce a property as invariant, we need to be able to _instantiate_ it with variable names. The instantiation of `X > 0` with `X` being instantiated to `a`, for instance, gets us `a > 0`. To this end, the function `instantiate_prop()` takes a property and a collection of variable names and instantiates the meta-variables left-to-right with the corresponding variables names in the collection. ###Code def instantiate_prop_ast(prop: str, var_names: Sequence[str]) -> ast.AST: class NameTransformer(ast.NodeTransformer): def visit_Name(self, node: ast.Name) -> ast.Name: if node.id not in mapping: return node return ast.Name(id=mapping[node.id], ctx=ast.Load()) meta_variables = metavars(prop) assert len(meta_variables) == len(var_names) mapping = {} for i in range(0, len(meta_variables)): mapping[meta_variables[i]] = var_names[i] prop_ast = ast.parse(prop, mode='eval') new_ast = NameTransformer().visit(prop_ast) return new_ast def instantiate_prop(prop: str, var_names: Sequence[str]) -> str: prop_ast = instantiate_prop_ast(prop, var_names) prop_text = astor.to_source(prop_ast).strip() while prop_text.startswith('(') and prop_text.endswith(')'): prop_text = prop_text[1:-1] return prop_text assert instantiate_prop("X > Y", ['a', 'b']) == 'a > b' assert instantiate_prop("X.startswith(Y)", ['x', 'y']) == 'x.startswith(y)' ###Output _____no_output_____ ###Markdown Evaluating PropertiesTo actually _evaluate_ properties, we do not need to instantiate them. Instead, we simply convert them into a boolean function, using `lambda`: ###Code def prop_function_text(prop: str) -> str: return "lambda " + ", ".join(metavars(prop)) + ": " + prop ###Output _____no_output_____ ###Markdown Here is a simple example: ###Code prop_function_text("X > Y") ###Output _____no_output_____ ###Markdown We can easily evaluate the function: ###Code def prop_function(prop: str) -> Callable: return eval(prop_function_text(prop)) ###Output _____no_output_____ ###Markdown Here is an example: ###Code p = prop_function("X > Y") quiz("What is p(100, 1)?", [ "False", "True" ], 'p(100, 1) + 1', globals()) p(100, 1) p(1, 100) ###Output _____no_output_____ ###Markdown Checking InvariantsTo extract invariants from an execution, we need to check them on all possible instantiations of arguments. If the function to be checked has two arguments `a` and `b`, we instantiate the property `X < Y` both as `a < b` and `b < a` and check each of them. To get all combinations, we use the Python `permutations()` function: ###Code import itertools for combination in itertools.permutations([1.0, 2.0, 3.0], 2): print(combination) ###Output _____no_output_____ ###Markdown The function `true_property_instantiations()` takes a property and a list of tuples (`var_name`, `value`). It then produces all instantiations of the property with the given values and returns those that evaluate to True. ###Code Invariants = Set[Tuple[str, Tuple[str, ...]]] def true_property_instantiations(prop: str, vars_and_values: Arguments, log: bool = False) -> Invariants: instantiations = set() p = prop_function(prop) len_metavars = len(metavars(prop)) for combination in itertools.permutations(vars_and_values, len_metavars): args = [value for var_name, value in combination] var_names = [var_name for var_name, value in combination] try: result = p(args) except: result = None if log: print(prop, combination, result) if result: instantiations.add((prop, tuple(var_names))) return instantiations ###Output _____no_output_____ ###Markdown Here is an example. If `x == -1` and `y == 1`, the property `X < Y` holds for `x < y`, but not for `y < x`: ###Code invs = true_property_instantiations("X < Y", [('x', -1), ('y', 1)], log=True) invs ###Output _____no_output_____ ###Markdown The instantiation retrieves the short form: ###Code for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Likewise, with values for `x` and `y` as above, the property `X < 0` only holds for `x`, but not for `y`: ###Code invs = true_property_instantiations("X < 0", [('x', -1), ('y', 1)], log=True) for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Extracting InvariantsLet us now run the above invariant extraction on function arguments and return values as observed during a function execution. To this end, we extend the `CallTracer` class into an `InvariantTracer` class, which automatically computes invariants for all functions and all calls observed during tracking. By default, an `InvariantTracer` uses the `INVARIANT_PROPERTIES` properties as defined above; however, one can specify alternate sets of properties. ###Code class InvariantTracer(CallTracer): def __init__(self, props: Optional[List[str]] = None, kwargs: Any) -> None: if props is None: props = INVARIANT_PROPERTIES self.props = props super().__init__(kwargs) ###Output _____no_output_____ ###Markdown The key method of the `InvariantTracer` is the `invariants()` method. This iterates over the calls observed and checks which properties hold. Only the intersection of properties – that is, the set of properties that hold for all calls – is preserved, and eventually returned. The special variable `return_value` is set to hold the return value. ###Code RETURN_VALUE = 'return_value' class InvariantTracer(InvariantTracer): def all_invariants(self) -> Dict[str, Invariants]: return {function_name: self.invariants(function_name) for function_name in self.all_calls()} def invariants(self, function_name: str) -> Invariants: invariants = None for variables, return_value in self.calls(function_name): vars_and_values = variables + [(RETURN_VALUE, return_value)] s = set() for prop in self.props: s \|= true_property_instantiations(prop, vars_and_values, self._log) if invariants is None: invariants = s else: invariants &= s assert invariants is not None return invariants ###Output _____no_output_____ ###Markdown Here's an example of how to use `invariants()`. We run the tracer on a small set of calls. ###Code with InvariantTracer() as tracer: y = square_root(25.0) y = square_root(10.0) tracer.all_calls() ###Output _____no_output_____ ###Markdown The `invariants()` method produces a set of properties that hold for the observed runs, together with their instantiations over function arguments. ###Code invs = tracer.invariants('square_root') invs ###Output _____no_output_____ ###Markdown As before, the actual instantiations are easier to read: ###Code def pretty_invariants(invariants: Invariants) -> List[str]: props = [] for (prop, var_names) in invariants: props.append(instantiate_prop(prop, var_names)) return sorted(props) pretty_invariants(invs) ###Output _____no_output_____ ###Markdown We see that the both `x` and the return value have a `float` type. We also see that both are always greater than zero. These are properties that may make useful pre- and postconditions, notably for symbolic analysis. However, there's also an invariant which does _not_ universally hold, namely `return_value <= x`, as the following example shows: ###Code square_root(0.01) ###Output _____no_output_____ ###Markdown Clearly, 0.1 > 0.01 holds. This is a case of us not learning from sufficiently diverse inputs. As soon as we have a call including `x = 0.1`, though, the invariant `return_value <= x` is eliminated: ###Code with InvariantTracer() as tracer: y = square_root(25.0) y = square_root(10.0) y = square_root(0.01) pretty_invariants(tracer.invariants('square_root')) ###Output _____no_output_____ ###Markdown We will discuss later how to ensure sufficient diversity in inputs. (Hint: This involves test generation.) Let us try out our invariant tracer on `sum3()`. We see that all types are well-defined; the properties that all arguments are non-zero, however, is specific to the calls observed. ###Code with InvariantTracer() as tracer: y = sum3(1, 2, 3) y = sum3(-4, -5, -6) pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with strings instead, we get different invariants. Notably, we obtain the postcondition that the returned string always starts with the string in the first argument `a` – a universal postcondition if strings are used. ###Code with InvariantTracer() as tracer: y = sum3('a', 'b', 'c') y = sum3('f', 'e', 'd') pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with both strings and numbers (and zeros, too), there are no properties left that would hold across all calls. That's the price of flexibility. ###Code with InvariantTracer() as tracer: y = sum3('a', 'b', 'c') y = sum3('c', 'b', 'a') y = sum3(-4, -5, -6) y = sum3(0, 0, 0) pretty_invariants(tracer.invariants('sum3')) ###Output _____no_output_____ ###Markdown Converting Mined Invariants to AnnotationsAs with types, above, we would like to have some functionality where we can add the mined invariants as annotations to existing functions. To this end, we introduce the `InvariantAnnotator` class, extending `InvariantTracer`. We start with a helper method. `params()` returns a comma-separated list of parameter names as observed during calls. ###Code class InvariantAnnotator(InvariantTracer): def params(self, function_name: str) -> str: arguments, return_value = self.calls(function_name)[0] return ", ".join(arg_name for (arg_name, arg_value) in arguments) with InvariantAnnotator() as annotator: y = square_root(25.0) y = sum3(1, 2, 3) annotator.params('square_root') annotator.params('sum3') ###Output _____no_output_____ ###Markdown Now for the actual annotation. `preconditions()` returns the preconditions from the mined invariants (i.e., those propertes that do not depend on the return value) as a string with annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = ("@precondition(lambda " + self.params(function_name) + ": " + inv + ")") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) annotator.preconditions('square_root') ###Output _____no_output_____ ###Markdown `postconditions()` does the same for postconditions: ###Code class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = (f"@postcondition(lambda {RETURN_VALUE}," f" {self.params(function_name)}: {inv})") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) annotator.postconditions('square_root') ###Output _____no_output_____ ###Markdown With these, we can take a function and add both pre- and postconditions as annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def functions_with_invariants(self) -> str: functions = "" for function_name in self.all_invariants(): try: function = self.function_with_invariants(function_name) except KeyError: continue functions += function return functions def function_with_invariants(self, function_name: str) -> str: function = globals()[function_name] # Can throw KeyError source = inspect.getsource(function) return '\n'.join(self.preconditions(function_name) + self.postconditions(function_name)) + \ '\n' + source ###Output _____no_output_____ ###Markdown Here comes `function_with_invariants()` in all its glory: ###Code with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) y = sum3(1, 2, 3) print_content(annotator.function_with_invariants('square_root'), '.py') ###Output _____no_output_____ ###Markdown Quite a number of invariants, isn't it? Further below (and in the exercises), we will discuss on how to focus on the most relevant properties. Avoiding OverspecializationMined specifications can only be as good as the executions they were mined from. If we only see a single call, for instance, we will be faced with several mined pre- and postconditions that _overspecialize_ towards the values seen. Let us illustrate this effect on a simple `sum2()` function which adds two numbers. ###Code def sum2(a, b): # type: ignore return a + b ###Output _____no_output_____ ###Markdown If we invoke `sum2()` with a variety of arguments, the invariants all capture the relationship between `a`, `b`, and the return value as `return_value == a + b` in all its variations. ###Code with InvariantAnnotator() as annotator: sum2(31, 45) sum2(0, 0) sum2(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown If, however, we see only a single call, the invariants will overspecialize to the single call seen: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown The mined precondition `a == b`, for instance, only holds for the single call observed; the same holds for the mined postcondition `return_value == a b`. Yet, `sum2()` can obviously be successfully called with other values that do not satisfy these conditions. To get out of this trap, we have to _learn from more and more diverse runs_. One way to obtain such runs is by _generating_ inputs. Indeed, a simple test generator for calls of `sum2()` will easily resolve the problem. ###Code import random with InvariantAnnotator() as annotator: for i in range(100): a = random.randrange(-10, +10) b = random.randrange(-10, +10) length = sum2(a, b) print_content(annotator.function_with_invariants('sum2'), '.py') ###Output _____no_output_____ ###Markdown Note, though, that an API test generator, such as above, will have to be set up such that it actually respects preconditions – in our case, we invoke `sum2()` with integers only, already assuming its precondition. In some way, one thus needs a specification (a model, a grammar) to mine another specification – a chicken-and-egg problem. However, there is one way out of this problem: If one can automatically generate tests at the system level, then one has an _infinite source of executions_ to learn invariants from. In each of these executions, all functions would be called with values that satisfy the (implicit) precondition, allowing us to mine invariants for these functions. This holds, because at the system level, invalid inputs must be rejected by the system in the first place. The meaningful precondition at the system level, ensuring that only valid inputs get through, thus gets broken down into a multitude of meaningful preconditions (and subsequent postconditions) at the function level. The big requirement for all this, though, is that one needs good test generators. This will be the subject of another book, namely [The Fuzzing Book](https://www.fuzzingbook.org/). Partial InvariantsFor debugging, it can be helpful to focus on invariants produced only by _failing_ runs, thus characterizing the _circumstances under which a function fails_. Let us illustrate this on an example. The `middle()` function from the [chapter on statistical debugging](StatisticalDebugger.ipynb) is supposed to return the middle of three integers `x`, `y`, and `z`. ###Code from StatisticalDebugger import middle # minor dependency with InvariantAnnotator() as annotator: for i in range(100): x = random.randrange(-10, +10) y = random.randrange(-10, +10) z = random.randrange(-10, +10) mid = middle(x, y, z) ###Output _____no_output_____ ###Markdown By default, our `InvariantAnnotator()` does not return any particular pre- or postcondition (other than the types observed). That is just fine, as the function indeed imposes no particular precondition; and the postcondition from `middle()` is not covered by the `InvariantAnnotator` patterns. ###Code print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Things get more interesting if we focus on a particular subset of runs only, though - say, a set of inputs where `middle()` fails. ###Code from StatisticalDebugger import MIDDLE_FAILING_TESTCASES # minor dependency with InvariantAnnotator() as annotator: for x, y, z in MIDDLE_FAILING_TESTCASES: mid = middle(x, y, z) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Now that's an intimidating set of pre- and postconditions. However, almost all of the preconditions are implied by the one precondition```python@precondition(lambda x, y, z: y < x < z, doc='y < x < z')```which characterizes the exact condition under which `middle()` fails (which also happens to be the condition under which the erroneous second `return y` is executed). By checking how _invariants for failing runs_ differ from _invariants for passing runs_, we can identify circumstances for function failures. ###Code quiz("Could `InvariantAnnotator` also determine a precondition " "that characterizes _passing_ runs?", [ "Yes", "No" ], 'int(math.exp(1))', globals()) ###Output _____no_output_____ ###Markdown Indeed, it cannot – the correct invariant for passing runs would be the _inverse_ of the invariant for failing runs, and `not A < B < C` is not part of our invariant library. We can easily test this: ###Code from StatisticalDebugger import MIDDLE_PASSING_TESTCASES # minor dependency with InvariantAnnotator() as annotator: for x, y, z in MIDDLE_PASSING_TESTCASES: mid = middle(x, y, z) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Some ExamplesLet us try out the `InvariantAnnotator` on a number of examples. Removing HTML MarkupRunning `InvariantAnnotator` on our ongoing example `remove_html_markup()` does not provide much, as our invariant properties are tailored towards numerical functions. ###Code from Intro_Debugging import remove_html_markup with InvariantAnnotator() as annotator: remove_html_markup("<foo>bar</foo>") remove_html_markup("bar") remove_html_markup('"bar"') print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown In the [chapter on DDSet](DDSetDebugger.ipynb), we will see how to express more complex properties for structured inputs. A Recursive FunctionHere's another example. `list_length()` recursively computes the length of a Python function. Let us see whether we can mine its invariants: ###Code def list_length(elems: List[Any]) -> int: if elems == []: length = 0 else: length = 1 + list_length(elems[1:]) return length with InvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Almost all these properties are relevant. Of course, the reason the invariants are so neat is that the return value is equal to `len(elems)` is that `X == len(Y)` is part of the list of properties to be checked. Sum of two NumbersThe next example is a very simple function: If we have a function without return value, the return value is `None` and we can only mine preconditions. (Well, we get a "postcondition" `not return_value` that the return value evaluates to False, which holds for `None`). ###Code def print_sum(a, b): # type: ignore print(a + b) with InvariantAnnotator() as annotator: print_sum(31, 45) print_sum(0, 0) print_sum(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Checking SpecificationsA function with invariants, as above, can be fed into the Python interpreter, such that all pre- and postconditions are checked. We create a function `square_root_annotated()` which includes all the invariants mined above. ###Code with InvariantAnnotator() as annotator: y = square_root(25.0) y = square_root(0.01) square_root_def = annotator.functions_with_invariants() square_root_def = square_root_def.replace('square_root', 'square_root_annotated') print_content(square_root_def, '.py') exec(square_root_def) ###Output _____no_output_____ ###Markdown The "annotated" version checks against invalid arguments – or more precisely, against arguments with properties that have not been observed yet: ###Code with ExpectError(): square_root_annotated(-1.0) # type: ignore ###Output _____no_output_____ ###Markdown This is in contrast to the original version, which just hangs on negative values: ###Code with ExpectTimeout(1): square_root(-1.0) ###Output _____no_output_____ ###Markdown If we make changes to the function definition such that the properties of the return value change, such _regressions_ are caught as violations of the postconditions. Let us illustrate this by simply inverting the result, and return $-2$ as square root of 4. ###Code square_root_def = square_root_def.replace('square_root_annotated', 'square_root_negative') square_root_def = square_root_def.replace('return approx', 'return -approx') print_content(square_root_def, '.py') exec(square_root_def) ###Output _____no_output_____ ###Markdown Technically speaking, $-2$ _is_ a square root of 4, since $(-2)^2 = 4$ holds. Yet, such a change may be unexpected by callers of `square_root()`, and hence, this would be caught with the first call: ###Code with ExpectError(): square_root_negative(2.0) # type: ignore ###Output _____no_output_____ ###Markdown We see how pre- and postconditions, as well as types, can serve as oracles during testing. In particular, once we have mined them for a set of functions, we can check them again and again with test generators – especially after code changes. The more checks we have, and the more specific they are, the more likely it is we can detect unwanted effects of changes. SynopsisThis chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator: ###Code def sum2(a, b): # type: ignore return a + b with TypeAnnotator() as type_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution. ###Code print(type_annotator.typed_functions()) ###Output _____no_output_____ ###Markdown The invariant annotator works in a similar fashion: ###Code with InvariantAnnotator() as inv_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values. ###Code print(inv_annotator.functions_with_invariants()) ###Output _____no_output_____ ###Markdown Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs). The chapter gives details on how to customize the properties checked for. Lessons Learned* Type annotations and explicit invariants allow for _checking_ arguments and results for expected data types and other properties.* One can automatically _mine_ data types and invariants by observing arguments and results at runtime.* The quality of mined invariants depends on the diversity of values observed during executions; this variety can be increased by generating tests. Next StepsIn the next chapter, we will explore [abstracting failure conditions](DDSetDebugger.ipynb). BackgroundThe [DAIKON dynamic invariant detector](https://plse.cs.washington.edu/daikon/) can be considered the mother of function specification miners. Continuously maintained and extended for more than 20 years, it mines likely invariants in the style of this chapter for a variety of languages, including C, C++, C, Eiffel, F, Java, Perl, and Visual Basic. On top of the functionality discussed above, it holds a rich catalog of patterns for likely invariants, supports data invariants, can eliminate invariants that are implied by others, and determines statistical confidence to disregard unlikely invariants. The corresponding paper \cite{Ernst2001} is one of the seminal and most-cited papers of Software Engineering. A multitude of works have been published based on DAIKON and detecting invariants; see this [curated list](http://plse.cs.washington.edu/daikon/pubs/) for details. The interaction between test generators and invariant detection is already discussed in \cite{Ernst2001} (incidentally also using grammars). The Eclat tool \cite{Pacheco2005} is a model example of tight interaction between a unit-level test generator and DAIKON-style invariant mining, where the mined invariants are used to produce oracles and to systematically guide the test generator towards fault-revealing inputs. Mining specifications is not restricted to pre- and postconditions. The paper "Mining Specifications" \cite{Ammons2002} is another classic in the field, learning state protocols from executions. Grammar mining \cite{Gopinath2020} can also be seen as a specification mining approach, this time learning specifications for input formats. As it comes to adding type annotations to existing code, the blog post ["The state of type hints in Python"](https://www.bernat.tech/the-state-of-type-hints-in-python/) gives a great overview on how Python type hints can be used and checked. To add type annotations, there are two important tools available that also implement our above approach:* [MonkeyType](https://instagram-engineering.com/let-your-code-type-hint-itself-introducing-open-source-monkeytype-a855c7284881) implements the above approach of tracing executions and annotating Python 3 arguments, returns, and variables with type hints.* [PyAnnotate](https://github.com/dropbox/pyannotate) does a similar job, focusing on code in Python 2. It does not produce Python 3-style annotations, but instead produces annotations as comments that can be processed by static type checkers.These tools have been created by engineers at Facebook and Dropbox, respectively, assisting them in checking millions of lines of code for type issues. ExercisesOur code for mining types and invariants is in no way complete. There are dozens of ways to extend our implementations, some of which we discuss in exercises. Exercise 1: Union TypesThe Python `typing` module allows to express that an argument can have multiple types. For `square_root(x)`, this allows to express that `x` can be an `int` or a `float`: ###Code def square_root_with_union_type(x: Union[int, float]) -> float: # type: ignore ... ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it supports union types for arguments and return values. Use `Optional[X]` as a shorthand for `Union[X, None]`. Solution. Left to the reader. Hint: extend `type_string()`. Exercise 2: Types for Local VariablesIn Python, one cannot only annotate arguments with types, but actually also local and global variables – for instance, `approx` and `guess` in our `square_root()` implementation: ###Code def square_root_with_local_types(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" approx: Optional[float] = None guess: float = x / 2 while approx != guess: approx: float = guess # type: ignore guess: float = (approx + x / approx) / 2 # type: ignore return approx ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it also annotates local variables with types. Search the function AST for assignments, determine the type of the assigned value, and make it an annotation on the left hand side. Solution. Left to the reader. Exercise 3: Verbose Invariant CheckersOur implementation of invariant checkers does not make it clear for the user which pre-/postcondition failed. ###Code @precondition(lambda s: len(s) > 0) def remove_first_char(s: str) -> str: return s[1:] with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown The following implementation adds an optional `doc` keyword argument which is printed if the invariant is violated: ###Code def my_condition(precondition: Optional[Callable] = None, postcondition: Optional[Callable] = None, doc: str = 'Unknown') -> Callable: def decorator(func: Callable) -> Callable: @functools.wraps(func) # preserves name, docstring, etc def wrapper(args: Any, kwargs: Any) -> Any: if precondition is not None: assert precondition(args, *kwargs), "Precondition violated: " + doc retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, kwargs), "Postcondition violated: " + doc return retval return wrapper return decorator def my_precondition(check: Callable, kwargs: Any) -> Callable: return my_condition(precondition=check, doc=kwargs.get('doc', 'Unknown')) def my_postcondition(check: Callable, kwargs: Any) -> Callable: return my_condition(postcondition=check, doc=kwargs.get('doc', 'Unknown')) @my_precondition(lambda s: len(s) > 0, doc="len(s) > 0") # type: ignore def remove_first_char(s: str) -> str: return s[1:] remove_first_char('abc') with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown Extend `InvariantAnnotator` such that it includes the conditions in the generated pre- and postconditions. Solution.** Here's a simple solution: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@my_precondition(lambda " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")" conditions.append(cond) return conditions class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name: str) -> List[str]: conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@my_postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")") conditions.append(cond) return conditions ###Output _____no_output_____ ###Markdown The resulting annotations are harder to read, but easier to diagnose: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown As an alternative, one may be able to use `inspect.getsource()` on the lambda expression or unparse it. This is left to the reader. Exercise 4: Save Initial ValuesIf the value of an argument changes during function execution, this can easily confuse our implementation: The values are tracked at the beginning of the function, but checked only when it returns. Extend the `InvariantAnnotator` and the infrastructure it uses such that* it saves argument values both at the beginning and at the end of a function invocation;* postconditions can be expressed over both _initial_ values of arguments as well as the _final_ values of arguments;* the mined postconditions refer to both these values as well. Solution. To be added. Exercise 5: ImplicationsSeveral mined invariant are actually _implied_ by others: If `x > 0` holds, then this implies `x >= 0` and `x != 0`. Extend the `InvariantAnnotator` such that implications between properties are explicitly encoded, and such that implied properties are no longer listed as invariants. See \cite{Ernst2001} for ideas. Solution. Left to the reader. Exercise 6: Local VariablesPostconditions may also refer to the values of local variables. Consider extending `InvariantAnnotator` and its infrastructure such that the values of local variables at the end of the execution are also recorded and made part of the invariant inference mechanism. Solution. Left to the reader. Exercise 7: Embedding Invariants as AssertionsRather than producing invariants as annotations for pre- and postconditions, insert them as `assert` statements into the function code, as in:```pythondef square_root(x): 'Computes the square root of x, using the Newton-Raphson method' assert isinstance(x, int), 'violated precondition' assert x > 0, 'violated precondition' approx = None guess = (x / 2) while (approx != guess): approx = guess guess = ((approx + (x / approx)) / 2) return_value = approx assert return_value < x, 'violated postcondition' assert isinstance(return_value, float), 'violated postcondition' return approx```Such a formulation may make it easier for test generators and symbolic analysis to access and interpret pre- and postconditions. Solution. Here is a tentative implementation that inserts invariants into function ASTs. Part 1: Embedding Invariants into Functions ###Code class EmbeddedInvariantAnnotator(InvariantTracer): def function_with_invariants_ast(self, function_name: str) -> ast.AST: return annotate_function_with_invariants(function_name, self.invariants(function_name)) def function_with_invariants(self, function_name: str) -> str: return astor.to_source(self.function_with_invariants_ast(function_name)) def annotate_invariants(invariants: Dict[str, Invariants]) -> Dict[str, ast.AST]: annotated_functions = {} for function_name in invariants: try: annotated_functions[function_name] = annotate_function_with_invariants(function_name, invariants[function_name]) except KeyError: continue return annotated_functions def annotate_function_with_invariants(function_name: str, function_invariants: Invariants) -> ast.AST: function = globals()[function_name] function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_invariants(function_ast, function_invariants) def annotate_function_ast_with_invariants(function_ast: ast.AST, function_invariants: Invariants) -> ast.AST: annotated_function_ast = EmbeddedInvariantTransformer(function_invariants).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Part 2: Preconditions ###Code class PreconditionTransformer(ast.NodeTransformer): def __init__(self, invariants: Invariants) -> None: self.invariants = invariants super().__init__() def preconditions(self) -> List[ast.stmt]: preconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated precondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) < 0: preconditions += assertion_ast.body return preconditions def insert_assertions(self, body: List[ast.stmt]) -> List[ast.stmt]: preconditions = self.preconditions() try: docstring = cast(ast.Constant, body[0]).value.s except: docstring = None if docstring: return [body[0]] + preconditions + body[1:] else: return preconditions + body def visit_FunctionDef(self, node: ast.FunctionDef) -> ast.FunctionDef: """Add invariants to function""" # print(ast.dump(node)) node.body = self.insert_assertions(node.body) return node class EmbeddedInvariantTransformer(PreconditionTransformer): pass with EmbeddedInvariantAnnotator() as annotator: square_root(5) print_content(annotator.function_with_invariants('square_root'), '.py') with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.function_with_invariants('sum3'), '.py') ###Output _____no_output_____ ###Markdown Part 3: PostconditionsWe make a few simplifying assumptions: * Variables do not change during execution.* There is a single `return` statement at the end of the function. ###Code class EmbeddedInvariantTransformer(EmbeddedInvariantTransformer): def postconditions(self) -> List[ast.stmt]: postconditions = [] for (prop, var_names) in self.invariants: assertion = ("assert " + instantiate_prop(prop, var_names) + ', "violated postcondition"') assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) >= 0: postconditions += assertion_ast.body return postconditions def insert_assertions(self, body: List[ast.stmt]) -> List[ast.stmt]: new_body = super().insert_assertions(body) postconditions = self.postconditions() body_ends_with_return = isinstance(new_body[-1], ast.Return) if body_ends_with_return: ret_val = cast(ast.Return, new_body[-1]).value saver = RETURN_VALUE + " = " + astor.to_source(ret_val) else: saver = RETURN_VALUE + " = None" saver_ast = cast(ast.stmt, ast.parse(saver)) postconditions = [saver_ast] + postconditions if body_ends_with_return: return new_body[:-1] + postconditions + [new_body[-1]] else: return new_body + postconditions with EmbeddedInvariantAnnotator() as annotator: square_root(5) square_root_def = annotator.function_with_invariants('square_root') ###Output _____no_output_____ ###Markdown Here's the full definition with included assertions: ###Code print_content(square_root_def, '.py') exec(square_root_def.replace('square_root', 'square_root_annotated')) with ExpectError(): square_root_annotated(-1) ###Output _____no_output_____ ###Markdown Here come some more examples: ###Code with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.function_with_invariants('sum3'), '.py') with EmbeddedInvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.function_with_invariants('list_length'), '.py') with EmbeddedInvariantAnnotator() as annotator: print_sum(31, 45) print_content(annotator.function_with_invariants('print_sum'), '.py') ###Output _____no_output_____ ###Markdown Our goal is to avoid such errors by _annotating_ functions with information that prevents errors like the above ones. The idea is to provide a _specification_ of expected properties – a specification that can then be checked at runtime or statically. \todo{Introduce the concept of contract.} Specifying and Checking Data TypesFor our Python code, one of the most important "specifications" we need is types. Python being a "dynamically" typed language means that all data types are determined at run time; the code itself does not explicitly state whether a variable is an integer, a string, an array, a dictionary – or whatever. As _writer_ of Python code, omitting explicit type declarations may save time (and allows for some fun hacks). It is not sure whether a lack of types helps in _reading_ and _understanding_ code for humans. For a _computer_ trying to analyze code, the lack of explicit types is detrimental. If, say, a constraint solver, sees `if x:` and cannot know whether `x` is supposed to be a number or a string, this introduces an _ambiguity_. Such ambiguities may multiply over the entire analysis in a combinatorial explosion – or in the analysis yielding an overly inaccurate result. Python 3.6 and later allows data types as _annotations_ to function arguments (actually, to all variables) and return values. We can, for instance, state that `my_sqrt()` is a function that accepts a floating-point value and returns one: ###Code def my_sqrt_with_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return my_sqrt(x) ###Output _____no_output_____ ###Markdown By default, such annotations are ignored by the Python interpreter. Therefore, one can still call `my_sqrt_typed()` with a string as an argument and get the exact same result as above. However, one can make use of special _typechecking_ modules that would check types – _dynamically_ at runtime or _statically_ by analyzing the code without having to execute it. Runtime Type CheckingThe Python `enforce` package provides a function decorator that automatically inserts type-checking code that is executed at runtime. Here is how to use it: ###Code import enforce @enforce.runtime_validation def my_sqrt_with_checked_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return my_sqrt(x) ###Output _____no_output_____ ###Markdown Now, invoking `my_sqrt_with_checked_type_annotations()` raises an exception when invoked with a type dfferent from the one declared: ###Code with ExpectError(): my_sqrt_with_checked_type_annotations(True) ###Output _____no_output_____ ###Markdown Note that this error is not caught by the "untyped" variant, where passing a boolean value happily returns $\sqrt{1}$ as result. ###Code my_sqrt(True) ###Output _____no_output_____ ###Markdown In Python (and other languages), the boolean values `True` and `False` can be implicitly converted to the integers 1 and 0; however, it is hard to think of a call to `sqrt()` where this would not be an error. Static Type CheckingType annotations can also be checked _statically_ – that is, without even running the code. Let us create a simple Python file consisting of the above `my_sqrt_typed()` definition and a bad invocation. ###Code import inspect import tempfile f = tempfile.NamedTemporaryFile(mode='w', suffix='.py') f.name f.write(inspect.getsource(my_sqrt)) f.write('\n') f.write(inspect.getsource(my_sqrt_with_type_annotations)) f.write('\n') f.write("print(my_sqrt_with_type_annotations('123'))\n") f.flush() ###Output _____no_output_____ ###Markdown These are the contents of our newly created Python file: ###Code from bookutils import print_file print_file(f.name) ###Output _____no_output_____ ###Markdown [Mypy](http://mypy-lang.org) is a type checker for Python programs. As it checks types statically, types induce no overhead at runtime; plus, a static check can be faster than a lengthy series of tests with runtime type checking enabled. Let us see what `mypy` produces on the above file: ###Code import subprocess result = subprocess.run(["mypy", "--strict", f.name], universal_newlines=True, stdout=subprocess.PIPE) del f # Delete temporary file print(result.stdout) ###Output _____no_output_____ ###Markdown We see that `mypy` complains about untyped function definitions such as `my_sqrt()`; most important, however, it finds that the call to `my_sqrt_with_type_annotations()` in the last line has the wrong type. With `mypy`, we can achieve the same type safety with Python as in statically typed languages – provided that we as programmers also produce the necessary type annotations. Is there a simple way to obtain these? Mining Type SpecificationsOur first task will be to mine type annotations (as part of the code) from _values_ we observe at run time. These type annotations would be _mined_ from actual function executions, _learning_ from (normal) runs what the expected argument and return types should be. By observing a series of calls such as these, we could infer that both `x` and the return value are of type `float`: ###Code y = my_sqrt(25.0) y y = my_sqrt(2.0) y ###Output _____no_output_____ ###Markdown How can we mine types from executions? The answer is simple: 1. We _observe_ a function during execution2. We track the _types_ of its arguments3. We include these types as _annotations_ into the code.To do so, we can make use of Python's tracing facility we already observed in the [chapter on coverage](Coverage.ipynb). With every call to a function, we retrieve the arguments, their values, and their types. Tracking CallsTo observe argument types at runtime, we define a _tracer function_ that tracks the execution of `my_sqrt()`, checking its arguments and return values. The `Tracker` class is set to trace functions in a `with` block as follows:```pythonwith Tracker() as tracker: function_to_be_tracked(...)info = tracker.collected_information()```As in the [chapter on coverage](Coverage.ipynb), we use the `sys.settrace()` function to trace individual functions during execution. We turn on tracking when the `with` block starts; at this point, the `__enter__()` method is called. When execution of the `with` block ends, `__exit()__` is called. ###Code import sys class Tracker(object): def __init__(self, log=False): self._log = log self.reset() def reset(self): self._calls = {} self._stack = [] def traceit(self): """Placeholder to be overloaded in subclasses""" pass # Start of `with` block def __enter__(self): self.original_trace_function = sys.gettrace() sys.settrace(self.traceit) return self # End of `with` block def __exit__(self, exc_type, exc_value, tb): sys.settrace(self.original_trace_function) ###Output _____no_output_____ ###Markdown The `traceit()` method does nothing yet; this is done in specialized subclasses. The `CallTracker` class implements a `traceit()` function that checks for function calls and returns: ###Code class CallTracker(Tracker): def traceit(self, frame, event, arg): """Tracking function: Record all calls and all args""" if event == "call": self.trace_call(frame, event, arg) elif event == "return": self.trace_return(frame, event, arg) return self.traceit ###Output _____no_output_____ ###Markdown `trace_call()` is called when a function is called; it retrieves the function name and current arguments, and saves them on a stack. ###Code class CallTracker(CallTracker): def trace_call(self, frame, event, arg): """Save current function name and args on the stack""" code = frame.f_code function_name = code.co_name arguments = get_arguments(frame) self._stack.append((function_name, arguments)) if self._log: print(simple_call_string(function_name, arguments)) def get_arguments(frame): """Return call arguments in the given frame""" # When called, all arguments are local variables arguments = [(var, frame.f_locals[var]) for var in frame.f_locals] arguments.reverse() # Want same order as call return arguments ###Output _____no_output_____ ###Markdown When the function returns, `trace_return()` is called. We now also have the return value. We log the whole call with arguments and return value (if desired) and save it in our list of calls. ###Code class CallTracker(CallTracker): def trace_return(self, frame, event, arg): """Get return value and store complete call with arguments and return value""" code = frame.f_code function_name = code.co_name return_value = arg # TODO: Could call get_arguments() here to also retrieve _final_ values of argument variables called_function_name, called_arguments = self._stack.pop() assert function_name == called_function_name if self._log: print(simple_call_string(function_name, called_arguments), "returns", return_value) self.add_call(function_name, called_arguments, return_value) ###Output _____no_output_____ ###Markdown `simple_call_string()` is a helper for logging that prints out calls in a user-friendly manner. ###Code def simple_call_string(function_name, argument_list, return_value=None): """Return function_name(arg[0], arg[1], ...) as a string""" call = function_name + "(" + \ ", ".join([var + "=" + repr(value) for (var, value) in argument_list]) + ")" if return_value is not None: call += " = " + repr(return_value) return call ###Output _____no_output_____ ###Markdown `add_call()` saves the calls in a list; each function name has its own list. ###Code class CallTracker(CallTracker): def add_call(self, function_name, arguments, return_value=None): """Add given call to list of calls""" if function_name not in self._calls: self._calls[function_name] = [] self._calls[function_name].append((arguments, return_value)) ###Output _____no_output_____ ###Markdown Using `calls()`, we can retrieve the list of calls, either for a given function, or for all functions. ###Code class CallTracker(CallTracker): def calls(self, function_name=None): """Return list of calls for function_name, or a mapping function_name -> calls for all functions tracked""" if function_name is None: return self._calls return self._calls[function_name] ###Output _____no_output_____ ###Markdown Let us now put this to use. We turn on logging to track the individual calls and their return values: ###Code with CallTracker(log=True) as tracker: y = my_sqrt(25) y = my_sqrt(2.0) ###Output _____no_output_____ ###Markdown After execution, we can retrieve the individual calls: ###Code calls = tracker.calls('my_sqrt') calls ###Output _____no_output_____ ###Markdown Each call is pair (`argument_list`, `return_value`), where `argument_list` is a list of pairs (`parameter_name`, `value`). ###Code my_sqrt_argument_list, my_sqrt_return_value = calls[0] simple_call_string('my_sqrt', my_sqrt_argument_list, my_sqrt_return_value) ###Output _____no_output_____ ###Markdown If the function does not return a value, `return_value` is `None`. ###Code def hello(name): print("Hello,", name) with CallTracker() as tracker: hello("world") hello_calls = tracker.calls('hello') hello_calls hello_argument_list, hello_return_value = hello_calls[0] simple_call_string('hello', hello_argument_list, hello_return_value) ###Output _____no_output_____ ###Markdown Getting TypesDespite what you may have read or heard, Python actually _is_ a typed language. It is just that it is _dynamically typed_ – types are used and checked only at runtime (rather than declared in the code, where they can be _statically checked_ at compile time). We can thus retrieve types of all values within Python: ###Code type(4) type(2.0) type([4]) ###Output _____no_output_____ ###Markdown We can retrieve the type of the first argument to `my_sqrt()`: ###Code parameter, value = my_sqrt_argument_list[0] parameter, type(value) ###Output _____no_output_____ ###Markdown as well as the type of the return value: ###Code type(my_sqrt_return_value) ###Output _____no_output_____ ###Markdown Hence, we see that (so far), `my_sqrt()` is a function taking (among others) integers and returning floats. We could declare `my_sqrt()` as: ###Code def my_sqrt_annotated(x: int) -> float: return my_sqrt(x) ###Output _____no_output_____ ###Markdown This is a representation we could place in a static type checker, allowing to check whether calls to `my_sqrt()` actually pass a number. A dynamic type checker could run such checks at runtime. And of course, any [symbolic interpretation](SymbolicFuzzer.ipynb) will greatly profit from the additional annotations. By default, Python does not do anything with such annotations. However, tools can access annotations from functions and other objects: ###Code my_sqrt_annotated.__annotations__ ###Output _____no_output_____ ###Markdown This is how run-time checkers access the annotations to check against. Accessing Function StructureOur plan is to annotate functions automatically, based on the types we have seen. To do so, we need a few modules that allow us to convert a function into a tree representation (called _abstract syntax trees_, or ASTs) and back; we already have seen these in the chapters on [concolic](ConcolicFuzzer.ipynb) and [symbolic](SymbolicFuzzer.ipynb) testing. ###Code import ast import inspect import astor ###Output _____no_output_____ ###Markdown We can get the source of a Python function using `inspect.getsource()`. (Note that this does not work for functions defined in other notebooks.) ###Code my_sqrt_source = inspect.getsource(my_sqrt) my_sqrt_source ###Output _____no_output_____ ###Markdown To view these in a visually pleasing form, our function `print_content(s, suffix)` formats and highlights the string `s` as if it were a file with ending `suffix`. We can thus view (and highlight) the source as if it were a Python file: ###Code from bookutils import print_content print_content(my_sqrt_source, '.py') ###Output _____no_output_____ ###Markdown Parsing this gives us an abstract syntax tree (AST) – a representation of the program in tree form. ###Code my_sqrt_ast = ast.parse(my_sqrt_source) ###Output _____no_output_____ ###Markdown What does this AST look like? The helper functions `astor.dump_tree()` (textual output) and `showast.show_ast()` (graphical output with [showast](https://github.com/hchasestevens/show_ast)) allow us to inspect the structure of the tree. We see that the function starts as a `FunctionDef` with name and arguments, followed by a body, which is a list of statements of type `Expr` (the docstring), type `Assign` (assignments), `While` (while loop with its own body), and finally `Return`. ###Code print(astor.dump_tree(my_sqrt_ast)) ###Output _____no_output_____ ###Markdown Too much text for you? This graphical representation may make things simpler. ###Code from bookutils import rich_output if rich_output(): import showast showast.show_ast(my_sqrt_ast) ###Output _____no_output_____ ###Markdown The function `astor.to_source()` converts such a tree back into the more familiar textual Python code representation. Comments are gone, and there may be more parentheses than before, but the result has the same semantics: ###Code print_content(astor.to_source(my_sqrt_ast), '.py') ###Output _____no_output_____ ###Markdown Annotating Functions with Given TypesLet us now go and transform these trees ti add type annotations. We start with a helper function `parse_type(name)` which parses a type name into an AST. ###Code def parse_type(name): class ValueVisitor(ast.NodeVisitor): def visit_Expr(self, node): self.value_node = node.value tree = ast.parse(name) name_visitor = ValueVisitor() name_visitor.visit(tree) return name_visitor.value_node print(astor.dump_tree(parse_type('int'))) print(astor.dump_tree(parse_type('[object]'))) ###Output _____no_output_____ ###Markdown We now define a helper function that actually adds type annotations to a function AST. The `TypeTransformer` class builds on the Python standard library `ast.NodeTransformer` infrastructure. It would be called as```python TypeTransformer({'x': 'int'}, 'float').visit(ast)```to annotate the arguments of `my_sqrt()`: `x` with `int`, and the return type with `float`. The returned AST can then be unparsed, compiled or analyzed. ###Code class TypeTransformer(ast.NodeTransformer): def __init__(self, argument_types, return_type=None): self.argument_types = argument_types self.return_type = return_type super().__init__() ###Output _____no_output_____ ###Markdown The core of `TypeTransformer` is the method `visit_FunctionDef()`, which is called for every function definition in the AST. Its argument `node` is the subtree of the function definition to be transformed. Our implementation accesses the individual arguments and invokes `annotate_args()` on them; it also sets the return type in the `returns` attribute of the node. ###Code class TypeTransformer(TypeTransformer): def visit_FunctionDef(self, node): """Add annotation to function""" # Set argument types new_args = [] for arg in node.args.args: new_args.append(self.annotate_arg(arg)) new_arguments = ast.arguments( new_args, node.args.vararg, node.args.kwonlyargs, node.args.kw_defaults, node.args.kwarg, node.args.defaults ) # Set return type if self.return_type is not None: node.returns = parse_type(self.return_type) return ast.copy_location(ast.FunctionDef(node.name, new_arguments, node.body, node.decorator_list, node.returns), node) ###Output _____no_output_____ ###Markdown Each argument gets its own annotation, taken from the types originally passed to the class: ###Code class TypeTransformer(TypeTransformer): def annotate_arg(self, arg): """Add annotation to single function argument""" arg_name = arg.arg if arg_name in self.argument_types: arg.annotation = parse_type(self.argument_types[arg_name]) return arg ###Output _____no_output_____ ###Markdown Does this work? Let us annotate the AST from `my_sqrt()` with types for the arguments and return types: ###Code new_ast = TypeTransformer({'x': 'int'}, 'float').visit(my_sqrt_ast) ###Output _____no_output_____ ###Markdown When we unparse the new AST, we see that the annotations actually are present: ###Code print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown Similarly, we can annotate the `hello()` function from above: ###Code hello_source = inspect.getsource(hello) hello_ast = ast.parse(hello_source) new_ast = TypeTransformer({'name': 'str'}, 'None').visit(hello_ast) print_content(astor.to_source(new_ast), '.py') ###Output _____no_output_____ ###Markdown Annotating Functions with Mined TypesLet us now annotate functions with types mined at runtime. We start with a simple function `type_string()` that determines the appropriate type of a given value (as a string): ###Code def type_string(value): return type(value).__name__ type_string(4) type_string([]) ###Output _____no_output_____ ###Markdown For composite structures, `type_string()` does not examine element types; hence, the type of `[3]` is simply `list` instead of, say, `list[int]`. For now, `list` will do fine. ###Code type_string([3]) ###Output _____no_output_____ ###Markdown `type_string()` will be used to infer the types of argument values found at runtime, as returned by `CallTracker.calls()`: ###Code with CallTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(2.0) tracker.calls() ###Output _____no_output_____ ###Markdown The function `annotate_types()` takes such a list of calls and annotates each function listed: ###Code def annotate_types(calls): annotated_functions = {} for function_name in calls: try: annotated_functions[function_name] = annotate_function_with_types(function_name, calls[function_name]) except KeyError: continue return annotated_functions ###Output _____no_output_____ ###Markdown For each function, we get the source and its AST and then get to the actual annotation in `annotate_function_ast_with_types()`: ###Code def annotate_function_with_types(function_name, function_calls): function = globals()[function_name] # May raise KeyError for internal functions function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_types(function_ast, function_calls) ###Output _____no_output_____ ###Markdown The function `annotate_function_ast_with_types()` invokes the `TypeTransformer` with the calls seen, and for each call, iterate over the arguments, determine their types, and annotate the AST with these. The universal type `Any` is used when we encounter type conflicts, which we will discuss below. ###Code from typing import Any def annotate_function_ast_with_types(function_ast, function_calls): parameter_types = {} return_type = None for calls_seen in function_calls: args, return_value = calls_seen if return_value is not None: if return_type is not None and return_type != type_string(return_value): return_type = 'Any' else: return_type = type_string(return_value) for parameter, value in args: try: different_type = parameter_types[parameter] != type_string(value) except KeyError: different_type = False if different_type: parameter_types[parameter] = 'Any' else: parameter_types[parameter] = type_string(value) annotated_function_ast = TypeTransformer(parameter_types, return_type).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Here is `my_sqrt()` annotated with the types recorded usign the tracker, above. ###Code print_content(astor.to_source(annotate_types(tracker.calls())['my_sqrt']), '.py') ###Output _____no_output_____ ###Markdown All-in-one AnnotationLet us bring all of this together in a single class `TypeAnnotator` that first tracks calls of functions and then allows to access the AST (and the source code form) of the tracked functions annotated with types. The method `typed_functions()` returns the annotated functions as a string; `typed_functions_ast()` returns their AST. ###Code class TypeTracker(CallTracker): pass class TypeAnnotator(TypeTracker): def typed_functions_ast(self, function_name=None): if function_name is None: return annotate_types(self.calls()) return annotate_function_with_types(function_name, self.calls(function_name)) def typed_functions(self, function_name=None): if function_name is None: functions = '' for f_name in self.calls(): try: f_text = astor.to_source(self.typed_functions_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions return astor.to_source(self.typed_functions_ast(function_name)) ###Output _____no_output_____ ###Markdown Here is how to use `TypeAnnotator`. We first track a series of calls: ###Code with TypeAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(2.0) ###Output _____no_output_____ ###Markdown After tracking, we can immediately retrieve an annotated version of the functions tracked: ###Code print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown This also works for multiple and diverse functions. One could go and implement an automatic type annotator for Python files based on the types seen during execution. ###Code with TypeAnnotator() as annotator: hello('type annotations') y = my_sqrt(1.0) print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown A content as above could now be sent to a type checker, which would detect any type inconsistency between callers and callees. Likewise, type annotations such as the ones above greatly benefit symbolic code analysis (as in the chapter on [symbolic fuzzing](SymbolicFuzzer.ipynb)), as they effectively constrain the set of values that arguments and variables can take. Multiple TypesLet us now resolve the role of the magic `Any` type in `annotate_function_ast_with_types()`. If we see multiple types for the same argument, we set its type to `Any`. For `my_sqrt()`, this makes sense, as its arguments can be integers as well as floats: ###Code with CallTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(4) print_content(astor.to_source(annotate_types(tracker.calls())['my_sqrt']), '.py') ###Output _____no_output_____ ###Markdown The following function `sum3()` can be called with floating-point numbers as arguments, resulting in the parameters getting a `float` type: ###Code def sum3(a, b, c): return a + b + c with TypeAnnotator() as annotator: y = sum3(1.0, 2.0, 3.0) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we call `sum3()` with integers, though, the arguments get an `int` type: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown And we can also call `sum3()` with strings, giving the arguments a `str` type: ###Code with TypeAnnotator() as annotator: y = sum3("one", "two", "three") y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we have multiple calls, but with different types, `TypeAnnotator()` will assign an `Any` type to both arguments and return values: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y = sum3("one", "two", "three") typed_sum3_def = annotator.typed_functions('sum3') print_content(typed_sum3_def, '.py') ###Output _____no_output_____ ###Markdown A type `Any` makes it explicit that an object can, indeed, have any type; it will not be typechecked at runtime or statically. To some extent, this defeats the power of type checking; but it also preserves some of the type flexibility that many Python programmers enjoy. Besides `Any`, the `typing` module supports several additional ways to define ambiguous types; we will keep this in mind for a later exercise. Specifying and Checking InvariantsBesides basic data types. we can check several further properties from arguments. We can, for instance, whether an argument can be negative, zero, or positive; or that one argument should be smaller than the second; or that the result should be the sum of two arguments – properties that cannot be expressed in a (Python) type.Such properties are called invariants, as they hold across all invocations of a function. Specifically, invariants come as _pre_- and _postconditions_ – conditions that always hold at the beginning and at the end of a function. (There are also _data_ and _object_ invariants that express always-holding properties over the state of data or objects, but we do not consider these in this book.) Annotating Functions with Pre- and PostconditionsThe classical means to specify pre- and postconditions is via _assertions_, which we have introduced in the [chapter on testing](Intro_Testing.ipynb). A precondition checks whether the arguments to a function satisfy the expected properties; a postcondition does the same for the result. We can express and check both using assertions as follows: ###Code def my_sqrt_with_invariants(x): assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown A nicer way, however, is to syntactically separate invariants from the function at hand. Using appropriate decorators, we could specify pre- and postconditions as follows:```python@precondition lambda x: x >= 0@postcondition lambda return_value, x: return_value * return_value == xdef my_sqrt_with_invariants(x): normal code without assertions ...```The decorators `@precondition` and `@postcondition` would run the given functions (specified as anonymous `lambda` functions) before and after the decorated function, respectively. If the functions return `False`, the condition is violated. `@precondition` gets the function arguments as arguments; `@postcondition` additionally gets the return value as first argument. It turns out that implementing such decorators is not hard at all. Our implementation builds on a [code snippet from StackOverflow](https://stackoverflow.com/questions/12151182/python-precondition-postcondition-for-member-function-how): ###Code import functools def condition(precondition=None, postcondition=None): def decorator(func): @functools.wraps(func) # preserves name, docstring, etc def wrapper(args, kwargs): if precondition is not None: assert precondition(args, *kwargs), "Precondition violated" retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, *kwargs), "Postcondition violated" return retval return wrapper return decorator def precondition(check): return condition(precondition=check) def postcondition(check): return condition(postcondition=check) ###Output _____no_output_____ ###Markdown With these, we can now start decorating `my_sqrt()`: ###Code @precondition(lambda x: x > 0) def my_sqrt_with_precondition(x): return my_sqrt(x) ###Output _____no_output_____ ###Markdown This catches arguments violating the precondition: ###Code with ExpectError(): my_sqrt_with_precondition(-1.0) ###Output _____no_output_____ ###Markdown Likewise, we can provide a postcondition: ###Code EPSILON = 1e-5 @postcondition(lambda ret, x: ret ret - x < EPSILON) def my_sqrt_with_postcondition(x): return my_sqrt(x) y = my_sqrt_with_postcondition(2.0) y ###Output _____no_output_____ ###Markdown If we have a buggy implementation of $\sqrt{x}$, this gets caught quickly: ###Code @postcondition(lambda ret, x: ret * ret - x < EPSILON) def buggy_my_sqrt_with_postcondition(x): return my_sqrt(x) + 0.1 with ExpectError(): y = buggy_my_sqrt_with_postcondition(2.0) ###Output _____no_output_____ ###Markdown While checking pre- and postconditions is a great way to catch errors, specifying them can be cumbersome. Let us try to see whether we can (again) _mine_ some of them. Mining InvariantsTo _mine_ invariants, we can use the same tracking functionality as before; instead of saving values for individual variables, though, we now check whether the values satisfy specific _properties_ or not. For instance, if all values of `x` seen satisfy the condition `x > 0`, then we make `x > 0` an invariant of the function. If we see positive, zero, and negative values of `x`, though, then there is no property of `x` left to talk about.The general idea is thus:1. Check all variable values observed against a set of predefined properties; and2. Keep only those properties that hold for all runs observed. Defining PropertiesWhat precisely do we mean by properties? Here is a small collection of value properties that would frequently be used in invariants. All these properties would be evaluated with the _metavariables_ `X`, `Y`, and `Z` (actually, any upper-case identifier) being replaced with the names of function parameters: ###Code INVARIANT_PROPERTIES = [ "X < 0", "X <= 0", "X > 0", "X >= 0", "X == 0", "X != 0", ] ###Output _____no_output_____ ###Markdown When `my_sqrt(x)` is called as, say `my_sqrt(5.0)`, we see that `x = 5.0` holds. The above properties would then all be checked for `x`. Only the properties `X > 0`, `X >= 0`, and `X != 0` hold for the call seen; and hence `x > 0`, `x >= 0`, and `x != 0` would make potential preconditions for `my_sqrt(x)`. We can check for many more properties such as relations between two arguments: ###Code INVARIANT_PROPERTIES += [ "X == Y", "X > Y", "X < Y", "X >= Y", "X <= Y", ] ###Output _____no_output_____ ###Markdown Types also can be checked using properties. For any function parameter `X`, only one of these will hold: ###Code INVARIANT_PROPERTIES += [ "isinstance(X, bool)", "isinstance(X, int)", "isinstance(X, float)", "isinstance(X, list)", "isinstance(X, dict)", ] ###Output _____no_output_____ ###Markdown We can check for arithmetic properties: ###Code INVARIANT_PROPERTIES += [ "X == Y + Z", "X == Y * Z", "X == Y - Z", "X == Y / Z", ] ###Output _____no_output_____ ###Markdown Here's relations over three values, a Python special: ###Code INVARIANT_PROPERTIES += [ "X < Y < Z", "X <= Y <= Z", "X > Y > Z", "X >= Y >= Z", ] ###Output _____no_output_____ ###Markdown Finally, we can also check for list or string properties. Again, this is just a tiny selection. ###Code INVARIANT_PROPERTIES += [ "X == len(Y)", "X == sum(Y)", "X.startswith(Y)", ] ###Output _____no_output_____ ###Markdown Extracting Meta-VariablesLet us first introduce a few _helper functions_ before we can get to the actual mining. `metavars()` extracts the set of meta-variables (`X`, `Y`, `Z`, etc.) from a property. To this end, we parse the property as a Python expression and then visit the identifiers. ###Code def metavars(prop): metavar_list = [] class ArgVisitor(ast.NodeVisitor): def visit_Name(self, node): if node.id.isupper(): metavar_list.append(node.id) ArgVisitor().visit(ast.parse(prop)) return metavar_list assert metavars("X < 0") == ['X'] assert metavars("X.startswith(Y)") == ['X', 'Y'] assert metavars("isinstance(X, str)") == ['X'] ###Output _____no_output_____ ###Markdown Instantiating PropertiesTo produce a property as invariant, we need to be able to _instantiate_ it with variable names. The instantiation of `X > 0` with `X` being instantiated to `a`, for instance, gets us `a > 0`. To this end, the function `instantiate_prop()` takes a property and a collection of variable names and instantiates the meta-variables left-to-right with the corresponding variables names in the collection. ###Code def instantiate_prop_ast(prop, var_names): class NameTransformer(ast.NodeTransformer): def visit_Name(self, node): if node.id not in mapping: return node return ast.Name(id=mapping[node.id], ctx=ast.Load()) meta_variables = metavars(prop) assert len(meta_variables) == len(var_names) mapping = {} for i in range(0, len(meta_variables)): mapping[meta_variables[i]] = var_names[i] prop_ast = ast.parse(prop, mode='eval') new_ast = NameTransformer().visit(prop_ast) return new_ast def instantiate_prop(prop, var_names): prop_ast = instantiate_prop_ast(prop, var_names) prop_text = astor.to_source(prop_ast).strip() while prop_text.startswith('(') and prop_text.endswith(')'): prop_text = prop_text[1:-1] return prop_text assert instantiate_prop("X > Y", ['a', 'b']) == 'a > b' assert instantiate_prop("X.startswith(Y)", ['x', 'y']) == 'x.startswith(y)' ###Output _____no_output_____ ###Markdown Evaluating PropertiesTo actually _evaluate_ properties, we do not need to instantiate them. Instead, we simply convert them into a boolean function, using `lambda`: ###Code def prop_function_text(prop): return "lambda " + ", ".join(metavars(prop)) + ": " + prop def prop_function(prop): return eval(prop_function_text(prop)) ###Output _____no_output_____ ###Markdown Here is a simple example: ###Code prop_function_text("X > Y") p = prop_function("X > Y") p(100, 1) p(1, 100) ###Output _____no_output_____ ###Markdown Checking InvariantsTo extract invariants from an execution, we need to check them on all possible instantiations of arguments. If the function to be checked has two arguments `a` and `b`, we instantiate the property `X < Y` both as `a < b` and `b < a` and check each of them. To get all combinations, we use the Python `permutations()` function: ###Code import itertools for combination in itertools.permutations([1.0, 2.0, 3.0], 2): print(combination) ###Output _____no_output_____ ###Markdown The function `true_property_instantiations()` takes a property and a list of tuples (`var_name`, `value`). It then produces all instantiations of the property with the given values and returns those that evaluate to True. ###Code def true_property_instantiations(prop, vars_and_values, log=False): instantiations = set() p = prop_function(prop) len_metavars = len(metavars(prop)) for combination in itertools.permutations(vars_and_values, len_metavars): args = [value for var_name, value in combination] var_names = [var_name for var_name, value in combination] try: result = p(args) except: result = None if log: print(prop, combination, result) if result: instantiations.add((prop, tuple(var_names))) return instantiations ###Output _____no_output_____ ###Markdown Here is an example. If `x == -1` and `y == 1`, the property `X < Y` holds for `x < y`, but not for `y < x`: ###Code invs = true_property_instantiations("X < Y", [('x', -1), ('y', 1)], log=True) invs ###Output _____no_output_____ ###Markdown The instantiation retrieves the short form: ###Code for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Likewise, with values for `x` and `y` as above, the property `X < 0` only holds for `x`, but not for `y`: ###Code invs = true_property_instantiations("X < 0", [('x', -1), ('y', 1)], log=True) for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Extracting InvariantsLet us now run the above invariant extraction on function arguments and return values as observed during a function execution. To this end, we extend the `CallTracker` class into an `InvariantTracker` class, which automatically computes invariants for all functions and all calls observed during tracking. By default, an `InvariantTracker` uses the properties as defined above; however, one can specify alternate sets of properties. ###Code class InvariantTracker(CallTracker): def __init__(self, props=None, kwargs): if props is None: props = INVARIANT_PROPERTIES self.props = props super().__init__(kwargs) ###Output _____no_output_____ ###Markdown The key method of the `InvariantTracker` is the `invariants()` method. This iterates over the calls observed and checks which properties hold. Only the intersection of properties – that is, the set of properties that hold for all calls – is preserved, and eventually returned. The special variable `return_value` is set to hold the return value. ###Code RETURN_VALUE = 'return_value' class InvariantTracker(InvariantTracker): def invariants(self, function_name=None): if function_name is None: return {function_name: self.invariants(function_name) for function_name in self.calls()} invariants = None for variables, return_value in self.calls(function_name): vars_and_values = variables + [(RETURN_VALUE, return_value)] s = set() for prop in self.props: s \|= true_property_instantiations(prop, vars_and_values, self._log) if invariants is None: invariants = s else: invariants &= s return invariants ###Output _____no_output_____ ###Markdown Here's an example of how to use `invariants()`. We run the tracker on a small set of calls. ###Code with InvariantTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(10.0) tracker.calls() ###Output _____no_output_____ ###Markdown The `invariants()` method produces a set of properties that hold for the observed runs, together with their instantiations over function arguments. ###Code invs = tracker.invariants('my_sqrt') invs ###Output _____no_output_____ ###Markdown As before, the actual instantiations are easier to read: ###Code def pretty_invariants(invariants): props = [] for (prop, var_names) in invariants: props.append(instantiate_prop(prop, var_names)) return sorted(props) pretty_invariants(invs) ###Output _____no_output_____ ###Markdown We see that the both `x` and the return value have a `float` type. We also see that both are always greater than zero. These are properties that may make useful pre- and postconditions, notably for symbolic analysis. However, there's also an invariant which does _not_ universally hold, namely `return_value <= x`, as the following example shows: ###Code my_sqrt(0.01) ###Output _____no_output_____ ###Markdown Clearly, 0.1 > 0.01 holds. This is a case of us not learning from sufficiently diverse inputs. As soon as we have a call including `x = 0.1`, though, the invariant `return_value <= x` is eliminated: ###Code with InvariantTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(10.0) y = my_sqrt(0.01) pretty_invariants(tracker.invariants('my_sqrt')) ###Output _____no_output_____ ###Markdown We will discuss later how to ensure sufficient diversity in inputs. (Hint: This involves test generation.) Let us try out our invariant tracker on `sum3()`. We see that all types are well-defined; the properties that all arguments are non-zero, however, is specific to the calls observed. ###Code with InvariantTracker() as tracker: y = sum3(1, 2, 3) y = sum3(-4, -5, -6) pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with strings instead, we get different invariants. Notably, we obtain the postcondition that the return value starts with the value of `a` – a universal postcondition if strings are used. ###Code with InvariantTracker() as tracker: y = sum3('a', 'b', 'c') y = sum3('f', 'e', 'd') pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with both strings and numbers (and zeros, too), there are no properties left that would hold across all calls. That's the price of flexibility. ###Code with InvariantTracker() as tracker: y = sum3('a', 'b', 'c') y = sum3('c', 'b', 'a') y = sum3(-4, -5, -6) y = sum3(0, 0, 0) pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown Converting Mined Invariants to AnnotationsAs with types, above, we would like to have some functionality where we can add the mined invariants as annotations to existing functions. To this end, we introduce the `InvariantAnnotator` class, extending `InvariantTracker`. We start with a helper method. `params()` returns a comma-separated list of parameter names as observed during calls. ###Code class InvariantAnnotator(InvariantTracker): def params(self, function_name): arguments, return_value = self.calls(function_name)[0] return ", ".join(arg_name for (arg_name, arg_value) in arguments) with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = sum3(1, 2, 3) annotator.params('my_sqrt') annotator.params('sum3') ###Output _____no_output_____ ###Markdown Now for the actual annotation. `preconditions()` returns the preconditions from the mined invariants (i.e., those propertes that do not depend on the return value) as a string with annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@precondition(lambda " + self.params(function_name) + ": " + inv + ")" conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) annotator.preconditions('my_sqrt') ###Output _____no_output_____ ###Markdown `postconditions()` does the same for postconditions: ###Code class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ")") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) annotator.postconditions('my_sqrt') ###Output _____no_output_____ ###Markdown With these, we can take a function and add both pre- and postconditions as annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def functions_with_invariants(self): functions = "" for function_name in self.invariants(): try: function = self.function_with_invariants(function_name) except KeyError: continue functions += function return functions def function_with_invariants(self, function_name): function = globals()[function_name] # Can throw KeyError source = inspect.getsource(function) return "\n".join(self.preconditions(function_name) + self.postconditions(function_name)) + '\n' + source ###Output _____no_output_____ ###Markdown Here comes `function_with_invariants()` in all its glory: ###Code with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) print_content(annotator.function_with_invariants('my_sqrt'), '.py') ###Output _____no_output_____ ###Markdown Quite a lot of invariants, is it? Further below (and in the exercises), we will discuss on how to focus on the most relevant properties. Some ExamplesHere's another example. `list_length()` recursively computes the length of a Python function. Let us see whether we can mine its invariants: ###Code def list_length(L): if L == []: length = 0 else: length = 1 + list_length(L[1:]) return length with InvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Almost all these properties (except for the very first) are relevant. Of course, the reason the invariants are so neat is that the return value is equal to `len(L)` is that `X == len(Y)` is part of the list of properties to be checked. The next example is a very simple function: ###Code def sum2(a, b): return a + b with InvariantAnnotator() as annotator: sum2(31, 45) sum2(0, 0) sum2(-1, -5) ###Output _____no_output_____ ###Markdown The invariants all capture the relationship between `a`, `b`, and the return value as `return_value == a + b` in all its variations. ###Code print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown If we have a function without return value, the return value is `None` and we can only mine preconditions. (Well, we get a "postcondition" that the return value is non-zero, which holds for `None`). ###Code def print_sum(a, b): print(a + b) with InvariantAnnotator() as annotator: print_sum(31, 45) print_sum(0, 0) print_sum(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Checking SpecificationsA function with invariants, as above, can be fed into the Python interpreter, such that all pre- and postconditions are checked. We create a function `my_sqrt_annotated()` which includes all the invariants mined above. ###Code with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) my_sqrt_def = annotator.functions_with_invariants() my_sqrt_def = my_sqrt_def.replace('my_sqrt', 'my_sqrt_annotated') print_content(my_sqrt_def, '.py') exec(my_sqrt_def) ###Output _____no_output_____ ###Markdown The "annotated" version checks against invalid arguments – or more precisely, against arguments with properties that have not been observed yet: ###Code with ExpectError(): my_sqrt_annotated(-1.0) ###Output _____no_output_____ ###Markdown This is in contrast to the original version, which just hangs on negative values: ###Code with ExpectTimeout(1): my_sqrt(-1.0) ###Output _____no_output_____ ###Markdown If we make changes to the function definition such that the properties of the return value change, such _regressions_ are caught as violations of the postconditions. Let us illustrate this by simply inverting the result, and return $-2$ as square root of 4. ###Code my_sqrt_def = my_sqrt_def.replace('my_sqrt_annotated', 'my_sqrt_negative') my_sqrt_def = my_sqrt_def.replace('return approx', 'return -approx') print_content(my_sqrt_def, '.py') exec(my_sqrt_def) ###Output _____no_output_____ ###Markdown Technically speaking, $-2$ _is_ a square root of 4, since $(-2)^2 = 4$ holds. Yet, such a change may be unexpected by callers of `my_sqrt()`, and hence, this would be caught with the first call: ###Code with ExpectError(): my_sqrt_negative(2.0) ###Output _____no_output_____ ###Markdown We see how pre- and postconditions, as well as types, can serve as oracles* during testing. In particular, once we have mined them for a set of functions, we can check them again and again with test generators – especially after code changes. The more checks we have, and the more specific they are, the more likely it is we can detect unwanted effects of changes. Mining Specifications from Generated TestsMined specifications can only be as good as the executions they were mined from. If we only see a single call to, say, `sum2()`, we will be faced with several mined pre- and postconditions that _overspecialize_ towards the values seen: ###Code def sum2(a, b): return a + b with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown The mined precondition `a == b`, for instance, only holds for the single call observed; the same holds for the mined postcondition `return_value == a * b`. Yet, `sum2()` can obviously be successfully called with other values that do not satisfy these conditions. To get out of this trap, we have to _learn from more and more diverse runs_. If we have a few more calls of `sum2()`, we see how the set of invariants quickly gets smaller: ###Code with InvariantAnnotator() as annotator: length = sum2(1, 2) length = sum2(-1, -2) length = sum2(0, 0) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown But where to we get such diverse runs from? This is the job of generating software tests. A simple grammar for calls of `sum2()` will easily resolve the problem. ###Code from GrammarFuzzer import GrammarFuzzer # minor dependency from Grammars import is_valid_grammar, crange, convert_ebnf_grammar # minor dependency SUM2_EBNF_GRAMMAR = { "<start>": ["<sum2>"], "<sum2>": ["sum2(<int>, <int>)"], "<int>": ["<_int>"], "<_int>": ["(-)?<leaddigit><digit>", "0"], "<leaddigit>": crange('1', '9'), "<digit>": crange('0', '9') } assert is_valid_grammar(SUM2_EBNF_GRAMMAR) sum2_grammar = convert_ebnf_grammar(SUM2_EBNF_GRAMMAR) sum2_fuzzer = GrammarFuzzer(sum2_grammar) [sum2_fuzzer.fuzz() for i in range(10)] with InvariantAnnotator() as annotator: for i in range(10): eval(sum2_fuzzer.fuzz()) print_content(annotator.function_with_invariants('sum2'), '.py') ###Output _____no_output_____ ###Markdown But then, writing tests (or a test driver) just to derive a set of pre- and postconditions may possibly be too much effort – in particular, since tests can easily be derived from given pre- and postconditions in the first place. Hence, it would be wiser to first specify invariants and then let test generators or program provers do the job. Also, an API grammar, such as above, will have to be set up such that it actually respects preconditions – in our case, we invoke `sqrt()` with positive numbers only, already assuming its precondition. In some way, one thus needs a specification (a model, a grammar) to mine another specification – a chicken-and-egg problem. However, there is one way out of this problem: If one can automatically generate tests at the system level, then one has an _infinite source of executions_ to learn invariants from. In each of these executions, all functions would be called with values that satisfy the (implicit) precondition, allowing us to mine invariants for these functions. This holds, because at the system level, invalid inputs must be rejected by the system in the first place. The meaningful precondition at the system level, ensuring that only valid inputs get through, thus gets broken down into a multitude of meaningful preconditions (and subsequent postconditions) at the function level. The big requirement for this, though, is that one needs good test generators at the system level. In [the next part](05_Domain-Specific_Fuzzing.ipynb), we will discuss how to automatically generate tests for a variety of domains, from configuration to graphical user interfaces. SynopsisThis chapter provides two classes that automatically extract specifications from a function and a set of inputs: `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator: ###Code def sum2(a, b): return a + b with TypeAnnotator() as type_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution. ###Code print(type_annotator.typed_functions()) ###Output _____no_output_____ ###Markdown The invariant annotator works in a similar fashion: ###Code with InvariantAnnotator() as inv_annotator: sum2(1, 2) sum2(-4, -5) sum2(0, 0) ###Output _____no_output_____ ###Markdown The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values. ###Code print(inv_annotator.functions_with_invariants()) ###Output _____no_output_____ ###Markdown Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs) as well as for all kinds of _symbolic code analyses_. The chapter gives details on how to customize the properties checked for. Lessons Learned* Type annotations and explicit invariants allow for _checking_ arguments and results for expected data types and other properties.* One can automatically _mine_ data types and invariants by observing arguments and results at runtime.* The quality of mined invariants depends on the diversity of values observed during executions; this variety can be increased by generating tests. Next StepsThis chapter concludes the [part on semantical fuzzing techniques](04_Semantical_Fuzzing.ipynb). In the next part, we will explore [domain-specific fuzzing techniques](05_Domain-Specific_Fuzzing.ipynb) from configurations and APIs to graphical user interfaces. BackgroundThe [DAIKON dynamic invariant detector](https://plse.cs.washington.edu/daikon/) can be considered the mother of function specification miners. Continuously maintained and extended for more than 20 years, it mines likely invariants in the style of this chapter for a variety of languages, including C, C++, C, Eiffel, F, Java, Perl, and Visual Basic. On top of the functionality discussed above, it holds a rich catalog of patterns for likely invariants, supports data invariants, can eliminate invariants that are implied by others, and determines statistical confidence to disregard unlikely invariants. The corresponding paper \cite{Ernst2001} is one of the seminal and most-cited papers of Software Engineering. A multitude of works have been published based on DAIKON and detecting invariants; see this [curated list](http://plse.cs.washington.edu/daikon/pubs/) for details. The interaction between test generators and invariant detection is already discussed in \cite{Ernst2001} (incidentally also using grammars). The Eclat tool \cite{Pacheco2005} is a model example of tight interaction between a unit-level test generator and DAIKON-style invariant mining, where the mined invariants are used to produce oracles and to systematically guide the test generator towards fault-revealing inputs. Mining specifications is not restricted to pre- and postconditions. The paper "Mining Specifications" \cite{Ammons2002} is another classic in the field, learning state protocols from executions. Grammar mining, as described in [our chapter with the same name](GrammarMiner.ipynb) can also be seen as a specification mining approach, this time learning specifications for input formats. As it comes to adding type annotations to existing code, the blog post ["The state of type hints in Python"](https://www.bernat.tech/the-state-of-type-hints-in-python/) gives a great overview on how Python type hints can be used and checked. To add type annotations, there are two important tools available that also implement our above approach:* [MonkeyType](https://instagram-engineering.com/let-your-code-type-hint-itself-introducing-open-source-monkeytype-a855c7284881) implements the above approach of tracing executions and annotating Python 3 arguments, returns, and variables with type hints.* [PyAnnotate](https://github.com/dropbox/pyannotate) does a similar job, focusing on code in Python 2. It does not produce Python 3-style annotations, but instead produces annotations as comments that can be processed by static type checkers.These tools have been created by engineers at Facebook and Dropbox, respectively, assisting them in checking millions of lines of code for type issues. ExercisesOur code for mining types and invariants is in no way complete. There are dozens of ways to extend our implementations, some of which we discuss in exercises. Exercise 1: Union TypesThe Python `typing` module allows to express that an argument can have multiple types. For `my_sqrt(x)`, this allows to express that `x` can be an `int` or a `float`: ###Code from typing import Union, Optional def my_sqrt_with_union_type(x: Union[int, float]) -> float: ... ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it supports union types for arguments and return values. Use `Optional[X]` as a shorthand for `Union[X, None]`. Solution. Left to the reader. Hint: extend `type_string()`. Exercise 2: Types for Local VariablesIn Python, one cannot only annotate arguments with types, but actually also local and global variables – for instance, `approx` and `guess` in our `my_sqrt()` implementation: ###Code def my_sqrt_with_local_types(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" approx: Optional[float] = None guess: float = x / 2 while approx != guess: approx: float = guess guess: float = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it also annotates local variables with types. Search the function AST for assignments, determine the type of the assigned value, and make it an annotation on the left hand side. Solution. Left to the reader. Exercise 3: Verbose Invariant CheckersOur implementation of invariant checkers does not make it clear for the user which pre-/postcondition failed. ###Code @precondition(lambda s: len(s) > 0) def remove_first_char(s): return s[1:] with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown The following implementation adds an optional `doc` keyword argument which is printed if the invariant is violated: ###Code def condition(precondition=None, postcondition=None, doc='Unknown'): def decorator(func): @functools.wraps(func) # preserves name, docstring, etc def wrapper(args, kwargs): if precondition is not None: assert precondition(args, *kwargs), "Precondition violated: " + doc retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, kwargs), "Postcondition violated: " + doc return retval return wrapper return decorator def precondition(check, kwargs): return condition(precondition=check, doc=kwargs.get('doc', 'Unknown')) def postcondition(check, kwargs): return condition(postcondition=check, doc=kwargs.get('doc', 'Unknown')) @precondition(lambda s: len(s) > 0, doc="len(s) > 0") def remove_first_char(s): return s[1:] remove_first_char('abc') with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown Extend `InvariantAnnotator` such that it includes the conditions in the generated pre- and postconditions. Solution.** Here's a simple solution: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@precondition(lambda " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")" conditions.append(cond) return conditions class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")") conditions.append(cond) return conditions ###Output _____no_output_____ ###Markdown The resulting annotations are harder to read, but easier to diagnose: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown As an alternative, one may be able to use `inspect.getsource()` on the lambda expression or unparse it. This is left to the reader. Exercise 4: Save Initial ValuesIf the value of an argument changes during function execution, this can easily confuse our implementation: The values are tracked at the beginning of the function, but checked only when it returns. Extend the `InvariantAnnotator` and the infrastructure it uses such that* it saves argument values both at the beginning and at the end of a function invocation;* postconditions can be expressed over both _initial_ values of arguments as well as the _final_ values of arguments;* the mined postconditions refer to both these values as well. Solution. To be added. Exercise 5: ImplicationsSeveral mined invariant are actually _implied_ by others: If `x > 0` holds, then this implies `x >= 0` and `x != 0`. Extend the `InvariantAnnotator` such that implications between properties are explicitly encoded, and such that implied properties are no longer listed as invariants. See \cite{Ernst2001} for ideas. Solution. Left to the reader. Exercise 6: Local VariablesPostconditions may also refer to the values of local variables. Consider extending `InvariantAnnotator` and its infrastructure such that the values of local variables at the end of the execution are also recorded and made part of the invariant inference mechanism. Solution. Left to the reader. Exercise 7: Exploring Invariant AlternativesAfter mining a first set of invariants, have a [concolic fuzzer](ConcolicFuzzer.ipynb) generate tests that systematically attempt to invalidate pre- and postconditions. How far can you generalize? Solution. To be added. Exercise 8: Grammar-Generated PropertiesThe larger the set of properties to be checked, the more potential invariants can be discovered. Create a _grammar_ that systematically produces a large set of properties. See \cite{Ernst2001} for possible patterns. Solution. Left to the reader. Exercise 9: Embedding Invariants as AssertionsRather than producing invariants as annotations for pre- and postconditions, insert them as `assert` statements into the function code, as in:```pythondef my_sqrt(x): 'Computes the square root of x, using the Newton-Raphson method' assert isinstance(x, int), 'violated precondition' assert (x > 0), 'violated precondition' approx = None guess = (x / 2) while (approx != guess): approx = guess guess = ((approx + (x / approx)) / 2) return_value = approx assert (return_value < x), 'violated postcondition' assert isinstance(return_value, float), 'violated postcondition' return approx```Such a formulation may make it easier for test generators and symbolic analysis to access and interpret pre- and postconditions. Solution. Here is a tentative implementation that inserts invariants into function ASTs. Part 1: Embedding Invariants into Functions ###Code class EmbeddedInvariantAnnotator(InvariantTracker): def functions_with_invariants_ast(self, function_name=None): if function_name is None: return annotate_functions_with_invariants(self.invariants()) return annotate_function_with_invariants(function_name, self.invariants(function_name)) def functions_with_invariants(self, function_name=None): if function_name is None: functions = '' for f_name in self.invariants(): try: f_text = astor.to_source(self.functions_with_invariants_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions return astor.to_source(self.functions_with_invariants_ast(function_name)) def function_with_invariants(self, function_name): return self.functions_with_invariants(function_name) def function_with_invariants_ast(self, function_name): return self.functions_with_invariants_ast(function_name) def annotate_invariants(invariants): annotated_functions = {} for function_name in invariants: try: annotated_functions[function_name] = annotate_function_with_invariants(function_name, invariants[function_name]) except KeyError: continue return annotated_functions def annotate_function_with_invariants(function_name, function_invariants): function = globals()[function_name] function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_invariants(function_ast, function_invariants) def annotate_function_ast_with_invariants(function_ast, function_invariants): annotated_function_ast = EmbeddedInvariantTransformer(function_invariants).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Part 2: Preconditions ###Code class PreconditionTransformer(ast.NodeTransformer): def __init__(self, invariants): self.invariants = invariants super().__init__() def preconditions(self): preconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated precondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) < 0: preconditions += assertion_ast.body return preconditions def insert_assertions(self, body): preconditions = self.preconditions() try: docstring = body[0].value.s except: docstring = None if docstring: return [body[0]] + preconditions + body[1:] else: return preconditions + body def visit_FunctionDef(self, node): """Add invariants to function""" # print(ast.dump(node)) node.body = self.insert_assertions(node.body) return node class EmbeddedInvariantTransformer(PreconditionTransformer): pass with EmbeddedInvariantAnnotator() as annotator: my_sqrt(5) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Part 3: PostconditionsWe make a few simplifying assumptions: * Variables do not change during execution.* There is a single `return` statement at the end of the function. ###Code class EmbeddedInvariantTransformer(PreconditionTransformer): def postconditions(self): postconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated postcondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) >= 0: postconditions += assertion_ast.body return postconditions def insert_assertions(self, body): new_body = super().insert_assertions(body) postconditions = self.postconditions() body_ends_with_return = isinstance(new_body[-1], ast.Return) if body_ends_with_return: saver = RETURN_VALUE + " = " + astor.to_source(new_body[-1].value) else: saver = RETURN_VALUE + " = None" saver_ast = ast.parse(saver) postconditions = [saver_ast] + postconditions if body_ends_with_return: return new_body[:-1] + postconditions + [new_body[-1]] else: return new_body + postconditions with EmbeddedInvariantAnnotator() as annotator: my_sqrt(5) my_sqrt_def = annotator.functions_with_invariants() ###Output _____no_output_____ ###Markdown Here's the full definition with included assertions: ###Code print_content(my_sqrt_def, '.py') exec(my_sqrt_def.replace('my_sqrt', 'my_sqrt_annotated')) with ExpectError(): my_sqrt_annotated(-1) ###Output _____no_output_____ ###Markdown Here come some more examples: ###Code with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: print_sum(31, 45) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Mining Function SpecificationsWhen testing a program, one not only needs to cover its several behaviors; one also needs to _check_ whether the result is as expected. In this chapter, we introduce a technique that allows us to _mine_ function specifications from a set of given executions, resulting in abstract and formal _descriptions_ of what the function expects and what it delivers. These so-called _dynamic invariants_ produce pre- and post-conditions over function arguments and variables from a set of executions. They are useful in a variety of contexts:* Dynamic invariants provide important information for [symbolic fuzzing](SymbolicFuzzer.ipynb), such as types and ranges of function arguments.* Dynamic invariants provide pre- and postconditions for formal program proofs and verification.* Dynamic invariants provide a large number of assertions that can check whether function behavior has changed* Checks provided by dynamic invariants can be very useful as _oracles_ for checking the effects of generated testsTraditionally, dynamic invariants are dependent on the executions they are derived from. However, when paired with comprehensive test generators, they quickly become very precise, as we show in this chapter. Prerequisites* You should be familiar with tracing program executions, as in the [chapter on coverage](Coverage.ipynb).* Later in this section, we access the internal _abstract syntax tree_ representations of Python programs and transform them, as in the [chapter on information flow](InformationFlow.ipynb). ###Code import bookutils import Coverage import Intro_Testing ###Output _____no_output_____ ###Markdown SynopsisTo [use the code provided in this chapter](Importing.ipynb), write```python>>> from fuzzingbook.DynamicInvariants import ```and then make use of the following features.This chapter provides two classes that automatically extract specifications from a function and a set of inputs:* `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator:```python>>> def sum(a, b):>>> return a + b>>> with TypeAnnotator() as type_annotator:>>> sum(1, 2)>>> sum(-4, -5)>>> sum(0, 0)```The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution.```python>>> print(type_annotator.typed_functions())def sum(a: int, b: int) -> int: return a + b```The invariant annotator works in a similar fashion:```python>>> with InvariantAnnotator() as inv_annotator:>>> sum(1, 2)>>> sum(-4, -5)>>> sum(0, 0)```The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values.```python>>> print(inv_annotator.functions_with_invariants())@precondition(lambda b, a: isinstance(a, int))@precondition(lambda b, a: isinstance(b, int))@postcondition(lambda return_value, b, a: a == return_value - b)@postcondition(lambda return_value, b, a: b == return_value - a)@postcondition(lambda return_value, b, a: isinstance(return_value, int))@postcondition(lambda return_value, b, a: return_value == a + b)@postcondition(lambda return_value, b, a: return_value == b + a)def sum(a, b): return a + b```Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs) as well as for all kinds of _symbolic code analyses_. The chapter gives details on how to customize the properties checked for. Specifications and AssertionsWhen implementing a function or program, one usually works against a _specification_ – a set of documented requirements to be satisfied by the code. Such specifications can come in natural language. A formal specification, however, allows the computer to check whether the specification is satisfied.In the [introduction to testing](Intro_Testing.ipynb), we have seen how _preconditions_ and _postconditions_ can describe what a function does. Consider the following (simple) square root function: ###Code def any_sqrt(x): assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown The assertion `assert p` checks the condition `p`; if it does not hold, execution is aborted. Here, the actual body is not yet written; we use the assertions as a specification of what `any_sqrt()` _expects_, and what it _delivers_.The topmost assertion is the _precondition_, stating the requirements on the function arguments. The assertion at the end is the _postcondition_, stating the properties of the function result (including its relationship with the original arguments). Using these pre- and postconditions as a specification, we can now go and implement a square root function that satisfies them. Once implemented, we can have the assertions check at runtime whether `any_sqrt()` works as expected; a [symbolic](SymbolicFuzzer.ipynb) or [concolic](ConcolicFuzzer.ipynb) test generator will even specifically try to find inputs where the assertions do _not_ hold. (An assertion can be seen as a conditional branch towards aborting the execution, and any technique that tries to cover all code branches will also try to invalidate as many assertions as possible.) However, not every piece of code is developed with explicit specifications in the first place; let alone does most code comes with formal pre- and post-conditions. (Just take a look at the chapters in this book.) This is a pity: As Ken Thompson famously said, "Without specifications, there are no bugs – only surprises". It is also a problem for testing, since, of course, testing needs some specification to test against. This raises the interesting question: Can we somehow _retrofit_ existing code with "specifications" that properly describe their behavior, allowing developers to simply _check_ them rather than having to write them from scratch? This is what we do in this chapter. Why Generic Error Checking is Not EnoughBefore we go into _mining_ specifications, let us first discuss why it could be useful to _have_ them. As a motivating example, consider the full implementation of a square root function from the [introduction to testing](Intro_Testing.ipynb): ###Code import bookutils def my_sqrt(x): """Computes the square root of x, using the Newton-Raphson method""" approx = None guess = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown `my_sqrt()` does not come with any functionality that would check types or values. Hence, it is easy for callers to make mistakes when calling `my_sqrt()`: ###Code from ExpectError import ExpectError, ExpectTimeout with ExpectError(): my_sqrt("foo") with ExpectError(): x = my_sqrt(0.0) ###Output _____no_output_____ ###Markdown At least, the Python system catches these errors at runtime. The following call, however, simply lets the function enter an infinite loop: ###Code with ExpectTimeout(1): x = my_sqrt(-1.0) ###Output _____no_output_____ ###Markdown Our goal is to avoid such errors by _annotating_ functions with information that prevents errors like the above ones. The idea is to provide a _specification_ of expected properties – a specification that can then be checked at runtime or statically. \todo{Introduce the concept of contract.} Specifying and Checking Data TypesFor our Python code, one of the most important "specifications" we need is types. Python being a "dynamically" typed language means that all data types are determined at run time; the code itself does not explicitly state whether a variable is an integer, a string, an array, a dictionary – or whatever. As _writer_ of Python code, omitting explicit type declarations may save time (and allows for some fun hacks). It is not sure whether a lack of types helps in _reading_ and _understanding_ code for humans. For a _computer_ trying to analyze code, the lack of explicit types is detrimental. If, say, a constraint solver, sees `if x:` and cannot know whether `x` is supposed to be a number or a string, this introduces an _ambiguity_. Such ambiguities may multiply over the entire analysis in a combinatorial explosion – or in the analysis yielding an overly inaccurate result. Python 3.6 and later allows data types as _annotations_ to function arguments (actually, to all variables) and return values. We can, for instance, state that `my_sqrt()` is a function that accepts a floating-point value and returns one: ###Code def my_sqrt_with_type_annotations(x: float) -> float: """Computes the square root of x, using the Newton-Raphson method""" return my_sqrt(x) ###Output _____no_output_____ ###Markdown By default, such annotations are ignored by the Python interpreter. Therefore, one can still call `my_sqrt_typed()` with a string as an argument and get the exact same result as above. However, one can make use of special _typechecking_ modules that would check types – _dynamically_ at runtime or _statically_ by analyzing the code without having to execute it. Excursion: Runtime Type Checking(Commented out as `enforce` is not supported by Python 3.9)The Python `enforce` package provides a function decorator that automatically inserts type-checking code that is executed at runtime. Here is how to use it: ###Code # import enforce # @enforce.runtime_validation # def my_sqrt_with_checked_type_annotations(x: float) -> float: # """Computes the square root of x, using the Newton-Raphson method""" # return my_sqrt(x) ###Output _____no_output_____ ###Markdown Now, invoking `my_sqrt_with_checked_type_annotations()` raises an exception when invoked with a type dfferent from the one declared: ###Code # with ExpectError(): # my_sqrt_with_checked_type_annotations(True) ###Output _____no_output_____ ###Markdown Note that this error is not caught by the "untyped" variant, where passing a boolean value happily returns $\sqrt{1}$ as result. ###Code # my_sqrt(True) ###Output _____no_output_____ ###Markdown In Python (and other languages), the boolean values `True` and `False` can be implicitly converted to the integers 1 and 0; however, it is hard to think of a call to `sqrt()` where this would not be an error. End of Excursion Static Type CheckingType annotations can also be checked _statically_ – that is, without even running the code. Let us create a simple Python file consisting of the above `my_sqrt_typed()` definition and a bad invocation. ###Code import inspect import tempfile f = tempfile.NamedTemporaryFile(mode='w', suffix='.py') f.name f.write(inspect.getsource(my_sqrt)) f.write('\n') f.write(inspect.getsource(my_sqrt_with_type_annotations)) f.write('\n') f.write("print(my_sqrt_with_type_annotations('123'))\n") f.flush() ###Output _____no_output_____ ###Markdown These are the contents of our newly created Python file: ###Code from bookutils import print_file print_file(f.name) ###Output _____no_output_____ ###Markdown [Mypy](http://mypy-lang.org) is a type checker for Python programs. As it checks types statically, types induce no overhead at runtime; plus, a static check can be faster than a lengthy series of tests with runtime type checking enabled. Let us see what `mypy` produces on the above file: ###Code import subprocess result = subprocess.run(["mypy", "--strict", f.name], universal_newlines=True, stdout=subprocess.PIPE) del f # Delete temporary file print(result.stdout) ###Output _____no_output_____ ###Markdown We see that `mypy` complains about untyped function definitions such as `my_sqrt()`; most important, however, it finds that the call to `my_sqrt_with_type_annotations()` in the last line has the wrong type. With `mypy`, we can achieve the same type safety with Python as in statically typed languages – provided that we as programmers also produce the necessary type annotations. Is there a simple way to obtain these? Mining Type SpecificationsOur first task will be to mine type annotations (as part of the code) from _values_ we observe at run time. These type annotations would be _mined_ from actual function executions, _learning_ from (normal) runs what the expected argument and return types should be. By observing a series of calls such as these, we could infer that both `x` and the return value are of type `float`: ###Code y = my_sqrt(25.0) y y = my_sqrt(2.0) y ###Output _____no_output_____ ###Markdown How can we mine types from executions? The answer is simple: 1. We _observe_ a function during execution2. We track the _types_ of its arguments3. We include these types as _annotations_ into the code.To do so, we can make use of Python's tracing facility we already observed in the [chapter on coverage](Coverage.ipynb). With every call to a function, we retrieve the arguments, their values, and their types. Tracking CallsTo observe argument types at runtime, we define a _tracer function_ that tracks the execution of `my_sqrt()`, checking its arguments and return values. The `Tracker` class is set to trace functions in a `with` block as follows:```pythonwith Tracker() as tracker: function_to_be_tracked(...)info = tracker.collected_information()```As in the [chapter on coverage](Coverage.ipynb), we use the `sys.settrace()` function to trace individual functions during execution. We turn on tracking when the `with` block starts; at this point, the `__enter__()` method is called. When execution of the `with` block ends, `__exit()__` is called. ###Code import sys class Tracker: def __init__(self, log=False): self._log = log self.reset() def reset(self): self._calls = {} self._stack = [] def traceit(self): """Placeholder to be overloaded in subclasses""" pass # Start of `with` block def __enter__(self): self.original_trace_function = sys.gettrace() sys.settrace(self.traceit) return self # End of `with` block def __exit__(self, exc_type, exc_value, tb): sys.settrace(self.original_trace_function) ###Output _____no_output_____ ###Markdown The `traceit()` method does nothing yet; this is done in specialized subclasses. The `CallTracker` class implements a `traceit()` function that checks for function calls and returns: ###Code class CallTracker(Tracker): def traceit(self, frame, event, arg): """Tracking function: Record all calls and all args""" if event == "call": self.trace_call(frame, event, arg) elif event == "return": self.trace_return(frame, event, arg) return self.traceit ###Output _____no_output_____ ###Markdown `trace_call()` is called when a function is called; it retrieves the function name and current arguments, and saves them on a stack. ###Code class CallTracker(CallTracker): def trace_call(self, frame, event, arg): """Save current function name and args on the stack""" code = frame.f_code function_name = code.co_name arguments = get_arguments(frame) self._stack.append((function_name, arguments)) if self._log: print(simple_call_string(function_name, arguments)) def get_arguments(frame): """Return call arguments in the given frame""" # When called, all arguments are local variables local_variables = dict(frame.f_locals) # explicit copy arguments = [(var, frame.f_locals[var]) for var in local_variables] arguments.reverse() # Want same order as call return arguments ###Output _____no_output_____ ###Markdown When the function returns, `trace_return()` is called. We now also have the return value. We log the whole call with arguments and return value (if desired) and save it in our list of calls. ###Code class CallTracker(CallTracker): def trace_return(self, frame, event, arg): """Get return value and store complete call with arguments and return value""" code = frame.f_code function_name = code.co_name return_value = arg # TODO: Could call get_arguments() here to also retrieve _final_ values of argument variables called_function_name, called_arguments = self._stack.pop() assert function_name == called_function_name if self._log: print(simple_call_string(function_name, called_arguments), "returns", return_value) self.add_call(function_name, called_arguments, return_value) ###Output _____no_output_____ ###Markdown `simple_call_string()` is a helper for logging that prints out calls in a user-friendly manner. ###Code def simple_call_string(function_name, argument_list, return_value=None): """Return function_name(arg[0], arg[1], ...) as a string""" call = function_name + "(" + \ ", ".join([var + "=" + repr(value) for (var, value) in argument_list]) + ")" if return_value is not None: call += " = " + repr(return_value) return call ###Output _____no_output_____ ###Markdown `add_call()` saves the calls in a list; each function name has its own list. ###Code class CallTracker(CallTracker): def add_call(self, function_name, arguments, return_value=None): """Add given call to list of calls""" if function_name not in self._calls: self._calls[function_name] = [] self._calls[function_name].append((arguments, return_value)) ###Output _____no_output_____ ###Markdown Using `calls()`, we can retrieve the list of calls, either for a given function, or for all functions. ###Code class CallTracker(CallTracker): def calls(self, function_name=None): """Return list of calls for function_name, or a mapping function_name -> calls for all functions tracked""" if function_name is None: return self._calls return self._calls[function_name] ###Output _____no_output_____ ###Markdown Let us now put this to use. We turn on logging to track the individual calls and their return values: ###Code with CallTracker(log=True) as tracker: y = my_sqrt(25) y = my_sqrt(2.0) ###Output _____no_output_____ ###Markdown After execution, we can retrieve the individual calls: ###Code calls = tracker.calls('my_sqrt') calls ###Output _____no_output_____ ###Markdown Each call is pair (`argument_list`, `return_value`), where `argument_list` is a list of pairs (`parameter_name`, `value`). ###Code my_sqrt_argument_list, my_sqrt_return_value = calls[0] simple_call_string('my_sqrt', my_sqrt_argument_list, my_sqrt_return_value) ###Output _____no_output_____ ###Markdown If the function does not return a value, `return_value` is `None`. ###Code def hello(name): print("Hello,", name) with CallTracker() as tracker: hello("world") hello_calls = tracker.calls('hello') hello_calls hello_argument_list, hello_return_value = hello_calls[0] simple_call_string('hello', hello_argument_list, hello_return_value) ###Output _____no_output_____ ###Markdown Getting TypesDespite what you may have read or heard, Python actually _is_ a typed language. It is just that it is _dynamically typed_ – types are used and checked only at runtime (rather than declared in the code, where they can be _statically checked_ at compile time). We can thus retrieve types of all values within Python: ###Code type(4) type(2.0) type([4]) ###Output _____no_output_____ ###Markdown We can retrieve the type of the first argument to `my_sqrt()`: ###Code parameter, value = my_sqrt_argument_list[0] parameter, type(value) ###Output _____no_output_____ ###Markdown as well as the type of the return value: ###Code type(my_sqrt_return_value) ###Output _____no_output_____ ###Markdown Hence, we see that (so far), `my_sqrt()` is a function taking (among others) integers and floats and returning floats. We could declare `my_sqrt()` as: ###Code def my_sqrt_annotated(x: float) -> float: return my_sqrt(x) ###Output _____no_output_____ ###Markdown This is a representation we could place in a static type checker, allowing to check whether calls to `my_sqrt()` actually pass a number. A dynamic type checker could run such checks at runtime. And of course, any [symbolic interpretation](SymbolicFuzzer.ipynb) will greatly profit from the additional annotations. By default, Python does not do anything with such annotations. However, tools can access annotations from functions and other objects: ###Code my_sqrt_annotated.__annotations__ ###Output _____no_output_____ ###Markdown This is how run-time checkers access the annotations to check against. Accessing Function StructureOur plan is to annotate functions automatically, based on the types we have seen. To do so, we need a few modules that allow us to convert a function into a tree representation (called _abstract syntax trees_, or ASTs) and back; we already have seen these in the chapters on [concolic](ConcolicFuzzer.ipynb) and [symbolic](SymbolicFuzzer.ipynb) testing. ###Code import ast import inspect ###Output _____no_output_____ ###Markdown We can get the source of a Python function using `inspect.getsource()`. (Note that this does not work for functions defined in other notebooks.) ###Code my_sqrt_source = inspect.getsource(my_sqrt) my_sqrt_source ###Output _____no_output_____ ###Markdown To view these in a visually pleasing form, our function `print_content(s, suffix)` formats and highlights the string `s` as if it were a file with ending `suffix`. We can thus view (and highlight) the source as if it were a Python file: ###Code from bookutils import print_content print_content(my_sqrt_source, '.py') ###Output _____no_output_____ ###Markdown Parsing this gives us an abstract syntax tree (AST) – a representation of the program in tree form. ###Code my_sqrt_ast = ast.parse(my_sqrt_source) ###Output _____no_output_____ ###Markdown What does this AST look like? The helper functions `ast.dump()` (textual output) and `showast.show_ast()` (graphical output with [showast](https://github.com/hchasestevens/show_ast)) allow us to inspect the structure of the tree. We see that the function starts as a `FunctionDef` with name and arguments, followed by a body, which is a list of statements of type `Expr` (the docstring), type `Assign` (assignments), `While` (while loop with its own body), and finally `Return`. ###Code print(ast.dump(my_sqrt_ast, indent=4)) ###Output _____no_output_____ ###Markdown Too much text for you? This graphical representation may make things simpler. ###Code from bookutils import rich_output if rich_output(): import showast showast.show_ast(my_sqrt_ast) ###Output _____no_output_____ ###Markdown The function `ast.unparse()` converts such a tree back into the more familiar textual Python code representation. Comments are gone, and there may be more parentheses than before, but the result has the same semantics: ###Code print_content(ast.unparse(my_sqrt_ast), '.py') ###Output _____no_output_____ ###Markdown Annotating Functions with Given TypesLet us now go and transform these trees ti add type annotations. We start with a helper function `parse_type(name)` which parses a type name into an AST. ###Code def parse_type(name): class ValueVisitor(ast.NodeVisitor): def visit_Expr(self, node): self.value_node = node.value tree = ast.parse(name) name_visitor = ValueVisitor() name_visitor.visit(tree) return name_visitor.value_node print(ast.dump(parse_type('int'))) print(ast.dump(parse_type('[object]'))) ###Output _____no_output_____ ###Markdown We now define a helper function that actually adds type annotations to a function AST. The `TypeTransformer` class builds on the Python standard library `ast.NodeTransformer` infrastructure. It would be called as```python TypeTransformer({'x': 'int'}, 'float').visit(ast)```to annotate the arguments of `my_sqrt()`: `x` with `int`, and the return type with `float`. The returned AST can then be unparsed, compiled or analyzed. ###Code class TypeTransformer(ast.NodeTransformer): def __init__(self, argument_types, return_type=None): self.argument_types = argument_types self.return_type = return_type super().__init__() ###Output _____no_output_____ ###Markdown The core of `TypeTransformer` is the method `visit_FunctionDef()`, which is called for every function definition in the AST. Its argument `node` is the subtree of the function definition to be transformed. Our implementation accesses the individual arguments and invokes `annotate_args()` on them; it also sets the return type in the `returns` attribute of the node. ###Code class TypeTransformer(TypeTransformer): def visit_FunctionDef(self, node): """Add annotation to function""" # Set argument types new_args = [] for arg in node.args.args: new_args.append(self.annotate_arg(arg)) new_arguments = ast.arguments( node.args.posonlyargs, new_args, node.args.vararg, node.args.kwonlyargs, node.args.kw_defaults, node.args.kwarg, node.args.defaults ) # Set return type if self.return_type is not None: node.returns = parse_type(self.return_type) return ast.copy_location( ast.FunctionDef(node.name, new_arguments, node.body, node.decorator_list, node.returns), node) ###Output _____no_output_____ ###Markdown Each argument gets its own annotation, taken from the types originally passed to the class: ###Code class TypeTransformer(TypeTransformer): def annotate_arg(self, arg): """Add annotation to single function argument""" arg_name = arg.arg if arg_name in self.argument_types: arg.annotation = parse_type(self.argument_types[arg_name]) return arg ###Output _____no_output_____ ###Markdown Does this work? Let us annotate the AST from `my_sqrt()` with types for the arguments and return types: ###Code new_ast = TypeTransformer({'x': 'int'}, 'float').visit(my_sqrt_ast) ###Output _____no_output_____ ###Markdown When we unparse the new AST, we see that the annotations actually are present: ###Code print_content(ast.unparse(new_ast), '.py') ###Output _____no_output_____ ###Markdown Similarly, we can annotate the `hello()` function from above: ###Code hello_source = inspect.getsource(hello) hello_ast = ast.parse(hello_source) new_ast = TypeTransformer({'name': 'str'}, 'None').visit(hello_ast) print_content(ast.unparse(new_ast), '.py') ###Output _____no_output_____ ###Markdown Annotating Functions with Mined TypesLet us now annotate functions with types mined at runtime. We start with a simple function `type_string()` that determines the appropriate type of a given value (as a string): ###Code def type_string(value): return type(value).__name__ type_string(4) type_string([]) ###Output _____no_output_____ ###Markdown For composite structures, `type_string()` does not examine element types; hence, the type of `[3]` is simply `list` instead of, say, `list[int]`. For now, `list` will do fine. ###Code type_string([3]) ###Output _____no_output_____ ###Markdown `type_string()` will be used to infer the types of argument values found at runtime, as returned by `CallTracker.calls()`: ###Code with CallTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(2.0) tracker.calls() ###Output _____no_output_____ ###Markdown The function `annotate_types()` takes such a list of calls and annotates each function listed: ###Code def annotate_types(calls): annotated_functions = {} for function_name in calls: try: annotated_functions[function_name] = annotate_function_with_types(function_name, calls[function_name]) except KeyError: continue return annotated_functions ###Output _____no_output_____ ###Markdown For each function, we get the source and its AST and then get to the actual annotation in `annotate_function_ast_with_types()`: ###Code def annotate_function_with_types(function_name, function_calls): function = globals()[function_name] # May raise KeyError for internal functions function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_types(function_ast, function_calls) ###Output _____no_output_____ ###Markdown The function `annotate_function_ast_with_types()` invokes the `TypeTransformer` with the calls seen, and for each call, iterate over the arguments, determine their types, and annotate the AST with these. The universal type `Any` is used when we encounter type conflicts, which we will discuss below. ###Code from typing import Any def annotate_function_ast_with_types(function_ast, function_calls): parameter_types = {} return_type = None for calls_seen in function_calls: args, return_value = calls_seen if return_value is not None: if return_type is not None and return_type != type_string(return_value): return_type = 'Any' else: return_type = type_string(return_value) for parameter, value in args: try: different_type = parameter_types[parameter] != type_string(value) except KeyError: different_type = False if different_type: parameter_types[parameter] = 'Any' else: parameter_types[parameter] = type_string(value) annotated_function_ast = TypeTransformer(parameter_types, return_type).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Here is `my_sqrt()` annotated with the types recorded usign the tracker, above. ###Code print_content(ast.unparse(annotate_types(tracker.calls())['my_sqrt']), '.py') ###Output _____no_output_____ ###Markdown All-in-one AnnotationLet us bring all of this together in a single class `TypeAnnotator` that first tracks calls of functions and then allows to access the AST (and the source code form) of the tracked functions annotated with types. The method `typed_functions()` returns the annotated functions as a string; `typed_functions_ast()` returns their AST. ###Code class TypeTracker(CallTracker): pass class TypeAnnotator(TypeTracker): def typed_functions_ast(self, function_name=None): if function_name is None: return annotate_types(self.calls()) return annotate_function_with_types(function_name, self.calls(function_name)) def typed_functions(self, function_name=None): if function_name is None: functions = '' for f_name in self.calls(): try: f_text = ast.unparse(self.typed_functions_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions return ast.unparse(self.typed_functions_ast(function_name)) ###Output _____no_output_____ ###Markdown Here is how to use `TypeAnnotator`. We first track a series of calls: ###Code with TypeAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(2.0) ###Output _____no_output_____ ###Markdown After tracking, we can immediately retrieve an annotated version of the functions tracked: ###Code print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown This also works for multiple and diverse functions. One could go and implement an automatic type annotator for Python files based on the types seen during execution. ###Code with TypeAnnotator() as annotator: hello('type annotations') y = my_sqrt(1.0) print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown A content as above could now be sent to a type checker, which would detect any type inconsistency between callers and callees. Likewise, type annotations such as the ones above greatly benefit symbolic code analysis (as in the chapter on [symbolic fuzzing](SymbolicFuzzer.ipynb)), as they effectively constrain the set of values that arguments and variables can take. Multiple TypesLet us now resolve the role of the magic `Any` type in `annotate_function_ast_with_types()`. If we see multiple types for the same argument, we set its type to `Any`. For `my_sqrt()`, this makes sense, as its arguments can be integers as well as floats: ###Code with CallTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(4) print_content(ast.unparse(annotate_types(tracker.calls())['my_sqrt']), '.py') ###Output _____no_output_____ ###Markdown The following function `sum3()` can be called with floating-point numbers as arguments, resulting in the parameters getting a `float` type: ###Code def sum3(a, b, c): return a + b + c with TypeAnnotator() as annotator: y = sum3(1.0, 2.0, 3.0) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we call `sum3()` with integers, though, the arguments get an `int` type: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown And we can also call `sum3()` with strings, giving the arguments a `str` type: ###Code with TypeAnnotator() as annotator: y = sum3("one", "two", "three") y print_content(annotator.typed_functions(), '.py') ###Output _____no_output_____ ###Markdown If we have multiple calls, but with different types, `TypeAnnotator()` will assign an `Any` type to both arguments and return values: ###Code with TypeAnnotator() as annotator: y = sum3(1, 2, 3) y = sum3("one", "two", "three") typed_sum3_def = annotator.typed_functions('sum3') print_content(typed_sum3_def, '.py') ###Output _____no_output_____ ###Markdown A type `Any` makes it explicit that an object can, indeed, have any type; it will not be typechecked at runtime or statically. To some extent, this defeats the power of type checking; but it also preserves some of the type flexibility that many Python programmers enjoy. Besides `Any`, the `typing` module supports several additional ways to define ambiguous types; we will keep this in mind for a later exercise. Specifying and Checking InvariantsBesides basic data types. we can check several further properties from arguments. We can, for instance, whether an argument can be negative, zero, or positive; or that one argument should be smaller than the second; or that the result should be the sum of two arguments – properties that cannot be expressed in a (Python) type.Such properties are called invariants, as they hold across all invocations of a function. Specifically, invariants come as _pre_- and _postconditions_ – conditions that always hold at the beginning and at the end of a function. (There are also _data_ and _object_ invariants that express always-holding properties over the state of data or objects, but we do not consider these in this book.) Annotating Functions with Pre- and PostconditionsThe classical means to specify pre- and postconditions is via _assertions_, which we have introduced in the [chapter on testing](Intro_Testing.ipynb). A precondition checks whether the arguments to a function satisfy the expected properties; a postcondition does the same for the result. We can express and check both using assertions as follows: ###Code def my_sqrt_with_invariants(x): assert x >= 0 # Precondition ... assert result * result == x # Postcondition return result ###Output _____no_output_____ ###Markdown A nicer way, however, is to syntactically separate invariants from the function at hand. Using appropriate decorators, we could specify pre- and postconditions as follows:```python@precondition lambda x: x >= 0@postcondition lambda return_value, x: return_value * return_value == xdef my_sqrt_with_invariants(x): normal code without assertions ...```The decorators `@precondition` and `@postcondition` would run the given functions (specified as anonymous `lambda` functions) before and after the decorated function, respectively. If the functions return `False`, the condition is violated. `@precondition` gets the function arguments as arguments; `@postcondition` additionally gets the return value as first argument. It turns out that implementing such decorators is not hard at all. Our implementation builds on a [code snippet from StackOverflow](https://stackoverflow.com/questions/12151182/python-precondition-postcondition-for-member-function-how): ###Code import functools def condition(precondition=None, postcondition=None): def decorator(func): @functools.wraps(func) # preserves name, docstring, etc def wrapper(args, kwargs): if precondition is not None: assert precondition(args, *kwargs), "Precondition violated" retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, *kwargs), "Postcondition violated" return retval return wrapper return decorator def precondition(check): return condition(precondition=check) def postcondition(check): return condition(postcondition=check) ###Output _____no_output_____ ###Markdown With these, we can now start decorating `my_sqrt()`: ###Code @precondition(lambda x: x > 0) def my_sqrt_with_precondition(x): return my_sqrt(x) ###Output _____no_output_____ ###Markdown This catches arguments violating the precondition: ###Code with ExpectError(): my_sqrt_with_precondition(-1.0) ###Output _____no_output_____ ###Markdown Likewise, we can provide a postcondition: ###Code EPSILON = 1e-5 @postcondition(lambda ret, x: ret ret - x < EPSILON) def my_sqrt_with_postcondition(x): return my_sqrt(x) y = my_sqrt_with_postcondition(2.0) y ###Output _____no_output_____ ###Markdown If we have a buggy implementation of $\sqrt{x}$, this gets caught quickly: ###Code @postcondition(lambda ret, x: ret * ret - x < EPSILON) def buggy_my_sqrt_with_postcondition(x): return my_sqrt(x) + 0.1 with ExpectError(): y = buggy_my_sqrt_with_postcondition(2.0) ###Output _____no_output_____ ###Markdown While checking pre- and postconditions is a great way to catch errors, specifying them can be cumbersome. Let us try to see whether we can (again) _mine_ some of them. Mining InvariantsTo _mine_ invariants, we can use the same tracking functionality as before; instead of saving values for individual variables, though, we now check whether the values satisfy specific _properties_ or not. For instance, if all values of `x` seen satisfy the condition `x > 0`, then we make `x > 0` an invariant of the function. If we see positive, zero, and negative values of `x`, though, then there is no property of `x` left to talk about.The general idea is thus:1. Check all variable values observed against a set of predefined properties; and2. Keep only those properties that hold for all runs observed. Defining PropertiesWhat precisely do we mean by properties? Here is a small collection of value properties that would frequently be used in invariants. All these properties would be evaluated with the _metavariables_ `X`, `Y`, and `Z` (actually, any upper-case identifier) being replaced with the names of function parameters: ###Code INVARIANT_PROPERTIES = [ "X < 0", "X <= 0", "X > 0", "X >= 0", "X == 0", "X != 0", ] ###Output _____no_output_____ ###Markdown When `my_sqrt(x)` is called as, say `my_sqrt(5.0)`, we see that `x = 5.0` holds. The above properties would then all be checked for `x`. Only the properties `X > 0`, `X >= 0`, and `X != 0` hold for the call seen; and hence `x > 0`, `x >= 0`, and `x != 0` would make potential preconditions for `my_sqrt(x)`. We can check for many more properties such as relations between two arguments: ###Code INVARIANT_PROPERTIES += [ "X == Y", "X > Y", "X < Y", "X >= Y", "X <= Y", ] ###Output _____no_output_____ ###Markdown Types also can be checked using properties. For any function parameter `X`, only one of these will hold: ###Code INVARIANT_PROPERTIES += [ "isinstance(X, bool)", "isinstance(X, int)", "isinstance(X, float)", "isinstance(X, list)", "isinstance(X, dict)", ] ###Output _____no_output_____ ###Markdown We can check for arithmetic properties: ###Code INVARIANT_PROPERTIES += [ "X == Y + Z", "X == Y * Z", "X == Y - Z", "X == Y / Z", ] ###Output _____no_output_____ ###Markdown Here's relations over three values, a Python special: ###Code INVARIANT_PROPERTIES += [ "X < Y < Z", "X <= Y <= Z", "X > Y > Z", "X >= Y >= Z", ] ###Output _____no_output_____ ###Markdown Finally, we can also check for list or string properties. Again, this is just a tiny selection. ###Code INVARIANT_PROPERTIES += [ "X == len(Y)", "X == sum(Y)", "X.startswith(Y)", ] ###Output _____no_output_____ ###Markdown Extracting Meta-VariablesLet us first introduce a few _helper functions_ before we can get to the actual mining. `metavars()` extracts the set of meta-variables (`X`, `Y`, `Z`, etc.) from a property. To this end, we parse the property as a Python expression and then visit the identifiers. ###Code def metavars(prop): metavar_list = [] class ArgVisitor(ast.NodeVisitor): def visit_Name(self, node): if node.id.isupper(): metavar_list.append(node.id) ArgVisitor().visit(ast.parse(prop)) return metavar_list assert metavars("X < 0") == ['X'] assert metavars("X.startswith(Y)") == ['X', 'Y'] assert metavars("isinstance(X, str)") == ['X'] ###Output _____no_output_____ ###Markdown Instantiating PropertiesTo produce a property as invariant, we need to be able to _instantiate_ it with variable names. The instantiation of `X > 0` with `X` being instantiated to `a`, for instance, gets us `a > 0`. To this end, the function `instantiate_prop()` takes a property and a collection of variable names and instantiates the meta-variables left-to-right with the corresponding variables names in the collection. ###Code def instantiate_prop_ast(prop, var_names): class NameTransformer(ast.NodeTransformer): def visit_Name(self, node): if node.id not in mapping: return node return ast.Name(id=mapping[node.id], ctx=ast.Load()) meta_variables = metavars(prop) assert len(meta_variables) == len(var_names) mapping = {} for i in range(0, len(meta_variables)): mapping[meta_variables[i]] = var_names[i] prop_ast = ast.parse(prop, mode='eval') new_ast = NameTransformer().visit(prop_ast) return new_ast def instantiate_prop(prop, var_names): prop_ast = instantiate_prop_ast(prop, var_names) prop_text = ast.unparse(prop_ast).strip() while prop_text.startswith('(') and prop_text.endswith(')'): prop_text = prop_text[1:-1] return prop_text assert instantiate_prop("X > Y", ['a', 'b']) == 'a > b' assert instantiate_prop("X.startswith(Y)", ['x', 'y']) == 'x.startswith(y)' ###Output _____no_output_____ ###Markdown Evaluating PropertiesTo actually _evaluate_ properties, we do not need to instantiate them. Instead, we simply convert them into a boolean function, using `lambda`: ###Code def prop_function_text(prop): return "lambda " + ", ".join(metavars(prop)) + ": " + prop def prop_function(prop): return eval(prop_function_text(prop)) ###Output _____no_output_____ ###Markdown Here is a simple example: ###Code prop_function_text("X > Y") p = prop_function("X > Y") p(100, 1) p(1, 100) ###Output _____no_output_____ ###Markdown Checking InvariantsTo extract invariants from an execution, we need to check them on all possible instantiations of arguments. If the function to be checked has two arguments `a` and `b`, we instantiate the property `X < Y` both as `a < b` and `b < a` and check each of them. To get all combinations, we use the Python `permutations()` function: ###Code import itertools for combination in itertools.permutations([1.0, 2.0, 3.0], 2): print(combination) ###Output _____no_output_____ ###Markdown The function `true_property_instantiations()` takes a property and a list of tuples (`var_name`, `value`). It then produces all instantiations of the property with the given values and returns those that evaluate to True. ###Code def true_property_instantiations(prop, vars_and_values, log=False): instantiations = set() p = prop_function(prop) len_metavars = len(metavars(prop)) for combination in itertools.permutations(vars_and_values, len_metavars): args = [value for var_name, value in combination] var_names = [var_name for var_name, value in combination] try: result = p(args) except: result = None if log: print(prop, combination, result) if result: instantiations.add((prop, tuple(var_names))) return instantiations ###Output _____no_output_____ ###Markdown Here is an example. If `x == -1` and `y == 1`, the property `X < Y` holds for `x < y`, but not for `y < x`: ###Code invs = true_property_instantiations("X < Y", [('x', -1), ('y', 1)], log=True) invs ###Output _____no_output_____ ###Markdown The instantiation retrieves the short form: ###Code for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Likewise, with values for `x` and `y` as above, the property `X < 0` only holds for `x`, but not for `y`: ###Code invs = true_property_instantiations("X < 0", [('x', -1), ('y', 1)], log=True) for prop, var_names in invs: print(instantiate_prop(prop, var_names)) ###Output _____no_output_____ ###Markdown Extracting InvariantsLet us now run the above invariant extraction on function arguments and return values as observed during a function execution. To this end, we extend the `CallTracker` class into an `InvariantTracker` class, which automatically computes invariants for all functions and all calls observed during tracking. By default, an `InvariantTracker` uses the properties as defined above; however, one can specify alternate sets of properties. ###Code class InvariantTracker(CallTracker): def __init__(self, props=None, kwargs): if props is None: props = INVARIANT_PROPERTIES self.props = props super().__init__(kwargs) ###Output _____no_output_____ ###Markdown The key method of the `InvariantTracker` is the `invariants()` method. This iterates over the calls observed and checks which properties hold. Only the intersection of properties – that is, the set of properties that hold for all calls – is preserved, and eventually returned. The special variable `return_value` is set to hold the return value. ###Code RETURN_VALUE = 'return_value' class InvariantTracker(InvariantTracker): def invariants(self, function_name=None): if function_name is None: return {function_name: self.invariants(function_name) for function_name in self.calls()} invariants = None for variables, return_value in self.calls(function_name): vars_and_values = variables + [(RETURN_VALUE, return_value)] s = set() for prop in self.props: s \|= true_property_instantiations(prop, vars_and_values, self._log) if invariants is None: invariants = s else: invariants &= s return invariants ###Output _____no_output_____ ###Markdown Here's an example of how to use `invariants()`. We run the tracker on a small set of calls. ###Code with InvariantTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(10.0) tracker.calls() ###Output _____no_output_____ ###Markdown The `invariants()` method produces a set of properties that hold for the observed runs, together with their instantiations over function arguments. ###Code invs = tracker.invariants('my_sqrt') invs ###Output _____no_output_____ ###Markdown As before, the actual instantiations are easier to read: ###Code def pretty_invariants(invariants): props = [] for (prop, var_names) in invariants: props.append(instantiate_prop(prop, var_names)) return sorted(props) pretty_invariants(invs) ###Output _____no_output_____ ###Markdown We see that the both `x` and the return value have a `float` type. We also see that both are always greater than zero. These are properties that may make useful pre- and postconditions, notably for symbolic analysis. However, there's also an invariant which does _not_ universally hold, namely `return_value <= x`, as the following example shows: ###Code my_sqrt(0.01) ###Output _____no_output_____ ###Markdown Clearly, 0.1 > 0.01 holds. This is a case of us not learning from sufficiently diverse inputs. As soon as we have a call including `x = 0.1`, though, the invariant `return_value <= x` is eliminated: ###Code with InvariantTracker() as tracker: y = my_sqrt(25.0) y = my_sqrt(10.0) y = my_sqrt(0.01) pretty_invariants(tracker.invariants('my_sqrt')) ###Output _____no_output_____ ###Markdown We will discuss later how to ensure sufficient diversity in inputs. (Hint: This involves test generation.) Let us try out our invariant tracker on `sum3()`. We see that all types are well-defined; the properties that all arguments are non-zero, however, is specific to the calls observed. ###Code with InvariantTracker() as tracker: y = sum3(1, 2, 3) y = sum3(-4, -5, -6) pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with strings instead, we get different invariants. Notably, we obtain the postcondition that the return value starts with the value of `a` – a universal postcondition if strings are used. ###Code with InvariantTracker() as tracker: y = sum3('a', 'b', 'c') y = sum3('f', 'e', 'd') pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown If we invoke `sum3()` with both strings and numbers (and zeros, too), there are no properties left that would hold across all calls. That's the price of flexibility. ###Code with InvariantTracker() as tracker: y = sum3('a', 'b', 'c') y = sum3('c', 'b', 'a') y = sum3(-4, -5, -6) y = sum3(0, 0, 0) pretty_invariants(tracker.invariants('sum3')) ###Output _____no_output_____ ###Markdown Converting Mined Invariants to AnnotationsAs with types, above, we would like to have some functionality where we can add the mined invariants as annotations to existing functions. To this end, we introduce the `InvariantAnnotator` class, extending `InvariantTracker`. We start with a helper method. `params()` returns a comma-separated list of parameter names as observed during calls. ###Code class InvariantAnnotator(InvariantTracker): def params(self, function_name): arguments, return_value = self.calls(function_name)[0] return ", ".join(arg_name for (arg_name, arg_value) in arguments) with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = sum3(1, 2, 3) annotator.params('my_sqrt') annotator.params('sum3') ###Output _____no_output_____ ###Markdown Now for the actual annotation. `preconditions()` returns the preconditions from the mined invariants (i.e., those propertes that do not depend on the return value) as a string with annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@precondition(lambda " + self.params(function_name) + ": " + inv + ")" conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) annotator.preconditions('my_sqrt') ###Output _____no_output_____ ###Markdown `postconditions()` does the same for postconditions: ###Code class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ")") conditions.append(cond) return conditions with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) annotator.postconditions('my_sqrt') ###Output _____no_output_____ ###Markdown With these, we can take a function and add both pre- and postconditions as annotations: ###Code class InvariantAnnotator(InvariantAnnotator): def functions_with_invariants(self): functions = "" for function_name in self.invariants(): try: function = self.function_with_invariants(function_name) except KeyError: continue functions += function return functions def function_with_invariants(self, function_name): function = globals()[function_name] # Can throw KeyError source = inspect.getsource(function) return "\n".join(self.preconditions(function_name) + self.postconditions(function_name)) + '\n' + source ###Output _____no_output_____ ###Markdown Here comes `function_with_invariants()` in all its glory: ###Code with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) y = sum3(1, 2, 3) print_content(annotator.function_with_invariants('my_sqrt'), '.py') ###Output _____no_output_____ ###Markdown Quite a lot of invariants, is it? Further below (and in the exercises), we will discuss on how to focus on the most relevant properties. Some ExamplesHere's another example. `list_length()` recursively computes the length of a Python function. Let us see whether we can mine its invariants: ###Code def list_length(L): if L == []: length = 0 else: length = 1 + list_length(L[1:]) return length with InvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Almost all these properties (except for the very first) are relevant. Of course, the reason the invariants are so neat is that the return value is equal to `len(L)` is that `X == len(Y)` is part of the list of properties to be checked. The next example is a very simple function: ###Code def sum2(a, b): return a + b with InvariantAnnotator() as annotator: sum2(31, 45) sum2(0, 0) sum2(-1, -5) ###Output _____no_output_____ ###Markdown The invariants all capture the relationship between `a`, `b`, and the return value as `return_value == a + b` in all its variations. ###Code print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown If we have a function without return value, the return value is `None` and we can only mine preconditions. (Well, we get a "postcondition" that the return value is non-zero, which holds for `None`). ###Code def print_sum(a, b): print(a + b) with InvariantAnnotator() as annotator: print_sum(31, 45) print_sum(0, 0) print_sum(-1, -5) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Checking SpecificationsA function with invariants, as above, can be fed into the Python interpreter, such that all pre- and postconditions are checked. We create a function `my_sqrt_annotated()` which includes all the invariants mined above. ###Code with InvariantAnnotator() as annotator: y = my_sqrt(25.0) y = my_sqrt(0.01) my_sqrt_def = annotator.functions_with_invariants() my_sqrt_def = my_sqrt_def.replace('my_sqrt', 'my_sqrt_annotated') print_content(my_sqrt_def, '.py') exec(my_sqrt_def) ###Output _____no_output_____ ###Markdown The "annotated" version checks against invalid arguments – or more precisely, against arguments with properties that have not been observed yet: ###Code with ExpectError(): my_sqrt_annotated(-1.0) ###Output _____no_output_____ ###Markdown This is in contrast to the original version, which just hangs on negative values: ###Code with ExpectTimeout(1): my_sqrt(-1.0) ###Output _____no_output_____ ###Markdown If we make changes to the function definition such that the properties of the return value change, such _regressions_ are caught as violations of the postconditions. Let us illustrate this by simply inverting the result, and return $-2$ as square root of 4. ###Code my_sqrt_def = my_sqrt_def.replace('my_sqrt_annotated', 'my_sqrt_negative') my_sqrt_def = my_sqrt_def.replace('return approx', 'return -approx') print_content(my_sqrt_def, '.py') exec(my_sqrt_def) ###Output _____no_output_____ ###Markdown Technically speaking, $-2$ _is_ a square root of 4, since $(-2)^2 = 4$ holds. Yet, such a change may be unexpected by callers of `my_sqrt()`, and hence, this would be caught with the first call: ###Code with ExpectError(): my_sqrt_negative(2.0) # type: ignore ###Output _____no_output_____ ###Markdown We see how pre- and postconditions, as well as types, can serve as oracles* during testing. In particular, once we have mined them for a set of functions, we can check them again and again with test generators – especially after code changes. The more checks we have, and the more specific they are, the more likely it is we can detect unwanted effects of changes. Mining Specifications from Generated TestsMined specifications can only be as good as the executions they were mined from. If we only see a single call to, say, `sum2()` as defined above, we will be faced with several mined pre- and postconditions that _overspecialize_ towards the values seen: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown The mined precondition `a == b`, for instance, only holds for the single call observed; the same holds for the mined postcondition `return_value == a * b`. Yet, `sum2()` can obviously be successfully called with other values that do not satisfy these conditions. To get out of this trap, we have to _learn from more and more diverse runs_. If we have a few more calls of `sum2()`, we see how the set of invariants quickly gets smaller: ###Code with InvariantAnnotator() as annotator: length = sum2(1, 2) length = sum2(-1, -2) length = sum2(0, 0) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown But where to we get such diverse runs from? This is the job of generating software tests. A simple grammar for calls of `sum2()` will easily resolve the problem. ###Code from GrammarFuzzer import GrammarFuzzer # minor dependency from Grammars import is_valid_grammar, crange # minor dependency from Grammars import convert_ebnf_grammar, Grammar # minor dependency SUM2_EBNF_GRAMMAR: Grammar = { "<start>": ["<sum2>"], "<sum2>": ["sum2(<int>, <int>)"], "<int>": ["<_int>"], "<_int>": ["(-)?<leaddigit><digit>", "0"], "<leaddigit>": crange('1', '9'), "<digit>": crange('0', '9') } assert is_valid_grammar(SUM2_EBNF_GRAMMAR) sum2_grammar = convert_ebnf_grammar(SUM2_EBNF_GRAMMAR) sum2_fuzzer = GrammarFuzzer(sum2_grammar) [sum2_fuzzer.fuzz() for i in range(10)] with InvariantAnnotator() as annotator: for i in range(10): eval(sum2_fuzzer.fuzz()) print_content(annotator.function_with_invariants('sum2'), '.py') ###Output _____no_output_____ ###Markdown But then, writing tests (or a test driver) just to derive a set of pre- and postconditions may possibly be too much effort – in particular, since tests can easily be derived from given pre- and postconditions in the first place. Hence, it would be wiser to first specify invariants and then let test generators or program provers do the job. Also, an API grammar, such as above, will have to be set up such that it actually respects preconditions – in our case, we invoke `sqrt()` with positive numbers only, already assuming its precondition. In some way, one thus needs a specification (a model, a grammar) to mine another specification – a chicken-and-egg problem. However, there is one way out of this problem: If one can automatically generate tests at the system level, then one has an _infinite source of executions_ to learn invariants from. In each of these executions, all functions would be called with values that satisfy the (implicit) precondition, allowing us to mine invariants for these functions. This holds, because at the system level, invalid inputs must be rejected by the system in the first place. The meaningful precondition at the system level, ensuring that only valid inputs get through, thus gets broken down into a multitude of meaningful preconditions (and subsequent postconditions) at the function level. The big requirement for this, though, is that one needs good test generators at the system level. In [the next part](05_Domain-Specific_Fuzzing.ipynb), we will discuss how to automatically generate tests for a variety of domains, from configuration to graphical user interfaces. SynopsisThis chapter provides two classes that automatically extract specifications from a function and a set of inputs: `TypeAnnotator` for _types_, and* `InvariantAnnotator` for _pre-_ and _postconditions_.Both work by _observing_ a function and its invocations within a `with` clause. Here is an example for the type annotator: ###Code def sum(a, b): return a + b with TypeAnnotator() as type_annotator: sum(1, 2) sum(-4, -5) sum(0, 0) ###Output _____no_output_____ ###Markdown The `typed_functions()` method will return a representation of `sum2()` annotated with types observed during execution. ###Code print(type_annotator.typed_functions()) ###Output _____no_output_____ ###Markdown The invariant annotator works in a similar fashion: ###Code with InvariantAnnotator() as inv_annotator: sum(1, 2) sum(-4, -5) sum(0, 0) ###Output _____no_output_____ ###Markdown The `functions_with_invariants()` method will return a representation of `sum2()` annotated with inferred pre- and postconditions that all hold for the observed values. ###Code print(inv_annotator.functions_with_invariants()) ###Output _____no_output_____ ###Markdown Such type specifications and invariants can be helpful as _oracles_ (to detect deviations from a given set of runs) as well as for all kinds of _symbolic code analyses_. The chapter gives details on how to customize the properties checked for. Lessons Learned* Type annotations and explicit invariants allow for _checking_ arguments and results for expected data types and other properties.* One can automatically _mine_ data types and invariants by observing arguments and results at runtime.* The quality of mined invariants depends on the diversity of values observed during executions; this variety can be increased by generating tests. Next StepsThis chapter concludes the [part on semantical fuzzing techniques](04_Semantical_Fuzzing.ipynb). In the next part, we will explore [domain-specific fuzzing techniques](05_Domain-Specific_Fuzzing.ipynb) from configurations and APIs to graphical user interfaces. BackgroundThe [DAIKON dynamic invariant detector](https://plse.cs.washington.edu/daikon/) can be considered the mother of function specification miners. Continuously maintained and extended for more than 20 years, it mines likely invariants in the style of this chapter for a variety of languages, including C, C++, C, Eiffel, F, Java, Perl, and Visual Basic. On top of the functionality discussed above, it holds a rich catalog of patterns for likely invariants, supports data invariants, can eliminate invariants that are implied by others, and determines statistical confidence to disregard unlikely invariants. The corresponding paper \cite{Ernst2001} is one of the seminal and most-cited papers of Software Engineering. A multitude of works have been published based on DAIKON and detecting invariants; see this [curated list](http://plse.cs.washington.edu/daikon/pubs/) for details. The interaction between test generators and invariant detection is already discussed in \cite{Ernst2001} (incidentally also using grammars). The Eclat tool \cite{Pacheco2005} is a model example of tight interaction between a unit-level test generator and DAIKON-style invariant mining, where the mined invariants are used to produce oracles and to systematically guide the test generator towards fault-revealing inputs. Mining specifications is not restricted to pre- and postconditions. The paper "Mining Specifications" \cite{Ammons2002} is another classic in the field, learning state protocols from executions. Grammar mining, as described in [our chapter with the same name](GrammarMiner.ipynb) can also be seen as a specification mining approach, this time learning specifications for input formats. As it comes to adding type annotations to existing code, the blog post ["The state of type hints in Python"](https://www.bernat.tech/the-state-of-type-hints-in-python/) gives a great overview on how Python type hints can be used and checked. To add type annotations, there are two important tools available that also implement our above approach:* [MonkeyType](https://instagram-engineering.com/let-your-code-type-hint-itself-introducing-open-source-monkeytype-a855c7284881) implements the above approach of tracing executions and annotating Python 3 arguments, returns, and variables with type hints.* [PyAnnotate](https://github.com/dropbox/pyannotate) does a similar job, focusing on code in Python 2. It does not produce Python 3-style annotations, but instead produces annotations as comments that can be processed by static type checkers.These tools have been created by engineers at Facebook and Dropbox, respectively, assisting them in checking millions of lines of code for type issues. ExercisesOur code for mining types and invariants is in no way complete. There are dozens of ways to extend our implementations, some of which we discuss in exercises. Exercise 1: Union TypesThe Python `typing` module allows to express that an argument can have multiple types. For `my_sqrt(x)`, this allows to express that `x` can be an `int` or a `float`: ###Code from typing import Union, Optional def my_sqrt_with_union_type(x: Union[int, float]) -> float: ... ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it supports union types for arguments and return values. Use `Optional[X]` as a shorthand for `Union[X, None]`. Solution. Left to the reader. Hint: extend `type_string()`. Exercise 2: Types for Local VariablesIn Python, one cannot only annotate arguments with types, but actually also local and global variables – for instance, `approx` and `guess` in our `my_sqrt()` implementation: ###Code def my_sqrt_with_local_types(x: Union[int, float]) -> float: """Computes the square root of x, using the Newton-Raphson method""" approx: Optional[float] = None guess: float = x / 2 while approx != guess: approx = guess guess = (approx + x / approx) / 2 return approx ###Output _____no_output_____ ###Markdown Extend the `TypeAnnotator` such that it also annotates local variables with types. Search the function AST for assignments, determine the type of the assigned value, and make it an annotation on the left hand side. Solution. Left to the reader. Exercise 3: Verbose Invariant CheckersOur implementation of invariant checkers does not make it clear for the user which pre-/postcondition failed. ###Code @precondition(lambda s: len(s) > 0) def remove_first_char(s): return s[1:] with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown The following implementation adds an optional `doc` keyword argument which is printed if the invariant is violated: ###Code def verbose_condition(precondition=None, postcondition=None, doc='Unknown'): def decorator(func): @functools.wraps(func) # preserves name, docstring, etc def wrapper(args, kwargs): if precondition is not None: assert precondition(args, *kwargs), "Precondition violated: " + doc retval = func(args, *kwargs) # call original function or method if postcondition is not None: assert postcondition(retval, args, kwargs), "Postcondition violated: " + doc return retval return wrapper return decorator def verbose_precondition(check, kwargs): # type: ignore return verbose_condition(precondition=check, doc=kwargs.get('doc', 'Unknown')) def verbose_postcondition(check, kwargs): # type: ignore return verbose_condition(postcondition=check, doc=kwargs.get('doc', 'Unknown')) @verbose_precondition(lambda s: len(s) > 0, doc="len(s) > 0") # type: ignore def remove_first_char(s): return s[1:] remove_first_char('abc') with ExpectError(): remove_first_char('') ###Output _____no_output_____ ###Markdown Extend `InvariantAnnotator` such that it includes the conditions in the generated pre- and postconditions. Solution.** Here's a simple solution: ###Code class InvariantAnnotator(InvariantAnnotator): def preconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) >= 0: continue # Postcondition cond = "@verbose_precondition(lambda " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")" conditions.append(cond) return conditions class InvariantAnnotator(InvariantAnnotator): def postconditions(self, function_name): conditions = [] for inv in pretty_invariants(self.invariants(function_name)): if inv.find(RETURN_VALUE) < 0: continue # Precondition cond = ("@verbose_postcondition(lambda " + RETURN_VALUE + ", " + self.params(function_name) + ": " + inv + ', doc=' + repr(inv) + ")") conditions.append(cond) return conditions ###Output _____no_output_____ ###Markdown The resulting annotations are harder to read, but easier to diagnose: ###Code with InvariantAnnotator() as annotator: y = sum2(2, 2) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown As an alternative, one may be able to use `inspect.getsource()` on the lambda expression or unparse it. This is left to the reader. Exercise 4: Save Initial ValuesIf the value of an argument changes during function execution, this can easily confuse our implementation: The values are tracked at the beginning of the function, but checked only when it returns. Extend the `InvariantAnnotator` and the infrastructure it uses such that* it saves argument values both at the beginning and at the end of a function invocation;* postconditions can be expressed over both _initial_ values of arguments as well as the _final_ values of arguments;* the mined postconditions refer to both these values as well. Solution. To be added. Exercise 5: ImplicationsSeveral mined invariant are actually _implied_ by others: If `x > 0` holds, then this implies `x >= 0` and `x != 0`. Extend the `InvariantAnnotator` such that implications between properties are explicitly encoded, and such that implied properties are no longer listed as invariants. See \cite{Ernst2001} for ideas. Solution. Left to the reader. Exercise 6: Local VariablesPostconditions may also refer to the values of local variables. Consider extending `InvariantAnnotator` and its infrastructure such that the values of local variables at the end of the execution are also recorded and made part of the invariant inference mechanism. Solution. Left to the reader. Exercise 7: Exploring Invariant AlternativesAfter mining a first set of invariants, have a [concolic fuzzer](ConcolicFuzzer.ipynb) generate tests that systematically attempt to invalidate pre- and postconditions. How far can you generalize? Solution. To be added. Exercise 8: Grammar-Generated PropertiesThe larger the set of properties to be checked, the more potential invariants can be discovered. Create a _grammar_ that systematically produces a large set of properties. See \cite{Ernst2001} for possible patterns. Solution. Left to the reader. Exercise 9: Embedding Invariants as AssertionsRather than producing invariants as annotations for pre- and postconditions, insert them as `assert` statements into the function code, as in:```pythondef my_sqrt(x): 'Computes the square root of x, using the Newton-Raphson method' assert isinstance(x, int), 'violated precondition' assert (x > 0), 'violated precondition' approx = None guess = (x / 2) while (approx != guess): approx = guess guess = ((approx + (x / approx)) / 2) return_value = approx assert (return_value < x), 'violated postcondition' assert isinstance(return_value, float), 'violated postcondition' return approx```Such a formulation may make it easier for test generators and symbolic analysis to access and interpret pre- and postconditions. Solution. Here is a tentative implementation that inserts invariants into function ASTs. Part 1: Embedding Invariants into Functions ###Code class EmbeddedInvariantAnnotator(InvariantTracker): def functions_with_invariants_ast(self, function_name=None): if function_name is None: return annotate_functions_with_invariants(self.invariants()) return annotate_function_with_invariants(function_name, self.invariants(function_name)) def functions_with_invariants(self, function_name=None): if function_name is None: functions = '' for f_name in self.invariants(): try: f_text = ast.unparse(self.functions_with_invariants_ast(f_name)) except KeyError: f_text = '' functions += f_text return functions return ast.unparse(self.functions_with_invariants_ast(function_name)) def function_with_invariants(self, function_name): return self.functions_with_invariants(function_name) def function_with_invariants_ast(self, function_name): return self.functions_with_invariants_ast(function_name) def annotate_invariants(invariants): annotated_functions = {} for function_name in invariants: try: annotated_functions[function_name] = annotate_function_with_invariants(function_name, invariants[function_name]) except KeyError: continue return annotated_functions def annotate_function_with_invariants(function_name, function_invariants): function = globals()[function_name] function_code = inspect.getsource(function) function_ast = ast.parse(function_code) return annotate_function_ast_with_invariants(function_ast, function_invariants) def annotate_function_ast_with_invariants(function_ast, function_invariants): annotated_function_ast = EmbeddedInvariantTransformer(function_invariants).visit(function_ast) return annotated_function_ast ###Output _____no_output_____ ###Markdown Part 2: Preconditions ###Code class PreconditionTransformer(ast.NodeTransformer): def __init__(self, invariants): self.invariants = invariants super().__init__() def preconditions(self): preconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated precondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) < 0: preconditions += assertion_ast.body return preconditions def insert_assertions(self, body): preconditions = self.preconditions() try: docstring = body[0].value.s except: docstring = None if docstring: return [body[0]] + preconditions + body[1:] else: return preconditions + body def visit_FunctionDef(self, node): """Add invariants to function""" # print(ast.dump(node)) node.body = self.insert_assertions(node.body) return node class EmbeddedInvariantTransformer(PreconditionTransformer): pass with EmbeddedInvariantAnnotator() as annotator: my_sqrt(5) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____ ###Markdown Part 3: PostconditionsWe make a few simplifying assumptions: * Variables do not change during execution.* There is a single `return` statement at the end of the function. ###Code class EmbeddedInvariantTransformer(PreconditionTransformer): def postconditions(self): postconditions = [] for (prop, var_names) in self.invariants: assertion = "assert " + instantiate_prop(prop, var_names) + ', "violated postcondition"' assertion_ast = ast.parse(assertion) if assertion.find(RETURN_VALUE) >= 0: postconditions += assertion_ast.body return postconditions def insert_assertions(self, body): new_body = super().insert_assertions(body) postconditions = self.postconditions() body_ends_with_return = isinstance(new_body[-1], ast.Return) if body_ends_with_return: saver = RETURN_VALUE + " = " + ast.unparse(new_body[-1].value) else: saver = RETURN_VALUE + " = None" saver_ast = ast.parse(saver) postconditions = [saver_ast] + postconditions if body_ends_with_return: return new_body[:-1] + postconditions + [new_body[-1]] else: return new_body + postconditions with EmbeddedInvariantAnnotator() as annotator: my_sqrt(5) my_sqrt_def = annotator.functions_with_invariants() ###Output _____no_output_____ ###Markdown Here's the full definition with included assertions: ###Code print_content(my_sqrt_def, '.py') exec(my_sqrt_def.replace('my_sqrt', 'my_sqrt_annotated')) with ExpectError(): my_sqrt_annotated(-1) ###Output _____no_output_____ ###Markdown Here come some more examples: ###Code with EmbeddedInvariantAnnotator() as annotator: y = sum3(3, 4, 5) y = sum3(-3, -4, -5) y = sum3(0, 0, 0) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: length = list_length([1, 2, 3]) print_content(annotator.functions_with_invariants(), '.py') with EmbeddedInvariantAnnotator() as annotator: print_sum(31, 45) print_content(annotator.functions_with_invariants(), '.py') ###Output _____no_output_____
ch01/Chapter1.ipynb	###Markdown And with the fact that conditions are also propagated to individual elements, we gain a very convenient way to access our data: ###Code a>4 a[a>4] ###Output _____no_output_____ ###Markdown We can use this feature to trim outliers: ###Code a[a>4] = 4 a ###Output _____no_output_____ ###Markdown This is a common use case, so there is a special clip function for it, clipping values at both ends of an interval with one function call: ###Code a.clip(0, 4) ###Output _____no_output_____ ###Markdown Handling nonexisting valuesThe power of NumPy's indexing capabilities comes in handy when preprocessing data that we have just read in from a text file. Most likely, that will contain invalid values that we will mark as not being a real number using numpy.NAN ###Code c = np.array([1,2,np.NAN,3,4]) # fake data np.isnan(c) c[~np.isnan(c)] np.mean(c[~np.isnan(c)]) ###Output _____no_output_____ ###Markdown Comparing the runtimeLet's compare the runtime behavior of NumPy compared with normal Python lists. In the following code, we will calculate the sum of all squared numbers from 1 to 1000 and see how much time it will take. ###Code import timeit normal_py_sec = timeit.timeit('sum(xx for x in range(1000))', number=10000) naive_np_sec = timeit.timeit('sum(nana)', setup="import numpy as np; na=np.arange(1000)", number=10000) good_np_sec = timeit.timeit('na.dot(na)', setup="import numpy as np; na=np.arange(1000)", number=10000) print("Normal Python: %f sec" % normal_py_sec) print("Naive NumPy: %f sec" %naive_np_sec) print("Good NumPy: %f sec" % good_np_sec) ###Output Normal Python: 3.576253 sec Naive NumPy: 4.167665 sec Good NumPy: 0.069332 sec ###Markdown There are some interesting observations:* Using NumPy as data storage takes more time, which is surprising since we believe it must be much faster as it is written as a C extension. But the explanation is on the access to individual elements from Python itself is rather costly. * The dot() function does exactly the same thing However we no longer have the incredible flexibility of Python lists, wich can hold basically anything. NumPy arrays always have only one data type. ###Code a = np.array([1,2,3]) a.dtype ###Output _____no_output_____ ###Markdown If we try to use elements of different types, shuch as the ones shown in the following code, NumPy will do its best to coerce them to be the most reasonable common data type: ###Code np.array([1, "stringy"]) np.array([1, "stringy", set([1,2,3])]) ###Output _____no_output_____ ###Markdown Learning SciPyOn top of the efficient data structures of NumPy, SciPy offers a magnitude of algorithms working on those arrays. Whatever numerical heavy algorithm you take from current books, on numerical recipes, most likely you will find support for them in SciPy on one way or the other. For convenience, the complete namespace of NumPy is also accessible via SciPy. You can check this easily comparing the function references of any base function, such as: ###Code import scipy, numpy scipy.version.full_version scipy.dot is numpy.dot ###Output _____no_output_____ ###Markdown Our first (tiny) application of machine learningLet's get our hands dirty and take a look at our hypothetical web start-up, MLaaS,which sells the service of providing machine learning algorithms via HTTP. Withincreasing success of our company, the demand for better infrastructure increasesto serve all incoming web requests successfully. We don't want to allocate toomany resources as that would be too costly. On the other side, we will lose money,if we have not reserved enough resources to serve all incoming requests. Now,the question is, when will we hit the limit of our current infrastructure, which weestimated to be at 100,000 requests per hour. We would like to know in advancewhen we have to request additional servers in the cloud to serve all the incomingrequests successfully without paying for unused ones. Reading in the dataWe have collected the web stats for the last month and aggregated them in ch01/data/web_traffic.tsv ( .tsv because it contains tab-separated values). They arestored as the number of hits per hour. Each line contains the hour consecutively andthe number of web hits in that hour.Using gentfromtxt(), we can easily read in the data using the following code: ###Code import scipy as sp data = sp.genfromtxt("data/web_traffic.tsv", delimiter="\t") ###Output _____no_output_____ ###Markdown We have to specify tab as the delimiter so that columns are correctly determined. A quick check shows that we have correctly read in the data: ###Code print(data[:10]) print(data.shape) ###Output (743, 2) ###Markdown As you can see, we have 743 data points with two dimensions. Preprocessing and cleaning the dataIt is more convenient for SciPy to separate the dimensions into two vectors, eachof size 743. The first vector, x , will contain the hours, and the other, y , will containthe Web hits in that particular hour. This splitting is done using the special indexnotation of SciPy, by which we can choose the columns individually: ###Code x = data[:,0] y = data[:,1] ###Output _____no_output_____ ###Markdown Let's check how many hours contain invaliddata, by running the following code: ###Code sp.sum(sp.isnan(y)) ###Output _____no_output_____ ###Markdown As you can see, we are missing only 8 out of 743 entries, so we can afford to removethem. ###Code x = x[~sp.isnan(y)] y = y[~sp.isnan(y)] ###Output _____no_output_____ ###Markdown We can plot our data using matplotlib which contains the pyplot package, wich tries to mimic MATLAB's interface, which is very convenient and easy to use as you can see in the following code: ###Code %matplotlib inline import matplotlib.pyplot as plt # plot the (x,y) points with dots of size 10 plt.scatter(x,y, s=10) plt.title("Web traffic over the last month") plt.xlabel("Time") plt.ylabel("Hits/hour") plt.xticks([w724 for w in range(10)], ['week %i' % w for w in range(10)]) plt.autoscale(tight=True) # draw a slightly opaque, dashed grid plt.grid(True, linestyle='-', color='0.75') plt.show() ###Output _____no_output_____ ###Markdown Choosing the right model and learning algorithmNow that we have a first impression of the data, we return to the initial question:How long will our server handle the incoming web traffic? To answer this we haveto do the following:1. Find the real model behind the noisy data points.2. Following this, use the model to extrapolate into the future to find the point in time where our infrastructure has to be extended. Before building our first model...When we talk about models, you can think of them as simplified theoreticalapproximations of complex reality. As such there is always some inferiorityinvolved, also called the approximation error. This error will guide us in choosingthe right model among the myriad of choices we have. And this error will becalculated as the squared distance of the model's prediction to the real data; forexample, for a learned model function f , the error is calculated as follows: ###Code def error(f, x, y): return sp.sum((f(x)-y)*2) ###Output _____no_output_____ ###Markdown The vectors x and y contain the web stats data that we have extracted earlier. It isthe beauty of SciPy's vectorized functions that we exploit here with f(x) . The trainedmodel is assumed to take a vector and return the results again as a vector of the samesize so that we can use it to calculate the difference to y . Starting with a simple straight line Let's assume for a second that the underlying model is a straight line. Then thechallenge is how to best put that line into the chart so that it results in the smallestapproximation error. SciPy's polyfit() function does exactly that. Given data x andy and the desired order of the polynomial (a straight line has order 1), it finds themodel function that minimizes the error function defined earlier: ###Code fp1, residuals, rank, sv, rcond = sp.polyfit(x, y, 1, full=True) ###Output _____no_output_____ ###Markdown The polyfit() function returns the parameters of the fitted model function, fp1 .And by setting full=True , we also get additional background information on thefitting process. Of this, only residuals are of interest, which is exactly the error ofthe approximation: ###Code print("Model parameters: %s" % fp1) print(residuals) ###Output [ 3.17389767e+08] ###Markdown This means the best straight line fit is the following functionf(x) = 2.59619213 x + 989.02487106We then use poly1d() to create a model function from the model parameters: ###Code f1 = sp.poly1d(fp1) print(error(f1, x, y)) ###Output 317389767.34 ###Markdown We have used full=True to retrieve more details on the fitting process. Normally,we would not need it, in which case only the model parameters would be returned.We can now use f1() to plot our first trained model. In addition to the precedingplotting instructions, we simply add the following code: ###Code import matplotlib.pyplot as plt # plot the (x,y) points with dots of size 10 plt.scatter(x,y, s=10) plt.title("Web traffic over the last month") plt.xlabel("Time") plt.ylabel("Hits/hour") plt.xticks([w724 for w in range(10)], ['week %i' % w for w in range(10)]) plt.autoscale(tight=True) # draw a slightly opaque, dashed grid plt.grid(True, linestyle='-', color='0.75') fx = sp.linspace(0,x[-1], 1000) # generate values for plotting plt.plot(fx, f1(fx), linewidth=4) plt.legend(["d=%i" % f1.order], loc="upper left") plt.show() ###Output _____no_output_____ ###Markdown It seems like the first 4 weeks are not that far off, although we clearly see that there issomething wrong with our initial assumption that the underlying model is a straightline. The absolute value of the error is seldom of use in isolation. However, whencomparing two competing models, we can use their errors to judge which one ofthem is better. Although our first model clearly is not the one we would use, it servesa very important purpose in the workflow. We will use it as our baseline until wefind a better one. Whatever model we come up with in the future, we will compare itagainst the current baseline. Towards some advanced stuffLet's now fit a more complex model, a polynomial of degree 2, to see whether itbetter understands our data: ###Code f2p = sp.polyfit(x, y, 2) print(f2p) f2 = sp.poly1d(f2p) print(error(f2, x, y)) import matplotlib.pyplot as plt # plot the (x,y) points with dots of size 10 plt.scatter(x,y, s=10) plt.title("Web traffic over the last month") plt.xlabel("Time") plt.ylabel("Hits/hour") plt.xticks([w724 for w in range(10)], ['week %i' % w for w in range(10)]) plt.autoscale(tight=True) # draw a slightly opaque, dashed grid plt.grid(True, linestyle='-', color='0.75') fx = sp.linspace(0,x[-1], 1000) # generate values for plotting plt.plot(fx, f2(fx), linewidth=4) plt.legend(["d=%i" % f2.order], loc="upper left") plt.show() ###Output _____no_output_____ ###Markdown The error is 179,983,507.878, which is almost half the error of the straight line model.This is good but unfortunately this comes with a price: We now have a more complexfunction, meaning that we have one parameter more to tune inside polyfit() . Thefitted polynomial is as follows: f(x) = 0.0105322215 * x*2 - 5.26545650 x + 1974.76082 So, if more complexity gives better results, why not increase the complexity evenmore? Let's try it for degrees 3, 10, and 100. ###Code f3p = sp.polyfit(x, y, 3) print(f3p) f3 = sp.poly1d(f3p) f10p = sp.polyfit(x, y, 10) print(f10p) f10 = sp.poly1d(f10p) f100p = sp.polyfit(x, y, 100) print(f100p) f100 = sp.poly1d(f100p) import matplotlib.pyplot as plt # plot the (x,y) points with dots of size 10 plt.scatter(x,y, s=10) plt.title("Web traffic over the last month") plt.xlabel("Time") plt.ylabel("Hits/hour") plt.xticks([w724 for w in range(10)], ['week %i' % w for w in range(10)]) plt.autoscale(tight=True) # draw a slightly opaque, dashed grid plt.grid(True, linestyle='-', color='0.75') fx = sp.linspace(0,x[-1], 1000) # generate values for plotting # plotting with a 1 order plt.plot(fx, f1(fx), linewidth=4, label="d1=%i" % f1.order) # plotting with a 2 order plt.plot(fx, f2(fx), linewidth=4, label="d2=%i" % f2.order) # plotting with a 3 order plt.plot(fx, f3(fx), linewidth=4, label="d3=%i" % f3.order) # plotting with a 10 order plt.plot(fx, f10(fx), linewidth=4, label="d10=%i" % f10.order) # plotting with a 100 order plt.plot(fx, f100(fx), linewidth=4, label="d100=%i" % f100.order) plt.legend(loc='upper left') plt.show() ###Output _____no_output_____ ###Markdown Interestingly, when you have plotted your graph that d100=53 this means that polyfit cannot determine a good fit with 100 degrees. Instead, it figured that 53 must be good enough. It seems like the curves capture and better the fitted data the more complex they get.And also, the errors seem to tell the same story: ###Code print("Error d=1: %f", error(f1, x, y)) print("Error d=2: %f", error(f2, x, y)) print("Error d=3: %f", error(f3, x, y)) print("Error d=10: %f", error(f10, x, y)) print("Error d=100: %f", error(f100, x, y)) ###Output Error d=1: %f 317389767.34 Error d=2: %f 179983507.878 Error d=3: %f 139350144.032 Error d=10: %f 121942326.364 Error d=100: %f 109452401.18 ###Markdown However, taking a closer look at the fitted curves, we start to wonder whether they alsocapture the true process that generated that data. Framed differently, do our modelscorrectly represent the underlying mass behavior of customers visiting our website?Looking at the polynomial of degree 10 and 53, we see wildly oscillating behavior. Itseems that the models are fitted too much to the data. So much that it is now capturingnot only the underlying process but also the noise. This is called overfitting. So we have the following choices:* Choosing one of the fitted polynomial models.* Switching to another more complex model class.* Thinking differently about the data and start again. Out of the five fitted models, the first order model clearly is too simple, and themodels of order 10 and 53 are clearly overfitting. Only the second and third ordermodels seem to somehow match the data. However, if we extrapolate them at bothborders, we see them going berserk.Switching to a more complex class seems also not to be the right way to go. Whatarguments would back which class? At this point, we realize that we probably havenot fully understood our data. Stepping back to go forward – another look at our dataSo, we step back and take another look at the data. It seems that there is an inflection point between weeks 3 and 4. So let's separate the data and train two lines using week 3.5 as a separation point: ###Code inflection = 3.5725 #calculate the inflection point in hours int_inflection = round(inflection) xa = x[:int_inflection] # data before the inflection point ya = y[:int_inflection] xb = x[int_inflection:] # data after yb = y[int_inflection:] fa = sp.poly1d(sp.polyfit(xa, ya, 1)) fb = sp.poly1d(sp.polyfit(xb, yb, 1)) fa_error = error(fa, xa, ya) fb_error = error(fb, xb, yb) print("Error inflection=%f" %(fa_error + fb_error)) import matplotlib.pyplot as plt # plot the (x,y) points with dots of size 10 plt.scatter(x,y, s=10) plt.title("Web traffic over the last month") plt.xlabel("Time") plt.ylabel("Hits/hour") plt.xticks([w724 for w in range(10)], ['week %i' % w for w in range(10)]) plt.autoscale(tight=True) # draw a slightly opaque, dashed grid plt.grid(True, linestyle='-', color='0.75') fx = sp.linspace(0,x[-1], 1000) # generate values for plotting # plotting with a 1 order plt.plot(fx, fa(fx), linewidth=4, label="d1=%i" % fa.order) # plotting with a 2 order plt.plot(fx, fb(fx), linewidth=4, label="d1=%i" % fb.order) plt.legend(loc='upper left') plt.show() ###Output _____no_output_____ ###Markdown Clearly, the combination of these two lines seems to be a much better fit to the datathan anything we have modeled before. But still, the combined error is higher thanthe higher order polynomials. Can we trust the error at the end? Asked differently, why do we trust the straight line fitted only at the last week of ourdata more than any of the more complex models? It is because we assume that it willcapture future data better. If we plot the models into the future, we see how right weare (d=1 is again our initial straight line). Training and testingIf we only had some data from the future that we could use to measure our modelsagainst, then we should be able to judge our model choice only on the resultingapproximation error.Although we cannot look into the future, we can and should simulate a similar effectby holding out a part of our data. Let's remove, for instance, a certain percentage ofthe data and train on the remaining one. Then we used the held-out data to calculatethe error. As the model has been trained not knowing the held-out data, we shouldget a more realistic picture of how the model will behave in the future.The test errors for the models trained only on the time after inflection point nowshow a completely different picture: ###Code inflection = 3.5725 #calculate the inflection point in hours int_inflection = inflection xb = x[int_inflection:] # data after yb = y[int_inflection:] fb1 = sp.poly1d(sp.polyfit(xb, yb, 1)) fb2 = sp.poly1d(sp.polyfit(xb, yb, 2)) fb3 = sp.poly1d(sp.polyfit(xb, yb, 3)) fb10 = sp.poly1d(sp.polyfit(xb, yb, 10)) fb53 = sp.poly1d(sp.polyfit(xb, yb, 53)) fb1_error = error(fb1, xb, yb) fb2_error = error(fb2, xb, yb) fb3_error = error(fb3, xb, yb) fb10_error = error(fb10, xb, yb) fb53_error = error(fb53, xb, yb) frac = 0.3 split_idx = int(frac * len(xb)) shuffled = sp.random.permutation(list(range(len(xb)))) test = sorted(shuffled[:split_idx]) train = sorted(shuffled[split_idx:]) fbt1 = sp.poly1d(sp.polyfit(xb[train], yb[train], 1)) fbt2 = sp.poly1d(sp.polyfit(xb[train], yb[train], 2)) fbt3 = sp.poly1d(sp.polyfit(xb[train], yb[train], 3)) fbt10 = sp.poly1d(sp.polyfit(xb[train], yb[train], 10)) fbt100 = sp.poly1d(sp.polyfit(xb[train], yb[train], 53)) print("Test errors for only the time after inflection point") for f in [fbt1, fbt2, fbt3, fbt10, fbt100]: print("Error d=%i: %f" % (f.order, error(f, xb[test], yb[test]))) ###Output Test errors for only the time after inflection point Error d=1: 3946251.726017 Error d=2: 3873979.021186 Error d=3: 3883897.384542 Error d=10: 4038394.035316 Error d=53: 4437453.980905 ###Markdown It seems that we finally have a clear winner: The model with degree 2 has the lowesttest error, which is the error when measured using data that the model did not seeduring training. And this gives us hope that we won't get bad surprises when futuredata arrives Answering our initial questionFinally we have arrived at a model which we think represents the underlyingprocess best; it is now a simple task of finding out when our infrastructure willreach 100,000 requests per hour. We have to calculate when our model functionreaches the value 100,000.Having a polynomial of degree 2, we could simply compute the inverse of thefunction and calculate its value at 100,000. Of course, we would like to have anapproach that is applicable to any model function easily.This can be done by subtracting 100,000 from the polynomial, which results inanother polynomial, and finding its root. SciPy's optimize module has the functionfsolve that achieves this, when providing an initial starting position with parameterx0 . As every entry in our input data file corresponds to one hour, and we have 743 ofthem, we set the starting position to some value after that. Let fbt2 be the winningpolynomial of degree 2. ###Code fbt2 = sp.poly1d(sp.polyfit(xb[train], yb[train], 2)) print("fbt2(x) = \n%s" %fbt2) print("fbt2(x)-100,000 = \n%s" %(fbt2-100000)) from scipy.optimize import fsolve reached_max = fsolve(fbt2-100000, x0=800)/(724) print("100,000 hits/hour expected at week %f" % reached_max[0]) ###Output 100,000 hits/hour expected at week 9.806430 ###Markdown Learning NumPy ###Code import numpy as np a = np.array([0, 1, 2, 3, 4, 5]) a a.ndim a.shape ###Output _____no_output_____ ###Markdown We just created an array like we would create a list in Python. However, the NumPy arrays have additional information about the shape. In this case, it is a one-dimensional array of six elements. We can now transform this array to a two-dimensional matrix: ###Code b = a.reshape((3, 2)) b b.ndim b.shape ###Output _____no_output_____ ###Markdown We have a trouble if we wan't to make a real copy, this shows how much the NumPy package is optimized. ###Code b[1][0] = 77 b ###Output _____no_output_____ ###Markdown But now if we see the values of a: ###Code a ###Output _____no_output_____ ###Markdown We see immediately the same change reflected in "a" as well. If we need a true copy we can perform: ###Code c = a.reshape((3, 2)).copy() c c[0][0] = -99 a c ###Output _____no_output_____ ###Markdown Another big advantage of NumPy arrays is that operations are propagated to the individual elements. ###Code d = np.array([1,2,3,4,5]) d2 ###Output _____no_output_____ ###Markdown Similarly, for other operations: ###Code d*2 ###Output _____no_output_____ ###Markdown What it's not the case with Python lists. ###Code [1,2,3,4,5]2 [1,2,3,4,5]**2 ###Output _____no_output_____ ###Markdown When using NumPy arrays, we sacrafice the agility Python lists offer. Simple operations such as adding or removing are bit complex for NumPy arrays. But we can choose the right tool for the task. IndexingNumpy allows you to use the arrays themselves as indices by performing: ###Code a[np.array([2,3,4])] ###Output _____no_output_____
content/en/wuhan-sir/wuhan-sir.ipynb	###Markdown When Will Coronavirous (COVID-19) End?by [Frank Zheng](http://frankzheng.me) This notebook is licensed under the MIT License. If you use the code or data visualization designs contained within this notebook, it would be greatly appreciated if proper attribution is given back to this notebook and/or myself. Thanks! :)Coronavirus Disease 2019 ([COVID-19](https://www.who.int/emergencies/diseases/novel-coronavirus-2019)) was identified as the cause of a cluster of pneumonia cases in Wuhan, a city in the Hubei Province of China, at the end of 2019. It subsequently spread throughout China and elsewhere, becoming a global health emergency. In February 2020, the World Health Organization (WHO) designated the disease COVID-19, which stands for coronavirus disease 2019. This post will use current data with SIR model and (try to) forcast when the number of coronavirous infected patients reaches its peak and eventually declines. SIR and SIRS ModelIn 1927, the SIR model for sperad of disease was first propsed in in a collection of three articles in the Proceedings of the Royal Society by [Anderson Gray](https://en.wikipedia.org/wiki/Anderson_Gray_McKendrick) McKendrick and [William Ogilvy Kermack](https://en.wikipedia.org/wiki/William_Ogilvy_Kermack); the resulting theory is known as [Kermack–McKendrick theory](https://en.wikipedia.org/wiki/Kermack%E2%80%93McKendrick_theory); now considered a subclass of a more general theory known as [compartmental models](https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology) in epidemiology. The three original articles were republished in 1991, in a special issue of the Bulletin of [Mathematical Biology](https://link.springer.com/journal/11538/53/1/page/1).SIR model stands for a (suspectible - infectious - recovered) model, while SIRS represents a (suspectible - infectious - recovered - susceptible) model. The main difference between these two is the latter does not confer lifelong immunity, so individual may become susceptible again. The SIR/SIRS diagram from [IDM](https://idmod.org/docs/hiv/model-si.html) below shows how individuals move through each compartment in the model. ![Image](https://idmod.org/docs/hiv/_images/SIR-SIRS.png) - $\beta$, the transmission rate, controls the rate of spread which represents the probability of transmitting disease between a susceptible and an infectious individual. - $\gamma$ = 1/D, recovery rate, is determined by the average duration, D, of infection. - $\xi$, only used for the SIRS model, is the rate which recovered individuals return to the susceptible statue due to loss of immunity.Besides the immunity issue, SIR model also considers the population changes. If the course of the infection is short (emergent outbreak) compared with the lifetime of an individual and the disease is non-fatal, vital dynamics (birth and death) can be ignored. SIR model with vital dynamics considers new births that can provide more susceptible individuals to the population, sustaining an epidemic or allowing new introductions to spread throughout the population. In our COVID-19 case, becuase the disease is such a outbreak, it's not likely to be fatal (3.4% death rate reported by [WHO](https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---3-march-2020)), and most patients who recoved from conronavirus gain immunity, therefore, SIR model without vital dynamics is more situable. In the deterministic form, the SIR model can be written as the following there ordinary differential equations (ODE), parameterized by two growth factors β and γ:$$\frac{dS}{dt} = - \frac{\beta S I}{N}$$$$\frac{dI}{dt} = \frac{\beta S I}{N} - \gamma I$$$$\frac{dR}{dt} = \gamma I$$where N is the population, and since each of S, I and R represent the number of people in mutually exclusive sets, we should have $$S+I+R=N$$Note that the right hand sides of the equations sum to zero, hence$$\frac{dS}{dt} + \frac{dI}{dt} + \frac{dR}{dt} = \frac{dN}{dt}=0$$which indicates that the population is constant.In a closed population with no vital dynamics, an epidemic will eventually die out due to an insufficient number of susceptible individuals to sustain the disease. Infected individuals who are added later will not start another epidemic due to the lifelong immunity of the existing population.A discrete model can be derived from the above equations for the evolution of the disease.$${S}_{n+1} = S_n − \frac{\beta}{N} S_n I_n$$$${I}_{n+1} = I_n + \frac{\beta}{N} S_n I_n - \gamma I_n$$$${R}_{n+1} = R_n + \gamma I_n$$- New infecteds, $I_{n+1}$, result from contact between the susceptibles, $S_n$, and infecteds, $I_n$, with rate of infection $\frac{\beta}{N}$.- Infecteds are cured at a rate proportional to the number of infecteds, $\gamma I_n$, which become recovered, $R_n$- The term $\frac{\beta}{N} S_n$ represents the proportion of contacts by an infected individual that result in the infection of a susceptible individual.- The ratio $1/\gamma$ is the average length of the infectious period of the disease.While these may look very confusing, once explained they make a lot of sense. For example, ${S}_{n+1} = S_n − \frac{\beta}{N} S_n I_n$the equation simply means that the number of susceptible people today(${S}_{n+1}$) would be the number of susceptible people yesterday $S_n$ deduct the number of people that got infected yesterday and today. We would calculate the number of people infected yesterday by multiplying by the rate of infection. Similarly, ${I}_{n+1} = I_n + \frac{\beta}{N} S_n I_n - \gamma I_n$ this simply means that the number of people that number of people infected today would be the number of people that were infected yesterday plus the number of people that got infected yesterday and today, then deduct the number of people that recovered yesterday. The final number is the number of people in the infected category today. Lastly, ${R}_{n+1} = R_n + \gamma I_n$ this equation simply means that the number of people recovered today are the number of people that were recovered yesterday as well as the number of infected people that recovered today.This model is clearly not applicable to all possible epidemics: there may be births and deaths, people may be re-infected, and so on. More complex models take these and other factors into account. However, based on we've learnt from coronavirous so far, I believe the SIR model without vital dynamics is the simplist but adequate model to use. Load packages ###Code import numpy as np import matplotlib.pyplot as plt import math ###Output _____no_output_____ ###Markdown Setup Parameters for SIR ModelUse current data to find {\gamma}(recovery rate) and {\beta}(transmission rate). On 01/24/2020, Wuhan has 258 cumulative total confirmed cases, 25 recovered case and 60 new confirmed cases. ###Code ### based on the data until 01/24/2020 for Wuhan # infected inf = 233 # recovered rec = 25 # recovery rate gamma = 25.0/258 # transmission rate beta = (60+25)/(258-25) # population of Wuhan n = 1100 * 10000 ###Output _____no_output_____ ###Markdown Build SIR Model ###Code class SIR: def __init__(self, inff, recc, suss, time): self.inff = inff self.recc = recc self.suss = suss self.time = time def sir(beta, gamma, n, inf, rec): sus = n - inf - rec t = 1 inff = [] recc = [] suss = [] time = [] inff.append(inf) recc.append(rec) suss.append(sus) time.append(t) while True: if t > 200: break t += 1 a = inf b = rec c = sus rec = b + gamma * a inf = (a + beta * a * c / n - gamma * a) sus = n - rec - inf inff.append(round(inf)) recc.append(rec) suss.append(round(sus)) time.append(t) return SIR(inff, recc, suss, time) ###Output _____no_output_____ ###Markdown Plot results ###Code p = sir(beta, gamma, n, inf, rec) fig = plt.figure(figsize=(12,4)) plt.plot(p.time, p.suss, 'y-', label = 'Suspectible') plt.plot(p.time, p.inff, 'r-', label = 'Infected') plt.plot(p.time, p.recc, 'g-', label = 'Recovered') plt.axvline(p.time[p.inff.index(max(p.inff))], ls = '--') plt.title('SIR Model Prediction on COVID-19 in Wuhan \n with 01/24/2020 as Day 1') plt.xlabel('Time(day) \n by Frank Zheng — frankzheng.me') plt.ylabel('Population') plt.xlim(0, 201) plt.legend(loc = 'best') plt.show() ###Output _____no_output_____
Lessons/Lesson06-opencv.ipynb	###Markdown Lesson 06: OpenCV OpenCV is a library that contains algorithms and functions that are related to and perform image processing and computer vision tasks. ###Code import cv2 ###Output _____no_output_____ ###Markdown Opening Images ###Code img = cv2.imread('../images/test-image.png') print(img.shape) cv2.imshow('img', img) # press 'q' to close image or else it will not be properly closed. cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Changing Color Space ###Code gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) cv2.imwrite('../images/gray.jpg', gray) cv2.imshow('img', gray) # press 'q' to close image or else it will not be properly closed. cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Resizing ###Code height, width = img.shape[:-1] big_image = cv2.resize(img, (2height, 2width)) cv2.imshow('img', big_image) cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Cropping ###Code img_crop = img[0:500, 300:500] cv2.imshow('img', img_crop) cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Thresholding Thresholding only takes grayscale image.The first argument is the grayscale image, the second argument is the threshold value which is used to classify the pixel values. The third argument is the maximum value which is assigned to pixel values exceeding the threshold. OpenCV provides different types of thresholding which is given by the fourth parameter of the function.The method returns two outputs. The first is the threshold that was used and the second output is the thresholded image. ###Code thresholded = cv2.threshold(gray, 120, 255, cv2.THRESH_BINARY) cv2.imshow('img', thresholded[1]) cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Filters ###Code import numpy as np kernel = np.array([ [1, 1, 1], [1, 1, 1], [1, 1, 1] ]) # here second argument means the depth of the output image. # If you set this argument to -1 then the output image will have the same depth as input image. filtered = cv2.filter2D(img, -1, kernel) cv2.imshow('img', filtered) cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Gaussian Blur Takes img, kernel size, standard deviation. If std is 0 then it is calculated from kernel size. ###Code gaussian = cv2.GaussianBlur(img, (5, 5), 0) cv2.imshow('img', gaussian) cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Edge Detection Canny Edge Detector First argument is grayscale image, then lower threshold, upper threshold and then kernel size which is by default 3.The edge pixels above the upper threshold are considered in an edge map and edge pixels below the threshold are discarded. The pixel in between the thresholds are considered only if they are connected to pixels in upper threshold. Thus we get a clean edge map. ###Code edges = cv2.Canny(gray, 100, 200, 3) cv2.imshow('img', edges) cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Feature Detection SIFT ###Code sift_img = cv2.imread('../images/test-image.png') sift_obj = cv2.xfeatures2d.SIFT_create() # you can also pass a mask in place of None if you want to find features in a specific region. keypoints = sift_obj.detect(gray) drawn = cv2.drawKeypoints(gray, keypoints, sift_img) cv2.imshow('img', sift_img) cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Feature Matching ###Code img_rot = cv2.imread('../images/test-image-rot.png') gray_rot = cv2.cvtColor(img_rot, cv2.COLOR_BGR2GRAY) import random sift = cv2.xfeatures2d.SIFT_create() # detectAndCompute will find keypoints as well as compute the descriptors # descriptors store information about keypoints that make them distinguishable kp, desc = sift.detectAndCompute(gray, None) kp_rot, desc_rot = sift.detectAndCompute(gray_rot, None) # this is will match the descriptors and find the ones that are similar bf = cv2.BFMatcher() matches = bf.knnMatch(desc, desc_rot, k=2) good = [] for m, n in matches: # applying the ratio test to filter out the bad matches due to noise # since we set k=2 in bf.knnMatch() we have two matches for each keypoint # the first one is the best and the second one of the second best # we are decreasing the value of the worst match and checking whether its # value becomes smaller then the best match. If it does then that match is discarded if m.distance < 0.4 * n.distance: good.append([m]) random.shuffle(good) image_match = cv2.drawMatchesKnn(img, kp, img_rot, kp_rot, good[:10], outImg=None) cv2.imshow('img', image_match) cv2.waitKey(0) cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Opening Videos ###Code cam = cv2.VideoCapture(0) while (cam.isOpened()): ret, frame = cam.read() cv2.imshow('frame', frame) if cv2.waitKey(1) & 0xFF == ord('q'): break cam.release() cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Converting to Grayscale ###Code cam = cv2.VideoCapture(0) while (cam.isOpened()): ret, frame = cam.read() gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY) cv2.imshow('gray', gray) cv2.imshow('frame', frame) if cv2.waitKey(1) & 0xFF == ord('q'): break cam.release() cv2.destroyAllWindows() ###Output _____no_output_____ ###Markdown Saving Video ###Code cam = cv2.VideoCapture(0) ret, frame = cam.read() h, w = frame.shape[:2] fourcc = cv2.VideoWriter_fourcc(*'DIVX') # 1st argument: where to save video, 2nd compression format, 3rd fps, 4th size of video video_writer = cv2.VideoWriter('../images/gray_vid.mp4', fourcc, 25.0, (w, h)) while (cam.isOpened()): ret, frame = cam.read() gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY) # gray = cv2.Canny(gray, 30, 35, 3) # have to convert back to BGR format because video needs 3 channels # this will not bring back the colors # gray = cv2.cvtColor(gray, cv2.COLOR_GRAY2BGR) video_writer.write(gray) cv2.imshow('frame', frame) cv2.imshow('gray', gray) if cv2.waitKey(1) & 0xFF == ord('q'): break cam.release() video_writer.release() cv2.destroyAllWindows() ###Output _____no_output_____
examples/DKT.ipynb	###Markdown Udacity - Machine Learning Engineer Nanodegree Capstone Project Title: Development of a LSTM Network to Predict Students’ Answers on Exam Questions Implementation of DKT: Part 1: Define constants ###Code fn = "data/ASSISTments_skill_builder_data.csv" # Dataset path verbose = 1 # Verbose = {0,1,2} best_model_weights = "weights/bestmodel" # File to save the model. log_dir = "logs" # Path to save the logs. optimizer = "adam" # Optimizer to use lstm_units = 100 # Number of LSTM units batch_size = 32 # Batch size epochs = 10 # Number of epochs to train dropout_rate = 0.3 # Dropout rate test_fraction = 0.2 # Portion of data to be used for testing validation_fraction = 0.2 # Portion of training data to be used for validation ###Output _____no_output_____ ###Markdown Part 2: Pre-processing ###Code from deepkt import deepkt, data_util, metrics dataset, length, nb_features, nb_skills = data_util.load_dataset(fn=fn, batch_size=batch_size, shuffle=True) train_set, test_set, val_set = data_util.split_dataset(dataset=dataset, total_size=length, test_fraction=test_fraction, val_fraction=validation_fraction) set_sz = length * batch_size test_set_sz = (set_sz * test_fraction) val_set_sz = (set_sz - test_set_sz) * validation_fraction train_set_sz = set_sz - test_set_sz - val_set_sz print("============= Data Summary =============") print("Total number of students: %d" % set_sz) print("Training set size: %d" % train_set_sz) print("Validation set size: %d" % val_set_sz) print("Testing set size: %d" % test_set_sz) print("Number of skills: %d" % nb_skills) print("Number of features in the input: %d" % nb_features) print("========================================") ###Output ============= Data Summary ============= Total number of students: 4160 Training set size: 2662 Validation set size: 665 Testing set size: 832 Number of skills: 123 Number of features in the input: 246 ======================================== ###Markdown Part 3: Building the model ###Code student_model = deepkt.DKTModel( nb_features=nb_features, nb_skills=nb_skills, hidden_units=lstm_units, dropout_rate=dropout_rate) student_model.compile( optimizer=optimizer, metrics=[ metrics.BinaryAccuracy(), metrics.AUC(), metrics.Precision(), metrics.Recall() ]) student_model.summary() ###Output Model: "DKTModel" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= inputs (InputLayer) [(None, None, 246)] 0 _________________________________________________________________ masking (Masking) (None, None, 246) 0 _________________________________________________________________ lstm (LSTM) (None, None, 100) 138800 _________________________________________________________________ outputs (TimeDistributed) (None, None, 123) 12423 ================================================================= Total params: 151,223 Trainable params: 151,223 Non-trainable params: 0 _________________________________________________________________ ###Markdown Part 4: Train the Model ###Code import tensorflow as tf history = student_model.fit(dataset=train_set, epochs=epochs, verbose=verbose, validation_data=val_set, callbacks=[ tf.keras.callbacks.CSVLogger(f"{log_dir}/train.log"), tf.keras.callbacks.ModelCheckpoint(best_model_weights, save_best_only=True, save_weights_only=True), tf.keras.callbacks.TensorBoard(log_dir=log_dir) ]) ###Output Epoch 1/10 83/83 [==============================] - 12s 146ms/step - loss: 0.0657 - binary_accuracy: 0.7288 - auc: 0.7076 - precision: 0.7478 - recall: 0.9222 - val_loss: 0.0000e+00 - val_binary_accuracy: 0.0000e+00 - val_auc: 0.0000e+00 - val_precision: 0.0000e+00 - val_recall: 0.0000e+00 Epoch 2/10 83/83 [==============================] - 9s 108ms/step - loss: 0.0557 - binary_accuracy: 0.7720 - auc: 0.8120 - precision: 0.7765 - recall: 0.9440 - val_loss: 0.0666 - val_binary_accuracy: 0.7878 - val_auc: 0.8344 - val_precision: 0.7908 - val_recall: 0.9487 Epoch 3/10 83/83 [==============================] - 9s 108ms/step - loss: 0.0612 - binary_accuracy: 0.7788 - auc: 0.8233 - precision: 0.7862 - recall: 0.9348 - val_loss: 0.0607 - val_binary_accuracy: 0.7715 - val_auc: 0.8289 - val_precision: 0.7733 - val_recall: 0.9310 Epoch 4/10 83/83 [==============================] - 9s 103ms/step - loss: 0.0596 - binary_accuracy: 0.7877 - auc: 0.8315 - precision: 0.7991 - recall: 0.9319 - val_loss: 0.0618 - val_binary_accuracy: 0.7871 - val_auc: 0.8322 - val_precision: 0.7917 - val_recall: 0.9436 Epoch 5/10 83/83 [==============================] - 9s 109ms/step - loss: 0.0532 - binary_accuracy: 0.7817 - auc: 0.8291 - precision: 0.7958 - recall: 0.9199 - val_loss: 0.0518 - val_binary_accuracy: 0.8046 - val_auc: 0.8671 - val_precision: 0.8093 - val_recall: 0.9352 Epoch 6/10 83/83 [==============================] - 8s 98ms/step - loss: 0.0584 - binary_accuracy: 0.7768 - auc: 0.8201 - precision: 0.7889 - recall: 0.9232 - val_loss: 0.0522 - val_binary_accuracy: 0.7863 - val_auc: 0.8385 - val_precision: 0.8047 - val_recall: 0.9141 Epoch 7/10 83/83 [==============================] - 9s 104ms/step - loss: 0.0536 - binary_accuracy: 0.7839 - auc: 0.8295 - precision: 0.7970 - recall: 0.9238 - val_loss: 0.0603 - val_binary_accuracy: 0.7838 - val_auc: 0.8345 - val_precision: 0.7932 - val_recall: 0.9277 Epoch 8/10 83/83 [==============================] - 9s 107ms/step - loss: 0.0546 - binary_accuracy: 0.7958 - auc: 0.8498 - precision: 0.8080 - recall: 0.9248 - val_loss: 0.0607 - val_binary_accuracy: 0.8053 - val_auc: 0.8586 - val_precision: 0.8169 - val_recall: 0.9346 Epoch 9/10 83/83 [==============================] - 9s 106ms/step - loss: 0.0543 - binary_accuracy: 0.7795 - auc: 0.8309 - precision: 0.7928 - recall: 0.9147 - val_loss: 0.0509 - val_binary_accuracy: 0.7806 - val_auc: 0.8216 - val_precision: 0.7891 - val_recall: 0.9329 Epoch 10/10 83/83 [==============================] - 9s 105ms/step - loss: 0.0547 - binary_accuracy: 0.7950 - auc: 0.8464 - precision: 0.8063 - recall: 0.9248 - val_loss: 0.0603 - val_binary_accuracy: 0.7717 - val_auc: 0.8144 - val_precision: 0.7823 - val_recall: 0.9200 ###Markdown Part 5: Load the Model with the Best Validation Loss ###Code student_model.load_weights(best_model_weights) ###Output _____no_output_____ ###Markdown Part 6: Test the Model ###Code result = student_model.evaluate(test_set, verbose=verbose) ###Output 26/Unknown - 2s 67ms/step - loss: 0.0529 - binary_accuracy: 0.8071 - auc: 0.8599 - precision: 0.8176 - recall: 0.9329 ###Markdown Confirm we can use a GPU to run the model ###Code import tensorflow as tf import pandas as pd import numpy as np ###Output _____no_output_____ ###Markdown Define constants ###Code data = "data/kuze_data/evaluations_per_ans_with_taxonomy_ids_PPL.csv" factorized_taxonomies = "data/kuze_data/factorized_math_taxonomies.csv" factorized_students = "data/kuze_data/factorized_student_ids.csv" verbose = 1 best_model_weights = "weights/bestmodel" log_dir = "logs" optimizer = "adam" lstm_units = 200 batch_size = 64 epochs = 1 dropout_rate = 0.3 test_fraction = 0.2 validation_fraction = 0.2 ###Output _____no_output_____ ###Markdown Pre-processing ###Code import sys sys.path.append('/home/grenouille/Documents/jenga/final_project/code/kuze_dkt_imp') from deepkt import deepkt, data_util, metrics dataset, length, nb_features, nb_taxonomies = data_util.load_dataset(data, factorized_taxonomies, factorized_students, batch_size=batch_size, shuffle=True) train_set, test_set, val_set = data_util.split_dataset(dataset=dataset, total_size=length, test_fraction=test_fraction, val_fraction=validation_fraction) set_size = length * batch_size test_set_size = (set_size * test_fraction) val_set_size = (set_size - test_set_size) * validation_fraction train_set_size = set_size - test_set_size - val_set_size print("============== Data Summary ==============") print("Total number of students: %d" % set_size) print("Training set size: %d" % train_set_size) print("Validation set size: %d" % val_set_size) print("Testing set size: %d" % test_set_size) print("Number of skills: %d" % nb_taxonomies) print("Number of features in the input: %d" % nb_features) print("========================================= ") ###Output _____no_output_____ ###Markdown Building the model ###Code student_model = deepkt.DKTModel( nb_features=nb_features, nb_taxonomies=nb_taxonomies, hidden_units=lstm_units, dropout_rate=dropout_rate) student_model.compile( optimizer=optimizer, metrics=[ metrics.BinaryAccuracy(), metrics.AUC(), metrics.Precision(), metrics.Recall() ]) student_model.summary() ###Output _____no_output_____ ###Markdown Train the model ###Code history = student_model.fit( dataset=train_set, epochs=epochs, verbose=verbose, validation_data=val_set, callbacks=[ tf.keras.callbacks.CSVLogger(f"{log_dir}/train.log"), tf.keras.callbacks.ModelCheckpoint(best_model_weights, save_best_only=True, save_weights_only=True), tf.keras.callbacks.TensorBoard(log_dir=log_dir) ] ) ###Output _____no_output_____ ###Markdown Load the model with the best validation loss ###Code student_model.load_weights(best_model_weights) ###Output _____no_output_____ ###Markdown Test the model ###Code result = student_model.evaluate(test_set, verbose=verbose) result student_model.save('student_prediction') student_model.input_shape student_model.output_shape ###Output _____no_output_____ ###Markdown Prediction ###Code def preprocess_for_prediction(dataframe): seq = dataframe.groupby('student_id').apply( lambda r: ( r['factorized_student_id'], r['factorized_taxonomy_id'] ) ) dataset = tf.data.Dataset.from_generator( generator=lambda: seq, output_types=(tf.int32, tf.int32) ) # Add 1 since indexing starts from 0 student_depth = int(students['factorized_student_id'].max() + 1) taxonomy_depth = int(taxonomies['factorized_taxonomy_code'].max() + 1) dataset = dataset.map( lambda factorized_student_id, factorized_taxonomy_code: ( tf.one_hot(factorized_student_id, depth=student_depth), tf.one_hot(factorized_taxonomy_code, depth=taxonomy_depth) ) ) dataset = dataset.padded_batch( batch_size=64, padding_values=( tf.constant(-1, dtype=tf.float32), tf.constant(-1, dtype=tf.float32)), padded_shapes=([None, None], [None, None]) ) return dataset def process_student_data(dataset): """Preprocess the tensorflow Dataset type used for prediction. The first item in the dataset corresponds to the student information. Dimensions: -> batch size -> number of elements per batch -> one-hot encoded data (number of students) We want to get the categorical student_id from the one-hot encoding. Return a list containing the categorical student_id """ student_id_list = [] student_val_list = [] for i in range(len(dataset[0][0])): for j in range(len(dataset[0][0][i])): array = dataset[0][0][i][j] idx = np.argmax(array) student_id_list.append(idx) student_val_list.append(array[idx].numpy()) return student_id_list, student_val_list def process_taxonomy_data(dataset): """Preprocess the tensorflow Dataset type used for prediction. The second item in the dataset corresponds to the taxonomy information. Dimensions: -> batch size -> number of elements per batch -> one-hot encoded data (number of students) We want to get the categorical student_id from the one-hot encoding. Return a list containing the categorical student_id """ taxonomy_id_list = [] taxonomy_val_list = [] for i in range(len(dataset[0][1])): for j in range(len(dataset[0][1][i])): array = dataset[0][1][i][j] idx = np.argmax(array) taxonomy_id_list.append(idx) taxonomy_val_list.append(array[idx].numpy()) return taxonomy_id_list, taxonomy_val_list def preprocess_prediction_data(predictions): """Expose relevant predictions from the predictions array. Dimensions: -> batch size -> number of elements per batch -> one-hot encoded data (number of taxonomies) Return one-hot encoded arrays sequentially ordered. """ prediction_array_list = [] for i in range(len(predictions)): for j in range(len(predictions[i])): prediction_array_list.append(predictions[i][j]) return prediction_array_list def process_prediction_data(predictions, taxonomy_id_list): """Get the predicted value for a taxonomy. Predictions is a list of arrays containing predictions for all taxonomies. The arrays within the list are sequentially ordered. To get the relevant array we index into the list of arrays with the index of the taxonomy_id of current interest within the taxonomy_id_list To get the prediction for the taxonomy of interest, we index into the array with the taxonomy_id. Return a list of predicted values. Length should be equal to that of taxonomy_id_list. """ taxonomy_predictions = [] for idx, taxonomy_code in enumerate(taxonomy_id_list): prediction_array = predictions[idx] taxonomy_predictions.append(prediction_array[taxonomy_code]) assert len(taxonomy_predictions) == len(taxonomy_id_list) return taxonomy_predictions def post_prediction_preprocessing(dataset, predictions): """Process the dataset and predictions into a pandas DataFrame. We want to take the input dataset and match it to the corresponding predictions. The dataset has paddings in order to conform to expected dimensions. Padding value is -1 and that is where the student_val_list and taxonomy_val_list come in handy. Any values with -1 in those 2 lists corresponds to a padding value and can therefore be dropped""" # convert the dataset into a list for easy access and manipulation dataset = list(dataset) student_id_list, student_val_list = process_student_data(dataset) taxonomy_id_list, taxonomy_val_list = process_taxonomy_data(dataset) preprocessed_prediction_list = preprocess_prediction_data(predictions) taxonomy_predictions = process_prediction_data( preprocessed_prediction_list, taxonomy_id_list) # round off all values in taxonomy_predictions to 2 decimal places # for readability taxonomy_predictions = [round(i, 4) for i in taxonomy_predictions] column_names = ['factorized_student_id', 'one-hot_student_value', 'factorized_taxonomy_id', 'one-hot_taxonomy_value', 'prediction'] prediction_df = pd.DataFrame(list(zip(student_id_list, student_val_list, taxonomy_id_list, taxonomy_val_list, taxonomy_predictions)), columns=column_names) # remove padding values from students and taxonomies prediction_df = prediction_df[prediction_df['one-hot_student_value'] != -1] prediction_df = prediction_df[prediction_df['one-hot_taxonomy_value'] != -1] # if the value of the prediction is greater than or equal to 0.5 # the predicted answer should be 1 else 0 # astype('int') converts a boolean value to an integer True == 1, False == 0 prediction_df['predicted_answer'] = prediction_df['prediction'].ge(0.5).astype('int') prediction_df['predicted_answer'] = prediction_df['predicted_answer'].astype('int') return prediction_df data = pd.read_csv('data/kuze_data/predictor_evaluations.csv') prediction_data = data[data['subject'] == 'math'] taxonomies = pd.read_csv(factorized_taxonomies) students = pd.read_csv(factorized_students) prediction_data['factorized_taxonomy_id'] = prediction_data['taxonomy_id_0'].map( taxonomies.set_index('taxonomy_id_0')['factorized_taxonomy_code']) prediction_data['factorized_student_id'] = prediction_data['student_id'].map( students.set_index('student_id')['factorized_student_id']) shape = prediction_data.shape[0] # due to limitations in dimensionality we want each dataframe we predict on to have # 95 items no_of_dataframes = shape // 95 # split the data into n number of dataframes each with at least 95 rows partitions = np.array_split(prediction_data, no_of_dataframes) # carry out prediction on a partition of the predicted data and append # the returned dataframe to a list predicted_partitions = [] for df in partitions: dataset = preprocess_for_prediction(df) predictions = student_model.predict(dataset) prediction_data = post_prediction_preprocessing(dataset, predictions) predicted_partitions.append(prediction_data) prediction_data = pd.concat(partitions, ignore_index=True) predictions = pd.concat(predicted_partitions, ignore_index=True) assert prediction_data.shape[0] == predictions.shape[0] rows = prediction_data.shape[0] answer_predictions = predictions['predicted_answer'].values for i in range(rows): prediction_data.at[i, 'answer_selection_prediction'] = answer_predictions[i] def get_aggregated_evaluation_performance(dataframe, with_preds=True): # Group data by student and evaluation id and calculate actual and predicted # performance on questions eval_id = [] student = [] total_questions = [] actual_performance = [] predicted_performance = [] date_of_evaluation = [] subject = [] student_full_name = [] class_name = [] class_grade = [] school_name = [] grouped_data = dataframe.groupby(['evaluation_id', 'student_id']) for item in grouped_data: evaluation_id, student_id = item[0] data = item[1] actual = data['answer_selection_correct'].value_counts() total_nu_questions = actual.sum() first_name = data['student_first_name'].unique()[0] last_name = data['student_last_name'].unique()[0] if first_name is np.nan: first_name = '' if last_name is np.nan: last_name = '' full_name = first_name + ' ' + last_name try: actual_correct = actual[1] except KeyError: # if a KeyError occurs it means the student got all of the # questions in that evaluation wrong actual_correct = 0 actual_perc = int((actual_correct / total_nu_questions) * 100) if with_preds: # if prediction data is included predicted = data['answer_selection_prediction'].astype('int').value_counts() # ensure acual no of questions done matches no of questions predicted assert actual.sum() == predicted.sum() predicted_correct = predicted[1] predicted_perc = int((predicted_correct/ total_nu_questions) * 100) predicted_performance.append(predicted_perc) else: predicted_performance.append(0) eval_id.append(evaluation_id) student.append(student_id) total_questions.append(total_nu_questions) actual_performance.append(actual_perc) date_of_evaluation.append(data['date_of_evaluation'].unique()[0].date()) subject.append(data['subject'].unique()[0]) student_full_name.append(full_name) class_name.append(data['class_name'].unique()[0]) class_grade.append(data['class_grade'].unique()[0]) school_name.append(data['school_name'].unique()[0]) column_names = ['evaluation_id', 'student_id', 'total_number_of_questions', 'actual_performance (%)', 'predicted_performance (%)', 'date_of_evaluation', 'subject', 'student_full_name', 'class_name', 'class_grade', 'school_name'] performance_df = pd.DataFrame(list(zip(eval_id, student, total_questions, actual_performance, predicted_performance, date_of_evaluation, subject, student_full_name, class_name, class_grade, school_name)), columns=column_names) return performance_df mask = (ds_evaluation_per_ans_sci_prediction_df['date_of_evaluation'] < '2021-07-01') training_data = ds_evaluation_per_ans_sci_prediction_df.loc[mask] # training_data.dropna(subset=['answer_selection_correct'], inplace=True) aggregated_training_data = get_aggregated_evaluation_performance(training_data, with_preds=False) performance_data = get_aggregated_evaluation_performance(prediction_data) aggregated_performance_data = pd.concat([aggregated_training_data, performance_data], ignore_index=True) ###Output _____no_output_____
lab/breast-cancer-classification.ipynb	###Markdown Predicting breast cancer tumor type: Benign or malignantApply a:- linear classifier, `SVC(kernel='linear')` - non-linear classifier, `RandomForestClassifier(random_state=82)` to the Wisconsin breast cancer dataset.The data is hosted on UCI https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)we will need `wdbc.names` and `wdbc.data` from the data folder on UCI. ###Code import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns ###Output _____no_output_____ ###Markdown 1. Download the data TODO: add base url and filenames. ###Code import os import requests #TODO: add base url and filenames base_url = ... file_names = [..., ...] # .names then .data for file_name in file_names: if not os.path.isfile(file_name): print(f"Downloading {file_name} from {base_url}") response = requests.get(base_url+file_name) with open(file_name, 'wb') as f: f.write(response.content) else: print(f"{file_name} found on disk") ###Output wdbc.names found on disk wdbc.data found on disk ###Markdown 2. Prepare the data 2.1 A look at the data files ###Code with open(file_names[0]) as f: print(f.read()) ###Output 1. Title: Wisconsin Diagnostic Breast Cancer (WDBC) 2. Source Information a) Creators: Dr. William H. Wolberg, General Surgery Dept., University of Wisconsin, Clinical Sciences Center, Madison, WI 53792 [email protected] W. Nick Street, Computer Sciences Dept., University of Wisconsin, 1210 West Dayton St., Madison, WI 53706 [email protected] 608-262-6619 Olvi L. Mangasarian, Computer Sciences Dept., University of Wisconsin, 1210 West Dayton St., Madison, WI 53706 [email protected] b) Donor: Nick Street c) Date: November 1995 3. Past Usage: first usage: W.N. Street, W.H. Wolberg and O.L. Mangasarian Nuclear feature extraction for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on Electronic Imaging: Science and Technology, volume 1905, pages 861-870, San Jose, CA, 1993. OR literature: O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and prognosis via linear programming. Operations Research, 43(4), pages 570-577, July-August 1995. Medical literature: W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994) 163-171. W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Image analysis and machine learning applied to breast cancer diagnosis and prognosis. Analytical and Quantitative Cytology and Histology, Vol. 17 No. 2, pages 77-87, April 1995. W.H. Wolberg, W.N. Street, D.M. Heisey, and O.L. Mangasarian. Computerized breast cancer diagnosis and prognosis from fine needle aspirates. Archives of Surgery 1995;130:511-516. W.H. Wolberg, W.N. Street, D.M. Heisey, and O.L. Mangasarian. Computer-derived nuclear features distinguish malignant from benign breast cytology. Human Pathology, 26:792--796, 1995. See also: http://www.cs.wisc.edu/~olvi/uwmp/mpml.html http://www.cs.wisc.edu/~olvi/uwmp/cancer.html Results: - predicting field 2, diagnosis: B = benign, M = malignant - sets are linearly separable using all 30 input features - best predictive accuracy obtained using one separating plane in the 3-D space of Worst Area, Worst Smoothness and Mean Texture. Estimated accuracy 97.5% using repeated 10-fold crossvalidations. Classifier has correctly diagnosed 176 consecutive new patients as of November 1995. 4. Relevant information Features are computed from a digitized image of a fine needle aspirate (FNA) of a breast mass. They describe characteristics of the cell nuclei present in the image. A few of the images can be found at http://www.cs.wisc.edu/~street/images/ Separating plane described above was obtained using Multisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree Construction Via Linear Programming." Proceedings of the 4th Midwest Artificial Intelligence and Cognitive Science Society, pp. 97-101, 1992], a classification method which uses linear programming to construct a decision tree. Relevant features were selected using an exhaustive search in the space of 1-4 features and 1-3 separating planes. The actual linear program used to obtain the separating plane in the 3-dimensional space is that described in: [K. P. Bennett and O. L. Mangasarian: "Robust Linear Programming Discrimination of Two Linearly Inseparable Sets", Optimization Methods and Software 1, 1992, 23-34]. This database is also available through the UW CS ftp server: ftp ftp.cs.wisc.edu cd math-prog/cpo-dataset/machine-learn/WDBC/ 5. Number of instances: 569 6. Number of attributes: 32 (ID, diagnosis, 30 real-valued input features) 7. Attribute information 1) ID number 2) Diagnosis (M = malignant, B = benign) 3-32) Ten real-valued features are computed for each cell nucleus: a) radius (mean of distances from center to points on the perimeter) b) texture (standard deviation of gray-scale values) c) perimeter d) area e) smoothness (local variation in radius lengths) f) compactness (perimeter^2 / area - 1.0) g) concavity (severity of concave portions of the contour) h) concave points (number of concave portions of the contour) i) symmetry j) fractal dimension ("coastline approximation" - 1) Several of the papers listed above contain detailed descriptions of how these features are computed. The mean, standard error, and "worst" or largest (mean of the three largest values) of these features were computed for each image, resulting in 30 features. For instance, field 3 is Mean Radius, field 13 is Radius SE, field 23 is Worst Radius. All feature values are recoded with four significant digits. 8. Missing attribute values: none 9. Class distribution: 357 benign, 212 malignant ###Markdown Data set summary Question 1: In the dataset, which columns are features, which column is the target?From the dataset desciption above, summarize how many features we have and what their column names are. State which column is the target, the values we would like to predict.Note, we will ignore the patient ID column and only consider columns 1-12. TODO: answer question below. ADD dataset summary The data ###Code with open(file_names[1]) as f: for _ in range(10): print(f.readline(), end="") ###Output 842302,M,17.99,10.38,122.8,1001,0.1184,0.2776,0.3001,0.1471,0.2419,0.07871,1.095,0.9053,8.589,153.4,0.006399,0.04904,0.05373,0.01587,0.03003,0.006193,25.38,17.33,184.6,2019,0.1622,0.6656,0.7119,0.2654,0.4601,0.1189 842517,M,20.57,17.77,132.9,1326,0.08474,0.07864,0.0869,0.07017,0.1812,0.05667,0.5435,0.7339,3.398,74.08,0.005225,0.01308,0.0186,0.0134,0.01389,0.003532,24.99,23.41,158.8,1956,0.1238,0.1866,0.2416,0.186,0.275,0.08902 84300903,M,19.69,21.25,130,1203,0.1096,0.1599,0.1974,0.1279,0.2069,0.05999,0.7456,0.7869,4.585,94.03,0.00615,0.04006,0.03832,0.02058,0.0225,0.004571,23.57,25.53,152.5,1709,0.1444,0.4245,0.4504,0.243,0.3613,0.08758 84348301,M,11.42,20.38,77.58,386.1,0.1425,0.2839,0.2414,0.1052,0.2597,0.09744,0.4956,1.156,3.445,27.23,0.00911,0.07458,0.05661,0.01867,0.05963,0.009208,14.91,26.5,98.87,567.7,0.2098,0.8663,0.6869,0.2575,0.6638,0.173 84358402,M,20.29,14.34,135.1,1297,0.1003,0.1328,0.198,0.1043,0.1809,0.05883,0.7572,0.7813,5.438,94.44,0.01149,0.02461,0.05688,0.01885,0.01756,0.005115,22.54,16.67,152.2,1575,0.1374,0.205,0.4,0.1625,0.2364,0.07678 843786,M,12.45,15.7,82.57,477.1,0.1278,0.17,0.1578,0.08089,0.2087,0.07613,0.3345,0.8902,2.217,27.19,0.00751,0.03345,0.03672,0.01137,0.02165,0.005082,15.47,23.75,103.4,741.6,0.1791,0.5249,0.5355,0.1741,0.3985,0.1244 844359,M,18.25,19.98,119.6,1040,0.09463,0.109,0.1127,0.074,0.1794,0.05742,0.4467,0.7732,3.18,53.91,0.004314,0.01382,0.02254,0.01039,0.01369,0.002179,22.88,27.66,153.2,1606,0.1442,0.2576,0.3784,0.1932,0.3063,0.08368 84458202,M,13.71,20.83,90.2,577.9,0.1189,0.1645,0.09366,0.05985,0.2196,0.07451,0.5835,1.377,3.856,50.96,0.008805,0.03029,0.02488,0.01448,0.01486,0.005412,17.06,28.14,110.6,897,0.1654,0.3682,0.2678,0.1556,0.3196,0.1151 844981,M,13,21.82,87.5,519.8,0.1273,0.1932,0.1859,0.09353,0.235,0.07389,0.3063,1.002,2.406,24.32,0.005731,0.03502,0.03553,0.01226,0.02143,0.003749,15.49,30.73,106.2,739.3,0.1703,0.5401,0.539,0.206,0.4378,0.1072 84501001,M,12.46,24.04,83.97,475.9,0.1186,0.2396,0.2273,0.08543,0.203,0.08243,0.2976,1.599,2.039,23.94,0.007149,0.07217,0.07743,0.01432,0.01789,0.01008,15.09,40.68,97.65,711.4,0.1853,1.058,1.105,0.221,0.4366,0.2075 ###Markdown 2.2 Loading the data with PandasSee `pandas.ipynb` for more information on the pandas python library. TODO: add the names of the 12 columns as a list to the names parameter. ###Code #TODO: add the names of the 12 columns as a list to the names parameter data = pd.read_csv( 'wdbc.data', index_col=False, names=[ ... ]) data.head() data.info() data.describe() data['diagnosis'].value_counts() ###Output _____no_output_____ ###Markdown renaming values in `'diagnosis'` column TODO: change 'B' to 'benign' and 'M' to 'malginant'. ###Code #TODO: change 'B' to 'benign' and 'M' to 'malginant' ... data['diagnosis'].value_counts() ###Output _____no_output_____ ###Markdown 2.3 Getting an overview by visualizing the dataSee `visualization.ipynb` for more information on plotting in python. Comparing healthy and diseased feature values TODO: create sns.histplot() for all columns in data except id and diagnosis. ###Code #TODO: create sns.histplot() for all columns in data except id and diagnosis plt.tight_layout() ###Output _____no_output_____ ###Markdown Pair-wise correlations of numerical features TODO: Create sns.pairplot() for columns 'radius', 'area', 'concavity', 'symmetry' in data using 'diagnosis' as hue. ###Code #TODO: Create sns.pairplot() for columns 'radius', 'area', 'concavity', 'symmetry' in data using 'diagnosis' as hue ###Output _____no_output_____ ###Markdown 2.4 Create feature matrix and target vector The feature matrix $X$ is the input to the model. The target vector $y$ contains the values the model should produce, the desired output. See [Python Data Science Handbook 05.02-Introducing-Scikit-Learn](https://github.com/jakevdp/PythonDataScienceHandbook/blob/8a34a4f653bdbdc01415a94dc20d4e9b97438965/notebooks/05.02-Introducing-Scikit-Learn.ipynb) for more information. TODO: use all columns except id and diagnosis for feature matrix X. assign diagnosis column to target vector y ###Code #TODO: use all columns except id and diagnosis for feature matrix X X = ... #TODO: assign diagnosis column to target vector y y = ... print(f"feature matrix X shape={X.shape}") print(f"target vector y shape={y.shape}") ###Output feature matrix X shape=(569, 10) target vector y shape=(569,) ###Markdown 2.5 Create training and validation setsWe split the data into two sets:1. Training set - used to create the machine learning model1. Validation set - used to evaluate model performance ###Code from sklearn.model_selection import train_test_split X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.1, stratify=y, random_state=31) print(f"train shape={X_train.shape}") print(f"val shape={X_val.shape}") print("training samples:") y_train.value_counts() print("validation samples:") y_val.value_counts() ###Output validation samples: ###Markdown 3. Machine learning: Supervised classification 3.1 Train a linear support vector classifier `SVC(kernel='linear')` See [Python Data Science Handbook 05.07-Support-Vector-Machines](https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.07-Support-Vector-Machines.ipynb) for more information on linear support vector classifiers. ###Code from sklearn.svm import SVC model_svc = SVC(kernel='linear') model_svc.fit(X_train, y_train) ###Output _____no_output_____ ###Markdown 3.2 Compare training and validation accuracyImportant: We assess the performance of the model on data the model has not seen yet. This set of data is called the validation set. The data used to create the model is used the training set.See [Python Data Science Handbook 05.03-Hyperparameters-and-Model-Validation](https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.03-Hyperparameters-and-Model-Validation.ipynb) for more information on interpreting model performance ###Code print(f"{model_svc} training accuracy={model_svc.score(X_train, y_train):.2f}") print(f"{model_svc} validation accuracy={model_svc.score(X_val, y_val):.2f}") ###Output SVC(kernel='linear') validation accuracy=0.89 ###Markdown Question 2: SVC - Are we over or underfitting? We are over-/under-fitting. We need more/less regularization and a higher/lower `C`. We will try `C=0.01`/`C=100` next. TODO: answer question below. ANSWER QUESTION HERE TODO: Re-train the model based on your answer. ###Code #TODO Re-train the model based on your answer print(f"{model_svc} training accuracy={model_svc.score(X_train, y_train):.2f}") print(f"{model_svc} validation accuracy={model_svc.score(X_val, y_val):.2f}") ###Output SVC(C=100, kernel='linear') training accuracy=0.93 SVC(C=100, kernel='linear') validation accuracy=0.93 ###Markdown Nice increase in accuracy. 3.3 Train a non-linear random forest classifier `RandomForestClassifier(random_state=82)` See [Python Data Science Handbook 05.08-Random-Forests](https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.08-Random-Forests.ipynb) for more information on random forest classifiers. ###Code from sklearn.ensemble import RandomForestClassifier model_rf = RandomForestClassifier(random_state=82) model_rf.fit(X_train, y_train) ###Output _____no_output_____ ###Markdown 3.4 Compare training and validation accuracyImportant: We assess the performance of the model on data the model has not seen yet. This set of data is called the validation set. The data used to create the model is used the training set.See [Python Data Science Handbook 05.03-Hyperparameters-and-Model-Validation](https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.03-Hyperparameters-and-Model-Validation.ipynb) for more information on interpreting model performance ###Code print(f"{model_rf} training accuracy={model_rf.score(X_train, y_train):.2f}") print(f"{model_rf} validation accuracy={model_rf.score(X_val, y_val):.2f}") ###Output RandomForestClassifier(random_state=82) validation accuracy=0.89 ###Markdown Question 3: RandomForest - Are we over or underfitting? We are over-/under-fitting. We need more/less regularization and adjust/not adjust `max_depth` or adjust/not adjust `max_features`. We will try `max_depth=3`/`max_features=None` next. TODO: answer question below. ANSWER QUESTION HERE TODO: Re-train the model based on your answer. ###Code #TODO: Re-train the model based on your answer print(f"{model_rf} training accuracy={model_rf.score(X_train, y_train):.2f}") print(f"{model_rf} validation accuracy={model_rf.score(X_val, y_val):.2f}") ###Output RandomForestClassifier(max_depth=3, random_state=82) training accuracy=0.96 RandomForestClassifier(max_depth=3, random_state=82) validation accuracy=0.91 ###Markdown This helped a little bit. 3.5 The confusion matrix More information on [wikipedia confusion matrix](https://en.wikipedia.org/wiki/Confusion_matrix) Using the svc model from step 3.2 ###Code from sklearn.metrics import confusion_matrix mat = confusion_matrix(y_val, model_svc.predict(X_val)) labels = ['benign', 'malignant'] sns.heatmap(mat, square=True, annot=True, cbar=False, xticklabels=labels, yticklabels=labels) plt.xlabel('predicted value') plt.ylabel('true value') plt.title(f'{model_svc}'); ###Output _____no_output_____ ###Markdown Using the random forest model from step 3.4 ###Code from sklearn.metrics import confusion_matrix mat = confusion_matrix(y_val, model_rf.predict(X_val)) labels = ['benign', 'malignant'] sns.heatmap(mat, square=True, annot=True, cbar=False, xticklabels=labels, yticklabels=labels) plt.xlabel('predicted value') plt.ylabel('true value') plt.title(f'{model_rf}'); ###Output _____no_output_____ ###Markdown Question 4: What kind of errors do SVC and RandomForest make?Based on the confusion matrices above, summarize false positives and false negatives of SVC and RandomForest make? TODO: answer question below. ANSWER QUESTION HERE 3.6 Summarize the different scores ###Code print(f'--- {model_svc} ---') print('training accuracy (all data) {:.3f}'.format(model_svc.score(X_train, y_train))) print('validation accuracy (new data) {:.3f}'.format(model_svc.score(X_val, y_val))) print(f'--- {model_rf} ---') print('training accuracy (all data) {:.3f}'.format(model_rf.score(X_train, y_train))) print('validation accuracy (new data) {:.3f}'.format(model_rf.score(X_val, y_val))) ###Output --- SVC(C=100, kernel='linear') --- training accuracy (all data) 0.926 validation accuracy (new data) 0.930 --- RandomForestClassifier(max_depth=3, random_state=82) --- training accuracy (all data) 0.965 validation accuracy (new data) 0.912
course1/.ipynb_checkpoints/Mnist1-LearningRateScheduler-checkpoint.ipynb	###Markdown Fashion Mnist: example with a Learning Rate (LR) scheduler ###Code import numpy as np import pandas as pd import tensorflow as tf import matplotlib.pyplot as plt # check TensorFlow version print(tf.__version__) data = tf.keras.datasets.fashion_mnist # globals EPOCHS = 60 BATCH_SIZE = 256 (train_images, train_labels), (test_images, test_labels) = data.load_data() print('Number of training images:', train_images.shape[0]) print('Number of test images:', test_images.shape[0]) # how many distinct classes np.unique(train_labels) # ok 10 distinct classes labeled as 0..9 # images are greyscale images train_images.shape ###Output _____no_output_____ ###Markdown first of all, normalize imagestrain_images /= 255.test_images /= 255. ###Code # let's sess one image plt.imshow(train_images[0], cmap = 'Greys'); # let's build a first classification model def build_model(): model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(28,28)), tf.keras.layers.Dense(128, activation = 'relu'), # adding these two intermediate layers I go from 0.85 to 0.87 validation accuracy tf.keras.layers.Dense(64, activation = 'relu'), tf.keras.layers.Dense(32, activation = 'relu'), tf.keras.layers.Dense(10, activation = 'softmax') ]) model.compile(optimizer='adam', loss = 'sparse_categorical_crossentropy', metrics = ['accuracy']) return model # let's see how many parameters, etc model = build_model() model.summary() # add a Callback that changes the learning rate during the training def lr_schedule(epoch): lr_initial = 0.001 ep_start_decay = 20 decay_rate = 0.9 if epoch > ep_start_decay: lr = lr_initial * decay_rate ** (epoch - ep_start_decay) else: lr = lr_initial return lr # let's plot it def plot_ls_scheduler(fn): vet_epochs = np.arange(EPOCHS) vet_lr = [fn(epoch) for epoch in vet_epochs] plt.plot(vet_epochs, vet_lr, 'b*') plt.grid() # here we plot plot_ls_scheduler(lr_schedule) # the callback for the LR cheduler cbk1 = tf.keras.callbacks.LearningRateScheduler(lr_schedule, verbose = 1) history = model.fit(train_images, train_labels, epochs = EPOCHS, batch_size = BATCH_SIZE, validation_split = 0.1, callbacks = [cbk1]) loss = history.history['loss'] val_loss = history.history['val_loss'] accuracy = history.history['accuracy'] val_accuracy = history.history['val_accuracy'] plt.xlabel('epoch') plt.ylabel('loss') plt.plot(loss, label = 'loss') plt.plot(val_loss, label = 'validation loss') plt.legend(loc = 'upper right') plt.grid(); # wants to see if it starts overfitting START = 20 plt.xlabel('epoch') plt.ylabel('loss') plt.plot(loss[START:], label = 'loss') plt.plot(val_loss[START:], label = 'validation loss') plt.legend(loc = 'upper right') plt.grid(); # ok it has slightly started overfitting.. as we can see from epochs 15 validation loss becomes higher and training loss is still decreasing plt.xlabel('epoch') plt.ylabel('accuracy') plt.plot(accuracy, label = 'accuracy') plt.plot(val_accuracy, label = 'validation accuracy') plt.legend(loc = 'lower right') plt.grid(); model.evaluate(test_images, test_labels) ###Output 313/313 [==============================] - 0s 925us/step - loss: 0.4801 - accuracy: 0.8766
.ipynb_checkpoints/Europeandataporta-checkpoint.ipynb	###Markdown Europeandataportal.eu Test access SPARQL endpoint ###Code import sys,json import pandas as pd from SPARQLWrapper import SPARQLWrapper, JSON endpoint_url = "https://www.europeandataportal.eu/sparql" query = """SELECT * WHERE { ?s ?p ?o } limit 100""" def get_sparql_dataframe(endpoint_url, query): # print (query) user_agent = "user: salgo60/%s.%s" % (sys.version_info[0], sys.version_info[1]) sparql = SPARQLWrapper(endpoint_url, agent=user_agent) sparql.setQuery(query) sparql.setReturnFormat(JSON) result = sparql.query().convert() print(type(result)) #print(results) column_names = ["s", "p", "q"] cols = results["head"] out = [] for row in processed_results['head']: item = [] print (cols) for c in cols: print(row) item.append(row.get(c, {}).get('value')) out.append(item) return pd.DataFrame(out, columns=cols) df = get_sparql_dataframe(endpoint_url, query) ###Output <class 'dict'> {'link': [], 'vars': ['s', 'p', 'o']} link
keras/keras_multiclass_classification.ipynb	###Markdown AbstractThis notebook is an example that shows how to build a multiclass classification model with the Keras API. References: - [Multiclass Classification with Keras](http://machinelearningmastery.com/multi-class-classification-tutorial-keras-deep-learning-library/)- [Display deep learning model training history with Keras](http://machinelearningmastery.com/display-deep-learning-model-training-history-in-keras/) Build Model ###Code import keras from keras.models import Sequential from keras.layers import Dense, Dropout, Activation from keras.optimizers import SGD # Generate dummy data import numpy as np import pandas as pd x_train = np.random.random((1000, 20)) y_train = keras.utils.to_categorical(np.random.randint(10, size=(1000, 1)), num_classes=10) x_test = np.random.random((100, 20)) y_test = keras.utils.to_categorical(np.random.randint(10, size=(100, 1)), num_classes=10) model = Sequential() # Dense(64) is a fully-connected layer with 64 hidden units. # in the first layer, you must specify the expected input data shape: # here, 20-dimensional vectors. model.add(Dense(64, activation='relu', input_dim=20)) model.add(Dropout(0.5)) model.add(Dense(64, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(10, activation='softmax')) sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9, nesterov=True) model.compile(loss='categorical_crossentropy', optimizer=sgd, metrics=['accuracy']) model.summary() print("stateful:", model.stateful) ###Output Using TensorFlow backend. ###Markdown Training ###Code # prevent the application from occupying all the memory in the GPU. import tensorflow as tf from keras.backend.tensorflow_backend import set_session config = tf.ConfigProto() #config.gpu_options.per_process_gpu_memory_fraction = 0.2 config.gpu_options.allow_growth=True session = tf.Session(config=config) set_session(session) history = model.fit(x_train, y_train, epochs=100, batch_size=128, verbose=0) history.history.keys() import matplotlib.pyplot as plt # configure notebook to display plots %matplotlib inline from matplotlib.pylab import rcParams rcParams['figure.figsize'] = 15,6 metrics = pd.DataFrame(history.history) def plot_metrics(metrics): ''' ''' ax = plt.subplot(211) # plot the evolution of loss and accurary during the training peroid ax.plot(metrics['loss'], color='r') #plt.plot(metrics['acc']) plt.ylabel('loss') plt.xlabel('epochs') ax = plt.subplot(212) ax.plot(metrics['acc']) plt.xlabel('epochs') _ = plt.ylabel('accuracy') plot_metrics(metrics) ###Output _____no_output_____ ###Markdown The evolution of `loss` and `accurary` metrics show that the model is constantly approaching to a more optimal values. Yet, there still certain potential to get to a more optimal point, if one adds more `epochs`.Indeed, as we see from the following experiment, on top of the model trained after `100 epochs`, we added another 100 epochs, the model continues to evolve torwards a more optimal position, i.e. loss decreases and accuracy increases. ###Code history = model.fit(x_train, y_train, epochs=100, batch_size=128, verbose=0) plot_metrics(pd.DataFrame(history.history)) ###Output _____no_output_____ ###Markdown Evaluation ###Code score = model.evaluate(x_test, y_test, batch_size=128) print(score) # as long as the Notebook is alive, the application would keep occupying the GPU memory. session.close() ###Output _____no_output_____
assignments/.ipynb_checkpoints/assignment-3-checkpoint.ipynb	###Markdown Assignment 3 - Handling arrays with NumPy Loan Pham and Brandan Owens Exercise 1 Import the data set “Boston_Housing.csv” Extract ['PRICE'] into an arrayPlot a histogram of housing priceFind the mean, max, 75th percentile of the housing price.Create an array of two rows, with the first row from [‘’RM”], and the second row from [“PRICE”]Find the number of houses with “RM” Find the mean of the housing price, with “RM” > 5 Plot a scatter plot to show the relationship between number of rooms and housing price (use plt.scatter()) ###Code # import the data set import os import pandas as pd import numpy as np data = pd.read_csv("../dataFiles/Boston_Housing.csv") data # extract price price = np.array(data["PRICE"]) price #plot histogram import matplotlib.pyplot as plt plt.hist(price) # find the mean, max, 75th percentile of the housing price print(price.max()) print(price.mean()) print(np.percentile(price,75)) # create an array of two rows from "RM" and "PRICE" rm = np.array(data["RM"]) rm first_row = rm[0:2] print(first_row) second_row = price[0:2] print(second_row) # Find the number of houses with “RM” < 5 # print(np.sum(rm < 5)) np.count_nonzero(rm < 5) # find the mean housing price where "RM" is greater than 5 np.mean(rm > 5) # plot scatterplot to show the relationship between number of rooms and housing price plt.scatter(rm, price) ###Output _____no_output_____ ###Markdown Exercise 2Create a 1000x1 array of numbers, x which divides the interval from -10 to 10 into equal widths.Reshape the array x into 20x50 array, then: (a) Find the shape, dimension, and data type of the array. (b) Access the last element of each row (c) Access first element and then every other elements of each row (d) Access the subarray 7th to 10th rows and 5th to 11th columns (e) find the sum of the 7th column (f) Print the elements in each column which is greater 0. (g) Replace all the negative numbers of the array with 0. (h) Sort each column of the array in descending order. ###Code # Create a 1000x1 array of numbers, x which divides the interval from -10 to 10 into equal widths. x = np.linspace(-10,10, num =1000) x.reshape((1000,1)) # reshape the array into 20x50 x_reshaped = x.reshape(20,50) x_reshaped # (a) Find the shape, dimension, and data type of the array. print(x_reshaped.shape) print(x_reshaped.ndim) print(x_reshaped.dtype) # (b) Access the last element of each row x_reshaped[:,-1] #(c) Access first element and then every other elements of each row x_reshaped[::,::2] # (d) Access the subarray 7th to 10th rows and 5th to 11th columns acc = x_reshaped[6:10, 4:11] acc # (e) find the sum of the 7th column sum_col = x_reshaped[:, 6].sum() sum_col # (f) print the elements in each column which is greater 0. for row in x_reshaped: for element in row: if element > 0: print(element) # (g) Replace all the negative numbers of the array with 0. num = x_reshaped print(np.where(num < 0, 0, num)) # (h) sort each column of the array in descending order. arrg = (-np.sort(-x_reshaped)) arrg ###Output _____no_output_____ ###Markdown Exercise 3 This exercise illustrates a simple machine learning algorithm. Suppose you have two arrays of numbers. You are going to teach the machine to learn the relationship between the two arrays. ###Code # - Create an array of 100 random numbers, x. Each number is between 0 and 1. x = np.random.uniform(0, 1, 100) x # Create an array, y, and y = 3x + 2 y = 3x + 2 y # - Create two numbers, a and b. Initialize them to be 0. a = 0 b = 0 # - Create 3 empty lists. list1 = [] list2 = [] list3 = [] # - the machine predicts the value of y, y_pred: y_pred = ax+b # calculate the cost value = sum of the square of difference between y_pred and actual y # Iterate the above optimization steps 1000 times. y_pred = ax +b for i in range(1000): cost = np.dot((y_pred - y), (y_pred - y)) # update the values of a and b da = 2np.dot((y_pred - y),(x)) db = 2np.sum(y_pred - y) a = a - 0.001da b = b - 0.001db y_pred = ax + b # - Store the values of a, b and cost in the 3 lists you created. list1.append(a) list2.append(b) list3.append(cost) # Plot a graph to show how the values of a and b change over iteration. plt.plot(list1, label='a') plt.plot(list2, label='b') plt.legend() plt.plot(list3, label='list3') plt.legend() ###Output _____no_output_____
notebooks/lstm-gait-classifier.ipynb	###Markdown Preparing dataset: ###Code def prepare_dataset(features: str = 'upcv1/train/coordinates'): print(f"Getting {features} features...") with open(file=f'{FEATURES_FOLDER}{features}.pickle', mode='rb+') as file: X, y = pickle.load(file=file) S, W, C = X.shape assert S == y.shape[0] print(f""" {X.shape}, {y.shape} Selected sequences: {S} Sequence window size: {W} Feature vector size: {C} Unique subjects: {len(np.unique(y))}""") return X, y """ -- dataset: upcv1, ks20, oumvlp -- augmentation: rotation and flipping -- feature combinations: coordinates, velocity, distance, orientation -- dimentionality reduction: PCA w/ varying dimension """ FEATURES = [ ('upcv1/train/coordinates', 'upcv1/test/coordinates'), ('upcv1/train/coordinates-augmented', 'upcv1/test/coordinates'), ('upcv1/train/velocity', 'upcv1/test/velocity'), ('upcv1/train/distance', 'upcv1/test/distance'), ('upcv1/train/orientation', 'upcv1/test/orientation'), ('upcv1/train/c-v', 'upcv1/test/c-v'), ('upcv1/train/d-o', 'upcv1/test/d-o'), ('upcv1/train/c-d-o', 'upcv1/test/c-d-o'), ('upcv1/train/c-v-d-o', 'upcv1/test/c-v-d-o'), ('ks20/train/coordinates', 'ks20/test/coordinates'), ('ks20/train/coordinates-augmented', 'ks20/test/coordinates'), ('ks20/train/velocity', 'ks20/test/velocity'), ('ks20/train/distance', 'ks20/test/distance'), ('ks20/train/orientation', 'ks20/test/orientation'), ('ks20/train/c-v', 'ks20/test/c-v'), ('ks20/train/d-o', 'ks20/test/d-o'), ('ks20/train/c-d-o', 'ks20/test/c-d-o'), ('ks20/train/c-v-d-o', 'ks20/test/c-v-d-o') ] train_features, test_features = FEATURES[7] X_train, y_train = prepare_dataset(features=train_features) X_test, y_test = prepare_dataset(features=test_features) def get_pca(X, R=None): """ R - desired reduced dimension size """ C, F, L = X.shape if R is None: R = L X = X.reshape(CF, L) pca = PCA(n_components=R).fit(X) return pca def transform_pca(pca, X): C, F, L = X.shape X = X.reshape(CF, -1) return pca.transform(X).reshape(C, F, -1) pca = get_pca(X_train, R=None) X_train = transform_pca(pca, X_train) X_test = transform_pca(pca, X_test) X_train.shape ###Output _____no_output_____ ###Markdown Set Parameters: ###Code n_classes = len(np.unique(y_train)) # n_steps - timesteps per series # n_input - num input parameters per timestep training_data_count, n_steps, n_input = X_train.shape test_data_count, _, _ = X_test.shape global_step = tf.Variable(0, trainable=False) learning_rate = tf.convert_to_tensor(0.001) # Hidden layer num of features n_hidden = 64 batch_size = 128 epochs = 3000 ###Output _____no_output_____ ###Markdown Utility functions for training: ###Code def LSTM(_X, _weights, _biases): # model architecture based on "guillaume-chevalier" and "aymericdamien" under the MIT license. _X = tf.transpose(_X, [1, 0, 2]) # permute n_steps and batch_size _X = tf.reshape(_X, [-1, n_input]) # Rectified Linear Unit activation function used _X = tf.nn.relu(tf.matmul(_X, _weights['hidden']) + _biases['hidden']) # Split data because rnn cell need a list of inputs for the RNN inner loop _X = tf.split(_X, n_steps, 0) # Define two stacked LSTM cells (two recurrent layers deep) with tensorflow lstm_cell_1 = tf.nn.rnn_cell.LSTMCell(n_hidden, forget_bias=1.0, state_is_tuple=True) lstm_cell_2 = tf.nn.rnn_cell.LSTMCell(n_hidden, forget_bias=1.0, state_is_tuple=True) lstm_cells = tf.nn.rnn_cell.MultiRNNCell([lstm_cell_1, lstm_cell_2], state_is_tuple=True) outputs, states = tf.nn.static_rnn(lstm_cells, _X, dtype=tf.float32) # A single output is produced, in style of "many to one" classifier, refer to http://karpathy.github.io/2015/05/21/rnn-effectiveness/ for details lstm_last_output = outputs[-1] # Linear activation return tf.matmul(lstm_last_output, _weights['out']) + _biases['out'] def extract_batch_size(_train, _labels, _unsampled, batch_size): # Fetch a "batch_size" amount of data and labels from "(X\|y)_train" data. # Elements of each batch are chosen randomly, without replacement, from X_train with corresponding label from Y_train # unsampled_indices keeps track of sampled data ensuring non-replacement. Resets when remaining datapoints < batch_size shape = list(_train.shape) shape[0] = batch_size batch_s = np.empty(shape) batch_labels = np.empty((batch_size,1)) for i in range(batch_size): # Loop index # index = random sample from _unsampled (indices) index = random.choice(_unsampled) batch_s[i] = _train[index] batch_labels[i] = _labels[index] _unsampled.remove(index) return batch_s, batch_labels, _unsampled def one_hot(y_): # One hot encoding of the network outputs # e.g.: [[5], [0], [3]] --> [[0, 0, 0, 0, 0, 1], [1, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0]] y_ = y_.reshape(len(y_)) n_values = int(np.max(y_)) + 1 return np.eye(n_values)[np.array(y_, dtype=np.int32)] # Returns FLOATS ###Output _____no_output_____ ###Markdown Build the network: ###Code # Graph input/output x = tf.placeholder(tf.float32, [None, n_steps, n_input]) y = tf.placeholder(tf.float32, [None, n_classes]) # Graph weights weights = { 'hidden': tf.Variable(tf.random_normal([n_input, n_hidden])), # Hidden layer weights 'out': tf.Variable(tf.random_normal([n_hidden, n_classes], mean=1.0)) } biases = { 'hidden': tf.Variable(tf.random_normal([n_hidden])), 'out': tf.Variable(tf.random_normal([n_classes])) } pred = LSTM(x, weights, biases) # Loss, optimizer and evaluation l2 = 0.001 * sum( tf.nn.l2_loss(tf_var) for tf_var in tf.trainable_variables() ) # L2 loss prevents this overkill neural network to overfit the data cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=pred)) + l2 # Softmax loss # if decaying_learning_rate: # learning_rate = tf.train.exponential_decay(init_learning_rate, global_stepbatch_size, decay_steps, decay_rate, staircase=True) #decayed_learning_rate = learning_rate decay_rate ^ (global_step / decay_steps) # exponentially decayed learning rate optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost,global_step=global_step) # Adam Optimizer correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1)) accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32)) ###Output WARNING:tensorflow:`tf.nn.rnn_cell.MultiRNNCell` is deprecated. This class is equivalent as `tf.keras.layers.StackedRNNCells`, and will be replaced by that in Tensorflow 2.0. WARNING:tensorflow:From <ipython-input-9-5a77964f3916>:15: static_rnn (from tensorflow.python.ops.rnn) is deprecated and will be removed in a future version. Instructions for updating: Please use `keras.layers.RNN(cell, unroll=True)`, which is equivalent to this API WARNING:tensorflow:From /home/user/.local/lib/python3.8/site-packages/keras/layers/legacy_rnn/rnn_cell_impl.py:979: calling Zeros.__init__ (from tensorflow.python.ops.init_ops) with dtype is deprecated and will be removed in a future version. Instructions for updating: Call initializer instance with the dtype argument instead of passing it to the constructor ###Markdown Train the network: ###Code print(f"Training on {train_features}") test_losses = [] test_accuracies = [] train_losses = [] train_accuracies = [] sess = tf.InteractiveSession(config=tf.ConfigProto(log_device_placement=True)) init = tf.global_variables_initializer() sess.run(init) # Perform Training steps with "batch_size" amount of data at each loop. # Elements of each batch are chosen randomly, without replacement, from X_train, # restarting when remaining datapoints < batch_size step = 1 time_start = time.time() unsampled_indices = list(range(0,len(X_train))) for i in range(epochs): if len(unsampled_indices) < batch_size: unsampled_indices = list(range(0,len(X_train))) batch_xs, raw_labels, unsampled_indicies = extract_batch_size(X_train, y_train, unsampled_indices, batch_size) batch_ys = one_hot(raw_labels) # check that encoded output is same length as num_classes, if not, pad it if len(batch_ys[0]) < n_classes: temp_ys = np.zeros((batch_size, n_classes)) temp_ys[:batch_ys.shape[0],:batch_ys.shape[1]] = batch_ys batch_ys = temp_ys # Fit training using batch data _, loss, acc = sess.run( [optimizer, cost, accuracy], feed_dict={ x: batch_xs, y: batch_ys } ) train_losses.append(loss) train_accuracies.append(acc) # Evaluation on the test set (no learning made here - just evaluation for diagnosis) test_loss, test_acc = sess.run( [cost, accuracy], feed_dict={ x: X_test, y: one_hot(y_test) } ) test_losses.append(test_loss) test_accuracies.append(test_acc) # print(f"Epoch #{i} Loss = {loss:.2f} Accuracy = {acc:.2f}") if i % 100 == 0: print(f"Epoch {i}/{epochs} Loss={loss:.2f} Accuracy={acc:.2f} Test Loss={test_loss:.2f} Test Accuracy={test_acc:.2f}") # Performance on test data one_hot_predictions, accuracy, final_loss = sess.run( [pred, accuracy, cost], feed_dict={ x: X_test, y: one_hot(y_test) } ) # test_losses.append(final_loss) # test_accuracies.append(accuracy) print(f"Training finished. Loss = {final_loss} Accuracy = {accuracy}") print(f"Duration: {time.time() - time_start} sec") ###Output Training on upcv1/train/c-d-o Device mapping: no known devices. Epoch 0/3000 Loss=45.71 Accuracy=0.01 Test Loss=45.23 Test Accuracy=0.05 Epoch 100/3000 Loss=34.90 Accuracy=1.00 Test Loss=35.30 Test Accuracy=0.86 Epoch 200/3000 Loss=30.04 Accuracy=1.00 Test Loss=30.42 Test Accuracy=0.88 Epoch 300/3000 Loss=25.87 Accuracy=1.00 Test Loss=26.25 Test Accuracy=0.88 Epoch 400/3000 Loss=22.29 Accuracy=1.00 Test Loss=22.67 Test Accuracy=0.88 Epoch 500/3000 Loss=19.21 Accuracy=1.00 Test Loss=19.59 Test Accuracy=0.89 Epoch 600/3000 Loss=16.56 Accuracy=1.00 Test Loss=16.94 Test Accuracy=0.88 Epoch 700/3000 Loss=14.27 Accuracy=1.00 Test Loss=14.65 Test Accuracy=0.89 Epoch 800/3000 Loss=12.29 Accuracy=1.00 Test Loss=12.66 Test Accuracy=0.90 Epoch 900/3000 Loss=10.58 Accuracy=1.00 Test Loss=10.93 Test Accuracy=0.90 Epoch 1000/3000 Loss=9.11 Accuracy=1.00 Test Loss=9.44 Test Accuracy=0.91 Epoch 1100/3000 Loss=7.83 Accuracy=1.00 Test Loss=8.15 Test Accuracy=0.92 Epoch 1200/3000 Loss=6.73 Accuracy=1.00 Test Loss=7.04 Test Accuracy=0.92 Epoch 1300/3000 Loss=5.88 Accuracy=1.00 Test Loss=6.10 Test Accuracy=0.92 Epoch 1400/3000 Loss=5.06 Accuracy=1.00 Test Loss=5.27 Test Accuracy=0.92 Epoch 1500/3000 Loss=4.37 Accuracy=1.00 Test Loss=4.60 Test Accuracy=0.92 Epoch 1600/3000 Loss=3.77 Accuracy=1.00 Test Loss=4.02 Test Accuracy=0.92 Epoch 1700/3000 Loss=3.26 Accuracy=1.00 Test Loss=3.51 Test Accuracy=0.92 Epoch 1800/3000 Loss=2.81 Accuracy=1.00 Test Loss=3.07 Test Accuracy=0.92 Epoch 1900/3000 Loss=2.42 Accuracy=1.00 Test Loss=2.69 Test Accuracy=0.92 Epoch 2000/3000 Loss=2.09 Accuracy=1.00 Test Loss=2.36 Test Accuracy=0.92 Epoch 2100/3000 Loss=1.80 Accuracy=1.00 Test Loss=2.08 Test Accuracy=0.91 Epoch 2200/3000 Loss=1.55 Accuracy=1.00 Test Loss=1.84 Test Accuracy=0.91 Epoch 2300/3000 Loss=1.33 Accuracy=1.00 Test Loss=1.65 Test Accuracy=0.91 Epoch 2400/3000 Loss=1.15 Accuracy=1.00 Test Loss=1.49 Test Accuracy=0.91 Epoch 2500/3000 Loss=0.99 Accuracy=1.00 Test Loss=1.33 Test Accuracy=0.90 Epoch 2600/3000 Loss=0.85 Accuracy=1.00 Test Loss=1.20 Test Accuracy=0.91 Epoch 2700/3000 Loss=0.89 Accuracy=0.97 Test Loss=1.21 Test Accuracy=0.88 Epoch 2800/3000 Loss=0.69 Accuracy=1.00 Test Loss=0.89 Test Accuracy=0.94 Epoch 2900/3000 Loss=0.60 Accuracy=1.00 Test Loss=0.81 Test Accuracy=0.94 Training finished. Loss = 0.7445202469825745 Accuracy = 0.9446367025375366 Duration: 610.8951778411865 sec ###Markdown Results: ###Code # summarize history for accuracy plt.plot(train_accuracies) plt.plot(test_accuracies) plt.title('model accuracy') plt.ylabel('accuracy') plt.xlabel('epoch') plt.legend(['train', 'test'], loc='lower right') plt.show() # summarize history for loss plt.plot(train_losses) plt.plot(test_losses) plt.title('model loss') plt.ylabel('loss') plt.xlabel('epoch') plt.legend(['train', 'test'], loc='upper right') plt.show() predictions = one_hot_predictions.argmax(1) print("Testing Accuracy: {}%".format(100accuracy)) print("Precision: {}%".format(100metrics.precision_score(y_test, predictions, average="weighted"))) print("Recall: {}%".format(100metrics.recall_score(y_test, predictions, average="weighted"))) print("f1_score: {}%".format(100metrics.f1_score(y_test, predictions, average="weighted"))) print("Confusion Matrix: Created using test set of {} datapoints, normalised to % of each class in the test dataset".format(len(y_test))) confusion_matrix = metrics.confusion_matrix(y_test, predictions) normalised_confusion_matrix = np.array(confusion_matrix, dtype=np.float32)/np.sum(confusion_matrix)*100 # Plot Results: plt.figure(figsize=(12, 12)) plt.imshow( normalised_confusion_matrix, interpolation='nearest', cmap=plt.cm.Blues ) plt.title("Confusion matrix \n(normalised to % of total test data)") plt.colorbar() plt.tight_layout() plt.ylabel('True label') plt.xlabel('Predicted label') plt.show() ###Output Testing Accuracy: 94.46367025375366% Precision: 95.23200383772824% Recall: 94.4636678200692% f1_score: 94.3922567745365% Confusion Matrix: Created using test set of 578 datapoints, normalised to % of each class in the test dataset
Notebooks/Implementations/JUP_SURGP_GLO_B_D__LEI_Evaluation.ipynb	###Markdown Calculate LEI ###Code for ghsl_file in GHSL_files: print(f'{ghsl_file}') out_file = ghsl_file.replace(".tif", "new_LEI_90_00.csv") if not os.path.exists(out_file): lei = calculate_LEI(ghsl_file, old_list = [5,6], new_list=[4]) xx = pd.DataFrame(lei, columns=['geometry', 'old', 'total']) xx['LEI'] = xx['old'] / xx['total'] xx.to_csv(out_file) # Process LEI results base_folder = '/home/wb411133/data/Projects/LEI' all_results_files = [] for root, folders, files in os.walk(base_folder): for f in files: if "GHSLnew_LEI_90_00" in f: all_results_files.append(os.path.join(root, f)) summarized_results = {} for res_file in all_results_files: res = summarize_LEI(res_file) baseName = os.path.basename(os.path.dirname(res_file)) summarized_results[baseName] = res all_results = pd.DataFrame(summarized_results).transpose() # Old test to determine which files were not processed correctly #bas_res = all_results[all_results['Expansion'] == 123282000.0].index all_results.head() all_results.to_csv(os.path.join(LEI_folder, "Summarized_LEI_Results_90_00.csv")) ###Output _____no_output_____ ###Markdown Summarize total built per city ###Code all_res = {} for g_file in GHSL_files: city = os.path.basename(os.path.dirname(g_file)) inR = rasterio.open(g_file) inD = inR.read() built2014 = (inD >= 3).sum() * (30 * 30) built2000 = (inD >= 4).sum() * (30 * 30) built1990 = (inD >= 5).sum() * (30 * 30) built1975 = (inD >= 6).sum() * (30 * 30) all_res[city] = [built1975, built1990, built2000, built2014] print(city) xx = pd.DataFrame(all_res).head().transpose() xx.columns = ['built75', 'built90', 'built00', 'built14'] #xx[xx.index.isin(['1'])] xx.head() xx.to_csv("/home/wb411133/temp/LEI_cities_built.csv") ###Output _____no_output_____ ###Markdown Combining results ###Code csv_files = [x for x in os.listdir(LEI_folder) if x[-4:] == ".csv"] lei0014 = pd.read_csv(os.path.join(LEI_folder, 'Summarized_LEI_Results.csv'),index_col=0) lei0014.columns = ["%s_0014" % x for x in lei0014.columns] lei9014 = pd.read_csv(os.path.join(LEI_folder, 'Summarized_LEI_Results_90_0014.csv'),index_col=0) lei9014.columns = ["%s_9014" % x for x in lei9014.columns] lei9000 = pd.read_csv(os.path.join(LEI_folder, 'Summarized_LEI_Results_90_00.csv'),index_col=0) lei9000.columns = ["%s_9000" % x for x in lei9000.columns] built_area = pd.read_csv("/home/wb411133/temp/LEI_cities_built.csv",index_col=0) built_area.columns = ["%s_BUILT" % x for x in built_area.columns] combined_results = lei0014.join(lei9014).join(lei9000).join(built_area) combined_results.to_csv(os.path.join(LEI_folder, 'LEI_COMBINED.csv')) combined_results['Expansion_0014'] + combined_results['Infill_0014'] + combined_results['Leapfrog_0014'] - (combined_results['built14_BUILT'] - combined_results['built00_BUILT']) built_area.head() ###Output _____no_output_____ ###Markdown Summarizing methods ###Code in_ghsl = "/home/wb411133/data/Projects/LEI/1/GHSL.tif" inR = rasterio.open(in_ghsl) inD = inR.read() # Get cell counts of each built category built2014 = (inD >= 3).sum() built2000 = (inD >= 4).sum() built1990 = (inD >= 5).sum() built1975 = (inD >= 6).sum() print("%s\n%s\n%s\n%s" % (built2014, built2000, built1990, built1975)) lei_2000_2014 = calculate_LEI(in_ghsl, old_list = [4,5,6], new_list=[3]) lei_1990_2000 = calculate_LEI(in_ghsl, old_list = [5,6], new_list=[4]) xx = pd.DataFrame(lei, columns=['geometry', 'old', 'total']) xx['LEI'] = xx['old'] / xx['total'] in_file = "/home/wb411133/data/Projects/LEI/1/GHSLnew_LEI_90_00.csv" inD = pd.read_csv(in_file, index_col=0) inD.head() summarize_LEI(in_file) ###Output _____no_output_____ ###Markdown DEBUGGING ###Code bad_files = [] for root, dirs, files in os.walk('/home/wb411133/data/Projects/LEI/'): for f in files: if "90_00.csv" in f: bad_files.append(os.path.join(root, f)) bad_files import shutil for b in bad_files: new_file = b.replace("_90_00", "_90_0014") shutil.move(b, new_file) ###Output _____no_output_____ ###Markdown Calculating LEIThis script is used for exploring LEI methods - in order to calculate LEI proper, look for the LEIFast.py script in GOST_Rocks/Urban; this implements multi-threading. ###Code import os, sys, logging import geojson, rasterio import rasterio.features import pandas as pd import numpy as np from shapely.geometry import shape, GeometryCollection from shapely.wkt import loads from matplotlib import pyplot from rasterio.plot import show, show_hist #Import GOST urban functions sys.path.append("../../") from src.LEI import * calculate_LEI? LEI_folder = '/home/wb411133/data/Projects/LEI' results = {} GHSL_files = [] for root, dirs, files in os.walk(LEI_folder): if os.path.exists(os.path.join(root, "GHSL.tif")): GHSL_files.append(os.path.join(root, "GHSL.tif")) try: results[os.path.basename(root)] = [len(files), os.stat(os.path.join(root, "GHSL.tif")).st_size] if len(files) != 6: print("%s - %s" % (os.path.basename(root), os.stat(os.path.join(root, "GHSL.tif")).st_size)) except: pass ###Output _____no_output_____ ###Markdown Vizualize raster data - GHSL ###Code root = '/home/wb411133/data/Projects/LEI/634/' inputGHSL = os.path.join(root, "GHSL.tif") inRaster = rasterio.open(inputGHSL) inR = inRaster.read() newR = (inR == 3).astype('int') oldR = (np.isin(inR, [4,5,6])).astype('int') fig, (axr, axg) = pyplot.subplots(1, 2, figsize=(20,20)) show(oldR, ax=axr, title='OLD') show(newR, ax=axg, title='NEW') #write out raster to file outProperties = inRaster.profile outRaster = outRaster.astype('int32') outProperties['dtype'] = 'int32' with rasterio.open(inputGHSL.replace(".tif", "_LEI.tif"), 'w', **outProperties) as out: out.write(outRaster) ###Output _____no_output_____
assets/sample/model-logger.ipynb	###Markdown Hey !! Let's get started ###Code !pip install modellogger from modellogger.modellogger import ModelLogger ###Output _____no_output_____ ###Markdown Setup model-logger ###Code # create an instance of modellogger ,It will automatically setup the db for you :) mlog = ModelLogger('mydb.db') import numpy as np import pandas as pd from matplotlib import rcParams from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error boston = load_boston() bos = pd.DataFrame(boston.data) bos.columns = boston.feature_names bos['PRICE'] = boston.target ###Output _____no_output_____ ###Markdown Train-->Predict-->Store-->Repeat ###Code #boston house pricing dataset X = bos.drop('PRICE', axis = 1) Y = bos['PRICE'] X_train, X_test, Y_train, Y_test =train_test_split(X, Y, test_size = 0.33, random_state = 5) #scoring def score(Y_test,Y_pred): return mean_squared_error(Y_test,Y_pred) #train the model as normal lr1 = LinearRegression() lr1.fit(X_train, Y_train) Y_pred = lr1.predict(X_test) #Store the model mlog.store_model('logistic_v1', lr1 , X_train , score(Y_test,Y_pred)) mlog.store_model('linear_v2', lr1 , X_train , score(Y_test,Y_pred)) # let's train another regression model with different set of columns X_train =X_train[['RM', 'AGE', 'DIS', 'RAD', 'TAX','PTRATIO', 'B', 'LSTAT']] X_test = X_test[['RM', 'AGE', 'DIS', 'RAD', 'TAX','PTRATIO', 'B', 'LSTAT']] lr2 = LinearRegression(n_jobs=11) lr2.fit(X_train,Y_train) Y_pred = lr2.predict(X_test) mlog.store_model( 'logistic_v2' , lr2 , X_train , score(Y_test,Y_pred)) #mlog.store_model( 'logistic_v3' , lr2 , X_train , score(Y_test,Y_pred)) mlog.store_model( 'linear_v1' , lr2 , X_train , score(Y_test,Y_pred)) ###Output _____no_output_____ ###Markdown Quick Sneak - peek ###Code mlog.view_results() ###Output _____no_output_____ ###Markdown Delete a model entry by 'model name' ###Code mlog.view_results() mlog.delete_model(Model_Name='logistic_v1') mlog.delete_model(Model_id= 4) mlog.delete_all() ###Output _____no_output_____ ###Markdown Model profiling - The fun part begins !! ###Code #sample database can be found in github modellogger.github.io/assests/sample run it local machine not in colab mlog = ModelLogger('financial.db') mlog.model_profiles() #Please refer to the documentaion if you face any issue with parameters mlog.info() ###Output _____no_output_____
Comparison_2015_2020_Notebook.ipynb	###Markdown Has the programming world changed over the past 5 years? Business understanding In order to investigate the changes occured in the programming world over the past 5 years, I would like to answer following questions:Is the programming industry showing more gender diversity in 2020 compared to 2015?Which programming languages are most common in 2020 and are they the same ones as in 2015?Are programmers nowadays having a formal computer science background and has this changed since 2015? Is programming a rewarding profession and has this changed since 2015? Data understanding The data used to answer the questions are the Stack Overflow Developer survey results from the years 2015 and 2020.First the relevant libraries and the datasets have been imported and examined to identify the columns needed for the analysis.Since the survey results are assumed to be a representative sample of the population, some demographics (age and location of respondents) have been evaluated and compared, in order to ensure that the data sets are similarly distributed. ###Code #Libraries import import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline %pylab inline #Import of Stack Overflow 2015 survey data df_2015 = pd.read_csv('2015 Stack Overflow Developer Survey Responses.csv', header=1) print(df_2015.shape) print(df_2015.head()) #Import of Stack Overflow 2020 survey data df_2020 = pd.read_csv('survey_results_public_2020.csv', header=0) print(df_2020.shape) print(df_2020.head()) #Check of age distribution of respondents in 2015 df_age_2015 = pd.DataFrame(df_2015.Age.value_counts().reset_index()) df_age_2015.columns = ('Age', 'Count') df_age_2015['Age'] = df_age_2015['Age'].str.replace('< 20','0-20') df_age_2015.sort_values(by=['Age']).plot.bar(x='Age', y='Count', legend=False) plt.show() #Check of geographical distribution of respondents in 2015 df_coun_2015 = pd.DataFrame(df_2015.Country.dropna().value_counts() / df_2015.Country.dropna().shape) df_coun_2015.reset_index(inplace = True) #For simplification purposes the countries having a percentage below 2% as well as the NaN values are aggregated as 'Other' df_coun_2015.rename(columns={'index': 'Country', 'Country': 'Count'}, inplace = True) df_coun_2015['Country_new'] = np.where((df_coun_2015['Count'] < 0.02) \| (df_coun_2015['Count'].isna()), 'Other',df_coun_2015['Country']) df_coun_2015 = pd.DataFrame(df_coun_2015.groupby('Country_new')['Count'].sum().reset_index()).sort_values(by=['Count'], ascending=False) df_coun_2015.plot.pie(y='Count', labels=df_coun_2015['Country_new'], legend = False, autopct='%1.1f%%', radius = 2) plt.show() #Check of age distribution of respondents in 2020; ages have been grouped in the same bins as in 2015 data to allow comparison bins=[0,20,24,29,34,39,50,60,100] df_age_2020 = pd.DataFrame(df_2020.groupby(pd.cut(df_2020['Age'], bins=bins, include_lowest=False)).size()) df_age_2020.reset_index(inplace = True) df_age_2020.columns = ('Age', 'Count') df_age_2020.plot.bar(x='Age', y='Count', legend=False) plt.show() #Check of geographical distribution of respondents in 2020 df_coun_2020 = pd.DataFrame(df_2020.Country.dropna().value_counts() / df_2020.Country.dropna().shape) df_coun_2020.reset_index(inplace = True) #For simplification purposes the countries having a percentage below 2% are aggregated as 'Other' df_coun_2020.rename(columns={'index': 'Country', 'Country': 'Count'}, inplace = True) df_coun_2020['Country_new'] = np.where((df_coun_2020['Count'] < 0.02) \| (df_coun_2020['Count'].isna()), 'Other',df_coun_2020['Country']) df_coun_2020 = pd.DataFrame(df_coun_2020.groupby('Country_new')['Count'].sum().reset_index()).sort_values(by=['Count'], ascending=False) df_coun_2020.plot.pie(y='Count', labels=df_coun_2020['Country_new'], legend = False, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() ###Output _____no_output_____ ###Markdown Prepare and Model data First step for data preparation is to check the error message shown upon import of the 2015 csv file, hinting at mixed data types: ###Code df_2015.iloc[:, [5,108,121,196,197,198]] ###Output _____no_output_____ ###Markdown Among the columns having mixed type the only column that will be used for the analysis is occupation, which will be formatted as string: ###Code df_2015['Occupation'] = df_2015['Occupation'].astype('str') ###Output _____no_output_____ ###Markdown 1. Question: Is the programming industry showing more gender diversity in 2020 compared to 2015? ###Code #Check for the percentage of NaN values in the column Gender in 2015 df_2015['Gender'].isna().sum() / df_2015.shape[0] * 100 #Since NaN represents around 1% of the total I will not consider them in the analysis df_gen_2015 = pd.DataFrame(df_2015.Gender.dropna().value_counts() / df_2015.Gender.dropna().shape) df_gen_2015.reset_index(inplace = True) df_gen_2015.rename(columns={'index': 'Gender', 'Gender': 'Count'}, inplace = True) #The occurences 'Other' and 'Prefer not to disclose' are aggregated as 'Other' and considered as non-binary genders df_gen_2015['Gender_agg'] = np.where((~df_gen_2015['Gender'].isin(('Male','Female'))), 'Other',df_gen_2015['Gender']) df_gen_2015 = pd.DataFrame(df_gen_2015.groupby('Gender_agg')['Count'].sum().reset_index()).sort_values(by=['Count'], ascending=False) df_gen_2015.plot.pie(y='Count', labels=df_gen_2015['Gender_agg'], legend=None, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() #Check for the percentage of NaN values in the column Gender in 2020 df_2020['Gender'].isna().sum() / df_2020.shape[0] * 100 #In this cases NaN values are around 21% but they cannot be interpretable and will therefore be dropped. #For transparency this will be declared in the results. df_gen_2020 = pd.DataFrame(df_2020.Gender.dropna().value_counts() /df_2020.Gender.dropna().shape) df_gen_2020.reset_index(inplace = True) df_gen_2020.rename(columns={'index': 'Gender', 'Gender': 'Count'}, inplace = True) df_gen_2020['Gender_agg'] = np.where((~df_gen_2020['Gender'].isin(('Man','Woman'))), 'Other',df_gen_2020['Gender']) df_gen_2020 = pd.DataFrame(df_gen_2020.groupby('Gender_agg')['Count'].sum().reset_index()).sort_values(by=['Count'], ascending=False) df_gen_2020.plot.pie(y='Count', labels=df_gen_2020['Gender_agg'], legend = False, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() ###Output _____no_output_____ ###Markdown 2. Question: Which programming languages are most common in 2020 and are they the same ones as in 2015? ###Code #Evaluation of the top 10 most common languages in the 2015 dataset df_lan_2015 = pd.DataFrame(df_2015.filter(like='Current Lang & Tech', axis=1).count().rename('Count').reset_index()).sort_values(by=['Count'], ascending=False) df_lan_2015.rename(columns={'index': 'Lang&Tech'}, inplace = True) df_lan_2015['Lang&Tech'] = df_lan_2015['Lang&Tech'].str.replace(r'Current Lang & Tech: ','') df_lan_2015.head(10).plot.barh(x='Lang&Tech',figsize=(15,5), legend=False) pylab.ylabel('') plt.show() df_lan_2015.plot.pie(y='Count', labels=df_lan_2015['Lang&Tech'], legend = False, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() #Evaluation of the top 10 languages to be learned in the future in the 2015 dataset df_lan_2015 = pd.DataFrame(df_2015.filter(like='Future Lang & Tech', axis=1).count().rename('Count').reset_index()).sort_values(by=['Count'], ascending=False) df_lan_2015.rename(columns={'index': 'Future_Lang&Tech'}, inplace = True) df_lan_2015['Future_Lang&Tech'] = df_lan_2015['Future_Lang&Tech'].str.replace(r'Future Lang & Tech: ','') df_lan_2015.head(10).plot.barh(x='Future_Lang&Tech',figsize=(15,5), legend=False) pylab.ylabel('') plt.show() df_lan_2015.plot.pie(y='Count', labels=df_lan_2015['Future_Lang&Tech'], legend = False, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() #Evaluation of the top 10 most common languages in the 2020 dataset df_lan_2020 = pd.DataFrame(df_2020.LanguageWorkedWith.str.split(';').explode('LanguageWorkedWith').reset_index(drop=True)) df_lan_2020 = pd.DataFrame(df_lan_2020['LanguageWorkedWith'].value_counts().rename('Count').reset_index()) df_lan_2020.rename(columns={'index': 'Language'}, inplace = True) df_lan_2020.head(10).plot.barh(x='Language',figsize=(15,5), legend=False) pylab.ylabel('') plt.show() df_lan_2020.plot.pie(y='Count', labels=df_lan_2020['Language'], legend = False, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() #Evaluation of the top 10 languages to be learned in the future in the 2020 dataset df_lan_2020 = df_2020[['LanguageDesireNextYear']] df_lan_2020 = pd.DataFrame(df_lan_2020.LanguageDesireNextYear.str.split(';').explode('LanguageDesireNextYear').reset_index(drop=True)) df_lan_2020 = pd.DataFrame(df_lan_2020['LanguageDesireNextYear'].value_counts().rename('Count').reset_index()) df_lan_2020.rename(columns={'index': 'Language'}, inplace = True) df_lan_2020.head(10).plot.barh(x='Language',figsize=(15,5), legend=False) pylab.ylabel('') plt.show() ###Output _____no_output_____ ###Markdown Question 3: Are coders having a formal computer science background and has this changed since 2015? ###Code #Computation of the percentage of respondents having no computer science background by counting the rows with all three fields related to computer science education left blank (NaN) df_educ_2015 = pd.DataFrame(df_2015[['Training & Education: BS in CS','Training & Education: Masters in CS', 'Training & Education: PhD in CS']].isna().sum(axis=1).rename('Count')) df_educ_2015[df_educ_2015.Count == 3].count()/df_2015.shape[0] #Visual representation of the academic background of the respondents in 2020 df_educ_2020 = pd.DataFrame(df_2020['UndergradMajor'].value_counts().rename('Count').reset_index()) df_educ_2020.rename(columns={'index': 'Major'}, inplace = True) df_educ_2020.plot.pie(y='Count', labels=df_educ_2020['Major'], legend = False, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() ###Output _____no_output_____ ###Markdown Question 4: Is the job satisfaction of programmers increasing as the technology advances? ###Code #Evaluation of the level of job satisfaction of programmers in 2015 df_satisf_2015 = df_2015[['Job Satisfaction']] df_satisf_2015 = pd.DataFrame(df_satisf_2015['Job Satisfaction'].value_counts().rename('Count').reset_index()) df_satisf_2015.rename(columns={'index': 'Job Satisfaction'}, inplace = True) df_satisf_2015.plot.pie(y='Count', labels=df_satisf_2015['Job Satisfaction'], legend = False, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() #Evaluation of the level of job satisfaction of programmers in 2020 df_satisf_2020 = df_2020[['JobSat']] df_satisf_2020 = pd.DataFrame(df_satisf_2020['JobSat'].value_counts().rename('Count').reset_index()) df_satisf_2020.rename(columns={'index': 'Job Satisfaction'}, inplace = True) df_satisf_2020.plot.pie(y='Count', labels=df_satisf_2020['Job Satisfaction'], legend = False, autopct='%1.1f%%', radius = 2) pylab.ylabel('') plt.show() ###Output _____no_output_____
examples/Engineering Metrics Example.ipynb	###Markdown Engineering Metrics Example In order to authenticate with the current Jira server we are required to use oauth with karhoo google apps credentials. To set this up you require the private and public keys of the Jira application for engineering metrics. Once you have these, set up your access as outlined here. Once config files are in place we can simple pass the path to the oauth config to an instance of the Engineering Metrics engine to gain access to all the juicy data stored in our Jira. ###Code import sys sys.path.append("..") from engineeringmetrics.engine import EngineeringMetrics from pathlib import Path config_dict = { 'jira_oauth_config_path': Path.home() } kem = EngineeringMetrics(config_dict) projects_data = kem.jirametrics.populate_projects(['INT'], max_results=110) import pandas as pd df = pd.DataFrame(projects_data['INT'].issues) df.shape df.head() oso_query = kem.jirametrics.populate_from_jql('project = "OSO" ORDER BY Rank ASC') oso_df = pd.DataFrame(oso_query.resolved_issues()) oso_df.shape oso_df.head() oso_df.set_index('created',drop=False,inplace=True) oso_df.cycle_time.plot(kind='line',style='ko-').set_title('Time between creation and resolution of OSO issues') closed_df = pd.DataFrame(projects_data['INT'].resolved_issues()) closed_df.shape closed_df.set_index('created',drop=False,inplace=True) closed_df.cycle_time.plot(kind='line',style='ko-').set_title('Time between creation and resolution of INT issues') ###Output _____no_output_____
Brandon_Rhodes_PyCon15/Exercises-5.ipynb	###Markdown Make a bar plot of the months in which movies with "Christmas" in their title tend to be released in the USA. ###Code r = release_dates r = r[r['title'].apply(lambda x:x.lower()).str.contains("christmas")] r = r[r['country']=='USA']['date'] r.dt.month.value_counts().sort_index().plot(kind='bar') ###Output _____no_output_____ ###Markdown Make a bar plot of the months in which movies whose titles start with "The Hobbit" are released in the USA. ###Code r = release_dates r = r[r['title'].str.startswith("The Hobbit")] r = r[r['country']=='USA']['date'] r.dt.month.value_counts().sort_index().plot(kind='bar') ###Output _____no_output_____ ###Markdown Make a bar plot of the day of the week on which movies with "Romance" in their title tend to be released in the USA. ###Code r = release_dates r = r[r['title'].apply(lambda x:x.lower()).str.contains("romance")] r = r[r['country']=='USA']['date'] r.dt.dayofweek.value_counts().sort_index().plot(kind='bar') ###Output _____no_output_____ ###Markdown Make a bar plot of the day of the week on which movies with "Action" in their title tend to be released in the USA. ###Code r = release_dates r = r[r['title'].apply(lambda x:x.lower()).str.contains("action")] r = r[r['country']=='USA']['date'] r.dt.dayofweek.value_counts().sort_index().plot(kind='bar') ###Output _____no_output_____ ###Markdown On which date was each Judi Dench movie from the 1990s released in the USA? ###Code c = cast r = release_dates r = r[r['country']=='USA'] c = c[(c['name']=='Judi Dench') & (c['year']//10*10== 1990)] c = c.merge(r) c.date.dt.day ###Output _____no_output_____ ###Markdown In which months do films with Judi Dench tend to be released in the USA? ###Code c = cast r = release_dates r = r[r['country']=='USA'] c = c[(c['name']=='Judi Dench')] c = c.merge(r) c.date.dt.month.value_counts().sort_index().plot(kind='bar') usa = release_dates[release_dates.country == 'USA'] c = cast c = c[c.name == 'Judi Dench'] m = c.merge(usa).sort_values('date') m.date.dt.month.value_counts().sort_index().plot(kind='bar') ###Output _____no_output_____ ###Markdown In which months do films with Tom Cruise tend to be released in the USA? ###Code c = cast r = release_dates r = r[r['country']=='USA'] c = c[(c['name']=='Tom Cruise') ] c = c.merge(r) c.date.dt.month.value_counts().sort_index().plot(kind='bar') ###Output _____no_output_____
4_4_Kalman_Filters/2_1. New Mean and Variance, exercise.ipynb	###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = (var2 * mean1 + var1 * mean2) / (var2 + var1) new_var = 1 / (1/var2 + 1/var1) return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output [11.0, 2.0] ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = None new_var = None return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output _____no_output_____ ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = (var2mean1 + var1mean2) / (var1 + var2) new_var = 1 / (1/var1 + 1/var2) return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output [11.0, 2.0] ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = (var2mean1+var1mean2)/(var1+var2) new_var = 1./(1/var1+1/var2) return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output [11.0, 2.0] ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: #print(mu, sigma2, x) g.append(f(mu, sigma2, x)) #print(g) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = ((var1mean1) + (var2mean2)) / (var1 + var2) new_var = 1 / (1/var1 + 1/var2) return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output [11.0, 2.0] ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = None new_var = None return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output _____no_output_____ ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = (mean1 * var2 + mean2 * var1) / (var1 + var2) new_var = 1 / (1/var1 + 1/var2) return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output [11.0, 2.0] ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = (var1mean2+var2mean1)/(var1+var2) new_var = 1/((1/var1)+(1/var2)) return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output [11.0, 2.0] ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## TODO: Calculate the new parameters new_mean = ((var1 * mean1) + (var2 * mean2)) / (var1 + var2) new_var = 1 / ((1/var1) + (1/var2)) return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output [11.0, 2.0] ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____ ###Markdown New Mean and VarianceNow let's take the formulas from the example below and use them to write a program that takes in two means and variances, and returns a new, updated mean and variance for a gaussian. This step is called the parameter or measurement update because it is the update that happens when an initial belief (represented by the blue Gaussian, below) is merged with a new piece of information, a measurement with some uncertainty (the orange Gaussian). As you've seen in the previous quizzes, the updated Gaussian will be a combination of these two Gaussians with a new mean that is in between both of theirs and a variance that is less than the smallest of the two given variances; this means that after a measurement, our new mean is more certain than that of the initial belief! Below is our usual Gaussian equation and imports. ###Code # import math functions from math import * import matplotlib.pyplot as plt import numpy as np # gaussian function def f(mu, sigma2, x): ''' f takes in a mean and squared variance, and an input x and returns the gaussian value.''' coefficient = 1.0 / sqrt(2.0 * pi sigma2) exponential = exp(-0.5 (x-mu) ** 2 / sigma2) return coefficient * exponential ###Output _____no_output_____ ###Markdown QUIZ: Write an `update` function that performs the measurement update.This function should combine the given Gaussian parameters and return new values for the mean and squared variance.This function does not have to perform any exponential math, it simply has to follow the equations for the measurement update as seen in the image at the top of this notebook. You may assume that the given variances `var1` and `var2` are squared terms. ###Code # the update function def update(mean1, var1, mean2, var2): ''' This function takes in two means and two squared variance terms, and returns updated gaussian parameters.''' ## Calculate the new parameters new_mean = (var2mean1 + var1mean2)/(var1+var2) new_var = 1/(1/var2 + 1/var1) return [new_mean, new_var] # test your implementation new_params = update(10, 4, 12, 4) print(new_params) ###Output [11.0, 2.0] ###Markdown Plot a GaussianPlot a Gaussian by looping through a range of x values and creating a resulting list of Gaussian values, `g`, as shown below. You're encouraged to see what happens if you change the values of `mu` and `sigma2`. ###Code # display a gaussian over a range of x values # define the parameters mu = new_params[0] sigma2 = new_params[1] # define a range of x values x_axis = np.arange(0, 20, 0.1) # create a corresponding list of gaussian values g = [] for x in x_axis: g.append(f(mu, sigma2, x)) # plot the result plt.plot(x_axis, g) ###Output _____no_output_____
01_startup.ipynb	###Markdown Dataset made using abalajiaus/oct_ca:latest-fastai-skl-ski-fire-onnx-mlflow ###Code #exports from fastai.vision import * import mlflow import model import pandas as pd import mlflow.pytorch as MYPY #exports def saveDictToConfigJSON(dictiontary, name): with open('/workspace/oct_ca_seg/oct/configs/'+ name, 'w') as file: json.dump(dictiontary, file) #exports def loadConfigJSONToDict(fn): with open('/workspace/oct_ca_seg/oct/configs/'+ fn, 'r') as file: config = json.load(file) return config #exports class DeepConfig(): def __init__(self, config_dict): self.config_dict = config_dict for k,v in self.config_dict.items(): setattr(self, k, DeepConfig(v) if isinstance(v, dict) else v) config_test = loadConfigJSONToDict('init_config.json') config = DeepConfig(config_test) config.DATSET.bs = 1 config.MODEL.dims1 = 8 config.MODEL.dims2 = 12 config.MODEL.dims3 = 16 config.MODEL.maps1 = 2 config.MODEL.maps2 = 8 config.MODEL.maps3 = 12 config.MODEL.f1dims = 8 config.MODEL.f2dims = 12 config.MODEL.f1maps = 2 config.MODEL.f2maps = 2 #this should be number of classes. background, lumen => 2 etc. config.LEARNER.lr = 0.01 cocodata_path = Path('/workspace/oct_ca_seg/COCOdata/') train_path = cocodata_path/'train/images' valid_path = cocodata_path/'valid/images' test_path = cocodata_path/'test/images' anno_name = 'medium_set_annotations.json' #or 'annotations.json' for full set train_anno = train_path/anno_name valid_anno = valid_path/anno_name test_anno = test_path/anno_name trainData = ImageList.from_folder(train_path) validData = ImageList.from_folder(valid_path) testData = ImageList.from_folder(test_path) #export binify = lambda x : x.point(lambda p: float(p>100.))#.point(lambda p: float(p)) fn = get_image_files(cocodata_path/'train/labels', recurse=True)[10] labal = open_mask(fn, after_open=binify, convert_mode='L') labal labal.data plt.hist(labal.data.flatten()) #export class SegCustomLabelList(SegmentationLabelList): def open(self, fn): return open_mask(fn, after_open=binify, convert_mode='L') #export class SegCustomItemList(SegmentationItemList): _label_cls = SegCustomLabelList src = SegCustomItemList.from_folder(cocodata_path, recurse=True, extensions='.jpg').filter_by_func(lambda fname: Path(fname).parent.name == 'images', ).split_by_folder('train', 'valid') codes = np.loadtxt(cocodata_path/'codes.txt', dtype=str) fn_get_y = lambda image_name: Path(image_name).parent.parent/('labels/'+Path(image_name).name) src.label_from_func(fn_get_y, classes=codes) tfms=get_transforms()[0].append(TfmPixel(to_float)) src.transform(tfms, size=256, tfm_y=True) src.train.y[0].data bs = config.DATSET.bs data = src.databunch(bs=bs, val_bs=bs2) #data.transform(get_transforms()[0], tfm_y=True) stats = [torch.tensor([0.2190, 0.1984, 0.1928]), torch.tensor([0.0645, 0.0473, 0.0434])] data.normalize(stats) src.train.y[0].data torch.argmax(src.train.x[0].data, 0, keepdim=True).size() #data.transform(tfms[0], tfm_y=True, size=(256, 256)) data.show_batch(10, ds_type=DatasetType.Train) data.one_batch() ###Output _____no_output_____ ###Markdown Metrics ###Code #export def sens(c, l): n_targs=l.size()[0] c = c.argmax(dim=1).view(n_targs,-1).float() l = l.view(n_targs, -1).float() inter = torch.sum(cl, dim=(1)) union = torch.sum(c, dim=(1)) + torch.sum(l, dim=1) - inter return (inter/union).mean() def spec(c, l): n_targs=l.size()[0] c = c.argmax(dim=1).view(n_targs,-1).float() l = l.view(n_targs, -1).float() c=1-c l=1-l inter = torch.sum(cl, dim=(1)) union = torch.sum(c, dim=(1)) + torch.sum(l, dim=1) - inter return (inter/union).mean() '''def acc(c, l): n_targs=l.size()[0] c = c.argmax(dim=1).view(n_targs,-1) l = l.view(n_targs, -1).float() return torch.sum(c,dim=(1)) / l.size()[-1]''' def acc(c, l): n_targs=l.size()[0] c = c.argmax(dim=1).view(n_targs,-1) l = l.argmax(dim=1).view(n_targs,-1) c = torch.sum(torch.eq(c,l).float(),dim=1) return (c/l.size()[-1]).mean() class Dice_Loss(torch.nn.Module): """This is a custom Dice Similarity Coefficient loss function that we use to the accuracy of the segmentation. it is defined as ; DSC = 2 (pred /intersect label) / (pred /union label) for the losss we use 1- DSC so gradient descent leads to better outputs.""" def __init__(self, weight=None, size_average=False): super(Dice_Loss, self).__init__() def forward(self, pred, label): label = label.float() smooth = 1. #helps with backprop intersection = torch.sum(pred * label) union = torch.sum(pred) + torch.sum(label) loss = (2. * intersection + smooth) / (union + smooth) #return 1-loss because we want to minimise dissimilarity return 1 - (loss) def my_Dice_Loss(pred, label): pred = torch.argmax(pred, dim=0,keepdim=True) label = label.float() smooth = 1. #helps with backprop intersection = torch.sum(pred * label) union = torch.sum(pred) + torch.sum(label) loss = (2. * intersection + smooth) / (union + smooth) #return 1-loss because we want to minimise dissimilarity return 1 - (loss) ###Output _____no_output_____ ###Markdown Model Deep Cap the way configs were originally set up needs some help to work here. just made a little recursive config class ###Code from model import CapsNet ###Output _____no_output_____ ###Markdown note these functions have the absolute path in the docker image to teh configs save dir ###Code torch.cuda.is_available() #saveDictToConfigJSON(config.config_dict, 'config_test_save.json') capsnet = CapsNet(config.MODEL).cuda() capsnet(data.one_batch()[0].cuda()).shape metrics = [sens, spec, acc, my_Dice_Loss, dice] learner = Learner(data, model=capsnet, metrics=metrics) lr = config.LEARNER.lr; lr ###Output _____no_output_____ ###Markdown Fastai UNET ###Code fast_unet_learner = unet_learner(data, models.resnet18, pretrained=False, y_range=[0,1], metrics=dice) fast_unet_learner.summary(); ###Output _____no_output_____ ###Markdown Fastai UNET with a resnet 18 backbone has 31,113,008 parameters. Let's make a capsnet with around that many parameters, train them both for an epoch and see which is better. MLFLOW Callback ###Code import mlflow #export clean_tensor_lists = lambda l : [x.item() for x in l] def saveResultsJSON(json, run_dir, name): #name = exp_name+'item name+ .json' with open(run_dir +'/'+ name, 'w') as file: file.write(json) def save_all_results(learner, run_dir, exp_name): #only call this function after training train_losses = pd.DataFrame(clean_tensor_lists(learner.recorder.losses)).to_json() valid_losses = pd.DataFrame(learner.recorder.val_losses).to_json() metrics = np.array([clean_tensor_lists(x) for x in learner.recorder.metrics]) metric_names = learner.recorder.metrics_names metrics = pd.DataFrame(metrics, columns=metric_names).to_json() saveResultsJSON(train_losses, run_dir,'trainL.json') saveResultsJSON(valid_losses, run_dir,'validL.json') saveResultsJSON(metrics, run_dir,'metrics.json') #export ## Tracking Class from mlflow.tracking import MlflowClient from mlflow.entities.run import Run class MLFlowTracker(LearnerCallback): "A `TrackerCallback` that tracks the loss and metrics into MLFlow" def __init__(self, learn:Learner, exp_name: str, params: dict, nb_path: str, log_model: bool,uri: str = "http://localhost:5000"): super().__init__(learn) self.learn = learn self.exp_name = exp_name self.params = params self.nb_path = nb_path self.log_model = log_model self.uri = uri self.metrics_names = ['train_loss', 'valid_loss'] + [o.__name__ for o in learn.metrics] def on_train_begin(self, kwargs: Any) -> None: "Prepare MLflow experiment and log params" self.client = mlflow.tracking.MlflowClient(self.uri) exp = self.client.get_experiment_by_name(self.exp_name) if exp is None: self.exp_id = self.client.create_experiment(self.exp_name) else: self.exp_id = exp.experiment_id run = self.client.create_run(experiment_id=self.exp_id) self.artifact_uri = run.info.artifact_uri self.run = run.info.run_uuid for k,v in self.params.items(): self.client.log_param(run_id=self.run, key=k, value=v) def on_epoch_end(self, epoch, kwargs:Any)->None: "Send loss and metrics values to MLFlow after each epoch" if kwargs['smooth_loss'] is None or kwargs["last_metrics"] is None: return metrics = [kwargs['smooth_loss']] + kwargs["last_metrics"] for name, val in zip(self.metrics_names, metrics): self.client.log_metric(self.run, name, np.float(val)) def on_train_end(self, *kwargs: Any) -> None: "Store the notebook and stop run" #self.client.log_artifact(run_id=self.run, local_path=self.nb_path) #if self.log_model: MYPY.log_model(self.learn.model, self.exp_name) self.client.set_terminated(run_id=self.run) !nbdev_install_git_hooks from nbdev.export import notebook2script() !nbdev_build_lib ###Output Converted 00_core.ipynb. Converted 01_startup.ipynb. Converted 01a_COCOnutte.ipynb. Converted 02_runs.ipynb. Converted index.ipynb.
colabs/intriguing_properties/generalized_contrastive_loss.ipynb	###Markdown Copyright 2020 Google LLC.Licensed under the Apache License, Version 2.0 (the "License");you may not use this file except in compliance with the License.You may obtain a copy of the License athttps://www.apache.org/licenses/LICENSE-2.0Unless required by applicable law or agreed to in writing, softwaredistributed under the License is distributed on an "AS IS" BASIS,WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.See the License for the specific language governing permissions andlimitations under the License. Generalized contrastive lossThis notebook contains implementation of generalized contrastive loss from *Intriguing Properties of Contrastive Losses. ###Code def generalized_contrastive_loss( hidden1, hidden2, lambda_weight=1.0, temperature=1.0, dist='normal', hidden_norm=True, loss_scaling=1.0): """Generalized contrastive loss. Both hidden1 and hidden2 should have shape of (n, d). Configurations to get following losses: decoupled NT-Xent loss: set dist='logsumexp', hidden_norm=True * SWD with normal distribution: set dist='normal', hidden_norm=False * SWD with uniform hypersphere: set dist='normal', hidden_norm=True * SWD with uniform hypercube: set dist='uniform', hidden_norm=False """ hidden_dim = hidden1.shape[-1] # get hidden dimension if hidden_norm: hidden1 = tf.math.l2_normalize(hidden1, -1) hidden2 = tf.math.l2_normalize(hidden2, -1) loss_align = tf.reduce_mean((hidden1 - hidden2)*2) / 2. hiddens = tf.concat([hidden1, hidden2], 0) if dist == 'logsumexp': loss_dist_match = get_logsumexp_loss(hiddens, temperature) else: initializer = tf.keras.initializers.Orthogonal() rand_w = initializer([hidden_dim, hidden_dim]) loss_dist_match = get_swd_loss(hiddens, rand_w, prior=dist, hidden_norm=hidden_norm) return loss_scaling (loss_align + lambda_weight * loss_dist_match) # Utilities for loss implementation. def get_logsumexp_loss(states, temperature): scores = tf.matmul(states, states, transpose_b=True) # (bsz, bsz) bias = tf.math.log(tf.cast(tf.shape(states)[1], tf.float32)) # a constant return tf.reduce_mean( tf.math.reduce_logsumexp(scores / temperature, 1) - bias) def sort(x): """Returns the matrix x where each row is sorted (ascending).""" xshape = tf.shape(x) rank = tf.reduce_sum( tf.cast(tf.expand_dims(x, 2) > tf.expand_dims(x, 1), tf.int32), axis=2) rank_inv = tf.einsum( 'dbc,c->db', tf.transpose(tf.cast(tf.one_hot(rank, xshape[1]), tf.float32), [0, 2, 1]), tf.range(xshape[1], dtype='float32')) # (dim, bsz) x = tf.gather(x, tf.cast(rank_inv, tf.int32), axis=-1, batch_dims=-1) return x def get_swd_loss(states, rand_w, prior='normal', stddev=1., hidden_norm=True): states_shape = tf.shape(states) states = tf.matmul(states, rand_w) states_t = sort(tf.transpose(states)) # (dim, bsz) if prior == 'normal': states_prior = tf.random.normal(states_shape, mean=0, stddev=stddev) elif prior == 'uniform': states_prior = tf.random.uniform(states_shape, -stddev, stddev) else: raise ValueError('Unknown prior {}'.format(prior)) if hidden_norm: states_prior = tf.math.l2_normalize(states_prior, -1) states_prior = tf.matmul(states_prior, rand_w) states_prior_t = sort(tf.transpose(states_prior)) # (dim, bsz) return tf.reduce_mean((states_prior_t - states_t)**2) ###Output _____no_output_____
EA_FORM1_ImpedanciaRadiacao.ipynb	###Markdown Circuito aproximado para impedância de radiação ###Code rho = 1.21 c = 343 pi = 3.141592653589793 ###Output _____no_output_____ ###Markdown ![Screenshot_20210615_085009.png](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAA7gAAAFwCAIAAAAdf0D8AAAACXBIWXMAAA7EAAAOxAGVKw4bAAAgAElEQVR4Xuzdd1gU1xYA8DO79C5dLKCilCgWUASVYkex9/jsiiUW7LELGiXGirHEXmJX7B1pIqCCLSiooKgUpXfYOu+PkXW4oFKXBc7v+957M+fcwTyz7J69c+dciqZpQAghhBBCCBXHIQMIIYQQQgghLJQRQgghhBAqFRbKCCGEEEIIlQILZYQQQgghhEqBhTJCCCGEEEKlwEIZIYQQQgihUmChjBBCCCGEUCmwUEYIIYQQQqgUWCgjhBBCCCFUCiyUEUIIIYQQKgUWygghhBBCCJUCC2WEEEIIIYRKgYUyQgghhBBCpcBCGSGEEEIIoVJgoYwQQgghhFApsFBGCCGEEEKoFHJkANVmQqHQ3LQlGUUIIYRQHRUT954MoaqDM8p1ipwcfvNBCCGE6hFTk2ZkCFUdrKvqGvxmicpFVVU9vyAXgHNo/6FJUyaQaYRkg6+vr4uLi1AocnR0CAgIINMI1UtYIksBzigjVK9RQAHNpWjg0AIyhxBCCNVvWCij+iL+UzwZQgAAYooSUQDqKspkBiGZQ5MBhBCqTlgoo/pi81+b+vd1iQgPJxP1Gw00TYMYxIViEZlDSGZQFMX8N3OAEELSgYUyqkdeR0ePGj4Cy2U2CiiKouQoiiPGJxaQ7KJpmvkfYA4QQkgqsFBG9Q6Wy2w0AA20iAZVTRUyh5CMoQEUyRhCCFUjnENC0hMRHn782DEyKi1hoaHsU6ZcNjM3v3ztKrbVA6BFhQVkDCHZgyuEEELShPUBkh5rGxtrGxsyKi3uc+deu3KVHZk3333KtGn1vUrm0EBTAHRqNhbKSPZRAsA1yggh6anfJQKqr5gSWUUFFxsw/eEAgKKx/kAyj/r6H4QQkhIslFH9giUyiQYaaAo4FAjJFEIy42uzCwoofLIGISRFWCij+mLw4CEbvLywRCaJmX5btEo9X4KCZBvT9YIG+mv7C4QQkgr8aET1hVN3ZzKEAL7u4EDTAjHWH0jm0RSIyRhCCFUfvImFUH1H0xQAJaSwUEa1Ai5SRghJDxbKCNVrcgBAiWmgVVRxUQqqBSj82EIISRG+4yBUr4mAAzQFX1dgICTjKAo7KSOEpAgLZYTqNRrEAEABReMaZSTDmK4XFEUD0/4CIYSkAh/mQ6hek4evhYc8H+sPJLu+dr2gaS52vUAISRHOKKPahFfIS0tLE4vxufcqI+QARQNNU4raDcgcQjKHSwYQQqg64YwyknXPnz275+v76OGjqFev8vLyAIDL5err6xubGLsOHOg6YICamhp5DSozmgM0UADilNTPZA4hmSMWkBGEEKpGWCgjGSUSic6fO3fsyNHX0dFKSko9evXs5uDQuEljAV/w8eOHu7fvhIWGhYWGrffwnOs+z23GDPJ6VEZCoJlSWYg78yGZR9F4HxQhJE1YKCNZ5O/n57VhQ2xMrJqa2qq1a4YOG6aurs4esGDRotMnT65ZtbqwsHCT15+vXr36c9NfikqK7DGoTLhAAcXsYk2mEJI1NPZnQQhJFRbKdUpEeDgAWNvYkInao6CgYN1aj7NnzgBAZ7vOmzZvNmrUiBwEAACjf/0VKGrlsuUAcO3K1QZaDdZ4epCD0E9RTKEMgDueIRlW1PWConDDEYSQFOEcUp2yeuWq1StXkdHaI/5T/CBXV6ZK7uvicuT48e9VyYxRo0e3MjNjjo8fO/bo4cPieVQGQqCBpmhQVJQnUwjJjK9dL4BmDhBCSDqwUK47IsLDX0dHv46OZuaVa53YmNhRw4e/i30HAH1dXLbv9JaT+8kdD4qifpszW3K63tOTlURlJAdMb1rOT/62Eap5WCQjhKQLC+W6QzKXXBsnlT9+/Dhm5MgvX74AgJm5+dYd239aJTNc+vVTVVVljl+9fPXq5aviefRTykBTNFAcvKONZB4H8GWKEJIqLJTrCGY6mTmudZPKubm506dMTU9PBwA5ObnNW7coKCiQg76Dw+EYmxhLTn0unGclUVkU0kAD0HzgkxmEZIyYYtbTI4SQlGChXEcQs8i1a1J58cKFb9++ZY7nzJtnYWlZPP8TJibNJMc4o1x+oq/3s8X4boBkHUXT+Ag6Qkia8KOxLmBPJzNq0aTytStX796+wxw3bNhw2nS34vmfU1RSkhwnJMSzMqgsxBQFFE2pUvhugGQX0/UCKIqicfEFQkh68KOxLih1/rjUoKzJzMz09PjW023qdLeyL7qQ+PL525ZyqSmprAz6OQ4A0BQNXBFg1wsku752vaCx6wVCSKrwJlZdcP3WTebgyqXLADBw8KBiaRm2+++/09PSmGMdXd3Ro8cUz5fJly/fCmW14vuSoJ8SU0wrZZGAxp35kKyjgHnJIoSQlOCMMqoxqSkpJ/89ITmdPGVyxbbW+5z0rVBuoKXFyqAyoIBDUzQNf2zYcPjIYTKLkCyhAfBjCyEkTfiOg2rMwQMHCwsLmWMulzts+PDi+TJJSU7Jy8uTnBqbmHzLoTJQ11AXU2IK6Devo2fOmPm///2PaT+CkEyiAERkDCGEqg0WyqhmiESiiz4XJKfdHBx09fRY+bIK8Pdnn1q1bcs+RT8VEhzSt7crh8ulOcDj8U+cONmuXbsDBw7w+dgtDskgGjspI4SkCQtlVDOCg+6zH7xz6dePlSwHv3u+7NMO1h3Yp+inmjdrfvmqz7ZtO5saNuEADUB/+vTpt99+Gz9+fEZGBjkaoRrCdL2gqK/dLxBCSDqwUEY1417xArdLt67s0zLi8XgPgh9ITrW1tTt26sTKozKRl5efM2dGQLDfyFGjmDKEz+efPXt25MiRSUlJ5GiEagJ2vUAI1QgslFHNePrkieS4WfPmhoaGrGRZhYWG5efnS0779e9fxo2vUUnNmjU/cPDgnTt+PXv2UlJSAoB79+5ZW1svW7ZMsh0MQgghVK9goYxqAK+Q9zr6teTUzMyMlSyHM6dPsU9Hjh7NPkXlpaqq2rOn0/Xr106fPm1qagoASUlJXl5etra269evT0xMJC9ACCGE6jQslFENSE1NEYvFklPTli1ZybJ6/+6dZEs/AHDu3t3yl/LtfY1KpaCgMGjQoIiICFdXV2YlRkZGxurVq//3v//5+wWSoxFCCKG6CwtlVAMyMjPZpwYG+uzTMtr/zz72asU58+aykqiy1NXVT5486enpqaGhAQA0Tfv7BwwdNmzZMs/s7GxyNEJSgp9ZCCGpwjcdVBOKP46jplbu7fSSk5MvXbwoOR0ybBg2hqtyampqy5cv9/HxsbKyAqAo4GZmpm3a5OHs7BwYGEyORqg6FXW9oLHtBUJImrBQRjVAW1ubfSoSl3sHAe/tOySNfhs0aLBsxfLieVQ1OBxOjx49bt26tWTJYlU1JaBALKafPnni6jowJzeLHI1QtSnqekFxsOsFQkiKsFBGNaChkZGmpqbk9NPHj6zkzwX4+Z8+eVJy6rF+HVF5o6rVsGHDP//8MzQ0dM6cuXp6ukBReXmZHdrbb9zo9fLlS3I0QtWIlicjCCFUjbBQRjWAoihbu86S048fylEop6WmLl2yRHI61c2tX//+rDyqLq1bt546dcLCRQvl5eRoGmJiXy1fvuz58+fkOISqDQW0kIwhhFA1wqazqGaMGDnyzq3bzPHjR49EIhGXyy0+pBQ0Tf++ZGla6tct/br36LF46beiGVWft2/fHj106MiRIwmfv1BAAdAcGowaN1ZRUSGHIlRtaAAhbmGNEJIiLJRRzXB0cjIzN38dHQ0A8fHx169eGzh4EDmoOJqmVy5b7u/nx5z26tN7x86dZSmvUYXl5+fHxMRs3Ljx7t276ekZNNAAQFNiDlC79+zt1MnWxKQpeQ1C1QrvgyKEpAjfclDN4HA4q9askZzu3bNHJPrRI31isXjlsuVnTp9mTseO+9/OXbsUFBSKj0JVKSQkZOrUqZ07dz59+nRaWhpF0xRNKyoqtG/ffu+ePdOnu7Vv37ZBgwbkZQhVg6KuF9j0AiEkVVgooxrT2a7zgkWLmOM3r1+vW+tRPP/Nhw8fxowcxVTJmpqau/bs8Vi3Dnerrj7v3r1buXLlgAEDTp06VVBQwARV1FSHjxpx/Pjx0JDQadOnF78CoepV1PWCpkXY9QIhJD1YaqCaNGv2bzRN79i2TSwW/3v8+MePHxYsXty6dWvJgDdv3pw9ffr0yVOFhYWKiorjJkyY+dssdscMVLUCAwL27dt319c3JSVFMnenpaXl6uo6bty4Hj164FoXhBBC9QcWyqiG/TZndmd7O+9t2x8EBwcFBgUFBunr6xs1MhIKRQnx8RkZGQDQysxs2PDhg4cO0dHRIa9HlVZYWPj06dN79+7dvHkzPDxcIBAAAEVRGhoajo6O/fr169u3b+PGjbFERjIAF14ghKQKC2VU86ytrY/+e/zTp08hDx784bkuOTm5hampsbGxo5OTmbmZtY2NgYEBeQ2qCp8+fQwNDfv7712hoSFCoQjg601tFRWV4cOHu7u7t2/fvvgVCNUsmsIVgwghKcJCGckKRUXF82fP8vn8tZ6e/xs/jkyjKvUq6mXg/aC/d/wdFRXFrP4EAKDA0MDQxcVl2rRpdnZ2xS5ASDbQICZDCCFUbbBQRjLh2dOns6bPEAqFx07828nWlkyjqlNQULBnz55/9h54GxNN0wBAAdAURTVp3GTm9JmTpk7C+XskgyRdLzjY9gIhJEV4DwvVvHNnzv46arSOrs7FK5crUCXHf4qf8L9xfD6fTKDixGLxkSNHbW27LF269E1sFA00BTSAuF27dt7e3nfu+v2+4neskpFsknS94EhugCCEUPXDGWVUk4RC4R+e644fO9avf/8/N/+lrKxMjviZz58/T5s8ed2GP7Cn8o9FPI2YNGFSZGQkTdMURXFp4CooWFlZTZs2rWPHjrgWGdUWHHyeDyEkRVgooxqTlpY2Z9Zvjx4+VFRUTEtLHTxgQH5+gYaGhp6enoWlZdt2ba2tbfT09cjLWC5dvLjew3PtOk+bjh3JHAIoKCj89Cn+YVjordu3bt68mZmZCQBcDse0eYsJY3/t0a+fjY0Nh4O3lVCtwQGKX/TIKUIISQEWyqhmREZGznSbnpSYCAA8Hu9h2EMmnpSY+Do6Ovj+fea0UeNGFhaWrczMmjVv1kCrgbqmBq+wMCUlJerlqxs3bmRnZ3us83QdMEDyYxFDKBS+evHir+3bb1y/np6eAQAU0Fw5uTZt2kybNm3SpElKSkrkNQjJPDHQuGAQISRNWCijGnDzxo0lCxcZNTJq265dfn7+589JOdk55CAAAEiIT0iIT/C9e5dMADg4OW7w8jI0NCQT9d7pU6cOHDz47NGjjBzmb5UDIJZXUDh08FC//v1w02lUu+GEMkJIirBQRjWgZctWt33vGjVqJIlkZma+jo6Ojo7+7/mLFy+ev3/3/lvPsuLU1NR69OzpOnCAc/fuZK7eS0lJcXd3P3/+PJ8vBBAzJbKyspKjo8Pq1aux4xuqvSRdLyhco4wQkiIslFENMG1pSkS0tLRsO3e27dyZOc3Ly4uOinr16lVCfEJaWhoAGBoaGBgYGpsYd7K1VVRULHYxKpKXl3fq1CkaaACKAlBWURr3668zZs1qh8/qoVpO0vXie1+hEUKoOmChjGSRqqqqtY2NtY0NmUA/xOFw1NXVc7JzaIoGGsRisYDHU8J+IKjuoHAXa4SQNOFjEQjVHQYGBvd8702cNFFPV5+iKD6Pd/jfE9adbHv16nX58mVyNEK1D83BRcoIISnCQhmhukNRUdGmo82hQ4fu3w/6be5szQZaNIjzC/J87/kOGTL8r02bRCIReQ1CtQpuYI0QkiYslBGqg8zMzLy3e9+8cXPo4CFKCsoUDRxa+PuyZT169Dh+/HhBQQF5AUK1BZcMIIRQ9cFCGaE6y9bW9oKPz+Vrl5x6O1PycmJaHBgYNHXq1D/W/5GVmUmORkiGYdcLhFCNwEIZoTqud8/e1y9dP75rFwcooIDP52/02ti9e8/9+/eLxXgfG9UOX7teFB0ghJB0YKGMUN2nrKw8eprbylWrDA0MACiapp88fTJ79uyhQ4f6+vqSoxGSWTSAGGeUEULSg4UyQvWFh4dHdHT04cOHLSwsKAoEAsGVK1f69+/fp0+fI0eOZGdnkxcgJHNo/NhCCEkTvuMgVI9oampOnDjh+vXr69ev19PTo2maz+ffuXNn8uTJVlZW3t7e8fHx5DUIyRbs3IIQkh4slBGqd0xMTJYvX3792vVhQ4ZpamoBANDw8cMHd3f3fv36nTt3rrCwkLwGIYQQqn+wUEaonrLpaHPuwrl79/xcXPpx5bgAFEXT//3339ixY0eOHHnz5k3yAoRqzreuFxSuUUYISQ8WygjVXxRFWVu3P3Hi38OHD1vbWNMUBQACgeDq1avDhw9fu3ZtZGQkeQ1CNeFr1wuaxq4XCCFpovBNpy65cukyAAwcPIhMIPQzhYWFa1asvnj5Usy7GOZtgcPh2NnZLVu2rG/fvlxuFW/zcOf2nYjwx2S0BAooRSUlNTVVNTW1xk2amJmb6+vrk4OQ7MnKyl6+fLlYLKIAaAA5ABGUfe9pZs642PDs7OzTp0+LxWJzc3MnJycAAKAooKmve/VRADTzZ3EBxOyLmeh3cSwtzefMmUOGEaoNTE2aMQcxce+LZ1CVwUK5TsFCGVVSUlKSt7f3/v3709LSKIqiaVpZWblr167Lly8vqk6qxpFDh4KCgp6ER+Tm5pK5H9LX1+8/wHXosGEWlpZkDsmMz0lJTZo2FQpFABwAMbNoggYRAFA0RQMA819AFfVHZupeoCgo+lBi1boU+6OKA5SYAmYchwaOpAinKOancQA4QAmBpimKommm7BbD15qZQ1HMtPTXCrpPnz63bt0q+uEI1SZYKEsBFsp1ChbKqEq8fPny9u3bu3btev/+65uvqqqqs7PzpElTunbpoqevW3x4xWVlZa1b63Hp4kUirq2jY2FhYdjQMDcn98OHDx8/fMjPzyfGjBo9eumyZRqaGkQcyYLk5C+NGzcRiUrtUPGTOd4y+jaH/HM/GEf16dP7xo0bZFgqRCJRzNu3iYmJmZmZWZmZCgqKDY0aGhkZmZg0U1RSJEcDpCSn+Fw4P3HS5FKzqB7CQlkKsFCuU7BQRlUoOTl5+/bte/fuzcjIAAAKOEDR5uaWixYtGjjQVVe3asplPp/v6uLyLvYdO7hpy+ahw4axI0GBgRvX//H27Vt2sJWZ2ckzp7W0tNhBJAvy8/OPHDnC7PxIUSoKChRfAHLyhQKegD1MTklOWCiUV5KnxWIhXwTk5PFXJYMKyoqiAp6KgmoOnwcgLBrGBVBWUKD4fA5N58orcoR8oeRCeSV5AV8AYlBSViws4El+lLGx8YABAySnUhAbE3vl8uVHDx9G/vdfQUEBmQZQUlKy79Kle88ezt27GxgYMMHUlJRxv47NzMwMffyo+HBUf2GhLAXkuw+q1bBQRlVLIBA8fvx49+7dFy5cKCwsBOBwgaY5VDsrq+CQEGVlZfKCCvFcs/bY0aPsyMPwxzolCnGRSLTJy+vg/gPsoE3HjqfOnsFOCEj28Xi882fPnTtzhv2MrKqq6i+tW+vo6Gg10JLjymVkZsS9j4t69UoyGd/B2tq2s212dvbtW7dSU1L7urj8vWe35HJUz2GhLAVyZAAhhIrIy8vb29t37tx53Lhxa9d6hoc/EoqEIOY8efZi/MTxSxYubN7CVEeHrGjLS8xMPBZpY2VVskoGAC6Xu2jJkqCAQPa8cvjjxz7nLwwbMZw1ECHZIhQKz587t8t7Z1JSEhMxMDAYMWpUX5e+rczMOByy/VReXt7Z02f+2bsnNSX1SUTEk4gISaqDtTVrIEKo2pG/nwghROBwOH369Ll58/q5c+daW/5CgYgC+vxZnz59Xf39A8jR5fcp/hP71MnZmX3KJi8vv2L1KiJ4/NgxIoKQ7IiIiHDp3WflsuVMlayto7Npy+agkAfuC+abW1iUrJIBQFVVddKUyTfv3Cn5u2Btg4UyQlJVyq8oQgiVRNPigoICgVBMU0ADF0CclZnO5/PJceVE0/SzJ0/ZESdnJ/YpoW27dkQk8r//UpJTiCBCNa6wsPCPdetGDx/x/t3XJfgDBw3y9fMbOmxYWfotNmjQYPc/e61tbCQRRUVFy19+YQ1BCFU7XHqBEPoRPp9/7do1Pz+/mzdvvn8fB0BTQAElGjZs5OjRIzt16kReUE5v37zJysqSnGpra7exsmLlSerq6np6eikpxSrjT58+6enrsSMI1azEhIQpkya/ffNGElmwaNGs2b+xhvycgoLCHxs3uvTuzTxN1LZdO3l5eXIQQqg6YaGMECrd+/fvT5w4cejQobi4uKKnfikOh2rVqtXI4cM91q0jxldMYEAA+9TB0bHUm9FsjRo3IgrljIx09ilCNetl5MupkyZJXqVcLneb945+/fsXH1Umpi1NbTt3DgsNBYAO1h3INEKommGhjBAiCQSCgIAAT0/P4OBgSZDD4bRv337ChAkTJkzQ0Kiy7sUB/v7s05KLMkvKzPw2A83ADnFIdoQ/fjx5wkR25+91G/6oWJXM6GDdgSmU2cswEELSgYUyQuib/Pz8kydOnDh5MjQ0VLL+mMPhtG3b1t3dfeDAgVVbkubk5ESEf3uin8PhdHN0YOVLIRKJkr98IYJGjRoREYRqxPt376ZPncaukue6zxs5ahRrSLlJ1uW374AzyghJGxbKCCEAgIz09FvXb/7xp9fr19FCoRAAKIqSk5OztrZeuHBhmzZtzM3NyWsq7UFwMPNnMdq1b6+pqcnKl+JJRASxS1/Lli0bNmzIjiBUI9LS0qZMnMRec9/NwWGuuztrSEVYWFgAgKmpadV+TUUIlQUWygjVdwkJCYGBgTt27Hj8+LFkByKKojp27Lhq1aq+ffvKyVXXG4W/nx/7tCzrLq5euUJEBg0ZQkQQqhFLFy3++PGj5FRNXX3Dn16sfAWpqqkBdlBGqIZU1+cfQkjGxb1//yoq6siRI2FhYfHx8UyQw+EYGhq2b9/ezc3N0dHxp/O7lUHTdFBAIDvy00L5w4cPZ0+fYUf09PQmTJrIjiBUIy5dvEgsuF+5alWV3OtQUlQCXKCMUA3BQhmheicjI+PEv/9u9PJKTEwEAAqABuBwOFZW7caOHTN58mRtbW3ymmrw8uVLdvMKfX19y18sWXkSr5C3aP589lINAPjDa2NV7aSNUIWlpaau9/BkR8zMzatqw0hFJcW+Li6d7TqTCYRQ9cNCGaF6hM/nX7p0ycvL69mzZ5JVFkBRv1haenqsc3Jy1NaRRonMCCw+/ebo5MQ+JfAKefPd5z0tvjXJwsWLu/fowY4gVCN2bN+emZnJjsxzd6coih2pjL/37CZDCCGpwEIZofri2LFj27dvf/HihVgspmmggJKTl7Oyspo3b56lpaW11FdAlr0x3Pt37+bNmfPq5St2cNmKFVOmTWVHEKoRSUlJ58+eY0csLC169enNjiBU5VKS08gQqgZYKCNU96Wmpvr7+0+aNFksFgEARVFKSiqOjg6TJk4YPGSwoqIieUH1y8jIePb0meRUTk6uS7eurDwAAJ/Pf/b06amTJ69fvSYWiyXxJk2arF23ztHJkTUW1Qu5ubkAoKamRiZq1D+79xB7uU+cNLkKp5MRKlVObgElrxQTG/374mVkDlUdLJQRqssyMjL37Ttw8uTxyMhIptbkAnS2td26ebN1585cLpe8QFqCAgO/rf0AAICJ48bp6empqWtwuZyszMy01LSXL1/yeDz2GGMTkzG//jpu/HhFpRoo7pE0icXimJiYR48e5eXlXbt2TUFBwc/PT0VFRV5eSVdXV1+3Qa++fUwszGzbdjAyNCQvlqLc3NxzZ8+yI4qKin1c+rIjCFUHsbiQokRAg0hU7MkNVLWwUEaoDkpNTb3h43Pu6tXw8PAvRdtzNG3adMCAgf369bO27mBgYFD8Cmkj1l0oKStH/hdJPKgn4eDoYG3TsbNd5w7W1jhRV8fk5uSGPQwzMDBITEx8/fpNWFjo58+fs7Ky4uLi+Hw+j8djXhXM16rMzEwA6sOHdxRF3bp9W05BXllZRVNDo1WrVoWFhUOHDnV0dMzPz7e2tlZRUSH/pOpx5/Zt4utcrz69ZW3OG9VdFABwuFjLVSP8y0Wo7hCLxTk5OZv/2nz02LH4+ASaFgPQABRFga2t3fnzZxvJxg52YrH4fmAQO3Lm3NlWZmbp6ekpycmfkz7PcHNjF83Tps+ws7djDUd1RHh4+K6dfwcEBX78+FEsFlMAQHFoGgC+rbQBAIqiOBwOc0tESUmJy+Xk5+fTQAn4YgE/Nzsr+9OnBAA6JCQEaFpdQ6N79+7Dhg2zs7dr0bwF++dUh2slGnt3744PmCJpoCgKgKYoCmeUqxUWygjVHUlJSc7Ozm/fvgVmngEoBQUFc3PzefPmDR06VHa29Xr29Bm7RYChoaGZuTkA6Ojo6OjomFtY2Nnb3w/6VknfvHEdC+U6Iz09PfHjJz9//xu3b4eFhWZnZzNxBQUFeXl5VVXVxo0b5+TkdOjQwcDAoGHDhkKhsGnTpjweb9asWSKRqEuXLl5eGz9//vz8+X9KyvIxb2OjoqKysrIyMjJSUlJ4PF5OTs7ly5cvX75saGjo2n/g8CGDzCwtjE1Miv1DVJG8vLwHwQ+IoJ29PRFBqDowt1lomubzC8kcqjpYKCNUdwgEgpiYWAAAoGigVFXVli1ZuGDRImVp3YYuI2LdRcnGcC79+7EL5du3bq/19ORwOKwhqPaJevPSzzdgz+49UVFRYloMNFAUZWho2Lq1lYtLH1NT044dOxp+Z8Gxr68vANBAi4QCGxsbAHB1dSXGJCZ+CX4Qej/I39//XnR0dFJS0oGD+/Yf/EdfT79Pnz5Dhw51cXGp2kdXX0ZGikQidqSFaQs9fT12BKHqVrnUVNkAACAASURBVOxpD1TVsFBGqO6Qk5Nr2bzZm9hYAJoDdF5+9o5t215HRs6cP9/OToZmZAP8i+1cXbJQ7tW796rlKyQlSFpq6qOHj3DDhdpLIBBs3OC9d8/Wz1++0EBTABRQunq6EyZMGPPrmA7tO5AXfA/9o5rAyMhg5IjBI0cMTk1NDQkJOXjwoK+vb35+fkpy6r/H/z179qylpWX37t1XrlxZVXdXXjx/QUTMzS2ICEKoVsMZGoTqDgMDgxu370yZMkVDQ1sM8kDLpWRlHT/v069f/ylTphQWysTtuZTkFHZHZDk5OfuuXVh5AIAGDRp0Ll7Z37xxnX2KapEPsTFTpk5Zt/73pJREmiPicqn2HdrNXzj/7t27np6e5aiSASgADvy8VYuuru7AgQPPnj179erVIUOGqKgqAwU8Hu/p06dbt251dXWNjo4mr6mQqFfFensDQPMW1b4qGiEWfLi52mGhjFDdIS8v36JF8wMHDgQE+I4cPkhDQ5WiaQpEmVkZhw4d+v3336OioshrpI5Yd2HT0abUFgEu/VzYp7dv3WK3Uka1Ap/Pv3//4aBhvx4/dkIkEuuo644a+uvlS5cjIiK2bN7Stm3b8m4/TgOIodhShx9QVFTs3r27j4/Pfy9eLHJf0Lq1lZycPE3TISEhvXv3Pnr0KNH8uALYe7AzmjVrRkQQqk4/uMWCqgYWygjVQe3btz9z7lxERMRGr01t23ZQUlSiKMrb27tLly6urq6+d/0qXyJUGLlA+Tsb8vXq04e9KDk1JfXxo0esPJJ1qamp7u7u/fv3evn8MVBiS0uLB2EPTp870d+1Pzm0XH4+oUxq1rz5pq2bw8JCzp8/17NnT4qiPn365ObmNn7S+A9xceTo8sjOyiIimpqaRAShasL0ysSOmdUNC2WE6ixT0xZLly5++jQiMDhgYL9+QNMZGRnXr1/v17/v8BHDg4KCiC0/pEAgEDwIDmZHSi5QZujo6HSytWVHbl6/wT5Fsuzd+/fdujns3bs3NzdPQ1tnzIhRN65fNzNvRY4rM0lNQFX0XrOqquqgQYOuXLmyYcMGIyMjgUBw9tRZ+y5dVq9anZ+fT44um6wShbKqmioRQaiaSLpeVPiXApUFFsoI1X2drG1Pnj7t5OQsJycHAEKh8PqVq3369BkyaNDDhw/J0dUp/HE4swsxo6GRUatW3y2e+vUvNvWIqy9qES1NzS9fPgNAz549/AOCTp453dTYmBxUHkU1AdDiSn27U1ZWXrp0qa+v76hRozgcTmJiYnj44wpvUVmyE0vVdtVAqCxUlMq3hAmVC/lLjhCqk1TU1C5e8nnw4IGr60A5OTkxxSksLLx89bqDg8PIkSOfPn2amppKXlMNAn/WGI6tT98+7LuKKSkpEeHhrDySXdra2qtXr13kvuD8ufNWbSzJdEVRAEBXwceWhYXFjh079uzZY2tr673du8LVrbq6OhGRtIVGSGrEnEp9e0Q/VgXvOAihWkFTU6tTp05Xr17evXt30yaNATgUAJ/PP3f+XNeuXceOHcu0qq1WxAJlJ2cn9ilBR1e3k20ndgRXX9Qi7u5zN23drKGpQSYqgQa6qh7z19fXnzZtWnBwsKlZSzJXZo0aNyYiGekZRASh6kWBiIeFcjXCQhmhemfq1KlBQUGrVq1saGQIQFE0lZ+ff+funSFDhvTq2fPOnTvkBVUkIT4+JiZGciovL//TPcz69uvHPr118yauvqj3ytr1oiyYxUgVZmFJdk3++PEjEUGoetEcvkgmWn/WVVgoI1QfGRsbe3isDX/8+OjRo64DBmhqalJA5eXl3fPzGzRokJ2d3V9//ZWUlEReVjn+fsWmkzt26qSq+pMnn/r2dWGvvkhOTn70UBq9L0QiUURExPat2/b/8w+ZQ6hI127diEhoSAgRQaia4dxB9cJCGaF6iqKohkZG48ePO3/+XEBAwNSpUzU0NGgaCgsLw8LClixZ0rVr1/3793/48IG8sqLuFV/a0c3RgX1aKj19PWsbG3bkyqVL7NMqd/7sud9mzLRu137UsOF/e3tzuZWacURV5VvXC1lqhtWuffuWLYut3IiICC8oKGBHKiMyMjL266b0CKGagYUyQvWdgoJCu3bt9u3bFxAQMHr0KA2Nr4tK379/P3369GHDhl28eDE5Obn4ReWWlpoa8uABO9K1a1f26fe49C+2+uLK5csle3JVoV9a/zJvwXzJthE/XkWNpEbSCUv6PQ1/bMSoUexTPo9/6sRJdqTC/O7dGzFkaG5uDpmoCrExsUcOHVq+9HcygWob7A1X3bBQRgh91a5du1OnTl26dKlv377Mvgk0TUdERIwYMWLkyJG3bt8UCATkNWV24fx5kajY6tIybvbb16XYFn2FhYWHDx5iR6qWhaVlq1atbG1tAaBx48Zl/IdE0iJzn1mDhw6Rl5dnR/b9s7fy28W/efNmwTz3GbNmtW3XjsxVQmhI6PKlv3ez79KnZ8/1nuvS0tLIEaj2ka2vjnWPzL3pIIRqlrOz85kzZy5evGhnZ8dERCJRYGDgoIGDXfr3v3r1egWm9PLz84nqVlFRUUFBgR35HgMDgw7W1uzIvn/2xrz99lBgdYiMjAQAp+/sGohqjswtx9TW1v5tzmx2JDUldfXKlexIeb1/92782LGt27QhfnLlNTRqOG26W7eipdV4w6QOoIEKDw9fs3qNt7f3tWvXrly5kpmZSQ5ClYCFMkKIpKGh4ezsfOTIkW3btpmbmzOrQvl8od/du8OGDenbt+/9+/fJa75PJBItW7o0JSWFHeTxeEGBQezID7gU733B5/EnTZgQFhrGDlahvLw8pmEzFsqoLGbNnt3ZrjM74nP+woF9+9mRsgsNCRk9cpSGhsbuvXsr2ZSjJBMTk2bNm/fq05s5/XEjcyTjihbuQ0RExLr169zd3QcOHDhs2LCmTZuamprOnTv3+fPnfD6fvAyVE3ft2rVkDNVar6NfA4CZuTmZQKj8dHR0OnfuPHXq1M6dO8vJySUlJebn54vF4nfv3h07dkxNRVkgFikrKZfauUIsFn+Ii3v79u3d27d/X7LkUVgp+//5+frm5OTweDyBUKisrEzcv2YzbGh4+OBBdiQ3J8fnwoVXL19lZGYU5BdoamlWeM+IkgL8/K9euaKgqLBuwx9VXqmginn37t2JEyfEYtrExHjixIlkukZRFNXVweHiBR/2Y3zB9+8LBAI7e/uyP30oFot37tixbMnSBtoNjv17Qk9fjxxRRa5fvRoWGtayZcuZv/1G5lDtkZubG3w/WJ7L0dbQoOTkOnTowOfzmTfVjIyMx48f79+//8qVK2pqalZWVuTFqMyoCtxFRTLryqXLADBw8CAygVClZWZment779u3LzEhkQYKQCwvL3/s2LHRo0eTQwFCHjwYP/Z/ZPT7Dh094uDoSEZZRgwd+vTJUzJa5OCRI45O372cpun4+PjPSUm/tG6toqICAOnp6Z+TPlv+UvqOccuX/n72zBkHR4dDR4+SOVRD7t2717dvX5FI5Ojo6F982xoZEf748W8zZ6UV3+HS0dlpxcqVZVnpHhERsW3zlrDQ0BamLY7++6+hoSE5ouowv01T3dx+X76MzKFa7tWrV9evXw8ICggKCMrNzQWgKIDuPbp7eHh06dKFHI3KACdLEEJlQtO0oaGhlpZWQkISgJgDIBAJvrf9h32XLjFx78loJZzz8SFDZSAWi69eubJ31+5fWrdu1rz5jm3be/Xu9fHjp6OHD/fr399719/kBQAAEBgQAACOuO5Clki6XlCyOrlj07HjtRs35s+by14UFOgfcD8waNDgwf1c+3e2s1NWVmZdAQCQmpJy/fr10ydPvX3zBgB69enttWkT8yhtNcnIyHj29Bnguos6ytLS0tLScvHixeFPw1evWX3v1j2+QHDvnv/Tp083bdo0ZcoU8gL0M1goI4R+Ii8v7++//z5+/HhUVJRYLGb2EG5ibDzdza1t27bkaJmRl5e3YJ772zdvDh453Kx5cwCYPnPGAJd+GZkZAPC9CeyoV6++fPkCuEBZVpXpCdAaoqevd+zECe/tO/bs2iXp8SIWiy/6+Fz08VFQUDBp1kxHR0dLSysrKysxMTEpMZHH4zHDdPV05y9cOKq0+zM/lZaW9i42tlmzZrp6egCQn5//7t27li1blroeKSgwkKZpNTU1m47FOpSjOsamvc25U+fOnTvn7e399OnT9PT0mTNnampqDh8+nByKfggLZYTQdz158uTChQtnzpx59+5d0TItDocDFhaWx44d69ChAzFediQlJU2ZOInH4508e0ZyF1tOTs60ZcubN24AgMN3lmoE+AcAgLGJibGxMZlDMkBIBmQLh8NxXzB/5OhRhw8evHzxUnp6uiTF5/PfvH7NGvtVKzOzYcOHjx33PyUlJTL3M8yCDS6X27FTx1MnTopEov6urrNmzNDR1Q17XPoelgH+/gBg37XLD54KQHWDqqrqxIkThw4dOnv27DNnzvAF/JkzZ7Zp08bMzIwcir4PC2WEUCn4fP6JEydWrlyZmJgoCXK5XGtr69GjR0+bNk1NTY01XLYIBILZM2fFxsRcuHyJWOspFAoAwMLSQl9fnx2XYMoInE6WWULgkiHZY2RktGLVqmUrVjx98uRh2MM3b17HvY/Lyc7Oy8+Tl5NXU1PTatDAtKWpubmFfRd75nZHBezcsWPf3n+27/Tu0bMnE1kwz91rwwYAcHBwKPUhQrFYHBx0H/AVXp9oaGjs27dv0qRJCxYseP78ec+ePffv39+7d28OB/uelQkWygihb/Lz81++fHn27Nm7d+9GRkaKxWKKorhcrpGR0aBBgyZMmGBmZibLJTJjk5fX82fP3GbMaN26NZFKSvoM31+dmZ2V/ezpU8D+srKs9ny4czgcaxsbYg/2KiEQCBa6z/e7d+/A4cPsznQdrK2vXL4M33+FP3v6LCPjR0uPUJ2kpKTk7OwcEBBgZ2cXFRU1ZsyYa9eu4bN9ZYSFMkIIACAnJ2ent/fVa9fCw8OFQiEAUBQlJyfXrVu3yZMnDxgwQLK1tYyLjoo6fPCQqqrqrNlk66v09PSXkZHw/Srh/v0gkUikpKTUydaWzKEaVdQylqI4pT8/Wq9s8vK6cf36qrVriP7NzA0TiqK6OnzdUoTA3DAxt7Co1q4aSDZpampOnz7d3X1+dmbm4sWLAwICyrjrUz1Xe76bI4SqR1pa2ubNmzt27Lh6zZqwh2GSKtna2vry5csXLlwYO3ZsbamSAeCfvXsBYMjQoSVnvi+cO8c8xkRs9SfBLFC2s7cv9SkoVIMkXS9okYx2vZAa37t3Dx881L5D+3HjxxOpz0mfAaBd+3ZaWlpEihEUEAB4w6Qemzt3roNDNzFAaGjomlWryDQqDRbKCNVfKSnJ+/fv79Gjx+LFS968fiMWiQCAw+GYmJhs3rw5KCjIxcXle5+4sik5OfnGtesAMGjIECKVk5Oz/599ANCla9dStxGhaTooMBBw+aZMo4Cu1x9bPB5v1fIVALBoyZKSa0yZLTO/d8MkNSWF2Zv9ewszUJ1HUdTy5cvV1dUB4OSJE8lfPpMjUAnkrxlCqD5Iik84vP9Qt26O06dPf/78OQDQQFMUZW5mPmPGjAcPHixYsKBkz1fZF/nff0xbrpatWhKp1StXMi0IvtfvIvK//5jdIrCMkF0UDVCvl15c9PFJSUlp2bKlbediiy4A4MXz56+jo+H7L+DAgEAAUNdQby/D/WpQdevateuwYcOAgvjExICQUDKNSihlWgUhVLdt3rxlz66/33/4INmYk6KoNm2s3N3n2dvb1+rOQbGxsQCgqqpKrLvYv29fbk4uc/y9+ba7d+4CgLGxceMmjckckhF0fZ/dOXLwEJR2wwQAtm7eAgDa2tqt27QhcwBQtEC5WzeHUu+ooHpCVVV11apVN2/eTE5OXrFkiX1Hm8aNm5CDEEs9f89BqB5JT8/w8wvo1NH+99+Xv/sQR9MAwJGTk7Ozszt27Oi1a1cnTZpUq6tkiby8vOioKOaYz+dv/OOP9LR0ZnsFU1NTPT297Vu3FbsAgKbp69euAUDbdu2IFJIlpbQ8qz/y8vJiYmIAoJVZKyJ1+tSp4Pv3AaBrt24ll2QAgFAoDA6+D9+fb0b1R/Pmzbt16wY0HRMTm5GRSaZRcfi1EqG6LzU1JSb23bSpU1+9esXMInM5XBMTk969e48aNarbdz5ZayMbm47MweQJE/83fnx+ft7N6zdGjRntNmOG+9y5ANCsRfP9/+zr59q/2GUAx44c+RAXBwC5uV8nnpFMKep6wfynnnoXG8sc6BsYsOOPHj70872npKRUWFjo+J0H9R49fJiTnQMA9l2xKRiCkSNHnj9/HoAOCwtr851bEIhRRz4dEUKlSkhMOOlzqmevXvZ2dpGRkWJaDABt27Y7d+7cixcvdu/e7ejoWGeqZABo36H9nHnzACA5OXnr5s0Pgh9s2b7NbcYMAFBWUgaAJxFPrG2sW7X6OiEnEAg816yd8L9x6zw8mYjfvXu/jhp95vTprz8RyYairhfALVovVJ9FPH4sOb7o4/PP3r2Tp04tLCwEgC5duuzYtl0gEHwbDQAAVy9fAQADA4OGDRsSKVQP9erVi8vlAkBOTg6ZQ8XhjDJCdU1+fv7u3buPHDkSFR0lFospmlnYSe3c6T1s2LA6/zE5b777oCGDY2NijI1NTFuaSuIr16zu59q/Xfv2zBPfDHl5+dUeayWnSPZx6vH8jmnLllpaWpmZmX9u9EpMTNTSanDP926Tpk137tp15dIlANDS0noZ+bKpcVNie+oXz59fungRAAQCAY/Hw+6HSEtLq0WLFm/evGHvvYpKhYUyQnVHdnb20aMnvHdsiYmNo4CiQMwBDsWlLCwshg8fPnv2bPKCOsrExMTExIQIqqqqdnNwIIKo1uGTgXpEWVl505bN7nPm5ufnH9x/oGHDhvMXLhg6fDgAKCkrA0BeXl7ch7gJEydKLjl04ODzZ8/u3rnDzDGnp6cP6u/azdFhBfbQrfcaNWr05s2b7OxsMoGKw0IZobojIyNjwYK5QqEQgKKB5nC5NjY2I0eOdHNzK7n7BkK1EE3X7/Zw3Xv08L8f9N/zF1oNtNpYWTF3zwFgwMCBhoYNmzZtYtSoEXv85KlT2KcISeTl5VEUVVBQQCZQcVgoI1R3cDgcPT29z5+ZHvKUubn5/PnzBw0apKSkRIxECNVSOjo6Tt3JPXG4XC6xnTVCP6apqUnTNLFKB5VUfxd7IVT3GBoa+vn5tW7dmgaapumXL1+OHTt2wIABL1++JIciVKsUdb2gmAOEUCWlpqYCAN5s/KkqmFE+sG9/SkoyGa0cJ+fudvZ2ZBQh9EPy8vLm5uZ379718vpz7949vMJCsUjk6+vbo0cPT891bm7TyAsQqiUkXS8ku+QghCpMJBK9efMGAAyKtxpEJVW2UE5LTf1z48Yqf+cyNW0JIKOFcn5+voqKChlFSGYYGBhs27a1e3fnZctWvHz5H1Dw5cuXmTNndO/ubGr6rQsEQrUOBTTeBkWo8u7du5eXlwdFX0HRD1S2UL5963bJv2VdPV1dXT0NDQ0VFRUlJSUulyt54IBQyCu8c+s2EezRs+fwkSOIoOzwvXP3n717Pdevs7axIXOy7czp0zwej4wWpyAvr6aurqOjY2FpqaWlRaZR7TFgwID27dtv8vLaf/AwvzAfxHTv3n3WrFk9ZswYBQUFcjRCtQENQEHpnyYIobILDg4GAADKAXsB/UxlC+WbN24wB8rKyv1c+w8eMqR9hw5lf3JowTx3ItK8RfPN27bK+Cq019HRo4aPMDM3r0XlslAoTEtN+/AhzvfO3aysLDJdGjNz85GjR40eMwabbtZSjRs39ly/3r5r19WrV7+NiX0f987Nzc3Hx+fQoUM6OjrkaIRkHwUiSkQGEULlkZGRcebMGYqijIyMWrRoQaZRcZUqlDMyMh49fAgArVu33v73zpKNS3/swL79Vy5fZkfU1NX/2b+fvR2ALKtd5bKcnNys2b8BQNbKrP59+hY1RgANDY3BQ4YYmxjr6OgqKSslJiZ+/PDhxrXrycnJr6Oj1631OPnvvzt37WplZlbsx6FaQktLa/To0fZd7a+dPT970SKBQHD16lUHB4cVK1aMGjXqe7d6EJJRND6CjlBlHTt27O3btzQN4//3v0bF+wmikipVKN+9c0ckEnXs1Onov8fLezP3QXDwJi8vIrh1+7ZmzZsTQRlXu8plANDU1Gxj1UZSKPfu26fkzmTzFy702rDh1ImTABAbE/u/X8ee87lgbGxMDEO1RdPGTWctWPDf27f//vtvbm5uVFTUuHHj9uzZs2XLlo4dO8r4DRyEgN31AvDlilDFxcfHe3v/DTStrq4+afIkMl02F318oqOiyGiRNlZWrgMGkNHKCfDzDw0NIaNFJk+dWn1PJVaqUL5144aBgcHOXX+Xt0r+9OnT3N9mi8XF+sbPX7ige48e7EgtUrvK5aTEJMmxkzPZjxMAVFVVPdatex0V/eTJEwBIT0tbvnTpidOnyXGoVtmzZ8+4cePmz1/w+PFjsZgODg4eOHCgp6fnr7/+ih2CkIz71vVCRD4Vg1D9JBKJUlJSYmJiCnmFaqpqzZs319HR+el9wpUrV7579x4oavSY0S1bVfBecdz7uKdPnkZHReXn55M5AAdHh6otlOPi4ubOnk38WUpKSi1btWpo1FC7gTY7XuUqXihnZ2WHPAj5a8sWXT09MvdD+fn5M6a5Ectke/ftM6v2769bK8plHo/3+vVr5lhOTq5L167F819xOJzf5s6dUrQV6sOwhy8jX/7S+pdig1BtY29vf+3a1Tlz5pw5c6aoG8bMmzdvenh4WFlZkaMRkjlYJaN6TSQS3bhxIyMjw9/P766vr6amZlZWlkgkkpeXV1dX5/F43bt379Wrl46OTvfu3cmLAR4/fnzq1CkAkYG+gaeHJ5kus/kLF8xfuIBXyLt06eK6tR6FhYXsbEJCAvu0kvh8vvvsOUSVPHDQII91nuoaGuxgNal4oezre1ffwMClfz8y8TNLFy1+HR3NjrRs1eqvLVvqzP1fGS+Xn0Q8EQgEzLG1jfUPVoSbmRf7rhkWGoqFch2gp6e3a9cuo8ZGu3bu4gv4YrH40qUr4eER//573NHRkRyNkGyhALteoHpJLBafPevj7b3t2bNnBQVfq0amJKUoStJ/LDY2dv/+/aqq6m3btlmzZk3v3r0lPwEAPDw8BHw+h8Px8vIyNDRkpypAUUlx1OjRTZsaT54wQVJXAEBCfFUWyn/9+WdkZCQ7Ymdv/9fWLT+dO68qFS+Uc7KzlyxdKidXvp+wZ9duSaMMhoaGxt79+1RVVdnBOkBmy+Xg+0GS41LXXUg00GrAPk1PT2OfotpLR0dn6+atvXv0XrRo4auoKBro+PhP8fHx5DiEZA4FgF0vUP3y4unTsxcvnTl1MjY2lono6Ojo6upaWFjq6enq6uoqKCgUFBRkZmbGx8dHRUWlpaXl5OSEhoa6uLgYGxuPHDnSzc2tsLBw0aJFt27dUlBU3Lhx48iRI4v/IRVnZ29n2tI06tW3JcuFhYXp6ena2lWwIiLAz//wwUNEcLXHWqlVyVCZQnnCpHKvAQ/0D9i6eTM7QlHU9p3edfgpMRkslwP8AyTHjj8slD99+sQ+bdSoMfsU1XZ9Xfradra1srJKSEgE6uvDUgjJtmJPtiBUtyUkJG7a9Oe+PXv4AqEYaHl5+U6dOnl4eDg4OMjLy5OjixQUFFy6dGn37t1hoaHv37//888/d+7cqaqqmpKSIicnt2HDhvnz55PXVEJKcgq7SmYkJiRUvlBOTk5esmgREbTp2LFly5ZEsFpJr9FO3Pv37vPmEruTLF66xKEe3O1lyuX+fV0iwsPJnHR9/vxZsu6loZFRq1atiueLefXyJfu0ldmPBqPaSEVZWU5OjqbFNI2LP5FM+9b1Ar/RoXpj1987vb29C4VCmqK6dOly6dKloKCgHj16/KBKBgBlZeUxY8b4+t7dt3+/mZkZAOTn56ekpABw3NzcFixYQF5QOQH+/mSoKlZfiMXiBfPc09PTiXgFVvxWkpQK5dzc3BnT3HKyc9jB/q6ubjNmsCN1myyUy+wXtJOz07dEac6cPiU5bmHaooO1NSuJ6gJJbUwBcLH+QDKsqOsFVWIrWITqLCUlJQAORdMA9JcvX+Lj4zmcspZtNEDch7iiZ+CYt3c6IyODPaZKlF4oV/p5vr2794SFhpJRgB49epKhalbWv/HKoGl68YIFMTEx7KC5hYXXX5vYkXqiZsvlwIAAyfGPFyhHREQ8DHsoOZ0zd17Zfz9RrcMBWk0J919Esk+M9z5Q/TF7zpylS5doNWhA03RMTMz06dN79Ojh4+MTHBzMfniOLS8v78aNG3v37v2l7S+enp6fPsUDgJ6errGxMQB9+vTpv/76i2hSURkCgeBBcDAAWFhasOOVLJQjIiJ2bNsGAL/8UqyFQAvTFo2bSHsVaMXXKJfdzh077t65y45oaWnt3bdPWVmZHaxXamTtskAgCAl+wBwrKCjY2dsXz3+TkZHhPnuO5HTYiOH9B7iy8qhOoQDEAGIaV3+iWgFvfaD6Qltb28tr48CBA5YtWxYSEiIUCv39/f39/Y2MjDQ1NXv27NmoUSNdXV1tbe2CgoLPnz8/e/YsJCQkJSUlKyuLojhAg7Ky0sCBA9euXUtR1JAhQ6Kjo1evXq2npzexqPdrJYU/Ds/NzVVUVBw6bPgfr9ZJ4okJFX86PDsre/7ceSKRaKqbW/D9++zUjyf4qkm1F8q+d+96b9/BjnA4HO9df0v/O8GPxX8q67/UDx/iyFBFSblcDn/8OC8vjznuZGuroqJSPP9VbEzsvDlzkpK+bkrSu2+fDV5euC6wl0b14wAAIABJREFUDmP+1RYW8ok4QjIJZ5RR/WJvb3/9+vXw8PCgoKBLly6/evUyMTExMTEx6vt742loaHTqZNu7d69BgwY1b96caVB29uxZN7fpYWGh7u7uTRoa9OjjQl5WfoH+/gDQ2d6ueYsW7HhlZpSX//57YkJCGyurcePHHdi3j51yci6lOXR1q95COTYmdtF8ctn478uX23fpQgRrnFO3bmRIWqRWLrMXEpmZm/H5fGJLxQ8fPlw4d/7QgQPMfRk1NbV58+ePnzhBmn1YkHRRAEADhwO0ksp3O2ojhBCqQWpqak5OTk5OTsuWLfPz809MTPAP8A8MCGzcuLFAKEhPT1dRVtHW1s3KyujVq5ezs7OiomLJDUdat269ffs2R0fH7KysEWPGhoSEmJubE2PKi6krnJydGzVqxI5X+GG+UydO3Lp5U1VVdftO7wcPvt4DZ6ipqdl0rMYa6XuqsVDOyc6ePm1abm4uOzho8ODJU6ewI4ghhXKZXSgf3H/g+NFjrczMjBoZqaurp6SkJCUkvn37lslqaWm59O83Z948fX19ySWo7qEooCguULQYKG41vhkgVFnY9QIhAJCXl+/TpzcATCp/i14A6NSp09KlSz08PDMyMr28vA4dOlSZp48S4uOZx8+cnJ11dXXZqaysrLy8vPJukfHmzZv1nusAwGP9OmNj400bvdjZbj9sild9Kv4X9GNisXj+PPe49+/ZwdatW2/wKvZ/GxGYcnn82P+RiUpLiI+Pjfnaq7xJkyYHDh2a6+5u0swkNTnlScSTt2/eKquo9Orda8KkSYePHQ0Lf7zujz+wSq7z6K8ooMUgxn0ckOwq6nqBbS8QqpRZs2ZZWloAh/a5cCEq5hWZLg9/P38AaNa8eZMmTZSVlbW0tNjZ8q6+KCwsnDd7Do/HGzxkyOAhQ4RCITGj7Ny9BhYoQ/XNKG/bsoXoGKKtrb173z+K+GT9D+nq6S5fsbKfa38yUWnsfUacu3d36u7sVEOvOSRjxABAA5WRi2uUkayjAIotF0MIlZO+vv68efNmzJiRl1vgvW3nP3v+IUeUWdG6CyfmtFGjRpmZmZJsYnzCj/dqIKz3XPf2zRtjY2OP9esAICI8PDenWE9hRycn9qnUVMuM8q2bN/fs2s2OcLncnbt3GRkZsYOITVdPd+v27cGhoQMHDyrvxuBlwf7e8uMN+VD9w0zRld5sCCHZQQMIyRhCqHzs7e0NDQ3FIPK941tQUECmy4ZXyGP6HEs6URg1Lr5MuTwzyrdu3jx98qScnNz2nd7Mgo3AgED2AKu2bXWKr+6QmqovyN68fr1kIbnl4IrVq2w7dyaCMmXr9u1k6Dv8/O5du3KVjFaCZBa5OupjBo/39QUNAEpKSp1l+98FkjIKaAo3HEG1BBbKCFVS69ate/Xqdfz48ffv46LevOrQtiK7iYWFhRUWFqqoqHTs1ImJEM/zJSaWtVBOiI9ftnQpACxasqSNlRUTJFYldO9BPpsoNVVcmWVlZc2Y5la0E8xXw0YMHz9hAjsigwYOHkSGvq+qCmUplMiMh2Fhkm+Nne3scAEMYqOBooEGDhbKqDaolvugCNUvkyZNOnbsGAB97fL1ihXKAX5+AGDfpYukfVajRsXa/pZxRlkoFM6fOy8nO6ebg8OUaVOZ4OfPn9+8fs0e5lSiiYfUVGV9JhKJ5s2e8/HjR3bQqm1bz/Xr2REEUiyRGexbGDXSrxvJJi6XK2kjIBbjM1JIdmHXC4SqkIODg4aGRnZ2doW7XjAb/UoWKEPJGeWydYjz3r79yZMnOrq6f23ZLPntJqaT9fT0iC36pKkqq7S/vP4k9lDR1dPd/c9eRUWcv/xGyiUyg/2aw0IZSYhEIpqWtBPAQhnJrqKXKUXjNzqEKo3D4bRs2TIiIuLLly9krgzexcYys6IOrAfsjBoVew6tLDPKoSGhzCNtm7du0dXTk8SZKlzCydm5Br8hV1mtdu3K1QP797Mj8vLyu/buNTQ0ZAfrsxopkQHgw4cPH+LimOMa2ScdyTysPFBtIcZXK0JVQkdHBwAk+/WWC9MYrmWrVuwmDUbFZ5STk5NL7mvGlp6evtDdnabpqdOmdXNwkMQFAkFIMNEYrsbWXUBVFcqvXr76fckSIrjGY621dUUWvtQ9NVUiM3A6Gf1YjX1PR6jc8NWKUNVITEwEAIGgIv2OJBvysYPa2trKysqSB6Jomv78+XPTpk3ZYyRoml6ycFFycnLrNm0WLlnMToU/DmeX7/Ly8l26dWXlpa2Ca1PY0tPTZ7i5MZseS4weM2b0r7+yI/VTdTd9K4u7t29Ljh0cHVkZhAAAaKBpAApLEFQL0FzgkjGEUPkZGhpSFFWBxbF5eXnhjx9D8QXKDHL1xfeXKR8+eCjA35/ZqprYb49Yd9HJ1ra8O/xVrcqWbkKhcO5vvyUWX4nSoUOH1R5r2ZF6qGZnkSVSklMePXzEHCsqKtp07Fg8jxAAAFAcOXkVMoiQ7BEBbiGJUBWIiYmhaZrYerosHgQ/EAgEaurq1jY2RKpRo0aSPYABgCgOJSIjI//6808AWLvO08TEhMgGFn+Sr6Y25JOobA23Yf0fYaFh7IiBgcGuvXt/sCqlzpOREplx4fx5sVjMHFu1bVuB746oDmN6CDAPSSirKJFphGRGUdcLDjb8Rqjyvnz5Eh8fDwBcbrlv0TCN4bp27VqyyDEyIvYciWefMvLy8ubNniMQCAYPGTJk6FAim5iY+PbtW3akBhvDMcj/k+Xic+HCsSNH2BEFBYVde/fo6X97dLEszpw+3ahRo67dupGJ2kamSmQAyMvLO3L4kOQUd0ZEBJrpeUEDTdE5eVlkGiGZUdT1Aihsz4JQpT169EgoFAKAhYUFmfuZosZwpUz0Es/zldr4Ys3KVR/i4oyNjdeu8yRzJaaTmzVvXnLKWcoqvkb5vxcvVi5fTgQ9169v1749EfyxxISEtatWa2pqkolaRRbWIhP+e/Fi6qTJqSmpkkhgQEBgQGDFVu6juo4GId7RRrKOomgOLqZHqNK2b98OABRFtWnThsz9UNSrV0xHOQenUh55akTsYl1ijfJFH59LFy8yW1WrqakRWSixc3WNr7uACs8op6WmznSbzufx2cFx48cPHzmCHSkL7x079A30JZsW1jqyNossEon69Oz56dMn4t8OAGRmZk6ZOJHD4TRp0uT2PV8Z+QdGNY4GoGjA+gPJPhpo/KKPUCXFx8czyxuaNm1qbGxMpn8owD8AACx/sdTX1ydzJfccKT6jHBcXt2blKgBYuGRxqVUfn88PeSBDjeEYFSmVBALBbzNnff78mR3sZGu7YvUqdqQsIv/7z+f8hclTp5KJ2kDWSmQGl8u97etLRhH6Di4NLYyNAWDliuUrV5D3iBCSHcaNGgPAp6Ku8AghPp+fnJzM4/HU1NR0dXXLsuBYIBAcOHAgPj6eoqjx48draWmRI37I388PvrPuAkosvUhKSqJpmnnAgM/nu8+ek5+f37Vbt6nTprGHSYQ//n979xUQ1bWFAXjtGbpIR0QQExMUC4oiKooUjQV7ixoV7CWxK4oltmgS7CUmdrFExIJdLGBBjGJBVLAgiA2UIh0GmHbuwxjucESUZMDB/N/TnLX2wXt9GP8c9tnrpkgkKr7U19dXhxMI/knC+2nRIsXJIMUsLS1/++P38ubFV0lJY0aOksvlnl09+T31pp4RGaC8PuGso88YRzIdPcO0lFQdfS0thq8IAFClsLDLgYGBKa/ToqJu5xfkSqVSjuOEQqFEIrGwsKhRw6JFC8fhI0Y6NC3lkS0RXb16dcWKFRzH1a9ff8KECfx2mbKzs+9ERRGR23uCsoWFhVAolMnebuSTSCSpqakWFhZEtGLZspiYGFMzs5WrV73vnx7ewXBtXVx4J8d9EuX+Et8fGLhvb4ByRUtba+OWzYoRLx/vTVraqBEj09LSallZNXVw4LfV2DedOiIiw+cBp6BUhEIpS3gUQ0TCbJ0vrDGaFABU4OWrpEvnLy9f7vcg5t7bo6wYMY44IsaY4m3XnJycuLj4v65eWbd+nXNr53nz5rVq1Ur5ALiioiJfX1+RSMQYGzlypCLCfrzwsMtyudzQ0NDhPbFNKBRa1KypvOMiKTHJwsLi0oWL/tt3ENGKVSuVR1XzKM9HI6L2HTooX34q5Ut7tyNvL5q/gFf8xc+vcTk3g58ODl4w78fMzEwiqnKPk/X0cNwsfD7inz3ll+DfWbtm/fTpUzkSWlmY4K8XAP4lkUi0e/furVu33omK4ujtEHctLS1ra+uCggIrK6vq1aunp6e/fv1aV1f31atXUqmUEYuIiOjVq5eDg8O0adO+++47gUBARFu2bLl+/ToRubu7T548ucQf8xEUQbadm2sZezysrKyUg/KrpCTr2tazfHyIaNSY0WVMPUtKTFQ+g5mI3Ep7X7DylSMop6SkTBg/nndmwohRI3v36aNcKUNRUdGlCxcPHNgfdvFScbGLZ9f/rwAAqOK0tLUYcRyT4v1IAPiXQkNDlyxZcuXKX3I5EXE6OjpOTi29vIaampvW+7pew4YNFQmYiMRi8d27d/Pz82NiYo4cOxIeFi6RyG9HRg4fPjwoKGjFihUmJiarV68mIjMzs59//llHp3xn58vl8sthYfT+DcoKVlZWyntzX758GbhvX0ZGRmN7e59Zs5Q6fKEhIcqX9k2alPHsuTJ9bFAWi8UTxo9PS0tTLjq3aTP7nRPiFAoKCkT5+bl5eelv3qSlpT17+uzRo4eXL4Xl5OQoL7O0tHRoVvoDfCLKyMgwMTFRfM7NyaluYFCy/7YuEAo/7XhDAIBiEk4iJyKOJG8f/QAAlJtMJps+3Wf79q2KnRKNGzfs0aPH6NGj69aty19KRERaWlpOTk5E5O7uPnHixNjY2E2bNp05cyY2Nvbo0aOXLl3S0tJKTU2tW7fujh07nJ2d+fd/yL27dzMyMoionasrv6eE9z7f9q1bs7Ky9PT03h1VzRNy7pzyZUUfDJeWmhYefjni2rUpU6daWVvz20o+Nigv/HH+nag7vGJk5C2Hxv/fdMFxnFwul8lkxfu4P6hLV89393SLxeJzZ8/u27v3esT1+GdP4+PifaZNi4mJsWvQYG/gPsWJy9H37m1Y/9uD+/e1tLSSkpL09fU7duo03cenvLNOAABUS5NpChjjiGm/8+UGAPCRtu7eun79WiKhlpbmxo0bR44cyV9Rpvr1669Zs2b58uWzZ89et3ZtZmYWEWdgYBASEvK+qF2286GhRNSoUaOy30njHaWclZVFRIuXLil7bkj6mzc3rt9QrlTQwXDPnj7dH7g//PLlRw8fEpGBgcGvy5bxF5X0UQNHXiUlHTxwgF8lEheJC5QUFhaKxeKPT8lE1KUrf9/Frp0727u6TZ00+XrEdSJKTU0d4e0dExNDRI8ePvzryhUiOnf2XN9evVNTU48HnzofdumviGvWtWsfPHDgu4EDi4qKeD8QAKBSMSbnOI7kYsyQA4B/SkuupSEUEsnEYvGGDRsuXLiQnV2++amFhYUBAQEHDx6UyRWv/7G8vLyDBw8qZvKVi1wuP3rkKBE5tWrJ75X07gzgXr17vzuqmic4OFj+9n8kEZGxsXF5X377SNUNDPr27zfUa6jisuz91gof9US5lpVVpb2SMmDgQC9vb+8hQyOuXSMiv59/Wf/779Wq6S34cX5hYaFzmzZyuXyury/HcYMGf2dsbExEpmZmU6ZNHTNy1LOnT29cv172LwUAACoU4+REjIj7qK9XAIDSeA/zlsqls33nZWZmRUXFeHp6Nm3UaOPWrY6OjvylpTl16pSfn19ERIQiFtvY1DYzM4uKilqwYEGNGjVGjBjBv6FMly+FvX71iog+mF95M0dsbGwWL12iXClV0IGDypeOLVq8u91AJUxNTU1NTa2srH6cO4+I3Nzd+SveoXbf5Lq6ukTU1KGpIig3dWjarHkzIgo8+PaRdlZWluI/qoyNjIvvsrWtp/jw+vXr4iIAQOWTkJSII46V+6ENAMDfNDQ0xo4Z27RJ00Vz5oRcviwWy25GRbVt27Z169a9evVq7tCUBEJHR8fiQdCZmZnXrl0zMTG5dOlSUNCRqKjbMpmMiNPS0vLw8Ni2bVv16tVbtGgRHx/v4zPzq6++ci3PU8U/NmxQfCh17rQy5T3KZYyqVnY5LEyxcaBYDYtSxv6p0P2//zi395/CUUztgrKCltbb412HeHmV7JCRkdF0H58n8fFt27kUFw0N377nV1BQUFwEAKh8uvr6jBHHMTlOvQCAf6dVq1bHTp/ZvGXnxo3rYmMficXisLDL4WGXScBq1qxpYGCQm5traGj45s0bQ0PD7OzstLQ0xZnKjDFNTY02bdr4+Ph0795d8dNmzpw5bty4jIz0hQsXnjp16mOOu5XJZOvXrrt9+7bi8nJY2DcdO5ZcUoKOjo6JqWlGejoRzZjp06RpU/6KkhJfJs6Z5csr3oi4XlBQoHhyWhEUk03smzQxVTpk+n3UNChraLzdMlLqXI/vJ/xQ/DkpMfHggYMnjh9XXMpl/9/jAgBQ+YQk5IiIOIZTLwDgX9PS1po0aezQod8mJCQcPnz4zJkzL1++zMrKev36teK36K9evSIixblkmpqaZmZmdevW7dq1a/fu3W1tbZWPgRs5cuTNmze3b98eFhb2888///zzz8UtZbm5uVlZWYkvE1+8eL57567YR4+KWwF/7k1JTvFo7/G1rW0NCwsbGxul+96ysrLKSE93addu9Nix/B6RVCrNyMjIyspKTUm5HBZ26MBB3nloRBQfH9/ds6v3MG/7Jk3NzM2MDI0M/n4eqhIXL1ykj9t3QWoblD9GTHT07xs2xD2O8xrmvTdwn0vrcp91AgCgcvl5+YwYMRJUzB47APgPMjY2dnR0dHR0/PnnnxMSEhITE3Nycl68eJGVlZWVlVWjRg1NTc369euLRKK2bdu+b+SehobGTz/9dP369ejo6LVr1w4fPqx456qy78eOU2x/LdX50FDFCRj16tcPPnuG3yaysrJKSkp636jqc2fPTp4wkV99x/Nnz5Ys/knx2Xv48AWLFpbsl5Cenp7w5MmXX36pOHpZJBIlJCTY2tqWOn02OTlZEf3dPdz5vdJUyaAsEokWL1x4/Oixmb6+v2/cKBAI8vPz+YsAAD6FAlEuccQxToBTLwCgAtStW/efHfFGRJaWljNmzBgxYoSoQPTLz7/67/TnryD6c18Av1QeGzb+wS8p6dqtW9du3fjVfyoyMnLNylVCodCppdO+vQEymaxb9+4/jB9vamYWcbPEeXPFFPMFjY2NP7gtRKHqBWWxWDxy2PBbN2+uXLP644cCAgBUEjlxRMQJSkwxBQBQDx06dKhdu/aLFy9Cz5/PzMpUPhqhavlt3botmzav/W19h2++UVSmT5nq98svROTq6lrq82wiCrt4kYhc3dyKhxqW7aMWqZWzp8/cunnT3NwcKRkA1JCpvj4RR4T3JQBAHVlbW9vb2wuIkpISX754yW9XBRKJZPKEiZs3btq6Y0dxSiai5o6OL168oPfvP5ZIJFf/ukrvX/CuqheUr129SkTvOyBaKsOJTADwKeXkiYgEpT/KAABQA99//z1HjDgqPs6ialnu5xd86tTM2b6tnVsr16VSCRExxlxc2ynXi928cSM/P58x1s7tY0/HU9OgXDze793Nxzq6ukSUnJysmNJHRJmZmXNnz1Z8Tk97w3Hcgf37i9cDAFSm6mZGxOQcsjIAqCs3Nze9anrE6MmTJ/ye2gsNCfHfvqNZ82Ze3t68VvLrZCJyaOZgZGTEaykoDoZzaOagmFj3MdQ0KD+4/0DxIeTcuZId6tyls+LD2FGjFy9Y6DtzZu8ePdw9PBTPmAMDA7/t27fUQ+UAACqBNDefEWOM02Bq+gULAP9x+vr6DRo04DhBZmYmv6feioqK5s+dR0Q+s2a9u8k4PDyciFzfP0ZE8Sbfx++7IDUMyoeDgoZ+Nzg0JERx6eszc9hQr8hbt4oXtGrdes68eRoaGkVFRXt2736a8HTXnj19+vbt1LkzERHHDR46tG+/fsXrAQAqUz0He+IYcZwEQ6wBQF2ZmpoSyUQiEb+h3o4cPpyWlmZra9uqdYlNF0R07+5dxblv78vBiS8Tn8Q/ISJ3Dw9+7/3U7nu8b79+H4y5o8aM7vdt/yfx8V988UXxVJXV69aO+358nTp1qhuo8lRqAIByiXn8kIjjSEAk5vcAANSDYkyJRFLFjufZuX0HEfUq7TiH1StXEZGJiUlje3t+j4j+fpxsambWqHFjfu/91O6J8kcyMjJybNFCefagpqZmY3t7pGQA+LSEEuKII4zlAwA1ZmVlRUSampr8hhrLz8+Pj48nonr1+XNSAvftuxIeTkQu7dq9uyVDQRGUXd3c3ndyXKlK/1kAAPDPaOtrEpXjWxgAoPIlJycTkb6+Pr+hxhL+fvWwRsnRgzeuX78Qel4xrNvtPfP28vPzFcemubRz4ffKhKAMAKBSAjkjRsQhLAOAesrMzIyNjWWMGRoa8ntVQeTNm8Wfjxw+vHnTppGjRxcWFhJR27Zt161Z++6WkpBz54qKioioqYMDr1U2tdujDABQpQkkQsIjZQBQY3v37i0oKCCiRo0a8Xtq7GtbWyMjo6ysrGW/+r169crIyPh8aEhtG5vffv/9+NGjRGRkZHQ/5r5NHRvelpL0N29+/22D4nNeXp5y64PwRBkAQJUEch1iHDEBlWcbHABApQkKCiIixljj8rzW9snp6uouX7VST09PLBZv37ot4M8/Bw8ZsmbdOj09PcWQjfz8/GfPn/Xp27f4losXLszy8enm6fk0IUFRGTV8xNTJkzMyMorXlA1PlAEAVCknX8YRCTghh/f5AED9PHz4MDY2loi++uqrL7/8kt9Wb+07dLgYfjn67j0jYyP7Jk2K5zT36NmzZk1LG5vatayslNd7tG/v0b69cqW8EJQBAFRJTgXEcXKS8xsAAGrg4sWLijf53N3dq1Wrxm+rPVNTU/f2/IOQhUIhb5y1qiAoAwCokrhQRIwYJ8c+ZQCoCBKJ5NatW49iH9t+/XV6+puMjAw9PT0TE5Pk5ORWrVrVq8c/Ok1ZYmLi+vXrOY7T19efPHkyvw3vQFAGAFAtGRERcRpyJGUAUI38/Py4uLjjx48fCDyYkpoiKsgvKiqSy0v85kooFOro6JiZmRkZGY0dO9bDw8POzk55gVgsnjFjxuPHjxljP/74Y9XaoPypICgDAKiSFhMQJyCSS0mX3wMAKL+9u3b9smxZXHy8VCrl3p48KWeMGRgYmJqampiYFBQWpCSnpqe/ycvLy8vPo2c0YcIEPT09d3f3mTNnurm5KX7Ozp07Dxw4QESdOnWaMGFCueZu/GchKAMAqBKnJWCMY8QEAqlcLn/fjCgAgA+6c+fO1t9+2+TvL+cERJyOjnbjxo1btmzZsWOXjh07VKump7w4MTHx4sWLhw4dio2Ne/IkTpQvCj51OjQ01Nvb28fHJykpafHixURkaWm5bt26qjVq5BNCUAYAUKXqxoaM4zgSpKS8GjrUa9WqlZaWlvxFAAAfcvhI0GzfOXHxcYxjQiG1dGrlt8zP1dWVv+5v1tbWXl5eXl5eRUVFgfsD/X75Nfbx46Ii8datW69fvy4Wi1+/fq2rq7t8+XLelgwoAx51AACokoZQk2OMI7lUIg0M3Ofu7n7t2jX+IgCAMt26dctrqHd8XBzjqKZlzQ0bNh4/eaqMlKxMW1t7mPews+fOrV271tKyJhHdu3fv0aNHjLFly5YNHDiQfwO8H4IyAIAqDezbf+Mfm2pb1eYExBE9fhzfs2fPbdu2icVi/lIAgPfw9/cXiUQcEUc0/vvxvfp2NzM15i8qk42NTf/+/fv06cOIKaaFmpubt2/fnje1DsomXLRoEb8GVVbso1giqo9fqQB8Opqami1aOHbs1Dk9JeNx7EOOkxUUFJw5c+bRo0dt2rSpXr06/wYAgHe0bt06Pz8/Pj6+qKjo0qVLR4OOvH6ZVMOihpGxsYbGB/bNikSiWzdvLZg/f/78+efPnydGFhY1DA0NU1JSzp8/7+LiUrNmTf498B6M4zA76vNx/OgxIurZuxe/AQCVTiQSHTt2dNYs36SkJI7jGGN2dnZLly719PTU1cWBGADwYffu3ZszZ865c+dkMhkx0tLUsrOz++67wW1btzUwNmjYsEFxaJZIJFFRUcnJyXfv3j1y5Eh09AOZtIgj0tHR8fb2XrBgQWpqapcuXVJTU2vVqnXq1CkHB4eSfxSUDkH5s4KgDKBuEhNfzZ8/PzAwoKioiIgEAoGHh8f48eN79OihpaXFXw0AUFJOTs6RI0e2bdt29epVjuOII46YUKhhYKAvFAoMDQ2rVauWk5OTl5cnkUhyc3PlcjkxYsSEQmHbtm3HjRs3YMAAxajnn376aeHChUTUo0eP48eP8/8kKA2C8mcFQRlADclkspMnT86cOTM+Pl7xlSsQCJycnPz9/Rs0aMBfDQBQmjNnzixbtuzWrVt5eflExIgjIo6IMcY4rnj0CGPMwMDQyanFsmXLmjdv/v/7ifLy8lxcXO7evUtE+/btGzRokHIXSoWg/FlBUAZQW7m5ub6+vnv27MnLy1NUGjduvH7dBo/2b2cBAAB80OXLlzMyMsLCwi5dulRUVCSTycRisba2tqampr6+ftu2bVu1amVjY9OqVSv+nUREFBQUNGTIkKKiokaNGl25csXIyIi/AkpCUP6sICgDqLmIiIipU6dev36diBhjhoYm48dPnjNnqoGBAX8pAECZRCJRcnJydna2mZmZhYXFx+zmKiwsHDp0aFBQkEAgOHToUJ8+ffgroCQE5c8KgjKA+nvx4sXmzZvXrVsnEhVynEwgEDg4OKxevc7NzYW/FABA1WJDGG+WAAAe/0lEQVRjY1u3bp2dne3o6HjmzBlTU1P+ClCCc5QBACqVjY2Nr6/vyZMnv/66LjGSy7mo27e7d+85w8cnNy+bvxoAQKXq16/fq1cvjuMiIyNTUlL4bSgJQRkAoLIZGBi4u7ufP39+0qTJ5uZmxFh+ftaa1aubN2tz7Ngx/moAAJVS7GDmOO727dv8HpSEoAwA8GnUrl179OhhM3xmaGpocBxxHBf/5MH+/fv56wAAVKpPnz6MMSKKi4vj96CkDwx3AQCAiiCRSDb+8cdyP7+k5BRGjIhjRIwjExMT/lIAAJWqWbOmjY3N8+fPFee7QxkQlAEAKtWbN28CAgL8/f2jo6NlcjkRcUwuIObQzGns2FGdO3fm3wAAoGp16tR5/vx5ZmYmvwElISgDAFSS6Ojos2fP7tq1KyYmhv4eE6Clrd2wUcPvx44bPXas4pehAAAVrbCwkDFWUFDAb0BJCMoAABUuISFhx44d/v7+r169Ki5qa2v36NXj237f9uzZU1tbW2k5AEDFMjY25jhOMdoayoCgDABQgbKzsxcvWvTn3r1paWnFRcaYvb39rFmzBg0ahH+oAKDyKTZdVKtWjd+AkhCUAQBULykp6cKFCyHnzl24eFHxFJkxpqGh0bBhw3bt2g0bNqxu3bp4bw8APgmZTPb48WMiMjc35/egJARlAACVkUql96Lv7f0zYPfuXenp6YrRp4wxXV3d/v37jxkzpkmTJphWDQCfVmRkZFZWFhHp6+vze1ASgjIAgGo8eHj/z4C9G9ZtyM3NZUQcETHS0tTq3LnznDlznJ2d+TcAAHwKR48eVXxwdHQs2QE+BGUAgH8rOjo6YG/A4cPH4uIfcdzbkyt0dXVd2rjMnTfXpZ2Lhga+bAFALWRlZQUHBzPGTExMatasyW9DSfjuBgD4554/fz537vyzZ09nZKRzjGPEGMmr6ev369dv8OChru3a6ejiOAsAUCNBQUHR0dEcx3Xv3t3Ozo7fhpIQlAEAyi0/P//s2bOHDh46fuJ4fn4+ETFiQo70DQ169+49cOBADw8PHR0d/m0AAJ/UvXv31q9fL5fLdXR0vLy8+G14B4IyAMDHKigofPky8XrEtV27d4WHh0skEiJijGlraze2s+vbq1f/IUNsbW35twEAqIdjx47du3ePiFxdXTt06MBvwzsQlAEAPkwqlT64d2/F2rXBp05lZGQyRhxHRJyRkVGPHj1mzJjRtGlT/j0AAOrkyZMnK1euJCJ9ff3Fixfz21AaBGUAgA8I3Ldv2/btd27cyMzNJSIiARFXp47Nd4MG9+7ds1Xr1rz1AABqaOnSpTk5OUQ0fvz41vji+jgIygAAZRkyZMihQ4fEYimRnEhAJNfV1Rk1auT06dO//PJL/moAAPWTl5e3dOnS3bt3C4XCKVOmzJ49m78C3gNBGQCgLPv27eOII2KMSFdPx2vw4PE//ODQrBl/HQCAWjp27NjChYvu3r0nENDSpUuRkssFQRkAoCzVq1fPzcnlGEccyeVySVGRjpYWfxEAgPpJTU09fPjwggUL0tLeELEBAwbMmjWLvwjKJOAXAABAyfnQ88NHDDc3q8EYExcV+f+517FlqxEjRsTGxvKXAgCojeDg4M6dO0+cODEtLY2Ia9GiuZ+fn0CA4Fc++PsCAChLC6cWO3bsCA+/PGHyRENjI47kooL8Xbt2NW/u2KtHjwcPHvBvAAD4dJ49exYeHt6zZ8/u3bvfuXNHJpPp6uoOGzbswoULderU4a+GD2Ecx/FrUGUdP3qMiHr27sVvAIAqXL9+ffmyZcHBZ8TiQsZxciJjE5PBgwf/8MMPDRo04K8GAKgwubm5ISGhOTnZYrFYT0/PzMzsyZMn586di46OfvnypUwm4ziOMebi4rJkyRI3Nzf+/fBxEJQ/KwjKAJXgXOi5mb4z70XdY0Qcx4hxdb+sO2f27G+//dbQyIi/GgCgAjx58qRHjx7x8fFCobCoqEi5xRirX79+t27d+vXrZ29vX61aNeUulAte5gMAKJ9O33SyP9Hopzlz9xwOEuWJOI4SEhLGjf9+48bNy1cu69Aew64AoMJxHCeVyiQSiVAoFAqFJiYmX331dVZW5ogRI+zt7Vu2bGliYsK/B8oPe5QBAMrNspbV7/7+x44e82jvoXg5Ri6X3Y66PWjgoIULF4pEIv4NAAAqJRBoKx53Tpw0USKRpKSkXL3614MHD2bOnNmlSxekZFVBUAYA+CcEAkGHDh3Onz9/LSJi4sRJFhYWjFF6evqSJUsaNmzo6+t7/fp1/j0AACoil4uJJEREHOP3QHUQlAEA/pWWTk6//bb+7JkzS5cuNTAw4Dju+fPny5cvd3Fx6dun7927d/GAGQAqwNt3zIQ48a0i4S8XAEAFmjo4zJ07d/Omzc2aOjLGiJhMKj1y9Iirq+u6desKCwv5NwAAqIBAykn5NVAdBGUAAJUZOGhgSOjZNWvW16plyRETEuXk5CxYsGDAgAGnT5/mrwYA+KcYY0TEGCcvQlCuQAjKAACqZGpmOmXKxEOHDs2YMV2venViJJPJTpw40b9//5EjR4aFheXk5PDvAQAop7fH+3KclJPze6A6OB4OAED1nJ2dnZ2d+/buu3jhwktXLovFYpFI5O/vf/LkyWHDhk2ZMsXa2pp/z79z7uy5yFs3+dV3MGLaOjr6+tX09fWta9eub2dXo0YN/iIAqCIwC6OiISgDAFSUNi5tzoSe27Rp0/z589PT04koLS1t1apVp06d6tSpk5+fn46ODv+ef+pVUmJcXNztW5F5eXn8Xplq1KjRrUf3vv36NWjYkN8DAPhvEy5atIhfgyor9lEsEdW3s+M3AOATYYw5OTl169btq6++Sk5OzsjIkMvlb968uXHjxoULF0xMzMxMzapV0+PfVn4OzZr16t37uyFDUlNSHj16xOuamJo2d3Rs2aqljY2NpqamSCSSSCSKVn5+/p2oqH17A1KSU5ycWmrraJe8FQDUUUZGxt69ezMyMlq1auXp6clvg4rgiTIAQIVr1KhRo0aNRo0adefOHV9f3xs3bsjl8mvXrvXr18fOrqGPj0/Pnt3NzMz4t5WfoaHhL8v87t27m/AkQbk+e+6cvv36KVcuh4X9uvTnuLi44sr+wMCoqKiA/YFGGMQNAEBEeJkPAKDSGBoaurm5HThwYMuWLfXr1ycijmOPHz4YM2ZU544dL168UFBQwL+n/LS0tFxc2vGKbm5uvIqrm9vJM6dHjRmtXHwcGzt+zNi3LwkBgBr7+9QLTBupWAjKAACVysbGZvTo0VevXv322wEaGgIZ4+RydvvOvS5dunoP937yJJ5/Q/nJ5SXegrdv0sS0tMfVQqHQZ9YsW1tb5eKtmzcPHwpSrgCAGlL8By3HcdV0q/F7oDoIygAAn4CJiYm//46DBw82btiIkYwRJxEXHTpw2M9vOX9p+b1MfKl86e7hoXypTFNTc96C+bzint27eRUAUFcCOcPxcBUIQRkA4NOQyWQFBQUSqZxjxJGQIyKSF4jy+evKieO4O7ejlCvuHu7KlzxNHRx4lZjo6LTUNF4RANSSvECkgi1b8D54mQ8AoLLFxcWdOHEiICDg9u0oIo4RIyYzNTV3d/eYPGUKf3U5xT1+nJ2dXXxpYmJi36SJUp+vevXq5ubmaWklkvHLly/Na5grVwAA/oMQlAEAKklBQUFwcPC2bdsuXrxYVFTEGOM4EghYvXr1BvTv/+2ggY0bNebfU35hly4pX7q6uQkEH/jloZW1FS8oZ2ZmKF8CAPw3ISgDAFQ4iURy6dKlTZs2BQcHFxYWKoqMsebNmw0bNmzYsGEGBgYl7/jnLl28qHxZxgblYllZ/38CrYAT4gDUHE69qBwIygAAFetMcPCyFSuuXbtWVFRUXDQzM5s4ceKUKVNUG0lzc3Mjb0UWXwoEgnZurkr9UshkstSUFF6xlpUVrwIAaqX41At+A1QKQRkAoELIZLIncfELFi4MPh2cm5urKDLGatSo0b9//6FDhzo4OKhwhLXCX1euSKXS4kuHZs0MDQ2V+qW4HRkpEomUK7a2tpaWlsoVAFBDcrHkqzpfBB8/sX79en4PVARBGQBAxaRS6d27d3fs2BEQEJCVlVX8G9I6deoMHTp03Lhx1tbW/HtU5OKFC8qXH7Pv4sTx47xKrz59eBUAgP8mBGUAAJWJfRR7+GjQ4aAjDx48UIzZY4wZGxs7OzuPHTu2VatWFhYW/HtUh+O4y5fClCsfDMrPnz8/ELhfuWJubj5sxHDlCgDAfxaCMgCACrx+9Too6NDCRYsyMjIZvd02aGxs0qlTp4ULFzRo0IC3viLcv39f+fCKGjVqNGzUUKnPV1RY5DNtmvJWDSL62e9XXV1d5QoAqCEbGxt+CSoAgjIAwL8SHx+/efPmwMDApKQkIiLiOCITE5NevXr7zvS1rf/1B09nU5WwkudduLm7K1/yFBUWTZs6JarkaJIZM2e279BBuQIA6klLS4tfggqAoAwA8E9kZmZGR0fv3LnzxIkT6enpimfIjFGNGjW6d+/u7e1tb29vYmLCv60iffzBcE8TEqZMmvTg/gPl4px580aNGa1cAQD4j0NQBgAot+fPny9atOjE8ePpGZlEiows0NHWHTCg/7x5c+vVq8e/oeJlZmbeibpTfKmhodG2nYtSn4hILBbfiYraFxBw6sRJuVxeXK9du/aiJUvc3N2U1gIAAIIyAEB5ZGZmbdmybdOm3589e0ZExEjAkbaubkcPj3lz57Zwdq60jRY8l8PCeCeqDvfyMjc3169uIBQKsrOy0t+k379/X/ksZyKq88UX3w0e7OXtra2jrVwHAABCUAYA+Bhv3rwJPnz44IkTt27dSklJISLGmJ6enpOTU+9evdu5trOzs9PT0+PfVol4+y50dHVjomN4L+oVc3VzdWzh1Nq5dXNHR0z2AgB4HwRlAICyZGdnr1yxctfu3YmJSRwnJ+KIWLVqeiNHjh45Ynhj+8YaGp/+i1Qul4eHXVau7D94oF79+hkZGWmpqcmvk8ePHascmseMG+/cxllpOQAAlOLTf78DAKgzJyenuLg4ImJERExLS8vOzs7Pz69jx47qEJEV7kTdycrKKr6sWbNmfTs7IjI1NTU1NbVr0MC5TZvwy/9P0qeDTyEoAwB80KfZSwcAUFXExz8hIiLGkaBateoL5s2LuHbN09NTfVIyvbPv4t2D4Ty7dVW+PHvmrPLLfAAAUCoEZQCAstjW/ZKIiDgByfNFOevWrBk3fPjjx495yz6tSxdLTK5+Nyh37NRJKBQWX6a/eXPj+g2lPgAAlAJBGQCgLMFnz40aNcrAwEROmsRppGVn7zl0uEuXLoGBgc+eP+Ov/hTSUtOUT0TW0NBo49JWqU9EZGxs3Nq5xF6L08GnlC8BAOBdCMoAAGX56qu627Ztu3QpdED/XgYG1RjHMZI9e/Zs8ODBQ4cMDQoKysvL499TuXj7Llo4tdDX11euKHh29VS+PHvmDHZfAACUDUEZAODDmjVrtv/gwcjIyF/9ljdt2lyxQfnq1auDBg1ydnaePn16TPR9sVjMv61S8Dcov2cgX8fOnZXPeH6T9ubmDey+AAAoC4IyAMDH+vrrr3x9Z0ZFRQYe3FfXxobjOJlUGhMTs2bNGscWzft/2//hg4f8eyqYRCL568oV5cq7G5QVTE1NW7ZqpVw5fSpY+RIAAHgQlAEAyq1vr377Dx786acllpaWRMRIIBWLTx0/4e7hvmL58srcjHHr5i3lP86yVq0yBmh37dZN+RK7LwAAyoagDADwTzg6Oc2f/+PNWzdXrFhhXduaY0zOBGlpab6z5zRr1mzDhg0JCQn8eypA2IcOhlPWuUtn5Tl8aWlpkbduKfUBAKAEBGUAgH+uVi0rHx+fyMhbP/74o01tayJGnDz+SfykSZPc3NxWrlyZmJjIv0eleBuU3T3clS95TM3MWrZqqVzB7gsAgDIgKAMA/Fvm5uY//fTT5cuXR40aKRAKiRMQUWJioq+vb8cOHTZt2sS/QUWSEhPj4+OLLzU1NZ3btFHql6JL1xKTR86cPl3Ruy+KioqCDh5avGDhgh9/DAwIEIlE/BUAAOoKQRkAQDXq1Kmzfv36Gzdu+PrOsrOzEwgEHMfFxsVNnjzZ2dl5xYoVKh9TcvFCicfJTi1bVqtWTbnyri5dPJV3X6Smplbo5JHrEREd3Nx9Z87cs3t3wJ97f5w7r3sXz4cP/n/qMwCAOkNQBgBQGV1d3ebNm/v5/RoaGhoQENCkSRMikkqlERERs2bNatmy5fDhw//66y9VHSR3PjRU+bKdm6vyZanMa5g7tmihXDl+9KjypQpFRkaOGj6iuoFB127dHJo5KEYDvnjxYtKEiYWFhfzVAADqB0EZAED1rKysBg4ceOfOHblcHh0d3aVLF0NDw+zs7F27drm4uGhra9esWXPTlk0SiYR/50dLf/Pm6l9/KVdcXFyUL9/Hs1uJ3RfHjx3Lzs5WrqiETCb7denS1WvXnj53dv3vGw4dORJ07KiFhQURPXv6NPgU5gICQBWAoAwAULEaNWq0f//+I0eOdO/eXU9PT1FMSUmZNGGSZ7duJ06c4jiu5B0fJejQIZlMplyp+9VXypfv08WzxIi+wsJC/+07lCsqkZqaOnnq1E5dOhdXGjduvHjpEsVn7L4AgCoBQRkAoMIZGBh4eHjs3r173759AwcO1NXVJSKZTHYhJKRfvz5dunQJDw/Pzy/H6csikYiXbrW1tbW0tJQr72NhYdHc0VG5smXzpvi4/78UqBKWlpaubm68YjtXV8V0QH396rwWAIAaQlAGAKgkxsbGPXv2DAwMjI6OXrlypa2tLTEmlUpDQkI8PDw6fPPN6pUrHsV+eLafTCab4+ublpamXCwqKrocdlm5UgbPkmdfiIvEI4YNi7gWoVysCFpaWoo036BBA34PAED9sH/2Kz9QT8ePHiOinr178RsAoH5EItHKlSu3bNnyKukVR4yII+KGDh26Z88e/lIiuVz+4vnztLS0+zExAXv3JjwpZZqJvr7+EK+hji1aWNeubW1tXbzN412vX79u51zKQXLfdOzYtp2LrW29Ro0bVa9e1kPf9PT0hCdPvvzySzNzcyISiUQJCQm2trba2tr8pUpevXrl2qatrq7upSvhpqam/DYAlMfXX3yp+BD/7GnJDqiMBr8AAACVguO4mjVrGhkZJSW9JpIzIkYkk5fYdlws4to17yFD+dWS8vLyNm98e2bzjl073935UMzS0rJZ82ZRt6N49dCQkNCQECLavnOnm3vpt0dGRq5ZuUooFDq1dNq3N0Amk3Xr3v2H8eNNzcwibn7gpLlLFy4S0djx45CSAaBKQFAGAPgEbt26NWPGjCtXrsjlciJGRBwjG5s6AwcM5C8lIqI2bduq9qHRwcOH+aWP8Nu6dVs2bV772/oO33yjqEyfMtXvl1+IyNXVVfmE5nfJZLJtW7bUt7MbM24cvwcAoJYQlAEAKk9OTs7p06f37NkTGhoqFos5jiMSCATUoEHDb7/9tkePHs2bN+ffox4kEsmMqdMunD+/zd+/tXPr4npzR8fjx44RkZu7e3GxVGtXr87Kytr55x4dHR1+DwBALSEoAwBUBrFYHBERsXDhwqtXryoGjjDGhEKho6PjoEGDxowZo6+vz79HnSz38ws+dWr+ooXKKZmIpFIJETHGXFzbKdd5LoeF+W/fsXXHdhsbG34PAEBdISgDAFSsBw8e+Pv7h4SEPHjwQCqVEhFjTF9f39PTc9asWfXr11fziExEoSEh/tt3NGvezMvbm9dKfp1MRA7NHIyMjHitYo9jY32mz9jwxx/ObUp5gxAAQG0hKAMAVJRrV6/8/vvGk6dOKY++s7a2/u677wYMGNCi5ChptVVUVDR/7jwi8pk1S3EKsrLw8HAiKuPFwVdJSaNHjlqydKl7ew9+DwBAvSEoAwCoWGFhYWxs7Pz58y9dCsvNy1W84MYYq1OnjpeX13fffVe1ThE+cvhwWlqara1tq9YlNl0Q0b27d2MfPaL3b1B+k5Y2aviImbNmdfbswu8BAKg9BGUAAJWRy+XXrl3bvn37gQMH8vMLBMQR44jYF198MWnSpNGjRxsYGPDvUXs7t+8gol59+vAbRKtXriIiExOTxvb2/B5RamrqyGHDp82YoTzIGgCgCkFQBgBQjdeJSZs2blm1blV+fv7fNWZoYOjp6blq1apatWopL64q8vPz4+Pjiahe/Xq8VuC+fVfCw4nIpV27d7dkJCcnjx89Zt78H3n7kqVSqYYG/ukBgKoB31YAAP9WakraosULz54+/fT587+nnTIDA4O+ffuOGjXSycmp7Hl16izhyRPFhxoWFsr1G9evXwg9r6OjU1hY6ObhrtwioufPn0+fMnXJLz/bN2miXN+wfr2NTR1MDwWAqgJBGQDgH5LL5QkJzzds2HDgQFByciJHMkaMMTIxMRs0aKC3t3ezZs00NTX5t1VNkTdvNm7cWPH5yOHDJ0+cGDN23IXz54mobdu269as/WHiBMX/2ZiYmEnf/zBrzmxtbe3HsbGKW9LTM0LOnTt18mT41b/+/pEAAOoOQRkAoNySU5JPnTx14sSJ8PArmZkZiqJQIHRwcPDy8ho6dOhnM6L5a1tbIyOjrKysZb/6vXr1ysjI+HxoSG0bm99+//340aNEZGRkdD/mvk0dG0VK/uvKlR/Gjc/Pz5/0wwT+zyL6YeIELS0tfhUAQF0hKAMAlEPSq6SwiMvzZsx9/uwZR0SMiCNdXd1WrVpPnjypW7dun1kQ1NXVXb5q5dRJk0Ui0fat2ywtLafNmN63f38i0tHVJaL8/Pxnz58NGz6ciB4/fjx6xEiJRFLyZ7wlEAgGDR7MrwIAqDHG/b2fDj4Dx48eIyLs/wOoCNnZ2UEHDqxevfbR40dyjlN8eerp6XXr1m3SpEmtW7f+bHZZvCs9PT367j0jYyP7Jk2EQqGiKJPJbt64aWNTu5aVVcnlAFAZvv7iS8WH+GdPS3ZAZfBEGQDgA0Qi0R9//LFz586Hjx7K5XLGETGBjo52p06d5s2b5+Dg8Jk9RX6Xqanpu+NChEIhb5w1AMBnBkEZAKAsv/22cf26VfFPnjFijOQCEjAha9u27aRJkzp06GBsbMy/AQAAPhcIygAAZZk+fbJUKiViHHECobBFixYDBgz44YcfdHR0+EsBAODzgqAMAFAWc3Pz5ORkIiJidnZ206ZN69WrF1IyAMB/AX+WEgAAKLtw4ULjxo054jiOu3///pAhQ3r06JGYmMhfBwAAnx0EZQCAstjZ2YWEhEydMk1HR4cRyWWy0NDQAQMGxsTE8JcCAMDnBUEZAOADLCws1qxZfeDAgYaN7BVnJ0dEXOvSpcuePXtEIhF/NQAAfC4QlAEAPkqPHj3OnAmeNGGCjrYeI3qd9GrUqFETJ0588OABfykAAHwWEJQBAD6WtbX1T0uX+vtvt6hZU85IIpX4+/t37dp148aN/KUAAFD1ISgDAJSDkZHRoEGDTp8OHtSnj66OHmPsxYsXkyZNateuXUBAgFwu598AAABVFoIyAEC5NW3qsPaPP3bu9HdyciIimUx25coVLy+vCRMm/H2WHAAAVHkIygAA/4SFhcWAAQMuXLgwd+5cff3qRAK5nNu8efOYMWMePnzIXw0AAFUQgjIAwD9XrVq1efPmnThxvGXLFkQcEZ08ebJ9+/br16+XSqX81QAAUKUgKAMA/Cu6urru7u6HDx+eNmOaUCgkRsnJKdOnz/D2HsZfCgAAVQqCMgCAClhZWa1euXr1qtW62jpETCaX3rp1k78IAACqFARlAACVmTR50uLFixljjBi/BwAAVY0GvwAAAP+CgaEhRzLiCE8iAACqOnyPAwCoFiOOiJiAOH4HAACqFARlAADVepuPNRCUAQCqOARlAAAVY0REHGb0AQBUdQjKAAAqpvhixdt8AABVHYIyAIBqKb5XhbwqAABUOTj1AgBAxeSMMZLL8UwZAKCKQ1D+rPTs3YtfAoDKJidOwJEMp14AAFR12HoBAKByMiKhhF8EAIAqBkEZAEDFOCIiHHoBAFDlISgDAKiekDh8vQIAVHX4JgcAUD0ZMTxSBgCo6vAyHwCAijGG8y4AAD4HeKIMAKBiHEfEISsDAFR5CMoAABUBOy8AAKo8BGUAAJXjMMEaAOAzgKAMAKB6HKaNAABUfQjKAAAqp3icrMmrAgBA1YJTLwAAVIwxImLYpgwAUNXhiTIAgIpxHEccIybjNwAAoEpBUAYAqAjYpQwAUOUxjsN3+edDKpXafW3LrwIAAMDnK/7ZU34JVARPlD8rGhrYdA4AAACgGgjKAAAAAFUVHidXKGy9AAAAAAAoBZ4oAwAAAACUAkEZAAAAAKAUCMoAAAAAAKVAUAYAAAAAKAWCMgAAAABAKRCUAQAAAABKgaAMAAAAAFAKBGUAAAAAgFIgKAMAAAAAlAJBGQAAAACgFAjKAAAAAAClQFAGAAAAACgFgjIAAAAAQCkQlAEAAAAASoGgDAAAAABQCgRlAAAAAIBSICgDAAAAAJQCQRkAAAAAoBT/Awy91PZRANY3AAAAAElFTkSuQmCC) Baffle infinito$R_{A1} = \large\frac{0.1404\rho_{0}c_{0}}{\pi a^{2}}$$R_{A2} = \large\frac{\rho_{0}c_{0}}{\pi a^{2}}$$C_{A1} = \large\frac{5.94a^{3}}{\rho_{0}c_{0}^{2}}$$M_{A1} = \large\frac{0.27\rho_{0}}{a}$ ###Code def zrad_baffle_infto(a): Ra1 = (0.1404 * rho * c) / (pi * a * a) Ra2 = (rho * c) / (pi * a * a) Ca1 = (5.94 * a * a * a) / (rho * c * c) Ma1 = (0.27 * rho) / a return Ra1, Ra2, Ca1, Ma1 ###Output _____no_output_____ ###Markdown Final de duto longo$R_{A1} = \large\frac{0.504\rho_{0}c_{0}}{\pi a^{2}}$$R_{A2} = \large\frac{\rho_{0}c_{0}}{\pi a^{2}}$$C_{A1} = \large\frac{5.44a^{3}}{\rho_{0}c_{0}^{2}}$$M_{A1} = \large\frac{0.1952\rho_{0}}{a}$ ###Code def zrad_duto_longo(a): Ra1 = (0.504 * rho * c) / (pi * a * a) Ra2 = (rho * c) / (pi * a * a) Ca1 = (5.44 * a * a * a) / (rho * c * c) Ma1 = (0.1952 * rho) / a return Ra1, Ra2, Ca1, Ma1 a12pol = 0.126 zrad_baffle_infto(a12pol) a6pol = 0.0133/2 zrad_baffle_infto(a6pol) ###Output _____no_output_____
d2l/tensorflow/chapter_convolutional-neural-networks/conv-layer.ipynb	###Markdown 图像卷积:label:`sec_conv_layer`上节我们解析了卷积层的原理，现在我们看看它的实际应用。由于卷积神经网络的设计是用于探索图像数据，本节我们将以图像为例。互相关运算严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation），而不是卷积运算。根据 :numref:`sec_why-conv`中的描述，在卷积层中，输入张量和核张量通过(互相关运算)产生输出张量。首先，我们暂时忽略通道（第三维）这一情况，看看如何处理二维图像数据和隐藏表示。在 :numref:`fig_correlation`中，输入是高度为$3$、宽度为$3$的二维张量（即形状为$3 \times 3$）。卷积核的高度和宽度都是$2$，而卷积核窗口（或卷积窗口）的形状由内核的高度和宽度决定（即$2 \times 2$）。![二维互相关运算。阴影部分是第一个输出元素，以及用于计算输出的输入张量元素和核张量元素：$0\times0+1\times1+3\times2+4\times3=19$.](../img/correlation.svg):label:`fig_correlation`在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，得到的张量再求和得到一个单一的标量值，由此我们得出了这一位置的输出张量值。在如上例子中，输出张量的四个元素由二维互相关运算得到，这个输出高度为$2$、宽度为$2$，如下所示：$$0\times0+1\times1+3\times2+4\times3=19,\\1\times0+2\times1+4\times2+5\times3=25,\\3\times0+4\times1+6\times2+7\times3=37,\\4\times0+5\times1+7\times2+8\times3=43.$$注意，输出大小略小于输入大小。这是因为卷积核的宽度和高度大于1，而卷积核只与图像中每个大小完全适合的位置进行互相关运算。所以，输出大小等于输入大小$n_h \times n_w$减去卷积核大小$k_h \times k_w$，即：$$(n_h-k_h+1) \times (n_w-k_w+1).$$这是因为我们需要足够的空间在图像上“移动”卷积核。稍后，我们将看到如何通过在图像边界周围填充零来保证有足够的空间移动内核，从而保持输出大小不变。接下来，我们在`corr2d`函数中实现如上过程，该函数接受输入张量`X`和卷积核张量`K`，并返回输出张量`Y`。 ###Code import tensorflow as tf from d2l import tensorflow as d2l def corr2d(X, K): #@save """计算二维互相关运算""" h, w = K.shape Y = tf.Variable(tf.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))) for i in range(Y.shape[0]): for j in range(Y.shape[1]): Y[i, j].assign(tf.reduce_sum( X[i: i + h, j: j + w] * K)) return Y ###Output _____no_output_____ ###Markdown 通过 :numref:`fig_correlation`的输入张量`X`和卷积核张量`K`，我们来[验证上述二维互相关运算的输出]。 ###Code X = tf.constant([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]]) K = tf.constant([[0.0, 1.0], [2.0, 3.0]]) corr2d(X, K) ###Output _____no_output_____ ###Markdown 卷积层卷积层对输入和卷积核权重进行互相关运算，并在添加标量偏置之后产生输出。所以，卷积层中的两个被训练的参数是卷积核权重和标量偏置。就像我们之前随机初始化全连接层一样，在训练基于卷积层的模型时，我们也随机初始化卷积核权重。基于上面定义的`corr2d`函数[实现二维卷积层]。在`__init__`构造函数中，将`weight`和`bias`声明为两个模型参数。前向传播函数调用`corr2d`函数并添加偏置。 ###Code class Conv2D(tf.keras.layers.Layer): def __init__(self): super().__init__() def build(self, kernel_size): initializer = tf.random_normal_initializer() self.weight = self.add_weight(name='w', shape=kernel_size, initializer=initializer) self.bias = self.add_weight(name='b', shape=(1, ), initializer=initializer) def call(self, inputs): return corr2d(inputs, self.weight) + self.bias ###Output _____no_output_____ ###Markdown 高度和宽度分别为$h$和$w$的卷积核可以被称为$h \times w$卷积或$h \times w$卷积核。我们也将带有$h \times w$卷积核的卷积层称为$h \times w$卷积层。图像中目标的边缘检测如下是[卷积层的一个简单应用：]通过找到像素变化的位置，来(检测图像中不同颜色的边缘)。首先，我们构造一个$6\times 8$像素的黑白图像。中间四列为黑色（$0$），其余像素为白色（$1$）。 ###Code X = tf.Variable(tf.ones((6, 8))) X[:, 2:6].assign(tf.zeros(X[:, 2:6].shape)) X ###Output _____no_output_____ ###Markdown 接下来，我们构造一个高度为$1$、宽度为$2$的卷积核`K`。当进行互相关运算时，如果水平相邻的两元素相同，则输出为零，否则输出为非零。 ###Code K = tf.constant([[1.0, -1.0]]) ###Output _____no_output_____ ###Markdown 现在，我们对参数`X`（输入）和`K`（卷积核）执行互相关运算。如下所示，[输出`Y`中的1代表从白色到黑色的边缘，-1代表从黑色到白色的边缘]，其他情况的输出为$0$。 ###Code Y = corr2d(X, K) Y ###Output _____no_output_____ ###Markdown 现在我们将输入的二维图像转置，再进行如上的互相关运算。其输出如下，之前检测到的垂直边缘消失了。不出所料，这个[卷积核`K`只可以检测垂直边缘]，无法检测水平边缘。 ###Code corr2d(tf.transpose(X), K) ###Output _____no_output_____ ###Markdown 学习卷积核如果我们只需寻找黑白边缘，那么以上`[1, -1]`的边缘检测器足以。然而，当有了更复杂数值的卷积核，或者连续的卷积层时，我们不可能手动设计过滤器。那么我们是否可以[学习由`X`生成`Y`的卷积核]呢？现在让我们看看是否可以通过仅查看“输入-输出”对来学习由`X`生成`Y`的卷积核。我们先构造一个卷积层，并将其卷积核初始化为随机张量。接下来，在每次迭代中，我们比较`Y`与卷积层输出的平方误差，然后计算梯度来更新卷积核。为了简单起见，我们在此使用内置的二维卷积层，并忽略偏置。 ###Code # 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核 conv2d = tf.keras.layers.Conv2D(1, (1, 2), use_bias=False) # 这个二维卷积层使用四维输入和输出格式（批量大小、高度、宽度、通道）， # 其中批量大小和通道数都为1 X = tf.reshape(X, (1, 6, 8, 1)) Y = tf.reshape(Y, (1, 6, 7, 1)) lr = 3e-2 # 学习率 Y_hat = conv2d(X) for i in range(10): with tf.GradientTape(watch_accessed_variables=False) as g: g.watch(conv2d.weights[0]) Y_hat = conv2d(X) l = (abs(Y_hat - Y)) 2 # 迭代卷积核 update = tf.multiply(lr, g.gradient(l, conv2d.weights[0])) weights = conv2d.get_weights() weights[0] = conv2d.weights[0] - update conv2d.set_weights(weights) if (i + 1) % 2 == 0: print(f'epoch {i+1}, loss {tf.reduce_sum(l):.3f}') ###Output epoch 2, loss 16.792 epoch 4, loss 5.780 epoch 6, loss 2.183 epoch 8, loss 0.863 epoch 10, loss 0.348 ###Markdown 在$10$次迭代之后，误差已经降到足够低。现在我们来看看我们[所学的卷积核的权重张量]。 ###Code tf.reshape(conv2d.get_weights()[0], (1, 2)) ###Output _____no_output_____ ###Markdown Convolutions for Images:label:`sec_conv_layer`Now that we understand how convolutional layers work in theory,we are ready to see how they work in practice.Building on our motivation of convolutional neural networksas efficient architectures for exploring structure in image data,we stick with images as our running example. The Cross-Correlation OperationRecall that strictly speaking, convolutional layersare a misnomer, since the operations they expressare more accurately described as cross-correlations.Based on our descriptions of convolutional layers in :numref:`sec_why-conv`,in such a layer, an input tensorand a kernel tensor are combinedto produce an output tensor through a (cross-correlation operation.*)Let us ignore channels for now and see how this workswith two-dimensional data and hidden representations.In :numref:`fig_correlation`,the input is a two-dimensional tensorwith a height of 3 and width of 3.We mark the shape of the tensor as $3 \times 3$ or ($3$, $3$).The height and width of the kernel are both 2.The shape of the kernel window* (or convolution window)is given by the height and width of the kernel(here it is $2 \times 2$).![Two-dimensional cross-correlation operation. The shaded portions are the first output element as well as the input and kernel tensor elements used for the output computation: $0\times0+1\times1+3\times2+4\times3=19$.](../img/correlation.svg):label:`fig_correlation`In the two-dimensional cross-correlation operation,we begin with the convolution window positionedat the upper-left corner of the input tensorand slide it across the input tensor,both from left to right and top to bottom.When the convolution window slides to a certain position,the input subtensor contained in that windowand the kernel tensor are multiplied elementwiseand the resulting tensor is summed upyielding a single scalar value.This result gives the value of the output tensorat the corresponding location.Here, the output tensor has a height of 2 and width of 2and the four elements are derived fromthe two-dimensional cross-correlation operation:$$0\times0+1\times1+3\times2+4\times3=19,\\1\times0+2\times1+4\times2+5\times3=25,\\3\times0+4\times1+6\times2+7\times3=37,\\4\times0+5\times1+7\times2+8\times3=43.$$Note that along each axis, the output sizeis slightly smaller than the input size.Because the kernel has width and height greater than one,we can only properly compute the cross-correlationfor locations where the kernel fits wholly within the image,the output size is given by the input size $n_h \times n_w$minus the size of the convolution kernel $k_h \times k_w$via$$(n_h-k_h+1) \times (n_w-k_w+1).$$This is the case since we need enough spaceto "shift" the convolution kernel across the image.Later we will see how to keep the size unchangedby padding the image with zeros around its boundaryso that there is enough space to shift the kernel.Next, we implement this process in the `corr2d` function,which accepts an input tensor `X` and a kernel tensor `K`and returns an output tensor `Y`. ###Code import tensorflow as tf from d2l import tensorflow as d2l def corr2d(X, K): #@save """Compute 2D cross-correlation.""" h, w = K.shape Y = tf.Variable(tf.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))) for i in range(Y.shape[0]): for j in range(Y.shape[1]): Y[i, j].assign(tf.reduce_sum( X[i: i + h, j: j + w] * K)) return Y ###Output _____no_output_____ ###Markdown We can construct the input tensor `X` and the kernel tensor `K`from :numref:`fig_correlation`to [validate the output of the above implementation]of the two-dimensional cross-correlation operation. ###Code X = tf.constant([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]]) K = tf.constant([[0.0, 1.0], [2.0, 3.0]]) corr2d(X, K) ###Output _____no_output_____ ###Markdown Convolutional LayersA convolutional layer cross-correlates the input and kerneland adds a scalar bias to produce an output.The two parameters of a convolutional layerare the kernel and the scalar bias.When training models based on convolutional layers,we typically initialize the kernels randomly,just as we would with a fully-connected layer.We are now ready to [implement a two-dimensional convolutional layer]based on the `corr2d` function defined above.In the `__init__` constructor function,we declare `weight` and `bias` as the two model parameters.The forward propagation functioncalls the `corr2d` function and adds the bias. ###Code class Conv2D(tf.keras.layers.Layer): def __init__(self): super().__init__() def build(self, kernel_size): initializer = tf.random_normal_initializer() self.weight = self.add_weight(name='w', shape=kernel_size, initializer=initializer) self.bias = self.add_weight(name='b', shape=(1, ), initializer=initializer) def call(self, inputs): return corr2d(inputs, self.weight) + self.bias ###Output _____no_output_____ ###Markdown In$h \times w$ convolutionor a $h \times w$ convolution kernel,the height and width of the convolution kernel are $h$ and $w$, respectively.We also refer toa convolutional layer with a $h \times w$convolution kernel simply as a $h \times w$ convolutional layer. Object Edge Detection in ImagesLet us take a moment to parse [a simple application of a convolutional layer:detecting the edge of an object in an image]by finding the location of the pixel change.First, we construct an "image" of $6\times 8$ pixels.The middle four columns are black (0) and the rest are white (1). ###Code X = tf.Variable(tf.ones((6, 8))) X[:, 2:6].assign(tf.zeros(X[:, 2:6].shape)) X ###Output _____no_output_____ ###Markdown Next, we construct a kernel `K` with a height of 1 and a width of 2.When we perform the cross-correlation operation with the input,if the horizontally adjacent elements are the same,the output is 0. Otherwise, the output is non-zero. ###Code K = tf.constant([[1.0, -1.0]]) ###Output _____no_output_____ ###Markdown We are ready to perform the cross-correlation operationwith arguments `X` (our input) and `K` (our kernel).As you can see, [we detect 1 for the edge from white to blackand -1 for the edge from black to white.]All other outputs take value 0. ###Code Y = corr2d(X, K) Y ###Output _____no_output_____ ###Markdown We can now apply the kernel to the transposed image.As expected, it vanishes. [The kernel `K` only detects vertical edges.] ###Code corr2d(tf.transpose(X), K) ###Output _____no_output_____ ###Markdown Learning a KernelDesigning an edge detector by finite differences `[1, -1]` is neatif we know this is precisely what we are looking for.However, as we look at larger kernels,and consider successive layers of convolutions,it might be impossible to specifyprecisely what each filter should be doing manually.Now let us see whether we can [learn the kernel that generated `Y` from `X`]by looking at the input--output pairs only.We first construct a convolutional layerand initialize its kernel as a random tensor.Next, in each iteration, we will use the squared errorto compare `Y` with the output of the convolutional layer.We can then calculate the gradient to update the kernel.For the sake of simplicity,in the followingwe use the built-in classfor two-dimensional convolutional layersand ignore the bias. ###Code # Construct a two-dimensional convolutional layer with 1 output channel and a # kernel of shape (1, 2). For the sake of simplicity, we ignore the bias here conv2d = tf.keras.layers.Conv2D(1, (1, 2), use_bias=False) # The two-dimensional convolutional layer uses four-dimensional input and # output in the format of (example, height, width, channel), where the batch # size (number of examples in the batch) and the number of channels are both 1 X = tf.reshape(X, (1, 6, 8, 1)) Y = tf.reshape(Y, (1, 6, 7, 1)) lr = 3e-2 # Learning rate Y_hat = conv2d(X) for i in range(10): with tf.GradientTape(watch_accessed_variables=False) as g: g.watch(conv2d.weights[0]) Y_hat = conv2d(X) l = (abs(Y_hat - Y)) 2 # Update the kernel update = tf.multiply(lr, g.gradient(l, conv2d.weights[0])) weights = conv2d.get_weights() weights[0] = conv2d.weights[0] - update conv2d.set_weights(weights) if (i + 1) % 2 == 0: print(f'epoch {i + 1}, loss {tf.reduce_sum(l):.3f}') ###Output epoch 2, loss 34.684 epoch 4, loss 11.937 epoch 6, loss 4.509 epoch 8, loss 1.783 epoch 10, loss 0.720 ###Markdown Note that the error has dropped to a small value after 10 iterations. Now we will [take a look at the kernel tensor we learned.**] ###Code tf.reshape(conv2d.get_weights()[0], (1, 2)) ###Output _____no_output_____
tutorials/tutorial.ipynb	###Markdown Introduction Key Problems with ML in Chemistry1. Translational Variance2. Rotational Variance3. Permutation VarianceTraditional ML algorithms struggle with making molecular predictions because of the nature of how we represent molecules. Typically, a molecule in space is represented as a 3D cartesian array, typically of shape (points, 3). Something like a Neural Network (NN) cannot operate on an array like this, because each position in the array doesn't mean something on it's own. For example, a molecule could have one cartesian array centered at (0, 0, 0), and another centered at (15, 15, 15). Both arrays represent the same molecule, but numerically they are very different. This is an example of translational variance. A similar example exists for rotational variance, but imagine rotating the molecule by $90^{\circ}$ instead of translating the molecule. In both of these examples, inputting the two different arrays which represent a single molecule would result in the NN seeing the arrays as representing different molecules, which they are not. Much work has gone into creating novel input representations for molecules in an attempt to resolve problems with translational and rotational variance. Translational Variance FixWe can solve the translational variance problem by computing the distance matrix of a molecule to obtain a representation of the molecule that is invariant to translation. However, in practice, a distance matrix array of shape (N, N) has a single number to characterize the distance between two points. Simply put, there is not enough explicit information contained within a distance matrix array to be useful to a NN. However, expanding that single number into a vector which probes various distances provides a more sparse representation, but one which is ultimately more explicit. An implementation of this idea, known as Atom-centered symmetry functions ([Behler, 2011](https://aip.scitation.org/doi/10.1063/1.3553717)) achieve this representation. These symmetry functions probe continuous space with gaussian functions centered on a grid, descretizing the provided molecular distance matrix. As each position on the grid explicitly means something (e.g. two points positioned exactly $1.42e^{-10}m$ apart), the network is capable of making inferences from each position in the array.Grid visualization: [desmos](https://www.desmos.com/calculator/4bncqy2bol) Basis Function Demonstration ###Code # Package written by Trevor Profitt, modified for TF 2.0 by Riley Jackson from tfn.layers.atomic_images import DistanceMatrix, GaussianBasis import numpy as np from matplotlib import pyplot as plt # batch, points, 3 np.random.seed(0) cartesians = np.random.randint(1, 5, size=(5, 15, 3)).astype('float32') print('cartesians shape: {}'.format(cartesians.shape)) distance_matrix = DistanceMatrix()(cartesians) print('distance_matrix shape: {}'.format(distance_matrix.shape)) image = GaussianBasis( width=0.2, spacing=0.2, min_value=-1.0, max_value=15.0 )(distance_matrix) print('image shape: {}'.format(image.shape)) # (batch, points, points, functions) plt.plot(image[0, 0, 1, :30]) plt.axis(xlim=16.0, ylim=1.0) plt.show() ###Output cartesians shape: (5, 15, 3) distance_matrix shape: (5, 15, 15) image shape: (5, 15, 15, 80) ###Markdown Permutation Variance FixThe ordering of points in an input tensor is meaningless in a molecular context, so we must be careful to avoid ever depending on this ordering. We can achieve this by only ever operating the network atom-wise to obtain atomic property predictions. Whenever we want to predict molecular properties, we must use cummulative combinations of these atomic predictions (e.g. summation). Rotational Variance FixAtom-centered symmetry functions are rotationally invariant because the distance matrix is invariant. The is fine for networks which predict scalar values from molecules, e.g. energy. However, for problems that are direction dependent, we want rotational equivariance, where the output of the network rotations the same as the input, e.g. force prediction, molecular dynamics, etc.Need a network that can encode directional information and feed it forward to influence outputs. Enter the Tensor Field Networks. Tensor Field NetworksTensor Field Networks (TFN) are Rotationally Equivariant Continuous Convolution Neural Networks which are capable of inputing continuous 3D point-clouds (e.g. molecules) and making scalar, vector, and higher order tensor predictions which rotate with the original input point-cloud ([Thomas et. al. 2018](https://arxiv.org/abs/1802.08219)).Ignoring the continuous convolution part, this means that TFNs are capable of knowing when an image has been rotated, something vanilla convolution nets are not capable of.For example, a traditional conv. net trained to recognize cats on non-rotated images would not identify a cat in the second picture:![cat](cat_pic.png) ![cat_rotated](cat_pic_rotated.png)While TFNs will still identify a cat in the rotated image, trained only on images in a single orientation. We can convince ourselves this is true by visualizing TFNs outputing a vector upon input of a molecule: Equivariance Demonstration ###Code import tensorflow as tf import numpy as np import math from matplotlib import pyplot as plt from tensorflow.python.keras.models import Model print('tensorflow version: {}\neager mode on: {}'.format(tf.__version__, tf.executing_eagerly())) def rotation_matrix(axis_matrix=None, theta=math.pi/2): """ Return the 3D rotation matrix associated with counterclockwise rotation about the given `axis` by `theta` radians. :param axis_matrix: np.ndarray. Defaults to [1, 0, 0], the x-axis. :param theta: float. Defaults to pi/2. Rotation in radians. """ axis_matrix = axis_matrix or [1, 0, 0] axis_matrix = np.asarray(axis_matrix) axis_matrix = axis_matrix / math.sqrt(np.dot(axis_matrix, axis_matrix)) a = math.cos(theta / 2.0) b, c, d = -axis_matrix * math.sin(theta / 2.0) aa, bb, cc, dd = a * a, b * b, c * c, d * d bc, ad, ac, ab, bd, cd = b * c, a * d, a * c, a * b, b * d, c * d return np.array([[aa + bb - cc - dd, 2 * (bc + ad), 2 * (bd - ac)], [2 * (bc - ad), aa + cc - bb - dd, 2 * (cd + ab)], [2 * (bd + ac), 2 * (cd - ab), aa + dd - bb - cc]]) class MyModel(Model): def __init__(self, max_z: int = 5): super().__init__(dynamic=True) self.max_z = max_z self.embedding = SelfInteraction(16) self.conv_0 = MolecularConvolution() self.conv_1 = MolecularConvolution(si_units=1, output_orders=[1]) def call(self, inputs, training=None, mask=None): r, z = inputs one_hot, image, vectors = Preprocessing(self.max_z)([r, z]) features = self.embedding(K.expand_dims(one_hot, axis=-1)) output = self.conv_0([one_hot, image, vectors] + features) output = self.conv_1([one_hot, image, vectors] + output)[0] output = K.squeeze(output, axis=-2) return K.mean(output, axis=1) # (batch, 3) def compute_output_shape(self, input_shape): r, z = input_shape batch, _ = r return tf.TensorShape([batch, 3]) # Set up random input/target data, instantiate model seed = 1 np.random.seed(seed) tf.random.set_seed(seed) cartesians = np.random.rand(5, 29, 3) atomic_nums = np.random.randint(0, 5, size=[5, 29]) vectors = np.random.rand(5, 3) model = MyModel() model.compile(optimizer='adam', loss='mae', run_eagerly=True) model.fit(x=[cartesians, atomic_nums], y=vectors, epochs=2, batch_size=5) # Make predictions on normal/rotated vectors predicted_vectors = model.predict([cartesians, atomic_nums]) R = rotation_matrix([1, 0, 0], theta=math.pi/4) rotated_cartesians = np.dot(cartesians, R) rotated_predicted_vectors = model.predict([rotated_cartesians, atomic_nums]) print('equivariance perserved: {}'.format( np.alltrue( np.isclose( np.dot(predicted_vectors, R), rotated_predicted_vectors, rtol=0., atol=1e-5 ) ) )) # Matplotlib display stuff fig = plt.figure() ax = fig.gca(projection='3d') ax.set_xlim3d(-1, 1) ax.set_ylim3d(-1, 1) ax.set_zlim3d(-1, 1) pv, rpv = predicted_vectors[0], rotated_predicted_vectors[0] ax.quiver( [0, 0], [0, 0], [0, 0], [pv[0], rpv[0]], [pv[1], rpv[1]], [pv[2], rpv[2]], length =2, normalize = True ) cosang = np.dot(pv, rpv) sinang = np.linalg.norm(np.cross(pv, rpv)) print('angle between predicted vectors: {}'.format(np.rad2deg(np.arctan2(sinang, cosang)))) plt.show() ###Output tensorflow version: 2.0.0 eager mode on: True Train on 5 samples Epoch 1/2 5/5 [==============================] - 3s 629ms/sample - loss: 0.4732 Epoch 2/2 5/5 [==============================] - 0s 72ms/sample - loss: 0.4692 equivariance perserved: True angle between predicted vectors: 44.04207229614258 ###Markdown Tensor Field Networks are powerful... How do they work?TFNs combine continuous convolution (i.e. a filter generating neural network) with the spherical harmonics to produce spherically symmetric filters* (dubbed Harmonic Filters) which are point-convolved with feature tensors associated with the 3D point-cloud. These Harmonic Filters are capable of convolving with features associated with the point-cloud (e.g. atom type information for molecules, mass, velocity, acceleration, etc.) to produce outputs which rotate equivariantly with the input point-cloud. Spherical HarmonicsThe Spherical Harmonics are a set of orthogonal basis functions defined on the surface of a sphere. They can be utilized to represent any function which exists on a sphere. They have many special properties, however, for our purposes, we are interested in their spherical symmetry. The filters of our network are composed of a directionless Radial function and the real component of the spherical harmonic function centered on the unit-vectors of our point-cloud.We're not mathematicians, so the important thing to know is that the spherical symmetry of the spherical harmonics provide the filters of our network with rotational equivariance. The implementation of these basis functions is quite simple due to a few shortcuts, which we'll see soon. Tensor Rotation OrderFeature tensors that are part of the group $S(O3)$ (i.e. tensors that rotate normally in 3D), require $2l + 1$ dimensions to be represented. "$l$" is referred to as the rotation order of that tensor. e.g. an array which represents a scalar value has rotation order $l=0$, and an array representing a vector has rotation order $l=1$.e.g. an energy (scalar) array for a batch of molecules would have the shape (molecules, points, 1), while a force (vector) array for a batch of molecules would have shape (molecules, points, 3).Once again, we're not mathematicians, so all we need to know is that rotation order refers to the rank of what our feature tensor represents, and that we can only combine tensors of varying rotation order in specific ways if we hope to conserve rotational equivariance. Equivariant Combination TypesThe combination rules are essentially the traditional ways of combining scalars, vectors, and higher order tensors. With notation $A \cdot B \rightarrow O$, the combinations are:$ L \cdot 0 \rightarrow L $; scalar multiplication$ 1 \cdot 1 \rightarrow 1 $; element-wise multiplication$ 1 \cdot 1 \rightarrow 0 $; dot product Equations of Tensor Field Networks The Harmonic Filter$$\Large{F^{(l_{f}l_{i})}_{cm}(\vec{r}) = R^{(l_{f}l_{i})}_{c}(r)Y^{l_{f}}_{m'}(\hat{r})}$$Where:$\vec{r}$ are the distance vectors for all points in the point-cloud,$F^{(l_{f}l_{i})}_{cm}$ is the Harmonic Filter of rotation order $l_{f}$ to be applied to feature of rotation order $l_{i}$$Y^{l_{f}}_{m'}(\hat{r})$ is the output of the spherical harmonic function applied to the unit vector $\hat{r}$ $R^{(l_{f}l_{i})}_{c}$ is the filter generating network, know as the Radial function.Some lucky shortcuts:$Y^{0}(\vec{r}) \propto 1$; since $Y^{0}$ is a sphere,$Y^{1}(\vec{r}) \propto \hat{r}$; since $Y^{1}$ is centered on the unit vectors, $\vec{r}$Some notes:the Radial takes as input the directionless discretized distance matrix, r, and outputs some learned representation of that distance matrix. The Radial function is isolated from either vectors or feature tensors, and as such is general to any function, so long as the output's shape matches with that of the feature tensor it will eventually be convolved with. The current default implementation is a multi-layer dense neural network, but could just as easily be replaced with a convolutional network, or some traditional architecture.A Harmonic Filter is created upon multiplying the output of the Radial with the output of the spherical harmonic function. Point ConvolutionCore function of the TFNs, contains 90%+ of the networks weights:$$\Large{ L^{l_{o}}_{acm_{o}}(\vec{r}_{a}, V^{(l_{\textit{i}})}_{acm_{i}}) := \sum_{m_{\textit{f}}, m_{\textit{i}}}C^{(l_{o}m_{o})}_{(l_{f},m_{f})(l_{i},m_{i})} \sum_{b \in S} F^{(l_{f},l_{i})}_{cm_{f}}(\vec{r}_{ab})V^{l_{i}}_{bcm_{i}}}$$Where:$\vec{r}_{a}$ is the image (discretized distance matrix),$V^{(l_{\textit{i}})}_{acm_{i}}$ is the collection of feature vectors, indexed by a, the point; c, the channel or feature of point a; m, the representation order of that feature.$F^{(l_{f},l_{i})}_{cm_{f}}(\vec{r}_{ab})$ is the Harmonic Filter$C^{(l_{o}m_{o})}_{(l_{f},m_{f})(l_{i},m_{i})}$ is the Clebsch-Gordan Coefficient for the convolution of Harmonic Filter and feature tensorSome Notes:The three indices $l_{i}$, $l_{f}$, and $l_{o}$ denote rotation order for input tensor (feature), Harmonic Filter, and output tensor, respectively. Based on the rules for combining tensors of varying rotation order (RO) described earlier, it may now be clear that there are multiple ways of combining filter and feature to obtain an output tensor. As such, usage of increasingly higher RO inputs and filters results in an explosion of total output tensors. For example, if you have a point-cloud with feature tensors representing mass and velocity for each point in the cloud, i.e. two feature tensors, one of RO 0 and the other RO 1, and convolve those feature tensors with Harmonic Filters of RO0 and RO1, there will be a total of 5 output tensors. Once tensors higher than vectors are introduced the space explodes. However, there are very few instances where tensors of RO higher than 1 are required.It is also import to note that each Harmonic Filter is indexed by $l_{i}$ and $l_{f}$. This means that for every convolution operation in a TFN, each input tensor is convolved with two full-fledged neural networks, both potentially quite large.On the surface, this is not much different from a traditional convolutional network. Typically, filters are small 3x3 weight arrays. The power of a conv. net comes from layering many of these filters, which serve as basic 'feature' detectors, on top of each other to build larger structure detection in data, typically images. TFNs are quite similar, only the filters are much larger than 3x3 arrays and they leverage symmetry from the Spherical Harmonics to gain rotational equivariance to input data. ConcatenationAs we saw in the last section, a point convolution can output many tensors of varying RO, depending on our choice of Harmonic Filter, and our input tensors. In the last example, we had 5 tensors, 3 of RO 0, 2 of RO 1. Only tensors of different RO must be stored seperately, so we can combine tensors of like RO by concatenating along the second last axis, the channels/feature dimension. So, following the same example, our list of 5 examples condenses to 2 tensors, one for RO 0 and another for RO 1. Self Interaction$$\Large{ \sum_{c'}W^{(l)}_{cc'}V^{(l)}_{ac'm}}$$Where:$W^{(l)}_{cc'}$ refers to a kernel matrix$V^{(l)}_{ac'm}$ refers to an input feature tensor indexed by representation index, mc' refers to the old channels dimension of the input tensor V, while c refers to the new channels dimensionSome Notes:This operation is analagous to a typical dense layer without biases. This operation can be thought of as a scalar transform, and is thus also rotationally equivariant. Equivariant Activation$$\Large{ \eta^{(0)}(V^{(0)}_{ac} + b^{(0)}_{c})}$$$$\Large{ \eta^{(l)}(\|\|V\|\|^{(l)}_{ac} + b^{(l)}_{c})V^{(l)}_{acm}}$$Where:$\eta$ refers to the nonlinear activation function applied to the tensors. This is typically a shifted softplus.$V^{(l)}_{ac'm}$ refers to the input tensors, indexed by the representation index, m.Some Notes:Much like the Self Interaction layer, this is a scalar transform operation, and is thus rotationally equivariant. Tensor Field Networks Implemented using Keras & TF 2.0All of these operations are contained nicely with the Keras Layer pattern. convenience layers, `tfn.layers.Convolution` and `tfn.layers.MolecularConvolution`, encapsulate all of the above operations with a very simple interface. Also contained in the `tfn.layers` package is `Preprocessing` layer, which takes as input cartesian and atomic number tensors and outputs the tensors: `one_hot`, which is used to identify the type of each atom; `image`, which is the discretized distance matrix of the cartesian tensor; `vectors`, which is the set of unit vectors between every point in the cartesian tensor. Below is an example script for setting up and training a TFN to predict molecular energies and atomic forces concurrently: ###Code import numpy as np from tensorflow.keras.models import Model from tensorflow.keras.layers import Input, Lambda from tensorflow.keras import backend as K # Package written by Riley Jackson from tfn.layers import MolecularConvolution, Preprocessing, SelfInteraction ### MODEL ### # Define inputs r = Input(shape=(29, 3), dtype='float32', name='r') z = Input(shape=(29,), dtype='int32', name='z') # Set up point-cloud/feature tensors one_hot, image, vectors = Preprocessing(max_z=6)([r, z]) expanded_onehot = Lambda(lambda x: K.expand_dims(x, axis=-1))(one_hot) feature_tensor = SelfInteraction(units=32)(expanded_onehot) # Neural Network output = MolecularConvolution(name='conv_0')([one_hot, image, vectors] + feature_tensor) output = MolecularConvolution(name='conv_1')([one_hot, image, vectors] + output) output = MolecularConvolution(name='conv_2', si_units=1)([one_hot, image, vectors] + output) # Reshape output tensors atomic_energies = Lambda(lambda x: K.squeeze(x, axis=-1))(output[0]) molecular_energies = Lambda(lambda x: K.sum(x, axis=-2), name='molecular_energies')(atomic_energies) # (batch, 1) forces = Lambda(lambda x: K.squeeze(x, axis=-2), name='forces')(output[1]) # (batch, points, 3) model = Model(inputs=[r, z], outputs=[molecular_energies, forces]) # Generate some random inputs/targets cartesians = np.random.rand(5, 29, 3) atomic_nums = np.random.randint(0, 5, size=(5, 29)) e = np.random.rand(5, 1) f = np.random.rand(5, 29, 3) # Compile and fit model.compile(loss='mae', optimizer='adam') model.fit(x=[cartesians, atomic_nums], y=[e, f], epochs=2) ###Output Train on 5 samples Epoch 1/2 5/5 [==============================] - 19s 4s/sample - loss: 6.6132 - molecular_energies_loss: 6.0510 - forces_loss: 0.5622 Epoch 2/2 5/5 [==============================] - 0s 27ms/sample - loss: 6.1962 - molecular_energies_loss: 5.6547 - forces_loss: 0.5415 ###Markdown Remember to install the package: pip install git+https://github.com/jrob93/nice_orbsAnd install dependencies! (see nice_orbs_env.yml) ###Code # If not pip installing add import path import sys import os print(os.getcwd()) sys.path.insert(0, os.path.abspath(os.path.join(os.getcwd(), '..'))) from nice_orbs.orb_class import BodyOrb import nice_orbs.orb_funcs as orb_funcs ###Output _____no_output_____ ###Markdown Create a blank body to add orbit values to ###Code bod = BodyOrb() ###Output _____no_output_____ ###Markdown Set some values manually. Note that by default nice_orbs accepts distances in units of semimajor axis, angles in radians. By default G=1 and M_sun=1 therefore time is in units of 1yr/2pi ###Code bod.a = 2.5 bod.e = 0.1 bod.inc = np.radians(5) bod.print_orb() ###Output a=2.5,e=0.1,inc=0.08726646259971647,peri=None,node=None,f=None ###Markdown An orbit can also be passed from a dictionary ###Code orb_dict = {"a":2.5, "e":0.1, "inc":np.radians(5), "peri":np.radians(10), "node":np.radians(15) } bod.load_dict(orb_dict) bod.print_orb() ###Output a=2.5,e=0.1,inc=0.08726646259971647,peri=0.17453292519943295,node=0.2617993877991494,f=None ###Markdown Note that we have only passed the 5 elements required to describe the shape and orientation of the elliptical orbit in 3d space. Also we need to call calc_orb_vectors in order to find the unit vectors of this ellipse from the elements ###Code bod.calc_orb_vectors() bod.calc_values() bod.ep,bod.eQ ###Output _____no_output_____ ###Markdown Now we can find the xyz positions that describe the elliptical orbit in space ###Code df_pos = bod.planet_orbit() fig = plt.figure() ax = plt.axes(projection='3d') ax.scatter3D(0,0,0,marker="+",c="k") # plot origin (sun) ax.plot3D(df_pos["x"],df_pos["y"],df_pos["z"],label = "bod") ax.set_box_aspect((np.ptp(df_pos["x"]), np.ptp(df_pos["y"]), np.ptp(df_pos["z"]))) # aspect ratio is 1:1:1 in data space ax.legend() ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("z") plt.show() ###Output _____no_output_____ ###Markdown We can also calculate the positions of an object from elements such as true_anomaly ###Code bod.f = np.radians(30) bod.n df_rv = bod.pos_vel_from_orbit(bod.f) fig = plt.figure() ax = plt.axes(projection='3d') ax.scatter3D(0,0,0,marker="+",c="k") # plot origin (sun) ax.plot3D(df_pos["x"],df_pos["y"],df_pos["z"],label = "bod") ax.scatter3D(df_rv["x"],df_rv["y"],df_rv["z"],label = "f_true = {:.2f} deg".format(np.degrees(bod.f))) ax.set_box_aspect((np.ptp(df_pos["x"]), np.ptp(df_pos["y"]), np.ptp(df_pos["z"]))) # aspect ratio is 1:1:1 in data space ax.legend() ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("z") plt.show() ###Output _____no_output_____ ###Markdown At time = 0 the object should be at its perihelion. Be wary of the time units, Kepler's second law (a^3 = T^2) gives the period from the semimajor axis in years (remember that 1 year = 2pi in these default units). ###Code t_list = np.linspace(0,2np.pi(bod.a*(3.0/2.0))) fig = plt.figure() ax = plt.axes(projection='3d') ax.scatter3D(0,0,0,marker="+",c="k") # plot origin (sun) ax.plot3D(df_pos["x"],df_pos["y"],df_pos["z"],label = "bod") for t in t_list: bod.f = orb_funcs.f_from_t(t,bod.e,bod.n,0,0) df_rv = bod.pos_vel_from_orbit(bod.f) s1 = ax.scatter3D(df_rv["x"],df_rv["y"],df_rv["z"],c=t,vmin = np.amin(t_list), vmax = np.amax(t_list)) cbar1=fig.colorbar(s1) cbar1.set_label("time") ax.set_box_aspect((np.ptp(df_pos["x"]), np.ptp(df_pos["y"]), np.ptp(df_pos["z"]))) # aspect ratio is 1:1:1 in data space ax.legend() ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("z") plt.show() ###Output _____no_output_____ ###Markdown synthtorch* tutorialTrain a network for a synthesis task with synthtorchAuthor: Jacob ReinholdDate: Mar 1, 2019 Setup notebook ###Code import logging import sys import matplotlib.pyplot as plt import nibabel as nib import numpy as np from PIL import Image import synthtorch ###Output _____no_output_____ ###Markdown Setup a logger (change the level here to control output logging information) ###Code logging.basicConfig(format='%(asctime)s - %(name)s - %(levelname)s - %(message)s', level=logging.getLevelName('INFO')) logger = logging.getLogger(__name__) ###Output _____no_output_____ ###Markdown Support in-notebook plotting ###Code %matplotlib inline ###Output _____no_output_____ ###Markdown Report versions ###Code print('numpy version: {}'.format(np.__version__)) from matplotlib import __version__ as mplver print('matplotlib version: {}'.format(mplver)) pv = sys.version_info print('python version: {}.{}.{}'.format(pv.major, pv.minor, pv.micro)) ###Output python version: 3.7.2 ###Markdown Reload packages where content for package development ###Code %load_ext autoreload %autoreload 2 ###Output _____no_output_____ ###Markdown Setup learnerIn this section, we instantiate a `learner` (inspired by the [fastai](https://github.com/fastai/fastai) library) which holds all the functions relevant to training and prediction; however, the library is tailored for experimentation with synthesis tasks, which is why we do not use fastai by itself.The easiest way to interface with the library is to create a configuration file (see [here](https://gist.github.com/jcreinhold/793d26387f6a8b9f6966b59c6705f249) for an example with instructions on how to fill out the file at the bottom) which holds the experimental parameters and setup.Below we import a configuration file for a T1-to-T1 (MPRAGE) task, i.e., a (denoising) autoencoder using a U-net architecture. In this case, I will actually load a pretrained model and continue training it (for one epoch). `synthtorch` knows to continue training if the configuration file field of `trained_model` is already an existing file, otherwise it will train a new network from scratch (and save it to the location in `trained_model`). ###Code config = synthtorch.ExperimentConfig.load_json('config.json') ###Output _____no_output_____ ###Markdown Now we create the model in a wrapper called `Learner` with the specified configuration. ###Code learner = synthtorch.Learner.train_setup(config) ###Output 2019-03-01 17:27:25,516 - synthnn.learn.learner - INFO - Number of trainable parameters in model: 531052 2019-03-01 17:27:25,544 - synthnn.learn.learner - INFO - Loaded checkpoint: tutorial.pth (epoch 30) 2019-03-01 17:27:25,546 - synthnn.learn.learner - INFO - Adding data augmentation transforms 2019-03-01 17:27:25,821 - synthnn.learn.learner - INFO - Number of training images: 57275 2019-03-01 17:27:25,856 - synthnn.learn.learner - INFO - Number of validation images: 7250 2019-03-01 17:27:25,857 - synthnn.learn.learner - INFO - LR: 0.00300 ###Markdown I can now train the model with the following command (I am only training for one epoch for this tutorial): ###Code learner.fit(1) ###Output 2019-03-01 13:12:28,931 - synthnn.learn.learner - INFO - Epoch: 1 - Training Loss: 4.70e+00, Validation Loss: 4.65e+00 ###Markdown Now we can save the model to `tutorial.pth` with the following command: ###Code learner.save('tutorial.pth') ###Output _____no_output_____ ###Markdown You can run the commands below without the following command; however, I will load a model here which produces ok results. ###Code learner.load('good.pth') ###Output _____no_output_____ ###Markdown Now we can do a prediction with either a `.tif` file (since this example is a 2D network) or a `.nii` file (or `.png`, if that is what was used for training). Note that the filename(s) must be in a list because `synthtorch` supports multiple modalities for input/output. In this case I use a `.tif` file for the convenience of displaying the result. ###Code test_fn = 'test_img.tif' out_img = learner.predict([test_fn]) orig = np.asarray(Image.open(test_fn)) synth = np.asarray(out_img) f, (ax1,ax2) = plt.subplots(1,2,figsize=(8,8)) ax1.imshow(orig,cmap='gray',vmax=synth.max()); ax1.axis('off'); ax1.set_title('Original') ax2.imshow(synth,cmap='gray'); ax2.axis('off'); ax2.set_title('Synthesized'); ###Output _____no_output_____ ###Markdown Example 1: Finding CRISPR-Cas systems in a cyanobacteria genome In this example, we will annotate and visualize CRISPR-Cas systems in the cyanobacteria species Rippkaea orientalis. CRISPR-Cas is a widespread bacterial defense system, found in at least 50% of all known prokaryotic species. This system is significant in that it can be leveraged as a precision gene editing tool, an advancement that was awarded the 2020 Nobel Prize in Chemistry. The genome of R. orientalis harbors two complete CRISPR-Cas loci (one chromosomal, and one extrachromosomal/plasmid).You can download the complete assembled genome [here](https://www.ncbi.nlm.nih.gov/assembly/GCF_000024045.1/); it is also available at https://github.com/wilkelab/Opfi in the `tutorials` folder (`tutorials/GCF_000024045.1_ASM2404v1_genomic.fna.gz`). This tutorial assumes the user has already installed Opfi and all dependencies (if installing with conda, this is done automatically). Some familiarity with BLAST and the basic homology search algorithm may also be helpful, but is not required. Note: This tutorial uses several input data files, all of which are provided in the `tutorials` directory. If running this notebook in another working directory, be sure copy over all three data files as well. 1. Use the makeblastdb utility to convert a Cas protein database to BLAST format We start by converting a Cas sequence database to a format that BLAST can recognize, using the command line utility `makeblastdb`, which is part of the core NCBI BLAST+ distribution. A set of ~20,000 non-redundant Cas sequences, downloaded from [Uniprot](https://www.uniprot.org/uniref/) is available as a tar archive (`tutorials/cas_database.tar.gz`). We'll make a new directory, "blastdb", and extract sequences there: ###Code ! mkdir blastdb ! cd blastdb && tar -xzf ../cas_database.tar.gz && cd .. ###Output _____no_output_____ ###Markdown Next, create two BLAST databases for the sequence data: one containing Cas1 sequences only, and another that contains the remaining Cas sequences. ###Code ! cd blastdb && cat cas1.fasta \| makeblastdb -dbtype prot -title cas1 -hash_index -out cas1_db && cd .. ! cd blastdb && cat cas[2-9].fasta cas1[0-2].fasta casphi.fasta \| makeblastdb -dbtype prot -title cas_all -hash_index -out cas_all_but_1_db ###Output _____no_output_____ ###Markdown `-dbtype prot` simply tells `makeblastdb` to expect amino acid sequences. We use `-title` and `-out` to name the database (required by BLAST) and to prefix the database files, respectively. `-hash_index` directs `makeblastdb` to generate a hash index of protein sequences, which can speed up computation time. 2. Use Opfi's Gene Finder module to search for CRISPR-Cas loci CRISPR-Cas systems are extremely diverse. The most recent [classification effort](https://www.nature.com/articles/s41579-019-0299-x) identifies 6 major types, and over 40 subtypes, of compositionally destinct systems. Although there is sufficent sequence similarity between subtypes to infer the existence of a common ancestor, the only protein family present in the majority of CRISPR-cas subtypes is the conserved endonuclease Cas1. For our search, we will define candidate CRISPR-cas loci as having, minimally, a cas1 gene. First, create another directory for output: ###Code ! mkdir example_1_output ###Output _____no_output_____ ###Markdown The following bit of code uses Opfi's Gene Finder module to search for CRISPR-Cas systems: ###Code from gene_finder.pipeline import Pipeline import os genomic_data = "GCF_000024045.1_ASM2404v1_genomic.fna.gz" output_directory = "example_1_output" p = Pipeline() p.add_seed_step(db="blastdb/cas1_db", name="cas1", e_val=0.001, blast_type="PROT", num_threads=1) p.add_filter_step(db="blastdb/cas_all_but_1_db", name="cas_all", e_val=0.001, blast_type="PROT", num_threads=1) p.add_crispr_step() # use the input filename as the job id # results will be written to the file <job id>_results.csv job_id = os.path.basename(genomic_data) results = p.run(job_id=job_id, data=genomic_data, output_directory=output_directory, min_prot_len=90, span=10000, gzip=True) ###Output _____no_output_____ ###Markdown First, we initialize a `Pipeline` object, which keeps track of all search parameters, as well as a running list of systems that meet search criteria. Next, we add three search steps to the pipeline:1. `add_seed_step`: BLAST is used to search the input genome against a database of Cas1 sequences. Regions around putative Cas1 hits become the intial candidates, and the rest of the genome is ignored.2. `add_filter_step`: Candidate regions are searched for any additional Cas genes. Candidates without at least one additional putative Cas gene are also discarded.3. `add_crispr_step`: Remaining candidates are annotated for CRISPR repeat sequences using PILER-CR. Finally, we run the pipeline, executing steps in the order they we added. `min_prot_len` sets the minimum length (in amino acid residues) of hits to keep (really short hits are unlikely real protein encoding genes). `span` is the region directly up- and downstream of initial hits. So, each candidate system will be about 20 kbp in length. Results are written to a single CSV file. Final candidate loci contain at least one putative Cas1 gene and one additional Cas gene. As we will see, this relatively permissive criteria captures some non-CRISPR-Cas loci. Opfi has additional modules for reducing unlikely systems after the gene finding stage. 3. Visualize annotated CRISPR-Cas gene clusters using Opfi's Operon Analyzer module It is sometimes useful to visualize candidate systems, especially during the exploratory phase of a genomics survey. Opfi provides a few functions for visualizing candidate systems as gene diagrams. We'll use these to visualize the CRISPR-Cas gene clusters in R. orientalis: ###Code import csv import sys from operon_analyzer import load, visualize feature_colors = { "cas1": "lightblue", "cas2": "seagreen", "cas3": "gold", "cas4": "springgreen", "cas5": "darkred", "cas6": "thistle", "cas7": "coral", "cas8": "red", "cas9": "palegreen", "cas10": "yellow", "cas11": "tan", "cas12": "orange", "cas13": "saddlebrown", "casphi": "olive", "CRISPR array": "purple" } # read in the output from Gene Finder and create a gene diagram for each cluster (operon) with open("example_1_output/GCF_000024045.1_ASM2404v1_genomic.fna.gz_results.csv", "r") as operon_data: operons = load.load_operons(operon_data) visualize.plot_operons(operons=operons, output_directory="example_1_output", feature_colors=feature_colors, nucl_per_line=25000) ###Output _____no_output_____ ###Markdown Looking at the gene diagrams, it is clear that we identified both CRISPR-Cas systems in this genome. We also see some systems that don't resemble functional CRISPR-Cas operons. Because we used a relatively permissive e-value threshhold of 0.001 when running BLAST, Opfi retained regions with very low sequence similarity to true CRISPR-Cas genes. In fact, these regions are likely not CRISPR-Cas loci at all. Using a lower e-value would likely eliminate these "false positive" systems, but Opfi also has additional functions for filtering out unlikely candidates _after_ the intial BLAST search. In general, we have found that using permissive BLAST parameters intially, and then filtering or eliminating candidates during the downstream analysis, is an effective way to search for gene clusters in large amounts of genomic/metagenomic data. In this toy example, we could re-run BLAST many times without significant cost. But on a more realistic dataset, needing to re-do the computationally expensive homology search could detrail a project. Since the optimal search parameters may not be known _a priori_, it can be better to do a permissive homology search initially, and then narrow down results later. Finally, clean up the temporary directories, if desired: ###Code ! rm -r example_1_output blastdb ###Output _____no_output_____ ###Markdown Example 2: Filter and classify CRISPR-Cas systems based on genomic composition As mentioned in the previous example, known CRISPR-Cas systems fall into 6 broad categories, based on the presence of particular "signature" genes, as well as overall composition and genomic architecture. In this example, we will use Opfi to search for and classify CRISPR-Cas systems in ~300 strains of fusobacteria. This dataset was chosen because it is more representative (in magnitude) of what would be encountered in a real genomics study. Additionally, the fusobacteria phylum contains a variety of CRISPR-Cas subtypes. Given that the homology search portion of the analysis takes several hours (using a single core) to complete, we have pre-run Gene Finder using the same setup as the previous example. 1. Make another temporary directory for output: ###Code ! mkdir example_2_output ###Output _____no_output_____ ###Markdown 2. Filter Gene Finder output and extract high-confidence CRISPR-Cas systems The following code reads in unfiltered Gene Finder output and applies a set of conditions ("rules") to accomplish two things:1. Select (and bin) systems according to type, and,2. Eliminate candidates that likely do not represent true CRISPR-Cas systems ###Code from operon_analyzer import analyze, rules fs = rules.FilterSet().pick_overlapping_features_by_bit_score(0.9) cas_types = ["I", "II", "III", "V"] rulesets = [] # type I rules rulesets.append(rules.RuleSet().contains_group(feature_names = ["cas5", "cas7"], max_gap_distance_bp = 1000, require_same_orientation = True) \ .require("cas3")) # type II rules rulesets.append(rules.RuleSet().contains_at_least_n_features(feature_names = ["cas1", "cas2", "cas9"], feature_count = 3) \ .minimum_size("cas9", 3000)) # type III rules rulesets.append(rules.RuleSet().contains_group(feature_names = ["cas5", "cas7"], max_gap_distance_bp = 1000, require_same_orientation = True) \ .require("cas10")) # type V rules rulesets.append(rules.RuleSet().contains_at_least_n_features(feature_names = ["cas1", "cas2", "cas12"], feature_count = 3)) for rs, cas_type in zip(rulesets, cas_types): with open("refseq_fusobacteria.csv", "r") as input_csv: with open(f"example_2_output/refseq_fuso_filtered_type{cas_type}.csv", "w") as output_csv: analyze.evaluate_rules_and_reserialize(input_csv, rs, fs, output_csv) ###Output _____no_output_____ ###Markdown The rule sets are informed by an established CRISPR-Cas classification system, which you can read more about [here](https://www.nature.com/articles/s41579-019-0299-x). The most recent system recognizes 6 major CRISPR-Cas types, but since fusobacteria doesn't contain type IV or VI systems that can be identified with our protein dataset, we didn't define the corresponding rule sets. 3. Verify results with additional visualizations Altogther, this analysis will identify several hundred systems. We won't look at each system individually (but you are free to do so!). For the sake of confirming that the code ran as expected, we'll create gene diagrams for just the type V systems, since there are only two: ###Code import csv import sys from operon_analyzer import load, visualize feature_colors = { "cas1": "lightblue", "cas2": "seagreen", "cas3": "gold", "cas4": "springgreen", "cas5": "darkred", "cas6": "thistle", "cas7": "coral", "cas8": "red", "cas9": "palegreen", "cas10": "yellow", "cas11": "tan", "cas12": "orange", "cas13": "saddlebrown", "casphi": "olive", "CRISPR array": "purple" } # read in the output from Gene Finder and create a gene diagram for each cluster (operon) with open("example_2_output/refseq_fuso_filtered_typeV.csv", "r") as operon_data: operons = load.load_operons(operon_data) visualize.plot_operons(operons=operons, output_directory="example_2_output", feature_colors=feature_colors, nucl_per_line=25000) ###Output _____no_output_____ ###Markdown Finally, clean up the temporary output directory, if desired: ###Code ! rm -r example_2_output ###Output _____no_output_____ ###Markdown Example 1: Finding CRISPR-Cas systems in a cyanobacteria genome In this example, we will annotate and visualize CRISPR-Cas systems in the cyanobacteria species Rippkaea orientalis. CRISPR-Cas is a widespread bacterial defense system, found in at least 50% of all known prokaryotic species. This system is significant in that it can be leveraged as a precision gene editing tool, an advancement that was awarded the 2020 Nobel Prize in Chemistry. The genome of R. orientalis harbors two complete CRISPR-Cas loci (one chromosomal, and one extrachromosomal/plasmid).You can download the complete assembled genome [here](https://www.ncbi.nlm.nih.gov/assembly/GCF_000024045.1/); it is also available at https://github.com/wilkelab/Opfi in the `tutorials` folder (`data/GCF_000024045.1_ASM2404v1_genomic.fna.gz`). This tutorial assumes the user has already cloned and built Opfi, installed NCBI BLAST+ and PILER-CR, and has set `tutorials` as the working directory. Some familiarity with BLAST and the basic homology search algorithm may also be helpful, but is not required. 1. Use the makeblastdb utility to convert a Cas protein database to BLAST format We start by converting a Cas sequence database to a format that BLAST can recognize, using the command line utility `makeblastdb`, which is part of the core NCBI BLAST+ distribution. A set of ~20,000 non-redundant Cas sequences, downloaded from [Uniprot](https://www.uniprot.org/uniref/) is available as a tar archive (`tutorials/data/cas_database.tar.gz`). We'll make a new directory, "blastdb", and extract sequences there: ###Code ! mkdir blastdb ! cd blastdb && tar -xzf ../data/cas_database.tar.gz && cd .. ###Output _____no_output_____ ###Markdown Next, create two BLAST databases for the sequence data: one containing Cas1 sequences only, and another that contains the remaining Cas sequences. ###Code ! cd blastdb && cat cas1.fasta \| makeblastdb -dbtype prot -title cas1 -hash_index -out cas1_db && cd .. ! cd blastdb && cat cas[2-9].fasta cas1[0-2].fasta casphi.fasta \| makeblastdb -dbtype prot -title cas_all -hash_index -out cas_all_but_1_db ###Output _____no_output_____ ###Markdown `-dbtype prot` simply tells `makeblastdb` to expect amino acid sequences. We use `-title` and `-out` to name the database (required by BLAST) and to prefix the database files, respectively. `-hash_index` directs `makeblastdb` to generate a hash index of protein sequences, which can speed up computation time. 2. Use Opfi's Gene Finder module to search for CRISPR-Cas loci CRISPR-Cas systems are extremely diverse. The most recent [classification effort](https://www.nature.com/articles/s41579-019-0299-x) identifies 6 major types, and over 40 subtypes, of compositionally destinct systems. Although there is sufficent sequence similarity between subtypes to infer the existence of a common ancestor, the only protein family present in the majority of CRISPR-cas subtypes is the conserved endonuclease Cas1. For our search, we will define candidate CRISPR-cas loci as having, minimally, a cas1 gene. First, create another directory for output: ###Code ! mkdir example_1_output ###Output _____no_output_____ ###Markdown The following bit of code uses Opfi's Gene Finder module to search for CRISPR-Cas systems: ###Code from gene_finder.pipeline import Pipeline import os genomic_data = "data/GCF_000024045.1_ASM2404v1_genomic.fna.gz" output_directory = "example_1_output" p = Pipeline() p.add_seed_step(db="blastdb/cas1_db", name="cas1", e_val=0.001, blast_type="PROT", num_threads=1) p.add_filter_step(db="blastdb/cas_all_but_1_db", name="cas_all", e_val=0.001, blast_type="PROT", num_threads=1) p.add_crispr_step() # use the input filename as the job id # results will be written to the file <job id>_results.csv job_id = os.path.basename(genomic_data) results = p.run(job_id=job_id, data=genomic_data, output_directory=output_directory, min_prot_len=90, span=10000, gzip=True) ###Output _____no_output_____ ###Markdown First, we initialize a `Pipeline` object, which keeps track of all search parameters, as well as a running list of systems that meet search criteria. Next, we add three search steps to the pipeline:1. `add_seed_step`: BLAST is used to search the input genome against a database of Cas1 sequences. Regions around putative Cas1 hits become the intial candidates, and the rest of the genome is ignored.2. `add_filter_step`: Candidate regions are searched for any additional Cas genes. Candidates without at least one additional putative Cas gene are also discarded.3. `add_crispr_step`: Remaining candidates are annotated for CRISPR repeat sequences using PILER-CR. Finally, we run the pipeline, executing steps in the order they we added. `min_prot_len` sets the minimum length (in amino acid residues) of hits to keep (really short hits are unlikely real protein encoding genes). `span` is the region directly up- and downstream of initial hits. So, each candidate system will be about 20 kbp in length. Results are written to a single CSV file. Final candidate loci contain at least one putative Cas1 gene and one additional Cas gene. As we will see, this relatively permissive criteria captures some non-CRISPR-Cas loci. Opfi has additional modules for reducing unlikely systems after the gene finding stage. 3. Visualize annotated CRISPR-Cas gene clusters using Opfi's Operon Analyzer module It is sometimes useful to visualize candidate systems, especially during the exploratory phase of a genomics survey. Opfi provides a few functions for visualizing candidate systems as gene diagrams. We'll use these to visualize the CRISPR-Cas gene clusters in R. orientalis: ###Code import csv import sys from operon_analyzer import load, visualize feature_colors = { "cas1": "lightblue", "cas2": "seagreen", "cas3": "gold", "cas4": "springgreen", "cas5": "darkred", "cas6": "thistle", "cas7": "coral", "cas8": "red", "cas9": "palegreen", "cas10": "yellow", "cas11": "tan", "cas12": "orange", "cas13": "saddlebrown", "casphi": "olive", "CRISPR array": "purple" } # read in the output from Gene Finder and create a gene diagram for each cluster (operon) with open("example_1_output/GCF_000024045.1_ASM2404v1_genomic.fna.gz_results.csv", "r") as operon_data: operons = load.load_operons(operon_data) visualize.plot_operons(operons=operons, output_directory="example_1_output", feature_colors=feature_colors, nucl_per_line=25000) ###Output _____no_output_____ ###Markdown Looking at the gene diagrams, it is clear that we identified both CRISPR-Cas systems in this genome. We also see some systems that don't resemble functional CRISPR-Cas operons. Because we used a relatively permissive e-value threshhold of 0.001 when running BLAST, Opfi retained regions with very low sequence similarity to true CRISPR-Cas genes. In fact, these regions are likely not CRISPR-Cas loci at all. Using a lower e-value would likely eliminate these "false positive" systems, but Opfi also has additional functions for filtering out unlikely candidates _after_ the intial BLAST search. In general, we have found that using permissive BLAST parameters intially, and then filtering or eliminating candidates during the downstream analysis, is an effective way to search for gene clusters in large amounts of genomic/metagenomic data. In this toy example, we could re-run BLAST many times without significant cost. But on a more realistic dataset, needing to re-do the computationally expensive homology search could detrail a project. Since the optimal search parameters may not be known _a priori_, it can be better to do a permissive homology search initially, and then narrow down results later. Finally, clean up the temporary directories, if desired: ###Code ! rm -r example_1_output blastdb ###Output _____no_output_____ ###Markdown Example 2: Filter and classify CRISPR-Cas systems based on genomic composition As mentioned in the previous example, known CRISPR-Cas systems fall into 6 broad categories, based on the presence of particular "signature" genes, as well as overall composition and genomic architecture. In this example, we will use Opfi to search for and classify CRISPR-Cas systems in ~300 strains of fusobacteria. This dataset was chosen because it is more representative (in magnitude) of what would be encountered in a real genomics study. Additionally, the fusobacteria phylum contains a variety of CRISPR-Cas subtypes. Given that the homology search portion of the analysis takes several hours (using a single core) to complete, we have pre-run Gene Finder using the same setup as the previous example. 1. Make another temporary directory for output: ###Code ! mkdir example_2_output ###Output _____no_output_____ ###Markdown 2. Filter Gene Finder output and extract high-confidence CRISPR-Cas systems The following code reads in unfiltered Gene Finder output and applies a set of conditions ("rules") to accomplish two things:1. Select (and bin) systems according to type, and,2. Eliminate candidates that likely do not represent true CRISPR-Cas systems ###Code from operon_analyzer import analyze, rules fs = rules.FilterSet().pick_overlapping_features_by_bit_score(0.9) cas_types = ["I", "II", "III", "V"] rulesets = [] # type I rules rulesets.append(rules.RuleSet().contains_group(feature_names = ["cas5", "cas7"], max_gap_distance_bp = 1000, require_same_orientation = True) \ .require("cas3")) # type II rules rulesets.append(rules.RuleSet().contains_at_least_n_features(feature_names = ["cas1", "cas2", "cas9"], feature_count = 3) \ .minimum_size("cas9", 3000)) # type III rules rulesets.append(rules.RuleSet().contains_group(feature_names = ["cas5", "cas7"], max_gap_distance_bp = 1000, require_same_orientation = True) \ .require("cas10")) # type V rules rulesets.append(rules.RuleSet().contains_at_least_n_features(feature_names = ["cas1", "cas2", "cas12"], feature_count = 3)) for rs, cas_type in zip(rulesets, cas_types): with open("data/refseq_fusobacteria.csv", "r") as input_csv: with open(f"example_2_output/refseq_fuso_filtered_type{cas_type}.csv", "w") as output_csv: analyze.evaluate_rules_and_reserialize(input_csv, rs, fs, output_csv) ###Output _____no_output_____ ###Markdown The rule sets are informed by an established CRISPR-Cas classification system, which you can read more about [here](https://www.nature.com/articles/s41579-019-0299-x). The most recent system recognizes 6 major CRISPR-Cas types, but since fusobacteria doesn't contain type IV or VI systems that can be identified with our protein dataset, we didn't define the corresponding rule sets. 3. Verify results with additional visualizations Altogther, this analysis will identify several hundred systems. We won't look at each system individually (but you are free to do so!). For the sake of confirming that the code ran as expected, we'll create gene diagrams for just the type V systems, since there are only two: ###Code import csv import sys from operon_analyzer import load, visualize feature_colors = { "cas1": "lightblue", "cas2": "seagreen", "cas3": "gold", "cas4": "springgreen", "cas5": "darkred", "cas6": "thistle", "cas7": "coral", "cas8": "red", "cas9": "palegreen", "cas10": "yellow", "cas11": "tan", "cas12": "orange", "cas13": "saddlebrown", "casphi": "olive", "CRISPR array": "purple" } # read in the output from Gene Finder and create a gene diagram for each cluster (operon) with open("example_2_output/refseq_fuso_filtered_typeV.csv", "r") as operon_data: operons = load.load_operons(operon_data) visualize.plot_operons(operons=operons, output_directory="example_2_output", feature_colors=feature_colors, nucl_per_line=25000) ###Output _____no_output_____ ###Markdown Finally, clean up the temporary output directory, if desired: ###Code ! rm -r example_2_output ###Output _____no_output_____ ###Markdown Note: restart runtime after this import before running the augmentations```>>> pip install dist/arizona-0.0.1-py3-none-any.whl``` ###Code import arizona arizona.__version__ ###Output _____no_output_____ ###Markdown Using by each input text ###Code from arizona.textmentations.functions import keyboard_func text = "giới thiệu về công ty ftech" results = keyboard_func( text, num_samples=5, intent='faq_company', tags='O O O B-work_unit I-word_unit I-work_unit', aug_char_percent=0.2, aug_word_percent=0.1, unikey_percent=0.5, config_file='../configs/unikey.json', ) from pprint import pprint pprint(results) from arizona.textmentations.functions import remove_accent_func text = 'giới thiệu về công ty ftech' results = remove_accent_func( text, num_samples=5, intent='faq_company', tags='O O O B-work_unit I-word_unit I-work_unit' ) from pprint import pprint pprint(results) from arizona.textmentations.functions import abbreviates_func text = "giới thiệu về công ty ftech" results = abbreviates_func( text, num_samples=10, intent='faq_company', tags='O O O B-work_unit I-word_unit I-work_unit', config_file='../configs/abbreviations.json' ) from pprint import pprint pprint(results) ###Output {'intent': ['faq_company', 'faq_company', 'faq_company', 'faq_company', 'faq_company', 'faq_company', 'faq_company', 'faq_company', 'faq_company', 'faq_company'], 'tags': ['O O B-work_unit I-work_unit', 'O O B-work_unit I-work_unit', 'O O B-work_unit I-word_unit I-work_unit', 'O O B-work_unit I-word_unit I-work_unit', 'O O B-work_unit I-work_unit', 'O O O B-work_unit I-work_unit', 'O O B-work_unit I-work_unit', 'O O B-work_unit I-work_unit', 'O O B-work_unit I-word_unit I-work_unit', 'O O B-work_unit I-word_unit I-work_unit'], 'text': ['gt về cty ftech', 'gthieu về cty ftech', 'gthieu về công ty ftech', 'gthieu về công ty ftech', 'gthieu về cty ftech', 'giới thiệu về cty ftech', 'gthieu về cty ftech', 'gthieu về cty ftech', 'gthieu về công ty ftech', 'gthieu về công ty ftech']} ###Markdown Using by a .csv file ###Code from arizona.textmentations import TextAugmentation data_path = '../data/nlu.csv' text_augs = TextAugmentation( data=data_path, text_col='text', intent_col='intent', tags_col='tags' ) df = text_augs.augment( methods=['remove_accent', 'abbreviation', 'keyboard'], without_origin_data=True, write_file=False ) df.head(10) ###Output 100%\|██████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████\| 10/10 [00:05<00:00, 1.92it/s] ###Markdown Reasonable Crowd Dataset Tutorial ###Code import json import geopandas as gpd import matplotlib.pyplot as plt import numpy as np from shapely.geometry import Polygon %matplotlib inline ###Output _____no_output_____ ###Markdown Simple manipulations Plotting a footprint In this section, we show a simple code snippet for plotting a footprint ###Code # Enter the path to a trajectory trajectory_path = "<INSERT_PATH_TO_DOWNLOADED_DATA>/reasonable_crowd_data/trajectories/U_27-a.json" # load the trajectory with open(trajectory_path, "r") as j_file: traj_states = json.load(j_file) # let's plot the footprint of the first state state = traj_states[0] fig = plt.figure() ax = fig.add_subplot(111) ax.set_aspect("equal") plt.axis("off") footprint = Polygon(state["footprint"]) ax.plot(footprint.exterior.xy) plt.show() ###Output _____no_output_____ ###Markdown Plotting a layer of the map Let's plot a layer of one of the maps. ###Code # Path to a gpkg file representing one of the layers map_path = "<INSERT_PATH_TO_DOWNLOADED_DATA>/reasonable_crowd_data/maps/S_boundaries.gpkg" # thanks to the wide support of the gpkg format, plotting is only a couple of lines map_df = gpd.read_file(map_path) fig, ax = plt.subplots(1, 1) map_df.plot(ax = ax) ax.set_aspect('equal') plt.axis("off") plt.show() ###Output _____no_output_____ ###Markdown More advanced manipulations To get better acquainted with the data, we wrote a small script: `visualize_realization.py` that visualizes a realization by making use of the map files and the trajectory files. The output of this script is something like `movie.mp4` in this directory. (Legend for the movie: the black polygon is ego, blue polygons are other cars, red polygons are pedestrians.)We highly recommend that you go through the code to become really familiar with the data. ###Code from visualize_realization import visualize_realization trajectory_path = "<INSERT_PATH_TO_DOWNLOADED_DATA>/reasonable_crowd_data/trajectories/S_1-a.json" map_path = "<INSERT_PATH_TO_DOWNLOADED_DATA>/reasonable_crowd_data/maps/S_boundaries.gpkg" # directory where to save the ouputs of this script (a video and an image for each frame) save_dir = "<INSERT_PATH_TO_DIRECTORY_WHERE_SAVE_PLOTS>" # NOTE: This might take a couple mins to run; visualize_realization(trajectory_path, map_path, save_dir) ###Output _____no_output_____ ###Markdown sconascona is a tool to perform network analysis over correlation networks of brain regions. This tutorial will go through the basic functionality of scona, taking us from our inputs (a matrix of structural regional measures over subjects) to a report of local network measures for each brain region, and network level comparisons to a cohort of random graphs of the same degree. ###Code import numpy as np import networkx as nx import scona as scn import scona.datasets as datasets ###Output _____no_output_____ ###Markdown Importing dataA scona analysis starts with four inputs. __regional_measures__ A pandas DataFrame with subjects as rows. The columns should include structural measures for each brain region, as well as any subject-wise covariates. * __names__ A list of names of the brain regions. This will be used to specify which columns of the __regional_measures__ matrix to want to correlate over.* __covars__ _(optional)_ A list of your covariates. This will be used to specify which columns of __regional_measure__ you wish to correct for. * __centroids__ A list of tuples representing the cartesian coordinates of brain regions. This list should be in the same order as the list of brain regions to accurately assign coordinates to regions. The coordinates are expected to obey the convention the the x=0 plane is the same plane that separates the left and right hemispheres of the brain. ###Code # Read in sample data from the NSPN WhitakerVertes PNAS 2016 paper. df, names, covars, centroids = datasets.NSPN_WhitakerVertes_PNAS2016.import_data() df.head() ###Output _____no_output_____ ###Markdown Create a correlation matrixWe calculate residuals of the matrix df for the columns of names, correcting for the columns in covars. ###Code df_res = scn.create_residuals_df(df, names, covars) df_res ###Output _____no_output_____ ###Markdown Now we create a correlation matrix over the columns of df_res ###Code M = scn.create_corrmat(df_res, method='pearson') ###Output _____no_output_____ ###Markdown Create a weighted graphA short sidenote on the BrainNetwork class: This is a very lightweight subclass of the [`Networkx.Graph`](https://networkx.github.io/documentation/stable/reference/classes/graph.html) class. This means that any methods you can use on a `Networkx.Graph` object can also be used on a `BrainNetwork` object, although the reverse is not true. We have added various methods which allow us to keep track of measures that have already been calculated, which, especially later on when one is dealing with 10^3 random graphs, saves a lot of time. All scona measures are implemented in such a way that they can be used on a regular `Networkx.Graph` object. For example, instead of `G.threshold(10)` you can use `scn.threshold_graph(G, 10)`. Also you can create a `BrainNetwork` from a `Networkx.Graph` `G`, using `scn.BrainNetwork(network=G)` Initialise a weighted graph `G` from the correlation matrix `M`. The `parcellation` and `centroids` arguments are used to label nodes with names and coordinates respectively. ###Code G = scn.BrainNetwork(network=M, parcellation=names, centroids=centroids) ###Output _____no_output_____ ###Markdown Threshold to create a binary graphWe threshold G at cost 10 to create a binary graph with 10% as many edges as the complete graph G. Ordinarily when thresholding one takes the 10% of edges with the highest weight. In our case, because we want the resulting graph to be connected, we calculate a minimum spanning tree first. If you want to omit this step, you can pass the argument `mst=False` to `threshold`.The threshold method does not edit objects inplace ###Code H = G.threshold(10) ###Output _____no_output_____ ###Markdown Calculate nodal summary. `calculate_nodal_measures` will compute and record the following nodal measures * average_dist (if centroids available)* total_dist (if centroids available)* betweenness* closeness* clustering coefficient* degree* interhem (if centroids are available)* interhem_proportion (if centroids are available)* nodal partition* participation coefficient under partition calculated above* shortest_path_length `export_nodal_measure` returns nodal attributes in a DataFrame. Let's try it now. ###Code H.report_nodal_measures().head() ###Output _____no_output_____ ###Markdown Use `calculate_nodal_measures` to fill in a bunch of nodal measures ###Code H.calculate_nodal_measures() H.report_nodal_measures().head() ###Output _____no_output_____ ###Markdown We can also add measures as one might normally add nodal attributes to a networkx graph ###Code nx.set_node_attributes(H, name="hat", values={x: x*2 for x in H.nodes}) ###Output _____no_output_____ ###Markdown These show up in our DataFrame too ###Code H.report_nodal_measures(columns=['name', 'degree', 'hat']).head() ###Output _____no_output_____ ###Markdown Calculate Global measures ###Code H.calculate_global_measures() H.rich_club(); ###Output _____no_output_____ ###Markdown Create a GraphBundleThe `GraphBundle` object is the scona way to handle across network comparisons. What is it? Essentially it's a python dictionary with `BrainNetwork` objects as values. ###Code brain_bundle = scn.GraphBundle([H], ['NSPN_cost=10']) ###Output _____no_output_____ ###Markdown This creates a dictionary-like object with BrainNetwork `H` keyed by `'NSPN_cost=10'` ###Code brain_bundle ###Output _____no_output_____ ###Markdown Now add a series of random_graphs created by edge swap randomisation of H (keyed by `'NSPN_cost=10'`) ###Code # Note that 10 is not usually a sufficient number of random graphs to do meaningful analysis, # it is used here for time considerations brain_bundle.create_random_graphs('NSPN_cost=10', 10) brain_bundle ###Output _____no_output_____ ###Markdown Report on a GraphBundleThe following method will calculate global measures ( if they have not already been calculated) for all of the graphs in `graph_bundle` and report the results in a DataFrame. We can do the same for rich club coefficients below. ###Code brain_bundle.report_global_measures() brain_bundle.report_rich_club() ###Output _____no_output_____ ###Markdown TutorialIn this little tutorial, we will show you how to use Moniker to sample from categorical distributions in constant time. We will also compare this to the famous `numpy.random.choice` function for sampling categorical distributions to get a sense of how much faster Alias sampling is!First, let's import our packages. ###Code import sys sys.path.append("../src/") import numpy as np import matplotlib.pyplot as plt import time from moniker import Sampler ###Output _____no_output_____ ###Markdown Let's use an array of four weights (unnormalized probabilities) to show that Moniker's samples and the samples from `numpy.random.choice` match the actual distribution. ###Code weights = np.array([4, 1, 5, 2]) sampler = Sampler(weights) num_samples = 100000 samples = sampler.sample(num_samples = num_samples) np_samples = np.zeros(num_samples) for s in range(num_samples): np_samples[s] = np.random.choice( range(weights.shape[0]), p=weights/np.sum(weights) ) my_uniques, my_counts = np.unique(samples, return_counts=True) np_uniques, np_counts = np.unique(np_samples, return_counts=True) plt.figure() plt.bar(my_uniques+0.25, my_counts/num_samples, color='blue', label="Moniker", align='center', width=0.25) plt.bar(range(weights.shape[0]), weights/np.sum(weights), color='black', label="True dist.", align='center', width=0.25) plt.bar(np_uniques-0.25, np_counts/num_samples, color='red', label="np.random.choice", align='center', width=0.25) plt.xlabel('Sample index') plt.ylabel('Sample frequency') plt.xticks(range(4)) plt.legend() plt.show() ###Output _____no_output_____ ###Markdown So, we know Moniker works! The distribution of its generated samples match with the true distribution and `numpy.random.choice`.Now, let's see how much faster Moniker is compared to `numpy.random.choice`. We will sample from randomly initialized distributions (`weights = np.random.uniform(size=num_weights`) of varying length (`num_weights`), and plot the time it takes to generate a varying number of samples (`num_samples`) using `numpy.random.choice` and Moniker. ###Code def colors_from_array(arr, c): # nice for plotting cmap = plt.get_cmap(c) colors = [cmap(i) for i in np.linspace(0.3,1,len(arr))] return colors, cmap num_samples_range = np.arange(10000,15000,1000) num_weights_range = np.arange(5,11) colors, my_cmap = colors_from_array(num_weights_range, "Blues") plt.figure() for w,num_weights in enumerate(num_weights_range): weights = np.random.uniform(size=num_weights) Δt = np.zeros_like(num_samples_range, dtype=np.float64) sampler = Sampler(weights) for n,num_samples in enumerate(num_samples_range): ti_moniker = time.time() samples = sampler.sample(num_samples=num_samples) t_moniker = time.time() - ti_moniker np_samples = np.zeros(num_samples) ti_numpy = time.time() for i in range(num_samples): np_samples[i] = np.random.choice( num_weights, p=weights/sum(weights) ) t_numpy = time.time() - ti_numpy Δt[n] = t_numpy - t_moniker plt.plot( num_samples_range, Δt, color=colors[w], label=r'$N = {}$'.format(num_weights) ) sm = plt.cm.ScalarMappable( cmap=my_cmap, norm=plt.Normalize( vmin=min(num_weights_range), vmax=max(num_weights_range) ) ) cbar = plt.colorbar(sm) cbar.set_label(r'$N$', rotation=0) plt.xlabel('Number of samples') plt.ylabel(r'$\Delta t$', rotation=0) plt.show() ###Output _____no_output_____ ###Markdown This module helps solve systems of linear equations. There are several ways of doing this. The first is to just pass the coefficients as a list of lists. Say we want to solve the system of equations:$$\begin{array}{c\|c\|c}x - y = 5\\x + y = -1\end{array}$$This is done with a simple call to linear_solver.solve_linear_system(), like so ###Code import linear_solver as ls xs = ls.solve_linear_system( [[1, -1, 5], [1, 1, -1]]) print(xs) ###Output [[ 2.] [-3.]] ###Markdown Clearly, the solution set $(2, -3)$ satisfies the two equations above.If a system of equations that has no unique solutions is given, a warning is printed and ```None``` is returned. ###Code xs = ls.solve_linear_system( [[1, 1, 0], [2, 2, 0]]) print(xs) xs = ls.solve_linear_system( [[1, 1, 0], [2, 2, 1]]) print(xs) ###Output Determinant of coefficients matrix is 0. No unique solution. None ###Markdown Additionally, the coefficients of the equation can be read from a text file, where expressions are evaluated before they are read. For example, consider the following system of equations:$$\begin{array}{c\|c\|c\|c}22m_1 + 22m_2 - m_3 = 0\\(0.1)(22)m_1 + (0.9)(22)m_2 - 0.6m_3 = 0\\\frac{22}{0.68} m_1 + \frac{22}{0.78} m_2 = (500)(3.785)\end{array}$$We can put these coefficients into a text file, ```'coefficients.txt'```, which has the contents\ contents of coefficients.txt22 22 -1 00.1\22 0.9\22 -0.6 022/0.68 22/0.78 0 500\3.785and then pass that file to the solver function. ###Code sol = ls.solve_linear_system('coefficients.txt') for i, row in enumerate(sol): print('m_{0} = {1:.2f}'.format(i, row[0,0])) ###Output m_0 = 23.85 m_1 = 39.74 m_2 = 1399.00 ###Markdown Simulate some source activity and EEG data ###Code sources_sim = run_simulations(pth_fwd, durOfTrial=0) eeg_sim = create_eeg(sources_sim, pth_fwd) ###Output _____no_output_____ ###Markdown Plot a simulated sample and corresponding EEG ###Code %matplotlib qt sample = 0 # index of the simulation title = f'Simulation {sample}' # Topographic plot eeg_sim[sample].average().plot_topomap([0.5]) # Source plot sources_sim.plot(hemi='both', initial_time=sample, surface='white', colormap='inferno', title=title, time_viewer=False) ###Output _____no_output_____ ###Markdown Load and train ConvDip with simulated data ###Code # Find out input and output dimensions based on the shape of the leadfield input_dim, output_dim = load_leadfield(pth_fwd).shape # Initialize the artificial neural network model model = get_model(input_dim, output_dim) # Train the model model, history = train_model(model, sources_sim, eeg_sim, delta=1) ###Output _____no_output_____ ###Markdown Evaluate ConvDipLet's evaluate our model! ###Code %matplotlib qt # Load some files from the forward model leadfield = load_leadfield(pth_fwd) info = load_info(pth_fwd) # Simulate a brand new sample: sources_eval = run_simulations(pth_fwd, 1, durOfTrial=0) eeg_eval = create_eeg(sources_eval, pth_fwd) # Calculate the ERP (average across trials): eeg_sample = np.squeeze( eeg_eval ) # Predict source_predicted = predict(model, eeg_sample, pth_fwd) # Visualize ground truth... title = f'Ground Truth' sources_eval.plot(hemi='both', initial_time=0.5, surface='white', colormap='inferno', title=title, time_viewer=False) # ... and prediction title = f'ConvDip Prediction' source_predicted.plot(hemi='both', initial_time=0.5, surface='white', colormap='inferno', title=title, time_viewer=False) # ... and the 'True' EEG topography title = f'Simulated EEG' eeg_eval[0].average().plot_topomap([0], title=title) ###Output _____no_output_____ ###Markdown sconascona is a tool to perform network analysis over correlation networks of brain regions. This tutorial will go through the basic functionality of scona, taking us from our inputs (a matrix of structural regional measures over subjects) to a report of local network measures for each brain region, and network level comparisons to a cohort of random graphs of the same degree. ###Code import numpy as np import networkx as nx import scona as scn import scona.datasets as datasets ###Output _____no_output_____ ###Markdown Importing dataA scona analysis starts with four inputs.* __regional_measures__ A pandas DataFrame with subjects as rows. The columns should include structural measures for each brain region, as well as any subject-wise covariates. * __names__ A list of names of the brain regions. This will be used to specify which columns of the __regional_measures__ matrix to want to correlate over.* __covars__ _(optional)_ A list of your covariates. This will be used to specify which columns of __regional_measure__ you wish to correct for. * __centroids__ A list of tuples representing the cartesian coordinates of brain regions. This list should be in the same order as the list of brain regions to accurately assign coordinates to regions. The coordinates are expected to obey the convention the the x=0 plane is the same plane that separates the left and right hemispheres of the brain. ###Code # Read in sample data from the NSPN WhitakerVertes PNAS 2016 paper. df, names, covars, centroids = datasets.NSPN_WhitakerVertes_PNAS2016.import_data() df.head() ###Output _____no_output_____ ###Markdown Create a correlation matrixWe calculate residuals of the matrix df for the columns of names, correcting for the columns in covars. ###Code df_res = scn.create_residuals_df(df, names, covars) df_res ###Output _____no_output_____ ###Markdown Now we create a correlation matrix over the columns of df_res ###Code M = scn.create_corrmat(df_res, method='pearson') ###Output _____no_output_____ ###Markdown Create a weighted graphA short sidenote on the BrainNetwork class: This is a very lightweight subclass of the [`Networkx.Graph`](https://networkx.github.io/documentation/stable/reference/classes/graph.html) class. This means that any methods you can use on a `Networkx.Graph` object can also be used on a `BrainNetwork` object, although the reverse is not true. We have added various methods which allow us to keep track of measures that have already been calculated, which, especially later on when one is dealing with 10^3 random graphs, saves a lot of time. All scona measures are implemented in such a way that they can be used on a regular `Networkx.Graph` object. For example, instead of `G.threshold(10)` you can use `scn.threshold_graph(G, 10)`. Also you can create a `BrainNetwork` from a `Networkx.Graph` `G`, using `scn.BrainNetwork(network=G)` Initialise a weighted graph `G` from the correlation matrix `M`. The `parcellation` and `centroids` arguments are used to label nodes with names and coordinates respectively. ###Code G = scn.BrainNetwork(network=M, parcellation=names, centroids=centroids) ###Output _____no_output_____ ###Markdown Threshold to create a binary graphWe threshold G at cost 10 to create a binary graph with 10% as many edges as the complete graph G. Ordinarily when thresholding one takes the 10% of edges with the highest weight. In our case, because we want the resulting graph to be connected, we calculate a minimum spanning tree first. If you want to omit this step, you can pass the argument `mst=False` to `threshold`.The threshold method does not edit objects inplace ###Code H = G.threshold(10) ###Output _____no_output_____ ###Markdown Calculate nodal summary. `calculate_nodal_measures` will compute and record the following nodal measures * average_dist (if centroids available)* total_dist (if centroids available)* betweenness* closeness* clustering coefficient* degree* interhem (if centroids are available)* interhem_proportion (if centroids are available)* nodal partition* participation coefficient under partition calculated above* shortest_path_length `export_nodal_measure` returns nodal attributes in a DataFrame. Let's try it now. ###Code H.report_nodal_measures().head() ###Output _____no_output_____ ###Markdown Use `calculate_nodal_measures` to fill in a bunch of nodal measures ###Code H.calculate_nodal_measures() H.report_nodal_measures().head() ###Output _____no_output_____ ###Markdown We can also add measures as one might normally add nodal attributes to a networkx graph ###Code nx.set_node_attributes(H, name="hat", values={x: x2 for x in H.nodes}) ###Output _____no_output_____ ###Markdown These show up in our DataFrame too ###Code H.report_nodal_measures(columns=['name', 'degree', 'hat']).head() ###Output _____no_output_____ ###Markdown Calculate Global measures ###Code H.calculate_global_measures() H.rich_club(); ###Output _____no_output_____ ###Markdown Create a GraphBundleThe `GraphBundle` object is the scona way to handle across network comparisons. What is it? Essentially it's a python dictionary with `BrainNetwork` objects as values. ###Code brain_bundle = scn.GraphBundle([H], ['NSPN_cost=10']) ###Output _____no_output_____ ###Markdown This creates a dictionary-like object with BrainNetwork `H` keyed by `'NSPN_cost=10'` ###Code brain_bundle ###Output _____no_output_____ ###Markdown Now add a series of random_graphs created by edge swap randomisation of H (keyed by `'NSPN_cost=10'`) ###Code # Note that 10 is not usually a sufficient number of random graphs to do meaningful analysis, # it is used here for time considerations brain_bundle.create_random_graphs('NSPN_cost=10', 10) brain_bundle ###Output _____no_output_____ ###Markdown Report on a GraphBundleThe following method will calculate global measures ( if they have not already been calculated) for all of the graphs in `graph_bundle` and report the results in a DataFrame. We can do the same for rich club coefficients below. ###Code brain_bundle.report_global_measures() brain_bundle.report_rich_club() ###Output _____no_output_____ ###Markdown Convert Calcium Imaging data from .mat to NWB fileMore details on [NWB Calcium imaging data](https://pynwb.readthedocs.io/en/stable/tutorials/domain/ophys.htmlcalcium-imaging-data).0. We start importing the relevant modules to read from .mat file and to manipulate NWB file groups and datasets ###Code from datetime import datetime from dateutil.tz import tzlocal from pynwb import NWBFile, NWBHDF5IO, ProcessingModule from pynwb.ophys import TwoPhotonSeries, OpticalChannel, ImageSegmentation, Fluorescence, DfOverF, MotionCorrection from pynwb.device import Device from pynwb.base import TimeSeries import scipy.io import numpy as np import h5py import os ###Output _____no_output_____ ###Markdown 1. Load the .mat files containing calcium imaging data ###Code path_to_files = '/Users/bendichter/Desktop/Axel Lab/data' #r'C:\Users\Luiz\Desktop\Axel' # Open info file fname0 = 'fly2_run1_info.mat' fpath0 = os.path.join(path_to_files, fname0) f_info = scipy.io.loadmat(fpath0, struct_as_record=False, squeeze_me=True) info = f_info['info'] # Open .mat file containing Calcium Imaging data fname1 = '2019_04_18_Nsyb_NLS6s_Su_walk_G_fly2_run1_8401reg.mat' fpath1 = os.path.join(path_to_files, fname1) file = h5py.File(fpath1, 'r') options = file['options'] landmarkThreshold = file['landmarkThreshold'] templates = file['templates'] R = file['R'] Y = file['Y'] ###Output _____no_output_____ ###Markdown 2. Create a new [NWB file instance](https://pynwb.readthedocs.io/en/stable/pynwb.file.htmlpynwb.file.NWBFile), fill it with all the relevant information ###Code #Create new NWB file nwb = NWBFile(session_description='my CaIm recording', identifier='EXAMPLE_ID', session_start_time=datetime.now(tzlocal()), experimenter='Dr. ABC', lab='My Lab', institution='My University', experiment_description='Some description.', session_id='IDX') print(nwb) ###Output _____no_output_____ ###Markdown 3. Create [Device](https://pynwb.readthedocs.io/en/stable/pynwb.device.htmlpynwb.device.Device) and [OpticalChannel](https://pynwb.readthedocs.io/en/stable/pynwb.ophys.htmlpynwb.ophys.OpticalChannel) containers to be used by a specific [ImagingPlane](https://pynwb.readthedocs.io/en/stable/pynwb.ophys.htmlpynwb.ophys.ImagingPlane). ###Code #Create and add device device = Device(info.objective.replace('/','_')) nwb.add_device(device) # Create an Imaging Plane for Yellow optical_channel_Y = OpticalChannel(name='optical_channel_Y', description='2P Optical Channel', emission_lambda=510.) imaging_plane_Y = nwb.create_imaging_plane(name='imaging_plane_Y', optical_channel=optical_channel_Y, description='Imaging plane', device=device, excitation_lambda=488., imaging_rate=info.daq.scanRate, indicator='NLS-GCaMP6s', location='whole central brain') # Create an Imaging Plane for Red optical_channel_R = OpticalChannel(name='optical_channel_R', description='2P Optical Channel', emission_lambda=633.) imaging_plane_R = nwb.create_imaging_plane(name='imaging_plane_R', optical_channel=optical_channel_R, description='Imaging plane', device=device, excitation_lambda=488., imaging_rate=info.daq.scanRate, indicator='redStinger', location='whole central brain') print(nwb) ###Output _____no_output_____ ###Markdown 4. Create a [TwoPhotonSeries](https://pynwb.readthedocs.io/en/stable/pynwb.ophys.htmlpynwb.ophys.TwoPhotonSeries) container to store the raw data. Raw data usually goes on the `acquisition` group of NWB files. ###Code #Stores raw data in acquisition group - dims=(X,Y,Z,T) raw_image_series_Y = TwoPhotonSeries(name='TwoPhotonSeries_Y', imaging_plane=imaging_plane_Y, rate=info.daq.scanRate, dimension=[36, 167, 257], data=Y[:,:,:,:]) raw_image_series_R = TwoPhotonSeries(name='TwoPhotonSeries_R', imaging_plane=imaging_plane_R, rate=info.daq.scanRate, dimension=[36, 167, 257], data=R[:,:,:,:]) nwb.add_acquisition(raw_image_series_Y) nwb.add_acquisition(raw_image_series_R) print(nwb.acquisition['TwoPhotonSeries']) ###Output _____no_output_____ ###Markdown 5. A very important data preprocessing step for calcium signals is motion correction. We can store the processed result data in the [MotionCorrection](https://pynwb.readthedocs.io/en/stable/pynwb.ophys.htmlpynwb.ophys.MotionCorrection) container, inside the `processing` group of NWB files. ###Code #Creates ophys ProcessingModule and add to file ophys_module = ProcessingModule(name='ophys', description='contains optical physiology processed data.') nwb.add_processing_module(ophys_module) #Stores corrected data in TwoPhotonSeries container corrected_image_series = TwoPhotonSeries(name='TwoPhotonSeries_corrected', imaging_plane=imaging_plane, rate=info.daq.scanRate, dimension=[36, 167, 257], data=Y[:,:,:,0]) #TimeSeries XY translation correction values xy_translation = TimeSeries(name='xy_translation', data=np.zeros((257,2)), rate=info.daq.scanRate) #Adds the corrected image stack to MotionCorrection container motion_correction = MotionCorrection() motion_correction.create_corrected_image_stack(corrected=corrected_image_series, original=raw_image_series, xy_translation=xy_translation) #Add MotionCorrection to processing group ophys_module.add_data_interface(motion_correction) ###Output _____no_output_____ ###Markdown 6. Any processed data should be stored in the `processing` group of NWB files. A list of available containers can be found [here](https://pynwb.readthedocs.io/en/stable/overview_nwbfile.htmlprocessing-modules). These include, for example, [DfOverF](https://pynwb.readthedocs.io/en/stable/pynwb.ophys.htmlpynwb.ophys.DfOverF), [ImageSegmentation](https://pynwb.readthedocs.io/en/stable/pynwb.ophys.htmlpynwb.ophys.ImageSegmentation), [Fluorescence](https://pynwb.readthedocs.io/en/stable/pynwb.ophys.htmlpynwb.ophys.Fluorescence) and others. ###Code #Stores processed data of different types in ProcessingModule group #Image segmentation img_seg = ImageSegmentation() ophys_module.add_data_interface(img_seg) #Fluorescence fl = Fluorescence() ophys_module.add_data_interface(fl) #DfOverF dfoverf = DfOverF() ophys_module.add_data_interface(dfoverf) print(nwb.processing['ophys']) ###Output _____no_output_____ ###Markdown 7. The NWB structure is is place, but we still need to save it to file: ###Code #Saves to NWB file fname_nwb = 'file_1.nwb' fpath_nwb = os.path.join(path_to_files, fname_nwb) with NWBHDF5IO(fpath_nwb, mode='w') as io: io.write(nwb) print('File saved with size: ', os.stat(fpath_nwb).st_size/1e6, ' mb') ###Output _____no_output_____ ###Markdown 8.** Finally, let's load it and check the file contents: ###Code #Loads NWB file with NWBHDF5IO(fpath_nwb, mode='r') as io: nwb = io.read() print(nwb) print(nwb.processing['ophys'].data_interfaces['MotionCorrection']) ###Output _____no_output_____ ###Markdown Evan Schaffer datafrom `.npz` files to NWB. ###Code from datetime import datetime from dateutil.tz import tzlocal from pynwb import NWBFile, NWBHDF5IO, ProcessingModule from pynwb.ophys import TwoPhotonSeries, OpticalChannel, ImageSegmentation, Fluorescence, DfOverF, MotionCorrection from pynwb.device import Device from pynwb.base import TimeSeries import scipy.io import numpy as np import h5py import os import matplotlib.pyplot as plt a = np.load('2019_07_01_Nsyb_NLS6s_walk_fly2.npz') print('First file:') print('Groups:', a.files) print('Dims (height,width,depth):', a['dims']) print('dFF shape: ', a['dFF'].shape) b = np.load('2019_07_01_Nsyb_NLS6s_walk_fly2_A.npz') print(' ') print('Second file - Sparse Matrix:') print('Groups:', b.files) print('Indices: ', b['indices'], ' \| Shape: ',b['indices'].shape) print('Indptr: ', b['indptr'], ' \| Shape: ',b['indptr'].shape) print('Format: ', b['format']) print('Shape: ', b['shape']) print('Data: ', b['data'], ' \| Shape: ',b['data'].shape) ###Output _____no_output_____ ###Markdown Start creating a new NWB file instance and populating it with fake raw data ###Code #Create new NWB file nwb = NWBFile(session_description='my CaIm recording', identifier='EXAMPLE_ID', session_start_time=datetime.now(tzlocal()), experimenter='Dr. ABC', lab='My Lab', institution='My University', experiment_description='Some description.', session_id='IDX') #Create and add device device = Device('MyDevice') nwb.add_device(device) # Create an Imaging Plane for Yellow optical_channel = OpticalChannel(name='optical_channel', description='2P Optical Channel', emission_lambda=510.) imaging_plane = nwb.create_imaging_plane(name='imaging_plane', optical_channel=optical_channel, description='Imaging plane', device=device, excitation_lambda=488., imaging_rate=1000., indicator='NLS-GCaMP6s', location='whole central brain', conversion=1.0) #Stores raw data in acquisition group - dims=(X,Y,Z,T) Xp = a['dims'][0][0] Yp = a['dims'][0][1] Zp = a['dims'][0][2] T = a['dFF'].shape[1] nCells = a['dFF'].shape[0] fake_data = np.random.randn(Xp,Yp,Zp,100) raw_image_series = TwoPhotonSeries(name='TwoPhotonSeries', imaging_plane=imaging_plane, rate=1000., dimension=[Xp,Yp,Zp], data=fake_data) nwb.add_acquisition(raw_image_series) #Creates ophys ProcessingModule and add to file ophys_module = ProcessingModule(name='ophys', description='contains optical physiology processed data.') nwb.add_processing_module(ophys_module) ###Output _____no_output_____ ###Markdown Now transform the lists of indices into (xp,yp,zp) masks. With the masks created, we can add them to a plane segmentation class. ###Code def make_voxel_mask(indices, dims): """ indices - List with voxels indices, e.g. [64371, 89300, 89301, ..., 3763753, 3763842, 3763843] dims - (height, width, depth) in pixels """ voxel_mask = [] for ind in indices: zp = np.floor(ind/(dims[0]dims[1])).astype('int') rest = ind%(dims[0]dims[1]) yp = np.floor(rest/dims[0]).astype('int') xp = rest%dims[0] voxel_mask.append((xp,yp,zp,1)) return voxel_mask #Call function indices = b['indices'] indptr = indices[b['indptr'][0:-1]] dims = np.squeeze(a['dims']) voxel_mask = make_voxel_mask(indptr, dims) #Create Image Segmentation compartment img_seg = ImageSegmentation() ophys_module.add_data_interface(img_seg) #Create plane segmentation and add ROIs ps = img_seg.create_plane_segmentation(description='plane segmentation', imaging_plane=imaging_plane, reference_images=raw_image_series) ps.add_roi(voxel_mask=voxel_mask) ###Output _____no_output_____ ###Markdown With the ROIs created, we can add the dF/F data ###Code #DFF measures dff = DfOverF(name='dff_interface') ophys_module.add_data_interface(dff) #create ROI regions roi_region = ps.create_roi_table_region(description='ROI table region', region=[0]) #create ROI response series dff_data = a['dFF'] dFF_series = dff.create_roi_response_series(name='df_over_f', data=dff_data, unit='NA', rois=roi_region, rate=1000.) ###Output _____no_output_____ ###Markdown The file contains two arrays with pixel indexing: one with all pixels at cells and one with only one reference pixel per cell. Let's see how it looks like in a 3D plot: ###Code #3D scatter with masks points from mpl_toolkits.mplot3d import Axes3D #Reference points xptr = [p[0] for p in voxel_mask] yptr = [p[1] for p in voxel_mask] zptr = [p[2] for p in voxel_mask] #All points in mask all_pt_mask = make_voxel_mask(indices, dims) x = [p[0] for p in all_pt_mask] y = [p[1] for p in all_pt_mask] z = [p[2] for p in all_pt_mask] %matplotlib notebook fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.scatter(x, y, z, c='k', marker='.', s=.5) ax.scatter(xptr, yptr, zptr, c='r', marker='o', s=20) #Saves to NWB file path_to_files = '' fname_nwb = 'file_1.nwb' fpath_nwb = os.path.join(path_to_files, fname_nwb) with NWBHDF5IO(fpath_nwb, mode='w') as io: io.write(nwb) print('File saved with size: ', os.stat(fpath_nwb).st_size/1e6, ' mb') #Loads NWB file with NWBHDF5IO(fpath_nwb, mode='r') as io: nwb = io.read() print(nwb) print(nwb.processing['ophys'].data_interfaces['dff_interface'].roi_response_series['df_over_f']) ###Output _____no_output_____ ###Markdown 데이터셋데이터는 영화 '라라랜드'의 네이버영화의 평점에 기록되어 있는 커멘트 15,603개 입니다. ###Code from pprint import pprint with open('./data/134963_norm.txt', encoding='utf-8') as f: docs = [doc.strip() for doc in f] print('n docs = %d' % len(docs)) pprint(docs[:5]) ###Output n docs = 15603 ['시사회에서 보고왔습니다동화와 재즈뮤지컬의 만남 지루하지않고 재밌습니다', '사랑과 꿈 그 흐름의 아름다움을 음악과 영상으로 최대한 담아놓았다 배우들 연기는 두말할것없고', '지금껏 영화 평가 해본 적이 없는데 진짜 최고네요 색감 스토리 음악 연기 모두ㅜㅜ최고입니다', '방금 시사회 보고 왔어요 배우들 매력이 눈을 뗄 수가 없게 만드네요 한편의 그림 같은 장면들도 많고 음악과 춤이 눈과 귀를 사로 잡았어요 ' '한번 더 보고 싶네요', '초반부터 끝까지 재미있게 잘보다가 결말에서 고국마 왕창먹음 힐링 받는 느낌들다가 막판에 기분 잡쳤습니다 마치 감독이 하고싶은 말은 ' '너희들이 원하는 결말은 이거지 하지만 현실은 이거다 라고 말하고 싶었나보군요'] ###Markdown PyCRFSuite spacing 학습데이터 만들기 ###Code import sys sys.path.append('../') from pycrfsuite_spacing import TemplateGenerator from pycrfsuite_spacing import CharacterFeatureTransformer from pycrfsuite_spacing import sent_to_chartags from pycrfsuite_spacing import sent_to_xy ###Output _____no_output_____ ###Markdown sent_to_chars는 띄어쓰기가 있는 문장을 글자와 띄어쓰기 태그로 변환해줍니다. 띄어쓰기/붙여쓰기의 태그를 지정할 수 있습니다. default는 space = 1, nonspace = 0으로 int 입니다. ###Code chars, tags = sent_to_chartags('이것도 너프해 보시지', space='1', nonspace='0') print(chars) print(tags) ###Output 이것도너프해보시지 ['0', '0', '1', '0', '0', '1', '0', '0', '1'] ###Markdown 빈 문자가 입력되면 빈 글자와 empty list 가 변환됩니다. ###Code sent_to_chartags('') ###Output _____no_output_____ ###Markdown TemplateGenerator는 앞 2 글자부터 뒤 2 글짜까지 길이가 3인 templates를 만든다는 의미입니다. 반드시 현재 글자 (index 0)가 포함된 부분만 template으로 만듭니다. ###Code TemplateGenerator(begin=-2, end=2, min_range_length=3,max_range_length=3).tolist() ###Output _____no_output_____ ###Markdown to_feature()는 template을 이용하여 문장에서 features를 만드는 함수입니다. CharacterFeatureTransformer의 instance는 callable 입니다. ###Code to_feature = CharacterFeatureTransformer( TemplateGenerator(begin=-2, end=2, min_range_length=3, max_range_length=3) ) x, y = sent_to_xy('이것도 너프해 보시지', to_feature) pprint(x) print(y) ###Output [['X[0,2]=이것도'], ['X[-1,1]=이것도', 'X[0,2]=것도너'], ['X[-2,0]=이것도', 'X[-1,1]=것도너', 'X[0,2]=도너프'], ['X[-2,0]=것도너', 'X[-1,1]=도너프', 'X[0,2]=너프해'], ['X[-2,0]=도너프', 'X[-1,1]=너프해', 'X[0,2]=프해보'], ['X[-2,0]=너프해', 'X[-1,1]=프해보', 'X[0,2]=해보시'], ['X[-2,0]=프해보', 'X[-1,1]=해보시', 'X[0,2]=보시지'], ['X[-2,0]=해보시', 'X[-1,1]=보시지'], ['X[-2,0]=보시지']] ['0', '0', '1', '0', '0', '1', '0', '0', '1'] ###Markdown PyCRFSuite spacing 모델 학습하기모델을 학습합니다. 사용할 수 있는 arguments 입니다. - feature_minfreq - 기본값은 0 입니다. 이 값이 지나치게 작으면 features 개수가 커집니다. 메모리가 많이 필요하니 적절한 수준으로 잡아줍니다. - max_iterations - 기본값은 100 입니다. - l1_cost, l2_cost - 기본값은 각각 l1_cost = 0, l2_cost=1.0 입니다. Lasso CRF 를 이용하려면 l2_cost = 0, l1_cost > 0 으로 설정합니다. - L1, L2 regularization 을 모두 이용하려면 l1_cost > 0 & l2_cost > 0 으로 설정합니다. default parameter 를 이용하려면 아래처럼 to_feature 만 입력합니다. correct = PyCRFSuiteSpacing(to_feature) ###Code from pycrfsuite_spacing import PyCRFSuiteSpacing correct = PyCRFSuiteSpacing( to_feature = to_feature, feature_minfreq=3, # default = 0 max_iterations=100, l1_cost=1.0, l2_cost=1.0 ) correct.train(docs, 'demo_model.crfsuite') ###Output _____no_output_____ ###Markdown 학습된 모델을 불러올 수도 있습니다. ###Code correct.load_tagger('demo_model.crfsuite') ###Output _____no_output_____ ###Markdown PyCRFSuite spacing 으로 띄어쓰기 오류 교정하기 ###Code correct('이건진짜좋은영화라라랜드진짜좋은영화') ###Output _____no_output_____
P09-RootFinding.ipynb	###Markdown Root Finding============This week we're exploring algorithms for finding roots of arbitrary functions.Any time you try to solve an algebraic problem and end up with a transcendental equation you can find yourself with root finding as the only viable means of extracting answers.As an example there's a nice quantum mechanical system (The finite square well , you don't need to follow this podcast, it's just an example for which the result of a transcendental equation is important) for which the bound energy states can be found by solving the two transcendental equations:$$\sin(z)=z/z_0$$and $$\cos(z)=z/z_0$$Where $z_0$ is a unitless real number that characterizes the depth and width of the potential well and $z$ is a unitless real number (less that $z_0$) that characterizes the energy level.Since the $\cos(z)$ version always has at least one solution, let's look at it first. ###Code %matplotlib inline import numpy as np import matplotlib.pyplot as pl N=100 z0=2.0 z=np.linspace(0,1.5,N) def leftS(z): return np.cos(z) def rightS(z,z0=z0): return z/z0 def f(z,z0=z0): return leftS(z)-rightS(z,z0) pl.grid() pl.title("Investigating $\cos(z)=z/z_0$") pl.ylabel("left, right and difference") pl.xlabel("$z$") pl.plot(z,leftS(z),'r-',label='$\cos(z)$') pl.plot(z, rightS(z),'b-',label='$z/z_0$') pl.plot(z, f(z),'g-', label='$\cos(z)-z/z_0$') pl.legend(loc=3) def fp(z): """ We need a function to evaluate the derivative of f(z) for Newton's method. """ return -np.sin(z)-1.0/z0 def newtonsMethod(f, fp, zi, eps=1e-15, Nmax=100, showCount=False): """ Very simple implementation of Newton's Method. Try to find a zero of 'f' near zi to within eps. Don't use up over Nmax iterations """ z=zi # start at zi y=f(z) # evaluate y count=0 # start count at zero while (abs(y)>eps) and count<Nmax: dz=y/fp(z) # evaluate dz z=z-dz # update z y=f(z) # update y count += 1 # update count if count>=Nmax: raise RuntimeError("Ack! I can't find a zero.") elif showCount: print( "Found root", z, "in", count, "iterations. y=", y) return z z = newtonsMethod(f, fp, 1.0, showCount=True) from scipy.optimize import brentq print (brentq(f, 0.9, 1.1)) ###Output 1.0298665293222566 ###Markdown Suppose we have some potential function and we want to find a "bound state" wavefunction that satisfies the boundary conditions of the potential. There are of course many different possible potentials that could be considered. Let's focus on a class that goes to infinity for $xL$. Between those limits the potential is defined by a function $V(x)$.We can ues RK4 to integrate from $x=0$ to $x=L$. What shall we integrate? The Schrodinger Wave Equation of course!$$-\frac{\hbar^2}{2m} \psi''(x) + V(x)\psi(x) = E\psi(x)$$$$\psi'' = \frac{2m}{\hbar^2}\left(V(x)-E\right)\psi(x)$$ ###Code def V(x, a=3.0): """ Here's an example potential V(x)=0.0 """ return 0.0 psi0, psip0 = 0.0, 1.0 # start psi and psi' at $x=0$. s=np.array([psi0, psip0]) hbar=1.0 # pick convenient units m=1.0 L=1.0 x=0.0 dx=L/20 E=0.90(hbar2/(2m))(np.pi/L)2 # start at 90% of known ground state energy. xList=[x] # put in the first value psiList=[psi0] def RK4Step(s, x, derivs, dx, E): """ Take a single RK4 step. (our old friend) But this time we're integrating in 'x', not 't'. """ dxh=dx/2.0 f1 = derivs(s, x, E) f2 = derivs(s+f1dxh, x+dxh, E) f3 = derivs(s+f2dxh, x+dxh, E) f4 = derivs(s+f3dx, x+dx, E) return s + (f1+2f2+2f3+f4)dx/6.0 def SWE_derivs(s, x, E): psi=s[0] psip=s[1] psipp =(2m/hbar*2)(V(x)-E)psi return np.array([psip, psipp]) while x<=L: s=RK4Step(s, x, SWE_derivs, dx, E) x+=dx xList.append(x) psiList.append(s[0]) pl.title("Test Wave Function at Energy %3.2f" % E) pl.ylabel("$\psi(x)$ (un-normalized)") pl.xlabel("$x$") pl.plot(xList, psiList, 'b-') def calcBC(E): """ Compute the value of psi(x) at x=L for a given value of E assuming psi(0) is zero. """ s=np.array([psi0, psip0]) x=0.0 while x<L: s=RK4Step(s, x, SWE_derivs, dx, E) x+=dx return s[0] print ("BC at E=4.4:",calcBC(4.4)) print ("BC at E=5.4:",calcBC(5.4)) Ezero = brentq(calcBC, 4.4, 5.4) # find "root" with brentq Ezero print( ((hbar2)/(2m))(np.pi/L)2 )# exact result def calcBC_wPsi(E): """ Compute the value of psi(x) at x=L for a given value of E assuming psi(0) is zero. """ s=np.array([psi0, psip0]) x=0.0 xList=[x] psiList=[psi0] while x<L: s=RK4Step(s, x, SWE_derivs, dx, E) x+=dx xList.append(x) psiList.append(s[0]) return xList, psiList xList, psiList = calcBC_wPsi(Ezero) pl.plot(xList, psiList, 'b-') pl.grid() ###Output _____no_output_____ ###Markdown Root Finding============This week we're exploring algorithms for finding roots of arbitrary functions.Any time you try to solve an algebraic problem and end up with a transcendental equation you can find yourself with root finding as the only viable means of extracting answers.As an example there's a nice quantum mechanical system (The finite square well , you don't need to follow this podcast, it's just an example for which the result of a transcendental equation is important) for which the bound energy states can be found by solving the two transcendental equations:$$\sin(z)=z/z_0$$and $$\cos(z)=z/z_0$$Where $z_0$ is a unitless real number that characterizes the depth and width of the potential well and $z$ is a unitless real number (less that $z_0$) that characterizes the energy level.Since the $\cos(z)$ version always has at least one solution, let's look at it first. ###Code %pylab inline N=100 z0=2.0 z=linspace(0,1.5,N) def leftS(z): return cos(z) def rightS(z,z0=z0): return z/z0 def f(z,z0=z0): return leftS(z)-rightS(z,z0) grid() title("Investigating $\cos(z)=z/z_0$") ylabel("left, right and difference") xlabel("$z$") plot(z,leftS(z),'r-',label='$\cos(z)$') plot(z, rightS(z),'b-',label='$z/z_0$') plot(z, f(z),'g-', label='$\cos(z)-z/z_0$') legend(loc=3) def fp(z): """ We need a function to evaluate the derivative of f(z) for Newton's method. """ return -sin(z)-1.0/z0 def newtonsMethod(f, fp, zi, eps=1e-15, Nmax=100, showCount=False): """ Very simple implementation of Newton's Method. Try to find a zero of 'f' near zi to within eps. Don't use up over Nmax iterations """ z=zi # start at zi y=f(z) # evaluate y count=0 # start count at zero while (abs(y)>eps) and count<Nmax: dz=y/fp(z) # evaluate dz z=z-dz # update z y=f(z) # update y count += 1 # update count if count>=Nmax: raise RuntimeError("Ack! I can't find a zero.") elif showCount: print( "Found root", z, "in", count, "iterations. y=", y) return z z = newtonsMethod(f, fp, 1.0, showCount=True) from scipy.optimize import brentq print (brentq(f, 0.9, 1.1)) ###Output 1.0298665293222566 ###Markdown Suppose we have some potential function and we want to find a "bound state" wavefunction that satisfies the boundary conditions of the potential. There are of course many different possible potentials that could be considered. Let's focus on a class that goes to infinity for $xL$. Between those limits the potential is defined by a function $V(x)$.We can ues RK4 to integrate from $x=0$ to $x=L$. What shall we integrate? The Schrodinger Wave Equation of course!$$-\frac{\hbar^2}{2m} \psi''(x) + V(x)\psi(x) = E\psi(x)$$$$\psi'' = \frac{2m}{\hbar^2}\left(V(x)-E\right)\psi(x)$$ ###Code def V(x, a=3.0): """ Here's an example potential V(x)=0.0 """ return 0.0 psi0, psip0 = 0.0, 1.0 # start psi and psi' at $x=0$. s=array([psi0, psip0]) hbar=1.0 # pick convenient units m=1.0 L=1.0 x=0.0 dx=L/20 E=0.90(hbar*2/(2m))(pi/L)2 # start at 90% of known ground state energy. xList=[x] # put in the first value psiList=[psi0] def RK4Step(s, x, derivs, dx, E): """ Take a single RK4 step. (our old friend) But this time we're integrating in 'x', not 't'. """ dxh=dx/2.0 f1 = derivs(s, x, E) f2 = derivs(s+f1dxh, x+dxh, E) f3 = derivs(s+f2dxh, x+dxh, E) f4 = derivs(s+f3dx, x+dx, E) return s + (f1+2f2+2f3+f4)dx/6.0 def SWE_derivs(s, x, E): psi=s[0] psip=s[1] psipp =(2m/hbar*2)(V(x)-E)psi return array([psip, psipp]) while x<=L: s=RK4Step(s, x, SWE_derivs, dx, E) x+=dx xList.append(x) psiList.append(s[0]) title("Test Wave Function at Energy %3.2f" % E) ylabel("$\psi(x)$ (un-normalized)") xlabel("$x$") plot(xList, psiList, 'b-') def calcBC(E): """ Compute the value of psi(x) at x=L for a given value of E assuming psi(0) is zero. """ s=array([psi0, psip0]) x=0.0 while x<L: s=RK4Step(s, x, SWE_derivs, dx, E) x+=dx return s[0] print ("BC at E=4.4:",calcBC(4.4)) print ("BC at E=5.4:",calcBC(5.4)) Ezero = brentq(calcBC, 4.4, 5.4) # find "root" with brentq Ezero print( ((hbar2)/(2m))(pi/L)*2 )# exact result def calcBC_wPsi(E): """ Compute the value of psi(x) at x=L for a given value of E assuming psi(0) is zero. """ s=array([psi0, psip0]) x=0.0 xList=[x] psiList=[psi0] while x<L: s=RK4Step(s, x, SWE_derivs, dx, E) x+=dx xList.append(x) psiList.append(s[0]) return xList, psiList xList, psiList = calcBC_wPsi(Ezero) plot(xList, psiList, 'b-') ###Output _____no_output_____
plot_history.ipynb	###Markdown Notebook to plot the history ###Code import numpy as np import json import os import matplotlib.pyplot as plt from matplotlib import rcParams class PlotStyler(): def __init__(self, n, cmap="Set1", change_linestyle=True): assert cmap in ["hsv", "Set1", "Accent"] self.cmap = cmap self.i = -1 self.n = n self.cm = plt.get_cmap(cmap) if change_linestyle: self.linestyles = [ "solid", "dotted", "dashed", "dashdot", (0, (3, 1, 1, 1, 1, 1)), (0, (5, 1)), (0, (3, 5, 1, 5, 1, 5)) ] else: self.linestyles = ["solid"] def get(self): self.i += 1 ls = self.linestyles[self.i % len(self.linestyles)] if self.cmap in ["hsv", "Accent"]: c = self.cm(self.i/self.n) else: c = self.cm(self.i) return c, ls def plot(d, xlim=None, ylim=None, title=None, plot_limbs=False, replace_reward_by_success_rate=False): generations = d["generations"] best_rewards = d["best_rewards"] mean_rewards = d["mean_rewards"] min_rewards = d["min_rewards"] species_mean_rewards = d["species_mean_rewards"] species_eval_rewards = d["species_eval_rewards"] num_limbs = d["num_limbs"] num_species = len(species_eval_rewards[0]) if replace_reward_by_success_rate: species_eval_rewards = d["success_rates"] ylim = (0, 1) plt.rcParams["font.size"] = 30 ps = PlotStyler(16) fig=plt.figure(figsize=(16, 10), dpi= 80, facecolor="w", edgecolor="k") if title is not None: fig.suptitle(title) ax1 = fig.add_subplot(111) # Decide the color and line style first styles = [] for i in range(num_species): styles.append(ps.get()) if plot_limbs: # rigid parts graph c, ls = ps.get() ax2 = ax1.twinx() ax2.plot(generations, num_limbs[:, 0], color=c, linestyle = ls, label="number of rigid parts") # reward graph for i in range(num_species): c, ls = styles[i] label = f"reward in worker {i+1}" if num_species == 1: label = "reward" ax1.plot(generations, species_mean_rewards[:, i], color=c, alpha=0.2) ax1.plot(generations, species_eval_rewards[:, i], color=c, linestyle = ls, label=label) h, l = ax1.get_legend_handles_labels() if plot_limbs: h2, l2 = ax2.get_legend_handles_labels() h += h2 l += l2 ax2.set_ylabel("num_limbs") plt.rcParams["font.size"] = 24 if "ax2" in locals(): # To eliminate overlap with ax2 graph ax2.legend(h, l, loc="upper left") else: ax1.legend(h, l, loc="upper left") ax1.set_xlabel("generation") ax1.set_ylabel("reward") if ylim is not None: ax1.set_ylim(ylim) if xlim is not None: ax1.set_xlim(xlim) if plot_limbs: ax2.set_xlim(xlim) def extract_data(d): generations = np.array([h["generation"] for h in d]) elapseds = np.array([h["elapsed"] for h in d]) best_species_eval_rewards = np.array([h["best_reward"] for h in d]) best_rewards = np.array([h["current_best_reward"] for h in d]) mean_rewards = np.array([h["current_mean_reward"] for h in d]) min_rewards = np.array([h["current_min_reward"] for h in d]) species_mean_rewards = np.array([h["current_mean_rewards"] for h in d]) species_eval_rewards = np.array([h["current_eval_rewards"] for h in d]) success_rates = np.mean(np.array([h["success_rate"] for h in d]), axis=2) num_limbs = np.array([h["num_limbs"] for h in d]) return { "generations": generations, "elapseds": elapseds, "best_species_eval_rewards": best_species_eval_rewards, "best_rewards": best_rewards, "mean_rewards": mean_rewards, "min_rewards": min_rewards, "species_mean_rewards": species_mean_rewards, "species_eval_rewards": species_eval_rewards, "success_rates": success_rates, "num_limbs": num_limbs } simname = "old/0.8.8_20220203_225723" # simname = "old/0.8.8_20220205_213427" # Data collection filename = os.path.join("log", simname, "history.json") with open(filename, "r") as f: d = extract_data(json.load(f)) plot(d) ###Output _____no_output_____ ###Markdown History ###Code experiments = !ls -1 ./checkpoints names = [ 'loss', # SSD 'conf_loss', 'loc_loss', #'pos_conf_loss', 'neg_conf_loss', 'pos_loc_loss', 'precision', 'recall', 'fmeasure', # SegLink 'seg_precision', 'seg_recall', 'seg_fmeasure', #'link_precision', 'link_recall', 'link_fmeasure', #'pos_seg_conf_loss', 'neg_seg_conf_loss', 'seg_loc_loss', 'pos_link_conf_loss', 'neg_link_conf_loss', #'num_pos_seg', 'num_neg_seg', 'num_pos_link', 'num_neg_link', #'seg_conf_loss', 'seg_loc_loss', 'link_conf_loss', ] #names = None plot_history(experiments[-4:], names) ###Output _____no_output_____ ###Markdown History ###Code d = experiments[1] checkpath = os.path.join('.', 'checkpoints', d) df = pd.read_csv(os.path.join(checkpath, 'history.csv')) epochs = np.arange(len(df)) + 1 ticks = epochs #print(list(df.keys())) plt.figure(figsize=(12,6)) plt.plot(epochs, df['loss']) plt.plot(epochs, df['val_loss']) plt.title('loss') plt.legend(['training','validation']) ax = plt.gca() ax.set_xticks(ticks) ax.set_xticklabels(ticks) plt.grid() #plt.ylim([0.0, 5.0]) #plt.ylim([0.0, 20.0]) if False: plotpath = os.path.join(checkpath, 'plots') os.makedirs(plotpath, exist_ok=True) plt.savefig(os.path.join(plotpath, 'history_loss.png'), bbox_inches='tight') # jpg/png/pgf plt.show() signals = [ # SSD #'conf_loss', 'loc_loss', #'pos_conf_loss', 'neg_conf_loss', 'pos_loc_loss', #'precision', 'recall', 'fmeasure', # SegLink 'seg_precision', 'seg_recall', 'seg_fmeasure', #'link_precision', 'link_recall', 'link_fmeasure', #'pos_seg_conf_loss', 'neg_seg_conf_loss', 'seg_loc_loss', 'pos_link_conf_loss', 'neg_link_conf_loss', #'num_pos_seg', 'num_neg_seg', 'num_pos_link', 'num_neg_link', #'seg_conf_loss', 'seg_loc_loss', 'link_conf_loss', ] fig, axs = plt.subplots(1, len(signals), figsize=(20,4)) for i, s in enumerate(signals): if s not in df.keys(): print('missing %s' %(s)) continue axs[i].plot(epochs, df[s]) axs[i].plot(epochs, df['val_'+s]) axs[i].set_title(s) if s.split('_')[-1] in ['precision', 'recall', 'fmeasure']: axs[i].set_ylim([0,1]) axs[i].set_xticks(ticks) axs[i].set_xticklabels(ticks) axs[i].grid() if False: plotpath = os.path.join(checkpath, 'plots') os.makedirs(plotpath, exist_ok=True) plt.savefig(os.path.join(plotpath, 'history_metrics.png'), bbox_inches='tight') # jpg/png/pgf plt.show() ###Output _____no_output_____ ###Markdown Compare History ###Code d1 = experiments[0] d2 = experiments[1] signals = [ #'loss', #'precision', #'recall', #'fmeasure', 'seg_fmeasure', 'link_fmeasure', ] df1 = pd.read_csv(os.path.join('.', 'checkpoints', d1, 'history.csv')) df2 = pd.read_csv(os.path.join('.', 'checkpoints', d2, 'history.csv')) epochs1 = np.arange(len(df1)) + 1 epochs2 = np.arange(len(df2)) + 1 ticks = np.arange(max(len(df1),len(df2))) + 1 fig, axs = plt.subplots(1, len(signals), figsize=(20,6)) for i, s in enumerate(signals): if s not in df1.keys() or s not in df2.keys(): print('missing %s' %(s)) continue ax = axs[i] if len(signals) > 1 else axs ax.plot(epochs1, df1[s]) ax.plot(epochs1, df1['val_'+s]) ax.plot(epochs2, df2[s]) ax.plot(epochs2, df2['val_'+s]) ax.set_title(s) if s.split('_')[-1] in ['precision', 'recall', 'fmeasure']: ax.set_ylim([0,1]) ax.set_xlim([0, ticks[-1]+1]) ax.set_xticks(ticks) ax.set_xticklabels(ticks) ax.grid() plt.show() ###Output _____no_output_____ ###Markdown History ###Code checkdir = experiments[-1] checkpath = os.path.join('.', 'checkpoints', checkdir) hist = pd.DataFrame.from_csv(os.path.join(checkpath, 'history.csv')) epochs = np.arange(len(hist)) + 1 ticks = epochs #print(list(hist.keys())) plt.figure(figsize=(12,6)) plt.plot(epochs, hist['loss']) plt.plot(epochs, hist['val_loss']) plt.title('loss') plt.legend(['training','validation']) ax = plt.gca() ax.set_xticks(ticks) ax.set_xticklabels(ticks) plt.grid() #plt.ylim([0.0, 5.0]) #plt.ylim([0.0, 20.0]) plotpath = os.path.join(checkpath, 'plots') os.makedirs(plotpath, exist_ok=True) plt.savefig(os.path.join(plotpath, 'history_loss.png'), bbox_inches='tight') # jpg/png/pgf plt.show() signals = [ # SSD #'conf_loss', 'loc_loss', #'pos_conf_loss', 'neg_conf_loss', 'pos_loc_loss', #'precision', 'recall', 'fmeasure', # SegLink 'seg_precision', 'seg_recall', 'seg_fmeasure', #'link_precision', 'link_recall', 'link_fmeasure', #'pos_seg_conf_loss', 'neg_seg_conf_loss', 'seg_loc_loss', 'pos_link_conf_loss', 'neg_link_conf_loss', #'num_pos_seg', 'num_neg_seg', 'num_pos_link', 'num_neg_link', #'seg_conf_loss', 'seg_loc_loss', 'link_conf_loss', ] fig, axs = plt.subplots(1, len(signals), figsize=(20,4)) for i, s in enumerate(signals): if s not in hist.keys(): print('missing %s' %(s)) continue axs[i].plot(epochs, hist[s]) axs[i].plot(epochs, hist['val_'+s]) axs[i].set_title(s) if s.split('_')[-1] in ['precision', 'recall', 'fmeasure']: axs[i].set_ylim([0,1]) axs[i].set_xticks(ticks) axs[i].set_xticklabels(ticks) axs[i].grid() plotpath = os.path.join(checkpath, 'plots') os.makedirs(plotpath, exist_ok=True) plt.savefig(os.path.join(plotpath, 'history_metrics.png'), bbox_inches='tight') # jpg/png/pgf plt.show() ###Output _____no_output_____ ###Markdown Compare History ###Code checkdir1 = experiments[-5] checkdir2 = experiments[-1] signals = [ #'loss', #'precision', #'recall', #'fmeasure', 'predictions_seg_fmeasure', 'predictions_inter_link_fmeasure', 'predictions_cross_link_fmeasure', ] hist1 = pd.DataFrame.from_csv(os.path.join('.', 'checkpoints', checkdir1, 'history.csv')) hist2 = pd.DataFrame.from_csv(os.path.join('.', 'checkpoints', checkdir2, 'history.csv')) epochs1 = np.arange(len(hist1)) + 1 epochs2 = np.arange(len(hist2)) + 1 ticks = np.arange(max(len(hist1),len(hist1))) + 1 fig, axs = plt.subplots(1, len(signals), figsize=(20,6)) for i, s in enumerate(signals): if s not in hist1.keys() or s not in hist2.keys(): print('missing %s' %(s)) continue ax = axs[i] if len(signals) > 1 else axs ax.plot(epochs1, hist1[s]) ax.plot(epochs1, hist1['val_'+s]) ax.plot(epochs2, hist2[s]) ax.plot(epochs2, hist2['val_'+s]) ax.set_title(s) if s.split('_')[-1] in ['precision', 'recall', 'fmeasure']: ax.set_ylim([0,1]) ax.set_xlim([0, ticks[-1]]) ax.set_xticks(ticks) ax.set_xticklabels(ticks) ax.grid() plt.show() ###Output _____no_output_____ ###Markdown History ###Code experiments = !ls -1 ./checkpoints names = [ 'loss', # SSD 'conf_loss', 'loc_loss', #'pos_conf_loss', 'neg_conf_loss', 'pos_loc_loss', 'precision', 'recall', 'fmeasure', # SegLink 'seg_precision', 'seg_recall', 'seg_fmeasure', #'link_precision', 'link_recall', 'link_fmeasure', #'pos_seg_conf_loss', 'neg_seg_conf_loss', 'seg_loc_loss', 'pos_link_conf_loss', 'neg_link_conf_loss', #'num_pos_seg', 'num_neg_seg', 'num_pos_link', 'num_neg_link', #'seg_conf_loss', 'seg_loc_loss', 'link_conf_loss', ] #names = None plot_history(experiments[-4:], names) ###Output _____no_output_____
examples/notebooks/generators/5_rest_api.ipynb	###Markdown Using the xcube generator REST API This notebook demonstrates direct use of the xcube generator REST API,without the higher-level Python client library. It performs the following steps:1. Use the xcube gen credentials to obtain an access token from the gen server.2. Issue a gen server request to generate a cube and store it in an S3 bucket.3. Monitor the status of the request until it has completed.4. Open the newly generated cube from the S3 bucket and plot an image using its data.This notebook reads the remote generator service configuration from the configuration file `edc_service.yml`, which may in turn contain references to environment variables. The notebook also requires the following environment variables to be set in order to write the generated cube into an S3 bucket:```AWS_ACCESS_KEY_IDAWS_SECRET_ACCESS_KEY``` First, import some necessary libraries. ###Code import os import requests import time import string import yaml from xcube.core.store import new_data_store ###Output _____no_output_____ ###Markdown Set the endpoint URL, client ID, and client secret for the generator service, reading the values from the `edc_service.yml` configuration file. ###Code with open('edc-service.yml', 'r') as fh: yaml_content = fh.read() yaml_substituted = string.Template(yaml_content).safe_substitute(os.environ) service_params = yaml.safe_load(yaml_substituted) client_id = service_params['client_id'] client_secret = service_params['client_secret'] endpoint = service_params['endpoint_url'] ###Output _____no_output_____ ###Markdown Post a request to the generator's authorization service to get an access token authorized by the client credentials. ###Code token_response = requests.post( endpoint + 'oauth/token', json = { 'audience': endpoint, 'client_id': client_id, 'client_secret': client_secret, 'grant_type': 'client-credentials', }, headers = {'Accept': 'application/json'}, ) access_token = token_response.json()['access_token'] ###Output _____no_output_____ ###Markdown Create and issue a request to generate a cube containing soil moisture data for the European region. Note the use of the access token to authorize the request. ###Code cubegen_request = { 'input_config': { 'store_id': '@cds', 'data_id': 'satellite-soil-moisture:saturation:monthly', 'open_params': {} }, 'cube_config': { 'variable_names': ['soil_moisture_saturation'], 'crs': 'WGS84', # 'bbox': [-13.00, 41.15, 21.79, 57.82], 'spatial_res': 0.25, 'time_range': ['2000-01-01', '2001-01-01'], 'time_period': '1M', 'chunks': {'lat': 65, 'lon': 139, 'time': 12}, }, 'output_config': { 'store_id': 's3', 'data_id': 'cds-soil-moisture.zarr', 'store_params': {'root': 'eurodatacube-scratch'}, 'replace': True, }, } cubegen_response = requests.put( endpoint + 'cubegens', json=cubegen_request, headers={ 'Accept': 'application/json', 'Authorization': 'Bearer ' + access_token }, ) ###Output _____no_output_____ ###Markdown Get the ID of the cube generation request so that we can monitor its progress. ###Code cubegen_id = cubegen_response.json()['job_id'] cubegen_id cubegen_response.json() ###Output _____no_output_____ ###Markdown Check the request status repeatedly at five-second intervals until the request completes, then show the status. ###Code while True: status_response = requests.get( endpoint + 'cubegens/' + cubegen_id, headers={ 'Accept': 'application/json', 'Authorization': 'Bearer ' + access_token } ) json_response = status_response.json() if json_response['job_status']['succeeded'] or json_response['job_status']['failed']: break time.sleep(5) json_response['job_status'] ###Output _____no_output_____ ###Markdown If the request was successful, the cube has now been written into an S3 bucket. Create an xcube data store to read the data from this bucket and list its contents. ###Code data_store = new_data_store( 's3', root='eurodatacube-scratch', storage_options={ 'key': os.environ['AWS_ACCESS_KEY_ID'], 'secret': os.environ['AWS_SECRET_ACCESS_KEY'] } ) list(data_store.get_data_ids()) ###Output _____no_output_____ ###Markdown Open our newly-created dataset from this store and show a summary of its properties and contents. ###Code dataset = data_store.open_data('cds-soil-moisture.zarr') dataset ###Output _____no_output_____ ###Markdown Plot a map showing the generated data at a particular point in time. ###Code dataset.sm.isel(time=6).plot.imshow() ###Output _____no_output_____
kudo-kubeflow/Anomaly-Detection-with-Serving.ipynb	###Markdown Function arguments specified with `InputPath` and `OutputPath` are the key to defining dependencies.For now, it suffices to think of them as the input and output of each step.How we can define dependencies is explained in the [next section](How-to-Combine-the-Components-into-a-Pipeline). Component 1: Download & Prepare the Data Set ###Code %%writefile minio_secret.yaml apiVersion: v1 kind: Secret metadata: name: minio-s3-secret annotations: serving.kubeflow.org/s3-endpoint: minio-service.kubeflow:9000 serving.kubeflow.org/s3-usehttps: "0" # Default: 1. Must be 0 when testing with MinIO! type: Opaque data: awsAccessKeyID: bWluaW8= awsSecretAccessKey: bWluaW8xMjM= --- apiVersion: v1 kind: ServiceAccount metadata: name: default secrets: - name: minio-s3-secret ! kubectl apply -f minio_secret.yaml def download_and_process_dataset(data_dir: OutputPath(str)): import pandas as pd import numpy as np import os if not os.path.exists(data_dir): os.makedirs(data_dir) # Generated training sequences for use in the model. def create_sequences(values, time_steps=288): output = [] for i in range(len(values) - time_steps): output.append(values[i : (i + time_steps)]) return np.stack(output) master_url_root = "https://raw.githubusercontent.com/numenta/NAB/master/data/" df_small_noise_url_suffix = "artificialNoAnomaly/art_daily_small_noise.csv" df_small_noise_url = master_url_root + df_small_noise_url_suffix df_small_noise = pd.read_csv( df_small_noise_url, parse_dates=True, index_col="timestamp" ) df_daily_jumpsup_url_suffix = "artificialWithAnomaly/art_daily_jumpsup.csv" df_daily_jumpsup_url = master_url_root + df_daily_jumpsup_url_suffix df_daily_jumpsup = pd.read_csv( df_daily_jumpsup_url, parse_dates=True, index_col="timestamp" ) # Normalize and save the mean and std we get, # for normalizing test data. training_mean = df_small_noise.mean() training_std = df_small_noise.std() df_training_value = (df_small_noise - training_mean) / training_std print("Number of training samples:", len(df_training_value)) x_train = create_sequences(df_training_value.values) print("Training input shape: ", x_train.shape) np.save(data_dir + "/x_train.npy", x_train) ###Output _____no_output_____ ###Markdown Component 2: Build the Model ###Code def build_and_train_model(data_dir: InputPath(str), model_dir: OutputPath(str)): import os import numpy as np from tensorflow import keras from keras import layers import tensorflow as tf x_train = np.load(data_dir + "/x_train.npy") print("Training input shape: ", x_train.shape) # TODO: make x_train into a layer so it can be used as input layer below class Conv1DTranspose(tf.keras.layers.Layer): def __init__(self, filters, kernel_size, strides=1, padding="valid"): super().__init__() self.conv2dtranspose = tf.keras.layers.Conv2DTranspose( filters, (kernel_size, 1), (strides, 1), padding ) def call(self, x): x = tf.expand_dims(x, axis=2) x = self.conv2dtranspose(x) x = tf.squeeze(x, axis=2) return x model = keras.Sequential( [ layers.Input(shape=(x_train.shape[1], x_train.shape[2])), layers.Conv1D( filters=32, kernel_size=7, padding="same", strides=2, activation="relu" ), layers.Dropout(rate=0.2), layers.Conv1D( filters=16, kernel_size=7, padding="same", strides=2, activation="relu" ), Conv1DTranspose(filters=16, kernel_size=7, padding="same", strides=2), layers.Dropout(rate=0.2), Conv1DTranspose(filters=32, kernel_size=7, padding="same", strides=2), Conv1DTranspose(filters=1, kernel_size=7, padding="same"), ] ) model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.001), loss="mse") model.summary() history = model.fit( x_train, x_train, epochs=50, batch_size=128, validation_split=0.1, callbacks=[ keras.callbacks.EarlyStopping(monitor="val_loss", patience=5, mode="min") ], ) model.save(model_dir) print(f"Model saved {model_dir}") print(os.listdir(model_dir)) ###Output _____no_output_____ ###Markdown Combine into pipeline ###Code def train_and_serve( data_dir: str, model_dir: str, export_bucket: str, model_name: str, model_version: int, ): # For GPU support, please add the "-gpu" suffix to the base image BASE_IMAGE = "mesosphere/kubeflow:1.0.1-0.3.1-tensorflow-2.2.0" downloadOp = components.func_to_container_op( download_and_process_dataset, base_image=BASE_IMAGE )() trainOp = components.func_to_container_op( build_and_train_model, base_image=BASE_IMAGE )(downloadOp.output) # evaluateOp = components.func_to_container_op(evaluate_model, base_image=BASE_IMAGE)( # downloadOp.output, trainOp.output # ) # exportOp = components.func_to_container_op(export_model, base_image=BASE_IMAGE)( # trainOp.output, evaluateOp.output, export_bucket, model_name, model_version # ) # # Create an inference server from an external component # kfserving_op = components.load_component_from_url( # "https://raw.githubusercontent.com/kubeflow/pipelines/8d738ea7ddc350e9b78719910982abcd8885f93f/components/kubeflow/kfserving/component.yaml" # ) # kfserving = kfserving_op( # action="create", # default_model_uri=f"s3://{export_bucket}/{model_name}", # model_name="mnist", # namespace=NAMESPACE, # framework="tensorflow", # ) # kfserving.after(exportOp) # See: https://github.com/kubeflow/kfserving/blob/master/docs/DEVELOPER_GUIDE.md#troubleshooting def op_transformer(op): op.add_pod_annotation(name="sidecar.istio.io/inject", value="false") return op @dsl.pipeline(name="anomaly-pipeline") def anomaly_pipeline( model_dir: str = "/train/model", data_dir: str = "/train/data", export_bucket: str = "airframe-anomaly", model_name: str = "airframe-anomaly", model_version: int = 1, ): train_and_serve( data_dir=data_dir, model_dir=model_dir, export_bucket=export_bucket, model_name=model_name, model_version=model_version, ) dsl.get_pipeline_conf().add_op_transformer(op_transformer) pipeline_func = anomaly_pipeline run_name = pipeline_func.__name__ + " run" experiment_name = "airframe-anomaly-detection" arguments = { "model_dir": "/train/model", "data_dir": "/train/data", # "export_bucket": "airframe-anomaly", "model_name": "airframe-anomaly", "model_version": "1", } client = kfp.Client() run_result = client.create_run_from_pipeline_func( pipeline_func, experiment_name=experiment_name, run_name=run_name, arguments=arguments, ) ###Output _____no_output_____ ###Markdown Component 3: Evaluate the ModelWith the following Python function the model is evaluated.The metrics [metadata](https://www.kubeflow.org/docs/pipelines/sdk/pipelines-metrics/) (loss and accuracy) is available to the Kubeflow Pipelines UI.Metadata can automatically be visualized with output viewer(s).Please go [here](https://www.kubeflow.org/docs/pipelines/sdk/output-viewer/) to see how to do that. ###Code def evaluate_model( data_dir: InputPath(str), model_dir: InputPath(str), metrics_path: OutputPath(str) ) -> NamedTuple("EvaluationOutput", [("mlpipeline_metrics", "Metrics")]): """Loads a saved model from file and uses a pre-downloaded dataset for evaluation. Model metrics are persisted to `/mlpipeline-metrics.json` for Kubeflow Pipelines metadata.""" import json import tensorflow as tf import tensorflow_datasets as tfds from collections import namedtuple def normalize_test(values, mean, std): values -= mean values /= std return values df_test_value = (df_daily_jumpsup - training_mean) / training_std # Create sequences from test values. x_test = create_sequences(df_test_value.values) print("Test input shape: ", x_test.shape) # Get test MAE loss. x_test_pred = model.predict(x_test) test_mae_loss = np.mean(np.abs(x_test_pred - x_test), axis=1) test_mae_loss = test_mae_loss.reshape((-1)) # Detect all the samples which are anomalies. anomalies = test_mae_loss > threshold print("Number of anomaly samples: ", np.sum(anomalies)) print("Indices of anomaly samples: ", np.where(anomalies)) ds_test, ds_info = tfds.load( "mnist", split="test", shuffle_files=True, as_supervised=True, withj_info=True, download=False, data_dir=data_dir, ) # See: https://www.tensorflow.org/datasets/keras_example#build_training_pipeline ds_test = ds_test.map( normalize_image, num_parallel_calls=tf.data.experimental.AUTOTUNE ) ds_test = ds_test.batch(128) ds_test = ds_test.cache() ds_test = ds_test.prefetch(tf.data.experimental.AUTOTUNE) model = tf.keras.models.load_model(model_dir) (loss, accuracy) = model.evaluate(ds_test) metrics = { "metrics": [ {"name": "loss", "numberValue": str(loss), "format": "PERCENTAGE"}, {"name": "accuracy", "numberValue": str(accuracy), "format": "PERCENTAGE"}, ] } with open(metrics_path, "w") as f: json.dump(metrics, f) out_tuple = namedtuple("EvaluationOutput", ["mlpipeline_metrics"]) return out_tuple(json.dumps(metrics)) ###Output _____no_output_____ ###Markdown Component 4: Export the Model ###Code def export_model( model_dir: InputPath(str), metrics: InputPath(str), export_bucket: str, model_name: str, model_version: int, ): import os import boto3 from botocore.client import Config s3 = boto3.client( "s3", endpoint_url="http://minio-service.kubeflow:9000", aws_access_key_id="minio", aws_secret_access_key="minio123", config=Config(signature_version="s3v4"), ) # Create export bucket if it does not yet exist response = s3.list_buckets() export_bucket_exists = False for bucket in response["Buckets"]: if bucket["Name"] == export_bucket: export_bucket_exists = True if not export_bucket_exists: s3.create_bucket(ACL="public-read-write", Bucket=export_bucket) # Save model files to S3 for root, dirs, files in os.walk(model_dir): for filename in files: local_path = os.path.join(root, filename) s3_path = os.path.relpath(local_path, model_dir) s3.upload_file( local_path, export_bucket, f"{model_name}/{model_version}/{s3_path}", ExtraArgs={"ACL": "public-read"}, ) response = s3.list_objects(Bucket=export_bucket) print(f"All objects in {export_bucket}:") for file in response["Contents"]: print("{}/{}".format(export_bucket, file["Key"])) ###Output _____no_output_____ ###Markdown How to Combine the Components into a PipelineNote that up to this point we have not yet used the Kubeflow Pipelines SDK!With our four components (i.e. self-contained funtions) defined, we can wire up the dependencies with Kubeflow Pipelines.The call [`components.func_to_container_op(f, base_image=img)(args)`](https://www.kubeflow.org/docs/pipelines/sdk/sdk-overview/) has the following ingredients:- `f` is the Python function that defines a component- `img` is the base (Docker) image used to package the function- `args` lists the arguments to `f`What the `*args` mean is best explained by going forward through the graph:- `downloadOp` is the very first step and has no dependencies; it therefore has no `InputPath`. Its output (i.e. `OutputPath`) is stored in `data_dir`.- `trainOp` needs the data downloaded from `downloadOp` and its signature lists `data_dir` (input) and `model_dir` (output). So, it _depends on_ `downloadOp.output` (i.e. the previous step's output) and stores its own outputs in `model_dir`, which can be used by another step. `downloadOp` is the parent of `trainOp`, as required.- `evaluateOp`'s function takes three arguments: `data_dir` (i.e. `downloadOp.output`), `model_dir` (i.e. `trainOp.output`), and `metrics_path`, which is where the function stores its evaluation metrics. That way, `evaluateOp` can only run after the successful completion of both `downloadOp` and `trainOp`.- `exportOp` runs the function `export_model`, which accepts five parameters: `model_dir`, `metrics`, `export_bucket`, `model_name`, and `model_version`. From where do we get the `model_dir`? It is nothing but `trainOp.output`. Similarly, `metrics` is `evaluateOp.output`. The remaining three arguments are regular Python arguments that are static for the pipeline: they do not depend on any step's output being available. Hence, they are defined without using `InputPath`. Since it is the last step of the pipeline, we also do not list any `OutputPath` for use in another step. ###Code def train_and_serve( data_dir: str, model_dir: str, export_bucket: str, model_name: str, model_version: int, ): # For GPU support, please add the "-gpu" suffix to the base image BASE_IMAGE = "mesosphere/kubeflow:1.0.1-0.3.1-tensorflow-2.2.0" downloadOp = components.func_to_container_op( download_dataset, base_image=BASE_IMAGE )() trainOp = components.func_to_container_op(train_model, base_image=BASE_IMAGE)( downloadOp.output ) evaluateOp = components.func_to_container_op(evaluate_model, base_image=BASE_IMAGE)( downloadOp.output, trainOp.output ) exportOp = components.func_to_container_op(export_model, base_image=BASE_IMAGE)( trainOp.output, evaluateOp.output, export_bucket, model_name, model_version ) # Create an inference server from an external component kfserving_op = components.load_component_from_url( "https://raw.githubusercontent.com/kubeflow/pipelines/8d738ea7ddc350e9b78719910982abcd8885f93f/components/kubeflow/kfserving/component.yaml" ) kfserving = kfserving_op( action="create", default_model_uri=f"s3://{export_bucket}/{model_name}", model_name="mnist", namespace=NAMESPACE, framework="tensorflow", ) kfserving.after(exportOp) ###Output _____no_output_____ ###Markdown Just in case it isn't obvious: this will build the Docker images for you.Each image is based on `BASE_IMAGE` and includes the Python functions as executable files.Each component _can_ use a different base image though.This may come in handy if you want to have reusable components for automatic data and/or model analysis (e.g. to investigate bias).Note that you did not have to use [Kubeflow Fairing](../fairing/Kubeflow%20Fairing.ipynb) or `docker build` locally at all! Remember when we said all dependencies have to be included in the base image? Well, that was not quite accurate. It's a good idea to have everything included and tested before you define and use your pipeline components to make sure that there are not dependency conflicts. There is, however, a way to add packages (packages_to_install) and additional code to execute before the function code (extra_code).Is that it?Not quite!We still have to define the pipeline itself.Our `train_and_serve` function defines dependencies but we must use the KFP domain-specific language (DSL) to register the pipeline with its four components: ###Code # See: https://github.com/kubeflow/kfserving/blob/master/docs/DEVELOPER_GUIDE.md#troubleshooting def op_transformer(op): op.add_pod_annotation(name="sidecar.istio.io/inject", value="false") return op @dsl.pipeline( name="End-to-End MNIST Pipeline", description="A sample pipeline to demonstrate multi-step model training, evaluation, export, and serving", ) def mnist_pipeline( model_dir: str = "/train/model", data_dir: str = "/train/data", export_bucket: str = "mnist", model_name: str = "mnist", model_version: int = 1, ): train_and_serve( data_dir=data_dir, model_dir=model_dir, export_bucket=export_bucket, model_name=model_name, model_version=model_version, ) dsl.get_pipeline_conf().add_op_transformer(op_transformer) ###Output _____no_output_____ ###Markdown With that in place, let's submit the pipeline directly from our notebook: ###Code pipeline_func = mnist_pipeline run_name = pipeline_func.__name__ + " run" experiment_name = "End-to-End MNIST Pipeline" arguments = { "model_dir": "/train/model", "data_dir": "/train/data", "export_bucket": "mnist", "model_name": "mnist", "model_version": "1", } client = kfp.Client() run_result = client.create_run_from_pipeline_func( pipeline_func, experiment_name=experiment_name, run_name=run_name, arguments=arguments, ) ###Output [I 200902 12:10:38 _client:267] Creating experiment End-to-End MNIST Pipeline. ###Markdown The graph will look like this:![Graph](./img/graph.png)If there are any issues with our pipeline definition, this is where they would flare up.So, until you submit it, you won't know if your pipeline definition is correct. We have so far claimed that Kubeflow Pipelines is for automation of multi-step (ad hoc) workflows and usage in CI/CD. You may have wondered why that is. After all, it is possible to set up recurring runs of pipelines. The reason is that these pipeline steps are one-offs. Even though you can parameterize each step, including the ones that kick off an entire pipeline, there is no orchestration of workflows. Stated differently, if a step fails, there is no mechanism for automatic retries. Nor is there any support for marking success: if the step is scheduled to be run again, it will be run again, whether or not the previous execution was successful, obviating any subsequent runs (except in cases where it may be warranted). Kubeflow Pipelines allows retries but it is not configurable out of the box. If you want Airflow- or Luigi-like behaviour for dependency management of workflows, Kubeflow Pipelines is not the tool. How to Predict with the Inference ServerThe simplest way to check that our inference server is up and running is to check it with `curl` ( pre-installed on the cluster).To do so, let's define a few helper functions for plotting and displaying images: ###Code import matplotlib.pyplot as plt def display_image(x_test, image_index): plt.imshow(x_test[image_index].reshape(28, 28), cmap="binary") def predict_number(model, x_test, image_index): pred = model.predict(x_test[image_index : image_index + 1]) print(pred.argmax()) import tensorflow as tf (x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data() x_test = x_test / 255.0 # We must transform the data in the same way as before! image_index = 1005 display_image(x_test, image_index) ###Output Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step ###Markdown The inference server expects a JSON payload: ###Code import codecs, json tf_serving_req = {"instances": x_test[image_index : image_index + 1].tolist()} with open("input.json", "w") as json_file: json.dump(tf_serving_req, json_file) model = "mnist" url = f"http://{model}-predictor-default.{NAMESPACE}.svc.cluster.local/v1/models/{model}:predict" ! curl -L $url [email protected] ###Output { "predictions": [[1.40836079e-07, 5.1750153e-06, 2.76334504e-06, 0.00259963516, 0.00124566338, 4.93358129e-06, 1.92605313e-07, 0.000128401283, 0.00166672678, 0.994346321] ] }
twitter_analysis2.ipynb	###Markdown snatwitter-searchhashtag.py ###Code from twitter import * import networkx as nx import json import os # Clear screen os.system('cls' if os.name=='nt' else 'clear') graph=nx.DiGraph() print("") print(".....................................................") print ("RT NETWORK OF AN HASHTAG") print("") hashtag = "#priyans49767484" # Log in OAUTH_TOKEN = "793203628429438978-o1Gs0rjBN3TesBu6cV5muiic15XeZpl" OAUTH_SECRET = "GVyujMi5n0gE0QE2R2fWK6R7wwxE3R2olAr4s0xd1NCnh" CONSUMER_KEY = "hCsfln5TQNt3p39CDC3dCJf6d" CONSUMER_SECRET = "7G3Q5a7Q33D8ENP2oI4ef1Earv4WfEldaPA1eaeR69NtblDQYY" auth = OAuth(OAUTH_TOKEN, OAUTH_SECRET, CONSUMER_KEY, CONSUMER_SECRET) twitter = Twitter(auth = auth) # search # https://dev.twitter.com/docs/api/1.1/get/search/tweets query = twitter.search.tweets(q=hashtag, count=100) # Debug line #print json.dumps(query, sort_keys=True, indent=4) # Print results print("Search complete (%f seconds)" % (query["search_metadata"]["completed_in"])) print("Found",len(query["statuses"]),"results.") # Get results and find retweets and mentions for result in query["statuses"]: print ("") print ("Tweet:",result["text"]) print ("By user:",result["user"]["name"]) if len(result["entities"]["user_mentions"]) != 0: print ("Mentions:") for i in result["entities"]["user_mentions"]: print (" - by",i["screen_name"]) graph.add_edge(i["screen_name"],result["user"]["name"]) if "retweeted_status" in result: if len(result["retweeted_status"]["entities"]["user_mentions"]) != 0: print( "Retweets:") for i in result["retweeted_status"]["entities"]["user_mentions"]: print (" - by",i["screen_name"]) graph.add_edge(i["screen_name"],result["user"]["name"]) else: pass # Save graph print( "") print ("The network of RT of the hashtag was analyzed succesfully.") print( "") print ("Saving the file as "+hashtag+"-rt-network.gexf...") nx.write_gexf(graph,"/home/"+ hashtag+"-rt-network.gexf") nx.write_gexf(graph,"/home/"+ hashtag+"-rt-network.txt") ###Output _____no_output_____
playbooks/windows/02_execution/T1035_service_execution/remote_service_creation.ipynb	###Markdown Remote Service Creation Playbook TagsID: WINEXEC190815181010Author: Roberto Rodriguez [@Cyb3rWard0g](https://twitter.com/Cyb3rWard0g)References: WINEXEC190813181010 ATT&CK TagsTactic: Execution, Lateral MovementTechnique: Service Execution (T1035) Applies To Technical DescriptionAdversaries may execute a binary, command, or script via a method that interacts with Windows services, such as the Service Control Manager. This can be done by by adversaries creating a new service. Adversaries can create services remotely to execute code and move lateraly across the environment. Permission RequiredAdministrator HypothesisAdversaries might be creating new services remotely to execute code and move laterally in my environment Attack Simulation Dataset\| Environment\| Name \| Description \|\|--------\|---------\|---------\|\| [Shire](https://github.com/Cyb3rWard0g/mordor/tree/acf9f6be6a386783a20139ceb2faf8146378d603/environment/shire) \| [empire_invoke_psexec](https://github.com/Cyb3rWard0g/mordor/blob/master/small_datasets/windows/execution/service_execution_T1035/empire_invoke_psexec.md) \| A mordor dataset to simulate an adversary creating a service \| Recommended Data Sources\| Event ID \| Event Name \| Log Provider \| Audit Category \| Audit Sub-Category \| ATT&CK Data Source \|\|---------\|---------\|----------\|----------\|---------\|---------\|\| [4697](https://docs.microsoft.com/en-us/windows/security/threat-protection/auditing/event-4697) \| A service was installed in the system \| Microsoft-Windows-Security-Auditing \| \| \| Windows Services \|\| [4624](https://github.com/Cyb3rWard0g/OSSEM/blob/master/data_dictionaries/windows/security/events/event-4624.md) \| An account was successfully logged on \| Microsoft-Windows-Security-Auditing \| Audit Logon/Logoff \| Audit Logon \| Windows Event Logs \| Data Analytics Initialize Analytics Engine ###Code from openhunt.logparser import winlogbeat from pyspark.sql import SparkSession win = winlogbeat() spark = SparkSession.builder.appName("Mordor").config("spark.sql.caseSensitive", "True").getOrCreate() print(spark) ###Output <pyspark.sql.session.SparkSession object at 0x7fe65115b198> ###Markdown Prepare & Process Mordor File ###Code mordor_file = win.extract_nested_fields("mordor/small_datasets/empire_invoke_psexec_2019-05-18210652.json",spark) ###Output [+] Processing a Spark DataFrame.. [+] Reading Mordor file.. [+] Processing Data from Winlogbeat version 6.. [+] DataFrame Returned ! ###Markdown Register Mordor DataFrame as a SQL temporary view ###Code mordor_file.createOrReplaceTempView("mordor_file") ###Output _____no_output_____ ###Markdown Validate Analytic I\| FP Rate \| Source \| Analytic Logic \| Description \|\|--------\|---------\|---------\|---------\|\| Low \| Sysmon \| SELECT o.`@timestamp`, o.computer_name, o.SubjectUserName, o.SubjectUserName, o.ServiceName, a.IpAddress FROM mordor_file o INNER JOIN (SELECT computer_name,TargetUserName,TargetLogonId,IpAddress FROM mordor_file WHERE channel = "Security" AND LogonType = 3 AND IpAddress is not null AND NOT TargetUserName LIKE "%$") a ON o.SubjectLogonId = a.TargetLogonId WHERE o.channel = "Security" AND o.event_id = 4697 \| Look for new services being created in your environment under a network logon session (3). That is a sign that the service creation was performed from another endpoint in the environment \| ###Code security_4697_4624_df = spark.sql( ''' SELECT o.`@timestamp`, o.computer_name, o.SubjectUserName, o.SubjectUserName, o.ServiceName, a.IpAddress FROM mordor_file o INNER JOIN ( SELECT computer_name,TargetUserName,TargetLogonId,IpAddress FROM mordor_file WHERE channel = "Security" AND LogonType = 3 AND IpAddress is not null AND NOT TargetUserName LIKE "%$" ) a ON o.SubjectLogonId = a.TargetLogonId WHERE o.channel = "Security" AND o.event_id = 4697 ''' ) security_4697_4624_df.show(20,False) ###Output +------------------------+---------------+---------------+---------------+-----------+-------------+ \|@timestamp \|computer_name \|SubjectUserName\|SubjectUserName\|ServiceName\|IpAddress \| +------------------------+---------------+---------------+---------------+-----------+-------------+ \|2019-05-18T21:07:23.035Z\|IT001.shire.com\|pgustavo \|pgustavo \|Updater \|172.18.39.106\| +------------------------+---------------+---------------+---------------+-----------+-------------+
gpt-pandas-code-generation.ipynb	###Markdown Adding Examples for GPT Model ###Code gpt.add_example(Example('How many unique values in Division Column?', 'df["Division"].nunique()')) gpt.add_example(Example('Find the Division of boy who scored 55 marks', 'df.loc[(df.loc[:, "Gender"] == "boy") & (df.loc[:, "Marks"] == 55), "Division"]')) gpt.add_example(Example('Find the average Marks scored by Girls', 'np.mean(df.loc[(df.loc[:, "Gender"] == "girl"), "Marks"])')) ###Output _____no_output_____ ###Markdown Example 1 ###Code prompt = "Display Division of girl who scored maximum marks" print(gpt.get_top_reply(prompt)) df.loc[(df.loc[:, "Gender"] == "girl") & (df.loc[:, "Marks"] == max(df.loc[:, "Marks"])), "Division"] ###Output _____no_output_____ ###Markdown Example 2 ###Code prompt = "Find the median Marks scored by Boys" print(gpt.get_top_reply(prompt)) np.median(df.loc[(df.loc[:, "Gender"] == "boy"), "Marks"]) ###Output _____no_output_____
US Stocks Performance Analysis/StockDataAnalysis.ipynb	###Markdown Extracting Stock Data Using a Python Library 1. Importing libraries ###Code !pip install yfinance==0.1.67 #!pip install pandas==1.3.3 import yfinance as yf import pandas as pd ###Output _____no_output_____ ###Markdown 2.1. Using the yfinance Library to Extract Stock Data of Apple Using the `Ticker` module we can create an object that will allow us to access functions to extract data. To do this we need to provide the ticker symbol for the stock, here the company is Apple and the ticker symbol is `AAPL`. ###Code apple = yf.Ticker("AAPL") ###Output _____no_output_____ ###Markdown Now we can access functions and variables to extract the type of data we need. You can view them and what they represent here [https://aroussi.com/post/python-yahoo-finance](https://aroussi.com/post/python-yahoo-finance?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkPY0220ENSkillsNetwork23455606-2021-01-01). Stock Info Using the attribute info we can extract information about the stock as a Python dictionary. ###Code apple_info=apple.info apple_info ###Output _____no_output_____ ###Markdown We can get the 'country' using the key country ###Code apple_info['country'] ###Output _____no_output_____ ###Markdown Extracting Share Price A share is the single smallest part of a company's stock that you can buy, the prices of these shares fluctuate over time. Using the history() method we can get the share price of the stock over a certain period of time. Using the `period` parameter we can set how far back from the present to get data. The options for `period` are 1 day (1d), 5d, 1 month (1mo) , 3mo, 6mo, 1 year (1y), 2y, 5y, 10y, ytd, and max. ###Code apple_share_price_data = apple.history(period="max") ###Output _____no_output_____ ###Markdown The format that the data is returned in is a Pandas DataFrame. With the `Date` as the index the share `Open`, `High`, `Low`, `Close`, `Volume`, and `Stock Splits` are given for each day. ###Code apple_share_price_data.head() ###Output _____no_output_____ ###Markdown We can reset the index of the DataFrame with the `reset_index` function. We also set the `inplace` paramter to `True` so the change takes place to the DataFrame itself. ###Code apple_share_price_data.reset_index(inplace=True) ###Output _____no_output_____ ###Markdown We can plot the `Open` price against the `Date`: ###Code apple_share_price_data.plot(x="Date", y="Open") ###Output _____no_output_____ ###Markdown Extracting Dividends Dividends are the distribution of a companys profits to shareholders. In this case they are defined as an amount of money returned per share an investor owns. Using the variable `dividends` we can get a dataframe of the data. The period of the data is given by the period defined in the 'history\` function. ###Code apple.dividends ###Output _____no_output_____ ###Markdown We can plot the dividends overtime: ###Code apple.dividends.plot() ###Output _____no_output_____ ###Markdown 2.2. Using the yfinance Library to Extract Stock Data of AMD Now using the `Ticker` module create an object for AMD (Advanced Micro Devices) with the ticker symbol is `AMD` called; name the object amd. ###Code AMD = yf.Ticker("amd") ###Output _____no_output_____ ###Markdown Question 1 Use the key 'country' to find the country the stock belongs to, remember it as it will be a quiz question. ###Code AMD_info=AMD.info AMD_info AMD_info['country'] ###Output _____no_output_____ ###Markdown Question 2 Use the key 'sector' to find the sector the stock belongs to, remember it as it will be a quiz question. ###Code AMD_info['sector'] ###Output _____no_output_____ ###Markdown Question 3 Obtain stock data for AMD using the `history` function, set the `period` to max. Find the `Volume` traded on the first day (first row). ###Code AMD_share_price_data = AMD.history(period="max") AMD_share_price_data.head() AMD_share_price_data.reset_index(inplace=True) AMD_share_price_data.plot(x="Date", y="Open") AMD.dividends #AMD.dividends.plot() ###Output _____no_output_____
04_HowTos/FileService/How_to_use_the_File_Services.ipynb	###Markdown How to Use the Data Lab Public File Services_Mike Fitzpatrick and Glenn Eychaner_Revised: Jan 03, 2019Files in the virtual storage are usually identified via the prefix "_vos://_". This shorthand identifier is resolved to a user's home directory of the storage space in the service. If the "_vos://_" prefix is instead the name of another user (e.g. "_geychaner://_", and the remainder of the path grants public or group read/write access, then the other user's spaces will be accessed. Most user spaces have a "_/public_" directory to facilitate file sharing (e.g. '_geychaner://public/foo.fits_' will access the '_foo.fits_' file from user '_geychaner_'). Users can make any file (or directory) public by moving it to (or creating a link in) their "/public" directory._Public file services_ are specially created areas where all files are world-readable, and are used for serving files from Data Lab datasets. ###Code # Make matplotlib plot inline %matplotlib inline # Standard DL imports, note we only need storeClient from dl import storeClient as sc # 3rd Party Imports import io import numpy as np from matplotlib import pyplot as p from astropy.io import fits ###Output _____no_output_____ ###Markdown Listing another user's 'public/' folder in their vospaceThe user in our example is 'demo00' ###Code print(sc.ls ('demo00://public', format='short')) ###Output test2.csv test3.csv test6.csv ###Markdown An example using the SDSS DR14 public file service.A 'file service' is a _public_ vospace, readable by all users. Set base directory and plate number ###Code # Set the base directory and plate number # These can be found by explring the SDSS DR14 space using 'sc.ls()' print(sc.ls ('sdss_dr14://')) print(sc.ls ('sdss_dr14://eboss')) print(sc.ls ('sdss_dr14://eboss/spectro')) print(sc.ls ('sdss_dr14://eboss/spectro/redux')) base = 'sdss_dr14://eboss/spectro/redux/v5_10_0/' plate = '3615' ###Output apo,apogee,eboss,env,manga,marvels,sdss calib,elg,lss,lya,photo,photoObj,qso,resolve,spectro,spiders,sweeps,target data,firefly,redux images,platelist-mjdsort.html,platelist-mjdsort.txt,platelist.fits,platelist.html,platelist.txt,platequality-mjdsort.html,platequality-mjdsort.txt,platequality.html,platequality.txt,redmonster,v5_10_0 ###Markdown List all available FITS plate files in the plate directory ###Code # Construct the vospace path to the plate directory spPlate = base + plate + '/spPlate-' + plate print(sc.ls (spPlate + '.fits', format='short')) ###Output spPlate-3615-55179.fits spPlate-3615-55208.fits spPlate-3615-55445.fits spPlate-3615-55856.fits spPlate-3615-56219.fits spPlate-3615-56544.fits ###Markdown Pick a modified Julian date and fiber ###Code mjd = '56544' fiber = 39 # Construct the vospace path to the plate file and verify spfile = spPlate + '-' + mjd + '.fits' print ('File: ' + spfile) print (sc.ls (spfile)) ###Output File: sdss_dr14://eboss/spectro/redux/v5_10_0/3615/spPlate-3615-56544.fits spPlate-3615-56544.fits ###Markdown Now read the spectrum from the file and construct the wavelength array ###Code try: with fits.open(sc.get(spfile, mode='fileobj')) as hdulist: hdr = hdulist[0].header flux = hdulist[0].data[fiber-1, :] ivar = hdulist[1].data[fiber-1, :] sky = hdulist[6].data[fiber-1, :] except Exception as e: raise ValueError("Could not find spPlate file for plate={0:s}, mjd={1:s}!".format(plate, mjd)) loglam = hdr['COEFF0'] + hdr['COEFF1']np.arange(hdr['NAXIS1'], dtype=flux.dtype) wavelength = 10.0*loglam print ("{} {} {}".format(len(flux),len(ivar),len(wavelength))) ###Output 4645 4645 4645 ###Markdown Make a plot of the spectrum ###Code p.plot(wavelength, flux (ivar > 0), 'k') p.xlabel('Angstroms') p.ylabel('Flux') ###Output _____no_output_____ ###Markdown List all available public file spacesThe '_sc.services()_' function allows a user to list all the available file services. ###Code print(sc.services()) ###Output name svc description -------- ---- -------- chandra vos ChaMPlane: Measuring the Faint X-ray Bin ... cosmic_dawn vos Cosmic DAWN survey deeprange vos Deeprange Survey deep_ecliptic vos Depp Ecliptic Survey dls vos Deep Lens Survey flamex vos FLAMINGOS Extragalactic Survey fls vos First Look Survey fsvs vos Faint Sky Variability Survey ir_bootes vos Infrared Bootes Imaging Survey lgs vos Local Group Survey lmc vos SuperMACHO Survey ls_dr1 vos DECam Legacy Survey DR1 ls_dr2 vos DECam Legacy Survey DR2 ls_dr3 vos DECam Legacy Survey DR3 ls_dr4 vos DECam Legacy Survey DR4 ls_dr5 vos DECam Legacy Survey DR5 ls_dr6 vos DECam Legacy Survey DR6 ls_dr7 vos DECam Legacy Survey DR7 ls_dr8 vos DECam Legacy Survey DR8 m31_newfirm vos M31 NEWFIRM Survey ndwfs vos NOAO Deep-Wide Survey nfp vos NOAO Fundamental Plane Survey nmbs vos NEWFIRM Medium Band Survey nmbs_2 vos NEWFIRM Medium Band Survey II nsc vos NOAO Source Catalog sdss_dr14 vos SDSS DR14 sdss_dr16 vos SDSS DR16 singg vos Survey for Ionization in Neutral-Gas Gal ... smash_dr1 vos SMASH DR1 smash_dr2 vos SMASH DR2 sze vos SZE+Optical Studies of the Cosmic Accele ... w_project vos The w Project zbootes vos z-band Photometry of the NOAO Deep-Wide ... ###Markdown How to Use the Data Lab Public File Services_Mike Fitzpatrick and Glenn Eychaner_Revised: Jan 03, 2019Files in the virtual storage are usually identified via the prefix "_vos://_". This shorthand identifier is resolved to a user's home directory of the storage space in the service. If the "_vos://_" prefix is instead the name of another user (e.g. "_geychaner://_", and the remainder of the path grants public or group read/write access, then the other user's spaces will be accessed. Most user spaces have a "_/public_" directory to facilitate file sharing (e.g. '_geychaner://public/foo.fits_' will access the '_foo.fits_' file from user '_geychaner_'). Users can make any file (or directory) public by moving it to (or creating a link in) their "/public" directory._Public file services_ are specially created areas where all files are world-readable, and are used for serving files from Data Lab datasets. ###Code # Make matplotlib plot inline %matplotlib inline # Standard DL imports, note we only need storeClient from dl import storeClient as sc # 3rd Party Imports import io import numpy as np from matplotlib import pyplot as p from astropy.io import fits ###Output _____no_output_____ ###Markdown Listing another user's public file space ###Code print(sc.ls ('geychaner://public', format='short')) ###Output grzw1_3sn10_29M.jpg grzw1_sn10_15M.jpg ###Markdown An example using the SDSS DR14 public file service. Set base directory and plate number ###Code # Set the base directory and plate number # These can be found by explring the SDSS DR14 space using 'sc.ls()' print(sc.ls ('sdss_dr14://')) print(sc.ls ('sdss_dr14://eboss')) print(sc.ls ('sdss_dr14://eboss/spectro')) print(sc.ls ('sdss_dr14://eboss/spectro/redux')) base = 'sdss_dr14://eboss/spectro/redux/v5_10_0/' plate = '3615' ###Output apo,apogee,eboss,env,manga,marvels,sdss calib,elg,lss,lya,photo,photoObj,qso,resolve,spectro,spiders,sweeps,target data,firefly,redux images,platelist-mjdsort.html,platelist-mjdsort.txt,platelist.fits,platelist.html,platelist.txt,platequality-mjdsort.html,platequality-mjdsort.txt,platequality.html,platequality.txt,redmonster,v5_10_0 ###Markdown List all available FITS plate files in the plate directory ###Code # Construct the vospace path to the plate directory spPlate = base + plate + '/spPlate-' + plate print(sc.ls (spPlate + '.fits', format='short')) ###Output spPlate-3615-55179.fits spPlate-3615-55208.fits spPlate-3615-55445.fits spPlate-3615-55856.fits spPlate-3615-56219.fits spPlate-3615-56544.fits ###Markdown Pick a modified Julian date and fiber ###Code mjd = '56544' fiber = 39 # Construct the vospace path to the plate file and verify spfile = spPlate + '-' + mjd + '.fits' print ('File: ' + spfile) print (sc.ls (spfile)) ###Output File: sdss_dr14://eboss/spectro/redux/v5_10_0/3615/spPlate-3615-56544.fits spPlate-3615-56544.fits ###Markdown Now read the spectrum from the file and construct the wavelength array ###Code try: with fits.open(sc.get(spfile, mode='fileobj')) as hdulist: hdr = hdulist[0].header flux = hdulist[0].data[fiber-1, :] ivar = hdulist[1].data[fiber-1, :] sky = hdulist[6].data[fiber-1, :] except Exception as e: raise ValueError("Could not find spPlate file for plate={0:s}, mjd={1:s}!".format(plate, mjd)) loglam = hdr['COEFF0'] + hdr['COEFF1']np.arange(hdr['NAXIS1'], dtype=flux.dtype) wavelength = 10.0*loglam print ("{} {} {}".format(len(flux),len(ivar),len(wavelength))) ###Output 4645 4645 4645 ###Markdown Make a plot of the spectrum ###Code p.plot(wavelength, flux (ivar > 0), 'k') p.xlabel('Angstroms') p.ylabel('Flux') ###Output _____no_output_____ ###Markdown List all available public file spacesThe '_sc.services()_' function allows a user to list all the available file services. ###Code print(sc.services()) ###Output name svc description -------- ---- -------- chandra vos ChaMPlane: Measuring the Faint X-ray Bin ... cosmic_dawn vos Cosmic DAWN survey deeprange vos Deeprange Survey deep_ecliptic vos Depp Ecliptic Survey dls vos Deep Lens Survey flamex vos FLAMINGOS Extragalactic Survey fls vos First Look Survey fsvs vos Faint Sky Variability Survey ir_bootes vos Infrared Bootes Imaging Survey lgs vos Local Group Survey lmc vos SuperMACHO Survey ls_dr1 vos DECam Legacy Survey DR1 ls_dr2 vos DECam Legacy Survey DR2 ls_dr3 vos DECam Legacy Survey DR3 ls_dr4 vos DECam Legacy Survey DR4 ls_dr5 vos DECam Legacy Survey DR5 ls_dr6 vos DECam Legacy Survey DR6 ls_dr7 vos DECam Legacy Survey DR7 m31_newfirm vos M31 NEWFIRM Survey ndwfs vos NOAO Deep-Wide Survey nfp vos NOAO Fundamental Plane Survey nmbs vos NEWFIRM Medium Band Survey nmbs_2 vos NEWFIRM Medium Band Survey II sdss_dr14 vos SDSS DR14 singg vos Survey for Ionization in Neutral-Gas Gal ... smash_dr1 vos SMASH DR1 sze vos SZE+Optical Studies of the Cosmic Accele ... w_project vos The w Project ###Markdown How to Use the Data Lab Public File Services_Mike Fitzpatrick, Glenn Eychaner, Robert Nikutta_Files in the virtual storage are usually identified via the prefix "_vos://_". This shorthand identifier is resolved to a user's home directory of the storage space in the service. If the "_vos://_" prefix is instead the name of another user (e.g. "_demo01://_", and the remainder of the path grants public or group read/write access, then the other user's spaces will be accessed. Most user spaces have a "_/public_" directory to facilitate file sharing (e.g. '_demo01://public/foo.fits_' will access the '_foo.fits_' file from user '_demo01_'). Users can make any file (or directory) public by moving it to (or creating a link in) their "/public" directory._Public file services_ are specially created areas where all files are world-readable, and are used for serving files from Data Lab datasets. ###Code # Make matplotlib plot inline %matplotlib inline # Standard DL imports, note we only need storeClient from dl import storeClient as sc # 3rd Party Imports import io import numpy as np from matplotlib import pyplot as p from astropy.io import fits ###Output _____no_output_____ ###Markdown Listing another user's 'public/' folder in their vospaceThe user in our example is 'demo00' ###Code print(sc.ls ('demo00://public', format='short')) ###Output test2.csv test3.csv test6.csv ###Markdown An example using the SDSS DR14 public file service.A 'file service' is a _public_ vospace, readable by all users. Set base directory and plate number ###Code # Set the base directory and plate number # These can be found by explring the SDSS DR14 space using 'sc.ls()' print(sc.ls ('sdss_dr14://')) print(sc.ls ('sdss_dr14://eboss')) print(sc.ls ('sdss_dr14://eboss/spectro')) print(sc.ls ('sdss_dr14://eboss/spectro/redux')) base = 'sdss_dr14://eboss/spectro/redux/v5_10_0/' plate = '3615' ###Output apo,apogee,eboss,env,manga,marvels,sdss calib,elg,lss,lya,photo,photoObj,qso,resolve,spectro,spiders,sweeps,target data,firefly,redux images,platelist-mjdsort.html,platelist-mjdsort.txt,platelist.fits,platelist.html,platelist.txt,platequality-mjdsort.html,platequality-mjdsort.txt,platequality.html,platequality.txt,redmonster,v5_10_0 ###Markdown List all available FITS plate files in the plate directory ###Code # Construct the vospace path to the plate directory spPlate = base + plate + '/spPlate-' + plate print(sc.ls (spPlate + '.fits', format='short')) ###Output spPlate-3615-55179.fits spPlate-3615-55208.fits spPlate-3615-55445.fits spPlate-3615-55856.fits spPlate-3615-56219.fits spPlate-3615-56544.fits ###Markdown Pick a modified Julian date and fiber ###Code mjd = '56544' fiber = 39 # Construct the vospace path to the plate file and verify spfile = spPlate + '-' + mjd + '.fits' print ('File: ' + spfile) print (sc.ls (spfile)) ###Output File: sdss_dr14://eboss/spectro/redux/v5_10_0/3615/spPlate-3615-56544.fits spPlate-3615-56544.fits ###Markdown Now read the spectrum from the file and construct the wavelength array ###Code try: with fits.open(sc.get(spfile, mode='fileobj')) as hdulist: hdr = hdulist[0].header flux = hdulist[0].data[fiber-1, :] ivar = hdulist[1].data[fiber-1, :] sky = hdulist[6].data[fiber-1, :] except Exception as e: raise ValueError("Could not find spPlate file for plate={0:s}, mjd={1:s}!".format(plate, mjd)) loglam = hdr['COEFF0'] + hdr['COEFF1']np.arange(hdr['NAXIS1'], dtype=flux.dtype) wavelength = 10.0*loglam print ("{} {} {}".format(len(flux),len(ivar),len(wavelength))) ###Output 4645 4645 4645 ###Markdown Make a plot of the spectrum ###Code p.plot(wavelength, flux (ivar > 0), 'k') p.xlabel('Angstroms') p.ylabel('Flux') ###Output _____no_output_____ ###Markdown List all available public file spacesThe '_sc.services()_' function allows a user to list all the available file services. ###Code print(sc.services()) ###Output name svc description -------- ---- -------- nfp vos NOAO Fundamental Plane Survey chandra vos ChaMPlane: Measuring the Faint X-ray Bin ... cosmic_dawn vos Cosmic DAWN survey deeprange vos Deeprange Survey deep_ecliptic vos Deep Ecliptic Survey des_dr2 vos Dark Energy Survey DR2 desi_ets vos DESI Early Target Selection dls vos Deep Lens Survey flamex vos FLAMINGOS Extragalactic Survey fls vos First Look Survey fsvs vos Faint Sky Variability Survey ir_bootes vos Infrared Bootes Imaging Survey lgs vos Local Group Survey gogreen_dr1 vos GOGREEN DR1 Survey lmc vos SuperMACHO Survey ls_dr1 vos DECam Legacy Survey DR1 ls_dr2 vos DECam Legacy Survey DR2 ls_dr3 vos DECam Legacy Survey DR3 ls_dr4 vos DECam Legacy Survey DR4 ls_dr5 vos DECam Legacy Survey DR5 ls_dr6 vos DECam Legacy Survey DR6 ls_dr7 vos DECam Legacy Survey DR7 ls_dr8 vos DECam Legacy Survey DR8 ls_dr9 vos DECam Legacy Survey DR9 ls_dr9sv vos DECam Legacy Survey DR9sv m31_newfirm vos M31 NEWFIRM Survey ndwfs vos NOAO Deep-Wide Survey nmbs vos NEWFIRM Medium Band Survey nmbs_2 vos NEWFIRM Medium Band Survey II nsc vos NOAO Source Catalog sdss_dr8 vos SDSS DR8 sdss_dr9 vos SDSS DR9 sdss_dr10 vos SDSS DR10 sdss_dr11 vos SDSS DR11 sdss_dr12 vos SDSS DR12 sdss_dr13 vos SDSS DR13 sdss_dr14 vos SDSS DR14 sdss_dr15 vos SDSS DR15 sdss_dr16 vos SDSS DR16 singg vos Survey for Ionization in Neutral-Gas Gal ... smash_dr1 vos SMASH DR1 smash_dr2 vos SMASH DR2 sze vos SZE+Optical Studies of the Cosmic Accele ... w_project vos The w Project zbootes vos z-band Photometry of the NOAO Deep-Wide ...
notebooks/ISIS Serial Numbers.ipynb	###Markdown Generate the dataThe next three cells take a directory of cleaned `.trn` files (extra values like AUTO or OPTIONAL removed) and generate a `data.db` database of ISIS serial number translations. ###Code # Database population and a declared class Base = declarative.declarative_base() class Translations(Base): __tablename__ = 'isis_translations' id = sqlalchemy.Column(sqlalchemy.INTEGER, primary_key=True) mission = sqlalchemy.Column(sqlalchemy.String) instrument = sqlalchemy.Column(sqlalchemy.String) translation = sqlalchemy.Column(NestedJsonObject) def __init__(self, mission, instrument, translation): self.mission = mission self.instrument = instrument self.translation = translation class StringToMission(Base): __tablename__ = 'isis_mission_to_standard' id = sqlalchemy.Column(sqlalchemy.INTEGER, primary_key=True) key = sqlalchemy.Column(sqlalchemy.String) value = sqlalchemy.Column(sqlalchemy.String) def __init__(self, key, value): self.key = key self.value = value engine = sqlalchemy.create_engine('sqlite:///data.db') Base.metadata.bind = engine Base.metadata.create_all() session = orm.sessionmaker(bind=engine)() files = glob.glob('../autocnet/examples/serial_number_translations/.trn') for f in files: p = pvl.load(f) name = os.path.basename(f[:-16]) try: v = re.findall("([a-z, 0-9])([A-Z, a-z, 0-9])", name)[0] mission, instrument = v except: v = re.findall("[a-z, 0-9]", name) mission = v[0] instrument = None r = Translations(mission, instrument, p) session.add(r) session.commit() # Build the mission names lookup table v = """ Group = MissionName InputKey = SpacecraftName InputGroup = "IsisCube,Instrument" InputPosition = (IsisCube, Instrument) Translation = (Aircraft, "Aircraft") Translation = (Apollo15, "APOLLO 15") Translation = (Apollo15, "APOLLO15") Translation = (Apollo16, "APOLLO 16") Translation = (Apollo16, "APOLLO16") Translation = (Apollo17, "APOLLO 17") Translation = (Apollo17, "APOLLO17") Translation = (Cassini, Cassini-Huygens) # Translation = (Chan1, "CHANDRAYAAN-1 ORBITER") # Translation = (Chan1, CHANDRAYAAN1_ORBITER) # Translation = (Chan1, CHANDRAYAAN-1) Translation = (Chandrayaan1, "CHANDRAYAAN-1 ORBITER") Translation = (Chandrayaan1, CHANDRAYAAN1_ORBITER) Translation = (Chandrayaan1, CHANDRAYAAN-1) Translation = (Clementine1, CLEMENTINE_1) Translation = (Clementine1, "CLEMENTINE 1") Translation = (Dawn, "DAWN") Translation = (Galileo, "Galileo Orbiter") Translation = (Hayabusa, HAYABUSA) Translation = (Ideal, IdealSpacecraft) Translation = (Kaguya, KAGUYA) Translation = (Kaguya, SELENE-M) Translation = (Lo, "Lunar Orbiter 3") Translation = (Lo, "Lunar Orbiter 4") Translation = (Lo, "Lunar Orbiter 5") Translation = (Lro, "LUNAR RECONNAISSANCE ORBITER") Translation = (Lro, "Lunar Reconnaissance Orbiter") Translation = (Mariner10, Mariner_10) Translation = (Mariner10, MARINER_10) Translation = (Mer, "MARS EXPLORATION ROVER 1") Translation = (Mer, MARS_EXPLORATION_ROVER_1) Translation = (Mer, "MARS EXPLORATION ROVER 2") Translation = (Mer, "SIMULATED MARS EXPLORATION ROVER 1") Translation = (Mer, "SIMULATED MARS EXPLORATION ROVER 2") Translation = (Messenger, MESSENGER) Translation = (Messenger, Messenger) Translation = (Mex, "MARS EXPRESS") Translation = (Mex, "Mars Express") Translation = (Mgs, MARSGLOBALSURVEYOR) Translation = (Mgs, "MARS GLOBAL SURVEYOR") Translation = (Mro, "MARS RECONNAISSANCE ORBITER") Translation = (Mro, Mars_Reconnaissance_Orbiter) Translation = (NewHorizons, "NEW HORIZONS") Translation = (Near, NEAR) Translation = (Near, "NEAR EARTH ASTEROID RENDEZVOUS") Translation = (Odyssey, MARS_ODYSSEY) Translation = (OsirisRex, OSIRIS-REX) Translation = (Smart1, SMART1) Translation = (Viking1, VIKING_ORBITER_1) Translation = (Viking2, VIKING_ORBITER_2) Translation = (Voyager1, VOYAGER_1) Translation = (Voyager2, VOYAGER_2) End_Group End """ p = pvl.loads(v) for k, v in p['MissionName'].items(): if k == 'Translation': r = StringToMission(v[1], v[0]) session.add(r) session.commit() ###Output _____no_output_____ ###Markdown Sample Query ###Code # Sample querying the database for i, j, t in session.query(Translations.mission, Translations.instrument, Translations.translation): print(i,j) d = PVLModule(t) print(d) break ###Output _____no_output_____ ###Markdown Testing code to prototype the functionality now in autocnet ###Code class SerialNumberDecoder(pvl.decoder.PVLDecoder): """ A PVL Decoder class to handle cube label parsing for the purpose of creating a valid ISIS serial number. Inherits from the PVLDecoder in planetarypy's pvl module. """ def cast_unquoated_string(self, value): """ Overrides the parent class's method so that any un-quoted string type value found in the parsed pvl will just return the original value. This is needed so that keyword values are not re-formatted from what is originally in the ISIS cube label. Note: This affects value types that are recognized as null, boolean, number, datetime, et at. """ return value.decode('utf-8') def get_isis_translation(label): """ Compute the ISIS serial number for a given image using the input cube or the label extracted from the cube. Parameters ---------- label : dict or str A PVL dict object or file name to extract the PVL object from Returns ------- translation : dict A PVLModule object containing the extracted translation file """ if not isinstance(label, PVLModule): label = pvl.load(label) cube_obj = find_in_dict(label, 'Instrument') # Grab the spacecraft name and run it through the ISIS lookup spacecraft_name = find_in_dict(cube_obj, 'SpacecraftName') for row in session.query(StringToMission).filter(StringToMission.key==spacecraft_name): spacecraft_name = row.value.lower() #Try and pull an instrument identifier try: instrumentid = find_in_dict(cube_obj, 'InstrumentId').capitalize() except: instrumentid = None # Grab the translation PVL object using the lookup for row in session.query(Translations).filter(Translations.mission==spacecraft_name, Translations.instrument==instrumentid): # Convert the JSON back to a PVL object translation = PVLModule(row.translation) return translation def extract_subgroup(data, key_list): return reduce(lambda d, k: d[k], key_list, data) def generate_serial_number(label): if not isinstance(label, PVLModule): label = pvl.load(label, cls=SerialNumberDecoder) # Get the translation information translation = get_isis_translation(label) serial_number = [] # Sort the keys to ensure proper iteration order keys = sorted(translation.keys()) for k in keys: group = translation[k] search_key = group['InputKey'] search_position = group['InputPosition'] search_translation = {group['Translation'][1]:group['Translation'][0]} print(search_key, search_position, search_translation) sub_group = extract_subgroup(label, search_position) serial_entry = sub_group[search_key] if serial_entry in search_translation.keys(): serial_entry = search_translation[serial_entry] elif '' in search_translation.keys() and search_translation[''] != '': serial_entry = search_translation[''] serial_number.append(serial_entry) return '/'.join(serial_number) ###Output SpacecraftName ['IsisCube', 'Instrument'] {'': 'APOLLO15'} InstrumentId ['IsisCube', 'Instrument'] {'': ''} StartTime ['IsisCube', 'Instrument'] {'': '*'} APOLLO15/METRIC/1971-07-31T01:24:36.970 ###Markdown Edit below code for the correct path to an Apollo cube and uncomment to test. Must remain commented out for a non-failing build server-side. ###Code #serial = generate_serial_number('/Users/jlaura/Desktop/Apollo15/AS15-M-0296_sub4.cub') #print(serial) ###Output _____no_output_____
Lab_1/Matplotlib_Lab_1.ipynb	###Markdown Introduction to Numerical Computing with Numpy and Matplotlib What is MatplotlibMatplotlib is a Python 2D plotting library which produces publication quality figures in a variety of hardcopy formats and interactive environments across platforms. Matplotlib can be used in Python scripts, the Python and IPython shells, the Jupyter notebook, web application servers, and four graphical user interface toolkits. Matplotlib tries to make easy things easy and hard things possible. You can generate plots, histograms, power spectra, bar charts, errorcharts, scatterplots, etc., with just a few lines of code.![Ref: Javatpoint ](https://static.javatpoint.com/tutorial/matplotlib/images/matplotlib-data-visualization2.png)For more infomration: [Matplotlib Webpage](https://matplotlib.org/) Malplotlib Object Model![alt text](https://matplotlib.org/_images/anatomy1.png) Matplotlib State's MachineMatplotlib behaves like a state machine. Any command is applied to the current plotting area. ###Code import matplotlib.pyplot as plt import numpy as np t = np.linspace(0, 2np.pi, 50) x = np.sin(t) y = np.cos(t) # Now create a figure plt.figure() # and plot x inside it plt.plot(x) # Now create a new figure plt.figure() # and plot y inside it... plt.plot(y) # Add a title plt.title("Cos") ###Output _____no_output_____ ###Markdown Line Plot ###Code x = np.linspace(0, 2np.pi, 50) y1 = np.sin(x) y2 = np.sin(2x) plt.figure() # Create figure plt.plot(y1) plt.plot(x, y1) # red dot-dash circle plt.plot(x, y1, 'r') # red marker only circle plt.plot(x, y1, 'r-o') # clear figure then plot 2 curves plt.clf() plt.plot(x, y1, 'g-o', x, y2, 'b-+') plt.legend(['sin(x)','sin(2x)']) ###Output _____no_output_____ ###Markdown Scatter Plot ###Code N = 50 # no. of points x = np.linspace(0, 10, N) #print(x) from numpy.random import rand e = rand(N)5.0 # noise y1 = x + e areas = rand(N)300 plt.scatter(x, y1, s=areas) colors = rand(N) plt.scatter(x, y1, s=areas,c=colors) plt.colorbar() plt.title("Random scatter") ###Output _____no_output_____ ###Markdown Image Plot: Correlation Plot ###Code # Create some data e1 = rand(100) e2 = rand(100)2 e3 = rand(100)50 e4 = rand(100)100 corrmatrix = np.corrcoef([e1, e2, e3, e4]) print(corrmatrix) # Plot corr matrix as image plt.imshow(corrmatrix, cmap='GnBu') plt.colorbar() ###Output [[ 1. 0.11927474 0.049266 0.02849791] [ 0.11927474 1. 0.02444701 0.0252238 ] [ 0.049266 0.02444701 1. -0.19692395] [ 0.02849791 0.0252238 -0.19692395 1. ]] ###Markdown Multiple plots using subplot ###Code t = np.linspace(0, 2np.pi) x = np.sin(t) y = np.cos(t) # To divide the plotting area plt.subplot(2, 1, 1) plt.plot(x) # Now activate a new plot # area. plt.subplot(2, 1, 2) plt.plot(y) ###Output _____no_output_____ ###Markdown Histogram plot ###Code # Create array of data from numpy.random import randint data = randint(10000, size=(10,1000)) # Approx norm distribution x = np.sum(data, axis=0) # Set up for stacked plots plt.subplot(2,1,1) plt.hist(x, color='r') # Plot cumulative dist plt.subplot(2,1,2) plt.hist(x, cumulative=True) ###Output _____no_output_____ ###Markdown Legend, Title, and Label Axis ###Code # Add labels in plot command. plt.plot(np.sin(t), label='sin') plt.plot(np.cos(t), label='cos') plt.legend() plt.plot(t, np.sin(t)) plt.xlabel('radians') # Keywords set text properties. plt.ylabel('amplitude',fontsize='large') plt.title('Sin(x)') ###Output _____no_output_____ ###Markdown Other Visualization Libraries: Seaborn: Better looking, high-level, plot-based on matplotlib [Seaborn](https://seaborn.pydata.org/)Bokeh: D3 like visulization in web browser [Bokeh](https://github.com/bokeh/bokeh) NumPy ArrayNumpy is the core library for scientific computing in Python. It provides a high-performance multidimensional array object, and tools for working with these arrays. A numpy array is a grid of values, all of the same type, and is indexed by a tuple of nonnegative integers. The number of dimensions is the rank of the array; the shape of an array is a tuple of integers giving the size of the array along each dimension.The Python core library provided Lists. A list is the Python equivalent of an array, but is resizeable and can contain elements of different types.Why NumPy array?Size - Numpy data structures take up less spacePerformance - they have a need for speed and are faster than listsFunctionality - SciPy and NumPy have optimized functions such as linear algebra operations built in. Introducing NumPy Array ###Code import numpy as np # Simple array creation a = np.array([0, 1, 2, 3, 4, 5]) print(a) # Checking the type and type of elements print(type(a)) print(a.dtype) # Check dimensions and shape print(a.ndim) print(a.shape) # Check Bytes per element and Bytes of memory use print(a.itemsize) print(a.nbytes) ###Output 8 48 ###Markdown Array Operations ###Code a = np.array([1, 2, 3, 4]) b = np.array([2, 3, 4, 5]) print(ab) print(a**b) print(a+b) print(a/b) # Setting array elements print(a[0]) a[0] = 10 print(a[0]) print(a) # Multi-dimensional array a = np.array([[ 0, 1, 2, 3], [10,11,12,13]]) print(a) print(a.shape) print(a.size) print(a.ndim) # Get and set elements in Multi-dimensional array print(a[1, 3]) a[1, 3] = -1 print(a[1, 3]) print(a[1]) ###Output [10 11 12 -1] ###Markdown Slicing array![Slicing array](https://scipy-lectures.org/_images/numpy_indexing.png) ###Code # Slicing array print(a) # print all row and 3rd column print(a[:,2]) # print first row and all column print(a[0,:]) # negative indices work also print(a) print(a[:,:-2]) ###Output [[ 0 1 2 3] [10 11 12 -1]] [ 2 12] [0 1 2 3] [[ 0 1 2 3] [10 11 12 -1]] [[ 0 1] [10 11]]
tarea_02/tarea_02.ipynb	###Markdown Tarea N°02 Instrucciones1.- Completa tus datos personales (nombre y rol USM) en siguiente celda.Nombre: Pedro PaillalefRol: 201304686-k2.- Debes pushear este archivo con tus cambios a tu repositorio personal del curso, incluyendo datos, imágenes, scripts, etc.3.- Se evaluará:- Soluciones- Código- Que Binder esté bien configurado.- Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error. I.- Clasificación de dígitosEn este laboratorio realizaremos el trabajo de reconocer un dígito a partir de una imagen. ![rgb](https://www.wolfram.com/language/11/neural-networks/assets.en/digit-classification/smallthumb_1.png) El objetivo es a partir de los datos, hacer la mejor predicción de cada imagen. Para ellos es necesario realizar los pasos clásicos de un proyecto de _Machine Learning_, como estadística descriptiva, visualización y preprocesamiento. * Se solicita ajustar al menos tres modelos de clasificación: * Regresión logística * K-Nearest Neighbours * Uno o más algoritmos a su elección [link](https://scikit-learn.org/stable/supervised_learning.htmlsupervised-learning) (es obligación escoger un _estimator_ que tenga por lo menos un hiperparámetro). * En los modelos que posean hiperparámetros es mandatorio buscar el/los mejores con alguna técnica disponible en `scikit-learn` ([ver más](https://scikit-learn.org/stable/modules/grid_search.htmltuning-the-hyper-parameters-of-an-estimator)).* Para cada modelo, se debe realizar _Cross Validation_ con 10 _folds_ utilizando los datos de entrenamiento con tal de determinar un intervalo de confianza para el _score_ del modelo.* Realizar una predicción con cada uno de los tres modelos con los datos _test_ y obtener el _score_. * Analizar sus métricas de error (accuracy, precision, recall, f-score) Exploración de los datosA continuación se carga el conjunto de datos a utilizar, a través del sub-módulo `datasets` de `sklearn`. ###Code import numpy as np import pandas as pd from sklearn import datasets import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import confusion_matrix import time from sklearn.ensemble import RandomForestClassifier from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import f1_score from sklearn.svm import SVC from sklearn.model_selection import validation_curve from itertools import cycle from sklearn import svm, datasets from sklearn.metrics import roc_curve, auc from sklearn.preprocessing import label_binarize from sklearn.multiclass import OneVsRestClassifier from scipy import interp from sklearn.metrics import roc_auc_score from sklearn import linear_model from sklearn.model_selection import cross_validate from sklearn.metrics import make_scorer from sklearn.feature_selection import SelectKBest, f_classif from sklearn.feature_selection import chi2 %matplotlib inline digits_dict = datasets.load_digits() print(digits_dict["DESCR"]) digits_dict digits_dict.keys() digits_dict["target"] ###Output _____no_output_____ ###Markdown A continuación se crea dataframe declarado como `digits` con los datos de `digits_dict` tal que tenga 65 columnas, las 6 primeras a la representación de la imagen en escala de grises (0-blanco, 255-negro) y la última correspondiente al dígito (`target`) con el nombre _target_. ###Code digits = ( pd.DataFrame( digits_dict["data"], ) .rename(columns=lambda x: f"c{x:02d}") .assign(target=digits_dict["target"]) .astype(int) ) digits.head() digits.describe() ###Output _____no_output_____ ###Markdown Ejercicio 1Análisis exploratorio: Realiza tu análisis exploratorio, no debes olvidar nada! Recuerda, cada análisis debe responder una pregunta.Algunas sugerencias:* ¿Cómo se distribuyen los datos?* ¿Cuánta memoria estoy utilizando?* ¿Qué tipo de datos son?* ¿Cuántos registros por clase hay?* ¿Hay registros que no se correspondan con tu conocimiento previo de los datos? ¿Cómo se distribuyen los datos? Los datos se distribuyen en un dataframe llamado digits, donde las columnas son string c+dígito desde 0 a 63. con un target que sirve para agrupar la base de datos y finalmente, estos últimos se dejan en formato int. DISCRIBUCUPIB BOMAL ¿Cuánta memoria estoy utilizando? ###Code digits.info ###Output _____no_output_____ ###Markdown En este data frame hay 456.4 KB de uso. ¿Qué tipo de datos son? Los datos son enteros ¿Cuántos registros por clase hay? 1797 ¿Hay registros que no se correspondan con tu conocimiento previo de los datos? no hay datos raros porque son int32 Ejercicio 2Visualización: Para visualizar los datos utilizaremos el método `imshow` de `matplotlib`. Resulta necesario convertir el arreglo desde las dimensiones (1,64) a (8,8) para que la imagen sea cuadrada y pueda distinguirse el dígito. Superpondremos además el label correspondiente al dígito, mediante el método `text`. Esto nos permitirá comparar la imagen generada con la etiqueta asociada a los valores. Realizaremos lo anterior para los primeros 25 datos del archivo. ###Code digits_dict["images"][0] ###Output _____no_output_____ ###Markdown Visualiza imágenes de los dígitos utilizando la llave `images` de `digits_dict`. Sugerencia: Utiliza `plt.subplots` y el método `imshow`. Puedes hacer una grilla de varias imágenes al mismo tiempo! ###Code nx, ny = 5, 5 fig, axs = plt.subplots(nx,ny, figsize=(12, 12)) for i in range(1, nxny +1): img = digits_dict["images"][i] fig.add_subplot(nx, ny, i) plt.imshow(img) plt.show() ###Output _____no_output_____ ###Markdown Ejercicio 3Machine Learning: En esta parte usted debe entrenar los distintos modelos escogidos desde la librería de `skelearn`. Para cada modelo, debe realizar los siguientes pasos: train-test * Crear conjunto de entrenamiento y testeo (usted determine las proporciones adecuadas). * Imprimir por pantalla el largo del conjunto de entrenamiento y de testeo. * modelo: * Instanciar el modelo objetivo desde la librería sklearn. * Hiper-parámetros: Utiliza `sklearn.model_selection.GridSearchCV` para obtener la mejor estimación de los parámetros del modelo objetivo.* Métricas: * Graficar matriz de confusión. * Analizar métricas de error.__Preguntas a responder:__* ¿Cuál modelo es mejor basado en sus métricas?* ¿Cuál modelo demora menos tiempo en ajustarse?* ¿Qué modelo escoges? ###Code X = digits.drop(columns="target").values y = digits["target"].values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42) ###Output _____no_output_____ ###Markdown Regresión logistica ###Code tiempos_ejecucion = [] lista_nombres = ["Logistic Regresor","Random Forest","knn","Logistic Regresor -","Random Forest-","knn-"] tiempo_inicial = time.time() clf = LogisticRegression() clf.fit(X_train,y_train) tiempo_final = time.time() tiempos_ejecucion.append(tiempo_final-tiempo_inicial) ###Output C:\Users\pedro\miniconda3\envs\mat281\lib\site-packages\sklearn\linear_model\_logistic.py:764: ConvergenceWarning: lbfgs failed to converge (status=1): STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. Increase the number of iterations (max_iter) or scale the data as shown in: https://scikit-learn.org/stable/modules/preprocessing.html Please also refer to the documentation for alternative solver options: https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression extra_warning_msg=_LOGISTIC_SOLVER_CONVERGENCE_MSG) ###Markdown Random Forest ###Code tiempo_inicial = time.time() rf = RandomForestClassifier(max_depth=12, random_state=0) rf.fit(X_train,y_train) tiempo_final = time.time() tiempos_ejecucion.append(tiempo_final-tiempo_inicial) ###Output _____no_output_____ ###Markdown KNN ###Code tiempo_inicial = time.time() knn = KNeighborsClassifier(n_neighbors=7) knn.fit(X_train,y_train) tiempo_final = time.time() tiempos_ejecucion.append(tiempo_final-tiempo_inicial) ###Output _____no_output_____ ###Markdown Score ###Code ### regresión logistica clf.score( X_test, y_test) #### matriz de contución regresión logistica y_pred = clf.predict(X_test) confusion_matrix(y_test, y_pred) ### Random Forest rf.score( X_test, y_test) #### Matriz de contusión random foret y_pred = rf.predict(X_test) confusion_matrix(y_test, y_pred) ### KNN knn.score( X_test, y_test) ### Matriz de contusión knn y_pred = knn.predict(X_test) confusion_matrix(y_test, y_pred) ###Output _____no_output_____ ###Markdown ¿Cuál modelo es mejor basado en sus métricas? El mejor modelo corresponde al KNN. ¿Cuál modelo demora menos tiempo en ajustarse? ###Code print(tiempos_ejecucion) ###Output [1.7783284187316895, 0.4449596405029297, 0.06295633316040039] ###Markdown El modelo que demora menos en ajustarse es el KNN con delta inicial 0.093 y luego con la reducción de dimensionalidad queda en 0.015. A modo complementario, el modelo cuyo ajusto no efecta practicamente nada corresponde al Random Forest con delta inicial 0.45 y luego obtuvo 0.42. ¿Qué modelo escoges? El modelo que escogo es KNN, por presentar mejores métricas. Ejercicio 4__Comprensión del modelo:__ Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, debe comprender e interpretar minuciosamente los resultados y gráficos asocados al modelo en estudio, para ello debe resolver los siguientes puntos: * Cross validation: usando cv (con n_fold = 10), sacar una especie de "intervalo de confianza" sobre alguna de las métricas estudiadas en clases: * $\mu \pm \sigma$ = promedio $\pm$ desviación estandar * Curva de Validación: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.htmlsphx-glr-auto-examples-model-selection-plot-validation-curve-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. * Curva AUC–ROC: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.htmlsphx-glr-auto-examples-model-selection-plot-roc-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. Cross validation ###Code cv_results = cross_validate(knn, X, y, cv=10) cv_results['test_score'] ###Output _____no_output_____ ###Markdown Curva de validación ###Code param_range = np.logspace(-6, -1, 5) train_scores, test_scores = validation_curve( SVC(), X, y, param_name="gamma", param_range=param_range, scoring="accuracy", n_jobs=1) train_scores_mean = np.mean(train_scores, axis=1) train_scores_std = np.std(train_scores, axis=1) test_scores_mean = np.mean(test_scores, axis=1) test_scores_std = np.std(test_scores, axis=1) plt.title("Validation Curve with SVM") plt.xlabel(r"$\gamma$") plt.ylabel("Score") plt.ylim(0.0, 1.1) lw = 2 plt.semilogx(param_range, train_scores_mean, label="Training score", color="darkorange", lw=lw) plt.fill_between(param_range, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.2, color="darkorange", lw=lw) plt.semilogx(param_range, test_scores_mean, label="Cross-validation score", color="navy", lw=lw) plt.fill_between(param_range, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.2, color="navy", lw=lw) plt.legend(loc="best") plt.show() ###Output _____no_output_____ ###Markdown Curva AUC–ROC ###Code # Binarize the output y = label_binarize(y, classes=[0, 1, 2,3,4,5,6,7,8,9]) n_classes = y.shape[1] # Add noisy features to make the problem harder random_state = np.random.RandomState(0) n_samples, n_features = X.shape X = np.c_[X, random_state.randn(n_samples, 200 * n_features)] # shuffle and split training and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5, random_state=0) # Learn to predict each class against the other classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True, random_state=random_state)) y_score = classifier.fit(X_train, y_train).decision_function(X_test) # Compute ROC curve and ROC area for each class fpr = dict() tpr = dict() roc_auc = dict() for i in range(n_classes): fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i]) roc_auc[i] = auc(fpr[i], tpr[i]) # Compute micro-average ROC curve and ROC area fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel()) roc_auc["micro"] = auc(fpr["micro"], tpr["micro"]) plt.figure() lw = 2 plt.plot(fpr[2], tpr[2], color='darkorange', lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2]) plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--') plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.title('Receiver operating characteristic example') plt.legend(loc="lower right") plt.show() ###Output _____no_output_____ ###Markdown La curva roc obtenida es típica y refleja buenos resultados (que se verán más adelante) Ejercicio 5__Reducción de la dimensión:__ Tomando en cuenta el mejor modelo encontrado en el `Ejercicio 3`, debe realizar una redcción de dimensionalidad del conjunto de datos. Para ello debe abordar el problema ocupando los dos criterios visto en clases: * Selección de atributos* Extracción de atributos__Preguntas a responder:__Una vez realizado la reducción de dimensionalidad, debe sacar algunas estadísticas y gráficas comparativas entre el conjunto de datos original y el nuevo conjunto de datos (tamaño del dataset, tiempo de ejecución del modelo, etc.) ###Code X = digits.drop(columns="target").values y = digits["target"].values X_new = SelectKBest(chi2, k=18).fit_transform(X, y) X = X_new X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42) ###Output _____no_output_____ ###Markdown Regresión logística ###Code tiempo_inicial = time.time() clf = LogisticRegression() clf.fit(X_test,y_test) tiempo_final = time.time() tiempos_ejecucion.append(tiempo_final-tiempo_inicial) ###Output C:\Users\pedro\miniconda3\envs\mat281\lib\site-packages\sklearn\linear_model\_logistic.py:764: ConvergenceWarning: lbfgs failed to converge (status=1): STOP: TOTAL NO. of ITERATIONS REACHED LIMIT. Increase the number of iterations (max_iter) or scale the data as shown in: https://scikit-learn.org/stable/modules/preprocessing.html Please also refer to the documentation for alternative solver options: https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression extra_warning_msg=_LOGISTIC_SOLVER_CONVERGENCE_MSG) ###Markdown Random forest ###Code tiempo_inicial = time.time() rf = RandomForestClassifier(max_depth=12, random_state=0) rf.fit(X_train,y_train) tiempo_final = time.time() tiempos_ejecucion.append(tiempo_final-tiempo_inicial) ###Output _____no_output_____ ###Markdown KNN ###Code tiempo_inicial = time.time() knn = KNeighborsClassifier(n_neighbors=7) knn.fit(X_train,y_train) tiempo_final = time.time() tiempos_ejecucion.append(tiempo_final-tiempo_inicial) ###Output _____no_output_____ ###Markdown Ejercicio 6__Visualizando Resultados:__ A continuación se provee código para comparar las etiquetas predichas vs las etiquetas reales del conjunto de _test_. ###Code def mostar_resultados(digits,model,nx=5, ny=5,label = "correctos"): """ Muestra los resultados de las prediciones de un modelo de clasificacion en particular. Se toman aleatoriamente los valores de los resultados. - label == 'correcto': retorna los valores en que el modelo acierta. - label == 'incorrecto': retorna los valores en que el modelo no acierta. Observacion: El modelo que recibe como argumento debe NO encontrarse 'entrenado'. :param digits: dataset 'digits' :param model: modelo de sklearn :param nx: numero de filas (subplots) :param ny: numero de columnas (subplots) :param label: datos correctos o incorrectos :return: graficos matplotlib """ X = digits.drop(columns="target").values y = digits["target"].values X_train, X_test, Y_train, Y_test = train_test_split(X, y, test_size=0.2, random_state = 42) model.fit(X_train, Y_train) # ajustando el modelo y_pred = list(model.predict(X_test)) # Mostrar los datos correctos if label=="correctos": mask = (y_pred == y_test) color = "green" # Mostrar los datos correctos elif label=="incorrectos": mask = (y_pred != y_test) color = "red" else: raise ValueError("Valor incorrecto") X_aux = X_test y_aux_true = y_test y_aux_pred = y_pred # We'll plot the first 100 examples, randomly choosen fig, ax = plt.subplots(nx, ny, figsize=(12,12)) for i in range(nx): for j in range(ny): index = j + ny * i data = X_aux[index, :].reshape(8,8) label_pred = str(int(y_aux_pred[index])) label_true = str(int(y_aux_true[index])) ax[i][j].imshow(data, interpolation='nearest', cmap='gray_r') ax[i][j].text(0, 0, label_pred, horizontalalignment='center', verticalalignment='center', fontsize=10, color=color) ax[i][j].text(7, 0, label_true, horizontalalignment='center', verticalalignment='center', fontsize=10, color='blue') ax[i][j].get_xaxis().set_visible(False) ax[i][j].get_yaxis().set_visible(False) plt.show() model=KNeighborsClassifier(n_neighbors=7) mostar_resultados(digits,model,nx=5, ny=5,label = "correctos") ###Output C:\Users\pedro\miniconda3\envs\mat281\lib\site-packages\ipykernel_launcher.py:33: DeprecationWarning: elementwise comparison failed; this will raise an error in the future. ###Markdown Pregunta* Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, grafique los resultados cuando: * el valor predicho y original son iguales * el valor predicho y original son distintos * Cuando el valor predicho y original son distintos , ¿Por qué ocurren estas fallas? ###Code #mostar_resultados(digits,knn,nx=5, ny=5,label = "correctos") model=KNeighborsClassifier(n_neighbors=7) mostar_resultados(digits,model,nx=3, ny=3,label = "incorrectos") ###Output C:\Users\pedro\miniconda3\envs\mat281\lib\site-packages\ipykernel_launcher.py:38: DeprecationWarning: elementwise comparison failed; this will raise an error in the future. ###Markdown Tarea N°02 Instrucciones1.- Completa tus datos personales (nombre y rol USM) en siguiente celda.Nombre: Gabriel Vergara SchifferliRol: 201510519-72.- Debes pushear este archivo con tus cambios a tu repositorio personal del curso, incluyendo datos, imágenes, scripts, etc.3.- Se evaluará:- Soluciones- Código- Que Binder esté bien configurado.- Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error. I.- Clasificación de dígitosEn este laboratorio realizaremos el trabajo de reconocer un dígito a partir de una imagen. ![rgb](https://www.wolfram.com/language/11/neural-networks/assets.en/digit-classification/smallthumb_1.png) El objetivo es a partir de los datos, hacer la mejor predicción de cada imagen. Para ellos es necesario realizar los pasos clásicos de un proyecto de _Machine Learning_, como estadística descriptiva, visualización y preprocesamiento. * Se solicita ajustar al menos tres modelos de clasificación: * Regresión logística * K-Nearest Neighbours * Uno o más algoritmos a su elección [link](https://scikit-learn.org/stable/supervised_learning.htmlsupervised-learning) (es obligación escoger un _estimator_ que tenga por lo menos un hiperparámetro). * En los modelos que posean hiperparámetros es mandatorio buscar el/los mejores con alguna técnica disponible en `scikit-learn` ([ver más](https://scikit-learn.org/stable/modules/grid_search.htmltuning-the-hyper-parameters-of-an-estimator)).* Para cada modelo, se debe realizar _Cross Validation_ con 10 _folds_ utilizando los datos de entrenamiento con tal de determinar un intervalo de confianza para el _score_ del modelo.* Realizar una predicción con cada uno de los tres modelos con los datos _test_ y obtener el _score_. * Analizar sus métricas de error (accuracy, precision, recall, f-score) Exploración de los datosA continuación se carga el conjunto de datos a utilizar, a través del sub-módulo `datasets` de `sklearn`. ###Code import numpy as np import pandas as pd from sklearn import datasets import matplotlib.pyplot as plt %matplotlib inline digits_dict = datasets.load_digits() print(digits_dict["DESCR"]) digits_dict.keys() digits_dict["target"] digits_dict["data"] ###Output _____no_output_____ ###Markdown A continuación se crea dataframe declarado como `digits` con los datos de `digits_dict` tal que tenga 65 columnas, las 6 primeras a la representación de la imagen en escala de grises (0-blanco, 255-negro) y la última correspondiente al dígito (`target`) con el nombre _target_. ###Code digits = ( pd.DataFrame( digits_dict["data"], ) .rename(columns=lambda x: f"c{x:02d}") .assign(target=digits_dict["target"]) .astype(int) ) digits.head() ###Output _____no_output_____ ###Markdown Ejercicio 1Análisis exploratorio: Realiza tu análisis exploratorio, no debes olvidar nada! Recuerda, cada análisis debe responder una pregunta.Algunas sugerencias:* ¿Cómo se distribuyen los datos?* ¿Cuánta memoria estoy utilizando?* ¿Qué tipo de datos son?* ¿Cuántos registros por clase hay?* ¿Hay registros que no se correspondan con tu conocimiento previo de los datos? ###Code numeros = [] for i in range(0,10): numeros.append( digits.loc[ digits["target"] == i ]) numeros[0].describe() numeros[0].describe().iloc[2] fig, ax = plt.subplots(2, 5, sharex='col', sharey='row') print("graficos de frecuencio número 0") for i in range(0,5): numeros[i].describe().iloc[2].hist(ax=ax[0,i]), numeros[i +5].describe().iloc[2].hist(ax=ax[1,i]) ###Output graficos de frecuencio número 0 ###Markdown Estos gráficos muestran la frecuencia que hay en la media para cada casilla de la imagen para los números 0 hasta 9. Entonces esto muestra el patron medio que tiene un número asociado a su dibujo. ###Code ### # LA MEMORIA UTILIZADA import sys Memoria = digits.memory_usage() total = (Memoria[1]65)/1000 print(total, 'kilobytes') for i in range(0,10): print("hay %f resgistros para la clase %s" % ( numeros[i].shape[0] , i ) ) ###Output hay 178.000000 resgistros para la clase 0 hay 182.000000 resgistros para la clase 1 hay 177.000000 resgistros para la clase 2 hay 183.000000 resgistros para la clase 3 hay 181.000000 resgistros para la clase 4 hay 182.000000 resgistros para la clase 5 hay 181.000000 resgistros para la clase 6 hay 179.000000 resgistros para la clase 7 hay 174.000000 resgistros para la clase 8 hay 180.000000 resgistros para la clase 9 ###Markdown Ejercicio 2Visualización:* Para visualizar los datos utilizaremos el método `imshow` de `matplotlib`. Resulta necesario convertir el arreglo desde las dimensiones (1,64) a (8,8) para que la imagen sea cuadrada y pueda distinguirse el dígito. Superpondremos además el label correspondiente al dígito, mediante el método `text`. Esto nos permitirá comparar la imagen generada con la etiqueta asociada a los valores. Realizaremos lo anterior para los primeros 25 datos del archivo. ###Code digits_dict["images"][0] ###Output _____no_output_____ ###Markdown Visualiza imágenes de los dígitos utilizando la llave `images` de `digits_dict`. Sugerencia: Utiliza `plt.subplots` y el método `imshow`. Puedes hacer una grilla de varias imágenes al mismo tiempo! ###Code fig, axs = plt.subplots(4, 4, figsize=(15, 15)) for i in range(1, 17): img = digits_dict["images"][i] fig.add_subplot(4, 4, i) plt.imshow(img) plt.axis('off') plt.show() ###Output _____no_output_____ ###Markdown Ejercicio 3Machine Learning: En esta parte usted debe entrenar los distintos modelos escogidos desde la librería de `skelearn`. Para cada modelo, debe realizar los siguientes pasos:* train-test * Crear conjunto de entrenamiento y testeo (usted determine las proporciones adecuadas). * Imprimir por pantalla el largo del conjunto de entrenamiento y de testeo. * modelo: * Instanciar el modelo objetivo desde la librería sklearn. * Hiper-parámetros: Utiliza `sklearn.model_selection.GridSearchCV` para obtener la mejor estimación de los parámetros del modelo objetivo.* Métricas: * Graficar matriz de confusión. * Analizar métricas de error.__Preguntas a responder:__* ¿Cuál modelo es mejor basado en sus métricas?* ¿Cuál modelo demora menos tiempo en ajustarse?* ¿Qué modelo escoges? ###Code x = digits.drop(columns="target").values y = digits["target"].values ###Output _____no_output_____ ###Markdown TRAIN-TEST SET ###Code from metrics_classification import summary_metrics as sm from sklearn.metrics import confusion_matrix from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.20, train_size=0.80, random_state=2020) print('cantidad de datos para entrenamiento : ',len(x_train)) print('cantidad de datos para testeo : ',len(x_test)) ###Output cantidad de datos para entrenamiento : 1437 cantidad de datos para testeo : 360 ###Markdown MODELO ###Code #REGRESIÓN LOGÍSTICA from sklearn.linear_model import LogisticRegression from sklearn.model_selection import GridSearchCV import time #Selección de hiperparámetros parameters = { 'penalty' : ['l2', None], 'class_weight' : ['balanced', None], 'solver' : ['liblinear', 'lbfgs'], 'random_state':[2020] } lr = LogisticRegression() lr_gridsearchcv = GridSearchCV(estimator = lr, param_grid = parameters, cv = 10) lr_grid_result = lr_gridsearchcv.fit(x_train, y_train) #KNN from sklearn.neighbors import KNeighborsClassifier knn = KNeighborsClassifier() knnparameters = { 'metric' : ['euclidean', 'manhattan'], 'weights' : ['uniform','distance'], 'algorithm' : ['auto', 'ball_tree', 'kd_tree'] } knn_gridsearchcv = GridSearchCV(estimator = knn, param_grid = knnparameters, cv = 10) knn_grid_result = knn_gridsearchcv.fit(x_train, y_train) #PERCEPTRON from sklearn.linear_model import Perceptron per = Perceptron() Pparameters ={ 'penalty' : ['l2','l1','elasticnet', None], 'tol':[1e-3,1e-5,1e-1], 'alpha' : [0.0001, 0.00001,0.000001] } scores = ['precision', 'recall'] P_gridsearchcv = GridSearchCV(estimator = per, param_grid = Pparameters, cv = 10) p_grid_result = P_gridsearchcv.fit(x_train, y_train) print("LOGISTIC REGRESSION") print("El mejor tiempo es de LR: %f usando %s" % (lr_grid_result.best_score_, lr_grid_result.best_params_)) #Calculo de métricas con matriz de confusión lr_predict = lr_gridsearchcv.predict(x_test) d = dict( y=y_test, yhat = lr_predict) df= pd.DataFrame.from_dict(d, orient='index').transpose() print(confusion_matrix(y_test,lr_predict)) print(sm(df)) print('') ######################################## print("KNN") print("El mejor tiempo es de KNN: %f usando %s" % (knn_grid_result.best_score_, knn_grid_result.best_params_)) knn_predict = knn_gridsearchcv.predict(x_test) d = dict( y=y_test, yhat = knn_predict) df= pd.DataFrame.from_dict(d, orient='index').transpose() print(confusion_matrix(y_test,knn_predict)) print(sm(df)) print('') ######################################### print("SGDR") print("El mejor tiempo es de SGDR: %f usando %s" % (p_grid_result.best_score_, p_grid_result.best_params_)) p_predict = P_gridsearchcv.predict(x_test) d = dict( y=y_test, yhat = p_predict) df= pd.DataFrame.from_dict(d, orient='index').transpose() print(confusion_matrix(y_test,p_predict)) print(sm(df)) print('') ###Output LOGISTIC REGRESSION El mejor tiempo es de LR: 0.959630 usando {'class_weight': 'balanced', 'penalty': 'l2', 'random_state': 2020, 'solver': 'lbfgs'} [[37 0 0 0 1 0 0 0 0 0] [ 0 34 0 0 0 0 1 0 0 0] [ 0 0 35 0 0 0 0 0 0 0] [ 0 0 0 35 0 0 0 0 0 1] [ 1 0 0 0 40 0 0 0 0 1] [ 0 0 0 0 1 35 0 0 0 1] [ 0 0 0 0 0 0 36 0 0 0] [ 0 0 0 0 0 0 0 37 0 0] [ 1 0 0 0 1 0 0 0 27 0] [ 0 0 0 0 1 0 0 0 1 33]] accuracy recall precision fscore 0 0.9694 0.969 0.9712 0.9698 KNN El mejor tiempo es de KNN: 0.985383 usando {'algorithm': 'auto', 'metric': 'euclidean', 'weights': 'uniform'} [[38 0 0 0 0 0 0 0 0 0] [ 0 35 0 0 0 0 0 0 0 0] [ 0 0 35 0 0 0 0 0 0 0] [ 0 0 0 36 0 0 0 0 0 0] [ 0 0 0 0 42 0 0 0 0 0] [ 0 0 0 0 0 36 0 0 0 1] [ 0 0 0 0 0 0 36 0 0 0] [ 0 0 0 0 0 0 0 37 0 0] [ 0 0 0 0 0 0 0 0 29 0] [ 0 0 0 0 0 0 0 0 0 35]] accuracy recall precision fscore 0 0.9972 0.9973 0.9972 0.9972 SGDR El mejor tiempo es de SGDR: 0.938068 usando {'alpha': 0.0001, 'penalty': 'l1', 'tol': 0.001} [[38 0 0 0 0 0 0 0 0 0] [ 0 32 0 2 1 0 0 0 0 0] [ 0 0 35 0 0 0 0 0 0 0] [ 0 0 0 32 0 0 0 0 3 1] [ 0 0 0 0 41 0 0 0 1 0] [ 0 2 0 0 0 35 0 0 0 0] [ 0 0 0 0 0 0 35 0 1 0] [ 0 0 0 0 0 0 0 37 0 0] [ 0 1 0 0 0 0 0 0 28 0] [ 1 0 0 0 0 0 0 1 9 24]] accuracy recall precision fscore 0 0.9361 0.9349 0.9406 0.9325 ###Markdown RESUMEN: el método knn y lr tienen un tiempo de ejecución similar, siendo lr el más rápido y perceptron el más lento.En cuanto a la cantidad de aciertos y errores, el método knn tiene la accuracy más alta y perceptron la peor. Esto se mantiene esta misma relación en cuanto a recall, presición y fscore.Por lo tanto el método que mejor se adapta en este caso es el KNN. Ejercicio 4__Comprensión del modelo:__ Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, debe comprender e interpretar minuciosamente los resultados y gráficos asocados al modelo en estudio, para ello debe resolver los siguientes puntos: * Cross validation: usando cv (con n_fold = 10), sacar una especie de "intervalo de confianza" sobre alguna de las métricas estudiadas en clases: * $\mu \pm \sigma$ = promedio $\pm$ desviación estandar * Curva de Validación: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.htmlsphx-glr-auto-examples-model-selection-plot-validation-curve-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. * Curva AUC–ROC: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.htmlsphx-glr-auto-examples-model-selection-plot-roc-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. ###Code #Cross Validation usando KNN from sklearn.model_selection import cross_val_score precision = cross_val_score(estimator=knn_gridsearchcv, X=x_train, y=y_train, cv=10) precision = [round(x,2) for x in precision] print('Precisiones: {} '.format(precision)) print('Precision promedio: {0: .3f} +/- {1: .3f}'.format(np.mean(precision), np.std(precision))) #curva de validación from sklearn.model_selection import validation_curve param_range = np.array([i for i in range(1, 10)]) #Validation curve usando los mejores hiperparámetros train_scores, test_scores = validation_curve( KNeighborsClassifier(weights = 'distance', metric = 'euclidean'), x_train, y_train, param_name="n_neighbors", param_range=param_range, scoring="accuracy", n_jobs=1) train_scores_mean = np.mean(train_scores, axis=1) train_scores_std = np.std(train_scores, axis=1) test_scores_mean = np.mean(test_scores, axis=1) test_scores_std = np.std(test_scores, axis=1) plt.title("Validation Curve with SVM") plt.xlabel(r"$\gamma$") plt.ylabel("Score") plt.ylim(0.0, 1.1) lw = 2 plt.semilogx(param_range, train_scores_mean, label="Training score", color="darkorange", lw=lw) plt.fill_between(param_range, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.2, color="darkorange", lw=lw) plt.semilogx(param_range, test_scores_mean, label="Cross-validation score", color="navy", lw=lw) plt.fill_between(param_range, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.2, color="navy", lw=lw) plt.legend(loc="best") plt.show() ###Output _____no_output_____ ###Markdown la curva de cross validation es practicamente constante, por lo tanto, se tiene que el modelo de knn se comporta de buena forma independiente de la cantidad de clusters dado que hay un leve decresimiento. ###Code from itertools import cycle from sklearn.metrics import roc_curve, auc from sklearn.preprocessing import label_binarize from sklearn.multiclass import OneVsRestClassifier from scipy import interp from sklearn.metrics import roc_auc_score index = np.argmax(test_scores_mean) param_range[index] y = label_binarize(y, classes=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) n_classes = y.shape[1] n_samples, n_features = x.shape x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.20, train_size=0.80, random_state=2020) classifier = KNeighborsClassifier(weights = 'distance',metric = 'euclidean', n_neighbors = param_range[index]) y_score = classifier.fit(x_train, y_train).predict(x_test) fpr = dict() tpr = dict() roc_auc = dict() for i in range(n_classes): fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i]) roc_auc[i] = auc(fpr[i], tpr[i]) # Compute micro-average ROC curve and ROC area fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel()) roc_auc["micro"] = auc(fpr["micro"], tpr["micro"]) #AOC-ROC para multiples clases (código también obtenido del link) all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)])) # Then interpolate all ROC curves at this points mean_tpr = np.zeros_like(all_fpr) for i in range(n_classes): mean_tpr += np.interp(all_fpr, fpr[i], tpr[i]) # Finally average it and compute AUC mean_tpr /= n_classes fpr["macro"] = all_fpr tpr["macro"] = mean_tpr roc_auc["macro"] = auc(fpr["macro"], tpr["macro"]) colors = cycle(['aqua', 'darkorange', 'cornflowerblue']) for i, color in zip(range(n_classes), colors): plt.plot(fpr[i], tpr[i], color=color, lw=lw, label='ROC curve of class {0} (area = {1:0.2f})' ''.format(i, roc_auc[i])) plt.plot([0, 1], [0, 1], 'k--', lw=lw) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.title('Some extension of Receiver operating characteristic to multi-class') plt.legend(loc="lower right") plt.show() #Curva promedio de las multi-clases import sys # First aggregate all false positive rates all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)])) # Then interpolate all ROC curves at this points mean_tpr = np.zeros_like(all_fpr) for i in range(n_classes): mean_tpr += np.interp(all_fpr, fpr[i], tpr[i]) # Finally average it and compute AUC mean_tpr /= n_classes fpr["macro"] = all_fpr tpr["macro"] = mean_tpr roc_auc["macro"] = auc(fpr["macro"], tpr["macro"]) plt.plot(fpr["macro"], tpr["macro"], label='macro-average ROC curve (area = {0:0.2f})' ''.format(roc_auc["macro"]), color='navy', linestyle='-', linewidth=4) plt.plot([0, 1], [0, 1], 'k--', lw=lw) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.title('Some extension of Receiver operating characteristic to multi-class') plt.legend(loc="lower right") plt.show() ###Output _____no_output_____ ###Markdown Ejercicio 5__Reducción de la dimensión:__ Tomando en cuenta el mejor modelo encontrado en el `Ejercicio 3`, debe realizar una redcción de dimensionalidad del conjunto de datos. Para ello debe abordar el problema ocupando los dos criterios visto en clases: * Selección de atributos* Extracción de atributos__Preguntas a responder:__Una vez realizado la reducción de dimensionalidad, debe sacar algunas estadísticas y gráficas comparativas entre el conjunto de datos original y el nuevo conjunto de datos (tamaño del dataset, tiempo de ejecución del modelo, etc.) ###Code #SELECCIÓN DE ATRIBUTOS from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import f_classif x_training = digits.drop(columns="target") y_training = digits["target"] x_training = x_training.drop(['c00','c32','c39'],axis=1) k = 30 # número de atributos a seleccionar columnas = list(x_training.columns.values) seleccionadas = SelectKBest(f_classif, k=k).fit(x_training, y_training) catrib = seleccionadas.get_support() atributos = [columnas[i] for i in list(catrib.nonzero()[0])] X_a=x_training[atributos] start_time = time.time() knn_grid_result = knn_gridsearchcv.fit(x_training, y_training) print("%s segundos, que demora antes de seleccionar atributos" % (time.time() - start_time)) start_time = time.time() knn_grid_result = knn_gridsearchcv.fit(X_a, y_training) print('%s segundos, que demora despues de seleccionar atributos' % (time.time() - start_time)) ###Output tiempo de 4.0168678760528564 segundos, que demora antes de seleccionar atributos tiempo de 2.3130300045013428 segundos, que demora despues de seleccionar atributos ###Markdown Ejercicio 6__Visualizando Resultados:__ A continuación se provee código para comparar las etiquetas predichas vs las etiquetas reales del conjunto de _test_. ###Code def mostar_resultados(digits,model,nx=5, ny=5,label = "correctos"): """ Muestra los resultados de las prediciones de un modelo de clasificacion en particular. Se toman aleatoriamente los valores de los resultados. - label == 'correcto': retorna los valores en que el modelo acierta. - label == 'incorrecto': retorna los valores en que el modelo no acierta. Observacion: El modelo que recibe como argumento debe NO encontrarse 'entrenado'. :param digits: dataset 'digits' :param model: modelo de sklearn :param nx: numero de filas (subplots) :param ny: numero de columnas (subplots) :param label: datos correctos o incorrectos :return: graficos matplotlib """ X = digits.drop(columns="target").values y = digits["target"].values X_train, X_test, Y_train, Y_test = train_test_split(X, y, test_size=0.2, random_state = 42) model.fit(X_train, Y_train) # ajustando el modelo y_pred = list(model.predict(X_test)) # Mostrar los datos correctos if label=="correctos": mask = (y_pred == Y_test) color = "green" # Mostrar los datos correctos elif label=="incorrectos": mask = (y_pred != Y_test) color = "red" else: raise ValueError("Valor incorrecto") X_aux = X_test[mask] y_aux_true = Y_test[mask] y_aux_pred = np.array(y_pred)[mask] # We'll plot the first 100 examples, randomly choosen fig, ax = plt.subplots(nx, ny, figsize=(12,12)) fix = X_aux.shape[0] for i in range(nx): for j in range(ny): index = j + ny * i if index < fix: data = X_aux[index, :].reshape(8,8) label_pred = str(int(y_aux_pred[index])) label_true = str(int(y_aux_true[index])) ax[i][j].imshow(data, interpolation='nearest', cmap='gray_r') ax[i][j].text(0, 0, label_pred, horizontalalignment='center', verticalalignment='center', fontsize=10, color=color) ax[i][j].text(7, 0, label_true, horizontalalignment='center', verticalalignment='center', fontsize=10, color='blue') ax[i][j].get_xaxis().set_visible(False) ax[i][j].get_yaxis().set_visible(False) plt.show() ###Output _____no_output_____ ###Markdown Pregunta* Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, grafique los resultados cuando: * el valor predicho y original son iguales * el valor predicho y original son distintos * Cuando el valor predicho y original son distintos , ¿Por qué ocurren estas fallas? ###Code mostar_resultados(digits,KNeighborsClassifier(),nx=5, ny=5,label = "correctos") mostar_resultados(digits,KNeighborsClassifier(),nx=5, ny=5,label = "incorrectos") ###Output _____no_output_____ ###Markdown Tarea N°02 Instrucciones1.- Completa tus datos personales (nombre y rol USM) en siguiente celda.Nombre: Lucas MonteroRol: 201473588-k2.- Debes pushear este archivo con tus cambios a tu repositorio personal del curso, incluyendo datos, imágenes, scripts, etc.3.- Se evaluará:- Soluciones- Código- Que Binder esté bien configurado.- Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error. I.- Clasificación de dígitosEn este laboratorio realizaremos el trabajo de reconocer un dígito a partir de una imagen. 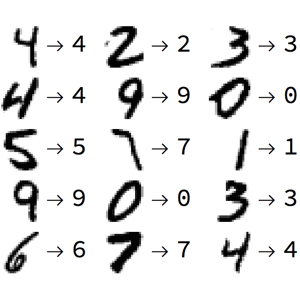![rgb](https://www.wolfram.com/language/11/neural-networks/assets.en/digit-classification/smallthumb_1.png) El objetivo es a partir de los datos, hacer la mejor predicción de cada imagen. Para ellos es necesario realizar los pasos clásicos de un proyecto de _Machine Learning_, como estadística descriptiva, visualización y preprocesamiento. * Se solicita ajustar al menos tres modelos de clasificación: * Regresión logística * K-Nearest Neighbours * Uno o más algoritmos a su elección [link](https://scikit-learn.org/stable/supervised_learning.htmlsupervised-learning) (es obligación escoger un _estimator_ que tenga por lo menos un hiperparámetro). * En los modelos que posean hiperparámetros es mandatorio buscar el/los mejores con alguna técnica disponible en `scikit-learn` ([ver más](https://scikit-learn.org/stable/modules/grid_search.htmltuning-the-hyper-parameters-of-an-estimator)).* Para cada modelo, se debe realizar _Cross Validation_ con 10 _folds_ utilizando los datos de entrenamiento con tal de determinar un intervalo de confianza para el _score_ del modelo.* Realizar una predicción con cada uno de los tres modelos con los datos _test_ y obtener el _score_. * Analizar sus métricas de error (accuracy, precision, recall, f-score) Exploración de los datosA continuación se carga el conjunto de datos a utilizar, a través del sub-módulo `datasets` de `sklearn`. ###Code import numpy as np import pandas as pd from sklearn import datasets import matplotlib.pyplot as plt %matplotlib inline digits_dict = datasets.load_digits() print(digits_dict["DESCR"]) digits_dict.keys() digits_dict["target"] ###Output _____no_output_____ ###Markdown A continuación se crea dataframe declarado como `digits` con los datos de `digits_dict` tal que tenga 65 columnas, las 6 primeras a la representación de la imagen en escala de grises (0-blanco, 255-negro) y la última correspondiente al dígito (`target`) con el nombre _target_. ###Code digits = ( pd.DataFrame( digits_dict["data"], ) .rename(columns=lambda x: f"c{x:02d}") .assign(target=digits_dict["target"]) .astype(int) ) digits.head() ###Output _____no_output_____ ###Markdown Ejercicio 1Análisis exploratorio: Realiza tu análisis exploratorio, no debes olvidar nada! Recuerda, cada análisis debe responder una pregunta.Algunas sugerencias:* ¿Cómo se distribuyen los datos?* ¿Cuánta memoria estoy utilizando?* ¿Qué tipo de datos son?* ¿Cuántos registros por clase hay?* ¿Hay registros que no se correspondan con tu conocimiento previo de los datos? ###Code #¿Cómo se distribuyen los datos? # Los datos se encuentran en el dataframe llamado "digits" # Se encuentran en columnas de string c+(dígito entre 00-63) # La ultima columna es un "target" que se utiliza para agrupar datos. #¿Cuánta memoria estoy utilizando? digits.info() #¿Qué tipo de datos son? # La información de la tabla es del formato int. #¿Cuántos registros por clase hay? #1797 #¿Hay registros que no se correspondan con tu conocimiento previo de los datos? #no ###Output _____no_output_____ ###Markdown Ejercicio 2Visualización: Para visualizar los datos utilizaremos el método `imshow` de `matplotlib`. Resulta necesario convertir el arreglo desde las dimensiones (1,64) a (8,8) para que la imagen sea cuadrada y pueda distinguirse el dígito. Superpondremos además el label correspondiente al dígito, mediante el método `text`. Esto nos permitirá comparar la imagen generada con la etiqueta asociada a los valores. Realizaremos lo anterior para los primeros 25 datos del archivo. ###Code digits_dict["images"][0] ###Output _____no_output_____ ###Markdown Visualiza imágenes de los dígitos utilizando la llave `images` de `digits_dict`. Sugerencia: Utiliza `plt.subplots` y el método `imshow`. Puedes hacer una grilla de varias imágenes al mismo tiempo! ###Code nx, ny = 5, 5 fig, axs = plt.subplots(nx,ny, figsize=(12, 12)) for i in range(1, nxny +1): img = digits_dict["images"][i] fig.add_subplot(nx, ny, i) plt.imshow(img) plt.show() ###Output _____no_output_____ ###Markdown Ejercicio 3Machine Learning: En esta parte usted debe entrenar los distintos modelos escogidos desde la librería de `skelearn`. Para cada modelo, debe realizar los siguientes pasos: train-test * Crear conjunto de entrenamiento y testeo (usted determine las proporciones adecuadas). * Imprimir por pantalla el largo del conjunto de entrenamiento y de testeo. * modelo: * Instanciar el modelo objetivo desde la librería sklearn. * Hiper-parámetros: Utiliza `sklearn.model_selection.GridSearchCV` para obtener la mejor estimación de los parámetros del modelo objetivo.* Métricas: * Graficar matriz de confusión. * Analizar métricas de error.__Preguntas a responder:__* ¿Cuál modelo es mejor basado en sus métricas?* ¿Cuál modelo demora menos tiempo en ajustarse?* ¿Qué modelo escoges? ###Code from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import confusion_matrix import time from sklearn.ensemble import RandomForestClassifier from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import f1_score from sklearn.svm import SVC from sklearn.model_selection import validation_curve from itertools import cycle from sklearn import svm, datasets from sklearn.metrics import roc_curve, auc from sklearn.preprocessing import label_binarize from sklearn.multiclass import OneVsRestClassifier from scipy import interp from sklearn.metrics import roc_auc_score from sklearn import linear_model from sklearn.model_selection import cross_validate from sklearn.metrics import make_scorer from sklearn.feature_selection import SelectKBest, f_classif from sklearn.feature_selection import chi2 X = digits.drop(columns="target").values y = digits["target"].values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42) tiempos = [] #Creamos una lista vacía para guardar los tiempos ########## Logistic Regresor ########## tiempo_i = time.time() #Guardamos el tiempo inicial LR = LogisticRegression() #Guardamos LogisticRegression() en LR LR.fit(X_train,y_train) #Usamos regresión logistica tiempo_f = time.time() #Guardamos el tiempo final tiempos.append(tiempo_f-tiempo_i) #Guardamos el tiempo que se demoró LR.score( X_test, y_test) #Vemos el score prediccion = LR.predict(X_test) #Guardamos la predicción confusion_matrix(y_test, prediccion) #Creamos la matriz de confusión f1_score(y_test, prediccion,average='micro') #Vemos el score final ########## Random Forest ########## tiempo_i = time.time() #Guardamos el tiempo inicial RF = RandomForestClassifier(max_depth=12, random_state=0) #Guardamos RandomForest en RF RF.fit(X_train,y_train) #Usamos random forest tiempo_f = time.time() #Guardamos el tiempo inicial tiempos.append(tiempo_f-tiempo_i) #Guardamos el tiempo que se demoró RF.score( X_test, y_test) #Vemos el score prediccion = RF.predict(X_test) #Guardamos la predicción confusion_matrix(y_test, prediccion) #Creamos la matriz de confusión f1_score(y_test, prediccion,average='micro') #Vemos el score final ########## KNN ########## tiempo_i = time.time() #Guardamos el tiempo inicial KNN = KNeighborsClassifier(n_neighbors=7) #Guardamos KNeighborsClassifier en KNN KNN.fit(X_train,y_train) #Usamos random forest tiempo_f = time.time() #Guardamos el tiempo inicial tiempos.append(tiempo_f-tiempo_i) #Guardamos el tiempo que se demoró KNN.score( X_test, y_test) #Vemos el score prediccion = KNN.predict(X_test) #Guardamos la predicción confusion_matrix(y_test, prediccion) #Creamos la matriz de confusión f1_score(y_test, prediccion,average='micro') #Vemos el score final ###Output _____no_output_____ ###Markdown Ejercicio 4__Comprensión del modelo:__ Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, debe comprender e interpretar minuciosamente los resultados y gráficos asocados al modelo en estudio, para ello debe resolver los siguientes puntos: * Cross validation: usando cv (con n_fold = 10), sacar una especie de "intervalo de confianza" sobre alguna de las métricas estudiadas en clases: * $\mu \pm \sigma$ = promedio $\pm$ desviación estandar * Curva de Validación: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.htmlsphx-glr-auto-examples-model-selection-plot-validation-curve-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. * Curva AUC–ROC: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.htmlsphx-glr-auto-examples-model-selection-plot-roc-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. ###Code cv_results = cross_validate(LR, X, y, cv=10) #Vemos la cross validation de regresión logistica cv_results['test_score'] cv_results = cross_validate(RF, X, y, cv=10) #Vemos la cross validation de random forest cv_results['test_score'] cv_results = cross_validate(KNN, X, y, cv=10) #Vemos la cross validation de knn cv_results['test_score'] ###Output _____no_output_____ ###Markdown Ejercicio 5__Reducción de la dimensión:__ Tomando en cuenta el mejor modelo encontrado en el `Ejercicio 3`, debe realizar una redcción de dimensionalidad del conjunto de datos. Para ello debe abordar el problema ocupando los dos criterios visto en clases: * Selección de atributos* Extracción de atributos__Preguntas a responder:__Una vez realizado la reducción de dimensionalidad, debe sacar algunas estadísticas y gráficas comparativas entre el conjunto de datos original y el nuevo conjunto de datos (tamaño del dataset, tiempo de ejecución del modelo, etc.) ###Code ## FIX ME PLEASE ###Output _____no_output_____ ###Markdown Ejercicio 6__Visualizando Resultados:__ A continuación se provee código para comparar las etiquetas predichas vs las etiquetas reales del conjunto de _test_. ###Code def mostar_resultados(digits,model,nx=5, ny=5,label = "correctos"): """ Muestra los resultados de las prediciones de un modelo de clasificacion en particular. Se toman aleatoriamente los valores de los resultados. - label == 'correcto': retorna los valores en que el modelo acierta. - label == 'incorrecto': retorna los valores en que el modelo no acierta. Observacion: El modelo que recibe como argumento debe NO encontrarse 'entrenado'. :param digits: dataset 'digits' :param model: modelo de sklearn :param nx: numero de filas (subplots) :param ny: numero de columnas (subplots) :param label: datos correctos o incorrectos :return: graficos matplotlib """ X = digits.drop(columns="target").values y = digits["target"].values X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state = 42) model.fit(X_train, Y_train) # ajustando el modelo y_pred = list(model.predict(X_test)) # Mostrar los datos correctos if label=="correctos": mask = (y_pred == y_test) color = "green" # Mostrar los datos correctos elif label=="incorrectos": mask = (y_pred != y_test) color = "red" else: raise ValueError("Valor incorrecto") X_aux = X_test[mask] y_aux_true = y_test[mask] y_aux_pred = y_pred[mask] # We'll plot the first 100 examples, randomly choosen fig, ax = plt.subplots(nx, ny, figsize=(12,12)) for i in range(nx): for j in range(ny): index = j + ny * i data = X_aux[index, :].reshape(8,8) label_pred = str(int(y_aux_pred[index])) label_true = str(int(y_aux_true[index])) ax[i][j].imshow(data, interpolation='nearest', cmap='gray_r') ax[i][j].text(0, 0, label_pred, horizontalalignment='center', verticalalignment='center', fontsize=10, color=color) ax[i][j].text(7, 0, label_true, horizontalalignment='center', verticalalignment='center', fontsize=10, color='blue') ax[i][j].get_xaxis().set_visible(False) ax[i][j].get_yaxis().set_visible(False) plt.show() ###Output _____no_output_____ ###Markdown Pregunta* Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, grafique los resultados cuando: * el valor predicho y original son iguales * el valor predicho y original son distintos * Cuando el valor predicho y original son distintos , ¿Por qué ocurren estas fallas? ###Code ## FIX ME PLEASE ###Output _____no_output_____ ###Markdown Tarea N°02 Instrucciones1.- Completa tus datos personales (nombre y rol USM) en siguiente celda.Nombre:Rol:2.- Debes pushear este archivo con tus cambios a tu repositorio personal del curso, incluyendo datos, imágenes, scripts, etc.3.- Se evaluará:- Soluciones- Código- Que Binder esté bien configurado.- Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error. I.- Clasificación de dígitosEn este laboratorio realizaremos el trabajo de reconocer un dígito a partir de una imagen. 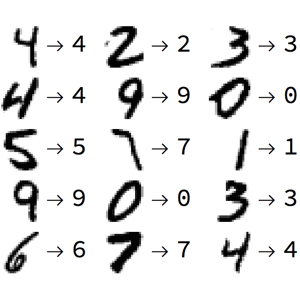![rgb](https://www.wolfram.com/language/11/neural-networks/assets.en/digit-classification/smallthumb_1.png) El objetivo es a partir de los datos, hacer la mejor predicción de cada imagen. Para ellos es necesario realizar los pasos clásicos de un proyecto de _Machine Learning_, como estadística descriptiva, visualización y preprocesamiento. * Se solicita ajustar al menos tres modelos de clasificación: * Regresión logística * K-Nearest Neighbours * Uno o más algoritmos a su elección [link](https://scikit-learn.org/stable/supervised_learning.htmlsupervised-learning) (es obligación escoger un _estimator_ que tenga por lo menos un hiperparámetro). * En los modelos que posean hiperparámetros es mandatorio buscar el/los mejores con alguna técnica disponible en `scikit-learn` ([ver más](https://scikit-learn.org/stable/modules/grid_search.htmltuning-the-hyper-parameters-of-an-estimator)).* Para cada modelo, se debe realizar _Cross Validation_ con 10 _folds_ utilizando los datos de entrenamiento con tal de determinar un intervalo de confianza para el _score_ del modelo.* Realizar una predicción con cada uno de los tres modelos con los datos _test_ y obtener el _score_. * Analizar sus métricas de error (accuracy, precision, recall, f-score) Exploración de los datosA continuación se carga el conjunto de datos a utilizar, a través del sub-módulo `datasets` de `sklearn`. ###Code import numpy as np import pandas as pd from sklearn import datasets import matplotlib.pyplot as plt %matplotlib inline digits_dict = datasets.load_digits() print(digits_dict["DESCR"]) digits_dict.keys() digits_dict["target"] ###Output _____no_output_____ ###Markdown A continuación se crea dataframe declarado como `digits` con los datos de `digits_dict` tal que tenga 65 columnas, las 6 primeras a la representación de la imagen en escala de grises (0-blanco, 255-negro) y la última correspondiente al dígito (`target`) con el nombre _target_. ###Code digits = ( pd.DataFrame( digits_dict["data"], ) .rename(columns=lambda x: f"c{x:02d}") .assign(target=digits_dict["target"]) .astype(int) ) digits.head() ###Output _____no_output_____ ###Markdown Ejercicio 1Análisis exploratorio: Realiza tu análisis exploratorio, no debes olvidar nada! Recuerda, cada análisis debe responder una pregunta.Algunas sugerencias:* ¿Cómo se distribuyen los datos?* ¿Cuánta memoria estoy utilizando?* ¿Qué tipo de datos son?* ¿Cuántos registros por clase hay?* ¿Hay registros que no se correspondan con tu conocimiento previo de los datos? ###Code ## FIX ME PLEASE digits.describe() digits.memory_usage() digits.dtypes len(digits.columns) ###Output _____no_output_____ ###Markdown Ejercicio 2Visualización: Para visualizar los datos utilizaremos el método `imshow` de `matplotlib`. Resulta necesario convertir el arreglo desde las dimensiones (1,64) a (8,8) para que la imagen sea cuadrada y pueda distinguirse el dígito. Superpondremos además el label correspondiente al dígito, mediante el método `text`. Esto nos permitirá comparar la imagen generada con la etiqueta asociada a los valores. Realizaremos lo anterior para los primeros 25 datos del archivo. ###Code digits_dict["images"][0] ###Output _____no_output_____ ###Markdown Visualiza imágenes de los dígitos utilizando la llave `images` de `digits_dict`. Sugerencia: Utiliza `plt.subplots` y el método `imshow`. Puedes hacer una grilla de varias imágenes al mismo tiempo! ###Code nx, ny = 5, 5 fig, axs = plt.subplots(nx, ny, figsize=(12, 12)) ## FIX ME PLEASE plt.imshow(digits_dict['images'][0]) ###Output _____no_output_____ ###Markdown Ejercicio 3Machine Learning: En esta parte usted debe entrenar los distintos modelos escogidos desde la librería de `skelearn`. Para cada modelo, debe realizar los siguientes pasos:* train-test * Crear conjunto de entrenamiento y testeo (usted determine las proporciones adecuadas). * Imprimir por pantalla el largo del conjunto de entrenamiento y de testeo. * modelo: * Instanciar el modelo objetivo desde la librería sklearn. * Hiper-parámetros: Utiliza `sklearn.model_selection.GridSearchCV` para obtener la mejor estimación de los parámetros del modelo objetivo.* Métricas: * Graficar matriz de confusión. * Analizar métricas de error.__Preguntas a responder:__* ¿Cuál modelo es mejor basado en sus métricas?* ¿Cuál modelo demora menos tiempo en ajustarse?* ¿Qué modelo escoges? ###Code X = digits.drop(columns="target").values y = digits["target"].values from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state = 2) model=LogisticRegression() len(X_train) len(X_test) len(y_train) len(y_test) from sklearn.linear_model import LogisticRegression rlog = LogisticRegression() rlog.fit(X_train, y_train) import sklearn as sk sk.model_selection.GridSearchCV import matplotlib.pyplot as plt # doctest: +SKIP from sklearn.datasets import make_classification from sklearn.metrics import plot_confusion_matrix from sklearn.model_selection import train_test_split from sklearn.svm import SVC X, y = make_classification(random_state=0) X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) clf = SVC(random_state=0) clf.fit(X_train, y_train) SVC(random_state=0) plot_confusion_matrix(clf, X_test, y_test) # doctest: +SKIP plt.show() # doctest: +SKIP # metrics from metrics_classification import * from sklearn.metrics import confusion_matrix y_true = list(y_test) y_pred = list(rlog.predict(X_test)) print('Valores:\n') print('originales: ', y_true) print('predicho: ', y_pred) print('\nMatriz de confusion:\n ') print(confusion_matrix(y_true,y_pred)) # ejemplo df_temp = pd.DataFrame( { 'y':y_true, 'yhat':y_pred } ) df_metrics = summary_metrics(df_temp) print("\nMetricas para los regresores : 'sepal length (cm)' y 'sepal width (cm)'") print("") print(df_metrics) #k-means # librerias import os import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from sklearn.datasets.samples_generator import make_blobs pd.set_option('display.max_columns', 500) # Ver más columnas de los dataframes # Ver gráficos de matplotlib en jupyter notebook/lab %matplotlib inline def init_blobs(N, k, seed=1): X, y = make_blobs(n_samples=N, centers=k, random_state=seed, cluster_std=0.60) return X digits.head() from sklearn.preprocessing import StandardScaler scaler = StandardScaler() columns = [i for i in digits.columns] digits[columns] = scaler.fit_transform(digits[columns]) digits.head() digits.describe() # graficar #un ejemplo sns.set(rc={'figure.figsize':(11.7,8.27)}) ax = sns.scatterplot( data=digits,x="c00", y="c01") # ajustar modelo: k-means from sklearn.cluster import KMeans kmeans = KMeans(n_clusters=4) kmeans.fit(X) centroids = kmeans.cluster_centers_ # centros clusters = kmeans.labels_ # clusters print(digits.columns) len(clusters) len(centroids) # etiquetar los datos con los clusters encontrados clusters=[clusters[i] for i in range(0,1797)] clusters=np.array(clusters) digits["cluster"] = clusters digits["cluster"] = digits["cluster"].astype('category') centroids_df = pd.DataFrame(centroids, columns=['c00','c01']) centroids_df["cluster"] = [0,1,2,3] # graficar los datos etiquetados con k-means fig, ax = plt.subplots(figsize=(11, 8.5)) sns.scatterplot( data=digits, x="c00", y="c01", hue="cluster", legend='full') sns.scatterplot(x="c00", y="c01", s=100, color="black", marker="x", data=centroids_df) #regresion logistica # librerias import os import numpy as np import pandas as pd from sklearn import datasets from sklearn.model_selection import train_test_split import matplotlib.pyplot as plt import seaborn as sns pd.set_option('display.max_columns', 500) # Ver más columnas de los dataframes # Ver gráficos de matplotlib en jupyter notebook/lab %matplotlib inline # datos from sklearn.linear_model import LogisticRegression X = digits[['c00', 'c01']] Y = digits['c02'] # split dataset X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.1, random_state = 1) # print rows train and test sets print('Separando informacion:\n') print('numero de filas data original : ',len(X)) print('numero de filas train set : ',len(X_train)) print('numero de filas test set : ',len(X_test)) # Creando el modelo rlog = LogisticRegression() rlog.fit(X_train, Y_train) # ajustando el modelo # grafica de la regresion logistica plt.figure(figsize=(12,4)) # dataframe a matriz X = X.values Y = Y.values x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5 y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5 h = .02 # step size in the mesh xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = rlog.predict(np.c_[xx.ravel(), yy.ravel()]) # Put the result into a color plot Z = Z.reshape(xx.shape) plt.figure(1, figsize=(4, 3)) plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired) # Plot also the training points plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolors='k', cmap=plt.cm.Paired) plt.xlabel('Sepal length') plt.ylabel('Sepal width') plt.show() ###Output _____no_output_____ ###Markdown Ejercicio 4__Comprensión del modelo:__ Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, debe comprender e interpretar minuciosamente los resultados y gráficos asocados al modelo en estudio, para ello debe resolver los siguientes puntos: * Cross validation: usando cv (con n_fold = 10), sacar una especie de "intervalo de confianza" sobre alguna de las métricas estudiadas en clases: * $\mu \pm \sigma$ = promedio $\pm$ desviación estandar * Curva de Validación: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.htmlsphx-glr-auto-examples-model-selection-plot-validation-curve-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. * Curva AUC–ROC: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.htmlsphx-glr-auto-examples-model-selection-plot-roc-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. ###Code from sklearn.model_selection import cross_val_score from sklearn.tree import DecisionTreeClassifier,DecisionTreeRegressor # separ los datos en train y eval X_train, X_eval, y_train, y_eval = train_test_split(X, y, test_size=0.35, train_size=0.65, random_state=1982) model = DecisionTreeClassifier(criterion='entropy', max_depth=5) precision = cross_val_score(estimator=model, X=X_train, y=y_train, cv=10) precision = [round(x,2) for x in precision] print('Precisiones: {} '.format(precision)) print('Precision promedio: {0: .3f} +/- {1: .3f}'.format(np.mean(precision),np.std(precision))) print(__doc__) import matplotlib.pyplot as plt import numpy as np import sklearn as sk from sklearn.datasets import load_digits from sklearn.svm import SVC from sklearn.model_selection import validation_curve param_range = np.logspace(-6, -1, 5) train_scores, test_scores = validation_curve( SVC(), X, y, "gamma", param_range, param_name='accuracy') train_scores_mean = np.mean(train_scores, axis=1) train_scores_std = np.std(train_scores, axis=1) test_scores_mean = np.mean(test_scores, axis=1) test_scores_std = np.std(test_scores, axis=1) plt.title("Validation Curve with SVM") plt.xlabel(r"$\gamma$") plt.ylabel("Score") plt.ylim(0.0, 1.1) lw = 2 plt.semilogx(param_range, train_scores_mean, label="Training score", color="darkorange", lw=lw) plt.fill_between(param_range, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.2, color="darkorange", lw=lw) plt.semilogx(param_range, test_scores_mean, label="Cross-validation score", color="navy", lw=lw) plt.fill_between(param_range, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.2, color="navy", lw=lw) plt.legend(loc="best") plt.show() sk.metrics.SCORERS.keys() ###Output _____no_output_____ ###Markdown Ejercicio 5__Reducción de la dimensión:__ Tomando en cuenta el mejor modelo encontrado en el `Ejercicio 3`, debe realizar una redcción de dimensionalidad del conjunto de datos. Para ello debe abordar el problema ocupando los dos criterios visto en clases: * Selección de atributos* Extracción de atributos__Preguntas a responder:__Una vez realizado la reducción de dimensionalidad, debe sacar algunas estadísticas y gráficas comparativas entre el conjunto de datos original y el nuevo conjunto de datos (tamaño del dataset, tiempo de ejecución del modelo, etc.) ###Code digits.columns = [f'V{k}' for k in range(1,digits.shape[1]+1)] digits['y']=y digits.head() from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import f_classif # Separamos las columnas objetivo x_training = digits.drop(['y'], axis=1) y_training = digits['y'] # Aplicando el algoritmo univariante de prueba F. k = 15 # número de atributos a seleccionar columnas = list(x_training.columns.values) seleccionadas = SelectKBest(f_classif, k=k).fit(x_training, y_training) catrib = digits['y'].get_support() atributos = [columnas[i] for i in list(catrib.nonzero()[0])] atributos ###Output _____no_output_____ ###Markdown Ejercicio 6__Visualizando Resultados:__ A continuación se provee código para comparar las etiquetas predichas vs las etiquetas reales del conjunto de _test_. ###Code def mostar_resultados(digits,model,nx=5, ny=5,label = "correctos"): """ Muestra los resultados de las prediciones de un modelo de clasificacion en particular. Se toman aleatoriamente los valores de los resultados. - label == 'correcto': retorna los valores en que el modelo acierta. - label == 'incorrecto': retorna los valores en que el modelo no acierta. Observacion: El modelo que recibe como argumento debe NO encontrarse 'entrenado'. :param digits: dataset 'digits' :param model: modelo de sklearn :param nx: numero de filas (subplots) :param ny: numero de columnas (subplots) :param label: datos correctos o incorrectos :return: graficos matplotlib """ X = digits.drop(columns="target").values y = digits["target"].values X_train, X_test, Y_train, Y_test = train_test_split(X, y, test_size=0.2, random_state = 42) model.fit(X_train, Y_train) # ajustando el modelo y_pred = list(model.predict(X_test)) # Mostrar los datos correctos if label=="correctos": mask = (y_pred == y_test) color = "green" # Mostrar los datos correctos elif label=="incorrectos": mask = (y_pred != y_test) color = "red" else: raise ValueError("Valor incorrecto") X_aux = X_test[mask] y_aux_true = y_test[mask] y_aux_pred = y_pred[mask] # We'll plot the first 100 examples, randomly choosen fig, ax = plt.subplots(nx, ny, figsize=(12,12)) for i in range(nx): for j in range(ny): index = j + ny * i data = X_aux[index, :].reshape(8,8) label_pred = str(int(y_aux_pred[index])) label_true = str(int(y_aux_true[index])) ax[i][j].imshow(data, interpolation='nearest', cmap='gray_r') ax[i][j].text(0, 0, label_pred, horizontalalignment='center', verticalalignment='center', fontsize=10, color=color) ax[i][j].text(7, 0, label_true, horizontalalignment='center', verticalalignment='center', fontsize=10, color='blue') ax[i][j].get_xaxis().set_visible(False) ax[i][j].get_yaxis().set_visible(False) plt.show() ###Output _____no_output_____ ###Markdown Pregunta* Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, grafique los resultados cuando: * el valor predicho y original son iguales * el valor predicho y original son distintos * Cuando el valor predicho y original son distintos , ¿Por qué ocurren estas fallas? ###Code mostar_resultados(digits,model,nx=5, ny=5,label = "correctos") ###Output _____no_output_____ ###Markdown Tarea N°02 Instrucciones1.- Completa tus datos personales (nombre y rol USM) en siguiente celda.Nombre:Andrés Montecinos LópezRol:201204515-02.- Debes pushear este archivo con tus cambios a tu repositorio personal del curso, incluyendo datos, imágenes, scripts, etc.3.- Se evaluará:- Soluciones- Código- Que Binder esté bien configurado.- Al presionar `Kernel -> Restart Kernel and Run All Cells` deben ejecutarse todas las celdas sin error. I.- Clasificación de dígitosEn este laboratorio realizaremos el trabajo de reconocer un dígito a partir de una imagen. 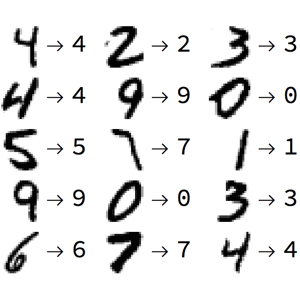![rgb](https://www.wolfram.com/language/11/neural-networks/assets.en/digit-classification/smallthumb_1.png) El objetivo es a partir de los datos, hacer la mejor predicción de cada imagen. Para ellos es necesario realizar los pasos clásicos de un proyecto de _Machine Learning_, como estadística descriptiva, visualización y preprocesamiento. * Se solicita ajustar al menos tres modelos de clasificación: * Regresión logística * K-Nearest Neighbours * Uno o más algoritmos a su elección [link](https://scikit-learn.org/stable/supervised_learning.htmlsupervised-learning) (es obligación escoger un _estimator_ que tenga por lo menos un hiperparámetro). * En los modelos que posean hiperparámetros es mandatorio buscar el/los mejores con alguna técnica disponible en `scikit-learn` ([ver más](https://scikit-learn.org/stable/modules/grid_search.htmltuning-the-hyper-parameters-of-an-estimator)).* Para cada modelo, se debe realizar _Cross Validation_ con 10 _folds_ utilizando los datos de entrenamiento con tal de determinar un intervalo de confianza para el _score_ del modelo.* Realizar una predicción con cada uno de los tres modelos con los datos _test_ y obtener el _score_. * Analizar sus métricas de error (accuracy, precision, recall, f-score) Exploración de los datosA continuación se carga el conjunto de datos a utilizar, a través del sub-módulo `datasets` de `sklearn`. ###Code import numpy as np import pandas as pd from sklearn import datasets import matplotlib.pyplot as plt %matplotlib inline digits_dict = datasets.load_digits() print(digits_dict["DESCR"]) digits_dict.keys() digits_dict["target"] ###Output _____no_output_____ ###Markdown A continuación se crea dataframe declarado como `digits` con los datos de `digits_dict` tal que tenga 65 columnas, las 6 primeras a la representación de la imagen en escala de grises (0-blanco, 255-negro) y la última correspondiente al dígito (`target`) con el nombre _target_. ###Code digits = ( pd.DataFrame( digits_dict["data"], ) .rename(columns=lambda x: f"c{x:02d}") .assign(target=digits_dict["target"]) .astype(int) ) digits.head() ###Output _____no_output_____ ###Markdown Ejercicio 1Análisis exploratorio: Realiza tu análisis exploratorio, no debes olvidar nada! Recuerda, cada análisis debe responder una pregunta.Algunas sugerencias:* ¿Cómo se distribuyen los datos?* ¿Cuánta memoria estoy utilizando?* ¿Qué tipo de datos son?* ¿Cuántos registros por clase hay?* ¿Hay registros que no se correspondan con tu conocimiento previo de los datos? ¿Qué pregunta (s) estás tratando de resolver (o probar que estás equivocado)? * Se intenta desarrollar un clasificador de digitos a partir de imagenes escritas a mano, empleando diferentes algoritmos de clasificación pertenecientes a la rama de Machine Learnig y que fueron vistos en clases. Para ello se provee de una matriz de datos previamente manipulada y normalizada, donde se reduce a una entrada de una matriz de 8x8 con datos que van del rango de 0 a 16 que representan el dígito entregado, además del valor objetivo. ¿Qué tipos de Datos son? * Inicialmente se observa que los datos a analizar son de tipo númerico, conformando un total de 1797 datos. De estos se consideran 64 variables de entrada, correspondiente a los pixeles de una imagen, con el objetivo de predecir un digito.* Por otro lado, cabe señalar que para elaborar la base de datos se consideraron digitos escritos por 43 personas donde 30 de ellas participaron generando digitos para la etapa de entrenamiento y el resto para la etapa de prueba. ###Code digits.info() digits.shape # En base a esto se y la información de la celda anterior se obtiene que la base de datos # no presenta valores nulos ###Output _____no_output_____ ###Markdown ¿Cuántos registros por clase hay?* En este caso se analizarán al menos 10 clases con digitos de 0 a 10. ###Code digits['target'].unique() ###Output _____no_output_____ ###Markdown Ejercicio 2Visualización: Para visualizar los datos utilizaremos el método `imshow` de `matplotlib`. Resulta necesario convertir el arreglo desde las dimensiones (1,64) a (8,8) para que la imagen sea cuadrada y pueda distinguirse el dígito. Superpondremos además el label correspondiente al dígito, mediante el método `text`. Esto nos permitirá comparar la imagen generada con la etiqueta asociada a los valores. Realizaremos lo anterior para los primeros 25 datos del archivo. ###Code #Ejemplo de digitos a=digits_dict["images"][0] plt.imshow(a, cmap=plt.cm.gray_r, interpolation='nearest') ###Output _____no_output_____ ###Markdown Visualiza imágenes de los dígitos utilizando la llave `images` de `digits_dict`. Sugerencia: Utiliza `plt.subplots` y el método `imshow`. Puedes hacer una grilla de varias imágenes al mismo tiempo! ###Code nx, ny = 5, 5 fig, ax = plt.subplots(nx, ny, figsize=(12, 12)) #plt.imshow(a, cmap=plt.cm.gray_r, interpolation='nearest') axes = [] for i in range(nxny): axes.append(fig.add_subplot(nx,ny,i+1)) a=digits_dict["images"][i] plt.imshow(a, cmap=plt.cm.gray_r, interpolation='nearest') plt.subplots_adjust(top = 0.9) fig.suptitle('Distribución variables numéricas', fontsize = 10, fontweight = "bold") ###Output _____no_output_____ ###Markdown Ejercicio 3Machine Learning: En esta parte usted debe entrenar los distintos modelos escogidos desde la librería de `skelearn`. Para cada modelo, debe realizar los siguientes pasos: train-test * Crear conjunto de entrenamiento y testeo (usted determine las proporciones adecuadas). * Imprimir por pantalla el largo del conjunto de entrenamiento y de testeo. * modelo: * Instanciar el modelo objetivo desde la librería sklearn. * Hiper-parámetros: Utiliza `sklearn.model_selection.GridSearchCV` para obtener la mejor estimación de los parámetros del modelo objetivo.* Métricas: * Graficar matriz de confusión. * Analizar métricas de error.__Preguntas a responder:__* ¿Cuál modelo es mejor basado en sus métricas?* ¿Cuál modelo demora menos tiempo en ajustarse?* ¿Qué modelo escoges? train-test ###Code X = digits.drop(columns="target").values y = digits["target"].values #División de Datos # Reparto de datos en train y test # ============================================================================== from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split( digits.drop('target', axis = 'columns'), digits['target'], train_size = 0.8, random_state = 1234, shuffle = True ) print('El conjuto de entrenamiento se conforma de:',y_train.size,'ejemplos') print('El conjuto de prueba se conforma de:',y_test.size,'ejemplos') print("Partición de entrenamento") print("-----------------------") print(y_train.describe()) print("Partición de test") print("-----------------------") print(y_test.describe()) ###Output Partición de test ----------------------- count 360.000000 mean 4.452778 std 2.774334 min 0.000000 25% 2.000000 50% 4.000000 75% 7.000000 max 9.000000 Name: target, dtype: float64 ###Markdown Metricas modelos analizados ###Code from sklearn.model_selection import GridSearchCV from sklearn import tree from sklearn.linear_model import LogisticRegression from sklearn.svm import SVC from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import RandomForestClassifier # nombre modelos names_models = [ "RBF SVM", "Decision Tree", "Random Forest" ] # modelos classifiers = [ SVC(kernel='poly',C=1), DecisionTreeClassifier(), RandomForestClassifier(), ] list_models = list(zip(names_models,classifiers)) hiperparametros={ 'RBF SVM': {'gamma': [0.01, 0.1, 2,10]}, 'Decision Tree' : {'max_depth':[2,3,4,5,6]}, 'Random Forest' : {'max_depth':[2,3,4,5,6]} } hiperparametros['RBF SVM'] from metrics_classification import* from sklearn.metrics import confusion_matrix from timeit import default_timer import seaborn as sns frames_metrics = pd.DataFrame([]) for nombre,modelo in list_models: inicio=default_timer() grid = GridSearchCV( estimator = modelo, #modelo a ajustar param_grid = hiperparametros[nombre], #función segúnel nombre del modelo arroje los hiperametros cargados anteriormente scoring = 'neg_root_mean_squared_error', n_jobs = - 1, cv = 10, verbose = 0, return_train_score = True) model_fit = grid.fit(X = X_train, y = y_train) modelo_final = grid.best_estimator_ print(modelo_final) preds = modelo_final.predict(X = X_test) df_temp = pd.DataFrame( { 'y':y_test, 'yhat': preds } ) a=summary_metrics(df_temp) fin=default_timer() a['name models']=nombre a['tiempo']=fin-inicio frames_metrics=pd.concat([frames_metrics,a],axis=0) matr=confusion_matrix(y_test,preds) ind=['0','1','2','3','4','5','6','7','8','9'] df_cn=pd.DataFrame(matr,index=ind,columns=ind) ax = plt.axes() grafica=sns.heatmap(df_cn, cmap="YlGnBu",annot=True) plt.xlabel='Digito' plt.ylabel='Digito' ax.set_title(nombre) plt.show() frames_metrics ###Output SVC(C=1, gamma=0.01, kernel='poly') ###Markdown * el mejor modelo basado en sus métricas es RBF SVM. Además respesto a random forest que tuvo buenas métricas, SVM es más rápido. Ejercicio 4__Comprensión del modelo:__ Tomando en cuenta el mejor modelo entontrado en el `Ejercicio 3`, debe comprender e interpretar minuciosamente los resultados y gráficos asocados al modelo en estudio, para ello debe resolver los siguientes puntos: * Cross validation: usando cv (con n_fold = 10), sacar una especie de "intervalo de confianza" sobre alguna de las métricas estudiadas en clases: * $\mu \pm \sigma$ = promedio $\pm$ desviación estandar * Curva de Validación: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.htmlsphx-glr-auto-examples-model-selection-plot-validation-curve-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. * Curva AUC–ROC: Replica el ejemplo del siguiente [link](https://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.htmlsphx-glr-auto-examples-model-selection-plot-roc-py) pero con el modelo, parámetros y métrica adecuada. Saque conclusiones del gráfico. Curva de Validación ###Code import matplotlib.pyplot as plt import numpy as np from matplotlib.pyplot import subplots, show from sklearn.datasets import load_digits from sklearn.svm import SVC from sklearn.model_selection import validation_curve X, y = load_digits(return_X_y=True) param_range = np.logspace(-6, 3, 5) train_scores, test_scores = validation_curve( SVC(kernel='poly',C=1), X, y, param_name="gamma", param_range=param_range, scoring="accuracy", n_jobs=1,cv=10) train_scores_mean = np.mean(train_scores, axis=1) train_scores_std = np.std(train_scores, axis=1) test_scores_mean = np.mean(test_scores, axis=1) test_scores_std = np.std(test_scores, axis=1) fig, ax = subplots() plt.title('Validation Curve with SVM') plt.ylim(0.0, 1.1) lw = 2 ax.semilogx(param_range, train_scores_mean, label="Training score", color="darkorange", lw=lw) ax.fill_between(param_range, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.2, color="darkorange", lw=lw) ax.semilogx(param_range, test_scores_mean, label="Cross-validation score", color="navy", lw=lw) ax.fill_between(param_range, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.2, color="navy", lw=lw) ax.legend(loc="best") ax.set_xlabel('gamma') ax.set_ylabel('Score') show() ###Output _____no_output_____ ###Markdown * se aprecia que del gráfico que para entrenamiento y cross-validation el mejor ajuste del parámetro gama es 0.01 Curva AUC–ROC ###Code import numpy as np import matplotlib.pyplot as plt from itertools import cycle from sklearn import svm, datasets from sklearn.metrics import roc_curve, auc from sklearn.model_selection import train_test_split from sklearn.preprocessing import label_binarize from sklearn.multiclass import OneVsRestClassifier from scipy import interp from sklearn.metrics import roc_auc_score # Import some data to play with X = digits.drop(columns="target").values y=digits["target"].values # Binarize the output y = label_binarize(y, classes=[0, 1, 2,3,4,5,6,7,8,9]) n_classes = y.shape[1] # shuffle and split training and test sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.2, random_state=0) # Learn to predict each class against the other classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True, random_state=0)) y_score = classifier.fit(X_train, y_train).decision_function(X_test) # Compute ROC curve and ROC area for each class fpr = dict() tpr = dict() roc_auc = dict() for i in range(n_classes): fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i]) roc_auc[i] = auc(fpr[i], tpr[i]) # Compute micro-average ROC curve and ROC area fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel()) roc_auc["micro"] = auc(fpr["micro"], tpr["micro"]) # First aggregate all false positive rates all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)])) # Then interpolate all ROC curves at this points mean_tpr = np.zeros_like(all_fpr) for i in range(n_classes): mean_tpr += interp(all_fpr, fpr[i], tpr[i]) # Finally average it and compute AUC mean_tpr /= n_classes fpr["macro"] = all_fpr tpr["macro"] = mean_tpr roc_auc["macro"] = auc(fpr["macro"], tpr["macro"]) # Plot all ROC curves fig, ax = subplots( figsize=(8,6)) ax.plot(fpr["micro"], tpr["micro"], label='micro-average ROC curve (area = {0:0.2f})' ''.format(roc_auc["micro"]), color='deeppink', linestyle=':', linewidth=4) ax.plot(fpr["macro"], tpr["macro"], label='macro-average ROC curve (area = {0:0.2f})' ''.format(roc_auc["macro"]), color='navy', linestyle=':', linewidth=4) colors = cycle(['aqua', 'darkorange', 'cornflowerblue']) for i, color in zip(range(n_classes), colors): ax.plot(fpr[i], tpr[i], color=color, lw=lw, label='ROC curve of class {0} (area = {1:0.2f})' ''.format(i, roc_auc[i])) ax.plot([0, 1], [0, 1], 'k--', lw=lw) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) ax.set_xlabel('False Positive Rate') ax.set_ylabel('True Positive Rate') plt.title('Some extension of Receiver operating characteristic to multi-class') ax.legend(bbox_to_anchor=(1.05, 1)) show() ###Output <ipython-input-20-4836a1f385bd>:7: DeprecationWarning: scipy.interp is deprecated and will be removed in SciPy 2.0.0, use numpy.interp instead mean_tpr += interp(all_fpr, fpr[i], tpr[i]) ###Markdown * Las mejores clasificaciones son hechas para la curva de clase 1-7-9.* Por otro lado existe tendencia a clasificar bien, esto dado que la razon de verdadero positivo es alta y se aleja de la diagonal. Ejercicio 5__Reducción de la dimensión:__ Tomando en cuenta el mejor modelo encontrado en el `Ejercicio 3`, debe realizar una redcción de dimensionalidad del conjunto de datos. Para ello debe abordar el problema ocupando los dos criterios visto en clases: * Selección de atributos* Extracción de atributos__Preguntas a responder:__Una vez realizado la reducción de dimensionalidad, debe sacar algunas estadísticas y gráficas comparativas entre el conjunto de datos original y el nuevo conjunto de datos (tamaño del dataset, tiempo de ejecución del modelo, etc.) ###Code from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import f_regression, mutual_info_regression from sklearn.feature_selection import chi2,mutual_info_classif X1 = digits.drop(columns="target") y1 = digits["target"] # Aplicando el algoritmo univariante de prueba F. k = 18 # número de atributos a seleccionar #columnas = list(X_train1.columns.values) seleccionadas = SelectKBest(mutual_info_classif, k=k).fit(X1, y1) selected_features_df = pd.DataFrame({'Feature':list(X1.columns), 'Scores MI':seleccionadas.scores_}) selected_features_df.sort_values(by='Scores MI', ascending=False).head(9) ###Output _____no_output_____ ###Markdown * aqui se muestran las mejores variables usando selección de atributos ###Code from sklearn.svm import SVC from sklearn.datasets import load_digits from sklearn.feature_selection import RFE import matplotlib.pyplot as plt # Load the digits dataset X2 = digits.drop(columns="target") y2 = digits["target"] # Create the RFE object and rank each pixel def error_rfe(n): svc = SVC(kernel="linear", C=1,gamma=2) rfe = RFE(estimator=svc, n_features_to_select=n, step=1) selec=rfe.fit(X2, y2) y_pr=selec.predict(X2) fina=pd.DataFrame({'pixel':list(range(0,64,1)),'Ranking':selec.ranking_}) df_temp = pd.DataFrame( { 'y':list(y2), 'yhat': list(y_pr) } ) a=summary_metrics(df_temp) return a error_rfe(2) error_rfe(4) error_rfe(6) error_rfe(8) error_rfe(10) error_rfe(12) error_rfe(14) error_rfe(18) ###Output _____no_output_____ ###Markdown Sobre 15 variables es suficiente para estimar. Ejercicio 6__Visualizando Resultados:__ A continuación se provee código para comparar las etiquetas predichas vs las etiquetas reales del conjunto de _test_. ###Code def mostar_resultados(digits,model,nx=5, ny=5,label = "correctos"): """ Muestra los resultados de las prediciones de un modelo de clasificacion en particular. Se toman aleatoriamente los valores de los resultados. - label == 'correcto': retorna los valores en que el modelo acierta. - label == 'incorrecto': retorna los valores en que el modelo no acierta. Observacion: El modelo que recibe como argumento debe NO encontrarse 'entrenado'. :param digits: dataset 'digits' :param model: modelo de sklearn :param nx: numero de filas (subplots) :param ny: numero de columnas (subplots) :param label: datos correctos o incorrectos :return: graficos matplotlib """ X = digits.drop(columns="target").values y = digits["target"].values X_train, X_test, Y_train, y_test = train_test_split(X, y, test_size=0.2, random_state = 42) model.fit(X_train, Y_train) # ajustando el modelo y_pred = list(model.predict(X_test)) # Mostrar los datos correctos if label=="correctos": mask = (y_pred == y_test) color = "green" # Mostrar los datos correctos elif label=="incorrectos": mask = (y_pred != y_test) color = "red" else: raise ValueError("Valor incorrecto") X_aux = X_test y_aux_true = y_test y_aux_pred = y_pred # We'll plot the first 100 examples, randomly choosen fig, ax = plt.subplots(nx, ny, figsize=(12,12)) for i in range(nx): for j in range(ny): index = j + ny * i data = X_aux[index, :].reshape(8,8) label_pred = str(int(y_aux_pred[index])) label_true = str(int(y_aux_true[index])) ax[i][j].imshow(data, interpolation='nearest', cmap='gray_r') ax[i][j].text(0, 0, label_pred, horizontalalignment='center', verticalalignment='center', fontsize=10, color=color) ax[i][j].text(7, 0, label_true, horizontalalignment='center', verticalalignment='center', fontsize=10, color='blue') ax[i][j].get_xaxis().set_visible(False) ax[i][j].get_yaxis().set_visible(False) plt.show() model=svm.SVC(C=1, gamma=0.01, kernel='poly') mostar_resultados(digits,model,nx=5, ny=5,label = "correctos") model=svm.SVC(C=1, gamma=0.01, kernel='poly') mostar_resultados(digits,model,nx=5, ny=5,label="incorrectos") ###Output _____no_output_____
tutorials/1_basis/1_basis.ipynb	###Markdown 1 - 机器学习基础``` 描述：机器学习基础作者：Chenyyx 时间：2019-12-23``````目录： 1 - 机器学习是什么？ 2 - 为什么使用机器学习？ 3 - 机器学习的类型 4 - 小实例 5 - 总结``` 1 - 机器学习是什么？机器学习是计算机编程的科学，它使得计算机可以从数据中学习。一个更加面向工程的定义：如果一个计算机在任务 T 上的性能由 P 这个指标来度量，并且随着经验 E 的提升而提升，那么我们就可以说这个计算机程序在任务 T 上使用 P 度量指标从经验 E 中学习。最简单的一个小例子，您的垃圾邮件过滤器就是一个机器学习程序，可以通过给出的垃圾邮件样本以及常规邮件样本来学习标记垃圾邮件。在这种情况下，任务 T 是为新的电子邮件标记垃圾邮件，经验 E 是训练数据集，并且需要定义性能度量 P。例如，您可以使用正确分类的电子邮件的比例。这种特殊的性能度量被称为准确性，经常用于分类任务。 2 - 为什么使用机器学习？ - 传统方法传统方法，我们会针对每一个模式写一个检测算法，如果检测到这些模式中的一些，我们的程序才会把目标检测出来。由于每次遇到的问题不会是很小的问题，我们的程序会发展为一个复杂的规则很长的列表，这在后期往往是很难进行维护的。![传统方法](../../imgs/1_1.png) - 机器学习方法相比之下，基于机器学习所编写的程序会更短，更加容易维护，而且可能会更加准确。![机器学习方法](../../imgs/1_2.png)就拿垃圾邮件分类任务举例来说，如果垃圾邮件发送者将垃圾邮件之前的规则调整一下，比如将 `4` 换成 `For` 。我们的传统方法则需要更新来标记 `For` 电子邮件，这样我们就需要不断写入新的规则。相比之下，基于机器学习技术的垃圾邮件过滤器会自动注意到 `For` 在用户标记的垃圾邮件中变得异常频繁，并且在没有我们干预的情况下开始对其进行标记。![自动适应变化](../../imgs/1_3.png)机器学习还对传统方法过于复杂或者没有已知算法的问题有些优势。例如，考虑语音识别：假如你想简单地开始写一个能区分单词 “one” 和 “two” 的程序。你可能会注意到 “two” 这个单词开头是一个高音（“T”），所以你可以硬编码一个测量高音强度的算法，并用它来区分 “one” 和 “two” 。很明显，这种技术不会在嘈杂的环境和数十种语言中扩展成千上万非常不同的人所说的话。最好的解决方案（至少是现在最好的）是编写一个自学习的算法，给出每个单词的许多示例记录。最后，机器学习可以帮助人类学习（图 1-4）：可以检查 ML 算法，看看他们已经学到了什么（尽管对于一些算法来说这可能很困难）。例如，一旦垃圾邮件过滤器已经接受足够的垃圾邮件训练，就可以很容易地检查垃圾邮件过滤器是否能够预测垃圾邮件的最佳预测效果。有时候，这将揭示出未知的相关性或新的趋势，从而导致对问题有更好的理解。应用 ML 技术挖掘大量的数据可以帮助发现那些并不明显的模式。这被称为数据挖掘。![帮助人类学习](../../imgs/1_4.png)总结一下，机器学习对于下面的问题有较好的表现： - 现有解决方案需要大量手动调整或长规则列表的问题：机器学习算法通常可以简化代码并且得到更好的效果。 - 使用传统的方法没有好的解决方案的复杂的问题：最好的机器学习技术可以找到一个解决方案。 - 不是很稳定，时常波动的环境：机器学习系统可以适应新的数据。 - 需要深入了解复杂的问题和数据量比较大的问题。 3 - 机器学习系统的类型 3.1 - 有监督学习在有监督学习中，提供给算法的训练数据包括其所需的分类或解决方案，称之为 label(标签) 。典型的监督学习任务是分类，垃圾邮件过滤器就是一个很好的例子：它与许多示例电子邮件和它们的类（垃圾邮件和常规邮件）一起训练，并且它必须学会如何分类新的电子邮件。![分类算法](../../imgs/1_5.png)另一个典型的任务是预测一个目标数值，如给定一组特征（里程，年限，品牌等），来预测一辆汽车的价格，称为预测。这种任务被称为回归。![回归算法](../../imgs/1_6.png)下面列出了一些比较重要的监督学习算法： - k-Nearest Neighbors（k近邻） - Linear Regression（线性回归） - Logistic Regression（Logistic 回归） - Support Vector Machines (SVMs)（支持向量机） - Decision Trees and Random Forests（决策树和随机森林） - Neural network（神经网络） 3.2 - 无监督学习在无监督学习中，训练数据是没有 label（标签）的。![](../../imgs/1_7.png)下面列出了一些重要的无监督学习算法： - 聚类 - k-Means（k均值） - Hierarchical Cluster Analysis (HCA)（分层聚类分析） - Expectation Maximization（期望最大化） - 可视化和降维 - Principal Component Analysis (PCA)（主成分分析） - Kernel PCA— Locally-Linear Embedding (LLE)（内核 PCA - 局部线性嵌入） - t-distributed Stochastic Neighbor Embedding (t-SNE)（t 分布的随机相邻嵌入） - 关联规则学习 - Apriori - Eclat![](../../imgs/1_8.png) 3.3 - 半监督学习还有一些算法可以处理部分标记的训练数据，通常是很多未标记的数据和一些标记的数据，这被称为半监督学习。![](../../imgs/1_9.png)大多数半监督学习算法是无监督和监督算法的组合。以无监督的方式训练模型，然后使用监督学习技术对整个系统进行微调。 3.4 - 强化学习在强化学习中，一个被称为 agent 的学习系统可以观察环境，选择和执行行动，并获取回报（或负面回报的惩罚）。然后，它必须自己学习什么是最好的策略，称为 policy，以获取最大的回报。一项 policy 规定了 agent 在特定情况下应该选择的行动。![](../../imgs/1_10.png) 4 - 小实例下面举个小例子，使用 scikit-learn 中的 k近邻算法进行分类。 ###Code from sklearn.neighbors import (NeighborhoodComponentsAnalysis, KNeighborsClassifier) from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.pipeline import Pipeline X, y = load_iris(return_X_y=True) X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.7, random_state=42) nca = NeighborhoodComponentsAnalysis(random_state=42) knn = KNeighborsClassifier(n_neighbors=3) nca_pipe = Pipeline([('nca', nca), ('knn', knn)]) nca_pipe.fit(X_train, y_train) print(nca_pipe.score(X_test, y_test)) ###Output 0.9619047619047619
run_locaNMF_notebooks/run_locaNMF_and_yongxu_original_code.ipynb	###Markdown User-defined Parameters ###Code ################################################################################################################## ## PARAMETERS THAT YOU SHOULD CHANGE ################################################################################################################## # Path to data and atlas mouse_name = 'IJ1' session_name = 'Mar3' root_dir = '/media/cat/4TBSSD/yuki/yongxu/data/' data_folder = root_dir+mouse_name+'/'+session_name+'/' # spatial_data_filename = "IA1_spatial.npy" # spatial_data_filename =mouse_name+'pm_'+session_name+'_30Hz_code_04_trial_ROItimeCourses_30sec_pca_0.95_spatial.npy' # temporal_data_filename = "IA1_temporal.npy" # temporal_data_filename = mouse_name+'pm_'+session_name+'_30Hz_code_04_trial_ROItimeCourses_30sec_pca_0.95.npy' # atlas_filename = "maskwarp_1.npy" # contains 'atlas' random_spatial_data_filename =mouse_name+'pm_'+session_name+'_30Hz_code_04_random_ROItimeCourses_30sec_pca_0.95_spatial.npy' # temporal_data_filename = "IA1_temporal.npy" # random_temporal_data_filename = mouse_name+'pm_'+session_name+'_30Hz_code_04_random_ROItimeCourses_30sec_pca_0.95.npy' atlas_filename = "atlas_split.npy" # maxrank = how many max components per brain region. Set maxrank to around 4 for regular dataset. maxrank = 1 # min_pixels = minimum number of pixels in Allen map for it to be considered a brain region # default min_pixels = 100 min_pixels = 200 # loc_thresh = Localization threshold, i.e. percentage of area restricted to be inside the 'Allen boundary' # default loc_thresh = 80 loc_thresh = 75 # r2_thresh = Fraction of variance in the data to capture with LocaNMF # default r2_thresh = 0.99 r2_thresh = 0.96 # Do you want nonnegative temporal components? The data itself should also be nonnegative in this case. # default nonnegative_temporal = False nonnegative_temporal = False ################################################################################################################## ## PARAMETERS THAT YOU SHOULD PROBABLY NOT CHANGE (unless you know what you're doing) ################################################################################################################## # maxiter_hals = Number of iterations in innermost loop (HALS). Keeping this low provides a sort of regularization. # default maxiter_hals = 20 maxiter_hals = 20 # maxiter_lambda = Number of iterations for the lambda loop. Keep this high for finding a good solution. # default maxiter_lambda = 100 maxiter_lambda = 150 # lambda_step = Amount to multiply lambda after every lambda iteration. # lambda_init = initial value of lambda. Keep this low. default lambda_init = 0.000001 # lambda_{i+1}=lambda_ilambda_step. lambda_0=lambda_init. default lambda_step = 1.35 lambda_step = 1.25 lambda_init = 1e-4 # # spatial_data_filename.shape # a=np.load(data_folder+spatial_data_filename) # print(a.shape) # b=np.load(data_folder+temporal_data_filename) # print(b.shape) ###Output _____no_output_____ ###Markdown Load & Format Data ###Code spatial = np.load(data_folder+spatial_data_filename) # spatial_random = np.load(data_folder+random_spatial_data_filename) # spatial=np.concatenate(spatial_trial,spatial_random,axis=0) spatial = np.transpose(spatial,[1,0]) denoised_spatial_name = np.reshape(spatial,[128,128,-1]) temporal_trial = np.load(data_folder+temporal_data_filename) temporal_random = np.load(data_folder+random_temporal_data_filename) temporal=np.concatenate((temporal_trial,temporal_random),axis=0) temporal = np.transpose(temporal,[1,0,2]) # denoised_temporal_name = np.reshape(temporal,[-1,42601]) denoised_temporal_name = np.reshape(temporal,[-1,temporal.shape[1]temporal.shape[2]]) print('loaded data\n',flush=True) atlas = np.load('/home/cat/code/widefieldPredict/locanmf/atlas_fixed_pixel.npy')#['atlas'].astype(float) #areanames = sio.loadmat(data_folder+atlas_filename)['areanames'] # atlas.shape fig = plt.figure() plt.imshow(atlas) # fig=plt.figure(figsize=(20,15)) # for it in np.unique(atlas): # plotmap=np.zeros((atlas.shape)); plotmap.fill(np.nan); plotmap[atlas==it]=atlas[atlas==it] # # plt.subplot(5,6,it+1) # plt.imshow(plotmap,cmap='Spectral'); plt.axis('off'); plt.title('Allen region map'); plt.show(); # plt.show() print(denoised_temporal_name.shape) print(denoised_spatial_name.shape) print(atlas.shape) fig = plt.figure() plt.plot(denoised_temporal_name[:,:601].T); plt.show() fig=plt.figure() for i in np.arange(7): plt.imshow(denoised_spatial_name[:,:,i]); plt.show() # Get data in the correct format V=denoised_temporal_name U=denoised_spatial_name # brainmask = np.ones(U.shape[:2],dtype=bool) # Load true areas if simulated data simulation=0 # Include nan values of U in brainmask, and put those values to 0 in U brainmask[np.isnan(np.sum(U,axis=2))]=False U[np.isnan(U)]=0 # Preprocess V: flatten and remove nans dimsV=V.shape keepinds=np.nonzero(np.sum(np.isfinite(V),axis=0))[0] V=V[:,keepinds] # del arrays # U.shape # Check that data has the correct shapes. V [K_d x T], U [X x Y x K_d], brainmask [X x Y] if V.shape[0]!=U.shape[-1]: print('Wrong dimensions of U and V!') print("Rank of video : %d" % V.shape[0]); print("Number of timepoints : %d" % V.shape[1]); # Plot the maximum of U # plotmap=np.zeros((atlas.shape)); plotmap.fill(np.nan); plotmap[brainmask]=atlas[brainmask] # fig=plt.figure() # plt.imshow(plotmap,cmap='Spectral'); plt.axis('off'); plt.title('Allen region map'); plt.show(); # fig=plt.figure() # plt.imshow(np.max(U,axis=2)); plt.axis('off'); plt.title('Max U'); plt.show() # Perform the LQ decomposition. Time everything. t0_global = time.time() t0 = time.time() if nonnegative_temporal: r = V.T else: q, r = np.linalg.qr(V.T) time_ests={'qr_decomp':time.time() - t0} ###Output _____no_output_____ ###Markdown Initialize LocaNMF ###Code # Put in data structure for LocaNMF video_mats = (np.copy(U[brainmask]), r.T) rank_range = (1, maxrank, 1) del U # region_mats[0] = [unique regions x pixels] the mask of each region # region_mats[1] = [unique regions x pixels] the distance penalty of each region # region_mats[2] = [unique regions] area code region_mats = LocaNMF.extract_region_metadata(brainmask, atlas, min_size=min_pixels) region_metadata = LocaNMF.RegionMetadata(region_mats[0].shape[0], region_mats[0].shape[1:], device=device) region_metadata.set(torch.from_numpy(region_mats[0].astype(np.uint8)), torch.from_numpy(region_mats[1]), torch.from_numpy(region_mats[2].astype(np.int64))) # print (region_mats[1].shape) # print (region_mats[2]) # print (region_mats[2].shape) # grab region names rois=np.load('/home/cat/code/widefieldPredict/locanmf/rois_50.npz') rois_name=rois['names'] # rois_name rois_ids=rois['ids'] # rois_ids # Do SVD as initialization if device=='cuda': torch.cuda.synchronize() # print('v SVD Initialization') t0 = time.time() region_videos = LocaNMF.factor_region_videos(video_mats, region_mats[0], rank_range[1], device=device) # if device=='cuda': torch.cuda.synchronize() print("\'-total : %f" % (time.time() - t0)) time_ests['svd_init'] = time.time() - t0 # low_rank_video = LocaNMF.LowRankVideo( (int(np.sum(brainmask)),) + video_mats[1].shape, device=device ) low_rank_video.set(torch.from_numpy(video_mats[0].T), torch.from_numpy(video_mats[1])) ###Output _____no_output_____ ###Markdown LocaNMF ###Code # if device=='cuda': torch.cuda.synchronize() # print('v Rank Line Search') t0 = time.time() #locanmf_comps,loc_save (nmf_factors, loc_save, save_lam, save_scale, save_per, save_spa, save_scratch) = LocaNMF.rank_linesearch(low_rank_video, region_metadata, region_videos, maxiter_rank=maxrank, maxiter_lambda=maxiter_lambda, # main param to tweak maxiter_hals=maxiter_hals, lambda_step=lambda_step, lambda_init=lambda_init, loc_thresh=loc_thresh, r2_thresh=r2_thresh, rank_range=rank_range, # nnt=nonnegative_temporal, verbose=[True, False, False], sample_prop=(1,1), device=device ) # if device=='cuda': torch.cuda.synchronize() # print("\'-total : %f" % (time.time() - t0)) time_ests['rank_linesearch'] = time.time() - t0 # print (loc_save.scale.data) # print (loc_save.spatial.data.shape) # print (loc_save.spatial.scratch.shape) # how much of spatial components is in each region ratio=torch.norm(loc_save.spatial.scratch,p=2,dim=-1)/torch.norm(loc_save.spatial.data,p=2,dim=-1) print ("ratio: ", ratio) # how much of the spatial component is inside the ROI per=100(ratio*2) print ('percentage; ', per) # print ("The threshold is 75%. all copmonents should be above, otherwise increase lambda iterations ") # # # print("Number of components : %d" % len(locanmf_comps)) # computing the variance in each component; print ("Compute the variance explained by each component ") mov = torch.matmul(low_rank_video.spatial.data.t(), low_rank_video.temporal.data) # var = torch.mean(torch.var(mov, dim=1, unbiased=False)) # TODO: Precompute this var_ests=np.zeros((len(nmf_factors))) for i in np.arange(len(nmf_factors)): mov = torch.matmul(torch.index_select(nmf_factors.spatial.data,0,torch.tensor([i])).t(), torch.index_select(nmf_factors.temporal.data,0,torch.tensor([i]))) var_i = torch.mean(torch.var(mov, dim=1, unbiased=False)) # mean(var(dataest))/mean(var(data)) var_ests[i] = var_i.item() / var.item() # to return to this; should sum to 1, perhaps plt.plot(var_ests); plt.show() # print (np.argsort(var_ests)) print (var_ests[np.argsort(var_ests)]) print (var_ests.sum()) print ("TODO: verify that locaNMF svm decoding is similar to pca") # compute the r-squared again mov = torch.matmul(low_rank_video.spatial.data.t(),low_rank_video.temporal.data) var = torch.mean(torch.var(mov, dim=1, unbiased=False)) # TODO: Precompute this torch.addmm(beta=1, input=mov, alpha=-1, mat1=nmf_factors.spatial.data.t(), mat2=nmf_factors.temporal.data, out=mov) r2_est = 1 - (torch.mean(mov.pow_(2)).item() / var.item()) print(r2_est); print ("TODO: Save rsquared components") # # for each component what is the rsquared - OPTIONAL - for checks # r2_ests=np.zeros((len(locanmf_comps))) # for i in np.arange(len(locanmf_comps)): # mov = torch.matmul(low_rank_video.spatial.data.t(),low_rank_video.temporal.data) # var = torch.mean(torch.var(mov, dim=1, unbiased=False)) # TODO: Precompute this # # mov = data-dataest = data-mat1mat2 # torch.addmm(beta=1, # input=mov, # alpha=-1, # mat1=torch.index_select(locanmf_comps.spatial.data, # 0, # torch.tensor([i])).t(), # mat2=torch.index_select(locanmf_comps.temporal.data, # 0, # torch.tensor([i])), # out=mov) # # r2_ests = 1-mean(var(data-dataest))/mean(var(data)) # r2_ests[i] = 1 - (torch.mean(mov.pow_(2)).item() / var.item()) # # for each component what is the rsquared - OPTIONAL - for checks # mov = torch.matmul(low_rank_video.spatial.data.t(),low_rank_video.temporal.data) # var = torch.mean(torch.var(mov, dim=1, unbiased=False)) # TODO: Precompute this # r2_ests_2=np.zeros((len(locanmf_comps))) # for i in np.arange(len(locanmf_comps)): # mov_i = torch.matmul(torch.index_select(locanmf_comps.spatial.data,0,torch.tensor([i])).t(), # torch.index_select(locanmf_comps.temporal.data,0,torch.tensor([i]))) # var_i = torch.mean(torch.var(mov-mov_i, dim=1, unbiased=False)) # # 1 - mean(var(data-dataest))/mean(var(data)) # r2_ests_2[i] = 1 - (var_i.item() / var.item()) # r2_ests_loo=np.zeros((len(locanmf_comps))) # for i in np.arange(len(locanmf_comps)): # mov = torch.matmul(low_rank_video.spatial.data.t(),low_rank_video.temporal.data) # var = torch.mean(torch.var(mov, dim=1, unbiased=False)) # TODO: Precompute this # torch.addmm(beta=1, # input=mov, # alpha=-1, # mat1=torch.index_select(locanmf_comps.spatial.data, # 0, # torch.tensor(np.concatenate((np.arange(0,i),np.arange(i+1,len(locanmf_comps)))))).t(), # mat2=torch.index_select(locanmf_comps.temporal.data, # 0, # torch.tensor(np.concatenate((np.arange(0,i),np.arange(i+1,len(locanmf_comps)))))), # out=mov) # r2_ests_loo[i] = 1 - (torch.mean(mov.pow_(2)).item() / var.item()) # _,r2_fit=LocaNMF.evaluate_fit_to_region(low_rank_video, # locanmf_comps, # region_metadata.support.data.sum(0), # sample_prop=(1, 1)) # Evaluate R^2 _,r2_fit=LocaNMF.evaluate_fit_to_region(low_rank_video, nmf_factors, region_metadata.support.data.sum(0), sample_prop=(1, 1) ) # print("R^2 fit on all data : %f" % r2_fit) time_ests['global_time'] = time.time()-t0_global # C is the temporal components C = np.matmul(q,nmf_factors.temporal.data.cpu().numpy().T).T print ("n_comps, n_time pts x n_trials: ", C.shape) qc, rc = np.linalg.qr(C.T) # back to visualizing variance print(np.sum(var_ests)) plt.bar(np.arange(len(nmf_factors)),var_ests); plt.show() # var_est=np.zeros((len(nmf_factors))) for i in np.arange(len(nmf_factors)): var_est[i]=np.var(C[i,:])/np.var(C) # locanmf_comps.regions.data ###Output _____no_output_____ ###Markdown Reformat spatial and temporal matrices, and save ###Code # Assigning regions to components region_ranks = []; region_idx = [] locanmf_comps = nmf_factors for rdx in torch.unique(locanmf_comps.regions.data, sorted=True): region_ranks.append(torch.sum(rdx == locanmf_comps.regions.data).item()) region_idx.append(rdx.item()) areas=region_metadata.labels.data[locanmf_comps.regions.data].cpu().numpy() # Get LocaNMF spatial and temporal components A=locanmf_comps.spatial.data.cpu().numpy().T A_reshape=np.zeros((brainmask.shape[0],brainmask.shape[1],A.shape[1])); A_reshape.fill(np.nan) A_reshape[brainmask,:]=A # C is already computed above delete above if nonnegative_temporal: C=locanmf_comps.temporal.data.cpu().numpy() else: C=np.matmul(q,locanmf_comps.temporal.data.cpu().numpy().T).T # Add back removed columns from C as nans C_reshape=np.full((C.shape[0],dimsV[1]),np.nan) C_reshape[:,keepinds]=C C_reshape=np.reshape(C_reshape,[C.shape[0],dimsV[1]]) # Get lambdas lambdas=np.squeeze(locanmf_comps.lambdas.data.cpu().numpy()) # A_reshape.shape # c_p is the trial sturcutre c_p=C_reshape.reshape(A_reshape.shape[2],int(C_reshape.shape[1]/1801),1801) # c_plot=c_p.transpose((1,0,2)) c_plot.shape # save LocaNMF data data_folder = root_dir+mouse_name+'/'+session_name+'/' areas_saved = [] for area in areas: idx = np.where(rois_ids==np.abs(area))[0] temp_name = str(rois_name[idx].squeeze()) if area <0: temp_name += " - right" else: temp_name += " - left" areas_saved.append(temp_name) np.savez(os.path.join(root_dir,mouse_name,session_name,'locanmf_trial.npz'), temporal = c_plot[:int(c_plot.shape[0]/2),:,:], areas = areas, names = areas_saved) np.savez(os.path.join(root_dir,mouse_name,session_name,'locanmf_random.npz'), temporal = c_plot[int(c_plot.shape[0]/2):,:,:], areas = areas, names = areas_saved) d = np.load('/media/cat/4TBSSD/yuki/yongxu/data/IJ1/Mar3/locanmf_trial.npz') temporal = d['temporal'] areas = d['areas'] names = d['names'] print (temporal.shape) print (areas) print (names) # from scipy.signal import savgol_filter # t = np.arange(temporal.shape[2])/30 - 30 # max_vals = [] # for k in range(temporal.shape[1]): # temp = temporal[:,k].mean(0) # #plt.plot(temp) # temp2 = savgol_filter(temp, 15, 2) # plt.subplot(121) # plt.xlim(-15,0) # plt.plot(t,temp2) # m = np.max(temp2[:temp2.shape[0]//2]) # max_vals.append(m) # plt.subplot(122) # plt.xlim(-15,0) # temp2 = temp2/np.max(temp2) # plt.plot(t,temp2) # #break # plt.show() # max_vals = np.array(max_vals) # args = np.argsort(max_vals)[::-1] # print (max_vals[args]) # print (names[args]) # temp componetns of behavior + control data vstacked t_plot=temporal.transpose((1,0,2)) print (temporal.shape) # Plot the distribution of lambdas. OPTIONAL # If lots of values close to the minimum, decrease lambda_init. # If lots of values close to the maximum, increase maxiter_lambda or lambda_step. plt.hist(locanmf_comps.lambdas.data.cpu(), bins=torch.unique(locanmf_comps.lambdas.data).shape[0]) plt.show() print(locanmf_comps.lambdas.data.cpu()) region_name=region_mats[2] region_name.shape region_name def parse_areanames_new(region_name,rois_name): areainds=[]; areanames=[]; for i,area in enumerate(region_name): areainds.append(area) areanames.append(rois_name[np.where(rois_ids==np.abs(area))][0]) sortvec=np.argsort(np.abs(areainds)) areanames=[areanames[i] for i in sortvec] areainds=[areainds[i] for i in sortvec] return areainds,areanames # region_name=region_mats[2] # Get area names for all components areainds,areanames_all = parse_areanames_new(region_name,rois_name) areanames_area=[] for i,area in enumerate(areas): areanames_area.append(areanames_all[areainds.index(area)]) # # Get area names for all components areainds,areanames_all =parse_areanames_new(region_name,rois_name) areanames_area=[] for i,area in enumerate(areas): areanames_area.append(areanames_all[areainds.index(area)]) # Save results! - USE .NPZ File print("LocaNMF completed successfully in "+ str(time.time()-t0_global) + "\n") print("Results saved in "+data_folder+'locanmf_decomp_loc'+str(loc_thresh)+'.mat') # Prefer to save c_p which is already converted sio.savemat(data_folder+'locanmf_decomp_loc'+str(loc_thresh)+'.mat', {'C':C_reshape, 'A':A_reshape, 'lambdas':lambdas, 'areas':areas, 'r2_fit':r2_fit, 'time_ests':time_ests, 'areanames':areanames_area }) torch.cuda.empty_cache() atlas_split=atlas itt=0 fig=plt.figure() #figsize=(10,10)) b_=[] for it in np.unique(atlas_split): if np.abs(it) !=0: plotmap=np.zeros((atlas_split.shape)); plotmap.fill(np.nan); plotmap[atlas_split==it]=atlas_split[atlas_split==it] plt.subplot(5,8,itt+1) plt.imshow(plotmap,cmap='Spectral'); plt.axis('off'); plt.title(rois_name[np.where(rois_ids==np.abs(it))][0],fontsize=6); b_.append(plotmap) # plt.show() itt=itt+1 plt.tight_layout(h_pad=0.5,w_pad=0.5) # how much of the spatial component is inside the ROI # per ###################################################### ##### PLACE TO LOOK FOR large spatial components ##### ###################################################### fig=plt.figure() for i in range(A_reshape.shape[2]): plt.subplot(5,8,i+1) plt.imshow(A_reshape[:,:,i]) plt.title(areanames_area[i],fontsize=6) plt.tight_layout(h_pad=0.5,w_pad=0.5) plt.show() # calculate ROI data roi_spatial=np.zeros((A_reshape.shape[2],denoised_spatial_name.shape[2])) for i in range(denoised_spatial_name.shape[2]): for j in range(A_reshape.shape[2]): A_masking=np.zeros((A_reshape[:,:,j].shape)) A_masking[A_reshape[:,:,j]!=0]=1 A_multiply=A_maskingdenoised_spatial_name[:,:,i] roi_spatial[j,i]=np.sum(A_multiply)/np.sum(A_masking) roi_data=[] for s in range(temporal_trial.shape[0]): roi_each=roi_spatial@temporal_trial[s] roi_data.append(roi_each) roi_save_trial=np.array(roi_data) roi_save_trial.shape # roi_spatial=np.zeros((A_reshape.shape[2],denoised_spatial_name.shape[2])) # for i in range(denoised_spatial_name.shape[2]): # for j in range(A_reshape.shape[2]): # A_masking=np.zeros((A_reshape[:,:,j].shape)) # A_masking[A_reshape[:,:,j]!=0]=1 # A_multiply=A_maskingdenoised_spatial_name[:,:,i] # roi_spatial[j,i]=np.sum(A_multiply)/np.sum(A_masking) # roi_data=[] # for s in range(temporal_random.shape[0]): # roi_each=roi_spatial@temporal_random[s] # roi_data.append(roi_each) # roi_save_random=np.array(roi_data) # roi_save_random.shape # save ROI data # np.save(save_folder+save_name+'trial.npy',roi_save_trial) # np.save(save_folder+save_name+'random.npy',roi_save_random) ###Output _____no_output_____ ###Markdown Visualization of components ###Code # CAT: Use actual averages not random data C_area_rois = c_plot[:int(c_plot.shape[0]/2),:,:].mean(0) print (C_area_rois.shape) t = np.arange(C_area_rois.shape[1])/30.-30 clrs_local = ['magenta','brown','pink','lightblue','darkblue'] fig = plt.figure(figsize=(12,16)) ############### SHREYA"S CODE #################### # Spatial and Temporal Components: Summary atlascolor=np.zeros((atlas.shape[0],atlas.shape[1],4)) A_color=np.zeros((A_reshape.shape[0],A_reshape.shape[1],4)) cmap=plt.cm.get_cmap('jet') colors=cmap(np.arange(len(areainds))/len(areainds)) # for i,area_i in enumerate(areainds): if area_i not in areas: continue atlascolor[atlas==area_i,:]=colors[i,:] C_area=C[np.where(areas==area_i)[0],:] # for z in range(len(names_plot)): if names_plot[z] in names_plot[z]: clr = clrs_local[z] break # for j in np.arange(colors.shape[1]): A_color[:,:,j]=A_color[:,:,j]+colors[i,j]A_reshape[:,:,np.where(areas==area_i)[0][0]] #fig=plt.figure(figsize=(15,8)) ax1=fig.add_subplot(2,2,1) ax1.imshow(atlascolor) #ax1.set_title('Atlas Regions') ax1.axis('off') ax2=fig.add_subplot(2,2,3) ax2.imshow(A_color) #ax2.set_title('Spatial Components (One per region)') ax2.axis('off') ax3=fig.add_subplot(1,2,2) axvar=0 print (areas) names_plot = ['Retrosplenial','barrel','limb','visual','motor'] for i,area_i in enumerate(areainds): if area_i not in areas: continue # C_area=C[np.where(areas==area_i)[0][0],:min(1000,C.shape[1])] C_area=C_area_rois[np.where(areas==area_i)[0][0]] #ax3.plot(1.5axvar+C_area/np.nanmax(np.abs(C_area)),color=colors[i,:]) for z in range(len(names_plot)): if names_plot[z] in names_plot[z]: clr = clrs_local[z] break ax3.plot(t, 1.5axvar+C_area23, #color=colors[i,:], color = clr, linewidth=3) print (C_area.shape) axvar+=1 ax3.set_xlim(-15,0) #ax3.set_title('Temporal Components (One per region)') ax3.axis('off') if True: plt.savefig('/home/cat/locanmf.svg',dpi=300) plt.close() else: plt.show() data1 = np.load('/media/cat/4TBSSD/yuki/AQ2/tif_files/AQ2am_Dec17_30Hz/AQ2am_Dec17_30Hz_locanmf.npz', allow_pickle=True) names_rois = data1['names'] print (names_rois) ids = data1['areas'] print (areas) # Plotting all the regions' components for i,area in enumerate(areas): try: fig=plt.figure(figsize=(20,4)) ax1 = fig.add_subplot(1,3,1) plotmap_area = np.zeros((atlas.shape)); plotmap_area.fill(np.nan); plotmap_area[brainmask] = atlas[brainmask]==area ax1.imshow(plotmap_area); ax1.set_title('Atlas '+areanames_area[i]) ax1.axis('off') ax2 = fig.add_subplot(1,3,2) ax2.imshow(A_reshape[:,:,i]) ax2.set_title('LocaNMF A [%s]'%(i+1)) ax2.axis('off') ax3 = fig.add_subplot(1,3,3) ax3.plot(C[i,:min(1000,C.shape[1])],'k') if simulation: ax3.plot(V[np.where(area==trueareas)[0][0],:min(1000,V.shape[1])],'r'); if i==0: ax3.legend(('LocaNMF','True')) ax3.set_title('LocaNMF C [%s]'%(i+1)) ax3.axis('off') plt.show() except: pass # Calculate Canonical Correlations between components in each pair of regions corrmat=np.zeros((len(areainds),len(areainds))) skipinds=[] for i,area_i in enumerate(areainds): for j,area_j in enumerate(areainds): if i==0 and area_j not in areas: skipinds.append(j) C_i=C[np.where(areas==area_i)[0],:].T C_j=C[np.where(areas==area_j)[0],:].T if i not in skipinds and j not in skipinds: cca=CCA(n_components=1) cca.fit(C_i,C_j) C_i_cca,C_j_cca=cca.transform(C_i,C_j) try: C_i_cca=C_i_cca[:,0] except: pass try: C_j_cca=C_j_cca[:,0] except: pass corrmat[i,j]=np.corrcoef(C_i_cca,C_j_cca)[0,1] corrmat=np.delete(corrmat,skipinds,axis=0); corrmat=np.delete(corrmat,skipinds,axis=1); corr_areanames=np.delete(areanames_all,skipinds) # Plot correlations fig=plt.figure() plt.imshow(corrmat,cmap=plt.cm.get_cmap('jet')); plt.clim(-1,1); plt.colorbar(shrink=0.8) plt.get_cmap('jet') plt.xticks(ticks=np.arange(len(areainds)-len(skipinds)),labels=corr_areanames,rotation=90); plt.yticks(ticks=np.arange(len(areainds)-len(skipinds)),labels=corr_areanames); plt.title('CCA between all regions',fontsize=12) plt.xlabel('Region i',fontsize=12) plt.ylabel('Region j',fontsize=12) plt.show() # Save visualized components and correlations # print('Saving postprocessing results!') # postprocess.plot_components(A_reshape,C,areas,atlas,areanames,data_folder) # postprocess.plot_correlations(A_reshape,C,areas,atlas,areanames,data_folder) import numpy as np data = np.load('/media/cat/4TBSSD/yuki/IA1/tif_files/IA1pm_Feb2_30Hz/IA1pm_Feb2_30Hz_locanmf.npz', allow_pickle=True) trials = data['temporal_trial'] random = data['temporal_random'] print (trials.shape, random.shape) trials = np.load('/media/cat/4TBSSD/yuki/IA1/tif_files/IA1am_Mar4_30Hz/IA1am_Mar4_30Hz_code_04_trial_ROItimeCourses_30sec_pca_0.95.npy') print (trials.shape) data = np.load('/media/cat/4TBSSD/yuki/IA1/tif_files/IA1am_Mar4_30Hz/IA1am_Mar4_30Hz_whole_stack_trial_ROItimeCourses_15sec_pca30components.npy') print (data.shape) spatial = np.load('/media/cat/4TBSSD/yuki/IA1/tif_files/IA1am_Mar4_30Hz/IA1am_Mar4_30Hz_whole_stack_trial_ROItimeCourses_15sec_pca30components_spatial.npy') print (spatial.shape) ###Output (40000, 30) (30, 16384)
Chapter_4/Chapter_4-5.ipynb	###Markdown Chapter4：実践的なアプリケーションを作ってみよう 4.5　テキストエディッタを作ってみよう① ###Code # リスト4.5.1：サブウインドウの作成例1 # tkinterのインポート import tkinter as tk ### GUI ### # ウインドウの作成 root = tk.Tk() # サブウインドウの作成 mini_window = tk.Toplevel(root) # ウインドウ状態の維持 root.mainloop() # リスト4.5.2：サブウインドウの作成例2 # tkinterのインポート import tkinter as tk ### 関数 ### def sub_window(): # サブウインドウの作成 mini_window = tk.Toplevel(root) # ボタン2 button2 = tk.Button(mini_window, text = "Push2") button2.pack(padx = 50, pady = 25) ### GUI ### # ウインドウの作成 root = tk.Tk() # ボタン1 button1 = tk.Button(root, text = "Push1", command = sub_window) button1.pack(padx = 100, pady = 50) # ウインドウ状態の維持 root.mainloop() ###Output _____no_output_____ ###Markdown Chapter4：実践的なアプリケーションを作ってみよう 4.5　テキストエディッタを作ってみよう① ###Code # リスト4.5.1：サブウインドウの作成例1 # tkinterのインポート import tkinter as tk ### GUI ### # ウインドウの作成 root = tk.Tk() # サブウインドウの作成 mini_window = tk.Toplevel(root) # ウインドウ状態の維持 root.mainloop() # リスト4.5.2：サブウインドウの作成例2 # tkinterのインポート import tkinter as tk ### 関数 ### def sub_window(): # サブウインドウの作成 mini_window = tk.Toplevel(root) # ボタン2 button2 = tk.Button(mini_window, text = "Push2") button2.pack(padx = 50, pady = 25) ### GUI ### # ウインドウの作成 root = tk.Tk() # ボタン1 button1 = tk.Button(root, text = "Push1", command = sub_window) button1.pack(padx = 100, pady = 50) # ウインドウ状態の維持 root.mainloop() ###Output _____no_output_____
python/example/dictionary-sentiment/sentiment.ipynb	###Markdown Rule-based Sentiment AnalysisIn the following example, we walk-through a simple use case for our straight forward SentimentDetector annotator.This annotator will work on top of a list of labeled sentences which can have any of the following features positive negative revert increment decrementEach of these sentences will be used for giving a score to text Spark `2.4` and Spark NLP `2.0.1` 1. Call necessary imports and set the resource path to read local data files ###Code #Imports import sys sys.path.append('../../') from pyspark.sql import SparkSession from pyspark.ml import Pipeline from pyspark.sql.functions import array_contains from sparknlp.annotator import * from sparknlp.common import RegexRule from sparknlp.base import DocumentAssembler, Finisher #Setting location of resource Directory resource_path= "../../../src/test/resources/" ###Output _____no_output_____ ###Markdown 2. Load SparkSession if not already there ###Code spark = SparkSession.builder \ .appName("SentimentDetector")\ .master("local[]")\ .config("spark.driver.memory","8G")\ .config("spark.driver.maxResultSize", "2G")\ .config("spark.jars.packages", "JohnSnowLabs:spark-nlp:2.0.1")\ .config("spark.kryoserializer.buffer.max", "500m")\ .getOrCreate() data = spark. \ read. \ parquet(resource_path+"sentiment.parquet"). \ limit(10000).cache() data.show() ###Output _____no_output_____ ###Markdown 3. Create appropriate annotators. We are using Sentence Detection, Tokenizing the sentences, and find the lemmas of those tokens. The Finisher will only output the Sentiment. ###Code document_assembler = DocumentAssembler() \ .setInputCol("text") sentence_detector = SentenceDetector() \ .setInputCols(["document"]) \ .setOutputCol("sentence") tokenizer = Tokenizer() \ .setInputCols(["sentence"]) \ .setOutputCol("token") lemmatizer = Lemmatizer() \ .setInputCols(["token"]) \ .setOutputCol("lemma") \ .setDictionary(resource_path+"lemma-corpus-small/lemmas_small.txt", key_delimiter="->", value_delimiter="\t") sentiment_detector = SentimentDetector() \ .setInputCols(["lemma", "sentence"]) \ .setOutputCol("sentiment_score") \ .setDictionary(resource_path+"sentiment-corpus/default-sentiment-dict.txt", ",") finisher = Finisher() \ .setInputCols(["sentiment_score"]) \ .setOutputCols(["sentiment"]) ###Output _____no_output_____ ###Markdown 4. Train the pipeline, which is only being trained from external resources, not from the dataset we pass on. The prediction runs on the target dataset ###Code pipeline = Pipeline(stages=[document_assembler, sentence_detector, tokenizer, lemmatizer, sentiment_detector, finisher]) model = pipeline.fit(data) result = model.transform(data) ###Output _____no_output_____ ###Markdown 5. filter the finisher output, to find the positive sentiment lines ###Code result.where(array_contains(result.sentiment, "positive")).show(10,False) ###Output _____no_output_____ ###Markdown Necessary imports ###Code #Imports import sys sys.path.append('../../') from pyspark.sql import SparkSession from pyspark.ml import Pipeline from sparknlp.annotator import from sparknlp.common import RegexRule from sparknlp.base import DocumentAssembler, Finisher ###Output _____no_output_____ ###Markdown Create a spark dataset ###Code data = spark. \ read. \ parquet("../../../src/test/resources/sentiment.parquet"). \ limit(10000) data.cache() data.count() ###Output _____no_output_____ ###Markdown Create appropriate annotators. We are using Sentence Detection, Tokenizing the sentences, and find the lemmas of those tokensThe Finisher will only output the Sentiment. ###Code document_assembler = DocumentAssembler() \ .setInputCol("text") sentence_detector = SentenceDetector() \ .setInputCols(["document"]) \ .setOutputCol("sentence") tokenizer = Tokenizer() \ .setInputCols(["sentence"]) \ .setOutputCol("token") lemmatizer = Lemmatizer() \ .setInputCols(["token"]) \ .setOutputCol("lemma") \ .setDictionary("../../../src/test/resources/lemma-corpus-small/lemmas_small.txt", key_delimiter="->", value_delimiter="\t") sentiment_detector = SentimentDetector() \ .setInputCols(["lemma", "sentence"]) \ .setOutputCol("sentiment_score") \ .setDictionary("../../../src/test/resources/sentiment-corpus/default-sentiment-dict.txt", ",") finisher = Finisher() \ .setInputCols(["sentiment_score"]) \ .setOutputCols(["sentiment"]) ###Output _____no_output_____ ###Markdown Train the pipeline, which is only being trained from external resources, not from the dataset we pass on.The prediction runs on the target dataset ###Code pipeline = Pipeline(stages=[document_assembler, sentence_detector, tokenizer, lemmatizer, sentiment_detector, finisher]) model = pipeline.fit(data) result = model.transform(data) ###Output _____no_output_____ ###Markdown We filter the finisher output, to find the positive sentiment lines ###Code result.filter("sentiment != 'positive'").show() ###Output _____no_output_____
python/08_keras_functional_api.ipynb	###Markdown Utilizando a API funcional do keras para criar uma rede neural MLPNesse notebook é utilizado o dataset [Concrete Compressive Strength Data Set](https://archive.ics.uci.edu/ml/datasets/concrete+compressive+strength), onde as features são:* Aglomerante: Cement (kg in a m3 mixture)* Escória de Alto Forno: Blast Furnace Slag (kg in a m3 mixture)* Cinzas volantes: Fly Ash (kg in a m3 mixture)* Água: Water (kg in a m3 mixture)* Superplastificante: Superplasticizer (kg in a m3 mixture)* Agregado graúdo: Coarse Aggregate (kg in a m3 mixture)* Agregado fino: Fine Aggregate (kg in a m3 mixture)* Idade: Age (Day (1~365))O objetivo é com essas features obter a resistência à compressão do concreto, em inglês: Concrete compressive strength (MPa).Primeiro são importadas as bibliotecas. ###Code import numpy as np import tensorflow as tf from tensorflow import keras from tensorflow.keras import layers from keras.models import Model from keras.layers import Input from keras.layers import Dense from sklearn.metrics import mean_absolute_error from sklearn.model_selection import cross_val_score import numpy as np import pandas as pd np.random.seed(0) tf.random.set_seed(0) ###Output _____no_output_____ ###Markdown O dataset é aberto usando o pandas. O formato original é em xls, então também é especificada a planilha aser aberta, a primeira. As features são renomeadas para facilitar as referências.São definidos os dataframes com features e variável de saída. ###Code url = "https://archive.ics.uci.edu/ml/machine-learning-databases/concrete/compressive/Concrete_Data.xls" df = pd.read_excel(url, sheet_name=0) df.columns = ['cement', 'slag', 'ash', 'water', 'superplasticizer', 'coarse_aggregate', 'fine_aggregate', 'age', 'compressive_strength'] X = (df.drop(['compressive_strength'], axis=1)) y = (df['compressive_strength']) ###Output _____no_output_____ ###Markdown O dataset é dividido em treino e teste. ###Code from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) from sklearn.preprocessing import StandardScaler scl = StandardScaler() X_train = scl.fit_transform(X_train) X_test = scl.transform(X_test) ###Output _____no_output_____ ###Markdown São definidas duas variáveis para a média e o desvio padrão da variável alvo. ###Code mean = y_train.mean() std = y_train.std() ###Output _____no_output_____ ###Markdown Uma função para ciração da rede é definida utilizando a API funcional do Keras. Isso permite com que o resultado final da rede seja multiplicado pelo desvio padrão e somado à média. Dessa forma os pesos são ajustados à variàvel objetivo padronizada. ###Code def create_model(): x = Input(shape=(X_train.shape[1],)) hidden1 = Dense(20, activation='relu')(x) hidden2 = Dense(100, activation='relu')(hidden1) hidden3 = Dense(20, activation='relu')(hidden2) hidden4 = Dense(1)(hidden3) output = hidden4 * std + mean model = Model(inputs=x, outputs=output) opt = keras.optimizers.Adam(learning_rate=1e-3) model.compile(loss="mean_absolute_error", optimizer=opt) return model ###Output _____no_output_____ ###Markdown O modelo é criado e as camadas são mostradas. ###Code model = create_model() model.summary() ###Output Model: "model" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= input_1 (InputLayer) [(None, 8)] 0 _________________________________________________________________ dense (Dense) (None, 20) 180 _________________________________________________________________ dense_1 (Dense) (None, 100) 2100 _________________________________________________________________ dense_2 (Dense) (None, 20) 2020 _________________________________________________________________ dense_3 (Dense) (None, 1) 21 _________________________________________________________________ tf.math.multiply (TFOpLambda (None, 1) 0 _________________________________________________________________ tf.__operators__.add (TFOpLa (None, 1) 0 ================================================================= Total params: 4,321 Trainable params: 4,321 Non-trainable params: 0 _________________________________________________________________ ###Markdown Um wraper é criado para utilizar a função de validação cruzado do Scikit-learn. ###Code from keras.wrappers.scikit_learn import KerasRegressor estimator = KerasRegressor(build_fn=create_model, epochs=300, batch_size=300, verbose=0) ###Output _____no_output_____ ###Markdown O score da validação cruzada é calculado. ###Code print(-cross_val_score(estimator, X_train, y_train, cv=5, scoring='neg_mean_absolute_error').mean()) ###Output WARNING:tensorflow:5 out of the last 5 calls to <function Model.make_predict_function.<locals>.predict_function at 0x7f5d4b7fc710> triggered tf.function retracing. Tracing is expensive and the excessive number of tracings could be due to (1) creating @tf.function repeatedly in a loop, (2) passing tensors with different shapes, (3) passing Python objects instead of tensors. For (1), please define your @tf.function outside of the loop. For (2), @tf.function has experimental_relax_shapes=True option that relaxes argument shapes that can avoid unnecessary retracing. For (3), please refer to https://www.tensorflow.org/guide/function#controlling_retracing and https://www.tensorflow.org/api_docs/python/tf/function for more details. 4.075838752319069 ###Markdown O score da validação cruzada no conjunto de treino é de 4.08 MPa. Por fim, o modelo é treinado utilizando todo o conjunto de treino. ###Code model.fit(x=X_train, y=y_train.values, epochs=300, batch_size=300) ###Output Epoch 1/300 3/3 [==============================] - 1s 8ms/step - loss: 13.0678 Epoch 2/300 3/3 [==============================] - 0s 6ms/step - loss: 12.3589 Epoch 3/300 3/3 [==============================] - 0s 3ms/step - loss: 11.7695 Epoch 4/300 3/3 [==============================] - 0s 4ms/step - loss: 11.4504 Epoch 5/300 3/3 [==============================] - 0s 3ms/step - loss: 10.9317 Epoch 6/300 3/3 [==============================] - 0s 5ms/step - loss: 10.5465 Epoch 7/300 3/3 [==============================] - 0s 5ms/step - loss: 10.2404 Epoch 8/300 3/3 [==============================] - 0s 5ms/step - loss: 9.9319 Epoch 9/300 3/3 [==============================] - 0s 4ms/step - loss: 9.5963 Epoch 10/300 3/3 [==============================] - 0s 4ms/step - loss: 9.3915 Epoch 11/300 3/3 [==============================] - 0s 5ms/step - loss: 9.4176 Epoch 12/300 3/3 [==============================] - 0s 4ms/step - loss: 9.1122 Epoch 13/300 3/3 [==============================] - 0s 5ms/step - loss: 8.9046 Epoch 14/300 3/3 [==============================] - 0s 4ms/step - loss: 8.8182 Epoch 15/300 3/3 [==============================] - 0s 7ms/step - loss: 8.8467 Epoch 16/300 3/3 [==============================] - 0s 5ms/step - loss: 8.5716 Epoch 17/300 3/3 [==============================] - 0s 4ms/step - loss: 8.1219 Epoch 18/300 3/3 [==============================] - 0s 6ms/step - loss: 7.9176 Epoch 19/300 3/3 [==============================] - 0s 4ms/step - loss: 7.9593 Epoch 20/300 3/3 [==============================] - 0s 8ms/step - loss: 7.7760 Epoch 21/300 3/3 [==============================] - 0s 5ms/step - loss: 7.5013 Epoch 22/300 3/3 [==============================] - 0s 6ms/step - loss: 7.2442 Epoch 23/300 3/3 [==============================] - 0s 3ms/step - loss: 7.1579 Epoch 24/300 3/3 [==============================] - 0s 7ms/step - loss: 6.9899 Epoch 25/300 3/3 [==============================] - 0s 6ms/step - loss: 6.9342 Epoch 26/300 3/3 [==============================] - 0s 5ms/step - loss: 6.6572 Epoch 27/300 3/3 [==============================] - 0s 5ms/step - loss: 6.5209 Epoch 28/300 3/3 [==============================] - 0s 6ms/step - loss: 6.5546 Epoch 29/300 3/3 [==============================] - 0s 5ms/step - loss: 6.3050 Epoch 30/300 3/3 [==============================] - 0s 4ms/step - loss: 6.2221 Epoch 31/300 3/3 [==============================] - 0s 5ms/step - loss: 6.0136 Epoch 32/300 3/3 [==============================] - 0s 3ms/step - loss: 5.8539 Epoch 33/300 3/3 [==============================] - 0s 3ms/step - loss: 5.7161 Epoch 34/300 3/3 [==============================] - 0s 3ms/step - loss: 5.6015 Epoch 35/300 3/3 [==============================] - 0s 4ms/step - loss: 5.4892 Epoch 36/300 3/3 [==============================] - 0s 4ms/step - loss: 5.5415 Epoch 37/300 3/3 [==============================] - 0s 4ms/step - loss: 5.5744 Epoch 38/300 3/3 [==============================] - 0s 4ms/step - loss: 5.4764 Epoch 39/300 3/3 [==============================] - 0s 4ms/step - loss: 5.2958 Epoch 40/300 3/3 [==============================] - 0s 8ms/step - loss: 5.2382 Epoch 41/300 3/3 [==============================] - 0s 5ms/step - loss: 5.1268 Epoch 42/300 3/3 [==============================] - 0s 6ms/step - loss: 5.0339 Epoch 43/300 3/3 [==============================] - 0s 4ms/step - loss: 5.1394 Epoch 44/300 3/3 [==============================] - 0s 5ms/step - loss: 4.8920 Epoch 45/300 3/3 [==============================] - 0s 4ms/step - loss: 4.7908 Epoch 46/300 3/3 [==============================] - 0s 4ms/step - loss: 4.7065 Epoch 47/300 3/3 [==============================] - 0s 6ms/step - loss: 4.7412 Epoch 48/300 3/3 [==============================] - 0s 5ms/step - loss: 4.6897 Epoch 49/300 3/3 [==============================] - 0s 5ms/step - loss: 4.7332 Epoch 50/300 3/3 [==============================] - 0s 5ms/step - loss: 4.6011 Epoch 51/300 3/3 [==============================] - 0s 5ms/step - loss: 4.5975 Epoch 52/300 3/3 [==============================] - 0s 5ms/step - loss: 4.5720 Epoch 53/300 3/3 [==============================] - 0s 4ms/step - loss: 4.3383 Epoch 54/300 3/3 [==============================] - 0s 4ms/step - loss: 4.4053 Epoch 55/300 3/3 [==============================] - 0s 4ms/step - loss: 4.2993 Epoch 56/300 3/3 [==============================] - 0s 4ms/step - loss: 4.2008 Epoch 57/300 3/3 [==============================] - 0s 4ms/step - loss: 4.0486 Epoch 58/300 3/3 [==============================] - 0s 4ms/step - loss: 4.1533 Epoch 59/300 3/3 [==============================] - 0s 4ms/step - loss: 4.1466 Epoch 60/300 3/3 [==============================] - 0s 4ms/step - loss: 4.0242 Epoch 61/300 3/3 [==============================] - 0s 6ms/step - loss: 4.0413 Epoch 62/300 3/3 [==============================] - 0s 4ms/step - loss: 4.0967 Epoch 63/300 3/3 [==============================] - 0s 11ms/step - loss: 3.9375 Epoch 64/300 3/3 [==============================] - 0s 5ms/step - loss: 3.8908 Epoch 65/300 3/3 [==============================] - 0s 5ms/step - loss: 3.8731 Epoch 66/300 3/3 [==============================] - 0s 4ms/step - loss: 3.9600 Epoch 67/300 3/3 [==============================] - 0s 5ms/step - loss: 3.8554 Epoch 68/300 3/3 [==============================] - 0s 5ms/step - loss: 3.9097 Epoch 69/300 3/3 [==============================] - 0s 7ms/step - loss: 3.8020 Epoch 70/300 3/3 [==============================] - 0s 5ms/step - loss: 3.7046 Epoch 71/300 3/3 [==============================] - 0s 4ms/step - loss: 3.6340 Epoch 72/300 3/3 [==============================] - 0s 4ms/step - loss: 3.6736 Epoch 73/300 3/3 [==============================] - 0s 5ms/step - loss: 3.6278 Epoch 74/300 3/3 [==============================] - 0s 4ms/step - loss: 3.5951 Epoch 75/300 3/3 [==============================] - 0s 5ms/step - loss: 3.5178 Epoch 76/300 3/3 [==============================] - 0s 4ms/step - loss: 3.6078 Epoch 77/300 3/3 [==============================] - 0s 7ms/step - loss: 3.4314 Epoch 78/300 3/3 [==============================] - 0s 5ms/step - loss: 3.5365 Epoch 79/300 3/3 [==============================] - 0s 7ms/step - loss: 3.4496 Epoch 80/300 3/3 [==============================] - 0s 3ms/step - loss: 3.4851 Epoch 81/300 3/3 [==============================] - 0s 3ms/step - loss: 3.5547 Epoch 82/300 3/3 [==============================] - 0s 4ms/step - loss: 3.4007 Epoch 83/300 3/3 [==============================] - 0s 4ms/step - loss: 3.3138 Epoch 84/300 3/3 [==============================] - 0s 3ms/step - loss: 3.4823 Epoch 85/300 3/3 [==============================] - 0s 4ms/step - loss: 3.4060 Epoch 86/300 3/3 [==============================] - 0s 5ms/step - loss: 3.2788 Epoch 87/300 3/3 [==============================] - 0s 4ms/step - loss: 3.3946 Epoch 88/300 3/3 [==============================] - 0s 9ms/step - loss: 3.1992 Epoch 89/300 3/3 [==============================] - 0s 4ms/step - loss: 3.3129 Epoch 90/300 3/3 [==============================] - 0s 3ms/step - loss: 3.1984 Epoch 91/300 3/3 [==============================] - 0s 5ms/step - loss: 3.1731 Epoch 92/300 3/3 [==============================] - 0s 4ms/step - loss: 3.1287 Epoch 93/300 3/3 [==============================] - 0s 6ms/step - loss: 3.2374 Epoch 94/300 3/3 [==============================] - 0s 6ms/step - loss: 3.1677 Epoch 95/300 3/3 [==============================] - 0s 3ms/step - loss: 3.1069 Epoch 96/300 3/3 [==============================] - 0s 6ms/step - loss: 3.3899 Epoch 97/300 3/3 [==============================] - 0s 3ms/step - loss: 3.2320 Epoch 98/300 3/3 [==============================] - 0s 8ms/step - loss: 3.1388 Epoch 99/300 3/3 [==============================] - 0s 6ms/step - loss: 3.0814 Epoch 100/300 3/3 [==============================] - 0s 8ms/step - loss: 3.1803 Epoch 101/300 3/3 [==============================] - 0s 6ms/step - loss: 3.1019 Epoch 102/300 3/3 [==============================] - 0s 6ms/step - loss: 3.0957 Epoch 103/300 3/3 [==============================] - 0s 4ms/step - loss: 3.0721 Epoch 104/300 3/3 [==============================] - 0s 4ms/step - loss: 3.0754 Epoch 105/300 3/3 [==============================] - 0s 5ms/step - loss: 2.9981 Epoch 106/300 3/3 [==============================] - 0s 5ms/step - loss: 2.9634 Epoch 107/300 3/3 [==============================] - 0s 5ms/step - loss: 2.8686 Epoch 108/300 3/3 [==============================] - 0s 6ms/step - loss: 2.8122 Epoch 109/300 3/3 [==============================] - 0s 4ms/step - loss: 2.8525 Epoch 110/300 3/3 [==============================] - 0s 4ms/step - loss: 2.9299 Epoch 111/300 3/3 [==============================] - 0s 10ms/step - loss: 2.7503 Epoch 112/300 3/3 [==============================] - 0s 6ms/step - loss: 2.8197 Epoch 113/300 3/3 [==============================] - 0s 7ms/step - loss: 2.8883 Epoch 114/300 3/3 [==============================] - 0s 7ms/step - loss: 2.9060 Epoch 115/300 3/3 [==============================] - 0s 4ms/step - loss: 2.9429 Epoch 116/300 3/3 [==============================] - 0s 5ms/step - loss: 2.8969 Epoch 117/300 3/3 [==============================] - 0s 6ms/step - loss: 2.8524 Epoch 118/300 3/3 [==============================] - 0s 5ms/step - loss: 2.8659 Epoch 119/300 3/3 [==============================] - 0s 9ms/step - loss: 2.7554 Epoch 120/300 3/3 [==============================] - 0s 7ms/step - loss: 2.7084 Epoch 121/300 3/3 [==============================] - 0s 5ms/step - loss: 2.7586 Epoch 122/300 3/3 [==============================] - 0s 7ms/step - loss: 2.8650 Epoch 123/300 3/3 [==============================] - 0s 5ms/step - loss: 2.8447 Epoch 124/300 3/3 [==============================] - 0s 5ms/step - loss: 2.7594 Epoch 125/300 3/3 [==============================] - 0s 5ms/step - loss: 2.7502 Epoch 126/300 3/3 [==============================] - 0s 3ms/step - loss: 2.6893 Epoch 127/300 3/3 [==============================] - 0s 5ms/step - loss: 2.6585 Epoch 128/300 3/3 [==============================] - 0s 4ms/step - loss: 2.7050 Epoch 129/300 3/3 [==============================] - 0s 9ms/step - loss: 2.7045 Epoch 130/300 3/3 [==============================] - 0s 5ms/step - loss: 2.6622 Epoch 131/300 3/3 [==============================] - 0s 4ms/step - loss: 2.6670 Epoch 132/300 3/3 [==============================] - 0s 5ms/step - loss: 2.6024 Epoch 133/300 3/3 [==============================] - 0s 5ms/step - loss: 2.5943 Epoch 134/300 3/3 [==============================] - 0s 6ms/step - loss: 2.6538 Epoch 135/300 3/3 [==============================] - 0s 5ms/step - loss: 2.6637 Epoch 136/300 3/3 [==============================] - 0s 5ms/step - loss: 2.6373 Epoch 137/300 3/3 [==============================] - 0s 4ms/step - loss: 2.6858 Epoch 138/300 3/3 [==============================] - 0s 4ms/step - loss: 2.5966 Epoch 139/300 3/3 [==============================] - 0s 6ms/step - loss: 2.6709 Epoch 140/300 3/3 [==============================] - 0s 5ms/step - loss: 2.6183 Epoch 141/300 3/3 [==============================] - 0s 6ms/step - loss: 2.6100 Epoch 142/300 3/3 [==============================] - 0s 6ms/step - loss: 2.5553 Epoch 143/300 3/3 [==============================] - 0s 5ms/step - loss: 2.5414 Epoch 144/300 3/3 [==============================] - 0s 9ms/step - loss: 2.5682 Epoch 145/300 3/3 [==============================] - 0s 6ms/step - loss: 2.5174 Epoch 146/300 3/3 [==============================] - 0s 6ms/step - loss: 2.5529 Epoch 147/300 3/3 [==============================] - 0s 4ms/step - loss: 2.5442 Epoch 148/300 3/3 [==============================] - 0s 4ms/step - loss: 2.4639 Epoch 149/300 3/3 [==============================] - 0s 5ms/step - loss: 2.4506 Epoch 150/300 3/3 [==============================] - 0s 8ms/step - loss: 2.4646 Epoch 151/300 3/3 [==============================] - 0s 4ms/step - loss: 2.4134 Epoch 152/300 3/3 [==============================] - 0s 5ms/step - loss: 2.4788 Epoch 153/300 3/3 [==============================] - 0s 5ms/step - loss: 2.5309 Epoch 154/300 3/3 [==============================] - 0s 5ms/step - loss: 2.4614 Epoch 155/300 3/3 [==============================] - 0s 5ms/step - loss: 2.4905 Epoch 156/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3991 Epoch 157/300 3/3 [==============================] - 0s 5ms/step - loss: 2.4559 Epoch 158/300 3/3 [==============================] - 0s 8ms/step - loss: 2.4049 Epoch 159/300 3/3 [==============================] - 0s 4ms/step - loss: 2.3743 Epoch 160/300 3/3 [==============================] - 0s 5ms/step - loss: 2.4227 Epoch 161/300 3/3 [==============================] - 0s 7ms/step - loss: 2.4768 Epoch 162/300 3/3 [==============================] - 0s 5ms/step - loss: 2.4126 Epoch 163/300 3/3 [==============================] - 0s 6ms/step - loss: 2.4278 Epoch 164/300 3/3 [==============================] - 0s 5ms/step - loss: 2.5466 Epoch 165/300 3/3 [==============================] - 0s 7ms/step - loss: 2.4127 Epoch 166/300 3/3 [==============================] - 0s 5ms/step - loss: 2.3923 Epoch 167/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3465 Epoch 168/300 3/3 [==============================] - 0s 5ms/step - loss: 2.3937 Epoch 169/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3169 Epoch 170/300 3/3 [==============================] - 0s 5ms/step - loss: 2.3969 Epoch 171/300 3/3 [==============================] - 0s 9ms/step - loss: 2.4319 Epoch 172/300 3/3 [==============================] - 0s 6ms/step - loss: 2.4004 Epoch 173/300 3/3 [==============================] - 0s 5ms/step - loss: 2.3470 Epoch 174/300 3/3 [==============================] - 0s 8ms/step - loss: 2.3041 Epoch 175/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3253 Epoch 176/300 3/3 [==============================] - 0s 5ms/step - loss: 2.3492 Epoch 177/300 3/3 [==============================] - 0s 5ms/step - loss: 2.3213 Epoch 178/300 3/3 [==============================] - 0s 4ms/step - loss: 2.3783 Epoch 179/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3139 Epoch 180/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3099 Epoch 181/300 3/3 [==============================] - 0s 5ms/step - loss: 2.3086 Epoch 182/300 3/3 [==============================] - 0s 5ms/step - loss: 2.2976 Epoch 183/300 3/3 [==============================] - 0s 6ms/step - loss: 2.2649 Epoch 184/300 3/3 [==============================] - 0s 5ms/step - loss: 2.1898 Epoch 185/300 3/3 [==============================] - 0s 6ms/step - loss: 2.2692 Epoch 186/300 3/3 [==============================] - 0s 3ms/step - loss: 2.2780 Epoch 187/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3409 Epoch 188/300 3/3 [==============================] - 0s 4ms/step - loss: 2.2484 Epoch 189/300 3/3 [==============================] - 0s 4ms/step - loss: 2.2649 Epoch 190/300 3/3 [==============================] - 0s 5ms/step - loss: 2.3110 Epoch 191/300 3/3 [==============================] - 0s 7ms/step - loss: 2.3460 Epoch 192/300 3/3 [==============================] - 0s 8ms/step - loss: 2.3201 Epoch 193/300 3/3 [==============================] - 0s 6ms/step - loss: 2.2863 Epoch 194/300 3/3 [==============================] - 0s 6ms/step - loss: 2.2222 Epoch 195/300 3/3 [==============================] - 0s 7ms/step - loss: 2.2940 Epoch 196/300 3/3 [==============================] - 0s 5ms/step - loss: 2.2871 Epoch 197/300 3/3 [==============================] - 0s 5ms/step - loss: 2.2805 Epoch 198/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3587 Epoch 199/300 3/3 [==============================] - 0s 6ms/step - loss: 2.1920 Epoch 200/300 3/3 [==============================] - 0s 4ms/step - loss: 2.3573 Epoch 201/300 3/3 [==============================] - 0s 4ms/step - loss: 2.3062 Epoch 202/300 3/3 [==============================] - 0s 6ms/step - loss: 2.3282 Epoch 203/300 3/3 [==============================] - 0s 7ms/step - loss: 2.2466 Epoch 204/300 3/3 [==============================] - 0s 7ms/step - loss: 2.2842 Epoch 205/300 3/3 [==============================] - 0s 8ms/step - loss: 2.2419 Epoch 206/300 3/3 [==============================] - 0s 11ms/step - loss: 2.2574 Epoch 207/300 3/3 [==============================] - 0s 6ms/step - loss: 2.1632 Epoch 208/300 3/3 [==============================] - 0s 9ms/step - loss: 2.1888 Epoch 209/300 3/3 [==============================] - 0s 5ms/step - loss: 2.1692 Epoch 210/300 3/3 [==============================] - 0s 5ms/step - loss: 2.1626 Epoch 211/300 3/3 [==============================] - 0s 5ms/step - loss: 2.1501 Epoch 212/300 3/3 [==============================] - 0s 4ms/step - loss: 2.1647 Epoch 213/300 3/3 [==============================] - 0s 4ms/step - loss: 2.1637 Epoch 214/300 3/3 [==============================] - 0s 5ms/step - loss: 2.1203 Epoch 215/300 3/3 [==============================] - 0s 4ms/step - loss: 2.1552 Epoch 216/300 3/3 [==============================] - 0s 8ms/step - loss: 2.0658 Epoch 217/300 3/3 [==============================] - 0s 5ms/step - loss: 2.1176 Epoch 218/300 3/3 [==============================] - 0s 7ms/step - loss: 2.1204 Epoch 219/300 3/3 [==============================] - 0s 5ms/step - loss: 2.2285 Epoch 220/300 3/3 [==============================] - 0s 4ms/step - loss: 2.1378 Epoch 221/300 3/3 [==============================] - 0s 6ms/step - loss: 2.0813 Epoch 222/300 3/3 [==============================] - 0s 11ms/step - loss: 2.1350 Epoch 223/300 3/3 [==============================] - 0s 7ms/step - loss: 2.0436 Epoch 224/300 3/3 [==============================] - 0s 7ms/step - loss: 2.1569 Epoch 225/300 3/3 [==============================] - 0s 7ms/step - loss: 2.0411 Epoch 226/300 3/3 [==============================] - 0s 5ms/step - loss: 2.0955 Epoch 227/300 3/3 [==============================] - 0s 5ms/step - loss: 2.1530 Epoch 228/300 3/3 [==============================] - 0s 4ms/step - loss: 2.1007 Epoch 229/300 3/3 [==============================] - 0s 6ms/step - loss: 2.0824 Epoch 230/300 3/3 [==============================] - 0s 6ms/step - loss: 2.1998 Epoch 231/300 3/3 [==============================] - 0s 4ms/step - loss: 2.1093 Epoch 232/300 3/3 [==============================] - 0s 4ms/step - loss: 2.1621 Epoch 233/300 3/3 [==============================] - 0s 4ms/step - loss: 1.9906 Epoch 234/300 3/3 [==============================] - 0s 6ms/step - loss: 2.0186 Epoch 235/300 3/3 [==============================] - 0s 4ms/step - loss: 2.0769 Epoch 236/300 3/3 [==============================] - 0s 7ms/step - loss: 1.9972 Epoch 237/300 3/3 [==============================] - 0s 5ms/step - loss: 2.1243 Epoch 238/300 3/3 [==============================] - 0s 5ms/step - loss: 2.0725 Epoch 239/300 3/3 [==============================] - 0s 3ms/step - loss: 2.0143 Epoch 240/300 3/3 [==============================] - 0s 4ms/step - loss: 2.2119 Epoch 241/300 3/3 [==============================] - 0s 6ms/step - loss: 2.0125 Epoch 242/300 3/3 [==============================] - 0s 7ms/step - loss: 2.0594 Epoch 243/300 3/3 [==============================] - 0s 5ms/step - loss: 2.0224 Epoch 244/300 3/3 [==============================] - 0s 6ms/step - loss: 2.0041 Epoch 245/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9769 Epoch 246/300 3/3 [==============================] - 0s 7ms/step - loss: 1.9534 Epoch 247/300 3/3 [==============================] - 0s 7ms/step - loss: 1.9638 Epoch 248/300 3/3 [==============================] - 0s 7ms/step - loss: 2.1759 Epoch 249/300 3/3 [==============================] - 0s 5ms/step - loss: 2.0925 Epoch 250/300 3/3 [==============================] - 0s 3ms/step - loss: 2.1773 Epoch 251/300 3/3 [==============================] - 0s 4ms/step - loss: 2.0704 Epoch 252/300 3/3 [==============================] - 0s 6ms/step - loss: 2.0607 Epoch 253/300 3/3 [==============================] - 0s 4ms/step - loss: 2.0396 Epoch 254/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9907 Epoch 255/300 3/3 [==============================] - 0s 4ms/step - loss: 1.9852 Epoch 256/300 3/3 [==============================] - 0s 4ms/step - loss: 2.0055 Epoch 257/300 3/3 [==============================] - 0s 5ms/step - loss: 1.9374 Epoch 258/300 3/3 [==============================] - 0s 6ms/step - loss: 2.0446 Epoch 259/300 3/3 [==============================] - 0s 3ms/step - loss: 1.9537 Epoch 260/300 3/3 [==============================] - 0s 5ms/step - loss: 2.0097 Epoch 261/300 3/3 [==============================] - 0s 4ms/step - loss: 2.0104 Epoch 262/300 3/3 [==============================] - 0s 4ms/step - loss: 2.0684 Epoch 263/300 3/3 [==============================] - 0s 4ms/step - loss: 2.0035 Epoch 264/300 3/3 [==============================] - 0s 5ms/step - loss: 1.9062 Epoch 265/300 3/3 [==============================] - 0s 4ms/step - loss: 2.0256 Epoch 266/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9907 Epoch 267/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9669 Epoch 268/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9967 Epoch 269/300 3/3 [==============================] - 0s 5ms/step - loss: 1.8749 Epoch 270/300 3/3 [==============================] - 0s 5ms/step - loss: 1.8846 Epoch 271/300 3/3 [==============================] - 0s 3ms/step - loss: 1.9608 Epoch 272/300 3/3 [==============================] - 0s 5ms/step - loss: 1.8159 Epoch 273/300 3/3 [==============================] - 0s 5ms/step - loss: 1.8787 Epoch 274/300 3/3 [==============================] - 0s 11ms/step - loss: 1.8671 Epoch 275/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9226 Epoch 276/300 3/3 [==============================] - 0s 6ms/step - loss: 2.0416 Epoch 277/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9772 Epoch 278/300 3/3 [==============================] - 0s 5ms/step - loss: 1.9869 Epoch 279/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9468 Epoch 280/300 3/3 [==============================] - 0s 8ms/step - loss: 1.9844 Epoch 281/300 3/3 [==============================] - 0s 5ms/step - loss: 1.9181 Epoch 282/300 3/3 [==============================] - 0s 5ms/step - loss: 1.9181 Epoch 283/300 3/3 [==============================] - 0s 5ms/step - loss: 2.0166 Epoch 284/300 3/3 [==============================] - 0s 4ms/step - loss: 1.9712 Epoch 285/300 3/3 [==============================] - 0s 5ms/step - loss: 1.9028 Epoch 286/300 3/3 [==============================] - 0s 5ms/step - loss: 1.9395 Epoch 287/300 3/3 [==============================] - 0s 4ms/step - loss: 1.9845 Epoch 288/300 3/3 [==============================] - 0s 5ms/step - loss: 1.8723 Epoch 289/300 3/3 [==============================] - 0s 3ms/step - loss: 1.8071 Epoch 290/300 3/3 [==============================] - 0s 4ms/step - loss: 1.8252 Epoch 291/300 3/3 [==============================] - 0s 7ms/step - loss: 1.8454 Epoch 292/300 3/3 [==============================] - 0s 8ms/step - loss: 1.9126 Epoch 293/300 3/3 [==============================] - 0s 6ms/step - loss: 1.8903 Epoch 294/300 3/3 [==============================] - 0s 6ms/step - loss: 1.9082 Epoch 295/300 3/3 [==============================] - 0s 6ms/step - loss: 1.8252 Epoch 296/300 3/3 [==============================] - 0s 6ms/step - loss: 1.8035 Epoch 297/300 3/3 [==============================] - 0s 6ms/step - loss: 1.8343 Epoch 298/300 3/3 [==============================] - 0s 5ms/step - loss: 1.8999 Epoch 299/300 3/3 [==============================] - 0s 4ms/step - loss: 1.9006 Epoch 300/300 3/3 [==============================] - 0s 6ms/step - loss: 1.8484 ###Markdown O erro médio absoluto final é então calculado. ###Code mean_absolute_error(y_test, model(X_test)) ###Output _____no_output_____ ###Markdown O modelo prevê a resistência à compressão do concreto com um erro médio absoluto de 3.845 MPa para o conunto de teste. ###Code ###Output _____no_output_____
statistics/nonparametric_methods/Distribution_Free_Methods.ipynb	###Markdown Creating Empirical Cumulative Distribution Function ###Code %matplotlib inline import numpy as np import matplotlib.pyplot as plt plt.style.use('ggplot') data = np.array([ 5.9, 6.0, 6.4, 6.4, 6.5, 6.5, 6.6, 6.7, 6.9, 7.0, 7.1, 7.2, 7.5, 7.5, 7.8, 7.9, 8.1, 8.1, 8.2, 8.9, 9.3, 9.3, 9.6, 10.4, 10.6, 11.8, 11.8, 12.6, 12.9, 14.3, 15.0, 16.2, 16.3, 17.0, 17.2, 22.8, 23.1, 33.0, 40.0, 42.8, 43.0, 44.8, 45.0, 45.8 ]) data len(data) ###Output _____no_output_____ ###Markdown The ECDF is generated with this function: $\large{\hat{F}(x) = \frac{\x_i \leq x}{n}}$ The above basically means for each value of x in your data set consisting of only unique values of x, the function is equal to the number of Xs that are less than or equal to the current X value. F(5.9) = 1/44 = 0.023F(6) = 2/44 = 0.045F(6.4) = 4/44 = 0.091...F(45.8) = 44/44 = 1.0 ###Code def ecdf(x): """Return empirical CDF of x.""" sx = np.sort(x) cdf = (1.0 + np.arange(len(sx)))/len(sx) return sx, cdf sx, y = ecdf(data) plt.step(sx, y) plt.title("Empirical CDF", fontsize=14, weight='bold') plt.show() ###Output _____no_output_____ ###Markdown Creating 95% confidence band based on [Dvoretzky–Kiefer–Wolfowitz](http://stats.stackexchange.com/questions/55500/confidence-intervals-for-empirical-cdf) inequality: $\large{ecdf\pm\sqrt{\frac{1}{2n}log(\frac{2}{\alpha})}}$ ###Code alpha = 0.05 nobs = 44 interval = np.sqrt(np.log(2./alpha) / (2 * nobs)) print("Confidence band width: " + str(interval)) lower = np.clip(y - interval, 0, 1) upper = np.clip(y + interval, 0, 1) plt.step(sx, y, sx, upper, sx, lower) plt.fill_between(sx, y, upper, color='grey', alpha=0.5, step='pre') plt.fill_between(sx, y, lower, color='grey',alpha=0.5, step='pre') plt.title("Emprical CDF with 95% Confidence Interval", fontsize=12, weight='bold') plt.show() ###Output Confidence band width: 0.204741507042 ###Markdown Found out that the [statsmodels](http://statsmodels.sourceforge.net/devel/_modules/statsmodels/distributions/empirical_distribution.html) package has ECDF function and function for making confidence interval. ###Code %matplotlib inline import numpy as np from statsmodels.distributions import ECDF from statsmodels.distributions.empirical_distribution import _conf_set import matplotlib.pyplot as plt data = np.array([ 5.9, 6.0, 6.4, 6.4, 6.5, 6.5, 6.6, 6.7, 6.9, 7.0, 7.1, 7.2, 7.5, 7.5, 7.8, 7.9, 8.1, 8.1, 8.2, 8.9, 9.3, 9.3, 9.6, 10.4, 10.6, 11.8, 11.8, 12.6, 12.9, 14.3, 15.0, 16.2, 16.3, 17.0, 17.2, 22.8, 23.1, 33.0, 40.0, 42.8, 43.0, 44.8, 45.0, 45.8 ]) cdf = ECDF(data) y = cdf.y x = cdf.x plt.step(x, y) lower, upper = _conf_set(y, alpha=0.05) plt.step(x, lower) plt.step(x, upper) plt.fill_between(x, y, upper, color='grey', alpha=0.5, interpolate=False, step='pre') plt.fill_between(x, y, lower, color='grey',alpha=0.5, interpolate=False, step='pre') plt.vlines(x, 0, .05) # show location of steps plt.title("Empirical CDF with 95% Confidence Interval", fontsize=12, weight='bold') plt.show() ###Output _____no_output_____
4-Condition.ipynb	###Markdown 4. Conditional Statements, If...Else Conditions are used a lot in programming. Sometimes, requirements could be broken down into some if-else statements. Let us try running some if-else statements. ###Code #compare strings, try replacing the name. name = "tom" if name == "tom": print("You are Tom.") else: print("You are not Tom.") ###Output _____no_output_____ ###Markdown You could compare numbers too. The following conditions check if a number is larger than 10 or smaller than 10, and also if the number is 10. ###Code a = 10 if a > 10: print("a is larger than 10") elif a < 10: print("a is lesser than 10") else: print("a is 10") ###Output _____no_output_____ ###Markdown We can also have multiple conditions such as the following, where we want to find a number larger than 10 and is an even number. ###Code a = 2 if a >= 10 or a % 2 == 0: print('a is either larger than or equals to 10 or it is an even number.') else: print('a is smaller than 10 and is not even.') ###Output _____no_output_____ ###Markdown Try it yourselfInstead of comparing with a fixed number, you can compare both variables. Try rewriting the above and replace 10 with a variable named "b". ###Code # Type in your code below ###Output _____no_output_____
InitialDataCleaning02.ipynb	###Markdown Initial Data CleaningThis script is designed to fill in nulls in important missing fields and to format and select the data which will be required to create a model later on. Import Statements ###Code import geopandas as gpd import folium import matplotlib.pyplot as plt import pandas as pd import numpy as np import sqlite3 from shapely.geometry import Point ###Output _____no_output_____ ###Markdown Filling in NullsTo fill in nulls in this process we need some background on the data itself and how I intend to use it. First off, the dataset of interest contains over 2 million rows - each of which pertains to a specific wildfire. For each fire there is a Latitude and Longitude point for where the fire originated. Also, in most rows there are county and state code identifiers, however, in many rows (approx. 600K) there are no county identifiers. The lack of those county identifiers is an issue since we intend to analyze and predict wildfires on a county level. To address the issue of the missing county identifiers we take the following actions:1. From an online source, get a data set which has Geofences (Polygons) for all the counties in the U.S. 2. From the U.S. Census Bureau get a correlation of all the counties and states with their correct code 3. Merge the county polygons to the county/state codes based on the county name and state abbreviation4. In the wildfire data create spatial Points out of the longitude and latitude columns5. Execute a Spatial merge between the wildfire Points and the county Polygons based on whether the Point is in the Polygon6. Extract the county/state codes from the merged dataframe and then subset to the desired columns for further cleaning Read in the .shp file which has all of the Polygons for the U.S. counties. Subset to just the three needed columns: county name, country/state/county abbreviation (which we extract state abbreviation from), and the Polygon for the county ###Code geodf = gpd.read_file("./Data/CountyGeoFences/gadm36_USA_2.shp")[["NAME_2", "HASC_2", 'geometry']] geodf.head(1) ###Output _____no_output_____ ###Markdown Create a new GeoDataFrame which reformats the county and state into the correct format to join on later ###Code new_df = gpd.GeoDataFrame() new_df['COUNTY'] = geodf['NAME_2'].str.upper().str.strip() new_df['STATE'] = geodf['HASC_2'].str.slice(3,5).str.strip() new_df['geometry'] = geodf['geometry'] new_df.head(1) ###Output _____no_output_____ ###Markdown Read in the Census data which correlates the county to the county/state code. In this data the whole states and the whole US are included, but are formatted so that their names are in all uppercase - whereas individual counties are in title case. So we filter out those rows which are already in upper case - as they are the whole states and whole US - which we are not interested in. ###Code lnd_data = pd.read_csv("./Data/CountyLandArea.csv")[['Areaname', 'STCOU']] lnd_data = lnd_data.loc[lnd_data['Areaname'] != lnd_data['Areaname'].str.upper()] lnd_data.head(1) ###Output _____no_output_____ ###Markdown Now format the data by separating the county name and the state abbreviation and by turning the code into a zero-padded five digit long value. For reference the code is built in a way such that the first two number indicate the state and the last three numbers indicate the county. ###Code new_lnd_data = pd.DataFrame() new_lnd_data['COUNTY'] = lnd_data['Areaname'].str.split(',').apply(lambda x: x[0].upper()).str.strip() new_lnd_data['STATE'] = lnd_data['Areaname'].str.split(',').apply(lambda x: x[1].upper()).str.strip() new_lnd_data['FIPS_CODE'] = lnd_data['STCOU'].astype(str).str.zfill(5) new_lnd_data.head(1) ###Output _____no_output_____ ###Markdown Merge the county Polygon data with the Census data to get the county/state code with the Polygons. Then ensure that the object is a Spatial DataFrame with the correct geospatial reference. ###Code comb = gpd.GeoDataFrame(pd.merge(new_lnd_data, new_df, on=['COUNTY', "STATE"], how='inner'), crs="EPSG:4326") ###Output _____no_output_____ ###Markdown Set that dataset aside. Read in the wildfire data from the .sqlite table, selecting (in SQL) only the few columns which we want ###Code cursor = sqlite3.connect('./Data/Fire/FPA_FOD_20210617.sqlite') query = "SELECT f.FOD_ID, f.DISCOVERY_DATE, f.FIRE_SIZE, f.LATITUDE, f.LONGITUDE, f.FIPS_CODE from Fires f" all_data = pd.read_sql_query(query, cursor) all_data.head(1) ###Output _____no_output_____ ###Markdown Take the wildfire data and turn it into a Spatial DataFrame and create the geometry columns to be the Lat/Long points and ensure that the Spatial DataFrame has the correct reference ###Code geo_fire_df = gpd.GeoDataFrame(all_data, geometry=gpd.points_from_xy(all_data.LONGITUDE, all_data.LATITUDE), crs="EPSG:4326") geo_fire_df.head(1) ###Output _____no_output_____ ###Markdown Now take both DataFrames - with the points (wildfire data) and with the polygons (county/state data)We will execute a spatial join such that we are joining the rows from the county/state data to the wildfire data wherever the Point in the wildfire data is within the Polygon of county/state data. ###Code merged = geo_fire_df.sjoin(comb, how='inner', predicate='within') ###Output _____no_output_____ ###Markdown There may be some duplicates because of overlap in counties or some edge cases within the data. So we remove those duplicates and retain only the first instance of the row. ###Code mgd = merged.drop_duplicates(subset=["DISCOVERY_DATE", "FIRE_SIZE", "FIPS_CODE_right"]) ###Output _____no_output_____ ###Markdown Formatting Now that we have the county/state codes filled in for all of our wildfire instances we can get to formatting the data. To format the data we will select just the few columns which we want and set the names correctly. Then we'll turn the discovery date into an actual date column and then finally calculate the discovery month of the fire - as we will be focused on monthly predictions of wildfires. ###Code final_mgd = mgd[["DISCOVERY_DATE", "FIRE_SIZE", "FIPS_CODE_right"]].rename({'FIPS_CODE_right': "FIPS_CODE"}, axis=1) final_mgd.loc[:, 'DISCOVERY_DATE'] = pd.to_datetime(final_mgd.loc[:, 'DISCOVERY_DATE']) final_mgd['MONTH'] = final_mgd['DISCOVERY_DATE'].to_numpy().astype('datetime64[M]') final_mgd.head(1) final_mgd.shape ###Output _____no_output_____ ###Markdown From this data we sum up all of the fire sizes for each month and county/state code (FIPS) ###Code agg_data = final_mgd.groupby(by=['MONTH', 'FIPS_CODE']).agg({'FIRE_SIZE': sum}).reset_index() agg_data.rename({'FIRE_SIZE': 'TOTAL_BURN_AREA'}, axis=1, inplace=True) ###Output _____no_output_____ ###Markdown Now - we want to standardize the area burned by the size of the county itself. This way we can better assess the actual impact of the fires on the county since some small fires may be very impactful in certain counties (i.e. small ones) but large fires may not matter at all since it's really only a small portion of the county (i.e. in Alaska where the counties are larger than most states)To do this standardization we turn back to the census bureau and we can find the land size (in Sq. Miles) for all of the counties and then merge it to our aggregated data and then divide the Fire Size by the county size. We will convert the Sq. Miles into Acres for a better apples-apples comparison of total area to area burned. Also note that some fires may extend beyond one county - or start in one county and then blow directly into the neighnoring county - and while this may lead some of our numbers to be decieving, as a whole the concept is still strong. However, from a data perspective this does mean that total area burned may be greater than county area. ###Code land_area_data = pd.read_csv("./Data/CountyLandArea.csv")[["STCOU", "LND010190D"]] land_area_data.rename({'STCOU': "FIPS_CODE", "LND010190D": "COUNTY_AREA"}, axis=1, inplace=True) land_area_data['FIPS_CODE'] = land_area_data["FIPS_CODE"].astype(str).str.zfill(5) land_area_data['COUNTY_AREA'] = land_area_data['COUNTY_AREA'] * 640 land_area_data = land_area_data.iloc[np.where(land_area_data['COUNTY_AREA'] != 0)] land_area_data.head(1) ###Output _____no_output_____ ###Markdown Now merge the aggregated data with the land area data and divide to get the burned to toal area ratio ###Code agg_and_area = pd.merge(agg_data, land_area_data, how='inner', on=['FIPS_CODE']) agg_and_area.head(1) ###Output _____no_output_____ ###Markdown We will keep the burn area and county data so that we can aggregate separately for state and national geographic areas. So output the data. ###Code agg_and_area.to_csv("./Data/clean_fire_data.csv", index=False) ###Output _____no_output_____ ###Markdown Our last step is to pull in some weather data, clean it and then join in based on the state for which the weather data pertains to. This data is kept separate for now but will be converted into a format where it can be easily joined into a state level aggregation of the wildfire data First read in the weather data csv file ###Code files = ["California", "Arizona", "Colorado", "Montana", "Nevada", "Oregon", "Washington", "Idaho", "Utah", "NewMexico", "Wyoming"] data = [] for f in files: df = pd.read_csv(f"./Data/Weather/{f}.csv", parse_dates=['DATE'])[["NAME", "DATE", "PRCP", "TMAX", "TMIN"]] df["STATE"] = df['NAME'].str.split(',').apply(lambda x: x[1]).str.strip().str.split(' ').apply(lambda x: x[0]).str.strip() df.drop('NAME', axis=1, inplace=True) data.append(df) weather_data = pd.concat(data, axis=0) ###Output _____no_output_____ ###Markdown Now, we will average out the measurements which we have for multiple stats down into measurements on a state level ###Code grped_weather = weather_data.groupby(by=["STATE", "DATE"]).mean().reset_index() grped_weather.rename({'DATE': 'MONTH'}, axis=1, inplace=True) ###Output _____no_output_____ ###Markdown Now, once again, read in the Census data to get state codes - there is a bit of logic to extract the state codes but not too bad since we can use work we have already done to format the file correctly. In the end we can see that we do indeed end up with codes for our 50 states ###Code census_data = pd.read_csv("./Data/CountyLandArea.csv")[["Areaname", "STCOU"]] census_data = census_data.loc[census_data['Areaname'] != census_data['Areaname'].str.upper()] census_data['STATE'] = census_data['Areaname'].str.split(',').apply(lambda x: x[1].upper()).str.strip() census_data['STATE_CODE'] = census_data['STCOU'].astype(str).str.zfill(5).str.slice(0,2) census_data = census_data.drop_duplicates(subset=['STATE_CODE', 'STATE'])[["STATE", "STATE_CODE"]].reset_index(drop=True) ###Output _____no_output_____ ###Markdown Now we will join the weather and census data together to get the state codes for our states ###Code weather_w_codes = pd.merge(grped_weather, census_data, how='inner', on='STATE') ###Output _____no_output_____ ###Markdown Now export the data to a csv file where we can pull it into our modelling efforts later on ###Code weather_w_codes.to_csv("./Data/cleaned_weather_data.csv", index=False) ###Output _____no_output_____
chapter_3/YELP_Dataset_full.ipynb	###Markdown Preprocessing Yelp Dataset (Full version) ###Code import re import collections import numpy as np import pandas as pd from tqdm.notebook import tqdm from argparse import Namespace tqdm.pandas(desc="Preprocessing Reviews") ###Output /opt/miniconda3/envs/notebook_env/lib/python3.7/site-packages/tqdm/std.py:668: FutureWarning: The Panel class is removed from pandas. Accessing it from the top-level namespace will also be removed in the next version from pandas import Panel ###Markdown Define configurations ###Code args = Namespace( raw_train_dataset_csv = "data/yelp/raw_train.csv", raw_test_dataset_csv = "data/yelp/raw_test.csv", output_munged_csv="data/yelp/reviews_with_splits_full.csv", seed=1337, ) ###Output _____no_output_____ ###Markdown Read Data ###Code train_reviews = pd.read_csv( args.raw_train_dataset_csv, header = None, names = ["rating", "review"] ) train_reviews = train_reviews[~pd.isnull(train_reviews.review)] test_reviews = pd.read_csv( args.raw_test_dataset_csv, header=None, names=["rating", "review"] ) test_reviews = test_reviews[~pd.isnull(test_reviews.review)] train_reviews.head() ###Output _____no_output_____ ###Markdown Split data into Train/Dev/Test ###Code from sklearn.model_selection import train_test_split train_reviews.rating.value_counts(), test_reviews.rating.value_counts() train, val = train_test_split(train_reviews, train_size=0.7, stratify=train_reviews.rating.values) train = train.copy() val = val.copy() train.rating.value_counts() # Have the same distribution val.rating.value_counts() # Have the same distribution test_reviews.rating.value_counts() # Have the same distribution train.reset_index(drop=True, inplace=True) val.reset_index(drop=True, inplace=True) test_reviews.reset_index(drop=True, inplace=True) train["split"] = "train" val["split"] = "val" test_reviews["split"] = "test" ###Output _____no_output_____ ###Markdown Final reviews ###Code final_reviews = pd.concat([train, val, test_reviews], axis=0, copy=True) final_reviews.reset_index(drop=True, inplace=True) final_reviews.split.value_counts() final_reviews.review.head() final_reviews[(final_reviews.review.isnull())] ###Output _____no_output_____ ###Markdown Preprocess Reviews ###Code # Preprocess the reviews def preprocess_text(text): text = text.lower() text = re.sub(r"([.,!?])", r" \1 ", text) text = re.sub(r"[^a-zA-Z.,!?]+", r" ", text) return text final_reviews.review = final_reviews.review.progress_apply( preprocess_text) final_reviews['rating'] = final_reviews.rating.progress_apply( {1: 'negative', 2: 'positive'}.get) final_reviews.head() final_reviews.to_csv(args.output_munged_csv, index=False) ###Output _____no_output_____
Reasearch Code - Jupyter Notebooks/Step2-Feature-Engineering.ipynb	###Markdown Machine Learning Model Building Pipeline: Feature Engineering1. Data Analysis2. Feature Engineering3. Feature Selection4. Model BuildingThis is the notebook for step 2: Feature EngineeringThe dataset used is the house price dataset available on [Kaggle.com](https://www.kaggle.com/c/house-prices-advanced-regression-techniques/data). See below for more details.=================================================================================================== Predicting Sale Price of HousesThe aim of the project is to build a machine learning model to predict the sale price of homes based on different explanatory variables describing aspects of residential houses. How do I download the dataset?To download the House Price dataset go this website:https://www.kaggle.com/c/house-prices-advanced-regression-techniques/dataDownload 'train.csv'. Rename the file as 'houseprice.csv' and save where you saved this jupyter notebook. House Prices dataset: Feature EngineeringIn the following cells, we will engineer / pre-process the variables of the House Price Dataset from Kaggle. We will engineer the variables so that we tackle:1. Missing values2. Temporal variables3. Non-Gaussian distributed variables4. Categorical variables: remove rare labels5. Categorical variables: convert strings to numbers5. Standarise the values of the variables to the same range Setting the seedIt is important to note that we are engineering variables and pre-processing data with the idea of deploying the model. Therefore, from now on, for each step that includes some element of randomness, it is extremely important that we set the seed. This way, we can obtain reproducibility between our research and our development code.Always set the seeds. ###Code # to handle datasets import pandas as pd import numpy as np # for plotting import matplotlib.pyplot as plt # to divide train and test set from sklearn.model_selection import train_test_split # feature scaling from sklearn.preprocessing import MinMaxScaler # to visualise al the columns in the dataframe pd.pandas.set_option('display.max_columns', None) import warnings warnings.simplefilter(action='ignore') # load dataset data = pd.read_csv('houseprice.csv') print(data.shape) data.head() ###Output (1460, 81) ###Markdown Separate dataset into train and testBefore beginning to engineer our features, it is important to separate our data intro training and testing set. When we engineer features, some techniques learn parameters from data. It is important to learn this parameters only from the train set. This is to avoid over-fitting. Separating the data into train and test involves randomness, therefore, we need to set the seed. ###Code # Let's separate into train and test set # Remember to set the seed (random_state for this sklearn function) X_train, X_test, y_train, y_test = train_test_split(data, data['SalePrice'], test_size=0.1, # we are setting the seed here: random_state=0) X_train.shape, X_test.shape ###Output _____no_output_____ ###Markdown Missing values Categorical variablesFor categorical variables, we will replace missing values with the string "missing". ###Code # make a list of the categorical variables that contain missing values vars_with_na = [ var for var in data.columns if X_train[var].isnull().sum() > 0 and X_train[var].dtypes == 'O' ] # print percentage of missing values per variable X_train[vars_with_na].isnull().mean() # replace missing values with new label: "Missing" X_train[vars_with_na] = X_train[vars_with_na].fillna('Missing') X_test[vars_with_na] = X_test[vars_with_na].fillna('Missing') # check that we have no missing information in the engineered variables X_train[vars_with_na].isnull().sum() # check that test set does not contain null values in the engineered variables [var for var in vars_with_na if X_test[var].isnull().sum() > 0] ###Output _____no_output_____ ###Markdown Numerical variablesTo engineer missing values in numerical variables, we will:- add a binary missing value indicator variable- and then replace the missing values in the original variable with the mode ###Code # make a list with the numerical variables that contain missing values vars_with_na = [ var for var in data.columns if X_train[var].isnull().sum() > 0 and X_train[var].dtypes != 'O' ] # print percentage of missing values per variable X_train[vars_with_na].isnull().mean() # replace engineer missing values as we described above for var in vars_with_na: # calculate the mode using the train set mode_val = X_train[var].mode()[0] # add binary missing indicator (in train and test) X_train[var+'_na'] = np.where(X_train[var].isnull(), 1, 0) X_test[var+'_na'] = np.where(X_test[var].isnull(), 1, 0) # replace missing values by the mode # (in train and test) X_train[var] = X_train[var].fillna(mode_val) X_test[var] = X_test[var].fillna(mode_val) # check that we have no more missing values in the engineered variables X_train[vars_with_na].isnull().sum() # check that test set does not contain null values in the engineered variables [vr for var in vars_with_na if X_test[var].isnull().sum() > 0] # check the binary missing indicator variables X_train[['LotFrontage_na', 'MasVnrArea_na', 'GarageYrBlt_na']].head() ###Output _____no_output_____ ###Markdown Temporal variables Capture elapsed timeThere are 4 variables that refer to the years in which the house or the garage were built or remodeled. We will capture the time elapsed between those variables and the year in which the house was sold: ###Code def elapsed_years(df, var): # capture difference between the year variable # and the year in which the house was sold df[var] = df['YrSold'] - df[var] return df for var in ['YearBuilt', 'YearRemodAdd', 'GarageYrBlt']: X_train = elapsed_years(X_train, var) X_test = elapsed_years(X_test, var) ###Output _____no_output_____ ###Markdown Numerical variable transformationIn the previous Jupyter notebook, we observed that the numerical variables are not normally distributed.We will log transform the positive numerical variables in order to get a more Gaussian-like distribution. This tends to help Linear machine learning models. ###Code for var in ['LotFrontage', 'LotArea', '1stFlrSF', 'GrLivArea', 'SalePrice']: X_train[var] = np.log(X_train[var]) X_test[var] = np.log(X_test[var]) # check that test set does not contain null values in the engineered variables [var for var in ['LotFrontage', 'LotArea', '1stFlrSF', 'GrLivArea', 'SalePrice'] if X_test[var].isnull().sum() > 0] # same for train set [var for var in ['LotFrontage', 'LotArea', '1stFlrSF', 'GrLivArea', 'SalePrice'] if X_train[var].isnull().sum() > 0] ###Output _____no_output_____ ###Markdown Categorical variables Removing rare labelsFirst, we will group those categories within variables that are present in less than 1% of the observations. That is, all values of categorical variables that are shared by less than 1% of houses, well be replaced by the string "Rare". ###Code # let's capture the categorical variables in a list cat_vars = [var for var in X_train.columns if X_train[var].dtype == 'O'] def find_frequent_labels(df, var, rare_perc): # function finds the labels that are shared by more than # a certain % of the houses in the dataset df = df.copy() tmp = df.groupby(var)['SalePrice'].count() / len(df) return tmp[tmp > rare_perc].index for var in cat_vars: # find the frequent categories frequent_ls = find_frequent_labels(X_train, var, 0.01) # replace rare categories by the string "Rare" X_train[var] = np.where(X_train[var].isin( frequent_ls), X_train[var], 'Rare') X_test[var] = np.where(X_test[var].isin( frequent_ls), X_test[var], 'Rare') ###Output _____no_output_____ ###Markdown Encoding of categorical variablesNext, we need to transform the strings of the categorical variables into numbers. We will do it so that we capture the monotonic relationship between the label and the target. ###Code # this function will assign discrete values to the strings of the variables, # so that the smaller value corresponds to the category that shows the smaller # mean house sale price def replace_categories(train, test, var, target): # order the categories in a variable from that with the lowest # house sale price, to that with the highest ordered_labels = train.groupby([var])[target].mean().sort_values().index # create a dictionary of ordered categories to integer values ordinal_label = {k: i for i, k in enumerate(ordered_labels, 0)} # use the dictionary to replace the categorical strings by integers train[var] = train[var].map(ordinal_label) test[var] = test[var].map(ordinal_label) for var in cat_vars: replace_categories(X_train, X_test, var, 'SalePrice') # check absence of na in the train set [var for var in X_train.columns if X_train[var].isnull().sum() > 0] # check absence of na in the test set [var for var in X_test.columns if X_test[var].isnull().sum() > 0] # let me show you what I mean by monotonic relationship # between labels and target def analyse_vars(df, var): # function plots median house sale price per encoded # category df = df.copy() df.groupby(var)['SalePrice'].median().plot.bar() plt.title(var) plt.ylabel('SalePrice') plt.show() for var in cat_vars: analyse_vars(X_train, var) ###Output _____no_output_____ ###Markdown The monotonic relationship is particularly clear for the variables MSZoning, Neighborhood, and ExterQual. Note how, the higher the integer that now represents the category, the higher the mean house sale price.(remember that the target is log-transformed, that is why the differences seem so small). Feature ScalingFor use in linear models, features need to be either scaled or normalised. In the next section, I will scale features to the minimum and maximum values: ###Code # capture all variables in a list # except the target and the ID train_vars = [var for var in X_train.columns if var not in ['Id', 'SalePrice']] # count number of variables len(train_vars) # create scaler scaler = MinMaxScaler() # fit the scaler to the train set scaler.fit(X_train[train_vars]) # transform the train and test set X_train[train_vars] = scaler.transform(X_train[train_vars]) X_test[train_vars] = scaler.transform(X_test[train_vars]) X_train.head() # let's now save the train and test sets for the next notebook! X_train.to_csv('xtrain.csv', index=False) X_test.to_csv('xtest.csv', index=False) ###Output _____no_output_____
is_square.ipynb	###Markdown TaskGiven an integral number, determine if it's a square number: ###Code def is_square(n): if (n * 1/2) * (n * 1/2) == n: return True return False ###Output _____no_output_____
old/Model-01.ipynb	###Markdown UCI Epileptic Seizure Recognition Data Set Link to the dataset: https://archive.ics.uci.edu/ml/datasets/Epileptic+Seizure+Recognition ###Code import os import numpy as np import pandas as pd import torch import torch.nn as nn import torch.optim as optim import torch.nn.functional as F from torchvision import transforms from torch.utils.data import Dataset, DataLoader from torch.utils.data.sampler import SubsetRandomSampler ###Output _____no_output_____ ###Markdown Hyperparamters ###Code batch_size = 64 test_split = .2 shuffle_dataset = True random_seed = 42 epochs = 100 learning_rate = 1e-3 ###Output _____no_output_____ ###Markdown Dataset ###Code class UCIEpilepsy(Dataset): def __init__(self, data_path): self.data = pd.read_csv(data_path).iloc[:, 1:].to_numpy().astype(np.single) def __len__(self): return len(self.data) def __getitem__(self, idx): data = torch.from_numpy(self.data[idx,2:178]) label = torch.from_numpy(self.data[idx,178:]) return data, label dataset = UCIEpilepsy(data_path='data/data.csv') dataset_size = len(dataset) indices = list(range(dataset_size)) split = int(np.floor(test_split * dataset_size)) if shuffle_dataset: np.random.seed(random_seed) np.random.shuffle(indices) test_indices, train_indices = indices[:split], indices[split:] train_sampler = SubsetRandomSampler(train_indices) test_sampler = SubsetRandomSampler(test_indices) train_dataloader = DataLoader(dataset, batch_size=batch_size, sampler=train_sampler) test_dataloader = DataLoader(dataset, batch_size=batch_size, sampler=test_sampler) ###Output _____no_output_____ ###Markdown Neural Network ###Code class NeuralNetwork(nn.Module): def __init__(self): super(NeuralNetwork, self).__init__() self.linear_relu_stack = nn.Sequential( nn.Linear(176, 128), nn.ReLU(), nn.Linear(128, 128), nn.ReLU(), nn.Linear(128, 5) ) def forward(self, x): return self.linear_relu_stack(x) ###Output _____no_output_____ ###Markdown Training Loop ###Code def train_loop(X,y, model, loss_fn, optimizer): size = len(X) # for batch, (X, y) in enumerate(dataloader, 0): outputs = model(X) loss = loss_fn(outputs, y.squeeze(1).long()-1) optimizer.zero_grad() loss.backward() optimizer.step() # if batch % 10 == 0: # loss, current = loss.item(), batch * len(X) print(f"loss: {loss:>7f}") ###Output _____no_output_____ ###Markdown Test Loop ###Code def test_loop(X, y, model, criterion): size = len(X) num_correct = 0 num_samples = 0 with torch.no_grad(): #for X, y in dataloader: outputs = model(X) _, predictions = outputs.max(1) num_correct += (predictions == y).sum() num_samples += predictions.size(0) print(f"Got {num_correct} / {num_samples} with {float(num_correct) / float(num_samples) * 100:.2f}") ###Output _____no_output_____ ###Markdown Execution ###Code model = NeuralNetwork() X, y = next(iter(train_dataloader)) textX, testy = next(iter(test_dataloader)) criterion = nn.CrossEntropyLoss() optimizer = optim.SGD(model.parameters(), lr=learning_rate, momentum=0.9) for epoch in range(epochs): print(f"Epoch [{epoch+1}/{epochs}]") train_loop(X, y, model, criterion, optimizer) test_loop(X, y, model, criterion) ###Output Epoch [1/100] loss: 18.408686 Got 9 / 64 with 14.06 Epoch [2/100] loss: 13.081454 Got 15 / 64 with 23.44 Epoch [3/100] loss: 13.784674 Got 345 / 64 with 539.06 Epoch [4/100] loss: 8.900457 Got 735 / 64 with 1148.44 Epoch [5/100] loss: 9.482249 Got 582 / 64 with 909.38 Epoch [6/100] loss: 6.394184 Got 543 / 64 with 848.44 Epoch [7/100] loss: 4.073208 Got 486 / 64 with 759.38 Epoch [8/100] loss: 2.911988 Got 495 / 64 with 773.44 Epoch [9/100] loss: 2.571485 Got 432 / 64 with 675.00 Epoch [10/100] loss: 1.705727 Got 414 / 64 with 646.88 Epoch [11/100] loss: 1.073463 Got 444 / 64 with 693.75 Epoch [12/100] loss: 0.786391 Got 510 / 64 with 796.88 Epoch [13/100] loss: 0.661567 Got 546 / 64 with 853.12 Epoch [14/100] loss: 0.446909 Got 567 / 64 with 885.94 Epoch [15/100] loss: 0.332226 Got 585 / 64 with 914.06 Epoch [16/100] loss: 0.268042 Got 597 / 64 with 932.81 Epoch [17/100] loss: 0.234971 Got 594 / 64 with 928.12 Epoch [18/100] loss: 0.207456 Got 591 / 64 with 923.44 Epoch [19/100] loss: 0.183676 Got 591 / 64 with 923.44 Epoch [20/100] loss: 0.157857 Got 585 / 64 with 914.06 Epoch [21/100] loss: 0.132126 Got 579 / 64 with 904.69 Epoch [22/100] loss: 0.107050 Got 579 / 64 with 904.69 Epoch [23/100] loss: 0.084840 Got 579 / 64 with 904.69 Epoch [24/100] loss: 0.067431 Got 579 / 64 with 904.69 Epoch [25/100] loss: 0.054594 Got 579 / 64 with 904.69 Epoch [26/100] loss: 0.045662 Got 579 / 64 with 904.69 Epoch [27/100] loss: 0.039722 Got 579 / 64 with 904.69 Epoch [28/100] loss: 0.035914 Got 579 / 64 with 904.69 Epoch [29/100] loss: 0.032929 Got 579 / 64 with 904.69 Epoch [30/100] loss: 0.029694 Got 579 / 64 with 904.69 Epoch [31/100] loss: 0.026613 Got 579 / 64 with 904.69 Epoch [32/100] loss: 0.024110 Got 579 / 64 with 904.69 Epoch [33/100] loss: 0.022154 Got 579 / 64 with 904.69 Epoch [34/100] loss: 0.020560 Got 579 / 64 with 904.69 Epoch [35/100] loss: 0.019147 Got 579 / 64 with 904.69 Epoch [36/100] loss: 0.017855 Got 579 / 64 with 904.69 Epoch [37/100] loss: 0.016668 Got 579 / 64 with 904.69 Epoch [38/100] loss: 0.015573 Got 579 / 64 with 904.69 Epoch [39/100] loss: 0.014584 Got 579 / 64 with 904.69 Epoch [40/100] loss: 0.013697 Got 579 / 64 with 904.69 Epoch [41/100] loss: 0.012875 Got 579 / 64 with 904.69 Epoch [42/100] loss: 0.012111 Got 579 / 64 with 904.69 Epoch [43/100] loss: 0.011405 Got 579 / 64 with 904.69 Epoch [44/100] loss: 0.010749 Got 579 / 64 with 904.69 Epoch [45/100] loss: 0.010141 Got 579 / 64 with 904.69 Epoch [46/100] loss: 0.009581 Got 579 / 64 with 904.69 Epoch [47/100] loss: 0.009067 Got 579 / 64 with 904.69 Epoch [48/100] loss: 0.008596 Got 579 / 64 with 904.69 Epoch [49/100] loss: 0.008165 Got 579 / 64 with 904.69 Epoch [50/100] loss: 0.007770 Got 579 / 64 with 904.69 Epoch [51/100] loss: 0.007410 Got 579 / 64 with 904.69 Epoch [52/100] loss: 0.007082 Got 579 / 64 with 904.69 Epoch [53/100] loss: 0.006781 Got 579 / 64 with 904.69 Epoch [54/100] loss: 0.006506 Got 579 / 64 with 904.69 Epoch [55/100] loss: 0.006254 Got 579 / 64 with 904.69 Epoch [56/100] loss: 0.006022 Got 579 / 64 with 904.69 Epoch [57/100] loss: 0.005809 Got 579 / 64 with 904.69 Epoch [58/100] loss: 0.005612 Got 579 / 64 with 904.69 Epoch [59/100] loss: 0.005430 Got 579 / 64 with 904.69 Epoch [60/100] loss: 0.005261 Got 579 / 64 with 904.69 Epoch [61/100] loss: 0.005104 Got 579 / 64 with 904.69 Epoch [62/100] loss: 0.004958 Got 579 / 64 with 904.69 Epoch [63/100] loss: 0.004822 Got 579 / 64 with 904.69 Epoch [64/100] loss: 0.004695 Got 579 / 64 with 904.69 Epoch [65/100] loss: 0.004576 Got 579 / 64 with 904.69 Epoch [66/100] loss: 0.004464 Got 579 / 64 with 904.69 Epoch [67/100] loss: 0.004359 Got 579 / 64 with 904.69 Epoch [68/100] loss: 0.004260 Got 579 / 64 with 904.69 Epoch [69/100] loss: 0.004166 Got 579 / 64 with 904.69 Epoch [70/100] loss: 0.004077 Got 579 / 64 with 904.69 Epoch [71/100] loss: 0.003993 Got 579 / 64 with 904.69 Epoch [72/100] loss: 0.003913 Got 579 / 64 with 904.69 Epoch [73/100] loss: 0.003837 Got 579 / 64 with 904.69 Epoch [74/100] loss: 0.003765 Got 579 / 64 with 904.69 Epoch [75/100] loss: 0.003696 Got 579 / 64 with 904.69 Epoch [76/100] loss: 0.003631 Got 579 / 64 with 904.69 Epoch [77/100] loss: 0.003568 Got 579 / 64 with 904.69 Epoch [78/100] loss: 0.003508 Got 579 / 64 with 904.69 Epoch [79/100] loss: 0.003451 Got 579 / 64 with 904.69 Epoch [80/100] loss: 0.003396 Got 579 / 64 with 904.69 Epoch [81/100] loss: 0.003343 Got 579 / 64 with 904.69 Epoch [82/100] loss: 0.003293 Got 579 / 64 with 904.69 Epoch [83/100] loss: 0.003244 Got 579 / 64 with 904.69 Epoch [84/100] loss: 0.003197 Got 579 / 64 with 904.69 Epoch [85/100] loss: 0.003152 Got 579 / 64 with 904.69 Epoch [86/100] loss: 0.003109 Got 579 / 64 with 904.69 Epoch [87/100] loss: 0.003067 Got 579 / 64 with 904.69 Epoch [88/100] loss: 0.003026 Got 579 / 64 with 904.69 Epoch [89/100] loss: 0.002987 Got 579 / 64 with 904.69 Epoch [90/100] loss: 0.002950 Got 579 / 64 with 904.69 Epoch [91/100] loss: 0.002913 Got 579 / 64 with 904.69 Epoch [92/100] loss: 0.002878 Got 579 / 64 with 904.69 Epoch [93/100] loss: 0.002844 Got 579 / 64 with 904.69 Epoch [94/100] loss: 0.002811 Got 579 / 64 with 904.69 Epoch [95/100] loss: 0.002779 Got 579 / 64 with 904.69 Epoch [96/100] loss: 0.002747 Got 579 / 64 with 904.69 Epoch [97/100] loss: 0.002717 Got 579 / 64 with 904.69 Epoch [98/100] loss: 0.002688 Got 579 / 64 with 904.69 Epoch [99/100] loss: 0.002659 Got 579 / 64 with 904.69 Epoch [100/100] loss: 0.002631 Got 579 / 64 with 904.69
doc/source/notebooks/ordinal.ipynb	###Markdown Ordinal Regression with GPflow Clement Tiennot, Camille Tiennot 2016 edits by James Hensman 2017 ###Code import gpflow import numpy as np import matplotlib %matplotlib inline matplotlib.rcParams['figure.figsize'] = (12, 6) plt = matplotlib.pyplot #make a one dimensional ordinal regression problem np.random.seed(1) num_data = 20 X = np.random.rand(num_data, 1) K = np.exp(-0.5np.square(X - X.T)/0.01) + np.eye(num_data)1e-6 f = np.dot(np.linalg.cholesky(K), np.random.randn(num_data, 1)) plt.plot(X, f, '.') plt.ylabel('latent function value') Y = np.round((f + f.min())3) Y = Y - Y.min() Y = np.asarray(Y, np.float64) plt.twinx() plt.plot(X, Y, 'kx', mew=1.5) plt.ylabel('observed data value') # construct ordinal likelihood bin_edges = np.array(np.arange(np.unique(Y).size + 1), dtype=float) bin_edges = bin_edges - bin_edges.mean() likelihood=gpflow.likelihoods.Ordinal(bin_edges) # build a model with this likelihood m = gpflow.models.VGP(X, Y, kern=gpflow.kernels.Matern32(1), likelihood=likelihood) #fit the model gpflow.train.ScipyOptimizer().minimize(m) # here we'll plot the expected value of Y +- 2 std deviations, as if the distribution were Gaussian plt.figure(figsize=(14, 6)) Xtest = np.linspace(m.X.read_value().min(), m.X.read_value().max(), 100).reshape(-1, 1) mu, var = m.predict_y(Xtest) line, = plt.plot(Xtest, mu, lw=2) col=line.get_color() plt.plot(Xtest, mu+2np.sqrt(var), '--', lw=2, color=col) plt.plot(Xtest, mu-2np.sqrt(var), '--', lw=2, color=col) plt.plot(m.X.read_value(), m.Y.read_value(), 'kx', mew=2) # to see the predictive density, try predicting every possible value. def pred_density(m): Xtest = np.linspace(m.X.read_value().min(), m.X.read_value().max(), 100).reshape(-1, 1) ys = np.arange(m.Y.read_value().max()+1) densities = [] for y in ys: Ytest = np.ones_like(Xtest) y densities.append(m.predict_density(Xtest, Ytest)) return np.hstack(densities).T plt.imshow(np.exp(pred_density(m)), interpolation='nearest', extent=[m.X.read_value().min(), m.X.read_value().max(), -0.5, m.Y.read_value().max()+0.5], origin='lower', aspect='auto', cmap=plt.cm.viridis) plt.colorbar() plt.plot(X, Y, 'kx', mew=2, scalex=False, scaley=False) ###Output _____no_output_____ ###Markdown Ordinal Regression with GPflow Clement Tiennot, Camille Tiennot 2016 edits by James Hensman 2017 ###Code import gpflow import numpy as np import matplotlib %matplotlib inline matplotlib.rcParams['figure.figsize'] = (12, 6) plt = matplotlib.pyplot #make a one dimensional ordinal regression problem np.random.seed(1) num_data = 20 X = np.random.rand(num_data, 1) K = np.exp(-0.5np.square(X - X.T)/0.01) + np.eye(num_data)1e-6 f = np.dot(np.linalg.cholesky(K), np.random.randn(num_data, 1)) plt.plot(X, f, '.') plt.ylabel('latent function value') Y = np.round((f + f.min())3) Y = Y - Y.min() Y = np.asarray(Y, np.float64) plt.twinx() plt.plot(X, Y, 'kx', mew=1.5) plt.ylabel('observed data value') # construct ordinal likelihood bin_edges = np.array(np.arange(np.unique(Y).size + 1), dtype=float) bin_edges = bin_edges - bin_edges.mean() likelihood=gpflow.likelihoods.Ordinal(bin_edges) # build a model with this likelihood m = gpflow.models.VGP(X, Y, kern=gpflow.kernels.Matern32(1), likelihood=likelihood) #fit the model gpflow.train.ScipyOptimizer().minimize(m) # here we'll plot the expected value of Y +- 2 std deviations, as if the distribution were Gaussian plt.figure(figsize=(14, 6)) Xtest = np.linspace(m.X.read_value().min(), m.X.read_value().max(), 100).reshape(-1, 1) mu, var = m.predict_y(Xtest) line, = plt.plot(Xtest, mu, lw=2) col=line.get_color() plt.plot(Xtest, mu+2np.sqrt(var), '--', lw=2, color=col) plt.plot(Xtest, mu-2np.sqrt(var), '--', lw=2, color=col) plt.plot(m.X.read_value(), m.Y.read_value(), 'kx', mew=2) # to see the predictive density, try predicting every possible value. def pred_density(m): Xtest = np.linspace(m.X.read_value().min(), m.X.read_value().max(), 100).reshape(-1, 1) ys = np.arange(m.Y.read_value().max()+1) densities = [] for y in ys: Ytest = np.ones_like(Xtest) y densities.append(m.predict_density(Xtest, Ytest)) return np.hstack(densities).T plt.imshow(np.exp(pred_density(m)), interpolation='nearest', extent=[m.X.read_value().min(), m.X.read_value().max(), -0.5, m.Y.read_value().max()+0.5], origin='lower', aspect='auto', cmap=plt.cm.viridis) plt.colorbar() plt.plot(X, Y, 'kx', mew=2, scalex=False, scaley=False) ###Output _____no_output_____ ###Markdown Ordinal Regression with GPflow ###Code import GPflow import tensorflow as tf import matplotlib import numpy as np %matplotlib inline matplotlib.style.use('ggplot') plt = matplotlib.pyplot #make a one dimensional ordinal regression problem np.random.seed(1) X = np.random.rand(100,1) K = np.exp(-0.5np.square(X - X.T)/0.01) + np.eye(100)1e-6 f = np.dot(np.linalg.cholesky(K), np.random.randn(100,1)) plt.plot(X, f, '.') Y = np.round((f + f.min())3) Y = Y - Y.min() Y = np.asarray(Y, np.int32) plt.twinx() plt.plot(X, Y, 'kx') # construct ordinal likelihood bin_edges = np.arange(np.unique(Y).size) bin_edges = bin_edges - bin_edges.mean() likelihood=GPflow.likelihoods.Ordinal(bin_edges) # build a model with this likelihood m = GPflow.vgp.VGP(X, Y, kern=GPflow.kernels.Matern32(1), likelihood=likelihood) #fit the model _ = m.optimize() # here we'll plot the expected value of Y +- 2 std deviations, as if the distribution were Gaussian plt.figure(figsize=(14, 6)) Xtest = np.linspace(m.X.value.min(), m.X.value.max(), 100).reshape(-1, 1) mu, var = m.predict_y(Xtest) line, = plt.plot(Xtest, mu, lw=2) col=line.get_color() plt.plot(Xtest, mu+2np.sqrt(var), '--', lw=2, color=col) plt.plot(Xtest, mu-2np.sqrt(var), '--', lw=2, color=col) plt.plot(m.X.value, m.Y.value, 'kx', mew=2) # to see the predictive density, try predicting every possible value. def pred_density(m): Xtest = np.linspace(m.X.value.min(), m.X.value.max(), 100).reshape(-1, 1) ys = np.arange(m.Y.value.max()+1) densities = [] for y in ys: Ytest = np.ones_like(Xtest) y densities.append(m.predict_density(Xtest, Ytest)) return np.hstack(densities).T plt.figure(figsize=(16,6)) plt.imshow(np.exp(pred_density(m)), interpolation='nearest', extent=[m.X.value.min(), m.X.value.max(), -0.5, m.Y.value.max()+0.5], origin='lower', aspect='auto', cmap=plt.cm.viridis) plt.colorbar() plt.plot(X, Y, 'kx', mew=2, scalex=False, scaley=False) ###Output _____no_output_____
Weatherpy/HM6 APi OpenWeather-Final.ipynb	###Markdown temperature(F) vs Latitude ###Code #temperature vs Latitude temp_lat_df = cities_df[['temperature','latitude']] fig,ax = plt.subplots() ax.scatter(temp_lat_df['latitude'],temp_lat_df['temperature'],marker='.') ax.set_xlabel('Latitude') ax.set_ylabel('Temperature(F)') plt.title('City Latitude vs Temperature(F)') ax.grid() fig.savefig('City Latitude vs Average Temperature(F).png') plt.show() ###Output _____no_output_____ ###Markdown First Oberservation: based on the graph above we can see that the tendency is that cities located at lower latitudes tend to have higher temperatures and cities located at higher latitudes tend to have lower temperatures. Humidity (%) vs. Latitude ###Code #Humidity (%) vs. Latitude hum_lat_df = cities_df[['humidity','latitude']] fig1,ax1 = plt.subplots() ax1.scatter(hum_lat_df['latitude'],hum_lat_df['humidity'],marker='.',color='g') ax1.set_xlabel('Latitude') ax1.set_ylabel('humidity(%)') plt.title('City Latitude vs Humidity(%)') ax1.grid() fig1.savefig('City Latitude vs Humidity(%).png') plt.show() ###Output _____no_output_____ ###Markdown Second Oberservation: Based on the graph above we can see that most of the cities located from equator up to a latitude of ~50 degrees have the highest humidity while those cities located below the equator tend to have less humidity. Cloudiness (%) vs. Latitude ###Code #Cloudiness (%) vs. Latitude cloud_lat_df = cities_df[['cloudiness','latitude']] fig2,ax2 = plt.subplots() ax2.scatter(cloud_lat_df['latitude'],cloud_lat_df['cloudiness'],marker='.',color='r') ax2.set_xlabel('Latitude') ax2.set_ylabel('cloudiness(%)') plt.title('City Latitude vs Cloudiness(%)') ax2.grid() fig2.savefig('City Latitude vs Cloudiness(%).png') plt.show() ###Output _____no_output_____ ###Markdown Third Observation: Based on the sample we have most of the cities where located from latitude from range 40 to 50 degrees. We can determine that at latitude 50 degrees we tend to have more cloudiness. Wind Speed (mph) vs. Latitude ###Code #Wind Speed (mph) vs. Latitude wind_lat_df = cities_df[['windspeed','latitude']] fig3,ax3 = plt.subplots() ax3.scatter(wind_lat_df['latitude'],wind_lat_df['windspeed'],marker='.',color='b') ax3.set_xlabel('Latitude') ax3.set_ylabel('windspeed(mph)') plt.title('City Latitude vs Windspeed(MPH)') ax3.grid() fig3.savefig('City Latitude vs Windspeed(MPH).png') plt.show() ###Output _____no_output_____
DSC 540 - Data Preparation/Week 3 & 4.ipynb	###Markdown Week 3 & 4TitleTitle -->H1 -->H2 -->H3 -->H4 -->Patrick Weatherford[Green]: (bce35b)[Purple]: (ae8bd5)[Coral]: (9c4957)[Grey]: (8c8c8c) **** Importing libraries ###Code import numpy as np import pandas as pd import matplotlib as mpl import matplotlib.pyplot as plt import os import requests from collections import deque as deq from itertools import permutations, dropwhile, zip_longest import re import math import io ## import custom config file with keys and change working directory class_path = os.path.expanduser('~') + '\\OneDrive - Bellevue University\\Bellevue_University\\DSC 540 - Data Preparation' bu_path = os.path.expanduser('~') + '\\OneDrive - Bellevue University\\Bellevue_University' os.chdir(bu_path); import config; os.chdir(class_path) ## matplotlib default settings plt.style.use('dark_background') mpl.rcParams.update({'lines.linewidth':3}) mpl.rcParams.update({'axes.labelsize':14}) mpl.rcParams.update({'axes.titlesize':16}) mpl.rcParams.update({'axes.titleweight':'bold'}) mpl.rcParams.update({'figure.autolayout':True}) mpl.rcParams.update({'axes.grid':True, 'grid.color':'#424242', 'grid.linestyle':'--'}) ## see list of current settings # plt.rcParams.keys() ###Output _____no_output_____ ###Markdown Instantiating random number generator ###Code rng_seed = 777 rng = np.random.default_rng(rng_seed) ###Output _____no_output_____ ###Markdown * Book ActivitiesTitleTitle -->H1 -->H2 -->H3 -->H4 -->Patrick Weatherford -->[Green]: (bce35b)[Purple]: (ae8bd5)[Coral]: (9c4957)[Grey]: (8c8c8c) Activity 5TitleTitle -->H1 -->H2 -->H3 -->H4 -->Patrick Weatherford -->[Green]: (bce35b)[Purple]: (ae8bd5)[Coral]: (9c4957)[Grey]: (8c8c8c)Boston Housing data set. ###Code ## get variable info def skip_logic(x): if 7 <= x <= 20: # get specific rows from website which hold variable info return False else: return True data_url = "http://lib.stat.cmu.edu/datasets/boston" var_df = pd.read_csv(data_url, sep=' +', skiprows=lambda x: skip_logic(x), header=None, engine='python', names=['VARIABLE','DESC']) # create DataFrame of variables var_df['VARIABLE'] = var_df['VARIABLE'].replace(' ', '') # remove whiate space from variable name var_df_disp = var_df.style.set_table_styles([dict(selector='th', props=[('text-align', 'left')])]) # lef-align headers var_df_disp.set_properties(subset=['DESC'], {'width': '400px'}) # widen description column var_df_disp.set_properties({'text-align': 'left'}) # left align all values var_df_disp ## get Boston Housing data raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None) # start data feed from 23 row data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :3]]) # data in rows on site is not on single row. Must skip every other row, hstack, then exclude NaN values from overlapping row labels = var_df['VARIABLE'].values # assign variable names to list bost_df = pd.DataFrame(data, columns=labels) # create df ## first 10 rows bost_df.head(10) ## drop specified columns bost_df.drop(['CHAS','NOX','B','LSTAT'], inplace=True, axis=1) bost_df ## last 7 rows in df bost_df.tail(7) ###Output _____no_output_____ ###Markdown Looping through df variables using pandas implementation. ###Code ## plot histogram of each variable bost_df.hist(figsize=(15,13), bins=30) plt.show() ###Output _____no_output_____ ###Markdown Custom function to loop through df and create histogram of each variable. ###Code def df_plot(df, plot_type, hist_bins=10, n_plot_cols=3, figsize=None): cols = df.columns # get list of column names n_vars = len(cols) # get number of variables in df n_plot_cols = n_plot_cols # get number of columns that will be in the subplot figure n_plot_rows = math.ceil(n_vars / n_plot_cols) # based on the number of columns in the subplot figure & number of df columns, calculate how many rows should be in the figure plt.figure(figsize=figsize) # set figure size graph_cnt = 1 # initiate counter for variable plots for r in range(1, n_plot_rows+1): # for row in subplot figure for c in range(1, n_plot_cols+1): # for col in subplot figure if graph_cnt > n_vars: # if variable counter is greater than the number of variables in the df, break the loop break else: # else plot each variable in the correct subplot location going from left->right, top->bottom plt.subplot(n_plot_rows, n_plot_cols, graph_cnt) if plot_type.lower() == 'hist': plt.hist(df.iloc[:, graph_cnt-1], bins=hist_bins) plt.title(cols[graph_cnt-1]) graph_cnt += 1 plt.show() df_plot(bost_df, plot_type='hist', hist_bins=30, figsize=(15,13)) ###Output _____no_output_____ ###Markdown Scatter plot ###Code plt.scatter( x=bost_df['RM'] , y=bost_df['MEDV'] , alpha=.7 ) plt.title('Median Home Value vs. Number of Rooms') plt.xlabel('Number of Rooms') plt.ylabel('Median Home Value ($1k)') plt.show() plt.scatter( x=np.log10(bost_df['CRIM']) , y=bost_df['MEDV'] , alpha=.7 ) plt.title('Median Home Value vs. Crime Rate') plt.xlabel('Crime Rate (log10)') plt.ylabel('Median Home Value ($1k)') plt.show() ###Output _____no_output_____ ###Markdown Summary statistics ###Code bost_df.describe() ###Output _____no_output_____ ###Markdown Percent (%) of houses < $20k ###Code p = round(100 * sum(bost_df['MEDV'] < 20) / len(bost_df), 2) print(f"{p}% of homes are less thatn $20k") ###Output 41.5% of homes are less thatn $20k ###Markdown Activity 6TitleTitle -->H1 -->H2 -->H3 -->H4 -->Patrick Weatherford -->[Green]: (bce35b)[Purple]: (ae8bd5)[Coral]: (9c4957)[Grey]: (8c8c8c)Adult Income Dataset (UCI) ###Code var_url = 'https://raw.githubusercontent.com/TrainingByPackt/Data-Wrangling-with-Python/master/Lesson04/Activity06/adult_income_names.txt' var_df = pd.read_csv(var_url, sep=':', engine='python', header=None, names=['VARIABLE','DESC']) var_df['VARIABLE'] = var_df['VARIABLE'].str.strip() var_df_disp = var_df.style.set_table_styles([dict(selector='th', props=[('text-align', 'left')])]) # lef-align headers var_df_disp.set_properties(subset=['DESC'], {'width': '800px'}) # widen description column var_df_disp.set_properties({'text-align': 'left'}) # left align all values var_df_disp cols = [i for i in var_df['VARIABLE']] cols.append('income') data_url = 'https://raw.githubusercontent.com/TrainingByPackt/Data-Wrangling-with-Python/master/Lesson04/Activity06/adult_income_data.csv' a6_df = pd.read_csv(data_url, header=None, names=cols) a6_df ###Output _____no_output_____ ###Markdown Read text file line-by-line ###Code def ReadText(file_path): with open(file_path, 'r') as TextFile: for line in TextFile: line = line.rstrip('\n') print(line) file_path = 'RandomTextFile.txt' ReadText(file_path) ###Output This is line 1 This is line 2 This is line 3 This is line 4 yo yo This is line 5 blahblah .-. \|_:_\| /(_Y_)\ . ( \/M\/ ) '. _.'-/'-'\-'._ ': _/.--'[[[[]'--.\_ ': /_' : \|::"\| : '.\ ': // ./ \|oUU\| \.' :\ ': _:'..' \_\|___\|_/ : :\| ':. .' \|_[___]_\| :.':\ [::\ \| : \| \| : ; : \ '-' \/'.\| \|.' \ .;.' \| \|\_ \ '-' : \| \| \ \ .: : \| \| \| \ \| '. : \ \| / \ :. .; \| / \| \| :__/ : \\ \| \| \| \: \| \ \| \|\| / \ : : \|: / \|__\| /\| \| : : :_/_\| /'._\ '--\|_\ /___.-/_\|-' \ \ '-' ###Markdown Find missing values row index locations. ###Code a6_df.isnull().sum() ###Output _____no_output_____ ###Markdown Create df with only age, education, and occupation ###Code df_sub = a6_df[['age','education','occupation']] df_sub plt.hist(a6_df['age'], bins=20) plt.title('Histogram of Age') plt.xlabel('Age (bins = 20)') plt.ylabel('Frequency') plt.show() ###Output _____no_output_____ ###Markdown Using apply(), strip white space from string columns ###Code def df_str_strip(df): for c in df.columns: if df[c].dtype == 'O': c_new = f"{c}_new" df[c_new] = df[c].apply(lambda x: x.strip()) df[c] = df[c_new] df.drop(labels=c_new, axis=1, inplace=True) else: continue df_str_strip(a6_df) a6_df ###Output _____no_output_____ ###Markdown Find people aged between 30 and 50. ###Code len((a6_df[(a6_df['age'] >=30) & (a6_df['age'] <= 50)]).index) ###Output _____no_output_____ ###Markdown Group records based on age and education to find how the mean age is distributed. ###Code pd.DataFrame(a6_df[['age','education']].groupby('education')['age'].mean()) occ_summ_df = a6_df.groupby('occupation')['age'].describe() occ_summ_df ###Output _____no_output_____ ###Markdown occupation with oldest workers ###Code occ_summ_df['mean'].max() ###Output _____no_output_____ ###Markdown occupation with highest share of 75% percentile ###Code occ_summ_df[occ_summ_df['75%'] == occ_summ_df['75%'].max()].index[0] ###Output _____no_output_____ ###Markdown Use subset and groupby to find outliers.- Are there classes with very few observations?- Are there extreme numerical values? ###Code for c in a6_df.columns: n_unique_vals = a6_df[[c]].nunique()[0] if n_unique_vals <= 20: pd.DataFrame(a6_df[[c]].groupby(c).size(), columns=[c]).plot.bar() else: pd.DataFrame(a6_df[[c]].groupby(c).size(), columns=[f"{c} (frequency)"]).plot.box() ###Output _____no_output_____ ###Markdown Joining based on values ###Code initial_df = a6_df[['age','workclass','education']] agg_df = a6_df[a6_df['income'] == '>50K'].loc[:,['workclass']] agg_df_grp = agg_df.groupby('workclass') agg_df = pd.DataFrame(agg_df_grp.size(), columns=['workclass >50K count']) pd.merge(left=initial_df, right=agg_df, left_on='workclass', right_index=True) ###Output _____no_output_____ ###Markdown * Series and Basic ArithmeticTitleTitle -->H1 -->H2 -->H3 -->H4 -->Patrick Weatherford -->[Green]: (bce35b)[Purple]: (ae8bd5)[Coral]: (9c4957)[Grey]: (8c8c8c) ###Code series1 = [7.3, -2.5, 3.4, 1.5] s1_index = ['a','c','d','e'] series2 = [-2.1, 3.6, -1.5, 4, 3.1] s2_index = ['a','c','e','f','g'] s1 = pd.Series(series1, index=s1_index) s2 = pd.Series(series2, index=s2_index) ###Output _____no_output_____ ###Markdown Add series 1 to series 2 ###Code s1 + s2 ###Output _____no_output_____ ###Markdown Subtract series 1 from series 2 ###Code s1 - s2 ###Output _____no_output_____ ###Markdown *Below code is for practice only ###Code np.arange(start=1, stop=20, step=2) np.arange(start=30, stop=-1, step=-2) np.linspace(start=1, stop=10, num=5) np.linspace(start=30, stop=0, num=20) a1 = rng.integers(1,100,30) a1 a1_re = a1.reshape(2,3,5) a1_re a1_re[1,0,3] ## index[1] in axis 0 ## index[0] in axis 1 ## index[3] in axis 2 a1_re.size, a1_re.shape, a1_re.ndim a1_rav = a1_re.ravel() a1_rav a2 = rng.integers(1,10,20).reshape(4,5) a2 df = pd.DataFrame(a2) df df1 = df.drop(0, axis=1) df1 rng.binomial(n=8, p=.6, size=10) url = "https://github.com/TrainingByPackt/Data-Wrangling-with-Python/raw/master/Lesson04/Exercise48-51/Sample%20-%20Superstore.xls" # Make sure the url is the raw version of the file on GitHub download = requests.get(url).content ss_df = pd.read_excel(io.BytesIO(download)) ss_df.drop(['Row ID'], inplace=True, axis=1) print(f""" {ss_df.shape} {ss_df.columns} """) ss_df_sub = ss_df.loc[ [i for i in range(5,10)] , ['Customer ID','Customer Name','City','Postal Code','Sales'] ] ss_df_sub ss_df.loc[ [i for i in range(100,200)] # axis 0 range(100,200) ,['Sales','Profit'] # axis 1 columns to include ].describe() unique_states = ss_df['State'].unique() n_unique_states = ss_df['State'].nunique() print(f""" States in DataFrame: {unique_states} Number of Distinct States in DataFrame: {n_unique_states} """) matrix_data = np.matrix([[22,66,140],[42,70,148],[30,62,125],[35,68,160],[25,62,152]]) row_labels = ['A','B','C','D','E'] column_headings = ['Age','Height','Weight'] matrix_data matrix_df = pd.DataFrame(data=matrix_data ,index=row_labels ,columns=column_headings) matrix_df matrix_df.reset_index(inplace=True, drop=True) matrix_df matrix_df['Profession'] = 'Student Teacher Engineer Doctor Nurse'.split() matrix_df matrix_df = matrix_df.set_index('Profession') matrix_df df_sub = ss_df.loc[ [i for i in range(10)] ,['Ship Mode','State','Sales'] ] df_sub by_state = df_sub.groupby('State') by_state.mean() pd.DataFrame(by_state.describe().loc['California']) df_sub.groupby('Ship Mode').describe().loc[['Second Class','Standard Class']] byStateCity = ss_df.groupby(['State','City'])['Sales'] byStateCity.describe() url = "https://github.com/TrainingByPackt/Data-Wrangling-with-Python/raw/master/Lesson04/Exercise48-51/Sample%20-%20Superstore.xls" # Make sure the url is the raw version of the file on GitHub download = requests.get(url).content miss_df = pd.read_excel(io.BytesIO(download), sheet_name='Missing') miss_df miss_df.isnull() for c in miss_df.columns: miss = miss_df[c].isnull().sum() if miss > 0: print(f"{c} has {miss} missing value(s)") else: print(f"{c} has NO missing value(s)!") ###Output Customer has 1 missing value(s) Product has 2 missing value(s) Sales has 1 missing value(s) Quantity has 1 missing value(s) Discount has NO missing value(s)! Profit has 1 missing value(s)
even-more-python-for-beginners-data-tools/15 - Visualizing data with Matplotlib/15 - Visualizing correlations.ipynb	###Markdown Visualizing data with matplotlib Somtimes graphs provide the best way to visualize dataThe matplotlib library allows you to draw graphs to help with visualizationIf we want to visualize data, we will need to load some data into a DataFrame ###Code import pandas as pd # Load our data from the csv file delays_df = pd.read_csv('Data/Lots_of_flight_data.csv') ###Output _____no_output_____ ###Markdown In order to display plots we need to import the matplotlib library ###Code import matplotlib.pyplot as plt ###Output _____no_output_____ ###Markdown A common plot used in data science is the scatter plot for checking the relationship between two columnsIf you see dots scattered everywhere, there is no correlation between the two columnsIf you see somethign resembling a line, there is a correlation between the two columnsYou can use the plot method of the DataFrame to draw the scatter plot* kind - the type of graph to draw* x - value to plot as x* y - value to plot as y* color - color to use for the graph points* alpha - opacity - useful to show density of points in a scatter plot* title - title of the graph ###Code #Check if there is a relationship between the distance of a flight and how late the flight arrives delays_df.plot( kind='scatter', x='DISTANCE', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and distance' ) plt.show() #Check if there is a relationship between the how late the flight leaves and how late the flight arrives delays_df.plot( kind='scatter', x='DEP_DELAY', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and departure delay' ) plt.show() ###Output _____no_output_____ ###Markdown Visualizing data with matplotlib Somtimes graphs provide the best way to visualize dataThe matplotlib library allows you to draw graphs to help with visualizationIf we want to visualize data, we will need to load some data into a DataFrame ###Code import pandas as pd # Load our data from the csv file delays_df = pd.read_csv('Data/Lots_of_flight_data.csv') ###Output _____no_output_____ ###Markdown In order to display plots we need to import the matplotlib library ###Code import matplotlib.pyplot as plt ###Output _____no_output_____ ###Markdown A common plot used in data science is the scatter plot for checking the relationship between two columnsIf you see dots scattered everywhere, there is no correlation between the two columnsIf you see somethign resembling a line, there is a correlation between the two columnsYou can use the plot method of the DataFrame to draw the scatter plot* kind - the type of graph to draw* x - value to plot as x* y - value to plot as y* color - color to use for the graph points* alpha - opacity - useful to show density of points in a scatter plot* title - title of the graph ###Code #Check if there is a relationship between the distance of a flight and how late the flight arrives delays_df.plot( kind='scatter', x='DISTANCE', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and distance' ) plt.show() #Check if there is a relationship between the how late the flight leaves and how late the flight arrives delays_df.plot( kind='scatter', x='DEP_DELAY', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and departure delay' ) plt.show() ###Output _____no_output_____ ###Markdown Visualizing data with matplotlib Somtimes graphs provide the best way to visualize dataThe matplotlib library allows you to draw graphs to help with visualizationIf we want to visualize data, we will need to load some data into a DataFrame ###Code import pandas as pd # Load our data from the csv file delays_df = pd.read_csv('Lots_of_flight_data.csv') ###Output _____no_output_____ ###Markdown In order to display plots we need to import the matplotlib library ###Code import matplotlib.pyplot as plt ###Output _____no_output_____ ###Markdown A common plot used in data science is the scatter plot for checking the relationship between two columnsIf you see dots scattered everywhere, there is no correlation between the two columnsIf you see somethign resembling a line, there is a correlation between the two columnsYou can use the plot method of the DataFrame to draw the scatter plot* kind - the type of graph to draw* x - value to plot as x* y - value to plot as y* color - color to use for the graph points* alpha - opacity - useful to show density of points in a scatter plot* title - title of the graph ###Code #Check if there is a relationship between the distance of a flight and how late the flight arrives delays_df.plot( kind='scatter', x='DISTANCE', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and distance' ) plt.show() #Check if there is a relationship between the how late the flight leaves and how late the flight arrives delays_df.plot( kind='scatter', x='DEP_DELAY', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and departure delay' ) plt.show() ###Output _____no_output_____ ###Markdown Visualizing data with matplotlib Somtimes graphs provide the best way to visualize dataThe matplotlib library allows you to draw graphs to help with visualizationIf we want to visualize data, we will need to load some data into a DataFrame ###Code import pandas as pd # Load our data from the csv file delays_df = pd.read_csv('Lots_of_flight_data.csv') ###Output _____no_output_____ ###Markdown In order to display plots we need to import the matplotlib library ###Code import matplotlib.pyplot as plt ###Output _____no_output_____ ###Markdown A common plot used in data science is the scatter plot for checking the relationship between two columnsIf you see dots scattered everywhere, there is no correlation between the two columnsIf you see somethign resembling a line, there is a correlation between the two columnsYou can use the plot method of the DataFrame to draw the scatter plot* kind - the type of graph to draw* x - value to plot as x* y - value to plot as y* color - color to use for the graph points* alpha - opacity - useful to show density of points in a scatter plot* title - title of the graph ###Code #Check if there is a relationship between the distance of a flight and how late the flight arrives delays_df.plot( kind='scatter', x='DISTANCE', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and distance' ) plt.show() #Check if there is a relationship between the how late the flight leaves and how late the flight arrives delays_df.plot( kind='scatter', x='DEP_DELAY', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and departure delay' ) plt.show() ###Output _____no_output_____ ###Markdown The scatter plot allows us to see there is no correlation between distance and arrival delay but there is a strong correlation between departure delay and arrival delay. ###Code plt.xlabel('Departure delay (minutes)') plt.ylabel('Arrival delay (minutes)') plt.title('Correlation Departure and Arrival Delay') plt.scatter(x=delays_df['DEP_DELAY'], y=delays_df['ARR_DELAY'], color='blue', alpha=0.3) plt.show() # Grab our libaries from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression # Remove rows with null values since those will crash our linear regression model training delays_df.dropna(inplace=True) # Move our features into the X DataFrame X = delays_df.loc[:,['DEP_DELAY']] # Move our labels into the y DataFrame y = delays_df.loc[:,['ARR_DELAY']] # Split our data into test and training DataFrames X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.3, random_state=42 ) regressor = LinearRegression() # Create a scikit learn LinearRegression object regressor.fit(X_train, y_train) # Use the fit method to train the model using your training data y_pred = regressor.predict(X_test) plt.xlabel('Departure delay (minutes)') plt.ylabel('Arrival delay (minutes)') plt.title('Predicted Arrival delays') plt.plot( X_test, y_pred, color='red', linewidth=1) plt.scatter(x=delays_df['DEP_DELAY'], y=delays_df['ARR_DELAY'], color='blue', alpha=0.3) plt.show() ###Output _____no_output_____ ###Markdown Matplotlib를 이용한 데이터 시각화 그래프는 데이터를 시각화하는 가장 좋은 방법입니다.matplotlib 라이브러리는 시각화를 돕는 그래프를 그리는 것을 제공합니다.데이터를 시각화하기 원한다면 DataFrame으로 데이터를 불러오는 것이 필요합니다. ###Code import pandas as pd # csv 파일로부터 데이터를 불러오기 delays_df = pd.read_csv('Data/Lots_of_flight_data.csv') ###Output _____no_output_____ ###Markdown plot을 표시하려면 matplotlib 라이브러리를 가져와야합니다. ###Code import matplotlib.pyplot as plt ###Output _____no_output_____ ###Markdown 데이터 과학에서 사용되는 일반적인 플롯은 두 열 간의 관계를 확인하기위한 산점도입니다.사방에 점이 흩어져있는 경우 두 열간에 상관 관계가없는 것입니다.선과 닮은 부분이 보이면 두 열 사이에 상관 관계가있는 것입니다.DataFrame의 plot 메서드를 사용하여 산점도를 그릴 수 있습니다.* kind - 그릴 그래프의 타입* x - x로 표시할 값* y - y로 표시할 값* color - 그래프 점에 사용할 색상* alpha - 불투명도 - 산점도에서 점의 밀도를 표시하는 데 유용합니다.* title - 그래프의 제목 ###Code # 항공편 거리와 항공편 도착 늦게 사이에 관계가 있는지 확인 delays_df.plot( kind='scatter', x='DISTANCE', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and distance' ) plt.show() # 항공편 출발 시간과 도착 시간 사이에 관계가 있는지 확인하세요. delays_df.plot( kind='scatter', x='DEP_DELAY', y='ARR_DELAY', color='blue', alpha=0.3, title='Correlation of arrival and departure delay' ) plt.show() ###Output _____no_output_____
shemi_piran_1990.ipynb	###Markdown [ADS Entry](http://adsabs.harvard.edu/abs/1990ApJ...365L..55S) ###Code import sympy sympy.init_printing() ###Output _____no_output_____ ###Markdown One difficulty that I had with equation 1 is that is assumes that the pair production cross section decreases quadratically with the photon energy. The cross section for pair production can be found in equation 32 in [Weaver 1976](https://journals.aps.org/pra/abstract/10.1103/PhysRevA.13.1563). The full calculation can be found in [Theory of Photons and Electrons by Jauch and Rohrlich (1955)](https://archive.org/details/TheoryOfPhotonsElectrons). Equation 1 ###Code sigma_T = sympy.Symbol('sigma_T') epsilon = sympy.Symbol('epsilon') n_gamma = sympy.Symbol('n_gamma') mathscrE = sympy.Symbol(r'\mathscr{E}') mathscrR = sympy.Symbol(r'\mathscr{R}') tau = sympy.Symbol('tau') hbar = sympy.Symbol('hbar', positive=True) c = sympy.Symbol('c',positive=True) m_e = sympy.Symbol('m_e', positive=True) R = sympy.Symbol('R', positive=True) alpha = sympy.Symbol('alpha') compton_wavelength = hbar/(m_ec) _ = sigma_Tn_gammaR/epsilon2 _ = _.subs(n_gamma,mathscrE/epsilon/R3) _ = _.subs(R,mathscrRcompton_wavelength) _ = _.subs(sigma_T,alpha*2compton_wavelength*2) eqn_1 = sympy.Eq(tau,_) eqn_1 ###Output _____no_output_____ ###Markdown To derive equation 2, we begin with the Fermi distribution function for electrons$n = \int_0^{\infty} \frac{p^2 dp}{\hbar^3} \left[1+\exp \left(\frac{\mu + \sqrt{p^2 c^2 + m_e^2 c^4}}{k T} \right)\right]^{-1} =$Since the electrons are in equilibrium with photons, the chemical potential vanishes $\mu = 0$$ = \int_0^{\infty} \frac{p^2 dp}{\hbar^3} \left[1+\exp \left(\frac{\sqrt{p^2 c^2 + m_e^2 c^4}}{k T} \right)\right]^{-1} \approx$Since we are dealing with temperatures much smaller than the electron rest mass energy, the exponential term in the denominator is much larger than unity$ \approx \int_0^{\infty} \frac{p^2 dp}{\hbar^3} \exp \left(-\frac{\sqrt{p^2 c^2 + m_e^2 c^4}}{k T} \right) \approx$Most of the contribution to the integral comes from the $p \ll m_e c$, so$ \approx \exp \left(-\frac{m_e c^2}{k T} \right) \int_0^{\infty} \frac{p^2 dp}{\hbar^3} \exp \left(-\frac{p^2}{m_e k T} \right) \approx \exp \left(-\frac{m_e c^2}{k T} \right) \left(\frac{m_e k T}{\hbar^2} \right)^{3/2}$ ###Code k = sympy.Symbol('k') T = sympy.Symbol('T') lambda_e = sympy.Symbol('lambda_e') mathscrT = sympy.Symbol(r'\mathscr{T}') n_pm = sympy.Symbol(r'n_{\pm}') _ = sympy.exp(-m_ec*2/k/T)(m_ekT/hbar2)sympy.Rational(3,2) _ = _.subs(T,mathscrTm_ec2/k) _ = _.subs(hbar,sympy.solve(sympy.Eq(lambda_e,compton_wavelength),hbar)[0]) eqn_2 = sympy.Eq(n_pm,_) eqn_2 ###Output _____no_output_____ ###Markdown Equation 3 ###Code _ = sympy.Eq(mathscrE,R3(kT)*4/(hbarc)*3/(m_ec*2)) _ = _.subs(T,mathscrTm_ec2/k) _ = _.subs(R, mathscrRcompton_wavelength) eqn_3 = _ eqn_3 ###Output _____no_output_____ ###Markdown The energy density in the fireball is comparable to the pressure $p$. The total energy in the fireball is therefore $R^3 p$. In order to escape, a photon has to travel a distance $R$. If the mean free path is $l$, then the number of scatterings it takes for a photon to reach the same is $\left(R/l \right)^2$, and so the actual path the photon travels before escaping is larger $R^2/l$. The photon moves all the while at the speed of light, so the escape time is $\tau \approx \frac{R^2}{c l} \approx \frac{R}{c} \tau$. The luminosity is therefore $L \approx \frac{p R^2 c}{\tau}$.The ratio between the luminosity and mechanical power is$\frac{L}{p dV/dt} \approx {p R^2 c}{p R^2 dR/dt} \frac{1}{\tau} \approx \frac{1}{\tau}$ Equation 5 ###Code V = sympy.Symbol('V') gamma = sympy.Symbol('gamma') _ = V*(gamma-1)T _ = _.subs(gamma,sympy.Rational(4,3)) _ = _.subs(V,R**3) _.simplify() ###Output _____no_output_____
notebooks/rna_graph_tutorial.ipynb	###Markdown Graphein RNA Graph Construction Tutorial[API Reference](https://graphein.ai/modules/graphein.rna.html)In this notebook we construct graphs of RNA secondary structures.The inputs we require are a sequence (optional) and a [dotbracket](https://www.tbi.univie.ac.at/RNA/ViennaRNA/doc/html/rna_structure_notations.html) specification of the secondary structure.The workflow we follow is similar to the other data modalities. The desired edge constructions are passed as a list of functions to the construction function.[![Open In Colab](https://colab.research.google.com/assets/colab-badge.svg)](https://colab.research.google.com/github/a-r-j/graphein/blob/master/notebooks/rna_graph_tutorial.ipynb)![](https://www.biorxiv.org/content/biorxiv/early/2021/10/12/2020.07.15.204701/F4.large.jpg?width=800&height=600&carousel=1]) ###Code # Install Graphein if necessary # !pip install graphein import logging logging.getLogger("matplotlib").setLevel(logging.WARNING) logging.getLogger("graphein").setLevel(logging.WARNING) from typing import List, Callable import networkx as nx from graphein.rna.graphs import construct_rna_graph from graphein.rna.edges import ( add_all_dotbracket_edges, add_pseudoknots, add_phosphodiester_bonds, add_base_pairing_interactions ) ###Output _____no_output_____ ###Markdown Construction with a DotbracketGraph construction is handled by the [`construct_rna_graph()`](https://graphein.ai/modules/graphein.rna.htmlgraphein.rna.graphs.construct_rna_graph) function. ###Code from graphein.rna.visualisation import plot_rna_graph edge_funcs_1: List[Callable] = [ add_base_pairing_interactions, add_phosphodiester_bonds, add_pseudoknots, ] edge_funcs_2: List[Callable] = [add_all_dotbracket_edges] g = construct_rna_graph( "......((((((......[[[))))))......]]]....", sequence=None, edge_construction_funcs=edge_funcs_1, ) nx.draw(g) plot_rna_graph(g, layout=nx.layout.spring_layout) ###Output WARNING:graphein.rna.visualisation:No sequence data found in graph. Skipping base type labelling. ###Markdown Construction with a dotbracket and sequence ###Code g = construct_rna_graph( sequence="CGUCUUAAACUCAUCACCGUGUGGAGCUGCGACCCUUCCCUAGAUUCGAAGACGAG", dotbracket="((((((...(((..(((...))))))...(((..((.....))..)))))))))..", edge_construction_funcs=edge_funcs_1, ) plot_rna_graph(g, layout=nx.layout.spring_layout) g = construct_rna_graph( sequence="CGUCUUAAACUCAUCACCGUGUGGAGCUGCGACCCUUCCCUAGAUUCGAAGACGAG", dotbracket="((((((...(((..(((...))))))...(((..((.....))..)))))))))..", edge_construction_funcs=edge_funcs_1, ) plot_rna_graph(g, layout=nx.layout.circular_layout) ###Output _____no_output_____ ###Markdown Graphein RNA Graph Construction TutorialIn this notebook we construct graphs of RNA secondary structures.The inputs we require are a sequence (optional) and a [dotbracket](https://www.tbi.univie.ac.at/RNA/ViennaRNA/doc/html/rna_structure_notations.html) specification of the secondary structure. The workflow we follow is similar to the other data modalities. The desired edge constructions are passed as a list of functions to the construction function. Construction with a dotbracket ###Code from graphein.rna.visualisation import plot_rna_graph edge_funcs_1: List[Callable] = [ add_base_pairing_interactions, add_phosphodiester_bonds, add_pseudoknots, ] edge_funcs_2: List[Callable] = [add_all_dotbracket_edges] g = construct_rna_graph( "......((((((......[[[))))))......]]]....", sequence=None, edge_construction_funcs=edge_funcs_1, ) nx.draw(g) ###Output _____no_output_____ ###Markdown Construction with a dotbracket and sequence ###Code g = construct_rna_graph( sequence="CGUCUUAAACUCAUCACCGUGUGGAGCUGCGACCCUUCCCUAGAUUCGAAGACGAG", dotbracket="((((((...(((..(((...))))))...(((..((.....))..)))))))))..", edge_construction_funcs=edge_funcs_1, ) plot_rna_graph(g) ###Output _____no_output_____
Scalable-Machine-Learning/spark_tutorial_student.ipynb	###Markdown ![Spark Logo](http://spark-mooc.github.io/web-assets/images/ta_Spark-logo-small.png) + ![Python Logo](http://spark-mooc.github.io/web-assets/images/python-logo-master-v3-TM-flattened_small.png) Spark Tutorial: Learning Apache Spark This tutorial will teach you how to use [Apache Spark](http://spark.apache.org/), a framework for large-scale data processing, within a notebook. Many traditional frameworks were designed to be run on a single computer. However, many datasets today are too large to be stored on a single computer, and even when a dataset can be stored on one computer (such as the datasets in this tutorial), the dataset can often be processed much more quickly using multiple computers. Spark has efficient implementations of a number of transformations and actions that can be composed together to perform data processing and analysis. Spark excels at distributing these operations across a cluster while abstracting away many of the underlying implementation details. Spark has been designed with a focus on scalability and efficiency. With Spark you can begin developing your solution on your laptop, using a small dataset, and then use that same code to process terabytes or even petabytes across a distributed cluster. During this tutorial we will cover: Part 1: Basic notebook usage and [Python](https://docs.python.org/2/) integration Part 2: An introduction to using [Apache Spark](https://spark.apache.org/) with the Python [pySpark API](https://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD) running in the browser Part 3: Using RDDs and chaining together transformations and actions Part 4: Lambda functions Part 5: Additional RDD actions Part 6: Additional RDD transformations Part 7: Caching RDDs and storage options Part 8: Debugging Spark applications and lazy evaluation The following transformations will be covered:* `map()`, `mapPartitions()`, `mapPartitionsWithIndex()`, `filter()`, `flatMap()`, `reduceByKey()`, `groupByKey()` The following actions will be covered:* `first()`, `take()`, `takeSample()`, `takeOrdered()`, `collect()`, `count()`, `countByValue()`, `reduce()`, `top()` Also covered:* `cache()`, `unpersist()`, `id()`, `setName()` Note that, for reference, you can look up the details of these methods in [Spark's Python API](https://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD) Part 1: Basic notebook usage and [Python](https://docs.python.org/2/) integration (1a) Notebook usage A notebook is comprised of a linear sequence of cells. These cells can contain either markdown or code, but we won't mix both in one cell. When a markdown cell is executed it renders formatted text, images, and links just like HTML in a normal webpage. The text you are reading right now is part of a markdown cell. Python code cells allow you to execute arbitrary Python commands just like in any Python shell. Place your cursor inside the cell below, and press "Shift" + "Enter" to execute the code and advance to the next cell. You can also press "Ctrl" + "Enter" to execute the code and remain in the cell. These commands work the same in both markdown and code cells. ###Code # This is a Python cell. You can run normal Python code here... print 'The sum of 1 and 1 is {0}'.format(1+1) # Here is another Python cell, this time with a variable (x) declaration and an if statement: x = 42 if x > 40: print 'The sum of 1 and 2 is {0}'.format(1+2) ###Output The sum of 1 and 2 is 3 ###Markdown (1b) Notebook state As you work through a notebook it is important that you run all of the code cells. The notebook is stateful, which means that variables and their values are retained until the notebook is detached (in Databricks Cloud) or the kernel is restarted (in IPython notebooks). If you do not run all of the code cells as you proceed through the notebook, your variables will not be properly initialized and later code might fail. You will also need to rerun any cells that you have modified in order for the changes to be available to other cells. ###Code # This cell relies on x being defined already. # If we didn't run the cells from part (1a) this code would fail. print x * 2 ###Output 84 ###Markdown (1c) Library imports We can import standard Python libraries ([modules](https://docs.python.org/2/tutorial/modules.html)) the usual way. An `import` statement will import the specified module. In this tutorial and future labs, we will provide any imports that are necessary. ###Code # Import the regular expression library import re m = re.search('(?<=abc)def', 'abcdef') m.group(0) # Import the datetime library import datetime print 'This was last run on: {0}'.format(datetime.datetime.now()) ###Output This was last run on: 2018-03-14 08:31:43.498335 ###Markdown Part 2: An introduction to using [Apache Spark](https://spark.apache.org/) with the Python [pySpark API](https://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD) running in the browser Spark Context In Spark, communication occurs between a driver and executors. The driver has Spark jobs that it needs to run and these jobs are split into tasks that are submitted to the executors for completion. The results from these tasks are delivered back to the driver. In part 1, we saw that normal python code can be executed via cells. When using Databricks Cloud this code gets executed in the Spark driver's Java Virtual Machine (JVM) and not in an executor's JVM, and when using an IPython notebook it is executed within the kernel associated with the notebook. Since no Spark functionality is actually being used, no tasks are launched on the executors. In order to use Spark and its API we will need to use a `SparkContext`. When running Spark, you start a new Spark application by creating a [SparkContext](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.SparkContext). When the `SparkContext` is created, it asks the master for some cores to use to do work. The master sets these cores aside just for you; they won't be used for other applications. When using Databricks Cloud or the virtual machine provisioned for this class, the `SparkContext` is created for you automatically as `sc`. (2a) Example Cluster The diagram below shows an example cluster, where the cores allocated for an application are outlined in purple.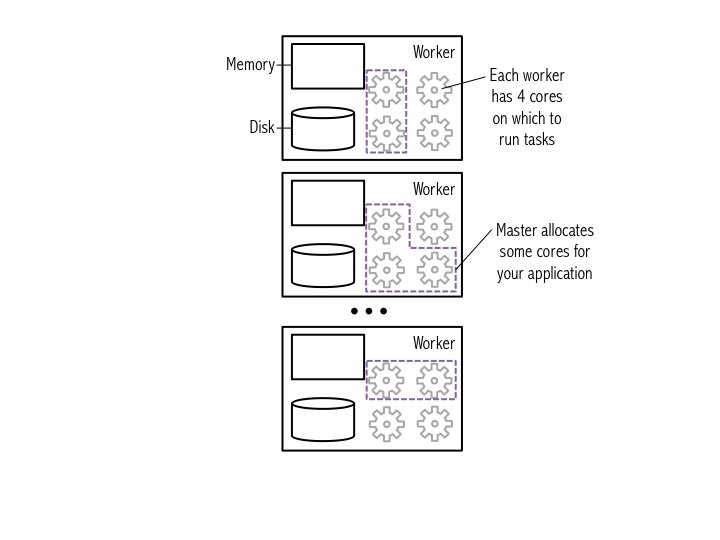![executors](http://spark-mooc.github.io/web-assets/images/executors.png) You can view the details of your Spark application in the Spark web UI. The web UI is accessible in Databricks cloud by going to "Clusters" and then clicking on the "View Spark UI" link for your cluster. When running locally you'll find it at [localhost:4040](http://localhost:4040). In the web UI, under the "Jobs" tab, you can see a list of jobs that have been scheduled or run. It's likely there isn't any thing interesting here yet because we haven't run any jobs, but we'll return to this page later. At a high level, every Spark application consists of a driver program that launches various parallel operations on executor Java Virtual Machines (JVMs) running either in a cluster or locally on the same machine. In Databricks Cloud, "Databricks Shell" is the driver program. When running locally, "PySparkShell" is the driver program. In all cases, this driver program contains the main loop for the program and creates distributed datasets on the cluster, then applies operations (transformations & actions) to those datasets. Driver programs access Spark through a SparkContext object, which represents a connection to a computing cluster. A Spark context object (`sc`) is the main entry point for Spark functionality. A Spark context can be used to create Resilient Distributed Datasets (RDDs) on a cluster. Try printing out `sc` to see its type. ###Code # Display the type of the Spark Context sc type(sc) ###Output _____no_output_____ ###Markdown (2b) `SparkContext` attributes You can use Python's [dir()](https://docs.python.org/2/library/functions.html?highlight=dirdir) function to get a list of all the attributes (including methods) accessible through the `sc` object. ###Code # List sc's attributes dir(sc) ###Output _____no_output_____ ###Markdown (2c) Getting help Alternatively, you can use Python's [help()](https://docs.python.org/2/library/functions.html?highlight=helphelp) function to get an easier to read list of all the attributes, including examples, that the `sc` object has. ###Code # Use help to obtain more detailed information help(sc) # After reading the help we've decided we want to use sc.version to see what version of Spark we are running sc.version # Help can be used on any Python object help(map) ###Output Help on built-in function map in module __builtin__: map(...) map(function, sequence[, sequence, ...]) -> list Return a list of the results of applying the function to the items of the argument sequence(s). If more than one sequence is given, the function is called with an argument list consisting of the corresponding item of each sequence, substituting None for missing values when not all sequences have the same length. If the function is None, return a list of the items of the sequence (or a list of tuples if more than one sequence). ###Markdown Part 3: Using RDDs and chaining together transformations and actions Working with your first RDD In Spark, we first create a base [Resilient Distributed Dataset](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD) (RDD). We can then apply one or more transformations to that base RDD. An RDD is immutable, so once it is created, it cannot be changed. As a result, each transformation creates a new RDD. Finally, we can apply one or more actions to the RDDs. Note that Spark uses lazy evaluation, so transformations are not actually executed until an action occurs. We will perform several exercises to obtain a better understanding of RDDs:* Create a Python collection of 10,000 integers* Create a Spark base RDD from that collection* Subtract one from each value using `map`* Perform action `collect` to view results* Perform action `count` to view counts* Apply transformation `filter` and view results with `collect`* Learn about lambda functions* Explore how lazy evaluation works and the debugging challenges that it introduces (3a) Create a Python collection of integers in the range of 1 .. 10000 We will use the [xrange()](https://docs.python.org/2/library/functions.html?highlight=xrangexrange) function to create a [list()](https://docs.python.org/2/library/functions.html?highlight=listlist) of integers. `xrange()` only generates values as they are needed. This is different from the behavior of [range()](https://docs.python.org/2/library/functions.html?highlight=rangerange) which generates the complete list upon execution. Because of this `xrange()` is more memory efficient than `range()`, especially for large ranges. ###Code data = xrange(1, 10001) # Data is just a normal Python list # Obtain data's first element data[0] # We can check the size of the list using the len() function len(data) ###Output _____no_output_____ ###Markdown (3b) Distributed data and using a collection to create an RDD In Spark, datasets are represented as a list of entries, where the list is broken up into many different partitions that are each stored on a different machine. Each partition holds a unique subset of the entries in the list. Spark calls datasets that it stores "Resilient Distributed Datasets" (RDDs). One of the defining features of Spark, compared to other data analytics frameworks (e.g., Hadoop), is that it stores data in memory rather than on disk. This allows Spark applications to run much more quickly, because they are not slowed down by needing to read data from disk. The figure below illustrates how Spark breaks a list of data entries into partitions that are each stored in memory on a worker.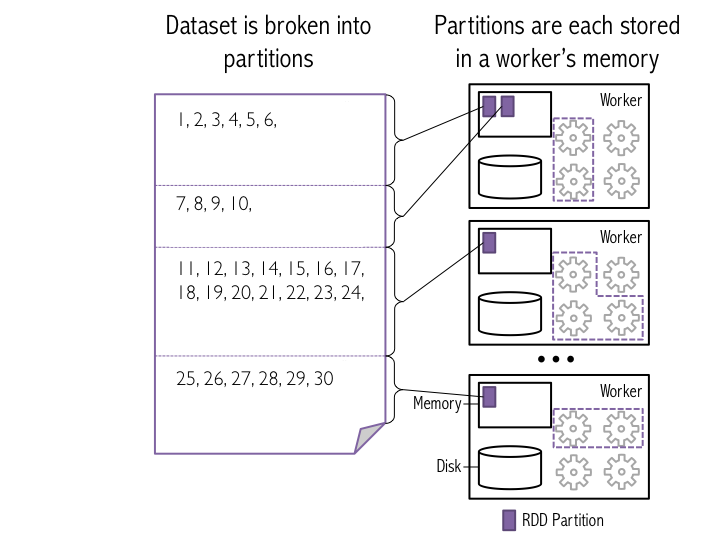![partitions](http://spark-mooc.github.io/web-assets/images/partitions.png) To create the RDD, we use `sc.parallelize()`, which tells Spark to create a new set of input data based on data that is passed in. In this example, we will provide an `xrange`. The second argument to the [sc.parallelize()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.SparkContext.parallelize) method tells Spark how many partitions to break the data into when it stores the data in memory (we'll talk more about this later in this tutorial). Note that for better performance when using `parallelize`, `xrange()` is recommended if the input represents a range. This is the reason why we used `xrange()` in 3a. There are many different types of RDDs. The base class for RDDs is [pyspark.RDD](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD) and other RDDs subclass `pyspark.RDD`. Since the other RDD types inherit from `pyspark.RDD` they have the same APIs and are functionally identical. We'll see that `sc.parallelize()` generates a `pyspark.rdd.PipelinedRDD` when its input is an `xrange`, and a `pyspark.RDD` when its input is a `range`. After we generate RDDs, we can view them in the "Storage" tab of the web UI. You'll notice that new datasets are not listed until Spark needs to return a result due to an action being executed. This feature of Spark is called "lazy evaluation". This allows Spark to avoid performing unnecessary calculations. ###Code # Parallelize data using 8 partitions # This operation is a transformation of data into an RDD # Spark uses lazy evaluation, so no Spark jobs are run at this point xrangeRDD = sc.parallelize(data, 8) # Let's view help on parallelize help(sc.parallelize) # Let's see what type sc.parallelize() returned print 'type of xrangeRDD: {0}'.format(type(xrangeRDD)) # How about if we use a range dataRange = range(1, 10001) rangeRDD = sc.parallelize(dataRange, 8) print 'type of dataRangeRDD: {0}'.format(type(rangeRDD)) # Each RDD gets a unique ID print 'xrangeRDD id: {0}'.format(xrangeRDD.id()) print 'rangeRDD id: {0}'.format(rangeRDD.id()) # We can name each newly created RDD using the setName() method xrangeRDD.setName('My first RDD') # Let's view the lineage (the set of transformations) of the RDD using toDebugString() print xrangeRDD.toDebugString() # Let's use help to see what methods we can call on this RDD help(xrangeRDD) # Let's see how many partitions the RDD will be split into by using the getNumPartitions() xrangeRDD.getNumPartitions() ###Output _____no_output_____ ###Markdown (3c): Subtract one from each value using `map` So far, we've created a distributed dataset that is split into many partitions, where each partition is stored on a single machine in our cluster. Let's look at what happens when we do a basic operation on the dataset. Many useful data analysis operations can be specified as "do something to each item in the dataset". These data-parallel operations are convenient because each item in the dataset can be processed individually: the operation on one entry doesn't effect the operations on any of the other entries. Therefore, Spark can parallelize the operation. `map(f)`, the most common Spark transformation, is one such example: it applies a function `f` to each item in the dataset, and outputs the resulting dataset. When you run `map()` on a dataset, a single stage of tasks is launched. A stage is a group of tasks that all perform the same computation, but on different input data. One task is launched for each partitition, as shown in the example below. A task is a unit of execution that runs on a single machine. When we run `map(f)` within a partition, a new task applies `f` to all of the entries in a particular partition, and outputs a new partition. In this example figure, the dataset is broken into four partitions, so four `map()` tasks are launched.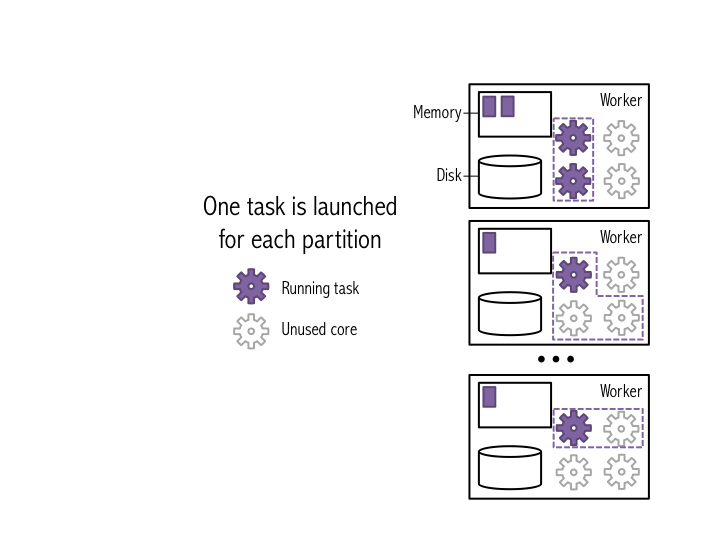![tasks](http://spark-mooc.github.io/web-assets/images/tasks.png) The figure below shows how this would work on the smaller data set from the earlier figures. Note that one task is launched for each partition.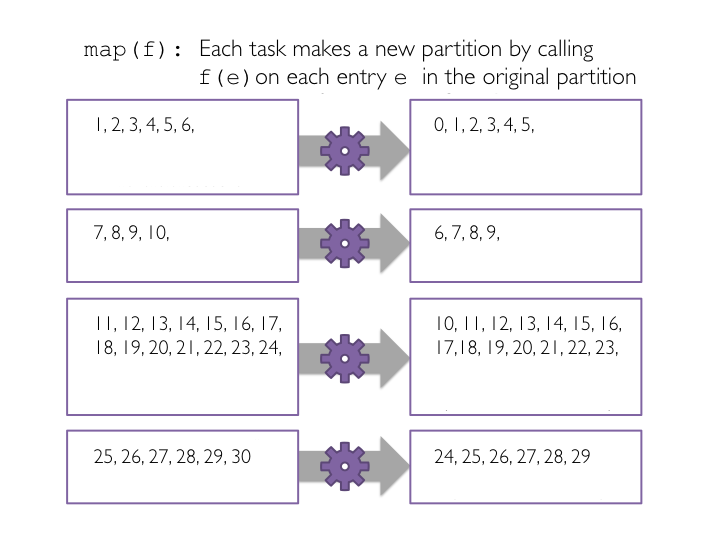![foo](http://spark-mooc.github.io/web-assets/images/map.png) When applying the `map()` transformation, each item in the parent RDD will map to one element in the new RDD. So, if the parent RDD has twenty elements, the new RDD will also have twenty items. Now we will use `map()` to subtract one from each value in the base RDD we just created. First, we define a Python function called `sub()` that will subtract one from the input integer. Second, we will pass each item in the base RDD into a `map()` transformation that applies the `sub()` function to each element. And finally, we print out the RDD transformation hierarchy using `toDebugString()`. ###Code # Create sub function to subtract 1 def sub(value): """"Subtracts one from `value`. Args: value (int): A number. Returns: int: `value` minus one. """ return (value - 1) # Transform xrangeRDD through map transformation using sub function # Because map is a transformation and Spark uses lazy evaluation, no jobs, stages, # or tasks will be launched when we run this code. subRDD = xrangeRDD.map(sub) # Let's see the RDD transformation hierarchy print subRDD.toDebugString() ###Output (8) PythonRDD[3] at RDD at PythonRDD.scala:43 [] \| ParallelCollectionRDD[0] at parallelize at PythonRDD.scala:392 [] ###Markdown (3d) Perform action `collect` to view results To see a list of elements decremented by one, we need to create a new list on the driver from the the data distributed in the executor nodes. To do this we call the `collect()` method on our RDD. `collect()` is often used after a filter or other operation to ensure that we are only returning a small amount of data to the driver. This is done because the data returned to the driver must fit into the driver's available memory. If not, the driver will crash. The `collect()` method is the first action operation that we have encountered. Action operations cause Spark to perform the (lazy) transformation operations that are required to compute the RDD returned by the action. In our example, this means that tasks will now be launched to perform the `parallelize`, `map`, and `collect` operations. In this example, the dataset is broken into four partitions, so four `collect()` tasks are launched. Each task collects the entries in its partition and sends the result to the SparkContext, which creates a list of the values, as shown in the figure below.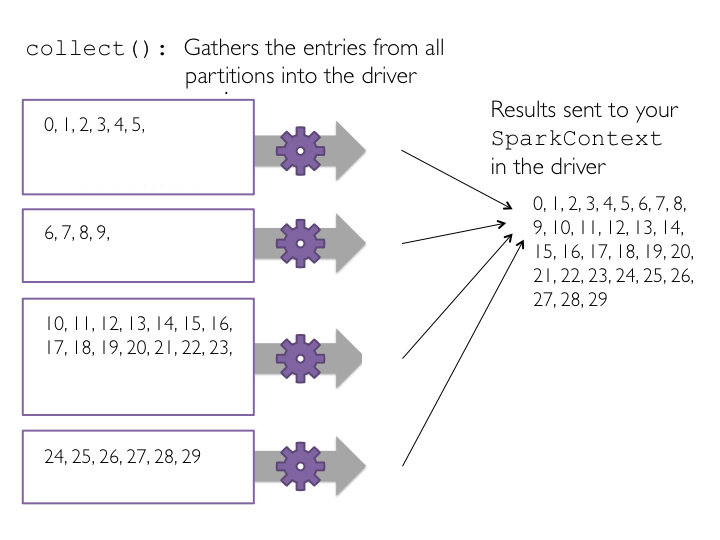![collect](http://spark-mooc.github.io/web-assets/images/collect.png) The above figures showed what would happen if we ran `collect()` on a small example dataset with just four partitions. Now let's run `collect()` on `subRDD`. ###Code # Let's collect the data print subRDD.collect() ###Output [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314, 315, 316, 317, 318, 319, 320, 321, 322, 323, 324, 325, 326, 327, 328, 329, 330, 331, 332, 333, 334, 335, 336, 337, 338, 339, 340, 341, 342, 343, 344, 345, 346, 347, 348, 349, 350, 351, 352, 353, 354, 355, 356, 357, 358, 359, 360, 361, 362, 363, 364, 365, 366, 367, 368, 369, 370, 371, 372, 373, 374, 375, 376, 377, 378, 379, 380, 381, 382, 383, 384, 385, 386, 387, 388, 389, 390, 391, 392, 393, 394, 395, 396, 397, 398, 399, 400, 401, 402, 403, 404, 405, 406, 407, 408, 409, 410, 411, 412, 413, 414, 415, 416, 417, 418, 419, 420, 421, 422, 423, 424, 425, 426, 427, 428, 429, 430, 431, 432, 433, 434, 435, 436, 437, 438, 439, 440, 441, 442, 443, 444, 445, 446, 447, 448, 449, 450, 451, 452, 453, 454, 455, 456, 457, 458, 459, 460, 461, 462, 463, 464, 465, 466, 467, 468, 469, 470, 471, 472, 473, 474, 475, 476, 477, 478, 479, 480, 481, 482, 483, 484, 485, 486, 487, 488, 489, 490, 491, 492, 493, 494, 495, 496, 497, 498, 499, 500, 501, 502, 503, 504, 505, 506, 507, 508, 509, 510, 511, 512, 513, 514, 515, 516, 517, 518, 519, 520, 521, 522, 523, 524, 525, 526, 527, 528, 529, 530, 531, 532, 533, 534, 535, 536, 537, 538, 539, 540, 541, 542, 543, 544, 545, 546, 547, 548, 549, 550, 551, 552, 553, 554, 555, 556, 557, 558, 559, 560, 561, 562, 563, 564, 565, 566, 567, 568, 569, 570, 571, 572, 573, 574, 575, 576, 577, 578, 579, 580, 581, 582, 583, 584, 585, 586, 587, 588, 589, 590, 591, 592, 593, 594, 595, 596, 597, 598, 599, 600, 601, 602, 603, 604, 605, 606, 607, 608, 609, 610, 611, 612, 613, 614, 615, 616, 617, 618, 619, 620, 621, 622, 623, 624, 625, 626, 627, 628, 629, 630, 631, 632, 633, 634, 635, 636, 637, 638, 639, 640, 641, 642, 643, 644, 645, 646, 647, 648, 649, 650, 651, 652, 653, 654, 655, 656, 657, 658, 659, 660, 661, 662, 663, 664, 665, 666, 667, 668, 669, 670, 671, 672, 673, 674, 675, 676, 677, 678, 679, 680, 681, 682, 683, 684, 685, 686, 687, 688, 689, 690, 691, 692, 693, 694, 695, 696, 697, 698, 699, 700, 701, 702, 703, 704, 705, 706, 707, 708, 709, 710, 711, 712, 713, 714, 715, 716, 717, 718, 719, 720, 721, 722, 723, 724, 725, 726, 727, 728, 729, 730, 731, 732, 733, 734, 735, 736, 737, 738, 739, 740, 741, 742, 743, 744, 745, 746, 747, 748, 749, 750, 751, 752, 753, 754, 755, 756, 757, 758, 759, 760, 761, 762, 763, 764, 765, 766, 767, 768, 769, 770, 771, 772, 773, 774, 775, 776, 777, 778, 779, 780, 781, 782, 783, 784, 785, 786, 787, 788, 789, 790, 791, 792, 793, 794, 795, 796, 797, 798, 799, 800, 801, 802, 803, 804, 805, 806, 807, 808, 809, 810, 811, 812, 813, 814, 815, 816, 817, 818, 819, 820, 821, 822, 823, 824, 825, 826, 827, 828, 829, 830, 831, 832, 833, 834, 835, 836, 837, 838, 839, 840, 841, 842, 843, 844, 845, 846, 847, 848, 849, 850, 851, 852, 853, 854, 855, 856, 857, 858, 859, 860, 861, 862, 863, 864, 865, 866, 867, 868, 869, 870, 871, 872, 873, 874, 875, 876, 877, 878, 879, 880, 881, 882, 883, 884, 885, 886, 887, 888, 889, 890, 891, 892, 893, 894, 895, 896, 897, 898, 899, 900, 901, 902, 903, 904, 905, 906, 907, 908, 909, 910, 911, 912, 913, 914, 915, 916, 917, 918, 919, 920, 921, 922, 923, 924, 925, 926, 927, 928, 929, 930, 931, 932, 933, 934, 935, 936, 937, 938, 939, 940, 941, 942, 943, 944, 945, 946, 947, 948, 949, 950, 951, 952, 953, 954, 955, 956, 957, 958, 959, 960, 961, 962, 963, 964, 965, 966, 967, 968, 969, 970, 971, 972, 973, 974, 975, 976, 977, 978, 979, 980, 981, 982, 983, 984, 985, 986, 987, 988, 989, 990, 991, 992, 993, 994, 995, 996, 997, 998, 999, 1000, 1001, 1002, 1003, 1004, 1005, 1006, 1007, 1008, 1009, 1010, 1011, 1012, 1013, 1014, 1015, 1016, 1017, 1018, 1019, 1020, 1021, 1022, 1023, 1024, 1025, 1026, 1027, 1028, 1029, 1030, 1031, 1032, 1033, 1034, 1035, 1036, 1037, 1038, 1039, 1040, 1041, 1042, 1043, 1044, 1045, 1046, 1047, 1048, 1049, 1050, 1051, 1052, 1053, 1054, 1055, 1056, 1057, 1058, 1059, 1060, 1061, 1062, 1063, 1064, 1065, 1066, 1067, 1068, 1069, 1070, 1071, 1072, 1073, 1074, 1075, 1076, 1077, 1078, 1079, 1080, 1081, 1082, 1083, 1084, 1085, 1086, 1087, 1088, 1089, 1090, 1091, 1092, 1093, 1094, 1095, 1096, 1097, 1098, 1099, 1100, 1101, 1102, 1103, 1104, 1105, 1106, 1107, 1108, 1109, 1110, 1111, 1112, 1113, 1114, 1115, 1116, 1117, 1118, 1119, 1120, 1121, 1122, 1123, 1124, 1125, 1126, 1127, 1128, 1129, 1130, 1131, 1132, 1133, 1134, 1135, 1136, 1137, 1138, 1139, 1140, 1141, 1142, 1143, 1144, 1145, 1146, 1147, 1148, 1149, 1150, 1151, 1152, 1153, 1154, 1155, 1156, 1157, 1158, 1159, 1160, 1161, 1162, 1163, 1164, 1165, 1166, 1167, 1168, 1169, 1170, 1171, 1172, 1173, 1174, 1175, 1176, 1177, 1178, 1179, 1180, 1181, 1182, 1183, 1184, 1185, 1186, 1187, 1188, 1189, 1190, 1191, 1192, 1193, 1194, 1195, 1196, 1197, 1198, 1199, 1200, 1201, 1202, 1203, 1204, 1205, 1206, 1207, 1208, 1209, 1210, 1211, 1212, 1213, 1214, 1215, 1216, 1217, 1218, 1219, 1220, 1221, 1222, 1223, 1224, 1225, 1226, 1227, 1228, 1229, 1230, 1231, 1232, 1233, 1234, 1235, 1236, 1237, 1238, 1239, 1240, 1241, 1242, 1243, 1244, 1245, 1246, 1247, 1248, 1249, 1250, 1251, 1252, 1253, 1254, 1255, 1256, 1257, 1258, 1259, 1260, 1261, 1262, 1263, 1264, 1265, 1266, 1267, 1268, 1269, 1270, 1271, 1272, 1273, 1274, 1275, 1276, 1277, 1278, 1279, 1280, 1281, 1282, 1283, 1284, 1285, 1286, 1287, 1288, 1289, 1290, 1291, 1292, 1293, 1294, 1295, 1296, 1297, 1298, 1299, 1300, 1301, 1302, 1303, 1304, 1305, 1306, 1307, 1308, 1309, 1310, 1311, 1312, 1313, 1314, 1315, 1316, 1317, 1318, 1319, 1320, 1321, 1322, 1323, 1324, 1325, 1326, 1327, 1328, 1329, 1330, 1331, 1332, 1333, 1334, 1335, 1336, 1337, 1338, 1339, 1340, 1341, 1342, 1343, 1344, 1345, 1346, 1347, 1348, 1349, 1350, 1351, 1352, 1353, 1354, 1355, 1356, 1357, 1358, 1359, 1360, 1361, 1362, 1363, 1364, 1365, 1366, 1367, 1368, 1369, 1370, 1371, 1372, 1373, 1374, 1375, 1376, 1377, 1378, 1379, 1380, 1381, 1382, 1383, 1384, 1385, 1386, 1387, 1388, 1389, 1390, 1391, 1392, 1393, 1394, 1395, 1396, 1397, 1398, 1399, 1400, 1401, 1402, 1403, 1404, 1405, 1406, 1407, 1408, 1409, 1410, 1411, 1412, 1413, 1414, 1415, 1416, 1417, 1418, 1419, 1420, 1421, 1422, 1423, 1424, 1425, 1426, 1427, 1428, 1429, 1430, 1431, 1432, 1433, 1434, 1435, 1436, 1437, 1438, 1439, 1440, 1441, 1442, 1443, 1444, 1445, 1446, 1447, 1448, 1449, 1450, 1451, 1452, 1453, 1454, 1455, 1456, 1457, 1458, 1459, 1460, 1461, 1462, 1463, 1464, 1465, 1466, 1467, 1468, 1469, 1470, 1471, 1472, 1473, 1474, 1475, 1476, 1477, 1478, 1479, 1480, 1481, 1482, 1483, 1484, 1485, 1486, 1487, 1488, 1489, 1490, 1491, 1492, 1493, 1494, 1495, 1496, 1497, 1498, 1499, 1500, 1501, 1502, 1503, 1504, 1505, 1506, 1507, 1508, 1509, 1510, 1511, 1512, 1513, 1514, 1515, 1516, 1517, 1518, 1519, 1520, 1521, 1522, 1523, 1524, 1525, 1526, 1527, 1528, 1529, 1530, 1531, 1532, 1533, 1534, 1535, 1536, 1537, 1538, 1539, 1540, 1541, 1542, 1543, 1544, 1545, 1546, 1547, 1548, 1549, 1550, 1551, 1552, 1553, 1554, 1555, 1556, 1557, 1558, 1559, 1560, 1561, 1562, 1563, 1564, 1565, 1566, 1567, 1568, 1569, 1570, 1571, 1572, 1573, 1574, 1575, 1576, 1577, 1578, 1579, 1580, 1581, 1582, 1583, 1584, 1585, 1586, 1587, 1588, 1589, 1590, 1591, 1592, 1593, 1594, 1595, 1596, 1597, 1598, 1599, 1600, 1601, 1602, 1603, 1604, 1605, 1606, 1607, 1608, 1609, 1610, 1611, 1612, 1613, 1614, 1615, 1616, 1617, 1618, 1619, 1620, 1621, 1622, 1623, 1624, 1625, 1626, 1627, 1628, 1629, 1630, 1631, 1632, 1633, 1634, 1635, 1636, 1637, 1638, 1639, 1640, 1641, 1642, 1643, 1644, 1645, 1646, 1647, 1648, 1649, 1650, 1651, 1652, 1653, 1654, 1655, 1656, 1657, 1658, 1659, 1660, 1661, 1662, 1663, 1664, 1665, 1666, 1667, 1668, 1669, 1670, 1671, 1672, 1673, 1674, 1675, 1676, 1677, 1678, 1679, 1680, 1681, 1682, 1683, 1684, 1685, 1686, 1687, 1688, 1689, 1690, 1691, 1692, 1693, 1694, 1695, 1696, 1697, 1698, 1699, 1700, 1701, 1702, 1703, 1704, 1705, 1706, 1707, 1708, 1709, 1710, 1711, 1712, 1713, 1714, 1715, 1716, 1717, 1718, 1719, 1720, 1721, 1722, 1723, 1724, 1725, 1726, 1727, 1728, 1729, 1730, 1731, 1732, 1733, 1734, 1735, 1736, 1737, 1738, 1739, 1740, 1741, 1742, 1743, 1744, 1745, 1746, 1747, 1748, 1749, 1750, 1751, 1752, 1753, 1754, 1755, 1756, 1757, 1758, 1759, 1760, 1761, 1762, 1763, 1764, 1765, 1766, 1767, 1768, 1769, 1770, 1771, 1772, 1773, 1774, 1775, 1776, 1777, 1778, 1779, 1780, 1781, 1782, 1783, 1784, 1785, 1786, 1787, 1788, 1789, 1790, 1791, 1792, 1793, 1794, 1795, 1796, 1797, 1798, 1799, 1800, 1801, 1802, 1803, 1804, 1805, 1806, 1807, 1808, 1809, 1810, 1811, 1812, 1813, 1814, 1815, 1816, 1817, 1818, 1819, 1820, 1821, 1822, 1823, 1824, 1825, 1826, 1827, 1828, 1829, 1830, 1831, 1832, 1833, 1834, 1835, 1836, 1837, 1838, 1839, 1840, 1841, 1842, 1843, 1844, 1845, 1846, 1847, 1848, 1849, 1850, 1851, 1852, 1853, 1854, 1855, 1856, 1857, 1858, 1859, 1860, 1861, 1862, 1863, 1864, 1865, 1866, 1867, 1868, 1869, 1870, 1871, 1872, 1873, 1874, 1875, 1876, 1877, 1878, 1879, 1880, 1881, 1882, 1883, 1884, 1885, 1886, 1887, 1888, 1889, 1890, 1891, 1892, 1893, 1894, 1895, 1896, 1897, 1898, 1899, 1900, 1901, 1902, 1903, 1904, 1905, 1906, 1907, 1908, 1909, 1910, 1911, 1912, 1913, 1914, 1915, 1916, 1917, 1918, 1919, 1920, 1921, 1922, 1923, 1924, 1925, 1926, 1927, 1928, 1929, 1930, 1931, 1932, 1933, 1934, 1935, 1936, 1937, 1938, 1939, 1940, 1941, 1942, 1943, 1944, 1945, 1946, 1947, 1948, 1949, 1950, 1951, 1952, 1953, 1954, 1955, 1956, 1957, 1958, 1959, 1960, 1961, 1962, 1963, 1964, 1965, 1966, 1967, 1968, 1969, 1970, 1971, 1972, 1973, 1974, 1975, 1976, 1977, 1978, 1979, 1980, 1981, 1982, 1983, 1984, 1985, 1986, 1987, 1988, 1989, 1990, 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022, 2023, 2024, 2025, 2026, 2027, 2028, 2029, 2030, 2031, 2032, 2033, 2034, 2035, 2036, 2037, 2038, 2039, 2040, 2041, 2042, 2043, 2044, 2045, 2046, 2047, 2048, 2049, 2050, 2051, 2052, 2053, 2054, 2055, 2056, 2057, 2058, 2059, 2060, 2061, 2062, 2063, 2064, 2065, 2066, 2067, 2068, 2069, 2070, 2071, 2072, 2073, 2074, 2075, 2076, 2077, 2078, 2079, 2080, 2081, 2082, 2083, 2084, 2085, 2086, 2087, 2088, 2089, 2090, 2091, 2092, 2093, 2094, 2095, 2096, 2097, 2098, 2099, 2100, 2101, 2102, 2103, 2104, 2105, 2106, 2107, 2108, 2109, 2110, 2111, 2112, 2113, 2114, 2115, 2116, 2117, 2118, 2119, 2120, 2121, 2122, 2123, 2124, 2125, 2126, 2127, 2128, 2129, 2130, 2131, 2132, 2133, 2134, 2135, 2136, 2137, 2138, 2139, 2140, 2141, 2142, 2143, 2144, 2145, 2146, 2147, 2148, 2149, 2150, 2151, 2152, 2153, 2154, 2155, 2156, 2157, 2158, 2159, 2160, 2161, 2162, 2163, 2164, 2165, 2166, 2167, 2168, 2169, 2170, 2171, 2172, 2173, 2174, 2175, 2176, 2177, 2178, 2179, 2180, 2181, 2182, 2183, 2184, 2185, 2186, 2187, 2188, 2189, 2190, 2191, 2192, 2193, 2194, 2195, 2196, 2197, 2198, 2199, 2200, 2201, 2202, 2203, 2204, 2205, 2206, 2207, 2208, 2209, 2210, 2211, 2212, 2213, 2214, 2215, 2216, 2217, 2218, 2219, 2220, 2221, 2222, 2223, 2224, 2225, 2226, 2227, 2228, 2229, 2230, 2231, 2232, 2233, 2234, 2235, 2236, 2237, 2238, 2239, 2240, 2241, 2242, 2243, 2244, 2245, 2246, 2247, 2248, 2249, 2250, 2251, 2252, 2253, 2254, 2255, 2256, 2257, 2258, 2259, 2260, 2261, 2262, 2263, 2264, 2265, 2266, 2267, 2268, 2269, 2270, 2271, 2272, 2273, 2274, 2275, 2276, 2277, 2278, 2279, 2280, 2281, 2282, 2283, 2284, 2285, 2286, 2287, 2288, 2289, 2290, 2291, 2292, 2293, 2294, 2295, 2296, 2297, 2298, 2299, 2300, 2301, 2302, 2303, 2304, 2305, 2306, 2307, 2308, 2309, 2310, 2311, 2312, 2313, 2314, 2315, 2316, 2317, 2318, 2319, 2320, 2321, 2322, 2323, 2324, 2325, 2326, 2327, 2328, 2329, 2330, 2331, 2332, 2333, 2334, 2335, 2336, 2337, 2338, 2339, 2340, 2341, 2342, 2343, 2344, 2345, 2346, 2347, 2348, 2349, 2350, 2351, 2352, 2353, 2354, 2355, 2356, 2357, 2358, 2359, 2360, 2361, 2362, 2363, 2364, 2365, 2366, 2367, 2368, 2369, 2370, 2371, 2372, 2373, 2374, 2375, 2376, 2377, 2378, 2379, 2380, 2381, 2382, 2383, 2384, 2385, 2386, 2387, 2388, 2389, 2390, 2391, 2392, 2393, 2394, 2395, 2396, 2397, 2398, 2399, 2400, 2401, 2402, 2403, 2404, 2405, 2406, 2407, 2408, 2409, 2410, 2411, 2412, 2413, 2414, 2415, 2416, 2417, 2418, 2419, 2420, 2421, 2422, 2423, 2424, 2425, 2426, 2427, 2428, 2429, 2430, 2431, 2432, 2433, 2434, 2435, 2436, 2437, 2438, 2439, 2440, 2441, 2442, 2443, 2444, 2445, 2446, 2447, 2448, 2449, 2450, 2451, 2452, 2453, 2454, 2455, 2456, 2457, 2458, 2459, 2460, 2461, 2462, 2463, 2464, 2465, 2466, 2467, 2468, 2469, 2470, 2471, 2472, 2473, 2474, 2475, 2476, 2477, 2478, 2479, 2480, 2481, 2482, 2483, 2484, 2485, 2486, 2487, 2488, 2489, 2490, 2491, 2492, 2493, 2494, 2495, 2496, 2497, 2498, 2499, 2500, 2501, 2502, 2503, 2504, 2505, 2506, 2507, 2508, 2509, 2510, 2511, 2512, 2513, 2514, 2515, 2516, 2517, 2518, 2519, 2520, 2521, 2522, 2523, 2524, 2525, 2526, 2527, 2528, 2529, 2530, 2531, 2532, 2533, 2534, 2535, 2536, 2537, 2538, 2539, 2540, 2541, 2542, 2543, 2544, 2545, 2546, 2547, 2548, 2549, 2550, 2551, 2552, 2553, 2554, 2555, 2556, 2557, 2558, 2559, 2560, 2561, 2562, 2563, 2564, 2565, 2566, 2567, 2568, 2569, 2570, 2571, 2572, 2573, 2574, 2575, 2576, 2577, 2578, 2579, 2580, 2581, 2582, 2583, 2584, 2585, 2586, 2587, 2588, 2589, 2590, 2591, 2592, 2593, 2594, 2595, 2596, 2597, 2598, 2599, 2600, 2601, 2602, 2603, 2604, 2605, 2606, 2607, 2608, 2609, 2610, 2611, 2612, 2613, 2614, 2615, 2616, 2617, 2618, 2619, 2620, 2621, 2622, 2623, 2624, 2625, 2626, 2627, 2628, 2629, 2630, 2631, 2632, 2633, 2634, 2635, 2636, 2637, 2638, 2639, 2640, 2641, 2642, 2643, 2644, 2645, 2646, 2647, 2648, 2649, 2650, 2651, 2652, 2653, 2654, 2655, 2656, 2657, 2658, 2659, 2660, 2661, 2662, 2663, 2664, 2665, 2666, 2667, 2668, 2669, 2670, 2671, 2672, 2673, 2674, 2675, 2676, 2677, 2678, 2679, 2680, 2681, 2682, 2683, 2684, 2685, 2686, 2687, 2688, 2689, 2690, 2691, 2692, 2693, 2694, 2695, 2696, 2697, 2698, 2699, 2700, 2701, 2702, 2703, 2704, 2705, 2706, 2707, 2708, 2709, 2710, 2711, 2712, 2713, 2714, 2715, 2716, 2717, 2718, 2719, 2720, 2721, 2722, 2723, 2724, 2725, 2726, 2727, 2728, 2729, 2730, 2731, 2732, 2733, 2734, 2735, 2736, 2737, 2738, 2739, 2740, 2741, 2742, 2743, 2744, 2745, 2746, 2747, 2748, 2749, 2750, 2751, 2752, 2753, 2754, 2755, 2756, 2757, 2758, 2759, 2760, 2761, 2762, 2763, 2764, 2765, 2766, 2767, 2768, 2769, 2770, 2771, 2772, 2773, 2774, 2775, 2776, 2777, 2778, 2779, 2780, 2781, 2782, 2783, 2784, 2785, 2786, 2787, 2788, 2789, 2790, 2791, 2792, 2793, 2794, 2795, 2796, 2797, 2798, 2799, 2800, 2801, 2802, 2803, 2804, 2805, 2806, 2807, 2808, 2809, 2810, 2811, 2812, 2813, 2814, 2815, 2816, 2817, 2818, 2819, 2820, 2821, 2822, 2823, 2824, 2825, 2826, 2827, 2828, 2829, 2830, 2831, 2832, 2833, 2834, 2835, 2836, 2837, 2838, 2839, 2840, 2841, 2842, 2843, 2844, 2845, 2846, 2847, 2848, 2849, 2850, 2851, 2852, 2853, 2854, 2855, 2856, 2857, 2858, 2859, 2860, 2861, 2862, 2863, 2864, 2865, 2866, 2867, 2868, 2869, 2870, 2871, 2872, 2873, 2874, 2875, 2876, 2877, 2878, 2879, 2880, 2881, 2882, 2883, 2884, 2885, 2886, 2887, 2888, 2889, 2890, 2891, 2892, 2893, 2894, 2895, 2896, 2897, 2898, 2899, 2900, 2901, 2902, 2903, 2904, 2905, 2906, 2907, 2908, 2909, 2910, 2911, 2912, 2913, 2914, 2915, 2916, 2917, 2918, 2919, 2920, 2921, 2922, 2923, 2924, 2925, 2926, 2927, 2928, 2929, 2930, 2931, 2932, 2933, 2934, 2935, 2936, 2937, 2938, 2939, 2940, 2941, 2942, 2943, 2944, 2945, 2946, 2947, 2948, 2949, 2950, 2951, 2952, 2953, 2954, 2955, 2956, 2957, 2958, 2959, 2960, 2961, 2962, 2963, 2964, 2965, 2966, 2967, 2968, 2969, 2970, 2971, 2972, 2973, 2974, 2975, 2976, 2977, 2978, 2979, 2980, 2981, 2982, 2983, 2984, 2985, 2986, 2987, 2988, 2989, 2990, 2991, 2992, 2993, 2994, 2995, 2996, 2997, 2998, 2999, 3000, 3001, 3002, 3003, 3004, 3005, 3006, 3007, 3008, 3009, 3010, 3011, 3012, 3013, 3014, 3015, 3016, 3017, 3018, 3019, 3020, 3021, 3022, 3023, 3024, 3025, 3026, 3027, 3028, 3029, 3030, 3031, 3032, 3033, 3034, 3035, 3036, 3037, 3038, 3039, 3040, 3041, 3042, 3043, 3044, 3045, 3046, 3047, 3048, 3049, 3050, 3051, 3052, 3053, 3054, 3055, 3056, 3057, 3058, 3059, 3060, 3061, 3062, 3063, 3064, 3065, 3066, 3067, 3068, 3069, 3070, 3071, 3072, 3073, 3074, 3075, 3076, 3077, 3078, 3079, 3080, 3081, 3082, 3083, 3084, 3085, 3086, 3087, 3088, 3089, 3090, 3091, 3092, 3093, 3094, 3095, 3096, 3097, 3098, 3099, 3100, 3101, 3102, 3103, 3104, 3105, 3106, 3107, 3108, 3109, 3110, 3111, 3112, 3113, 3114, 3115, 3116, 3117, 3118, 3119, 3120, 3121, 3122, 3123, 3124, 3125, 3126, 3127, 3128, 3129, 3130, 3131, 3132, 3133, 3134, 3135, 3136, 3137, 3138, 3139, 3140, 3141, 3142, 3143, 3144, 3145, 3146, 3147, 3148, 3149, 3150, 3151, 3152, 3153, 3154, 3155, 3156, 3157, 3158, 3159, 3160, 3161, 3162, 3163, 3164, 3165, 3166, 3167, 3168, 3169, 3170, 3171, 3172, 3173, 3174, 3175, 3176, 3177, 3178, 3179, 3180, 3181, 3182, 3183, 3184, 3185, 3186, 3187, 3188, 3189, 3190, 3191, 3192, 3193, 3194, 3195, 3196, 3197, 3198, 3199, 3200, 3201, 3202, 3203, 3204, 3205, 3206, 3207, 3208, 3209, 3210, 3211, 3212, 3213, 3214, 3215, 3216, 3217, 3218, 3219, 3220, 3221, 3222, 3223, 3224, 3225, 3226, 3227, 3228, 3229, 3230, 3231, 3232, 3233, 3234, 3235, 3236, 3237, 3238, 3239, 3240, 3241, 3242, 3243, 3244, 3245, 3246, 3247, 3248, 3249, 3250, 3251, 3252, 3253, 3254, 3255, 3256, 3257, 3258, 3259, 3260, 3261, 3262, 3263, 3264, 3265, 3266, 3267, 3268, 3269, 3270, 3271, 3272, 3273, 3274, 3275, 3276, 3277, 3278, 3279, 3280, 3281, 3282, 3283, 3284, 3285, 3286, 3287, 3288, 3289, 3290, 3291, 3292, 3293, 3294, 3295, 3296, 3297, 3298, 3299, 3300, 3301, 3302, 3303, 3304, 3305, 3306, 3307, 3308, 3309, 3310, 3311, 3312, 3313, 3314, 3315, 3316, 3317, 3318, 3319, 3320, 3321, 3322, 3323, 3324, 3325, 3326, 3327, 3328, 3329, 3330, 3331, 3332, 3333, 3334, 3335, 3336, 3337, 3338, 3339, 3340, 3341, 3342, 3343, 3344, 3345, 3346, 3347, 3348, 3349, 3350, 3351, 3352, 3353, 3354, 3355, 3356, 3357, 3358, 3359, 3360, 3361, 3362, 3363, 3364, 3365, 3366, 3367, 3368, 3369, 3370, 3371, 3372, 3373, 3374, 3375, 3376, 3377, 3378, 3379, 3380, 3381, 3382, 3383, 3384, 3385, 3386, 3387, 3388, 3389, 3390, 3391, 3392, 3393, 3394, 3395, 3396, 3397, 3398, 3399, 3400, 3401, 3402, 3403, 3404, 3405, 3406, 3407, 3408, 3409, 3410, 3411, 3412, 3413, 3414, 3415, 3416, 3417, 3418, 3419, 3420, 3421, 3422, 3423, 3424, 3425, 3426, 3427, 3428, 3429, 3430, 3431, 3432, 3433, 3434, 3435, 3436, 3437, 3438, 3439, 3440, 3441, 3442, 3443, 3444, 3445, 3446, 3447, 3448, 3449, 3450, 3451, 3452, 3453, 3454, 3455, 3456, 3457, 3458, 3459, 3460, 3461, 3462, 3463, 3464, 3465, 3466, 3467, 3468, 3469, 3470, 3471, 3472, 3473, 3474, 3475, 3476, 3477, 3478, 3479, 3480, 3481, 3482, 3483, 3484, 3485, 3486, 3487, 3488, 3489, 3490, 3491, 3492, 3493, 3494, 3495, 3496, 3497, 3498, 3499, 3500, 3501, 3502, 3503, 3504, 3505, 3506, 3507, 3508, 3509, 3510, 3511, 3512, 3513, 3514, 3515, 3516, 3517, 3518, 3519, 3520, 3521, 3522, 3523, 3524, 3525, 3526, 3527, 3528, 3529, 3530, 3531, 3532, 3533, 3534, 3535, 3536, 3537, 3538, 3539, 3540, 3541, 3542, 3543, 3544, 3545, 3546, 3547, 3548, 3549, 3550, 3551, 3552, 3553, 3554, 3555, 3556, 3557, 3558, 3559, 3560, 3561, 3562, 3563, 3564, 3565, 3566, 3567, 3568, 3569, 3570, 3571, 3572, 3573, 3574, 3575, 3576, 3577, 3578, 3579, 3580, 3581, 3582, 3583, 3584, 3585, 3586, 3587, 3588, 3589, 3590, 3591, 3592, 3593, 3594, 3595, 3596, 3597, 3598, 3599, 3600, 3601, 3602, 3603, 3604, 3605, 3606, 3607, 3608, 3609, 3610, 3611, 3612, 3613, 3614, 3615, 3616, 3617, 3618, 3619, 3620, 3621, 3622, 3623, 3624, 3625, 3626, 3627, 3628, 3629, 3630, 3631, 3632, 3633, 3634, 3635, 3636, 3637, 3638, 3639, 3640, 3641, 3642, 3643, 3644, 3645, 3646, 3647, 3648, 3649, 3650, 3651, 3652, 3653, 3654, 3655, 3656, 3657, 3658, 3659, 3660, 3661, 3662, 3663, 3664, 3665, 3666, 3667, 3668, 3669, 3670, 3671, 3672, 3673, 3674, 3675, 3676, 3677, 3678, 3679, 3680, 3681, 3682, 3683, 3684, 3685, 3686, 3687, 3688, 3689, 3690, 3691, 3692, 3693, 3694, 3695, 3696, 3697, 3698, 3699, 3700, 3701, 3702, 3703, 3704, 3705, 3706, 3707, 3708, 3709, 3710, 3711, 3712, 3713, 3714, 3715, 3716, 3717, 3718, 3719, 3720, 3721, 3722, 3723, 3724, 3725, 3726, 3727, 3728, 3729, 3730, 3731, 3732, 3733, 3734, 3735, 3736, 3737, 3738, 3739, 3740, 3741, 3742, 3743, 3744, 3745, 3746, 3747, 3748, 3749, 3750, 3751, 3752, 3753, 3754, 3755, 3756, 3757, 3758, 3759, 3760, 3761, 3762, 3763, 3764, 3765, 3766, 3767, 3768, 3769, 3770, 3771, 3772, 3773, 3774, 3775, 3776, 3777, 3778, 3779, 3780, 3781, 3782, 3783, 3784, 3785, 3786, 3787, 3788, 3789, 3790, 3791, 3792, 3793, 3794, 3795, 3796, 3797, 3798, 3799, 3800, 3801, 3802, 3803, 3804, 3805, 3806, 3807, 3808, 3809, 3810, 3811, 3812, 3813, 3814, 3815, 3816, 3817, 3818, 3819, 3820, 3821, 3822, 3823, 3824, 3825, 3826, 3827, 3828, 3829, 3830, 3831, 3832, 3833, 3834, 3835, 3836, 3837, 3838, 3839, 3840, 3841, 3842, 3843, 3844, 3845, 3846, 3847, 3848, 3849, 3850, 3851, 3852, 3853, 3854, 3855, 3856, 3857, 3858, 3859, 3860, 3861, 3862, 3863, 3864, 3865, 3866, 3867, 3868, 3869, 3870, 3871, 3872, 3873, 3874, 3875, 3876, 3877, 3878, 3879, 3880, 3881, 3882, 3883, 3884, 3885, 3886, 3887, 3888, 3889, 3890, 3891, 3892, 3893, 3894, 3895, 3896, 3897, 3898, 3899, 3900, 3901, 3902, 3903, 3904, 3905, 3906, 3907, 3908, 3909, 3910, 3911, 3912, 3913, 3914, 3915, 3916, 3917, 3918, 3919, 3920, 3921, 3922, 3923, 3924, 3925, 3926, 3927, 3928, 3929, 3930, 3931, 3932, 3933, 3934, 3935, 3936, 3937, 3938, 3939, 3940, 3941, 3942, 3943, 3944, 3945, 3946, 3947, 3948, 3949, 3950, 3951, 3952, 3953, 3954, 3955, 3956, 3957, 3958, 3959, 3960, 3961, 3962, 3963, 3964, 3965, 3966, 3967, 3968, 3969, 3970, 3971, 3972, 3973, 3974, 3975, 3976, 3977, 3978, 3979, 3980, 3981, 3982, 3983, 3984, 3985, 3986, 3987, 3988, 3989, 3990, 3991, 3992, 3993, 3994, 3995, 3996, 3997, 3998, 3999, 4000, 4001, 4002, 4003, 4004, 4005, 4006, 4007, 4008, 4009, 4010, 4011, 4012, 4013, 4014, 4015, 4016, 4017, 4018, 4019, 4020, 4021, 4022, 4023, 4024, 4025, 4026, 4027, 4028, 4029, 4030, 4031, 4032, 4033, 4034, 4035, 4036, 4037, 4038, 4039, 4040, 4041, 4042, 4043, 4044, 4045, 4046, 4047, 4048, 4049, 4050, 4051, 4052, 4053, 4054, 4055, 4056, 4057, 4058, 4059, 4060, 4061, 4062, 4063, 4064, 4065, 4066, 4067, 4068, 4069, 4070, 4071, 4072, 4073, 4074, 4075, 4076, 4077, 4078, 4079, 4080, 4081, 4082, 4083, 4084, 4085, 4086, 4087, 4088, 4089, 4090, 4091, 4092, 4093, 4094, 4095, 4096, 4097, 4098, 4099, 4100, 4101, 4102, 4103, 4104, 4105, 4106, 4107, 4108, 4109, 4110, 4111, 4112, 4113, 4114, 4115, 4116, 4117, 4118, 4119, 4120, 4121, 4122, 4123, 4124, 4125, 4126, 4127, 4128, 4129, 4130, 4131, 4132, 4133, 4134, 4135, 4136, 4137, 4138, 4139, 4140, 4141, 4142, 4143, 4144, 4145, 4146, 4147, 4148, 4149, 4150, 4151, 4152, 4153, 4154, 4155, 4156, 4157, 4158, 4159, 4160, 4161, 4162, 4163, 4164, 4165, 4166, 4167, 4168, 4169, 4170, 4171, 4172, 4173, 4174, 4175, 4176, 4177, 4178, 4179, 4180, 4181, 4182, 4183, 4184, 4185, 4186, 4187, 4188, 4189, 4190, 4191, 4192, 4193, 4194, 4195, 4196, 4197, 4198, 4199, 4200, 4201, 4202, 4203, 4204, 4205, 4206, 4207, 4208, 4209, 4210, 4211, 4212, 4213, 4214, 4215, 4216, 4217, 4218, 4219, 4220, 4221, 4222, 4223, 4224, 4225, 4226, 4227, 4228, 4229, 4230, 4231, 4232, 4233, 4234, 4235, 4236, 4237, 4238, 4239, 4240, 4241, 4242, 4243, 4244, 4245, 4246, 4247, 4248, 4249, 4250, 4251, 4252, 4253, 4254, 4255, 4256, 4257, 4258, 4259, 4260, 4261, 4262, 4263, 4264, 4265, 4266, 4267, 4268, 4269, 4270, 4271, 4272, 4273, 4274, 4275, 4276, 4277, 4278, 4279, 4280, 4281, 4282, 4283, 4284, 4285, 4286, 4287, 4288, 4289, 4290, 4291, 4292, 4293, 4294, 4295, 4296, 4297, 4298, 4299, 4300, 4301, 4302, 4303, 4304, 4305, 4306, 4307, 4308, 4309, 4310, 4311, 4312, 4313, 4314, 4315, 4316, 4317, 4318, 4319, 4320, 4321, 4322, 4323, 4324, 4325, 4326, 4327, 4328, 4329, 4330, 4331, 4332, 4333, 4334, 4335, 4336, 4337, 4338, 4339, 4340, 4341, 4342, 4343, 4344, 4345, 4346, 4347, 4348, 4349, 4350, 4351, 4352, 4353, 4354, 4355, 4356, 4357, 4358, 4359, 4360, 4361, 4362, 4363, 4364, 4365, 4366, 4367, 4368, 4369, 4370, 4371, 4372, 4373, 4374, 4375, 4376, 4377, 4378, 4379, 4380, 4381, 4382, 4383, 4384, 4385, 4386, 4387, 4388, 4389, 4390, 4391, 4392, 4393, 4394, 4395, 4396, 4397, 4398, 4399, 4400, 4401, 4402, 4403, 4404, 4405, 4406, 4407, 4408, 4409, 4410, 4411, 4412, 4413, 4414, 4415, 4416, 4417, 4418, 4419, 4420, 4421, 4422, 4423, 4424, 4425, 4426, 4427, 4428, 4429, 4430, 4431, 4432, 4433, 4434, 4435, 4436, 4437, 4438, 4439, 4440, 4441, 4442, 4443, 4444, 4445, 4446, 4447, 4448, 4449, 4450, 4451, 4452, 4453, 4454, 4455, 4456, 4457, 4458, 4459, 4460, 4461, 4462, 4463, 4464, 4465, 4466, 4467, 4468, 4469, 4470, 4471, 4472, 4473, 4474, 4475, 4476, 4477, 4478, 4479, 4480, 4481, 4482, 4483, 4484, 4485, 4486, 4487, 4488, 4489, 4490, 4491, 4492, 4493, 4494, 4495, 4496, 4497, 4498, 4499, 4500, 4501, 4502, 4503, 4504, 4505, 4506, 4507, 4508, 4509, 4510, 4511, 4512, 4513, 4514, 4515, 4516, 4517, 4518, 4519, 4520, 4521, 4522, 4523, 4524, 4525, 4526, 4527, 4528, 4529, 4530, 4531, 4532, 4533, 4534, 4535, 4536, 4537, 4538, 4539, 4540, 4541, 4542, 4543, 4544, 4545, 4546, 4547, 4548, 4549, 4550, 4551, 4552, 4553, 4554, 4555, 4556, 4557, 4558, 4559, 4560, 4561, 4562, 4563, 4564, 4565, 4566, 4567, 4568, 4569, 4570, 4571, 4572, 4573, 4574, 4575, 4576, 4577, 4578, 4579, 4580, 4581, 4582, 4583, 4584, 4585, 4586, 4587, 4588, 4589, 4590, 4591, 4592, 4593, 4594, 4595, 4596, 4597, 4598, 4599, 4600, 4601, 4602, 4603, 4604, 4605, 4606, 4607, 4608, 4609, 4610, 4611, 4612, 4613, 4614, 4615, 4616, 4617, 4618, 4619, 4620, 4621, 4622, 4623, 4624, 4625, 4626, 4627, 4628, 4629, 4630, 4631, 4632, 4633, 4634, 4635, 4636, 4637, 4638, 4639, 4640, 4641, 4642, 4643, 4644, 4645, 4646, 4647, 4648, 4649, 4650, 4651, 4652, 4653, 4654, 4655, 4656, 4657, 4658, 4659, 4660, 4661, 4662, 4663, 4664, 4665, 4666, 4667, 4668, 4669, 4670, 4671, 4672, 4673, 4674, 4675, 4676, 4677, 4678, 4679, 4680, 4681, 4682, 4683, 4684, 4685, 4686, 4687, 4688, 4689, 4690, 4691, 4692, 4693, 4694, 4695, 4696, 4697, 4698, 4699, 4700, 4701, 4702, 4703, 4704, 4705, 4706, 4707, 4708, 4709, 4710, 4711, 4712, 4713, 4714, 4715, 4716, 4717, 4718, 4719, 4720, 4721, 4722, 4723, 4724, 4725, 4726, 4727, 4728, 4729, 4730, 4731, 4732, 4733, 4734, 4735, 4736, 4737, 4738, 4739, 4740, 4741, 4742, 4743, 4744, 4745, 4746, 4747, 4748, 4749, 4750, 4751, 4752, 4753, 4754, 4755, 4756, 4757, 4758, 4759, 4760, 4761, 4762, 4763, 4764, 4765, 4766, 4767, 4768, 4769, 4770, 4771, 4772, 4773, 4774, 4775, 4776, 4777, 4778, 4779, 4780, 4781, 4782, 4783, 4784, 4785, 4786, 4787, 4788, 4789, 4790, 4791, 4792, 4793, 4794, 4795, 4796, 4797, 4798, 4799, 4800, 4801, 4802, 4803, 4804, 4805, 4806, 4807, 4808, 4809, 4810, 4811, 4812, 4813, 4814, 4815, 4816, 4817, 4818, 4819, 4820, 4821, 4822, 4823, 4824, 4825, 4826, 4827, 4828, 4829, 4830, 4831, 4832, 4833, 4834, 4835, 4836, 4837, 4838, 4839, 4840, 4841, 4842, 4843, 4844, 4845, 4846, 4847, 4848, 4849, 4850, 4851, 4852, 4853, 4854, 4855, 4856, 4857, 4858, 4859, 4860, 4861, 4862, 4863, 4864, 4865, 4866, 4867, 4868, 4869, 4870, 4871, 4872, 4873, 4874, 4875, 4876, 4877, 4878, 4879, 4880, 4881, 4882, 4883, 4884, 4885, 4886, 4887, 4888, 4889, 4890, 4891, 4892, 4893, 4894, 4895, 4896, 4897, 4898, 4899, 4900, 4901, 4902, 4903, 4904, 4905, 4906, 4907, 4908, 4909, 4910, 4911, 4912, 4913, 4914, 4915, 4916, 4917, 4918, 4919, 4920, 4921, 4922, 4923, 4924, 4925, 4926, 4927, 4928, 4929, 4930, 4931, 4932, 4933, 4934, 4935, 4936, 4937, 4938, 4939, 4940, 4941, 4942, 4943, 4944, 4945, 4946, 4947, 4948, 4949, 4950, 4951, 4952, 4953, 4954, 4955, 4956, 4957, 4958, 4959, 4960, 4961, 4962, 4963, 4964, 4965, 4966, 4967, 4968, 4969, 4970, 4971, 4972, 4973, 4974, 4975, 4976, 4977, 4978, 4979, 4980, 4981, 4982, 4983, 4984, 4985, 4986, 4987, 4988, 4989, 4990, 4991, 4992, 4993, 4994, 4995, 4996, 4997, 4998, 4999, 5000, 5001, 5002, 5003, 5004, 5005, 5006, 5007, 5008, 5009, 5010, 5011, 5012, 5013, 5014, 5015, 5016, 5017, 5018, 5019, 5020, 5021, 5022, 5023, 5024, 5025, 5026, 5027, 5028, 5029, 5030, 5031, 5032, 5033, 5034, 5035, 5036, 5037, 5038, 5039, 5040, 5041, 5042, 5043, 5044, 5045, 5046, 5047, 5048, 5049, 5050, 5051, 5052, 5053, 5054, 5055, 5056, 5057, 5058, 5059, 5060, 5061, 5062, 5063, 5064, 5065, 5066, 5067, 5068, 5069, 5070, 5071, 5072, 5073, 5074, 5075, 5076, 5077, 5078, 5079, 5080, 5081, 5082, 5083, 5084, 5085, 5086, 5087, 5088, 5089, 5090, 5091, 5092, 5093, 5094, 5095, 5096, 5097, 5098, 5099, 5100, 5101, 5102, 5103, 5104, 5105, 5106, 5107, 5108, 5109, 5110, 5111, 5112, 5113, 5114, 5115, 5116, 5117, 5118, 5119, 5120, 5121, 5122, 5123, 5124, 5125, 5126, 5127, 5128, 5129, 5130, 5131, 5132, 5133, 5134, 5135, 5136, 5137, 5138, 5139, 5140, 5141, 5142, 5143, 5144, 5145, 5146, 5147, 5148, 5149, 5150, 5151, 5152, 5153, 5154, 5155, 5156, 5157, 5158, 5159, 5160, 5161, 5162, 5163, 5164, 5165, 5166, 5167, 5168, 5169, 5170, 5171, 5172, 5173, 5174, 5175, 5176, 5177, 5178, 5179, 5180, 5181, 5182, 5183, 5184, 5185, 5186, 5187, 5188, 5189, 5190, 5191, 5192, 5193, 5194, 5195, 5196, 5197, 5198, 5199, 5200, 5201, 5202, 5203, 5204, 5205, 5206, 5207, 5208, 5209, 5210, 5211, 5212, 5213, 5214, 5215, 5216, 5217, 5218, 5219, 5220, 5221, 5222, 5223, 5224, 5225, 5226, 5227, 5228, 5229, 5230, 5231, 5232, 5233, 5234, 5235, 5236, 5237, 5238, 5239, 5240, 5241, 5242, 5243, 5244, 5245, 5246, 5247, 5248, 5249, 5250, 5251, 5252, 5253, 5254, 5255, 5256, 5257, 5258, 5259, 5260, 5261, 5262, 5263, 5264, 5265, 5266, 5267, 5268, 5269, 5270, 5271, 5272, 5273, 5274, 5275, 5276, 5277, 5278, 5279, 5280, 5281, 5282, 5283, 5284, 5285, 5286, 5287, 5288, 5289, 5290, 5291, 5292, 5293, 5294, 5295, 5296, 5297, 5298, 5299, 5300, 5301, 5302, 5303, 5304, 5305, 5306, 5307, 5308, 5309, 5310, 5311, 5312, 5313, 5314, 5315, 5316, 5317, 5318, 5319, 5320, 5321, 5322, 5323, 5324, 5325, 5326, 5327, 5328, 5329, 5330, 5331, 5332, 5333, 5334, 5335, 5336, 5337, 5338, 5339, 5340, 5341, 5342, 5343, 5344, 5345, 5346, 5347, 5348, 5349, 5350, 5351, 5352, 5353, 5354, 5355, 5356, 5357, 5358, 5359, 5360, 5361, 5362, 5363, 5364, 5365, 5366, 5367, 5368, 5369, 5370, 5371, 5372, 5373, 5374, 5375, 5376, 5377, 5378, 5379, 5380, 5381, 5382, 5383, 5384, 5385, 5386, 5387, 5388, 5389, 5390, 5391, 5392, 5393, 5394, 5395, 5396, 5397, 5398, 5399, 5400, 5401, 5402, 5403, 5404, 5405, 5406, 5407, 5408, 5409, 5410, 5411, 5412, 5413, 5414, 5415, 5416, 5417, 5418, 5419, 5420, 5421, 5422, 5423, 5424, 5425, 5426, 5427, 5428, 5429, 5430, 5431, 5432, 5433, 5434, 5435, 5436, 5437, 5438, 5439, 5440, 5441, 5442, 5443, 5444, 5445, 5446, 5447, 5448, 5449, 5450, 5451, 5452, 5453, 5454, 5455, 5456, 5457, 5458, 5459, 5460, 5461, 5462, 5463, 5464, 5465, 5466, 5467, 5468, 5469, 5470, 5471, 5472, 5473, 5474, 5475, 5476, 5477, 5478, 5479, 5480, 5481, 5482, 5483, 5484, 5485, 5486, 5487, 5488, 5489, 5490, 5491, 5492, 5493, 5494, 5495, 5496, 5497, 5498, 5499, 5500, 5501, 5502, 5503, 5504, 5505, 5506, 5507, 5508, 5509, 5510, 5511, 5512, 5513, 5514, 5515, 5516, 5517, 5518, 5519, 5520, 5521, 5522, 5523, 5524, 5525, 5526, 5527, 5528, 5529, 5530, 5531, 5532, 5533, 5534, 5535, 5536, 5537, 5538, 5539, 5540, 5541, 5542, 5543, 5544, 5545, 5546, 5547, 5548, 5549, 5550, 5551, 5552, 5553, 5554, 5555, 5556, 5557, 5558, 5559, 5560, 5561, 5562, 5563, 5564, 5565, 5566, 5567, 5568, 5569, 5570, 5571, 5572, 5573, 5574, 5575, 5576, 5577, 5578, 5579, 5580, 5581, 5582, 5583, 5584, 5585, 5586, 5587, 5588, 5589, 5590, 5591, 5592, 5593, 5594, 5595, 5596, 5597, 5598, 5599, 5600, 5601, 5602, 5603, 5604, 5605, 5606, 5607, 5608, 5609, 5610, 5611, 5612, 5613, 5614, 5615, 5616, 5617, 5618, 5619, 5620, 5621, 5622, 5623, 5624, 5625, 5626, 5627, 5628, 5629, 5630, 5631, 5632, 5633, 5634, 5635, 5636, 5637, 5638, 5639, 5640, 5641, 5642, 5643, 5644, 5645, 5646, 5647, 5648, 5649, 5650, 5651, 5652, 5653, 5654, 5655, 5656, 5657, 5658, 5659, 5660, 5661, 5662, 5663, 5664, 5665, 5666, 5667, 5668, 5669, 5670, 5671, 5672, 5673, 5674, 5675, 5676, 5677, 5678, 5679, 5680, 5681, 5682, 5683, 5684, 5685, 5686, 5687, 5688, 5689, 5690, 5691, 5692, 5693, 5694, 5695, 5696, 5697, 5698, 5699, 5700, 5701, 5702, 5703, 5704, 5705, 5706, 5707, 5708, 5709, 5710, 5711, 5712, 5713, 5714, 5715, 5716, 5717, 5718, 5719, 5720, 5721, 5722, 5723, 5724, 5725, 5726, 5727, 5728, 5729, 5730, 5731, 5732, 5733, 5734, 5735, 5736, 5737, 5738, 5739, 5740, 5741, 5742, 5743, 5744, 5745, 5746, 5747, 5748, 5749, 5750, 5751, 5752, 5753, 5754, 5755, 5756, 5757, 5758, 5759, 5760, 5761, 5762, 5763, 5764, 5765, 5766, 5767, 5768, 5769, 5770, 5771, 5772, 5773, 5774, 5775, 5776, 5777, 5778, 5779, 5780, 5781, 5782, 5783, 5784, 5785, 5786, 5787, 5788, 5789, 5790, 5791, 5792, 5793, 5794, 5795, 5796, 5797, 5798, 5799, 5800, 5801, 5802, 5803, 5804, 5805, 5806, 5807, 5808, 5809, 5810, 5811, 5812, 5813, 5814, 5815, 5816, 5817, 5818, 5819, 5820, 5821, 5822, 5823, 5824, 5825, 5826, 5827, 5828, 5829, 5830, 5831, 5832, 5833, 5834, 5835, 5836, 5837, 5838, 5839, 5840, 5841, 5842, 5843, 5844, 5845, 5846, 5847, 5848, 5849, 5850, 5851, 5852, 5853, 5854, 5855, 5856, 5857, 5858, 5859, 5860, 5861, 5862, 5863, 5864, 5865, 5866, 5867, 5868, 5869, 5870, 5871, 5872, 5873, 5874, 5875, 5876, 5877, 5878, 5879, 5880, 5881, 5882, 5883, 5884, 5885, 5886, 5887, 5888, 5889, 5890, 5891, 5892, 5893, 5894, 5895, 5896, 5897, 5898, 5899, 5900, 5901, 5902, 5903, 5904, 5905, 5906, 5907, 5908, 5909, 5910, 5911, 5912, 5913, 5914, 5915, 5916, 5917, 5918, 5919, 5920, 5921, 5922, 5923, 5924, 5925, 5926, 5927, 5928, 5929, 5930, 5931, 5932, 5933, 5934, 5935, 5936, 5937, 5938, 5939, 5940, 5941, 5942, 5943, 5944, 5945, 5946, 5947, 5948, 5949, 5950, 5951, 5952, 5953, 5954, 5955, 5956, 5957, 5958, 5959, 5960, 5961, 5962, 5963, 5964, 5965, 5966, 5967, 5968, 5969, 5970, 5971, 5972, 5973, 5974, 5975, 5976, 5977, 5978, 5979, 5980, 5981, 5982, 5983, 5984, 5985, 5986, 5987, 5988, 5989, 5990, 5991, 5992, 5993, 5994, 5995, 5996, 5997, 5998, 5999, 6000, 6001, 6002, 6003, 6004, 6005, 6006, 6007, 6008, 6009, 6010, 6011, 6012, 6013, 6014, 6015, 6016, 6017, 6018, 6019, 6020, 6021, 6022, 6023, 6024, 6025, 6026, 6027, 6028, 6029, 6030, 6031, 6032, 6033, 6034, 6035, 6036, 6037, 6038, 6039, 6040, 6041, 6042, 6043, 6044, 6045, 6046, 6047, 6048, 6049, 6050, 6051, 6052, 6053, 6054, 6055, 6056, 6057, 6058, 6059, 6060, 6061, 6062, 6063, 6064, 6065, 6066, 6067, 6068, 6069, 6070, 6071, 6072, 6073, 6074, 6075, 6076, 6077, 6078, 6079, 6080, 6081, 6082, 6083, 6084, 6085, 6086, 6087, 6088, 6089, 6090, 6091, 6092, 6093, 6094, 6095, 6096, 6097, 6098, 6099, 6100, 6101, 6102, 6103, 6104, 6105, 6106, 6107, 6108, 6109, 6110, 6111, 6112, 6113, 6114, 6115, 6116, 6117, 6118, 6119, 6120, 6121, 6122, 6123, 6124, 6125, 6126, 6127, 6128, 6129, 6130, 6131, 6132, 6133, 6134, 6135, 6136, 6137, 6138, 6139, 6140, 6141, 6142, 6143, 6144, 6145, 6146, 6147, 6148, 6149, 6150, 6151, 6152, 6153, 6154, 6155, 6156, 6157, 6158, 6159, 6160, 6161, 6162, 6163, 6164, 6165, 6166, 6167, 6168, 6169, 6170, 6171, 6172, 6173, 6174, 6175, 6176, 6177, 6178, 6179, 6180, 6181, 6182, 6183, 6184, 6185, 6186, 6187, 6188, 6189, 6190, 6191, 6192, 6193, 6194, 6195, 6196, 6197, 6198, 6199, 6200, 6201, 6202, 6203, 6204, 6205, 6206, 6207, 6208, 6209, 6210, 6211, 6212, 6213, 6214, 6215, 6216, 6217, 6218, 6219, 6220, 6221, 6222, 6223, 6224, 6225, 6226, 6227, 6228, 6229, 6230, 6231, 6232, 6233, 6234, 6235, 6236, 6237, 6238, 6239, 6240, 6241, 6242, 6243, 6244, 6245, 6246, 6247, 6248, 6249, 6250, 6251, 6252, 6253, 6254, 6255, 6256, 6257, 6258, 6259, 6260, 6261, 6262, 6263, 6264, 6265, 6266, 6267, 6268, 6269, 6270, 6271, 6272, 6273, 6274, 6275, 6276, 6277, 6278, 6279, 6280, 6281, 6282, 6283, 6284, 6285, 6286, 6287, 6288, 6289, 6290, 6291, 6292, 6293, 6294, 6295, 6296, 6297, 6298, 6299, 6300, 6301, 6302, 6303, 6304, 6305, 6306, 6307, 6308, 6309, 6310, 6311, 6312, 6313, 6314, 6315, 6316, 6317, 6318, 6319, 6320, 6321, 6322, 6323, 6324, 6325, 6326, 6327, 6328, 6329, 6330, 6331, 6332, 6333, 6334, 6335, 6336, 6337, 6338, 6339, 6340, 6341, 6342, 6343, 6344, 6345, 6346, 6347, 6348, 6349, 6350, 6351, 6352, 6353, 6354, 6355, 6356, 6357, 6358, 6359, 6360, 6361, 6362, 6363, 6364, 6365, 6366, 6367, 6368, 6369, 6370, 6371, 6372, 6373, 6374, 6375, 6376, 6377, 6378, 6379, 6380, 6381, 6382, 6383, 6384, 6385, 6386, 6387, 6388, 6389, 6390, 6391, 6392, 6393, 6394, 6395, 6396, 6397, 6398, 6399, 6400, 6401, 6402, 6403, 6404, 6405, 6406, 6407, 6408, 6409, 6410, 6411, 6412, 6413, 6414, 6415, 6416, 6417, 6418, 6419, 6420, 6421, 6422, 6423, 6424, 6425, 6426, 6427, 6428, 6429, 6430, 6431, 6432, 6433, 6434, 6435, 6436, 6437, 6438, 6439, 6440, 6441, 6442, 6443, 6444, 6445, 6446, 6447, 6448, 6449, 6450, 6451, 6452, 6453, 6454, 6455, 6456, 6457, 6458, 6459, 6460, 6461, 6462, 6463, 6464, 6465, 6466, 6467, 6468, 6469, 6470, 6471, 6472, 6473, 6474, 6475, 6476, 6477, 6478, 6479, 6480, 6481, 6482, 6483, 6484, 6485, 6486, 6487, 6488, 6489, 6490, 6491, 6492, 6493, 6494, 6495, 6496, 6497, 6498, 6499, 6500, 6501, 6502, 6503, 6504, 6505, 6506, 6507, 6508, 6509, 6510, 6511, 6512, 6513, 6514, 6515, 6516, 6517, 6518, 6519, 6520, 6521, 6522, 6523, 6524, 6525, 6526, 6527, 6528, 6529, 6530, 6531, 6532, 6533, 6534, 6535, 6536, 6537, 6538, 6539, 6540, 6541, 6542, 6543, 6544, 6545, 6546, 6547, 6548, 6549, 6550, 6551, 6552, 6553, 6554, 6555, 6556, 6557, 6558, 6559, 6560, 6561, 6562, 6563, 6564, 6565, 6566, 6567, 6568, 6569, 6570, 6571, 6572, 6573, 6574, 6575, 6576, 6577, 6578, 6579, 6580, 6581, 6582, 6583, 6584, 6585, 6586, 6587, 6588, 6589, 6590, 6591, 6592, 6593, 6594, 6595, 6596, 6597, 6598, 6599, 6600, 6601, 6602, 6603, 6604, 6605, 6606, 6607, 6608, 6609, 6610, 6611, 6612, 6613, 6614, 6615, 6616, 6617, 6618, 6619, 6620, 6621, 6622, 6623, 6624, 6625, 6626, 6627, 6628, 6629, 6630, 6631, 6632, 6633, 6634, 6635, 6636, 6637, 6638, 6639, 6640, 6641, 6642, 6643, 6644, 6645, 6646, 6647, 6648, 6649, 6650, 6651, 6652, 6653, 6654, 6655, 6656, 6657, 6658, 6659, 6660, 6661, 6662, 6663, 6664, 6665, 6666, 6667, 6668, 6669, 6670, 6671, 6672, 6673, 6674, 6675, 6676, 6677, 6678, 6679, 6680, 6681, 6682, 6683, 6684, 6685, 6686, 6687, 6688, 6689, 6690, 6691, 6692, 6693, 6694, 6695, 6696, 6697, 6698, 6699, 6700, 6701, 6702, 6703, 6704, 6705, 6706, 6707, 6708, 6709, 6710, 6711, 6712, 6713, 6714, 6715, 6716, 6717, 6718, 6719, 6720, 6721, 6722, 6723, 6724, 6725, 6726, 6727, 6728, 6729, 6730, 6731, 6732, 6733, 6734, 6735, 6736, 6737, 6738, 6739, 6740, 6741, 6742, 6743, 6744, 6745, 6746, 6747, 6748, 6749, 6750, 6751, 6752, 6753, 6754, 6755, 6756, 6757, 6758, 6759, 6760, 6761, 6762, 6763, 6764, 6765, 6766, 6767, 6768, 6769, 6770, 6771, 6772, 6773, 6774, 6775, 6776, 6777, 6778, 6779, 6780, 6781, 6782, 6783, 6784, 6785, 6786, 6787, 6788, 6789, 6790, 6791, 6792, 6793, 6794, 6795, 6796, 6797, 6798, 6799, 6800, 6801, 6802, 6803, 6804, 6805, 6806, 6807, 6808, 6809, 6810, 6811, 6812, 6813, 6814, 6815, 6816, 6817, 6818, 6819, 6820, 6821, 6822, 6823, 6824, 6825, 6826, 6827, 6828, 6829, 6830, 6831, 6832, 6833, 6834, 6835, 6836, 6837, 6838, 6839, 6840, 6841, 6842, 6843, 6844, 6845, 6846, 6847, 6848, 6849, 6850, 6851, 6852, 6853, 6854, 6855, 6856, 6857, 6858, 6859, 6860, 6861, 6862, 6863, 6864, 6865, 6866, 6867, 6868, 6869, 6870, 6871, 6872, 6873, 6874, 6875, 6876, 6877, 6878, 6879, 6880, 6881, 6882, 6883, 6884, 6885, 6886, 6887, 6888, 6889, 6890, 6891, 6892, 6893, 6894, 6895, 6896, 6897, 6898, 6899, 6900, 6901, 6902, 6903, 6904, 6905, 6906, 6907, 6908, 6909, 6910, 6911, 6912, 6913, 6914, 6915, 6916, 6917, 6918, 6919, 6920, 6921, 6922, 6923, 6924, 6925, 6926, 6927, 6928, 6929, 6930, 6931, 6932, 6933, 6934, 6935, 6936, 6937, 6938, 6939, 6940, 6941, 6942, 6943, 6944, 6945, 6946, 6947, 6948, 6949, 6950, 6951, 6952, 6953, 6954, 6955, 6956, 6957, 6958, 6959, 6960, 6961, 6962, 6963, 6964, 6965, 6966, 6967, 6968, 6969, 6970, 6971, 6972, 6973, 6974, 6975, 6976, 6977, 6978, 6979, 6980, 6981, 6982, 6983, 6984, 6985, 6986, 6987, 6988, 6989, 6990, 6991, 6992, 6993, 6994, 6995, 6996, 6997, 6998, 6999, 7000, 7001, 7002, 7003, 7004, 7005, 7006, 7007, 7008, 7009, 7010, 7011, 7012, 7013, 7014, 7015, 7016, 7017, 7018, 7019, 7020, 7021, 7022, 7023, 7024, 7025, 7026, 7027, 7028, 7029, 7030, 7031, 7032, 7033, 7034, 7035, 7036, 7037, 7038, 7039, 7040, 7041, 7042, 7043, 7044, 7045, 7046, 7047, 7048, 7049, 7050, 7051, 7052, 7053, 7054, 7055, 7056, 7057, 7058, 7059, 7060, 7061, 7062, 7063, 7064, 7065, 7066, 7067, 7068, 7069, 7070, 7071, 7072, 7073, 7074, 7075, 7076, 7077, 7078, 7079, 7080, 7081, 7082, 7083, 7084, 7085, 7086, 7087, 7088, 7089, 7090, 7091, 7092, 7093, 7094, 7095, 7096, 7097, 7098, 7099, 7100, 7101, 7102, 7103, 7104, 7105, 7106, 7107, 7108, 7109, 7110, 7111, 7112, 7113, 7114, 7115, 7116, 7117, 7118, 7119, 7120, 7121, 7122, 7123, 7124, 7125, 7126, 7127, 7128, 7129, 7130, 7131, 7132, 7133, 7134, 7135, 7136, 7137, 7138, 7139, 7140, 7141, 7142, 7143, 7144, 7145, 7146, 7147, 7148, 7149, 7150, 7151, 7152, 7153, 7154, 7155, 7156, 7157, 7158, 7159, 7160, 7161, 7162, 7163, 7164, 7165, 7166, 7167, 7168, 7169, 7170, 7171, 7172, 7173, 7174, 7175, 7176, 7177, 7178, 7179, 7180, 7181, 7182, 7183, 7184, 7185, 7186, 7187, 7188, 7189, 7190, 7191, 7192, 7193, 7194, 7195, 7196, 7197, 7198, 7199, 7200, 7201, 7202, 7203, 7204, 7205, 7206, 7207, 7208, 7209, 7210, 7211, 7212, 7213, 7214, 7215, 7216, 7217, 7218, 7219, 7220, 7221, 7222, 7223, 7224, 7225, 7226, 7227, 7228, 7229, 7230, 7231, 7232, 7233, 7234, 7235, 7236, 7237, 7238, 7239, 7240, 7241, 7242, 7243, 7244, 7245, 7246, 7247, 7248, 7249, 7250, 7251, 7252, 7253, 7254, 7255, 7256, 7257, 7258, 7259, 7260, 7261, 7262, 7263, 7264, 7265, 7266, 7267, 7268, 7269, 7270, 7271, 7272, 7273, 7274, 7275, 7276, 7277, 7278, 7279, 7280, 7281, 7282, 7283, 7284, 7285, 7286, 7287, 7288, 7289, 7290, 7291, 7292, 7293, 7294, 7295, 7296, 7297, 7298, 7299, 7300, 7301, 7302, 7303, 7304, 7305, 7306, 7307, 7308, 7309, 7310, 7311, 7312, 7313, 7314, 7315, 7316, 7317, 7318, 7319, 7320, 7321, 7322, 7323, 7324, 7325, 7326, 7327, 7328, 7329, 7330, 7331, 7332, 7333, 7334, 7335, 7336, 7337, 7338, 7339, 7340, 7341, 7342, 7343, 7344, 7345, 7346, 7347, 7348, 7349, 7350, 7351, 7352, 7353, 7354, 7355, 7356, 7357, 7358, 7359, 7360, 7361, 7362, 7363, 7364, 7365, 7366, 7367, 7368, 7369, 7370, 7371, 7372, 7373, 7374, 7375, 7376, 7377, 7378, 7379, 7380, 7381, 7382, 7383, 7384, 7385, 7386, 7387, 7388, 7389, 7390, 7391, 7392, 7393, 7394, 7395, 7396, 7397, 7398, 7399, 7400, 7401, 7402, 7403, 7404, 7405, 7406, 7407, 7408, 7409, 7410, 7411, 7412, 7413, 7414, 7415, 7416, 7417, 7418, 7419, 7420, 7421, 7422, 7423, 7424, 7425, 7426, 7427, 7428, 7429, 7430, 7431, 7432, 7433, 7434, 7435, 7436, 7437, 7438, 7439, 7440, 7441, 7442, 7443, 7444, 7445, 7446, 7447, 7448, 7449, 7450, 7451, 7452, 7453, 7454, 7455, 7456, 7457, 7458, 7459, 7460, 7461, 7462, 7463, 7464, 7465, 7466, 7467, 7468, 7469, 7470, 7471, 7472, 7473, 7474, 7475, 7476, 7477, 7478, 7479, 7480, 7481, 7482, 7483, 7484, 7485, 7486, 7487, 7488, 7489, 7490, 7491, 7492, 7493, 7494, 7495, 7496, 7497, 7498, 7499, 7500, 7501, 7502, 7503, 7504, 7505, 7506, 7507, 7508, 7509, 7510, 7511, 7512, 7513, 7514, 7515, 7516, 7517, 7518, 7519, 7520, 7521, 7522, 7523, 7524, 7525, 7526, 7527, 7528, 7529, 7530, 7531, 7532, 7533, 7534, 7535, 7536, 7537, 7538, 7539, 7540, 7541, 7542, 7543, 7544, 7545, 7546, 7547, 7548, 7549, 7550, 7551, 7552, 7553, 7554, 7555, 7556, 7557, 7558, 7559, 7560, 7561, 7562, 7563, 7564, 7565, 7566, 7567, 7568, 7569, 7570, 7571, 7572, 7573, 7574, 7575, 7576, 7577, 7578, 7579, 7580, 7581, 7582, 7583, 7584, 7585, 7586, 7587, 7588, 7589, 7590, 7591, 7592, 7593, 7594, 7595, 7596, 7597, 7598, 7599, 7600, 7601, 7602, 7603, 7604, 7605, 7606, 7607, 7608, 7609, 7610, 7611, 7612, 7613, 7614, 7615, 7616, 7617, 7618, 7619, 7620, 7621, 7622, 7623, 7624, 7625, 7626, 7627, 7628, 7629, 7630, 7631, 7632, 7633, 7634, 7635, 7636, 7637, 7638, 7639, 7640, 7641, 7642, 7643, 7644, 7645, 7646, 7647, 7648, 7649, 7650, 7651, 7652, 7653, 7654, 7655, 7656, 7657, 7658, 7659, 7660, 7661, 7662, 7663, 7664, 7665, 7666, 7667, 7668, 7669, 7670, 7671, 7672, 7673, 7674, 7675, 7676, 7677, 7678, 7679, 7680, 7681, 7682, 7683, 7684, 7685, 7686, 7687, 7688, 7689, 7690, 7691, 7692, 7693, 7694, 7695, 7696, 7697, 7698, 7699, 7700, 7701, 7702, 7703, 7704, 7705, 7706, 7707, 7708, 7709, 7710, 7711, 7712, 7713, 7714, 7715, 7716, 7717, 7718, 7719, 7720, 7721, 7722, 7723, 7724, 7725, 7726, 7727, 7728, 7729, 7730, 7731, 7732, 7733, 7734, 7735, 7736, 7737, 7738, 7739, 7740, 7741, 7742, 7743, 7744, 7745, 7746, 7747, 7748, 7749, 7750, 7751, 7752, 7753, 7754, 7755, 7756, 7757, 7758, 7759, 7760, 7761, 7762, 7763, 7764, 7765, 7766, 7767, 7768, 7769, 7770, 7771, 7772, 7773, 7774, 7775, 7776, 7777, 7778, 7779, 7780, 7781, 7782, 7783, 7784, 7785, 7786, 7787, 7788, 7789, 7790, 7791, 7792, 7793, 7794, 7795, 7796, 7797, 7798, 7799, 7800, 7801, 7802, 7803, 7804, 7805, 7806, 7807, 7808, 7809, 7810, 7811, 7812, 7813, 7814, 7815, 7816, 7817, 7818, 7819, 7820, 7821, 7822, 7823, 7824, 7825, 7826, 7827, 7828, 7829, 7830, 7831, 7832, 7833, 7834, 7835, 7836, 7837, 7838, 7839, 7840, 7841, 7842, 7843, 7844, 7845, 7846, 7847, 7848, 7849, 7850, 7851, 7852, 7853, 7854, 7855, 7856, 7857, 7858, 7859, 7860, 7861, 7862, 7863, 7864, 7865, 7866, 7867, 7868, 7869, 7870, 7871, 7872, 7873, 7874, 7875, 7876, 7877, 7878, 7879, 7880, 7881, 7882, 7883, 7884, 7885, 7886, 7887, 7888, 7889, 7890, 7891, 7892, 7893, 7894, 7895, 7896, 7897, 7898, 7899, 7900, 7901, 7902, 7903, 7904, 7905, 7906, 7907, 7908, 7909, 7910, 7911, 7912, 7913, 7914, 7915, 7916, 7917, 7918, 7919, 7920, 7921, 7922, 7923, 7924, 7925, 7926, 7927, 7928, 7929, 7930, 7931, 7932, 7933, 7934, 7935, 7936, 7937, 7938, 7939, 7940, 7941, 7942, 7943, 7944, 7945, 7946, 7947, 7948, 7949, 7950, 7951, 7952, 7953, 7954, 7955, 7956, 7957, 7958, 7959, 7960, 7961, 7962, 7963, 7964, 7965, 7966, 7967, 7968, 7969, 7970, 7971, 7972, 7973, 7974, 7975, 7976, 7977, 7978, 7979, 7980, 7981, 7982, 7983, 7984, 7985, 7986, 7987, 7988, 7989, 7990, 7991, 7992, 7993, 7994, 7995, 7996, 7997, 7998, 7999, 8000, 8001, 8002, 8003, 8004, 8005, 8006, 8007, 8008, 8009, 8010, 8011, 8012, 8013, 8014, 8015, 8016, 8017, 8018, 8019, 8020, 8021, 8022, 8023, 8024, 8025, 8026, 8027, 8028, 8029, 8030, 8031, 8032, 8033, 8034, 8035, 8036, 8037, 8038, 8039, 8040, 8041, 8042, 8043, 8044, 8045, 8046, 8047, 8048, 8049, 8050, 8051, 8052, 8053, 8054, 8055, 8056, 8057, 8058, 8059, 8060, 8061, 8062, 8063, 8064, 8065, 8066, 8067, 8068, 8069, 8070, 8071, 8072, 8073, 8074, 8075, 8076, 8077, 8078, 8079, 8080, 8081, 8082, 8083, 8084, 8085, 8086, 8087, 8088, 8089, 8090, 8091, 8092, 8093, 8094, 8095, 8096, 8097, 8098, 8099, 8100, 8101, 8102, 8103, 8104, 8105, 8106, 8107, 8108, 8109, 8110, 8111, 8112, 8113, 8114, 8115, 8116, 8117, 8118, 8119, 8120, 8121, 8122, 8123, 8124, 8125, 8126, 8127, 8128, 8129, 8130, 8131, 8132, 8133, 8134, 8135, 8136, 8137, 8138, 8139, 8140, 8141, 8142, 8143, 8144, 8145, 8146, 8147, 8148, 8149, 8150, 8151, 8152, 8153, 8154, 8155, 8156, 8157, 8158, 8159, 8160, 8161, 8162, 8163, 8164, 8165, 8166, 8167, 8168, 8169, 8170, 8171, 8172, 8173, 8174, 8175, 8176, 8177, 8178, 8179, 8180, 8181, 8182, 8183, 8184, 8185, 8186, 8187, 8188, 8189, 8190, 8191, 8192, 8193, 8194, 8195, 8196, 8197, 8198, 8199, 8200, 8201, 8202, 8203, 8204, 8205, 8206, 8207, 8208, 8209, 8210, 8211, 8212, 8213, 8214, 8215, 8216, 8217, 8218, 8219, 8220, 8221, 8222, 8223, 8224, 8225, 8226, 8227, 8228, 8229, 8230, 8231, 8232, 8233, 8234, 8235, 8236, 8237, 8238, 8239, 8240, 8241, 8242, 8243, 8244, 8245, 8246, 8247, 8248, 8249, 8250, 8251, 8252, 8253, 8254, 8255, 8256, 8257, 8258, 8259, 8260, 8261, 8262, 8263, 8264, 8265, 8266, 8267, 8268, 8269, 8270, 8271, 8272, 8273, 8274, 8275, 8276, 8277, 8278, 8279, 8280, 8281, 8282, 8283, 8284, 8285, 8286, 8287, 8288, 8289, 8290, 8291, 8292, 8293, 8294, 8295, 8296, 8297, 8298, 8299, 8300, 8301, 8302, 8303, 8304, 8305, 8306, 8307, 8308, 8309, 8310, 8311, 8312, 8313, 8314, 8315, 8316, 8317, 8318, 8319, 8320, 8321, 8322, 8323, 8324, 8325, 8326, 8327, 8328, 8329, 8330, 8331, 8332, 8333, 8334, 8335, 8336, 8337, 8338, 8339, 8340, 8341, 8342, 8343, 8344, 8345, 8346, 8347, 8348, 8349, 8350, 8351, 8352, 8353, 8354, 8355, 8356, 8357, 8358, 8359, 8360, 8361, 8362, 8363, 8364, 8365, 8366, 8367, 8368, 8369, 8370, 8371, 8372, 8373, 8374, 8375, 8376, 8377, 8378, 8379, 8380, 8381, 8382, 8383, 8384, 8385, 8386, 8387, 8388, 8389, 8390, 8391, 8392, 8393, 8394, 8395, 8396, 8397, 8398, 8399, 8400, 8401, 8402, 8403, 8404, 8405, 8406, 8407, 8408, 8409, 8410, 8411, 8412, 8413, 8414, 8415, 8416, 8417, 8418, 8419, 8420, 8421, 8422, 8423, 8424, 8425, 8426, 8427, 8428, 8429, 8430, 8431, 8432, 8433, 8434, 8435, 8436, 8437, 8438, 8439, 8440, 8441, 8442, 8443, 8444, 8445, 8446, 8447, 8448, 8449, 8450, 8451, 8452, 8453, 8454, 8455, 8456, 8457, 8458, 8459, 8460, 8461, 8462, 8463, 8464, 8465, 8466, 8467, 8468, 8469, 8470, 8471, 8472, 8473, 8474, 8475, 8476, 8477, 8478, 8479, 8480, 8481, 8482, 8483, 8484, 8485, 8486, 8487, 8488, 8489, 8490, 8491, 8492, 8493, 8494, 8495, 8496, 8497, 8498, 8499, 8500, 8501, 8502, 8503, 8504, 8505, 8506, 8507, 8508, 8509, 8510, 8511, 8512, 8513, 8514, 8515, 8516, 8517, 8518, 8519, 8520, 8521, 8522, 8523, 8524, 8525, 8526, 8527, 8528, 8529, 8530, 8531, 8532, 8533, 8534, 8535, 8536, 8537, 8538, 8539, 8540, 8541, 8542, 8543, 8544, 8545, 8546, 8547, 8548, 8549, 8550, 8551, 8552, 8553, 8554, 8555, 8556, 8557, 8558, 8559, 8560, 8561, 8562, 8563, 8564, 8565, 8566, 8567, 8568, 8569, 8570, 8571, 8572, 8573, 8574, 8575, 8576, 8577, 8578, 8579, 8580, 8581, 8582, 8583, 8584, 8585, 8586, 8587, 8588, 8589, 8590, 8591, 8592, 8593, 8594, 8595, 8596, 8597, 8598, 8599, 8600, 8601, 8602, 8603, 8604, 8605, 8606, 8607, 8608, 8609, 8610, 8611, 8612, 8613, 8614, 8615, 8616, 8617, 8618, 8619, 8620, 8621, 8622, 8623, 8624, 8625, 8626, 8627, 8628, 8629, 8630, 8631, 8632, 8633, 8634, 8635, 8636, 8637, 8638, 8639, 8640, 8641, 8642, 8643, 8644, 8645, 8646, 8647, 8648, 8649, 8650, 8651, 8652, 8653, 8654, 8655, 8656, 8657, 8658, 8659, 8660, 8661, 8662, 8663, 8664, 8665, 8666, 8667, 8668, 8669, 8670, 8671, 8672, 8673, 8674, 8675, 8676, 8677, 8678, 8679, 8680, 8681, 8682, 8683, 8684, 8685, 8686, 8687, 8688, 8689, 8690, 8691, 8692, 8693, 8694, 8695, 8696, 8697, 8698, 8699, 8700, 8701, 8702, 8703, 8704, 8705, 8706, 8707, 8708, 8709, 8710, 8711, 8712, 8713, 8714, 8715, 8716, 8717, 8718, 8719, 8720, 8721, 8722, 8723, 8724, 8725, 8726, 8727, 8728, 8729, 8730, 8731, 8732, 8733, 8734, 8735, 8736, 8737, 8738, 8739, 8740, 8741, 8742, 8743, 8744, 8745, 8746, 8747, 8748, 8749, 8750, 8751, 8752, 8753, 8754, 8755, 8756, 8757, 8758, 8759, 8760, 8761, 8762, 8763, 8764, 8765, 8766, 8767, 8768, 8769, 8770, 8771, 8772, 8773, 8774, 8775, 8776, 8777, 8778, 8779, 8780, 8781, 8782, 8783, 8784, 8785, 8786, 8787, 8788, 8789, 8790, 8791, 8792, 8793, 8794, 8795, 8796, 8797, 8798, 8799, 8800, 8801, 8802, 8803, 8804, 8805, 8806, 8807, 8808, 8809, 8810, 8811, 8812, 8813, 8814, 8815, 8816, 8817, 8818, 8819, 8820, 8821, 8822, 8823, 8824, 8825, 8826, 8827, 8828, 8829, 8830, 8831, 8832, 8833, 8834, 8835, 8836, 8837, 8838, 8839, 8840, 8841, 8842, 8843, 8844, 8845, 8846, 8847, 8848, 8849, 8850, 8851, 8852, 8853, 8854, 8855, 8856, 8857, 8858, 8859, 8860, 8861, 8862, 8863, 8864, 8865, 8866, 8867, 8868, 8869, 8870, 8871, 8872, 8873, 8874, 8875, 8876, 8877, 8878, 8879, 8880, 8881, 8882, 8883, 8884, 8885, 8886, 8887, 8888, 8889, 8890, 8891, 8892, 8893, 8894, 8895, 8896, 8897, 8898, 8899, 8900, 8901, 8902, 8903, 8904, 8905, 8906, 8907, 8908, 8909, 8910, 8911, 8912, 8913, 8914, 8915, 8916, 8917, 8918, 8919, 8920, 8921, 8922, 8923, 8924, 8925, 8926, 8927, 8928, 8929, 8930, 8931, 8932, 8933, 8934, 8935, 8936, 8937, 8938, 8939, 8940, 8941, 8942, 8943, 8944, 8945, 8946, 8947, 8948, 8949, 8950, 8951, 8952, 8953, 8954, 8955, 8956, 8957, 8958, 8959, 8960, 8961, 8962, 8963, 8964, 8965, 8966, 8967, 8968, 8969, 8970, 8971, 8972, 8973, 8974, 8975, 8976, 8977, 8978, 8979, 8980, 8981, 8982, 8983, 8984, 8985, 8986, 8987, 8988, 8989, 8990, 8991, 8992, 8993, 8994, 8995, 8996, 8997, 8998, 8999, 9000, 9001, 9002, 9003, 9004, 9005, 9006, 9007, 9008, 9009, 9010, 9011, 9012, 9013, 9014, 9015, 9016, 9017, 9018, 9019, 9020, 9021, 9022, 9023, 9024, 9025, 9026, 9027, 9028, 9029, 9030, 9031, 9032, 9033, 9034, 9035, 9036, 9037, 9038, 9039, 9040, 9041, 9042, 9043, 9044, 9045, 9046, 9047, 9048, 9049, 9050, 9051, 9052, 9053, 9054, 9055, 9056, 9057, 9058, 9059, 9060, 9061, 9062, 9063, 9064, 9065, 9066, 9067, 9068, 9069, 9070, 9071, 9072, 9073, 9074, 9075, 9076, 9077, 9078, 9079, 9080, 9081, 9082, 9083, 9084, 9085, 9086, 9087, 9088, 9089, 9090, 9091, 9092, 9093, 9094, 9095, 9096, 9097, 9098, 9099, 9100, 9101, 9102, 9103, 9104, 9105, 9106, 9107, 9108, 9109, 9110, 9111, 9112, 9113, 9114, 9115, 9116, 9117, 9118, 9119, 9120, 9121, 9122, 9123, 9124, 9125, 9126, 9127, 9128, 9129, 9130, 9131, 9132, 9133, 9134, 9135, 9136, 9137, 9138, 9139, 9140, 9141, 9142, 9143, 9144, 9145, 9146, 9147, 9148, 9149, 9150, 9151, 9152, 9153, 9154, 9155, 9156, 9157, 9158, 9159, 9160, 9161, 9162, 9163, 9164, 9165, 9166, 9167, 9168, 9169, 9170, 9171, 9172, 9173, 9174, 9175, 9176, 9177, 9178, 9179, 9180, 9181, 9182, 9183, 9184, 9185, 9186, 9187, 9188, 9189, 9190, 9191, 9192, 9193, 9194, 9195, 9196, 9197, 9198, 9199, 9200, 9201, 9202, 9203, 9204, 9205, 9206, 9207, 9208, 9209, 9210, 9211, 9212, 9213, 9214, 9215, 9216, 9217, 9218, 9219, 9220, 9221, 9222, 9223, 9224, 9225, 9226, 9227, 9228, 9229, 9230, 9231, 9232, 9233, 9234, 9235, 9236, 9237, 9238, 9239, 9240, 9241, 9242, 9243, 9244, 9245, 9246, 9247, 9248, 9249, 9250, 9251, 9252, 9253, 9254, 9255, 9256, 9257, 9258, 9259, 9260, 9261, 9262, 9263, 9264, 9265, 9266, 9267, 9268, 9269, 9270, 9271, 9272, 9273, 9274, 9275, 9276, 9277, 9278, 9279, 9280, 9281, 9282, 9283, 9284, 9285, 9286, 9287, 9288, 9289, 9290, 9291, 9292, 9293, 9294, 9295, 9296, 9297, 9298, 9299, 9300, 9301, 9302, 9303, 9304, 9305, 9306, 9307, 9308, 9309, 9310, 9311, 9312, 9313, 9314, 9315, 9316, 9317, 9318, 9319, 9320, 9321, 9322, 9323, 9324, 9325, 9326, 9327, 9328, 9329, 9330, 9331, 9332, 9333, 9334, 9335, 9336, 9337, 9338, 9339, 9340, 9341, 9342, 9343, 9344, 9345, 9346, 9347, 9348, 9349, 9350, 9351, 9352, 9353, 9354, 9355, 9356, 9357, 9358, 9359, 9360, 9361, 9362, 9363, 9364, 9365, 9366, 9367, 9368, 9369, 9370, 9371, 9372, 9373, 9374, 9375, 9376, 9377, 9378, 9379, 9380, 9381, 9382, 9383, 9384, 9385, 9386, 9387, 9388, 9389, 9390, 9391, 9392, 9393, 9394, 9395, 9396, 9397, 9398, 9399, 9400, 9401, 9402, 9403, 9404, 9405, 9406, 9407, 9408, 9409, 9410, 9411, 9412, 9413, 9414, 9415, 9416, 9417, 9418, 9419, 9420, 9421, 9422, 9423, 9424, 9425, 9426, 9427, 9428, 9429, 9430, 9431, 9432, 9433, 9434, 9435, 9436, 9437, 9438, 9439, 9440, 9441, 9442, 9443, 9444, 9445, 9446, 9447, 9448, 9449, 9450, 9451, 9452, 9453, 9454, 9455, 9456, 9457, 9458, 9459, 9460, 9461, 9462, 9463, 9464, 9465, 9466, 9467, 9468, 9469, 9470, 9471, 9472, 9473, 9474, 9475, 9476, 9477, 9478, 9479, 9480, 9481, 9482, 9483, 9484, 9485, 9486, 9487, 9488, 9489, 9490, 9491, 9492, 9493, 9494, 9495, 9496, 9497, 9498, 9499, 9500, 9501, 9502, 9503, 9504, 9505, 9506, 9507, 9508, 9509, 9510, 9511, 9512, 9513, 9514, 9515, 9516, 9517, 9518, 9519, 9520, 9521, 9522, 9523, 9524, 9525, 9526, 9527, 9528, 9529, 9530, 9531, 9532, 9533, 9534, 9535, 9536, 9537, 9538, 9539, 9540, 9541, 9542, 9543, 9544, 9545, 9546, 9547, 9548, 9549, 9550, 9551, 9552, 9553, 9554, 9555, 9556, 9557, 9558, 9559, 9560, 9561, 9562, 9563, 9564, 9565, 9566, 9567, 9568, 9569, 9570, 9571, 9572, 9573, 9574, 9575, 9576, 9577, 9578, 9579, 9580, 9581, 9582, 9583, 9584, 9585, 9586, 9587, 9588, 9589, 9590, 9591, 9592, 9593, 9594, 9595, 9596, 9597, 9598, 9599, 9600, 9601, 9602, 9603, 9604, 9605, 9606, 9607, 9608, 9609, 9610, 9611, 9612, 9613, 9614, 9615, 9616, 9617, 9618, 9619, 9620, 9621, 9622, 9623, 9624, 9625, 9626, 9627, 9628, 9629, 9630, 9631, 9632, 9633, 9634, 9635, 9636, 9637, 9638, 9639, 9640, 9641, 9642, 9643, 9644, 9645, 9646, 9647, 9648, 9649, 9650, 9651, 9652, 9653, 9654, 9655, 9656, 9657, 9658, 9659, 9660, 9661, 9662, 9663, 9664, 9665, 9666, 9667, 9668, 9669, 9670, 9671, 9672, 9673, 9674, 9675, 9676, 9677, 9678, 9679, 9680, 9681, 9682, 9683, 9684, 9685, 9686, 9687, 9688, 9689, 9690, 9691, 9692, 9693, 9694, 9695, 9696, 9697, 9698, 9699, 9700, 9701, 9702, 9703, 9704, 9705, 9706, 9707, 9708, 9709, 9710, 9711, 9712, 9713, 9714, 9715, 9716, 9717, 9718, 9719, 9720, 9721, 9722, 9723, 9724, 9725, 9726, 9727, 9728, 9729, 9730, 9731, 9732, 9733, 9734, 9735, 9736, 9737, 9738, 9739, 9740, 9741, 9742, 9743, 9744, 9745, 9746, 9747, 9748, 9749, 9750, 9751, 9752, 9753, 9754, 9755, 9756, 9757, 9758, 9759, 9760, 9761, 9762, 9763, 9764, 9765, 9766, 9767, 9768, 9769, 9770, 9771, 9772, 9773, 9774, 9775, 9776, 9777, 9778, 9779, 9780, 9781, 9782, 9783, 9784, 9785, 9786, 9787, 9788, 9789, 9790, 9791, 9792, 9793, 9794, 9795, 9796, 9797, 9798, 9799, 9800, 9801, 9802, 9803, 9804, 9805, 9806, 9807, 9808, 9809, 9810, 9811, 9812, 9813, 9814, 9815, 9816, 9817, 9818, 9819, 9820, 9821, 9822, 9823, 9824, 9825, 9826, 9827, 9828, 9829, 9830, 9831, 9832, 9833, 9834, 9835, 9836, 9837, 9838, 9839, 9840, 9841, 9842, 9843, 9844, 9845, 9846, 9847, 9848, 9849, 9850, 9851, 9852, 9853, 9854, 9855, 9856, 9857, 9858, 9859, 9860, 9861, 9862, 9863, 9864, 9865, 9866, 9867, 9868, 9869, 9870, 9871, 9872, 9873, 9874, 9875, 9876, 9877, 9878, 9879, 9880, 9881, 9882, 9883, 9884, 9885, 9886, 9887, 9888, 9889, 9890, 9891, 9892, 9893, 9894, 9895, 9896, 9897, 9898, 9899, 9900, 9901, 9902, 9903, 9904, 9905, 9906, 9907, 9908, 9909, 9910, 9911, 9912, 9913, 9914, 9915, 9916, 9917, 9918, 9919, 9920, 9921, 9922, 9923, 9924, 9925, 9926, 9927, 9928, 9929, 9930, 9931, 9932, 9933, 9934, 9935, 9936, 9937, 9938, 9939, 9940, 9941, 9942, 9943, 9944, 9945, 9946, 9947, 9948, 9949, 9950, 9951, 9952, 9953, 9954, 9955, 9956, 9957, 9958, 9959, 9960, 9961, 9962, 9963, 9964, 9965, 9966, 9967, 9968, 9969, 9970, 9971, 9972, 9973, 9974, 9975, 9976, 9977, 9978, 9979, 9980, 9981, 9982, 9983, 9984, 9985, 9986, 9987, 9988, 9989, 9990, 9991, 9992, 9993, 9994, 9995, 9996, 9997, 9998, 9999] ###Markdown (3d) Perform action `count` to view counts One of the most basic jobs that we can run is the `count()` job which will count the number of elements in an RDD using the `count()` action. Since `map()` creates a new RDD with the same number of elements as the starting RDD, we expect that applying `count()` to each RDD will return the same result. Note that because `count()` is an action operation, if we had not already performed an action with `collect()`, then Spark would now perform the transformation operations when we executed `count()`. Each task counts the entries in its partition and sends the result to your SparkContext, which adds up all of the counts. The figure below shows what would happen if we ran `count()` on a small example dataset with just four partitions.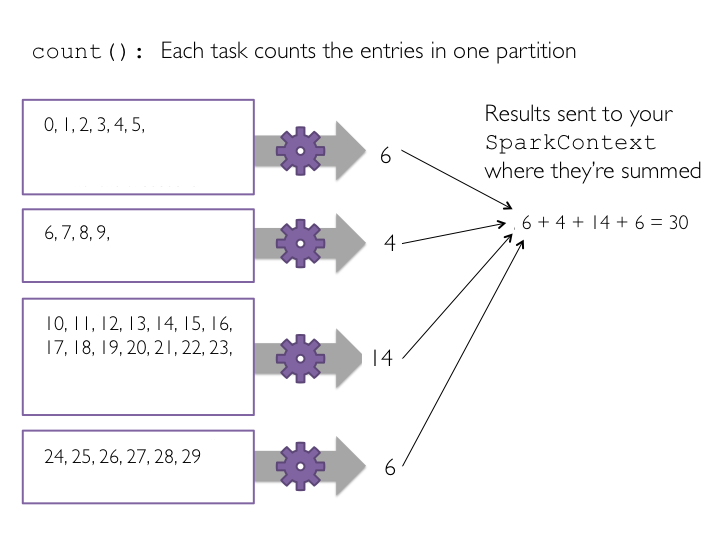![count](http://spark-mooc.github.io/web-assets/images/count.png) ###Code print xrangeRDD.count() print subRDD.count() ###Output 10000 10000 ###Markdown (3e) Apply transformation `filter` and view results with `collect` Next, we'll create a new RDD that only contains the values less than ten by using the `filter(f)` data-parallel operation. The `filter(f)` method is a transformation operation that creates a new RDD from the input RDD by applying filter function `f` to each item in the parent RDD and only passing those elements where the filter function returns `True`. Elements that do not return `True` will be dropped. Like `map()`, filter can be applied individually to each entry in the dataset, so is easily parallelized using Spark. The figure below shows how this would work on the small four-partition dataset.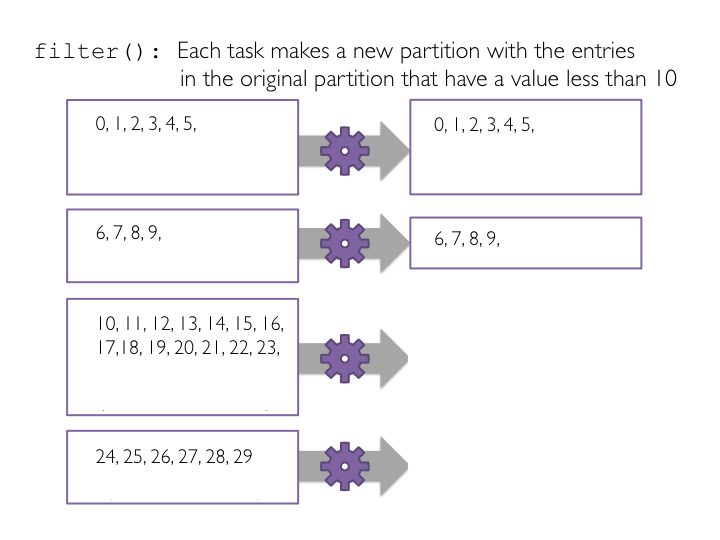![filter](http://spark-mooc.github.io/web-assets/images/filter.png) To filter this dataset, we'll define a function called `ten()`, which returns `True` if the input is less than 10 and `False` otherwise. This function will be passed to the `filter()` transformation as the filter function `f`. To view the filtered list of elements less than ten, we need to create a new list on the driver from the distributed data on the executor nodes. We use the `collect()` method to return a list that contains all of the elements in this filtered RDD to the driver program. ###Code # Define a function to filter a single value def ten(value): """Return whether value is below ten. Args: value (int): A number. Returns: bool: Whether `value` is less than ten. """ if (value < 10): return True else: return False # The ten function could also be written concisely as: def ten(value): return value < 10 # Pass the function ten to the filter transformation # Filter is a transformation so no tasks are run filteredRDD = subRDD.filter(ten) # View the results using collect() # Collect is an action and triggers the filter transformation to run print filteredRDD.collect() ###Output [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] ###Markdown Part 4: Lambda Functions (4a) Using Python `lambda()` functions Python supports the use of small one-line anonymous functions that are not bound to a name at runtime. Borrowed from LISP, these `lambda` functions can be used wherever function objects are required. They are syntactically restricted to a single expression. Remember that `lambda` functions are a matter of style and using them is never required - semantically, they are just syntactic sugar for a normal function definition. You can always define a separate normal function instead, but using a `lambda()` function is an equivalent and more compact form of coding. Ideally you should consider using `lambda` functions where you want to encapsulate non-reusable code without littering your code with one-line functions. Here, instead of defining a separate function for the `filter()` transformation, we will use an inline `lambda()` function. ###Code lambdaRDD = subRDD.filter(lambda x: x < 10) lambdaRDD.collect() # Let's collect the even values less than 10 evenRDD = lambdaRDD.filter(lambda x: x % 2 == 0) evenRDD.collect() ###Output _____no_output_____ ###Markdown Part 5: Additional RDD actions (5a) Other common actions Let's investigate the additional actions: [first()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.first), [take()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.take), [top()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.top), [takeOrdered()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.takeOrdered), and [reduce()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.reduce) One useful thing to do when we have a new dataset is to look at the first few entries to obtain a rough idea of what information is available. In Spark, we can do that using the `first()`, `take()`, `top()`, and `takeOrdered()` actions. Note that for the `first()` and `take()` actions, the elements that are returned depend on how the RDD is partitioned. Instead of using the `collect()` action, we can use the `take(n)` action to return the first n elements of the RDD. The `first()` action returns the first element of an RDD, and is equivalent to `take(1)`. The `takeOrdered()` action returns the first n elements of the RDD, using either their natural order or a custom comparator. The key advantage of using `takeOrdered()` instead of `first()` or `take()` is that `takeOrdered()` returns a deterministic result, while the other two actions may return differing results, depending on the number of partions or execution environment. `takeOrdered()` returns the list sorted in ascending order. The `top()` action is similar to `takeOrdered()` except that it returns the list in descending order. The `reduce()` action reduces the elements of a RDD to a single value by applying a function that takes two parameters and returns a single value. The function should be commutative and associative, as `reduce()` is applied at the partition level and then again to aggregate results from partitions. If these rules don't hold, the results from `reduce()` will be inconsistent. Reducing locally at partitions makes `reduce()` very efficient. ###Code # Let's get the first element print filteredRDD.first() # The first 4 print filteredRDD.take(4) # Note that it is ok to take more elements than the RDD has print filteredRDD.take(12) # Retrieve the three smallest elements print filteredRDD.takeOrdered(3) # Retrieve the five largest elements print filteredRDD.top(5) # Pass a lambda function to takeOrdered to reverse the order filteredRDD.takeOrdered(4, lambda s: -s) # Obtain Python's add function from operator import add # Efficiently sum the RDD using reduce print filteredRDD.reduce(add) # Sum using reduce with a lambda function print filteredRDD.reduce(lambda a, b: a + b) # Note that subtraction is not both associative and commutative print filteredRDD.reduce(lambda a, b: a - b) print filteredRDD.repartition(4).reduce(lambda a, b: a - b) # While addition is print filteredRDD.repartition(4).reduce(lambda a, b: a + b) ###Output 45 45 -45 21 45 ###Markdown (5b) Advanced actions Here are two additional actions that are useful for retrieving information from an RDD: [takeSample()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.takeSample) and [countByValue()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.countByValue) The `takeSample()` action returns an array with a random sample of elements from the dataset. It takes in a `withReplacement` argument, which specifies whether it is okay to randomly pick the same item multiple times from the parent RDD (so when `withReplacement=True`, you can get the same item back multiple times). It also takes an optional `seed` parameter that allows you to specify a seed value for the random number generator, so that reproducible results can be obtained. The `countByValue()` action returns the count of each unique value in the RDD as a dictionary that maps values to counts. ###Code # takeSample reusing elements print filteredRDD.takeSample(withReplacement=True, num=6) # takeSample without reuse print filteredRDD.takeSample(withReplacement=False, num=6) # Set seed for predictability print filteredRDD.takeSample(withReplacement=False, num=6, seed=500) # Try reruning this cell and the cell above -- the results from this cell will remain constant # Use ctrl-enter to run without moving to the next cell # Create new base RDD to show countByValue repetitiveRDD = sc.parallelize([1, 2, 3, 1, 2, 3, 1, 2, 1, 2, 3, 3, 3, 4, 5, 4, 6]) print repetitiveRDD.countByValue() ###Output defaultdict(<type 'int'>, {1: 4, 2: 4, 3: 5, 4: 2, 5: 1, 6: 1}) ###Markdown Part 6: Additional RDD transformations (6a) `flatMap` When performing a `map()` transformation using a function, sometimes the function will return more (or less) than one element. We would like the newly created RDD to consist of the elements outputted by the function. Simply applying a `map()` transformation would yield a new RDD made up of iterators. Each iterator could have zero or more elements. Instead, we often want an RDD consisting of the values contained in those iterators. The solution is to use a [flatMap()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.flatMap) transformation, `flatMap()` is similar to `map()`, except that with `flatMap()` each input item can be mapped to zero or more output elements. To demonstrate `flatMap()`, we will first emit a word along with its plural, and then a range that grows in length with each subsequent operation. ###Code # Let's create a new base RDD to work from wordsList = ['cat', 'elephant', 'rat', 'rat', 'cat'] wordsRDD = sc.parallelize(wordsList, 4) # Use map singularAndPluralWordsRDDMap = wordsRDD.map(lambda x: (x, x + 's')) # Use flatMap singularAndPluralWordsRDD = wordsRDD.flatMap(lambda x: (x, x + 's')) # View the results print singularAndPluralWordsRDDMap.collect() print singularAndPluralWordsRDD.collect() # View the number of elements in the RDD print singularAndPluralWordsRDDMap.count() print singularAndPluralWordsRDD.count() simpleRDD = sc.parallelize([2, 3, 4]) print simpleRDD.map(lambda x: range(1, x)).collect() print simpleRDD.flatMap(lambda x: range(1, x)).collect() ###Output [[1], [1, 2], [1, 2, 3]] [1, 1, 2, 1, 2, 3] ###Markdown (6b) `groupByKey` and `reduceByKey` Let's investigate the additional transformations: [groupByKey()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.groupByKey) and [reduceByKey()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.reduceByKey). Both of these transformations operate on pair RDDs. A pair RDD is an RDD where each element is a pair tuple (key, value). For example, `sc.parallelize([('a', 1), ('a', 2), ('b', 1)])` would create a pair RDD where the keys are 'a', 'a', 'b' and the values are 1, 2, 1. The `reduceByKey()` transformation gathers together pairs that have the same key and applies a function to two associated values at a time. `reduceByKey()` operates by applying the function first within each partition on a per-key basis and then across the partitions. While both the `groupByKey()` and `reduceByKey()` transformations can often be used to solve the same problem and will produce the same answer, the `reduceByKey()` transformation works much better for large distributed datasets. This is because Spark knows it can combine output with a common key on each partition before shuffling (redistributing) the data across nodes. Only use `groupByKey()` if the operation would not benefit from reducing the data before the shuffle occurs. Look at the diagram below to understand how `reduceByKey` works. Notice how pairs on the same machine with the same key are combined (by using the lamdba function passed into reduceByKey) before the data is shuffled. Then the lamdba function is called again to reduce all the values from each partition to produce one final result.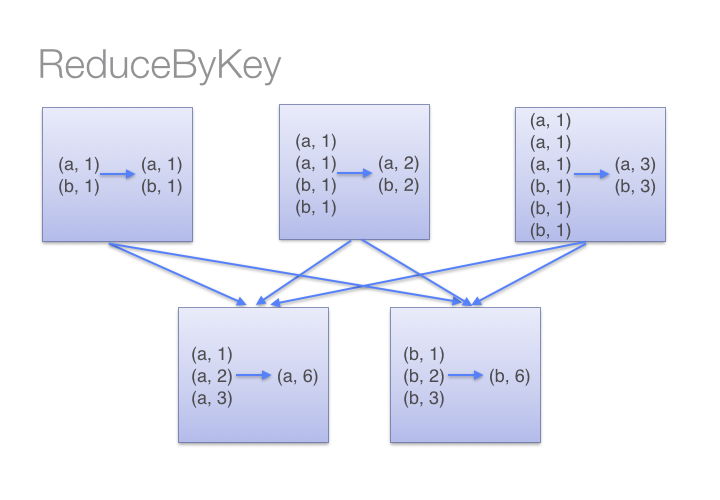![reduceByKey() figure](http://spark-mooc.github.io/web-assets/images/reduce_by.png) On the other hand, when using the `groupByKey()` transformation - all the key-value pairs are shuffled around, causing a lot of unnecessary data to being transferred over the network. To determine which machine to shuffle a pair to, Spark calls a partitioning function on the key of the pair. Spark spills data to disk when there is more data shuffled onto a single executor machine than can fit in memory. However, it flushes out the data to disk one key at a time, so if a single key has more key-value pairs than can fit in memory an out of memory exception occurs. This will be more gracefully handled in a later release of Spark so that the job can still proceed, but should still be avoided. When Spark needs to spill to disk, performance is severely impacted.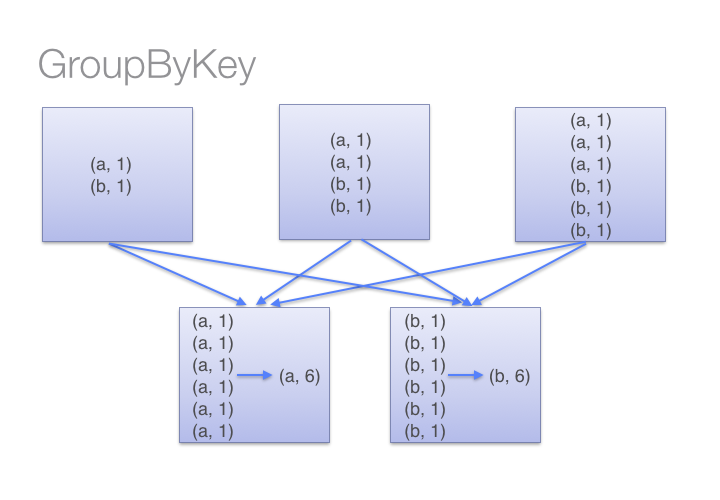![groupByKey() figure](http://spark-mooc.github.io/web-assets/images/group_by.png) As your dataset grows, the difference in the amount of data that needs to be shuffled, between the `reduceByKey()` and `groupByKey()` transformations, becomes increasingly exaggerated. Here are more transformations to prefer over `groupByKey()`: + [combineByKey()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.combineByKey) can be used when you are combining elements but your return type differs from your input value type. + [foldByKey()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.foldByKey) merges the values for each key using an associative function and a neutral "zero value". Now let's go through a simple `groupByKey()` and `reduceByKey()` example. ###Code pairRDD = sc.parallelize([('a', 1), ('a', 2), ('b', 1)]) # mapValues only used to improve format for printing print pairRDD.groupByKey().mapValues(lambda x: list(x)).collect() # Different ways to sum by key print pairRDD.groupByKey().map(lambda (k, v): (k, sum(v))).collect() # Using mapValues, which is recommended when they key doesn't change print pairRDD.groupByKey().mapValues(lambda x: sum(x)).collect() # reduceByKey is more efficient / scalable print pairRDD.reduceByKey(add).collect() ###Output [('a', [1, 2]), ('b', [1])] [('a', 3), ('b', 1)] [('a', 3), ('b', 1)] [('a', 3), ('b', 1)] ###Markdown (6c) Advanced transformations [Optional] Let's investigate the advanced transformations: [mapPartitions()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.mapPartitions) and [mapPartitionsWithIndex()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.mapPartitionsWithIndex) The `mapPartitions()` transformation uses a function that takes in an iterator (to the items in that specific partition) and returns an iterator. The function is applied on a partition by partition basis. The `mapPartitionsWithIndex()` transformation uses a function that takes in a partition index (think of this like the partition number) and an iterator (to the items in that specific partition). For every partition (index, iterator) pair, the function returns a tuple of the same partition index number and an iterator of the transformed items in that partition. ###Code # mapPartitions takes a function that takes an iterator and returns an iterator print wordsRDD.collect() itemsRDD = wordsRDD.mapPartitions(lambda iterator: [','.join(iterator)]) print itemsRDD.collect() itemsByPartRDD = wordsRDD.mapPartitionsWithIndex(lambda index, iterator: [(index, list(iterator))]) # We can see that three of the (partitions) workers have one element and the fourth worker has two # elements, although things may not bode well for the rat... print itemsByPartRDD.collect() # Rerun without returning a list (acts more like flatMap) itemsByPartRDD = wordsRDD.mapPartitionsWithIndex(lambda index, iterator: (index, list(iterator))) print itemsByPartRDD.collect() ###Output [(0, ['cat']), (1, ['elephant']), (2, ['rat']), (3, ['rat', 'cat'])] [0, ['cat'], 1, ['elephant'], 2, ['rat'], 3, ['rat', 'cat']] ###Markdown Part 7: Caching RDDs and storage options (7a) Caching RDDs For efficiency Spark keeps your RDDs in memory. By keeping the contents in memory, Spark can quickly access the data. However, memory is limited, so if you try to keep too many RDDs in memory, Spark will automatically delete RDDs from memory to make space for new RDDs. If you later refer to one of the RDDs, Spark will automatically recreate the RDD for you, but that takes time. So, if you plan to use an RDD more than once, then you should tell Spark to cache that RDD. You can use the `cache()` operation to keep the RDD in memory. However, if you cache too many RDDs and Spark runs out of memory, it will delete the least recently used (LRU) RDD first. Again, the RDD will be automatically recreated when accessed. You can check if an RDD is cached by using the `is_cached` attribute, and you can see your cached RDD in the "Storage" section of the Spark web UI. If you click on the RDD's name, you can see more information about where the RDD is stored. ###Code # Name the RDD filteredRDD.setName('My Filtered RDD') # Cache the RDD filteredRDD.cache() # Is it cached print filteredRDD.is_cached ###Output True ###Markdown (7b) Unpersist and storage options Spark automatically manages the RDDs cached in memory and will save them to disk if it runs out of memory. For efficiency, once you are finished using an RDD, you can optionally tell Spark to stop caching it in memory by using the RDD's `unpersist()` method to inform Spark that you no longer need the RDD in memory. You can see the set of transformations that were applied to create an RDD by using the `toDebugString()` method, which will provide storage information, and you can directly query the current storage information for an RDD using the `getStorageLevel()` operation. Advanced: Spark provides many more options for managing how RDDs are stored in memory or even saved to disk. You can explore the API for RDD's [persist()](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.RDD.persist) operation using Python's [help()](https://docs.python.org/2/library/functions.html?highlight=helphelp) command. The `persist()` operation, optionally, takes a pySpark [StorageLevel](http://spark.apache.org/docs/latest/api/python/pyspark.htmlpyspark.StorageLevel) object. ###Code # Note that toDebugString also provides storage information print filteredRDD.toDebugString() # If we are done with the RDD we can unpersist it so that its memory can be reclaimed filteredRDD.unpersist() # Storage level for a non cached RDD print filteredRDD.getStorageLevel() filteredRDD.cache() # Storage level for a cached RDD print filteredRDD.getStorageLevel() ###Output Serialized 1x Replicated Memory Serialized 1x Replicated ###Markdown Part 8: Debugging Spark applications and lazy evaluation How Python is Executed in Spark Internally, Spark executes using a Java Virtual Machine (JVM). pySpark runs Python code in a JVM using [Py4J](http://py4j.sourceforge.net). Py4J enables Python programs running in a Python interpreter to dynamically access Java objects in a Java Virtual Machine. Methods are called as if the Java objects resided in the Python interpreter and Java collections can be accessed through standard Python collection methods. Py4J also enables Java programs to call back Python objects. Because pySpark uses Py4J, coding errors often result in a complicated, confusing stack trace that can be difficult to understand. In the following section, we'll explore how to understand stack traces. (8a) Challenges with lazy evaluation using transformations and actions Spark's use of lazy evaluation can make debugging more difficult because code is not always executed immediately. To see an example of how this can happen, let's first define a broken filter function. Next we perform a `filter()` operation using the broken filtering function. No error will occur at this point due to Spark's use of lazy evaluation. The `filter()` method will not be executed until an action operation is invoked on the RDD. We will perform an action by using the `collect()` method to return a list that contains all of the elements in this RDD. ###Code def brokenTen(value): """Incorrect implementation of the ten function. Note: The `if` statement checks an undefined variable `val` instead of `value`. Args: value (int): A number. Returns: bool: Whether `value` is less than ten. Raises: NameError: The function references `val`, which is not available in the local or global namespace, so a `NameError` is raised. """ if (val < 10): return True else: return False brokenRDD = subRDD.filter(brokenTen) # Now we'll see the error brokenRDD.collect() ###Output _____no_output_____ ###Markdown (8b) Finding the bug When the `filter()` method is executed, Spark evaluates the RDD by executing the `parallelize()` and `filter()` methods. Since our `filter()` method has an error in the filtering function `brokenTen()`, an error occurs. Scroll through the output "Py4JJavaError Traceback (most recent call last)" part of the cell and first you will see that the line that generated the error is the `collect()` method line. There is nothing wrong with this line. However, it is an action and that caused other methods to be executed. Continue scrolling through the Traceback and you will see the following error line: NameError: global name 'val' is not defined Looking at this error line, we can see that we used the wrong variable name in our filtering function `brokenTen()`. (8c) Moving toward expert style As you are learning Spark, I recommend that you write your code in the form: RDD.transformation1() RDD.action1() RDD.transformation2() RDD.action2() Using this style will make debugging your code much easier as it makes errors easier to localize - errors in your transformations will occur when the next action is executed. Once you become more experienced with Spark, you can write your code with the form: RDD.transformation1().transformation2().action() We can also use `lambda()` functions instead of separately defined functions when their use improves readability and conciseness. ###Code # Cleaner code through lambda use subRDD.filter(lambda x: x < 10).collect() # Even better by moving our chain of operators into a single line. sc.parallelize(data).map(lambda y: y - 1).filter(lambda x: x < 10).collect() ###Output _____no_output_____ ###Markdown (8d) Readability and code style To make the expert coding style more readable, enclose the statement in parentheses and put each method, transformation, or action on a separate line. ###Code # Final version (sc .parallelize(data) .map(lambda y: y - 1) .filter(lambda x: x < 10) .collect()) ###Output _____no_output_____
Insee/notebooks/02.Filtering_data.ipynb	###Markdown 2 Filtering dataIn chapter 1, we have seen how to retrieve data with select. Now you may want to know how can we only retrieve the data that interest us,but not all the rows. We can use the where statement to filter data that satisfied certain conditions. ###Code %load_ext sql %config SqlMagic.autocommit=False %config SqlMagic.autolimit=20 %config SqlMagic.displaylimit=20 %sql postgresql://user-pengfei:gv8eba5xmsw4kt2uk1mn@postgresql-124499/test %%sql SELECT * from orders limit 5; ###Output * postgresql://user-pengfei:**@postgresql-124499/test 5 rows affected. ###Markdown 2.1 Filtering digit columnsTo filter digit column, we need to build a boolean expression such as column_name comparator valuePossible comparators:- equality : =- inequality : !=, or - greater than: >- less than : <- Greater than equal to : >=- Less than equal to : <=Below query is an example, in the boolean expression column name is order_date (we extract the year from the date), comparator is =, value is 1996This query should only return records where the order_date equals to 1996 ###Code %%sql select from orders where extract(year from order_date)=1996 limit 5 ###Output * postgresql://user-pengfei:*@postgresql-124499/test 5 rows affected. ###Markdown What if I want to get all records where year is not equals to 2010. There are two possible ways (!=, or ) to express inequality. Most database servers such as Mysql, Postgresql, SQLite, etc. support both. However, some database server such as Microsoft Access and IBM DB2 only support *. ###Code %%sql select from orders where extract(year from order_date)!=1996 limit 5 %%sql select * from orders where extract(year from order_date)<>1996 limit 5 ###Output * postgresql://pliu:**@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown These two queries do the same thing. You should see the same output. We can also qualify inclusive ranges using a BETWEEN statement, as shown here(“inclusive” means that 1996 and 1997 are included in the range): ###Code %%sql select from orders where extract(year from order_date) between 1996 and 1997 limit 5 ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown 2.2 Combining multiple filtering condition 2.2.1 And operatorWe can express the "between and" range with another expression. For instance the year must be greater than or equal to 2005 and less than or equal to 2010. We need to add two filter and combine the result of the two filter with an and*.Below query should return exactly the same result as the above query ###Code %%sql select from orders where extract(year from order_date) >= 1996 and extract(year from order_date)<= 1997 limit 5 ###Output * postgresql://user-pengfei:**@postgresql-124499/test 5 rows affected. ###Markdown Note the "between and" express an inclusive range, for not inclusive range, we can not use it. As a result, evaluate the and of two filters become very useful. Below query returns orders that order_date > 1996 and < 1998. ###Code %%sql select from orders where extract(year from order_date) > 1996 and extract(year from order_date)< 1998 limit 5 ###Output * postgresql://pliu:**@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown 2.2.2 Or operatorThe OR operator will return the record if at least one of the criteria is true for the record. For instance, if we wanted only orders with months 3, 6, 9, or 12, we can use below query: ###Code %%sql select from orders where extract(month from order_date)=3 or extract(month from order_date)=6 or extract(month from order_date)=9 or extract(month from order_date)=12 limit 5; ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown 2.2.3 In operatorIn the above example, we tested column month with a list of possible value. In this kind of situation, we can use the In** operator. ###Code %%sql select * from orders where extract(month from order_date) in (3,6,9,12) limit 5; ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown We can also express the negation of the in operator by adding not in front of in** operator. ###Code %%sql select * from orders where extract(month from order_date) not in (3,6,9,12) limit 5; ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown 2.2.4 Arithmetic operatorsWe can notice 3,6,9,12 can all be divided by 3. So we can also use another way to get the same records as above examples.Note some database such as Oracle does not support the modulus operator. It instead uses the MOD() function.** ###Code %%sql select * from orders where cast(extract(month from order_date) as integer ) %3=0 limit 5; ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown 2.3 Filtering text columnsThe rules for qualifying text fields follow the same structure, although there are subtle(small) differences. You canuse =, AND, OR, and IN statements with text. However, when using text, you must wrap literals (or text values you specify) in single quotes*. ###Code %%sql SELECT FROM orders WHERE ship_city = 'Paris' limit 5; ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 4 rows affected. ###Markdown Note postgresql does not support double quote** on string value. So below query will return error in postgresql. It works for Mysql or Sqlite ###Code %%sql SELECT * FROM orders WHERE ship_city = "Paris" limit 5; ###Output * postgresql://pliu:**@127.0.0.1:5432/north_wind (psycopg2.errors.UndefinedColumn) column "Paris" does not exist LINE 2: WHERE ship_city = "Paris" ^ [SQL: SELECT FROM orders WHERE ship_city = "Paris" limit 5;] (Background on this error at: https://sqlalche.me/e/14/f405) ###Markdown If we do not add " or ' on Paris, the database server will get confused and think Paris is a column name rather than a text value. This single-quote rule applies to all text operations. For example, below query will return error. ###Code %%sql SELECT * FROM orders WHERE ship_city = Paris limit 5; ###Output * postgresql://pliu:**@127.0.0.1:5432/north_wind (psycopg2.errors.UndefinedColumn) column "paris" does not exist LINE 2: WHERE ship_city = Paris ^ [SQL: SELECT FROM orders WHERE ship_city = Paris limit 5;] (Background on this error at: https://sqlalche.me/e/14/f405) ###Markdown We can also use string value in other filter operations. Below query will return all rows that the ship_city is Paris, London, or Madrid. ###Code %%sql SELECT * FROM orders WHERE ship_city in ('Paris','London','Madrid') limit 5; ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown 2.3.1 Other useful functions filter by using lengthlength** operator can get the length of a text field. For instance, below query will filter all rows that ship_country length is <=2 (e.g. UK). ###Code %%sql SELECT * FROM orders WHERE length(ship_country) <= 2 limit 5 ###Output * postgresql://pliu:**@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown Wild card text filtering with like operatorAnother common operation is to use wildcards with LIKE followed by a regular expression, in the regular expression:- % : means any number of characters an- _ : means any single character.- Any other character is interpreted literally.So, if you wanted to find all orders that have ship_country start with the letter “C” you would run below query to find all text start with “C” and followed by any characters ###Code %%sql select from orders where ship_country like 'C%' limit 5; ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown If you want find all text that have a “C” as the first character and a “n” as the third character, you can run below query.Note the character inside '' is case-sensitive unlike the query command*. Try change below query to 'C_N' and see what happens. ###Code %%sql select from orders where ship_country like 'C_n%' limit 5; ###Output * postgresql://pliu:*@127.0.0.1:5432/north_wind 5 rows affected. ###Markdown 2.4 Handling nullYou may have noticed that in table orders the ship_region column have null values. A null is a value that has no value. It is the complete absence of any content. It is a vacuous state.In sql, Null values cannot be determined with an = . You need to use the IS NULL or IS NOT NULL statements to identify null values*Below query returns all rows that snow_depth is null ###Code %%sql select from orders where ship_region is null limit 5; ###Output * postgresql://user-pengfei:*@postgresql-124499/test 5 rows affected. ###Markdown 2.4.1 Why we even have null values in the database? The null values is useful for some use case. For example, for a table of weather station, the column such as snow_depth or precipitation, it does make sense. Not because it was a sunny day (in this case, it is better to record the values as 0), but rather because some stations might not have the necessary instruments to take those measurements. Can we replace null by 0 for snow_depth?No, It might be misleading to set those values to 0 (which implies data was recorded), so those measurements should be left null.In some columns, we can not have null values. For example, the order_id column should be designed that it never allows nulls. Because if it's null, all the rest columns of this row become orphan data that belongs to no order.We can see that nulls values are ambiguous and it can be difficult to determine their business meaning. It is important that nullable columns (columns that are allowed to have null values) have documented what a null value means from a business perspective. Otherwise, nulls should be banned from those table columns.Do not confuse nulls with empty text(i.e., '' ). This also applies to whitespace text (i.e., ' ') . These will be treated as values andnever will be considered null. A null is definitely not the same as 0 either, because 0 is a value, whereas null is an absence of a value. 2.4.2 Problems caused by null valuesWe know that freight column has null values, try to run the following query. You can notice that the returned rows do not contain any null values. Because null is not 0 or any number, it will not qualify to any condition. So the freight <= 6** filtered out all rows that contain null value. ###Code %%sql SELECT order_id, freight FROM orders WHERE freight <= 6 limit 5 ###Output * postgresql://user-pengfei:**@postgresql-124499/test 5 rows affected. ###Markdown But having a null value does not mean the freight > 6, so we may want to keep those rows that have null values. We can have them by using the following query ###Code %%sql SELECT order_id, freight FROM orders WHERE freight is null or freight <= 6 limit 5 ###Output postgresql://user-pengfei:*@postgresql-124499/test 5 rows affected. ###Markdown The above query works, but we have a more elegant way of handling null values. We can use the coalesce() function*- coalesce(col_name,replacement_value): It takes a column name that may have null value, if the row value is null, then replace it with the given replacement_value.Below query use coalesce to replace all null value of column freight by 0 than compare them with <=6. This will not modify the origin table. ###Code %%sql SELECT order_id, freight FROM orders WHERE coalesce(freight,0) <= 6 limit 5 ###Output postgresql://user-pengfei:**@postgresql-124499/test 5 rows affected. ###Markdown If we want the other user can use the replaced value, we can create a new column by using below query ###Code %%sql SELECT order_id, coalesce(freight, 0) as freight_without_null FROM orders limit 5; ###Output postgresql://user-pengfei:**@postgresql-124499/test 5 rows affected. ###Markdown 2.5 Grouping ConditionsWhen you start chaining "AND" and "OR" together, you need to make sure that you organize each set of conditions between each OR in a way that groups related conditions.For example, we need to find all orders that shipped by company 2 and freight is not bigger than 6 or the . We could write below query. ###Code %%sql select from orders where ship_via = 2 and freight <=6 or ship_city = 'Paris' limit 5; ###Output * postgresql://user-pengfei:*@postgresql-124499/test 5 rows affected. ###Markdown We are lucky this works, because AND, OR have the same priority, sql resolve from left to right. So ship_via = 2 and freight <=6 resolved to a value, then this value get resolved with or ship_city = 'Paris'*. But for a begginer, this can be confusing, he will wonder if AND condition get resolved first or the OR condition get resolved first.To avoid this, we can explicitly group conditions in parentheses. This makes not only makes the semantics clearer, but also the execution safer. ###Code %%sql select from orders where (ship_via = 2 and freight <=6) or ship_city = 'Paris' limit 5; ###Output * postgresql://user-pengfei:***@postgresql-124499/test 5 rows affected.
Notebooks/plots_for_midpoint_presentation.ipynb	###Markdown Some Prior Draws ###Code lh = gpytorch.likelihoods.GaussianLikelihood() model = Surrogate(test_x, true_y, lh, RBFKernel) model.train() lh.train(); n_samples = 4 samples = model(test_x).sample(sample_shape=torch.Size((n_samples,))).squeeze() label_fs = 18 title_fs = 20 leg_fs = 16 lwd = 3. plt.figure(figsize=(10, 6)) sns.set_style("white") colors = sns.color_palette("muted") for smp in range(n_samples): plt.plot(test_x, samples[smp, :].detach(), color=colors[0], linewidth=lwd) # plt.plot(train_x, train_y.detach(), marker="o", linestyle="None", # label="Observations", color=colors[1], markersize=5) # plt.plot(test_x, pred_mean.detach(), label="Predicted Mean", color=colors[0], # linewidth=lwd) # plt.fill_between(test_x, lower.detach(), upper.detach(), # alpha=0.2) plt.title("Prior Samples From Gaussian Process", fontsize=title_fs) plt.xlabel("Input", fontsize=label_fs) plt.ylabel("Response", fontsize=label_fs) plt.xticks([]) plt.yticks([]) sns.despine() plt.legend( fontsize=leg_fs) plt.show() ###Output _____no_output_____ ###Markdown Train and Get Posterior Samples ###Code lh = gpytorch.likelihoods.GaussianLikelihood() model = Surrogate(train_x, train_y, lh, RBFKernel) model.train() lh.train() optimizer = torch.optim.Adam(model.parameters(), lr=0.01) mll = gpytorch.mlls.ExactMarginalLogLikelihood(lh, model) for i in range(500): # Zero gradients from previous iteration optimizer.zero_grad() # Output from model output = model(train_x) # Calc loss and backprop gradients loss = -mll(output, train_y) loss.backward() optimizer.step() # print(loss.item()) model.eval() lh.eval() pred_dist = lh(model(test_x)) pred_mean = pred_dist.mean.detach() lower, upper = pred_dist.confidence_region() import seaborn as sns label_fs = 18 title_fs = 20 leg_fs = 16 lwd = 3. plt.figure(figsize=(10, 6)) sns.set_style("white") colors = sns.color_palette("muted") plt.plot(test_x, true_y.detach(), label="Ground Truth", color=colors[2], linewidth=lwd) plt.plot(train_x, train_y.detach(), marker="o", linestyle="None", label="Observations", color=colors[1], markersize=5) plt.plot(test_x, pred_mean.detach(), label="Predicted Mean", color=colors[0], linewidth=lwd) plt.fill_between(test_x, lower.detach(), upper.detach(), alpha=0.2) plt.xlabel("Input", fontsize=label_fs) plt.ylabel("Response", fontsize=label_fs) plt.title("Posterior Gaussian Process Distribution", fontsize=title_fs) plt.xticks([]) plt.yticks([]) sns.despine() plt.legend(fontsize=leg_fs) plt.show() ###Output _____no_output_____ ###Markdown Bayesian Optimization ###Code train_x = torch.rand(5) * 5 train_y = true_func(train_x) bayesopt = BayesOpt(train_x, train_y, normalize=False, normalize_y=False, max_x=5.) # bayesopt.surrogate.train() # bayesopt.surrogate_lh.train() # optimizer = torch.optim.Adam(bayesopt.surrogate.parameters(), lr=0.01) # mll = gpytorch.mlls.ExactMarginalLogLikelihood(bayesopt.surrogate_lh, # bayesopt.surrogate) # for i in range(200): # # Zero gradients from previous iteration # optimizer.zero_grad() # # Output from model # output = bayesopt.surrogate(bayesopt.train_x) # # Calc loss and backprop gradients # loss = -mll(output, bayesopt.train_y) # loss.backward() # optimizer.step() # print(loss.item()) bayesopt.train_surrogate(200) bayesopt.surrogate next_query = bayesopt.acquire() bayesopt.surrogate.eval(); bayesopt.surrogate_lh.eval(); pred_dist = bayesopt.surrogate_lh(bayesopt.surrogate(test_x)) pred_mean = pred_dist.mean.detach() lower, upper = pred_dist.confidence_region() label_fs = 18 title_fs = 20 leg_fs = 16 lwd = 3. plt.figure(figsize=(10, 6)) sns.set_style("white") colors = sns.color_palette("muted") plt.plot(test_x, true_y.detach(), label="Ground Truth", color=colors[2], linewidth=lwd, linestyle="--") plt.plot(train_x, train_y.detach(), marker="o", linestyle="None", label="Observations", color=colors[1], markersize=8) plt.plot(test_x, pred_mean.detach(), label="Predictive Distribution", color=colors[0], linewidth=lwd) plt.fill_between(test_x, lower.detach(), upper.detach(), alpha=0.2) plt.scatter(next_query, true_func(next_query, 0.).detach(), marker="P", s=200, label="Next Query") plt.xlabel("Input", fontsize=label_fs) plt.ylabel("Response", fontsize=label_fs) plt.title("Optimization", fontsize=title_fs) plt.xticks([]) plt.yticks([]) plt.ylim(-2.5, 2.5) sns.despine() plt.legend(fontsize=leg_fs) plt.show() bayesopt.update_obs(next_query.unsqueeze(0), true_func(next_query).unsqueeze(0)) bayesopt.train_surrogate(200); next_query = bayesopt.acquire() bayesopt.surrogate.eval(); bayesopt.surrogate_lh.eval(); pred_dist = bayesopt.surrogate_lh(bayesopt.surrogate(test_x)) pred_mean = pred_dist.mean.detach() lower, upper = pred_dist.confidence_region() label_fs = 18 title_fs = 20 leg_fs = 16 lwd = 3. plt.figure(figsize=(10, 6)) sns.set_style("white") colors = sns.color_palette("muted") plt.plot(test_x, true_y.detach(), label="Ground Truth", color=colors[2], linewidth=lwd, linestyle="--") plt.plot(bayesopt.train_x, bayesopt.train_y.detach(), marker="o", linestyle="None", label="Observations", color=colors[1], markersize=8) plt.plot(test_x, pred_mean.detach(), label="Predictive Distribution", color=colors[0], linewidth=lwd) plt.fill_between(test_x, lower.detach(), upper.detach(), alpha=0.2) plt.scatter(next_query, true_func(next_query, 0.).detach(), marker="P", s=200, label="Next Query") plt.xlabel("Input", fontsize=label_fs) plt.ylabel("Response", fontsize=label_fs) plt.title("Optimization", fontsize=title_fs) plt.xticks([]) plt.yticks([]) plt.ylim(-2.5, 2.5) sns.despine() plt.legend(fontsize=leg_fs) plt.show() bayesopt.update_obs(next_query.unsqueeze(0), true_func(next_query).unsqueeze(0)) bayesopt.train_surrogate(200); next_query = bayesopt.acquire() bayesopt.surrogate.eval(); bayesopt.surrogate_lh.eval(); pred_dist = bayesopt.surrogate_lh(bayesopt.surrogate(test_x)) pred_mean = pred_dist.mean.detach() lower, upper = pred_dist.confidence_region() label_fs = 18 title_fs = 20 leg_fs = 16 lwd = 3. plt.figure(figsize=(10, 6)) sns.set_style("white") colors = sns.color_palette("muted") plt.plot(test_x, true_y.detach(), label="Ground Truth", color=colors[2], linewidth=lwd, linestyle="--") plt.plot(bayesopt.train_x, bayesopt.train_y.detach(), marker="o", linestyle="None", label="Observations", color=colors[1], markersize=8) plt.plot(test_x, pred_mean.detach(), label="Predictive Distribution", color=colors[0], linewidth=lwd) plt.fill_between(test_x, lower.detach(), upper.detach(), alpha=0.2) plt.scatter(next_query, true_func(next_query, 0.).detach(), marker="P", s=200, label="Next Query") plt.xlabel("Input", fontsize=label_fs) plt.ylabel("Response", fontsize=label_fs) plt.title("Optimization", fontsize=title_fs) plt.xticks([]) plt.yticks([]) plt.ylim(-2.5, 2.5) sns.despine() plt.legend(fontsize=leg_fs) plt.show() ###Output _____no_output_____ ###Markdown Network Plots ###Code import sys sys.path.append("../ntwrk/gym/") import network_sim import gym env = gym.make("PccNs-v0") env.reset() send_rates = torch.arange(1, 1000, 25) n_trial = 100 rwrds = torch.zeros(send_rates.numel(), n_trial) for ind, sr in enumerate(send_rates): for tt in range(n_trial): rwrds[ind, tt] = env.step(sr.unsqueeze(0))[1] env.reset() mean_rwrd = rwrds.mean(1).unsqueeze(-1) std_rwrd = rwrds.std(1).unsqueeze(-1) mean_rwrd.shape sns.set_style("white") sns.set_palette("muted") label_fs = 20 title_fs = 24 tick_fs = 16 plt.figure(figsize=(10, 6)) plt.errorbar(x=send_rates, y=mean_rwrd, yerr=std_rwrd, linestyle="None", marker='o', capsize=3) plt.tick_params(labelsize=tick_fs) plt.title("Reward At Initialization", fontsize=title_fs) plt.xlabel("Send Rate (packets/sec)", fontsize=label_fs) plt.ylabel("Scaled Reward", fontsize=label_fs) sns.despine() plt.show() # init_send_rate = torch.tensor(850).unsqueeze(0) # n_init_send = 20 # n_trial = 100 # rwrds = torch.zeros(send_rates.numel(), n_trial) # for ind, sr in enumerate(send_rates): # for tt in range(n_trial): # for snd in range(n_init_send): # env.step(init_send_rate) # rwrds[ind, tt] = env.step(sr.unsqueeze(0))[1] # env.reset() # mean_rwrd = rwrds.mean(1).unsqueeze(-1) # std_rwrd = rwrds.std(1).unsqueeze(-1) # sns.set_style("white") # sns.set_palette("muted") # label_fs = 20 # title_fs = 24 # tick_fs = 16 # plt.figure(figsize=(10, 6)) # plt.errorbar(x=send_rates, y=mean_rwrd, yerr=std_rwrd, # linestyle="None", marker='o', # capsize=3) # plt.tick_params(labelsize=tick_fs) # plt.title("Reward After 20 Time Steps", fontsize=title_fs) # plt.xlabel("Send Rate (packets/sec)", fontsize=label_fs) # plt.ylabel("Scaled Reward", fontsize=label_fs) # sns.despine() # plt.show() ###Output _____no_output_____ ###Markdown Bayesian Optimization for Network ###Code env = gym.make("PccNs-v0") env.reset() env.senders[0].rate = env.senders[0].starting_rate rate = torch.tensor(env.senders[0].rate).unsqueeze(0) rwrd = torch.tensor(env.step(rate)[1]).unsqueeze(0) max_x = 1000. bayes_opt = BayesOpt(rate, rwrd, normalize=True, normalize_y=False, max_x=max_x, max_jump=400) bayes_opt.surrogate_lh.noise.data = torch.tensor([-1.]) rnds = 10 max_obs = 3 test_points = torch.arange(1, 1000).float().div(max_x) rate_history = torch.zeros(rnds, max_obs + 1) rwrd_history = torch.zeros(rnds, max_obs + 1) pred_means = torch.zeros(rnds, test_points.numel()) pred_lower = torch.zeros(rnds, test_points.numel()) pred_upper = torch.zeros(rnds, test_points.numel()) for ii in range(rnds): bayes_opt.train_surrogate(iters=200, overwrite=True) next_rate = bayes_opt.acquire(explore=0.5).unsqueeze(0) # next_rate = torch.rand(1) rwrd = torch.tensor(env.step(next_rate.mul(bayes_opt.max_x))[1]).unsqueeze(0) print(next_rate, rwrd) rate_history[ii, :bayes_opt.train_x.numel()] = bayes_opt.train_x.clone() rwrd_history[ii, :bayes_opt.train_y.numel()] = bayes_opt.train_y.clone() bayes_opt.update_obs(next_rate, rwrd, max_obs=max_obs) print("train x = ", bayes_opt.train_x) bayes_opt.surrogate_lh.eval() bayes_opt.surrogate.eval() test_dist = bayes_opt.surrogate_lh(bayes_opt.surrogate(test_points)) pred_means[ii, :] = test_dist.mean.detach() pred_lower[ii, :], pred_upper[ii, :] = test_dist.confidence_region() rate_history[ii, -1] = bayes_opt.train_x[-1].clone() rwrd_history[ii, -1] = bayes_opt.train_y[-1].clone() # plt.plot(bayes_opt.train_x[:-1], bayes_opt.train_y[:-1], marker='.', linestyle="None") # plt.plot(bayes_opt.train_x[-1], bayes_opt.train_y[-1], marker='*', linestyle="None") # plt.plot(test_points, test_dist.mean.detach()) # plt.show() # sns.set_style("white") # colors = sns.color_palette("muted") label_fs = 20 title_fs = 24 tick_fs = 16 leg_fs = 18 marksize=15 lwd = 2.5 for rnd in range(rnds): plt.figure(figsize=(10, 6)) plt.plot(rate_history[rnd, :-1], rwrd_history[rnd, :-1], marker=".", linestyle="None", label="Observations", color=colors[1], markersize=marksize) plt.plot(test_points, pred_means[rnd, :], label="Predictive Distribution", linewidth=lwd) plt.scatter(rate_history[rnd, -1], rwrd_history[rnd, -1], marker="P",s=200, label="Next Query", linestyle="None", color=colors[2]) plt.tick_params(labelsize=tick_fs) plt.title("Reward vs Rate Optimization", fontsize=title_fs) plt.xlabel("Send Rate (normalized packets/sec)", fontsize=label_fs) plt.ylabel("Scaled Reward", fontsize=label_fs) plt.legend(loc='upper left') sns.despine() plt.ylim(0, 0.6) plt.show() ###Output _____no_output_____
EDA/EDA_items.ipynb	###Markdown Análisis exploratorio de items_ordered_2years En este cuadeerno se detalla el proceso de análisis de datos de los pedidos realizados Índice de Contenidos 1. Importación de paquetes2. Carga de datos3. Análisis de los datos 3.1. Variables 3.2. Duplicados 3.3. Clientes 3.4. Ventas totales 3.5. Ventas por localización 4. Conclusiones Importación de paquetes Cargamos las librerías a usar. ###Code import pandas as pd import plotly.express as px import random seed = 124 random.seed(seed) ###Output _____no_output_____ ###Markdown Carga de datos Abrimos el fichero y lo cargamos para poder manejar la información ###Code df_items = pd.read_csv('../Data/items_ordered_2years.txt', sep='\|', on_bad_lines='skip',parse_dates=['created_at']) df_items.sample(5, random_state=seed) ###Output _____no_output_____ ###Markdown Análisis de los datos En este apartado se analizarán todas las características de las variables ###Code print("Dimensiones de los datos:", df_items.shape) df_items.isna().sum() ###Output _____no_output_____ ###Markdown Existen datos perdidos o no proporcionados de 3 variables distintas ###Code percent_missing = df_items.isnull().sum() * 100 / df_items.shape[0] df_missing_values = pd.DataFrame({ 'column_name': df_items.columns, 'percent_missing': percent_missing }) df_missing_values.sort_values(by='percent_missing',ascending=False,inplace=True) print(df_missing_values.to_string(index=False)) ###Output column_name percent_missing city 0.323019 zipcode 0.322697 base_cost 0.258028 num_order 0.000000 item_id 0.000000 created_at 0.000000 product_id 0.000000 qty_ordered 0.000000 price 0.000000 discount_percent 0.000000 customer_id 0.000000 ###Markdown Aunque haya datos perdidos, estos no representan una gran proporción respecto al dataset ###Code df_items.info() ###Output <class 'pandas.core.frame.DataFrame'> RangeIndex: 930905 entries, 0 to 930904 Data columns (total 11 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 num_order 930905 non-null object 1 item_id 930905 non-null object 2 created_at 930905 non-null datetime64[ns] 3 product_id 930905 non-null int64 4 qty_ordered 930905 non-null int64 5 base_cost 928503 non-null float64 6 price 930905 non-null float64 7 discount_percent 930905 non-null float64 8 customer_id 930905 non-null object 9 city 927898 non-null object 10 zipcode 927901 non-null object dtypes: datetime64[ns](1), float64(3), int64(2), object(5) memory usage: 60.4+ MB ###Markdown Podemos observar que tenemos 1 variable de tipo fecha, 2 variables que son números enteros (el identificador de producto y la cantidad pedida), 3 variables son números decimales (precio base, precio de venta y porcentaje de descuento) y las demás variables que son clásificadas como tipo object también las podemos considerar de tipo string ###Code df_items.describe() ###Output _____no_output_____ ###Markdown Al echar un vistazo por encima nos podemos dar cuenta de un par de cosas un tanto extrañas:* El mínimo precio base es negativo* El mínimo precio de venta es 0* El mínimo porcentaje de descuento es 1, por lo tanto no hay ningún pedido que no tenga aplicado un porcentaje de descuento ###Code df_items.describe(include=object) ###Output _____no_output_____ ###Markdown Vemos que el número de pedido se repite y esto se debe a que por cada producto distinto que existen dentro de un pedido necesitamos un registro nuevo, y por eso se repide el identificador de pedido Variables Ahora realizaremos un análisis más específico de cada variable num_order Esta variable es el identificador de los pedidos y la podemos ver repetida ya que en un mismo pedido puede haber diferentes productos, y para cada producto distinto dentro de un mismo pedido se usan distintas entradas. ###Code orders = df_items['num_order'].nunique() print(f'Hay {orders} pedidos registrados') df_items['num_order'].value_counts() ###Output _____no_output_____ ###Markdown El máximo de líneas de pedidos son 60, mientras que hay pedidos con tan solo una línea. item_id La variable item_id se usa para identificar el producto dentro del pedido, por lo tanto un mismo producto que este en pedidos distintos tendrá distintos item_id ###Code items = df_items['item_id'].nunique() print(f'Identificadores : {items}') print(f'Registros : {df_items.shape[0]}') ###Output Identificadores : 906266 Registros : 930905 ###Markdown Como se ve no tenemos identificadores de items como registros del dataset lo que nos lleva a pensar que podría haber registros repetidos ###Code df_items['item_id'].value_counts() df_items[df_items['item_id'] == '642b9b87df5b13e91ce86962684c2613'] ###Output _____no_output_____ ###Markdown Nuestras sospechas se confirman, ya que vemos que el mismo pedido tiene las tres mismas líneas. Por tanto, se trata de datos duplicados created_at Instante en el que se realizó el pedido ###Code df_items['created_at'].sample(1,random_state=seed) ###Output _____no_output_____ ###Markdown El formato de la fecha y tiempo es YYYY-MM-DD HH:MM:SS product_id Identificador del producto ###Code products = df_items['product_id'].nunique() print(f'Hay {products} identificadores de productos') # Productos en más frecuentas en los pedidos df_items['product_id'].value_counts() ###Output _____no_output_____ ###Markdown Los productos más comunes en los pedidos, no son exactamente los mismos que los que más cantidad se piden. ###Code # Productos más vendidos (cantidad) df_best_products = df_items.groupby("product_id",as_index=False).agg({"num_order":"count", "qty_ordered":"sum"}).sort_values("qty_ordered", ascending=False) df_best_products.head() ###Output _____no_output_____ ###Markdown qty_ordered Cantidad pedida de cierto producto para un cierto pedido ###Code df_q = df_items.groupby('num_order',as_index=False).agg(total_qty=('qty_ordered','sum'),n_items=('item_id','count')).sort_values('total_qty',ascending=False) df_q.head(10) df_q.tail(10) ###Output _____no_output_____ ###Markdown En el resumen de la descripción del conjunto de datos, ya veíamos que los mínimos y máximos de las cantidades que se piden eran bastante dispares. Con esta tabla vemos como se reparten las cantidades pedidas respecto a los productos dentro del pedido. ###Code df_q['total_qty'].value_counts().head(10) df_q[df_q['total_qty'] > 10].shape[0] ###Output _____no_output_____ ###Markdown Vemos que lo más común es que en los pedidos haya entre 2 y 10 unidades de productos. Aun así hay un número sustancia del pedidos que tienen cantidades superiores a las 10 unidades. base_cost Precio de coste de una unidad de producto sin IVA Como vimos al principio esta columna tiene valores perdidos. Veamos si sería posible recuperarlos mirando base_cost del mismo producto en otros pedidos. ###Code products = df_items[df_items['base_cost'].isna()]['product_id'].drop_duplicates().to_list() print(f'Nº productos con precios nulos: {len(products)}') df_pr = df_items[(df_items['product_id'].isin(products)) & (df_items['base_cost'].notna())][['product_id','base_cost']] print(f"Nº productos que se puede recuperar base_cost: {df_pr['product_id'].nunique()}") df_pr.groupby('product_id',as_index=False).agg(n_cost=('base_cost','count'),mean_cost=('base_cost','mean')).sort_values('n_cost',ascending=False) ###Output Nº productos con precios nulos: 564 Nº productos que se puede recuperar base_cost: 499 ###Markdown Parece ser que se puede recuperar bastantes valores, eso sí hay que decidir que valores imputar porque los productos varían de precio en los diferentes pedidos. Lo más extraño a mencionar es que el precio de coste medio de uno de los productos sea directamente un cero. ###Code neg_bcost = df_items[df_items['base_cost'] < 0].shape[0] print(f'Registros con base_cost negativo: {neg_bcost}') ###Output Registros con base_cost negativo: 46 ###Markdown price Precio unitario de los productos. ###Code pr_zero = df_items[df_items['price'] == 0].shape[0] null_benefits = df_items[(df_items['price'] < df_items['base_cost'])][['product_id','base_cost','price','discount_percent']] print(f'Productos con precio cero: {pr_zero}') print(f'Líneas pedido sin beneficios: {null_benefits.shape[0]}') ###Output Productos con precio cero: 61 Líneas pedido sin beneficios: 10729 ###Markdown Existen registros con precios nulos y también bastantes líneas de pedidos en los que nos se generan beneficios. Puede que estas últimas se traten de descuentos aplicados. ###Code null_benefits.corr() ###Output _____no_output_____ ###Markdown Donde nos surge la gran duda es en que no hay correspondencia entre los costes, precios y descuentos de los productos. Por tanto, podemos intuir que los precios sobre los que se aplican los descuentos no son estos, sino otros, ya que nosotros tenemos los precios finales. discount_percent Porcentaje de descuento aplicado, pero no al precio con el que contamos nosotros. ###Code print(f"Líneas con descuento: {df_items[df_items['discount_percent'] > 0].shape[0]}") print(f'Lineas total: {df_items.shape[0]}') ###Output Líneas con descuento: 930905 Lineas total: 930905 ###Markdown Algo que llama la atención es que todos las líneas de pedidos tienen descuentos ###Code print(f"Cantidad de porc. desc.: {df_items['discount_percent'].nunique()}") df_items['discount_percent'].value_counts().sort_values(ascending=False).head(10) df_items['discount_percent'].value_counts().sort_values(ascending=False).tail(10) ###Output _____no_output_____ ###Markdown Los porcentajes de descuento más comunes son por debajo de 25%, mientras que los menos comunes oscilan entre el 30% y 50%. customer_id El identificador del cliente que ha realizado el pedido ###Code clients = df_items['customer_id'].nunique() print(f'{clients} clientes han realizado pedidos') df_items['customer_id'].sample(5,random_state=seed) ###Output _____no_output_____ ###Markdown Este campo es un hash con el fin de anonimizar los datos personales. city y zipcode Estas variables indican la ciudad en la cuál se han realizado el pedido ###Code print(f"Nº de ciudades: {df_items['city'].nunique()}") print(f"Nº de ciudades: {df_items['zipcode'].nunique()}") ###Output Nº de ciudades: 20993 Nº de ciudades: 11116 ###Markdown Vimos antes que estas dos columnas tienen un número similar de registros nulos, lo que da a entender que puede que coincidan. ###Code df_items[(df_items.city.isna()) & (df_items.zipcode.isna())].shape[0] ###Output _____no_output_____ ###Markdown Tenemos 2910 registros donde no tenemos ninguna información de la dirección, ni la ciudad ni el código postal. A pesar de que no son demasiados registros, es información que no podremos recuperar de ninguna manera, ya que los datos están anonimizados ###Code cities = df_items[(df_items['city'].notna()) & (df_items['city'].str.contains('alba'))]['city'] cities.value_counts() ###Output _____no_output_____ ###Markdown Haciendo una búsqueda sencilla de cadenas, vemos que el campo no está normalizado y hay nombres de ciudades escritos de diferentes maneras. ###Code # Normalizamos los nombres de ciudades indexes = df_items['city'].notna().index df_items.loc[indexes, 'city'] = df_items.loc[indexes, 'city'].apply(lambda x: str(x).lower().strip()) print(f"Nº de ciudades: {df_items['city'].nunique()}") ###Output Nº de ciudades: 11569 ###Markdown Cuando normalizamos vemos que el número de ciudades disminuye. Aun así, faltarían muchos más métodos que aplicar para llegar a normalizar el campo. NOTA Por otro lado, mientras que estabamos limpiando datos, nos dimos cuenta que hay valores númericos para ciudades y códigos postales imputados como nombres. ###Code df_city = df_items[(df_items['city'].notna()) & (df_items['city'].str.isnumeric())] print(f"Nº ciudad con dígitos: {df_city.shape[0]}") df_city[['num_order','city','zipcode']].sample(5,random_state=seed) df_zip = df_items[(df_items['zipcode'].notna()) & (df_items['zipcode'].notna())] df_zip = df_zip[(df_zip['city'].str.isnumeric()) & (~df_zip['zipcode'].str.isnumeric())] print(f"Nº códigos postales y ciudad invertidos: {df_zip.shape[0]}") df_zip[['city','zipcode']].sample(10,random_state=seed) ###Output Nº códigos postales y ciudad invertidos: 357 ###Markdown Duplicados En apartados anteriores intuimos la presencia de registros duplicados, veamos a que se debe. ###Code print(f"Regitros duplicados: {df_items.duplicated().sum()}") df_items[df_items.duplicated()].head(5) ###Output Regitros duplicados: 17599 ###Markdown Clientes que más compran Clientes que más pedidos hacen ###Code df_clients = df_items.groupby(['customer_id', 'num_order'],as_index=False).agg({'qty_ordered':'sum'}) # num_order se repite, por tanto no se puede agregar por el de primeras df_clients = df_clients.groupby(['customer_id'],as_index=False).agg({'num_order':'count', 'qty_ordered':'sum'}) df_clients = df_clients.sort_values('num_order',ascending=False) df_clients.head() ###Output _____no_output_____ ###Markdown Clientes que han comprado una mayor cantidad de productos ###Code df_clientes = df_clients.sort_values('qty_ordered',ascending=False) df_clientes.head() ###Output _____no_output_____ ###Markdown Ventas totales En este apartado veremos las fechas en las cuáles se producen más ventas ###Code # Modificamos la columna para que solo muestre la fecha sin la hora df_items.loc[:, 'date'] = df_items['created_at'].dt.date df_items[['created_at','date']].sample(5,random_state=seed) ###Output _____no_output_____ ###Markdown Agrupamos por fecha para saber la cantidad de productos y el número de pedidos realizados por cada día ###Code df_temp = df_items.groupby(['date', 'num_order']).agg({'qty_ordered':'sum'}).reset_index() # num_order se repite, por tanto no se puede agregar por el de primeras df_temp = df_temp.groupby(['date']).agg({'num_order':'count', 'qty_ordered':'sum'}).reset_index() df_temp.sample(5,random_state=seed) fig = px.area(df_temp, x="date", y="num_order", title='Pedidos realizados por día',) fig.show() ###Output _____no_output_____ ###Markdown Vemos los picos de pedidos en los meses como Noviembre (BlackFriday) y picos en las rebajas tanto de invierno como de verano ###Code fig = px.area(df_temp, x="date", y="qty_ordered", title='Cantidad de productos pedidos por día') fig.show() ###Output _____no_output_____ ###Markdown La cantidad de productos pedidos por día es muy similar en forma a la anterior gráfica, por lo que tienen cierta correlación. Aun así, nos debemos fijar en la escala del eje Y. ###Code df_temp.corr() ###Output _____no_output_____ ###Markdown Ventas por localización Puesto que hemos sacado las coordenadas de cada localización podemos mostrar visualmente donde se han producido más ventas ###Code df_temp = df_items.groupby(['city', 'num_order'],as_index=False).agg({'qty_ordered':'sum'}) # num_order se repite, por tanto no se puede agregar por el de primeras df_temp = df_temp.groupby(['city'],as_index=False).agg({'num_order':'count', 'qty_ordered':'sum'}) df_temp.sort_values('num_order',ascending=False).head(10) ###Output _____no_output_____
conditionals.ipynb	###Markdown Conditionals A very simple program might just be a sequence of statements: a = 1 print(a) a = 2 print(a) But virtually nothing interesting can be written this way -- because what happens can never change. The program cannot change depending on what button you clicked on screen, what packets have come in over the network, what bytes you have read from a file or upon calculations done in advance.We can use simple diagrams to show how branching affects programs. Consider the sequence of statements above. We can draw that as:This is pretty boring, so we can simplify all the statements to just:where the arrow is assumed to include a sequence of statements without branches.If we add a branch to our program, we now have two possible exits at some block in the code:Here, true_path is only executed if some condition was true at the `if` block. Learning to see the structure of programs as graphs like this is a key part of understanding how programs will run. We'll see several of these graphs in this lecture. ConditionalsA conditional is an expression that evaluates to True or False (i.e. a boolean expression). `if` takes a conditional to decide which branch of code to execute.The comparison operators are used to test values and the boolean operators combine sub-expressions together.Valid conditional expressions include: x == 0 [equality] x > 5 [comparison] status == "alive" or status == "dead" [boolean operator] The expression following an if statement must be a conditional. It must evaluate to either `True` or `False`. Block syntax: indentationIn Python, we denote the section of code following `if` by indenting it (putting spaces in front of the following lines). The `if` continues until the code indentation moves back to where it was before. An indented block always starts with a colon `:`.All blocks of code in Python are denoted this way. Python is whitespace-sensitive. There are no block markers like braces `{ }` or `begin` and `end` in Python. The block of code is defined by the colon followed by the indentation (spacing) alone. The code that "belongs" to a `if` statement is everything which has the matching indentation. All other language features which deal with blocks of code (i.e. need to work with multiple statements) use indentation to mark the blocks of code. ###Code # this is fine x = False if x: print("hello") print("there") print("after") # this is an indentation error -- it will not run! x = True if x: print ("hello") print ("there") # ^ # \| does not match any possible indentation! # this is also an indentation error -- it will not run! x = True if x: print ("hello") print ("there") ###Output _____no_output_____ ###Markdown ifHow do we introduce such branches in our programs. The simplest branching statement is `if`. `if` takes an expression and executes one sequence of code only if the given expression is `True`. if : ... elseWe can have a branch with two different paths using `else`. One of the two paths is always executed; the `if` path if the expression is True or the `else` path if it is False. if : else: ###Code #If the if condition is true, the if statement is executed. #The program then continues after the else statement. exam = 28 if exam < 40: print("You failed", end = " ") else: print("You passed", end = " ") print("the exams") ###Output You failed the exams ###Markdown if....elif....elseSometimes we need to have more than two branches. For example, we might have a temperature scale in a recipe in Celsius, and we need to work out what Gas Mark to put our oven at: We can use `elif` to combine an `else` and an `if` together. We can still use a final `else` statement. ###Code temp = 150 if temp<135: gas_mark=1 elif temp<149: gas_mark =2 elif temp<163: gas_mark = 3 else: # if it's hotter than that, just turn the burner on full blast! gas_mark = 100 print(gas_mark) ###Output 3 ###Markdown 5. Compound Boolean ExpressionsThe can have more than one condition on an if statement. The conditions need to be joined together with `and` , `or` or `not` operators to create a large boolean expression. `and` All the conditions need to be true for the expression to be true. `or` Any of the conditions need to be true for the expression to be true. ###Code #Both conditions of the or expression are true. weather = "wet" temp = 24 if weather == "wet" or temp < 0: print("I'm not going outside today") elif weather == "sunny" and temp > 20: print("I'm going to need suncream today") else: print("Not sure what I'll do today") ###Output I'm not going outside today
Lesson_5/convolution_visualization/conv_visualization.ipynb	###Markdown Convolutional LayerIn this notebook, we visualize four filtered outputs (a.k.a. activation maps) of a convolutional layer. In this example, we are defining four filters that are applied to an input image by initializing the weights of a convolutional layer, but a trained CNN will learn the values of these weights. Import the image ###Code import cv2 import matplotlib.pyplot as plt %matplotlib inline # TODO: Feel free to try out your own images here by changing img_path # to a file path to another image on your computer! img_path = 'data/udacity_sdc.png' # load color image bgr_img = cv2.imread(img_path) # convert to grayscale gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY) # normalize, rescale entries to lie in [0,1] gray_img = gray_img.astype("float32")/255 # plot image plt.imshow(gray_img, cmap='gray') plt.show() ###Output _____no_output_____ ###Markdown Define and visualize the filters ###Code import numpy as np ## TODO: Feel free to modify the numbers here, to try out another filter! filter_vals = np.array([[-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1]]) print('Filter shape: ', filter_vals.shape) # Defining four different filters, # all of which are linear combinations of the `filter_vals` defined above # define four filters filter_1 = filter_vals filter_2 = -filter_1 filter_3 = filter_1.T filter_4 = -filter_3 filters = np.array([filter_1, filter_2, filter_3, filter_4]) # For an example, print out the values of filter 1 print('Filter 1: \n', filter_1) #filter 3 print('Filter 3: \n', filter_3) # visualize all four filters fig = plt.figure(figsize=(10, 5)) for i in range(4): ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[]) ax.imshow(filters[i], cmap='gray') ax.set_title('Filter %s' % str(i+1)) width, height = filters[i].shape for x in range(width): for y in range(height): ax.annotate(str(filters[i][x][y]), xy=(y,x), horizontalalignment='center', verticalalignment='center', color='white' if filters[i][x][y]<0 else 'black') ###Output _____no_output_____ ###Markdown Define a convolutional layer The various layers that make up any neural network are documented, [here](http://pytorch.org/docs/stable/nn.html). For a convolutional neural network, we'll start by defining a:* Convolutional layerInitialize a single convolutional layer so that it contains all your created filters. Note that you are not training this network; you are initializing the weights in a convolutional layer so that you can visualize what happens after a forward pass through this network! `__init__` and `forward`To define a neural network in PyTorch, you define the layers of a model in the function `__init__` and define the forward behavior of a network that applyies those initialized layers to an input (`x`) in the function `forward`. In PyTorch we convert all inputs into the Tensor datatype, which is similar to a list data type in Python. Below, I define the structure of a class called `Net` that has a convolutional layer that can contain four 3x3 grayscale filters. ###Code import torch import torch.nn as nn import torch.nn.functional as F # define a neural network with a single convolutional layer with four filters class Net(nn.Module): def __init__(self, weight): super(Net, self).__init__() # initializes the weights of the convolutional layer to be the weights of the 4 defined filters k_height, k_width = weight.shape[2:] # assumes there are 4 grayscale filters self.conv = nn.Conv2d(1, 4, kernel_size=(k_height, k_width), bias=False) self.conv.weight = torch.nn.Parameter(weight) def forward(self, x): # calculates the output of a convolutional layer # pre- and post-activation conv_x = self.conv(x) activated_x = F.relu(conv_x) # returns both layers return conv_x, activated_x # instantiate the model and set the weights weight = torch.from_numpy(filters).unsqueeze(1).type(torch.FloatTensor) model = Net(weight) # print out the layer in the network print(model) ###Output Net( (conv): Conv2d(1, 4, kernel_size=(4, 4), stride=(1, 1), bias=False) ) ###Markdown Visualize the output of each filterFirst, we'll define a helper function, `viz_layer` that takes in a specific layer and number of filters (optional argument), and displays the output of that layer once an image has been passed through. ###Code # helper function for visualizing the output of a given layer # default number of filters is 4 def viz_layer(layer, n_filters= 4): fig = plt.figure(figsize=(20, 20)) for i in range(n_filters): ax = fig.add_subplot(1, n_filters, i+1, xticks=[], yticks=[]) # grab layer outputs ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray') ax.set_title('Output %s' % str(i+1)) ###Output _____no_output_____ ###Markdown Let's look at the output of a convolutional layer, before and after a ReLu activation function is applied. ###Code # plot original image plt.imshow(gray_img, cmap='gray') # visualize all filters fig = plt.figure(figsize=(12, 6)) fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05) for i in range(4): ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[]) ax.imshow(filters[i], cmap='gray') ax.set_title('Filter %s' % str(i+1)) # convert the image into an input Tensor gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1) # get the convolutional layer (pre and post activation) conv_layer, activated_layer = model(gray_img_tensor) # visualize the output of a conv layer viz_layer(conv_layer) ###Output _____no_output_____ ###Markdown ReLu activationIn this model, we've used an activation function that scales the output of the convolutional layer. We've chose a ReLu function to do this, and this function simply turns all negative pixel values in 0's (black). See the equation pictured below for input pixel values, `x`. ###Code # after a ReLu is applied # visualize the output of an activated conv layer viz_layer(activated_layer) ###Output _____no_output_____
Basic/PythonNegativeIndexing.ipynb	###Markdown We can index single characters in strings using the bracket notation. The first character has index 0, the second index 1, and so on. Did you ever want to access the last element in a string? Counting the indices can be a real pain for long strings with more than 8-10 characters.But no worries, Python has a language feature for this.Instead of starting counting from the left, you can also start from the right. Access the last character with the negative index -1, the second last with the index -2, and so on.In summary, there are two ways to index sequence positions, from the left and from the right: ###Code x = 'cool' print(x[-1] + x[-2] + x[-4] + x[-3]) ###Output _____no_output_____
Exercise py/07-Sets and Booleans.ipynb	###Markdown Set and BooleansThere are two other object types in Python that we should quickly cover: Sets and Booleans. SetsSets are an unordered collection of unique elements. We can construct them by using the set() function. Let's go ahead and make a set to see how it works ###Code x = set() # We add to sets with the add() method x.add(1) #Show x ###Output _____no_output_____ ###Markdown Note the curly brackets. This does not indicate a dictionary! Although you can draw analogies as a set being a dictionary with only keys.We know that a set has only unique entries. So what happens when we try to add something that is already in a set? ###Code # Add a different element x.add(2) #Show x # Try to add the same element x.add(1) #Show x ###Output _____no_output_____ ###Markdown Notice how it won't place another 1 there. That's because a set is only concerned with unique elements! We can cast a list with multiple repeat elements to a set to get the unique elements. For example: ###Code # Create a list with repeats list1 = [1,1,2,2,3,4,5,6,1,1] # Cast as set to get unique values set(list1) ###Output _____no_output_____ ###Markdown BooleansPython comes with Booleans (with predefined True and False displays that are basically just the integers 1 and 0). It also has a placeholder object called None. Let's walk through a few quick examples of Booleans (we will dive deeper into them later in this course). ###Code # Set object to be a boolean a = True #Show a ###Output _____no_output_____ ###Markdown We can also use comparison operators to create booleans. We will go over all the comparison operators later on in the course. ###Code # Output is boolean 1 > 2 ###Output _____no_output_____ ###Markdown We can use None as a placeholder for an object that we don't want to reassign yet: ###Code # None placeholder b = None # Show print(b) ###Output None
files/IO/06.Protobuf.ipynb	###Markdown [Protobuf](https://developers.google.com/protocol-buffers/docs/pythontutorial?hl=rucompiling-your-protocol-buffers) ###Code 40*10000/1024 !sudo apt-get install protobuf-compiler !pip install protobuf !mkdir proto_example !touch proto_example/__init__.py !protoc --python_out=proto_example example.proto from proto_example.example_pb2 import ParticleList particle_list = ParticleList() with open("build/example.bin", "rb") as fin: particle_list.ParseFromString(fin.read()) for indx, particle in enumerate(particle_list.particle): if indx > 100: md = particle.momentum_direction print(particle.id, particle.energy) print(md.x, md.y, md.z) break ###Output 101 317.14 -1.0 1.0 1.0
docs/memo/notebooks/data/zacks.broker_ratings/notebook.ipynb	###Markdown Zack's Broker Ratings Revision HistoryIn this notebook, we'll take a look at Zack's Broker Ratings Revision History dataset, available on [Quantopian](https://www.quantopian.com/store). This dataset spans 2002 through the current day and provides Analyst Ratings History for Securities.Update time: Zacks updates this dataset sometime during the first week of each month. In pipeline, your data will be updated close to midnight. So on the 27th, you will have data with a maximum asof_date of the 26th. Notebook ContentsThere are two ways to access the data and you'll find both of them listed below. Just click on the section you'd like to read through.- Interactive overview: This is only available on Research and uses blaze to give you access to large amounts of data. Recommended for exploration and plotting.- Pipeline overview: Data is made available through pipeline which is available on both the Research & Backtesting environment. Recommended for custom factor development and moving back & forth between research/backtesting. Free samples and limitsOne key caveat: we limit the number of results returned from any given expression to 10,000 to protect against runaway memory usage. To be clear, you have access to all the data server side. We are limiting the size of the responses back from Blaze.There is a free version of this dataset as well as a paid one. The free sample includes data until 2 months prior to the current date.To access the most up-to-date values for this data set for trading a live algorithm (as with other partner sets), you need to purchase acess to the full set.With preamble in place, let's get started:Interactive Overview Accessing the data with Blaze and Interactive on ResearchPartner datasets are available on Quantopian Research through an API service known as [Blaze](http://blaze.pydata.org). Blaze provides the Quantopian user with a convenient interface to access very large datasets, in an interactive, generic manner.Blaze provides an important function for accessing these datasets. Some of these sets are many millions of records. Bringing that data directly into Quantopian Research directly just is not viable. So Blaze allows us to provide a simple querying interface and shift the burden over to the server side.It is common to use Blaze to reduce your dataset in size, convert it over to Pandas and then to use Pandas for further computation, manipulation and visualization.Helpful links:* [Query building for Blaze](http://blaze.readthedocs.io/en/latest/queries.html)* [Pandas-to-Blaze dictionary](http://blaze.readthedocs.io/en/latest/rosetta-pandas.html)* [SQL-to-Blaze dictionary](http://blaze.readthedocs.io/en/latest/rosetta-sql.html).Once you've limited the size of your Blaze object, you can convert it to a Pandas DataFrames using:> `from odo import odo` > `odo(expr, pandas.DataFrame)`To see how this data can be used in your algorithm, search for the `Pipeline Overview` section of this notebook or head straight to Pipeline Overview ###Code # import the free sample of the dataset from quantopian.interactive.data.zacks import broker_ratings as dataset # import data operations from odo import odo # import other libraries we will use import pandas as pd import matplotlib.pyplot as plt # Let's use blaze to understand the data a bit using Blaze dshape() dataset.timestamp.min() # And how many rows are there? # N.B. we're using a Blaze function to do this, not len() dataset.count() # Let's see what the data looks like. We'll grab three rows dataset.tail(3) ###Output _____no_output_____ ###Markdown Let's go over the columns:- file_prod_date: File production date- m_ticker: Master ticker or trading symbol- symbol: Ticker- comp_name: Company name- comp_name_2: Company name 2- exchange: Exchange traded- currency_code: Currency code- rating_cnt_strong_buys: Number of analysts with a strong buy rating- rating_cnt_mod_buys: Number of analysts with a moderate buy rating- rating_cnt_holds: Number of analysts with a hold rating- rating_cnt_mod_sells: Number of analysts with a moderate sell rating- rating_cnt_strong_sells: Number of analysts with a strong sell rating- rating_mean_recom: Average rating recommendation- rating_cnt_with: Number of analysts with a rating- rating_cnt_without: Number of analysts with no rating- asof_date: Observation date- timestamp: This is our timestamp on when we registered the data.We've done much of the data processing for you. Fields like `timestamp` and `sid` are standardized across all our Store Datasets, so the datasets are easy to combine. We have standardized the `sid` across all our equity databases.We can select columns and rows with ease. Below, we'll fetch all rows for Apple (sid 24) and explore the scores a bit with a chart. ###Code aapl_data = dataset_100[dataset_100.symbol == 'AAPL'] aapl = odo(aapl_data, pd.DataFrame) # suppose we want the rows to be indexed by timestamp. aapl.index = list(aapl['asof_date']) aapl.drop('asof_date',1,inplace=True) aapl[-3:] ###Output _____no_output_____ ###Markdown Pipeline Overview Accessing the data in your algorithms & researchThe only method for accessing partner data within algorithms running on Quantopian is via the pipeline API. Different data sets work differently but in the case of this data, you can add this data to your pipeline as follows: ###Code # Import necessary Pipeline modules from quantopian.pipeline import Pipeline from quantopian.research import run_pipeline from quantopian.pipeline.factors import AverageDollarVolume # For use in your algorithms # Using the full/sample paid dataset in your pipeline algo from quantopian.pipeline.data.zacks import broker_ratings ###Output _____no_output_____ ###Markdown Now that we've imported the data, let's take a look at which fields are available for each dataset.You'll find the dataset, the available fields, and the datatypes for each of those fields. ###Code print "Here are the list of available fields per dataset:" print "---------------------------------------------------\n" def _print_fields(dataset): print "Dataset: %s\n" % dataset.__name__ print "Fields:" for field in list(dataset.columns): print "%s - %s" % (field.name, field.dtype) print "\n" for data in (broker_ratings,): _print_fields(data) print "---------------------------------------------------\n" ###Output Here are the list of available fields per dataset: --------------------------------------------------- Dataset: broker_ratings Fields: comp_name - object exchange - object currency_code - object symbol - object m_ticker - object rating_mean_recom - float64 rating_cnt_without - float64 rating_cnt_strong_buys - float64 asof_date - datetime64[ns] rating_cnt_mod_buys - float64 rating_cnt_holds - float64 file_prod_date - datetime64[ns] rating_cnt_mod_sells - float64 comp_name_2 - object rating_cnt_strong_sells - float64 rating_cnt_with - float64 --------------------------------------------------- ###Markdown Now that we know what fields we have access to, let's see what this data looks like when we run it through Pipeline.This is constructed the same way as you would in the backtester. For more information on using Pipeline in Research view this thread:https://www.quantopian.com/posts/pipeline-in-research-build-test-and-visualize-your-factors-and-filters ###Code # Let's see what this data looks like when we run it through Pipeline # This is constructed the same way as you would in the backtester. For more information # on using Pipeline in Research view this thread: # https://www.quantopian.com/posts/pipeline-in-research-build-test-and-visualize-your-factors-and-filters columns = {'Strong Sells': broker_ratings.rating_cnt_strong_sells.latest, 'Strong Buys': broker_ratings.rating_cnt_strong_buys.latest} pipe = Pipeline(columns=columns, screen=broker_ratings.rating_cnt_mod_sells.latest.notnan()) # The show_graph() method of pipeline objects produces a graph to show how it is being calculated. pipe.show_graph(format='png') # run_pipeline will show the output of your pipeline pipe_output = run_pipeline(pipe, start_date='2013-11-01', end_date='2013-11-25') pipe_output ###Output _____no_output_____ ###Markdown Zack's Broker Ratings Revision HistoryIn this notebook, we'll take a look at Zack's Broker Ratings Revision History dataset, available on [Quantopian](https://www.quantopian.com/store). This dataset spans 2002 through the current day and provides Analyst Ratings History for Securities.Update time: Zacks updates this dataset sometime during the first week of each month. In pipeline, your data will be updated close to midnight. So on the 27th, you will have data with a maximum asof_date of the 26th. Notebook ContentsThere are two ways to access the data and you'll find both of them listed below. Just click on the section you'd like to read through.- Interactive overview: This is only available on Research and uses blaze to give you access to large amounts of data. Recommended for exploration and plotting.- Pipeline overview: Data is made available through pipeline which is available on both the Research & Backtesting environment. Recommended for custom factor development and moving back & forth between research/backtesting. Free samples and limitsOne key caveat: we limit the number of results returned from any given expression to 10,000 to protect against runaway memory usage. To be clear, you have access to all the data server side. We are limiting the size of the responses back from Blaze.There is a free version of this dataset as well as a paid one. The free sample includes data until 2 months prior to the current date.To access the most up-to-date values for this data set for trading a live algorithm (as with other partner sets), you need to purchase acess to the full set.With preamble in place, let's get started:Interactive Overview Accessing the data with Blaze and Interactive on ResearchPartner datasets are available on Quantopian Research through an API service known as [Blaze](http://blaze.pydata.org). Blaze provides the Quantopian user with a convenient interface to access very large datasets, in an interactive, generic manner.Blaze provides an important function for accessing these datasets. Some of these sets are many millions of records. Bringing that data directly into Quantopian Research directly just is not viable. So Blaze allows us to provide a simple querying interface and shift the burden over to the server side.It is common to use Blaze to reduce your dataset in size, convert it over to Pandas and then to use Pandas for further computation, manipulation and visualization.Helpful links:* [Query building for Blaze](http://blaze.readthedocs.io/en/latest/queries.html)* [Pandas-to-Blaze dictionary](http://blaze.readthedocs.io/en/latest/rosetta-pandas.html)* [SQL-to-Blaze dictionary](http://blaze.readthedocs.io/en/latest/rosetta-sql.html).Once you've limited the size of your Blaze object, you can convert it to a Pandas DataFrames using:> `from odo import odo` > `odo(expr, pandas.DataFrame)`To see how this data can be used in your algorithm, search for the `Pipeline Overview` section of this notebook or head straight to Pipeline Overview ###Code # import the free sample of the dataset from quantopian.interactive.data.zacks import broker_ratings as dataset # import data operations from odo import odo # import other libraries we will use import pandas as pd import matplotlib.pyplot as plt # Let's use blaze to understand the data a bit using Blaze dshape() dataset.timestamp.min() # And how many rows are there? # N.B. we're using a Blaze function to do this, not len() dataset.count() # Let's see what the data looks like. We'll grab three rows dataset.tail(3) ###Output _____no_output_____ ###Markdown Let's go over the columns:- file_prod_date: File production date- m_ticker: Master ticker or trading symbol- symbol: Ticker- comp_name: Company name- comp_name_2: Company name 2- exchange: Exchange traded- currency_code: Currency code- rating_cnt_strong_buys: Number of analysts with a strong buy rating- rating_cnt_mod_buys: Number of analysts with a moderate buy rating- rating_cnt_holds: Number of analysts with a hold rating- rating_cnt_mod_sells: Number of analysts with a moderate sell rating- rating_cnt_strong_sells: Number of analysts with a strong sell rating- rating_mean_recom: Average rating recommendation- rating_cnt_with: Number of analysts with a rating- rating_cnt_without: Number of analysts with no rating- asof_date: Observation date- timestamp: This is our timestamp on when we registered the data.We've done much of the data processing for you. Fields like `timestamp` and `sid` are standardized across all our Store Datasets, so the datasets are easy to combine. We have standardized the `sid` across all our equity databases.We can select columns and rows with ease. Below, we'll fetch all rows for Apple (sid 24) and explore the scores a bit with a chart. ###Code aapl_data = dataset_100[dataset_100.symbol == 'AAPL'] aapl = odo(aapl_data, pd.DataFrame) # suppose we want the rows to be indexed by timestamp. aapl.index = list(aapl['asof_date']) aapl.drop('asof_date',1,inplace=True) aapl[-3:] ###Output _____no_output_____ ###Markdown Pipeline Overview Accessing the data in your algorithms & researchThe only method for accessing partner data within algorithms running on Quantopian is via the pipeline API. Different data sets work differently but in the case of this data, you can add this data to your pipeline as follows: ###Code # Import necessary Pipeline modules from quantopian.pipeline import Pipeline from quantopian.research import run_pipeline from quantopian.pipeline.factors import AverageDollarVolume # For use in your algorithms # Using the full/sample paid dataset in your pipeline algo from quantopian.pipeline.data.zacks import broker_ratings ###Output _____no_output_____ ###Markdown Now that we've imported the data, let's take a look at which fields are available for each dataset.You'll find the dataset, the available fields, and the datatypes for each of those fields. ###Code print "Here are the list of available fields per dataset:" print "---------------------------------------------------\n" def _print_fields(dataset): print "Dataset: %s\n" % dataset.__name__ print "Fields:" for field in list(dataset.columns): print "%s - %s" % (field.name, field.dtype) print "\n" for data in (broker_ratings,): _print_fields(data) print "---------------------------------------------------\n" ###Output Here are the list of available fields per dataset: --------------------------------------------------- Dataset: broker_ratings Fields: comp_name - object exchange - object currency_code - object symbol - object m_ticker - object rating_mean_recom - float64 rating_cnt_without - float64 rating_cnt_strong_buys - float64 asof_date - datetime64[ns] rating_cnt_mod_buys - float64 rating_cnt_holds - float64 file_prod_date - datetime64[ns] rating_cnt_mod_sells - float64 comp_name_2 - object rating_cnt_strong_sells - float64 rating_cnt_with - float64 --------------------------------------------------- ###Markdown Now that we know what fields we have access to, let's see what this data looks like when we run it through Pipeline.This is constructed the same way as you would in the backtester. For more information on using Pipeline in Research view this thread:https://www.quantopian.com/posts/pipeline-in-research-build-test-and-visualize-your-factors-and-filters ###Code # Let's see what this data looks like when we run it through Pipeline # This is constructed the same way as you would in the backtester. For more information # on using Pipeline in Research view this thread: # https://www.quantopian.com/posts/pipeline-in-research-build-test-and-visualize-your-factors-and-filters columns = {'Strong Sells': broker_ratings.rating_cnt_strong_sells.latest, 'Strong Buys': broker_ratings.rating_cnt_strong_buys.latest} pipe = Pipeline(columns=columns, screen=broker_ratings.rating_cnt_mod_sells.latest.notnan()) # The show_graph() method of pipeline objects produces a graph to show how it is being calculated. pipe.show_graph(format='png') # run_pipeline will show the output of your pipeline pipe_output = run_pipeline(pipe, start_date='2013-11-01', end_date='2013-11-25') pipe_output ###Output _____no_output_____
RankingIntermediateChanges.ipynb	###Markdown Application of ML in Ranking Application of ML in Ranking of Search Engines Downloading Data From Kaggle Might Take a while ###Code from google.colab import drive drive.mount('/content/drive', force_remount=True) # Download Data !pip install kaggle import json import os from pprint import pprint with open('/content/drive/My Drive/kaggle.json') as kc: kaggle_config = json.load(kc) os.environ['KAGGLE_USERNAME'] = kaggle_config['username'] os.environ['KAGGLE_KEY'] = kaggle_config['key'] !kaggle competitions download -c text-relevance-competition-ir-2-itmo-fall-2019 !unzip docs.tsv.zip !rm docs.tsv.zip ###Output Requirement already satisfied: kaggle in /usr/local/lib/python3.6/dist-packages (1.5.6) Requirement already satisfied: six>=1.10 in /usr/local/lib/python3.6/dist-packages (from kaggle) (1.12.0) Requirement already satisfied: urllib3<1.25,>=1.21.1 in /usr/local/lib/python3.6/dist-packages (from kaggle) (1.24.3) Requirement already satisfied: requests in /usr/local/lib/python3.6/dist-packages (from kaggle) (2.21.0) Requirement already satisfied: certifi in /usr/local/lib/python3.6/dist-packages (from kaggle) (2019.11.28) Requirement already satisfied: python-dateutil in /usr/local/lib/python3.6/dist-packages (from kaggle) (2.6.1) Requirement already satisfied: python-slugify in /usr/local/lib/python3.6/dist-packages (from kaggle) (4.0.0) Requirement already satisfied: tqdm in /usr/local/lib/python3.6/dist-packages (from kaggle) (4.41.1) Requirement already satisfied: idna<2.9,>=2.5 in /usr/local/lib/python3.6/dist-packages (from requests->kaggle) (2.8) Requirement already satisfied: chardet<3.1.0,>=3.0.2 in /usr/local/lib/python3.6/dist-packages (from requests->kaggle) (3.0.4) Requirement already satisfied: text-unidecode>=1.3 in /usr/local/lib/python3.6/dist-packages (from python-slugify->kaggle) (1.3) Warning: Looks like you're using an outdated API Version, please consider updating (server 1.5.6 / client 1.5.4) Downloading docs.tsv.zip to /content 100% 1.17G/1.17G [00:31<00:00, 39.1MB/s] 100% 1.17G/1.17G [00:31<00:00, 39.7MB/s] Downloading sample.submission.txt to /content 0% 0.00/434k [00:00<?, ?B/s] 100% 434k/434k [00:00<00:00, 59.8MB/s] Downloading queries.numerate.txt to /content 0% 0.00/31.9k [00:00<?, ?B/s] 100% 31.9k/31.9k [00:00<00:00, 32.2MB/s] Archive: docs.tsv.zip inflating: docs.tsv ###Markdown Code ###Code !pip install -U tqdm !pip install rank_bm25 !pip install keyw import os import gzip import nltk import random import pickle import pandas as pd import logging import keyw import itertools import re import time import numpy as np import pandas as pd from rank_bm25 import BM25Okapi from nltk.corpus import stopwords nltk.download("stopwords") from string import punctuation from collections import defaultdict from collections import OrderedDict from tqdm.notebook import tqdm logging.basicConfig(level=logging.DEBUG) logging.debug('Test Logger') indexing_data_location = '/content/docs.tsv' queries_list = '/content/queries.numerate.txt' db_directory_name = 'database' ###Output _____no_output_____ ###Markdown Convert Docs from memory load to IO operations ###Code # database = pd.read_csv(indexing_data_location, sep='\t', header=None, # names=['id', 'subject', 'content'], # dtype = {'id': int,'subject': str, # 'content': str}) os.mkdir(db_directory_name) with open(indexing_data_location, "rb") as f: for line in tqdm(f): line = line.decode().split('\t') file_number = line[0] subject = line[1] text = line[2] line = subject + ' ' + text with open(os.path.join(db_directory_name, file_number), 'w') as output: output.write(line) ###Output _____no_output_____ ###Markdown Building Inverted Index Inverted Indexer Class ###Code class InvertedIndexer: """ This class makes inverted index """ def __init__(self, filename=False): self.filename = filename self.stemmer_ru = nltk.SnowballStemmer("russian") self.stopwords = set(stopwords.words("russian")) \| set(stopwords.words("english")) self.punctuation = punctuation # from string import punctuation if filename: self.inverted_index = self._build_index(self.filename) else: self.inverted_index = defaultdict(set) def preprocess(self, sentence): """ Method to remove stop words and punctuations return tokens """ NONTEXT = re.compile('[^0-9 a-z#+_а-яё]') sentence = sentence.lower() sentence = sentence.translate(str.maketrans('', '', punctuation)) sentence = re.sub(NONTEXT,'',sentence) # Heavy Operation Taking lot of time will move it outside # tokens = [self.stemmer_ru.stem(word) for word in sentence.split()] tokens = [token for token in sentence.split() if token not in self.stopwords] return tokens def stem_keys(self, inverted_index): """ Called after index is built to stem all the keys and normalize them """ logging.debug('Indexing Complete will not Stem keys and remap indexes') temp_dict = defaultdict(set) i = 0 for word in tqdm(inverted_index): stemmed_key = keyw.engrus(word) stemmed_key = self.stemmer_ru.stem(stemmed_key) temp_dict[stemmed_key].update(inverted_index[word]) inverted_index[word] = None inverted_index = temp_dict logging.debug('Done Stemmping Indexes') return inverted_index def _build_index(self, indexing_data_location): """ This method builds the inverted index and returns the invrted index dictionary """ inverted_index = defaultdict(set) with open(indexing_data_location, "rb") as f: for line in tqdm(f): line = line.decode().split('\t') file_number = line[0] subject = line[1] text = line[2] line = subject + ' ' + text for word in self.preprocess(line): inverted_index[word].add(int(file_number)) inverted_index = self.stem_keys(inverted_index) return inverted_index def save(self, filename_to_save): """ Save method to save the inverted indexes """ with open(filename_to_save, mode='wb') as f: pickle.dump(self.inverted_index, f) def load(self, filelocation_to_load): """ Load method to load the inverted indexes """ with open(filelocation_to_load, mode='rb') as f: self.inverted_index = pickle.load(f) ###Output _____no_output_____ ###Markdown SolutionPredictor Class ###Code class SolutionPredictor: """ This classes uses object of Hw1SolutionIndexer to make boolean search """ def __init__(self, indexer): """ indexer : object of class Hw1SolutionIndexer """ self.indexer = indexer def find_docs(self, query): """ This method provides booleaen search query : string with text of query Returns Python set with documents which contain query words Should return maximum 100 docs """ query = keyw.engrus(query) tokens = self.indexer.preprocess(query) tokens = [self.indexer.stemmer_ru.stem(word) for word in tokens] docs_list = set() for word in tokens: if len(docs_list) > 0: docs_list.intersection_update(self.indexer.inverted_index[word]) # changed from intersection_update else: docs_list.update(self.indexer.inverted_index[word]) # Handling case when no set is returned by intersection # if len(docs_list) < 10: # for word in tokens: # docs_list.update(self.indexer.inverted_index[word]) # changed from intersection_update return docs_list ###Output _____no_output_____ ###Markdown Generate Index Run Only when Index is not generated Otherwise use the Loading code block ###Code logging.debug('Index is creating...') start = time.time() new_index = InvertedIndexer(indexing_data_location) end = time.time() logging.debug('Index has been created and saved as inverted_index.pickle in {:.4f}s'.format(end-start)) len(new_index.inverted_index) new_index.save('inverted_index_all_rus.pickle') !cp inverted_index.pickle '/content/drive/My Drive/Homeworks/InformationRetrieval/inverted_index_temp.pickle' ###Output _____no_output_____ ###Markdown Load IndexRun when Index is not generated ###Code index_location = '/content/drive/My Drive/Homeworks/InformationRetrieval/inverted_index_4.pickle' logging.debug('Loading Index...') start = time.time() new_index = InvertedIndexer() new_index.load(index_location) end = time.time() logging.debug('Index has been loaded from inverted_index.pickle in {:.4f}s'.format(end-start)) len(new_index.inverted_index) ###Output _____no_output_____ ###Markdown Testing Block ###Code test_sentence = 'бандиты боятся ли ментов' boolean_model = SolutionPredictor(new_index) start = time.time() print(boolean_model.find_docs(test_sentence)) logging.debug('Search Time: {}'.format(time.time() - start)) test_docs = boolean_model.find_docs(test_sentence) test_dict = {} for doc in test_docs: with open(os.path.join(db_directory_name, str(doc))) as f: test_dict[doc] = f.readlines()[0] ###Output _____no_output_____ ###Markdown Loading File to DataFrameWe are doing this for faster search based on index numbers ###Code # %%time # database = pd.read_csv(indexing_data_location, sep='\t', header=None, # names=['id', 'subject', 'content'], # dtype = {'id': int,'subject': str, # 'content': str}) # database.head() ###Output _____no_output_____ ###Markdown Implementing BM25 (When all data in memory) ###Code # # boolean_model = SolutionPredictor(new_index) # output=open('submission.csv', 'w') # with open(queries_list) as queries: # output.write('QueryId,DocumentId\n') # for line in tqdm(queries.readlines()): # line = line.split('\t') # id = int(line[0]) # query = line[1] # value_present = boolean_model.find_docs(query) # data = database[database['id'].isin(list(value_present))].copy() # data.loc[:, 'content'] = data[['subject', 'content']].astype(str).apply(' '.join, axis=1) # del data['subject'] # data = OrderedDict(data.set_index('id')['content'].to_dict()) # for key in data: # data[key] = new_index.preprocess(data[key]) # if data: # bm25 = BM25Okapi(data.values()) # rankings = sorted(list(zip(data.keys(), bm25.get_scores(new_index.preprocess(query)))), key=lambda x: x[1], reverse=True)[:10] # for rank in rankings: # output.write('{},{}\n'.format(id, rank[0])) # if (not data) or len(rankings) < 10: # if not data: # rankings = [] # logging.debug('Found Some values with no query results or less than 10 {} ranking'.format(id, len(rankings))) # print(id, query) # for i in range(10 - len(rankings)): # output.write('{},{}\n'.format(id, random.randrange(50000))) # output.close() # !cp submission.csv '/content/drive/My Drive/Homeworks/InformationRetrieval/submission.csv' ###Output _____no_output_____ ###Markdown Implementing BM25 when all data on disk ###Code corpus = { 1: "Hello there good man!", 2: "It is quite windy in London", 3: "How is the weather today?" } tokenized_corpus = [doc.split(" ") for doc in corpus.values()] print(tokenized_corpus) bm25 = BM25Okapi(tokenized_corpus) query = "windy London" tokenized_query = query.split(" ") doc_scores = bm25.get_scores(tokenized_query) print(sorted(list(zip(corpus.keys(),doc_scores)), key=lambda x: x[1], reverse=True)) output=open('submission.csv', 'w') with open(queries_list) as queries: output.write('QueryId,DocumentId\n') for line in tqdm(queries.readlines()): line = line.split('\t') id = int(line[0]) query = line[1] value_present = boolean_model.find_docs(query) logging.debug('Found Value {}'.format(len(value_present))) data = OrderedDict() for doc in value_present: with open(os.path.join(db_directory_name, str(doc))) as f: data[doc] = new_index.preprocess(f.readlines()[0]) logging.debug('Loaded Data') if data: bm25 = BM25Okapi(data.values()) start = time.time() rankings = sorted(list(zip(data.keys(), bm25.get_scores(new_index.preprocess(query)))), key=lambda x: x[1], reverse=True)[:100] for rank in rankings: output.write('{},{}\n'.format(id, rank[0])) logging.debug('Calculated ranking in {}'.format(time.time()- start)) if (not data) or len(rankings) < 10: if not data: rankings = [] logging.debug('Found Some values with no query results or less than 10 {} ranking'.format(id, len(rankings))) print(id, query) for i in range(10 - len(rankings)): output.write('{},{}\n'.format(id, random.randrange(50000))) output.close() data = OrderedDict() with open(queries_list) as queries: for line in tqdm(queries.readlines()): line = line.split('\t') id = int(line[0]) query = line[1] value_present = boolean_model.find_docs(query) data[id] = value_present i = 0 for k in data: print(k, data[k]) if i == 5: break i += 1 for key in data: if len(data[key]) < 10: print(key, data[key]) ###Output _____no_output_____
lessons/NLP Pipelines/tokenization_practice.ipynb	###Markdown Note on NLTK data downloadRun the cell below to download the necessary nltk data packages. Note, because we are working in classroom workspaces, we will be downloading specific packages in each notebook throughout the lesson. However, you can download all packages by entering `nltk.download()` on your computer. Keep in mind this does take up a bit more space. You can learn more about nltk data installation [here](https://www.nltk.org/data.html). ###Code import nltk nltk.download('punkt') ###Output [nltk_data] Downloading package punkt to /Users/zacks/nltk_data... [nltk_data] Package punkt is already up-to-date! ###Markdown TokenizationTry out the tokenization methods in nltk to split the following text into words and then sentences.Note: All solution notebooks can be found by clicking on the Jupyter icon on the top left of this workspace. ###Code # import statements from nltk.tokenize import word_tokenize from nltk.tokenize import sent_tokenize text = "Dr. Smith graduated from the University of Washington. He later started an analytics firm called Lux, which catered to enterprise customers." print(text) # Split text into words using NLTK word_tokenize(text) # Split text into sentences sent_tokenize(text) ###Output _____no_output_____ ###Markdown Table of Contents1  Note on NLTK data download2  Tokenization Note on NLTK data downloadRun the cell below to download the necessary nltk data packages. Note, because we are working in classroom workspaces, we will be downloading specific packages in each notebook throughout the lesson. However, you can download all packages by entering `nltk.download()` on your computer. Keep in mind this does take up a bit more space. You can learn more about nltk data installation [here](https://www.nltk.org/data.html). ###Code import nltk ###Output _____no_output_____ ###Markdown TokenizationTry out the tokenization methods in nltk to split the following text into words and then sentences.Note: All solution notebooks can be found by clicking on the Jupyter icon on the top left of this workspace. ###Code # import statements from nltk.tokenize import word_tokenize from nltk.tokenize import sent_tokenize text = "Dr. Smith graduated from the University of Washington. He later started an analytics firm called Lux, which catered to enterprise customers." print(text) # Split text into words using NLTK word_tokens = word_tokenize(text) #word_tokens # Split text into sentences sent_tokenize = sent_tokenize(text) sent_tokenize ###Output _____no_output_____ ###Markdown Note on NLTK data downloadRun the cell below to download the necessary nltk data packages. Note, because we are working in classroom workspaces, we will be downloading specific packages in each notebook throughout the lesson. However, you can download all packages by entering `nltk.download()` on your computer. Keep in mind this does take up a bit more space. You can learn more about nltk data installation [here](https://www.nltk.org/data.html). ###Code import nltk nltk.download('punkt') ###Output [nltk_data] Downloading package punkt to [nltk_data] C:\Users\amira\AppData\Roaming\nltk_data... [nltk_data] Unzipping tokenizers\punkt.zip. ###Markdown TokenizationTry out the tokenization methods in nltk to split the following text into words and then sentences.Note: All solution notebooks can be found by clicking on the Jupyter icon on the top left of this workspace. ###Code # import statements from nltk.tokenize import word_tokenize from nltk.tokenize import sent_tokenize text = "Dr. Smith graduated from the University of Washington. He later started an analytics firm called Lux, which catered to enterprise customers." print(text) # Split text into words using NLTK words = word_tokenize(text) print(words) # Split text into sentences sentences = sent_tokenize(text) print(sentences) ###Output ['Dr. Smith graduated from the University of Washington.', 'He later started an analytics firm called Lux, which catered to enterprise customers.'] ###Markdown Note on NLTK data downloadRun the cell below to download the necessary nltk data packages. Note, because we are working in classroom workspaces, we will be downloading specific packages in each notebook throughout the lesson. However, you can download all packages by entering `nltk.download()` on your computer. Keep in mind this does take up a bit more space. You can learn more about nltk data installation [here](https://www.nltk.org/data.html). ###Code import nltk nltk.download('punkt') ###Output _____no_output_____ ###Markdown TokenizationTry out the tokenization methods in nltk to split the following text into words and then sentences.Note: All solution notebooks can be found by clicking on the Jupyter icon on the top left of this workspace. ###Code # import statements text = "Dr. Smith graduated from the University of Washington. He later started an analytics firm called Lux, which catered to enterprise customers." print(text) # Split text into words using NLTK # Split text into sentences ###Output _____no_output_____ ###Markdown Note on NLTK data downloadRun the cell below to download the necessary nltk data packages. Note, because we are working in classroom workspaces, we will be downloading specific packages in each notebook throughout the lesson. However, you can download all packages by entering `nltk.download()` on your computer. Keep in mind this does take up a bit more space. You can learn more about nltk data installation [here](https://www.nltk.org/data.html). ###Code import nltk nltk.download('punkt') ###Output [nltk_data] Downloading package punkt to /home/jovyan/nltk_data... [nltk_data] Unzipping tokenizers/punkt.zip. ###Markdown TokenizationTry out the tokenization methods in nltk to split the following text into words and then sentences.Note: All solution notebooks can be found by clicking on the Jupyter icon on the top left of this workspace. ###Code # import statements from nltk.tokenize import word_tokenize text = "Dr. Smith graduated from the University of Washington. He later started an analytics firm called Lux, which catered to enterprise customers." print(text) # Split text into words using NLTK word_tokenize(text) # Split text into sentences text.split() ###Output _____no_output_____
Final Problem 1 - Double Pendulum(1).ipynb	###Markdown Problem 1: Double Pendulum Solved Using Lagrangian Method Physics 5700 Final, Spring 2021 Alex Bumgarner.187 Part 1: Python Setup: Here, I import the packages needed for the rest of the notebook: ###Code %matplotlib inline from IPython.display import Image #Allows us to display images from the web import numpy as np #For our more complicated math from scipy.integrate import solve_ivp #Allows us to solve first-order ODE's import matplotlib.pyplot as plt #For plotting ###Output _____no_output_____ ###Markdown Part 2: Problem Setup: ###Code Image(url = 'https://upload.wikimedia.org/wikipedia/commons/7/78/Double-Pendulum.svg') ###Output _____no_output_____ ###Markdown Fig. 1: Double PendulumSource: Wikimedia Commons A mass $m_1$ is attached to the ceiling by a massless rope of length $L_1$. A second mass $m_2$ is attached to the first mass by a massless string of length $m_2$, forming the double pendulum shown in Fig. 1. Our goal is to predict the motion of these two masses given a set of initial conditions. We define our Cartesian axes such that $\hat{x}$ points to the right and $\hat{y}$ points up. Part 3: Solving the Euler-Lagrange Equations The Lagrangian is defined as $\mathscr{L} = T - U$, where $T$ is the kinetic energy and $U$ is the potential energy of the system. We will define these energies in terms of our general coordinates $\theta_1$ and $\theta_2$ Assuming $m_1$ is $h_1$ high off the ground when $\theta_1 = 0$, the height of $m_1$ is equal to $h_1 + L_1 - L_1\cos{\theta_1}$. Thus, the potential energy of $m_1$ is given by: $$U_1 = m_1 g [L_1 (1-\cos{\theta_1})+ h_1]$$ Assuming $m_2$ is $h_2$ high ff the ground with $\theta_1 = \theta_2 = 0$, the height of $m_2$ is given by $h_1 + L_1 - L_1\cos{\theta_1} + h_2 + L_2 - L_2\cos{\theta_2}$. Thus, the potential energy of $m_2$ is given by: $$U_2 = m_2 g [L_1 (1-\cos{\theta_1}) + h_1 + L_2 (1-\cos{\theta_2})+h_2]$$ Summing these two potential energies (and omitting the $h$'s, as they will "disappear" when differentiating), we get an expression for the total potential energy: $$U = (m_1 + m_2) g L_1 (1-\cos{\theta_1}) + m_2 g L_2 (1-\cos{\theta_2})$$ The kinetic energy of $m_1$ is given by $\frac{1}{2} m_1 v_1^2$, where $v_1$ is the magnitdue of the mass's velocity. $v_1 = L_1 \dot{\theta_1}$, so the kinetic energy is: $$ T_1 = \frac{1}{2} m_1 L_1^2 \dot{\theta_1}^2 $$ The kinetic energy of $m_2$ is given by $\frac{1}{2} m_2 v_2^2$. Like $m_1$, $m_2$ moves with a tangential velocity $L_2 \dot{\theta_2}$. However, it is also affected by the velocity of $m_1$. As such, we must find the velocity of $m_2$ in each Carteian direction and add them in quadreture to get the magnitude. In the x-direction, the velocity is $v_2,x = L_1 \dot{\theta_1} \cos{\theta_1} + L_2 \dot{\theta_2} \cos{\theta_2}$ In the y-direction, the velocity is $v_2,y = L_1 \dot{\theta_1} \sin{\theta_1} + L_2 \dot{\theta_2} \sin{\theta_2}$ Thus, the kinetic energy of $m_2$ is given by: $$T_2 = \frac{1}{2} m_2 [(L_1 \dot\theta_1 \cos{\theta_1} + L_2 \dot\theta_2 \cos{\theta_2})^2 + (L_1 \dot\theta_1 \sin{\theta_1} + L_2 \dot\theta_2 \sin{\theta_2})^2]$$ This can be expanded and simplified: $$T_2 = \frac{1}{2} m_2 (L_1^2 \dot\theta_1^2 +L_2^2 \dot\theta_2^2 + 2 L_1 L_2 \dot\theta_1 \dot\theta_2 (\sin{\theta_1} \sin{\theta_2} + \cos{\theta_1} \cos{\theta_2}))$$ $$T_2 = \frac{1}{2} m_2 (L_1^2 \dot\theta_1^2 +L_2^2 \dot\theta_2^2 + 2 L_1 L_2 \dot\theta_1 \dot\theta_2 \cos{(\theta_1-\theta_2))}$$ Summing these energies gives us the total kinetic energy of the system: $$ T = \frac{1}{2}(m_1 + m_2) L_1^2 \dot\theta_1^2 + \frac{1}{2} m_2 L_2^2 \dot\theta_2^2 + m_2 L_1 L_2 \dot\theta_1 \dot\theta_2 \cos{(\theta_1 - \theta_2)}$$ Thus, the Lagrangian $\mathscr{L} = T - U$ is given by: $$\mathscr{L} = \frac{1}{2}(m_1 + m_2) L_1^2 \dot\theta_1^2 + \frac{1}{2} m_2 L_2^2 \dot\theta_2^2 + m_2 L_1 L_2 \dot\theta_1 \dot\theta_2 \cos{(\theta_1 - \theta_2)} - (m_1 + m_2) g L_1 (1-\cos{\theta_1}) - m_2 g L_2 (1-\cos{\theta_2})$$ The Euler-Lagrange equations for our generalized variables, $\theta_1$ and $\theta_2$, are: $$\frac{d}{dt} (\frac{\partial\mathscr{L}}{\partial \dot\theta_1}) = \frac{\partial\mathscr{L}}{\partial\theta_1} $$ $$\frac{d}{dt} (\frac{\partial\mathscr{L}}{\partial \dot\theta_2}) = \frac{\partial\mathscr{L}}{\partial\theta_2} $$ Plugging in our Lagrangian and simplifying gives us: $$ \ddot\theta_1 (m_1+m_2) L_1 + m_2 L_2 \ddot\theta_2 \cos(\theta_1 - \theta_2) + \dot\theta_2^2 m_2 L_2 \sin(\theta_1 - \theta_2) = -(m_1 + m_2) g \sin(\theta_1)$$ $$ \ddot\theta_2 m_2 L_2 + m_2 L_1 \ddot\theta_1 \cos(\theta_1-\theta_2) -m_2 L_1 \dot\theta_1^2 \sin(\theta_1 - \theta_2) = -m_2 g \sin(\theta_2) $$ To solve with scipy, we need these as first-order ordinary differential equations. We rewrite the above equations using $z_i = \dot\theta_i$ and $\dot{z_i} = \ddot\theta_i$. Solving for $\dot z_1$ and $\dot z_2$, we get: $$ \dot{z_1} = \frac{-(m_1+m2)g\sin(\theta_1) - m_2 \sin(\theta_1 - \theta_2) (L_2 z_2^2 + L_1 z_1^2 \cos(\theta_1 - \theta_2)) + g m_2 \cos(\theta_1 - \theta_2) \sin(\theta_2)}{L_1 (m_1 + m_2 \sin^2(\theta_1 - \theta_2))}$$ $$ \dot{z_2} = \frac{(m_1 + m_2) [g \cos(\theta_1 - \theta_2) \sin(\theta_1) + L_1 z_1^2 \sin(\theta_1 - \theta_2) - g \sin(\theta_2)] + L_2 m_2 z_2^2 \cos(\theta_1-\theta_2)\sin(\theta_1-\theta_2)}{L_2 (m_1 + m_2 \sin^2(\theta_1 - \theta_2))}$$ Part 4: Solving for the Motion The following is largely adapted from the Lagrangian_pendulum.ipynb notebook provided in class We now want to solve our system of differntial equations and plot the course of the masses given initial conditions: ###Code class Pendulum(): """ This class creates and solves for the motion of a pendulum of two masses using Lagrange's equations Parameters ------------ L1: float length of first pendulum L2: float length of second pendulum m1: float mass of first object m2: float mass of second object g: float gravitational acceleration at the Earth's surface """ def __init__(self, L1 = 1., L2 = 1., m1 = 1., m2 = 1., g = 1.): """ Initializes the pendulum and provides default values if none are provided by user """ self.L1 = L1 self.L2 = L2 self.m1 = m1 self.m2 = m2 self.g = g def dy_dt(self,t,y): """ Inputs a four component vector y[theta1,theta1dot,theta2,thetadot2] and outputs the time derivative of each component """ theta1 = y[0] theta1dot = y[1] theta2 = y[2] theta2dot = y[3] z1 = theta1dot #We defined these in the last section to get 1st order ODE's z2 = theta2dot #Below, a handful of common functions to simplify formula input (thanks for the idea!) c = np.cos(theta1-theta2) s = np.sin(theta1-theta2) denom = (self.m1 + self.m2s2) #Now, the equations from above: z1_dot = (-(self.m1 + self.m2)gnp.sin(theta1)-self.m2s(self.L2z2*2 + self.L1z1*2 c)+self.gself.m2cnp.sin(theta2))/(self.L1denom) z2_dot = ((self.m1+self.m2)(self.gcnp.sin(theta1)+self.L1z1*2 s - gnp.sin(theta2))+self.L2self.m2z22 cs)/(self.L2denom) return(z1,z1_dot,z2,z2_dot) def solve_ode(self, t_pts, theta1_0, theta1dot_0, theta2_0, theta2dot_0, abserr=1.0e-10,relerr = 1.0e-10): """ As the name suggests, this function inputs initial values for each theta and theta dot and solves the ODE along the specified t_pts """ #initial position y-vector: y = [theta1_0, theta1dot_0, theta2_0, theta2dot_0] #Below, we use the solve_ivp function to solve for the motion over our set of t_pts solution = solve_ivp(self.dy_dt, (t_pts[0], t_pts[-1]), y, t_eval=t_pts, atol = abserr, rtol = relerr) theta1, theta1dot, theta2, theta2dot = solution.y return(theta1,theta1dot,theta2,theta2dot) ###Output _____no_output_____ ###Markdown Now, a few plotting functions: ###Code def plot_y_vs_x(x, y, axis_labels=None, label=None, title=None, color=None, linestyle=None, semilogy=False, loglog=False, ax=None): """ Simple plot of points y vs. points x, found in Lagrangian_pendulum.ipynb """ if ax is None: ax = plt.gca() if (semilogy): line, = ax.semilogy(x, y, label=label, color=color, linestyle=linestyle) elif (loglog): line, = ax.loglog(x, y, label=label, color=color, linestyle=linestyle) else: line, = ax.plot(x, y, label=label, color=color, linestyle=linestyle) if label is not None: ax.legend() if title is not None: ax.set_title(title) if axis_labels is not None: ax.set_xlabel(axis_labels[0]) ax.set_ylabel(axis_labels[1]) return ax, line def start_stop_indices(t_pts, plot_start, plot_stop): start_index = (np.fabs(t_pts-plot_start)).argmin() stop_index = (np.fabs(t_pts-plot_stop)).argmin() return start_index, stop_index ###Output _____no_output_____ ###Markdown Finally, some labels for our plots: ###Code theta_vs_time_labels = (r'$t$', r'$\theta(t)$') ###Output _____no_output_____ ###Markdown Part 5: Plotting the Motion Below, we'll make some representative plots of the motion for various parameters and initial conditions: ###Code # Define plotting time t_start = 0. t_end = 50. delta_t = 0.001 t_pts = np.arange(t_start, t_end+delta_t, delta_t) ###Output _____no_output_____ ###Markdown Pendulum 1: Basic parameters, initially at rest ###Code #Parameters: L1 = 1.0 L2 = 1.0 m1 = 1.0 m2 = 1.0 g = 1.0 #Initial conditions: theta1_0 = np.pi/2 theta1dot_0 = 0.0 theta2_0 = np.pi theta2dot_0 = 0.0 #Create the pendulum: p1 = Pendulum(L1,L2,m1,m2,g) theta1, theta1dot, theta2, theta2dot = p1.solve_ode(t_pts,theta1_0,theta1dot_0,theta2_0,theta2dot_0) fig = plt.figure(figsize = (10,5)) overall_title = 'Double Pendulum: ' + \ rf' $\theta_1(0) = {theta1_0:.2f},$' + \ rf' $\dot\theta_1(0) = {theta1dot_0:.2f},$' + \ rf' $\theta_2(0) = {theta2_0:.2f},$' + \ rf' $\dot\theta_2(0) = {theta2dot_0:.2f}$' fig.suptitle(overall_title, va='baseline') ax_a = fig.add_subplot(1,1,1) start,stop = start_stop_indices(t_pts,t_start,t_end) plot_y_vs_x(t_pts[start:stop],theta1[start:stop], axis_labels = theta_vs_time_labels, label = r'$\theta_1(t)$', ax = ax_a) plot_y_vs_x(t_pts[start:stop],theta2[start:stop], axis_labels = theta_vs_time_labels, label = r'$\theta_2(t)$', ax = ax_a) ###Output _____no_output_____ ###Markdown Here, we see the first mass stays fairly close to its initial conditions, while the second mass moves around for a bit then abruptly makes multiple full rotations before settling down, again. Pendulum 2: Basic parameters, begin by pulling back and releasing bottom mass ###Code #Parameters: L1 = 1.0 L2 = 1.0 m1 = 1.0 m2 = 1.0 g = 1.0 #Initial conditions: theta1_0 = 0 theta1dot_0 = 0.0 theta2_0 = np.pi/4 theta2dot_0 = 0.0 #Create the pendulum: p2 = Pendulum(L1,L2,m1,m2,g) theta1, theta1dot, theta2, theta2dot = p2.solve_ode(t_pts,theta1_0,theta1dot_0,theta2_0,theta2dot_0) fig = plt.figure(figsize = (10,5)) overall_title = 'Double Pendulum: ' + \ rf' $\theta_1(0) = {theta1_0:.2f},$' + \ rf' $\dot\theta_1(0) = {theta1dot_0:.2f},$' + \ rf' $\theta_2(0) = {theta2_0:.2f},$' + \ rf' $\dot\theta_2(0) = {theta2dot_0:.2f}$' fig.suptitle(overall_title, va='baseline') ax_a = fig.add_subplot(1,1,1) start,stop = start_stop_indices(t_pts,t_start,t_end) plot_y_vs_x(t_pts[start:stop],theta1[start:stop], axis_labels = theta_vs_time_labels, label = r'$\theta_1(t)$', ax = ax_a) plot_y_vs_x(t_pts[start:stop],theta2[start:stop], axis_labels = theta_vs_time_labels, label = r'$\theta_2(t)$', ax = ax_a) ###Output _____no_output_____ ###Markdown While neither mass appears periodic, they both stay quite close to their initial starting positions, never making full rotations. Pendulum 3: $m_2 > m_1$ ###Code #Parameters: L1 = 1.0 L2 = 1.0 m1 = 1.0 m2 = 10.0 g = 1.0 #Initial conditions (same as Pendulum 1): theta1_0 = np.pi/2 theta1dot_0 = 0.0 theta2_0 = np.pi theta2dot_0 = 0.0 #Create the pendulum: p3 = Pendulum(L1,L2,m1,m2,g) theta1, theta1dot, theta2, theta2dot = p3.solve_ode(t_pts,theta1_0,theta1dot_0,theta2_0,theta2dot_0) fig = plt.figure(figsize = (10,5)) overall_title = 'Double Pendulum: ' + \ rf' $\theta_1(0) = {theta1_0:.2f},$' + \ rf' $\dot\theta_1(0) = {theta1dot_0:.2f},$' + \ rf' $\theta_2(0) = {theta2_0:.2f},$' + \ rf' $\dot\theta_2(0) = {theta2dot_0:.2f}$' fig.suptitle(overall_title, va='baseline') ax_a = fig.add_subplot(1,1,1) start,stop = start_stop_indices(t_pts,t_start,t_end) plot_y_vs_x(t_pts[start:stop],theta1[start:stop], axis_labels = theta_vs_time_labels, label = r'$\theta_1(t)$', ax = ax_a) plot_y_vs_x(t_pts[start:stop],theta2[start:stop], axis_labels = theta_vs_time_labels, label = r'$\theta_2(t)$', ax = ax_a) ###Output _____no_output_____ ###Markdown In this case, both masses make full rotations, with the first mass making multiple rotations before finally settling down. Part 6: Investigating Chaos Some of the signature features of chaotic system include a lack of periodicity and an exponential sensitivity to initial conditions. In this section, I show that the double pendulum is chaotic for initial conditions outside of the small-angle approximation. We'll start by initializing a pendulum with fairly large initial angles: ###Code #Parameters: L1 = 1.0 L2 = 1.0 m1 = 1.0 m2 = 1.0 g = 1.0 #Initial conditions (same as Pendulum 1): theta1_0 = np.pi/4 theta1dot_0 = 0 theta2_0 = np.pi theta2dot_0 = 0.0 #Create the pendulum: p4 = Pendulum(L1,L2,m1,m2,g) theta1, theta1dot, theta2, theta2dot = p4.solve_ode(t_pts,theta1_0,theta1dot_0,theta2_0,theta2dot_0) fig = plt.figure(figsize = (10,5)) overall_title = 'Double Pendulum: ' + \ rf' $\theta_1(0) = {theta1_0:.2f},$' + \ rf' $\dot\theta_1(0) = {theta1dot_0:.2f},$' + \ rf' $\theta_2(0) = {theta2_0:.2f},$' + \ rf' $\dot\theta_2(0) = {theta2dot_0:.2f}$' fig.suptitle(overall_title, va='baseline') ax_a = fig.add_subplot(1,1,1) start,stop = start_stop_indices(t_pts,t_start,t_end) plot_y_vs_x(t_pts[start:stop],theta1[start:stop], axis_labels = theta_vs_time_labels, label = r'$\theta_1(t)$', ax = ax_a) plot_y_vs_x(t_pts[start:stop],theta2[start:stop], axis_labels = theta_vs_time_labels, label = r'$\theta_2(t)$', ax = ax_a) ###Output _____no_output_____ ###Markdown Already, it appears that neither mass is periodic with time, indicating chaos. However, we need a bit more evidence. Below, we'll plot the state space plot of each mass with respect to time. If either plot closes on itself, the mass's motion is periodic. ###Code state_space_labels = (r'$\theta$', r'$d\theta/dt$') #New labels for comparing thetadot to theta fig = plt.figure(figsize = (10,5)) overall_title = 'Double Pendulum: ' + \ rf' $\theta_1(0) = {theta1_0:.2f},$' + \ rf' $\dot\theta_1(0) = {theta1dot_0:.2f},$' + \ rf' $\theta_2(0) = {theta2_0:.2f},$' + \ rf' $\dot\theta_2(0) = {theta2dot_0:.2f}$' fig.suptitle(overall_title, va='baseline') ax_a = fig.add_subplot(1,2,1) #1 row, 2 columns, position 1 ax_b = fig.add_subplot(1,2,2) #1 row, 2 columns, position 2 start,stop = start_stop_indices(t_pts,t_start,t_end) plot_y_vs_x(theta1[start:stop],theta1dot[start:stop], axis_labels = state_space_labels, label = r'$\theta_1(t)$', ax = ax_a) plot_y_vs_x(theta2[start:stop],theta2dot[start:stop], axis_labels = state_space_labels, label = r'$\theta_2(t)$', ax = ax_b) ###Output _____no_output_____ ###Markdown As expected, neither plot closes on itself, indicating that the motion is chaotic. B As a final check for chaos, we'll plot the difference between each $\theta$ for two pendulums with almost identical initial positions. In other words, we will create a second pendulum with initial conditions only slighly different than the first. If the difference between respective $\theta$ increases exponentially with time, we have a chaotic system. ###Code # Our first pendulum is p4, created above. Here, we create the slightly different pendulum: #Parameters: L1 = 1.0 L2 = 1.0 m1 = 1.0 m2 = 1.0 g = 1.0 #Initial conditions (slightly different than Pendulum 4): theta1_0 = np.pi/4 + 0.001 theta1dot_0 = 0 theta2_0 = np.pi + 0.001 theta2dot_0 = 0.0 #Create the pendulum: p5 = Pendulum(L1,L2,m1,m2,g) theta1_diff, theta1dot_diff, theta2_diff, theta2dot_diff = p5.solve_ode(t_pts,theta1_0,theta1dot_0,theta2_0,theta2dot_0) #Labels for our new plots: delta_labels = (r'$t$', r'$\Delta\theta$') #Define variables to plot, the difference between each theta diff1 = np.abs(theta1-theta1_diff) diff2 = np.abs(theta2-theta2_diff) #Plot our functions: fig = plt.figure(figsize = (10,5)) overall_title = 'Double Pendulum: ' + \ rf' $\theta_1(0) = {theta1_0:.2f},$' + \ rf' $\dot\theta_1(0) = {theta1dot_0:.2f},$' + \ rf' $\theta_2(0) = {theta2_0:.2f},$' + \ rf' $\dot\theta_2(0) = {theta2dot_0:.2f}$' fig.suptitle(overall_title, va='baseline') ax_a = fig.add_subplot(1,1,1) #1 row, 1 columns, position 1 start,stop = start_stop_indices(t_pts,t_start,t_end) plot_y_vs_x(t_pts[start:stop],diff1[start:stop], axis_labels = delta_labels, label = r'$\Delta\theta_1(t)$', semilogy = True, #Semi log plot ax = ax_a) plot_y_vs_x(t_pts[start:stop],diff2[start:stop], axis_labels = delta_labels, label = r'$\Delta\theta_2(t)$', semilogy = True, #Semi log plot ax = ax_a) ###Output _____no_output_____
tutorials/regression/03-CurveFitting-TensorFlow.ipynb	###Markdown 3 Curve Fitting (TensorFlow)Two methods are used to fit a curve in this tutorial, using [TensorFlow](https://www.tensorflow.org/):- Direct solution using least-squares method - this is the same method used in the previous tutorial that uses NumPy - Iterative optimisation using stochastic gradient descent 3.1 DataFirst, we sample $n$ observed data from the underlying polynomial defined by weights $w$: ###Code import random import numpy as np # get ground-truth data from the "true" model n = 100 w = [4, 3, 2, 1] deg = len(w)-1 x = np.linspace(-1,1,n)[:,np.newaxis] t = np.matmul(np.power(np.reshape(x,[-1,1]), np.linspace(deg,0,deg+1)), w) std_noise = 0.2 t_observed = np.reshape( [t[idx]+random.gauss(0,std_noise) for idx in range(n)], [-1,1]) ###Output _____no_output_____ ###Markdown 3.2 Least-Squares SolutionThis is mathematcally the same method used in previous NumPy tutorial. The advantage using TensorFlow here is not particularly obvious. ###Code import tensorflow as tf X = tf.pow(x, tf.linspace(deg,0,deg+1)) w_lstsq = tf.linalg.lstsq(X, t_observed) print(w_lstsq) ###Output tf.Tensor( [[4.05248568] [2.95396288] [1.956563 ] [1.00741483]], shape=(4, 1), dtype=float64) ###Markdown 3.3 Stochastic Gradient Descend MethodInstead of least-squares, weights can be optimised by minimising a loss function between the predicted- and observed target values, using [SGD](https://en.wikipedia.org/wiki/Stochastic_gradient_descent). It is not an efficient method for this curve fitting problem, is only for the purpose of demonstrating how an iterative method can be implemented in TensorFlow. ###Code w_sgd = tf.Variable(initial_value=tf.zeros([deg+1,1],tf.float64)) polynomial = lambda x_input : tf.matmul(x_input, w_sgd) optimizer = tf.optimizers.SGD(5e-3) total_iter = int(2e4) for step in range(total_iter): index = step % n with tf.GradientTape() as g: loss = tf.reduce_mean((polynomial(X[None,index,:])-t_observed[index])**2) #MSE gradients = g.gradient(loss, [w_sgd]) optimizer.apply_gradients(zip(gradients, [w_sgd])) if (step%1000)==0: print('Step %d: Loss=%f' % (step, loss)) print(w_sgd) ###Output Step 0: Loss=4.267816 Step 1000: Loss=0.037259 Step 2000: Loss=0.042375 Step 3000: Loss=0.133096 Step 4000: Loss=0.154306 Step 5000: Loss=0.136392 Step 6000: Loss=0.108063 Step 7000: Loss=0.081463 Step 8000: Loss=0.060006 Step 9000: Loss=0.043758 Step 10000: Loss=0.031807 Step 11000: Loss=0.023136 Step 12000: Loss=0.016880 Step 13000: Loss=0.012372 Step 14000: Loss=0.009123 Step 15000: Loss=0.006774 Step 16000: Loss=0.005071 Step 17000: Loss=0.003832 Step 18000: Loss=0.002925 Step 19000: Loss=0.002258 <tf.Variable 'Variable:0' shape=(4, 1) dtype=float64, numpy= array([[3.99621521], [2.96221558], [1.99494511], [1.00508842]])>
tests/test_vae_ts.ipynb	###Markdown Identifiability Test of Linear VAE on Synthetic Dataset ###Code %load_ext autoreload %autoreload 2 import torch import torch.nn.functional as F from torch.utils.data import DataLoader, random_split import ltcl import numpy as np from ltcl.datasets.sim_dataset import SimulationDatasetTSTwoSample from ltcl.modules.srnn import SRNNSynthetic from ltcl.tools.utils import load_yaml import random import seaborn as sns import matplotlib.pyplot as plt %matplotlib inline use_cuda = True device = torch.device("cuda:0" if use_cuda else "cpu") latent_size = 8 data = SimulationDatasetTSTwoSample(directory = '/srv/data/ltcl/data/', transition='linear_nongaussian_ts') num_validation_samples = 2500 train_data, val_data = random_split(data, [len(data)-num_validation_samples, num_validation_samples]) train_loader = DataLoader(train_data, batch_size=12800, shuffle=True, pin_memory=True) val_loader = DataLoader(val_data, batch_size=16, shuffle=False, pin_memory=True) cfg = load_yaml('../ltcl/configs/toy_linear_ts.yaml') model = SRNNSynthetic.load_from_checkpoint(checkpoint_path="/srv/data/ltcl/log/weiran/toy_linear_ts/lightning_logs/version_1/checkpoints/epoch=299-step=228599.ckpt", input_dim=cfg['VAE']['INPUT_DIM'], length=cfg['VAE']['LENGTH'], z_dim=cfg['VAE']['LATENT_DIM'], lag=cfg['VAE']['LAG'], hidden_dim=cfg['VAE']['ENC']['HIDDEN_DIM'], trans_prior=cfg['VAE']['TRANS_PRIOR'], bound=cfg['SPLINE']['BOUND'], count_bins=cfg['SPLINE']['BINS'], order=cfg['SPLINE']['ORDER'], beta=cfg['VAE']['BETA'], gamma=cfg['VAE']['GAMMA'], sigma=cfg['VAE']['SIGMA'], lr=cfg['VAE']['LR'], bias=cfg['VAE']['BIAS'], use_warm_start=cfg['SPLINE']['USE_WARM_START'], spline_pth=cfg['SPLINE']['PATH'], decoder_dist=cfg['VAE']['DEC']['DIST'], correlation=cfg['MCC']['CORR']) ###Output Load pretrained spline flow ###Markdown Load model checkpoint ###Code model.eval() model.to('cpu') ###Output _____no_output_____ ###Markdown Compute permutation and sign flip ###Code for batch in train_loader: break batch_size = batch['s1']['xt'].shape[0] zs.shape zs, mu, logvar = model.forward(batch['s1']) mu = mu.view(batch_size, -1, latent_size) A = mu[:,0,:].detach().cpu().numpy() B = batch['s1']['yt'][:,0,:].detach().cpu().numpy() C = np.zeros((latent_size,latent_size)) for i in range(latent_size): C[i] = -np.abs(np.corrcoef(B, A, rowvar=False)[i,latent_size:]) from scipy.optimize import linear_sum_assignment row_ind, col_ind = linear_sum_assignment(C) A = A[:, col_ind] mask = np.ones(latent_size) for i in range(latent_size): if np.corrcoef(B, A, rowvar=False)[i,latent_size:][i] > 0: mask[i] = -1 print("Permutation:",col_ind) print("Sign Flip:", mask) fig = plt.figure(figsize=(4,4)) sns.heatmap(-C, vmin=0, vmax=1, annot=True, fmt=".2f", linewidths=.5, cbar=False, cmap='Greens') plt.xlabel("Estimated latents ") plt.ylabel("True latents ") plt.title("MCC=%.3f"%np.abs(C[row_ind, col_ind]).mean()); figure_path = '/home/weiran/figs/' from matplotlib.backends.backend_pdf import PdfPages with PdfPages(figure_path + '/mcc_var.pdf') as pdf: fig = plt.figure(figsize=(4,4)) sns.heatmap(-C, vmin=0, vmax=1, annot=True, fmt=".2f", linewidths=.5, cbar=False, cmap='Greens') plt.xlabel("Estimated latents ") plt.ylabel("True latents ") plt.title("MCC=%.3f"%np.abs(C[row_ind, col_ind]).mean()); pdf.savefig(fig, bbox_inches="tight") # Permute column here mu = mu[:,:,col_ind] # Flip sign here mu = mu * torch.Tensor(mask, device=mu.device).view(1,1,latent_size) mu = -mu fig = plt.figure(figsize=(8,2)) col = 0 plt.plot(mu[:250,-1,col].detach().cpu().numpy(), color='b', label='True', alpha=0.75) plt.plot(batch['yt_'].squeeze()[:250,col].detach().cpu().numpy(), color='r', label="Estimated", alpha=0.75) plt.legend() plt.title("Current latent variable $z_t$") fig = plt.figure(figsize=(8,2)) col = 3 l = 1 plt.plot(batch['yt'].squeeze()[:250,l,col].detach().cpu().numpy(), color='b', label='True') plt.plot(mu[:,:-1,:][:250,l,col].detach().cpu().numpy(), color='r', label="Estimated") plt.xlabel("Sample index") plt.ylabel("Latent variable value") plt.legend() plt.title("Past latent variable $z_l$") fig = plt.figure(figsize=(2,2)) eps = model.sample(batch["xt"].cpu()) eps = eps.detach().cpu().numpy() component_idx = 4 sns.distplot(eps[:,component_idx], hist=False, kde=True, bins=None, hist_kws={'edgecolor':'black'}, kde_kws={'linewidth': 2}); plt.title("Learned noise prior") ###Output /home/cmu_wyao/anaconda3/envs/py37/lib/python3.7/site-packages/seaborn/distributions.py:2557: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `kdeplot` (an axes-level function for kernel density plots). warnings.warn(msg, FutureWarning) ###Markdown System identification (causal discovery) ###Code from ltcl.modules.components.base import GroupLinearLayer trans_func = GroupLinearLayer(din = 8, dout = 8, num_blocks = 2, diagonal = False) b = torch.nn.Parameter(0.001 * torch.randn(1, 8)) opt = torch.optim.Adam(trans_func.parameters(),lr=0.01) lossfunc = torch.nn.L1Loss() max_iters = 2 counter = 0 for step in range(max_iters): for batch in train_loader: batch_size = batch['yt'].shape[0] x_recon, mu, logvar, z = model.forward(batch) mu = mu.view(batch_size, -1, 8) # Fix permutation before training mu = mu[:,:,col_ind] # Fix sign flip before training mu = mu * torch.Tensor(mask, device=mu.device).view(1,1,8) mu = -mu pred = trans_func(mu[:,:-1,:]).sum(dim=1) + b true = mu[:,-1,:] loss = lossfunc(pred, true) #+ torch.mean(adaptive.lossfun((pred - true))) opt.zero_grad() loss.backward() opt.step() if counter % 100 == 0: print(loss.item()) counter += 1 ###Output 1.0767319202423096 0.213593527674675 ###Markdown Visualize causal matrix ###Code B2 = model.transition_prior.transition.w[0][col_ind][:, col_ind].detach().cpu().numpy() B1 = model.transition_prior.transition.w[1][col_ind][:, col_ind].detach().cpu().numpy() B1 = B1 * mask.reshape(1,-1) * (mask).reshape(-1,1) B2 = B2 * mask.reshape(1,-1) * (mask).reshape(-1,1) BB2 = np.load("/srv/data/ltcl/data/linear_nongaussian_ts/W2.npy") BB1 = np.load("/srv/data/ltcl/data/linear_nongaussian_ts/W1.npy") # b = np.concatenate((B1,B2), axis=0) # bb = np.concatenate((BB1,BB2), axis=0) # b = b / np.linalg.norm(b, axis=0).reshape(1, -1) # bb = bb / np.linalg.norm(bb, axis=0).reshape(1, -1) # pred = (b / np.linalg.norm(b, axis=0).reshape(1, -1)).reshape(-1) # true = (bb / np.linalg.norm(bb, axis=0).reshape(1, -1)).reshape(-1) bs = [B1, B2] bbs = [BB1, BB2] with PdfPages(figure_path + '/entries.pdf') as pdf: fig, axs = plt.subplots(1,2, figsize=(4,2)) for tau in range(2): ax = axs[tau] b = bs[tau] bb = bbs[tau] b = b / np.linalg.norm(b, axis=0).reshape(1, -1) bb = bb / np.linalg.norm(bb, axis=0).reshape(1, -1) pred = (b / np.linalg.norm(b, axis=0).reshape(1, -1)).reshape(-1) true = (bb / np.linalg.norm(bb, axis=0).reshape(1, -1)).reshape(-1) ax.scatter(pred, true, s=10, cmap=plt.cm.coolwarm, zorder=10, color='b') lims = [-0.75,0.75 ] # now plot both limits against eachother ax.plot(lims, lims, '-.', alpha=0.75, zorder=0) # ax.set_xlim(lims) # ax.set_ylim(lims) ax.set_xlabel("Estimated weight") ax.set_ylabel("Truth weight") ax.set_title(r"Entries of $\mathbf{B}_%d$"%(tau+1)) plt.tight_layout() pdf.savefig(fig, bbox_inches="tight") fig, axs = plt.subplots(2,4, figsize=(4,2)) for i in range(8): row = i // 4 col = i % 4 ax = axs[row,col] ax.scatter(B[:,i], A[:,i], s=4, color='b', alpha=0.25) ax.axis('off') # ax.set_xlabel('Ground truth latent') # ax.set_ylabel('Estimated latent') # ax.grid('..') fig.tight_layout() import numpy as numx def calculate_amari_distance(matrix_one, matrix_two, version=1): """ Calculate the Amari distance between two input matrices. :param matrix_one: the first matrix :type matrix_one: numpy array :param matrix_two: the second matrix :type matrix_two: numpy array :param version: Variant to use. :type version: int :return: The amari distance between two input matrices. :rtype: float """ if matrix_one.shape != matrix_two.shape: return "Two matrices must have the same shape." product_matrix = numx.abs(numx.dot(matrix_one, numx.linalg.inv(matrix_two))) product_matrix_max_col = numx.array(product_matrix.max(0)) product_matrix_max_row = numx.array(product_matrix.max(1)) n = product_matrix.shape[0] """ Formula from ESLII Here they refered to as "amari error" The value is in [0, N-1]. reference: Bach, F. R.; Jordan, M. I. Kernel Independent Component Analysis, J MACH LEARN RES, 2002, 3, 1--48 """ amari_distance = product_matrix / numx.tile(product_matrix_max_col, (n, 1)) amari_distance += product_matrix / numx.tile(product_matrix_max_row, (n, 1)).T amari_distance = amari_distance.sum() / (2 * n) - 1 amari_distance = amari_distance / (n-1) return amari_distance print("Amari distance for B1:", calculate_amari_distance(B1, BB1)) print("Amari distance for B2:", calculate_amari_distance(B2, BB2)) ###Output Amari distance for B1: 0.16492316394918433 Amari distance for B2: 0.352378050478662 ###Markdown Identifiability Test of Linear VAE on Synthetic Dataset ###Code %load_ext autoreload %autoreload 2 import torch import torch.nn.functional as F from torch.utils.data import DataLoader, random_split import leap import numpy as np from leap.datasets.sim_dataset import SimulationDatasetTSTwoSample from leap.modules.srnn import SRNNSynthetic from leap.tools.utils import load_yaml import random import seaborn as sns import matplotlib.pyplot as plt %matplotlib inline use_cuda = True device = torch.device("cuda:0" if use_cuda else "cpu") latent_size = 8 data = SimulationDatasetTSTwoSample(directory = '/srv/data/leap/data/', transition='linear_nongaussian_ts') num_validation_samples = 2500 train_data, val_data = random_split(data, [len(data)-num_validation_samples, num_validation_samples]) train_loader = DataLoader(train_data, batch_size=12800, shuffle=True, pin_memory=True) val_loader = DataLoader(val_data, batch_size=16, shuffle=False, pin_memory=True) cfg = load_yaml('../leap/configs/toy_linear_ts.yaml') model = SRNNSynthetic.load_from_checkpoint(checkpoint_path="/srv/data/ltcl/log/weiran/toy_linear_ts/lightning_logs/version_1/checkpoints/epoch=299-step=228599.ckpt", input_dim=cfg['VAE']['INPUT_DIM'], length=cfg['VAE']['LENGTH'], z_dim=cfg['VAE']['LATENT_DIM'], lag=cfg['VAE']['LAG'], hidden_dim=cfg['VAE']['ENC']['HIDDEN_DIM'], trans_prior=cfg['VAE']['TRANS_PRIOR'], bound=cfg['SPLINE']['BOUND'], count_bins=cfg['SPLINE']['BINS'], order=cfg['SPLINE']['ORDER'], beta=cfg['VAE']['BETA'], gamma=cfg['VAE']['GAMMA'], sigma=cfg['VAE']['SIGMA'], lr=cfg['VAE']['LR'], bias=cfg['VAE']['BIAS'], use_warm_start=cfg['SPLINE']['USE_WARM_START'], spline_pth=cfg['SPLINE']['PATH'], decoder_dist=cfg['VAE']['DEC']['DIST'], correlation=cfg['MCC']['CORR']) ###Output Load pretrained spline flow ###Markdown Load model checkpoint ###Code model.eval() model.to('cpu') ###Output _____no_output_____ ###Markdown Compute permutation and sign flip ###Code for batch in train_loader: break batch_size = batch['s1']['xt'].shape[0] zs.shape zs, mu, logvar = model.forward(batch['s1']) mu = mu.view(batch_size, -1, latent_size) A = mu[:,0,:].detach().cpu().numpy() B = batch['s1']['yt'][:,0,:].detach().cpu().numpy() C = np.zeros((latent_size,latent_size)) for i in range(latent_size): C[i] = -np.abs(np.corrcoef(B, A, rowvar=False)[i,latent_size:]) from scipy.optimize import linear_sum_assignment row_ind, col_ind = linear_sum_assignment(C) A = A[:, col_ind] mask = np.ones(latent_size) for i in range(latent_size): if np.corrcoef(B, A, rowvar=False)[i,latent_size:][i] > 0: mask[i] = -1 print("Permutation:",col_ind) print("Sign Flip:", mask) fig = plt.figure(figsize=(4,4)) sns.heatmap(-C, vmin=0, vmax=1, annot=True, fmt=".2f", linewidths=.5, cbar=False, cmap='Greens') plt.xlabel("Estimated latents ") plt.ylabel("True latents ") plt.title("MCC=%.3f"%np.abs(C[row_ind, col_ind]).mean()); figure_path = '/home/weiran/figs/' from matplotlib.backends.backend_pdf import PdfPages with PdfPages(figure_path + '/mcc_var.pdf') as pdf: fig = plt.figure(figsize=(4,4)) sns.heatmap(-C, vmin=0, vmax=1, annot=True, fmt=".2f", linewidths=.5, cbar=False, cmap='Greens') plt.xlabel("Estimated latents ") plt.ylabel("True latents ") plt.title("MCC=%.3f"%np.abs(C[row_ind, col_ind]).mean()); pdf.savefig(fig, bbox_inches="tight") # Permute column here mu = mu[:,:,col_ind] # Flip sign here mu = mu * torch.Tensor(mask, device=mu.device).view(1,1,latent_size) mu = -mu fig = plt.figure(figsize=(8,2)) col = 0 plt.plot(mu[:250,-1,col].detach().cpu().numpy(), color='b', label='True', alpha=0.75) plt.plot(batch['yt_'].squeeze()[:250,col].detach().cpu().numpy(), color='r', label="Estimated", alpha=0.75) plt.legend() plt.title("Current latent variable $z_t$") fig = plt.figure(figsize=(8,2)) col = 3 l = 1 plt.plot(batch['yt'].squeeze()[:250,l,col].detach().cpu().numpy(), color='b', label='True') plt.plot(mu[:,:-1,:][:250,l,col].detach().cpu().numpy(), color='r', label="Estimated") plt.xlabel("Sample index") plt.ylabel("Latent variable value") plt.legend() plt.title("Past latent variable $z_l$") fig = plt.figure(figsize=(2,2)) eps = model.sample(batch["xt"].cpu()) eps = eps.detach().cpu().numpy() component_idx = 4 sns.distplot(eps[:,component_idx], hist=False, kde=True, bins=None, hist_kws={'edgecolor':'black'}, kde_kws={'linewidth': 2}); plt.title("Learned noise prior") ###Output /home/cmu_wyao/anaconda3/envs/py37/lib/python3.7/site-packages/seaborn/distributions.py:2557: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `kdeplot` (an axes-level function for kernel density plots). warnings.warn(msg, FutureWarning) ###Markdown System identification (causal discovery) ###Code from leap.modules.components.base import GroupLinearLayer trans_func = GroupLinearLayer(din = 8, dout = 8, num_blocks = 2, diagonal = False) b = torch.nn.Parameter(0.001 * torch.randn(1, 8)) opt = torch.optim.Adam(trans_func.parameters(),lr=0.01) lossfunc = torch.nn.L1Loss() max_iters = 2 counter = 0 for step in range(max_iters): for batch in train_loader: batch_size = batch['yt'].shape[0] x_recon, mu, logvar, z = model.forward(batch) mu = mu.view(batch_size, -1, 8) # Fix permutation before training mu = mu[:,:,col_ind] # Fix sign flip before training mu = mu * torch.Tensor(mask, device=mu.device).view(1,1,8) mu = -mu pred = trans_func(mu[:,:-1,:]).sum(dim=1) + b true = mu[:,-1,:] loss = lossfunc(pred, true) #+ torch.mean(adaptive.lossfun((pred - true))) opt.zero_grad() loss.backward() opt.step() if counter % 100 == 0: print(loss.item()) counter += 1 ###Output 1.0767319202423096 0.213593527674675 ###Markdown Visualize causal matrix ###Code B2 = model.transition_prior.transition.w[0][col_ind][:, col_ind].detach().cpu().numpy() B1 = model.transition_prior.transition.w[1][col_ind][:, col_ind].detach().cpu().numpy() B1 = B1 * mask.reshape(1,-1) * (mask).reshape(-1,1) B2 = B2 * mask.reshape(1,-1) * (mask).reshape(-1,1) BB2 = np.load("/srv/data/ltcl/data/linear_nongaussian_ts/W2.npy") BB1 = np.load("/srv/data/ltcl/data/linear_nongaussian_ts/W1.npy") # b = np.concatenate((B1,B2), axis=0) # bb = np.concatenate((BB1,BB2), axis=0) # b = b / np.linalg.norm(b, axis=0).reshape(1, -1) # bb = bb / np.linalg.norm(bb, axis=0).reshape(1, -1) # pred = (b / np.linalg.norm(b, axis=0).reshape(1, -1)).reshape(-1) # true = (bb / np.linalg.norm(bb, axis=0).reshape(1, -1)).reshape(-1) bs = [B1, B2] bbs = [BB1, BB2] with PdfPages(figure_path + '/entries.pdf') as pdf: fig, axs = plt.subplots(1,2, figsize=(4,2)) for tau in range(2): ax = axs[tau] b = bs[tau] bb = bbs[tau] b = b / np.linalg.norm(b, axis=0).reshape(1, -1) bb = bb / np.linalg.norm(bb, axis=0).reshape(1, -1) pred = (b / np.linalg.norm(b, axis=0).reshape(1, -1)).reshape(-1) true = (bb / np.linalg.norm(bb, axis=0).reshape(1, -1)).reshape(-1) ax.scatter(pred, true, s=10, cmap=plt.cm.coolwarm, zorder=10, color='b') lims = [-0.75,0.75 ] # now plot both limits against eachother ax.plot(lims, lims, '-.', alpha=0.75, zorder=0) # ax.set_xlim(lims) # ax.set_ylim(lims) ax.set_xlabel("Estimated weight") ax.set_ylabel("Truth weight") ax.set_title(r"Entries of $\mathbf{B}_%d$"%(tau+1)) plt.tight_layout() pdf.savefig(fig, bbox_inches="tight") fig, axs = plt.subplots(2,4, figsize=(4,2)) for i in range(8): row = i // 4 col = i % 4 ax = axs[row,col] ax.scatter(B[:,i], A[:,i], s=4, color='b', alpha=0.25) ax.axis('off') # ax.set_xlabel('Ground truth latent') # ax.set_ylabel('Estimated latent') # ax.grid('..') fig.tight_layout() import numpy as numx def calculate_amari_distance(matrix_one, matrix_two, version=1): """ Calculate the Amari distance between two input matrices. :param matrix_one: the first matrix :type matrix_one: numpy array :param matrix_two: the second matrix :type matrix_two: numpy array :param version: Variant to use. :type version: int :return: The amari distance between two input matrices. :rtype: float """ if matrix_one.shape != matrix_two.shape: return "Two matrices must have the same shape." product_matrix = numx.abs(numx.dot(matrix_one, numx.linalg.inv(matrix_two))) product_matrix_max_col = numx.array(product_matrix.max(0)) product_matrix_max_row = numx.array(product_matrix.max(1)) n = product_matrix.shape[0] """ Formula from ESLII Here they refered to as "amari error" The value is in [0, N-1]. reference: Bach, F. R.; Jordan, M. I. Kernel Independent Component Analysis, J MACH LEARN RES, 2002, 3, 1--48 """ amari_distance = product_matrix / numx.tile(product_matrix_max_col, (n, 1)) amari_distance += product_matrix / numx.tile(product_matrix_max_row, (n, 1)).T amari_distance = amari_distance.sum() / (2 * n) - 1 amari_distance = amari_distance / (n-1) return amari_distance print("Amari distance for B1:", calculate_amari_distance(B1, BB1)) print("Amari distance for B2:", calculate_amari_distance(B2, BB2)) ###Output Amari distance for B1: 0.16492316394918433 Amari distance for B2: 0.352378050478662
Semana1-Projeto.ipynb	###Markdown Descrição: As a data scientist working for an investment firm, you will extract the revenue data for Tesla and GameStop and build a dashboard to compare the price of the stock vs the revenue. Tarefas:- Question 1 - Extracting Tesla Stock Data Using yfinance - 2 Points- Question 2 - Extracting Tesla Revenue Data Using Webscraping - 1 Points- Question 3 - Extracting GameStop Stock Data Using yfinance - 2 Points- Question 4 - Extracting GameStop Revenue Data Using Webscraping - 1 Points- Question 5 - Tesla Stock and Revenue Dashboard - 2 Points- Question 6 - GameStop Stock and Revenue Dashboard- 2 Points- Question 7 - Sharing your Assignment Notebook - 2 Points ###Code # installing dependencies !pip install yfinance pandas bs4 # importing modules import yfinance as yf import pandas as pd import requests from bs4 import BeautifulSoup # needed to cast datetime values from datetime import datetime ###Output Requirement already satisfied: yfinance in /opt/conda/lib/python3.8/site-packages (0.1.63) Requirement already satisfied: pandas in /opt/conda/lib/python3.8/site-packages (1.2.4) Requirement already satisfied: bs4 in /opt/conda/lib/python3.8/site-packages (0.0.1) Requirement already satisfied: beautifulsoup4 in /opt/conda/lib/python3.8/site-packages (from bs4) (4.9.3) Requirement already satisfied: python-dateutil>=2.7.3 in /opt/conda/lib/python3.8/site-packages (from pandas) (2.8.1) Requirement already satisfied: pytz>=2017.3 in /opt/conda/lib/python3.8/site-packages (from pandas) (2021.1) Requirement already satisfied: numpy>=1.16.5 in /opt/conda/lib/python3.8/site-packages (from pandas) (1.20.2) Requirement already satisfied: six>=1.5 in /opt/conda/lib/python3.8/site-packages (from python-dateutil>=2.7.3->pandas) (1.15.0) Requirement already satisfied: multitasking>=0.0.7 in /opt/conda/lib/python3.8/site-packages (from yfinance) (0.0.9) Requirement already satisfied: requests>=2.20 in /opt/conda/lib/python3.8/site-packages (from yfinance) (2.25.1) Requirement already satisfied: lxml>=4.5.1 in /opt/conda/lib/python3.8/site-packages (from yfinance) (4.6.3) Requirement already satisfied: urllib3<1.27,>=1.21.1 in /opt/conda/lib/python3.8/site-packages (from requests>=2.20->yfinance) (1.26.4) Requirement already satisfied: chardet<5,>=3.0.2 in /opt/conda/lib/python3.8/site-packages (from requests>=2.20->yfinance) (4.0.0) Requirement already satisfied: idna<3,>=2.5 in /opt/conda/lib/python3.8/site-packages (from requests>=2.20->yfinance) (2.10) Requirement already satisfied: certifi>=2017.4.17 in /opt/conda/lib/python3.8/site-packages (from requests>=2.20->yfinance) (2020.12.5) Requirement already satisfied: soupsieve>1.2 in /opt/conda/lib/python3.8/site-packages (from beautifulsoup4->bs4) (2.0.1) ###Markdown Question 1 - Extracting Tesla Stock Data Using yfinance ###Code # making Ticker object tesla_ticker = yf.Ticker("TSLA") # creating a dataframe with history values tesla_data = tesla_ticker.history(period="max") # now we need to reset dataframe index and show first values tesla_data.reset_index(inplace=True) tesla_data.head() ###Output _____no_output_____ ###Markdown Question 2 - Extracting Tesla Revenue Data Using Webscraping ###Code # getting TSLA revenue data from https://www.macrotrends.net/stocks/charts/TSLA/tesla/revenue tesla_revenue_url="https://www.macrotrends.net/stocks/charts/TSLA/tesla/revenue" html_data=requests.get(tesla_revenue_url).text # parsing html data soup = BeautifulSoup(html_data,"html.parser") # now we need to create a dataframe with columns "date" and "revenue", using data scrapped from soup tesla_revenue_table = soup.find("table", class_="historical_data_table") # now we will create an empty dataframe tesla_revenue_data = pd.DataFrame(columns=["Date", "Revenue"]) # now we will loop through table and populate the dataframe for row in tesla_revenue_table.tbody.find_all("tr"): col = row.find_all("td") if (col != []): row_date = col[0].text row_date = datetime.strptime(row_date, '%Y') row_revenue = col[1].text # we need to strip "," and "$" chars from revenue value row_revenue = row_revenue.replace(",","").replace("$","") row_revenue = int(row_revenue) # printing var types # print(type(row_date), type(row_revenue) ) tesla_revenue_data = tesla_revenue_data.append( { 'Date': row_date, 'Revenue': row_revenue }, ignore_index=True) tesla_revenue_data.head() ###Output _____no_output_____ ###Markdown Question 3 - Extracting GameStop Stock Data Using yfinance ###Code # making Ticker object gme_ticker = yf.Ticker("GME") # creating a dataframe with history values gme_data = gme_ticker.history(period="max") # now we need to reset dataframe index and show first values gme_data.reset_index(inplace=True) gme_data.head() ###Output _____no_output_____ ###Markdown Question 4 - Extracting GameStop Revenue Data Using Webscraping ###Code # getting GME revenue data from https://www.macrotrends.net/stocks/charts/GME/gamestop/revenue gme_revenue_url="https://www.macrotrends.net/stocks/charts/GME/gamestop/revenue" html_data=requests.get(gme_revenue_url).text # parsing html data soup = BeautifulSoup(html_data,"html.parser") # now we need to create a dataframe with columns "date" and "revenue", using data scrapped from soup gme_revenue_table = soup.find("table", class_="historical_data_table") # now we will create an empty dataframe gme_revenue_data = pd.DataFrame(columns=["Date", "Revenue"]) # now we will loop through table and populate the dataframe for row in gme_revenue_table.tbody.find_all("tr"): col = row.find_all("td") if (col != []): row_date = col[0].text row_date = datetime.strptime(row_date, '%Y') row_revenue = col[1].text # we need to strip "," and "$" chars from revenue value row_revenue = row_revenue.replace(",","").replace("$","") row_revenue = int(row_revenue) # printing var types # print(type(row_date), type(row_revenue) ) gme_revenue_data = gme_revenue_data.append( { 'Date': row_date, 'Revenue': row_revenue }, ignore_index=True) gme_revenue_data.head() ###Output _____no_output_____ ###Markdown Question 5 - Tesla Stock and Revenue Dashboard ###Code # plotting tesla stock data tesla_data.plot(x="Date", y="Open") # plotting tesla revenue data tesla_revenue_data.plot(x="Date", y="Revenue") ###Output _____no_output_____ ###Markdown Question 6 - GameStop Stock and Revenue Dashboard ###Code # plotting gamestop stock data gme_data.plot(x="Date", y="Open") # plotting gamestop revenue data gme_revenue_data.plot(x="Date", y="Revenue") ###Output _____no_output_____
program/.ipynb_checkpoints/2_6_Qlearning-checkpoint.ipynb	###Markdown 2.6 Q学習で迷路を攻略 ###Code # 使用するパッケージの宣言 import numpy as np import matplotlib.pyplot as plt %matplotlib inline # 初期位置での迷路の様子 # 図を描く大きさと、図の変数名を宣言 fig = plt.figure(figsize=(5, 5)) ax = plt.gca() # 赤い壁を描く plt.plot([1, 1], [0, 1], color='red', linewidth=2) plt.plot([1, 2], [2, 2], color='red', linewidth=2) plt.plot([2, 2], [2, 1], color='red', linewidth=2) plt.plot([2, 3], [1, 1], color='red', linewidth=2) # 状態を示す文字S0～S8を描く plt.text(0.5, 2.5, 'S0', size=14, ha='center') plt.text(1.5, 2.5, 'S1', size=14, ha='center') plt.text(2.5, 2.5, 'S2', size=14, ha='center') plt.text(0.5, 1.5, 'S3', size=14, ha='center') plt.text(1.5, 1.5, 'S4', size=14, ha='center') plt.text(2.5, 1.5, 'S5', size=14, ha='center') plt.text(0.5, 0.5, 'S6', size=14, ha='center') plt.text(1.5, 0.5, 'S7', size=14, ha='center') plt.text(2.5, 0.5, 'S8', size=14, ha='center') plt.text(0.5, 2.3, 'START', ha='center') plt.text(2.5, 0.3, 'GOAL', ha='center') # 描画範囲の設定と目盛りを消す設定 ax.set_xlim(0, 3) ax.set_ylim(0, 3) plt.tick_params(axis='both', which='both', bottom='off', top='off', labelbottom='off', right='off', left='off', labelleft='off') # 現在地S0に緑丸を描画する line, = ax.plot([0.5], [2.5], marker="o", color='g', markersize=60) # 初期の方策を決定するパラメータtheta_0を設定 # 行は状態0～7、列は移動方向で↑、→、↓、←を表す theta_0 = np.array([[np.nan, 1, 1, np.nan], # s0 [np.nan, 1, np.nan, 1], # s1 [np.nan, np.nan, 1, 1], # s2 [1, 1, 1, np.nan], # s3 [np.nan, np.nan, 1, 1], # s4 [1, np.nan, np.nan, np.nan], # s5 [1, np.nan, np.nan, np.nan], # s6 [1, 1, np.nan, np.nan], # s7、※s8はゴールなので、方策はなし ]) # 方策パラメータtheta_0をランダム方策piに変換する関数の定義 def simple_convert_into_pi_from_theta(theta): '''単純に割合を計算する''' [m, n] = theta.shape # thetaの行列サイズを取得 pi = np.zeros((m, n)) for i in range(0, m): pi[i, :] = theta[i, :] / np.nansum(theta[i, :]) # 割合の計算 pi = np.nan_to_num(pi) # nanを0に変換 return pi # ランダム行動方策pi_0を求める pi_0 = simple_convert_into_pi_from_theta(theta_0) # 初期の行動価値関数Qを設定 [a, b] = theta_0.shape # 行と列の数をa, bに格納 Q = np.random.rand(a, b) * theta_0 * 0.1 # theta0をすることで要素ごとに掛け算をし、Qの壁方向の値がnanになる # ε-greedy法を実装 def get_action(s, Q, epsilon, pi_0): direction = ["up", "right", "down", "left"] # 行動を決める if np.random.rand() < epsilon: # εの確率でランダムに動く next_direction = np.random.choice(direction, p=pi_0[s, :]) else: # Qの最大値の行動を採用する next_direction = direction[np.nanargmax(Q[s, :])] # 行動をindexに if next_direction == "up": action = 0 elif next_direction == "right": action = 1 elif next_direction == "down": action = 2 elif next_direction == "left": action = 3 return action def get_s_next(s, a, Q, epsilon, pi_0): direction = ["up", "right", "down", "left"] next_direction = direction[a] # 行動aの方向 # 行動から次の状態を決める if next_direction == "up": s_next = s - 3 # 上に移動するときは状態の数字が3小さくなる elif next_direction == "right": s_next = s + 1 # 右に移動するときは状態の数字が1大きくなる elif next_direction == "down": s_next = s + 3 # 下に移動するときは状態の数字が3大きくなる elif next_direction == "left": s_next = s - 1 # 左に移動するときは状態の数字が1小さくなる return s_next # Q学習による行動価値関数Qの更新 def Q_learning(s, a, r, s_next, Q, eta, gamma): if s_next == 8: # ゴールした場合 Q[s, a] = Q[s, a] + eta (r - Q[s, a]) else: Q[s, a] = Q[s, a] + eta * (r + gamma * np.nanmax(Q[s_next,: ]) - Q[s, a]) return Q # Q学習で迷路を解く関数の定義、状態と行動の履歴および更新したQを出力 def goal_maze_ret_s_a_Q(Q, epsilon, eta, gamma, pi): s = 0 # スタート地点 a = a_next = get_action(s, Q, epsilon, pi) # 初期の行動 s_a_history = [[0, np.nan]] # エージェントの移動を記録するリスト while (1): # ゴールするまでループ a = a_next # 行動更新 s_a_history[-1][1] = a # 現在の状態（つまり一番最後なのでindex=-1）に行動を代入 s_next = get_s_next(s, a, Q, epsilon, pi) # 次の状態を格納 s_a_history.append([s_next, np.nan]) # 次の状態を代入。行動はまだ分からないのでnanにしておく # 報酬を与え,　次の行動を求めます if s_next == 8: r = 1 # ゴールにたどり着いたなら報酬を与える a_next = np.nan else: r = 0 a_next = get_action(s_next, Q, epsilon, pi) # 次の行動a_nextを求めます。 # 価値関数を更新 Q = Q_learning(s, a, r, s_next, Q, eta, gamma) # 終了判定 if s_next == 8: # ゴール地点なら終了 break else: s = s_next return [s_a_history, Q] # Q学習で迷路を解く eta = 0.1 # 学習率 gamma = 0.9 # 時間割引率 epsilon = 0.5 # ε-greedy法の初期値 v = np.nanmax(Q, axis=1) # 状態ごとに価値の最大値を求める is_continue = True episode = 1 V = [] # エピソードごとの状態価値を格納する V.append(np.nanmax(Q, axis=1)) # 状態ごとに行動価値の最大値を求める while is_continue: # is_continueがFalseになるまで繰り返す print("エピソード:" + str(episode)) # ε-greedyの値を少しずつ小さくする epsilon = epsilon / 2 # Q学習で迷路を解き、移動した履歴と更新したQを求める [s_a_history, Q] = goal_maze_ret_s_a_Q(Q, epsilon, eta, gamma, pi_0) # 状態価値の変化 new_v = np.nanmax(Q, axis=1) # 状態ごとに行動価値の最大値を求める print(np.sum(np.abs(new_v - v))) # 状態価値関数の変化を出力 v = new_v V.append(v) # このエピソード終了時の状態価値関数を追加 print("迷路を解くのにかかったステップ数は" + str(len(s_a_history) - 1) + "です") # 100エピソード繰り返す episode = episode + 1 if episode > 100: break # 状態価値の変化を可視化します # 参考URL http://louistiao.me/posts/notebooks/embedding-matplotlib-animations-in-jupyter-notebooks/ from matplotlib import animation from IPython.display import HTML import matplotlib.cm as cm # color map def init(): # 背景画像の初期化 line.set_data([], []) return (line,) def animate(i): # フレームごとの描画内容 # 各マスに状態価値の大きさに基づく色付きの四角を描画 line, = ax.plot([0.5], [2.5], marker="s", color=cm.jet(V[i][0]), markersize=85) # S0 line, = ax.plot([1.5], [2.5], marker="s", color=cm.jet(V[i][1]), markersize=85) # S1 line, = ax.plot([2.5], [2.5], marker="s", color=cm.jet(V[i][2]), markersize=85) # S2 line, = ax.plot([0.5], [1.5], marker="s", color=cm.jet(V[i][3]), markersize=85) # S3 line, = ax.plot([1.5], [1.5], marker="s", color=cm.jet(V[i][4]), markersize=85) # S4 line, = ax.plot([2.5], [1.5], marker="s", color=cm.jet(V[i][5]), markersize=85) # S5 line, = ax.plot([0.5], [0.5], marker="s", color=cm.jet(V[i][6]), markersize=85) # S6 line, = ax.plot([1.5], [0.5], marker="s", color=cm.jet(V[i][7]), markersize=85) # S7 line, = ax.plot([2.5], [0.5], marker="s", color=cm.jet(1.0), markersize=85) # S8 return (line,) #　初期化関数とフレームごとの描画関数を用いて動画を作成 anim = animation.FuncAnimation( fig, animate, init_func=init, frames=len(V), interval=200, repeat=False) HTML(anim.to_jshtml()) ###Output _____no_output_____
doc/examples/Simple Live plotting example with DDH5.ipynb	###Markdown The idea is pretty simple:We first define the structure of the datadict (you can also use a datadict that is already populated); this is equivalent to the idea of registering parameters in qcodes.You can then use the DDH5 writer to start saving data -- it'll determine file location automatically, within the base directory that is the first argument.To look at the data, you can use the `autoplot_ddh5` app. The easiest way might be to copy the file `apps/templates/autoplot_ddh5.bat` to some location of your choice, and edit the pathname variable to the correct folder in which `autoplot_ddh5.py` is located, such as:`` @set "APPPATH=c:\code\plottr\apps"``(note: this is the apps directory in the plottr base repository, not in the package). You can then associate opening `.ddh5` files with that batch file. ###Code data = dd.DataDict( x = dict(unit='A'), y = dict(unit='B'), z = dict(axes=['x', 'y']), ) data.validate() nrows = 100 with dds.DDH5Writer(r"d:\data", data) as writer: for n in range(nrows): writer.add_data(x=[n], y=np.linspace(0,1,11).reshape(1,-1), z=np.random.rand(11).reshape(1,-1) ) time.sleep(1) ###Output _____no_output_____
practice/cython-demo.ipynb	###Markdown Compare speed between native and cythonized math functions ###Code %load_ext Cython %%cython from libc.math cimport log, sqrt def log_c(float x): return log(x)/2.302585092994046 def sqrt_c(float x): return sqrt(x) import os from os.path import expanduser import pandas as pd import pandas.io.sql as pd_sql import math from functions.auth.connections import postgres_connection connection_uri = postgres_connection('mountain_project') def transform_features(df): """ Add log and sqrt values """ # add log values for ols linear regression df['log_star_ratings'] = df['star_ratings'].apply(lambda x: math.log(x+1, 10)) df['log_ticks'] = df['ticks'].apply(lambda x: math.log(x+1, 10)) df['log_avg_stars'] = df['avg_stars'].apply(lambda x: math.log(x+1, 10)) df['log_length'] = df['length_'].apply(lambda x: math.log(x+1, 10)) df['log_grade'] = df['grade'].apply(lambda x: math.log(x+2, 10)) df['log_on_to_do_lists'] = df['on_to_do_lists'].apply(lambda x: math.log(x+1, 10)) # Target # add sqrt values for Poisson regression df['sqrt_star_ratings'] = df['star_ratings'].apply(lambda x: math.sqrt(x)) df['sqrt_ticks'] = df['ticks'].apply(lambda x: math.sqrt(x)) df['sqrt_avg_stars'] = df['avg_stars'].apply(lambda x: math.sqrt(x)) df['sqrt_length'] = df['length_'].apply(lambda x: math.sqrt(x)) df['sqrt_grade'] = df['grade'].apply(lambda x: math.sqrt(x+1)) return df def transform_features_cythonized(df): """ Add log and sqrt values using cythonized math functions """ # add log values for ols linear regression df['log_star_ratings'] = df.star_ratings.apply(lambda x: log_c(x+1)) df['log_ticks'] = df.ticks.apply(lambda x: log_c(x+1)) df['log_avg_stars'] = df.avg_stars.apply(lambda x: log_c(x+1)) df['log_length'] = df.length_.apply(lambda x: log_c(x+1)) df['log_grade'] = df.grade.apply(lambda x: log_c(x+2)) df['log_on_to_do_lists'] = df.on_to_do_lists.apply(lambda x: log_c(x+1)) # add sqrt values for Poisson regression df['sqrt_star_ratings'] = df.star_ratings.apply(lambda x: sqrt_c(x)) df['sqrt_ticks'] = df.ticks.apply(lambda x: sqrt_c(x)) df['sqrt_avg_stars'] = df.avg_stars.apply(lambda x: sqrt_c(x)) df['sqrt_length'] = df.length_.apply(lambda x: sqrt_c(x)) df['sqrt_grade'] = df.grade.apply(lambda x: sqrt_c(x+1)) return df query = """ SELECT b.avg_stars, b.your_stars, b.length_, b.grade, r.star_ratings, r.suggested_ratings, r.on_to_do_lists, r.ticks FROM routes b LEFT JOIN ratings r ON b.url_id = r.url_id WHERE b.area_name = 'buttermilks' AND length_ IS NOT NULL """ df = pd_sql.read_sql(query, connection_uri) # grab data as a dataframe df.head() %%timeit transform_features(df) %%timeit transform_features_cythonized(df) # Cythonized math functions are only barely faster ###Output 2.98 ms ± 31.3 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
cleared-demos/ivp_odes/Dissipation in Runge-Kutta Methods.ipynb	###Markdown Dissipation in Runge-Kutta MethodsCopyright (C) 2020 Andreas KloecknerMIT LicensePermission is hereby granted, free of charge, to any person obtaining a copyof this software and associated documentation files (the "Software"), to dealin the Software without restriction, including without limitation the rightsto use, copy, modify, merge, publish, distribute, sublicense, and/or sellcopies of the Software, and to permit persons to whom the Software isfurnished to do so, subject to the following conditions:The above copyright notice and this permission notice shall be included inall copies or substantial portions of the Software.THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS ORIMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THEAUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHERLIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS INTHE SOFTWARE. ###Code import numpy as np import matplotlib.pyplot as pt def rk4_step(y, t, h, f): k1 = f(t, y) k2 = f(t+h/2, y + h/2k1) k3 = f(t+h/2, y + h/2k2) k4 = f(t+h, y + hk3) return y + h/6(k1 + 2k2 + 2k3 + k4) ###Output _____no_output_____ ###Markdown Consider the second-order harmonic oscillator$$u''=-u$$with initial conditions $u(0) = 1$ and $u'(0)=0$.$\cos(x)$ is a solution to this problem.`f` below gives the right-hand side for this ODE converted to first-order form: ###Code def f(t, y): u, up = y return np.array([up, -u]) ###Output _____no_output_____ ###Markdown Now, we use 4th-order Runge Kutta to integrate this system over "many" time steps: ###Code times = [0] y_values = [np.array([1,0])] h = 0.5 t_end = 800 while times[-1] < t_end: y_values.append(rk4_step(y_values[-1], times[-1], h, f)) times.append(times[-1]+h) ###Output _____no_output_____ ###Markdown Lastly, plot the computed solution: ###Code y_values = np.array(y_values) pt.figure(figsize=(15,5)) pt.plot(times, y_values[:, 0]) ###Output _____no_output_____
assignments/assignment9/Assignment9_Model1_NarrativeQA_dataset.ipynb	###Markdown 2 - Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine TranslationIn this second notebook on sequence-to-sequence models using PyTorch and TorchText, we'll be implementing the model from [Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation](https://arxiv.org/abs/1406.1078). This model will achieve improved test perplexity whilst only using a single layer RNN in both the encoder and the decoder. IntroductionLet's remind ourselves of the general encoder-decoder model.![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq1.png?raw=1)We use our encoder (green) over the embedded source sequence (yellow) to create a context vector (red). We then use that context vector with the decoder (blue) and a linear layer (purple) to generate the target sentence.In the previous model, we used an multi-layered LSTM as the encoder and decoder.![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq4.png?raw=1)One downside of the previous model is that the decoder is trying to cram lots of information into the hidden states. Whilst decoding, the hidden state will need to contain information about the whole of the source sequence, as well as all of the tokens have been decoded so far. By alleviating some of this information compression, we can create a better model!We'll also be using a GRU (Gated Recurrent Unit) instead of an LSTM (Long Short-Term Memory). Why? Mainly because that's what they did in the paper (this paper also introduced GRUs) and also because we used LSTMs last time. To understand how GRUs (and LSTMs) differ from standard RNNS, check out [this](https://colah.github.io/posts/2015-08-Understanding-LSTMs/) link. Is a GRU better than an LSTM? [Research](https://arxiv.org/abs/1412.3555) has shown they're pretty much the same, and both are better than standard RNNs. Preparing DataAll of the data preparation will be (almost) the same as last time, so we'll very briefly detail what each code block does. See the previous notebook for a recap.We'll import PyTorch, TorchText, spaCy and a few standard modules. ###Code import torch import torch.nn as nn import torch.optim as optim from torchtext.datasets import Multi30k from torchtext.data import Field, BucketIterator, Example, Dataset import spacy import numpy as np import random import math import time ###Output _____no_output_____ ###Markdown Then set a random seed for deterministic results/reproducability. ###Code SEED = 1234 random.seed(SEED) np.random.seed(SEED) torch.manual_seed(SEED) torch.cuda.manual_seed(SEED) torch.backends.cudnn.deterministic = True ###Output _____no_output_____ ###Markdown Instantiate our German and English spaCy models. Previously we reversed the source (German) sentence, however in the paper we are implementing they don't do this, so neither will we. Create our fields to process our data. This will append the "start of sentence" and "end of sentence" tokens as well as converting all words to lowercase. ###Code SRC = Field(tokenize='spacy', init_token='<sos>', eos_token='<eos>', lower=True) TRG = Field(tokenize = 'spacy', init_token='<sos>', eos_token='<eos>', lower=True) ###Output _____no_output_____ ###Markdown Load our data. ###Code import pandas as pd #Read and preprocess the data docs_index = pd.read_csv('https://raw.githubusercontent.com/deepmind/narrativeqa/master/documents.csv') qapair = pd.read_csv('https://raw.githubusercontent.com/deepmind/narrativeqa/master/qaps.csv') wiki_summary = pd.read_csv("https://raw.githubusercontent.com/deepmind/narrativeqa/master/third_party/wikipedia/summaries.csv") wiki_summary.head(2) docs_index.head() qapair docs_index.shape, qapair.shape, wiki_summary.shape qapair.columns, wiki_summary.columns mapped_ads = qapair.merge(wiki_summary[['document_id', 'summary']], on='document_id', how='left') mapped_ads_filtered = mapped_ads[['question', 'answer1', 'summary', 'set']] mapped_ads_filtered['question'][0] mapped_ads_filtered['summary'][0][:400] MAX_LEN = 400 mapped_ads_filtered['summary_question'] = mapped_ads_filtered['summary'].apply(lambda x: x[:MAX_LEN]) + mapped_ads_filtered['question'] mapped_ads_filtered['answer'] = mapped_ads_filtered['answer1'] len(mapped_ads_filtered['summary_question'][0]) mapped_ads_filtered[mapped_ads_filtered['summary'].isna()] df= mapped_ads_filtered[['summary_question', 'answer', 'set']] test_df, train_df, valid_df = [group for _, group in df.groupby('set')] test_df.reset_index(drop=True, inplace=True) train_df.reset_index(drop=True, inplace=True) valid_df.reset_index(drop=True, inplace=True) len(train_df['summary_question'][10]) # This pandas dataframe should be mapped to the list of fields object # formed the list of fields object fields = [('src',SRC), ('trg', TRG)] # map operation to map the rows of pandas dataframe to torchdataset field train_mapped_rows_to_torchtext = [Example.fromlist([train_df['summary_question'][i], train_df['answer'][i]], fields) for i in range(train_df.shape[0])] test_mapped_rows_to_torchtext = [Example.fromlist([test_df['summary_question'][i], test_df['answer'][i]], fields) for i in range(test_df.shape[0])] valid_mapped_rows_to_torchtext = [Example.fromlist([valid_df['summary_question'][i], valid_df['answer'][i]], fields) for i in range(valid_df.shape[0])] train_data = Dataset(train_mapped_rows_to_torchtext, fields) valid_data = Dataset(valid_mapped_rows_to_torchtext, fields) test_data = Dataset(test_mapped_rows_to_torchtext, fields) ###Output _____no_output_____ ###Markdown We'll also print out an example just to double check they're not reversed. ###Code print(vars(valid_data.examples[0])) print(vars(train_data.examples[0])) ###Output {'src': [' ', 'at', 'madeline', 'hall', ',', 'an', 'old', 'mansion', '-', 'house', 'near', 'southampton', 'belonging', 'to', 'the', 'wealthy', 'de', 'versely', 'family', ',', 'lives', 'an', 'elderly', 'spinster', 'miss', 'delmar', ',', 'the', 'aunt', 'of', 'the', 'earl', 'de', 'versely', 'and', 'captain', 'delmar', '.', 'miss', 'delmar', 'invites', 'arabella', 'mason', ',', 'the', 'daughter', 'of', 'a', 'deceased', ',', 'well', '-', 'liked', 'steward', 'to', 'stay', 'with', 'her', 'as', 'a', 'lower', '-', 'class', 'guest', 'in', 'the', 'house', '.', 'captain', 'delmar', 'is', 'known', 'to', 'visit', 'his', 'aunt', 'at', 'madeline', 'hall', 'frequently', ',', 'who', 'is', 'miss', 'delmer', '?'], 'trg': ['the', 'elderly', 'spinster', 'aunt', 'of', 'the', 'earl', 'de', 'verseley', 'and', 'captain', 'delmar']} ###Markdown Then create our vocabulary, converting all tokens appearing less than twice into `` tokens. ###Code SRC.build_vocab(train_data, min_freq = 2) TRG.build_vocab(train_data, min_freq = 2) ###Output _____no_output_____ ###Markdown Finally, define the `device` and create our iterators. ###Code device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') BATCH_SIZE = 128 train_iterator, valid_iterator, test_iterator = BucketIterator.splits( (train_data, valid_data, test_data), batch_size = BATCH_SIZE, device = device, sort=False) print("dataload complete") ###Output dataload complete ###Markdown Building the Seq2Seq Model EncoderThe encoder is similar to the previous one, with the multi-layer LSTM swapped for a single-layer GRU. We also don't pass the dropout as an argument to the GRU as that dropout is used between each layer of a multi-layered RNN. As we only have a single layer, PyTorch will display a warning if we try and use pass a dropout value to it.Another thing to note about the GRU is that it only requires and returns a hidden state, there is no cell state like in the LSTM.$$\begin{align}h_t &= \text{GRU}(e(x_t), h_{t-1})\\(h_t, c_t) &= \text{LSTM}(e(x_t), h_{t-1}, c_{t-1})\\h_t &= \text{RNN}(e(x_t), h_{t-1})\end{align}$$From the equations above, it looks like the RNN and the GRU are identical. Inside the GRU, however, is a number of gating mechanisms that control the information flow in to and out of the hidden state (similar to an LSTM). Again, for more info, check out [this](https://colah.github.io/posts/2015-08-Understanding-LSTMs/) excellent post. The rest of the encoder should be very familar from the last session, it takes in a sequence, $X = \{x_1, x_2, ... , x_T\}$, passes it through the embedding layer, recurrently calculates hidden states, $H = \{h_1, h_2, ..., h_T\}$, and returns a context vector (the final hidden state), $z=h_T$.$$h_t = \text{EncoderGRU}(e(x_t), h_{t-1})$$This is identical to the encoder of the general seq2seq model, with all the "magic" happening inside the GRU (green).![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq5.png?raw=1) ###Code class Encoder(nn.Module): def __init__(self, input_dim, emb_dim, hid_dim, dropout): super().__init__() self.hid_dim = hid_dim self.embedding = nn.Embedding(input_dim, emb_dim) #no dropout as only one layer! self.rnn = nn.GRU(emb_dim, hid_dim) self.dropout = nn.Dropout(dropout) def forward(self, src): #src = [src len, batch size] embedded = self.dropout(self.embedding(src)) #embedded = [src len, batch size, emb dim] outputs, hidden = self.rnn(embedded) #no cell state! #outputs = [src len, batch size, hid dim * n directions] #hidden = [n layers * n directions, batch size, hid dim] #outputs are always from the top hidden layer return hidden ###Output _____no_output_____ ###Markdown DecoderThe decoder is where the implementation differs significantly from the previous model and we alleviate some of the information compression.Instead of the GRU in the decoder taking just the embedded target token, $d(y_t)$ and the previous hidden state $s_{t-1}$ as inputs, it also takes the context vector $z$. $$s_t = \text{DecoderGRU}(d(y_t), s_{t-1}, z)$$Note how this context vector, $z$, does not have a $t$ subscript, meaning we re-use the same context vector returned by the encoder for every time-step in the decoder. Before, we predicted the next token, $\hat{y}_{t+1}$, with the linear layer, $f$, only using the top-layer decoder hidden state at that time-step, $s_t$, as $\hat{y}_{t+1}=f(s_t^L)$. Now, we also pass the embedding of current token, $d(y_t)$ and the context vector, $z$ to the linear layer.$$\hat{y}_{t+1} = f(d(y_t), s_t, z)$$Thus, our decoder now looks something like this:![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq6.png?raw=1)Note, the initial hidden state, $s_0$, is still the context vector, $z$, so when generating the first token we are actually inputting two identical context vectors into the GRU.How do these two changes reduce the information compression? Well, hypothetically the decoder hidden states, $s_t$, no longer need to contain information about the source sequence as it is always available as an input. Thus, it only needs to contain information about what tokens it has generated so far. The addition of $y_t$ to the linear layer also means this layer can directly see what the token is, without having to get this information from the hidden state. However, this hypothesis is just a hypothesis, it is impossible to determine how the model actually uses the information provided to it (don't listen to anyone that says differently). Nevertheless, it is a solid intuition and the results seem to indicate that this modifications are a good idea!Within the implementation, we will pass $d(y_t)$ and $z$ to the GRU by concatenating them together, so the input dimensions to the GRU are now `emb_dim + hid_dim` (as context vector will be of size `hid_dim`). The linear layer will take $d(y_t), s_t$ and $z$ also by concatenating them together, hence the input dimensions are now `emb_dim + hid_dim2`. We also don't pass a value of dropout to the GRU as it only uses a single layer.`forward` now takes a `context` argument. Inside of `forward`, we concatenate $y_t$ and $z$ as `emb_con` before feeding to the GRU, and we concatenate $d(y_t)$, $s_t$ and $z$ together as `output` before feeding it through the linear layer to receive our predictions, $\hat{y}_{t+1}$. ###Code class Decoder(nn.Module): def __init__(self, output_dim, emb_dim, hid_dim, dropout): super().__init__() self.hid_dim = hid_dim self.output_dim = output_dim self.embedding = nn.Embedding(output_dim, emb_dim) self.rnn = nn.GRU(emb_dim + hid_dim, hid_dim) self.fc_out = nn.Linear(emb_dim + hid_dim 2, output_dim) self.dropout = nn.Dropout(dropout) def forward(self, input, hidden, context): #input = [batch size] #hidden = [n layers * n directions, batch size, hid dim] #context = [n layers * n directions, batch size, hid dim] #n layers and n directions in the decoder will both always be 1, therefore: #hidden = [1, batch size, hid dim] #context = [1, batch size, hid dim] input = input.unsqueeze(0) #input = [1, batch size] embedded = self.dropout(self.embedding(input)) #embedded = [1, batch size, emb dim] emb_con = torch.cat((embedded, context), dim = 2) #emb_con = [1, batch size, emb dim + hid dim] output, hidden = self.rnn(emb_con, hidden) #output = [seq len, batch size, hid dim * n directions] #hidden = [n layers * n directions, batch size, hid dim] #seq len, n layers and n directions will always be 1 in the decoder, therefore: #output = [1, batch size, hid dim] #hidden = [1, batch size, hid dim] output = torch.cat((embedded.squeeze(0), hidden.squeeze(0), context.squeeze(0)), dim = 1) #output = [batch size, emb dim + hid dim * 2] prediction = self.fc_out(output) #prediction = [batch size, output dim] return prediction, hidden ###Output _____no_output_____ ###Markdown Seq2Seq ModelPutting the encoder and decoder together, we get:![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq7.png?raw=1)Again, in this implementation we need to ensure the hidden dimensions in both the encoder and the decoder are the same.Briefly going over all of the steps:- the `outputs` tensor is created to hold all predictions, $\hat{Y}$- the source sequence, $X$, is fed into the encoder to receive a `context` vector- the initial decoder hidden state is set to be the `context` vector, $s_0 = z = h_T$- we use a batch of `` tokens as the first `input`, $y_1$- we then decode within a loop: - inserting the input token $y_t$, previous hidden state, $s_{t-1}$, and the context vector, $z$, into the decoder - receiving a prediction, $\hat{y}_{t+1}$, and a new hidden state, $s_t$ - we then decide if we are going to teacher force or not, setting the next input as appropriate (either the ground truth next token in the target sequence or the highest predicted next token) ###Code class Seq2Seq(nn.Module): def __init__(self, encoder, decoder, device): super().__init__() self.encoder = encoder self.decoder = decoder self.device = device assert encoder.hid_dim == decoder.hid_dim, \ "Hidden dimensions of encoder and decoder must be equal!" def forward(self, src, trg, teacher_forcing_ratio = 0.5): #src = [src len, batch size] #trg = [trg len, batch size] #teacher_forcing_ratio is probability to use teacher forcing #e.g. if teacher_forcing_ratio is 0.75 we use ground-truth inputs 75% of the time batch_size = trg.shape[1] trg_len = trg.shape[0] trg_vocab_size = self.decoder.output_dim #tensor to store decoder outputs outputs = torch.zeros(trg_len, batch_size, trg_vocab_size).to(self.device) #last hidden state of the encoder is the context context = self.encoder(src) #context also used as the initial hidden state of the decoder hidden = context #first input to the decoder is the <sos> tokens input = trg[0,:] for t in range(1, trg_len): #insert input token embedding, previous hidden state and the context state #receive output tensor (predictions) and new hidden state output, hidden = self.decoder(input, hidden, context) #place predictions in a tensor holding predictions for each token outputs[t] = output #decide if we are going to use teacher forcing or not teacher_force = random.random() < teacher_forcing_ratio #get the highest predicted token from our predictions top1 = output.argmax(1) #if teacher forcing, use actual next token as next input #if not, use predicted token input = trg[t] if teacher_force else top1 return outputs ###Output _____no_output_____ ###Markdown Training the Seq2Seq ModelThe rest of this session is very similar to the previous one. We initialise our encoder, decoder and seq2seq model (placing it on the GPU if we have one). As before, the embedding dimensions and the amount of dropout used can be different between the encoder and the decoder, but the hidden dimensions must remain the same. ###Code INPUT_DIM = len(SRC.vocab) OUTPUT_DIM = len(TRG.vocab) ENC_EMB_DIM = 256 DEC_EMB_DIM = 256 HID_DIM = 512 ENC_DROPOUT = 0.5 DEC_DROPOUT = 0.5 enc = Encoder(INPUT_DIM, ENC_EMB_DIM, HID_DIM, ENC_DROPOUT) dec = Decoder(OUTPUT_DIM, DEC_EMB_DIM, HID_DIM, DEC_DROPOUT) device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') model = Seq2Seq(enc, dec, device).to(device) ###Output _____no_output_____ ###Markdown Next, we initialize our parameters. The paper states the parameters are initialized from a normal distribution with a mean of 0 and a standard deviation of 0.01, i.e. $\mathcal{N}(0, 0.01)$. It also states we should initialize the recurrent parameters to a special initialization, however to keep things simple we'll also initialize them to $\mathcal{N}(0, 0.01)$. ###Code def init_weights(m): for name, param in m.named_parameters(): nn.init.normal_(param.data, mean=0, std=0.01) model.apply(init_weights) ###Output _____no_output_____ ###Markdown We print out the number of parameters.Even though we only have a single layer RNN for our encoder and decoder we actually have more parameters than the last model. This is due to the increased size of the inputs to the GRU and the linear layer. However, it is not a significant amount of parameters and causes a minimal amount of increase in training time (~3 seconds per epoch extra). ###Code def count_parameters(model): return sum(p.numel() for p in model.parameters() if p.requires_grad) print(f'The model has {count_parameters(model):,} trainable parameters') ###Output The model has 24,638,663 trainable parameters ###Markdown We initiaize our optimizer. ###Code optimizer = optim.Adam(model.parameters()) ###Output _____no_output_____ ###Markdown We also initialize the loss function, making sure to ignore the loss on `` tokens. ###Code TRG_PAD_IDX = TRG.vocab.stoi[TRG.pad_token] criterion = nn.CrossEntropyLoss(ignore_index = TRG_PAD_IDX) ###Output _____no_output_____ ###Markdown We then create the training loop... ###Code def train(model, iterator, optimizer, criterion, clip): model.train() epoch_loss = 0 for i, batch in enumerate(iterator): src = batch.src trg = batch.trg optimizer.zero_grad() output = model(src, trg) #trg = [trg len, batch size] #output = [trg len, batch size, output dim] output_dim = output.shape[-1] output = output[1:].view(-1, output_dim) trg = trg[1:].view(-1) #trg = [(trg len - 1) * batch size] #output = [(trg len - 1) * batch size, output dim] loss = criterion(output, trg) loss.backward() torch.nn.utils.clip_grad_norm_(model.parameters(), clip) optimizer.step() epoch_loss += loss.item() return epoch_loss / len(iterator) ###Output _____no_output_____ ###Markdown ...and the evaluation loop, remembering to set the model to `eval` mode and turn off teaching forcing. ###Code def evaluate(model, iterator, criterion): model.eval() epoch_loss = 0 with torch.no_grad(): for i, batch in enumerate(iterator): src = batch.src trg = batch.trg output = model(src, trg, 0) #turn off teacher forcing #trg = [trg len, batch size] #output = [trg len, batch size, output dim] output_dim = output.shape[-1] output = output[1:].view(-1, output_dim) trg = trg[1:].view(-1) #trg = [(trg len - 1) * batch size] #output = [(trg len - 1) * batch size, output dim] loss = criterion(output, trg) epoch_loss += loss.item() return epoch_loss / len(iterator) ###Output _____no_output_____ ###Markdown We'll also define the function that calculates how long an epoch takes. ###Code def epoch_time(start_time, end_time): elapsed_time = end_time - start_time elapsed_mins = int(elapsed_time / 60) elapsed_secs = int(elapsed_time - (elapsed_mins * 60)) return elapsed_mins, elapsed_secs ###Output _____no_output_____ ###Markdown Then, we train our model, saving the parameters that give us the best validation loss. ###Code N_EPOCHS = 10 CLIP = 1 best_valid_loss = float('inf') for epoch in range(N_EPOCHS): start_time = time.time() train_loss = train(model, train_iterator, optimizer, criterion, CLIP) valid_loss = evaluate(model, test_iterator, criterion) end_time = time.time() epoch_mins, epoch_secs = epoch_time(start_time, end_time) if valid_loss < best_valid_loss: best_valid_loss = valid_loss torch.save(model.state_dict(), 'tut2-model.pt') print(f'Epoch: {epoch+1:02} \| Time: {epoch_mins}m {epoch_secs}s') print(f'\tTrain Loss: {train_loss:.3f} \| Train PPL: {math.exp(train_loss):7.3f}') print(f'\t Val. Loss: {valid_loss:.3f} \| Val. PPL: {math.exp(valid_loss):7.3f}') ###Output Epoch: 01 \| Time: 1m 4s Train Loss: 6.010 \| Train PPL: 407.627 Val. Loss: 5.360 \| Val. PPL: 212.814 Epoch: 02 \| Time: 1m 5s Train Loss: 5.555 \| Train PPL: 258.535 Val. Loss: 5.364 \| Val. PPL: 213.547 Epoch: 03 \| Time: 1m 5s Train Loss: 5.425 \| Train PPL: 227.036 Val. Loss: 5.355 \| Val. PPL: 211.694 Epoch: 04 \| Time: 1m 6s Train Loss: 5.304 \| Train PPL: 201.061 Val. Loss: 5.408 \| Val. PPL: 223.160 Epoch: 05 \| Time: 1m 7s Train Loss: 5.162 \| Train PPL: 174.467 Val. Loss: 5.323 \| Val. PPL: 205.019 Epoch: 06 \| Time: 1m 6s Train Loss: 5.028 \| Train PPL: 152.612 Val. Loss: 5.317 \| Val. PPL: 203.845 Epoch: 07 \| Time: 1m 7s Train Loss: 4.871 \| Train PPL: 130.504 Val. Loss: 5.354 \| Val. PPL: 211.498 Epoch: 08 \| Time: 1m 7s Train Loss: 4.684 \| Train PPL: 108.236 Val. Loss: 5.360 \| Val. PPL: 212.657 Epoch: 09 \| Time: 1m 7s Train Loss: 4.406 \| Train PPL: 81.967 Val. Loss: 5.458 \| Val. PPL: 234.543 Epoch: 10 \| Time: 1m 6s Train Loss: 4.103 \| Train PPL: 60.502 Val. Loss: 5.606 \| Val. PPL: 271.940 ###Markdown Finally, we test the model on the test set using these "best" parameters. ###Code model.load_state_dict(torch.load('tut2-model.pt')) test_loss = evaluate(model, test_iterator, criterion) print(f'\| Test Loss: {test_loss:.3f} \| Test PPL: {math.exp(test_loss):7.3f} \|') ###Output \| Test Loss: 5.317 \| Test PPL: 203.845 \| ###Markdown 2 - Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine TranslationIn this second notebook on sequence-to-sequence models using PyTorch and TorchText, we'll be implementing the model from [Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation](https://arxiv.org/abs/1406.1078). This model will achieve improved test perplexity whilst only using a single layer RNN in both the encoder and the decoder. IntroductionLet's remind ourselves of the general encoder-decoder model.![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq1.png?raw=1)We use our encoder (green) over the embedded source sequence (yellow) to create a context vector (red). We then use that context vector with the decoder (blue) and a linear layer (purple) to generate the target sentence.In the previous model, we used an multi-layered LSTM as the encoder and decoder.![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq4.png?raw=1)One downside of the previous model is that the decoder is trying to cram lots of information into the hidden states. Whilst decoding, the hidden state will need to contain information about the whole of the source sequence, as well as all of the tokens have been decoded so far. By alleviating some of this information compression, we can create a better model!We'll also be using a GRU (Gated Recurrent Unit) instead of an LSTM (Long Short-Term Memory). Why? Mainly because that's what they did in the paper (this paper also introduced GRUs) and also because we used LSTMs last time. To understand how GRUs (and LSTMs) differ from standard RNNS, check out [this](https://colah.github.io/posts/2015-08-Understanding-LSTMs/) link. Is a GRU better than an LSTM? [Research](https://arxiv.org/abs/1412.3555) has shown they're pretty much the same, and both are better than standard RNNs. Preparing DataAll of the data preparation will be (almost) the same as last time, so we'll very briefly detail what each code block does. See the previous notebook for a recap.We'll import PyTorch, TorchText, spaCy and a few standard modules. ###Code import torch import torch.nn as nn import torch.optim as optim from torchtext.datasets import Multi30k from torchtext.data import Field, BucketIterator, Example, Dataset import spacy import numpy as np import random import math import time ###Output _____no_output_____ ###Markdown Then set a random seed for deterministic results/reproducability. ###Code SEED = 1234 random.seed(SEED) np.random.seed(SEED) torch.manual_seed(SEED) torch.cuda.manual_seed(SEED) torch.backends.cudnn.deterministic = True ###Output _____no_output_____ ###Markdown Instantiate our German and English spaCy models. Previously we reversed the source (German) sentence, however in the paper we are implementing they don't do this, so neither will we. Create our fields to process our data. This will append the "start of sentence" and "end of sentence" tokens as well as converting all words to lowercase. ###Code SRC = Field(tokenize='spacy', init_token='<sos>', eos_token='<eos>', lower=True) TRG = Field(tokenize = 'spacy', init_token='<sos>', eos_token='<eos>', lower=True) ###Output _____no_output_____ ###Markdown Load our data. ###Code import pandas as pd #Read and preprocess the data docs_index = pd.read_csv('https://raw.githubusercontent.com/deepmind/narrativeqa/master/documents.csv') qapair = pd.read_csv('https://raw.githubusercontent.com/deepmind/narrativeqa/master/qaps.csv') wiki_summary = pd.read_csv("https://raw.githubusercontent.com/deepmind/narrativeqa/master/third_party/wikipedia/summaries.csv") wiki_summary.head(2) docs_index.head() qapair docs_index.shape, qapair.shape, wiki_summary.shape qapair.columns, wiki_summary.columns mapped_ads = qapair.merge(wiki_summary[['document_id', 'summary']], on='document_id', how='left') mapped_ads_filtered = mapped_ads[['question', 'answer1', 'summary', 'set']] mapped_ads_filtered['question'][0] mapped_ads_filtered['summary'][0][:400] MAX_LEN = 400 mapped_ads_filtered['summary_question'] = mapped_ads_filtered['summary'].apply(lambda x: x[:MAX_LEN]) + mapped_ads_filtered['question'] mapped_ads_filtered['answer'] = mapped_ads_filtered['answer1'] len(mapped_ads_filtered['summary_question'][0]) mapped_ads_filtered[mapped_ads_filtered['summary'].isna()] df= mapped_ads_filtered[['summary_question', 'answer', 'set']] test_df, train_df, valid_df = [group for _, group in df.groupby('set')] test_df.reset_index(drop=True, inplace=True) train_df.reset_index(drop=True, inplace=True) valid_df.reset_index(drop=True, inplace=True) len(train_df['summary_question'][10]) # This pandas dataframe should be mapped to the list of fields object # formed the list of fields object fields = [('src',SRC), ('trg', TRG)] # map operation to map the rows of pandas dataframe to torchdataset field train_mapped_rows_to_torchtext = [Example.fromlist([train_df['summary_question'][i], train_df['answer'][i]], fields) for i in range(train_df.shape[0])] test_mapped_rows_to_torchtext = [Example.fromlist([test_df['summary_question'][i], test_df['answer'][i]], fields) for i in range(test_df.shape[0])] valid_mapped_rows_to_torchtext = [Example.fromlist([valid_df['summary_question'][i], valid_df['answer'][i]], fields) for i in range(valid_df.shape[0])] train_data = Dataset(train_mapped_rows_to_torchtext, fields) valid_data = Dataset(valid_mapped_rows_to_torchtext, fields) test_data = Dataset(test_mapped_rows_to_torchtext, fields) ###Output _____no_output_____ ###Markdown We'll also print out an example just to double check they're not reversed. ###Code print(vars(valid_data.examples[0])) print(vars(train_data.examples[0])) ###Output {'src': [' ', 'at', 'madeline', 'hall', ',', 'an', 'old', 'mansion', '-', 'house', 'near', 'southampton', 'belonging', 'to', 'the', 'wealthy', 'de', 'versely', 'family', ',', 'lives', 'an', 'elderly', 'spinster', 'miss', 'delmar', ',', 'the', 'aunt', 'of', 'the', 'earl', 'de', 'versely', 'and', 'captain', 'delmar', '.', 'miss', 'delmar', 'invites', 'arabella', 'mason', ',', 'the', 'daughter', 'of', 'a', 'deceased', ',', 'well', '-', 'liked', 'steward', 'to', 'stay', 'with', 'her', 'as', 'a', 'lower', '-', 'class', 'guest', 'in', 'the', 'house', '.', 'captain', 'delmar', 'is', 'known', 'to', 'visit', 'his', 'aunt', 'at', 'madeline', 'hall', 'frequently', ',', 'who', 'is', 'miss', 'delmer', '?'], 'trg': ['the', 'elderly', 'spinster', 'aunt', 'of', 'the', 'earl', 'de', 'verseley', 'and', 'captain', 'delmar']} ###Markdown Then create our vocabulary, converting all tokens appearing less than twice into `` tokens. ###Code SRC.build_vocab(train_data, min_freq = 2) TRG.build_vocab(train_data, min_freq = 2) ###Output _____no_output_____ ###Markdown Finally, define the `device` and create our iterators. ###Code device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') BATCH_SIZE = 128 train_iterator, valid_iterator, test_iterator = BucketIterator.splits( (train_data, valid_data, test_data), batch_size = BATCH_SIZE, device = device, sort=False) print("dataload complete") ###Output dataload complete ###Markdown Building the Seq2Seq Model EncoderThe encoder is similar to the previous one, with the multi-layer LSTM swapped for a single-layer GRU. We also don't pass the dropout as an argument to the GRU as that dropout is used between each layer of a multi-layered RNN. As we only have a single layer, PyTorch will display a warning if we try and use pass a dropout value to it.Another thing to note about the GRU is that it only requires and returns a hidden state, there is no cell state like in the LSTM.$$\begin{align}h_t &= \text{GRU}(e(x_t), h_{t-1})\\(h_t, c_t) &= \text{LSTM}(e(x_t), h_{t-1}, c_{t-1})\\h_t &= \text{RNN}(e(x_t), h_{t-1})\end{align}$$From the equations above, it looks like the RNN and the GRU are identical. Inside the GRU, however, is a number of gating mechanisms that control the information flow in to and out of the hidden state (similar to an LSTM). Again, for more info, check out [this](https://colah.github.io/posts/2015-08-Understanding-LSTMs/) excellent post. The rest of the encoder should be very familar from the last session, it takes in a sequence, $X = \{x_1, x_2, ... , x_T\}$, passes it through the embedding layer, recurrently calculates hidden states, $H = \{h_1, h_2, ..., h_T\}$, and returns a context vector (the final hidden state), $z=h_T$.$$h_t = \text{EncoderGRU}(e(x_t), h_{t-1})$$This is identical to the encoder of the general seq2seq model, with all the "magic" happening inside the GRU (green).![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq5.png?raw=1) ###Code class Encoder(nn.Module): def __init__(self, input_dim, emb_dim, hid_dim, dropout): super().__init__() self.hid_dim = hid_dim self.embedding = nn.Embedding(input_dim, emb_dim) #no dropout as only one layer! self.rnn = nn.GRU(emb_dim, hid_dim) self.dropout = nn.Dropout(dropout) def forward(self, src): #src = [src len, batch size] embedded = self.dropout(self.embedding(src)) #embedded = [src len, batch size, emb dim] outputs, hidden = self.rnn(embedded) #no cell state! #outputs = [src len, batch size, hid dim * n directions] #hidden = [n layers * n directions, batch size, hid dim] #outputs are always from the top hidden layer return hidden ###Output _____no_output_____ ###Markdown DecoderThe decoder is where the implementation differs significantly from the previous model and we alleviate some of the information compression.Instead of the GRU in the decoder taking just the embedded target token, $d(y_t)$ and the previous hidden state $s_{t-1}$ as inputs, it also takes the context vector $z$. $$s_t = \text{DecoderGRU}(d(y_t), s_{t-1}, z)$$Note how this context vector, $z$, does not have a $t$ subscript, meaning we re-use the same context vector returned by the encoder for every time-step in the decoder. Before, we predicted the next token, $\hat{y}_{t+1}$, with the linear layer, $f$, only using the top-layer decoder hidden state at that time-step, $s_t$, as $\hat{y}_{t+1}=f(s_t^L)$. Now, we also pass the embedding of current token, $d(y_t)$ and the context vector, $z$ to the linear layer.$$\hat{y}_{t+1} = f(d(y_t), s_t, z)$$Thus, our decoder now looks something like this:![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq6.png?raw=1)Note, the initial hidden state, $s_0$, is still the context vector, $z$, so when generating the first token we are actually inputting two identical context vectors into the GRU.How do these two changes reduce the information compression? Well, hypothetically the decoder hidden states, $s_t$, no longer need to contain information about the source sequence as it is always available as an input. Thus, it only needs to contain information about what tokens it has generated so far. The addition of $y_t$ to the linear layer also means this layer can directly see what the token is, without having to get this information from the hidden state. However, this hypothesis is just a hypothesis, it is impossible to determine how the model actually uses the information provided to it (don't listen to anyone that says differently). Nevertheless, it is a solid intuition and the results seem to indicate that this modifications are a good idea!Within the implementation, we will pass $d(y_t)$ and $z$ to the GRU by concatenating them together, so the input dimensions to the GRU are now `emb_dim + hid_dim` (as context vector will be of size `hid_dim`). The linear layer will take $d(y_t), s_t$ and $z$ also by concatenating them together, hence the input dimensions are now `emb_dim + hid_dim2`. We also don't pass a value of dropout to the GRU as it only uses a single layer.`forward` now takes a `context` argument. Inside of `forward`, we concatenate $y_t$ and $z$ as `emb_con` before feeding to the GRU, and we concatenate $d(y_t)$, $s_t$ and $z$ together as `output` before feeding it through the linear layer to receive our predictions, $\hat{y}_{t+1}$. ###Code class Decoder(nn.Module): def __init__(self, output_dim, emb_dim, hid_dim, dropout): super().__init__() self.hid_dim = hid_dim self.output_dim = output_dim self.embedding = nn.Embedding(output_dim, emb_dim) self.rnn = nn.GRU(emb_dim + hid_dim, hid_dim) self.fc_out = nn.Linear(emb_dim + hid_dim 2, output_dim) self.dropout = nn.Dropout(dropout) def forward(self, input, hidden, context): #input = [batch size] #hidden = [n layers * n directions, batch size, hid dim] #context = [n layers * n directions, batch size, hid dim] #n layers and n directions in the decoder will both always be 1, therefore: #hidden = [1, batch size, hid dim] #context = [1, batch size, hid dim] input = input.unsqueeze(0) #input = [1, batch size] embedded = self.dropout(self.embedding(input)) #embedded = [1, batch size, emb dim] emb_con = torch.cat((embedded, context), dim = 2) #emb_con = [1, batch size, emb dim + hid dim] output, hidden = self.rnn(emb_con, hidden) #output = [seq len, batch size, hid dim * n directions] #hidden = [n layers * n directions, batch size, hid dim] #seq len, n layers and n directions will always be 1 in the decoder, therefore: #output = [1, batch size, hid dim] #hidden = [1, batch size, hid dim] output = torch.cat((embedded.squeeze(0), hidden.squeeze(0), context.squeeze(0)), dim = 1) #output = [batch size, emb dim + hid dim * 2] prediction = self.fc_out(output) #prediction = [batch size, output dim] return prediction, hidden ###Output _____no_output_____ ###Markdown Seq2Seq ModelPutting the encoder and decoder together, we get:![](https://github.com/bentrevett/pytorch-seq2seq/blob/master/assets/seq2seq7.png?raw=1)Again, in this implementation we need to ensure the hidden dimensions in both the encoder and the decoder are the same.Briefly going over all of the steps:- the `outputs` tensor is created to hold all predictions, $\hat{Y}$- the source sequence, $X$, is fed into the encoder to receive a `context` vector- the initial decoder hidden state is set to be the `context` vector, $s_0 = z = h_T$- we use a batch of `` tokens as the first `input`, $y_1$- we then decode within a loop: - inserting the input token $y_t$, previous hidden state, $s_{t-1}$, and the context vector, $z$, into the decoder - receiving a prediction, $\hat{y}_{t+1}$, and a new hidden state, $s_t$ - we then decide if we are going to teacher force or not, setting the next input as appropriate (either the ground truth next token in the target sequence or the highest predicted next token) ###Code class Seq2Seq(nn.Module): def __init__(self, encoder, decoder, device): super().__init__() self.encoder = encoder self.decoder = decoder self.device = device assert encoder.hid_dim == decoder.hid_dim, \ "Hidden dimensions of encoder and decoder must be equal!" def forward(self, src, trg, teacher_forcing_ratio = 0.5): #src = [src len, batch size] #trg = [trg len, batch size] #teacher_forcing_ratio is probability to use teacher forcing #e.g. if teacher_forcing_ratio is 0.75 we use ground-truth inputs 75% of the time batch_size = trg.shape[1] trg_len = trg.shape[0] trg_vocab_size = self.decoder.output_dim #tensor to store decoder outputs outputs = torch.zeros(trg_len, batch_size, trg_vocab_size).to(self.device) #last hidden state of the encoder is the context context = self.encoder(src) #context also used as the initial hidden state of the decoder hidden = context #first input to the decoder is the <sos> tokens input = trg[0,:] for t in range(1, trg_len): #insert input token embedding, previous hidden state and the context state #receive output tensor (predictions) and new hidden state output, hidden = self.decoder(input, hidden, context) #place predictions in a tensor holding predictions for each token outputs[t] = output #decide if we are going to use teacher forcing or not teacher_force = random.random() < teacher_forcing_ratio #get the highest predicted token from our predictions top1 = output.argmax(1) #if teacher forcing, use actual next token as next input #if not, use predicted token input = trg[t] if teacher_force else top1 return outputs ###Output _____no_output_____ ###Markdown Training the Seq2Seq ModelThe rest of this session is very similar to the previous one. We initialise our encoder, decoder and seq2seq model (placing it on the GPU if we have one). As before, the embedding dimensions and the amount of dropout used can be different between the encoder and the decoder, but the hidden dimensions must remain the same. ###Code INPUT_DIM = len(SRC.vocab) OUTPUT_DIM = len(TRG.vocab) ENC_EMB_DIM = 256 DEC_EMB_DIM = 256 HID_DIM = 512 ENC_DROPOUT = 0.5 DEC_DROPOUT = 0.5 enc = Encoder(INPUT_DIM, ENC_EMB_DIM, HID_DIM, ENC_DROPOUT) dec = Decoder(OUTPUT_DIM, DEC_EMB_DIM, HID_DIM, DEC_DROPOUT) device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') model = Seq2Seq(enc, dec, device).to(device) ###Output _____no_output_____ ###Markdown Next, we initialize our parameters. The paper states the parameters are initialized from a normal distribution with a mean of 0 and a standard deviation of 0.01, i.e. $\mathcal{N}(0, 0.01)$. It also states we should initialize the recurrent parameters to a special initialization, however to keep things simple we'll also initialize them to $\mathcal{N}(0, 0.01)$. ###Code def init_weights(m): for name, param in m.named_parameters(): nn.init.normal_(param.data, mean=0, std=0.01) model.apply(init_weights) ###Output _____no_output_____ ###Markdown We print out the number of parameters.Even though we only have a single layer RNN for our encoder and decoder we actually have more parameters than the last model. This is due to the increased size of the inputs to the GRU and the linear layer. However, it is not a significant amount of parameters and causes a minimal amount of increase in training time (~3 seconds per epoch extra). ###Code def count_parameters(model): return sum(p.numel() for p in model.parameters() if p.requires_grad) print(f'The model has {count_parameters(model):,} trainable parameters') ###Output The model has 24,638,663 trainable parameters ###Markdown We initiaize our optimizer. ###Code optimizer = optim.Adam(model.parameters()) ###Output _____no_output_____ ###Markdown We also initialize the loss function, making sure to ignore the loss on `` tokens. ###Code TRG_PAD_IDX = TRG.vocab.stoi[TRG.pad_token] criterion = nn.CrossEntropyLoss(ignore_index = TRG_PAD_IDX) ###Output _____no_output_____ ###Markdown We then create the training loop... ###Code def train(model, iterator, optimizer, criterion, clip): model.train() epoch_loss = 0 for i, batch in enumerate(iterator): src = batch.src trg = batch.trg optimizer.zero_grad() output = model(src, trg) #trg = [trg len, batch size] #output = [trg len, batch size, output dim] output_dim = output.shape[-1] output = output[1:].view(-1, output_dim) trg = trg[1:].view(-1) #trg = [(trg len - 1) * batch size] #output = [(trg len - 1) * batch size, output dim] loss = criterion(output, trg) loss.backward() torch.nn.utils.clip_grad_norm_(model.parameters(), clip) optimizer.step() epoch_loss += loss.item() return epoch_loss / len(iterator) ###Output _____no_output_____ ###Markdown ...and the evaluation loop, remembering to set the model to `eval` mode and turn off teaching forcing. ###Code def evaluate(model, iterator, criterion): model.eval() epoch_loss = 0 with torch.no_grad(): for i, batch in enumerate(iterator): src = batch.src trg = batch.trg output = model(src, trg, 0) #turn off teacher forcing #trg = [trg len, batch size] #output = [trg len, batch size, output dim] output_dim = output.shape[-1] output = output[1:].view(-1, output_dim) trg = trg[1:].view(-1) #trg = [(trg len - 1) * batch size] #output = [(trg len - 1) * batch size, output dim] loss = criterion(output, trg) epoch_loss += loss.item() return epoch_loss / len(iterator) ###Output _____no_output_____ ###Markdown We'll also define the function that calculates how long an epoch takes. ###Code def epoch_time(start_time, end_time): elapsed_time = end_time - start_time elapsed_mins = int(elapsed_time / 60) elapsed_secs = int(elapsed_time - (elapsed_mins * 60)) return elapsed_mins, elapsed_secs ###Output _____no_output_____ ###Markdown Then, we train our model, saving the parameters that give us the best validation loss. ###Code N_EPOCHS = 10 CLIP = 1 best_valid_loss = float('inf') for epoch in range(N_EPOCHS): start_time = time.time() train_loss = train(model, train_iterator, optimizer, criterion, CLIP) valid_loss = evaluate(model, test_iterator, criterion) end_time = time.time() epoch_mins, epoch_secs = epoch_time(start_time, end_time) if valid_loss < best_valid_loss: best_valid_loss = valid_loss torch.save(model.state_dict(), 'tut2-model.pt') print(f'Epoch: {epoch+1:02} \| Time: {epoch_mins}m {epoch_secs}s') print(f'\tTrain Loss: {train_loss:.3f} \| Train PPL: {math.exp(train_loss):7.3f}') print(f'\t Val. Loss: {valid_loss:.3f} \| Val. PPL: {math.exp(valid_loss):7.3f}') ###Output Epoch: 01 \| Time: 1m 4s Train Loss: 6.010 \| Train PPL: 407.627 Val. Loss: 5.360 \| Val. PPL: 212.814 Epoch: 02 \| Time: 1m 5s Train Loss: 5.555 \| Train PPL: 258.535 Val. Loss: 5.364 \| Val. PPL: 213.547 Epoch: 03 \| Time: 1m 5s Train Loss: 5.425 \| Train PPL: 227.036 Val. Loss: 5.355 \| Val. PPL: 211.694 Epoch: 04 \| Time: 1m 6s Train Loss: 5.304 \| Train PPL: 201.061 Val. Loss: 5.408 \| Val. PPL: 223.160 Epoch: 05 \| Time: 1m 7s Train Loss: 5.162 \| Train PPL: 174.467 Val. Loss: 5.323 \| Val. PPL: 205.019 Epoch: 06 \| Time: 1m 6s Train Loss: 5.028 \| Train PPL: 152.612 Val. Loss: 5.317 \| Val. PPL: 203.845 Epoch: 07 \| Time: 1m 7s Train Loss: 4.871 \| Train PPL: 130.504 Val. Loss: 5.354 \| Val. PPL: 211.498 Epoch: 08 \| Time: 1m 7s Train Loss: 4.684 \| Train PPL: 108.236 Val. Loss: 5.360 \| Val. PPL: 212.657 Epoch: 09 \| Time: 1m 7s Train Loss: 4.406 \| Train PPL: 81.967 Val. Loss: 5.458 \| Val. PPL: 234.543 Epoch: 10 \| Time: 1m 6s Train Loss: 4.103 \| Train PPL: 60.502 Val. Loss: 5.606 \| Val. PPL: 271.940 ###Markdown Finally, we test the model on the test set using these "best" parameters. ###Code model.load_state_dict(torch.load('tut2-model.pt')) test_loss = evaluate(model, test_iterator, criterion) print(f'\| Test Loss: {test_loss:.3f} \| Test PPL: {math.exp(test_loss):7.3f} \|') ###Output \| Test Loss: 5.317 \| Test PPL: 203.845 \|
urls.ipynb	###Markdown Extract already-prepared urls dataData overview [in this py notebook](https://github.com/sisudata/coloring/blob/master/coloring.ipynb) ###Code %%bash cd /tmp test -e coloring \|\| git clone https://github.com/sisudata/coloring cd coloring if ! [ -d url_svmlight ] ; then wget --quiet "http://www.sysnet.ucsd.edu/projects/url/url_svmlight.tar.gz" tar xzf url_svmlight.tar.gz fi if ! [ -f parallelSort.o ] \|\| ! [ -f u4_sort.so ] \|\| ! [ -f u8_sort.so ]; then ./build.sh 2>/dev/null fi import os orig_wd = os.getcwd() os.chdir('/tmp/coloring') import numpy as np import random np.random.seed(1234) random.seed(1234) import utils_graph_coloring as urlutils Xcontinuous, Xcsr, _, y, nrows, ncols = urlutils.get_all_data() os.chdir(orig_wd) from svmlight_loader_install import dump_svmlight_file ixs = np.arange(nrows, dtype=int) # malicious urls is temporally correlated, only 1 split to make cut = int(.7 * nrows) train_ixs, test_ixs = ixs[:cut], ixs[cut:] Xcontinuous_train = Xcontinuous[:cut, :] Xcontinuous_test = Xcontinuous[cut:, :] Xcsr_train = Xcsr[:cut, :] Xcsr_test = Xcsr[cut:, :] y_train = y[:cut] y_test = y[cut:] print('urls-data/cont00.svm') dump_svmlight_file(Xcontinuous_train, y_train, 'urls-data/cont00.svm') print('urls-data/sps00.svm') dump_svmlight_file(Xcsr_train, y_train, 'urls-data/sps00.svm') print('urls-data/cont01.svm') dump_svmlight_file(Xcontinuous_test, y_test, 'urls-data/cont01.svm') print('urls-data/sps01.svm') dump_svmlight_file(Xcsr_test, y_test, 'urls-data/sps01.svm') Xcsr_train.shape # (1677291, 3381345) Xcontinuous_train.shape # (1677291, 64) ###Output _____no_output_____ ###Markdown From [Feature Engineering and Analysis on kaggle.com](https://www.kaggle.com/br0kej/feature-engineering-and-analysis/notebook). Adapted to save the split and feature engineered dataset as csv and to only use xgboost. ###Code import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt import re from tld import get_tld from typing import Tuple, Union, Any from sklearn.preprocessing import OrdinalEncoder from sklearn.model_selection import train_test_split from sklearn.metrics import classification_report, confusion_matrix, accuracy_score df = pd.read_csv('data/malicious_phish.csv') df.head() df.shape df.type.value_counts() sns.countplot(x = 'type', data = df, order = df['type'].value_counts().index) def is_url_ip_address(url: str) -> bool: return re.search( # IPv4 '(([01]?\\d\\d?\|2[0-4]\\d\|25[0-5])\\.([01]?\\d\\d?\|2[0-4]\\d\|25[0-5])\\.([01]?\\d\\d?\|2[0-4]\\d\|25[0-5])\\.' '([01]?\\d\\d?\|2[0-4]\\d\|25[0-5])\\/)\|' # IPv4 with port '(([01]?\\d\\d?\|2[0-4]\\d\|25[0-5])\\.([01]?\\d\\d?\|2[0-4]\\d\|25[0-5])\\.([01]?\\d\\d?\|2[0-4]\\d\|25[0-5])\\.' '([01]?\\d\\d?\|2[0-4]\\d\|25[0-5])\\/)\|' # IPv4 in hexadecimal '((0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\.(0x[0-9a-fA-F]{1,2})\\/)' # Ipv6 '(?:[a-fA-F0-9]{1,4}:){7}[a-fA-F0-9]{1,4}\|' '([0-9]+(?:\.[0-9]+){3}:[0-9]+)\|' '((?:(?:\d\|[01]?\d\d\|2[0-4]\d\|25[0-5])\.){3}(?:25[0-5]\|2[0-4]\d\|[01]?\d\d\|\d)(?:\/\d{1,2})?)', url) is not None df['is_ip'] = df['url'].apply(lambda i: is_url_ip_address(i)) df['is_ip'].value_counts() def process_tld(url: str, fix_protos: bool = False) -> Tuple[str, str, str, str]: """ Takes a URL string and uses the tld library to extract subdomain, domain, top level domain and full length domain """ res = get_tld(url, as_object=True, fail_silently=False, fix_protocol=fix_protos) subdomain = res.subdomain domain = res.domain tld = res.tld fld = res.fld return subdomain, domain, tld, fld def process_url_with_tld(row: pd.Series) -> Tuple[str, str, str, str]: """ Takes in a dataframe row, checks to see if rows `is_ip` column is False. If it is false, continues to process the URL and extract the features, otherwise sets four features to None before returning. This processing is wrapped in a try/except block to enable debugging and it prints out the inputs that caused a failure as well as a failure counter. """ try: if not row['is_ip']: if str(row['url']).startswith('http:'): return process_tld(row['url']) else: return process_tld(row['url'], fix_protos=True) else: subdomain = None domain = None tld = None fld = None return subdomain, domain, tld, fld except: idx = row.name url = row['url'] type = row['type'] print(f'Failed - {idx}: {url} is a {type} example') return None, None, None, None df[['subdomain', 'domain', 'tld', 'fld']] = df.apply(lambda x: process_url_with_tld(x), axis=1, result_type="expand") df[['subdomain', 'domain', 'tld', 'fld']].value_counts() df[['subdomain', 'domain', 'tld', 'fld']].isna().sum(), df['is_ip'].value_counts() df[['subdomain', 'domain', 'tld', 'fld']].isna().sum()[0] - \ df['is_ip'].value_counts()[1] df.head() def get_url_path(url: str) -> Union[str, None]: """ Get's the path from a URL For example: If the URL was "www.google.co.uk/my/great/path" The path returned would be "my/great/path" """ try: res = get_tld(url, as_object=True, fail_silently=False, fix_protocol=True) if res.parsed_url.query: joined = res.parsed_url.path + res.parsed_url.query return joined else: return res.parsed_url.path except: return None def alpha_count(url: str) -> int: """ Counts the number of alpha characters in a URL """ alpha = 0 for i in url: if i.isalpha(): alpha += 1 return alpha def digit_count(url: str) -> int: """ Counts the number of digit characters in a URL """ digits = 0 for i in url: if i.isnumeric(): digits += 1 return digits def count_dir_in_url_path(url_path: Union[str, None]) -> int: """ Counts number of / in url path to count number of sub directories """ if url_path: n_dirs = url_path.count('/') return n_dirs else: return 0 def get_first_dir_len(url_path: Union[str, None]) -> int: """ Counts the length of the first directory within the URL provided """ if url_path: if len(url_path.split('/')) > 1: first_dir_len = len(url_path.split('/')[1]) return first_dir_len else: return 0 def contains_shortening_service(url: str) -> int: """ Checks to see whether URL contains a shortening service """ return re.search('bit\.ly\|goo\.gl\|shorte\.st\|go2l\.ink\|x\.co\|ow\.ly\|t\.co\|tinyurl\|tr\.im\|is\.gd\|cli\.gs\|' 'yfrog\.com\|migre\.me\|ff\.im\|tiny\.cc\|url4\.eu\|twit\.ac\|su\.pr\|twurl\.nl\|snipurl\.com\|' 'short\.to\|BudURL\.com\|ping\.fm\|post\.ly\|Just\.as\|bkite\.com\|snipr\.com\|fic\.kr\|loopt\.us\|' 'doiop\.com\|short\.ie\|kl\.am\|wp\.me\|rubyurl\.com\|om\.ly\|to\.ly\|bit\.do\|t\.co\|lnkd\.in\|' 'db\.tt\|qr\.ae\|adf\.ly\|goo\.gl\|bitly\.com\|cur\.lv\|tinyurl\.com\|ow\.ly\|bit\.ly\|ity\.im\|' 'q\.gs\|is\.gd\|po\.st\|bc\.vc\|twitthis\.com\|u\.to\|j\.mp\|buzurl\.com\|cutt\.us\|u\.bb\|yourls\.org\|' 'x\.co\|prettylinkpro\.com\|scrnch\.me\|filoops\.info\|vzturl\.com\|qr\.net\|1url\.com\|tweez\.me\|v\.gd\|' 'tr\.im\|link\.zip\.net', url) is not None # General Features df['url_path'] = df['url'].apply(lambda x: get_url_path(x)) df['contains_shortener'] = df['url'].apply( lambda x: contains_shortening_service(x)) # URL component length df['url_len'] = df['url'].apply(lambda x: len(str(x))) df['subdomain_len'] = df['subdomain'].apply(lambda x: len(str(x))) df['tld_len'] = df['tld'].apply(lambda x: len(str(x))) df['fld_len'] = df['fld'].apply(lambda x: len(str(x))) df['url_path_len'] = df['url_path'].apply(lambda x: len(str(x))) # Simple count features df['url_alphas'] = df['url'].apply(lambda i: alpha_count(i)) df['url_digits'] = df['url'].apply(lambda i: digit_count(i)) df['url_puncs'] = (df['url_len'] - (df['url_alphas'] + df['url_digits'])) df['count.'] = df['url'].apply(lambda x: x.count('.')) df['count@'] = df['url'].apply(lambda x: x.count('@')) df['count-'] = df['url'].apply(lambda x: x.count('-')) df['count%'] = df['url'].apply(lambda x: x.count('%')) df['count?'] = df['url'].apply(lambda x: x.count('?')) df['count='] = df['url'].apply(lambda x: x.count('=')) df['count_dirs'] = df['url_path'].apply(lambda x: count_dir_in_url_path(x)) df['first_dir_len'] = df['url_path'].apply(lambda x: get_first_dir_len(x)) # Binary Label df['binary_label'] = df['type'].apply(lambda x: 0 if x == 'benign' else 1) # Binned Features groups = ['Short', 'Medium', 'Long', 'Very Long'] # URL Lengths in 4 bins df['url_len_q'] = pd.qcut(df['url_len'], q=4, labels=groups) # FLD Lengths in 4 bins df['fld_len_q'] = pd.qcut(df['fld_len'], q=4, labels=groups) # Percentage Features df['pc_alphas'] = df['url_alphas'] / df['url_len'] df['pc_digits'] = df['url_digits'] / df['url_len'] df['pc_puncs'] = df['url_puncs'] / df['url_len'] df[["url_len_q", "fld_len_q"]] = OrdinalEncoder().fit_transform( df[["url_len_q", "fld_len_q"]]) df.head() df.describe() fig, axes = plt.subplots(2, 2, figsize=(20, 10), sharey=False) sns.boxplot(ax=axes[0, 0], x='type', y='url_len', data=df) axes[0, 0].set_title('URL Length') sns.boxplot(ax=axes[0, 1], x='type', y='subdomain_len', data=df) axes[0, 1].set_title('Subdomain Length') sns.boxplot(ax=axes[1, 0], x='type', y='tld_len', data=df) axes[1, 0].set_title('Top-Level Domain Length') sns.boxplot(ax=axes[1, 1], x='type', y='fld_len', data=df) axes[1, 1].set_title('Full Length Domain Length') fig, axes = plt.subplots(1, 3, figsize=(20, 5), sharey=True) sns.boxplot(ax=axes[0], x='type', y='pc_alphas', data=df) axes[0].set_title('Ratio of Alpha Characeters to URL') sns.boxplot(ax=axes[1], x='type', y='pc_puncs', data=df) axes[1].set_title('Ratio of Puncutation to URL') sns.boxplot(ax=axes[2], x='type', y='pc_digits', data=df) axes[2].set_title('Ratio of Digits to URL') fig, axes = plt.subplots(1, 3, figsize=(20, 5), sharey=True) fig.suptitle('% of Character Type in URL - with length quartiles') sns.boxplot(ax=axes[0], x='type', y='pc_alphas', hue='url_len_q', data=df) axes[0].set_title('Ratio of Alpha Characeters to URL') sns.boxplot(ax=axes[1], x='type', y='pc_puncs', hue='url_len_q', data=df) axes[1].set_title('Ratio of Puncutation to URL') sns.boxplot(ax=axes[2], x='type', y='pc_digits', hue='url_len_q', data=df) axes[2].set_title('Ratio of Digits to URL') fig, axes = plt.subplots(3, 1, figsize=(20, 15), sharey=True) sns.kdeplot(ax=axes[0], data=df, x="pc_alphas", hue='type') sns.kdeplot(ax=axes[1], data=df, x="pc_puncs", hue='type') sns.kdeplot(ax=axes[2], data=df, x="pc_digits", hue='type') X = df[['is_ip', 'url_len', 'subdomain_len', 'tld_len', 'fld_len', 'url_path_len', 'url_alphas', 'url_digits', 'url_puncs', 'count.', 'count@', 'count-', 'count%', 'count?', 'count=', 'pc_alphas', 'pc_digits', 'pc_puncs', 'count_dirs', 'contains_shortener', 'first_dir_len', 'url_len_q', 'fld_len_q']] y = df['binary_label'] X.isna().sum() X[X.isnull().any(axis=1)] df[df['first_dir_len'].isnull()] X['first_dir_len'].value_counts() X = X.fillna(0) X.isna().sum() X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, shuffle=True, random_state=5) def make_binary(X): df = X df['is_ip'] = df['is_ip'] \ .apply(lambda x: 1 if x else 0) df['contains_shortener'] = df['contains_shortener'] \ .apply(lambda x: 1 if x else 0) return df make_binary(X_train).to_csv( 'data/malicious_phish_X_train.csv', index=False) make_binary(X_test).to_csv('data/malicious_phish_X_test.csv', index=False) y_train.to_csv('data/malicious_phish_y_train.csv', index=False) y_test.to_csv('data/malicious_phish_y_test.csv', index=False) from xgboost import XGBClassifier model = XGBClassifier(n_estimators=100, use_label_encoder=False) model.fit(X_train, y_train) print(model) y_pred = model.predict(X_test) print(classification_report(y_test, y_pred)) score = accuracy_score(y_test, y_pred) print("accuracy: %0.3f" % score) sns.heatmap(confusion_matrix(y_test, y_pred), annot=True, fmt='g', cmap='Blues') xgb_features = model.feature_importances_.tolist() cols = X.columns feature_importances = pd.DataFrame({'features': cols, 'xgb': xgb_features}) feature_importances['mean_importance'] = feature_importances.mean(axis=1) feature_importances = feature_importances.sort_values( by='mean_importance', ascending=False) feature_importances fig, axes = plt.subplots(1, figsize=(20, 10)) sns.barplot(data=feature_importances, x="mean_importance", y='features', ax=axes) ###Output _____no_output_____
Machine Learning/tasks/1 term/HW_2_Texts/homework2_texts.ipynb	###Markdown Homework 2. Simple text processing. ###Code import numpy as np import matplotlib.pyplot as plt %matplotlib inline ###Output _____no_output_____ ###Markdown Prohibited Comment ClassificationThis part of assigment is fully based on YSDA NLP_course homework. Special thanks to YSDA team for making it available on github.![img](https://github.com/yandexdataschool/nlp_course/raw/master/resources/banhammer.jpg)__In this part__ you will build an algorithm that classifies social media comments into normal or toxic.Like in many real-world cases, you only have a small (10^3) dataset of hand-labeled examples to work with. We'll tackle this problem using both classical nlp methods and embedding-based approach. ###Code # In colab uncomment this cell # ! wget https://raw.githubusercontent.com/ml-mipt/ml-mipt/basic/homeworks/homework2_texts/comments.tsv import pandas as pd data = pd.read_csv("comments.tsv", sep='\t') texts = data['comment_text'].values target = data['should_ban'].values data[50::200] from sklearn.model_selection import train_test_split texts_train, texts_test, y_train, y_test = train_test_split(texts, target, test_size=0.5, random_state=42) ###Output _____no_output_____ ###Markdown __Note:__ it is generally a good idea to split data into train/test before anything is done to them.It guards you against possible data leakage in the preprocessing stage. For example, should you decide to select words present in obscene tweets as features, you should only count those words over the training set. Otherwise your algoritm can cheat evaluation. Preprocessing and tokenizationComments contain raw text with punctuation, upper/lowercase letters and even newline symbols.To simplify all further steps, we'll split text into space-separated tokens using one of nltk tokenizers.Generally, library `nltk` [link](https://www.nltk.org) is widely used in NLP. It is not necessary in here, but mentioned to intoduce it to you. ###Code from nltk.tokenize import TweetTokenizer tokenizer = TweetTokenizer() preprocess = lambda text: ' '.join(tokenizer.tokenize(text.lower())) text = 'How to be a grown-up at work: replace "I don\'t want to do that" with "Ok, great!".' print("before:", text,) print("after:", preprocess(text),) # task: preprocess each comment in train and test texts_train = pd.DataFrame(texts_train)[0].apply(preprocess).values texts_test = pd.DataFrame(texts_test)[0].apply(preprocess).values # Small check that everything is done properly assert texts_train[5] == 'who cares anymore . they attack with impunity .' assert texts_test[89] == 'hey todds ! quick q ? why are you so gay' assert len(texts_test) == len(y_test) ###Output _____no_output_____ ###Markdown Solving it: bag of words![img](http://www.novuslight.com/uploads/n/BagofWords.jpg)One traditional approach to such problem is to use bag of words features:1. build a vocabulary of frequent words (use train data only)2. for each training sample, count the number of times a word occurs in it (for each word in vocabulary).3. consider this count a feature for some classifier__Note:__ in practice, you can compute such features using sklearn. __Please don't do that in the current assignment, though.__* `from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer` ###Code import re import operator all_words_train = ' '.join(texts_train).split() word_frequency = {word: all_words_train.count(word) for word in set(all_words_train)} word_frequency_sorted = dict(sorted(word_frequency.items(), key = operator.itemgetter(1), reverse = True)) # task: find up to k most frequent tokens in texts_train, # sort them by number of occurences (highest first) k = min(10000, len(set(' '.join(texts_train).split()))) bow_vocabulary = list(word_frequency_sorted)[:k] print('example features:', sorted(bow_vocabulary)[::100]) def text_to_bow(text): """ convert text string to an array of token counts. Use bow_vocabulary. """ word_freq_text = [text.split().count(word) for word in bow_vocabulary] return np.array(word_freq_text, 'float32') X_train_bow = np.stack(list(map(text_to_bow, texts_train))) X_test_bow = np.stack(list(map(text_to_bow, texts_test))) # Small check that everything is done properly k_max = len(set(' '.join(texts_train).split())) assert X_train_bow.shape == (len(texts_train), min(k, k_max)) assert X_test_bow.shape == (len(texts_test), min(k, k_max)) assert np.all(X_train_bow[5:10].sum(-1) == np.array([len(s.split()) for s in texts_train[5:10]])) assert len(bow_vocabulary) <= min(k, k_max) assert X_train_bow[6, bow_vocabulary.index('.')] == texts_train[6].split().count('.') ###Output _____no_output_____ ###Markdown Machine learning stuff: fit, predict, evaluate. You know the drill. ###Code from sklearn.linear_model import LogisticRegression from sklearn.model_selection import GridSearchCV bow_model = LogisticRegression(solver = 'liblinear', max_iter=1000).fit(X_train_bow, y_train) from sklearn.metrics import roc_auc_score, roc_curve def plotting(X_train_bow, X_test_bow, y_train, y_test, bow_model): for name, X, y, model in [ ('train', X_train_bow, y_train, bow_model), ('test ', X_test_bow, y_test, bow_model) ]: proba = model.predict_proba(X)[:, 1] auc = roc_auc_score(y, proba) plt.plot(roc_curve(y, proba)[:2], label='%s AUC=%.4f' % (name, auc)) plt.plot([0, 1], [0, 1], '--', color='black',) plt.legend(fontsize='large') plt.grid() plotting(X_train_bow, X_test_bow, y_train, y_test, bow_model) ###Output _____no_output_____ ###Markdown Try to vary the number of tokens `k` and check how the model performance changes. Show it on a plot. ###Code import tqdm aucs = [] tokens = np.arange(4500, 6000, 100) for token in tqdm.tqdm_notebook(tokens): bow_vocabulary = list(word_frequency_sorted)[:token] X_train_bow = np.stack(list(map(text_to_bow, texts_train))) X_test_bow = np.stack(list(map(text_to_bow, texts_test))) bow_model = LogisticRegression(solver = 'liblinear', max_iter=1000).fit(X_train_bow, y_train) proba = bow_model.predict_proba(X_test_bow)[:, 1] aucs.append(roc_auc_score(y_test, proba)) plt.plot(tokens, aucs, label = 'Test') plt.xlabel('Number of tokens') plt.ylabel('AUC Score') plt.title('AUC') plt.legend() plt.grid() ###Output _____no_output_____ ###Markdown Task: implement TF-IDF featuresNot all words are equally useful. One can prioritize rare words and downscale words like "and"/"or" by using __tf-idf features__. This abbreviation stands for __text frequency/inverse document frequence__ and means exactly that:$$ feature_i = { Count(word_i \in x) \times { log {N \over Count(word_i \in D) + \alpha} }}, $$where x is a single text, D is your dataset (a collection of texts), N is a total number of documents and $\alpha$ is a smoothing hyperparameter (typically 1). And $Count(word_i \in D)$ is the number of documents where $word_i$ appears.It may also be a good idea to normalize each data sample after computing tf-idf features.__Your task:__ implement tf-idf features, train a model and evaluate ROC curve. Compare it with basic BagOfWords model from above.__Please don't use sklearn/nltk builtin tf-idf vectorizers in your solution :)__ You can still use 'em for debugging though. Blog post about implementing the TF-IDF features from scratch: https://triton.ml/blog/tf-idf-from-scratch ###Code # Your beautiful code here alpha = 0.95 def idf(word): freq = sum(1 for text in texts_train if word in text.split()) return np.log(len(texts_train) / (freq + alpha)) def tf_idf(text): features = [text.split().count(word) idf(word) if word in text.split() else 0 for word in bow_vocabulary] return np.array(features) X_train_feat = np.stack(list(map(tf_idf, texts_train))) X_test_feat = np.stack(list(map(tf_idf, texts_test))) feat_model = LogisticRegression(solver = 'liblinear', max_iter=1000).fit(X_train_feat, y_train) plotting(X_train_feat, X_test_feat, y_train, y_test, feat_model) ###Output _____no_output_____
winner.ipynb	###Markdown for i in range(len(y)): if y[i]==X[i][0]: y[i]=0 else: y[i]=1 imbalanced dataset so it is going to print(np.unique(y, return_counts=True)) ###Code zeros = 0 for i in range(len(X)): if y[i] == X[i][0]: if zeros <= 250: y[i] = 0 zeros = zeros + 1 else: y[i] = 1 t = X[i][0] X[i][0] = X[i][1] X[i][1] = t else: y[i] = 1 for i in range(len(X)): if X[i][3]==X[i][0]: X[i][3]=0 else: X[i][3]=1 X = np.array(X , dtype='int32') y = np.array(y , dtype='int32') y = y.ravel() print(np.unique(y, return_counts=True)) # now balanced dataset from sklearn.model_selection import train_test_split X_train, X_test, y_train,y_test = train_test_split(X, y, test_size=0.2 , random_state=0) alg1 = LogisticRegression(solver='liblinear') start = time.time() alg1.fit(X_train , y_train) end = time.time() total_time1 = end - start y_pred1 = alg1.predict(X_test) print('accuracy : ', alg1.score(X_test , y_test)) print('time : ' , total_time1) print(classification_report(y_test , y_pred1)) print(confusion_matrix(y_test , y_pred1)) alg2 = RandomForestClassifier(n_estimators=60) start = time.time() alg2.fit(X_train , y_train) end = time.time() total_time2 = end - start y_pred2 = alg2.predict(X_test) print('accuracy : ', alg2.score(X_test , y_test)) print('time : ' , total_time2) print(classification_report(y_test , y_pred2)) print(confusion_matrix(y_test , y_pred2)) alg3 = DecisionTreeClassifier(max_depth=1 , criterion='gini') start = time.time() alg3.fit(X_train , y_train) end = time.time() total_time3 = end - start y_pred3 = alg3.predict(X_test) print('accuracy : ', alg3.score(X_test , y_test)) print('time : ' , total_time3) print(classification_report(y_test , y_pred3)) print(confusion_matrix(y_test , y_pred3)) # Printing tree alongwith class names dot_data = StringIO() export_graphviz(alg3, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = ['team1', 'team2', 'venue','toss_winner', 'toss_decision']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png()) dot_data = export_graphviz(alg3, out_file=None, feature_names=['team1', 'team2', 'venue', 'toss_winner', 'toss_decision']) graph = pydotplus.graph_from_dot_data(dot_data) graph.write_pdf("ipl_winner_decision_tree.pdf") alg4 = BernoulliNB() start = time.time() alg4.fit(X_train,y_train) end = time.time() total_time4 = end - start y_pred4 = alg4.predict(X_test) print('accuracy : ', alg4.score(X_test , y_test)) print('time : ' , total_time4) print(classification_report(y_test , y_pred4)) print(confusion_matrix(y_test , y_pred4)) alg5 = GaussianNB() start = time.time() alg5.fit(X_train,y_train) end = time.time() total_time5 = end - start y_pred5 = alg5.predict(X_test) print('accuracy : ', alg5.score(X_test , y_test)) print('time : ' , total_time5) print(classification_report(y_test , y_pred5)) print(confusion_matrix(y_test , y_pred5)) alg6 = MultinomialNB() start = time.time() alg6.fit(X_train,y_train) end = time.time() total_time6 = end - start y_pred6 = alg6.predict(X_test) print('accuracy : ', alg6.score(X_test , y_test)) print('time : ' , total_time6) print(classification_report(y_test , y_pred6)) print(confusion_matrix(y_test , y_pred6)) x_axis = [] y_axis = [] for k in range(1, 26, 2): clf = KNeighborsClassifier(n_neighbors = k) score = cross_val_score(clf, X_train, y_train, cv = KFold(n_splits=5, shuffle=True, random_state=0)) x_axis.append(k) y_axis.append(score.mean()) import matplotlib.pyplot as plt plt.plot(x_axis, y_axis) plt.xlabel("k") plt.ylabel("cross_val_score") plt.title("variation of score on different values of k") plt.show() alg7 = KNeighborsClassifier(n_neighbors=19, weights='distance', algorithm='auto', p=2, metric='minkowski') start = time.time() alg7.fit(X_train, y_train) end = time.time() total_time7 = end - start y_pred7 = alg7.predict(X_test) print('accuracy : ', alg7.score(X_test , y_test)) print('time : ' , total_time7) print(classification_report(y_test , y_pred7)) print(confusion_matrix(y_test , y_pred7)) clf = SVC(kernel='rbf') grid = {'C': [1e2,1e3, 5e3, 1e4, 5e4, 1e5], 'gamma': [1e-3, 5e-4, 1e-4, 5e-3]} alg8 = GridSearchCV(clf, grid) start = time.time() alg8.fit(X_train, y_train) end = time.time() total_time8 = end - start y_pred8 = alg8.predict(X_test) print(alg8.best_estimator_) print('accuracy : ', alg8.score(X_test , y_test)) print('time : ' , total_time8) print(classification_report(y_test , y_pred8)) print(confusion_matrix(y_test , y_pred8)) alg9 = LinearSVC(multi_class='crammer_singer') start = time.time() alg9.fit(X_train, y_train) end = time.time() total_time9 = end - start y_pred9 = alg9.predict(X_test) print('accuracy : ', alg9.score(X_test , y_test)) print('time : ' , total_time9) print(classification_report(y_test , y_pred9)) print(confusion_matrix(y_test , y_pred9)) ridge = RidgeClassifier() parameters={'alpha':[1e-15,1e-10,1e-8,1e-3,1e-2,1,5,10,20,30,35,40]} alg10=GridSearchCV(ridge,parameters) start = time.time() alg10.fit(X_train, y_train) end = time.time() total_time10 = end - start y_pred10 = alg10.predict(X_test) print('accuracy : ', alg10.score(X_test , y_test)) print('time : ' , total_time10) print(classification_report(y_test , y_pred10)) print(confusion_matrix(y_test , y_pred10)) test = np.array([2, 4, 1, 1, 1]).reshape(1,-1) print('alg1 : ' , alg1.predict(test)) print('alg2 : ' , alg2.predict(test)) print('alg3 : ' , alg3.predict(test)) print('alg4 : ' , alg4.predict(test)) print('alg5 : ' , alg5.predict(test)) print('alg6 : ' , alg6.predict(test)) print('alg7 : ' , alg7.predict(test)) print('alg8 : ' , alg8.predict(test)) print('alg9 : ' , alg9.predict(test)) print('alg10 :' , alg10.predict(test)) test = np.array([4, 2, 1, 0, 1]).reshape(1,-1) print('alg1 : ' , alg1.predict(test)) print('alg2 : ' , alg2.predict(test)) print('alg3 : ' , alg3.predict(test)) print('alg4 : ' , alg4.predict(test)) print('alg5 : ' , alg5.predict(test)) print('alg6 : ' , alg6.predict(test)) print('alg7 : ' , alg7.predict(test)) print('alg8 : ' , alg8.predict(test)) print('alg9 : ' , alg9.predict(test)) print('alg10 :' , alg10.predict(test)) df_model=pd.DataFrame({ 'Model_Applied':['Logistic_Regression', 'Random_Forest', 'Decision_tree', 'BernoulliNB', 'GausianNB', 'MultinomialNB', 'KNN', 'SVC', 'Linear_SVC', 'Ridge_Classifier'], 'Accuracy':[alg1.score(X_test,y_test), alg2.score(X_test,y_test), alg3.score(X_test,y_test), alg4.score(X_test,y_test), alg5.score(X_test,y_test), alg6.score(X_test,y_test), alg7.score(X_test,y_test), alg8.score(X_test,y_test), alg9.score(X_test,y_test), alg10.score(X_test,y_test)], 'Training_Time':[total_time1, total_time2, total_time3, total_time4, total_time5, total_time6, total_time7, total_time8, total_time9, total_time10]}) df_model df_model.plot(kind='bar',x='Model_Applied', ylim=[0,1] , y='Accuracy', figsize=(10,10) , ylabel='Accuracy', title='Accurcy comparison of different Models') df_model.plot(kind='bar',x='Model_Applied', ylim=[0,0.14] , y='Training_Time', figsize=(10,10), ylabel='Training Time', title='Training time comparison of different Models') import pickle as pkl with open('winner.pkl', 'wb') as f: pkl.dump(alg3, f) with open('winner.pkl', 'rb') as f: model = pkl.load(f) model.predict(test) ###Output _____no_output_____
pytorch3d_render.ipynb	###Markdown Attempt 2 (Using PyTorch3D) ###Code import sys import torch pyt_version_str=torch.__version__.split("+")[0].replace(".", "") # print(pyt_version_str) version_str="".join([ f"py3{sys.version_info.minor}_cu", torch.version.cuda.replace(".",""), f"_pyt{pyt_version_str}" ]) !pip install --no-index --no-cache-dir pytorch3d -f https://dl.fbaipublicfiles.com/pytorch3d/packaging/wheels/{version_str}/download.html import pytorch3d as p3d print(p3d.__version__) !pip uninstall pytorch3d import os import torch import numpy as np from tqdm.notebook import tqdm import imageio import torch.nn as nn import torch.nn.functional as F import matplotlib.pyplot as plt from skimage import img_as_ubyte # io utils from pytorch3d.io import load_obj,load_objs_as_meshes # datastructures from pytorch3d.structures import Meshes # 3D transformations functions from pytorch3d.transforms import Rotate, Translate # rendering components from pytorch3d.renderer import ( FoVPerspectiveCameras, look_at_view_transform, look_at_rotation, RasterizationSettings, MeshRenderer, MeshRasterizer, BlendParams, SoftSilhouetteShader, HardPhongShader, PointLights, TexturesVertex, ) # verts_l, faces_l, aux_l = load_obj(f'{data_path}/{fname}/{fname}_lower.obj') # verts_u, faces_u, aux_u = load_obj(f'{data_path}/{fname}/{fname}_upper.obj') # verts_u, faces_u, _= load_obj('/content/016KWDMV_upper.obj') !wget https://dl.fbaipublicfiles.com/pytorch3d/data/teapot/teapot.obj # verts_u, faces_u, _ = load_obj("/content/teapot.obj") verts_u, faces_u, _= load_obj('/content/016KWDMV_upper.obj') print(verts_u.shape) print(faces_u.textures_idx.shape) # print(aux_u) # !rm -rf /content/data # device = torch.device("cuda:0") # verts_u, faces_u, _= load_obj('/content/016KWDMV_upper.obj') faces = faces_u.verts_idx # Initialize each vertex to be white in color. verts_rgb = torch.ones_like(verts_u)[None] # (1, V, 3) textures = TexturesVertex(verts_features=verts_rgb.to('cuda')) # Create a Meshes object for the teapot. Here we have only one mesh in the batch. mesh = Meshes( verts=[verts_u.to('cuda')], faces=[faces.to('cuda')], textures=textures ) print(verts_u) print(verts_rgb) # plt.figure(figsize=(7,7)) # print(mesh.textures) # # texturesuv_image_matplotlib(mesh.textures, subsample=None) # plt.axis("off"); # Initialize a perspective camera. cameras = FoVPerspectiveCameras(device='cuda') # To blend the 100 faces we set a few parameters which control the opacity and the sharpness of # edges. Refer to blending.py for more details. blend_params = BlendParams(sigma=1e-4, gamma=1e-4) # Define the settings for rasterization and shading. Here we set the output image to be of size # 256x256. To form the blended image we use 100 faces for each pixel. We also set bin_size and max_faces_per_bin to None which ensure that # the faster coarse-to-fine rasterization method is used. Refer to rasterize_meshes.py for # explanations of these parameters. Refer to docs/notes/renderer.md for an explanation of # the difference between naive and coarse-to-fine rasterization. raster_settings = RasterizationSettings( image_size=256, blur_radius=np.log(1. / 1e-4 - 1.) * blend_params.sigma, faces_per_pixel=100, ) # Create a silhouette mesh renderer by composing a rasterizer and a shader. silhouette_renderer = MeshRenderer( rasterizer=MeshRasterizer( cameras=cameras, raster_settings=raster_settings ), shader=SoftSilhouetteShader(blend_params=blend_params) ) # We will also create a Phong renderer. This is simpler and only needs to render one face per pixel. raster_settings = RasterizationSettings( image_size=256, blur_radius=0.0, faces_per_pixel=1, ) # We can add a point light in front of the object. lights = PointLights(device='cuda', location=((2.0, 2.0, -2.0),)) phong_renderer = MeshRenderer( rasterizer=MeshRasterizer( cameras=cameras, raster_settings=raster_settings ), shader=HardPhongShader(device='cuda', cameras=cameras, lights=lights) ) # Select the viewpoint using spherical angles distance = 10 # distance from camera to the object elevation = 0.0 # angle of elevation in degrees azimuth = 0.0 # No rotation so the camera is positioned on the +Z axis. # Get the position of the camera based on the spherical angles R, T = look_at_view_transform(distance, elevation, azimuth, device='cuda') # Render the teapot providing the values of R and T. silhouette = silhouette_renderer(meshes_world=mesh, R=R, T=T) image_ref = phong_renderer(meshes_world=mesh, R=R, T=T) silhouette = silhouette.cpu().numpy() image_ref = image_ref.cpu().numpy() plt.figure(figsize=(16, 16)) plt.subplot(1, 2, 1) plt.imshow(silhouette.squeeze()[..., 3]) # only plot the alpha channel of the RGBA image plt.grid(False) plt.subplot(1, 2, 2) plt.imshow(image_ref.squeeze()) plt.grid(False) ###Output _____no_output_____
noteboooks/dispersion.ipynb	###Markdown FODO dispersion ###Code cirumference = 1000 # meters proton_energy = 15 # GeV dipole_length = 5 # meters dipole_B_max = 2 # T n_cells = 8 # ?? dipole_angle = np.pi / 16 # ?? quad_length = 3 quad_strength = 8.89e-3 / quad_length dipole_length = 5 dipole_angle = np.pi / 16 dipole_bending_radius = dipole_length / dipole_angle # reduce the drift lengths to compensate for the now thick elements drift_length = (cirumference / n_cells - (2 * quad_length) - (4 * dipole_length)) / 6 half_quad_f = Quadrupole(quad_strength, quad_length/2, name="quad_f") quad_d = Quadrupole(-quad_strength, quad_length, name="quad_d") dipole = Dipole(dipole_bending_radius, dipole_angle) drift = Drift(drift_length) # We take the same FODO as exercise 1 and add some quadupoles FODO_thick = Lattice([half_quad_f, drift, dipole, drift, dipole, drift, quad_d, drift, dipole, drift, dipole, drift, half_quad_f]) FODO_thick.plot() FODO_thick.m FODO_thick.dispersion_solution() (FODO_thick * 8).plot.top_down() tracked = FODO_thick.dispersion() plt.plot(tracked.s, tracked.x, label="dispersion") plt.legend() ###Output _____no_output_____ ###Markdown particles with energy spread ###Code beam = Beam(n_particles=50, sigma_energy=1e-6) beam transported = FODO_thick.transport(beam.match(FODO_thick.twiss_solution())) plt.plot(transported.s, transported.x.T); s, disp, _ = FODO_thick.dispersion() plt.plot(s, disp) FODO_thick.plot() ###Output _____no_output_____ ###Markdown dp/p orbit ###Code lat = Lattice([Dipole(1, np.pi/2)]) tracked = lat.slice(Dipole, 100).transport([[0, 0.1], [0, 0], [0, 0], [0, 0], [0, 0.1]]) plt.plot(tracked.s, tracked.x.T) # top down view, projecting around the bend x_circle = np.cos(tracked.s) + tracked.x np.cos(tracked.s) y_circle = np.sin(tracked.s) + tracked.x * np.sin(tracked.s) fig, ax = plt.subplots(1, 1) ax.plot(x_circle.T, y_circle.T) ax.set_aspect("equal") ###Output _____no_output_____
.ipynb_checkpoints/hypothesis-checkpoint.ipynb	###Markdown Hypothesis Testing==================Copyright 2016 Allen DowneyLicense: [Creative Commons Attribution 4.0 International](http://creativecommons.org/licenses/by/4.0/) ###Code from __future__ import print_function, division import numpy import scipy.stats import matplotlib.pyplot as pyplot from ipywidgets import interact, interactive, fixed import ipywidgets as widgets import first # seed the random number generator so we all get the same results numpy.random.seed(19) # some nicer colors from http://colorbrewer2.org/ COLOR1 = '#7fc97f' COLOR2 = '#beaed4' COLOR3 = '#fdc086' COLOR4 = '#ffff99' COLOR5 = '#386cb0' %matplotlib inline ###Output _____no_output_____ ###Markdown Part One Suppose you observe an apparent difference between two groups and you want to check whether it might be due to chance.As an example, we'll look at differences between first babies and others. The `first` module provides code to read data from the National Survey of Family Growth (NSFG). ###Code live, firsts, others = first.MakeFrames() ###Output _____no_output_____ ###Markdown We'll look at a couple of variables, including pregnancy length and birth weight. The effect size we'll consider is the difference in the means.Other examples might include a correlation between variables or a coefficient in a linear regression. The number that quantifies the size of the effect is called the "test statistic". ###Code def TestStatistic(data): group1, group2 = data test_stat = abs(group1.mean() - group2.mean()) return test_stat ###Output _____no_output_____ ###Markdown For the first example, I extract the pregnancy length for first babies and others. The results are pandas Series objects. ###Code group1 = firsts.prglngth group2 = others.prglngth ###Output _____no_output_____ ###Markdown The actual difference in the means is 0.078 weeks, which is only 13 hours. ###Code actual = TestStatistic((group1, group2)) actual ###Output _____no_output_____ ###Markdown The null hypothesis is that there is no difference between the groups. We can model that by forming a pooled sample that includes first babies and others. ###Code n, m = len(group1), len(group2) pool = numpy.hstack((group1, group2)) ###Output _____no_output_____ ###Markdown Then we can simulate the null hypothesis by shuffling the pool and dividing it into two groups, using the same sizes as the actual sample. ###Code def RunModel(): numpy.random.shuffle(pool) data = pool[:n], pool[n:] return data ###Output _____no_output_____ ###Markdown The result of running the model is two NumPy arrays with the shuffled pregnancy lengths: ###Code RunModel() ###Output _____no_output_____ ###Markdown Then we compute the same test statistic using the simulated data: ###Code TestStatistic(RunModel()) ###Output _____no_output_____ ###Markdown If we run the model 1000 times and compute the test statistic, we can see how much the test statistic varies under the null hypothesis. ###Code test_stats = numpy.array([TestStatistic(RunModel()) for i in range(1000)]) test_stats.shape ###Output _____no_output_____ ###Markdown Here's the sampling distribution of the test statistic under the null hypothesis, with the actual difference in means indicated by a gray line. ###Code pyplot.vlines(actual, 0, 300, linewidth=3, color='0.8') pyplot.hist(test_stats, color=COLOR5) pyplot.xlabel('difference in means') pyplot.ylabel('count') None ###Output _____no_output_____ ###Markdown The p-value is the probability that the test statistic under the null hypothesis exceeds the actual value. ###Code pvalue = sum(test_stats >= actual) / len(test_stats) pvalue ###Output _____no_output_____ ###Markdown In this case the result is about 15%, which means that even if there is no difference between the groups, it is plausible that we could see a sample difference as big as 0.078 weeks.We conclude that the apparent effect might be due to chance, so we are not confident that it would appear in the general population, or in another sample from the same population.STOP HERE--------- Part Two========We can take the pieces from the previous section and organize them in a class that represents the structure of a hypothesis test. ###Code class HypothesisTest(object): """Represents a hypothesis test.""" def __init__(self, data): """Initializes. data: data in whatever form is relevant """ self.data = data self.MakeModel() self.actual = self.TestStatistic(data) self.test_stats = None def PValue(self, iters=1000): """Computes the distribution of the test statistic and p-value. iters: number of iterations returns: float p-value """ self.test_stats = numpy.array([self.TestStatistic(self.RunModel()) for _ in range(iters)]) count = sum(self.test_stats >= self.actual) return count / iters def MaxTestStat(self): """Returns the largest test statistic seen during simulations. """ return max(self.test_stats) def PlotHist(self, label=None): """Draws a Cdf with vertical lines at the observed test stat. """ ys, xs, patches = pyplot.hist(ht.test_stats, color=COLOR4) pyplot.vlines(self.actual, 0, max(ys), linewidth=3, color='0.8') pyplot.xlabel('test statistic') pyplot.ylabel('count') def TestStatistic(self, data): """Computes the test statistic. data: data in whatever form is relevant """ raise UnimplementedMethodException() def MakeModel(self): """Build a model of the null hypothesis. """ pass def RunModel(self): """Run the model of the null hypothesis. returns: simulated data """ raise UnimplementedMethodException() ###Output _____no_output_____ ###Markdown `HypothesisTest` is an abstract parent class that encodes the template. Child classes fill in the missing methods. For example, here's the test from the previous section. ###Code class DiffMeansPermute(HypothesisTest): """Tests a difference in means by permutation.""" def TestStatistic(self, data): """Computes the test statistic. data: data in whatever form is relevant """ group1, group2 = data test_stat = abs(group1.mean() - group2.mean()) return test_stat def MakeModel(self): """Build a model of the null hypothesis. """ group1, group2 = self.data self.n, self.m = len(group1), len(group2) self.pool = numpy.hstack((group1, group2)) def RunModel(self): """Run the model of the null hypothesis. returns: simulated data """ numpy.random.shuffle(self.pool) data = self.pool[:self.n], self.pool[self.n:] return data ###Output _____no_output_____ ###Markdown Now we can run the test by instantiating a DiffMeansPermute object: ###Code data = (firsts.prglngth, others.prglngth) ht = DiffMeansPermute(data) p_value = ht.PValue(iters=1000) print('\nmeans permute pregnancy length') print('p-value =', p_value) print('actual =', ht.actual) print('ts max =', ht.MaxTestStat()) ###Output means permute pregnancy length p-value = 0.169 actual = 0.07803726677754952 ts max = 0.20696822841 ###Markdown And we can plot the sampling distribution of the test statistic under the null hypothesis. ###Code ht.PlotHist() ###Output _____no_output_____ ###Markdown Difference in standard deviationExercize 1: Write a class named `DiffStdPermute` that extends `DiffMeansPermute` and overrides `TestStatistic` to compute the difference in standard deviations. Is the difference in standard deviations statistically significant? ###Code # Solution goes here ###Output _____no_output_____ ###Markdown Here's the code to test your solution to the previous exercise. ###Code data = (firsts.prglngth, others.prglngth) ht = DiffStdPermute(data) p_value = ht.PValue(iters=1000) print('\nstd permute pregnancy length') print('p-value =', p_value) print('actual =', ht.actual) print('ts max =', ht.MaxTestStat()) ###Output std permute pregnancy length p-value = 0.156 actual = 0.1760490642294399 ts max = 0.503028294469 ###Markdown Difference in birth weightsNow let's run DiffMeansPermute again to see if there is a difference in birth weight between first babies and others. ###Code data = (firsts.totalwgt_lb.dropna(), others.totalwgt_lb.dropna()) ht = DiffMeansPermute(data) p_value = ht.PValue(iters=1000) print('\nmeans permute birthweight') print('p-value =', p_value) print('actual =', ht.actual) print('ts max =', ht.MaxTestStat()) ###Output means permute birthweight p-value = 0.0 actual = 0.12476118453549034 ts max = 0.0924976865499
Inferential_Statistical_Analysis_with_Python-master/week1/week1_assessment.ipynb	###Markdown You will use the values of what you find in this assignment to answer questions in the quiz that follows. You may want to open this notebook to be displayed side-by-side on screen with this next quiz. 1. Write a function that inputs an integers and returns the negative ###Code # Write your function here def some_function(Int_input): return -Int_input # Test your function with input x x = 4 Output = some_function(x) print(Output) ###Output -4 ###Markdown 2. Write a function that inputs a list of integers and returns the minimum value ###Code # Write your function here def ListFun(lst): return min(lst) # Test your function with input lst lst = [-3, 0, 2, 100, -1, 2] print(ListFun(lst)) # Create you own input list to test with my_lst = [324,-234,284,34975,0,-23,34978,-213] print(ListFun(my_lst)) ###Output -3 -234 ###Markdown Challenge problem: Write a function that take in four arguments: lst1, lst2, str1, str2, and returns a pandas DataFrame that has the first column labeled str1 and the second column labaled str2, that have values lst1 and lst2 scaled to be between 0 and 1.For example```lst1 = [1, 2, 3]lst2 = [2, 4, 5]str1 = 'one'str2 = 'two'my_function(lst1, lst2, str1, str2)``` should return a DataFrame that looks like:\| \| one \| two \|\| --- \| --- \| --- \|\| 0 \| 0 \| 0 \|\| 1 \| .5 \| .666 \|\| 2 \| 1 \| 1 \| ###Code import pandas as pd def Challenge(lst1, lst2, str1, str2): df = pd.DataFrame({str1:lst1, str2:lst2}) return df # test your challenge problem function import numpy as np lst1 = np.random.randint(-234, 938, 100) lst2 = np.random.randint(-522, 123, 100) str1 = 'one' str2 = 'alpha' print(Challenge(lst1, lst2, str1, str2)) ###Output one alpha 0 795 -52 1 637 -241 2 665 -46 3 655 -104 4 417 -486 5 497 57 6 773 -370 7 824 -128 8 111 -170 9 479 102 10 -103 -450 11 439 -385 12 151 -266 13 621 -104 14 582 41 15 -116 -431 16 -94 -24 17 332 -239 18 184 -262 19 232 4 20 344 -349 21 634 -35 22 920 -107 23 -117 -275 24 871 -380 25 828 -252 26 371 -496 27 893 -224 28 687 -103 29 734 -223 .. ... ... 70 355 -194 71 743 -142 72 464 -73 73 536 -219 74 323 -21 75 714 36 76 -84 -37 77 -111 -180 78 -155 -143 79 702 54 80 -125 67 81 -180 -35 82 339 -119 83 325 -368 84 127 -488 85 116 -78 86 265 -190 87 138 -315 88 763 -123 89 754 -286 90 595 61 91 769 -49 92 -228 -501 93 76 -110 94 811 8 95 149 -415 96 850 -60 97 258 25 98 774 -426 99 393 -440 [100 rows x 2 columns]
notebooks/firefox_p2/tc_br_tracing/bm25-model.ipynb	###Markdown IntroductionIn this notebook we demonstrate the use of BM25 (Best Matching 25) Information Retrieval technique to make trace link recovery between Test Cases and Bug Reports.We model our study as follows:* Each bug report title, summary and description compose a single query.* We use each test case content as an entire document that must be returned to the query made Import Libraries ###Code %load_ext autoreload %autoreload 2 from mod_finder_util import mod_finder_util mod_finder_util.add_modules_origin_search_path() import pandas as pd from modules.models_runner.tc_br_models_runner import TC_BR_Runner from modules.models_runner.tc_br_models_runner import TC_BR_Models_Hyperp from modules.utils import aux_functions from modules.utils import firefox_dataset_p2 as fd from modules.utils import tokenizers as tok from modules.models.bm25 import BM_25 from IPython.display import display import warnings; warnings.simplefilter('ignore') ###Output _____no_output_____ ###Markdown Load Datasets ###Code tcs = [x for x in range(37,59)] orc = fd.Tc_BR_Oracles.read_oracle_expert_df() orc_subset = orc[orc.index.isin(tcs)] #aux_functions.highlight_df(orc_subset) tcs = [13,37,60] brs = [1267501] testcases = fd.Datasets.read_testcases_df() testcases = testcases[testcases.TC_Number.isin(tcs)] bugreports = fd.Datasets.read_selected_bugreports_df() bugreports = bugreports[bugreports.Bug_Number.isin(brs)] print('tc.shape: {}'.format(testcases.shape)) print('br.shape: {}'.format(bugreports.shape)) ###Output TestCases.shape: (195, 12) SelectedBugReports.shape: (91, 18) tc.shape: (3, 12) br.shape: (1, 18) ###Markdown Running BM25 Model ###Code corpus = testcases.tc_desc query = bugreports.br_desc test_cases_names = testcases.tc_name bug_reports_names = bugreports.br_name bm25_hyperp = TC_BR_Models_Hyperp.get_bm25_model_hyperp() bm25_model = BM_25(**bm25_hyperp) bm25_model.set_name('BM25_Model_TC_BR') bm25_model.recover_links(corpus, query, test_cases_names, bug_reports_names) bm25_model.get_sim_matrix().shape sim_matrix_normalized = bm25_model.get_sim_matrix() aux_functions.highlight_df(sim_matrix_normalized) sim_matrix_origin = bm25_model._sim_matrix_origin aux_functions.highlight_df(sim_matrix_origin) df = pd.DataFrame() df['tc'] = corpus df.index = test_cases_names df.index.name = '' #df = df.T df.head(10) ###Output _____no_output_____ ###Markdown Query Vector ###Code tokenizer = tok.PorterStemmerBased_Tokenizer() query_vec = [tokenizer.__call__(doc) for doc in query] df_q = pd.DataFrame(query_vec) df_q.index = bug_reports_names df_q.index.name = '' df_q = df_q.T df_q.head(10) ###Output _____no_output_____ ###Markdown Average Document Length ###Code bm25_model.bm25.avgdl ###Output _____no_output_____ ###Markdown Number of documents ###Code bm25_model.bm25.corpus_size ###Output _____no_output_____ ###Markdown Term frequency by document ###Code bm25_model.bm25.df['apz'] ###Output _____no_output_____ ###Markdown Most Relevant Words ###Code bm25_model.mrw_tcs bm25_model.docs_feats_df ###Output _____no_output_____
ICCT_en/examples/01/M-01_Complex_numbers_Cartesian_form.ipynb	###Markdown Complex numbers in Cartesian formFeel free to use this interactive example to visualize complex numbers in a complex plane, utilizing the Cartesian form. Also, you can test basic mathematical operators while working with complex numbers: addition, subtraction, multiplying, and dividing. All results are presented in the respective plot, as well as in the typical mathematical notation.You can manipulate complex numbers directly on the plot (by simple clicking), or/and use input fields at the same time. In order to provide better visibility of the respective vectors in the plot widget, the complex number coefficients are limited to $\pm10$. ###Code %matplotlib notebook import matplotlib.pyplot as plt import matplotlib.patches as mpatches import numpy as np import ipywidgets as widgets from IPython.display import display red_patch = mpatches.Patch(color='red', label='z1') blue_patch = mpatches.Patch(color='blue', label='z2') green_patch = mpatches.Patch(color='green', label='z1 + z2') yellow_patch = mpatches.Patch(color='yellow', label='z1 - z2') black_patch = mpatches.Patch(color='black', label='z1 * z2') magenta_patch = mpatches.Patch(color='magenta', label='z1 / z2') # Init values XLIM = 5 YLIM = 5 vectors_index_first = False; V = [None, None] V_complex = [None, None] # Complex plane fig = plt.figure(num='Complex numbers in Cartesian form') ax = fig.add_subplot(1, 1, 1) def get_interval(lim): if lim <= 10: return 1 if lim < 75: return 5 if lim > 100: return 25 return 10 def set_ticks(): XLIMc = int((XLIM / 10) + 1) * 10 YLIMc = int((YLIM / 10) + 1) * 10 if XLIMc > 150: XLIMc += 10 if YLIMc > 150: YLIMc += 10 xstep = get_interval(XLIMc) ystep = get_interval(YLIMc) #print(stepx, stepy) major_ticks = np.arange(-XLIMc, XLIMc, xstep) major_ticks_y = np.arange(-YLIMc, YLIMc, ystep) ax.set_xticks(major_ticks) ax.set_yticks(major_ticks_y) ax.grid(which='both') def clear_plot(): plt.cla() set_ticks() ax.set_xlabel('Re') ax.set_ylabel('Im') plt.ylim([-YLIM, YLIM]) plt.xlim([-XLIM, XLIM]) plt.legend(handles=[red_patch, blue_patch, green_patch, yellow_patch, black_patch, magenta_patch]) clear_plot() set_ticks() plt.show() set_ticks() # Set a complex number using direct manipulation on the plot def set_vector(i, data_x, data_y): clear_plot() V.pop(i) V.insert(i, (0, 0, round(data_x, 2), round(data_y, 2))) V_complex.pop(i) V_complex.insert(i, complex(round(data_x, 2), round(data_y, 2))) if i == 0: ax.arrow(V[0], head_width=0.25, head_length=0.5, color="r", length_includes_head=True) a1.value = round(data_x, 2) b1.value = round(data_y, 2) if V[1] != None: ax.arrow(V[1], head_width=0.25, head_length=0.5, color="b", length_includes_head=True) elif i == 1: ax.arrow(V[1], head_width=0.25, head_length=0.5, color="b", length_includes_head=True) a2.value = round(data_x, 2) b2.value = round(data_y, 2) if V[0] != None: ax.arrow(V[0], head_width=0.25, head_length=0.5, color="r", length_includes_head=True) max_bound() def onclick(event): global vectors_index_first vectors_index_first = not vectors_index_first x = event.xdata y = event.ydata if (x > 10): x = 10.0 if (x < - 10): x = -10.0 if (y > 10): y = 10.0 if (y < - 10): y = -10.0 if vectors_index_first: set_vector(0, x, y) else: set_vector(1, x, y) fig.canvas.mpl_connect('button_press_event', onclick) # Widgets a1 = widgets.BoundedFloatText(layout=widgets.Layout(width='10%'), min = -10, max = 10, step = 0.5) b1 = widgets.BoundedFloatText(layout=widgets.Layout(width='10%'), min = -10, max = 10, step = 0.5) button_set_z1 = widgets.Button(description="Plot z1") a2 = widgets.BoundedFloatText(layout=widgets.Layout(width='10%'), min = -10, max = 10, step = 0.5) b2 = widgets.BoundedFloatText(layout=widgets.Layout(width='10%'), min = -10, max = 10, step = 0.5) button_set_z2 = widgets.Button(description="Plot z2") box_layout_z1 = widgets.Layout(border='solid red', padding='10px') box_layout_z2 = widgets.Layout(border='solid blue', padding='10px') box_layout_opers = widgets.Layout(border='solid black', padding='10px') items_z1 = [widgets.Label("z1 = "), a1, widgets.Label("+ j * "), b1, button_set_z1] items_z2 = [widgets.Label("z2 = "), a2, widgets.Label("+ j * "), b2, button_set_z2] display(widgets.Box(children=items_z1, layout=box_layout_z1)) display(widgets.Box(children=items_z2, layout=box_layout_z2)) button_add = widgets.Button(description="Add") button_substract = widgets.Button(description="Subtract") button_multiply = widgets.Button(description="Multiply") button_divide = widgets.Button(description="Divide") button_reset = widgets.Button(description="Reset") output = widgets.Output() print('Complex number operations:') items_operations = [button_add, button_substract, button_multiply, button_divide, button_reset] display(widgets.Box(children=items_operations)) display(output) # Set complex number using input widgets (Text and Button) def on_button_set_z1_clicked(b): z1_old = V[0]; z1_new = (0, 0, a1.value, b1.value) if z1_old != z1_new: set_vector(0, a1.value, b1.value) change_lims() def on_button_set_z2_clicked(b): z2_old = V[1]; z2_new = (0, 0, a2.value, b2.value) if z2_old != z2_new: set_vector(1, a2.value, b2.value) change_lims() # Complex number operations: def perform_operation(oper): global XLIM, YLIM if (V_complex[0] != None) and (V_complex[1] != None): if (oper == '+'): result = V_complex[0] + V_complex[1] v_color = "g" elif (oper == '-'): result = V_complex[0] - V_complex[1] v_color = "y" elif (oper == ''): result = V_complex[0] V_complex[1] v_color = "black" elif (oper == '/'): result = V_complex[0] / V_complex[1] v_color = "magenta" result = complex(round(result.real, 2), round(result.imag, 2)) ax.arrow(0, 0, result.real, result.imag, head_width=0.25, head_length=0.5, color=v_color, length_includes_head=True) if abs(result.real) > XLIM: XLIM = round(abs(result.real) + 1) if abs(result.imag) > YLIM: YLIM = round(abs(result.imag) + 1) change_lims() with output: print(V_complex[0], oper, V_complex[1], "=", result) def on_button_add_clicked(b): perform_operation("+") def on_button_substract_clicked(b): perform_operation("-") def on_button_multiply_clicked(b): perform_operation("*") def on_button_divide_clicked(b): perform_operation("/") # Plot init methods def on_button_reset_clicked(b): global V, V_complex, XLIM, YLIM with output: output.clear_output() clear_plot() vectors_index_first = False; V = [None, None] V_complex = [None, None] a1.value = 0 b1.value = 0 a2.value = 0 b2.value = 0 XLIM = 5 YLIM = 5 change_lims() def clear_plot(): plt.cla() set_ticks() ax.set_xlabel('Re') ax.set_ylabel('Im') plt.ylim([-YLIM, YLIM]) plt.xlim([-XLIM, XLIM]) plt.legend(handles=[red_patch, blue_patch, green_patch, yellow_patch, black_patch, magenta_patch]) def change_lims(): set_ticks() plt.ylim([-YLIM, YLIM]) plt.xlim([-XLIM, XLIM]) set_ticks() def max_bound(): global XLIM, YLIM mx = 0 my = 0 if V_complex[0] != None: z = V_complex[0] if abs(z.real) > mx: mx = abs(z.real) if abs(z.imag) > my: my = abs(z.imag) if V_complex[1] != None: z = V_complex[1] if abs(z.real) > mx: mx = abs(z.real) if abs(z.imag) > my: my = abs(z.imag) if mx > XLIM: XLIM = round(mx + 1) elif mx <=5: XLIM = 5 if my > YLIM: YLIM = round(my + 1) elif my <=5: YLIM = 5 change_lims() # Button events button_set_z1.on_click(on_button_set_z1_clicked) button_set_z2.on_click(on_button_set_z2_clicked) button_add.on_click(on_button_add_clicked) button_substract.on_click(on_button_substract_clicked) button_multiply.on_click(on_button_multiply_clicked) button_divide.on_click(on_button_divide_clicked) button_reset.on_click(on_button_reset_clicked) ###Output _____no_output_____
backend.ipynb	###Markdown Backend Data Generation---This notebook generates the backend data needed for the app to fetch latest stat of a fighter ###Code import pandas as pd import numpy as np pd.set_option('display.max_columns', 100) df = pd.read_csv("data/UFC_processed.csv") df["date"] = pd.to_datetime(df["date"]) # date as datetime features = ["date","fighter"] for name in df.columns[4:25]: # slice string to separate prefix (e.g: R_) features.append(name[2:]) # add more to features # separate fighters blueFighter = pd.concat([df.iloc[:,[0,1]],df.iloc[:,4:25]],axis=1) redFighter = pd.concat([df.iloc[:,[0,2]],df.iloc[:,25:]],axis=1) # rename columns blueFighter.columns = features redFighter.columns = features # join them in one table fighters = pd.concat([redFighter,blueFighter],axis=0,).reset_index(drop=True) # as each fighter has fought multiple matches, in order to get the latest stat for each fighter, we have to group them by name # and get the details of their latest match: l = fighters.groupby("fighter") fighters_detail = [] # for each unique fighter: # 1- groupby fighter's name to get all their fights # 2- sort the values by data in newest to oldest format # 3- get the first element (i.e: iloc0) which is the newest for fighter in fighters["fighter"].unique(): fighters_detail.append(l.get_group(fighter).sort_values(by=["date"],ascending=False).iloc[0]) fighter_stat = pd.DataFrame(fighters_detail).sort_values(by="fighter") fighter_stat.insert(0, 'ID', np.arange(1,len(fighter_stat.index)+1)) fighter_stat.reset_index(drop=True, inplace=True) # export dataset fighter_stat.to_csv("data/FIGHTER_STAT.csv",index=False) ###Output _____no_output_____
1.- Fundamentos de Pandas/1.1 Colab/Creando_el_primer_DataFrame_desde_un_csv.ipynb	###Markdown Descargando y consumiendo un csv ###Code # Descargamos el Dataset ! wget http://srea64.github.io/msan622/project/pokemon.csv """ Importamos la librería pandas """ import pandas """ pd: responde al alias read_csv: Función de Pandas que permite trabajar con csv """ pandas.read_csv('pokemon.csv') """ Importamos la librería pandas y le colocamos el alias pd para ser llamada más adelante """ import pandas as pd """ pd: responde al alias read_csv: Función de Pandas que permite trabajar con csv """ df_pokemon = pd.read_csv('pokemon.csv') df_pokemon ###Output _____no_output_____ ###Markdown Leemos directamente de la URL origen ###Code import pandas as pd url = "http://srea64.github.io/msan622/project/pokemon.csv" pd.read_csv(url) ###Output _____no_output_____ ###Markdown Columna con valores NA ###Code # Saber que columna del dataframe tiene valores NA df_pokemon.isnull().sum() ###Output _____no_output_____ ###Markdown Nombre de las columnas ###Code # Saber los nombres de las columnas que conforman mi dataframe list(df_pokemon) ###Output _____no_output_____ ###Markdown Consultar datos en base al nombre de la columna ###Code # Extraer información de la columna con su nombre df_pokemon['id'] # En vase al nombre de la columna extraemos el mismo elemento df_pokemon['Name'][1] ###Output _____no_output_____ ###Markdown Consultar datos en base a la posición de la columna ###Code # Extraer el nombre de la columna por su posición df_pokemon.columns[1] """ 1.- Extraemos el nombre de la columna por su posición 2.- Usamos ese nombre para extraer la información """ df_pokemon[df_pokemon.columns[1]] """ 1.- Extraemos el nombre de la columna por su posición 2.- Usamos ese nombre para extraer la información 3.- Tomamos el primer elemento de la información extraída """ df_pokemon[df_pokemon.columns[1]][1] ###Output _____no_output_____ ###Markdown Extraer información en base a los datos de una fila ###Code # Extraer información en base a la primera columna en este caso 'id' df_pokemon.loc[0] # Extraer información en base a la columna seleccionada por el usuario en este caso 'Name' df_pokemon.loc[df_pokemon['Name'] == 'Bulbasaur'] # Extraer información en base a la posición de columna en este caso 'Name' df_pokemon.loc[df_pokemon[df_pokemon.columns[1]] == 'Bulbasaur'] ###Output _____no_output_____ ###Markdown Ejemplo de uso para filtrar datos de un dataframe ###Code """ Otro ejemplo Extraemos los pokemons que tengan un ataque mayor o igual a 50 """ df_pokemon.loc[df_pokemon['Attack'] >= 50] ###Output _____no_output_____
LHS_PRCC.ipynb	###Markdown Latin Hypercube Sampling & Partial Rank Correlation Coefficients ~ a method for analyzing model sensitivity to parameters ~ Importing packages that will be used. ###Code import numpy as np from scipy import special import random from ipywidgets import interact, interactive, fixed, interact_manual import ipywidgets as widgets from IPython.display import display import pandas as pd import matplotlib.pyplot as plt ###Output _____no_output_____ ###Markdown Specify the number of parameters to sample and the number of samples to draw from each parameter distribution. Do not include any parameters that should be left fixed in parameterCount - those will be specified later. When choosing number of samples to draw, note that more samples (~ 1000) yields better results while fewer (~50) is faster for testing, since it requires fewer model solves. ###Code # Number of parameters to sample parameterCount = 2; # Number of samples to draw for each parameter sampleCount = 100; ###Output _____no_output_____ ###Markdown This defines functions for specifying sampled parameters' names and distributions as well as drawing samples from a user-specified parameter distribution. Does not need any user edits. ###Code def parNameDist(Name,Distribution): paramTemp = {} paramTemp['Name']=Name paramTemp['Dist']=Distribution return paramTemp def sampleDistrib(modelParamName,distrib,distribSpecs): if distrib == 'uniform': mmin = distribSpecs[0].value mmax = distribSpecs[1].value intervalwidth = (mmax - mmin) / sampleCount # width of each # sampling interval samples = [] for sample in range(sampleCount): lower = mmin + intervalwidth * (sample-1) # lb of interval upper = mmin + intervalwidth * (sample) # ub of interval sampleVal = np.random.uniform(lower, upper) # draw a random sample # within the interval samples.append(sampleVal) elif distrib == 'normal': mmean= distribSpecs[0].value mvar = distribSpecs[1].value lower = mvarnp.sqrt(2)special.erfinv(-0.9999)+mmean # set lb of 1st # sample interval samples = [] for sample in range(sampleCount): n = sample + 1 if n != sampleCount: upper = (np.sqrt(2mvar)special.erfinv(2n/sampleCount-1) + mmean) # ub of sample interval else: upper = np.sqrt(2mvar)special.erfinv(0.9999) + mmean sampleVal = np.random.uniform(lower, upper) # draw a random sample # within the interval samples.append(sampleVal) lower = upper # set current ub as the lb for next interval elif distrib == 'triangle': mmin = distribSpecs[0].value mmax = distribSpecs[1].value mmode= distribSpecs[2].value samples = [] for sample in range(sampleCount): n = sample + 1 intervalarea = 1/sampleCount ylower = intervalarea(n-1) # use cdf to read off area as y's & yupper = intervalarea(n) # get corresponding x's for the pdf # Check to see if y values = cdf(x <= mmode) # for calculating correxponding x values: if ylower <= ((mmode - mmin)/(mmax - mmin)): lower = np.sqrt(ylower(mmax - mmin)(mmode - mmin)) + mmin else: lower = mmax-np.sqrt((1 - ylower)(mmax - mmin)(mmax - mmode)) if yupper <= ((mmode - mmin)/(mmax - mmin)): upper = np.sqrt(yupper(mmax - mmin)(mmode - mmin)) + mmin; else: upper = mmax-np.sqrt((1 - yupper)(mmax - mmin)(mmax - mmode)) sampleVal = np.random.uniform(lower, upper) samples.append(sampleVal) b = int(np.ceil(sampleCount/10)) plt.hist(samples, density = 1, bins = b) B=str(b) plt.title('Histogram of ' + modelParamName + ' parameter samples for ' + B + ' bins') plt.ylabel('proportion of samples'); plt.xlabel(modelParamName + ' value') plt.show() return samples ###Output _____no_output_____ ###Markdown Calls the function to ask for user input to name parameters and specify distributions. Type these in text input boxes and dropdowns that will appear below after running the cell. ###Code params = {} for i in range(parameterCount): s=str(i) params[i] = interactive(parNameDist, Name='Type parameter ' + s + ' name', Distribution=['uniform','normal','triangle']) display(params[i]) ###Output _____no_output_____ ###Markdown Input parameter distribution specifics in the interactive boxes that appear below after running this cell. ###Code distribSpecs={} for i in range(parameterCount): parName = params[i].result['Name'] print('Enter distribution specifics for parameter ' + parName + ':') if params[i].result['Dist'] == 'normal': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=2, description='Mean:' ) distribSpecs[parName][1] = widgets.FloatText( value=1, description='Variance:' ) display(distribSpecs[parName][0], distribSpecs[parName][1]) elif params[i].result['Dist'] == 'uniform': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=0, description='Minimum:' ) distribSpecs[parName][1] = widgets.FloatText( value=2, description='Maximum:' ) display(distribSpecs[parName][0], distribSpecs[parName][1]) elif params[i].result['Dist'] == 'triangle': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=0, description='Minimum:' ) distribSpecs[parName][1] = widgets.FloatText( value=2, description='Maximum:' ) distribSpecs[parName][2] = widgets.FloatText( value=1, description='Mode:' ) display(distribSpecs[parName][0], distribSpecs[parName][1], distribSpecs[parName][2]) ###Output _____no_output_____ ###Markdown This passes the distributions to the code for generating parameter samples, and histogram plots of samples for each parameter will appear below. ###Code parameters = {} for j in range(parameterCount): parameters[params[j].result['Name']] = sampleDistrib(params[j].result['Name'], params[j].result['Dist'], distribSpecs[params[j].result['Name']]) ###Output _____no_output_____ ###Markdown Randomly permute each set of parameter samples in order to randomly pair the samples to more fully sample the parameter space for the Monte Carlo simulations. ###Code LHSparams=[] for p in parameters: temp = parameters[p] random.shuffle(temp) LHSparams.append(temp) ###Output _____no_output_____ ###Markdown Define your model function. Two examples have been provided below: (1) a linear function with two sampled parameters: slope and intercept, and (2) a Lotka-Volterra predator - prey model.Note that the order and number of the parameters needs to match the order and number of parameters speficied above to ensure accuracy when the model is solved below. ###Code def testlinear(x,sampledParams,unsampledParams): m = sampledParams[0] b = sampledParams[1] a = unsampledParams y = m x + b + a; return y def myodes(y, t, sampledParams, unsampledParams): q, r = y # unpack current values of y alpha, beta = sampledParams # unpack sampled parameters delta, lambdaa, gamma = unsampledParams # unpack unsampled parameters derivs = [alphaqr - lambdaaq, # list of dy/dt=f functions betar - gammaqr - deltar] return derivs ###Output _____no_output_____ ###Markdown Run Monte Carlo simulations for each parameter sample set. Be sure to specify a call to your model function and any necessary arguments below.* ###Code # EDIT THE FOLLOWING VARIABLES, UNSAMPLED PARAMETERS, & ANY OTHER ARGS HERE, # AS WELL AS THE CALL TO YOUR OWN MODEL FUNCTION INSIDE THE FOR LOOP BELOW x = np.linspace(0, 10, num=101) unsampledParams = 2; Output = [] for j in range(sampleCount): sampledParams=[i[j] for i in LHSparams] sol = testlinear(x,sampledParams,unsampledParams) Output.append(sol) # EDIT THE STRING TO NAME YOUR SIM OUTPUT (for fig labels, filenames): labelstring = 'y' # # EXAMPLE CODE FOR A COUPLED ODE MODEL: # import scipy.integrate as spi # t = np.linspace(0,17,num=171) # time domain for myodes # # odesic = [q0, r0] # odesic = [500,1000] # lambdaa = np.log(2)/7 # delta = 0.5 # gamma = 1 # unsampledParams = [lambdaa, delta, gamma] # Simdata={} # Output = [] # for i in range(sampleCount): # Simdata[i]={} # Simdata[i]['q']=[] # Simdata[i]['r']=[] # for j in range(sampleCount): # sampledParams=[i[j] for i in LHSparams] # sol=spi.odeint(myodes, odesic, t, args=(sampledParams,unsampledParams)) # Simdata[j]['q'] = sol[:,0] # solution to the equation for variable r # Simdata[j]['r'] = sol[:,1] # solution to the equation for variable s # Ratio = np.divide(sol[:,0],sol[:,1]) # compute ratio to compare w/ param samples # Output.append(Ratio) # labelstring = 'predator to prey ratio (q/r)'; # id for fig labels, filenames ###Output _____no_output_____ ###Markdown Plot the range of simulation output generated by the all of the Monte Carlo simulations using errorbars. ###Code yavg = np.mean(Output, axis=0) yerr = np.std(Output, axis=0) plt.errorbar(t,yavg,yerr) plt.xlabel('x') # plt.xlabel('time (days)') # for myodes plt.ylabel(labelstring) plt.title('Error bar plot of ' + labelstring + ' from LHS simulations') plt.show() ###Output _____no_output_____ ###Markdown Compute partial rank correlation coefficients to compare simulation outputs with parameters ###Code SampleResult=[] x_idx = 11 # time or location index of sim results x_idx2= x_idx+1 # to compare w/ param sample vals LHS=[zip(LHSparams)] LHSarray=np.array(LHS) Outputarray=np.array(Output) subOut=Outputarray[0:,x_idx:x_idx2] LHSout = np.hstack((LHSarray,subOut)) SampleResult = LHSout.tolist() Ranks=[] for s in range(sampleCount): indices = list(range(len(SampleResult[s]))) indices.sort(key=lambda k: SampleResult[s][k]) r = [0] * len(indices) for i, k in enumerate(indices): r[k] = i Ranks.append(r) C=np.corrcoef(Ranks); if np.linalg.det(C) < 1e-16: # determine if singular Cinv = np.linalg.pinv(C) # may need to use pseudo inverse else: Cinv = np.linalg.inv(C) resultIdx = parameterCount+1 prcc=np.zeros(resultIdx) for w in range(parameterCount): # compute PRCC btwn each param & sim result prcc[w]=-Cinv[w,resultIdx]/np.sqrt(Cinv[w,w]Cinv[resultIdx,resultIdx]) ###Output _____no_output_____ ###Markdown Plot the PRCCs for each parameter ###Code xp=[i for i in range(parameterCount)] plt.bar(xp,prcc[0:parameterCount], align='center') bLabels=list(parameters.keys()) plt.xticks(xp, bLabels) plt.ylabel('PRCC value'); N=str(sampleCount) loc=str(x_idx) plt.title('Partial rank correlation of params with ' + labelstring + ' results \n from ' + N + ' LHS sims, at x = ' +loc); plt.show() ###Output _____no_output_____ ###Markdown Can also do PRCCs over time... ###Code SampleResult=[] resultIdx = parameterCount+1 prcc=np.zeros((resultIdx,len(x))) LHS=[zip(LHSparams)] LHSarray=np.array(LHS) Outputarray=np.array(Output) for xi in range(len(x)): # loop through time or location of sim results xi2 = xi+1 # to compare w/ parameter sample vals subOut = Outputarray[0:,xi:xi2] LHSout = np.hstack((LHSarray,subOut)) SampleResult = LHSout.tolist() Ranks=[] for s in range(sampleCount): indices = list(range(len(SampleResult[s]))) indices.sort(key=lambda k: SampleResult[s][k]) r = [0] len(indices) for i, k in enumerate(indices): r[k] = i Ranks.append(r) C=np.corrcoef(Ranks); if np.linalg.det(C) < 1e-16: # determine if singular Cinv = np.linalg.pinv(C) # may need to use pseudo inverse else: Cinv = np.linalg.inv(C) for w in range(parameterCount): # compute PRCC btwn each param & sim result prcc[w,xi]=-Cinv[w,resultIdx]/np.sqrt(Cinv[w,w]Cinv[resultIdx,resultIdx]) ###Output _____no_output_____ ###Markdown Plot PRCC values as they vary over time or space. Notice PRCC can change with respect to the independent variable (x-axis). This may be helpful for certain applications, as opposed to only looking at a "snapshot."* ###Code for p in range(parameterCount): plt.plot(x,prcc[p,]) labels=list(parameters.keys()) plt.legend(labels) plt.ylabel('PRCC value'); plt.xlabel('x') N=str(sampleCount) plt.title('Partial rank correlation of params with ' + labelstring + ' results \n from ' + N + ' LHS sims'); plt.show() ###Output _____no_output_____ ###Markdown Latin Hypercube Sampling & Partial Rank Correlation Coefficients ~ a method for analyzing model sensitivity to parameters ~ Importing packages that will be used. ###Code import numpy as np from scipy import special import random from ipywidgets import interact, interactive, fixed, interact_manual import ipywidgets as widgets from IPython.display import display import pandas as pd import matplotlib.pyplot as plt ###Output _____no_output_____ ###Markdown Specify the number of parameters to sample and the number of samples to draw from each parameter distribution. Do not include any parameters that should be left fixed in parameterCount - those will be specified later. When choosing number of samples to draw, note that more samples (~ 1000) yields better results while fewer (~50) is faster for testing, since it requires fewer model solves. ###Code # Number of parameters to sample parameterCount = 2; # Number of samples to draw for each parameter sampleCount = 100; ###Output _____no_output_____ ###Markdown This defines functions for specifying sampled parameters' names and distributions as well as drawing samples from a user-specified parameter distribution. Does not need any user edits. ###Code def parNameDist(Name,Distribution): paramTemp = {} paramTemp['Name']=Name paramTemp['Dist']=Distribution return paramTemp def sampleDistrib(modelParamName,distrib,distribSpecs): if distrib == 'uniform': mmin = distribSpecs[0].value mmax = distribSpecs[1].value intervalwidth = (mmax - mmin) / sampleCount # width of each # sampling interval samples = [] for sample in range(sampleCount): lower = mmin + intervalwidth * (sample-1) # lb of interval upper = mmin + intervalwidth * (sample) # ub of interval sampleVal = np.random.uniform(lower, upper) # draw a random sample # within the interval samples.append(sampleVal) elif distrib == 'normal': mmean= distribSpecs[0].value mvar = distribSpecs[1].value lower = mvarnp.sqrt(2)special.erfinv(-0.9999)+mmean # set lb of 1st # sample interval samples = [] for sample in range(sampleCount): n = sample + 1 if n != sampleCount: upper = (np.sqrt(2mvar)special.erfinv(2n/sampleCount-1) + mmean) # ub of sample interval else: upper = np.sqrt(2mvar)special.erfinv(0.9999) + mmean sampleVal = np.random.uniform(lower, upper) # draw a random sample # within the interval samples.append(sampleVal) lower = upper # set current ub as the lb for next interval elif distrib == 'triangle': mmin = distribSpecs[0].value mmax = distribSpecs[1].value mmode= distribSpecs[2].value samples = [] for sample in range(sampleCount): n = sample + 1 intervalarea = 1/sampleCount ylower = intervalarea(n-1) # use cdf to read off area as y's & yupper = intervalarea(n) # get corresponding x's for the pdf # Check to see if y values = cdf(x <= mmode) # for calculating correxponding x values: if ylower <= ((mmode - mmin)/(mmax - mmin)): lower = np.sqrt(ylower(mmax - mmin)(mmode - mmin)) + mmin else: lower = mmax-np.sqrt((1 - ylower)(mmax - mmin)(mmax - mmode)) if yupper <= ((mmode - mmin)/(mmax - mmin)): upper = np.sqrt(yupper(mmax - mmin)(mmode - mmin)) + mmin; else: upper = mmax-np.sqrt((1 - yupper)(mmax - mmin)(mmax - mmode)) sampleVal = np.random.uniform(lower, upper) samples.append(sampleVal) b = int(np.ceil(sampleCount/10)) plt.hist(samples, density = 1, bins = b) B=str(b) plt.title('Histogram of ' + modelParamName + ' parameter samples for ' + B + ' bins') plt.ylabel('proportion of samples'); plt.xlabel(modelParamName + ' value') plt.show() return samples ###Output _____no_output_____ ###Markdown Calls the function to ask for user input to name parameters and specify distributions. Type these in text input boxes and dropdowns that will appear below after running the cell. ###Code params = {} for i in range(parameterCount): s=str(i) params[i] = interactive(parNameDist, Name='Type parameter ' + s + ' name', Distribution=['uniform','normal','triangle']) display(params[i]) ###Output _____no_output_____ ###Markdown Input parameter distribution specifics in the interactive boxes that appear below after running this cell. ###Code distribSpecs={} for i in range(parameterCount): parName = params[i].result['Name'] print('Enter distribution specifics for parameter ' + parName + ':') if params[i].result['Dist'] == 'normal': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=2, description='Mean:' ) distribSpecs[parName][1] = widgets.FloatText( value=1, description='Variance:' ) display(distribSpecs[parName][0], distribSpecs[parName][1]) elif params[i].result['Dist'] == 'uniform': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=0, description='Minimum:' ) distribSpecs[parName][1] = widgets.FloatText( value=2, description='Maximum:' ) display(distribSpecs[parName][0], distribSpecs[parName][1]) elif params[i].result['Dist'] == 'triangle': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=0, description='Minimum:' ) distribSpecs[parName][1] = widgets.FloatText( value=2, description='Maximum:' ) distribSpecs[parName][2] = widgets.FloatText( value=1, description='Mode:' ) display(distribSpecs[parName][0], distribSpecs[parName][1], distribSpecs[parName][2]) ###Output Enter distribution specifics for parameter Type parameter 0 name: ###Markdown This passes the distributions to the code for generating parameter samples, and histogram plots of samples for each parameter will appear below. ###Code parameters = {} for j in range(parameterCount): parameters[params[j].result['Name']] = sampleDistrib(params[j].result['Name'], params[j].result['Dist'], distribSpecs[params[j].result['Name']]) ###Output _____no_output_____ ###Markdown Randomly permute each set of parameter samples in order to randomly pair the samples to more fully sample the parameter space for the Monte Carlo simulations. ###Code LHSparams=[] for p in parameters: temp = parameters[p] random.shuffle(temp) LHSparams.append(temp) ###Output _____no_output_____ ###Markdown Define your model function. Two examples have been provided below: (1) a linear function with two sampled parameters: slope and intercept, and (2) a Lotka-Volterra predator - prey model.Note that the order and number of the parameters needs to match the order and number of parameters speficied above to ensure accuracy when the model is solved below. ###Code def testlinear(x,sampledParams,unsampledParams): m = sampledParams[0] b = sampledParams[1] a = unsampledParams y = m x + b + a; return y def myodes(y, t, sampledParams, unsampledParams): q, r = y # unpack current values of y alpha, beta = sampledParams # unpack sampled parameters delta, lambdaa, gamma = unsampledParams # unpack unsampled parameters derivs = [alphaqr - lambdaaq, # list of dy/dt=f functions betar - gammaqr - deltar] return derivs ###Output _____no_output_____ ###Markdown Run Monte Carlo simulations for each parameter sample set. Be sure to specify a call to your model function and any necessary arguments below.* ###Code # EDIT THE FOLLOWING VARIABLES, UNSAMPLED PARAMETERS, & ANY OTHER ARGS HERE, # AS WELL AS THE CALL TO YOUR OWN MODEL FUNCTION INSIDE THE FOR LOOP BELOW x = np.linspace(0, 10, num=101) unsampledParams = 2; Output = [] for j in range(sampleCount): sampledParams=[i[j] for i in LHSparams] sol = testlinear(x,sampledParams,unsampledParams) Output.append(sol) # EDIT THE STRING TO NAME YOUR SIM OUTPUT (for fig labels, filenames): labelstring = 'y' # # EXAMPLE CODE FOR A COUPLED ODE MODEL: # import scipy.integrate as spi # t = np.linspace(0,17,num=171) # time domain for myodes # # odesic = [q0, r0] # odesic = [500,1000] # lambdaa = np.log(2)/7 # delta = 0.5 # gamma = 1 # unsampledParams = [lambdaa, delta, gamma] # Simdata={} # Output = [] # for i in range(sampleCount): # Simdata[i]={} # Simdata[i]['q']=[] # Simdata[i]['r']=[] # for j in range(sampleCount): # sampledParams=[i[j] for i in LHSparams] # sol=spi.odeint(myodes, odesic, t, args=(sampledParams,unsampledParams)) # Simdata[j]['q'] = sol[:,0] # solution to the equation for variable r # Simdata[j]['r'] = sol[:,1] # solution to the equation for variable s # Ratio = np.divide(sol[:,0],sol[:,1]) # compute ratio to compare w/ param samples # Output.append(Ratio) # labelstring = 'predator to prey ratio (q/r)'; # id for fig labels, filenames ###Output _____no_output_____ ###Markdown Plot the range of simulation output generated by the all of the Monte Carlo simulations using errorbars. ###Code yavg = np.mean(Output, axis=0) yerr = np.std(Output, axis=0) plt.errorbar(t,yavg,yerr) plt.xlabel('x') # plt.xlabel('time (days)') # for myodes plt.ylabel(labelstring) plt.title('Error bar plot of ' + labelstring + ' from LHS simulations') plt.show() ###Output _____no_output_____ ###Markdown Compute partial rank correlation coefficients to compare simulation outputs with parameters ###Code SampleResult=[] x_idx = 11 # time or location index of sim results x_idx2= x_idx+1 # to compare w/ param sample vals LHS=[zip(LHSparams)] LHSarray=np.array(LHS) Outputarray=np.array(Output) subOut=Outputarray[0:,x_idx:x_idx2] LHSout = np.hstack((LHSarray,subOut)) SampleResult = LHSout.tolist() Ranks=[] for s in range(sampleCount): indices = list(range(len(SampleResult[s]))) indices.sort(key=lambda k: SampleResult[s][k]) r = [0] * len(indices) for i, k in enumerate(indices): r[k] = i Ranks.append(r) C=np.corrcoef(Ranks); if np.linalg.det(C) < 1e-16: # determine if singular Cinv = np.linalg.pinv(C) # may need to use pseudo inverse else: Cinv = np.linalg.inv(C) resultIdx = parameterCount+1 prcc=np.zeros(resultIdx) for w in range(parameterCount): # compute PRCC btwn each param & sim result prcc[w]=-Cinv[w,resultIdx]/np.sqrt(Cinv[w,w]Cinv[resultIdx,resultIdx]) ###Output _____no_output_____ ###Markdown Plot the PRCCs for each parameter ###Code xp=[i for i in range(parameterCount)] plt.bar(xp,prcc[0:parameterCount], align='center') bLabels=list(parameters.keys()) plt.xticks(xp, bLabels) plt.ylabel('PRCC value'); N=str(sampleCount) loc=str(x_idx) plt.title('Partial rank correlation of params with ' + labelstring + ' results \n from ' + N + ' LHS sims, at x = ' +loc); plt.show() ###Output _____no_output_____ ###Markdown Can also do PRCCs over time... ###Code SampleResult=[] resultIdx = parameterCount+1 prcc=np.zeros((resultIdx,len(x))) LHS=[zip(LHSparams)] LHSarray=np.array(LHS) Outputarray=np.array(Output) for xi in range(len(x)): # loop through time or location of sim results xi2 = xi+1 # to compare w/ parameter sample vals subOut = Outputarray[0:,xi:xi2] LHSout = np.hstack((LHSarray,subOut)) SampleResult = LHSout.tolist() Ranks=[] for s in range(sampleCount): indices = list(range(len(SampleResult[s]))) indices.sort(key=lambda k: SampleResult[s][k]) r = [0] len(indices) for i, k in enumerate(indices): r[k] = i Ranks.append(r) C=np.corrcoef(Ranks); if np.linalg.det(C) < 1e-16: # determine if singular Cinv = np.linalg.pinv(C) # may need to use pseudo inverse else: Cinv = np.linalg.inv(C) for w in range(parameterCount): # compute PRCC btwn each param & sim result prcc[w,xi]=-Cinv[w,resultIdx]/np.sqrt(Cinv[w,w]Cinv[resultIdx,resultIdx]) ###Output _____no_output_____ ###Markdown Plot PRCC values as they vary over time or space. Notice PRCC can change with respect to the independent variable (x-axis). This may be helpful for certain applications, as opposed to only looking at a "snapshot."* ###Code for p in range(parameterCount): plt.plot(x,prcc[p,]) labels=list(parameters.keys()) plt.legend(labels) plt.ylabel('PRCC value'); plt.xlabel('x') N=str(sampleCount) plt.title('Partial rank correlation of params with ' + labelstring + ' results \n from ' + N + ' LHS sims'); plt.show() ###Output _____no_output_____ ###Markdown Latin Hypercube Sampling & Partial Rank Correlation Coefficients ~ a method for analyzing model sensitivity to parameters ~ Importing packages that will be used. ###Code import numpy as np from scipy import special import random from ipywidgets import interact, interactive, fixed, interact_manual import ipywidgets as widgets from IPython.display import display import pandas as pd import matplotlib.pyplot as plt ###Output _____no_output_____ ###Markdown Specify the number of parameters to sample and the number of samples to draw from each parameter distribution. Do not include any parameters that should be left fixed in parameterCount - those will be specified later. When choosing number of samples to draw, note that more samples (~ 1000) yields better results while fewer (~50) is faster for testing, since it requires fewer model solves. ###Code # Number of parameters to sample parameterCount = 4; # Number of samples to draw for each parameter sampleCount = 100; # 1000 plus ###Output _____no_output_____ ###Markdown This defines functions for specifying sampled parameters' names and distributions as well as drawing samples from a user-specified parameter distribution. Does not need any user edits. ###Code def parNameDist(Name,Distribution): paramTemp = {} paramTemp['Name']=Name paramTemp['Dist']=Distribution return paramTemp def sampleDistrib(modelParamName,distrib,distribSpecs): if distrib == 'uniform': mmin = distribSpecs[0].value mmax = distribSpecs[1].value intervalwidth = (mmax - mmin) / sampleCount # width of each # sampling interval samples = [] for sample in range(sampleCount): lower = mmin + intervalwidth * (sample-1) # lb of interval upper = mmin + intervalwidth * (sample) # ub of interval sampleVal = np.random.uniform(lower, upper) # draw a random sample # within the interval samples.append(sampleVal) elif distrib == 'normal': mmean= distribSpecs[0].value mvar = distribSpecs[1].value lower = mvarnp.sqrt(2)special.erfinv(-0.9999)+mmean # set lb of 1st # sample interval samples = [] for sample in range(sampleCount): n = sample + 1 if n != sampleCount: upper = (np.sqrt(2mvar)special.erfinv(2n/sampleCount-1) + mmean) # ub of sample interval else: upper = np.sqrt(2mvar)special.erfinv(0.9999) + mmean sampleVal = np.random.uniform(lower, upper) # draw a random sample # within the interval samples.append(sampleVal) lower = upper # set current ub as the lb for next interval elif distrib == 'triangle': mmin = distribSpecs[0].value mmax = distribSpecs[1].value mmode= distribSpecs[2].value samples = [] for sample in range(sampleCount): n = sample + 1 intervalarea = 1/sampleCount ylower = intervalarea(n-1) # use cdf to read off area as y's & yupper = intervalarea(n) # get corresponding x's for the pdf # Check to see if y values = cdf(x <= mmode) # for calculating correxponding x values: if ylower <= ((mmode - mmin)/(mmax - mmin)): lower = np.sqrt(ylower(mmax - mmin)(mmode - mmin)) + mmin else: lower = mmax-np.sqrt((1 - ylower)(mmax - mmin)(mmax - mmode)) if yupper <= ((mmode - mmin)/(mmax - mmin)): upper = np.sqrt(yupper(mmax - mmin)(mmode - mmin)) + mmin; else: upper = mmax-np.sqrt((1 - yupper)(mmax - mmin)(mmax - mmode)) sampleVal = np.random.uniform(lower, upper) samples.append(sampleVal) b = int(np.ceil(sampleCount/10)) plt.hist(samples, density = 1, bins = b) B=str(b) plt.title('Histogram of ' + modelParamName + ' parameter samples for ' + B + ' bins') plt.ylabel('proportion of samples'); plt.xlabel(modelParamName + ' value') plt.show() return samples ###Output _____no_output_____ ###Markdown Calls the function to ask for user input to name parameters and specify distributions. Type these in text input boxes and dropdowns that will appear below after running the cell. ###Code params = {} for i in range(parameterCount): s=str(i) params[i] = interactive(parNameDist, Name='Type parameter ' + s + ' name', Distribution=['uniform','normal','triangle']) display(params[i]) params ###Output _____no_output_____ ###Markdown Input parameter distribution specifics in the interactive boxes that appear below after running this cell. ###Code distribSpecs={} for i in range(parameterCount): parName = params[i].result['Name'] print('Enter distribution specifics for parameter ' + parName + ':') if params[i].result['Dist'] == 'normal': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=2, description='Mean:' ) distribSpecs[parName][1] = widgets.FloatText( value=1, description='Variance:' ) display(distribSpecs[parName][0], distribSpecs[parName][1]) elif params[i].result['Dist'] == 'uniform': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=0, description='Minimum:' ) distribSpecs[parName][1] = widgets.FloatText( value=2, description='Maximum:' ) display(distribSpecs[parName][0], distribSpecs[parName][1]) elif params[i].result['Dist'] == 'triangle': distribSpecs[parName] = {} distribSpecs[parName][0] = widgets.FloatText( value=0, description='Minimum:' ) distribSpecs[parName][1] = widgets.FloatText( value=2, description='Maximum:' ) distribSpecs[parName][2] = widgets.FloatText( value=1, description='Mode:' ) display(distribSpecs[parName][0], distribSpecs[parName][1], distribSpecs[parName][2]) # parameter of interest a=1.5 b = 1.64 delta = 4.0 beta = 2 lf = 0.50 uf = 2 varbound=np.array([[alf,auf],[blf,buf],[lfdelta,ufdelta],[lfbeta,ufbeta]]) varbound ###Output _____no_output_____ ###Markdown This passes the distributions to the code for generating parameter samples, and histogram plots of samples for each parameter will appear below. ###Code parameters = {} for j in range(parameterCount): parameters[params[j].result['Name']] = sampleDistrib(params[j].result['Name'], params[j].result['Dist'], distribSpecs[params[j].result['Name']]) ###Output _____no_output_____ ###Markdown Randomly permute each set of parameter samples in order to randomly pair the samples to more fully sample the parameter space for the Monte Carlo simulations. ###Code LHSparams=[] for p in parameters: temp = parameters[p] random.shuffle(temp) LHSparams.append(temp) # parameters # LHSparams ###Output _____no_output_____ ###Markdown Our IDM/FIDM model packages ###Code #!/usr/bin/env python3 # -- coding: utf-8 -- """ Created on Mon Jan 24 15:17:39 2022 @author: rafiul """ # import scipy.integrate as integrate # from scipy.integrate import odeint import sys import os # from geneticalgorithm import geneticalgorithm as ga #from geneticalgorithm_pronto import geneticalgorithm as ga # from ga import ga import numpy as np import scipy.integrate as integrate from scipy import special from scipy.interpolate import interp1d import pandas as pd ###Output _____no_output_____ ###Markdown Functions ###Code def RK4(func, X0, ts): """ Runge Kutta 4 solver. """ dt = ts[1] - ts[0] nt = len(ts) X = np.zeros((nt, X0.shape[0]),dtype=np.float64) X[0] = X0 for i in range(nt-1): k1 = func(X[i], ts[i]) k2 = func(X[i] + dt/2. k1, ts[i] + dt/2.) k3 = func(X[i] + dt/2. * k2, ts[i] + dt/2.) k4 = func(X[i] + dt * k3, ts[i] + dt) X[i+1] = X[i] + dt / 6. * (k1 + 2. * k2 + 2. * k3 + k4) return X # see this link for model and paramterts https://en.wikipedia.org/wiki/Intelligent_driver_model # DOI: 10.1098/rsta.2010.0084 # @jit(nopython=True) def idm_model(x,t): X,V = x[0],x[1] dX,dV = np.zeros(1,dtype=np.float64), np.zeros(1,dtype=np.float64) dX = V # Differtial Equation 1 ### s = position_LV(t) - X - 5 # 5 = length of the car deltaV = V - speed_LV(t) sstar = s0+VT + (VdeltaV)/(2np.sqrt(ab)) # ### dV = a(1-(V/V_0)delta - (sstar/s)2) # Differtial Equation 2 return np.array([dX,dV],dtype=np.float64) # @jit(nopython=True) def speed_LV(t): return interp1d(nth_car_data['time'],nth_car_data['speed'],bounds_error=False)(t) def position_LV(t): return interp1d(nth_car_data['time'],postion_of_the_LV,bounds_error=False)(t) def fractional_idm_model_1d(V,t,X): # index = round(t) #convert into integer number current_position_of_follower = X ### s = position_LV(t) - current_position_of_follower - 5 # 5 = length of the car deltaV = V - speed_LV(t) sstar = s0+VT + (VdeltaV)/(2np.sqrt(ab)) # ### dV = a(1-(V/V_0)delta - (sstar/s)2) # Differtial Equation 2 return dV def speed_error(sol,nth_car_speed): return np.sum((sol[1,:-1]-nth_car_speed[1:])2) def gap_error(sol,postion_of_the_LV): return np.sum((sol[0,:]-postion_of_the_LV)2) def caputoEuler_1d(a, f, y0, tspan, x0_f): """Use one-step Adams-Bashforth (Euler) method to integrate Caputo equation D^a y(t) = f(y,t) Args: a: fractional exponent in the range (0,1) f: callable(y,t) returning a numpy array of shape (d,) Vector-valued function to define the right hand side of the system y0: array of shape (d,) giving the initial state vector y(t==0) tspan (array): The sequence of time points for which to solve for y. These must be equally spaced, e.g. np.arange(0,10,0.005) tspan[0] is the intial time corresponding to the initial state y0. Returns: y: array, with shape (len(tspan), len(y0)) With the initial value y0 in the first row Raises: FODEValueError See also: K. Diethelm et al. (2004) Detailed error analysis for a fractional Adams method C. Li and F. Zeng (2012) Finite Difference Methods for Fractional Differential Equations """ #(d, a, f, y0, tspan) = _check_args(a, f, y0, tspan) N = len(tspan) h = (tspan[N-1] - tspan[0])/(N - 1) c = special.rgamma(a) * np.power(h, a) / a w = c * np.diff(np.power(np.arange(N), a)) fhistory = np.zeros(N - 1, dtype=np.float64) y = np.zeros(N, dtype=np.float64) x = np.zeros(N, dtype=np.float64) y[0] = y0; x[0] = x0_f; for n in range(0, N - 1): tn = tspan[n] yn = y[n] fhistory[n] = f(yn, tn, x[n]) y[n+1] = y0 + np.dot(w[0:n+1], fhistory[n::-1]) x[n+1] = x[n] + y[n+1] * h return np.array([x,y]) def error_func_idm(variable_X): # varbound=np.array([[alf,auf],[lfdelta,ufdelta],[lfbeta,ufbeta]]) a = variable_X[0] delta = variable_X[1] beta = variable_X[2] x0 = np.array([initial_position,initial_velocity],dtype=np.float64) #initial position and velocity # Classical ODE # sol = integrate.odeint(idm_model, x0, time_span) sol = RK4(idm_model, x0, time_span) sol = sol.transpose(1,0) # print(np.sum((sol[1,:-1]-nth_car_speed[1:])2)) return np.sum((sol[1,1:]-nth_car_speed[:-1])2) def error_func_fidm(variable_X): # varbound=np.array([[alf,auf],[lfdelta,ufdelta],[lfbeta,ufbeta]]) a = variable_X[0] delta = variable_X[1] beta = variable_X[2] alpha = variable_X[3] if alpha > .99999: alpha = .99999 sol = caputoEuler_1d(alpha,fractional_idm_model_1d, initial_velocity, time_span, initial_position) #, args=(number_groups,beta_P,beta_C,beta_A,v,w,mu_E,mu_A,mu_P,mu_C,p,q,contact_by_group)) return np.sum((sol[1,1:]-nth_car_speed[:-1])*2) # np.array(Output).reshape(len(Output),1) ###Output _____no_output_____ ###Markdown Run Monte Carlo simulations for each parameter sample set. Be sure to specify a call to your model function and any necessary arguments below.* ###Code ###################################### # Global variables # see this link for model and paramterts https://en.wikipedia.org/wiki/Intelligent_driver_model V_0 = 20 # desired speed m/s s0 = 30 T = 1.5 nth_car = 3 # a=1.5 # b = 1.67 # delta = 4.0 # beta = 2 # find best values for our model # a_alpha = 1.2 # ###################################### # Actual data # df = pd.read_csv('RAllCarDataTime350.csv') git_raw_url = 'https://raw.githubusercontent.com/m-rafiul-islam/driver-behavior-model/main/RAllCarDataTime350.csv' df = pd.read_csv(git_raw_url) nth_car_data = df.loc[df['nthcar'] == nth_car, :] nth_car_speed = np.array(df.loc[df['nthcar'] == nth_car,'speed']) # leader vehicle profile # 7 m/s - 25.2 km/h 11 m/s - 39.6 km/h 18 m/s - 64.8 km/h 22 m/s - 79.2 km/h # 25 km/h -- 6.95 m/s 40 km/h -- 11.11 m/s 60 km/h -- 16.67 m/s # dt=1 #time step -- 1 sec time_span = np.array(nth_car_data['time']) dt = time_span[1]-time_span[0] # speed_of_the_LV = 15np.ones(600+1) # we will need data # speed_of_the_LV = np.concatenate((np.linspace(0,7,60),7np.ones(120),np.linspace(7,11,60), 11np.ones(120), np.linspace(11,0,60) ))# we will need data speed_of_the_LV = nth_car_speed num_points = len(speed_of_the_LV) postion_of_the_LV = np.zeros(num_points) initla_position_of_the_LV = 18.45 # 113 postion_of_the_LV[0] = initla_position_of_the_LV for i in range(1,num_points): postion_of_the_LV[i] = postion_of_the_LV[i-1] + dt(speed_of_the_LV[i]+speed_of_the_LV[i-1])/2 initial_position = 0. initial_velocity = 6.72 x0 = np.array([initial_position,initial_velocity],dtype=np.float64) #initial position and velocity alpha =1 # a=1.5 b = 1.67 # delta = 4.0 # beta = 2 Output = [] for j in range(sampleCount): sampledParams=[i[j] for i in LHSparams] SSE = error_func_idm(sampledParams) Output.append(SSE) ###Output _____no_output_____ ###Markdown Plot the range of simulation output generated by the all of the Monte Carlo simulations using errorbars. ###Code # yavg = np.mean(Output, axis=0) # yerr = np.std(Output, axis=0) # plt.errorbar(t,yavg,yerr) # plt.xlabel('x') # # plt.xlabel('time (days)') # for myodes # plt.ylabel(labelstring) # plt.title('Error bar plot of ' + labelstring + ' from LHS simulations') # plt.show() ###Output _____no_output_____ ###Markdown Compute partial rank correlation coefficients to compare simulation outputs with parameters ###Code # LHSout = np.hstack((LHSarray,np.array(Output).reshape(len(Output),1))) SampleResult = LHSout.tolist() Ranks=[] for s in range(sampleCount): indices = list(range(len(SampleResult[s]))) indices.sort(key=lambda k: SampleResult[s][k]) r = [0] * len(indices) for i, k in enumerate(indices): r[k] = i Ranks.append(r) C=np.corrcoef(Ranks); if np.linalg.det(C) < 1e-16: # determine if singular Cinv = np.linalg.pinv(C) # may need to use pseudo inverse else: Cinv = np.linalg.inv(C) resultIdx = parameterCount+1 prcc=np.zeros(resultIdx) for w in range(parameterCount): # compute PRCC btwn each param & sim result prcc[w]=-Cinv[w,resultIdx]/np.sqrt(Cinv[w,w]*Cinv[resultIdx,resultIdx]) xp=[i for i in range(parameterCount)] plt.bar(xp,prcc[0:parameterCount], align='center') bLabels=list(parameters.keys()) plt.xticks(xp, bLabels) plt.ylabel('PRCC value'); plt.show() ###Output _____no_output_____
notebooks/tutorials/landscape_evolution/smooth_threshold_eroder/stream_power_smooth_threshold_eroder.ipynb	###Markdown The `StreamPowerSmoothThresholdEroder` componentLandlab's `StreamPowerSmoothThresholdEroder` (here SPSTE for short) is a fluvial landscape evolution component that uses a thresholded form of the stream power erosion law. The novel aspect is that the threshold takes a smoothed form rather than an abrupt mathematical discontinuity: as long as slope and drainage area are greater than zero, there is always some erosion rate even if the erosive potential function is below the nominal threshold value. This approach is motivated by the finding that mathematically discontinuous functions in numerical models can lead to "numerical daemons": non-smooth functional behavior that can greatly complicate optimization (Clark & Kavetski, 2010; Kavetski & Clark, 2010, 2011). The SPSTE is one of the fluvial erosion components used in the terrainBento collection of landscape evolution models (Barnhart et al., 2019).This tutorial provides a brief overview of how to use the SPSTE component.(G.E. Tucker, 2021) TheoryThe SPSTE formulation is as follows. Consider a location on a stream channel that has local downstream slope gradient $S$ and drainage area $A$. We define an erosion potential function $\omega$ as$$\omega = KA^mS^n$$where $K$ is an erodibility coefficient with dimensions of $[L^{(1-2m)}/T]$. The erosion potential function has dimensions of erosion (lowering) rate, [L/T], and it represents the rate of erosion that would occur if there were no threshold term. The expression takes the form of the familiar area-slope erosion law, also known as the "stream power law" because the exponents can be configured to represent an erosion law that depends on stream power per unit bed area (Whipple & Tucker, 1999). A common choice of exponents is $m=1/2$, $n=1$, but other combinations are possible depending on one's assumptions about process, hydrology, channel geometry, and other factors (e.g., Howard et al., 1994; Whipple et al., 2000).We also define a threshold erosion potential function, $\omega_c$, below which erosion rate declines precipitously. Given these definitions, a mathematically discontinuous threshold erosion function would look like this:$$E = \max (\omega - \omega_c, 0)$$This kind of formulation is mathematically simple, and given data on $E$ and $\omega$, one could easily find $K$ and $\omega_c$ empirically by fitting a line. Yet even in the case of sediment transport, where the initial motion of grains is usually represented by a threshold shear stress (often referred to as the critical shear stress for initiation of sediment motion), we know that some transport still occurs below the nominal threshold (e.g, Wilcock & McArdell, 1997). Although it is undeniably true that the rate of sediment transport declines rapidly when the average shear stress drops below a critical value, the strictly linear-with-threshold formulation is really more of convenient mathematical fiction than an accurate reflection of geophysical reality. In bed-load sediment transport, reality seems to be smoother than this mathematical fiction, if one transport rates averaged over a suitably long time period. The same is likely true for the hydraulic detachment and removal of cohesive/rocky material as well. Furthermore, as alluded to above, a strict threshold expression for transport or erosion can create numerical daemons that complicate model analysis.To avoid the mathematical discontinuity at $\omega=\omega_c$, SPSTE uses a smoothed version of the above function:$$E = \omega - \omega_c \left( 1 - e^{-\omega / \omega_c} \right)$$The code below generates a plot that compares the strict threshold and smooth threshold erosion laws. ###Code import numpy as np import matplotlib.pyplot as plt from landlab import RasterModelGrid, imshow_grid from landlab.components import FlowAccumulator, StreamPowerSmoothThresholdEroder omega = np.arange(0, 5.01, 0.01) omegac = 1.0 Eabrupt = np.maximum(omega - omegac, 0.0) Esmooth = omega - omegac * (1.0 - np.exp(-omega / omegac)) plt.plot(omega, Esmooth, "k", label="Smoothed threshold") plt.plot(omega, Eabrupt, "k--", label="Hard threshold") plt.plot([1.0, 1.0], [0.0, 4.0], "g:", label=r"$\omega=\omega_c$") plt.xlabel(r"Erosion potential function ($\omega$)") plt.ylabel("Erosion rate") plt.legend() ###Output _____no_output_____ ###Markdown Notice that the SPSTE formulation effectively smooths over the sharp discontinuity at $\omega = \omega_c$. EquilibriumConsider a case of steady, uniform fluvial erosion. Let the ratio of the erosion potential function to its threshold value be a constant, as$$\beta = \omega / \omega_c$$This allows us to replace instances of $\omega_c$ with $(1/\beta) \omega$,$$E = KA^m S^n - \frac{1}{\beta} KA^m S^n \left( 1 - e^{-\beta} \right)$$$$ = K A^m S^n \left( 1 - \frac{1}{\beta} \left( 1 - e^{-\beta} \right)\right)$$Let$$\alpha = \left( 1 - \frac{1}{\beta} \left( 1 - e^{-\beta} \right)\right)$$Then we can solve for the steady-state slope as$$\boxed{S = \left( \frac{E}{\alpha K A^m} \right)^{1/n}}$$We can relate $\beta$ and $\omega_c$ via$$\omega_c = E / (1-\beta (1 - e^{-\beta} ))$$ UsageHere we get a summary of the component's usage and input parameters by printing out the component's header docstring: ###Code print(StreamPowerSmoothThresholdEroder.__doc__) ###Output _____no_output_____ ###Markdown ExampleHere we'll run a steady-state example with $\beta = 1$. To do this, we'll start with a slightly inclined surface with some superimposed random noise, and subject it to a steady rate of rock uplift relative to baselevel, $U$, until it reaches a steady state. ###Code # Parameters K = 0.0001 # erodibility coefficient, 1/yr m = 0.5 # drainage area exponent beta = 1.0 # ratio of w / wc [-] uplift_rate = 0.001 # rate of uplift relative to baselevel, m/yr nrows = 16 # number of grid rows (small for speed) ncols = 25 # number of grid columns (") dx = 100.0 # grid spacing, m dt = 1000.0 # time-step duration, yr run_duration = 2.5e5 # duration of run, yr init_slope = 0.001 # initial slope gradient of topography, m/m noise_amplitude = 0.1 # amplitude of random noise on init. topo. # Derived parameters omega_c = uplift_rate / (beta - (1 - np.exp(-beta))) nsteps = int(run_duration / dt) # Create grid and elevation field with initial ramp grid = RasterModelGrid((nrows, ncols), xy_spacing=dx) grid.set_closed_boundaries_at_grid_edges(True, True, True, False) elev = grid.add_zeros("topographic__elevation", at="node") elev[:] = init_slope * grid.y_of_node np.random.seed(0) elev[grid.core_nodes] += noise_amplitude * np.random.rand(grid.number_of_core_nodes) # Display starting topography imshow_grid(grid, elev) # Instantiate the two components # (note that m=0.5, n=1 are the defaults for SPSTE) fa = FlowAccumulator(grid, flow_director="D8") spste = StreamPowerSmoothThresholdEroder(grid, K_sp=K, threshold_sp=omega_c) # Run the model for i in range(nsteps): # flow accumulation fa.run_one_step() # uplift / baselevel elev[grid.core_nodes] += uplift_rate * dt # erosion spste.run_one_step(dt) # Display the final topopgraphy imshow_grid(grid, elev) # Calculate the analytical solution in slope-area space alpha = 1.0 - (1.0 / beta) * (1.0 - np.exp(-beta)) area_pred = np.array([1.0e4, 1.0e6]) slope_pred = uplift_rate / (alpha * K * area_pred ** m) # Plot the slope-area relation and compare with analytical area = grid.at_node["drainage_area"] slope = grid.at_node["topographic__steepest_slope"] cores = grid.core_nodes plt.loglog(area[cores], slope[cores], "k.") plt.plot(area_pred, slope_pred) plt.legend(["Numerical", "Analytical"]) plt.title("Equilibrium slope-area relation") plt.xlabel(r"Drainage area (m$^2$)") _ = plt.ylabel("Slope (m/m)") ###Output _____no_output_____ ###Markdown The above plot shows that the simulation has reached steady state, and that the slope-area relation matches the analytical solution.We can also inspect the erosion potential function, which should be uniform in space, and (because $\beta = 1$ in this example) equal to the threshold $\omega_c$. We can also compare this with the uplift rate and the erosion-rate function: ###Code # Plot the erosion potential function omega = K * area[cores] ** m * slope[cores] plt.plot([0.0, 1.0e6], [omega_c, omega_c], "g", label=r"$\omega_c$") plt.plot(area[cores], omega, ".", label=r"$\omega$") plt.plot([0.0, 1.0e6], [uplift_rate, uplift_rate], "r", label=r"$U$") erorate = omega - omega_c * (1.0 - np.exp(-omega / omega_c)) plt.plot( area[cores], erorate, "k+", label=r"$\omega - \omega_c (1 - e^{-\omega/\omega_c})$" ) plt.ylim([0.0, 2 * omega_c]) plt.legend() plt.title("Erosion potential function vs. threshold term") plt.xlabel(r"Drainage area (m$^2$)") _ = plt.ylabel("Erosion potential function (m/yr)") ###Output _____no_output_____ ###Markdown The `StreamPowerSmoothThresholdEroder` componentLandlab's `StreamPowerSmoothThresholdEroder` (here SPSTE for short) is a fluvial landscape evolution component that uses a thresholded form of the stream power erosion law. The novel aspect is that the threshold takes a smoothed form rather than an abrupt mathematical discontinuity: as long as slope and drainage area are greater than zero, there is always some erosion rate even if the erosive potential function is below the nominal threshold value. This approach is motivated by the finding that mathematically discontinuous functions in numerical models can lead to "numerical daemons": non-smooth functional behavior that can greatly complicate optimization (Clark & Kavetski, 2010; Kavetski & Clark, 2010, 2011). The SPSTE is one of the fluvial erosion components used in the terrainBento collection of landscape evolution models (Barnhart et al., 2019).This tutorial provides a brief overview of how to use the SPSTE component.(G.E. Tucker, 2021) TheoryThe SPSTE formulation is as follows. Consider a location on a stream channel that has local downstream slope gradient $S$ and drainage area $A$. We define an erosion potential function $\omega$ as$$\omega = KA^mS^n$$where $K$ is an erodibility coefficient with dimensions of $[L^{(1-2m)}/T]$. The erosion potential function has dimensions of erosion (lowering) rate, [L/T], and it represents the rate of erosion that would occur if there were no threshold term. The expression takes the form of the familiar area-slope erosion law, also known as the "stream power law" because the exponents can be configured to represent an erosion law that depends on stream power per unit bed area (Whipple & Tucker, 1999). A common choice of exponents is $m=1/2$, $n=1$, but other combinations are possible depending on one's assumptions about process, hydrology, channel geometry, and other factors (e.g., Howard et al., 1994; Whipple et al., 2000).We also define a threshold erosion potential function, $\omega_c$, below which erosion rate declines precipitously. Given these definitions, a mathematically discontinuous threshold erosion function would look like this:$$E = \max (\omega - \omega_c, 0)$$This kind of formulation is mathematically simple, and given data on $E$ and $\omega$, one could easily find $K$ and $\omega_c$ empirically by fitting a line. Yet even in the case of sediment transport, where the initial motion of grains is usually represented by a threshold shear stress (often referred to as the critical shear stress for initiation of sediment motion), we know that some transport still occurs below the nominal threshold (e.g, Wilcock & McArdell, 1997). Although it is undeniably true that the rate of sediment transport declines rapidly when the average shear stress drops below a critical value, the strictly linear-with-threshold formulation is really more of convenient mathematical fiction than an accurate reflection of geophysical reality. In bed-load sediment transport, reality seems to be smoother than this mathematical fiction, if one transport rates averaged over a suitably long time period. The same is likely true for the hydraulic detachment and removal of cohesive/rocky material as well. Furthermore, as alluded to above, a strict threshold expression for transport or erosion can create numerical daemons that complicate model analysis.To avoid the mathematical discontinuity at $\omega=\omega_c$, SPSTE uses a smoothed version of the above function:$$E = \omega - \omega_c \left( 1 - e^{-\omega / \omega_c} \right)$$The code below generates a plot that compares the strict threshold and smooth threshold erosion laws. ###Code import numpy as np import matplotlib.pyplot as plt from landlab import RasterModelGrid, imshow_grid from landlab.components import (FlowAccumulator, StreamPowerSmoothThresholdEroder) omega = np.arange(0, 5.01, 0.01) omegac = 1.0 Eabrupt = np.maximum(omega - omegac, 0.0) Esmooth = omega - omegac * (1.0 - np.exp(-omega / omegac)) plt.plot(omega, Esmooth, 'k', label='Smoothed threshold') plt.plot(omega, Eabrupt, 'k--', label='Hard threshold') plt.plot([1., 1.], [0., 4.], 'g:', label=r'$\omega=\omega_c$') plt.xlabel(r'Erosion potential function ($\omega$)') plt.ylabel('Erosion rate') plt.legend() ###Output _____no_output_____ ###Markdown Notice that the SPSTE formulation effectively smooths over the sharp discontinuity at $\omega = \omega_c$. EquilibriumConsider a case of steady, uniform fluvial erosion. Let the ratio of the erosion potential function to its threshold value be a constant, as$$\beta = \omega / \omega_c$$This allows us to replace instances of $\omega_c$ with $(1/\beta) \omega$,$$E = KA^m S^n - \frac{1}{\beta} KA^m S^n \left( 1 - e^{-\beta} \right)$$$$ = K A^m S^n \left( 1 - \frac{1}{\beta} \left( 1 - e^{-\beta} \right)\right)$$Let$$\alpha = \left( 1 - \frac{1}{\beta} \left( 1 - e^{-\beta} \right)\right)$$Then we can solve for the steady-state slope as$$\boxed{S = \left( \frac{E}{\alpha K A^m} \right)^{1/n}}$$We can relate $\beta$ and $\omega_c$ via$$\omega_c = E / (1-\beta (1 - e^{-\beta} ))$$ UsageHere we get a summary of the component's usage and input parameters by printing out the component's header docstring: ###Code print(StreamPowerSmoothThresholdEroder.__doc__) ###Output _____no_output_____ ###Markdown ExampleHere we'll run a steady-state example with $\beta = 1$. To do this, we'll start with a slightly inclined surface with some superimposed random noise, and subject it to a steady rate of rock uplift relative to baselevel, $U$, until it reaches a steady state. ###Code # Parameters K = 0.0001 # erodibility coefficient, 1/yr m = 0.5 # drainage area exponent beta = 1.0 # ratio of w / wc [-] uplift_rate = 0.001 # rate of uplift relative to baselevel, m/yr nrows = 16 # number of grid rows (small for speed) ncols = 25 # number of grid columns (") dx = 100.0 # grid spacing, m dt = 1000.0 # time-step duration, yr run_duration = 2.5e5 # duration of run, yr init_slope = 0.001 # initial slope gradient of topography, m/m noise_amplitude = 0.1 # amplitude of random noise on init. topo. # Derived parameters omega_c = uplift_rate / (beta - (1 - np.exp(-beta))) nsteps = int(run_duration / dt) # Create grid and elevation field with initial ramp grid = RasterModelGrid((nrows, ncols), xy_spacing=dx) grid.set_closed_boundaries_at_grid_edges(True, True, True, False) elev = grid.add_zeros('topographic__elevation', at='node') elev[:] = init_slope * grid.y_of_node np.random.seed(0) elev[grid.core_nodes] += (noise_amplitude * np.random.rand(grid.number_of_core_nodes)) # Display starting topography imshow_grid(grid, elev) # Instantiate the two components # (note that m=0.5, n=1 are the defaults for SPSTE) fa = FlowAccumulator(grid, flow_director='D8') spste = StreamPowerSmoothThresholdEroder( grid, K_sp=K, threshold_sp=omega_c ) # Run the model for i in range(nsteps): # flow accumulation fa.run_one_step() # uplift / baselevel elev[grid.core_nodes] += uplift_rate * dt # erosion spste.run_one_step(dt) # Display the final topopgraphy imshow_grid(grid, elev) # Calculate the analytical solution in slope-area space alpha = (1.0 - (1.0 / beta) * (1.0 - np.exp(-beta))) area_pred = np.array([1.0e4, 1.0e6]) slope_pred = (uplift_rate / (alpha * K * area_pred*m)) # Plot the slope-area relation and compare with analytical area = grid.at_node['drainage_area'] slope = grid.at_node['topographic__steepest_slope'] cores = grid.core_nodes plt.loglog(area[cores], slope[cores], 'k.') plt.plot(area_pred, slope_pred) plt.legend(['Numerical', 'Analytical']) plt.title('Equilibrium slope-area relation') plt.xlabel(r'Drainage area (m$^2$)') _ = plt.ylabel('Slope (m/m)') ###Output _____no_output_____ ###Markdown The above plot shows that the simulation has reached steady state, and that the slope-area relation matches the analytical solution.We can also inspect the erosion potential function, which should be uniform in space, and (because $\beta = 1$ in this example) equal to the threshold $\omega_c$. We can also compare this with the uplift rate and the erosion-rate function: ###Code # Plot the erosion potential function omega = K area[cores]*m slope[cores] plt.plot([0.0, 1.0e6], [omega_c, omega_c], 'g', label=r'$\omega_c$') plt.plot(area[cores], omega, '.', label=r'$\omega$') plt.plot([0.0, 1.0e6], [uplift_rate, uplift_rate], 'r', label=r'$U$' ) erorate = omega - omega_c * (1.0 - np.exp(-omega / omega_c)) plt.plot(area[cores], erorate, 'k+', label=r'$\omega - \omega_c (1 - e^{-\omega/\omega_c})$') plt.ylim([0.0, 2 * omega_c]) plt.legend() plt.title('Erosion potential function vs. threshold term') plt.xlabel(r'Drainage area (m$^2$)') _ = plt.ylabel('Erosion potential function (m/yr)') ###Output _____no_output_____
YgroupChallenge.ipynb	###Markdown Librerias utilizadas ###Code import pandas as pd import matplotlib.pyplot as plt import ipywidgets as widgets from ipywidgets import interact from area import area import ipydatetime ###Output _____no_output_____ ###Markdown Histograma de tiempos de viaje para un año dado ###Code def histograma_por_año(año): df = pd.read_csv("Data/OD_{}.csv".format(año)) duration = df["duration_sec"] plt.hist(duration, bins=20 ,histtype='bar', edgecolor='k') plt.xlabel('Duracion del viaje(segundos)') plt.ylabel('Numero de viajes') plt.title('Histograma de tiempos de viaje año {}'.format(año)) return plt.show() interact(histograma_por_año, año=[2014,2015,2016,2017]) ###Output _____no_output_____ ###Markdown Listado del Top N de estaciones más utilizadas para un año dado. Dividirlo en:- Estaciones de salida- Estaciones de llegada- En general ###Code def listado_top_estaciones_año(año,N): df = pd.read_csv("Data/OD_{}.csv".format(año)) start_st = pd.DataFrame({'station_code': df['start_station_code']}) end_st = pd.DataFrame({'station_code': df['end_station_code']}) general_st = start_st.append(end_st) start_st = start_st.groupby('station_code').size().reset_index(name='counts') start_st = start_st.sort_values(by=['counts'],ascending=False) start_st = start_st.head(int(N)) start_st.index = range(1, int(N)+1) end_st = end_st.groupby('station_code').size().reset_index(name='counts') end_st = end_st.sort_values(by=['counts'],ascending=False) end_st = end_st.head(int(N)) end_st.index = range(1, int(N)+1) general_st = general_st.groupby('station_code').size().reset_index(name='counts') general_st = general_st.sort_values(by=['counts'],ascending=False) general_st = general_st.head(int(N)) general_st.index = range(1, int(N)+1) informe = pd.concat([start_st,end_st,general_st],axis=1) informe.columns = ["start_station_code","start_count","end_station_code","end_count","general_station_code","general_count"] informe.to_csv("listado_top{}_estaciones_{}.csv".format(int(N),año),index=False) return informe interact(listado_top_estaciones_año, año=[2014,2015,2016,2017],N=(0.0,200.0,1)) ###Output _____no_output_____ ###Markdown Listado del Top N de viajes más comunes para un año dado. Donde un viaje se define por su estación de salida y de llegada ###Code def listado_top_viajes_año(año,N): df = pd.read_csv("Data/OD_{}.csv".format(año)) viajes = pd.DataFrame({'start_station_code': df['start_station_code'], 'end_station_code': df['end_station_code']}) viajes["viaje"] = viajes["start_station_code"].astype(str) + '-' + viajes["end_station_code"].astype(str) viajes = viajes.groupby('viaje').size().reset_index(name='counts') viajes = viajes.sort_values(by=['counts'],ascending=False) viajes = viajes.head(int(N)) viajes.index = range(1, int(N)+1) viajes.to_csv("listado_top{}_viajes_{}.csv".format(int(N),año),index=False) return viajes interact(listado_top_viajes_año, año=[2014,2015,2016,2017],N=(0.0,200.0,1)) ###Output _____no_output_____ ###Markdown Identificación de horas punta para un año determinado sin tener en cuenta el día. Es decir, si es día de semana, fin de semana, festivo o temporada del año. ###Code def histograma_horas_por_año(año): df = pd.read_csv("Data/OD_{}.csv".format(año)) hours = pd.to_datetime(df["start_date"]).dt.hour plt.hist(hours, bins=24 ,histtype='bar', edgecolor='k') plt.xlabel('Hora del viage') plt.xticks(range(0,24)) plt.xlabel('Hora') plt.ylabel('Numero de viajes') plt.title('Histograma de horas puntas de viaje año {}'.format(año)) return plt.show() interact(histograma_horas_por_año, año=[2014,2015,2016,2017]) ###Output _____no_output_____ ###Markdown Comparación de utilización del sistema entre dos años cualesquiera. La utilización del sistema se puede medir como:- Cantidad de viajes totales- Tiempo total de utilización del sistema- Cantidad de viajes por estaciones/bicicletas disponibles ###Code def comparacion_sistema_año(año1,año2,medida): df1 = pd.read_csv("Data/OD_{}.csv".format(año1)) df2 = pd.read_csv("Data/OD_{}.csv".format(año2)) if medida=="viajes totales": plt.bar([str(año1),str(año2)],[len(df1),len(df2)]) plt.xlabel('Año') plt.ylabel('Numero de viajes') plt.title('Comparacion Nº viajes entre el {} y el {}'.format(año1,año2)) return plt.show() if medida=="tiempo de uso": uso1 = str(pd.Timedelta(df1["duration_sec"].sum(), unit ='s')) uso2 = str(pd.Timedelta(df2["duration_sec"].sum(), unit ='s')) usoTotal = pd.DataFrame({str(año1):uso1, str(año2):uso2},index=[0]) return usoTotal else: start_st1 = pd.DataFrame({'station_code': df1['start_station_code']}) end_st1 = pd.DataFrame({'station_code': df1['end_station_code']}) general_st1 = start_st1.append(end_st1) start_st2 = pd.DataFrame({'station_code': df2['start_station_code']}) end_st2 = pd.DataFrame({'station_code': df2['end_station_code']}) general_st2 = start_st2.append(end_st2) st1 = general_st1.groupby('station_code').size().reset_index(name='counts') st1.index = range(1, len(st1)+1) st2 = general_st2.groupby('station_code').size().reset_index(name='counts') st2.index = range(1, len(st2)+1) comp_est = pd.concat([st1,st2],axis=1) comp_est.columns = ["station_code_"+str(año1),"count_"+str(año1),"station_code_"+str(año2),"count_"+str(año2)] comp_est.to_csv("comparacion_{}_{}_{}.csv".format(año1,año2,medida),index=False) return comp_est interact(comparacion_sistema_año, año1=[2014,2015,2016,2017],año2=[2014,2015,2016,2017], medida=["viajes totales","tiempo de uso", "cantidad de viajes por estacion"]) ###Output _____no_output_____ ###Markdown Capacidad instalada total (suma de la capacidad total de cada estación) ###Code stations = pd.read_json("Data/stations.json") capacity = pd.json_normalize(stations["stations"]) print("\nCapacidad total : {}".format(capacity['ba'].sum())) ###Output Capacidad total : 4925 ###Markdown Cambio en la capacidad instalada entre dos años puntuales ###Code def comparacion_capacidad_año(año1,año2): df1 = pd.read_csv("Data/Stations_{}.csv".format(año1)) df2 = pd.read_csv("Data/Stations_{}.csv".format(año2)) stations = pd.read_json("Data/stations.json") capacity = pd.json_normalize(stations["stations"]) sum1 = capacity[capacity.n.astype(int).isin(df1["code"])] sum2 = capacity[capacity.n.astype(int).isin(df2["code"])] change = sum2['ba'].sum() - sum1['ba'].sum() print("El cambio de capacidad entre los años {} y {} ha sido de : {} unidades".format(año1,año2,change)) interact(comparacion_capacidad_año, año1=[2014,2015,2016,2017],año2=[2014,2015,2016,2017]) ###Output _____no_output_____ ###Markdown Ampliación de la cobertura de la red entre dos años puntuales. La misma se puede medir como el área total que generan las estaciones. ###Code def ampliacion_red_año(año1,año2): df1 = pd.read_csv("Data/Stations_{}.csv".format(año1)) df2 = pd.read_csv("Data/Stations_{}.csv".format(año2)) coordinates1 = [] for i in range(len(df1)): coordinates1.append([df1["latitude"][i],df1["longitude"][i]]) coordinates2 = [] for i in range(len(df2)): coordinates2.append([df2["latitude"][i],df2["longitude"][i]]) coordinates1.sort(key = lambda x: (-x[0], x[1])) coordinates2.sort(key = lambda x: (-x[0], x[1])) obj1 = {'type':'Polygon','coordinates':[coordinates1]} obj2 = {'type':'Polygon','coordinates':[coordinates2]} area1 = area(obj1) area2 = area(obj2) print("La diferencia entre la cobertura de la red entre el {} y el {} es: {} m".format(año1,año2,area2-area1)) interact(ampliacion_red_año, año1=[2014,2015,2016,2017],año2=[2014,2015,2016,2017]) ###Output _____no_output_____ ###Markdown Comparación de densidad de la red para un par de años puntuales. La densidad de la red se mide como el área que abarcan todas las estaciones,dividida la cantidad de estaciones. ###Code def densidad_red_año(año1,año2): df1 = pd.read_csv("Data/Stations_{}.csv".format(año1)) df2 = pd.read_csv("Data/Stations_{}.csv".format(año2)) coordinates1 = [] for i in range(len(df1)): coordinates1.append([df1["latitude"][i],df1["longitude"][i]]) coordinates2 = [] for i in range(len(df2)): coordinates2.append([df2["latitude"][i],df2["longitude"][i]]) coordinates1.sort(key = lambda x: (-x[0], x[1])) coordinates2.sort(key = lambda x: (-x[0], x[1])) obj1 = {'type':'Polygon','coordinates':[coordinates1]} obj2 = {'type':'Polygon','coordinates':[coordinates2]} densidad1 = area(obj1) / len(df1) densidad2 = area(obj2) / len(df2) print("La diferencia entre la densidad de la red entre el {} y el {} es: {}".format(año1,año2,densidad2-densidad1)) interact(densidad_red_año, año1=[2014,2015,2016,2017],año2=[2014,2015,2016,2017]) ###Output _____no_output_____ ###Markdown Velocidad promedio de los ciclistas para un año determinado ###Code from math import sin, cos, sqrt, atan2, radians def velocidad_año(año): df = pd.read_csv("Data/OD_{}.csv".format(año)) stations = pd.read_json("Data/stations.json") stations = pd.json_normalize(stations["stations"]) stations.n = stations.n.astype(int) start = pd.DataFrame({'n': df["start_station_code"]}) result_start = pd.merge(start,stations,on='n',how="left") end = pd.DataFrame({'n': df["end_station_code"]}) result_end = pd.merge(end,stations,on='n',how="left") combine = pd.concat([result_start[["n","id","la","lo"]],result_end[["n","id","la","lo"]],df["duration_sec"]],axis=1) combine.columns = ["start_station_code","id","start_station_la","start_station_lo", "end_station_code","end_station_id","end_station_la","end_station_lo","duration_sec"] R = 6373.0 lat1 = combine["start_station_la"].map(radians) lon1 = combine["start_station_lo"].map(radians) lat2 = combine["end_station_la"].map(radians) lon2 = combine["end_station_lo"].map(radians) dlon = lon2 - lon1 dlat = lat2 - lat1 a = (dlat/2).map(sin)*2 + lat1.map(cos) lat2.map(cos) * (dlon/2).map(sin)*2 c = 2 a.map(sqrt).map(asin) distance = R * c combine["speed"] = distance / (combine["duration_sec"]/3600) print("La velocidad media de los ciclistas en el año {} es: {} km/h".format(año,combine["speed"].mean())) interact(velocidad_año, año=[2014,2015,2016,2017]) ###Output _____no_output_____ ###Markdown Cantidad de bicicletas totales para un momento dado. Considerando la misma como la cantidad de bicicletas que hay en todas las estaciones activas para ese momento, más todos los viajes que se estén realizando. ###Code from datetime import datetime import pytz datetime_picker = ipydatetime.DatetimePicker() def total_bikes_at_date(date): if date!=None: df = pd.read_csv("Data/OD_{}.csv".format(date.year)) df.start_date = pd.to_datetime(df.start_date) df.end_date = pd.to_datetime(df.end_date) date = pd.to_datetime(date).tz_localize(tz=None) total = len(df[(date>df.start_date) & (date<df.end_date)]) print("En el momento {} hay {} bicicletas".format(str(date),total)) else: return 0 interact(total_bikes_at_date,date=datetime_picker) ###Output _____no_output_____
docs/_static/notebooks/old_quickstart.ipynb	###Markdown Quickstart ===================================In this notebook, we will explore `visual`, a companion package to `torchbearer` that enables complex feature visualisation with minimal work. We shall first show how easy it is to get a feature visualisation going using visual. ###Code !pip install -q torchbearer-visual ###Output _____no_output_____ ###Markdown We import a couple things from visual and then print the layer names of squeezenet v1.1 so that we can decide which layer to ascend on. ###Code from visual.models import inception_v3 from visual import BasicAscent, Channel, image from visual.transforms import RandomRotate, RandomScale, SpatialJitter, Compose from visual.models.utils import IntermediateLayerGetter return_layers = {'Mixed_5b': 'feat1'} model = IntermediateLayerGetter(inception_v3(True, False), return_layers) print(model.layer_names) ###Output ['Conv2d_1a_3x3', 'Conv2d_1a_3x3_conv', 'Conv2d_1a_3x3_bn', 'Conv2d_1a_3x3_relu', 'Conv2d_2a_3x3', 'Conv2d_2a_3x3_conv', 'Conv2d_2a_3x3_bn', 'Conv2d_2a_3x3_relu', 'Conv2d_2b_3x3', 'Conv2d_2b_3x3_conv', 'Conv2d_2b_3x3_bn', 'Conv2d_2b_3x3_relu', 'MaxPool2b', 'Conv2d_3b_1x1', 'Conv2d_3b_1x1_conv', 'Conv2d_3b_1x1_bn', 'Conv2d_3b_1x1_relu', 'Conv2d_4a_3x3', 'Conv2d_4a_3x3_conv', 'Conv2d_4a_3x3_bn', 'Conv2d_4a_3x3_relu', 'MaxPool4a', 'Mixed_5b', 'Mixed_5b_branch1x1', 'Mixed_5b_branch1x1_conv', 'Mixed_5b_branch1x1_bn', 'Mixed_5b_branch1x1_relu', 'Mixed_5b_branch5x5_1', 'Mixed_5b_branch5x5_1_conv', 'Mixed_5b_branch5x5_1_bn', 'Mixed_5b_branch5x5_1_relu', 'Mixed_5b_branch5x5_2', 'Mixed_5b_branch5x5_2_conv', 'Mixed_5b_branch5x5_2_bn', 'Mixed_5b_branch5x5_2_relu', 'Mixed_5b_branch3x3dbl_1', 'Mixed_5b_branch3x3dbl_1_conv', 'Mixed_5b_branch3x3dbl_1_bn', 'Mixed_5b_branch3x3dbl_1_relu', 'Mixed_5b_branch3x3dbl_2', 'Mixed_5b_branch3x3dbl_2_conv', 'Mixed_5b_branch3x3dbl_2_bn', 'Mixed_5b_branch3x3dbl_2_relu', 'Mixed_5b_branch3x3dbl_3', 'Mixed_5b_branch3x3dbl_3_conv', 'Mixed_5b_branch3x3dbl_3_bn', 'Mixed_5b_branch3x3dbl_3_relu', 'Mixed_5b_AvgPool', 'Mixed_5b_branch_pool', 'Mixed_5b_branch_pool_conv', 'Mixed_5b_branch_pool_bn', 'Mixed_5b_branch_pool_relu', 'Mixed_5c', 'Mixed_5c_branch1x1', 'Mixed_5c_branch1x1_conv', 'Mixed_5c_branch1x1_bn', 'Mixed_5c_branch1x1_relu', 'Mixed_5c_branch5x5_1', 'Mixed_5c_branch5x5_1_conv', 'Mixed_5c_branch5x5_1_bn', 'Mixed_5c_branch5x5_1_relu', 'Mixed_5c_branch5x5_2', 'Mixed_5c_branch5x5_2_conv', 'Mixed_5c_branch5x5_2_bn', 'Mixed_5c_branch5x5_2_relu', 'Mixed_5c_branch3x3dbl_1', 'Mixed_5c_branch3x3dbl_1_conv', 'Mixed_5c_branch3x3dbl_1_bn', 'Mixed_5c_branch3x3dbl_1_relu', 'Mixed_5c_branch3x3dbl_2', 'Mixed_5c_branch3x3dbl_2_conv', 'Mixed_5c_branch3x3dbl_2_bn', 'Mixed_5c_branch3x3dbl_2_relu', 'Mixed_5c_branch3x3dbl_3', 'Mixed_5c_branch3x3dbl_3_conv', 'Mixed_5c_branch3x3dbl_3_bn', 'Mixed_5c_branch3x3dbl_3_relu', 'Mixed_5c_AvgPool', 'Mixed_5c_branch_pool', 'Mixed_5c_branch_pool_conv', 'Mixed_5c_branch_pool_bn', 'Mixed_5c_branch_pool_relu', 'Mixed_5d', 'Mixed_5d_branch1x1', 'Mixed_5d_branch1x1_conv', 'Mixed_5d_branch1x1_bn', 'Mixed_5d_branch1x1_relu', 'Mixed_5d_branch5x5_1', 'Mixed_5d_branch5x5_1_conv', 'Mixed_5d_branch5x5_1_bn', 'Mixed_5d_branch5x5_1_relu', 'Mixed_5d_branch5x5_2', 'Mixed_5d_branch5x5_2_conv', 'Mixed_5d_branch5x5_2_bn', 'Mixed_5d_branch5x5_2_relu', 'Mixed_5d_branch3x3dbl_1', 'Mixed_5d_branch3x3dbl_1_conv', 'Mixed_5d_branch3x3dbl_1_bn', 'Mixed_5d_branch3x3dbl_1_relu', 'Mixed_5d_branch3x3dbl_2', 'Mixed_5d_branch3x3dbl_2_conv', 'Mixed_5d_branch3x3dbl_2_bn', 'Mixed_5d_branch3x3dbl_2_relu', 'Mixed_5d_branch3x3dbl_3', 'Mixed_5d_branch3x3dbl_3_conv', 'Mixed_5d_branch3x3dbl_3_bn', 'Mixed_5d_branch3x3dbl_3_relu', 'Mixed_5d_AvgPool', 'Mixed_5d_branch_pool', 'Mixed_5d_branch_pool_conv', 'Mixed_5d_branch_pool_bn', 'Mixed_5d_branch_pool_relu', 'Mixed_6a', 'Mixed_6a_branch3x3', 'Mixed_6a_branch3x3_conv', 'Mixed_6a_branch3x3_bn', 'Mixed_6a_branch3x3_relu', 'Mixed_6a_branch3x3dbl_1', 'Mixed_6a_branch3x3dbl_1_conv', 'Mixed_6a_branch3x3dbl_1_bn', 'Mixed_6a_branch3x3dbl_1_relu', 'Mixed_6a_branch3x3dbl_2', 'Mixed_6a_branch3x3dbl_2_conv', 'Mixed_6a_branch3x3dbl_2_bn', 'Mixed_6a_branch3x3dbl_2_relu', 'Mixed_6a_branch3x3dbl_3', 'Mixed_6a_branch3x3dbl_3_conv', 'Mixed_6a_branch3x3dbl_3_bn', 'Mixed_6a_branch3x3dbl_3_relu', 'Mixed_6a_MaxPool', 'Mixed_6b', 'Mixed_6b_branch1x1', 'Mixed_6b_branch1x1_conv', 'Mixed_6b_branch1x1_bn', 'Mixed_6b_branch1x1_relu', 'Mixed_6b_branch7x7_1', 'Mixed_6b_branch7x7_1_conv', 'Mixed_6b_branch7x7_1_bn', 'Mixed_6b_branch7x7_1_relu', 'Mixed_6b_branch7x7_2', 'Mixed_6b_branch7x7_2_conv', 'Mixed_6b_branch7x7_2_bn', 'Mixed_6b_branch7x7_2_relu', 'Mixed_6b_branch7x7_3', 'Mixed_6b_branch7x7_3_conv', 'Mixed_6b_branch7x7_3_bn', 'Mixed_6b_branch7x7_3_relu', 'Mixed_6b_branch7x7dbl_1', 'Mixed_6b_branch7x7dbl_1_conv', 'Mixed_6b_branch7x7dbl_1_bn', 'Mixed_6b_branch7x7dbl_1_relu', 'Mixed_6b_branch7x7dbl_2', 'Mixed_6b_branch7x7dbl_2_conv', 'Mixed_6b_branch7x7dbl_2_bn', 'Mixed_6b_branch7x7dbl_2_relu', 'Mixed_6b_branch7x7dbl_3', 'Mixed_6b_branch7x7dbl_3_conv', 'Mixed_6b_branch7x7dbl_3_bn', 'Mixed_6b_branch7x7dbl_3_relu', 'Mixed_6b_branch7x7dbl_4', 'Mixed_6b_branch7x7dbl_4_conv', 'Mixed_6b_branch7x7dbl_4_bn', 'Mixed_6b_branch7x7dbl_4_relu', 'Mixed_6b_branch7x7dbl_5', 'Mixed_6b_branch7x7dbl_5_conv', 'Mixed_6b_branch7x7dbl_5_bn', 'Mixed_6b_branch7x7dbl_5_relu', 'Mixed_6b_AvgPool', 'Mixed_6b_branch_pool', 'Mixed_6b_branch_pool_conv', 'Mixed_6b_branch_pool_bn', 'Mixed_6b_branch_pool_relu', 'Mixed_6c', 'Mixed_6c_branch1x1', 'Mixed_6c_branch1x1_conv', 'Mixed_6c_branch1x1_bn', 'Mixed_6c_branch1x1_relu', 'Mixed_6c_branch7x7_1', 'Mixed_6c_branch7x7_1_conv', 'Mixed_6c_branch7x7_1_bn', 'Mixed_6c_branch7x7_1_relu', 'Mixed_6c_branch7x7_2', 'Mixed_6c_branch7x7_2_conv', 'Mixed_6c_branch7x7_2_bn', 'Mixed_6c_branch7x7_2_relu', 'Mixed_6c_branch7x7_3', 'Mixed_6c_branch7x7_3_conv', 'Mixed_6c_branch7x7_3_bn', 'Mixed_6c_branch7x7_3_relu', 'Mixed_6c_branch7x7dbl_1', 'Mixed_6c_branch7x7dbl_1_conv', 'Mixed_6c_branch7x7dbl_1_bn', 'Mixed_6c_branch7x7dbl_1_relu', 'Mixed_6c_branch7x7dbl_2', 'Mixed_6c_branch7x7dbl_2_conv', 'Mixed_6c_branch7x7dbl_2_bn', 'Mixed_6c_branch7x7dbl_2_relu', 'Mixed_6c_branch7x7dbl_3', 'Mixed_6c_branch7x7dbl_3_conv', 'Mixed_6c_branch7x7dbl_3_bn', 'Mixed_6c_branch7x7dbl_3_relu', 'Mixed_6c_branch7x7dbl_4', 'Mixed_6c_branch7x7dbl_4_conv', 'Mixed_6c_branch7x7dbl_4_bn', 'Mixed_6c_branch7x7dbl_4_relu', 'Mixed_6c_branch7x7dbl_5', 'Mixed_6c_branch7x7dbl_5_conv', 'Mixed_6c_branch7x7dbl_5_bn', 'Mixed_6c_branch7x7dbl_5_relu', 'Mixed_6c_AvgPool', 'Mixed_6c_branch_pool', 'Mixed_6c_branch_pool_conv', 'Mixed_6c_branch_pool_bn', 'Mixed_6c_branch_pool_relu', 'Mixed_6d', 'Mixed_6d_branch1x1', 'Mixed_6d_branch1x1_conv', 'Mixed_6d_branch1x1_bn', 'Mixed_6d_branch1x1_relu', 'Mixed_6d_branch7x7_1', 'Mixed_6d_branch7x7_1_conv', 'Mixed_6d_branch7x7_1_bn', 'Mixed_6d_branch7x7_1_relu', 'Mixed_6d_branch7x7_2', 'Mixed_6d_branch7x7_2_conv', 'Mixed_6d_branch7x7_2_bn', 'Mixed_6d_branch7x7_2_relu', 'Mixed_6d_branch7x7_3', 'Mixed_6d_branch7x7_3_conv', 'Mixed_6d_branch7x7_3_bn', 'Mixed_6d_branch7x7_3_relu', 'Mixed_6d_branch7x7dbl_1', 'Mixed_6d_branch7x7dbl_1_conv', 'Mixed_6d_branch7x7dbl_1_bn', 'Mixed_6d_branch7x7dbl_1_relu', 'Mixed_6d_branch7x7dbl_2', 'Mixed_6d_branch7x7dbl_2_conv', 'Mixed_6d_branch7x7dbl_2_bn', 'Mixed_6d_branch7x7dbl_2_relu', 'Mixed_6d_branch7x7dbl_3', 'Mixed_6d_branch7x7dbl_3_conv', 'Mixed_6d_branch7x7dbl_3_bn', 'Mixed_6d_branch7x7dbl_3_relu', 'Mixed_6d_branch7x7dbl_4', 'Mixed_6d_branch7x7dbl_4_conv', 'Mixed_6d_branch7x7dbl_4_bn', 'Mixed_6d_branch7x7dbl_4_relu', 'Mixed_6d_branch7x7dbl_5', 'Mixed_6d_branch7x7dbl_5_conv', 'Mixed_6d_branch7x7dbl_5_bn', 'Mixed_6d_branch7x7dbl_5_relu', 'Mixed_6d_AvgPool', 'Mixed_6d_branch_pool', 'Mixed_6d_branch_pool_conv', 'Mixed_6d_branch_pool_bn', 'Mixed_6d_branch_pool_relu', 'Mixed_6e', 'Mixed_6e_branch1x1', 'Mixed_6e_branch1x1_conv', 'Mixed_6e_branch1x1_bn', 'Mixed_6e_branch1x1_relu', 'Mixed_6e_branch7x7_1', 'Mixed_6e_branch7x7_1_conv', 'Mixed_6e_branch7x7_1_bn', 'Mixed_6e_branch7x7_1_relu', 'Mixed_6e_branch7x7_2', 'Mixed_6e_branch7x7_2_conv', 'Mixed_6e_branch7x7_2_bn', 'Mixed_6e_branch7x7_2_relu', 'Mixed_6e_branch7x7_3', 'Mixed_6e_branch7x7_3_conv', 'Mixed_6e_branch7x7_3_bn', 'Mixed_6e_branch7x7_3_relu', 'Mixed_6e_branch7x7dbl_1', 'Mixed_6e_branch7x7dbl_1_conv', 'Mixed_6e_branch7x7dbl_1_bn', 'Mixed_6e_branch7x7dbl_1_relu', 'Mixed_6e_branch7x7dbl_2', 'Mixed_6e_branch7x7dbl_2_conv', 'Mixed_6e_branch7x7dbl_2_bn', 'Mixed_6e_branch7x7dbl_2_relu', 'Mixed_6e_branch7x7dbl_3', 'Mixed_6e_branch7x7dbl_3_conv', 'Mixed_6e_branch7x7dbl_3_bn', 'Mixed_6e_branch7x7dbl_3_relu', 'Mixed_6e_branch7x7dbl_4', 'Mixed_6e_branch7x7dbl_4_conv', 'Mixed_6e_branch7x7dbl_4_bn', 'Mixed_6e_branch7x7dbl_4_relu', 'Mixed_6e_branch7x7dbl_5', 'Mixed_6e_branch7x7dbl_5_conv', 'Mixed_6e_branch7x7dbl_5_bn', 'Mixed_6e_branch7x7dbl_5_relu', 'Mixed_6e_AvgPool', 'Mixed_6e_branch_pool', 'Mixed_6e_branch_pool_conv', 'Mixed_6e_branch_pool_bn', 'Mixed_6e_branch_pool_relu', 'AuxLogits', 'AuxLogits_AvgPool0', 'AuxLogits_conv0', 'AuxLogits_conv0_conv', 'AuxLogits_conv0_bn', 'AuxLogits_conv0_relu', 'AuxLogits_conv1', 'AuxLogits_conv1_conv', 'AuxLogits_conv1_bn', 'AuxLogits_conv1_relu', 'AuxLogits_AvgPool1', 'AuxLogits_fc', 'Mixed_7a', 'Mixed_7a_branch3x3_1', 'Mixed_7a_branch3x3_1_conv', 'Mixed_7a_branch3x3_1_bn', 'Mixed_7a_branch3x3_1_relu', 'Mixed_7a_branch3x3_2', 'Mixed_7a_branch3x3_2_conv', 'Mixed_7a_branch3x3_2_bn', 'Mixed_7a_branch3x3_2_relu', 'Mixed_7a_branch7x7x3_1', 'Mixed_7a_branch7x7x3_1_conv', 'Mixed_7a_branch7x7x3_1_bn', 'Mixed_7a_branch7x7x3_1_relu', 'Mixed_7a_branch7x7x3_2', 'Mixed_7a_branch7x7x3_2_conv', 'Mixed_7a_branch7x7x3_2_bn', 'Mixed_7a_branch7x7x3_2_relu', 'Mixed_7a_branch7x7x3_3', 'Mixed_7a_branch7x7x3_3_conv', 'Mixed_7a_branch7x7x3_3_bn', 'Mixed_7a_branch7x7x3_3_relu', 'Mixed_7a_branch7x7x3_4', 'Mixed_7a_branch7x7x3_4_conv', 'Mixed_7a_branch7x7x3_4_bn', 'Mixed_7a_branch7x7x3_4_relu', 'Mixed_7a_MaxPool', 'Mixed_7b', 'Mixed_7b_branch1x1', 'Mixed_7b_branch1x1_conv', 'Mixed_7b_branch1x1_bn', 'Mixed_7b_branch1x1_relu', 'Mixed_7b_branch3x3_1', 'Mixed_7b_branch3x3_1_conv', 'Mixed_7b_branch3x3_1_bn', 'Mixed_7b_branch3x3_1_relu', 'Mixed_7b_branch3x3_2a', 'Mixed_7b_branch3x3_2a_conv', 'Mixed_7b_branch3x3_2a_bn', 'Mixed_7b_branch3x3_2a_relu', 'Mixed_7b_branch3x3_2b', 'Mixed_7b_branch3x3_2b_conv', 'Mixed_7b_branch3x3_2b_bn', 'Mixed_7b_branch3x3_2b_relu', 'Mixed_7b_branch3x3dbl_1', 'Mixed_7b_branch3x3dbl_1_conv', 'Mixed_7b_branch3x3dbl_1_bn', 'Mixed_7b_branch3x3dbl_1_relu', 'Mixed_7b_branch3x3dbl_2', 'Mixed_7b_branch3x3dbl_2_conv', 'Mixed_7b_branch3x3dbl_2_bn', 'Mixed_7b_branch3x3dbl_2_relu', 'Mixed_7b_branch3x3dbl_3a', 'Mixed_7b_branch3x3dbl_3a_conv', 'Mixed_7b_branch3x3dbl_3a_bn', 'Mixed_7b_branch3x3dbl_3a_relu', 'Mixed_7b_branch3x3dbl_3b', 'Mixed_7b_branch3x3dbl_3b_conv', 'Mixed_7b_branch3x3dbl_3b_bn', 'Mixed_7b_branch3x3dbl_3b_relu', 'Mixed_7b_AvgPool', 'Mixed_7b_branch_pool', 'Mixed_7b_branch_pool_conv', 'Mixed_7b_branch_pool_bn', 'Mixed_7b_branch_pool_relu', 'Mixed_7c', 'Mixed_7c_branch1x1', 'Mixed_7c_branch1x1_conv', 'Mixed_7c_branch1x1_bn', 'Mixed_7c_branch1x1_relu', 'Mixed_7c_branch3x3_1', 'Mixed_7c_branch3x3_1_conv', 'Mixed_7c_branch3x3_1_bn', 'Mixed_7c_branch3x3_1_relu', 'Mixed_7c_branch3x3_2a', 'Mixed_7c_branch3x3_2a_conv', 'Mixed_7c_branch3x3_2a_bn', 'Mixed_7c_branch3x3_2a_relu', 'Mixed_7c_branch3x3_2b', 'Mixed_7c_branch3x3_2b_conv', 'Mixed_7c_branch3x3_2b_bn', 'Mixed_7c_branch3x3_2b_relu', 'Mixed_7c_branch3x3dbl_1', 'Mixed_7c_branch3x3dbl_1_conv', 'Mixed_7c_branch3x3dbl_1_bn', 'Mixed_7c_branch3x3dbl_1_relu', 'Mixed_7c_branch3x3dbl_2', 'Mixed_7c_branch3x3dbl_2_conv', 'Mixed_7c_branch3x3dbl_2_bn', 'Mixed_7c_branch3x3dbl_2_relu', 'Mixed_7c_branch3x3dbl_3a', 'Mixed_7c_branch3x3dbl_3a_conv', 'Mixed_7c_branch3x3dbl_3a_bn', 'Mixed_7c_branch3x3dbl_3a_relu', 'Mixed_7c_branch3x3dbl_3b', 'Mixed_7c_branch3x3dbl_3b_conv', 'Mixed_7c_branch3x3dbl_3b_bn', 'Mixed_7c_branch3x3dbl_3b_relu', 'Mixed_7c_AvgPool', 'Mixed_7c_branch_pool', 'Mixed_7c_branch_pool_conv', 'Mixed_7c_branch_pool_bn', 'Mixed_7c_branch_pool_relu', 'AvgPool', 'fc'] ###Markdown Let's choose the final layer, where we have 1000 channels, each corresponding to 1 imagenet class. We'll choose the 256th feature, which is the class "Newfoundland Dog". After running a `BasicAscent` and viewing it in pyplot, you can confirm for yourself that we indeed see things that look like dogs. ###Code transforms = Compose([ RandomRotate(list(range(-30, 30, 5))), RandomScale([0.9, 0.95, 1.0, 1.05, 1.1, 1.15, 1.2]), ]) crit = Channel(10, 'feat1') img = image((3, 256, 256), transform=transforms, correlate=True, fft=True) a = BasicAscent(img, crit, verbose=2).to_pyplot().run(model, device='cuda') ###Output _____no_output_____ ###Markdown So, we have seen how quick it is to get a simple visualisation running, but what were did we actually do to get there? We'll now introduce, one at a time, the abstractions that visual uses:- Images- Transforms- Criterions- Ascenders- Models ###Code ###Output _____no_output_____
trial.ipynb	###Markdown Define Muskingum coefficients Parameters ###Code K1 = 7.722 X1 = 0.3 delta_t = 1560 alpha1 = (delta_t-2K1X1)/(2K1(1-X1)+delta_t) beta1 = (delta_t+2K1X1)/(2K1(1-X1)+delta_t) xi1 = (2K1(1-X1)-delta_t)/(2K1(1-X1)+delta_t) K2 = 7.3317 X2 = 0.5 delta_t = 1560 alpha2 = (delta_t-2K2X2)/(2K2(1-X2)+delta_t) beta2 = (delta_t+2K1X1)/(2K2(1-X2)+delta_t) xi2 = (2K2(1-X1)-delta_t)/(2K2(1-X2)+delta_t) K3 = 7.722 X3 = 0.2 delta_t = 1560 alpha3 = (delta_t-2K2X2)/(2K2(1-X2)+delta_t) beta3 = (delta_t+2K2X2)/(2K2(1-X2)+delta_t) xi3 = (2K2(1-X2)-delta_t)/(2K2(1-X2)+delta_t) ###Output _____no_output_____ ###Markdown Define state space system Matrices ###Code #Define the matrices import numpy as np import pandas as pd import matplotlib.pyplot as plt from matplotlib.dates import DateFormatter B_I = np.array([0,0,0,0,0,0,beta1,beta2,0]).reshape(3,3) X_I = np.array([0,0,0,0,0,0,xi1,xi2,0]).reshape(3,3) B_O = np.array([beta1,0,0,0,beta2,0,alpha3beta1,alpha3beta2,beta3]).reshape(3,3) X_O = np.array([xi1,0,0,0,xi2,0,alpha3xi1,alpha3xi2,xi3]).reshape(3,3) P_I = np.array([1,0,0,0,1,0,alpha1,alpha2,1]).reshape(3,3) P_O = np.array([alpha1,0,0,0,alpha2,0,alpha3alpha1,alpha3alpha2,alpha3]).reshape(3,3) ###Output _____no_output_____ ###Markdown Create block Matrices ###Code df = pd.read_csv('Total_inflow.csv') mat_6x6 = np.block([[B_I,X_I],[B_O,X_O]]) # Creating 6x6 Matrix mat_6x3 = np.block([[P_I],[P_O]]) # Creating 6 3 matrix I_intial=np.array([0,0,0]).reshape(3,1) # Intializing I matrix O_intial=np.array([0,0,0]).reshape(3,1) # Initializing O matrix IO_mat_6x1 = np.block([[I_intial],[O_intial]]) # Creating a block matrix eig = np.linalg.eig(mat_6x6) eig ###Output _____no_output_____ ###Markdown Finding the State Space System Solution ###Code P1 = np.array(df['Inflow_1']) P2 = np.array(df['Inflow_2']) P3 = np.array(df['Inflow_3']) time = df['Time'] # P_t = np.array([[P1[0]],[P2[0]],[P3[0]]]) result = IO_mat_6x1.reshape(1,6) # Initialing result with initial value for Input and output for idx in range(len(P1)): # running till the length of P1 i.e. the number of time steps P_t = np.array([[P1[idx]],[P2[idx]],[P3[idx]]]) # extracting value of each arrary for each time step val = mat_6x6@result[-1,:].reshape(6,1)+mat_6x3@P_t # selecting the last value of result and reshaping it to 6x1 val = val.reshape(1,6) result = np.concatenate((result,val),axis=0) # each row result for each time step df_nwm = pd.read_csv('Total_Discharge_nwm.csv') # plot the discharge time series import matplotlib.pyplot as plt from matplotlib.dates import DateFormatter time= pd.to_datetime(time) plt.figure(facecolor='white') plt.plot(time, result[1:,3]) plt.plot(df_nwm['Outflow1'],label = 'NWM') date_form = DateFormatter("%b %d") plt.legend() plt.figure(facecolor = 'white') plt.plot(result[1:,4],label = 'Model') plt.plot(df_nwm['Outflow2'],label = 'NWM') plt.legend() plt.figure(facecolor = 'white') plt.plot(result[1:,5],label = 'Model') plt.plot(df_nwm['Outflow3'],label = 'NWM') plt.legend() # # plt.rc('font', size=14) # fig, ax = plt.subplots(figsize=(10, 6)) # ax.plot(result[:,3], time, color='tab:blue', label='Q') type(time) #Load the sensor data and model data sensor = pd.read_csv('D:/Sujana/Project/ce397/DD6_sensor.csv') Y = np.array(sensor['DD6_discharge']) X = pd.read_csv('D:/Sujana/Project/ce397/result_outflow_kalman.csv') I1 = np.array(X['I1']) I2 = np.array(X['I2']) I3 = np.array(X['I3']) O1 = np.array(X['O1']) O2 = np.array(X['O2']) O3 = np.array(X['O3']) C = np.array([1/4,0,0,3/4,0,0]).reshape(1,6) #Define noise parameters sigma_v = 0.05 # Measurement noise std. dev sigma_w = 0.5 # Process noise std. dev add_v = 0 # Add measurement noise by setting to 1 add_w = 0 # Add process noise by setting to 1 #Generate y_hat values # for i in range(len(I1)): # x_h = np.array([[I1[i]],[I2[i]],[I3[i]],[O1[i]],[O2[i]],[O3[i]]]) # value = C@x_h.reshape(6,1) # y_hat = np.concatenate((result,val),axis=0) # y_hat += add_v * sigma_v * np.random.randn(y_hat.shape) ###Output _____no_output_____ ###Markdown Kalman Filter ###Code A = np.block([[B_I,X_I],[B_O,X_O]]) B = np.block([[P_I],[P_O]]) V = sigma_v2 np.eye(len(C)) # Measurement noise covariance W = sigma_w*2 np.eye(len(A)) # Process noise covariance S = 1e-2 * np.eye(len(A)) # Initial estimate of error covariance x_hat = np.zeros(6).reshape(1,6) # Estimate of initial state # X_hat = [x_hat] for k in range(len(I1)): y = Y[k] u = np.array([[P1[k]],[P2[k]],[P3[k]]]) # u += add_w * sigma_w * np.random.randn(B.shape[1]) S = A @ (S - S @ C.T @ np.linalg.inv(C @ S @ C.T + V) @ C @ S) @ A.T + W L = S @ C.T @ np.linalg.inv(C @ S @ C.T + V) y_hat = C @ (A @ x_hat[-1,:].reshape(6,1) + B @ u) x = A @ x_hat[-1,:].reshape(6,1) + B @ u + L @ (y - y_hat) x = x.reshape(1,6) x_hat = np.concatenate((x_hat,x),axis=0) X_hat = x_hat # X_hat = np.vstack(X_hat) # for idx in range(len(P1)): # running till the length of P1 i.e. the number of time steps # P_t = np.array([[P1[idx]],[P2[idx]],[P3[idx]]]) # extracting value of each arrary for each time step # val = mat_6x6@result[-1,:].reshape(6,1)+mat_6x3@P_t # selecting the last value of result and reshaping it to 6x1 # val = val.reshape(1,6) # result = np.concatenate((result,val),axis=0) # plot the discharge time series # Outflow1 plt.figure(facecolor='white') plt.plot(O1) plt.plot(Y, label = 'sensor') plt.plot(X_hat[:,3]) # plt.plot(df_nwm['Outflow1'],label = 'NWM') date_form = DateFormatter("%b %d") plt.legend() # Outflow3 plt.figure(facecolor = 'white') plt.plot(result[1:,5],label = 'Model') plt.plot(df_nwm['Outflow3'],label = 'NWM') plt.legend() # # plt.rc('font', size=14) # fig, ax = plt.subplots(figsize=(10, 6)) # ax.plot(result[:,3], time, color='tab:blue', label='Q') # plot the discharge time series import matplotlib.pyplot as plt from matplotlib.dates import DateFormatter plt.figure(facecolor='white') plt.plot(time, result[1:,3]) plt.plot(df_nwm['Outflow1'],label = 'NWM') date_form = DateFormatter("%b %d") ax.xaxis.set_major_formatter(date_form) plt.legend() import matplotlib.pyplot as plt from matplotlib.dates import DateFormatter plt.figure(facecolor='white') plt.rc('font', size=14) fig, ax = plt.subplots(figsize=(10, 6)) ax.plot(X['O1'], color='tab:blue', label='Q') # ax.line(X.index.values, # X['O1'], # color='purple') ax.set(xlabel='Date', ylabel='Discharge [cms]', title='Outflow 1') date_form = DateFormatter("%b %d") ax.xaxis.set_major_formatter(date_form) ax.legend() ax.grid(True) plt.show() X = X.set_index('Time') m = type(X.index.values) ###Output _____no_output_____ ###Markdown Check the path of your csv files before loading the data ###Code col_types = {'Id': 'int', 'OwnerUserId': 'float', 'CreationDate': 'str', 'ParentId': 'int', 'Score': 'int', 'Title': 'str', 'Body':'str'} questions = pd.read_csv('/pythonquestions/Questions.csv', encoding = "ISO-8859-1", dtype=col_types) answers = pd.read_csv('/pythonquestions/Answers.csv', encoding = "ISO-8859-1", dtype=col_types) # question to answer: (ans_id, score, owner_id) q_to_a = load_obj('obj/q_to_a.pkl') if not q_to_a: q_to_a = dict() for _, row in answers[['Id', 'ParentId', 'Score', 'OwnerUserId']].iterrows(): q_id = row['ParentId'] a_id = row['Id'] a_score = row['Score'] a_owner_id = row['OwnerUserId'] if not np.isnan(row['OwnerUserId']) else None if q_id not in q_to_a: q_to_a[q_id] = [(a_id, a_score, a_owner_id)] else: q_to_a[q_id].append((a_id, a_score, a_owner_id)) save_obj(q_to_a, 'obj/q_to_a.pkl') # Keep only the questions with 4-10 answers and a distinguishable answer q_to_a = {k:v for k, v in q_to_a.items() if len(v)>3 and len(v)<11 and max(v, key=lambda x: x[1])[1]>0} # keep only qualified questions questions = questions[questions['Id'].isin(q_to_a)] # Keep only answers related to a qualified question def answer_in_use(answer): if answer['ParentId'] in q_to_a: for item in q_to_a[answer['ParentId']]: if answer['Id'] == item[0]: return True return False answers = answers[answers.apply(lambda x: answer_in_use(x), axis=1)] questions.info() answers.info() ###Output <class 'pandas.core.frame.DataFrame'> Int64Index: 215203 entries, 0 to 987106 Data columns (total 6 columns): Id 215203 non-null int32 OwnerUserId 213419 non-null float64 CreationDate 215203 non-null object ParentId 215203 non-null int32 Score 215203 non-null int32 Body 215203 non-null object dtypes: float64(1), int32(3), object(2) memory usage: 9.0+ MB ###Markdown Semantic features: Question-Ans similarity and Ans-Ans similarity (It took 1.5 hr to run on my Core-i7-7700 / 32GB RAM laptop) ###Code #t_start = time.time() def compute_sim(q_to_a, df_questions, df_answers): a_sim = dict() tokenizer = RegexpTokenizer(r'\w+') print(len(q_to_a)) c = 0 for q_id, a_list in q_to_a.items(): c+=1 print(str(c) + ' ' + str(len(a_list)), end='\r') # get split body text for a question and the answers q_body = df_questions[df_questions['Id']==q_id].iloc[0]['Body'] q_body = BeautifulSoup(q_body, 'html.parser').get_text()#.split() q_body = tokenizer.tokenize(q_body.lower()) q_body = [w for w in q_body if w not in stopwords.words('english')] #print(q_body) a_bodies = list() for a_id, _, _ in a_list: a_body = df_answers[df_answers['Id']==a_id].iloc[0]['Body'] a_body = BeautifulSoup(a_body, 'html.parser').get_text()#.split() a_body = tokenizer.tokenize(a_body.lower()) a_body = [w for w in a_body if w not in stopwords.words('english')] a_bodies.append(a_body) #print(a_bodies) # apply a series of transformations to the answers: bag-of-word, tf-idf, and lsi dictionary = corpora.Dictionary(a_bodies) corpus = [dictionary.doc2bow(a) for a in a_bodies] #print(a_bodies[0], len(a_bodies[0])) #print(corpus[0], len(corpus[0])) tfidf = models.TfidfModel(corpus) corpus_tfidf = tfidf[corpus] #print(corpus_tfidf[0], len(corpus_tfidf[0])) lsi = models.LsiModel(corpus_tfidf, id2word=dictionary, num_topics=4) corpus_lsi = lsi[corpus_tfidf] #print(corpus_lsi[0], len(corpus_lsi[0])) index = similarities.MatrixSimilarity(corpus_lsi) # question-to-answer similarity q_bow = dictionary.doc2bow(q_body) q_lsi = lsi[q_bow] q_to_a_sim = index[q_lsi] #print(q_to_a_sim) # ans-to-ans similarity, excluding the answer itself for idx, a_lsi in enumerate(corpus_lsi): a_to_a_sim = index[a_lsi] a_to_a_sim = [a_to_a_sim[i] for i in range(len(a_to_a_sim)) if i != idx] # exclude itself # construct the dictionary a_sim a_id = a_list[idx][0] sim_to_q = q_to_a_sim[idx] max_sim_to_a = max(a_to_a_sim) min_sim_to_a = min(a_to_a_sim) a_sim[a_id] = (sim_to_q, max_sim_to_a, min_sim_to_a) return a_sim # a_sim: a_id -> (sim_to_question, max_sim_to_other_ans, min_sim_to_other_ans) a_sim = load_obj('obj/a_sim.pkl') if not a_sim: a_sim = compute_sim(q_to_a, questions, answers) save_obj(a_sim, 'obj/a_sim.pkl') #t_end = time.time() #print('time elapsed: %f minutes', ((t_end-t_start)/60.0)) answers = answers.assign(SimToQ = answers['Id'].apply(lambda a_id: a_sim[a_id][0])) answers = answers.assign(MaxSimToA = answers['Id'].apply(lambda a_id: a_sim[a_id][1])) answers = answers.assign(MinSimToA = answers['Id'].apply(lambda a_id: a_sim[a_id][2])) answers.head(3) ###Output _____no_output_____ ###Markdown Shallow Features ###Code def strip_code(html): bs = BeautifulSoup(html, 'html.parser') [s.extract() for s in bs('code')] return bs.get_text() answers = answers.assign(BodyEnglishText = answers['Body'].apply(strip_code)) answers = answers.assign(EnglishCount = answers['BodyEnglishText'].apply(lambda x: len(x.split()))) answers.head(3) def count_links(html): bs = BeautifulSoup(html, 'html.parser') return len(bs.find_all('a')) answers = answers.assign(LinkCount = answers['Body'].apply(count_links)) answers.head(3) def has_code(html): bs = BeautifulSoup(html, 'html.parser') return 1 if bs.find('code') else 0 answers = answers.assign(HasCode = answers['Body'].apply(has_code)) answers.head(3) def code_length(html): bs = BeautifulSoup(html, 'html.parser') contents = [tag.text.split() for tag in bs.find_all('code')] return sum(len(item) for item in contents) answers = answers.assign(CodeLength = answers['Body'].apply(code_length)) answers = answers.assign(TotalLength = answers.apply(lambda row: row['EnglishCount'] + row['CodeLength'], axis=1)) answers.head(3) def get_order(qid, aid): ids = [i[0] for i in q_to_a[qid]] return ids.index(aid)+1 answers = answers.assign(PostOrder = answers.apply(lambda row: get_order(row['ParentId'], row['Id']), axis=1)) answers.head(3) def is_answer(qid, aid): if aid == max(q_to_a[qid], key=lambda item: item[1])[0]: return 1 else: return 0 answers = answers.assign(IsAnswer = answers.apply(lambda row: is_answer(row['ParentId'], row['Id']), axis=1)) answers.head(3) # calculate reputation scores for users user_rep = dict() for ans_list in q_to_a.values(): for _, score, owner_id in ans_list: if owner_id: if owner_id in user_rep: user_rep[owner_id] += score else: user_rep[owner_id] = score def get_reputation(userId): if not np.isnan(userId) and userId in user_rep: return user_rep[userId] else: return 0 answers = answers.assign(Reputation = answers['OwnerUserId'].apply(get_reputation)) answers.head(3) ###Output _____no_output_____ ###Markdown Training: RandomForest ###Code q_train, q_validation = model_selection.train_test_split(questions, test_size=0.2, random_state=42) a_train = answers[answers['ParentId'].isin(q_train['Id'])] a_validation = answers[answers['ParentId'].isin(q_validation['Id'])] x_train = a_train[['TotalLength','LinkCount', 'CodeLength', 'PostOrder', 'Reputation', 'SimToQ', 'MaxSimToA', 'MinSimToA']] y_train = a_train[['IsAnswer']] x_val = a_validation[['Id', 'TotalLength','LinkCount', 'CodeLength', 'PostOrder', 'Reputation', 'SimToQ', 'MaxSimToA', 'MinSimToA']] y_val = a_validation[['IsAnswer']] rf_classifier = RandomForestClassifier( n_estimators=1000, min_samples_leaf=4, n_jobs=-1, oob_score=True, random_state=42) rf_classifier.fit(x_train, y_train.values.ravel()) y_pred = rf_classifier.predict_proba(x_val.iloc[:, 1:]) def get_accuracy(q_ids, a_ids, prob_pred): a_to_prob = dict() for idx, a_id in enumerate(a_ids): prob = prob_pred[:, 1][idx] a_to_prob[a_id] = prob count = 0 for q_id in q_ids: right_answer = max(q_to_a[q_id], key=lambda item: item[1])[0] predict_answer = 0 highest_score = 0 for a_id, score, _ in q_to_a[q_id]: pred_score = a_to_prob[a_id] if pred_score > highest_score: predict_answer = a_id highest_score = pred_score if right_answer==predict_answer: count += 1 return count/len(q_ids) print('RF model accuracy:', get_accuracy(q_validation['Id'].tolist(), a_validation['Id'].tolist(), y_pred)) ###Output RF model accuracy: 0.4722190788729207 ###Markdown Baseline ###Code def baseline(q_ids, a_val): count_first = 0 count_last = 0 count_long = 0 for q_id in q_ids: right_answer = max(q_to_a[q_id], key=lambda item: item[1])[0] first_answer = q_to_a[q_id][0][0] if right_answer==first_answer: count_first += 1 last_answer = q_to_a[q_id][-1][0] if right_answer==last_answer: count_last += 1 longest_answer = -1 max_length = 0 for a_id, score, _ in q_to_a[q_id]: leng = a_val[a_val.Id==a_id].iloc[0]['TotalLength'] if leng > max_length: longest_answer = a_id max_length = leng if right_answer==longest_answer: count_long += 1 print('Baseline for the first answer:', count_first/len(q_ids)) print('Baseline for the last answer:', count_last/len(q_ids)) print('Baseline for the longest answer:', count_long/len(q_ids)) baseline(q_validation['Id'].tolist(), a_validation) ###Output Baseline for the first answer: 0.3969672965938667 Baseline for the last answer: 0.07649654860246691 Baseline for the longest answer: 0.29885707819395724 ###Markdown Explaintion of important features ###Code x_val = x_val.assign(PredictProba = y_pred[:, 1]) x_val.head(10) importances = rf_classifier.feature_importances_ std = np.std([tree.feature_importances_ for tree in rf_classifier.estimators_], axis=0) indices = np.argsort(importances)[::-1] # Print the feature ranking print("Feature ranking:") for f in range(x_val.shape[1]-2): print("%d. feature %d (%f)" % (f + 1, indices[f], importances[indices[f]])) import matplotlib.pyplot as plt plt.figure() plt.title("Feature importances") plt.bar(range(x_val.shape[1]-2), importances[indices], color="r", yerr=std[indices], align="center") plt.xticks(range(x_val.shape[1]-2), indices) plt.xlim([-1, x_val.shape[1]-2]) plt.show() ###Output _____no_output_____ ###Markdown Checking installation. ###Code import numpy as np from scipy import special as sp import matplotlib.pyplot as plt import pandas as pd %matplotlib inline ###Output _____no_output_____ ###Markdown Parabola ###Code x = np.array([0,1,2,3,4,5,15,25,35,50]) y = np.sqrt(4x) plt.plot(x, y, label='up') plt.plot(x, -y, label='down') plt.xlabel('X') plt.ylabel('Y') plt.legend() ###Output _____no_output_____ ###Markdown Factorial square ###Code x = np.array([0,1,2,3,4,5,15,25,35,50]) y = (x/sp.factorial(5))2 plt.plot(x, y, label='up') plt.plot(x, -y, label='down') plt.xlabel('X') plt.ylabel('Y') plt.legend() ###Output _____no_output_____ ###Markdown Use of pandas ###Code pd.DataFrame.from_dict({'students':['a','b', 'c'], 'marks':[95,30,40]}) ###Output _____no_output_____ ###Markdown ###Code print('mont ra mad an traoù ?') ###Output mont ra mad an traoù ? ###Markdown Import Packages ###Code # Importing Packages import numpy as np import pandas as pd #Importing packages for cross_validation from sklearn.model_selection import cross_val_score #for modeling from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import RandomForestClassifier from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier import xgboost as xgb from sklearn.model_selection import train_test_split from collections import Counter #for feature selection from sklearn.feature_selection import SelectKBest, f_classif ## Grid search cross validation from sklearn.model_selection import GridSearchCV from sklearn.model_selection import StratifiedKFold import seaborn as sns import matplotlib.pyplot as plt import matplotlib from scipy import stats import pickle ###Output _____no_output_____ ###Markdown Read Test and Train Data ###Code train = pd.read_csv('./data/train.csv') test = pd.read_csv('./data/test.csv') ###Output _____no_output_____ ###Markdown Exploratory Data Analysis ###Code train.info() train.describe() train.tail() test.info() train.isnull().sum().sum() test.isnull().sum().sum() %config InlineBackend.figure_format = 'retina' features = ['var_0', 'var_1','var_2','var_3', 'var_4', 'var_5'] train_sub = train[features] sns.pairplot(train_sub) %config InlineBackend.figure_format = 'retina' sns.countplot(x= "target", data=train) t0 = train.loc[train['target'] == 0].drop(['target'], axis=1) t1 = train.loc[train['target'] == 1].drop(['target'], axis=1) features = t0.columns.values[1:51] t0.columns.values[1] x = features.shape[0] rows = np.int((np.ceil(x/5.0))) %config InlineBackend.figure_format = 'retina' f, axes = plt.subplots(rows, 5, figsize=(20, rows 3), sharex=True) font = {'family' : 'Times new roman', 'weight' : 'bold', 'size' : 18} matplotlib.rc('font', font) for i, ax in enumerate(axes.flatten()): sns.kdeplot(t0.iloc[:, i+1], Label='0', ax=ax) sns.kdeplot(t1.iloc[:, i+1], Label='1', ax=ax) ax.set_xlabel(features[i]) # ax.legend(fontsize=18) plt.tight_layout() %config InlineBackend.figure_format = 'retina' font = {'family' : 'Times new roman', 'weight' : 'bold', 'size' : 22} matplotlib.rc('font', font) f, axes = plt.subplots(1, 2, figsize=(20, 8)) #features = train.columns.values[2:202] sns.distplot(t0.mean(axis=1),color="green", kde=True,bins=120, label='target 0', hist_kws={"alpha" : 0.4}, ax=axes[0]) sns.distplot(t1.mean(axis=1),color="blue", kde=True,bins=120, label='target 1', hist_kws={"alpha" : 0.4}, ax=axes[0]) axes[0].set_title("Distribution of mean values per row in the \n training set for target 0 and target 1", fontsize=20) axes[0].legend() sns.distplot(t0.mean(axis=0),color="green", kde=True,bins=120, label='target 0', hist_kws={"alpha" : 0.4}, ax=axes[1]) sns.distplot(t1.mean(axis=0),color="blue", kde=True,bins=120, label='target 1', hist_kws={"alpha" : 0.4}, ax=axes[1]) axes[1].set_title("Distribution of mean values per column in the \n training set for target 0 and target 1", fontsize=20) axes[1].legend() plt.show() plt.tight_layout() %config InlineBackend.figure_format = 'retina' font = {'family' : 'Times new roman', 'weight' : 'bold', 'size' : 22} matplotlib.rc('font', font) f, axes = plt.subplots(1, 2, figsize=(20, 8)) #features = train.columns.values[2:202] sns.distplot(t0.std(axis=1),color="green", kde=True,bins=120, label='target 0', hist_kws={"alpha" : 0.4}, ax=axes[0]) sns.distplot(t1.std(axis=1),color="blue", kde=True,bins=120, label='target 1', hist_kws={"alpha" : 0.4}, ax=axes[0]) axes[0].set_title("Distribution of standard deviations per row in the \n training set for target 0 and target 1", fontsize=20) axes[0].legend() sns.distplot(t0.std(axis=0),color="green", kde=True,bins=120, label='target 0', hist_kws={"alpha" : 0.4}, ax=axes[1]) sns.distplot(t1.std(axis=0),color="blue", kde=True,bins=120, label='target 1', hist_kws={"alpha" : 0.4}, ax=axes[1]) axes[1].set_title("Distribution of standard deviations per column in the \n training set for target 0 and target 1", fontsize=20) axes[1].legend() plt.show() plt.tight_layout() %config InlineBackend.figure_format = 'retina' font = {'family' : 'Times new roman', 'weight' : 'bold', 'size' : 22} matplotlib.rc('font', font) f, axes = plt.subplots(1, 2, figsize=(20, 8)) #features = train.columns.values[2:202] sns.distplot(t0.min(axis=1),color="green", kde=True,bins=120, label='target 0', hist_kws={"alpha" : 0.4}, ax=axes[0]) sns.distplot(t1.min(axis=1),color="blue", kde=True,bins=120, label='target 1', hist_kws={"alpha" : 0.4}, ax=axes[0]) axes[0].set_title("Distribution of minimum values per row in the \n training set for target 0 and target 1", fontsize=20) axes[0].legend() sns.distplot(t0.max(axis=1),color="green", kde=True,bins=120, label='target 0', hist_kws={"alpha" : 0.4}, ax=axes[1]) sns.distplot(t1.max(axis=1),color="blue", kde=True,bins=120, label='target 1', hist_kws={"alpha" : 0.4}, ax=axes[1]) axes[1].set_title("Distribution of maximum values per row in the \n training set for target 0 and target 1", fontsize=20) axes[1].legend() plt.show() plt.tight_layout() %%time correlations = train[features].corr().abs().unstack().sort_values(kind="quicksort").reset_index() correlations = correlations[correlations['level_0'] != correlations['level_1']] correlation = correlations[correlations.index % 2 != 0].reset_index() correlation.tail() features = t0.columns.values[1:202] duplicate = [] # dups_shape = train['var_68'].nunique() for fea in features: dups_shape = train.pivot_table(index=[fea], aggfunc='size') duplicate.append([fea, dups_shape.max(), dups_shape.idxmax()]) duplicate_df = pd.DataFrame(duplicate,columns=['Features', 'Max_duplicates', 'Value']) np.transpose(duplicate_df.sort_values(by = 'Max_duplicates', ascending=False).head(20)) ###Output _____no_output_____ ###Markdown 4. Feature Selection* [Feature selection algorithms](https://www.analyticsvidhya.com/blog/2016/12/introduction-to-feature-selection-methods-with-an-example-or-how-to-select-the-right-variables/) help to determine which features significantly influence the output variable and then eliminate the remaining features from consideration. This step was useful as this dataset has large number of features, being able to eliminate features that have little to no impact on the analysis reduced the complexity of the model and enabled machine learning algortihms to train faster. * The scikit module provides [several ways](https://scikit-learn.org/stable/modules/feature_selection.html) for identifying significant features either by evaluating the statistical correlation with the outcome variable (e.g. univariate feature selection method) or by measuring the usefulness of a subset of feature by actually training a machine learning model on it (e.g. recursive feature elimination). * Considering the size of this particular dataset and the computational time usually required for recursive feature elimination, the universal feature seleciton method was adopted to select the top 25 features that are critical for modeling. Later, submissions were also made by selecting top 50, 100 and 150 features to check the effect of feature selection on accuracy and time required for computation. * Define Target Variable and Test Variables for Modeling ###Code import numpy as np from sklearn.feature_selection import SelectKBest, f_classif feature_data = train.drop(columns=['target','ID_code'],axis=1) target_data = train['target'] X_train, X_test, y_train, y_test = train_test_split( feature_data, target_data, test_size=0.3, random_state=40) X_train ###Output _____no_output_____ ###Markdown * Select Features to be Considered for Modeling ###Code selector = SelectKBest(f_classif, k=50) X_new=selector.fit_transform(X_train, y_train) mask = selector.get_support(indices=True) colname = X_train.columns[mask]# Names of the selected columns scores = -np.log10(selector.pvalues_) # def plot_joint_plot(df, feature, target): # j = sns.jointplot(feature, target, data = df, kind = 'reg') # j.annotate(stats.pearsonr) # return plt.show() pearson_r = [] for column in X_train.columns: corr_tuple = stats.pearsonr(X_train[column], y_train) pearson_r.append([column, corr_tuple[0], corr_tuple[1]]) corr_df = pd.DataFrame(pearson_r, columns = ['Features', 'Correlation', 'P_value' ]) corr_df.head(5) corr_df.sort_values(by = ['P_value'], inplace=True) corr_df.head(5) ###Output _____no_output_____ ###Markdown * Redifining Train and Test Data Using the Selected Features ###Code X_train_new = X_train[colname] X_test_new = X_test[colname] ###Output _____no_output_____ ###Markdown 5. Train Different Classification Models using Selected Features* All models (KNN, Logistic Regresson, Decision Tree,XGBoost and Random Forest) were trained using the train dataset with selected features. * To estimate the accuracy of these models when applied to unseen data, cross validation was performed for each model by splitting the train dataset (80%/20% for train/test split), fitting the model and computing the score 5 consecutive times (with different splits each time) based on ROC_AUC score. The mean of the accuracies for the 5 trials were then reported as the CV score for each model. * Defining models ###Code #Random Forest, Decision Tree, Logistic Regression and K Nearest Neighbours, and XGBoost models RFmodel=RandomForestClassifier(random_state=1) DTmodel=DecisionTreeClassifier(random_state=1) logreg = LogisticRegression(solver='newton-cg', max_iter=1000) knn = KNeighborsClassifier(n_neighbors = 3) xgbm = xgb.XGBClassifier(silent=True, scale_pos_weight=1,learning_rate=0.01, colsample_bytree = 0.4, subsample = 0.8, objective='binary:logistic', n_estimators=1000, reg_alpha = 0.3, max_depth=4, gamma=10) ###Output _____no_output_____ ###Markdown * Training the Models ###Code # RFmodel.fit(X_train_new, y_train) # print("RF done") # filename = 'RF_model.sav' # pickle.dump(RFmodel, open(filename, 'wb')) # DTmodel.fit(X_train_new, y_train) # print("DT done") # filename = 'DT_model.sav' # pickle.dump(DTmodel, open(filename, 'wb')) # logreg.fit(X_train_new, y_train) # print("logreg done") # filename = 'logreg_model.sav' # pickle.dump(logreg, open(filename, 'wb')) # knn.fit(X_train_new, y_train) # print("knn done") # filename = 'knn_model.sav' # pickle.dump(knn, open(filename, 'wb')) # xgbm.fit(X_train_new, y_train)# print("xgbm done") # filename = 'xgbm_model.sav' # pickle.dump(xgbm, open(filename, 'wb')) from sklearn import metrics from sklearn.metrics import roc_curve def model_performance(model_name, file_name, test_X, test_Y): loaded_model = pickle.load(open(file_name, 'rb')) y_pred = loaded_model.predict(test_X) y_pred_prob = loaded_model.predict_proba(test_X)[:,1] fpr, tpr, thresholds = roc_curve(test_Y, y_pred_prob) cnf_matrix = metrics.confusion_matrix(test_Y, y_pred) print("Accuracy:",metrics.accuracy_score(y_test, y_pred)) print("Precision:",metrics.precision_score(y_test, y_pred)) print("Recall:",metrics.recall_score(y_test, y_pred)) %config InlineBackend.figure_format = 'retina' fig, axes = plt.subplots(1, 2, figsize=(20, 8)) sns.set(font_scale=2) sns.heatmap(pd.DataFrame(cnf_matrix), annot=True, annot_kws={"size": 20}, cmap="viridis", fmt='g', ax = axes[0]) axes[0].xaxis.set_label_position("top") axes[0].set_title('Confusion matrix for {}'.format(model), y=1.1, fontsize=20) axes[0].set_ylabel('Actual label', fontsize=20) axes[0].set_xlabel('Predicted label', fontsize=20) axes[0].xaxis.set_tick_params(labelsize=20) axes[0].yaxis.set_tick_params(labelsize=20) axes[1].plot([0, 1], [0, 1], 'k--', linewidth=3.0) axes[1].plot(fpr,tpr, label='Logistic Regression', linewidth=3.0) axes[1].set_xlabel('False Positive Rate') axes[1].set_ylabel('True Positive Rate') axes[1].set_title('ROC Curve') plt.tight_layout() model = 'Random Forest' file_name = 'RF_model.sav' model_performance(model, file_name, X_test_new, y_test) model = 'Logistic Regression' file_name = 'logreg_model.sav' model_performance(model, file_name, X_test_new, y_test) ###Output Accuracy: 0.9066833333333333 Precision: 0.6394453004622496 Recall: 0.13923838282167422 ###Markdown * Calculating Cross Validation Scores ###Code #define a function that can be called to calculate cross validation score for each model def cross_val(X,x,y): scores = cross_val_score(X, x, y, cv=5, scoring = "roc_auc") return scores.mean() #Calculate Cross Validation Score based on ROC_AUC by calling th ecross_val function defined before RF_score = round(cross_val(RFmodel, X_train_new, y_train) * 100, 2) print("RF done") DT_score =round(cross_val(DTmodel, X_train_new, y_train) * 100, 2) print("DT done") logreg_score = round(cross_val(logreg, X_train_new, y_train) * 100, 2) print("logreg done") knn_score = round(cross_val(knn, X_train_new, y_train) * 100, 2) print("knn done") xgb_score = round(cross_val(xgbm,X_train_new, y_train) * 100, 2) print("xgb done") RF_score ###Output _____no_output_____ ###Markdown * Tabulating the CV Scores for Different Models ###Code results = pd.DataFrame({'Model': ['XGB', 'Logistic Regression', 'Random_Forest','KNN','DT' ],'Score': [xgb_score , logreg_score,RF_score,knn_score,DT_score]}) results = results.sort_values(['Score'], ascending=[False]) results.head() ###Output _____no_output_____ ###Markdown 6. Hyperparameter Tuning for Logistic RegressionResults from the previous step shows that XGBoost and Logistic Regression have the best CV scores (this was also found to be true when the iteration was repeated with 50,100 and 150 features). To reduce the possibility of overfitting, the GridSearchCV method from scikit is used to perform a hyper-paramter optimization on these two models to check if it improves the accuracy of prediction. Below is the code used for a hyperparamter search for logistic regression. * Grid Search to Optimize the Parameters ###Code grid={"C":np.logspace(-2,3,7), "penalty":["l1","l2"]}# l1 lasso l2 ridge logreg1=LogisticRegression() logreg_hp=GridSearchCV(logreg1,grid,cv=3,verbose=0) logreg_hp.fit(train_X_new,train_Y) print("tuned hpyerparameters :(best parameters) ",logreg_hp.best_params_) print("accuracy :",logreg_hp.best_score_) ###Output _____no_output_____ ###Markdown * Modeling with the Best Parameters from GridSearch ###Code logreg2=LogisticRegression(C=1000,penalty="l2")#Grid Search Result C:1000 l2 Accuracy :0.902095 logreg2.fit(train_X_new,train_Y) logreg2_score = round(cross_val(logreg2,train_X_new, train_Y) * 100, 2) print("Accuracy for logical regression after doing a GridSearchCV: ", logreg2_score) ###Output _____no_output_____ ###Markdown 7. Hyperparameter Tuning for XGBoost The code below is commented out as Kaggle timed out before the grid search is complete for these paramters. ###Code #xgbm_h = xgb.XGBClassifier(silent=False, scale_pos_weight=1,learning_rate=0.01, colsample_bytree = 0.4,subsample = 0.8,objective='binary:logistic', n_estimators=1000, reg_alpha = 0.3, max_depth=4, gamma=10) #params = { # 'min_child_weight': [1, 5, 10], # 'gamma': [0.5, 1, 1.5, 2, 5], # 'subsample': [0.6, 0.8, 1.0], # 'colsample_bytree': [0.6, 0.8, 1.0], # 'max_depth': [3, 4, 5] } #xgbm_hp= GridSearchCV(estimator = xgbm, param_grid = params, scoring='roc_auc',n_jobs=1,iid=False, cv=3) #xgbm_hp.fit(train_X_new,train_Y) #xgbm_hp.best_params_, xgbm_hp.best_score_ ###Output _____no_output_____ ###Markdown Training XGB Model with Best Parameters from GridSearch ###Code #xgbm2 = xgb.XGBClassifier(silent=1, # scale_pos_weight=1, # learning_rate=0.01, # colsample_bytree = 0.4, # subsample = 0.8, # objective='binary:logistic', # n_estimators=1000, # reg_alpha = 0.3, # max_depth=4, # gamma=10) #xgbm2.fit(train_X_new,train_Y) #xgb2_score = round(cross_val(xgbm2,train_X_new, train_Y) * 100, 2) ###Output _____no_output_____ ###Markdown 8. Prediction on Test Data using the Best Performing Model ###Code #Comment out the models you wont use in this iteration #logreg_pred = logreg.predict_proba(test_X_new)[:,1] #logreg2_pred = logreg2.predict_proba(test_X_new)[:,1] xgb_pred =xgbm.predict_proba (test_X_new)[:,1] #xgb2_pred =xgbm2.predict_proba (test_X_new)[:,1] ###Output _____no_output_____ ###Markdown 8. Generate Output File for Submission ###Code #The lines below shows you how to save your data in the format needed to score it in the competition output = pd.DataFrame({'ID_code': test.ID_code, 'target': xgb_pred}) output.to_csv('submission.csv', index=False) ###Output _____no_output_____ ###Markdown 不完備情報2社参入ゲームのサンプルデータを作る。利得関数に入るのはPop, Dist, sigma（相手の参入確率）で、それぞれにつくパラメータとサンプルマーケットの数を指定してオブジェクトを作ることを考える。 ###Code import numpy as np import matplotlib.pyplot as plt % matplotlib inline class Seim: def __init__(self, alpha, beta, delta, Market_num): self.alpha, self.beta, self.delta, self.Market_num = alpha, beta, delta, Market_num def pop(self): Population = np.random.uniform(size = (self.Merket_num, 1)) return Population def dist(self): Distance = np.random.uniform(size = (self.Merket_num, 2)) return Distance def fixedpoint(self, error): # ここで初期値に依存して到達する均衡が異なる。→今のモデルであれば具体的にそのthresholdが求められる。 ###Output _____no_output_____ ###Markdown このモデルにおいて別々の均衡に到達する初期値の場所を探す ###Code # PopとDistを固定した一つの市場に注目する。 def update(sigma1, sigma2, pop, dist, alpha, beta, delta): updatesigma1 = np.exp(alphapop + betadist[0] + deltasigma2)/(1 + np.exp(alphapop + betadist[0] + deltasigma2)) updatesigma2 = np.exp(alphapop + betadist[1] + deltasigma1)/(1 +np.exp(alphapop + betadist[1] + deltasigma1)) return [updatesigma1, updatesigma2] def fixpoint(sigma1, sigma2, pop, dist, alpha, beta, delta, error): diff = (update(sigma1, sigma2, pop, dist, alpha, beta, delta)[0] - sigma1)2 + (update(sigma1, sigma2, pop, dist, alpha, beta, delta)[1] - sigma2)2 while diff > error: sigma1 = update(sigma1, sigma2, pop, dist, alpha, beta, delta)[0] sigma2 = update(sigma1, sigma2, pop, dist, alpha, beta, delta)[1] diff = (update(sigma1, sigma2, pop, dist, alpha, beta, delta)[0] - sigma1)2 + (update(sigma1, sigma2, pop, dist, alpha, beta, delta)[1] - sigma2)2 return [sigma1, sigma2] # 　設定 pop = 1 dist = [1, 2] alpha = 0.5 beta = -0.7 delta = -0.3 error = 1.0e-20 fixpoint(0, 0, pop, dist, alpha, beta, delta, error) fixpoint(1,1, pop, dist, alpha, beta, delta, error) fixpoint(0, 1, pop, dist, alpha, beta, delta, error) fixpoint(1, 0, pop, dist, alpha, beta, delta, error) ###Output _____no_output_____ ###Markdown 単一っぽい。updateの過程を描く ###Code point_num = 100 sigmas = np.zeros((point_num, 2)) sigma1 = 0 sigma2 = 0 initial = [sigma1, sigma2] sigmas[0, :] = initial for i in range(point_num-1): sigmas[i+1 , :] = update(sigmas[i, 0], sigmas[i, 1], pop, dist, alpha, beta, delta) sigmas[0:5, :] ###Output _____no_output_____ ###Markdown 一瞬で収束しちゃうね。　複数均衡が現れる過程を描く。そのためにbest response functionをお互いについて書く。設定はpop = 1dist = [1, 2]alpha = 0.5beta = -0.7delta = -0.3error = 1.0e-20 ###Code # 　設定1 pop = 1 dist = [1, 1] alpha = 0 beta = 0 delta = 0.3 error = 1.0e-20 def br1(sigma2, pop, dist, alpha, beta, delta): return np.exp(alphapop + betadist[0] + deltasigma2)/(1 + np.exp(alphapop + betadist[0] + deltasigma2)) def br2(sigma1, pop, dist, alpha, beta, delta): return np.exp(alphapop + betadist[1] + deltasigma1)/(1 +np.exp(alphapop + betadist[1] + deltasigma1)) grid_num = 200 grid = np.linspace(0,1,grid_num) BRs = np.zeros((grid_num, 2)) for i in range(grid_num): BRs[i, :] = [br1(grid[i], pop, dist, alpha, beta, delta), br2(grid[i], pop, dist, alpha, beta, delta)] plt.plot(grid, BRs[:, 1], label = "player 2's BR function") plt.plot(BRs[:, 0], grid, label = "player 1's BR function") plt.legend() plt.xlabel("player 1's entry probability") plt.ylabel("player 2's entry probability") # 　設定2　複数均衡を出す pop = 1 dist = [1, 1] alpha = 0 beta = 3 delta = -6 for i in range(grid_num): BRs[i, :] = [br1(grid[i], pop, dist, alpha, beta, delta), br2(grid[i], pop, dist, alpha, beta, delta)] plt.plot(grid, BRs[:, 1], label = "player 2's BR function") plt.plot(BRs[:, 0], grid, label = "player 1's BR function") plt.legend() plt.xlabel("player 1's entry probability") plt.ylabel("player 2's entry probability") # 　設定3　deltaが正、つまりstrategic somplemetaryな時 pop = 1 dist = [1, 1] alpha = 0 beta = -3 delta = 6 for i in range(grid_num): BRs[i, :] = [br1(grid[i], pop, dist, alpha, beta, delta), br2(grid[i], pop, dist, alpha, beta, delta)] plt.plot(grid, BRs[:, 1], label = "player 2's BR function") plt.plot(BRs[:, 0], grid, label = "player 1's BR function") plt.legend() plt.xlabel("player 1's entry probability") plt.ylabel("player 2's entry probability") ###Output _____no_output_____ ###Markdown 若干の知見- alphaは均衡の数にほぼ関係ない。（BRを上下にシフトさせるだけ）- betaは逆にかなり重要。betaを0のままdeltaを弄って複数の均衡を存在させるにはdeltaがかなり大きくないといけない。しかも、それで均衡が出せるのはdeltaが負の時、すなわちstarategic substituteの時だけっぽい。（証明はなし）- betaの値は重要っぽいが、別にplayerごとにdistが異なってなくても構わない。 ###Code # 設定4 betaを0のままdeltaだけを弄って複数の均衡を生み出す pop = 1 dist = [1, 1] alpha = 0 beta = 0 delta = -10 for i in range(grid_num): BRs[i, :] = [br1(grid[i], pop, dist, alpha, beta, delta), br2(grid[i], pop, dist, alpha, beta, delta)] plt.plot(grid, BRs[:, 1], label = "player 2's BR function") plt.plot(BRs[:, 0], grid, label = "player 1's BR function") plt.legend() plt.xlabel("player 1's entry probability") plt.ylabel("player 2's entry probability") ###Output _____no_output_____
notebooks/rotating tetrahedron.ipynb	###Markdown Adapted from https://www.tutorialspoint.com/webgl/webgl_sample_application.htm ###Code import feedWebGL2.feedback as fd from ipywidgets import interact, interactive, fixed, interact_manual import numpy as np fd.widen_notebook() np.set_printoptions(precision=4) corners = 0.5 * np.array([ [1, 1, 1], [1, -1, -1], [-1, -1, 1], [-1, 1, -1], ]) colors = corners + 0.5 def tetrahedron_triangles(corners): triangles = np.zeros([4, 3, 3], dtype=np.float) for i in range(4): triangles[i, :i] = corners[:i] triangles[i, i:] = corners[i+1:] return triangles triangles = tetrahedron_triangles(corners) tcolors = tetrahedron_triangles(colors) # make faces "flat colored" if 0: for i in range(4): for j in range(3): tcolors[i,j] = colors[i] def matrix1(phi, i=0): result = np.eye(4) result[0,0] = np.cos(phi) result[i,i] = np.cos(phi) result[0,i] = np.sin(phi) result[i,0] = -np.sin(phi) return result def matrix(phi=0.0, theta=0.0, xt=0, yt=0, zt=0): M1 = matrix1(phi, 1) #print(M1) M2 = matrix1(theta, 2) #print(M2) M12 = M1.dot(M2) Mt = np.eye(4) Mt[3,0] = xt Mt[3,1] = yt Mt[3,2] = zt return M12.dot(Mt) M = matrix(1.0, 2.0, 0.1, -0.1, 0.2) M vertices = triangles.ravel() def rotate(phi=-0.5, theta=0.0, xt=0.0, yt=0.0, zt=0.0): M = matrix(phi * np.pi, theta * np.pi, xt, yt, zt) assert np.abs(np.linalg.det(M) - 1.0) < 0.0001 feedback_program.change_uniform_vector("rotation_matrix", M.ravel()) feedback_program.run() return M vertex_shader = """#version 300 es uniform mat4 rotation_matrix; in vec3 coordinates; in vec3 vcolor; out vec3 output_vertex; out vec3 coord_color; void main() { coord_color = vcolor; gl_Position = vec4(coordinates, 1.0); gl_Position = rotation_matrix * gl_Position; gl_Position[3] = 1.0; output_vertex = gl_Position.xyz; } """ fragment_shader = """#version 300 es // For some reason it is required to specify precision, otherwise error. precision highp float; in vec3 coord_color; //out vec4 color; out vec4 fragmentColor; void main() { fragmentColor = vec4(coord_color, 1.0); } """ feedback_program = fd.FeedbackProgram( program = fd.Program( vertex_shader = vertex_shader, fragment_shader = fragment_shader, feedbacks = fd.Feedbacks( output_vertex = fd.Feedback(num_components=3), ), ), runner = fd.Runner( vertices_per_instance = 3 * len(triangles), run_type = "TRIANGLES", uniforms = fd.Uniforms( rotation_matrix = fd.Uniform( default_value = list(M.ravel()), vtype = "4fv", is_matrix = True, ), ), inputs = fd.Inputs( coordinates = fd.Input( num_components = 3, from_buffer = fd.BufferLocation( name = "coordinates_buffer", # start at the beginning, don't skip any values... ), ), vcolor = fd.Input( num_components = 3, from_buffer = fd.BufferLocation( name = "colors_buffer", # start at the beginning, don't skip any values... ), ), ), ), context = fd.Context( buffers = fd.Buffers( coordinates_buffer = fd.Buffer( array=list(vertices), ), colors_buffer = fd.Buffer( array=list(tcolors.ravel()), ) ), width = 600, show = True, ), ) # display the widget and debugging information feedback_program.debugging_display() #feedback_program #feedback_program.run() interact(rotate, phi=(-1.0, 1.0), theta=(-1.0, 1.0), xt=(-1.0, 1.0), yt=(-1.0, 1.0), zt=(-1.0, 1.0)) #move_corner(x=-0.1) A1 = np.array(feedback_program.get_feedback("output_vertex")) A1 A2 = np.array(feedback_program.get_feedback("output_vertex")) A2 A1 - A2 colors np.abs(np.linalg.det(M)) ###Output _____no_output_____
itertools.ipynb	###Markdown exploring itertools- itertools https://docs.python.org/3/library/itertools.html- more itertools https://more-itertools.readthedocs.io/en/stable/index.html itertools ###Code import itertools as it inf=['count', 'cycle', 'repeat'] iter_short=['accumulate', 'chain', 'chain.from_iterable', 'compress', 'dropwhile', 'filterfalse', 'groupby', 'islice', 'pairwise', 'starmap', 'takewhile', 'tee', 'zip_longest'] combinatoric = ['product', 'permutations', 'combinations', 'combinations_with_replacement'] notes="pairwise is new in vesrion 3.10 but exists in more-itertools for earlier versions" recipes=['take', 'prepend', 'tabulate', 'tail', 'consume', 'nth', 'all_equal', 'quantify', 'pad_none', 'ncycles', 'flatten', 'repeatfunc', 'grouper', 'triplewise', 'sliding_window', 'roundrobin', 'partition', 'before_and_after', 'powerset', 'unique_everseen', 'unique_justseen', 'iter_except', 'first_true', 'random_product', 'random_combination_with_replacement', 'nth_combination'] for x in combinatoric: print(x) help(it.__dict__[x]) for x in inf: print(x) help(it.__dict__[x]) for x in iter_short: print(x) help(it.__dict__[x]) help(it.chain.from_iterable) for x in combinatoric: print(x) help(it.__dict__[x]) ###Output product Help on class product in module itertools: class product(builtins.object) \| product(iterables, repeat=1) --> product object \| \| Cartesian product of input iterables. Equivalent to nested for-loops. \| \| For example, product(A, B) returns the same as: ((x,y) for x in A for y in B). \| The leftmost iterators are in the outermost for-loop, so the output tuples \| cycle in a manner similar to an odometer (with the rightmost element changing \| on every iteration). \| \| To compute the product of an iterable with itself, specify the number \| of repetitions with the optional repeat keyword argument. For example, \| product(A, repeat=4) means the same as product(A, A, A, A). \| \| product('ab', range(3)) --> ('a',0) ('a',1) ('a',2) ('b',0) ('b',1) ('b',2) \| product((0,1), (0,1), (0,1)) --> (0,0,0) (0,0,1) (0,1,0) (0,1,1) (1,0,0) ... \| \| Methods defined here: \| \| __getattribute__(self, name, /) \| Return getattr(self, name). \| \| __iter__(self, /) \| Implement iter(self). \| \| __next__(self, /) \| Implement next(self). \| \| __reduce__(...) \| Return state information for pickling. \| \| __setstate__(...) \| Set state information for unpickling. \| \| __sizeof__(...) \| Returns size in memory, in bytes. \| \| ---------------------------------------------------------------------- \| Static methods defined here: \| \| __new__(args, *kwargs) from builtins.type \| Create and return a new object. See help(type) for accurate signature. permutations Help on class permutations in module itertools: class permutations(builtins.object) \| permutations(iterable, r=None) \| \| Return successive r-length permutations of elements in the iterable. \| \| permutations(range(3), 2) --> (0,1), (0,2), (1,0), (1,2), (2,0), (2,1) \| \| Methods defined here: \| \| __getattribute__(self, name, /) \| Return getattr(self, name). \| \| __iter__(self, /) \| Implement iter(self). \| \| __next__(self, /) \| Implement next(self). \| \| __reduce__(...) \| Return state information for pickling. \| \| __setstate__(...) \| Set state information for unpickling. \| \| __sizeof__(...) \| Returns size in memory, in bytes. \| \| ---------------------------------------------------------------------- \| Static methods defined here: \| \| __new__(args, *kwargs) from builtins.type \| Create and return a new object. See help(type) for accurate signature. combinations Help on class combinations in module itertools: class combinations(builtins.object) \| combinations(iterable, r) \| \| Return successive r-length combinations of elements in the iterable. \| \| combinations(range(4), 3) --> (0,1,2), (0,1,3), (0,2,3), (1,2,3) \| \| Methods defined here: \| \| __getattribute__(self, name, /) \| Return getattr(self, name). \| \| __iter__(self, /) \| Implement iter(self). \| \| __next__(self, /) \| Implement next(self). \| \| __reduce__(...) \| Return state information for pickling. \| \| __setstate__(...) \| Set state information for unpickling. \| \| __sizeof__(...) \| Returns size in memory, in bytes. \| \| ---------------------------------------------------------------------- \| Static methods defined here: \| \| __new__(args, *kwargs) from builtins.type \| Create and return a new object. See help(type) for accurate signature. combinations_with_replacement Help on class combinations_with_replacement in module itertools: class combinations_with_replacement(builtins.object) \| combinations_with_replacement(iterable, r) \| \| Return successive r-length combinations of elements in the iterable allowing individual elements to have successive repeats. \| \| combinations_with_replacement('ABC', 2) --> AA AB AC BB BC CC" \| \| Methods defined here: \| \| __getattribute__(self, name, /) \| Return getattr(self, name). \| \| __iter__(self, /) \| Implement iter(self). \| \| __next__(self, /) \| Implement next(self). \| \| __reduce__(...) \| Return state information for pickling. \| \| __setstate__(...) \| Set state information for unpickling. \| \| __sizeof__(...) \| Returns size in memory, in bytes. \| \| ---------------------------------------------------------------------- \| Static methods defined here: \| \| __new__(args, *kwargs) from builtins.type \| Create and return a new object. See help(type) for accurate signature. ###Markdown more_itertools ###Code import more_itertools as mi grouping="chunked, ichunked, sliced, distribute, divide, split_at, split_before, split_after, split_into, split_when, bucket, unzip, grouper, partition" look_ahead_behind="spy, peekable, seekable" windowing="windowed, substrings, substrings_indexes, stagger, windowed_complete, pairwise, triplewise, sliding_window" Augmenting="count_cycle, intersperse, padded, mark_ends, repeat_last, adjacent, groupby_transform, pad_none, ncycles" Combining="collapse, sort_together, interleave, interleave_longest, interleave_evenly, zip_offset, zip_equal, zip_broadcast, dotproduct, convolve, flatten, roundrobin, prepend, value_chain" Summarizing="ilen, unique_to_each, sample, consecutive_groups, run_length, map_reduce, exactly_n, is_sorted, all_equal, all_unique, minmax, first_true, quantify" Selecting="islice_extended, first, last, one, only, strictly_n, strip, lstrip, rstrip, filter_except, map_except, nth_or_last, unique_in_window, before_and_after, nth, take, tail, unique_everseen, unique_justseen, duplicates_everseen, duplicates_justseen" Combinatorics="distinct_permutations, distinct_combinations, circular_shifts, partitions, set_partitions, product_index, combination_index, permutation_index, powerset, random_product, random_permutation, random_combination, random_combination_with_replacement, nth_product, nth_permutation, nth_combination" Wrapping="always_iterable, always_reversible, countable, consumer, with_iter, iter_except" Others = "locate, rlocate, replace, numeric_range, side_effect, iterate, difference, make_decorator, SequenceView, time_limited, consume, tabulate, repeatfunc" names = 'grouping, look_ahead_behind, windowing, Augmenting, Combining, Summarizing, Selecting, Combinatorics, Wrapping, Others'.replace(',','').split() names recipes_in_more = [] recipes_in_more.extend([x for x in grouping.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in look_ahead_behind.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in windowing.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in Augmenting.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in Combining.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in Summarizing.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in Selecting.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in Combinatorics.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in Wrapping.replace(",","").split() if x in recipes]) recipes_in_more.extend([x for x in Others.replace(",","").split() if x in recipes]) recipes_in_more set(recipes)-set(recipes_in_more) for n in [x.strip() for x in grouping.split(',')]: print(n) help(mi.__dict__[n]) for n in [x.strip() for x in look_ahead_behind.split(',')]: print(n) help(mi.__dict__[n]) for n in [x.strip() for x in windowing.split(',')]: print(n) help(mi.__dict__[n]) for n in [x.strip() for x in Augmenting.split(',')]: print(n) help(mi.__dict__[n]) for n in [x.strip() for x in Combining.split(',')]: print(n) help(mi.__dict__[n]) for n in [x.strip() for x in Summarizing.split(',')]: print(n) help(mi.__dict__[n]) for n in [x.strip() for x in Selecting.split(',')]: print(n) help(mi.__dict__[n]) for n in [x.strip() for x in Combinatorics.split(',')]: print(n) help(mi.__dict__[n]) re.sub? import re worditer = re.sub(r'[\,\.]','', "Slices with negative values require some caching of iterable, but this").lower().split() print(repr(worditer)) import random random.shuffle(worditer) print(repr(worditer)) from queue import i = [1,2,78, 'fred', ['nested', 'list', 1], 22.56] mi.random_combination_with_replacement(i, 5) for n in [x.strip() for x in Wrapping.split(',')]: print(n) help(mi.__dict__[n]) for n in [x.strip() for x in Others.split(',')]: print(n) help(mi.__dict__[n]) ###Output locate Help on function locate in module more_itertools.more: locate(iterable, pred=<class 'bool'>, window_size=None) Yield the index of each item in iterable for which pred returns ``True``. pred defaults to :func:`bool`, which will select truthy items: >>> list(locate([0, 1, 1, 0, 1, 0, 0])) [1, 2, 4] Set pred to a custom function to, e.g., find the indexes for a particular item. >>> list(locate(['a', 'b', 'c', 'b'], lambda x: x == 'b')) [1, 3] If window_size is given, then the pred function will be called with that many items. This enables searching for sub-sequences: >>> iterable = [0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3] >>> pred = lambda args: args == (1, 2, 3) >>> list(locate(iterable, pred=pred, window_size=3)) [1, 5, 9] Use with :func:`seekable` to find indexes and then retrieve the associated items: >>> from itertools import count >>> from more_itertools import seekable >>> source = (3 n + 1 if (n % 2) else n // 2 for n in count()) >>> it = seekable(source) >>> pred = lambda x: x > 100 >>> indexes = locate(it, pred=pred) >>> i = next(indexes) >>> it.seek(i) >>> next(it) 106 rlocate Help on function rlocate in module more_itertools.more: rlocate(iterable, pred=<class 'bool'>, window_size=None) Yield the index of each item in iterable for which pred returns ``True``, starting from the right and moving left. pred defaults to :func:`bool`, which will select truthy items: >>> list(rlocate([0, 1, 1, 0, 1, 0, 0])) # Truthy at 1, 2, and 4 [4, 2, 1] Set pred to a custom function to, e.g., find the indexes for a particular item: >>> iterable = iter('abcb') >>> pred = lambda x: x == 'b' >>> list(rlocate(iterable, pred)) [3, 1] If window_size is given, then the pred function will be called with that many items. This enables searching for sub-sequences: >>> iterable = [0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3] >>> pred = lambda args: args == (1, 2, 3) >>> list(rlocate(iterable, pred=pred, window_size=3)) [9, 5, 1] Beware, this function won't return anything for infinite iterables. If iterable* is reversible, ``rlocate`` will reverse it and search from the right. Otherwise, it will search from the left and return the results in reverse order. See :func:`locate` to for other example applications. replace Help on function replace in module more_itertools.more: replace(iterable, pred, substitutes, count=None, window_size=1) Yield the items from iterable, replacing the items for which pred returns ``True`` with the items from the iterable substitutes. >>> iterable = [1, 1, 0, 1, 1, 0, 1, 1] >>> pred = lambda x: x == 0 >>> substitutes = (2, 3) >>> list(replace(iterable, pred, substitutes)) [1, 1, 2, 3, 1, 1, 2, 3, 1, 1] If count is given, the number of replacements will be limited: >>> iterable = [1, 1, 0, 1, 1, 0, 1, 1, 0] >>> pred = lambda x: x == 0 >>> substitutes = [None] >>> list(replace(iterable, pred, substitutes, count=2)) [1, 1, None, 1, 1, None, 1, 1, 0] Use window_size to control the number of items passed as arguments to pred. This allows for locating and replacing subsequences. >>> iterable = [0, 1, 2, 5, 0, 1, 2, 5] >>> window_size = 3 >>> pred = lambda args: args == (0, 1, 2) # 3 items passed to pred >>> substitutes = [3, 4] # Splice in these items >>> list(replace(iterable, pred, substitutes, window_size=window_size)) [3, 4, 5, 3, 4, 5] numeric_range Help on class numeric_range in module more_itertools.more: class numeric_range(collections.abc.Sequence, collections.abc.Hashable) \| numeric_range(args) \| \| An extension of the built-in ``range()`` function whose arguments can \| be any orderable numeric type. \| \| With only stop specified, start defaults to ``0`` and step \| defaults to ``1``. The output items will match the type of stop: \| \| >>> list(numeric_range(3.5)) \| [0.0, 1.0, 2.0, 3.0] \| \| With only start and stop specified, step defaults to ``1``. The \| output items will match the type of start: \| \| >>> from decimal import Decimal \| >>> start = Decimal('2.1') \| >>> stop = Decimal('5.1') \| >>> list(numeric_range(start, stop)) \| [Decimal('2.1'), Decimal('3.1'), Decimal('4.1')] \| \| With start, stop, and step specified the output items will match \| the type of ``start + step``: \| \| >>> from fractions import Fraction \| >>> start = Fraction(1, 2) # Start at 1/2 \| >>> stop = Fraction(5, 2) # End at 5/2 \| >>> step = Fraction(1, 2) # Count by 1/2 \| >>> list(numeric_range(start, stop, step)) \| [Fraction(1, 2), Fraction(1, 1), Fraction(3, 2), Fraction(2, 1)] \| \| If step is zero, ``ValueError`` is raised. Negative steps are supported: \| \| >>> list(numeric_range(3, -1, -1.0)) \| [3.0, 2.0, 1.0, 0.0] \| \| Be aware of the limitations of floating point numbers; the representation \| of the yielded numbers may be surprising. \| \| ``datetime.datetime`` objects can be used for start and stop, if step \| is a ``datetime.timedelta`` object: \| \| >>> import datetime \| >>> start = datetime.datetime(2019, 1, 1) \| >>> stop = datetime.datetime(2019, 1, 3) \| >>> step = datetime.timedelta(days=1) \| >>> items = iter(numeric_range(start, stop, step)) \| >>> next(items) \| datetime.datetime(2019, 1, 1, 0, 0) \| >>> next(items) \| datetime.datetime(2019, 1, 2, 0, 0) \| \| Method resolution order: \| numeric_range \| collections.abc.Sequence \| collections.abc.Reversible \| collections.abc.Collection \| collections.abc.Sized \| collections.abc.Iterable \| collections.abc.Container \| collections.abc.Hashable \| builtins.object \| \| Methods defined here: \| \| __bool__(self) \| \| __contains__(self, elem) \| \| __eq__(self, other) \| Return self==value. \| \| __getitem__(self, key) \| \| __hash__(self) \| Return hash(self). \| \| __init__(self, args) \| Initialize self. See help(type(self)) for accurate signature. \| \| __iter__(self) \| \| __len__(self) \| \| __reduce__(self) \| Helper for pickle. \| \| __repr__(self) \| Return repr(self). \| \| __reversed__(self) \| \| count(self, value) \| S.count(value) -> integer -- return number of occurrences of value \| \| index(self, value) \| S.index(value, [start, [stop]]) -> integer -- return first index of value. \| Raises ValueError if the value is not present. \| \| Supporting start and stop arguments is optional, but \| recommended. \| \| ---------------------------------------------------------------------- \| Data descriptors defined here: \| \| __dict__ \| dictionary for instance variables (if defined) \| \| __weakref__ \| list of weak references to the object (if defined) \| \| ---------------------------------------------------------------------- \| Data and other attributes defined here: \| \| __abstractmethods__ = frozenset() \| \| ---------------------------------------------------------------------- \| Class methods inherited from collections.abc.Reversible: \| \| __subclasshook__(C) from abc.ABCMeta \| Abstract classes can override this to customize issubclass(). \| \| This is invoked early on by abc.ABCMeta.__subclasscheck__(). \| It should return True, False or NotImplemented. If it returns \| NotImplemented, the normal algorithm is used. Otherwise, it \| overrides the normal algorithm (and the outcome is cached). side_effect Help on function side_effect in module more_itertools.more: side_effect(func, iterable, chunk_size=None, before=None, after=None) Invoke func* on each item in iterable (or on each chunk_size group of items) before yielding the item. `func` must be a function that takes a single argument. Its return value will be discarded. before and after are optional functions that take no arguments. They will be executed before iteration starts and after it ends, respectively. `side_effect` can be used for logging, updating progress bars, or anything that is not functionally "pure." Emitting a status message: >>> from more_itertools import consume >>> func = lambda item: print('Received {}'.format(item)) >>> consume(side_effect(func, range(2))) Received 0 Received 1 Operating on chunks of items: >>> pair_sums = [] >>> func = lambda chunk: pair_sums.append(sum(chunk)) >>> list(side_effect(func, [0, 1, 2, 3, 4, 5], 2)) [0, 1, 2, 3, 4, 5] >>> list(pair_sums) [1, 5, 9] Writing to a file-like object: >>> from io import StringIO >>> from more_itertools import consume >>> f = StringIO() >>> func = lambda x: print(x, file=f) >>> before = lambda: print(u'HEADER', file=f) >>> after = f.close >>> it = [u'a', u'b', u'c'] >>> consume(side_effect(func, it, before=before, after=after)) >>> f.closed True iterate Help on function iterate in module more_itertools.more: iterate(func, start) Return ``start``, ``func(start)``, ``func(func(start))``, ... >>> from itertools import islice >>> list(islice(iterate(lambda x: 2x, 1), 10)) [1, 2, 4, 8, 16, 32, 64, 128, 256, 512] difference Help on function difference in module more_itertools.more: difference(iterable, func=<built-in function sub>, , initial=None) This function is the inverse of :func:`itertools.accumulate`. By default it will compute the first difference of iterable using :func:`operator.sub`: >>> from itertools import accumulate >>> iterable = accumulate([0, 1, 2, 3, 4]) # produces 0, 1, 3, 6, 10 >>> list(difference(iterable)) [0, 1, 2, 3, 4] func defaults to :func:`operator.sub`, but other functions can be specified. They will be applied as follows:: A, B, C, D, ... --> A, func(B, A), func(C, B), func(D, C), ... For example, to do progressive division: >>> iterable = [1, 2, 6, 24, 120] >>> func = lambda x, y: x // y >>> list(difference(iterable, func)) [1, 2, 3, 4, 5] If the initial keyword is set, the first element will be skipped when computing successive differences. >>> it = [10, 11, 13, 16] # from accumulate([1, 2, 3], initial=10) >>> list(difference(it, initial=10)) [1, 2, 3] make_decorator Help on function make_decorator in module more_itertools.more: make_decorator(wrapping_func, result_index=0) Return a decorator version of wrapping_func, which is a function that modifies an iterable. result_index is the position in that function's signature where the iterable goes. This lets you use itertools on the "production end," i.e. at function definition. This can augment what the function returns without changing the function's code. For example, to produce a decorator version of :func:`chunked`: >>> from more_itertools import chunked >>> chunker = make_decorator(chunked, result_index=0) >>> @chunker(3) ... def iter_range(n): ... return iter(range(n)) ... >>> list(iter_range(9)) [[0, 1, 2], [3, 4, 5], [6, 7, 8]] To only allow truthy items to be returned: >>> truth_serum = make_decorator(filter, result_index=1) >>> @truth_serum(bool) ... def boolean_test(): ... return [0, 1, '', ' ', False, True] ... >>> list(boolean_test()) [1, ' ', True] The :func:`peekable` and :func:`seekable` wrappers make for practical decorators: >>> from more_itertools import peekable >>> peekable_function = make_decorator(peekable) >>> @peekable_function() ... def str_range(args): ... return (str(x) for x in range(args)) ... >>> it = str_range(1, 20, 2) >>> next(it), next(it), next(it) ('1', '3', '5') >>> it.peek() '7' >>> next(it) '7' SequenceView Help on class SequenceView in module more_itertools.more: class SequenceView(collections.abc.Sequence) \| SequenceView(target) \| \| Return a read-only view of the sequence object target. \| \| :class:`SequenceView` objects are analogous to Python's built-in \| "dictionary view" types. They provide a dynamic view of a sequence's items, \| meaning that when the sequence updates, so does the view. \| \| >>> seq = ['0', '1', '2'] \| >>> view = SequenceView(seq) \| >>> view \| SequenceView(['0', '1', '2']) \| >>> seq.append('3') \| >>> view \| SequenceView(['0', '1', '2', '3']) \| \| Sequence views support indexing, slicing, and length queries. They act \| like the underlying sequence, except they don't allow assignment: \| \| >>> view[1] \| '1' \| >>> view[1:-1] \| ['1', '2'] \| >>> len(view) \| 4 \| \| Sequence views are useful as an alternative to copying, as they don't \| require (much) extra storage. \| \| Method resolution order: \| SequenceView \| collections.abc.Sequence \| collections.abc.Reversible \| collections.abc.Collection \| collections.abc.Sized \| collections.abc.Iterable \| collections.abc.Container \| builtins.object \| \| Methods defined here: \| \| __getitem__(self, index) \| \| __init__(self, target) \| Initialize self. See help(type(self)) for accurate signature. \| \| __len__(self) \| \| __repr__(self) \| Return repr(self). \| \| ---------------------------------------------------------------------- \| Data descriptors defined here: \| \| __dict__ \| dictionary for instance variables (if defined) \| \| __weakref__ \| list of weak references to the object (if defined) \| \| ---------------------------------------------------------------------- \| Data and other attributes defined here: \| \| __abstractmethods__ = frozenset() \| \| ---------------------------------------------------------------------- \| Methods inherited from collections.abc.Sequence: \| \| __contains__(self, value) \| \| __iter__(self) \| \| __reversed__(self) \| \| count(self, value) \| S.count(value) -> integer -- return number of occurrences of value \| \| index(self, value, start=0, stop=None) \| S.index(value, [start, [stop]]) -> integer -- return first index of value. \| Raises ValueError if the value is not present. \| \| Supporting start and stop arguments is optional, but \| recommended. \| \| ---------------------------------------------------------------------- \| Class methods inherited from collections.abc.Reversible: \| \| __subclasshook__(C) from abc.ABCMeta \| Abstract classes can override this to customize issubclass(). \| \| This is invoked early on by abc.ABCMeta.__subclasscheck__(). \| It should return True, False or NotImplemented. If it returns \| NotImplemented, the normal algorithm is used. Otherwise, it \| overrides the normal algorithm (and the outcome is cached). time_limited Help on class time_limited in module more_itertools.more: class time_limited(builtins.object) \| time_limited(limit_seconds, iterable) \| \| Yield items from iterable until limit_seconds have passed. \| If the time limit expires before all items have been yielded, the \| ``timed_out`` parameter will be set to ``True``. \| \| >>> from time import sleep \| >>> def generator(): \| ... yield 1 \| ... yield 2 \| ... sleep(0.2) \| ... yield 3 \| >>> iterable = time_limited(0.1, generator()) \| >>> list(iterable) \| [1, 2] \| >>> iterable.timed_out \| True \| \| Note that the time is checked before each item is yielded, and iteration \| stops if the time elapsed is greater than limit_seconds. If your time \| limit is 1 second, but it takes 2 seconds to generate the first item from \| the iterable, the function will run for 2 seconds and not yield anything. \| \| Methods defined here: \| \| __init__(self, limit_seconds, iterable) \| Initialize self. See help(type(self)) for accurate signature. \| \| __iter__(self) \| \| __next__(self) \| \| ---------------------------------------------------------------------- \| Data descriptors defined here: \| \| __dict__ \| dictionary for instance variables (if defined) \| \| __weakref__ \| list of weak references to the object (if defined) consume Help on function consume in module more_itertools.recipes: consume(iterator, n=None) Advance iterable by n steps. If n is ``None``, consume it entirely. Efficiently exhausts an iterator without returning values. Defaults to consuming the whole iterator, but an optional second argument may be provided to limit consumption. >>> i = (x for x in range(10)) >>> next(i) 0 >>> consume(i, 3) >>> next(i) 4 >>> consume(i) >>> next(i) Traceback (most recent call last): File "<stdin>", line 1, in <module> StopIteration If the iterator has fewer items remaining than the provided limit, the whole iterator will be consumed. >>> i = (x for x in range(3)) >>> consume(i, 5) >>> next(i) Traceback (most recent call last): File "<stdin>", line 1, in <module> StopIteration tabulate Help on function tabulate in module more_itertools.recipes: tabulate(function, start=0) Return an iterator over the results of ``func(start)``, ``func(start + 1)``, ``func(start + 2)``... func should be a function that accepts one integer argument. If start is not specified it defaults to 0. It will be incremented each time the iterator is advanced. >>> square = lambda x: x ** 2 >>> iterator = tabulate(square, -3) >>> take(4, iterator) [9, 4, 1, 0] repeatfunc Help on function repeatfunc in module more_itertools.recipes: repeatfunc(func, times=None, args) Call func* with args repeatedly, returning an iterable over the results. If times is specified, the iterable will terminate after that many repetitions: >>> from operator import add >>> times = 4 >>> args = 3, 5 >>> list(repeatfunc(add, times, args)) [8, 8, 8, 8] If times* is ``None`` the iterable will not terminate: >>> from random import randrange >>> times = None >>> args = 1, 11 >>> take(6, repeatfunc(randrange, times, args)) # doctest:+SKIP [2, 4, 8, 1, 8, 4] ###Markdown itertools> This module implements a number of iterator building blocks inspired by constructs from APL, Haskell, and SML. Each has been recast in a form suitable for Python. The module standardizes a core set of fast, memory efficient tools that are useful by themselves or in combination. Together, they form an “iterator algebra” making it possible to construct specialized tools succinctly and efficiently in pure Python.[Python 3 Standard Library - itertools](https://docs.python.org/3/library/itertools.html)Infinite iterators - count() - cycle() - repeat()Iterators terminating on the shortest input sequence: - accumulate() - chain() - chain.from_iterable() - compress() - dropwhile() - filterfalse() - groupby() - islice() - starmap() - takewhile() - tee() - zip_longest()Combinatoric iterators: - product() - permutations() - combinations() - combinations_with_replacement() accumulate()Return series of accumulated sums (or other binary function results).[Python 3 Standard Library - itertools.accumulate](https://docs.python.org/3/library/itertools.htmlitertools.accumulate) ###Code from itertools import accumulate accumulations = accumulate([1, 2, 3]) list(accumulations) ###Output _____no_output_____ ###Markdown chain()Return a chain object whose __next__() method returns elements from the first iterable until it is exhausted, then elements from the next iterable, until all of the iterables are exhausted.[Python 3 Standard Library - itertools.chain](https://docs.python.org/3/library/itertools.htmlitertools.chain) ###Code # Example (slightly modified) from: # https://realpython.com/python-itertools/#section-recap_2 from itertools import chain chained_iterator = chain('abc', [1, 2, 3]) chained_iterator list(chained_iterator) ###Output _____no_output_____ ###Markdown chain.from_iterable()Alternate constructor for chain(). Gets chained inputs from a single iterable argument.[Python 3 Standard Library - itertools.chain.from_iterable](https://docs.python.org/3/library/itertools.htmlitertools.chain.from_iterable) ###Code from itertools import chain chained_iterator = chain.from_iterable(['ABC', 'DEF']) chained_iterator list(chained_iterator) ###Output _____no_output_____ ###Markdown combinations()Return successive n-length combinations of elements in the iterable.[Python 3 Standard Library - itertools.combinations](https://docs.python.org/3/library/itertools.htmlitertools.combinations) ###Code # Example (slightly modified) from: # https://realpython.com/python-itertools/#section-recap from itertools import combinations combinations = combinations([1, 2, 3], 2) list(combinations) ###Output _____no_output_____ ###Markdown combinations_with_replacement()Return successive n-length combinations of elements in the iterable allowing individual elements to have successive repeats.[Python 3 Standard Library - itertools.combinations_with_replacement](https://docs.python.org/3/library/itertools.htmlitertools.combinations_with_replacement) ###Code # Example (slightly modified) from: # https://realpython.com/python-itertools/#section-recap from itertools import combinations_with_replacement combinations = combinations_with_replacement([1, 2, 3], 2) list(combinations) ###Output _____no_output_____ ###Markdown compress()Make an iterator that filters elements from data returning only those that have a corresponding element in selectors that evaluates to True.[Python 3 Standard Library - itertools.compress](https://docs.python.org/3/library/itertools.htmlitertools.compress) ###Code from itertools import compress filtered_values = compress('ABCDEF', [1,0,1,0,1,1]) filtered_values list(filtered_values) ###Output _____no_output_____ ###Markdown count()Return a count object whose .__next__() method returns consecutive values.[Python 3 Standard Library - itertools.count](https://docs.python.org/3/library/itertools.htmlitertools.count)``` Example from: https://realpython.com/python-itertools/section-recap>>> from itertools import count>>> count(start=1, step=2)1, 3, 5, 7, 9, ...``` cycle()Return elements from the iterable until it is exhausted. Then repeat the sequence indefinitely.[Python 3 Standard Library - itertools.cycle](https://docs.python.org/3/library/itertools.htmlitertools.cycle)```>>> from itertools import cycle>>> cycle('ABCD')A B C D A B C D A B C D ...``` dropwhile()Drop items from the iterable while pred(item) is true. Afterwards, return every element until the iterable is exhausted.[Python 3 Standard Library - itertools.dropwhile](https://docs.python.org/3/library/itertools.htmlitertools.dropwhile) ###Code from itertools import dropwhile filtered_values = dropwhile(lambda x: x<5, [1,4,6,4,1]) filtered_values list(filtered_values) ###Output _____no_output_____ ###Markdown islice()Return an iterator whose __next__() method returns selected values from an iterable. Works like a slice() on a list but returns an iterator.[Python 3 Standard Library - itertools.islice](https://docs.python.org/3/library/itertools.htmlitertools.islice) ###Code from itertools import islice iterable = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] sliced_iterator = islice(iterable, 1, 7, 2) # iterable, start, stop, step sliced_iterator list(sliced_iterator) ###Output _____no_output_____ ###Markdown filterfalse()Return those items of sequence for which pred(item) is false. If pred is None, return the items that are false.[Python 3 Standard Library - itertools.filterfalse](https://docs.python.org/3/library/itertools.htmlitertools.filterfalse) ###Code # Example from: # https://docs.python.org/3/library/itertools.html#itertools.filterfalse from itertools import filterfalse even_numbers = filterfalse(lambda x: x%2, range(10)) even_numbers list(even_numbers) ###Output _____no_output_____ ###Markdown groupby()Make an iterator that returns consecutive keys and groups from the iterable.[Python 3 Standard Library - itertools.groupby](https://docs.python.org/3/library/itertools.htmlitertools.groupby) ###Code from itertools import groupby grouped_values = (k for k, g in groupby('AAAABBBCCDAABBB')) grouped_values list(grouped_values) ###Output _____no_output_____ ###Markdown permutations()Return successive n-length permutations of elements in the iterable.[Python 3 Standard Library - itertools.permutations](https://docs.python.org/3/library/itertools.htmlitertools.permutations) ###Code # Example (slightly modified) from: # https://realpython.com/python-itertools/#section-recap from itertools import permutations permutations = permutations('abc') list(permutations) ###Output _____no_output_____ ###Markdown product()Cartesian product of input iterables. Equivalent to nested for-loops. ((x,y) for x in A for y in B)[Python 3 Standard Library - itertools.product](https://docs.python.org/3/library/itertools.htmlitertools.product) ###Code # Example (slightly modified) from: # https://realpython.com/python-itertools/#section-recap_2 from itertools import product product = product([1, 2], ['a', 'b']) product list(product) # Example (slightly modified) from: # https://docs.python.org/3/library/itertools.html#itertools.product same_product = ((x,y) for x in [1, 2] for y in ['a', 'b']) same_product list(same_product) ###Output _____no_output_____ ###Markdown repeat()Create an iterator which returns the object for the specified number of times. If not specified, returns the object endlessly.[Python 3 Standard Library - itertools.repeat](https://docs.python.org/3/library/itertools.htmlitertools.repeat) ###Code # Example (slightly modified) from: # https://realpython.com/python-itertools/#section-recap from itertools import repeat repetitions = repeat(2, 5) list(repetitions) ###Output _____no_output_____ ###Markdown starmap()Make an iterator that computes the function using arguments obtained from the iterable. Used instead of [map()](https://docs.python.org/3/library/functions.htmlmap) when argument parameters are already grouped in tuples from a single iterable (the data has been “pre-zipped”)[Python 3 Standard Library - itertools.starmap](https://docs.python.org/3/library/itertools.htmlitertools.starmap) ###Code from itertools import starmap powers = starmap(pow, [(2,5), (3,2), (10,3)]) powers list(powers) ###Output _____no_output_____ ###Markdown takewhile()Make an iterator that returns elements from the iterable as long as the predicate is true.[Python 3 Standard Library - itertools.takewhile](https://docs.python.org/3/library/itertools.htmlitertools.takewhile) ###Code # Example from: # https://docs.python.org/3/library/itertools.html#itertools.takewhile from itertools import takewhile filtered_values = takewhile(lambda x: x<5, [1,4,6,4,1]) filtered_values list(filtered_values) ###Output _____no_output_____ ###Markdown tee()Create any number of independent iterators from a single input iterable.[Python 3 Standard Library - itertools.tee](https://docs.python.org/3/library/itertools.htmlitertools.tee) ###Code # Example (slightly modified) from: # https://realpython.com/python-itertools/#section-recap_2 from itertools import tee iterable = ['a', 'b', 'c'] clone_1, clone_2 = tee(iterable, 2) list(clone_1) list(clone_2) ###Output _____no_output_____ ###Markdown zip_longest()Make an iterator that aggregates elements from each of the iterables.[Python 3 Standard Library - itertools.zip_longest](https://docs.python.org/3/library/itertools.htmlitertools.zip_longest) ###Code from itertools import zip_longest zipped = zip_longest('ABCD', 'xy', fillvalue='-') zipped list(zipped) ###Output _____no_output_____ ###Markdown How do we loop over the elements on a list? ###Code numbers = [1, 2, 3, 4, 5] for n in numbers: print(n) ###Output 1 2 3 4 5 ###Markdown We all agree that's much better than: ###Code for index in range(0, len(numbers)): print(numbers[index]) ###Output 1 2 3 4 5 ###Markdown Every time somebody loops over the indexes, a kitten dies. ... or, even worse: ###Code index = 0 while index < len(numbers): print(numbers[index]) index += 1 ###Output 1 2 3 ###Markdown This is going to get at least two* kittens dead. Python's for loop- Known as 'for-each' in other programming languages.- Higher abstraction level $\rightarrow$ more readable and clear.- We don't care about indexes or implementation details.- We just say "loop over this" (whatever it is) Recommended talk: [Loop Like a Native](https://www.youtube.com/watch?v=EnSu9hHGq5o), by Ned Batchelder. It's safer- Not manipulating indexes $\rightarrow$ fewer places were we can make mistakes.- Actually, we can arguably err nowhere using a for-each loop. ###Code index = 0 while index <= len(numbers): # Ooops! print(numbers[index]) index += 1 ###Output 1 2 3 ###Markdown The for loop not only works with lists Strings ###Code for letter in "aeiou": print(letter) ###Output a e i o u ###Markdown Sets ###Code numbers = {"one", "two", "three"} for n in numbers: print(n) ###Output two three one ###Markdown Note: no guarantees as for the order. See [All Your Ducks In A Row](https://www.youtube.com/watch?v=fYlnfvKVDoM), by Brandon Rhodes Dictionaries ###Code numbers = {1 : "one", 2 : "two", 3 : "three"} for key, value in numbers.items(): print(key, "->", value) ###Output 1 -> one 2 -> two 3 -> three ###Markdown Files ###Code with open("quixote.txt") as fd: for line in fd: print(line, end="") # line already includes a newline ###Output In a village of La Mancha, the name of which I have no desire to call to mind, there lived not long since one of those gentlemen that keep a lance in the lance-rack, an old buckler, a lean hack, and a greyhound for coursing. ###Markdown We can use the for loop with anything that's iterable Advanced tip: we can use [Abstract Base Classes](https://docs.python.org/3/library/abc.html).[collections.abc.Iterable](https://docs.python.org/3/library/collections.abc.htmlcollections.abc.Iterable) is an ABC for classes that are iterable. ###Code import collections.abc print(issubclass(list, collections.abc.Iterable)) print(issubclass(str, collections.abc.Iterable)) isinstance({1, 2}, collections.Iterable) isinstance("abcd", collections.Iterable) ###Output _____no_output_____ ###Markdown Detour: What's an iterable? From the [Glossary](https://docs.python.org/3/glossary.htmlterm-iterable):> An object capable of returning its members one at a time. Examples of iterables include all sequence types (such as `list`, `str`, and `tuple`) and some non-sequence types like dict, file objects, and objects of any classes you define with an `__iter__()` or `__getitem__()` method. So our object will be iterable if it implements `__iter__()` [``] [``] ... or `__getitem__()`, but let's focus on `__iter__()`. What's `__iter__()`? Again, [from the docs](https://docs.python.org/3/reference/datamodel.htmlobject.__iter__):> This method is called when an iterator is required for a container. This method should return a new iteratorobject that can iterate over all the objects in the container. For mappings, it should iterate over the keys of the container.- So we need to implement `__iter__()` and make it return an iterator- This method is called implicitly by the built-in `iter()` I don't believe you ###Code numbers = [1, 2, 3] print(numbers.__iter__) ###Output <method-wrapper '__iter__' of list object at 0x7fdbbc074788> ###Markdown OK, `__iter__()` exists. ###Code it = iter(numbers) # calls __iter__() print(it) ###Output <list_iterator object at 0x7fdb9e410860> ###Markdown ... and it returns an iterator. But... what's an iterator?It's an object that conforms to the [Iterator Protocol](https://docs.python.org/3/library/stdtypes.htmliterator-types), implementing two methods. `iterator.__iter__()`> Return the iterator object itself. This is required to allow both containers and iterators to be used with the for and in statements. This method corresponds to the `tp_iter` slot of the type structure for Python objects in the Python/C API.- TL;DR: implement `__iter__()`, make it return `self`.- We need to do this, for... whatever reasons. I'll follow the instructions, then. ###Code class MyIterator(object): def __iter__(self): return self ###Output _____no_output_____ ###Markdown This feels pointless. `iterator.__next__()` > Return the next item from the container. If there are no further items, raise the `StopIteration` exception. This method corresponds to the `tp_iternext` slot of the type structure for Python objects in the Python/C API.- No, I did not understand the second sentence either.- This was `.next()` in the now long-forgotten, barely remembered Python 2. ###Code class MyIterator(object): def __init__(self, elements): self.elements = elements self.index = 0 def __iter__(self): return self def __next__(self): # No elements left, so raise exception. if self.index >= len(self.elements): raise StopIteration result = self.elements[self.index] self.index += 1 return result it = MyIterator([1, 2, 3]) print(next(it)) # calls __next__() print(next(it)) print(next(it)) ###Output 1 2 3 ###Markdown - We've built our own ugly, awkward iterator object. Yay!- Recommended reading: [Understanding Python Iterables and Iterators](http://www.shutupandship.com/2012/01/understanding-python-iterables-and.html) The fourth time we call `next()`, `StopIteration` happens: ###Code print(next(it)) ###Output _____no_output_____ ###Markdown `next()` must be used on iteratorsEven if our class is iterable, we need an iterator to loop over it: ###Code numbers = [1, 2, 3] next(numbers) numbers = [1, 2, 3] it = iter(numbers) # calls __iter__(), returns iterator print("Iterator:", it) # it is an iterator indeed print(next(it)) # returns 1 print(next(it)) # returns 2 print(next(it)) # returns 3 print(next(it)) # raises StopIteration ###Output 1 2 3 ###Markdown This is exactly what the `for` loop does under the hood- Uses `iter()` to get an iterator.- Repeatedly calls `next()`.- Stops when `StopIteration` is raised. ###Code numbers = [1, 2, 3] def awkward_for(iterable): it = iter(iterable) while True: try: print(next(it)) except StopIteration: break awkward_for(numbers) ###Output 1 2 3 ###Markdown I'm so happy we have the built-in `for` instead of this monster. `for` and `StopIteration`- Although the iterator will raise StopIteration, we don't have to worry about it.- It turns out that the for loop listens for StopIteration explicitly.- It doesn't catch other exceptions raised by the iterator...- ... or `StopIteration` raised within the body of the loop. ###Code numbers = [1, 2, 3] for n in numbers: raise StopIteration # break stuff ###Output _____no_output_____ ###Markdown Detour: GeneratorsGenerators are a special type of iterator.How a normal function works:- The execution starts at the function's first line.- It continues until we reach a `return` statement...- ... or the end of the function — that returns `None` implicitly.- Whatever result we return, must be returned at once. Recommended readings:- ['yield' and Generators Explained](https://jeffknupp.com/blog/2013/04/07/improve-your-python-yield-and-generators-explained/)- [Generator Tricks for Systems Programmers](http://www.dabeaz.com/generators/) Single exit point ###Code def foo(x): """Add one, then square.""" y = x + 1 # we first do this z = y 2 # then we do this return z # exit the function here print(foo(4)) ###Output 25 ###Markdown Multiple exit points ###Code import random def spam(x): """Square if even, halve if odd.""" if x % 2 == 0: return x 2 # we may exit here... return x / 2 # ... or here. print(spam(4)) # 4 2 = 16 print(spam(7)) # 7 / 2 = 3.5 ###Output 16 3.5 ###Markdown Implicit `None` ###Code def foobar(x): y = x + 1 # do nothing with 'y' # implicit `return None` print(foobar(2)) ###Output None ###Markdown Let's say that we want to work with even numbers. ###Code def get_even(stop): """Return all the even numbers <= stop.""" numbers = [] n = 0 while n <= stop: numbers.append(n) n += 2 return numbers ###Output _____no_output_____ ###Markdown ... or, of course, simply: ###Code def get_even(stop): return list(range(0, stop + 1, 2)) print(get_even(10)) # [2 ... 10] print("Sum:", sum(get_even(10))) ###Output [0, 2, 4, 6, 8, 10] Sum: 30 ###Markdown When problems arise- The problem is that we're building the list...- ... and returning all the elements at once.- Working with large intervals becomes impractical, to say the least. ###Code sum(get_even(int(1e18))) # not enough RAM modules ###Output _____no_output_____ ###Markdown Generators to the rescue- Generators are functions that are able to return values one by one.- The state of the function is frozen until the next value is requested.- They use they `yield` keyword instead of `return`.- If there's $\gt 1$ `yield` in our function, it becomes a `generator function`.- Generator functions return generator iterators (generators, for short) ###Code def simple_generator(): yield 1 # will return this the first time yield 2 # this the second time yield 3 # and this the third time g = simple_generator() print(g) print(next(g)) # returns 1 print(next(g)) # returns 2 print(next(g)) # returns 3 print(next(g)) # raises StopIteration ###Output <generator object simple_generator at 0x7fdbe0916a20> 1 2 3 ###Markdown Let's say that we want a function that returns all** natural numbers: ###Code def count(): n = 1 while True: yield n n += 1 numbers = count() print(numbers) # again, it's a generator print(next(numbers)) # 1 print(next(numbers)) # 2 print(next(numbers)) # 3 ###Output <generator object count at 0x7fdbe0930828> 1 2 3 ###Markdown ... and so on, up to infinity and beyond. This is not possible with a normal function — we can't return all the natural numbers. ###Code def count(): """Try to return all natural numbers, and fail.""" result = [] n = 1 while True: result.append(n) n += 1 ###Output _____no_output_____ ###Markdown Don't run this code. Extra points: generator expressions- Like comprehension lists, but with lazy evaluation.- They generate the elements one by one, as needed. ###Code g = (x 2 for x in range(1, 1000000)) print(g) # it's a generator indeed print(next(g)) # computes the square of 1 print(next(g)) # computes the square of 2 print(next(g)) # computes the square of 3 ###Output <generator object <genexpr> at 0x7fdb9e428ab0> 1 4 9 ###Markdown Even more extra points:- `range()` is not a generator- In the old world of Python 2 it returned a list.- But now, in Python3, generates elements one by one. ###Code numbers = range(1, 100) print(numbers) # range(1, 100) print(type(numbers)) # it's a 'range' object it = iter(numbers) print(next(it)) # returns the first element print(next(it)) # returns the second element ###Output 1 2 ###Markdown So...- `range` is a `sequence object` that produces numbers on demand.- `sequences` in Python are object that support random access.- It can also contain if the number is part of the range in $\mathcal{O}(1)$...- ... instead of the $\mathcal{O}(n)$ that it would take to scan through all of them. ###Code odd = range(1, int(1e50), 2) print(odd) # a really large range indeed ###Output range(1, 100000000000000007629769841091887003294964970946560, 2) ###Markdown print(odd[9]) tell me what's the 10th odd number ###Code print(int(1e48) in odd) # completes before the heat death of the Universe ###Output False ###Markdown Summary- Iterators are objects on which we can call `next()`- Generators generate elements one by one.- Every generator is an iterator, but not vice versa.- We could achieve the same with a custom iterator — but this is nicer.Recommended reading: [this answer by Alex Martelli on Stack Owerflow](http://stackoverflow.com/a/2776865). Extra: Measuring a generatorHow do we calculate the number of elements of a generator? ###Code g = (x 2 for x in range(1, 101)) ###Output _____no_output_____ ###Markdown This doesn't work. ###Code len(g) # TypeError ###Output _____no_output_____ ###Markdown Idea: cast to list ###Code g = (x 2 for x in range(1, 101)) len(list(g)) ###Output _____no_output_____ ###Markdown But we need a temporary list. Better: use `sum()` ###Code g = (x 2 for x in range(1, 101)) sum(1 for x in g) # use another generator ###Output _____no_output_____ ###Markdown Or more idiomatic, as we don't care about the vale of the numbers: ###Code g = (x 2 for x in range(1, 101)) sum(1 for _ in g) ###Output _____no_output_____ ###Markdown Use `_` as a throwaway variable. Finally, time for some Kung Fu[Photo](https://www.flickr.com/photos/kurt-b/9453209945/) by Kurt Bauschardt / [CC BY-SA 2.0](https://creativecommons.org/licenses/by-sa/2.0/) Prime numbersHow do we determine whether a number is prime? ###Code def is_prime(n): """Checks whether a number is prime.""" divisor = 2 while divisor < n: if n % divisor == 0: return False divisor += 1 return True print(is_prime(2)) # True print(is_prime(3)) # True print(is_prime(8)) # False ###Output True True False ###Markdown But we already now there's a much better way with `range()`! ###Code def is_prime(n): """Checks whether a number is prime.""" for divisor in range(2, n): if n % divisor == 0: return False divisor += 1 return True print(is_prime(5)) # True print(is_prime(6)) # False print(is_prime(7)) # True ###Output True False True ###Markdown Mandatory optimization: check divisors only until $\sqrt{n}$- Because a non-prime number $n$ will have a divisor $\le \sqrt{n}$- Brings us down from $\mathcal{O}(n)$ to $\mathcal{O}(\sqrt{n})$. Not bad.- Recommended reading, with proof for humans: [this answer on Stack Overflow](http://stackoverflow.com/a/5811176) ###Code import math def is_prime(n): """Checks whether a number is prime.""" stop = int(math.sqrt(n)) + 1 for divisor in range(2, stop): if n % divisor == 0: return False divisor += 1 return True print(is_prime(10)) print(is_prime(13)) ###Output False True ###Markdown Integer factorization- Now we want to decompose a number into its prime factors.- For example, $8 = 2 \times 2 \times 2 = 2^3$, and $30 = 2 \times 3 \times 5$- Simplest method: [trial division](https://en.wikipedia.org/wiki/Trial_division), one by one- For this we'll need to loop over prime numbers Getting the first n prime numbers Attempt 1 ###Code def get_primes(how_many): """Return the first 'how_many' prime numbers.""" primes = [] n = 2 while len(primes) < how_many: if is_prime(n): primes.append(n) n += 1 return primes print(get_primes(5)) ###Output [2, 3, 5, 7, 11] ###Markdown Problem:** we need to generate all the prime numbers at once.Let's use a generator instead! Attempt 2 ###Code def get_primes(how_many): """Return the first 'how_many' prime numbers.""" counter = 0 n = 2 while counter < how_many: if is_prime(n): yield n counter += 1 n += 1 ###Output <generator object get_primes at 0x7fdbe0941120> [2, 3, 5, 7, 11] ###Markdown Twice as many places where we can commit a mistake, as we're keeping track of:- How many prime numbers we have generated so far.- What's the next number we need to evaluate.`range()` is not an option because we don't know what the stop is. But we can use... itertools.count()- Makes an iterator that returns evenly spaced values starting with $n$.- By default, we start counting from zero.- The default step is one. ###Code import itertools numbers = itertools.count() print(numbers) # tells us what the next element will be print(next(numbers)) # 0 print(next(numbers)) # 1 print(next(numbers)) # 2 odd = itertools.count(1, step=2) print(next(odd)) # first odd number print(next(odd)) # second odd number ###Output 1 3 ###Markdown Attempt 3We can thus simplify our code a little bit: ###Code def get_primes(how_many): """Return the first 'how_many' prime numbers.""" counter = 0 for n in itertools.count(2): if is_prime(n): yield n counter += 1 if counter == how_many: break ###Output _____no_output_____ ###Markdown However, this is still awkward, as our function does two things:- Generates prime numbers- Keeps track if how many we have generated so far. Let's split it in two different steps. Attempt 4 ###Code def primes(): """An endless generator of prime numbers.""" for n in itertools.count(2): if is_prime(n): yield n def get_primes(how_many): """Return the first 'how_many' prime numbers.""" counter = 0 all_primes = primes() while counter < how_many: yield next(all_primes) counter += 1 ###Output _____no_output_____ ###Markdown Good! But this can be simplified even further! To get all the prime numbers we can use a generator expression ###Code primes = (n for n in itertools.count(2) if is_prime(n)) ###Output _____no_output_____ ###Markdown ... or `filter()`: ###Code primes = filter(is_prime, itertools.count(2)) ###Output _____no_output_____ ###Markdown Notes:- generator expressions are usually shorter and more readable- But in this case `filter()` is arguably better — we're taking the value as it is.- `filter()` was `itertools.ifilter()` before...- ... but nobody uses Python 2 anymore. Attempt 5 ###Code def get_primes(how_many): """Return the first 'how_many' prime numbers.""" counter = 0 primes = filter(is_prime, itertools.count(2)) while counter < how_many: yield next(all_primes) counter += 1 ###Output _____no_output_____ ###Markdown Take how many?- This thing that we're doing in `get_primes()` is a common pattern.- "Give me the first n elements of this iterable"- We cannot use slice notation: ###Code numbers = [1, 2, 3, 4, 5] print(numbers[:3]) # the first three print(get_primes(10)[:5]) # slicing doesn't work with generators ###Output [1, 2, 3] ###Markdown itertools.islice()- Like slice notation, but works with all things iterable.- Lazy evaluation, of course, asking for elements once at a time. ###Code for n in itertools.islice(itertools.count(), 5): print(n) word = "abcde" print(list(itertools.islice(word, 3))) # the first three letters # If start != 0, skip elements until it's reached squares = (x ** 2 for x in itertools.count(1)) print(list(itertools.islice(squares, 10, 15))) # start=10, stop=15 # We can use a step other than one. numbers = range(100000) print(list(itertools.islice(numbers, 0, 20, 2))) # step=2 ###Output [0, 2, 4, 6, 8, 10, 12, 14, 16, 18] ###Markdown So if we want the first $n$ prime numbers: ###Code primes = filter(is_prime, itertools.count(2)) for n in itertools.islice(primes, 10): print(n) ###Output 2 3 5 7 11 13 17 19 23 29 ###Markdown Attempt 6Let's rewrite our function: ###Code def get_primes(how_many): """Return the first 'how_many' prime numbers.""" primes = filter(is_prime, itertools.count(2)) for n in itertools.islice(primes, how_many): yield n for n in get_primes(5): print(n) ###Output 2 3 5 7 11 ###Markdown We're just looping over the elements of a iterator and in turn `yield`ing them. This is what `yield from` was invented for! yield from- Allows a generator to delegate part of its operations to another generator.- That is, each `next()` which ask the sub-generator for another value.- Usually we delegate to subgenerators, but it works with anything iterable.- `yield from iterable` $\approx$ `for item in iterable: yield item`- It is also a transparent two-way channel from the caller to the sub-generator. ###Code def foo(): yield 1 yield 2 yield 3 def spam(): yield from foo() # for x in foo(): yield x print(list(spam())) def vowels(): # Works with anything iterable yield from "aeiou" print(list(vowels())) ###Output ['a', 'e', 'i', 'o', 'u'] ###Markdown Recommended reading:[A Curious Course on Coroutines and Concurrency](http://dabeaz.com/coroutines/) Attempt 7So we can rewrite our function as: ###Code def get_primes(how_many): """Return the first 'how_many' prime numbers.""" primes = filter(is_prime, itertools.count(2)) yield from itertools.islice(primes, how_many) for n in get_primes(5): print(n) ###Output 2 3 5 7 11 ###Markdown Yet we can make this even shorter.- We're just defining a generator that delegates all the work to another generator.- The first argument to `islice()` is always the same: `primes`.- The only thing that changes is the second one, `how_many`. This is what `functools.partial()` was invented for! functools.partial()- Used for partial function application. That's formal language for...- ... "freezing some portion of a function's arguments".- It also supports freezing keyword arguments.- Allows us to simplifying a function signature.- You don't know you need it in your life until you come across it. ###Code import functools power_two = functools.partial(math.pow, 2) # freeze 'math.pow(2, ...' print(power_two) print(power_two(3)) # math.pow(2, 3) print(power_two(5)) # math.pow(2, 5) print(power_two(9)) # math.pow(2, 9) ###Output 8.0 32.0 512.0 ###Markdown Used in real life to create handy shortcuts for a function we'll call repeatedly, and where some arguments are always the same: ###Code import os.path src_dir = "/home/vterron/src/" print(os.path.join(src_dir, "file1.py")) print(os.path.join(src_dir, "file2.py")) print(os.path.join(src_dir, "file3.py")) # This is getting a little tedious... ###Output /home/vterron/src/file1.py /home/vterron/src/file2.py /home/vterron/src/file3.py ###Markdown We can do instead: ###Code get_src = functools.partial(os.path.join, "/home/vterron/src/") print(get_src("file1.py")) # os.path.join("/home/vterron/src/", "file1.py") print(get_src("file2.py")) print(get_src("file3.py")) ###Output /home/vterron/src/file1.py /home/vterron/src/file2.py /home/vterron/src/file3.py ###Markdown ... or as a shorcut to define a function: ###Code import random def bonoloto(): """Get a random ticket to play BonoLoto.""" return random.sample(range(1, 50), 6) bonoloto() import functools import random bonoloto = functools.partial(random.sample, range(1, 50), 6) bonoloto() ###Output _____no_output_____ ###Markdown Attempt 8So going back to our function... ###Code def get_primes(how_many): """Return the first 'how_many' prime numbers.""" primes = filter(is_prime, itertools.count(2)) yield from itertools.islice(primes, how_many) ###Output _____no_output_____ ###Markdown We can do instead: ###Code primes = filter(is_prime, itertools.count(2)) get_primes = functools.partial(itertools.islice, primes) for n in get_primes(5): print(n) ###Output 2 3 5 7 11 ###Markdown Integer factorization, Part II- This is all neat and good, but not exactly what we need here.- We don't want the first whatever prime numbers...- ... but all the prime numbers $\le \sqrt{n}$.- For example, to factorize 15 we need to test all the primes until $\left \lceil{\sqrt{15}}\right \rceil = 3$: Generating all the divisors $\le x$ Naive attempt ###Code def primes_until(stop): """Return all the prime numbers <= stop.""" primes = filter(is_prime, itertools.count(2)) for p in primes: if p <= stop: yield p else: break print(list(primes_until(15))) ###Output [2, 3, 5, 7, 11, 13] ###Markdown This is also a common pattern: loop over the elements of an iterable, stopping as soon as some condition is no longer satisfied. And this is what `takewhile()` was invented for! `itertools.takewhile()`- Make an iterator that returns elements.- Stop when the predicate is no longer `True`.- Frequently used in conjunction with lambda functions. ###Code numbers = range(1, 10000) # Take numbers as long as they're < 4 it = itertools.takewhile(lambda x: x < 4, numbers) print(next(it)) # 1 is < 4, so we return it print(next(it)) # 2 is < 4, so we return it print(next(it)) # 3 is < 4, so we return it print(next(it)) # 4 is not < 4, so stop ###Output 1 2 3 ###Markdown Lambda functions are not mandatory ###Code def smaller_than_ten(x): """Checks whether the number is < 10.""" return x < 10 numbers = range(0, int(1e12), 2) list(itertools.takewhile(smaller_than_ten, numbers)) ###Output _____no_output_____ ###Markdown But since we're at it... ###Code def is_smaller(x, than=float("inf")): return x < than numbers = range(0, int(1e18), 2) # functools.partial() + keyword argument = more readable! for n in itertools.takewhile(functools.partial(is_smaller, than=10), numbers): print(n) ###Output 0 2 4 6 8 ###Markdown `operator`This [must-know module](https://docs.python.org/3/library/operator.html) exports all standard operators as functions. ###Code import operator print(operator.lt(3, 5)) # 3 < 5 -> True print(operator.not_(True)) # not True -> False print(operator.add(2, 1)) # 2 + 1 -> 3 print(operator.neg(-1)) # -(-1) -> 1 # In-place addition x = [1, 2, 3] operator.iadd(x, [4, 5]) # x += [4, 5] print(x) # [1, 2, 3, 4, 5] ###Output True False 3 1 [1, 2, 3, 4, 5] ###Markdown So we can rewrite our solution as... ###Code numbers = range(0, int(1e24), 2) smaller_than_ten = functools.partial(operator.gt, 10) for n in itertools.takewhile(smaller_than_ten, numbers): print(n) ###Output 0 2 4 6 8 ###Markdown - Note that with `partial()` we have to bind arguments left to right.- Instead of testing whether $x < 10$...- ... we're rewriting it as $10 > x$Anyway. Generating all the divisors $\le x$ Kung Fu version ###Code def primes_until(stop): """Return all the prime numbers <= stop.""" primes = filter(is_prime, itertools.count(2)) yield from itertools.takewhile(lambda p: p < stop, primes) for x in primes_until(15): print(x) ###Output 2 3 5 7 11 13 ###Markdown Woo-hoo! And what about the opposite? `itertools.dropwhile()`- Make an iterator that returns elements.- Ignore elements as long as the predicate is `True`.- As soon as it's not anymore, return everything. ###Code numbers = range(1, 10000) # Ignore numbers as long as they're < 4 it = itertools.dropwhile(lambda x: x < 4, numbers) print(next(it)) # 'it' returns 1 -> 1 < 4, so we drop it, so ... # 'it' returns 2 -> 2 < 4, so we drop it, so ... # 'it' returns 3 -> 3 < 4, so we drop it, so ... # returns 4 print(next(it)) # returns 5 print(next(it)) # returns 6 print(next(it)) # returns 7 print(next(it)) # returns 8 # ... and so on until we exhaust 'numbers' ###Output 4 5 6 7 8 ###Markdown Prime numbers within a rangeUsing both `takewhile()` and `dropwhile()` gets us this: ###Code def primes_range(start=2, stop=float("inf")): """Return all the prime numbers start <= x < stop.""" primes = filter(is_prime, itertools.count(2)) it = itertools.dropwhile(lambda x: x < start, primes) yield from itertools.takewhile(lambda y: y < stop, it) print(list(primes_range(100, 125))) # 100 <= x < 125 print(list(primes_range(stop=20))) # all primes < 20 it = primes_range(start=1000) # all primes >= 1000 print(next(it)) # 1009 print(next(it)) # 1013 print(next(it)) # 1019 print(next(it)) # 1021 # ... and so on until infinity. ###Output 1009 1013 1019 1021 ###Markdown Integer factorization: The Algorithm- Iterate over the prime numbers $p \le \sqrt{n}$- If $n$ is divisible by $p$, then $p$ is a factor.- Divide $n$ by $p$ and factorize the quotient, recursively.- Base case: we ran out of prime numbers, so $n$ is prime too.- The factorization is all found factors. Example: factorize $30$- Is $30$ divisible by $2$? Yes.- Therefore, $2$ is a factor.Factorize now the quotient, $30 \div 2 = 15$:- Is $15$ divisible by $2$? No.- Is $15$ divisible by $3$? Yes.- Therefore, $3$ is a factor.Factorize now the quotient, $15 \div 3 = 5$:- There're no primes $\le \sqrt{5}$, so $5$ is prime too.- $30 = 2 \times 3 \times 5$ Show me the code ###Code import math def factorize(n): """Decompose n into prime numbers.""" for p in primes_until(int(math.sqrt(n))): quotient, remainder = divmod(n, p) if remainder == 0: # 'p' is a prime factor return [p] + factorize(quotient) # Base case, reached only if we run out of primes return [n] # n is prime print(factorize(30)) # [2, 3, 5] print(factorize(70)) # [2, 3, 7] print(factorize(78)) # [2, 3, 13] print(factorize(11)) # we hit the base case directly ###Output [2, 3, 5] [2, 5, 7] [2, 3, 13] [11] ###Markdown The `uniq` commandA Unix command that collapses adjacent identical lines into one. ###Code %%bash cat ~/letters.txt %%bash uniq ~/letters.txt ###Output a b a ###Markdown Note that we're only removing consecutive duplicates. Our own version Padawan attemptFor simplicity's sake, let's accept only strings as input. ###Code def uniq(word): """Remove consecutive duplicates letters.""" # Don't break if string is empty if not word: return '' result = [word[0]] for letter in word[1:]: if letter != result[-1]: result.append(letter) return ''.join(result) print(uniq("a")) # 'a' print(uniq("bbb")) # 'b' print(uniq("abc")) # 'abc' print(uniq("aabbbccccdee")) # 'abcde' ###Output a b abc abcde ###Markdown itertools.groupby()- Make an iterator that returns consecutive `keys` and `groups` from the iterable.- A new `group` starts every time the value of the key changes.- The `group` objects are a sub-iterator over the elements in the group. ###Code word = "aabccc" groups = itertools.groupby(word) print(groups) # a 'groupby' object — an iterable key1, group1 = next(groups) # give me the first group print("Key:", key1) # 'a' print("Group:", group1) # a '_grouper' object... another iterable print("Next:", next(group1)) # the first 'a' print("Next:", next(group1)) # the second 'a' print("Next:", next(group1)) # StopIteration ###Output Next: a Next: a ###Markdown - Each call to `next()` will return two elements: the `key` and the `group`.- The `key` is what this group contains — e.g., the letter a. - The `group` are the actual occurrences of the key — e.g., "aa".Let's keep going on... ###Code print("Word", word) # 'aabcc' key2, group2 = next(groups) # give me the second group print("Key:", key2) # ok, so this group contains 'b' # And how many occurrences of 'b' are there? print("Group:", group2) # the occurrences of 'b' print(list(group2)) # ['b'] — oh, only one. # The third and last group key3, group3 = next(groups) print("Key:", key3) # 'c' print(list(group3)) # ['c', 'c', 'c'] ###Output Key: c ['c', 'c', 'c'] ###Markdown Using a `for` loop instead ###Code word = "aabccc" for key, group in itertools.groupby(word): print(key, "->", list(group)) ###Output a -> ['a', 'a'] b -> ['b'] c -> ['c', 'c', 'c'] ###Markdown This might seem silly, but it's very powerful indeed. Our `uniq` command Kung Fu version ###Code def uniq(word): result = [] # We don't need the group for all, hence the '_' for key, _ in itertools.groupby(word): result.append(key) return ''.join(result) word = "aaabbcccccdee" print(uniq(word)) ###Output abcde ###Markdown ... or even more succinct: ###Code def uniq(word): return ''.join(key for key, _ in itertools.groupby(word)) print(uniq(word)) ###Output abcde ###Markdown A (rudimentary) compression algorithm- Let's implement a very basic string compression function...- ... using the counts of repeated characters.- For example, "aaabbcccccdee" returns "a3b2c5d1e2" Without `itertools`, the solution brings us pain and misery. ###Code def compress(word): """Return a compressed version of the string.""" result = [] current = word[0] counter = 1 for letter in word[1:]: if letter == current: # We're still in the same group counter += 1 else: # We need to start a new group result += [current, str(counter)] current = letter # start a new group counter = 1 result += [current, str(counter)] return ''.join(result) word = "aaabbcccccdee" print(compress(word)) # 'a3b2c5d1e2' ###Output a3b2c5d1e2 ###Markdown Kung Fu version ###Code def compress(word): """Return a compressed version of the string.""" result = [] for key, group in itertools.groupby(word): result.append("{}{}".format(key, len(list(group)))) return ''.join(result) word = "aaabbcccccdee" print(compress(word)) # 'a3b2c5d1e2' ###Output a3b2c5d1e2 ###Markdown Making it case case-insensitiveA problem is that letters in different case are considered to be different. ###Code print(compress("aaAAAA")) # 'a2A4' ###Output a2A4 ###Markdown This might make sense, but we're into compressing our strings so much that we decide to ignore the case... respecting the case of the first occurrence — otherwise, we would just `.upper()` or `.lower()` the entire string. That is:- "aaAAAA" $\rightarrow$ "a6"- "AAaaaa" $\rightarrow$ "A6"- "BbBccC" $\rightarrow$ "B3c3".How do we do this? The `key` function- By default, `groupby()` compares the elements as they are seen.- The keyword argument `key` allows us to specify a different criteria.- It is a function that transforms each elements before it's compared.- This is known as the "key value for each element" How is this useful? Let's do this: ###Code def compress_more(word): """Return an even more compressed version of the string.""" result = [] # Make the comparison between letters case-insensitive. for _, group in itertools.groupby(word, key=lambda x: x.upper()): group = list(group) # Take first element to respect case of the first occurrence. result.append("{}{}".format(group[0], len(group))) return ''.join(result) print(compress_more("aaAAAA")) # 'a6' print(compress_more("AAaaaa")) # 'A6' print(compress_more("BbBccC")) # 'B3c3' ###Output a6 A6 B3c3 ###Markdown - We can't use the key, as they will always be in upper case.- 'group' is an iterator, so we store it as a list to use slices and `len()`. Grouping letters by lengthLet's say that we have a series of words, and we want to group them by their length. ###Code words = "red orange yellow green blue indigo violet gray".split() ###Output _____no_output_____ ###Markdown Rookie version ###Code # Map each length to a list of words lengths = collections.defaultdict(list) for w in words: lengths[len(w)].append(w) for key, value in lengths.items(): print(key, '->', value) ###Output 3 -> ['red'] 4 -> ['blue', 'gray'] 5 -> ['green'] 6 -> ['orange', 'yellow', 'indigo', 'violet'] ###Markdown Kung Fu version ###Code words.sort(key=len) for key, group in itertools.groupby(words, key=len): print(key, '->', list(group)) ###Output 3 -> ['red'] 4 -> ['blue', 'gray'] 5 -> ['green'] 6 -> ['orange', 'yellow', 'indigo', 'violet'] ###Markdown Two things to note:- We have to sort the list first; otherwise it only groups consecutive items.- The first solution is $\mathcal{O}(n)$ vs $\mathcal{O}(n \log n)$, because we have to sort the list. But `groupby()` is arguably better here as it's shorter and clearly conveys what we're doing: grouping the words according to a criteria. AnagramsHow do we find anagrams in a list of wors? ###Code words = ['listen', 'meteor', 'dawn', 'remote', 'silent'] # If two words are an anagram, sorted() returns the same print(sorted('listen')) # ['e', 'i', 'l', 'n', 's', 't'] print(sorted('silent')) # ['e', 'i', 'l', 'n', 's', 't'] ###Output ['e', 'i', 'l', 'n', 's', 't'] ['e', 'i', 'l', 'n', 's', 't'] ###Markdown Neophyte version ###Code anagrams = collections.defaultdict(list) for w in words: # Because lists are not hashable anagrams[tuple(sorted(w))].append(w) for words_ in anagrams.values(): # 'dawn' doesn't match anything else if len(words_) >= 2: print(words_) ###Output ['listen', 'silent'] ['meteor', 'remote'] ###Markdown Kung Fu version ###Code words.sort(key=sorted) for _, group in itertools.groupby(words, key=sorted): words_ = list(group) if len(words_) >= 2: print(words_) %matplotlib inline ###Output _____no_output_____ ###Markdown Consecutive values over a thresholdLet's say we have this function:$\frac{x^3}{14} + \frac{x^2}{14} - \frac{13 x}{14} - \frac{1}{14}$ ###Code import numpy # Build polynomial from coefficients coeffs = [1/14, 1/14, -13/14, -1/14] func = numpy.poly1d(coeffs) func(0.5) # evaluate function at 0.5 ###Output _____no_output_____ ###Markdown Maths! Run for your lives! It looks like this ###Code from matplotlib import pyplot xp = numpy.linspace(-4, 4.5, 100) pyplot.plot(xp, func(xp), 'b', alpha = 0.7) pyplot.grid(True) ###Output _____no_output_____ ###Markdown Let's say it's time versus some value we're monitoring We want to trigger an alarm if we spent $>= 3$ seconds below zero. ###Code import numpy from matplotlib import pyplot coeffs = [1/14, 1/14, -13/14, -1/14] func = numpy.poly1d(coeffs) print(numpy.roots(coeffs)) xp = numpy.linspace(-4, 4.5, 100) xzero = numpy.linspace(-0.077, 3.183, 100) yzero = func(xzero) pyplot.plot(xp, func(xp), 'b', alpha = 0.7) pyplot.grid(True) pyplot.xlabel("Time") pyplot.ylabel("Important Thing") pyplot.fill_between(xzero, 0, func(xzero), facecolor='red') pyplot.savefig("images/curve-three.svg") ###Output [-4.106 3.183 -0.077] ###Markdown We know that the answer is yes...How do we do it... in code? ###Code # Use three decimal digits numpy.set_printoptions(precision=3) ###Output _____no_output_____ ###Markdown For simplicity, evaluate it only at integers. ###Code xp = range(-4, 5) yp = func(xp) for x, y in zip(xp, yp): print("f({}) -> {:.3f}".format(x, y)) ###Output f(-4) -> 0.214 f(-3) -> 1.429 f(-2) -> 1.500 f(-1) -> 0.857 f(0) -> -0.071 f(1) -> -0.857 f(2) -> -1.071 f(3) -> -0.286 f(4) -> 1.929 ###Markdown Are there three consecutive points here with negative sign? It's as simple as this ###Code # Group the func(x) values by whether they're negative or not. for is_negative, group in itertools.groupby(yp, key=lambda x: x < 0): values = numpy.array(list(group)) print(is_negative, "->", values) if is_negative and len(values) >= 3: print("Trigger alarm!!") break ###Output False -> [ 0.214 1.429 1.5 0.857] True -> [-0.071 -0.857 -1.071 -0.286] Trigger alarm!! ###Markdown Don't even try to implement this without `groupby()`. [Photo](https://en.wikipedia.org/wiki/File:Wushu_dao.jpg) by AEMHZ~commonswiki / [CC BY-SA 3.0](https://creativecommons.org/licenses/by-sa/3.0/deed.en) / Cropped from original [Photo](https://en.wikipedia.org/wiki/File:Wushu_dao.jpg) by Alexandre Ferreira / [CC BY-SA 2.0](https://creativecommons.org/licenses/by-sa/2.0/) / Cropped from original Iterators are a one-way roadIn order to check how many elements there are in a iterator we need to consume it. ###Code g = (x 2 for x in range(1, 101)) sum(1 for _ in g) ###Output _____no_output_____ ###Markdown Which... works, but the generator is now exhausted, so we can't use it anymore. ###Code list(g) # iterator is empty, so empty list ###Output _____no_output_____ ###Markdown There is no way we can go backwards in the traversal of the iterator. There's no going backEvery time we call `next()` the iterator moves one step forward — forever. ###Code it = iter("abcdefghijk") next(it) # 'a' next(it) # now b, we'll never see 'a' again ###Output _____no_output_____ ###Markdown That's why, if we'll need each element more than once, we need to store them in a list. `itertools.tee()`- Returns $n$ independent iterators from a single iterable.- This allows us to move forward using of these iterators...- ... while the rest still point at the same place. ###Code even = itertools.count(2, step=2) a, b = itertools.tee(even) print(next(a)) # 2 print(next(a)) # 4 ###Output 2 4 ###Markdown We haven't yet called `next()` with `b`, to it's still at $2$. ###Code print(next(b)) # 2 ###Output 4 ###Markdown Measuring an iterator, Part IIWe could be tempted to do something like this: ###Code g = (x 2 for x in range(1, 101)) # Fork the iterator, rebind name 'g' g, tmp = itertools.tee(g) length = sum(1 for _ in tmp) print("Length:", length) ###Output Length: 100 ###Markdown - We have exahusted the original iterator `g`...- ... but we use the same name for one of the copies.- The other copy, `tmp`, is the one we use for counting. However...This is a bad idea. From [the documentation](https://docs.python.org/3/library/itertools.htmlitertools.tee):> This itertool may require significant auxiliary storage (depending on how much temporary data needs to be stored). In general, if one iterator uses most or all of the data before another iterator starts, it is faster to use `list()` instead of `tee()`.These independent iterators need to store the elements in memory until they've been consumed by all the elements, so if we are going to exahust one of the iterators we're better off by simply using a list. ###Code g = (x 2 for x in range(1, 11)) g = list(g) print(len(g)) print(g) ###Output [1, 4, 9, 16, 25, 36, 49, 64, 81, 100] ###Markdown When is this iseful, then?When the independent generators are going to be used more or less at the same time.For example, if we need to compute the difference between consecutive elements in list: ###Code numbers = [1, 5, 7] # The output will be [4, 2], because 5 - 1 = 4 and 7 - 5 = 2 def diff(sequence): # Pair element with the previous one pairs = zip(sequence, sequence[1:]) return [p[1] - p[0] for p in pairs] diff(numbers) ###Output _____no_output_____ ###Markdown However, we can't use this with a generator, because we can't use slicing. ###Code numbers = (x 2 for x in [1, 5, 7]) diff(numbers) ###Output _____no_output_____ ###Markdown `tee()` to the rescueThis is a job `tee()` was designed for: ###Code def diff(iterable): a, b = itertools.tee(iterable) next(b) return [p[1] - p[0] for p in zip(a, b)] numbers = (x for x in [1, 5, 7]) diff(numbers) ###Output _____no_output_____ ###Markdown NumPy already did itBy the way, if we're working with sequences NumPy already includes [a function for this](http://docs.scipy.org/doc/numpy/reference/generated/numpy.diff.html): ###Code import numpy numpy.diff([1, 5, 7]) ###Output _____no_output_____ ###Markdown Don't reinvent the wheel! A NeverEnding StoryHow do we alternate indefinitely between -1 and 1? Absolute n00b version ###Code x = 1 while True: print(x) if x == 1: x = -1 else: x = 1 ###Output _____no_output_____ ###Markdown An infinite loop, of catastrophic consequences if executed. A little-less-beginner version ###Code x = 1 while True: print(x) x = -1 ###Output _____no_output_____ ###Markdown We're all still going to die if we run this. The FIFO versionUsing a [first in, first out](https://en.wikipedia.org/wiki/FIFO_(computing_and_electronics) queue. ###Code import collections class Alternate(object): """Alternate between 1 and -1 endlessly, via pop().""" def __init__(self): self.values = collections.deque() self._refill() def _refill(self): """Insert some 1's and -1's in the queue.""" self.values.extend([1, -1] 10) def __len__(self): return len(self.values) def pop(self): """Return the next 1 or -1 value.""" # We ran out of values, so generate a few more. if not len(self): self._refill() return self.values.popleft() ###Output _____no_output_____ ###Markdown The [`collections`](https://docs.python.org/3/library/collections.htmlcollections.deque) module is awesome, but this is totally overkill. The pr0 versionThe "I was paying attention, so I know we have to use a generator" approach: ###Code def alternate(): """Alternate between 1 and -1 endlessly.""" x = 1 while True: yield x x = -1 ones = alternate() print(next(ones)) # 1 print(next(ones)) # -1 print(next(ones)) # 1 # ... ###Output 1 -1 1 ###Markdown Kung Fu version ###Code ones = itertools.cycle([1, -1]) print(next(ones)) # 1 print(next(ones)) # -1 print(next(ones)) # 1 print(next(ones)) # -1 print(next(ones)) # 1 # ... ###Output 1 -1 1 -1 1 ###Markdown `itertools.cycle()`- Make an iterator returning elements from the iterable...- ... and save a copy of each of the returned elements.- When the iterable is exhausted, iterate over the saved copy.- Repeat indefinitely, until the end of time. ###Code vowels = itertools.cycle("aeiou") # Endless generator, so we need islice() for v in itertools.islice(vowels, 10): print(v) g = (x * 2 for x in range(1, 4)) squares = itertools.cycle(g) print(list(itertools.islice(squares, 11))) # We've exahusted the generator... next(g) # StopIteration # ... but 'cycle' still keeps a copy. next(squares) # 9 ###Output _____no_output_____ ###Markdown Waiting patientlyA real-life case where `cycle()` proves useful: ###Code import itertools import sys import time def sleep(seconds): """Show an animated spinner while we sleep.""" symbols = itertools.cycle('-\\|/') tend = time.time() + seconds while time.time() < tend: # '\r' is carriage return: return cursor to the start of the line. sys.stdout.write('\rPlease wait... ' + next(symbols)) # no newline sys.stdout.flush() time.sleep(0.1) print() # newline if __name__ == "__main__": sleep(20) ###Output _____no_output_____ ###Markdown [![asciicast](https://asciinema.org/a/8ocljajktav6nkm3lbtrv7i8l.png)](https://asciinema.org/a/8ocljajktav6nkm3lbtrv7i8l?size=medium&t=3&autoplay=1) Iterating over two (or more) iterablesLet's count from $1$ to $10$, then down to $1$ again, and so on. ###Code up = list(range(1, 11)) down = list(reversed(range(2, 10))) print("Up :", up) print("Down:", down) itertools.cycle(numbers, vowels) ###Output _____no_output_____ ###Markdown We have a problem — `cycle()` only accepts an iterable. And, by extension, what do we do if we want to loop over two iterables? This? ###Code numbers = [1, 2, 3] vowels = "aeiou" for item in numbers: print(item) for item in vowels: print(item) ###Output 1 2 3 a e i o u ###Markdown There must be a better way — as [Raymond Hettinger always reminds us](https://youtu.be/wf-BqAjZb8M?t=23m7s). `itertools.chain()`- Make an iterator returning elements from the first iterable...- ... then proceed to the next iterable...- ... and so on until all of the iterables are exhausted. ###Code numbers = [1, 2, 3] vowels = "aeiou" for item in itertools.chain(numbers, vowels): print(item) ###Output 1 2 3 a e i o u ###Markdown So going back to what we wanted to do... ###Code up = range(1, 11) down = reversed(range(2, 10)) numbers = itertools.cycle(itertools.chain(up, down)) list(itertools.islice(numbers, 25)) ###Output _____no_output_____ ###Markdown Doing it lazilyAnd the other way around? What it we have our iterables already in a list? ###Code words = "Past glories are poor feeding".split() # ― Isaac Asimov print(words) ###Output ['Past', 'glories', 'are', 'poor', 'feeding'] ###Markdown We want to loop other the letters of all the words. I'll use `chain()` then ###Code for letter in itertools.chain(words): print(letter) ###Output Past glories are poor feeding ###Markdown It doesn't work! `chain()` iterates over the strings of the single iterable (the list) it receives. What we want is to chain the letters in each word — so each word will need to be an input argument. Unpacking Arguments- Here's where we would normally use argument unpacking.- From list or tuple to separate positional arguments...- ... using the `` operator to unpack the arguments out. ###Code def add(x, y): return x + y values = [2, 3] # Works, but terribly ugly add(values[0], values[1]) # values[0] becomes the first positional argument... # ... and values[1] becomes the second one. add(values) ###Output _____no_output_____ ###Markdown Unpacking our words ###Code words = "Past glories are poor feeding".split() # ― Isaac Asimov letters = itertools.chain(words) # notice the list(itertools.islice(letters, 15)) ###Output _____no_output_____ ###Markdown Works! But — Intertwining iterators ###Code squares = (x 2 for x in range(2, 100000000)) # 1e8 sep = itertools.cycle(["->"]) powers = zip(squares, sep) print(next(powers)) # (4, '->') print(next(powers)) # (9, '->') print(next(powers)) # (16, '->') ###Output (4, '->') (9, '->') (16, '->') ###Markdown How do we chain these values? That is: $4 \rightarrow 9 \rightarrow 16 \rightarrow$... Do we... unpack it, as we just said? ###Code squares = (x 2 for x in range(2, 100000000)) # 1e8 sep = itertools.cycle(["->"]) powers = zip(squares, sep) it = itertools.chain(powers) # unpacks 1e8 arguments ###Output _____no_output_____ ###Markdown Blood, toil, tears, and sweat ensue. `itertools.chain.from_iterable()`- Alternate constructor for `chain()`- Chained inputs from a single iterable argument...- ... that is evaluated lazily. ###Code numbers = [1, 2, 3] vowels = "aeiou" things = [numbers, vowels] # Instead of chain() + argument unpacking for item in itertools.chain.from_iterable(things): print(item) ###Output 1 2 3 a e i o u ###Markdown Since the evaluation is lazy, we could even chain an infinite* number of iterables. ###Code squares = (x ** 2 for x in range(2, 100000000)) # 1e8 sep = itertools.cycle(["->"]) powers = zip(squares, sep) it = itertools.chain.from_iterable(powers) # doesn't explode list(itertools.islice(it, 10)) # just the first ten elements ###Output _____no_output_____ ###Markdown [Photo](https://commons.wikimedia.org/wiki/File:Steven_ho_about.jpg) by Jane Davees / [CC BY 3.0](https://creativecommons.org/licenses/by/3.0/) Rolling dicesIf we roll two six-sided dices, how many unique combinations are there? ###Code def product(first, second): """A generator of the Cartesian product of two iterables.""" for x in first: for y in second: yield (x, y) dice = range(1, 7) pairs = list(product(dice, dice)) pairs[:8] # set() needed because (1, 3) is the same result as (3, 1) len(set(pairs)) ###Output _____no_output_____ ###Markdown What if it's three dices? Three (or more) dicesWe need to generalize our solution. For example, via recursion: ###Code def product(args): """A generator of the Cartesian product of multiple iterables.""" # Base case if not args: yield () return for element in args[0]: for subproduct in product(args[1:]): yield (element,) + subproduct dice = range(1, 7) triplets = product(dice, dice, dice) for x in itertools.islice(triplets, 7): print(x) ###Output (1, 1, 1) (1, 1, 2) (1, 1, 3) (1, 1, 4) (1, 1, 5) (1, 1, 6) (1, 2, 1) ###Markdown `itertools.product()`- Make an iterator returning the Cartesian product of the input iterables.- Cycles with the rightmost element advancing on every iteration.- To compute the product of an iterable with itself, we use `repeat`. ###Code g = itertools.product([1, 2], "ab") print(g) for pair in g: print(pair) ###Output (1, 'a') (1, 'b') (2, 'a') (2, 'b') ###Markdown `repeat` keyword argumentInstead of writing several times the same input iterable: ###Code dice = range(1, 7) pairs = itertools.product(dice, repeat=2) for pair in itertools.islice(pairs, 10): print(pair) ###Output (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) (2, 1) (2, 2) (2, 3) (2, 4) ###Markdown An easy questionIf we roll four six-sided dices, in how many outcomes they add up to 5? ###Code results = itertools.product(range(1, 7), repeat=4) results = filter(lambda x: sum(x) == 5, results) for x in results: print(x) ###Output (1, 1, 1, 2) (1, 1, 2, 1) (1, 2, 1, 1) (2, 1, 1, 1) ###Markdown That is — we need a $2$ in one dice and $1$ in the other three. PixelsLet's say we need to work with pixels — lots of them! ###Code class Pixel(object): def __init__(self, row, column): self.row = row self.column = column def __repr__(self): """Return a nicely formatted representation string.""" return "Pixel(row={}, column={})".format(self.row, self.column) p = Pixel(2, 3) print(p) ###Output Pixel(row=2, column=3) ###Markdown [`collections.namedtuple()`](https://docs.python.org/3/library/collections.htmlcollections.namedtuple)- Factory function for creating tuple subclasses with named fields.- Makes our live much easier if we don't need our class to be mutable...- ... because we get `__init__()`, `__repr__()` and others for free.- We can add our own methods via inheritance. ###Code Pixel = collections.namedtuple("Pixel", "row, column") ###Output _____no_output_____ ###Markdown That's all. ###Code p = Pixel(5, 1) print(p) ###Output Pixel(row=5, column=1) ###Markdown Adding a methodTo compute the distance between two points: ###Code class Pixel(collections.namedtuple("Pixel", "row, column")): def distance(self, other): """Return the Euclidean distance between two picels.""" delta_x = self.row - other.row delta_y = self.column - other.column return math.sqrt(delta_x 2 + delta_y 2) p1 = Pixel(2, 3) p2 = Pixel(5, 1) print("Distance:", p1.distance(p2), "pixels") ###Output Distance: 3.605551275463989 pixels ###Markdown Getting the neighborsLet's add a method to get the eight neighbors, lateral and diagonal: Naive version: ###Code class Pixel(collections.namedtuple("Pixel", "row, column")): def neighbours(self): """Return a generator of the eight neighbours of the Pixel.""" yield Pixel(self.row - 1, self.column - 1) yield Pixel(self.row - 1, self.column ) yield Pixel(self.row - 1, self.column + 1) yield Pixel(self.row , self.column - 1) yield Pixel(self.row , self.column + 1) yield Pixel(self.row + 1, self.column - 1) yield Pixel(self.row + 1, self.column ) yield Pixel(self.row + 1, self.column + 1) ###Output _____no_output_____ ###Markdown That's a lot of code. Kung Fu version ###Code class Pixel(collections.namedtuple("Pixel", "row column")): def neighbours(self): """Return a generator of the eight neighbours of the Pixel.""" for x_delta, y_delta in itertools.product([-1, 0, 1], repeat=2): if x_delta or y_delta: # ignore delta (0, 0) yield Pixel(self.row + x_delta, self.column + y_delta) for p in Pixel(3, 4).neighbours(): print(p) ###Output Pixel(row=2, column=3) Pixel(row=2, column=4) Pixel(row=2, column=5) Pixel(row=3, column=3) Pixel(row=3, column=5) Pixel(row=4, column=3) Pixel(row=4, column=4) Pixel(row=4, column=5) ###Markdown Kung Fu Master versionDon't hardcode the class name. ###Code class Pixel(collections.namedtuple("Pixel", "row column")): def neighbours(self): """Return a generator of the eight neighbours of the Pixel.""" cls = type(self) # we can use now 'cls' to create new objects for x_delta, y_delta in itertools.product([-1, 0, 1], repeat=2): if x_delta or y_delta: # ignore delta (0, 0) yield cls(self.row + x_delta, self.column + y_delta) for p in Pixel(4, 7).neighbours(): print(p) ###Output Pixel(row=3, column=6) Pixel(row=3, column=7) Pixel(row=3, column=8) Pixel(row=4, column=6) Pixel(row=4, column=8) Pixel(row=5, column=6) Pixel(row=5, column=7) Pixel(row=5, column=8)
provider/docs/tutorial/notebooks/01-register-features.ipynb	###Markdown Copyright (c) Microsoft Corporation.Licensed under the MIT license. Feast Azure Provider Tutorial: Register FeaturesIn this notebook you will connect to your feature store and register features into a central repository hosted on Azure Blob Storage. It should be noted that best practice for registering features would be through a CI/CD process e.g. GitHub Actions, or Azure DevOps. Configure Feature RepoThe cell below connects to your feature store. __You need to update the feature_repo/feature_store.yaml file so that the registry path points to your blob location__ ###Code import os from feast import FeatureStore from azureml.core import Workspace # access key vault to get secrets ws = Workspace.from_config() kv = ws.get_default_keyvault() # update with your connection string os.environ['SQL_CONN']=kv.get_secret("FEAST-SQL-CONN") os.environ['REDIS_CONN']=kv.get_secret("FEAST-REDIS-CONN") # connect to feature store fs = FeatureStore("./feature_repo") ###Output _____no_output_____ ###Markdown Define the data source (offline store)The data source refers to raw underlying data (a table in Azure SQL DB or Synapse SQL). Feast uses a time-series data model to represent data. This data model is used to interpret feature data in data sources in order to build training datasets or when materializing features into an online store. ###Code from feast_azure_provider.mssqlserver_source import MsSqlServerSource orders_table = "orders" driver_hourly_table = "driver_hourly" customer_profile_table = "customer_profile" driver_source = MsSqlServerSource( table_ref=driver_hourly_table, event_timestamp_column="datetime", created_timestamp_column="created", ) customer_source = MsSqlServerSource( table_ref=customer_profile_table, event_timestamp_column="datetime", created_timestamp_column="", ) ###Output _____no_output_____ ###Markdown Define Feature ViewsA feature view is an object that represents a logical group of time-series feature data as it is found in a data source. Feature views consist of one or more entities, features, and a data source. Feature views allow Feast to model your existing feature data in a consistent way in both an offline (training) and online (serving) environment.Feature views are used during:- The generation of training datasets by querying the data source of feature views in order to find historical feature values. A single training dataset may consist of features from multiple feature views. - Loading of feature values into an online store. Feature views determine the storage schema in the online store.- Retrieval of features from the online store. Feature views provide the schema definition to Feast in order to look up features from the online store.__NOTE: Feast does not generate feature values. It acts as the ingestion and serving system. The data sources described within feature views should reference feature values in their already computed form.__ ###Code from feast import Feature, FeatureView, ValueType from datetime import timedelta driver_fv = FeatureView( name="driver_stats", entities=["driver"], features=[ Feature(name="conv_rate", dtype=ValueType.FLOAT), Feature(name="acc_rate", dtype=ValueType.FLOAT), Feature(name="avg_daily_trips", dtype=ValueType.INT32), ], batch_source=driver_source, ttl=timedelta(hours=2), ) customer_fv = FeatureView( name="customer_profile", entities=["customer_id"], features=[ Feature(name="current_balance", dtype=ValueType.FLOAT), Feature(name="avg_passenger_count", dtype=ValueType.FLOAT), Feature(name="lifetime_trip_count", dtype=ValueType.INT32), ], batch_source=customer_source, ttl=timedelta(days=2), ) ###Output _____no_output_____ ###Markdown Define entitiesAn entity is a collection of semantically related features. Users define entities to map to the domain of their use case. For example, a ride-hailing service could have customers and drivers as their entities, which group related features that correspond to these customers and drivers.Entities are defined as part of feature views. Entities are used to identify the primary key on which feature values should be stored and retrieved. These keys are used during the lookup of feature values from the online store and the join process in point-in-time joins. It is possible to define composite entities (more than one entity object) in a feature view.Entities should be reused across feature views. Entity keyA related concept is an entity key. These are one or more entity values that uniquely describe a feature view record. In the case of an entity (like a driver) that only has a single entity field, the entity is an entity key. However, it is also possible for an entity key to consist of multiple entity values. For example, a feature view with the composite entity of (customer, country) might have an entity key of (1001, 5).Entity keys act as primary keys. They are used during the lookup of features from the online store, and they are also used to match feature rows across feature views during point-in-time joins. ###Code from feast import Entity driver = Entity(name="driver", join_key="driver_id", value_type=ValueType.INT64) customer = Entity(name="customer_id", value_type=ValueType.INT64) ###Output _____no_output_____ ###Markdown Feast `apply()`Feast `apply` will:1. Feast will scan Python files in your feature repository and find all Feast object definitions, such as feature views, entities, and data sources.1. Feast will validate your feature definitions1. Feast will sync the metadata about Feast objects to the registry. If a registry does not exist, then it will be instantiated. The standard registry is a simple protobuf binary file that is stored on Azure Blob Storage.1. Feast CLI will create all necessary feature store infrastructure. The exact infrastructure that is deployed or configured depends on the provider configuration that you have set in feature_store.yaml. ###Code fs.apply([driver, driver_fv, customer, customer_fv]) ###Output _____no_output_____ ###Markdown Copyright (c) Microsoft Corporation.Licensed under the MIT license. Feast Azure Provider Tutorial: Register FeaturesIn this notebook you will connect to your feature store and register features into a central repository hosted on Azure Blob Storage. It should be noted that best practice for registering features would be through a CI/CD process e.g. GitHub Actions, or Azure DevOps. Configure Feature RepoThe cell below connects to your feature store. The `registry_blob_url` should point to the location on blob where you want your feature repsository to be stored. ###Code from feast import FeatureStore, RepoConfig from feast.registry import RegistryConfig from feast_azure_provider.mssqlserver import MsSqlServerOfflineStoreConfig from feast.infra.online_stores.redis import RedisOnlineStoreConfig from azureml.core import Workspace # update this to your location on blob registry_blob_url = "https://<ACCOUNT_NAME>.blob.core.windows.net/<CONTAINER>/<PATH>/registry.db" # access key vault to get secrets ws = Workspace.from_config() kv = ws.get_default_keyvault() # update with your connection string offline_conn_str = kv.get_secret("FEAST-SQL-CONN") online_conn_str = kv.get_secret("FEAST-REDIS-CONN") # set RegistryConfig reg_config = RegistryConfig( registry_store_type="feast_azure_provider.registry_store.AzBlobRegistryStore", path=registry_blob_url, ) # set RepoConfig repo_cfg = RepoConfig( registry=reg_config, project="production", provider="feast_azure_provider.azure_provider.AzureProvider", offline_store=MsSqlServerOfflineStoreConfig(connection_string=offline_conn_str), online_store=RedisOnlineStoreConfig(connection_string=online_conn_str), ) # connect to feature store store = FeatureStore(config=repo_cfg) ###Output _____no_output_____ ###Markdown Define the data source (offline store)The data source refers to raw underlying data (a table in Azure SQL DB or Synapse SQL). Feast uses a time-series data model to represent data. This data model is used to interpret feature data in data sources in order to build training datasets or when materializing features into an online store. ###Code from feast_azure_provider.mssqlserver_source import MsSqlServerSource orders_table = "orders" driver_hourly_table = "driver_hourly" customer_profile_table = "customer_profile" driver_source = MsSqlServerSource( table_ref=driver_hourly_table, event_timestamp_column="datetime", created_timestamp_column="created", ) customer_source = MsSqlServerSource( table_ref=customer_profile_table, event_timestamp_column="datetime", created_timestamp_column="", ) ###Output _____no_output_____ ###Markdown Define Feature ViewsA feature view is an object that represents a logical group of time-series feature data as it is found in a data source. Feature views consist of one or more entities, features, and a data source. Feature views allow Feast to model your existing feature data in a consistent way in both an offline (training) and online (serving) environment.Feature views are used during:- The generation of training datasets by querying the data source of feature views in order to find historical feature values. A single training dataset may consist of features from multiple feature views. - Loading of feature values into an online store. Feature views determine the storage schema in the online store.- Retrieval of features from the online store. Feature views provide the schema definition to Feast in order to look up features from the online store.__NOTE: Feast does not generate feature values. It acts as the ingestion and serving system. The data sources described within feature views should reference feature values in their already computed form.__ ###Code from feast import Feature, FeatureView, ValueType from datetime import timedelta driver_fv = FeatureView( name="driver_stats", entities=["driver"], features=[ Feature(name="conv_rate", dtype=ValueType.FLOAT), Feature(name="acc_rate", dtype=ValueType.FLOAT), Feature(name="avg_daily_trips", dtype=ValueType.INT32), ], batch_source=driver_source, ttl=timedelta(hours=2), ) customer_fv = FeatureView( name="customer_profile", entities=["customer_id"], features=[ Feature(name="current_balance", dtype=ValueType.FLOAT), Feature(name="avg_passenger_count", dtype=ValueType.FLOAT), Feature(name="lifetime_trip_count", dtype=ValueType.INT32), ], batch_source=customer_source, ttl=timedelta(days=2), ) ###Output _____no_output_____ ###Markdown Define entitiesAn entity is a collection of semantically related features. Users define entities to map to the domain of their use case. For example, a ride-hailing service could have customers and drivers as their entities, which group related features that correspond to these customers and drivers.Entities are defined as part of feature views. Entities are used to identify the primary key on which feature values should be stored and retrieved. These keys are used during the lookup of feature values from the online store and the join process in point-in-time joins. It is possible to define composite entities (more than one entity object) in a feature view.Entities should be reused across feature views. Entity keyA related concept is an entity key. These are one or more entity values that uniquely describe a feature view record. In the case of an entity (like a driver) that only has a single entity field, the entity is an entity key. However, it is also possible for an entity key to consist of multiple entity values. For example, a feature view with the composite entity of (customer, country) might have an entity key of (1001, 5).Entity keys act as primary keys. They are used during the lookup of features from the online store, and they are also used to match feature rows across feature views during point-in-time joins. ###Code from feast import Entity driver = Entity(name="driver", join_key="driver_id", value_type=ValueType.INT64) customer = Entity(name="customer_id", value_type=ValueType.INT64) ###Output _____no_output_____ ###Markdown Feast `apply()`Feast `apply` will:1. Feast will scan Python files in your feature repository and find all Feast object definitions, such as feature views, entities, and data sources.1. Feast will validate your feature definitions1. Feast will sync the metadata about Feast objects to the registry. If a registry does not exist, then it will be instantiated. The standard registry is a simple protobuf binary file that is stored on Azure Blob Storage.1. Feast CLI will create all necessary feature store infrastructure. The exact infrastructure that is deployed or configured depends on the provider configuration that you have set in feature_store.yaml. ###Code store.apply([driver, driver_fv, customer, customer_fv]) ###Output _____no_output_____
TypeDataStructures/Nesting Dictionary.ipynb	###Markdown Nesting Dictionary ###Code Y1 ={ 'bb':11} Y10 = {'hhh':555} Y7 = { 'ff':44, 'gg': Y10} Y = {'a': Y1, 'c':2, 'd':3, 'e': Y7 } print(Y) ###Output {'a': {'bb': 11}, 'd': 3, 'e': {'gg': {'hhh': 555}, 'ff': 44}, 'c': 2}
misc/day44_querying_database.ipynb	###Markdown Questions to answer- What kind of projects are popular on Kickstarter?- How much are people asking for?- What kind of projects tend to be more funded? Connect to database ###Code dbname="kick" tblname="info" engine = create_engine( 'postgresql://localhost:5432/{dbname}'.format(dbname=dbname)) # Connect to database conn = psycopg2.connect(dbname=dbname) cur = conn.cursor() ###Output _____no_output_____ ###Markdown Remind myself of the columns in the table: ###Code cur.execute("SELECT column_name,data_type FROM information_schema.columns WHERE table_name = '{table}';".format(table=tblname)) rows = cur.fetchall() pd.DataFrame(rows, columns=["column_name", "data_type"]) ###Output _____no_output_____ ###Markdown Number of records in table: ###Code cur.execute("SELECT COUNT() from {table}".format(table=tblname)) cur.fetchone() ###Output _____no_output_____ ###Markdown --- Question 1: Project topics- How many different types of projects are on Kickstarter?- What is most popular?- What is most rare? ###Code cur.execute("SELECT topic, COUNT() from {table} GROUP BY topic ORDER BY count DESC;".format(table=tblname)) rows = cur.fetchall() df = pd.DataFrame(rows, columns=["topic", "count"]) # Plot findings plt.rcParams["figure.figsize"] = [17,5] df.plot(kind="bar", x="topic", y="count", legend=False) plt.ylabel("Kickstarter projects") plt.xlabel("Topic") plt.title("Kickstarter projects by topic") plt.tick_params(axis='x', labelsize=7) "There are {num_topics} different types of Kickstarter projects".format(num_topics=df.shape[0]) # Most popular project topic is df[df["count"] == df["count"].max()] # Most rare project topic is df[df["count"] == df["count"].min()] ###Output _____no_output_____ ###Markdown What are the rare projects? ###Code cur.execute("SELECT id, blurb, goalstatic_usd_rate as goal_usd FROM {table} WHERE topic = '{topic}'".format(table=tblname, topic="Taxidermy")) rows = cur.fetchall() for row in rows: row_id, blurb, goal = row print(">>> $%d \| id: %s" % (goal, row_id), blurb, sep="\n") ###Output >>> $8319 \| id: 2009417734 Master prop maker and creator of the dead fairy hoax that captured the world’s imagination invites you into his studio to reveal all! >>> $4300 \| id: 874566085 Gallery \| Public Dissections \| Events \| A space in downtown San Francisco to reflect upon the less considered means of living & dying. >>> $5000 \| id: 304809544 TaxiClear transforms biology into brilliant works of art that illustrate the beauty and complexity of life >>> $500 \| id: 1111529080 Insects: the most abundant and intriguing organisms on Earth. May be seen as pests but are works of art that I will add to wreaths. >>> $3000 \| id: 48529158 I take my passion for leather working and create hand carved notebook covers to honor a person's legacy and career accomplishments. >>> $2000 \| id: 588593322 Casting skulls from rare and unique species of animal. To include miniature skulls in the future. >>> $705 \| id: 1539840572 The "Meteor Grip" ergonomic craft, taxidermy knife fro precise accurate cutting. This hand specific design is a leader in grip design. >>> $456 \| id: 1450117214 Creating beautiful and unique statement pieces with the use of taxidermy, skulls and ornate frames. >>> $15450 \| id: 1370425060 Bringing art and science together through hand made ethically sourced bone jewellery and art sculptures >>> $5464 \| id: 1052896826 A new and creative way to display the beauty of ocean,swamp and land creatures of the world by electroless silver plating. >>> $7208 \| id: 1208011665 Hollow Earth is slated to be Perth's 1st true Oddity/Collectables store. Selling anything from hand-made trinkets to occult items. >>> $250000 \| id: 1984141754 I want to go into the wilds to find and subsequently kill sasquatch. Donors will be sent a small piece of his hide if I succeed. ###Markdown Question 2: Project funding goals- How much are people asking for in general? by topics? ###Code sql = "SELECT id, topic, goalstatic_usd_rate as goal_usd FROM {table}".format(table=tblname) cur.execute(sql) rows = cur.fetchall() df = pd.DataFrame(rows, columns=["id", "topic", "goal_usd"]) # Asking average np.log10(df.goal_usd).plot.kde() plt.xlabel("log(funding goal in USD)") "Most projects are asking for: $%d - $%d" % (102.5, 105) sns.barplot(x="topic", y="goal_usd", data=df.groupby("topic").mean().reset_index().sort_values(by="goal_usd", ascending=False)) _ = plt.xticks(rotation='vertical') plt.ylabel("Average goal (USD)") plt.xlabel("Kickstarter project topic") plt.title("Funding goals on Kickstarter by topic") plt.tick_params(axis='x', labelsize=7) ###Output _____no_output_____ ###Markdown "Movie Theaters" and "Space exploration" have the average higest funding goals Question 3: Funding successWhat tends to get funded? ###Code sql = "SELECT id, topic, goal, pledged, pledged/goal as progress FROM info ORDER BY progress DESC;" cur.execute(sql) rows = cur.fetchall() df = pd.DataFrame(rows, columns=["id", "topic", "goal", "pledged", "progress"]) df["well_funded"] = df.progress >= 1 plt.rcParams["figure.figsize"] = [17,5] sns.boxplot(x="topic", y="progress", data=df[df.well_funded].sort_values(by="topic")) _ = plt.xticks(rotation='vertical') plt.yscale('log') plt.ylabel("Percent of funding goal") plt.xlabel("Topic") plt.title("Projects that were successfully funded by Topic") plt.tick_params(axis='x', labelsize=7) sns.barplot(x="topic", y="progress", data=df[df.well_funded].groupby("topic").count().reset_index().sort_values(by="progress", ascending=False)) _ = plt.xticks(rotation='vertical') plt.ylabel("Project that were successfully funded") plt.xlabel("Topic") plt.title("Projects that were successfully funded by Topic") plt.tick_params(axis='x', labelsize=7) plt.rcParams["figure.figsize"] = [17,5] sns.boxplot(x="topic", y="progress", data=df[np.invert(df.well_funded)].sort_values(by="topic")) _ = plt.xticks(rotation='vertical') plt.ylabel("Percent of funding goal met") plt.xlabel("Topic") plt.title("Pojects that have yet to meet their funding goals") plt.tick_params(axis='x', labelsize=7) sns.barplot(x="topic", y="progress", data=df[np.invert(df.well_funded)].groupby("topic").count().reset_index().sort_values(by="progress", ascending=False)) _ = plt.xticks(rotation='vertical') plt.ylabel("Project that were not yet successfully funded") plt.xlabel("Topic") plt.title("Pojects that have yet to meet their funding goals") plt.tick_params(axis='x', labelsize=7) ###Output _____no_output_____ ###Markdown Close connection ###Code # close communication with the PostgreSQL database server cur.close() # commit the changes conn.commit() # close connection conn.close() ###Output _____no_output_____

Subsets and Splits

No community queries yet

The top public SQL queries from the community will appear here once available.