licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 11379 | @testset "Lanczos - eigsolve full ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n)) .- one(T) / 2
A = (A + A') / 2
v = rand(T, (n,))
n1 = div(n, 2)
D1, V1, info = @test_logs (:info,) eigsolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), n1, :SR;
krylovdim=n,
maxiter=1, tol=tolerance(T),
verbosity=1)
@test KrylovKit.eigselector(wrapop(A, Val(mode)), scalartype(v); krylovdim=n,
maxiter=1,
tol=tolerance(T), ishermitian=true) isa Lanczos
n2 = n - n1
alg = Lanczos(; krylovdim=2 * n, maxiter=1, tol=tolerance(T))
D2, V2, info = @constinferred eigsolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)),
n2, :LR, alg)
@test vcat(D1[1:n1], reverse(D2[1:n2])) ≊ eigvals(A)
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test U1' * U1 ≈ I
@test U2' * U2 ≈ I
@test A * U1 ≈ U1 * Diagonal(D1)
@test A * U2 ≈ U2 * Diagonal(D2)
@test_logs (:warn,) eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n + 1,
:LM;
krylovdim=2n,
maxiter=1, tol=tolerance(T), verbosity=0)
end
end
end
@testset "Lanczos - eigsolve iteratively ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (N, N)) .- one(T) / 2
A = (A + A') / 2
v = rand(T, (N,))
alg = Lanczos(; krylovdim=2 * n, maxiter=10,
tol=tolerance(T), eager=true)
D1, V1, info1 = @constinferred eigsolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), n, :SR, alg)
D2, V2, info2 = eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n, :LR,
alg)
l1 = info1.converged
l2 = info2.converged
@test l1 > 0
@test l2 > 0
@test D1[1:l1] ≈ eigvals(A)[1:l1]
@test D2[1:l2] ≈ eigvals(A)[N:-1:(N - l2 + 1)]
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test U1' * U1 ≈ I
@test U2' * U2 ≈ I
R1 = stack(unwrapvec, info1.residual)
R2 = stack(unwrapvec, info2.residual)
@test A * U1 ≈ U1 * Diagonal(D1) + R1
@test A * U2 ≈ U2 * Diagonal(D2) + R2
end
end
end
@testset "Arnoldi - eigsolve full ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n)) .- one(T) / 2
v = rand(T, (n,))
n1 = div(n, 2)
D1, V1, info1 = @test_logs (:info,) eigsolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), n1, :SR;
orth=orth, krylovdim=n,
maxiter=1, tol=tolerance(T),
verbosity=1)
@test KrylovKit.eigselector(wrapop(A, Val(mode)), eltype(v); orth=orth,
krylovdim=n, maxiter=1,
tol=tolerance(T)) isa Arnoldi
n2 = n - n1
alg = Arnoldi(; orth=orth, krylovdim=2 * n, maxiter=1, tol=tolerance(T))
D2, V2, info2 = @constinferred eigsolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), n2, :LR, alg)
D = sort(sort(eigvals(A); by=imag, rev=true); alg=MergeSort, by=real)
D2′ = sort(sort(D2; by=imag, rev=true); alg=MergeSort, by=real)
@test vcat(D1[1:n1], D2′[(end - n2 + 1):end]) ≈ D
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test A * U1 ≈ U1 * Diagonal(D1)
@test A * U2 ≈ U2 * Diagonal(D2)
if T <: Complex
n1 = div(n, 2)
D1, V1, info = eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n1,
:SI,
alg)
n2 = n - n1
D2, V2, info = eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n2,
:LI,
alg)
D = sort(eigvals(A); by=imag)
@test vcat(D1[1:n1], reverse(D2[1:n2])) ≊ D
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test A * U1 ≈ U1 * Diagonal(D1)
@test A * U2 ≈ U2 * Diagonal(D2)
end
@test_logs (:warn,) eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n + 1,
:LM; orth=orth,
krylovdim=2n,
maxiter=1, tol=tolerance(T), verbosity=0)
end
end
end
@testset "Arnoldi - eigsolve iteratively ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (N, N)) .- one(T) / 2
v = rand(T, (N,))
alg = Arnoldi(; krylovdim=3 * n, maxiter=20,
tol=tolerance(T), eager=true)
D1, V1, info1 = @constinferred eigsolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), n, :SR, alg)
D2, V2, info2 = eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n, :LR,
alg)
D3, V3, info3 = eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n, :LM,
alg)
D = sort(eigvals(A); by=imag, rev=true)
l1 = info1.converged
l2 = info2.converged
l3 = info3.converged
@test l1 > 0
@test l2 > 0
@test l3 > 0
@test D1[1:l1] ≊ sort(D; alg=MergeSort, by=real)[1:l1]
@test D2[1:l2] ≊ sort(D; alg=MergeSort, by=real, rev=true)[1:l2]
# sorting by abs does not seem very reliable if two distinct eigenvalues are close
# in absolute value, so we perform a second sort afterwards using the real part
@test D3[1:l3] ≊ sort(D; by=abs, rev=true)[1:l3]
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
U3 = stack(unwrapvec, V3)
R1 = stack(unwrapvec, info1.residual)
R2 = stack(unwrapvec, info2.residual)
R3 = stack(unwrapvec, info3.residual)
@test A * U1 ≈ U1 * Diagonal(D1) + R1
@test A * U2 ≈ U2 * Diagonal(D2) + R2
@test A * U3 ≈ U3 * Diagonal(D3) + R3
if T <: Complex
D1, V1, info1 = eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n,
:SI, alg)
D2, V2, info2 = eigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n,
:LI, alg)
D = eigvals(A)
l1 = info1.converged
l2 = info2.converged
@test l1 > 0
@test l2 > 0
@test D1[1:l1] ≈ sort(D; by=imag)[1:l1]
@test D2[1:l2] ≈ sort(D; by=imag, rev=true)[1:l2]
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
R1 = stack(unwrapvec, info1.residual)
R2 = stack(unwrapvec, info2.residual)
@test A * U1 ≈ U1 * Diagonal(D1) + R1
@test A * U2 ≈ U2 * Diagonal(D2) + R2
end
end
end
end
@testset "Arnoldi - realeigsolve iteratively ($mode)" for mode in
(:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64) : (Float64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
V = exp(randn(T, (N, N)) / 10)
D = randn(T, N)
A = V * Diagonal(D) / V
v = rand(T, (N,))
alg = Arnoldi(; krylovdim=3 * n, maxiter=20,
tol=tolerance(T), eager=true)
D1, V1, info1 = @constinferred realeigsolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), n, :SR, alg)
D2, V2, info2 = realeigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n,
:LR,
alg)
D3, V3, info3 = realeigsolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n,
:LM,
alg)
l1 = info1.converged
l2 = info2.converged
l3 = info3.converged
@test l1 > 0
@test l2 > 0
@test l3 > 0
@test D1[1:l1] ≊ sort(D; alg=MergeSort)[1:l1]
@test D2[1:l2] ≊ sort(D; alg=MergeSort, rev=true)[1:l2]
# sorting by abs does not seem very reliable if two distinct eigenvalues are close
# in absolute value, so we perform a second sort afterwards using the real part
@test D3[1:l3] ≊ sort(D; by=abs, rev=true)[1:l3]
@test eltype(D1) == T
@test eltype(D2) == T
@test eltype(D3) == T
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
U3 = stack(unwrapvec, V3)
R1 = stack(unwrapvec, info1.residual)
R2 = stack(unwrapvec, info2.residual)
R3 = stack(unwrapvec, info3.residual)
@test A * U1 ≈ U1 * Diagonal(D1) + R1
@test A * U2 ≈ U2 * Diagonal(D2) + R2
@test A * U3 ≈ U3 * Diagonal(D3) + R3
end
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 8447 | function ϕ(A, v, p)
m = LinearAlgebra.checksquare(A)
length(v) == m ||
throw(DimensionMismatch("second dimension of A, $m, does not match length of x, $(length(v))"))
p == 0 && return exp(A) * v
A′ = fill!(similar(A, m + p, m + p), 0)
copyto!(view(A′, 1:m, 1:m), A)
copyto!(view(A′, 1:m, m + 1), v)
for k in 1:(p - 1)
A′[m + k, m + k + 1] = 1
end
return exp(A′)[1:m, end]
end
@testset "Lanczos - expintegrator full ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n)) .- one(T) / 2
A = (A + A') / 2
V = one(A)
W = zero(A)
alg = Lanczos(; orth=orth, krylovdim=n, maxiter=2, tol=tolerance(T),
verbosity=2)
for k in 1:n
w, = @test_logs (:info,) (:info,) exponentiate(wrapop(A, Val(mode)), 1,
wrapvec(view(V, :, k),
Val(mode)), alg)
W[:, k] = unwrapvec(w)
end
@test W ≈ exp(A)
pmax = 5
alg = Lanczos(; orth=orth, krylovdim=n, maxiter=2, tol=tolerance(T),
verbosity=0)
for t in (rand(real(T)), -rand(real(T)), im * randn(real(T)),
randn(real(T)) + im * randn(real(T)))
for p in 1:pmax
u = ntuple(i -> rand(T, n), p + 1)
w, info = @constinferred expintegrator(wrapop(A, Val(mode)), t,
wrapvec.(u, Ref(Val(mode))), alg)
w2 = exp(t * A) * u[1]
for j in 1:p
w2 .+= t^j * ϕ(t * A, u[j + 1], j)
end
@test info.converged > 0
@test w2 ≈ unwrapvec(w)
end
end
end
end
end
@testset "Arnoldi - expintegrator full ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n)) .- one(T) / 2
V = one(A)
W = zero(A)
alg = Arnoldi(; orth=orth, krylovdim=n, maxiter=2, tol=tolerance(T),
verbosity=2)
for k in 1:n
w, = @test_logs (:info,) (:info,) exponentiate(wrapop(A, Val(mode)), 1,
wrapvec(view(V, :, k),
Val(mode)), alg)
W[:, k] = unwrapvec(w)
end
@test W ≈ exp(A)
pmax = 5
alg = Arnoldi(; orth=orth, krylovdim=n, maxiter=2, tol=tolerance(T),
verbosity=0)
for t in (rand(real(T)), -rand(real(T)), im * randn(real(T)),
randn(real(T)) + im * randn(real(T)))
for p in 1:pmax
u = ntuple(i -> rand(T, n), p + 1)
w, info = @constinferred expintegrator(wrapop(A, Val(mode)), t,
wrapvec.(u, Ref(Val(mode))), alg)
w2 = exp(t * A) * u[1]
for j in 1:p
w2 .+= t^j * ϕ(t * A, u[j + 1], j)
end
@test info.converged > 0
@test w2 ≈ unwrapvec(w)
end
end
end
end
end
@testset "Lanczos - expintegrator iteratively ($mode)" for mode in
(:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (N, N)) .- one(T) / 2
A = (A + A') / 2
s = norm(eigvals(A), 1)
rmul!(A, 1 / (10 * s))
pmax = 5
for t in (rand(real(T)), -rand(real(T)), im * randn(real(T)),
randn(real(T)) + im * randn(real(T)))
for p in 1:pmax
u = ntuple(i -> rand(T, N), p + 1)
w1, info = @constinferred expintegrator(wrapop(A, Val(mode)), t,
wrapvec.(u, Ref(Val(mode)))...;
maxiter=100, krylovdim=n,
eager=true)
@assert info.converged > 0
w2 = exp(t * A) * u[1]
for j in 1:p
w2 .+= t^j * ϕ(t * A, u[j + 1], j)
end
@test w2 ≈ unwrapvec(w1)
w1, info = @constinferred expintegrator(wrapop(A, Val(mode)), t,
wrapvec.(u, Ref(Val(mode)))...;
maxiter=100, krylovdim=n,
tol=1e-3, eager=true)
@test unwrapvec(w1) ≈ w2 atol = 1e-2 * abs(t)
end
end
end
end
end
@testset "Arnoldi - expintegrator iteratively ($mode)" for mode in
(:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (N, N)) .- one(T) / 2
s = norm(eigvals(A), 1)
rmul!(A, 1 / (10 * s))
pmax = 5
for t in (rand(real(T)), -rand(real(T)), im * randn(real(T)),
randn(real(T)) + im * randn(real(T)))
for p in 1:pmax
u = ntuple(i -> rand(T, N), p + 1)
w1, info = @constinferred expintegrator(wrapop(A, Val(mode)), t,
wrapvec.(u, Ref(Val(mode)))...;
maxiter=100, krylovdim=n,
eager=true)
@test info.converged > 0
w2 = exp(t * A) * u[1]
for j in 1:p
w2 .+= t^j * ϕ(t * A, u[j + 1], j)
end
@test w2 ≈ unwrapvec(w1)
w1, info = @constinferred expintegrator(wrapop(A, Val(mode)), t,
wrapvec.(u, Ref(Val(mode)))...;
maxiter=100, krylovdim=n,
tol=1e-3, eager=true)
@test unwrapvec(w1) ≈ w2 atol = 1e-2 * abs(t)
end
end
end
end
end
@testset "Arnoldi - expintegrator fixed point branch" begin
@testset for T in (ComplexF32, ComplexF64) # less probable that :LR eig is degenerate
A = rand(T, (N, N))
v₀ = rand(T, N)
λs, vs, infoR = eigsolve(A, v₀, 1, :LR)
@test infoR.converged > 0
r = vs[1]
A = A - λs[1] * I
λs, vs, infoL = eigsolve(A', v₀, 1, :LR)
@test infoL.converged > 0
l = vs[1]
w1, info1 = expintegrator(A, 1000.0, v₀)
@test info1.converged > 0
@test abs(dot(r, w1)) / norm(r) / norm(w1) ≈ 1 atol = 1e-4
v₁ = rand(T, N)
v₁ -= r * dot(l, v₁) / dot(l, r)
w2, info2 = expintegrator(A, 1000.0, v₀, v₁)
@test info2.converged > 0
@test A * w2 ≈ -v₁
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 6780 | # Test complete Lanczos factorization
@testset "Complete Lanczos factorization ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (cgs2,)
@testset for T in scalartypes
@testset for orth in orths # tests fail miserably for cgs and mgs
A = rand(T, (n, n))
v = rand(T, (n,))
A = (A + A')
iter = LanczosIterator(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), orth)
verbosity = 3
fact = @constinferred initialize(iter; verbosity=verbosity)
@constinferred expand!(iter, fact; verbosity=verbosity)
verbosity = 1
while length(fact) < n
if verbosity == 1
@test_logs (:info,) expand!(iter, fact; verbosity=verbosity)
else
@test_logs expand!(iter, fact; verbosity=verbosity)
end
verbosity = 1 - verbosity # flipflop
end
V = stack(unwrapvec, basis(fact))
H = rayleighquotient(fact)
@test normres(fact) < 10 * n * eps(real(T))
@test V' * V ≈ I
@test A * V ≈ V * H
@constinferred initialize!(iter, deepcopy(fact); verbosity=1)
states = collect(Iterators.take(iter, n)) # collect tests size and eltype?
@test rayleighquotient(last(states)) ≈ H
end
end
end
# Test complete Arnoldi factorization
@testset "Complete Arnoldi factorization ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs, mgs, cgs2, mgs2, cgsr, mgsr) : (cgs2,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n))
v = rand(T, (n,))
iter = ArnoldiIterator(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), orth)
verbosity = 3
fact = @constinferred initialize(iter; verbosity=verbosity)
@constinferred expand!(iter, fact; verbosity=verbosity)
verbosity = 1
while length(fact) < n
if verbosity == 1
@test_logs (:info,) expand!(iter, fact; verbosity=verbosity)
else
@test_logs expand!(iter, fact; verbosity=verbosity)
end
verbosity = 1 - verbosity # flipflop
end
V = stack(unwrapvec, basis(fact))
H = rayleighquotient(fact)
factor = (orth == cgs || orth == mgs ? 250 : 10)
@test normres(fact) < factor * n * eps(real(T))
@test V' * V ≈ I
@test A * V ≈ V * H
@constinferred initialize!(iter, deepcopy(fact); verbosity=1)
states = collect(Iterators.take(iter, n)) # collect tests size and eltype?
@test rayleighquotient(last(states)) ≈ H
end
end
end
# Test incomplete Lanczos factorization
@testset "Incomplete Lanczos factorization ($mode)" for mode in
(:vector, :inplace, :outplace)
scalartypes = mode === :vector ?
(Float32, Float64, ComplexF32, ComplexF64, Complex{Int}) : (ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (cgs2,)
@testset for T in scalartypes
@testset for orth in orths # tests fail miserably for cgs and mgs
if T === Complex{Int}
A = rand(-100:100, (N, N)) + im * rand(-100:100, (N, N))
v = rand(-100:100, (N,))
else
A = rand(T, (N, N))
v = rand(T, (N,))
end
A = (A + A')
iter = @constinferred LanczosIterator(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)),
orth)
krylovdim = n
fact = @constinferred initialize(iter)
while normres(fact) > eps(float(real(T))) && length(fact) < krylovdim
@constinferred expand!(iter, fact)
Ṽ, H, r̃, β, e = fact
V = stack(unwrapvec, Ṽ)
r = unwrapvec(r̃)
@test V' * V ≈ I
@test norm(r) ≈ β
@test A * V ≈ V * H + r * e'
end
fact = @constinferred shrink!(fact, div(n, 2))
V = stack(unwrapvec, @constinferred basis(fact))
H = @constinferred rayleighquotient(fact)
r = @constinferred unwrapvec(residual(fact))
β = @constinferred normres(fact)
e = @constinferred rayleighextension(fact)
@test V' * V ≈ I
@test norm(r) ≈ β
@test A * V ≈ V * H + r * e'
end
end
end
# Test incomplete Arnoldi factorization
@testset "Incomplete Arnoldi factorization ($mode)" for mode in
(:vector, :inplace, :outplace)
scalartypes = mode === :vector ?
(Float32, Float64, ComplexF32, ComplexF64, Complex{Int}) : (ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (cgs2,)
@testset for T in scalartypes
@testset for orth in orths
if T === Complex{Int}
A = rand(-100:100, (N, N)) + im * rand(-100:100, (N, N))
v = rand(-100:100, (N,))
else
A = rand(T, (N, N))
v = rand(T, (N,))
end
iter = @constinferred ArnoldiIterator(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), orth)
krylovdim = 3 * n
fact = @constinferred initialize(iter)
while normres(fact) > eps(float(real(T))) && length(fact) < krylovdim
@constinferred expand!(iter, fact)
Ṽ, H, r̃, β, e = fact
V = stack(unwrapvec, Ṽ)
r = unwrapvec(r̃)
@test V' * V ≈ I
@test norm(r) ≈ β
@test A * V ≈ V * H + r * e'
end
fact = @constinferred shrink!(fact, div(n, 2))
V = stack(unwrapvec, @constinferred basis(fact))
H = @constinferred rayleighquotient(fact)
r = unwrapvec(@constinferred residual(fact))
β = @constinferred normres(fact)
e = @constinferred rayleighextension(fact)
@test V' * V ≈ I
@test norm(r) ≈ β
@test A * V ≈ V * H + r * e'
end
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 3973 |
@testset "GolubYe - geneigsolve full ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n)) .- one(T) / 2
A = (A + A') / 2
B = rand(T, (n, n)) .- one(T) / 2
B = sqrt(B * B')
v = rand(T, (n,))
alg = GolubYe(; orth=orth, krylovdim=n, maxiter=1, tol=tolerance(T),
verbosity=1)
n1 = div(n, 2)
D1, V1, info = @constinferred geneigsolve((wrapop(A, Val(mode)),
wrapop(B, Val(mode))),
wrapvec(v, Val(mode)),
n1, :SR; orth=orth, krylovdim=n,
maxiter=1, tol=tolerance(T),
ishermitian=true, isposdef=true,
verbosity=2)
@test KrylovKit.geneigselector((wrapop(A, Val(mode)), wrapop(B, Val(mode))),
scalartype(v); orth=orth, krylovdim=n,
maxiter=1, tol=tolerance(T), ishermitian=true,
isposdef=true) isa GolubYe
n2 = n - n1
D2, V2, info = @constinferred geneigsolve((wrapop(A, Val(mode)),
wrapop(B, Val(mode))),
wrapvec(v, Val(mode)),
n2, :LR, alg)
@test vcat(D1[1:n1], reverse(D2[1:n2])) ≈ eigvals(A, B)
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test U1' * B * U1 ≈ I
@test U2' * B * U2 ≈ I
@test A * U1 ≈ B * U1 * Diagonal(D1)
@test A * U2 ≈ B * U2 * Diagonal(D2)
end
end
end
@testset "GolubYe - geneigsolve iteratively ($mode)" for mode in
(:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float64, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (N, N)) .- one(T) / 2
A = (A + A') / 2
B = rand(T, (N, N)) .- one(T) / 2
B = sqrt(B * B')
v = rand(T, (N,))
alg = GolubYe(; orth=orth, krylovdim=3 * n, maxiter=100,
tol=cond(B) * tolerance(T))
D1, V1, info1 = @constinferred geneigsolve((wrapop(A, Val(mode)),
wrapop(B, Val(mode))),
wrapvec(v, Val(mode)),
n, :SR, alg)
D2, V2, info2 = geneigsolve((wrapop(A, Val(mode)), wrapop(B, Val(mode))),
wrapvec(v, Val(mode)), n, :LR, alg)
l1 = info1.converged
l2 = info2.converged
@test l1 > 0
@test l2 > 0
@test D1[1:l1] ≊ eigvals(A, B)[1:l1]
@test D2[1:l2] ≊ eigvals(A, B)[N:-1:(N - l2 + 1)]
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test U1' * B * U1 ≈ I
@test U2' * B * U2 ≈ I
R1 = stack(unwrapvec, info1.residual)
R2 = stack(unwrapvec, info2.residual)
@test A * U1 ≈ B * U1 * Diagonal(D1) + R1
@test A * U2 ≈ B * U2 * Diagonal(D2) + R2
end
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 3918 | # Test complete Golub-Kahan-Lanczos factorization
@testset "Complete Golub-Kahan-Lanczos factorization ($mode)" for mode in
(:vector, :inplace,
:outplace, :mixed)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n))
v = A * rand(T, (n,)) # ensure v is in column space of A
iter = GKLIterator(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), orth)
verbosity = 3
fact = @constinferred initialize(iter; verbosity=verbosity)
@constinferred expand!(iter, fact; verbosity=verbosity)
verbosity = 1
while length(fact) < n
if verbosity == 1
@test_logs (:info,) expand!(iter, fact; verbosity=verbosity)
else
@test_logs expand!(iter, fact; verbosity=verbosity)
end
verbosity = 1 - verbosity # flipflop
end
U = stack(unwrapvec, basis(fact, :U))
V = stack(unwrapvec, basis(fact, :V))
B = rayleighquotient(fact)
@test normres(fact) < 10 * n * eps(real(T))
@test U' * U ≈ I
@test V' * V ≈ I
@test A * V ≈ U * B
@test A' * U ≈ V * B'
@constinferred initialize!(iter, deepcopy(fact); verbosity=1)
states = collect(Iterators.take(iter, n)) # collect tests size and eltype?
@test rayleighquotient(last(states)) ≈ B
end
end
end
# Test incomplete Golub-Kahan-Lanczos factorization
@testset "Incomplete Golub-Kahan-Lanczos factorization ($mode)" for mode in
(:vector, :inplace,
:outplace, :mixed)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
if T == Complex{Int}
A = rand(-100:100, (N, N)) + im * rand(-100:100, (N, N))
v = rand(-100:100, (N,))
else
A = rand(T, (N, N))
v = rand(T, (N,))
end
iter = @constinferred GKLIterator(wrapop(A, Val(mode)), wrapvec(v, Val(mode)),
orth)
krylovdim = 3 * n
fact = @constinferred initialize(iter)
while normres(fact) > eps(float(real(T))) && length(fact) < krylovdim
@constinferred expand!(iter, fact)
Ũ, Ṽ, B, r̃, β, e = fact
U = stack(unwrapvec, Ũ)
V = stack(unwrapvec, Ṽ)
r = unwrapvec(r̃)
@test U' * U ≈ I
@test V' * V ≈ I
@test norm(r) ≈ β
@test A * V ≈ U * B + r * e'
@test A' * U ≈ V * B'
end
fact = @constinferred shrink!(fact, div(n, 2))
U = stack(unwrapvec, @constinferred basis(fact, :U))
V = stack(unwrapvec, @constinferred basis(fact, :V))
B = @constinferred rayleighquotient(fact)
r = unwrapvec(@constinferred residual(fact))
β = @constinferred normres(fact)
e = @constinferred rayleighextension(fact)
@test U' * U ≈ I
@test V' * V ≈ I
@test norm(r) ≈ β
@test A * V ≈ U * B + r * e'
@test A' * U ≈ V * B'
end
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 3037 | using KrylovKit: OrthonormalBasis, householder, rows, cols, hschur!, schur2eigvals,
schur2eigvecs, permuteschur!
@testset "Orthonormalize with algorithm $alg" for alg in (cgs, mgs, cgs2, mgs2, cgsr, mgsr)
@testset for S in (Float32, Float64, ComplexF32, ComplexF64)
b = OrthonormalBasis{Vector{S}}()
A = randn(S, (n, n))
v, r, x = orthonormalize(A[:, 1], b, alg)
@test r ≈ norm(A[:, 1])
@test norm(v) ≈ 1
@test length(x) == 0
push!(b, v)
for i in 2:n
v, r, x = orthonormalize(A[:, i], b, alg)
@test norm([r, norm(x)]) ≈ norm(A[:, i])
@test norm(v) ≈ 1
@test length(x) == i - 1
push!(b, v)
end
U = hcat(b...)
@test U' * U ≈ I
v = randn(S, n)
@test U * v ≈ b * v
end
end
@testset "Givens and Householder" begin
@testset for S in (Float32, Float64, ComplexF32, ComplexF64)
U, = svd!(randn(S, (n, n)))
b = OrthonormalBasis(map(copy, cols(U)))
v = randn(S, (n,))
g, r = givens(v, 1, n)
@test rmul!(U, g) ≈ hcat(rmul!(b, g)...)
h, r = householder(v, axes(v, 1), 3)
@test r ≈ norm(v)
v2 = lmul!(h, copy(v))
v3 = zero(v2)
v3[3] = r
@test v2 ≈ v3
@test lmul!(h, one(U)) ≈ rmul!(one(U), h)
@test lmul!(h, one(U))' ≈ lmul!(h', one(U))
@test rmul!(U, h) ≈ hcat(rmul!(b, h)...)
end
end
@testset "Rows and cols iterator" begin
@testset for S in (Float32, Float64, ComplexF32, ComplexF64)
A = randn(S, (n, n))
rowiter = rows(A)
@test typeof(first(rowiter)) == eltype(rowiter)
@test all(t -> t[1] == t[2], zip(rowiter, [A[i, :] for i in 1:n]))
coliter = cols(A)
@test typeof(first(coliter)) == eltype(coliter)
@test all(t -> t[1] == t[2], zip(coliter, [A[:, i] for i in 1:n]))
end
end
@testset "Dense Schur factorisation and associated methods" begin
@testset for S in (Float32, Float64, ComplexF32, ComplexF64)
H = convert(Matrix, hessenberg(rand(S, n, n)).H) # convert for compatibility with 1.3
# schur factorisation of Hessenberg matrix
T, U, w = hschur!(copy(H))
@test H * U ≈ U * T
@test schur2eigvals(T) ≈ w
# full eigenvector computation
V = schur2eigvecs(T)
@test T * V ≈ V * Diagonal(w)
# selected eigenvector computation
p = randperm(n)
select = p[1:(n >> 1)]
V2 = schur2eigvecs(T, select)
@test T * V2 ≈ V2 * Diagonal(w[select])
# permuting / reordering schur: take permutations that keep 2x2 blocks together in real case
p = sortperm(w; by=real)
T2, U2 = permuteschur!(copy(T), copy(U), p)
@test H * U2 ≈ U2 * T2
@test schur2eigvals(T2) ≈ w[p]
p = sortperm(w; by=abs)
T2, U2 = permuteschur!(copy(T), copy(U), p)
@test H * U2 ≈ U2 * T2
@test schur2eigvals(T2) ≈ w[p]
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 6680 | # Test CG complete
@testset "CG small problem ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
@testset for T in scalartypes
A = rand(T, (n, n))
A = sqrt(A * A')
b = rand(T, n)
alg = CG(; maxiter=2n, tol=tolerance(T) * norm(b), verbosity=2) # because of loss of orthogonality, we choose maxiter = 2n
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode));
ishermitian=true, isposdef=true, maxiter=2n,
krylovdim=1, rtol=tolerance(T),
verbosity=1)
@test info.converged > 0
@test unwrapvec(b) ≈ A * unwrapvec(x)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)), x;
ishermitian=true, isposdef=true, maxiter=2n,
krylovdim=1, rtol=tolerance(T))
@test info.numops == 1
A = rand(T, (n, n))
A = sqrt(A * A')
α₀ = rand(real(T)) + 1
α₁ = rand(real(T))
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)),
wrapvec(zerovector(b), Val(mode)), alg, α₀, α₁)
@test unwrapvec(b) ≈ (α₀ * I + α₁ * A) * unwrapvec(x)
@test info.converged > 0
end
end
# Test CG complete
@testset "CG large problem ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
@testset for T in scalartypes
A = rand(T, (N, N))
A = sqrt(sqrt(A * A')) / N
b = rand(T, N)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode));
isposdef=true, maxiter=1, krylovdim=N,
rtol=tolerance(T))
@test unwrapvec(b) ≈ A * unwrapvec(x) + unwrapvec(info.residual)
α₀ = rand(real(T)) + 1
α₁ = rand(real(T))
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)),
α₀, α₁;
isposdef=true, maxiter=1, krylovdim=N,
rtol=tolerance(T))
@test unwrapvec(b) ≈ (α₀ * I + α₁ * A) * unwrapvec(x) + unwrapvec(info.residual)
end
end
# Test GMRES complete
@testset "GMRES full factorization ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
@testset for T in scalartypes
A = rand(T, (n, n)) .- one(T) / 2
b = rand(T, n)
alg = GMRES(; krylovdim=n, maxiter=2, tol=tolerance(T) * norm(b), verbosity=2)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode));
krylovdim=n, maxiter=2,
rtol=tolerance(T), verbosity=1)
@test info.converged > 0
@test unwrapvec(b) ≈ A * unwrapvec(x)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)), x;
krylovdim=n, maxiter=2,
rtol=tolerance(T))
@test info.numops == 1
A = rand(T, (n, n))
α₀ = rand(T)
α₁ = -rand(T)
x, info = @constinferred(linsolve(A, b, zerovector(b), alg, α₀, α₁))
@test unwrapvec(b) ≈ (α₀ * I + α₁ * A) * unwrapvec(x)
@test info.converged > 0
end
end
# Test GMRES with restart
@testset "GMRES with restarts ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
@testset for T in scalartypes
A = rand(T, (N, N)) .- one(T) / 2
A = I - T(9 / 10) * A / maximum(abs, eigvals(A))
b = rand(T, N)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode));
krylovdim=3 * n,
maxiter=50, rtol=tolerance(T))
@test unwrapvec(b) ≈ A * unwrapvec(x) + unwrapvec(info.residual)
A = rand(T, (N, N)) .- one(T) / 2
α₀ = maximum(abs, eigvals(A))
α₁ = -rand(T)
α₁ *= T(9) / T(10) / abs(α₁)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)), α₀,
α₁; krylovdim=3 * n,
maxiter=50, rtol=tolerance(T))
@test unwrapvec(b) ≈ (α₀ * I + α₁ * A) * unwrapvec(x) + unwrapvec(info.residual)
end
end
# Test BICGStab
@testset "BiCGStab ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
@testset for T in scalartypes
A = rand(T, (n, n)) .- one(T) / 2
A = I - T(9 / 10) * A / maximum(abs, eigvals(A))
b = rand(T, n)
alg = BiCGStab(; maxiter=4n, tol=tolerance(T) * norm(b), verbosity=2)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)),
wrapvec(zerovector(b), Val(mode)), alg)
@test info.converged > 0
@test unwrapvec(b) ≈ A * unwrapvec(x)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)), x,
alg)
@test info.numops == 1
A = rand(T, (N, N)) .- one(T) / 2
b = rand(T, N)
α₀ = maximum(abs, eigvals(A))
α₁ = -rand(T)
α₁ *= T(9) / T(10) / abs(α₁)
alg = BiCGStab(; maxiter=2, tol=tolerance(T) * norm(b), verbosity=1)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)),
wrapvec(zerovector(b), Val(mode)), alg, α₀,
α₁)
@test unwrapvec(b) ≈ (α₀ * I + α₁ * A) * unwrapvec(x) + unwrapvec(info.residual)
alg = BiCGStab(; maxiter=10 * N, tol=tolerance(T) * norm(b), verbosity=0)
x, info = @constinferred linsolve(wrapop(A, Val(mode)), wrapvec(b, Val(mode)), x,
alg, α₀, α₁)
@test info.converged > 0
@test unwrapvec(b) ≈ (α₀ * I + α₁ * A) * unwrapvec(x)
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 1796 | @testset "RecursiveVec - singular values full" begin
@testset for T in (Float32, Float64, ComplexF32, ComplexF64)
@testset for orth in (cgs2, mgs2, cgsr, mgsr)
A = rand(T, (n, n))
v = rand(T, (n,))
v2 = RecursiveVec(v, zero(v))
alg = Lanczos(; orth=orth, krylovdim=2 * n, maxiter=1, tol=tolerance(T))
D, V, info = eigsolve(v2, n, :LR, alg) do x
x1, x2 = x
y1 = A * x2
y2 = A' * x1
return RecursiveVec(y1, y2)
end
@test info.converged >= n
S = D[1:n]
@test S ≈ svdvals(A)
UU = hcat((sqrt(2 * one(T)) * v[1] for v in V[1:n])...)
VV = hcat((sqrt(2 * one(T)) * v[2] for v in V[1:n])...)
@test UU * Diagonal(S) * VV' ≈ A
end
end
end
@testset "RecursiveVec - singular values iteratively" begin
@testset for T in (Float32, Float64, ComplexF32, ComplexF64)
@testset for orth in (cgs2, mgs2, cgsr, mgsr)
A = rand(T, (N, 2 * N))
v = rand(T, (N,))
w = rand(T, (2 * N,))
v2 = RecursiveVec(v, w)
alg = Lanczos(; orth=orth, krylovdim=n, maxiter=300, tol=tolerance(T))
n1 = div(n, 2)
D, V, info = eigsolve(v2, n1, :LR, alg) do x
x1, x2 = x
y1 = A * x2
y2 = A' * x1
return RecursiveVec(y1, y2)
end
@test info.converged >= n1
S = D[1:n1]
@test S ≈ svdvals(A)[1:n1]
UU = hcat((sqrt(2 * one(T)) * v[1] for v in V[1:n1])...)
VV = hcat((sqrt(2 * one(T)) * v[2] for v in V[1:n1])...)
@test Diagonal(S) ≈ UU' * A * VV
end
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 1145 | using Random
Random.seed!(76543210)
using Test, TestExtras
using LinearAlgebra
using KrylovKit
using VectorInterface
include("testsetup.jl")
using ..TestSetup
# Parameters
# ----------
const n = 10
const N = 100
const η₀ = 0.75 # seems to be necessary to get sufficient convergence for GKL iteration with Float32 precision
const cgs = ClassicalGramSchmidt()
const mgs = ModifiedGramSchmidt()
const cgs2 = ClassicalGramSchmidt2()
const mgs2 = ModifiedGramSchmidt2()
const cgsr = ClassicalGramSchmidtIR(η₀)
const mgsr = ModifiedGramSchmidtIR(η₀)
# Tests
# -----
t = time()
include("factorize.jl")
include("gklfactorize.jl")
include("linsolve.jl")
include("eigsolve.jl")
include("schursolve.jl")
include("geneigsolve.jl")
include("svdsolve.jl")
include("expintegrator.jl")
include("linalg.jl")
include("recursivevec.jl")
include("ad.jl")
t = time() - t
println("Tests finished in $t seconds")
module AquaTests
using KrylovKit
using Aqua
Aqua.test_all(KrylovKit; ambiguities=false)
# treat ambiguities special because of ambiguities between ChainRulesCore and Base
Aqua.test_ambiguities([KrylovKit, Base, Core]; exclude=[Base.:(==)])
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 5025 | @testset "Arnoldi - schursolve full ($mode)" for mode in (:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n)) .- one(T) / 2
v = rand(T, (n,))
alg = Arnoldi(; orth=orth, krylovdim=n, maxiter=1, tol=tolerance(T))
n1 = div(n, 2)
T1, V1, D1, info1 = @constinferred schursolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), n1, :SR,
alg)
n2 = n - n1
T2, V2, D2, info2 = schursolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n2,
:LR, alg)
D = sort(sort(eigvals(A); by=imag, rev=true); alg=MergeSort, by=real)
D2′ = sort(sort(D2; by=imag, rev=true); alg=MergeSort, by=real)
@test vcat(D1[1:n1], D2′[(end - n2 + 1):end]) ≈ D
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test U1' * U1 ≈ I
@test U2' * U2 ≈ I
@test A * U1 ≈ U1 * T1
@test A * U2 ≈ U2 * T2
if T <: Complex
T1, V1, D1, info = schursolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)),
n1, :SI, alg)
T2, V2, D2, info = schursolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)),
n2, :LI, alg)
D = sort(eigvals(A); by=imag)
@test vcat(D1[1:n1], reverse(D2[1:n2])) ≈ D
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test U1' * U1 ≈ I
@test U2' * U2 ≈ I
@test A * U1 ≈ U1 * T1
@test A * U2 ≈ U2 * T2
end
end
end
end
@testset "Arnoldi - schursolve iteratively ($mode)" for mode in
(:vector, :inplace, :outplace)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (N, N)) .- one(T) / 2
v = rand(T, (N,))
alg = Arnoldi(; orth=orth, krylovdim=3 * n, maxiter=10, tol=tolerance(T))
T1, V1, D1, info1 = @constinferred schursolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)), n, :SR,
alg)
T2, V2, D2, info2 = schursolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n,
:LR, alg)
T3, V3, D3, info3 = schursolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)), n,
:LM, alg)
D = sort(eigvals(A); by=imag, rev=true)
l1 = info1.converged
l2 = info2.converged
l3 = info3.converged
@test D1[1:l1] ≊ sort(D; alg=MergeSort, by=real)[1:l1]
@test D2[1:l2] ≊ sort(D; alg=MergeSort, by=real, rev=true)[1:l2]
@test D3[1:l3] ≊ sort(D; alg=MergeSort, by=abs, rev=true)[1:l3]
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
U3 = stack(unwrapvec, V3)
@test U1' * U1 ≈ one(U1' * U1)
@test U2' * U2 ≈ one(U2' * U2)
@test U3' * U3 ≈ one(U3' * U3)
R1 = stack(unwrapvec, info1.residual)
R2 = stack(unwrapvec, info2.residual)
R3 = stack(unwrapvec, info3.residual)
@test A * U1 ≈ U1 * T1 + R1
@test A * U2 ≈ U2 * T2 + R2
@test A * U3 ≈ U3 * T3 + R3
if T <: Complex
T1, V1, D1, info1 = schursolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)),
n, :SI, alg)
T2, V2, D2, info2 = schursolve(wrapop(A, Val(mode)), wrapvec(v, Val(mode)),
n, :LI, alg)
D = eigvals(A)
l1 = info1.converged
l2 = info2.converged
@test D1[1:l1] ≊ sort(D; by=imag)[1:l1]
@test D2[1:l2] ≊ sort(D; by=imag, rev=true)[1:l2]
U1 = stack(unwrapvec, V1)
U2 = stack(unwrapvec, V2)
@test U1[:, 1:l1]' * U1[:, 1:l1] ≈ I
@test U2[:, 1:l2]' * U2[:, 1:l2] ≈ I
R1 = stack(unwrapvec, info1.residual)
R2 = stack(unwrapvec, info2.residual)
@test A * U1 ≈ U1 * T1 + R1
@test A * U2 ≈ U2 * T2 + R2
end
end
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 2166 | @testset "GKL - svdsolve full ($mode)" for mode in (:vector, :inplace, :outplace, :mixed)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (n, n))
alg = GKL(; orth=orth, krylovdim=2 * n, maxiter=1, tol=tolerance(T))
S, lvecs, rvecs, info = @constinferred svdsolve(wrapop(A, Val(mode)),
wrapvec(A[:, 1], Val(mode)), n,
:LR, alg)
@test S ≈ svdvals(A)
U = stack(unwrapvec, lvecs)
V = stack(unwrapvec, rvecs)
@test U' * U ≈ I
@test V' * V ≈ I
@test A * V ≈ U * Diagonal(S)
end
end
end
@testset "GKL - svdsolve iteratively ($mode)" for mode in
(:vector, :inplace, :outplace, :mixed)
scalartypes = mode === :vector ? (Float32, Float64, ComplexF32, ComplexF64) :
(ComplexF64,)
orths = mode === :vector ? (cgs2, mgs2, cgsr, mgsr) : (mgsr,)
@testset for T in scalartypes
@testset for orth in orths
A = rand(T, (2 * N, N))
v = rand(T, (2 * N,))
n₁ = div(n, 2)
alg = GKL(; orth=orth, krylovdim=n, maxiter=10, tol=tolerance(T), eager=true)
S, lvecs, rvecs, info = @constinferred svdsolve(wrapop(A, Val(mode)),
wrapvec(v, Val(mode)),
n₁, :LR, alg)
l = info.converged
@test S[1:l] ≈ svdvals(A)[1:l]
U = stack(unwrapvec, lvecs)
V = stack(unwrapvec, rvecs)
@test U[:, 1:l]' * U[:, 1:l] ≈ I
@test V[:, 1:l]' * V[:, 1:l] ≈ I
R = stack(unwrapvec, info.residual)
@test A' * U ≈ V * Diagonal(S)
@test A * V ≈ U * Diagonal(S) + R
end
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | code | 3967 | module TestSetup
export tolerance, ≊, MinimalVec, isinplace, stack
export wrapop, wrapvec, unwrapvec
import VectorInterface as VI
using VectorInterface
using LinearAlgebra: LinearAlgebra
# Utility functions
# -----------------
"function for determining the precision of a type"
tolerance(T::Type{<:Number}) = eps(real(T))^(2 / 3)
"function for comparing sets of eigenvalues"
function ≊(list1::AbstractVector, list2::AbstractVector)
length(list1) == length(list2) || return false
n = length(list1)
ind2 = collect(1:n)
p = sizehint!(Int[], n)
for i in 1:n
j = argmin(abs.(view(list2, ind2) .- list1[i]))
p = push!(p, ind2[j])
ind2 = deleteat!(ind2, j)
end
return list1 ≈ view(list2, p)
end
# Minimal vector type
# -------------------
"""
MinimalVec{T<:Number,IP}
Minimal interface for a vector. Can support either in-place assignments or not, depending on
`IP=true` or `IP=false`.
"""
struct MinimalVec{IP,V<:AbstractVector}
vec::V
function MinimalVec{IP}(vec::V) where {IP,V}
return new{IP,V}(vec)
end
end
const InplaceVec{V} = MinimalVec{true,V}
const OutplaceVec{V} = MinimalVec{false,V}
isinplace(::Type{MinimalVec{IP,V}}) where {V,IP} = IP
isinplace(v::MinimalVec) = isinplace(typeof(v))
VI.scalartype(::Type{<:MinimalVec{IP,V}}) where {IP,V} = scalartype(V)
function VI.zerovector(v::MinimalVec, S::Type{<:Number})
return MinimalVec{isinplace(v)}(zerovector(v.vec, S))
end
function VI.zerovector!(v::InplaceVec{V}) where {V}
zerovector!(v.vec)
return v
end
VI.zerovector!!(v::MinimalVec) = isinplace(v) ? zerovector!(v) : zerovector(v)
function VI.scale(v::MinimalVec, α::Number)
return MinimalVec{isinplace(v)}(scale(v.vec, α))
end
function VI.scale!(v::InplaceVec{V}, α::Number) where {V}
scale!(v.vec, α)
return v
end
function VI.scale!!(v::MinimalVec, α::Number)
return isinplace(v) ? scale!(v, α) : scale(v, α)
end
function VI.scale!(w::InplaceVec{V}, v::InplaceVec{W}, α::Number) where {V,W}
scale!(w.vec, v.vec, α)
return w
end
function VI.scale!!(w::MinimalVec, v::MinimalVec, α::Number)
isinplace(w) && return scale!(w, v, α)
return MinimalVec{false}(scale!!(copy(w.vec), v.vec, α))
end
function VI.add(y::MinimalVec, x::MinimalVec, α::Number, β::Number)
return MinimalVec{isinplace(y)}(add(y.vec, x.vec, α, β))
end
function VI.add!(y::InplaceVec{W}, x::InplaceVec{V}, α::Number, β::Number) where {W,V}
add!(y.vec, x.vec, α, β)
return y
end
function VI.add!!(y::MinimalVec, x::MinimalVec, α::Number, β::Number)
return isinplace(y) ? add!(y, x, α, β) : add(y, x, α, β)
end
VI.inner(x::MinimalVec, y::MinimalVec) = inner(x.vec, y.vec)
VI.norm(x::MinimalVec) = LinearAlgebra.norm(x.vec)
# Wrappers
# --------
# dispatch on val is necessary for type stability
function wrapvec(v, ::Val{mode}) where {mode}
return mode === :vector ? v :
mode === :inplace ? MinimalVec{true}(v) :
mode === :outplace ? MinimalVec{false}(v) :
mode === :mixed ? MinimalVec{false}(v) :
throw(ArgumentError("invalid mode ($mode)"))
end
function wrapvec2(v, ::Val{mode}) where {mode}
return mode === :mixed ? MinimalVec{true}(v) : wrapvec(v, mode)
end
unwrapvec(v::MinimalVec) = v.vec
unwrapvec(v) = v
function wrapop(A, ::Val{mode}) where {mode}
if mode === :vector
return A
elseif mode === :inplace || mode === :outplace
return function (v, flag=Val(false))
if flag === Val(true)
return wrapvec(A' * unwrapvec(v), Val(mode))
else
return wrapvec(A * unwrapvec(v), Val(mode))
end
end
elseif mode === :mixed
return (x -> wrapvec(A * unwrapvec(x), Val(mode)),
y -> wrapvec2(A' * unwrapvec(y), Val(mode)))
else
throw(ArgumentError("invalid mode ($mode)"))
end
end
if VERSION < v"1.9"
stack(f, itr) = mapreduce(f, hcat, itr)
end
end
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 5165 | # KrylovKit.jl
A Julia package collecting a number of Krylov-based algorithms for linear problems, singular
value and eigenvalue problems and the application of functions of linear maps or operators
to vectors.
| **Documentation** | **Build Status** | **Digital Object Idenitifier** | **License** |
|:-----------------:|:----------------:|:---------------:|:-----------:|
| [![][docs-stable-img]][docs-stable-url] [![][docs-dev-img]][docs-dev-url] | [![][aqua-img]][aqua-url] [![CI][github-img]][github-url] [![][codecov-img]][codecov-url] | [![DOI][doi-img]][doi-url] | [![license][license-img]][license-url] |
[docs-dev-img]: https://img.shields.io/badge/docs-dev-blue.svg
[docs-dev-url]: https://jutho.github.io/KrylovKit.jl/latest
[docs-stable-img]: https://img.shields.io/badge/docs-stable-blue.svg
[docs-stable-url]: https://jutho.github.io/KrylovKit.jl/stable
[github-img]: https://github.com/Jutho/KrylovKit.jl/workflows/CI/badge.svg
[github-url]: https://github.com/Jutho/KrylovKit.jl/actions?query=workflow%3ACI
[aqua-img]: https://raw.githubusercontent.com/JuliaTesting/Aqua.jl/master/badge.svg
[aqua-url]: https://github.com/JuliaTesting/Aqua.jl
[codecov-img]: https://codecov.io/gh/Jutho/KrylovKit.jl/branch/master/graph/badge.svg
[codecov-url]: https://codecov.io/gh/Jutho/KrylovKit.jl
[license-img]: http://img.shields.io/badge/license-MIT-brightgreen.svg?style=flat
[license-url]: LICENSE.md
[doi-img]: https://zenodo.org/badge/DOI/10.5281/zenodo.10622234.svg
[doi-url]: https://doi.org/10.5281/zenodo.10622234
## Release notes for the latest version
### v0.7
This version now depends on and uses [VectorInterface.jl](https://github.com/Jutho/VectorInterface.jl)
to define the vector-like behavior of the input vectors, rather than some minimal set of
methods from `Base` and `LinearAlgebra`. The advantage is that many more types from standard
Julia are now supported out of the box, such as nested vectors or immutable objects such as
tuples. For custom user types for which the old set of required methods was implemented, there
are fallback definitions of the methods in VectorInferace.jl such that these types should still
be supported, but this might result in warnings being printed. It is recommend to implement full
support for at least the methods in VectorInterface without bang or with double bang, where the
latter set of methods can use in-place mutation if your type supports this behavior.
In particular, tuples are now supported:
```julia
julia> values, vectors, info = eigsolve(t -> cumsum(t) .+ 0.5 .* reverse(t), (1,0,0,0));
julia> values
4-element Vector{ComplexF64}:
2.5298897746721303 + 0.0im
0.7181879189193713 + 0.4653321688070444im
0.7181879189193713 - 0.4653321688070444im
0.03373438748912972 + 0.0im
julia> vectors
4-element Vector{NTuple{4, ComplexF64}}:
(0.25302539267845964 + 0.0im, 0.322913174072047 + 0.0im, 0.48199234088257203 + 0.0im, 0.774201921982351 + 0.0im)
(0.08084058845575778 + 0.46550907490257704im, 0.16361072959559492 - 0.20526827902633993im, -0.06286027036719286 - 0.6630573167350086im, -0.47879640378455346 - 0.18713670961291684im)
(0.08084058845575778 - 0.46550907490257704im, 0.16361072959559492 + 0.20526827902633993im, -0.06286027036719286 + 0.6630573167350086im, -0.47879640378455346 + 0.18713670961291684im)
(0.22573986355213632 + 0.0im, -0.5730667760748933 + 0.0im, 0.655989711683001 + 0.0im, -0.4362493350466509 + 0.0im)
```
## Overview
KrylovKit.jl accepts general functions or callable objects as linear maps, and general Julia
objects with vector like behavior (as defined in the docs) as vectors.
The high level interface of KrylovKit is provided by the following functions:
* `linsolve`: solve linear systems
* `eigsolve`: find a few eigenvalues and corresponding eigenvectors
* `geneigsolve`: find a few generalized eigenvalues and corresponding vectors
* `svdsolve`: find a few singular values and corresponding left and right singular vectors
* `exponentiate`: apply the exponential of a linear map to a vector
* `expintegrator`: [exponential integrator](https://en.wikipedia.org/wiki/Exponential_integrator)
for a linear non-homogeneous ODE, computes a linear combination of the `ϕⱼ` functions which generalize `ϕ₀(z) = exp(z)`.
## Installation
`KrylovKit.jl` can be installed with the Julia package manager.
From the Julia REPL, type `]` to enter the Pkg REPL mode and run:
```
pkg> add KrylovKit
```
Or, equivalently, via the `Pkg` API:
```julia
julia> import Pkg; Pkg.add("KrylovKit.jl")
```
## Documentation
- [**STABLE**][docs-stable-url] - **documentation of the most recently tagged version.**
- [**DEVEL**][docs-dev-url] - *documentation of the in-development version.*
## Project Status
The package is tested against Julia `1.0`, the current stable and the nightly builds of the Julia `master` branch on Linux, macOS, and Windows, 32- and 64-bit architecture and with `1` and `4` threads.
## Questions and Contributions
Contributions are very welcome, as are feature requests and suggestions. Please open an [issue][issues-url] if you encounter any problems.
[issues-url]: https://github.com/Jutho/KrylovKit.jl/issues
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 8670 | # KrylovKit.jl
A Julia package collecting a number of Krylov-based algorithms for linear problems, singular
value and eigenvalue problems and the application of functions of linear maps or operators
to vectors.
## Overview
KrylovKit.jl accepts general functions or callable objects as linear maps, and general Julia
objects with vector like behavior (see below) as vectors.
The high level interface of KrylovKit is provided by the following functions:
* [`linsolve`](@ref): solve linear systems `A*x = b`
* [`eigsolve`](@ref): find a few eigenvalues and corresponding eigenvectors of an
eigenvalue problem `A*x = λ x`
* [`geneigsolve`](@ref): find a few eigenvalues and corresponding vectors of a
generalized eigenvalue problem `A*x = λ*B*x`
* [`svdsolve`](@ref): find a few singular values and corresponding left and right
singular vectors `A*x = σ * y` and `A'*y = σ*x`
* [`exponentiate`](@ref): apply the exponential of a linear map to a vector `x=exp(t*A)*x₀`
* [`expintegrator`](@ref): exponential integrator for a linear non-homogeneous ODE
(generalization of `exponentiate`)
## Package features and alternatives
This section could also be titled "Why did I create KrylovKit.jl"?
There are already a fair number of packages with Krylov-based or other iterative methods, such as
* [IterativeSolvers.jl](https://github.com/JuliaMath/IterativeSolvers.jl): part of the
[JuliaMath](https://github.com/JuliaMath) organisation, solves linear systems and least
square problems, eigenvalue and singular value problems
* [Krylov.jl](https://github.com/JuliaSmoothOptimizers/Krylov.jl): part of the
[JuliaSmoothOptimizers](https://github.com/JuliaSmoothOptimizers) organisation, solves
linear systems and least square problems, specific for linear operators from
[LinearOperators.jl](https://github.com/JuliaSmoothOptimizers/LinearOperators.jl).
* [KrylovMethods.jl](https://github.com/lruthotto/KrylovMethods.jl): specific for sparse
matrices
* [Expokit.jl](https://github.com/acroy/Expokit.jl): application of the matrix
exponential to a vector
* [ArnoldiMethod.jl](https://github.com/haampie/ArnoldiMethod.jl): Implicitly restarted
Arnoldi method for eigenvalues of a general matrix
* [JacobiDavidson.jl](https://github.com/haampie/JacobiDavidson.jl): Jacobi-Davidson
method for eigenvalues of a general matrix
* [ExponentialUtilities.jl](https://github.com/JuliaDiffEq/ExponentialUtilities.jl): Krylov
subspace methods for matrix exponentials and `phiv` exponential integrator products. It
has specialized methods for subspace caching, time stepping, and error testing which are
essential for use in high order exponential integrators.
* [OrdinaryDiffEq.jl](https://github.com/JuliaDiffEq/OrdinaryDiffEq.jl):
contains implementations of [high order exponential integrators](https://docs.juliadiffeq.org/latest/solvers/split_ode_solve/#OrdinaryDiffEq.jl-2)
with adaptive Krylov-subspace calculations for solving semilinear and nonlinear ODEs.
These packages have certainly inspired and influenced the development of KrylovKit.jl.
However, KrylovKit.jl distinguishes itself from the previous packages in the following ways:
1. KrylovKit accepts general functions to represent the linear map or operator that defines
the problem, without having to wrap them in a
[`LinearMap`](https://github.com/Jutho/LinearMaps.jl) or
[`LinearOperator`](https://github.com/JuliaSmoothOptimizers/LinearOperators.jl) type.
Of course, subtypes of `AbstractMatrix` are also supported. If the linear map (always
the first argument) is a subtype of `AbstractMatrix`, matrix vector multiplication is
used, otherwise it is applied as a function call.
2. KrylovKit does not assume that the vectors involved in the problem are actual subtypes
of `AbstractVector`. Any Julia object that behaves as a vector is supported, so in
particular higher-dimensional arrays or any custom user type that supports the
interface as defined in
[`VectorInterface.jl`](https://github.com/Jutho/VectorInterface.jl)
Algorithms in KrylovKit.jl are tested against such a minimal implementation (named
`MinimalVec`) in the test suite. This type is only defined in the tests. However,
KrylovKit provides two types implementing this interface and slightly more, to make
them behave more like `AbstractArrays` (e.g. also `Base.:+` etc), which can facilitate
certain applications:
* [`RecursiveVec`](@ref) can be used for grouping a set of vectors into a single
vector like structure (can be used recursively). This is more robust than trying to
use nested `Vector{<:Vector}` types.
* [`InnerProductVec`](@ref) can be used to redefine the inner product (i.e. `inner`)
and corresponding norm (`norm`) of an already existing vector like object. The
latter should help with implementing certain type of preconditioners.
3. Since version 0.8, KrylovKit.jl supports reverse-mode AD by defining `ChainRulesCore.rrule`
definitions for the most common functionality (`linsolve`, `eigsolve`, `svdsolve`).
Hence, reverse mode AD engines that are compatible with the [ChainRules](https://juliadiff.org/ChainRulesCore.jl/dev/)
ecosystem will be able to benefit from an optimized implementation of the adjoint
of these functions. The `rrule` definitions for the remaining functionality
(`geneigsolve` and `expintegrator`, of which `exponentiate` is a special case) will be
added at a later stage. There is a dedicated documentation page on how to configure these
`rrule`s, as they also require to solve large-scale linear or eigenvalue problems.
## Current functionality
The following algorithms are currently implemented
* `linsolve`: [`CG`](@ref), [`GMRES`](@ref), [`BiCGStab`](@ref)
* `eigsolve`: a Krylov-Schur algorithm (i.e. with tick restarts) for extremal eigenvalues
of normal (i.e. not generalized) eigenvalue problems, corresponding to
[`Lanczos`](@ref) for real symmetric or complex hermitian linear maps, and to
[`Arnoldi`](@ref) for general linear maps.
* `geneigsolve`: an customized implementation of the inverse-free algorithm of Golub and
Ye for symmetric / hermitian generalized eigenvalue problems with positive definite
matrix `B` in the right hand side of the generalized eigenvalue problem ``A v = B v λ``.
The Matlab implementation was described by Money and Ye and is known as `EIGIFP`; in
particular it extends the Krylov subspace with a vector corresponding to the step
between the current and previous estimate, analogous to the locally optimal
preconditioned conjugate gradient method (LOPCG). In particular, with Krylov dimension
2, it becomes equivalent to the latter.
* `svdsolve`: finding largest singular values based on Golub-Kahan-Lanczos
bidiagonalization (see [`GKL`](@ref))
* `exponentiate`: a [`Lanczos`](@ref) or [`Arnoldi`](@ref) based algorithm for the action
of the exponential of linear map.
* `expintegrator`: [exponential integrator](https://en.wikipedia.org/wiki/Exponential_integrator)
for a linear non-homogeneous ODE, computes a linear combination of the `ϕⱼ` functions which generalize `ϕ₀(z) = exp(z)`.
## Future functionality?
Here follows a wish list / to-do list for the future. Any help is welcomed and appreciated.
* More algorithms, including biorthogonal methods:
- for `linsolve`: L-GMRES, MINRES, BiCG, IDR(s), ...
- for `eigsolve`: BiLanczos, Jacobi-Davidson JDQR/JDQZ, subspace iteration (?), ...
- for `geneigsolve`: trace minimization, ...
* Support both in-place / mutating and out-of-place functions as linear maps
* Reuse memory for storing vectors when restarting algorithms (related to previous)
* Support non-BLAS scalar types using GeneralLinearAlgebra.jl and GeneralSchur.jl
* Least square problems
* Nonlinear eigenvalue problems
* Preconditioners
* Refined Ritz vectors, Harmonic Ritz values and vectors
* Block versions of the algorithms
* More relevant matrix functions
Partially done:
* Improved efficiency for the specific case where `x` is `Vector` (i.e. BLAS level 2
operations): any vector `v::AbstractArray` which has `IndexStyle(v) == IndexLinear()`
now benefits from a multithreaded (use `export JULIA_NUM_THREADS = x` with `x` the
number of threads you want to use) implementation that resembles BLAS level 2 style for
the vector operations, provided `ClassicalGramSchmidt()`, `ClassicalGramSchmidt2()` or
`ClassicalGramSchmidtIR()` is chosen as orthogonalization routine.
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 584 | # Available algorithms
## Orthogonalization algorithms
```@docs
KrylovKit.Orthogonalizer
ClassicalGramSchmidt
ModifiedGramSchmidt
ClassicalGramSchmidt2
ModifiedGramSchmidt2
ClassicalGramSchmidtIR
ModifiedGramSchmidtIR
```
## General Krylov algorithms
```@docs
Lanczos
Arnoldi
```
## Specific algorithms for linear systems
```@docs
CG
KrylovKit.MINRES
GMRES
KrylovKit.BiCG
BiCGStab
```
## Specific algorithms for generalized eigenvalue problems
```@docs
GolubYe
```
## Specific algorithms for singular value problems
```@docs
GKL
```
## Default values
```@docs
KrylovDefaults
```
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 6038 | # Eigenvalue problems
## Eigenvalues and eigenvectors
Finding a selection of eigenvalues and corresponding (right) eigenvectors of a linear map
can be accomplished with the `eigsolve` routine:
```@docs
eigsolve
```
Which eigenvalues are targeted can be specified using one of the symbols `:LM`, `:LR`,
`:SR`, `:LI` and `:SI` for largest magnitude, largest and smallest real part, and largest
and smallest imaginary part respectively. Alternatively, one can just specify a general
sorting operation using `EigSorter`
```@docs
EigSorter
```
For a general matrix, eigenvalues and eigenvectors will always be returned with complex
values for reasons of type stability. However, if the linear map and initial guess are
real, most of the computation is actually performed using real arithmetic, as in fact the
first step is to compute an approximate partial Schur factorization. If one is not
interested in the eigenvectors, one can also just compute this partial Schur factorization
using `schursolve`, for which only an 'expert' method call is available
```@docs
schursolve
```
Note that, for symmetric or hermitian linear maps, the eigenvalue and Schur factorization
are equivalent, and one should only use `eigsolve`. There is no `schursolve` using the `Lanczos` algorithm.
Another example of a possible use case of `schursolve` is if the linear map is known to have
a unique eigenvalue of, e.g. largest magnitude. Then, if the linear map is real valued, that
largest magnitude eigenvalue and its corresponding eigenvector are also real valued.
`eigsolve` will automatically return complex valued eigenvectors for reasons of type
stability. However, as the first Schur vector will coincide with the first eigenvector, one
can instead use
```julia
T, vecs, vals, info = schursolve(A, x₀, 1, :LM, Arnoldi(...))
```
and use `vecs[1]` as the real valued eigenvector (after checking `info.converged`)
corresponding to the largest magnitude eigenvalue of `A`.
More generally, if you want to compute several eigenvalues of a real linear map, and you know
that all of them are real, so that also the associated eigenvectors will be real, then you
can use the `realeigsolve` method, which is also restricted to the 'expert' method call and
which will error if any of the requested eigenvalues turn out to be complex
```@docs
realeigsolve
```
## Automatic differentation
The `eigsolve` (and `realeigsolve`) routine can be used in conjunction with reverse-mode automatic
differentiation, using AD engines that are compatible with the [ChainRules](https://juliadiff.org/ChainRulesCore.jl/dev/)
ecosystem. The adjoint problem of an eigenvalue problem is a linear problem, although it can also
be formulated as an eigenvalue problem. Details about this approach will be published in a
forthcoming manuscript.
In either case, the adjoint problem requires the adjoint[^1] of the linear map. If the linear map is
an `AbstractMatrix` instance, its `adjoint` will be used in the `rrule`. If the linear map is implemented
as a function `f`, then the AD engine itself is used to compute the corresponding adjoint via
`ChainRulesCore.rrule_via_ad(config, f, x)`. The specific base point `x` at which this adjoint is
computed should not affect the result if `f` properly represents a linear map. Furthermore, the linear
map is the only argument that affects the `eigsolve` output (from a theoretical perspective, the
starting vector and algorithm parameters should have no effect), so that this is where the adjoint
variables need to be propagated to and have a nonzero effect.
The adjoint problem (also referred to as cotangent problem) can thus be solved as a linear problem
or as an eigenvalue problem. Note that this eigenvalue problem is never symmetric or Hermitian,
even if the primal problem is. The different implementations of the `rrule` can be selected using
the `alg_rrule` keyword argument. If a linear solver such as `GMRES` or `BiCGStab` is specified,
the adjoint problem requires solving a number of linear problems equal to the number of requested
eigenvalues and eigenvectors. If an eigenvalue solver is specified, for which `Arnoldi` is essentially
the only option, then the adjoint problem is solved as a single (but larger) eigenvalue problem.
Note that the phase of an eigenvector is not uniquely determined. Hence, a well-defined cost function
constructed from eigenvectors should depend on these in such a way that its value is not affected
by changing the phase of those eigenvectors, i.e. the cost function should be 'gauge invariant'.
If this is not the case, the cost function is said to be 'gauge dependent', and this can be detected
in the resulting adjoint variables for those eigenvectors. The KrylovKit `rrule` for `eigsolve`
will print a warning if it detects from the incoming adjoint variables that the cost function is gauge
dependent. This warning can be suppressed by passing `alg_rrule` an algorithm with `verbosity=-1`.
## Generalized eigenvalue problems
Generalized eigenvalues `λ` and corresponding vectors `x` of the generalized eigenvalue
problem ``A x = λ B x`` can be obtained using the method `geneigsolve`. Currently, there is
only one algorithm, which does not require inverses of `A` or `B`, but is restricted to
symmetric or hermitian generalized eigenvalue problems where the matrix or linear map `B`
is positive definite. Note that this is not reflected in the default values for the keyword
arguments `issymmetric`, `ishermitian` and `isposdef`, so that these should be set
explicitly in order to comply with this restriction. If `A` and `B` are actual instances of
`AbstractMatrix`, the default value for the keyword arguments will try to check these
properties explicitly.
```@docs
geneigsolve
```
Currently, there is `rrule` and thus no automatic differentiation support for `geneigsolve`.
[^1]: For a linear map, the adjoint or pullback required in the reverse-order chain rule coincides
with its (conjugate) transpose, at least with respect to the standard Euclidean inner product.
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 3444 | # Implementation details
## Orthogonalization
To denote a basis of vectors, e.g. to represent a given Krylov subspace, there is an
abstract type `Basis{T}`
```@docs
KrylovKit.Basis
```
Many Krylov based algorithms use an orthogonal basis to parameterize the Krylov subspace. In
that case, the specific implementation `OrthonormalBasis{T}` can be used:
```@docs
KrylovKit.OrthonormalBasis
```
We can orthogonalize or orthonormalize a given vector to another vector (assumed normalized)
or to a given [`KrylovKit.OrthonormalBasis`](@ref) using
```@docs
KrylovKit.orthogonalize
KrylovKit.orthonormalize
```
or using the possibly in-place versions
```@docs
KrylovKit.orthogonalize!!
KrylovKit.orthonormalize!!
```
The expansion coefficients of a general vector in terms of a given orthonormal basis can be obtained as
```@docs
KrylovKit.project!!
```
whereas the inverse calculation is obtained as
```@docs
KrylovKit.unproject!!
```
An orthonormal basis can be transformed using a rank-1 update using
```@docs
KrylovKit.rank1update!
```
Note that this changes the subspace. A mere rotation of the basis, which does not change
the subspace spanned by it, can be computed using
```@docs
KrylovKit.basistransform!
```
## Dense linear algebra
KrylovKit relies on Julia's `LinearAlgebra` module from the standard library for most of its
dense linear algebra dependencies.
## Factorization types
The central ingredient in a Krylov based algorithm is a Krylov factorization or
decomposition of a linear map. Such partial factorizations are represented as a
`KrylovFactorization`, of which `LanczosFactorization` and `ArnoldiFactorization` are two
concrete implementations:
```@docs
KrylovKit.KrylovFactorization
KrylovKit.LanczosFactorization
KrylovKit.ArnoldiFactorization
KrylovKit.GKLFactorization
```
A `KrylovFactorization` or `GKLFactorization` can be destructured into its defining
components using iteration, but these can also be accessed using the following functions
```@docs
basis
rayleighquotient
residual
normres
rayleighextension
```
As the `rayleighextension` is typically a simple basis vector, we have created a dedicated
type to represent this without having to allocate an actual vector, i.e.
```@docs
KrylovKit.SimpleBasisVector
```
Furthermore, to store the Rayleigh quotient of the Arnoldi factorization in a manner that
can easily be expanded, we have constructed a custom matrix type to store the Hessenberg
matrix in a packed format (without zeros):
```@docs
KrylovKit.PackedHessenberg
```
## Factorization iterators
Given a linear map ``A`` and a starting vector ``x₀``, a Krylov factorization is obtained
by sequentially building a Krylov subspace ``{x₀, A x₀, A² x₀, ...}``. Rather then using
this set of vectors as a basis, an orthonormal basis is generated by a process known as
Lanczos or Arnoldi iteration (for symmetric/hermitian and for general matrices,
respectively). These processes are represented as iterators in Julia:
```@docs
KrylovKit.KrylovIterator
KrylovKit.LanczosIterator
KrylovKit.ArnoldiIterator
```
Similarly, there is also an iterator for the Golub-Kahan-Lanczos bidiagonalization proces:
```@docs
KrylovKit.GKLIterator
```
As an alternative to the standard iteration interface from Julia Base (using `iterate`),
these iterative processes and the factorizations they produce can also be manipulated
using the following functions:
```@docs
expand!
shrink!
initialize
initialize!
```
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 3097 | # Introduction
```@contents
Pages = ["man/intro.md", "man/linear.md", "man/eig.md", "man/svd.md", "man/matfun.md",
"man/algorithms.md", "man/implementation.md"]
Depth = 2
```
## Installing
Install KrylovKit.jl via the package manager:
```julia
using Pkg
Pkg.add("KrylovKit")
```
KrylovKit.jl is a pure Julia package; no dependencies (aside from the Julia standard
library) are required.
## Getting started
After installation, start by loading `KrylovKit`
```julia
using KrylovKit
```
The help entry of the `KrylovKit` module states
```@docs
KrylovKit
```
## Common interface
The for high-level function [`linsolve`](@ref), [`eigsolve`](@ref), [`geneigsolve`](@ref),
[`svdsolve`](@ref), [`exponentiate`](@ref) and [`expintegrator`](@ref) follow a common interface
```julia
results..., info = problemsolver(A, args...; kwargs...)
```
where `problemsolver` is one of the functions above. Here, `A` is the linear map in the
problem, which could be an instance of `AbstractMatrix`, or any function or callable object
that encodes the action of the linear map on a vector. In particular, one can write the
linear map using Julia's `do` block syntax as
```julia
results..., info = problemsolver(args...; kwargs...) do x
y = # implement linear map on x
return y
end
```
Read the documentation for problems that require both the linear map and its adjoint to be
implemented, e.g. [`svdsolve`](@ref), or that require two different linear maps, e.g.
[`geneigsolve`](@ref).
Furthermore, `args` is a set of additional arguments to specify the problem. The keyword
arguments `kwargs` contain information about the linear map (`issymmetric`, `ishermitian`,
`isposdef`) and about the solution strategy (`tol`, `krylovdim`, `maxiter`). Finally, there
is a keyword argument `verbosity` that determines how much information is printed to
`STDOUT`. The default value `verbosity = 0` means that no information will be printed. With
`verbosity = 1`, a single message at the end of the algorithm will be displayed, which is a
warning if the algorithm did not succeed in finding the solution, or some information if it
did. For `verbosity = 2`, information about the current state is displayed after every
iteration of the algorithm. Finally, for `verbosity > 2`, information about the individual Krylov expansion steps is displayed.
The return value contains one or more entries that define the solution, and a final
entry `info` of type `ConvergeInfo` that encodes information about the solution, i.e.
whether it has converged, the residual(s) and the norm thereof, the number of operations
used:
```@docs
KrylovKit.ConvergenceInfo
```
There is also an expert interface where the user specifies the algorithm that should be used
explicitly, i.e.
```julia
results..., info = problemsolver(A, args..., algorithm(; kwargs...))
```
Most `algorithm` constructions take the same keyword arguments (`tol`, `krylovdim`,
`maxiter` and `verbosity`) discussed above.
As mentioned before, there are two auxiliary structs that can be used to define new vectors,
namely
```@docs
RecursiveVec
InnerProductVec
```
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 1906 | # Linear problems
Linear systems are of the form `A*x=b` where `A` should be a linear map that has the same
type of output as input, i.e. the solution `x` should be of the same type as the right hand
side `b`. They can be solved using the function `linsolve`:
```@docs
linsolve
```
## Automatic differentation
The `linsolve` routine can be used in conjunction with reverse-mode automatic differentiation,
using AD engines that are compatible with the [ChainRules](https://juliadiff.org/ChainRulesCore.jl/dev/)
ecosystem. The adjoint problem of a linear problem is again a linear problem, that requires the
adjoint[^1] of the linear map. If the linear map is an `AbstractMatrix` instance, its `adjoint`
will be used in the `rrule`. If the linear map is implemented as a function `f`, then the AD engine
itself is used to compute the corresponding adjoint via `ChainRulesCore.rrule_via_ad(config, f, x)`.
The specific base point `x` at which this adjoint is computed should not affect the result if `f`
properly represents a linear map. Furthermore, the `linsolve` output is only affected by the linear
map argument and the right hand side argument `b` (from a theoretical perspective, the starting vector
and algorithm parameters should have no effect), so that these two arguments are where the adjoint
variables need to be propagated to and have a nonzero effect.
The adjoint linear problem (also referred to as cotangent problem) is by default solved using the
same algorithms as the primal problem. However, the `rrule` can be customized to use a different
Krylov algorithm, by specifying the `alg_rrule` keyword argument. Its value can take any of the values
as the `algorithm` argument in `linsolve`.
[^1]: For a linear map, the adjoint or pullback required in the reverse-order chain rule coincides
with its (conjugate) transpose, at least with respect to the standard Euclidean inner product. | KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 1004 | # Functions of matrices and linear maps
Applying a function of a matrix or linear map to a given vector can in some cases also be
computed using Krylov methods. One example is the inverse function, which exactly
corresponds to what `linsolve` computes: ``A^{-1} * b``. There are other functions ``f``
for which ``f(A) * b`` can be computed using Krylov techniques, i.e. where ``f(A) * b`` can
be well approximated in the Krylov subspace spanned by ``{b, A * b, A^2 * b, ...}``.
Currently, the only family of functions of a linear map for which such a method is
available are the `ϕⱼ(z)` functions which generalize the exponential function
`ϕ₀(z) = exp(z)` and arise in the context of linear non-homogeneous ODEs. The corresponding
Krylov method for computing is an exponential integrator, and is thus available under the
name `expintegrator`. For a linear homogeneous ODE, the solution is a pure exponential, and
the special wrapper `exponentiate` is available:
```@docs
exponentiate
expintegrator
```
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 0.8.1 | 3c2a016489c38f35160a246c91a3f3353c47bb68 | docs | 2733 | # Singular value problems
It is possible to iteratively compute a few singular values and corresponding left and
right singular vectors using the function `svdsolve`:
```@docs
svdsolve
```
## Automatic differentation
The `svdsolve` routine can be used in conjunction with reverse-mode automatic differentiation,
using AD engines that are compatible with the [ChainRules](https://juliadiff.org/ChainRulesCore.jl/dev/)
ecosystem. The adjoint problem of a singular value problem contains a linear problem, although it
can also be formulated as an eigenvalue problem. Details about this approach will be published in a
forthcoming manuscript.
Both `svdsolve` and the adjoint problem associated with it require the action of the linear map as
well as of its adjoint[^1]. Hence, no new information about the linear map is required for the adjoint
problem. However, the linear map is the only argument that affects the `svdsolve` output (from a
theoretical perspective, the starting vector and algorithm parameters should have no effect), so that
this is where the adjoint variables need to be propagated to.
The adjoint problem (also referred to as cotangent problem) can thus be solved as a linear problem
or as an eigenvalue problem. Note that this eigenvalue problem is never symmetric or Hermitian.
The different implementations of the `rrule` can be selected using the `alg_rrule` keyword argument.
If a linear solver such as `GMRES` or `BiCGStab` is specified, the adjoint problem requires solving a]
number of linear problems equal to the number of requested singular values and vectors. If an
eigenvalue solver is specified, for which `Arnoldi` is essentially the only option, then the adjoint
problem is solved as a single (but larger) eigenvalue problem.
Note that the common pair of left and right singular vectors has an arbitrary phase freedom.
Hence, a well-defined cost function constructed from singular should depend on these in such a way
that its value is not affected by simultaneously changing the left and right singular vector with
a common phase factor, i.e. the cost function should be 'gauge invariant'. If this is not the case,
the cost function is said to be 'gauge dependent', and this can be detected in the resulting adjoint
variables for those singular vectors. The KrylovKit `rrule` for `svdsolve` will print a warning if
it detects from the incoming adjoint variables that the cost function is gauge dependent. This
warning can be suppressed by passing `alg_rrule` an algorithm with `verbosity=-1`.
[^1]: For a linear map, the adjoint or pullback required in the reverse-order chain rule coincides
with its (conjugate) transpose, at least with respect to the standard Euclidean inner product.
| KrylovKit | https://github.com/Jutho/KrylovKit.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | code | 392 | using Documenter, StanQuap
makedocs(
modules = [StanQuap],
format = Documenter.HTML(; prettyurls = get(ENV, "CI", nothing) == "true"),
authors = "Rob J Goedman",
sitename = "StanQuap.jl",
pages = Any["index.md"]
# strict = true,
# clean = true,
# checkdocs = :exports,
)
deploydocs(
repo = "github.com/goedman/StanQuap.jl.git",
push_preview = true
)
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | code | 807 | using CSV, DataFrames, Statistics, Test
using StanQuap
ProjDir = @__DIR__
df = CSV.read(joinpath(ProjDir, "..", "data", "Howell1.csv"), DataFrame)
df = filter(row -> row[:age] >= 18, df);
stan4_1 = "
// Inferring the mean and std
data {
int N;
array[N] real<lower=0> h;
}
parameters {
real<lower=0.1> sigma;
real<lower=100,upper=180> mu;
}
model {
// Priors for mu and sigma
mu ~ normal(178, 20);
sigma ~ exponential(1);
// Observed heights
h ~ normal(mu, sigma);
}
";
data = (N = size(df, 1), h = df.height)
init = (mu = 160.0, sigma = 10.0)
qm, sm, om = stan_quap("s4.1s", stan4_1; data, init)
println()
qm |> display
println()
println()
om.optim |> display
println()
println()
mean(Array(sample(qm)), dims=1) |> display
println()
ka =read_samples(sm)
ka |> display
println()
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | code | 291 | module StanQuap
using Reexport
@reexport using StanOptimize, StanSample
using StatsBase
using CSV, DataFrames, Distributions
using NamedTupleTools
using MonteCarloMeasurements
using DocStringExtensions, Statistics
using OrderedCollections, LinearAlgebra
include("quap.jl")
end # module
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | code | 4075 | import StatsBase: stderror, sample
"""
QuapResult
$(FIELDS)
where:
coef : NamedTuple with parameter MAP estimates,
vcov : Covariance matric,
converged : Simple check that multiple chains converged,
distr : Distributike to sample from (Normal or MvNormal),
params : Vector of parameter symbols.
"""
struct QuapResult{
N <: NamedTuple
} <: StatsBase.StatisticalModel
coef :: N
vcov :: Array{Float64, 2}
converged :: Bool
distr :: Union{Normal, MvNormal}
params :: Array{Symbol, 1}
end
"""
Compute the quadratic approximation to the posterior distribution.
$(SIGNATURES)
### Required arguments
```julia
* `name::String` : Name for SampleModel
* `model::String` : Stan Language model
```
### Keyword arguments
```julia
* `data` : Data for model (NamedTuple or Duct)
* `init` : Initial values for parameters (NamedTuple or Dict)
```
### Reyrns
```julia
* `res::QuapResult` : Returned object
```
In general using `init` results in better behavior.
"""
function stan_quap(
name::AbstractString,
model::AbstractString;
kwargs...)
om = OptimizeModel(name, model)
rc = stan_optimize(om; kwargs...)
if success(rc)
tmp, cnames = read_optimize(om)
optim = Dict()
for key in keys(tmp)
if !(key in ["lp__", :stan_version])
optim[Symbol(key)] = tmp[key]
end
end
sm = SampleModel(name, model, om.tmpdir)
rc2 = stan_sample(sm; kwargs...)
else
return ((nothing, nothing, nothing))
end
if success(rc2)
qm = quap(sm, optim, cnames)
return((qm, sm, (optim=optim, cnames=cnames)))
else
return((nothing, sm, nothing))
end
end
"""
Compute the quadratic approximation to the posterior distribution.
$(SIGNATURES)
Not exported
"""
function quap(
sm_sam::SampleModel,
optim::Dict,
cnames::Vector{String})
samples = read_samples(sm_sam, :dataframe)
n = Symbol.(names(samples))
coefnames = tuple(n...,)
c = [optim[Symbol(coefname)][1] for coefname in coefnames]
cvals = reshape(c, 1, length(n))
coefvalues = reshape(c, length(n))
v = Statistics.covm(Array(samples[:, n]), cvals)
distr = if length(coefnames) == 1
Normal(coefvalues[1], √v[1]) # Normal expects stddev
else
MvNormal(coefvalues, v) # MvNormal expects variance matrix
end
converged = true
for coefname in coefnames
o = optim[Symbol(coefname)]
converged = abs(sum(o) - 4 * o[1]) < 0.001 * abs(o[1])
!converged && break
end
ntcoef = namedtuple(coefnames, coefvalues)
return(QuapResult(ntcoef, v, converged, distr, n))
end
"""
Sample from a quadratic approximation to the posterior distribution.
$(SIGNATURES)
### Required arguments
```julia
* `qm` : QuapResult object (see: `?QuapResult`)
```
### Keyword arguments
```julia
* `nsamples = 4000` : Number of smaples taken from distribution
```
"""
function sample(qm::QuapResult; nsamples=4000)
df = DataFrame()
p = Particles(nsamples, qm.distr)
for (indx, coef) in enumerate(qm.params)
if length(qm.params) == 1
df[!, coef] = p.particles
else
df[!, coef] = p[indx].particles
end
end
df
end
# TEMPORARILY:
# Used by Max. Need to check if this works in general
function sample(qr::QuapResult, count::Int)::DataFrame
names = qr.params # StatsBase.coefnames(mode_result) in Turing
means = values(qr.coef) # StatsBase.coef(mode_result) in Turing
sigmas = Diagonal(qr.vcov) # StatsBase.stderr(mode_result) in Turing
DataFrame([
name => rand(Normal(μ, σ), count)
for (name, μ, σ) ∈ zip(names, means, sigmas)
])
end
export
QuapResult,
stan_quap,
sample
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | code | 62 | using StanQuap
using Test
include("./../scripts/howell1.jl")
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | code | 363 | ####
#### Coverage summary, printed as "(percentage) covered".
####
#### Useful for CI environments that just want a summary (eg a Gitlab setup).
####
using Coverage
cd(joinpath(@__DIR__, "..", "..")) do
covered_lines, total_lines = get_summary(process_folder())
percentage = covered_lines / total_lines * 100
println("($(percentage)%) covered")
end
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | code | 266 | # only push coverage from one bot
get(ENV, "TRAVIS_OS_NAME", nothing) == "linux" || exit(0)
get(ENV, "TRAVIS_JULIA_VERSION", nothing) == "1.3" || exit(0)
using Coverage
cd(joinpath(@__DIR__, "..", "..")) do
Codecov.submit(Codecov.process_folder())
end
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | docs | 1775 | # StanQuap.jl
| **Project Status** | **Build Status** |
|:---------------------------:|:-----------------:|
|![][project-status-img] | ![][CI-build] |
[docs-dev-img]: https://img.shields.io/badge/docs-dev-blue.svg
[docs-dev-url]: https://stanjulia.github.io/StanQuap.jl/latest
[docs-stable-img]: https://img.shields.io/badge/docs-stable-blue.svg
[docs-stable-url]: https://stanjulia.github.io/StanQuap.jl/stable
[CI-build]: https://github.com/stanjulia/StanQuap.jl/workflows/CI/badge.svg?branch=master
[issues-url]: https://github.com/stanjulia/StanQuap.jl/issues
[project-status-img]: https://img.shields.io/badge/lifecycle-stable-green.svg
## Purpose of package
This package is created to simplify the usage of quadratic approximations in [StatisticalRethinking.jl](https://github.com/StatisticalRethinkingJulia).
As such, it is intended for initial learning purposes.
Many better (and certainly more efficient!) ways of obtaining a quadratic approximation to the posterior distribution are available in Julia (and demonstrated in the project StatisticalRethinkingStan.jl) but none used a vanilla Stan Language program as used in Statistical Rethinking.
## Installation
Once this package is registered, install with
```julia
pkg> add StanQuap.jl
```
You need a working [Stan's cmdstan](https://mc-stan.org/users/interfaces/cmdstan.html) installation, the path of which you should specify either in `CMDSTAN` or `JULIA_CMDSTAN_HOME`, eg in your `~/.julia/config/startup.jl` have a line like
```julia
# CmdStan setup
ENV["CMDSTAN"] = expanduser("~/src/cmdstan-2.35.0/") # replace with your path
```
It is recommended that you start your Julia process with multiple worker processes to take advantage of parallel sampling, eg
```sh
julia -p auto
```
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 4.4.1 | bb591abb7d9d2353ae69a929bfafd8dff3dbe2a3 | docs | 39 | # StanQuap
*Documentation goes here.*
| StanQuap | https://github.com/StanJulia/StanQuap.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | code | 413 | push!(LOAD_PATH,"../src/")
using Documenter, HolidayCalendars
makedocs(
modules = [HolidayCalendars],
clean = false,
format = Documenter.HTML(),
sitename = "HolidayCalendars.jl",
authors = "Iain Skett",
pages = [
"Holiday Calendars" => "index.md",
],
)
deploydocs(
repo = "github.com/InfiniteChai/HolidayCalendars.jl.git",
devbranch = "main",
devurl = "latest"
)
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | code | 322 | module HolidayCalendars
import RDates
include("rules.jl")
const CALENDARS = RDates.SimpleCalendarManager()
RDates.setcachedcalendar!(CALENDARS, "WEEKEND", RDates.WeekendCalendar())
include("calendars/unitedkingdom.jl")
include("calendars/unitedstates.jl")
include("calendars/target.jl")
export CALENDARS
end # module
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | code | 4639 | import RDates: RDates, CalendarManager, RDate, Calendar, apply, NullCalendarManager
import Dates: Dates, Date
abstract type CalendarRule end
includehols(::CalendarRule, from::Date, to::Date) = repeat([false], (to-from).value + 1)
excludehols(::CalendarRule, from::Date, to::Date) = repeat([false], (to-from).value + 1)
"""
WindowCalendarRule(rule; from::Union{Nothing,Date}=nothing, to::Union{Nothing,Date}=nothing)
Restrict another calendar rule to within a window of [from, to].
"""
struct WindowCalendarRule <: CalendarRule
rule::CalendarRule
from::Union{Nothing,Date}
to::Union{Nothing,Date}
WindowCalendarRule(rule; from=nothing, to=nothing) = new(rule, from, to)
end
function includehols(rule::WindowCalendarRule, from::Date, to::Date)
rule.from != nothing && rule.from > to && return repeat([false], (to-from).value + 1)
rule.to != nothing && rule.to < from && return repeat([false], (to-from).value + 1)
hols = includehols(rule.rule, from, to)
r1 = rule.from != nothing ? (1:(rule.from-from).value) : []
r2 = rule.to != nothing ? ((rule.to-from).value+2:(to-from).vaue+1) : []
for i in Iterators.flatten([r1,r2])
@inbounds hols[i] = false
end
hols
end
function excludehols(rule::WindowCalendarRule, from::Date, to::Date)
rule.from != nothing && rule.from > to && return repeat([false], (to-from).value + 1)
rule.to != nothing && rule.to < from && return repeat([false], (to-from).value + 1)
hols = excludehols(rule.rule, from, to)
r1 = rule.from != nothing ? (1:(rule.from-from).value) : []
r2 = rule.to != nothing ? ((rule.to-from).value+2:(to-from).vaue+1) : []
for i in Iterators.flatten([r1,r2])
@inbounds hols[i] = false
end
hols
end
"""
PeriodicCalendarRule(period::RDate, increment::RDate; include::Bool=true, cal_mgr::CalendarManager=NullCalendarManager())
A calendar rule which is generated by iterating on a `period` and then applying an `increment`. To mark
the calendar rule is an exclusion then can set the `include` parameter to false.
```julia-repl
julia> PeriodicCalendarRule(rd"1y", rd"1MAY+Last MON");
```
"""
struct PeriodicCalendarRule <: CalendarRule
period::RDate
increment::RDate
include::Bool
cal_mgr::CalendarManager
PeriodicCalendarRule(period::RDate, increment::RDate; include=true, cal_mgr=NullCalendarManager()) = new(period, increment, include, cal_mgr)
end
function holidays(rule::PeriodicCalendarRule, from::Date, to::Date)
hols = repeat([false], (to-from).value + 1)
for d in RDates.range(from, to, rule.period; cal_mgr=rule.cal_mgr)
d1 = apply(rule.increment, d, rule.cal_mgr)
if from <= d1 <= to
@inbounds hols[(d1-from).value+1] = true
end
end
hols
end
includehols(rule::PeriodicCalendarRule, from::Date, to::Date) = rule.include ? holidays(rule, from, to) : repeat([false], (to-from).value + 1)
excludehols(rule::PeriodicCalendarRule, from::Date, to::Date) = rule.include ? repeat([false], (to-from).value + 1) : holidays(rule, from, to)
"""
ExplicitDateRule(;inclusions::Vector{Date}=[], exclusions::Vector{Date}=[])
A calendar rule to mark an explicit set of dates as holiday or not holidays.
"""
struct ExplicitDateRule <: CalendarRule
inclusions::Vector{Date}
exclusions::Vector{Date}
ExplicitDateRule(;inclusions=Vector{Date}(), exclusions=Vector{Date}()) = new(inclusions, exclusions)
end
function includehols(rule::ExplicitDateRule, from::Date, to::Date)
hols = repeat([false], (to-from).value + 1)
for d in rule.inclusions
if from <= d <= to
@inbounds hols[(d-from).value+1] = true
end
end
hols
end
function excludehols(rule::ExplicitDateRule, from::Date, to::Date)
hols = repeat([false], (to-from).value + 1)
for d in rule.exclusions
if from <= d <= to
@inbounds hols[(d-from).value+1] = true
end
end
hols
end
"""
RuleBasedCalendar(rules::Vector{CalendarRule})
A calendar system which is calculated by applying a set of of rules in order.
"""
struct RuleBasedCalendar <: Calendar
rules::Vector{CalendarRule}
end
function RDates.holidays(cal::RuleBasedCalendar, from::Date, to::Date)
hols = repeat([false], (to-from).value + 1)
for rule in cal.rules
hols = hols .| includehols(rule, from, to)
hols = hols .& (.! excludehols(rule, from, to))
end
hols
end
function RDates.is_holiday(cal::RuleBasedCalendar, date::Date)
year = Dates.year(date); from = Date(year,1,1); to = Date(year,12,31)
holidays(cal, from, to)[(date-from).value + 1]
end
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | code | 824 | import RDates: WeekendCalendar, @rd_str, setcachedcalendar!
import Dates: Date
setcachedcalendar!(CALENDARS, "TARGET", WeekendCalendar() + RuleBasedCalendar([
# New Years Day
PeriodicCalendarRule(rd"1y", rd"1JAN"),
# Labour Day
WindowCalendarRule(PeriodicCalendarRule(rd"1y", rd"1MAY"); from=Date(2000,1,1)),
# Good Friday
WindowCalendarRule(PeriodicCalendarRule(rd"1y", rd"0E-1FRI"); from=Date(2000,1,1)),
# Easter Monday
WindowCalendarRule(PeriodicCalendarRule(rd"1y", rd"0E+1MON"); from=Date(2000,1,1)),
# Christmas Day
PeriodicCalendarRule(rd"1y", rd"25DEC"),
# Day of Goodwill
WindowCalendarRule(PeriodicCalendarRule(rd"1y", rd"26DEC"); from=Date(2000,1,1)),
# End of Year
ExplicitDateRule(inclusions=[Date(1998,12,31), Date(1999,12,31), Date(2001,12,31)]),
]))
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | code | 4695 | import RDates: WeekendCalendar, @rd_str, setcachedcalendar!, calendar
import Dates: Date
setcachedcalendar!(CALENDARS, "UK/SETTLEMENT", WeekendCalendar() + RuleBasedCalendar([
# New Year's Day
PeriodicCalendarRule(rd"1y", rd"1JAN@WEEKEND[NBD]"; cal_mgr=CALENDARS),
# Good Friday
PeriodicCalendarRule(rd"1y", rd"0E-1FRI"),
# Easter Monday
PeriodicCalendarRule(rd"1y", rd"0E+1MON"),
# Early May Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1MAY+1st MON"),
# Spring Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1MAY+Last MON"),
# Late Summer Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1AUG+Last MON"),
# Christmas Day
PeriodicCalendarRule(rd"1y", rd"25DEC+0b@WEEKEND"; cal_mgr=CALENDARS),
# Boxing Day
PeriodicCalendarRule(rd"1y", rd"25DEC+1b@WEEKEND"; cal_mgr=CALENDARS),
# 50th VE Day Anniversary
ExplicitDateRule(inclusions=[Date(1995,5,8)], exclusions=[Date(1995,5,1)]),
# Golden Jubilee
ExplicitDateRule(inclusions=[Date(2002,6,3), Date(2002,6,4)], exclusions=[Date(2002,5,27)]),
# 2011 Royal Wedding
ExplicitDateRule(inclusions=[Date(2011,4,29)]),
# Diamond Jubilee
ExplicitDateRule(inclusions=[Date(2012,6,4), Date(2012,6,5)], exclusions=[Date(2002,5,28)]),
# 75th VE Day Anniversary
ExplicitDateRule(inclusions=[Date(2020,5,8)], exclusions=[Date(2020,5,4)]),
# Platinum Jubilee
ExplicitDateRule(inclusions=[Date(2022,6,2), Date(2022,6,3)], exclusions=[Date(2022,5,30)])
]))
setcachedcalendar!(CALENDARS, "LONDON", calendar(CALENDARS, "UK/SETTLEMENT"))
setcachedcalendar!(CALENDARS, "UK/STOCK EXCHANGE", WeekendCalendar() + RuleBasedCalendar([
# New Year's Day
PeriodicCalendarRule(rd"1y", rd"1JAN@WEEKEND[NBD]"; cal_mgr=CALENDARS),
# Good Friday
PeriodicCalendarRule(rd"1y", rd"0E-1FRI"),
# Easter Monday
PeriodicCalendarRule(rd"1y", rd"0E+1MON"),
# Early May Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1MAY+1st MON"),
# Spring Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1MAY+Last MON"),
# Late Summer Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1AUG+Last MON"),
# Christmas Day
PeriodicCalendarRule(rd"1y", rd"25DEC+0b@WEEKEND"; cal_mgr=CALENDARS),
# Boxing Day
PeriodicCalendarRule(rd"1y", rd"25DEC+1b@WEEKEND"; cal_mgr=CALENDARS),
# 50th VE Day Anniversary
ExplicitDateRule(inclusions=[Date(1995,5,8)], exclusions=[Date(1995,5,1)]),
# Golden Jubilee
ExplicitDateRule(inclusions=[Date(2002,6,3), Date(2002,6,4)], exclusions=[Date(2002,5,27)]),
# 2011 Royal Wedding
ExplicitDateRule(inclusions=[Date(2011,4,29)]),
# Diamond Jubilee
ExplicitDateRule(inclusions=[Date(2012,6,4), Date(2012,6,5)], exclusions=[Date(2002,5,28)]),
# 75th VE Day Anniversary
ExplicitDateRule(inclusions=[Date(2020,5,8)], exclusions=[Date(2020,5,4)]),
# Platinum Jubilee
ExplicitDateRule(inclusions=[Date(2022,6,2), Date(2022,6,3)], exclusions=[Date(2022,5,30)]),
# 31Dec1999
ExplicitDateRule(inclusions=[Date(1999,12,31)])
]))
setcachedcalendar!(CALENDARS, "UK/LSE", calendar(CALENDARS, "UK/STOCK EXCHANGE"))
setcachedcalendar!(CALENDARS, "UK/METAL EXCHANGE", WeekendCalendar() + RuleBasedCalendar([
# New Year's Day
PeriodicCalendarRule(rd"1y", rd"1JAN@WEEKEND[NBD]"; cal_mgr=CALENDARS),
# Good Friday
PeriodicCalendarRule(rd"1y", rd"0E-1FRI"),
# Easter Monday
PeriodicCalendarRule(rd"1y", rd"0E+1MON"),
# Early May Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1MAY+1st MON"),
# Spring Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1MAY+Last MON"),
# Late Summer Bank Holiday
PeriodicCalendarRule(rd"1y", rd"1AUG+Last MON"),
# Christmas Day
PeriodicCalendarRule(rd"1y", rd"25DEC+0b@WEEKEND"; cal_mgr=CALENDARS),
# Boxing Day
PeriodicCalendarRule(rd"1y", rd"25DEC+1b@WEEKEND"; cal_mgr=CALENDARS),
# 50th VE Day Anniversary
ExplicitDateRule(inclusions=[Date(1995,5,8)], exclusions=[Date(1995,5,1)]),
# Golden Jubilee
ExplicitDateRule(inclusions=[Date(2002,6,3), Date(2002,6,4)], exclusions=[Date(2002,5,27)]),
# 2011 Royal Wedding
ExplicitDateRule(inclusions=[Date(2011,4,29)]),
# Diamond Jubilee
ExplicitDateRule(inclusions=[Date(2012,6,4), Date(2012,6,5)], exclusions=[Date(2002,5,28)]),
# 75th VE Day Anniversary
ExplicitDateRule(inclusions=[Date(2020,5,8)], exclusions=[Date(2020,5,4)]),
# Platinum Jubilee
ExplicitDateRule(inclusions=[Date(2022,6,2), Date(2022,6,3)], exclusions=[Date(2022,5,30)]),
# 31Dec1999
ExplicitDateRule(inclusions=[Date(1999,12,31)])
]))
setcachedcalendar!(CALENDARS, "UK/LME", calendar(CALENDARS, "UK/METAL EXCHANGE"))
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | code | 1456 | import RDates: WeekendCalendar, @rd_str, setcachedcalendar!, calendar
import Dates: Date
setcachedcalendar!(CALENDARS, "US/SETTLEMENT", WeekendCalendar() + RuleBasedCalendar([
# New Year's Day
PeriodicCalendarRule(rd"1y", rd"1JAN@WEEKEND[NEAR]"; cal_mgr=CALENDARS),
# New Year's Day (handle case where day falls back into this year)
PeriodicCalendarRule(rd"1y", rd"1y+1JAN@WEEKEND[NEAR]"; cal_mgr=CALENDARS),
# # Martin Luther King Jr Birthday
WindowCalendarRule(PeriodicCalendarRule(rd"1y", rd"1JAN+3rd MON"); from=Date(1983,1,1)),
# # Washingthon's Birthday
PeriodicCalendarRule(rd"1y", rd"1FEB+3rd MON"),
# # Memorial Day
PeriodicCalendarRule(rd"1y", rd"1MAY+Last MON"),
# # Juneteenth
WindowCalendarRule(PeriodicCalendarRule(rd"1y", rd"19JUN@WEEKEND[NEAR]"; cal_mgr=CALENDARS); from=Date(2021,1,1)),
# # Independence Day
PeriodicCalendarRule(rd"1y", rd"4JUL@WEEKEND[NEAR]"; cal_mgr=CALENDARS),
# # Labor Day
PeriodicCalendarRule(rd"1y", rd"1SEP+1st MON"),
# # Columbus Day
PeriodicCalendarRule(rd"1y", rd"1OCT+2nd MON"),
# # Veteran's Day
PeriodicCalendarRule(rd"1y", rd"11NOV@WEEKEND[NEAR]"; cal_mgr=CALENDARS),
# # Thanksgiving Day
PeriodicCalendarRule(rd"1y", rd"1NOV+4th THU"),
# # Christmas
PeriodicCalendarRule(rd"1y", rd"25DEC@WEEKEND[NEAR]"; cal_mgr=CALENDARS),
]))
setcachedcalendar!(CALENDARS, "NEW YORK", calendar(CALENDARS, "US/SETTLEMENT"))
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | code | 2111 | using Test
using HolidayCalendars
using Dates: Date, dayofweek
using RDates
@testset "Holiday Calendars" verbose=true begin
@testset "United Kingdom → Settlements" begin
holidays_2004 = Set([
Date(2004,1,1),
Date(2004,4,9),
Date(2004,4,12),
Date(2004,5,3),
Date(2004,5,31),
Date(2004,8,30),
Date(2004,12,27),
Date(2004,12,28),
])
cal = RDates.calendar(CALENDARS, ["UK/SETTLEMENT"])
for d in range(Date(2004,1,1), Date(2004,12,31), rd"1b@WEEKEND"; cal_mgr=CALENDARS)
@test is_holiday(cal, d) == (d in holidays_2004 || dayofweek(d) > 5)
end
holidays_2005 = Set([
Date(2005,1,3),
Date(2005,3,25),
Date(2005,3,28),
Date(2005,5,2),
Date(2005,5,30),
Date(2005,8,29),
Date(2005,12,26),
Date(2005,12,27),
])
for d in range(Date(2005,1,1), Date(2005,12,31), rd"1b@WEEKEND"; cal_mgr=CALENDARS)
@test is_holiday(cal, d) == (d in holidays_2005 || dayofweek(d) > 5)
end
holidays_2021 = Set([
Date(2021,1,1),
Date(2021,4,2),
Date(2021,4,5),
Date(2021,5,3),
Date(2021,5,31),
Date(2021,8,30),
Date(2021,12,27),
Date(2021,12,28),
])
for d in range(Date(2021,1,1), Date(2021,12,31), rd"1b@WEEKEND"; cal_mgr=CALENDARS)
@test is_holiday(cal, d) == (d in holidays_2021 || dayofweek(d) > 5)
end
holidays_2022 = Set([
Date(2022,1,3),
Date(2022,4,15),
Date(2022,4,18),
Date(2022,5,2),
Date(2022,6,2),
Date(2022,6,3),
Date(2022,8,29),
Date(2022,12,26),
Date(2022,12,27),
])
for d in range(Date(2022,1,1), Date(2022,12,31), rd"1b@WEEKEND"; cal_mgr=CALENDARS)
@test is_holiday(cal, d) == (d in holidays_2022 || dayofweek(d) > 5)
end
end
end
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | docs | 2092 | # HolidayCalendars
*A holiday calendar suite to integrate with the [RDates](https://github.com/InfiniteChai/RDates.jl) library*
| **Documentation** | **Build Status** |
|:-------------------------------------------------------------------------:|:-------------------------------------------------------------:|
| [![][docs-stable-img]][docs-stable-url] [![][docs-latest-img]][docs-latest-url] | [![][travis-img]][travis-url] [![][codecov-img]][codecov-url] |
This provides a set of the financial holiday calendars that can be integrated with [RDates](https://github.com/InfiniteChai/RDates.jl), the relative date library. It is built to be easy to understand but heavily optimised for
integration with financial models.
## Installation
`HolidayCalendars` can be installed using the Julia package manager. From the Julia REPL, type `]` to enter the Pkg REPL mode and run
```julia-repl
pkg> add HolidayCalendars
```
## Basic Usage
At this point you can now start using `HolidayCalendars` in your current Julia session using the following command
```julia-repl
julia> using HolidayCalendars
```
To work with the RDates library you then just need to use the `CALENDARS` calendar manager
```julia-repl
julia> using RDates, Dates
julia> apply(rd"1b@LONDON", Date(2021,7,16), CALENDARS)
2021-07-19
```
[docs-latest-img]: https://img.shields.io/badge/docs-latest-blue.svg
[docs-latest-url]: https://infinitechai.github.io/HolidayCalendars.jl/latest
[docs-stable-img]: https://img.shields.io/badge/docs-stable-blue.svg
[docs-stable-url]: https://infinitechai.github.io/HolidayCalendars.jl/stable
[travis-img]: https://travis-ci.com/InfiniteChai/HolidayCalendars.jl.svg?branch=master
[travis-url]: https://travis-ci.com/InfiniteChai/HolidayCalendars.jl
[codecov-img]: https://codecov.io/gh/InfiniteChai/HolidayCalendars.jl/branch/master/graph/badge.svg
[codecov-url]: https://codecov.io/gh/InfiniteChai/HolidayCalendars.jl
[issues-url]: https://github.com/JuliaDocs/Documenter.jl/issues
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"MIT"
] | 0.1.0 | cd545c06384a7994dc67f81ec1c4370234601f97 | docs | 3320 | # Holiday Calendars
*A holiday calendar suite to integrate with the [RDates](https://github.com/InfiniteChai/RDates.jl) library*
This provides a set of the financial holiday calendars that can be integrated with [RDates](https://github.com/InfiniteChai/RDates.jl), the relative date library. It is built to be easy to understand but heavily optimised for
integration with financial models.
## Installation
`HolidayCalendars` can be installed using the Julia package manager. From the Julia REPL, type `]` to enter the Pkg REPL mode and run
```julia-repl
pkg> add HolidayCalendars
```
## Basic Usage
At this point you can now start using `HolidayCalendars` in your current Julia session using the following command
```julia-repl
julia> using HolidayCalendars
```
To work with the RDates library you then just need to use the `CALENDARS` calendar manager
```julia-repl
julia> using RDates, Dates
julia> apply(rd"1b@LONDON", Date(2021,7,16), CALENDARS)
2021-07-19
```
## Calendar Definitions
This package provides the following set of holiday calendars.
### General Calendars
- **WEEKEND** will mark Saturday and Sunday as holidays.
### United Kingdom Calendars
- **UK/SETTLEMENT** or **LONDON** is the bank holiday (and swap settlement) calendar for England and Wales.
- **UK/STOCK EXCHANGE** or **UK/LSE** is the holiday calendar for the London Stock Exchange.
- **UK/METAL EXCHANGE** or **UK/LME** is the holiday calendar for the London Metal Exchange.
### European Calendars
- **TARGET** is the [TARGET](https://www.ecb.europa.eu/paym/target/target2/profuse/calendar/html/index.en.html) holiday calendar.
### United States Calendars
- **US/SETTLEMENT** or **NEW YORK** is the bank holiday (and swap settlement) calendar for United States.
## Benchmarks
When working with financial models, it's important to optimise the performance for
high frequency of calls.
We use the cached calendar model by default so that we can perform a million calculations
of holiday functions in under a second.
First we can check out the performance of calculating the number of business days within
an 85 year period.
```@example
using HolidayCalendars, RDates, Dates, BenchmarkTools
d0 = Dates.Date(2015,1,1)
d1 = Dates.Date(2100,12,31)
cal = calendar(CALENDARS, "LONDON")
bizdaycount(cal, d0, d1)
res = @benchmark for _ in 1:1000000 bizdaycount(cal, d0, d1) end
println(IOContext(stdout, :compact => false), res)
```
Next lets check out the performance of calculating the next business day.
```@example
using HolidayCalendars, RDates, Dates, BenchmarkTools
d0 = Dates.Date(2015,1,1)
d1 = rd"1b@LONDON"
res = @benchmark for _ in 1:1000000 apply(d1, d0, CALENDARS) end
println(IOContext(stdout, :compact => false), res)
```
## Registering a Calendar
To register a new calendar, then you can use calendar rules for defining it
```@docs
HolidayCalendars.PeriodicCalendarRule
HolidayCalendars.ExplicitDateRule
HolidayCalendars.WindowCalendarRule
```
You can then register these together into `RuleBasedCalendar`.
```@docs
HolidayCalendars.RuleBasedCalendar
```
When registering your calendar, use `setcachedcalendar!` to make sure we're getting
the necessary performance characteristics within financial models.
```julia
setcachedcalendar!(CALENDARS, "CAL NAME", WeekendCalendar() + RuleBasedCalendar([]))
```
| HolidayCalendars | https://github.com/InfiniteChai/HolidayCalendars.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 735 | # Copyright 2017 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
module KernelMethods
include("scores.jl")
include("cv.jl")
include("kernels.jl")
include("supervised.jl")
include("kmap/kmap.jl")
# include("nets.jl")
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 2003 | # Copyright 2017 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
module CrossValidation
using Random
export montecarlo, kfolds
function montecarlo(evalfun::Function, X::Vector{ItemType}, y::Vector{LabelType}; runs::Int=3, trainratio=0.7, testratio=0.3) where {ItemType, LabelType}
Z = zip(X, y) |> collect
R = Float64[]
for i in 1:runs
shuffle!(Z)
sep = floor(Int, length(Z) * trainratio)
last = min(length(Z), sep + 1 + floor(Int, length(Z) * testratio))
train = @view Z[1:sep]
test = @view Z[1+sep:last]
s = evalfun([z[1] for z in train], [z[2] for z in train], [z[1] for z in test], [z[2] for z in test])
push!(R, s)
end
return R
end
function kfolds(evalfun::Function, X::Vector{ItemType}, y::Vector{LabelType}; folds::Int=3, shuffle=true) where {ItemType, LabelType}
Z = zip(X, y) |> collect
if shuffle
shuffle!(Z)
end
R = Float64[]
bsize = floor(Int, length(Z) / folds)
begin
test = @view Z[1:bsize]
train = @view Z[bsize+1:end]
s = evalfun([z[1] for z in train], [z[2] for z in train], [z[1] for z in test], [z[2] for z in test])
push!(R, s)
end
for i in 1:folds-1
train = vcat(Z[1:bsize*i], Z[bsize*(i+1)+1:end])
test = @view Z[bsize*i+1:bsize*(i+1)]
s = evalfun([z[1] for z in train], [z[2] for z in train], [z[1] for z in test], [z[2] for z in test])
push!(R, s)
end
return R
end
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1471 | module Kernels
export gaussian_kernel, sigmoid_kernel, cauchy_kernel, linear_kernel
"""
Creates a Gaussian kernel with the given distance function and `sigma` value
"""
function gaussian_kernel(dist, sigma=1.0)
sigma2 = sigma * 2
function fun(obj, ref)::Float64
d = dist(obj, ref)
(d == 0 || sigma == 0) && return 1.0
exp(-d / sigma2)
end
fun
end
"""
Creates a sigmoid kernel with the given `sigma` value and distance function
"""
function sigmoid_kernel(dist, sigma=1.0)
sqrtsigma = sqrt(sigma)
function fun(obj, ref)::Float64
x = dist(obj, ref)
2 * sqrtsigma / (1 + exp(-x))
end
fun
end
"""
Creates a Cauchy's kernel with the given `sigma` value and distance function
"""
function cauchy_kernel(dist, sigma=1.0)
sqsigma = sigma^2
function fun(obj, ref)::Float64
x = dist(obj, ref)
(x == 0 || sqsigma == 0) && return 1.0
1 / (1 + x^2 / sqsigma)
end
fun
end
"""
Creates a tanh kernel with the given `sigma` value and distance function
"""
function tanh_kernel(dist, sigma=1.0)
function fun(obj, ref)::Float64
x = dist(obj, ref)
(exp(x-sigma) - exp(-x+sigma)) / (exp(x-sigma) + exp(-x+sigma))
end
fun
end
"""
Creates a linear kernel with the given distance function and `sigma` slope
"""
function linear_kernel(dist, sigma=1.0)
function fun(obj, ref)::Float64
dist(obj, ref) * sigma
end
fun
end
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 5196 | # Copyright 2017,2018 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
using SimilaritySearch:
Sequential, KnnResult
import SimilaritySearch: optimize!
import KernelMethods.CrossValidation: montecarlo, kfolds
export NearNeighborClassifier, optimize!, predict, predict_proba
mutable struct NearNeighborClassifier{IndexType,LabelType}
dist::Function
X::IndexType
y::Vector{Int}
k::Int
le::LabelEncoder{LabelType}
weight
function NearNeighborClassifier(dist::Function, X::AbstractVector{ItemType}, y::AbstractVector{LabelType}, k::Int=1, weight=:uniform, create_index=nothing) where {ItemType, LabelType}
le = LabelEncoder(y)
y_ = [transform(le, l) for l in y]
if create_index == nothing
index = fit(Sequential, X)
else
index = create_index(X)
end
new{typeof(index), LabelType}(dist, index, y_, k, le, weight)
end
end
function predict(nnc::NearNeighborClassifier{IndexType,LabelType}, vector) where {IndexType,LabelType}
[predict_one(nnc, item) for item in vector]
end
function predict_proba(nnc::NearNeighborClassifier{IndexType,LabelType}, vector::AbstractVector; smoothing=0.0) where {IndexType,LabelType}
[predict_one_proba(nnc, item, smoothing=smoothing) for item in vector]
end
function _predict_one(nnc::NearNeighborClassifier{IndexType,LabelType}, item) where {IndexType,LabelType}
res = KnnResult(nnc.k)
search(nnc.X, nnc.dist, item, res)
w = zeros(Float64, length(nnc.le.labels))
if nnc.weight == :uniform
for p in res
l = nnc.y[p.objID]
w[l] += 1.0
end
elseif nnc.weight == :distance
for p in res
l = nnc.y[p.objID]
w[l] += 1.0 / (1.0 + p.dist)
end
else
throw(ArgumentError("Unknown weighting scheme $(nnc.weight)"))
end
w
end
function predict_one(nnc::NearNeighborClassifier{IndexType,LabelType}, item) where {IndexType,LabelType}
score, i = findmax(_predict_one(nnc, item))
inverse_transform(nnc.le, i)
end
function predict_one_proba(nnc::NearNeighborClassifier{IndexType,LabelType}, item; smoothing=0.0) where {IndexType,LabelType}
w = _predict_one(nnc, item)
t = sum(w)
s = t * smoothing
ss = s * length(w)
for i in 1:length(w)
w[i] = (w[i] + s) / (t + ss) # overriding previous w
end
w
end
function _train_create_table(dist::Function, train_X, train_y, test_X, k::Int)
index = fit(Sequential, train_X)
tab = Vector{Vector{Tuple{Int,Float64}}}(undef, length(test_X))
for i in 1:length(test_X)
res = search(index, dist, test_X[i], KnnResult(k))
tab[i] = [(train_y[p.objID], p.dist) for p in res]
end
tab
end
function _train_predict(nnc::NearNeighborClassifier{IndexType,LabelType}, table, test_X, k) where {IndexType,LabelType}
A = Vector{LabelType}(undef, length(test_X))
w = Vector{Float64}(undef, length(nnc.le.labels))
for i in 1:length(test_X)
w .= 0.0
row = table[i]
for j in 1:k
label, _d = row[j]
if nnc.weight == :uniform
w[label] += 1
else
w[label] += 1.0 / (1.0 + _d)
end
end
score, label = findmax(w)
A[i] = inverse_transform(nnc.le, label)
end
A
end
function optimize!(nnc::NearNeighborClassifier, scorefun::Function; runs=3, trainratio=0.5, testratio=0.5, folds=0, folds_shuffle=true)
mem = Dict{Tuple,Float64}()
function f(train_X, train_y, test_X, test_y)
_nnc = NearNeighborClassifier(nnc.dist, train_X, train_y)
kmax = sqrt(length(train_y)) |> round |> Int
table = _train_create_table(_nnc.dist, train_X, train_y, test_X, kmax)
k = 2
while k <= kmax
for weight in (:uniform, :distance)
_nnc.weight = weight
_nnc.k = k - 1
pred_y = _train_predict(_nnc, table, test_X, _nnc.k)
score = scorefun(test_y, pred_y)
key = (k - 1, weight)
mem[key] = get(mem, key, 0.0) + score
end
k += k
end
0
end
if folds > 1
kfolds(f, nnc.X.db, nnc.y, folds=folds, shuffle=folds_shuffle)
bestlist = [(score/folds, conf) for (conf, score) in mem]
else
montecarlo(f, nnc.X.db, nnc.y, runs=runs, trainratio=trainratio, testratio=testratio)
bestlist = [(score/runs, conf) for (conf, score) in mem]
end
sort!(bestlist, by=x -> (-x[1], x[2][1]))
best = bestlist[1]
nnc.k = best[2][1]
nnc.weight = best[2][2]
bestlist
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 3705 | # Copyright 2017,2018 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
export NearNeighborRegression, optimize!, predict, predict_proba
import KernelMethods.CrossValidation: montecarlo, kfolds
using Statistics
using SimilaritySearch:
Sequential, KnnResult, empty!, fit
mutable struct NearNeighborRegression{IndexType,DataType}
dist::Function
X::IndexType
y::Vector{DataType}
k::Int
summarize::Function
function NearNeighborRegression(dist::Function, X::AbstractVector{ItemType}, y::AbstractVector{DataType}; summarize=mean, k::Int=1) where {ItemType, DataType}
index = fit(Sequential, X)
new{typeof(index), DataType}(dist, index, y, k, summarize)
end
end
function predict(nnc::NearNeighborRegression{IndexType,DataType}, vector) where {IndexType,DataType}
[predict_one(nnc, item) for item in vector]
end
function predict_one(nnc::NearNeighborRegression{IndexType,DataType}, item) where {IndexType,DataType}
res = KnnResult(nnc.k)
search(nnc.X, nnc.dist, item, res)
DataType[nnc.y[p.objID] for p in res] |> nnc.summarize
end
function _train_create_table_reg(dist::Function, train_X, train_y, test_X, k::Int)
index = fit(Sequential, train_X)
res = KnnResult(k)
function f(x)
empty!(res) # this is thread unsafe
search(index, dist, x, res)
[train_y[p.objID] for p in res]
end
f.(test_X)
end
function _train_predict(nnc::NearNeighborRegression{IndexType,DataType}, table, test_X, k) where {IndexType,DataType}
A = Vector{DataType}(undef, length(test_X))
for i in 1:length(test_X)
row = table[i]
A[i] = nnc.summarize(row[1:k])
end
A
end
function gmean(X)
prod(X)^(1/length(X))
end
function hmean(X)
d = 0.0
for x in X
d += 1.0 / x
end
length(X) / d
end
function optimize!(nnr::NearNeighborRegression, scorefun::Function; summarize_list=[mean, median, gmean, hmean], runs=3, trainratio=0.5, testratio=0.5, folds=0, shufflefolds=true)
mem = Dict{Tuple,Float64}()
function f(train_X, train_y, test_X, test_y)
_nnr = NearNeighborRegression(nnr.dist, train_X, train_y)
kmax = sqrt(length(train_y)) |> round |> Int
table = _train_create_table_reg(nnr.dist, train_X, train_y, test_X, kmax)
k = 2
while k <= kmax
_nnr.k = k - 1
for summarize in summarize_list
_nnr.summarize = summarize
pred_y = _train_predict(_nnr, table, test_X, _nnr.k)
score = scorefun(test_y, pred_y)
key = (k - 1, summarize)
mem[key] = get(mem, key, 0.0) + score
end
k += k
end
0
end
if folds > 1
kfolds(f, nnr.X.db, nnr.y, folds=folds, shuffle=shufflefolds)
bestlist = [(score/folds, conf) for (conf, score) in mem]
else
montecarlo(f, nnr.X.db, nnr.y, runs=runs, trainratio=trainratio, testratio=testratio)
bestlist = [(score/runs, conf) for (conf, score) in mem]
end
sort!(bestlist, by=x -> (-x[1], x[2][1]))
best = bestlist[1]
nnr.k = best[2][1]
nnr.summarize = best[2][2]
bestlist
end | KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1429 | # Copyright 2017 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
export LabelEncoder, transform, inverse_transform
import Base: broadcastable
struct LabelEncoder{LabelType}
imap::Dict{LabelType,Int}
labels::Vector{LabelType}
freqs::Vector{Int}
function LabelEncoder(y::AbstractVector{LabelType}) where LabelType
L = Dict{LabelType,Int}()
for c in y
L[c] = get(L, c, 0) + 1
end
labels = collect(keys(L))
sort!(labels)
freqs = [L[c] for c in labels]
imap = Dict(c => i for (i, c) in enumerate(labels))
new{LabelType}(imap, labels, freqs)
end
end
function transform(le::LabelEncoder{LabelType}, y::LabelType)::Int where LabelType
le.imap[y]
end
function inverse_transform(le::LabelEncoder{LabelType}, y::Int)::LabelType where LabelType
le.labels[y]
end
function broadcastable(le::LabelEncoder)
[le]
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 3734 | # Copyright 2017,2018 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import SimilaritySearch: optimize!
export NaiveBayesClassifier, NaiveBayesKernel, kernel_prob, predict, predict_proba, optimize!
abstract type NaiveBayesKernel end
mutable struct NaiveBayesClassifier{ItemType,LabelType}
kernel::NaiveBayesKernel
probs::Vector{Float64}
le::LabelEncoder{LabelType}
end
include("nbgaussian.jl")
include("nbmultinomial.jl")
function NaiveBayesClassifier(X::AbstractVector{ItemType}, y::AbstractVector{LabelType}; kernel=GaussianKernel) where {ItemType,LabelType}
le = LabelEncoder(y)
# y_ = [transform(le, l) for l in y]
y_ = transform.(le, y)
probs = Float64[freq/length(y) for freq in le.freqs]
kernel_ = kernel(X, y_, length(le.labels))
NaiveBayesClassifier{ItemType,LabelType}(kernel_, probs, le)
end
function predict(nbc::NaiveBayesClassifier{ItemType,LabelType}, vector)::Vector{LabelType} where {ItemType,LabelType}
y = Vector{LabelType}(undef, length(vector))
for i in 1:length(vector)
y[i] = predict_one(nbc, vector[i])
end
y
end
function predict_one_proba(nbc::NaiveBayesClassifier{ItemType,LabelType}, x) where {ItemType,LabelType}
w = kernel_prob(nbc, nbc.kernel, x)
ws = sum(w)
@inbounds for i in 1:length(w)
w[i] /= ws
end
w
end
function predict_one(nbc::NaiveBayesClassifier{ItemType,LabelType}, x) where {ItemType,LabelType}
p, i = findmax(kernel_prob(nbc, nbc.kernel, x))
inverse_transform(nbc.le, i)
end
function optimize!(nbc::NaiveBayesClassifier{ItemType,LabelType}, X::AbstractVector{ItemType}, y::AbstractVector{LabelType}, scorefun::Function; runs=3, trainratio=0.5, testratio=0.5, folds=0, shufflefolds=true) where {ItemType,LabelType}
@info "optimizing nbc $(typeof(nbc))"
# y::Vector{Int} = transform.(nbc.le, y)
mem = Dict{Any,Float64}()
function f(train_X, train_y, test_X, test_y)
tmp = NaiveBayesClassifier(train_X, train_y, kernel=MultinomialKernel)
for smoothing in [0.0, 0.1, 0.3, 1.0]
tmp.kernel.smoothing = smoothing
pred_y = predict(tmp, test_X)
score = scorefun(test_y, pred_y)
mem[(MultinomialKernel, smoothing)] = get(mem, (MultinomialKernel, smoothing), 0.0) + score
end
tmp.kernel = GaussianKernel(train_X, transform.(tmp.le, train_y), length(tmp.le.labels))
pred_y = predict(tmp, test_X)
score = scorefun(test_y, pred_y)
mem[(GaussianKernel, -1)] = get(mem, (GaussianKernel, -1), 0.0) + score
0
end
if folds > 1
kfolds(f, X, y, folds=folds, shuffle=shufflefolds)
bestlist = [(score/folds, conf) for (conf, score) in mem]
else
montecarlo(f, X, y, runs=runs, trainratio=trainratio, testratio=testratio)
bestlist = [(score/runs, conf) for (conf, score) in mem]
end
sort!(bestlist, by=x -> (-x[1], x[2][2]))
best = bestlist[1][2]
if best[1] == GaussianKernel
nbc.kernel = GaussianKernel(X, transform.(nbc.le, y), length(nbc.le.labels))
else
nbc.kernel = MultinomialKernel(X, transform.(nbc.le, y), length(nbc.le.labels), smoothing=best[2])
end
bestlist
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1946 | # Copyright 2017 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
export GaussianKernel
# using Distributions
struct GaussianKernel <: NaiveBayesKernel
mean_given_y::Matrix{Float64}
var_given_y::Matrix{Float64}
end
function GaussianKernel(X::AbstractVector{ItemType}, y::AbstractVector{Int}, nlabels::Int) where ItemType
dim = length(X[1])
occ = ones(Float64, dim, nlabels)
C = zeros(Float64, dim, nlabels)
V = zeros(Float64, dim, nlabels)
# α = 1 / length(X)
@inbounds for i in 1:length(X)
label = y[i]
for (j, x) in enumerate(X[i])
C[j, label] += x
occ[j, label] += 1
end
end
C = C ./ occ
@inbounds for i in 1:length(X)
label = y[i]
for (j, x) in enumerate(X[i])
V[j, label] += (x - C[j, label])^2
end
end
V = V ./ occ
GaussianKernel(C, V)
end
function kernel_prob(nbc::NaiveBayesClassifier, kernel::GaussianKernel, x::AbstractVector{Float64})::Vector{Float64}
n = length(nbc.le.labels)
scores = zeros(Float64, n)
@inbounds for i in 1:n
pxy = 1.0
py = nbc.probs[i]
for j in 1:length(x)
var2 = 2 * kernel.var_given_y[j, i]
a = 1 / sqrt(pi * var2)
# a = 1/sqrt(pi * abs(var2))
pxy *= a * exp(-(x[j] - kernel.mean_given_y[j, i])^2 / var2)
end
scores[i] = py * pxy
end
scores
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1537 | # Copyright 2017 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
export MultinomialKernel
mutable struct MultinomialKernel <: NaiveBayesKernel
acc_given_y::Matrix{Float64}
smoothing::Float64
end
function MultinomialKernel(X::AbstractVector{ItemType}, y::AbstractVector{Int}, nlabels::Int; smoothing::Float64=0.0) where ItemType
C = zeros(Float64, length(X[1]), nlabels)
@inbounds for i in 1:length(X)
label = y[i]
for (j, x) in enumerate(X[i])
C[j, label] += x
end
end
MultinomialKernel(C, smoothing)
end
function kernel_prob(nbc::NaiveBayesClassifier, kernel::MultinomialKernel, x::AbstractVector{Float64})::Vector{Float64}
n = length(nbc.le.labels)
scores = zeros(Float64, n)
for i in 1:n
pxy = 1.0
py = nbc.probs[i]
for j in 1:length(x)
den = kernel.acc_given_y[j, i] + kernel.smoothing * n
pxy *= (x[j] + kernel.smoothing) / den
end
scores[i] = py * pxy
end
scores
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 14432 | # Copyright 2017 Jose Ortiz-Bejar
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
module Nets
export Net, enet, kmnet, dnet, gen_features, KernelClassifier
import KernelMethods.Kernels: sigmoid, gaussian, linear, cauchy
import KernelMethods.Scores: accuracy, recall
import KernelMethods.Supervised: NearNeighborClassifier, NaiveBayesClassifier, optimize!, predict_one, predict_one_proba, LabelEncoder, transform, inverse_transform
using SimilaritySearch: KnnResult, L2Distance, L2SquaredDistance, CosineDistance, DenseCosine, JaccardDistance
using TextModel
using PyCall
@pyimport sklearn.naive_bayes as nb
@pyimport sklearn.model_selection as ms
#using JSON
#using DataStructures
mutable struct Net{ItemType,LabelType}
data::Vector{ItemType}
labels::Vector{Int}
le::LabelEncoder{LabelType}
references::Vector{Int32}
partitions::Vector{Int32}
centers::Vector{ItemType}
centroids::Vector{ItemType}
dists::Vector{Float64}
csigmas::Vector{Float64}
sigmas::Dict{Int,Float64}
stats::Dict{LabelType,Float64}
reftype::Symbol
distance
kernel
end
function Net(data::Vector{ItemType},labels::Vector{LabelType}) where {ItemType, LabelType}
le = LabelEncoder(labels)
y = transform.(le, labels)
Net(data,y,le,
Int32[],Int32[],ItemType[],
ItemType[],Float64[],Float64[],
Dict{Int,Float64}(), Dict{LabelType,Float64}(),:centroids,L2SquaredDistance(),gaussian)
end
function cosine(x1,x2)::Float64
xc1=DenseCosine(x1)
xc2=DenseCosine(x2)
d=CosineDistance()
return d(xc1,xc2)
end
function maxmin(data,centers,ind,index::KnnResult,distance,partitions)::Tuple{Int64,Float64}
c=last(centers)
if length(index)==0
for i in ind
if i!=c
push!(index,i,Inf)
end
end
end
nindex=KnnResult(length(index))
for fn in index
dist=distance(data[fn.objID],data[c])
#push!(lK[fn.objID],dist)
dist = if (dist<fn.dist) dist else fn.dist end
partitions[fn.objID] = if (dist<fn.dist) c else partitions[fn.objID] end
if fn.objID!=c
push!(nindex,fn.objID,dist)
end
end
index.k=nindex.k
index.pool=nindex.pool
fn=pop!(index)
return fn.objID,fn.dist
end
function get_centroids(data::Vector{T}, partitions::Vector{Int})::Vector{T} where T
centers=[j for j in Set(partitions)]
sort!(centers)
centroids=Vector{T}(length(centers))
for (ic,c) in enumerate(centers)
ind=[i for (i,v) in enumerate(partitions) if v==c]
centroids[ic]=mean(data[ind])
end
return centroids
end
# Epsilon Network using farthest first traversal Algorithm
function enet(N::Net,num_of_centers::Int; distance=L2SquaredDistance(),
per_class=false,reftype=:centroids, kernel=linear)
N.distance=distance
N.kernel=kernel
n=length(N.data)
partitions=[0 for i in 1:n]
gcenters,dists,sigmas=Vector{Int}(0),Vector{Float64}(num_of_centers-1),Dict{Int,Float64}()
indices=[[i for i in 1:n]]
for ind in indices
centers=Vector{Int}(0)
s=rand(1:length(ind))
push!(centers,ind[s])
#ll=N.labels[ind[s]]
index=KnnResult(length(ind))
partitions[ind[s]]=ind[s]
k=1
while k<=num_of_centers-1 && k<=length(ind)
fnid,d=maxmin(N.data,centers,ind,index,distance,partitions)
push!(centers,fnid)
dists[k]=d
partitions[fnid]=fnid
k+=1
end
sigmas[0]=minimum(dists)
gcenters=vcat(gcenters,centers)
end
N.references,N.partitions,N.dists,N.sigmas=gcenters,partitions,dists,sigmas
N.centers,N.centroids=N.data[gcenters],get_centroids(N.data,partitions)
N.csigmas,N.stats=get_csigmas(N.data,N.centroids,N.partitions,distance=N.distance)
N.reftype=reftype
end
# KMeans ++ seeding Algorithm
function kmpp(N::Net,num_of_centers::Int)::Vector{Int}
n=length(N.data)
s=rand(1:n)
centers, d = Vector{Int}(num_of_centers), L2SquaredDistance()
centers[1]=s
D=[d(N.data[j],N.data[s]) for j in 1:n]
for i in 1:num_of_centers-1
cp=cumsum(D/sum(D))
r=rand()
sl=[j for j in 1:length(cp) if cp[j]>=r]
s=sl[1]
centers[i+1]=s
for j in 1:n
dist=d(N.data[j],N.data[s])
if dist<D[j]
D[j]=dist
end
end
end
centers
end
#Assign Elementes to thier nearest centroid
function assign(data,centroids,partitions;distance=L2SquaredDistance())
d=distance
for i in 1:length(data)
partitions[i]=sortperm([d(data[i],c) for c in centroids])[1]
end
end
#Distances for each element to its nearest cluster centroid
function get_distances(data,centroids,partitions;distance=L2SquaredDistance())::Vector{Float64}
dists=Vector{Float64}(length(centroids))
for i in 1:length(centroids)
ind=[j for (j,l) in enumerate(partitions) if l==i]
if length(ind)>0
X=data[ind]
dd=[distance(centroids[i],x) for x in X]
dists[i]=maximum(dd)
end
end
sort!(dists)
return dists
end
#Calculated the sigma for each ball
function get_csigmas(data,centroids,partitions;distance=L2SquaredDistance())::Tuple{Vector{Float64},Dict{String,Float64}}
stats=Dict("SSE"=>0.0,"BSS"=>0.0)
refs=[j for j in Set(partitions)]
sort!(refs)
csigmas=Vector{Float64}(length(refs))
df=distance
m=mean(data)
for (ii,i) in enumerate(refs)
ind=[j for (j,l) in enumerate(partitions) if l==i]
#if length(ind)>0
X=data[ind]
dd=[df(data[i],x) for x in X]
csigmas[ii]=max(0,maximum(dd))
stats["SSE"]+=sum(dd)
stats["BSS"]+=length(X)*(sum(mean(X)-m))^2
#end
end
return csigmas,stats
end
#Feature generator using kmeans centroids
function kmnet(N::Net,num_of_centers::Int; max_iter=1000,kernel=linear,distance=L2SquaredDistance(),reftype=:centroids)
n=length(N.data)
#lK,partitions=[[] for i in 1:n],[0 for i in 1:n],[0 for i in 1:n]
partitions=[0 for i in 1:n]
dists=Vector{Float64}
init=kmpp(N,num_of_centers)
centroids=N.data[init]
i,aux=1,Vector{Float64}(length(centroids))
while centroids != aux && i < max_iter
i=i+1
aux = centroids
assign(N.data,centroids,partitions)
centroids=get_centroids(N.data,partitions)
end
N.distance=distance
dists=get_distances(N.data,centroids,partitions,distance=N.distance)
N.partitions,N.dists=partitions,dists
N.centroids,N.sigmas[0]=centroids,maximum(N.dists)
N.csigmas,N.stats=get_csigmas(N.data,N.centroids,N.partitions,distance=N.distance)
N.sigmas[0]=maximum(N.csigmas)
N.reftype=:centroids
N.kernel=kernel
end
#Feature generator using naive algorithm for density net
function dnet(N::Net,num_of_elements::Int64; distance=L2SquaredDistance(),kernel=linear,reftype=:centroids)
n,d,k=length(N.data),distance,num_of_elements
partitions,references=[0 for i in 1:n],Vector{Int}(0)
pk=1
dists,sigmas=Vector{Float64},Dict{Int,Float64}()
while 0 in partitions
pending=[j for (j,v) in enumerate(partitions) if partitions[j]==0]
s=rand(pending)
partitions[s]=s
pending=[j for (j,v) in enumerate(partitions) if partitions[j]==0]
push!(references,s)
pc=sortperm([d(N.data[j],N.data[s]) for j in pending])
if length(pc)>=k
partitions[pending[pc[1:k]]]=s
else
partitions[pending[pc]]=s
end
end
N.references,N.partitions=references,partitions
N.centers,N.centroids=N.data[references],get_centroids(N.data,partitions)
N.csigmas,N.stats=get_csigmas(N.data,N.centroids,N.partitions,distance=N.distance)
N.sigmas[0]=maximum(N.csigmas)
N.reftype=:centroids
N.distance=distance
N.kernel=kernel
end
#Generates feature espace using cluster centroids or centers
function gen_features(Xo::Vector{T},N::Net)::Vector{Vector{Float64}} where T
n=length(Xo)
sigmas,Xr=N.csigmas,Vector{T}(n)
Xm = N.reftype==:centroids || length(N.centers)==0 ? N.centroids : N.centers
nf=length(Xm[1])
kernel=N.kernel
for i in 1:n
xd=Vector{Float64}(nf)
for j in 1:nf
xd[j]=kernel(Xo[i],Xm[j],sigma=sigmas[j],distance=N.distance)
end
Xr[i]=xd
end
Xr
end
function traintest(N; op_function=recall, runs=3, folds=0, trainratio=0.7, testratio=0.3)
clf, avg = nb.GaussianNB(), Vector{Float64}(runs)
skf = ms.ShuffleSplit(n_splits=runs, train_size=trainratio, test_size=testratio)
X=gen_features(N.data,N)
y=N.labels
skf[:get_n_splits](X,y)
for (ei,vi) in skf[:split](X,y)
ei,vi=ei+1,vi+1
xt,xv=X[ei],X[vi]
yt,yv=y[ei],y[vi]
clf[:fit](xt,yt)
y_pred=clf[:predict](xv)
push!(avg,op_function(yv,y_pred))
end
#println("========== ",length(N.centroids) ," ",avg/folds)
#@show typeof(clf)
clf[:fit](X,y)
return clf,mean(avg)
end
#function transductive(){
# continue
#}
function predict_test(xt,y,xv,desc,cl)::Vector{Int64}
y_pred=[]
if contains(desc,"KNN")
#@show typeof(xt), typeof(y), typeof(cl.X.dist), Symbol(cl.X.dist)
cln=NearNeighborClassifier(xt,y,cl.X.dist,cl.k,cl.weight)
y_pred=[predict_one(cln,x)[1] for x in xv]
else
cln=nb.GaussianNB()
cln[:fit](xt,y)
y_pred=cln[:predict](xv)
end
y_pred
end
HammingDistance(x1,x2)::Float64 = length(x1)-sum(x1.==x2)
L2Squared = L2SquaredDistance()
function KlusterClassifier(Xe, Ye; op_function=recall,
K=[4, 8, 16, 32],
kernels=[:gaussian, :sigmoid, :linear, :cauchy],
runs=3,
trainratio=0.6,
testratio=0.4,
folds=0,
top_k=32,
threshold=0.03,
distances=[:cosine, :L2Squared],
nets=[:enet, :kmnet, :dnet], nsplits=3)::Vector{Tuple{Tuple{Any,Net},Float64,String}}
top=Vector{Tuple{Float64,String}}(0)
DNNC=Dict()
for (k, nettype, reftype, kernel, distancek) in zip(K, nets, [:centers, :centroids], kernels, distances)
if (distancek==:L2Squared || reftype==:centers) && nettype=="kmeans"
continue
else
N=Net(Xe,Ye)
eval(nettype)(N, k, kernel=eval(kernel), distance = eval(distancek), reftype=reftype)
X=gen_features(N.data, N)
end
for distance in distances
nnc = NearNeighborClassifier(X,Ye, eval(distance))
opval,_tmp=optimize!(nnc, op_function,runs=runs, trainratio=trainratio,
testratio=testratio,folds=folds)[1]
kknn,w = _tmp
key="$nettype/$kernel/$k/KNN$kknn/$reftype/$distance/$w"
push!(top,(opval,key))
DNNC[key]=(nnc,N)
end
key="$nettype/$kernel/$k/NaiveBayes/$reftype/NA"
nbc,opval=traintest(N,op_function=op_function,folds=folds,
trainratio=trainratio,testratio=testratio)
push!(top,(opval,key))
DNNC[key]=(nbc,N)
end
sort!(top, rev=true)
top=top[1:min(12, length(top))]
# if top_k>0
# top=ctop[1:k]
# else
# top=[t for t in top if (ctop[1][1]-t[1])<threshold]
# end
# @show length(top)
LN=[(DNNC[t[2]],t[1],t[2]) for t in top ]
#@show typeof(LN)
end
function ensemble_cfft(knc,k::Int64=7;testratio=0.4,distance=HammingDistance)::Vector{Tuple{Tuple{Any,Net},Float64,String}}
(cl,n),opv,desc=knc[1]
data=Vector{Vector{String}}(length(knc))
for i in 1:length(knc)
kc,opv,desc=knc[i]
v=split(desc,"/")[1:6]
data[i]=v
end
ind=[i for (i,x) in enumerate(data)]
partitions,centers,index=[0 for x in ind],[1],KnnResult(k)
while length(centers)<k && length(centers)<=length(ind)
oid,dist=maxmin(data,centers,ind,index,distance,partitions)
push!(centers,oid)
end
knc[centers]
end
function ensemble_pfft(knc,k::Int64=7;trainratio=0.6,distance=HammingDistance)::Vector{Tuple{Tuple{Any,Net},Float64,String}}
(cl,N),opv,desc=knc[1]
n=length(N.data)
tn=Int(trunc(n*trainratio));
data=Vector{Vector{Int}}(length(knc))
perm=randperm(n)
ti,vi=perm[1:tn],perm[tn+1:n]
for i in 1:length(knc)
(cl,N),opv,desc=knc[i]
xv=gen_features(N.data[vi],N)
xt=gen_features(N.data[ti],N)
y=N.labels[ti]
data[i]=predict_test(xt,y,xv,desc,cl)
end
ind=[i for (i,x) in enumerate(data)]
partitions,centers,index=[0 for x in ind],[1],KnnResult(k)
while length(centers)<k && length(centers)<=length(ind)
oid,dist=maxmin(data,centers,ind,index,distance,partitions)
push!(centers,oid)
end
knc[centers]
end
function predict(knc,X;ensemble_k=1)::Vector{Int64}
y_t=Vector{Int}(0)
for i in 1:ensemble_k
kc,opv,desc=knc[i]
cl,N=kc
xv=gen_features(X,N)
if contains(desc,"KNN")
y_i=[predict_one(cl,x)[1] for x in xv]
else
y_i=cl[:predict](xv)
end
y_t = length(y_t)>0 ? hcat(y_t,y_i) : hcat(y_i)
end
y_pred=Vector{Int}(length(X))
for i in 1:length(y_t[:,1])
y_r=y_t[i,:]
y_pred[i]=last(sort([(count(x->x==k,y_r),k) for k in unique(y_r)]))[2]
end
y_pred
end
function predict_proba(knc,X;ensemble_k=1):Vector{Vector{Float64}}
kc,opv,desc=knc[1]
cl,N=kc
xv=gen_features(X,N)
if contains(desc,"KNN")
y_pred=[predict_one_proba(cl,x) for x in xv]
else
y_pred=cl[:predict_proba](xv)
end
y_pred
end
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 6445 | # Copyright 2017,2018 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
module Scores
using StatsBase
export accuracy, precision_recall, precision, recall, f1, scores
"""
It computes the recall between the gold dataset and the list of predictions `predict`
It applies the desired weighting scheme for binary and multiclass problems
- `:macro` performs a uniform weigth to each class
- `:weigthed` the weight of each class is proportional to its population in gold
- `:micro` returns the global recall, without distinguishing among classes
"""
function recall(gold, predict; weight=:macro)::Float64
precision, recall, precision_recall_per_class = precision_recall(gold, predict)
if weight == :macro
mean(x -> x.second[2], precision_recall_per_class)
elseif weight == :weighted
mean(x -> x.second[2] * x.second[3] / length(gold), precision_recall_per_class)
elseif :micro
recall
else
throw(Exception("Unknown weighting method $weight"))
end
end
"""
It computes the precision between the gold dataset and the list of predictions `predict`
It applies the desired weighting scheme for binary and multiclass problems
- `:macro` performs a uniform weigth to each class
- `:weigthed` the weight of each class is proportional to its population in gold
- `:micro` returns the global precision, without distinguishing among classes
"""
function precision(gold, predict; weight=:macro)::Float64
precision, recall, precision_recall_per_class = precision_recall(gold, predict)
if weight == :macro
mean(x -> x.second[1], precision_recall_per_class)
elseif weight == :weighted
mean(x -> x.second[1] * x.second[3] / length(gold), precision_recall_per_class)
elseif weight == :micro
precision
else
throw(Exception("Unknown weighting method $weight"))
end
end
"""
It computes the F1 score between the gold dataset and the list of predictions `predict`
It applies the desired weighting scheme for binary and multiclass problems
- `:macro` performs a uniform weigth to each class
- `:weigthed` the weight of each class is proportional to its population in gold
- `:micro` returns the global F1, without distinguishing among classes
"""
function f1(gold, predict; weight=:macro)::Float64
precision, recall, precision_recall_per_class = precision_recall(gold, predict)
if weight == :macro
mean(x -> 2 * x.second[1] * x.second[2] / (x.second[1] + x.second[2]), precision_recall_per_class)
elseif weight == :weighted
mean(x -> 2 * x.second[1] * x.second[2] / (x.second[1] + x.second[2]) * x.second[3]/length(gold), precision_recall_per_class)
elseif weight == :micro
2 * (precision * recall) / (precision + recall)
else
throw(Exception("Unknown weighting method $weight"))
end
end
"""
Computes precision, recall, and f1 scores, for global and per-class granularity
"""
function scores(gold, predicted)
precision, recall, precision_recall_per_class = precision_recall(gold, predicted)
m = Dict(
:micro_f1 => 2 * precision * recall / (precision + recall),
:precision => precision,
:recall => recall,
:class_f1 => Dict(),
:class_precision => Dict(),
:class_recall => Dict()
)
for (k, v) in precision_recall_per_class
m[:class_f1][k] = 2 * v[1] * v[2] / (v[1] + v[2])
m[:class_precision][k] = v[1]
m[:class_recall][k] = v[2]
end
m[:macro_recall] = mean(values(m[:class_recall]))
m[:macro_f1] = mean(values(m[:class_f1]))
m[:accuracy] = accuracy(gold, predicted)
m
end
"""
It computes the global and per-class precision and recall values between the gold standard
and the predicted set
"""
function precision_recall(gold, predicted)
labels = unique(gold)
M = Dict{typeof(labels[1]), Tuple}()
tp_ = 0
tn_ = 0
fn_ = 0
fp_ = 0
for label in labels
lgold = label .== gold
lpred = label .== predicted
tp = 0
tn = 0
fn = 0
fp = 0
for i in 1:length(lgold)
if lgold[i] == lpred[i]
if lgold[i]
tp += 1
else
tn += 1
end
else
if lgold[i]
fn += 1
else
fp += 1
end
end
end
tp_ += tp
tn_ += tn
fn_ += fn
fp_ += fp
M[label] = (tp / (tp + fp), tp / (tp + fn), sum(lgold) |> Int) # precision, recall, class-population
end
tp_ / (tp_ + fp_), tp_ / (tp_ + fn_), M
end
"""
It computes the accuracy score between the gold and the predicted sets
"""
function accuracy(gold, predicted)
# mean(gold .== predicted)
c = 0
for i in 1:length(gold)
c += (gold[i] == predicted[i])
end
c / length(gold)
end
######### Regression ########
export pearson, spearman, isqerror
"""
Pearson correlation score
"""
function pearson(X::AbstractVector{F}, Y::AbstractVector{F}) where {F <: AbstractFloat}
X̄ = mean(X)
Ȳ = mean(Y)
n = length(X)
sumXY = 0.0
sumX2 = 0.0
sumY2 = 0.0
for i in 1:n
x, y = X[i], Y[i]
sumXY += x * y
sumX2 += x * x
sumY2 += y * y
end
num = sumXY - n * X̄ * Ȳ
den = sqrt(sumX2 - n * X̄^2) * sqrt(sumY2 - n * Ȳ^2)
num / den
end
"""
Spearman rank correleation score
"""
function spearman(X::AbstractVector{F}, Y::AbstractVector{F}) where {F <: AbstractFloat}
n = length(X)
x = invperm(sortperm(X))
y = invperm(sortperm(Y))
d = x - y
1 - 6 * sum(d.^2) / (n * (n^2 - 1))
end
"""
Negative squared error (to be used for maximizing algorithms)
"""
function isqerror(X::AbstractVector{F}, Y::AbstractVector{F}) where {F <: AbstractFloat}
n = length(X)
d = 0.0
@inbounds for i in 1:n
d += (X[i] - Y[i])^2
end
-d
end
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 830 | # Copyright 2017 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
module Supervised
using SimilaritySearch
import StatsBase: fit, predict
export fit, predict
# classifiers
include("labelencoder.jl")
include("knn.jl")
include("naivebayes.jl")
# regression
include("knnreg.jl")
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1725 | export size_criterion, sqrt_criterion, change_criterion, log_criterion, epsilon_criterion
"""
Stops when the distance between far items achieves the given `e`
"""
function epsilon_criterion(e)
(dmaxlist, database) -> dmaxlist[end] < e
end
"""
Stops when the number of far items are equal or larger than the given `maxsize`
"""
function size_criterion(maxsize)
(dmaxlist, database) -> length(dmaxlist) >= maxsize
end
"""
Stops when the number of far items are equal or larger than the square root of the size of the database
"""
function sqrt_criterion()
(dmaxlist, database) -> length(dmaxlist) >= Int(length(database) |> sqrt |> round)
end
"""
Stops when the number of far items are equal or larger than logarithm-2 of the size of the database
"""
function log_criterion()
(dmaxlist, database) -> length(dmaxlist) >= Int(length(database) |> log2 |> round)
end
"""
Stops the process whenever the maximum distance converges, i.e., after `window` far items the maximum distance
change is below or equal to the allowed tolerance `tol`
"""
function change_criterion(tol=0.001, window=3)
mlist = Float64[]
count = 0.0
function stop(dmaxlist, database)
count += dmaxlist[end]
if length(dmaxlist) % window != 1
return false
end
push!(mlist, count)
count = 0.0
if length(dmaxlist) < 2
return false
end
s = abs(mlist[end] - mlist[end-1])
return s <= tol
end
return stop
end
"""
It nevers stops by side, it explores the entire dataset making a full farthest first traversal
"""
function salesman_criterion()
function stop(dmaxlist, dataset)
return false
end
end | KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1140 | using SimilaritySearch
import SimilaritySearch: fit
using Random
export dnet
"""
A `k`-net is a set of points `M` such that each object in `X` can be:
- It is in `M`
- It is in the knn set of an object in `M` (defined with the distance function `dist`)
The size of `M` is determined by ``\\leftceil|X|/k\\rightceil``
The dnet function uses the `callback` function as an output mechanism. This function is called on each center as `callback(centerId, res)` where
res is a `KnnResult` object (from SimilaritySearch.jl).
"""
function dnet(callback::Function, dist::Function, X::Vector{T}, k) where {T}
N = length(X)
metadist = (a::Int, b::Int) -> dist(X[a], X[b])
I = fit(Sequential, shuffle!(collect(1:N)))
res = KnnResult(k)
i = 0
while length(I.db) > 0
i += 1
empty!(res)
c = pop!(I.db)
search(I, metadist, c, res)
callback(c, res)
@info "computing dnet point $i, dmax: $(covrad(res))"
j = 0
for p in res
I.db[p.objID] = I.db[end-j]
j += 1
end
for p in res
pop!(I.db)
end
end
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 3158 | using SimilaritySearch
export fftraversal, fftclustering
function _ignore3(a, b, c)
end
"""
Selects a number of farthest points in `X`, using a farthest first traversal
- The callback function is called on each selected far point as `callback(centerID, dmax)` where `dmax` is the distance to the nearest previous reported center (the first is reported with typemax)
- The selected objects are far under the `dist` distance function with signature (T, T) -> Float64
- The number of points is determined by the stop criterion function with signature (Float64[], T[]) -> Bool
- The first argument corresponds to the list of known distances (far objects)
- The second argument corresponds to the database
- Check `criterions.jl` for basic implementations of stop criterions
- The callbackdist function is called on each distance evaluation between pivots and items in the dataset
`callbackdist(index-pivot, index-item, distance)`
"""
function fftraversal(callback::Function, dist::Function, X::AbstractVector{T}, stop, callbackdist=_ignore3) where {T}
N = length(X)
D = Vector{Float64}(undef, N)
dmaxlist = Float64[]
dset = [typemax(Float64) for i in 1:N]
imax::Int = rand(1:N)
dmax::Float64 = typemax(Float64)
if N == 0
return
end
k::Int = 0
@inbounds while k <= N
k += 1
pivot = X[imax]
push!(dmaxlist, dmax)
callback(imax, dmax)
println(stderr, "computing fartest point $k, dmax: $dmax, imax: $imax, stop: $stop")
dmax = 0.0
ipivot = imax
imax = 0
D .= 0.0
Threads.@threads for i in 1:N
D[i] = dist(X[i], pivot)
end
for i in 1:N
# d = dist(X[i], pivot)
d = D[i]
callbackdist(i, ipivot, d)
if d < dset[i]
dset[i] = d
end
if dset[i] > dmax
dmax = dset[i]
imax = i
end
end
if dmax == 0 || stop(dmaxlist, X)
break
end
end
end
"""
fftclustering(dist::Function, X::Vector{T}, numcenters::Int, k::Int) where T
Clustering algorithm based on Farthest First Traversal (an efficient solution for the K-centers problem).
- `dist` distance function
- `X` contains the objects to be clustered
- `numcenters` number of centers to be computed
- `k` number of nearest references per object (k=1 makes a partition)
Returns a named tuple ``(NN, irefs, dmax)``.
- `NN` contains the ``k`` nearest references for each object in ``X``.
- `irefs` contains the list of centers (indexes to ``X``)
- `dmax` smallest distance among centers
"""
function fftclustering(dist::Function, X::Vector{T}, numcenters::Int; k::Int=1) where T
# refs = Vector{Float64}[]
irefs = Int[]
NN = [KnnResult(k) for i in 1:length(X)]
dmax = 0.0
function callback(c, _dmax)
push!(irefs, c)
dmax = _dmax
end
function capturenn(i, refID, d)
push!(NN[i], refID, d)
end
fftraversal(callback, dist, X, size_criterion(numcenters), capturenn)
return (NN=NN, irefs=irefs, dmax=dmax)
end | KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 7696 | # Copyright 2018,2019 Eric S. Tellez <[email protected]>
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
export KernelClassifier, KConfigurationSpace, predict, predict_one
using KernelMethods
import KernelMethods.Scores: accuracy, recall, precision, f1, precision_recall
import KernelMethods.CrossValidation: montecarlo, kfolds
import KernelMethods.Supervised: NearNeighborClassifier, NaiveBayesClassifier, optimize!, predict, predict_one, transform, inverse_transform
import SimilaritySearch: l2_distance, angle_distance
# import KernelMethods.KMap: sqrt_criterion, log_criterion, change_criterion
# using KernelMethods.KMap: fftraversal, sqrt_criterion, change_criterion, log_criterion, kmap
using KernelMethods.Kernels: gaussian_kernel, cauchy_kernel, sigmoid_kernel, tanh_kernel, linear_kernel
struct KConfigurationSpace
normalize
distances
kdistances
sampling
kernels
reftypes
classifiers
function KConfigurationSpace(;
normalize=[true, false],
distances=[l2_distance, cosine_distance],
kdistances=[l2_distance, cosine_distance],
sampling=vcat(
[(method=fftraversal, stop=x) for x in (sqrt_criterion, log_criterion, change_criterion)],
[(method=dnet, kfun=x) for x in (log2, x -> min(x, log2(x)^2))]
),
#kernels=[linear_kernel, gaussian_kernel, sigmoid_kernel, cauchy_kernel, tanh_kernel],
kernels=[linear_kernel, gaussian_kernel, tanh_kernel],
#reftypes=[:centroids, :centers],
reftypes=[:centroids, :centers],
#classifiers=[NearNeighborClassifier, NaiveBayesClassifier]
classifiers=[NearNeighborClassifier]
)
new(normalize, distances, kdistances, sampling, kernels, reftypes, classifiers)
end
end
struct KConfiguration
normalize
dist
kdist
kernel
net
reftype
classifier
end
function randconf(space::KConfigurationSpace)
kdist = rand(space.kdistances)
normalize = (kdist in (cosine_distance, angle_distance)) || rand(space.normalize)
c = KConfiguration(
normalize,
rand(space.distances),
kdist,
rand(space.kernels),
rand(space.sampling),
rand(space.reftypes),
rand(space.classifiers)
)
c
end
function randconf(space::KConfigurationSpace, num::Integer)
[randconf(space) for i in 1:num]
end
struct KernelClassifierType{ItemType}
kernel
refs::Vector{ItemType}
classifier
conf::KConfiguration
end
"""
Searches for a competitive configuration in a parameter space using random search
"""
function KernelClassifier(X, y;
folds=3,
score=recall,
size=32,
ensemble_size=3,
space=KConfigurationSpace()
)
bestlist = []
tabu = Set()
dtype = typeof(X[1])
for conf in randconf(space, size)
if conf in tabu
continue
end
@info "testing configuration $(conf), data-type $(typeof(X))"
push!(tabu, conf)
dist = conf.dist
kdist = conf.kdist
refs = Vector{dtype}()
dmax = 0.0
if conf.kernel in (cauchy_kernel, gaussian_kernel, sigmoid_kernel, tanh_kernel)
kernel = conf.kernel(dist, dmax/2)
elseif conf.kernel == linear_kernel
kernel = conf.kernel(dist)
else
kernel = conf.kernel
end
if conf.net.method == fftraversal
function pushcenter1(c, _dmax)
push!(refs, X[c])
dmax = _dmax
end
fftraversal(pushcenter1, dist, X, conf.net.stop())
# after fftraversal refs is populated
R = fit(Sequential, refs)
@info "computing kmap, conf: $conf"
if conf.reftype == :centroids
a = [centroid!(X[plist]) for plist in invindex(dist, X, R) if length(plist) > 0]
M = kmap(X, kernel, a)
else
M = kmap(X, kernel, refs)
end
elseif conf.net.method == dnet
function pushcenter2(c, dmaxlist)
if conf.reftype == :centroids
a = vcat([X[c]], X[[p.objID for p in dmaxlist]]) |> centroid!
push!(refs, a)
else
push!(refs, X[c])
end
dmax += last(dmaxlist).dist
end
k = conf.net.kfun(length(X)) |> ceil |> Int
dnet(pushcenter2, dist, X, k)
if k == length(refs)
@info "$k != $(length(refs))"
@info refs
error("incorrect number of references, $conf")
end
@info "computing kmap, conf: $conf"
M = kmap(X, kernel, refs)
dmax /= length(refs)
end
if conf.normalize
for m in M
normalize!(m)
end
end
@info "creating and optimizing classifier, conf: $conf"
if conf.classifier == NearNeighborClassifier
classifier = NearNeighborClassifier(kdist, M, y)
best = optimize!(classifier, score, folds=folds)[1]
else
classifier = NaiveBayesClassifier(M, y)
best = optimize!(classifier, M, y, score, folds=folds)[1]
end
model = KernelClassifierType(kernel, refs, classifier, conf)
push!(bestlist, (best[1], model))
@info "score: $(best[1]), conf: $conf"
sort!(bestlist, by=x->-x[1])
if length(bestlist) > ensemble_size
bestlist = bestlist[1:ensemble_size]
end
end
@info "final scores: ", [b[1] for b in bestlist]
# @show [b[1] for b in bestlist]
[b[2] for b in bestlist]
end
function predict(kmodel::AbstractVector{KernelClassifierType{ItemType}}, vector) where {ItemType}
[predict_one(kmodel, x) for x in vector]
end
function predict_one(kmodel::AbstractVector{KernelClassifierType{ItemType}}, x) where {ItemType}
C = Dict()
for m in kmodel
label = predict_one(m, x)
C[label] = get(C, label, 0) + 1
end
counter = [(c, label) for (label, c) in C]
sort!(counter, by=x->-x[1])
# @show counter
counter[1][end]
end
function predict_one(kmodel::KernelClassifierType{ItemType}, x) where {ItemType}
kernel = kmodel.kernel
refs = kmodel.refs
vec = Vector{Float64}(undef, length(refs))
for i in 1:length(refs)
vec[i] = kernel(x, refs[i])
end
if kmodel.conf.normalize
normalize!(vec)
end
predict_one(kmodel.classifier, vec)
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 3537 | module KMap
import StatsBase: fit, predict
using SimilaritySearch:
Sequential, KnnResult, search, empty!, Item, Index
#using TextModel
export kmap, centroid!, partition, knearestreferences, sequence, fit, predict
include("criterions.jl")
include("fftraversal.jl")
include("dnet.jl")
include("kclass.jl")
include("oneclass.jl")
"""
Transforms `objects` to a new representation space induced by ``(refs, dist, kernel)``
- `refs` a list of references
- `kernel` a kernel function (and an embedded distance) with signature ``(T, T) \\rightarrow Float64``
"""
function kmap(objects::AbstractVector{T}, kernel, refs::AbstractVector{T}) where {T}
# X = Vector{T}(length(objects))
m = Vector{Vector{Float64}}(undef, length(objects))
@inbounds for i in 1:length(objects)
u = Vector{Float64}(undef, length(refs))
obj = objects[i]
for j in 1:length(refs)
u[j] = kernel(obj, refs[j])
end
m[i] = u
end
return m
end
"""
Groups items in `objects` using a nearest neighbor rule over `refs`.
The output is controlled using a callback function. The call is performed in `objects` order.
- `callback` is a function that is called for each `(objID, refItem)`
- `objects` is the input dataset
- `dist` a distance function ``(T, T) \\rightarrow \\mathbb{R}``
- `refs` the list of references
- `k` specifies the number of nearest neighbors to use
- `indexclass` specifies the kind of index to be used, a function receiving `(refs, dist)` as arguments,
and returning the new metric index
Please note that each object can be related to more than one group ``k > 1`` (default ``k=1``)
"""
function partition(callback::Function, dist::Function, objects::AbstractVector{T}, refs::Index; k::Int=1) where T
res = KnnResult(k)
for i in 1:length(objects)
empty!(res)
callback(i, search(refs, dist, objects[i], res))
end
end
"""
Creates an inverted index from references to objects.
So, an object ``u`` is in ``r``'s posting list iff ``r``
is among the ``k`` nearest references of ``u``.
"""
function invindex(dist::Function, objects::AbstractVector{T}, refs::Index; k::Int=1) where T
π = [Vector{Int}() for i in 1:length(refs.db)]
# partition((i, p) -> push!(π[p.objID], i), dist, objects, refs, k=k)
partition(dist, objects, refs, k=k) do i, res
for p in res
push!(π[p.objID], i)
end
end
π
end
"""
Returns the nearest reference (identifier) of each item in the dataset
"""
function sequence(dist::Function, objects::AbstractVector{T}, refs::Index) where T
s = Vector{Int}(length(objects))
partition(dist, objects, refs) do i, res
s[i] = first(res).objID
end
s
end
"""
Returns an array of k-nearest neighbors for `objects`
"""
function knearestreferences(dist::Function, objects::AbstractVector{T}, refs::Index) where T
s = Vector{Vector{Int}}(length(objects))
partition(dist, objects, refs) do i, res
s[i] = [p.objID for p in res]
end
s
end
"""
Computes the centroid of the list of objects
- Use the dot operator (broadcast) to convert several groups of objects
"""
function centroid!(objects::AbstractVector{Vector{F}})::Vector{F} where {F <: AbstractFloat}
u = copy(objects[1])
@inbounds for i in 2:length(objects)
w = objects[i]
@simd for j in 1:length(u)
u[j] += w[j]
end
end
f = 1.0 / length(objects)
@inbounds @simd for j in 1:length(u)
u[j] *= f
end
return u
end
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1506 | using StatsBase: countmap
export OneClassClassifier, regions, centroid, fit, predict
mutable struct OneClassClassifier{T}
centers::Vector{T}
freqs::Vector{Int}
n::Int
epsilon::Float64
end
function fit(::Type{OneClassClassifier}, dist::Function, X::AbstractVector{T}, m::Int; centroids=true) where T
Q = fftclustering(dist, X, m)
C = X[Q.irefs]
P = Dict(Q.irefs[i] => i for i in eachindex(Q.irefs))
freqs = zeros(Int, length(Q.irefs))
for nn in Q.NN
freqs[P[first(nn).objID]] += 1
end
if centroids
CC = centroid_correction(dist, X, C)
OneClassClassifier(CC, freqs, length(X), Q.dmax)
else
OneClassClassifier(C, freqs, length(X), Q.dmax)
end
end
function regions(dist::Function, X, refs::Index)
I = KMap.invindex(dist, X, refs, k=1)
(freqs=[length(lst) for lst in I], regions=I)
end
function regions(dist::Function, X, refs)
regions(dist, X, fit(Sequential, refs))
end
function centroid(D)
sum(D) ./ length(D)
end
function centroid_correction(dist::Function, X, C)
[centroid(X[lst]) for lst in regions(dist, X, C).regions if length(lst) > 0]
end
function predict(occ::OneClassClassifier{T}, dist::Function, q::T) where T
seq = fit(Sequential, occ.centers)
res = search(seq, dist, q, KnnResult(1))
#1.0 - first(res).dist / occ.epsilon
(similarity=max(0.0, 1.0 - first(res).dist / occ.epsilon), freq=occ.freqs[first(res).objID])
#occ.freqs[first(res).objID] / occ.n
end | KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1019 | # Copyright 2017,2018 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
using Test
using StatsBase
include("loaddata.jl")
@testset "encode by farthest points" begin
using KernelMethods.KMap: KernelClassifier, predict
using KernelMethods.Scores: accuracy, recall
X, y = loadiris()
kmodel = KernelClassifier(X, y, folds=3, ensemble_size=3, size=31, score=accuracy)
yh = predict(kmodel, X)
acc = mean(y .== yh)
@info "===== KernelClassifier accuracy: $acc"
@test acc > 0.9
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 4205 | # Copyright 2017,2018 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
using Test
include("loaddata.jl")
@testset "encode by farthest points" begin
using KernelMethods.KMap: fftraversal, sqrt_criterion, change_criterion, log_criterion, kmap
using KernelMethods.Scores: accuracy
using KernelMethods.Supervised: NearNeighborClassifier, optimize!
using SimilaritySearch: l2_distance, normalize!
using KernelMethods.Kernels: gaussian_kernel, cauchy_kernel, sigmoid_kernel
X, y = loadiris()
dist = l2_distance
# criterion = change_criterion(0.01)
refs = Vector{typeof(X[1])}()
dmax = 0.0
function callback(c, _dmax)
push!(refs, X[c])
dmax = _dmax
end
fftraversal(callback, dist, X, sqrt_criterion())
g = cauchy_kernel(dist, dmax/2)
M = kmap(X, g, refs)
nnc = NearNeighborClassifier(l2_distance, M, y)
@test optimize!(nnc, accuracy, folds=2)[1][1] > 0.9
@test optimize!(nnc, accuracy, folds=3)[1][1] > 0.9
@test optimize!(nnc, accuracy, folds=5)[1][1] > 0.93
@test optimize!(nnc, accuracy, folds=10)[1][1] > 0.93
@show optimize!(nnc, accuracy, folds=5)
end
@testset "Clustering and centroid computation (with cosine)" begin
using KernelMethods.KMap: fftraversal, sqrt_criterion, invindex, centroid!
using SimilaritySearch: l2_distance, l1_distance, angle_distance, cosine_distance
X, y = loadiris()
dist = l2_distance
refs = Vector{typeof(X[1])}()
dmax = 0.0
function callback(c, _dmax)
push!(refs, X[c])
dmax = _dmax
end
fftraversal(callback, dist, X, sqrt_criterion())
R = fit(Sequential, refs)
a = [centroid!(X[plist]) for plist in invindex(dist, X, R)]
g = gaussian_kernel(dist, dmax/4)
M = kmap(X, g, a)
nnc = NearNeighborClassifier(cosine_distance, [normalize!(w) for w in M], y)
@test optimize!(nnc, accuracy, folds=2)[1][1] > 0.8
@test optimize!(nnc, accuracy, folds=3)[1][1] > 0.8
@show optimize!(nnc, accuracy, folds=10)
end
@testset "encode with dnet" begin
using KernelMethods.KMap: dnet, sqrt_criterion, change_criterion, log_criterion, kmap, fftclustering
using KernelMethods.Scores: accuracy
using KernelMethods.Supervised: NearNeighborClassifier, optimize!
using SimilaritySearch: l2_distance, normalize!, angle_distance
using KernelMethods.Kernels: gaussian_kernel, sigmoid_kernel, cauchy_kernel, tanh_kernel
using Statistics
X, y = loadiris()
dist = l2_distance
# criterion = change_criterion(0.01)
refs = Vector{typeof(X[1])}()
dmax = 0.0
function callback(c, dmaxlist)
push!(refs, X[c])
dmax += last(dmaxlist).dist
end
dnet(callback, dist, X, 14)
_dmax = dmax / length(refs)
g = tanh_kernel(dist, _dmax)
M = kmap(X, g, refs)
nnc = NearNeighborClassifier(l2_distance, M, y)
@test optimize!(nnc, accuracy, folds=2)[1][1] > 0.9
@test optimize!(nnc, accuracy, folds=3)[1][1] > 0.9
@test optimize!(nnc, accuracy, folds=5)[1][1] > 0.9
@test optimize!(nnc, accuracy, folds=10)[1][1] > 0.9
@show optimize!(nnc, accuracy, folds=5)
C = fftclustering(angle_distance, [normalize!(x) for x in X], 21, k=3)
matches = 0
for (i, res) in enumerate(C.NN)
label = Dict{eltype(typeof(y)),Float64}()
for (pos, p) in enumerate(res)
l = y[p.objID]
label[l] = get(label, l, 0) + 1 / pos
end
L = [(v, k) for (k, v) in label]
sort!(L)
if y[i] == L[end][end]
matches += 1
end
end
@info "===== accuracy by fftclustering: $(matches/length(y))"
@test matches/length(y) > 0.9
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1577 | # Copyright 2017 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
using KernelMethods
import KernelMethods.Scores: pearson, spearman, isqerror
import KernelMethods.CrossValidation: montecarlo, kfolds
import KernelMethods.Supervised: NearNeighborRegression, optimize!, predict, predict_proba, transform, inverse_transform
import SimilaritySearch: l2_distance
# import KernelMethods.Nets: KlusterClassifier
using Test
include("loaddata.jl")
@testset "KNN Regression" begin
X, y = loadlinearreg()
nnr = NearNeighborRegression(l2_distance, X, y)
@test optimize!(nnr, pearson, folds=3)[1][1] > 0.95
@test optimize!(nnr, spearman, folds=3)[1][1] > 0.95
@show optimize!(nnr, isqerror, folds=5)
#@test optimize!(nnr, accuracy, runs=5, trainratio=0.3, testratio=0.3)[1][1] > 0.9
#@test sum([maximum(x) for x in predict_proba(nnr, X, smoothing=0)])/ length(X) > 0.9 ## close to have all ones, just in case
#@test sum([maximum(x) for x in predict_proba(nnr, X, smoothing=0.01)])/ length(X) > 0.9 ## close to have all ones, just in case
end
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 1092 | # Copyright 2017,2018 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
using Test
using DelimitedFiles
function loadiris()
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
filename = basename(url)
if !isfile(filename)
download(url, filename)
end
data = readdlm(filename, ',')
X = data[:, 1:4]
X = [Float64.(X[i, :]) for i in 1:size(X, 1)]
y = String.(data[:, 5])
X, y
end
function loadlinearreg()
X = [rand(2) .+ i for i in 1:100]
y = range(1, stop=100, length=100) .+ rand(100)
X, y
end | KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 726 | using Test
include("loaddata.jl")
@testset "encode by farthest points" begin
using KernelMethods.KMap
using SimilaritySearch
using KernelMethods.Scores
using StatsBase: mean
X, ylabels = loadiris()
dist = lp_distance(3.3)
L = Float64[]
for label in ["Iris-setosa", "Iris-versicolor", "Iris-virginica"]
y = ylabels .== label
A = X[y]
B = X[.~y]
occ = fit(OneClassClassifier, dist, A, 21)
ypred = [predict(occ, dist, x).similarity > 0 for x in X]
push!(L, mean(ypred .== y))
println(stderr, "==> $label: $(L[end])")
end
macrorecall = mean(L)
println(stderr, "===> macro-recall: $macrorecall")
@test macrorecall > 0.9
end | KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | code | 3786 | # Copyright 2017 Eric S. Tellez
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
using KernelMethods
import KernelMethods.Scores: accuracy, recall, precision, f1, precision_recall
import KernelMethods.CrossValidation: montecarlo, kfolds
import KernelMethods.Supervised: NearNeighborClassifier, NaiveBayesClassifier, optimize!, predict, predict_proba, transform, inverse_transform
import SimilaritySearch: l2_distance, fit, Sequential
# import KernelMethods.Nets: KlusterClassifier
using Test
@testset "Scores" begin
@test accuracy([1,1,1,1,1], [1,1,1,1,1]) == 1.0
@test accuracy([1,1,1,1,1], [0,0,0,0,0]) == 0.0
@test accuracy([1,1,1,1,0], [0,1,1,1,1]) == 0.6
@test precision_recall([0,1,1,1,0,1], [0,1,1,1,1,1]) == (0.8333333333333334, 0.8333333333333334, Dict(0 => (1.0, 0.5, 2), 1 => (0.8, 1.0, 4)))
@test precision([0,1,1,1,0,1], [0,1,1,1,1,1]) == 0.9
@test recall([0,1,1,1,0,1], [0,1,1,1,1,1]) == 0.75
@test precision([0,1,1,1,0,1], [0,1,1,1,1,1], weight=:weighted) == (1.0 * 2/6 + 0.8 * 4/6) / 2
@test recall([0,1,1,1,0,1], [0,1,1,1,1,1], weight=:weighted) == (0.5 * 2/6 + 1.0 * 4/6) / 2
@test f1([0,1,1,1,0,1], [0,1,1,1,1,1], weight=:macro) ≈ (2 * 0.5 / 1.5 + 2 * 0.8 / 1.8) / 2
#@show f1([0,1,1,1,0,1], [0,1,1,1,1,1], weight=:weighted) # ≈ (2/6 * 2 * 0.5 / 1.5 + 4 / 6 * 2 * 0.8 / 1.8) / 2
end
@testset "CrossValidation" begin
data = collect(1:100)
function f(train_X, train_y, test_X, test_y)
@test train_X == train_y
@test test_X == test_y
@test length(train_X ∩ test_X) == 0
@test length(train_X ∪ test_X) >= 99
1
end
@test montecarlo(f, data, data, runs=10) |> sum == 10
@test kfolds(f, data, data, folds=10, shuffle=true) |> sum == 10
end
include("oneclass.jl")
include("loaddata.jl")
@testset "KNN" begin
X, y = loadiris()
nnc = NearNeighborClassifier(l2_distance, X, y)
@test optimize!(nnc, accuracy, runs=5, trainratio=0.2, testratio=0.2)[1][1] > 0.8
@test optimize!(nnc, accuracy, runs=5, trainratio=0.3, testratio=0.3)[1][1] > 0.8
@test optimize!(nnc, accuracy, runs=5, trainratio=0.7, testratio=0.3)[1][1] > 0.8
@test optimize!(nnc, accuracy, folds=2)[1][1] > 0.8
@test optimize!(nnc, accuracy, folds=3)[1][1] > 0.8
@test optimize!(nnc, accuracy, folds=5)[1][1] > 0.85
@test optimize!(nnc, accuracy, folds=10)[1][1] > 0.85
@show optimize!(nnc, accuracy, folds=5)
@test sum([maximum(x) for x in predict_proba(nnc, X, smoothing=0)])/ length(X) > 0.8 ## close to have all ones, just in case
@test sum([maximum(x) for x in predict_proba(nnc, X, smoothing=0.01)])/ length(X) > 0.8 ## close to have all ones, just in case
end
@testset "NB" begin
X, y = loadiris()
nbc = NaiveBayesClassifier(X, y)
@test optimize!(nbc, X, y, accuracy, runs=5, trainratio=0.2, testratio=0.2)[1][1] > 0.8
@test optimize!(nbc, X, y, accuracy, runs=5, trainratio=0.3, testratio=0.3)[1][1] > 0.8
@test optimize!(nbc, X, y, accuracy, runs=5, trainratio=0.5, testratio=0.5)[1][1] > 0.8
@test optimize!(nbc, X, y, accuracy, runs=5, trainratio=0.7, testratio=0.3)[1][1] > 0.8
@show optimize!(nbc, X, y, accuracy, runs=5, trainratio=0.7, testratio=0.3)
end
include("knnreg.jl")
include("kmap.jl")
include("kclass.jl")
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"Apache-2.0"
] | 0.1.3 | 965c7f1abbcb8d9500b6aeed46f95ca816213014 | docs | 1734 | [](https://travis-ci.org/sadit/KernelMethods.jl)
[](https://coveralls.io/github/sadit/KernelMethods.jl?branch=master)
[](https://codecov.io/gh/sadit/KernelMethods.jl)
# Kernel Methods
KernelMethods.jl is a library that implements and explores Kernel-Based Methods for _supervised learning_ and _semi-supervised learning_.
## Install
To start using `KernelMethods.jl` just type into an active Julia session
```julia
using Pkg
pkg"add https://github.com/sadit/KernelMethods.jl"
using KernelMethods
```
## Usage
`KernelMethods.jl` consists of a few modules
- `KernelMethods.Scores`. It contains several common performance measures, i.e., accuracy, recall, precision, f1, precision_recall.
- `KernelMethods.CrossValidation`. Some methods to perform cross validation, all of them work through callback functions:
- `montecarlo`
- `kfolds`
- `KernelMethods.Supervised`. It contains methods related to supervised learning
- `NearNeighborClassifier`. It defines a `KNN` classifier
- `optimize!`
- `predict`
- `predict_proba`
The distance functions are mostly taken from:
- `SimilaritySearch`
### Dependencies
KernelMethods.jl depends on
- [SimilaritySearch.jl](https://github.com/sadit/SimilaritySearch.jl)
## Final notes ##
To reach maximum performance, please ensure that Julia has access to the specific instruction set of your CPUs
[http://docs.julialang.org/en/latest/devdocs/sysimg/](http://docs.julialang.org/en/latest/devdocs/sysimg/)
| KernelMethods | https://github.com/sadit/KernelMethods.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 1038 | #=
function solve_poisson(model, u, f, order)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, u)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * f) * dx
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
writevtk(Ω, "Lshaped_soln", cellfields = ["uh" => uh, "∇uh" => ∇(uh)])
uh
end
function compute_estimator(σ, 𝐀ₕ, model, order)
degree = 2 * order + 1
Ω = Triangulation(model)
dx = Measure(Ω, degree)
#η = ∫((σ + 𝐀ₕ) ⋅ (σ + 𝐀ₕ)) * dx
η = L2_norm_int(σ + 𝐀ₕ, dx)
writevtk(Ω, "Estimator", cellfields = ["η" => σ + 𝐀ₕ])
get_array(η)
end
function error_estimate(model, u, uh, 𝐀ₕ, σ, f, order)
degree = 2 * order
Ω = Triangulation(model)
dx = Measure(Ω, degree)
#H1err = sum(∫(∇(u - uh) ⋅ ∇(u - uh)) * dx)
H1err = L2_norm(∇(u - uh), dx)
div_check = L2_norm(∇ ⋅ σ - f, dx)
est = L2_norm(σ + 𝐀ₕ, dx)
@show div_check
@show H1err
@show est
@show est / H1err
(H1err, est)
end
=#
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 1028 | #!/usr/bin/env -S julia --startup-file=no
import Pkg
Pkg.activate(@__DIR__)
Pkg.resolve()
using Literate
function update(fname, target=nothing)
@info "running code in `$fname`"
include(abspath(fname))
Literate.markdown(fname, pwd(),
flavor=Literate.CommonMarkFlavor())
Literate.notebook(fname, pwd())
name, _ = splitext(fname)
@show name
run(`pandoc -s --mathjax=https://cdnjs.cloudflare.com/ajax/libs/mathjax/3.2.2/es5/tex-mml-chtml.min.js $name.md -o $name.html`)
if target !== nothing
@info "writing result to target directory `$target`"
contents = read("$name.md", String)
cd(target) do
write("$name.md", contents)
run(`pandoc -s --mathjax=https://cdnjs.cloudflare.com/ajax/libs/mathjax/3.2.2/es5/tex-mml-chtml.min.js $name.md -o $name.html`)
end
end
end
if abspath(PROGRAM_FILE) == @__FILE__
fname = get(ARGS, 1, "README.jl")
target = get(ARGS, 2, nothing)
update(fname, target)
end
true
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 687 | using GLMakie
using Gridap
using GridapMakie
using Gridap.CellData
using Gridap.Adaptivity
let
domain = (0,1,0,1)
fields = CellField[]
for i = 1:5
n = 2^i
# This works
#n = 8
parition = (n, n)
model = CartesianDiscreteModel(domain, parition) |> simplexify
#model = model.model
Ω = Triangulation(model)
field = CellField(rand(num_cells(model)), Ω)
push!(fields, field)
end
idx = Observable(1)
field_plot = lift(idx) do idx
fields[idx]
end
fig, ax, plt = plot(field_plot)
framerate = 5
idxs = 1:length(fields)
record(fig, "animation.gif", idxs; framerate=framerate, compression=0) do this_idx
idx[] = this_idx
end
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 5885 | # # EqFlux.jl
# This package is based on the
# [Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide tools to calculate a
# posteriori error estimates for numerical solutions of
# partial differential equations (PDEs). More precisely, if we solving an abstract PDE of the
# form: find $u$ such that
# $$-\nabla\cdot\mathbf{A}(\nabla u) = f.$$
# If we compute an approximation $u_h$ to the solution $u$ in Gridap.jl,
# the `EqFlux.jl` library provides the tools to compute an estimator
# $\eta(u_h)$ such that the error measured in some norm $\|\cdot\|$ can be
# bounded by
# $$\|u - u_h\| \le \eta(u_h),$$
# which we refer to as reliability, as well as the bound
# $$\eta(u_h) \lesssim \|u - u_h\|$$
# which we refer to as efficiency. The main ingredient in computing this estimator
# is an reconstructed flux obtained by postprocessing that is an approximation
# to the to the numerical flux, i.e., $\sigma_h\approx \mathbf{A}(\nabla u_h)$. This
# flux has the important property of being "conservative" in the sense
# that
# $$\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).$$
# we provide two functions to obtain this object:
# `build_equilibrated_flux` and `build_average_flux`. In addition, for the
# eq_field flux the so-called equilibrium condition is satisfied, i.e.,
# $$\nabla\cdot\sigma_h = \Pi_pf$$
# where $\Pi_p$ is the orthogonal projection onto polynomials of degree at most
# $p$.
#
# We first load the required packages
import Pkg #hide
Pkg.activate(joinpath(@__DIR__, "..")) #hide
Pkg.resolve(io=devnull) #hide
using Gridap
using Gridap.Geometry
using Gridap.Adaptivity
using GridapMakie, GLMakie
using EqFlux
using JLD2
# Define some helper functions
L2_inner_product(f, g, dx) = ∫(f ⋅ g) * dx
L2_norm_squared(f, dx) = L2_inner_product(f, f, dx)
function L2_norm_squared(f, model, order)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
L2_norm_squared(f, dx)
end
function L²_projection_f(model, reffe, f, dx)
V = TestFESpace(model, reffe; conformity = :L2)
m(u, v) = ∫(u * v)*dx
b(v) = ∫(v * f) * dx
op_proj = AffineFEOperator(m, b, V, V)
solve(op_proj)
end
let
# Now we consider the Laplace problem
# $$\begin{align}
# -\Delta u &= f &&\text{ in }\Omega\\
# u &= g &&\text{ on }\partial\Omega
# \end{align}$$
# on the L-shaped domain. In this case, we know the true solution
# is given by the following formula in polar coordinates:
u(x) = sin(2*pi*x[1])*sin(2*pi*x[2])
# The right hand side is zero for the Laplace equation
f(x) = 8*pi^2*u(x)
#u(x) = x[1] * (x[1] - 1) * x[2] * (x[2] - 1)
#f(x) = (-2 * (x[1] * x[1] + x[2] * x[2]) + 2 * (x[1] + x[2]))
# Now we find an approximate solution using Gridap.jl
order = 1
n = 10
domain = (0,1,0,1)
partition = (n, n)
model = CartesianDiscreteModel(domain, partition) |> simplexify
trian = Triangulation(model)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, u)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * f) * dx
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
# We then plot the approximate solution
fig_soln, _ , plt = plot(trian, uh, colormap=:viridis)
Colorbar(fig_soln[1,2], plt)
save("solution_fig.png", fig_soln) #src
#md # 
# We now compute the two fluxes.
𝐀ₕ = ∇(uh)
σeq = build_equilibrated_flux(𝐀ₕ, f, model, order)
σave = build_averaged_flux(𝐀ₕ, model)
ηeq² = L2_norm_squared(σeq + 𝐀ₕ, dx)
ηeq_arr = sqrt.(getindex(ηeq², Ω))
H1err² = L2_norm_squared(∇(u - uh), dx)
H1err_arr = sqrt.(getindex(H1err², Ω))
ηave² = L2_norm_squared(σave + 𝐀ₕ, dx)
ηave_arr = sqrt.(getindex(ηave², Ω))
max_val = maximum([ηave_arr..., ηeq_arr..., H1err_arr...])
min_val = minimum([ηave_arr..., ηeq_arr..., H1err_arr...])
ηave_vis = CellField(ηave_arr, Ω)
ηeq_vis = CellField(ηeq_arr, Ω)
H1err_vis = CellField(H1err_arr, Ω)
fig = Figure(resolution = (700, 600))
ga = fig[1, 1] = GridLayout()
axerr = Axis(ga[1, 1], xlabel = L"x", ylabel = L"y", title = L"$H_0^1$ seminorm error")
axeq = Axis(ga[2, 1], xlabel = L"x", ylabel = L"y", title = L"$$Equilibrated flux esitmator")
axave = Axis(ga[2, 2], xlabel = L"x", ylabel = L"y", title = L"$$Averaged flux esitmator")
plot_error = plot!(axerr, trian, H1err_vis, colorrange=(min_val,max_val), colormap=:viridis)
plot_eq = plot!(axeq, trian, ηeq_vis, colorrange=(min_val,max_val), colormap=:viridis)
plot_aver = plot!(axave, trian, ηave_vis, colorrange=(min_val,max_val), colormap=:viridis)
Colorbar(fig[1,2], limits=(min_val, max_val), colormap=:viridis)
#display(fig)
save("comparison.png", fig) #src
#md # 
fig = Figure(resolution = (1600, 800))
ga = fig[1, 1] = GridLayout()
axdiveq = Axis(ga[1, 1], xlabel = L"x", ylabel = L"y", title = L"$$ Divergence misfit equilibrated flux")
axdivave= Axis(ga[1, 3], xlabel = L"x", ylabel = L"y", title = L"$$ Divergence misfit averaged flux")
f_proj = L²_projection_f(model, reffe, f, dx)
eq_div = L2_norm_squared(∇ ⋅ σeq - f_proj, dx)
ave_div = L2_norm_squared(∇ ⋅ σave - f_proj, dx)
eq_div_vis = CellField(sqrt.(getindex(eq_div, Ω)), Ω)
ave_div_vis = CellField(sqrt.(getindex(ave_div, Ω)), Ω)
plot_div_eq = plot!(axdiveq, trian, eq_div_vis, colormap=:viridis)
Colorbar(ga[1,2], plot_div_eq)
plot_div_ave = plot!(axdivave, trian, ave_div_vis, colormap=:viridis)
Colorbar(ga[1,4], plot_div_ave)
save("comparison_div.png", fig) #src
#md # 
div_check² = L2_norm_squared(∇ ⋅ σeq - f_proj, dx)
@show √sum(div_check²)
@show √sum(H1err²)
@show eff_eq = √sum(ηeq²)/ √sum(H1err²)
@show eff_ave = √sum(ηave²)/ √sum(H1err²)
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 1488 | using EquilibratedFlux
using Documenter
using Literate
for name in ("readme", "Lshaped")
cd(joinpath(@__DIR__, "src", "examples", name)) do
Literate.markdown("$name.jl")
Literate.notebook("$name.jl")
if name == "readme"
@info "running script `$name.jl`"
include(joinpath(pwd(), "$name.jl"))
end
end
end
DocMeta.setdocmeta!(EquilibratedFlux, :DocTestSetup, :(using EquilibratedFlux); recursive=true)
on_CI = get(ENV, "CI", "false") == "true"
makedocs(;
modules=[EquilibratedFlux],
authors="Ari Rappaport <[email protected]>",
repo="https://github.com/aerappa/EquilibratedFlux.jl/blob/{commit}{path}#{line}",
sitename="EquilibratedFlux.jl",
format=Documenter.HTML(;
prettyurls=get(ENV, "CI", "false") == "true",
canonical="https://aerappa.github.io/EquilibratedFlux.jl",
edit_link="main",
assets=String[],
),
pages=[
"Home" => "index.md",
"Tutorials" => [
"examples/readme/readme.md",
"examples/Lshaped/Lshaped.md",
],
],
warnonly = on_CI ? false : Documenter.except(:linkcheck_remotes),
)
deploydocs(;
repo="github.com/aerappa/EquilibratedFlux.jl",
devbranch="main",
)
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 6025 | # # Mesh refinement
#
#md # [](Lshaped.ipynb)
#md # [](@__NBVIEWER_ROOT_URL__/examples/Lshaped/Lshaped.ipynb)
# In this tutorial, we use the estimator obtained by the equilibrated flux to
# drive an adative mesh refinement (AMR) procedure. We consider the Laplace
# problem
#
# ```math
# \begin{align}
# -\Delta u &= 0 &&\text{ in }\Omega\\
# u &= g &&\text{ on }\partial\Omega
# \end{align}
# ```
#
# on an L-shaped domain $\Omega = (-1,1)^2 \setminus [(0,1)\times(-1,0)]$. We
# load this domain from a json file.
using Gridap, GridapMakie, CairoMakie
model = DiscreteModelFromFile("Lshaped.json")
Ω = Triangulation(model)
fig = plot(Ω)
wireframe!(Ω, color=:black, linewidth=2);
fig
#-
# In this case, we know the true solution $u$ is given by the following formula
# in polar coordinates:
"Have to convert from -[π, π] to [0, 2π]"
function θ(x)
θt = atan(x[2], x[1])
(θt >= 0) * θt + (θt < 0) * (θt + 2 * π)
end
r(x) = sqrt(x[1]^2 + x[2]^2)
α = 2 / 3
u(x) = r(x)^α * sin(θ(x) * α)
u_fig, _ , plt = plot(Ω, u, colormap=:viridis)
Colorbar(u_fig[1,2], plt)
u_fig
#-
using Gridap.Geometry
using Gridap.Adaptivity
using EquilibratedFlux
# We define some helper functions for computing the L² norm in Gridap
L2_inner_product(f, g, dx) = ∫(f ⋅ g) * dx
L2_norm_squared(f, dx) = L2_inner_product(f, f, dx)
function L2_norm_squared(f, model, order)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
L2_norm_squared(f, dx)
end
# Next, we define the Dörfler marking[1]
function dorfler_marking(η_arr)
if η_arr isa Gridap.Arrays.LazyArray
η_arr = EquilibratedFlux.smart_collect(η_arr)
end
θ = 0.3 # Marking parameter
η_tot = sum(η_arr)
sorted_inds = sortperm(η_arr, rev = true)
sorted = η_arr[sorted_inds]
η_partial = 0.0
i = 1
while η_partial <= θ * η_tot
η_partial += sorted[i]
i += 1
end
sorted_inds[1:i]
end
# As a small example, we show the result of calling
# `dorfler_marking`
#
# This step just corresponds almost exact to the contents of the [first
# Gridap.jl
# tutorial](https://gridap.github.io/Tutorials/dev/pages/t001_poisson/#Tutorial-1:-Poisson-equation-1).
function solve_laplace(model, order, g)
Ω = Triangulation(model)
degree = 2 * order + 2
dx = Measure(Ω, degree)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * 0.0) * dx
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, g)
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
dofs = num_free_dofs(V0)
uh, dx, dofs
end
# This function uses the EquilibratedFlux.jl package to obtain an error estimation on each
# cell of the mesh.
function estimate_laplace(uh, dx, model, order)
σ = build_equilibrated_flux(-∇(uh), x -> 0.0, model, order)
#σ = build_averaged_flux(∇(uh), model)
η² = L2_norm_squared(σ + ∇(uh), dx)
Ω = Triangulation(model)
getindex(η², Ω)
end
# Finally, this function puts the previous functions together into the standard
# Solve -> Estimate -> Mark -> Refine loop of AFEM. The refinement step using
# newest vertex bisection can be selected using "nvb" with the keyword argument
# refinement_method. $g$ is the function on the Dirichlet boundary.
function solve_estimate_mark_refine_laplace(model, tol, order; g)
η = Inf
estimators = Float64[]
errors = Float64[]
num_dofs = Float64[]
error_fields = CellField[]
while η > tol
## We extract the internal model from the refined model
if model isa AdaptedDiscreteModel
model = model.model
end
## SOLVE
uh, dx, dofs = solve_laplace(model, order, g)
push!(num_dofs, dofs)
## ESTIMATE
η_arr = estimate_laplace(uh, dx, model, order)
H1err² = L2_norm_squared(∇(u - uh), dx)
Ω = Triangulation(model)
error_field = CellField(sqrt.(getindex(H1err², Ω)), Ω)
push!(error_fields, error_field)
H1err = √sum(H1err²)
η = √(sum(η_arr))
push!(estimators, η)
push!(errors, H1err)
## MARK
cells_to_refine = dorfler_marking(η_arr)
## REFINE
model = refine(model, refinement_method = "nvb", cells_to_refine = cells_to_refine)
end
return error_fields, num_dofs, estimators, errors
end
# We can change the polynomial order here as well as the tolerance for the
# estimator.
order = 2
tol = 1e-4
# We pass the true solution as the Dirichlet function $g$
error_fields, num_dofs, estimators, errors = solve_estimate_mark_refine_laplace(model, tol, order, g = u);
# We now show that the AFEM refinement achieves the optimal rate of convergence
# of $\mathrm{DOFs}^{-p/d} = \mathrm{DOFs}^{-p/2}$ in 2D.
fig = Figure()
axis = Axis(fig[1,1], xscale = log10, yscale = log10, title = "Order p=$order", xlabel = "DOFs")
lines!(axis, num_dofs, errors, label = "Error")
lines!(axis, num_dofs, estimators, label = "Estimator")
lines!(axis, num_dofs, num_dofs.^(-order / 2), label = "Optimal rate")
axislegend()
fig
# Finally, the following animation shows the sequence of meshes generated by the
# adaptive refinement procedure. The refinement is clearly concentrated to the
# re-entrant corner.
let
idx = Observable(1)
Ωᵢ = lift(idx) do i
error_fields[i].trian
end
nDOFᵢ = lift(idx) do i
"Iteration $i\n$(Int(num_dofs[i])) DOFs"
end
fig, ax, plt = plot(Ωᵢ)
wireframe!(Ωᵢ, color=:black, linewidth=2)
text!(ax, (0.5, -0.5), text=nDOFᵢ, align=(:center, :center), justification=:left)
record(fig, "animation.gif", eachindex(error_fields); framerate=2, compression=0) do i
idx[] = i
end
display(MIME"image/gif"(), read("animation.gif")) #nb
end
#md # 
# [1] Dörfler, W. A convergent adaptive algorithm for Poisson’s equation. SIAM
# Journal on Numerical Analysis 33, 3 (1996), 1106–1124
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 2219 | using Gridap
using LaTeXStrings
using GridapMakie, CairoMakie
# Define some helper functions
L2_inner_product(f, g, dx) = ∫(f ⋅ g) * dx
L2_norm_squared(f, dx) = L2_inner_product(f, f, dx)
function L2_norm_squared(f, model, order)
degree = 2 * order + 2
trian = Triangulation(model)
dx = Measure(trian, degree)
L2_norm_squared(f, dx)
end
function L²_projection(model, reffe, f, dx)
V = TestFESpace(model, reffe; conformity = :L2)
m(u, v) = ∫(u * v)*dx
b(v) = ∫(v * f) * dx
op_proj = AffineFEOperator(m, b, V, V)
solve(op_proj)
end
function plot_error_and_estimator(trian, ηave_arr, ηeq_arr, H1err_arr)
max_val = maximum([ηave_arr..., ηeq_arr..., H1err_arr...])
min_val = minimum([ηave_arr..., ηeq_arr..., H1err_arr...])
ηave_vis = CellField(ηave_arr, trian)
ηeq_vis = CellField(ηeq_arr, trian)
H1err_vis = CellField(H1err_arr, trian)
fig = Figure(resolution = (700, 600))
ga = fig[1, 1] = GridLayout()
axerr = Axis(ga[1, 1], xlabel = L"x", ylabel = L"y", title = L"$H_0^1$ seminorm error")
axeq = Axis(ga[2, 1], xlabel = L"x", ylabel = L"y", title = L"$$Equilibrated flux estimator")
axave = Axis(ga[2, 2], xlabel = L"x", ylabel = L"y", title = L"$$Averaged flux estimator")
plot_error = plot!(axerr, trian, H1err_vis, colorrange=(min_val,max_val), colormap=:viridis)
plot_eq = plot!(axeq, trian, ηeq_vis, colorrange=(min_val,max_val), colormap=:viridis)
plot_aver = plot!(axave, trian, ηave_vis, colorrange=(min_val,max_val), colormap=:viridis)
Colorbar(fig[1,2], limits=(min_val, max_val), colormap=:viridis)
fig
end
#save("comparison.png", fig) #src
#
function plot_divergence_misfit(trian, eq_div_vis, ave_div_vis)
fig = Figure(resolution = (1600, 800))
ga = fig[1, 1] = GridLayout()
axdiveq = Axis(ga[1, 1], xlabel = L"x", ylabel = L"y", title = L"$$ Divergence misfit equilibrated flux")
axdivave= Axis(ga[1, 3], xlabel = L"x", ylabel = L"y", title = L"$$ Divergence misfit averaged flux")
plot_div_eq = plot!(axdiveq, trian, eq_div_vis, colormap=:viridis)
Colorbar(ga[1,2], plot_div_eq)
plot_div_ave = plot!(axdivave, trian, ave_div_vis, colormap=:viridis)
Colorbar(ga[1,4], plot_div_ave)
fig
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 5172 | # # [Error estimation](@id tuto-error-estimation)
#
#md # [](readme.ipynb)
#md # [](@__NBVIEWER_ROOT_URL__/examples/readme/readme.ipynb)
#=
This package is based on the
[Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide tools to
calculate a posteriori error estimates for numerical solutions of partial
differential equations (PDEs). For simplicity, we consider here the Poisson
equation
```math
\begin{align}
- \Delta u &= f &&\text{in }\Omega\\
u &= g &&\text{on }\partial\Omega.
\end{align}
```
We suppose we have already computed a conforming approximation $u_h \in
V_h\subset H^1_0(\Omega)$ to the solution $u$ in Gridap.jl by solving
```math
(\nabla u_h, \nabla v_h) = (f, v_h)\quad\forall v_h\in V_h,
```
for this see for example the [first Gridap.jl
tutorial](https://gridap.github.io/Tutorials/dev/pages/t001_poisson/#Tutorial-1:-Poisson-equation-1).
The `EquilibratedFlux.jl` library then provides the tools to compute an
estimator $\eta(u_h)$ such that the error measured in the $H^1_0$-seminorm can
be bounded as
```math
\|\nabla(u - u_h)\| \le \eta(u_h),
```
which we refer to as reliability of the estimator. We also can prove the bound
```math
\eta(u_h) \lesssim \|\nabla(u - u_h)\|
```
which we refer to as efficiency. The main ingredient in computing this estimator
is a reconstructed flux obtained by postprocessing that is an approximation to
the numerical flux, i.e., $\sigma_h\approx -\nabla u_h$. This flux has the
important property of being "conservative over faces" in the sense that
```math
\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).
```
We provide two functions to obtain this object: `build_equilibrated_flux` and
`build_average_flux` which we denote by $\sigma_{\mathrm{eq},h}$ and
$\sigma_{\mathrm{ave},h}$ respectively.
In addition, for the equilibrated flux $\sigma_{\mathrm{eq},h}$ satisfies the
so-called equilibrium condition, i.e., for piecewise polynomial $f$, we have
```math
\nabla\cdot\sigma_{\mathrm{eq},h} = f.
```
In either case,the estimator takes the form
```math
\eta(u_h) = \| \sigma_{\cdot,h} + \nabla u_h\|.
```
=#
# We set $\Omega = (0,1)^2$ to be the unit square in 2D. We use a uniform
# simplicial mesh $\mathcal{T}_h$ to discretize this domain by the following in Gridap.jl
using Gridap
using GridapMakie
using CairoMakie
n = 10 # Number of elements in x and y for square mesh
domain = (0,1,0,1)
partition = (n, n)
model = CartesianDiscreteModel(domain, partition)
## Change to triangles
model = simplexify(model)
𝓣ₕ = Triangulation(model)
plt = plot(𝓣ₕ)
wireframe!(𝓣ₕ, color=:black)
plt
# We manufacture the solution $u = \sin(2\pi x)\sin(\pi y)$ by choosing the
# right hand side:
u(x) = sin(2*pi*x[1]) * sin(pi*x[2])
f(x) = 5 * pi^2 * u(x) # = -Δu
# We consider the discrete space
#
# ```math
# V_h = \{v_h\in H_0^1(\Omega): v_h|_K \in\mathbb{P}_k(K),\quad\forall K\in \mathcal{T}_h\}.
# ```
#
# This is achieved through the following with Gridap.jl:
## Polynomial order
order = 1
degree = 2 * order + 2
dx = Measure(𝓣ₕ, degree)
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, u)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * f) * dx
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
fig_soln, _ , plt = plot(𝓣ₕ, uh, colormap=:viridis)
Colorbar(fig_soln[1,2], plt)
fig_soln
# We can then build the fluxes $\sigma_{\mathrm{eq},h}$ and
# $\sigma_{\mathrm{ave},h}$ via the following:
using EquilibratedFlux
σ_eq = build_equilibrated_flux(-∇(uh), f, model, order);
σ_ave = build_averaged_flux(-∇(uh), model);
# First we calculate the estimators and the error using the fluxes and the
# approximate solution $u_h$.
include("helpers.jl")
H1err² = L2_norm_squared(∇(u - uh), dx)
@show sqrt(sum(H1err²))
H1err_arr = sqrt.(getindex(H1err², 𝓣ₕ));
η_eq² = L2_norm_squared(σ_eq + ∇(uh), dx)
@show sqrt(sum(η_eq²))
ηeq_arr = sqrt.(getindex(η_eq², 𝓣ₕ));
η_ave² = L2_norm_squared(σ_ave + ∇(uh), dx)
@show sqrt(sum(η_ave²))
ηave_arr = sqrt.(getindex(η_ave², 𝓣ₕ));
# Now we plot the estimators and errors restricted to each element (the full
# code can be found in `helpers.jl`)
fig = plot_error_and_estimator(𝓣ₕ, ηave_arr, ηeq_arr, H1err_arr)
save("estimator.png", fig) #src
# We see that both estimators provide a good cellwise approximation of the
# error, but the one based on the equilibrated flux is closer visually. Next, we
# consider the divergence error, i.e., how well the reconstructed object
# satisfies $\nabla\cdot\sigma = \Pi_1 f$. In particular, in the following plot
# we can see that the equilibrated flux estimator satisfies the divergence
# constraint up to machine precision, but the flux based on averaging does not.
f_proj = L²_projection(model, reffe, f, dx)
eq_div = L2_norm_squared(∇ ⋅ σ_eq - f_proj, dx)
ave_div = L2_norm_squared(∇ ⋅ σ_ave - f_proj, dx)
eq_div_vis = CellField(sqrt.(getindex(eq_div, 𝓣ₕ)), 𝓣ₕ)
ave_div_vis = CellField(sqrt.(getindex(ave_div, 𝓣ₕ)), 𝓣ₕ)
fig = plot_divergence_misfit(𝓣ₕ, eq_div_vis, ave_div_vis)
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 3080 | using Gridap.Geometry
using Gridap
using FillArrays
average(xs) = sum(xs) / length(xs)
midpoint(xs) = average(xs)
function get_positive_normals(trian)
n = get_normal_vector(trian)
edge_endpoints = get_cell_points(trian)
n.plus(edge_endpoints)
# plus == ⁺ is the positively oriented normal: outward on boundary and from
# low to high GID in the interior
normals = evaluate(n.plus, edge_endpoints)
lazy_map(midpoint, normals) |> parallel_smart_collect
end
function get_cell_field_at_midpoints(𝓣ₕ, 𝐀ₕ)
reffe_mid = VectorValue(0.5, 0.5)
mid_cellpoint = CellPoint(Fill(reffe_mid, num_cells(𝓣ₕ)), 𝓣ₕ, ReferenceDomain())
evaluate(𝐀ₕ, mid_cellpoint) |> parallel_smart_collect
end
function get_edge_lengths(edge_to_nodes, node_coords)
num_edges = length(edge_to_nodes)
edge_to_nodes_cache = array_cache(edge_to_nodes)
edge_lengths = zeros(num_edges)
for edge_ind in 1:num_edges
node = getindex!(edge_to_nodes_cache, edge_to_nodes, edge_ind)
edge_lengths[edge_ind] = norm(node_coords[node[1]] - node_coords[node[2]])
end
edge_lengths
end
function scatter_to_σ!(σ_arr, edge_inds, edge_to_cells, edge_lengths, normals, 𝐀ₕ_at_midpoints)
normals_cache = array_cache(normals)
edge_to_cells_cache = array_cache(edge_to_cells)
#𝐀ₕ_average = zero(𝐀ₕ_at_midpoints[1])
for (i, edge_ind) in enumerate(edge_inds)
# Cells that share this vertex
cell_inds = getindex!(edge_to_cells_cache, edge_to_cells, edge_ind)
#n_F = n_all[edge_ind]
normal = getindex!(normals_cache, normals, i)
#𝐀ₕ_average += getindex!(𝐀ₕ_at_midpoints_cache, 𝐀ₕ_at_midpoints, 1)
#for cell_ind in cell_inds
# 𝐀ₕ_average += getindex!(𝐀ₕ_at_midpoints_cache, 𝐀ₕ_at_midpoints, cell_ind)
#end
#𝐀ₕ_average /= length(𝐀ₕ_average)
𝐀ₕ_average = average(𝐀ₕ_at_midpoints[cell_inds])
σ_arr[edge_ind] = edge_lengths[edge_ind]*(𝐀ₕ_average ⋅ normal) # -|F|{∇uh} ⋅ n_F
end
end
"""
build_averaged_flux(𝐀ₕ, model)
TODO: relevant docstring
"""
function build_averaged_flux(𝐀ₕ, model)
𝓣ₕ = Triangulation(model)
𝓢ₕ = SkeletonTriangulation(model)
𝓑ₕ = BoundaryTriangulation(model)
grid = get_grid(𝓣ₕ)
topo = Geometry.GridTopology(grid)
edge_to_cells = Geometry.get_faces(topo, 1, 2)
edge_to_nodes = Geometry.get_faces(topo, 1, 0)
num_edges = length(edge_to_nodes)
node_coords = Geometry.get_node_coordinates(model)
edge_lengths = get_edge_lengths(edge_to_nodes, node_coords)
n_skel = get_positive_normals(𝓢ₕ)
n_bdry = get_positive_normals(𝓑ₕ)
bdry_edge_inds = findall(map(cells -> length(cells)==1, edge_to_cells))
skel_edge_inds = setdiff(1:length(edge_to_cells), bdry_edge_inds)
reffe_RT₀ = ReferenceFE(raviart_thomas, Float64, 0)
RT₀ = FESpace(model, reffe_RT₀)
𝓣ₕ = Triangulation(model)
𝐀ₕ_at_midpoints = get_cell_field_at_midpoints(𝓣ₕ, 𝐀ₕ)
σ_arr = zeros(num_edges)
# Bdry
scatter_to_σ!(σ_arr, bdry_edge_inds, edge_to_cells, edge_lengths, n_bdry, 𝐀ₕ_at_midpoints)
# Skeleton
scatter_to_σ!(σ_arr, skel_edge_inds, edge_to_cells, edge_lengths, n_skel, 𝐀ₕ_at_midpoints)
FEFunction(RT₀, σ_arr)
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 2811 | using Gridap.CellData
function _get_hat_function_cellfield(i, basis_data, model)
Ω = Triangulation(model)
cell_to_ith_node(c) = c[i]
A = lazy_map(cell_to_ith_node, basis_data)
GenericCellField(A, Ω, ReferenceDomain())
end
function _get_hat_functions_on_cells(model)
# Always order 1
reffe = ReferenceFE(lagrangian, Float64, 1)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
fe_basis = get_fe_basis(V0)
bd = Gridap.CellData.get_data(fe_basis)
#@show typeof(bd)
bd
end
function _build_patch_RHS_vectors(𝐀ₕ, f, model, weight, dvRT, dvp, Qₕ)
hat_fns_on_cells = _get_hat_functions_on_cells(model)
RHS_RT_form(ψ) = ∫(ψ * (weight ⋅ 𝐀ₕ ⋅ dvRT))*Qₕ
RHS_L²_form(ψ) = ∫((f * ψ + 𝐀ₕ ⋅ ∇(ψ))*dvp)*Qₕ
cur_num_cells = num_cells(model)
# Hardcoded for triangles
nodes_per_cell = 3
# TODO: find eltype of the vectors
cell_RHS_RTs = Matrix{Vector{Float64}}(undef, cur_num_cells, nodes_per_cell)
cell_RHS_L²s = Matrix{Vector{Float64}}(undef, cur_num_cells, nodes_per_cell)
Ω = Triangulation(model)
for i = 1:nodes_per_cell
ψᵢ = _get_hat_function_cellfield(i, hat_fns_on_cells, model)
#writevtk(Ω, "psi$(i)", cellfields=["ψᵢ" => ψᵢ])
cell_RHS_RT = RHS_RT_form(ψᵢ)
cell_RHS_L² = RHS_L²_form(ψᵢ)
#@show typeof(parallel_smart_collect(cell_RHS_RT))
cell_RHS_RTs[:, i] = lazy_map(vec, parallel_smart_collect(cell_RHS_RT))
cell_RHS_L²s[:, i] = lazy_map(vec, parallel_smart_collect(cell_RHS_L²))
end
cell_RHS_RTs, cell_RHS_L²s
end
function _build_cellwise_matrices(duRT, weight, dvRT, dvp, Qₕ)
cell_mass_mats = ∫(weight ⋅ duRT ⋅ dvRT) * Qₕ
cell_mixed_mats = ∫((∇ ⋅ duRT) * dvp) * Qₕ
cell_mass_mats = parallel_smart_collect(cell_mass_mats)
cell_mixed_mats = parallel_smart_collect(cell_mixed_mats)
cell_mass_mats, cell_mixed_mats
end
function _build_lagange_row(dvp, Qₕ)
#cur_num_cells = num_cells(model)
#cell_Λ_vecs = Matrix{Vector{Float64}}(undef, cur_num_cells, 1)
cell_Λ_vecs = ∫(1 * dvp) * Qₕ
#cell_Λ_vecs = cell_Λ_cells
cell_Λ_vecs = map(vec, parallel_smart_collect(cell_Λ_vecs))
end
function build_all_cellwise_objects(𝐀ₕ, f, weight, spaces, model, RT_order, measure)
Tₕ = Triangulation(model)
if isnothing(measure)
measure = Measure(Tₕ, 2 * RT_order + 2)
end
Qₕ = CellData.get_cell_quadrature(measure)
#Qₕ = CellQuadrature(Tₕ, quad_order)
dvp = get_trial_fe_basis(spaces.L²_space)
duRT = get_fe_basis(spaces.RT_space)
dvRT = get_trial_fe_basis(spaces.RT_space)
args = (weight, dvRT, dvp, Qₕ)
cell_mass_mats, cell_mixed_mats = _build_cellwise_matrices(duRT, args...)
cell_RHS_RTs, cell_RHS_L²s = _build_patch_RHS_vectors(𝐀ₕ, f, model, args...)
cell_Λ_vecs = _build_lagange_row(dvp, Qₕ)
(; cell_mass_mats, cell_Λ_vecs, cell_mixed_mats, cell_RHS_RTs, cell_RHS_L²s)
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 4521 | #using TimerOutputs
struct DOFManager{T, M <: Matrix{T}, V <: Vector{T}} # TODO: get rid of these types
# All the cell dofs stored as a matrix
all_cell_dofs_gl::M
# The current patch dofs in the global ennumeration
patch_dofs_gl::V
# The current free dofs in patch local ennumeration for slicing
# into the patch local objects
free_patch_dofs_loc::V
# The current cell's dofs in the patch local ennumeration
cell_dofs_loc::V
end
function DOFManager(space)
all_cell_dofs_gl = make_matrix_from_lazy(get_cell_dof_ids(space))
patch_dofs_RT_gl = sizehint!(eltype(all_cell_dofs_gl)[], 256)
push!(patch_dofs_RT_gl, 0)
cell_dofs_loc = sizehint!(eltype(all_cell_dofs_gl)[], 256)
push!(cell_dofs_loc, 0)
free_patch_dofs_loc = sizehint!(eltype(all_cell_dofs_gl)[], 256)
push!(free_patch_dofs_loc, 0)
DOFManager(all_cell_dofs_gl, patch_dofs_RT_gl, free_patch_dofs_loc, cell_dofs_loc)
end
DOFManager(dm::DOFManager) = DOFManager(
copy(dm.all_cell_dofs_gl),
copy(dm.patch_dofs_gl),
copy(dm.free_patch_dofs_loc),
copy(dm.cell_dofs_loc),
)
function update_cell_local_dofs!(dm::DOFManager, cellid)
cur_cell_dofs_gl = @view dm.all_cell_dofs_gl[cellid, :]
empty!(dm.cell_dofs_loc)
for id in cur_cell_dofs_gl
new_id = findfirst(n -> n == id, dm.patch_dofs_gl)
new_id isa Nothing && error("Cannot update cell local dofs!")
push!(dm.cell_dofs_loc, new_id)
end
end
function make_matrix_from_lazy(lazy)
rows = length(lazy)
cols = length(lazy[1])
matrix = zeros(eltype(eltype(lazy)), rows, cols)
lazy_cache = array_cache(lazy)
for i = 1:rows
matrix[i, :] = getindex!(lazy_cache, lazy, i)
end
matrix
end
#function _get_edge_dofs(edge_ids, dofs_per_edge)
# edge_dofs = eltype(edge_ids)[]
# for edge_id in edge_ids
# # Enumerate all dofs on the given edge
# for i = 0:(dofs_per_edge-1)
# edge_dof = (edge_id * dofs_per_edge) - i
# push!(edge_dofs, edge_dof)
# end
# end
# edge_dofs
#end
function remove_homogeneous_neumann_dofs!(dm, patch_data, RT_order)
dofs_per_edge = RT_order + 1
# TODO: for the moment, there are two loops, first to remove the local
# edge dofs, and then to remove the global edge dofs. The problem is that
# the global edge dofs cannot be modied in the first loop because their
# positions are being checked to get the local_edge_dofs.
patch_dofs_gl = dm.patch_dofs_gl
free_patch_dofs_loc = dm.free_patch_dofs_loc
bdry_edge_ids = patch_data.bdry_edge_ids
for edge_id in bdry_edge_ids
#for edge_id in patch_data.bdry_edge_ids
# Enumerate all dofs on the given edge
for i = 0:(dofs_per_edge-1)
bdry_edge_dof = (edge_id * dofs_per_edge) - i
local_edge_dof = findfirst(n -> n == bdry_edge_dof, patch_dofs_gl)
local_edge_dof isa Nothing && error("local_edge_dof cannot be computed!")
local_edge_dof_idx = findfirst(n -> n == local_edge_dof, free_patch_dofs_loc)
local_edge_dof_idx isa Nothing && error("local_edge_dof cannot be computed!")
deleteat!(free_patch_dofs_loc, local_edge_dof_idx)
#@timeit to "filter" filter!(n -> n ≠ local_edge_dof, free_patch_dofs_loc)
end
end
for edge_id in bdry_edge_ids
#for edge_id in patch_data.bdry_edge_ids
# Enumerate all dofs on the given edge
for i = 0:(dofs_per_edge-1)
bdry_edge_dof = (edge_id * dofs_per_edge) - i
edge_dof_idx = findfirst(n -> n == bdry_edge_dof, patch_dofs_gl)
edge_dof_idx isa Nothing && error("local_edge_dof cannot be computed!")
deleteat!(patch_dofs_gl, edge_dof_idx)
#filter!(n -> n ≠ edge_dof, patch_dofs_gl)
end
end
#@show length(dm.patch_dofs_gl)
#@show length(dm.free_patch_dofs_loc)
#@assert length(dm.patch_dofs_gl) == length(dm.free_patch_dofs_loc)
end
function update_global_patch_dofs!(dm::DOFManager, patch_data)
empty!(dm.patch_dofs_gl)
patch_cell_ids = patch_data.patch_cell_ids
#RT_dofs_all = unique(foldl(union, patch_cell_dof_RT))
for i ∈ patch_cell_ids
cell_dofs = @view dm.all_cell_dofs_gl[i, :]
for j ∈ cell_dofs
if j ∉ dm.patch_dofs_gl
push!(dm.patch_dofs_gl, j)
end
end
end
end
function update_free_patch_dofs!(dm, patch_data)
empty!(dm.free_patch_dofs_loc)
# TODO: possibly for RT only handle removing edge DOFs
for i = 1:length(dm.patch_dofs_gl)
push!(dm.free_patch_dofs_loc, i)
end
end
function update_patch_dofs!(dm::DOFManager, patch_data)
update_global_patch_dofs!(dm, patch_data)
update_free_patch_dofs!(dm, patch_data)
nothing
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 362 | module EquilibratedFlux
using Gridap
using Gridap.Geometry
#using BenchmarkTools
include("SpaceManager.jl")
include("CellwiseAssembler.jl")
include("Patch.jl")
include("Util.jl")
include("DOFManager.jl")
include("LinAlgAssembler.jl")
include("AveragedFlux.jl")
include("FluxBuilder.jl")
export build_equilibrated_flux
export build_averaged_flux
end # module
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 7051 | using LinearAlgebra
using Gridap.Adaptivity
using ChunkSplitters
#using TimerOutputs
#
#macro timeit(timer, title, body)
# esc(body)
#end
#const to = TimerOutput()
#
function build_equilibrated_flux(𝐀ₕ, f, model::AdaptedDiscreteModel, RT_order;
measure = nothing, weight = 1.0)
build_equilibrated_flux(𝐀ₕ, f, model.model, RT_order, measure = measure, weight = weight)
end
"""
build_equilibrated_flux(𝐀ₕ, f, model, RT_order; measure = nothing, weight= 1.0)
TODO: relevant docstring
"""
function build_equilibrated_flux(𝐀ₕ, f, model, RT_order; measure = nothing, weight= 1.0)
topo = get_grid_topology(model)
@assert all(p->p==TRI,get_polytopes(topo))
patches, metadata = create_patches(model, RT_order)
spaces = build_global_spaces(model, RT_order)
cell_objects = build_all_cellwise_objects(𝐀ₕ, f, weight, spaces, model, RT_order, measure)
linalgs = [instantiate_linalg(RT_order, 2, metadata) for i = 1:Threads.nthreads()]
dms = build_DOFManagers(spaces)
σ_gl = zero(spaces.RT_space)
diri_patches::Vector{DirichletPatch{Int32}} =
filter(patch -> patch isa DirichletPatch, patches)
int_patches::Vector{InteriorPatch{Int32}} =
filter(patch -> patch isa InteriorPatch, patches)
build_equilibrated_flux(diri_patches, σ_gl.free_values, linalgs, cell_objects, RT_order, dms)
build_equilibrated_flux(int_patches, σ_gl.free_values, linalgs, cell_objects, RT_order, dms)
σ_gl
end
function matrix_scatter!(patch_mat, cell_mats, dm_col, dm_row, patch_data)
fill!(patch_mat, 0)
for cellid in patch_data.patch_cell_ids
update_cell_local_dofs!(dm_row, cellid)
update_cell_local_dofs!(dm_col, cellid)
cell_mat = cell_mats[cellid]
for i in axes(cell_mat, 1)
for j in axes(cell_mat, 2)
patch_mat[dm_row.cell_dofs_loc[i], dm_col.cell_dofs_loc[j]] += cell_mat[i, j]
end
end
end
end
function single_vector_scatter!(patch_vec, cell_vecs, dm, patch_data)
fill!(patch_vec, 0)
for cellid in patch_data.patch_cell_ids
update_cell_local_dofs!(dm, cellid)
cell_vec = cell_vecs[cellid]
for i in axes(cell_vec, 1)
patch_vec[dm.cell_dofs_loc[i]] += cell_vec[i]
end
end
end
function vector_scatter!(patch_vec, cell_vecs, dm, patch_data)
fill!(patch_vec, 0)
node_to_offsets = patch_data.node_to_offsets
for (i, cellid) in enumerate(patch_data.patch_cell_ids)
cell_vec_all_nodes = @view cell_vecs[cellid, :]
offset = node_to_offsets[i]
update_cell_local_dofs!(dm, cellid)
cell_vec = cell_vec_all_nodes[offset]
for i in axes(cell_vec, 1)
patch_vec[dm.cell_dofs_loc[i]] += cell_vec[i]
end
end
end
function setup_patch_system!(A, RHS, linalg, dm_RT, dm_L²)
A .= 0
RHS .= 0
free_patch_dofs_RT = dm_RT.free_patch_dofs_loc
free_patch_dofs_L² = dm_L².free_patch_dofs_loc
ndofs_RT = length(free_patch_dofs_RT)
ndofs_L² = length(free_patch_dofs_L²)
ndofs = ndofs_RT + ndofs_L²
RHS[1:ndofs_RT] = @view linalg.RHS_RT[free_patch_dofs_RT]
RHS[ndofs_RT+1:ndofs] = @view linalg.RHS_L²[free_patch_dofs_L²]
A[1:ndofs_RT, 1:ndofs_RT] = @view linalg.M[free_patch_dofs_RT, free_patch_dofs_RT]
A[1:ndofs_RT, ndofs_RT+1:ndofs] = @view linalg.B[free_patch_dofs_RT, free_patch_dofs_L²]
A[ndofs_RT+1:ndofs, 1:ndofs_RT] =
transpose(@view linalg.B[free_patch_dofs_RT, free_patch_dofs_L²])
end
function count_free_dofs(dm::DOFManager)
free_patch_dofs = dm.free_patch_dofs_loc
length(free_patch_dofs)
end
function add_lagrange!(A, dm_RT, dm_L², Λ)
ndofs_RT = count_free_dofs(dm_RT)
ndofs_L² = count_free_dofs(dm_L²)
ndofs = ndofs_RT + ndofs_L²
A[ndofs+1, ndofs_RT+1:ndofs] = @view Λ[1:ndofs_L²]
A[ndofs_RT+1:ndofs, ndofs+1] = transpose(@view Λ[1:ndofs_L²])
end
function scatter_to_global_σ!(σ_gl, dm_RT, σ_patch, n_free_dofs_RT)
for i = 1:n_free_dofs_RT
σ_gl[dm_RT.patch_dofs_gl[i]] += σ_patch[i]
end
end
function solve_patch!(linalg, n_free_dofs)
# Extract free dofs slices of the monolithic objects
# Solve the patch problem in place
A_free_dofs = @view linalg.A[1:n_free_dofs, 1:n_free_dofs]
RHS_free_dofs = @view linalg.RHS[1:n_free_dofs]
σ_free_dofs = @view linalg.σ_loc[1:n_free_dofs]
ldiv!(σ_free_dofs, LU(LAPACK.getrf!(linalg.ws, A_free_dofs)...), RHS_free_dofs)
end
function build_DOFManagers(spaces)
dm_RTs = [DOFManager(spaces.RT_space) for i = 1:Threads.nthreads()]
dm_L²s = [DOFManager(spaces.L²_space) for i = 1:Threads.nthreads()]
(dm_RTs, dm_L²s)
end
#The convention will be that
# global := dof ordering for all the dofs
# local := dof ordering for the patch
# an underscore _gl at the end of a variable indicates global dof index
# and similarly for _loc always patch local
#
function build_equilibrated_flux(
patches::AbstractVector{<:Patch},
σ_gl,
linalgs,
cell_objects,
RT_order,
(dm_RTs, dm_L²s);
nchunks=Threads.nthreads() # TODO: Consider different chunk sizes?
)
#println("Loop on patches")
co = cell_objects
BLAS_nthreads = BLAS.get_num_threads()
BLAS.set_num_threads(1)
σ_gls = [zeros(size(σ_gl)) for i = 1:Threads.nthreads()]
#for patch in patches # Serial
Threads.@threads for (patchid_range, ichunk) in chunks(1:length(patches), nchunks)
for patchid in patchid_range
#tid = Threads.threadid()
linalg = linalgs[ichunk]
dm_L² = dm_L²s[ichunk]
dm_RT = dm_RTs[ichunk]
σ_gl_chunk = σ_gls[ichunk]
patch = patches[patchid]
# Change the local numbering for the current patch
update_patch_dofs!(dm_RT, patch.data)
update_patch_dofs!(dm_L², patch.data)
## Scatter the cell based matrices in cell_objects to the reused matrices in
## linalg
matrix_scatter!(linalg.M, co.cell_mass_mats, dm_RT, dm_RT, patch.data)
matrix_scatter!(linalg.B, co.cell_mixed_mats, dm_L², dm_RT, patch.data)
## Idem for vectors
vector_scatter!(linalg.RHS_RT, co.cell_RHS_RTs, dm_RT, patch.data)
vector_scatter!(linalg.RHS_L², co.cell_RHS_L²s, dm_L², patch.data)
single_vector_scatter!(linalg.Λ, co.cell_Λ_vecs, dm_L², patch.data)
## Now that scatter to local system is complete, remove fixed dofs
remove_homogeneous_neumann_dofs!(dm_RT, patch.data, RT_order)
## Count the free dofs for this patch once the BCs are imposed
n_free_dofs_RT = count_free_dofs(dm_RT)
n_free_dofs_L² = count_free_dofs(dm_L²)
n_free_dofs = n_free_dofs_RT + n_free_dofs_L²
## Use the sub-matrices and vectors generated from the scatters to build
## the monolithic objects
setup_patch_system!(linalg.A, linalg.RHS, linalg, dm_RT, dm_L²)
## Handle the pure Neumann case
if patch isa InteriorPatch
add_lagrange!(linalg.A, dm_RT, dm_L², linalg.Λ)
n_free_dofs += 1
end
solve_patch!(linalg, n_free_dofs)
## Scatter to the global FE object's free_values
scatter_to_global_σ!(σ_gl_chunk, dm_RT, linalg.σ_loc, n_free_dofs_RT)
end
end
σ_gl .+= sum(σ_gls)
#patch::DirichletPatch = patches[1]
#@show to
BLAS.set_num_threads(BLAS_nthreads)
σ_gl
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 2423 | using SparseArrays
using Gridap.FESpaces
using Gridap.Arrays
using FastLapackInterface
struct LinAlgObjs end
instantiate_M(RT_dofs_per_cell, max_patch_cells) =
zeros(RT_dofs_per_cell * max_patch_cells, RT_dofs_per_cell * max_patch_cells)
instantiate_B(RT_dofs_per_cell, L²_dofs_per_cell, max_patch_cells) =
zeros(RT_dofs_per_cell * max_patch_cells, L²_dofs_per_cell * max_patch_cells)
instantiate_A(M, B) = [M B; transpose(B) zeros(size(B)[2], size(B)[2])]
instantiate_RHS_RT(RT_dofs_per_cell, max_patch_cells) =
zeros(max_patch_cells * RT_dofs_per_cell)
instantiate_RHS_L²(L²_dofs_per_cell, max_patch_cells) =
zeros(max_patch_cells * L²_dofs_per_cell)
instantiate_RHS(RHS_RT, RHS_L²) = [RHS_RT; RHS_L²]
instantiate_Λ(RHS_L²) = zeros(length(RHS_L²))
function get_dofs_per_cell(k, d)
RT_dofs_per_cell = (k + d + 1) * binomial(k + d - 1, k)
L²_dofs_per_cell = binomial(k + d, k)
(RT_dofs_per_cell, L²_dofs_per_cell)
end
function test_dofs_per_cell(k, d, spaces)
RT_cell_dof_ids = get_cell_dof_ids(spaces.RT_space)
L²_cell_dof_ids = get_cell_dof_ids(spaces.L²_space)
num_dofs_per_cell_RTs = lazy_map(length, RT_cell_dof_ids)
num_dofs_per_cell_L²s = lazy_map(length, L²_cell_dof_ids)
RT_dofs_per_cell_formula = (k + d + 1) * binomial(k + d - 1, k)
L²_dofs_per_cell_formula = binomial(k + d, k)
cache_RT = array_cache(num_dofs_per_cell_RTs)
cache_L² = array_cache(num_dofs_per_cell_L²s)
for i = 1:length(num_dofs_per_cell_RTs)
cell_dofs_RT = getindex!(cache_RT, num_dofs_per_cell_RTs, i)
@assert cell_dofs_RT == RT_dofs_per_cell_formula
end
for i = 1:length(num_dofs_per_cell_L²s)
cell_dofs_L² = getindex!(cache_L², num_dofs_per_cell_L²s, i)
@assert cell_dofs_L² == L²_dofs_per_cell_formula
end
end
function instantiate_linalg(RT_order, dim, metadata)
(RT_dofs_per_cell, L²_dofs_per_cell) = get_dofs_per_cell(RT_order, dim)
max_patch_cells = metadata.max_num_patch_cells
M = instantiate_M(RT_dofs_per_cell, max_patch_cells)
B = instantiate_B(RT_dofs_per_cell, L²_dofs_per_cell, max_patch_cells)
A = instantiate_A(M, B)
# Pre-allocate the pivot vector for the matrix A
ws = LUWs(A)
RHS_RT = instantiate_RHS_RT(RT_dofs_per_cell, max_patch_cells)
RHS_L² = instantiate_RHS_L²(L²_dofs_per_cell, max_patch_cells)
RHS = instantiate_RHS(RHS_RT, RHS_L²)
Λ = similar(RHS_L²)
σ_loc = similar(RHS)
(; M, B, A, ws, Λ, RHS_RT, RHS_L², RHS, σ_loc)
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 6193 | using Gridap.Geometry
abstract type Patch{T} end
struct PatchData{T}
node_to_offsets::Vector{T}
patch_cell_ids::Vector{T}
bdry_edge_ids::Vector{T}
all_edge_ids::Vector{T}
end
struct DirichletPatch{T} <: Patch{T}
data::PatchData{T}
end
struct InteriorPatch{T} <: Patch{T}
data::PatchData{T}
end
# TODO: Implement
struct NeumannPatch{T} <: Patch{T}
data::PatchData{T}
bdry_data::Vector{Float64}
end
function _is_interior_object(i, d, labels)
entity_idx_i = labels.d_to_dface_to_entity[d][i]
labels.tag_to_name[entity_idx_i] == "interior"
end
_is_boundary_node_labels(i, labels) = !_is_interior_object(i, 1, labels)
_is_boundary_edge_labels(e, labels) = !_is_interior_object(e, 2, labels)
_is_boundary_edge_patch_i_e2n(e, i, edge_to_node) = i ∉ edge_to_node[e]
#=
This function constructs the map from a given node to the indices
in the cell_to_node array which it appears. For example with
cell_to_node = [[1, 2, 4], [2, 4, 5], [2, 3, 5], [3, 5, 6],
[4, 5, 7], [5, 7, 8], [5, 6, 8], [6, 8, 9]]
The first few entries of node_to_offsets are
node_to_offsets = [[1], [2, 1, 1], [2, 1], [3, 2, 1],..
The idea is that eventually we will want to slice into a cell_RHS arrays
with certain cells e.g.
patch_cell_RHS_RTs = cell_RHS_RTs[patch_cells]
and then next extract the current patch via
patch_RT_cell_RHS_RTs = patch_cell_RHS_RTs[node_to_offsets[patchid]]
=#
function _get_nodes_to_offsets(model)
topo = get_grid_topology(model)
cell_to_node = Geometry.get_faces(topo, 2, 0)
node_to_cell = Geometry.get_faces(topo, 0, 2)
cell_to_node_cache = array_cache(cell_to_node)
node_to_cell_cache = array_cache(node_to_cell)
num_nodes = length(node_to_cell)
node_to_offsets = [[] for i = 1:num_nodes]
for nodeid = 1:num_nodes
cellids = getindex!(node_to_cell_cache, node_to_cell, nodeid)
for cellid in cellids
nodeids = getindex!(cell_to_node_cache, cell_to_node, cellid)
node_offset = findfirst(i -> i == nodeid, nodeids)
push!(node_to_offsets[nodeid], node_offset)
end
end
node_to_offsets
end
function _get_node_to_offsets(
nodeid,
cell_to_node,
node_to_cell,
cell_to_node_cache,
node_to_cell_cache,
)
node_to_offsets = typeof(nodeid)[]
cellids = getindex!(node_to_cell_cache, node_to_cell, nodeid)
for cellid in cellids
nodeids = getindex!(cell_to_node_cache, cell_to_node, cellid)
node_offset = findfirst(i -> i == nodeid, nodeids)
push!(node_to_offsets, node_offset)
end
node_to_offsets
end
function _get_patch_edge_ids(patch_cell_ids, cell_to_edge, cell_to_edge_cache)
patch_edge_ids = getindex!(cell_to_edge_cache, cell_to_edge, patch_cell_ids)
unique!(patch_edge_ids.data)
end
function _get_boundary_edges(patch_edge_ids, edge_to_node, edge_to_node_cache, i)
bdry_edge_ids = eltype(patch_edge_ids)[]
for e in patch_edge_ids
nodes = getindex!(edge_to_node_cache, edge_to_node, e)
if i ∉ nodes
push!(bdry_edge_ids, e)
end
end
bdry_edge_ids
end
function test_edge_dof_consistency(model, RT_order, RT_space)
topo = get_grid_topology(model)
dofs_per_edge = RT_order + 1
node_to_cell = Geometry.get_faces(topo, 0, 2)
cell_to_edge = Geometry.get_faces(topo, 2, 1)
node_to_cell_cache = array_cache(node_to_cell)
cell_to_edge_cache = array_cache(cell_to_edge)
cell_dofs_RT = get_cell_dof_ids(RT_space)
num_nodes = length(node_to_cell)
for i = 1:num_nodes
patch_cell_ids = getindex!(node_to_cell_cache, node_to_cell, i)
patch_edge_ids = _get_patch_edge_ids(patch_cell_ids, cell_to_edge, cell_to_edge_cache)
patch_edge_dofs = _get_edge_dofs(patch_edge_ids, dofs_per_edge)
sort!(patch_edge_dofs)
RT_dofs = unique!(cell_dofs_RT[patch_cell_ids].data)
sort!(RT_dofs)
nedofs = length(patch_edge_dofs)
@assert RT_dofs[1:nedofs] == patch_edge_dofs
end
end
function create_patches(model, RT_order)
labels = get_face_labeling(model)
#is_boundary_edge(e) = _is_boundary_edge_labels(e, labels)
is_boundary_node(i) = _is_boundary_node_labels(i, labels)
dofs_per_edge = RT_order + 1
#dofs_per_cell = RT_order * (RT_order + 1)
topo = get_grid_topology(model)
node_to_cell = Geometry.get_faces(topo, 0, 2)
cell_to_node = Geometry.get_faces(topo, 2, 0)
cell_to_edge = Geometry.get_faces(topo, 2, 1)
edge_to_node = Geometry.get_faces(topo, 1, 0)
#nodes_to_offsets = _get_nodes_to_offsets(model)
# Type of the table, Int32 it seems
T = eltype(cell_to_edge[1])
patches = Patch[]
# Need to declare caches first to prevent reinstatiation
node_to_cell_cache = array_cache(node_to_cell)
cell_to_edge_cache = array_cache(cell_to_edge)
cell_to_node_cache = array_cache(cell_to_node)
edge_to_node_cache = array_cache(edge_to_node)
num_nodes = length(node_to_cell)
max_num_patch_cells = 0
for i::T = 1:num_nodes
#is_boundary_edge_patch(e) = _is_boundary_edge_patch_i(e, i)
patch_cell_ids = getindex!(node_to_cell_cache, node_to_cell, i)
all_edge_ids = _get_patch_edge_ids(patch_cell_ids, cell_to_edge, cell_to_edge_cache)
max_num_patch_cells = max(max_num_patch_cells, length(patch_cell_ids))
# TODO: For now the connectivity is always giving the correct boundary
# edges because it only includes nodes that are not adjacent to the current
# node. This is asssuming Dirichlet boundary conditions everywhere
bdry_edge_ids = _get_boundary_edges(all_edge_ids, edge_to_node, edge_to_node_cache, i)
#all_dofs = _get_edge_dofs(patch_edge_ids, dofs_per_edge)
node_to_offsets = _get_node_to_offsets(
i,
cell_to_node,
node_to_cell,
cell_to_node_cache,
node_to_cell_cache,
)
# Copy needed because otherwise modifying the underlying array
data = PatchData(node_to_offsets, copy(patch_cell_ids), bdry_edge_ids, all_edge_ids)
if is_boundary_node(i)
patch = DirichletPatch(data)
#filter!(!is_boundary_edge, bdry_edge_ids)
else
patch = InteriorPatch(data)
end
push!(patches, patch)
end
#metadata = (; nodes_to_offsets, max_num_patch_cells)
# Can probably delete this is max_num_patch_cells can be known a priori
metadata = (; max_num_patch_cells)
patches, metadata
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 433 | using Gridap
function build_triangle_model(n)
domain = (0, 1, 0, 1)
partition = (n, n)
CartesianDiscreteModel(domain, partition) |> simplexify
end
function build_global_spaces(model, k)
reffeRT = ReferenceFE(raviart_thomas, Float64, k)
reffeP = ReferenceFE(lagrangian, Float64, k)
RT_space = FESpace(model, reffeRT, conformity = :HDiv)
L²_space = FESpace(model, reffeP, conformity = :L2)
(; RT_space, L²_space)
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 759 | using ChunkSplitters
function parallel_smart_collect(lazy_array; nchunks=Threads.nthreads())
n = length(lazy_array)
ntids = Threads.nthreads()
non_lazy = Array{eltype(lazy_array)}(undef, n)
caches = [array_cache(lazy_array) for _ = 1:ntids]
#Threads.@threads for i = 1:n
Threads.@threads for (id_range, ichunk) in chunks(1:n, nchunks)
for i in id_range
cache = caches[ichunk]
non_lazy[i] = copy(getindex!(cache, lazy_array, i))
end
end
non_lazy
end
function smart_collect(lazy_array)
n = length(lazy_array)
non_lazy = Array{eltype(lazy_array)}(undef, n)
cache = array_cache(lazy_array)
for i = 1:n
non_lazy[i] = copy(getindex!(cache, lazy_array, i))
#getindex!(cache, lazy_array, i)
end
non_lazy
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | code | 105 | using EquilibratedFlux
using Test
@testset "EquilibratedFlux.jl" begin
# Write your tests here.
end
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 3207 | # EquilibratedFlux.jl
[](https://aerappa.github.io/EquilibratedFlux.jl/stable/)
[](https://aerappa.github.io/EquilibratedFlux.jl/dev/)
[](https://github.com/aerappa/EquilibratedFlux.jl/actions/workflows/CI.yml?query=branch%3Amain)
<!-- [](https://codecov.io/gh/triscale-innov/DataViewer.jl) -->
This package is based on
[Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide
post-processing tools to calculate reconstructed fluxes associated to the given
approximate solution of a PDE.
For simplicity, we consider here the Poisson equation
```math
\begin{align}
- \Delta u &= f &&\text{in }\Omega\\
u &= g &&\text{on }\partial\Omega.
\end{align}
```
We suppose we have already computed a conforming approximation $u_h \in
V_h\subset H^1_0(\Omega)$ to the solution $u$ in Gridap.jl by solving
```math
(\nabla u_h, \nabla v_h) = (f, v_h)\quad\forall v_h\in V_h,
```
The `EquilibratedFlux.jl` library then provides the tools to compute a reconstructed flux
associated to $u_h$. This flux, obtained by postprocessing, is an approximation to the numerical flux, i.e.
```math
\sigma_h \approx -\nabla u_h.
```
This flux has the important property of being "conservative over faces" in the
sense that
```math
\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).
```
We provide two functions to obtain such an object:
[`build_equilibrated_flux`](https://aerappa.github.io/EquilibratedFlux.jl/dev/#EquilibratedFlux.build_equilibrated_flux-NTuple{4,%20Any})
and
[`build_averaged_flux`](https://aerappa.github.io/EquilibratedFlux.jl/dev/#EquilibratedFlux.build_averaged_flux-Tuple{Any,%20Any})
both provide reconstructed fluxes, which we denote by $\sigma_{\mathrm{eq},h}$
and $\sigma_{\mathrm{ave},h}$ respectively.
In addition to the properties listed above, the equilibrated flux
$\sigma_{\mathrm{eq},h}$ satisfies the so-called equilibrium condition, i.e.,
for piecewise polynomial $f$, we have
```math
\nabla\cdot\sigma_{\mathrm{eq},h} = f.
```
More details can be found in the [documentation](https://aerappa.github.io/EquilibratedFlux.jl/dev/).
## Examples / Tutorials
### Error estimation
The reconstructed flux is the main ingredient in computing [*a posteriori* error
estimators](https://aerappa.github.io/EquilibratedFlux.jl/dev/examples/readme/readme/).
[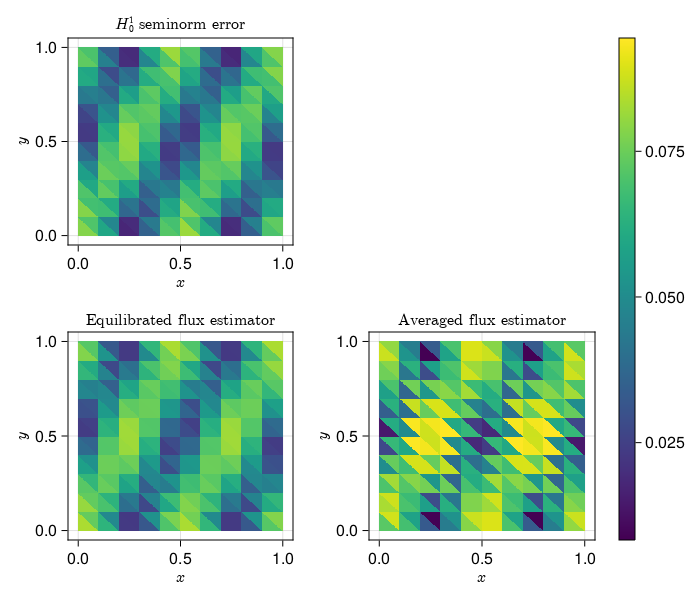](https://aerappa.github.io/EquilibratedFlux.jl/dev/examples/readme/readme/)
### Mesh refinement
Estimators obtained using the equilibrated flux can be used to drive an Adaptive
Mesh Refinement (AMR) precedure, demonstrated here for the Laplace problem in an
[L-shaped domain](https://aerappa.github.io/EquilibratedFlux.jl/dev/examples/Lshaped/Lshaped/).
[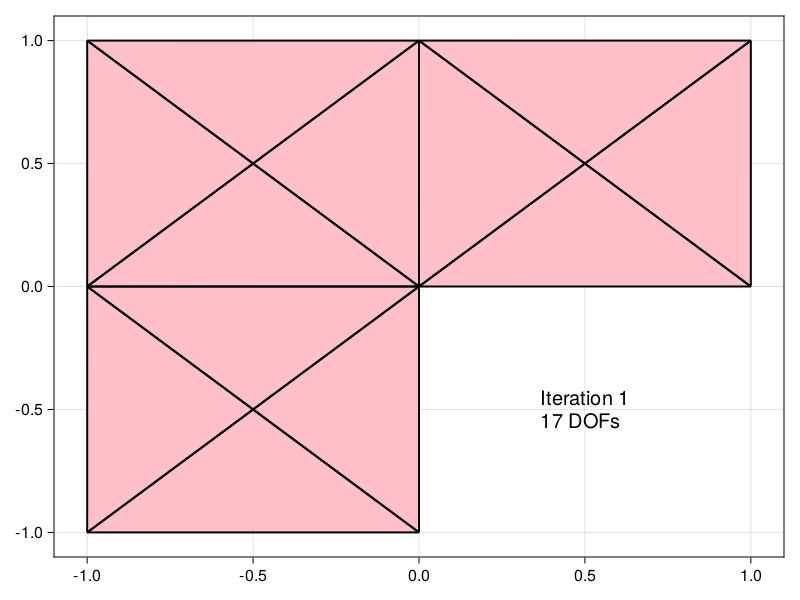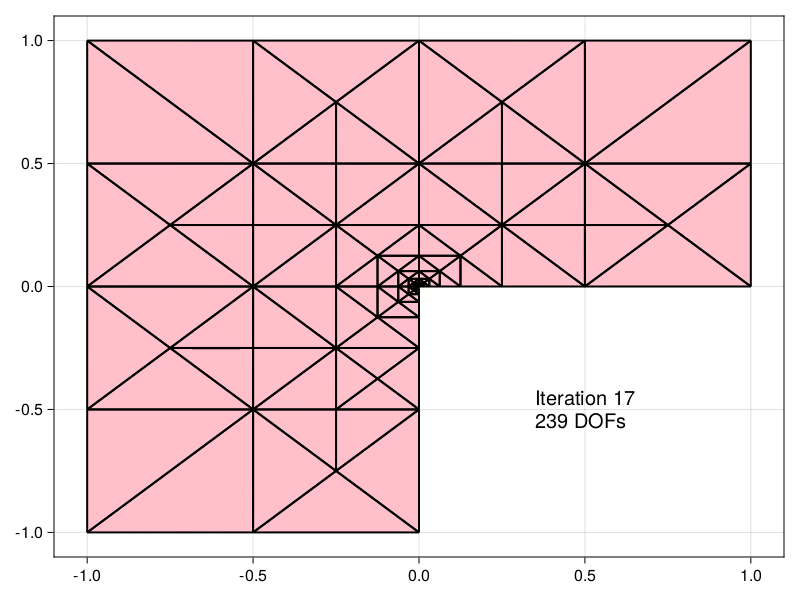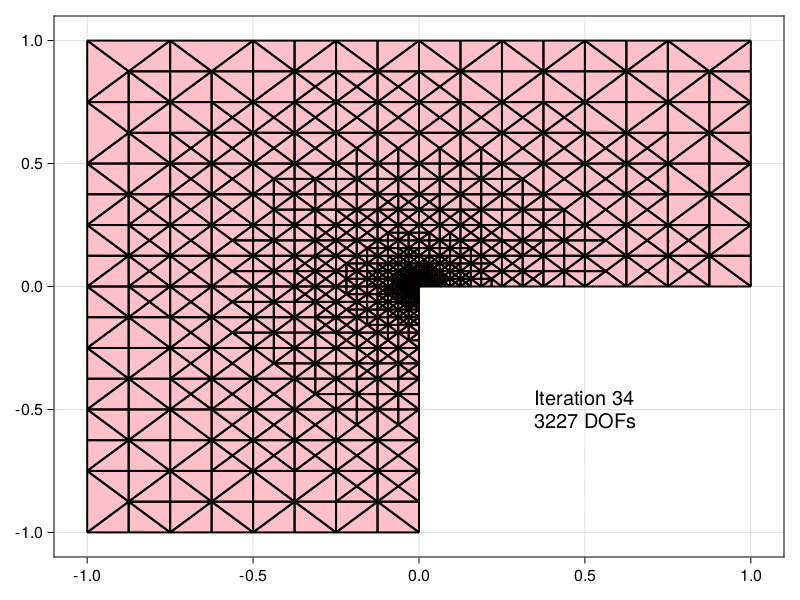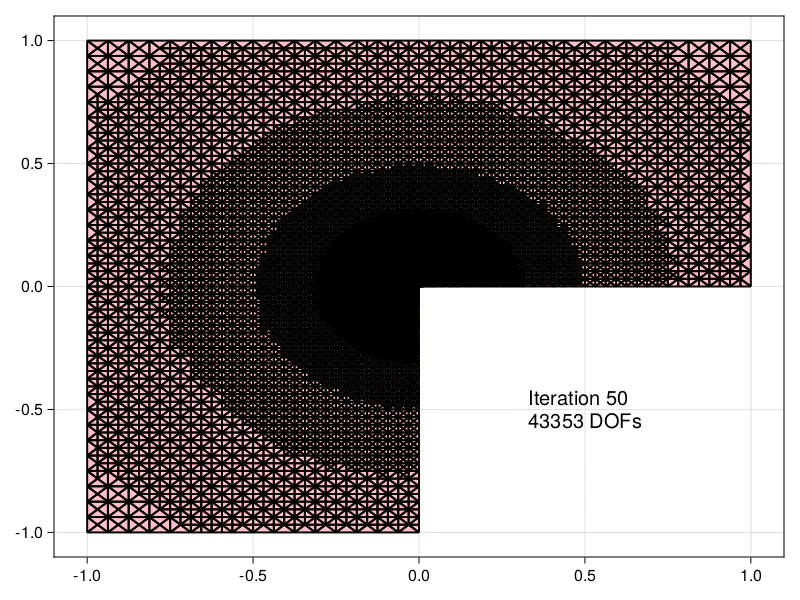](https://aerappa.github.io/EquilibratedFlux.jl/dev/examples/Lshaped/Lshaped/)
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 5851 | # Refinement test
In this tutorial, we use the estimator obtained by the equilibrated flux
to drive an adative mesh refinement (AMR) procedure.
We consider the Laplace problem
$$\begin{align}
-\Delta u &= 0 &&\text{ in }\Omega\\
u &= g &&\text{ on }\partial\Omega
\end{align}$$
on an L-shaped domain $\Omega = (-1,1)^2 \setminus [(0,1)\times(-1,0)]$.
We load this domain from a json file.
````julia
using Gridap
model = DiscreteModelFromFile("Lshaped.json")
Ω = Triangulation(model)
using GridapMakie, GLMakie
Ω_fig = plot(Ω)
wireframe!(Ω, color=:black, linewidth=2);
````

In this case, we know the true solution $u$
is given by the following formula in polar coordinates:
````julia
"Have to convert from -[π, π] to [0, 2π]"
function θ(x)
θt = atan(x[2], x[1])
(θt >= 0) * θt + (θt < 0) * (θt + 2 * π)
end
r(x) = sqrt(x[1]^2 + x[2]^2)
α = 2 / 3
u(x) = r(x)^α * sin(θ(x) * α)
u_fig, _ , plt = plot(Ω, u, colormap=:viridis)
Colorbar(u_fig[1,2], plt)
````

````julia
using Gridap
using Gridap.Geometry
using Gridap.Adaptivity
using EqFlux
````
We define some helper functions for computing the L² norm in Gridap
````julia
L2_inner_product(f, g, dx) = ∫(f ⋅ g) * dx
L2_norm_squared(f, dx) = L2_inner_product(f, f, dx)
function L2_norm_squared(f, model, order)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
L2_norm_squared(f, dx)
end
````
Next, we define the Dörfler marking[1]
````julia
function dorfler_marking(η_arr)
if η_arr isa Gridap.Arrays.LazyArray
η_arr = EqFlux.smart_collect(η_arr)
end
θ = 0.3 # Marking parameter
η_tot = sum(η_arr)
sorted_inds = sortperm(η_arr, rev = true)
sorted = η_arr[sorted_inds]
η_partial = 0.0
i = 1
while η_partial <= θ * η_tot
η_partial += sorted[i]
i += 1
end
sorted_inds[1:i]
end
````
As a small example, we show the result of calling
`dorfler_marking
This step just corresponds to the contents of the [first Gridap.jl tutorial](https://gridap.github.io/Tutorials/dev/pages/t001_poisson/#Tutorial-1:-Poisson-equation-1).
````julia
function solve_laplace(model, order, g)
Ω = Triangulation(model)
degree = 2 * order + 2
dx = Measure(Ω, degree)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * 0.0) * dx
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, g)
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
dofs = num_free_dofs(V0)
uh, dx, dofs
end
````
This function uses the EqFlux.jl package to obtain an error estimation on each cell
of the mesh.
````julia
function estimate_laplace(uh, dx, model, order)
σ = build_equilibrated_flux(∇(uh), x -> 0.0, model, order)
#σ = build_averaged_flux(∇(uh), model)
η² = L2_norm_squared(σ + ∇(uh), dx)
Ω = Triangulation(model)
getindex(η², Ω)
end
using Gridap.Adaptivity
````
Finally, this function puts the previous functions together into the standard
Solve -> Estimate -> Mark -> Refine
loop of AFEM. The refinement step using newest vertex bisection can
be selected using "nvb" with the keyword argument refinement_method.
g is the function on the Dirichlet boundary.
````julia
function solve_estimate_mark_refine_laplace(model, tol, order; g)
η = Inf
estimators = Float64[]
errors = Float64[]
num_dofs = Float64[]
error_fields = CellField[]
while η > tol
# We extract the internal model from the refined model
if model isa AdaptedDiscreteModel
model = model.model
end
# SOLVE
uh, dx, dofs = solve_laplace(model, order, g)
#@show dofs
push!(num_dofs, dofs)
# ESTIMATE
η_arr = estimate_laplace(uh, dx, model, order)
H1err² = L2_norm_squared(∇(u - uh), dx)
Ω = Triangulation(model)
error_field = CellField(sqrt.(getindex(H1err², Ω)), Ω)
push!(error_fields, error_field)
H1err = √sum(H1err²)
η = √(sum(η_arr))
#@show η
push!(estimators, η)
push!(errors, H1err)
# MARK
cells_to_refine = dorfler_marking(η_arr)
# REFINE
model = refine(model, refinement_method = "nvb", cells_to_refine = cells_to_refine)
end
return error_fields, num_dofs, estimators, errors
end
````
We can change the polynomial order here as well as the tolerance for the
estimator.
````julia
let
order = 3
tol = 1e-4
````
We pass the true solution as the Dirichlet function $g$
````julia
error_fields, num_dofs, estimators, errors = solve_estimate_mark_refine_laplace(model, tol, order, g = u)
fig = Figure()
axis = Axis(fig[1,1], xscale = log10, yscale = log10, title = "Order p=$order", xlabel = "DOFs")
lines!(axis, num_dofs, errors, label = "Error")
lines!(axis, num_dofs, estimators, label = "Estimator")
lines!(axis, num_dofs, num_dofs.^(-order / 2), label = "Optimal rate")
axislegend()
````
We now show that the AFEM refinement achieves the optimat rate of convergence
of $\mathrm{DOFs}^{-p/d} = \mathrm{DOFs}^{-p/2}$ in 2D.
````julia
@show estimators[end]
````

Finally, we plot a .gif that shows sequence of meshes generated by the
adaptive refinement procedure. The refinement is clearly concentrated to the
re-entrant corner.
````julia
idx = Observable(1)
errors_plot = lift(idx) do idx
error_fields[idx].trian
end
fig, ax, plt = plot(errors_plot)
#display(fig)
wireframe!(errors_plot, color=:black, linewidth=2)
framerate = 5
idxs = 1:length(error_fields)
record(fig, "animation.gif", idxs; framerate=framerate, compression=0) do this_idx
idx[] = this_idx
end
end
````

````julia
#wireframe!(Ω, color=:black, linewidth=2);
````
[1] Dörfler, W. A convergent adaptive algorithm for Poisson’s equation. SIAM Journal on Numerical
Analysis 33, 3 (1996), 1106–1124
---
*This page was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 4157 | # EqFlux.jl
This package is based on the
[Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide tools to calculate a
posteriori error estimates for numerical solutions of
partial differential equations (PDEs). For simplicity, we consider here the
Poisson equation
\begin{align}
- \Delta u &= f &&\text{in }\Omega\\
u &= g &&\text{on }\partial\Omega.
\end{align}
We suppose we have already computed a conforming approximation
$u_h \in V_h\subset H^1_0(\Omega)$ to the solution $u$ in Gridap.jl by solving
$$(\nabla u_h, \nabla v_h) = (f, v_h)\quad\forall v_h\in V_h,$$
for this see for example the
[first Gridap.jl tutorial](https://gridap.github.io/Tutorials/dev/pages/t001_poisson/#Tutorial-1:-Poisson-equation-1).
The `EqFlux.jl` library then provides the tools to compute an estimator
$\eta(u_h)$ such that the error measured in the $H^1_0$-seminorm
can be bounded as
$$\|\nabla(u - u_h)\| \le \eta(u_h),$$
which we refer to as reliability of the estimator. We also can prove the bound
$$\eta(u_h) \lesssim \|\nabla(u - u_h)\|$$
which we refer to as efficiency. The main ingredient in computing this estimator
is a reconstructed flux obtained by postprocessing that is an approximation
to the numerical flux, i.e., $\sigma_h\approx -\nabla u_h$. This
flux has the important property of being "conservative over faces" in the sense
that
$$\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).$$
we provide two functions to obtain this object:
`build_equilibrated_flux` and `build_average_flux` which we denote by
$\sigma_{\mathrm{eq},h}$ and $\sigma_{\mathrm{ave},h}$ respectively.
. In addition, for the
equilibrated flux $\sigma_{\mathrm{eq},h}$ satisfies the so-called equilibrium
condition, i.e., for piecewise polynomial $f$, we have
$$\nabla\cdot\sigma_{\mathrm{eq},h} = f.$$
In either case,the estimator takes the form
$$\eta(u_h) = \| \sigma_{\cdot,h} + \nabla u_h\|.$$
# Demonstration
We set $\Omega = (0,1)^2$ to be the unit square in 2D. We use a uniform
simplicial mesh $\mathcal{T}_h$ to discretize this domain by the following in Gridap.jl
````julia
using Gridap
n = 10 # Number of elements in x and y for square mesh
domain = (0,1,0,1)
partition = (n, n)
model = CartesianDiscreteModel(domain, partition)
# Change to triangles
model = simplexify(model)
𝓣ₕ = Triangulation(model)
````
We manufacture the solution $u = \sin(2\pi x)\sin(2\pi y)$ by choosing the right hand side:
````julia
u(x) = sin(2*pi*x[1])*sin(2*pi*x[2])
f(x) = 8*pi^2*u(x)
````
We consider the discrete space
$$V_h = \{v_h\in H_0^1(\Omega): v_h|_K \in\mathbb{P}_k(K),\quad\forall K\in
\mathcal{T}_h\}.$$ This is achieved through the following with Gridap.jl:
````julia
# Polynomial order
order = 1
degree = 2 * order + 2
dx = Measure(𝓣ₕ, degree)
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, u)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * f) * dx
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
````
We can then build the fluxes $\sigma_{\mathrm{eq},h}$ and
$\sigma_{\mathrm{ave},h}$ via the following:
````julia
using EqFlux
σ_eq = build_equilibrated_flux(∇(uh), f, model, order)
σ_ave = build_averaged_flux(∇(uh), model)
include(joinpath(@__DIR__, "helpers.jl"))
ηeq_arr, H1err_arr, ηave_arr = calculate_error_and_estimator(𝓣ₕ, uh, u, σ_eq, σ_ave, dx)
plot_error_and_estimator(𝓣ₕ, ηave_arr, ηeq_arr, H1err_arr)
````
We compare the estimators with the error they are estimating in the
following figure (the rest of the full code can be founde here TODO)

We see that both estimators provide a good cellwise approximation of the
error, but the one based on the equilibrated flux is closer visually. Next,
we consider the divergence error, i.e., how well the reconstructed object
satisfies $\nabla\cdot\sigma = \Pi_1 f$. In particular, in the following plot we can
see that the equilibrated flux estimator satisfies the divergence constraint
up to machine precision, but the flux based on averaging does not.

---
*This page was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 5713 | # eq_field flux
This package is based on the
[Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide tools to calculate a
posteriori error estimates for numerical solutions of
partial differential equations (PDEs). More precisely, if we solving an abstract PDE of the
form: find $u$ such that
$$-\nabla\cdot\mathbf{A}(u) = f.$$
If we compute an approximation $u_h$ to the solution $u$ in Gridap.jl,
the `EqFlux.jl` library provides the tools to compute an estimator
$\eta(u_h)$ such that the error measured in some norm $\|\cdot\|$ can be
bounded by
$$\|u - u_h\| \le \eta(u_h),$$
which we refer to as reliability, as well as the bound
$$\eta(u_h) \lesssim \|u - u_h\|$$
which we refer to as efficiency. The main ingredient in computing this estimator
is an reconstructed flux obtained by postprocessing that is an approximation
to the to the numerical flux, i.e., $\sigma_h\approx \mathbf{A}(u_h)$. This
flux has the important property of being "mass conservative" in the sense
that
$$\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).$$
we provide two functions to obtain this object:
`build_equilibrated_flux` and `build_average_flux`. In addition, for the
eq_field flux the so-called equilibrium condition is satisfied, i.e.,
$$\nabla\cdot\sigma_h = \Pi_pf$$
where $\Pi_p$ is the orthogonal projection onto polynomials of degree at most
$p$.
We first load the required packages
````julia
using Gridap
using Gridap.Geometry
using Gridap.Adaptivity
using GridapMakie, GLMakie
using EqFlux
using JLD2
````
Define some helper functions
````julia
L2_inner_product(f, g, dx) = ∫(f ⋅ g) * dx
L2_norm_squared(f, dx) = L2_inner_product(f, f, dx)
function L2_norm_squared(f, model, order)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
L2_norm_squared(f, dx)
end
function L²_projection_f(model, reffe, f, dx)
V = TestFESpace(model, reffe; conformity = :L2)
m(u, v) = ∫(u * v)*dx
b(v) = ∫(v * f) * dx
op_proj = AffineFEOperator(m, b, V, V)
solve(op_proj)
end
max_cell_fields(cell_fields, cell_point) =
max(maximum(map(maximum, evaluate(cell_field, cell_point)) for cell_field in cell_fields)...)
min_cell_fields(cell_fields, cell_point) =
min(minimum(map(minimum, evaluate(cell_field, cell_point)) for cell_field in cell_fields)...)
````
Now we consider the Laplace problem
$$\begin{align}
-\Delta u &= f &&\text{ in }\Omega\\
u &= g &&\text{ on }\partial\Omega
\end{align}$$
on the L-shaped domain. In this case, we know the true solution
is given by the following formula in polar coordinates:
````julia
#u(x) = sin(2*pi*x[1])*sin(2*pi*x[2])
````
The right hand side is zero for the Laplace equation
````julia
#f(x) = 8*pi^2*u(x)
u(x) = 30*x[1] * (x[1] - 1) * x[2] * (x[2] - 1)
f(x) = 30*(-2 * (x[1] * x[1] + x[2] * x[2]) + 2 * (x[1] + x[2]))
````
Now we find an approximate solution using Gridap.jl
````julia
order = 1
n = 10
domain = (0,1,0,1)
partition = (n, n)
model = CartesianDiscreteModel(domain, partition) |> simplexify
#model = refine(model)
trian = Triangulation(model)
#trian_fig = plot(trian)
#wireframe!(trian, color=:black, linewidth=2);
#@time uh, dofs = solve_poisson(model, u, f, order)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, u)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * f) * dx
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
fig_soln, _ , plt = plot(trian, uh)
Colorbar(fig_soln[1,2], plt)
````

````julia
Qₕ = CellQuadrature(Ω,degree)
Qₕ_cell_point = get_cell_points(Qₕ)
𝐀ₕ = ∇(uh)
σ = build_equilibrated_flux(𝐀ₕ, f, model, order)
σ_ave = build_averaged_flux(𝐀ₕ, model)
η² = L2_norm_squared(σ + 𝐀ₕ, dx)
H1err² = L2_norm_squared(∇(u - uh), dx)
````
Cell fields
````julia
eq_field = norm ∘ (σ + 𝐀ₕ)
av_field = norm ∘ (σ_ave + 𝐀ₕ)
H1err_field = norm ∘ ∇(u - uh)
max_val = max_cell_fields([eq_field, av_field, H1err_field], Qₕ_cell_point)
min_val = min_cell_fields([eq_field, av_field, H1err_field], Qₕ_cell_point)
fig = Figure(resolution = (800, 600))
ga = fig[1, 1] = GridLayout()
axerr = Axis(ga[1, 1], xlabel = L"x", ylabel = L"y", title = L"$H_0^1$ seminorm error")
axeq = Axis(ga[2, 1], xlabel = L"x", ylabel = L"y", title = L"$$Equilibrated flux esitmator")
axave = Axis(ga[2, 2], xlabel = L"x", ylabel = L"y", title = L"$$Averaged flux esitmator")
plot_error = plot!(axerr, trian, H1err_field, colorrange=(min_val,max_val), colormap=:viridis)
plot_eq = plot!(axeq, trian, eq_field, colorrange=(min_val,max_val), colormap=:viridis)
plot_aver = plot!(axave, trian, av_field, colorrange=(min_val,max_val), colormap=:viridis)
Colorbar(fig[1,2], limits=(min_val, max_val), colormap=:viridis)
display(fig)
````

````julia
fig = Figure(resolution = (800, 1400))
ga = fig[1, 1] = GridLayout()
axdiveq = Axis(ga[1, 1], xlabel = L"x", ylabel = L"y", title = "Div error equilibrated flux")
axdivave= Axis(ga[2, 1], xlabel = L"x", ylabel = L"y", title = "Div error averaged flux")
f_proj = L²_projection_f(model, reffe, f, dx)
eq_div_field = norm ∘ (∇ ⋅ σ - f_proj)
ave_div_field = norm ∘ (∇ ⋅ σ_ave - f_proj)
plot_div_eq = plot!(axdiveq, trian, eq_div_field, colormap=:viridis)
Colorbar(ga[1,2], plot_div_eq)
plot_div_ave = plot!(axdivave, trian, ave_div_field, colormap=:viridis)
Colorbar(ga[2,2], plot_div_ave)
````

````julia
div_check² = L2_norm_squared(∇ ⋅ σ - f_proj, dx)
@show √sum(div_check²)
@show √sum(H1err²)
@show eff = √sum(η²)/ √sum(H1err²)
````
---
*This page was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 5801 | # Refinement test
In this tutorial, we use the estimator obtained by the equilibrated flux
to drive an adative mesh refinement (AMR) procedure.
We consider the Laplace problem
$$\begin{align}
-\Delta u &= 0 &&\text{ in }\Omega\\
u &= g &&\text{ on }\partial\Omega
\end{align}$$
on an L-shaped domain $\Omega = (-1,1)^2 \setminus [(0,1)\times(-1,0)]$.
We load this domain from a json file.
````julia
using Gridap
model = DiscreteModelFromFile("Lshaped.json")
Ω = Triangulation(model)
using GridapMakie, GLMakie
fig = plot(Ω)
wireframe!(Ω, color=:black, linewidth=2);
fig
````
In this case, we know the true solution $u$
is given by the following formula in polar coordinates:
````julia
"Have to convert from -[π, π] to [0, 2π]"
function θ(x)
θt = atan(x[2], x[1])
(θt >= 0) * θt + (θt < 0) * (θt + 2 * π)
end
r(x) = sqrt(x[1]^2 + x[2]^2)
α = 2 / 3
u(x) = r(x)^α * sin(θ(x) * α)
u_fig, _ , plt = plot(Ω, u, colormap=:viridis)
Colorbar(u_fig[1,2], plt)
````

````julia
using Gridap
using Gridap.Geometry
using Gridap.Adaptivity
using EqFlux
````
We define some helper functions for computing the L² norm in Gridap
````julia
L2_inner_product(f, g, dx) = ∫(f ⋅ g) * dx
L2_norm_squared(f, dx) = L2_inner_product(f, f, dx)
function L2_norm_squared(f, model, order)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
L2_norm_squared(f, dx)
end
````
Next, we define the Dörfler marking[1]
````julia
function dorfler_marking(η_arr)
if η_arr isa Gridap.Arrays.LazyArray
η_arr = EqFlux.smart_collect(η_arr)
end
θ = 0.3 # Marking parameter
η_tot = sum(η_arr)
sorted_inds = sortperm(η_arr, rev = true)
sorted = η_arr[sorted_inds]
η_partial = 0.0
i = 1
while η_partial <= θ * η_tot
η_partial += sorted[i]
i += 1
end
sorted_inds[1:i]
end
````
As a small example, we show the result of calling
`dorfler_marking
This step just corresponds to the contents of the [first Gridap.jl tutorial](https://gridap.github.io/Tutorials/dev/pages/t001_poisson/#Tutorial-1:-Poisson-equation-1).
````julia
function solve_laplace(model, order, g)
Ω = Triangulation(model)
degree = 2 * order + 2
dx = Measure(Ω, degree)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * 0.0) * dx
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, g)
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
dofs = num_free_dofs(V0)
uh, dx, dofs
end
````
This function uses the EqFlux.jl package to obtain an error estimation on each cell
of the mesh.
````julia
function estimate_laplace(uh, dx, model, order)
σ = build_equilibrated_flux(-∇(uh), x -> 0.0, model, order)
#σ = build_averaged_flux(∇(uh), model)
η² = L2_norm_squared(σ + ∇(uh), dx)
Ω = Triangulation(model)
getindex(η², Ω)
end
using Gridap.Adaptivity
````
Finally, this function puts the previous functions together into the standard
Solve -> Estimate -> Mark -> Refine
loop of AFEM. The refinement step using newest vertex bisection can
be selected using "nvb" with the keyword argument refinement_method.
g is the function on the Dirichlet boundary.
````julia
function solve_estimate_mark_refine_laplace(model, tol, order; g)
η = Inf
estimators = Float64[]
errors = Float64[]
num_dofs = Float64[]
error_fields = CellField[]
while η > tol
# We extract the internal model from the refined model
if model isa AdaptedDiscreteModel
model = model.model
end
# SOLVE
uh, dx, dofs = solve_laplace(model, order, g)
push!(num_dofs, dofs)
# ESTIMATE
η_arr = estimate_laplace(uh, dx, model, order)
H1err² = L2_norm_squared(∇(u - uh), dx)
Ω = Triangulation(model)
error_field = CellField(sqrt.(getindex(H1err², Ω)), Ω)
push!(error_fields, error_field)
H1err = √sum(H1err²)
η = √(sum(η_arr))
push!(estimators, η)
push!(errors, H1err)
# MARK
cells_to_refine = dorfler_marking(η_arr)
# REFINE
model = refine(model, refinement_method = "nvb", cells_to_refine = cells_to_refine)
end
return error_fields, num_dofs, estimators, errors
end
````
We can change the polynomial order here as well as the tolerance for the
estimator.
````julia
order = 2
tol = 1e-4
````
We pass the true solution as the Dirichlet function $g$
````julia
error_fields, num_dofs, estimators, errors = solve_estimate_mark_refine_laplace(model, tol, order, g = u)
fig = Figure()
axis = Axis(fig[1,1], xscale = log10, yscale = log10, title = "Order p=$order", xlabel = "DOFs")
lines!(axis, num_dofs, errors, label = "Error")
lines!(axis, num_dofs, estimators, label = "Estimator")
lines!(axis, num_dofs, num_dofs.^(-order / 2), label = "Optimal rate")
axislegend()
fig
````
We now show that the AFEM refinement achieves the optimat rate of convergence
of $\mathrm{DOFs}^{-p/d} = \mathrm{DOFs}^{-p/2}$ in 2D.
````julia
@show estimators[end]
````

Finally, we plot a .gif that shows sequence of meshes generated by the
adaptive refinement procedure. The refinement is clearly concentrated to the
re-entrant corner.
````julia
idx = Observable(1)
errors_plot = lift(idx) do idx
error_fields[idx].trian
end
fig, ax, plt = plot(errors_plot)
#display(fig)
wireframe!(errors_plot, color=:black, linewidth=2)
framerate = 5
idxs = 1:length(error_fields)
record(fig, "animation.gif", idxs; framerate=framerate, compression=0) do this_idx
idx[] = this_idx
end
````

````julia
#wireframe!(Ω, color=:black, linewidth=2);
````
[1] Dörfler, W. A convergent adaptive algorithm for Poisson’s equation. SIAM Journal on Numerical
Analysis 33, 3 (1996), 1106–1124
---
*This page was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 5036 | # EqFlux.jl
This package is based on the
[Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide tools to calculate a
posteriori error estimates for numerical solutions of
partial differential equations (PDEs). For simplicity, we consider here the
Poisson equation
\begin{align}
- \Delta u &= f &&\text{in }\Omega\\
u &= g &&\text{on }\partial\Omega.
\end{align}
We suppose we have already computed a conforming approximation
$u_h \in V_h\subset H^1_0(\Omega)$ to the solution $u$ in Gridap.jl by solving
$$(\nabla u_h, \nabla v_h) = (f, v_h)\quad\forall v_h\in V_h,$$
for this see for example the
[first Gridap.jl tutorial](https://gridap.github.io/Tutorials/dev/pages/t001_poisson/#Tutorial-1:-Poisson-equation-1).
The `EqFlux.jl` library then provides the tools to compute an estimator
$\eta(u_h)$ such that the error measured in the $H^1_0$-seminorm
can be bounded as
$$\|\nabla(u - u_h)\| \le \eta(u_h),$$
which we refer to as reliability of the estimator. We also can prove the bound
$$\eta(u_h) \lesssim \|\nabla(u - u_h)\|$$
which we refer to as efficiency. The main ingredient in computing this estimator
is a reconstructed flux obtained by postprocessing that is an approximation
to the numerical flux, i.e., $\sigma_h\approx -\nabla u_h$. This
flux has the important property of being "conservative over faces" in the sense
that
$$\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).$$
we provide two functions to obtain this object:
`build_equilibrated_flux` and `build_average_flux` which we denote by
$\sigma_{\mathrm{eq},h}$ and $\sigma_{\mathrm{ave},h}$ respectively.
. In addition, for the
equilibrated flux $\sigma_{\mathrm{eq},h}$ satisfies the so-called equilibrium
condition, i.e., for piecewise polynomial $f$, we have
$$\nabla\cdot\sigma_{\mathrm{eq},h} = f.$$
In either case,the estimator takes the form
$$\eta(u_h) = \| \sigma_{\cdot,h} + \nabla u_h\|.$$
# Demonstration
We set $\Omega = (0,1)^2$ to be the unit square in 2D. We use a uniform
simplicial mesh $\mathcal{T}_h$ to discretize this domain by the following in Gridap.jl
````julia
using Gridap
using GridapMakie
using GLMakie
n = 10 # Number of elements in x and y for square mesh
domain = (0,1,0,1)
partition = (n, n)
model = CartesianDiscreteModel(domain, partition)
# Change to triangles
model = simplexify(model)
𝓣ₕ = Triangulation(model)
plt = plot(𝓣ₕ)
wireframe!(𝓣ₕ, color=:black)
plt
````
We manufacture the solution $u = \sin(2\pi x)\sin(2\pi y)$ by choosing the right hand side:
````julia
u(x) = sin(2*pi*x[1])*sin(2*pi*x[2])
f(x) = 8*pi^2*u(x) # = -Δu
````
We consider the discrete space
$$V_h = \{v_h\in H_0^1(\Omega): v_h|_K \in\mathbb{P}_k(K),\quad\forall K\in
\mathcal{T}_h\}.$$ This is achieved through the following with Gridap.jl:
````julia
# Polynomial order
order = 1
degree = 2 * order + 2
dx = Measure(𝓣ₕ, degree)
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, u)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * f) * dx
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
fig_soln, _ , plt = plot(𝓣ₕ, uh, colormap=:viridis)
Colorbar(fig_soln[1,2], plt)
fig_soln
````
We can then build the fluxes $\sigma_{\mathrm{eq},h}$ and
$\sigma_{\mathrm{ave},h}$ via the following:
````julia
using EqFlux
σ_eq = build_equilibrated_flux(-∇(uh), f, model, order)
σ_ave = build_averaged_flux(-∇(uh), model)
include(joinpath(@__DIR__, "helpers.jl"))
````
First we calculate the estimators and the error using the fluxes and the
approximate solution uh.
````julia
H1err² = L2_norm_squared(∇(u - uh), dx)
@show sqrt(sum(H1err²))
H1err_arr = sqrt.(getindex(H1err², 𝓣ₕ))
η_eq² = L2_norm_squared(σ_eq + ∇(uh), dx)
@show sqrt(sum(η_eq²))
ηeq_arr = sqrt.(getindex(η_eq², 𝓣ₕ))
η_ave² = L2_norm_squared(σ_ave + ∇(uh), dx)
@show sqrt(sum(η_ave²))
ηave_arr = sqrt.(getindex(η_ave², 𝓣ₕ));
````
Now we plot the estimators and errors restricted to each element
(the full code can be found in helpers.jl)
````julia
fig = plot_error_and_estimator(𝓣ₕ, ηave_arr, ηeq_arr, H1err_arr)
````

````julia
#fig
````
We see that both estimators provide a good cellwise approximation of the
error, but the one based on the equilibrated flux is closer visually. Next,
we consider the divergence error, i.e., how well the reconstructed object
satisfies $\nabla\cdot\sigma = \Pi_1 f$. In particular, in the following plot we can
see that the equilibrated flux estimator satisfies the divergence constraint
up to machine precision, but the flux based on averaging does not.
````julia
f_proj = L²_projection(model, reffe, f, dx)
eq_div = L2_norm_squared(∇ ⋅ σ_eq - f_proj, dx)
ave_div = L2_norm_squared(∇ ⋅ σ_ave - f_proj, dx)
eq_div_vis = CellField(sqrt.(getindex(eq_div, 𝓣ₕ)), 𝓣ₕ)
ave_div_vis = CellField(sqrt.(getindex(ave_div, 𝓣ₕ)), 𝓣ₕ)
fig = plot_divergence_mismatch(𝓣ₕ, eq_div_vis, ave_div_vis)
````

---
*This page was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 3967 | # EqFlux.jl
This package is based on the
[Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide tools to calculate a
posteriori error estimates for numerical solutions of
partial differential equations (PDEs). For simplicity, we consider here the
Poisson equation
\begin{align}
- \Delta u &= f &&\text{in }\Omega\\
u &= g &&\text{on }\partial\Omega.
\end{align}
We suppose we have already computed a conforming approximation
$u_h \in V_h\subset H^1_0(\Omega)$ to the solution $u$ in Gridap.jl by solving
$$(\nabla u_h, \nabla v_h) = (f, v_h)\quad\forall v_h\in V_h,$$
for this see for example the
[first Gridap.jl tutorial](https://gridap.github.io/Tutorials/dev/pages/t001_poisson/#Tutorial-1:-Poisson-equation-1).
The `EqFlux.jl` library then provides the tools to compute an estimator
$\eta(u_h)$ such that the error measured in the $H^1_0$-seminorm
can be bounded as
$$\|\nabla(u - u_h)\| \le \eta(u_h),$$
which we refer to as reliability of the estimator. We also can prove the bound
$$\eta(u_h) \lesssim \|\nabla(u - u_h)\|$$
which we refer to as efficiency. The main ingredient in computing this estimator
is a reconstructed flux obtained by postprocessing that is an approximation
to the numerical flux, i.e., $\sigma_h\approx -\nabla u_h$. This
flux has the important property of being "conservative over faces" in the sense
that
$$\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).$$
we provide two functions to obtain this object:
`build_equilibrated_flux` and `build_average_flux` which we denote by
$\sigma_{\mathrm{eq},h}$ and $\sigma_{\mathrm{ave},h}$ respectively.
. In addition, for the
equilibrated flux $\sigma_{\mathrm{eq},h}$ satisfies the so-called equilibrium
condition, i.e., for piecewise polynomial $f$, we have
$$\nabla\cdot\sigma_{\mathrm{eq},h} = f.$$
In either case,the estimator takes the form
$$\eta(u_h) = \| \sigma_{\cdot,h} + \nabla u_h\|.$$
# Demonstration
We set $\Omega = (0,1)^2$ to be the unit square in 2D. We use a uniform
simplicial mesh $\mathcal{T}_h$ to discretize this domain by the following in Gridap.jl
````julia
using Gridap
n = 10 # Number of elements in x and y for square mesh
domain = (0,1,0,1)
partition = (n, n)
model = CartesianDiscreteModel(domain, partition)
# Change to triangles
model = simplexify(model)
𝓣ₕ = Triangulation(model)
````
We manufacture the solution $u = \sin(2\pi x)\sin(2\pi y)$ by choosing the right hand side:
````julia
u(x) = sin(2*pi*x[1])*sin(2*pi*x[2])
f(x) = 8*pi^2*u(x)
````
We consider the discrete space
$$V_h = \{v_h\in H_0^1(\Omega): v_h|_K \in\mathbb{P}_k(K),\quad\forall K\in
\mathcal{T}_h\}.$$ This is achieved through the following with Gridap.jl:
````julia
# Polynomial order
order = 1
degree = 2 * order + 2
dx = Measure(𝓣ₕ, degree)
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, u)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * f) * dx
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
````
We can then build the fluxes $\sigma_{\mathrm{eq},h}$ and
$\sigma_{\mathrm{ave},h}$ via the following:
````julia
using EqFlux
σ_eq = build_equilibrated_flux(∇(uh), f, model, order)
σ_ave = build_averaged_flux(∇(uh), model)
````
We compare the estimators with the error they are estimating in the
following figure (the rest of the full code can be founde here TODO)

We see that both estimators provide a good cellwise approximation of the
error, but the one based on the equilibrated flux is closer visually. Next,
we consider the divergence error, i.e., how well the reconstructed object
satisfies $\nabla\cdot\sigma = \Pi_1 f$. In particular, in the following plot we can
see that the equilibrated flux estimator satisfies the divergence constraint
up to machine precision, but the flux based on averaging does not.

---
*This page was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 5906 | # EqFlux.jl
This package is based on the
[Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide tools to calculate a
posteriori error estimates for numerical solutions of
partial differential equations (PDEs). More precisely, if we solving an abstract PDE of the
form: find $u$ such that
$$-\nabla\cdot\mathbf{A}(\nabla u) = f.$$
If we compute an approximation $u_h$ to the solution $u$ in Gridap.jl,
the `EqFlux.jl` library provides the tools to compute an estimator
$\eta(u_h)$ such that the error measured in some norm $\|\cdot\|$ can be
bounded by
$$\|u - u_h\| \le \eta(u_h),$$
which we refer to as reliability, as well as the bound
$$\eta(u_h) \lesssim \|u - u_h\|$$
which we refer to as efficiency. The main ingredient in computing this estimator
is an reconstructed flux obtained by postprocessing that is an approximation
to the to the numerical flux, i.e., $\sigma_h\approx \mathbf{A}(\nabla u_h)$. This
flux has the important property of being "conservative" in the sense
that
$$\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).$$
we provide two functions to obtain this object:
`build_equilibrated_flux` and `build_average_flux`. In addition, for the
eq_field flux the so-called equilibrium condition is satisfied, i.e.,
$$\nabla\cdot\sigma_h = \Pi_pf$$
where $\Pi_p$ is the orthogonal projection onto polynomials of degree at most
$p$.
We first load the required packages
````julia
using Gridap
using Gridap.Geometry
using Gridap.Adaptivity
using GridapMakie, GLMakie
using EqFlux
using JLD2
````
Define some helper functions
````julia
L2_inner_product(f, g, dx) = ∫(f ⋅ g) * dx
L2_norm_squared(f, dx) = L2_inner_product(f, f, dx)
function L2_norm_squared(f, model, order)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
L2_norm_squared(f, dx)
end
function L²_projection_f(model, reffe, f, dx)
V = TestFESpace(model, reffe; conformity = :L2)
m(u, v) = ∫(u * v)*dx
b(v) = ∫(v * f) * dx
op_proj = AffineFEOperator(m, b, V, V)
solve(op_proj)
end
let
````
Now we consider the Laplace problem
$$\begin{align}
-\Delta u &= f &&\text{ in }\Omega\\
u &= g &&\text{ on }\partial\Omega
\end{align}$$
on the L-shaped domain. In this case, we know the true solution
is given by the following formula in polar coordinates:
````julia
u(x) = sin(2*pi*x[1])*sin(2*pi*x[2])
````
The right hand side is zero for the Laplace equation
````julia
f(x) = 8*pi^2*u(x)
#u(x) = x[1] * (x[1] - 1) * x[2] * (x[2] - 1)
#f(x) = (-2 * (x[1] * x[1] + x[2] * x[2]) + 2 * (x[1] + x[2]))
````
Now we find an approximate solution using Gridap.jl
````julia
order = 1
n = 10
domain = (0,1,0,1)
partition = (n, n)
model = CartesianDiscreteModel(domain, partition) |> simplexify
trian = Triangulation(model)
degree = 2 * order + 2
Ω = Triangulation(model)
dx = Measure(Ω, degree)
reffe = ReferenceFE(lagrangian, Float64, order)
V0 = TestFESpace(model, reffe; conformity = :H1, dirichlet_tags = "boundary")
U = TrialFESpace(V0, u)
a(u, v) = ∫(∇(v) ⊙ ∇(u)) * dx
b(v) = ∫(v * f) * dx
op = AffineFEOperator(a, b, U, V0)
uh = solve(op)
````
We then plot the approximate solution
````julia
fig_soln, _ , plt = plot(trian, uh, colormap=:viridis)
Colorbar(fig_soln[1,2], plt)
#md # 
````
We now compute the two fluxes.
````julia
𝐀ₕ = ∇(uh)
σeq = build_equilibrated_flux(𝐀ₕ, f, model, order)
σave = build_averaged_flux(𝐀ₕ, model)
ηeq² = L2_norm_squared(σeq + 𝐀ₕ, dx)
ηeq_arr = sqrt.(getindex(ηeq², Ω))
H1err² = L2_norm_squared(∇(u - uh), dx)
H1err_arr = sqrt.(getindex(H1err², Ω))
ηave² = L2_norm_squared(σave + 𝐀ₕ, dx)
ηave_arr = sqrt.(getindex(ηave², Ω))
reffe0 = ReferenceFE(lagrangian, Float64, 0)
Vint0 = TestFESpace(model, reffe0; conformity=:L2)
max_val = maximum([ηave_arr..., ηeq_arr..., H1err_arr...])
min_val = minimum([ηave_arr..., ηeq_arr..., H1err_arr...])
#ηave_vis = FEFunction(Vint0, ηave_arr)
ηave_vis = CellField(ηave_arr, Ω)
ηeq_vis = FEFunction(Vint0, ηeq_arr)
H1err_vis = FEFunction(Vint0, H1err_arr)
fig = Figure(resolution = (700, 600))
ga = fig[1, 1] = GridLayout()
axerr = Axis(ga[1, 1], xlabel = L"x", ylabel = L"y", title = L"$H_0^1$ seminorm error")
axeq = Axis(ga[2, 1], xlabel = L"x", ylabel = L"y", title = L"$$Equilibrated flux esitmator")
axave = Axis(ga[2, 2], xlabel = L"x", ylabel = L"y", title = L"$$Averaged flux esitmator")
plot_error = plot!(axerr, trian, H1err_vis, colorrange=(min_val,max_val), colormap=:viridis)
plot_eq = plot!(axeq, trian, ηeq_vis, colorrange=(min_val,max_val), colormap=:viridis)
plot_aver = plot!(axave, trian, ηave_vis, colorrange=(min_val,max_val), colormap=:viridis)
Colorbar(fig[1,2], limits=(min_val, max_val), colormap=:viridis)
#display(fig)
#md # 
fig = Figure(resolution = (1600, 800))
ga = fig[1, 1] = GridLayout()
axdiveq = Axis(ga[1, 1], xlabel = L"x", ylabel = L"y", title = L"$$ Divergence misfit equilibrated flux")
axdivave= Axis(ga[1, 3], xlabel = L"x", ylabel = L"y", title = L"$$ Divergence misfit averaged flux")
f_proj = L²_projection_f(model, reffe, f, dx)
eq_div = L2_norm_squared(∇ ⋅ σeq - f_proj, dx)
ave_div = L2_norm_squared(∇ ⋅ σave - f_proj, dx)
eq_div_vis = FEFunction(Vint0, sqrt.(getindex(eq_div, Ω)))
ave_div_vis = FEFunction(Vint0, sqrt.(getindex(ave_div, Ω)))
plot_div_eq = plot!(axdiveq, trian, eq_div_vis, colormap=:viridis)
Colorbar(ga[1,2], plot_div_eq)
plot_div_ave = plot!(axdivave, trian, ave_div_vis, colormap=:viridis)
Colorbar(ga[1,4], plot_div_ave)
#md # 
div_check² = L2_norm_squared(∇ ⋅ σeq - f_proj, dx)
@show √sum(div_check²)
@show √sum(H1err²)
@show eff_eq = √sum(ηeq²)/ √sum(H1err²)
@show eff_ave = √sum(ηave²)/ √sum(H1err²)
end
````
---
*This page was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.0 | 2c532e19fbd25f43acbb11aafccbb5dad75e2f21 | docs | 1772 | ```@meta
CurrentModule = EquilibratedFlux
```
# EquilibratedFlux.jl
This package is based on
[Gridap.jl](https://github.com/gridap/Gridap.jl/tree/master) to provide
post-processing tools to calculate reconstructed fluxes associated to the given
approximate solution of a PDE.
For simplicity, we consider here the Poisson equation
```math
\begin{align}
- \Delta u &= f &&\text{in }\Omega\\
u &= g &&\text{on }\partial\Omega.
\end{align}
```
We suppose we have already computed a conforming approximation $u_h \in
V_h\subset H^1_0(\Omega)$ to the solution $u$ in Gridap.jl by solving
```math
(\nabla u_h, \nabla v_h) = (f, v_h)\quad\forall v_h\in V_h,
```
The `EquilibratedFlux.jl` library then provides the tools to compute a reconstructed flux
associated to $u_h$. This flux, obtained by postprocessing, is an approximation to the numerical flux, i.e.
```math
\sigma_h \approx -\nabla u_h.
```
This flux has the important property of being "conservative over faces" in the
sense that
```math
\sigma_h \in \mathbf{H}(\mathrm{div},\Omega).
```
We provide two functions to obtain such an object:
[`build_equilibrated_flux`](@ref) and [`build_averaged_flux`](@ref) both provide
reconstructed fluxes, which we denote by $\sigma_{\mathrm{eq},h}$ and
$\sigma_{\mathrm{ave},h}$ respectively.
In addition to the properties listed above, the equilibrated flux
$\sigma_{\mathrm{eq},h}$ satisfies the so-called equilibrium condition, i.e.,
for piecewise polynomial $f$, we have
```math
\nabla\cdot\sigma_{\mathrm{eq},h} = f.
```
The reconstructed flux is the main ingredient in computing *a posteriori* error
estimators. See the [first tutorial](@ref tuto-error-estimation) for a complete
demonstration of how to do this.
```@autodocs
Modules = [EquilibratedFlux]
```
| EquilibratedFlux | https://github.com/aerappa/EquilibratedFlux.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | code | 608 | using Fetch
using Documenter
DocMeta.setdocmeta!(Fetch, :DocTestSetup, :(using Fetch); recursive=true)
makedocs(;
modules=[Fetch],
authors="JingYu Ning <[email protected]> and contributors",
repo="https://github.com/foldfelis/Fetch.jl/blob/{commit}{path}#{line}",
sitename="Fetch.jl",
format=Documenter.HTML(;
prettyurls=get(ENV, "CI", "false") == "true",
canonical="https://foldfelis.github.io/Fetch.jl",
assets=String[],
),
pages=[
"Home" => "index.md",
],
)
deploydocs(;
repo="github.com/foldfelis/Fetch.jl",
devbranch="main"
)
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | code | 167 | module Fetch
using Random: randstring
using HTTP
using JSON3
using StructTypes
using Base64
include("gdrive.jl")
include("kaggle.jl")
end
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | code | 3448 | export gdownload
const SPREADSHEET_PATTERN = "docs.google.com/spreadsheets"
const DRIVE_PATTERN = "drive.google.com/file/d"
const DOCS_PATTERN = "docs.google.com"
is_gsheet(url) = occursin(SPREADSHEET_PATTERN, url)
is_gfile(url) = occursin(DRIVE_PATTERN, url)
is_gdoc(url) = occursin(DOCS_PATTERN, url)
"""
unshortlink(url)
return unshorten url or the url if it is not a short link
"""
function unshortlink(url; kw...)
rq = HTTP.request("HEAD", url; redirect=false, status_exception=false, kw...)
while !(is_gdoc(url) || is_gfile(url)) && (rq.status ÷ 100 == 3)
url = HTTP.header(rq, "Location")
rq = HTTP.request("HEAD", url; redirect=false, status_exception=false, kw...)
end
return url
end
function gsheet_handler(url; format=:csv)
link, expo = splitdir(url)
if startswith(expo, "edit") || (expo == "")
url = link * "/export?format=$format"
elseif startswith(expo, "export")
url = replace(url, r"format=([a-zA-Z]*)(.*)"=>SubstitutionString("format=$format\\2"))
end
return url
end
function gfile_handler(url)
# pattern of file path in google drive:
# https://drive.google.com/file/d/<hash>/view?usp=sharing
h = match(r"/file/d/([^\/]+)/", url)
isnothing(h) && throw(ErrorException("Can't find google drive file ID in the url"))
return "https://docs.google.com/uc?export=download&id=$(h.captures[])"
end
function find_filename(header)
m = match(r"filename=\\\"(.*)\\\"", header)
if isnothing(m)
filename = "gdrive_downloaded-$(randstring())"
@warn "File name not found, use `$filename`"
else
filename = m.captures[]
end
return filename
end
function download_gdrive(url, localdir)
m = match(r"confirm=([^;&]+)", url)
isnothing(m) && (url = "$url&confirm=pbef")
r = HTTP.head(url; status_exception = false)
HTTP.iserror(r) && r.status != 303 && throw(HTTP.StatusError(r.status, r.request.method, r.request.target, r))
r.status == 303 && (url = r["Location"])
filepath = Ref{String}("")
HTTP.open(
"GET", url, ["Range"=>"bytes=0-"], redirect_limit=10
) do stream
response = HTTP.startread(stream)
eof(stream) && return
header = HTTP.header(response, "Content-Disposition")
isempty(header) && return
filepath[] = joinpath(localdir, find_filename(header))
total_bytes = tryparse(Int64, rsplit(HTTP.header(response, "Content-Range"), '/'; limit=2)[end])
isnothing(total_bytes) && (total_bytes = NaN)
println("Total: $total_bytes bytes")
downloaded_bytes = progress = 0
print("Downloaded:\e[s")
Base.open(filepath[], "w") do fh
while !eof(stream)
downloaded_bytes += write(fh, readavailable(stream))
new_progress = 100downloaded_bytes ÷ total_bytes
(new_progress > progress) && print("\e[u $downloaded_bytes bytes ($new_progress%)")
progress = new_progress
end
println()
end
end
return filepath[]
end
"""
gdownload(url, localdir)
Download file or Google Sheet from Google drive.
"""
function gdownload(url, localdir)
url = unshortlink(url)
if is_gfile(url)
url = gfile_handler(url)
elseif is_gsheet(url)
url = gsheet_handler(url)
end
is_gdoc(url) || throw("invalid url")
download_gdrive(url, localdir)
end
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | code | 2086 | export kdownload
const KAGGLE_DOMAIN = "www.kaggle.com"
const KAGGLE_API = "https://www.kaggle.com/api/v1/datasets/download"
struct Auth
username::String
key::String
end
StructTypes.StructType(::Type{Auth}) = StructTypes.Struct()
function gen_auth_key()
auth_file = joinpath(homedir(), ".kaggle", "kaggle.json")
if isfile(auth_file)
f = open(auth_file, "r")
auth = JSON3.read(f, Auth)
close(f)
else
auth = Auth(ENV["KAGGLE_USERNAME"], ENV["KAGGLE_KEY"])
end
auth_str = Base64.base64encode("$(auth.username):$(auth.key)")
return "Basic $(auth_str)"
end
function gen_kaggle_url(dataset)
return "$KAGGLE_API/$dataset"
end
function kaggle_url2dataset(url_or_dataset)
if contains(url_or_dataset, KAGGLE_DOMAIN)
user_name, dataset_name = match(Regex("$KAGGLE_DOMAIN/([^/]+)/([^/]+)"), url_or_dataset).captures
dataset = "$user_name/$dataset_name"
else
dataset = url_or_dataset
end
@assert HTTP.request("HEAD", "https://$KAGGLE_DOMAIN/$dataset").status == 200
return dataset
end
function kdownload(url_or_dataset, localdir)
dataset = kaggle_url2dataset(url_or_dataset)
url = gen_kaggle_url(dataset)
filepath = joinpath(localdir, "$(replace(dataset, '/'=>'_')).zip")
HTTP.open("GET", url, ["Authorization"=>gen_auth_key()]) do stream
HTTP.startread(stream)
eof(stream) && return
total_bytes = tryparse(Int64, HTTP.header(stream, "Content-Length"))
(total_bytes === nothing) && (total_bytes = NaN)
println("Total: $total_bytes bytes")
downloaded_bytes = progress = 0
print("Downloaded:\e[s")
Base.open(filepath, "w") do f
while !eof(stream)
downloaded_bytes += write(f, readavailable(stream))
new_progress = 100downloaded_bytes ÷ total_bytes
(new_progress > progress) && print("\e[u $downloaded_bytes bytes ($new_progress%)")
progress = new_progress
end
end
end
return filepath
end
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | code | 1334 | const LARGE_GFILE = "https://drive.google.com/file/d/1OiX6gEWRm57kb1H8L0K_HWN_pzc-sk8y/view?usp=sharing"
const SMALL_GDRIVE = "https://drive.google.com/file/d/1BENwlCOlGEMF8zsM4rC-SYVxyL7f8xw0/view?usp=sharing"
const GFILE_NAME = "FetchTest"
@testset "large file" begin
f = gdownload(LARGE_GFILE, pwd())
unpack(f)
open(joinpath(pwd(), GFILE_NAME, "$GFILE_NAME.txt"), "r") do file
@test readline(file) == "Test"
end
rm(GFILE_NAME, recursive=true, force=true)
end
@testset "small file" begin
gdownload(SMALL_GDRIVE, pwd())
open(joinpath(pwd(), "$GFILE_NAME.txt"), "r") do file
@test readline(file) == "Test"
end
rm("$GFILE_NAME.txt", recursive=true, force=true)
end
const GSHEET = "https://docs.google.com/spreadsheets/d/1rwoDt5HrcP6TTgBe3BWxp7kPdVMWuS1cGVZp7BXhPwc/edit?usp=sharing"
const GSHEET_NAME = "FetchTest"
@testset "sheet" begin
gdownload(GSHEET, pwd())
open(joinpath(pwd(), "$GSHEET_NAME-1.csv"), "r") do file
@test readline(file) == "Test,1"
end
rm("$GSHEET_NAME-1.csv", recursive=true, force=true)
end
@testset "unshortlink" begin
@test Fetch.unshortlink("https://bit.ly/3ir0gYu") == LARGE_GFILE
@test Fetch.unshortlink("https://bit.ly/3yqqdwK") == SMALL_GDRIVE
@test Fetch.unshortlink("https://bit.ly/3yDDi69") == GSHEET
end
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | code | 1071 | @testset "kaggle dataset" begin
dataset = "ningjingyu/fetchtest"
f = kdownload(dataset, pwd())
unpack(f)
open(joinpath(pwd(), "FetchTest", "FetchTest.txt"), "r") do file
@test readline(file) == "Test"
end
rm(joinpath(pwd(), "FetchTest"), recursive=true, force=true)
end
@testset "kaggle url" begin
urls = [
"https://www.kaggle.com/ningjingyu/fetchtest",
"https://www.kaggle.com/ningjingyu/fetchtest/tasks",
"https://www.kaggle.com/ningjingyu/fetchtest/code",
"https://www.kaggle.com/ningjingyu/fetchtest/discussion",
"https://www.kaggle.com/ningjingyu/fetchtest/activity",
"https://www.kaggle.com/ningjingyu/fetchtest/metadata",
"https://www.kaggle.com/ningjingyu/fetchtest/settings",
]
for url in urls
f = kdownload(url, pwd())
unpack(f)
open(joinpath(pwd(), "FetchTest", "FetchTest.txt"), "r") do file
@test readline(file) == "Test"
end
rm(joinpath(pwd(), "FetchTest"), recursive=true, force=true)
end
end
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | code | 146 | using Fetch
using Test
include(joinpath(@__DIR__, "unpack.jl"))
@testset "Fetch.jl" begin
include("gdrive.jl")
include("kaggle.jl")
end
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | code | 1044 | using p7zip_jll
# https://github.com/oxinabox/DataDeps.jl/blob/v0.7.8/src/post_fetch_helpers.jl
# This file is a part of DataDeps.jl. License is MIT.
function unpack_cmd(file,directory,extension,secondary_extension)
p7zip() do exe7z
if secondary_extension == ".tar" || extension == ".tgz" || extension == ".tbz"
# special handling for compressed tarballs
return pipeline(`$exe7z x $file -y -so`, `$exe7z x -si -y -ttar -o$directory`)
else
return `$exe7z x $file -y -o$directory`
end
end
end
"""
unpack(f; keep_originals=false)
Extracts the content of an archive in the current directory;
deleting the original archive, unless the `keep_originals` flag is set.
"""
function unpack(f; keep_originals=false)
run(unpack_cmd(f, pwd(), last(splitext(f)), last(splitext(first(splitext(f))))))
rm("pax_global_header"; force=true) # Non-compliant tarball extractors dump out this file. It is meaningless (google it's filename for more)
!keep_originals && rm(f)
end
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
|
[
"MIT"
] | 0.1.4 | 781292162fd5bfe8d001210f9dddbb6baa509bf4 | docs | 2617 | # Fetch
[](https://foldfelis.github.io/Fetch.jl/dev)
[](https://github.com/foldfelis/Fetch.jl/actions)
[](https://codecov.io/gh/foldfelis/Fetch.jl)
## Quick start
The package can be installed with the Julia package manager.
From the Julia REPL, type ] to enter the Pkg REPL mode and run:
```julia
pkg> add Fetch
```
## Download file from Google drive
Download file or Google Sheet from Google drive via the share link:
```julia
using Fetch
link = "https://drive.google.com/file/d/1OiX6gEWRm57kb1H8L0K_HWN_pzc-sk8y/view?usp=sharing"
gdownload(link, pwd())
```
## Download dataset from Kaggle
Download dataset from Kaggle via the name of dataset:
```julia
using Fetch
dataset = "ningjingyu/fetchtest"
kdownload(dataset, pwd())
```
Or via the url of the home page of the dataset:
```julia
using Fetch
url = "https://www.kaggle.com/ningjingyu/fetchtest"
kdownload(url, pwd())
```
## Intergrate with DataDeps.jl
According to [DataDeps.jl](https://github.com/oxinabox/DataDeps.jl),
`DataDep` can be construct as following:
```julia
DataDep(
name::String,
message::String,
remote_path::Union{String,Vector{String}...},
[checksum::Union{String,Vector{String}...},];
fetch_method=fetch_default
post_fetch_method=identity
)
```
By using `Fetch.jl`, one can upload their dataset to Google drive,
and construct `DataDep` by setting `fetch_method=gdownload`.
```julia
using DataDeps
using Fetch
register(DataDep(
"FetchTest",
"""Test dataset""",
"https://drive.google.com/file/d/1OiX6gEWRm57kb1H8L0K_HWN_pzc-sk8y/view?usp=sharing",
"b083597a25bec4c82c2060651be40c0bb71075b472d3b0fabd85af92cc4a7076",
fetch_method=gdownload,
post_fetch_method=unpack
))
datadep"FetchTest"
```
Or to Kaggle
```julia
using DataDeps
using Fetch
register(DataDep(
"FetchTest",
"""Test dataset""",
"ningjingyu/fetchtest",
"65492e1f4c6affb7955125e5e4cece2bb547e482627f3af9812c06448dae40a9",
fetch_method=kdownload,
post_fetch_method=unpack
))
datadep"FetchTest"
```
According to the document of [Kaggle-api](https://github.com/Kaggle/kaggle-api#api-credentials)
one needs to set their environment variables `KAGGLE_USERNAME` and `KAGGLE_KEY`,
or simply download the api token from Kaggle, and place this file in the location `~/.kaggle/kaggle.json`
(on Windows in the location `C:\Users\<Windows-username>\.kaggle\kaggle.json`).
| Fetch | https://github.com/foldfelis/Fetch.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.