licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 843 | cd(@__DIR__); include("setups/path128.jl")
gr(dpi = 200)
##
f = 1.5 * 𝚽[:, 11] + 𝚽[:, 31] .* characteristic(1:32, N) +
𝚽[:, 61] .* characteristic(1:64, N) + 0.5 * 𝚽[:, 111]
## (a)
plot(f, c = :black, grid = false, legend = false, frame = :box, lw = 1.5)
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
plt = plot!(xlab = latexstring("x"), ylab = latexstring("f"),
size = (600, 400), guidefontsize = 18, xlim = [1, N])
savefig(plt, "../figs/Path128_Spectrogram_f.png")
## (b)
plot(0:N-1, 𝚽' * f, c = :black, grid = false, legend = false, frame = :box, lw = 1.5)
xticks!([0; 15:16:127], vcat(string("DC"), [string(k) for k in 15:16:127]))
plt = plot!(xlab = latexstring("l"), ylab = latexstring("g"),
size = (600, 400), guidefontsize = 18, xlim = [1, N])
savefig(plt, "../figs/Path128_Spectrogram_g.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 684 | cd(@__DIR__); include("setups/path128.jl")
gr(dpi = 200)
##
f = 1.5 * 𝚽[:, 11] + 𝚽[:, 31] .* characteristic(1:32, N) +
𝚽[:, 61] .* characteristic(1:64, N) + 0.5 * 𝚽[:, 111]
## (a)
plt = path_spectrogram(f, distDCT, 𝚽; c = 0.01)
savefig(plt, "../figs/Path128_Spectrogram_CoeffEnergy_sig001dmax.png")
## (b)
plt = path_spectrogram(f, distDCT, 𝚽; c = 0.02)
savefig(plt, "../figs/Path128_Spectrogram_CoeffEnergy_sig002dmax.png")
## (c)
plt = path_spectrogram(f, distDCT, 𝚽; c = 0.05)
savefig(plt, "../figs/Path128_Spectrogram_CoeffEnergy_sig005dmax.png")
## (d)
plt = path_spectrogram(f, distDCT, 𝚽; c = 0.1)
savefig(plt, "../figs/Path128_Spectrogram_CoeffEnergy_sig01dmax.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 652 | cd(@__DIR__); include("setups/grid23x22.jl")
gr(dpi = 200)
##
frame = sgwt_frame(W; nf = 6)
filters = sgwt_filter_banks(W, 𝛌; nf = 6)
plot(𝛌, filters', lw = 3, size = (800, 450), grid = false, frame = :box,
legendfontsize = 14, xlab = latexstring("\\lambda"), xguidefontsize = 14,
lab = [latexstring("h(\\lambda)") latexstring("g(s_{1}\\lambda)") latexstring("g(s_{2}\\lambda)") latexstring("g(s_{3}\\lambda)") latexstring("g(s_{4}\\lambda)") latexstring("g(s_{5}\\lambda)")])
# plot!(𝛌, sum(filters, dims = 1)[:]/6, c = :black, lw = 3, lab = "partition of unity")
plt = current()
savefig(plt, "../figs/Grid$(Nx)x$(Ny)_SGWT_filter_banks.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 331 | cd(@__DIR__); include("setups/grid23x22.jl")
gr(dpi = 200)
##
frame = sgwt_frame(W; nf = 6)
x = 242
for j = 1:6
plt = heatmap(reshape(frame[:, x, j], (Nx, Ny))', c = :viridis, ratio = 1,
frame = :none, xlim = [1, Nx], size = (500, 400))
savefig(plt, "../figs/Grid$(Nx)x$(Ny)_SGWT_frame_j$(j-1)_x$(x).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 793 | cd(@__DIR__); include("setups/grid23x22.jl")
gr(dpi = 200)
##
x = 242
## (a)
l = 11 # vertical
plt = grid_eigenvector_plot(l)
savefig(plt, "../figs/Grid$(Nx)x$(Ny)_eigenvector_l$(l-1).png")
## (d)
plt = grid_NGWFvector_plot(l, x, D, 𝚽)
savefig(plt, "../figs/Grid$(Nx)x$(Ny)_NGWF_DAG_sig02_l$(l-1)_x$(x).png")
## (b)
l = 16 # horizontal
plt = grid_eigenvector_plot(l)
savefig(plt, "../figs/Grid$(Nx)x$(Ny)_eigenvector_l$(l-1).png")
## (e)
plt = grid_NGWFvector_plot(l, x, D, 𝚽)
savefig(plt, "../figs/Grid$(Nx)x$(Ny)_NGWF_DAG_sig02_l$(l-1)_x$(x).png")
## (c)
l = 30 # mix
plt = grid_eigenvector_plot(l)
savefig(plt, "../figs/Grid$(Nx)x$(Ny)_eigenvector_l$(l-1).png")
## (f)
plt = grid_NGWFvector_plot(l, x, D, 𝚽)
savefig(plt, "../figs/Grid$(Nx)x$(Ny)_NGWF_DAG_sig02_l$(l-1)_x$(x).png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1077 | cd(@__DIR__); include("setups/grid23x22.jl")
gr(dpi = 200)
## assemble frames
frame = sgwt_frame(W; nf = 6)
SGWT = reshape(frame, (N, :))
SGWT_dual = (SGWT * SGWT') \ SGWT
rNGWF, dic_l2x = rngwf_all_vectors(D, 𝚽; σ = 0.2 * maximum(D), thres = 0.15)
rNGWF_dual = (rNGWF * rNGWF') \ rNGWF
Γ = rngwf_lx(dic_l2x)
## (a)
f = digit_img[:]
plt = heatmap(reshape(f, (Nx, Ny))', c = :viridis, ratio = 1,
frame = :none, xlim = [1, Nx], size = (600, 500))
savefig(plt, "../figs/grid23x22_fdigit3.png")
## (b)
rel_approx_sgwt, f_approx_sgwt = frame_approx(f, SGWT, SGWT_dual; num_kept = 3 * N)
rel_approx_rngwf, f_approx_rngwf = frame_approx(f, rNGWF, rNGWF_dual; num_kept = 3 * N)
plot(0:length(rel_approx_rngwf)-1, [rel_approx_sgwt rel_approx_rngwf],
grid = false, lw = 2, c = [:blue :green],
xlab = "Number of Coefficients Retained",
ylab = "Relative Approximation Error", yaxis = :log,
lab = ["SGWT" "rNGWF"])
plt = plot!(xguidefontsize = 14, yguidefontsize = 14, legendfontsize = 11, size = (600, 500))
savefig(plt, "../figs/grid23x22_approx_fdigit3.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 505 | cd(@__DIR__); include("setups/grid23x22.jl")
gr(dpi = 200)
## build SGWT frame
frame = sgwt_frame(W; nf = 6)
SGWT = reshape(frame, (N, :))
SGWT_dual = (SGWT * SGWT') \ SGWT
f = digit_img[:]
important_idx = sortperm((SGWT' * f).^2; rev = true)
plot(layout = Plots.grid(10,10), size = (2300, 2800))
for i = 1:100
grid_vector_plot!(important_idx[i], i, SGWT)
if i == 90
plot_square!(Nx, Ny; subplot = i)
end
end
plt = current()
savefig(plt, "../figs/Grid23x22_fdigit3_sgwt_top100.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 780 | cd(@__DIR__); include("setups/grid23x22.jl")
gr(dpi = 200)
## build rNGWF
rNGWF, dic_l2x = rngwf_all_vectors(D, 𝚽; σ = 0.2 * maximum(D), thres = 0.15)
rNGWF_dual = (rNGWF * rNGWF') \ rNGWF
Γ = rngwf_lx(dic_l2x)
f = digit_img[:]
important_idx = sortperm((rNGWF' * f).^2; rev = true)
red_box_inds = [41, 43, 66, 69, 71, 73, 75, 84, 85, 86, 89, 99]
orange_box_inds = [40, 53, 54, 55, 72]
plot(layout = Plots.grid(10,10), size = (2300, 2800))
for i = 1:100
plot!(clims = (-0.002, 0.02))
grid_vector_plot!(important_idx[i], i, rNGWF)
if i in red_box_inds
plot_square!(Nx, Ny; subplot = i)
elseif i in orange_box_inds
plot_square!(Nx, Ny; subplot = i, c = :orange)
end
end
plt = current()
savefig(plt, "../figs/Grid23x22_fdigit3_rngwf_top100.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 974 | cd(@__DIR__); include("setups/grid7x3.jl")
pyplot(dpi = 200)
## (a) eigenvectors by nondecreasing eigenvalue ordering
plot(layout = Plots.grid(3, 7))
for i in 1:N
heatmap!(reshape(𝚽[:, i], (Nx, Ny))', c = :viridis, cbar = false,
clims = (-0.4,0.4), frame = :none, ratio = 1, ylim = [0, Ny + 1],
title = latexstring("\\phi_{", i-1, "}"), titlefont = 12,
subplot = i)
end
plt = current()
savefig(plt, "../figs/grid7x3_evsp_title.png")
## (b) eigenvectors by natural frequency ordering
plot(layout = Plots.grid(3, 7))
for i in 1:N
k = grid2eig_ind[i]
heatmap!(reshape(𝚽[:,k], (Nx, Ny))', c = :viridis, cbar = false,
clims = (-0.4,0.4), frame = :none, ratio = 1, ylim = [0, Ny + 1],
title = latexstring("\\varphi_{", string(eig2dct[k,1]),
",", string(eig2dct[k,2]), "}"), titlefont = 12, subplot = i)
end
plt = current()
savefig(plt, "../figs/grid7x3_dct_title2.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 189 | cd(@__DIR__); include("setups/rgc100.jl")
plotlyjs(dpi = 200)
gplot(W, X3; grid = true, shape = :circle, mcolor = :yellow)
plot!(xlab = "x", ylab = "y", zlab = "z", size = (500, 500))
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 315 | cd(@__DIR__); include("setups/rgc100.jl")
gr(dpi = 200)
plt = plot(0:(N - 1), 𝛌, c = :black, lw = 1, ylims = [0, 5], legend = false,
shape = :circle, frame = :box, xlab = latexstring("l"),
ylab = latexstring("\\tilde{\\lambda}_l"), size = (500, 400))
savefig(plt, "../figs/RGC100_eigenvalues.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 662 | cd(@__DIR__); include("setups/rgc100.jl")
gr(dpi = 200)
plt = gplot(W, X; width = 1); scatter_gplot!(X; marker = 𝚽[:, 1142], ms = 4)
plot!(xlims = [-180, 220], xlabel = "x(μm)", ylabel = "y(μm)",
clims = (-0.12, 0.12), frame = :box, size = (550, 500), right_margin = 5mm)
savefig(plt, "../figs/RGC100_twotypes_semi_oscillation.png")
plt = gplot(W, X; width = 1); scatter_gplot!(X; marker = 𝚽[:, 1143], ms = 4,
plotOrder = :s2l); plot!(xlims = [-180, 220], xlabel = "x(μm)",
ylabel = "y(μm)", clims = (-0.3, 0.3), frame = :box, size = (550, 500),
right_margin = 5mm)
savefig(plt, "../figs/RGC100_twotypes_localized.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1204 | cd(@__DIR__); include("setups/distROT_distTSD_ratio.jl")
gr(dpi = 200)
## (a) P64
include("setups/path64.jl")
ρ1 = generate_ROT_TSD_ratio(nsim, 𝚽, ∇𝚽, 𝛌, Q)
# plt = ROT_TSD_ratio_histogram(ρ1)
# savefig(plt, "../figs/Path64_ROT_TSD.png")
## (b) P₇ x P₃
include("setups/grid7x3.jl")
ρ2 = generate_ROT_TSD_ratio(nsim, 𝚽, ∇𝚽, 𝛌, Q)
# plt = ROT_TSD_ratio_histogram(ρ2)
# savefig(plt, "../figs/Grid7x3_ROT_TSD.png")
## (c) Erdos Rényi
include("setups/er.jl")
ρ3 = generate_ROT_TSD_ratio(nsim, 𝚽, ∇𝚽, 𝛌, Q)
# plt = ROT_TSD_ratio_histogram(ρ3)
# savefig(plt, "../figs/Erdos_Renyi_ROT_TSD.png")
## (d) weighted RGC100
include("setups/rgc100.jl")
ρ4 = generate_ROT_TSD_ratio(nsim, 𝚽, ∇𝚽, 𝛌, Q; edge_length = edge_length)
# plt = ROT_TSD_ratio_histogram(ρ4)
# savefig(plt, "../figs/wRGC100_ROT_TSD.png")
## boxplot
plt = boxplot(["(a) Path" "(b) Grid" "(c) ER" "(d) RGC100"], [ρ1, ρ2, ρ3, ρ4];
legend = false, frame = :box, ylim = [0.9, 1.9], tickfontsize = 11,
outliers = true, grid = false, range = 3, lw = 1, size = (800, 600),
ylab = "ρ", yguidefontsize = 14, xtickfontsize = 12, color = :white)
savefig(plt, "../figs/ROT_TSD_boxplots.png")
## Table 4.1
display_basic_stats([ρ1, ρ2, ρ3, ρ4])
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 316 | cd(@__DIR__); include("setups/grid7x3.jl");
## ROT1 + pmf1
D = natural_eigdist(𝚽, 𝛌, Q; α = 0.5, input_format = :pmf1, distance = :ROT)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
plt = grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot)
savefig(plt, "../figs/Grid7x3_MDS_ROT1_pmf1_alpha05.png")
display(plt)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 321 | cd(@__DIR__); include("setups/simpletree.jl");
gr(dpi=200)
plt = plot(0:(N - 1), 𝛌, c = :black, lw = 1, ylims = [0, 5], legend = false,
shape = :circle, frame = :box, xlab = latexstring("l"), ms = 4,
ylab = latexstring("\\lambda_l"), size = (500, 400))
savefig(plt, "../figs/SimpleTree_eigenvalues.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 337 | cd(@__DIR__); include("setups/simpletree.jl");
pyplot(dpi=200)
for l = 97:100
local plt
plot(size = (200, 500), framestyle = :none)
gplot!(W, X, width = 1)
scatter_gplot!(X; marker = 𝚽[:, l], ms = 5)
plt = plot!(cbar = false, clims = (-0.3, 0.3))
savefig(plt, "../figs/SimpleTree_eigenvector$(l-1)_red.png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 740 | cd(@__DIR__); include("setups/simpletree.jl");
plotlyjs(dpi = 200)
## (a)
D = natural_eigdist(𝚽, 𝛌, Q; α = 1.0, input_format = :pmf1, distance = :ROT)
E = transform(fit(MDS, D, maxoutdim=3, distances=true))
E[1, :] .*= 1; E[2, :] .*= -1; E[3, :] .*= 1;
plt = simpletree_mds_plot(E, ieb1, ieb2, ieb3, ieb4, iejc); plot!(camera=(210,-37), xlims = [-18, 15])
# savefig(plt, "../figs/SimpleTree_MDS_ROT1_pmf1_alpha1.html")
savefig(plt, "../figs/SimpleTree_MDS_ROT1_pmf1_alpha1.pdf")
## (b)
D = dist_sROT
E = transform(fit(MDS, D, maxoutdim=3, distances=true))
plt = simpletree_mds_plot(E, ieb1, ieb2, ieb3, ieb4, iejc)
# savefig(plt, "../figs/SimpleTree_MDS_sROT_pmf1_alpha1.html")
savefig(plt, "../figs/SimpleTree_MDS_sROT_pmf1_alpha1.pdf")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 370 | cd(@__DIR__); include("setups/grid7x3.jl");
## ROT1 + pmf2
D = natural_eigdist(𝚽, 𝛌, Q; α = 0.1, input_format = :pmf2, distance = :ROT)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
E[1, :] .*= sign(E[1, 2]); E[2, :] .*= -sign(E[1, 2])
plt = grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot)
savefig(plt, "../figs/Grid7x3_MDS_ROT1_pmf2_alpha01.png")
display(plt)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 336 | cd(@__DIR__); include("setups/grid7x3.jl");
## ROT2
D = natural_eigdist(𝚽, 𝛌, Q; α = 0.1, distance = :ROT)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
E[1, :] .*= sign(E[1, 2]); E[2, :] .*= -sign(E[1, 2])
plt = grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot)
savefig(plt, "../figs/Grid7x3_MDS_ROT2_alpha01.png")
display(plt)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 263 | cd(@__DIR__); include("setups/grid7x3.jl");
## HAD
D = natural_eigdist(𝚽, 𝛌, Q; distance = :HAD)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
plt = grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot)
savefig(plt, "../figs/Grid7x3_MDS_HAD.png")
display(plt)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 263 | cd(@__DIR__); include("setups/grid7x3.jl");
## DAG
D = natural_eigdist(𝚽, 𝛌, Q; distance = :DAG)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
plt = grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot)
savefig(plt, "../figs/Grid7x3_MDS_DAG.png")
display(plt)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 342 | cd(@__DIR__); include("setups/grid7x3.jl");
## TSD (T = 0.1)
D = natural_eigdist(𝚽, 𝛌, Q; T = 0.1, distance = :TSD)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
# E[1, :] .*= sign(E[1, 2]); E[2, :] .*= -sign(E[1, 2])
plt = grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot)
savefig(plt, "../figs/Grid7x3_MDS_TSD_T01.png")
display(plt)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1126 | cd(@__DIR__); include("setups/grid7x3.jl");
## ROT2
D = natural_eigdist(𝚽, 𝛌, Q; α = 1.0, distance = :ROT)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
plt = grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot,
annotate_ind = vcat(1:6, 8, 10, 11), plotOrder = N:-1:1)
savefig(plt, "../figs/Grid7x3_MDS_ROT2_alpha1.png")
display(plt)
## TSD (T = :Inf)
D = natural_eigdist(𝚽, 𝛌, Q; T = :Inf, distance = :TSD)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
E[1, :] .*= sign(E[1, 2]); E[2, :] .*= -sign(E[1, 2])
plt = grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot,
annotate_ind = vcat(1:8, 11), plotOrder = vcat(N:-1:9, 6:8, 5:-1:1))
savefig(plt, "../figs/Grid7x3_MDS_TSD_Tinfty.png")
display(plt)
## TSD T from 0.1 to 10
anim = @animate for t ∈ 0.1:0.1:10
D = natural_eigdist(𝚽, 𝛌, Q; T = t, distance = :TSD)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
E[1, :] .*= sign(E[1, 2])
E[2, :] .*= sign(E[2, 2]) * ((t <= 1) * 2 - 1)
grid7x3_mds_heatmaps(E, 𝚽; backend = :pyplot)
title!("T = $(t)")
end
gif(anim, "../gifs/Grid7x3_MDS_TSD_T01_inf.gif", fps = 5)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1103 | cd(@__DIR__); include("setups/simpletree.jl");
pyplot(dpi = 200)
## (a)
plot(size = (200,500))
gplot!(W, X, width = 1)
scatter_gplot!(X[ib1, :]; c = :pink, ms = 5)
scatter_gplot!(X[ib2, :]; c = :orange, ms = 5)
scatter_gplot!(X[ib3, :]; c = :green, ms = 5)
scatter_gplot!(X[ib4, :]; c = :yellow, ms = 5)
scatter_gplot!(X[ijc, :]; c = :red, ms = 5)
scatter_gplot!(X[ir, :]; c = :grey, ms = 5)
plot!(framestyle = :none)
plot!([0, 0], [0.3, 2], line = :arrow, c = :black, lw = 1)
plt = annotate!(0, 3, text("root", 9))
savefig(plt, "../figs/SimpleTree.png")
## (b)
plot(size = (200, 500))
gplot!(Ws, Xs, width = 1)
scatter_gplot!(Xs[11:11, :]; c = :pink, ms = 5)
scatter_gplot!(Xs[10:10, :]; c = :orange, ms = 5)
scatter_gplot!(Xs[13:13, :]; c = :green, ms = 5)
scatter_gplot!(Xs[12:12, :]; c = :yellow, ms = 5)
scatter_gplot!(Xs[[2,4,6,8], :]; c = :red, ms = 5)
scatter_gplot!(Xs[[1,3,5,7,9], :]; c = :grey, ms = 5)
plt = plot!(framestyle = :none, xlims = [minimum(X[:, 1]), maximum(X[:, 1])],
ylims = [minimum(X[:, 2]), maximum(X[:, 2])])
savefig(plt, "../figs/SimpleTree_simplified.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1294 | cd(@__DIR__); include("setups/simpletree.jl");
pyplot(dpi = 200)
## (a)
println("l = $(ieb1[end] - 1) and λₗ = $(𝛌[ieb1[end] - 1])")
plot(size = (200, 500), framestyle = :none)
gplot!(W, X, width = 1)
scatter_gplot!(X; marker = 𝚽[:, ieb1[end]], ms = 5)
plt = plot!(cbar = false, clims = (-0.3, 0.3))
savefig(plt, "../figs/SimpleTree_eigenvector$(ieb1[end]-1)_pink.png")
## (b)
println("l = $(ieb2[end] - 1) and λₗ = $(𝛌[ieb2[end] - 1])")
plot(size = (200, 500), framestyle = :none)
gplot!(W, X, width = 1)
scatter_gplot!(X; marker = 𝚽[:, ieb2[end]], ms = 5)
plt = plot!(cbar = false, clims = (-0.3, 0.3))
savefig(plt, "../figs/SimpleTree_eigenvector$(ieb2[end]-1)_orange.png")
## (c)
println("l = $(ieb3[end] - 1) and λₗ = $(𝛌[ieb3[end] - 1])")
plot(size = (200, 500), framestyle = :none)
gplot!(W, X, width = 1)
scatter_gplot!(X; marker = 𝚽[:, ieb3[end]], ms = 5)
plt = plot!(cbar = false, clims = (-0.3, 0.3))
savefig(plt, "../figs/SimpleTree_eigenvector$(ieb3[end]-1)_green.png")
## (d)
println("l = $(ieb4[end] - 1) and λₗ = $(𝛌[ieb4[end] - 1])")
plot(size = (200, 500), framestyle = :none)
gplot!(W, X, width = 1)
scatter_gplot!(X; marker = 𝚽[:, ieb4[end]], ms = 5)
plt = plot!(cbar = false, clims = (-0.3, 0.3))
savefig(plt, "../figs/SimpleTree_eigenvector$(ieb4[end]-1)_yellow.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1241 | cd(@__DIR__); include("setups/grid7x3.jl");
pyplot(dpi = 200)
# DAG pseudo-metric
distDAG = eigDAG_Distance(𝚽, Q, N)
# MDS embedding into R²
D = distDAG
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
# set up all heatmap plots' positions
dx = 0.01; dy = dx;
xej = zeros(Nx, N); yej=zeros(Ny, N);
a = 5.0; b = 9.0;
for k = 1:N
xej[:,k] = LinRange(E[1,k] - Ny * a * dx, E[1, k] + Ny * a * dx, Nx)
yej[:,k] = LinRange(E[2,k] - a * dy, E[2, k] + a * dy, Ny)
end
##
plot()
for k=1:N
heatmap!(xej[:, k], yej[:, k], reshape(𝚽[:, k], (Nx, Ny))', c = :viridis,
colorbar = false, ratio = 1, annotations = (xej[4, k],
yej[3, k] + b*dy, text(latexstring("\\varphi_{",
string(eig2dct[k, 1]), ",", string(eig2dct[k, 2]), "}"), 10)))
end
plt = plot!(xlim = [-1.4, 1.3], ylim = [-1.4, 1.3], grid = false, clims = (-0.4, 0.4))
# first level partition
p1x = [-0.2, 1.0, NaN]; p1y = [1.3, -1.0, NaN];
plot!(p1x, p1y, c = :red, legend = false, width = 3)
# second level partition
p2x = [-1.0, 0.2, NaN, 0.4, 1.2, NaN]; p2y = [-0.8, 0.45, NaN, 0.25, 0.2, NaN];
plot!(p2x, p2y, c=:orange, legend = false, width = 2)
plt = current()
savefig(plt, "../figs/Grid7x3_DAG_2levels_partition.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 444 | cd(@__DIR__); include("setups/path512.jl");
gr(dpi = 200)
## Build VM-NGWP
@time VM_NGWP = vm_ngwp(𝚽, GP_dual)
#################### Fig.5
j = 5
for k in [1, 2, 5]
WW = sort_wavelets(VM_NGWP[GP_dual.rs[k, j]:(GP_dual.rs[k + 1, j] - 1), j, :]')
sc = 0.75
if k == 1
sc = 0.5
end
if k == 2
WW[:, end] *= -1
end
plt = wiggle(WW; sc = sc)
savefig(plt, "../figs/Path512_VM_NGWP_j$(j-1)k$(k-1).png")
end
current()
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1961 | cd(@__DIR__); include("setups/grid7x3.jl");
pyplot(dpi = 200)
# DAG pseudo-metric
distDAG = eigDAG_Distance(𝚽, Q, N)
# MDS embedding into R²
D = distDAG
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
# set up all heatmap plots' positions
dx = 0.01; dy = dx;
xej = zeros(Nx, N); yej=zeros(Ny, N);
a = 5.0; b = 9.0;
for k = 1:N
xej[:,k] = LinRange(E[1,k] - Ny * a * dx, E[1, k] + Ny * a * dx, Nx)
yej[:,k] = LinRange(E[2,k] - a * dy, E[2, k] + a * dy, Ny)
end
## Build Dual Graph
Gstar_Sig = dualgraph(distDAG)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
VM_NGWP = vm_ngwp(𝚽, GP_dual)
## level 2 VM-NGWP vectors
j = 3; W_VM = VM_NGWP[:, j, :]'
wav_kl = [[0 0];[0 1];[0 2];[1 0];[1 1];[1 2];[1 3];[2 0];[2 1];[2 2];[3 0];
[3 1];[3 2];[3 3];[2 3];[2 4];[2 5];[2 6];[3 4];[3 5];[3 6]];
wav_kl = wav_kl[eig2grid_ind,:];
# reorder_ind = [2,3,1,5,7,4,6, 16,17,15, 9,11,8,10, 18,20,21,19, 13,14,12]
reorder_ind = [1,3,2,5,7,4,6, 8,10,9,17,15,18,16, 11,13,14,12,20,21,19]
W_VM = W_VM[:,reorder_ind[eig2grid_ind]];
sgn = ones(N); sgn[grid2eig_ind[[4,6,8,11,12,14]]] .= -1; W_VM = W_VM * Diagonal(sgn);
#################### Fig. 6
plot()
for k=1:N
heatmap!(xej[:, k], yej[:, k], reshape(W_VM[:,k], (Nx, Ny))', c = :viridis,
colorbar = false, ratio = 1, annotations = (xej[4, k], yej[3, k] + b * dy,
text(latexstring("\\psi_{", string(wav_kl[k,1]), ",", string(wav_kl[k,2]), "}"), 10)))
end
plot!(aspect_ratio = 1, xlim = [-1.4, 1.3], ylim = [-1.4, 1.3], grid = false, clims=(-0.34, 0.34))
# first level partition
p1x = [-0.2, 1.0, NaN]; p1y = [1.3, -1.0, NaN]; plot!(p1x, p1y, c = :red, legend = false, width = 3)
# second level partition
p2x = [-1.0, 0.2, NaN, 0.4, 1.2, NaN]; p2y = [-0.8, 0.45, NaN, 0.25, 0.2, NaN];
plot!(p2x, p2y, c = :orange, legend = false, width = 2)
plt = current()
savefig(plt, "../figs/Grid7x3_DAG_VM_NGWP_lvl2_wavelets.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1145 | cd(@__DIR__); include("setups/path16.jl");
gr(dpi = 250)
plot(size = (800, 250), framestyle = :none, xlim = [-10.5, N+13], ylim = [-5, 1])
path_pc_plot!(W, X; c = :yellow)
k = 1
path_pc_plot!(W, X .- [12 4]; c = :yellow,
ind = GP_primal.inds[GP_primal.rs[k, 2]:GP_primal.rs[k+1, 2] - 1, 2])
k = 2
path_pc_plot!(W, X .- [-12 4]; c = :yellow,
ind = GP_primal.inds[GP_primal.rs[k, 2]:GP_primal.rs[k+1, 2] - 1, 2])
plot!([6, -1], [-0.8, -3.3], line = :solid, c = :black, lw = 0.65)
plot!([11, 18], [-0.8, -3.3], line = :solid, c = :black, lw = 0.65)
annotate!(mean(X[:, 1]), 0.5,
text(latexstring("V= \\{ \\delta_{1}, ..., \\delta_{16} \\}"), :bottom, 11))
annotate!(mean(X[:, 1]) - 12, -4 - 0.7,
text(latexstring("V_{0}= \\{ \\delta_{1}, \\delta_{3}, \\delta_{5}, \\delta_{7}, \\delta_{10}, \\delta_{12}, \\delta_{14}, \\delta_{16} \\}"), :top, 11))
annotate!(mean(X[:, 1]) + 12, -4 - 0.7,
text(latexstring("V_{1}= \\{ \\delta_{2}, \\delta_{4}, \\delta_{6}, \\delta_{8}, \\delta_{9}, \\delta_{11}, \\delta_{13}, \\delta_{15} \\}"), :top, 11))
plt = current()
savefig(plt, "../figs/Path16_1lev_PC.png")
display(plt)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 975 | cd(@__DIR__); include("setups/path512.jl")
pyplot(dpi = 200)
## construct full HGLET and Lapped-HGLET dictionaries
@time HGLET_dic = HGLET_dictionary(GP, G_Sig; gltype = :L)
@time LPHGLET_dic = LPHGLET_dictionary(GP, G_Sig; gltype = :L, ϵ = 0.3)
j = 3; k = 2; l = 6;
WH = HGLET_dic[GP.rs[k, j]:(GP.rs[k + 1, j] - 1), j, :]'
WlH = LPHGLET_dic[GP.rs[k, j]:(GP.rs[k + 1, j] - 1), j, :]'
plt = plot(WH[:, l], c = :black, grid = false, frame = :box, lw = 0.8,
legendfontsize = 11, legend = false, size = (500, 400), ylim = [-0.15, 0.15])
xticks!([1; 64:64:N], vcat(string(1), [string(k) for k in 64:64:N]))
savefig(plt, "../figs/Path512_HGLET_j$(j-1)k$(k-1)l$(l-1).png")
plt = plot(WlH[:, l], c = :black, grid = false, frame = :box, lw = 0.8,
legendfontsize = 11, legend = false, size = (500, 400), ylim = [-0.15, 0.15])
xticks!([1; 64:64:N], vcat(string(1), [string(k) for k in 64:64:N]))
savefig(plt, "../figs/Path512_LPHGLET_j$(j-1)k$(k-1)l$(l-1).png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1932 | cd(@__DIR__); include("setups/path512.jl")
pyplot(dpi = 200)
##
@time VM_NGWP = vm_ngwp(𝚽, GP_dual)
@time LP_NGWP = lp_ngwp(𝚽, Gstar_Sig.W, GP_dual; ϵ = 0.3)
dict_VM = Dict()
dict_LP = Dict()
for j in [3, 4, 5]
for k in [1, 2, 3]
if GP_dual.rs[k + 1, j] - GP_dual.rs[k, j] < 1
continue
end
WW_VM = sort_wavelets(VM_NGWP[GP_dual.rs[k, j]:(GP_dual.rs[k + 1, j] - 1), j, :]')
WW_LP = sort_wavelets(LP_NGWP[GP_dual.rs[k, j]:(GP_dual.rs[k + 1, j] - 1), j, :]')
Y = [-0.5, 0.6]
l = Int(floor(size(WW_LP, 2) / 2))
dict_VM[(j-1, k-1, l-1)] = WW_VM[:, l]
dict_LP[(j-1, k-1, l-1)] = WW_LP[:, l]
plt = plot(size = (400, 350), layout = Plots.grid(2, 1), ylim = Y)
plot!(WW_VM[:, l], c = :black, grid = false, frame = :box, lw = 0.8, xtick = false,
lab = latexstring("\\psi^{($(j-1))}_{$(k-1), $(l-1)} (\\mathrm{VM})"), legendfontsize = 11)
plot!(WW_LP[:, l], c = :black, grid = false, frame = :box, lw = 0.8,
lab = latexstring("\\psi^{($(j-1))}_{$(k-1), $(l-1)} (\\mathrm{LP})"), legendfontsize = 11,
subplot = 2)
xticks!([1; 64:64:N], vcat(string(1), [string(k) for k in 64:64:N]),
subplot = 2)
savefig(plt, "../figs/Path512_VM_LP_j$(j-1)k$(k-1)l$(l-1).png")
end
end
## Table 8.2
using PrettyTables
header = ["basis vector" "main support width" "sidelobe attenuation"]
res = Matrix{String}(undef, 0, 3)
iter = sort(collect(keys(dict_VM)))
for γ in iter
global res
ms = find_mainsupport(dict_VM[γ]; ϵ = 0.01)
sa = sidelobe_attenuation(dict_VM[γ])
j, k, l = γ
res = vcat(res, ["ψ^{$(j)}_{$(k), $(l)} (VM)" ms[2] - ms[1] + 1 round(sa; digits = 4)])
ms = find_mainsupport(dict_LP[γ]; ϵ = 0.01)
sa = sidelobe_attenuation(dict_LP[γ])
res = vcat(res, ["ψ^{$(j)}_{$(k), $(l)} (LP)" ms[2] - ms[1] + 1 round(sa; digits = 4)])
end
pretty_table(res; header = tuple(header), alignment = :c)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1362 | cd(@__DIR__); include("setups/path128.jl");
gr(dpi = 200)
## (a)
plt = plot(size = (400, 480), layout = Plots.grid(2, 1), ylim = [-0.3, 1.3])
scatter!(χ(1:64, N), c = :black, grid = false, legend = false, frame = :box,
lw = 1.5, ms = 3)
bar!(χ(1:64, N); bar_width = 0.02, c = :black)
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
scatter!(χ(65:N, N), c = :black, grid = false, legend = false, frame = :box,
lw = 1.5, subplot = 2, ms = 3)
bar!(χ(65:N, N); bar_width = 0.02, c = :black, subplot = 2)
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]),
subplot = 2)
savefig(plt, "../figs/Path128_hard_bipart_restric_j1.png")
## (b)
plt = plot(size = (400, 480), layout = Plots.grid(2, 1), ylim = [-0.3, 1.3])
scatter!(P0 * ones(N), c = :black, grid = false, legend = false, frame = :box,
lw = 1.5, ms = 3)
bar!(P0 * ones(N); bar_width = 0.02, c = :black)
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
scatter!(P1 * ones(N), c = :black, grid = false, legend = false, frame = :box,
lw = 1.5, ms = 3, subplot = 2)
bar!(P1 * ones(N); bar_width = 0.02, c = :black, subplot = 2)
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]),
subplot = 2)
savefig(plt, "../figs/Path128_soft_bipart_PSO_j1.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1099 | cd(@__DIR__); include("setups/path128.jl");
gr(dpi = 200)
## (a)
plt = plot(size = (500, 400))
heatmap!(Uf, c = :viridis, ratio = 1, yflip = true, xlim = [1, N], clims = (-1, 1))
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
yticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
savefig(plt, "../figs/Path128_Uf_j1.png")
## (b)
plt = plot(size = (500, 560), layout = Plots.grid(2, 1))
scatter!(diag(Uf), ylim = [-1, 1], c = :black, grid = false, legend = false,
frame = :box, lw = 1.5, ms = 3)
bar!(diag(Uf); bar_width = 0.02, c = :black)
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
title!("Diagonal entries")
scatter!(anti_diag(Uf), ylim = [-1, 1], c = :black, grid = false, legend = false,
frame = :box, lw = 1.5, ms = 3, subplot = 2)
bar!(anti_diag(Uf); bar_width = 0.02, c = :black, subplot = 2)
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
title!("Antidiagonal entries", subplot = 2)
savefig(plt, "../figs/Path128_Uf_diag_entries.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 833 | cd(@__DIR__); include("setups/path128.jl");
gr(dpi = 200)
## (a)
Uf = unitary_folding_operator(W, GP; ϵ = 0.38, J = 2)' # ϵa ≈ 0.38⋅∥𝛟₁∥_{∞}
plt = plot(size = (500, 400))
heatmap!(Uf, c = :viridis, ratio = 1, yflip = true, xlim = [1, N], clims = (-1, 1))
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
yticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
savefig(plt, "../figs/Path128_Uf_j2.png")
## (b)
Uf = unitary_folding_operator(W, GP; ϵ = 0.38, J = 3)'
plt = plot(size = (500, 400))
heatmap!(Uf, c = :viridis, ratio = 1, yflip = true, xlim = [1, N], clims = (-1, 1))
xticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
yticks!([1; 16:16:128], vcat(string(1), [string(k) for k in 16:16:128]))
savefig(plt, "../figs/Path128_Uf_j3.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 761 | cd(@__DIR__); include("setups/rgc100.jl");
##
ϵ = 0.3
pair_inds, 𝛟1 = find_pairinds(W; ϵ = ϵ)
## (a) fiedler vector on RGC100
gr(dpi = 200)
plt = gplot(W, X; width = 1)
scatter_gplot!(X; marker = 𝛟1, plotOrder = :l2s)
plot!(xlims = [-180, 220], xlabel = "x(μm)", ylabel = "y(μm)", frame = :box,
size = (520, 500), right_margin = 5mm)
savefig(plt, "../figs/RGC100_fiedler.png")
## (b) fiedler embedding
pyplot(dpi = 200)
plt = plot(size = (520, 150))
plot!(-0.055:0.11:0.055, zeros(2), c = :black, lw = 2, yticks = false,
xlab = latexstring("\\phi^{rw}_1(v)"))
scatter!(𝛟1, 0:0, ylim = [-0.2, 0.2], grid = false,
ms = 4, mswidth = 0, legend = false, frame = :box, c = :black)
savefig(plt, "../figs/RGC100_fiedler_embedding.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 4246 | cd(@__DIR__); include("setups/rgc100.jl");
pyplot(dpi = 200)
##
ϵ = 0.3
pair_inds, 𝛟1 = find_pairinds(W; ϵ = ϵ)
v_bar = (𝛟1[pair_inds[1, end-1:end]] - 𝛟1[pair_inds[2, end-1:end]]) ./ 2
band = ϵ * norm(𝛟1, Inf)
pos_ar = findall(0 .< 𝛟1 .< band)
neg_ar = findall(-band .< 𝛟1 .<= 0)
# soft partition 1D
plt = plot(layout = Plots.grid(2, 1), size = (520, 500))
plot!(-0.055:0.11:0.055, zeros(2), c = :black, lw = 2, yticks = false,
subplot = 1)
plot!(zeros(2), [-0.1, 0.1], lw = 3, c = :grey, linestyle = :solid,
xlab = latexstring("\\phi^{rw}_1(v)"), subplot = 1)
scatter!(𝛟1[𝛟1 .> 0], 0:0, ylim = [-0.2, 0.2], grid = false,
ms = 4, mswidth = 0, legend = false, frame = :box, c = :red, subplot = 1)
scatter!(𝛟1[𝛟1 .< 0], 0:0, m = (1, 4), mswidth = 0, c = :blue, subplot = 1)
plot!(ones(2) * ϵ * norm(𝛟1, Inf), [-0.08, 0.08], lw = 2, c = :grey,
linestyle = :dash, subplot = 1)
plot!(-ones(2) * ϵ * norm(𝛟1, Inf), [-0.08, 0.08], lw = 2, c = :grey,
linestyle = :dash, subplot = 1)
annotate!(0.02, -0.12,
text(latexstring("\\epsilon \\cdot \\Vert \\phi^{rw}_1 \\Vert_{\\infty}"), 11),
subplot = 1)
annotate!(-0.02, -0.12,
text(latexstring("-\\epsilon \\cdot \\Vert \\phi^{rw}_1 \\Vert_{\\infty}"), 11),
subplot = 1)
annotate!(0, 0.15, text("action region", 10), subplot = 1)
plot!(-0.016:0.032:0.016, zeros(2), c = :black, lw = 2, yticks = false,
subplot = 2)
plot!(zeros(2), [-0.1, 0.1], lw = 3, c = :grey, linestyle = :solid,
xlab = latexstring("\\phi^{rw}_1(v)"), subplot = 2)
scatter!(𝛟1[pos_ar], 0:0, ylim = [-0.2, 0.2], grid = false,
ms = 4, mswidth = 0, legend = false, frame = :box, c = :red, subplot = 2)
scatter!(𝛟1[neg_ar], 0:0, m = (1, 4), mswidth = 0, c = :blue, subplot = 2)
plot!(ones(2) * ϵ * norm(𝛟1, Inf), [-0.08, 0.08], lw = 2, c = :grey,
linestyle = :dash, subplot = 2)
plot!(-ones(2) * ϵ * norm(𝛟1, Inf), [-0.08, 0.08], lw = 2, c = :grey,
linestyle = :dash, subplot = 2)
annotate!(0.012, -0.12,
text(latexstring("\\epsilon \\cdot \\Vert \\phi^{rw}_1 \\Vert_{\\infty}"), 11),
subplot = 2)
annotate!(-0.012, -0.12,
text(latexstring("-\\epsilon \\cdot \\Vert \\phi^{rw}_1 \\Vert_{\\infty}"), 11),
subplot = 2)
annotate!(-0.0075, 0.15, text("negative action region", 10), subplot = 2)
annotate!(0.0075, 0.15, text("positive action region", 10), subplot = 2)
savefig(plt, "../figs/RGC100_fiedler_embedding_soft_clustering.png")
# zoom-in: find relection points about the nodal point
plt = plot(layout = Plots.grid(2, 1), size = (520, 500))
plot!(-0.005:0.01:0.005, zeros(2), c = :black, lw = 2, yticks = false,
subplot = 1)
scatter!(𝛟1[pair_inds[1, end-1:end]], 0:0, ylim = [-0.2, 0.2], grid = false,
ms = 6, mswidth = 0, legend = false, frame = :box, c = :red, subplot = 1)
scatter!(𝛟1[pair_inds[2, end-1:end]], 0:0, ms = 6, mswidth = 0, c = :blue,
subplot = 1)
plot!(zeros(2), [-0.1, 0.1], lw = 3, c = :grey, linestyle = :solid,
xlab = latexstring("\\phi^{rw}_1(v)"), subplot = 1)
annotate!(𝛟1[pair_inds[1, end]], 0.05, text(latexstring("v^{+}_{1}"), 11),
subplot = 1)
annotate!(𝛟1[pair_inds[1, end-1]], 0.05, text(latexstring("v^{+}_{2}"), 11),
subplot = 1)
annotate!(𝛟1[pair_inds[2, end]], 0.05, text(latexstring("v^{-}_{1}"), 11),
subplot = 1)
annotate!(𝛟1[pair_inds[2, end-1]], 0.05, text(latexstring("v^{-}_{2}"), 11),
subplot = 1)
plot!(vec(-0.005:0.01:0.005), zeros(2), c = :black, lw = 2,
yticks = false, subplot = 2)
scatter!(vcat(v_bar, -v_bar), 0:0, ylim = [-0.2, 0.2], grid = false,
ms = 6, mswidth = 0, legend = false, frame = :box, c = :purple, subplot = 2)
plot!(zeros(2), [-0.1, 0.1], lw = 3, c = :grey, linestyle = :solid,
xlab = latexstring("r"), subplot = 2)
annotate!(v_bar[end], -0.05, text(latexstring("r_{1}"), 11),
subplot = 2)
annotate!(v_bar[end-1], -0.05, text(latexstring("r_{2}"), 11),
subplot = 2)
annotate!(-v_bar[end], -0.05, text(latexstring("-r_{1}"), 11),
subplot = 2)
annotate!(-v_bar[end-1], -0.05, text(latexstring("-r_{2}"), 11),
subplot = 2)
savefig(plt, "../figs/RGC100_fiedler_embedding_find_reflection_points.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 438 | cd(@__DIR__); include("setups/rgc100.jl");
pyplot(dpi = 200)
##
ϵ = 0.3
for J = 1:2
Uf = unitary_folding_operator(W, GP; ϵ = ϵ, J = J)
gplot(W, X; width = 1)
scatter_gplot!(X; marker = diag(Uf), plotOrder = :l2s, ms = 4)
plt = plot!(xlims = [-180, 220], xlabel = "x(μm)", ylabel = "y(μm)",
clims = (0.6, 1), frame = :box, size = (520, 500))
savefig(plt, "../figs/RGC100_unitary_folding_diag_J$(J).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1934 | cd(@__DIR__); include("setups/rgc100.jl")
gr(dpi = 200)
## construct full HGLET and Lapped-HGLET dictionaries
@time HGLET_dic = HGLET_dictionary(GP, G_Sig; gltype = :L)
@time LPHGLET_dic = LPHGLET_dictionary(GP, G_Sig; gltype = :L, ϵ = 0.3)
## generate figures
# pre-selected (j, k, l)s
T = [(2, 1, 1), (2, 1, 12), (3, 1, 3), (3, 1, 5),
(4, 5, 6), (6, 23, 3), (7, 5, 2), (8, 15, 1)]
XLs = [
[-50, 50], [-50, 50], [-110, 40], [-110, 40],
[-20, 50], [50, 120], [-80, -20], [-40, -10]
]
YLs = [
[-50, 50], [-50, 50], [-50, 100], [-50, 100],
[-50, 20], [-70, 0], [-90, -30], [-160, -130]
]
for i in 1:length(T)
(j, k, l) = T[i]
𝚽H = HGLET_dic[GP.rs[k, j]:(GP.rs[k + 1, j] - 1), j, :]'
𝚽lH = LPHGLET_dic[GP.rs[k, j]:(GP.rs[k + 1, j] - 1), j, :]'
p1 = gplot(W, X; width = 1)
scatter_gplot!(X; marker = 𝚽H[:, l], plotOrder = :s2l, ms = 5)
plot!(xlims = [-180, 220], xlabel = "x(μm)", ylabel = "y(μm)", frame = :box, cbar = false)
plot!(left_margin = 3mm, bottom_margin = 3mm, clims = (-0.05, 0.05))
p2 = gplot(W, X; width = 1)
scatter_gplot!(X; marker = 𝚽lH[:, l], plotOrder = :s2l, ms = 5)
plot!(xlims = [-180, 220], xlabel = "x(μm)", ylabel = "y(μm)", frame = :box, cbar = false)
plot!(left_margin = 3mm, bottom_margin = 3mm, clims = (-0.05, 0.05))
plt = plot(p1, p2, size = (640, 300), layout = Plots.grid(1, 2),
xlims = XLs[i], ylims = YLs[i])
# xlims = [-120, 120], ylims = [-150, 150])
# gplot(W, X; width = 1)
# ord = :s2l
# if i == 8
# ord = :l2s
# end
# scatter_gplot!(X; marker = 𝚽lH[:, l] - 𝚽H[:, l], plotOrder = ord, ms = 4)
# plot!(xlabel = "x(μm)", ylabel = "y(μm)", frame = :box, cbar = true)
# plot!(left_margin = 3mm, bottom_margin = 3mm, right_margin = 3mm)
# plt = plot!(size = (500, 500))
savefig(plt, "../figs/RGC100_HGLET_LPHGLET_j$(j-1)k$(k-1)l$(l-1).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 542 | cd(@__DIR__); runapprox = false; include("setups/sunflower.jl")
gr(dpi = 200)
## (a) sunflower graph
gplot(W, X; width = 1)
scatter_gplot!(X; c = :red, ms = LinRange(1, 9, N))
plt = plot!(frame = :none)
savefig(plt, "../figs/SunFlower.png")
## (b) voronoi tessellation
xx, yy = getplotxy(voronoiedges(tess))
plt = plot(xx, yy, xlim = [1, 2], ylim = [1, 2], linestyle = :auto, linewidth = 1,
linecolor = :blue, grid = false, label = "", ratio = 1, frame = :box, ticks = false)
savefig(plt, "../figs/Sunflower_Barbara_Voronoi_cells.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1039 | cd(@__DIR__); allNGWPs = false; include("setups/toronto.jl")
gr(dpi = 200)
## pedestrian signal 16 most important PC-NGWP vectors
PC_NGWP = pc_ngwp(𝚽, GP_dual, GP_primal)
fp = load("../datasets/new_toronto.jld", "fp")
G_Sig.f = reshape(fp, (N, 1))
dmatrix_PC = ngwp_analysis(G_Sig, PC_NGWP)
dvec_pc_ngwp, BS_pc_ngwp = ngwp_bestbasis(dmatrix_PC, GP_dual)
important_idx = sortperm(dvec_pc_ngwp[:].^2; rev = true)
println("================fp-PC-NGWP-top-basis-vectors=================")
for i in 1:16
dr, dc = BS_pc_ngwp.levlist[important_idx[i]]
w = PC_NGWP[dr, dc, :]
j, k, l = NGWP_jkl(GP_dual, dr, dc)
print("(j, k, l) = ($(j), $(k), $(l)) ")
if j == jmax
print("φ_{$(GP_dual.ind[dr]-1)}")
end
println()
sgn = (maximum(w) > -minimum(w)) * 2 - 1
gplot(A, X; width=1)
scatter_gplot!(X; marker = sgn .* w, plotOrder = :s2l, ms = 3)
plt = plot!(cbar = false, clims = (-0.075,0.075))
savefig(plt,
"../figs/Toronto_fp_DAG_PC_NGWP_ibv$(lpad(i,2,"0"))_j$(j)_k$(k)_l$(l).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 969 | cd(@__DIR__); allNGWPs = false; include("setups/toronto.jl")
gr(dpi = 200)
## pedestrian signal 16 most important LP-NGWP vectors
LP_NGWP = lp_ngwp(𝚽, Gstar_Sig.W, GP_dual; ϵ = 0.3)
fp = load("../datasets/new_toronto.jld", "fp")
G_Sig.f = reshape(fp, (N, 1))
dmatrix_LP = ngwp_analysis(G_Sig, LP_NGWP)
dvec_lp_ngwp, BS_lp_ngwp = ngwp_bestbasis(dmatrix_LP, GP_dual)
important_idx = sortperm(dvec_lp_ngwp[:].^2; rev = true)
println("================fp-LP-NGWP-top-basis-vectors=================")
for i in 1:16
dr, dc = BS_lp_ngwp.levlist[important_idx[i]]
w = LP_NGWP[dr, dc, :]
j, k, l = NGWP_jkl(GP_dual, dr, dc)
println("(j, k, l) = ($(j), $(k), $(l))")
sgn = (maximum(w) > -minimum(w)) * 2 - 1
gplot(A, X; width=1)
scatter_gplot!(X; marker = sgn .* w, plotOrder = :s2l, ms = 3)
plt = plot!(cbar = false, clims = (-0.075,0.075))
savefig(plt,
"../figs/Toronto_fp_DAG_LP_NGWP_ibv$(lpad(i,2,"0"))_j$(j)_k$(k)_l$(l).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1117 | cd(@__DIR__); runapprox = true; allNGWPs = true; include("setups/sunflower.jl")
gr(dpi = 200)
## (a) barbara sunflower eye
heatmap(barbara, yflip = true, ratio = 1, c = :greys)
scatter_gplot!(transform2D(X; s = 20, t = [395, 100]); ms = 2, c = :red)
sample_location_plt = plot!(cbar = false, frame = :none)
savefig(sample_location_plt, "../figs/barb_sunflower_eye.png")
## (b) barbara eye graph signal
f = matread("../datasets/sunflower_barbara_voronoi.mat")["f_eye_voronoi"]
G_Sig.f = reshape(f, (N, 1))
scatter_gplot(X; marker = f, ms = LinRange(4.0, 14.0, N), c = :greys);
plt = plot!(xlim = [-1.2,1.2], ylim = [-1.2,1.2], frame = :none)
savefig(plt, "../figs/SunFlower_barbara_feye.png")
## (c) barbara eye relative l2 approximation error by various methods
DVEC = getall_expansioncoeffs2(G_Sig, GP_dual, GP_dual_Lsym, VM_NGWP, PC_NGWP, LP_NGWP,
VM_NGWP_Lsym, PC_NGWP_Lsym, LP_NGWP_Lsym, 𝚽, 𝚽sym)
approx_error_plot2(DVEC);
plt = plot!(xguidefontsize = 14, yguidefontsize = 14, legendfontsize = 11, size = (600, 600))
savefig(plt, "../figs/SunFlower_barbara_feye_DAG_approx.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1118 | cd(@__DIR__); runapprox = true; allNGWPs = false; include("setups/sunflower.jl")
gr(dpi = 200)
##
VM_NGWP_Lsym = vm_ngwp(𝚽sym, GP_dual_Lsym)
f = matread("../datasets/sunflower_barbara_voronoi.mat")["f_eye_voronoi"]
G_Sig.f = reshape(f, (N, 1))
dmatrix_VM_Lsym = ngwp_analysis(G_Sig, VM_NGWP_Lsym)
dvec_vm_ngwp_Lsym, BS_vm_ngwp_Lsym = ngwp_bestbasis(dmatrix_VM_Lsym, GP_dual_Lsym)
important_idx = sortperm(dvec_vm_ngwp_Lsym[:].^2; rev = true)
println("================feye-VM-NGWP-Lsym-top-basis-vectors=================")
for i in 2:17
dr, dc = BS_vm_ngwp_Lsym.levlist[important_idx[i]]
w = VM_NGWP_Lsym[dr, dc, :]
j, k, l = NGWP_jkl(GP_dual_Lsym, dr, dc)
print("(j, k, l) = ($(j), $(k), $(l)) ")
if j == jmax_Lsym
print("φ_{$(GP_dual_Lsym.ind[dr]-1)}")
end
println()
scatter_gplot(X; marker = w, ms = LinRange(4.0, 14.0, N), c = :greys)
plt = plot!(xlim = [-1.2, 1.2], ylim = [-1.2, 1.2], frame = :none,
cbar = false, clims = (-0.15, 0.15))
savefig(plt,
"../figs/SunFlower_feye_DAG_VM_NGWP_Lsym_ibv$(lpad(i,2,"0"))_j$(j)_k$(k)_l$(l).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1127 | cd(@__DIR__); runapprox = true; allNGWPs = true; include("setups/sunflower.jl")
gr(dpi = 200)
## (a) barbara sunflower pants
heatmap(barbara, yflip=true, ratio=1, c=:greys)
scatter_gplot!(transform2D(X; s = 20, t = [280, 320]); ms = 2, c = :red)
sample_location_plt = plot!(cbar = false, frame = :none)
savefig(sample_location_plt, "../figs/barb_sunflower_pants.png")
## (b) barbara eye graph signal
f = matread("../datasets/sunflower_barbara_voronoi.mat")["f_trouser_voronoi"]
G_Sig.f = reshape(f, (N, 1))
scatter_gplot(X; marker = f, ms = LinRange(4.0, 14.0, N), c = :greys);
plt = plot!(xlim = [-1.2,1.2], ylim = [-1.2,1.2], frame = :none)
savefig(plt, "../figs/SunFlower_barbara_ftrouser.png")
## (c) barbara eye relative l2 approximation error by various methods
DVEC = getall_expansioncoeffs2(G_Sig, GP_dual, GP_dual_Lsym, VM_NGWP, PC_NGWP, LP_NGWP,
VM_NGWP_Lsym, PC_NGWP_Lsym, LP_NGWP_Lsym, 𝚽, 𝚽sym)
approx_error_plot2(DVEC);
plt = plot!(xguidefontsize = 14, yguidefontsize = 14, legendfontsize = 11, size = (600, 600))
savefig(plt, "../figs/SunFlower_barbara_ftrouser_DAG_approx.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1047 | cd(@__DIR__); runapprox = true; allNGWPs = false; include("setups/sunflower.jl")
gr(dpi = 200)
##
VM_NGWP = vm_ngwp(𝚽, GP_dual)
f = matread("../datasets/sunflower_barbara_voronoi.mat")["f_trouser_voronoi"]
G_Sig.f = reshape(f, (N, 1))
dmatrix_VM = ngwp_analysis(G_Sig, VM_NGWP)
dvec_vm_ngwp, BS_vm_ngwp = ngwp_bestbasis(dmatrix_VM, GP_dual)
important_idx = sortperm(dvec_vm_ngwp[:].^2; rev = true)
println("================ftrouser-VM-NGWP-top-basis-vectors=================")
for i in 2:17
dr, dc = BS_vm_ngwp.levlist[important_idx[i]]
w = VM_NGWP[dr, dc, :]
j, k, l = NGWP_jkl(GP_dual, dr, dc)
print("(j, k, l) = ($(j), $(k), $(l)) ")
if j == jmax
print("φ_{$(GP_dual.ind[dr]-1)}")
end
println()
scatter_gplot(X; marker = w, ms = LinRange(4.0, 14.0, N), c = :greys)
plt = plot!(xlim = [-1.2, 1.2], ylim = [-1.2, 1.2], frame = :none,
cbar = false, clims = (-0.15, 0.15))
savefig(plt,
"../figs/SunFlower_ftrouser_DAG_VM_NGWP_ibv$(lpad(i,2,"0"))_j$(j)_k$(k)_l$(l).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1017 | cd(@__DIR__); allNGWPs = false; include("setups/toronto.jl")
gr(dpi = 200)
## (a) a smooth spatial distribution of the street intersections graph signal
f = zeros(N); for i in 1:N; f[i] = length(findall(dist_X[:,i] .< 1/minimum(edge_weight))); end
G_Sig.f = reshape(f, (N, 1))
gplot(A, X; width=1); plot!(size = (600, 600))
signal_plt = scatter_gplot!(X; marker = f, plotOrder = :s2l, ms = 3)
savefig(signal_plt, "../figs/Toronto_fdensity.png")
## (b) spatial distribution signal relative l2 approximation error by various methods
# uncomment the following if `allNGWPs` = true
# DVEC = getall_expansioncoeffs2(G_Sig, GP_dual, GP_dual_Lsym, VM_NGWP, PC_NGWP, LP_NGWP,
# VM_NGWP_Lsym, PC_NGWP_Lsym, LP_NGWP_Lsym, 𝚽, 𝚽sym)
# use precomputed results
DVEC = load("../datasets/Toronto_fdensity_DVEC.jld", "DVEC")
approx_error_plot2(DVEC);
plt = plot!(xguidefontsize = 14, yguidefontsize = 14, legendfontsize = 11, size = (600, 600))
savefig(plt, "../figs/Toronto_fdensity_DAG_approx.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1049 | cd(@__DIR__); allNGWPs = false; include("setups/toronto.jl")
gr(dpi = 200)
## fdensity 16 most important VM-NGWP vectors (ignore the DC vector)
VM_NGWP = vm_ngwp(𝚽, GP_dual)
f = zeros(N); for i in 1:N; f[i] = length(findall(dist_X[:,i] .< 1/minimum(edge_weight))); end
G_Sig.f = reshape(f, (N, 1))
dmatrix_VM = ngwp_analysis(G_Sig, VM_NGWP)
dvec_vm_ngwp, BS_vm_ngwp = ngwp_bestbasis(dmatrix_VM, GP_dual)
important_idx = sortperm(dvec_vm_ngwp[:].^2; rev = true)
println("================fdensity-VM-NGWP-top-basis-vectors=================")
for i in 2:17
dr, dc = BS_vm_ngwp.levlist[important_idx[i]]
w = VM_NGWP[dr, dc, :]
j, k, l = NGWP_jkl(GP_dual, dr, dc)
print("(j, k, l) = ($(j), $(k), $(l)) ")
if j == jmax
print("φ_{$(GP_dual.ind[dr]-1)}")
end
println()
gplot(A, X; width=1)
scatter_gplot!(X; marker = w, plotOrder = :s2l, ms = 3)
plt = plot!(cbar = false, clims = (-0.075,0.075))
savefig(plt,
"../figs/Toronto_fdensity_DAG_VM_NGWP_ibv$(lpad(i,2,"0"))_j$(j)_k$(k)_l$(l).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 948 | cd(@__DIR__); allNGWPs = false; include("setups/toronto.jl")
using Plots.PlotMeasures
gr(dpi = 200)
## (a) pedestrian volume graph signal
fp = load("../datasets/new_toronto.jld", "fp")
G_Sig.f = reshape(fp, (N, 1))
gplot(A, X; width=1); plot!(size = (600, 600), right_margin = 5mm)
signal_plt = scatter_gplot!(X; marker = fp, plotOrder = :s2l, ms = 3)
savefig(signal_plt, "../figs/Toronto_fp.png")
## (b) pedestrian signal relative l2 approximation error by various methods
# uncomment the following if `allNGWPs` = true
# DVEC = getall_expansioncoeffs2(G_Sig, GP_dual, GP_dual_Lsym, VM_NGWP, PC_NGWP, LP_NGWP,
# VM_NGWP_Lsym, PC_NGWP_Lsym, LP_NGWP_Lsym, 𝚽, 𝚽sym)
# use precomputed results
DVEC = load("../datasets/Toronto_fp_DVEC.jld", "DVEC")
approx_error_plot2(DVEC);
plt = plot!(xguidefontsize = 14, yguidefontsize = 14, legendfontsize = 11, size = (600, 600))
savefig(plt, "../figs/Toronto_fp_DAG_approx.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 978 | cd(@__DIR__); allNGWPs = false; include("setups/toronto.jl")
gr(dpi = 200)
## pedestrian signal 16 most important VM-NGWP vectors
VM_NGWP = vm_ngwp(𝚽, GP_dual)
fp = load("../datasets/new_toronto.jld", "fp")
G_Sig.f = reshape(fp, (N, 1))
dmatrix_VM = ngwp_analysis(G_Sig, VM_NGWP)
dvec_vm_ngwp, BS_vm_ngwp = ngwp_bestbasis(dmatrix_VM, GP_dual)
important_idx = sortperm(dvec_vm_ngwp[:].^2; rev = true)
println("================fp-VM-NGWP-top-basis-vectors=================")
for i in 1:16
dr, dc = BS_vm_ngwp.levlist[important_idx[i]]
w = VM_NGWP[dr, dc, :]
j, k, l = NGWP_jkl(GP_dual, dr, dc)
print("(j, k, l) = ($(j), $(k), $(l)) ")
if j == jmax
print("φ_{$(GP_dual.ind[dr]-1)}")
end
println()
gplot(A, X; width = 1)
scatter_gplot!(X; marker = w, plotOrder = :s2l, ms = 3)
plt = plot!(cbar = false, clims = (-0.075,0.075))
savefig(plt,
"../figs/Toronto_fp_DAG_VM_NGWP_ibv$(lpad(i,2,"0"))_j$(j)_k$(k)_l$(l).png")
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1055 | using MultiscaleGraphSignalTransforms, Plots, Graphs, Random
using PrettyTables, StatsPlots
nsim = 500
function generate_ROT_TSD_ratio(nsim, 𝚽, ∇𝚽, 𝛌, Q; edge_length = 1)
Random.seed!(1234)
ρ = zeros(nsim)
for i = 1:nsim
p = rand(N); p ./= norm(p, 1)
q = rand(N); q ./= norm(q, 1)
W1 = ROT_Distance(p, q, Q; edge_length = edge_length)
K = K_functional(p, q, 𝚽, ∇𝚽, 𝛌; length = edge_length)[1]
ρ[i] = K / W1
end
return ρ
end
function display_basic_stats(ρs)
header = ["min" "max" "mean" "std"]
basic_stats = zeros(0, 4)
for ρ in ρs
basic_stats = vcat(
basic_stats,
round.([minimum(ρ) maximum(ρ) mean(ρ) std(ρ)]; digits = 4)
)
end
pretty_table(basic_stats; header = tuple([header[i] for i = 1:length(header)]))
end
function ROT_TSD_ratio_histogram(ρ)
plt = histogram(ρ, grid = false, legend = false, c = :teal,
xlims = [minimum(ρ) - std(ρ), maximum(ρ) + std(ρ)],
xlab = "ρ")
return plt
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 246 | Random.seed!(1234)
N, M = 50, 200
G = erdos_renyi(N, M)
# println("Is the ER graph connected: ", is_connected(G))
L = Matrix(laplacian_matrix(G))
𝛌, 𝚽 = eigen(L); standardize_eigenvectors!(𝚽)
Q = incidence_matrix(G; oriented = true)
∇𝚽 = Q' * 𝚽
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1917 | using MLDatasets, Graphs, Plots, LaTeXStrings, MultiscaleGraphSignalTransforms
# Load local module
push!(LOAD_PATH, @__DIR__)
using pSGWT
example, label = MNIST.traindata(Float64, 28)
digit_img = example[4:26, 26:-1:5]
# heatmap(digit_img', ratio = 1, c=:viridis, frame = :none, xlim = [1, 22])
Nx, Ny = size(digit_img)
G = Graphs.grid([Nx, Ny]); N = nv(G);
W = Matrix(adjacency_matrix(G))
L = Matrix(laplacian_matrix(G))
Q = incidence_matrix(G; oriented = true)
𝛌, 𝚽 = eigen(L); 𝚽 = 𝚽 .* sign.(𝚽[1, :])';
D = natural_eigdist(𝚽, 𝛌, Q; distance = :DAG)
function grid_eigenvector_plot(l)
heatmap(reshape(𝚽[:, l], (Nx, Ny))', c = :viridis, ratio = 1, frame = :none,
xlim = [1, Nx], size = (500, 400), cbar = true)
end
function grid_NGWFvector_plot(l, x, D, 𝚽; σ = 0.2 * maximum(D))
heatmap(reshape(ngwf_vector(D, l, x, 𝚽; σ = σ)', (Nx, Ny))',
c = :viridis, ratio = 1, frame = :none, xlim = [1, Nx], size = (500, 400))
end
function plot_edge!(A, B; style = :solid, subplot = 1, c = :red)
plot!([A[1], B[1], NaN], [A[2], B[2], NaN], c = c, legend = false,
width = 10, style = style, subplot = subplot)
end
function plot_square!(Nx, Ny; subplot = 1, c = :red)
plot_edge!([-0.33, 0], [Nx + 1.24, 0]; subplot = subplot, c = c)
plot_edge!([0, 0], [0, Ny + 1]; subplot = subplot, c = c)
plot_edge!([-0.33, Ny + 1], [Nx + 1.24, Ny + 1]; subplot = subplot, c = c)
plot_edge!([Nx + 0.92, 0], [Nx + 0.92, Ny + 1]; subplot = subplot, c = c)
end
function grid_vector_plot!(l, i, VECs)
v = deepcopy(VECs[:, l])
v ./= norm(v, 1)
heatmap!(reshape(v, (Nx, Ny))', c = :viridis, ratio = 1, frame = :none,
xlim = [-0.5, Nx+1.5], cbar = false, subplot = i)
end
function grid_vec_heatmap(VEC, Nx, Ny; l = 1)
v = VEC[:, l]
heatmap(reshape(v, (Nx, Ny))', c = :viridis, ratio = 1, frame = :none,
xlim = [1, Nx], size = (500, 400), cbar = true)
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 2358 | using MultiscaleGraphSignalTransforms, Plots, Graphs, MultivariateStats
using LaTeXStrings
Nx, Ny = 7, 3
G = Graphs.grid([Nx, Ny]); N = nv(G);
L = Matrix(laplacian_matrix(G))
Q = incidence_matrix(G; oriented = true)
𝛌, 𝚽 = eigen(L); 𝚽 = 𝚽.*sign.(𝚽[1,:])'; # sign of DCT
∇𝚽 = Q' * 𝚽
W = 1.0 * adjacency_matrix(G)
grid2eig_ind = [1,2,3,6,8,12,15,4,5,7,9,13,16,18,10,11,14,17,19,20,21];
eig2grid_ind = sortperm(grid2eig_ind);
eig2dct = Array{Int64,3}(undef, Nx, Ny, 2);
for i = 1:Nx; for j = 1:Ny; eig2dct[i,j,1] = i-1; eig2dct[i,j,2] = j-1; end; end
eig2dct = reshape(eig2dct, (N, 2)); eig2dct = eig2dct[eig2grid_ind, :];
function grid7x3_mds_heatmaps(E, 𝚽; Nx = 7, Ny = 3, backend = :pyplot,
annotate_ind = 1:N, plotOrder = 1:N)
# set up all heatmap plots' positions
max_x = maximum(E[1, :]); min_x = minimum(E[1, :])
width_x = max_x - min_x
max_y = maximum(E[2, :]); min_y = minimum(E[2, :])
width_y = max_y - min_y
dx = 0.005 * width_x; dy = dx;
xej = zeros(Nx, N); yej=zeros(Ny, N);
a = 5.0; b = 7.0;
for k = 1:N
xej[:,k] = LinRange(E[1,k] - Ny * a * dx, E[1, k] + Ny * a * dx, Nx)
yej[:,k] = LinRange(E[2,k] - a * dy, E[2, k] + a * dy, Ny)
end
# generate Grid7x3 2D MDS heatmaps plot
if backend == :gr
gr(dpi = 200)
elseif backend == :pyplot
pyplot(dpi = 200)
elseif backend == :plotlyjs
plotlyjs(dpi = 200)
else
@error("backend does not support $(backend)!")
end
plot()
for k in plotOrder
if k in annotate_ind
heatmap!(xej[:, k], yej[:, k], reshape(𝚽[:, k], (Nx, Ny))', c = :viridis,
colorbar = false, ratio = 1, annotations = (xej[4, k],
yej[3, k] + b*dy, text(latexstring("\\varphi_{",
string(eig2dct[k, 1]), ",", string(eig2dct[k, 2]), "}"), 10)))
else
heatmap!(xej[:, k], yej[:, k], reshape(𝚽[:, k], (Nx, Ny))', c = :viridis,
colorbar = false, ratio = 1)
end
end
plt = plot!(xlim = [min_x - 0.12 * width_x, max_x + 0.12 * width_x],
ylim = [min_y - 0.16 * width_y, max_y + 0.16 * width_y],
grid = false, clims = (-0.4, 0.4),
xlab = "X₁", ylab = "X₂")
return plt
end
# display(vcat((1:N)', eig2dct'))
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1192 | module pSGWT
using PyCall
export sgwt_frame, sgwt_filter_banks
const pygsp = PyNULL()
function __init__()
copy!(pygsp, pyimport_conda("pygsp", "pygsp", "conda-forge"))
end
function init_Graph(W)
G = pygsp.graphs.Graph(PyReverseDims(W))
return G
end
"""
sgwt_transform(loc, nf, W)
SGWT\\_TRANSFORM perform the SGWT transform with MexicanHat filter as a python wrapper.
See https://pygsp.readthedocs.io/en/stable/tutorials/wavelet.html
# Input Arguments
- `loc::Int64`: the vertex index that the output wavelet centered at.
- `W::Matrix{Float64}`: weighted adjacency matrix.
- `nf::Int64`: default is 6. Number of filters.
# Output Argument
- `frame::Array{Float64, 3}`: a N x N x nf matrix.
"""
function sgwt_frame(W; nf = 6)
G = init_Graph(W)
G.estimate_lmax()
g = pygsp.filters.MexicanHat(G, Nf = nf)
# np = pyimport("numpy")
# s = np.zeros(G.N); s[loc] = 1
# s = g.filter(s, method="chebyshev")
return g.compute_frame()
end
function sgwt_filter_banks(W, 𝛌; nf = 6)
G = init_Graph(W)
G.estimate_lmax()
g = pygsp.filters.MexicanHat(G, Nf = nf)
np = pyimport("numpy")
e = np.array(𝛌)
return g.evaluate(e)
end
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1660 | using MultiscaleGraphSignalTransforms, Graphs, Plots, LaTeXStrings
## Build Graph
N = 128; G = path_graph(N)
X = zeros(N,2); X[:, 1] = 1:N
L = Matrix(laplacian_matrix(G))
𝛌, 𝚽 = eigen(L); standardize_eigenvectors!(𝚽)
W = 1.0 * adjacency_matrix(G)
G_Sig = GraphSig(W, xy = X)
GP = partition_tree_fiedler(G_Sig; swapRegion = false)
function anti_diag(A)
N = size(A, 1)
return [A[i, N+1-i] for i = 1:N]
end
## construct 1D smooth orthogonal projector
ϵa = 16
pair_inds = vcat(vec((64 + ϵa):-1:65)', vec((64 - ϵa + 1):64)')
Uf = Matrix{Float64}(I, N, N)
β = 64.5
for i in 1:size(pair_inds, 2)
pv, nv = pair_inds[:, i]
t = abs(pv - β) / ϵa
Uf[pv, pv] = rising_cutoff(t)
Uf[pv, nv] = rising_cutoff(-t)
Uf[nv, pv] = -rising_cutoff(-t)
Uf[nv, nv] = rising_cutoff(t)
end
P0 = Uf' * diagm(χ(1:64, N)) * Uf
P1 = Uf' * diagm(χ(65:N, N)) * Uf
##
distDCT = zeros(N,N)
for i in 1:N-1, j = i+1:N
distDCT[i,j] = abs(i-j)
end
distDCT = distDCT + distDCT'
function path_spectrogram(f, D, 𝚽; c = 0.01)
N = length(f)
dmatrix = zeros(N, N)
for l = 1:N
P = 𝚽 * diagm(nat_spec_filter(l, D; σ = c * maximum(D))) * 𝚽'
for x = 1:N
ψ = P * spike(x, N)
ψ ./= norm(ψ, 2)
dmatrix[l, x] = ψ' * f
end
end
heatmap(abs.(dmatrix), c = :thermal, ratio = 1, xlim = [0.5, N+1],
ylim = [0.5, N], xlab = latexstring("x"), ylab = latexstring("l"),
guidefontsize = 18)
xticks!([16:16:128;], [string(k) for k in 16:16:128])
yticks!([1;16:16:128], vcat("DC", [string(k) for k in 15:16:127]))
plt = plot!(size = (500, 400))
return plt
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 859 | using MultiscaleGraphSignalTransforms, Graphs, Plots, LaTeXStrings
## Build Graph
N = 16; G = path_graph(N)
X = zeros(N,2); X[:, 1] = 1:N
L = Matrix(laplacian_matrix(G))
𝛌, 𝚽 = eigen(L); 𝚽 = 𝚽 .* sign.(𝚽[1,:])'
W = 1.0 * adjacency_matrix(G)
## preliminaries for PC-NGWP
Gstar_Sig = GraphSig(W)
G_Sig = GraphSig(W, xy = X)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
## Plots
function path_pc_plot!(W, X; ind = 1:size(X, 1), c = :teal)
# plot(size = (500, 50), framestyle = :none, xlim = [1, N+1.5], ylim = [-0.2, 0.3])
gplot!(W, X, width = 1, color = :blue, style = :solid)
scatter_gplot!(X; ms = 6, c = :teal)
annotate!(X[:, 1], X[:, 2] .- 0.2, [text(string(n), :top, 7) for n = 1:N])
scatter_gplot!(X[ind, :]; ms = 6, c = c)
plt = plot!(ratio = :auto)
return plt
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1333 | using MultiscaleGraphSignalTransforms, Graphs, Plots, LaTeXStrings
import WaveletsExt: wiggle
## Build Graph
N = 512; G = path_graph(N)
X = zeros(N,2); X[:, 1] = 1:N
L = Matrix(laplacian_matrix(G))
𝛌, 𝚽 = eigen(L); 𝚽 = 𝚽 .* sign.(𝚽[1,:])'
W = 1.0 * adjacency_matrix(G)
Gstar_Sig = GraphSig(W)
G_Sig = GraphSig(W, xy = X)
GP = partition_tree_fiedler(G_Sig; swapRegion = false)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
## utility functions
function find_mainsupport(w; ϵ = 0.01)
N = length(w)
l, r = 1, N
for i in 1:N
if abs(w[i]) >= ϵ
l = i
break
end
end
for i in N:-1:l
if abs(w[i]) >= ϵ
r = i
break
end
end
return [l, r]
end
function findlocalmaxima(signal::Vector)
inds = Int[]
if length(signal)>1
if signal[1]>signal[2]
push!(inds,1)
end
for i=2:length(signal)-1
if signal[i-1]<signal[i]>signal[i+1]
push!(inds,i)
end
end
if signal[end]>signal[end-1]
push!(inds,length(signal))
end
end
inds
end
function sidelobe_attenuation(w)
locmax_ind = findlocalmaxima(w)
locmax_val = sort(w[locmax_ind]; rev = true)
return locmax_val[2] / locmax_val[1]
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 152 | N = 64; G = path_graph(N)
L = Matrix(laplacian_matrix(G))
𝛌, 𝚽 = eigen(L); 𝚽 = 𝚽 .* sign.(𝚽[1,:])'
Q = incidence_matrix(G; oriented = true)
∇𝚽 = Q' * 𝚽
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 663 | using Plots, Graphs, JLD, LaTeXStrings, MultiscaleGraphSignalTransforms, Distances
using Plots.PlotMeasures
G = loadgraph("../datasets/RGC100.lgz"); N = nv(G)
X = load("../datasets/RGC100_xyz.jld", "xyz")[:, 1:2]
X3 = load("../datasets/RGC100_xyz.jld", "xyz")
L = Matrix(laplacian_matrix(G))
𝛌, 𝚽 = eigen(L)
standardize_eigenvectors!(𝚽)
dist_X = pairwise(Euclidean(1e-12), X3; dims = 1)
A = 1.0 .* adjacency_matrix(G)
W = zeros(N, N); W[A .> 0] = 1 ./ dist_X[A .> 0]; W = A .* W
Q = incidence_matrix(G; oriented = true)
∇𝚽 = Q' * 𝚽
edge_length = sqrt.(sum((Q' * X3).^2, dims = 2)[:])
G_Sig = GraphSig(W)
GP = partition_tree_fiedler(G_Sig; swapRegion = false)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1996 | using MultiscaleGraphSignalTransforms, JLD, Plots, Graphs, MultivariateStats
using LaTeXStrings
push!(LOAD_PATH, @__DIR__)
using pSGWT
G = loadgraph("../datasets/simple_tree_graph.lgz")
X = load("../datasets/simple_tree_xy.jld", "xy")
N = nv(G)
L = Matrix(laplacian_matrix(G))
𝛌, 𝚽 = eigen(L)
standardize_eigenvectors!(𝚽)
W = 1.0 * adjacency_matrix(G)
Q = incidence_matrix(G; oriented = true)
ib1 = 36:56
ib2 = 21:35
ib3 = 71:100
ib4 = 57:70
ijc = [3,5,12,16]
ir = setdiff(1:N, ib1, ib2, ib3, ib4, ijc)
##
P = 𝚽.^2
# P = exp.(𝚽) ./ sum(exp.(𝚽), dims = 1)
dist_sROT, Ws, Xs, 𝚯 = eigsROT_Distance(P, W, X; α = 1.0)
##
function find_active_eigenvectors(P, interest_locs; threshold = 0.5)
N = size(P, 1)
energy = zeros(N)
for k=1:N
energy[k] = norm(P[interest_locs, k], 1) / norm(P[:, k], 1)
end
ind = findall(energy .> threshold)
return ind
end
# index of eigenvectors active at branch k (k = 1,2,3,4)
ieb1 = find_active_eigenvectors(𝚽.^2, ib1)
ieb2 = find_active_eigenvectors(𝚽.^2, ib2)
ieb3 = find_active_eigenvectors(𝚽.^2, ib3)
ieb4 = find_active_eigenvectors(𝚽.^2, ib4)
iejc = find_active_eigenvectors(𝚽.^2, ijc; threshold = 0.1)
function simpletree_mds_plot(E, ieb1, ieb2, ieb3, ieb4, iejc)
scatter_gplot(E'; c = :grey, ms = 2)
scatter_gplot!(E[:, ieb1]'; c = :pink, ms = 2)
scatter_gplot!(E[:, ieb2]'; c = :orange, ms = 2)
scatter_gplot!(E[:, ieb3]'; c = :green, ms = 2)
scatter_gplot!(E[:, ieb4]'; c = :yellow, ms = 2)
scatter_gplot!(E[:, iejc]'; c = :red, ms = 2)
scatter_gplot!(E[:, 1:1]'; c = :magenta, ms = 4)
plt = plot!(xaxis = "X₁", yaxis = "X₂", zaxis = "X₃", legend = false,
cbar = false, grid = true)
return plt
end
##
f = zeros(N)
ib1 = 36:56; ib2 = 21:35; ib3 = 71:100; ib4 = 57:70; ijc = [3,5,12,16]
f[ib1] = sin.(0.3 * (0:(length(ib1) - 1)))
f[ib2] = cos.(0.4 * (0:(length(ib2) - 1)))
f[ib3] = sin.(0.5 * (0:(length(ib3) - 1)))
f[ib4] = cos.(0.6 * (0:(length(ib4) - 1)))
f[ijc] .= 1;
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 2822 | using MultiscaleGraphSignalTransforms, Plots, Graphs, JLD, MAT
barbara = JLD.load("../datasets/barbara_gray_matrix.jld", "barbara")
## Build weighted graph
G, L, X = SunFlowerGraph(N = 400); N = nv(G)
W = 1.0 * adjacency_matrix(G)
if runapprox
Q = incidence_matrix(G; oriented = true)
edge_weight = [e.weight for e in edges(G)]
## eigenvectors of L(G)
𝛌, 𝚽 = eigen(Matrix(L))
standardize_eigenvectors!(𝚽)
## eigenvectors of Lsym(G)
deg = sum(W, dims = 1)[:] # weighted degree vector
Lsym = diagm(deg.^(-1/2)) * (diagm(deg) - W) * diagm(deg.^(-1/2))
𝛌sym, 𝚽sym = eigen(Lsym)
standardize_eigenvectors!(𝚽sym)
## Build Dual Graph by DAG metric
distDAG = eigDAG_Distance(𝚽, Q, N; edge_weight = edge_weight)
Gstar_Sig = dualgraph(distDAG)
G_Sig = GraphSig(W, xy = X)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
jmax = size(GP_dual.rs, 2) - 1 # zero-indexed
if allNGWPs
# 54.986524 seconds (1.19 M allocations: 25.127 GiB, 2.36% gc time)
@time VM_NGWP = vm_ngwp(𝚽, GP_dual)
# 0.611176 seconds (225.41 k allocations: 844.488 MiB, 11.71% gc time)
@time PC_NGWP = pc_ngwp(𝚽, GP_dual, GP_primal)
# 50.939912 seconds (7.67 M allocations: 28.051 GiB, 3.11% gc time)
@time LP_NGWP = lp_ngwp(𝚽, Gstar_Sig.W, GP_dual; ϵ = 0.3)
end
## Build Dual Graph by DAG metric (Lsym)
distDAG_Lsym = eigDAG_Distance(𝚽sym, Q, N; edge_weight = edge_weight)
Gstar_Sig_Lsym = dualgraph(distDAG_Lsym)
GP_dual_Lsym = partition_tree_fiedler(Gstar_Sig_Lsym; swapRegion = false)
GP_primal_Lsym = pairclustering(𝚽sym, GP_dual_Lsym)
jmax_Lsym = size(GP_dual_Lsym.rs, 2) - 1
if allNGWPs
# 61.328441 seconds (1.34 M allocations: 29.058 GiB, 2.30% gc time)
@time VM_NGWP_Lsym = vm_ngwp(𝚽sym, GP_dual_Lsym)
# 0.605507 seconds (237.87 k allocations: 876.689 MiB, 10.83% gc time)
@time PC_NGWP_Lsym = pc_ngwp(𝚽sym, GP_dual_Lsym, GP_primal_Lsym)
# 77.918189 seconds (2.12 M allocations: 42.872 GiB, 2.91% gc time)
@time LP_NGWP_Lsym = lp_ngwp(𝚽sym, Gstar_Sig_Lsym.W, GP_dual_Lsym; ϵ = 0.3)
end
else
using VoronoiDelaunay, VoronoiCells, GeometricalPredicates
## Voronoi tessellation
width_x = maximum(abs.(X[:, 1])) * 2; width_y = maximum(abs.(X[:, 2])) * 2;
width = VoronoiDelaunay.max_coord - VoronoiDelaunay.min_coord
center_coord = (VoronoiDelaunay.min_coord + VoronoiDelaunay.max_coord)/2
X_transform = zeros(N,2)
for i in 1:N
X_transform[i,:] = X[i,:] ./ [width_x/width, width_y/width] + [center_coord, center_coord]
end
pts = [Point2D(X_transform[i,1], X_transform[i,2]) for i in 1:N]
tess = DelaunayTessellation(N)
push!(tess, pts)
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1943 | using MultiscaleGraphSignalTransforms, JLD, Plots, Graphs, Distances
## Build weighted toronto street network graph
G = loadgraph("../datasets/new_toronto_graph.lgz"); N = nv(G)
X = load("../datasets/new_toronto.jld", "xy")
dist_X = pairwise(Euclidean(), X; dims = 1)
A = 1.0 .* adjacency_matrix(G)
W = zeros(N, N); W[A .> 0] = 1 ./ dist_X[A .> 0]; W = A .* W
Q = incidence_matrix(G; oriented = true)
edge_weight = 1 ./ sqrt.(sum((Q' * X).^2, dims = 2)[:])
## eigenvectors of L(G)
deg = sum(W, dims = 1)[:] # weighted degree vector
L = diagm(deg) - W
𝛌, 𝚽 = eigen(L)
standardize_eigenvectors!(𝚽)
## eigenvectors of Lsym(G)
Lsym = diagm(deg.^(-1/2)) * (diagm(deg) - W) * diagm(deg.^(-1/2))
𝛌sym, 𝚽sym = eigen(Lsym)
standardize_eigenvectors!(𝚽sym)
## Build Dual Graph by DAG metric
distDAG = eigDAG_Distance(𝚽, Q, N; edge_weight = edge_weight) #52.375477 seconds
Gstar_Sig = dualgraph(distDAG)
G_Sig = GraphSig(A, xy = X); G_Sig = Adj2InvEuc(G_Sig)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
jmax = size(GP_dual.rs, 2) - 1 # zero-indexed
if allNGWPs
#1315.821724 seconds (3.05 M allocations: 495.010 GiB, 7.04% gc time)
@time VM_NGWP = vm_ngwp(𝚽, GP_dual)
#119.590168 seconds (12.14 M allocations: 158.035 GiB, 13.89% gc time)
@time PC_NGWP = pc_ngwp(𝚽, GP_dual, GP_primal)
@time LP_NGWP = lp_ngwp(𝚽, Gstar_Sig.W, GP_dual; ϵ = 0.3)
end
## Build Dual Graph by DAG metric (Lsym)
distDAG_Lsym = eigDAG_Distance(𝚽sym, Q, N; edge_weight = edge_weight)
Gstar_Sig_Lsym = dualgraph(distDAG_Lsym)
GP_dual_Lsym = partition_tree_fiedler(Gstar_Sig_Lsym; swapRegion = false)
GP_primal_Lsym = pairclustering(𝚽sym, GP_dual_Lsym)
jmax_Lsym = size(GP_dual_Lsym.rs, 2) - 1
if allNGWPs
VM_NGWP_Lsym = vm_ngwp(𝚽sym, GP_dual_Lsym)
PC_NGWP_Lsym = pc_ngwp(𝚽sym, GP_dual_Lsym, GP_primal_Lsym)
LP_NGWP_Lsym = lp_ngwp(𝚽sym, Gstar_Sig_Lsym.W, GP_dual_Lsym; ϵ = 0.3)
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1264 | #Figure 2.5
#Run function "Glevel" at bottom of file first
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
JLD2.@load "../data/Toronto.jld2"
tmp1 = toronto["G"]
G=GraphSig(tmp1["W"],xy=tmp1["xy"],f=tmp1["f"],name =tmp1["name"],plotspecs = tmp1["plotspecs"])
G = Adj2InvEuc(G)
GP = partition_tree_fiedler(G,:Lrw)
dmatrix = ghwt_analysis!(G, GP=GP)
j = 1
GraphSig_Plot(Glevel(G,GP,1), linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0., notitle = true, nocolorbar = true)
plot!(axis = false)
#savefig("G1.pdf")
j = 2
GraphSig_Plot(Glevel(G,GP,2), linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0., notitle = true, nocolorbar = true)
plot!(axis = false)
#savefig("G2.pdf")
j = 3
GraphSig_Plot(Glevel(G,GP,3), linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0., notitle = true, nocolorbar = true)
plot!(axis = false)
#savefig("G3.pdf")
function Glevel(G::GraphSig, GP::GraphPart, j::Int64)
f = zeros(size(G.f))
for k in 1:size(GP.rs,1)
a = GP.rs[k,j]
b = GP.rs[k+1,j] - 1
if b == -1
break
end
f[a:b] .= k*1.0
end
Gsub = deepcopy(G)
Gsub.f[GP.ind] = f
return Gsub
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1578 | #Figure 3.2
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
include("../../../../src/utils.jl")
JLD2.@load "../data/Toronto.jld2"
tmp1 = toronto["G"]
G=GraphSig(tmp1["W"],xy=tmp1["xy"],f=tmp1["f"],name =tmp1["name"],plotspecs = tmp1["plotspecs"])
G = Adj2InvEuc(G)
GP = partition_tree_fiedler(G,:Lrw)
dmatrix = ghwt_analysis!(G, GP=GP)
N = length(G.f)
j = 1
loc = 1
BS = bs_level(GP, j)
dvec = zeros(N,1)
dvec[loc,1] = 1
(f, GS) = ghwt_synthesis(dvec, GP, BS, G)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markerstrokealpha =0., notitle = true, clim = (-0.1, 0.1))
plot!(axis = false,colorbar = false)
k,l = BS.levlist[loc][1], BS.levlist[loc][2]
print(j," ",(rs_to_region(GP.rs, GP.tag))[k,l]," ",GP.tag[k,l])
#savefig("Toronto100.pdf")
j = 2
loc = 2
BS = bs_level(GP, j)
dvec = zeros(N,1)
dvec[loc,1] = 1
(f, GS) = ghwt_synthesis(dvec, GP, BS, G)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markerstrokealpha =0., notitle = true, clim = (-0.1, 0.1))
plot!(axis = false,colorbar = false)
k,l = BS.levlist[loc][1], BS.levlist[loc][2]
print(j," ",(rs_to_region(GP.rs, GP.tag))[k,l]," ",GP.tag[k,l])
#savefig("Toronto201.pdf")
j = 5
loc = 100
BS = bs_level(GP, j)
dvec = zeros(N,1)
dvec[loc,1] = 1
(f, GS) = ghwt_synthesis(dvec, GP, BS, G)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markerstrokealpha =0., notitle = true, clim = (-0.1, 0.1))
plot!(axis = false,colorbar = false)
k,l = BS.levlist[loc][1], BS.levlist[loc][2]
print(j," ",(rs_to_region(GP.rs, GP.tag))[k,l]," ",GP.tag[k,l])
#savefig("Toronto5134.pdf")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 5055 | #Figure 5.4, 5.5
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
JLD2.@load "../data/spie_data.jld2"
matrix = vars["barbara"]
#face
row_zoom = 1:180
col_zoom = 330:450
#right leg
row_zoom = 300:512
col_zoom = 400:512
#full image
row_zoom = 1:512
col_zoom = 1:512
heatmap(matrix[row_zoom, col_zoom],ratio=1, yaxis =:flip, axis = false, color = :grays)
#savefig("original.pdf")
### initialize the regular balanced binary partition and compute the expanding coefficients
dmatrix, GProws, GPcols = ghwt_tf_init_2d_Lindberg(matrix)
### Compute the coefficients of different basis we will compare
############# Haar
BS_haar_rows = bs_haar(GProws)
BS_haar_cols = bs_haar(GPcols)
dvec_haar, loc_haar = BS2loc(dmatrix, GProws, GPcols, BS_haar_rows, BS_haar_cols)
############# Walsh
BS_walsh_rows = bs_walsh(GProws)
BS_walsh_cols = bs_walsh(GPcols)
dvec_walsh, loc_walsh = BS2loc(dmatrix, GProws, GPcols, BS_walsh_rows, BS_walsh_cols)
############# GHWT (i.e., regular haar-walsh wavelet packet dictionary)
fcols, jmax_col = size(GProws.tag);
frows, jmax_row = size(GPcols.tag);
dmatrix_rows = reshape(dmatrix, (frows, jmax_row, fcols*jmax_col))
dmatrix_cols = Array{Float64,3}(reshape(dmatrix',(fcols, jmax_col, frows*jmax_row)))
############# c2f bestbasis
dvec_c2f_rows, BS_c2f_rows = ghwt_c2f_bestbasis(dmatrix_rows, GProws)
dvec_c2f_cols, BS_c2f_cols = ghwt_c2f_bestbasis(dmatrix_cols, GPcols)
dvec_c2f, loc_c2f = BS2loc(dmatrix, GProws, GPcols, BS_c2f_rows, BS_c2f_cols)
############# f2c bestbasis
dvec_f2c_rows, BS_f2c_rows = ghwt_f2c_bestbasis(dmatrix_rows, GProws)
dvec_f2c_cols, BS_f2c_cols = ghwt_f2c_bestbasis(dmatrix_cols, GPcols)
dvec_f2c, loc_f2c = BS2loc(dmatrix, GProws, GPcols, BS_f2c_rows, BS_f2c_cols)
#############
##################### tf bestbasis
dvec_tf, loc_tf = ghwt_tf_bestbasis_2d(matrix, GProws, GPcols)
################################################################################
##################### Visualize the results of synthesis########################
################################################################################
### function to plot the image synthesized by top p vectors
function top_vectors_synthesis_2d(p::Int64, dvec::Vector{Float64}, loc::Matrix{Int64}, GProws::GraphPart, GPcols::GraphPart, dmatrix::Matrix{Float64})
sorted_dvec = sort(abs.(dvec[:]), rev = true)
dvecT = copy(dvec)
dvecT[abs.(dvec) .< sorted_dvec[p]].= 0
matrix_syn = ghwt_tf_synthesis_2d(dvecT, loc, GProws, GPcols)
heatmap(matrix_syn[row_zoom, col_zoom],ratio=1, yaxis =:flip, axis = false, color = :grays)
mse = norm(matrix - matrix_syn,2)^2/length(matrix)
psnr = -10*log10(mse)
return psnr
end
################################################################################
percent = 1/32;
p = Int64(floor(percent*length(matrix)))
### haar
# Figure 5.4(a)
top_vectors_synthesis_2d(p, dvec_haar, loc_haar, GProws, GPcols, dmatrix)
#savefig("synthesis_haar_1_32.pdf")
### walsh
top_vectors_synthesis_2d(p, dvec_walsh, loc_walsh, GProws, GPcols, dmatrix)
#savefig("synthesis_walsh_1_32.pdf")
### c2f
# Figure 5.4(b)
top_vectors_synthesis_2d(p, dvec_c2f, loc_c2f, GProws, GPcols, dmatrix)
#savefig("synthesis_c2f_1_32.pdf")
### f2c
# Figure 5.4(c)
top_vectors_synthesis_2d(p, dvec_f2c, loc_f2c, GProws, GPcols, dmatrix)
#savefig("synthesis_f2c_1_32.pdf")
### tf
# Figure 5.4(d)
top_vectors_synthesis_2d(p, dvec_tf, loc_tf, GProws, GPcols, dmatrix)
#savefig("synthesis_tf_1_32.pdf")
# To generate Figure 5.5, just change the row_zoom, and col_zoom at the head of this file.
################################################################################
####################### Approximation error plot################################
################################################################################
function approx_error(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0:0.01:0.3
T = ["Haar","Walsh","GHWT_c2f", "GHWT_f2c", "eGHWT"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :red),(:solid, :green),(:solid, :black)]
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
er = fill(0., length(frac))
for j = 1:length(frac)
p = Int64(floor(frac[j]*N))
er[j] = sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm
end
plot!(frac, er, yaxis=:log, xlims = (0.,0.3), label = T[i], line = L[i])
end
end
approx_error([dvec_haar, dvec_walsh, dvec_c2f, dvec_f2c, dvec_tf])
current()
#################
### Generate the relative l2 error when approximating by 1/32 coefficients
################
DVEC = [dvec_haar, dvec_walsh, dvec_c2f, dvec_f2c, dvec_tf];
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
p = Int64(floor(N./32))
print(sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm)
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 3700 | #Figure 5.7, 5.8
using TestImages, Plots, SparseArrays, LinearAlgebra, Wavelets, MultiscaleGraphSignalTransforms
img = testimage("camera");
matrix = convert(Array{Float64,2}, img)[1:4:512,1:4:512]
heatmap(matrix,ratio=1, yaxis =:flip, axis = false, color = :grays, clim = (0,1), colorbar = false)
matrix_gt = matrix[:]
sigma = 0.007
#sigma = 0.07
m, n = size(matrix)
############### Get the neighbors for affinity matrix computing
r = 5; # specify radius of neighbors
l = 2*r + 1
temp_x, temp_y = fill(1,l^2), fill(1,l^2)
temp_xy = CartesianIndices((1:l,1:l))
for i = 1:l^2
temp_x[i], temp_y[i] = temp_xy[i][1], temp_xy[i][2]
end
temp_ind = ((temp_x .- (r + 1)).^2 + (temp_y .- (r + 1)).^2).<= r^2
neighbor_x = temp_x[temp_ind] .- (r + 1)
neighbor_y = temp_y[temp_ind] .- (r + 1)
# for any index(x,y), (x + neighbor_x, y - neigbor_y) are the neighbors to calculate affinity
################ Create affinity matrix
W = fill(0., (m*n,m*n))
for i = 1:m*n
cur = CartesianIndices((m,n))[i]
for j = 1:length(neighbor_x)
if 1 <= cur[1] + neighbor_x[j] <= m && 1 <= cur[2] + neighbor_y[j] <= n
tempd = LinearIndices((m,n))[cur[1] + neighbor_x[j], cur[2] + neighbor_y[j]]
W[i,tempd] = exp(-(matrix_gt[i] - matrix_gt[tempd])^2/sigma)
end
end
end
W = sparse(W)
############### Preprocess to get G and GP
G = GraphSig(W, f = reshape(matrix,(length(matrix_gt),1)))
GP = partition_tree_fiedler(G)
dmatrix = ghwt_analysis!(G, GP=GP)
############# Construct or search the specific basis
############# Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
############# eGHWT
dvec_eghwt, BS_eghwt = ghwt_tf_bestbasis(dmatrix, GP)
####################
function top_vectors_plot(dvec::Array{Float64, 2}, BS::BasisSpec, GP::GraphPart; clims::Tuple{Float64,Float64} = (-0.02,0.02))
sorted_ind = sortperm(abs.(dvec[:]), rev = true);
plot(9,layout=(3,3),framestyle=:none, legend=false)
for i=1:9
dvecT = fill(0., size(dvec))
#dvecT[sorted_ind[i]] = dvec_ghwt[sorted_ind[i]]
dvecT[sorted_ind[i]] = 1
f = ghwt_synthesis(dvecT, GP, BS)
#print((maximum(f), minimum(f)))
heatmap!(reshape(f, size(matrix)), subplot=i, ratio=1, yaxis=:flip, axis=false, color = :grays, clims = clims)
end
current()
end
#Figure 5.8a (re-run the code with sigma = 0.07 to generate figure 5.8b)
top_vectors_plot(dvec_eghwt, BS_eghwt, GP)
dvec_haar0007 = dvec_haar
dvec_eghwt0007 = dvec_eghwt
#re-run the code with sigma = 0.07 to generate dvec_haar007 and dvec_eghwt007
# dvec_haar007 = dvec_haar
# dvec_eghwt007 = dvec_eghwt
function approx_error2(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0.3
T = ["Classical Haar transform", "eGHWT Haar basis (sigma = 0.07)", "eGHWT best basis (sigma = 0.07)", "eGHWT Haar basis (sigma = 0.007)", "eGHWT best basis (sigma = 0.007)"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :red),(:dashdot,:purple),(:solid,:black)]
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2) # the smallest first
er = sqrt.(reverse(cumsum(dvec_sort)))/dvec_norm # this is the relative L^2 error of the whole thing, i.e., its length is N
p = Int64(floor(frac*N)) + 1 # upper limit
plot!(frac*(0:(p-1))/(p-1), er[1:p], yaxis=:log, xlims = (0.,frac), label = T[i], line = L[i])
end
end
dvec_classichaar = dwt(matrix, wavelet(WT.haar))
#Figure 5.7
approx_error2([dvec_classichaar[:], dvec_haar007[:], dvec_eghwt007[:], dvec_haar0007[:], dvec_eghwt0007[:]])
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 3779 | #Figure 5.9, 5.10
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms, PyCall
py"""
import numpy
xs = numpy.load('../data/texture_mask.npy')
"""
xs = PyArray(py"xs"o)
matrix_gt = reshape(xs,(512,512))[1:4:512,1:4:512]
heatmap(matrix_gt,ratio=1, yaxis =:flip, axis = false, color = :grays, colorbar = false)
max1 = maximum(matrix_gt[:])
min1 = minimum(matrix_gt[:])
matrix_gt = (matrix_gt[:] .- min1)./(max1 - min1)
JLD2.@load "../data/handcut_images.jld2"
heatmap(tmp["block5"],ratio=1, yaxis =:flip, axis = false, color = :grays, colorbar = false)
matrix = tmp["block5"]
########################
sigma = 0.001
m, n = size(matrix)
############### Get the neighbors for affinity matrix computing
r = 5; # specify radius of neighbors
l = 2*r + 1
temp_x, temp_y = fill(1,l^2), fill(1,l^2)
temp_xy = CartesianIndices((1:l,1:l))
for i = 1:l^2
temp_x[i], temp_y[i] = temp_xy[i][1], temp_xy[i][2]
end
temp_ind = ((temp_x .- (r + 1)).^2 + (temp_y .- (r + 1)).^2).<= r^2
neighbor_x = temp_x[temp_ind] .- (r + 1)
neighbor_y = temp_y[temp_ind] .- (r + 1)
# for any index(x,y), (x + neighbor_x, y - neigbor_y) are the neighbors to calculate affinity
################ Create affinity matrix
W = fill(0., (m*n,m*n))
for i = 1:m*n
cur = CartesianIndices((m,n))[i]
for j = 1:length(neighbor_x)
if 1 <= cur[1] + neighbor_x[j] <= m && 1 <= cur[2] + neighbor_y[j] <= n
tempd = LinearIndices((m,n))[cur[1] + neighbor_x[j], cur[2] + neighbor_y[j]]
W[i,tempd] = exp(-(matrix_gt[i] - matrix_gt[tempd])^2/sigma)
end
end
end
W = sparse(W)
############### Preprocess to get G and GP
G = GraphSig(W, f = reshape(matrix,(length(matrix_gt),1)))
GP = partition_tree_fiedler(G)
dmatrix = ghwt_analysis!(G, GP=GP)
#####################
############# Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
############# Walsh
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
############# GHWT_c2f
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
############# GHWT_f2c
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
############# eGHWT
dvec_eghwt, BS_eghwt = ghwt_tf_bestbasis(dmatrix, GP)
function top_vectors_plot(dvec::Array{Float64, 2}, BS::BasisSpec, GP::GraphPart; clims::Tuple{Float64,Float64} = (-0.01,0.01))
sorted_ind = sortperm(abs.(dvec[:]), rev = true);
plot(9,layout=(3,3),framestyle=:none, legend=false)
for i=1:9
dvecT = fill(0., size(dvec))
#dvecT[sorted_ind[i]] = dvec_ghwt[sorted_ind[i]]
dvecT[sorted_ind[i]] = 1
f = ghwt_synthesis(dvecT, GP, BS)
#print((maximum(f), minimum(f)))
heatmap!(reshape(f, size(matrix)), subplot=i, ratio=1, yaxis=:flip, axis=false, color = :grays, clims = clims)
end
current()
end
#Figure 5.10b
top_vectors_plot(dvec_eghwt, BS_eghwt, GP)
function approx_error2(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0.3
T = ["eGHWT Haar basis","eGHWT Walsh basis","GHWT_c2f", "GHWT_f2c", "eGHWT best basis"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :red),(:solid, :green),(:solid, :black)]
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2) # the smallest first
er = sqrt.(reverse(cumsum(dvec_sort)))/dvec_norm # this is the relative L^2 error of the whole thing, i.e., its length is N
p = Int64(floor(frac*N)) + 1 # upper limit
plot!(frac*(0:(p-1))/(p-1), er[1:p], yaxis=:log, xlims = (0.,frac), label = T[i], line = L[i])
end
end
#Figure 5.10a
approx_error2([dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:]])
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 4672 | #Figure 5.1, 5.2, 5.3
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
JLD2.@load "../data/Toronto.jld2"
tmp1 = toronto["G"]
G=GraphSig(tmp1["W"],xy=tmp1["xy"],f=tmp1["f"],name =tmp1["name"],plotspecs = tmp1["plotspecs"])
GraphSig_Plot(G, linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0.)
G = Adj2InvEuc(G)
GP = partition_tree_fiedler(G,:Lrw)
dmatrix = ghwt_analysis!(G, GP=GP)
############# Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
############# Walsh
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
############# GHWT_c2f
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
############# GHWT_f2c
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
############# eGHWT
dvec_eghwt, BS_eghwt = ghwt_tf_bestbasis(dmatrix, GP)
################################################################################
####################### Approximation error plot################################
################################################################################
function approx_error(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0:0.01:0.3
T = ["Haar","Walsh","GHWT_c2f", "GHWT_f2c", "eGHWT"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :red),(:solid, :green),(:solid, :black)]
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
er = fill(0., length(frac))
for j = 1:length(frac)
p = Int64(floor(frac[j]*N))
er[j] = sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm
end
plot!(frac, er, yaxis=:log, xlims = (0.,0.3), label = T[i], line = L[i])
print(er[26])
end
end
################################################################################
######################### Synthesized by top vectors###########################
################################################################################
color_limit_residual = (0., 0.15)
function top_vectors_residual(p::Int64, dvec::Array{Float64,2}, BS::BasisSpec, GP::GraphPart, G::GraphSig)
sorted_dvec = sort(abs.(dvec[:]), rev = true)
dvecT = copy(dvec)
dvecT[abs.(dvec) .< sorted_dvec[p]].= 0
(f, GS) = ghwt_synthesis(dvecT, GP, BS, G)
GS.name = "Square of the residual"
#GS.f = (G.f - GS.f).^2
#print((maximum(GS.f), minimum(GS.f)))
#GraphSig_Plot(GS)
GS.f = (G.f - GS.f).^2 ./(G.f.^2)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0., clim = color_limit_residual)
current()
end
################################
### Generate results
################################
# Figure 5.1(b)
approx_error([dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:]])
current()
###
frac = 1/4
p = Int64(ceil(frac*G.length))
### original (Figure )
# Figure 5.1(a)
GraphSig_Plot(G, linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0., clim = (2000., 110000.))
### haar
# Figure 5.2(a)
top_vectors_residual(p, dvec_haar, BS_haar, GP, G)
### walsh
# Figure 5.2(b)
top_vectors_residual(p, dvec_walsh, BS_walsh, GP, G)
### c2f
# Figure 5.2(b)
top_vectors_residual(p, dvec_c2f, BS_c2f, GP, G)
### f2c
# Figure 5.2(c)
top_vectors_residual(p, dvec_f2c, BS_f2c, GP, G)
### eghwt
# Figure 5.2(d)
top_vectors_residual(p, dvec_eghwt, BS_eghwt, GP, G)
################################ Figure 5.3 and 5.4
################################
using JLD;
tmp = load("../data/new_toronto.jld");
G=GraphSig(SparseMatrixCSC{Float64,Int64}(tmp["W"]),xy=tmp["xy"],f=reshape(tmp["fp"],(length(tmp["fp"]),1)))
GraphSig_Plot(G, linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0.)
G = Adj2InvEuc(G)
GP = partition_tree_fiedler(G,:Lrw)
dmatrix = ghwt_analysis!(G, GP=GP)
############# Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
############# Walsh
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
############# GHWT_c2f
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
############# GHWT_f2c
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
############# eGHWT
dvec_eghwt, BS_eghwt = ghwt_tf_bestbasis(dmatrix, GP)
########## Figure 5.3a
GraphSig_Plot(G, linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0.)
#savefig("5_3a.pdf")
########## Figure 5.3b
approx_error([dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:]])
current()
#savefig("5_3b.pdf")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 5750 | #Table 6.2
#Run uility functions at bottom
#Change the setting of Lambda if necessary
using NMF, LinearAlgebra, MultiscaleGraphSignalTransforms, ScikitLearn
@sk_import linear_model:Lasso
########################### utility functions ###########################
function create_scaling_vectors(GProws::GraphPart)
GP = GProws
### creating scaling vectors
temp = GP.tag.== 0;
scaling_index = findall(temp);# index of the scaling vectors .i.e. vectors with tag == 0
num_scaling = length(scaling_index);
scaling_vectors = fill(0., (size(GP.tag,1), num_scaling));
for i = 1:num_scaling
ind = scaling_index[i]
dvec = fill(0., (size(GP.tag,1),1))
dvec[ind[1],1] = 1.;
BS = bs_level(GP, ind[2] - 1)
scaling_vectors[:,i] = ghwt_synthesis(dvec, GP, BS)
end
return scaling_vectors
end
function create_PHI(scaling_vectors_rows, scaling_vectors_cols, m, n)
PHI_right = repeat(scaling_vectors_cols[:,1:n], outer = (1, m))
PHI_left = repeat(scaling_vectors_rows[:,1:m], inner = (1, n))
return PHI_left, PHI_right
end
function ghwtinit(matrix, k)
GProws, GPcols = partition_tree_matrixDhillon(matrix)
dmatrix = ghwt_analysis_2d(matrix, GProws, GPcols)
scaling_vectors_rows = create_scaling_vectors(GProws)
scaling_vectors_cols = create_scaling_vectors(GPcols)
PHI_left, PHI_right = create_PHI(scaling_vectors_rows, scaling_vectors_cols, 10, 10)
scaling_vectors = fill(0., (length(matrix[:]), size(PHI_left,2)))
for i = 1:size(PHI_left,2)
scaling_vectors[:,i] = (PHI_left[:,i]*PHI_right[:,i]')[:]
end
##########################
####################################### perform lasso
f = matrix[:]
#Lambda = range(0.00001,stop = 0.0001, length = 10)
Lambda = range(0.001,stop = 0.01, length = 10)# m=125,n=25,k=5,sigma = 0.5,
#Lambda = range(0.001, stop = 0.01, length = 10)
B = fill(0., (size(scaling_vectors,2), length(Lambda))) ### initialize coefficients
for i = 1:length(Lambda)
lasso_out = Lasso(alpha = Lambda[i], positive = true, fit_intercept = false)
ScikitLearn.fit!(lasso_out, scaling_vectors, f)
B[:,i] = lasso_out.coef_
end
j = 1
if sum((B[:,j].!=0)) < k
return false, false
else
while j <10 && sum(B[:,j+1].!=0) >= k
j += 1
end
end
index = findall(B[:,j].!=0)[1:k]
rescaleW = repeat(sqrt.(B[index,j]'),size(PHI_left,1),1)
rescaleH = repeat(sqrt.(B[index,j]'),size(PHI_right,1),1)
Wtilda = PHI_left[:,index].*rescaleW
Htilda = Array{Float64,2}((PHI_right[:,index].*rescaleH)')
return Wtilda, Htilda
end
function improved_NNDSVD(matrix, k)
m,n = size(matrix)
U,S,V = svd(matrix)
W = zeros(m,k)
H = zeros(k,n)
Y = U*sqrt.(Diagonal(S))
Z = sqrt.(Diagonal(S))*transpose(V)
W[:,1] = abs.(Y[:,1])
H[1,:] = abs.(Z[1,:])
j = 2
for i = 2:k
if mod(i,2) == 0
W[:,i] = Y[:,j]
H[i,:] = Z[i,:]
else
W[:,i] = .-Y[:,j]
H[i,:] = .-Z[i,:]
j += 1
end
W[W[:,i] .< 0,i] .= 0
H[i,H[i,:] .< 0] .= 0
end
return W, H
end
########################### end of utility functions ###########################
### Now the start of the actual NMF experiments.
k = 5
m = 125
n = 25
sigma = 0.5 #noise parameter
#methodid = 1 corresponds to ALSPGRAD.
#methodid = 2 corresponds to HALS.
methodid = 2
num_pos_eghwt_svd = 0
num_neg_eghwt_svd = 0
num_pos_eghwt_rand = 0
num_neg_eghwt_rand = 0
num_pos_svd_rand = 0
num_neg_svd_rand = 0
num_pos_svd_newsvd = 0
num_neg_svd_newsvd = 0
num_pos_eghwt_newsvd = 0
num_neg_eghwt_newsvd = 0
for i = 1:50
Wtrue = rand(m,k)
Htrue = rand(k,n)
X = Wtrue*Htrue + sigma*rand(m,n)
#X = rand(m,n)
################
######################################
Wtilda, Htilda = ghwtinit(X, k)
if Wtilda == false
continue
end
Wsvd, Hsvd = NMF.nndsvd(X, k)
Wrand, Hrand = NMF.randinit(X, k)
Wnewsvd, Hnewsvd = improved_NNDSVD(X, k)
iters = 1000000
method = [NMF.ALSPGrad{Float64}(maxiter=iters, tolg=1.0e-6), NMF.CoordinateDescent{Float64}(maxiter=iters, α=0.5, l₁ratio=0.5)]
a = NMF.solve!(method[methodid], X, copy(Wtilda), copy(Htilda))
b = NMF.solve!(method[methodid], X, copy(Wsvd), copy(Hsvd))
c = NMF.solve!(method[methodid], X, copy(Wrand), copy(Hrand))
d = NMF.solve!(method[methodid], X, copy(Wnewsvd), copy(Hnewsvd))
#println("initial norm ",norm(X - Wtilda*Htilda)," ",norm(X-Wsvd*Hsvd)," ",norm(X - Wrand*Hrand)," ", norm(X - Wnewsvd*Hnewsvd))
#println(" ",a.niters," ",b.niters," ",c.niters," ",d.niters)
#println("final norm",norm(X - a.W*a.H)," ",norm(X-b.W*b.H)," ",norm(X - c.W*c.H)," ", norm(X - d.W*d.H))
if a.niters < b.niters
global num_pos_eghwt_svd += 1
else
global num_neg_eghwt_svd += 1
end
if a.niters < c.niters
global num_pos_eghwt_rand += 1
else
global num_neg_eghwt_rand += 1
end
if b.niters < c.niters
global num_pos_svd_rand += 1
else
global num_neg_svd_rand += 1
end
if a.niters < d.niters
global num_pos_eghwt_newsvd += 1
else
global num_neg_eghwt_newsvd += 1
end
if b.niters < d.niters
global num_pos_svd_newsvd += 1
else
global num_neg_svd_newsvd += 1
end
end
println("compare eGHWT with NNDSVD ", num_pos_eghwt_svd/(num_pos_eghwt_svd + num_neg_eghwt_svd))
println("compare eGHWT with Random ", num_pos_eghwt_rand/(num_pos_eghwt_rand + num_neg_eghwt_rand))
println("compare eGHWT with NNSVD-LRC ", num_pos_eghwt_newsvd/(num_pos_eghwt_newsvd + num_neg_eghwt_newsvd))
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 4418 | # script for Fig.1, Fig.2, Fig.4, Fig.6
using MultiscaleGraphSignalTransforms, Graphs, Plots, LaTeXStrings, MultivariateStats
pyplot(dpi = 200)
Nx, Ny = 7, 3
G = Graphs.grid([Nx, Ny]); N = nv(G);
L = Matrix(laplacian_matrix(G))
Q = incidence_matrix(G; oriented = true)
𝛌, 𝚽 = eigen(L); 𝚽 = 𝚽 .* sign.(𝚽[1, :])';
#################### Fig. 1(a) eigenvectors by nondecreasing eigenvalue ordering
plot(layout = Plots.grid(3, 7))
for i in 1:N
heatmap!(reshape(𝚽[:, i],(Nx, Ny))', c = :viridis, cbar = false,
clims = (-0.4,0.4), frame = :none, ratio = 1,
title = latexstring("\\phi_{", i-1, "}"), titlefont = 12,
subplot = i)
end
plt = current()
# savefig(plt, joinpath(@__DIR__, "../paperfigs/grid7x3_evsp_title.png"))
#################### Fig. 1(b) eigenvectors by natural frequency ordering
# find correct 2D index
grid2eig_ind = [1,2,3,6,8,12,15,4,5,7,9,13,16,18,10,11,14,17,19,20,21];
eig2grid_ind = sortperm(grid2eig_ind);
eig2dct = Array{Int64,3}(undef, Nx, Ny, 2);
for i = 1:Nx; for j = 1:Ny; eig2dct[i,j,1] = i-1; eig2dct[i,j,2] = j-1; end; end
eig2dct = reshape(eig2dct, (N, 2)); eig2dct = eig2dct[eig2grid_ind, :];
plot(layout = Plots.grid(3, 7))
for i in 1:N
k = grid2eig_ind[i]
heatmap!(reshape(𝚽[:,k],(Nx,Ny))', c = :viridis, cbar = false,
clims = (-0.4,0.4), frame = :none, ratio = 1,
title = latexstring("\\varphi_{", string(eig2dct[k,1]),
",", string(eig2dct[k,2]), "}"), titlefont = 12, subplot = i)
end
plt = current()
# savefig(plt, joinpath(@__DIR__, "../paperfigs/grid7x3_dct_title2.png"))
# DAG pseudo-metric
distDAG = eigDAG_Distance(𝚽, Q, N)
# MDS embedding into R²
D = distDAG
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
# set up all heatmap plots' positions
dx = 0.01; dy = dx;
xej = zeros(Nx, N); yej=zeros(Ny, N);
a = 5.0; b = 9.0;
for k = 1:N
xej[:,k] = LinRange(E[1,k] - Ny * a * dx, E[1, k] + Ny * a * dx, Nx)
yej[:,k] = LinRange(E[2,k] - a * dy, E[2, k] + a * dy, Ny)
end
#################### Fig. 2
plot()
for k=1:N
heatmap!(xej[:, k], yej[:, k], reshape(𝚽[:, k], (Nx, Ny))', c = :viridis,
colorbar = false, ratio = 1, annotations = (xej[4, k],
yej[3, k] + b*dy, text(latexstring("\\varphi_{",
string(eig2dct[k, 1]), ",", string(eig2dct[k, 2]), "}"), 10)))
end
plt = plot!(xlim = [-1.4, 1.3], ylim = [-1.4, 1.3], grid = false, clims = (-0.4, 0.4))
# savefig(plt, joinpath(@__DIR__, "../paperfigs/Grid7x3_DAG_MDS.png"))
#################### Fig. 4
# first level partition
p1x = [-0.2, 1.0, NaN]; p1y = [1.3, -1.0, NaN];
plot!(p1x, p1y, c = :red, legend = false, width = 3)
# second level partition
p2x = [-1.0, 0.2, NaN, 0.4, 1.2, NaN]; p2y = [-0.8, 0.45, NaN, 0.25, 0.2, NaN];
plot!(p2x, p2y, c=:orange, legend = false, width = 2)
plt = current()
# savefig(plt, joinpath(@__DIR__, "../paperfigs/Grid7x3_DAG_2levels_partition.png"))
## Build Dual Graph
Gstar_Sig = dualgraph(distDAG)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
@time VM_NGWP = vm_ngwp(𝚽, GP_dual)
## level 2 VM-NGWP vectors
j = 3; W_VM = VM_NGWP[:, j, :]'
wav_kl = [[0 0];[0 1];[0 2];[1 0];[1 1];[1 2];[1 3];[2 0];[2 1];[2 2];[3 0];
[3 1];[3 2];[3 3];[2 3];[2 4];[2 5];[2 6];[3 4];[3 5];[3 6]];
wav_kl = wav_kl[eig2grid_ind,:];
# reorder_ind = [2,3,1,5,7,4,6, 16,17,15, 9,11,8,10, 18,20,21,19, 13,14,12]
reorder_ind = [1,3,2,5,7,4,6, 9,10,8,16,18,15,17, 11,13,14,12,20,21,19]
W_VM = W_VM[:,reorder_ind[eig2grid_ind]];
sgn = ones(N); sgn[grid2eig_ind[[4,6,8,10,14]]] .= -1; W_VM = W_VM * Diagonal(sgn);
#################### Fig. 6
plot()
for k=1:N
heatmap!(xej[:,k],yej[:,k],reshape(W_VM[:,k],(Nx,Ny))',c=:viridis,colorbar=false,ratio=1,annotations=(xej[4,k], yej[3,k]+b*dy, text(latexstring("\\psi_{", string(wav_kl[k,1]), ",", string(wav_kl[k,2]), "}"),10)))
end
plot!(aspect_ratio = 1, xlim = [-1.4, 1.3], ylim = [-1.4, 1.3], grid = false, clims=(-0.34,0.34))
# first level partition
p1x = [-0.2, 1.0, NaN]; p1y = [1.3, -1.0, NaN]; plot!(p1x, p1y, c = :red, legend = false, width = 3)
# second level partition
p2x = [-1.0, 0.2, NaN, 0.4, 1.2, NaN]; p2y = [-0.8, 0.45, NaN, 0.25, 0.2, NaN]; plot!(p2x, p2y, c=:orange, legend = false, width = 2)
plt = current()
# savefig(plt, joinpath(@__DIR__, "../paperfigs/Grid7x3_DAG_VM_NGWP_lvl2_wavelets.png"))
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 812 | # script for Fig.5
using MultiscaleGraphSignalTransforms, Graphs, Plots; gr(dpi = 200)
import WaveletsExt: wiggle
## Build Graph
N = 512; G = path_graph(N)
X = zeros(N,2); X[:, 1] = 1:N
L = Matrix(laplacian_matrix(G))
𝛌, 𝚽 = eigen(L); 𝚽 = 𝚽 .* sign.(𝚽[1,:])'
W = 1.0 * adjacency_matrix(G)
## Build NGWPs
Gstar_Sig = GraphSig(W)
G_Sig = GraphSig(W, xy = X)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
@time VM_NGWP = vm_ngwp(𝚽, GP_dual)
#################### Fig.5
j = 5
for k in [1, 2, 5]
WW = sort_wavelets(VM_NGWP[GP_dual.rs[k, j]:(GP_dual.rs[k + 1, j] - 1), j, :]')
if k == 2
WW[:, end] *= -1
end
plt = wiggle(WW; sc = 0.75)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/Path512_VM_NGWP_j$(j-1)k$(k-1).png"))
end
current()
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 3959 | # script for Fig.8(b)(c), Fig.9, Fig.10(b)(c), Fig.11
using MultiscaleGraphSignalTransforms, Graphs, Plots; gr(dpi = 200)
## Build weighted graph
G, L, X = SunFlowerGraph(N = 400); N = nv(G)
𝛌, 𝚽 = eigen(Matrix(L))
sgn = (maximum(𝚽, dims = 1)[:] .> -minimum(𝚽, dims = 1)[:]) .* 2 .- 1
𝚽 = 𝚽 * Diagonal(sgn)
Q = incidence_matrix(G; oriented = true)
W = 1.0 * adjacency_matrix(G)
edge_weight = [e.weight for e in edges(G)]
## Build Dual Graph by DAG metric
distDAG = eigDAG_Distance(𝚽, Q, N; edge_weight = edge_weight)
Gstar_Sig = dualgraph(distDAG)
G_Sig = GraphSig(W, xy = X)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
@time VM_NGWP = vm_ngwp(𝚽, GP_dual) #54.986524 seconds (1.19 M allocations: 25.127 GiB, 2.36% gc time)
@time PC_NGWP = pc_ngwp(𝚽, GP_dual, GP_primal) #0.611176 seconds (225.41 k allocations: 844.488 MiB, 11.71% gc time)
#################### Fig. 8(b) barbara eye graph signal
using MAT
f = matread(joinpath(@__DIR__, "../datasets",
"sunflower_barbara_voronoi.mat"))["f_eye_voronoi"]
G_Sig.f = reshape(f, (N, 1))
scatter_gplot(X; marker = f, ms = LinRange(4.0, 14.0, N), c = :greys);
plt = plot!(xlim = [-1.2,1.2], ylim = [-1.2,1.2], frame = :none)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/SunFlower_barbara_feye.png"))
#################### Fig. 8(c) barbara eye relative l2 approximation error by various methods
DVEC = getall_expansioncoeffs(G_Sig, GP_dual, VM_NGWP, PC_NGWP, 𝚽)
approx_error_plot(DVEC);
plt = plot!(xguidefontsize = 16, yguidefontsize = 16, legendfontsize = 12)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/SunFlower_barbara_feye_DAG_approx.png"))
#################### Fig. 9 barbara eye 16 most important VM-NGWP vectors (ignore the DC vector)
dmatrix_VM = ngwp_analysis(G_Sig, VM_NGWP)
dvec_vm_ngwp, BS_vm_ngwp = ngwp_bestbasis(dmatrix_VM, GP_dual)
important_idx = sortperm(dvec_vm_ngwp[:].^2; rev = true)
for i in 2:17
dr, dc = BS_vm_ngwp.levlist[important_idx[i]]
w = VM_NGWP[dr, dc, :]
println("(j, k, l) = ", NGWP_jkl(GP_dual, dr, dc))
scatter_gplot(X; marker = w, ms = LinRange(4.0, 14.0, N), c = :greys)
plt = plot!(xlim = [-1.2, 1.2], ylim = [-1.2, 1.2], frame = :none,
cbar = false, clims = (-0.15, 0.15))
# savefig(plt, joinpath(@__DIR__,
# "../paperfigs/SunFlower_barbara_feye_DAG_VM_NGW_important_basis_vector$(lpad(i,2,"0")).png"))
end
#################### Fig. 10(b) barbara pants graph signal
f = matread(joinpath(@__DIR__, "../datasets",
"sunflower_barbara_voronoi.mat"))["f_trouser_voronoi"]
scatter_gplot(X; marker = f, ms = LinRange(4.0, 14.0, N), c = :greys);
plt = plot!(xlim = [-1.2,1.2], ylim = [-1.2,1.2], frame = :none)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/SunFlower_barbara_ftrouser.png"))
#################### Fig. 10(c) barbara eye relative l2 approximation error by various methods
G_Sig.f = reshape(f, (N, 1))
DVEC = getall_expansioncoeffs(G_Sig, GP_dual, VM_NGWP, PC_NGWP, 𝚽)
approx_error_plot(DVEC);
plt = plot!(xguidefontsize = 16, yguidefontsize = 16, legendfontsize = 12)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/SunFlower_barbara_ftrouser_DAG_approx.png"))
#################### Fig. 11 barbara pants 16 most important VM-NGWP vectors (ignore the DC vector)
dmatrix_VM = ngwp_analysis(G_Sig, VM_NGWP)
dvec_vm_ngwp, BS_vm_ngwp = ngwp_bestbasis(dmatrix_VM, GP_dual)
important_idx = sortperm(dvec_vm_ngwp[:].^2; rev = true)
for i in 2:17
dr, dc = BS_vm_ngwp.levlist[important_idx[i]]
w = VM_NGWP[dr, dc, :]
println("(j, k, l) = ", NGWP_jkl(GP_dual, dr, dc))
scatter_gplot(X; marker = w, ms = LinRange(4.0, 14.0, N), c = :greys)
plt = plot!(xlim = [-1.2, 1.2], ylim = [-1.2, 1.2], frame = :none,
cbar = false, clims = (-0.15, 0.15))
# savefig(plt, joinpath(@__DIR__,
# "../paperfigs/SunFlower_barbara_ftrouser_DAG_VM_NGW_important_basis_vector$(lpad(i,2,"0")).png"))
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 1996 | ## script for Fig.7, Fig.8(a), Fig.10(a)
using VoronoiDelaunay, VoronoiCells, GeometricalPredicates
using MultiscaleGraphSignalTransforms, Plots, Graphs, JLD; gr(dpi = 200)
barbara = JLD.load(joinpath(@__DIR__, "..", "datasets", "barbara_gray_matrix.jld"), "barbara")
G, L, X = SunFlowerGraph(); N = nv(G)
#################### Fig. 7(a) sunflower graph
gplot(1.0*adjacency_matrix(G),X; width=1); scatter_gplot!(X; c = :red, ms = LinRange(1,9,N)); plt = plot!(frame = :none)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/SunFlower.png"))
## Voronoi tessellation
width_x = maximum(abs.(X[:,1])) * 2; width_y = maximum(abs.(X[:,2])) * 2;
width = VoronoiDelaunay.max_coord - VoronoiDelaunay.min_coord
center_coord = (VoronoiDelaunay.min_coord + VoronoiDelaunay.max_coord)/2
X_transform = zeros(N,2)
for i in 1:N
X_transform[i,:] = X[i,:] ./ [width_x/width, width_y/width] + [center_coord, center_coord]
end
pts = [Point2D(X_transform[i,1], X_transform[i,2]) for i in 1:N]
tess = DelaunayTessellation(N)
push!(tess, pts)
#################### Fig. 7(b) voronoi tessellation
xx, yy = getplotxy(voronoiedges(tess))
plt = plot(xx, yy, xlim=[1,2], ylim=[1,2], linestyle=:auto, linewidth=1, linecolor=:blue, grid=false, label="", aspect_ratio=1, frame=:box)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/Sunflower_Barbara_Voronoi_cells.png"))
#################### Fig. 8(a) barbara sunflower eye
heatmap(barbara, yflip=true, ratio=1, c=:greys); scatter_gplot!(transform2D(X; s = 20, t = [395, 100]); ms = 2, c = :red); sample_location_plt = plot!(cbar = false, frame = :none)
# savefig(sample_location_plt, joinpath(@__DIR__, "../paperfigs/barb_sunflower_eye.png"))
#################### Fig. 10(a) barbara sunflower pants
heatmap(barbara, yflip=true, ratio=1, c=:greys); scatter_gplot!(transform2D(X; s = 20, t = [280, 320]); ms = 2, c = :red); sample_location_plt = plot!(cbar = false, frame = :none)
# savefig(sample_location_plt, joinpath(@__DIR__, "../paperfigs/barb_sunflower_pants.png"))
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 4789 | # script for Fig.12, Fig.13, Fig.14, Fig.15, Fig.16
using MultiscaleGraphSignalTransforms, JLD, Plots, Graphs, Distances
gr(dpi = 200)
## Build weighted toronto street network graph
G = loadgraph(joinpath(@__DIR__, "../datasets", "new_toronto_graph.lgz")); N = nv(G)
X = load(joinpath(@__DIR__, "../datasets", "new_toronto.jld"), "xy")
dist_X = pairwise(Euclidean(), X; dims = 1)
W = 1.0 .* adjacency_matrix(G)
Weight = zeros(N, N); Weight[W .> 0] = 1 ./ dist_X[W .> 0]; Weight = W .* Weight
L = Matrix(Diagonal(sum(Weight; dims = 1)[:]) - Weight)
𝛌, 𝚽 = eigen(L);
sgn = (maximum(𝚽, dims = 1)[:] .> -minimum(𝚽, dims = 1)[:]) .* 2 .- 1; 𝚽 = 𝚽 .* sgn';
Q = incidence_matrix(G; oriented = true)
edge_weight = 1 ./ sqrt.(sum((Q' * X).^2, dims = 2)[:])
## Build Dual Graph by DAG metric
distDAG = eigDAG_Distance(𝚽, Q, N; edge_weight = edge_weight) #52.375477 seconds
Gstar_Sig = dualgraph(distDAG)
G_Sig = GraphSig(W, xy = X); G_Sig = Adj2InvEuc(G_Sig)
GP_dual = partition_tree_fiedler(Gstar_Sig; swapRegion = false)
GP_primal = pairclustering(𝚽, GP_dual)
@time PC_NGWP = pc_ngwp(𝚽, GP_dual, GP_primal) #119.590168 seconds (12.14 M allocations: 158.035 GiB, 13.89% gc time)
@time VM_NGWP = vm_ngwp(𝚽, GP_dual) #1315.821724 seconds (3.05 M allocations: 495.010 GiB, 7.04% gc time)
#################### Fig. 12(a) a smooth spatial distribution of the street intersections graph signal
f = zeros(N); for i in 1:N; f[i] = length(findall(dist_X[:,i] .< 1/minimum(edge_weight))); end #fneighbor
G_Sig.f = reshape(f, (N, 1))
gplot(W, X; width=1); signal_plt = scatter_gplot!(X; marker = f, plotOrder = :s2l, ms = 3)
# savefig(signal_plt, joinpath(@__DIR__, "../paperfigs/Toronto_fdensity.png"))
#################### Fig. 12(b) spatial distribution signal relative l2 approximation error by various methods
DVEC = getall_expansioncoeffs(G_Sig, GP_dual, VM_NGWP, PC_NGWP, 𝚽)
approx_error_plot(DVEC);
plt = plot!(xguidefontsize = 14, yguidefontsize = 14, legendfontsize = 10)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/Toronto_fdensity_DAG_approx.png"))
#################### Fig. 13 fdensity 16 most important VM-NGWP vectors (ignore the DC vector)
dmatrix_VM = ngwp_analysis(G_Sig, VM_NGWP)
dvec_vm_ngwp, BS_vm_ngwp = ngwp_bestbasis(dmatrix_VM, GP_dual)
important_idx = sortperm(dvec_vm_ngwp[:].^2; rev = true)
for i in 2:17
dr, dc = BS_vm_ngwp.levlist[important_idx[i]]
w = VM_NGWP[dr, dc, :]
println("(j, k, l) = ", NGWP_jkl(GP_dual, dr, dc))
gplot(W, X; width=1)
scatter_gplot!(X; marker = w, plotOrder = :s2l, ms = 3)
plt = plot!(cbar = false, clims = (-0.075,0.075))
# savefig(plt, joinpath(@__DIR__,
# "../paperfigs/Toronto_fdensity_DAG_VM_NGW_important_basis_vector$(lpad(i,2,"0")).png"))
end
#################### Fig. 14(a) pedestrian volume graph signal
fp = load(joinpath(@__DIR__, "../datasets", "new_toronto.jld"), "fp")
G_Sig.f = reshape(fp, (N, 1))
gplot(W, X; width=1); signal_plt = scatter_gplot!(X; marker = fp, plotOrder = :s2l, ms = 3)
# savefig(signal_plt, joinpath(@__DIR__, "../paperfigs/Toronto_fp.png"))
#################### Fig. 14(b) pedestrian signal relative l2 approximation error by various methods
DVEC = getall_expansioncoeffs(G_Sig, GP_dual, VM_NGWP, PC_NGWP, 𝚽)
approx_error_plot(DVEC)
plt = plot!(xguidefontsize = 14, yguidefontsize = 14, legendfontsize = 10)
# savefig(plt, joinpath(@__DIR__, "../paperfigs/Toronto_fp_DAG_approx.png"))
#################### Fig. 15 pedestrian signal 16 most important VM-NGWP vectors
dmatrix_VM = ngwp_analysis(G_Sig, VM_NGWP)
dvec_vm_ngwp, BS_vm_ngwp = ngwp_bestbasis(dmatrix_VM, GP_dual)
important_idx = sortperm(dvec_vm_ngwp[:].^2; rev = true)
for i in 1:16
dr, dc = BS_vm_ngwp.levlist[important_idx[i]]
w = VM_NGWP[dr, dc, :]
println("(j, k, l) = ", NGWP_jkl(GP_dual, dr, dc))
gplot(W, X; width=1)
scatter_gplot!(X; marker = w, plotOrder = :s2l, ms = 3)
plt = plot!(cbar = false, clims = (-0.075,0.075))
# savefig(plt, joinpath(@__DIR__,
# "../paperfigs/Toronto_fp_DAG_VM_NGW_important_basis_vector$(lpad(i,2,"0")).png"))
end
#################### Fig. 16 pedestrian signal 16 most important PC-NGWP vectors
dmatrix_PC = ngwp_analysis(G_Sig, PC_NGWP)
dvec_pc_ngwp, BS_pc_ngwp = ngwp_bestbasis(dmatrix_PC, GP_dual)
important_idx = sortperm(dvec_pc_ngwp[:].^2; rev = true)
for i in 1:16
dr, dc = BS_pc_ngwp.levlist[important_idx[i]]
w = PC_NGWP[dr, dc, :]
println("(j, k, l) = ", NGWP_jkl(GP_dual, dr, dc))
sgn = (maximum(w) > -minimum(w)) * 2 - 1
gplot(W, X; width=1)
scatter_gplot!(X; marker = sgn .* w, plotOrder = :s2l, ms = 3)
plt = plot!(cbar = false, clims = (-0.075,0.075))
# savefig(plt, joinpath(@__DIR__,
# "../paperfigs/Toronto_fp_DAG_PC_NGW_important_basis_vector$(lpad(i,2,"0")).png"))
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 5877 | ################################################################################
####################### Approximation error plot ###############################
################################################################################
function approx_error2(DVEC::Array{Array{Float64,1},1},
T::Vector{String}, L::Vector{Tuple{Symbol,Symbol}},
frac::Float64 = 0.30)
# This version plots the relative L2 errors against
# the FRACTION of coefficients retained.
plot(xaxis = "Fraction of Coefficients Retained",
yaxis = "Relative Approximation Error")
for i = 1:length(DVEC)
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2) # the smallest first
er = sqrt.(reverse(cumsum(dvec_sort)))/dvec_norm
er[er .== 0.0] .= minimum(er[er .!= 0.0]) # avoid blowup by taking log in the plot below
# er is the relative L^2 error of the whole thing: length(er)=N.
p = Int64(floor(frac*N)) + 1 # upper limit
plot!(frac*(0:(p-1))/(p-1), er[1:p], yaxis=:log, xlims = (0.,frac),
label = T[i], line = L[i], linewidth = 2, grid = false)
end
display(current())
end
function approx_error3(DVEC::Array{Array{Float64,1},1},
T::Vector{String}, L::Vector{Tuple{Symbol,Symbol}},
N::Int64)
# This version plots the relative L2 errors against
# the NUMBER of coefficients retained.
plot(xaxis = "Number of Coefficients Retained",
yaxis = "Relative Approximation Error")
for i = 1:length(DVEC)
dvec = DVEC[i]
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2) # the smallest first
er = sqrt.(reverse(cumsum(dvec_sort)))/dvec_norm
er[er .== 0.0] .= minimum(er[er .!= 0.0]) # avoid blowup by taking log in the plot below
# er is the relative L^2 error of the whole thing: length(er)=N.
plot!(0:N-1, er[1:N], yaxis=:log, label = T[i], line = L[i],
linewidth = 2, grid = false)
end
display(current())
end
################################################################################
############ Computing a weight matrix using the Gaussian affinity #############
################################################################################
function image_Gaussian_affinity(img::Matrix{Float64}, r::Int64, σ::Float64)
# Get the neighbors for affinity matrix computation
l = 2*r + 1
temp_x, temp_y = fill(1,l^2), fill(1,l^2)
temp_xy = CartesianIndices((1:l,1:l))
for i = 1:l^2
temp_x[i], temp_y[i] = temp_xy[i][1], temp_xy[i][2]
end
# (r+1, r+1) is the index of the center location.
temp_ind = ((temp_x .- (r + 1)).^2 + (temp_y .- (r + 1)).^2) .<= r^2
# Now, temp_ind indicates those points withinin the circle of radius r
# from the center while neighbor_x, neighbor_y represent relative positions
# of those points from the center.
neighbor_x = temp_x[temp_ind] .- (r + 1)
neighbor_y = temp_y[temp_ind] .- (r + 1)
# So, for any index (x, y), points within (x ± neighbor_x, y ± neighbor_y) are
# its neighbors for the purpose of calculating affinity
# Create affinity matrix
m, n = size(img)
sig = img[:]
W = fill(0., (m*n,m*n))
for i = 1:m*n
cur = CartesianIndices((m,n))[i]
for j = 1:length(neighbor_x) # assuming dim(neighbor_x) == dim(neighbor_y)
if 1 <= cur[1] + neighbor_x[j] <= m && 1 <= cur[2] + neighbor_y[j] <= n
tempd = LinearIndices((m,n))[cur[1] + neighbor_x[j], cur[2] + neighbor_y[j]]
W[i,tempd] = exp(-(sig[i] - sig[tempd])^2/σ)
end
end
end
return sparse(W)
end # end of the image_Gaussian_affinity function
################################################################################
######## Display top 9 basis vectors of various bases for an image data ########
################################################################################
function top_vectors_plot2(dvec::Array{Float64, 2}, m::Int64, n::Int64, BS::BasisSpec, GP::GraphPart;
clims::Tuple{Float64,Float64} = (-0.01, 0.01))
# Get the indices from max to min in terms of absolute value of the coefs
# Note that m*n == length(dvec); m and n are the image size.
sorted_ind = sortperm(abs.(dvec[:]), rev = true);
# Set up the layout as 3 x 3 subplots
plot(9, layout = (3,3), framestyle = :none, legend = false)
# Do the display!
for i=1:9
dvecT = fill(0., size(dvec))
dvecT[sorted_ind[i]] = 1
f = ghwt_synthesis(dvecT, GP, BS)
heatmap!(reshape(f, (m,n)), subplot=i, ratio=1, yaxis=:flip,
showaxis=false, ticks = false, color = :grays, clims = clims)
end
display(current())
end
################################################################################
function top_vectors_plot3(dvec::Array{Float64, 2}, m::Int64, n::Int64, BS::BasisSpec,
GP::GraphPart; clims::Tuple{Float64,Float64} = (-0.01, 0.01), K::Int64 = 9)
# Get the indices from max to min in terms of absolute value of the coefs
# Note that m*n == length(dvec); m and n are the image size.
sorted_ind = sortperm(abs.(dvec[:]), rev = true);
# Set up the layout as 3 x 3 subplots
plot(K, layout = (Int(sqrt(K)), Int(sqrt(K))), framestyle = :none, legend = false)
# Do the display!
for i=1:K
dvecT = fill(0., size(dvec))
dvecT[sorted_ind[i]] = 1
f = ghwt_synthesis(dvecT, GP, BS)
heatmap!(reshape(f, (m,n)), subplot=i, ratio=1, yaxis=:flip,
showaxis=false, ticks = false, color = :grays, clims = clims)
end
display(current())
end
################################################################################
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 2041 | # Script to generate figures in Figure 2.
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
# First define a utility function "Glevel", which generate a Graph Signal that
# are piecewise constants whose values are actual region indices "k".
function Glevel(G::GraphSig, GP::GraphPart, j::Int64)
f = zeros(size(G.f))
for k in 1:size(GP.rs,1)
a = GP.rs[k,j+1]
b = GP.rs[k+1,j+1] - 1
if b == -1
break
end
f[a:b] .= k*1.0
end
Gsub = deepcopy(G)
Gsub.f[GP.ind] = f
return Gsub
end
# Set up the resolution and display size
gr(dpi=200, size=(800,600))
# Load the Toronto street network (vehicular volume counts as its graph signal)
JLD2.@load "Toronto_new.jld2"
tmp1 = toronto["G"]
G=GraphSig(tmp1["W"],xy=tmp1["xy"],f=tmp1["f"],name =tmp1["name"],
plotspecs = tmp1["plotspecs"])
# Assign correct edge weights via 1/Euclidean distance
G = Adj2InvEuc(G)
# Perform the hierarchical graph partitioning using the Fiedler vectors
GP = partition_tree_fiedler(G) # Lrw by default
# Compute the expansion coefficients of the full GHWT c2f dictionary
dmatrix = ghwt_analysis!(G, GP=GP)
N = length(G.f)
# Fig. 2a: Level 1 first since Level 0 is not interesting
j = 1
GraphSig_Plot(Glevel(G,GP,j), linewidth = 1., markersize = 4.,
markercolor = :viridis, markerstrokealpha =0., notitle = true, nocolorbar = true)
plot!(showaxis = false, ticks = false)
savefig("toronto_j1.pdf")
savefig("toronto_j1.png")
# Fig. 2b: Level 2
j = 2
GraphSig_Plot(Glevel(G,GP,j), linewidth = 1., markersize = 4.,
markercolor = :viridis, markerstrokealpha =0., notitle = true, nocolorbar = true)
plot!(showaxis = false, ticks = false)
savefig("toronto_j2.pdf")
savefig("toronto_j2.png")
# Fig. 2c: Level 3
j = 3
GraphSig_Plot(Glevel(G,GP,j), linewidth = 1., markersize = 4.,
markercolor = :viridis, markerstrokealpha =0., notitle = true, nocolorbar = true)
plot!(showaxis = false, ticks = false)
savefig("toronto_j3.pdf")
savefig("toronto_j3.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 2388 | # Script to generate figures in Figure 4.
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
# Set up the resolution and display size
gr(dpi=200, size=(800,600))
# Load the Toronto street network (vehicular volume counts as its graph signal)
JLD2.@load "Toronto_new.jld2"
tmp1 = toronto["G"]
G=GraphSig(tmp1["W"],xy=tmp1["xy"],f=tmp1["f"],name =tmp1["name"],
plotspecs = tmp1["plotspecs"])
# Assign correct edge weights via 1/Euclidean distance
G = Adj2InvEuc(G)
# Perform the hierarchical graph partitioning using the Fiedler vectors
GP = partition_tree_fiedler(G) # Lrw by default
# Compute the expansion coefficients of the full GHWT c2f dictionary
dmatrix = ghwt_analysis!(G, GP=GP)
N = length(G.f)
# Fig. 4a: Sacling vector ψ^1_{0,0}, i.e., (j,k,l)=(1,0,0).
j = 1
loc = 1
BS = bs_level(GP, j)
dvec = zeros(N, 1)
dvec[loc,1] = 1.0
(f, GS) = ghwt_synthesis(dvec, GP, BS, G)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markerstrokealpha = 0.,
markercolor = :viridis, notitle = true, nocolorbar = true, clim = (-0.01, 0.01))
plot!(showaxis = false, ticks = false)
k, l = BS.levlist[loc][1], BS.levlist[loc][2]
print(j," ",(rs_to_region(GP.rs, GP.tag))[k,l]," ",GP.tag[k,l])
savefig("toronto_psi100.pdf")
savefig("toronto_psi100.png")
# Fig. 4b: Haar vector ψ^2_{0,1}, i.e., (j,k,l)=(2,0,1).
j = 2
loc = 2
BS = bs_level(GP, j)
dvec = zeros(N, 1)
dvec[loc,1] = 1.0
(f, GS) = ghwt_synthesis(dvec, GP, BS, G)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markerstrokealpha = 0.,
markercolor = :viridis, notitle = true, nocolorbar = true, clim = (-0.01, 0.01))
plot!(showaxis = false, ticks = false)
k, l = BS.levlist[loc][1], BS.levlist[loc][2]
print(j," ",(rs_to_region(GP.rs, GP.tag))[k,l]," ",GP.tag[k,l])
savefig("toronto_psi201.pdf")
savefig("toronto_psi201.png")
# Fig. 4c: Walsh vector ψ^3_{0,9}, i.e., (j,k,l)=(3,0,9).
#j = 5
#loc = 1000
j = 3
loc = 10
BS = bs_level(GP, j)
dvec = zeros(N, 1)
dvec[loc,1] = 1
(f, GS) = ghwt_synthesis(dvec, GP, BS, G)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markerstrokealpha = 0.,
markercolor = :viridis, notitle = true, nocolorbar = true, clim = (-0.01, 0.01))
plot!(showaxis = false, ticks = false)
k, l = BS.levlist[loc][1], BS.levlist[loc][2]
print(j," ",(rs_to_region(GP.rs, GP.tag))[k,l]," ",GP.tag[k,l])
savefig("toronto_psi309.pdf")
savefig("toronto_psi309.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 2644 | # Script to generate Figure 15.
using Plots, SparseArrays, JLD2, LinearAlgebra, Wavelets, MultiscaleGraphSignalTransforms
include("auxilaries.jl")
include("../../../src/unbalanced_haar_image.jl")
# Set up the resolution and display size
gr(dpi=200, size=(800,600))
# Load the Barbara image data
JLD2.@load "barbara.jld2"
# smaller face region of size 100x100
row_zoom = 71:170
col_zoom = 341:440
display(heatmap(barbara[row_zoom, col_zoom],ratio=1, yaxis =:flip,
showaxis = false, ticks = false, color = :grays, clims = (0,1)))
# Extract that portion of the image
matrix = deepcopy(barbara[row_zoom, col_zoom])
#
# Perform the image partition using the penalized total variation and then
# compute the expansion coefficients
#
p = 3.0
maxlev = 9 # need this to reach the single node leaves
GPcols = PartitionTreeMatrix_unbalanced_haar_binarytree(matrix, maxlev, p)
maxlev = 8 # need this to reach the single node leaves
GProws = PartitionTreeMatrix_unbalanced_haar_binarytree(copy(matrix'), maxlev, p)
# copy() is necessary to switch the Adjoint type to a regular Matrix{Float64}.
dmatrix = ghwt_analysis_2d(matrix, GProws, GPcols)
#
# Compute the graph Haar coefficients from the previous PTV partition tree
#
BS_haar_rows = bs_haar(GProws)
BS_haar_cols = bs_haar(GPcols)
dvec_haar, loc_haar = BS2loc(dmatrix, GProws, GPcols, BS_haar_rows, BS_haar_cols)
#
# Compute the eGHWT best basis
#
dvec_eghwt, loc_eghwt = eghwt_bestbasis_2d(matrix, GProws, GPcols)
#
# Classical Haar transform via Wavelets.jl with direct input
#
dvec_classichaar = dwt(matrix, wavelet(WT.haar))
#
# Classical Haar transform via Wavelets.jl via putting in the dyadic image
#
matrix2 = zeros(128,128)
matrix2[15:114,15:114] = deepcopy(matrix)
dvec_classichaar2 = dwt(matrix2, wavelet(WT.haar))
#
# Classical Haar transform via Wavelets.jl via putting in the dyadic image
#
matrix3 = zeros(128,128)
matrix3[1:100,1:100] = deepcopy(matrix)
matrix3[101:end,1:100] = deepcopy(matrix[end:-1:end-27,1:100])
matrix3[:,101:end] = matrix3[:,100:-1:73]
dvec_classichaar3 = dwt(matrix3, wavelet(WT.haar))
# Figure 15 (Approximation error plot up to the top 5000 coefficients)
DVEC = [ dvec_classichaar[:], dvec_classichaar2[:], dvec_classichaar3[:],
dvec_haar[:], dvec_eghwt[:] ]
T = [ "Classic Haar (direct)", "Classic Haar (zero pad)",
"Classic Haar (even refl)", "Graph Haar (PTV cost)", "eGHWT (PTV cost)" ]
L = [ (:dashdot, :orange), (:dashdot, :red), (:dashdot, :green),
(:solid, :blue), (:solid, :black) ]
approx_error3(DVEC, T, L, 5000)
savefig("barbara_face100_nondyadic_haar_error.pdf")
savefig("barbara_face100_nondyadic_haar_error.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 5153 | # Generate figures on the Toronto street network
# Load necessary packages
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
include("auxilaries.jl")
# Set up the resolution and display size
gr(dpi=200, size=(800,600))
# Load the Toronto street network (vehicular volume counts as its graph signal)
JLD2.@load "Toronto_new.jld2"
tmp1 = toronto["G"]
G=GraphSig(tmp1["W"],xy=tmp1["xy"],f=tmp1["f"],name =tmp1["name"],
plotspecs = tmp1["plotspecs"])
# Generate Fig. 10a
# GraphSig_Plot(G, linewidth = 1., markersize = 4.,
# markercolor = :viridis, markerstrokealpha = 0., notitle = true)
gplot(G.W, G.xy; width=1);
plt = scatter_gplot!(G.xy; marker = G.f, plotOrder = :s2l,
ms = G.f*8/maximum(G.f), mswidth=1)
display(plt)
savefig("toronto_vv.pdf")
savefig("toronto_vv.png")
# Assign correct edge weights via 1/Euclidean distance
G = Adj2InvEuc(G)
# Perform the hierarchical graph partitioning using the Fiedler vectors
GP = partition_tree_fiedler(G) # Lrw by default
# Compute the expansion coefficients of the full GHWT c2f dictionary
dmatrix = ghwt_analysis!(G, GP=GP)
# Extract the coefficients corresponding to the Haar basis
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
# Extract the coefficients corresponding to the Walsh basis
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
# Compute the c2f GHWT best basis and the coefficients
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
# Compute the f2c GHWT best basis and the coefficients
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
# Compute the eGHWT best basis and the coefficients
dvec_eghwt, BS_eghwt = eghwt_bestbasis(dmatrix, GP)
################################################################################
###################### Generate approximaation errors ##########################
################################################################################
# Generate Fig. 10b up to 50% of the coefficients retained.
DVEC = [ dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:] ]
T = [ "Graph Haar","Graph Walsh","GHWT_c2f", "GHWT_f2c", "eGHWT" ]
L = [ (:dashdot, :orange), (:dashdot, :blue), (:solid, :red), (:solid, :green),
(:solid, :black) ]
approx_error2(DVEC, T, L, 0.5)
savefig("toronto_vv_approx_error.pdf")
savefig("toronto_vv_approx_error.png")
################################################################################
######################### Synthesis by top vectors #############################
################################################################################
color_limit_residual = (0., 0.15)
function top_vectors_residual(p::Int64, dvec::Array{Float64,2},
BS::BasisSpec, GP::GraphPart, G::GraphSig)
sorted_dvec = sort(abs.(dvec[:]), rev = true)
dvecT = copy(dvec)
dvecT[abs.(dvec) .< sorted_dvec[p]].= 0
(recon, GS)= ghwt_synthesis(dvecT, GP, BS, G)
GS.name = "Square of the residual"
#GS.f = (G.f - GS.f).^2
#print((maximum(GS.f), minimum(GS.f)))
#GraphSig_Plot(GS)
GS.f = (G.f - recon).^2 ./(G.f.^2)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markercolor = :viridis,
markerstrokealpha =0., clim = color_limit_residual)
display(current())
end
################################################################################
############## Visuallization of Top basis vectors #############################
################################################################################
### function to plot the basis vectors of user specified range
# Recommended number of basis vectors are squared numbers, e.g., 9, 16, 25.
function top_vectors_plot(dvec::Array{Float64, 2}, BS::BasisSpec, GP::GraphPart,
G::GraphSig; istart = 2, iend = 17, ms = 2)
sorted_ind = sortperm(dvec[:].^2; rev = true)
ibs = iend-istart+1
n1 = Int64(sqrt(ibs))
plot(layout = Plots.grid(n1, n1))
idsp = 1
for ib in istart:iend
dvecT = fill(0., size(dvec))
dvecT[sorted_ind[ib]] = 1
bv = ghwt_synthesis(dvecT, GP, BS)
gplot!(G.W, G.xy; width=0.25, subplot=idsp, color=:gray)
scatter_gplot!(G.xy; marker = bv, plotOrder = :propabs, ms, subplot=idsp)
plt = plot!(cbar = false, clims = (-0.001,0.001), axis=([], false), subplot=idsp)
idsp += 1
end
display(current())
end # of top_vectors_plot
### Fig. 11a: Haar
top_vectors_plot(dvec_haar, BS_haar, GP, G, iend=10)
savefig("toronto_vv_haar09.png")
savefig("toronto_vv_haar09.pdf")
### Walsh
top_vectors_plot(dvec_walsh, BS_walsh, GP, G, iend=10)
savefig("toronto_vv_walsh09.png")
savefig("toronto_vv_walsh09.pdf")
### Fig. 11b: GHWT_c2f (= Walsh in this case)
top_vectors_plot(dvec_c2f, BS_c2f, GP, G, iend=10)
savefig("toronto_vv_c2f09.png")
savefig("toronto_vv_c2f09.pdf")
### Fig. 11c: GHWT_f2c
top_vectors_plot(dvec_f2c, BS_f2c, GP, G, iend=10)
savefig("toronto_vv_f2c09.png")
savefig("toronto_vv_f2c09.pdf")
### Fig. 11d: eGHWT
top_vectors_plot(dvec_eghwt, BS_eghwt, GP, G, iend=10)
savefig("toronto_vv_eghwt09.png")
savefig("toronto_vv_eghwt09.pdf")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 7477 | # Script to generate Figures 12, 13, and 14.
using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
include("auxilaries.jl")
# Set up the resolution and display size
gr(dpi=200, size=(800,600))
# Load the Barbara image data
JLD2.@load "barbara.jld2"
matrix = deepcopy(barbara)
# Here are the list of local regions of interest:
# full image
row_zoom = 1:512
col_zoom = 1:512
# Generate the original Barbara image as a reference.
heatmap(matrix[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, color = :grays)
savefig("barbara.pdf")
savefig("barbara.png")
#
# Initialize the regular balanced binary partition and compute the expansion coefficients
#
dmatrix, GProws, GPcols = eghwt_init_2d_Lindberg(matrix)
#
# Compute the coefficients of different bases with which we compare
#
# Haar
BS_haar_rows = bs_haar(GProws)
BS_haar_cols = bs_haar(GPcols)
dvec_haar, loc_haar = BS2loc(dmatrix, GProws, GPcols, BS_haar_rows, BS_haar_cols)
# Walsh
BS_walsh_rows = bs_walsh(GProws)
BS_walsh_cols = bs_walsh(GPcols)
dvec_walsh, loc_walsh = BS2loc(dmatrix, GProws, GPcols, BS_walsh_rows, BS_walsh_cols)
# GHWT c2f
fcols, jmax_col = size(GProws.tag);
frows, jmax_row = size(GPcols.tag);
dmatrix_rows = reshape(dmatrix, (frows, jmax_row, fcols*jmax_col))
dmatrix_cols = Array{Float64,3}(reshape(dmatrix',(fcols, jmax_col, frows*jmax_row)))
dvec_c2f_rows, BS_c2f_rows = ghwt_c2f_bestbasis(dmatrix_rows, GProws)
dvec_c2f_cols, BS_c2f_cols = ghwt_c2f_bestbasis(dmatrix_cols, GPcols)
dvec_c2f, loc_c2f = BS2loc(dmatrix, GProws, GPcols, BS_c2f_rows, BS_c2f_cols)
# GHWT f2c
dvec_f2c_rows, BS_f2c_rows = ghwt_f2c_bestbasis(dmatrix_rows, GProws)
dvec_f2c_cols, BS_f2c_cols = ghwt_f2c_bestbasis(dmatrix_cols, GPcols)
dvec_f2c, loc_f2c = BS2loc(dmatrix, GProws, GPcols, BS_f2c_rows, BS_f2c_cols)
# eGHWT
dvec_eghwt, loc_eghwt = eghwt_bestbasis_2d(matrix, GProws, GPcols)
################################################################################
##################### Visualize the results of synthesis #######################
################################################################################
### function to plot the image synthesized by top p vectors
function top_vectors_synthesis_2d(p::Int64, dvec::Vector{Float64}, loc::Matrix{Int64},
GProws::GraphPart, GPcols::GraphPart, dmatrix::Matrix{Float64})
sorted_dvec = sort(abs.(dvec[:]), rev = true)
dvecT = copy(dvec)
dvecT[abs.(dvec) .< sorted_dvec[p]].= 0
matrix_syn = eghwt_synthesis_2d(dvecT, loc, GProws, GPcols)
display(heatmap(matrix_syn[row_zoom, col_zoom],ratio=1, yaxis =:flip,
showaxis = false, ticks = false, colorbar= false,
clims = (minimum(matrix), maximum(matrix)), color = :grays))
mse = norm(matrix - matrix_syn,2)^2/length(matrix)
snr = 20 * log10(norm(matrix,2)/norm(matrix - matrix_syn,2))
psnr = 10 * log10(maximum(matrix)^2/mse)
println("MSE: ", mse, "SNR (dB): ", snr, "PSNR (dB): ", psnr)
return matrix_syn
end
################################################################################
percent = 1/32;
p = Int64(floor(percent*length(matrix)))
# Fig. 13a: Haar
haar32 = top_vectors_synthesis_2d(p, dvec_haar, loc_haar, GProws, GPcols, dmatrix)
savefig("barbara_haar32.pdf")
savefig("barbara_haar32.png")
# Walsh
walsh32 = top_vectors_synthesis_2d(p, dvec_walsh, loc_walsh, GProws, GPcols, dmatrix)
savefig("barbara_walsh32.pdf")
savefig("barbara_walsh32.png")
# Fig. 13b: GHWT c2f
c2f32 = top_vectors_synthesis_2d(p, dvec_c2f, loc_c2f, GProws, GPcols, dmatrix)
savefig("barbara_c2f32.pdf")
savefig("barbara_c2f32.png")
# Fig. 13c: GHWT f2c
f2c32 = top_vectors_synthesis_2d(p, dvec_f2c, loc_f2c, GProws, GPcols, dmatrix)
savefig("barbara_f2c32.pdf")
savefig("barbara_f2c32.png")
# Fig. 13d: eGHWT
eghwt32 = top_vectors_synthesis_2d(p, dvec_eghwt, loc_eghwt, GProws, GPcols, dmatrix)
savefig("barbara_eghwt32.pdf")
savefig("barbara_eghwt32.png")
#
# Zoom up the face region of those approximations (Fig. 14a)
#
row_zoom = 1:180
col_zoom = 330:450
# Haar
display(heatmap(haar32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_face_haar32.pdf")
savefig("barbara_face_haar32.png")
# Walsh
display(heatmap(walsh32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_face_walsh32.pdf")
savefig("barbara_face_walsh32.png")
# GHWT c2f
display(heatmap(c2f32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_face_c2f32.pdf")
savefig("barbara_face_c2f32.png")
# GHWT f2c
display(heatmap(f2c32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_face_f2c32.pdf")
savefig("barbara_face_f2c32.png")
# eGHWT
display(heatmap(eghwt32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_face_eghwt32.pdf")
savefig("barbara_face_eghwt32.png")
#
# Zoom up the left leg region of those approximations (Fig. 14b)
#
row_zoom = 300:512
col_zoom = 400:512
# Haar
display(heatmap(haar32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_lleg_haar32.pdf")
savefig("barbara_lleg_haar32.png")
# Walsh
display(heatmap(walsh32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_lleg_walsh32.pdf")
savefig("barbara_lleg_walsh32.png")
# GHWT c2f
display(heatmap(c2f32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_lleg_c2f32.pdf")
savefig("barbara_lleg_c2f32.png")
# GHWT f2c
display(heatmap(f2c32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_lleg_f2c32.pdf")
savefig("barbara_lleg_f2c32.png")
# eGHWT
display(heatmap(eghwt32[row_zoom, col_zoom],ratio=1, yaxis =:flip, showaxis = false,
ticks = false, colorbar = false, clims = (minimum(matrix), maximum(matrix)), color = :grays))
savefig("barbara_lleg_eghwt32.pdf")
savefig("barbara_lleg_eghwt32.png")
################################################################################
###################### Generate approximaation errors ##########################
################################################################################
# Generate Fig. 12b up to 50% of the coefficients retained.
DVEC =[ dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:] ]
T = [ "Graph Haar","Graph Walsh","GHWT_c2f", "GHWT_f2c", "eGHWT" ]
L = [ (:dashdot, :orange), (:dashdot, :blue), (:solid, :red), (:solid, :green),
(:solid, :black)]
approx_error2(DVEC, T, L, 0.5)
savefig("barbara_approx_error.pdf")
savefig("barbara_approx_error.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 2856 | # Script to generate Figures 16 and 17
using TestImages, Plots, SparseArrays, LinearAlgebra, Wavelets, MultiscaleGraphSignalTransforms
include("auxilaries.jl")
# Set up the resolution and display size
gr(dpi=200, size=(800,600))
# Load the cameraman image and subsample it to make it as 128x128 image
img = testimage("camera");
matrix = convert(Array{Float64,2}, img)[1:4:512,1:4:512]
m, n = size(matrix)
# Fig. 16a
display(heatmap(matrix, ratio=1, yaxis =:flip, showaxis = false, ticks = false,
color = :grays, clim = (0,1), colorbar = false))
savefig("cameraman.pdf")
savefig("cameraman.png")
# Now, let's compute the weight matrix based on the Gaussian affinity
# of the small windows (or radius r) around pixels and the pixel locations.
# Set up the key parameters
r = 5; # specify radius of neighbors
σ = 0.007
# Do the weight matrix computation
W007 = image_Gaussian_affinity(matrix, r, σ)
# Preprocess to generate G (GraphSig struct) and GP (GraphPart struct)
# Note that GraphSig requires a matrix data even if it is just a one vector, i.e.,
# f = matrix[:] does not work!
G007 = GraphSig(W007, f = reshape(matrix, (length(matrix), 1)))
GP007 = partition_tree_fiedler(G007)
dmatrix007 = ghwt_analysis!(G007, GP=GP007)
# Construct or search the specific basis
# Haar
BS_haar007 = bs_haar(GP007)
dvec_haar007 = dmatrix2dvec(dmatrix007, GP007, BS_haar007)
# eGHWT
dvec_eghwt007, BS_eghwt007 = eghwt_bestbasis(dmatrix007, GP007)
# Generate Fig. 17a
top_vectors_plot2(dvec_eghwt007, m, n, BS_eghwt007, GP007)
savefig("cameraman_eghwt09_sigma007.pdf")
savefig("cameraman_eghwt09_sigma007.png")
# Now change the σ value
σ = 0.07
W07 = image_Gaussian_affinity(matrix, r, σ)
# Preprocess to generate G (GraphSig struct) and GP (GraphPart struct)
G07 = GraphSig(W07, f = reshape(matrix, (length(matrix), 1)))
GP07 = partition_tree_fiedler(G07)
dmatrix07 = ghwt_analysis!(G07, GP=GP07)
# Construct or search the specific basis
# Haar
BS_haar07 = bs_haar(GP07)
dvec_haar07 = dmatrix2dvec(dmatrix07, GP07, BS_haar07)
# eGHWT
dvec_eghwt07, BS_eghwt07 = eghwt_bestbasis(dmatrix07, GP07)
# Generate Fig. 17b
top_vectors_plot2(dvec_eghwt07, m, n, BS_eghwt07, GP07)
savefig("cameraman_eghwt09_sigma07.pdf")
savefig("cameraman_eghwt09_sigma07.png")
# Finally, do the classical Haar transform in Wavelets.jl
dvec_classichaar = dwt(matrix, wavelet(WT.haar))
# Fig. 16b (Approximation error plot)
DVEC = [ dvec_classichaar[:], dvec_haar07[:], dvec_eghwt07[:],
dvec_haar007[:], dvec_eghwt007[:] ]
T = [ "Classical Haar", "Graph Haar (σ = 0.07)",
"eGHWT (σ = 0.07)", "Graph Haar (σ = 0.007)",
"eGHWT (σ = 0.007)"]
L = [ (:dashdot,:orange), (:dashdot, :red), (:dashdot, :black),
(:solid, :red), (:solid, :black) ]
approx_error2(DVEC, T, L, 0.5)
savefig("cameraman_approx_error.pdf")
savefig("cameraman_approx_error.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 5925 | # Script to generate Figures 18 and 19
using FileIO, Images, ImageFiltering, JLD2, MultiscaleGraphSignalTransforms, MultivariateStats, Plots, StatsBase
include("auxilaries.jl")
# Set up the resolution and display size
gr(dpi=200, size=(800,600))
# Load the original 512x512 composite texture image and its mastge
textures = FileIO.load("5block.png")
textures = Matrix{Float64}(textures) # convert it to a regular matrix
# Compute the mask image using the Gabor features + PCA
#
# Step 1: Parameter setups
# Orientations
ndir = 2
Θ = [ π/3; 5*π/6 ]
# Spatial frequencies
Ξ = [0.2; 0.3; 0.4; 0.5]
# Convert them to wavelengths
Λ = 1.0 ./ Ξ
# Gaussian bandwidth for Gabor filters
bw = 1.0
σ = 1.0/π * sqrt(log(2)/2) * (2^bw+1)/(2^bw-1)
# Spatial aspect ratio: σx = σ; σy = σ/γ
γ = 1.0
# Step 2: Apply Gabor filters; the same size as the input image.
m, n = size(textures)
K = length(Θ) *length(Λ) # K should be square number
F = zeros(m, n, K) # This is the space for the Gabor filtered images
Fg = zeros(m, n, K) # This is the space for the Gaussian smoothed version of F
kr = zeros(m+1, n+1, K)
ki = zeros(m+1, n+1, K)
k = 1
kl = (0, 0)
for θ in Θ
for λ in Λ
kernel = Kernel.gabor(m, n, λ*σ, θ, λ, γ, 0.0)
kernel[1] ./= 2*π*σ*σ/γ
kernel[2] ./= 2*π*σ*σ/γ
global kl = size(kernel[1])
kr[1:kl[1],1:kl[2],k] = kernel[1]
ki[1:kl[1],1:kl[2],k] = kernel[2]
cker = (centered(kernel[1]), centered(kernel[2]))
F[:,:,k] = sqrt.(imfilter(textures, reflect(cker[1])).^2 +
imfilter(textures, reflect(cker[2])).^2)
# "reflect"ing the kernel is necessary for convolution;
# otherwise it does the correlation.
Fg[:,:,k] = imfilter(F[:,:,k], Kernel.gaussian(3.0*λ))
global k += 1
end
end
# Display those Gabor features
plot(K, layout=(length(Θ),length(Λ)), framestyle=:none, legend=false)
for k = 1:K
heatmap!(kr[226:286,226:286,k], subplot=k, ratio=1, yaxis=:flip, showaxis=false,
ticks=false, c=:grays, clims=(minimum(kr), maximum(kr)), colorbar=false)
end
display(current())
# Displaying the imaginary part of Gabor kernels may not be necessary...
#plot(K, layout=(Int(sqrt(K)),Int(sqrt(K))), framestyle=:none, legend=false)
#for k = 1:K
# heatmap!(ki[:,:,k], subplot=k, ratio=1, yaxis=:flip, showaxis=false,
# ticks=false, c=:grays, clims=(minimum(ki), maximum(ki)), colorbar=false)
#end
#display(current())
plot(K, layout=(length(Θ),length(Λ)), framestyle=:none, legend=false)
for k = 1:K
heatmap!(Fg[:,:,k], subplot=k, ratio=1, yaxis=:flip, showaxis=false,
ticks=false, c=:grays, clims=(0, maximum(F)), colorbar=false)
end
display(current())
# Step 3. Compute the PCA and extract the first principal component
Xtr=reshape(Fg, (m*n, K))
Xtr=Xtr'
dt=StatsBase.fit(ZScoreTransform, Xtr) # Each variable is standardized to have
# mean 0, stddev 1
Xtr=StatsBase.transform(dt, Xtr)
M = MultivariateStats.fit(PCA, Xtr)
Ytr=MultivariateStats.transform(M, Xtr)
Ytr=Ytr'
Ytr=reshape(Ytr, (m, n, size(Ytr, 2)))
plot(K, layout=(length(Θ),length(Λ)), framestyle=:none, legend=false)
for k = 1:outdim(M)
heatmap!(Ytr[:,:,k], subplot=k, ratio=1, yaxis=:flip, showaxis=false,
ticks=false, c=:grays, clims=(minimum(Ytr), maximum(Ytr)), colorbar=false)
end
display(current())
mask = Ytr[:,:,1]
display(heatmap(mask, ratio=1, c=:grays, yaxis=:flip))
# End of 512 x 512 mask generation.
#
# Subsample both the original and mask images to 128 x 128
#
textures = deepcopy(textures[1:4:end,1:4:end])
mask = deepcopy(mask[1:4:end,1:4:end])
m, n = size(textures) # recapture the subsampled matrix size
#
# Normalize the mask
#
mask = (mask.-minimum(mask))./(maximum(mask)-minimum(mask));
#
# Generate Fig. 18a
#
display(heatmap(textures, ratio=1, yaxis =:flip, showaxis = false, ticks = false,
color = :grays, colorbar = false))
savefig("textures_orig.pdf")
savefig("textures_orig.png")
#
# Generate Fig. 18b
#
display(heatmap(mask, ratio=1, yaxis =:flip, showaxis = false, ticks = false,
color = :grays, colorbar = false))
savefig("textures_mask.pdf")
savefig("textures_mask.png")
#
# Now, let's compute the weight matrix based on the Gaussian affinity
# of the small windows (or radius r) around pixels and the pixel locations.
#
# Set up the key parameters
r = 3 # specify radius of neighbors; so far the best
σ = 0.0005 # the best so far with r=3 or r=5
# Do the weight matrix computation
W = image_Gaussian_affinity(mask, r, σ)
#
# Generate G (GraphSig object) and GP (GraphPart object) using the computed
# weight matrix W, and the subsampled texture image as a graph signal.
# Note that GraphSig requires a matrix data even if it is just a one vector, i.e., f = textures[:] does not work!
G = GraphSig(W, f = reshape(textures, (length(textures), 1)))
GP = partition_tree_fiedler(G)
dmatrix = ghwt_analysis!(G, GP=GP)
#
# Construct or search the specific basis
#
# Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
# Walsh
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
# GHWT_c2f
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
# GHWT_f2c
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
# eGHWT
dvec_eghwt, BS_eghwt = eghwt_bestbasis(dmatrix, GP)
#
# Generate Figure 19a (Approximation error plot)
#
DVEC = [ dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:] ]
T = [ "Graph Haar", "Graph Walsh", "GHWT_c2f ", "GHWT_f2c", "eGHWT" ]
L = [ (:dashdot,:orange), (:dashdot,:blue), (:solid, :red), (:solid, :green),
(:solid, :black) ]
approx_error2(DVEC, T, L, 0.5)
savefig("textures_approx_error_r3_sigma0005.pdf")
savefig("textures_approx_error_r3_sigma0005.png")
#
# Generate Figure 19b (Top 9 eGHWT basis vectors)
#
top_vectors_plot3(dvec_eghwt, m, n, BS_eghwt, GP)
savefig("textures_eghwt09_r3_sigma0005.pdf")
savefig("textures_eghwt09_r3_sigma0005.png")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 3665 | using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
#@load "MN_MutGauss.jld2"
#tmp1 = G["G"]
#G=GraphSig(tmp1["W"],xy=tmp1["xy"],f=tmp1["f"],name =tmp1["name"],plotspecs = tmp1["plotspecs"])
#color_limit = (-0.2,2.2)
JLD2.@load "Toronto.jld2"
tmp1 = toronto["G"]
G=GraphSig(tmp1["W"],xy=tmp1["xy"],f=tmp1["f"],name =tmp1["name"],plotspecs = tmp1["plotspecs"])
GraphSig_Plot(G, linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0.)
G = Adj2InvEuc(G)
GP = partition_tree_fiedler(G,:Lrw)
dmatrix = ghwt_analysis!(G, GP=GP)
############# Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
############# Walsh
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
############# GHWT_c2f
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
############# GHWT_f2c
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
############# eGHWT
dvec_eghwt, BS_eghwt = ghwt_tf_bestbasis(dmatrix, GP)
################################################################################
####################### Approximation error plot################################
################################################################################
function approx_error(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0:0.01:0.3
T = ["Haar","Walsh","GHWT_c2f", "GHWT_f2c", "eGHWT"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :red),(:solid, :green),(:solid, :black)]
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
er = fill(0., length(frac))
for j = 1:length(frac)
p = Int64(floor(frac[j]*N))
er[j] = sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm
end
plot!(frac, er, yaxis=:log, xlims = (0.,0.3), label = T[i], line = L[i])
print(er[26])
end
end
################################################################################
######################### Synthesized by top vectors###########################
################################################################################
color_limit_residual = (0., 0.15)
function top_vectors_residual(p::Int64, dvec::Array{Float64,2}, BS::BasisSpec, GP::GraphPart, G::GraphSig)
sorted_dvec = sort(abs.(dvec[:]), rev = true)
dvecT = copy(dvec)
dvecT[abs.(dvec) .< sorted_dvec[p]].= 0
(f, GS) = ghwt_synthesis(dvecT, GP, BS, G)
GS.name = "Square of the residual"
#GS.f = (G.f - GS.f).^2
#print((maximum(GS.f), minimum(GS.f)))
#GraphSig_Plot(GS)
GS.f = (G.f - GS.f).^2 ./(G.f.^2)
GraphSig_Plot(GS, linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0., clim = color_limit_residual)
current()
end
################################
### Generate results
################################
# Figure 3(b)
approx_error([dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:]])
current()
###
frac = 1/4
p = Int64(ceil(frac*G.length))
### original (Figure )
# Figure 3(a)
GraphSig_Plot(G, linewidth = 1., markersize = 4., markercolor = :viridis, markerstrokealpha =0., clim = (2000., 110000.))
### haar
# Figure 4(a)
top_vectors_residual(p, dvec_haar, BS_haar, GP, G)
### walsh
# Figure 4(b)
top_vectors_residual(p, dvec_walsh, BS_walsh, GP, G)
### c2f
# Figure 4(b)
top_vectors_residual(p, dvec_c2f, BS_c2f, GP, G)
### f2c
# Figure 4(c)
top_vectors_residual(p, dvec_f2c, BS_f2c, GP, G)
### eghwt
# Figure 4(d)
top_vectors_residual(p, dvec_eghwt, BS_eghwt, GP, G)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 5018 | using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
@load "../spie_data.jld2"
matrix = vars["barbara"]
#face
row_zoom = 1:180
col_zoom = 330:450
#right leg
row_zoom = 300:512
col_zoom = 400:512
#full image
row_zoom = 1:512
col_zoom = 1:512
heatmap(matrix[row_zoom, col_zoom],ratio=1, yaxis =:flip, axis = false, color = :grays)
#savefig("original.pdf")
### initialize the regular balanced binary partition and compute the expanding coefficients
dmatrix, GProws, GPcols = ghwt_tf_init_2d_Lindberg(matrix)
### Compute the coefficients of different basis we will compare
############# Haar
BS_haar_rows = bs_haar(GProws)
BS_haar_cols = bs_haar(GPcols)
dvec_haar, loc_haar = BS2loc(dmatrix, GProws, GPcols, BS_haar_rows, BS_haar_cols)
############# Walsh
BS_walsh_rows = bs_walsh(GProws)
BS_walsh_cols = bs_walsh(GPcols)
dvec_walsh, loc_walsh = BS2loc(dmatrix, GProws, GPcols, BS_walsh_rows, BS_walsh_cols)
############# GHWT (i.e., regular haar-walsh wavelet packet dictionary)
fcols, jmax_col = size(GProws.tag);
frows, jmax_row = size(GPcols.tag);
dmatrix_rows = reshape(dmatrix, (frows, jmax_row, fcols*jmax_col))
dmatrix_cols = Array{Float64,3}(reshape(dmatrix',(fcols, jmax_col, frows*jmax_row)))
############# c2f bestbasis
dvec_c2f_rows, BS_c2f_rows = ghwt_c2f_bestbasis(dmatrix_rows, GProws)
dvec_c2f_cols, BS_c2f_cols = ghwt_c2f_bestbasis(dmatrix_cols, GPcols)
dvec_c2f, loc_c2f = BS2loc(dmatrix, GProws, GPcols, BS_c2f_rows, BS_c2f_cols)
############# f2c bestbasis
dvec_f2c_rows, BS_f2c_rows = ghwt_f2c_bestbasis(dmatrix_rows, GProws)
dvec_f2c_cols, BS_f2c_cols = ghwt_f2c_bestbasis(dmatrix_cols, GPcols)
dvec_f2c, loc_f2c = BS2loc(dmatrix, GProws, GPcols, BS_f2c_rows, BS_f2c_cols)
#############
##################### tf bestbasis
dvec_tf, loc_tf = ghwt_tf_bestbasis_2d(matrix, GProws, GPcols)
################################################################################
##################### Visualize the results of synthesis########################
################################################################################
### function to plot the image synthesized by top p vectors
function top_vectors_synthesis_2d(p::Int64, dvec::Vector{Float64}, loc::Matrix{Int64}, GProws::GraphPart, GPcols::GraphPart, dmatrix::Matrix{Float64})
sorted_dvec = sort(abs.(dvec[:]), rev = true)
dvecT = copy(dvec)
dvecT[abs.(dvec) .< sorted_dvec[p]].= 0
matrix_syn = ghwt_tf_synthesis_2d(dvecT, loc, GProws, GPcols)
heatmap(matrix_syn[row_zoom, col_zoom],ratio=1, yaxis =:flip, axis = false, color = :grays)
mse = norm(matrix - matrix_syn,2)^2/length(matrix)
psnr = -10*log10(mse)
return psnr
end
################################################################################
percent = 1/32;
p = Int64(floor(percent*length(matrix)))
### haar
# Figure 5(a)
top_vectors_synthesis_2d(p, dvec_haar, loc_haar, GProws, GPcols, dmatrix)
#savefig("synthesis_haar_1_32.pdf")
### walsh
top_vectors_synthesis_2d(p, dvec_walsh, loc_walsh, GProws, GPcols, dmatrix)
#savefig("synthesis_walsh_1_32.pdf")
### c2f
# Figure 5(b)
top_vectors_synthesis_2d(p, dvec_c2f, loc_c2f, GProws, GPcols, dmatrix)
#savefig("synthesis_c2f_1_32.pdf")
### f2c
# Figure 5(c)
top_vectors_synthesis_2d(p, dvec_f2c, loc_f2c, GProws, GPcols, dmatrix)
#savefig("synthesis_f2c_1_32.pdf")
### tf
# Figure 5(d)
top_vectors_synthesis_2d(p, dvec_tf, loc_tf, GProws, GPcols, dmatrix)
#savefig("synthesis_tf_1_32.pdf")
# To generate Figure 6. Just change the row_zoom, and col_zoom at the head of this file.
################################################################################
####################### Approximation error plot################################
################################################################################
function approx_error(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0:0.01:0.3
T = ["Haar","Walsh","GHWT_c2f", "GHWT_f2c", "eGHWT"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :red),(:solid, :green),(:solid, :black)]
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
er = fill(0., length(frac))
for j = 1:length(frac)
p = Int64(floor(frac[j]*N))
er[j] = sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm
end
plot!(frac, er, yaxis=:log, xlims = (0.,0.3), label = T[i], line = L[i])
end
end
approx_error([dvec_haar, dvec_walsh, dvec_c2f, dvec_f2c, dvec_tf])
current()
#################
### Generate the relative l2 error when approximating by 1/32 coefficients
################
DVEC = [dvec_haar, dvec_walsh, dvec_c2f, dvec_f2c, dvec_tf];
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
p = Int64(floor(N./32))
print(sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm)
end
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 4320 | using Plots, SparseArrays, JLD2, LinearAlgebra, Wavelets, MultiscaleGraphSignalTransforms
@load "../spie_data.jld2"
matrix = vars["barbara"]
#face
row_zoom = 1:180
col_zoom = 330:450
#right leg
row_zoom = 300:512
col_zoom = 400:512
#full image
row_zoom = 1:512
col_zoom = 1:512
#face_smaller
row_zoom = 71:170
col_zoom = 341:440
heatmap(matrix[row_zoom, col_zoom],ratio=1, yaxis =:flip, axis = false, color = :grays)
#savefig("original.pdf")
matrix = matrix[row_zoom, col_zoom]
### initialize the regular balanced binary partition and compute the expanding coefficients
GPcols = PartitionTreeMatrix_unbalanced_haar_binarytree(matrix, 9, 3.)
GProws = PartitionTreeMatrix_unbalanced_haar_binarytree(Matrix{Float64}(transpose(matrix)), 8, 3.)
dmatrix = ghwt_analysis_2d(matrix, GProws, GPcols)
### Compute the coefficients of different basis we will compare
############# Haar
BS_haar_rows = bs_haar(GProws)
BS_haar_cols = bs_haar(GPcols)
dvec_haar, loc_haar = BS2loc(dmatrix, GProws, GPcols, BS_haar_rows, BS_haar_cols)
# ############# Walsh
# BS_walsh_rows = bs_walsh(GProws)
# BS_walsh_cols = bs_walsh(GPcols)
# dvec_walsh, loc_walsh = BS2loc(dmatrix, GProws, GPcols, BS_walsh_rows, BS_walsh_cols)
#
# ############# GHWT (i.e., regular haar-walsh wavelet packet dictionary)
# fcols, jmax_col = size(GProws.tag);
# frows, jmax_row = size(GPcols.tag);
# dmatrix_rows = reshape(dmatrix, (frows, jmax_row, fcols*jmax_col))
# dmatrix_cols = Array{Float64,3}(reshape(dmatrix',(fcols, jmax_col, frows*jmax_row)))
# ############# c2f bestbasis
# dvec_c2f_rows, BS_c2f_rows = ghwt_c2f_bestbasis(dmatrix_rows, GProws)
# dvec_c2f_cols, BS_c2f_cols = ghwt_c2f_bestbasis(dmatrix_cols, GPcols)
# dvec_c2f, loc_c2f = BS2loc(dmatrix, GProws, GPcols, BS_c2f_rows, BS_c2f_cols)
#
# ############# f2c bestbasis
# dvec_f2c_rows, BS_f2c_rows = ghwt_f2c_bestbasis(dmatrix_rows, GProws)
# dvec_f2c_cols, BS_f2c_cols = ghwt_f2c_bestbasis(dmatrix_cols, GPcols)
# dvec_f2c, loc_f2c = BS2loc(dmatrix, GProws, GPcols, BS_f2c_rows, BS_f2c_cols)
#############
##################### tf bestbasis
dvec_tf, loc_tf = ghwt_tf_bestbasis_2d(matrix, GProws, GPcols)
##################### classical haar
dvec_classichaar = dwt(matrix, wavelet(WT.haar))
################################################################################
#########################
function approx_error(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0:0.01:0.3
T = ["Classical Haar transform", "eGHWT Haar basis", "eGHWT best basis"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :black)]
for i = 1:3
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
er = fill(0., length(frac))
for j = 1:length(frac)
p = Int64(floor(frac[j]*N))
er[j] = sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm
end
plot!(frac, er, yaxis=:log, xlims = (0.,0.3), label = T[i], line = L[i])
print(er[26])
end
end
################################################################################
####################### Approximation error plot################################
################################################################################
### function to plot the approximation error curve
function approx_error2(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0.3
T = ["Classical Haar transform", "eGHWT Haar basis", "eGHWT best basis"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :black)]
for i = 1:3
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2) # the smallest first
er = sqrt.(reverse(cumsum(dvec_sort)))/dvec_norm # this is the relative L^2 error of the whole thing, i.e., its length is N
p = Int64(floor(frac*N)) + 1 # upper limit
plot!(frac*(0:(p-1))/(p-1), er[1:p], yaxis=:log, xlims = (0.,frac), label = T[i], line = L[i])
end
end
### Figure 7
#approx_error([dvec_classichaar[:], dvec_haar[:], dvec_tf[:]])
approx_error2([dvec_classichaar[:], dvec_haar[:], dvec_tf[:]])
current()
savefig("figure7.pdf")
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 6818 | using Plots, SparseArrays, JLD2, LinearAlgebra, Wavelets, MultiscaleGraphSignalTransforms
#img = load("test\\8.jpg")
#heatmap(img,ratio=1, yaxis =:flip, axis = false, color = :gray)
JLD2.@load "../spie_data.jld2"
matrix = vars["barbara"][1:4:512,1:4:512]
heatmap(matrix,ratio=1, yaxis =:flip, axis = false, color = :grays, clim = (0,1))
matrix_gt = matrix[:]
sigma = 0.01
m, n = size(matrix)
############### Get the neighbors for affinity matrix computing
r = 5; # specify radius of neighbors
l = 2*r + 1
temp_x, temp_y = fill(1,l^2), fill(1,l^2)
temp_xy = CartesianIndices((1:l,1:l))
for i = 1:l^2
temp_x[i], temp_y[i] = temp_xy[i][1], temp_xy[i][2]
end
temp_ind = ((temp_x .- (r + 1)).^2 + (temp_y .- (r + 1)).^2).<= r^2
neighbor_x = temp_x[temp_ind] .- (r + 1)
neighbor_y = temp_y[temp_ind] .- (r + 1)
# for any index(x,y), (x + neighbor_x, y - neigbor_y) are the neighbors to calculate affinity
################ Create affinity matrix
W = fill(0., (m*n,m*n))
for i = 1:m*n
cur = CartesianIndices((m,n))[i]
for j = 1:length(neighbor_x)
if 1 <= cur[1] + neighbor_x[j] <= m && 1 <= cur[2] + neighbor_y[j] <= n
tempd = LinearIndices((m,n))[cur[1] + neighbor_x[j], cur[2] + neighbor_y[j]]
W[i,tempd] = exp(-(matrix_gt[i] - matrix_gt[tempd])^2/sigma)
end
end
end
W = sparse(W)
############### Preprocess to get G and GP
G = GraphSig(W, f = reshape(matrix,(length(matrix_gt),1)))
GP = partition_tree_fiedler(G)
dmatrix = ghwt_analysis!(G, GP=GP)
G_tmp = Glevel(G,GP,4)
heatmap(reshape(G_tmp.f[:],(128,128)))
############# Construct or search the specific basis
############# Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
############# eGHWT
dvec_eghwt, BS_eghwt = ghwt_tf_bestbasis(dmatrix, GP)
############# Walsh
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
############# GHWT_c2f
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
############# GHWT_f2c
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
###################################################################################
############## Visuallization of Top basis vector (multiple)#######################
###################################################################################
### visualization fo the first 12 vectors
### function to plot top 12 vectors
function top_vectors_plot(dvec::Array{Float64, 2}, BS::BasisSpec, GP::GraphPart; clims::Tuple{Float64,Float64} = (-0.02,0.02))
sorted_ind = sortperm(abs.(dvec[:]), rev = true);
plot(12,layout=(3,4),framestyle=:none, legend=false)
for i=1:12
dvecT = fill(0., size(dvec))
#dvecT[sorted_ind[i]] = dvec_ghwt[sorted_ind[i]]
dvecT[sorted_ind[i]] = 1
f = ghwt_synthesis(dvecT, GP, BS)
#print((maximum(f), minimum(f)))
heatmap!(reshape(f, size(matrix)), subplot=i, ratio=1, yaxis=:flip, axis=false, color = :balance, clims = clims)
end
current()
end
### haar
top_vectors_plot(dvec_haar, BS_haar, GP)
### walsh
top_vectors_plot(dvec_walsh, BS_walsh, GP)
### c2f
top_vectors_plot(dvec_c2f, BS_c2f, GP)
### f2c
top_vectors_plot(dvec_f2c, BS_f2c, GP)
### eghwt
top_vectors_plot(dvec_eghwt, BS_eghwt, GP)
###################################################################################
############## Visuallization of Top basis vector (single)#########################
###################################################################################
### function to plot the first i-th vector
### Note that here only one vector is plotted instead of multiple vectors.
function top_vector_plot(dvec::Array{Float64, 2}, BS::BasisSpec, GP::GraphPart, G::GraphSig, i::Int64; clims::Tuple{Float64,Float64} = (-0.02,0.02))
sorted_ind = sortperm(abs.(dvec[:]), rev = true);
dvecT = fill(0., size(dvec))
#dvecT[sorted_ind[i]] = dvec_ghwt[sorted_ind[i]]
dvecT[sorted_ind[i]] = 1
f, GS = ghwt_synthesis(dvecT, GP, BS, G)
heatmap(reshape(f, size(matrix)), ratio=1, yaxis=:flip, axis=false, color = :grays, clims = clims)
end
########################## plot top i-th vector
i = 2
### haar
top_vector_plot(dvec_haar, BS_haar, GP, G, i)
### walsh
top_vector_plot(dvec_walsh, BS_walsh, GP, G, i)
### c2f
top_vector_plot(dvec_c2f, BS_c2f, GP, G, i)
### f2c
top_vector_plot(dvec_f2c, BS_f2c, GP, G, i)
### eghwt
top_vector_plot(dvec_eghwt, BS_eghwt, GP, G, i)
#######################################################################################
### generate figure used for spie paper
##########################################################################################
# Figure 8b
sorted_ind = sortperm(abs.(dvec_eghwt[:]), rev = true)
plot(4, layout=(2,2), framestyle=:none, legend=false)
for i = 1:4
dvec_T = fill(0., size(dvec_eghwt))
dvec_T[sorted_ind[i+1]] = 1
f = ghwt_synthesis(dvec_T, GP, BS_eghwt)
heatmap!(reshape(f, size(matrix)), subplot=i, ratio=1, yaxis=:flip, axis=false, color = :grays, clims = (-0.01,0.01))
end
current()
savefig("barbara_top4.pdf")
#########################
function approx_error(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0:0.01:0.3
T = ["Classical Haar transform", "eGHWT Haar basis", "eGHWT best basis"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :black)]
for i = 1:3
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
er = fill(0., length(frac))
for j = 1:length(frac)
p = Int64(floor(frac[j]*N))
er[j] = sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm
end
plot!(frac, er, yaxis=:log, xlims = (0.,0.3), label = T[i], line = L[i])
print(er[26])
end
end
#########################
function approx_error2(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0.3
T = ["Classical Haar transform", "eGHWT Haar basis", "eGHWT best basis"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :black)]
for i = 1:3
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2) # the smallest first
er = sqrt.(reverse(cumsum(dvec_sort)))/dvec_norm # this is the relative L^2 error of the whole thing, i.e., its length is N
p = Int64(floor(frac*N)) + 1 # upper limit
plot!(frac*(0:(p-1))/(p-1), er[1:p], yaxis=:log, xlims = (0.,frac), label = T[i], line = L[i])
end
end
dvec_classichaar = dwt(matrix, wavelet(WT.haar))
### Figure 8(a)
#approx_error([dvec_classichaar[:], dvec_haar[:], dvec_eghwt[:]])
approx_error2([dvec_classichaar[:], dvec_haar[:], dvec_eghwt[:]])
current()
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | code | 5984 | using Plots, SparseArrays, JLD2, LinearAlgebra, MultiscaleGraphSignalTransforms
JLD2.@load "handcut_images.jld2"
heatmap(tmp["block5"],ratio=1, yaxis =:flip, axis = false, color = :grays)
#savefig("original.pdf")
heatmap(tmp["block5_gt"],ratio=1, yaxis =:flip, axis = false, color = :grays)
#savefig("ground_truth.pdf")
matrix = tmp["block5"]
matrix_gt = tmp["block5_gt"][:]
sigma = 0.0001
m, n = size(matrix)
############### Get the neighbors for affinity matrix computing
r = 5; # specify radius of neighbors
l = 2*r + 1
temp_x, temp_y = fill(1,l^2), fill(1,l^2)
temp_xy = CartesianIndices((1:l,1:l))
for i = 1:l^2
temp_x[i], temp_y[i] = temp_xy[i][1], temp_xy[i][2]
end
temp_ind = ((temp_x .- (r + 1)).^2 + (temp_y .- (r + 1)).^2).<= r^2
neighbor_x = temp_x[temp_ind] .- (r + 1)
neighbor_y = temp_y[temp_ind] .- (r + 1)
# for any index(x,y), (x + neighbor_x, y - neigbor_y) are the neighbors to calculate affinity
################ Create affinity matrix
W = fill(0., (m*n,m*n))
for i = 1:m*n
cur = CartesianIndices((m,n))[i]
for j = 1:length(neighbor_x)
if 1 <= cur[1] + neighbor_x[j] <= m && 1 <= cur[2] + neighbor_y[j] <= n
tempd = LinearIndices((m,n))[cur[1] + neighbor_x[j], cur[2] + neighbor_y[j]]
W[i,tempd] = exp(-(matrix_gt[i] - matrix_gt[tempd])^2/sigma)
end
end
end
W = sparse(W)
############### Preprocess to get G and GP
G = GraphSig(W, f = reshape(matrix,(length(matrix_gt),1)))
GP = partition_tree_fiedler(G)
dmatrix = ghwt_analysis!(G, GP=GP)
############# Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
############# Walsh
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
############# GHWT_c2f
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
############# GHWT_f2c
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
############# eGHWT
dvec_eghwt, BS_eghwt = ghwt_tf_bestbasis(dmatrix, GP)
################################################################################
############## Visuallization of Top basis vectors##############################
################################################################################
### function to plot top 9 vectors
function top_vectors_plot(dvec::Array{Float64, 2}, BS::BasisSpec, GP::GraphPart; clims::Tuple{Float64,Float64} = (-0.01,0.01))
sorted_ind = sortperm(abs.(dvec[:]), rev = true);
plot(9,layout=(3,3),framestyle=:none, legend=false)
for i=1:9
dvecT = fill(0., size(dvec))
#dvecT[sorted_ind[i]] = dvec_ghwt[sorted_ind[i]]
dvecT[sorted_ind[i]] = 1
f = ghwt_synthesis(dvecT, GP, BS)
#print((maximum(f), minimum(f)))
heatmap!(reshape(f, size(matrix)), subplot=i, ratio=1, yaxis=:flip, axis=false, color = :grays, clims = clims)
end
current()
end
########################## plot top vectors
### haar
top_vectors_plot(dvec_haar, BS_haar, GP)
#savefig("top9_haar.pdf")
### walsh
top_vectors_plot(dvec_walsh, BS_walsh, GP)
#savefig("top9_walsh.pdf")
### c2f
top_vectors_plot(dvec_c2f, BS_c2f, GP)
#savefig("top9_c2f.pdf")
### f2c
top_vectors_plot(dvec_f2c, BS_f2c, GP)
#savefig("top9_f2c.pdf")
### eghwt
top_vectors_plot(dvec_eghwt, BS_eghwt, GP)
################################################################################
####################### Approximation error plot################################
################################################################################
### function to plot the approximation error curve
function approx_error(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0:0.01:0.3
T = ["Haar","Walsh","GHWT_c2f", "GHWT_f2c", "eGHWT"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :red),(:solid, :green),(:solid, :black)]
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2, rev = true)
er = fill(0., length(frac))
for j = 1:length(frac)
p = Int64(floor(frac[j]*N))
er[j] = sqrt(dvec_norm^2 - sum(dvec_sort[1:p]))/dvec_norm
end
plot!(frac, er, yaxis=:log, xlims = (0.,0.3), label = T[i], line = L[i])
end
end
#approx_error([dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:]])
#current()
#savefig("approx_error.pdf")
################################################################################
####################### Approximation error plot################################
################################################################################
### function to plot the approximation error curve
function approx_error2(DVEC::Array{Array{Float64,1},1})
plot(xaxis = "Fraction of Coefficients Retained", yaxis = "Relative Approximation Error")
frac = 0.3
T = ["Haar","Walsh","GHWT_c2f", "GHWT_f2c", "eGHWT"]
L = [(:dashdot,:orange),(:dashdot,:blue),(:solid, :red),(:solid, :green),(:solid, :black)]
for i = 1:5
dvec = DVEC[i]
N = length(dvec)
dvec_norm = norm(dvec,2)
dvec_sort = sort(dvec.^2) # the smallest first
er = sqrt.(reverse(cumsum(dvec_sort)))/dvec_norm # this is the relative L^2 error of the whole thing, i.e., its length is N
p = Int64(floor(frac*N)) + 1 # upper limit
plot!(frac*(0:(p-1))/(p-1), er[1:p], yaxis=:log, xlims = (0.,frac),ylims = (10^(-2.5),1), label = T[i], line = L[i])
end
end
############################
### spie figures
############################
# Figure 9(a)
heatmap(tmp["block5"],ratio=1, yaxis =:flip, axis = false, color = :grays)
# Figure 9(b)
#approx_error([dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:]])
approx_error2([dvec_haar[:], dvec_walsh[:], dvec_c2f[:], dvec_f2c[:], dvec_eghwt[:]])
current()
savefig("figure9b.pdf")
# Figure 10(a)
top_vectors_plot(dvec_haar, BS_haar, GP)
# Figure 10(b)
top_vectors_plot(dvec_eghwt, BS_eghwt, GP)
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 4386 | # MultiscaleGraphSignalTransforms.jl
| Doc | Build | Test |
|------|-------|------|
| [](https://ucd4ids.github.io/MultiscaleGraphSignalTransforms.jl/dev/) | [](https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl/actions) | [](https://codecov.io/gh/UCD4IDS/MultiscaleGraphSignalTransforms.jl) |

## COPYRIGHT
Copyright 2015-2022 The Regents of the University of California
Implemented by Jeff Irion, Haotian Li, Naoki Saito, and Yiqun Shao
## SETUP
To install the MultiscaleGraphSignalTransforms.jl, run
```julia
julia> import Pkg; Pkg.add("MultiscaleGraphSignalTransforms")
julia> using MultiscaleGraphSignalTransforms
```
## GETTING STARTED
Currently, you can run a set of very small tests via ```] test MultiscaleGraphSignalTransforms```; see the actual file ```test/runtest.jl``` as well as [the documentation](https://ucd4ids.github.io/MultiscaleGraphSignalTransforms.jl/dev) for further information.
## REFERENCES
1. J. Irion and N. Saito, [Hierarchical graph Laplacian eigen transforms](https://www.math.ucdavis.edu/~saito/publications/hglets.html), *Japan SIAM Letters*, vol. 6, pp. 21-24, 2014.
2. J. Irion and N. Saito, [The generalized Haar-Walsh transform](https://www.math.ucdavis.edu/~saito/publications/ghwt.html), *Proc. 2014 IEEE Statistical Signal Processing Workshop*, pp. 488-491, 2014.
3. J. Irion and N. Saito, [Applied and computational harmonic analysis on
graphs and networks](https://www.math.ucdavis.edu/~saito/publications/spie15.html), *Wavelets and Sparsity XVI*, (M. Papadakis, V. K. Goyal, D. Van De Ville, eds.), *Proc. SPIE 9597*, Paper #95971F, Invited paper, 2015.
4. J. Irion, [Multiscale Transforms for Signals on Graphs: Methods and Applications](https://jefflirion.github.io/publications_and_presentations/irion_dissertation.pdf), Ph.D. dissertation, University of California, Davis, Dec. 2015.
5. J. Irion and N. Saito, [Learning sparsity and structure of matrices with multiscale graph basis dictionaries](https://www.math.ucdavis.edu/~saito/publications/matanal.html), *Proc. 2016 IEEE 26th International Workshop on Machine Learning for Signal Processing (MLSP)*, (A. Uncini, K. Diamantaras, F. A. N. Palmieri, and J. Larsen, eds.), 2016.
6. J. Irion and N. Saito, [Efficient approximation and denoising of graph signals using the multiscale basis dictionaries](https://www.math.ucdavis.edu/~saito/publications/eadgsumbd.html), *IEEE Transactions on Signal and Information Processing over Networks*, Vol. 3, no. 3, pp. 607-616, 2017.
7. N. Saito, [How can we naturally order and organize graph Laplacian eigenvectors?](https://www.math.ucdavis.edu/~saito/publications/lapeigport.html) *Proc. 2018 IEEE Workshop on Statistical Signal Processing*, pp. 483-487, 2018.
8. Y. Shao and N. Saito, [The extended Generalized Haar-Walsh Transform and applications](https://www.math.ucdavis.edu/~saito/publications/eghwt.html), *Wavelets and Sparsity XVIII*, (D. Van De Ville, M. Papadakis, and Y. M. Lu, eds.), *Proc. SPIE 11138*, Paper #111380C, 2019.
9. H. Li and N. Saito, [Metrics of graph Laplacian eigenvectors](https://www.math.ucdavis.edu/~saito/publications/metgraphlap.html), *Wavelets and Sparsity XVIII*, (D. Van De Ville, M. Papadakis, and Y. M. Lu, eds.), *Proc. SPIE 11138*, Paper #111381K, 2019.
10. Y. Shao, [The Extended Generalized Haar-Walsh Transform and Applications](https://www.math.ucdavis.edu/~tdenena/dissertations/202008_Shao_Yiqun_dissertation.pdf), Ph.D. dissertation, University of California, Davis, Sep. 2020.
11. A. Cloninger, H. Li and N. Saito, [Natural graph wavelet packet dictionaries](https://www.math.ucdavis.edu/~saito/publications/ngwp.html), *J. Fourier Anal. Appl.*, vol. 27, Article \#41, 2021.
12. H. Li, Natural Graph Wavelet Dictionaries: Methods and Applications, Ph.D. dissertation, University of California, Davis, Jun. 2021.
13. N. Saito and Y. Shao, [eGHWT: The extended Generalized Haar-Walsh Transform](https://www.math.ucdavis.edu/~saito/publications/eghwt21.html), *J. Math. Imaging Vis.*, vol. 64, no. 3, pp. 261-283, 2022.
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 3689 | # MultiscaleGraphSignalTransforms.jl
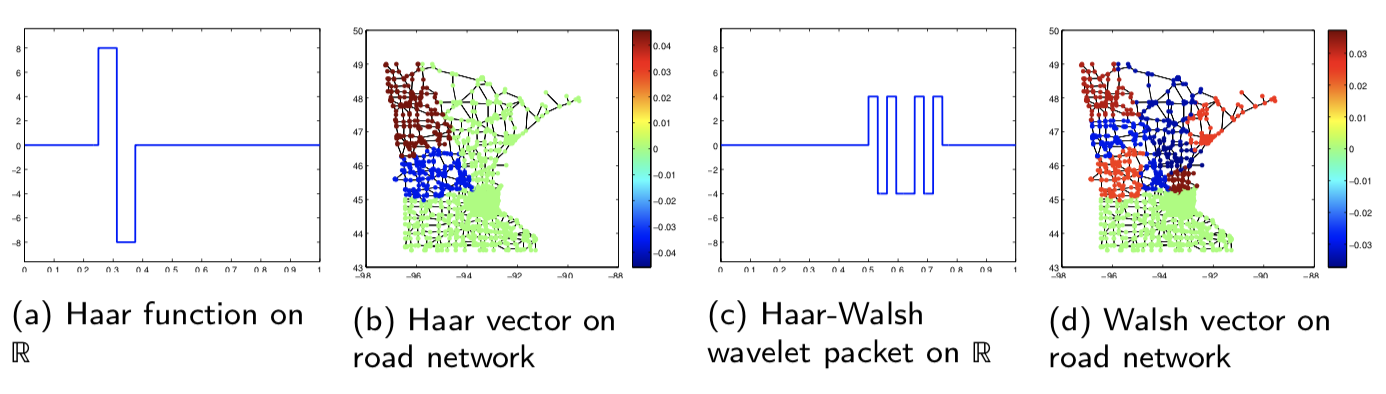
MultiscaleGraphSignalTransforms.jl is a collection of tools for graph signal processing including HGLET, GHWT, eGHWT, NGWP, Lapped NGWP, and Lapped HGLET. Some of them were originally written in MATLAB by Jeff Irion, but we added more functionalities, e.g., eGHWT, NGWP, etc.
## COPYRIGHT
Copyright 2015-2021 The Regents of the University of California
Implemented by Jeff Irion, Haotian Li, Naoki Saito, and Yiqun Shao
## SETUP
To install the MultiscaleGraphSignalTransforms.jl, run
```julia
julia> import Pkg; Pkg.add("MultiscaleGraphSignalTransforms")
julia> using MultiscaleGraphSignalTransforms
```
## GETTING STARTED
Currently, you can run a set of very small tests via ```] test MultiscaleGraphSignalTransforms```; see the actual file [`test/runtest.jl`](https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl/blob/master/test/runtests.jl) for more details.
You can also check out the examples we provided in the sidebar.
## REFERENCES
1. J. Irion and N. Saito, [Hierarchical graph Laplacian eigen transforms](http://doi.org/10.14495/jsiaml.6.21), *Japan SIAM Letters*, vol. 6, pp. 21-24, 2014.
2. J. Irion and N. Saito, [The generalized Haar-Walsh transform](http://dx.doi.org/10.1109/SSP.2014.6884678), *Proc. 2014 IEEE Statistical Signal Processing Workshop*, pp. 488-491, 2014.
3. J. Irion and N. Saito, [Applied and computational harmonic analysis on graphs and networks](http://dx.doi.org/10.1117/12.2186921), *Wavelets and Sparsity XVI*, (M. Papadakis, V. K. Goyal, D. Van De Ville, eds.), *Proc. SPIE 9597*, Paper #95971F, Invited paper, 2015.
4. J. Irion, [Multiscale Transforms for Signals on Graphs: Methods and Applications](https://jefflirion.github.io/publications_and_presentations/irion_dissertation.pdf), Ph.D. dissertation, University of California, Davis, Dec. 2015.
5. J. Irion and N. Saito, [Learning sparsity and structure of matrices with multiscale graph basis dictionaries](http://dx.doi.org/10.1109/MLSP.2016.7738892), *Proc. 2016 IEEE 26th International Workshop on Machine Learning for Signal Processing (MLSP)*, (A. Uncini, K. Diamantaras, F. A. N. Palmieri, and J. Larsen, eds.), 2016.
6. J. Irion and N. Saito, [Efficient approximation and denoising of graph signals using the multiscale basis dictionaries](http://dx.doi.org/10.1109/TSIPN.2016.2632039), *IEEE Transactions on Signal and Information Processing over Networks*, Vol. 3, no. 3, pp. 607-616, 2017.
7. Y. Shao and N. Saito, [The extended Generalized Haar-Walsh Transform and applications](https://www.math.ucdavis.edu/~saito/publications/saito_eghwt.pdf), *Wavelets and Sparsity XVIII*, (D. Van De Ville, M. Papadakis, and Y. M. Lu, eds.), *Proc. SPIE 11138*, Paper #111380C, 2019.
8. Y. Shao, [The Extended Generalized Haar-Walsh Transform and Applications](https://www.math.ucdavis.edu/~tdenena/dissertations/202008_Shao_Yiqun_dissertation.pdf), Ph.D. dissertation, University of California, Davis, Sep. 2020.
9. H. Li and N. Saito, [Metrics of graph Laplacian eigenvectors](https://www.math.ucdavis.edu/~saito/publications/metgraphlap.html), *Wavelets and Sparsity XVIII*, (D. Van De Ville, M. Papadakis, and Y. M. Lu, eds.), *Proc. SPIE 11138*, Paper #111381K, 2019.
10. C. Alexander, H. Li and N. Saito, [Natural graph wavelet packet dictionaries](https://link.springer.com/article/10.1007/s00041-021-09832-3), *J. Fourier Anal. Appl.*, vol. 27, Article \#41, 2021.
11. H. Li, Natural Graph Wavelet Dictionaries: Methods and Applications, Ph.D. dissertation, University of California, Davis, Jun. 2021.
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 4765 | # Metrics of Graph Laplacian Eigenvectors on ``P_7 \times P_3``
## Set up
```@example grid
using MultiscaleGraphSignalTransforms, LightGraphs, MultivariateStats
using Plots, LaTeXStrings, LinearAlgebra
# compute the graph related quantities
Nx, Ny = 7, 3
G = LightGraphs.grid([Nx, Ny])
N = nv(G)
L = Matrix(laplacian_matrix(G))
Q = incidence_matrix(G; oriented = true)
𝛌, 𝚽 = eigen(L)
𝚽 = 𝚽 .* sign.(𝚽[1, :])' # sign of DCT
∇𝚽 = Q' * 𝚽
W = 1.0 * adjacency_matrix(G)
# manually set up the mapping between 1D ordering and 2D ordering
grid2eig_ind = [1,2,3,6,8,12,15,4,5,7,9,13,16,18,10,11,14,17,19,20,21];
eig2grid_ind = sortperm(grid2eig_ind);
eig2dct = Array{Int64,3}(undef, Nx, Ny, 2);
for i = 1:Nx; for j = 1:Ny; eig2dct[i,j,1] = i-1; eig2dct[i,j,2] = j-1; end; end
eig2dct = reshape(eig2dct, (N, 2)); eig2dct = eig2dct[eig2grid_ind, :];
nothing # hide
```
Let us see the comparison between 1D ordering vs. 2D ordering of the eigenvectors.
```@example grid
## 1D ordering: non-decreasing eigenvalue ordering
plot(layout = Plots.grid(3, 7))
for i in 1:N
heatmap!(reshape(𝚽[:, i], (Nx, Ny))', c = :viridis, cbar = false,
clims = (-0.4,0.4), frame = :none, ratio = 1, ylim = [0, Ny + 1],
title = latexstring("\\phi_{", i-1, "}"), titlefont = 12,
subplot = i)
end
plot!(size = (815, 350)) # hide
```
```@example grid
## 2D ordering: natural frequency ordering
plot(layout = Plots.grid(3, 7))
for i in 1:N
k = grid2eig_ind[i]
heatmap!(reshape(𝚽[:,k], (Nx, Ny))', c = :viridis, cbar = false,
clims = (-0.4,0.4), frame = :none, ratio = 1, ylim = [0, Ny + 1],
title = latexstring("\\varphi_{", string(eig2dct[k,1]),
",", string(eig2dct[k,2]), "}"), titlefont = 12, subplot = i)
end
plot!(size = (815, 350)) # hide
```
What we really want to do is to *organize* those eigenvectors based on their natural frequencies or their behaviors instead of their eigenvalues.
To do that, we utilize the metrics discussed in the [paper](https://www.math.ucdavis.edu/~saito/publications/metgraphlap.html) as follows.
But first, we create a custom plotting function for later use.
```@example grid
function grid7x3_mds_heatmaps(E, 𝚽; Nx = 7, Ny = 3, annotate_ind = 1:N, plotOrder = 1:N)
# set up all heatmap plots' positions
max_x = maximum(E[1, :]); min_x = minimum(E[1, :])
width_x = max_x - min_x
max_y = maximum(E[2, :]); min_y = minimum(E[2, :])
width_y = max_y - min_y
dx = 0.005 * width_x; dy = dx;
xej = zeros(Nx, N); yej=zeros(Ny, N);
a = 5.0; b = 7.0;
for k = 1:N
xej[:,k] = LinRange(E[1,k] - Ny * a * dx, E[1, k] + Ny * a * dx, Nx)
yej[:,k] = LinRange(E[2,k] - a * dy, E[2, k] + a * dy, Ny)
end
plot()
for k in plotOrder
if k in annotate_ind
heatmap!(xej[:, k], yej[:, k], reshape(𝚽[:, k], (Nx, Ny))', c = :viridis,
colorbar = false, ratio = 1, annotations = (xej[4, k],
yej[3, k] + b*dy, text(latexstring("\\varphi_{",
string(eig2dct[k, 1]), ",", string(eig2dct[k, 2]), "}"), 10)))
else
heatmap!(xej[:, k], yej[:, k], reshape(𝚽[:, k], (Nx, Ny))', c = :viridis,
colorbar = false, ratio = 1)
end
end
plt = plot!(xlim = [min_x - 0.12 * width_x, max_x + 0.12 * width_x],
ylim = [min_y - 0.16 * width_y, max_y + 0.16 * width_y],
grid = false, clims = (-0.4, 0.4),
xlab = "X₁", ylab = "X₂")
return plt
end
nothing # hide
```
## ROT distance
Before we measure the ROT distance between the eigenvectors, we convert them to probability mass functions by taking entrywise squares.
After we got the ROT distance matrix of the eigenvectors, we visualize the arrangement of the eigenvectors in ``\mathbb{R}^{2}`` via [the classical MDS embedding](https://en.wikipedia.org/wiki/Multidimensional_scaling#Classical_multidimensional_scaling).
```@example grid
## ROT distance
D = natural_eigdist(𝚽, 𝛌, Q; α = 0.5, input_format = :pmf1, distance = :ROT)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
grid7x3_mds_heatmaps(E, 𝚽)
plot!(size = (815, 611)) # hide
```
## DAG distance
We organize the eigenvectors by the DAG distance.
```@example grid
D = natural_eigdist(𝚽, 𝛌, Q; distance = :DAG)
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
grid7x3_mds_heatmaps(E, 𝚽)
plot!(size = (815, 611)) # hide
```
## TSD distance
We organize the eigenvectors by the TSD distance with the parameter ``T = 0.1``.
```@example grid
D = natural_eigdist(𝚽, 𝛌, Q; T = 0.1, distance = :TSD) # T = 0.1
E = transform(fit(MDS, D, maxoutdim=2, distances=true))
grid7x3_mds_heatmaps(E, 𝚽)
plot!(size = (815, 611)) # hide
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 7377 | # [Multiscale Graph Signal Transforms on 1D Path](@id p64)
Let us use the *unweighted* 1D path with a synthetic signal as a simple example to demonstrate the usage of the MultiscaleGraphSignalTransforms.jl.
## Set up
We first construct the `GraphSig` and `GraphPart` objects of the *primal* graph ``G = P_{64}``.
```@example path
using MultiscaleGraphSignalTransforms, Plots, LinearAlgebra
import WaveletsExt: wiggle
using Plots.PlotMeasures # hide
# construct P64
N = 64
G = gpath(N)
# compute graph Laplacian eigenvectors
W = G.W
L = diagm(sum(W; dims = 1)[:]) - W # unnormalized graph Laplacian
𝛌, 𝚽 = eigen(L)
𝚽 = 𝚽 .* sign.(𝚽[1,:])'
# perform recursive bipartitioning of G by the Fiedler vectors of Lrw
GP = partition_tree_fiedler(G; swapRegion = false)
# use Chebyshev polynomial T₅(x) (x ∈ [0, 1]) as an example signal
G.f = reshape([16 * x^5 - 20 * x^3 + 5 * x for x in LinRange(0, 1, N)], (N, 1))
plot(G.f; c = :black, lw = 2, legend = false, grid = false, size = (815, 300))
xticks!([1; 8:8:64], vcat(string("1"), [string(k) for k in 8:8:64])) # hide
plot!(left_margin = 5mm) # hide
```
## Graph Signal Processing via HGLET/LP-HGLET
```@example path
## analyze the signal via HGLET
dmatrixH, dmatrixHrw, dmatrixHsym = HGLET_Analysis_All(G, GP)
dvec_hglet, BS_hglet, trans_hglet = HGLET_GHWT_BestBasis(GP, dmatrixH = dmatrixH,
dmatrixHrw = dmatrixHrw, dmatrixHsym = dmatrixHsym, costfun = 1)
## LP-HGLET
dmatrixsH, dmatrixsHsym = LPHGLET_Analysis_All(G, GP; ϵ = 0.3)
dvec_lphglet, BS_lphglet, trans_lphglet = HGLET_GHWT_BestBasis(GP, dmatrixH = dmatrixsH,
dmatrixHsym = dmatrixsHsym, costfun = 1)
# find the top 10 HGLET basis vectors
important_idx = sortperm(dvec_hglet[:].^2; rev = true)
hglet_top10 = zeros(N, 10)
for i in 1:10
w, _ = HGLET_Synthesis(reshape(spike(important_idx[i], N), (N, 1)),
GP, BS_hglet, G, method = :L)
hglet_top10[:, i] = w[:]
end
wiggle(hglet_top10; sc = 0.45)
p1 = title!("Top 10 HGLET basis vectors")
# find the top 10 LP-HGLET basis vectors
important_idx = sortperm(dvec_lphglet[:].^2; rev = true)
lphglet_top10 = zeros(N, 10)
for i in 1:10
w, _ = LPHGLET_Synthesis(reshape(spike(important_idx[i], N), (N, 1)),
GP, BS_lphglet, G; method = :L, ϵ = 0.3)
lphglet_top10[:, i] = w[:]
end
wiggle(lphglet_top10; sc = 0.45)
p2 = title!("Top 10 LP-HGLET basis vectors")
plot(p1, p2, layout = Plots.grid(2, 1), size = (815, 600))
xticks!([1; 8:8:64], vcat(string("1"), [string(k) for k in 8:8:64])) # hide
yticks!([0; 1:10], vcat(string(""), [string(k) for k in 1:10])) # hide
plot!(left_margin = 5mm) # hide
```
## Graph Signal Processing via GHWT, eGHWT, etc.
```@example path
## analyze the signal via GHWT
dmatrix = ghwt_analysis!(G, GP = GP)
## Haar
BS_haar = bs_haar(GP)
dvec_haar = dmatrix2dvec(dmatrix, GP, BS_haar)
## Walsh
BS_walsh = bs_walsh(GP)
dvec_walsh = dmatrix2dvec(dmatrix, GP, BS_walsh)
## GHWT_c2f
dvec_c2f, BS_c2f = ghwt_c2f_bestbasis(dmatrix, GP)
## GHWT_f2c
dvec_f2c, BS_f2c = ghwt_f2c_bestbasis(dmatrix, GP)
## eGHWT
dvec_eghwt, BS_eghwt = ghwt_tf_bestbasis(dmatrix, GP)
nothing # hide
```
We then find the top 10 basis vectors in each case.
```@example path
## Haar
important_idx = sortperm(dvec_haar[:].^2; rev = true)
haar_top10 = zeros(N, 10)
for i in 1:10
w = ghwt_synthesis(reshape(spike(important_idx[i], N), (N, 1)), GP, BS_haar)
haar_top10[:, i] = w[:]
end
wiggle(haar_top10; sc = 0.45)
p1 = title!("Top 10 Haar basis vectors")
## Walsh
important_idx = sortperm(dvec_walsh[:].^2; rev = true)
walsh_top10 = zeros(N, 10)
for i in 1:10
w = ghwt_synthesis(reshape(spike(important_idx[i], N), (N, 1)), GP, BS_walsh)
walsh_top10[:, i] = w[:]
end
wiggle(walsh_top10; sc = 0.45)
p2 = title!("Top 10 Walsh basis vectors")
## GHWT_c2f
important_idx = sortperm(dvec_c2f[:].^2; rev = true)
ghwt_c2f_top10 = zeros(N, 10)
for i in 1:10
w = ghwt_synthesis(reshape(spike(important_idx[i], N), (N, 1)), GP, BS_c2f)
ghwt_c2f_top10[:, i] = w[:]
end
wiggle(ghwt_c2f_top10; sc = 0.45)
p3 = title!("Top 10 GHWT c2f best basis vectors")
## GHWT_f2c
important_idx = sortperm(dvec_f2c[:].^2; rev = true)
ghwt_f2c_top10 = zeros(N, 10)
for i in 1:10
w = ghwt_synthesis(reshape(spike(important_idx[i], N), (N, 1)), GP, BS_f2c)
ghwt_f2c_top10[:, i] = w[:]
end
wiggle(ghwt_f2c_top10; sc = 0.45)
p4 = title!("Top 10 GHWT f2c best basis vectors")
## eGHWT
important_idx = sortperm(dvec_eghwt[:].^2; rev = true)
eghwt_top10 = zeros(N, 10)
for i in 1:10
w = ghwt_synthesis(reshape(spike(important_idx[i], N), (N, 1)), GP, BS_eghwt)
eghwt_top10[:, i] = w[:]
end
wiggle(eghwt_top10; sc = 0.45)
p5 = title!("Top 10 eGHWT best basis vectors")
# display the top 10 basis vectors
plot(p1, p2, p3, p4, p5, layout = Plots.grid(5, 1), size = (815, 1500))
xticks!([1; 8:8:64], vcat(string("1"), [string(k) for k in 8:8:64])) # hide
yticks!([0; 1:10], vcat(string(""), [string(k) for k in 1:10])) # hide
plot!(left_margin = 5mm) # hide
```
## Graph Signal Processing via the NGWP dictionaries
To perform the NGWP transforms, we set up the *dual* graph ``G^{\star}`` (which is also ``P_{64}``).
```@example path
# build the dual graph object
Gstar = GraphSig(W)
# perform recursive bipartitioning of Gstar by the Fiedler vectors of Lrw
GstarP = partition_tree_fiedler(Gstar; swapRegion = false)
# perform the pair-clustering algorithm to recursively bipartition G
GP_pc = pairclustering(𝚽, GstarP) # for PC-NGWP
nothing # hide
```
Now, let us construct the three NGWP dictionaries (i.e., the VM-NGWP, the PC-NGWP, and the LP-NGWP) and use them to analyze the signal, respectively.
```@example path
VM_NGWP = vm_ngwp(𝚽, GstarP)
PC_NGWP = pc_ngwp(𝚽, GstarP, GP_pc)
LP_NGWP = lp_ngwp(𝚽, W, GstarP; ϵ = 0.3) # relative action region bandwidth ϵ
# NGWP analysis, i.e., get the expansion coefficient matrix and apply the best
# basis algorithm.
dmatrix_VM = ngwp_analysis(G, VM_NGWP)
dvec_vm_ngwp, BS_vm_ngwp = ngwp_bestbasis(dmatrix_VM, GstarP)
dmatrix_PC = ngwp_analysis(G, PC_NGWP)
dvec_pc_ngwp, BS_pc_ngwp = ngwp_bestbasis(dmatrix_PC, GstarP)
dmatrix_LP = ngwp_analysis(G, LP_NGWP)
dvec_lp_ngwp, BS_lp_ngwp = ngwp_bestbasis(dmatrix_LP, GstarP)
nothing # hide
```
Then, the top 10 NGWP basis vectors selected from each dictionary can be displayed as follows.
```@example path
important_idx = sortperm(dvec_vm_ngwp[:].^2; rev = true)
wav_vm_top10 = zeros(N, 10)
for i in 1:10
dr, dc = BS_vm_ngwp.levlist[important_idx[i]]
wav_vm_top10[:, i] = VM_NGWP[dr, dc, :]
end
wiggle(wav_vm_top10; sc = 0.45)
p1 = title!("Top 10 VM-NGWP basis vectors")
important_idx = sortperm(dvec_pc_ngwp[:].^2; rev = true)
wav_pc_top10 = zeros(N, 10)
for i in 1:10
dr, dc = BS_pc_ngwp.levlist[important_idx[i]]
wav_pc_top10[:, i] = PC_NGWP[dr, dc, :]
end
wiggle(wav_pc_top10; sc = 0.45)
p2 = title!("Top 10 PC-NGWP basis vectors")
important_idx = sortperm(dvec_lp_ngwp[:].^2; rev = true)
wav_lp_top10 = zeros(N, 10)
for i in 1:10
dr, dc = BS_lp_ngwp.levlist[important_idx[i]]
wav_lp_top10[:, i] = LP_NGWP[dr, dc, :]
end
wiggle(wav_lp_top10; sc = 0.45)
p3 = title!("Top 10 LP-NGWP basis vectors")
plot(p1, p2, p3, layout = Plots.grid(3, 1), size = (815, 900))
xticks!([1; 8:8:64], vcat(string("1"), [string(k) for k in 8:8:64])) # hide
yticks!([0; 1:10], vcat(string(""), [string(k) for k in 1:10])) # hide
plot!(left_margin = 5mm) # hide
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 840 | # Visualization of the Sunflower Graph
```@docs
SunFlowerGraph
```
Let us see how to visualize the sunflower graph by `gplot()` and `scatter_gplot()`.
```@example sunflower
using MultiscaleGraphSignalTransforms, LightGraphs, Plots
# construct the sunflower graph
G, L, X = SunFlowerGraph(); N = nv(G)
# display the sunflower graph (node radii vary for visualization purpose)
gplot(1.0 * adjacency_matrix(G), X; width = 1)
scatter_gplot!(X; c = :red, ms = LinRange(1, 9, N))
plot!(frame = :none, size = (815, 500)) # hide
```
One can also represent a signal on the graph by colors. For example,
```@example sunflower
f = zeros(N)
f[1:200] .= 1
f[301:N] .= -1
# display the graph signal
gplot(1.0 * adjacency_matrix(G), X; width = 1)
scatter_gplot!(X; marker = f, ms = LinRange(1, 9, N))
plot!(frame = :none, size = (815, 500)) # hide
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 146 | # Generalized Haar-Walsh Transform
```@index
Pages = ["GHWT.md"]
```
```@autodocs
Modules = [GHWT, GHWT_2d]
Pages = ["GHWT.jl", "GHWT_2d.jl"]
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 232 | # (Lapped) Hierarchical Graph Laplacian Eigen Transform
```@index
Pages = ["HGLET.md"]
```
```@autodocs
Modules = [HGLET]
Pages = ["HGLET.jl"]
```
```@autodocs
Modules = [MultiscaleGraphSignalTransforms]
Pages = ["LP-HGLET.jl"]
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 872 | # Natural Graph Wavelet Dictionaries
```@index
Pages = ["NGWD.md"]
```
## Metrics of graph Laplacian eigenvectors
```@autodocs
Modules = [MultiscaleGraphSignalTransforms]
Pages = ["natural_distances.jl", "eigROT_Distance.jl", "eigsROT_Distance.jl", "eigDAG_Distance.jl", "eigHAD_Distance.jl", "eigDAG_Distance.jl", "eigTSD_Distance.jl"]
```
## Dual Graph
```@docs
dualgraph
```
## Varimax Natural Graph Wavelet Packet
```@docs
varimax
```
```@docs
vm_ngwp
```
## Pair-Clustering Natural Graph Wavelet Packet
```@docs
pairclustering
```
```@docs
mgslp
```
```@docs
pc_ngwp
```
## Lapped Natural Graph Wavelet Packet
```@docs
lp_ngwp
```
## Graph Signal Processing via NGWP
```@docs
ngwp_analysis
```
```@docs
ngwp_bestbasis
```
```@docs
NGWP_jkl
```
## Natural Graph Wavelet Frame
```@autodocs
Modules = [MultiscaleGraphSignalTransforms]
Pages = ["NGWF.jl"]
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 208 | # Recursive Graph Partitioning
```@index
Pages = ["Partition.md"]
```
## Graph Partition
```@autodocs
Modules = [GraphPartition]
Pages = ["GraphPartition.jl"]
```
## BasisSpec Object
```@docs
BasisSpec
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 204 | ## Visualization
```@docs
gplot
```
```@docs
scatter_gplot
```
```@docs
GraphSig_Plot
```
## Best Basis Related
```@docs
cost_functional
```
```@docs
dmatrix_flatten
```
```@docs
dmatrix_ldb_flatten
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"BSD-3-Clause"
] | 1.7.3 | b7903b11d1aa4a96fc63d04de036236099cf8608 | docs | 174 | # extended Generalized Haar-Walsh Transform
```@index
Pages = ["eGHWT.md"]
```
```@autodocs
Modules = [GHWT_tf_1d, GHWT_tf_2d]
Pages = ["GHWT_tf_1d.jl", "GHWT_tf_2d.jl"]
```
| MultiscaleGraphSignalTransforms | https://github.com/UCD4IDS/MultiscaleGraphSignalTransforms.jl.git |
|
[
"MIT"
] | 0.0.1 | e2da55f31e0a03f2fc04109ea5534108163d4eee | code | 709 | using MetapopulationDynamics
using Plots
sl = StochasticLogistic(dt = 0.01, σ = 1.0)
rm = RickerModel()
sg = SpatialGraph()
djdm = DeterministicJumpDispersalModel(
0.8,
DispersalPotential(ExponentialDispersalKernel(decay = 10.0, threshold = 0.01), sg),
)
sjdm = StochasticJumpDispersalModel(
0.1,
DispersalPotential(ExponentialDispersalKernel(decay = 1, threshold = 0.01), sg),
)
fullmodel = modelset(djdm, rm)
results = simulate(fullmodel, sg; numtimesteps = 100)
computepcc(results)
plt = plot(legend = :outerright, xlabel = "time", ylabel = "Abundance")
for i = 1:size(results.timeseries, 1)
plot!(1:size(results.timeseries, 2), results.timeseries[i, :], label = "Pop $i")
end
plt
| MetapopulationDynamics | https://github.com/EcoJulia/MetapopulationDynamics.jl.git |
|
[
"MIT"
] | 0.0.1 | e2da55f31e0a03f2fc04109ea5534108163d4eee | code | 475 | using Documenter, MetapopulationDynamics
# For GR docs bug
ENV["GKSwstype"] = "100"
makedocs(
sitename="MetapopulationDynamics.jl",
authors="Michael Catchen",
modules=[MetapopulationDynamics],
pages=[
"Index" => "index.md",
],
checkdocs=:all,
strict=true,
)
deploydocs(
deps=Deps.pip("pygments", "python-markdown-math"),
repo="github.com/EcoJulia/MetapopulationDyanmics.jl.git",
devbranch="main",
push_preview=true
) | MetapopulationDynamics | https://github.com/EcoJulia/MetapopulationDynamics.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.