licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | code | 467 | module UnderwaterAcoustics
using Requires
using DocStringExtensions
using DSP: amp2db, db2amp, pow2db, db2pow
using Printf
export °
const ° = π/180.0
# basic underwater acoustics
include("uw_basic.jl")
# propagation modeling
include("pm_core.jl")
include("pm_basic.jl")
include("pm_pekeris.jl")
include("pm_all.jl")
# plot recipes
function __init__()
@require Plots="91a5bcdd-55d7-5caf-9e0b-520d859cae80" begin
include("plot.jl")
end
end
end # module
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | code | 3459 | using RecipesBase
using Colors
@recipe function plot(env::UnderwaterEnvironment;
sources=[], receivers=[], transmissionloss=[], rays=[], xmargin=0.0, dynamicrange=42.0,
colors=range(colorant"darkred", colorant"deepskyblue"; length=256)
)
if length(transmissionloss) > 0
size(transmissionloss) == size(receivers) || throw(ArgumentError("Mismatched receivers and transmissionloss"))
receivers isa AcousticReceiverGrid2D || throw(ArgumentError("Receivers must be an instance of AcousticReceiverGrid2D"))
minloss = minimum(transmissionloss)
clims --> (-minloss-dynamicrange, -minloss)
colorbar --> true
cguide --> "dB"
@series begin
seriestype := :heatmap
receivers.xrange, receivers.zrange, -transmissionloss'
end
end
xmin = Inf64
xmax = -Inf64
length(rays) > 0 && (xmin = min(xmin, minimum(minimum(r1[1] for r1 ∈ r.raypath) for r ∈ rays)))
length(rays) > 0 && (xmax = max(xmax, maximum(maximum(r1[1] for r1 ∈ r.raypath) for r ∈ rays)))
length(sources) > 0 && (xmin = min(xmin, minimum(p[1] for p ∈ location.(sources))))
length(sources) > 0 && (xmax = max(xmax, maximum(p[1] for p ∈ location.(sources))))
length(receivers) > 0 && (xmin = min(xmin, minimum(p[1] for p ∈ location.(receivers))))
length(receivers) > 0 && (xmax = max(xmax, maximum(p[1] for p ∈ location.(receivers))))
isinf(xmin) && (xmin = 0.0)
isinf(xmax) && (xmax = 1000.0)
xmin -= xmargin
xmax += xmargin
xrange = range(xmin, xmax; length=1000)
ticks --> :native
legend --> false
xguide --> "x (m)"
yguide --> "z (m) "
z = altimetry(env)
@series begin
seriestype := :line
linecolor := :royalblue
xrange, [altitude(z, x, 0.0) for x ∈ xrange]
end
z = bathymetry(env)
@series begin
seriestype := :line
linecolor := :brown
xrange, [-depth(z, x, 0.0) for x ∈ xrange]
end
if length(rays) > 0
reverse!(rays)
ampl = [r.phasor === missing ? -(r.surface + 3*r.bottom) : amp2db(abs.(r.phasor)) for r ∈ rays]
ampl .-= minimum(ampl)
if maximum(ampl) > 0.0
cndx = round.(Int, 1 .+ (length(colors)-1) .* ampl ./ maximum(ampl))
else
cndx = ones(Int, length(ampl)) .* length(colors)
end
for (j, eigenray) ∈ enumerate(rays)
r = eigenray.raypath
@series begin
seriestype := :line
linecolor := colors[cndx[j]]
[r[i][1] for i ∈ 1:length(r)], [r[i][3] for i ∈ 1:length(r)]
end
end
end
if length(sources) > 0
@series begin
seriestype := :scatter
marker := :star
seriescolor := :red
[p[1] for p ∈ location.(sources)], [p[3] for p ∈ location.(sources)]
end
end
if length(receivers) > 0 && length(transmissionloss) == 0
@series begin
seriestype := :scatter
seriescolor := :blue
[p[1] for p ∈ location.(receivers)], [p[3] for p ∈ location.(receivers)]
end
end
end
@recipe function plot(ssp::SoundSpeedProfile; maxdepth=missing, x=0.0)
D = 10.0
if maxdepth === missing
ssp isa SampledSSP && (D = maximum(-ssp.z))
else
D = maxdepth
end
d = 0.0:-0.1:-D
c = [soundspeed(ssp, x, 0.0, d1) for d1 ∈ d]
clim = extrema(c)
if clim[2] - clim[1] > 50.0
clim = (round(clim[1]-5.0), round(clim[2]+5.0))
else
μ = (clim[2] + clim[1]) / 2.0
clim = (round(μ - 30.0), round(μ + 30.0))
end
ticks --> :native
xlims --> clim
xguide --> "soundspeed (m/s)"
yguide --> "z (m) "
@series begin
c, d
end
end
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | code | 467 | export models
const allmodels = [
PekerisRayModel
]
"""
models()
models(env::UnderwaterEnvironment)
List available models, optionally for a given environment.
"""
function models(env=missing)
mlist = []
for m ∈ allmodels
try
check(m, env)
push!(mlist, m)
catch ex
# don't add to list
end
end
mlist
end
"""
$(SIGNATURES)
Register model in the list of available models.
"""
addmodel!(mtype) = push!(allmodels, mtype)
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | code | 20459 | using Interpolations
using SignalAnalysis
using DSP: hilbert
export IsoSSP, MunkSSP, SampledSSP, ConstantDepth, SampledDepth, SampledAltitude
export ReflectionCoef, FlatSurface, RayleighReflectionCoef, SurfaceLoss
export Rock, Pebbles, SandyGravel, CoarseSand, MediumSand, FineSand, VeryFineSand
export ClayeySand, CoarseSilt, SandySilt, Silt, FineSilt, SandyClay, SiltyClay, Clay
export Vacuum, SeaState0, SeaState1, SeaState2, SeaState3, SeaState4
export SeaState5, SeaState6, SeaState7, SeaState8, SeaState9
export AcousticReceiverGrid2D, AcousticReceiverGrid3D, NarrowbandAcousticSource
export WhiteGaussianNoise, RedGaussianNoise, Pinger, SampledAcousticSource
### sound speed profiles
"""
$(TYPEDEF)
Isovelocity sound speed profile.
---
IsoSSP(c)
Create an isovelocity sound speed profile with sound speed `c`.
"""
struct IsoSSP{T} <: SoundSpeedProfile
c::T
end
soundspeed(ssp::IsoSSP, x, y, z) = ssp.c
"""
$(TYPEDEF)
Munk sound speed profile.
"""
struct MunkSSP <: SoundSpeedProfile end
function soundspeed(::MunkSSP, x, y, z)
ϵ = 0.00737
z̃ = 2.0 * (-z - 1300.0) / 1300.0
1500.0 * (1.0 + ϵ * (z̃ - 1 + exp(-z̃)))
end
"""
$(TYPEDEF)
Sound speed profile based on discrete measurements.
"""
abstract type SampledSSP <: SoundSpeedProfile end
"""
$(TYPEDEF)
Sound speed profile based on measurements at discrete depths.
"""
struct SampledSSP1D{T1,T2,T3} <: SampledSSP
z::Vector{T1}
c::Vector{T2}
interp::Symbol
f::T3
function SampledSSP1D(depth, c, interp)
if interp === :smooth
depth isa AbstractRange || throw(ArgumentError("depth must be sampled uniformly and specified as an AbstractRange"))
f = cubic_spline_interpolation(depth, c; extrapolation_bc=Line())
elseif interp === :linear
f = linear_interpolation(depth, c; extrapolation_bc=Line())
else
throw(ArgumentError("Unknown interpolation"))
end
new{eltype(depth),eltype(c),typeof(f)}(-depth, c, interp, f)
end
end
"""
$(TYPEDEF)
Sound speed profile based on measurements at discrete depths and ranges.
"""
struct SampledSSP2D{T1,T2,T3,T4} <: SampledSSP
x::Vector{T1}
z::Vector{T2}
c::Matrix{T3}
interp::Symbol
f::T4
function SampledSSP2D(range, depth, c, interp)
if interp === :linear
f = extrapolate(interpolate((range, depth), c, Gridded(Linear())), Line())
else
throw(ArgumentError("Unknown interpolation"))
end
new{eltype(range),eltype(depth),eltype(c),typeof(f)}(range, -depth, c, interp, f)
end
end
"""
SampledSSP(depth, c)
SampledSSP(depth, c, interp)
SampledSSP(range, depth, c)
SampledSSP(range, depth, c, interp)
Create a sound speed profile based on measurements at discrete depths.
`interp` may be either `:linear` or `:smooth`, and defaults to `:linear`
if unspecified. `:smooth` is currently only supported for range-independent
sound speed profiles.
"""
SampledSSP(depth, c) = SampledSSP1D(depth, c, :linear)
SampledSSP(depth, c, interp::Symbol) = SampledSSP1D(depth, c, interp)
SampledSSP(range, depth, c) = SampledSSP2D(range, depth, c, :linear)
SampledSSP(range, depth, c, interp::Symbol) = SampledSSP2D(range, depth, c, interp)
soundspeed(ssp::SampledSSP1D, x, y, z) = ssp.f(-z)
soundspeed(ssp::SampledSSP2D, x, y, z) = ssp.f(x, -z)
function Base.show(io::IO, ssp::SampledSSP1D{T1,T2,T3}) where {T1,T2,T3}
print(io, "SampledSSP1D{", T1, ",", T2, ",", ssp.interp, "}(", length(ssp.z), " points)")
end
function Base.show(io::IO, ssp::SampledSSP2D{T1,T2,T3,T4}) where {T1,T2,T3,T4}
print(io, "SampledSSP2D{", T1, ",", T2, ",", T3, ",", ssp.interp, "}(", length(ssp.x), " × ", length(ssp.z), " points)")
end
### bathymetry models
"""
$(TYPEDEF)
Bathymetry with constant depth.
---
ConstantDepth(depth)
Create a constant depth bathymetry.
"""
struct ConstantDepth{T} <: Bathymetry
depth::T
end
depth(bathy::ConstantDepth, x, y) = bathy.depth
maxdepth(bathy::ConstantDepth) = bathy.depth
"""
$(TYPEDEF)
Bathymetry based on depth samples.
"""
struct SampledDepth{T1,T2,T3} <: Bathymetry
x::Vector{T1}
depth::Vector{T2}
interp::Symbol
f::T3
function SampledDepth(x, depth, interp)
if interp === :smooth
x isa AbstractRange || throw(ArgumentError("x must be sampled uniformly and specified as an AbstractRange"))
f = cubic_spline_interpolation(x, depth; extrapolation_bc=Line())
elseif interp === :linear
f = linear_interpolation(x, depth; extrapolation_bc=Line())
else
throw(ArgumentError("Unknown interpolation"))
end
new{eltype(x),eltype(depth),typeof(f)}(x, depth, interp, f)
end
end
"""
SampledDepth(x, depth)
SampledDepth(x, depth, interp)
Create a bathymetry given discrete depth measurements at locations given in `x`.
`interp` may be either `:linear` or `:smooth`, and defaults to `:linear`
if unspecified.
"""
SampledDepth(x, depth) = SampledDepth(x, depth, :linear)
depth(bathy::SampledDepth, x, y) = bathy.f(x)
maxdepth(bathy::SampledDepth) = maximum(bathy.depth)
function Base.show(io::IO, b::SampledDepth{T1,T2,T3}) where {T1,T2,T3}
print(io, "SampledDepth{", T1, ",", T2, ",", b.interp, "}(", length(b.x), " points)")
end
### altimetry models
"""
$(TYPEDEF)
Altimetry for a flat surface with constant altitude of zero.
"""
struct FlatSurface <: Altimetry end
altitude(::FlatSurface, x, y) = 0.0
"""
$(TYPEDEF)
Altimetry based on altitude samples.
"""
struct SampledAltitude{T1,T2,T3} <: Altimetry
x::Vector{T1}
altitude::Vector{T2}
interp::Symbol
f::T3
function SampledAltitude(x, altitude, interp)
if interp === :smooth
x isa AbstractRange || throw(ArgumentError("x must be sampled uniformly and specified as an AbstractRange"))
f = cubic_spline_interpolation(x, altitude; extrapolation_bc=Line())
elseif interp === :linear
f = linear_interpolation(x, altitude; extrapolation_bc=Line())
else
throw(ArgumentError("Unknown interpolation"))
end
new{eltype(x),eltype(altitude),typeof(f)}(x, altitude, interp, f)
end
end
"""
SampledAltitude(x, altitude)
SampledAltitude(x, altitude, interp)
Create an altimetry given discrete altitude measurements at locations given in `x`.
`interp` may be either `:linear` or `:smooth`, and defaults to `:linear`
if unspecified.
"""
SampledAltitude(x, altitude) = SampledAltitude(x, altitude, :linear)
altitude(a::SampledAltitude, x, y) = a.f(x)
function Base.show(io::IO, a::SampledAltitude{T1,T2,T3}) where {T1,T2,T3}
print(io, "SampledAltitude{", T1, ",", T2, ",", a.interp, "}(", length(a.x), " points)")
end
### reflection models
"""
$(TYPEDEF)
Reflection model for a surface with a constant reflection coefficient.
---
ReflectionCoef(coef)
Create a reflection model for a surface with a constant reflection coefficient `coef`.
"""
struct ReflectionCoef{T<:Number} <: ReflectionModel
coef::T
end
reflectioncoef(rm::ReflectionCoef, f, θ) = rm.coef
"""
$(TYPEDEF)
Reflection model for a surface with a Rayleigh reflection coefficient.
---
RayleighReflectionCoef(ρᵣ, cᵣ, δ)
RayleighReflectionCoef(ρᵣ, cᵣ)
Create a reflection model for a surface with a Rayleigh reflection coefficient
with relative density `ρᵣ`, relative sound speed `cᵣ`, and dimensionless
attentuation `δ`. If attentuation `δ` is unspecified, it is assumed to be zero.
See `reflectioncoef()` for more details.
"""
struct RayleighReflectionCoef{T1,T2,T3} <: ReflectionModel
ρᵣ::T1
cᵣ::T2
δ::T3
end
RayleighReflectionCoef(ρᵣ, cᵣ) = RayleighReflectionCoef(ρᵣ, cᵣ, 0.0)
# from APL-UW TR 9407 (1994), IV-6 Table 2
const Rock = RayleighReflectionCoef(2.5, 2.5, 0.01374)
const Pebbles = RayleighReflectionCoef(2.5, 1.8, 0.01374)
const SandyGravel = RayleighReflectionCoef(2.492, 1.3370, 0.01705)
const CoarseSand = RayleighReflectionCoef(2.231, 1.2503, 0.01638)
const MediumSand = RayleighReflectionCoef(1.845, 1.1782, 0.01624)
const FineSand = RayleighReflectionCoef(1.451, 1.1073, 0.01602)
const VeryFineSand = RayleighReflectionCoef(1.268, 1.0568, 0.01875)
const ClayeySand = RayleighReflectionCoef(1.224, 1.0364, 0.02019)
const CoarseSilt = RayleighReflectionCoef(1.195, 1.0179, 0.02158)
const SandySilt = RayleighReflectionCoef(1.169, 0.9999, 0.01261)
const Silt = RayleighReflectionCoef(1.149, 0.9873, 0.00386)
const FineSilt = RayleighReflectionCoef(1.148, 0.9861, 0.00306)
const SandyClay = RayleighReflectionCoef(1.147, 0.9849, 0.00242)
const SiltyClay = RayleighReflectionCoef(1.146, 0.9824, 0.00163)
const Clay = RayleighReflectionCoef(1.145, 0.98, 0.00148)
reflectioncoef(rm::RayleighReflectionCoef, f, θ) = reflectioncoef(θ, rm.ρᵣ, rm.cᵣ, rm.δ)
"""
$(TYPEDEF)
Reflection model for a water surface affected by wind.
---
SurfaceLoss(windspeed)
Create a reflection model for a surface affected by wind. `windspeed` is
given in m/s.
"""
struct SurfaceLoss{T} <: ReflectionModel
windspeed::T
end
reflectioncoef(rm::SurfaceLoss, f, θ) = complex(-surfaceloss(rm.windspeed, f, θ), 0.0)
const Vacuum = ReflectionCoef(complex(-1.0, 0.0))
# WMO sea states
# from APL-UW TR 9407 (1994), II-4 Table 2 (median windspeed)
const SeaState0 = SurfaceLoss(0.8)
const SeaState1 = SurfaceLoss(2.6)
const SeaState2 = SurfaceLoss(4.4)
const SeaState3 = SurfaceLoss(6.9)
const SeaState4 = SurfaceLoss(9.8)
const SeaState5 = SurfaceLoss(12.6)
const SeaState6 = SurfaceLoss(19.3)
const SeaState7 = SurfaceLoss(26.5)
const SeaState8 = SurfaceLoss(30.6)
const SeaState9 = SurfaceLoss(32.9)
### basic environmental model
Base.@kwdef struct BasicUnderwaterEnvironment{T1<:Altimetry, T2<:Bathymetry, T3<:SoundSpeedProfile, T4<:Number, T5<:ReflectionModel, T6<:ReflectionModel, T7} <: UnderwaterEnvironment
altimetry::T1 = FlatSurface()
bathymetry::T2 = ConstantDepth(20.0)
ssp::T3 = IsoSSP(soundspeed())
salinity::T4 = 35.0
waterdensity::T4 = waterdensity()
seasurface::T5 = Vacuum
seabed::T6 = SandySilt
noise::T7 = RedGaussianNoise(db2amp(120.0))
end
"""
UnderwaterEnvironment(; altimetry, bathymetry, ssp, salinity, seasurface, seabed, noise)
Create an underwater environment.
"""
UnderwaterEnvironment(; kwargs...) = BasicUnderwaterEnvironment(; kwargs...)
altimetry(env::BasicUnderwaterEnvironment) = env.altimetry
bathymetry(env::BasicUnderwaterEnvironment) = env.bathymetry
ssp(env::BasicUnderwaterEnvironment) = env.ssp
salinity(env::BasicUnderwaterEnvironment) = env.salinity
waterdensity(env::BasicUnderwaterEnvironment) = env.waterdensity
seasurface(env::BasicUnderwaterEnvironment) = env.seasurface
seabed(env::BasicUnderwaterEnvironment) = env.seabed
noise(env::BasicUnderwaterEnvironment) = env.noise
### noise models
"""
$(TYPEDEF)
Ambient noise model with Gaussian noise with a flat power spectral density.
---
WhiteGaussianNoise(σ)
Create an white Gaussian ambient noise model with variance `σ²`.
"""
struct WhiteGaussianNoise{T} <: NoiseModel
σ::T
end
function record(noisemodel::WhiteGaussianNoise, duration, fs; start=0.0)
n = round(Int, duration*fs)
signal(complex.(randn(n), randn(n)) .* (noisemodel.σ / √2), fs)
end
"""
$(TYPEDEF)
Ambient noise model with Gaussian noise with a `1/f²` power spectral density.
---
RedGaussianNoise(σ)
Create an ambient noise model with variance `σ²` and `1/f²` power spectral density.
"""
struct RedGaussianNoise{T} <: NoiseModel
σ::T
end
function record(noisemodel::RedGaussianNoise, duration, fs; start=0.0)
analytic(signal(rand(RedGaussian(; n=round(Int, duration*fs), σ=noisemodel.σ)), fs))
end
### basic source & recevier models
"""
$(TYPEDEF)
Narrowband acoustic source.
"""
struct NarrowbandAcousticSource{T1,T2,T3,T4} <: AcousticSource
pos::NTuple{3,T1}
f::T2
A::T3
ϕ::T4
end
"""
$(SIGNATURES)
Create a narrowband acoustic source with frequency `f` Hz at location (`x`, `y`, `z`).
The `sourcelevel` is in µPa @ 1m. A phase `ϕ` may be optionlly specified.
"""
NarrowbandAcousticSource(x, y, z, f; sourcelevel=db2amp(180.0), ϕ=0.0) = NarrowbandAcousticSource(promote(x, y, z), f, sourcelevel, ϕ)
"""
$(SIGNATURES)
Create a narrowband acoustic source with frequency `f` Hz at location (`x`, z`).
The `sourcelevel` is in µPa @ 1m. A phase `ϕ` may be optionlly specified.
"""
NarrowbandAcousticSource(x, z, f; sourcelevel=db2amp(180.0), ϕ=0.0) = NarrowbandAcousticSource(promote(x, 0, z), f, sourcelevel, ϕ)
"""
$(SIGNATURES)
Create a narrowband acoustic source with frequency `f` Hz at location (`x`, `y`, `z`).
The `sourcelevel` is in µPa @ 1m. A phase `ϕ` may be optionlly specified.
"""
AcousticSource(x, y, z, f; sourcelevel=db2amp(180.0), ϕ=0.0) = NarrowbandAcousticSource(promote(x, y, z), f, sourcelevel, ϕ)
"""
$(SIGNATURES)
Create a narrowband acoustic source with frequency `f` Hz at location (`x`, `y`, `z`).
The `sourcelevel` is in µPa @ 1m. A phase `ϕ` may be optionlly specified.
"""
AcousticSource(x, z, f; sourcelevel=db2amp(180.0), ϕ=0.0) = NarrowbandAcousticSource(promote(x, 0, z), f, sourcelevel, ϕ)
location(tx::NarrowbandAcousticSource) = tx.pos
nominalfrequency(tx::NarrowbandAcousticSource) = tx.f
phasor(tx::NarrowbandAcousticSource) = tx.A * cis(tx.ϕ)
record(tx::NarrowbandAcousticSource, duration, fs; start=0.0) = signal(tx.A .* cis.(2π .* tx.f .* (start:1/fs:start+duration-1/fs) .+ tx.ϕ), fs)
"""
$(TYPEDEF)
Narrowband pulsed acoustic source.
"""
Base.@kwdef struct Pinger{T1,T2,T3,T4,T5,T6,T7,T8} <: AcousticSource
pos::NTuple{3,T1}
frequency::T2
sourcelevel::T3 = db2amp(180.0)
phase::T4 = 0.0
duration::T5 = 0.02
start::T6 = 0.0
interval::T7 = 1.0
window::T8 = nothing
end
"""
Pinger(x, y, z, f; sourcelevel, phase, duration, start, interval, window)
Create a pulsed narrowband acoustic source with frequency `f` Hz at location (`x`, `y`, `z`).
Additional parameters that may be specified:
- `sourcelevel` in µPa @ 1m (default 180 dB)
- `phase` of the narrowband signal (default 0)
- `duration` of the pulse in seconds (default 20 ms)
- `start` time of one of the pulses in seconds (default 0)
- pulse repetition `interval` in seconds (default 1 second)
- `window` type (from `DSP.jl`) (default `nothing`)
"""
Pinger(x, y, z, f; kwargs...) = Pinger(; pos=promote(x, y, z), frequency=f, kwargs...)
"""
Pinger(x, z, f; sourcelevel, phase, duration, start, interval, window)
Create a pulsed narrowband acoustic source with frequency `f` Hz at location (`x`, `z`).
Additional parameters that may be specified:
- `sourcelevel` in µPa @ 1m (default 180 dB)
- `phase` of the narrowband signal (default 0)
- `duration` of the pulse in seconds (default 20 ms)
- `start` time of one of the pulses in seconds (default 0)
- pulse repetition `interval` in seconds (default 1 second)
- `window` type (from `DSP.jl`) (default `nothing`)
"""
Pinger(x, z, f; kwargs...) = Pinger(; pos=promote(x, 0, z), frequency=f, kwargs...)
location(tx::Pinger) = tx.pos
nominalfrequency(tx::Pinger) = tx.frequency
phasor(tx::Pinger) = tx.sourcelevel * cis(tx.phase)
function record(pinger::Pinger, duration, fs; start=0.0)
nsamples = round(Int, duration * fs)
ping = cw(pinger.frequency, pinger.duration, fs; phase=pinger.phase, window=pinger.window)
x = zeros(eltype(ping), nsamples)
k1 = ceil(Int, (start - pinger.start - pinger.duration) / pinger.interval)
k2 = floor(Int, (start - pinger.start + duration) / pinger.interval)
n = length(ping)
for k ∈ k1:k2
ndx = round(Int, (pinger.start + k * pinger.interval - start) * fs) + 1
if ndx > 0 && ndx + n ≤ nsamples
x[ndx:ndx+n-1] .= ping
elseif ndx > 0
x[ndx:end] .= ping[1:nsamples-ndx+1]
elseif ndx + n ≤ nsamples
x[1:n+ndx-1] .= ping[2-ndx:end]
else
x .= ping[2-ndx:1-ndx+nsamples]
end
end
signal(pinger.sourcelevel * x, fs)
end
"""
$(TYPEDEF)
Acoustic source transmitting a sampled signal.
"""
struct SampledAcousticSource{T1,T2,T3<:AbstractArray} <: AcousticSource
pos::NTuple{3,T1}
frequency::T2
signal::T3
end
"""
SampledAcousticSource(x, y, z, sig; fs, frequency)
Create a sampled acoustic source transmitting signal `sig` at location (`x`, `y`, `z`). The
samples are assumed to be in µPa @ 1m from the source.
Additional parameters that may be specified:
- `fs` is the sampling rate of the signal `sig`
- nominal `frequency` in Hz (`nothing` to auto-estimate)
"""
function SampledAcousticSource(x, y, z, sig::AbstractArray; fs=framerate(sig), frequency=nothing)
s = signal(sig, fs)
SampledAcousticSource(promote(x, y, z), frequency === nothing ? meanfrequency(s) : frequency, s)
end
"""
SampledAcousticSource(x, z, sig; fs, frequency)
Create a sampled acoustic source transmitting signal `sig` at location (`x`, `z`). The
samples are assumed to be in µPa @ 1m from the source.
Additional parameters that may be specified:
- `fs` is the sampling rate of signal `sig`
- nominal `frequency` in Hz (`nothing` to auto-estimate)
"""
function SampledAcousticSource(x, z, sig::AbstractArray; fs=framerate(sig), frequency=nothing)
s = signal(sig, fs)
SampledAcousticSource(promote(x, 0, z), frequency === nothing ? meanfrequency(s) : frequency, s)
end
location(tx::SampledAcousticSource) = tx.pos
nominalfrequency(tx::SampledAcousticSource) = tx.frequency
phasor(tx::SampledAcousticSource) = throw(ArgumentError("phasor is undefined for a SampledAcousticSource"))
function record(tx::SampledAcousticSource, duration, fs=framerate(tx.signal); start=0.0)
fs == framerate(tx.signal) || throw(ArgumentError("Resampling of SampledAcousticSource is not supported"))
t1 = toframe(start, tx.signal)
t2 = toframe(start+duration, tx.signal) - 1
y = padded(tx.signal, (max(t1-1, 0), max(t2-t1+1-length(tx.signal), 0)); delay=-t1+1)
@view y[1:t2-t1+1]
end
"""
$(TYPEDEF)
Omnidirectional acoustic receiver.
"""
struct BasicAcousticReceiver{T} <: AcousticReceiver
pos::NTuple{3,T}
end
"""
$(SIGNATURES)
Create an omnidirectional acoustic receiver at location (`x`, `y`, `z`).
"""
BasicAcousticReceiver(x, y, z) = BasicAcousticReceiver(promote(x, y, z))
"""
$(SIGNATURES)
Create an omnidirectional acoustic receiver at location (`x`, `z`).
"""
BasicAcousticReceiver(x, z) = BasicAcousticReceiver(promote(x, 0, z))
"""
$(SIGNATURES)
Create an omnidirectional acoustic receiver at location (`x`, `y`, `z`).
"""
AcousticReceiver(x, y, z) = BasicAcousticReceiver(promote(x, y, z))
"""
$(SIGNATURES)
Create an omnidirectional acoustic receiver at location (`x`, `z`).
"""
AcousticReceiver(x, z) = BasicAcousticReceiver(promote(x, 0, z))
location(rx::BasicAcousticReceiver) = rx.pos
### receiver grids for transmission loss computation
"""
$(TYPEDEF)
A 2D Cartesian grid of omnidirectional acoustic receivers.
"""
struct AcousticReceiverGrid2D{T} <: AbstractArray{BasicAcousticReceiver{T},2}
xrange::StepRangeLen{T,T,T}
zrange::StepRangeLen{T,T,T}
end
"""
$(SIGNATURES)
Create a 2D Cartesian grid of omnidirectional acoustic receivers with `nx` × `nz`
receviers starting (`xmin`, `zmin`) with step sizes `xstep` and `zstep`.
"""
function AcousticReceiverGrid2D(xmin, xstep, nx, zmin, zstep, nz)
xmin, xstep, zmin, zstep = promote(xmin, xstep, zmin, zstep)
AcousticReceiverGrid2D(StepRangeLen(xmin, xstep, nx), StepRangeLen(zmin, zstep, nz))
end
Base.size(g::AcousticReceiverGrid2D) = (g.xrange.len, g.zrange.len)
Base.getindex(g::AcousticReceiverGrid2D, I::Vararg{Int,2}) = AcousticReceiver(g.xrange[I[1]], g.zrange[I[2]])
Base.setindex!(g::AcousticReceiverGrid2D, v, I::Vararg{Int,2}) = throw(ArgumentError("AcousticReceiverGrid2D is readonly"))
"""
$(TYPEDEF)
A 3D Cartesian grid of omnidirectional acoustic receivers.
"""
struct AcousticReceiverGrid3D{T} <: AbstractArray{BasicAcousticReceiver{T},3}
xrange::StepRangeLen{T,T,T}
yrange::StepRangeLen{T,T,T}
zrange::StepRangeLen{T,T,T}
end
"""
$(SIGNATURES)
Create a 3D Cartesian grid of omnidirectional acoustic receivers with `nx` × `ny` × `nz`
receviers starting (`xmin`, `ymin`, `zmin`) with step sizes `xstep`, `ystep`, and `zstep`.
"""
function AcousticReceiverGrid3D(xmin, xstep, nx, ymin, ystep, ny, zmin, zstep, nz)
xmin, xstep, ymin, ystep, zmin, zstep = promote(xmin, xstep, ymin, ystep, zmin, zstep)
AcousticReceiverGrid3D(StepRangeLen(xmin, xstep, nx), StepRangeLen(ymin, ystep, ny), StepRangeLen(zmin, zstep, nz))
end
Base.size(g::AcousticReceiverGrid3D) = (g.xrange.len, g.yrange.len, g.zrange.len)
Base.getindex(g::AcousticReceiverGrid3D, I::Vararg{Int,3}) = AcousticReceiver(g.xrange[I[1]], g.yrange[I[2]], g.zrange[I[3]])
Base.setindex!(g::AcousticReceiverGrid3D, v, I::Vararg{Int,3}) = throw(ArgumentError("AcousticReceiverGrid3D is readonly"))
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | code | 17997 | using SignalAnalysis: signal
using FFTW: ifft!
using DSP: nextfastfft
using ToeplitzMatrices: TriangularToeplitz
export SoundSpeedProfile, soundspeed
export Bathymetry, depth, maxdepth
export Altimetry, altitude
export ReflectionModel, reflectioncoef
export UnderwaterEnvironment, altimetry, bathymetry, ssp, salinity, seasurface, seabed, noise
export AcousticSource, AcousticReceiver, location, nominalfrequency, phasor, record, recorder
export PropagationModel, arrivals, transfercoef, transmissionloss, eigenrays, rays
export NoiseModel
export impulseresponse, channelmatrix
### interface: SoundSpeedProfile
abstract type SoundSpeedProfile end
"""
soundspeed(ssp::SoundSpeedProfile, x, y, z)
Get sound speed at location (`x`, `y`, `z`). If a sound speed profile is range
independent, `x` and `y` may be ignored. `z` is generally negative, since the
sea surface is the datum and z-axis points upwards.
"""
function soundspeed end
### interface: Bathymetry
abstract type Bathymetry end
"""
depth(bathy::Bathymetry, x, y)
Get water depth at location (`x`, `y`).
"""
function depth end
"""
maxdepth(bathy::Bathymetry)
Get the maximum water depth.
"""
function maxdepth end
### interface: Altimetry
abstract type Altimetry end
"""
altitude(alt::Altimetry, x, y)
Get water surface altitude at location (`x`, `y`). The nominal water surface
is considered to have an altitude of zero. However, the water surface may
not be flat, and the Altimetry provisions for variations of altitude around the
nominal altitutde of zero.
"""
function altitude end
### interface: ReflectionModel
abstract type ReflectionModel end
"""
reflectioncoef(rm::ReflectionModel, f, θ)
Get complex reflection coefficient at frequency `f` Hz and incidence angle `θ`
(w.r.t. the surface normal).
"""
function reflectioncoef end
### interface: UnderwaterEnvironment
abstract type UnderwaterEnvironment end
"""
altimetry(env::UnderwaterEnvironment)::Altimetry
Get the altimetry for the underwater environment.
"""
function altimetry end
"""
bathymetry(env::UnderwaterEnvironment)::Bathymetry
Get the bathymetry for the underwater environment.
"""
function bathymetry end
"""
ssp(env::UnderwaterEnvironment)::SoundSpeedProfile
Get the sound speed profile for the underwater environment.
"""
function ssp end
"""
salinity(env::UnderwaterEnvironment)
Get the salinity of the underwater environment.
"""
function salinity end
"""
waterdensity(env::UnderwaterEnvironment)
Get the nominal water density for the underwater environment.
"""
function waterdensity end
"""
seasurface(env::UnderwaterEnvironment)::ReflectionModel
Get the sea surface reflection model for the underwater environment.
"""
function seasurface end
"""
seabed(env::UnderwaterEnvironment)::ReflectionModel
Get the seabed reflection model for the underwater environment.
"""
function seabed end
"""
noise(env::UnderwaterEnvironment)::NoiseModel
Get the noise model for the underwater environment.
"""
function noise end
### interface: AcousticSource
abstract type AcousticSource end
"""
location(src::AcousticSource)
location(src::AcousticReceiver)
Get the location of an acoustic source or receiver as a 3-tuple (`x`, `y`, `z`).
"""
function location end
"""
nominalfrequency(src::AcousticSource)
Get the nominal frequency of an acoustic source in Hz.
"""
function nominalfrequency end
"""
nominalfrequency(src::AcousticSource)
Get the complex phasor representation (amplitude & phase) of a narrowband
acoustic source at the nominal frequency.
"""
function phasor end
"""
record(src::AcousticSource, duration, fs; start=0.0)
record(noise::NoiseModel, duration, fs; start=0.0)
record(model::PropagationModel, tx, rx, duration, fs; start=0.0)
record(model::PropagationModel, tx, rx, sig; reltime=true)
Make a recording of an acoustic source or ambient noise. The `start` time and
`duration` are specified in seconds, and the recording is made at a sampling
rate of `fs` Hz.
For an recording of an acoustic source, free space propagation is assumed,
and the recording is made at a nominal range of 1 meter from the acoustic
center of the source.
For a recording through a propagation model, `tx` and `rx` may be single `AcousticSource`
and `AcousticReceiver`, or an array each. The returned signal is always complex,
irrespective of whether the source is real or complex.
When a `sig` is specified, the sources are assumed to transmit the sampled signal in `sig`.
The number of channels in `sig` must match the number of sources. The returned signal
is the same type as the input signal (real or complex). If `reltime` is `true`, the
recorded signal starts at the first arrival, otherwise it starts at the beginning of the
transmission.
"""
function record end
### interface: AcousticReceiver
abstract type AcousticReceiver end
function location end
### interface: NoiseModel
abstract type NoiseModel end
function record end
### interface: PropagationModel
abstract type PropagationModel{T<:UnderwaterEnvironment} end
"""
environment(pm::PropagationModel)
Get the environment associated with the propagation model.
"""
function environment end
"""
check(pm::Type{<:PropagationModel}, env::UnderwaterEnvironment)
check(pm::Type{<:PropagationModel}, env=missing)
Check if an propagation model is available, and can simulate the specified
environment. Returns the environment if it can be simulated, or throws an
error with a descriptive error message if it cannot be simulated.
This function is internally used by the propagation modeling toolbox to choose
a model or offer a selection of models to the user.
"""
function check end
"""
arrivals(pm::PropagationModel, tx1::AcousticSource, rx1::AcousticReceiver)
Compute the arrivals from `tx1` to `rx1`. Returns an array of `Arrival` structs.
"""
function arrivals end
"""
transfercoef(pm::PropagationModel, tx1::AcousticSource, rx1::AcousticReceiver; mode=:coherent)
transfercoef(pm::PropagationModel, tx1::AcousticSource, rx::AbstractArray{<:AcousticReceiver}; mode=:coherent)
Compute the complex transfer coefficients from `tx1` to `rx1` or all receivers in `rx`.
The mode may be `:coherent` or `:incoherent`.
"""
function transfercoef end
"""
transmissionloss(pm::PropagationModel, tx1::AcousticSource, rx1::AcousticReceiver; mode=:coherent)
transmissionloss(pm::PropagationModel, tx1::AcousticSource, rx::AbstractArray{<:AcousticReceiver}; mode=:coherent)
Compute the transmission loss in dB from `tx1` to `rx1` or all receivers in `rx`.
The mode may be `:coherent` or `:incoherent`.
"""
function transmissionloss end
"""
eigenrays(pm::PropagationModel, tx1::AcousticSource, rx1::AcousticReceiver)
Compute the eigenrays from `tx1` to `rx1`. Returns an array of `RayArrival` structs.
"""
function eigenrays end
"""
rays(pm::PropagationModel, tx1::AcousticSource, θ::Real, rmax)
Compute the rays from `tx1` launched at angle `θ` (or all angles in `θ`, if it is a vector).
Returns an array of `RayArrival` datatypes. `rmax` is the maximum horizontal range in meters
to track the rays over.
"""
function rays end
function record end
"""
recorder(model::PropagationModel, tx, rx)
Create a recorder function that may be called later to make an acoustic recording
of sources in `tx` at receviers `rx`. `tx` and `rx` may be single `AcousticSource` and
`AcousticReceiver`, or an array each.
The recorder function may be called later with `duration`, `fs`, and optionally a `start`
time. Alternatively, the recorder function may also be called with a sampled signal.
It functions in a similar way as the `record()` function.
# Examples:
```julia-repl
julia> rec = recorder(pm, tx, rx);
julia> s = rec(1.0, 44100.0; start=0.0); # make a recording of 1 second at 44.1 kHz
julia> s = rec(signal(randn(44100), 44100)); # transmit a random 1 second signal
```
"""
function recorder end
### arrival types
abstract type Arrival end
struct RayArrival{T1,T2} <: Arrival
time::T1
phasor::Complex{T1}
surface::Int
bottom::Int
launchangle::T1
arrivalangle::T1
raypath::Union{Vector{NTuple{3,T2}},Missing}
end
function RayArrival(time::T1, phasor::Complex{T1}, surface::Int, bottom::Int, launchangle::T1, arrivalangle::T1, raypath::Vector{NTuple{3,T2}}) where {T1,T2}
RayArrival{T1,T2}(time, phasor, surface, bottom, launchangle, arrivalangle, raypath)
end
function RayArrival(time, phasor, surface::Int, bottom::Int, launchangle, arrivalangle, raypath::Vector{NTuple{3,T}}) where T
t, r, i, θ1, θ2 = promote(time, real(phasor), imag(phasor), launchangle, arrivalangle)
RayArrival{typeof(t),T}(t, Complex(r, i), surface, bottom, θ1, θ2, raypath)
end
function RayArrival(time, phasor, surface::Int, bottom::Int, launchangle, arrivalangle)
t, r, i, θ1, θ2 = promote(time, real(phasor), imag(phasor), launchangle, arrivalangle)
RayArrival{typeof(t),Missing}(t, Complex(r, i), surface, bottom, θ1, θ2, missing)
end
phasortype(::Type{RayArrival{T1,T2}}) where {T1,T2} = T1
### fallbacks & helpers
location(x::NTuple{3,T}) where T = x
location(x::NTuple{2,T}) where T = (x[1], zero(T), x[2])
check(model::PropagationModel, env) = env
environment(model::PropagationModel) = model.env
function transfercoef(model::PropagationModel, tx1::AcousticSource, rx1::AcousticReceiver; mode=:coherent)
arr = arrivals(model, tx1, rx1)
length(arr) == 0 && return zero(phasortype(eltype(arr)))
if mode === :coherent
f = nominalfrequency(tx1)
tc = sum(a.phasor * cis(2π * a.time * f) for a ∈ arr)
elseif mode === :incoherent
tc = Complex(√sum(abs2(a.phasor) for a ∈ arr), 0)
else
throw(ArgumentError("Unknown mode :" * string(mode)))
end
tc
end
function transfercoef(model::PropagationModel, tx1::AcousticSource, rx::AbstractArray{<:AcousticReceiver}; mode=:coherent)
tmap(rx1 -> transfercoef(model, tx1, rx1; mode), rx)
end
function rays(model::PropagationModel, tx1::AcousticSource, θ::AbstractArray, rmax)
tmap(θ1 -> rays(model, tx1, θ1, rmax), θ)
end
transmissionloss(model, tx, rx; mode=:coherent) = -amp2db.(abs.(transfercoef(model, tx, rx; mode)))
struct Recorder{T1,T2,T3,T4}
noisemodel::T1
tx::T2 # always an array of sources
rx::T3 # could be an array or a single recevier
arr::Matrix{T4}
end
function (rec::Recorder)(duration, fs; start=0.0)
mindelay, maxdelay = extrema(Iterators.flatten([[a1.time for a1 ∈ a] for a ∈ rec.arr]))
src = [analytic(record(tx1, duration + (maxdelay-mindelay) + 1/fs, fs; start=start-maxdelay)) for tx1 ∈ rec.tx]
nsamples = round(Int, duration * fs)
x = zeros(Base.promote_eltype(src...), nsamples, size(rec.arr, 2))
for j = 1:size(rec.arr, 1)
for k = 1:size(rec.arr, 2)
for a ∈ rec.arr[j,k]
t = round(Int, (maxdelay - a.time) * fs)
x[:,k] .+= a.phasor .* src[j][t+1:t+nsamples]
end
end
end
if rec.noisemodel !== missing && rec.noisemodel !== nothing
for k = 1:size(rec.arr, 2)
x[:,k] .+= record(rec.noisemodel, duration, fs; start)
end
end
x̄ = rec.rx isa AbstractArray ? x : dropdims(x; dims=2)
signal(x̄, fs)
end
function (rec::Recorder)(sig; fs=framerate(sig), reltime=true)
nchannels(sig) == length(rec.tx) || throw(ArgumentError("Input signal must have $(length(rec.tx)) channel(s)"))
mindelay, maxdelay = extrema(Iterators.flatten([[a1.time for a1 ∈ a] for a ∈ rec.arr]))
n1 = round(Int, maxdelay * fs)
n2 = round(Int, (maxdelay - mindelay) * fs) + 1
src = [analytic(vcat(zeros(eltype(sig), n1), sig[:,i], zeros(eltype(sig), n2))) for i ∈ eachindex(rec.tx)]
nsamples = nframes(sig) + n1
x = zeros(Base.promote_eltype(src...), nsamples, size(rec.arr, 2))
for j = 1:size(rec.arr, 1)
for k = 1:size(rec.arr, 2)
for a ∈ rec.arr[j,k]
t = round(Int, (maxdelay - a.time) * fs)
x[:,k] .+= a.phasor .* src[j][t+1:t+nsamples]
end
end
end
if rec.noisemodel !== missing && rec.noisemodel !== nothing
for k = 1:size(rec.arr, 2)
x[:,k] .+= record(rec.noisemodel, nsamples/fs, fs)
end
end
n3 = reltime ? round(Int, mindelay * fs) : 1
x̄ = rec.rx isa AbstractArray ? @view(x[n3:end,:]) : dropdims(@view x[n3:end,:]; dims=2)
isanalytic(sig) ? signal(x̄, fs) : signal(convert.(eltype(sig), real.(x̄) .* √2), fs)
end
"""
channelmatrix(rec::Recorder, fs, ntaps=0; tx=1, rx=1, approx=false)
channelmatrix(rec::Vector{<:Arrival}, fs, ntaps=0; approx=false)
Generate a sampled channel matrix at a sampling rate of `fs` Hz. If `ntaps` is zero,
the number of taps of the channel matrix are chosen automatically.
If `approx` is `true`, a fast algorithm is used to generate a sparse channel matrix
that assigns an arrival to the nearest sampling time.
"""
function channelmatrix(rec::Recorder, fs, ntaps=0; tx=1, rx=1, approx=false)
ir = impulseresponse(rec.arr[tx,rx], fs, ntaps; reltime=true, approx)
TriangularToeplitz(ir, :L)
end
function channelmatrix(arrivals::Vector{<:Arrival}, fs, ntaps=0; approx=false)
ir = impulseresponse(arrivals, fs, ntaps; reltime=true, approx)
TriangularToeplitz(ir, :L)
end
function recorder(model::PropagationModel, tx::AcousticSource, rx::AcousticReceiver)
arr = [arrivals(model, tx1, rx1) for tx1 ∈ [tx], rx1 ∈ [rx]]
Recorder(noise(environment(model)), [tx], rx, arr)
end
function recorder(model::PropagationModel, tx::AcousticSource, rx::AbstractArray{<:AcousticReceiver})
arr = [arrivals(model, tx1, rx1) for tx1 ∈ [tx], rx1 ∈ rx]
Recorder(noise(environment(model)), [tx], rx, arr)
end
function recorder(model::PropagationModel, tx::AbstractArray{<:AcousticSource}, rx::AcousticReceiver)
arr = [arrivals(model, tx1, rx1) for tx1 ∈ tx, rx1 ∈ [rx]]
Recorder(noise(environment(model)), tx, rx, arr)
end
function recorder(model::PropagationModel, tx::AbstractArray{<:AcousticSource}, rx::AbstractArray{<:AcousticReceiver})
arr = [arrivals(model, tx1, rx1) for tx1 ∈ tx, rx1 ∈ rx]
Recorder(noise(environment(model)), tx, rx, arr)
end
# delegate recording task to an ephemeral recorder
record(model::PropagationModel, tx, rx, duration, fs; start=0.0) = recorder(model, tx, rx)(duration, fs; start)
record(model::PropagationModel, tx, rx, sig; reltime=true) = recorder(model, tx, rx)(sig; reltime)
"""
$(SIGNATURES)
Convert a vector of arrivals to a sampled impulse response time series at a
sampling rate of `fs` Hz. If `ntaps` is zero, the number of taps of the impulse
response are chosen automatically.
If `reltime` is `true`, the impulse response start time is relative to the
first arrival, otherwise it is relative to the absolute time. If `approx`
is `true`, a fast algorithm is used to generate a sparse impulse response
that assigns an arrival to the nearest sampling time.
"""
function impulseresponse(arrivals::Vector{<:Arrival}, fs, ntaps=0; reltime=false, approx=false)
length(arrivals) == 0 && throw(ArgumentError("No arrivals"))
mintime, maxtime = extrema(a.time for a ∈ arrivals)
reltime || (mintime = zero(typeof(arrivals[1].time)))
mintaps = ceil(Int, (maxtime-mintime) * fs) + 1
if approx
ntaps == 0 && (ntaps = mintaps)
ir = zeros(typeof(arrivals[1].phasor), ntaps)
for a ∈ arrivals
ndx = round(Int, (a.time - mintime) * fs) + 1
ndx ≤ ntaps && (ir[ndx] = a.phasor)
end
else
N = nextfastfft(4*max(256, mintaps))
x = zeros(typeof(arrivals[1].phasor), N)
for a ∈ arrivals
δ = (a.time - mintime) * fs
for i ∈ 1:N
x[i] += a.phasor * cis(-2π * (i-1)/N * δ)
end
end
ifft!(x)
if ntaps == 0
ndx = findfirst(abs.(x[mintaps+1:end]) .≤ abs(arrivals[1].phasor)/100)
ndx === nothing && (ndx = argmin(abs.(x[mintaps+1:end])))
ir = x[1:mintaps+ndx]
elseif ntaps ≤ N/2
ir = x[1:ntaps]
else
Nby2 = floor(Int, N/2)
ir = vcat(x[1:Nby2], zeros(typeof(arrivals[1].phasor), ntaps-Nby2))
end
end
ir
end
# fast threaded map, assuming all entries have the same result type
function tmap(f, x)
x1 = first(x)
y1 = f(x1)
y = Array{typeof(y1)}(undef, size(x))
Threads.@threads for i ∈ eachindex(x)
y[i] = x1 === x[i] ? y1 : f(x[i])
end
y
end
function envrealtype(env::UnderwaterEnvironment)
a = altitude(altimetry(env), 0.0, 0.0)
b = depth(bathymetry(env), 0.0, 0.0)
c = soundspeed(ssp(env), 0.0, 0.0, 0.0)
s = salinity(env)
d = waterdensity(env)
r1 = real(reflectioncoef(seasurface(env), 1000.0, 0.0))
r2 = real(reflectioncoef(seabed(env), 1000.0, 0.0))
promote_type(typeof(a), typeof(b), typeof(c), typeof(s), typeof(d), typeof(r1), typeof(r2))
end
### pretty printing
function Base.show(io::IO, env::UnderwaterEnvironment)
s = replace(replace(string(typeof(env)), r"\{.*$" => ""), r"^[^\.]*\." => "")
println(io, s, ":")
println(io, " altimetry = ", altimetry(env))
println(io, " bathymetry = ", bathymetry(env))
println(io, " ssp = ", ssp(env))
println(io, " salinity = ", salinity(env))
println(io, " waterdensity = ", waterdensity(env))
println(io, " seasurface = ", seasurface(env))
println(io, " seabed = ", seabed(env))
println(io, " noise = ", noise(env))
end
function Base.show(io::IO, model::PropagationModel)
s = replace(string(typeof(model)), r"\{.*$" => "")
print(io, s, " with ")
show(io, environment(model))
end
function Base.show(io::IO, a::Arrival)
if isnan(a.time) || isnan(a.phasor)
@printf(io, "∠%5.1f° %2d↑ %2d↓%s",
rad2deg(a.launchangle), a.surface, a.bottom, a.raypath === missing || length(a.raypath) == 0 ? "" : " ⤷")
else
@printf(io, "∠%5.1f° %2d↑ %2d↓ ∠%5.1f° | %6.2f ms | %5.1f dB ϕ%6.1f°%s",
rad2deg(a.launchangle), a.surface, a.bottom, rad2deg(a.arrivalangle),
1000*a.time, amp2db(abs(a.phasor)), rad2deg(angle(a.phasor)),
a.raypath === missing || length(a.raypath) == 0 ? "" : " ⤷")
end
end
function Base.show(io::IO, rec::Recorder)
s = replace(string(typeof(rec)), r"\{.*$" => "")
print(io, "$s($(size(rec.arr, 1)) => $(size(rec.arr, 2)))")
end
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | code | 4426 | export PekerisRayModel
"""
struct PekerisRayModel{T} <: PropagationModel{T}
A fast differentiable ray model that only supports isovelocity constant depth
environments.
---
PekerisRayModel(env, rays)
Create a Pekeris ray propagation model with a maximum of `rays` ray arrivals.
"""
struct PekerisRayModel{T} <: PropagationModel{T}
env::T
rays::Int
function PekerisRayModel(env, rays=7)
rays > 0 || throw(ArgumentError("Number of rays should be more than 0"))
new{typeof(env)}(check(PekerisRayModel, env), rays)
end
end
### interface functions
function check(::Type{PekerisRayModel}, env::Union{<:UnderwaterEnvironment,Missing})
if env !== missing
altimetry(env) isa FlatSurface || throw(ArgumentError("PekerisRayModel only supports environments with flat sea surface"))
bathymetry(env) isa ConstantDepth || throw(ArgumentError("PekerisRayModel only supports constant depth environments"))
ssp(env) isa IsoSSP || throw(ArgumentError("PekerisRayModel only supports isovelocity environments"))
end
env
end
function arrivals(model::PekerisRayModel, tx1::AcousticSource, rx1::AcousticReceiver)
# based on Chitre (2007)
c = soundspeed(ssp(model.env), 0.0, 0.0, 0.0)
h = depth(bathymetry(model.env), 0.0, 0.0)
f = nominalfrequency(tx1)
p1 = location(tx1)
p2 = location(rx1)
R² = abs2(p1[1] - p2[1]) + abs2(p1[2] - p2[2])
R = R² == 0 ? R² : √R² # ForwardDiff compatible version of √R²
d1 = -p1[3]
d2 = -p2[3]
[arrival(j, model, R, R², d1, d2, h, c, f) for j ∈ 1:model.rays]
end
function eigenrays(model::PekerisRayModel, tx1::AcousticSource, rx1::AcousticReceiver)
# based on Chitre (2007)
c = soundspeed(ssp(model.env), 0.0, 0.0, 0.0)
h = depth(bathymetry(model.env), 0.0, 0.0)
f = nominalfrequency(tx1)
p1 = location(tx1)
p2 = location(rx1)
R² = abs2(p1[1] - p2[1]) + abs2(p1[2] - p2[2])
R = R² == 0 ? R² : √R² # ForwardDiff compatible version of √R²
d1 = -p1[3]
d2 = -p2[3]
[arrival(j, model, R, R², d1, d2, h, c, f, p1, p2) for j ∈ 1:model.rays]
end
function rays(model::PekerisRayModel, tx1::AcousticSource, θ::Real, rmax)
-π/2 < θ < π/2 || throw(ArgumentError("θ must be between -π/2 and π/2"))
c = soundspeed(ssp(model.env), 0.0, 0.0, 0.0)
h = depth(bathymetry(model.env), 0.0, 0.0)
f = nominalfrequency(tx1)
p1 = location(tx1)
d1 = -p1[3]
d2 = d1 - rmax * tan(θ)
s = 0
b = 0
while true
if d2 < 0
s += 1
d2 = -d2
elseif d2 > h
b += 1
d2 = 2h - d2
else
break
end
end
if 4s - 2 == 4b + 2
j = 4s - 2
elseif 4s + 3 == 4b - 1
j = 4s + 3
else
@assert s == b
j = θ > 0 ? 4s : 4s + 1
end
p2 = (p1[1] + rmax, p1[2], -d2)
arrival(j, model, rmax, rmax*rmax, d1, d2, h, c, f, p1, p2)
end
### helper functions
# memoized version of absorption
const cached_absorption = Ref{Tuple{Float64,Float64,Float64}}()
function fast_absorption(f::Float64, D, S::Float64)
if cached_absorption[][1:2] == (f, S)
db2amp(cached_absorption[][3] * D)
else
dBperm = amp2db(absorption(f, 1.0, S))
cached_absorption[] = (f, S, dBperm)
db2amp(dBperm * D)
end
end
# fallback
fast_absorption(f, D, S) = absorption(f, D, S)
# complex ForwardDiff friendly version of x^n
ipow(x, n::Int) = prod(x for _ ∈ 1:n)
function arrival(j, model, R, R², d1, d2, h, c, f, p1=missing, p2=missing)
upward = iseven(j)
s1 = 2*upward - 1
n = div(j, 2)
s = div(n + upward, 2)
b = div(n + (1-upward), 2)
s2 = 2*iseven(n) - 1
dz = 2*b*h + s1*d1 - s1*s2*d2
D = √(R² + abs2(dz))
θ = atan(R, dz)
t = D/c
A = Complex(1.0, 0.0) / D * fast_absorption(f, D, salinity(model.env))
s > 0 && (A *= ipow(reflectioncoef(seasurface(model.env), f, θ), s))
b > 0 && (A *= ipow(reflectioncoef(seabed(model.env), f, θ), b))
λ = π/2 - θ
if typeof(p1) === Missing
RayArrival(t, conj(A), s, b, s1*λ, -s1*s2*λ) # conj(A) needed to match with Bellhop
else
raypath = Array{typeof(p1)}(undef, 2+s+b)
raypath[1] = p1
if s + b > 0
dx = p2[1] - p1[1]
dy = p2[2] - p1[2]
z = (1-upward) * h
r = abs(z-d1) * tan(θ)
raypath[2] = (p1[1] + r/R * dx, p1[2] + r/R * dy, -z)
for i ∈ 3:length(raypath)-1
r += h * tan(θ)
z = h - z
raypath[i] = (p1[1] + r/R * dx, p1[2] + r/R * dy, -z)
end
end
raypath[end] = p2
RayArrival(t, conj(A), s, b, s1*λ, -s1*s2*λ, raypath)
end
end
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | code | 5466 | export soundspeed, absorption, waterdensity, reflectioncoef, surfaceloss, doppler, bubbleresonance
export dBperλ, indBperλ
"""
$(SIGNATURES)
Compute sound speed in water in m/s, given:
- water `temperature` in °C
- `salinity` in ppt
- `depth` in meters
- void fraction (`voidfrac`) in bubbly water
- sound speed in gas (`cgas`), if `voidfrac` > 0
- ratio of density of water to gas (`reldensity`), if `voidfrac` > 0
Implementation based on Mackenzie (1981), Wood (1964) and Buckingham (1997).
"""
function soundspeed(temperature=27.0, salinity=35.0, depth=10.0; voidfrac=0.0, cgas=340.0, reldensity=1000.0)
c = 1448.96 + 4.591*temperature - 5.304e-2*temperature^2 + 2.374e-4*temperature^3
c += 1.340*(salinity-35) + 1.630e-2*depth + 1.675e-7*depth^2
c += -1.025e-2*temperature*(salinity-35) - 7.139e-13*temperature*depth^3
if voidfrac > 0.0
m = √reldensity
c = 1.0/(1.0/c*√((voidfrac*(c/cgas)^2*m+(1.0-voidfrac)/m)*(voidfrac/m+(1-voidfrac)*m)))
end
return c
end
"""
$(SIGNATURES)
Compute volume acoustic absorption coefficient in water, given:
- `frequency` in Hz
- `distance` in meters
- `salinity` in ppm
- water `temperature` in °C
- `depth` in meters
- `pH` of water
The result is a unitless linear scale factor for sound pressure over the given `distance`. To get
absorption in terms of dB / m, set `distance = 1.0` and convert the result to decibels. For instance,
at a frequency of 100 kHz:
```julia-repl
julia> A = absorption(100e3, 1.0)
0.9959084838594522
julia> α = -20log10(A)
0.035611359656810865
```
Implementation based on the Francois and Garrison (1982) model.
"""
function absorption(frequency, distance=1000.0, salinity=35.0, temperature=27.0, depth=10.0, pH=8.1)
f = frequency/1000.0
d = distance/1000.0
c = 1412.0 + 3.21*temperature + 1.19*salinity + 0.0167*depth
A1 = 8.86/c * 10.0^(0.78*pH-5.0)
P1 = 1.0
f1 = 2.8*√(salinity/35.0) * 10.0^(4.0-1245.0/(temperature+273.0))
A2 = 21.44*salinity/c*(1.0+0.025*temperature)
P2 = 1.0 - 1.37e-4*depth + 6.2e-9*depth*depth
f2 = 8.17 * 10^(8.0-1990.0/(temperature+273.0)) / (1.0+0.0018*(salinity-35.0))
P3 = 1.0 - 3.83e-5*depth + 4.9e-10*depth*depth
if temperature < 20.0
A3 = 4.937e-4 - 2.59e-5*temperature + 9.11e-7*temperature^2 - 1.5e-8*temperature^3
else
A3 = 3.964e-4 - 1.146e-5*temperature + 1.45e-7*temperature^2 - 6.5e-10*temperature^3
end
a = A1*P1*f1*f*f/(f1*f1+f*f) + A2*P2*f2*f*f/(f2*f2+f*f) + A3*P3*f*f
db2amp(-a*d)
end
"""
$(SIGNATURES)
Compute density of water (kg/m^3), given `temperature` in °C and `salinity` in ppm.
Implementation based on Fofonoff (1985 - IES 80).
"""
function waterdensity(temperature=27, salinity=35)
t = temperature
A = 1.001685e-04 + t * (-1.120083e-06 + t * 6.536332e-09)
A = 999.842594 + t * (6.793952e-02 + t * (-9.095290e-03 + t * A))
B = 7.6438e-05 + t * (-8.2467e-07 + t * 5.3875e-09)
B = 0.824493 + t * (-4.0899e-03 + t * B)
C = -5.72466e-03 + t * (1.0227e-04 - t * 1.6546e-06)
D = 4.8314e-04
A + salinity * (B + C*√(salinity) + D*salinity)
end
"""
$(SIGNATURES)
Compute complex reflection coefficient at a fluid-fluid boundary, given:
- angle of incidence `θ` (angle to the surface normal)
- relative density of the reflecting medium to incidence medium `ρᵣ`
- relative sound speed of the reflecting medium to incidence medium `cᵣ`
- dimensionless absorption coefficient `δ`
Implementation based on Brekhovskikh & Lysanov. Dimensionless absorption
coefficient based on APL-UW Technical Report 9407.
"""
function reflectioncoef(θ, ρᵣ, cᵣ, δ=0.0)
n = Complex(1.0, δ) / cᵣ
t1 = ρᵣ * cos(θ)
t2 = n*n - sin(θ)^2
t3 = √abs(t2) * cis(angle(t2)/2) # ForwardDiff friendly complex √
(t1 - t3) / (t1 + t3)
end
"""
$(SIGNATURES)
Compute dimensionless absorption coefficient `δ` from dB/λ.
Implementation based on APL-UW TR 9407 (1994), IV-9 equation (4).
"""
dBperλ(x) = x / (40π / log(10))
"""
$(SIGNATURES)
Compute dB/λ from dimensionless absorption coefficient `δ`.
Implementation based on APL-UW TR 9407 (1994), IV-9 equation (4).
"""
indBperλ(δ) = δ * 40π / log(10)
"""
$(SIGNATURES)
Compute surface reflection coefficient, given:
- `windspeed` in m/s
- `frequency` in Hz
- angle of incidence `θ` (angle to the surface normal)
Implementation based on the APL-UW Technical Report 9407 II-21.
"""
function surfaceloss(windspeed, frequency, θ)
β = π/2 - θ
f = frequency/1000.0
if windspeed >= 6.0
a = 1.26e-3/sin(β) * windspeed^1.57 * f^0.85
else
a = 1.26e-3/sin(β) * 6^1.57 * f^0.85 * exp(1.2*(windspeed-6.0))
end
db2amp(-a)
end
"""
$(SIGNATURES)
Compute Doppler frequency, given relative speed between transmitter and
receiver in m/s. `c` is the nominal sound speed in water.
"""
doppler(speed, frequency, c=soundspeed()) = (1.0+speed/c)*frequency
"""
$(SIGNATURES)
Compute resonance frequency of a freely oscillating has bubble in water, given:
- bubble `radius` in meters
- `depth` of bubble in water in meters
- gas ratio of specific heats 'γ', default: 1.4 (for air)
- atmospheric pressure 'p0', default: 1.013e5
- density of water 'ρ' in kg/m³, default: 1022.476
This ignores surface-tension, thermal, viscous and acoustic damping effects, and the pressure-volume relationship is taken to be adiabatic.
Implementation based on Medwin & Clay (1998).
"""
function bubbleresonance(radius, depth=0.0, γ=1.4, p0=1.013e5, ρ=1022.476)
g = 9.80665 # acceleration due to gravity
pₐ = p0 + ρ*g*depth
1 / (2π * radius) * √(3γ * pₐ/ρ)
end
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | code | 23978 | using Test
using UnderwaterAcoustics
using UnderwaterAcoustics: amp2db, db2amp, pow2db
using Statistics
import ForwardDiff, ReverseDiff, Zygote
@testset "basic" begin
@test soundspeed() ≈ 1539.0 atol=0.1
@test soundspeed(; voidfrac=1e-5) ≈ 1402.1 atol=0.1
@test soundspeed(; voidfrac=1.0) ≈ 340.0
@test amp2db(absorption(10000, 1000.0, 35.0, 15.0)) ≈ -1.0 atol=0.5
@test amp2db(absorption(50000)) ≈ -11.0 atol=0.5
@test amp2db(absorption(100000)) ≈ -36.0 atol=0.5
@test amp2db(absorption(100000, 1000.0, 38.5, 14.0, 0.0)) ≈ -40.0 atol=0.5
@test amp2db(absorption(100000, 1000.0, 38.5, 14.0, 2000.0)) ≈ -30.0 atol=0.5
@test amp2db(absorption(100000, 1000.0, 38.5, 14.0, 6000.0)) ≈ -16.0 atol=0.5
@test waterdensity() ≈ 1022.7 atol=0.1
@test reflectioncoef(0.0, 1200.0/1023.0, 1600.0/1540.0, 0.0) isa Complex
@test reflectioncoef(0.0, 1200.0/1023.0, 1600.0/1540.0, 0.0) ≈ 0.0986 atol=0.0001
@test amp2db(abs(reflectioncoef(0.0, 2.5, 2.5, 0.01374))) ≈ -2.8 atol=0.1
@test amp2db(abs(reflectioncoef(0.0, 2.492, 1.3370, 0.01705))) ≈ -5 atol=0.5
@test amp2db(abs(reflectioncoef(0.0, 1.195, 1.0179, 0.02158))) ≈ -20 atol=0.5
@test amp2db(abs(reflectioncoef(1.22, 1.149, 0.9873, 0.00386))) ≈ -32 atol=0.5
@test amp2db(surfaceloss(15.0, 20000.0, 80°)) ≈ -6.5 atol=0.1
@test amp2db(surfaceloss(10.0, 20000.0, 80°)) ≈ -3.4 atol=0.1
@test amp2db(surfaceloss(5.0, 20000.0, 80°)) ≈ -0.5 atol=0.1
@test doppler(0.0, 50000.0) == 50000.0
@test doppler(10.0, 50000.0) ≈ 50325 atol=0.5
@test doppler(-10.0, 50000.0) ≈ 49675 atol=0.5
@test bubbleresonance(100e-6) ≈ 32465.562964 atol=0.1
@test bubbleresonance(32e-6) ≈ 101454.8842 atol=0.1
@test bubbleresonance(100e-6, 10.0) ≈ 45796.45437634176 atol=0.1
end
@testset "pm-core-basic" begin
env = UnderwaterEnvironment()
@test models() isa AbstractArray
@test models(env) isa AbstractArray
@test env isa UnderwaterAcoustics.BasicUnderwaterEnvironment
@test altimetry(env) isa Altimetry
@test bathymetry(env) isa Bathymetry
@test ssp(env) isa SoundSpeedProfile
@test salinity(env) isa Real
@test seasurface(env) isa ReflectionModel
@test seabed(env) isa ReflectionModel
@test noise(env) isa NoiseModel
@test altitude(altimetry(env), 0.0, 0.0) isa Real
@test depth(bathymetry(env), 0.0, 0.0) isa Real
@test soundspeed(ssp(env), 0.0, 0.0, 0.0) isa Real
@test reflectioncoef(seasurface(env), 1000.0, 0.0) isa Complex
@test reflectioncoef(seabed(env), 1000.0, 0.0) isa Complex
sig = record(noise(env), 1.0, 44100.0)
@test length(sig) == 44100
@test sum(abs2.(sig)) > 0.0
@test AcousticReceiver(0.0, 0.0) isa AcousticReceiver
@test location(AcousticReceiver(100.0, 10.0, -50.0)) == (100, 10.0, -50.0)
@test location(AcousticReceiver(100.0, -50.0)) == (100, 0.0, -50.0)
src = AcousticSource(100.0, 10.0, -50.0, 4410.0; sourcelevel=1.0)
sig = record(src, 1.0, 44100.0)
@test src isa NarrowbandAcousticSource
@test location(src) == (100.0, 10.0, -50.0)
@test location(AcousticSource(100.0, -50.0, 1000.0)) == (100.0, 0.0, -50.0)
@test nominalfrequency(src) == 4410.0
@test phasor(src) == complex(1.0, 0.0)
@test length(sig) == 44100
@test eltype(sig) <: Complex
@test sum(abs2.(sig))/44100.0 ≈ 1.0 atol=1e-4
@test sig[1] != sig[2]
@test sig[1] ≈ sig[11]
@test sig[2] ≈ sig[12]
src = Pinger(10.0, -10.0, 1000.0; sourcelevel=1.0, interval=0.5)
sig = record(src, 1.0, 44100.0)
@test src isa AcousticSource
@test location(src) == (10.0, 0.0, -10.0)
@test nominalfrequency(src) == 1000.0
@test phasor(src) == complex(1.0, 0.0)
@test length(sig) == 44100
@test eltype(sig) <: Complex
@test sum(abs2.(sig))/44100.0 ≈ 0.04 atol=1e-4
@test maximum(abs2.(sig)) ≈ 1.0 atol=1e-4
src = SampledAcousticSource(10.0, -10.0, ones(1000); fs=1000.0, frequency=100.0)
@test src isa SampledAcousticSource
@test location(src) == (10.0, 0.0, -10.0)
@test nominalfrequency(src) == 100.0
sig = record(src, 1.0, 1000.0)
@test length(sig) == 1000
@test eltype(sig) === Float64
@test all(sig .== 1.0)
sig = record(src, 1.0, 1000.0; start=-0.5)
@test length(sig) == 1000
@test eltype(sig) === Float64
@test all(sig[1:500] .== 0.0)
@test all(sig[501:1000] .== 1.0)
sig = record(src, 1.0, 1000.0; start=0.5)
@test length(sig) == 1000
@test eltype(sig) === Float64
@test all(sig[1:500] .== 1.0)
@test all(sig[501:1000] .== 0.0)
sig = record(src, 1.0, 1000.0; start=-2.0)
@test length(sig) == 1000
@test eltype(sig) === Float64
@test all(sig .== 0.0)
sig = record(src, 1.0, 1000.0; start=2.0)
@test length(sig) == 1000
@test eltype(sig) === Float64
@test all(sig .== 0.0)
@test_throws ArgumentError record(src, 1.0, 2000.0)
src = SampledAcousticSource(10.0, 5.0, -10.0, cis.(2π * 1000 * (0:999) ./ 10000.0); fs=10000.0)
@test src isa SampledAcousticSource
@test location(src) == (10.0, 5.0, -10.0)
@test nominalfrequency(src) == 1000.0
sig = record(src, 0.1, 10000.0)
@test length(sig) == 1000
@test eltype(sig) === ComplexF64
@test IsoSSP(1500.0) isa SoundSpeedProfile
@test soundspeed(IsoSSP(1500.0), 100.0, 10.0, -50.0) == 1500.0
@test MunkSSP() isa SoundSpeedProfile
@test soundspeed(MunkSSP(), 0.0, 0.0, -2000.0) ≈ 1505.0 atol=1.0
@test soundspeed(MunkSSP(), 0.0, 0.0, -3000.0) ≈ 1518.0 atol=1.0
s = SampledSSP(0.0:500.0:1000.0, [1500.0, 1520.0, 1510.0])
@test s isa SoundSpeedProfile
@test soundspeed(s, 0.0, 0.0, 0.0) ≈ 1500.0
@test soundspeed(s, 0.0, 0.0, -250.0) ≈ 1510.0
@test soundspeed(s, 0.0, 0.0, -500.0) ≈ 1520.0
@test soundspeed(s, 0.0, 0.0, -750.0) ≈ 1515.0
@test soundspeed(s, 0.0, 0.0, -1000.0) ≈ 1510.0
s = SampledSSP(0.0:500.0:1000.0, [1500.0, 1520.0, 1510.0], :smooth)
@test s isa SoundSpeedProfile
@test soundspeed(s, 0.0, 0.0, 0.0) ≈ 1500.0
@test soundspeed(s, 0.0, 0.0, -250.0) > 1510.0
@test soundspeed(s, 0.0, 0.0, -500.0) ≈ 1520.0
@test soundspeed(s, 0.0, 0.0, -750.0) > 1515.0
@test soundspeed(s, 0.0, 0.0, -1000.0) ≈ 1510.0
s = SampledSSP(0.0:50.0:100.0, 0.0:500.0:1000.0, [1400.0 1420.0 1410.0; 1500.0 1520.0 1510.0; 1300.0 1320.0 1310.0])
@test s isa SoundSpeedProfile
@test soundspeed(s, 50.0, 0.0, 0.0) ≈ 1500.0
@test soundspeed(s, 50.0, 0.0, -250.0) ≈ 1510.0
@test soundspeed(s, 50.0, 0.0, -500.0) ≈ 1520.0
@test soundspeed(s, 50.0, 0.0, -750.0) ≈ 1515.0
@test soundspeed(s, 50.0, 0.0, -1000.0) ≈ 1510.0
@test soundspeed(s, 0.0, 0.0, 0.0) ≈ 1400.0
@test soundspeed(s, 0.0, 0.0, -250.0) ≈ 1410.0
@test soundspeed(s, 0.0, 0.0, -500.0) ≈ 1420.0
@test soundspeed(s, 0.0, 0.0, -750.0) ≈ 1415.0
@test soundspeed(s, 0.0, 0.0, -1000.0) ≈ 1410.0
@test ConstantDepth(20.0) isa Bathymetry
@test depth(ConstantDepth(20.0), 0.0, 0.0) == 20.0
@test maxdepth(ConstantDepth(20.0)) == 20.0
b = SampledDepth(0.0:500.0:1000.0, [20.0, 25.0, 15.0])
@test b isa Bathymetry
@test depth(b, 0.0, 0.0) ≈ 20.0
@test depth(b, 250.0, 0.0) ≈ 22.5
@test depth(b, 500.0, 0.0) ≈ 25.0
@test depth(b, 750.0, 0.0) ≈ 20.0
@test depth(b, 1000.0, 0.0) ≈ 15.0
@test maxdepth(b) ≈ 25.0
b = SampledDepth(0.0:500.0:1000.0, [20.0, 25.0, 15.0], :smooth)
@test b isa Bathymetry
@test depth(b, 0.0, 0.0) ≈ 20.0
@test depth(b, 250.0, 0.0) > 22.5
@test depth(b, 500.0, 0.0) ≈ 25.0
@test depth(b, 750.0, 0.0) > 20.0
@test depth(b, 1000.0, 0.0) ≈ 15.0
@test maxdepth(b) ≈ 25.0
@test FlatSurface() isa Altimetry
@test altitude(FlatSurface(), 0.0, 0.0) == 0.0
a = SampledAltitude(0.0:500.0:1000.0, [0.0, 1.0, -1.0])
@test a isa Altimetry
@test altitude(a, 0.0, 0.0) ≈ 0.0
@test altitude(a, 250.0, 0.0) ≈ 0.5
@test altitude(a, 500.0, 0.0) ≈ 1.0
@test altitude(a, 750.0, 0.0) ≈ 0.0
@test altitude(a, 1000.0, 0.0) ≈ -1.0
a = SampledAltitude(0.0:500.0:1000.0, [0.0, 1.0, -1.0], :smooth)
@test a isa Altimetry
@test altitude(a, 0.0, 0.0) ≈ 0.0 atol=1e-6
@test altitude(a, 250.0, 0.0) > 0.5
@test altitude(a, 500.0, 0.0) ≈ 1.0 atol=1e-6
@test altitude(a, 1000.0, 0.0) ≈ -1.0 atol=1e-6
@test ReflectionCoef(0.5 + 0.3im) isa ReflectionModel
@test reflectioncoef(ReflectionCoef(0.5 + 0.3im), 1000.0, 0.0) == 0.5 + 0.3im
@test RayleighReflectionCoef(1.0, 1.0) isa ReflectionModel
@test RayleighReflectionCoef(1.0, 1.0, 0.0) isa ReflectionModel
@test reflectioncoef(RayleighReflectionCoef(1.0, 1.0, 0.0), 1000.0, 0.0) ≈ 0.0
@test reflectioncoef(RayleighReflectionCoef(0.0, 1.0, 0.0), 1000.0, 0.0) ≈ -1.0
@test Rock isa RayleighReflectionCoef
@test Pebbles isa RayleighReflectionCoef
@test SandyGravel isa RayleighReflectionCoef
@test CoarseSand isa RayleighReflectionCoef
@test MediumSand isa RayleighReflectionCoef
@test FineSand isa RayleighReflectionCoef
@test VeryFineSand isa RayleighReflectionCoef
@test ClayeySand isa RayleighReflectionCoef
@test CoarseSilt isa RayleighReflectionCoef
@test SandySilt isa RayleighReflectionCoef
@test Silt isa RayleighReflectionCoef
@test FineSilt isa RayleighReflectionCoef
@test SandyClay isa RayleighReflectionCoef
@test SiltyClay isa RayleighReflectionCoef
@test Clay isa RayleighReflectionCoef
@test Vacuum isa ReflectionModel
@test reflectioncoef(Vacuum, 1000.0, 0.0) ≈ -1.0
@test 0.0 < abs(reflectioncoef(Rock, 1000.0, 0.0)) < 1.0
@test abs(reflectioncoef(Silt, 1000.0, 0.0)) < abs(reflectioncoef(SandyGravel, 1000.0, 0.0))
@test abs(reflectioncoef(CoarseSilt, 1000.0, 0.0)) < abs(reflectioncoef(Rock, 1000.0, 0.0))
@test SurfaceLoss(5.0) isa ReflectionModel
@test SeaState0 isa SurfaceLoss
@test SeaState1 isa SurfaceLoss
@test SeaState2 isa SurfaceLoss
@test SeaState3 isa SurfaceLoss
@test SeaState4 isa SurfaceLoss
@test SeaState5 isa SurfaceLoss
@test SeaState6 isa SurfaceLoss
@test SeaState7 isa SurfaceLoss
@test SeaState8 isa SurfaceLoss
@test SeaState9 isa SurfaceLoss
@test 0.0 < abs(reflectioncoef(SeaState2, 1000.0, 0.0)) < 1.0
@test abs(reflectioncoef(SeaState2, 1000.0, 0.0)) > abs(reflectioncoef(SeaState5, 1000.0, 0.0))
@test abs(reflectioncoef(SeaState5, 1000.0, 0.0)) > abs(reflectioncoef(SeaState5, 2000.0, 0.0))
rx = AcousticReceiverGrid2D(100.0, 2.0, 100, -100.0, 5.0, 10)
@test rx isa AcousticReceiverGrid2D
@test rx isa AbstractMatrix
@test size(rx) == (100, 10)
@test rx[1,1] == AcousticReceiver(100.0, -100.0)
@test rx[end,end] == AcousticReceiver(298.0, -55.0)
rx = AcousticReceiverGrid3D(100.0, 2.0, 100, 0.0, 1.0, 100, -100.0, 5.0, 10)
@test rx isa AcousticReceiverGrid3D
@test rx isa AbstractArray
@test size(rx) == (100, 100, 10)
@test rx[1,1,1] == AcousticReceiver(100.0, 0.0, -100.0)
@test rx[end,end,end] == AcousticReceiver(298.0, 99.0, -55.0)
end
@testset "pm-pekeris" begin
@test PekerisRayModel in models()
env = UnderwaterEnvironment()
pm = PekerisRayModel(env, 7)
@test pm isa PekerisRayModel
arr = arrivals(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiver(100.0, -10.0))
@test arr isa AbstractArray{<:UnderwaterAcoustics.RayArrival}
@test length(arr) == 7
@test arr[1].time ≈ 0.0650 atol=0.0001
@test arr[2].time ≈ 0.0657 atol=0.0001
@test arr[3].time ≈ 0.0670 atol=0.0001
@test all([arr[j].time > arr[j-1].time for j ∈ 2:7])
@test abs(arr[1].phasor) ≈ 0.01 atol=0.001
@test real(arr[2].phasor) < 0.0
@test imag(arr[2].phasor) ≈ 0.0
@test all([abs(arr[j].phasor) < abs(arr[j-1].phasor) for j ∈ 2:7])
@test [(arr[j].surface, arr[j].bottom) for j ∈ 1:7] == [(0,0), (1,0), (0,1), (1,1), (1,1), (2,1), (1,2)]
@test all([abs(arr[j].arrivalangle) == abs(arr[j].launchangle) for j ∈ 1:7])
r = eigenrays(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiver(100.0, -10.0))
@test r isa AbstractArray{<:UnderwaterAcoustics.RayArrival}
@test length(r) == 7
@test all([abs(r[j].arrivalangle) == abs(r[j].launchangle) for j ∈ 1:7])
@test all([r[j].raypath[1] == (0.0, 0.0, -5.0) for j ∈ 1:7])
@test all([r[j].raypath[end] == (100.0, 0.0, -10.0) for j ∈ 1:7])
@test all([length(r[j].raypath) == r[j].surface + r[j].bottom + 2 for j ∈ 1:7])
r = rays(pm, AcousticSource(0.0, -5.0, 1000.0), -60°:15°:60°, 100.0)
@test r isa AbstractArray{<:UnderwaterAcoustics.RayArrival}
@test length(r) == 9
@test all([r[j].launchangle for j ∈ 1:9] .≈ -60°:15°:60°)
@test all([abs(r[j].arrivalangle) == abs(r[j].launchangle) for j ∈ 1:9])
@test all([r[j].raypath[1] == (0.0, 0.0, -5.0) for j ∈ 1:9])
@test all([r[j].raypath[end][1] ≥ 100.0 for j ∈ 1:9])
@test all([length(r[j].raypath) == r[j].surface + r[j].bottom + 2 for j ∈ 1:9])
ir1 = impulseresponse(arr, 10000.0; reltime=true, approx=true)
ir2 = impulseresponse(arr, 10000.0; reltime=false, approx=true)
@test length(ir2) ≈ length(ir1) + round(Int, 10000.0 * arr[1].time) atol=1
@test length(ir2) == round(Int, 10000.0 * arr[end].time) + 1
@test sum(ir1 .!= 0.0) == 7
@test sum(ir2 .!= 0.0) == 7
ndx = findall(abs.(ir1) .> 0)
@test (ndx .- 1) ./ 10000.0 ≈ [arr[j].time - arr[1].time for j ∈ 1:7] atol=1e-4
ndx = findall(abs.(ir2) .> 0)
@test (ndx .- 1) ./ 10000.0 ≈ [arr[j].time for j ∈ 1:7] atol=1e-4
ir1a = impulseresponse(arr, 10000.0; reltime=true)
ir2a = impulseresponse(arr, 10000.0; reltime=false)
@test length(ir2a) ≈ length(ir1a) + round(Int, 10000.0 * arr[1].time) atol=1
@test length(ir2a) ≥ length(ir2)
@test sum(abs2.(ir1a))/sum(abs2.(ir1)) ≈ 1.0 atol=0.05
@test sum(abs2.(ir2a))/sum(abs2.(ir2)) ≈ 1.0 atol=0.05
@test length(impulseresponse(arr, 10000.0, 256; reltime=true, approx=true)) == 256
@test length(impulseresponse(arr, 10000.0, 64; reltime=true, approx=true)) == 64
@test length(impulseresponse(arr, 10000.0, 256; reltime=true, approx=false)) == 256
@test length(impulseresponse(arr, 10000.0, 64; reltime=true, approx=false)) == 64
@test length(impulseresponse(arr, 10000.0, 1024; reltime=false, approx=true)) == 1024
@test length(impulseresponse(arr, 10000.0, 700; reltime=false, approx=true)) == 700
@test length(impulseresponse(arr, 10000.0, 1024; reltime=false, approx=false)) == 1024
@test length(impulseresponse(arr, 10000.0, 700; reltime=false, approx=false)) == 700
env = UnderwaterEnvironment(ssp=IsoSSP(1500.0))
pm = PekerisRayModel(env, 2)
d = (√1209.0)/4.0
x = transfercoef(pm, AcousticSource(0.0, -d, 1000.0), AcousticReceiver(100.0, -d))
@test x isa Complex
@test abs(x) ≈ 0.0 atol=0.0002
x′ = transfercoef(pm, AcousticSource(0.0, -d, 1000.0), AcousticReceiver(100.0, -d); mode=:incoherent)
@test x′ isa Complex
@test imag(x′) == 0.0
@test abs(x′) > 1/100.0
d = (√2409.0)/8.0
x = transfercoef(pm, AcousticSource(0.0, -d, 1000.0), AcousticReceiver(100.0, -d))
@test abs(x) > abs(x′)
y = transmissionloss(pm, AcousticSource(0.0, -d, 1000.0), AcousticReceiver(100.0, -d))
@test -10 * log10(abs2(x)) ≈ y atol=0.1
x = transfercoef(pm, AcousticSource(0.0, -d, 1000.0), AcousticReceiver(100.0, -d); mode=:incoherent)
@test abs(x) ≈ abs(x′) atol=0.0001
y = transmissionloss(pm, AcousticSource(0.0, -d, 1000.0), AcousticReceiver(100.0, -d); mode=:incoherent)
@test -10 * log10(abs2(x)) ≈ y atol=0.1
x1 = transfercoef(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiver(100.0, -5.0))
x2 = transfercoef(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiver(100.0, -10.0))
x3 = transfercoef(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiver(100.0, -15.0))
x = transfercoef(pm, AcousticSource(0.0, -5.0, 1000.0), [AcousticReceiver(100.0, -d) for d ∈ 5.0:5.0:15.0])
@test x isa AbstractVector
@test [x1, x2, x3] == x
x = transfercoef(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiverGrid2D(100.0, 0.0, 1, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (1, 3)
@test [x1 x2 x3] == x
x = transfercoef(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiverGrid2D(100.0, 10.0, 3, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (3, 3)
@test [x1, x2, x3] == x[1,:]
x1 = transmissionloss(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiver(100.0, -5.0))
x2 = transmissionloss(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiver(100.0, -10.0))
x3 = transmissionloss(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiver(100.0, -15.0))
x = transmissionloss(pm, AcousticSource(0.0, -5.0, 1000.0), [AcousticReceiver(100.0, -d) for d ∈ 5.0:5.0:15.0])
@test x isa AbstractVector
@test [x1, x2, x3] == x
x = transmissionloss(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiverGrid2D(100.0, 0.0, 1, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (1, 3)
@test [x1 x2 x3] == x
x = transmissionloss(pm, AcousticSource(0.0, -5.0, 1000.0), AcousticReceiverGrid2D(100.0, 10.0, 3, -5.0, -5.0, 3))
@test x isa AbstractMatrix
@test size(x) == (3, 3)
@test [x1, x2, x3] == x[1,:]
env = UnderwaterEnvironment()
pm = PekerisRayModel(env, 7)
tx = AcousticSource(0.0, -5.0, 1000.0)
rx = AcousticReceiver(100.0, -10.0)
sig = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig) == (44100,)
sig = record(pm, tx, rx, 1.0, 44100.0; start=0.5)
@test size(sig) == (44100,)
sig = recorder(pm, tx, rx)(1.0, 44100.0)
@test size(sig) == (44100,)
sig = recorder(pm, tx, rx)(1.0, 44100.0; start=0.5)
@test size(sig) == (44100,)
tx = [AcousticSource(0.0, -5.0, 1000.0), AcousticSource(0.0, -10.0, 2000.0)]
rx = AcousticReceiver(100.0, -10.0)
sig = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig) == (44100,)
sig = record(pm, tx, rx, 1.0, 44100.0; start=0.5)
@test size(sig) == (44100,)
sig = recorder(pm, tx, rx)(1.0, 44100.0)
@test size(sig) == (44100,)
sig = recorder(pm, tx, rx)(1.0, 44100.0; start=0.5)
@test size(sig) == (44100,)
tx = [AcousticSource(0.0, -5.0, 1000.0), AcousticSource(0.0, -10.0, 2000.0)]
rx = [AcousticReceiver(100.0, -10.0), AcousticReceiver(100.0, -15.0)]
sig = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig) == (44100,2)
sig = record(pm, tx, rx, 1.0, 44100.0; start=0.5)
@test size(sig) == (44100,2)
sig = recorder(pm, tx, rx)(1.0, 44100.0)
@test size(sig) == (44100,2)
sig = recorder(pm, tx, rx)(1.0, 44100.0; start=0.5)
@test size(sig) == (44100,2)
tx = AcousticSource(0.0, -5.0, 1000.0)
rx = [AcousticReceiver(100.0, -10.0), AcousticReceiver(100.0, -15.0)]
sig = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig) == (44100,2)
sig = record(pm, tx, rx, 1.0, 44100.0; start=0.5)
@test size(sig) == (44100,2)
sig = recorder(pm, tx, rx)(1.0, 44100.0)
@test size(sig) == (44100,2)
sig = recorder(pm, tx, rx)(1.0, 44100.0; start=0.5)
@test size(sig) == (44100,2)
env = UnderwaterEnvironment(noise=missing)
pm = PekerisRayModel(env, 7)
tx = Pinger(0.0, -5.0, 1000.0; interval=0.3)
rx = AcousticReceiver(100.0, -10.0)
sig1 = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig1) == (44100,)
sig2 = record(pm, tx, rx, 1.0, 44100.0; start=0.5)
@test size(sig2) == (44100,)
@test sig1[22051:end] ≈ sig2[1:22050]
rx = AcousticReceiver(100.0, -11.0)
sig3 = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig3) == (44100,)
@test !(sig1 ≈ sig3)
rx = AcousticReceiver(100.0/√2, 100.0/√2, -10.0)
sig3 = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig3) == (44100,)
@test sig1 ≈ sig3
tx = [Pinger(0.0, -5.0, 1000.0; interval=0.3), Pinger(1.0, -5.0, 2000.0; interval=0.5)]
rx = AcousticReceiver(100.0, 0.0, -10.0)
sig1 = record(pm, tx, rx, 1.0, 44100.0)
rx = AcousticReceiver(100.0/√2, 100.0/√2, -10.0)
sig2 = record(pm, tx, rx, 1.0, 44100.0)
@test !(sig1 ≈ sig2)
env = UnderwaterEnvironment(noise=WhiteGaussianNoise(db2amp(120.0)))
pm = PekerisRayModel(env, 7)
tx = SampledAcousticSource(0.0, -5.0, sin.(10000π .* (1:44100) ./ 44100.0); fs=44100.0)
@test tx.frequency ≈ 5000.0 atol=10.0
rx = AcousticReceiver(100.0, -10.0)
sig = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig) == (44100,)
@test eltype(sig) === ComplexF64
tx = SampledAcousticSource(0.0, -5.0, cis.(10000π .* (1:44100) ./ 44100.0); fs=44100.0)
@test tx.frequency ≈ 5000.0 atol=10.0
sig = record(pm, tx, rx, 1.0, 44100.0)
@test size(sig) == (44100,)
@test eltype(sig) === ComplexF64
tx = SampledAcousticSource(0.0, -5.0, zeros(44100); fs=44100.0, frequency=5000.0)
sig = record(pm, tx, [rx, rx], 1.0, 44100.0)
@test pow2db(mean(abs2, sig[:,1])) ≈ 120.0 atol=0.5
@test pow2db(mean(abs2, sig[:,2])) ≈ 120.0 atol=0.5
env = UnderwaterEnvironment()
pm = PekerisRayModel(env)
tx = AcousticSource(0.0, -5.0, 10000.0)
rx = AcousticReceiver(100.0, -10.0)
rec = recorder(pm, tx, rx)
sig = rec(zeros(44100); fs=44100.0)
@test sig isa AbstractVector
@test eltype(sig) === Float64
@test 44100 < length(sig) < 44700
sig = rec(zeros(44100); fs=44100.0, reltime=false)
@test sig isa AbstractVector
@test eltype(sig) === Float64
@test 47000 < length(sig) < 47600
sig = rec(zeros(ComplexF64, 44100); fs=44100.0)
@test sig isa AbstractVector
@test eltype(sig) === ComplexF64
sig = rec(zeros(ComplexF32, 44100); fs=44100.0)
@test sig isa AbstractVector
@test eltype(sig) === ComplexF32
sig = rec(zeros(Float32, 44100); fs=44100.0)
@test sig isa AbstractVector
@test eltype(sig) === Float32
rec = recorder(pm, [tx, tx], rx)
sig = rec(zeros(44100, 2); fs=44100.0)
@test sig isa AbstractVector
rec = recorder(pm, tx, [rx, rx])
sig = rec(zeros(44100); fs=44100.0)
@test sig isa AbstractMatrix
@test size(sig, 2) == 2
rec = recorder(pm, [tx, tx], [rx, rx])
sig = rec(zeros(44100, 2); fs=44100.0)
@test sig isa AbstractMatrix
@test size(sig, 2) == 2
env = UnderwaterEnvironment(noise=nothing)
pm = PekerisRayModel(env)
tx = AcousticSource(0.0, -5.0, 10000.0)
rx = AcousticReceiver(100.0, -10.0)
rec = recorder(pm, tx, rx)
ir = impulseresponse(arrivals(pm, tx, rx), 44100.0, 500; approx=true, reltime=true)
X1 = channelmatrix(rec, 44100.0, 500; approx=true)
X2 = channelmatrix(arrivals(pm, tx, rx), 44100.0, 500; approx=true)
@test X1 == X2
@test X1 * vcat([1.0], zeros(size(X1,1)-1)) ≈ ir
end
function ∂(f, x, i, ϵ)
x1 = copy(x)
x1[i] = x[i] + ϵ
f1 = f(x1)
x1[i] = x[i] - ϵ
(f1 - f(x1)) / (2ϵ)
end
@testset "pm-∂pekeris" begin
function ℳ(x)
D, R, d1, d2, f, c = x
env = UnderwaterEnvironment(ssp=IsoSSP(c), bathymetry=ConstantDepth(D))
pm = PekerisRayModel(env, 7)
transmissionloss(pm, AcousticSource(0.0, -d1, f), AcousticReceiver(R, -d2))
end
x = [20.0, 100.0, 5.0, 10.0, 5000.0, 1500.0]
∇ℳ = ForwardDiff.gradient(ℳ, x)
for i ∈ 1:length(x)
@test ∇ℳ[i] ≈ ∂(ℳ, x, i, 0.0001) atol=0.1
end
x = [25.0, 200.0, 10.0, 8.0, 1000.0, 1540.0]
∇ℳ = ForwardDiff.gradient(ℳ, x)
for i ∈ 1:length(x)
@test ∇ℳ[i] ≈ ∂(ℳ, x, i, 0.0001) atol=0.1
end
x = [20.0, 100.0, 5.0, 10.0, 5000.0, 1500.0]
∇ℳ = ReverseDiff.gradient(ℳ, x)
for i ∈ 1:length(x)
@test ∇ℳ[i] ≈ ∂(ℳ, x, i, 0.0001) atol=0.1
end
x = [25.0, 200.0, 10.0, 8.0, 1000.0, 1540.0]
∇ℳ = ReverseDiff.gradient(ℳ, x)
for i ∈ 1:length(x)
@test ∇ℳ[i] ≈ ∂(ℳ, x, i, 0.0001) atol=0.1
end
x = [20.0, 100.0, 5.0, 10.0, 5000.0, 1500.0]
∇ℳ = Zygote.gradient(ℳ, x) |> first
for i ∈ 1:length(x)
@test ∇ℳ[i] ≈ ∂(ℳ, x, i, 0.0001) atol=0.1
end
x = [25.0, 200.0, 10.0, 8.0, 1000.0, 1540.0]
∇ℳ = Zygote.gradient(ℳ, x) |> first
for i ∈ 1:length(x)
@test ∇ℳ[i] ≈ ∂(ℳ, x, i, 0.0001) atol=0.1
end
function ℳ2(x)
D, R, d1, d2, f, c = x
env = UnderwaterEnvironment(ssp=IsoSSP(c), bathymetry=ConstantDepth(D))
pm = PekerisRayModel(env, 7)
# FIXME: approx=true needed because FFT is not yet differentiable
X = channelmatrix(arrivals(pm, AcousticSource(0.0, -d1, f), AcousticReceiver(R, -d2)), 44100.0, 500; approx=true)
sum(abs2, X)
end
x = [25.0, 200.0, 10.0, 8.0, 1000.0, 1540.0]
∇ℳ = ForwardDiff.gradient(ℳ2, x)
for i ∈ 1:length(x)
@test ∇ℳ[i] ≈ ∂(ℳ2, x, i, 0.0001) atol=0.1
end
∇ℳ = ReverseDiff.gradient(ℳ2, x)
for i ∈ 1:length(x)
@test ∇ℳ[i] ≈ ∂(ℳ2, x, i, 0.0001) atol=0.1
end
# FIXME: Zygote.gradient fails due to mutation in impulseresponse() and no adjoint for TriangularToeplitz
end
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 13580 | # Contributing to UnderwaterAcoustics.jl
Contributions in terms of bug reports, feature requests, ideas/suggestions, documentation improvements, bug fixes, and new feature implementations are most welcome! Even contributions on improving this document are welcome!
If you intend to contribute, please read the guidelines below:
## Getting started
We assume familiarity with git, Github, markdown and Julia. If you need to brush up on these, here are some good starting points:
* [Github](https://docs.github.com/en/get-started/quickstart/set-up-git)
* [Markdown](https://guides.github.com/features/mastering-markdown/)
* [Julia](https://julialang.org/learning/)
While we haven't adopted a formal code of conduct, there is an implicit expectation that all of us shall be professional, respectful of differing opinions and viewpoints, empathetic and kind, and open to giving and gracefully accepting constructive feedback. By contributing, you accept to abide by this code.
Finally, read and understand the [ROADMAP](ROADMAP.md) document to understand what UnderwaterAcoustics.jl is meant to be, and meant not to be, so that all of us work from a common set of expectations. If you have suggestions on the scope, directions or roadmap for the project, we are open to [discussing](https://github.com/org-arl/UnderwaterAcoustics.jl/discussions) those too.
## Bug reports, features requests & discussions
### Bug reports
Bug reports are an important part of making UnderwaterAcoustics.jl more stable and reliable. Having a good bug report will allow others to reproduce it and provide insight into fixing. See [this stackoverflow article](https://stackoverflow.com/help/mcve) for tips on writing a good bug report.
Trying out the bug-producing code on the `master` branch is often a worthwhile exercise to confirm that the bug still exists. You'd also want to search for existing bug reports and pull requests to see if the issue has already been reported and/or fixed before [filing a new issue](https://github.com/org-arl/UnderwaterAcoustics.jl/issues/new/choose).
### Feature requests
If you have ideas for new features that fit within the [scope of the project](ROADMAP.md), feel free to [file a new issue](https://github.com/org-arl/UnderwaterAcoustics.jl/issues/new/choose) with your idea. Providing some background on the motivation behind the feature request, and some use cases of how the feature might be used, is very valuable for others to understand your idea.
### Discussions
If you have things you'd like to talk about that don't naturally fit in as a bug report or feature request, [open a new discussion](https://github.com/org-arl/UnderwaterAcoustics.jl/discussions) for it. Discussions may include Q&A, project scope/roadmap discussions, ideas that aren't concrete enough to be feature requests yet, cool things you've done with UnderwaterAcoustics.jl that you'd want to show others, etc.
### Triage
The convention used to tag what's planned is as follows:
- Issues assigned to a milestone are prioritized for inclusion in an upcoming milestone. These issues will always be assigned to a person.
- Issues assigned to a person but not tagged for a milestone are under consideration for future milestones by the person.
- Issues unassigned to anyone are not under consideration at present for any milestone.
- Issues marked `high-priority` or `low-priority` are prioritized as such. Issues not marked with either label are considered "normal priority".
If you wish to take up an issue for a PR, please indicate so in the issue, so that we can assign it to you and track the relevant PR.
## Bug fixes, new features & documentation enhancements
In order to contribute to the code and/or documentation for UnderwaterAcoustics.jl, you'll need to be familiar with git and have a Github account. We have some useful links in the [Getting Started](#getting-started) section above, if you're new to git or Github.
The general process to contribute code or documentation is as follows:
1. Fork the repository, and make a clone of the fork on your own machine.
2. Create a new branch based on `master` and checkout the new branch. The name of the branch should be descriptive but short, with only lowercase letters and hyphens in it. Each branch should only contain changes for a specific issue, or a related set of isses.
3. Make changes to the codebase (`src` folder) and/or documentation (`docs/src` folder) locally. You may find it useful to have [VSCode](https://code.visualstudio.com) with the [Julia extension](https://github.com/julia-vscode/julia-vscode) installed to work with the codebase, although this is not strictly necessary.
4. If you're fixing a bug, it may be worth adding test cases (`test` folder) that catch the bug before you fix it, and then running those test cases to ensure that your fix works.
5. If you're adding a new feature, you may want to develop test cases for the feature before or along with your development. Include your test cases in the test suite (in the `test` folder). You'd also want to add documentation in the form of [docstrings](https://docs.julialang.org/en/v1/manual/documentation/) within your code and/or markdown documentation (`docs/src` folder). We use [Documenter.jl](https://github.com/JuliaDocs/Documenter.jl) to generate the online documentation automatically.
6. Test the changes locally, making sure that your code works as advertised, and that you haven't broken anything else. In order to do that:
- Run the regression test suite locally:
```sh
$ julia --project # run Julia
julia> # press ] for package mode
(UnderwaterAcoustics) pkg> test # start the test
```
Make sure that all tests pass.
- Build the documentation locally and check it:
```sh
$ cd docs
$ julia --project make.jl
```
After the build process, the documentation is in the `docs/build` folder. Open it with a browser and check it.
7. Commit your changes (you may want to do this often during your development and testing phases) and push them to your forked repository. Ensure you use [good commit messages](#commit-messages).
8. Raise a [pull request (PR)](https://docs.github.com/en/github/collaborating-with-pull-requests/proposing-changes-to-your-work-with-pull-requests/about-pull-requests) from your branch in your forked repository to the `master` branch in the main repository. Provide details of your changes, and links to one or more original issues that may have led to this PR. You may raise PRs before you are ready with the final changes, but please mark them as _draft_ (Github allows you to create a _draft PR_) until it's ready for others to review.
9. Once your PR is ready for review, one of the maintainers of the repository will assign a reviewer. The job of the reviewer is to ensure code and documentation quality before the PR is merged. The reviewer will provide constructive feedback to help address any concerns with the PR.
10. Once all concerns are addressed and marked _resolved_, the PR will be ready for merging. One of the maintainers will merge the PR, and the changes will become part of the next release of UnderwaterAcoustics.jl.
## Commit messages
We have guidelines on how our git commit messages should be formatted. This leads to more readable messages that are easy to follow when looking through the project history, and also allow automated generation of change logs.
Each commit message consists of a **header**, and optionally, a **body**. The header has a special format that includes a **type**, a **scope** and a **summary**:
```
type(scope): summary
body
```
The summary should be kept to about 50 characters, and each line in the body should not exceed 80 characters. If the commit fixes or addresses any issue, it should be referenced in the summary or the body. Subject lines should be succint and use imperative voice and present tense. For the subject line, don't capitalize the first letter and don't add a dot (.) at the end.
We should strive to maintain backward compatibility as much as possible. However, if a commit breaks backward compatibility, it MUST be flagged. To do so, start the body with `"BREAKING CHANGE:"`.
Allowable **type**s include:
- **feat**: new feature
- **fix**: bug fix
- **docs**: documentation-only changes
- **test**: new test cases or fixes to existing test cases
- **perf**: code changes that improve performance
- **refactor**: code change that improves codebase without adding features or fixing bugs
- **style**: changes that do not affect the code (e.g. whitespace, indentation, etc)
- **chore**: changes to build scripts, CI configuration, gitignore, etc.
- **revert**: commit reverts a previous commit (provide SHA of previous commit)
Allowable **scope** include:
- **uwa**: basic underwater acoustic functionality
- **pm**: core infrastructure for propagation modeling
- **pekeris**: Pekeris ray propagation model
- **plot**: plotting support functionality
NOTE: As we evolve the UnderwaterAcoustics.jl library, the allowable scope list will evolve. If you find something you're doing doesn't fit in this scope list, please [open an issue](https://github.com/org-arl/UnderwaterAcoustics.jl/issues/new/choose) to propose addition of a new scope.
In some cases, the scope of a commit cuts across multiple scopes. In that case, a comma-separated scope list may be used. In cases, where all scopes are affected, a "`*`" may be used as scope, or the scope may be omitted.
Some examples of good commit messages:
```
fix(pekeris): fix type instability for Float32 (issue #17)
```
```
feat(uwa): add bubble resonance calculator
Compute resonance frequency of a freely oscillating has bubble in water
using equation from based on Medwin & Clay (1998).
```
```
fix(pm): return complex transmission loss from models
BREAKING CHANGE: Propagation models used to return just the magnitude of
transmission loss, and ignore phase. We have updated the API to now return
complex transmission loss instead, and let users take the `abs()`
of it, if they need only the magnitude.
```
## Coding standards
We have not evolved a formal coding standard yet, but good coding practices common in the Julia community are adopted in this project. At minimum, you should be familiar (and comply to the extent reasonable) with [Julia style guide](https://docs.julialang.org/en/v1/manual/style-guide/), [Julia performance tips](https://docs.julialang.org/en/v1/manual/performance-tips/) and the [Julia documentation guidelines](https://docs.julialang.org/en/v1/manual/documentation/).
### Some guidelines:
- Properly format and indent your code. Use 2 spaces for indentation (DO NOT use tabs).
- Use blank lines and/or comments to separate code sections for readability. But do not use excess whitespace or blank lines, as this limits the amount of visible code on the screen and makes the code harder to navigate.
- Do not leave chunks of commented code in the codebase. Delete unused code, and rely on git history for access to old code when necessary.
- Type names start with a capital letter and use CamelCase (e.g. `RaySolver`).
- Function and variable names are generally all lowercase. Multiple words are concatenated together without a underscore. However, the use of underscore or uppercase is permitted when concatenated words are difficult to read (e.g. `bubbleresonance()`, `surfaceloss`, `transmissionloss_dB()`).
- Use descriptive function and variable names, and avoid abbreviations unless obvious or common (e.g. prefer `count` over `cnt`). Local index variables may use single letter variables (e.g. `i`, `j`, `k`, etc).
- When implementing mathematical algorithms, it is fine to use the notation used in the original papers, including single letter variables, Greek letters, unicode characters, and capital letters for matrices. When doing so, however, it is recommended that a citation to the original paper be made available in the code as a comment, or in the docstring.
- Code should be as self-documenting as possible, and comments that could go out of sync with code should be avoided. However, in cases where additional information would be useful for the reader, comments may be included.
- Comments may be prefixed with `NOTE:`, `FIXME:` or `TODO:`, if the developer wishes to leave some thoughts for oneself or a later developer to be reminded of, understand or address.
- When docstrings are included, they MUST either include the method signature, or the text "`$(SIGNATURES)`" (or equivalent). We use [DocStringExtensions.jl](https://juliadocs.github.io/DocStringExtensions.jl/stable/) to expand "`$(SIGNATURES)`" out into the method signatures, when generating the online documentation.
- Be mindful of performance (memory organization, type stability, etc) when coding, as much of the code in this project gets used in computationally sensitive applications. The [Julia performance tips](https://docs.julialang.org/en/v1/manual/performance-tips/) section provides a good guidelines on this.
- When in doubt, be guided by other parts of the existing codebase. If still unsure, [ask](https://github.com/org-arl/UnderwaterAcoustics.jl/discussions).
## Acknowledgments
In preparing this document, we used the following references:
- [Contributing to xarray](http://xarray.pydata.org/en/stable/contributing.html)
- [Contributing to Github](https://github.com/github/docs/blob/main/CONTRIBUTING.md)
- [Angular commit format reference sheet](https://gist.github.com/brianclements/841ea7bffdb01346392c)
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 2444 | [](https://github.com/org-arl/UnderwaterAcoustics.jl/actions)
[](https://org-arl.github.io/UnderwaterAcoustics.jl/stable)
[](https://org-arl.github.io/UnderwaterAcoustics.jl/dev)
[](https://codecov.io/gh/org-arl/UnderwaterAcoustics.jl)
[](CONTRIBUTING.md)
# UnderwaterAcoustics.jl
### Julia toolbox for underwater acoustic modeling

## Highlights
- Underwater acoustic propagation modeling with pluggable models
- 2D/3D underwater acoustic simulation tools
- Differentiable and probabilistic underwater acoustic modeling
- Underwater acoustics utility functions
## Installation
```julia-repl
julia>]
pkg> add UnderwaterAcoustics
```
## Related packages
**NOTE: In version 0.2, `RaySolver` and `Bellhop` models have been moved out to separate packages.**
- Install [`AcousticRayTracers.jl`](https://github.com/org-arl/AcousticRayTracers.jl) for `RaySolver` model
- Install [`AcousticsToolbox.jl`](https://github.com/org-arl/AcousticsToolbox.jl) for `Bellhop` and `Kraken` models
- Install [`DataDrivenAcoustics.jl`](https://github.com/org-arl/DataDrivenAcoustics.jl) for `RayBasis` and `GPR` family of models
## Getting started
- Propagation modeling toolkit -- [quickstart guide](https://org-arl.github.io/UnderwaterAcoustics.jl/stable/pm_basic.html)
- Probabilistic propagation modeling -- [tutorial](https://org-arl.github.io/UnderwaterAcoustics.jl/stable/tut_turing.html)
- Differentiable propagation modeling -- [tutorial](https://org-arl.github.io/UnderwaterAcoustics.jl/stable/tut_autodiff.html)
## Contributing
Contributions in the form of bug reports, feature requests, ideas/suggestions, bug fixes, code enhancements, and documentation updates are most welcome. Please read [contribution guidelines](CONTRIBUTING.md) if you wish to start contributing.
## Talks & publications
- Mandar Chitre, "[Underwater Acoustics in the age of differentiable and probabilistic programming](https://www.facebook.com/watch/live/?v=2473971036238315)", UComms 2020 webinar, 3 December 2020.
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 38 | # Project roadmap
(work in progress)
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 736 | # UnderwaterAcoustics.jl
### Julia toolbox for underwater acoustic modeling
```@meta
CurrentModule = UnderwaterAcoustics
```
## Highlights
- Underwater acoustic propagation modeling with pluggable models
- Differentiable and probabilistic underwater acoustic modeling
- Underwater acoustics utility functions
## Installation
```julia-repl
julia>]
pkg> add UnderwaterAcoustics
```
## Getting started
- [Propagation modeling toolkit](@ref) quickstart guide.
- [Underwater acoustics](@ref) utility functions.
## Talks & publications
- Mandar Chitre, "[Underwater Acoustics in the age of differentiable and probabilistic programming](https://www.facebook.com/watch/live/?v=2473971036238315)", UComms 2020 webinar, 3 December 2020.
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 408 | # Propagation modeling API
## Model database
```@autodocs
Modules = [UnderwaterAcoustics]
Pages = ["pm_all.jl"]
```
## Core interfaces
```@autodocs
Modules = [UnderwaterAcoustics]
Pages = ["pm_core.jl"]
```
# Common models
```@autodocs
Modules = [UnderwaterAcoustics]
Pages = ["pm_basic.jl"]
```
# Propagation models
```@autodocs
Modules = [UnderwaterAcoustics]
Pages = ["pm_pekeris.jl"]
```
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 13468 | # Propagation modeling toolkit
## Overview
The _underwater acoustic propagation modeling & simulation toolkit_ provides a framework for modeling and simulating underwater acoustic environments with multiple sources and receivers. The toolkit provides a pluggable interface that allows different propagation models to be used with the same scene description. While `UnderwaterAcoustics.jl` provides several propagation model implementations that can be used out-of-the-box, the interface is designed to allow third party propagation models to be easily plugged in to the toolkit as well.
Available models:
| Model | Description | Language | Strengths | Limitations |
|-------|-------------|----------|-----------|-------------|
| [PekerisRayModel](@ref) | Analytical ray model for Pekeris waveguides | Julia | Fast, differentiable, multi-threaded | Isovelocity, range independent |
| [RaySolver](https://github.com/org-arl/AcousticRayTracers.jl) | Ray/Gaussian beam model | Julia | Differentiable, multi-threaded | Tell us and we'll fix them! |
| [Bellhop](https://github.com/org-arl/AcousticsToolbox.jl) | Interface to [OALIB Bellhop model](http://oalib.hlsresearch.com/AcousticsToolbox/) | FORTRAN | Well established benchmark model | Does not support automatic differentiation |
| [Kraken](https://github.com/org-arl/AcousticsToolbox.jl) | Interface to [OALIB Kraken model](http://oalib.hlsresearch.com/AcousticsToolbox/) | FORTRAN | Well established benchmark model | Does not support automatic differentiation |
| [RayBasis](https://github.com/org-arl/DataDrivenAcoustics.jl) | Ray-basis neural network models | Julia | Data-driven models | Requires training data |
| [GPR](https://github.com/org-arl/DataDrivenAcoustics.jl) | Gaussian process regression models | Julia | Data-driven model | Requires training data |
## Quickstart guide
Let's get started:
```julia-repl
julia> using UnderwaterAcoustics
```
### Define an environment
First, let's setup an environment description.
```julia-repl
julia> env = UnderwaterEnvironment()
BasicUnderwaterEnvironment:
altimetry = FlatSurface()
bathymetry = ConstantDepth{Float64}(20.0)
ssp = IsoSSP{Float64}(1539.0866009307247)
salinity = 35.0
seasurface = SurfaceLoss{Float64}(2.6)
seabed = RayleighReflectionCoef{Float64,Float64,Float64}(1.169, 0.9999, 0.01261)
noise = RedGaussianNoise{Float64}(1.0e6)
```
Environments are immutable, so you have to customize them during construction. For example:
```julia-repl
julia> env = UnderwaterEnvironment(
seasurface = Vacuum,
seabed = SandyClay,
ssp = SampledSSP(0.0:20.0:40.0, [1500.0, 1490.0, 1520.0], :smooth),
bathymetry = ConstantDepth(40.0)
)
BasicUnderwaterEnvironment:
altimetry = FlatSurface()
bathymetry = ConstantDepth{Float64}(40.0)
ssp = SampledSSP{Float64,Float64,linear}(3 points)
salinity = 35.0
seasurface = ReflectionCoef{Float64}(-1.0)
seabed = RayleighReflectionCoef{Float64,Float64,Float64}(1.147, 0.9849, 0.00242)
noise = RedGaussianNoise{Float64}(1.0e6)
```
If you have `Plots.jl` installed, you can use plot recipes to plot the environment or the soundspeed profile. For example:
```julia-repl
julia> using Plots
julia> plot(ssp(env))
```

### Selecting a model
Once you have an environment, you need to select a propagation model. To get a list of all available models:
```julia-repl
julia> models()
3-element Array{Any,1}:
PekerisRayModel
RaySolver
Bellhop
```
NOTE: `Bellhop` will only be available if you have a working copy of OALIB `bellhop.exe` available on your PATH.
Once you have an environment, you can select a model that can work with that environment:
```julia-repl
julia> models(env)
2-element Array{Any,1}:
RaySolver
Bellhop
```
In this case, we got a shorter list back because the `PekerisRayModel` can't deal with non-isovelocity SSP. We can confirm this by creating an iso-velocity environment:
```julia-repl
julia> env = UnderwaterEnvironment()
BasicUnderwaterEnvironment:
altimetry = FlatSurface()
bathymetry = ConstantDepth{Float64}(20.0)
ssp = IsoSSP{Float64}(1539.0866009307247)
salinity = 35.0
seasurface = SurfaceLoss{Float64}(2.6)
seabed = RayleighReflectionCoef{Float64,Float64,Float64}(1.169, 0.9999, 0.01261)
noise = RedGaussianNoise{Float64}(1.0e6)
julia> models(env)
2-element Array{Any,1}:
PekerisRayModel
RaySolver
```
This time you see that `Bellhop` wasn't included, as it assumes a `Vacuum` surface by default and we have a `SeaState1` surface as our default.
Let's pick a 7-ray Pakeris ray model for now:
```julia-repl
julia> pm = PekerisRayModel(env, 7)
PekerisRayModel with BasicUnderwaterEnvironment:
altimetry = FlatSurface()
bathymetry = ConstantDepth{Float64}(20.0)
ssp = IsoSSP{Float64}(1539.0866009307247)
salinity = 35.0
seasurface = SurfaceLoss{Float64}(2.6)
seabed = RayleighReflectionCoef{Float64,Float64,Float64}(1.169, 0.9999, 0.01261)
noise = RedGaussianNoise{Float64}(1.0e6)
```
If you wanted the ray solver instead, you'd do `pm = RaySolver(env)`, or for a Bellhop model, you'd do `pm = Bellhop(env)`. Both models can take additional keyword parameters that can customize the solver.
### Defining sources and receivers
Now, we need a source and a receiver:
```julia-repl
julia> tx = AcousticSource(0.0, -5.0, 1000.0);
julia> rx = AcousticReceiver(100.0, -10.0);
```
This defines an omnidirectional 1 kHz transmitter `tx` at a depth of 5 m at the origin, and an omnidirectional receiver at a range of 100 m and a depth of 10 m.
NOTE: All coordinates are specified in meters as (x, y, z) for 3D or (x, z) for 2D. The coordinate system has `x` and `y` axis in the horizontal plane, and `z` axis pointing upwards, with the nominal water surface being at 0 m. This means that all `z` coordinates in water are negative.
### Ray tracing
Now that we have an environment, a propation model, a transmitter and a receiver, we can modeling. First, we ask for all eigenrays between the transmitter and receiver:
```julia-repl
julia> r = eigenrays(pm, tx, rx)
7-element Array{UnderwaterAcoustics.RayArrival{Float64,Float64},1}:
∠ -2.9° 0↑ 0↓ ∠ 2.9° | 65.05 ms | -40.0 dB ϕ -0.0° ⤷
∠ 8.5° 1↑ 0↓ ∠ 8.5° | 65.70 ms | -40.1 dB ϕ-180.0° ⤷
∠-14.0° 0↑ 1↓ ∠-14.0° | 66.97 ms | -59.0 dB ϕ 60.5° ⤷
∠ 19.3° 1↑ 1↓ ∠-19.3° | 68.84 ms | -61.3 dB ϕ-141.7° ⤷
∠-24.2° 1↑ 1↓ ∠ 24.2° | 71.25 ms | -62.3 dB ϕ-153.8° ⤷
∠ 28.8° 2↑ 1↓ ∠ 28.8° | 74.15 ms | -63.0 dB ϕ 19.4° ⤷
∠-33.0° 1↑ 2↓ ∠-33.0° | 77.49 ms | -85.4 dB ϕ-149.4° ⤷
```
For each eigenray, this shows us the launch angle, number of surface bounces, number of bottom bounces, arrival angle, travel time, transmission loss along that ray, and phase change. The last "`⤷`" symbol indicates that the complete ray path is also available. We can plot the ray paths:
```julia-repl
julia> plot(env; sources=[tx], receivers=[rx], rays=r)
```

Th red star is the transmitter and the blue circle is the receiver. The stronger eigenrays are shown in blue, while the weaker ones are shown in red.
We might sometimes want to see all rays from the transmitter at certain angular spacing (-45°:5°:45°) and a given range (100 m):
```julia-repl
julia> r = rays(pm, tx, -45°:5°:45°, 100.0)
19-element Array{UnderwaterAcoustics.RayArrival{Float64,Float64},1}:
∠-45.0° 2↑ 3↓ ∠-45.0° | 91.89 ms | -109.6 dB ϕ 27.5° ⤷
∠-40.0° 2↑ 2↓ ∠ 40.0° | 84.82 ms | -86.8 dB ϕ 22.1° ⤷
∠-35.0° 1↑ 2↓ ∠-35.0° | 79.32 ms | -85.9 dB ϕ-152.3° ⤷
∠-30.0° 1↑ 2↓ ∠-30.0° | 75.03 ms | -85.2 dB ϕ-143.9° ⤷
∠-25.0° 1↑ 1↓ ∠ 25.0° | 71.69 ms | -62.8 dB ϕ-155.2° ⤷
∠-20.0° 1↑ 1↓ ∠ 20.0° | 69.14 ms | -61.9 dB ϕ-143.9° ⤷
∠-15.0° 0↑ 1↓ ∠-15.0° | 67.27 ms | -59.6 dB ϕ 55.5° ⤷
⋮
∠ 15.0° 1↑ 1↓ ∠-15.0° | 67.27 ms | -60.0 dB ϕ-124.5° ⤷
∠ 20.0° 1↑ 1↓ ∠-20.0° | 69.14 ms | -61.9 dB ϕ-143.9° ⤷
∠ 25.0° 2↑ 1↓ ∠ 25.0° | 71.69 ms | -63.1 dB ϕ 24.8° ⤷
∠ 30.0° 2↑ 1↓ ∠ 30.0° | 75.03 ms | -63.6 dB ϕ 18.1° ⤷
∠ 35.0° 2↑ 2↓ ∠-35.0° | 79.32 ms | -86.2 dB ϕ 27.7° ⤷
∠ 40.0° 2↑ 2↓ ∠-40.0° | 84.82 ms | -86.8 dB ϕ 22.1° ⤷
∠ 45.0° 3↑ 2↓ ∠ 45.0° | 91.89 ms | -87.7 dB ϕ-161.7° ⤷
julia> plot(env; sources=[tx], rays=r)
```

### Arrivals & transmission loss
Often, we are interested in the arrival structure or transmission loss at a receiver. Getting the arrivals is quite similar to getting eigenrays, but the ray paths are not stored:
```julia-repl
julia> a = arrivals(pm, tx, rx)
7-element Array{UnderwaterAcoustics.RayArrival{Float64,Missing},1}:
∠ -2.9° 0↑ 0↓ ∠ 2.9° | 65.05 ms | -40.0 dB ϕ -0.0°
∠ 8.5° 1↑ 0↓ ∠ 8.5° | 65.70 ms | -40.1 dB ϕ-180.0°
∠-14.0° 0↑ 1↓ ∠-14.0° | 66.97 ms | -59.0 dB ϕ 60.5°
∠ 19.3° 1↑ 1↓ ∠-19.3° | 68.84 ms | -61.3 dB ϕ-141.7°
∠-24.2° 1↑ 1↓ ∠ 24.2° | 71.25 ms | -62.3 dB ϕ-153.8°
∠ 28.8° 2↑ 1↓ ∠ 28.8° | 74.15 ms | -63.0 dB ϕ 19.4°
∠-33.0° 1↑ 2↓ ∠-33.0° | 77.49 ms | -85.4 dB ϕ-149.4°
```
If we prefer, we can plot these arrivals as an impulse response (sampled at 44.1 kSa/s, in this case):
```julia-repl
julia> plot(abs.(impulseresponse(a, 44100; reltime=true)); xlabel="Sample #", legend=false)
```

The `reltime=true` option generates an impulse response with time relative to the first arrival (default is relative to transmission time).
If we want, we can also get the complex transfer coefficient or the transmission loss in dB:
```julia-repl
julia> transfercoef(pm, tx, rx)
0.013183979186458052 - 0.012267750240848727im
julia> transmissionloss(pm, tx, rx)
34.89032959932541
```
You can also pass in arrays of sources and receivers, if you want many transmission losses to be computed simultanously. Some models are able to compute transmission loss on a Cartesion grid very efficiently. This is useful to plot transmission loss as a function of space.
To define a 1000×200 Cartesion grid with 0.1 m spacing:
```julia-repl
julia> rx = AcousticReceiverGrid2D(1.0, 0.1, 1000, -20.0, 0.1, 200)
1000×200 AcousticReceiverGrid2D{Float64}:
BasicAcousticReceiver((1.0, 0.0, -20.0)) … BasicAcousticReceiver((1.0, 0.0, -0.1))
BasicAcousticReceiver((1.1, 0.0, -20.0)) BasicAcousticReceiver((1.1, 0.0, -0.1))
BasicAcousticReceiver((1.2, 0.0, -20.0)) BasicAcousticReceiver((1.2, 0.0, -0.1))
⋮ ⋱
BasicAcousticReceiver((100.7, 0.0, -20.0)) BasicAcousticReceiver((100.7, 0.0, -0.1))
BasicAcousticReceiver((100.8, 0.0, -20.0)) BasicAcousticReceiver((100.8, 0.0, -0.1))
BasicAcousticReceiver((100.9, 0.0, -20.0)) BasicAcousticReceiver((100.9, 0.0, -0.1))
```
We can then compute the transmission loss over the grid:
```julia-repl
julia> x = transmissionloss(pm, tx, rx)
1000×200 Array{Float64,2}:
19.0129 19.12 19.5288 … 9.02602 8.23644 8.86055 11.1436 16.4536
19.017 19.1239 19.5324 9.02506 8.26487 8.90641 11.2 16.5155
19.0217 19.1284 19.5366 … 9.02392 8.29514 8.95536 11.2602 16.5817
19.0271 19.1336 19.5415 9.0226 8.32706 9.00713 11.3239 16.6519
⋮ ⋮ ⋱ ⋮ ⋮
35.5238 35.4909 35.4954 56.1556 57.7909 59.9858 63.1631 68.5643
35.5742 35.5448 35.5526 … 56.5185 58.1488 60.3365 63.5039 68.8852
35.6261 35.6 35.611 56.8971 58.522 60.7023 63.8594 69.2206
35.6793 35.6565 35.6704 57.2926 58.9118 61.0841 64.2306 69.5712
julia> plot(env; receivers=rx, transmissionloss=x)
```

### Acoustic simulations
Apart from propagation modeling, we can also setup a simulation with various sources and receviers.
We demonstrate this by setting up a scenario with two pingers (1 kHz, 10 ms pulse with 1 Hz PRR; 2 kHz, 20 ms pulse with 2 Hz PRR) with a source level of 170 dB re µPa @ 1m, at two locations, and deploying two omnidirectional receviers to record them:
```julia-repl
julia> using DSP: db2amp
julia> tx = [
Pinger(0.0, 0.0, -5.0, 1000.0; interval=1.0, duration=10e-3, sourcelevel=db2amp(170)),
Pinger(0.0, 100.0, -5.0, 2000.0; interval=0.5, duration=20e-3, sourcelevel=db2amp(170))
]
julia> rx = [
AcousticReceiver(100.0, 0.0, -10.0);
AcousticReceiver(50.0, 20.0, -5.0)
];
```
To carry out the simulation, we can for a 2-second long recording (at 8 kSa/s) at the receivers:
```julia-repl
julia> s = record(pm, tx, rx, 2.0, 8000.0)
SampledSignal @ 8000.0 Hz, 16000×2 Array{Complex{Float64},2}:
127308.0+884666.0im 1.15927e6-548579.0im
-263820.0+1.16962e6im 1.1377e6+541803.0im
-80980.6+1.16562e6im 657226.0+738712.0im
⋮
-447370.0+910253.0im 163952.0-436691.0im
-431239.0+903852.0im 100509.0-118066.0im
-391797.0+582705.0im 49383.0-679981.0im
```
The signals are returned as complex analytic signals, but can be easily converted to real signals, if desired:
```julia-repl
julia> s = real(s)
SampledSignal @ 8000.0 Hz, 16000×2 Array{Float64,2}:
-672702.0 318731.0
-825049.0 377382.0
-984626.0 214490.0
⋮
66193.3 -497239.0
-144031.0 -321312.0
-260200.0 -235680.0
```
To visualize the recording, we plot a spectrogram of the signal at the first receiver with the `SignalAnalysis.jl` package:
```julia-repl
julia> using SignalAnalysis
julia> specgram(s[:,1])
```

We can clearly see the two pingers, as well as the ambient noise generated with the noise model defined in the environment description.
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 2486 | # Environmental model reference
```@meta
CurrentModule = UnderwaterAcoustics
```
## Environmental model
*Interface*:
- `abstract type UnderwaterEnvironment`
- [`altimetry`](@ref)`()`
- [`bathymetry`](@ref)`()`
- [`ssp`](@ref)`()`
- [`salinity`](@ref)`()`
- [`seasurface`](@ref)`()`
- [`seabed`](@ref)`()`
- [`noise`](@ref)`()`
*Standard models:*
- [`UnderwaterEnvironment`](@ref)
## Sound speed profiles
*Interface*:
- `abstract type SoundSpeedProfile`
- [`soundspeed`](@ref)`()`
*Standard models:*
- [`IsoSSP`](@ref)
- [`MunkSSP`](@ref)
- [`SampledSSP`](@ref)
## Bathymetry
*Interface*:
- `abstract type Bathymetry`
- [`depth`](@ref)`()`
- [`maxdepth`](@ref)`()`
*Standard models:*
- [`ConstantDepth`](@ref)
- [`SampledDepth`](@ref)
## Altimetry
*Interface*:
- `abstract type Altimetry`
- [`altitude`](@ref)`()`
*Standard models:*
- [`FlatSurface`](@ref)
- [`SampledAltitude`](@ref)
## Sea surface
*Interface*:
- `abstract type ReflectionModel`
- [`reflectioncoef`](@ref)`()`
*Standard models:*
- [`ReflectionCoef`](@ref)
- [`RayleighReflectionCoef`](@ref)
- [`SurfaceLoss`](@ref)
- `const Vacuum`
- `const SeaState0`
- `const SeaState1`
- `const SeaState2`
- `const SeaState3`
- `const SeaState4`
- `const SeaState5`
- `const SeaState6`
- `const SeaState7`
- `const SeaState8`
- `const SeaState9`
## Seabed
*Interface*:
- `abstract type ReflectionModel`
- [`reflectioncoef`](@ref)`()`
*Standard models:*
- [`ReflectionCoef`](@ref)
- [`RayleighReflectionCoef`](@ref)
- `const Rock`
- `const Pebbles`
- `const SandyGravel`
- `const CoarseSand`
- `const MediumSand`
- `const FineSand`
- `const VeryFineSand`
- `const ClayeySand`
- `const CoarseSilt`
- `const SandySilt`
- `const Silt`
- `const FineSilt`
- `const SandyClay`
- `const SiltyClay`
- `const Clay`
## Acoustic sources
*Interface*:
- [`AcousticSource`](@ref)
- [`location`](@ref)`()`
- [`nominalfrequency`](@ref)`()`
- [`phasor`](@ref)`()`
- [`record`](@ref)`()`
- [`recorder`](@ref)`()`
*Standard models:*
- [`NarrowbandAcousticSource`](@ref)
- [`Pinger`](@ref)
- [`SampledAcousticSource`](@ref)
# Acoustic receivers
*Interface*:
- [`AcousticReceiver`](@ref)
- [`location`](@ref)`()`
*Standard models:*
- [`AcousticReceiver`](@ref)
- [`AcousticReceiverGrid2D`](@ref)
- [`AcousticReceiverGrid3D`](@ref)
# Ambient noise
*Interface*:
- `abstact type NoiseModel`
- [`record`](@ref)`()`
*Standard models:*
- [`RedGaussianNoise`](@ref)
- any other distribution that works with `rand()`
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 760 | # PekerisRayModel
```@meta
CurrentModule = UnderwaterAcoustics
```
The Pekeris ray model is a very fast fully differentiable 2D/3D ray model for isovelocity range-independent environments. The only parameter that has to be specified when creating the model is the desired number of rays.
**Example:**
```julia
using UnderwaterAcoustics
using Plots
env = UnderwaterEnvironment(
seasurface = SeaState2,
seabed = SandyClay
)
pm = PekerisRayModel(env, 7) # 7-ray model
tx = AcousticSource(0.0, -5.0, 1000.0)
rx = AcousticReceiver(100.0, -10.0)
r = eigenrays(pm, tx, rx)
plot(env; sources=[tx], receivers=[rx], rays=r)
```

For more information on how to use the propagation models, see [Propagation modeling toolkit](@ref).
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 4369 | # Differentiable modeling
!!! note
This tutorial is adapted from the example presented in the UComms 2020 webinar talk "[Underwater Acoustics in the age of differentiable and probabilistic programming](https://www.facebook.com/watch/live/?v=2473971036238315)".
## Problem statement
Let us consider a scenario where a drifting probe acoustically transmits its sensor data periodically to a static receiver. The initial position of the sensor is perfectly known, and so is the environment. But the path of the sensor as it drifts is not known, but we'd like to get an estimate of it from the received acoustic signal. Due to the high data rate requirements, the receiver uses an equalization technique that requires an accurate estimate of the channel impulse response. We want to generate that using a propagation model and an accurate estimate of the location of the probe.
The environment is an isovelocity channel with a constant depth of 20 m and known seabed parameters (relative density `ρ` = 1.5, relative soundspeed `c` = 1.2, and attenuation `δ` = 0.001). The probe uses a 1-2 kHz band for data transmission, and includes 101 pilots at 10 Hz spacing to aid with channel estimation. The transmission loss can be accurately measured at those pilot frequencies, since the transmit source level is assumed to be known, but phase information is assumed to be unavailable at each pilot.

## Dataset
To illustrate the idea, we generate a 60-transmission dataset with a linearly drifting path for the transmitter. Since we have an range-independent isovelocity environment, we can use the `PekerisRayModel` (otherwise we could use the `RaySolver`):
```julia
using UnderwaterAcoustics
using DataFrames
function 𝒴(θ)
r, d, f, ρ, c, δ = θ
env = UnderwaterEnvironment(seabed = RayleighReflectionCoef(ρ, c, δ))
tx = AcousticSource(0.0, -5.0, f)
rx = AcousticReceiver(r, -d)
pm = PekerisRayModel(env, 7)
transmissionloss(pm, tx, rx)
end
data = [(
range=100.0 + 0.5t,
depth=6.0 + 0.01t,
pilots=[𝒴([100.0 + 0.5t, 6.0 + 0.01t, f, 1.5, 1.2, 0.001]) for f ∈ 1000.0:10.0:2000.0]
) for t ∈ 0.0:1.0:59.0]
data = DataFrame(vec(data))
```
## Gradient descent
In order to recover the drift path of the probe, we build a simple error model for the measured pilots. We initialize the model with the known starting location of the probe, and track the probe by minimizing the error through gradient descent.
Since our propagation model is differentiable, the gradient of the error can be automatically computed during the optimization using [`ForwardDiff.jl`](https://github.com/JuliaDiff/ForwardDiff.jl).
```julia
using ForwardDiff
# channel model for pilots
pilots(r, d) = [
𝒴([r, d, f, 1.5, 1.2, 0.001]) for f ∈ 1000.0:10.0:2000.0
]
# gradient descent optimization
function chparams(data)
history = []
θ = [100.0, 6.0] # known initial location
η = [1e-4, 1e-6] # learning rate
for row ∈ eachrow(data)
err(θ) = sum(abs2, pilots(θ[1], θ[2]) .- row.pilots) # error model
for i ∈ 1:100 # iterations of simple gradient descent
θ .-= η .* ForwardDiff.gradient(err, θ)
end
push!(history, (range=θ[1], depth=θ[2]))
end
DataFrame(history)
end
p = chparams(data)
```
Now that we have a path estimate, let's check it against the ground truth:
```julia
using Plots
plot(data.range, -data.depth; xlabel="Range (m)", ylabel="Depth (m)", label="Ground truth")
scatter!(p.range, -p.depth; label="Estimated")
```

We have a pretty good match!
## Impulse response estimation
Now we can generate the impulse response for each of the 60 received data packets:
```julia
# compute impulse response
function iresp(r, d)
env = UnderwaterEnvironment(
seabed = RayleighReflectionCoef(1.5, 1.2, 0.001)
)
tx = AcousticSource(0.0, -5.0, 1500.0)
rx = AcousticReceiver(r, -d)
pm = PekerisRayModel(env, 7)
impulseresponse(arrivals(pm, tx, rx), 8000; reltime=true)[1:72]
end
ir = hcat([iresp(row.range, row.depth) for row ∈ eachrow(p)]...)'
heatmap(20*log10.(abs.(ir)); clim=(-60, -30), xlabel="Delay (samples)", ylabel="Transmission #", yflip=true)
```

We see the impulse response evolve over time as the probe drifts. This can then be used for channel equalization and to recover the transmitted data!
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 3762 | # Probabilistic modeling
!!! note
This tutorial is based on the example presented in the UComms 2020 webinar talk "[Underwater Acoustics in the age of differentiable and probabilistic programming](https://www.facebook.com/watch/live/?v=2473971036238315)".
## Problem statement
Let us consider a geoacoustic inversion problem where we have a static omnidirectional broadband acoustic source transmitting in a 5-7 kHz band. A single omnidirectional receiver picks up the signal at a fixed range, but profiles the water column, and therefore makes transmission loss measurements at various depths. We would like to estimate seabed parameters from these transmission loss measurements.
## Dataset
To illustrate this idea, let us generate a synthetic dataset for a known set of seabed parameters (relative density `ρ` = 1.5, relative soundspeed `c` = 1.2, and attenuation `δ` = 0.001).
The environment is assumed to be an isovelocity and with a constant depth of 20 m. The source is at a depth of 5 m. The receiver is at a range of 100 m from the source, and makes measurements at depths from 10 to 19 m in steps of 1 m.

Since we have an range-independent isovelocity environment, we can use the `PekerisRayModel` (otherwise we could use the `RaySolver`):
```julia
using UnderwaterAcoustics
using DataFrames
function 𝒴(θ)
r, d, f, ρ, c, δ = θ
env = UnderwaterEnvironment(seabed = RayleighReflectionCoef(ρ, c, δ))
tx = AcousticSource(0.0, -5.0, f)
rx = AcousticReceiver(r, -d)
pm = PekerisRayModel(env, 7)
transmissionloss(pm, tx, rx)
end
data = [
(depth=d, frequency=f, xloss=𝒴([100.0, d, f, 1.5, 1.2, 0.001]))
for d ∈ 10.0:1.0:19.0, f ∈ 5000.0:100.0:7000.0
]
data = DataFrame(vec(data))
```
## Probabilistic model
We use some very loose uniform priors for `ρ`, `c` and `δ`, and estimate the transmission loss using the same model 𝒴, as used in the data generation, but without information on the actual seabed parameters. We assume that the measurements of transmission loss are normally distributed around the modeled transmission loss, with a covariance of 0.5 dB.
We define the probabilistic model as a [`Turing.jl`](https://github.com/TuringLang/Turing.jl) model:
```julia
using Turing
# depths d, frequencies f, transmission loss measurements x
@model function geoacoustic(d, f, x)
ρ ~ Uniform(1.0, 3.0)
c ~ Uniform(0.5, 2.5)
δ ~ Uniform(0.0, 0.003)
μ = [𝒴([100.0, d[i], f[i], ρ, c, δ]) for i ∈ 1:length(d)]
x ~ MvNormal(μ, 0.5)
end
```
## Variational inference
Once we have the model defined, we can run Bayesian inference on it. We could either use MCMC methods from Turing, or variational inference. Since our model is differentiable, we choose to use the automatic differentiation variational inference (ADVI):
```julia
using Turing: Variational
q = vi(
geoacoustic(data.depth, data.frequency, data.xloss),
ADVI(100, 10000)
)
```
The returned `q` is a 3-dimensional posterior probability distribution over the parameters `ρ`, `c` and `δ`. We can estimate the mean of the distribution by drawing random variates and taking the sample mean:
```julia-repl
julia> mean(rand(q, 10000); dims=2)
3×1 Array{Float64,2}:
1.4989510476936188
1.2000012848664092
0.0009835578241605488
```
We see that the estimated parameter means for `ρ`, `c` and `δ` are quite close to the actual values used in generating the data.
We can also plot the conditional distributions of each parameter:
```julia-repl
using StatsPlots
plot(ρ -> pdf(q, [ρ, 1.2, 0.001]), 1.3, 1.7; xlabel="ρ")
plot(c -> pdf(q, [1.5, c, 0.001]), 1.1, 1.3; xlabel="c")
plot(δ -> pdf(q, [1.5, 1.2, δ]), 0.0, 0.003; xlabel="δ")
```



| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.3.4 | 4c11fcf40b7cd7015b82e1ff7d5426fd7f145eb9 | docs | 119 | # Underwater acoustics
Utility functions:
```@autodocs
Modules = [UnderwaterAcoustics]
Pages = ["uw_basic.jl"]
```
| UnderwaterAcoustics | https://github.com/org-arl/UnderwaterAcoustics.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | code | 298 | using Documenter, Harbest
makedocs(
sitename = "Harbest.jl",
authors = "José Díaz",
pages = [
"Home" => "index.md",
"Docstrings" => "lib/docstrings.md"
]
)
deploydocs(
repo = "https://github.com/jdiaz97/Harbest.jl.git",
push_preview = true
) | Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | code | 2096 | using Harbest, DataFrames, PlotlyJS
function get_scores(html)
score = html_elements(html,".ipl-rating-star__rating") |> html_text3 ## Read scores from HTML
score = score[score .!= "Rate" .&& occursin.(".",score)] ## Get actual scores
scores::Vector{Float64} = parse.(Float64,score)
return scores
end
function get_names(html)
names::Vector{String} = html_elements(html,[".info","strong"]) |> html_text3
return names
end
function get_imgs(html)
data = html_elements(html,["img",".zero-z-index"])
imgs::Vector{String} = html_attrs(data,"src")
return imgs
end
function get_n_season(html)
data = read_html(html)
data = html_elements(data,["select","option"])[2] |> html_text3
n_season::Int = parse(Int,data)
return n_season
end
function get_df(url)
df::DataFrame = DataFrame()
n_seasons = get_n_season(url)
urls = url.*"episodes?season=".*string.(1:n_seasons)
for i in eachindex(urls)
html = read_html(urls[i])
temp_df = DataFrame(scores = get_scores(html),
names = get_names(html),
season = i,
images = get_imgs(html))
df = [df;temp_df]
end
df[!,"N"]= rownumber.(eachrow(df))
return df
end
function plot_df(df,title)
return plot(df,
x = :N,
y = :scores,
text = :names,
color = :season,
mode = "lines",
labels=Dict(
:N => "Episode number",
:scores => "Score",
:season => "Season"
),
Layout(title = title* " score on IMDb")
)
end
community_df = get_df("https://www.imdb.com/title/tt1439629/")
plot_community = plot_df(community_df,"Community")
bojack_df = get_df("https://www.imdb.com/title/tt3398228/")
plot_bojack = plot_df(bojack_df,"Bojack Horseman")
savefig(plot_community,"examples/plot_community.html")
savefig(plot_bojack,"examples/plot_bojack.html")
| Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | code | 206 | module Harbest
using HTTP, Cascadia, Gumbo, DataFrames
export read_html, html_elements, html_attrs
export html_text, html_text2, html_text3
export html_table
include("resources.jl")
end # module Harbest | Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | code | 668 | function parse_rows(rows)
rows.children .|> html_text3
end
function transpose(df::DataFrame)
df = permutedims(df,1)
return select!(df, Not(:x1))
end
"""
Takes some HTML and turns it into a DataFrame, only if there is a very clear HTML Table.
html_table(table_html)
### Input:
- `table_html` -- Vector{HTMLNode}
### Output
A DataFrame
"""
function html_table(table_html::Vector{HTMLNode})::DataFrame
rows = html_elements(table_html, "tr")
t = parse_rows.(rows)
t = t[length.(t) .== length(t[1])]
df = DataFrame(t,:auto)
df = transpose(df) ## Not great, will have to replace later
return df
end | Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | code | 3304 | """
Returns the text of an HTML.
html_text3(html)
### Input:
- `html` -- HTMLDocument, HTMLElement or Vector{HTMLNode}
### Output
A single String or a Vector{String} depending on the input
If you want/need whitespaces and other things, you can use html_text or html_text2
"""
function html_text3(html::HTMLDocument)
text = nodeText(html.root)
return replace(text, '\n' => "")
end
function html_text3(html::HTMLElement)
text = nodeText(html)
return replace(text, '\n' => "")
end
function html_text3(html::Vector{HTMLNode})
text = nodeText.(html)
return replace.(text, '\n' => "")
end
function get_text(htmlstring)
test = htmlstring
vector = []
start = 0
for i in eachindex(test)
if test[i] == '>'
start = i+1
end
if test[i] == '<' && start != 0
final = i-1
vector = vcat(vector,(start,final))
start = nothing
final = nothing
end
end
text = []
for i in eachindex(vector)
temptext = test[vector[i][1]:vector[i][2]]
text = vcat(text,temptext)
end
return text
## return reduce(string,text)
end
"""
Returns the text of an HTML but with some whitespaces
"""
function html_text(html::HTMLDocument)
html = repr(html.root)
text = get_text(html)
text = reduce(string,text)
return text
end
function html_text(html::Vector{HTMLNode})
html = repr.(html)
text = get_text.(html)
text = reduce.(string,text)
return text
end
function html_text(html::HTMLElement)
html = repr(html)
text = get_text(html)
text = reduce(string,text)
return text
end
function cleantext(vectortext)
text = vectortext
finaltext = []
for i in eachindex(text)
temptext = text[i]
linebreak1 = true
for j in eachindex(temptext)
linebreak0 = temptext[j] == '\n' || temptext[j] == ' '
linebreak1 = linebreak0*linebreak1
end
if linebreak1 == false
finaltext = vcat(finaltext,temptext)
end
end
breakline = []
for k in eachindex(finaltext)
test = finaltext[k]
for i in eachindex(test)
bool = test[i] == '\n' || test[i] == ' '
if bool == false
breakline = vcat(breakline,i)
break
end
end
end
ftext = []
for i in eachindex(finaltext)
text = finaltext[i]
ftext = vcat(ftext, text[breakline[i]:length(text)])
end
if ftext == []
return ""
else
return reduce(string, ftext)
end
end
"""
Returns the text of an HTML, but cleaner than html_text
"""
function html_text2(html::HTMLDocument)
html = repr(html.root)
text = get_text(html)
text = cleantext(text)
return text
end
function html_text2(html::Vector{HTMLNode})
html = repr.(html)
text = get_text.(html)
text = cleantext.(text)
return text
end
function html_text2(html::HTMLElement)
html = repr(html)
text = get_text(html)
text = cleantext(text)
return text
end
html_text3 | Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | code | 2637 | include("html_text.jl")
include("html_table.jl")
"""
Returns a parsed HTML from an url
read_html(url::String)
### Input:
- `url::String`
### Output
HTMLDocument
"""
function read_html(url::String)::HTMLDocument
r = HTTP.get(url)
return parsehtml(String(r.body))
end
"""
Returns HTML elements
html_elements(html,string)
### Input:
- `html` -- It can be HTMLDocument, HTMLElement or Vector{HTMLNode}
- `string` -- It's the element in the HTML that you want to find. It can be a String or Vector{String}, if the latter, it will apply the function in sequence
### Output
Your HTML reduced to the element that you indicated
"""
function html_elements(html::HTMLDocument,string::String)
elements = eachmatch(Selector(string),html.root)
return elements
end
function html_elements(html::HTMLElement,string::String)
elements = eachmatch(Selector(string),html)
return elements
end
function html_elements(html::Vector{HTMLNode},string::String)
elements = eachmatch.([Selector(string)],html)
return reduce(vcat,elements) ## will solve the Vector of Vectors problem
end
function html_elements(html::HTMLDocument,strings::Vector{String})
result = html
for string in strings
result = html_elements(result,string)
end
return result
end
function html_elements(html::HTMLElement,strings::Vector{String})
result = html
for string in strings
result = html_elements(result,string)
end
return result
end
function html_elements(html::Vector{HTMLNode},strings::Vector{String})
result = html
for string in strings
result = html_elements(result,string)
end
return result
end
"""
Get an attribute
html_attrs(html,string)
### Input:
- `html` -- It can be HTMLDocument, HTMLElement or Vector{HTMLNode}
- `string::String` (optional) -- Define the attribute that you want to return, if not provided, it would try to return a list of the attributes.
### Output
Indicated attribute or a list of the available attributes
"""
function html_attrs(html::HTMLDocument)
return attrs(html.root)
end
function html_attrs(html::Vector{HTMLNode})
return attrs.(html)
end
function html_attrs(html::HTMLElement)
return attrs(html)
end
function html_attrs(html::HTMLDocument,string::String)
return getattr(html.root,string)
end
function html_attrs(html::Vector{HTMLNode},string::String)
return getattr.(html,string)
end
function html_attrs(html::HTMLElement,string::String)
return getattr(html,string)
end
| Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | code | 1851 | include("../src/Harbest.jl")
using .Harbest
starwars = read_html("https://rvest.tidyverse.org/articles/starwars.html")
films = html_elements(starwars, "section")
title = html_elements(films,"h2")
html_text3(title)
# 7-element Vector{String}:
# "The Phantom Menace"
# "Attack of the Clones"
# "Revenge of the Sith"
# ⋮
# "Return of the Jedi"
# "The Force Awakens"
html = read_html("https://en.wikipedia.org/w/index.php?title=The_Lego_Movie&oldid=998422565")
table = html_elements(html, ".tracklist") |> html_table
# 28×4 DataFrame
# Row │ No. Title Performer(s) Length
# │ String String String String
# ─────┼──────────────────────────────────────────────────────────────────────────────────────
# 1 │ 1. "Everything Is Awesome" Tegan and Sara featuring The Lon… 2:43
# 2 │ 2. "Prologue" 2:28
# 3 │ 3. "Emmett's Morning" 2:00
# 4 │ 4. "Emmett Falls in Love" 1:11
# 5 │ 5. "Escape" 3:26
# ⋮ │ ⋮ ⋮ ⋮ ⋮
# 25 │ 25. "Everything Is Awesome" Jo Li (Joshua Bartholomew and Li… 1:26
# 26 │ 26. "Everything Is Awesome (unplugge… Shawn Patterson and Sammy Allen 1:24
# 27 │ 27. "Untitled Self Portrait" Will Arnett 1:08
# 28 │ 28. "Everything Is Awesome (instrume… 2:41
# 19 rows omitted | Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | code | 550 | include("../../src/Harbest.jl")
using .Harbest
url = "https://www.imdb.com/title/tt1439629/episodes?season=1"
html = Harbest.read_html(url)
score = Harbest.html_elements(html,".ipl-rating-star__rating") |> Harbest.html_text3 ## Read scores from HTML
score = score[score .!= "Rate" .&& occursin.(".",score)] ## Get actual scores
score = parse.(Float64,score)
b = Harbest.html_elements(html,".info")
b = Harbest.html_elements(b,"strong") |> Harbest.html_text3
Harbest.html_elements(html,[".info","strong"]) |> Harbest.html_text3 | Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | docs | 2529 | # Harbest.jl
## Simple web scraping with Julia
This library combines HTTP, Gumbo and Cascadia for a more simple way to scrape data.
Early version. Based on [tidyverse/rvest](https://github.com/tidyverse/rvest).
## Usage
```julia
using Harbest
starwars = read_html("https://rvest.tidyverse.org/articles/starwars.html")
titles = html_elements(starwars, ["section", "h2"]) |> html_text3
titles
# 7-element Vector{String}:
# "The Phantom Menace"
# "Attack of the Clones"
# "Revenge of the Sith"
# ⋮
# "Return of the Jedi"
# "The Force Awakens"
html = read_html("https://en.wikipedia.org/w/index.php?title=The_Lego_Movie&oldid=998422565")
table = html_elements(html, ".tracklist") |> html_table
table
# 28×4 DataFrame
# Row │ No. Title Performer(s) Length
# │ String String String String
# ─────┼──────────────────────────────────────────────────────────────────────────────────────
# 1 │ 1. "Everything Is Awesome" Tegan and Sara featuring The Lon… 2:43
# 2 │ 2. "Prologue" 2:28
# 3 │ 3. "Emmett's Morning" 2:00
# 4 │ 4. "Emmett Falls in Love" 1:11
# 5 │ 5. "Escape" 3:26
# ⋮ │ ⋮ ⋮ ⋮ ⋮
# 25 │ 25. "Everything Is Awesome" Jo Li (Joshua Bartholomew and Li… 1:26
# 26 │ 26. "Everything Is Awesome (unplugge… Shawn Patterson and Sammy Allen 1:24
# 27 │ 27. "Untitled Self Portrait" Will Arnett 1:08
# 28 │ 28. "Everything Is Awesome (instrume… 2:41
# 19 rows omitted
```
## Functions
### `read_html`
Read an url
### `html_elements`
Get the elements you want from an html
### `html_text`
Get the text, you can also use `html_text2` or `html_text3` for cleaner text
### `html_attrs`
Get the content of an attribute, if string not provided it would try to get you an attribute
### `html_table`
Create a DataFrame from an HTML Table node
## Notes
- I'm actively accepting suggestions | Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | docs | 4630 | # Harbest.jl
Web Scraping is a technique to get data from the internet. In this package you can do this to get data from a static HTML.
This is a port form [tidyverse/Rvest](https://github.com/tidyverse/rvest)
# Usage
```julia
using Harbest
starwars = read_html("https://rvest.tidyverse.org/articles/starwars.html")
titles = html_elements(starwars, ["section", "h2"]) |> html_text3
titles
# 7-element Vector{String}:
# "The Phantom Menace"
# "Attack of the Clones"
# "Revenge of the Sith"
# ⋮
# "Return of the Jedi"
# "The Force Awakens"
html = read_html("https://en.wikipedia.org/w/index.php?title=The_Lego_Movie&oldid=998422565")
table = html_elements(html, ".tracklist") |> html_table
table
# 28×4 DataFrame
# Row │ No. Title Performer(s) Length
# │ String String String String
# ─────┼──────────────────────────────────────────────────────────────────────────────────────
# 1 │ 1. "Everything Is Awesome" Tegan and Sara featuring The Lon… 2:43
# 2 │ 2. "Prologue" 2:28
# 3 │ 3. "Emmett's Morning" 2:00
# 4 │ 4. "Emmett Falls in Love" 1:11
# 5 │ 5. "Escape" 3:26
# ⋮ │ ⋮ ⋮ ⋮ ⋮
# 25 │ 25. "Everything Is Awesome" Jo Li (Joshua Bartholomew and Li… 1:26
# 26 │ 26. "Everything Is Awesome (unplugge… Shawn Patterson and Sammy Allen 1:24
# 27 │ 27. "Untitled Self Portrait" Will Arnett 1:08
# 28 │ 28. "Everything Is Awesome (instrume… 2:41
# 19 rows omitted
```
# Functions
- read_html(url)
- html_elements(html,string) or html_elements(html,strings)
- html_attrs(html,string) or html_attrs(html)
- html_text(html) or html_text2(html) or html_text3(html)
- html_table(html)
# Tutorial
First, we import
```julia
using Harbest, DataFrames, PlotlyJS
```
Then, scrape the data with `html_elements`, `html_attrs` and `html_text3`
```julia
function get_scores(html)
score = html_elements(html,".ipl-rating-star__rating") |> html_text3 ## Read scores from HTML
score = score[score .!= "Rate" .&& occursin.(".",score)] ## Get actual scores
scores::Vector{Float64} = parse.(Float64,score)
return scores
end
function get_names(html)
names::Vector{String} = html_elements(html,[".info","strong"]) |> html_text3
return names
end
function get_imgs(html)
data = html_elements(html,["img",".zero-z-index"])
imgs::Vector{String} = html_attrs(data,"src")
return imgs
end
function get_n_season(html)
data = read_html(html)
data = html_elements(data,["select","option"])[2] |> html_text3
n_season::Int = parse(Int,data)
return n_season
end
function get_df(url)
df::DataFrame = DataFrame()
n_seasons = get_n_season(url)
urls = url.*"episodes?season=".*string.(1:n_seasons)
for i in eachindex(urls)
html = read_html(urls[i])
temp_df = DataFrame(scores = get_scores(html),
names = get_names(html),
season = i,
images = get_imgs(html))
df = [df;temp_df]
end
df[!,"N"]= rownumber.(eachrow(df))
return df
end
function plot_df(df,title)
return plot(df,
x = :N,
y = :scores,
text = :names,
color = :season,
mode = "lines",
labels=Dict(
:N => "Episode number",
:scores => "Score",
:season => "Season"
),
Layout(title = title* " score on IMDb")
)
end
```
```julia
community_df = get_df("https://www.imdb.com/title/tt1439629/")
plot_df(community_df,"Community")
```
```@raw html
<iframe src="plot_community.html" style="height:500px;width:100%;"></iframe>
```
```julia
bojack_df = get_df("https://www.imdb.com/title/tt3398228/")
plot_df(bojack_df,"Bojack Horseman")
```
```@raw html
<iframe src="plot_bojack.html" style="height:500px;width:100%;"></iframe>
```
| Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.2 | 7789df56a6bd384f9ce1bca6ea100b35c80d0abe | docs | 156 | # Docstrings
```@meta
CurrentModule = Harbest
```
```@docs
read_html
html_elements
html_attrs
html_table
html_text3
html_text2
html_text
``` | Harbest | https://github.com/jdiaz97/Harbest.jl.git |
|
[
"MIT"
] | 0.4.5 | 2a51ded195d93974975a3448df7df37a675081a4 | code | 163 | module FIB
using POMDPs
using POMDPTools
using Printf
import POMDPs: Solver, Policy, solve
export
FIBSolver,
solve
include("vanilla.jl")
end # module
| FIB | https://github.com/JuliaPOMDP/FIB.jl.git |
|
[
"MIT"
] | 0.4.5 | 2a51ded195d93974975a3448df7df37a675081a4 | code | 2514 | # tolerance is ||alpha^k - alpha^k+1||_infty
mutable struct FIBSolver <: Solver
max_iterations::Int64
tolerance::Float64
verbose::Bool
end
function FIBSolver(;max_iterations::Int64=100, tolerance::Float64=1e-3, verbose::Bool=false)
return FIBSolver(max_iterations, tolerance, verbose)
end
function solve(solver::FIBSolver, pomdp::POMDP; kwargs...)
if !isempty(kwargs)
@warn("Keyword args for solve(::FIBSolver, ::MDP) are no longer supported. For verbose output, use the verbose option in the FIBSolver")
end
state_list = ordered_states(pomdp)
obs_list = observations(pomdp)
action_list = ordered_actions(pomdp)
ns = length(state_list)
na = length(action_list)
alphas = zeros(ns,na)
old_alphas = zeros(ns,na)
for i = 1:solver.max_iterations
# copyto!(dest, src)
copyto!(old_alphas, alphas)
residual = 0.0
for (ai, a) in enumerate(action_list)
for (si, s) in enumerate(state_list)
sp_dist = transition(pomdp, s, a)
r = 0.0
for (sp, p_sp) in weighted_iterator(sp_dist)
r += p_sp*reward(pomdp, s, a, sp)
end
# Sum_o max_a' Sum_s' O(o | s',a) T(s'|s,a) alpha_a^k(s')
o_sum = 0.0
for o in obs_list
# take maximum over ap
ap_sum = -Inf
for (api, ap) in enumerate(action_list)
# Sum_s' O(o | s',a) T(s'|s,a) alpha_a^k(s')
temp_ap_sum = 0.0
for (sp, p_sp) in weighted_iterator(sp_dist)
o_dist = observation(pomdp, s, a, sp)
p_o = pdf(o_dist, o)
spi = stateindex(pomdp, sp)
temp_ap_sum += p_o * p_sp * old_alphas[spi,api]
end
ap_sum = max(temp_ap_sum, ap_sum)
end
o_sum += ap_sum
end
alphas[si, ai] = r + discount(pomdp) * o_sum
alpha_diff = abs(alphas[si, ai] - old_alphas[si, ai])
residual = max(alpha_diff, residual)
end
end
solver.verbose ? @printf("[Iteration %-4d] residual: %10.3G \n", i, residual) : nothing
residual < solver.tolerance ? break : nothing
end
return AlphaVectorPolicy(pomdp, alphas, action_list)
end
| FIB | https://github.com/JuliaPOMDP/FIB.jl.git |
|
[
"MIT"
] | 0.4.5 | 2a51ded195d93974975a3448df7df37a675081a4 | code | 1073 | using FIB
using POMDPs
using POMDPModels
using POMDPTools
using POMDPLinter: show_requirements, get_requirements
using Test
pomdp = BabyPOMDP()
solver = FIBSolver()
policy = solve(solver, pomdp)
@testset "all" begin
@test_skip @requirements_info solver pomdp
show_requirements(get_requirements(POMDPs.solve, (solver, pomdp)))
# test that alpha vectors turn out mostly correct
@testset "alpha vectors" begin
alphas = Vector{Float64}[]
push!(alphas, [-16.0629, -36.5093])
push!(alphas, [-19.4557, -29.4557])
@test isapprox(policy.alphas, alphas, atol=1e-4)
@test policy.action_map == [false, true]
end
@testset "action value functions" begin
# create uniform belief (0.5,0.5)
bu = updater(policy)
b = uniform_belief(pomdp)
# check that the action and value functions work
a = action(policy, b)
v = value(policy, b)
@test a # feed is the best action at this belief
@test isapprox(v, -24.4557, atol=1e-4)
end
@testset "solver" begin
test_solver(solver, BabyPOMDP())
test_solver(solver, TigerPOMDP())
end
end
| FIB | https://github.com/JuliaPOMDP/FIB.jl.git |
|
[
"MIT"
] | 0.4.5 | 2a51ded195d93974975a3448df7df37a675081a4 | docs | 1191 | # FIB
[](https://github.com/JuliaPOMDP/FIB.jl/actions/workflows/CI.yml/)
[](https://codecov.io/gh/JuliaPOMDP/FIB.jl)
Implements the fast informed bound (FIB) solver for POMDPs. FIB is discussed in Sec. 21.2 of:
* M. J. Kochenderfer, T. A. Wheeler, and K. H. Wray, [Algorithms for Decision Making](https://algorithmsbook.com/decisionmaking), MIT Press, 2022.
## Installation
```julia
Pkg.add("FIB")
```
```julia
using FIB
using POMDPModels
pomdp = TigerPOMDP() # initialize POMDP
solver = FIBSolver()
# run the solver
policy = solve(solver, pomdp) # policy is of type AlphaVectorPolicy
```
The result of `solve` is an `AlphaVectorPolicy`. This policy type is implemented in [POMDPTools.jl](https://juliapomdp.github.io/POMDPs.jl/stable/POMDPTools/policies/#Alpha-Vector-Policy).
FIB.jl solves problems implemented using the [POMDPs.jl interface](https://github.com/JuliaPOMDP/POMDPs.jl). See the [documentation for POMDPs.jl](http://juliapomdp.github.io/POMDPs.jl/latest/) for more information.
| FIB | https://github.com/JuliaPOMDP/FIB.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | code | 188 | using Documenter
using Traceur
makedocs(
sitename = "Traceur",
format = Documenter.HTML(),
modules = [Traceur]
)
deploydocs(
repo = "github.com/JunoLab/Traceur.jl.git"
)
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | code | 314 | module Traceur
using MacroTools
# using Vinyl: @primitive, overdub
# using ASTInterpreter2: linearize!
import Core.MethodInstance
export @trace, @trace_static, @should_not_warn, @check
include("util.jl")
include("analysis.jl")
include("trace.jl")
# include("trace_static.jl")
include("check.jl")
end # module
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | code | 5399 | abstract type Call end
method_expr(f, Ts::Type{<:Tuple}) =
:($f($([:(::$T) for T in Ts.parameters]...)))
function loc(c::Call)
meth = method(c)
"$(meth.file):$(meth.line)"
end
struct DynamicCall{F,A} <: Call
f::F
a::A
DynamicCall{F,A}(f,a...) where {F,A} = new(f, a)
end
DynamicCall(f, a...) = DynamicCall{typeof(f),typeof(a)}(f, a...)
argtypes(c::DynamicCall) = Base.typesof(c.a...)
types(c::DynamicCall) = (typeof(c.f), argtypes(c).parameters...)
method(c::DynamicCall) = which(c.f, argtypes(c))
method_expr(c::DynamicCall) = method_expr(c.f, argtypes(c))
function code(c::DynamicCall; optimize = false)
codeinfo = @static if VERSION >= v"1.1.0"
code_typed(c.f, argtypes(c), optimize = optimize, debuginfo=:source)
else
code_typed(c.f, argtypes(c), optimize = optimize)
end
@assert length(codeinfo) == 1
codeinfo = codeinfo[1]
return codeinfo
end
# struct StaticCall <: Call
# method_instance::MethodInstance
# end
#
# argtypes(c::StaticCall) = Tuple{c.method_instance.specTypes.parameters[2:end]...}
# types(c::StaticCall) = c.method_instance.specTypes
# method(c::StaticCall) = c.method_instance.def
#
# method_expr(c::StaticCall) = method_expr(method(c).name, argtypes(c))
#
# function code(c::StaticCall; optimize = false)
# # TODO static call graph can only be computed with optimize=true, so analyzing with optimized=false will skip inlined methods
# codeinfo = get_code_info(c.method_instance, optimize=true)
# linearize!(codeinfo[1])
# return codeinfo
# end
function eachline(f, code, line = -1)
for (i, l) in enumerate(code.code)
ind = code.codelocs[i]
1 <= ind <= length(code.linetable) ?
line = code.linetable[ind].line :
line = -1
f(line, l)
end
end
exprtype(code, x) = typeof(x)
exprtype(code, x::Core.TypedSlot) = x.typ
exprtype(code, x::QuoteNode) = typeof(x.value)
exprtype(code, x::Core.SSAValue) = code.ssavaluetypes[x.id+1]
# exprtype(code, x::Core.SlotNumber) = code.slottypes[x.id]
rebuild(code, x) = x
rebuild(code, x::QuoteNode) = x.value
rebuild(code, x::Expr) = Expr(x.head, rebuild.(Ref(code), x.args)...)
rebuild(code, x::Core.SlotNumber) = code.slotnames[x.id]
struct Warning
call::Call
line::Int
message::String
stack::Vector{Call}
end
getmod(w::Warning) = method(w.call).module
Warning(call, message) = Warning(call, -1, message)
Warning(call, line, message) = Warning(call, line, message, Call[])
function warning_printer(modules=[])
(w) -> begin
meth = method(w.call)
if isempty(modules) || getmod(w) in modules
@safe_warn w.message _file=String(meth.file) _line=w.line _module=nothing
end
end
end
# global variables
function globals(warn, call)
c = code(call)[1]
eachline(c) do line, ex
ex isa Expr || return
for ref in ex.args
ref isa GlobalRef || continue
isconst(ref.mod, ref.name) && continue
getfield(ref.mod, ref.name) isa Module && continue
warn(call, line, "uses global variable $(ref.mod).$(ref.name)")
end
end
end
# fields
function fields(warn, call)
c = code(call)[1]
eachline(c) do line, x
(isexpr(x, :(=)) && isexpr(x.args[2], :call) &&
rebuild(c, x.args[2].args[1]) == GlobalRef(Core,:getfield)) ||
return
x, field = x.args[2].args[2:3]
x, x_expr, field = exprtype(c, x), rebuild(c, x), rebuild(c, field)
(isconcretetype(x) && !(x.name.wrapper == Type) && field isa Symbol) ||
return
isconcretetype(fieldtype(x, field)) || warn(call, line, "field $x_expr.$field::$(fieldtype(x, field)), $x_expr::$x")
end
end
# local variables
function assignments(code, l = -1)
assigns = Dict()
idx = 0
eachline(code, l) do line, ex
idx += 1
(isexpr(ex, :(=)) && isexpr(ex.args[1], Core.SlotNumber)) || return
typ = Core.Compiler.widenconst(code.ssavaluetypes[idx])
push!(get!(assigns, ex.args[1], []), (line, typ))
end
return assigns
end
function locals(warn, call)
c = code(call)[1]
as = assignments(c)
for (x, as) in as
(length(unique(map(x->x[2],as))) == 1 && (isconcretetype(as[1][2]) || istype(as[1][2]))) && continue
var = c.slotnames[x.id]
startswith(string(var), '#') && continue
for (l, t) in as
warn(call, l, "$(var) is assigned as $(t)")
end
end
end
# dynamic dispatch
rebuild(code, x::Core.SSAValue) = rebuild(code, code.code[x.id])
function dispatch(warn, call)
c = code(call, optimize = true)[1]
eachline(c) do line, ex
isexpr(ex, :(=)) && (ex = ex.args[2])
isexpr(ex, :call) || return
callex = rebuild(c, ex)
f = callex.args[1]
(f isa GlobalRef && isprimitive(getfield(f.mod, f.name)) || isprimitive(f)) && return
warn(call, line, string("dynamic dispatch to ", callex))
end
end
# return type
function issmallunion(t)
ts = Base.uniontypes(t)
length(ts) == 1 && isconcretetype(first(ts)) && return true
length(ts) > 2 && return false
(Missing in ts || Nothing in ts) && return true
return false
end
istype(::Type{T}) where T = true
istype(::Union) = false
istype(x) = false
function rettype(warn, call)
c, out = code(call)
if out == Any || !(issmallunion(out) || isconcretetype(out) || istype(out))
warn(call, method(call).line, "$(call.f) returns $out")
end
end
# overall analysis
function analyse(warn, call)
globals(warn, call)
locals(warn, call)
fields(warn, call)
dispatch(warn, call)
rettype(warn, call)
end
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | code | 2388 | const should_not_warn = Set{Function}()
"""
@should_not_warn function foo(x)
...
end
Add `foo` to the list of functions in which no warnings may occur (checkd by `@check`).
"""
macro should_not_warn(expr)
quote
fun = $(esc(expr))
push!(should_not_warn, fun)
fun
end
end
"""
check(f::Function; nowarn=[], except=[], kwargs...)
Run Traceur on `f`, and throw an error if any warnings occur inside functions
tagged with `@should_not_warn` or specified in `nowarn`.
To throw an error if any warnings occur inside any functions, set
`nowarn=:all`.
To throw an error if any warnings occur inside any functions EXCEPT for a
certain set of functions, list the exceptions in the `except` variable,
for example `except=[g,h]`
"""
function check(f; nowarn=Any[], except=Any[], kwargs...)
if !isempty(except) # if `except` is provided, we ignore the value of `nowarn`
_nowarn = Any[]
_nowarn_all = false
_nowarn_allexcept = true
elseif nowarn isa Symbol
_nowarn = Any[]
_nowarn_all = nowarn == :all
_nowarn_allexcept = false
else
_nowarn = nowarn
_nowarn_all = false
_nowarn_allexcept = false
end
failed = false
wp = warning_printer()
result = trace(f; kwargs...) do warning
ix = findfirst(warning.stack) do call
_nowarn_all || call.f in should_not_warn || call.f in _nowarn || (_nowarn_allexcept && !(call.f in except))
end
if ix != nothing
tagged_function = warning.stack[ix].f
message = "$(warning.message) (called from $(tagged_function))"
warning = Warning(warning.call, warning.line, message, warning.stack)
wp(warning)
failed = true
end
end
@assert !failed "One or more warnings occured inside functions tagged with `@should_not_warn` or specified with `nowarn`"
result
end
"""
@check fun(args...) nowarn=[] except=[] maxdepth=typemax(Int)
Run Traceur on `fun`, and throw an error if any warnings occur inside functions
tagged with `@should_not_warn` or specified in `nowarn`.
To throw an error if any warnings occur inside any functions, set
`nowarn=:all`.
To throw an error if any warnings occur inside any functions EXCEPT for a
certain set of functions, list the exceptions in the `except` variable,
for example `except=[g,h]`
"""
macro check(expr, args...)
quote
check(() -> $(esc(expr)); $(map(esc, args)...))
end
end
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | code | 2484 | using Cassette, InteractiveUtils
Cassette.@context TraceurCtx
struct Trace
seen::Set
stack::Vector{Call}
warn
maxdepth::Int
end
function Trace(w; maxdepth=typemax(Int))
Trace(Set(), Vector{Call}(), w, maxdepth)
end
isprimitive(f) = f isa Core.Builtin || f isa Core.IntrinsicFunction
const ignored_methods = Set([@which((1,2)[1])])
const ignored_functions = Set([getproperty, setproperty!])
function Cassette.prehook(ctx::TraceurCtx, f, args...)
tra = ctx.metadata
C = DynamicCall(f, args...)
push!(tra.stack, C)
nothing
end
function Cassette.posthook(ctx::TraceurCtx, out, f, args...)
tra = ctx.metadata
C = tra.stack[end]
f = C.f
T = typeof.((f, args))
if !(f ∈ ignored_functions || T ∈ tra.seen || isprimitive(f) ||
method(C) ∈ ignored_methods || method(C).module ∈ (Core, Core.Compiler))
push!(tra.seen, T)
analyse((a...) -> tra.warn(Warning(a..., copy(tra.stack))), C)
end
pop!(tra.stack)
nothing
end
function Cassette.overdub(ctx::TraceurCtx, f, args...)
tra = ctx.metadata
if (length(tra.stack) > tra.maxdepth)
return f(args...)
else
invoke(Cassette.overdub, Tuple{Cassette.Context, typeof(f), typeof.(args)...}, ctx, f, args...)
end
end
trace(w, f; kwargs...) = Cassette.recurse(TraceurCtx(metadata=Trace(w; kwargs...)), f)
function warntrace(f; modules=[], kwargs...)
trace(warning_printer(modules), f; kwargs...)
end
"""
warnings(f; kwargs...)::Vector{Traceur.Warnings}
Collect all warnings generated by Traceur's analysis of the execution of the
no-arg function `f` and return them.
Possible keyword arguments:
- `maxdepth=typemax(Int)` constrols how far Traceur recurses through the call stack.
- If `modules` is nonempty, only warnings for methods defined in one of the modules specified will be printed.
"""
function warnings(f; modules=[], kwargs...)
warnings = Warning[]
trace(w -> push!(warnings, w), f; kwargs...)
if !isempty(modules)
filter!(x -> getmod(x) in modules, warnings)
end
return warnings
end
"""
@trace(functioncall(args...), maxdepth=2, modules=[])
Analyse `functioncall(args...)` for common performance problems and print them to
the terminal.
Optional arguments:
- `maxdepth` constrols how far Traceur recurses through the call stack.
- If `modules` is nonempty, only warnings for methods defined in one of the modules specified will be printed.
"""
macro trace(ex, args...)
quote
warntrace(() -> $(esc(ex)); $(map(esc, args)...))
end
end
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | code | 4663 | function get_method_instance(f, typs) ::MethodInstance
world = ccall(:jl_get_world_counter, UInt, ())
tt = typs isa Type ? Tuple{typeof(f), typs.parameters...} : Tuple{typeof(f), typs...}
results = Base._methods_by_ftype(tt, -1, world)
@assert length(results) == 1 "get_method_instance should return one method, instead returned $(length(results)) methods: $results"
(_, _, meth) = results[1]
# TODO not totally sure what jl_match_method is needed for - I think it's just extracting type parameters like `where {T}`
(ti, env) = ccall(:jl_match_method, Any, (Any, Any), tt, meth.sig)::SimpleVector
meth = Base.func_for_method_checked(meth, tt)
linfo = ccall(:jl_specializations_get_linfo, Ref{MethodInstance}, (Any, Any, Any, UInt), meth, tt, env, world)
end
function get_code_info(method_instance::MethodInstance; optimize=true) ::Tuple{CodeInfo, Type}
world = ccall(:jl_get_world_counter, UInt, ())
# TODO inlining=false would make analysis easier to follow, but it seems to break specialization on function types
params = Core.Inference.InferenceParams(world)
optimize = true
cache = false # not sure if cached copies use the same params
(_, code_info, return_typ) = Core.Inference.typeinf_code(method_instance, optimize, cache, params)
(code_info, return_typ)
end
"Does this look like error reporting code ie not worth looking inside?"
function is_error_path(expr)
expr == :throw ||
expr == :throw_boundserror ||
expr == :error ||
expr == :assert ||
(expr isa QuoteNode && is_error_path(expr.value)) ||
(expr isa Expr && expr.head == :(.) && is_error_path(expr.args[2])) ||
(expr isa GlobalRef && is_error_path(expr.name)) ||
(expr isa MethodInstance && is_error_path(expr.def.name))
end
"Is it pointless to look inside this expression?"
function should_ignore(expr::Expr)
is_error_path(expr.head) ||
(expr.head == :call && is_error_path(expr.args[1])) ||
(expr.head == :invoke && is_error_path(expr.args[1]))
end
"Return all function calls in the method whose argument types can be determined statically"
function get_child_calls(method_instance::MethodInstance)
code_info, return_typ = get_code_info(method_instance, optimize=true)
calls = Set{MethodInstance}()
function walk_expr(expr)
if isa(expr, MethodInstance)
push!(calls, expr)
elseif isa(expr, Expr)
if !should_ignore(expr)
foreach(walk_expr, expr.args)
end
end
end
foreach(walk_expr, code_info.code)
calls
end
"A node in the call graph"
struct CallNode
call::MethodInstance
parent_calls::Set{MethodInstance}
child_calls::Set{MethodInstance}
end
"Return as much of the call graph of `method_instance` as can be determined statically"
function get_call_graph(method_instance::MethodInstance, max_calls=1000::Int64) ::Vector{CallNode}
all = Dict{MethodInstance, CallNode}()
ordered = Vector{MethodInstance}()
unexplored = Set{Tuple{Union{Void, MethodInstance}, MethodInstance}}(((nothing, method_instance),))
for _ in 1:max_calls
if isempty(unexplored)
return [all[call] for call in ordered]
end
(parent, call) = pop!(unexplored)
child_calls= get_child_calls(call)
parent_calls = parent == nothing ? Set() : Set((parent,))
all[call] = CallNode(call, parent_calls, child_calls)
push!(ordered, call)
for child_call in child_calls
if !haskey(all, child_call)
push!(unexplored, (call, child_call))
else
push!(all[child_call].parent_calls, call)
end
end
end
error("get_call_graph reached $max_calls calls and gave up")
end
@generated function show_structure(x)
quote
@show x
$([:(isdefined(x, $(Expr(:quote, fieldname))) ? (@show x.$fieldname) : nothing) for fieldname in fieldnames(x)]...)
x
end
end
function trace_static(filter::Function, warn::Function, f::Function, typs)
for call_node in get_call_graph(get_method_instance(f, typs))
if filter(call_node.call)
analyse((a...) -> warn(Warning(a...)), StaticCall(call_node.call))
end
end
end
warntrace_static(filter::Function, f::Function, typs) = trace_static(filter, warning_printer(), f, typs)
warntrace_static(f::Function, typs) = warntrace_static((_) -> true, f, typs)
@eval begin
macro trace_static(ex0)
Base.gen_call_with_extracted_types($(Expr(:quote, :warntrace_static)), ex0)
end
macro trace_static(filter, ex0)
expr = Base.gen_call_with_extracted_types($(Expr(:quote, :warntrace_static)), ex0)
insert!(expr.args, 2, esc(filter))
expr
end
end
function warnings_static(f)
warnings = Warning[]
trace_static((_) -> true, w -> push!(warnings, w), f, ())
return warnings
end
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | code | 708 | using Logging
# define safe loggers that use raw streams,
# since we can't use regular streams that lock upon use
for level in [:trace, :debug, :info, :warn, :error, :fatal]
@eval begin
macro $(Symbol("safe_$level"))(ex...)
macrocall = :(@placeholder $(ex...))
# NOTE: `@placeholder` in order to avoid hard-coding @__LINE__ etc
macrocall.args[1] = Symbol($"@$level")
quote
old_logger = global_logger()
global_logger(Logging.ConsoleLogger(Core.stderr, old_logger.min_level))
ret = $(esc(macrocall))
global_logger(old_logger)
ret
end
end
end
end | Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | code | 3924 | using Traceur, Test
warns_for(ws, x) = any(w -> occursin(x, w.message), ws)
warns_for(ws, x, xs...) = warns_for(ws, x) && warns_for(ws, xs...)
y = 1
const cy = 2
naive_relu(x) = x < 0 ? 0 : x
randone() = rand() < 0.5 ? Int(1) : rand() < 0.5 ? Float64(1) : BigInt(1)
function naive_sum(xs)
s = 0
for x in xs
s += x
end
return s
end
f(x) = x+y
function f2(x)
foo = y
sin(x)+y
end
g(x) = x+cy
naive_sum_wrapper(x) = naive_sum(x)
x = 1
my_add(y) = x + y
module Foo
module Bar
function naive_sum(xs)
s = 0
for x in xs
s += x
end
return s
end
end
naive_sum_wrapper(x) = Bar.naive_sum(x)
end
@should_not_warn my_stable_add(y) = my_add(y)
my_stable_add_undecorated(y) = my_add(y)
@testset "Traceur" begin
ws = Traceur.warnings(() -> naive_relu(1))
@test isempty(ws)
ws = Traceur.warnings(() -> naive_relu(1.0))
@test warns_for(ws, "returns")
ws = Traceur.warnings(() -> randone())
@test warns_for(ws, "returns")
ws = Traceur.warnings(() -> naive_sum([1]))
if Base.VERSION >= v"1.2.0"
@test length(ws) == 4
@test warns_for(ws, "assigned")
else
@test isempty(ws)
end
ws = Traceur.warnings(() -> naive_sum([1.0]))
@test warns_for(ws, "assigned", "returns")
ws = Traceur.warnings(() -> f(1))
@test warns_for(ws, "global", "dispatch", "returns")
ws = Traceur.warnings(() -> f2(1))
@test warns_for(ws, "global", "dispatch", "returns")
ws = Traceur.warnings(() -> g(1))
@test isempty(ws)
@testset "depth limiting" begin
ws = Traceur.warnings(() -> naive_sum_wrapper(rand(3)); maxdepth = 0)
@test length(ws) == 1
@test warns_for(ws, "returns")
ws = Traceur.warnings(() -> naive_sum_wrapper(rand(3)); maxdepth = 1)
if Base.VERSION >= v"1.2.0"
@test length(ws) == 6
else
@test length(ws) == 4
end
@test warns_for(ws, "assigned", "returns")
end
@testset "module specific" begin
ws = Traceur.warnings(() -> Foo.naive_sum_wrapper(rand(3)); maxdepth = 2, modules=[Foo])
@test length(ws) == 1
@test warns_for(ws, "returns")
ws = Traceur.warnings(() -> Foo.naive_sum_wrapper(rand(3)); maxdepth = 2, modules=[Foo.Bar])
if Base.VERSION >= v"1.2.0"
@test length(ws) == 5
else
@test length(ws) == 3
end
@test warns_for(ws, "assigned", "returns")
ws = Traceur.warnings(() -> Foo.naive_sum_wrapper(rand(3)); maxdepth = 2, modules=[Foo, Foo.Bar])
if Base.VERSION >= v"1.2.0"
@test length(ws) == 6
else
@test length(ws) == 4
end
@test warns_for(ws, "assigned", "returns")
end
@testset "test utilities" begin
@test_nowarn @check my_add(1)
@test_throws AssertionError @check my_stable_add(1)
@test_throws AssertionError @check my_stable_add_undecorated(1) nowarn=[my_stable_add_undecorated]
@test_throws AssertionError @check my_stable_add_undecorated(1) nowarn=:all
function bar(x)
x > 0 ? 1.0 : 1
end
@test_nowarn @check(bar(2)) == 1.0
@test_nowarn @check(bar(2), maxdepth=100) == 1.0
@test_nowarn @check(bar(2), nowarn=[]) == 1.0
@test_nowarn @check(bar(2), nowarn=[], maxdepth=100) == 1.0
@test_nowarn @check(bar(2), nowarn=Any[]) == 1.0
@test_nowarn @check(bar(2), nowarn=Any[], maxdepth=100) == 1.0
@test_throws AssertionError @check(bar(2), nowarn=[bar])
@test_throws AssertionError @check(bar(2), nowarn=[bar], maxdepth=100)
@test_throws AssertionError @check(bar(2), nowarn=Any[bar])
@test_throws AssertionError @check(bar(2), nowarn=Any[bar], maxdepth=100)
@test_throws AssertionError @check(bar(2), nowarn=:all)
@test_throws AssertionError @check(bar(2), nowarn=:all, maxdepth=100)
@test_nowarn @check(bar(2), except=[bar]) == 1.0
@test_nowarn @check(bar(2), except=[bar], maxdepth=100) == 1.0
@test_nowarn @check(bar(2), except=Any[bar]) == 1.0
@test_nowarn @check(bar(2), except=Any[bar], maxdepth=100) == 1.0
end
end
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | docs | 1735 | # Traceur
[](https://travis-ci.org/JunoLab/Traceur.jl) [](https://JunoLab.github.io/Traceur.jl/latest)
Traceur is essentially a codified version of the [Julia performance tips](https://docs.julialang.org/en/v1/manual/performance-tips/). You run your code, it tells you about any obvious performance traps.
```julia
julia> using Traceur
julia> naive_relu(x) = x < 0 ? 0 : x
julia> @trace naive_relu(1.0)
naive_relu(::Float64) at none:1
returns Union{Float64, Int64}
1.0
julia> function naive_sum(xs)
s = 0
for x in xs
s += x
end
return s
end
julia> @trace naive_sum([1.])
Base.indexed_next(::Tuple{Int64,Bool}, ::Int64, ::Int64) at tuple.jl:54
returns Tuple{Union{Bool, Int64},Int64}
naive_sum(::Array{Float64,1}) at none:2
s is assigned as Int64 at line 2
s is assigned as Float64 at line 4
dynamic dispatch to s + x at line 4
returns Union{Float64, Int64}
1.0
julia> y = 1
julia> f(x) = x+y
julia> @trace f(1)
f(::Int64) at none:1
uses global variable Main.y
dynamic dispatch to x + Main.y at line 1
returns Any
2
```
### Mechanics
The heavily lifting is done by [`analyse`](https://github.com/MikeInnes/Traceur.jl/blob/a107a2d9646675441e4e7c8d5f3be14d8bae86ad/src/analysis.jl#L127), which takes a `Call` (essentially a `(f, args...)` tuple for each function called in the code). Most of the analysis steps work by retrieving the `code_typed` of the function, inspecting it for issues and emitting any warnings.
Suggestions for (or better, implementations of!) further analysis passes are welcome.
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 0.3.1 | c61e04e7e3592c3dba1a282bab66af79f3f69674 | docs | 221 | # Traceur.jl
Performance linting for Julia.
## Normal Use
```@docs
Traceur.@trace
```
```@docs
Traceur.warnings
```
## Tests
```@docs
Traceur.@check
```
```@docs
Traceur.check
```
```@docs
Traceur.@should_not_warn
```
| Traceur | https://github.com/JunoLab/Traceur.jl.git |
|
[
"MIT"
] | 1.1.1 | ce1566720fd6b19ff3411404d4b977acd4814f9f | code | 505 | module Indexing
import Base: getindex, setindex!, view, IndexStyle, @propagate_inbounds, keys, haskey,
parent, length, iterate, axes, size
export getindices, setindices!, ViewArray, ViewVector, ViewMatrix, ViewDict
_valtype(a::AbstractDict) = Base.valtype(a)
_valtype(a) = Base.eltype(a)
include("getindices.jl")
include("setindices.jl")
include("view.jl")
# TODO:
#
# * Deal better with bounds checking and @inbounds
# * Accelerate for Base containers where necessary?
end # module
| Indexing | https://github.com/andyferris/Indexing.jl.git |
|
[
"MIT"
] | 1.1.1 | ce1566720fd6b19ff3411404d4b977acd4814f9f | code | 1659 | # Possible syntax: container.[indices]
"""
getindices(container, indices)
Return an indexable container with indices `keys(indices)` and values `container[i]` for
`i ∈ values(indices)`. This generalizes scalar `getindex(container, index)` for multiple
indices, for dictionaries, tuples, named tuples, etc.
# Examples
```julia
julia> d = Dict(:a => "Alice", :b => "Bob", :c => "Charlie")
Dict{Symbol,String} with 3 entries:
:a => "Alice"
:b => "Bob"
:c => "Charlie"
julia> getindices(d, [:a, :c])
2-element Array{String,1}:
"Alice"
"Charlie"
julia> getindices(d, (:a, :c))
("Alice", "Charlie")
julia> getindices(d, Dict("Wife" => :a, "Husband" => :c))
Dict{String,String} with 2 entries:
"Wife" => "Alice"
"Husband" => "Charlie"
```
"""
function getindices(container, indices)
# TODO figure out how to do @inbounds
return map(i -> container[i], indices)
end
getindices(container, ::Colon) = getindices(container, keys(container))
getindices(t::Tuple, ::Colon) = t
getindices(nt::NamedTuple, ::Colon) = nt
function getindices(container, indices::AbstractDict)
out = empty(indices, keytype(indices), _valtype(container))
for (i, v) in indices
out[i] = container[v]
end
return out
end
function getindices(d::AbstractDict, ::Colon)
return copy(d)
end
# Make a 0-D array instead of scalar
Base.@propagate_inbounds function getindices(a::AbstractArray, is::Int...)
out = similar(a, eltype(a), ())
out[] = a[is...]
return out
end
# Ambiguities
Base.@propagate_inbounds getindices(a::AbstractArray, is::Union{Int,Colon,AbstractArray}...) = a[is...]
getindices(a::AbstractVector, ::Colon) = a[:] | Indexing | https://github.com/andyferris/Indexing.jl.git |
|
[
"MIT"
] | 1.1.1 | ce1566720fd6b19ff3411404d4b977acd4814f9f | code | 659 |
# Possible syntax: container.[indices] = value
"""
setindices!(container, value, indices)
Store the given `value` at all the indices in `values(indices)` of `container`. This
generalizes scalar `setindex!` for dictionaries, etc.
"""
function setindices!(container, value, indices)
foreach(i -> (container[i] = value), indices)
return container # Traditionally for setindex! this is value, but that's crazy
end
setindices!(container, value, ::Colon) = setindices!(container, value, keys(container))
function setindices!(container, value, indices::AbstractDict)
for (i, v) in indices
container[v] = value
end
return container
end
| Indexing | https://github.com/andyferris/Indexing.jl.git |
|
[
"MIT"
] | 1.1.1 | ce1566720fd6b19ff3411404d4b977acd4814f9f | code | 5374 | ## Array views of other indexable containers
"""
ViewArray(parent, indices)
Create an array `out` which is a lazy view of `parent`. The indices of `out` match the
indices of `indices`, and the values of `indices` are used to index `parent`. Unlike
`SubArray`, the parent type could be any indexable container (for instance, we can create an
`AbstractArray` view of the values stored in an `AbstractDict`).
See also `ViewDict`, `view`.
# Examples
```julia
julia> d = Dict(:a => 11, :b => 12, :c => 13)
Dict{Symbol,Int64} with 3 entries:
:a => 11
:b => 12
:c => 13
julia> ViewArray(d, [:a, :c])
2-element ViewArray{Int64,1,Dict{Symbol,Int64},Array{Symbol,1}}:
11
13
```
"""
struct ViewArray{T, N, A, I <: AbstractArray{<:Any, N}} <: AbstractArray{T, N}
parent::A
indices::I
end
ViewArray(a, indices::AbstractArray) = ViewArray{_valtype(a)}(a, indices)
ViewArray{T}(a, indices::AbstractArray) where {T} = ViewArray{T, ndims(indices)}(a, indices)
ViewArray{T, N}(a, indices::AbstractArray) where {T, N} = ViewArray{T, N, typeof(a)}(a, indices)
ViewArray{T, N, A}(a, indices::AbstractArray) where {T, N, A} = ViewArray{T, N, A, typeof(indices)}(a, indices)
# vector & matrix versions
const ViewVector{T, A, I <: AbstractVector} = ViewArray{T, 1, A, I}
ViewVector(a, indices::AbstractVector) = ViewVector{_valtype(a)}(a, indices)
const ViewMatrix{T, A, I <: AbstractMatrix} = ViewArray{T, 2, A, I}
ViewMatrix(a, indices::AbstractMatrix) = ViewMatrix{_valtype(a)}(a, indices)
# `AbstractArray` implementation (no resizing)
IndexStyle(::Type{ViewArray{T, N, A, I}}) where {T, N, A, I} = IndexStyle(I)
axes(a::ViewArray) = axes(a.indices)
size(a::ViewArray) = size(a.indices)
@propagate_inbounds getindex(a::ViewArray, i::Int) = a.parent[a.indices[i]]
@propagate_inbounds getindex(a::ViewArray, is::Int...) = a.parent[a.indices[is...]]
@propagate_inbounds setindex!(a::ViewArray, v, i::Int) = (a.parent[a.indices[i]] = v)
@propagate_inbounds setindex!(a::ViewArray, v, is::Int...) = (a.parent[a.indices[is...]] = v)
# Connect with `view`
"""
view(d::AbstractDict, inds::AbstractArray)
Create an array view over the dictionary `d` with the indices stored in `inds`.
See also `ViewArray`.
# Examples
```julia
julia> d = Dict(:a => 11, :b => 12, :c => 13)
Dict{Symbol,Int64} with 3 entries:
:a => 11
:b => 12
:c => 13
julia> view(d, [:a, :c])
2-element ViewArray{Int64,1,Dict{Symbol,Int64},Array{Symbol,1}}:
11
13
```
"""
view(d::AbstractDict, inds::AbstractArray) = ViewArray{_valtype(d), ndims(inds)}(d, inds)
parent(a::ViewArray) = a.parent
## Dictionary views of indexable containers
"""
ViewDict(parent, indices)
Create an array `out` which is a lazy view of `parent`. The indices of `out` match the
indices of `indices`, and the values of `indices` are used to index `parent`. The parent
must be an indexable type - for instance, an array or dictionary.
See also `ViewArray`, `view`.
# Examples
```julia
julia> d = Dict(:a => "Alice", :b => "Bob", :c => "Charlie")
Dict{Symbol,String} with 3 entries:
:a => "Alice"
:b => "Bob"
:c => "Charlie"
julia> ViewDict(d, Dict(:aa => :a, :cc => :c))
ViewDict{Symbol,String,Dict{Symbol,String},Dict{Symbol,Symbol}} with 2 entries:
:aa => "Alice"
:cc => "Charlie"
julia> v = [11, 12, 13]
3-element Array{Int64,1}:
11
12
13
julia> ViewDict(v, Dict(:a =>1 , :c => 3))
ViewDict{Symbol,Int64,Array{Int64,1},Dict{Symbol,Int64}} with 2 entries:
:a => 11
:c => 13
```
"""
struct ViewDict{K, V, A, I} <: AbstractDict{K, V}
parent::A
indices::I
end
ViewDict(a, indices) = ViewDict{keytype(indices)}(a, indices)
ViewDict{K}(a, indices) where {K} = ViewDict{K, _valtype(a)}(a, indices)
ViewDict{K, V}(a, indices) where {K, V} = ViewDict{K, V, typeof(a)}(a, indices)
ViewDict{K, V, A}(a, indices) where {K, V, A} = ViewDict{K, V, A, typeof(indices)}(a, indices)
# `AbstractDict` implementation (immutable keys)
keys(d::ViewDict) = keys(d.indices)
haskey(d::ViewDict, i) = haskey(d.indices, i)
length(d::ViewDict) = length(d.indices)
@propagate_inbounds getindex(d::ViewDict, i) = d.parent[d.indices[i]]
@propagate_inbounds setindex!(d::ViewDict, v, i) = (d.parent[d.indices[i]] = v)
function iterate(d::ViewDict, state...)
tmp = iterate(d.indices, state...)
if tmp === nothing
return tmp
end
(kv, state2) = tmp
return (kv.first => d.parent[kv.second], state2)
end
# Connect with `view`
"""
view(parent, inds::AbstractDict)
Create a dictionary view over the indexable container `parent`. The indices of the output
are the indices of `inds`, and the values are the corresponding `parent[i]` for
`i in values(inds)`.
See also `ViewDict`.
# Examples
```julia
julia> d = Dict(:a => "Alice", :b => "Bob", :c => "Charlie")
Dict{Symbol,String} with 3 entries:
:a => "Alice"
:b => "Bob"
:c => "Charlie"
julia> view(d, Dict(:aa => :a, :cc => :c))
ViewDict{Symbol,String,Dict{Symbol,String},Dict{Symbol,Symbol}} with 2 entries:
:aa => "Alice"
:cc => "Charlie"
julia> v = [11, 12, 13]
3-element Array{Int64,1}:
11
12
13
julia> view(v, Dict(:a =>1 , :c => 3))
ViewDict{Symbol,Int64,Array{Int64,1},Dict{Symbol,Int64}} with 2 entries:
:a => 11
:c => 13
```
"""
view(d, inds::AbstractDict) = ViewDict(d, inds)
view(d::AbstractArray, inds::AbstractDict) = ViewDict(d, inds) # disambiguation
parent(d::ViewDict) = d.parent
| Indexing | https://github.com/andyferris/Indexing.jl.git |
|
[
"MIT"
] | 1.1.1 | ce1566720fd6b19ff3411404d4b977acd4814f9f | code | 4364 | using Indexing
if VERSION < v"0.7-"
using Base.Test
else
using Test
end
@testset "getindices" begin
d = Dict(:a => "Alice", :b => "Bob", :c => "Charlie")
@test getindices(d, [:a, :c]) == ["Alice", "Charlie"]
@test getindices(d, (:a, :c)) == ("Alice", "Charlie")
@test getindices(d, Dict(:aa => :a, :cc => :c)) == Dict(:aa => "Alice", :cc => "Charlie")
@static if VERSION > v"0.7-"
@test getindices(d, (aa = :a, cc = :c)) == (aa = "Alice", cc = "Charlie")
end
@test getindices(d, :) == d
v = [11, 12, 13]
@test (getindices(v, 2)::Array{Int, 0})[] == 12
@test getindices(v, [1, 3]) == [11, 13]
@test getindices(v, Dict(:a => 1, :c => 3)) == Dict(:a => 11, :c => 13)
@test getindices(v, (1, 3)) === (11, 13)
@static if VERSION > v"0.7-"
@test getindices(v, (a = 1, c = 3)) === (a = 11, c = 13)
end
@test getindices(v, :) == v
t = (11, 12, 13)
@test getindices(t, [1, 3]) == [11, 13]
@test getindices(t, Dict(:a => 1, :c => 3)) == Dict(:a => 11, :c => 13)
@test getindices(t, (1, 3)) == (11, 13)
@static if VERSION > v"0.7-"
@test getindices(t, (a = 1, c = 3)) === (a = 11, c = 13)
end
@test getindices(t, :) == t
@static if VERSION > v"0.7-"
nt = (a = 1, b = 2.0, c = "three")
@test getindices(nt, [:a, :c]) == [1, "three"]
@test getindices(nt, Dict(:aa => :a, :cc => :c)) == Dict(:aa => 1, :cc => "three")
@test getindices(nt, (:a, :c)) == (1, "three")
@test getindices(nt, (aa = :a, cc = :c)) == (aa = 1, cc = "three")
@test getindices(nt, :) == nt
end
end
@testset "setindices!" begin
d = Dict(:a => "Alice", :b => "Bob", :c => "Charlie")
d2 = copy(d)
setindices!(d2, "Someone", [:a, :c])
@test d2 == Dict(:a => "Someone", :b => "Bob", :c => "Someone")
d3 = copy(d)
setindices!(d3, "Someone", (:a, :c))
@test d3 == Dict(:a => "Someone", :b => "Bob", :c => "Someone")
d4 = copy(d)
setindices!(d4, "Someone", Dict(:aa => :a, :cc => :c))
@test d4 == Dict(:a => "Someone", :b => "Bob", :c => "Someone")
@static if VERSION > v"0.7-"
d5 = copy(d)
setindices!(d5, "Someone", (aa = :a, cc = :c))
@test d5 == Dict(:a => "Someone", :b => "Bob", :c => "Someone")
end
d6 = copy(d)
setindices!(d6, "Someone", :)
@test d6 == Dict(:a => "Someone", :b => "Someone", :c => "Someone")
v = [11, 12, 13]
v2 = copy(v)
setindices!(v2, 20, [1, 3])
@test v2 == [20, 12, 20]
v3 = copy(v)
setindices!(v3, 20, (1, 3))
@test v3 == [20, 12, 20]
v4 = copy(v)
setindices!(v4, 20, Dict(:a => 1, :c => 3))
@test v4 == [20, 12, 20]
@static if VERSION > v"0.7-"
v5 = copy(v)
setindices!(v5, 20, (a = 1, c = 3))
@test v5 == [20, 12, 20]
end
v6 = copy(v)
setindices!(v6, 20, :)
@test v6 == [20, 20, 20]
end
@testset "view" begin
d = Dict(:a => "Alice", :b => "Bob", :c => "Charlie")
d2 = copy(d)
@test view(d, [:a, :c])::ViewArray == ["Alice", "Charlie"]
@test view(d, Dict(:aa => :a, :cc => :c))::ViewDict == Dict(:aa => "Alice", :cc => "Charlie")
av = view(d, [:a, :c])
@test parent(av) === d
@test av[1] == "Alice"
@test Indexing.axes(av) === (Base.OneTo(2),)
av[1] = "Someone"
@test d == Dict(:a => "Someone", :b => "Bob", :c => "Charlie")
dv = view(d2, Dict(:aa => :a, :cc => :c))
@test parent(dv) === d2
@test dv[:aa] == "Alice"
@test keys(dv) ⊆ [:aa, :cc] # Probably will want to change this
@test length(keys(dv)) == 2
@test haskey(dv, :aa)
dv[:aa] = "No-one"
@test d2 == Dict(:a => "No-one", :b => "Bob", :c => "Charlie")
v = [11, 12, 13]
@test view(v, Dict(:a =>1 , :c => 3))::ViewDict == Dict(:a => 11, :c => 13)
dv2 = view(v, Dict(:a =>1 , :c => 3))
@test parent(dv2) === v
@test dv2[:a] == 11
@test keys(dv2) ⊆ [:a, :c]
@test length(keys(dv2)) == 2
@test haskey(dv2, :a)
@test first(dv2) === (:a => 11) || first(dv2) === (:c => 13)
dv2[:a] = 21
@test v == [21, 12, 13]
@test ViewArray(d, [:b, :c])::ViewArray == ["Bob", "Charlie"]
@test ViewVector(d, [:b, :c])::ViewVector == ["Bob", "Charlie"]
@test ViewMatrix(d, [:b :c; :c :b])::ViewMatrix == ["Bob" "Charlie"; "Charlie" "Bob"]
end
| Indexing | https://github.com/andyferris/Indexing.jl.git |
|
[
"MIT"
] | 1.1.1 | ce1566720fd6b19ff3411404d4b977acd4814f9f | docs | 2632 | # Indexing
*Generalized indexing for Julia*
[](https://github.com/andyferris/Indexing.jl/actions?query=workflow%3ACI)
[](http://codecov.io/github/andyferris/Indexing.jl?branch=master)
-----------
This package defines functions for getting multiple indices out of dictionaries, tuples,
etc, extending this ability beyond `AbstractArray`.
To acheive this, we introduce new functions and methods:
* `getindices(container, indices)` - generalizes `getindex(container, index)` to multiple indices.
* `setindices!(container, value, indices)` - generalizes `setindex!(container, value, index)` to multiple indices. The same `value` is set for
each index in `indices`.
* `view(container, indices)` - lazy versions of `getindices(container, indices)` defined for dictionaries.
## Quick start
You can install Indexing via Julia's package manager:
```
julia> using Pkg
julia> Pkg.add("Indexing")
julia> using Indexing
julia> d = Dict(:a => "Alice", :b => "Bob", :c => "Charlie")
Dict{Symbol,String} with 3 entries:
:a => "Alice"
:b => "Bob"
:c => "Charlie"
julia> getindices(d, [:a, :c]) # Preserves type/keys of index collection - an array of length 2
2-element Array{String,1}:
"Alice"
"Charlie"
julia> getindices(d, (:a, :c)) # Preserves type/keys of index collection - a tuple of length 2
("Alice", "Charlie")
julia> getindices(d, Dict("Wife" => :a, "Husband" => :c)) # Preserves type/keys of index collection - a dictionary with keys "Wife" and "Husband"
Dict{String,String} with 2 entries:
"Wife" => "Alice"
"Husband" => "Charlie"
```
Similarly, `view` works as a lazy version of `getindices`, and `setindices!` works by
setting *the same* value to each specified index.
## TODO
This package is a work-in-progress. To complete the package, we need to:
* Performance improvements and propagation of `@inbounds` annotations.
## Future thoughts
Perhaps these could be intergrated into future Julia syntax. One suggestion:
```julia
a[i] --> getindex(a, i) # scalar only
a.[inds] --> getindices(a, inds)
a[i] = v --> setindex!(a, v, i) # scalar only
a.[inds] = v --> setindices!(a, v, inds)
a[i] .= v --> broadcast!(identity, a[i], v)
a.[inds] .= values --> broadcast!(identity, view(a, inds), values)
```
Note the lack of `dotview` and `maybeview`. The last two could support dot-fusion on the RHS.
Also, the default for `a.[inds]` could potentially move to `view`.
| Indexing | https://github.com/andyferris/Indexing.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 1118 | using EquationsOfStateOfSolids
using Documenter
DocMeta.setdocmeta!(EquationsOfStateOfSolids, :DocTestSetup, :(using EquationsOfStateOfSolids); recursive=true)
makedocs(;
modules=[EquationsOfStateOfSolids],
authors="Reno <[email protected]>",
repo="https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl/blob/{commit}{path}#{line}",
sitename="EquationsOfStateOfSolids.jl",
format=Documenter.HTML(;
prettyurls=get(ENV, "CI", "false") == "true",
canonical="https://MineralsCloud.github.io/EquationsOfStateOfSolids.jl",
assets=String[],
),
pages=[
"Home" => "index.md",
"Manual" => ["Installation" => "installation.md", "Development" => "develop.md"],
"API" => [
"Collections" => "api/collections.md",
"Fitting" => "api/fitting.md",
"Portability" => "portability.md",
"Interoperability" => "interoperability.md",
"Plotting" => "plotting.md",
],
"FAQ" => "faq.md",
],
)
deploydocs(;
repo="github.com/MineralsCloud/EquationsOfStateOfSolids.jl",
)
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 1600 | module EquationsOfStateOfSolids
using Unitful: AbstractQuantity, NoUnits, ħ, me
const FERMI_GAS_CONSTANT = (3π^2)^(2 / 3) * ħ^2 / 5 / me
# See https://discourse.julialang.org/t/is-there-a-way-to-include-in-function-name/45378/3
abstract type Power end
struct TwoThirds <: Power end
struct OneThird <: Power end
struct FiveHalves <: Power end
struct ThreeHalves <: Power end
const _⅔ = TwoThirds()
const _⅓ = OneThird()
const _2½ = FiveHalves()
const _1½ = ThreeHalves()
Base.:(^)(x, ::TwoThirds) = x^(2 // 3)
Base.:(^)(x::Union{Complex,AbstractQuantity{<:Complex}}, ::TwoThirds) = x^(2 / 3)
Base.:(^)(x::Union{Real,AbstractQuantity{<:Real}}, ::TwoThirds) =
_isnegative(x) ? complex(x)^(2 / 3) : x^(2 / 3)
Base.:(^)(x, ::OneThird) = x^(1 // 3)
Base.:(^)(x::Union{Complex,AbstractQuantity{<:Complex}}, ::OneThird) = x^(1 / 3)
Base.:(^)(x::Union{Real,AbstractQuantity{<:Real}}, ::OneThird) =
_isnegative(x) ? complex(x)^(1 / 3) : x^(1 / 3)
Base.:(^)(x, ::FiveHalves) = x^(5 // 2)
Base.:(^)(x::Union{Complex,AbstractQuantity{<:Complex}}, ::FiveHalves) = sqrt(x^5)
Base.:(^)(x::Union{Real,AbstractQuantity{<:Real}}, ::FiveHalves) =
_isnegative(x) ? sqrt(complex(x^5)) : sqrt(x^5)
Base.:(^)(x, ::ThreeHalves) = x^(3 // 2)
Base.:(^)(x::Union{Complex,AbstractQuantity{<:Complex}}, ::ThreeHalves) = sqrt(x^3)
Base.:(^)(x::Union{Real,AbstractQuantity{<:Real}}, ::ThreeHalves) =
_isnegative(x) ? sqrt(complex(x^3)) : sqrt(x^3)
_isnegative(x) = x < zero(x) # Do not export!
include("FiniteStrains.jl")
include("collections/collections.jl")
include("vsolve.jl")
include("Fitting.jl")
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 3681 | module FiniteStrains
using ..EquationsOfStateOfSolids: _⅔, _⅓, _1½
abstract type FiniteStrain end
struct EulerianStrain <: FiniteStrain end
struct LagrangianStrain <: FiniteStrain end
struct NaturalStrain <: FiniteStrain end
struct InfinitesimalStrain <: FiniteStrain end
"""
ToEulerianStrain(v0)(v)
ToLagrangianStrain(v0)(v)
ToNaturalStrain(v0)(v)
ToInfinitesimalStrain(v0)(v)
Calculate the finite strain of `v` based on the reference volume `v0`.
!!! info
See the formulae on the [`Gibbs2` paper](https://www.sciencedirect.com/science/article/pii/S0010465511001470) Table 3.
"""
struct ToStrain{S<:FiniteStrain,T}
v0::T
end
ToStrain{S}(v0::T) where {S,T} = ToStrain{S,T}(v0)
const ToEulerianStrain = ToStrain{EulerianStrain}
const ToLagrangianStrain = ToStrain{LagrangianStrain}
const ToNaturalStrain = ToStrain{NaturalStrain}
const ToInfinitesimalStrain = ToStrain{InfinitesimalStrain}
(x::ToEulerianStrain)(v) = ((x.v0 / v)^_⅔ - 1) / 2
(x::ToLagrangianStrain)(v) = ((v / x.v0)^_⅔ - 1) / 2
(x::ToNaturalStrain)(v) = log(v / x.v0) / 3
(x::ToInfinitesimalStrain)(v) = 1 - (x.v0 / v)^_⅓
"""
FromEulerianStrain(v0)(f)
FromLagrangianStrain(v0)(f)
FromNaturalStrain(v0)(f)
FromInfinitesimalStrain(v0)(f)
Calculate the original volume `v` from the finite strain `f` based on the reference volume `v0`.
!!! info
See the formulae on the [`Gibbs2` paper](https://www.sciencedirect.com/science/article/pii/S0010465511001470) Table 3.
"""
struct FromStrain{S<:FiniteStrain,T}
v0::T
end
FromStrain{S}(v0::T) where {S,T} = FromStrain{S,T}(v0)
const FromEulerianStrain = FromStrain{EulerianStrain}
const FromLagrangianStrain = FromStrain{LagrangianStrain}
const FromNaturalStrain = FromStrain{NaturalStrain}
const FromInfinitesimalStrain = FromStrain{InfinitesimalStrain}
# Eulerian strain
function (x::FromEulerianStrain)(f)
v = x.v0 / (2f + 1)^_1½
return isreal(v) ? real(v) : v
end
# Lagrangian strain
function (x::FromLagrangianStrain)(f)
v = x.v0 * (2f + 1)^_1½
return isreal(v) ? real(v) : v
end
# Natural strain
function (x::FromNaturalStrain)(f)
v = x.v0 * exp(3f)
return isreal(v) ? real(v) : v
end
# Infinitesimal strain
function (x::FromInfinitesimalStrain)(f)
v = x.v0 / (1 - f)^3
return isreal(v) ? real(v) : v
end
"""
Dⁿᵥf(s::EulerianStrain, deg, v0)
Dⁿᵥf(s::LagrangianStrain, deg, v0)
Dⁿᵥf(s::NaturalStrain, deg, v0)
Dⁿᵥf(s::InfinitesimalStrain, deg, v0)
Return a function of `v` that calculates the `deg`th order derivative of strain wrt volume from `v0`.
!!! info
See the formulae on Ref. 1 Table 3.
"""
function Dⁿᵥf(s::EulerianStrain, deg, v0)
function (v)
if isone(deg) # Stop recursion
return -(v0 / v)^_⅔ / 3 / v
else # Recursion
return -(3deg - 1) / 3 / v * Dⁿᵥf(s, deg - 1, v0)(v)
end
end
end
function Dⁿᵥf(s::LagrangianStrain, deg, v0)
function (v)
if isone(deg) # Stop recursion
return -(v / v0)^_⅔ / 3 / v
else # Recursion
return -(3deg - 5) / 3 / v * Dⁿᵥf(s, deg - 1, v0)(v)
end
end
end
function Dⁿᵥf(s::NaturalStrain, deg, v0)
function (v)
if isone(deg) # Stop recursion
return 1 / 3 / v
else # Recursion
return -(deg - 1) / v * Dⁿᵥf(s, deg - 1, v0)(v)
end
end
end
function Dⁿᵥf(s::InfinitesimalStrain, deg, v0)
function (v)
if isone(deg) # Stop recursion
return (1 - ToInfinitesimalStrain(v0)(v))^4 / 3 / v0
else # Recursion
return -(3deg - 2) / 3 / v * Dⁿᵥf(s, deg - 1, v0)(v)
end
end
end
function straintype end
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 9692 | module Fitting
using ConstructionBase: constructorof, setproperties
using LsqFit: curve_fit, coef
using PolynomialRoots: roots
using Polynomials: fit, derivative, coeffs, derivative
using Unitful: AbstractQuantity, NoUnits, ustrip, unit, uconvert
using ..EquationsOfStateOfSolids:
EquationOfStateOfSolids,
FiniteStrainParameters,
Parameters,
PressureEquation,
EnergyEquation,
BulkModulusEquation,
orderof,
_ispositive,
getparam
using ..FiniteStrains: FiniteStrain, ToStrain, FromStrain, Dⁿᵥf, straintype
import Unitful
export linfit, nonlinfit, eosfit
# See https://github.com/JuliaMath/Roots.jl/blob/bf0da62/src/utils.jl#L9-L11
struct ConvergenceFailed
msg::String
end
struct CriterionNotMet
msg::String
end
eosfit(eos::EnergyEquation{<:FiniteStrainParameters}, volumes, energies; kwargs...) =
linfit(eos, volumes, energies; kwargs...)
eosfit(eos, xs, ys; kwargs...) = nonlinfit(eos, xs, ys; kwargs...)
# ================================== Linear fitting ==================================
"""
linfit(eos::EnergyEquation{<:FiniteStrainParameters}, volumes, energies; kwargs...)
Fit an equation of state using linear algorithms.
# Arguments
- `maxiter::Integer=1000`: .
- `conv_thr::AbstractFloat=1e-12`: .
- `root_thr::AbstractFloat=1e-20`: .
- `verbose::Bool=false`: .
!!! note
If you want to fit with `BigFloat` data, you need to install
[`GenericSVD.jl`](https://github.com/JuliaLinearAlgebra/GenericSVD.jl) and `using
GenericSVD` before fittting!
"""
function linfit(
eos::EnergyEquation{<:FiniteStrainParameters},
volumes,
energies;
maxiter = 1000,
conv_thr = 1e-12,
root_thr = 1e-20,
verbose = false,
)::FiniteStrainParameters
deg = orderof(getparam(eos))
S = straintype(getparam(eos))
v0 = iszero(getparam(eos).v0) ? volumes[findmin(energies)[2]] : getparam(eos).v0 # Initial v0
uv, ue = unit(v0), unit(energies[1])
uvrule = uconvert(unit(volumes[1]), 1 * uv)
v0 = ustrip(v0)
volumes = collect(map(x -> ustrip(uv, x), volumes)) # `parent` is needed to unwrap `DimArray`
energies = collect(map(x -> ustrip(ue, x), energies))
for i in 1:maxiter # Self consistent loop
strains = map(ToStrain{S}(v0), volumes)
if !(isreal(strains) && isreal(energies))
throw(DomainError("the strains or the energies are complex!"))
end
poly = fit(real(strains), real(energies), deg)
f0, e0 = _minofmin(poly, root_thr)
v0_prev, v0 = v0, FromStrain{S}(v0)(f0) # Record v0 to v0_prev, then update v0
if abs((v0_prev - v0) / v0_prev) <= conv_thr
if verbose
@info "convergence reached after $i steps!"
end
fᵥ = map(deg -> Dⁿᵥf(S(), deg, v0)(v0), 1:4)
e_f = map(deg -> derivative(poly, deg)(f0), 1:4)
b0, b′0, b″0 = _Dₚb(fᵥ, e_f)
return _update(
getparam(eos);
v0 = v0 * uv,
b0 = b0(v0) * ue / uv,
b′0 = b′0(v0),
b″0 = b″0(v0) * uv / ue,
e0 = e0 * ue,
)
end
end
throw(ConvergenceFailed("convergence not reached after $maxiter steps!"))
end
function _islocalmin(x, y) # `x` & `y` are both real
y″ₓ = derivative(y, 2)(x) # Must be real
return _ispositive(real(y″ₓ)) # If 2nd derivative at x > 0, (x, y(x)) is a local minimum
end
function _localmin(y, root_thr = 1e-20) # `y` is a polynomial (could be complex)
y′ = derivative(y, 1)
pool = roots(coeffs(y′); polish = true, epsilon = root_thr)
real_roots = real(filter(isreal, pool)) # Complex volumes are meaningless
if isempty(real_roots)
throw(CriterionNotMet("no real extrema found! Consider changing `root_thr`!")) # For some polynomials, could be all complex
else
localminima = filter(x -> _islocalmin(x, y), real_roots)
if isempty(localminima)
throw(CriterionNotMet("no local minima found!"))
else
return localminima
end
end
end
# https://stackoverflow.com/a/21367608/3260253
function _minofmin(y, root_thr = 1e-20) # Find the minimum of the local minima
localminima = _localmin(y, root_thr)
y0, i = findmin(map(y, localminima)) # `y0` must be real, or `findmap` will error
x0 = localminima[i]
return x0, y0
end
# See Eq. (55) - (57) in Ref. 1.
function _Dₚb(fᵥ, e_f) # Bulk modulus & its derivatives
e″ᵥ = _D²ᵥe(fᵥ, e_f)
e‴ᵥ = _D³ᵥe(fᵥ, e_f)
b0 = v -> v * e″ᵥ
b′0 = v -> -v * e‴ᵥ / e″ᵥ - 1
b″0 = v -> (v * (_D⁴ᵥe(fᵥ, e_f) * e″ᵥ - e‴ᵥ^2) + e‴ᵥ * e″ᵥ) / e″ᵥ^3
return b0, b′0, b″0 # 3 lazy functions
end
# Energy-volume derivatives, see Eq. (50) - (53) in Ref. 1.
_D¹ᵥe(fᵥ, e_f) = e_f[1] * fᵥ[1]
_D²ᵥe(fᵥ, e_f) = e_f[2] * fᵥ[1]^2 + e_f[1] * fᵥ[2]
_D³ᵥe(fᵥ, e_f) = e_f[3] * fᵥ[1]^3 + 3fᵥ[1] * fᵥ[2] * e_f[2] + e_f[1] * fᵥ[3]
_D⁴ᵥe(fᵥ, e_f) =
e_f[4] * fᵥ[1]^4 +
6fᵥ[1]^2 * fᵥ[2] * e_f[3] +
(4fᵥ[1] * fᵥ[3] + 3fᵥ[3]^2) * e_f[2] +
e_f[1] * fᵥ[4]
function _update(x::FiniteStrainParameters; kwargs...)
patch = (; (f => kwargs[f] for f in propertynames(x))...)
return setproperties(x, patch)
end
# ================================== Nonlinear fitting ==================================
"""
nonlinfit(eos::EquationOfStateOfSolids, xs, ys; kwargs...)
Fit an equation of state using nonlinear algorithms.
# Arguments
- `xtol::AbstractFloat=1e-16`: .
- `gtol::AbstractFloat=1e-16`: .
- `maxiter::Integer=1000`: .
- `min_step_quality::AbstractFloat=1e-16`: .
- `good_step_quality::AbstractFloat=0.75`: .
- `verbose::Bool=false`: .
"""
function nonlinfit(
eos::EquationOfStateOfSolids,
xdata,
ydata;
xtol = 1e-16,
gtol = 1e-16,
maxiter = 1000,
min_step_quality = 1e-16,
good_step_quality = 0.75,
verbose = false,
)::Parameters
model = buildmodel(eos)
p0, xdata, ydata = _preprocess(eos, xdata, ydata)
fit = curve_fit( # See https://github.com/JuliaNLSolvers/LsqFit.jl/blob/f687631/src/levenberg_marquardt.jl#L3-L28
model,
xdata,
ydata,
p0;
x_tol = xtol,
g_tol = gtol,
maxIter = maxiter,
min_step_quality = min_step_quality,
good_step_quality = good_step_quality,
show_trace = verbose,
)
if fit.converged
result = _postprocess(coef(fit), getparam(eos))
checkresult(result)
return result
else
throw(ConvergenceFailed("convergence not reached after $maxiter steps!"))
end
end
# Do not export!
buildmodel(eos::EquationOfStateOfSolids{T}) where {T} =
(x, p) -> constructorof(typeof(eos))(constructorof(T)(p...)).(x)
function checkresult(x::Parameters) # Do not export!
if x.v0 <= zero(x.v0) || x.b0 <= zero(x.b0)
@error "either v0 ($(x.v0)) or b0 ($(x.b0)) is not positive!"
end
if PressureEquation(x)(x.v0) >= x.b0 && x isa FiniteStrainParameters
@warn "consider using higher order EOS!"
end
end
function _preprocess(eos, xdata, ydata) # Do not export!
p = getparam(eos)
if eos isa EnergyEquation && iszero(p.e0)
eos = EnergyEquation(setproperties(p; e0 = uconvert(unit(p.e0), minimum(ydata)))) # Energy minimum as e0, `uconvert` is important to keep the unit right!
end
return map(_float_collect, _unify(eos, xdata, ydata)) # `xs` & `ys` may not be arrays
end
function _unify(eos, xdata, ydata) # Unify units of data
p = getparam(eos)
uy(eos::EnergyEquation) = unit(p.e0)
uy(eos::Union{PressureEquation,BulkModulusEquation}) = unit(p.e0) / unit(p.v0)
return ustrip.(_unormal(p)), ustrip.(unit(p.v0), xdata), ustrip.(uy(eos), ydata)
end
_unormal(p::Parameters) = collect(getfield(p, i) for i in 1:nfields(p))
function _unormal(p::Parameters{<:AbstractQuantity}) # Normalize units of `p`
up = unit(p.e0) / unit(p.v0) # Pressure/bulk modulus unit
return map(fieldnames(typeof(p))) do f
x = getfield(p, f)
if f == :b0
x |> up
elseif f == :b″0
x |> up^(-1)
elseif f == :b‴0
x |> up^(-2)
elseif f in (:v0, :b′0, :e0)
x
else
error("unknown field `$f`!")
end
end
end
_postprocess(p, p0::Parameters) = constructorof(typeof(p0))(p...)
function _postprocess(p, p0::Parameters{<:AbstractQuantity})
up = unit(p0.e0) / unit(p0.v0) # Pressure/bulk modulus unit
param = map(enumerate(fieldnames(typeof(p0)))) do (i, f)
x = p[i]
u = unit(getfield(p0, f))
if f == :b0
x * up |> u
elseif f == :b″0
x * up^(-1) |> u
elseif f == :b‴0
x * up^(-2) |> u
elseif f in (:v0, :b′0, :e0)
x * u
else
error("unknown field `$f`!")
end
end
return constructorof(typeof(p0))(param...)
end
_float_collect(x) = collect(float.(x)) # Do not export!
_fmap(f, x) = constructorof(typeof(x))((f(getfield(x, i)) for i in 1:nfields(x))...) # Do not export!
"Convert all elements of a `Parameters` to floating point data types."
Base.float(p::Parameters) = _fmap(float, p) # Not used here but may be useful
"Test whether all `p`'s elements are numerically equal to some real number."
Base.isreal(p::Parameters) = all(isreal(getfield(p, i)) for i in 1:nfields(p)) # Not used here but may be useful
"Construct a real `Parameters` from the real parts of the elements of p."
Base.real(p::Parameters) = _fmap(real, p) # Not used here but may be useful
"""
ustrip(p::Parameters)
Strip units from a `Parameters`.
"""
Unitful.ustrip(p::Parameters) = _fmap(ustrip, p)
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 7694 | using PolynomialRoots: roots
using Roots: Order2, Newton, newton, find_zeros, find_zero
using .FiniteStrains: FromEulerianStrain, FromNaturalStrain
export vsolve
function vsolve(
eos::PressureEquation{<:Murnaghan1st},
p;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
)
@unpack v0, b0, b′0 = getparam(eos)
soln = [v0 * (1 + b′0 / b0 * p)^(-1 / b′0)]
return _clamp(soln, bounds)
end
function vsolve(
eos::PressureEquation{<:Murnaghan2nd},
p;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
)
@unpack v0, b0, b′0, b″0 = getparam(eos)
h = sqrt(2b0 * b″0 - b′0^2)
k = b″0 * p + b′0
numerator = exp(-2 / h * atan(p * h / (2b0 + p * b′0))) * v0
denominator = (abs((k - h) / (k + h) * (b′0 + h) / (b′0 - h)))^(1 / h)
soln = [numerator / denominator]
return _clamp(soln, bounds)
end
function vsolve(
eos::EnergyEquation{<:BirchMurnaghan2nd},
e;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
)
@unpack v0, b0, e0 = getparam(eos)
Δ = (e - e0) / v0 / b0
if Δ >= 0
f = sqrt(2 / 9 * Δ)
soln = map(FromEulerianStrain(v0), [f, -f])
return _clamp(soln, bounds)
elseif Δ < 0
return typeof(v0)[] # Complex strains
else
@assert false "Δ == (e - e0) / v0 / b0 == $Δ. this should never happen!"
end
end
function vsolve(
eos::PressureEquation{<:BirchMurnaghan2nd},
p;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
stopping_criterion = 1e-20, # Unitless
chop = eps(),
rtol = sqrt(eps()),
)
@unpack v0, b0 = getparam(eos)
# Solve f for (3 B0 f (2f + 1))^2 == p^2
fs = roots(
[-(p / 3b0)^2, 0, 1, 10, 40, 80, 80, 32];
polish = true,
epsilon = stopping_criterion,
)
soln = _strain2volume(eos, v0, fs, p, chop, rtol)
return _clamp(soln, bounds)
end
function vsolve(
eos::BulkModulusEquation{<:BirchMurnaghan2nd},
b;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
stopping_criterion = 1e-20, # Unitless
chop = eps(),
rtol = sqrt(eps()),
)
@unpack v0, b0 = getparam(eos)
# Solve f for ((7f + 1) * (2f + 1)^(5/2))^2 == (b/b0)^2
fs = roots(
[1 - (b / b0)^2, 24, 229, 1130, 3160, 5072, 4368, 1568];
polish = true,
epsilon = stopping_criterion,
)
soln = _strain2volume(eos, v0, fs, b, chop, rtol)
return _clamp(soln, bounds)
end
function vsolve(
eos::EnergyEquation{<:BirchMurnaghan3rd},
e;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
chop = eps(),
rtol = sqrt(eps()),
)
@unpack v0, b0, b′0, e0 = getparam(eos)
# Constrcut ax^3 + bx^2 + d = 0, see https://zh.wikipedia.org/wiki/%E4%B8%89%E6%AC%A1%E6%96%B9%E7%A8%8B#%E6%B1%82%E6%A0%B9%E5%85%AC%E5%BC%8F%E6%B3%95
if b′0 == 4
@warn "`b′0 == 4` for a `BirchMurnaghan3rd` is just a `BirchMurnaghan2nd`!"
return vsolve(EnergyEquation(BirchMurnaghan2nd(v0, b0, e0)), e; bounds = bounds)
else
a = b′0 - 4
r = 1 / 3a # b = 1
d = (e0 - e) / (9 / 2 * b0 * v0)
p, q = -r^3 - d / 2a, -r^2
Δ = p^2 + q^3
fs = -r .+ if Δ > 0
[cbrt(p + √Δ) + cbrt(p - √Δ)] # Only 1 real solution
elseif Δ < 0
SIN, COS = sincos(acos(p / abs(r)^3) / 3)
[2COS, -COS - √3 * SIN, -COS + √3 * SIN] .* abs(r) # Verified
elseif Δ == 0
if p == q == 0
[0] # 3 reals are equal
else # p == -q != 0
[2cbrt(p), -cbrt(p)] # 2 real roots are equal, leaving 2 solutions
end
else
@assert false "Δ == p^2 + q^3 == $Δ. this should never happen!"
end # solutions are strains
soln = _strain2volume(eos, v0, fs, e, chop, rtol)
return _clamp(soln, bounds)
end
end
function vsolve(
eos::PressureEquation{<:BirchMurnaghan3rd},
p;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
stopping_criterion = 1e-20, # Unitless
chop = eps(),
rtol = sqrt(eps()),
)
@unpack v0, b0, b′0 = getparam(eos)
# Solve f for (f (2f + 1)^(5/2) [2 + 3f (b′0 - 4)])^2 - (p / (3b0/2))^2 = 0
fs = roots(
[
-(2p / 3 / b0)^2,
0,
4,
12b′0 - 8,
9b′0^2 + 48b′0 - 176,
90b′0^2 - 80(2 + 3b′0),
360b′0^2 + 320(7 - 6b′0),
720b′0^2 + 64(122 - 75b′0),
720b′0^2 + 768(13 - 7b′0),
288b′0^2 + 2304(2 - b′0),
];
polish = true,
epsilon = stopping_criterion,
)
soln = _strain2volume(eos, v0, fs, p, chop, rtol)
return _clamp(soln, bounds)
end
function vsolve(
eos::EnergyEquation{<:BirchMurnaghan4th},
e;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
stopping_criterion = 1e-20, # Unitless
chop = eps(),
rtol = sqrt(eps()),
)
@unpack v0, b0, b′0, b″0, e0 = getparam(eos)
h = b0 * b″0 + b′0^2
fs = roots(
[(e0 - e) / (3 / 8 * v0 * b0), 0, 12, 12(b′0 - 4), 143 - 63b′0 + 9h];
polish = true,
epsilon = stopping_criterion,
)
soln = _strain2volume(eos, v0, fs, e, chop, rtol)
return _clamp(soln, bounds)
end
function vsolve(
eos::EnergyEquation{<:PoirierTarantola2nd},
e;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
)
@unpack v0, b0, e0 = getparam(eos)
Δ = (e - e0) / v0 / b0
if Δ >= 0
f = sqrt(2 / 9 * Δ)
soln = map(FromNaturalStrain(v0), [f, -f])
return _clamp(soln, bounds)
elseif Δ < 0
return typeof(v0)[] # Complex strains
else
@assert false "Δ == (e - e0) / v0 / b0 == $Δ. this should never happen!"
end
end
function vsolve(
eos::EquationOfStateOfSolids,
y;
bounds = (zero(eos.param.v0), 4 * eos.param.v0),
xrtol = eps(),
rtol = 4eps(),
)
# Bisection method
try
return find_zeros(v -> eos(v) - y, bounds; xrtol = xrtol, rtol = rtol)
catch e
@error "cannot find solution! Come across `$e`!"
return typeof(eos.param.v0)[]
end
end
function vsolve(
eos::EquationOfStateOfSolids,
y,
vᵢ,
method = Order2();
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
maxiter = 40,
verbose = false,
xrtol = eps(),
rtol = 4eps(),
)
try
vᵣ = find_zero(
v -> eos(v) - y,
vᵢ,
method;
maxevals = maxiter,
verbose = verbose,
xrtol = xrtol,
rtol = rtol,
)
return _clamp([vᵣ], bounds)
catch e
@error "cannot find solution! Come across `$e`!"
return typeof(vᵢ)[]
end
end
function vsolve(
eos::EnergyEquation,
e,
vᵢ,
::Newton;
bounds = (zero(eos.param.v0), Inf * eos.param.v0),
kwargs...,
)
try
vᵣ = newton(v -> eos(v) - e, v -> -PressureEquation(eos)(v), vᵢ; kwargs...)
return _clamp([vᵣ], bounds)
catch e
@error "cannot find solution! Come across `$e`!"
return typeof(vᵢ)[]
end
end
function _strain2volume(
eos::EquationOfStateOfSolids{<:BirchMurnaghan},
v0,
fs,
y,
chop = eps(),
rtol = sqrt(eps()),
)
@assert _ispositive(chop) && _ispositive(rtol) "either `chop` or `rtol` is less than 0!"
return fs |>
Base.Fix1(map, FromEulerianStrain(v0)) |>
Base.Fix1(filter, x -> abs(imag(x)) < chop * oneunit(imag(x))) .|> # If `x` has unit
real |>
Base.Fix1(filter, x -> isapprox(eos(x), y; rtol = rtol)) |> # In case of duplicate values
unique
end
function _clamp(soln, bounds)
low, high = extrema(bounds)
return filter(v -> low <= v <= high, soln)
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 1904 | (eos::BulkModulusEquation{<:Murnaghan1st})(v) = getparam(eos).b0 + PressureEquation(eos)(v)
function (eos::BulkModulusEquation{<:BirchMurnaghan2nd})(v)
@unpack v0, b0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
return b0 * (7f + 1) * (2f + 1)^_2½
end
# The formula in the Gibbs2 paper is wrong! See the EosFit7c paper!
function (eos::BulkModulusEquation{<:BirchMurnaghan3rd})(v)
@unpack v0, b0, b′0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
return b0 * (2f + 1)^_2½ * (27f^2 / 2 * (b′0 - 4) + (3b′0 - 5) * f + 1)
end
function (eos::BulkModulusEquation{<:BirchMurnaghan4th})(v)
@unpack v0, b0, b′0, b″0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
h = b″0 * b0 + b′0^2
return b0 / 6 *
(2f + 1)^_2½ *
((99h - 693b′0 + 1573) * f^3 + (27h - 108b′0 + 105) * f^2 + 6f * (3b′0 - 5) + 6)
end
function (eos::BulkModulusEquation{<:PoirierTarantola2nd})(v)
@unpack v0, b0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
return b0 * (1 - 3f) * exp(-3f)
end
function (eos::BulkModulusEquation{<:PoirierTarantola3rd})(v)
@unpack v0, b0, b′0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
return -b0 / 2 * exp(-3f) * (9f^2 * (b′0 - 2) - 6f * (b′0 + 1) - 2)
end
function (eos::BulkModulusEquation{<:PoirierTarantola4th})(v)
@unpack v0, b0, b′0, b″0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
h = b″0 * b0 + b′0^2
return -b0 / 2 *
exp(-3f) *
(9f^3 * (h + 3b′0 + 3) - 9f^2 * (h + 2b′0 + 1) - 6f * (b′0 + 1) - 2)
end
function (eos::BulkModulusEquation{<:Vinet})(v)
@unpack v0, b0, b′0 = getparam(eos)
x, ξ = (v / v0)^_⅓, 3 / 2 * (b′0 - 1)
return -b0 / (2 * x^2) * (3x * (x - 1) * (b′0 - 1) + 2 * (x - 2)) * exp(-ξ * (x - 1))
end
function (eos::BulkModulusEquation{<:AntonSchmidt})(v)
@unpack v0, b0, b′0 = getparam(eos)
x, n = v / v0, -b′0 / 2
return b0 * x^n * (1 + n * log(x))
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 1541 | using UnPack: @unpack
using .FiniteStrains: ToEulerianStrain, ToNaturalStrain, EulerianStrain, NaturalStrain
import .FiniteStrains: straintype
export getparam, orderof
include("types.jl")
include("ev.jl")
include("pv.jl")
include("bv.jl")
_ispositive(x) = x > zero(x) # Do not export!
# Ref: https://github.com/JuliaLang/julia/blob/4a2830a/base/array.jl#L125
"""
orderof(x::FiniteStrainParameters)
Return the order of a `FiniteStrainParameters`.
# Examples
```jldoctest
julia> orderof(BirchMurnaghan(40, 0.5, 4, 0)) == 3
true
```
"""
orderof(::Type{<:FiniteStrainParameters{N}}) where {N} = N
orderof(x::FiniteStrainParameters) = orderof(typeof(x))
function Base.show(io::IO, param::Parameters) # Ref: https://github.com/mauro3/Parameters.jl/blob/3c1d72b/src/Parameters.jl#L542-L549
if get(io, :compact, false)
Base.show_default(IOContext(io, :limit => true), param)
else
# just dumping seems to give ok output, in particular for big data-sets:
T = typeof(param)
println(io, T)
for f in propertynames(param)
println(io, " ", f, " = ", getproperty(param, f))
end
end
end
"""
getparam(eos::EquationOfStateOfSolids)
Get the `Parameters` from an `EquationOfStateOfSolids`.
"""
getparam(eos::EquationOfStateOfSolids) = eos.param
straintype(::Type{<:BirchMurnaghan}) = EulerianStrain
straintype(::Type{<:PoirierTarantola}) = NaturalStrain
straintype(x::FiniteStrainParameters) = straintype(typeof(x))
Base.eltype(::Type{<:Parameters{T}}) where {T} = T
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 1796 | function (eos::EnergyEquation{<:Murnaghan1st})(v)
@unpack v0, b0, b′0, e0 = getparam(eos)
x, y = b′0 - 1, (v0 / v)^b′0
return e0 + b0 / b′0 * v * (y / x + 1) - v0 * b0 / x
end
function (eos::EnergyEquation{<:BirchMurnaghan2nd})(v)
@unpack v0, b0, e0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
return e0 + 9b0 * v0 * f^2 / 2
end
function (eos::EnergyEquation{<:BirchMurnaghan3rd})(v)
@unpack v0, b0, b′0, e0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
return e0 + 9b0 * v0 * f^2 / 2 * (1 + f * (b′0 - 4))
end
function (eos::EnergyEquation{<:BirchMurnaghan4th})(v)
@unpack v0, b0, b′0, b″0, e0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
h = b″0 * b0 + b′0^2
return e0 + 3b0 * v0 / 8 * f^2 * ((9h - 63b′0 + 143) * f^2 + 12f * (b′0 - 4) + 12)
end
function (eos::EnergyEquation{<:PoirierTarantola2nd})(v)
@unpack v0, b0, e0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
return e0 + 9b0 * v0 * f^2 / 2
end
function (eos::EnergyEquation{<:PoirierTarantola3rd})(v)
@unpack v0, b0, b′0, e0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
return e0 + 9b0 * v0 * f^2 / 2 * ((2 - b′0) * f + 1)
end
function (eos::EnergyEquation{<:PoirierTarantola4th})(v)
@unpack v0, b0, b′0, b″0, e0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
h = b″0 * b0 + b′0^2
return e0 + 9b0 * v0 * f^2 * (3f^2 * (h + 3b′0 + 3) + 4f * (b′0 + 2) + 4)
end
function (eos::EnergyEquation{<:Vinet})(v)
@unpack v0, b0, b′0, e0 = getparam(eos)
x, y = 1 - (v / v0)^_⅓, 3 / 2 * (b′0 - 1)
return e0 + 9b0 * v0 / y^2 * (1 + (x * y - 1) * exp(x * y))
end
function (eos::EnergyEquation{<:AntonSchmidt})(v)
@unpack v0, b0, b′0, e∞ = getparam(eos)
n₊₁ = -b′0 / 2 + 1
x = v / v0
return e∞ + b0 * v0 / n₊₁ * x^n₊₁ * (log(x) - 1 / n₊₁)
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 2193 | function (eos::PressureEquation{<:Murnaghan1st})(v)
@unpack v0, b0, b′0 = getparam(eos)
return b0 / b′0 * ((v0 / v)^b′0 - 1)
end
function (eos::PressureEquation{<:Murnaghan2nd})(v)
@unpack v0, b0, b′0, b″0 = getparam(eos)
h = b′0^2 - 2b0 * b″0
r = (v0 / v)^h
return 2b0 / b′0 / (h / b′0 * ((r + 1) / (r - 1)) - 1)
end
function (eos::PressureEquation{<:BirchMurnaghan2nd})(v)
@unpack v0, b0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
return 3b0 * f * (2f + 1)^_2½
end
function (eos::PressureEquation{<:BirchMurnaghan3rd})(v)
@unpack v0, b0, b′0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
return 3f / 2 * b0 * (2f + 1)^_2½ * (2 + 3f * (b′0 - 4))
end
function (eos::PressureEquation{<:BirchMurnaghan4th})(v)
@unpack v0, b0, b′0, b″0 = getparam(eos)
f = ToEulerianStrain(v0)(v)
h = b″0 * b0 + b′0^2
return b0 / 2 * (2f + 1)^_2½ * ((9h - 63b′0 + 143) * f^2 + 9f * (b′0 - 4) + 6)
end
function (eos::PressureEquation{<:PoirierTarantola2nd})(v)
@unpack v0, b0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
return -3b0 * f * exp(-3f)
end
function (eos::PressureEquation{<:PoirierTarantola3rd})(v)
@unpack v0, b0, b′0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
return -3b0 / 2 * f * exp(-3f) * (3f * (b′0 - 2) + 1)
end
function (eos::PressureEquation{<:PoirierTarantola4th})(v)
@unpack v0, b0, b′0, b″0 = getparam(eos)
f = ToNaturalStrain(v0)(v)
h = b″0 * b0 + b′0^2
return -3b0 / 2 * f * exp(-3f) * (3f^2 * (h + 3b′0 + 3) + 3f * (b′0 - 2) + 2)
end
function (eos::PressureEquation{<:Vinet})(v)
@unpack v0, b0, b′0 = getparam(eos)
x, y = (v / v0)^_⅓, 3 / 2 * (b′0 - 1)
return 3b0 / x^2 * (1 - x) * exp(y * (1 - x))
end
function (eos::PressureEquation{<:AntonSchmidt})(v)
@unpack v0, b0, b′0 = getparam(eos)
x, n = v / v0, -b′0 / 2
return -b0 * x^n * log(x)
end
function (eos::PressureEquation{<:Holzapfel{Z}})(v) where {Z}
@unpack v0, b0, b′0 = getparam(eos)
η = (v / v0)^_⅓
p0 = FERMI_GAS_CONSTANT * (Z / v0)^(5 / 3)
c0 = -log(3b0 / p0 |> NoUnits)
c2 = 3 / 2 * (b′0 - 3) - c0
return 3b0 * (1 - η) / η^5 * exp(c0 * (1 - η)) * (1 + c2 * η * (1 - η))
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 10989 | using ConstructionBase: constructorof
using EquationsOfState: Parameters, EquationOfState
using StructHelpers: @batteries
export Murnaghan,
Murnaghan1st,
BirchMurnaghan,
BirchMurnaghan2nd,
BirchMurnaghan3rd,
BirchMurnaghan4th,
PoirierTarantola,
PoirierTarantola2nd,
PoirierTarantola3rd,
# PoirierTarantola4th,
Vinet,
EnergyEquation,
PressureEquation,
BulkModulusEquation
abstract type FiniteStrainParameters{N,T} <: Parameters{T} end
abstract type BirchMurnaghan{N,T} <: FiniteStrainParameters{N,T} end
abstract type PoirierTarantola{N,T} <: FiniteStrainParameters{N,T} end
abstract type Murnaghan{T} <: Parameters{T} end
"""
Murnaghan1st(v0, b0, b′0, e0=zero(v0 * b0))
Create a Murnaghan first order equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `b′0`: the first-order pressure-derivative bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
"""
struct Murnaghan1st{T} <: Murnaghan{T}
v0::T
b0::T
b′0::T
e0::T
Murnaghan1st{T}(v0, b0, b′0, e0 = zero(v0 * b0)) where {T} = new(v0, b0, b′0, e0)
end
"""
Murnaghan2nd(v0, b0, b′0, b″0, e0=zero(v0 * b0))
Create a Murnaghan second order equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `b′0`: the first-order pressure-derivative bulk modulus of solid at zero pressure.
- `b″0`: the second-order pressure-derivative bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
"""
struct Murnaghan2nd{T} <: Murnaghan{T}
v0::T
b0::T
b′0::T
b″0::T
e0::T
Murnaghan2nd{T}(v0, b0, b′0, b″0, e0 = zero(v0 * b0)) where {T} =
new(v0, b0, b′0, b″0, e0)
end
"""
BirchMurnaghan2nd(v0, b0, e0=zero(v0 * b0))
Create a Birch–Murnaghan second order equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
"""
struct BirchMurnaghan2nd{T} <: BirchMurnaghan{2,T}
v0::T
b0::T
e0::T
BirchMurnaghan2nd{T}(v0, b0, e0 = zero(v0 * b0)) where {T} = new(v0, b0, e0)
end
"""
BirchMurnaghan3rd(v0, b0, b′0, e0=zero(v0 * b0))
Create a Birch–Murnaghan third order equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `b′0`: the first-order pressure-derivative bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
!!! note
The third-order equation (Equation (22)) becomes identical to the second-order equation
when ``b′0 = 4`` (not ``0``!).
"""
struct BirchMurnaghan3rd{T} <: BirchMurnaghan{3,T}
v0::T
b0::T
b′0::T
e0::T
BirchMurnaghan3rd{T}(v0, b0, b′0, e0 = zero(v0 * b0)) where {T} = new(v0, b0, b′0, e0)
end
"""
BirchMurnaghan4th(v0, b0, b′0, b″0, e0=zero(v0 * b0))
Create a Birch–Murnaghan fourth order equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `b′0`: the first-order pressure-derivative bulk modulus of solid at zero pressure.
- `b″0`: the second-order pressure-derivative bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
!!! note
The fourth-order equation becomes identical to the third-order equation when
```math
b″0 = -\\frac{ 1 }{ 9b0 } (9b′0^2 - 63b′0 + 143).
```
"""
struct BirchMurnaghan4th{T} <: BirchMurnaghan{4,T}
v0::T
b0::T
b′0::T
b″0::T
e0::T
BirchMurnaghan4th{T}(v0, b0, b′0, b″0, e0 = zero(v0 * b0)) where {T} =
new(v0, b0, b′0, b″0, e0)
end
"""
PoirierTarantola2nd(v0, b0, e0=zero(v0 * b0))
Create a Poirier–Tarantola second order equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
"""
struct PoirierTarantola2nd{T} <: PoirierTarantola{2,T}
v0::T
b0::T
e0::T
PoirierTarantola2nd{T}(v0, b0, e0 = zero(v0 * b0)) where {T} = new(v0, b0, e0)
end
"""
PoirierTarantola3rd(v0, b0, b′0, e0=zero(v0 * b0))
Create a Poirier–Tarantola third order equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `b′0`: the first-order pressure-derivative bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
"""
struct PoirierTarantola3rd{T} <: PoirierTarantola{3,T}
v0::T
b0::T
b′0::T
e0::T
PoirierTarantola3rd{T}(v0, b0, b′0, e0 = zero(v0 * b0)) where {T} = new(v0, b0, b′0, e0)
end
"""
PoirierTarantola4th(v0, b0, b′0, b″0, e0=zero(v0 * b0))
Create a Poirier–Tarantola fourth order equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `b′0`: the first-order pressure-derivative bulk modulus of solid at zero pressure.
- `b″0`: the second-order pressure-derivative bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
"""
struct PoirierTarantola4th{T} <: PoirierTarantola{4,T}
v0::T
b0::T
b′0::T
b″0::T
e0::T
PoirierTarantola4th{T}(v0, b0, b′0, b″0, e0 = zero(v0 * b0)) where {T} =
new(v0, b0, b′0, b″0, e0)
end
"""
Vinet(v0, b0, b′0, e0=zero(v0 * b0))
Create a Vinet equation of state.
This equation of state can have units. The units are specified in
[`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl)'s `@u_str` style.
# Arguments
- `v0`: the volume of solid at zero pressure.
- `b0`: the bulk modulus of solid at zero pressure.
- `b′0`: the first-order pressure-derivative bulk modulus of solid at zero pressure.
- `e0`: the energy of solid at zero pressure.
"""
struct Vinet{T} <: Parameters{T}
v0::T
b0::T
b′0::T
e0::T
Vinet{T}(v0, b0, b′0, e0 = zero(v0 * b0)) where {T} = new(v0, b0, b′0, e0)
end
struct AntonSchmidt{T} <: Parameters{T}
v0::T
b0::T
b′0::T
e∞::T
AntonSchmidt{T}(v0, b0, b′0, e∞ = zero(v0 * b0)) where {T} = new(v0, b0, b′0, e∞)
end
struct Holzapfel{Z,T} <: Parameters{T}
v0::T
b0::T
b′0::T
e0::T
function Holzapfel{Z,T}(v0, b0, b′0, e0 = zero(v0 * b0)) where {Z,T}
@assert 1 <= Z <= 118 "elements are between 1 and 118!"
return new(v0, b0, b′0, e0)
end
end
@batteries Murnaghan1st eq = true hash = true
@batteries Murnaghan2nd eq = true hash = true
@batteries BirchMurnaghan2nd eq = true hash = true
@batteries BirchMurnaghan3rd eq = true hash = true
@batteries BirchMurnaghan4th eq = true hash = true
@batteries PoirierTarantola2nd eq = true hash = true
@batteries PoirierTarantola3rd eq = true hash = true
@batteries PoirierTarantola4th eq = true hash = true
@batteries Vinet eq = true hash = true
@batteries AntonSchmidt eq = true hash = true
@batteries Holzapfel eq = true hash = true
function (::Type{T})(args...) where {T<:Parameters}
E = Base.promote_typeof(args...)
return constructorof(T){E}(args...) # Cannot use `T.(args...)`! For `AbstractQuantity` they will fail!
end
function Murnaghan(args...)
N = length(args)
if N == 4
return Murnaghan1st(args...)
elseif N == 5
return Murnaghan2nd(args...)
else
throw(ArgumentError("unknown number of arguments $N."))
end
end
"""
BirchMurnaghan(args...)
Construct a `BirchMurnaghan` based on the length of arguments, where `e0` must be provided.
See also: [`BirchMurnaghan2nd`](@ref), [`BirchMurnaghan3rd`](@ref), [`BirchMurnaghan4th`](@ref)
"""
function BirchMurnaghan(args...)
N = length(args)
if N == 3
return BirchMurnaghan2nd(args...)
elseif N == 4
return BirchMurnaghan3rd(args...)
elseif N == 5
return BirchMurnaghan4th(args...)
else
throw(ArgumentError("unknown number of arguments $N."))
end
end
"""
PoirierTarantola(args...)
Construct a `PoirierTarantola` based on the length of arguments, where `e0` must be provided.
See also: [`PoirierTarantola2nd`](@ref), [`PoirierTarantola3rd`](@ref), [`PoirierTarantola4th`](@ref)
"""
function PoirierTarantola(args...)
N = length(args)
if N == 3
return PoirierTarantola2nd(args...)
elseif N == 4
return PoirierTarantola3rd(args...)
elseif N == 5
return PoirierTarantola4th(args...)
else
throw(ArgumentError("unknown number of arguments $N."))
end
end
"""
EquationOfStateOfSolids{T<:Parameters}
Represent an equation of state of solids.
"""
abstract type EquationOfStateOfSolids{T} <: EquationOfState{T} end
"""
EnergyEquation{T} <: EquationOfStateOfSolids{T}
EnergyEquation(parameters::Parameters)
Construct an equation of state which evaluates the energy of the given `parameters`.
"""
struct EnergyEquation{T} <: EquationOfStateOfSolids{T}
param::T
end
EnergyEquation(eos::EquationOfStateOfSolids) = EnergyEquation(getparam(eos))
"""
PressureEquation{T} <: EquationOfStateOfSolids{T}
PressureEquation(parameters::Parameters)
Construct an equation of state which evaluates the pressure of the given `parameters`.
"""
struct PressureEquation{T} <: EquationOfStateOfSolids{T}
param::T
end
PressureEquation(eos::EquationOfStateOfSolids) = PressureEquation(getparam(eos))
"""
BulkModulusEquation{T} <: EquationOfStateOfSolids{T}
BulkModulusEquation(parameters::Parameters)
Construct an equation of state which evaluates the bulk modulus of the given `parameters`.
"""
struct BulkModulusEquation{T} <: EquationOfStateOfSolids{T}
param::T
end
BulkModulusEquation(eos::EquationOfStateOfSolids) = BulkModulusEquation(getparam(eos))
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 25000 | module Fitting
using GenericSVD
using Test
using Unitful: EnergyUnits, PressureUnits, ustrip, @u_str
using UnitfulAtomic
using YAML
using EquationsOfStateOfSolids:
Parameters,
Murnaghan1st,
BirchMurnaghan2nd,
BirchMurnaghan3rd,
BirchMurnaghan4th,
PoirierTarantola3rd,
Vinet,
EnergyEquation
using EquationsOfStateOfSolids.Fitting: nonlinfit, linfit
import Unitful
Unitful.promote_unit(::S, ::T) where {S<:EnergyUnits,T<:EnergyUnits} = u"eV"
Unitful.promote_unit(::S, ::T) where {S<:PressureUnits,T<:PressureUnits} = u"GPa"
# Do not export! Only for internal use!
function _isapprox(a::T, b::T; kwargs...) where {T<:Parameters}
x, y = [], []
for f in fieldnames(T)
pa, pb = map(ustrip, promote(getfield(a, f), getfield(b, f)))
push!(x, pa)
push!(y, pb)
end
return isapprox(x, y; kwargs...)
end
# Data from https://github.com/materialsproject/pymatgen/blob/19c4d98/pymatgen/analysis/tests/test_eos.py#L17-L73
@testset "Test data from Pymatgen" begin
data = open("data/si.yml", "r") do io
YAML.load(io)
end
@testset "With `Float64`" begin
volumes, energies = data["volume"], data["energy"]
@test _isapprox(
nonlinfit(EnergyEquation(BirchMurnaghan3rd(40, 0.5, 4)), volumes, energies),
BirchMurnaghan3rd(
40.98926572528106,
0.5369258245417454,
4.178644235500821,
-10.842803908240892,
),
)
@test _isapprox(
linfit(EnergyEquation(BirchMurnaghan3rd(40, 0.5, 4)), volumes, energies),
BirchMurnaghan3rd(
40.98926572528106,
0.5369258245417454,
4.178644235500821,
-10.842803908240892,
),
)
@test _isapprox(
nonlinfit(EnergyEquation(Murnaghan1st(41, 0.5, 4)), volumes, energies),
Murnaghan1st(
41.13757930387086,
0.5144967693786603,
3.9123862262572264,
-10.836794514626673,
),
)
@test _isapprox(
nonlinfit(EnergyEquation(PoirierTarantola3rd(41, 0.5, 4)), volumes, energies),
PoirierTarantola3rd(
40.86770643373908,
0.5667729960804602,
4.331688936974368,
-10.851486685041658,
),
)
@test _isapprox(
linfit(EnergyEquation(PoirierTarantola3rd(41, 0.5, 4)), volumes, energies),
PoirierTarantola3rd(
40.86770643373908,
0.5667729960804602,
4.331688936974368,
-10.851486685041658,
),
)
@test _isapprox(
nonlinfit(EnergyEquation(Vinet(41, 0.5, 4)), volumes, energies),
Vinet(
40.916875663779784,
0.5493839425156859,
4.3051929654936885,
-10.846160810560756,
),
)
end
@testset "`linfit` for `BigFloat` parameters" begin
volumes, energies = data["volume"], data["energy"]
@test _isapprox(
linfit(
EnergyEquation(BirchMurnaghan3rd(40, 0.5, 4)),
big.(volumes),
big.(energies),
),
BirchMurnaghan3rd{BigFloat}(
40.98926572528106,
0.5369258245417454,
4.178644235500821,
-10.842803908240892,
);
atol = 1e-8,
)
@test _isapprox(
linfit(EnergyEquation(BirchMurnaghan3rd{BigInt}(40, 1, 4)), volumes, energies),
BirchMurnaghan3rd{BigFloat}(
40.98926572528106,
0.5369258245417454,
4.178644235500821,
-10.842803908240892,
);
atol = 1e-8,
)
@test _isapprox(
linfit(
EnergyEquation(PoirierTarantola3rd(41, 0.5, 4)),
big.(volumes),
big.(energies),
),
PoirierTarantola3rd{BigFloat}(
40.86770643373908,
0.5667729960804602,
4.331688936974368,
-10.851486685041658,
);
atol = 1e-8,
)
@test _isapprox(
linfit(
EnergyEquation(PoirierTarantola3rd{BigFloat}(41, 1 // 2, 4)),
volumes,
energies,
),
PoirierTarantola3rd{BigFloat}(
40.86770643373908,
0.5667729960804602,
4.331688936974368,
-10.851486685041658,
);
atol = 1e-8,
)
end
end
# Data from https://github.com/materialsproject/pymatgen/blob/19c4d98/pymatgen/analysis/tests/test_eos.py#L92-L167
@testset "Test Mg dataset" begin
data = open("data/mp153.yml", "r") do io
YAML.load(io)
end
@testset "without unit" begin
volumes, energies, known_energies_vinet =
data["volume"], data["energy"], data["known_energy_vinet"]
fitted_eos = nonlinfit(EnergyEquation(Vinet(23, 0.5, 4)), volumes, energies)
@test _isapprox(
fitted_eos,
Vinet(22.957645593, 0.22570911414, 4.06054339, -1.59442926062),
)
@test isapprox(
map(EnergyEquation(fitted_eos), volumes),
known_energies_vinet;
atol = 1e-6,
)
end
@testset "with units" begin
volumes, energies, known_energies_vinet = data["volume"] * u"angstrom^3",
data["energy"] * u"eV",
data["known_energy_vinet"] * u"eV"
fitted_eos = nonlinfit(
EnergyEquation(Vinet(23u"angstrom^3", 36.16u"GPa", 4)),
volumes,
energies,
)
@test _isapprox(
fitted_eos,
Vinet(
22.957645593u"angstrom^3",
36.16258657649159u"GPa", # https://github.com/materialsproject/pymatgen/blob/19c4d98/pymatgen/analysis/tests/test_eos.py#L181
4.06054339,
-1.59442926062u"eV",
),
)
@test isapprox(
map(EnergyEquation(fitted_eos), volumes),
known_energies_vinet;
atol = 1e-6u"eV",
)
end
end
# Data from https://github.com/materialsproject/pymatgen/blob/19c4d98/pymatgen/analysis/tests/test_eos.py#L185-L260
@testset "Test Si dataset" begin
data = open("data/mp149.yml", "r") do io
YAML.load(io)
end
@testset "without unit" begin
volumes, energies, known_energies_vinet =
data["volume"], data["energy"], data["known_energy_vinet"]
fitted_eos = nonlinfit(EnergyEquation(Vinet(20, 0.5, 4)), volumes, energies)
@test _isapprox(
fitted_eos,
Vinet(20.446696754, 0.55166385214, 4.32437391, -5.42496338987),
)
@test isapprox(
map(EnergyEquation(fitted_eos), volumes),
known_energies_vinet;
atol = 1e-5,
)
end
@testset "with units" begin
volumes, energies, known_energies_vinet = data["volume"] * u"angstrom^3",
data["energy"] * u"eV",
data["known_energy_vinet"] * u"eV"
fitted_eos = nonlinfit(
EnergyEquation(Vinet(20u"angstrom^3", 88.39u"GPa", 4)),
volumes,
energies,
)
@test _isapprox(
fitted_eos,
Vinet(
20.446696754u"angstrom^3",
88.38629264585195u"GPa", # https://github.com/materialsproject/pymatgen/blob/19c4d98/pymatgen/analysis/tests/test_eos.py#L274
4.32437391,
-5.42496338987u"eV",
),
)
@test isapprox(
map(EnergyEquation(fitted_eos), volumes),
known_energies_vinet;
atol = 1e-6u"eV",
)
end
end
# Data from https://github.com/materialsproject/pymatgen/blob/19c4d98/pymatgen/analysis/tests/test_eos.py#L278-L353
@testset "Test Ti dataset" begin
data = open("data/mp72.yml", "r") do io
YAML.load(io)
end
@testset "without unit" begin
volumes, energies, known_energies_vinet =
data["volume"], data["energy"], data["known_energy_vinet"]
fitted_eos = nonlinfit(EnergyEquation(Vinet(17, 0.5, 4)), volumes, energies)
@test _isapprox(
fitted_eos,
Vinet(17.1322302613, 0.70297662247, 3.638807756, -7.89741495912),
)
@test isapprox(
map(EnergyEquation(fitted_eos), volumes),
known_energies_vinet;
atol = 1e-5,
)
end
@testset "with units" begin
volumes, energies, known_energies_vinet = data["volume"] * u"angstrom^3",
data["energy"] * u"eV",
data["known_energy_vinet"] * u"eV"
fitted_eos = nonlinfit(
EnergyEquation(Vinet(17u"angstrom^3", 112.63u"GPa", 4)),
volumes,
energies,
)
@test _isapprox(
fitted_eos,
Vinet(
17.1322302613u"angstrom^3",
112.62927094503254u"GPa", # https://github.com/materialsproject/pymatgen/blob/19c4d98/pymatgen/analysis/tests/test_eos.py#L367
3.638807756,
-7.89741495912u"eV",
),
)
@test isapprox(
map(EnergyEquation(fitted_eos), volumes),
known_energies_vinet;
atol = 1e-7u"eV",
)
end
end
@testset "Test `w2k-lda-na.dat` from `Gibbs2`" begin
data = open("data/w2k-lda-na.yml", "r") do io
YAML.load(io)
end
@testset "without unit" begin
volumes, energies = data["volume"], data["energy"]
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L117-L122
@test _isapprox(
nonlinfit(EnergyEquation(Murnaghan1st(224, 6e-4, 4)), volumes, energies),
Murnaghan1st(224.501825, 6.047952315268776e-4, 3.723835, -323.417686);
atol = 1e-5,
)
# No reference data, I run on my computer.
@test _isapprox(
nonlinfit(EnergyEquation(BirchMurnaghan2nd(224, 6e-4)), volumes, energies),
BirchMurnaghan2nd(223.7192539523166, 6.268341030294978e-4, -323.4177121144877);
atol = 1e-8,
)
# No reference data, I run on my computer.
@test _isapprox(
linfit(EnergyEquation(BirchMurnaghan2nd(224, 6e-4)), volumes, energies),
BirchMurnaghan2nd(223.7192539523166, 6.268341030294978e-4, -323.4177121144877),
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L15-L20
@test _isapprox(
nonlinfit(EnergyEquation(BirchMurnaghan3rd(224, 6e-4, 4)), volumes, energies),
BirchMurnaghan3rd(224.444565, 6.250619105057268e-4, 3.740369, -323.417714),
)
@test _isapprox(
linfit(EnergyEquation(BirchMurnaghan3rd(224, 6e-4, 4)), volumes, energies),
BirchMurnaghan3rd(224.444565, 6.250619105057268e-4, 3.740369, -323.417714),
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L30-L36
@test _isapprox(
nonlinfit(
EnergyEquation(BirchMurnaghan4th(224, 6e-4, 4, -5460)), # bohr^3, Ry/bohr^3, 1, bohr^3/Ry, Ry
volumes,
energies,
),
BirchMurnaghan4th(
224.457562, # bohr^3
6.229381129795094e-4, # Ry/bohr^3
3.730992,
-5322.7030547560435, # bohr^3/Ry
-323.417712, # Ry
);
rtol = 1e-5,
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L30-L36
# @test _isapprox(
# linfit(
# EnergyEquation(BirchMurnaghan4th(224, 6e-4, 4, -5460)), # bohr^3, Ry/bohr^3, 1, bohr^3/Ry, Ry
# volumes,
# energies,
# ),
# BirchMurnaghan4th(
# 224.457562, # bohr^3
# 6.229381129795094e-4, # Ry/bohr^3
# 3.730992,
# -5322.7030547560435, # bohr^3/Ry
# -323.417712, # Ry
# );
# rtol = 1e-5,
# )
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L98-L105
# @test _isapprox(
# nonlinfit(
# EnergyEquation( # BirchMurnaghan5th(224.445371, 0.0006, 4, -5500, 3.884535907971559e7, -323)),
# volumes,
# energies,
# ),
# BirchMurnaghan5th(
# 224.451813,
# 0.0006228893043314733,
# 3.736723,
# -5292.414119096362,
# 6.3542116050611705e7,
# -323.417712,
# );
# atol = 1,
# ) # FIXME: result is wrong
# # No reference data, I run on my computer.
@test _isapprox(
nonlinfit(EnergyEquation(Vinet(224, 6e-4, 4)), volumes, energies),
Vinet(
224.45278665796354,
6.313500637481759e-4,
3.7312381477678853,
-323.4177229576912,
),
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L66-L71
@test _isapprox(
nonlinfit(EnergyEquation(PoirierTarantola3rd(224, 6e-4, 4)), volumes, energies),
PoirierTarantola3rd(224.509208, 6.3589226415983795e-4, 3.690448, -323.41773);
atol = 1e-5,
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L66-L71
@test _isapprox(
linfit(EnergyEquation(PoirierTarantola3rd(224, 6e-4, 4)), volumes, energies),
PoirierTarantola3rd(224.509208, 6.3589226415983795e-4, 3.690448, -323.41773);
atol = 1e-5,
)
# # FIXME: This cannot go through
# @test _isapprox(
# nonlinfit(
# EnergyEquation( # PoirierTarantola4th(220, 0.0006, 3.7, -5500, -323)),
# volumes,
# energies,
# ),
# PoirierTarantola4th(
# 224.430182,
# 0.0006232241765069493,
# 3.758360,
# -5493.859729817176,
# -323.417712,
# ),
# )
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L98-L105
# @test _isapprox(
# nonlinfit(
# EnergyEquation(PoirierTarantola5th(
# 224.445371,
# 0.0006,
# 3.8,
# -5500,
# 6e7,
# -323,
# )),
# volumes,
# energies,
# ),
# PoirierTarantola5th(
# 224.451250,
# 0.000622877204137392,
# 3.737484,
# -5283.999708607125,
# 6.296000262990379e7,
# -323.417712,
# );
# rtol = 0.05,
# )
end
@testset "with units" begin
volumes, energies = data["volume"] * u"bohr^3", data["energy"] * u"Ry"
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L117-L122
@test _isapprox(
nonlinfit(
EnergyEquation(Murnaghan1st(224u"bohr^3", 9u"GPa", 4)),
volumes,
energies,
),
Murnaghan1st(224.501825u"bohr^3", 8.896845u"GPa", 3.723835, -323.417686u"Ry");
atol = 1e-5,
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L15-L20
@test _isapprox(
nonlinfit(
EnergyEquation(BirchMurnaghan3rd(224u"bohr^3", 9u"GPa", 4)),
volumes,
energies,
),
BirchMurnaghan3rd(
224.444565u"bohr^3",
9.194978u"GPa",
3.740369,
-323.417714u"Ry",
),
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L15-L20
@test _isapprox(
linfit(
EnergyEquation(BirchMurnaghan3rd(224u"bohr^3", 9u"GPa", 4)),
volumes,
energies,
),
BirchMurnaghan3rd(
224.444565u"bohr^3",
6.250619009766436e-4u"Ry/bohr^3",
3.740369,
-323.417714u"Ry",
),
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L30-L36
@test _isapprox(
nonlinfit(
EnergyEquation(BirchMurnaghan4th(224u"bohr^3", 9u"GPa", 4, -0.3u"1/GPa")),
volumes,
energies,
),
BirchMurnaghan4th(
224.457562u"bohr^3",
9.163736u"GPa",
3.730992,
-0.361830u"1/GPa",
-323.417712u"Ry", # Ry
);
rtol = 1e-7,
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L66-L71
@test _isapprox(
nonlinfit(
EnergyEquation(PoirierTarantola3rd(224u"bohr^3", 9u"GPa", 4)),
volumes,
energies,
),
PoirierTarantola3rd(
224.509208u"bohr^3",
9.354298u"GPa",
3.690448,
-323.41773u"Ry",
),
)
# See https://github.com/aoterodelaroza/asturfit/blob/4de9b41/test/test03.out#L66-L71
@test _isapprox(
linfit(
EnergyEquation(PoirierTarantola3rd(224u"bohr^3", 9u"GPa", 4)),
volumes,
energies,
),
PoirierTarantola3rd(
224.509208u"bohr^3",
6.3589226415983795e-4u"Ry/bohr^3",
3.690448,
-323.41773u"Ry",
);
atol = 1e-5,
)
end
end
@testset "Test `w2k-lda-k.dat` from `Gibbs2`" begin
data = open("data/w2k-lda-k.yml", "r") do io
YAML.load(io)
end
@testset "without unit" begin
volumes, energies = data["volume"], data["energy"]
@test _isapprox(
nonlinfit(EnergyEquation(Murnaghan1st(430, 3e-4, 4)), volumes, energies),
Murnaghan1st(
435.05782299050884,
2.8297159355249786e-4,
3.5705032675000785,
-1201.2082739321822,
),
)
@test _isapprox(
nonlinfit(EnergyEquation(BirchMurnaghan2nd(430, 3e-4)), volumes, energies),
BirchMurnaghan2nd(430.10027687726716, 3.02451215462375e-4, -1201.2083221436026),
)
@test _isapprox(
nonlinfit(EnergyEquation(BirchMurnaghan3rd(430, 3e-4, 4)), volumes, energies),
BirchMurnaghan3rd(
432.67139080209046,
3.0508544859901674e-4,
3.7894868450211923,
-1201.2083959943404,
),
)
@test _isapprox(
nonlinfit(
EnergyEquation(BirchMurnaghan4th(432, 3e-4, 3.8, -11773)),
volumes,
energies,
),
BirchMurnaghan4th(
432.8012195854224,
3.041889904166284e-4,
3.774020919355492,
-11773.192574765615,
-1201.2083912308235,
);
rtol = 1e-4,
)
@test _isapprox(
nonlinfit(EnergyEquation(Vinet(432, 3e-4, 3.8)), volumes, energies),
Vinet(
432.04609865398015,
3.137631070690569e-4,
3.837666939407128,
-1201.2084453225773,
),
)
end
@testset "with units" begin
volumes, energies = data["volume"] * u"bohr^3", data["energy"] * u"Ry"
@test _isapprox(
nonlinfit(
EnergyEquation(BirchMurnaghan3rd(430u"bohr^3", 3e-4u"Ry/bohr^3", 4)),
volumes,
energies,
),
BirchMurnaghan3rd(
432.6713907942206u"bohr^3",
3.0508544859901674e-4u"Ry/bohr^3",
3.789486849598267,
-1201.208395994332u"Ry",
),
)
@test _isapprox(
linfit(
EnergyEquation(BirchMurnaghan3rd(430u"bohr^3", 3e-4u"Ry/bohr^3", 4)),
volumes,
energies,
),
BirchMurnaghan3rd(
432.6713907942206u"bohr^3",
3.0508544859901674e-4u"Ry/bohr^3",
3.789486849598267,
-1201.208395994332u"Ry",
),
)
end
end
# Data from http://tutorials.crystalsolutions.eu/tutorial.html?td=eos&tf=eos_tut
@testset "Test MgO data" begin
volumes = [17.789658, 18.382125, 18.987603, 19.336585, 19.606232, 20.238155, 20.883512]
energies = [
-275.3023029137,
-275.3039525749,
-275.3047829172,
-275.3049167772,
-275.3048617406,
-275.3042539881,
-275.3030141001,
]
@testset "without unit" begin
@test _isapprox(
nonlinfit(EnergyEquation(Murnaghan1st(19, 100, 4)), volumes, energies),
Murnaghan1st(19.3620, 0.035786498967406696, 3.70, -275.30491639);
atol = 1e-2,
)
@test _isapprox(
nonlinfit(EnergyEquation(BirchMurnaghan3rd(19, 100, 4)), volumes, energies),
BirchMurnaghan3rd(19.3618, 0.035859897760315104, 3.72, -275.30491678);
atol = 1e-2,
)
@test _isapprox(
nonlinfit(EnergyEquation(PoirierTarantola3rd(19, 100, 4)), volumes, energies),
PoirierTarantola3rd(19.3617, 0.0358988908690477, 3.73, -275.30491699);
atol = 1e-2,
)
@test _isapprox(
nonlinfit(EnergyEquation(Vinet(19, 100, 4)), volumes, energies),
Vinet(19.3617, 0.035880541170820596, 3.73, -275.30491690);
atol = 1e-4,
)
end
@testset "with units" begin
volumes *= u"angstrom^3"
energies *= u"Eh_au"
@test _isapprox(
nonlinfit(
EnergyEquation(Murnaghan1st(19u"angstrom^3", 100u"GPa", 4)),
volumes,
energies,
),
Murnaghan1st(19.3620u"angstrom^3", 156.02u"GPa", 3.70, -275.30491639u"Eh_au");
rtol = 1e-6,
)
@test _isapprox(
nonlinfit(
EnergyEquation(BirchMurnaghan3rd(19u"angstrom^3", 100u"GPa", 4)),
volumes,
energies,
),
BirchMurnaghan3rd(
19.3618u"angstrom^3",
156.34u"GPa",
3.72,
-275.30491678u"Eh_au",
);
rtol = 1e-6,
)
@test _isapprox(
nonlinfit(
EnergyEquation(PoirierTarantola3rd(19u"angstrom^3", 100u"GPa", 4)),
volumes,
energies,
),
PoirierTarantola3rd(
19.3617u"angstrom^3",
156.51u"GPa",
3.73,
-275.30491699u"Eh_au",
);
rtol = 1e-6,
)
@test _isapprox(
nonlinfit(
EnergyEquation(Vinet(19u"angstrom^3", 100u"GPa", 4)),
volumes,
energies,
),
Vinet(19.3617u"angstrom^3", 156.43u"GPa", 3.73, -275.30491690u"Eh_au");
rtol = 1e-6,
)
@test _isapprox(
linfit(
EnergyEquation(BirchMurnaghan3rd(19u"angstrom^3", 100u"GPa", 4)),
volumes,
energies,
),
BirchMurnaghan3rd(
19.3618u"angstrom^3",
0.035859897760315104u"Eh_au / angstrom^3",
3.72,
-275.30491678u"Eh_au",
);
rtol = 1e-4,
)
@test _isapprox(
linfit(
EnergyEquation(PoirierTarantola3rd(19u"angstrom^3", 150u"GPa", 3.7)),
volumes,
energies,
),
PoirierTarantola3rd(
19.3617u"angstrom^3",
0.0358988908690477u"Eh_au / angstrom^3",
3.73,
-275.30491699u"Eh_au",
);
rtol = 1e-5,
)
end
end
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 11696 | using Measurements: Measurement, measurement
using SymEngine: Basic, symbols
using Test: @test, @testset, @test_throws
using Unitful: Quantity, DimensionlessQuantity, @u_str
using EquationsOfStateOfSolids:
Murnaghan,
Murnaghan1st,
BirchMurnaghan,
BirchMurnaghan2nd,
BirchMurnaghan3rd,
BirchMurnaghan4th,
PoirierTarantola,
PoirierTarantola2nd,
PoirierTarantola3rd,
PoirierTarantola4th,
Vinet,
AntonSchmidt
@testset "Promoting `eltype`" begin
@testset "Promoting to floating-point numbers" begin
@test eltype(Murnaghan1st(1, 2, 3.0, 0)) === Float64
@test eltype(BirchMurnaghan2nd(1, 2.0, 0)) === Float64
@test eltype(BirchMurnaghan3rd(1, 2, 3.0, 0)) === Float64
@test eltype(BirchMurnaghan4th(1, 2.0, 3, 4, 0)) === Float64
@test eltype(PoirierTarantola2nd(1, 2.0, 0)) === Float64
@test eltype(PoirierTarantola3rd(1, 2, 3.0, 0)) === Float64
@test eltype(Vinet(1, 2, 3.0, 0)) === Float64
@test eltype(AntonSchmidt(1, 2, 3.0, 0)) === Float64
# @test eltype(BreenanStacey(1, 2, 3.0, 0)) === Float64
@test eltype(Murnaghan1st{Float32}(Int(1), 2 // 1, Int8(3), Float64(4))) === Float32
@test eltype(Murnaghan1st{BigFloat}(Int(1), 2 // 1, Int8(3), Float64(4))) ===
BigFloat
@test eltype(PoirierTarantola4th{Float16}(Int8(1), 2 // 1, 4, Int16(5), 6)) ===
Float16
@test eltype(BirchMurnaghan4th(Int8(1), 2 // 1, big(4.0), Int16(5), 6)) === BigFloat
@test eltype(BirchMurnaghan4th(Int8(1), 2 // 1, big(4), Int16(5), 6.0)) === BigFloat
@test_throws InexactError Vinet{Float64}(41 + 0.1im, 1.2, 4)
end
@testset "Promoting to rationals" begin
@test eltype(PoirierTarantola4th(1, 2, 3, 4, 0)) === Int
@test eltype(Murnaghan1st(Int32(1), Int16(2), Int8(3), 0)) === Int
@test eltype(Murnaghan1st(1, 2 // 1, Int8(3), 0)) === Rational{Int}
@test eltype(BirchMurnaghan2nd(1, Int8(2), 0)) === Int
@test eltype(BirchMurnaghan2nd(1 // 1, Int32(2))) === Rational{Int}
@test eltype(BirchMurnaghan3rd(Int8(1), 2, 4, 0)) === Int
@test eltype(BirchMurnaghan3rd(Int8(1), 2 // 1, 4, 0)) === Rational{Int}
@test eltype(BirchMurnaghan4th(Int8(1), 2, 4, Int16(5), 6)) === Int
@test eltype(BirchMurnaghan4th(Int8(1), 2 // 1, 4, Int16(5), 6)) === Rational{Int}
@test eltype(BirchMurnaghan4th(Int8(1), 2 // 1, big(4), Int16(5), 6)) ===
Rational{BigInt}
@test eltype(PoirierTarantola2nd(Int8(1), 2, 3)) === Int
@test eltype(PoirierTarantola2nd(Int8(1), 2 // 1, 3)) === Rational{Int}
@test eltype(PoirierTarantola3rd(Int8(1), 2, 3, Int16(4))) === Int
@test eltype(PoirierTarantola3rd(Int8(1), 2 // 1, 3 // 1, Int16(4))) ===
Rational{Int}
@test eltype(PoirierTarantola4th(Int8(1), 2, 3, Int16(4), 5)) === Int
@test eltype(PoirierTarantola4th(Int8(1), 2 // 1, 3, Int16(4), 5)) === Rational{Int}
@test eltype(Vinet(Int8(1), 2, 3, Int16(4))) === Int
@test eltype(Vinet(Int8(1), 2 // 1, 3, Int16(4))) === Rational{Int}
@test eltype(AntonSchmidt(Int8(1), 2, 3, 0)) === Int
@test eltype(AntonSchmidt(Int8(1), 2 // 1, 3, 0)) === Rational{Int}
@test_throws InexactError PoirierTarantola3rd{BigInt}(41, 1 // 2, 4)
@test_throws InexactError PoirierTarantola3rd{BigInt}(41, 1, 2.2)
end
@testset "Promoting with units" begin
@test Murnaghan1st(1u"angstrom^3", 2u"eV/angstrom^3", 3.0, 4u"eV") ===
Murnaghan1st(1.0u"angstrom^3", 2.0u"eV/angstrom^3", 3.0, 4.0u"eV")
@test Murnaghan1st(1u"angstrom^3", 2u"eV/nm^3", 3 // 2, 4u"eV") ===
Murnaghan1st((1 // 1)u"angstrom^3", (2 // 1)u"eV/nm^3", 3 // 2, (4 // 1)u"eV")
@test BirchMurnaghan2nd(1u"angstrom^3", 2u"eV/angstrom^3", 3.0u"J") ===
BirchMurnaghan2nd(1.0u"angstrom^3", 2.0u"eV/angstrom^3", 3.0u"J")
BirchMurnaghan2nd((1 // 1)u"pm^3", (2 // 1)u"eV/angstrom^3", (3 // 1)u"eV")
@test BirchMurnaghan3rd(1u"angstrom^3", 2u"GPa", 4.0, 3u"eV") ===
BirchMurnaghan3rd(1.0u"angstrom^3", 2.0u"GPa", 4.0, 3.0u"eV")
@test BirchMurnaghan3rd(1u"angstrom^3", 2u"GPa", 4 // 1, 3u"eV") ===
BirchMurnaghan3rd(
(1 // 1)u"angstrom^3",
(2 // 1)u"GPa",
4 // 1,
(3 // 1)u"eV",
)
@test BirchMurnaghan4th(1u"nm^3", 2u"GPa", 3.0, 4u"GPa^-1", 5u"eV") ===
BirchMurnaghan4th(1.0u"nm^3", 2.0u"GPa", 3.0, 4.0u"GPa^-1", 5.0u"eV")
@test BirchMurnaghan4th(1u"nm^3", 2u"GPa", 3 // 1, 4u"1/GPa", 5u"J") ===
BirchMurnaghan4th(
(1 // 1)u"nm^3",
(2 // 1)u"GPa",
3 // 1,
(4 // 1)u"1/GPa",
(5 // 1)u"J",
)
@test PoirierTarantola2nd(1u"pm^3", 2u"GPa", 3.0u"eV") ===
PoirierTarantola2nd(1.0u"pm^3", 2.0u"GPa", 3.0u"eV")
@test PoirierTarantola2nd(1u"nm^3", 2u"GPa", (3 // 1)u"eV") ===
PoirierTarantola2nd((1 // 1)u"nm^3", (2 // 1)u"GPa", (3 // 1)u"eV")
@test PoirierTarantola3rd(1u"nm^3", 2u"GPa", 3, 4.0u"eV") ===
PoirierTarantola3rd(1.0u"nm^3", 2.0u"GPa", 3, 4.0u"eV")
@test PoirierTarantola3rd(1u"nm^3", 2u"GPa", 3, (4 // 1)u"eV") ===
PoirierTarantola3rd((1 // 1)u"nm^3", (2 // 1)u"GPa", 3 // 1, (4 // 1)u"eV")
@test PoirierTarantola4th(1u"nm^3", 2u"GPa", 3, 1 / 0.25u"Pa", 5.0u"eV") ===
PoirierTarantola4th(1.0u"nm^3", 2.0u"GPa", 3.0, 4.0u"1/Pa", 5.0u"eV")
@test PoirierTarantola4th(1u"nm^3", 2u"GPa", 3 // 1, 4u"GPa^(-1)", 5u"eV") ===
PoirierTarantola4th(
(1 // 1)u"nm^3",
(2 // 1)u"GPa",
3 // 1,
(4 // 1)u"GPa^(-1)",
(5 // 1)u"eV",
)
@test Vinet(1u"nm^3", 2u"GPa", 3, 4.0u"eV") ===
Vinet(1.0u"nm^3", 2.0u"GPa", 3.0, 4.0u"eV")
@test Vinet(1u"nm^3", 2u"GPa", 3, (4 // 1)u"eV") ===
Vinet((1 // 1)u"nm^3", (2 // 1)u"GPa", 3 // 1, (4 // 1)u"eV")
@test AntonSchmidt(1u"nm^3", 2u"GPa", 3.0, 4u"eV") ===
AntonSchmidt(1.0u"nm^3", 2.0u"GPa", 3.0, 4.0u"eV")
@test AntonSchmidt(1u"nm^3", 2u"GPa", 3 // 1, 4u"eV") ===
AntonSchmidt((1 // 1)u"nm^3", (2 // 1)u"GPa", 3 // 1, (4 // 1)u"eV")
# @test BreenanStacey(1u"nm^3", 2u"GPa", 3.0, 0u"eV") ===
# BreenanStacey{Quantity{Float64}}
# @test BreenanStacey(1u"nm^3", 2u"GPa", 3 // 1, 0u"eV") ===
# BreenanStacey{Quantity{Rational{Int}}}
@test BirchMurnaghan3rd(1u"angstrom^3", 2u"GPa", 4 // 1, 3u"eV").b′0 isa
DimensionlessQuantity
@test AntonSchmidt(1u"nm^3", 2u"GPa", 3.0, 4u"eV").b′0 isa DimensionlessQuantity
end
end
@testset "Parameter `e0` and promotion" begin
@test Murnaghan1st(1, 2, 3.0) === Murnaghan1st(1.0, 2.0, 3.0, 0.0)
@test BirchMurnaghan2nd(1, 2.0) === BirchMurnaghan2nd(1.0, 2.0, 0.0)
@test BirchMurnaghan3rd(1, 2, 3.0) === BirchMurnaghan3rd(1.0, 2.0, 3.0, 0.0)
@test BirchMurnaghan4th(1, 2.0, 3, 4) === BirchMurnaghan4th(1.0, 2.0, 3.0, 4.0, 0.0)
@test Vinet(1, 2, 3.0) === Vinet(1.0, 2.0, 3.0, 0.0)
@test PoirierTarantola2nd(1, 2.0) === PoirierTarantola2nd(1.0, 2.0, 0.0)
@test PoirierTarantola3rd(1, 2, 3.0) === PoirierTarantola3rd(1.0, 2.0, 3.0, 0.0)
@test PoirierTarantola4th(1, 2, 3, 4) === PoirierTarantola4th(1, 2, 3, 4, 0)
@test AntonSchmidt(1, 2, 3.0) === AntonSchmidt(1.0, 2.0, 3.0, 0.0)
# @test BreenanStacey(1, 2, 3.0) === BreenanStacey(1.0, 2.0, 3.0, 0.0)
@test eltype(Murnaghan1st(1u"angstrom^3", 2u"eV/angstrom^3", 3)) === Quantity{Int}
@test eltype(Murnaghan1st(1u"angstrom^3", 2u"eV/angstrom^3", 3.0)) === Quantity{Float64}
@test eltype(BirchMurnaghan2nd(1u"nm^3", 2u"GPa")) === Quantity{Int}
@test eltype(BirchMurnaghan2nd(1u"nm^3", 2.0u"GPa")) === Quantity{Float64}
@test eltype(BirchMurnaghan3rd(1u"nm^3", 2u"GPa", 4)) === Quantity{Int}
@test eltype(BirchMurnaghan3rd(1u"nm^3", 2u"GPa", 4.0)) === Quantity{Float64}
@test eltype(BirchMurnaghan4th(1u"nm^3", 2u"GPa", 3, 4u"1/GPa")) === Quantity{Int}
@test eltype(BirchMurnaghan4th(1u"nm^3", 2u"GPa", 3, 4.0u"1/GPa")) === Quantity{Float64}
@test eltype(PoirierTarantola2nd(1u"nm^3", 2u"GPa")) === Quantity{Int}
@test eltype(PoirierTarantola2nd(1u"nm^3", 2.0u"GPa")) === Quantity{Float64}
@test eltype(PoirierTarantola3rd(1u"nm^3", 2u"GPa", 3)) === Quantity{Int}
@test eltype(PoirierTarantola3rd(1u"nm^3", 2u"GPa", 3.0)) === Quantity{Float64}
@test eltype(PoirierTarantola4th(1u"nm^3", 2u"GPa", 3, 4u"1/GPa")) === Quantity{Int}
@test eltype(PoirierTarantola4th(1u"nm^3", 2u"GPa", 3, 4.0u"1/GPa")) ===
Quantity{Float64}
@test eltype(Vinet(1u"nm^3", 2u"GPa", 3)) === Quantity{Int}
@test eltype(Vinet(1u"nm^3", 2u"GPa", 3.0)) === Quantity{Float64}
@test eltype(AntonSchmidt(1u"nm^3", 2u"GPa", 3)) === Quantity{Int}
@test eltype(AntonSchmidt(1u"nm^3", 2u"GPa", 3.0)) === Quantity{Float64}
#@test eltype(BreenanStacey(1u"nm^3", 2u"GPa", 3))
#@test eltype(BreenanStacey(1u"nm^3", 2u"GPa", 3.0)
end
@testset "Constructors" begin
@test_throws ArgumentError Murnaghan(1, 2, 3.0)
@test_throws ArgumentError Murnaghan(1, 2, 3.0, 4, 5 // 1, Int32(6))
@test Murnaghan(1, 2, 3.0, 4) === Murnaghan1st(1.0, 2.0, 3.0, 4.0)
@test Murnaghan(1u"angstrom^3", 2u"eV/angstrom^3", 3.0, 4u"eV") ===
Murnaghan1st(1.0u"angstrom^3", 2.0u"eV/angstrom^3", 3.0, 4.0u"eV")
@test_throws ArgumentError BirchMurnaghan(1, 2)
@test BirchMurnaghan(1, 2 // 1, 3.0) === BirchMurnaghan2nd(1.0, 2.0, 3.0)
@test BirchMurnaghan(1, 2, 3.0, 4) === BirchMurnaghan3rd(1.0, 2.0, 3.0, 4.0)
@test BirchMurnaghan(1, 2, 3.0, 4, Int32(5)) ===
BirchMurnaghan4th(1.0, 2.0, 3.0, 4.0, 5.0)
@test BirchMurnaghan(1u"angstrom^3", 2u"eV/angstrom^3", 3.0, 4u"eV") ===
BirchMurnaghan3rd(1.0u"angstrom^3", 2.0u"eV/angstrom^3", 3.0, 4.0u"eV")
@test_throws ArgumentError PoirierTarantola(1, 2)
@test PoirierTarantola(1, 2 // 1, 3.0) === PoirierTarantola2nd(1.0, 2.0, 3.0)
@test PoirierTarantola(1, 2, 3.0, 4) === PoirierTarantola3rd(1.0, 2.0, 3.0, 4.0)
@test PoirierTarantola(1, 2, 3.0, 4, Int32(5)) ===
PoirierTarantola4th(1.0, 2.0, 3.0, 4.0, 5.0)
@test PoirierTarantola(1u"angstrom^3", 2u"eV/angstrom^3", 3.0, 4u"eV") ===
PoirierTarantola3rd(1.0u"angstrom^3", 2.0u"eV/angstrom^3", 3.0, 4.0u"eV")
end
@testset "`float` on an EOS" begin
@test eltype(float(Vinet(1, 2, 3))) === Float64
@test eltype(float(Vinet(1u"nm^3", 2u"GPa", 3))) === Quantity{Float64}
@test eltype(float(Murnaghan1st(big(2), 3, 4, 5))) === BigFloat
end
@testset "Other element types" begin
@test eltype(
BirchMurnaghan4th(measurement("1 +- 0.1"), 3 // 1, 2, measurement("-123.4(56)")),
) === Measurement{Float64}
@testset "`SymEngine.Basic`" begin
v0, b0, b′0, b″0, e0 = symbols("v0, b0, b′0, b″0, e0")
@test eltype(BirchMurnaghan4th(v0, b0, b′0, b″0, e0)) === Basic
@test eltype(BirchMurnaghan4th(v0, b0, b′0, b″0)) === Basic
@test iszero(BirchMurnaghan4th(v0, b0, b′0, b″0).e0)
end
end
@testset "Test equality" begin
@test BirchMurnaghan3rd(1, 2, 3, 4) == BirchMurnaghan3rd(1.0, 2.0, 3.0, 4.0)
@test BirchMurnaghan3rd(1 // 1, 2 // 1, 6 // 2, 12 // 3) ==
BirchMurnaghan3rd(1.0, 2.0, 3.0, 4.0)
@test BirchMurnaghan3rd(1u"angstrom^3", 2u"GPa", 3) ==
BirchMurnaghan3rd(1.0u"angstrom^3", 2.0u"GPa", 3.0)
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | code | 148 | using EquationsOfStateOfSolids
using Test
@testset "EquationsOfStateOfSolids.jl" begin
include("collections.jl")
include("Fitting.jl")
end
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 3531 | <div align="center">
<img src="./docs/src/assets/logo.png" height="200"><br>
</div>
# EquationsOfStateOfSolids
[](https://MineralsCloud.github.io/EquationsOfStateOfSolids.jl/stable)
[](https://MineralsCloud.github.io/EquationsOfStateOfSolids.jl/dev)
[](https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl/actions)
[](https://gitlab.com/singularitti/equationsofstateofsolids.jl/-/pipelines)
[](https://ci.appveyor.com/project/singularitti/EquationsOfStateOfSolids-jl)
[](https://cirrus-ci.com/github/MineralsCloud/EquationsOfStateOfSolids.jl)
[](https://codecov.io/gh/MineralsCloud/EquationsOfStateOfSolids.jl)
[](https://JuliaCI.github.io/NanosoldierReports/pkgeval_badges/report.html)
[](https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl/blob/master/LICENSE)
This package implements some _equations of state_ (EOS) of solids which are
useful in research. It currently includes:
1. `Murnaghan1st` EOS
2. Birch–Murnaghan EOS family:
1. `BirchMurnaghan2nd`
2. `BirchMurnaghan3rd`
3. `BirchMurnaghan4th`
3. `Vinet` EOS
4. Poirier–Tarantola EOS family:
1. `PoirierTarantola2nd`
2. `PoirierTarantola3rd`
The formulae are referenced from Ref. 1.
This package also includes linear and nonlinear fitting methods, also referenced
from Ref. 1.
See its
[documentation](https://mineralscloud.github.io/EquationsOfStateOfSolids.jl/stable).
## Compatibility
- [Julia version: above `v1.0.0`](https://julialang.org/downloads/)
- Dependencies:
- [`StructHelpers.jl`](https://github.com/jw3126/StructHelpers.jl) `v0.1.0` and above
- [`ConstructionBase.jl`](https://github.com/JuliaObjects/ConstructionBase.jl) `v1.0` and above
- [`EquationsOfState.jl`](https://github.com/MineralsCloud/EquationsOfState.jl) `v4.0.0` and above
- [`LsqFit.jl`](https://github.com/JuliaNLSolvers/LsqFit.jl) `v0.8.0` and above
- [`PolynomialRoots.jl`](https://github.com/giordano/PolynomialRoots.jl) `v1.0.0` and above
- [`Polynomials.jl`](https://github.com/JuliaMath/Polynomials.jl) `v0.8.0` and above
- [`Roots.jl`](https://github.com/JuliaMath/Roots.jl) `v0.8.0` and above
- [`UnPack.jl`](https://github.com/mauro3/UnPack.jl) `v1.0.0` and above
- [`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl) `v0.18.0` and above
- OS: macOS, Linux, Windows, and FreeBSD
- Architecture: x86, x64, ARM
## References
1. [A. Otero-De-La-Roza, V. Luaña, _Comput. Phys. Commun._ **182**, 1708–1720 (2011).](https://www.sciencedirect.com/science/article/pii/S0010465511001470)
2. [R. J. Angel, M. Alvaro, J. Gonzalez-Platas, *Zeitschrift Für Kristallographie - Cryst Mater*. **229**, 405–419 (2014).](https://www.degruyter.com/document/doi/10.1515/zkri-2013-1711/html)
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 759 | ---
name: Bug report
about: Create a report to help us improve
title: ''
labels: bug
assignees: singularitti
---
**Describe the bug**
A clear and concise description of what the bug is.
**To Reproduce**
Steps to reproduce the behavior:
1. Go to '...'
2. Click on '....'
3. Scroll down to '....'
4. See error
5. Run code
```julia
julia> using Pkg
```
**Expected behavior**
A clear and concise description of what you expected to happen.
**Screenshots**
If applicable, paste screenshots to help explain your problem.
**Desktop (please complete the following information):**
- OS: [e.g. macOS 10.14.6]
- Julia version: [e.g. 1.0.4, 1.1.1]
- Package version: [e.g. 2.0.0]
**Additional context**
Add any other context about the problem here.
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 614 | ---
name: Feature request
about: Suggest an idea for this project
title: ''
labels: enhancement
assignees: singularitti
---
**Is your feature request related to a problem? Please describe.**
A clear and concise description of what the problem is. Ex. I'm always frustrated when [...]
**Describe the solution you'd like**
A clear and concise description of what you want to happen.
**Describe alternatives you've considered**
A clear and concise description of any alternative solutions or features you've considered.
**Additional context**
Add any other context or screenshots about the feature request here.
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 1397 | # How to contribute
## Download the project
Similar to section "[Installation](@ref)", run
```julia
julia> using Pkg
julia> pkg"dev EquationsOfStateOfSolids"
```
in Julia REPL.
Then the package will be cloned to your local machine at a path. On macOS, by default is
located at `~/.julia/dev/EquationsOfStateOfSolids` unless you modify the `JULIA_DEPOT_PATH`
environment variable. (See [Julia's official documentation](http://docs.julialang.org/en/v1/manual/environment-variables/#JULIA_DEPOT_PATH-1)
on how to do this.) In the following text, we will call it `PKGROOT`.
## [Instantiate the project](@id instantiating)
Go to `PKGROOT`, start a new Julia session and run
```julia
julia> using Pkg; Pkg.instantiate()
```
## How to build docs
Usually, the up-to-state doc is available in
[here](https://MineralsCloud.github.io/EquationsOfStateOfSolids.jl/dev), but there are cases
where users need to build the doc themselves.
After [instantiating](@ref) the project, go to `PKGROOT`, run (without the `$` prompt)
```bash
$ julia --color=yes docs/make.jl
```
in your terminal. In a while a folder `PKGROOT/docs/build` will appear. Open
`PKGROOT/docs/build/index.html` with your favorite browser and have fun!
## How to run tests
After [instantiating](@ref) the project, go to `PKGROOT`, run (without the `$` prompt)
```bash
$ julia --color=yes test/runtests.jl
```
in your terminal.
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 1104 | # FAQ
## How to make a `Vector` from a `Parameters`?
A suggested way is to use the
[`IterTools.fieldvalues` function](https://juliacollections.github.io/IterTools.jl/latest/index.html#IterTools.fieldvalues):
```julia
julia> using IterTools
julia> eos = BirchMurnaghan4th(1, 2.0, 3, 4)
BirchMurnaghan4th{Float64}
v0 = 1.0
b0 = 2.0
b′0 = 3.0
b″0 = 4.0
e0 = 0.0
julia> collect(fieldvalues(eos))
5-element Array{Float64,1}:
1.0
2.0
3.0
4.0
0.0
```
It is lazy and fast.
Or to write a non-lazy version of `fieldvalues` manually:
```julia
julia> fieldvalues(eos::EquationOfState) = [getfield(eos, i) for i in 1:nfields(eos)]
fieldvalues (generic function with 1 method)
julia> fieldvalues(eos)
5-element Array{Float64,1}:
1.0
2.0
3.0
4.0
0.0
```
It is slower than `IterTools.fieldvalues`. Use it with care.
## `linfit` does not work with `BigFloat`?
`LinearAlgebra` by default does not support SVD for matrices with `BigFloat`
elements. You need to install
[`GenericSVD.jl`](https://github.com/JuliaLinearAlgebra/GenericSVD.jl) first
then `using GenericSVD`. And then it should work.
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 2463 | ```@meta
CurrentModule = EquationsOfStateOfSolids
```
# EquationsOfStateOfSolids
Documentation for [EquationsOfStateOfSolids](https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl).
## Package Features
- Calculate energy, pressure, and bulk modulus of an EOS `Parameters` on a (an)
volume (array of volumes).
- Fit an `EquationOfState` on a series of volumes using least-squares fitting
method.
- Fit an `EquationOfState` on a series of volumes linearly.
- Find the corresponding volume of an EOS `Parameters` given an (a) energy,
pressure, and bulk modulus.
- Handle unit conversion automatically in the above features, take any unit.
See the [Index](@ref main-index) for the complete list of documented functions
and types.
The old [`EquationsOfState.jl`](https://github.com/MineralsCloud/EquationsOfState.jl)
package has been superseded by `EquationsOfStateOfSolids.jl`.
So please just use `EquationsOfStateOfSolids.jl`.
The code is [hosted on GitHub](https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl),
with some continuous integration services to test its validity.
This repository is created and maintained by [singularitti](https://github.com/singularitti).
You are very welcome to contribute.
## Compatibility
- [Julia version: above `v1.0.0`](https://julialang.org/downloads/)
- Dependencies:
- [`StructHelpers.jl`](https://github.com/jw3126/StructHelpers.jl) `v0.1.0` and above
- [`ConstructionBase.jl`](https://github.com/JuliaObjects/ConstructionBase.jl) `v1.0` and above
- [`EquationsOfState.jl`](https://github.com/MineralsCloud/EquationsOfState.jl) `v4.0.0` and above
- [`LsqFit.jl`](https://github.com/JuliaNLSolvers/LsqFit.jl) `v0.8.0` and above
- [`PolynomialRoots.jl`](https://github.com/giordano/PolynomialRoots.jl) `v1.0.0` and above
- [`Polynomials.jl`](https://github.com/JuliaMath/Polynomials.jl) `v0.8.0` and above
- [`Roots.jl`](https://github.com/JuliaMath/Roots.jl) `v0.8.0` and above
- [`UnPack.jl`](https://github.com/mauro3/UnPack.jl) `v1.0.0` and above
- [`Unitful.jl`](https://github.com/PainterQubits/Unitful.jl) `v0.18.0` and above
- OS: macOS, Linux, Windows, and FreeBSD
- Architecture: x86, x64, ARM
## Manual Outline
```@contents
Pages = [
"installation.md",
"develop.md",
"portability.md",
"interoperability.md",
"plotting.md",
"faq.md",
"api/collections.md",
"api/fitting.md",
]
Depth = 3
```
## [Index](@id main-index)
```@index
```
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 2457 | # Installation
## Install Julia
First, you should install Julia. We recommend downloading it from
[its official website](https://julialang.org/downloads/). Versions higher than `v1.3`,
especially `v1.6`, are strongly recommended. This package may not work on `v0.7` and below.
Please follow the detailed instructions on its website if you have to
[build Julia from source](https://github.com/JuliaLang/julia/blob/master/doc/build/build.md).
Some computing centers provide preinstalled Julia. Please contact your administrator for
more information in that case.
If you have [Homebrew](https://brew.sh) installed, open
`Terminal.app` and type
```shell
$ brew install --cask julia # on macOS
```
or
```shell
$ brew install julia # on other operating systems
```
If you want to install multiple Julia versions in the same operating system,
a suggested way is to use a version manager such as
[`asdf`](https://asdf-vm.com/guide/introduction.html).
First, [install `asdf`](https://asdf-vm.com/guide/getting-started.html#_3-install-asdf).
Then, run
```shell
$ asdf install julia 1.6.2 # or other versions of Julia
$ asdf global julia 1.6.2
```
to install Julia and
[set `v1.6.2` as a global version](https://asdf-vm.com/guide/getting-started.html#_6-set-a-version).
## Install `EquationsOfStateOfSolids`
Now I am using [macOS](https://en.wikipedia.org/wiki/MacOS) as a standard
platform to explain the following steps:
1. Open `Terminal.app`, and type `julia` to start an interactive session (known as
[REPL](https://docs.julialang.org/en/v1/stdlib/REPL/)).
2. Run the following commands and wait for them to finish:
```julia
julia> using Pkg; Pkg.update()
julia> Pkg.add("EquationsOfStateOfSolids")
```
3. Run
```julia
julia> using EquationsOfStateOfSolids
```
and have fun!
4. While using, please keep this Julia session alive. Restarting might recompile
the package and cost some time.
If you want to install the latest in development (maybe buggy) version of `EquationsOfStateOfSolids`, type
```julia
julia> using Pkg; Pkg.update()
julia> pkg"add EquationsOfStateOfSolids#master"
```
in the second step instead.
## Uninstall and reinstall `EquationsOfStateOfSolids`
1. To uninstall, in a Julia session, run
```julia
julia> Pkg.rm("EquationsOfStateOfSolids"); Pkg.gc()
```
2. Press `ctrl+d` to quit the current session. Start a new Julia session and
reinstall `EquationsOfStateOfSolids`.
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 2196 | # How to use `EquationsOfStateOfSolids` in Python?
It may be attempting for [Pythonistas](https://en.wiktionary.org/wiki/Pythonista)
to use this package in Python, without
writing too much code. Luckily, Julia provides such a feature.
1. First, install [`PyCall.jl`](https://github.com/JuliaPy/PyCall.jl), following their [instructions](https://github.com/JuliaPy/PyCall.jl/blob/master/README.md). Notice on macOS, that if you want to install Python from [`pyenv`](https://github.com/pyenv/pyenv), you may need to run
```shell
env PYTHON_CONFIGURE_OPTS="--enable-framework" pyenv install 3.6.9
```
in terminal to install your `python`, or else Julia will throw an
```julia
ImportError: No module named site
```
See [this issue](https://github.com/JuliaPy/PyCall.jl/issues/122) and [another issue](https://github.com/JuliaPy/PyCall.jl/issues/597) for details.
2. Install [`PyJulia`](https://pyjulia.readthedocs.io/en/stable/index.html) in Python. Please see [its official tutorial](https://pyjulia.readthedocs.io/en/stable/installation.html#step-2-install-pyjulia) for instructions.
3. Open a (an) Python (IPython) session, start playing!
```python
In [1]: from julia import Unitful
In [2]: from julia.EquationsOfStateOfSolids import *
In [3]: from julia.EquationsOfStateOfSolids.Fitting import *
In [4]: Murnaghan(1, 2, 3.0, 4)
Out[4]: <PyCall.jlwrap EquationsOfStateOfSolids.Murnaghan1st{Float64}(1.0, 2.0, 3.0, 4.0)>
In [5]: result = nonlinfit(
...: PressureEquation(BirchMurnaghan3rd(1, 2, 3.0, 0)),
...: [1, 2, 3, 4, 5],
...: [5, 6, 9, 8, 7],
...: )
In [6]: result.v0, result.b0, result.b′0
Out[6]: (1.1024687826913997, 29.308616965851673, 12.689089874230556)
In [7]: from julia import Main
In [8]: volumes = Main.eval("data[:, 1] .* u\"bohr^3\"")
In [9]: energies = Main.eval("data[:, 2] .* u\"Ry\"")
```
where `data` is copied from Julia:
```python
In [1]: data = Main.eval("""
...: [
...: 159.9086 -323.4078898
⋮ ⋮
...: 319.8173 -323.4105393
...: ]
...: """
...: )
```
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 888 | # Plotting
Package
[`EquationOfStateRecipes.jl`](https://github.com/MineralsCloud/EquationOfStateRecipes.jl)
provides some default themes for plotting an `EquationOfStateOfSolids`.
First, try to install the [`Plots.jl`](https://github.com/JuliaPlots/Plots.jl) package by
```julia
julia> using Pkg
julia> Pkg.add("Plots")
julia> using Plots
```
Then install `EquationOfStateRecipes.jl` with
```julia
julia> Pkg.add("EquationOfStateRecipes")
julia> using EquationOfStateRecipes
```
Finally, load `EquationsOfStateOfSolids.jl` and plot:
```julia
julia> using EquationsOfStateOfSolids
julia> eos = EnergyEquation(Murnaghan(224.501825u"bohr^3", 8.896845u"GPa", 3.723835, -323.417686u"Ry"));
julia> plot(eos)
julia> plot!(eos, (0.8:0.01:1.2) * eos.param.v0)
julia> scatter!(eos, (0.5:0.1:1) * eos.param.v0)
```
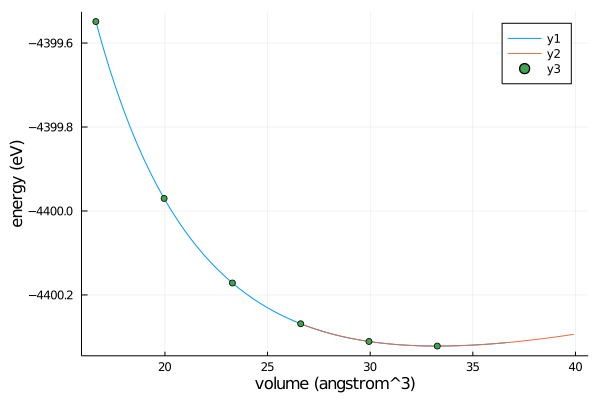
Have fun!
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 1908 | # How to make your data portable?
After an equation-of-state-fitting, for instance, you want to save the returned
`EquationsOfStateOfSolids` to share with a colleague or for future use. Julia provides
several ways to do this. Below I will list one recommended way: saving it to
a JLD format by [`JLD2.jl`](https://github.com/JuliaIO/JLD2.jl) package.
> JLD is a specific "dialect" of HDF5, a cross-platform, multi-language data storage format most frequently used for scientific data.
1. Install [`JLD2.jl`](https://github.com/JuliaIO/JLD2.jl) and
[`FileIO.jl`](https://github.com/JuliaIO/FileIO.jl) packages.
```julia
julia> using Pkg
julia> Pkg.add("FileIO"); Pkg.add("JLD2")
```
2. Create some `EquationsOfStateOfSolids`s:
```julia
julia> using EquationsOfStateOfSolids, Unitful, UnitfulAtomic
julia> m = Murnaghan(224.501825, 0.00060479524074699499, 3.723835, -323.417686);
julia> bm = BirchMurnaghan3rd(224.4445656763778u"bohr^3", 9.194980249913018u"GPa", 3.7403684211716297, -161.70885710742223u"hartree");
```
3. Save them to file `"eos.jld2"`:
```julia
julia> using JLD2, FileIO
julia> @save "/some/path/eos.jld2" m bm
```
4. On another computer, or some days later, load them into REPL:
```julia
julia> using EquationsOfStateOfSolids, Unitful, UnitfulAtomic
julia> @load "/some/path/eos.jld2" m bm
```
Now variables `m` and `bm` represent the original `Parameters`:
```julia
julia> m.b0
0.000604795240746995
julia> m.b′0
3.723835
julia> bm.v0
224.4445656763778 a₀^3
julia> bm.b0
9.194980249913018 GPa
```
For more details on the JLD format, please refer to
[`JLD.jl`'s doc](https://github.com/JuliaIO/JLD.jl/blob/master/doc/jld.md),
[`JLD2.jl`'s doc](https://github.com/JuliaIO/JLD2.jl/blob/master/README.md) or
[this discussion](https://discourse.julialang.org/t/jld-jl-vs-jld2-jl/15287).
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 7082 | ```@meta
CurrentModule = EquationsOfStateOfSolids
```
# Collections
```@contents
Pages = ["collections.md"]
Depth = 3
```
The current `Parameters`s contain
```
EquationsOfState.EquationOfStateOfSolidsParameters
├─ EquationsOfStateOfSolids.AntonSchmidt
├─ EquationsOfStateOfSolids.FiniteStrainParameters
│ ├─ BirchMurnaghan
│ │ ├─ BirchMurnaghan2nd
│ │ ├─ BirchMurnaghan3rd
│ │ └─ BirchMurnaghan4th
│ └─ PoirierTarantola
│ ├─ EquationsOfStateOfSolids.PoirierTarantola4th
│ ├─ PoirierTarantola2nd
│ └─ PoirierTarantola3rd
├─ EquationsOfStateOfSolids.Holzapfel
├─ Murnaghan
│ ├─ EquationsOfStateOfSolids.Murnaghan2nd
│ └─ Murnaghan1st
└─ Vinet
```
Here the leaves of the type tree are concrete types and can be constructed.
## Usage
### Construct a `Parameters` instance
We will use `BirchMurnaghan3rd` as an example.
A `BirchMurnaghan3rd` can be constructed from scratch, as shown above. It can
also be constructed from an existing `BirchMurnaghan3rd`, with
[`Setfield.jl`](https://github.com/jw3126/Setfield.jl)
[`@set!`](https://jw3126.github.io/Setfield.jl/stable/#Setfield.@set!-Tuple{Any})
macro:
```julia
julia> using Setfield
julia> eos = Murnaghan(1, 2, 3.0)
Murnaghan{Float64}(1.0, 2.0, 3.0, 0.0)
julia> @set! eos.v0 = 4
Murnaghan{Float64}(4.0, 2.0, 3.0, 0.0)
julia> eos
Murnaghan{Float64}(4.0, 2.0, 3.0, 0.0)
```
To modify multiple fields (say, `:v0`, `:b′0`, `:b′′0`, `:e0`) at a time, use
[`@batchlens`](https://tkf.github.io/Kaleido.jl/stable/#Kaleido.@batchlens) from
[`Kaleido.jl`](https://github.com/tkf/Kaleido.jl):
```julia
julia> using Setfield, Kaleido
julia> lens = @batchlens(begin
_.v0
_.b′0
_.b″0
_.e0
end)
IndexBatchLens(:v0, :b′0, :b″0, :e0)
julia> eos = BirchMurnaghan4th(1, 2.0, 3, 4)
BirchMurnaghan4th{Float64}(1.0, 2.0, 3.0, 4.0, 0.0)
julia> set(eos, lens, (5, 6, 7, 8))
BirchMurnaghan4th{Float64}(5.0, 2.0, 6.0, 7.0, 8.0)
```
Users can access `BirchMurnaghan3rd`'s elements by "dot notation":
```julia
julia> eos = BirchMurnaghan3rd(1, 2, 3, 4.0)
4-element BirchMurnaghan3rd{Float64}:
1.0
2.0
3.0
4.0
julia> eos.v0
1.0
```
### Evaluate energy
The $E(V)$ relation of equations of state are listed as below:
1. `Murnaghan`:
```math
E(V) = E_{0}+K_{0} V_{0}\left[\frac{1}{K_{0}^{\prime}\left(K_{0}^{\prime}-1\right)}\left(\frac{V}{V_{0}}\right)^{1-K_{0}^{\prime}}+\frac{1}{K_{0}^{\prime}} \frac{V}{V_{0}}-\frac{1}{K_{0}^{\prime}-1}\right].
```
2. `BirchMurnaghan2nd`:
```math
E(V) = E_{0} + \frac{9}{8} B_{0} V_{0} \left(\left( V / V_0 \right)^{-2 / 3}-1\right)^{2}.
```
3. `BirchMurnaghan3rd`:
```math
E(V) = E_{0}+\frac{9}{16} V_{0} B_{0} \frac{\left(x^{2 / 3}-1\right)^{2}}{x^{7 / 3}}\left\{x^{1 / 3}\left(B_{0}^{\prime}-4\right)-x\left(B_{0}^{\prime}-6\right)\right\}.
```
where `x = V / V_0`, and
`f = \frac{ 1 }{ 2 } \bigg[ \bigg( \frac{ V_0 }{ V } \bigg)^{2/3} - 1 \bigg]`.
4. `BirchMurnaghan4th`:
```math
E(V) = E_{0}+\frac{3}{8} V_{0} B_{0} f^{2}\left[\left(9 H-63 B_{0}^{\prime}+143\right) f^{2}+12\left(B_{0}^{\prime}-4\right) f+12\right].
```
where `H = B_0 B_0'' + (B_0')^2`.
5. `PoirierTarantola2nd`:
```math
E(V) = E_{0}+\frac{1}{2} B_{0} V_{0} \ln ^{2} x.
```
6. `PoirierTarantola3rd`:
```math
E(V) = E_{0}+\frac{1}{6} B_{0} V_{0} \ln ^{2} x\left[\left(B_{0}^{\prime}+2\right) \ln x+3\right].
```
7. `PoirierTarantola4th`:
```math
E(V) = E_{0}+\frac{1}{24} B_{0} V_{0} \ln ^{2} x\left\{\left(H+3 B_{0}^{\prime}+3\right) \ln ^{2} x\right. \left.+4\left(B_{0}^{\prime}+2\right) \ln x+12\right\}.
```
where `H = B_0 B_0'' + (B_0')^2`.
8. `Vinet`:
```math
E(V) = E_{0}+\frac{9}{16} V_{0} B_{0} \frac{\left(x^{2 / 3}-1\right)^{2}}{x^{7 / 3}}\left\{x^{1 / 3}\left(B_{0}^{\prime}-4\right)-x\left(B_{0}^{\prime}-6\right)\right\}.
```
9. `AntonSchmidt`:
```math
E(V)=\frac{\beta V_{0}}{n+1}\left(\frac{V}{V_{0}}\right)^{n+1}\left[\ln \left(\frac{V}{V_{0}}\right)-\frac{1}{n+1}\right]+E_{\infty}.
```
### Evaluate pressure
The $P(V)$ relation of equations of state are listed as below:
1. `Murnaghan`:
```math
P(V) = \frac{B_{0}}{B_{0}^{\prime}}\left[\left(\frac{V_{0}}{V}\right)^{B_{0}^{\prime}}-1\right].
```
2. `BirchMurnaghan2nd`:
```math
P(V) = \frac{3}{2} B_{0}\left(x^{-7 / 3}-x^{-5 / 3}\right).
```
3. `BirchMurnaghan3rd`:
```math
P(V) = \frac{3}{8} B_{0} \frac{x^{2 / 3}-1}{x^{10 / 3}}\left\{3 B_{0}^{\prime} x-16 x-3 x^{1 / 3}\left(B_{0}^{\prime}-4\right)\right\}.
```
4. `BirchMurnaghan4th`:
```math
P(V) = \frac{1}{2} B_{0}(2 f+1)^{5 / 2}\left\{\left(9 H-63 B_{0}^{\prime}+143\right) f^{2}\right.\left.+9\left(B_{0}^{\prime}-4\right) f+6\right\}.
```
5. `PoirierTarantola2nd`:
```math
P(V) = -\frac{B_{0}}{x} \ln x.
```
6. `PoirierTarantola3rd`:
```math
P(V) = -\frac{B_{0} \ln x}{2 x}\left[\left(B_{0}^{\prime}+2\right) \ln x+2\right].
```
7. `PoirierTarantola4th`:
```math
P(V) = -\frac{B_{0} \ln x}{6 x}\left\{\left(H+3 B_{0}^{\prime}+3\right) \ln ^{2} x+3\left(B_{0}^{\prime}+6\right) \ln x+6\right\}.
```
8. `Vinet`:
```math
P(V) = 3 B_{0} \frac{1-\eta}{\eta^{2}} \exp \left\{-\frac{3}{2}\left(B_{0}^{\prime}-1\right)(\eta-1)\right\}.
```
9. `AntonSchmidt`:
```math
P(V) = -\beta\left(\frac{V}{V_{0}}\right)^{n} \ln \left(\frac{V}{V_{0}}\right).
```
### Evaluate bulk modulus
The $B(V)$ relation of equations of state are listed as below:
1. `BirchMurnaghan2nd`:
```math
B(V) = B_{0}(7 f+1)(2 f+1)^{5 / 2}.
```
2. `BirchMurnaghan3rd`:
```math
B(V) = B_{0}(2 f+1)^{5 / 2} \left\{ 1 + (3B_{0}^{\prime} - 5) f + \frac{ 27 }{ 2 }(B_{0}^{\prime} - 4) f^2 \right\}
```
3. `BirchMurnaghan4th`:
```math
B(V) = \frac{1}{6} B_{0}(2 f+1)^{5 / 2}\left\{\left(99 H-693 B_{0}^{\prime}+1573\right) f^{3}\right.\left.+\left(27 H-108 B_{0}^{\prime}+105\right) f^{2}+6\left(3 B_{0}^{\prime}-5\right) f+6\right\}.
```
4. `PoirierTarantola2nd`:
```math
B(V) = \frac{B_{0}}{x}(1-\ln x).
```
5. `PoirierTarantola3rd`:
```math
B(V) = -\frac{B_{0}}{2 x}\left[\left(B_{0}^{\prime}+2\right) \ln x(\ln x-1)-2\right].
```
6. `PoirierTarantola4th`:
```math
B(V) = -\frac{B_{0}}{6 x}\left\{\left(H+3 B_{0}^{\prime}+3\right) \ln ^{3} x-3\left(H+2 B_{0}^{\prime}+1\right) \ln ^{2} x\right.\left.-6\left(B_{0}^{\prime}+1\right) \ln x-6\right\}.
```
7. `Vinet`:
```math
B(V) = -\frac{B_{0}}{2 \eta^{2}}\left[3 \eta(\eta-1)\left(B_{0}^{\prime}-1\right)+2(\eta-2)\right]\times \exp \left\{-\frac{3}{2}\left(B_{0}^{\prime}-1\right)(\eta-1)\right\}.
```
8. `AntonSchmidt`:
```math
B(V) = \beta\left(\frac{V}{V_{0}}\right)^{n}\left[1+n \ln \frac{V}{V_{0}}\right].
```
## Public interfaces
```@docs
Murnaghan1st
BirchMurnaghan
BirchMurnaghan2nd
BirchMurnaghan3rd
BirchMurnaghan4th
PoirierTarantola
PoirierTarantola2nd
PoirierTarantola3rd
Vinet
EnergyEquation
PressureEquation
BulkModulusEquation
getparam
orderof
real
isreal
float
```
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.4.2 | 101ee1ca55db9b5bf4265613eac836af151b3f8f | docs | 3730 | ```@meta
CurrentModule = EquationsOfStateOfSolids.Fitting
```
# Nonlinear fitting
From Ref. 1,
> The equations of state depend nonlinearly on a collection of parameters,
> $E_0$, $V_0$, $B_0$, $B_0'$, ..., that represent physical properties of the
> solid at equilibrium and can, in principle, be obtained experimentally by
> independent methods. The use of a given analytical EOS may have significant
> influence on the results obtained, particularly because the parameters are far
> from being independent. The number of parameters has to be considered in
> comparing the goodness of fit of functional forms with different analytical
> flexibility. The possibility of using too many parameters, beyond what is
> physically justified by the information contained in the experimental data, is
> a serious aspect that deserves consideration.
In [`EquationsOfStateOfSolids`](https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl),
the nonlinear fitting is currently implemented by
[`LsqFit`](https://github.com/JuliaNLSolvers/LsqFit.jl), a small library that
provides basic least-squares fitting in pure Julia. It only utilizes the
_Levenberg–Marquardt algorithm_ for non-linear fitting. See its
[documentation](https://github.com/JuliaNLSolvers/LsqFit.jl/blob/master/README.md)
for more information.
## Usage
We provide API `nonlinfit` currently.
```julia
using EquationsOfStateOfSolids
using EquationsOfStateOfSolids.Fitting
volumes = [
25.987454833,
26.9045702104,
27.8430241908,
28.8029649591,
29.7848370694,
30.7887887064,
31.814968055,
32.8638196693,
33.9353435494,
35.0299842495,
36.1477417695,
37.2892088485,
38.4543854865,
39.6437162376,
40.857201102,
42.095136449,
43.3579668329,
44.6456922537,
45.9587572656,
47.2973100535,
48.6614988019,
50.0517680652,
51.4682660281,
52.9112890601,
54.3808371612,
55.8775030703,
57.4014349722,
58.9526328669,
];
energies = [
-7.63622156576,
-8.16831294894,
-8.63871612686,
-9.05181213218,
-9.41170988374,
-9.72238224345,
-9.98744832526,
-10.210309552,
-10.3943401353,
-10.5427238068,
-10.6584266073,
-10.7442240979,
-10.8027285713,
-10.8363890521,
-10.8474912964,
-10.838157792,
-10.8103477586,
-10.7659387815,
-10.7066179666,
-10.6339907853,
-10.5495538639,
-10.4546677714,
-10.3506386542,
-10.2386366017,
-10.1197772808,
-9.99504030111,
-9.86535084973,
-9.73155247952,
];
```
```julia
nonlinfit(EnergyEquation(BirchMurnaghan3rd(40, 0.5, 4, 0)), volumes, energies)
# BirchMurnaghan3rd{Float64}
# v0 = 40.98926572792904
# b0 = 0.5369258245610551
# b′0 = 4.178644231924164
# e0 = -10.84280390829923
nonlinfit(EnergyEquation(Murnaghan(41, 0.5, 4, 0)), volumes, energies)
# Murnaghan1st{Float64}
# v0 = 41.137579246216546
# b0 = 0.5144967654207855
# b′0 = 3.9123863218932553
# e0 = -10.836794510856276
nonlinfit(EnergyEquation(PoirierTarantola3rd(41, 0.5, 4, 0)), volumes, energies)
# PoirierTarantola3rd{Float64}
# v0 = 40.86770643566912
# b0 = 0.5667729960007934
# b′0 = 4.331688934950856
# e0 = -10.851486685029291
nonlinfit(EnergyEquation(Vinet(41, 0.5, 4, 0)), volumes, energies)
# Vinet{Float64}
# v0 = 40.91687567401044
# b0 = 0.5493839427843428
# b′0 = 4.305192949379345
# e0 = -10.846160810983534
```
Then 4 different equations of state will be fitted.
## Public interfaces
```@docs
linfit
nonlinfit
```
## References
1. [A. Otero-De-La-Roza, V. Luaña, _Computer Physics Communications_. **182**, 1708–1720 (2011), doi:10.1016/j.cpc.2011.04.016.](https://www.sciencedirect.com/science/article/pii/S0010465511001470)
| EquationsOfStateOfSolids | https://github.com/MineralsCloud/EquationsOfStateOfSolids.jl.git |
|
[
"MIT"
] | 0.2.1 | bfc6b52f75b4720581e3e49ae786da6764e65b6a | code | 334 | using BinaryProvider
using Pkg
tarball_url = "https://github.com/kdheepak/FIGletFonts/archive/v0.5.0.tar.gz"
hash = "39f46c840ba035ba3b52aebf46123e6eda7393a7a18c5e6e02fb68c8cb50a33d"
prefix = Prefix(@__DIR__)
!isdefined(Pkg, :Artifacts) && !isinstalled(tarball_url, hash, prefix=prefix) && install(tarball_url, hash, prefix=prefix)
| FIGlet | https://github.com/kdheepak/FIGlet.jl.git |
|
[
"MIT"
] | 0.2.1 | bfc6b52f75b4720581e3e49ae786da6764e65b6a | code | 609 | using Documenter, FIGlet, DocumenterMarkdown
cp(joinpath(@__DIR__, "../README.md"), joinpath(@__DIR__, "./src/index.md"), force=true, follow_symlinks=true)
makedocs(
sitename="FIGlet.jl documentation",
format = Markdown()
)
deploydocs(;
repo="github.com/kdheepak/FIGlet.jl",
deps = Deps.pip(
"mkdocs==0.17.5",
"mkdocs-material==2.9.4",
"python-markdown-math",
"pygments",
"pymdown-extensions",
),
make = () -> run(`mkdocs build`),
target = "site",
)
| FIGlet | https://github.com/kdheepak/FIGlet.jl.git |
|
[
"MIT"
] | 0.2.1 | bfc6b52f75b4720581e3e49ae786da6764e65b6a | code | 16306 | module FIGlet
import Base
using Pkg
if isdefined(Pkg, :Artifacts)
using Pkg.Artifacts
@eval fontsroot = artifact"fonts"
else
fontsroot = normpath(@__DIR__, "..", "deps")
end
const FONTSDIR = abspath(normpath(joinpath(fontsroot, "FIGletFonts-0.5.0", "fonts")))
const UNPARSEABLES = [
"nvscript.flf",
]
const DEFAULTFONT = "Standard"
abstract type FIGletError <: Exception end
"""
Width is not sufficient to print a character
"""
struct CharNotPrinted <: FIGletError end
"""
Font can't be located
"""
struct FontNotFoundError <: FIGletError
msg::String
end
Base.showerror(io::IO, e::FontNotFoundError) = print(io, "FontNotFoundError: $(e.msg)")
"""
Problem parsing a font file
"""
struct FontError <: FIGletError
msg::String
end
Base.showerror(io::IO, e::FontError) = print(io, "FontError: $(e.msg)")
"""
Color is invalid
"""
struct InvalidColorError <: FIGletError end
Base.@enum(Layout,
FullWidth = -1,
HorizontalSmushingRule1 = 1,
HorizontalSmushingRule2 = 2,
HorizontalSmushingRule3 = 4,
HorizontalSmushingRule4 = 8,
HorizontalSmushingRule5 = 16,
HorizontalSmushingRule6 = 32,
HorizontalFitting = 64,
HorizontalSmushing = 128,
VerticalSmushingRule1 = 256,
VerticalSmushingRule2 = 512,
VerticalSmushingRule3 = 1024,
VerticalSmushingRule4 = 2048,
VerticalSmushingRule5 = 4096,
VerticalFitting = 8192,
VerticalSmushing = 16384,
)
struct FIGletHeader
hardblank::Char
height::Int
baseline::Int
max_length::Int
old_layout::Int
comment_lines::Int
print_direction::Int
full_layout::Int
codetag_count::Int
function FIGletHeader(
hardblank,
height,
baseline,
max_length,
old_layout,
comment_lines,
print_direction=0,
full_layout=-2,
codetag_count=0,
args...,
)
length(args) >0 && @warn "Received unknown header attributes: `$args`."
if full_layout == -2
full_layout = old_layout
if full_layout == 0
full_layout = Int(HorizontalFitting)
elseif full_layout == -1
full_layout = 0
else
full_layout = ( full_layout & 63 ) | Int(HorizontalSmushing)
end
end
height < 1 && ( height = 1 )
max_length < 1 && ( max_length = 1 )
print_direction < 0 && ( print_direction = 0 )
# max_length += 100 # Give ourselves some extra room
new(hardblank, height, baseline, max_length, old_layout, comment_lines, print_direction, full_layout, codetag_count)
end
end
function FIGletHeader(
hardblank,
height::AbstractString,
baseline::AbstractString,
max_length::AbstractString,
old_layout::AbstractString,
comment_lines::AbstractString,
print_direction::AbstractString="0",
full_layout::AbstractString="-2",
codetag_count::AbstractString="0",
args...,
)
return FIGletHeader(
hardblank,
parse(Int, height),
parse(Int, baseline),
parse(Int, max_length),
parse(Int, old_layout),
parse(Int, comment_lines),
parse(Int, print_direction),
parse(Int, full_layout),
parse(Int, codetag_count),
args...,
)
end
struct FIGletChar
ord::Char
thechar::Matrix{Char}
end
struct FIGletFont
header::FIGletHeader
font_characters::Dict{Char,FIGletChar}
version::VersionNumber
end
Base.show(io::IO, ff::FIGletFont) = print(io, "FIGletFont(n=$(length(ff.font_characters)))")
function readmagic(io)
magic = read(io, 5)
magic[1:4] != UInt8['f', 'l', 'f', '2'] && throw(FontError("File is not a valid FIGlet Lettering Font format. Magic header values must start with `flf2`."))
magic[5] != UInt8('a') && @warn "File may be a FLF format but not flf2a."
return magic # File has valid FIGlet Lettering Font format magic header.
end
function readfontchar(io, ord, height)
s = readline(io)
width = length(s)-1
width == -1 && throw(FontError("Unable to find character `$ord` in FIGlet Font."))
thechar = Matrix{Char}(undef, height, width)
for (w, c) in enumerate(s)
w > width && break
thechar[1, w] = c
end
for h in 2:height
s = readline(io)
for (w, c) in enumerate(s)
w > width && break
thechar[h, w] = c
end
end
return FIGletChar(ord, thechar)
end
Base.show(io::IO, fc::FIGletChar) = print(io, "FIGletChar(ord='$(fc.ord)')")
function getfontpath(s::AbstractString)
name = s
if !isfile(name)
name = abspath(normpath(joinpath(FONTSDIR, name)))
if !isfile(name)
name = "$name.flf"
!isfile(name) && throw(FontNotFoundError("Cannot find font `$s`."))
end
end
return name
end
function readfont(s::AbstractString)
name = getfontpath(s)
font = open(name) do f
readfont(f)
end
return font
end
function readfont(io)
magic = readmagic(io)
header = split(readline(io))
fig_header = FIGletHeader(
header[1][1],
header[2:end]...,
)
for i in 1:fig_header.comment_lines
discard = readline(io)
end
fig_font = FIGletFont(
fig_header,
Dict{Char, FIGletChar}(),
v"2.0.0",
)
for c in ' ':'~'
fig_font.font_characters[c] = readfontchar(io, c, fig_header.height)
end
for c in ['Ä', 'Ö', 'Ü', 'ä', 'ö', 'ü', 'ß']
if bytesavailable(io) > 1
fig_font.font_characters[c] = readfontchar(io, c, fig_header.height)
end
end
while bytesavailable(io) > 1
s = readline(io)
strip(s) == "" && continue
s = split(s)[1]
c = if '-' in s
Char(-(parse(UInt16, strip(s, '-'))))
else
Char(parse(Int, s))
end
fig_font.font_characters[c] = readfontchar(io, c, fig_header.height)
end
return fig_font
end
function availablefonts(substring)
fonts = String[]
for (root, dirs, files) in walkdir(FONTSDIR)
for file in files
if !(file in UNPARSEABLES)
if occursin(lowercase(substring), lowercase(file)) || substring == ""
push!(fonts, replace(file, ".flf"=>""))
end
end
end
end
sort!(fonts)
return fonts
end
"""
availablefonts() -> Vector{String}
availablefonts(substring::AbstractString) -> Vector{String}
Returns all available fonts.
If `substring` is passed, returns available fonts that contain the case insensitive `substring`.
Example:
julia> availablefonts()
680-element Array{String,1}:
"1943____"
"1row"
⋮
"zig_zag_"
"zone7___"
julia> FIGlet.availablefonts("3d")
5-element Array{String,1}:
"3D Diagonal"
"3D-ASCII"
"3d"
"Henry 3D"
"Larry 3D"
julia>
"""
availablefonts() = availablefonts("")
raw"""
smushem(lch::Char, rch::Char, fh::FIGletHeader) -> Char
Given 2 characters, attempts to smush them into 1, according to
smushmode. Returns smushed character or '\0' if no smushing can be
done.
smushmode values are sum of following (all values smush blanks):
1: Smush equal chars (not hardblanks)
2: Smush '_' with any char in hierarchy below
4: hierarchy: "|", "/\", "[]", "{}", "()", "<>"
Each class in hier. can be replaced by later class.
8: [ + ] -> |, { + } -> |, ( + ) -> |
16: / + \ -> X, > + < -> X (only in that order)
32: hardblank + hardblank -> hardblank
"""
function smushem(lch::Char, rch::Char, fh::FIGletHeader)
smushmode = fh.full_layout
hardblank = fh.hardblank
right2left = fh.print_direction
lch==' ' && return rch
rch==' ' && return lch
# TODO: Disallow overlapping if the previous character or the current character has a width of 0 or 1
# if previouscharwidth < 2 || currcharwidth < 2 return '\0' end
if ( smushmode & Int(HorizontalSmushing::Layout) ) == 0 return '\0' end
if ( smushmode & 63 ) == 0
# This is smushing by universal overlapping.
# Ensure overlapping preference to visible characters.
if lch == hardblank return rch end
if rch == hardblank return lch end
# Ensures that the dominant (foreground) fig-character for overlapping is the latter in the user's text, not necessarily the rightmost character.
if right2left == 1 return lch end
# Catch all exceptions
return rch
end
if smushmode & Int(HorizontalSmushingRule6::Layout) != 0
if lch == hardblank && rch == hardblank return lch end
end
if lch == hardblank || rch == hardblank return '\0' end
if smushmode & Int(HorizontalSmushingRule1::Layout) != 0
if lch == rch return lch end
end
if smushmode & Int(HorizontalSmushingRule2::Layout) != 0
if lch == '_' && rch in "|/\\[]{}()<>" return rch end
if rch == '_' && lch in "|/\\[]{}()<>" return lch end
end
if smushmode & Int(HorizontalSmushingRule3::Layout) != 0
if lch == '|' && rch in "/\\[]{}()<>" return rch end
if rch == '|' && lch in "/\\[]{}()<>" return lch end
if lch in "/\\" && rch in "[]{}()<>" return rch end
if rch in "/\\" && lch in "[]{}()<>" return lch end
if lch in "[]" && rch in "{}()<>" return rch end
if rch in "[]" && lch in "{}()<>" return lch end
if lch in "{}" && rch in "()<>" return rch end
if rch in "{}" && lch in "()<>" return lch end
if lch in "()" && rch in "<>" return rch end
if rch in "()" && lch in "<>" return lch end
end
if smushmode & Int(HorizontalSmushingRule4::Layout) != 0
if lch == '[' && rch == ']' return '|' end
if rch == '[' && lch == ']' return '|' end
if lch == '{' && rch == '}' return '|' end
if rch == '{' && lch == '}' return '|' end
if lch == '(' && rch == ')' return '|' end
if rch == '(' && lch == ')' return '|' end
end
if smushmode & Int(HorizontalSmushingRule5::Layout) != 0
if lch == '/' && rch == '\\' return '|' end
if rch == '/' && lch == '\\' return 'Y' end
# Don't want the reverse of below to give 'X'.
if lch == '>' && rch == '<' return 'X' end
end
return '\0'
end
function smushamount(current::Matrix{Char}, thechar::Matrix{Char}, fh::FIGletHeader)
smushmode = fh.full_layout
right2left = fh.print_direction
if (smushmode & (Int(HorizontalSmushing::Layout) | Int(HorizontalFitting::Layout)) == 0)
return 0
end
nrows_l, ncols_l = size(current)
_, ncols_r = size(thechar)
maximum_smush = ncols_r
smush = ncols_l
for row in 1:nrows_l
cl = '\0'
cr = '\0'
linebd = 0
charbd = 0
if right2left == 1
if maximum_smush > ncols_l
maximum_smush = ncols_l
end
for col_r in ncols_r:-1:1
cr = thechar[row, col_r]
if cr == ' '
charbd += 1
continue
else
break
end
end
for col_l in 1:ncols_l
cl = current[row, col_l]
if cl == '\0' || cl == ' '
linebd += 1
continue
else
break
end
end
else
for col_l in ncols_l:-1:1
cl = current[row, col_l]
if col_l > 1 && ( cl == '\0' || cl == ' ' )
linebd += 1
continue
else
break
end
end
for col_r in 1:ncols_r
cr = thechar[row, col_r]
if cr == ' '
charbd += 1
continue
else
break
end
end
end
smush = linebd + charbd
if cl == '\0' || cl == ' '
smush += 1
elseif (cr != '\0')
if smushem(cl, cr, fh) != '\0'
smush += 1
end
end
if smush < maximum_smush
maximum_smush = smush
end
end
return maximum_smush
end
function addchar(current::Matrix{Char}, thechar::Matrix{Char}, fh::FIGletHeader)
right2left = fh.print_direction
current = copy(current)
thechar = copy(thechar)
maximum_smush = smushamount(current, thechar, fh)
_, ncols_l = size(current)
nrows_r, ncols_r = size(thechar)
for row in 1:nrows_r
if right2left == 1
for smush in 1:maximum_smush
col_r = ncols_r - maximum_smush + smush
col_r < 1 && ( col_r = 1 )
thechar[row, col_r] = smushem(thechar[row, col_r], current[row, smush], fh)
end
else
for smush in 1:maximum_smush
col_l = ncols_l - maximum_smush + smush
col_l < 1 && ( col_l = 1 )
current[row, col_l] = smushem(current[row, col_l], thechar[row, smush], fh)
end
end
end
if right2left == 1
current = hcat(
thechar,
current[:, ( maximum_smush + 1 ):end],
)
else
current = hcat(
current,
thechar[:, ( maximum_smush + 1 ):end],
)
end
return current
end
function render(io, text::AbstractString, ff::FIGletFont)
(HEIGHT, WIDTH) = Base.displaysize(io)
words = Matrix{Char}[]
for word in split(text)
current = fill(' ', ff.header.height, 1)
for c in word
current = addchar(current, ff.font_characters[c].thechar, ff.header)
end
current = addchar(current, ff.font_characters[' '].thechar, ff.header)
push!(words, current)
end
lines = Matrix{Char}[]
current = fill('\0', ff.header.height, 0)
for word in words
if size(current)[2] + size(word)[2] < WIDTH
if ff.header.print_direction == 1
current = hcat(word, current)
else
current = hcat(current, word)
end
else
push!(lines, current)
current = fill('\0', ff.header.height, 0)
if ff.header.print_direction == 1
current = hcat(word, current)
else
current = hcat(current, word)
end
end
end
push!(lines, current)
for line in lines
nrows, ncols = size(line)
for r in 1:nrows
s = join(line[r, :])
s = replace(s, ff.header.hardblank=>' ') |> rstrip
print(io, s)
println(io)
end
println(io)
end
end
render(io, text::AbstractString, ff::AbstractString) = render(io, text, readfont(ff))
"""
render(text::AbstractString, font::Union{AbstractString, FIGletFont})
Renders `text` using `font` to `stdout`
Example:
render("hello world", "standard")
render("hello world", readfont("standard"))
"""
render(text::AbstractString, font=DEFAULTFONT) = render(stdout, text, font)
end # module
| FIGlet | https://github.com/kdheepak/FIGlet.jl.git |
|
[
"MIT"
] | 0.2.1 | bfc6b52f75b4720581e3e49ae786da6764e65b6a | code | 6866 | using FIGlet
using Test
function generate_output(s::AbstractString, font::AbstractString="Standard")
fontpath = FIGlet.getfontpath(font)
io = IOContext(IOBuffer())
FIGlet.render(io, s, FIGlet.readfont(fontpath))
jl_output = String(take!(io.io))
cli_output = read(`figlet -f $fontpath $s`, String)
return strip(join(strip.(split(jl_output, '\n')), '\n')), strip(join(strip.(split(cli_output, '\n')), '\n'))
end
@testset "FIGlet.jl" begin
iob = IOBuffer(b"flf2a", read=true);
@test FIGlet.readmagic(iob) == UInt8['f', 'l', 'f', '2', 'a']
@test FIGlet.FIGletHeader('$', 6, 5, 16, 15, 11) == FIGlet.FIGletHeader('$', 6, 5, 16, 15, 11, 0, 143, 0)
@test FIGlet.availablefonts() |> length == 680
for font in FIGlet.availablefonts()
@test FIGlet.readfont(font) isa FIGlet.FIGletFont
end
ff = FIGlet.readfont("jiskan16")
iob = IOBuffer()
print(iob, ff)
@test String(take!(iob)) == "FIGletFont(n=7098)"
iob = IOBuffer()
print(iob, ff.font_characters['㙤'])
@test String(take!(iob)) == "FIGletChar(ord='㙤')"
@test_throws FIGlet.FontNotFoundError FIGlet.readfont("wat")
@test_throws FIGlet.FontError FIGlet.readfont(joinpath(@__DIR__, "..", "README.md"))
iob = IOBuffer()
FIGlet.render(iob, "the quick brown fox jumps over the lazy dog", "standard")
@test String(take!(iob)) == raw"""
_ _ _ _ _
| |_| |__ ___ __ _ _ _(_) ___| | __ | |__ _ __ _____ ___ __
| __| '_ \ / _ \ / _` | | | | |/ __| |/ / | '_ \| '__/ _ \ \ /\ / / '_ \
| |_| | | | __/ | (_| | |_| | | (__| < | |_) | | | (_) \ V V /| | | |
\__|_| |_|\___| \__, |\__,_|_|\___|_|\_\ |_.__/|_| \___/ \_/\_/ |_| |_|
|_|
__ _
/ _| _____ __ (_)_ _ _ __ ___ _ __ ___ _____ _____ _ __
| |_ / _ \ \/ / | | | | | '_ ` _ \| '_ \/ __| / _ \ \ / / _ \ '__|
| _| (_) > < | | |_| | | | | | | |_) \__ \ | (_) \ V / __/ |
|_| \___/_/\_\ _/ |\__,_|_| |_| |_| .__/|___/ \___/ \_/ \___|_|
|__/ |_|
_ _ _ _
| |_| |__ ___ | | __ _ _____ _ __| | ___ __ _
| __| '_ \ / _ \ | |/ _` |_ / | | | / _` |/ _ \ / _` |
| |_| | | | __/ | | (_| |/ /| |_| | | (_| | (_) | (_| |
\__|_| |_|\___| |_|\__,_/___|\__, | \__,_|\___/ \__, |
|___/ |___/
"""
iob = IOBuffer()
FIGlet.render(iob, uppercase("the quick brown fox jumps over the lazy dog"), "standard")
@test String(take!(iob)) == raw"""
_____ _ _ _____ ___ _ _ ___ ____ _ __
|_ _| | | | ____| / _ \| | | |_ _/ ___| |/ /
| | | |_| | _| | | | | | | || | | | ' /
| | | _ | |___ | |_| | |_| || | |___| . \
|_| |_| |_|_____| \__\_\\___/|___\____|_|\_\
____ ____ _____ ___ _ _____ _____ __
| __ )| _ \ / _ \ \ / / \ | | | ___/ _ \ \/ /
| _ \| |_) | | | \ \ /\ / /| \| | | |_ | | | \ /
| |_) | _ <| |_| |\ V V / | |\ | | _|| |_| / \
|____/|_| \_\\___/ \_/\_/ |_| \_| |_| \___/_/\_\
_ _ _ __ __ ____ ____ _____ _______ ____
| | | | | \/ | _ \/ ___| / _ \ \ / / ____| _ \
_ | | | | | |\/| | |_) \___ \ | | | \ \ / /| _| | |_) |
| |_| | |_| | | | | __/ ___) | | |_| |\ V / | |___| _ <
\___/ \___/|_| |_|_| |____/ \___/ \_/ |_____|_| \_\
_____ _ _ _____ _ _ _______ __ ____ ___ ____
|_ _| | | | ____| | | / \ |__ /\ \ / / | _ \ / _ \ / ___|
| | | |_| | _| | | / _ \ / / \ V / | | | | | | | | _
| | | _ | |___ | |___ / ___ \ / /_ | | | |_| | |_| | |_| |
|_| |_| |_|_____| |_____/_/ \_\/____| |_| |____/ \___/ \____|
"""
iob = IOBuffer()
FIGlet.render(iob, "the quick brown fox jumps over the lazy dog", "mirror")
@test String(take!(iob)) == raw"""
_ _ _ _ _
__ ___ _____ __ _ __| | __ | |___ (_)_ _ _ __ ___ __| |_| |
/ _` \ \ /\ / / _ \__` |/ _` | \ \| |__ \| | | | | '_ \ / _ \ / _` |__ |
| | | |\ V V / (_) | | | (_| | > |__) | | |_| | |_) | \__ | | | |_| |
|_| |_| \_/\_/ \___/ |_|\__,_| /_/|_|___/|_|_.__/| .__/ |___/|_| |_|__/
|_|
_ __
__ _ _____ _____ ___ __ _ ___ __ _ _ _(_) __ _____ |_ \
|__` / _ \ \ / / _ \ |__ \/ _` |/ _ ' _` | | | | | \ \/ / _ \ _| |
| \__ \ V / (_) | / __/ (_| | | | | | | |_| | | > < (_) |_ |
|_|___/ \_/ \___/ \___|\__, |_| |_| |_|_.__/| \_ /_/\_\___/ |_|
|_| \__|
_ _ _ _
_ __ ___ | |__ _ _____ _ __ | | ___ __| |_| |
| '_ \ / _ \| '_ \ | | | \ _| '_ \| | / _ \ / _` |__ |
| |_) | (_) | |_) | | |_| |\ \| |_) | | \__ | | | |_| |
| .__/ \___/|_.__/ | .__/|___\_.__/|_| |___/|_| |_|__/
\___| \___|
"""
iob = IOBuffer()
FIGlet.render(iob, uppercase("the quick brown fox jumps over the lazy dog"), "mirror")
@test String(take!(iob)) == raw"""
__ _ ____ ___ _ _ ___ _____ _ _ _____
\ \| |___ \_ _| | | |/ _ \ |____ | | | |_ _|
\ ` | | | || | | | | | | |_ | |_| | | |
/ . |___| | || |_| | |_| | ___| | _ | | |
/_/|_|____/___|\___//_/__/ |_____|_| |_| |_|
__ _____ _____ _ ___ _____ ____ ____
\ \/ / _ \___ | | | / \ \ / / _ \ / _ |( __ |
\ / | | | _| | | |/ |\ \ /\ / / | | | (_| |/ _ |
/ \ |_| ||_ | | /| | \ V V /| |_| |> _ | (_| |
/_/\_\___/ |_| |_/ |_| \_/\_/ \___//_/ |_|\____|
____ _______ _____ ____ ____ __ __ _ _ _
/ _ |____ \ \ / / _ \ |___ \/ _ | \/ | | | | |
| (_| | |_ |\ \ / / | | | / ___/ (_| | |\/| | | | | | _
> _ |___| | \ V /| |_| | | (___ \__ | | | | |_| | |_| |
/_/ |_|_____| \_/ \___/ \____| |_|_| |_|\___/ \___/
____ ___ ____ __ _______ _ _ _____ _ _ _____
|___ \ / _ \ / _ | \ \ / /\ __| / \ | | |____ | | | |_ _|
_ | | | | | | | | \ V / \ \ / _ \ | | |_ | |_| | | |
| |_| | |_| | |_| | | | _\ \ / ___ \ ___| | ___| | _ | | |
|____/ \___/ \____| |_| |____\/_/ \_\_____| |_____|_| |_| |_|
"""
@testset "Render all fonts" begin
for (i, font) in enumerate(FIGlet.availablefonts())
try
iob = IOBuffer()
sentence = "the quick brown fox jumps over the lazy dog"
FIGlet.render(iob, sentence, font)
FIGlet.render(iob, uppercase(sentence), font)
@test length(String(take!(iob))) > 0
catch
println("Cannot render font: number = $i, name = \"$font\"")
end
end
end
end
| FIGlet | https://github.com/kdheepak/FIGlet.jl.git |
|
[
"MIT"
] | 0.2.1 | bfc6b52f75b4720581e3e49ae786da6764e65b6a | docs | 1770 | ```
███████████ █████ █████████ ████ █████ ███ ████
░░███░░░░░░█░░███ ███░░░░░███░░███ ░░███ ░░░ ░░███
░███ █ ░ ░███ ███ ░░░ ░███ ██████ ███████ █████ ░███
░███████ ░███ ░███ ░███ ███░░███░░░███░ ░░███ ░███
░███░░░█ ░███ ░███ █████ ░███ ░███████ ░███ ░███ ░███
░███ ░ ░███ ░░███ ░░███ ░███ ░███░░░ ░███ ███ ░███ ░███
█████ █████ ░░█████████ █████░░██████ ░░█████ ██ ░███ █████
░░░░░ ░░░░░ ░░░░░░░░░ ░░░░░ ░░░░░░ ░░░░░ ░░ ░███ ░░░░░
███ ░███
░░██████
░░░░░░
```
[](https://kdheepak.github.io/FIGlet.jl/stable)
[](https://kdheepak.github.io/FIGlet.jl/dev)
[](https://travis-ci.com/kdheepak/FIGlet.jl)
[](https://codecov.io/gh/kdheepak/FIGlet.jl)
[](https://coveralls.io/github/kdheepak/FIGlet.jl?branch=master)
FIGlet.jl is a Julia port of [FIGlet](http://www.figlet.org/).

| FIGlet | https://github.com/kdheepak/FIGlet.jl.git |
|
[
"MIT"
] | 0.2.1 | bfc6b52f75b4720581e3e49ae786da6764e65b6a | docs | 1193820 | # Examples
**1943____**
```
### ### #### ## ## #### ### # #
## ## ## ## ## #### ### # #
## ## ## #### ### # #
## ## ## ## ### # ## #### ### # #
## ## ## ## # ### ## ## ### # #
## ## ## ## ### #### ### #### ### # #
#### #### ## ## ### #### ## ## ### # #
# # ### ## ## ### # #
```
**1row**
```
/= | (_, |_ [- ~|~
```
**3-d**
```
******** ** ******** ** **
/**///// /** **//////** /** /**
/** /** ** // /** ***** ******
/******* /**/** /** **///**///**/
/**//// /**/** ***** /**/******* /**
/** /**//** ////** /**/**//// /**
/** /** //******** ***//****** //**
// // //////// /// ////// //
```
**3D Diagonal**
```
,---,. ,---, ,----.. ,--, ___
,' .' |,`--.' | / / \ ,--.'| ,--.'|_
,---.' || : :| : : | | : | | :,'
| | .': | '. | ;. / : : ' : : ' :
: : : | : |. ; /--` | ' | ,---. .;__,' /
: | |-,' ' ;; | ; __ ' | | / \ | | |
| : ;/|| | || : |.' .'| | : / / |:__,'| :
| | .'' : ;. | '_.' :' : |__ . ' / | ' : |__
' : ' | | '' ; : \ || | '.'|' ; /| | | '.'|
| | | ' : |' | '/ .'; : ;' | / | ; : ;
| : \ ; |.' | : / | , / | : | | , /
| | ,' '---' \ \ .' ---`-' \ \ / ---`-'
`----' `---` `----'
```
**3D-ASCII**
```
________ ___ ________ ___ _______ _________
|\ _____\\ \|\ ____\|\ \ |\ ___ \|\___ ___\
\ \ \__/\ \ \ \ \___|\ \ \ \ \ __/\|___ \ \_|
\ \ __\\ \ \ \ \ __\ \ \ \ \ \_|/__ \ \ \
\ \ \_| \ \ \ \ \|\ \ \ \____\ \ \_|\ \ \ \ \
\ \__\ \ \__\ \_______\ \_______\ \_______\ \ \__\
\|__| \|__|\|_______|\|_______|\|_______| \|__|
```
**3d**
```
████████ ██ ████████ ██ ██
░██░░░░░ ░██ ██░░░░░░██ ░██ ░██
░██ ░██ ██ ░░ ░██ █████ ██████
░███████ ░██░██ ░██ ██░░░██░░░██░
░██░░░░ ░██░██ █████ ░██░███████ ░██
░██ ░██░░██ ░░░░██ ░██░██░░░░ ░██
░██ ░██ ░░████████ ███░░██████ ░░██
░░ ░░ ░░░░░░░░ ░░░ ░░░░░░ ░░
```
**3x5**
```
### ### ## # #
# # # # ### ###
## # # # # ## #
# # # # ## ### ##
# ### ##
```
**4max**
```
888888 88 dP""b8 88 888888 888888
88__ 88 dP `" 88 88__ 88
88"" 88 Yb "88 88 .o 88"" 88
88 88 YboodP 88ood8 888888 88
```
**4x4_offr**
```
###### #### #### ## ## ####
## ## ## ## ## ######## ## ## ##
## ## ## ## ######## ## ## ###
#### ## ## ### ## ## ## ###
## ## ## ## ## ## ##
## ## ## ## ## ## ## #
## #### #### ######## ## ####
######## ##
```
**5 Line Oblique**
```
___ ___
// / / / / // ) )
//___ / / // // ___ __ ___
/ ___ / / // ____ // //___) ) / /
// / / // / / // // / /
// __/ /___ ((____/ / // ((____ / /
```
**5x7**
```
#### ### ## ## #
# # # # # #
### # # # ## ###
# # # ## # # ## #
# # # # # ## #
# ### ### ### ## ##
```
**5x8**
```
#### ### ## ## #
# # # # # #
### # # # ## ###
# # # ## # #### #
# # # # # # # #
# ### ## ### ## #
```
**64f1____**
```
####### ####### ##### # # ### ##
#### ### ### ## # # # ## ###
###### ### ### ## ## ## # ## # #
#### ### ### ## ## ### # ### # ####
#### ### ### ## ## # ### # ### ###
#### ####### ####### # #### # ### # ## #
#### ####### ####### ## # #### # #
#### ####### ##### # # # # # #
```
**6x10**
```
##### ### ### ## #
# # # # # #
# # # # ### ####
#### # # # # # #
# # # ## # ##### #
# # # # # # # #
# ### ### ### ### ##
```
**6x9**
```
#
#### ### ## ## #
# # # # # ###
### # # # ## #
# # # ## # # ## # #
# # # # # ## # #
# ### ## ### ### #
```
**AMC 3 Line**
```
.-. .-. .-. . .-. .-.
|- | |.. | |- |
' `-' `-' `-' `-' '
```
**AMC 3 Liv1**
```
.: ;:. :. .
S S .:;s;:' S ' S S S S S S:;s;:'
`:;S;:' `:;S;:' `:;S;:' `:;S;:' `
```
**AMC AAA01**
```
sSSs .S sSSSSs S. sSSs sdSS_SSSSSSbs
d%%SP .SS d%%%%SP SS. d%%SP YSSS~S%SSSSSP
d%S' S%S d%S' S%S d%S' S%S
S%S S%S S%S S%S S%S S%S
S&S S&S S&S S&S S&S S&S
S&S_Ss S&S S&S S&S S&S_Ss S&S
S&S~SP S&S S&S S&S S&S~SP S&S
S&S S&S S&S sSSs S&S S&S S&S
S*b S*S S*b `S%% S*b S*b S*S
S*S S*S S*S S% S*S. S*S. S*S
S*S S*S SS_sSSS SSSbs SSSbs S*S
S*S S*S Y~YSSY YSSP YSSP S*S
SP SP SP
Y Y Y
```
**AMC Neko**
```
.sSSSSs. SSSSS .sSSSSs.
SSSSSSSSSs. SSSSS SSSSSSSSSs. SSSSS .sSSSSs. .sSSSSSSSSSSSSSs.
S SSS SSSS' S SSS S SSS SSSSS S SSS S SSSSSSSs. SSSSS S SSS SSSSS
S SS S SS S SS SSSS' S SS S SS SSSS' SSSSS S SS SSSSS
S..SSsss S..SS S..SS S..SS S..SS `:S:' S..SS `:S:'
S:::SSSS S:::S S:::S`sSSs. S:::S S:::SSSS S:::S
S;;;S S;;;S S;;;S SSSSS S;;;S S;;;S S;;;S
S%%%S S%%%S S%%%S SSSSS S%%%S SSSSS S%%%S SSSSS S%%%S
SSSSS SSSSS SSSSSsSSSSS SSSSSsSS;:' SSSSSsSS;:' SSSSS
```
**AMC Razor**
```
___ ___ ___ ___ ___ ___
.'|=|_.' .'| .'|=|_.' .'| .'|=|_.' `._|=| |=|_.'
.' | ___ .' | .' |___ .' | .' | ___ | |
| |=|_.' | | | |`._|=. | | | |=|_.' | |
| | | | `. | __|| | | ___ | | ___ `. |
|___| |___| `.|=|_.'' |___|=|_.' |___|=|_.' `.|
```
**AMC Razor2**
```
. . . . . . . . . . .
.+'|=|`+. |`+. .+'|=|`+. .+'| .+'|=|`+. .+'|=|`+.=|`+.
| | `+.| | | | | `+.| | | | | `+.| |.+' | | `+.|
| |=|`. | | | | . | | | |=|`. | |
| | `.| | | | | |`+. | | | | `.| | |
| | | | | | `. | | | . | | . | |
| | | | | | .+ | | | .+'| | | .+'| | |
`+.| |.+' `+.|=|.+' `+.|=|.+' `+.|=|.+' |.+'
```
**AMC Slash**
```
.s5SSSs. s. .s5SSSs.
SS. SS. .s .s5SSSs. .s5SSSSs.
sS S%S sS `:; SS. SSS
SS S%S SS sS sS `:; S%S
SSSs. S%S SS SS SSSs. S%S
SS S%S SS SS SS S%S
SS `:; SS ``:; SS SS `:;
SS ;,. SS ;,. SS ;,. SS ;,. ;,.
:; ;:' `:;;;;;:' `:;;;;;:' `:;;;;;:' ;:'
```
**AMC Slider**
```
___________ _____ ____
| | .-~ ~. | | `````|`````
|______ | : | |______ |
| | : _____ | | |
| | `-._____.'| |_______ |___________ |
```
**AMC Thin**
```
.-..--. .-. .-..--. .-. .-..--. .-..-..-.
| | ~~ | | | | ~~ | | | | ~~ ~ | | ~
| | _ | | | | __ | | | | _ | |
| |`-' | | | | `. | | | | |`-' | |
| | | | | | _| | | | __ | | __ | |
`-' `-' `-'`---' `-'`--' `-'`--' `-'
```
**AMC Tubes**
```
d sss d sSSSs d d sss sss sssss
S S S S S S S
S S S S S S
S sSSs S S S S sSSs S
S S S ssSb S S S
S S S S S S S
P P "sss" P sSSs P sSSss P
```
**AMC Untitled**
```
,'',,'', ,'', ,'',,'',
; ;',,' ; ; ; ;',,'
; ;,'', ; ; ; ; ,'', ,'',,'', ,'',,'',,'',
; ;',,' ; ; ; ;,'', ; ; ; ;',,' ',,'; ;',,'
; ; ; ; ; ;', ; ; ; ; ;',,' ; ;
; ; ; ; ; ;,' ; ; ;,'', ; ; ,, ; ;
',,' ',,' ',,'',,' ',,'',,' ',,'',,' ',,'
```
**ANSI Regular**
```
███████ ██ ██████ ██ ███████ ████████
██ ██ ██ ██ ██ ██
█████ ██ ██ ███ ██ █████ ██
██ ██ ██ ██ ██ ██ ██
██ ██ ██████ ███████ ███████ ██
```
**ANSI Shadow**
```
███████╗██╗ ██████╗ ██╗ ███████╗████████╗
██╔════╝██║██╔════╝ ██║ ██╔════╝╚══██╔══╝
█████╗ ██║██║ ███╗██║ █████╗ ██║
██╔══╝ ██║██║ ██║██║ ██╔══╝ ██║
██║ ██║╚██████╔╝███████╗███████╗ ██║
╚═╝ ╚═╝ ╚═════╝ ╚══════╝╚══════╝ ╚═╝
```
**ASCII New Roman**
```
____,__, ____, __, ____,____,
(-|_,(-| (-/ _,(-| (-|_,(-|
_| _|_,_\__| _|__,_|__,_|,
( ( ( ( ( (
```
**B1FF**
```
F16|_3T
```
**Big Chief**
```
____________________________________________
_____ __ __
/ ' / / ) /
---/__--------/----/--------/----__--_/_----
/ / / --, / /___) /
_/________ _/_ __(____/___/___(___ _(_ _____
```
**Big Money-ne**
```
/$$$$$$$$ /$$$$$$ /$$$$$$ /$$ /$$
| $$_____/|_ $$_/ /$$__ $$| $$ | $$
| $$ | $$ | $$ \__/| $$ /$$$$$$ /$$$$$$
| $$$$$ | $$ | $$ /$$$$| $$ /$$__ $$|_ $$_/
| $$__/ | $$ | $$|_ $$| $$| $$$$$$$$ | $$
| $$ | $$ | $$ \ $$| $$| $$_____/ | $$ /$$
| $$ /$$$$$$| $$$$$$/| $$| $$$$$$$ | $$$$/
|__/ |______/ \______/ |__/ \_______/ \___/
```
**Big Money-nw**
```
$$$$$$$$\ $$$$$$\ $$$$$$\ $$\ $$\
$$ _____|\_$$ _|$$ __$$\ $$ | $$ |
$$ | $$ | $$ / \__|$$ | $$$$$$\ $$$$$$\
$$$$$\ $$ | $$ |$$$$\ $$ |$$ __$$\\_$$ _|
$$ __| $$ | $$ |\_$$ |$$ |$$$$$$$$ | $$ |
$$ | $$ | $$ | $$ |$$ |$$ ____| $$ |$$\
$$ | $$$$$$\ \$$$$$$ |$$ |\$$$$$$$\ \$$$$ |
\__| \______| \______/ \__| \_______| \____/
```
**Big Money-se**
```
________ ______ ______ __ __
| \| \ / \ | \ | \
| $$$$$$$$ \$$$$$$| $$$$$$\| $$ ______ _| $$_
| $$__ | $$ | $$ __\$$| $$ / \| $$ \
| $$ \ | $$ | $$| \| $$| $$$$$$\\$$$$$$
| $$$$$ | $$ | $$ \$$$$| $$| $$ $$ | $$ __
| $$ _| $$_ | $$__| $$| $$| $$$$$$$$ | $$| \
| $$ | $$ \ \$$ $$| $$ \$$ \ \$$ $$
\$$ \$$$$$$ \$$$$$$ \$$ \$$$$$$$ \$$$$
```
**Big Money-sw**
```
________ ______ ______ __ __
/ |/ | / \ / | / |
$$$$$$$$/ $$$$$$/ /$$$$$$ |$$ | ______ _$$ |_
$$ |__ $$ | $$ | _$$/ $$ | / \ / $$ |
$$ | $$ | $$ |/ |$$ |/$$$$$$ |$$$$$$/
$$$$$/ $$ | $$ |$$$$ |$$ |$$ $$ | $$ | __
$$ | _$$ |_ $$ \__$$ |$$ |$$$$$$$$/ $$ |/ |
$$ | / $$ |$$ $$/ $$ |$$ | $$ $$/
$$/ $$$$$$/ $$$$$$/ $$/ $$$$$$$/ $$$$/
```
**Bloody**
```
█████▒██▓ ▄████ ██▓ ▓█████▄▄▄█████▓
▓██ ▒▓██▒ ██▒ ▀█▒▓██▒ ▓█ ▀▓ ██▒ ▓▒
▒████ ░▒██▒▒██░▄▄▄░▒██░ ▒███ ▒ ▓██░ ▒░
░▓█▒ ░░██░░▓█ ██▓▒██░ ▒▓█ ▄░ ▓██▓ ░
░▒█░ ░██░░▒▓███▀▒░██████▒░▒████▒ ▒██▒ ░
▒ ░ ░▓ ░▒ ▒ ░ ▒░▓ ░░░ ▒░ ░ ▒ ░░
░ ▒ ░ ░ ░ ░ ░ ▒ ░ ░ ░ ░ ░
░ ░ ▒ ░░ ░ ░ ░ ░ ░ ░
░ ░ ░ ░ ░ ░
```
**Broadway KB**
```
____ _ __ _ ____ _____
| |_ | | / /`_ | | | |_ | |
|_| |_| \_\_/ |_|__ |_|__ |_|
```
**Caligraphy2**
```
##### ## ##### # # ### ###
###### /### / ###### / / /### / ###
/# / / ##/ /# / / / / ###/ ## #
/ / / # / / / / ## ## ## ##
/ / / / / ### ## ##
## ## ## ## ## ## ## /## ########
## ## ## ## ## ## ### ## / ### ########
## ###### /### ## ## ## /### / ## / ### ##
## ##### / ### ## ## ## / ###/ ## ## ### ##
## ## ## ## ## ##/ ## ## ######## ##
# ## ## ## ## ## ## # ## ####### ##
# ### # / ## # / ## ## ##
/#### ### / ### / ## #### / ##
/ ##### #####/ ######/ ### / ######/ ##
/ ### ### ### ##/ ##### ##
#
##
```
**Calvin S**
```
╔═╗╦╔═╗┬ ┌─┐┌┬┐
╠╣ ║║ ╦│ ├┤ │
╚ ╩╚═╝┴─┘└─┘ ┴
```
**Crawford2**
```
_____ ____ ____ _ ___ ______
| || | / || | / _] |
| __| | | | __|| | / [_| |
| |_ | | | | || |___ | _]_| |_|
| _] | | | |_ || || [_ | |
| | | | | || || | | |
|__| |____||___,_||_____||_____| |__|
```
**DANC4**
```
O/# \O/#'\ /` |_O \O/ '\ /`
|_ .___Y \ / _|> Y \ /
/ | | Y _| \ / \ X
./ |_ |_ /O# |_./ \, /O\
```
**DOS Rebel**
```
███████████ █████ █████████ ████ █████
░░███░░░░░░█░░███ ███░░░░░███░░███ ░░███
░███ █ ░ ░███ ███ ░░░ ░███ ██████ ███████
░███████ ░███ ░███ ░███ ███░░███░░░███░
░███░░░█ ░███ ░███ █████ ░███ ░███████ ░███
░███ ░ ░███ ░░███ ░░███ ░███ ░███░░░ ░███ ███
█████ █████ ░░█████████ █████░░██████ ░░█████
░░░░░ ░░░░░ ░░░░░░░░░ ░░░░░ ░░░░░░ ░░░░░
```
**Dancing Font**
```
_____ ____ _ U _____ u _____
|" ___| ___ U /"___|u |"| \| ___"|/ |_ " _|
U| |_ u |_"_| \| | _ /U | | u | _|" | |
\| _|/ | | | |_| | \| |/__ | |___ /| |\
|_| U/| |\u \____| |_____| |_____| u |_|U
)(\\,-.-,_|___|_,-._)(|_ // \\ << >> _// \\_
(__)(_/ \_)-' '-(_/(__)__) (_")("_)(__) (__)(__) (__)
```
**Def Leppard**
```
,
Et
E#t ,;
E##t t .Gt i f#i
E#W#t Ej j#W: LE .E#t GEEEEEEEL
E#tfL. E#, ;K#f L#E i#W, ,;;L#K;;.
E#t E#t .G#D. G#W. L#D. t#E
,ffW#Dffj. E#t j#K; D#K. :K#Wfff; t#E
;LW#ELLLf. E#t ,K#f ,GD; E#K. i##WLLLLt t#E
E#t E#t j#Wi E#t .E#E. .E#L t#E
E#t E#t .G#D: E#t .K#E f#E: t#E
E#t E#t ,K#fK#t .K#D ,WW; t#E
E#t E#t j###t .W#G .D#; t#E
E#t E#t .G#t :W##########Wt tt fE
;#t ,;. ;; :,,,,,,,,,,,,,. :
:;
```
**Delta Corps Priest 1**
```
▄████████ ▄█ ▄██████▄ ▄█ ▄████████ ███
███ ███ ███ ███ ███ ███ ███ ███ ▀█████████▄
███ █▀ ███▌ ███ █▀ ███ ███ █▀ ▀███▀▀██
▄███▄▄▄ ███▌ ▄███ ███ ▄███▄▄▄ ███ ▀
▀▀███▀▀▀ ███▌ ▀▀███ ████▄ ███ ▀▀███▀▀▀ ███
███ ███ ███ ███ ███ ███ █▄ ███
███ ███ ███ ███ ███▌ ▄ ███ ███ ███
███ █▀ ████████▀ █████▄▄██ ██████████ ▄████▀
▀
```
**Diet Cola**
```
.-._.---'.----. .-. .
(_) / / `.--.`-' / /
/--. / / (_; / .-.---/---
/ / / / ./.-'_ /
.-/ / ( --;-_/_.-(__.' /
(_/ .---------'`.___.'
```
**Dot Matrix**
```
_ _ _ _ _ _ _ _ _ _ _ _ _ _
(_)(_)(_)(_)(_)(_)(_)(_)_ (_)(_)(_) _ (_)(_) (_)
(_) (_) (_) (_) (_) _ _ _ _ _ (_) _ _
(_) _ _ (_) (_) _ _ _ (_) (_)(_)(_)(_)_(_)(_)(_)(_)
(_)(_)(_) (_) (_) (_)(_)(_) (_) (_) _ _ _ (_) (_)
(_) (_) (_) (_) (_) (_)(_)(_)(_)(_) (_) _
(_) _ (_) _(_) _ _ _ (_) _ (_) _(_)_ _ _ _ (_)_ _(_)
(_) (_)(_)(_) (_)(_)(_)(_)(_)(_)(_) (_)(_)(_)(_) (_)(_)
```
**Double Shorts**
```
_____ __ ____ __ _____ _____
||== || (( ___ || ||== ||
|| || \\_|| ||__| ||___ ||
```
**Dr Pepper**
```
___ _ ___ _ _
| __>| |/ _> | | ___ _| |_
| _> | || <_/\| |/ ._> | |
|_| |_|`____/|_|\___. |_|
```
**Efti Chess**
```
##################
##|:+:|####[`'`']#
##(o:o)#####|::|##
###(:)######|::|##
##################
```
**Efti Font**
```
___ _ __
| __|| |/ _|||_||
| _| | ( |_n|/o\ ]
|_| |_|\__/L\(L|
```
**Efti Italic**
```
____ __ __
/ __// /,'_/ /7 __ /7
/ _/ / // /_n //,'o//_7
/_/ /_/ |__,'// |_(//
```
**Efti Piti**
```
__() __
[|-[](|_;let
```
**Efti Robot**
```
____ _ ____ _ _
( __)( )( __)( ) ( )
| |_ | || | _ | | ___ | |
( __) ( )( )_))( )( o_)( _)
/_\ /_\/____\/_\ \( /_\
```
**Efti Wall**
```
_ _ |"|
### ||| -*~*- o' \,=./ `o _|_|_ ()_()
(o o) (o o) (o o) (o o) (o o) (o o)
ooO--(_)--Ooo-ooO--(_)--Ooo-ooO--(_)--Ooo-ooO--(_)--Ooo-ooO--(_)--Ooo-ooO--`o'--Ooo----
```
**Efti Water**
```
___ _ ___ _ _
)L )) ))_ )) __ )L
(( (( ((_((( (('((
```
**Electronic**
```
▄▄▄▄▄▄▄▄▄▄▄ ▄▄▄▄▄▄▄▄▄▄▄ ▄▄▄▄▄▄▄▄▄▄▄ ▄ ▄▄▄▄▄▄▄▄▄▄▄ ▄▄▄▄▄▄▄▄▄▄▄
▐░░░░░░░░░░░▌▐░░░░░░░░░░░▌▐░░░░░░░░░░░▌▐░▌ ▐░░░░░░░░░░░▌▐░░░░░░░░░░░▌
▐░█▀▀▀▀▀▀▀▀▀ ▀▀▀▀█░█▀▀▀▀ ▐░█▀▀▀▀▀▀▀▀▀ ▐░▌ ▐░█▀▀▀▀▀▀▀▀▀ ▀▀▀▀█░█▀▀▀▀
▐░▌ ▐░▌ ▐░▌ ▐░▌ ▐░▌ ▐░▌
▐░█▄▄▄▄▄▄▄▄▄ ▐░▌ ▐░▌ ▄▄▄▄▄▄▄▄ ▐░▌ ▐░█▄▄▄▄▄▄▄▄▄ ▐░▌
▐░░░░░░░░░░░▌ ▐░▌ ▐░▌▐░░░░░░░░▌▐░▌ ▐░░░░░░░░░░░▌ ▐░▌
▐░█▀▀▀▀▀▀▀▀▀ ▐░▌ ▐░▌ ▀▀▀▀▀▀█░▌▐░▌ ▐░█▀▀▀▀▀▀▀▀▀ ▐░▌
▐░▌ ▐░▌ ▐░▌ ▐░▌▐░▌ ▐░▌ ▐░▌
▐░▌ ▄▄▄▄█░█▄▄▄▄ ▐░█▄▄▄▄▄▄▄█░▌▐░█▄▄▄▄▄▄▄▄▄ ▐░█▄▄▄▄▄▄▄▄▄ ▐░▌
▐░▌ ▐░░░░░░░░░░░▌▐░░░░░░░░░░░▌▐░░░░░░░░░░░▌▐░░░░░░░░░░░▌ ▐░▌
▀ ▀▀▀▀▀▀▀▀▀▀▀ ▀▀▀▀▀▀▀▀▀▀▀ ▀▀▀▀▀▀▀▀▀▀▀ ▀▀▀▀▀▀▀▀▀▀▀ ▀
```
**Elite**
```
·▄▄▄▪ ▄▄ • ▄▄▌ ▄▄▄ .▄▄▄▄▄
▐▄▄·██ ▐█ ▀ ▪██• ▀▄.▀·•██
██▪ ▐█·▄█ ▀█▄██▪ ▐▀▀▪▄ ▐█.▪
██▌.▐█▌▐█▄▪▐█▐█▌▐▌▐█▄▄▌ ▐█▌·
▀▀▀ ▀▀▀·▀▀▀▀ .▀▀▀ ▀▀▀ ▀▀▀
```
**Fire Font-k**
```
( (
)\ ) )\ ) ( ( )
(()/( (()/( )\ ) )\ ( ( /(
/(_)) /(_))(()/( ((_) ))\ )\())
(_))_|(_)) /(_))_ _ /((_)(_))/
| |_ |_ _| (_)) __|| |(_)) | |_
| __| | | | (_ || |/ -_) | _|
|_| |___| \___||_|\___| \__|
```
**Flower Power**
```
________ .-./`) .-_'''-. .---. .-''-. ,---------.
| |\ .-.') '_( )_ \ | ,_| .'_ _ \\ \
| .----'/ `-' \|(_ o _)| ' ,-./ ) / ( ` ) '`--. ,---'
| _|____ `-'`"`. (_,_)/___| \ '_ '`) . (_ o _) | | \
|_( )_ | .---. | | .-----. > (_) ) | (_,_)___| :_ _:
(_ o._)__| | | ' \ '- .'( . .-' ' \ .---. (_I_)
|(_,_) | | \ `-'` | `-'`-'|___\ `-' / (_(=)_)
| | | | \ / | \\ / (_I_)
'---' '---' `'-...-' `--------` `'-..-' '---'
```
**Four Tops**
```
|~~~|~/~~\| |
|-- || __|/~/~|~
| _|_\__/|\/_ |
```
**Fun Face**
```
wW Ww \/ W W (o)__(o)
wWw(O)(O) (OO) (O)(O) wWw(__ __)
(O)_(..) ,'.--.) || (O)_ ( )
.' __)|| / /|_|_\ | \ .' __) )(
( _) _||_ | \_.--. | `.( _) ( )
)/ (_/\_)'. \) \(.-.__)`.__) )/
( `-.(_.' `-' (
```
**Fun Faces**
```
wWw wW Ww \/ W W wWw (o)__(o)
(O)_(O)(O) (OO) (O)(O) (O)_(__ __)
/ __)(..) ,'.--.) || / __) ( )
/ ( || / /|_|_\ | \ / ( )(
( _) _||_ | \_.--. | `.( _) ( )
/ / (_/\_)'. \) \(.-.__)\ \_ )/
)/ `-.(_.' `-' \__) (
```
**Georgia11**
```
,,
`7MM"""YMM `7MMF' .g8"""bgd `7MM mm
MM `7 MM .dP' `M MM MM
MM d MM dM' ` MM .gP"Ya mmMMmm
MM""MM MM MM MM ,M' Yb MM
MM Y MM MM. `7MMF' MM 8M"""""" MM
MM MM `Mb. MM MM YM. , MM
.JMML. .JMML. `"bmmmdPY .JMML.`Mbmmd' `Mbmo
```
**Heart Left**
```
.-.-. .-.-. .-.-. .-.-. .-.-. .-.-.
( F .'( I .'( G .'( l .'( e .'( t .'.-.-.
`.( `.( `.( `.( `.( `.( '._.'
```
**Heart Right**
```
.-.-. .-.-. .-.-. .-.-. .-.-. .-.-.
'. F )'. I )'. G )'. l )'. e )'. t ).-.-.
).' ).' ).' ).' ).' ).' '._.'
```
**Henry 3D**
```
____ __ ___ __ _
F ___J FJ ,"___". LJ ____ FJ_
J |___: J L FJ---L] FJ F __ J J _|
| _____|| | J | [""LJ L | _____J | |-'
F |____JF J | \___] |J L F L___--.F |__-.
J__F J____LJ\_____/FJ__LJ\______/F\_____/
|__| |____| J_____F |__| J______F J_____F
```
**Horizontal Left**
```
_______ _ _ _______ _______ _______ _
| _ ___| | |___| | / .---. \ /______ \ | ._ _. | | /_____
| ||_\ | ___ | | \ .-`_/ / | | \ v / | | ______/
|_/ |_| |_| \_/ |.` \_| |_/ \_| |_\
```
**Horizontal Right**
```
_______ _ _ _______ _______ _______ _
|___ _ | | |___| | / .---. \ / ______\ | ._ _. | _____\ |
/_|| | | ___ | \_'-. / | | \ | \ v / | \______ |
\_| |_| |_| '.| \_/ |_/ |_/ \_| /_|
```
**ICL-1900**
```
FIGlet
*** *
*
*
* *
*
*
*
*
```
**JS Block Letters**
```
____ _ ____ _ ____ _____
| ===|| |/ (_,`| |__ | ===||_ _|
|__| |_|\____)|____||____| |_|
```
**JS Bracket Letters**
```
.----..-. .---. .-. .----..---.
| {_ | |/ __}| | | {_ {_ _}
| | | |\ {_ }| `--.| {__ | |
`-' `-' `---' `----'`----' `-'
```
**JS Capital Curves**
```
____, ____, ____ __ ____, ____,
(-|_, (-| (-/ `_,(-| (-|_, (-|
_| _|__, \___) _|__, _|__, _|
( ( ( ( (
```
**JS Cursive**
```
_
/) . __ // _ -/-
_//__/__(_/__(/__(/__/_
_/ _/_
/) (/
`
```
**JS Stick Letters**
```
___ __ ___ ___
|__ | / _` | |__ |
| | \__> |___ |___ |
```
**Konto Slant**
```
/?? / /? / /.? ?/?
/? / /.T /. /.. /
```
**Larry 3D**
```
____ ______ ____ ___ __
/\ _`\ /\__ _\ /\ _`\ /\_ \ /\ \__
\ \ \L\_\/_/\ \/ \ \ \L\_\//\ \ __\ \ ,_\
\ \ _\/ \ \ \ \ \ \L_L \ \ \ /'__`\ \ \/
\ \ \/ \_\ \__\ \ \/, \\_\ \_/\ __/\ \ \_
\ \_\ /\_____\\ \____//\____\ \____\\ \__\
\/_/ \/_____/ \/___/ \/____/\/____/ \/__/
```
**Lil Devil**
```
_ (`-') _(`-')
<-. (_) .-> <-. ( OO).-/( OO).->
(`-')-----.,-(`-') ,---(`-') ,--. ) (,------./ '._
(OO|(_\---'| ( OO)' .-(OO ) | (`-') | .---'|'--...__)
/ | '--. | | )| | .-, \ | |OO )(| '--. `--. .--'
\_) .--'(| |_/ | | '.(_/(| '__ | | .--' | |
`| |_) | |'->| '-' | | |' | `---. | |
`--' `--' `-----' `-----' `------' `--'
```
**Line Blocks**
```
______ _____ ______ _ ______ _______
| | | | | | ____ | | | | | |
| |---- | | | | | | | | _ | |---- | |
|_| _|_|_ |_|__|_| |_|__|_| |_|____ |_|
```
**NT Greek**
```
_ ___ _______
_| |_( ) ___) \
/ \| || | \ \ ___ ___
( (| |) ) || | > \ / __| )
\_ _/| || | / ^ \> _) | |
|_| (___)_| /_/ \_\___) \_)
```
**NV Script**
```
,gggggggggggggg ,a8a, ,gg,
dP""""""88"""""",8" "8, i8""8i ,dPYb, I8
Yb,_ 88 d8 8b `8,,8' IP'`Yb I8
`"" 88 88 88 `Y88aaad8 I8 8I 88888888
ggg88gggg 88 88 d8""""Y8, I8 8' I8
88 8 Y8 8P ,8P 8b I8 dP ,ggg, I8
88 `8, ,8' dP Y8 I8dP i8" "8i I8
gg, 88 8888 "8,8" _ ,dP' I8 I8P I8, ,8I ,I8,
"Yb,,8P `8b, ,d8b, "888,,_____,dP,d8b,_ `YbadP' ,d88b,
"Y8P' "Y88P" "Y8a8P"Y888888P" 8P'"Y88888P"Y8888P""Y8
```
**Obanner1**
```
@ @ @ @ @ @ @
```
**Obanner10**
```
# ##
# # # #
# # # # #
## ## # #
```
**Obanner100**
```
### ###
### ### ###################
### ### ############################
### ### ##################################
##################################################################### #######################################
##################################################################### ############################################## #############
##################################################################### ################################################# #####################
##################################################################### #################################################### ########################
##################################################################### ################### ################ ###########################
##################################################################### ################ ############## ################################# ###
### ### ### ### ### ############## ########## ################################### ###
### ### ### ### ### ########### ######## ########## ### ########## ###
### ### ### ### ### ######### ###### ### ### ##### ### ###### ##########################################
### ### ### ### ####### ##### ### ### ##### ### #### ###############################################
### ### ##################################################################### ###### ### ##################################################################### #### ### ### #################################################
### ### ##################################################################### ###### #### ##################################################################### ### ### ### #################################################
### ### ##################################################################### ###### #### ##################################################################### ### ### ### ###################################################
### ### ##################################################################### ##### ### ##################################################################### ### ### ### ###################################################
### ### ##################################################################### #### ### ##################################################################### ### ### #### ######### ###
##### ### ##################################################################### #### ### ##################################################################### ## ### ### ###### ###
####### ### ### ### #### ### #### ### ### ### #### ##### ###
############# ### ### ### #### ### ### ### ### ### ####### #####
############# ### ### ### ##### ### ### #### ### ########## ####
############# ### ####### ### ##### ### ################### ###
### ######### ### ##### ### ################# ###
#### ############ ### ###### ### ###############
#### ################################ ############# ##############
##### ############################### ############# ########
###### ############################## #############
############# ############################ #############
############# #######################
############# ####################
#############
```
**Obanner101**
```
#### ### ###################
#### ### ############################
#### ### ##################################
#### ### #######################################
###################################################################### ############################################### ##############
###################################################################### ################################################## ######################
###################################################################### ##################################################### ########################
###################################################################### ################### ################ ############################
###################################################################### ################ ############# ################################## ###
###################################################################### #### ### ############## ########## ################################### ###
#### ### ### #### ### ########## ######## ########## ### ######### ###
#### ### ### #### ### ######### ####### #### ### ##### ### ##### ###########################################
#### ### ### #### ### ######## ##### #### ### ##### ### ##### ################################################
#### ### ### ###################################################################### ######## #### ###################################################################### #### ### #### #################################################
### ### ###################################################################### ####### #### ###################################################################### #### ### ### ##################################################
### ### ###################################################################### ###### #### ###################################################################### #### ### ### ####################################################
### ### ###################################################################### ##### ### ###################################################################### #### ### ### ####################################################
### ### ###################################################################### #### ### ###################################################################### #### ### ### ######### ###
### ### ###################################################################### #### ### ###################################################################### ### ### #### ####### ###
### ### #### ### #### ### #### ### ### ##### ###### ###
######## ### #### ### #### ### ### #### ## ### ##### #####
############## ### #### ### ##### ### #### ### ### ######### ####
############## ### #### ### ##### ### #### ### ################### ###
############## ### ######## ### ##### #### ################## ##
### ########### ### ####### ### ###############
### ################################## ######### #############
#### ################################# ############## ############
##### ############################### ##############
###### ############################# ##############
######## ###########################
############## #####################
############## ##############
##############
```
**Obanner102**
```
### ###
### ### ###################
### ### ############################
### ### ###################################
###################################################################### ########################################
###################################################################### ############################################### #############
###################################################################### ################################################## #####################
###################################################################### ##################################################### #########################
###################################################################### ################### ################ ###########################
###################################################################### ################# ############## ################################## ###
###################################################################### ### ### ############# ########### ################################### ###
### ### ### ### ### ############ ######### ########## ### ########## ###
### ### ### ### ### ######### ###### ### ### ###### ### ###### ###########################################
### ### ### ### ### ######## #### ### ### ##### ### ##### ###############################################
### ### ###################################################################### ######## #### ###################################################################### #### ### #### #################################################
### ### ###################################################################### ###### #### ###################################################################### #### ### ### ##################################################
### ### ###################################################################### ##### #### ###################################################################### ### ### ### ###################################################
### ### ###################################################################### #### ### ###################################################################### ### ### ### ###################################################
### ### ###################################################################### #### ### ###################################################################### ### ### ### ######## ###
### ### ###################################################################### #### ### ###################################################################### ### ### #### ####### ###
#### ### ###################################################################### #### ### ### #### ### ##### ###### ###
############## ### ### ### #### #### #### ### ### ### ###### #####
############## ### ### ### ##### #### #### ### ### ########## ####
############## ### ### ### ###### #### ### ### ################### ###
### ####### #### ##### ### ################### ##
### ########### #### ####### #### #################
#### ################################## ######### ##############
#### ################################## ############## ############
###### ################################ ############## ########
######### ############################## ##############
############## ############################
############## ########################
############## ##############
```
**Obanner103**
```
### ### ###################
### ### #############################
### ### ###################################
### ### #######################################
####################################################################### ############################################### ##############
####################################################################### ################################################### ######################
####################################################################### ###################################################### #########################
####################################################################### ######################################################### ############################
####################################################################### ################ ############## ################################## ###
####################################################################### ### ### ############## ########### #################################### ###
####################################################################### ### ### ############# ######### ########## #### ########## ###
### ### ### ### ### ########## ###### ### ### ####### #### ####### ############################################
### ### ### ### ### ######## #### ### ### #### #### #### ################################################
### ### ### ####################################################################### ####### ##### ####################################################################### #### #### #### ##################################################
### ### ####################################################################### ###### #### ####################################################################### #### #### #### ###################################################
### ### ####################################################################### ##### #### ####################################################################### ### #### ### ###################################################
### ### ####################################################################### ##### ### ####################################################################### ### #### ### ####################################################
### ### ####################################################################### ##### ### ####################################################################### ### #### ### ######## ###
### ### ####################################################################### #### ### ####################################################################### ### #### #### ####### ###
### ### ####################################################################### #### ### ### ### #### #### ##### ###
##### ### ### ### #### ### #### ### ### #### ##### ####
####### ### ### ### #### ### ### #### #### ####### ####
############### ### ### ### ###### ### #### ### #################### ####
############### ### ####### ### ##### #### ################### ##
############### ### ######### ### ###### #### ##################
### ################################## ######### ### ################
#### ################################# ############## #############
#### ################################ ############## #########
###### ############################### ##############
######### ###########################
############## ########################
############## #####################
##############
```
**Obanner104**
```
### ### ####################
### ### ##############################
### ### ####################################
### ### ########################################
######################################################################## ################################################ ##############
######################################################################## #################################################### ######################
######################################################################## ###################################################### #########################
######################################################################## ########################################################## #############################
######################################################################## ################ ############## ################################### ###
######################################################################## ### ### ############## ########### ##################################### ###
######################################################################## ### ### ############# ######### ########### ### ########## ###
### ### ### ### ### ############ ####### ### ### ####### ### ####### ############################################
### ### ### ### ### ######## #### ### ### ##### ### ##### #################################################
### ### ### ######################################################################## ######## ##### ######################################################################## #### ### #### ###################################################
### ### ######################################################################## ###### #### ######################################################################## #### ### #### ###################################################
### ### ######################################################################## ###### #### ######################################################################## ### ### ### ####################################################
### ### ######################################################################## ##### ### ######################################################################## ### ### ### #####################################################
### ### ######################################################################## ##### ### ######################################################################## ### ### ### ######### ###
### ### ######################################################################## #### ### ######################################################################## ### ### #### ####### ###
### ### ######################################################################## #### ### ### ### ### ##### ###### ###
#### ### ### ### #### ### #### ### ## ### ##### #####
######## ### ### ### #### ### ### ### ### ####### ####
############## ### ### ### ##### ### #### #### ### ########## ####
############## ### ####### ### #### #### ################### ###
############## ### ######### ### ###### #### #################
### ############ ### ####### ### ################
#### ################################## ############## ##############
#### ################################# ############## ########
###### ################################ ##############
###### ############################## ##############
############## #########################
############## ######################
############## ##############
##############
```
**Obanner105**
```
#### ### ###################
#### ### #############################
#### ### ###################################
#### ### #########################################
######################################################################### #################################################
######################################################################### ################################################### ##############
######################################################################### ####################################################### ######################
######################################################################### ########################################################## ##########################
######################################################################### ################# ############## ############################
######################################################################### ############### ########### ################################### ###
######################################################################### #### ### ############ ######### #################################### ###
#### ### ### #### ### ########### ######## ########## ### ########## ###
#### ### ### #### ### ######## ##### #### ### ####### ### ####### #############################################
#### ### ### #### ### ######## ##### #### ### ##### ### ##### ##################################################
### ### ######################################################################### ####### #### ######################################################################### #### ### #### ###################################################
### ### ######################################################################### ####### #### ######################################################################### #### ### #### ####################################################
### ### ######################################################################### ##### ### ######################################################################### #### ### ### #####################################################
### ### ######################################################################### ##### ### ######################################################################### #### ### ### ######################################################
### ### ######################################################################### #### ### ######################################################################### #### ### ### ######### ###
### ### ######################################################################### #### ### ######################################################################### #### ### #### ######## ###
##### ### ######################################################################### #### ### #### #### ### ### #### ####### ###
######## ### #### ### #### ### ### #### ## ### ###### #####
############## ### #### ### ##### ### #### ### ### ####### ####
############## ### #### ### ###### ### #### ### ### ########## ####
############## ### ######## ### ###### ### #################### ####
### ########### ### ####### #### ##################
### ################################### ########## ### ################
#### ################################## ############### ###############
###### ############################### ############### #############
####### ############################## ###############
######### ############################
############### ########################
############### ##############
###############
```
**Obanner106**
```
### #### ####################
### #### ##############################
### #### ####################################
### #### #########################################
######################################################################### ##############################################
######################################################################### #################################################### ##############
######################################################################### ######################################################## #######################
######################################################################### ########################################################## ##########################
######################################################################### #################### ################# #############################
######################################################################### ############## ############ ################################ ###
######################################################################### ### #### ############# ######## ##################################### ###
### ### #### ### #### ########### ######## ########## ### ########### ###
### ### #### ### #### ########## ###### ### #### ####### ### ####### #############################################
### ### #### ### #### ######## ##### ### #### ###### ### ##### ################################################
### #### ######################################################################### ####### #### ######################################################################### #### ### #### ###################################################
### #### ######################################################################### ###### #### ######################################################################### #### ### #### ####################################################
### #### ######################################################################### ##### #### ######################################################################### ### ### ### #####################################################
### #### ######################################################################### #### #### ######################################################################### ### ### ### #####################################################
### #### ######################################################################### #### #### ######################################################################### ### ### ### ######## ###
### #### ######################################################################### #### #### ######################################################################### ### ### #### ####### ###
### #### ######################################################################### #### #### ######################################################################### ### ### #### ###### ###
######## #### ### #### #### ### ### ### #### ### ##### ###### ###
############### #### ### #### ##### ### #### ### ### ####### ####
############### #### ### #### ###### ### #### ### ### ########### ####
############### #### ####### ### ##### ### #################### ###
#### ############ ### ######## #### ################### ##
#### ################################### ########## ### ################
#### ################################### ############### ##############
#### ################################# ############### #############
####### ############################### ############### ########
######### ############################
############### #########################
############### ######################
###############
```
**Obanner107**
```
### #### ####################
### #### ##############################
### #### #####################################
### #### #########################################
########################################################################## ##############################################
########################################################################## ##################################################### ###############
########################################################################## ######################################################## #######################
########################################################################## ########################################################### ##########################
########################################################################## ##################### ################# #############################
########################################################################## ############## ############ ################################# ####
########################################################################## ### #### ############# ######### ##################################### ####
### #### #### ### #### ############ ######## ########### ### ########## ####
### #### #### ### #### ########## ####### ### #### ######## ### ####### #############################################
### #### #### ### #### ######## ##### ### #### ###### ### ###### #################################################
#### #### ########################################################################## ###### #### ########################################################################## #### ### #### ####################################################
#### #### ########################################################################## ###### #### ########################################################################## #### ### #### #####################################################
#### #### ########################################################################## ##### #### ########################################################################## ### ### #### #####################################################
#### #### ########################################################################## ##### #### ########################################################################## ### ### #### ######################################################
#### #### ########################################################################## #### #### ########################################################################## ### ### #### ######### ####
#### #### ########################################################################## #### #### ########################################################################## ### ### #### ####### ####
#### #### ########################################################################## #### #### ########################################################################## ## ### #### ###### ####
#### #### ### #### #### #### #### ### ### ### ##### ##### ####
############## #### ### #### #### #### #### ### ### ###### ####
############## #### ### #### ###### #### #### ### ### ########## ####
############## #### ######## #### ##### ### #################### ###
############## #### ######### #### ##### #### #################### ###
#### #################################### ########## ##### ##################
#### ################################### ############### ###############
#### ################################## ############### #############
###### ################################# ############### #########
######### #############################
############### ##########################
############### ######################
############### ###############
###############
```
**Obanner108**
```
### ### ####################
### ### ##############################
### ### #####################################
### ### ##########################################
########################################################################## ###############################################
########################################################################## ##################################################### ##############
########################################################################## ######################################################## #######################
########################################################################## ############################################################ ##########################
########################################################################## #################### ################# ##############################
########################################################################## ############### ########### ################################ ###
########################################################################## ### ### ############# ######### ###################################### ###
### ### ### ### ### ############ ######## ########### #### ########### ###
### ### ### ### ### ######### ####### ### ### ####### #### ######## ##############################################
### ### ### ### ### ######## ##### ### ### ##### #### ###### #################################################
### ### ########################################################################## ###### #### ########################################################################## #### #### #### #####################################################
### ### ########################################################################## ####### #### ########################################################################## #### #### #### #####################################################
### ### ########################################################################## ###### #### ########################################################################## ### #### ### ######################################################
### ### ########################################################################## ##### ### ########################################################################## ### #### ### #######################################################
### ### ########################################################################## #### ### ########################################################################## ### #### ### ######### ###
### ### ########################################################################## #### ### ########################################################################## ### #### #### ####### ###
### ### ########################################################################## #### ### ########################################################################## ## #### #### ####### ###
##### ### ### ### #### ### #### ### ### #### ##### ###### ###
######### ### ### ### #### ### #### ## #### ###### #####
############### ### ### ### ##### ### #### #### #### ########### #####
############### ### ####### ### ##### #### ##################### ###
############### ### ######### ### ###### #### #################### ##
### ############# ### ####### #### ##################
#### ################################### ############## #### #################
#### ################################# ############## ##############
##### ################################# ############## #########
###### ############################### ##############
######### #############################
############## ######################
############## ###############
##############
```
**Obanner109**
```
#### ###
#### ### ####################
#### ### ##############################
#### ### #####################################
########################################################################### ##########################################
########################################################################### ############################################### ###############
########################################################################### ###################################################### #######################
########################################################################### ######################################################### ###########################
########################################################################### ############################################################ #############################
########################################################################### ##################### ################## ################################# ###
########################################################################### ################## ############## ###################################### ###
#### ### ### #### ### ############# ######### ########## ### ########## ###
#### ### ### #### ### ########### ######## ####### ### ####### ###############################################
#### ### ### #### ### ########## ####### #### ### ###### ### ###### ##################################################
#### ### ### #### ### ######## ##### #### ### ##### ### ##### #####################################################
### ### ########################################################################### ######## ##### ########################################################################### #### ### #### ######################################################
### ### ########################################################################### ####### #### ########################################################################### #### ### ### #######################################################
### ### ########################################################################### ###### #### ########################################################################### #### ### ### ########################################################
### ### ########################################################################### ##### ### ########################################################################### #### ### ### ########################################################
### ### ########################################################################### ##### ### ########################################################################### #### ### ### ######## ###
### ### ########################################################################### #### ### ########################################################################### ### ### #### ####### ###
##### ### ########################################################################### #### ### ########################################################################### ### ### ##### ###### ###
######## ### #### ### #### #### #### #### ## ### ###### #####
############### ### #### ### #### #### #### ### ### ####### ####
############### ### #### ### ##### #### ##### ### ##################### ####
############### ### #### ### ####### #### ##### ##### #################### ##
### ######### #### ###### #### ##################
### ############ #### ####### ### ################
#### ##################################### ######### ###############
##### #################################### ############## #########
###### ################################# ##############
######### ################################ ##############
############## #############################
############## ##########################
############## #######################
```
**Obanner11**
```
# ## ##
######## # ## # #
# ######## # # ## #
# ### ##
```
**Obanner110**
```
#### ###
#### ### #####################
#### ### ###############################
#### ### #####################################
############################################################################ ###########################################
############################################################################ ############################################### ###############
############################################################################ ###################################################### ########################
############################################################################ ######################################################### ##########################
############################################################################ ############################################################# ##############################
############################################################################ ##################### ################## ################################## ###
############################################################################ ################## ############### ###################################### ###
#### ### ### #### ### ############# ######### ########### #### ########### ###
#### ### ### #### ### ############ ######### ######## #### ######## ##############################################
#### ### ### #### ### ########## ####### #### ### ###### #### ###### ##################################################
#### ### ### #### ### ######## ##### #### ### ##### #### ##### #####################################################
### ### ############################################################################ ######### ##### ############################################################################ ##### #### #### ######################################################
### ### ############################################################################ ####### #### ############################################################################ #### #### ### #######################################################
### ### ############################################################################ ###### #### ############################################################################ #### #### ### ########################################################
### ### ############################################################################ ##### ### ############################################################################ #### #### ### ########################################################
### ### ############################################################################ ##### ### ############################################################################ #### #### ### ######## ###
### ### ############################################################################ ##### ### ############################################################################ ### #### ##### ####### ###
##### ### ############################################################################ ##### ### ############################################################################ #### #### ##### ###### ###
######## ### #### ### ##### ### #### #### ### #### ###### #####
############### ### #### ### #### ### ### ### #### ######## ####
############### ### #### ### ##### ### #### ### #### ########### ###
############### ### #### ### ###### ### ##### #### #################### ###
### ######### ### ###### #### ###################
### ############ ### ####### ### #################
#### #################################### ########## ###############
#### #################################### ############### ##############
###### ################################## ###############
######### ############################### ###############
############### #############################
############### ##########################
############### ######################
###############
```
**Obanner111**
```
### ### #####################
### ### ################################
### ### ######################################
### ### ##########################################
############################################################################ ################################################
############################################################################ #################################################### ###############
############################################################################ ########################################################## #######################
############################################################################ ############################################################## ###########################
############################################################################ ##################### ################## ###############################
############################################################################ ################# ############### ################################# ###
############################################################################ ### ### ############### ############ ##################################### ###
### ### ### ### ### ############ ######### ########### ### ########### ###
### ### ### ### ### ########## ####### ######## ### ####### ###############################################
### ### ### ### ### ######### ##### ### ### ###### ### ##### ##################################################
### ### ### ############################################################################ ######## ##### ### ### ##### ### ##### ####################################################
### ### ############################################################################ ###### #### ############################################################################ #### ### #### #######################################################
### ### ############################################################################ ###### #### ############################################################################ ### ### ### #######################################################
### ### ############################################################################ ##### ### ############################################################################ ### ### ### ########################################################
### ### ############################################################################ ##### ### ############################################################################ ### ### ### ########################################################
### ### ############################################################################ #### ### ############################################################################ ### ### ### ######### ###
### ### ############################################################################ #### ### ############################################################################ ### ### #### ###### ###
### ### ### ### #### ### ############################################################################ ### ### ##### ##### ###
######### ### ### ### #### ### ### ### ### ### ##### #####
############### ### ### ### ##### ### #### ### #### ### ####### #####
############### ### ### ### ###### ### ##### #### ### ########### ####
############### ### ######## ### ##### ### ##################### ###
############### ### ######### ### ###### #### ####################
### ##################################### ########## #### #################
#### #################################### ############### ###############
#### ################################### ############### #############
###### ################################## ############### #########
###### ################################ ###############
############### ##########################
############### #######################
############### ###############
###############
```
**Obanner112**
```
### ###
### ### #####################
### ### ###############################
### ### #######################################
############################################################################# ###########################################
############################################################################# ################################################# ###############
############################################################################# ################################################### ########################
############################################################################# ########################################################### ###########################
############################################################################# ############################################################## ##############################
############################################################################# ##################### ################# ##################################
############################################################################# ################## ############### ###################################### ####
############################################################################# ### ### ############### ############ ############ #### ########### ####
### #### ### ### ### ############## ########## ####### #### ######## ####
### #### ### ### ### ########## ###### ### ### ###### #### ###### ################################################
### #### ### ### ### ######## ##### ### ### ##### #### ##### ###################################################
#### ### ############################################################################# ######## ##### ############################################################################# #### #### #### #####################################################
#### ### ############################################################################# ####### #### ############################################################################# #### #### #### #######################################################
#### ### ############################################################################# ####### #### ############################################################################# ### #### #### ########################################################
#### ### ############################################################################# ##### ### ############################################################################# ### #### #### #########################################################
#### ### ############################################################################# ##### ### ############################################################################# ### #### #### #########################################################
#### ### ############################################################################# #### ### ############################################################################# ### #### #### ######### ####
#### ### ############################################################################# #### ### ############################################################################# ## #### #### ######## ####
##### ### ############################################################################# #### ### ### ## #### ###### ###### ####
################ ### ### ### #### #### #### ### ### #### ######## #####
################ ### ### ### ##### #### #### #### #### ########### ####
################ ### ### ### ###### #### #### #### ##################### #####
################ ### ####### #### ##### #### ##################### ####
### ########## #### ###### #### ###################
#### ############# #### ######## ###############
#### ##################################### ############### ##############
###### ################################### ############### #########
####### ################################## ###############
######### ################################# ###############
############### ##############################
############### ###########################
############### ################
```
**Obanner113**
```
#### ###
#### ### ######################
#### ### ################################
#### ### ######################################
############################################################################## ############################################
############################################################################## ################################################# ###############
############################################################################## #################################################### ########################
############################################################################## ########################################################### ###########################
############################################################################## ############################################################## ###############################
############################################################################## ##################### ################## ##################################
############################################################################## ################## ############### ###################################### ###
############################################################################## #### ### ################ ############ ########### ### ########### ###
#### ### ### #### ### ############# ########## ######## ### ######## ###
#### ### ### #### ### ########## ###### #### ### ###### ### ###### ################################################
#### ### ### #### ### ######## ##### #### ### ##### ### ###### ####################################################
### ### ############################################################################## ######### ##### ############################################################################## #### ### ##### ######################################################
### ### ############################################################################## ####### #### ############################################################################## #### ### #### ########################################################
### ### ############################################################################## ####### #### ############################################################################## #### ### ### #########################################################
### ### ############################################################################## ###### #### ############################################################################## #### ### ### ##########################################################
### ### ############################################################################## ##### ### ############################################################################## #### ### ### ##########################################################
### ### ############################################################################## #### ### ############################################################################## #### ### #### ########## ###
### ### ############################################################################## #### ### ############################################################################## ### ### ##### ######## ###
##### ### ############################################################################## #### ### #### ### ### ###### ###### ###
######### ### #### ### #### ### #### #### ### ### ######## #####
############### ### #### ### #### ### ### ### ### ########### ####
############### ### #### ### ###### ### #### ### ##################### ####
############### ### ######## ### ###### ##### #################### ####
### ######### ### ###### #### ################## ###
### ############ ### ######## ### #################
#### ###################################### ########## #############
###### ##################################### ############### #########
####### ################################## ###############
######### ################################ ###############
############### ##############################
############### ##########################
############### #######################
###############
```
**Obanner114**
```
#### ###
#### ### #####################
#### ### ################################
#### ### #######################################
############################################################################### ############################################
############################################################################### #################################################
############################################################################### ##################################################### ###############
############################################################################### ######################################################## ########################
############################################################################### ############################################################### ############################
############################################################################### ###################### ################## ###############################
############################################################################### ################## ################ ################################### ###
############################################################################### #### ### ############### ############ ###################################### ###
#### ### ### #### ### ############## ########## ######################################## ###
#### ### ### #### ### ############ ######## #### ### ######## ### ####### ################################################
#### ### ### #### ### ######### ##### #### ### ###### ### ###### ####################################################
### ### ############################################################################### ######### ##### ############################################################################### ##### ### ##### #####################################################
### ### ############################################################################### ####### #### ############################################################################### ##### ### #### #######################################################
### ### ############################################################################### ####### #### ############################################################################### ##### ### #### #########################################################
### ### ############################################################################### ###### #### ############################################################################### #### ### ### ##########################################################
### ### ############################################################################### ###### ### ############################################################################### #### ### ### ##########################################################
### ### ############################################################################### ##### ### ############################################################################### #### ### ### ########## ###
### ### ############################################################################### ##### ### ############################################################################### #### ### #### ######## ###
##### ### ############################################################################### ##### ### #### ### ### #### ####### ###
######### ### #### ### ##### #### #### #### #### ### ##### #####
############### ### #### ### ##### #### ### ### ### ###### ####
############### ### #### ### ##### #### #### ### ### ########### ####
############### ### ###### #### #### ### ###################### ###
### ######### #### ####### #### ##################### ###
### ############# #### ######## ##### ###################
#### ###################################### ########### #### #################
#### ##################################### ################ ################
###### #################################### ################ ##############
########## ################################### ################
################ ###############################
################ ###########################
################ ########################
################ ################
```
**Obanner115**
```
### ####
### #### ######################
### #### ################################
### #### #######################################
############################################################################### ############################################
############################################################################### ################################################## ################
############################################################################### ##################################################### ########################
############################################################################### ######################################################### ############################
############################################################################### ################################################################ ################################
############################################################################### ##################### ################## ###################################
############################################################################### ################## ################ ###################################### ####
############################################################################### ### #### ################ ############# ######################################## ####
### #### #### ### #### ############## ######### ######## #### ######## ####
### #### #### ### #### ############ ######## ### #### ###### #### ###### #################################################
### #### #### ### #### ########### ####### ### #### ##### #### ##### ####################################################
#### #### ############################################################################### ######## ##### ############################################################################### #### #### ##### ######################################################
#### #### ############################################################################### ###### #### ############################################################################### #### #### ##### ########################################################
#### #### ############################################################################### ####### #### ############################################################################### ### #### #### #########################################################
#### #### ############################################################################### ###### #### ############################################################################### ### #### #### ##########################################################
#### #### ############################################################################### ##### #### ############################################################################### ### #### #### ##########################################################
#### #### ############################################################################### ##### #### ############################################################################### ### #### ##### ######### ####
#### #### ############################################################################### #### #### ############################################################################### ## #### ##### ####### ####
###### #### ############################################################################### #### #### ### ### #### ##### ####### ####
######## #### ### #### #### ### #### ### ### #### ###### ###### ####
################ #### ### #### #### ### ### #### #### ######## #####
################ #### ### #### ##### ### #### #### #### ########### #####
################ #### ###### ### #### #### ##################### ###
################ #### ######## ### ##### #### #################### ##
#### ########## ### ###### #### ##################
#### ###################################### ########### ################
#### ##################################### ################ ##############
###### ################################### ################ ##########
####### ################################### ################
########## ################################# ################
################ ##############################
################ #######################
################ ###############
```
**Obanner116**
```
### #### ######################
### #### ################################
### #### ########################################
### #### #############################################
################################################################################ ##################################################
################################################################################ ###################################################### ###############
################################################################################ ######################################################### #########################
################################################################################ ############################################################ ############################
################################################################################ ###################### ################### ###############################
################################################################################ ################### ################ ################################### ###
################################################################################ ################ ############ ####################################### ###
################################################################################ ### #### ############## ######### ######################################### ###
### ### #### ### #### ############# ######### ############ ### ############ #################################################
### ### #### ### #### ########## ####### ### #### ###### ### ####### #####################################################
### ### #### ### #### ######## ##### ### #### ##### ### ##### #######################################################
### #### ################################################################################ ####### #### ################################################################################ #### ### #### #########################################################
### #### ################################################################################ ####### ##### ################################################################################ #### ### #### #########################################################
### #### ################################################################################ ###### ##### ################################################################################ ### ### ### ###########################################################
### #### ################################################################################ ##### #### ################################################################################ ### ### ### ###########################################################
### #### ################################################################################ ##### #### ################################################################################ ### ### ### ########## ###
### #### ################################################################################ #### #### ################################################################################ ### ### #### ######## ###
### #### ################################################################################ #### #### ################################################################################ ## ### #### ####### ###
##### #### ################################################################################ #### #### ##### ### ### ### ##### ###### ###
######### #### ### #### #### #### #### ### ## ### ####### #####
############### #### ### #### ##### #### #### ### ### ######## #####
############### #### ### #### ###### #### #### #### ### ############ ####
############### #### ######## #### ##### #### ###################### ###
############### #### ########## #### ###### #### ###################
#### ############## #### ####### ### #################
##### ###################################### ################ ################
##### #################################### ################ ##############
###### ################################### ################ #########
####### ################################# ################
########## ###############################
################ ###########################
################ ########################
################ ################
```
**Obanner117**
```
#### ####
#### #### ######################
#### #### #################################
#### #### ########################################
################################################################################# #############################################
################################################################################# ###################################################
################################################################################# ###################################################### ################
################################################################################# ######################################################### ########################
################################################################################# ############################################################# ############################
################################################################################# ###################### ################### ################################
################################################################################# ################### ################ #################################### ####
################################################################################# ############### ############ ####################################### ####
#### #### #### #### #### ############## ########## ######################################## ####
#### #### #### #### #### ############ ######### ########### #### ########### #################################################
#### #### #### #### #### ########## ####### #### #### ###### #### ###### #####################################################
#### #### #### #### #### ######### ##### #### #### ##### #### ##### ######################################################
#### #### ################################################################################# ######### ##### ################################################################################# #### #### #### ########################################################
#### #### ################################################################################# ####### ##### ################################################################################# ##### #### #### #########################################################
#### #### ################################################################################# ###### ##### ################################################################################# #### #### #### ###########################################################
#### #### ################################################################################# ##### #### ################################################################################# #### #### #### ###########################################################
#### #### ################################################################################# ##### #### ################################################################################# #### #### #### ########## ####
#### #### ################################################################################# ##### #### ################################################################################# #### #### #### ######## ####
#### #### ################################################################################# ##### #### ################################################################################# ### #### #### ####### ####
##### #### ################################################################################# ##### #### #### #### #### ##### ###### ####
################ #### #### #### ##### #### ##### #### ### #### ###### #####
################ #### #### #### ##### #### ##### ### #### ######## ####
################ #### #### #### ###### #### #### ### #### ########### ###
################ #### #### #### ######## #### ##### ### ###################### ###
#### ######### #### ###### #### ######################
#### ############# #### ######## ##### ####################
##### ####################################### ########## ################
##### ####################################### ################ ##############
####### ##################################### ################ ##########
########## ################################## ################
################ ################################
################ ############################
################ ########################
################ ################
```
**Obanner118**
```
#### #### ######################
#### #### ##################################
#### #### ########################################
#### #### ##############################################
################################################################################## ##################################################
################################################################################## ###################################################### ################
################################################################################## ########################################################## #########################
################################################################################## ############################################################## #############################
################################################################################## ################################################################## #################################
################################################################################## ################## ################ ###################################
################################################################################## ################ ############ ####################################### ####
################################################################################## #### #### ############## ########## ######################################### ####
#### #### #### #### #### ############# ######### ############ ### ############ ####
#### #### #### #### #### ########### ####### #### #### ######## ### ######## ##################################################
#### #### #### #### #### ######### ##### #### #### ###### ### ###### #####################################################
#### #### #### ################################################################################## ######### ###### ################################################################################## ##### ### ##### #######################################################
#### #### ################################################################################## ####### ##### ################################################################################## ##### ### ##### #########################################################
#### #### ################################################################################## ####### ##### ################################################################################## #### ### #### ##########################################################
#### #### ################################################################################## ###### #### ################################################################################## #### ### #### ###########################################################
#### #### ################################################################################## ###### #### ################################################################################## #### ### #### ############################################################
#### #### ################################################################################## ##### #### ################################################################################## #### ### #### ########## ####
#### #### ################################################################################## ##### #### ################################################################################## #### ### ##### ######## ####
#### #### ################################################################################## ##### #### #### #### ### ###### ####### ####
##### #### #### #### ##### ### ##### #### ### ### ###### ###### ####
######### #### #### #### ##### ### #### #### ### ######## ######
################ #### #### #### ###### ### ##### #### ### ############ #####
################ #### #### #### ######## ### ##### ### ###################### ####
################ #### ########## ### ###### #### ##################### ###
#### ############# ### ######## #### ###################
#### ####################################### ########## #### ##################
##### ###################################### ################ ################
##### ##################################### ################ #########
####### #################################### ################
####### ################################## ################
################ ############################
################ ########################
################ ################
################
```
**Obanner119**
```
### #### #######################
### #### #################################
### #### #########################################
### #### ##############################################
################################################################################## ###################################################
################################################################################## ####################################################### ################
################################################################################## ########################################################### ##########################
################################################################################## ############################################################### #############################
################################################################################## ################################################################# ################################
################################################################################## ###################### ################### ####################################
################################################################################## ################ ############# ######################################## ###
################################################################################## ### #### ############### ########## ########################################## ###
### ### #### ### #### ############# ######### ############ #### ############ ###
### ### #### ### #### ########### ####### ### #### ######## #### ######## ###################################################
### ### #### ### #### ######### ###### ### #### ####### #### ###### ######################################################
### ### #### ################################################################################## ######### ###### ################################################################################## ##### #### #### ########################################################
### #### ################################################################################## ######## ##### ################################################################################## #### #### #### ##########################################################
### #### ################################################################################## ####### ##### ################################################################################## ### #### ### ###########################################################
### #### ################################################################################## ###### ##### ################################################################################## ### #### ### ############################################################
### #### ################################################################################## ##### #### ################################################################################## ### #### ### ############################################################
### #### ################################################################################## #### #### ################################################################################## ### #### ### ######### ###
### #### ################################################################################## #### #### ################################################################################## ### #### #### ######## ###
### #### ################################################################################## #### #### ################################################################################## ### #### #### ####### ###
##### #### ### #### #### #### ##### ### #### #### ##### ####### ###
######### #### ### #### ##### #### #### #### #### ######## ######
################# #### ### #### ###### #### ##### #### #### ############ #####
################# #### ### #### ####### #### ##### #### ####################### #####
################# #### ######## #### ###### ##### ###################### ####
#### ############## #### ######## #### #################### ##
#### ######################################## ########### ### ##################
##### ####################################### ################# ################
##### ##################################### ################# ###############
####### #################################### ################# ##########
######## ################################### #################
########## ################################
################# ############################
################# #########################
#################
```
**Obanner12**
```
# ## #
######## # # # # # #
######## # # # # # #
#### #
```
**Obanner120**
```
### ### ######################
### ### ##################################
### ### #########################################
### ### ##############################################
################################################################################## ####################################################
################################################################################## ######################################################## ################
################################################################################## ########################################################### #########################
################################################################################## ############################################################## #############################
################################################################################## ################################################################## #################################
################################################################################## ####################### ################### ####################################
################################################################################## ################# ############# ######################################## ####
################################################################################## ### ### ############### ########## ########################################## ####
### #### ### ### ### ############# ######### ############ #### ############ ####
### #### ### ### ### ########## ######## ######## #### ######## ###################################################
### #### ### ### ### ######### ###### ### ### ###### #### ###### #######################################################
### #### ### ################################################################################## ######### ###### ### ### #### #### ##### #########################################################
#### ### ################################################################################## ####### ##### ################################################################################## #### #### ##### ###########################################################
#### ### ################################################################################## ####### #### ################################################################################## ### #### #### ###########################################################
#### ### ################################################################################## ###### #### ################################################################################## ### #### #### ############################################################
#### ### ################################################################################## ##### ### ################################################################################## ### #### #### #############################################################
#### ### ################################################################################## #### ### ################################################################################## ### #### #### ########## ####
#### ### ################################################################################## #### ### ################################################################################## ### #### ##### ######## ####
#### ### ################################################################################## #### ### ################################################################################## ## #### ##### ####### ####
###### ### ### ### #### ### #### ################################################################################## ### #### ###### ###### ####
########## ### ### ### #### ### #### ### ## #### ###### #####
################ ### ### ### ##### ### ##### #### #### ############ ####
################ ### ### ### ###### ### ##### #### ####################### #####
################ ### ######## ### ###### ##### ###################### ####
################ ### ########## ### ####### ##### #################### ###
### ############## ### ######## #### ###################
#### ####################################### ################ #################
#### ##################################### ################ ###############
###### #################################### ################ ##########
####### ################################## ################
########## ################################
################ ############################
################ ########################
################ ################
################
```
**Obanner121**
```
#### ### #######################
#### ### ##################################
#### ### #########################################
#### ### ###############################################
################################################################################### ####################################################
################################################################################### ######################################################## #################
################################################################################### ########################################################### ##########################
################################################################################### ############################################################### #############################
################################################################################### ################################################################### #################################
################################################################################### ####################### ################### #####################################
################################################################################### #################### ################# ######################################## ###
################################################################################### #### ### ############## ########## ########################################## ###
#### ### ### #### ### ############# ########## ############ #### ############ ###
#### ### ### #### ### ########### ######## ######## #### ######### ###################################################
#### ### ### #### ### ######### ###### #### ### ###### #### ####### #######################################################
#### ### ### ################################################################################### ######### ##### #### ### ##### #### ###### ########################################################
### ### ################################################################################### ####### #### ################################################################################### ##### #### #### ##########################################################
### ### ################################################################################### ####### #### ################################################################################### #### #### ### ###########################################################
### ### ################################################################################### ###### #### ################################################################################### #### #### ### ############################################################
### ### ################################################################################### ##### ### ################################################################################### #### #### ### #############################################################
### ### ################################################################################### ##### ### ################################################################################### #### #### ### #############################################################
### ### ################################################################################### ##### ### ################################################################################### #### #### #### ######## ###
### ### ################################################################################### ##### ### ################################################################################### ### #### ##### ####### ###
##### ### #### ### ##### #### #### ################################################################################### #### #### ###### ###### ###
######### ### #### ### #### #### ### #### ### #### ####### #####
################# ### #### ### ##### #### #### ### #### ######### ####
################# ### #### ### ###### #### ##### ### #### ############ ####
################# ### ######## #### ###### #### ###################### ###
################# ### ########## #### ####### ##### #################### ###
### ############# #### ######## #### ##################
### ######################################## ########### ################
#### ######################################## ################ ###############
#### ###################################### ################ ##########
####### ################################### ################
########## ################################
################ #############################
################ #########################
################ #################
################
```
**Obanner122**
```
#### ###
#### ### #######################
#### ### ##################################
#### ### ##########################################
#################################################################################### ###############################################
#################################################################################### #####################################################
#################################################################################### ######################################################## ################
#################################################################################### ############################################################ ##########################
#################################################################################### ################################################################ ##############################
#################################################################################### ################################################################### #################################
#################################################################################### ####################### ################### ##################################### ####
#################################################################################### ################### ################# ######################################### ####
#################################################################################### #### ### ################ ############# ########################################## ####
#### #### ### #### ### ############### ########### ############ #### ############ ####################################################
#### #### ### #### ### ########### ####### #### ### ######## #### ######## #######################################################
#### #### ### #### ### ######### ##### #### ### ####### #### ###### #########################################################
#### ### #################################################################################### ######### ##### #################################################################################### ###### #### ##### ###########################################################
#### ### #################################################################################### ######## #### #################################################################################### ##### #### #### ############################################################
#### ### #################################################################################### ######## #### #################################################################################### ##### #### #### #############################################################
#### ### #################################################################################### ####### #### #################################################################################### #### #### #### ##############################################################
#### ### #################################################################################### ###### ### #################################################################################### #### #### #### ##############################################################
#### ### #################################################################################### ###### ### #################################################################################### #### #### #### ########## ####
#### ### #################################################################################### ##### ### #################################################################################### #### #### #### ######### ####
#### ### #################################################################################### ##### ### #################################################################################### ### #### #### ####### ####
##### ### #################################################################################### ##### ### #### #### #### ##### ######
################# ### #### ### ##### #### #### #### ### #### ###### #####
################# ### #### ### ###### #### #### #### #### ######## #####
################# ### #### ### ####### #### #### #### #### ############ ####
################# ### ######## #### ###### #### ####################### ##
### ########## #### ####### #### #######################
### ############## #### ######### #### #####################
#### ######################################### ########### #################
#### ######################################## ################ ###############
###### ###################################### ################ ##########
####### ##################################### ################
########## #################################### ################
################ #################################
################ #############################
################ #################
```
**Obanner123**
```
#### ### #######################
#### ### ##################################
#### ### ##########################################
#### ### ################################################
##################################################################################### #####################################################
##################################################################################### #########################################################
##################################################################################### ############################################################ #################
##################################################################################### ################################################################ ##########################
##################################################################################### #################################################################### ##############################
##################################################################################### ####################### #################### #################################
##################################################################################### #################### ################# ##################################### ####
##################################################################################### ################# ############# ######################################### ####
##################################################################################### #### ### ############### ########### ########################################### ####
#### #### ### #### ### ############# ######### ############ ### ############ ####################################################
#### #### ### #### ### ########## ##### #### ### ######### ### ######## ########################################################
#### #### ### #### ### ########## ##### #### ### ####### ### ####### ##########################################################
#### ### ##################################################################################### ######## #### ##################################################################################### ###### ### ###### ############################################################
#### ### ##################################################################################### ######## #### ##################################################################################### ##### ### ##### #############################################################
#### ### ##################################################################################### ####### #### ##################################################################################### ##### ### ##### ##############################################################
#### ### ##################################################################################### ###### ### ##################################################################################### #### ### #### ###############################################################
#### ### ##################################################################################### ###### ### ##################################################################################### #### ### #### ###############################################################
#### ### ##################################################################################### ##### ### ##################################################################################### #### ### #### ########### ####
#### ### ##################################################################################### ##### ### ##################################################################################### #### ### ##### ######### ####
#### ### ##################################################################################### ##### ### ##################################################################################### ### ### ##### ######## ####
###### ### ##################################################################################### ##### #### #### #### #### ### ###### ######
########## ### #### ### ##### #### ### #### ### ### ####### #####
################ ### #### ### ###### #### #### #### ### ######## #####
################ ### #### ### ####### #### #### #### ### ############ ####
################ ### ########## #### ####### #### ####################### ###
### ############## #### ######### ##### ######################
### ######################################### ############ ##### ####################
#### ######################################## ################# #### ##################
#### ###################################### ################# #################
###### ##################################### ################# ###############
####### ################################### #################
########## #################################
################# #############################
################# #########################
################# #################
#################
```
**Obanner124**
```
### ####
### #### #######################
### #### ###################################
### #### ###########################################
##################################################################################### ################################################
##################################################################################### #####################################################
##################################################################################### ######################################################### ################
##################################################################################### ############################################################# ##########################
##################################################################################### ################################################################# ##############################
##################################################################################### ##################################################################### ##################################
##################################################################################### ######################## #################### ######################################
##################################################################################### #################### ################# ########################################## ###
##################################################################################### ### #### ################# ############# ############################################ ###
### ### #### ### #### ############### ########## ############# #### ############# ###
### ### #### ### #### ############## ######### ### #### ######## #### ######### #####################################################
### ### #### ### #### ########### ####### ### #### ###### #### ####### #########################################################
### #### ##################################################################################### ######### ##### ##################################################################################### ##### #### ##### ###########################################################
### #### ##################################################################################### ####### #### ##################################################################################### #### #### #### #############################################################
### #### ##################################################################################### ####### ##### ##################################################################################### #### #### #### #############################################################
### #### ##################################################################################### ###### ##### ##################################################################################### ### #### ### ##############################################################
### #### ##################################################################################### ##### #### ##################################################################################### ### #### ### ###############################################################
### #### ##################################################################################### ##### #### ##################################################################################### ### #### ### ###############################################################
### #### ##################################################################################### #### #### ##################################################################################### ### #### #### ########## ###
### #### ##################################################################################### #### #### ##################################################################################### ## #### #### ######## ###
##### #### ##################################################################################### #### #### ### ### #### ##### ####### ###
######### #### ### #### #### #### ##### ### ## #### ####### ###### ###
################# #### ### #### #### #### #### ### #### ######### #####
################# #### ### #### ##### #### #### #### #### ############# #####
################# #### ###### #### #### #### ######################## ####
################# #### ######## #### ##### ##### ####################### ###
#### ########### #### ###### ##### #####################
##### ############### #### ######## #### ###################
##### ######################################### ################# #################
###### ####################################### ################# ###############
####### ###################################### ################# ##########
########## #################################### #################
################# #################################
################# #############################
################# ##########################
################# #################
```
**Obanner125**
```
#### ####
#### #### ########################
#### #### ####################################
#### #### ##########################################
###################################################################################### ################################################
###################################################################################### ######################################################
###################################################################################### ########################################################## #################
###################################################################################### ############################################################## ###########################
###################################################################################### ################################################################## ###############################
###################################################################################### ###################################################################### ###################################
###################################################################################### ######################## #################### #####################################
###################################################################################### ################### ################# ######################################### ####
###################################################################################### #### #### ################# ############# ########################################### ####
#### #### #### #### #### ############### ########## ############ ### ############ ####
#### #### #### #### #### ############# ######### #### #### ######## ### ######## #####################################################
#### #### #### #### #### ########### ####### #### #### ###### ### ###### ########################################################
#### #### #### ###################################################################################### ######### ##### ###################################################################################### ###### ### ###### ##########################################################
#### #### ###################################################################################### ######### ###### ###################################################################################### ##### ### ##### ############################################################
#### #### ###################################################################################### ####### ##### ###################################################################################### ##### ### ##### #############################################################
#### #### ###################################################################################### ####### ##### ###################################################################################### #### ### #### ##############################################################
#### #### ###################################################################################### ###### #### ###################################################################################### #### ### #### ###############################################################
#### #### ###################################################################################### ###### #### ###################################################################################### #### ### #### ###############################################################
#### #### ###################################################################################### ##### #### ###################################################################################### #### ### #### ########## ####
#### #### ###################################################################################### ##### #### ###################################################################################### #### ### ##### ######## ####
###### #### ###################################################################################### ##### #### #### #### ### ###### ####### ####
########## #### #### #### ##### ### ##### #### ### ### ###### ###### ####
################# #### #### #### ##### ### #### #### ### ######## ######
################# #### #### #### ###### ### ##### #### ### ############ #####
################# #### #### #### ###### ### ##### ### ####################### ####
################# #### ######## ### ##### #### ###################### ###
#### ########## ### ###### #### ####################
#### ############## ### ######## #### ###################
##### ######################################### ########### #################
##### ######################################## ################# ###############
####### ####################################### ################# ##########
####### ###################################### #################
################# #################################### #################
################# #############################
################# #########################
################# #################
```
**Obanner126**
```
#### ####
#### #### #######################
#### #### ###################################
#### #### ###########################################
####################################################################################### #################################################
####################################################################################### #######################################################
####################################################################################### ########################################################### #################
####################################################################################### ############################################################## ##########################
####################################################################################### ################################################################# ##############################
####################################################################################### ##################################################################### ##################################
####################################################################################### ######################## #################### ######################################
####################################################################################### #################### ################# ########################################## ####
####################################################################################### #### #### ################# ############# ############################################ ####
#### #### #### #### #### ############### ########## ############ #### ############# ####
#### #### #### #### #### ############# ######### ######### #### ######### #####################################################
#### #### #### #### #### ########### ######## #### #### ####### #### ####### #########################################################
#### #### #### ####################################################################################### ########## ###### #### #### ###### #### ###### ###########################################################
#### #### ####################################################################################### ########## ###### ####################################################################################### ##### #### ##### #############################################################
#### #### ####################################################################################### ######## ##### ####################################################################################### ##### #### ##### ##############################################################
#### #### ####################################################################################### ######## ##### ####################################################################################### #### #### #### ###############################################################
#### #### ####################################################################################### ####### ##### ####################################################################################### #### #### #### ################################################################
#### #### ####################################################################################### ###### #### ####################################################################################### #### #### #### ################################################################
#### #### ####################################################################################### ##### #### ####################################################################################### #### #### #### ########### ####
#### #### ####################################################################################### ##### #### ####################################################################################### #### #### ##### ######### ####
###### #### ####################################################################################### ##### #### ####################################################################################### ### #### ##### ######## ####
########## #### #### #### ##### #### ##### #### #### #### ###### ####### ####
################# #### #### #### ##### #### #### #### ### #### ####### ######
################# #### #### #### ###### #### ##### #### #### ############# #####
################# #### #### #### ####### #### ##### #### ######################## #####
################# #### ######### #### ###### ##### ####################### ####
#### ########## #### ####### ##### ##################### ###
#### ############## #### ######## #### ###################
##### ########################################## ########### #################
##### ######################################### ################# ###############
####### ####################################### ################# ##########
######## ###################################### #################
########### #################################### #################
################# ##################################
################# ##############################
################# ##########################
################# #################
```
**Obanner127**
```
#### ####
#### #### ########################
#### #### ####################################
#### #### ############################################
######################################################################################## #################################################
######################################################################################## #######################################################
######################################################################################## ########################################################## #################
######################################################################################## ############################################################## ###########################
######################################################################################## ################################################################## ###############################
######################################################################################## ###################################################################### ###################################
######################################################################################## ######################## #################### #######################################
######################################################################################## #################### ################# ########################################### ####
######################################################################################## #### #### ################# ############# ############################################ ####
#### #### #### #### #### ################ ########### ############# #### ############ ####
#### #### #### #### #### ############## ########## ######### #### ######## ######################################################
#### #### #### #### #### ############ ######## #### #### ####### #### ###### ##########################################################
#### #### #### ######################################################################################## ########## ###### #### #### ###### #### ##### ############################################################
#### #### ######################################################################################## ########## ###### ######################################################################################## ##### #### #### ##############################################################
#### #### ######################################################################################## ######## ##### ######################################################################################## ##### #### #### ###############################################################
#### #### ######################################################################################## ######## ##### ######################################################################################## #### #### #### ################################################################
#### #### ######################################################################################## ####### ##### ######################################################################################## #### #### #### #################################################################
#### #### ######################################################################################## ###### #### ######################################################################################## #### #### #### #################################################################
#### #### ######################################################################################## ###### #### ######################################################################################## #### #### #### ########### ####
#### #### ######################################################################################## ##### #### ######################################################################################## #### #### #### ######### ####
#### #### ######################################################################################## ##### #### ######################################################################################## ### #### #### ######## ####
##### #### #### #### ##### #### #### #### #### ##### ####### ####
################# #### #### #### ##### #### ##### #### ### #### ###### ######
################# #### #### #### ###### #### ##### #### #### ######## #####
################# #### #### #### ####### #### ##### #### #### ############ #####
################# #### ######### #### ###### #### ######################## ####
#### ########### #### ####### ##### ######################## ###
#### ############### #### ######### ##### ######################
##### ########################################### ########### ##################
##### ########################################## ################# ################
####### ######################################## ################# ###########
######## ####################################### #################
########### ##################################### #################
################# ##################################
################# ##############################
################# ##########################
################# ##################
```
**Obanner128**
```
### #### ########################
### #### ####################################
### #### ############################################
### #### #################################################
######################################################################################## #######################################################
######################################################################################## ########################################################### #################
######################################################################################## ############################################################### ###########################
######################################################################################## ################################################################### ###############################
######################################################################################## ####################################################################### ###################################
######################################################################################## ######################### #################### #######################################
######################################################################################## ##################### ################# ########################################### ####
######################################################################################## ################## ############## ############################################# ####
######################################################################################## ### #### ################ ########### ############# #### ############# ####
### #### #### ### #### ############## ########## ######## #### ######### #######################################################
### #### #### ### #### ########### ######## ### #### ###### #### ####### ###########################################################
### #### #### ### #### ######### ###### ### #### ##### #### ###### #############################################################
### #### #### ######################################################################################## ######### ###### ######################################################################################## #### #### ##### ###############################################################
#### #### ######################################################################################## ####### ##### ######################################################################################## #### #### ##### ###############################################################
#### #### ######################################################################################## ####### ##### ######################################################################################## ### #### #### ################################################################
#### #### ######################################################################################## ###### ##### ######################################################################################## ### #### #### #################################################################
#### #### ######################################################################################## ##### #### ######################################################################################## ### #### #### #################################################################
#### #### ######################################################################################## ##### #### ######################################################################################## ### #### #### ########## ####
#### #### ######################################################################################## #### #### ######################################################################################## ### #### ##### ######## ####
#### #### ######################################################################################## #### #### ######################################################################################## ## #### ##### ####### ####
#### #### ######################################################################################## #### #### ### ### #### ###### ###### ####
###### #### ### #### #### #### ##### ### ## #### ####### #####
########## #### ### #### #### #### #### ### #### ######### ####
################## #### ### #### ##### #### ##### #### #### ############# #####
################## #### ### #### ###### #### ##### #### ######################## ####
################## #### ######## #### ###### ##### ####################### ###
################## #### ########### #### ####### ##### #####################
#### ############### #### ######### #### ###################
##### ########################################## ################## #################
##### ######################################## ################## ###############
####### ####################################### ################## ##########
######## ##################################### ##################
########### ##################################
################## ##############################
################## ##########################
################## #################
##################
```
**Obanner129**
```
#### ####
#### #### ########################
#### #### ####################################
#### #### ############################################
######################################################################################### ##################################################
######################################################################################### ########################################################
######################################################################################### ############################################################ ##################
######################################################################################### ############################################################### ###########################
######################################################################################### ################################################################### ###############################
######################################################################################### ####################################################################### ###################################
######################################################################################### ######################## ##################### #######################################
######################################################################################### #################### ################## ########################################### ####
######################################################################################### ################# ############## ############################################# ####
#### #### #### #### #### ############### ########### ############ #### ############# ####
#### #### #### #### #### ############# ########## ######### #### ######### ######################################################
#### #### #### #### #### ########### ######## #### #### ####### #### ####### ##########################################################
#### #### #### #### #### ########## ###### #### #### ###### #### ###### ############################################################
#### #### ######################################################################################### ########## ###### ######################################################################################### ##### #### ##### ##############################################################
#### #### ######################################################################################### ######## ##### ######################################################################################### ##### #### ##### ###############################################################
#### #### ######################################################################################### ######## ##### ######################################################################################### #### #### #### ################################################################
#### #### ######################################################################################### ####### ##### ######################################################################################### #### #### #### #################################################################
#### #### ######################################################################################### ###### #### ######################################################################################### #### #### #### #################################################################
#### #### ######################################################################################### ###### #### ######################################################################################### #### #### #### ########### ####
#### #### ######################################################################################### ##### #### ######################################################################################### #### #### ##### ######### ####
#### #### ######################################################################################### ##### #### ######################################################################################### ### #### ##### ######## ####
###### #### ######################################################################################### ##### #### #### #### #### ###### ####### ####
########## #### #### #### ##### #### ##### #### ### #### ####### ######
################# #### #### #### ##### #### #### #### #### ######### #####
################# #### #### #### ###### #### ##### #### #### ############# #####
################# #### #### #### ####### #### ##### #### ######################### ####
################# #### ######### #### ###### ##### ######################## ###
#### ########## #### ####### ##### ######################
#### ############## #### ######### #### ####################
##### ########################################### ############ ##################
##### ########################################## ################## ################
####### ######################################## ################## ###########
######## ####################################### ##################
########### ##################################### ##################
################## ###################################
################## ###############################
################## ###########################
################## ##################
```
**Obanner13**
```
# ## ##
######### # ## ## # # #
# ######### # # # #######
# # #
# #
```
**Obanner130**
```
#### #### ########################
#### #### ####################################
#### #### ############################################
#### #### ##################################################
########################################################################################## ########################################################
########################################################################################## ############################################################
########################################################################################## ################################################################ #################
########################################################################################## #################################################################### ###########################
########################################################################################## ######################################################################## ###############################
########################################################################################## ######################### ##################### ###################################
########################################################################################## ##################### ################## #######################################
########################################################################################## ################## ############## ########################################### ####
########################################################################################## #### #### ################ ########### ############################################# ####
#### #### #### #### #### ############## ########## ############# #### ############# ####
#### #### #### #### #### ############ ######## ######### #### ######### #######################################################
#### #### #### #### #### ########## ###### #### #### ####### #### ####### ###########################################################
#### #### #### ########################################################################################## ########## ###### #### #### ###### #### ###### #############################################################
#### #### ########################################################################################## ######## ##### ########################################################################################## ##### #### ##### ###############################################################
#### #### ########################################################################################## ######## ##### ########################################################################################## ##### #### ##### ################################################################
#### #### ########################################################################################## ####### ##### ########################################################################################## #### #### #### #################################################################
#### #### ########################################################################################## ###### #### ########################################################################################## #### #### #### ##################################################################
#### #### ########################################################################################## ###### #### ########################################################################################## #### #### #### ##################################################################
#### #### ########################################################################################## ##### #### ########################################################################################## #### #### #### ########### ####
#### #### ########################################################################################## ##### #### ########################################################################################## #### #### ##### ######### ####
#### #### ########################################################################################## ##### #### ########################################################################################## ### #### ##### ######## ####
###### #### #### #### ##### #### ##### #### #### #### ###### ####### ####
########## #### #### #### ##### #### #### #### ### #### ####### ######
################## #### #### #### ###### #### ##### #### #### ######### #####
################## #### #### #### ####### #### ##### #### #### ############# #####
################## #### ######### #### ###### #### ######################## ####
################## #### ########### #### ####### ##### ####################### ###
#### ############### #### ######### ##### #####################
#### ########################################### ############ #### ###################
##### ########################################## ################## #################
##### ######################################## ################## ###############
####### ####################################### ################## ##########
######## ##################################### ##################
########### ##################################
################## ##############################
################## ##########################
################## #################
##################
```
**Obanner131**
```
#### #### #########################
#### #### #####################################
#### #### #############################################
#### #### ###################################################
########################################################################################### #########################################################
########################################################################################### #############################################################
########################################################################################### ################################################################# ##################
########################################################################################### ##################################################################### ############################
########################################################################################### ######################################################################### ################################
########################################################################################### ######################### ##################### ####################################
########################################################################################### ##################### ################## ########################################
########################################################################################### ################## ############## ############################################ ####
########################################################################################### #### #### ################ ########### ############################################## ####
#### #### #### #### #### ############## ########## ############# #### ############# ####
#### #### #### #### #### ############ ######## ######### #### ######### ########################################################
#### #### #### #### #### ########## ###### #### #### ####### #### ####### ############################################################
#### #### #### ########################################################################################### ########## ###### #### #### ###### #### ###### ##############################################################
#### #### ########################################################################################### ######## ##### ########################################################################################### ##### #### ##### ################################################################
#### #### ########################################################################################### ######## ##### ########################################################################################### ##### #### ##### #################################################################
#### #### ########################################################################################### ####### ##### ########################################################################################### #### #### #### ##################################################################
#### #### ########################################################################################### ###### #### ########################################################################################### #### #### #### ###################################################################
#### #### ########################################################################################### ###### #### ########################################################################################### #### #### #### ###################################################################
#### #### ########################################################################################### ##### #### ########################################################################################### #### #### #### ########### ####
#### #### ########################################################################################### ##### #### ########################################################################################### #### #### ##### ######### ####
#### #### ########################################################################################### ##### #### ########################################################################################### ### #### ##### ######## ####
###### #### #### #### ##### #### ##### #### #### #### ###### ####### ####
########## #### #### #### ##### #### #### #### ### #### ####### ######
################## #### #### #### ###### #### ##### #### #### ######### #####
################## #### #### #### ####### #### ##### #### #### ############# #####
################## #### ######### #### ###### #### ######################### ####
################## #### ########### #### ####### ##### ######################## ###
#### ############### #### ######### ##### ######################
#### ############################################ ############ #### ####################
##### ########################################### ################## ##################
##### ######################################### ################## ################
####### ######################################## ################## ###########
######## ###################################### ##################
########### ###################################
################## ###############################
################## ###########################
################## ##################
##################
```
**Obanner14**
```
### #
######### ## ## # # #
######### # ######### # #######
## # # ## #
# ####
```
**Obanner15**
```
##
########## ######## ##
########## # # # ########
# # ########## # #
# #### ## ##
```
**Obanner16**
```
# ###
########### # ######### ## #
# # ########### # # # # # # ########
# # # ########### # # # #
##### ## ###
##
```
**Obanner17**
```
# ###
############ ######### ##
# # # # # # ##
############ # ############ # ########
# ## # # ### #
## ####
```
**Obanner18**
```
# ###
############ ######### ##
# # # # # # ## # ## #
# # ############ # ############ # # #########
### # # # # # # ## # #
# ##### ## #
```
**Obanner19**
```
# ###
############# ######### ###
# # # ## # ####### #
# # ############# # # # # # #########
### # # # # # ############# # # # # #
# ###### ### ###
###
```
**Obanner2**
```
@ @ #@ @ @ @ @
```
**Obanner20**
```
# # ####
############## ########## ##
# # # # ### # #######
# ############## # # # # # ##########
## # # # # # ############## # # #
# ###### ### # ### #
### ####
```
**Obanner21**
```
# # ###
############### ########### ### #
############### # # ## ## # # ####### ##########
# # ############### ## # ############### # # # ## #
# # ############### # # # # # # #
# ## # # # ####
## ######
```
**Obanner22**
```
# #
################ #### ###
################ ########## ########
# # # ### ## # # # ###########
# ################ ## # ################ # ##
### # ################ # # # #### #
## ## # #
####### ###
```
**Obanner23**
```
# #####
################ ########### ###
################ # ### ### ####### #
# # ################ # # # # # ##########
# # ################ # # ################ # # ## #
### # # # # # ### #
# ####### #### ###
#### ###
```
**Obanner24**
```
# ####
################ ########### ###
################ # ### ### # ######## #
# # ################ ## # ################ # # # ###########
# ################ # # # # # ## #
### # # # # # # ## #
######## ### ####
### ######
```
**Obanner25**
```
#
################# #####
################# ############ ###
# # #### ### # ########
################# # # ################# ## # # ############
## ################# # # # # #############
# # # # ## ##
# ### # # ####
####### ###
```
**Obanner26**
```
# #####
################## ############ ###
################## # #### ### ######### #
# # ################## ## # # # # # #############
# ################## ## ################## # # # ##############
# # # # # # # ## #
### ## # ## # #####
# ######## ###
### ###
```
**Obanner27**
```
# #####
################## ############ ####
################## # ##### ##### ######## #
# # ################## ## ## # # # # ############
# # ################## # # ################## # # #############
# # # # # ################## # # # # #
#### # ## # ## # ##### #
# ######### ### ##
### ######
```
**Obanner28**
```
# # #####
################### ############# ###
################### ##### #### ######### #
# # # # # ### ## # # ## # ## #############
# # ################### ## # ################### # # # ##############
# # ################### # # ################### # # # ## #
#### # # # ## # # # ##### #
# ######### #### ####
## #######
```
**Obanner29**
```
# # ######
#################### ############ ####
#################### ##### #### ######## #
# # # # # ### ## # # # ## #############
# # #################### ## # #################### # # ###############
# # #################### # # #################### # # ## #
### # # # ## # # # ### #
# ### # ## ####
## ######## ####
#### ####
```
**Obanner3**
```
```
**Obanner30**
```
# # #####
##################### ############# ####
##################### ################# #########
# # # # # ### ## ## # ## #
# # ##################### # # # # # # # ##############
# # ##################### # # ##################### # # ## ###############
## # # # # # ##################### # # ### ## #
#### # ## ## # ##### #
## ######### ####
#### ######
```
**Obanner31**
```
# ######
##################### ############# ####
##################### ################# ##########
##################### # #### ### # ## # ## #
# # ##################### ## # ##################### # # # ##############
# # ##################### # # ##################### # # ###############
# # ##################### # # # # # ## ## #
#### # ## # # # ###### #
# ########## #### ###
#### #######
```
**Obanner32**
```
# # ######
###################### ##############
###################### ################## ####
###################### # # #### ### ########## #
# # # ###################### ## ## # # ## # ## ###############
# # ###################### # # ###################### # # # ################
# # ###################### # # ###################### # # # ## #
##### # # # ## # # # # # #
# ########### ##### # ######
### ######### ####
#####
```
**Obanner33**
```
# # ######
####################### ##############
####################### ################## #####
####################### # # #### ### ########## #
# # # ####################### ### # # # ### # ## ###############
# # ####################### # # ####################### # # # #################
# # ####################### # # ####################### # # # ## #
#### # # # ## # # # # ## ##
# ########### ### # ######
## ######### ##### ####
##### ####
```
**Obanner34**
```
# #
# # ######
######################## ############## ####
######################## ################## ######### #
# # # # # #### ### # # ### # ### ##############
# # # # ## # ######################## ## # # ################
# # ######################## ## ## ######################## # # # ### #
##### # ######################## ## # # ## # ## ##
# # # ## # # # ###### #
## #### # ## ####
##### ########### #####
########
```
**Obanner35**
```
## # #######
## # #############
######################### ################### #####
######################### ##### ### ######### #
## # # ## # ### ## ## # #### # ### ###############
# # ## # ### ## ######################### # # ## #################
# # ######################### ## # ######################### ## # # ### #
### # ######################### # # # ## # # ## #
##### # ## # ### # ## # # ### #
## ########### ##### # #####
### #########
#####
```
**Obanner36**
```
# # ######
# # ############## ####
######################## ################## ##########
######################## # # ##### #### #### ## #### #
# # # # # ### ## # # # ## # ###############
# # ######################## ## # ######################## # ## # ##################
# # ######################## # # ######################## # ## # ### #
## # # # # # # # ## ## #### ## #
##### # ### # ## # ###### #
# ############ #### ###
## ########## ####
#### #####
```
**Obanner37**
```
# #
# # #######
######################### ############## #####
######################### ################### ###########
# # # # # ##### ##### ### # ### #
# # # # #### ## # # ## # ## ################
# # ######################### ## # ######################### # # # ###################
# # ######################### ## # ######################### # # # ###################
##### # # # # # # ## # ## ## #
# ## # ## ## ####### #
## ############# #### ####
##### ############ #####
########
```
**Obanner38**
```
# # #######
# # ###############
########################## ################### #####
########################## # # ###### ###### ########## #
# # # # # #### ## # # ############## ################
# # ########################## ### # ########################## ## # # ##################
# # ########################## ## # ########################## # # # ###################
# # # # ## # # # # ## ## #
##### # ## # # # # ## #
# ##### # ### # #######
# ############ ##### ######
##### #########
#####
```
**Obanner39**
```
## # #######
## # ############### #####
########################### ################### ###########
########################### ## # ###### ##### ############# #
## # # ## # #### ### ## # # # ## ################
## # # ########################### ### ## ########################### ## # # ###################
# # ########################### ## # ########################### ## # # ####################
# # ## # ## # ## # # ## ### #
##### # ## # # # ## # ####### #
##### # ### # ## #####
# ############# #####
### ###########
##### #####
```
**Obanner4**
```
# # # #
#
```
**Obanner40**
```
# # #######
# # ###############
########################### ################### #####
########################### ######## ####### ########### #
# # # # # ##### ### ############## #################
# # # # # ### ## # # ## # ## ####################
# # ########################### ## # ########################### # # # ####################
# # ########################### # # ########################### # # # ## #
### # # # # # # ########################### # # ## ##
##### # # # ### # ## # ######## #
# ############# ##### ## ######
## ########### ##### ###
##### ########
```
**Obanner41**
```
# # ########
# # ################
############################ #################### ######
############################ ######## ####### ########### ##
############################ # # ##### #### # # ############## ##################
# ## # # # ### ## ############################ ### # ## ####################
## # ############################ ## # ############################ # # ## #####################
## # ############################ # # ############################ # # ## ### ##
## # ############################ # # # # # ## ##
###### # # # ### # # # # #### #
# ############## #### ## ######
## ############ ###### #####
###### ##########
######
```
**Obanner42**
```
# # #######
# # #################
############################# ##################### #####
############################# ######## ###### ###########
############################# # # ##### #### ############### #
# # # # # ### ## # # ## # ### #################
# # ############################# ### ## ############################# ## # # ####################
# # ############################# ## # ############################# # # # #####################
## # ############################# ## ## ## ############################# # # ## ### #
##### # # # ## ## # # # #### ##
# ##### ## ## ## ####### #
## ############# ###### #####
#### ############
###### ######
```
**Obanner43**
```
## # ########
## # ################
############################## ##################### ######
############################## ######## ####### ############
############################## ## # ##### #### ############### #
## # # ## # ### ## ## # ## ## ## ##################
# # ############################## ### ## ############################## ## ## ## #####################
# # ############################## ## # ############################## ## ## # ######################
# # ############################## ## # ############################## # ## ## ### #
###### # ## # ## # ## # ## ### ##
###### # #### # ### ## ######## #
## ############## ###### ######
### ############ ######
###### #########
```
**Obanner44**
```
## ## #########
## ## #################
############################### ##################### ######
############################### ######## ####### ############
############################### ## ## ##### ### ############### #
## # ## ## ## ### ## ## ## ## # ### ###################
# ## ############################### ### ## ############################### ## # # ######################
# ## ############################### ## ## ############################### ## # # #######################
# ## ############################### ## ## ############################### # # ## ### #
###### ## ## ## ## ## # # # ### ##
###### ## #### ## ## ## ######## #
## ############### ###### ######
### ############# ######
###### #########
```
**Obanner45**
```
# ## ########
# ## ###############
############################### ##################### ######
############################### ######################### ###########
############################### # ## ####### ##### ############### #
# # ## # ## #### ### # ## ### ## ### #
# ## ############################### ### # ############################### ## ## ## ######################
# ## ############################### ## ## ############################### # ## # #######################
# ## ############################### # ## ############################### # ## ## ### #
### ## # ## ## # # # # ## ## ## #
####### ## ### # ## # ######### #
## ############### #### # #######
### ############# ###### ####
###### ##########
######
```
**Obanner46**
```
# ## #########
# ## ################
################################ ##################### ######
################################ ########################## ###########
################################ # ## ###### ##### ############### ##
# ## ## # ## #### ### # ## ### # ### ##
## ## ################################ ### # ################################ ## # # #####################
## ## ################################ ## ## ################################ # # ## #######################
## ## ################################ ## ## ################################ # # ## #### ##
## ## # ## ## # ## # # # ## ### ##
###### ## ## # ## # # ##### ##
## ###### # ### ## #######
## ############## ####### #####
#### ############
####### ######
```
**Obanner47**
```
## ##
## ## #########
################################# ################ ######
################################# ##################### ###########
################################# ########################## ################ #
## # ## ## ## ###### ##### ### ## #### #
## # ## ## ## #### ### ## ## # ## ## ######################
# ## ################################# ### ## ################################# ## ## # #######################
# ## ################################# ### ## ################################# ## ## # #### #
## ## ################################# ## ## ################################# # ## ## ## #
####### ## ## ## ## ## ## ## ## ## #### ##
####### ## ## ## ## ## ## # ######## #
## #### ## ## ######
### ################ #######
####### ############## #######
##########
```
**Obanner48**
```
## # #########
## # ################
################################# ###################### ######
################################# ########################## ############
################################# ####### ##### ################ #
## # # ## # ###### ### ### ## ### #
## # # ## # ### ## ## # ## ## ## #######################
# # ################################# ### # ################################# ## ## # ########################
# # ################################# ## # ################################# ## ## # #### #
# # ################################# ## # ################################# # ## ### ### #
####### # ## # ## # ## ## ## ## ##### ##
####### # ## # #### # ### ## ######### #
# ############### ###### #######
## ############## ######
###### ###########
######
```
**Obanner49**
```
# # #########
# # #################
################################# ####################### #######
################################# ########################### ############
################################# # # ######## ###### ################# ##
# ## # # # ##### ### # # #### # ### ##
# ## # ################################# #### ## ################################# ## # ## ########################
## # ################################# ### # ################################# # # ## #########################
## # ################################# ## # ################################# # # ## #########################
## # # # # # # # # ## ### ##
#### # # # ## ## # ## # ### ##
###### # #### ## ## ## ######### ##
# ################# #### # #######
## ############### ###### ####
#### #############
###### #######
```
**Obanner5**
```
# #
#
```
**Obanner50**
```
# #
# # ##########
################################## #################
################################## ####################### ######
################################## ########################## ############
# # # # # ######## ####### ################ #
# # # # # ##### #### # # ##### ## ##### #
# # ################################## ### ### ################################## ### ## ## #######################
# # ################################## ### ## ################################## # ## # ########################
# # ################################## ## # ################################## # ## # #########################
### # # # ## # # # ## ## ### #
####### # # # ## # ## # ## #### ###
# ### # ## ## ########## #
## ###### # ### ## ########
### ############### ###### ####
###### ############## ######
##########
```
**Obanner51**
```
## # #########
## # #################
################################### ####################### #######
################################### ########################### #############
################################### ######### ####### ################# ##
################################### ## # ###### ##### ## # ##### # ##### ##
## ## # ## # #### ## ################################### ### # ### ########################
## # ################################### ### ## ################################### ## # ## #########################
## # ################################### ## # ################################### ## # ## ##########################
## # ################################### ## # ## ## # ## #### ##
## # ################################### ## ## ## # # ### ###
####### # ## # ### ## # # ######### ##
# ##### ## ### ## ########
## ################# ####### ######
### ############### #######
####### ############
#######
```
**Obanner52**
```
## # ##########
## # ##################
#################################### ######################## #######
#################################### ########################### ############
#################################### ## # ######## ####### ################## ##
#################################### ## # ###### ##### ## # ###### ## ##### ##
## ## # #################################### #### ## #################################### ## ## ## #########################
## # #################################### ### ## #################################### ## ## ## ##########################
## # #################################### ### # #################################### ## ## ## ###########################
## # #################################### ## # ## ## ## ## #### ##
## # ## # ## ## ## # ## ### ##
####### # ## ## ## ## ## ##### ##
####### # ##### ## ### ## #########
## ################# ####### #######
### ################ #######
####### #############
####### #######
```
**Obanner53**
```
# ## ##########
# ## ##################
#################################### ####################### #######
#################################### ############################ #############
#################################### ########## ######### ################ #
#################################### # ## ####### #### ##### # ##### #
# # ## # ## ##### ### # ## ### # ## ########################
# ## #################################### ### ## #################################### ## # ## ##########################
# ## #################################### ## ## #################################### # # # ##########################
# ## #################################### ## ## #################################### # # ## ### #
# ## #################################### ## ## #################################### ## # ### ### #
####### ## # ## ## # ## # # ##### ##
####### ## #### # ### ## ######### #
## ################# ##### #######
## ################ ####### ####
#### ##############
####### ###########
```
**Obanner54**
```
# ## ##########
# ## ###################
##################################### ####################### #######
##################################### ############################ #############
##################################### ########## ######### ################ ##
##################################### # ## ####### #### ##### ## ###### ##
# ## ## # ## #### ### # ## ## ## ### ########################
## ## ##################################### ### ## ##################################### ## ## ## ##########################
## ## ##################################### ### ## ##################################### # ## ## ###########################
## ## ##################################### ## ## ##################################### # ## ## ### ##
## ## ##################################### ## ## ##################################### ## ## ## ### ##
#### ## # ## ## ## ## ## ## ###### ##
######## ## ### ## ### ## ########## #
## ####### ## #### ## ########
## ################# ####### ####
### ################ #######
####### ###########
#######
```
**Obanner55**
```
## ## ##########
## ## ##################
###################################### ########################
###################################### ############################ ########
###################################### ########### ######### #############
###################################### ## ## ###### #### ################# #
## # ## ## ## ##### ### ## ## ###### ## ##### #
## # ## ###################################### ##### ## ###################################### ### ## ### #########################
# ## ###################################### ### ## ###################################### ## ## ## ###########################
# ## ###################################### ## ## ###################################### ## ## # ############################
# ## ###################################### ## ## ###################################### ## ## # #### #
#### ## ## ## ## # # ## ## ## ### #
####### ## ## ## ### # ## # ## #### ##
## ###### # #### ## ########## ##
## ################## ######## # #########
### ############### ######## #######
######## #############
######## #######
```
**Obanner56**
```
## ## ###########
## ## ###################
####################################### ######################### #######
####################################### ############################# #############
####################################### ########## ######## #################
####################################### ## ## ######## ###### ###### ## ###### ##
## ## ## ## ## ##### ### ## ## ### ## ### ##
## ## ## ####################################### #### ## ####################################### ## ## ## ##########################
## ## ####################################### #### ## ####################################### ## ## ## ############################
## ## ####################################### ### ## ####################################### ## ## ## #############################
## ## ####################################### ## ## ####################################### # ## ## ##### ##
### ## ## ## ## ## ## ## ## ## #### ### ##
######## ## ## ## ### ## ## ## ########## ##
######## ## ##### ## ### ## ######### ##
## ################## ######## #######
### ################# ########
##### ###############
######## ########
```
**Obanner57**
```
## ## ##########
## ## ####################
######################################## ########################
######################################## ############################ ########
######################################## ########### ######### ##############
######################################## ####### ###### ################## ##
## ## ## ## ## ###### #### #################### ##
## ## ## ## ## #### ## ## ## ### ## ### ##########################
## ## ######################################## #### ## ######################################## ## ## ## ###########################
## ## ######################################## ### ## ######################################## ## ## ## #############################
## ## ######################################## ### ## ######################################## ## ## ## ##### ##
## ## ######################################## ### ## ## ######################################## # ## ## #### ##
######## ## ## ## ## ## ## ## ## ## ### ##
######## ## ## ## #### ## ### ## ########### #
## ################### ##### ### ##########
## ################## ######## ########
##### ################
######## ############
########
```
**Obanner58**
```
# ## ###########
# ## ####################
######################################## #########################
######################################## ############################# #######
######################################## ########### ######### ##############
######################################## ######## ###### ################# #
# # ## # ## ###### #### ##################### #
# # ## # ## #### ### # ## ### # #### ##########################
# ## ######################################## ### ### ######################################## ## # ## ############################
# ## ######################################## ## ## ######################################## # # # #############################
# ## ######################################## ## ## ######################################## # # # ##### #
### ## ######################################## ## ## ### ######################################## # # ## ### #
####### ## # ## ### ## ## # # # #### ###
####### ## # ## #### ## ## ## # ###### ##
## ####### ## ### ## #########
### ################## ######## ########
#### ################ ######## ####
######## #############
######## ########
```
**Obanner59**
```
## ##
## ## ###########
######################################### ####################
######################################### ######################### ########
######################################### ############################# ##############
######################################### ################################# ################## ##
## ## ## ## ## ######## ###### #################### ##
## ## ## ## ## ####### #### ## ## #### ## #### ###########################
## ## ######################################### #### ### ######################################### ### ## ### #############################
## ## ######################################### #### ## ######################################### ## ## ## ##############################
## ## ######################################### ### ## ######################################### ## ## ## ##### ##
## ## ######################################### ## ## ######################################### ## ## ## ### ##
#### ## ## ## ## ## ## # ## ### ###
######## ## ## ## ### ## ## ## ## ###### ##
## #### ## ## ## ###########
### ###### ## #### ## #########
#### ################### ######## #####
######## ################## ########
######## ##############
########
```
**Obanner6**
```
#
```
**Obanner60**
```
## # ###########
## # ####################
######################################### ##########################
######################################### ############################## ########
######################################### ################################# ###############
######################################### ######### ###### ################## ##
## ## # ## # ####### #### ##################### ##
## ## # ## # ##### ### ## # #### ## #### ############################
## # ######################################### ### ## ######################################### ## ## ## ##############################
## # ######################################### ### ## ######################################### ## ## ## ##############################
## # ######################################### ## # ######################################### ## ## ## ##### ##
## # ######################################### ## # ######################################### ## ## ### #### ##
##### # ## # ## # ## ## # ## ### ##
######## # ## # ### # ### ## ## ###### ###
######## # ##### # #### ### ########### #
## ################### ######## ## ##########
### ################## ######## ########
##### ################
######## ############
########
```
**Obanner61**
```
## # ###########
## # #####################
########################################## ########################### ########
########################################## ############################## ###############
########################################## ################################# ##################
########################################## ## # ########## ######### ##################### ##
########################################## ## # ######## ###### ## # #### ## #### ##
## ## # ########################################## ##### ## ########################################## ### ## ### ###########################
## # ########################################## #### ## ########################################## ### ## ## #############################
## # ########################################## #### ## ########################################## ## ## ## ##############################
## # ########################################## ### # ########################################## ## ## ## ###############################
## # ########################################## ### # ## ## ## ### ##### ##
### # ## # ### ## ## ## ## #### ###
######### # #### ## ## ## ########### ##
######### # ##### ## #### ## ########## #
# #################### ###### #######
## ################### ########
### ################## ########
######## ##############
########
```
**Obanner62**
```
# ##
# ## ############
########################################## ######################
########################################## ########################## ########
########################################## ############################## ###############
########################################## ################################## ###################
########################################## # ## ########## ######### ###################### ##
# ## ## # ## ######## ##### # ## #### ## #### ##
## ## ########################################## ##### ### ########################################## ### ## ## ############################
## ## ########################################## #### ## ########################################## ## ## ## ##############################
## ## ########################################## ### ## ########################################## # ## ## ###############################
## ## ########################################## ## ## ########################################## # ## ## ###############################
## ## ########################################## ## ## # ## ## ## #### ##
######## ## # ## ## ## ## # ## #### ### ##
######## ## ### ## ## ## ############ ##
## #### ## ### ## ########### ##
## ######## ## #### #########
### #################### ######## #####
######## ################## ########
######## ###############
#########
```
**Obanner63**
```
## ## ###########
## ## #####################
########################################### ###########################
########################################### ############################### #########
########################################### ################################### ###############
########################################### ########## ######## ################### ##
########################################### ## ## ####### ##### ###################### ##
## ## ## ## ## ##### #### ## ## #### ## ##### #############################
## ## ## ########################################### ##### ### ########################################### ### ## ### ###############################
## ## ########################################### #### ## ########################################### ## ## ### ################################
## ## ########################################### ### ## ########################################### ## ## ## ################################
## ## ########################################### ## ## ########################################### ## ## ## #### ##
### ## ########################################### ## ## ## ## ## ## ## #### ##
######### ## ## ## ### ## ### # ## #### ##
######### ## ## ## #### ## ### ## ############ ##
## ####### ## #### ### ##########
## #################### ######## ########
### ################### ######## #####
##### #################
######## #############
########
```
**Obanner64**
```
## ## ############
## ## ######################
############################################ ############################ ########
############################################ ################################ ################
############################################ #################################### ####################
############################################ ########## ######## ###################### ##
############################################ ## ## ######## ##### #### ## #### ##
## ## ## ## ## ###### #### ## ## ## ## ### ##############################
## ## ## ############################################ #### ### ############################################ ## ## ## ################################
## ## ############################################ #### ## ############################################ ## ## ## ################################
## ## ############################################ ### ## ############################################ ## ## ## #################################
## ## ############################################ ## ## ############################################ # ## ### #### ##
## ## ############################################ ## ## ## # ## ### ### ##
##### ## ## ## ## ## ## ## ## ####### ##
######### ## ## ## ### ## ## ### ############ ##
######### ## ###### ## ### ## ##########
## ##################### ######### ########
### #################### #########
##### #################
######### #############
#########
```
**Obanner65**
```
## ## ############
## ## ######################
############################################# ############################
############################################# ################################ #########
############################################# #################################### ###############
############################################# ########### ######### ################### ##
############################################# ## ## ######## ##### ####################### ##
## ## ## ## ## ###### #### ## ## ##### ## ##### #############################
## ## ## ############################################# ##### ### ############################################# ### ## ### ###############################
## ## ############################################# #### ## ############################################# ### ## ### ################################
## ## ############################################# ### ## ############################################# ## ## ## #################################
## ## ############################################# ### ## ############################################# ## ## ## ##### ##
## ## ############################################# ### ## ## # ## ## ### ##
##### ## ## ## ## ## ## ## ## #### ###
######### ## ## ## #### ## ## ## ## ###### ##
######### ## ##### ## ### ## ###########
## ##################### ###### ## #########
## #################### ######### #######
#### ################## #########
######### ###############
######### ########
```
**Obanner66**
```
## ## ############
## ## ######################
############################################## ############################
############################################## ################################ #########
############################################## #################################### ################
############################################## ########### ######### #################### ##
############################################## ## ## ######## ###### ####################### ##
## ## ## ## ## ###### #### ## ## ##### ## #### ##############################
## ## ## ############################################## ##### ### ############################################## ### ## ### ################################
## ## ############################################## #### ### ############################################## ### ## ## #################################
## ## ############################################## ### ## ############################################## ## ## ## ##################################
## ## ############################################## ### ## ############################################## ## ## ## ##### ##
## ## ############################################## ### ## ## # ## ### ### ##
##### ## ## ## ## ## ## ## ## ### ###
######### ## ## ## #### ## ### ## ## ####### ##
######### ## ##### ## #### ## ############
## ###################### ###### ## ##########
### ##################### ######### ########
#### ################### #########
######### ################
######### #########
```
**Obanner67**
```
## ## #############
## ## ###################
## ## ##########################
############################################## ############################### #########
############################################## ################################### ###############
############################################## ############ ########### ################### ##
############################################## ## ## ######### ####### ####################### ##
## ## ## ## ## ####### ##### ## ## ####### ## ####### #############################
## ## ## ## ## ##### ### ## ## ### ## ### ################################
## ## ############################################## #### ## ############################################## ### ## ### #################################
## ## ############################################## ### ### ############################################## ## ## ## ##################################
## ## ############################################## ### ## ############################################## ## ## ## ##### ##
## ## ############################################## ## ## ############################################## ## ## ## #### ##
### ## ## ## ## ## ### ## ## ## ### ###
######### ## ## ## ### ## ## ## ## #### ###
######### ## #### ## ### ## ############# #
## ####### ## #### ### ############
### ###################### ######### ##########
#### ##################### ######### ######
###### ##################
######### ##############
#########
```
**Obanner68**
```
## ## #############
## ## ###################
## ## ###########################
############################################### ############################### #########
############################################### ################################### ##############
############################################### ############# ########### ##################
############################################### ## ## ######### ####### ###################### ##
## ## ## ## ## ######## ##### ####### ## ###### ##
## ## ## ## ## ##### ### ## ## #### ## #### ############################
## ## ############################################### ##### ## ## ## ### ## ## ###############################
## ## ############################################### #### ### ############################################### ## ## ## #################################
## ## ############################################### ### ## ############################################### ## ## ## ##################################
## ## ############################################### ### ## ############################################### ## ## ### ###### ##
### ## ## ## ### ## ### ############################################### ### ## ### #### ##
######### ## ## ## #### ## ## ## ## ## ##### ####
######### ## ##### ## ### ## ############# ###
## ######## ## #### ## ########### ##
### ###################### ######### #########
### ##################### ######### #####
#### ################### #########
######### ################
######### #########
```
**Obanner69**
```
## ## #############
## ## ####################
## ## ##########################
################################################ ################################ #########
################################################ #################################### ###############
################################################ ############# ########### ###################
################################################ ## ## ######### ####### ####################### ##
## ## ## ## ## ####### ##### ####### ## ####### ##
## ## ## ## ## ##### ### ## ## #### ## ### #############################
## ## ################################################ #### ## ## ## ## ## ### ################################
## ## ################################################ #### ### ################################################ ## ## ## ##################################
## ## ################################################ ### ## ################################################ ## ## ## ###################################
## ## ################################################ ### ## ################################################ ## ## ## ###### ##
## ## ## ## ### ## ################################################ ## ## ### #### ##
##### ## ## ## ## ## ## ## ## ## #### ###
######### ## #### ## ### ## ## ####### ##
######### ## ##### ## #### ## ############# ##
## ####################### ####### ## ###########
### ###################### ########## #########
#### #################### ##########
########## ################
########## ##########
```
**Obanner7**
```
#
# #
# ## # #
```
**Obanner70**
```
### ## #############
### ## ###################
### ## ###########################
################################################# ################################# #########
################################################# ##################################### ###############
################################################# ############# ########### ###################
################################################# ########## ####### ####################### ##
### ## ## ### ## ####### ##### ####### ## ###### ##
### ## ## ### ## ###### #### ### ## #### ## #### ##############################
### ## ## ### ## ##### ### ### ## ### ## ### #################################
## ## ################################################# ##### ### ################################################# ### ## ## ###################################
## ## ################################################# #### ## ################################################# ### ## ## ####################################
## ## ################################################# ### ## ################################################# ### ## ## ###### ##
## ## ################################################# ### ## ################################################# ## ## ### ##### ##
###### ## ### ## ### ## ## ### ## ## #### ###
########## ## ### ## #### ## ### ## ## ###### ###
########## ## ### ## ###### ## #### ### ############ ##
## ####################### ###### ## ##########
### ###################### ########## ########
#### ##################### ##########
###### ##################
########## ##############
##########
```
**Obanner71**
```
## ### ##############
## ### ####################
## ### ############################
################################################# ################################# ##########
################################################# ##################################### ###############
################################################# ############# ########### ####################
################################################# ########## ######## ######################## ##
## ## ### ## ### ######## ##### ####### ## ####### ##
## ## ### ## ### ###### ##### ## ### ### ## #### ##############################
## ## ### ## ### ###### ### ## ### ### ## ### ##################################
## ### ################################################# #### ### ################################################# ## ## ## ###################################
## ### ################################################# ### ### ################################################# ## ## ## ####################################
## ### ################################################# ## ### ################################################# ## ## ## ###### ##
## ### ################################################# ## ### ################################################# ## ## ### #### ##
##### ### ## ### ### ## ## ## # ## #### #### ##
######### ### ## ### ### ## ### ## ## ####### ##
######### ### ## ### ##### ## ### ### ############# ##
### ######## ## ##### ### ###########
### ####################### ########## ##########
#### ###################### ########## ######
###### ###################
########## ###############
########## ##########
```
**Obanner72**
```
## ##
## ## #############
## ## ####################
################################################# ############################
################################################# ################################# #########
################################################# ##################################### ###############
################################################# ############## ########### ################### ##
################################################# ## ## ######### ######## ######################## ##
## ## ## ## ## ######### ###### ## ## ######## ### ####### ##############################
## ## ## ## ## ###### #### ## ## #### ### #### #################################
## ## ################################################# ###### ### ################################################# ### ### ### ###################################
## ## ################################################# #### ## ################################################# ### ### ## ####################################
## ## ################################################# ### ## ################################################# ## ### ## ###### ##
## ## ################################################# ### ## ################################################# ## ### ## ##### ##
### ## ################################################# ### ## ## ## ### ### #### ##
########## ## ## ## ### ### ## ## ### #### ###
########## ## ## ## #### ### ### ### ### ####### ##
## ##### ### ### ## ##############
## ######## ### ##### ## ############
## ######################## ######### ##########
#### ####################### ######### ######
######### ##################### #########
######### #################
##########
```
**Obanner73**
```
## ## ##############
## ## ####################
## ## ############################
################################################## ################################## ##########
################################################## ###################################### ################
################################################## ############# ############ ####################
################################################## ############ ########## ######################## ##
################################################## ## ## ######### ###### ####### ## ####### ##
## ## ## ## ## ####### #### ## ## #### ## #### ###############################
## ## ## ## ## ##### ### ## ## ### ## ### ##################################
## ## ################################################## ##### ## ################################################## ### ## ### ####################################
## ## ################################################## #### ## ################################################## ## ## ## #####################################
## ## ################################################## ### ## ################################################## ## ## ## #####################################
## ## ################################################## ### ## ################################################## # ## ## ##### ##
#### ## ################################################## ### ## ## ## ## ## ### #### ##
########## ## ## ## ### ## ### ## ## ##### ###
########## ## ## ## #### ## ## ### ############## ##
########## ## ###### ## #### ### ############ #
## ######################## ####### ##########
## ###################### ########## #########
#### ##################### ##########
###### ###################
########## ###############
##########
```
**Obanner74**
```
### ##
### ## ##############
### ## #####################
################################################### ############################
################################################### ################################## ##########
################################################### ####################################### ###############
################################################### ######################################### #####################
################################################### ### ## ########### ########## ######################### ###
### ### ## ### ## ######### ###### ####### ### ####### ###
### ### ## ### ## ####### #### ### ## ##### ### ##### ################################
### ## ################################################### ##### #### ### ## ### ### ### ###################################
### ## ################################################### #### ### ################################################### ### ### ### #####################################
### ## ################################################### #### ## ################################################### ### ### ### #####################################
### ## ################################################### #### ## ################################################### ### ### ### ######################################
### ## ################################################### ### ## ################################################### ### ### ### ##### ###
##### ## ### ## ### ## ### ## ### ### #### ###
########### ## ### ## ### ## ## ### ### ##### ###
########### ## #### ## ### ## ############## ###
## ###### ## #### ### ############## #
## ######################### ####### ### ############
#### ######################## ########## #########
###### ####################### ##########
########## ####################
########## ###############
```
**Obanner75**
```
## ##
## ## ##############
## ## #####################
################################################### #############################
################################################### ################################### ##########
################################################### ####################################### ################
################################################### ######################################### ####################
################################################### ## ## ############ ########## ######################### ##
## ## ## ## ## ######### ###### ######## ## ######## ##
## ## ## ## ## ###### #### ## ## ##### ## ##### ################################
## ## ################################################### ##### ### ## ## #### ## #### ####################################
## ## ################################################### ##### ### ################################################### ## ## ### #####################################
## ## ################################################### #### ### ################################################### ## ## ## ######################################
## ## ################################################### ### ## ################################################### ## ## ## ######################################
## ## ################################################### ## ## ################################################### ## ## ### ##### ##
###### ## ## ## ## ## ## ## ## #### #### ##
########## ## ## ## ### ## ### ## ## ##### ####
########## ## #### ## ### ### ## ######## ###
## ##### ## #### ### ############# ##
### ######## ## ##### ## ###########
#### ######################## ########## #########
#### ###################### ########## ######
########## ##################### ##########
########## #################
##########
```
**Obanner76**
```
## ## ##############
## ## ######################
## ## ##############################
#################################################### #################################### ##########
#################################################### ###################################### ################
#################################################### ########################################## #####################
#################################################### ############ ########### ######################### ##
#################################################### ## ## ######### ###### ########################### ##
## ## ## ## ## ######### ##### ## ## ##### ## ##### ################################
## ## ## ## ## ###### ### ## ## #### ## ### ###################################
## ## #################################################### ##### ### #################################################### ### ## ### #####################################
## ## #################################################### #### ### #################################################### ## ## ## ######################################
## ## #################################################### ### ## #################################################### ## ## ## ######################################
## ## #################################################### ### ## #################################################### ## ## ### ##### ##
## ## #################################################### ### ## ## ### ## ### #### ##
###### ## ## ## ### ## ### ## ## #### ####
########## ## ## ## #### ## ### ### ## ####### ###
########## ## ##### ## ### ### ############## ##
## ######### ## ##### ## ############
### ######################### ########## ###########
### ######################## ########## ######
#### ###################### ##########
########## ##################
########## ################
##########
```
**Obanner77**
```
## ##
## ## ###############
## ## #####################
##################################################### #############################
##################################################### ################################### ###########
##################################################### ##################################### ################
##################################################### ########################################### #####################
##################################################### ############# ########### ########################## ##
## ## ## ## ## ########## ####### ########################### ##
## ## ## ## ## ######## ###### ## ## ##### ## ##### #################################
## ## ## ## ###### #### ## ## ### ## #### ####################################
## ## ##################################################### #### ## ##################################################### ### ## ## #####################################
## ## ##################################################### ##### ### ##################################################### ## ## ## ######################################
## ## ##################################################### ### ## ##################################################### ## ## ## #######################################
## ## ##################################################### ### ## ##################################################### ## ## ## ##### ##
### ## ##################################################### ### ## ## # ## ### ##### ##
########### ## ## ## ### ### ### ## ## #### ###
########### ## ## ## ### ### ## ## ## ######## ###
########### ## ##### ### ### ### ############## ##
## ###### ### #### ### ############
### ########################## ####### ##########
##### ######################## ########## ######
###### ####################### ##########
########## #####################
########## ################
```
**Obanner78**
```
### ## ##############
### ## ######################
### ## ##############################
###################################################### #################################### ##########
###################################################### ###################################### ################
###################################################### ########################################### #####################
###################################################### ############ ########## ########################## ##
###################################################### ### ## ########### ######## ########################### ##
### ## ## ### ## ######## ###### ###### ## ##### #################################
### ## ## ### ## ###### #### ### ## ### ## #### #####################################
### ## ## ###################################################### ###### ### ### ## ### ## ### ######################################
## ## ###################################################### ##### ### ###################################################### ### ## ## #######################################
## ## ###################################################### #### ## ###################################################### ### ## ## ########################################
## ## ###################################################### ### ## ###################################################### ### ## ## ####### ##
## ## ###################################################### ### ## ###################################################### ## ## ### ##### ##
#### ## ### ## ### ## ### ### ## ## #### ###
########## ## ### ## ### ## ### ### ## ## ####### ###
########## ## ### ## ##### ## ### ## ############### ###
########## ## ###### ## ##### ### #############
## ########################## ####### ###########
### ######################### ########### #########
#### ####################### ###########
####### #####################
########### ##################
########### ##########
```
**Obanner79**
```
### ## ###############
### ## ######################
### ## ###############################
####################################################### ##################################### ###########
####################################################### ####################################### #################
####################################################### ############################################ #####################
####################################################### ############# ########## ########################### ###
####################################################### ### ## ########### ######## ########################### ###
### ### ## ### ## ######### ###### ##### ### ###### ##################################
### ### ## ### ## ###### #### ### ## #### ### ### ######################################
### ### ## ####################################################### ###### ### ### ## ### ### ### #######################################
### ## ####################################################### ##### ### ####################################################### ### ### ### ########################################
### ## ####################################################### #### ## ####################################################### ### ### ### #########################################
### ## ####################################################### #### ## ####################################################### ### ### ### ####### ###
### ## ####################################################### ### ## ####################################################### ## ### ### ##### ###
### ## ### ## ### ### ### ### # ### ##### ####
###### ## ### ## ### ### ## ### ## ### ###### ###
########### ## ### ## #### ### ### ## ############### ###
########### ## ####### ### ##### ### ##############
## ######### ### ##### ## ############
### ########################## ########### ##########
#### ######################## ###########
##### ####################### ###########
########### ###################
########### ###########
###########
```
**Obanner8**
```
# ##
# # # # # # # #
# ## # # # #
```
**Obanner80**
```
## ### ###############
## ### ######################
## ### ###############################
####################################################### ###################################
####################################################### ####################################### ##########
####################################################### ############################################ #################
####################################################### ############### ############# ######################
####################################################### ########### ######### ######################## ##
## ## ### ## ### ######### ###### ############################ ##
## ## ### ## ### ####### ##### ## ### ##### ## ##### ##################################
## ## ### ## ### ###### ### ## ### #### ## #### ####################################
## ### ####################################################### ##### ### ####################################################### ### ## ### #######################################
## ### ####################################################### #### ### ####################################################### ## ## ## ########################################
## ### ####################################################### ### ### ####################################################### ## ## ## ########################################
## ### ####################################################### ### ### ####################################################### ## ## ## ###### ##
## ### ####################################################### ### ### ####################################################### ## ## ### ##### ##
###### ### ## ### ### ## ## ## ### ## #### ##### ##
########### ### ## ### #### ## ### ## ## ##### ###
########### ### ## ### ##### ## #### ### ############### ##
### ######### ## ###### ### ############## #
### ########################## ########### ### ############
### ######################## ########### ##########
##### ####################### ########### ######
####### #####################
########### ################
###########
```
**Obanner81**
```
## ### ###############
## ### #######################
## ### ###############################
######################################################## ################################### ###########
######################################################## ######################################## #################
######################################################## ############################################# #######################
######################################################## ############### ############# #########################
######################################################## ## ### ########### ######### ############################# ##
## ## ### ## ### ######## ###### ###### ### ###### ##
## ## ### ## ### ####### ##### ## ### #### ### #### ##################################
## ## ### ######################################################## ###### #### ## ### ### ### ### #####################################
## ### ######################################################## #### ### ######################################################## ## ### ## #######################################
## ### ######################################################## #### ### ######################################################## ## ### ## ########################################
## ### ######################################################## #### ### ######################################################## ## ### ## #########################################
## ### ######################################################## ### ### ######################################################## ## ### ### ####### ##
## ### ## ### ### ### ######################################################## ## ### ### ##### ##
###### ### ## ### ### ## ## ## ### ### ###### #### ##
########### ### ## ### ### ## ### ## ### ######## ###
########### ### ###### ## #### ### ############### ###
########### ### ###### ## #### ### ############# ##
### ########################### ####### ###########
### ######################### ########### #######
##### ######################### ###########
####### ######################
########### #################
########### ###########
```
**Obanner82**
```
### ### ###############
### ### #######################
### ### ###############################
######################################################### ###################################
######################################################### ######################################### ###########
######################################################### ############################################# ##################
######################################################### ################ ############# ######################
######################################################### ########### ######### ######################### ###
######################################################### ### ### ########## ####### ############################ ###
### ### ### ### ### ######## ##### ### ### ###### ## ##### ###################################
### ### ### ### ### ###### #### ### ### ##### ## #### ######################################
### ### ######################################################### ##### ### ######################################################### ### ## ### ########################################
### ### ######################################################### #### ### ######################################################### ### ## ### #########################################
### ### ######################################################### #### ### ######################################################### ### ## ### ##########################################
### ### ######################################################### ### ### ######################################################### ### ## ### ####### ###
### ### ######################################################### ### ### ######################################################### ### ## ### ###### ###
### ### ######################################################### ### ### ### ### ## ## #### #### ###
########### ### ### ### ### ### ### ## ## #### ###
########### ### ### ### ##### ### ### ## ## ######## ###
########### ### ####### ### #### ### ############### ##
### ############################ ######## #### #############
### ########################### ############ ###########
##### ######################### ############ ##########
####### ######################
############ ####################
############ ############
############
```
**Obanner83**
```
### ### ################
### ### ########################
### ### ################################
########################################################## ####################################
########################################################## ######################################## ###########
########################################################## ############################################ #################
########################################################## ################ ############## #######################
########################################################## ########### ######## ######################### ##
########################################################## ### ### ########## ####### ############################# ##
### ## ### ### ### ####### ##### ### ### ######## ### ######## ###################################
### ## ### ### ### ###### ### ### ### #### ### #### #####################################
## ### ########################################################## ##### ### ########################################################## ### ### ### ########################################
## ### ########################################################## ##### #### ########################################################## #### ### ### ########################################
## ### ########################################################## #### ### ########################################################## ### ### ## ##########################################
## ### ########################################################## #### ### ########################################################## ### ### ## ####### ##
## ### ########################################################## #### ### ########################################################## ### ### ### ###### ##
#### ### ########################################################## #### ## #### ### ### ### #### #### ##
############ ### ### ### #### ## ### ## ### #### ####
############ ### ### ### #### ## ### ### ### ######## ###
############ ### ####### ## #### ## ################ ##
### ######### ## ##### ### ##############
#### ########################### ############ ###########
#### ########################## ############ ##########
##### ######################## ############
############ ###################
############ #################
############
```
**Obanner84**
```
## ##
## ## ###############
## ## #######################
######################################################### #################################
######################################################### ##################################### ###########
######################################################### ######################################### ##################
######################################################### ########################################### #######################
######################################################### ################ ############# ######################### ###
######################################################### ## ## ########### ######### ############################# ###
## ### ## ## ## ########## ####### ######### ### ######## ###################################
## ### ## ## ## ####### ##### ## ## #### ### ##### ######################################
### ## ######################################################### ###### #### ## ## ### ### ### #########################################
### ## ######################################################### ##### ### ######################################################### ### ### ### #########################################
### ## ######################################################### ##### ### ######################################################### ## ### ### ##########################################
### ## ######################################################### ### ## ######################################################### ## ### ### ####### ###
### ## ######################################################### ### ## ######################################################### ## ### ### ##### ###
#### ## ######################################################### ### ## ######################################################### ## ### ### ##### ###
####### ## ## ## ### ### ### ## ## ### ##### ####
########### ## ## ## ### ### ### ### ### ######## ####
########### ## #### ### ### ### ################ ##
## ###### ### #### ### ##############
### ########## ### ##### ### #############
### ############################ ########### ###########
##### ########################## ########### #######
####### ######################## ###########
########### #######################
########### #################
############
```
**Obanner85**
```
## ## ################
## ## ########################
## ## #################################
########################################################## ####################################
########################################################## ########################################## ############
########################################################## ############################################ ##################
########################################################## ################ ############# #######################
########################################################## ############# ############ ########################## ###
########################################################## ## ## ########### ####### ############################## ###
## ### ## ## ## ######### ###### ######## ## ######### ####################################
## ### ## ## ## ####### #### ## ## ##### ## #### #######################################
### ## ########################################################## ###### ### ## ## #### ## #### #########################################
### ## ########################################################## ##### ### ########################################################## ### ## #### ##########################################
### ## ########################################################## #### ## ########################################################## ## ## ### ###########################################
### ## ########################################################## #### ## ########################################################## ## ## ### ###########################################
### ## ########################################################## ### ## ########################################################## ## ## #### ###### ###
### ## ########################################################## ### ## ########################################################## ## ## ### ##### ###
####### ## ## ## #### ## ### ## ## ## #### ####
########### ## ## ## #### ## ### ### ## ##### ###
########### ## ###### ## ### ### ################ ###
## ########## ## ###### ### ###############
## ############################ ######## ## #############
### ########################## ########### ############
#### ######################### ########### #######
####### ######################
########### ####################
########### ###########
###########
```
**Obanner86**
```
### ##
### ## ################
### ## ########################
########################################################### #################################
########################################################### ##################################### ###########
########################################################### ########################################## ##################
########################################################### ############################################# #######################
########################################################### ################# ############## ##########################
########################################################### ############## ########### ############################## ##
### ## ## ### ## ########## ####### ######## ### ######## ##
### ## ## ### ## ######### ###### ### ## ##### ### ##### #####################################
### ## ## ### ## ####### #### ### ## #### ### #### #######################################
## ## ########################################################### ###### #### ########################################################### ### ### ### ##########################################
## ## ########################################################### ##### ### ########################################################### ### ### ## ###########################################
## ## ########################################################### ##### ### ########################################################### ### ### ## ############################################
## ## ########################################################### #### ## ########################################################### ### ### ## ############################################
## ## ########################################################### ### ## ########################################################### ## ### #### ###### ##
###### ## ########################################################### ### ## ### ## ### #### ##### ##
############ ## ### ## ### ### ### ### ### ###### ####
############ ## ### ## #### ### #### ## ################# ####
############ ## ### ## ###### ### #### #### ################ ###
## ####### ### ##### ### ############# ##
### ############################# ####### ############
#### ############################ ########### #######
##### ########################## ###########
########### ######################### ###########
########### ####################
########### ##################
```
**Obanner87**
```
### ##
### ## ################
### ## ########################
############################################################ ##################################
############################################################ ###################################### ############
############################################################ ########################################### ##################
############################################################ ############################################# ########################
############################################################ ################ ############## ##########################
############################################################ ############## ############ ############################## ###
### ### ## ### ## ########## ######## ######### ## ######### ###
### ### ## ### ## ######### ###### ### ## #### ## ##### ####################################
### ### ## ### ## ###### #### ### ## #### ## #### #######################################
### ## ############################################################ ####### #### ############################################################ #### ## ### ##########################################
### ## ############################################################ ###### ### ############################################################ ### ## ### ##########################################
### ## ############################################################ ##### ### ############################################################ ### ## ### ############################################
### ## ############################################################ #### ## ############################################################ ### ## ### ############################################
### ## ############################################################ #### ## ############################################################ ## ## ### ###### ###
#### ## ############################################################ #### ## ### ### ## #### ###### ###
########### ## ### ## #### ### ### ## ## ###### ####
########### ## ### ## #### ### #### ### ## ######### ###
########### ## ### ## #### ### ### ### ################ ##
## ####### ### ##### ### ############## ##
### ########## ### ###### ############
### ############################# ############ ##########
##### ########################### ############
####### ######################### ############
############ ########################
############ ##################
############
```
**Obanner88**
```
### ###
### ### #################
### ### #########################
############################################################# ##################################
############################################################# ###################################### ############
############################################################# ########################################### ###################
############################################################# ############################################## ########################
############################################################# ################ ############## ###########################
############################################################# ############## ############ ############################### ##
### ## ### ### ### ########### ####### ######### ### ######## ##
### ## ### ### ### ########## ####### ### ### #### ### ##### #####################################
### ## ### ### ### ###### #### ### ### #### ### #### ########################################
## ### ############################################################# ####### #### ############################################################# #### ### ### ###########################################
## ### ############################################################# ###### ### ############################################################# ### ### ## ###########################################
## ### ############################################################# ##### ### ############################################################# ### ### ## #############################################
## ### ############################################################# #### ### ############################################################# ### ### ## #############################################
## ### ############################################################# #### ### ############################################################# ## ### #### ###### ##
#### ### ############################################################# #### ### ### ### ### #### ###### ##
############ ### ### ### #### ### ### ## ### ###### ####
############ ### ### ### #### ### ### ### ### ######## ###
############ ### ### ### #### ### #### ### ################ ##
### ######## ### #### ### ############### ##
### ########## ### ###### ############
### ############################# ############ ###########
##### ########################### ############
####### ######################### ############
############ #######################
############ ##################
############
```
**Obanner89**
```
## ### #################
## ### #########################
## ### ###############################
############################################################# #######################################
############################################################# ######################################### ############
############################################################# ############################################### ###################
############################################################# ################################################# ######################
############################################################# ############## ############ ########################### ###
############################################################# ## ### ############ ########## ############################## ###
## ### ### ## ### ######### ####### ######### ## ######### ###
## ### ### ## ### ######## ###### ## ### ###### ## ###### #########################################
## ### ### ############################################################# ####### #### ## ### #### ## #### ##########################################
### ### ############################################################# ###### ### ############################################################# #### ## ### ############################################
### ### ############################################################# #### ### ############################################################# ## ## ### #############################################
### ### ############################################################# #### ### ############################################################# ## ## ### #############################################
### ### ############################################################# ### ### ############################################################# ## ## ### ####### ###
### ### ############################################################# ### ### ############################################################# ## ## ### ##### ###
#### ### ## ### ### ### ### ## ### ## #### ##### ###
####### ### ## ### #### ### ## ## ## ## ##### ###
############ ### ## ### ##### ### #### ## ## ######### ###
############ ### ###### ### #### ### ################ ##
### ########### ### ###### #### ##############
### ############################## ######## ## #############
### ############################ ############ ##########
##### ########################### ############ #######
####### ########################
############ #####################
############ ############
############
```
**Obanner9**
```
# # # #
# # # # #
## # # #
```
**Obanner90**
```
### ###
### ### #################
### ### ##########################
############################################################## ##############################
############################################################## ###################################### ############
############################################################## ########################################## ###################
############################################################## ############################################### ######################
############################################################## ################################################## ###########################
############################################################## ############## ############ ############################## ###
### ### ### ### ### ############# ########## ######### ### ######### ###
### ### ### ### ### ########## ####### ###### ### ###### ###
### ### ### ### ### ######## ###### ### ### #### ### #### #########################################
### ### ############################################################## ###### #### ### ### ### ### ### ###########################################
### ### ############################################################## ##### ### ############################################################## ### ### ### #############################################
### ### ############################################################## ##### ### ############################################################## ### ### ### #############################################
### ### ############################################################## #### ### ############################################################## ### ### ### ##############################################
### ### ############################################################## ### ### ############################################################## ### ### #### ####### ###
### ### ############################################################## ### ### ############################################################## ## ### #### ##### ###
####### ### ### ### ### ### ### ## ### #### #### ###
############# ### ### ### ### ## ## ### ### ### ######### ####
############# ### ### ### #### ## ### ## ################# ###
############# ### ###### ## #### #### ################ ##
### ####### ## ##### ### ##############
### ############################## ######## ############
##### ############################# ############ #######
##### ########################### ############
############ ########################## ############
############ #####################
############ ##################
```
**Obanner91**
```
### ### #################
### ### #########################
### ### ###############################
############################################################### #######################################
############################################################### ########################################## ############
############################################################### ############################################### ###################
############################################################### ################################################### ######################
############################################################### ############### ############# ############################ ##
############################################################### ### ### ############ ######### ############################## ##
### ## ### ### ### ########## ####### ######### ### ######### ##
### ## ### ### ### ######## ###### ### ### ###### ### ###### #########################################
### ## ### ############################################################### ###### ##### ### ### #### ### #### ##########################################
## ### ############################################################### ##### ### ############################################################### ### ### #### ############################################
## ### ############################################################### ###### #### ############################################################### ### ### ## #############################################
## ### ############################################################### #### ### ############################################################### ### ### ## ##############################################
## ### ############################################################### #### ### ############################################################### ### ### ## ######## ##
## ### ############################################################### #### ### ############################################################### ### ### ### ###### ##
## ### ### ### #### ### ### ## ### #### ##### ##
###### ### ### ### ### ### ### ### ## ### ##### ####
############ ### ### ### #### ### ### ## ### ###### ####
############ ### ###### ### #### ### ################## ##
############ ### ######## ### ##### ### #################
### ########## ### ###### ### ##############
#### ############################## ############ #############
#### ############################ ############ ########
###### ########################## ############
######## ########################
############ ###################
############ ############
```
**Obanner92**
```
### ### ##################
### ### ##########################
### ### ################################
################################################################ ########################################
################################################################ ########################################## ############
################################################################ ################################################ ####################
################################################################ ################################################### ######################
################################################################ ############## ############# ############################ ###
################################################################ ### ### ############ ######### ############################### ###
################################################################ ### ### ########### ######## ########## ### ######### ###
### ### ### ### ### ######## ##### ### ### ###### ### ####### ##########################################
### ### ### ################################################################ ####### #### ### ### #### ### #### ###########################################
### ### ################################################################ ###### ### ################################################################ #### ### ### #############################################
### ### ################################################################ ###### #### ################################################################ #### ### ### ##############################################
### ### ################################################################ ##### ### ################################################################ ### ### ### ###############################################
### ### ################################################################ ##### ### ################################################################ ### ### ### ######## ###
### ### ################################################################ #### ### ################################################################ ### ### ### ####### ###
### ### ################################################################ #### ### ### ## ### ### ##### ###
#### ### ### ### #### ### #### ### ## ### ##### ####
############# ### ### ### #### ### ### ### ### ####### ####
############# ### ##### ### ### ### ### ######### ###
############# ### ######## ### ##### ### #################
### ########### ### ###### #### ###############
#### ############################## ############# ############
#### ############################# ############# ###########
##### ############################ #############
######## #########################
############# ######################
############# #############
#############
```
**Obanner93**
```
## ### #################
## ### ##########################
## ### ################################
################################################################ ########################################
################################################################ ########################################### #############
################################################################ ################################################# ####################
################################################################ ################################################### #######################
################################################################ ################## ############### ############################
################################################################ ############# ########## ############################### ###
################################################################ ## ### ############ ######## ######### ### ########## ###
## ### ### ## ### ######## ##### ## ### ###### ### ###### ###
## ### ### ## ### ####### #### ## ### ##### ### ##### ##########################################
### ### ################################################################ ###### ### ################################################################ #### ### #### ############################################
### ### ################################################################ ##### #### ################################################################ ### ### #### ##############################################
### ### ################################################################ ##### #### ################################################################ ## ### ### ###############################################
### ### ################################################################ #### ### ################################################################ ## ### ### ###############################################
### ### ################################################################ ### ### ################################################################ ## ### #### ####### ###
### ### ################################################################ ### ### ################################################################ ## ### #### ###### ###
#### ### ################################################################ ### ### #### ## ### ### #### ##### ###
####### ### ## ### #### ### ### ### ### ###### #####
############# ### ## ### ##### ### ### ### ### ########## ###
############# ### ###### ### ##### #### ################# ###
### ########### ### ###### ### ################ ##
### ############################### ######### ### ##############
#### ############################# ############# ############
##### ############################ ############# ########
###### ########################### #############
############# ######################
############# ###################
#############
```
**Obanner94**
```
### ### ##################
### ### ##########################
### ### ################################
################################################################# #########################################
################################################################# ########################################### ############
################################################################# ################################################# ####################
################################################################# #################################################### ######################
################################################################# ################# ############### ############################
################################################################# ############# ########## ################################ ###
################################################################# ### ### ########### ######## ######### ### ######### ###
### ### ### ### ### ######### ##### ### ### ####### ### ####### ###
### ### ### ### ### ####### #### ### ### ##### ### ##### ###########################################
### ### ### ################################################################# ####### #### ################################################################# ### ### #### #############################################
### ### ################################################################# ###### #### ################################################################# ### ### ### ###############################################
### ### ################################################################# ##### #### ################################################################# ### ### ### ###############################################
### ### ################################################################# #### ### ################################################################# ### ### ### ################################################
### ### ################################################################# ### ### ################################################################# ### ### ### ######## ###
### ### ################################################################# ### ### ################################################################# ## ### #### ###### ###
#### ### ################################################################# ### ### #### ### ## ### ##### ##### ###
####### ### ### ### ### ### ### ### ### ####### ####
############# ### ### ### ##### ### ### ### ### ######### ####
############# ### ### ### ####### ### ##### ### ################# ###
############# ### ######## ### ##### ### ############### ##
### ################################ ######## ### ##############
#### ############################### ############# ###########
##### ############################# ############# #######
###### ########################### #############
######## #########################
############# ###################
############# #############
```
**Obanner95**
```
### ### ##################
### ### ##########################
### ### ################################
################################################################## #########################################
################################################################## ############################################ #############
################################################################## ############################################### #####################
################################################################## #################################################### #######################
################################################################## ################## ############### #############################
################################################################## ############# ########## ############################### ###
################################################################## ### ### ########### ######## ################################# ###
### ### ### ### ### ########## ####### ###### ### ####### ###
### ### ### ### ### ####### #### ### ### ##### ### ###### ###########################################
### ### ### ################################################################## ####### #### ### ### ### ### ### ############################################
### ### ################################################################## ###### #### ################################################################## #### ### #### ##############################################
### ### ################################################################## ##### #### ################################################################## ### ### ### ###############################################
### ### ################################################################## #### ### ################################################################## ### ### ### ################################################
### ### ################################################################## #### ### ################################################################## ### ### ### ######## ###
### ### ################################################################## #### ### ################################################################## ## ### ### ####### ###
##### ### ################################################################## #### ### #### ################################################################## ### ### #### ###### ###
####### ### ### ### ### ### ### ### ## ### ###### ####
############# ### ### ### #### ### #### ### ### ########## ###
############# ### ### ### ###### ### #### ### ################## ###
############# ### ######## ### ##### #### ################ ##
### ########### ### ###### ## ##############
#### ############################### ############# #############
#### ############################# ############# ########
###### ########################### #############
######## #########################
############# ######################
############# #############
#############
```
**Obanner96**
```
### ## ##################
### ## ###########################
### ## #################################
################################################################## #########################################
################################################################## ############################################# #############
################################################################## ############################################### ####################
################################################################## ##################################################### ########################
################################################################## ################## ################ #############################
################################################################## ############# ########## ################################ ###
################################################################## ### ## ############ ######## ################################## ###
### ### ## ### ## ########### ####### ###### ### ###### ###
### ### ## ### ## ####### #### ### ## ##### ### ##### ############################################
### ### ## ################################################################## ####### ##### ### ## #### ### #### #############################################
### ## ################################################################## ###### #### ################################################################## #### ### #### ###############################################
### ## ################################################################## ##### ### ################################################################## ### ### ### ################################################
### ## ################################################################## ##### ## ################################################################## ### ### ### #################################################
### ## ################################################################## #### ## ################################################################## ### ### ### ######## ###
### ## ################################################################## #### ## ################################################################## ### ### #### ####### ###
### ## ################################################################## #### ## ################################################################## ### ### ##### ###### ###
######## ## ### ## #### ### ### ### ## ### ##### ####
############# ## ### ## #### ### #### ### ### ######### ###
############# ## ### ## ##### ### #### ### ################### ####
############# ## ######## ### ###### #### ################## ##
## ########### ### ####### ### ###############
### ############################### ############# ##############
### ############################## ############# ############
##### ############################# #############
######## ##########################
############# #######################
############# ####################
#############
```
**Obanner97**
```
## ###
## ### ##################
## ### ############################
################################################################## ##################################
################################################################## ##########################################
################################################################## ############################################ #############
################################################################## ################################################ #####################
################################################################## ###################################################### #######################
################################################################## ################### ################ ############################# ###
################################################################## ## ### ############### ############# ################################# ###
## ### ### ## ### ############ ######## ################################## ###
## ### ### ## ### ########## ####### ## ### ####### ### ####### ############################################
## ### ### ################################################################## ######### ###### ## ### ##### ### ##### ##############################################
### ### ################################################################## ######## ##### ################################################################## ##### ### #### ###############################################
### ### ################################################################## ###### #### ################################################################## ### ### ### #################################################
### ### ################################################################## ##### ### ################################################################## ## ### ### #################################################
### ### ################################################################## #### ### ################################################################## ## ### ### #################################################
### ### ################################################################## #### ### ################################################################## ## ### ### ###### ###
### ### ################################################################## ### ### ################################################################## ## ### ### ##### ###
#### ### ## ### ### ### ## ### ### #### ##### ###
############# ### ## ### ### ### ### ## ### ##### ####
############# ### ## ### ##### ### #### ### ### ####### ###
############# ### ##### ### #### ### ################## ###
### ####### ### #### #### ##################
### ############ ### ####### ### ################
### ################################# ######### #############
##### ############################### ############# ############
##### ############################## ############# ########
############# ############################ #############
############# #######################
############# ####################
##############
```
**Obanner98**
```
### ### ###################
### ### ###########################
### ### #################################
################################################################### ###########################################
################################################################### ############################################# #############
################################################################### ################################################# #####################
################################################################### ####################################################### ########################
################################################################### ################## ############### ##############################
################################################################### ################ ############# ################################# ###
################################################################### ### ### ############ ######## ################################## ###
### ### ### ### ### ########## ####### ####### ### ###### ###
### ### ### ### ### ######### ###### ### ### ##### ### ##### #############################################
### ### ### ################################################################### ####### ##### ### ### #### ### #### ###############################################
### ### ################################################################### ##### #### ################################################################### ### ### #### ################################################
### ### ################################################################### ###### ### ################################################################### ### ### ### #################################################
### ### ################################################################### #### ### ################################################################### ### ### ### ##################################################
### ### ################################################################### #### ### ################################################################### ### ### ### ##################################################
### ### ################################################################### ### ### ################################################################### ### ### #### ###### ###
### ### ################################################################### ### ### ################################################################### ## ### #### ###### ###
##### ### ### ### ### ### ### ### ## ### ##### ##### ###
####### ### ### ### ### ### ### ### ### ###### ####
############# ### ### ### ##### ### #### ### ### ########## ####
############# ### ####### ### #### #### ################## ###
############# ### ######## ### ##### #### #################
### ################################# ######### ### ###############
### ################################ ############# ############
##### ############################## ############# ########
###### ############################ #############
######## ##########################
############# ####################
############# #############
#############
```
**Obanner99**
```
### ###
### ### ##################
### ### ############################
#################################################################### ##################################
#################################################################### ##########################################
#################################################################### ############################################## ##############
#################################################################### ################################################ #####################
#################################################################### ###################################################### ########################
#################################################################### ################### ################ ##############################
#################################################################### ################ ############## ################################# ###
### ### ### ### ### ############ ######## ################################## ###
### ### ### ### ### ########### ######## ####### ### ####### ###
### ### ### ### ### ######### ###### ### ### ###### ### ##### #############################################
### ### #################################################################### ####### #### ### ### #### ### ##### ##############################################
### ### #################################################################### ###### ### #################################################################### #### ### ### ################################################
### ### #################################################################### ###### #### #################################################################### ### ### ### #################################################
### ### #################################################################### #### ### #################################################################### ### ### ### ##################################################
### ### #################################################################### #### ### #################################################################### ### ### ### ##################################################
### ### #################################################################### #### ### #################################################################### ### ### ### ####### ###
#### ### #################################################################### #### ### #################################################################### ## ### #### ###### ###
######## ### ### ### #### ### #### ### ### ### ##### ##### ###
############## ### ### ### ### ### ### ### ### ####### ####
############## ### ### ### ###### ### #### ### ### ########## ####
############## ### ####### ### ##### ### ################## ###
### ######## ### ##### #### ################
#### ################################# ######### ### ###############
#### ################################# ############# ############
###### ############################### ############# ########
######## ############################# #############
############# ###########################
############# ########################
############# ##############
```
**Old Banner**
```
####### ### #####
# # # # # ###### #####
# # # # # #
##### # # #### # ##### #
# # # # # # #
# # # # # # #
# ### ##### ###### ###### #
```
**Patorjk's Cheese**
```
_____ ____ _____ ____ ______ _________________
____|\ \ | | ___|\ \ | | ___|\ \ / \
| | \ \| | / /\ \ | | | \ \\______ ______/
| |______/| || | |____| | | | ,_____/| \( / / )/
| |----'\ | || | ____ | | ____ | \--'\_|/ ' | | '
| |_____/ | || | | || | | || /___/| | |
| | | || | |_, || | | || \____|\ / //
|____| |____||\ ___\___/ /||____|/____/||____ ' /| /___//
| | | || | /____ / || | ||| /_____/ | |` |
|____| |____| \|___| | / |____|_____|/|____| | / |____|
)/ \( \( |____|/ \( )/ \( |_____|/ \(
' ' ' )/ ' ' ' )/ '
' '
```
**Patorjk-HeX**
```
_____ _____
____ \ \ ____________ _____ _____ _____\ \ ________ ________
\ \ /____/| / \ _____\ \_ |\ \ / / | | / \ / \
| |/_____|/|\___/\ \\___/| / /| | \\ \ / / /___/||\ \/ /|
| | ___ \|____\ \___|// / /____/| \\ \ | |__ |___|/| \ /\____/ |
| \__/ \ | | | | |_____|/ \| | ______ | \ | \______/\ \ | |
/ /\___/| __ / / __ | | |_________ | |/ \| __/ __ \ | | \ \____|/
/ /| | | |/ \/ /_/ ||\ \|\ \ / ||\ \ / \ \|______| \ \
|_____| /\|_|/|____________/|| \_____\| |\__/| /_____/\_____/|| \____\/ | \ \___\
| |/ | | /| | /____/| | ||| | | ||| | |____/| \ | |
|_____| |___________|/ \|_____| |\|_|/|______|/|____|/ \|____| | | \|___|
|____/ |___|/
```
**Peaks Slant**
```
_/\/\/\/\/\/\__/\/\/\/\____/\/\/\/\/\__/\/\__________________/\/\_________
_/\/\____________/\/\____/\/\__________/\/\______/\/\/\____/\/\/\/\/\_____
_/\/\/\/\/\______/\/\____/\/\__/\/\/\__/\/\____/\/\/\/\/\____/\/\_________
_/\/\____________/\/\____/\/\____/\/\__/\/\____/\/\__________/\/\_________
_/\/\__________/\/\/\/\____/\/\/\/\/\__/\/\/\____/\/\/\/\____/\/\/\_______
__________________________________________________________________________
```
**Red Phoenix**
```
___________.___ ________ .__ __
\_ _____/| | / _____/ | | ____ _/ |_
| __) | |/ \ ___ | | _/ __ \\ __\
| \ | |\ \_\ \| |__\ ___/ | |
\___ / |___| \______ /|____/ \___ >|__|
\/ \/ \/
```
**Rowan Cap**
```
dMMMMMP dMP .aMMMMP dMP dMMMMMP dMMMMMMP
dMP amr dMP" dMP dMP dMP
dMMMP dMP dMP MMP"dMP dMMMP dMP
dMP dMP dMP.dMP dMP dMP dMP
dMP dMP VMMMP" dMMMMMP dMMMMMP dMP
```
**S Blood**
```
@@@@@@@@ @@@ @@@@@@@ @@@ @@@@@@@@ @@@@@@@
@@! @@! !@@ @@! @@! @@!
@!!!:! !!@ !@! @!@!@ @!! @!!!:! @!!
!!: !!: :!! !!: !!: !!: !!:
: : :: :: : : ::.: : : :: ::: :
```
**SL Script**
```
_____ _ () , _
/ ' | ) /`-'| // _/_
,-/-,,---|/ / / // _ /
(_/ \_/ \_/__-<_</_</_<__
```
**Santa Clara**
```
_________ ,___ _
( / ( / / /// _/_
-/-- / / __// _ /
_/ _/_(___/(/_(/_(__
```
**Slant Relief**
```
__/\\\\\\\\\\\\\\\__/\\\\\\\\\\\_____/\\\\\\\\\\\\__/\\\\\\___________________________________________
_\/\\\///////////__\/////\\\///____/\\\//////////__\////\\\___________________________________________
_\/\\\_________________\/\\\______/\\\________________\/\\\_______________________/\\\________________
_\/\\\\\\\\\\\_________\/\\\_____\/\\\____/\\\\\\\____\/\\\________/\\\\\\\\___/\\\\\\\\\\\___________
_\/\\\///////__________\/\\\_____\/\\\___\/////\\\____\/\\\______/\\\/////\\\_\////\\\////____________
_\/\\\_________________\/\\\_____\/\\\_______\/\\\____\/\\\_____/\\\\\\\\\\\_____\/\\\________________
_\/\\\_________________\/\\\_____\/\\\_______\/\\\____\/\\\____\//\\///////______\/\\\_/\\____________
_\/\\\______________/\\\\\\\\\\\_\//\\\\\\\\\\\\/___/\\\\\\\\\__\//\\\\\\\\\\____\//\\\\\_____________
_\///______________\///////////___\////////////____\/////////____\//////////______\/////______________
```
**Small Caps**
```
___ ___ ____ _ ___ _____
) __( )_ _( ).-._( ) | ) __( )__ __(
| _) _| |_ |( ,-. | (__ | _) | |
)_( )_____()_`__( )____( )___( )_(
```
**Small Isometric1**
```
___ ___ ___ ___ ___ ___
/\ \ /\ \ /\ \ /\__\ /\ \ /\ \
/::\ \ _\:\ \ /::\ \ /:/ / /::\ \ \:\ \
/::\:\__\ /\/::\__\ /:/\:\__\ /:/__/ /::\:\__\ /::\__\
\/\:\/__/ \::/\/__/ \:\:\/__/ \:\ \ \:\:\/ / /:/\/__/
\/__/ \:\__\ \::/ / \:\__\ \:\/ / \/__/
\/__/ \/__/ \/__/ \/__/
```
**Small Keyboard**
```
____ ____ ____ ____ ____ ____ _________
||F |||I |||G |||l |||e |||t ||| ||
||__|||__|||__|||__|||__|||__|||_______||
|/__\|/__\|/__\|/__\|/__\|/__\|/_______\|
```
**Small Poison**
```
@@@@@@@@ @@@ @@@@@@@ @@@ @@@@@@@@ @@@@@@@
@@! @@! !@@ @@! @@! @!!
@!!!:! !!@ !@! @!@!@ @!! @!!!:! @!!
!!: !!: :!! !!: !!: !!: !!:
: : :: :: : : ::.: : : :: :: :
```
**Small Script**
```
_____
() |_ |\ () ||\ __|_
/| |_ |/ /\/||/ |/ |
(/ \_/\//(_/ |_/|_/|_/
```
**Small Shadow**
```
__|_ _| __| | |
_| | (_ | | -_) _|
_| ___|\___|_|\___|\__|
```
**Small Slant**
```
_______________ __
/ __/ _/ ___/ /__ / /_
/ _/_/ // (_ / / -_) __/
/_/ /___/\___/_/\__/\__/
```
**Small Tengwar**
```
|_ ' _____ ,'
|_) | (_(_| --- | |~)
| (_, |
```
**Star Strips**
```
------------ -------- ------------ ---- ------------ ------------
************ ******** ************ **** ************ ************
---- ---- ---- ---- ---- ------------
************ **** **** ****** **** ************ ****
------------ ---- ---- ------ ---- ------------ ----
**** **** **** **** ************ **** ****
---- -------- ------------ ------------ ------------ ----
**** ******** ************ ************ ************ ****
```
**Star Wars**
```
_______ __ _______ __ _______ .___________.
| ____|| | / _____|| | | ____|| |
| |__ | | | | __ | | | |__ `---| |----`
| __| | | | | |_ | | | | __| | |
| | | | | |__| | | `----.| |____ | |
|__| |__| \______| |_______||_______| |__|
```
**Stick Letters**
```
___ __ ___ ___
|__ | / _` | |__ |
| | \__> |___ |___ |
```
**Stronger Than All**
```
._______.___ ._____ .___ .____________._
:_ ____/: __|:_ ___\ | | : .____/\__ _:|
| _/ | : || |___| | | : _/\ | :|
| | | || / || |/\ | / \ | |
|_. | | ||. __ || / \|_.: __/ | |
:/ |___| :/ |. ||______/ :/ |___|
: : :/
:
```
**Swamp Land**
```
______ ________ _______ __ ______ _________
/_____/\ /_______/\/______/\ /_/\ /_____/\ /________/\
\::::_\/_\__.::._\/\::::__\/__\:\ \ \::::_\/_\__.::.__\/
\:\/___/\ \::\ \ \:\ /____/\\:\ \ \:\/___/\ \::\ \
\:::._\/ _\::\ \__\:\\_ _\/ \:\ \____\::___\/_ \::\ \
\:\ \ /__\::\__/\\:\_\ \ \ \:\/___/\\:\____/\ \::\ \
\_\/ \________\/ \_____\/ \_____\/ \_____\/ \__\/
```
**THIS**
```
▄▀▀▀█▄ ▄▀▀█▀▄ ▄▀▀▀▀▄ ▄▀▀▀▀▄ ▄▀▀█▄▄▄▄ ▄▀▀▀█▀▀▄
█ ▄▀ ▀▄ █ █ █ █ █ █ ▐ ▄▀ ▐ █ █ ▐
▐ █▄▄▄▄ ▐ █ ▐ █ ▀▄▄ ▐ █ █▄▄▄▄▄ ▐ █
█ ▐ █ █ █ █ █ █ ▌ █
█ ▄▀▀▀▀▀▄ ▐▀▄▄▄▄▀ ▐ ▄▀▄▄▄▄▄▄▀ ▄▀▄▄▄▄ ▄▀
█ █ █ ▐ █ █ ▐ █
▐ ▐ ▐ ▐ ▐ ▐
```
**The Edge**
```
▄████ ▄█ ▄▀ █ ▄███▄ ▄▄▄▄▀
█▀ ▀ ██ ▄▀ █ █▀ ▀ ▀▀▀ █
█▀▀ ██ █ ▀▄ █ ██▄▄ █
█ ▐█ █ █ ███▄ █▄ ▄▀ █
█ ▐ ███ ▀ ▀███▀ ▀
▀
```
**Thorned**
```
__, ___, _, , _, ___,
'|_,' | / _ | /_,' |
| _|_,'\_|`'|__'\_ |
' ' _| ' ` '
'
```
**Three Point**
```
|~~|~/~_| _ _|_
|~_|_\_/|(/_ |
```
**Two Point**
```
|~||~_| __|_
|~||_||}_ |
```
**USA Flag**
```
:::===== ::: :::===== ::: :::===== :::====
::: ::: ::: ::: ::: :::====
====== === === ===== === ====== ===
=== === === === === === ===
=== === ======= ======== ======== ===
```
**Wet Letter**
```
,---.,-. ,--, ,-. ,---. _______
| .-'|(|.' .' | | | .-'|__ __|
| `-.(_)| | __ | | | `-. )| |
| .-'| |\ \ ( _)| | | .-' (_) |
| | | | \ `-) )| `--. | `--. | |
)\| `-' )\____/ |( __.'/( __.' `-'
(__) (__) (_) (__)
```
**a_zooloo**
```
###### #### ##### ###### ### ## #####
###### ###### ####### ###### ### ## #####
## ### ### ###### ### ### #######
###### ### ## ### ###### ### ### #######
###### ### ## ## ## ####### ###
### ### ### ### ## ####### ###
#### ##### ####### ###### ###### ##
### ##### ###### ###### ###### ##
```
**acrobatic**
```
o__ __o__/_ __o__ o__ __o o o
<| v | /v v\ <|> <|>
< > / \ /> <\ / \ < >
| \o/ o/ \o/ o__ __o |
o__/_ | <| _\__o__ | /v |> o__/_
| < > \\ | / \ /> // |
<o> | \ / \o/ \o o/ |
| o o o | v\ /v __o o
/ \ __|>_ <\__ __/> / \ <\/> __/> <\__
```
**advenger**
```
####### ###### ##### ###### # ###### ###
## # ## ## ## ###### # ####### ###
## ## ## ##### ## ####### ###
#### ## ## #### ##### ## ######## ###
## ## ## ## ##### # ######## ##
## ## ## ## #### # ####### ##
#### ###### ##### #### # ####### #
### # ######
```
**alligator**
```
:::::::::: ::::::::::: :::::::: ::: :::::::::: :::::::::::
:+: :+: :+: :+: :+: :+: :+:
+:+ +:+ +:+ +:+ +:+ +:+
:#::+::# +#+ :#: +#+ +#++:++# +#+
+#+ +#+ +#+ +#+# +#+ +#+ +#+
#+# #+# #+# #+# #+# #+# #+#
### ########### ######## ########## ########## ###
```
**alligator2**
```
:::::::::: ::::::::::: :::::::: ::: :::::::::: :::::::::::
:+: :+: :+: :+: :+: :+: :+:
+:+ +:+ +:+ +:+ +:+ +:+
:#::+::# +#+ :#: +#+ +#++:++# +#+
+#+ +#+ +#+ +#+# +#+ +#+ +#+
#+# #+# #+# #+# #+# #+# #+#
### ########### ######## ########## ########## ###
```
**alligator3**
```
:::::::::: ::::::::::: :::::::: ::: :::::::::: :::::::::::
:+: :+: :+: :+: :+: :+: :+:
+:+ +:+ +:+ +:+ +:+ +:+
:#::+::# +#+ :#: +#+ +#++:++# +#+
+#+ +#+ +#+ +#+# +#+ +#+ +#+
#+# #+# #+# #+# #+# #+# #+#
### ########### ######## ########## ########## ###
```
**alpha**
```
_____ _____ _____ _____ _____ _____
/\ \ /\ \ /\ \ /\ \ /\ \ /\ \
/::\ \ /::\ \ /::\ \ /::\____\ /::\ \ /::\ \
/::::\ \ \:::\ \ /::::\ \ /:::/ / /::::\ \ \:::\ \
/::::::\ \ \:::\ \ /::::::\ \ /:::/ / /::::::\ \ \:::\ \
/:::/\:::\ \ \:::\ \ /:::/\:::\ \ /:::/ / /:::/\:::\ \ \:::\ \
/:::/__\:::\ \ \:::\ \ /:::/ \:::\ \ /:::/ / /:::/__\:::\ \ \:::\ \
/::::\ \:::\ \ /::::\ \ /:::/ \:::\ \ /:::/ / /::::\ \:::\ \ /::::\ \
/::::::\ \:::\ \ ____ /::::::\ \ /:::/ / \:::\ \ /:::/ / /::::::\ \:::\ \ /::::::\ \
/:::/\:::\ \:::\ \ /\ \ /:::/\:::\ \ /:::/ / \:::\ ___\ /:::/ / /:::/\:::\ \:::\ \ /:::/\:::\ \
/:::/ \:::\ \:::\____\/::\ \/:::/ \:::\____\/:::/____/ ___\:::| |/:::/____/ /:::/__\:::\ \:::\____\ /:::/ \:::\____\
\::/ \:::\ \::/ /\:::\ /:::/ \::/ /\:::\ \ /\ /:::|____|\:::\ \ \:::\ \:::\ \::/ / /:::/ \::/ /
\/____/ \:::\ \/____/ \:::\/:::/ / \/____/ \:::\ /::\ \::/ / \:::\ \ \:::\ \:::\ \/____/ /:::/ / \/____/
\:::\ \ \::::::/ / \:::\ \:::\ \/____/ \:::\ \ \:::\ \:::\ \ /:::/ /
\:::\____\ \::::/____/ \:::\ \:::\____\ \:::\ \ \:::\ \:::\____\ /:::/ /
\::/ / \:::\ \ \:::\ /:::/ / \:::\ \ \:::\ \::/ / \::/ /
\/____/ \:::\ \ \:::\/:::/ / \:::\ \ \:::\ \/____/ \/____/
\:::\ \ \::::::/ / \:::\ \ \:::\ \
\:::\____\ \::::/ / \:::\____\ \:::\____\
\::/ / \::/____/ \::/ / \::/ /
\/____/ \/____/ \/____/
```
**alphabet**
```
FFFF III GGG l t
F I G l t
FFF I G GG l eee ttt
F I G G l e e t
F III GGG l ee tt
```
**aquaplan**
```
###### #### #### #####
## ## ## ## ####### ##
## ## ## ######## ##
#### ## ## ### ######## # # ##
## ## ## ## ####### # #
## ## ## ## ######## # # #
## #### #### ##### # # ##
# ### # # #
```
**arrows**
```
>=======> >=> >===> >=> >=>
>=> >=> >> >=> >=> >=>
>=> >=> >=> >=> >==> >=>>==>
>=====> >=> >=> >=> >> >=> >=>
>=> >=> >=> >===> >=> >>===>>=> >=>
>=> >=> >=> >> >=> >> >=>
>=> >=> >====> >==> >====> >=>
```
**asc_____**
```
###### # ######
# # # #
# # # # ####### #######
##### ## ## ### # # #
## ## ## # # #### #
## ## ## # # # #
## ## ####### ####### ####### #
```
**ascii___**
```
### ## #### ####### ######
## ## ## ## # # ## #
# ### ### ## ## ## # ##
#### ## ## ## ## #### ##
## ## ## ## ## # ## # ##
## ## ##### ## ## ## # ##
#### #### ## ####### ####### ####
#####
```
**assalt_m**
```
####### ####### ####### # ##
## ### ## ## ## ### ## ####
## ### ## ## ## ## ## ##
####### ### ## #### ### ## # ## ## ##
### ### ## ### ### ## ## ## ## ##
### ### ## ### #### #### ## ## ##
### ####### ####### ##### ## #######
## ### ##
```
**asslt__m**
```
####### ####### ####### # ##
## ### ## ## ## ### ## ####
## ### ## ## ## ## ## ##
####### ### ## #### ### ## # ## ## ##
### ### ## ### ### ## ## ## ## ##
### ### ## ### #### #### ## ## ##
### ####### ####### ##### ## #######
## ### ##
```
**atc_____**
```
# ## # # # # ## # ### # ########
# ## ### ## # ## ### # # ## # # ########
# #### ### ## # #### # ### # # ########
# ## ### ## # #### ### # # # # ## ########
# #### ### ## # # ## # # ## # # ########
# #### ### ## # ## ### # # ### ## # ########
# #### ## # # # # # ########
######## ######## ######## # # ## # # ########
```
**atc_gran**
```
# ## # # # ## # ### # ########
# ## ### ## # ## # # # # ## # # ########
# #### ### ## # #### # ## # ## # ########
# ## ### ## # #### # # # ## # #### ########
# #### ### ## # # #### # ## # # ########
# #### ### ## # ## # ## ## # # # ########
# #### ## # # ### ## ##### # ########
######## ######## ######## ###### # # # # # # # ########
```
**avatar**
```
_____ _ _____ _ _____ _____
/ // \/ __// \ / __//__ __\
| __\| || | _| | | \ / \
| | | || |_//| |_/\| /_ | |
\_/ \_/\____\\____/\____\ \_/
```
**b_m__200**
```
####
## # #
## # # #
##
##
##
####
```
**banner**
```
####### ### #####
# # # # # ###### #####
# # # # # #
##### # # #### # ##### #
# # # # # # #
# # # # # # #
# ### ##### ###### ###### #
```
**banner3**
```
######## #### ###### ## ######## ########
## ## ## ## ## ## ##
## ## ## ## ## ##
###### ## ## #### ## ###### ##
## ## ## ## ## ## ##
## ## ## ## ## ## ##
## #### ###### ######## ######## ##
```
**banner3-D**
```
'########:'####::'######:::'##:::::::'########:'########::::
##.....::. ##::'##... ##:: ##::::::: ##.....::... ##..:::::
##:::::::: ##:: ##:::..::: ##::::::: ##:::::::::: ##:::::::
######:::: ##:: ##::'####: ##::::::: ######:::::: ##:::::::
##...::::: ##:: ##::: ##:: ##::::::: ##...::::::: ##:::::::
##:::::::: ##:: ##::: ##:: ##::::::: ##:::::::::: ##:::::::
##:::::::'####:. ######::: ########: ########:::: ##:::::::
..::::::::....:::......::::........::........:::::..::::::::
```
**banner4**
```
.########.####..######...##.......########.########...
.##........##..##....##..##.......##..........##......
.##........##..##........##.......##..........##......
.######....##..##...####.##.......######......##......
.##........##..##....##..##.......##..........##......
.##........##..##....##..##.......##..........##......
.##.......####..######...########.########....##......
```
**barbwire**
```
><<<<<<<<><< ><<<< ><< ><<
><< ><< >< ><< ><< ><<
><< ><<><< ><< ><< ><>< ><
><<<<<< ><<><< ><< >< ><< ><<
><< ><<><< ><<<< ><<><<<<< ><< ><<
><< ><< ><< >< ><<>< ><<
><< ><< ><<<<< ><<< ><<<< ><<
```
**basic**
```
d88888b d888888b d888b db d88888b d888888b
88' `88' 88' Y8b 88 88' `~~88~~'
88ooo 88 88 88 88ooooo 88
88~~~ 88 88 ooo 88 88~~~~~ 88
88 .88. 88. ~8~ 88booo. 88. 88
YP Y888888P Y888P Y88888P Y88888P YP
```
**battlesh**
```
####### #### ###### # ###### ####### ######
####### #### ####### # # # # # ##### ## ##
## ## ## ## ## # # ### # ### # ## #
#### ## ## # # # # # # # # #
#### ## ## ### # # # # # ### # # #
## ## ## ## # # # # ##### # ## # ## #
#### #### ####### #### # ### # ## ## ##
#### #### ###### #### ##### ### ######
```
**baz__bil**
```
###### #### #### ######## # ######
## ## ## # ######## ### ##
## ## ## ######## ##### ##
#### ## ## ######## ##### #####
## ## ## ### # # ###### ####### ##
## ## ## ## # #### #### ######## ##
## ## ## ## # ##### ######## ####### # ##
## #### #### # ##### #### ####### ####
```
**bear**
```
_ _ _ _ _ _ _ _ _ _ _ _
(c).-.(c) (c).-.(c) (c).-.(c) (c).-.(c) (c).-.(c) (c).-.(c)
/ ._. \ / ._. \ / ._. \ / ._. \ / ._. \ / ._. \
__\( Y )/__ __\( Y )/__ __\( Y )/__ __\( Y )/__ __\( Y )/__ __\( Y )/__
(_.-/'-'\-._)(_.-/'-'\-._)(_.-/'-'\-._)(_.-/'-'\-._)(_.-/'-'\-._)(_.-/'-'\-._)
|| F || || I || || G || || L || || E || || T ||
_.' `-' '._ _.' `-' '._ _.' `-' '._ _.' `-' '._ _.' `-' '._ _.' `-' '._
(.-./`-'\.-.)(.-./`-'\.-.)(.-./`-'\.-.)(.-./`-'\.-.)(.-./`-'\.-.)(.-./`-'\.-.)
`-' `-' `-' `-' `-' `-' `-' `-' `-' `-' `-' `-'
```
**beer_pub**
```
####### ###### ##### # # # # ######## ##
### ## ## ### ## # # # # ### # # ###
### ## ### # # # # ### # # ########
##### ## ### ### # # # # ### # # ########
### ## ### ## ######## ### # # ########
### ## ### ## #### ### # # ########
### ###### ##### #### ## # # # ###
######## ##
```
**bell**
```
.____ _ ___ . .
/ | .' \ | ___ _/_
|__. | | | .' ` |
| | | _ | |----' |
/ / `.___| /\__ `.___, \__/
```
**benjamin**
```
|=@|@[,@|_@[-@"|"@ @
```
**big**
```
______ _____ _____ _ _
| ____|_ _/ ____| | | |
| |__ | || | __| | ___| |_
| __| | || | |_ | |/ _ \ __|
| | _| || |__| | | __/ |_
|_| |_____\_____|_|\___|\__|
```
**bigfig**
```
_____ __
|_ | /__ | _ _|_
| _|_\_| | (/_ |_
```
**binary**
```
01000110 01001001 01000111 01101100 01100101 01110100
```
**block**
```
_|_|_|_| _|_|_| _|_|_| _| _|
_| _| _| _| _|_| _|_|_|_|
_|_|_| _| _| _|_| _| _|_|_|_| _|
_| _| _| _| _| _| _|
_| _|_|_| _|_|_| _| _|_|_| _|_|
```
**blocks**
```
.----------------. .----------------. .----------------. .----------------. .----------------. .----------------.
| .--------------. || .--------------. || .--------------. || .--------------. || .--------------. || .--------------. |
| | _________ | || | _____ | || | ______ | || | _____ | || | _________ | || | _________ | |
| | |_ ___ | | || | |_ _| | || | .' ___ | | || | |_ _| | || | |_ ___ | | || | | _ _ | | |
| | | |_ \_| | || | | | | || | / .' \_| | || | | | | || | | |_ \_| | || | |_/ | | \_| | |
| | | _| | || | | | | || | | | ____ | || | | | _ | || | | _| _ | || | | | | |
| | _| |_ | || | _| |_ | || | \ `.___] _| | || | _| |__/ | | || | _| |___/ | | || | _| |_ | |
| | |_____| | || | |_____| | || | `._____.' | || | |________| | || | |_________| | || | |_____| | |
| | | || | | || | | || | | || | | || | | |
| '--------------' || '--------------' || '--------------' || '--------------' || '--------------' || '--------------' |
'----------------' '----------------' '----------------' '----------------' '----------------' '----------------'
```
**bolger**
```
888~~ 888 e88~~\ 888 d8
888___ 888 d888 888 e88~~8e _d88__
888 888 8888 __ 888 d888 88b 888
888 888 8888 | 888 8888__888 888
888 888 Y888 | 888 Y888 , 888
888 888 "88__/ 888 "88___/ "88_/
```
**braced**
```
.----..-..----..-. .----..-----.
} |__}{ || |--'} | } |__}`-' '-'
} '_} | }| }-`}} '--.} '__} } {
`--' `-'`----'`----'`----' `-'
```
**bright**
```
.######..######...####...##......######..######.........
.##........##....##......##......##........##...........
.####......##....##.###..##......####......##...........
.##........##....##..##..##......##........##...........
.##......######...####...######..######....##...........
........................................................
```
**brite**
```
#### ### #### ## #
# # # ## # # #
## # # # ## ###
# # # ### # ### #
# # ## # # # #
# ### #### ### ## ##
```
**briteb**
```
##### ### #### ## #
# # # ## # # #
### # # # ## ###
# # # ### # #### #
# # ## # # # #
## ### #### ### ### ##
```
**britebi**
```
#### ### #### ## #
# # # ## # # #
### # ## # ### ###
# ## # ### # # # ##
# # ## # # #### #
## ### #### ## ### ##
```
**britei**
```
#### ## ### ## #
# # # # # # #
### # # # ## ###
# # # ## # # # #
# # # # # #### #
## ## ### ## ### ##
```
**broadway**
```
8 8888888888 8 8888 ,o888888o. 8 8888 8 8888888888 8888888 8888888888
8 8888 8 8888 8888 `88. 8 8888 8 8888 8 8888
8 8888 8 8888 ,8 8888 `8. 8 8888 8 8888 8 8888
8 8888 8 8888 88 8888 8 8888 8 8888 8 8888
8 888888888888 8 8888 88 8888 8 8888 8 888888888888 8 8888
8 8888 8 8888 88 8888 8 8888 8 8888 8 8888
8 8888 8 8888 88 8888 8888888 8 8888 8 8888 8 8888
8 8888 8 8888 `8 8888 .8' 8 8888 8 8888 8 8888
8 8888 8 8888 8888 ,88' 8 8888 8 8888 8 8888
8 8888 8 8888 `8888888P' 8 888888888888 8 888888888888 8 8888
```
**broadway_kb**
```
____ _ __ _ ____ _____
| |_ | | / /`_ | | | |_ | |
|_| |_| \_\_/ |_|__ |_|__ |_|
```
**bubble**
```
_ _ _ _ _ _
/ \ / \ / \ / \ / \ / \
( F | I | G | l | e | t )
\_/ \_/ \_/ \_/ \_/ \_/
```
**bubble__**
```
#### ### ### ####### ######
##### ###### ### #### ######
### ### ### ### ### ### ##
##### ### ### ### ### ##### ##
##### ### ###### ### ### ##
### ### ### ###### #### ##
### #### ###### ####### ####### ##
######
```
**bubble_b**
```
###### ###### #### ## #### ###### #
## ## ## ## ###### #### ###### ## #
## ## ## ###### #### ###### ## #
#### ## ## ### ###### #### ###### ## #
## ## ## ## ###### ## ###### ## #
## ## ## ## ###### ## ###### ## # #
## ###### #### ###### ###### ## # #
###### ## #### # #
```
**bulbhead**
```
____ ____ ___ __ ____ ____
( ___)(_ _)/ __)( ) ( ___)(_ _)
)__) _)(_( (_-. )(__ )__) )(
(__) (____)\___/(____)(____) (__)
```
**c1______**
```
####### ###### ##### ## ##
## ## ## ## ## ## ######## ##
## ## ## ## ######## ##
#### ## ## ## ##
## ## ## ### ## ##
## ## ## ## ## ##
#### ###### ##### ######## ##
######## ##
```
**c2______**
```
####### #### #####
####### #### #######
##### ## ## ####
## ## ## ##
## #### #######
## #### #####
```
**c_ascii_**
```
### ## #### ####### ######
## ## ## ## # # ## #
## ### ### ## ## ## # ##
#### ## ## ## ## #### ##
## ## ## ## ## # ## # ##
## ## ##### ## ## ## # ##
#### #### ## ####### ####### ####
#####
```
**c_consen**
```
### #### ###
# # #### # ##
##### #### ##### # # # # ## ### ####
## ## ## ### ### ### ## ##
#### ## ## ### ### ### ### ## ##
## ## ## ## ### ### ### ## ##
## #### #### ### ### # ### ## ##
# #### ### ## ##
```
**caligraphy**
```
***** ** ***** * * *** ***
****** **** * ****** * * **** * *** *
** * * *** ** * * * * **** ** **
* * * * * * * * ** ** ** **
* * * * * *** ** ********
** ** ** ** ** ** ** *** ********
** ** ** ** ** ** *** ** * *** **
** ****** **** ** ** ** **** * ** * *** **
** ***** * *** ** ** ** * **** ** ** *** **
** ** ** ** ** *** ** ** ******** **
* ** ** ** ** ** ** * ** ******* **
* *** * * ** * * ** ** **
***** *** * *** * ** **** * **
* ***** ****** ******* *** * ******* **
* *** *** *** *** *****
*
**
```
**cards**
```
.------..------..------..------..------..------.
|F.--. ||I.--. ||G.--. ||L.--. ||E.--. ||T.--. |.-.
| :(): || (\/) || :/\: || :/\: || (\/) || :/\: ((5))
| ()() || :\/: || :\/: || (__) || :\/: || (__) |'-.-.
| '--'F|| '--'I|| '--'G|| '--'L|| '--'E|| '--'T| ((1))
`------'`------'`------'`------'`------'`------' '-'
```
**catwalk**
```
_////////_// _//// _// _//
_// _// _/ _// _// _//
_// _//_// _// _// _/_/ _/
_////// _//_// _// _/ _// _//
_// _//_// _//// _//_///// _// _//
_// _// _// _/ _//_/ _//
_// _// _///// _/// _//// _//
```
**caus_in_**
```
####### ####### ####### ##
####### ####### ####### ##
### # # # ### # ### # # ####### ##
##### # # ### # ### ### ## ##
### # # # ### # ### ### ## ##
### # # ####### ####### #### ## ##
### # # ####### ####### ## ## ##
# # # # # # # # # # # # #### ## ## ##
```
**char1___**
```
## ##
###### ###### ##### ## ######## ##
## ## ## ## ######## ##
##### ## ## ## ##
## ## ## ### ## ##
## ## ## ## ## ##
## ###### ##### ######## ##
######## ##
```
**char2___**
```
###### ## ###### ## ###### #####
## ## ## ## ## ####### ######
## ## ## ## ## ##
##### ### ### ### ## ####### ##
### ### ### ## ## ## ##
### ### ### ## ####### ####### ##
### ### ####### ###### ###### ##
```
**char3___**
```
####### #### #### # ###### #####
## # ## ## ## # # #
## ## ## # # #
#### ## ## ### # #### #
## ## ## ## # # #
## ## ## ### # # #
#### #### ### # ###### ###### #
```
**char4___**
```
### #### ###
##### ## #####
## ## ##
#### ## ##
## ## ## ####
## ## ## ###
### #### #####
```
**charact1**
```
#### ## ### ###### ######
## ###### ### ###### ######
###### ### ## ## ### ## ##
## ## ## ## ### #### ##
## ## ###### ### ## ##
#### ###### ## ###### ###### ##
######
```
**charact2**
```
### ## ## ##### ######
## ## ## ##
###### ### ##### ## #### ##
## ## ## ## ## ## ##
## ## ##### ## ## ##
#### ###### ## ###### ##### ##
#####
```
**charact3**
```
### ## ### ###### ######
## ## ### ### ## ##
## ## ###### ## #### ##
###### ## ## ## ### ## ##
## ## ###### ## ## ### ## ##
## ##### ## ####### ####### ##
####
```
**charact4**
```
##### ## ## ###### ######
### ## ## ######
##### ## ###### ## #### ##
### ## ## ### ### ### ##
### ### ###### ### ### ##
### ### ## ###### ###### ##
######
```
**charact5**
```
### ### ##### ####### ######
#### ### ### ######
## ### ##### ### ##### # ## #
#### ## ## ## ### ### ##
## ## ##### ### ## ### ##
#### ###### ### ####### ####### ####
#####
```
**charact6**
```
### ## ## ###### ######
## ##### ## ## ##
##### ### ## ## ## #### ##
## ## ## ## ## ## ##
## ## ##### ## ## ##
## #### ## ###### ###### ##
#####
```
**characte**
```
#### ## ## ###### ######
## ## ## ##
###### ### ###### ## #### ##
## ## ## ## ## ## ##
## ## ###### ## ## ##
#### ###### ## ###### ###### ##
######
```
**charset_**
```
####### ####### ###### ## ###### ######
####### ####### ####### ## ###### ######
#### #### #### ## ## ##
####### #### #### ## #### ##
####### #### #### ## ## ##
#### ####### ####### ###### ###### ##
#### ####### ###### ###### ###### ##
```
**chartr**
```
#### # ### #
# # # # # #
### # # # # ##
# # # # ## # ### #
# # ## # # # #
# # ### # ## ##
```
**chartri**
```
#### ## ### #
# # ## # # #
### # # # # ###
# # # # ## # ### #
# # # # # ## #
## ## ### # ### ##
```
**chiseled**
```
_,---. .=-.-. _,---. ,----. ,--.--------.
.-`.' , \ /==/_ /_.='.'-, \ _.-. ,-.--` , \/==/, - , -\
/==/_ _.-'|==|, |/==.'- / .-,.'| |==|- _.-`\==\.-. - ,-./
/==/- '..-.|==| /==/ - .-' |==|, | |==| `.-. `--`\==\- \
|==|_ , /|==|- |==|_ /_,-.|==|- | /==/_ , / \==\_ \
|==| .--' |==| ,|==| , \_.' )==|, | |==| .-' |==|- |
|==|- | |==|- \==\- , (|==|- `-._|==|_ ,`-._ |==|, |
/==/ \ /==/. //==/ _ , //==/ - , ,/==/ , / /==/ -/
`--`---' `--`-` `--`------' `--`-----'`--`-----`` `--`--`
```
**chunky**
```
_______ _______ _______ __ __
| ___|_ _| __| |.-----.| |_
| ___|_| |_| | | || -__|| _|
|___| |_______|_______|__||_____||____|
```
**clb6x10**
```
### ##
##### #### ### ## ##
## ## ## ## ## ##
## ## ## ## ### ####
#### ## ##### ## ## ## ##
## ## ## ## ## ##### ##
## ## ## ## ## ## ##
## #### #### #### ### ##
```
**clb8x10**
```
### ##
####### ###### #### ## ##
## ## ## ## ## ##
## ## ## ## ##### ######
##### ## ## ## ## ## ##
## ## ## ### ## ####### ##
## ## ## ## ## ## ##
## ###### ##### #### ##### ###
```
**clb8x8**
```
####### ###### #### ### ##
## ## ## ## ## ##
## ## ## ## ##### ######
##### ## ## ## ## ## ##
## ## ## ### ## ####### ##
## ## ## ## ## ## ##
## ###### ##### #### ##### ###
```
**cli8x8**
```
###### ##### ### ### ##
## ## ## ## ## ##
## ## ## ## #### #######
##### ## ## ## ## ## ##
## ## ## #### ## ######## ##
## ## ## ## ## ## ##
## ##### #### #### #### ###
```
**clr4x6**
```
### ### ## # #
# # # # ## ###
## # # # # ### #
# # # # # # #
# ### ## # ## #
```
**clr5x10**
```
#### ### ## ##
# # # # # #
# # # # ## ####
### # # ## # # # #
# # # # # #### #
# # # # # # #
# ### ### ### ## ##
```
**clr5x6**
```
#### ### ### ## #
# # # # ## ####
### # # ## # #### #
# # # # # # #
# ### ### ### ## ##
```
**clr5x8**
```
#### ### ## ##
# # # # # #
# # # # ## ####
### # # ## # # # #
# # # # # #### #
# # # # # # #
# ### ### ### ## ##
```
**clr6x10**
```
## #
##### ##### ### # #
# # # # # #
# # # # ### #####
#### # # ## # # # #
# # # # # ##### #
# # # # # # #
# ##### #### ### ### ##
```
**clr6x6**
```
##### ### #### ## #
# # # # ### ####
#### # # ## # ##### #
# # # # # # #
# ### #### ### ### ##
```
**clr6x8**
```
##### ##### ### ## #
# # # # # #
# # # # ### #####
#### # # ## # # # #
# # # # # ##### #
# # # # # # #
# ##### #### ### ### ##
```
**clr7x10**
```
## #
###### ##### ### # #
# # # # # #
# # # # #### #####
#### # # ### # # # #
# # # # # ###### #
# # # # # # #
# ##### #### ### #### ###
```
**clr7x8**
```
###### ##### ### ## #
# # # # # #
# # # # #### #####
#### # # ### # # # #
# # # # # ###### #
# # # # # # #
# ##### #### ### #### ###
```
**clr8x10**
```
## #
####### ##### #### # #
# # # # # #
# # # # ##### ######
##### # # ### # # # #
# # # # # ####### #
# # # # # # #
# ##### ##### ### ##### ###
```
**clr8x8**
```
####### ##### #### ## #
# # # # # #
# # # # ##### ######
##### # # ### # # # #
# # # # # ####### #
# # # # # # #
# ##### ##### ### ##### ###
```
**cns**
```
```
**coil_cop**
```
####### ###### #####
## # ## ## ##
## ## ##
#### ## ## ####
## ## ## ##
## ## ## ##
#### ###### #####
```
**coinstak**
```
O))))))))O)) O)))) O)) O))
O)) O)) O) O)) O)) O))
O)) O))O)) O)) O)) O)O) O)
O)))))) O))O)) O)) O) O)) O))
O)) O))O)) O)))) O))O))))) O)) O))
O)) O)) O)) O) O))O) O))
O)) O)) O))))) O))) O)))) O))
```
**cola**
```
.-._.;;;'.;;;;. .-. .; .
(_).; ' .;' ` .;;.`-' .;' ...;...
.:--. .;' ;; (_; .; .-. .'
.:' .;' ;; :: .;.-' .;
.-: .;' ;; `;;'_;;_.-`:::'.;
(_/ .;;;;;;;;;'`;.___.'
```
**colossal**
```
8888888888 8888888 .d8888b. 888 888
888 888 d88P Y88b 888 888
888 888 888 888 888 888
8888888 888 888 888 .d88b. 888888
888 888 888 88888 888 d8P Y8b 888
888 888 888 888 888 88888888 888
888 888 Y88b d88P 888 Y8b. Y88b.
888 8888888 "Y8888P88 888 "Y8888 "Y888
```
**com_sen_**
```
### ## #### ####### ######
## ## ## ##
## ### ##### ## ## ##
###### ## ## ## ## #### ##
## ## ## ## ## ## ##
## ## ##### ## ## ##
## #### ## ####### ####### ##
#####
```
**computer**
```
8"""" 8 8""""8
8 8 8 " e eeee eeeee
8eeee 8e 8e 8 8 8
88 88 88 ee 8e 8eee 8e
88 88 88 8 88 88 88
88 88 88eee8 88eee 88ee 88
```
**contessa**
```
.___._..__ . ,
[__ | [ __| _ -+-
| _|_[_./|(/, |
```
**contrast**
```
.%%%%%%..%%%%%%...%%%%...%%......%%%%%%..%%%%%%.........
.%%........%%....%%......%%......%%........%%...........
.%%%%......%%....%%.%%%..%%......%%%%......%%...........
.%%........%%....%%..%%..%%......%%........%%...........
.%%......%%%%%%...%%%%...%%%%%%..%%%%%%....%%...........
........................................................
```
**convoy__**
```
###### ###### ###### # # # # # # ###
### ### ### # # # # # # ###
### ### ### # # ## ##### #
###### ### ### # # # ## ## # # # # #
### ### ### # # # # # # # # #
### ### ### # # # ## # ## # # # #
### ###### ###### # # # ## #######
# ## # # # # # ######
```
**cosmic**
```
.-:::::'::: .,-:::::/ ::: .,::::::::::::::::::
;;;'''' ;;;,;;-'````' ;;; ;;;;'''';;;;;;;;''''
[[[,,== [[[[[[ [[[[[[/ [[[ [[cccc [[
`$$$"`` $$$"$$c. "$$ $$' $$"""" $$
888 888 `Y8bo,,,o88oo88oo,.__888oo,__ 88,
"MM, MMM `'YMUP"YMM""""YUMMM""""YUMMM MMM
```
**cosmike**
```
.-:::::'::: .,-:::::/ ::: .,::::::::::::::::::
;;;'''' ;;;,;;-'````' ;;; ;;;;'''';;;;;;;;''''
[[[,,== [[[[[[ [[[[[[/ [[[ [[cccc [[
`$$$"`` $$$"$$c. "$$ $$' $$"""" $$
888 888 `Y8bo,,,o88oo88oo,.__888oo,__ 88,
"MM, MMM `'YMUP"YMM""""YUMMM""""YUMMM MMM
```
**cour**
```
## #
#### ### ## # #
# # # # # ## ####
## # ### # ### #
# # # # # # # #
## ### ## ### ## ##
```
**courb**
```
## #
#### ### ### # #
# # # ## # ### ####
## # ## # # #### #
# # ## # # ## #
### ### ### ### ### ###
```
**courbi**
```
## #
#### #### ### # ##
# ## # # ### ####
### # ## # # ##### #
# ## ## # ## ## ## #
## #### ### #### ### ##
```
**couri**
```
## #
#### ### ### # #
# # ## # ### ####
### # # ## # #### #
# # # # # # #
## ### ## #### ## ###
```
**crawford**
```
_____ ____ ____ _ ___ ______
| |l j / T| T / _]| T
| __j | T Y __j| | / [_ | |
| l_ | | | T || l___ Y _]l_j l_j
| _] | | | l_ || T| [_ | |
| T j l | || || T | |
l__j |____jl___,_jl_____jl_____j l__j
```
**crazy**
```
.---.
.--. | | __.....__
_.._ |__| .--./) | | .-'' '.
.' .._|.--. /.''\\ | | / .-''"'-. `. .|
| ' | || | | | | |/ /________\ \ .' |_
__| |__ | | \`-' / | || | .' |
|__ __| | | /("'` | |\ .-------------''--. .-'
| | | | \ '---. | | \ '-.____...---. | |
| | |__| /'""'.\ | | `. .' | |
| | || ||'---' `''-...... -' | '.'
| | \'. __// | /
|_| `'---' `'-'
```
**cricket**
```
_______ ___ _______ __ __
| _ | | _ | .-----| |_
|. 1___|. |. |___| | -__| _|
|. __) |. |. | |__|_____|____|
|: | |: |: 1 |
|::.| |::.|::.. . |
`---' `---`-------'
```
**cursive**
```
_____ _ () , _
/ ' | ) /`-'| // _/_
,-/-,,---|/ / / // _ /
(_/ \_/ \_/__-<_</_</_<__
```
**cyberlarge**
```
_______ _____ ______ _______ _______
|______ | | ____ | |______ |
| __|__ |_____| |_____ |______ |
```
**cybermedium**
```
____ _ ____ _ ____ ___
|___ | | __ | |___ |
| | |__] |___ |___ |
```
**cybersmall**
```
____ _ ____ _ ____ ___
|--- | |__, |___ |=== |
```
**cygnet**
```
.---.-.-.. .
|- | |-.| .-,-|-
' -'-'-''-`'- '-
#
```
**d_dragon**
```
####### ####### ####### ## ##### ######## # # ###
## ### ## ## ######## ######## ##### #
## ### ## ######## ######## #### ###
####### ### ## #### ######## ######## ## #####
### ### ## ### ######## ######## ########
### ### ## ### ######## ######## ########
### ####### ####### ######## ######## ########
######## ######## ########
```
**dcs_bfmo**
```
# # # # # #### # # # # #
####### ####### ##### # # # # # # ## # ### #
#### ### ### # ## # ##### #
###### ### ### ## ## ###### #
#### ### ### ## ###### #
#### ####### ####### ###### #
#### ####### ####### ###### #
#### ####### ##### ###### #
```
**decimal**
```
70 73 71 108 101 116
```
**deep_str**
```
### ### ### # ### ## ######## #######
### # ### ## ## ### ###
### ### ### # #### ## ##
### ## ### ### #### ###
### ### ### ### ###### ## ###
### ### ## ### ##### ### ###
### ### # ## # #### ## ##
## ####
```
**demo_1__**
```
### ### #### # ###
## ## ## ## ## ## ###### ######
## ## ### ## ## ##
## ## ## ### ### ## ## ##
## ## ### ## # #### ##
## ## ## ## ## ## ##
#### #### # ## ## ## ##
####### ####### ##
```
**demo_2__**
```
###### #### ####
## ## ## ## ## # # #### #######
## ## ## # # ## ## ##
#### ## ## ### # # #
## ## ## ## ## ## ## #
## ## ## ## ## ## ##
#### #### ##### ## ## ## ### ##
## #### ## ### ##
```
**demo_m__**
```
##### ## ##### ## ##### ######
## ## ## ## ## ##
## ## ## ## ## ##
##### ## ### ## ## #### ##
## ## ## ## ## ## ##
## ## ## ## ## ## ##
## ## ###### ##### ##### ##
```
**devilish**
```
####### ##### ##### ## # ##
## ### ### ## ## ## # ##
## ## ## ## # ## ### ##
### ## ## ## ### ## ##
#### ### ## ### ## ## ## ##
### ### ### ## ## # # ##
### #### ##### ######## # ##
######## ##
```
**diamond**
```
/\\\\\\\\/\\ /\\\\ /\\ /\\
/\\ /\\ /\ /\\ /\\ /\\
/\\ /\\/\\ /\\ /\\ /\/\ /\
/\\\\\\ /\\/\\ /\\ /\ /\\ /\\
/\\ /\\/\\ /\\\\ /\\/\\\\\ /\\ /\\
/\\ /\\ /\\ /\ /\\/\ /\\
/\\ /\\ /\\\\\ /\\\ /\\\\ /\\
```
**digital**
```
+-+-+-+-+-+-+
|F|I|G|l|e|t|
+-+-+-+-+-+-+
```
**doh**
```
FFFFFFFFFFFFFFFFFFFFFFIIIIIIIIII GGGGGGGGGGGGGlllllll tttt
F::::::::::::::::::::FI::::::::I GGG::::::::::::Gl:::::l ttt:::t
F::::::::::::::::::::FI::::::::I GG:::::::::::::::Gl:::::l t:::::t
FF::::::FFFFFFFFF::::FII::::::IIG:::::GGGGGGGG::::Gl:::::l t:::::t
F:::::F FFFFFF I::::I G:::::G GGGGGG l::::l eeeeeeeeeeee ttttttt:::::ttttttt
F:::::F I::::IG:::::G l::::l ee::::::::::::ee t:::::::::::::::::t
F::::::FFFFFFFFFF I::::IG:::::G l::::l e::::::eeeee:::::eet:::::::::::::::::t
F:::::::::::::::F I::::IG:::::G GGGGGGGGGG l::::l e::::::e e:::::etttttt:::::::tttttt
F:::::::::::::::F I::::IG:::::G G::::::::G l::::l e:::::::eeeee::::::e t:::::t
F::::::FFFFFFFFFF I::::IG:::::G GGGGG::::G l::::l e:::::::::::::::::e t:::::t
F:::::F I::::IG:::::G G::::G l::::l e::::::eeeeeeeeeee t:::::t
F:::::F I::::I G:::::G G::::G l::::l e:::::::e t:::::t tttttt
FF:::::::FF II::::::IIG:::::GGGGGGGG::::Gl::::::le::::::::e t::::::tttt:::::t
F::::::::FF I::::::::I GG:::::::::::::::Gl::::::l e::::::::eeeeeeee tt::::::::::::::t
F::::::::FF I::::::::I GGG::::::GGG:::Gl::::::l ee:::::::::::::e tt:::::::::::tt
FFFFFFFFFFF IIIIIIIIII GGGGGG GGGGllllllll eeeeeeeeeeeeee ttttttttttt
```
**doom**
```
______ _____ _____ _ _
| ___|_ _| __ \ | | |
| |_ | | | | \/ | ___| |_
| _| | | | | __| |/ _ \ __|
| | _| |_| |_\ \ | __/ |_
\_| \___/ \____/_|\___|\__|
```
**double**
```
____ __ ___ __ ____ ______
|| || // \\ || || | || |
||== || (( ___ || ||== ||
|| || \\_|| ||__| ||___ ||
```
**druid___**
```
#### ######
####### ## #### #### #
# ## ## ## ## # #####
## ## ### ## # # ####
####### ## ### ### ## ### ## ##
## ## ### # ## # ###
## ## ### ### # #
## ## #### ###
```
**dwhistled**
```
I l t
x x X
x x X
x x X
x . X
. . X
. . .
FIGlet
```
**e__fist_**
```
# # ## # ## ###### ######
## # ## ## ##
# # # ## ## ##
# ## ##### ##
## ## ##
## ## ##
# ###### ###### ##
#
```
**ebbs_1__**
```
### ## ## ###### ######
## ##### ## ## ##
##### ### ## ## ## #### ##
## ## ## ## ## ## ##
## ## ##### ## ## ##
## #### ## ###### ###### ##
#####
```
**ebbs_2__**
```
### ## #### ####### ######
## ## ## ##
## ### ##### ## ## ##
###### ## ## ## ## #### ##
## ## ## ## ## ## ##
## ## ##### ## ## ##
## #### ## ####### ####### ##
#####
```
**eca_____**
```
#### ### #### ####### #######
### ## ## #### #### ###
###### #### ### ### #### ###### ###
### ### ### ### #### #### ###
### ### ###### #### #### ###
### ##### ### # ##### ####### ###
######
```
**epic**
```
_______ _________ _______ _ _______ _________
( ____ \\__ __/( ____ \( \ ( ____ \\__ __/
| ( \/ ) ( | ( \/| ( | ( \/ ) (
| (__ | | | | | | | (__ | |
| __) | | | | ____ | | | __) | |
| ( | | | | \_ )| | | ( | |
| ) ___) (___| (___) || (____/\| (____/\ | |
|/ \_______/(_______)(_______/(_______/ )_(
```
**etcrvs__**
```
# ### # # # ###
###### ####### ###### # # ## # # # # # ## #
## ## ## ## ## # # ### #
####### ## ## ### # ### ## # ## ##
## ## ## ## # # ## # ## # # ## #
## ###### ##### ## # # # ## #
## # # ## ### # #
# ## # # # # #
```
**f15_____**
```
######## ######## ######## ######## ######## ######## ########
# # ## ## ## ## ### ## ## ### ########
# ##### ### ### # ## # ### ## ## ### ###### ########
# ### ### ### # ##### ### ## ## ###### ########
# ##### ### ### # # # ### ## ## ### ###### ########
# ##### ### ### # ## # ### ## ## ### ###### ########
# ##### ## ## ## ## ### ## ###### ########
######## ######## ######## ######## ######## ######## ########
```
**faces_of**
```
## ##
###### #### ##### # ## ##
## ### ## ## ### ## ## ##
## # ## ## ### ## ##
##### ## ## ## ## # ## ##
## ## ## ## ## ## # ## ##
## ## ## ## ## # ## ##
## #### ####### ## # ######## ##
```
**fair_mea**
```
###### # ###### # ###### # # # # # # ########
## # # # ### # # ## # # # # # # # # ########
## # # # ### # # ## # # # # # # # ########
#### # # ### # # ## ### # # # # # # ########
## # # # ### # # ## ### # # # # # # ########
## # # # ### # # ## ### # # # # ########
## # # # ###### # ###### # # # # # # ########
# # # # # # # # # # # # # # # # # # # #
```
**fairligh**
```
####### ###### ##### ## # #
### ## # ### # #
## ## ## #### # ## #
##### ## ## ### ## # # # #
## ## ## ## # # ### # #
## ## ## ### #### # # # #
## ##### ##### # # # #
# # # # #
```
**fantasy_**
```
### # # ### # ## ##
## # ## ## # ## ######## ##
## ## ## ## ######## ##
#### ## ## #### ## ##
## ## ## # ## ##
## ## ## # ## ##
# # ### ## ######## ##
# # #### # ######## ##
```
**fbr12___**
```
### ### ### # ## ###
#### #### #### ## # ## ###
## ## ## # # # # ## ###
## ## ## ########
###### ## ## ### # # ## # # ###
## ## ## # # # ###
## ### ####### ## # ## ###
## # #### # ## ###
```
**fbr1____**
```
###### #### #### # # # # # # # ## #
## # ## ## ## # ## # # # # # ## #
### ## ### ## # # # # # # #
## ## #### ## # # # # # # # #### #
#### #### ####### # #### # # # # # ##
#### #### ####### # # # # # #
#### #### ### ## # # # # # # # ## #
# ## # # # # # ## # ##
```
**fbr2____**
```
#### ###### ########
##### ### ### ### ## # ###
### # ##### ### ### ###
###### #### ### ## ### ##### ###
### ### ### ## ### ### ###
### ### ##### ### # ### ## ###
### ##### ## ## ####### ###### ###
#####
```
**fbr_stri**
```
###### ###### #### # # ## # # ## #
###### ###### ###### ## ## # #
## ## ## ## # ## # # ### # #
## ## ## # #### # # # # # #
#### ## ## ### # # ## # ## ### #
## ## ## ## ## ### # # # # # #
## ###### #### # # ## ## #
# # # # # ## #
```
**fbr_tilt**
```
### ### ### # ## ###
#### #### #### ## # ## ###
## ## ## # # # # ## ###
## ## ## ## ###
###### ## ## ### # # ## ## ###
## ## ## # ## ###
## ### ####### ## # ## ###
## # #### # ## ###
```
**fender**
```
'||''''| |''||''| .|'''''| '||` ||
|| . || || . || ||
||''| || || |''|| || .|''|, ''||''
|| || || || || ||..|| ||
.||. |..||..| `|....|' .||. `|... `|..'
```
**filter**
```
o8boooo 8888 888PPP8b 888 ,d8PPPP 888888888
88booop 8888 d88 ` 888 d88ooo '88d
88b 8888 d8b PPY8 888 ,88' '888
88P 8888 Y8PPPPPP 888PPPPP 88bdPPP '88p
```
**finalass**
```
####### ###### ##### ## ##
## ## ## ## ## ## ######## ##
## ## ## ## ######## ##
#### ## ## ### ## ##
## ## ## ## ## ##
## ## ## ## ## ##
#### ###### ##### ######## ##
######## ##
```
**fireing_**
```
#### # # ###### ######
# #
# # #### # #
##### # # # # ###### #
# # # # # # #
# # ## # # # #
# # # ###### ###### #####
#####
```
**flipped**
```
____ ____ ____ _
|_ | ____ | _ | ____ | | __| |
|| ||____|| \|_|| __|||_| ||__ |
|_| \__| |_| |_||_| |_|
```
**flyn_sh**
```
####### ##### # ## ## # # ## ## # #######
### ### # ##### ## ## ### ###### # ## # #######
## ## ## # ### ## # ## # ## # # ## ##
## ## ####### ###### ### # ## # # # ## ##
## ### ## ###### #### # ###### ## ##### ## ##
## ## ## ## ## ##### ## ### ####### ## ##
####### ##### ## ## #### ### ###### #######
### ### # ### ## ## # ## ## # #### #######
```
**fp1_____**
```
####### #### ####### ## ##
## ######## ##
## ## ## ## ######## ##
#### ## ## ### ## ##
## ## ## ## ## ##
## ## ## ## ## ##
## #### ###### ######## ##
######## ##
```
**fp2_____**
```
####### ###### ##### ## ##
## ## ## # ## ## ######## ##
## ## ## ## ######## ##
#### ## ## ### ## ##
## ## ## ## ## ##
# ## # ## ## ##
#### ###### ##### ######## ##
######## ##
```
**fraktur**
```
..... ..... . .... . .. s
.H8888888x. '`+ .d88888Neu. 'L .x88" `^x~ xH(` x .d88" :8
:888888888888x. ! F""""*8888888F X888 x8 ` 8888h 5888R .88
8~ `"*88888888" * `"*88*" 88888 888. %8888 '888R .u :888ooo
! . `f"""" -.... ue=:. <8888X X8888 X8? 888R ud8888. -*8888888
~:...-` :8L <)88: :88N ` X8888> 488888>"8888x 888R :888'8888. 8888
. :888:>X88! 9888L X8888> 888888 '8888L 888R d888 '88%" 8888
:~"88x 48888X ^` uzu. `8888L ?8888X ?8888>'8888X 888R 8888.+" 8888
< :888k'88888X ,""888i ?8888 8888X h 8888 '8888~ 888R 8888L .8888Lu=
d8888f '88888X 4 9888L %888> ?888 -:8*" <888" .888B . '8888c. .+ ^%888*
:8888! ?8888> ' '8888 '88% `*88. :88% ^*888% "88888% 'Y"
X888! 8888~ "*8Nu.z*" ^"~====""` "% "YP'
'888 X88f
'%8: .8*"
^----~"`
```
**funky_dr**
```
##
##
###### ## ##### ## ###### ######
## ## ## ## ## ## ### #
## ### ## ## ### ## ## ##
## ## ## ## ## ## ## ###
## ## ##### ## ###### ## ##
## # ## ##
```
**future_1**
```
####### ###### ##### ## ##
## ## ## ## ## ## ######## ##
## ## ## ## ######## ##
#### ## ## ### ## ##
## ## ## ## ## ##
## ## ## ## ## ##
#### ###### ##### ######## ##
######## ##
```
**future_2**
```
####### ###### ##### ##
####### ###### ####### # ## ####
## # #### ## ### ### ## ## #
###### ## ## ### # ## # ## ## ## ## #
## ## ## ## # ## # ## #### ## ## #
## ###### ####### # ## # ## ## ##### #
## ###### # ### # ## # ## ## ## #
#### # ## ### ##
```
**future_3**
```
####### #### ####### ## ##
## ######## ##
## ## ## ## ######## ##
#### ## ## ### ## ##
## ## ## ## ## ##
## ## ## ## ## ##
## #### ###### ######## ##
######## ##
```
**future_4**
```
### # ## # # # # #
## # ## # ## # # ## ##
## ## ## # ## # # # # ##
##### ## ## ## ## ## ## # #
## ### ## ## # ## # # # # ## #
## ### ### ## ## ## ## ## ##
## ### #### # ## # # # # ## #
## ## ## ## ##
```
**future_5**
```
###### #### ##### # # # #
## ## ### ### # ## # # #
## ## ### ## # ## ###
##### ### ## #### ## #### ########
## ## ## # # ###### #
## ## ## # # ####
## # ## #### #####
#######
```
**future_6**
```
###### #### ##### # # # #
## #### #### ## #### #######
## #### ## #######
#### ## ## ### ########
## # ## ## ## ########
## ## ### ### #######
# # ##### #######
# # # #
```
**future_7**
```
###### ###### #### ## ##
## # ## # # ## ## ######## ##
## ## ## ## ######## ##
##### ## ## ### ## ##
## ## ## ## ## ##
## # ## # # ## ## ##
## ###### #### ######## ##
######## ##
```
**future_8**
```
## ##
## ######## ##
####### ###### ####### ## ######## ##
## ## ##
#### ## ## ## ## ##
## ## ## # ## ##
## ###### ####### ######## ##
######## ##
```
**fuzzy**
```
.---. .-. .--. .-. .-.
: .--': :: .--': : .' `.
: `; : :: : _ : : .--.`. .'
: : : :: :; :: :_ ' '_.': :
:_; :_;`.__.'`.__;`.__.':_;
```
**gauntlet**
```
# # # ### #
### ### # # # # ######## #### ## #### #
## ## ### # # # # ######## #### ### #### #
### ## # ### # #### #### # #### #
### ## ### ### #### #### # #### #
## #### ## ## #### #### #### # ### #
## ## ### ###### #### # #### # ### #
### ## ### #### #### # #### # ### #
```
**gb16fs**
```
####### ####### ## # ####
# # # # ## # #
# # # # # # #
# # # # #
# # # # # ### ######
# # # # # # # #
#### # # #### # # # #
# # # # # # ####### #
# # # # # # # #
# # # # # # #
# # # # # # # # #
# # ## ## # # # # #
#### ####### ## # ######## #### ###
```
**gb16st**
```
####### ####### ## # ####
# # # # ## # #
# # # # # # #
# # # # #
# # # # # ### ######
# # # # # # # #
#### # # #### # # # #
# # # # # # ####### #
# # # # # # # #
# # # # # # #
# # # # # # # # #
# # ## ## # # # # #
#### ####### ## # ######## #### ###
```
**georgi16**
```
________ ____ ____ ___
`MMMMMMM `MM' 6MMMMb/ `MM
MM \ MM 8P YM MM /
MM MM 6M Y MM ____ /M
MM , MM MM MM 6MMMMb /MMMMM
MMMMMM MM MM MM 6M' `Mb MM
MM ` MM MM ___ MM MM MM MM
MM MM MM `M' MM MMMMMMMM MM
MM MM YM M MM MM MM
MM MM 8b d9 MM YM d9 YM. ,
_MM_ _MM_ YMMMM9 _MM_ YMMMM9 YMMM9
```
**ghost**
```
('-. .-') _
_( OO) ( OO) )
,------.,-.-') ,----. ,--. (,------./ '._
('-| _.---'| |OO) ' .-./-') | |.-') | .---'|'--...__)
(OO|(_\ | | \ | |_( O- ) | | OO ) | | '--. .--'
/ | '--. | |(_/ | | .--, \ | |`-' |(| '--. | |
\_)| .--',| |_.'(| | '. (_/(| '---.' | .--' | |
\| |_)(_| | | '--' | | | | `---. | |
`--' `--' `------' `------' `------' `--'
```
**ghost_bo**
```
# #### ###### #####
####### ###### #######
## ##
###### ## ## ###
## ## ## ##
## ###### #######
## ###### #####
```
**ghoulish**
```
)`-.--. .'( )\.-. .') )\.---. .-,.-.,-.
) ,-._( \ ) ,' ,-,_) ( / ( ,-._( ) ,, ,. (
\ `-._ ) ( ( . __ )) \ '-, \( |( )/
) ,_( \ ) ) '._\ _) )'._.-. ) ,-` ) \
( \ ) \ ( , ( ( ) ( ``-. \ (
).' )/ )/'._.' )/,__.' )..-.( )/
```
**glenyn**
```
____ ____ ____ __ ____ ____
| _\|___\| _\| | | __\|_ _\
| _\ | / | [ \| |__| ]_ ||
|/ |/ |___/|___/|___/ |/
```
**goofy**
```
___ ____ ___ ____ ___ _____
\ ___) (_ _) ) ____) \ | \ ___) (__ __)
| (__ | | / / __ | | | (__ | |
| __) | | ( ( ( \ | | | __) | |
| ( _| |_ \ \__) ) | |__ | (___ | |
/ \____( )___) (__/ )_/ )____| |_______
```
**gothic**
```
_ , __ ,
,- - _-_, ,-| ~ ,, ,
_||_ // ('||/__, || ||
' || || (( ||| | || _-_ =||=
|| ~|| (( |||==| || || \\ ||
|, || ( / | , || ||/ ||
_-/ _-_, -____/ \\ \\,/ \\,
```
**gothic__**
```
## # ## ### # ### ## #### ###
# ## ## # ## ## # #
## # ### ## ## ## # #
## ### ## ## ## #### ## #
##### ## ## ## ## ## ## # #
## ## ## ## ### ## ### ## ## ##
## #### ## # #### # #### #####
## ####
```
**graceful**
```
____ __ ___ __ ____ ____
( __)( )/ __)( ) ( __)(_ _)
) _) )(( (_ \/ (_/\ ) _) )(
(__) (__)\___/\____/(____) (__)
```
**gradient**
```
eeeeee.eee..eeeeee..eee....eeeeee.eeeeeeeee....
@@@@@@:@@@:@@@@@@@@:@@@::::@@@@@@:@@@@@@@@@::::
%%%----%%%-%%%------%%%----%%%-------%%%-------
&&&&&++&&&+&&&++++++&&&++++&&&&&+++++&&&+++++++
|||||**|||*|||*||||*|||****|||||*****|||*******
!!!====!!!=!!!==!!!=!!!====!!!=======!!!=======
:::####:::#::::::::#::::::#::::::####:::#######
...@@@@...@@......@@......@......@@@@...@@@@@@@
```
**graffiti**
```
___________.___ ________.__ __
\_ _____/| |/ _____/| | _____/ |_
| __) | / \ ___| | _/ __ \ __\
| \ | \ \_\ \ |_\ ___/| |
\___ / |___|\______ /____/\___ >__|
\/ \/ \/
```
**grand_pr**
```
###### ###### ## ## ##### # ### # # #
## ## ## ## # # # # # #
## ## ## # # # ### # #
#### ## ## ## ## # # # # # # # #
## ## ## ## ## #### ## # #
## ## ## ## ######## ###### ## # # # #
## ###### #### ### ## ######## # # # #
######## ######## # ### # #
```
**green_be**
```
### ### #### # ### #### ########
## ## ## ## ## #### # ######
## ## ### # # #### #
## ## ## ### ### # # ## # #
## ## ### ## #### # # # # #
## ## ## ## #### # # # # # #
#### #### # ## # ## # # # # # #
#### # # # # # #
```
**hades___**
```
####### ##### ##### #### #### # ####
## ### ### ## ## #### # ####
## ## ## ## # ######## #### ########
### ## ## #### ###### # ####
#### ### ## ### #### ### ####
### ### ### ## ###### # ## ########
### #### ##### # # ######## # #
#### ## ####
```
**hanglg16**
```
####### ####### ## # ####
# # # # ## # #
# # # # # # #
# # # # #
# # # # # ### ######
# # # # # # # #
#### # # #### # # # #
# # # # # # ####### #
# # # # # # # #
# # # # # # #
# # # # # # # # #
# # ## ## # # # # #
#### ####### ## # ######## #### ###
```
**hanglm16**
```
####### ####### ## # ####
# # # # ## # #
# # # # # # #
# # # # #
# # # # # ### ######
# # # # # # # #
#### # # #### # # # #
# # # # # # ####### #
# # # # # # # #
# # # # # # #
# # # # # # # # #
# # ## ## # # # # #
#### ####### ## # ######## #### ###
```
**heavy_me**
```
####### ###### #### # # # ##
## ## ## ## ## #### ####
## ## ## ### #####
#### ## ## ### # # # #
## ## ## ## ######
## ## ## ## ###
#### ###### ##### #####
########
```
**helv**
```
# #
#### # ### # #
# # # # # ###
### # # ## # # # #
# # # # # ### #
# # # # # # #
# # ### # ## #
```
**helvb**
```
# #
#### # #### # ##
## # ## # # ## ####
#### # ## # ## # ##
## # ## ## # #### ##
## # ## # # ## ##
## # #### # ## ##
```
**helvbi**
```
#### # #### # #
## # ## # ## ####
### # ## # ## # ##
## # ## ### # ##### ##
## # ## ## # ## #
## # #### # ### ##
```
**helvi**
```
#
##### # ### # #
# # # # # ## ####
### # # # # # #
# # # ### # ### #
# # ## # # # #
# # ### # ## ##
```
**heroboti**
```
# # # ## # # # # # # ####
##### ## ##### # # # ## # # # # # ##### ######
####### ## ####### # # # ## # # # # ##### # #######
## ## ## ## # # # ## # # # # ### # # ##
## ## ####### # # # ## # # # ## # # # # ######
#### ## ## # # # ## # # #### # # # # ## ##
#### ## ###### # # #### # ##### # # # # #######
## ## ##### # # #### ##### # # # # # #####
```
**hex**
```
46 49 47 6C 65 74
```
**hieroglyphs**
```
;. ______ ,-. ,-.
\/ ; | '-.--.-' <,- \_____/ ` ||
`-'_ `.| /::::\ / ___. \ .... || .-==-.
`---. | )_/\_( ,_(__/ ,_(__\ `=.`''===.' /______\
```
**high_noo**
```
######## ######## ######## # ## ## # # # # ########
# ## # ## # # # # # # #
#### # #### # ## # # # # # # # # # ### #
###### #### # #### ## ### ## # # # # ### #
## # # ### ### ###### # ## # # # # # # ### #
#### # ###### # ## #### ###### # ## # # # # # # # #
#### # #### # # ##### # ##### # # # # # # #
# ## # ## #### # ####### # ### #
```
**hills___**
```
# ### ####
# ## # #####
# ## ### # ######
# ##### ## ### ###
# # ### ### # ### #
# ## # ### ## ### ####
# # # # # # ### # ### ##
# # # # ### # # # # ###
```
**hollywood**
```
_ _ _ _
/' `\ ' /' `/' `\ /' /'
/' ._)/' /' ) /' --/'--
,/' /' /' /' ____ /'
/`---, /' /' _ /' /' ) /'
/' /' /' ' )/' /(___,/' /'
(,/' (,/(_, (_____,/'(__(________(__
```
**home_pak**
```
## ##
### ### #### ####### #######
### ### #### # ## ###
### ### #### ###### ###
### ## ### # ## #### ###
### ### ### #### #### ###
### #### ### ####### ####### ###
## #### ##
```
**house_of**
```
# # # # ## ##
###### ##### #### # # # # ######## ####
## ## ## ## # # # ## # ## ## ##
## ## ## # # #### ## ## ## ##
#### ## ###### # # #### ## ## ######## ##
## ## ### ## # # #### ######## ######## ## ##
## ##### ##### # # #### ## ## ######## ####
# # #### ## ## ########
```
**hypa_bal**
```
###### ###### ###### # # ## # # # #### # ## #
## ## ## ## ## # # ### # ## ## # #
## ## ## ### # # # ## # # ## # ## #
#### ## ## #### ## # ## # # ## ### ## #
## ## ## ## # # ### # ### # # ##
## ## ## ## # ## # #### # # ## # # #
## ###### ###### ## ## # # # ## #### ## #
### # ## ### ### # # ## #
```
**hyper___**
```
###### ###### #### ## ##
## # ## # ## ## ## ######## ##
## ## ## ## ######## ##
##### ## ## ### ## ##
## ## ## ## ## ##
## # ## # ## ## ## ##
## ###### #### ######## ##
######## ##
```
**impossible**
```
_ _ _ _ _ _
/\ \ /\ \ /\ \ _\ \ /\ \ /\ \
/ \ \ \ \ \ / \ \ /\__ \ / \ \ \_\ \
/ /\ \ \ /\ \_\ / /\ \_\ / /_ \_\ / /\ \ \ /\__ \
/ / /\ \_\ / /\/_/ / / /\/_/ / / /\/_/ / / /\ \_\ / /_ \ \
/ /_/_ \/_// / / / / / ______ / / / / /_/_ \/_/ / / /\ \ \
/ /____/\ / / / / / / /\_____\ / / / / /____/\ / / / \/_/
/ /\____\/ / / / / / / \/____ // / / ____ / /\____\/ / / /
/ / / ___/ / /__ / / /_____/ / // /_/_/ ___/\ / / /______ / / /
/ / / /\__\/_/___\/ / /______\/ //_______/\__\// / /_______\/_/ /
\/_/ \/_________/\/___________/ \_______\/ \/__________/\_\/
```
**inc_raw_**
```
##### ### ##### ## ##### ## # ## #
## ## ## ## # ##### # ##### ### ###
## ## ## # ##### # ##### ### ###
#### ## ## ### # ##### # ### ### ###
## ## ## ## # ##### # ##### ### ###
## ## ## ## # ##### # ##### ### ###
## ## ## ## # ##### # ##### ### ###
## ### ##### # ## # ## ### ####
```
**invita**
```
________) _____ _____)
(, / (, / / /)
/___, / / ___ // _ _/_
) / ___/__/ / ) (/__(/_(__
(_/ (__ / (____ /
```
**isometric1**
```
___ ___ ___ ___ ___
/\ \ ___ /\ \ /\__\ /\ \ /\ \
/::\ \ /\ \ /::\ \ /:/ / /::\ \ \:\ \
/:/\:\ \ \:\ \ /:/\:\ \ /:/ / /:/\:\ \ \:\ \
/::\~\:\ \ /::\__\ /:/ \:\ \ /:/ / /::\~\:\ \ /::\ \
/:/\:\ \:\__\ __/:/\/__/ /:/__/_\:\__\ /:/__/ /:/\:\ \:\__\ /:/\:\__\
\/__\:\ \/__/ /\/:/ / \:\ /\ \/__/ \:\ \ \:\~\:\ \/__/ /:/ \/__/
\:\__\ \::/__/ \:\ \:\__\ \:\ \ \:\ \:\__\ /:/ /
\/__/ \:\__\ \:\/:/ / \:\ \ \:\ \/__/ \/__/
\/__/ \::/ / \:\__\ \:\__\
\/__/ \/__/ \/__/
```
**isometric2**
```
___ ___ ___
/\__\ /\__\ /\__\
/:/ _/_ ___ /:/ _/_ /:/ _/_ ___
/:/ /\__\ /\__\ /:/ /\ \ /:/ /\__\ /\__\
/:/ /:/ / /:/__/ /:/ /::\ \ ___ ___ /:/ /:/ _/_ /:/ /
/:/_/:/ / /::\ \ /:/__\/\:\__\ /\ \ /\__\ /:/_/:/ /\__\ /:/__/
\:\/:/ / \/\:\ \__ \:\ \ /:/ / \:\ \ /:/ / \:\/:/ /:/ / /::\ \
\::/__/ ~~\:\/\__\ \:\ /:/ / \:\ /:/ / \::/_/:/ / /:/\:\ \
\:\ \ \::/ / \:\/:/ / \:\/:/ / \:\/:/ / \/__\:\ \
\:\__\ /:/ / \::/ / \::/ / \::/ / \:\__\
\/__/ \/__/ \/__/ \/__/ \/__/ \/__/
```
**isometric3**
```
___ ___ ___
/ /\ ___ / /\ / /\ ___
/ /:/_ / /\ / /:/_ / /:/_ / /\
/ /:/ /\ / /:/ / /:/ /\ ___ ___ / /:/ /\ / /:/
/ /:/ /:/ /__/::\ / /:/_/::\ /__/\ / /\ / /:/ /:/_ / /:/
/__/:/ /:/ \__\/\:\__ /__/:/__\/\:\ \ \:\ / /:/ /__/:/ /:/ /\ / /::\
\ \:\/:/ \ \:\/\ \ \:\ /~~/:/ \ \:\ /:/ \ \:\/:/ /:/ /__/:/\:\
\ \::/ \__\::/ \ \:\ /:/ \ \:\/:/ \ \::/ /:/ \__\/ \:\
\ \:\ /__/:/ \ \:\/:/ \ \::/ \ \:\/:/ \ \:\
\ \:\ \__\/ \ \::/ \__\/ \ \::/ \__\/
\__\/ \__\/ \__\/
```
**isometric4**
```
___ ___ ___
___ ___ / /\ / /\ / /\ ___
/ /\ /__/\ / /::\ / /:/ / /::\ /__/\
/ /::\ \__\:\ / /:/\:\ / /:/ / /:/\:\ \ \:\
/ /:/\:\ / /::\ / /:/ \:\ / /:/ / /::\ \:\ \__\:\
/ /::\ \:\ __/ /:/\/ /__/:/_\_ \:\ /__/:/ /__/:/\:\ \:\ / /::\
/__/:/\:\ \:\ /__/\/:/~~ \ \:\__/\_\/ \ \:\ \ \:\ \:\_\/ / /:/\:\
\__\/ \:\_\/ \ \::/ \ \:\ \:\ \ \:\ \ \:\ \:\ / /:/__\/
\ \:\ \ \:\ \ \:\/:/ \ \:\ \ \:\_\/ /__/:/
\__\/ \__\/ \ \::/ \ \:\ \ \:\ \__\/
\__\/ \__\/ \__\/
```
**italic**
```
___ __
(_ // _ /_ _/
/ ((__)((- /
```
**italics_**
```
# # #### ######
### # # # #
# #### # # #
# # # # # #### #
#### # # # # # # #
# # #### # # #
# # # ###### ##### #
####
```
**ivrit**
```
_ _ ____ ___ _____
| |_ ___| |/ ___|_ _| ___|
| __/ _ \ | | _ | || |_
| || __/ | |_| || || _|
\__\___|_|\____|___|_|
```
**jacky**
```
_________ _____ _____ _____ _____ ________
(_ _____) (_ _) / ___ \ (_ _) / ___/ (___ ___)
) (___ | | / / \_) | | ( (__ ) )
( ___) | | ( ( ____ | | ) __) ( (
) ( | | ( ( (__ ) | | __ ( ( ) )
( ) _| |__ \ \__/ / __| |___) ) \ \___ ( (
\_/ /_____( \____/ \________/ \____\ /__\
```
**jazmine**
```
ooooo o .oPYo. 8 o
8 8 8 8 8 8
o8oo 8 8 8 .oPYo. o8P
8 8 8 oo 8 8oooo8 8
8 8 8 8 8 8. 8
8 8 `YooP8 8 `Yooo' 8
:..::::..:....8 ..:.....:::..:::
::::::::::::::8 ::::::::::::::::
::::::::::::::..::::::::::::::::
```
**jerusalem**
```
__ ________ _______ ____ ___ _____
\ \ / /____ |____ ./ ___|_ _| ___|
| V / _ | | | | | _ | || |_
| |\ \ | | |_| | | |_| || || _|
|_| \_\| | | |\____|___|_|
|_| |_|
```
**jiskan16**
```
####### ####### ## # ####
# # # # ## # #
# # # # # # #
# # # # #
# # # # # ### ######
# # # # # # # #
#### # # #### # # # #
# # # # # # ####### #
# # # # # # # #
# # # # # # #
# # # # # # # # #
# # ## ## # # # # #
#### ####### ## # ######## #### ###
```
**joust___**
```
##### ## ###### #### # #
## ## ## ## # # ###
#### ## ## ######## ########
## ## ## ### ## # ###
## ## ## ## ## ######## ##### #
## ## ###### ## # # # # ##### #
## # # # # ## ## #
# # # #
```
**katakana**
```
# # # # #
########## ######## # # ###### ########## #######
# # # # # # # # # # #
# # # # # # # # #
# # # # # # # # ##########
# # # # # # ########## # #
# # # # # #
```
**kban**
```
'||''''| '||' ..|'''.| '|| .
|| . || .|' ' || .... .||.
||''| || || .... || .|...|| ||
|| || '|. || || || ||
.||. .||. ''|...'| .||. '|...' '|.'
```
**keyboard**
```
_______ _______ _______ _______ _______ _______
|\ /|\ /|\ /|\ /|\ /|\ /|
| +---+ | +---+ | +---+ | +---+ | +---+ | +---+ |
| | | | | | | | | | | | | | | | | | |
| |F | | |I | | |G | | |l | | |e | | |t | |
| +---+ | +---+ | +---+ | +---+ | +---+ | +---+ |
|/_____\|/_____\|/_____\|/_____\|/_____\|/_____\|
```
**kgames_i**
```
### # # ##### # #####
###### ###### ##### ### # # # ## # ######
## ## ## ### # # ##### # ####
##### ## ## ### # # # ## # ####
## ## ## ### ### # # ######## ##### # ####
## ## ## ## ### # # ###### # # ## # ####
## ###### ##### ### # # # # # # ##### # ####
### # # # # # # # ## # ######
```
**kik_star**
```
###### ###### ##### ### #
## ## ## ## # # ### #
## ## ## ### # # ######
##### ## ## ### # ## ## # ## ###
## ## ## ## # ### ### # ### ##
## ## ## ## ## ## ### # ## ##
## ###### ##### ### ### ### # ######
## ##### # # #######
```
**knob**
```
_________ _______ _ _________ _________ _________ _
(___ _ )(_______(_)( _____ )( _______)( _ _ ) _______| |
| | | | | |_ | || | | | | | | |(_______ |
(_) (_) (___) (_)(_) (_) (_) (_) |_|
```
**konto**
```
I?? I ,?? I I.` ??T??
I? I `.7 L.. I.. I
```
**krak_out**
```
# # # # # # ## #
####### ##### #### # # ##### # # ##
## # ## # ##### # # ## #
###### # ## ###### # # ## ##
## # ## ## ## # # # # #
## # ## # # ## # ### ## ##
## ##### ####### # # # ## # ### ## #
# # # # # # ## ##
```
**l4me**
```
F@!@6@|@3@t@ @
```
**lazy_jon**
```
####### ###### ##### ### # #
## ## ## ## ## ### ####
## ## ## ##### ### ####
##### ## ## ####### ### ####
## ## ## ### ## ## ####### # #
## ## ## ## ## ####### ####
## ## ## ## ## ####
## ###### ##### #### ####
```
**lcd**
```
___ ___ ___
| | | | |
|-+- + | +- + - -+-
| | | | | |/ |
--- --- - -- -
```
**lean**
```
_/_/_/_/ _/_/_/ _/_/_/ _/ _/
_/ _/ _/ _/ _/_/ _/_/_/_/
_/_/_/ _/ _/ _/_/ _/ _/_/_/_/ _/
_/ _/ _/ _/ _/ _/ _/
_/ _/_/_/ _/_/_/ _/ _/_/_/ _/_/
```
**letter_w**
```
####### #### ####### ## ##
## ######## #
## ## ## ## ######## ##
#### ## ## ### ## ##
## ## ## ## ## ##
## ## ## ## ## ##
## #### ###### ######## ##
######## ##
```
**letters**
```
FFFFFFF IIIII GGGG lll tt
FF III GG GG lll eee tt
FFFF III GG lll ee e tttt
FF III GG GG lll eeeee tt
FF IIIII GGGGGG lll eeeee tttt
```
**letterw3**
```
###### ###### #### ## ##
## # ## # ## ## ## ######## ##
## ## ## ## ######## ##
##### ## ## ### ## ##
## ## ## ## ## ##
## # ## # ## ## ## ##
## ###### #### ######## ##
######## ##
```
**lexible_**
```
####### ### #####
####### ### ######
### ###
##### ### ## ###
### ### ### #
### ### ######
### ### ####
```
**linux**
```
.---..-..---..-. .---..---.
| |- | || |'_| |__ | |- `| |'
`-' `-'`-'-/`----'`---' `-'
```
**lockergnome**
```
::::::|::::::| :::::\:| :|
::::> ::| ::> ==:| :~~/ :::|
::| ::::::| :::::/:| :::, :|
```
**mad_nurs**
```
####### ###### ##### # ## ## ## ##
## ## ## ## ## ## ## ## ##
## ## ## ## ## ## ## ##
###### ## ## #### ## ## ## ## ##
## ## ## ## # ## ## ## ##
## ## ## ## ## ## ## ## ##
## ## ## ## ####### ###### ##
## ###### ##### ####### ###### ##
```
**madrid**
```
/=\ | /=\ | |-
|= = | _ | /=\ |
| | \=/ \= \= \=
```
**magic_ma**
```
## ####### ##### ##
#### ####### ##### ####### ### #####
##### ##### ####### ##### ##### #
##### ### ### ##### ### #
#### ### ####### ##### #### #
## ### ####### ##### ## ##
##### ####### #######
## ####### ##### # # # #
```
**marquee**
```
.::::::::.:: .:::: .:: .::
.:: .:: .: .:: .:: .::
.:: .::.:: .:: .:: .:.: .:
.:::::: .::.:: .:: .: .:: .::
.:: .::.:: .:::: .::.::::: .:: .::
.:: .:: .:: .: .::.: .::
.:: .:: .::::: .::: .:::: .::
```
**master_o**
```
####### #### #### ##### ###
## # ## ## # ##### ###
## # ## ## ###### ###
#### ## ## #### ###### # ####
## # ## ## ## ##### # ######
## ## ## ## ###### ####
#### #### #### ##### ###
##### ###
```
**maxfour**
```
|~~~|~/~~\| |
|-- || __|/~/~|~
| _|_\__/|\/_ |
```
**maxiwi**
```
█
███ ███ ███ █ █
█ █ █ █ ███ ███
███ █ █ █ ███ █
█ █ █ █ █ █ █
█ ███ ███ ██ ███ ██
```
**mayhem_d**
```
###### ###### #####
## ## ## ##
## ## ##
##### ## ## ##
## ## ## ### ##
## ## ## ## ##
## ###### ##### ####
# ##
```
**mcg_____**
```
### # # # ###
## # ## # # # #
## #### ##### # # #
#### ## ## ## # #
## ## ## ## # # ### #
## ## ## ## # # #
#### #### #### # ## # # #
# ## ### #
```
**merlin1**
```
_______ __ _______ ___ _______ ___________
/" "||" \ /" _ "| |" | /" "|(" _ ")
(: ______)|| | (: ( \___) || | (: ______) )__/ \\__/
\/ | |: | \/ \ |: | \/ | \\_ /
// ___) |. | // \ ___ \ |___ // ___)_ |. |
(: ( /\ |\(: _( _|( \_|: \(: "| \: |
\__/ (__\_|_)\_______) \_______)\_______) \__|
```
**merlin2**
```
_ _ _ _ _ _
__/\\___ _/\\_ __/\\__ _/\\_ __/\\___ __/\\__
(_ ____))(____))(_ ___))(_ _)) (_ ____))(__ __))
/ ||__ / \\ / || _ / \\ / ._)) / \\
/:. ._)) /:. \\/:. \/ \\/:. \\__ /:. ||___ /:. \\
\ _)) \__ //\ ____//\__ ____))\ _____)) \__ //
\// \// \// \// \// \//
```
**mig_ally**
```
###### #### #### # # #### # # # # #####
## ## ## ## # # #### # # # # #######
## ## ## # # #### # # # ##
#### ## ## ### # # # ## # # #### ######
## ## ## ## # # # ## # # #### #####
## ## ## ## # # # ## # # #### #######
## #### #### # # # # # # # ## #####
# # # # # # # #
```
**mike**
```
|\ | _ _
| _| /| | |/ |
|
```
**mini**
```
____ __
|_ | /__| __|_
| _|_\_||(/_|_
```
**miniwi**
```
▄▖▄▖▄▖▜ ▗
▙▖▐ ▌ ▐ █▌▜▘
▌ ▟▖▙▌▐▖▙▖▐▖
```
**mirror**
```
_ _ ____ ___ _____
_| |___ | |___ \_ _|___ |
|__ / _ \| |_ | | | _| |
_| \__ | | |_| | | |_ |
|__/|___/|_|____/___| |_|
```
**mnemonic**
```
F@I@G@l@e@t@&SP@
```
**modern__**
```
### ### #### ## ### ## ##
### ## #### ### ## ## ######## ##
### # # #### ### # ## ######## ##
##### #### ### ## ##
### # #### ### ### ## ##
### #### ### ### ## ##
### #### ## ## ######## ##
######## ##
```
**modular**
```
_______ ___ _______ ___ _______ _______
| || | | || | | || |
| ___|| | | ___|| | | ___||_ _|
| |___ | | | | __ | | | |___ | |
| ___|| | | || || |___ | ___| | |
| | | | | |_| || || |___ | |
|___| |___| |_______||_______||_______| |___|
```
**moscow**
```
# # # ##### ##### ##### #####
### # ## # # # # # #
# # # # # # # # # #### #
### ## # # # # # #
# # # # # # ##### #
```
**mshebrew210**
```
\>""|""|
L\| ' |
| |
```
**muzzle**
```
__ __ __
| > | | | >>|<<
|<< | | >> | |<< |
| | '__| |<< |__ |
```
**nancyj**
```
88888888b dP .88888. dP dP
88 88 d8' `88 88 88
a88aaaa 88 88 88 .d8888b. d8888P
88 88 88 YP88 88 88ooood8 88
88 88 Y8. .88 88 88. ... 88
dP dP `88888' dP `88888P' dP
```
**nancyj-fancy**
```
MM""""""""`M M""M MM'"""""`MM dP dP
MM mmmmmmmM M M M' .mmm. `M 88 88
M' MMMM M M M MMMMMMMM 88 .d8888b. d8888P
MM MMMMMMMM M M M MMM `M 88 88ooood8 88
MM MMMMMMMM M M M. `MMM' .M 88 88. ... 88
MM MMMMMMMM M M MM. .MM dP `88888P' dP
MMMMMMMMMMMM MMMM MMMMMMMMMMM
```
**nancyj-improved**
```
88888888b dP .88888. dP dP
88 88 d8' `88 88 88
a88aaaa 88 88 88 .d8888b. d8888P
88 88 88 YP88 88 88ooood8 88
88 88 Y8. .88 88 88. ... 88
dP dP `88888' dP `88888P' dP
```
**nancyj-underlined**
```
88888888b dP .88888. dP dP
88 88 d8' `88 88 88
a88aaaa 88 88 88 .d8888b. d8888P
88 88 88 YP88 88 88ooood8 88
88 88 Y8. .88 88 88. ... 88
dP dP `88888' dP `88888P' dP
oooooooooooooooooooooooooooooooooooooooooooooo
```
**nfi1____**
```
#### ## #### #### ########
#### ## ## #### #### #### ####
#### #### #### #### #### ####
#### #### #### ######## ######
#### #### #### #### ####
###### #### #### #### #### ####
###### #### #### #### ########
```
**nipples**
```
{________{__ {____ {__ {__
{__ {__ {_ {__ {__ {__
{__ {__{__ {__ {__ {_{_ {_
{______ {__{__ {__ {_ {__ {__
{__ {__{__ {____ {__{_____ {__ {__
{__ {__ {__ {_ {__{_ {__
{__ {__ {_____ {___ {____ {__
```
**notie_ca**
```
######## ### ### ## # ## # # ## ###
######## #### # #### # ## # ## ####
######## #### # #### # # ## # # ## ## #
# ### # ## ## ##
# ### ####### # ## ##
# ### # ### # #### # ## ## ## ##
# ### # ### ######## # ## ## ##
# ### # ### # ##### # ## ## ##
```
**npn_____**
```
###
####### ### ###### ### ######## ########
### ### ### ###
####### ### ### ## ### ####### ###
## ### ### ## ### ### ###
## ### ###### ####### ####### ###
```
**nscript**
```
,gggggggggggggg ,a8a, ,gg,
dP""""""88"""""" ,8" "8, i8""8i ,dPYb, I8
Yb,_ 88 d8 8b `8,,8' IP'`Yb I8
`"" 88 88 88 `Y88aaad8 I8 8I 88888888
ggg88gggg 88 88 d8""""Y8, I8 8' I8
88 8 Y8 8P ,8P 8b I8 dP ,ggg, I8
88 `8, ,8' dP Y8 I8dP i8" "8i I8
gg, 88 8888 "8,8" _ ,dP' I8 I8P I8, ,8I ,I8,
"Yb,,8P `8b, ,d8b, "888,,_____,dP,d8b,_ `YbadP' ,d88b,
"Y8P' "Y88P" "Y8a8P"Y888888P" 8P'"Y88888P"Y88888P""Y88
```
**o8**
```
ooooooooooo ooooo ooooooo8 o888 o8
888 88 888 o888 88 888 ooooooooo8 o888oo
888ooo8 888 888 oooo 888 888oooooo8 888
888 888 888o 88 888 888 888
o888o o888o 888ooo888 o888o 88oooo888 888o
```
**octal**
```
106 111 107 154 145 164
```
**odel_lak**
```
## ###### ######
### ## ## ## ##
## ##### ## ## ##
##### ### ## ## ## #### ##
## ## ## ## ## ## ##
## ## ##### ## ## ##
## #### ## ###### ###### ##
#####
```
**ogre**
```
________ ___ _ _
/ __\_ \/ _ \ | ___| |_
/ _\ / /\/ /_\/ |/ _ \ __|
/ / /\/ /_/ /_\\| | __/ |_
\/ \____/\____/|_|\___|\__|
```
**ok_beer_**
```
### ###### ###
### ### ###
####### ##### ##### ### ### ###
### ### ### ## ###### ####### ###
###### ### ###
### ### ### ###
### ### ### ##
### ##### #####
```
**os2**
```
ooooooo_oooo____oooo___ooo____________oo_______
oo_______oo___oo____oo__oo____ooooo___oo_______
oooo_____oo__oo_________oo___oo____o_oooo______
oo_______oo__oo____ooo__oo___ooooooo__oo_______
oo_______oo___oo____oo__oo___oo_______oo__o____
oo______oooo____oooo___ooooo__ooooo____ooo_____
_______________________________________________
```
**outrun__**
```
###### #### #### # # # ## ## # ##
###### #### ###### # ### ## ## # ##
## ## ## ## ##### ## # # # # ## # ##
## # ## ## ### # # # # # # ## ##
#### ## ## ### # # # # ### # # ## #
## # ## ## ### # # # # ##### ## # #
## #### ###### # # # ##
## #### #### ##### ##
```
**p_s_h_m_**
```
# # # # ## # # ######## ######## ########
# # # # ## ######## # ##### # # # #
# # # # ## # ##### # # # #
## # # ## # ##### # ##### ### ###
## # ### # ##### # ### ### ###
# # ## ## # ##### # ##### ### ###
# # # # ## # # # # ### ###
# # # # ## ######## # # # # ### ###
```
**p_skateb**
```
# # # # # ## # #
####### #### ##### # # # ## #
## ## ## ## # ## # # # ## #
## ## ## # ### # # ## # ####
##### ## ## ### # ## # # # ## # ## ##
## ## ## ## ### # # ## # #####
## ## ## ## #### # ## # ##
## #### ##### ##### # ####
```
**pacos_pe**
```
####### # ## #######
###### #### #### ### # # ## ### # #
###### #### ###### # #### # # # #### #
## ## ## ### ## # ### ##
#### ## ## ### ###### # #######
#### ## ## ## #### ## #### ##
## #### ###### ## ## ## ##
## #### #### ### # ### #
```
**panther_**
```
####### ####### ##### # # # # ## ## #######
####### ####### ####### ###### ####### ###### ### ###
### ### ### ## # # ### ### ###
####### ### ####### ## # # ### #### ### ###
### ### ### #### # # ### ## # # # #
### ####### ####### ## # # ### ## #### #
### ####### ##### ## # # ### ## #######
###### # # ### ## ### ###
```
**pawn_ins**
```
## ### ## ### ## ##
## ### ## #### ## ######## ##
## ## ### ## ######## ##
## ### ## ## ### ## ##
## ### ## ## ### ## ##
## ## ### ## ##
## ## ##### ######## ##
## ## ### ######## ##
```
**pawp**
```
______ _______ _____ __ _
(______)(_______)(_____)(__) ____ (_)_
(_)__ (_) (_) ___ (_) (____)(___)
(____) (_) (_) (___)(_)(_)_(_)(_)
(_) __(_)__(_)___(_)(_)(__)__ (_)_
(_) (_______)(_____)(___)(____) (__)
```
**peaks**
```
/^^^^^^^^/^^ /^^^^ /^^ /^^
/^^ /^^ /^ /^^ /^^ /^^
/^^ /^^/^^ /^^ /^^ /^/^ /^
/^^^^^^ /^^/^^ /^^ /^ /^^ /^^
/^^ /^^/^^ /^^^^ /^^/^^^^^ /^^ /^^
/^^ /^^ /^^ /^ /^^/^ /^^
/^^ /^^ /^^^^^ /^^^ /^^^^ /^^
```
**pebbles**
```
OOooOoO ooOoOOo .oOOOo. o
o O .O o O
O o o o O
oOooO O O O oOo
O o O .oOOo o .oOo. o
o O o. O O OooO' O
o O O. oO o O o
O' ooOOoOo `OooO' Oo `OoO' `oO
```
**pepper**
```
_ _
/_`// `/_ _/_
/ //_;//_'/
```
**phonix__**
```
###### ###### ##### # # #
# # # # ### #
## ## ## #### #####
## ## ## ###
##### ## ## ### # # # # # # # # # #
## ## ## ## # # # # # # #
## ## ## ## ######## #### # ### #
## ###### ###### # ###
```
**platoon2**
```
# # # # # ### # # # ### #####
# # # # ## # ## ## ## ## ## ####### #######
### ## # #### ### #### ######## ## #######
# ##### # #### ####### # ###### ###### ###
# # ### # ###### ######## ####### ###### ###
#### ## ######## # ###### # ###### ## ###
# ## ## ######## ##### ## ### #### ####### ###
## #### ######## ######## ######## ##### ###
```
**platoon_**
```
##### ## #### # ### ## ######
### # ### ### ### # # #####
## # ## ## # # ## #####
#### ## ## ### ####
## # ## ## #### # # ####
## ## ### ## ####
#### #### ###### #####
#######
```
**pod_____**
```
###### ## ###### # #### # # # ######## ###
## ## ## ## ## # #### # # # ######## ####
#### ## ## ###### # # # ######## ## ##
### ### ### ### ######## # # # ######## ## ##
### ### ### ## ## # # # ## ##
### ### ### ## ## # # # ## # # # #######
### ### ####### ## # # # ## # # ###
## # # ## #
```
**poison**
```
@@@@@@@@ @@@ @@@@@@@@ @@@ @@@@@@@@ @@@@@@@
@@@@@@@@ @@@ @@@@@@@@@ @@@ @@@@@@@@ @@@@@@@
@@! @@! !@@ @@! @@! @@!
!@! !@! !@! !@! !@! !@!
@!!!:! !!@ !@! @!@!@ @!! @!!!:! @!!
!!!!!: !!! !!! !!@!! !!! !!!!!: !!!
!!: !!: :!! !!: !!: !!: !!:
:!: :!: :!: !:: :!: :!: :!:
:: :: ::: :::: :: :::: :: :::: ::
: : :: :: : : :: : : : :: :: :
```
**puffy**
```
___ _ ___ _ _
( _`\ (_)( _`\ (_ ) ( )_
| (_(_)| || ( (_) | | __ | ,_)
| _) | || |___ | | /'__`\| |
| | | || (_, ) | | ( ___/| |_
(_) (_)(____/'(___)`\____)`\__)
```
**puzzle**
```
_ _ _ _ _ _ _
_( )__ _( )__ _( )__ _( )__ _( )__ _( )__ _( )__
_| _| _| _| _| _| _| _| _| _| _| _| _| _|
(_ F _ (_ (_ I _ (_ (_ G _ (_ (_ L _ (_ (_ E _ (_ (_ T _ (_ (_ _ (_
|_( )__| |_( )__| |_( )__| |_( )__| |_( )__| |_( )__| |_( )__|
```
**pyramid**
```
^ ^ ^ ^ ^ ^
/F\ /I\ /G\ /l\ /e\ /t\
<___><___><___><___><___><___>
```
**r2-d2___**
```
##### #### #### ######## ########
## # # # ####### # # # # # #
## ### ##### ## # # # # ##### ### ###
# # # # # ## # # # # # # #
## ### ## # ## # # # # ### # #
# # ## ## ##### # # ##### # ##### # #
# # # # # ## # # # # # #
#### ###### ###### ######## ######## ####
```
**rad_____**
```
####### ####### ####### # # # # # ##
## ### ## ## # ## # # ###
## ### ## #### ### ####
####### ### ## #### # # ### # ###
### ### ## ### # ## # ## #
### ### ## ### #### # #
### ####### ####### # ## # # # ## #
##### #### #
```
**rad_phan**
```
###### #### ##### ##### # # # ## ##
### ## ### ### ## ## # # # # # # ##
### ### ### # ### # ### ## # # ####
##### ### ### ### # # ## ###### ## #
### ### ### ## # ## # ## # ## ##
### ### ### ## #### # ### #### # # #
### ### ##### # ### # ### # # ##
# # # # # # ## ####
```
**radical_**
```
###### ### ###### ## ###### ######
### ### #### ## ## ##
### ### ### ## ## ##
##### ### ### ## ##### ##
### ### ### ## ## ## ##
### ### ## ## ##
#### ### ##### ## ###### ###### ##
```
**rainbow_**
```
### ## # ### ## # ### # # ### # #####
### #### # ### ## # ### # # ### # #####
## # ## ## # ### ## ##### # # ### ## #####
#### ### ## ## # ### ## ### # # ###### #####
## ## ### ## # ### ## ## ### ## ### #####
## ## ## ## # ###### # ### # ### # #####
### # ### ### ######## # ### # ##### # #####
## ## ###### # ### ## # ### # # ### # #####
```
**rally_s2**
```
##### ##### ####### ## ####### # # ######
### ### ## ### ## ###### # # ### ##
###### ###### #### ##### ##### ###### # ##
## ## ### #### ## ##### # ## # #######
####### ####### ##### #### ###### ## # ######
####### ###### ##### ## ####### # # # ####
##### ##### ##### ##### ###### ## ####
## ## ###### # #
```
**rally_sp**
```
####### ##### ### ## ## ##### #######
####### ##### ####### ## ###### # # # ### ###
### ##### ##### #### ####### ## ### ##
###### ####### # # # #
####### ##### ##### ## ###### ## # #####
### ### ### ### ## ##### # # # ### ##
###### ##### ###### #### #### ## # ### ##
## ### ### ### ## ## ## ### # # # # ### ##
```
**rammstein**
```
_____ _____ _____
__|___ |__ __|_ |__ __|___ |__ ____ ______ __
| ___| || | || ___| || | | ___| _| |_
| ___| || | || | | || |_ | ___||_ _|
|___| __||____| __||______| __||______||______| |__|
|_____| |_____| |_____|
```
**rampage_**
```
###### #### ##### #### ## #### ##
## ## ## ## #### ##
## ## ## ## #### ##
#### ## ## ### ## ## #### ##
## ## ## # #### ##
## ## ## # #### ##
## #### ##### #### #### ####
```
**rastan__**
```
###### #### #### ###
## ## ## # # ###
## ## ## ######## # #
#### ## ## ### ### ### ## #
## ## ## ## ### ### ## #
## ## ### ## ### ### ### #
### #### ##### ### ### # #
######## # #
```
**raw_recu**
```
###### #### #### ########
###### #### ###### ######## ##
## ## ## # ######## #
#### ## ## ### # ######## # #
## ## ## ## ######## # #
## #### ###### ######## # #
## #### #### ######## #
######## ##
```
**rci_____**
```
######## ########
######## ########
####### ### ###### ######## ########
### ### ######
####### ### ### ## ####
### ### ### ## ##
### ### ###### ####
####
```
**rectangles**
```
_____ _____ _____ _ _
| __| | __| |___| |_
| __|- -| | | | -_| _|
|__| |_____|_____|_|___|_|
```
**relief**
```
___________________________________________________________________
/~~~~~~~~\_/~~~~\__/~~~~~~\__/~~\_______/~~~~~~~~\_/~~~~~~~~\______
/~~\________/~~\__/~~\__/~~\_/~~\_______/~~\__________/~~\_________
/~~~~~~\____/~~\__/~~\_______/~~\_______/~~~~~~\______/~~\_________
/~~\________/~~\__/~~\__/~~\_/~~\_______/~~\__________/~~\_________
/~~\_______/~~~~\__/~~~~~~~\_/~~~~~~~~\_/~~~~~~~~\____/~~\_________
________________________/~~\_______________________________________
```
**relief2**
```
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
///////// \///// \\/////// \\/// \\\\\\\///////// \///////// \\\\\\
/// \\\\\\\\/// \\/// \\/// \/// \\\\\\\/// \\\\\\\\\\/// \\\\\\\\\
/////// \\\\/// \\/// \\\\\\\/// \\\\\\\/////// \\\\\\/// \\\\\\\\\
/// \\\\\\\\/// \\/// \\/// \/// \\\\\\\/// \\\\\\\\\\/// \\\\\\\\\
/// \\\\\\\///// \\//////// \///////// \///////// \\\\/// \\\\\\\\\
\\\\\\\\\\\\\\\\\\\\\\\\/// \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
```
**reverse**
```
================================================
= == === === ===================
= ========= === == == ===================
= ========= === ==== == ========== =======
= ========= === ======== === === ======
= ===== === ======== == = === =======
= ========= === === == == === =======
= ========= === ==== == == ====== =======
= ========= === == == == = === =======
= ======== === === === ==== ======
================================================
```
**ripper!_**
```
###### ## #### ######
### # ### # ### ### ########
## ## ## ###### ########
##### ## ## ######## ########
## ## ## ### ######## ########
## ## ### ## ###### ######## ########
#### ### ##### ######## ######## ########
######## ######## ########
```
**road_rai**
```
# # # # ### #
###### ###### #### ### # ## # # # #
## ## ## ## # # # ## # # # #
#### ## ## # ## ### # # # #
## ## ## ### # # # # #
## ## ## ## ## # # # # # # #
## ###### #### # # ### # #
# # #### ## # #
```
**rockbox_**
```
### # ##
## # ## #
## ## ##
##### ## ##
## ### ## ##
## ### ### ##
## ### ####
```
**rok_____**
```
####### #### ######
## ## ##
##### ## ## ###
## ## ## ##
## #### #####
```
**roman**
```
oooooooooooo ooooo .oooooo. oooo .
`888' `8 `888' d8P' `Y8b `888 .o8
888 888 888 888 .ooooo. .o888oo
888oooo8 888 888 888 d88' `88b 888
888 " 888 888 ooooo 888 888ooo888 888
888 888 `88. .88' 888 888 .o 888 .
o888o o888o `Y8bood8P' o888o `Y8bod8P' "888"
```
**roman___**
```
#### ## ## #### ####### ########
## # ##### ## ## # # ## #
## ### ## ## ## ## ##
##### ## ##### ## ##### ##
## ## ## ## # ## ##
## ## ##### ## ## ## # ##
#### ###### ## ## ####### ####### ####
#####
```
**rot13**
```
SVTyrg
```
**rotated**
```
____ |___| ___ ___ _ _,_
' || |( ) (|) ( '
`|
```
**rounded**
```
_______ _ _______ _
(_______) (_______) | _
_____ | |_ ___| | _____ _| |_
| ___) | | | (_ | || ___ (_ _)
| | | | |___) | || ____| | |_
|_| |_|\_____/ \_)_____) \__)
```
**rozzo**
```
888'Y88 888 e88'Y88 888 d8
888 ,'Y 888 d888 'Y 888 ,e e, d88
888C8 888 C8888 eeee 888 d88 88b d88888
888 " 888 Y888 888P 888 888 , 888
888 888 "88 88" 888 "YeeP" 888
```
**runic**
```
| / / | \ /
|/ / | \ /
| / | \/ _
|/ | /\ |_|
| | / \
| | / \
```
**runyc**
```
| / / | \ /
|/ / | \ /
| / | \/ _
|/ | /\ |\ |\/| /|\ |_|
| | / \ | | | |
| | / \ | | | |
```
**sans**
```
### # #### # #
# # ## # #
# # # # ## ###
### # # # # #### #
# # ## # # # #
# # #### # ### ##
```
**sansb**
```
### # #### # #
# # ## # #
# # # # ### ##
### # # # # #### #
# # ## # # ## #
# # #### # ### ##
```
**sansbi**
```
#### ## #### ## #
# ## # ## #
# # # # ### ###
#### # # # # ### ##
## ## # ## ## ## # #
## ## #### ## #### ###
```
**sansi**
```
### # ### # #
# # # # #
# # # # ## ###
### # # # # # # #
# # # # # ### #
# # ### # ### ##
```
**sbook**
```
##### ### #### ## #
# # # # # #
### # # # ## ###
# # # ### # ### #
# # # # # # #
### ### #### ### ## ##
```
**sbookb**
```
##### ### #### ### ##
## ## ## # ## ##
#### ## ## ## ## ###
## ## ## ## ## #### ##
## ## ## # ## ## ##
#### ### #### ### ### ##
```
**sbookbi**
```
##### #### #### ## #
# ## ## # ## ##
### ## ## ## ## ###
## # ## ## ### ## ### #
## ## ## ## ## ## ##
### #### ## # ### ### ##
```
**sbooki**
```
##### ### #### ## #
# # # # # # #
## # # # ## ###
# # # ### # ### #
# # # # # # #
### ### #### # ## ##
```
**script**
```
______ _ _
(_) | | | () || |
_|_ | | /\/|| | _ _|_
/ | |_ |/ / ||/ |/ |
(_/ \_/\//(__/ |__/|__/|_/
```
**script__**
```
### ## # ### # ##### #######
## # ## ## # ## # # ## ## # ##
## ## ## ### # ## # ### # ## ##
## ## ## ## ### # ### ##
##### ## ## ## ## # ## ##
## ## # ## # #### ### ## ## ### ##
## ### ## ## ### # ## # # ##
### ##### ## ##### ###### #####
```
**serifcap**
```
___ __ __ __ ___ ____
( _)( )/ _)( ) ( _)(_ _)
) _) )(( (/\ )(__ ) _) )(
(_) (__)\__/(____)(___) (__)
```
**shadow**
```
____|_ _| ___| | |
| | | | _ \ __|
__| | | | | __/ |
_| ___|\____|_|\___|\__|
```
**shimrod**
```
,--. , ,-. . .
| | / | |
|- | | -. | ,-. |-
| | \ | | |-' |
' ' `-' ' `-' `-'
```
**short**
```
[~|/~ | _ |-
| |\_||(/_|_
```
**skate_ro**
```
### ## ### #####
## # ## # # ### #####
# ## # ##### #####
### ## # ## ##### ##### #
# ## # ### ##### ##### #
# ## # # ##### ### # #
# ## ### ##### # # #
##### # ##
```
**skateord**
```
####### ## ##### ## ## # # # # ## ##
## ## ## ## ## ## # # # # ## ##
## ## ## ## ## ###### # ## ##
##### ## ## ### ## ## ####### ## ##
## ## ## ## ## ## ####### ## ##
## ## ## ## ## ## # # # # ## ##
## ## ##### ## ## # # # # ## ##
## ## # # # # ## ##
```
**skateroc**
```
### ## ### #####
## # ## # # ### #####
# ## # ##### #####
### ## # ## ##### ##### #
# ## # ### ##### ##### #
# ## # # ##### ### # #
# ## ### ##### # # #
##### # ##
```
**sketch_s**
```
# ###### #####
### # #
# #### # #
# # # # # ###### #
### # # # # #
# # ##### # # #
# # # # ### ###### #
#####
```
**slant**
```
__________________ __
/ ____/ _/ ____/ /__ / /_
/ /_ / // / __/ / _ \/ __/
/ __/ _/ // /_/ / / __/ /_
/_/ /___/\____/_/\___/\__/
```
**slide**
```
##HH||#HH|#HH||#| #|
## #|## #| #H|##HH|
##HH| #|## H||#|##HH|#|
## #|## ||#|## #|
## #HH|#HH||#H|#HH|#H|
```
**sm______**
```
######## ######## ######## # # # ## # # # # ########
# # ## ## # ## # # # ## # # # # ########
###### ### ### ### # # # # ## # # # # ########
# ### ### ### ###### # # # ## # # # # ########
###### ### ### ## # # # # ## # # # # ########
###### ### ### ### # # # # ## # # # # ########
###### ## ## # # ######## # # # ## # # #### ########
###### ######## ##### # # # # # # # # ## # # ## # ########
```
**small**
```
___ ___ ___ _ _
| __|_ _/ __| |___| |_
| _| | | (_ | / -_) _|
|_| |___\___|_\___|\__|
```
**soft**
```
,------.,--. ,----. ,--. ,--.
| .---'| |' .-./ | | ,---. ,-' '-.
| `--, | || | .---.| || .-. :'-. .-'
| |` | |' '--' || |\ --. | |
`--' `--' `------' `--' `----' `--'
```
**space_op**
```
### #### #### # ########
### ### ##### # ### # ## ####### ####### ########
## # ##### # ### ### ## ## ## ########
## #### #### ## ## # ## ###### ## ########
## #### #### ## ## # ## ## ## ########
# #### ### # ## # ####### ####### ## ########
# ##### ######## ######## ########
######## ######## ######## ########
```
**spc_demo**
```
### # ## #######
## # ## # #######
## ## ## ##
##### ## ## ##
## ### ## ## ##
## ### ### ## ### #######
## ### #### ### ######
```
**speed**
```
______________________________ _____
___ ____/___ _/_ ____/__ /______ /_
__ /_ __ / _ / __ __ /_ _ \ __/
_ __/ __/ / / /_/ / _ / / __/ /_
/_/ /___/ \____/ /_/ \___/\__/
```
**spliff**
```
_____ ___ _____ ____ _____ ____
/ __\/___\/ __\/ _/ / __\/ \
| __|| || |_ || |---| __|\- -/
\__/ \___/\_____/\_____/\_____/ |__|
```
**stacey**
```
______________________ _______________
7 77 77 77 7 7 77 7
| ___!| || __!| | | ___!!__ __!
| __| | || ! 7| !___| __|_ 7 7
| 7 | || || 7| 7 | |
!__! !__!!_____!!_____!!_____! !__!
```
**stampate**
```
`.--- ,-_/ ,---. . .
|__ ' | | -' | ,-. |-
,| .- | | ,-' | |-' |
`' `--' `---| `' `-' `'
,-.|
`-+'
```
**stampatello**
```
.-,--' ,-_/ ,---. . .
\|__ ' | | -' | ,-. |-
| .^ | | ,-' | |-' |
`' `--' `---| `' `-' `'
,-.|
`-+'
```
**standard**
```
_____ ___ ____ _ _
| ___|_ _/ ___| | ___| |_
| |_ | | | _| |/ _ \ __|
| _| | | |_| | | __/ |_
|_| |___\____|_|\___|\__|
```
**star_war**
```
###### ###### ###### # #### # # ## # # #
## ## ## # # # ### # ##
## ## ## # # # # ### # # #
###### ## ## ## # ## # #### # ###
## ## ## ## # # ### # # ## ##
## ## ## ## # # # # ## ####
## ###### ###### # ### # ### # # # #
# # ### # #
```
**stealth_**
```
####### ###### ##### #
####### ###### ####### # ## ####
## ## #### ## ### ### ## ## #
###### ## ## ### # ## # ## ## ## ## #
## ## ## ## # ## # # #### ## ## #
## ###### ####### # ## # ## ## ##### #
## ###### ##### # ## # ## ## ## #
#### # ## ### ##
```
**stellar**
```
`........`.. `.... `.. `..
`.. `.. `. `.. `.. `..
`.. `..`.. `.. `.. `.`. `.
`...... `..`.. `.. `. `.. `..
`.. `..`.. `.... `..`..... `.. `..
`.. `.. `.. `. `..`. `..
`.. `.. `..... `... `.... `..
```
**stencil1**
```
#### #### ## #### ## # ## # #### ######## ####
#### #### #### # ## # #### ######## ####
#### #### # ## # #### ######## ####
#### ## #### # ## # #### ######## ####
#### #### # ## # #### ######
#### #### # # # # #### ######
#### #### #### # # # # #### ######
#### #### ## #### ## # # # # #### ######
```
**stencil2**
```
#### #### ## #### ## # ## # #### # # # # ####
#### #### #### # ## # #### # # # # ####
#### #### # ## # #### # # # # ####
#### ## #### # ## # #### # ## # ####
#### #### # ## # #### ## #
#### #### # # # # #### ## #
#### #### #### # # # # #### ## #
#### #### ## #### ## # # # # #### ## #
```
**stforek**
```
___ _ __ _ ___ _____
| __| |/ _] | | __|_ _|
| _|| | [/\ |_| _| | |
|_| |_|\__/___|___| |_|
```
**stop**
```
_______ _____ ______ _
(_______|_____) _____) | _
_____ _ | / ___| | ____| |_
| ___) | || | (___) |/ _ ) _)
| | _| || \____/| ( (/ /| |__
|_| (_____)_____/|_|\____)\___)
```
**straight**
```
__ __
|_ |/ _ | _|_
| |\__)|(-|_
```
**street_s**
```
####### ####### ##### ######## ######
####### ####### ####### ######## ##### ########
### ### ### ######## ##### ####
####### ### ####### ##### # ##### ##
### ### ### ### ## ##### #####
### ####### ####### ######## #####
### ####### ##### ######## #####
######## #####
```
**sub-zero**
```
______ __ ______ __ ______ ______
/\ ___\ /\ \ /\ ___\ /\ \ /\ ___\ /\__ _\
\ \ __\ \ \ \ \ \ \__ \ \ \ \____ \ \ __\ \/_/\ \/
\ \_\ \ \_\ \ \_____\ \ \_____\ \ \_____\ \ \_\
\/_/ \/_/ \/_____/ \/_____/ \/_____/ \/_/
```
**subteran**
```
### # ### # ### # ## ## # ## # ##
## #### ## ### ## #### # # ### ### ## ### ### #
# ##### # # ### # ##### # ## # # ## ######
## ### ## ### ###### ## ### # ### ######
# #### ### ### ## # # # ## # # ##
##### ### # # ### # # ## #### ##### #
###### ### ## # ## # ## ## # # ### #
###### # #### #### # ### # ## # ##
```
**super_te**
```
###### ###### #### # #### #
## # ## # ## ## # ####
## ## ## # ######
##### ## ## ### # ###### #### #
## ## ## ## # ###### ##
## # ## # ## ## ## ##### ##
## ###### #### ## # ##
###### ## #
```
**swan**
```
.---.--.-- .--.. .
| | : | _|_
|--- | | --.| .-. |
| | : ||(.-' |
' --'-- `--'`-`--'`-'
```
**sweet**
```
.-. ___ ___
/ \ .-. ( ) ( )
| .`. ; ( __) .--. | | .--. | |_
| |(___) (''") / \ | | / \ ( __)
| |_ | | ; ,-. ' | | | .-. ; | |
( __) | | | | | | | | | | | | | | ___
| | | | | | | | | | | |/ | | |( )
| | | | | | | | | | | ' _.' | | | |
| | | | | ' | | | | | .'.-. | ' | |
| | | | ' `-' | | | ' `-' / ' `-' ;
(___) (___) `.__. | (___) `.__.' `.__.
( `-' ;
`.__.
```
**t__of_ap**
```
### ##### #######
### ## # ## ### # ## #
## ## ### ##### ## ## ##
## ## ## ## ## #### ##
###### ## ##### ## ## ##
## ## ## # ### ## ### ##
## ### ## ## ##### ##### ###
## #### # # #
```
**tanja**
```
F)ffffff I)iiii G)gggg l)L t)
F) I) G) l) t)tTTT
F)fffff I) G) ggg l) e)EEEEE t)
F) I) G) gg l) e)EEEE t)
F) I) G) gg l) e) t)
F) I)iiii G)ggg l)LL e)EEEE t)T
```
**tav1____**
```
### # ## ###### ######
## # ## # ######## ######
## ## ## ####
##### ## ## #### ######
## ### ## ## ####
## ### ### ## ######## ######
## ### #### ###### ######
```
**taxi____**
```
## ###### ######
### ## ## ## ##
## ##### ## ## ##
##### ### ## ## ## #### ##
## ## ## ## ## ## ##
## ## ##### ## ## ##
## #### ## ###### ###### ##
#####
```
**tec1____**
```
# ### # # # ###
###### ####### ###### # # ## # # # # # ## #
## ## ## ## ## # # ### #
####### ## ## ### # ### ## # ## ##
## ## ## ## # # ## # ## # # ## #
## ###### ##### ## # # # ## #
## # # ## ### # #
# ## # # # # #
```
**tec_7000**
```
# ### # # # ###
###### ####### ###### # # ## # # # # # ## #
## ## ## ## ## # # ### #
####### ## ## ### # ### ## # ## ##
## ## ## ## # # ## # ## # # ## #
## ###### ##### ## # # # ## #
## # # ## ### # #
# ## # # # # #
```
**tecrvs__**
```
# ### # # # ###
###### ####### ###### # # ## # # # # # ## #
## ## ## ## ## # # ### #
####### ## ## ### # ### ## # ## ##
## ## ## ## # # ## # ## # # ## #
## ###### ##### ## # # # ## #
## # # ## ### # #
# ## # # # # #
```
**tengwar**
```
`Yb .dP'
88 db dP'
88 "Ybaaaaaaaaad8'
88.d88b. 'Yb .dP' dP' 88 `Y8888888b. 'Yb `Yb.d888b
88P' Y8 88 88 88 88 .dP' 88 88' 8Y
88 8P 88 Y8 Y8 .88 ,dP 88 88 8P
88 ,dP .8P `Y88P`Y88P'88 88 . .8P 88 ,dP
.888888888b. 88 `Yb...dP 88
88 `"""' 88
Y8. .8P
```
**term**
```
FIGlet
```
**test1**
```
_________________________________ __________ _________
/ /_____/\__/ \__/ /_____/ /_____/ /_____//__ __\
\___\%%%%%'_`%\_/%'\___\%%%%.]___\_____\___\%%%%%'`%%|___|%%'
`BB' `BBBBBBB'`BBBBBBBB'`BBBBBBBB'`BBBBBBBB' `B'
```
**thick**
```
8888 888 .d88b 8 w
8www 8 8P www 8 .d88b w8ww
8 8 8b d8 8 8.dP' 8
8 888 `Y88P' 8 `Y88P Y8P
```
**thin**
```
,---.|,---.| |
|__. || _.| ,---.|---
| || || |---'|
` ``---'`---'`---'`---'
```
**ti_pan__**
```
#### # #### #
## # ## ## # # # # # # # # # # #
## ## ## # # #
##### #### ### ### # # # ##
## ## ## # # # # ####
## ## ## # # # # ####
# # #### # # # # ##
# # # # # #
```
**ticks**
```
_/\/\/\/\/\/\__/\/\/\/\____/\/\/\/\/\__/\/\__________________/\/\_________
_/\/\____________/\/\____/\/\__________/\/\______/\/\/\____/\/\/\/\/\_____
_/\/\/\/\/\______/\/\____/\/\__/\/\/\__/\/\____/\/\/\/\/\____/\/\_________
_/\/\____________/\/\____/\/\____/\/\__/\/\____/\/\__________/\/\_________
_/\/\__________/\/\/\/\____/\/\/\/\/\__/\/\/\____/\/\/\/\____/\/\/\_______
__________________________________________________________________________
```
**tiles**
```
[........[.. [.... [.. [..
[.. [.. [. [.. [.. [..
[.. [..[.. [.. [.. [.[. [.
[...... [..[.. [.. [. [.. [..
[.. [..[.. [.... [..[..... [.. [..
[.. [.. [.. [. [..[. [..
[.. [.. [..... [... [.... [..
```
**times**
```
#
##### #### ### # #
## ## ## # ## ###
#### ## ## ## # ### #
## ## ## ## # ## #
#### #### ### # ## #
```
**timesofl**
```
##### # ######## ######## #### ## # # ########
#### ## ### ### ######## # ##### # ### # # # # # ########
#### ### ######## ## # # # ##### # ##### ### ### ########
## # ## ### # ## # # ##### # ### ### ### ########
### ### # # ### # # # # ### # # ### # ### ### ########
### ### ### # # ## # # # ## # # ## # ### ### ########
### ### ### ## #### ## # # ## ## ########
## #### ######## # ### ######## ######## ######## ########
```
**tinker-toy**
```
o--o o-O-o o-o o o
| | o | |
O-o | | -o | o-o -o-
| | o | | |-' |
o o-O-o o-o o o-o o
```
**tomahawk**
```
# ### # ##### ## ##
####### ###### #### ## ## ### # # #
## # ## ## ## # #### # # ## # #
## # ## ## ##### # ## # # ### # # # # #
#### ## ## #### ## # ### # # # #
## # ## ## ### # #### # # # # # ## # # # # #
## ## ## ## # # # ## ## ## ###
#### ###### ##### ## # # # # #### ### # # # #
```
**tombstone**
```
__, _ _, _, __, ___
|_ | / _ | |_ |
| | \ / | , | |
~ ~ ~ ~~~ ~~~ ~
```
**top_duck**
```
###### #### ##### # # # ######## # ## #
## ## ### ## # # # ####### # ## #
## ## ## # # # ##### # # ## #
#### ## ## ### # # # ## # # ## #
## ## ## ## # # # # ## # # ## #
## ## ## ## # # # # ## # # ## #
## #### #### # # # # # ## # # ##
# # # # # ## # # #
```
**train**
```
___ ___ ___ _ _
| __| |_ _| / __| | | ___ | |_ o O O
| _| | | | (_ | | | / -_) | _| o
_|_|_ |___| \___| _|_|_ \___| _\__| TS__[O]
_| """ |_|"""""|_|"""""|_|"""""|_|"""""|_|"""""| {======|
"`-0-0-'"`-0-0-'"`-0-0-'"`-0-0-'"`-0-0-'"`-0-0-'./o--000'
```
**trashman**
```
### ## ## ### ##
## # ## ## ## ##
## # # ## ## #### ######
### # ## ## ## ## ##
### ## ## ## ###### ##
## ## ## ## ## ##
####### ## #### ##### ###
#### # ##
```
**trek**
```
dBBBBP dBP dBBBBb dBP dBBBP dBBBBBBP
dBBBP dBP dBBBB dBP dBBP dBP
dBP dBP dB' BB dBP dBP dBP
dBP dBP dBBBBBB dBBBBP dBBBBP dBP
```
**triad_st**
```
###### ###### #### ##### # ## # ##
###### ###### ###### # # # #
## ## ## ## # # # # # #
## ## ## # ### # # #
#### ## ## ### # # # #
## ## ## ## # # # # ## # ## #
## ###### #### #### # #### #
# ## # # # #
```
**ts1_____**
```
####### #### #### ### ### ##### # #### ###
## # ## ### ## # # #
## ## ## # # # ####
##### ## ## ### ## #### #### ## ## ####
## ## ## ## # #
## ## ### ## # # ##
### #### #### # # # # ## # ####
##
```
**tsalagi**
```
_ _ __ ___ ___ ___
` | () / ' / \ | | / \
|-_| /~\ | |" | |_, ` |
| | | | | | . | ' |
_|_ \_/ \__/ `__' _|_ \_/
```
**tsm_____**
```
###### ## #### ## #
## ## ### ## #
## ## ## ## ## ##
##### ## ## ## #
## ## ## ### # ##
## ## ## ## # # ##
## ## ###### # ## ###
# ## ###
```
**tsn_base**
```
# ## ### ##
###### #### ##### ##### # ## ## ##
## ## ## ## # ## ## ##
#### ## ## ### ## ### # ## ### ######
## ## ## ## ## ## # ## ##
## #### #### #### #### ## ##
## ##
######## #### ## ###
```
**tty**
```
#### ### ### ### #
# # ## # #
# # # # ### ####
#### # # # # #### #
# # ## # # # #
# ### ### # ### ###
```
**ttyb**
```
#### ### #### ### #
# # ## # #
# # # # ## ####
#### # # # # #### #
# # ## # # # #
# ### #### # ### ###
```
**tubular**
```
O~~~~~~~~O~~ O~~~~ O~~ O~~
O~~ O~~ O~ O~~ O~~ O~~
O~~ O~~O~~ O~~ O~~ O~O~ O~
O~~~~~~ O~~O~~ O~~ O~ O~~ O~~
O~~ O~~O~~ O~~~~ O~~O~~~~~ O~~ O~~
O~~ O~~ O~~ O~ O~~O~ O~~
O~~ O~~ O~~~~~ O~~~ O~~~~ O~~
```
**twin_cob**
```
### ### #### ## ###
## # ## ## # ## ####### #######
## # ## ## ## ## ##
## ## ## ## ### ## ###### ##
## # ## ## ## ## ## ##
## ## ## ## ####### ####### ##
### #### ## ##
```
**twisted**
```
_____ __ ______ __ _____ _______
/\_____\/\_\ /_/\___\ /\_\ /\_____\/\_______)\
( ( ___/\/_/ ) ) ___/ ( ( ( ( (_____/\(___ __\/
\ \ \_ /\_\/_/ / ___ \ \_\ \ \__\ / / /
/ / /_\ / / /\ \ \_/\__\ / / /__ / /__/_ ( ( (
/ /____/( (_( )_) \/ _/( (_____(( (_____\ \ \ \
\/_/ \/_/ \_\____/ \/_____/ \/_____/ /_/_/
```
**type_set**
```
## # # ###### #####
# # # # #
# ## ### # # # #
##### # # ## # #### #
# # # ## # # #
# # ### # # # #
# ### # ###### ###### #
####
```
**ucf_fan_**
```
### ####### #######
#### ### ### ### ## ###
### ###### ### ### ###
###### ### ### ## ### ###### ###
### ### ### ## ### ### ###
### ### ###### ### ## ### ## ###
### ### ## ####### ####### ###
#####
```
**ugalympi**
```
# # # ### # # # #
##### ## ## # # ### ## # ####
## ##### ##### ## # #### # #### # # #
#### ## ## # ## # # ## # ## # ## # # ####
#### ## # # # ## # # ### # #### #
## ### # ### # # # # # # ### ### # #
##### ## ## # ## # ## ### # # ### # #
#### # ## # ## ## # # # # #
```
**unarmed_**
```
####### ###### ##### #### #######
## ## ## ## ## # #
## ## ## ##### # # ## ###
##### ## ## ### # #####
## ## ## ## ## ## # ### #### #
## ## ## ## # ## # # ### ####
## ###### ##### ## ## #### #### ##
# ## #######
```
**univers**
```
88888888888 88 ,ad8888ba, 88
88 88 d8"' `"8b 88 ,d
88 88 d8' 88 88
88aaaaa 88 88 88 ,adPPYba, MM88MMM
88""""" 88 88 88888 88 a8P_____88 88
88 88 Y8, 88 88 8PP""""""" 88
88 88 Y8a. .a88 88 "8b, ,aa 88,
88 88 `"Y88888P" 88 `"Ybbd8"' "Y888
```
**usa_____**
```
# # # #
## # # ## # #
####### ###### ####### ## # # ## # #
## # #
#### ## ## ## ## # # ## # #
## ## ## # # ## # ## # #
## ###### ####### # #
## # # ## # #
```
**usa_pq__**
```
# # ### #### ###
######## # ## ### ## # # #
####### ###### ####### ######## ## #### # # # #
## #### ### # # ###
#### ## ## ## # # # # # ## ### ## #####
## ## ## # # # # # ## #### ########
## ###### ####### # ## ### #### ###
# ## ### ## ####
```
**utopia**
```
##
##### ### #### #
# # # # # # #
# # # # ## ###
### # # # # # #
# # # ### # #### #
# # # # # # #
### ### #### ### ### ##
```
**utopiab**
```
###
###### #### ##### ## #
## # ## ## # ## ##
## ## ## ## ### ####
#### ## ## ## ## ## ##
## ## ## ### ## ##### ##
## ## ## ## ## ## ##
#### #### ##### #### #### ##
```
**utopiabi**
```
###
###### #### #### ## #
## # ## ## ## ## ##
## # ## ### ## ## ####
##### ## ## ## # ## ##
## # ## ## #### ## #### ##
## ## ## ## ## ## ##
#### #### #### ## #### ###
```
**utopiai**
```
##
##### ### #### #
# # # # # # #
# # # # ## ###
#### # # # # # #
# # # ### # ### #
# # # # # # #
### ### #### ## ## ##
```
**varsity**
```
________ _____ ______ __ _
|_ __ ||_ _|.' ___ |[ | / |_
| |_ \_| | | / .' \_| | | .---.`| |-'
| _| | | | | ____ | |/ /__\\| |
_| |_ _| |_\ `.___] || || \__.,| |,
|_____| |_____|`._____.'[___]'.__.'\__/
```
**vortron_**
```
##### #### ####
## ## ## ## #### # # ####
## ## ## ## # ## ## #######
###### ## ## ## ## ## #### #######
## ## ## ## ## ## ## #######
## ## ## ## #### ## ####
## #### #####
```
**war_of_w**
```
####### ###### #####
## # ## ##
#### ## ##
## # ## ## ###
## # ## # ## ##
### ###### ######
```
**wavy**
```
___ ___ _
)_ ) / _ ) _ _)_
( _(_ (__/ ( )_) (_
(_
```
**weird**
```
___ __
/ / / / /
(___ ( ( __ ( ___ (___
| | | )| |___)|
| | |__/ | |__ |__
```
**whimsy**
```
,d8888b d8, d8b
88P' `8P 88P d8P
d888888P d88 d888888P
?88' 88b d888b8b 888 d8888b ?88'
88P 88Pd8P' ?88 ?88 d8b_,dP 88P
d88 d88 88b ,88b 88b 88b 88b
d88' d88' `?88P'`88b 88b`?888P' `?8b
)88
,88P
`?8888P
```
**wow**
```
][= #]][ #((6 #][_ #]E #`][` # #
```
**xbrite**
```
##### ### #### ## #
# # # # # # #
# # # # # #
### # # # ## ###
# # # # ### # # # #
# # # # # #### #
# # # # # # #
## ### #### ### ### ##
```
**xbriteb**
```
###### ### #### ## #
# # # # # # #
# # # # # #
#### # # # ### ###
# # # # ### # # # #
# # # # # ##### #
# # # # # # #
### ### #### ### #### ##
```
**xbritebi**
```
###### #### ##### ## #
## # # ## # # ##
# # # # # ##
#### # # # ## ####
## # # # #### # # # #
## ## # # # ### #
## ## ## ## # # # #
### #### ##### ## #### ###
```
**xbritei**
```
##### ### #### ## #
# # # ## # # #
# # # # # #
#### # # # ## ###
# # # # ### # # # #
# # # # # ### #
# # ## # # # # #
### ### ##### ## #### ##
```
**xchartr**
```
#
##### ### ### #
# # # # # # #
# # # # # ## ##
### # # ### # # # #
# # # # # # #### #
# # # # # # #
## ### ### # ### ##
```
**xchartri**
```
##
##### ### #### #
# # # ## # # #
# # # # # # ###
#### # # ### # ### #
# # # # # # ## #
# # # # # # # #
### ### ### ## ## ##
```
**xcour**
```
## #
##### ##### ## # #
# # # # # # ## ####
### # # # # # #
# # # # ## # ### #
# # # # # # # #
### ##### ## ##### ### ##
```
**xcourb**
```
### ##
###### #### ### ## ##
## # ## ## ## ## ### #####
#### ## ## ## ## ## ##
## ## ##### ## ##### ##
## ## ## ## ## ## ## ##
#### #### #### ###### #### ###
```
**xcourbi**
```
### ##
##### ##### #### ## ##
# ## ## ## # ## ### #####
#### ## ## ## ## ## ##
## # ## ## ### ## ###### ##
## ## ## # ## ## ## ##
### ##### #### ##### #### ###
```
**xcouri**
```
## #
###### ##### ### # #
# # # # # # ## #####
### # # # # # #
# # # ## # ##### #
# # # # # # # #
### ##### ### ##### ### ##
```
**xhelv**
```
##### # #### # #
# # # # # #
# # # # ## ###
#### # # # # # #
# # # ## # #### #
# # # # # # #
# # # ## # # # #
# # ### # # ## ##
```
**xhelvb**
```
##### ## #### ## ##
## ## ## ## ## ##
## ## ## # ## ### ###
#### ## ## ## ## ## ##
## ## ## ### ## ##### ##
## ## ## ## ## ## ##
## ## ## ## ## ## ## ##
## ## ### # ## ### ##
```
**xhelvbi**
```
##### ## #### ## ##
## ## ## ## ## ##
## ## ## ## ### #####
#### ## ## ## ## ## ##
## ## ## #### ## ##### ##
## ## ## ## ## ## ##
## ## ## ## ## ## ## ##
## ## ##### ## ### ##
```
**xhelvi**
```
##### # #### # #
# # # # # #
# # # # ### ####
#### # # # # # #
# # # ### # #### #
# # # # # # #
# # # # # # # #
# # ##### # ## ##
```
**xsans**
```
#
#### # ### # #
# # # # ## ####
# # # # # # #
### # # # #### #
# # # # # # #
# # # # # # #
# # ### # ### ##
```
**xsansb**
```
##
##### ## #### ## ##
## ## ## ## ### ####
## ## ## ## ## ## ##
#### ## ## ## ## ## ## ##
## ## ## ## ## ##### ##
## ## ## ## ## ## ##
## ## #### ## #### ##
```
**xsansbi**
```
##
##### ## #### ## ##
## ## ### ## ### #####
## ## ## ## # ## ##
##### ### ## ## ## ## ## ##
## ## ## ## ## #### ##
## ## ### ## ## ## ##
## ## #### ## ### ###
```
**xsansi**
```
#
#### # #### # #
# # # # ### ####
# # # # # # #
#### ## # # # # # #
# # # # # ### #
# # # # # # #
# # ### # ### ##
```
**xsbook**
```
###### ### #### ##
# # # # # # #
# # # # # # #
### # # # ## ###
# # # # ### # # # #
# # # # # #### #
# # # # # # #
### ### ### ### ### ##
```
**xsbookb**
```
###### #### ### # ###
## # ## # ## ## #
## # ## ## # ## ##
#### ## ## ## ### ####
## # ## ## ### ## ## ## ##
## ## ## ## ## ##### ##
## ## # ## ## ## ##
#### #### ### # #### #### ##
```
**xsbookbi**
```
###### #### ##### ###
## # ## ## # ## ##
## # ## ## ## ##
#### ## ## ## ### ####
## # ## ## ### ## # # ##
## ## ## ## ## #### ##
## ## ## ## ## ## # ##
#### #### ### # ### ### ###
```
**xsbooki**
```
###### ### ##### ##
# # # # # # #
# # # # # #
### # # # ## ###
# # # # ### # # # #
# # # # # ### #
# # # ## # # # #
### ### ### # ## ## ##
```
**xtimes**
```
###### #### ##### ## #
## # ## ## ## ## ##
## # ## ## ## ### ###
#### ## ## ### ## ## # ##
## # ## ## ## ## #### ##
## ## ## ## ## ## ##
#### #### #### ## ### ##
```
**xtty**
```
###
#### ### ### # #
# # # # # ## ####
# # # # # # #
### # # # #### #
# # # # # # #
# # # # # # #
# ### ### # ### ##
```
**xttyb**
```
####
##### #### #### ## ##
## ## ### ## ### #####
## ## ## ## ## ## ##
#### ## ## # ## ## ## ##
## ## ## # ## ##### ##
## ## ### # ## ## ##
## #### #### ## #### ###
```
**yie-ar__**
```
###### #### ##### # # # #
## #### #### ## #### #######
## #### ## #######
#### ## ## ### ########
## # ## ## ## ########
## ## ### ### #######
# # ##### #######
# # # #
```
**yie_ar_k**
```
###### #### ##### # # # #
## #### #### ## #### #######
## #### ## #######
#### ## ## ### ########
## # ## ## ## ########
## ## ### ### #######
# # ##### #######
# # # #
```
**z-pilot_**
```
## ### ## ### #### ######## ########
## ### ## #### ###### ###### # ########
## ## ### #### ### # # ########
## ### ## ## ### ###### ### # # ########
## ### ## ## ### #### ### # # ########
## ## # ###### ### # # ########
## ## ##### #### ## # # # # ######
## ## ### ## # # # # # ######
```
**zig_zag_**
```
####### #### #### ### # #
####### ## ###### # ## ##
## # ## ### ## # # ### #
#### ## ## # # ##
## ## ## ### # #
## #### ## ## # # #
## #### #### # # ##
# # # ## ##
```
**zone7___**
```
####### #### ##### ########
####### #### ####### ### ## #
#### # # #
##### ## ## #### # ### #
## ## ## ## ######## # ### #
## #### ####### ######## # # ####
## #### ##### ## ###
########
```
| FIGlet | https://github.com/kdheepak/FIGlet.jl.git |
|
[
"MIT"
] | 0.2.1 | bfc6b52f75b4720581e3e49ae786da6764e65b6a | docs | 76 | # Usage
### API
```@autodocs
Modules = [FIGlet]
Order = [:function]
```
| FIGlet | https://github.com/kdheepak/FIGlet.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 1513 | using Documenter
using Literate
@info "Loading Petri"
using Petri
# Set Literate.jl config if not being compiled on recognized service.
config = Dict{String,String}()
if !(haskey(ENV, "GITHUB_ACTIONS") || haskey(ENV, "GITLAB_CI"))
config["nbviewer_root_url"] = "https://nbviewer.jupyter.org/github/mehalter/Petri.jl/blob/gh-pages/dev"
config["repo_root_url"] = "https://github.com/mehalter/Petri.jl/blob/master/docs"
end
const literate_dir = joinpath(@__DIR__, "..", "examples")
const generated_dir = joinpath(@__DIR__, "src", "examples")
for (root, dirs, files) in walkdir(literate_dir)
out_dir = joinpath(generated_dir, relpath(root, literate_dir))
for file in files
f,l = splitext(file)
if l == ".jl" && !startswith(f, "_")
Literate.markdown(joinpath(root, file), out_dir;
config=config, documenter=true, credit=false)
Literate.notebook(joinpath(root, file), out_dir;
execute=true, documenter=true, credit=false)
end
end
end
@info "Building Documenter.jl docs"
makedocs(
modules = [Petri],
format = Documenter.HTML(
assets = ["assets/analytics.js"],
),
sitename = "Petri.jl",
doctest = false,
checkdocs = :none,
pages = Any[
"Petri.jl" => "index.md",
"Examples" => Any[
"examples/epidemiology.md",
"examples/lotka-volterra.md",
],
"Library Reference" => "api.md",
]
)
@info "Deploying docs"
deploydocs(
target = "build",
repo = "github.com/mehalter/Petri.jl.git",
branch = "gh-pages"
)
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 3495 | # # [Basic Epidemiology Models](@id epidemiology_example)
#
#md # [](@__NBVIEWER_ROOT_URL__/examples/epidemiology.ipynb)
using Petri
using LabelledArrays
using Plots
using JumpProcesses
using StochasticDiffEq
using OrdinaryDiffEq
# ### SIR Model
#
# The SIR model represents the epidemiological dynamics of an infectious disease
# that causes immunity in its victims. There are three *states:* `Suceptible
# ,Infected, Recovered`. These states interact through two *transitions*.
# Infection has the form `S+I -> 2I` where a susceptible person meets an
# infected person and results in two infected people. The second transition is
# recovery `I -> R` where an infected person recovers spontaneously.
S = [:S,:I,:R]
Δ = LVector(
inf=(LVector(S=1, I=1), LVector(I=2)),
rec=(LVector(I=1), LVector(R=1)),
)
sir = Petri.Model(S, Δ)
Graph(sir)
# Once a model is defined, we can define out initial parameters `u0`, a time
# span `tspan`, and the transition rates of the interactions `β`
u0 = LVector(S=990.0, I=10.0, R=0.0)
tspan = (0.0,40.0)
# add a dynamic transition rate for infection
# where the rate of infection decreases over time
# as is dependent on the current state of the system
β = LVector(inf=((u,t)->((3/sum(u))/(t+1))), rec=0.25);
# each transition rates can one of three options:
#
# - constant: `β = [.25]`
# - where the rate is specified by a value of type `Number`
# - time dependent: `β = [t->((3/1000)/(t+1))]`
# - where `t` is the current time step
# - state and time dependent: `β = [(u,t)->((3/sum(u))/(t+1))]`
# - where `u` is the current state of `u0` and `t` is the current time step
# Petri.jl provides interfaces to StochasticDiffEq.jl, JumpProcesses.jl, and
# OrdinaryDiffEq.jl Here, we call the `JumpProblem` function that returns an
# JumpProcesses problem object that can be passed to the JumpProcesses solver which
# can then be plotted and visualized
prob = JumpProblem(sir, u0, tspan, β)
sol = JumpProcesses.solve(prob,SSAStepper())
plot(sol)
# Similarly, we can generated `SDEProblem` statements that can be used with
# StochasticDiffEq solvers
prob, cb = SDEProblem(sir, u0, tspan, β)
sol = StochasticDiffEq.solve(prob,LambaEM(),callback=cb)
plot(sol)
# Lastly, we can generated `ODEProblem` statements that can be used with
# OrdinOrdinaryDiffEq solvers
prob = ODEProblem(sir, u0, tspan, β)
sol = OrdinaryDiffEq.solve(prob,Tsit5(),reltol=1e-8,abstol=1e-8)
plot(sol)
# ### SEIR Model
S = [:S,:E,:I,:R]
Δ = LVector(
exp=(LVector(S=1, I=1), LVector(I=1, E=1)),
inf=(LVector(E=1), LVector(I=1)),
rec=(LVector(I=1), LVector(R=1)),
)
seir = Petri.Model(S, Δ)
Graph(seir)
#-
u0 = LVector(S=990.0, E=10.0, I=0.0, R=0.0)
tspan = (0.0,40.0)
β = LVector(exp=0.7/sum(u0), inf=0.5, rec=0.25)
prob, cb = SDEProblem(seir, u0, tspan, β)
sol = StochasticDiffEq.solve(prob,LambaEM(),callback=cb)
plot(sol)
# ### SEIRD Model
S = [:S,:E,:I,:R, :D]
Δ = LVector(
exp=(LVector(S=1, I=1), LVector(I=1, E=1)),
inf=(LVector(E=1), LVector(I=1)),
rec=(LVector(I=1), LVector(R=1)),
die=(LVector(I=1), LVector(D=1)),
)
seird = Petri.Model(S, Δ)
Graph(seird)
#-
u0 = LVector(S=990.0, E=10.0, I=0.0, R=0.0, D=0.0)
tspan = (0.0,40.0)
β = LVector(exp=0.9/sum(u0), inf=0.9, rec=0.25, die=0.03)
prob, cb = SDEProblem(seird, u0, tspan, β)
sol = StochasticDiffEq.solve(prob,LambaEM(),callback=cb)
plot(sol)
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 1222 | # # [Lotka-Volterra Model](@id lotka_volterra_example)
#
#md # [](@__NBVIEWER_ROOT_URL__/examples/lotka-volterra.ipynb)
using Petri
using LabelledArrays
using Plots
using OrdinaryDiffEq
# **Step 1:** Define the states and transitions of the Petri Net
#
# Here we have 2 states, wolves and rabbits, and transitions to
# model predation between the two species in the system
S = [:rabbits, :wolves]
Δ = LVector(
birth=(LVector(rabbits=1), LVector(rabbits=2)),
predation=(LVector(wolves=1, rabbits=1), LVector(wolves=2)),
death=(LVector(wolves=1), LVector()),
)
lotka = Petri.Model(S, Δ)
Graph(lotka)
# **Step 2:** Define the parameters and transition rates
#
# Once a model is defined, we can define out initial parameters `u0`, a time
# span `tspan`, and the transition rates of the interactions `β`
u0 = LVector(wolves=10.0, rabbits=100.0)
tspan = (0.0,100.0)
β = LVector(birth=.3, predation=.015, death=.7);
# **Step 3:** Generate a solver and solve
#
# Finally we can generate a solver and solve the simulation
prob = ODEProblem(lotka, u0, tspan, β)
sol = OrdinaryDiffEq.solve(prob,Tsit5(),reltol=1e-8,abstol=1e-8)
plot(sol) | Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 247 | """
Petri
Provides a modeling framework for representing and solving stochastic petri nets
"""
module Petri
export Model, NullPetri, EmptyPetri, vectorfield, Graph
include("types.jl")
include("solvers.jl")
include("visualization.jl")
end
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 3676 | using DiffEqBase
using OrdinaryDiffEq
using SteadyStateDiffEq
using StochasticDiffEq
using JumpProcesses
using SparseArrays
import OrdinaryDiffEq: ODEProblem
import SteadyStateDiffEq: SteadyStateProblem
import StochasticDiffEq: SDEProblem
import JumpProcesses: JumpProblem
funcindex!(list, key, f, vals...) = list[key] = f(list[key],vals...)
valueat(x::Number, u, t) = x
valueat(f::Function, u, t) = try f(u,t) catch e f(t) end
transitionrate(S, T, k, rate, t) = exp(reduce((x,y)->x+log(S[y] <= 0 ? 0 : S[y]),
keys(first(T[k]));
init=log(valueat(rate[k],S,t))))
""" vectorfield(m::Model)
Convert a petri model into a differential equation function that can
be passed into DifferentialEquation.jl or OrdinaryDiffEq.jl solvers
"""
function vectorfield(m::Model)
S = m.S
T = m.Δ
ϕ = Dict()
f(du, u, p, t) = begin
for k in keys(T)
ϕ[k] = transitionrate(u, T, k, p, t)
end
for s in S
du[s] = 0
end
for k in keys(T)
l,r = T[k]
for s in keys(l)
funcindex!(du, s, -, ϕ[k] * l[s])
end
for s in keys(r)
funcindex!(du, s, +, ϕ[k] * r[s])
end
end
return du
end
return f
end
""" ODEProblem(m::Model, u0, tspan, β)
Generate an OrdinaryDiffEq ODEProblem
"""
ODEProblem(m::Model, u0, tspan, β) = ODEProblem(vectorfield(m), u0, tspan, β)
""" SteadyStateProblem(m::Model, u0, tspan, β)
Generate an SteadyStateDiffEq SteadyStateProblem
"""
SteadyStateProblem(m::Model, u0, tspan, β) = SteadyStateProblem(ODEProblem(m, u0, tspan, β))
function statecb(s)
cond = (u,t,integrator) -> u[s]
aff = (integrator) -> integrator.u[s] = 0.0
return ContinuousCallback(cond, aff)
end
""" SDEProblem(m::Model, u0, tspan, β)
Generate an StochasticDiffEq SDEProblem and an appropriate CallbackSet
"""
function SDEProblem(m::Model, u0, tspan, β)
S = m.S
T = m.Δ
ϕ = Dict()
Spos = Dict(S[k]=>k for k in keys(S))
T_keys = collect(keys(T))
Tpos = Dict(T_keys[k]=>k for k in keys(T_keys))
nu = spzeros(Float64, length(S), length(T))
for k in T_keys
l,r = T[k]
for i in keys(l)
nu[Spos[i],Tpos[k]] -= l[i]
end
for i in keys(r)
nu[Spos[i],Tpos[k]] += r[i]
end
end
noise(du, u, p, t) = begin
sum_u = sum(u)
for k in keys(T)
ins = first(T[k])
ϕ[k] = transitionrate(u, T, k, p, t)
end
for k in keys(T)
l,r = T[k]
rate = sqrt(abs(ϕ[k]))
for i in keys(l)
du[Spos[i],Tpos[k]] = -rate
end
for i in keys(r)
du[Spos[i],Tpos[k]] = rate
end
end
return du
end
return SDEProblem(vectorfield(m),noise,u0,tspan,β,noise_rate_prototype=nu),
CallbackSet([statecb(s) for s in S]...)
end
jumpTransitionRate(T, k) = (u,p,t) -> transitionrate(u, T, k, p, t)
function jumpTransitionFunction(t)
return (integrator) -> begin
l,r = t
for i in keys(l)
integrator.u[i] -= l[i]
end
for i in keys(r)
integrator.u[i] += r[i]
end
end
end
""" JumpProblem(m::Model, u0, tspan, β)
Generate an JumpProcesses JumpProblem
"""
function JumpProblem(m::Model, u0, tspan, β)
T = m.Δ
prob = DiscreteProblem(u0, tspan, β)
return JumpProblem(prob, Direct(), [ConstantRateJump(jumpTransitionRate(T, k),
jumpTransitionFunction(T[k])
) for k in keys(T)]...)
end
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 864 | using StructEquality
"""
Model{S,D}
Structure for representing the petri net model
represented by states and transition functions
"""
@struct_hash_equal struct Model{S,D}
S::S # states
Δ::D # transition function
end
Model(s::S, Δ) where S<:UnitRange = Model(collect(s), Δ)
Model(s::S, Δ) where S<:Int = Model(1:s, Δ)
"""
NullPetri
create a Petri net of no states and no transitions
"""
const NullPetri = Model(Int[], Vector{Tuple{Dict{Int, Number},Dict{Int, Number}}}())
"""
EmptyPetri(n::Int)
create a Petri net of ``n`` states with no transitions
"""
EmptyPetri(n::Int) = Model(collect(1:n), Vector{Tuple{Dict{Int, Number},Dict{Int, Number}}}())
"""
EmptyPetri(s::Vector{T})
create a Petri net with states ``s`` with no transitions
"""
EmptyPetri(s::Vector{T}) where T = Model(s, Vector{Tuple{Dict{T, Number},Dict{T, Number}}}())
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 1372 | import Base.Iterators: flatten
using Catlab.Graphics.Graphviz
import Catlab.Graphics.Graphviz: Graph, Edge
graph_attrs = Attributes(:rankdir=>"LR")
node_attrs = Attributes(:shape=>"plain", :style=>"filled", :color=>"white")
edge_attrs = Attributes(:splines=>"splines")
function edgify(δ, transition, reverse::Bool)
return [Edge(reverse ? ["T_$transition", "S_$k"] :
["S_$k", "T_$transition"],
Attributes(:label=>"$(δ[k])", :labelfontsize=>"6"))
for k in collect(keys(δ)) if δ[k] != 0]
end
"""
Graph(model::Model)
convert a Model into a GraphViz Graph. Transition are green boxes and states are blue circles. Arrows go from the input states to the output states for each transition.
"""
function Graph(model::Model)
ks = collect(keys(model.Δ))
statenodes = [Node(string("S_$s"), Attributes(:shape=>"circle", :color=>"#6C9AC3")) for s in model.S]
transnodes = [Node(string("T_$k"), Attributes(:shape=>"square", :color=>"#E28F41")) for k in ks]
stmts = vcat(statenodes, transnodes)
edges = map(ks) do k
vcat(edgify(first(model.Δ[k]), k, false),
edgify(last(model.Δ[k]), k, true))
end |> flatten |> collect
stmts = vcat(stmts, edges)
g = Graphviz.Digraph("G", stmts; graph_attrs=graph_attrs, node_attrs=node_attrs, edge_attrs=edge_attrs)
return g
end
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 1418 | using Test
using Petri
using LabelledArrays
@testset "Equality" begin
sir_1 = Petri.Model([1,2,3],[([1,1], [2]),
([1], [1])])
sir_2 = Petri.Model(1:3,[([1,1], [2]),
([1], [1])])
sir_3 = Petri.Model(3,[([1,1], [2]),
([1], [1])])
@test typeof(Graph(sir_1)) == Graph
@test sir_1 == sir_2
@test sir_1 == sir_3
@test EmptyPetri(5) == Petri.Model(1:5, [])
@test EmptyPetri(5) == EmptyPetri(collect(1:5))
sir = Petri.Model([:S,:I,:R],[(LVector(S=1,I=1), LVector(I=2)),
(LVector(I=1), LVector(R=1))])
@test sir == sir
seir = Petri.Model([:S,:E,:I,:R],[(LVector(S=1,I=1), LVector(I=1,E=1)),
(LVector(E=1), LVector(I=1)),
(LVector(I=1), LVector(R=1))])
x = Petri.Model([:S,:E,:I,:R],[(LVector(S=1,I=1), LVector(I=2)),
(LVector(I=1), LVector(R=1))])
y = Petri.Model([:S,:E,:I,:R],[(LVector(S=1,I=1), LVector(I=1,E=1)),
(LVector(E=1), LVector(I=1)),
(LVector(I=1), LVector(R=1)),
(LVector(R=1), LVector(S=1))])
@test sir != seir
@test seir != x
@test seir != y
end
include("solvers.jl")
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | code | 2822 | using Test
using Petri
using LabelledArrays
using OrdinaryDiffEq
using SteadyStateDiffEq
using StochasticDiffEq
using JumpProcesses
@testset "Generation of ODE formulas" begin
sir = Petri.Model([:S,:I,:R],[(LVector(S=1,I=1), LVector(I=2)),
(LVector(I=1), LVector(R=1))])
sirf = vectorfield(sir)
rates = sirf(LVector(S=0.0, I=0.0, R=0.0), LVector(S=100.0,I=1.0,R=0.0), [0.5/101,0.25],0.0)
@test rates.S ≈ -.495 atol=1e-2
@test rates.I ≈ .24505 atol=1e-2
@test rates.R ≈ .25 atol=1e-2
end
@testset "Generation of ODE solutions" begin
@testset "SIR Solving" begin
sir = Petri.Model([:S,:I,:R],[(LVector(S=1,I=1), LVector(I=2)),
(LVector(I=1), LVector(R=1))])
u0 = LVector(S=990.0,I=10.0,R=0.0)
p = [(u,t)->0.5/sum(u), 0.25]
prob = ODEProblem(sir,u0,(0.0,40.0),p)
sol = OrdinaryDiffEq.solve(prob,Tsit5())
@test sum(sol[end]) ≈ 1000 atol=1
@test sol[end].S ≈ 210 atol=1
@test sol[end].I ≈ 14.5 atol=1
@test sol[end].R ≈ 775.5 atol=1
end
end
@testset "Generation of SDE solutions" begin
@testset "SIR Solving" begin
sir = Petri.Model([:S,:I,:R],[(LVector(S=1,I=1), LVector(I=2)),
(LVector(I=1), LVector(R=1))])
u0 = LVector(S=990.0,I=10.0,R=0.0)
p = [(u,t)->(0.5/sum(u)), 0.25]
prob,cb = SDEProblem(sir,u0,(0.0,40.0),p)
sol = StochasticDiffEq.solve(prob,SRA1(),callback=cb)
@test sum(sol[end]) ≈ 1000 atol=1
@test sol[end].S > 0
@test sol[end].I > 0
@test sol[end].R > 0
end
end
@testset "Generation of Jump solutions" begin
@testset "SIR Solving" begin
sir = Petri.Model([:S,:I,:R],[(LVector(S=1,I=1), LVector(I=2)),
(LVector(I=1), LVector(R=1))])
u0 = LVector(S=990.0,I=10.0,R=0.0)
p = [0.5/sum(u0), 0.25]
prob = JumpProblem(sir,u0,(0.0,40.0),p)
sol = JumpProcesses.solve(prob,SSAStepper())
@test sum(sol[end]) == 1000
@test sol[end].S > 0
@test sol[end].I > 0
@test sol[end].R > 0
end
end
@testset "Generation of SteadyState solutions" begin
@testset "SIR Steady State Solving" begin
sir = Petri.Model([:S,:I,:R],[(LVector(S=1,I=1), LVector(I=2)),
(LVector(I=1), LVector(R=1))])
u0 = LVector(S=990.0,I=0.0,R=0.0)
p = [(u,t)->0.5/sum(u), 0.25]
prob = SteadyStateProblem(sir,u0,(0.0,40.0),p)
sol = OrdinaryDiffEq.solve(prob,DynamicSS(Tsit5()))
@test sum(sol.u) ≈ 990 atol=1e-2
@test sol.u.S ≈ 990 atol=1e-2
@test sol.u.I ≈ 0 atol=1e-2
@test sol.u.R ≈ 0 atol=1e-2
end
end
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | docs | 1870 | 
[](https://mehalter.github.io/Petri.jl/stable/)

[](https://codecov.io/gh/mehalter/Petri.jl)
[](https://zenodo.org/badge/latestdoi/203420191)
`Petri.jl` is a Petri net modeling framework for the Julia programming language.
`Petri` makes it easy to build complex reaction networks using a simple DSL.
Once a model is defined, `Petri.jl` has support to generate ODE solutions and
stochastic simulations using `DifferentialEquations.jl`. Examples and basic
usage can be found in the documentation.
## Goals
This is related to the
[DiffeqBiological](https://github.com/JuliaDiffEq/DiffEqBiological.jl) Reaction
DSL, but takes a different implementation approach. Instead of building our
framework around symbolic algebra and standard chemical notion, we are working
off the Applied Category Theory approach to reaction networks [[Baez Pollard, 2017](http://math.ucr.edu/home/baez/RxNet.pdf)].
There are operations that are easy to do on the `Petri.Model` like "add a
transition from R to S" that require simultaneously changing multiple parts of
the algebraic formulation. Applied Category Theory gives a sound theoretical
framework for manipulating Petri Nets as a model in terms of the given domain.
`Petri` is a Julia package primarily intended to investigate how we can
operationalize this theory into practical scientific software.
See [AlgebraicPetri](https://github.com/AlgebraicJulia/AlgebraicPetri.jl) for
tools that work with Petri net models and manipulating them with higher level
APIs based on Applied Category Theory.
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | docs | 56 | # Library Reference
```@autodocs
Modules = [Petri]
```
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 1.3.0 | 7387d445305178e9814bf3f693c6fdedb081316a | docs | 1407 | 
```@meta
CurrentModule = Petri
```
`Petri.jl` is a Petri net modeling framework for the Julia programming language.
`Petri` makes it easy to build complex reaction networks using a simple DSL.
Once a model is defined, `Petri.jl` has support to generate ODE solutions and
stochastic simulations using `DifferentialEquations.jl`.
## Goals
This is related to the
[DiffeqBiological](https://github.com/JuliaDiffEq/DiffEqBiological.jl) Reaction
DSL, but takes a different implementation approach. Instead of building our
framework around symbolic algebra and standard chemical notion, we are working
off the Applied Category Theory approach to reaction networks [[Baez Pollard, 2017](http://math.ucr.edu/home/baez/RxNet.pdf)].
There are operations that are easy to do on the `Petri.Model` like "add a
transition from R to S" that require simultaneously changing multiple parts of
the algebraic formulation. Applied Category Theory gives a sound theoretical
framework for manipulating Petri Nets as a model in terms of the given domain.
`Petri` is a Julia package primarily intended to investigate how we can
operationalize this theory into practical scientific software.
See [AlgebraicPetri](https://github.com/AlgebraicJulia/AlgebraicPetri.jl) for
tools that work with Petri net models and manipulating them with higher level
APIs based on Applied Category Theory.
| Petri | https://github.com/AlgebraicJulia/Petri.jl.git |
|
[
"MIT"
] | 0.1.0 | 8830ae3d26179ed6fc177335b4c252158192c0e5 | code | 907 | using UnionFind
function floodfill(grid, wrap=false)
uf = UnionFinder(length(grid))
height, width = size(grid)
for x in 1:width
for y in 1:height
# Look rightwards.
if x != width && grid[x, y] == grid[x + 1, y]
union!(uf, flatten(x, y, grid), flatten(x + 1, y, grid))
elseif wrap && grid[x, y] == grid[1, y]
union!(uf, flatten(x, y, grid), flatten(1, y, grid))
end
# Look upwards.
if y != height && grid[x, y] == grid[x, y + 1]
union!(uf, flatten(x, y, grid), flatten(x, y + 1, grid))
elseif wrap && grid[x, y] == grid[x, 1]
union!(uf, flatten(x, y, grid), flatten(x, 1, grid))
end
end
end
cf = CompressedFinder(uf)
return reshape(cf.ids, size(grid))
end
flatten(x, y, grid) = y + (x - 1)size(grid)[1]
| UnionFind | https://github.com/epatters/UnionFind.jl.git |
|
[
"MIT"
] | 0.1.0 | 8830ae3d26179ed6fc177335b4c252158192c0e5 | code | 364 | using UnionFind
# edges must be pre-sorted according to weight.
function kruskal{T <: Integer}(nodes :: T, edges :: Array{(T, T)})
uf = UnionFinder(nodes)
mst = Array{(T, T)}
for i in 1:length(edges)
(u, v) = edges[i]
if find!(uf, u) != find!(uf, v)
union!(uf, u, v)
push!(mst, (u, v))
end
end
end
| UnionFind | https://github.com/epatters/UnionFind.jl.git |
|
[
"MIT"
] | 0.1.0 | 8830ae3d26179ed6fc177335b4c252158192c0e5 | code | 1523 | # `CompressedFinder{T <: Integer}` is an optimized variant of UnionFinder{T}
# which does not support the addition of more edges. `CompressedFinder` also
# tracks the number of groups in the graph and garuantees that all group IDs
# will be between 1 and the total group number, inclusive.
mutable struct CompressedFinder{T <: Integer}
ids :: Vector{T}
groups :: T
# `CompressedFinder(uf)` creates a `CompressedFinder` instance from the
# groups within `uf`.
function CompressedFinder{T}(uf :: UnionFinder{T}) where T
groups = zero(T)
ids = zeros(T, length(uf.parents))
for i in one(T):convert(T, length(uf.parents))
root = find!(uf, i)
if ids[root] == 0
groups += 1
ids[root] = groups
end
ids[i] = ids[root]
end
return new(ids, convert(T, groups))
end
end
CompressedFinder(uf :: UnionFinder) = CompressedFinder{eltype(uf.sizes)}(uf)
# `find(cf, node)` returns the group ID of `node`. `node` must be a valid
# index into `uf`.
function find(cf :: CompressedFinder{T}, node :: T) where T <: Integer
if node <= 0 || node > length(cf.ids)
throw(BoundsError())
end
return cf.ids[node]
end
# `length(cf)` returns the number of nodes in `cf`.
function Base.length(cf :: CompressedFinder)
return length(cf.ids)
end
# `groups(cf)` returns the number of groups in `cf`.
function groups(cf :: CompressedFinder)
return cf.groups
end
| UnionFind | https://github.com/epatters/UnionFind.jl.git |
|
[
"MIT"
] | 0.1.0 | 8830ae3d26179ed6fc177335b4c252158192c0e5 | code | 251 | module UnionFind
import Base: union!
if VERSION < VersionNumber("1.0.0")
import Base: find
end
export UnionFinder, CompressedFinder
export reset!, union!, find!, size!, find, groups
include("UnionFinder.jl")
include("CompressedFinder.jl")
end
| UnionFind | https://github.com/epatters/UnionFind.jl.git |
|
[
"MIT"
] | 0.1.0 | 8830ae3d26179ed6fc177335b4c252158192c0e5 | code | 4065 | # `UnionFinder{T <: Integer}` is a graph containing a constant number of nodes
# which allows for union-find operations. All nodes are indexed by an integer
# of type `T` which is between 1 an the number of internal nodes.
mutable struct UnionFinder{T <: Integer}
sizes :: Vector{T}
parents :: Vector{T}
# `UnionFinder(nodes)` returns a `UnionFinder` with `nodes` unconnected
# internal nodes.
function UnionFinder{T}(nodes :: T) where T
if nodes <= 0
throw(ArgumentError("Non-positive nodes, $nodes."))
end
uf = new(Vector{T}(undef, Int(nodes)), Vector{T}(undef, Int(nodes)))
reset!(uf)
return uf
end
end
UnionFinder(nodes :: Integer) = UnionFinder{typeof(nodes)}(nodes)
# `reset(uf)` disconnects all the nodes within `uf`.
function reset!(uf :: UnionFinder)
for i in 1:length(uf.parents)
uf.sizes[i] = 1
uf.parents[i] = i
end
end
# `union!(uf, iterator)` iterates through `iterator` which returns integer
# edges, (`u`, `v`), and connects them within `uf`. `u` and `v` must be valid
# node indices for `uf`.
function union!(uf :: UnionFinder{T}, iterator) where T <: Integer
for (u, v) in iterator
union!(uf, u, v)
end
end
# `union!(uf, us, vs)` connects nodes within `uf` which are bridged by
# the edges (`us[i]`, `vs[i]`). All values in `us` and `vs` must be valid node
# indices for `uf` and `us` and `vs` must be the same length.
function union!(uf :: UnionFinder{T},
us :: Vector{T}, vs :: Vector{T}) where T <: Integer
if length(us) != length(vs)
throw(ArgumentError("us and vs not of the same length."))
end
for i in 1:length(us)
union!(uf, us[i], vs[i])
end
end
# `union!(uf, edges)` conncts all nodes within `uf` which are bridged by an
# edge within `edges`. Both vertices for each edge must be valid node indices
# into `uf`.
function union!(uf :: UnionFinder{T},
edges :: Vector{Tuple{T,T}}) where T <: Integer
for (u, v) in edges
union!(uf, u, v)
end
end
# `union!(uf, node1, node2)` connects the nodes within `uf` with indices
# `node1` and `node2`. `node1` and `node2` must be valid indices into `uf`.
function union!(uf :: UnionFinder{T}, node1 :: T, node2 :: T) where T <: Integer
root1 = find!(uf, node1)
root2 = find!(uf, node2)
# TODO: Test whether using rank or using size is better for performance.
if root1 == root2
return
elseif uf.sizes[root1] < uf.sizes[root2]
uf.parents[root1] = root2
uf.sizes[root2] += uf.sizes[root1]
else
uf.parents[root2] = root1
uf.sizes[root1] += uf.sizes[root2]
end
end
# `find!(uf, node)` returns the group ID of `node`. `node` must be a valid
# index into `uf`.
function find!(uf :: UnionFinder{T}, node :: T) where T <: Integer
if node > length(uf.parents) || node <= 0
throw(BoundsError())
end
if uf.parents[node] != uf.parents[uf.parents[node]]
compress!(uf, node)
end
return uf.parents[node]
end
# `compress(uf, node)` compresses the internal parental node tree so that
# all nodes between `node` and the root of its group will point directly to the
# root. `node` must be a valid index into `uf`.
#
# Not publicly exported.
function compress!(uf :: UnionFinder{T}, node :: T) where T <: Integer
child = node
parent = uf.parents[child]
while child != parent
child = parent
parent = uf.parents[child]
end
root = child
child = node
parent = uf.parents[child]
uf.parents[child] = root
while child != parent
child = parent
parent = uf.parents[child]
uf.parents[child] = root
end
end
# `length(uf)` returns the number of nodes in `uf`.
function Base.length(uf :: UnionFinder)
return length(uf.parents)
end
# `size!(uf, node)` returns the size of the group containing `node`.
function size!(uf :: UnionFinder{T}, node :: T) where T <: Integer
return uf.sizes[find!(uf, node)]
end
| UnionFind | https://github.com/epatters/UnionFind.jl.git |
|
[
"MIT"
] | 0.1.0 | 8830ae3d26179ed6fc177335b4c252158192c0e5 | code | 2545 | function time_unit(t)
units = ["hr", "min", "s", "ms", "us", "ns", "ps"]
sizes = [60.0 * 60.0, 60.0, 1.0, 1e-3, 1e-6, 1e-9, 1e-12]
for (unit, size) in zip(units, sizes)
if t / 10 > size
return unit, size
end
end
return units[end], sizes[end]
end
function fmt_time(ts)
avg = sum(ts) / length(ts)
unit, size = time_unit(avg)
return @sprintf "%d %s" (avg / size) unit
end
function bench_graph_union(nodes :: Int, edges :: Int)
us = [convert(Int, floor(nodes * rand()) + 1) for e in 1:edges]
vs = [convert(Int, floor(nodes * rand()) + 1) for e in 1:edges]
uf = UnionFinder(nodes)
t = @elapsed union!(uf, us, vs)
return uf, t
end
function bench_grid_union(nodes :: Int, edges :: Int)
width = convert(Int, ceil(sqrt(nodes)))
us = [convert(Int, floor(nodes * rand()) + 1) for e in 1:edges]
dirs = [1, nodes - 1, width, nodes - width]
vs = [(dirs[convert(Int, floor(4 * rand()) + 1)] + us[e]) % nodes + 1
for e in 1:edges]
uf = UnionFinder(nodes)
t = @elapsed union!(uf, us, vs)
return uf, t
end
function bench_avg(nodes :: Int, frac :: Float64, sweeps :: Int, f :: Function)
uts = Vector{Float64}(undef, sweeps)
cts = Vector{Float64}(undef, sweeps)
edges = convert(Int, ceil(nodes * frac))
for i in 1:sweeps
uf, uts[i] = f(nodes, edges)
cts[i] = @elapsed CompressedFinder(uf)
uts[i] = edges == 0 ? uts[i] : uts[i] / edges
cts[i] = cts[i] / nodes
end
@printf "%12s/edge %12s/node\n" fmt_time(uts) fmt_time(cts)
end
function benchmark_main()
@printf "%30s%17s %17s\n" " " "UnionFinder" "CompressedFinder"
@printf "%30s" "Sparse 1,000 node graph"
bench_avg(1000, 0.1, 1000, bench_graph_union)
@printf "%30s" "Dense 1,000 node graph"
bench_avg(1000, 0.8, 1000, bench_graph_union)
@printf "%30s" "Sparse 1,000,000 node graph"
bench_avg(1000 * 1000, 0.1, 10, bench_graph_union)
@printf "%30s" "Dense 1,000,000 node graph"
bench_avg(1000 * 1000, 0.8, 10, bench_graph_union)
println()
@printf "%30s" "Sparse 1,000 node grid"
bench_avg(1000, 0.1, 1000, bench_grid_union)
@printf "%30s" "Dense 1,000 node grid"
bench_avg(1000, 0.8, 1000, bench_grid_union)
@printf "%30s" "Sparse 1,000,000 node grid"
bench_avg(1000 * 1000, 0.1, 10, bench_grid_union)
@printf "%30s" "Dense 1,000,000 node grid"
bench_avg(1000 * 1000, 0.8, 10, bench_grid_union)
end
benchmark_main()
| UnionFind | https://github.com/epatters/UnionFind.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.