code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
```
%run ../setup/nb_setup
%matplotlib inline
```
# Compute a Galactic orbit for a star using Gaia data
Author(s): Adrian Price-Whelan
## Learning goals
In this tutorial, we will retrieve the sky coordinates, astrometry, and radial velocity for a star — [Kepler-444](https://en.wikipedia.org/wiki/Kepler-444) — and compute its orbit in the default Milky Way mass model implemented in Gala. We will compare the orbit of Kepler-444 to the orbit of the Sun and a random sample of nearby stars.
### Notebook Setup and Package Imports
```
import astropy.coordinates as coord
import astropy.units as u
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from pyia import GaiaData
# Gala
import gala.dynamics as gd
import gala.potential as gp
```
## Define a Galactocentric Coordinate Frame
We will start by defining a Galactocentric coordinate system using `astropy.coordinates`. We will adopt the latest parameter set assumptions for the solar Galactocentric position and velocity as implemented in Astropy, but note that these parameters are customizable by passing parameters into the `Galactocentric` class below (e.g., you could change the sun-galactic center distance by setting `galcen_distance=...`).
```
with coord.galactocentric_frame_defaults.set("v4.0"):
galcen_frame = coord.Galactocentric()
galcen_frame
```
## Define the Solar Position and Velocity
In this coordinate system, the sun is along the $x$-axis (at a negative $x$ value), and the Galactic rotation at this position is in the $+y$ direction. The 3D position of the sun is therefore given by:
```
sun_xyz = u.Quantity(
[-galcen_frame.galcen_distance, 0 * u.kpc, galcen_frame.z_sun] # x,y,z
)
```
We can combine this with the solar velocity vector (defined in the `astropy.coordinates.Galactocentric` frame) to define the sun's phase-space position, which we will use as initial conditions shortly to compute the orbit of the Sun:
```
sun_vxyz = galcen_frame.galcen_v_sun
sun_vxyz
sun_w0 = gd.PhaseSpacePosition(pos=sun_xyz, vel=sun_vxyz)
```
To compute the sun's orbit, we need to specify a mass model for the Galaxy. Here, we will use the default Milky Way mass model implemented in Gala, which is defined in detail in the Gala documentation: [Defining a Milky Way model](define-milky-way-model.html). Here, we will initialize the potential model with default parameters:
```
mw_potential = gp.MilkyWayPotential()
mw_potential
```
This potential is composed of four mass components meant to represent simple models of the different structural components of the Milky Way:
```
for k, pot in mw_potential.items():
print(f"{k}: {pot!r}")
```
With a potential model for the Galaxy and initial conditions for the sun, we can now compute the Sun's orbit using the default integrator (Leapfrog integration): We will compute the orbit for 4 Gyr, which is about 16 orbital periods.
```
sun_orbit = mw_potential.integrate_orbit(sun_w0, dt=0.5 * u.Myr, t1=0, t2=4 * u.Gyr)
```
Let's plot the Sun's orbit in 3D to get a feel for the geometry of the orbit:
```
fig, ax = sun_orbit.plot_3d()
lim = (-12, 12)
ax.set(xlim=lim, ylim=lim, zlim=lim)
```
## Retrieve Gaia Data for Kepler-444
As a comparison, we will compute the orbit of the exoplanet-hosting star "Kepler-444." To get Gaia data for this star, we first have to retrieve its sky coordinates so that we can do a positional cross-match query on the Gaia catalog. We can retrieve the sky position of Kepler-444 from Simbad using the `SkyCoord.from_name()` classmethod, which queries Simbad under the hood to resolve the name:
```
star_sky_c = coord.SkyCoord.from_name("Kepler-444")
star_sky_c
```
We happen to know a priori that Kepler-444 has a large proper motion, so the sky position reported by Simbad could be off from the Gaia sky position (epoch=2016) by many arcseconds. To run and retrieve the Gaia data, we will use the [pyia](http://pyia.readthedocs.io/) package: We can pass in an ADQL query, which `pyia` uses to query the Gaia science archive using `astroquery`, and returns the data as a `pyia.GaiaData` object. To run the query, we will do a sky position cross-match with a large positional tolerance by setting the cross-match radius to 15 arcseconds, but we will take the brightest cross-matched source within this region as our match:
```
star_gaia = GaiaData.from_query(
f"""
SELECT TOP 1 * FROM gaiaedr3.gaia_source
WHERE 1=CONTAINS(
POINT('ICRS', {star_sky_c.ra.degree}, {star_sky_c.dec.degree}),
CIRCLE('ICRS', ra, dec, {(15*u.arcsec).to_value(u.degree)})
)
ORDER BY phot_g_mean_mag
"""
)
star_gaia
```
We will assume (and hope!) that this source is Kepler-444, but we know that it is fairly bright compared to a typical Gaia source, so we should be safe.
We can now use the returned `pyia.GaiaData` object to retrieve an astropy `SkyCoord` object with all of the position and velocity measurements taken from the Gaia archive record for this source:
```
star_gaia_c = star_gaia.get_skycoord()
star_gaia_c
```
To compute this star's Galactic orbit, we need to convert its observed, Heliocentric (actually solar system barycentric) data into the Galactocentric coordinate frame we defined above. To do this, we will use the `astropy.coordinates` transformation framework using the `.transform_to()` method, and we will pass in the `Galactocentric` coordinate frame we defined above:
```
star_galcen = star_gaia_c.transform_to(galcen_frame)
star_galcen
```
Let's print out the Cartesian position and velocity for Kepler-444:
```
print(star_galcen.cartesian)
print(star_galcen.velocity)
```
Now with Galactocentric position and velocity components for Kepler-444, we can create Gala initial conditions and compute its orbit on the time grid used to compute the Sun's orbit above:
```
star_w0 = gd.PhaseSpacePosition(star_galcen.data)
star_orbit = mw_potential.integrate_orbit(star_w0, t=sun_orbit.t)
```
We can now compare the orbit of Kepler-444 to the solar orbit we computed above. We will plot the two orbits in two projections: First in the $x$-$y$ plane (Cartesian positions), then in the *meridional plane*, showing the cylindrical $R$ and $z$ position dependence of the orbits:
```
fig, axes = plt.subplots(1, 2, figsize=(10, 5), constrained_layout=True)
sun_orbit.plot(["x", "y"], axes=axes[0])
star_orbit.plot(["x", "y"], axes=axes[0])
axes[0].set_xlim(-10, 10)
axes[0].set_ylim(-10, 10)
sun_orbit.cylindrical.plot(
["rho", "z"],
axes=axes[1],
auto_aspect=False,
labels=["$R$ [kpc]", "$z$ [kpc]"],
label="Sun",
)
star_orbit.cylindrical.plot(
["rho", "z"],
axes=axes[1],
auto_aspect=False,
labels=["$R$ [kpc]", "$z$ [kpc]"],
label="Kepler-444",
)
axes[1].set_xlim(0, 10)
axes[1].set_ylim(-5, 5)
axes[1].set_aspect("auto")
axes[1].legend(loc="best", fontsize=15)
```
### Exercise: How does Kepler-444's orbit differ from the Sun's?
- What are the guiding center radii of the two orbits?
- What is the maximum $z$ height reached by each orbit?
- What are their eccentricities?
- Can you guess which star is older based on their kinematics?
- Which star do you think has a higher metallicity?
### Exercise: Compute orbits for Monte Carlo sampled initial conditions using the Gaia error distribution
*Hint: Use the `pyia.GaiaData.get_error_samples()` method to generate samples from the Gaia error distribution*
- Generate 128 samples from the error distribution
- Construct a `SkyCoord` object with all of these Monte Carlo samples
- Transform the error sample coordinates to the Galactocentric frame and define Gala initial conditions (a `PhaseSpacePosition` object)
- Compute orbits for all error samples using the same time grid we used above
- Compute the eccentricity and $L_z$ for all samples: what is the standard deviation of the eccentricity and $L_z$ values?
- With what fractional precision can we measure this star's eccentricity and $L_z$? (i.e. what is $\textrm{std}(e) / \textrm{mean}(e)$ and the same for $L_z$)
### Exercise: Comparing these orbits to the orbits of other Gaia stars
Retrieve Gaia data for a set of 100 random Gaia stars within 200 pc of the sun with measured radial velocities and well-measured parallaxes using the query:
SELECT TOP 100 * FROM gaiaedr3.gaia_source
WHERE dr2_radial_velocity IS NOT NULL AND
parallax_over_error > 10 AND
ruwe < 1.2 AND
parallax > 5
ORDER BY random_index
```
# random_stars_g = ..
```
Compute orbits for these stars for the same time grid used above to compute the sun's orbit:
```
# random_stars_c = ...
# random_stars_galcen = ...
# random_stars_w0 = ...
# random_stars_orbits = ...
```
Plot the initial (present-day) positions of all of these stars in Galactocentric Cartesian coordinates:
Now plot the orbits of these stars in the x-y and R-z planes:
```
fig, axes = plt.subplots(1, 2, figsize=(10, 5), constrained_layout=True)
random_stars_orbits.plot(["x", "y"], axes=axes[0])
axes[0].set_xlim(-15, 15)
axes[0].set_ylim(-15, 15)
random_stars_orbits.cylindrical.plot(
["rho", "z"],
axes=axes[1],
auto_aspect=False,
labels=["$R$ [kpc]", "$z$ [kpc]"],
)
axes[1].set_xlim(0, 15)
axes[1].set_ylim(-5, 5)
axes[1].set_aspect("auto")
```
Compute maximum $z$ heights ($z_\textrm{max}$) and eccentricities for all of these orbits. Compare the Sun, Kepler-444, and this random sampling of nearby stars. Where do the Sun and Kepler-444 sit relative to the random sample of nearby stars in terms of $z_\textrm{max}$ and eccentricity? (Hint: plot $z_\textrm{max}$ vs. eccentricity and highlight the Sun and Kepler-444!) Are either of them outliers in any way?
```
# rand_zmax = ...
# rand_ecc = ...
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(
rand_ecc, rand_zmax, color="k", alpha=0.4, s=14, lw=0, label="random nearby stars"
)
ax.scatter(sun_orbit.eccentricity(), sun_orbit.zmax(), color="tab:orange", label="Sun")
ax.scatter(
star_orbit.eccentricity(), star_orbit.zmax(), color="tab:cyan", label="Kepler-444"
)
ax.legend(loc="best", fontsize=14)
ax.set_xlabel("eccentricity, $e$")
ax.set_ylabel(r"max. $z$ height, $z_{\rm max}$ [kpc]")
```
| github_jupyter |
```
import os
import tarfile
import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_PATH = os.path.join("datasets","housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url = HOUSING_URL,housing_path = HOUSING_PATH):
os.makedirs(housing_path,exist_ok=True)
tgz_path = os.path.join(housing_path,"housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
fetch_housing_data()
import pandas as pd
def load_housing_data(housing_path = HOUSING_PATH):
csv_path = os.path.join(housing_path,"housing.csv")
return pd.read_csv(csv_path)
housing = load_housing_data()
housing.head()
housing.info()
housing["ocean_proximity"].value_counts()
housing.describe()
import matplotlib.pyplot as plt
%matplotlib inline
housing.hist(bins=50, figsize=(20,15))
plt.show()
import numpy as np
def split_test_data(data,test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data)*test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_test_data(housing,0.2)
len(train_set)
len(test_set)
from zlib import crc32
def test_set_check(identifier, test_ratio):
return crc32(np.int64(identifier)) & 0xffffffff < test_ratio * 2**32
def split_train_test_by_id(data, test_ratio, id_column):
ids = data[id_column]
in_test_set = ids.apply(lambda id_ : test_set_check(id_ , test_ratio))
return data.loc[~in_test_set], data.loc[in_test_set]
housing_with_id = housing.reset_index()
train_set, test_set = split_train_test_by_id(housing_with_id,0.2,"index")
housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
train_set, test_set = split_train_test_by_id(housing_with_id,0.2,"id")
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing,test_size = 0.2, random_state = 42)
housing["income_cat"] = pd.cut(housing["median_income"],bins=[0.,1.5,3.0,4.5,6.,np.inf],labels=[1,2,3,4,5])
housing["income_cat"].hist()
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits = 1,test_size=0.2,random_state=42)
for train_index, test_index in split.split(housing,housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
strat_test_set["income_cat"].value_counts()/len(strat_test_set)
strat_train_set["income_cat"].value_counts()/len(strat_train_set)
for set_ in (strat_train_set,strat_test_set):
set_.drop("income_cat",axis=1,inplace=True)
housing = strat_train_set.copy()
housing.plot(kind="scatter",x="longitude",y="latitude")
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.1)
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.4,s=housing["population"]/100,label = "population",figsize =(10,7),c="median_house_value",cmap=plt.get_cmap("jet"),colorbar=True)
plt.legend()
housing.plot(kind="scatter",x="longitude",y="latitude",alpha=0.4,s=housing["population"]/100,label = "population",figsize =(10,7),c="median_house_value",cmap=plt.get_cmap("jet"),colorbar=True)
plt.legend()
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
corr_matrix
from pandas.plotting import scatter_matrix
attributes = ["median_house_value","median_income","total_rooms","housing_median_age"]
scatter_matrix(housing[attributes],figsize=(12,8))
housing.plot(kind="scatter",x="median_income",y="median_house_value",alpha = 0.1)
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"] = housing["population"]/housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
housing = strat_train_set.drop("median_house_value",axis=1)
housing_labels = strat_train_set["median_house_value"].copy()
# housing.dropna(subset=["total_bedrooms"]) //option 1
# housing.drop("total_bedrooms",axis=1) //option 2
median = housing["total_bedrooms"].median() #//option 3
housing["total_bedrooms"].fillna(median,inplace=True)
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy="median")
housing_num = housing.drop("ocean_proximity",axis=1)
imputer.fit(housing_num)
imputer.statistics_
housing_num.median().values
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X,columns=housing_num.columns,index=housing_num.index)
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(10)
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat_encoded[0:10]
ordinal_encoder.categories_
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
housing_cat_1hot.toarray()
cat_encoder.categories_
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, households_ix = 3,4,5,6
class CombinedAttributesAdder(BaseEstimator,TransformerMixin):
def __init__(self,add_bedrooms_per_room=True):
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self,X,y=None):
return self
def transform(self,X,y=None):
rooms_per_households = X[:,rooms_ix]/X[:,households_ix]
population_per_household = X[:,population_ix]/X[:,households_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:,bedrooms_ix]/X[:,rooms_ix]
return np.c_[X,rooms_per_households,population_per_household,bedrooms_per_room]
else:
return np.c_[X,rooms_per_households,population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attribs = attr_adder.transform(housing.values)
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeine = Pipeline([('imputer',SimpleImputer(strategy="median")),("attribs_adder",CombinedAttributesAdder()),("std_scaler",StandardScaler())])
housing_num_tr = num_pipeine.fit_transform(housing_num)
from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([("num",num_pipeine,num_attribs),("cat",OneHotEncoder(),cat_attribs)])
housing_prepared = full_pipeline.fit_transform(housing)
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print("Predictions:",lin_reg.predict(some_data_prepared))
print("Labels:",list(some_labels))
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels,housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse)
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared,housing_labels)
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
scores = cross_val_score(tree_reg, housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
tree_rmse_scores = np.sqrt(-scores)
def display_scores(scores):
print("Scores:",scores)
print("Mean:",scores.mean())
print("Standard deviation:",scores.std())
display_scores(tree_rmse_scores)
lin_scores = cross_val_score(lin_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared,housing_labels)
housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels,housing_predictions)
forest_rmse = np.sqrt(forest_mse)
print(forest_rmse)
forest_scores = cross_val_score(forest_reg,housing_prepared,housing_labels,scoring="neg_mean_squared_error",cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)
# imp+
```
| github_jupyter |
# Image Denoising with Autoencoders
## Introduction and Importing Libraries
___
Note: If you are starting the notebook from this task, you can run cells from all previous tasks in the kernel by going to the top menu and then selecting Kernel > Restart and Run All
___
```
import numpy as np
from tensorflow.keras.datasets import mnist
from matplotlib import pyplot as plt
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Dense, Input
from tensorflow.keras.callbacks import EarlyStopping, LambdaCallback
from tensorflow.keras.utils import to_categorical
%matplotlib inline
```
## Data Preprocessing
___
Note: If you are starting the notebook from this task, you can run cells from all previous tasks in the kernel by going to the top menu and then selecting Kernel > Restart and Run All
___
```
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float')/255.
x_test = x_test.astype('float')/255.
x_train = np.reshape(x_train, (60000, 784))
x_test = np.reshape(x_test, (10000, 784))
```
## Adding Noise
___
Note: If you are starting the notebook from this task, you can run cells from all previous tasks in the kernel by going to the top menu and then selecting Kernel > Restart and Run All
___
```
x_train_noisy = x_train + np.random.rand(60000, 784)*0.9
x_test_noisy = x_test + np.random.rand(10000, 784)*0.9
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
def Plot(x, p, labels = False):
plt.figure(figsize = (20, 2))
for i in range(10):
plt.subplot(1, 10, i + 1)
plt.imshow(x[i].reshape(28,28), cmap = 'viridis')
plt.xticks([])
plt.yticks([])
if labels:
plt.xlabel(np.argmax(p[i]))
plt.show()
Plot(x_train, None)
Plot(x_train_noisy, None)
```
## Building and Training a Classifier
___
Note: If you are starting the notebook from this task, you can run cells from all previous tasks in the kernel by going to the top menu and then selecting Kernel > Restart and Run All
___
```
classifier = Sequential([
Dense(256, activation = 'relu', input_shape = (784,)),
Dense(256, activation = 'relu'),
Dense(256, activation = 'softmax')
])
classifier.compile(optimizer = 'adam',
loss = 'sparse_categorical_crossentropy',
metrics = ['accuracy'])
classifier.fit(x_train, y_train, batch_size = 512, epochs = 3)
loss, acc = classifier.evaluate(x_test, y_test)
print(acc)
loss, acc = classifier.evaluate(x_test_noisy, y_test)
print(acc)
```
## Building the Autoencoder
___
Note: If you are starting the notebook from this task, you can run cells from all previous tasks in the kernel by going to the top menu and then selecting Kernel > Restart and Run All
___
```
input_image = Input(shape = (784,))
encoded = Dense(64, activation = 'relu')(input_image)
decoded = Dense(784, activation = 'sigmoid')(encoded)
autoencoder = Model(input_image, decoded)
autoencoder.compile(loss = 'binary_crossentropy', optimizer = 'adam')
```
## Training the Autoencoder
___
Note: If you are starting the notebook from this task, you can run cells from all previous tasks in the kernel by going to the top menu and then selecting Kernel > Restart and Run All
___
```
autoencoder.fit(
x_train_noisy,
x_train,
epochs = 100,
batch_size = 512,
validation_split = 0.2,
verbose = False,
callbacks = [
EarlyStopping(monitor = 'val_loss', patience = 5),
LambdaCallback(on_epoch_end = lambda e,l: print('{:.3f}'.format(l['val_loss']), end = ' _ '))
]
)
print(' _ ')
print('Training is complete!')
```
## Denoised Images
___
Note: If you are starting the notebook from this task, you can run cells from all previous tasks in the kernel by going to the top menu and then selecting Kernel > Restart and Run All
___
```
preds = autoencoder.predict(x_test_noisy)
Plot(x_test_noisy, None)
Plot(preds, None)
loss, acc = classifier.evaluate(preds, y_test)
print(acc)
```
## Composite Model
___
Note: If you are starting the notebook from this task, you can run cells from all previous tasks in the kernel by going to the top menu and then selecting Kernel > Restart and Run All
___
```
input_image=Input(shape=(784,))
x=autoencoder(input_image)
y=classifier(x)
denoise_and_classfiy = Model(input_image, y)
predictions=denoise_and_classfiy.predict(x_test_noisy)
Plot(x_test_noisy, predictions, True)
Plot(x_test, to_categorical(y_test), True)
```
| github_jupyter |
# Lab 04 : Train vanilla neural network -- solution
# Training a one-layer net on FASHION-MNIST
```
# For Google Colaboratory
import sys, os
if 'google.colab' in sys.modules:
from google.colab import drive
drive.mount('/content/gdrive')
file_name = 'train_vanilla_nn_solution.ipynb'
import subprocess
path_to_file = subprocess.check_output('find . -type f -name ' + str(file_name), shell=True).decode("utf-8")
print(path_to_file)
path_to_file = path_to_file.replace(file_name,"").replace('\n',"")
os.chdir(path_to_file)
!pwd
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from random import randint
import utils
```
### Download the TRAINING SET (data+labels)
```
from utils import check_fashion_mnist_dataset_exists
data_path=check_fashion_mnist_dataset_exists()
train_data=torch.load(data_path+'fashion-mnist/train_data.pt')
train_label=torch.load(data_path+'fashion-mnist/train_label.pt')
print(train_data.size())
print(train_label.size())
```
### Download the TEST SET (data only)
```
test_data=torch.load(data_path+'fashion-mnist/test_data.pt')
print(test_data.size())
```
### Make a one layer net class
```
class one_layer_net(nn.Module):
def __init__(self, input_size, output_size):
super(one_layer_net , self).__init__()
self.linear_layer = nn.Linear( input_size, output_size , bias=False)
def forward(self, x):
y = self.linear_layer(x)
prob = F.softmax(y, dim=1)
return prob
```
### Build the net
```
net=one_layer_net(784,10)
print(net)
```
### Take the 4th image of the test set:
```
im=test_data[4]
utils.show(im)
```
### And feed it to the UNTRAINED network:
```
p = net( im.view(1,784))
print(p)
```
### Display visually the confidence scores
```
utils.show_prob_fashion_mnist(p)
```
### Train the network (only 5000 iterations) on the train set
```
criterion = nn.NLLLoss()
optimizer=torch.optim.SGD(net.parameters() , lr=0.01 )
for iter in range(1,5000):
# choose a random integer between 0 and 59,999
# extract the corresponding picture and label
# and reshape them to fit the network
idx=randint(0, 60000-1)
input=train_data[idx].view(1,784)
label=train_label[idx].view(1)
# feed the input to the net
input.requires_grad_()
prob=net(input)
# update the weights (all the magic happens here -- we will discuss it later)
log_prob=torch.log(prob)
loss = criterion(log_prob, label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
```
### Take the 34th image of the test set:
```
im=test_data[34]
utils.show(im)
```
### Feed it to the TRAINED net:
```
p = net( im.view(1,784))
print(p)
```
### Display visually the confidence scores
```
utils.show_prob_fashion_mnist(prob)
```
### Choose image at random from the test set and see how good/bad are the predictions
```
# choose a picture at random
idx=randint(0, 10000-1)
im=test_data[idx]
# diplay the picture
utils.show(im)
# feed it to the net and display the confidence scores
prob = net( im.view(1,784))
utils.show_prob_fashion_mnist(prob)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/TerradasExatas/IA_e_Machine_Learning/blob/main/IA_ConvNN_classificacao_MNIST.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#https://machinelearningmastery.com/how-to-develop-a-convolutional-neural-network-from-scratch-for-mnist-handwritten-digit-classification/
#https://towardsdatascience.com/convolutional-neural-networks-for-beginners-using-keras-and-tensorflow-2-c578f7b3bf25
#https://github.com/jorditorresBCN/python-deep-learning/blob/master/08_redes_neuronales_convolucionales.ipynb
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#importa o dataset (as imagens da base "mnist")
mnist = tf.keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
#inspeciona o data set
print('train imagens original shape:',train_images.shape)
print('train labels original shape:',train_labels.shape)
plt.rcParams.update({'font.size':14})
plt.figure(figsize=(8,4))
for i in range(2*4):
plt.subplot(2,4,i+1)
plt.xticks([]);plt.yticks([])
plt.imshow(train_images[i],cmap=plt.cm.binary)
plt.xlabel(str(train_labels[i]))
plt.show()
#prepara o data set
train_images = train_images.reshape((60000, 28, 28, 1))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28, 28, 1))
test_images = test_images.astype('float32') / 255
#inspeciona os dados preparados
print ('train images new shape:',train_images.shape)
N_class=10
#Criando a rede neural
model = tf.keras.Sequential(name='rede_IF_CNN_MNIST')
#Adicionando as camadas
model.add(tf.keras.layers.Conv2D(12, (5, 5),
activation='relu', input_shape=(28, 28, 1)))
model.add(tf.keras.layers.MaxPooling2D((2, 2)))
model.add(tf.keras.layers.Conv2D(24, (3, 3), activation='relu'))
model.add(tf.keras.layers.MaxPooling2D((2, 2)))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(N_class, activation='softmax'))
#compilando a rede
opt=tf.keras.optimizers.Adam(learning_rate=0.002)
model.compile(optimizer=opt, loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.summary()
# treinando a rede
history=model.fit(train_images, train_labels,epochs=8,verbose=1)
#mostra a performace do treinamento da rede
plt.figure()
plt.subplot(2,1,1);plt.semilogy(history.history['loss'],'k')
plt.legend(['loss'])
plt.subplot(2,1,2);plt.plot(history.history['accuracy'],'k')
plt.legend(['acuracia'])
plt.tight_layout()
#testando a rede com os dados de teste
pred = model.predict(test_images)
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print('\n accuracia dos dados de teste: ', test_acc)
#encontra a classe de maior probabilidade
labels_pred=np.argmax(pred,axis=1)
#mostra 15 resultados esperados e os alcançados lado a lado
print('data and pred = \n',np.concatenate(
(test_labels[None].T[0:15], labels_pred[None].T[0:15]),axis=1))
```
| github_jupyter |
```
from pandas import read_csv
import cv2
import glob
import os
import numpy as np
import logging
import coloredlogs
logger = logging.getLogger(__name__)
coloredlogs.install(level='DEBUG')
coloredlogs.install(level='DEBUG', logger=logger)
IM_EXTENSIONS = ['png', 'jpg', 'jpeg', 'bmp']
def read_img(img_path, img_shape=(128, 128)):
"""
load image file and divide by 255.
"""
img = cv2.imread(img_path)
img = cv2.resize(img, img_shape)
img = img.astype('float')
img /= 255.
return img
dataset_dir = './data/images/'
label_path = './data/label.csv'
batch_size=32,
img_shape=(128, 128)
label_df = read_csv(label_path)
# img_files = glob.glob(dataset_dir + '*')
# img_files = [f for f in img_files if f[-3:] in IM_EXTENSIONS]
label_idx = label_df.set_index('filename')
img_files = label_idx.index.unique().values
label_idx.loc['0_Parade_Parade_0_628.jpg'].head()
label_idx.iloc[0:5]
len(img_files)
def append_zero(arr):
return np.append([0], arr)
# temp = label_idx.loc[img_files[0]].values[:, :4] #[0, 26, 299, 36, 315]
# np.apply_along_axis(append_zero, 1, temp)
"""
data loader
return image, [class_label, class_and_location_label]
"""
numofData = len(img_files) # endwiths(png,jpg ...)
data_idx = np.arange(numofData)
while True:
batch_idx = np.random.choice(data_idx, size=batch_size, replace=False)
batch_img = []
batch_label = []
batch_label_cls = []
for i in batch_idx:
img = read_img(dataset_dir + img_files[i], img_shape=img_shape)
label_idx = label_df.set_index('filename')
img_files = label_idx.index.unique().values
label = label_idx.loc[img_files[i]].values
label = np.array(label, ndmin=2)
label = label[:, :4]
cls_loc_label = np.apply_along_axis(append_zero, 1, label)
batch_img.append(img)
batch_label.append(label)
batch_label_cls.append(0) # label[0:1]) ---> face
# yield ({'input_1': np.array(batch_img, dtype=np.float32)},
# {'clf_output': np.array(batch_label_cls, dtype=np.float32),
# 'bb_output': np.array(batch_label, dtype=np.float32)})
import tensorflow as tf
def dataloader(dataset_dir, label_path, batch_size=1000, img_shape=(128, 128)):
"""
data loader
return image, [class_label, class_and_location_label]
"""
label_df = read_csv(label_path)
label_idx = label_df.set_index('filename')
img_files = label_idx.index.unique().values
numofData = len(img_files) # endwiths(png,jpg ...)
data_idx = np.arange(numofData)
while True:
batch_idx = np.random.choice(data_idx, size=batch_size, replace=False)
batch_img = []
batch_label = []
batch_class = []
for i in batch_idx:
img = read_img(dataset_dir + img_files[i], img_shape=img_shape)
label = label_idx.loc[img_files[i]].values
label = np.array(label, ndmin=2)
label = label[:, :4]
cls_loc_label = np.apply_along_axis(append_zero, 1, label)
batch_img.append(img)
batch_label.append(cls_loc_label) # face + bb
batch_class.append(cls_loc_label[:, 0:1]) # label[:, 0:1]) ---> face
# yield {'input_1': np.array(batch_img, dtype=np.float32)}, {'clf_output': np.array(batch_class, dtype=np.float32),'bb_output': np.array(batch_label, dtype=np.float32)}
yield np.array(batch_img, dtype=np.float32), [np.array(batch_class, dtype=np.float32), np.array(batch_label, dtype=np.float32)]
data_gen = dataloader(dataset_dir, label_path, batch_size=1, img_shape=(128, 128))
data = next(data_gen)
len(data)
```
| github_jupyter |
<font color = "mediumblue">Note: Notebook was updated July 2, 2019 with bug fixes.</font>
#### If you were working on the older version:
* Please click on the "Coursera" icon in the top right to open up the folder directory.
* Navigate to the folder: Week 3/ Planar data classification with one hidden layer. You can see your prior work in version 5: Planar data classification with one hidden layer v5.ipynb
#### List of bug fixes and enhancements
* Clarifies that the classifier will learn to classify regions as either red or blue.
* compute_cost function fixes np.squeeze by casting it as a float.
* compute_cost instructions clarify the purpose of np.squeeze.
* compute_cost clarifies that "parameters" parameter is not needed, but is kept in the function definition until the auto-grader is also updated.
* nn_model removes extraction of parameter values, as the entire parameter dictionary is passed to the invoked functions.
# Planar data classification with one hidden layer
Welcome to your week 3 programming assignment. It's time to build your first neural network, which will have a hidden layer. You will see a big difference between this model and the one you implemented using logistic regression.
**You will learn how to:**
- Implement a 2-class classification neural network with a single hidden layer
- Use units with a non-linear activation function, such as tanh
- Compute the cross entropy loss
- Implement forward and backward propagation
## 1 - Packages ##
Let's first import all the packages that you will need during this assignment.
- [numpy](https://www.numpy.org/) is the fundamental package for scientific computing with Python.
- [sklearn](http://scikit-learn.org/stable/) provides simple and efficient tools for data mining and data analysis.
- [matplotlib](http://matplotlib.org) is a library for plotting graphs in Python.
- testCases provides some test examples to assess the correctness of your functions
- planar_utils provide various useful functions used in this assignment
```
# Package imports
import numpy as np
import matplotlib.pyplot as plt
from testCases_v2 import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
%matplotlib inline
np.random.seed(1) # set a seed so that the results are consistent
```
## 2 - Dataset ##
First, let's get the dataset you will work on. The following code will load a "flower" 2-class dataset into variables `X` and `Y`.
```
X, Y = load_planar_dataset()
```
Visualize the dataset using matplotlib. The data looks like a "flower" with some red (label y=0) and some blue (y=1) points. Your goal is to build a model to fit this data. In other words, we want the classifier to define regions as either red or blue.
```
# Visualize the data:
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);
```
You have:
- a numpy-array (matrix) X that contains your features (x1, x2)
- a numpy-array (vector) Y that contains your labels (red:0, blue:1).
Lets first get a better sense of what our data is like.
**Exercise**: How many training examples do you have? In addition, what is the `shape` of the variables `X` and `Y`?
**Hint**: How do you get the shape of a numpy array? [(help)](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.shape.html)
```
### START CODE HERE ### (≈ 3 lines of code)
shape_X = None
shape_Y = None
m = X.shape[1] # training set size
### END CODE HERE ###
print ('The shape of X is: ' + str(shape_X))
print ('The shape of Y is: ' + str(shape_Y))
print ('I have m = %d training examples!' % (m))
```
**Expected Output**:
<table style="width:20%">
<tr>
<td>**shape of X**</td>
<td> (2, 400) </td>
</tr>
<tr>
<td>**shape of Y**</td>
<td>(1, 400) </td>
</tr>
<tr>
<td>**m**</td>
<td> 400 </td>
</tr>
</table>
## 3 - Simple Logistic Regression
Before building a full neural network, lets first see how logistic regression performs on this problem. You can use sklearn's built-in functions to do that. Run the code below to train a logistic regression classifier on the dataset.
```
# Train the logistic regression classifier
clf = sklearn.linear_model.LogisticRegressionCV();
clf.fit(X.T, Y.T);
```
You can now plot the decision boundary of these models. Run the code below.
```
# Plot the decision boundary for logistic regression
plot_decision_boundary(lambda x: clf.predict(x), X, Y)
plt.title("Logistic Regression")
# Print accuracy
LR_predictions = clf.predict(X.T)
print ('Accuracy of logistic regression: %d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +
'% ' + "(percentage of correctly labelled datapoints)")
```
**Expected Output**:
<table style="width:20%">
<tr>
<td>**Accuracy**</td>
<td> 47% </td>
</tr>
</table>
**Interpretation**: The dataset is not linearly separable, so logistic regression doesn't perform well. Hopefully a neural network will do better. Let's try this now!
## 4 - Neural Network model
Logistic regression did not work well on the "flower dataset". You are going to train a Neural Network with a single hidden layer.
**Here is our model**:
<img src="images/classification_kiank.png" style="width:600px;height:300px;">
**Mathematically**:
For one example $x^{(i)}$:
$$z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1]}\tag{1}$$
$$a^{[1] (i)} = \tanh(z^{[1] (i)})\tag{2}$$
$$z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2]}\tag{3}$$
$$\hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{ [2] (i)})\tag{4}$$
$$y^{(i)}_{prediction} = \begin{cases} 1 & \mbox{if } a^{[2](i)} > 0.5 \\ 0 & \mbox{otherwise } \end{cases}\tag{5}$$
Given the predictions on all the examples, you can also compute the cost $J$ as follows:
$$J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large\left(\small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large \right) \small \tag{6}$$
**Reminder**: The general methodology to build a Neural Network is to:
1. Define the neural network structure ( # of input units, # of hidden units, etc).
2. Initialize the model's parameters
3. Loop:
- Implement forward propagation
- Compute loss
- Implement backward propagation to get the gradients
- Update parameters (gradient descent)
You often build helper functions to compute steps 1-3 and then merge them into one function we call `nn_model()`. Once you've built `nn_model()` and learnt the right parameters, you can make predictions on new data.
### 4.1 - Defining the neural network structure ####
**Exercise**: Define three variables:
- n_x: the size of the input layer
- n_h: the size of the hidden layer (set this to 4)
- n_y: the size of the output layer
**Hint**: Use shapes of X and Y to find n_x and n_y. Also, hard code the hidden layer size to be 4.
```
# GRADED FUNCTION: layer_sizes
def layer_sizes(X, Y):
"""
Arguments:
X -- input dataset of shape (input size, number of examples)
Y -- labels of shape (output size, number of examples)
Returns:
n_x -- the size of the input layer
n_h -- the size of the hidden layer
n_y -- the size of the output layer
"""
### START CODE HERE ### (≈ 3 lines of code)
n_x = None # size of input layer
n_h = None
n_y = None # size of output layer
### END CODE HERE ###
return (n_x, n_h, n_y)
X_assess, Y_assess = layer_sizes_test_case()
(n_x, n_h, n_y) = layer_sizes(X_assess, Y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))
```
**Expected Output** (these are not the sizes you will use for your network, they are just used to assess the function you've just coded).
<table style="width:20%">
<tr>
<td>**n_x**</td>
<td> 5 </td>
</tr>
<tr>
<td>**n_h**</td>
<td> 4 </td>
</tr>
<tr>
<td>**n_y**</td>
<td> 2 </td>
</tr>
</table>
### 4.2 - Initialize the model's parameters ####
**Exercise**: Implement the function `initialize_parameters()`.
**Instructions**:
- Make sure your parameters' sizes are right. Refer to the neural network figure above if needed.
- You will initialize the weights matrices with random values.
- Use: `np.random.randn(a,b) * 0.01` to randomly initialize a matrix of shape (a,b).
- You will initialize the bias vectors as zeros.
- Use: `np.zeros((a,b))` to initialize a matrix of shape (a,b) with zeros.
```
# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
params -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.
### START CODE HERE ### (≈ 4 lines of code)
W1 = None
b1 = None
W2 = None
b2 = None
### END CODE HERE ###
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
n_x, n_h, n_y = initialize_parameters_test_case()
parameters = initialize_parameters(n_x, n_h, n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
```
**Expected Output**:
<table style="width:90%">
<tr>
<td>**W1**</td>
<td> [[-0.00416758 -0.00056267]
[-0.02136196 0.01640271]
[-0.01793436 -0.00841747]
[ 0.00502881 -0.01245288]] </td>
</tr>
<tr>
<td>**b1**</td>
<td> [[ 0.]
[ 0.]
[ 0.]
[ 0.]] </td>
</tr>
<tr>
<td>**W2**</td>
<td> [[-0.01057952 -0.00909008 0.00551454 0.02292208]]</td>
</tr>
<tr>
<td>**b2**</td>
<td> [[ 0.]] </td>
</tr>
</table>
### 4.3 - The Loop ####
**Question**: Implement `forward_propagation()`.
**Instructions**:
- Look above at the mathematical representation of your classifier.
- You can use the function `sigmoid()`. It is built-in (imported) in the notebook.
- You can use the function `np.tanh()`. It is part of the numpy library.
- The steps you have to implement are:
1. Retrieve each parameter from the dictionary "parameters" (which is the output of `initialize_parameters()`) by using `parameters[".."]`.
2. Implement Forward Propagation. Compute $Z^{[1]}, A^{[1]}, Z^{[2]}$ and $A^{[2]}$ (the vector of all your predictions on all the examples in the training set).
- Values needed in the backpropagation are stored in "`cache`". The `cache` will be given as an input to the backpropagation function.
```
# GRADED FUNCTION: forward_propagation
def forward_propagation(X, parameters):
"""
Argument:
X -- input data of size (n_x, m)
parameters -- python dictionary containing your parameters (output of initialization function)
Returns:
A2 -- The sigmoid output of the second activation
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
"""
# Retrieve each parameter from the dictionary "parameters"
### START CODE HERE ### (≈ 4 lines of code)
W1 = None
b1 = None
W2 = None
b2 = None
### END CODE HERE ###
# Implement Forward Propagation to calculate A2 (probabilities)
### START CODE HERE ### (≈ 4 lines of code)
Z1 = None
A1 = None
Z2 = None
A2 = None
### END CODE HERE ###
assert(A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
X_assess, parameters = forward_propagation_test_case()
A2, cache = forward_propagation(X_assess, parameters)
# Note: we use the mean here just to make sure that your output matches ours.
print(np.mean(cache['Z1']) ,np.mean(cache['A1']),np.mean(cache['Z2']),np.mean(cache['A2']))
```
**Expected Output**:
<table style="width:50%">
<tr>
<td> 0.262818640198 0.091999045227 -1.30766601287 0.212877681719 </td>
</tr>
</table>
Now that you have computed $A^{[2]}$ (in the Python variable "`A2`"), which contains $a^{[2](i)}$ for every example, you can compute the cost function as follows:
$$J = - \frac{1}{m} \sum\limits_{i = 1}^{m} \large{(} \small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large{)} \small\tag{13}$$
**Exercise**: Implement `compute_cost()` to compute the value of the cost $J$.
**Instructions**:
- There are many ways to implement the cross-entropy loss. To help you, we give you how we would have implemented
$- \sum\limits_{i=0}^{m} y^{(i)}\log(a^{[2](i)})$:
```python
logprobs = np.multiply(np.log(A2),Y)
cost = - np.sum(logprobs) # no need to use a for loop!
```
(you can use either `np.multiply()` and then `np.sum()` or directly `np.dot()`).
Note that if you use `np.multiply` followed by `np.sum` the end result will be a type `float`, whereas if you use `np.dot`, the result will be a 2D numpy array. We can use `np.squeeze()` to remove redundant dimensions (in the case of single float, this will be reduced to a zero-dimension array). We can cast the array as a type `float` using `float()`.
```
# GRADED FUNCTION: compute_cost
def compute_cost(A2, Y, parameters):
"""
Computes the cross-entropy cost given in equation (13)
Arguments:
A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
Y -- "true" labels vector of shape (1, number of examples)
parameters -- python dictionary containing your parameters W1, b1, W2 and b2
[Note that the parameters argument is not used in this function,
but the auto-grader currently expects this parameter.
Future version of this notebook will fix both the notebook
and the auto-grader so that `parameters` is not needed.
For now, please include `parameters` in the function signature,
and also when invoking this function.]
Returns:
cost -- cross-entropy cost given equation (13)
"""
m = Y.shape[1] # number of example
# Compute the cross-entropy cost
### START CODE HERE ### (≈ 2 lines of code)
logprobs = None
cost = None
### END CODE HERE ###
cost = float(np.squeeze(cost)) # makes sure cost is the dimension we expect.
# E.g., turns [[17]] into 17
assert(isinstance(cost, float))
return cost
A2, Y_assess, parameters = compute_cost_test_case()
print("cost = " + str(compute_cost(A2, Y_assess, parameters)))
```
**Expected Output**:
<table style="width:20%">
<tr>
<td>**cost**</td>
<td> 0.693058761... </td>
</tr>
</table>
Using the cache computed during forward propagation, you can now implement backward propagation.
**Question**: Implement the function `backward_propagation()`.
**Instructions**:
Backpropagation is usually the hardest (most mathematical) part in deep learning. To help you, here again is the slide from the lecture on backpropagation. You'll want to use the six equations on the right of this slide, since you are building a vectorized implementation.
<img src="images/grad_summary.png" style="width:600px;height:300px;">
<!--
$\frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } = \frac{1}{m} (a^{[2](i)} - y^{(i)})$
$\frac{\partial \mathcal{J} }{ \partial W_2 } = \frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } a^{[1] (i) T} $
$\frac{\partial \mathcal{J} }{ \partial b_2 } = \sum_i{\frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)}}}$
$\frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)} } = W_2^T \frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } * ( 1 - a^{[1] (i) 2}) $
$\frac{\partial \mathcal{J} }{ \partial W_1 } = \frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)} } X^T $
$\frac{\partial \mathcal{J} _i }{ \partial b_1 } = \sum_i{\frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)}}}$
- Note that $*$ denotes elementwise multiplication.
- The notation you will use is common in deep learning coding:
- dW1 = $\frac{\partial \mathcal{J} }{ \partial W_1 }$
- db1 = $\frac{\partial \mathcal{J} }{ \partial b_1 }$
- dW2 = $\frac{\partial \mathcal{J} }{ \partial W_2 }$
- db2 = $\frac{\partial \mathcal{J} }{ \partial b_2 }$
!-->
- Tips:
- To compute dZ1 you'll need to compute $g^{[1]'}(Z^{[1]})$. Since $g^{[1]}(.)$ is the tanh activation function, if $a = g^{[1]}(z)$ then $g^{[1]'}(z) = 1-a^2$. So you can compute
$g^{[1]'}(Z^{[1]})$ using `(1 - np.power(A1, 2))`.
```
# GRADED FUNCTION: backward_propagation
def backward_propagation(parameters, cache, X, Y):
"""
Implement the backward propagation using the instructions above.
Arguments:
parameters -- python dictionary containing our parameters
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
X -- input data of shape (2, number of examples)
Y -- "true" labels vector of shape (1, number of examples)
Returns:
grads -- python dictionary containing your gradients with respect to different parameters
"""
m = X.shape[1]
# First, retrieve W1 and W2 from the dictionary "parameters".
### START CODE HERE ### (≈ 2 lines of code)
W1 = None
W2 = None
### END CODE HERE ###
# Retrieve also A1 and A2 from dictionary "cache".
### START CODE HERE ### (≈ 2 lines of code)
A1 = None
A2 = None
### END CODE HERE ###
# Backward propagation: calculate dW1, db1, dW2, db2.
### START CODE HERE ### (≈ 6 lines of code, corresponding to 6 equations on slide above)
dZ2 = None
dW2 = None
db2 = None
dZ1 = None
dW1 = None
db1 = None
### END CODE HERE ###
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
parameters, cache, X_assess, Y_assess = backward_propagation_test_case()
grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))
```
**Expected output**:
<table style="width:80%">
<tr>
<td>**dW1**</td>
<td> [[ 0.00301023 -0.00747267]
[ 0.00257968 -0.00641288]
[-0.00156892 0.003893 ]
[-0.00652037 0.01618243]] </td>
</tr>
<tr>
<td>**db1**</td>
<td> [[ 0.00176201]
[ 0.00150995]
[-0.00091736]
[-0.00381422]] </td>
</tr>
<tr>
<td>**dW2**</td>
<td> [[ 0.00078841 0.01765429 -0.00084166 -0.01022527]] </td>
</tr>
<tr>
<td>**db2**</td>
<td> [[-0.16655712]] </td>
</tr>
</table>
**Question**: Implement the update rule. Use gradient descent. You have to use (dW1, db1, dW2, db2) in order to update (W1, b1, W2, b2).
**General gradient descent rule**: $ \theta = \theta - \alpha \frac{\partial J }{ \partial \theta }$ where $\alpha$ is the learning rate and $\theta$ represents a parameter.
**Illustration**: The gradient descent algorithm with a good learning rate (converging) and a bad learning rate (diverging). Images courtesy of Adam Harley.
<img src="images/sgd.gif" style="width:400;height:400;"> <img src="images/sgd_bad.gif" style="width:400;height:400;">
```
# GRADED FUNCTION: update_parameters
def update_parameters(parameters, grads, learning_rate = 1.2):
"""
Updates parameters using the gradient descent update rule given above
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients
Returns:
parameters -- python dictionary containing your updated parameters
"""
# Retrieve each parameter from the dictionary "parameters"
### START CODE HERE ### (≈ 4 lines of code)
W1 = None
b1 = None
W2 = None
b2 = None
### END CODE HERE ###
# Retrieve each gradient from the dictionary "grads"
### START CODE HERE ### (≈ 4 lines of code)
dW1 = None
db1 = None
dW2 = None
db2 = None
## END CODE HERE ###
# Update rule for each parameter
### START CODE HERE ### (≈ 4 lines of code)
W1 = None
b1 = None
W2 = None
b2 = None
### END CODE HERE ###
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
```
**Expected Output**:
<table style="width:80%">
<tr>
<td>**W1**</td>
<td> [[-0.00643025 0.01936718]
[-0.02410458 0.03978052]
[-0.01653973 -0.02096177]
[ 0.01046864 -0.05990141]]</td>
</tr>
<tr>
<td>**b1**</td>
<td> [[ -1.02420756e-06]
[ 1.27373948e-05]
[ 8.32996807e-07]
[ -3.20136836e-06]]</td>
</tr>
<tr>
<td>**W2**</td>
<td> [[-0.01041081 -0.04463285 0.01758031 0.04747113]] </td>
</tr>
<tr>
<td>**b2**</td>
<td> [[ 0.00010457]] </td>
</tr>
</table>
### 4.4 - Integrate parts 4.1, 4.2 and 4.3 in nn_model() ####
**Question**: Build your neural network model in `nn_model()`.
**Instructions**: The neural network model has to use the previous functions in the right order.
```
# GRADED FUNCTION: nn_model
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
"""
Arguments:
X -- dataset of shape (2, number of examples)
Y -- labels of shape (1, number of examples)
n_h -- size of the hidden layer
num_iterations -- Number of iterations in gradient descent loop
print_cost -- if True, print the cost every 1000 iterations
Returns:
parameters -- parameters learnt by the model. They can then be used to predict.
"""
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# Initialize parameters
### START CODE HERE ### (≈ 1 line of code)
parameters = None
### END CODE HERE ###
# Loop (gradient descent)
for i in range(0, num_iterations):
### START CODE HERE ### (≈ 4 lines of code)
# Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
A2, cache = None
# Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
cost = None
# Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
grads = None
# Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
parameters = None
### END CODE HERE ###
# Print the cost every 1000 iterations
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters
X_assess, Y_assess = nn_model_test_case()
parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=True)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
```
**Expected Output**:
<table style="width:90%">
<tr>
<td>
**cost after iteration 0**
</td>
<td>
0.692739
</td>
</tr>
<tr>
<td>
<center> $\vdots$ </center>
</td>
<td>
<center> $\vdots$ </center>
</td>
</tr>
<tr>
<td>**W1**</td>
<td> [[-0.65848169 1.21866811]
[-0.76204273 1.39377573]
[ 0.5792005 -1.10397703]
[ 0.76773391 -1.41477129]]</td>
</tr>
<tr>
<td>**b1**</td>
<td> [[ 0.287592 ]
[ 0.3511264 ]
[-0.2431246 ]
[-0.35772805]] </td>
</tr>
<tr>
<td>**W2**</td>
<td> [[-2.45566237 -3.27042274 2.00784958 3.36773273]] </td>
</tr>
<tr>
<td>**b2**</td>
<td> [[ 0.20459656]] </td>
</tr>
</table>
### 4.5 Predictions
**Question**: Use your model to predict by building predict().
Use forward propagation to predict results.
**Reminder**: predictions = $y_{prediction} = \mathbb 1 \text{{activation > 0.5}} = \begin{cases}
1 & \text{if}\ activation > 0.5 \\
0 & \text{otherwise}
\end{cases}$
As an example, if you would like to set the entries of a matrix X to 0 and 1 based on a threshold you would do: ```X_new = (X > threshold)```
```
# GRADED FUNCTION: predict
def predict(parameters, X):
"""
Using the learned parameters, predicts a class for each example in X
Arguments:
parameters -- python dictionary containing your parameters
X -- input data of size (n_x, m)
Returns
predictions -- vector of predictions of our model (red: 0 / blue: 1)
"""
# Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.
### START CODE HERE ### (≈ 2 lines of code)
A2, cache = None
predictions = None
### END CODE HERE ###
return predictions
parameters, X_assess = predict_test_case()
predictions = predict(parameters, X_assess)
print("predictions mean = " + str(np.mean(predictions)))
```
**Expected Output**:
<table style="width:40%">
<tr>
<td>**predictions mean**</td>
<td> 0.666666666667 </td>
</tr>
</table>
It is time to run the model and see how it performs on a planar dataset. Run the following code to test your model with a single hidden layer of $n_h$ hidden units.
```
# Build a model with a n_h-dimensional hidden layer
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
# Plot the decision boundary
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
```
**Expected Output**:
<table style="width:40%">
<tr>
<td>**Cost after iteration 9000**</td>
<td> 0.218607 </td>
</tr>
</table>
```
# Print accuracy
predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')
```
**Expected Output**:
<table style="width:15%">
<tr>
<td>**Accuracy**</td>
<td> 90% </td>
</tr>
</table>
Accuracy is really high compared to Logistic Regression. The model has learnt the leaf patterns of the flower! Neural networks are able to learn even highly non-linear decision boundaries, unlike logistic regression.
Now, let's try out several hidden layer sizes.
### 4.6 - Tuning hidden layer size (optional/ungraded exercise) ###
Run the following code. It may take 1-2 minutes. You will observe different behaviors of the model for various hidden layer sizes.
```
# This may take about 2 minutes to run
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i+1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))
```
**Interpretation**:
- The larger models (with more hidden units) are able to fit the training set better, until eventually the largest models overfit the data.
- The best hidden layer size seems to be around n_h = 5. Indeed, a value around here seems to fits the data well without also incurring noticeable overfitting.
- You will also learn later about regularization, which lets you use very large models (such as n_h = 50) without much overfitting.
**Optional questions**:
**Note**: Remember to submit the assignment by clicking the blue "Submit Assignment" button at the upper-right.
Some optional/ungraded questions that you can explore if you wish:
- What happens when you change the tanh activation for a sigmoid activation or a ReLU activation?
- Play with the learning_rate. What happens?
- What if we change the dataset? (See part 5 below!)
<font color='blue'>
**You've learnt to:**
- Build a complete neural network with a hidden layer
- Make a good use of a non-linear unit
- Implemented forward propagation and backpropagation, and trained a neural network
- See the impact of varying the hidden layer size, including overfitting.
Nice work!
## 5) Performance on other datasets
If you want, you can rerun the whole notebook (minus the dataset part) for each of the following datasets.
```
# Datasets
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {"noisy_circles": noisy_circles,
"noisy_moons": noisy_moons,
"blobs": blobs,
"gaussian_quantiles": gaussian_quantiles}
### START CODE HERE ### (choose your dataset)
dataset = "noisy_moons"
### END CODE HERE ###
X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])
# make blobs binary
if dataset == "blobs":
Y = Y%2
# Visualize the data
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);
```
Congrats on finishing this Programming Assignment!
Reference:
- http://scs.ryerson.ca/~aharley/neural-networks/
- http://cs231n.github.io/neural-networks-case-study/
| github_jupyter |
<a href="https://cognitiveclass.ai/">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Ad/CCLog.png" width="200" align="center">
</a>
<h1>2D <code>Numpy</code> in Python</h1>
<p><strong>Welcome!</strong> This notebook will teach you about using <code>Numpy</code> in the Python Programming Language. By the end of this lab, you'll know what <code>Numpy</code> is and the <code>Numpy</code> operations.</p>
<h2>Table of Contents</h2>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<ul>
<li><a href="create">Create a 2D Numpy Array</a></li>
<li><a href="access">Accessing different elements of a Numpy Array</a></li>
<li><a href="op">Basic Operations</a></li>
</ul>
<p>
Estimated time needed: <strong>20 min</strong>
</p>
</div>
<hr>
<h2 id="create">Create a 2D Numpy Array</h2>
```
# Import the libraries
import numpy as np
import matplotlib.pyplot as plt
```
Consider the list <code>a</code>, the list contains three nested lists **each of equal size**.
```
# Create a list
a = [[11, 12, 13], [21, 22, 23], [31, 32, 33]]
a
```
We can cast the list to a Numpy Array as follow
```
# Convert list to Numpy Array
# Every element is the same type
A = np.array(a)
A
```
We can use the attribute <code>ndim</code> to obtain the number of axes or dimensions referred to as the rank.
```
# Show the numpy array dimensions
A.ndim
```
Attribute <code>shape</code> returns a tuple corresponding to the size or number of each dimension.
```
# Show the numpy array shape
A.shape
```
The total number of elements in the array is given by the attribute <code>size</code>.
```
# Show the numpy array size
A.size
```
<hr>
<h2 id="access">Accessing different elements of a Numpy Array</h2>
We can use rectangular brackets to access the different elements of the array. The correspondence between the rectangular brackets and the list and the rectangular representation is shown in the following figure for a 3x3 array:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoEg.png" width="500" />
We can access the 2nd-row 3rd column as shown in the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFT.png" width="400" />
We simply use the square brackets and the indices corresponding to the element we would like:
```
# Access the element on the second row and third column
A[1, 2]
```
We can also use the following notation to obtain the elements:
```
# Access the element on the second row and third column
A[1][2]
```
Consider the elements shown in the following figure
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFF.png" width="400" />
We can access the element as follows
```
# Access the element on the first row and first column
A[0][0]
```
We can also use slicing in numpy arrays. Consider the following figure. We would like to obtain the first two columns in the first row
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFSF.png" width="400" />
This can be done with the following syntax
```
# Access the element on the first row and first and second columns
A[0][0:2]
```
Similarly, we can obtain the first two rows of the 3rd column as follows:
```
# Access the element on the first and second rows and third column
A[0:2, 2]
```
Corresponding to the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoTST.png" width="400" />
<hr>
<h2 id="op">Basic Operations</h2>
We can also add arrays. The process is identical to matrix addition. Matrix addition of <code>X</code> and <code>Y</code> is shown in the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoAdd.png" width="500" />
The numpy array is given by <code>X</code> and <code>Y</code>
```
# Create a numpy array X
X = np.array([[1, 0], [0, 1]])
X
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
```
We can add the numpy arrays as follows.
```
# Add X and Y
Z = X + Y
Z
```
Multiplying a numpy array by a scaler is identical to multiplying a matrix by a scaler. If we multiply the matrix <code>Y</code> by the scaler 2, we simply multiply every element in the matrix by 2 as shown in the figure.
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoDb.png" width="500" />
We can perform the same operation in numpy as follows
```
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
# Multiply Y with 2
Z = 2 * Y
Z
```
Multiplication of two arrays corresponds to an element-wise product or Hadamard product. Consider matrix <code>X</code> and <code>Y</code>. The Hadamard product corresponds to multiplying each of the elements in the same position, i.e. multiplying elements contained in the same color boxes together. The result is a new matrix that is the same size as matrix <code>Y</code> or <code>X</code>, as shown in the following figure.
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoMul.png" width="500" />
We can perform element-wise product of the array <code>X</code> and <code>Y</code> as follows:
```
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
# Create a numpy array X
X = np.array([[1, 0], [0, 1]])
X
# Multiply X with Y
Z = X * Y
Z
```
We can also perform matrix multiplication with the numpy arrays <code>A</code> and <code>B</code> as follows:
First, we define matrix <code>A</code> and <code>B</code>:
```
# Create a matrix A
A = np.array([[0, 1, 1], [1, 0, 1]])
A
# Create a matrix B
B = np.array([[1, 1], [1, 1], [-1, 1]])
B
```
We use the numpy function <code>dot</code> to multiply the arrays together.
```
# Calculate the dot product
Z = np.dot(A,B)
Z
# Calculate the sine of Z
np.sin(Z)
```
We use the numpy attribute <code>T</code> to calculate the transposed matrix
```
# Create a matrix C
C = np.array([[1,1],[2,2],[3,3]])
C
# Get the transposed of C
C.T
```
<hr>
<h2>The last exercise!</h2>
<p>Congratulations, you have completed your first lesson and hands-on lab in Python. However, there is one more thing you need to do. The Data Science community encourages sharing work. The best way to share and showcase your work is to share it on GitHub. By sharing your notebook on GitHub you are not only building your reputation with fellow data scientists, but you can also show it off when applying for a job. Even though this was your first piece of work, it is never too early to start building good habits. So, please read and follow <a href="https://cognitiveclass.ai/blog/data-scientists-stand-out-by-sharing-your-notebooks/" target="_blank">this article</a> to learn how to share your work.
<hr>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<h2>Get IBM Watson Studio free of charge!</h2>
<p><a href="https://cocl.us/bottemNotebooksPython101Coursera"><img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Ad/BottomAd.png" width="750" align="center"></a></p>
</div>
<h3>About the Authors:</h3>
<p><a href="https://www.linkedin.com/in/joseph-s-50398b136/" target="_blank">Joseph Santarcangelo</a> is a Data Scientist at IBM, and holds a PhD in Electrical Engineering. His research focused on using Machine Learning, Signal Processing, and Computer Vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.</p>
Other contributors: <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
<hr>
<p>Copyright © 2018 IBM Developer Skills Network. This notebook and its source code are released under the terms of the <a href="https://cognitiveclass.ai/mit-license/">MIT License</a>.</p>
| github_jupyter |
```
import scipy.special as sps
import pyro
import pyro.distributions as dist
import torch
from torch.distributions import constraints
from pyro.infer import MCMC, NUTS
from scipy.stats import norm
from torch import nn
from pyro.infer.autoguide import AutoDiagonalNormal
from pyro.nn import PyroModule
from pyro import optim
from pyro.infer import SVI, Trace_ELBO
from pyro.nn import PyroSample
from pyro.infer import Predictive
pyro.enable_validation(True)
pyro.set_rng_seed(1)
pyro.enable_validation(True)
import os
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import statsmodels.api as sm
import statsmodels
#import HNSCC_analysis_pipeline_lib as lib
import pickle as pkl
import seaborn as sbn
print(pyro.__version__)
assert pyro.__version__.startswith('1.1.0')
import time
from __future__ import print_function
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from scipy.stats import norm, gamma, poisson, beta
%matplotlib inline
```
# Hill-Langmuir Bayesian Regression
Goals similar to: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3773943/pdf/nihms187302.pdf
However, they use a different paramerization that does not include Emax
# Bayesian Hill Model Regression
The Hill model is defined as:
$$ F(c, E_{max}, E_0, EC_{50}, H) = E_0 + \frac{E_{max} - E_0}{1 + (\frac{EC_{50}}{C})^H} $$
Where concentration, $c$ is in uM, and is *not* in logspace.
To quantify uncertainty in downstream modeling, and to allow placement of priors on the relevant variables, we will do this in a bayesian framework.
# Building Intuition with the Hill Equation
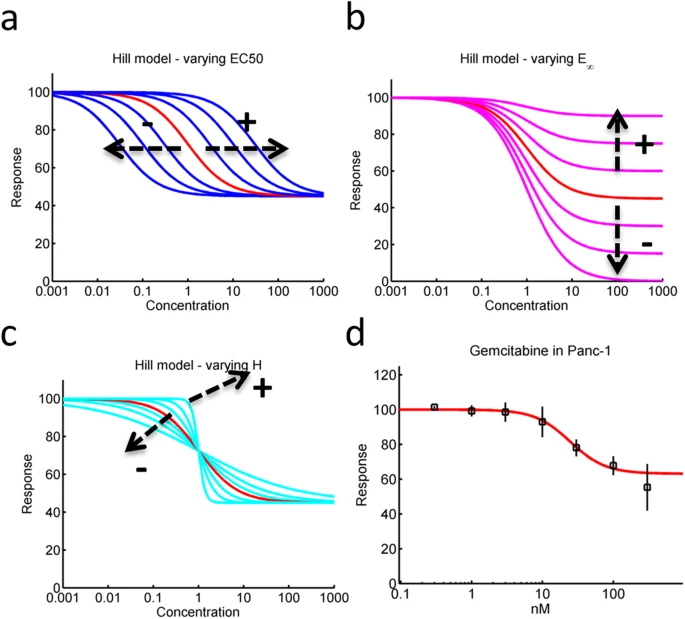
1. Di Veroli GY, Fornari C, Goldlust I, Mills G, Koh SB, Bramhall JL, et al. An automated fitting procedure and software for dose-response curves with multiphasic features. Scientific Reports. 2015 Oct 1;5(1):1–11.
```
# https://ipywidgets.readthedocs.io/en/latest/examples/Using%20Interact.html
def f(E0=2.5, Emax=0, log_EC50=-2, H=1):
EC50 = 10**log_EC50
plt.figure(2, figsize=(10,5))
xx = np.logspace(-4, 1, 100)
yy = E0 + (Emax - E0)/(1+(EC50/xx)**H)
plt.plot(np.log10(xx),yy, 'r-')
plt.ylim(-0.2, 3)
plt.xlabel('log10 [Concentration (uM)] ')
plt.ylabel('cell response')
plt.show()
interactive_plot = interactive(f, E0=(0,3,0.5), Emax=(0.,1.,0.05), log_EC50=(-5,2,0.1), H=(1,5,1))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
```
# Define Model + Guide
```
class plotter:
def __init__(self, params, figsize=(20,10), subplots = (2,7)):
'''
'''
assert len(params) <= subplots[0]*subplots[1], 'wrong number of subplots for given params to report'
self.fig, self.axes = plt.subplots(*subplots,figsize=figsize, sharex='col', sharey='row')
self.vals = {p:[] for p in params}
self.params = params
def record(self):
'''
'''
for p in self.params:
self.vals[p].append(pyro.param(p).item())
def plot_all(self):
'''
'''
for p, ax in zip(self.params, self.axes.flat):
ax.plot(self.vals[p], 'b-')
ax.set_title(p, fontsize=25)
ax.set_xlabel('step', fontsize=20)
ax.set_ylabel('param value', fontsize=20)
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=None, hspace=0.35)
plt.show()
def model(X, Y=None):
'''
'''
E0 = pyro.sample('E0', dist.Normal(1., E0_std))
Emax = pyro.sample('Emax', dist.Beta(a_emax, b_emax))
H = pyro.sample('H', dist.Gamma(alpha_H, beta_H))
EC50 = 10**pyro.sample('log_EC50', dist.Normal(mu_ec50, std_ec50))
obs_sigma = pyro.sample("obs_sigma", dist.Gamma(a_obs, b_obs))
obs_mean = E0 + (Emax - E0)/(1+(EC50/X)**H)
with pyro.plate("data", X.shape[0]):
obs = pyro.sample("obs", dist.Normal(obs_mean.squeeze(-1), obs_sigma), obs=Y)
return obs_mean
def guide(X, Y=None):
_E0_mean = pyro.param('E0_mean', torch.tensor(0.))
_E0_std = pyro.param('E0_std', torch.tensor(E0_std), constraint=constraints.positive)
E0 = pyro.sample('E0', dist.Normal(_E0_mean, _E0_std))
_a_emax = pyro.param('_a_emax', torch.tensor(a_emax), constraint=constraints.positive)
_b_emax = pyro.param('_b_emax', torch.tensor(b_emax), constraint=constraints.positive)
Emax = pyro.sample('Emax', dist.Beta(_a_emax, _b_emax))
_alpha_H = pyro.param('_alpha_H', torch.tensor(alpha_H), constraint=constraints.positive)
_beta_H = pyro.param('_beta_H', torch.tensor(beta_H), constraint=constraints.positive)
H = pyro.sample('H', dist.Gamma(_alpha_H, _beta_H))
_mu_ec50 = pyro.param('_mu_ec50', torch.tensor(mu_ec50))
_std_ec50 = pyro.param('_std_ec50', torch.tensor(std_ec50), constraint=constraints.positive)
EC50 = pyro.sample('log_EC50', dist.Normal(_mu_ec50, _std_ec50))
_a_obs = pyro.param('_a_obs', torch.tensor(a_obs), constraint=constraints.positive)
_b_obs = pyro.param('_b_obs', torch.tensor(b_obs), constraint=constraints.positive)
obs_sigma = pyro.sample("obs_sigma", dist.Gamma(_a_obs, _b_obs))
obs_mean = E0 + (Emax - E0)/(1+(EC50/X)**H)
return obs_mean
```
## choosing priors
### $E_0$
The upper bound or maximum value of our function, $E_0$ should be centered at 1, although it's possible to be a little above or below that, we'll model this with a Normal distribution and a fairly tight variance around 1.
$$ E_0 \propto N(1, \sigma_{E_0}) $$
### $E_{max}$
$E_{max}$ is the lower bound, or minimum value of our function, and is expected to be at 0, however, for some inhibitors it's significantly above this.
$$ E_{max} \propto Beta(a_{E_{max}}, b_{E_{max}}) $$
$$ e[E_{max}] = \frac{a}{a+b} $$
### H
Hill coefficient, $H$ should be a positive integer, however, we're going to approximate this as gamma since a poisson is not flexible enough to characterize this properly.
$$ H \propto gamma(\alpha_{H}, \beta_{H}) $$
$$ Mean = E[gamma] = \frac{ \alpha_{H} }{\beta_{H}} $$
### $EC_{50}$
EC50 was actually a little tough, we could imagine encoding IC50 as a gamma distribution in concentration space, however, this results in poor behavior when used in logspace. Therefore, it actually works much better to encode this as a Normal distribution in logspace.
$$ log10(EC50) \propto Normal(\mu_{EC50}, \sigma_{EC50}) $$
### cell viability ($Y$)
We'll assume this is a normal distribution, centered around the hill function with standard deviation $\sigma_{obs}$.
$$ \mu_{obs} = E_0 + \frac{E_{max} - E_0}{1 + (\frac{EC_{50}}{C})^H} $$
$$ Y \propto N(\mu_{obs}, \sigma_{obs}) $$
# Building Prior Intuition
## E0 Prior
```
def f(E0_std):
plt.figure(2)
xx = np.linspace(-2, 4, 50)
rv = norm(1, E0_std)
yy = rv.pdf(xx)
plt.ylim(0,1)
plt.title('E0 parameter')
plt.xlabel('E0')
plt.ylabel('probability')
plt.plot(xx, yy, 'r-')
plt.show()
interactive_plot = interactive(f, E0_std=(0.1,4,0.1))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
```
## Expecation, Variance to Alpha,Beta for Gamma
```
def gamma_modes_to_params(E, S):
'''
'''
beta = E/S
alpha = E**2/S
return alpha, beta
```
## Emax Prior
```
# TODO: Have inputs be E[] and Var[] rather than a,b... more useful for setting up priors.
def f(emax_mean=1, emax_var=3):
a_emax, b_emax = gamma_modes_to_params(emax_mean, emax_var)
plt.figure(2)
xx = np.linspace(0, 1.2, 100)
rv = gamma(a_emax, scale=1/b_emax, loc=0)
yy = rv.pdf(xx)
plt.title('Emax Parameter')
plt.xlabel('Emax')
plt.ylabel('probability')
plt.ylim(0,5)
plt.plot(xx, yy, 'r-', label=f'alpha={a_emax:.2f}, beta={b_emax:.2f}')
plt.legend()
plt.show()
interactive_plot = interactive(f, emax_mean=(0.1,1.2,0.05), emax_var=(0.01,1,0.05))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
def f(alpha_H=1, beta_H=0.5):
f, axes = plt.subplots(1,1,figsize=(5,5))
xx = np.linspace(0, 5, 100)
g = gamma(alpha_H, scale=1/beta_H, loc=0)
yy = g.pdf(xx)
axes.set_xlabel('H')
axes.set_ylabel('probability')
plt.xlim(0,5)
plt.ylim(0,5)
axes.plot(xx,yy, 'r-')
plt.tight_layout()
plt.title('Hill Coefficient')
plt.show()
interactive_plot = interactive(f, alpha_H=(1,10,1), beta_H=(0.1,5,0.1))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
def f(mu_ec50=-1, std_ec50=0.5):
f, axes = plt.subplots(1,1,figsize=(5,5))
xx = np.log10( np.logspace(-5, 2, 100) )
g = norm(mu_ec50, std_ec50)
yy = g.pdf(xx)
axes.plot(xx,yy, 'r-')
plt.xlabel('log10 EC50')
plt.ylabel('probability')
plt.title('EC50 parameter')
plt.tight_layout()
plt.show()
interactive_plot = interactive(f, mu_ec50=(-5,2,0.1), std_ec50=(0.01,5,0.1))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
def f(a_obs=1, b_obs=1):
plt.figure(2)
xx = np.linspace(0, 3, 50)
rv = gamma(a_obs, scale=1/b_obs, loc=0)
yy = rv.pdf(xx)
plt.ylim(0,5)
plt.plot(xx, yy, 'r-')
plt.xlabel('std_obs')
plt.ylabel('probability')
plt.title('Observation (Y) std')
plt.show()
interactive_plot = interactive(f, a_obs=(1,100,1), b_obs=(1,100,1))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
```
# Define Priors
```
############ PRIORS ###############
E0_std = 0.05
# uniform
# 50,100 -> example if we have strong support for Emax around 0.5
a_emax = 50. #2.
b_emax = 100. #8.
# H gamma prior
alpha_H = 1
beta_H = 1
#EC50
# this is in logspace, so in uM -> 10**mu_ec50
mu_ec50 = -2.
std_ec50 = 3.
# obs error
a_obs = 1
b_obs = 1
###################################
```
# Define Data
We'll use fake data for now.
```
Y = torch.tensor([1., 1., 1., 0.9, 0.7, 0.6, 0.5], dtype=torch.float)
X = torch.tensor([10./3**i for i in range(7)][::-1], dtype=torch.float).unsqueeze(-1)
```
# Fit model with MCMC
https://forum.pyro.ai/t/need-help-with-very-simple-model/600
https://pyro.ai/examples/bayesian_regression_ii.html
```
torch.manual_seed(99999)
nuts_kernel = NUTS(model, adapt_step_size=True)
mcmc_run = MCMC(nuts_kernel, num_samples=400, warmup_steps=100, num_chains=1)
mcmc_run.run(X,Y)
```
## visualize results
```
samples = {k: v.detach().cpu().numpy() for k, v in mcmc_run.get_samples().items()}
f, axes = plt.subplots(3,2, figsize=(10,5))
for ax, key in zip(axes.flat, samples.keys()):
ax.set_title(key)
ax.hist(samples[key], bins=np.linspace(min(samples[key]), max(samples[key]), 50), density=True)
ax.set_xlabel(key)
ax.set_ylabel('probability')
axes.flat[-1].hist(10**samples['log_EC50'], bins=np.linspace(min(10**(samples['log_EC50'])), max(10**(samples['log_EC50'])), 50))
axes.flat[-1].set_title('EC50')
axes.flat[-1].set_xlabel('EC50 [uM]')
plt.tight_layout()
plt.show()
```
## plot fitted hill f-n
```
plt.figure(figsize=(7,7))
xx = np.logspace(-7, 6, 200)
for i,s in pd.DataFrame(samples).iterrows():
yy = s.E0 + (s.Emax - s.E0)/(1+(10**s.log_EC50/xx)**s.H)
plt.plot(np.log10(xx), yy, 'ro', alpha=0.01)
plt.plot(np.log10(X), Y, 'b.', label='data')
plt.xlabel('log10 Concentration')
plt.ylabel('cell_viability')
plt.ylim(0,1.2)
plt.legend()
plt.title('MCMC results')
plt.show()
```
# Deprecated
## EC50 example - gamma in concentration space
```
def f(alpha_ec50=1, beta_ec50=0.5):
f, axes = plt.subplots(1,2,figsize=(8,4))
xx = np.logspace(-5, 2, 100)
g = gamma(alpha_ec50, scale=1/beta_ec50, loc=0)
yy = g.pdf(xx)
g_samples = g.rvs(1000)
axes[0].plot(xx,yy, 'r-')
axes[1].plot(np.log10(xx), yy, 'b-')
plt.tight_layout()
plt.show()
interactive_plot = interactive(f, alpha_ec50=(1,10,1), beta_ec50=(0.01,5,0.1))
output = interactive_plot.children[-1]
output.layout.height = '350px'
interactive_plot
```
# Fit Model with `stochastic variational inference`
```
adam = optim.Adam({"lr": 1e-1})
svi = SVI(model, guide, adam, loss=Trace_ELBO())
tic = time.time()
STEPS = 2500
pyro.clear_param_store()
myplotter = plotter(['_alpha_H', '_beta_H', '_a_emax', '_b_emax', '_a_obs', '_b_obs', '_mu_ec50', '_std_ec50'], figsize=(12, 8), subplots=(2,5))
_losses = []
last=0
loss = 0
n = 100
try:
for j in range(STEPS):
loss += svi.step(X, Y)
myplotter.record()
if j % n == 0:
print(f"[iteration {j}] loss: {(loss / n) :.2f} [change={(loss/n - last/n):.2f}]", end='\t\t\t\r')
_losses.append(np.log10(loss))
last = loss
loss = 0
myplotter.plot_all()
except:
myplotter.plot_all()
raise
plt.figure()
plt.plot(_losses)
plt.xlabel('steps')
plt.ylabel('loss')
plt.show()
toc = time.time()
print(f'time to train {STEPS} iterations: {toc-tic:.2g}s')
x_data = torch.tensor(np.logspace(-5, 5, 200)).unsqueeze(-1)
def summary(samples):
site_stats = {}
for k, v in samples.items():
site_stats[k] = {
"mean": torch.mean(v, 0),
"std": torch.std(v, 0),
"5%": v.kthvalue(int(len(v) * 0.05), dim=0)[0],
"95%": v.kthvalue(int(len(v) * 0.95), dim=0)[0],
}
return site_stats
predictive = Predictive(model, guide=guide, num_samples=800,
return_sites=("linear.weight", "obs", "_RETURN"))
samples = predictive(x_data)
pred_summary = summary(samples)
y_mean = pred_summary['obs']['mean'].detach().numpy()
y_5 = pred_summary['obs']['5%'].detach().numpy()
y_95 = pred_summary['obs']['95%'].detach().numpy()
plt.figure(figsize=(7,7))
plt.plot(np.log10(X),Y, 'k*', label='data')
plt.plot(np.log10(x_data), y_mean, 'r-')
plt.plot(np.log10(x_data), y_5, 'g-', label='95% Posterior Predictive CI')
plt.plot(np.log10(x_data), y_95, 'g-')
plt.ylim(0,1.2)
plt.legend()
plt.show()
```
| github_jupyter |
```
import pdfkit
from string import Template
import numpy as np
from PyPDF2 import PdfFileReader, PdfFileMerger
import glob
temp_address = r'C:\Users\Ol\Documents\EXPERIMENTS\ACT_ID\Materials\projectsListTemp_pl.html'
# Import content
with open(r'C:\Users\Ol\Documents\EXPERIMENTS\ACT_ID\Materials\progs_.txt', 'r', encoding='utf-8') as f:
content = f.readlines()
# Strip newline characters
content = [x.strip('\n') for x in content]
header = """  Poniżej znajdziesz 10 krótkich opisów projektów naukowych
i edukacyjnych, które będą dostępne dla studentów Florida Atlantic University i Uniwersytetu
Warszawskiego w ramach międzynarodowego projektu
realizowanego przy współpracy Instytutu Studiów Społecznych UW (ISS UW) oraz
Departament of Psychology at Florida Atlantic University.
<br><br>
Chcemy Cię prosić o ich ocenę. Uporządkuj je według Twoich
preferencji.
<br><br>
<b>1</b> oznacza, że przyznajesz pierwsze miejsce, <b>10</b>, że ostatnie.
<br><br>
Udział w którym projekcie byłby dla Ciebie najbardziej atrakcyjny? <br><br>
"""
def fill_temp(template_location, content):
with open(template_location) as f:
template = f.read()
template = Template(template[6:])
filled = template.safe_substitute(HEADER = header,
DESCR = 'Skrócony opis projektu',
POS = 'Pozycja',
P1 = content[choice[0]],
P2 = content[choice[1]],
P3 = content[choice[2]],
P4 = content[choice[3]],
P5 = content[choice[4]],
P6 = content[choice[5]],
P7 = content[choice[6]],
P8 = content[choice[7]],
P9 = content[choice[8]],
P10 = content[choice[9]])
return filled
# Define options
options = {'page-size': 'A4',
'encoding': "utf-8"}
# Generate pdfs
for i in range(50):
choice = np.random.choice(10, 10, replace=False)
quest_ready = fill_temp(temp_address, content)
pdfkit.from_string(quest_ready, r'C:\Users\Ol\Documents\EXPERIMENTS\ACT_ID\Materials\Pdf\pList{:02}.pdf'.format(50+i), options=options)
```
## Merge files
into one printable pdf
```
# Define naming pattern
pattern = r'C:\Users\Ol\Documents\EXPERIMENTS\ACT_ID\Materials\PDF\2\*.pdf'
# Generate files list
pdfs_list = glob.glob(pattern)
# Merge and write the output file
merger = PdfFileMerger()
for f in pdfs_list:
merger.append(PdfFileReader(f), 'rb')
merger.write(r'C:\Users\Ol\Documents\EXPERIMENTS\ACT_ID\Materials\PDF\FAU_UW_project2.pdf')
```
| github_jupyter |
```
%matplotlib inline
```
# About Dipoles in MEG and EEG
For an explanation of what is going on in the demo and background information
about magentoencephalography (MEG) and electroencephalography (EEG) in
general, let's walk through some code. To execute this code, you'll need
to have a working version of python with ``mne`` installed, see the
`quick-start` documentation for instructions. You'll need the development
version, so you'll need to do
``pip install git+https://github.com/mne-tools/mne-python.git`` You'll also
need to install the requirements such as with
``pip install -r requirements.txt``.
```
# Author: Alex Rockhill <[email protected]>
#
# License: BSD-3-Clause
```
Let's start by importing the dependencies we'll need.
```
import os.path as op # comes with python and helps naviagte to files
import numpy as np # a scientific computing package with arrays
import matplotlib.pyplot as plt # a plotting library
import mne # our main analysis software package
from nilearn.plotting import plot_anat # this package plots brains
```
## Background
MEG and EEG researchers record very small electromagentic potentials
generated by the brain from outside the head. When it comes from the
recording devices, it looks like this (there are a lot of channels
so only a subset are shown):
```
data_path = mne.datasets.sample.data_path() # get the sample data path
raw = mne.io.read_raw( # navigate to some raw sample data
op.join(data_path, 'MEG', 'sample', 'sample_audvis_raw.fif'))
raw_plot = raw.copy() # make a copy to modify for plotting
raw_plot.pick_channels(raw.ch_names[::10]) # pick only every tenth channel
raw_plot.plot(n_channels=len(raw_plot.ch_names),
duration=1, # only a small, 1 second time window
start=50, # start part way in
)
```
The goal of MEG and EEG researchers is to try and understand how activity
in the brain changes as we respond to stimuli in our environment and
perform behaviors. To do that, researchers will often use magnetic resonance
(MR) to create an image of the research subject's brain. These images
look like this:
```
# first, get a T1-weighted MR scan file from the MNE example dataset
T1_fname = op.join(data_path, 'subjects', 'sample', 'mri', 'T1.mgz')
plot_anat(T1_fname) # now we can plot it
```
The T1 MR image can be used to figure out where the surfaces of the
brain skull and scalp are as well as label the parts of the brain
in the image using Freesurfer. The command below does this (it takes
8 hours so I wouldn't recommend executing it now but it has already
been done for you in the mne sample data, see `here
<https://surfer.nmr.mgh.harvard.edu/fswiki/DownloadAndInstall>`_ for
how to install Freesurfer):
.. code-block:: bash
recon-all -subjid sample -sd $DATA_PATH/subjects -i $T1_FNAME -all
Now let's put it all together and see the problem that MEG and EEG
researchers face in figuring out what's going on inside the brain from
electromagnetic potentials on the surface of the scalp. As you can see below,
there are a lot of MEG and EEG sensors and they cover a large portion of the
head but its not readily apparent how much of each brain area each sensor
records from and how to separate the summed activity from all the brain areas
that is recorded by each sensor into components for each brain area:
<div class="alert alert-info"><h4>Note</h4><p>The sensor positions don't come aligned to the MR image since they are
recorded by a different device so we need to a transformation matrix to
transform them from the coordinate frame they are in to MR coordinates.
This can be done with :func:`mne.gui.coregistration` to generate the
``trans`` file that is loaded below.</p></div>
```
# the subjects_dir is where Freesurfer stored all the surface files
subjects_dir = op.join(data_path, 'subjects')
trans = mne.read_trans(op.join(data_path, 'MEG', 'sample',
'sample_audvis_raw-trans.fif'))
# the main plotter for mne, the brain object
brain = mne.viz.Brain(subject_id='sample', hemi='both', surf='pial',
subjects_dir=subjects_dir)
brain.add_skull(alpha=0.5) # alpha sets transparency
brain.add_head(alpha=0.5)
brain.add_sensors(raw.info, trans)
# set a nice view to show
brain.show_view(azimuth=120, elevation=90, distance=500)
```
## Making a Source Space and Forward Model
First let's setup a space of vertices within the brain that we will consider
as the sources of signal. In a real brain, there are hundreds of billions
of cells but we don't have the resolution with only hundreds of sensors to
determine the activity of each cell, so, instead, we'll choose a regularly
sampled grid of sources that represent the summed activity of tens of
thousands of cells. In most analyses in publications, the source space has
around 8000 vertices, but, for this example, we'll use a smaller source
space for demonstration.
First, we would need to make a boundary element model (BEM) to account for
differences in conductivity of the brain, skull and scalp. This can be
done with :func:`mne.make_bem_model` but, in this case, we'll just load
a pre-computed model. We'll also load the solution to the BEM model for how
different conductivities of issues effect current dipoles as they pass
through each of the layers, but this can be computed with
:func:`mne.make_bem_solution`.
```
bem_fname = op.join(subjects_dir, 'sample', 'bem',
'sample-5120-5120-5120-bem.fif')
# load a pre-computed solution the how the sources within the brain will
# be affected by the different conductivities
bem_sol = op.join(subjects_dir, 'sample', 'bem',
'sample-5120-5120-5120-bem-sol.fif')
# plot it, it's saved out in a standard location,
# so we don't have to pass the path
mne.viz.plot_bem(subject='sample', subjects_dir=op.join(data_path, 'subjects'),
slices=np.linspace(45, 200, 12).round().astype(int))
```
## Making a Dipole
Now, we're ready to make a dipole and see how its current will be recorded
at the scalp with MEG and EEG.
<div class="alert alert-info"><h4>Note</h4><p>You can use ``print(mne.Dipole.__doc__)`` to print the arguments that
are required by ``mne.Dipole`` or any other class, method or function.</p></div>
```
# make a dipole within the temporal lobe pointing superiorly,
# fake a goodness-of-fit number
dip_pos = [-0.0647572, 0.01315963, 0.07091921]
dip = mne.Dipole(times=[0], pos=[dip_pos], amplitude=[3e-8],
ori=[[0, 0, 1]], gof=50)
# plot it!
brain = mne.viz.Brain(subject_id='sample', hemi='both', surf='pial',
subjects_dir=subjects_dir, alpha=0.25)
brain.add_dipole(dip, trans, scales=10)
brain.show_view(azimuth=150, elevation=60, distance=500)
```
## Simulating Sensor Data
We're ready to compute a forward operator using the BEM to make the so-called
leadfield matrix which multiplies activity at the dipole to give the
modelled the activity at the sensors. We can then use this to simulate evoked
data.
```
fwd, stc = mne.make_forward_dipole(
dipole=dip, bem=bem_sol, info=raw.info, trans=trans)
# we don't have a few things like the covarience matrix or a number of epochs
# to average so we use these arguments for a reasonable solution
evoked = mne.simulation.simulate_evoked(
fwd, stc, raw.info, cov=None, nave=np.inf)
# Now we can see what it would look like at the sensors
fig, axes = plt.subplots(1, 3, figsize=(6, 4)) # make a figure with 3 subplots
# use zip to iterate over axes and channel types at the same time
for ax, ch_type in zip(axes, ('grad', 'mag', 'eeg')):
# we're just looking at the relative pattern so we won't use a colorbar
evoked.plot_topomap(times=[0], ch_type=ch_type, axes=ax, colorbar=False)
ax.set_title(ch_type)
```
## Wrapping Up
We covered some good intuition but there's lots more to learn! The main thing
is that MEG and EEG researchers generally don't have the information about
what's going on inside the brain, that's what they are trying to predict. To
reverse this process, you need to invert the forward solution (tutorial:
`tut-viz-stcs`). There is tons more to explore in the MNE `tutorials
<https://mne.tools/dev/auto_tutorials/index.html>`_ and `examples
<https://mne.tools/dev/auto_examples/index.html>`_ pages. Let's leave off by
setting up a source space of many different dipoles and seeing their
different activities manifest on the scalp as measured by the sensors.
```
src = mne.setup_volume_source_space(
subject='sample', pos=20, # in mm
bem=bem_fname, subjects_dir=subjects_dir)
# make the leadfield matrix
fwd = mne.make_forward_solution(
raw.info, trans=trans, src=src, bem=bem_sol)
# plot our setup
brain = mne.viz.Brain(subject_id='sample', hemi='both', surf='pial',
subjects_dir=subjects_dir, alpha=0.25)
brain.add_volume_labels(alpha=0.25, colors='gray')
brain.add_forward(fwd, trans, scale=3)
brain.show_view(azimuth=30, elevation=90, distance=500)
```
Plot the same solution using a source space of dipoles
```
# take the source space from the forward model because some of the
# vertices are excluded from the vertices in src
n_dipoles = fwd['source_rr'].shape[0] # rr is the vertex positions
# find the closest dipole to the one we used before (it was in this
# source space) using the euclidean distance (np.linalg.norm)
idx = np.argmin(np.linalg.norm(fwd['source_rr'] - dip_pos, axis=1))
# make an empty matrix of zeros
data = np.zeros((n_dipoles, 3, 1))
data[idx, 2, 0] = 3e-8 # make the same dipole as before
# this is the format that vertiex numbers are stored in
vertices = [fwd['src'][0]['vertno']]
stc = mne.VolVectorSourceEstimate(data, vertices=vertices,
subject='sample', tmin=0, tstep=1)
evoked = mne.simulation.simulate_evoked(
fwd, stc, raw.info, cov=None, nave=np.inf)
# confirm our replication
fig, axes = plt.subplots(1, 3, figsize=(6, 4)) # make a figure with 3 subplots
for ax, ch_type in zip(axes, ('grad', 'mag', 'eeg')):
evoked.plot_topomap(times=[0], ch_type=ch_type, axes=ax, colorbar=False)
ax.set_title(ch_type)
```
Now, go crazy and simulate a bunch of random dipoles
```
np.random.seed(88) # always seed random number generation for reproducibility
stc.data = np.random.random(stc.data.shape) * 3e-8 - 1.5e-8
evoked = mne.simulation.simulate_evoked(
fwd, stc, raw.info, cov=None, nave=np.inf)
# now that's a complicated faked brain pattern, fortunately brain activity
# is much more correlated (neighboring areas have similar activity) which
# makes results a bit easier to interpret
fig, axes = plt.subplots(1, 3, figsize=(6, 4)) # make a figure with 3 subplots
for ax, ch_type in zip(axes, ('grad', 'mag', 'eeg')):
evoked.plot_topomap(times=[0], ch_type=ch_type, axes=ax, colorbar=False)
ax.set_title(ch_type)
```
| github_jupyter |
# Segmentation
This notebook shows how to use Stardist (Object Detection with Star-convex Shapes) as a part of a segmentation-classification-tracking analysis pipeline.
The sections of this notebook are as follows:
1. Load images
2. Load model of choice and segment an initial image to test Stardist parameters
3. Batch segment a sequence of images
The data used in this notebook is timelapse microscopy data with h2b-gfp/rfp markers that show the spatial extent of the nucleus and it's mitotic state.
This notebook uses the dask octopuslite image loader from the CellX/Lowe lab project.
```
import matplotlib.pyplot as plt
import numpy as np
import os
from octopuslite import DaskOctopusLiteLoader
from stardist.models import StarDist2D
from stardist.plot import render_label
from csbdeep.utils import normalize
from tqdm.auto import tqdm
from skimage.io import imsave
import json
from scipy import ndimage as nd
%matplotlib inline
plt.rcParams['figure.figsize'] = [18,8]
```
## 1. Load images
```
# define experiment ID and select a position
expt = 'ND0011'
pos = 'Pos6'
# point to where the data is
root_dir = '/home/nathan/data'
image_path = f'{root_dir}/{expt}/{pos}/{pos}_images'
# lazily load imagesdd
images = DaskOctopusLiteLoader(image_path,
remove_background = True)
images.channels
```
Set segmentation channel and load test image
```
# segmentation channel
segmentation_channel = images.channels[3]
# set test image index
frame = 1000
# load test image
irfp = images[segmentation_channel.name][frame].compute()
# create 1-channel XYC image
img = np.expand_dims(irfp, axis = -1)
img.shape
```
## 2. Load model and test segment single image
```
model = StarDist2D.from_pretrained('2D_versatile_fluo')
model
```
### 2.1 Test run and display initial results
```
# initialise test segmentation
labels, details = model.predict_instances(normalize(img))
# plot input image and prediction
plt.clf()
plt.subplot(1,2,1)
plt.imshow(normalize(img[:,:,0]), cmap="PiYG")
plt.axis("off")
plt.title("input image")
plt.subplot(1,2,2)
plt.imshow(render_label(labels, img = img))
plt.axis("off")
plt.title("prediction + input overlay")
plt.show()
```
## 3. Batch segment a whole stack of images
When you segment a whole data set you do not want to apply any image transformation. This is so that when you load images and masks later on you can apply the same transformation. You can apply a crop but note that you need to be consistent with your use of the crop from this point on, otherwise you'll get a shift.
```
for expt in tqdm(['ND0009', 'ND0010', 'ND0011']):
for pos in tqdm(['Pos0', 'Pos1', 'Pos2', 'Pos3', 'Pos4']):
print('Starting experiment position:', expt, pos)
# load images
image_path = f'{root_dir}/{expt}/{pos}/{pos}_images'
images = DaskOctopusLiteLoader(image_path,
remove_background = True)
# iterate over images filenames
for fn in tqdm(images.files(segmentation_channel.name)):
# compile 1-channel into XYC array
img = np.expand_dims(imread(fn), axis = -1)
# predict labels
labels, details = model.predict_instances(normalize(img))
# set filename as mask format (channel099)
fn = fn.replace(f'channel00{segmentation_channel.value}', 'channel099')
# save out labelled image
imsave(fn, labels.astype(np.uint16), check_contrast=False)
```
| github_jupyter |
# Introduction to Language Processing Concepts
### Original tutorial by Brain Lehman, with updates by Fiona Pigott
The goal of this tutorial is to introduce a few basical vocabularies, ideas, and Python libraries for thinking about topic modeling, in order to make sure that we have a good set of vocabulary to talk more in-depth about processing languge with Python later. We'll spend some time on defining vocabulary for topic modeling and using basic topic modeling tools.
A big thank-you to the good people at the Stanford NLP group, for their informative and helpful online book: https://nlp.stanford.edu/IR-book/.
### Definitions.
1. **Document**: a body of text (eg. tweet)
2. **Tokenization**: dividing a document into pieces (and maybe throwing away some characters), in English this often (but not necessarily) means words separated by spaces and puctuation.
3. **Text corpus**: the set of documents that contains the text for the analysis (eg. many tweets)
4. **Stop words**: words that occur so frequently, or have so little topical meaning, that they are excluded (e.g., "and")
5. **Vectorize**: Turn some documents into vectors
6. **Vector corpus**: the set of documents transformed such that each token is a tuple (token_id , doc_freq)
```
# first, get some text:
import fileinput
try:
import ujson as json
except ImportError:
import json
documents = []
for line in fileinput.FileInput("example_tweets.json"):
documents.append(json.loads(line)["text"])
```
### 1) Document
In the case of the text that we just imported, each entry in the list is a "document"--a single body of text, hopefully with some coherent meaning.
```
print("One document: \"{}\"".format(documents[0]))
```
### 2) Tokenization
We split each document into smaller pieces ("tokens") in a process called tokenization. Tokens can be counted, and most importantly, compared between documents. There are potentially many different ways to tokenize text--splitting on spaces, removing punctionation, diving the document into n-character pieces--anything that gives us tokens that we can, hopefully, effectively compare across documents and derive meaning from.
Related to tokenization are processes called *stemming* and *lemmatiztion* which can help when using tokens to model topics based on the meaning of a word. In the phrases "they run" and "he runs" (space separated tokens: ["they", "run"] and ["he", "runs"]) the words "run" and "run*s*" mean basically the same thing, but are two different tokens. Stemming and/or lemmatization help us compare tokens with the same meaning but different spelling/suffixes.
#### Lemmatization:
Uses a dictionary of words and their possible morphologies to map many different forms of a base word ("lemma") to a single lemma, comparable across documents. E.g.: "run", "ran", "runs", and "running" might all map to the lemma "run"
#### Stemming:
Uses a set of heuristic rules to try to approximate lemmatization, without knowing the words in advance. For the English language, a simple and effective stemming algorithm might simply be to remove an "s" from the ends of words, or an "ing" from the end of words. E.g.: "run", "runs", and "running" all map to "run," but "ran" (an irregularrly conjugated verb) would not.
Stemming is particularly interesting and applicable in social data, because while some words are decidely *not* standard English, conventinoal rules of grammar still apply. A fan of the popular singer Justin Bieber might call herself a "belieber," while a group of fans call themselves "beliebers." You won't find "belieber" in any English lemmatization dictionary, but a good stemming algorithm will still map "belieber" and "beliebers" to the same token ("belieber", or even "belieb", if we remover the common suffix "er").
```
from nltk.stem import porter
from nltk.tokenize import TweetTokenizer
# tokenize the documents
# find good information on tokenization:
# https://nlp.stanford.edu/IR-book/html/htmledition/tokenization-1.html
# find documentation on pre-made tokenizers and options here:
# http://www.nltk.org/api/nltk.tokenize.html
tknzr = TweetTokenizer(reduce_len = True)
# stem the documents
# find good information on stemming and lemmatization:
# https://nlp.stanford.edu/IR-book/html/htmledition/stemming-and-lemmatization-1.html
# find documentation on available pre-implemented stemmers here:
# http://www.nltk.org/api/nltk.stem.html
stemmer = porter.PorterStemmer()
for doc in documents[0:10]:
tokenized = tknzr.tokenize(doc)
stemmed = [stemmer.stem(x) for x in tokenized]
print("Original document:\n{}\nTokenized result:\n{}\nStemmed result:\n{}\n".format(
doc, tokenized, stemmed))
```
### 3) Text corpus
The text corpus is a collection of all of the documents (Tweets) that we're interested in modeling. Topic modeling and/or clustering on a corpus tends to work best if that corpus has some similar themes--this will mean that some tokens overlap, and we can get signal out of when documents share (or do not share) tokens.
Modeling text tends to get much harder the more different, uncommon and unrelated tokens appear in a text, especially when we are working with social data, where tokens don't necessarily appear in a dictionary. This difficultly (of having many, many unrelated tokens as dimension in our model) is one example of the [curse of dimensionality](https://en.wikipedia.org/wiki/Curse_of_dimensionality).
```
# number of documents in the corpus
print("There are {} documents in the corpus.".format(len(documents)))
```
### 4) Stop words:
Stop words are simply tokens that we've chosen to remove from the corpus, for any reason. In English, removing words like "and", "the", "a", "at", and "it" are common choices for stop words. Stop words can also be edited per project requirement, in case some words are too common in a particular dataset to be meaningful (another way to do stop word removal is to simply remove any word that appears in more than some fixed percentage of documents).
```
from nltk.corpus import stopwords
stopset = set(stopwords.words('english'))
print("The English stop words list provided by NLTK: ")
print(stopset)
stopset.update(["twitter"]) # add token
stopset.remove("i") # remove token
print("\nAdd or remove stop words form the set: ")
print(stopset)
```
### 5) Vectorize:
Transform each document into a vector. There are several good choices that you can make about how to do this transformation, and I'll talk about each of them in a second.
In order to vectorize documents in a corpus (without any dimensional reduction around the vocabulary), think of each document as a row in a matrix, and each column as a word in the vocabulary of the entire corpus. In order to vectorize a corpus, we must read the entire corpus, assign one word to each column, and then turn each document into a row.
**Example**:
**Documents**: "I love cake", "I hate chocolate", "I love chocolate cake", "I love cake, but I hate chocolate cake"
**Stopwords**: Say, because the word "but" is a conjunction, we want to make it a stop word (not include it in our document vectors)
**Vocabulary**: "I" (column 1), "love" (column 2), "cake" (column 3), "hate" (column 4), "chocolate" (column 5)
\begin{equation*}
\begin{matrix}
\text{"I love cake" } & =\\
\text{"I hate chocolate" } & =\\
\text{"I love chocolate cake" } & = \\
\text{"I love cake, but I hate chocolate cake"} & =
\end{matrix}
\qquad
\begin{bmatrix}
1 & 1 & 1 & 0 & 0\\
1 & 0 & 0 & 1 & 1\\
1 & 1 & 1 & 0 & 1\\
2 & 1 & 2 & 1 & 1
\end{bmatrix}
\end{equation*}
Vectorization like this don't take into account word order (we call this property "bag of words"), and in the above example I am simply counting the frequency of each term in each document.
```
# we're going to use the vectorizer functions that scikit learn provides
# define the tokenizer that we want to use
# must be a callable function that takes a document and returns a list of tokens
tknzr = TweetTokenizer(reduce_len = True)
stemmer = porter.PorterStemmer()
def myTokenizer(doc):
return [stemmer.stem(x) for x in tknzr.tokenize(doc)]
# choose the stopword set that we want to use
stopset = set(stopwords.words('english'))
stopset.update(["http","https","twitter","amp"])
# vectorize
# we're using the scikit learn CountVectorizer function, which is very handy
# documentation here:
# http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
vectorizer = CountVectorizer(tokenizer = myTokenizer, stop_words = stopset)
vectorized_documents = vectorizer.fit_transform(documents)
vectorized_documents
import matplotlib.pyplot as plt
%matplotlib inline
_ = plt.hist(vectorized_documents.todense().sum(axis = 1))
_ = plt.title("Number of tokens per document")
_ = plt.xlabel("Number of tokens")
_ = plt.ylabel("Number of documents with x tokens")
from numpy import logspace, ceil, histogram, array
# get the token frequency
token_freq = sorted(vectorized_documents.todense().astype(bool).sum(axis = 0).tolist()[0], reverse = False)
# make a histogram with log scales
bins = array([ceil(x) for x in logspace(0, 3, 5)])
widths = (bins[1:] - bins[:-1])
hist = histogram(token_freq, bins=bins)
hist_norm = hist[0]/widths
# plot (notice that most tokens only appear in one document)
plt.bar(bins[:-1], hist_norm, widths)
plt.xscale('log')
plt.yscale('log')
_ = plt.title("Number of documents in which each token appears")
_ = plt.xlabel("Number of documents")
_ = plt.ylabel("Number of tokens")
```
#### Bag of words
Taking all the words from a document, and sticking them in a bag. Order does not matter, which could cause a problem. "Alice loves cake" might have a different meaning than "Cake loves Alice."
#### Frequency
Counting the number of times a word appears in a document.
#### Tf-Idf (term frequency inverse document frequency):
A statistic that is intended to reflect how important a word is to a document in a collection or corpus. The Tf-Idf value increases proportionally to the number of times a word appears in the document and is inversely proportional to the frequency of the word in the corpus--this helps control words that are generally more common than others.
There are several different possibilities for computing the tf-idf statistic--choosing whether to normalize the vectors, choosing whether to use counts or the logarithm of counts, etc. I'm going to show how scikit-learn computed the tf-idf statistic by default, with more information available in the documentation of the sckit-learn [TfidfVectorizer](http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.TfidfTransformer.html).
$tf(t)$ : Term Frequency, count of the number of times each term appears in the document.
$idf(d,t)$ : Inverse document frequency.
$df(d,t)$ : Document frequency, the count of the number of documents in which the term appears.
$$
tfidf(t) = tf(t) * \log\big(\frac{1 + n}{1 + df(d, t)}\big) + 1
$$
We also then take the Euclidean ($l2$) norm of each document vector, so that long documents (documents with many non-stopword tokens) have the same norm as shorter documents.
```
# documentation on this sckit-learn function here:
# http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.TfidfTransformer.html
tfidf_vectorizer = TfidfVectorizer(tokenizer = myTokenizer, stop_words = stopset)
tfidf_vectorized_documents = tfidf_vectorizer.fit_transform(documents)
tfidf_vectorized_documents
# you can look at two vectors for the same document, from 2 different vectorizers:
tfidf_vectorized_documents[0].todense().tolist()[0]
vectorized_documents[0].todense().tolist()[0]
```
## That's all for now!
| github_jupyter |
<a href="https://colab.research.google.com/github/saanaz379/user-comment-classifier/blob/main/solution_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
This is the first of three solutions to identify offensive language or hate speech in a set of user comments. The code is tested on actual data provided from a day's user comments. This solution utilizes a dictionary that stores all common offensive words and identifies them in any given review, which is then flagged for review. The dictionary is extracted from a Kaggle dataset of offensive tweets.
*Note: This code is incapable of detecting sentence patterns that may predict hate speech.
```
! pip install nltk
! python -m textblob.download_corpora
import nltk
import csv
import collections
import pandas as pd
from collections import Counter
from nltk.corpus import stopwords
# extracting offensive language from twitter kaggle data to final_list
nltk.download('stopwords')
raw_reviews = []
reviews_filename = '/content/drive/MyDrive/labeled_data.csv'
with open(reviews_filename, 'r') as reviews_csvfile:
csvreader = csv.reader(reviews_csvfile)
next(csvreader)
for i in range(1000): # 10399
row = next(csvreader)
if int(row[3]) != 0:
review = row[-1]
review_arr = review.split(":")
raw_reviews.append(review_arr[-1])
review_words = []
for review in raw_reviews:
review_arr = review.split(" ")
for review_word in review_arr:
if "\"" not in review_word and review_word != "" and not "&" in review_word and review_word != "-" and review_word != "love" and "I" not in review_word and "'" not in review_word and review_word != "got":
review_words.append(review_word)
stop_words = set(stopwords.words('english'))
with open('/content/drive/MyDrive/common_words.txt','r') as file:
common_words = file.read()
words_list = [word for word in review_words if not word in stop_words and not word in common_words]
final_list = []
for word in Counter(words_list).most_common(9):
final_list.append(word[0])
# adding reviews to formatted Data Frame
raw_reviews = []
reviews_filename = '/content/drive/MyDrive/reviews.csv.txt'
with open(reviews_filename, 'r') as reviews_csvfile:
csvreader = csv.reader(reviews_csvfile)
next(csvreader)
next(csvreader)
for i in range(10397):
row = next(csvreader)
if (len(row) >= 5):
row.pop(0)
row.pop(-1)
row[2] = ''.join(row[2].split())
if row[2].replace('.', '', 1).isdigit():
row[2] = float(row[2])
row[1] = row[1].rstrip()
if not row[1] == "" and isinstance(row[2], float):
raw_reviews.append(row)
table = pd.DataFrame(data = raw_reviews, columns = ['ID', 'Comments', 'Recommend'])
table
# Return flagged comments for human review. In
# this case, the comments marked only contain
# contain words that are made up of a word in the
# dictionary.
for col, row in table.iterrows():
curr_review = row['Comments']
for word in final_list:
word = word + "."
if word in curr_review:
print("offensive lang")
print(curr_review)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W1D3_ModelFitting/W1D3_Tutorial3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Neuromatch Academy: Week 1, Day 3, Tutorial 3
# Model Fitting: Confidence intervals and bootstrapping
**Content creators**: Pierre-Étienne Fiquet, Anqi Wu, Alex Hyafil with help from Byron Galbraith
**Content reviewers**: Lina Teichmann, Saeed Salehi, Patrick Mineault, Ella Batty, Michael Waskom
#Tutorial Objectives
This is Tutorial 3 of a series on fitting models to data. We start with simple linear regression, using least squares optimization (Tutorial 1) and Maximum Likelihood Estimation (Tutorial 2). We will use bootstrapping to build confidence intervals around the inferred linear model parameters (Tutorial 3). We'll finish our exploration of regression models by generalizing to multiple linear regression and polynomial regression (Tutorial 4). We end by learning how to choose between these various models. We discuss the bias-variance trade-off (Tutorial 5) and Cross Validation for model selection (Tutorial 6).
In this tutorial, we wil discuss how to gauge how good our estimated model parameters are.
- Learn how to use bootstrapping to generate new sample datasets
- Estimate our model parameter on these new sample datasets
- Quantify the variance of our estimate using confidence intervals
```
#@title Video 1: Confidence Intervals & Bootstrapping
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="hs6bVGQNSIs", width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
```
Up to this point we have been finding ways to estimate model parameters to fit some observed data. Our approach has been to optimize some criterion, either minimize the mean squared error or maximize the likelihood while using the entire dataset. How good is our estimate really? How confident are we that it will generalize to describe new data we haven't seen yet?
One solution to this is to just collect more data and check the MSE on this new dataset with the previously estimated parameters. However this is not always feasible and still leaves open the question of how quantifiably confident we are in the accuracy of our model.
In Section 1, we will explore how to implement bootstrapping. In Section 2, we will build confidence intervals of our estimates using the bootstrapping method.
---
# Setup
```
import numpy as np
import matplotlib.pyplot as plt
#@title Figure Settings
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
#@title Helper Functions
def solve_normal_eqn(x, y):
"""Solve the normal equations to produce the value of theta_hat that minimizes
MSE.
Args:
x (ndarray): An array of shape (samples,) that contains the input values.
y (ndarray): An array of shape (samples,) that contains the corresponding
measurement values to the inputs.
thata_hat (float): An estimate of the slope parameter.
Returns:
float: the value for theta_hat arrived from minimizing MSE
"""
theta_hat = (x.T @ y) / (x.T @ x)
return theta_hat
```
---
# Section 1: Bootstrapping
[Bootstrapping](https://en.wikipedia.org/wiki/Bootstrapping_(statistics)) is a widely applicable method to assess confidence/uncertainty about estimated parameters, it was originally [proposed](https://projecteuclid.org/euclid.aos/1176344552) by [Bradley Efron](https://en.wikipedia.org/wiki/Bradley_Efron). The idea is to generate many new synthetic datasets from the initial true dataset by randomly sampling from it, then finding estimators for each one of these new datasets, and finally looking at the distribution of all these estimators to quantify our confidence.
Note that each new resampled datasets will be the same size as our original one, with the new data points sampled with replacement i.e. we can repeat the same data point multiple times. Also note that in practice we need a lot of resampled datasets, here we use 2000.
To explore this idea, we will start again with our noisy samples along the line $y_n = 1.2x_n + \epsilon_n$, but this time only use half the data points as last time (15 instead of 30).
```
#@title
#@markdown Execute this cell to simulate some data
# setting a fixed seed to our random number generator ensures we will always
# get the same psuedorandom number sequence
np.random.seed(121)
# Let's set some parameters
theta = 1.2
n_samples = 15
# Draw x and then calculate y
x = 10 * np.random.rand(n_samples) # sample from a uniform distribution over [0,10)
noise = np.random.randn(n_samples) # sample from a standard normal distribution
y = theta * x + noise
fig, ax = plt.subplots()
ax.scatter(x, y) # produces a scatter plot
ax.set(xlabel='x', ylabel='y');
```
### Exercise 1: Resample Dataset with Replacement
In this exercise you will implement a method to resample a dataset with replacement. The method accepts $x$ and $y$ arrays. It should return a new set of $x'$ and $y'$ arrays that are created by randomly sampling from the originals.
We will then compare the original dataset to a resampled dataset.
TIP: The [numpy.random.choice](https://numpy.org/doc/stable/reference/random/generated/numpy.random.choice.html) method would be useful here.
```
def resample_with_replacement(x, y):
"""Resample data points with replacement from the dataset of `x` inputs and
`y` measurements.
Args:
x (ndarray): An array of shape (samples,) that contains the input values.
y (ndarray): An array of shape (samples,) that contains the corresponding
measurement values to the inputs.
Returns:
ndarray, ndarray: The newly resampled `x` and `y` data points.
"""
#######################################################
## TODO for students: resample dataset with replacement
# Fill out function and remove
raise NotImplementedError("Student exercise: resample dataset with replacement")
#######################################################
# Get array of indices for resampled points
sample_idx = ...
# Sample from x and y according to sample_idx
x_ = ...
y_ = ...
return x_, y_
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 5))
ax1.scatter(x, y)
ax1.set(title='Original', xlabel='x', ylabel='y')
# Uncomment below to test your function
#x_, y_ = resample_with_replacement(x, y)
#ax2.scatter(x_, y_, color='c')
ax2.set(title='Resampled', xlabel='x', ylabel='y',
xlim=ax1.get_xlim(), ylim=ax1.get_ylim());
# to_remove solution
def resample_with_replacement(x, y):
"""Resample data points with replacement from the dataset of `x` inputs and
`y` measurements.
Args:
x (ndarray): An array of shape (samples,) that contains the input values.
y (ndarray): An array of shape (samples,) that contains the corresponding
measurement values to the inputs.
Returns:
ndarray, ndarray: The newly resampled `x` and `y` data points.
"""
# Get array of indices for resampled points
sample_idx = np.random.choice(len(x), size=len(x), replace=True)
# Sample from x and y according to sample_idx
x_ = x[sample_idx]
y_ = y[sample_idx]
return x_, y_
with plt.xkcd():
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 5))
ax1.scatter(x, y)
ax1.set(title='Original', xlabel='x', ylabel='y')
x_, y_ = resample_with_replacement(x, y)
ax2.scatter(x_, y_, color='c')
ax2.set(title='Resampled', xlabel='x', ylabel='y',
xlim=ax1.get_xlim(), ylim=ax1.get_ylim());
```
In the resampled plot on the right, the actual number of points is the same, but some have been repeated so they only display once.
Now that we have a way to resample the data, we can use that in the full bootstrapping process.
### Exercise 2: Bootstrap Estimates
In this exercise you will implement a method to run the bootstrap process of generating a set of $\hat\theta$ values from a dataset of $x$ inputs and $y$ measurements. You should use `resample_with_replacement` here, and you may also invoke helper function `solve_normal_eqn` from Tutorial 1 to produce the MSE-based estimator.
We will then use this function to look at the theta_hat from different samples.
```
def bootstrap_estimates(x, y, n=2000):
"""Generate a set of theta_hat estimates using the bootstrap method.
Args:
x (ndarray): An array of shape (samples,) that contains the input values.
y (ndarray): An array of shape (samples,) that contains the corresponding
measurement values to the inputs.
n (int): The number of estimates to compute
Returns:
ndarray: An array of estimated parameters with size (n,)
"""
theta_hats = np.zeros(n)
##############################################################################
## TODO for students: implement bootstrap estimation
# Fill out function and remove
raise NotImplementedError("Student exercise: implement bootstrap estimation")
##############################################################################
# Loop over number of estimates
for i in range(n):
# Resample x and y
x_, y_ = ...
# Compute theta_hat for this sample
theta_hats[i] = ...
return theta_hats
np.random.seed(123) # set random seed for checking solutions
# Uncomment below to test function
# theta_hats = bootstrap_estimates(x, y, n=2000)
# print(theta_hats[0:5])
# to_remove solution
def bootstrap_estimates(x, y, n=2000):
"""Generate a set of theta_hat estimates using the bootstrap method.
Args:
x (ndarray): An array of shape (samples,) that contains the input values.
y (ndarray): An array of shape (samples,) that contains the corresponding
measurement values to the inputs.
n (int): The number of estimates to compute
Returns:
ndarray: An array of estimated parameters with size (n,)
"""
theta_hats = np.zeros(n)
# Loop over number of estimates
for i in range(n):
# Resample x and y
x_, y_ = resample_with_replacement(x, y)
# Compute theta_hat for this sample
theta_hats[i] = solve_normal_eqn(x_, y_)
return theta_hats
np.random.seed(123) # set random seed for checking solutions
theta_hats = bootstrap_estimates(x, y, n=2000)
print(theta_hats[0:5])
```
You should see `[1.27550888 1.17317819 1.18198819 1.25329255 1.20714664]` as the first five estimates.
Now that we have our bootstrap estimates, we can visualize all the potential models (models computed with different resampling) together to see how distributed they are.
```
#@title
#@markdown Execute this cell to visualize all potential models
fig, ax = plt.subplots()
# For each theta_hat, plot model
theta_hats = bootstrap_estimates(x, y, n=2000)
for i, theta_hat in enumerate(theta_hats):
y_hat = theta_hat * x
ax.plot(x, y_hat, c='r', alpha=0.01, label='Resampled Fits' if i==0 else '')
# Plot observed data
ax.scatter(x, y, label='Observed')
# Plot true fit data
y_true = theta * x
ax.plot(x, y_true, 'g', linewidth=2, label='True Model')
ax.set(
title='Bootstrapped Slope Estimation',
xlabel='x',
ylabel='y'
)
# Change legend line alpha property
handles, labels = ax.get_legend_handles_labels()
handles[0].set_alpha(1)
ax.legend();
```
This looks pretty good! The bootstrapped estimates spread around the true model, as we would have hoped. Note that here we have the luxury to know the ground truth value for $\theta$, but in applications we are trying to guess it from data. Therefore, assessing the quality of estimates based on finite data is a task of fundamental importance in data analysis.
---
# Section 2: Confidence Intervals
Let us now quantify how uncertain our estimated slope is. We do so by computing [confidence intervals](https://en.wikipedia.org/wiki/Confidence_interval) (CIs) from our bootstrapped estimates. The most direct approach is to compute percentiles from the empirical distribution of bootstrapped estimates. Note that this is widely applicable as we are not assuming that this empirical distribution is Gaussian.
```
#@title
#@markdown Execute this cell to plot bootstrapped CI
theta_hats = bootstrap_estimates(x, y, n=2000)
print(f"mean = {np.mean(theta_hats):.2f}, std = {np.std(theta_hats):.2f}")
fig, ax = plt.subplots()
ax.hist(theta_hats, bins=20, facecolor='C1', alpha=0.75)
ax.axvline(theta, c='g', label=r'True $\theta$')
ax.axvline(np.percentile(theta_hats, 50), color='r', label='Median')
ax.axvline(np.percentile(theta_hats, 2.5), color='b', label='95% CI')
ax.axvline(np.percentile(theta_hats, 97.5), color='b')
ax.legend()
ax.set(
title='Bootstrapped Confidence Interval',
xlabel=r'$\hat{{\theta}}$',
ylabel='count',
xlim=[1.0, 1.5]
);
```
Looking at the distribution of bootstrapped $\hat{\theta}$ values, we see that the true $\theta$ falls well within the 95% confidence interval, wich is reinsuring. We also see that the value $\theta = 1$ does not fall within the confidence interval. From this we would reject the hypothesis that the slope was 1.
---
# Summary
- Bootstrapping is a resampling procedure that allows to build confidence intervals around inferred parameter values
- it is a widely applicable and very practical method that relies on computational power and pseudo-random number generators (as opposed to more classical approaches than depend on analytical derivations)
**Suggested readings**
Computer Age Statistical Inference: Algorithms, Evidence and Data Science, by Bradley Efron and Trevor Hastie
| github_jupyter |
## Dependencies
```
import warnings, math, json, glob
import pandas as pd
import tensorflow.keras.layers as L
import tensorflow.keras.backend as K
from tensorflow.keras import Model
from transformers import TFAutoModelForSequenceClassification, TFAutoModel, AutoTokenizer
from commonlit_scripts import *
seed = 0
seed_everything(seed)
warnings.filterwarnings('ignore')
pd.set_option('display.max_colwidth', 150)
```
### Hardware configuration
```
strategy, tpu = get_strategy()
AUTO = tf.data.AUTOTUNE
REPLICAS = strategy.num_replicas_in_sync
print(f'REPLICAS: {REPLICAS}')
```
# Load data
```
base_path = '/kaggle/input/'
test_filepath = base_path + 'commonlitreadabilityprize/test.csv'
test = pd.read_csv(test_filepath)
print(f'Test samples: {len(test)}')
display(test.head())
```
# Model parameters
```
input_noteboks = [x for x in os.listdir(base_path) if '-commonlit-' in x]
input_base_path = f'{base_path}{input_noteboks[0]}/'
with open(input_base_path + 'config.json') as json_file:
config = json.load(json_file)
config
```
## Auxiliary functions
```
# Datasets utility functions
def custom_standardization(text, is_lower=True):
if is_lower:
text = text.lower() # if encoder is uncased
text = text.strip()
return text
def sample_target(features, target):
mean, stddev = target
sampled_target = tf.random.normal([], mean=tf.cast(mean, dtype=tf.float32),
stddev=tf.cast(stddev, dtype=tf.float32), dtype=tf.float32)
return (features, sampled_target)
def get_dataset(pandas_df, tokenizer, labeled=True, ordered=False, repeated=False,
is_sampled=False, batch_size=32, seq_len=128, is_lower=True):
"""
Return a Tensorflow dataset ready for training or inference.
"""
text = [custom_standardization(text, is_lower) for text in pandas_df['excerpt']]
# Tokenize inputs
tokenized_inputs = tokenizer(text, max_length=seq_len, truncation=True,
padding='max_length', return_tensors='tf')
if labeled:
dataset = tf.data.Dataset.from_tensor_slices(({'input_ids': tokenized_inputs['input_ids'],
'attention_mask': tokenized_inputs['attention_mask']},
(pandas_df['target'], pandas_df['standard_error'])))
if is_sampled:
dataset = dataset.map(sample_target, num_parallel_calls=tf.data.AUTOTUNE)
else:
dataset = tf.data.Dataset.from_tensor_slices({'input_ids': tokenized_inputs['input_ids'],
'attention_mask': tokenized_inputs['attention_mask']})
if repeated:
dataset = dataset.repeat()
if not ordered:
dataset = dataset.shuffle(2048)
dataset = dataset.batch(batch_size)
dataset = dataset.cache()
dataset = dataset.prefetch(tf.data.AUTOTUNE)
return dataset
model_path_list = glob.glob(f'{input_base_path}*.h5')
model_path_list.sort()
print('Models to predict:')
print(*model_path_list, sep='\n')
```
# Model
```
def model_fn(encoder, seq_len=256):
input_ids = L.Input(shape=(seq_len,), dtype=tf.int32, name='input_ids')
input_attention_mask = L.Input(shape=(seq_len,), dtype=tf.int32, name='attention_mask')
outputs = encoder({'input_ids': input_ids,
'attention_mask': input_attention_mask})
last_hidden_state = outputs['last_hidden_state']
cls_token = last_hidden_state[:, 0, :]
output = L.Dense(1, name='output')(cls_token)
model = Model(inputs=[input_ids, input_attention_mask],
outputs=[output])
return model
with strategy.scope():
encoder = TFAutoModel.from_pretrained(config['BASE_MODEL'])
# Freeze embeddings
encoder.layers[0].embeddings.trainable = False
model = model_fn(encoder, config['SEQ_LEN'])
model.summary()
```
# Test set predictions
```
tokenizer = AutoTokenizer.from_pretrained(config['BASE_MODEL'])
test_pred = []
for model_path in model_path_list:
print(model_path)
if tpu: tf.tpu.experimental.initialize_tpu_system(tpu)
K.clear_session()
model.load_weights(model_path)
# Test predictions
test_ds = get_dataset(test, tokenizer, labeled=False, ordered=True,
batch_size=config['BATCH_SIZE'], seq_len=config['SEQ_LEN'])
x_test = test_ds.map(lambda sample: sample)
test_pred.append(model.predict(x_test))
```
# Test set predictions
```
submission = test[['id']]
submission['target'] = np.mean(test_pred, axis=0)
submission.to_csv('submission.csv', index=False)
display(submission.head(10))
```
| github_jupyter |
# Load raw data
```
import numpy as np
data = np.loadtxt('SlowSteps1.csv', delimiter = ',') # load the raw data, change the filename as required!
```
# Find spikes
```
time_s = (data[:,8]-data[0,8])/1000000 # set the timing array to seconds and subtract 1st entry to zero it
n_spikes = 0
spike_times = [] # in seconds
spike_points = [] # in timepoints
for x in range(1, data.shape[0]-1):
if (data[x,0]>10 and data[x-1,0]<10): # looks for all instances where subsequent Vm points jump from <10 to >10
spike_times.append(time_s[x])
spike_points.append(x)
n_spikes+=1
print(n_spikes, "spikes detected")
```
# Compute spike rate
```
spike_rate = np.zeros(data.shape[0])
for x in range(0, n_spikes-1):
current_rate = 1/(spike_times[x+1]-spike_times[x])
spike_rate[spike_points[x]:spike_points[x+1]]=current_rate
```
# Plot raw data and spike rate
```
from bokeh.plotting import figure, output_file, show
from bokeh.layouts import column
from bokeh.models import Range1d
output_file("RawDataPlot.html")
spike_plot = figure(plot_width=1200, plot_height = 100)
spike_plot.line(time_s[:],spike_rate[:], line_width=1, line_color="black") # Spike rate
spike_plot.yaxis[0].axis_label = 'Rate (Hz)'
spike_plot.xgrid.grid_line_color =None
spike_plot.ygrid.grid_line_color =None
spike_plot.xaxis.major_label_text_font_size = '0pt' # turn off x-axis tick labels
spike_plot.yaxis.minor_tick_line_color = None # turn off y-axis minor ticks
vm_plot = figure(plot_width=1200, plot_height = 300, y_range=Range1d(-100, 50),x_range=spike_plot.x_range)
vm_plot.line(time_s[:],data[:,0], line_width=1, line_color="black") # Vm
vm_plot.scatter(spike_times[:],45, line_color="black") # Rasterplot over spikes
vm_plot.yaxis[0].axis_label = 'Vm (mV)'
vm_plot.xgrid.grid_line_color =None
vm_plot.ygrid.grid_line_color =None
vm_plot.xaxis.major_label_text_font_size = '0pt' # turn off x-axis tick labels
itotal_plot = figure(plot_width=1200, plot_height = 200, x_range=spike_plot.x_range)
itotal_plot.line(time_s[:], data[:,1], line_width=1, line_color="black") # Itotal
itotal_plot.yaxis[0].axis_label = 'I total (a.u.)'
itotal_plot.xgrid.grid_line_color =None
itotal_plot.xaxis.major_label_text_font_size = '0pt' # turn off x-axis tick labels
in_spikes_plot = figure(plot_width=1200, plot_height = 80, y_range=Range1d(-0.1,1.1), x_range=spike_plot.x_range)
in_spikes_plot.line(time_s[:], data[:,3], line_width=1, line_color="black") # Spikes in from Port 1
in_spikes_plot.line(time_s[:], data[:,4], line_width=1, line_color="grey") # Spikes in from Port 2
in_spikes_plot.yaxis[0].axis_label = 'Input spikes'
in_spikes_plot.xgrid.grid_line_color =None
in_spikes_plot.ygrid.grid_line_color =None
in_spikes_plot.yaxis.major_tick_line_color = None # turn off y-axis major ticks
in_spikes_plot.yaxis.minor_tick_line_color = None # turn off y-axis minor ticks
in_spikes_plot.xaxis.major_label_text_font_size = '0pt' # turn off x-axis tick labels
in_spikes_plot.yaxis.major_label_text_font_size = '0pt' # turn off y-axis tick labels
stim_plot = figure(plot_width=1200, plot_height = 100,y_range=Range1d(-0.1,1.1), x_range=spike_plot.x_range)
stim_plot.line(time_s[:], data[:,2], line_width=1, line_color="black") # Stimulus
stim_plot.yaxis[0].axis_label = 'Stimulus'
stim_plot.xaxis[0].axis_label = 'Time (s)'
stim_plot.xgrid.grid_line_color =None
stim_plot.ygrid.grid_line_color =None
stim_plot.yaxis.major_tick_line_color = None # turn off y-axis major ticks
stim_plot.yaxis.minor_tick_line_color = None # turn off y-axis minor ticks
stim_plot.yaxis.major_label_text_font_size = '0pt' # turn off y-axis tick labels
show(column(spike_plot,vm_plot,itotal_plot,in_spikes_plot,stim_plot))
```
# Analysis Option 1: Trigger stimuli and align
```
stimulus_times = []
stimulus_times_s = []
for x in range(0, data.shape[0]-1): # goes through each timepoint
if (data[x,2]<data[x+1,2]): # checks if the stimulus went from 0 to 1
stimulus_times.append(x) ## make a list of times (in points) when stimulus increased
stimulus_times_s.append(time_s[x]) ## also make a list of times (in seconds)
loop_duration = stimulus_times[1]-stimulus_times[0] # compute arraylength for single stimulus
loop_duration_s = stimulus_times_s[1]-stimulus_times_s[0] # compute arraylength for single stimulus also in s
print(loop_duration, "points per loop;", loop_duration_s, "seconds")
sr_loops = []
vm_loops = []
itotal_loops = []
stim_loops = []
stimulus_times = np.where(data[:,2]>np.roll(data[:,2], axis = 0, shift = 1)) ## make a list of times when stimulus increased (again)
sr_loops = np.vstack([spike_rate[x:x+loop_duration] for x in stimulus_times[0][:-1]])
vm_loops = np.vstack([data[x:x+loop_duration, 0] for x in stimulus_times[0][:-1]])
itotal_loops = np.vstack([data[x:x+loop_duration, 1] for x in stimulus_times[0][:-1]])
stim_loops = np.vstack([data[x:x+loop_duration, 2] for x in stimulus_times[0][:-1]])
st_loops = []
for i, x in enumerate(stimulus_times[0][:-1]):
st_loops.append([time_s[sp]-time_s[x] for sp in spike_points if sp > x and sp < x+loop_duration])
loops = vm_loops.shape[0]
print(loops, "loops")
```
# Make average arrays
```
sr_mean = np.mean(sr_loops, axis=0)
vm_mean = np.mean(vm_loops, axis=0)
itotal_mean = np.mean(itotal_loops, axis=0)
stim_mean = np.mean(stim_loops, axis=0)
```
# Plot stimulus aligned data
```
from bokeh.plotting import figure, output_file, show
from bokeh.layouts import column
from bokeh.models import Range1d
output_file("AlignedDataPlot.html")
spike_plot = figure(plot_width=400, plot_height = 100)
for i in range(0,loops-1):
spike_plot.line(time_s[0:loop_duration],sr_loops[i,:], line_width=1, line_color="gray") # Vm individual repeats
spike_plot.line(time_s[0:loop_duration],sr_mean[:], line_width=1.5, line_color="black") # Vm mean
spike_plot.yaxis[0].axis_label = 'Rate (Hz)'
spike_plot.xgrid.grid_line_color =None
spike_plot.ygrid.grid_line_color =None
spike_plot.xaxis.major_label_text_font_size = '0pt' # turn off x-axis tick labels
dot_plot = figure(plot_width=400, plot_height = 100, x_range=spike_plot.x_range)
for i in range(0,loops-1):
dot_plot.scatter(st_loops[i],i, line_color="black") # Rasterplot
dot_plot.yaxis[0].axis_label = 'Repeat'
dot_plot.xgrid.grid_line_color =None
dot_plot.ygrid.grid_line_color =None
dot_plot.xaxis.major_label_text_font_size = '0pt' # turn off x-axis tick labels
vm_plot = figure(plot_width=400, plot_height = 300, y_range=Range1d(-100, 40),x_range=spike_plot.x_range)
for i in range(0,loops-1):
vm_plot.line(time_s[0:loop_duration],vm_loops[i,:], line_width=1, line_color="gray") # Vm individual repeats
vm_plot.line(time_s[0:loop_duration],vm_mean[:], line_width=1.5, line_color="black") # Vm mean
vm_plot.yaxis[0].axis_label = 'Vm (mV)'
vm_plot.xgrid.grid_line_color =None
vm_plot.ygrid.grid_line_color =None
vm_plot.xaxis.major_label_text_font_size = '0pt' # turn off x-axis tick labels
itotal_plot = figure(plot_width=400, plot_height = 200, x_range=spike_plot.x_range)
for i in range(0,loops-1):
itotal_plot.line(time_s[0:loop_duration], itotal_loops[i,:], line_width=1, line_color="gray") # Itotal individual repeats
itotal_plot.line(time_s[0:loop_duration], itotal_mean[:], line_width=1.5, line_color="black") # Itotal mean
itotal_plot.yaxis[0].axis_label = 'Itotal (a.u.)'
itotal_plot.xgrid.grid_line_color =None
itotal_plot.xaxis.major_label_text_font_size = '0pt' # turn off x-axis tick labels
stim_plot = figure(plot_width=400, plot_height = 100,y_range=Range1d(-0.1,1.1), x_range=spike_plot.x_range)
for i in range(0,loops-1):
stim_plot.line(time_s[0:loop_duration], stim_loops[i,:], line_width=1, line_color="gray") # Stimulus individual repeats
stim_plot.line(time_s[0:loop_duration], stim_mean[:], line_width=1.5, line_color="black") # Stimulus mean
stim_plot.yaxis[0].axis_label = 'Stimulus'
stim_plot.xaxis[0].axis_label = 'Time (s)'
stim_plot.xgrid.grid_line_color =None
stim_plot.ygrid.grid_line_color =None
stim_plot.yaxis.major_tick_line_color = None # turn off y-axis major ticks
stim_plot.yaxis.minor_tick_line_color = None # turn off y-axis minor ticks
stim_plot.yaxis.major_label_text_font_size = '0pt' # turn off y-axis tick labels
show(column(spike_plot,dot_plot,vm_plot,itotal_plot,stim_plot))
```
# Analysis option 2: Spike triggered average (STA)
```
sta_points = 200 # number of points computed
sta_individual = []
sta_individual = np.vstack([data[x-sta_points:x,2] for x in spike_points[2:-1]])
sta = np.mean(sta_individual, axis=0)
import matplotlib.pyplot as plt
plt.plot(time_s[0:200],sta[:])
plt.ylabel('Kernel amplitude')
plt.xlabel('Time before spike (s)')
plt.show()
```
| github_jupyter |
# Convolutional Neural Networks: Step by Step
Welcome to Course 4's first assignment! In this assignment, you will implement convolutional (CONV) and pooling (POOL) layers in numpy, including both forward propagation and (optionally) backward propagation.
By the end of this notebook, you'll be able to:
* Explain the convolution operation
* Apply two different types of pooling operation
* Identify the components used in a convolutional neural network (padding, stride, filter, ...) and their purpose
* Build a convolutional neural network
**Notation**:
- Superscript $[l]$ denotes an object of the $l^{th}$ layer.
- Example: $a^{[4]}$ is the $4^{th}$ layer activation. $W^{[5]}$ and $b^{[5]}$ are the $5^{th}$ layer parameters.
- Superscript $(i)$ denotes an object from the $i^{th}$ example.
- Example: $x^{(i)}$ is the $i^{th}$ training example input.
- Subscript $i$ denotes the $i^{th}$ entry of a vector.
- Example: $a^{[l]}_i$ denotes the $i^{th}$ entry of the activations in layer $l$, assuming this is a fully connected (FC) layer.
- $n_H$, $n_W$ and $n_C$ denote respectively the height, width and number of channels of a given layer. If you want to reference a specific layer $l$, you can also write $n_H^{[l]}$, $n_W^{[l]}$, $n_C^{[l]}$.
- $n_{H_{prev}}$, $n_{W_{prev}}$ and $n_{C_{prev}}$ denote respectively the height, width and number of channels of the previous layer. If referencing a specific layer $l$, this could also be denoted $n_H^{[l-1]}$, $n_W^{[l-1]}$, $n_C^{[l-1]}$.
You should be familiar with `numpy` and/or have completed the previous courses of the specialization. Let's get started!
## Table of Contents
- [1 - Packages](#1)
- [2 - Outline of the Assignment](#2)
- [3 - Convolutional Neural Networks](#3)
- [3.1 - Zero-Padding](#3-1)
- [Exercise 1 - zero_pad](#ex-1)
- [3.2 - Single Step of Convolution](#3-2)
- [Exercise 2 - conv_single_step](#ex-2)
- [3.3 - Convolutional Neural Networks - Forward Pass](#3-3)
- [Exercise 3 - conv_forward](#ex-3)
- [4 - Pooling Layer](#4)
- [4.1 - Forward Pooling](#4-1)
- [Exercise 4 - pool_forward](#ex-4)
- [5 - Backpropagation in Convolutional Neural Networks (OPTIONAL / UNGRADED)](#5)
- [5.1 - Convolutional Layer Backward Pass](#5-1)
- [5.1.1 - Computing dA](#5-1-1)
- [5.1.2 - Computing dW](#5-1-2)
- [5.1.3 - Computing db](#5-1-3)
- [Exercise 5 - conv_backward](#ex-5)
- [5.2 Pooling Layer - Backward Pass](#5-2)
- [5.2.1 Max Pooling - Backward Pass](#5-2-1)
- [Exercise 6 - create_mask_from_window](#ex-6)
- [5.2.2 - Average Pooling - Backward Pass](#5-2-2)
- [Exercise 7 - distribute_value](#ex-7)
- [5.2.3 Putting it Together: Pooling Backward](#5-2-3)
- [Exercise 8 - pool_backward](#ex-8)
<a name='1'></a>
## 1 - Packages
Let's first import all the packages that you will need during this assignment.
- [numpy](www.numpy.org) is the fundamental package for scientific computing with Python.
- [matplotlib](http://matplotlib.org) is a library to plot graphs in Python.
- np.random.seed(1) is used to keep all the random function calls consistent. This helps to grade your work.
```
import numpy as np
import h5py
import matplotlib.pyplot as plt
from public_tests import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2
np.random.seed(1)
```
<a name='2'></a>
## 2 - Outline of the Assignment
You will be implementing the building blocks of a convolutional neural network! Each function you will implement will have detailed instructions to walk you through the steps:
- Convolution functions, including:
- Zero Padding
- Convolve window
- Convolution forward
- Convolution backward (optional)
- Pooling functions, including:
- Pooling forward
- Create mask
- Distribute value
- Pooling backward (optional)
This notebook will ask you to implement these functions from scratch in `numpy`. In the next notebook, you will use the TensorFlow equivalents of these functions to build the following model:
<img src="images/model.png" style="width:800px;height:300px;">
**Note**: For every forward function, there is a corresponding backward equivalent. Hence, at every step of your forward module you will store some parameters in a cache. These parameters are used to compute gradients during backpropagation.
<a name='3'></a>
## 3 - Convolutional Neural Networks
Although programming frameworks make convolutions easy to use, they remain one of the hardest concepts to understand in Deep Learning. A convolution layer transforms an input volume into an output volume of different size, as shown below.
<img src="images/conv_nn.png" style="width:350px;height:200px;">
In this part, you will build every step of the convolution layer. You will first implement two helper functions: one for zero padding and the other for computing the convolution function itself.
<a name='3-1'></a>
### 3.1 - Zero-Padding
Zero-padding adds zeros around the border of an image:
<img src="images/PAD.png" style="width:600px;height:400px;">
<caption><center> <u> <font color='purple'> <b>Figure 1</b> </u><font color='purple'> : <b>Zero-Padding</b><br> Image (3 channels, RGB) with a padding of 2. </center></caption>
The main benefits of padding are:
- It allows you to use a CONV layer without necessarily shrinking the height and width of the volumes. This is important for building deeper networks, since otherwise the height/width would shrink as you go to deeper layers. An important special case is the "same" convolution, in which the height/width is exactly preserved after one layer.
- It helps us keep more of the information at the border of an image. Without padding, very few values at the next layer would be affected by pixels at the edges of an image.
<a name='ex-1'></a>
### Exercise 1 - zero_pad
Implement the following function, which pads all the images of a batch of examples X with zeros. [Use np.pad](https://docs.scipy.org/doc/numpy/reference/generated/numpy.pad.html). Note if you want to pad the array "a" of shape $(5,5,5,5,5)$ with `pad = 1` for the 2nd dimension, `pad = 3` for the 4th dimension and `pad = 0` for the rest, you would do:
```python
a = np.pad(a, ((0,0), (1,1), (0,0), (3,3), (0,0)), mode='constant', constant_values = (0,0))
```
```
# GRADED FUNCTION: zero_pad
def zero_pad(X, pad):
"""
Pad with zeros all images of the dataset X. The padding is applied to the height and width of an image,
as illustrated in Figure 1.
Argument:
X -- python numpy array of shape (m, n_H, n_W, n_C) representing a batch of m images
pad -- integer, amount of padding around each image on vertical and horizontal dimensions
Returns:
X_pad -- padded image of shape (m, n_H + 2 * pad, n_W + 2 * pad, n_C)
"""
#(≈ 1 line)
# X_pad = None
# YOUR CODE STARTS HERE
X_pad = np.pad(X, ((0, 0), (pad, pad), (pad, pad), (0, 0)), mode='constant', constant_values = 0)
# YOUR CODE ENDS HERE
return X_pad
np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
x_pad = zero_pad(x, 3)
print ("x.shape =\n", x.shape)
print ("x_pad.shape =\n", x_pad.shape)
print ("x[1,1] =\n", x[1, 1])
print ("x_pad[1,1] =\n", x_pad[1, 1])
fig, axarr = plt.subplots(1, 2)
axarr[0].set_title('x')
axarr[0].imshow(x[0, :, :, 0])
axarr[1].set_title('x_pad')
axarr[1].imshow(x_pad[0, :, :, 0])
zero_pad_test(zero_pad)
```
<a name='3-2'></a>
### 3.2 - Single Step of Convolution
In this part, implement a single step of convolution, in which you apply the filter to a single position of the input. This will be used to build a convolutional unit, which:
- Takes an input volume
- Applies a filter at every position of the input
- Outputs another volume (usually of different size)
<img src="images/Convolution_schematic.gif" style="width:500px;height:300px;">
<caption><center> <u> <font color='purple'> <b>Figure 2</b> </u><font color='purple'> : <b>Convolution operation</b><br> with a filter of 3x3 and a stride of 1 (stride = amount you move the window each time you slide) </center></caption>
In a computer vision application, each value in the matrix on the left corresponds to a single pixel value. You convolve a 3x3 filter with the image by multiplying its values element-wise with the original matrix, then summing them up and adding a bias. In this first step of the exercise, you will implement a single step of convolution, corresponding to applying a filter to just one of the positions to get a single real-valued output.
Later in this notebook, you'll apply this function to multiple positions of the input to implement the full convolutional operation.
<a name='ex-2'></a>
### Exercise 2 - conv_single_step
Implement `conv_single_step()`.
[Hint](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.sum.html).
**Note**: The variable b will be passed in as a numpy array. If you add a scalar (a float or integer) to a numpy array, the result is a numpy array. In the special case of a numpy array containing a single value, you can cast it as a float to convert it to a scalar.
```
# GRADED FUNCTION: conv_single_step
def conv_single_step(a_slice_prev, W, b):
"""
Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation
of the previous layer.
Arguments:
a_slice_prev -- slice of input data of shape (f, f, n_C_prev)
W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)
b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)
Returns:
Z -- a scalar value, the result of convolving the sliding window (W, b) on a slice x of the input data
"""
#(≈ 3 lines of code)
# Element-wise product between a_slice_prev and W. Do not add the bias yet.
# s = None
# Sum over all entries of the volume s.
# Z = None
# Add bias b to Z. Cast b to a float() so that Z results in a scalar value.
# Z = None
# YOUR CODE STARTS HERE
s = np.multiply(a_slice_prev, W)
Z = np.sum(s)
Z = Z + float(b)
# YOUR CODE ENDS HERE
return Z
np.random.seed(1)
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)
Z = conv_single_step(a_slice_prev, W, b)
print("Z =", Z)
conv_single_step_test(conv_single_step)
assert (type(Z) == np.float64 or type(Z) == np.float32), "You must cast the output to float"
assert np.isclose(Z, -6.999089450680221), "Wrong value"
```
<a name='3-3'></a>
### 3.3 - Convolutional Neural Networks - Forward Pass
In the forward pass, you will take many filters and convolve them on the input. Each 'convolution' gives you a 2D matrix output. You will then stack these outputs to get a 3D volume:
<center>
<video width="620" height="440" src="images/conv_kiank.mp4" type="video/mp4" controls>
</video>
</center>
<a name='ex-3'></a>
### Exercise 3 - conv_forward
Implement the function below to convolve the filters `W` on an input activation `A_prev`.
This function takes the following inputs:
* `A_prev`, the activations output by the previous layer (for a batch of m inputs);
* Weights are denoted by `W`. The filter window size is `f` by `f`.
* The bias vector is `b`, where each filter has its own (single) bias.
You also have access to the hyperparameters dictionary, which contains the stride and the padding.
**Hint**:
1. To select a 2x2 slice at the upper left corner of a matrix "a_prev" (shape (5,5,3)), you would do:
```python
a_slice_prev = a_prev[0:2,0:2,:]
```
Notice how this gives a 3D slice that has height 2, width 2, and depth 3. Depth is the number of channels.
This will be useful when you will define `a_slice_prev` below, using the `start/end` indexes you will define.
2. To define a_slice you will need to first define its corners `vert_start`, `vert_end`, `horiz_start` and `horiz_end`. This figure may be helpful for you to find out how each of the corners can be defined using h, w, f and s in the code below.
<img src="images/vert_horiz_kiank.png" style="width:400px;height:300px;">
<caption><center> <u> <font color='purple'> <b>Figure 3</b> </u><font color='purple'> : <b>Definition of a slice using vertical and horizontal start/end (with a 2x2 filter)</b> <br> This figure shows only a single channel. </center></caption>
**Reminder**:
The formulas relating the output shape of the convolution to the input shape are:
$$n_H = \Bigl\lfloor \frac{n_{H_{prev}} - f + 2 \times pad}{stride} \Bigr\rfloor +1$$
$$n_W = \Bigl\lfloor \frac{n_{W_{prev}} - f + 2 \times pad}{stride} \Bigr\rfloor +1$$
$$n_C = \text{number of filters used in the convolution}$$
For this exercise, don't worry about vectorization! Just implement everything with for-loops.
#### Additional Hints (if you're stuck):
* Use array slicing (e.g.`varname[0:1,:,3:5]`) for the following variables:
`a_prev_pad` ,`W`, `b`
- Copy the starter code of the function and run it outside of the defined function, in separate cells.
- Check that the subset of each array is the size and dimension that you're expecting.
* To decide how to get the `vert_start`, `vert_end`, `horiz_start`, `horiz_end`, remember that these are indices of the previous layer.
- Draw an example of a previous padded layer (8 x 8, for instance), and the current (output layer) (2 x 2, for instance).
- The output layer's indices are denoted by `h` and `w`.
* Make sure that `a_slice_prev` has a height, width and depth.
* Remember that `a_prev_pad` is a subset of `A_prev_pad`.
- Think about which one should be used within the for loops.
```
# GRADED FUNCTION: conv_forward
def conv_forward(A_prev, W, b, hparameters):
"""
Implements the forward propagation for a convolution function
Arguments:
A_prev -- output activations of the previous layer,
numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
W -- Weights, numpy array of shape (f, f, n_C_prev, n_C)
b -- Biases, numpy array of shape (1, 1, 1, n_C)
hparameters -- python dictionary containing "stride" and "pad"
Returns:
Z -- conv output, numpy array of shape (m, n_H, n_W, n_C)
cache -- cache of values needed for the conv_backward() function
"""
# Retrieve dimensions from A_prev's shape (≈1 line)
# (m, n_H_prev, n_W_prev, n_C_prev) = None
# Retrieve dimensions from W's shape (≈1 line)
# (f, f, n_C_prev, n_C) = None
# Retrieve information from "hparameters" (≈2 lines)
# stride = None
# pad = None
# Compute the dimensions of the CONV output volume using the formula given above.
# Hint: use int() to apply the 'floor' operation. (≈2 lines)
# n_H = None
# n_W = None
# Initialize the output volume Z with zeros. (≈1 line)
# Z = None
# Create A_prev_pad by padding A_prev
# A_prev_pad = None
# for i in range(None): # loop over the batch of training examples
# a_prev_pad = None # Select ith training example's padded activation
# for h in range(None): # loop over vertical axis of the output volume
# Find the vertical start and end of the current "slice" (≈2 lines)
# vert_start = None
# vert_end = None
# for w in range(None): # loop over horizontal axis of the output volume
# Find the horizontal start and end of the current "slice" (≈2 lines)
# horiz_start = None
# horiz_end = None
# for c in range(None): # loop over channels (= #filters) of the output volume
# Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line)
# a_slice_prev = None
# Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈3 line)
# weights = None
# biases = None
# Z[i, h, w, c] = None
# YOUR CODE STARTS HERE
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
(f, f, n_C_prev, n_C) = W.shape
stride = hparameters["stride"]
pad = hparameters["pad"]
n_H = int((n_H_prev - f + 2 * pad)/stride) + 1
n_W = int((n_W_prev - f + 2 * pad)/stride) + 1
Z = np.zeros((m, n_H, n_W, n_C))
A_prev_pad = zero_pad(A_prev, pad)
for i in range(m):
a_prev_pad = A_prev_pad[i,:,:,:]
for h in range(n_H):
vert_start = h*stride
vert_end = vert_start + f
for w in range(n_W):
horiz_start = w*stride
horiz_end = horiz_start + f
for c in range(n_C):
a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
weights = W[:,:,:,c]
biases = b[:,:,:,c]
Z[i, h, w, c] = conv_single_step(a_slice_prev, weights, biases)
# YOUR CODE ENDS HERE
# Save information in "cache" for the backprop
cache = (A_prev, W, b, hparameters)
return Z, cache
np.random.seed(1)
A_prev = np.random.randn(2, 5, 7, 4)
W = np.random.randn(3, 3, 4, 8)
b = np.random.randn(1, 1, 1, 8)
hparameters = {"pad" : 1,
"stride": 2}
Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
print("Z's mean =\n", np.mean(Z))
print("Z[0,2,1] =\n", Z[0, 2, 1])
print("cache_conv[0][1][2][3] =\n", cache_conv[0][1][2][3])
conv_forward_test(conv_forward)
```
Finally, a CONV layer should also contain an activation, in which case you would add the following line of code:
```python
# Convolve the window to get back one output neuron
Z[i, h, w, c] = ...
# Apply activation
A[i, h, w, c] = activation(Z[i, h, w, c])
```
You don't need to do it here, however.
<a name='4'></a>
## 4 - Pooling Layer
The pooling (POOL) layer reduces the height and width of the input. It helps reduce computation, as well as helps make feature detectors more invariant to its position in the input. The two types of pooling layers are:
- Max-pooling layer: slides an ($f, f$) window over the input and stores the max value of the window in the output.
- Average-pooling layer: slides an ($f, f$) window over the input and stores the average value of the window in the output.
<table>
<td>
<img src="images/max_pool1.png" style="width:500px;height:300px;">
<td>
<td>
<img src="images/a_pool.png" style="width:500px;height:300px;">
<td>
</table>
These pooling layers have no parameters for backpropagation to train. However, they have hyperparameters such as the window size $f$. This specifies the height and width of the $f \times f$ window you would compute a *max* or *average* over.
<a name='4-1'></a>
### 4.1 - Forward Pooling
Now, you are going to implement MAX-POOL and AVG-POOL, in the same function.
<a name='ex-4'></a>
### Exercise 4 - pool_forward
Implement the forward pass of the pooling layer. Follow the hints in the comments below.
**Reminder**:
As there's no padding, the formulas binding the output shape of the pooling to the input shape is:
$$n_H = \Bigl\lfloor \frac{n_{H_{prev}} - f}{stride} \Bigr\rfloor +1$$
$$n_W = \Bigl\lfloor \frac{n_{W_{prev}} - f}{stride} \Bigr\rfloor +1$$
$$n_C = n_{C_{prev}}$$
```
# GRADED FUNCTION: pool_forward
def pool_forward(A_prev, hparameters, mode = "max"):
"""
Implements the forward pass of the pooling layer
Arguments:
A_prev -- Input data, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
hparameters -- python dictionary containing "f" and "stride"
mode -- the pooling mode you would like to use, defined as a string ("max" or "average")
Returns:
A -- output of the pool layer, a numpy array of shape (m, n_H, n_W, n_C)
cache -- cache used in the backward pass of the pooling layer, contains the input and hparameters
"""
# Retrieve dimensions from the input shape
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# Retrieve hyperparameters from "hparameters"
f = hparameters["f"]
stride = hparameters["stride"]
# Define the dimensions of the output
n_H = int(1 + (n_H_prev - f) / stride)
n_W = int(1 + (n_W_prev - f) / stride)
n_C = n_C_prev
# Initialize output matrix A
A = np.zeros((m, n_H, n_W, n_C))
# for i in range(None): # loop over the training examples
# for h in range(None): # loop on the vertical axis of the output volume
# Find the vertical start and end of the current "slice" (≈2 lines)
# vert_start = None
# vert_end = None
# for w in range(None): # loop on the horizontal axis of the output volume
# Find the vertical start and end of the current "slice" (≈2 lines)
# horiz_start = None
# horiz_end = None
# for c in range (None): # loop over the channels of the output volume
# Use the corners to define the current slice on the ith training example of A_prev, channel c. (≈1 line)
# a_prev_slice = None
# Compute the pooling operation on the slice.
# Use an if statement to differentiate the modes.
# Use np.max and np.mean.
# if mode == "max":
# A[i, h, w, c] = None
# elif mode == "average":
# A[i, h, w, c] = None
# YOUR CODE STARTS HERE
for i in range(m):
for h in range(n_H):
vert_start = h*stride
vert_end = vert_start + f
for w in range(n_W):
horiz_start = w*stride
horiz_end = horiz_start + f
for c in range(n_C):
a_prev_slice = A_prev[i, vert_start:vert_end, horiz_start:horiz_end, c]
if mode == "max":
A[i, h, w, c] = np.max(a_prev_slice)
elif mode == "average":
A[i, h, w, c] = np.mean(a_prev_slice)
# YOUR CODE ENDS HERE
# Store the input and hparameters in "cache" for pool_backward()
cache = (A_prev, hparameters)
# Making sure your output shape is correct
#assert(A.shape == (m, n_H, n_W, n_C))
return A, cache
# Case 1: stride of 1
np.random.seed(1)
A_prev = np.random.randn(2, 5, 5, 3)
hparameters = {"stride" : 1, "f": 3}
A, cache = pool_forward(A_prev, hparameters, mode = "max")
print("mode = max")
print("A.shape = " + str(A.shape))
print("A[1, 1] =\n", A[1, 1])
A, cache = pool_forward(A_prev, hparameters, mode = "average")
print("mode = average")
print("A.shape = " + str(A.shape))
print("A[1, 1] =\n", A[1, 1])
pool_forward_test(pool_forward)
```
**Expected output**
```
mode = max
A.shape = (2, 3, 3, 3)
A[1, 1] =
[[1.96710175 0.84616065 1.27375593]
[1.96710175 0.84616065 1.23616403]
[1.62765075 1.12141771 1.2245077 ]]
mode = average
A.shape = (2, 3, 3, 3)
A[1, 1] =
[[ 0.44497696 -0.00261695 -0.31040307]
[ 0.50811474 -0.23493734 -0.23961183]
[ 0.11872677 0.17255229 -0.22112197]]
```
```
# Case 2: stride of 2
np.random.seed(1)
A_prev = np.random.randn(2, 5, 5, 3)
hparameters = {"stride" : 2, "f": 3}
A, cache = pool_forward(A_prev, hparameters)
print("mode = max")
print("A.shape = " + str(A.shape))
print("A[0] =\n", A[0])
print()
A, cache = pool_forward(A_prev, hparameters, mode = "average")
print("mode = average")
print("A.shape = " + str(A.shape))
print("A[1] =\n", A[1])
```
**Expected Output:**
```
mode = max
A.shape = (2, 2, 2, 3)
A[0] =
[[[1.74481176 0.90159072 1.65980218]
[1.74481176 1.6924546 1.65980218]]
[[1.13162939 1.51981682 2.18557541]
[1.13162939 1.6924546 2.18557541]]]
mode = average
A.shape = (2, 2, 2, 3)
A[1] =
[[[-0.17313416 0.32377198 -0.34317572]
[ 0.02030094 0.14141479 -0.01231585]]
[[ 0.42944926 0.08446996 -0.27290905]
[ 0.15077452 0.28911175 0.00123239]]]
```
<font color='blue'>
**What you should remember**:
* A convolution extracts features from an input image by taking the dot product between the input data and a 3D array of weights (the filter).
* The 2D output of the convolution is called the feature map
* A convolution layer is where the filter slides over the image and computes the dot product
* This transforms the input volume into an output volume of different size
* Zero padding helps keep more information at the image borders, and is helpful for building deeper networks, because you can build a CONV layer without shrinking the height and width of the volumes
* Pooling layers gradually reduce the height and width of the input by sliding a 2D window over each specified region, then summarizing the features in that region
**Congratulations**! You have now implemented the forward passes of all the layers of a convolutional network. Great work!
The remainder of this notebook is optional, and will not be graded. If you carry on, just remember to hit the Submit button to submit your work for grading first.
<a name='5'></a>
## 5 - Backpropagation in Convolutional Neural Networks (OPTIONAL / UNGRADED)
In modern deep learning frameworks, you only have to implement the forward pass, and the framework takes care of the backward pass, so most deep learning engineers don't need to bother with the details of the backward pass. The backward pass for convolutional networks is complicated. If you wish, you can work through this optional portion of the notebook to get a sense of what backprop in a convolutional network looks like.
When in an earlier course you implemented a simple (fully connected) neural network, you used backpropagation to compute the derivatives with respect to the cost to update the parameters. Similarly, in convolutional neural networks you can calculate the derivatives with respect to the cost in order to update the parameters. The backprop equations are not trivial and were not derived in lecture, but are briefly presented below.
<a name='5-1'></a>
### 5.1 - Convolutional Layer Backward Pass
Let's start by implementing the backward pass for a CONV layer.
<a name='5-1-1'></a>
#### 5.1.1 - Computing dA:
This is the formula for computing $dA$ with respect to the cost for a certain filter $W_c$ and a given training example:
$$dA \mathrel{+}= \sum _{h=0} ^{n_H} \sum_{w=0} ^{n_W} W_c \times dZ_{hw} \tag{1}$$
Where $W_c$ is a filter and $dZ_{hw}$ is a scalar corresponding to the gradient of the cost with respect to the output of the conv layer Z at the hth row and wth column (corresponding to the dot product taken at the ith stride left and jth stride down). Note that at each time, you multiply the the same filter $W_c$ by a different dZ when updating dA. We do so mainly because when computing the forward propagation, each filter is dotted and summed by a different a_slice. Therefore when computing the backprop for dA, you are just adding the gradients of all the a_slices.
In code, inside the appropriate for-loops, this formula translates into:
```python
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]
```
<a name='5-1-2'></a>
#### 5.1.2 - Computing dW:
This is the formula for computing $dW_c$ ($dW_c$ is the derivative of one filter) with respect to the loss:
$$dW_c \mathrel{+}= \sum _{h=0} ^{n_H} \sum_{w=0} ^ {n_W} a_{slice} \times dZ_{hw} \tag{2}$$
Where $a_{slice}$ corresponds to the slice which was used to generate the activation $Z_{ij}$. Hence, this ends up giving us the gradient for $W$ with respect to that slice. Since it is the same $W$, we will just add up all such gradients to get $dW$.
In code, inside the appropriate for-loops, this formula translates into:
```python
dW[:,:,:,c] \mathrel{+}= a_slice * dZ[i, h, w, c]
```
<a name='5-1-3'></a>
#### 5.1.3 - Computing db:
This is the formula for computing $db$ with respect to the cost for a certain filter $W_c$:
$$db = \sum_h \sum_w dZ_{hw} \tag{3}$$
As you have previously seen in basic neural networks, db is computed by summing $dZ$. In this case, you are just summing over all the gradients of the conv output (Z) with respect to the cost.
In code, inside the appropriate for-loops, this formula translates into:
```python
db[:,:,:,c] += dZ[i, h, w, c]
```
<a name='ex-5'></a>
### Exercise 5 - conv_backward
Implement the `conv_backward` function below. You should sum over all the training examples, filters, heights, and widths. You should then compute the derivatives using formulas 1, 2 and 3 above.
```
def conv_backward(dZ, cache):
"""
Implement the backward propagation for a convolution function
Arguments:
dZ -- gradient of the cost with respect to the output of the conv layer (Z), numpy array of shape (m, n_H, n_W, n_C)
cache -- cache of values needed for the conv_backward(), output of conv_forward()
Returns:
dA_prev -- gradient of the cost with respect to the input of the conv layer (A_prev),
numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
dW -- gradient of the cost with respect to the weights of the conv layer (W)
numpy array of shape (f, f, n_C_prev, n_C)
db -- gradient of the cost with respect to the biases of the conv layer (b)
numpy array of shape (1, 1, 1, n_C)
"""
# Retrieve information from "cache"
# (A_prev, W, b, hparameters) = None
# Retrieve dimensions from A_prev's shape
# (m, n_H_prev, n_W_prev, n_C_prev) = None
# Retrieve dimensions from W's shape
# (f, f, n_C_prev, n_C) = None
# Retrieve information from "hparameters"
# stride = None
# pad = None
# Retrieve dimensions from dZ's shape
# (m, n_H, n_W, n_C) = None
# Initialize dA_prev, dW, db with the correct shapes
# dA_prev = None
# dW = None
# db = None
# Pad A_prev and dA_prev
# A_prev_pad = zero_pad(A_prev, pad)
# dA_prev_pad = zero_pad(dA_prev, pad)
#for i in range(m): # loop over the training examples
# select ith training example from A_prev_pad and dA_prev_pad
# a_prev_pad = None
# da_prev_pad = None
#for h in range(n_H): # loop over vertical axis of the output volume
# for w in range(n_W): # loop over horizontal axis of the output volume
# for c in range(n_C): # loop over the channels of the output volume
# Find the corners of the current "slice"
# vert_start = None
# vert_end = None
# horiz_start = None
# horiz_end = None
# Use the corners to define the slice from a_prev_pad
# a_slice = None
# Update gradients for the window and the filter's parameters using the code formulas given above
# da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += None
# dW[:,:,:,c] += None
# db[:,:,:,c] += None
# Set the ith training example's dA_prev to the unpadded da_prev_pad (Hint: use X[pad:-pad, pad:-pad, :])
# dA_prev[i, :, :, :] = None
# YOUR CODE STARTS HERE
# YOUR CODE ENDS HERE
# Making sure your output shape is correct
assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
return dA_prev, dW, db
# We'll run conv_forward to initialize the 'Z' and 'cache_conv",
# which we'll use to test the conv_backward function
np.random.seed(1)
A_prev = np.random.randn(10, 4, 4, 3)
W = np.random.randn(2, 2, 3, 8)
b = np.random.randn(1, 1, 1, 8)
hparameters = {"pad" : 2,
"stride": 2}
Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
# Test conv_backward
dA, dW, db = conv_backward(Z, cache_conv)
print("dA_mean =", np.mean(dA))
print("dW_mean =", np.mean(dW))
print("db_mean =", np.mean(db))
assert type(dA) == np.ndarray, "Output must be a np.ndarray"
assert type(dW) == np.ndarray, "Output must be a np.ndarray"
assert type(db) == np.ndarray, "Output must be a np.ndarray"
assert dA.shape == (10, 4, 4, 3), f"Wrong shape for dA {dA.shape} != (10, 4, 4, 3)"
assert dW.shape == (2, 2, 3, 8), f"Wrong shape for dW {dW.shape} != (2, 2, 3, 8)"
assert db.shape == (1, 1, 1, 8), f"Wrong shape for db {db.shape} != (1, 1, 1, 8)"
assert np.isclose(np.mean(dA), 1.4524377), "Wrong values for dA"
assert np.isclose(np.mean(dW), 1.7269914), "Wrong values for dW"
assert np.isclose(np.mean(db), 7.8392325), "Wrong values for db"
print("\033[92m All tests passed.")
```
**Expected Output**:
<table>
<tr>
<td>
dA_mean
</td>
<td>
1.45243777754
</td>
</tr>
<tr>
<td>
dW_mean
</td>
<td>
1.72699145831
</td>
</tr>
<tr>
<td>
db_mean
</td>
<td>
7.83923256462
</td>
</tr>
</table>
<a name='5-2'></a>
## 5.2 Pooling Layer - Backward Pass
Next, let's implement the backward pass for the pooling layer, starting with the MAX-POOL layer. Even though a pooling layer has no parameters for backprop to update, you still need to backpropagate the gradient through the pooling layer in order to compute gradients for layers that came before the pooling layer.
<a name='5-2-1'></a>
### 5.2.1 Max Pooling - Backward Pass
Before jumping into the backpropagation of the pooling layer, you are going to build a helper function called `create_mask_from_window()` which does the following:
$$ X = \begin{bmatrix}
1 && 3 \\
4 && 2
\end{bmatrix} \quad \rightarrow \quad M =\begin{bmatrix}
0 && 0 \\
1 && 0
\end{bmatrix}\tag{4}$$
As you can see, this function creates a "mask" matrix which keeps track of where the maximum of the matrix is. True (1) indicates the position of the maximum in X, the other entries are False (0). You'll see later that the backward pass for average pooling is similar to this, but uses a different mask.
<a name='ex-6'></a>
### Exercise 6 - create_mask_from_window
Implement `create_mask_from_window()`. This function will be helpful for pooling backward.
Hints:
- [np.max()]() may be helpful. It computes the maximum of an array.
- If you have a matrix X and a scalar x: `A = (X == x)` will return a matrix A of the same size as X such that:
```
A[i,j] = True if X[i,j] = x
A[i,j] = False if X[i,j] != x
```
- Here, you don't need to consider cases where there are several maxima in a matrix.
```
def create_mask_from_window(x):
"""
Creates a mask from an input matrix x, to identify the max entry of x.
Arguments:
x -- Array of shape (f, f)
Returns:
mask -- Array of the same shape as window, contains a True at the position corresponding to the max entry of x.
"""
# (≈1 line)
# mask = None
# YOUR CODE STARTS HERE
# YOUR CODE ENDS HERE
return mask
np.random.seed(1)
x = np.random.randn(2, 3)
mask = create_mask_from_window(x)
print('x = ', x)
print("mask = ", mask)
x = np.array([[-1, 2, 3],
[2, -3, 2],
[1, 5, -2]])
y = np.array([[False, False, False],
[False, False, False],
[False, True, False]])
mask = create_mask_from_window(x)
assert type(mask) == np.ndarray, "Output must be a np.ndarray"
assert mask.shape == x.shape, "Input and output shapes must match"
assert np.allclose(mask, y), "Wrong output. The True value must be at position (2, 1)"
print("\033[92m All tests passed.")
```
**Expected Output:**
<table>
<tr>
<td>
**x =**
</td>
<td>
[[ 1.62434536 -0.61175641 -0.52817175] <br>
[-1.07296862 0.86540763 -2.3015387 ]]
</td>
</tr>
<tr>
<td>
mask =
</td>
<td>
[[ True False False] <br>
[False False False]]
</td>
</tr>
</table>
Why keep track of the position of the max? It's because this is the input value that ultimately influenced the output, and therefore the cost. Backprop is computing gradients with respect to the cost, so anything that influences the ultimate cost should have a non-zero gradient. So, backprop will "propagate" the gradient back to this particular input value that had influenced the cost.
<a name='5-2-2'></a>
### 5.2.2 - Average Pooling - Backward Pass
In max pooling, for each input window, all the "influence" on the output came from a single input value--the max. In average pooling, every element of the input window has equal influence on the output. So to implement backprop, you will now implement a helper function that reflects this.
For example if we did average pooling in the forward pass using a 2x2 filter, then the mask you'll use for the backward pass will look like:
$$ dZ = 1 \quad \rightarrow \quad dZ =\begin{bmatrix}
1/4 && 1/4 \\
1/4 && 1/4
\end{bmatrix}\tag{5}$$
This implies that each position in the $dZ$ matrix contributes equally to output because in the forward pass, we took an average.
<a name='ex-7'></a>
### Exercise 7 - distribute_value
Implement the function below to equally distribute a value dz through a matrix of dimension shape.
[Hint](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ones.html)
```
def distribute_value(dz, shape):
"""
Distributes the input value in the matrix of dimension shape
Arguments:
dz -- input scalar
shape -- the shape (n_H, n_W) of the output matrix for which we want to distribute the value of dz
Returns:
a -- Array of size (n_H, n_W) for which we distributed the value of dz
"""
# Retrieve dimensions from shape (≈1 line)
# (n_H, n_W) = None
# Compute the value to distribute on the matrix (≈1 line)
# average = None
# Create a matrix where every entry is the "average" value (≈1 line)
# a = None
# YOUR CODE STARTS HERE
# YOUR CODE ENDS HERE
return a
a = distribute_value(2, (2, 2))
print('distributed value =', a)
assert type(a) == np.ndarray, "Output must be a np.ndarray"
assert a.shape == (2, 2), f"Wrong shape {a.shape} != (2, 2)"
assert np.sum(a) == 2, "Values must sum to 2"
a = distribute_value(100, (10, 10))
assert type(a) == np.ndarray, "Output must be a np.ndarray"
assert a.shape == (10, 10), f"Wrong shape {a.shape} != (10, 10)"
assert np.sum(a) == 100, "Values must sum to 100"
print("\033[92m All tests passed.")
```
**Expected Output**:
<table>
<tr>
<td>
distributed_value =
</td>
<td>
[[ 0.5 0.5]
<br\>
[ 0.5 0.5]]
</td>
</tr>
</table>
<a name='5-2-3'></a>
### 5.2.3 Putting it Together: Pooling Backward
You now have everything you need to compute backward propagation on a pooling layer.
<a name='ex-8'></a>
### Exercise 8 - pool_backward
Implement the `pool_backward` function in both modes (`"max"` and `"average"`). You will once again use 4 for-loops (iterating over training examples, height, width, and channels). You should use an `if/elif` statement to see if the mode is equal to `'max'` or `'average'`. If it is equal to 'average' you should use the `distribute_value()` function you implemented above to create a matrix of the same shape as `a_slice`. Otherwise, the mode is equal to '`max`', and you will create a mask with `create_mask_from_window()` and multiply it by the corresponding value of dA.
```
def pool_backward(dA, cache, mode = "max"):
"""
Implements the backward pass of the pooling layer
Arguments:
dA -- gradient of cost with respect to the output of the pooling layer, same shape as A
cache -- cache output from the forward pass of the pooling layer, contains the layer's input and hparameters
mode -- the pooling mode you would like to use, defined as a string ("max" or "average")
Returns:
dA_prev -- gradient of cost with respect to the input of the pooling layer, same shape as A_prev
"""
# Retrieve information from cache (≈1 line)
# (A_prev, hparameters) = None
# Retrieve hyperparameters from "hparameters" (≈2 lines)
# stride = None
# f = None
# Retrieve dimensions from A_prev's shape and dA's shape (≈2 lines)
# m, n_H_prev, n_W_prev, n_C_prev = None
# m, n_H, n_W, n_C = None
# Initialize dA_prev with zeros (≈1 line)
# dA_prev = None
# for i in range(None): # loop over the training examples
# select training example from A_prev (≈1 line)
# a_prev = None
# for h in range(n_H): # loop on the vertical axis
# for w in range(n_W): # loop on the horizontal axis
# for c in range(n_C): # loop over the channels (depth)
# Find the corners of the current "slice" (≈4 lines)
# vert_start = None
# vert_end = None
# horiz_start = None
# horiz_end = None
# Compute the backward propagation in both modes.
# if mode == "max":
# Use the corners and "c" to define the current slice from a_prev (≈1 line)
# a_prev_slice = None
# Create the mask from a_prev_slice (≈1 line)
# mask = None
# Set dA_prev to be dA_prev + (the mask multiplied by the correct entry of dA) (≈1 line)
# dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += None
# elif mode == "average":
# Get the value da from dA (≈1 line)
# da = None
# Define the shape of the filter as fxf (≈1 line)
# shape = None
# Distribute it to get the correct slice of dA_prev. i.e. Add the distributed value of da. (≈1 line)
# dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += None
# YOUR CODE STARTS HERE
# YOUR CODE ENDS HERE
# Making sure your output shape is correct
assert(dA_prev.shape == A_prev.shape)
return dA_prev
np.random.seed(1)
A_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride" : 1, "f": 2}
A, cache = pool_forward(A_prev, hparameters)
print(A.shape)
print(cache[0].shape)
dA = np.random.randn(5, 4, 2, 2)
dA_prev1 = pool_backward(dA, cache, mode = "max")
print("mode = max")
print('mean of dA = ', np.mean(dA))
print('dA_prev1[1,1] = ', dA_prev1[1, 1])
print()
dA_prev2 = pool_backward(dA, cache, mode = "average")
print("mode = average")
print('mean of dA = ', np.mean(dA))
print('dA_prev2[1,1] = ', dA_prev2[1, 1])
assert type(dA_prev1) == np.ndarray, "Wrong type"
assert dA_prev1.shape == (5, 5, 3, 2), f"Wrong shape {dA_prev1.shape} != (5, 5, 3, 2)"
assert np.allclose(dA_prev1[1, 1], [[0, 0],
[ 5.05844394, -1.68282702],
[ 0, 0]]), "Wrong values for mode max"
assert np.allclose(dA_prev2[1, 1], [[0.08485462, 0.2787552],
[1.26461098, -0.25749373],
[1.17975636, -0.53624893]]), "Wrong values for mode average"
print("\033[92m All tests passed.")
```
**Expected Output**:
mode = max:
<table>
<tr>
<td>
**mean of dA =**
</td>
<td>
0.145713902729
</td>
</tr>
<tr>
<td>
dA_prev[1,1] =
</td>
<td>
[[ 0. 0. ] <br>
[ 5.05844394 -1.68282702] <br>
[ 0. 0. ]]
</td>
</tr>
</table>
mode = average
<table>
<tr>
<td>
mean of dA =
</td>
<td>
0.145713902729
</td>
</tr>
<tr>
<td>
dA_prev[1,1] =
</td>
<td>
[[ 0.08485462 0.2787552 ] <br>
[ 1.26461098 -0.25749373] <br>
[ 1.17975636 -0.53624893]]
</td>
</tr>
</table>
**Congratulations**! You've completed the assignment and its optional portion. You now understand how convolutional neural networks work, and have implemented all the building blocks of a neural network. In the next assignment you will implement a ConvNet using TensorFlow. Nicely done! See you there.
| github_jupyter |
# Choosing the number of segments - Elbow chart method
This document illustrates how to decide the number of segments (optimal $k$) using elbow charts.
## Introducing elbow chart method
**When we should (not) add more clusters**: Ideally, the lower the $SSE$ is, the better is the clustering. Although adding more clusters (a higher $k$) always reduces $SSE$, adding too many clusters can be managerially cumbersome (e.g., when designing individual strategies for each segment) and redundant (e.g., nearby clusters have little differences). Hence, we want to add more clusters if doing so can **significantly** reduce $SSE$, and stop adding clusters if doing so **doesn't reduce $SSE$ by much**.
**How elbow chart works**: The elbow chart plots a curve of how SSE changes with the number of clusters. Because adding more clusters will reduce SSE, the curve will be downward sloping, and the curve is steeper if adding one more cluster ($k \rightarrow k+1$) reduces SSE by a greater amount. We should choose the cluster number $k$ that corresponds to the "elbow point" in the plot (the kink where the curve exhibits an "L" shape). The elbow point indicates that the curve is steeper on the left ($SSE$ decreases a lot from $k-1$ to $k$), and is flatter on the right ($SSE$ decreases not much from $k$ to $k+1$).
**Procedure**: Suppose we want to create no more than $K$ segments. The procedure is as follows:
1. For $k$ from $1$ to $K$: run k-mean algorithm with $k$ clusters, and calculate and record the $SSE$.
2. Plot $SSE$ over the number of segments $k$ to get the elbow chart.
3. Find $k$ that corresponds to the elbow point. This is the optimal number of segments to segment consumers.
4. Use the optimal $k$ to run k-mean algorithm to segment consumers.
We will use "MallCustomersTwoVariables.csv" for analysis.
## Loading data and preprocessing
This section will generate the normalized dataframe, `df_normalized`, for k-mean algorithm.
```
# importing packages
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans # Use "sklearn/cluster/KMeans" for clustering analysis
# importing data and renaming variables
url = "https://raw.githubusercontent.com/zoutianxin1992/MarketingAnalyticsPython/main/Marketing%20Analytics%20in%20Python/Segmentation/Datasets/MallCustomersTwoVariables.csv"
df = pd.read_csv(url,index_col=0) # use the first column (customer id) as index
df = df.rename(columns = {"Annual Income (k$)":"annual_income","Spending Score (1-100)":"spending_score"})
# normalizing the data for k-mean algorithm
df_normalized = (df-df.min())/(df.max()-df.min()) # By default, pandas calculate maximums and minimums by columns, which serves our purpose.
```
## Calculate $SSE$ for each $k$
For exposition, we will create no more than $K = 10$ clusters, and calculate $SSE$s when $k = 1,2,3,...,K$. This can be achieved with a for loop.
<br />
(If you use Windows, you may see a warning of "KMeans is known to have a memory leak...." Don't worry in our case because both our data size and the number of clusters are much smaller than when the problem will happen.)
```
K = 10 # K is the maximum number of clusters we will check
store_SSE = np.zeros(K) # create a vector to store SSE's. The k-th entry will be the SSE with k clusters.
for k in range(1, K+1): # try k from 1 to K
kmeanSpec = KMeans(n_clusters = k, n_init = 100) # set up k-mean model with k clusters
kmean_result = kmeanSpec.fit(df_normalized) # run k-mean on normalized data
store_SSE[k-1] = kmeanSpec.inertia_ # store the SSE (.inertia_) in the k-th entry of store_SSE
```
## Generate elbow chart
```
from matplotlib import pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = [12,8] # set figure size to be 12*8 inch
plt.plot(range(1, K+1), store_SSE)
plt.xticks(range(1, K+1), fontsize = 18)
plt.yticks(fontsize = 18)
plt.ylabel("SSE",fontsize = 18)
plt.xlabel("number of clusters", fontsize = 18)
```
As we can see, the elbow point (kink of "L" shape) appears at $k = 5$, which will be the optimal number of segments to use.
## Potential Problems of the elbow-chart method
- There may be no apparent elbow points or multiple elbow points in the chart
- Choice of elbow points is rather subjective
| github_jupyter |
# DIMAML for Autoencoder models
Training is on Celeba. Evaluation is on Tiny ImageNet
```
%load_ext autoreload
%autoreload 2
%env CUDA_VISIBLE_DEVICES=0
import os, sys, time
sys.path.insert(0, '..')
import lib
import math
import numpy as np
from copy import deepcopy
import torch, torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('seaborn-darkgrid')
plt.rcParams['pdf.fonttype'] = 42
plt.rcParams['ps.fonttype'] = 42
# For reproducibility
import random
seed = random.randint(0, 2 ** 32 - 1)
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
print(seed)
```
## Setting
```
model_type = 'AE'
# Dataset
data_dir = './data'
train_batch_size = 128
valid_batch_size = 256
test_batch_size = 128
num_workers = 3
pin_memory = True
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# AE
latent_dim = 64
loss_function = F.mse_loss
# MAML
max_steps = 1500
inner_loop_steps_in_epoch = 200
inner_loop_epochs = 3
inner_loop_steps = inner_loop_steps_in_epoch * inner_loop_epochs
meta_grad_clip = 10.
loss_kwargs={'reduction':'mean'}
loss_interval = 50
first_val_step = 200
assert (inner_loop_steps - first_val_step) % loss_interval == 0
validation_steps = int((inner_loop_steps - first_val_step) / loss_interval + 1)
# Inner optimizer
inner_optimizer_type='momentum'
inner_optimizer_kwargs = dict(
lr=0.01, momentum=0.9,
nesterov=False, weight_decay=0.0
)
# Meta optimizer
meta_learning_rate = 1e-4
meta_betas = (0.9, 0.997)
meta_decay_interval = max_steps
checkpoint_steps = 15
recovery_step = None
kwargs = dict(
first_valid_step=first_val_step,
valid_loss_interval=loss_interval,
loss_kwargs=loss_kwargs,
)
exp_name = f"{model_type}{latent_dim}_celeba_{inner_optimizer_type}" + \
f"_steps{inner_loop_steps}_interval{loss_interval}" + \
f"_tr_bs{train_batch_size}_val_bs{valid_batch_size}_seed_{seed}"
print("Experiment name: ", exp_name)
logs_path = "./logs/{}".format(exp_name)
assert recovery_step is not None or not os.path.exists(logs_path)
# !rm -rf {logs_path}
```
## Prepare the CelebA dataset
```
import pandas as pd
import shutil
celeba_data_dir = 'data/celeba/'
data = pd.read_csv(os.path.join(celeba_data_dir, 'list_eval_partition.csv'))
try:
for partition in ['train', 'val', 'test']:
os.makedirs(os.path.join(celeba_data_dir, partition))
os.makedirs(os.path.join(celeba_data_dir, partition, 'images'))
for i in data.index:
partition = data.loc[i].partition
src_path = os.path.join(celeba_data_dir, 'img_align_celeba/img_align_celeba', data.loc[i].image_id)
if partition == 0:
shutil.copyfile(src_path, os.path.join(celeba_data_dir, 'train', 'images', data.loc[i].image_id))
elif partition == 1:
shutil.copyfile(src_path, os.path.join(celeba_data_dir, 'val', 'images', data.loc[i].image_id))
elif partition == 2:
shutil.copyfile(src_path, os.path.join(celeba_data_dir, 'test', 'images', data.loc[i].image_id))
except FileExistsError:
print('\'train\', \'val\', \'test\' already exist. Probably, you do not want to copy data again')
from torchvision import transforms, datasets
from torch.utils.data import DataLoader
celeba_transforms = transforms.Compose([
transforms.Resize((64, 64)),
transforms.ToTensor(),
])
# Create the train set
celeba_train_dataset = datasets.ImageFolder(celeba_data_dir+'train', transform=celeba_transforms)
celeba_train_images = torch.cat([celeba_train_dataset[i][0][None] for i in range(len(celeba_train_dataset))])
celeba_mean_image = celeba_train_images.mean(0)
celeba_std_image = celeba_train_images.std(0)
celeba_train_images = (celeba_train_images - celeba_mean_image) / celeba_std_image
# Create the val set
celeba_valid_dataset = datasets.ImageFolder(celeba_data_dir+'val', celeba_transforms)
celeba_valid_images = torch.cat([celeba_valid_dataset[i][0][None] for i in range(len(celeba_valid_dataset))])
celeba_valid_images = (celeba_valid_images - celeba_mean_image) / celeba_std_image
# Create the test set
celeba_test_dataset = datasets.ImageFolder(celeba_data_dir+'test', celeba_transforms)
celeba_test_images = torch.cat([celeba_test_dataset[i][0][None] for i in range(len(celeba_test_dataset))])
celeba_test_images = (celeba_test_images - celeba_mean_image) / celeba_std_image
# Create data loaders
train_loader = torch.utils.data.DataLoader(celeba_train_images, batch_size=train_batch_size, shuffle=True,
pin_memory=pin_memory, num_workers=num_workers)
valid_loader = torch.utils.data.DataLoader(celeba_valid_images, batch_size=valid_batch_size, shuffle=True,
pin_memory=pin_memory, num_workers=num_workers)
test_loader = torch.utils.data.DataLoader(celeba_test_images, batch_size=test_batch_size,
pin_memory=pin_memory, num_workers=num_workers)
```
## Create the model and meta-optimizer
```
optimizer = lib.make_inner_optimizer(inner_optimizer_type, **inner_optimizer_kwargs)
model = lib.models.AE(latent_dim)
maml = lib.MAML(model, model_type, optimizer=optimizer,
checkpoint_steps=checkpoint_steps,
loss_function=loss_function
).to(device)
```
## Trainer
```
def samples_batches(dataloader, num_batches):
x_batches = []
for batch_i, x_batch in enumerate(dataloader):
if batch_i >= num_batches: break
x_batches.append(x_batch)
return x_batches
class TrainerAE(lib.Trainer):
def train_on_batch(self, train_loader, valid_loader, prefix='train/', **kwargs):
""" Performs a single gradient update and reports metrics """
# Sample train and val batches
x_batches = []
for _ in range(inner_loop_epochs):
x_batches.extend(samples_batches(train_loader, inner_loop_steps_in_epoch))
x_val_batches = samples_batches(valid_loader, validation_steps)
# Perform a meta training step
self.meta_optimizer.zero_grad()
with lib.training_mode(self.maml, is_train=True):
self.maml.resample_parameters()
_updated_model, train_loss_history, valid_loss_history, *etc = \
self.maml.forward(x_batches, x_batches, x_val_batches, x_val_batches,
device=self.device, **kwargs)
train_loss = torch.cat(train_loss_history).mean()
valid_loss = torch.cat(valid_loss_history).mean() if len(valid_loss_history) > 0 else torch.zeros(1)
valid_loss.backward()
# Check gradients
grad_norm = lib.utils.total_norm_frobenius(self.maml.initializers.parameters())
self.writer.add_scalar(prefix + "grad_norm", grad_norm, self.total_steps)
bad_grad = not math.isfinite(grad_norm)
if not bad_grad:
nn.utils.clip_grad_norm_(list(self.maml.initializers.parameters()), meta_grad_clip)
else:
print("Fix bad grad. Loss {} | Grad {}".format(train_loss.item(), grad_norm))
for param in self.maml.initializers.parameters():
param.grad = torch.where(torch.isfinite(param.grad),
param.grad, torch.zeros_like(param.grad))
self.meta_optimizer.step()
return self.record(train_loss=train_loss.item(),
valid_loss=valid_loss.item(), prefix=prefix)
def evaluate_metrics(self, train_loader, test_loader, prefix='val/', **kwargs):
""" Predicts and evaluates metrics over the entire dataset """
torch.cuda.empty_cache()
print('Baseline')
self.maml.resample_parameters(initializers=self.maml.untrained_initializers, is_final=True)
base_model = deepcopy(self.maml.model)
base_train_loss_history, base_test_loss_history = eval_model(base_model, train_loader, test_loader,
device=self.device, **kwargs)
print('DIMAML')
self.maml.resample_parameters(is_final=True)
maml_model = deepcopy(self.maml.model)
maml_train_loss_history, maml_test_loss_history = eval_model(maml_model, train_loader, test_loader,
device=self.device, **kwargs)
lib.utils.ae_draw_plots(base_train_loss_history, base_test_loss_history,
maml_train_loss_history, maml_test_loss_history)
self.writer.add_scalar(prefix + "train_AUC", sum(maml_train_loss_history), self.total_steps)
self.writer.add_scalar(prefix + "test_AUC", sum(maml_test_loss_history), self.total_steps)
self.writer.add_scalar(prefix + "test_loss", maml_test_loss_history[-1], self.total_steps)
########################
# Generate Train Batch #
########################
def generate_train_batches(train_loader, batches_in_epoch=150):
x_batches = []
for batch_i, x_batch in enumerate(train_loader):
if batch_i >= batches_in_epoch: break
x_batches.append(x_batch)
assert len(x_batches) == batches_in_epoch
local_x = torch.cat(x_batches, dim=0)
return DataLoader(local_x, batch_size=train_batch_size, shuffle=True,
num_workers=num_workers, pin_memory=pin_memory)
##################
# Eval functions #
##################
@torch.no_grad()
def compute_test_loss(model, loss_function, test_loader, device='cuda'):
model.eval()
test_loss = 0.
for batch_test in test_loader:
if isinstance(batch_test, (list, tuple)):
x_test = batch_test[0].to(device)
elif isinstance(batch_test, torch.Tensor):
x_test = batch_test.to(device)
else:
raise Exception("Wrong batch")
preds = model(x_test)
test_loss += loss_function(preds, x_test) * x_test.shape[0]
test_loss /= len(test_loader.dataset)
model.train()
return test_loss.item()
def eval_model(model, train_loader, test_loader, batches_in_epoch=150,
epochs=3, test_loss_interval=50, device='cuda', **kwargs):
optimizer = lib.optimizers.make_eval_inner_optimizer(
maml, model, inner_optimizer_type,
**inner_optimizer_kwargs
)
train_loss_history = []
test_loss_history = []
training_mode = model.training
total_iters = 0
for epoch in range(1, epochs + 1):
model.train()
for x_batch in train_loader:
optimizer.zero_grad()
x_batch = x_batch.to(device)
preds = model(x_batch)
loss = loss_function(preds, x_batch)
loss.backward()
optimizer.step()
train_loss_history.append(loss.item())
if (total_iters == 0) or (total_iters + 1) % test_loss_interval == 0:
model.eval()
test_loss = compute_test_loss(model, loss_function, test_loader, device=device)
print("Epoch {} | Total Iteration {} | Loss {}".format(epoch, total_iters+1, test_loss))
test_loss_history.append(test_loss)
model.train()
total_iters += 1
model.train(training_mode)
return train_loss_history, test_loss_history
train_loss_history = []
valid_loss_history = []
trainer = TrainerAE(maml, meta_lr=meta_learning_rate,
meta_betas=meta_betas, meta_grad_clip=meta_grad_clip,
exp_name=exp_name, recovery_step=recovery_step)
from IPython.display import clear_output
lib.free_memory()
t0 = time.time()
while trainer.total_steps <= max_steps:
local_train_loader = generate_train_batches(train_loader, inner_loop_steps_in_epoch)
with lib.activate_context_batchnorm(maml.model):
metrics = trainer.train_on_batch(
local_train_loader, valid_loader, **kwargs
)
train_loss = metrics['train_loss']
train_loss_history.append(train_loss)
valid_loss = metrics['valid_loss']
valid_loss_history.append(valid_loss)
if trainer.total_steps % 20 == 0:
clear_output(True)
print("Step: %d | Time: %f | Train Loss %.5f | Valid loss %.5f"
% (trainer.total_steps, time.time()-t0, train_loss, valid_loss))
plt.figure(figsize=[16, 5])
plt.subplot(1,2,1)
plt.title('Train Loss over time')
plt.plot(lib.utils.moving_average(train_loss_history, span=50))
plt.scatter(range(len(train_loss_history)), train_loss_history, alpha=0.1)
plt.subplot(1,2,2)
plt.title('Valid Loss over time')
plt.plot(lib.utils.moving_average(valid_loss_history, span=50))
plt.scatter(range(len(valid_loss_history)), valid_loss_history, alpha=0.1)
plt.show()
trainer.evaluate_metrics(local_train_loader, test_loader, epochs=inner_loop_epochs,
test_loss_interval=loss_interval)
lib.utils.ae_visualize_pdf(maml)
t0 = time.time()
if trainer.total_steps % 100 == 0:
trainer.save_model()
trainer.total_steps += 1
```
## Probability Functions
```
lib.utils.ae_visualize_pdf(maml)
```
# Evaluation
```
torch.backends.cudnn.deterministic = False
torch.backends.cudnn.benchmark = True
def genOrthgonal(dim):
a = torch.zeros((dim, dim)).normal_(0, 1)
q, r = torch.qr(a)
d = torch.diag(r, 0).sign()
diag_size = d.size(0)
d_exp = d.view(1, diag_size).expand(diag_size, diag_size)
q.mul_(d_exp)
return q
def makeDeltaOrthogonal(weights, gain):
rows = weights.size(0)
cols = weights.size(1)
if rows < cols:
print("In_filters should not be greater than out_filters.")
weights.data.fill_(0)
dim = max(rows, cols)
q = genOrthgonal(dim)
mid1 = weights.size(2) // 2
mid2 = weights.size(3) // 2
with torch.no_grad():
weights[:, :, mid1, mid2] = q[:weights.size(0), :weights.size(1)]
weights.mul_(gain)
def gradient_quotient(loss, params, eps=1e-5):
grad = torch.autograd.grad(loss, params, retain_graph=True, create_graph=True)
prod = torch.autograd.grad(sum([(g**2).sum() / 2 for g in grad]),
params, retain_graph=True, create_graph=True)
out = sum([((g - p) / (g + eps * (2*(g >= 0).float() - 1).detach()) - 1).abs().sum()
for g, p in zip(grad, prod)])
return out / sum([p.data.nelement() for p in params])
def metainit(model, criterion, x_size, lr=0.1, momentum=0.9, steps=200, eps=1e-5):
model.eval()
params = [p for p in model.parameters()
if p.requires_grad and len(p.size()) >= 2]
memory = [0] * len(params)
for i in range(steps):
input = torch.Tensor(*x_size).normal_(0, 1).cuda()
loss = criterion(model(input), input)
gq = gradient_quotient(loss, list(model.parameters()), eps)
grad = torch.autograd.grad(gq, params)
for j, (p, g_all) in enumerate(zip(params, grad)):
norm = p.data.norm().item()
g = torch.sign((p.data * g_all).sum() / norm)
memory[j] = momentum * memory[j] - lr * g.item()
new_norm = norm + memory[j]
p.data.mul_(new_norm / (norm + eps))
print("%d/GQ = %.2f" % (i, gq.item()))
```
## Evalution on Tiny Imagenet
```
class PixelNormalize(object):
def __init__(self, mean_image, std_image):
self.mean_image = mean_image
self.std_image = std_image
def __call__(self, image):
normalized_image = (image - self.mean_image) / self.std_image
return normalized_image
class Flip(object):
def __call__(self, image):
if random.random() > 0.5:
return image.flip(-1)
else:
return image
class CustomTensorDataset(torch.utils.data.Dataset):
""" TensorDataset with support of transforms """
def __init__(self, *tensors, transform=None):
assert all(tensors[0].size(0) == tensor.size(0) for tensor in tensors)
self.tensors = tensors
self.transform = transform
def __getitem__(self, index):
x = self.tensors[0][index]
if self.transform:
x = self.transform(x)
return x
def __len__(self):
return self.tensors[0].size(0)
# Load train and valid data
from torchvision import transforms, datasets
from torch.utils.data import DataLoader
data_dir = 'data/tiny-imagenet-200/'
train_image_dataset = datasets.ImageFolder(os.path.join(data_dir, 'train'), transforms.ToTensor())
train_images = torch.cat([train_image_dataset[i][0][None] for i in range(len(train_image_dataset))], dim=0)
mean_image = train_images.mean(0)
std_image = train_images.std(0)
train_transforms = transforms.Compose([
Flip(),
PixelNormalize(mean_image, std_image),
])
eval_transforms = transforms.Compose([
PixelNormalize(mean_image, std_image),
])
ti_train_dataset = CustomTensorDataset(train_images, transform=train_transforms)
valid_image_dataset = datasets.ImageFolder(os.path.join(data_dir, 'val'), transforms.ToTensor())
valid_images = torch.cat([valid_image_dataset[i][0][None] for i in range(len(valid_image_dataset))], dim=0)
ti_valid_dataset = CustomTensorDataset(valid_images, transform=eval_transforms)
test_image_dataset = datasets.ImageFolder(os.path.join(data_dir, 'test'), transforms.ToTensor())
test_images = torch.cat([test_image_dataset[i][0][None] for i in range(len(test_image_dataset))], dim=0)
ti_test_dataset = CustomTensorDataset(test_images, transform=eval_transforms)
# Create data loaders
ti_train_loader = DataLoader(
ti_train_dataset, batch_size=train_batch_size, shuffle=True,
num_workers=num_workers, pin_memory=pin_memory,
)
ti_valid_loader = DataLoader(
ti_valid_dataset, batch_size=valid_batch_size, shuffle=True,
num_workers=num_workers, pin_memory=pin_memory,
)
ti_test_loader = DataLoader(
ti_test_dataset, batch_size=test_batch_size, shuffle=False,
num_workers=num_workers, pin_memory=pin_memory
)
num_reruns = 10
ti_batches_in_epoch = len(ti_train_loader) #782 - full epoch
assert ti_batches_in_epoch == 782
ti_base_runs_10 = []
ti_base_runs_50 = []
ti_base_runs_100 = []
ti_metainit_runs_10 = []
ti_metainit_runs_50 = []
ti_metainit_runs_100 = []
ti_deltaorthogonal_runs_10 = []
ti_deltaorthogonal_runs_50 = []
ti_deltaorthogonal_runs_100 = []
ti_maml_runs_10 = []
ti_maml_runs_50 = []
ti_maml_runs_100 = []
for _ in range(num_reruns):
print("Baseline")
maml.resample_parameters(initializers=maml.untrained_initializers, is_final=True)
base_model = deepcopy(maml.model)
base_train_loss_history, base_test_loss_history = \
eval_model(base_model, ti_train_loader, ti_test_loader, epochs=100,
test_loss_interval=10*ti_batches_in_epoch, device=device)
print("MetaInit")
batch_x = next(iter(ti_train_loader))
maml.resample_parameters(initializers=maml.untrained_initializers, is_final=True)
metainit_model = deepcopy(maml.model)
metainit(metainit_model, loss_function, batch_x.shape, steps=200)
metainit_train_loss_history, metainit_test_loss_history = \
eval_model(metainit_model, ti_train_loader, ti_test_loader,
batches_in_epoch=ti_batches_in_epoch, epochs=100,
test_loss_interval=10*ti_batches_in_epoch, device=device)
print("Delta Orthogonal")
maml.resample_parameters(initializers=maml.untrained_initializers, is_final=True)
deltaorthogonal_model = deepcopy(maml.model)
for param in deltaorthogonal_model.parameters():
if len(param.size()) >= 4:
makeDeltaOrthogonal(param, nn.init.calculate_gain('relu'))
deltaorthogonal_train_loss_history, deltaorthogonal_test_loss_history = \
eval_model(deltaorthogonal_model, ti_train_loader, ti_test_loader,
batches_in_epoch=ti_batches_in_epoch, epochs=100,
test_loss_interval=10*ti_batches_in_epoch, device=device)
ti_deltaorthogonal_runs_10.append(deltaorthogonal_test_loss_history[1])
ti_deltaorthogonal_runs_50.append(deltaorthogonal_test_loss_history[5])
ti_deltaorthogonal_runs_100.append(deltaorthogonal_test_loss_history[10])
print("DIMAML")
maml.resample_parameters(is_final=True)
maml_model = deepcopy(maml.model)
maml_train_loss_history, maml_test_loss_history = \
eval_model(maml_model, ti_train_loader, ti_test_loader, epochs=100,
test_loss_interval=10*ti_batches_in_epoch, device=device)
ti_base_runs_10.append(base_test_loss_history[1])
ti_base_runs_50.append(base_test_loss_history[5])
ti_base_runs_100.append(base_test_loss_history[10])
ti_metainit_runs_10.append(metainit_test_loss_history[1])
ti_metainit_runs_50.append(metainit_test_loss_history[5])
ti_metainit_runs_100.append(metainit_test_loss_history[10])
ti_maml_runs_10.append(maml_test_loss_history[1])
ti_maml_runs_50.append(maml_test_loss_history[5])
ti_maml_runs_100.append(maml_test_loss_history[10])
print("Baseline 10 epoch: ", np.mean(ti_base_runs_10), np.std(ti_base_runs_10, ddof=1))
print("Baseline 50 epoch: ", np.mean(ti_base_runs_50), np.std(ti_base_runs_50, ddof=1))
print("Baseline 100 epoch: ", np.mean(ti_base_runs_100), np.std(ti_base_runs_100, ddof=1))
print()
print("DeltaOrthogonal 10 epoch: ", np.mean(ti_deltaorthogonal_runs_10), np.std(ti_deltaorthogonal_runs_10, ddof=1))
print("DeltaOrthogonal 50 epoch: ", np.mean(ti_deltaorthogonal_runs_50), np.std(ti_deltaorthogonal_runs_50, ddof=1))
print("DeltaOrthogonal 100 epoch: ", np.mean(ti_deltaorthogonal_runs_100), np.std(ti_deltaorthogonal_runs_100, ddof=1))
print()
print("MetaInit 10 epoch: ", np.mean(ti_metainit_runs_10), np.std(ti_metainit_runs_10, ddof=1))
print("MetaInit 50 epoch: ", np.mean(ti_metainit_runs_50), np.std(ti_metainit_runs_50, ddof=1))
print("MetaInit 100 epoch: ", np.mean(ti_metainit_runs_100), np.std(ti_metainit_runs_100, ddof=1))
print()
print("DIMAML 10 epoch: ", np.mean(ti_maml_runs_10), np.std(ti_maml_runs_10, ddof=1))
print("DIMAML 50 epoch: ", np.mean(ti_maml_runs_50), np.std(ti_maml_runs_50, ddof=1))
print("DIMAML 100 epoch: ", np.mean(ti_maml_runs_100), np.std(ti_maml_runs_100, ddof=1))
```
| github_jupyter |
# Autonomous Driving - Car Detection
Welcome to the Week 3 programming assignment! In this notebook, you'll implement object detection using the very powerful YOLO model. Many of the ideas in this notebook are described in the two YOLO papers: [Redmon et al., 2016](https://arxiv.org/abs/1506.02640) and [Redmon and Farhadi, 2016](https://arxiv.org/abs/1612.08242).
**By the end of this assignment, you'll be able to**:
- Detect objects in a car detection dataset
- Implement non-max suppression to increase accuracy
- Implement intersection over union
- Handle bounding boxes, a type of image annotation popular in deep learning
## Table of Contents
- [Packages](#0)
- [1 - Problem Statement](#1)
- [2 - YOLO](#2)
- [2.1 - Model Details](#2-1)
- [2.2 - Filtering with a Threshold on Class Scores](#2-2)
- [Exercise 1 - yolo_filter_boxes](#ex-1)
- [2.3 - Non-max Suppression](#2-3)
- [Exercise 2 - iou](#ex-2)
- [2.4 - YOLO Non-max Suppression](#2-4)
- [Exercise 3 - yolo_non_max_suppression](#ex-3)
- [2.5 - Wrapping Up the Filtering](#2-5)
- [Exercise 4 - yolo_eval](#ex-4)
- [3 - Test YOLO Pre-trained Model on Images](#3)
- [3.1 - Defining Classes, Anchors and Image Shape](#3-1)
- [3.2 - Loading a Pre-trained Model](#3-2)
- [3.3 - Convert Output of the Model to Usable Bounding Box Tensors](#3-3)
- [3.4 - Filtering Boxes](#3-4)
- [3.5 - Run the YOLO on an Image](#3-5)
- [4 - Summary for YOLO](#4)
- [5 - References](#5)
<a name='0'></a>
## Packages
Run the following cell to load the packages and dependencies that will come in handy as you build the object detector!
```
import argparse
import os
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
import scipy.io
import scipy.misc
import numpy as np
import pandas as pd
import PIL
from PIL import ImageFont, ImageDraw, Image
import tensorflow as tf
from tensorflow.python.framework.ops import EagerTensor
from tensorflow.keras.models import load_model
from yad2k.models.keras_yolo import yolo_head
from yad2k.utils.utils import draw_boxes, get_colors_for_classes, scale_boxes, read_classes, read_anchors, preprocess_image
%matplotlib inline
```
<a name='1'></a>
## 1 - Problem Statement
You are working on a self-driving car. Go you! As a critical component of this project, you'd like to first build a car detection system. To collect data, you've mounted a camera to the hood (meaning the front) of the car, which takes pictures of the road ahead every few seconds as you drive around.
<center>
<video width="400" height="200" src="nb_images/road_video_compressed2.mp4" type="video/mp4" controls>
</video>
</center>
<caption><center> Pictures taken from a car-mounted camera while driving around Silicon Valley. <br> Dataset provided by <a href="https://www.drive.ai/">drive.ai</a>.
</center></caption>
You've gathered all these images into a folder and labelled them by drawing bounding boxes around every car you found. Here's an example of what your bounding boxes look like:
<img src="nb_images/box_label.png" style="width:500px;height:250;">
<caption><center> <u><b>Figure 1</u></b>: Definition of a box<br> </center></caption>
If there are 80 classes you want the object detector to recognize, you can represent the class label $c$ either as an integer from 1 to 80, or as an 80-dimensional vector (with 80 numbers) one component of which is 1, and the rest of which are 0. The video lectures used the latter representation; in this notebook, you'll use both representations, depending on which is more convenient for a particular step.
In this exercise, you'll discover how YOLO ("You Only Look Once") performs object detection, and then apply it to car detection. Because the YOLO model is very computationally expensive to train, the pre-trained weights are already loaded for you to use.
<a name='2'></a>
## 2 - YOLO
"You Only Look Once" (YOLO) is a popular algorithm because it achieves high accuracy while also being able to run in real time. This algorithm "only looks once" at the image in the sense that it requires only one forward propagation pass through the network to make predictions. After non-max suppression, it then outputs recognized objects together with the bounding boxes.
<a name='2-1'></a>
### 2.1 - Model Details
#### Inputs and outputs
- The **input** is a batch of images, and each image has the shape (m, 608, 608, 3)
- The **output** is a list of bounding boxes along with the recognized classes. Each bounding box is represented by 6 numbers $(p_c, b_x, b_y, b_h, b_w, c)$ as explained above. If you expand $c$ into an 80-dimensional vector, each bounding box is then represented by 85 numbers.
#### Anchor Boxes
* Anchor boxes are chosen by exploring the training data to choose reasonable height/width ratios that represent the different classes. For this assignment, 5 anchor boxes were chosen for you (to cover the 80 classes), and stored in the file './model_data/yolo_anchors.txt'
* The dimension for anchor boxes is the second to last dimension in the encoding: $(m, n_H,n_W,anchors,classes)$.
* The YOLO architecture is: IMAGE (m, 608, 608, 3) -> DEEP CNN -> ENCODING (m, 19, 19, 5, 85).
#### Encoding
Let's look in greater detail at what this encoding represents.
<img src="nb_images/architecture.png" style="width:700px;height:400;">
<caption><center> <u><b> Figure 2 </u></b>: Encoding architecture for YOLO<br> </center></caption>
If the center/midpoint of an object falls into a grid cell, that grid cell is responsible for detecting that object.
Since you're using 5 anchor boxes, each of the 19 x19 cells thus encodes information about 5 boxes. Anchor boxes are defined only by their width and height.
For simplicity, you'll flatten the last two dimensions of the shape (19, 19, 5, 85) encoding, so the output of the Deep CNN is (19, 19, 425).
<img src="nb_images/flatten.png" style="width:700px;height:400;">
<caption><center> <u><b> Figure 3 </u></b>: Flattening the last two last dimensions<br> </center></caption>
#### Class score
Now, for each box (of each cell) you'll compute the following element-wise product and extract a probability that the box contains a certain class.
The class score is $score_{c,i} = p_{c} \times c_{i}$: the probability that there is an object $p_{c}$ times the probability that the object is a certain class $c_{i}$.
<img src="nb_images/probability_extraction.png" style="width:700px;height:400;">
<caption><center> <u><b>Figure 4</u></b>: Find the class detected by each box<br> </center></caption>
##### Example of figure 4
* In figure 4, let's say for box 1 (cell 1), the probability that an object exists is $p_{1}=0.60$. So there's a 60% chance that an object exists in box 1 (cell 1).
* The probability that the object is the class "category 3 (a car)" is $c_{3}=0.73$.
* The score for box 1 and for category "3" is $score_{1,3}=0.60 \times 0.73 = 0.44$.
* Let's say you calculate the score for all 80 classes in box 1, and find that the score for the car class (class 3) is the maximum. So you'll assign the score 0.44 and class "3" to this box "1".
#### Visualizing classes
Here's one way to visualize what YOLO is predicting on an image:
- For each of the 19x19 grid cells, find the maximum of the probability scores (taking a max across the 80 classes, one maximum for each of the 5 anchor boxes).
- Color that grid cell according to what object that grid cell considers the most likely.
Doing this results in this picture:
<img src="nb_images/proba_map.png" style="width:300px;height:300;">
<caption><center> <u><b>Figure 5</u></b>: Each one of the 19x19 grid cells is colored according to which class has the largest predicted probability in that cell.<br> </center></caption>
Note that this visualization isn't a core part of the YOLO algorithm itself for making predictions; it's just a nice way of visualizing an intermediate result of the algorithm.
#### Visualizing bounding boxes
Another way to visualize YOLO's output is to plot the bounding boxes that it outputs. Doing that results in a visualization like this:
<img src="nb_images/anchor_map.png" style="width:200px;height:200;">
<caption><center> <u><b>Figure 6</u></b>: Each cell gives you 5 boxes. In total, the model predicts: 19x19x5 = 1805 boxes just by looking once at the image (one forward pass through the network)! Different colors denote different classes. <br> </center></caption>
#### Non-Max suppression
In the figure above, the only boxes plotted are ones for which the model had assigned a high probability, but this is still too many boxes. You'd like to reduce the algorithm's output to a much smaller number of detected objects.
To do so, you'll use **non-max suppression**. Specifically, you'll carry out these steps:
- Get rid of boxes with a low score. Meaning, the box is not very confident about detecting a class, either due to the low probability of any object, or low probability of this particular class.
- Select only one box when several boxes overlap with each other and detect the same object.
<a name='2-2'></a>
### 2.2 - Filtering with a Threshold on Class Scores
You're going to first apply a filter by thresholding, meaning you'll get rid of any box for which the class "score" is less than a chosen threshold.
The model gives you a total of 19x19x5x85 numbers, with each box described by 85 numbers. It's convenient to rearrange the (19,19,5,85) (or (19,19,425)) dimensional tensor into the following variables:
- `box_confidence`: tensor of shape $(19, 19, 5, 1)$ containing $p_c$ (confidence probability that there's some object) for each of the 5 boxes predicted in each of the 19x19 cells.
- `boxes`: tensor of shape $(19, 19, 5, 4)$ containing the midpoint and dimensions $(b_x, b_y, b_h, b_w)$ for each of the 5 boxes in each cell.
- `box_class_probs`: tensor of shape $(19, 19, 5, 80)$ containing the "class probabilities" $(c_1, c_2, ... c_{80})$ for each of the 80 classes for each of the 5 boxes per cell.
<a name='ex-1'></a>
### Exercise 1 - yolo_filter_boxes
Implement `yolo_filter_boxes()`.
1. Compute box scores by doing the elementwise product as described in Figure 4 ($p \times c$).
The following code may help you choose the right operator:
```python
a = np.random.randn(19, 19, 5, 1)
b = np.random.randn(19, 19, 5, 80)
c = a * b # shape of c will be (19, 19, 5, 80)
```
This is an example of **broadcasting** (multiplying vectors of different sizes).
2. For each box, find:
- the index of the class with the maximum box score
- the corresponding box score
**Useful References**
* [tf.math.argmax](https://www.tensorflow.org/api_docs/python/tf/math/argmax)
* [tf.math.reduce_max](https://www.tensorflow.org/api_docs/python/tf/math/reduce_max)
**Helpful Hints**
* For the `axis` parameter of `argmax` and `reduce_max`, if you want to select the **last** axis, one way to do so is to set `axis=-1`. This is similar to Python array indexing, where you can select the last position of an array using `arrayname[-1]`.
* Applying `reduce_max` normally collapses the axis for which the maximum is applied. `keepdims=False` is the default option, and allows that dimension to be removed. You don't need to keep the last dimension after applying the maximum here.
3. Create a mask by using a threshold. As a reminder: `([0.9, 0.3, 0.4, 0.5, 0.1] < 0.4)` returns: `[False, True, False, False, True]`. The mask should be `True` for the boxes you want to keep.
4. Use TensorFlow to apply the mask to `box_class_scores`, `boxes` and `box_classes` to filter out the boxes you don't want. You should be left with just the subset of boxes you want to keep.
**One more useful reference**:
* [tf.boolean mask](https://www.tensorflow.org/api_docs/python/tf/boolean_mask)
**And one more helpful hint**: :)
* For the `tf.boolean_mask`, you can keep the default `axis=None`.
```
# GRADED FUNCTION: yolo_filter_boxes
def yolo_filter_boxes(boxes, box_confidence, box_class_probs, threshold = 0.6):
"""Filters YOLO boxes by thresholding on object and class confidence.
Arguments:
boxes -- tensor of shape (19, 19, 5, 4)
box_confidence -- tensor of shape (19, 19, 5, 1)
box_class_probs -- tensor of shape (19, 19, 5, 80)
threshold -- real value, if [ highest class probability score < threshold],
then get rid of the corresponding box
Returns:
scores -- tensor of shape (None,), containing the class probability score for selected boxes
boxes -- tensor of shape (None, 4), containing (b_x, b_y, b_h, b_w) coordinates of selected boxes
classes -- tensor of shape (None,), containing the index of the class detected by the selected boxes
Note: "None" is here because you don't know the exact number of selected boxes, as it depends on the threshold.
For example, the actual output size of scores would be (10,) if there are 10 boxes.
"""
x = 10
y = tf.constant(100)
# YOUR CODE STARTS HERE
# Step 1: Compute box scores
##(≈ 1 line)
box_scores = box_class_probs*box_confidence
# Step 2: Find the box_classes using the max box_scores, keep track of the corresponding score
##(≈ 2 lines)
box_classes = tf.math.argmax(box_scores,axis=-1)
box_class_scores = tf.math.reduce_max(box_scores,axis=-1)
# Step 3: Create a filtering mask based on "box_class_scores" by using "threshold". The mask should have the
# same dimension as box_class_scores, and be True for the boxes you want to keep (with probability >= threshold)
## (≈ 1 line)
filtering_mask = (box_class_scores >= threshold)
# Step 4: Apply the mask to box_class_scores, boxes and box_classes
## (≈ 3 lines)
scores = tf.boolean_mask(box_class_scores,filtering_mask)
boxes = tf.boolean_mask(boxes,filtering_mask)
classes = tf.boolean_mask(box_classes,filtering_mask)
# YOUR CODE ENDS HERE
return scores, boxes, classes
tf.random.set_seed(10)
box_confidence = tf.random.normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1)
boxes = tf.random.normal([19, 19, 5, 4], mean=1, stddev=4, seed = 1)
box_class_probs = tf.random.normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_filter_boxes(boxes, box_confidence, box_class_probs, threshold = 0.5)
print("scores[2] = " + str(scores[2].numpy()))
print("boxes[2] = " + str(boxes[2].numpy()))
print("classes[2] = " + str(classes[2].numpy()))
print("scores.shape = " + str(scores.shape))
print("boxes.shape = " + str(boxes.shape))
print("classes.shape = " + str(classes.shape))
assert type(scores) == EagerTensor, "Use tensorflow functions"
assert type(boxes) == EagerTensor, "Use tensorflow functions"
assert type(classes) == EagerTensor, "Use tensorflow functions"
assert scores.shape == (1789,), "Wrong shape in scores"
assert boxes.shape == (1789, 4), "Wrong shape in boxes"
assert classes.shape == (1789,), "Wrong shape in classes"
assert np.isclose(scores[2].numpy(), 9.270486), "Values are wrong on scores"
assert np.allclose(boxes[2].numpy(), [4.6399336, 3.2303846, 4.431282, -2.202031]), "Values are wrong on boxes"
assert classes[2].numpy() == 8, "Values are wrong on classes"
print("\033[92m All tests passed!")
```
**Expected Output**:
<table>
<tr>
<td>
<b>scores[2]</b>
</td>
<td>
9.270486
</td>
</tr>
<tr>
<td>
<b>boxes[2]</b>
</td>
<td>
[ 4.6399336 3.2303846 4.431282 -2.202031 ]
</td>
</tr>
<tr>
<td>
<b>classes[2]</b>
</td>
<td>
8
</td>
</tr>
<tr>
<td>
<b>scores.shape</b>
</td>
<td>
(1789,)
</td>
</tr>
<tr>
<td>
<b>boxes.shape</b>
</td>
<td>
(1789, 4)
</td>
</tr>
<tr>
<td>
<b>classes.shape</b>
</td>
<td>
(1789,)
</td>
</tr>
</table>
**Note** In the test for `yolo_filter_boxes`, you're using random numbers to test the function. In real data, the `box_class_probs` would contain non-zero values between 0 and 1 for the probabilities. The box coordinates in `boxes` would also be chosen so that lengths and heights are non-negative.
<a name='2-3'></a>
### 2.3 - Non-max Suppression
Even after filtering by thresholding over the class scores, you still end up with a lot of overlapping boxes. A second filter for selecting the right boxes is called non-maximum suppression (NMS).
<img src="nb_images/non-max-suppression.png" style="width:500px;height:400;">
<caption><center> <u> <b>Figure 7</b> </u>: In this example, the model has predicted 3 cars, but it's actually 3 predictions of the same car. Running non-max suppression (NMS) will select only the most accurate (highest probability) of the 3 boxes. <br> </center></caption>
Non-max suppression uses the very important function called **"Intersection over Union"**, or IoU.
<img src="nb_images/iou.png" style="width:500px;height:400;">
<caption><center> <u> <b>Figure 8</b> </u>: Definition of "Intersection over Union". <br> </center></caption>
<a name='ex-2'></a>
### Exercise 2 - iou
Implement `iou()`
Some hints:
- This code uses the convention that (0,0) is the top-left corner of an image, (1,0) is the upper-right corner, and (1,1) is the lower-right corner. In other words, the (0,0) origin starts at the top left corner of the image. As x increases, you move to the right. As y increases, you move down.
- For this exercise, a box is defined using its two corners: upper left $(x_1, y_1)$ and lower right $(x_2,y_2)$, instead of using the midpoint, height and width. This makes it a bit easier to calculate the intersection.
- To calculate the area of a rectangle, multiply its height $(y_2 - y_1)$ by its width $(x_2 - x_1)$. Since $(x_1,y_1)$ is the top left and $x_2,y_2$ are the bottom right, these differences should be non-negative.
- To find the **intersection** of the two boxes $(xi_{1}, yi_{1}, xi_{2}, yi_{2})$:
- Feel free to draw some examples on paper to clarify this conceptually.
- The top left corner of the intersection $(xi_{1}, yi_{1})$ is found by comparing the top left corners $(x_1, y_1)$ of the two boxes and finding a vertex that has an x-coordinate that is closer to the right, and y-coordinate that is closer to the bottom.
- The bottom right corner of the intersection $(xi_{2}, yi_{2})$ is found by comparing the bottom right corners $(x_2,y_2)$ of the two boxes and finding a vertex whose x-coordinate is closer to the left, and the y-coordinate that is closer to the top.
- The two boxes **may have no intersection**. You can detect this if the intersection coordinates you calculate end up being the top right and/or bottom left corners of an intersection box. Another way to think of this is if you calculate the height $(y_2 - y_1)$ or width $(x_2 - x_1)$ and find that at least one of these lengths is negative, then there is no intersection (intersection area is zero).
- The two boxes may intersect at the **edges or vertices**, in which case the intersection area is still zero. This happens when either the height or width (or both) of the calculated intersection is zero.
**Additional Hints**
- `xi1` = **max**imum of the x1 coordinates of the two boxes
- `yi1` = **max**imum of the y1 coordinates of the two boxes
- `xi2` = **min**imum of the x2 coordinates of the two boxes
- `yi2` = **min**imum of the y2 coordinates of the two boxes
- `inter_area` = You can use `max(height, 0)` and `max(width, 0)`
```
#########################################################################
######################## USELESS BELOW ##################################
#########################################################################
# GRADED FUNCTION: iou
def iou(box1, box2):
"""Implement the intersection over union (IoU) between box1 and box2
Arguments:
box1 -- first box, list object with coordinates (box1_x1, box1_y1, box1_x2, box_1_y2)
box2 -- second box, list object with coordinates (box2_x1, box2_y1, box2_x2, box2_y2)
"""
(box1_x1, box1_y1, box1_x2, box1_y2) = box1
(box2_x1, box2_y1, box2_x2, box2_y2) = box2
# YOUR CODE STARTS HERE
# Calculate the (yi1, xi1, yi2, xi2) coordinates of the intersection of box1 and box2. Calculate its Area.
##(≈ 7 lines)
xi1 = max(box1_x1,box2_x1)
yi1 = max(box1_y1,box2_y1)
xi2 = min(box1_x2,box2_x2)
yi2 = min(box1_y2,box2_y2)
inter_width = max(0,yi2 - yi1)
inter_height = max(0,xi2 - xi1)
inter_area = inter_width*inter_height
# Calculate the Union area by using Formula: Union(A,B) = A + B - Inter(A,B)
## (≈ 3 lines)
box1_area = (box1_x2-box1_x1)*((box1_y2-box1_y1))
box2_area = (box2_x2-box2_x1)*((box2_y2-box2_y1))
union_area = box1_area + box2_area - inter_area
# compute the IoU
## (≈ 1 line)
iou = inter_area/union_area
# YOUR CODE ENDS HERE
return iou
## Test case 1: boxes intersect
box1 = (2, 1, 4, 3)
box2 = (1, 2, 3, 4)
print("iou for intersecting boxes = " + str(iou(box1, box2)))
assert iou(box1, box2) < 1, "The intersection area must be always smaller or equal than the union area."
assert np.isclose(iou(box1, box2), 0.14285714), "Wrong value. Check your implementation. Problem with intersecting boxes"
## Test case 2: boxes do not intersect
box1 = (1,2,3,4)
box2 = (5,6,7,8)
print("iou for non-intersecting boxes = " + str(iou(box1,box2)))
assert iou(box1, box2) == 0, "Intersection must be 0"
## Test case 3: boxes intersect at vertices only
box1 = (1,1,2,2)
box2 = (2,2,3,3)
print("iou for boxes that only touch at vertices = " + str(iou(box1,box2)))
assert iou(box1, box2) == 0, "Intersection at vertices must be 0"
## Test case 4: boxes intersect at edge only
box1 = (1,1,3,3)
box2 = (2,3,3,4)
print("iou for boxes that only touch at edges = " + str(iou(box1,box2)))
assert iou(box1, box2) == 0, "Intersection at edges must be 0"
print("\033[92m All tests passed!")
```
**Expected Output**:
```
iou for intersecting boxes = 0.14285714285714285
iou for non-intersecting boxes = 0.0
iou for boxes that only touch at vertices = 0.0
iou for boxes that only touch at edges = 0.0
```
<a name='2-4'></a>
### 2.4 - YOLO Non-max Suppression
You are now ready to implement non-max suppression. The key steps are:
1. Select the box that has the highest score.
2. Compute the overlap of this box with all other boxes, and remove boxes that overlap significantly (iou >= `iou_threshold`).
3. Go back to step 1 and iterate until there are no more boxes with a lower score than the currently selected box.
This will remove all boxes that have a large overlap with the selected boxes. Only the "best" boxes remain.
<a name='ex-3'></a>
### Exercise 3 - yolo_non_max_suppression
Implement `yolo_non_max_suppression()` using TensorFlow. TensorFlow has two built-in functions that are used to implement non-max suppression (so you don't actually need to use your `iou()` implementation):
**Reference documentation**:
- [tf.image.non_max_suppression()](https://www.tensorflow.org/api_docs/python/tf/image/non_max_suppression)
```
tf.image.non_max_suppression(
boxes,
scores,
max_output_size,
iou_threshold=0.5,
name=None
)
```
Note that in the version of TensorFlow used here, there is no parameter `score_threshold` (it's shown in the documentation for the latest version) so trying to set this value will result in an error message: *got an unexpected keyword argument `score_threshold`.*
- [tf.gather()](https://www.tensorflow.org/api_docs/python/tf/gather)
```
keras.gather(
reference,
indices
)
```
```
# GRADED FUNCTION: yolo_non_max_suppression
def yolo_non_max_suppression(scores, boxes, classes, max_boxes = 10, iou_threshold = 0.5):
"""
Applies Non-max suppression (NMS) to set of boxes
Arguments:
scores -- tensor of shape (None,), output of yolo_filter_boxes()
boxes -- tensor of shape (None, 4), output of yolo_filter_boxes() that have been scaled to the image size (see later)
classes -- tensor of shape (None,), output of yolo_filter_boxes()
max_boxes -- integer, maximum number of predicted boxes you'd like
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (, None), predicted score for each box
boxes -- tensor of shape (4, None), predicted box coordinates
classes -- tensor of shape (, None), predicted class for each box
Note: The "None" dimension of the output tensors has obviously to be less than max_boxes. Note also that this
function will transpose the shapes of scores, boxes, classes. This is made for convenience.
"""
max_boxes_tensor = tf.Variable(max_boxes, dtype='int32') # tensor to be used in tf.image.non_max_suppression()
# Use tf.image.non_max_suppression() to get the list of indices corresponding to boxes you keep
##(≈ 1 line)
nms_indices = tf.image.non_max_suppression(boxes,scores,max_boxes_tensor,iou_threshold)
# Use tf.gather() to select only nms_indices from scores, boxes and classes
##(≈ 3 lines)
scores = tf.gather(scores,nms_indices)
boxes = tf.gather(boxes,nms_indices)
classes = tf.gather(classes,nms_indices)
# YOUR CODE STARTS HERE
# YOUR CODE ENDS HERE
return scores, boxes, classes
tf.random.set_seed(10)
scores = tf.random.normal([54,], mean=1, stddev=4, seed = 1)
boxes = tf.random.normal([54, 4], mean=1, stddev=4, seed = 1)
classes = tf.random.normal([54,], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes)
assert type(scores) == EagerTensor, "Use tensoflow functions"
print("scores[2] = " + str(scores[2].numpy()))
print("boxes[2] = " + str(boxes[2].numpy()))
print("classes[2] = " + str(classes[2].numpy()))
print("scores.shape = " + str(scores.numpy().shape))
print("boxes.shape = " + str(boxes.numpy().shape))
print("classes.shape = " + str(classes.numpy().shape))
assert type(scores) == EagerTensor, "Use tensoflow functions"
assert type(boxes) == EagerTensor, "Use tensoflow functions"
assert type(classes) == EagerTensor, "Use tensoflow functions"
assert scores.shape == (10,), "Wrong shape"
assert boxes.shape == (10, 4), "Wrong shape"
assert classes.shape == (10,), "Wrong shape"
assert np.isclose(scores[2].numpy(), 8.147684), "Wrong value on scores"
assert np.allclose(boxes[2].numpy(), [ 6.0797963, 3.743308, 1.3914018, -0.34089637]), "Wrong value on boxes"
assert np.isclose(classes[2].numpy(), 1.7079165), "Wrong value on classes"
print("\033[92m All tests passed!")
```
**Expected Output**:
<table>
<tr>
<td>
<b>scores[2]</b>
</td>
<td>
8.147684
</td>
</tr>
<tr>
<td>
<b>boxes[2]</b>
</td>
<td>
[ 6.0797963 3.743308 1.3914018 -0.34089637]
</td>
</tr>
<tr>
<td>
<b>classes[2]</b>
</td>
<td>
1.7079165
</td>
</tr>
<tr>
<td>
<b>scores.shape</b>
</td>
<td>
(10,)
</td>
</tr>
<tr>
<td>
<b>boxes.shape</b>
</td>
<td>
(10, 4)
</td>
</tr>
<tr>
<td>
<b>classes.shape</b>
</td>
<td>
(10,)
</td>
</tr>
</table>
<a name='2-5'></a>
### 2.5 - Wrapping Up the Filtering
It's time to implement a function taking the output of the deep CNN (the 19x19x5x85 dimensional encoding) and filtering through all the boxes using the functions you've just implemented.
<a name='ex-4'></a>
### Exercise 4 - yolo_eval
Implement `yolo_eval()` which takes the output of the YOLO encoding and filters the boxes using score threshold and NMS. There's just one last implementational detail you have to know. There're a few ways of representing boxes, such as via their corners or via their midpoint and height/width. YOLO converts between a few such formats at different times, using the following functions (which are provided):
```python
boxes = yolo_boxes_to_corners(box_xy, box_wh)
```
which converts the yolo box coordinates (x,y,w,h) to box corners' coordinates (x1, y1, x2, y2) to fit the input of `yolo_filter_boxes`
```python
boxes = scale_boxes(boxes, image_shape)
```
YOLO's network was trained to run on 608x608 images. If you are testing this data on a different size image -- for example, the car detection dataset had 720x1280 images -- this step rescales the boxes so that they can be plotted on top of the original 720x1280 image.
Don't worry about these two functions; you'll see where they need to be called below.
```
def yolo_boxes_to_corners(box_xy, box_wh):
"""Convert YOLO box predictions to bounding box corners."""
box_mins = box_xy - (box_wh / 2.)
box_maxes = box_xy + (box_wh / 2.)
return tf.keras.backend.concatenate([
box_mins[..., 1:2], # y_min
box_mins[..., 0:1], # x_min
box_maxes[..., 1:2], # y_max
box_maxes[..., 0:1] # x_max
])
# GRADED FUNCTION: yolo_eval
def yolo_eval(yolo_outputs, image_shape = (720, 1280), max_boxes=10, score_threshold=.6, iou_threshold=.5):
"""
Converts the output of YOLO encoding (a lot of boxes) to your predicted boxes along with their scores, box coordinates and classes.
Arguments:
yolo_outputs -- output of the encoding model (for image_shape of (608, 608, 3)), contains 4 tensors:
box_xy: tensor of shape (None, 19, 19, 5, 2)
box_wh: tensor of shape (None, 19, 19, 5, 2)
box_confidence: tensor of shape (None, 19, 19, 5, 1)
box_class_probs: tensor of shape (None, 19, 19, 5, 80)
image_shape -- tensor of shape (2,) containing the input shape, in this notebook we use (608., 608.) (has to be float32 dtype)
max_boxes -- integer, maximum number of predicted boxes you'd like
score_threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (None, ), predicted score for each box
boxes -- tensor of shape (None, 4), predicted box coordinates
classes -- tensor of shape (None,), predicted class for each box
"""
# Retrieve outputs of the YOLO model (≈1 line)
box_xy, box_wh, box_confidence, box_class_probs = yolo_outputs
# Convert boxes to be ready for filtering functions (convert boxes box_xy and box_wh to corner coordinates)
boxes = yolo_boxes_to_corners(box_xy, box_wh)
# Use one of the functions you've implemented to perform Score-filtering with a threshold of score_threshold (≈1 line)
scores, boxes, classes = yolo_filter_boxes(boxes, box_confidence, box_class_probs, score_threshold)
# Scale boxes back to original image shape (720, 1280 or whatever)
boxes = scale_boxes(boxes, image_shape) # Network was trained to run on 608x608 images
# Use one of the functions you've implemented to perform Non-max suppression with
# maximum number of boxes set to max_boxes and a threshold of iou_threshold (≈1 line)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes, max_boxes, iou_threshold)
# YOUR CODE STARTS HERE
# YOUR CODE ENDS HERE
return scores, boxes, classes
tf.random.set_seed(10)
yolo_outputs = (tf.random.normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random.normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random.normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1),
tf.random.normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1))
scores, boxes, classes = yolo_eval(yolo_outputs)
print("scores[2] = " + str(scores[2].numpy()))
print("boxes[2] = " + str(boxes[2].numpy()))
print("classes[2] = " + str(classes[2].numpy()))
print("scores.shape = " + str(scores.numpy().shape))
print("boxes.shape = " + str(boxes.numpy().shape))
print("classes.shape = " + str(classes.numpy().shape))
assert type(scores) == EagerTensor, "Use tensoflow functions"
assert type(boxes) == EagerTensor, "Use tensoflow functions"
assert type(classes) == EagerTensor, "Use tensoflow functions"
assert scores.shape == (10,), "Wrong shape"
assert boxes.shape == (10, 4), "Wrong shape"
assert classes.shape == (10,), "Wrong shape"
assert np.isclose(scores[2].numpy(), 171.60194), "Wrong value on scores"
assert np.allclose(boxes[2].numpy(), [-1240.3483, -3212.5881, -645.78, 2024.3052]), "Wrong value on boxes"
assert np.isclose(classes[2].numpy(), 16), "Wrong value on classes"
print("\033[92m All tests passed!")
```
**Expected Output**:
<table>
<tr>
<td>
<b>scores[2]</b>
</td>
<td>
171.60194
</td>
</tr>
<tr>
<td>
<b>boxes[2]</b>
</td>
<td>
[-1240.3483 -3212.5881 -645.78 2024.3052]
</td>
</tr>
<tr>
<td>
<b>classes[2]</b>
</td>
<td>
16
</td>
</tr>
<tr>
<td>
<b>scores.shape</b>
</td>
<td>
(10,)
</td>
</tr>
<tr>
<td>
<b>boxes.shape</b>
</td>
<td>
(10, 4)
</td>
</tr>
<tr>
<td>
<b>classes.shape</b>
</td>
<td>
(10,)
</td>
</tr>
</table>
<a name='3'></a>
## 3 - Test YOLO Pre-trained Model on Images
In this section, you are going to use a pre-trained model and test it on the car detection dataset.
<a name='3-1'></a>
### 3.1 - Defining Classes, Anchors and Image Shape
You're trying to detect 80 classes, and are using 5 anchor boxes. The information on the 80 classes and 5 boxes is gathered in two files: "coco_classes.txt" and "yolo_anchors.txt". You'll read class names and anchors from text files. The car detection dataset has 720x1280 images, which are pre-processed into 608x608 images.
```
class_names = read_classes("model_data/coco_classes.txt")
anchors = read_anchors("model_data/yolo_anchors.txt")
model_image_size = (608, 608) # Same as yolo_model input layer size
```
<a name='3-2'></a>
### 3.2 - Loading a Pre-trained Model
Training a YOLO model takes a very long time and requires a fairly large dataset of labelled bounding boxes for a large range of target classes. You are going to load an existing pre-trained Keras YOLO model stored in "yolo.h5". These weights come from the official YOLO website, and were converted using a function written by Allan Zelener. References are at the end of this notebook. Technically, these are the parameters from the "YOLOv2" model, but are simply referred to as "YOLO" in this notebook.
Run the cell below to load the model from this file.
```
yolo_model = load_model("model_data/", compile=False)
```
This loads the weights of a trained YOLO model. Here's a summary of the layers your model contains:
```
yolo_model.summary()
```
**Note**: On some computers, you may see a warning message from Keras. Don't worry about it if you do -- this is fine!
**Reminder**: This model converts a preprocessed batch of input images (shape: (m, 608, 608, 3)) into a tensor of shape (m, 19, 19, 5, 85) as explained in Figure (2).
<a name='3-3'></a>
### 3.3 - Convert Output of the Model to Usable Bounding Box Tensors
The output of `yolo_model` is a (m, 19, 19, 5, 85) tensor that needs to pass through non-trivial processing and conversion. You will need to call `yolo_head` to format the encoding of the model you got from `yolo_model` into something decipherable:
`yolo_model_outputs = yolo_model(image_data)`
`yolo_outputs = yolo_head(yolo_model_outputs, anchors, len(class_names))`
The variable `yolo_outputs` will be defined as a set of 4 tensors that you can then use as input by your yolo_eval function. If you are curious about how yolo_head is implemented, you can find the function definition in the file `keras_yolo.py`. The file is also located in your workspace in this path: `yad2k/models/keras_yolo.py`.
<a name='3-4'></a>
### 3.4 - Filtering Boxes
`yolo_outputs` gave you all the predicted boxes of `yolo_model` in the correct format. To perform filtering and select only the best boxes, you will call `yolo_eval`, which you had previously implemented, to do so:
out_scores, out_boxes, out_classes = yolo_eval(yolo_outputs, [image.size[1], image.size[0]], 10, 0.3, 0.5)
<a name='3-5'></a>
### 3.5 - Run the YOLO on an Image
Let the fun begin! You will create a graph that can be summarized as follows:
`yolo_model.input` is given to `yolo_model`. The model is used to compute the output `yolo_model.output`
`yolo_model.output` is processed by `yolo_head`. It gives you `yolo_outputs`
`yolo_outputs` goes through a filtering function, `yolo_eval`. It outputs your predictions: `out_scores`, `out_boxes`, `out_classes`.
Now, we have implemented for you the `predict(image_file)` function, which runs the graph to test YOLO on an image to compute `out_scores`, `out_boxes`, `out_classes`.
The code below also uses the following function:
image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
which opens the image file and scales, reshapes and normalizes the image. It returns the outputs:
image: a python (PIL) representation of your image used for drawing boxes. You won't need to use it.
image_data: a numpy-array representing the image. This will be the input to the CNN.
```
def predict(image_file):
"""
Runs the graph to predict boxes for "image_file". Prints and plots the predictions.
Arguments:
image_file -- name of an image stored in the "images" folder.
Returns:
out_scores -- tensor of shape (None, ), scores of the predicted boxes
out_boxes -- tensor of shape (None, 4), coordinates of the predicted boxes
out_classes -- tensor of shape (None, ), class index of the predicted boxes
Note: "None" actually represents the number of predicted boxes, it varies between 0 and max_boxes.
"""
# Preprocess your image
image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
yolo_model_outputs = yolo_model(image_data) # It's output is of shape (m, 19, 19, 5, 85)
# But yolo_eval takes input a tensor contains 4 tensors: box_xy,box_wh, box_confidence & box_class_probs
yolo_outputs = yolo_head(yolo_model_outputs, anchors, len(class_names))
out_scores, out_boxes, out_classes = yolo_eval(yolo_outputs, [image.size[1], image.size[0]], 10, 0.3, 0.5)
# Print predictions info
print('Found {} boxes for {}'.format(len(out_boxes), "images/" + image_file))
# Generate colors for drawing bounding boxes.
colors = get_colors_for_classes(len(class_names))
# Draw bounding boxes on the image file
#draw_boxes2(image, out_scores, out_boxes, out_classes, class_names, colors, image_shape)
draw_boxes(image, out_boxes, out_classes, class_names, out_scores)
# Save the predicted bounding box on the image
image.save(os.path.join("out", str(image_file).split('.')[0]+"_annotated." +str(image_file).split('.')[1] ), quality=100)
# Display the results in the notebook
output_image = Image.open(os.path.join("out", str(image_file).split('.')[0]+"_annotated." +str(image_file).split('.')[1] ))
imshow(output_image)
return out_scores, out_boxes, out_classes
```
Run the following cell on the "test.jpg" image to verify that your function is correct.
```
out_scores, out_boxes, out_classes = predict("0001.jpg")
```
**Expected Output**:
<table>
<tr>
<td>
<b>Found 10 boxes for images/test.jpg</b>
</td>
</tr>
<tr>
<td>
<b>car</b>
</td>
<td>
0.89 (367, 300) (745, 648)
</td>
</tr>
<tr>
<td>
<b>car</b>
</td>
<td>
0.80 (761, 282) (942, 412)
</td>
</tr>
<tr>
<td>
<b>car</b>
</td>
<td>
0.74 (159, 303) (346, 440)
</td>
</tr>
<tr>
<td>
<b>car</b>
</td>
<td>
0.70 (947, 324) (1280, 705)
</td>
</tr>
<tr>
<td>
<b>bus</b>
</td>
<td>
0.67 (5, 266) (220, 407)
</td>
</tr>
<tr>
<td>
<b>car</b>
</td>
<td>
0.66 (706, 279) (786, 350)
</td>
</tr>
<tr>
<td>
<b>car</b>
</td>
<td>
0.60 (925, 285) (1045, 374)
</td>
</tr>
<tr>
<td>
<b>car</b>
</td>
<td>
0.44 (336, 296) (378, 335)
</td>
</tr>
<tr>
<td>
<b>car</b>
</td>
<td>
0.37 (965, 273) (1022, 292)
</td>
</tr>
<tr>
<td>
<b>traffic light</b>
</td>
<td>
00.36 (681, 195) (692, 214)
</td>
</tr>
</table>
The model you've just run is actually able to detect 80 different classes listed in "coco_classes.txt". To test the model on your own images:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Write your image's name in the cell above code
4. Run the code and see the output of the algorithm!
If you were to run your session in a for loop over all your images. Here's what you would get:
<center>
<video width="400" height="200" src="nb_images/pred_video_compressed2.mp4" type="video/mp4" controls>
</video>
</center>
<caption><center> Predictions of the YOLO model on pictures taken from a camera while driving around the Silicon Valley <br> Thanks to <a href="https://www.drive.ai/">drive.ai</a> for providing this dataset! </center></caption>
<a name='4'></a>
## 4 - Summary for YOLO
- Input image (608, 608, 3)
- The input image goes through a CNN, resulting in a (19,19,5,85) dimensional output.
- After flattening the last two dimensions, the output is a volume of shape (19, 19, 425):
- Each cell in a 19x19 grid over the input image gives 425 numbers.
- 425 = 5 x 85 because each cell contains predictions for 5 boxes, corresponding to 5 anchor boxes, as seen in lecture.
- 85 = 5 + 80 where 5 is because $(p_c, b_x, b_y, b_h, b_w)$ has 5 numbers, and 80 is the number of classes we'd like to detect
- You then select only few boxes based on:
- Score-thresholding: throw away boxes that have detected a class with a score less than the threshold
- Non-max suppression: Compute the Intersection over Union and avoid selecting overlapping boxes
- This gives you YOLO's final output.
<font color='blue'>
**What you should remember**:
- YOLO is a state-of-the-art object detection model that is fast and accurate
- It runs an input image through a CNN, which outputs a 19x19x5x85 dimensional volume.
- The encoding can be seen as a grid where each of the 19x19 cells contains information about 5 boxes.
- You filter through all the boxes using non-max suppression. Specifically:
- Score thresholding on the probability of detecting a class to keep only accurate (high probability) boxes
- Intersection over Union (IoU) thresholding to eliminate overlapping boxes
- Because training a YOLO model from randomly initialized weights is non-trivial and requires a large dataset as well as lot of computation, previously trained model parameters were used in this exercise. If you wish, you can also try fine-tuning the YOLO model with your own dataset, though this would be a fairly non-trivial exercise.
**Congratulations!** You've come to the end of this assignment.
Here's a quick recap of all you've accomplished.
You've:
- Detected objects in a car detection dataset
- Implemented non-max suppression to achieve better accuracy
- Implemented intersection over union as a function of NMS
- Created usable bounding box tensors from the model's predictions
Amazing work! If you'd like to know more about the origins of these ideas, spend some time on the papers referenced below.
<a name='5'></a>
## 5 - References
The ideas presented in this notebook came primarily from the two YOLO papers. The implementation here also took significant inspiration and used many components from Allan Zelener's GitHub repository. The pre-trained weights used in this exercise came from the official YOLO website.
- Joseph Redmon, Santosh Divvala, Ross Girshick, Ali Farhadi - [You Only Look Once: Unified, Real-Time Object Detection](https://arxiv.org/abs/1506.02640) (2015)
- Joseph Redmon, Ali Farhadi - [YOLO9000: Better, Faster, Stronger](https://arxiv.org/abs/1612.08242) (2016)
- Allan Zelener - [YAD2K: Yet Another Darknet 2 Keras](https://github.com/allanzelener/YAD2K)
- The official YOLO website (https://pjreddie.com/darknet/yolo/)
### Car detection dataset
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons License" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/88x31.png" /></a><br /><span xmlns:dct="http://purl.org/dc/terms/" property="dct:title">The Drive.ai Sample Dataset</span> (provided by drive.ai) is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License</a>. Thanks to Brody Huval, Chih Hu and Rahul Patel for providing this data.
| github_jupyter |
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Eager execution basics
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/2/tutorials/eager/eager_basics"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/tutorials/eager/eager_basics.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/tutorials/eager/eager_basics.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
This is an introductory TensorFlow tutorial shows how to:
* Import the required package
* Create and use tensors
* Use GPU acceleration
* Demonstrate `tf.data.Dataset`
```
!pip install tf-nightly-2.0-preview
```
## Import TensorFlow
Import the `tensorflow` module to get started. [Eager execution](../../guide/eager.ipynb) is enabled by default.
```
import tensorflow as tf
```
## Tensors
A Tensor is a multi-dimensional array. Similar to NumPy `ndarray` objects, `tf.Tensor` objects have a data type and a shape. Additionally, `tf.Tensor`s can reside in accelerator memory (like a GPU). TensorFlow offers a rich library of operations ([tf.add](https://www.tensorflow.org/api_docs/python/tf/add), [tf.matmul](https://www.tensorflow.org/api_docs/python/tf/matmul), [tf.linalg.inv](https://www.tensorflow.org/api_docs/python/tf/linalg/inv) etc.) that consume and produce `tf.Tensor`s. These operations automatically convert native Python types, for example:
```
print(tf.add(1, 2))
print(tf.add([1, 2], [3, 4]))
print(tf.square(5))
print(tf.reduce_sum([1, 2, 3]))
print(tf.io.encode_base64("hello world"))
# Operator overloading is also supported
print(tf.square(2) + tf.square(3))
```
Each `tf.Tensor` has a shape and a datatype:
```
x = tf.matmul([[1]], [[2, 3]])
print(x.shape)
print(x.dtype)
```
The most obvious differences between NumPy arrays and `tf.Tensor`s are:
1. Tensors can be backed by accelerator memory (like GPU, TPU).
2. Tensors are immutable.
### NumPy Compatibility
Converting between a TensorFlow `tf.Tensor`s and a NumPy `ndarray` is easy:
* TensorFlow operations automatically convert NumPy ndarrays to Tensors.
* NumPy operations automatically convert Tensors to NumPy ndarrays.
Tensors are explicitly converted to NumPy ndarrays using their `.numpy()` method. These conversions are typically cheap since the array and `tf.Tensor` share the underlying memory representation, if possible. However, sharing the underlying representation isn't always possible since the `tf.Tensor` may be hosted in GPU memory while NumPy arrays are always backed by host memory, and the conversion involves a copy from GPU to host memory.
```
import numpy as np
ndarray = np.ones([3, 3])
print("TensorFlow operations convert numpy arrays to Tensors automatically")
tensor = tf.multiply(ndarray, 42)
print(tensor)
print("And NumPy operations convert Tensors to numpy arrays automatically")
print(np.add(tensor, 1))
print("The .numpy() method explicitly converts a Tensor to a numpy array")
print(tensor.numpy())
```
## GPU acceleration
Many TensorFlow operations are accelerated using the GPU for computation. Without any annotations, TensorFlow automatically decides whether to use the GPU or CPU for an operation—copying the tensor between CPU and GPU memory, if necessary. Tensors produced by an operation are typically backed by the memory of the device on which the operation executed, for example:
```
x = tf.random.uniform([3, 3])
print("Is there a GPU available: "),
print(tf.test.is_gpu_available())
print("Is the Tensor on GPU #0: "),
print(x.device.endswith('GPU:0'))
```
### Device Names
The `Tensor.device` property provides a fully qualified string name of the device hosting the contents of the tensor. This name encodes many details, such as an identifier of the network address of the host on which this program is executing and the device within that host. This is required for distributed execution of a TensorFlow program. The string ends with `GPU:<N>` if the tensor is placed on the `N`-th GPU on the host.
### Explicit Device Placement
In TensorFlow, *placement* refers to how individual operations are assigned (placed on) a device for execution. As mentioned, when there is no explicit guidance provided, TensorFlow automatically decides which device to execute an operation and copies tensors to that device, if needed. However, TensorFlow operations can be explicitly placed on specific devices using the `tf.device` context manager, for example:
```
import time
def time_matmul(x):
start = time.time()
for loop in range(10):
tf.matmul(x, x)
result = time.time()-start
print("10 loops: {:0.2f}ms".format(1000*result))
# Force execution on CPU
print("On CPU:")
with tf.device("CPU:0"):
x = tf.random.uniform([1000, 1000])
assert x.device.endswith("CPU:0")
time_matmul(x)
# Force execution on GPU #0 if available
if tf.test.is_gpu_available():
with tf.device("GPU:0"): # Or GPU:1 for the 2nd GPU, GPU:2 for the 3rd etc.
x = tf.random.uniform([1000, 1000])
assert x.device.endswith("GPU:0")
time_matmul(x)
```
## Datasets
This section uses the [`tf.data.Dataset` API](https://www.tensorflow.org/guide/datasets) to build a pipeline for feeding data to your model. The `tf.data.Dataset` API is used to build performant, complex input pipelines from simple, re-usable pieces that will feed your model's training or evaluation loops.
### Create a source `Dataset`
Create a *source* dataset using one of the factory functions like [`Dataset.from_tensors`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#from_tensors), [`Dataset.from_tensor_slices`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#from_tensor_slices), or using objects that read from files like [`TextLineDataset`](https://www.tensorflow.org/api_docs/python/tf/data/TextLineDataset) or [`TFRecordDataset`](https://www.tensorflow.org/api_docs/python/tf/data/TFRecordDataset). See the [TensorFlow Dataset guide](https://www.tensorflow.org/guide/datasets#reading_input_data) for more information.
```
ds_tensors = tf.data.Dataset.from_tensor_slices([1, 2, 3, 4, 5, 6])
# Create a CSV file
import tempfile
_, filename = tempfile.mkstemp()
with open(filename, 'w') as f:
f.write("""Line 1
Line 2
Line 3
""")
ds_file = tf.data.TextLineDataset(filename)
```
### Apply transformations
Use the transformations functions like [`map`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#map), [`batch`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#batch), and [`shuffle`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#shuffle) to apply transformations to dataset records.
```
ds_tensors = ds_tensors.map(tf.square).shuffle(2).batch(2)
ds_file = ds_file.batch(2)
```
### Iterate
`tf.data.Dataset` objects support iteration to loop over records:
```
print('Elements of ds_tensors:')
for x in ds_tensors:
print(x)
print('\nElements in ds_file:')
for x in ds_file:
print(x)
```
| github_jupyter |
```
# Header starts here.
from sympy.physics.units import *
from sympy import *
# Rounding:
import decimal
from decimal import Decimal as DX
from copy import deepcopy
def iso_round(obj, pv, rounding=decimal.ROUND_HALF_EVEN):
import sympy
"""
Rounding acc. to DIN EN ISO 80000-1:2013-08
place value = Rundestellenwert
"""
assert pv in set([
# place value # round to:
1, # 1
0.1, # 1st digit after decimal
0.01, # 2nd
0.001, # 3rd
0.0001, # 4th
0.00001, # 5th
0.000001, # 6th
0.0000001, # 7th
0.00000001, # 8th
0.000000001, # 9th
0.0000000001, # 10th
])
objc = deepcopy(obj)
try:
tmp = DX(str(float(objc)))
objc = tmp.quantize(DX(str(pv)), rounding=rounding)
except:
for i in range(len(objc)):
tmp = DX(str(float(objc[i])))
objc[i] = tmp.quantize(DX(str(pv)), rounding=rounding)
return objc
# LateX:
kwargs = {}
kwargs["mat_str"] = "bmatrix"
kwargs["mat_delim"] = ""
# kwargs["symbol_names"] = {FB: "F^{\mathsf B}", }
# Units:
(k, M, G ) = ( 10**3, 10**6, 10**9 )
(mm, cm) = ( m/1000, m/100 )
Newton = kg*m/s**2
Pa = Newton/m**2
MPa = M*Pa
GPa = G*Pa
kN = k*Newton
deg = pi/180
half = S(1)/2
# Header ends here.
#
# https://colab.research.google.com/github/kassbohm/wb-snippets/blob/master/ipynb/TEM_10/ESA/a1_cc.ipynb
F,l = var("F,l")
R = 3*F/2
lu = l/sqrt(3)
Ah,Av,Bh,Bv,Ch,Cv = var("Ah,Av,Bh,Bv,Ch,Cv")
e1 = Eq(Ah + Bh + F)
e2 = Eq(Av + Bv - R)
e3 = Eq(Bv*l - Bh*l - F*l/2 - R*7/18*l)
e4 = Eq(Ch - Bh)
e5 = Eq(Cv - F - Bv)
e6 = Eq(F*lu/2 + Bv*lu + Bh*l)
eqs = [e1,e2,e3,e4,e5,e6]
unknowns = [Ah,Av,Bh,Bv,Ch,Cv]
pprint("\nEquations:")
for e in eqs:
pprint(e)
pprint("\n")
# Alternative Solution (also correct):
# Ah,Av,Bh,Bv,Gh,Gv = var("Ah,Av,Bh,Bv,Gh,Gv")
#
# e1 = Eq(Av + Gv - R)
# e2 = Eq(Ah + F - Gh)
# e3 = Eq(F/2 + 7*R/18 - Gv - Gh)
# e4 = Eq(-Gv -F + Bv)
# e5 = Eq(Gh - Bh)
# e6 = Eq(Gh - sqrt(3)*F/6 - Gv/sqrt(3))
#
# eqs = [e1,e2,e3,e4,e5,e6]
# unknowns = [Ah,Av,Bh,Bv,Gh,Gv]
sol = solve(eqs,unknowns)
pprint("\nReactions:")
pprint(sol)
pprint("\nReactions / F (rounded to 0.01):")
for v in sorted(sol,key=default_sort_key):
pprint("\n\n")
s = sol[v]
tmp = (s/F)
tmp = tmp.simplify()
# pprint(tmp)
pprint([v, tmp, iso_round(tmp,0.01)])
# Reactions / F:
#
# ⎡ 43 19⋅√3 ⎤
# ⎢Ah, - ── + ─────, -0.42⎥
# ⎣ 24 24 ⎦
#
#
# ⎡ 3 19⋅√3 ⎤
# ⎢Av, - ─ + ─────, 1.0⎥
# ⎣ 8 24 ⎦
#
#
# ⎡ 19⋅√3 19 ⎤
# ⎢Bh, - ───── + ──, -0.58⎥
# ⎣ 24 24 ⎦
#
#
# ⎡ 19⋅√3 15 ⎤
# ⎢Bv, - ───── + ──, 0.5⎥
# ⎣ 24 8 ⎦
#
#
# ⎡ 19⋅√3 19 ⎤
# ⎢Ch, - ───── + ──, -0.58⎥
# ⎣ 24 24 ⎦
#
#
# ⎡ 19⋅√3 23 ⎤
# ⎢Cv, - ───── + ──, 1.5⎥
# ⎣ 24 8 ⎦
```
| github_jupyter |
# Introduction to programming for Geoscientists through Python
### [Gerard Gorman](http://www.imperial.ac.uk/people/g.gorman), [Nicolas Barral](http://www.imperial.ac.uk/people/n.barral)
# Lecture 6: Files, strings, and dictionaries
Learning objectives: You will learn how to:
* Read data in from a file
* Parse strings to extract specific data of interest.
* Use dictionaries to index data using any type of key.
```
from client.api.notebook import Notebook
from client.api import assignment
from client.utils import auth
args = assignment.Settings(server='okpyic.azurewebsites.net')
ok = Notebook('./lecture6.ok', args)
var1 = 4
var2 = 3
var3 = 3
def funct1():
return 0
def funct2():
return 0
ok.grade('lect6-q0')
```
## Reading data from a plain text file
We can read text from a [text file](http://en.wikipedia.org/wiki/Text_file) into strings in a program. This is a common (and simple) way for a program to get input data. The basic recipe is:
Let's look at the file [data1.txt](https://raw.githubusercontent.com/ggorman/Introduction-to-programming-for-geoscientists/master/notebook/data/data1.txt) (all of the data files in this lecture are stored in the sub-folder *data/* of this notebook library). The files has a column of numbers:
The goal is to read this file and calculate the mean:
```
# Open data file
infile = open("data/data1.txt", "r")
# Initialise values
mean = 0
n=0
# Loop to perform sum
for number in infile:
number = float(number)
mean = mean + number
n += 1
# It is good practice to close a file when you are finished.
infile.close()
# Calculate the mean.
mean = mean/n
print(mean)
```
Let's make this example more interesting. There is a **lot** of data out there for you to discover all kinds of interesting facts - you just need to be interested in learning a little analysis. For this case I have downloaded tidal gauge data for the port of Avonmouth from the [BODC](http://www.bodc.ac.uk/). If you look at the header of file [data/2012AVO.txt](https://raw.githubusercontent.com/ggorman/Introduction-to-programming-for-geoscientists/master/notebook/data/2012AVO.txt) you will see the [metadata](http://en.wikipedia.org/wiki/Metadata):
Let's read the column ASLVTD02 (the surface elevation) and plot it:
```
from pylab import *
tide_file = open("data/2012AVO.txt", "r")
# We know from inspecting the file that the first 11 lines are just
# header information so lets just skip those lines.
for i in range(11):
line = tide_file.readline()
# Initialise an empty list to store the elevation
elevation = []
days = []
# Now we start reading the interesting data
n=0
while True: # This will keep looping until we break out.
# Here we use a try/except block to try to read the data as normal
# and to break out if unsuccessful - ie when we reach the end of the file.
try:
# Read the next line
line = tide_file.readline()
# Split this line into words.
words = line.split()
# If we do not have 5 words then it must be blank lines at the end of the file.
if len(words)!=5:
break
except:
# If we failed to read a line then we must have got to the end.
break
n+=1 # Count number of data points
try:
# The elevation data is on the 4th column. However, the BODC
# appends a "M" when a value is improbable and an "N" when
# data is missing (maybe a ship dumped into it during rough weather!)
# Therefore, we put this conversion from a string into a float in a
# try/except block.
level = float(words[3])
elevation.append(level)
# There is a measurement every quarter hour.
days.append(n*0.25/24)
except:
continue
# For plotting lets convert the list to a NumPy array.
elevation = array(elevation)
days = array(days)
plot(days, elevation)
xlabel("Days")
ylabel("Elevation (meters)")
show()
```
Quiz time:
* What tidal constituents can you identify by looking at this plot?
* Is this primarily a diurnal or semi-diurnal tidal region? (hint - change the x-axis range on the plot above).
You will notice in the above example that we used the *split()* string member function. This is a very useful function for grabbing individual words on a line. When called without any arguments it assumes that the [delimiter](http://en.wikipedia.org/wiki/Delimiter) is a blank space. However, you can use this to split a string with any delimiter, *e.g.*, *line.split(';')*, *line.split(':')*.
## <span style="color:blue">Exercise 6.1: Read a two-column data file</span>
The file [data/xy.dat](https://raw.githubusercontent.com/ggorman/Introduction-to-programming-for-geoscientists/master/notebook/data/xy.dat) contains two columns of numbers, corresponding to *x* and *y* coordinates on a curve. The start of the file looks like this:
-1.0000 -0.0000</br>
-0.9933 -0.0087</br>
-0.9867 -0.0179</br>
-0.9800 -0.0274</br>
-0.9733 -0.0374</br>
Make a program that reads the first column into a list `xlist_61` and the second column into a list `ylist_61`. Then convert the lists to arrays named `xarray_61` and `yarray_61`, and plot the curve. Store the maximum and minimum y coordinates in two variables named `ymin_61` and `ymax_61`. (Hint: Read the file line by line, split each line into words, convert to float, and append to `xlist_61` and `ylist_61`.)</br>
```
# Open data file
infile = open("data/xy.dat", "r") # "r" is for read
# Initialise empty lists
xlist_61 = []
ylist_61 = []
# Loop through infile and write to x and y lists
for line in infile:
line = line.split() # convert to list by dropping spaces
xlist_61.append(float(line[0])) # take 0th element and covert to float
ylist_61.append(float(line[1])) # take 1st element and covert to float
# Close the filehandle
infile.close()
xarray_61 = np.array(xlist_61)
yarray_61 = np.array(ylist_61)
ymin_61 = yarray_61.min()
ymax_61 = yarray_61.max()
grade = ok.grade('lect6-q1')
print("===", grade, "===")
```
## <span style="color:blue">Exercise 6.2: Read a data file</span>
The files [data/density_water.dat](https://raw.githubusercontent.com/ggorman/Introduction-to-programming-for-geoscientists/master/notebook/data/density_water.dat) and [data/density_air.dat](https://raw.githubusercontent.com/ggorman/Introduction-to-programming-for-geoscientists/master/notebook/data/density_air.dat) contain data about the density of water and air (respectively) for different temperatures. The data files have some comment lines starting with # and some lines are blank. The rest of the lines contain density data: the temperature in the first column and the corresponding density in the second column. The goal of this exercise is to read the data in such a file, discard commented or blank lines, and plot the density versus the temperature as distinct (small) circles for each data point. Write a function `readTempDenFile` that takes a filename as argument and returns two lists containing respectively the temperature and the density. Call this function on both files, and store the temperature and density in lists called `temp_air_list`, `dens_air_list`, `temp_water_list` and `dens_water_list`.
```
def readTempDenFile(filename):
infile = open(filename, "r")
temp = []
dens = []
for line in infile:
try:
t, d = line.split()
t = float(t)
d = float(d)
except:
continue
temp.append(t) # N.B. we're now filling out temp and dens lists
dens.append(d)
infile.close()
plot(array(temp), array(dens))
xlabel("Temperature (C)")
ylabel("Density (kg/m^3)")
show()
return temp,dens
# run function
temp_air_list, dens_air_list = readTempDenFile("data/density_air.dat")
temp_water_list, dens_water_list = readTempDenFile("data/density_water.dat")
ok.grade("lect6-q2")
```
## <span style="color:blue">Exercise 6.3: Read acceleration data and find velocities</span>
A file [data/acc.dat](https://raw.githubusercontent.com/ggorman/Introduction-to-programming-for-geoscientists/master/notebook/data/acc.dat) contains measurements $a_0, a_1, \ldots, a_{n-1}$ of the acceleration of an object moving along a straight line. The measurement $a_k$ is taken at time point $t_k = k\Delta t$, where $\Delta t$ is the time spacing between the measurements. The purpose of the exercise is to load the acceleration data into a program and compute the velocity $v(t)$ of the object at some time $t$.
In general, the acceleration $a(t)$ is related to the velocity $v(t)$ through $v^\prime(t) = a(t)$. This means that
$$
v(t) = v(0) + \int_0^t{a(\tau)d\tau}
$$
If $a(t)$ is only known at some discrete, equally spaced points in time, $a_0, \ldots, a_{n-1}$ (which is the case in this exercise), we must compute the integral above numerically, for example by the Trapezoidal rule:
$$
v(t_k) \approx v(0) + \Delta t \left(\frac{1}{2}a_0 + \frac{1}{2}a_k + \sum_{i=1}^{k-1}a_i \right), \ \ 1 \leq k \leq n-1.
$$
We assume $v(0) = 0$ so that also $v_0 = 0$.
Read the values $a_0, \ldots, a_{n-1}$ from file into an array `acc_array_63` and plot the acceleration versus time for $\Delta_t = 0.5$. The time should be stored in an array named `time_array_63`.
Then write a function `compute_velocity(dt, k, a)` that takes as arguments a time interval $\Delta_t$ `dt`, an index `k` and a list of accelerations `a`, uses the Trapezoidal rule to compute one $v(t_k)$ value and return this value. Experiment with different values of $\Delta t$ and $k$.
```
dt = 0.5
# read in acceleration
infile = open("data/acc.dat", "r")
alist = []
for line in infile:
alist.append(float(line))
infile.close()
acc_array_63 = array(alist)
time_array_63 = array([e*dt for e in range(len(alist))]) # time is specified by dt and the number of elements in acc.dat
#print(time_array_63, acc_array_63)
# plot
plot(time_array_63, acc_array_63)
xlabel("Time")
ylabel("Acceleration")
show()
def compute_velocity(dt, k, alist):
if not (1 <= k <= (len(alist) - 1)):
raise ValueError
return dt*(.5*alist[0] + .5*alist[k] + sum(alist[:k]))
dt = 2
k = 4
print(compute_velocity(2, 4, alist))
print(compute_velocity(3, 5, alist))
print(compute_velocity(12, 21, alist))
ok.grade('lect6-q3')
```
## Python dictionaries
Suppose we need to store the temperatures in Oslo, London and Paris. The Python list solution might look like:
```
temps = [13, 15.4, 17.5]
# temps[0]: Oslo
# temps[1]: London
# temps[2]: Paris
```
In this case we need to remember the mapping between the index and the city name. It would be easier to specify name of city to get the temperature. Containers such as lists and arrays use a continuous series of integers to index elements. However, for many applications such an integer index is not useful.
**Dictionaries** are containers where any Python object can be used
as an index. Let's rewrite the previous example using a Python dictionary:
```
temps = {"Oslo": 13, "London": 15.4, "Paris": 17.5}
print("The temperature in London is", temps["London"])
```
Add a new element to a dictionary:
```
temps["Madrid"] = 26.0
print(temps)
```
Loop (iterate) over a dictionary:
```
for city in temps:
print("The temperature in %s is %g" % (city, temps[city]))
```
The index in a dictionary is called the **key**. A dictionary is said to hold key–value pairs. So in general:
Does the dictionary have a particular key (*i.e.* a particular data entry)?
```
if "Berlin" in temps:
print("We have Berlin and its temperature is ", temps["Berlin"])
else:
print("I don't know Berlin' termperature.")
print("Oslo" in temps) # i.e. standard boolean expression
```
The keys and values can be reached as lists:
```
print("Keys = ", temps.keys())
print("Values = ", temps.values())
```
Note that the sequence of keys is **arbitrary**! Never rely on it, if you need a specific order of the keys then you should explicitly sort:
```
for key in sorted(temps):
value = temps[key]
print(key, value)
```
Remove Oslo key:value:
```
del temps["Oslo"] # remove Oslo key w/value
print(temps, len(temps))
```
Similarly to what we saw for arrays, two variables can refer to the same dictionary:
```
t1 = temps
t1["Stockholm"] = 10.0
print(temps)
```
So we can see that while we modified *t1*, the *temps* dictionary was also changed.
Let's look at a simple example of reading the same data from a file and putting it into a dictionary. We will be reading the file *data/deg2.dat*.
```
infile = open("data/deg2.dat", "r")
# Start with empty dictionary
temps = {}
for line in infile:
# If you examine the file you will see a ':' after the city name,
# so let's use this as the delimiter for splitting the line.
city, temp = line.split(":")
temps[city] = float(temp)
infile.close()
print(temps)
```
## <span style="color:blue">Exercise 6.4: Make a dictionary from a table</span>
The file [data/constants.txt](https://raw.githubusercontent.com/ggorman/Introduction-to-programming-for-geoscientists/master/notebook/data/constants.txt) contains a table of the values and the dimensions of some fundamental constants from physics. We want to load this table into a dictionary *constants*, where the keys are the names of the constants. For example, *constants['gravitational constant']* holds the value of the gravitational constant (6.67259 $\times$ 10$^{-11}$) in Newton's law of gravitation. Make a function `read_constants(file_path)` that that reads and interprets the text in the file passed as argument, and thereafter returns the dictionary.
```
def read_constants(file_path):
infile = open(file_path, "r")
constants = {} # An empty dictionary to store the constants that are read in from the file
infile.readline(); infile.readline() # Skip the first two lines of the file, since these just contain the column names and the separator.
for line in infile:
words = line.split() # Split each line up into individual words
dimension = words.pop() # pop is a list operation that removes the last element from a list and returns it
value = float(words.pop()) # Again, use pop to obtain the constant itself.
name = " ".join(words) # After the two 'pop' operations above, the words remaining in the 'words' list must be the name of the constant. Join the individual words together, with spaces inbetween, using .join.
constants[name] = value # Create a new key-value pair in the dictionary
return constants
print(read_constants('data/constants.txt'))
ok.grade('lect6-q4')
```
## <span style="color:blue">Exercise 6.5: Explore syntax differences: lists vs. dictionaries</span>
Consider this code:
```
t1 = {}
t1[0] = -5
t1[1] = 10.5
```
Explain why the lines above work fine while the ones below do not:
```
t2 = []
#t2[0] = -5
#t2[1] = 10.5
```
What must be done in the last code snippet to make it work properly?
## <span style="color:blue">Exercise 6.6: Compute the area of a triangle</span>
An arbitrary triangle can be described by the coordinates of its three vertices: $(x_1, y_1), (x_2, y_2), (x_3, y_3)$, numbered in a counterclockwise direction. The area of the triangle is given by the formula:
$A = \frac{1}{2}|x_2y_3 - x_3y_2 - x_1y_3 + x_3y_1 + x_1y_2 - x_2y_1|.$
Write a function `triangle_area(vertices)` that returns the area of a triangle whose vertices are specified by the argument vertices, which is a nested list of the vertex coordinates. For example, vertices can be [[0,0], [1,0], [0,2]] if the three corners of the triangle have coordinates (0, 0), (1, 0), and (0, 2).
Then, assume that the vertices of the triangle are stored in a dictionary and not a list. The keys in the dictionary correspond to the vertex number (1, 2, or 3) while the values are 2-tuples with the x and y coordinates of the vertex. For example, in a triangle with vertices (0, 0), (1, 0), and (0, 2) the vertices argument becomes:
```
def triangle_area(vertices):
# nb. vertices = {v1: (x,y)}
x2y3 = vertices[2][0] * vertices[3][1]
x3y2 = vertices[3][0] * vertices[2][1]
x1y3 = vertices[1][0] * vertices[3][1]
x3y1 = vertices[3][0] * vertices[1][1]
x1y2 = vertices[1][0] * vertices[2][1]
x2y1 = vertices[2][0] * vertices[1][1]
return .5*(x2y3 - x3y2 - x1y3 + x3y1 + x1y2 - x2y1)
print(triangle_area({1: (0,0), 2: (1,0), 3: (0,1)}))
ok.grade('lect6-q6')
```
## String manipulation
Text in Python is represented as **strings**. Programming with strings is therefore the key to interpret text in files and construct new text (*i.e.* **parsing**). First we show some common string operations and then we apply them to real examples. Our sample string used for illustration is:
```
s = "Berlin: 18.4 C at 4 pm"
```
Strings behave much like lists/tuples - they are simply a sequence of characters:
```
print("s[0] = ", s[0])
print("s[1] = ", s[1])
```
Substrings are just slices of lists and arrays:
```
# from index 8 to the end of the string
print(s[8:])
# index 8, 9, 10 and 11 (not 12!)
print(s[8:12])
# from index 8 to 8 from the end of the string
print(s[8:-8])
```
You can also find the start of a substring:
```
# where does "Berlin" start?
print(s.find("Berlin"))
print(s.find("pm"))
print (s.find("Oslo"))
```
In this last example, Oslo does not exist in the list so the return value is -1.
We can also check if a substring is contained in a string:
```
print ("Berlin" in s)
print ("Oslo" in s)
if "C" in s:
print("C found")
else:
print("C not found")
```
### Search and replace
Strings also support substituting a substring by another string. In general this looks like *s.replace(s1, s2)*, which replaces string *s1* in *s* by string *s2*, *e.g.*:
```
s = s.replace(" ", "_")
print(s)
s = s.replace("Berlin", "Bonn")
print(s)
# Replace the text before the first colon by 'London'
s = s.replace(s[:s.find(":")], "London")
print(s)
```
Notice that in all these examples we assign the new result back to *s*. One of the reasons we are doing this is strings are actually constant (*i.e* immutable) and therefore cannot be modified *inplace*. We **cannot** write for example:
We also encountered examples above where we used the split function to break up a line into separate substrings for a given separator (where a space is the default delimiter). Sometimes we want to split a string into lines - *i.e.* the delimiter is the [carriage return](http://en.wikipedia.org/wiki/Carriage_return). This can be surprisingly tricky because different computing platforms (*e.g.* Windows, Linux, Mac) use different characters to represent a carriage return. For example, Unix uses '\n'. Luckly Python provides a *cross platform* way of doing this so regardless of what platform created the data file, or what platform you are running Python on, it will do the *right thing*:
```
t = "1st line\n2nd line\n3rd line"
print ("""original t =
""", t)
# This works here but will give you problems if you are switching
# files between Windows and either Mac or Linux.
print (t.split("\n"))
# Cross platform (ie better) solution
print(t.splitlines())
```
### Stripping off leading/trailing whitespace
When processing text from a file and composing new strings, we frequently need to trim leading and trailing whitespaces:
```
s = " text with leading and trailing spaces \n"
print("-->%s<--"%s.strip())
# left strip
print("-->%s<--"%s.lstrip())
# right strip
print("-->%s<--"%s.rstrip())
```
### join() (the opposite of split())
We can join a list of substrings to form a new string. Similarly to *split()* we put strings together with a delimiter inbetween:
```
strings = ["Newton", "Secant", "Bisection"]
print(", ".join(strings))
```
You can prove to yourself that these are inverse operations:
As an example, let's split off the first two words on a line:
```
line = "This is a line of words separated by space"
words = line.split()
print("words = ", words)
line2 = " ".join(words[2:])
print("line2 = ", line2)
```
## <span style="color:blue">Exercise 6.7: Improve a program</span>
The file [data/densities.dat](https://raw.githubusercontent.com/ggorman/Introduction-to-programming-for-geoscientists/master/notebook/data/densities.dat) contains a table of densities of various substances measured in g/cm$^3$. The following program reads the data in this file and produces a dictionary whose keys are the names of substances, and the values are the corresponding densities.
```
def read_densities(filename):
infile = open(filename, 'r')
densities = {}
for line in infile:
words = line.split()
density = float(words[-1])
if len(words[:-1]) == 2:
substance = words[0] + ' ' + words[1]
else:
substance = words[0]
densities[substance] = density
infile.close()
return densities
densities = read_densities('data/densities.dat')
print(densities)
```
One problem we face when implementing the program above is that the name of the substance can contain one or two words, and maybe more words in a more comprehensive table. The purpose of this exercise is to use string operations to shorten the code and make it more general. Implement the following two methods in separate functions `read_densities_join` and `read_densities_substrings`, and control that they give the same result.
1. Let *substance* consist of all the words but the last, using the join method in string objects to combine the words.
2. Observe that all the densities start in the same column file and use substrings to divide line into two parts. (Hint: Remember to strip the first part such that, e.g., the density of ice is obtained as *densities['ice']* and not *densities['ice ']*.)
```
def read_densities_join(filename):
infile = open(filename, 'r')
densities = {}
for line in infile:
words = line.split()
density = float(words.pop()) # pop is a list operation that removes the last element from a list and returns it
substance = "_".join(words) # join the remaining words with _
densities[substance] = density
infile.close()
return densities
def read_densities_substrings(filename):
infile = open(filename, 'r')
densities = {}
for line in infile:
density = float(line[12:]) # column 13 onwards
substance = line[:12] # upto coumn 12
substance = substance.strip() # remove trailing spaces
substance = substance.replace(" ", "_") # replace spaces with _
densities[substance] = density
infile.close()
return densities
densities_join = read_densities_join('data/densities.dat')
densities_substrings = read_densities_substrings('data/densities.dat')
print(densities_join)
print(densities_substrings)
ok.grade('lect6-q7')
```
## File writing
Writing a file in Python is simple. You just collect the text you want to write in one or more strings and, for each string, use a statement along the lines of
The write function does not add a newline character so you may have to do that explicitly:
That’s it! Compose the strings and write! Let's do an example. Write a nested list (table) to a file:
```
# Let's define some table of data
data = [[ 0.75, 0.29619813, -0.29619813, -0.75 ],
[ 0.29619813, 0.11697778, -0.11697778, -0.29619813],
[-0.29619813, -0.11697778, 0.11697778, 0.29619813],
[-0.75, -0.29619813, 0.29619813, 0.75 ]]
# Open the file for writing. Notice the "w" indicates we are writing!
outfile = open("tmp_table.dat", "w")
for row in data:
for column in row:
outfile.write("%14.8f" % column)
outfile.write("\n") # ensure newline
outfile.close()
```
And that's it - run the above cell and take a look at the file that was generated in your Azure library clone.
## <span style="color:blue">Exercise 6.8: Write function data to a file</span>
We want to dump $x$ and $f(x)$ values to a file named function_data.dat, where the $x$ values appear in the first column and the $f(x)$ values appear in the second. Choose $n$ equally spaced $x$ values in the interval [-4, 4]. Here, the function $f(x)$ is given by:
$f(x) = \frac{1}{\sqrt{2\pi}}\exp(-0.5x^2)$
```
from math import pi
# define our function
def f(x):
return (1.0/sqrt(2.0*pi))*exp(-.5*x**2.0)
# let's make our x
xarray = linspace(-4.0, 4.0, 100)
fxs = f(xarray)
fxs[-1] += 1
# let's zip them up for a simple for loop when writing out
data = zip(xarray, fxs) # this combines each element into a tuple e.g. [(xarray1, fxs1), (xarray2, fxs2) ...]
# write out
outfile = open("ex8_out.dat", "w") # w is for writing!
for x,y in data:
outfile.write("X = %.2f Y = %.2f" % (x, y))
outfile.write("\n") # ensure newline
outfile.close()
ok.grade('lect6-q8')
ok.score()
```
| github_jupyter |
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
!pip install tf-nightly-2.0-preview
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
def trend(time, slope=0):
return slope * time
def seasonal_pattern(season_time):
"""Just an arbitrary pattern, you can change it if you wish"""
return np.where(season_time < 0.4,
np.cos(season_time * 2 * np.pi),
1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):
"""Repeats the same pattern at each period"""
season_time = ((time + phase) % period) / period
return amplitude * seasonal_pattern(season_time)
def noise(time, noise_level=1, seed=None):
rnd = np.random.RandomState(seed)
return rnd.randn(len(time)) * noise_level
time = np.arange(4 * 365 + 1, dtype="float32")
baseline = 10
series = trend(time, 0.1)
baseline = 10
amplitude = 40
slope = 0.05
noise_level = 5
# Create the series
series = baseline + trend(time, slope) + seasonality(time, period=365, amplitude=amplitude)
# Update with noise
series += noise(time, noise_level, seed=42)
split_time = 1000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
window_size = 20
batch_size = 32
shuffle_buffer_size = 1000
def windowed_dataset(series, window_size, batch_size, shuffle_buffer):
dataset = tf.data.Dataset.from_tensor_slices(series)
dataset = dataset.window(window_size + 1, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_size + 1))
dataset = dataset.shuffle(shuffle_buffer).map(lambda window: (window[:-1], window[-1]))
dataset = dataset.batch(batch_size).prefetch(1)
return dataset
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
tf.keras.backend.clear_session()
dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1),
input_shape=[None]),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32)),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 100.0)
])
lr_schedule = tf.keras.callbacks.LearningRateScheduler(
lambda epoch: 1e-8 * 10**(epoch / 20))
optimizer = tf.keras.optimizers.SGD(lr=1e-8, momentum=0.9)
model.compile(loss=tf.keras.losses.Huber(),
optimizer=optimizer,
metrics=["mae"])
history = model.fit(dataset, epochs=100, callbacks=[lr_schedule])
plt.semilogx(history.history["lr"], history.history["loss"])
plt.axis([1e-8, 1e-4, 0, 30])
tf.keras.backend.clear_session()
tf.random.set_seed(51)
np.random.seed(51)
tf.keras.backend.clear_session()
dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1),
input_shape=[None]),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32)),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 100.0)
])
model.compile(loss="mse", optimizer=tf.keras.optimizers.SGD(lr=1e-5, momentum=0.9),metrics=["mae"])
history = model.fit(dataset,epochs=500,verbose=0)
forecast = []
results = []
for time in range(len(series) - window_size):
forecast.append(model.predict(series[time:time + window_size][np.newaxis]))
forecast = forecast[split_time-window_size:]
results = np.array(forecast)[:, 0, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, results)
tf.keras.metrics.mean_absolute_error(x_valid, results).numpy()
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
mae=history.history['mae']
loss=history.history['loss']
epochs=range(len(loss)) # Get number of epochs
#------------------------------------------------
# Plot MAE and Loss
#------------------------------------------------
plt.plot(epochs, mae, 'r')
plt.plot(epochs, loss, 'b')
plt.title('MAE and Loss')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["MAE", "Loss"])
plt.figure()
epochs_zoom = epochs[200:]
mae_zoom = mae[200:]
loss_zoom = loss[200:]
#------------------------------------------------
# Plot Zoomed MAE and Loss
#------------------------------------------------
plt.plot(epochs_zoom, mae_zoom, 'r')
plt.plot(epochs_zoom, loss_zoom, 'b')
plt.title('MAE and Loss')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["MAE", "Loss"])
plt.figure()
tf.keras.backend.clear_session()
dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1),
input_shape=[None]),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32)),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 100.0)
])
model.compile(loss="mse", optimizer=tf.keras.optimizers.SGD(lr=1e-6, momentum=0.9))
model.fit(dataset,epochs=100, verbose=0)
tf.keras.backend.clear_session()
dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Lambda(lambda x: tf.expand_dims(x, axis=-1),
input_shape=[None]),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32, return_sequences=True)),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(32)),
tf.keras.layers.Dense(1),
tf.keras.layers.Lambda(lambda x: x * 100.0)
])
model.compile(loss="mse", optimizer=tf.keras.optimizers.SGD(lr=1e-6, momentum=0.9))
model.fit(dataset,epochs=100)
```
| github_jupyter |
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
```
# Reflect Tables into SQLAlchemy ORM
```
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, inspect
from sqlalchemy import desc
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
conn = engine.connect()
inspector = inspect(engine)
inspector.get_table_names()
# reflect an existing database into a new model
# reflect the tables
Base = automap_base()
Base.prepare(engine, reflect=True)
# We can view all of the classes that automap found
Base.classes.keys()
# Save references to each table
ME = Base.classes.measurement
ST = Base.classes.station
# Create our session (link) from Python to the DB
session = Session(engine)
```
# Exploratory Climate Analysis
```
first_row = session.query(ME).first()
first_row.__dict__
first_row = session.query(ST).first()
first_row.__dict__
columns = inspector.get_columns('measurement')
for column in columns:
print(column["name"], column["type"])
columns = inspector.get_columns('station')
for column in columns:
print(column["name"], column["type"])
session.query(func.min(ME.date)).all()
session.query(func.max(ME.date)).all()
# Design a query to retrieve the last 12 months of precipitation data and plot the results
# Calculate the date 1 year ago from the last data point in the database
# Perform a query to retrieve the data and precipitation scores
# Save the query results as a Pandas DataFrame and set the index to the date column
# Sort the dataframe by date
# Use Pandas Plotting with Matplotlib to plot the data
previous_year = dt.date(2017, 8, 23) - dt.timedelta(days=365)
# print(previous_year)
year_query = session.query(ME.date, ME.prcp).\
filter(ME.date >= previous_year).\
order_by(ME.date).all()
# year_query
year_data = pd.DataFrame(year_query)
year_data.set_index('date', inplace = True)
year_data.plot()
plt.xticks(rotation = 'vertical')
# plt.title('Last 12 Months of Precipitation')
plt.xlabel('Date')
plt.ylabel('Inches')
plt.tight_layout()
plt.show()
# Use Pandas to calcualte the summary statistics for the precipitation data
year_data.describe()
# Design a query to show how many stations are available in this dataset?
sel = [func.count(ST.station)]
stations = session.query(*sel).all()
stations
# What are the most active stations? (i.e. what stations have the most rows)?
# List the stations and the counts in descending order.
sel = [ME.station, func.count(ME.station)]
most_active = session.query(*sel).\
group_by(ME.station).\
order_by(func.count(ME.station).desc()).all()
most_active
# Using the station id from the previous query, calculate the lowest temperature recorded,
# highest temperature recorded, and average temperature of the most active station?
#once i find the station with the most count from the measurment table we can query the min and max for that station
sel = [func.min(ME.tobs), func.max(ME.tobs), func.avg(ME.tobs)]
session.query(*sel).\
filter(ME.station == 'USC00519281').all()
# Choose the station with the highest number of temperature observations.
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
#can use the same query as above but do a date filter
sel = [ME.tobs]
tobs_data = pd.DataFrame(session.query(*sel).\
filter(ME.date >= previous_year).\
filter(ME.station == 'USC00519281').all())
# tobs_data
tobs_data.plot.hist(bins=12)
plt.xlabel('Temperature')
plt.tight_layout()
plt.show()
```
## Bonus Challenge Assignment
```
# This function called `calc_temps` will accept start date and end date in the format '%Y-%m-%d'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(ME.tobs), func.avg(ME.tobs), func.max(ME.tobs)).\
filter(ME.date >= start_date).filter(ME.date <= end_date).all()
# function usage example
print(calc_temps('2012-02-28', '2012-03-05'))
# Use your previous function `calc_temps` to calculate the tmin, tavg, and tmax
# for your trip using the previous year's data for those same dates.
start_date = dt.date(2012, 2, 28) - dt.timedelta(days=365)
end_date = dt.date(2012, 3, 5) - dt.timedelta(days=365)
trip_temps = calc_temps(start_date, end_date)
trip_temps
# Plot the results from your previous query as a bar chart.
# Use "Trip Avg Temp" as your Title
# Use the average temperature for the y value
# Use the peak-to-peak (tmax-tmin) value as the y error bar (yerr)
fig, ax = plt.subplots(figsize=plt.figaspect(2.))
avg_temp = trip_temps[0][1]
xpos = 1
bar = ax.bar(xpos, avg_temp, yerr=error, alpha=0.5, color='red', align='center')
ax.set(xticks=range(xpos), title="Trip Avg Temp", ylabel="Temperature (F)")
ax.margins(.5, .5)
fig.tight_layout()
fig.show()
# Calculate the total amount of rainfall per weather station for your trip dates using the previous year's matching dates.
# Sort this in descending order by precipitation amount and list the station, name, latitude, longitude, and elevation
# Create a query that will calculate the daily normals
# (i.e. the averages for tmin, tmax, and tavg for all historic data matching a specific month and day)
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
daily_normals("01-01")
# calculate the daily normals for your trip
# push each tuple of calculations into a list called `normals`
# Set the start and end date of the trip
# Use the start and end date to create a range of dates
# Stip off the year and save a list of %m-%d strings
# Loop through the list of %m-%d strings and calculate the normals for each date
# Load the previous query results into a Pandas DataFrame and add the `trip_dates` range as the `date` index
# Plot the daily normals as an area plot with `stacked=False`
```
| github_jupyter |
# Remote Sensing Hands-On Lesson, using TGO
EPSC Conference, Berlin, September 18, 2018
## Overview
In this lesson you will develop a series of simple programs that
demonstrate the usage of SpiceyPy to compute a variety of different
geometric quantities applicable to experiments carried out by a remote
sensing instrument flown on an interplanetary spacecraft. This
particular lesson focuses on a spectrometer flying on the ExoMars2016 TGO
spacecraft, but many of the concepts are easily extended and generalized
to other scenarios.
## Importing SpiceyPy and Loading the Kernels
## Time Conversion
Write a program that prompts the user for an input UTC time string,
converts it to the following time systems and output formats:
* Ephemeris Time (ET) in seconds past J2000
* Calendar Ephemeris Time
* Spacecraft Clock Time
and displays the results. Use the program to convert "2018 JUN 11
19:32:00" UTC into these alternate systems.
## Obtaining Target States and Positions
Write a program that prompts the user for an input UTC time string,
computes the following quantities at that epoch:
* The apparent state of Mars as seen from ExoMars2016 TGO in the J2000 frame, in kilometers and kilometers/second. This vector itself is not of any particular interest, but it is a useful intermediate quantity in some geometry calculations.
* The apparent position of the Earth as seen from ExoMars2016 TGO in the J2000 frame, in kilometers.
* The one-way light time between ExoMars2016 TGO and the apparent position of Earth, in seconds.
* The apparent position of the Sun as seen from Mars in the J2000 frame (J2000), in kilometers.
* The actual (geometric) distance between the Sun and Mars, in astronomical units.
and displays the results. Use the program to compute these quantities at
"2018 JUN 11 19:32:00" UTC.
## Spacecraft Orientation and Reference Frames
Write a program that prompts the user for an input time string, and
computes and displays the following at the epoch of interest:
* The apparent state of Mars as seen from ExoMars2016 TGO in the IAU_MARS body-fixed frame. This vector itself is not of any particular interest, but it is a useful intermediate quantity in some geometry calculations.
* The angular separation between the apparent position of Mars as seen from ExoMars2016 TGO and the nominal instrument view direction.
* The nominal instrument view direction is not provided by any kernel variable, but it is indicated in the ExoMars2016 TGO frame kernel.
Use the program to compute these quantities at the epoch 2018 JUN 11
19:32:00 UTC.
## Computing Sub-s/c and Sub-solar Points on an Ellipsoid and a DSK
Write a program that prompts the user for an input UTC time string and computes the following quantities at that epoch:
* The apparent sub-observer point of ExoMars2016 TGO on Mars, in the body fixed frame IAU_MARS, in kilometers.
* The apparent sub-solar point on Mars, as seen from ExoMars2016 TGO in the body fixed frame IAU_MARS, in kilometers.
The program computes each point twice: once using an ellipsoidal shape model and the
near point/ellipsoid
definition, and once using a DSK shape model and the
nadir/dsk/unprioritized
definition.
The program displays the results. Use the program to compute these
quantities at 2018 JUN 11 19:32:00 UTC.
## Intersecting Vectors with an Ellipsoid and a DSK (fovint)
Write a program that prompts the user for an input UTC time string and,
for that time, computes the intersection of the ExoMars-16 TGO NOMAD LNO
Nadir aperture boresight and field of view (FOV) boundary vectors with
the surface of Mars. Compute each intercept twice: once with Mars' shape
modeled as an ellipsoid, and once with Mars' shape modeled by DSK data.
The program presents each point of intersection as
* A Cartesian vector in the IAU_MARS frame
* Planetocentric (latitudinal) coordinates in the IAU_MARS frame.
For each of the camera FOV boundary and boresight vectors, if an
intersection is found, the program displays the results of the above
computations, otherwise it indicates no intersection exists.
At each point of intersection compute the following:
* Phase angle
* Solar incidence angle
* Emission angle
These angles should be computed using both ellipsoidal and DSK shape
models.
Additionally compute the local solar time at the intercept of the
spectrometer aperture boresight with the surface of Mars, using both
ellipsoidal and DSK shape models.
Use this program to compute values at 2018 JUN 11 19:32:00 UTC
| github_jupyter |
```
import numpy
from context import vaeqst
import numpy
from context import base
base.RandomCliffordGate(0,1)
```
# Random Clifford Circuit
## RandomCliffordGate
`RandomClifordGate(*qubits)` represents a random Clifford gate acting on a set of qubits. There is no further parameter to specify, as it is not any particular gate, but a placeholder for a generic random Clifford gate.
**Parameters**
- `*qubits`: indices of the set of qubits on which the gate acts on.
Example:
```
gate = vaeqst.RandomCliffordGate(0,1)
gate
```
`RandomCliffordGate.random_clifford_map()` evokes a random sampling of the Clifford unitary, return in the form of operator mapping table $M$ and the corresponding sign indicator $h$. Such that under the mapping, any Pauli operator $\sigma_g$ specified by the binary representation $g$ (and localized within the gate support) gets mapped to
$$\sigma_g \to \prod_{i=1}^{2n} (-)^{h_i}\sigma_{M_i}^{g_i}.$$
The binary representation is in the $g=(x_0,z_0,x_1,z_1,\cdots)$ basis.
```
gate.random_clifford_map()
```
## RandomCliffordLayer
`RandomCliffordLayer(*gates)` represents a layer of random Clifford gates.
**Parameters:**
* `*gates`: quantum gates contained in the layer.
The gates in the same layer should not overlap with each other (all gates need to commute). To ensure this, we do not manually add gates to the layer, but using the higher level function `.gate()` provided by `RandomCliffordCircuit` (see discussion later).
Example:
```
layer = vaeqst.RandomCliffordLayer(vaeqst.RandomCliffordGate(0,1),vaeqst.RandomCliffordGate(3,5))
layer
```
It hosts a list of gates:
```
layer.gates
```
Given the total number of qubits $N$, the layer can sample the Clifford unitary (as product of each gate) $U=\prod_{a}U_a$, and represent it as a single operator mapping (because gates do not overlap, so they maps operators in different supports independently).
```
layer.random_clifford_map(6)
```
## RandomCliffordCircuit
`RandomCliffordCircuit()` represents a quantum circuit of random Clifford gates.
### Methods
#### Construct the Circuit
Example: create a random Clifford circuit.
```
circ = vaeqst.RandomCliffordCircuit()
```
Use `.gate(*qubits)` to add random Clifford gates to the circuit.
```
circ.gate(0,1)
circ.gate(2,4)
circ.gate(1,4)
circ.gate(0,2)
circ.gate(3,5)
circ.gate(3,4)
circ
```
Gates will automatically arranged into layers. Each new gate added to the circuit will commute through the layers if it is not blocked by the existing gates.
If the number of qubits `.N` is not explicitly defined, it will be dynamically infered from the circuit width, as the largest qubit index of all gates + 1.
```
circ.N
```
#### Navigate in the Circuit
`.layers_forward()` and `.layers_backward()` provides two generators to iterate over layers in forward and backward order resepctively.
```
list(circ.layers_forward())
list(circ.layers_backward())
```
`.first_layer` and `.last_layer` points to the first and the last layers.
```
circ.first_layer
circ.last_layer
```
Use `.next_layer` and `.prev_layer` to move forward and backward.
```
circ.first_layer.next_layer, circ.last_layer.prev_layer
```
Locate a gate in the circuit.
```
circ.first_layer.next_layer.next_layer.gates[0]
```
#### Apply Circuit to State
`.forward(state)` and `.backward(state)` applies the circuit to transform the state forward / backward.
* Each call will sample a new random realization of the random Clifford circuit.
* The transformation will create a new state, the original state remains untouched.
```
rho = vaeqst.StabilizerState(6, r=0)
rho
circ.forward(rho)
circ.backward(rho)
```
#### POVM
`.povm(nsample)` provides a generator to sample $n_\text{sample}$ from the prior POVM based on the circuit by back evolution.
```
list(circ.povm(3))
```
## BrickWallRCC
`BrickWallRCC(N, depth)` is a subclass of `RandomCliffordCircuit`. It represents the circuit with 2-qubit gates arranged following a brick wall pattern.
```
circ = vaeqst.BrickWallRCC(16,2)
circ
```
Create an inital state as a computational basis state.
```
rho = vaeqst.StabilizerState(16, r=0)
rho
```
Backward evolve the state to obtain the measurement operator.
```
circ.backward(rho)
```
## OnSiteRCC
`OnSiteRCC(N)` is a subclass of `RandomCliffordCircuit`. It represents the circuit of a single layer of on-site Clifford gates. It can be used to generate random Pauli states.
```
circ = vaeqst.OnSiteRCC(16)
circ
rho = vaeqst.StabilizerState(16, r=0)
circ.backward(rho)
```
## GlobalRCC
`GlobalRCC(N)` is a subclass of `RandomCliffordCircuit`. It represents the circuit consists of a global Clifford gate. It can be used to generate Clifford states.
```
circ = vaeqst.GlobalRCC(16)
circ
rho = vaeqst.StabilizerState(16, r=0)
circ.backward(rho)
```
| github_jupyter |
<div style="text-align:center;">
<img alt="" <img src="./images/logo_default.png"/><br/>
</div>
<h2 style="color: #6b4e3d;">Amicable numbers</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 21</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>Let d(<i>n</i>) be defined as the sum of proper divisors of <i>n</i> (numbers less than <i>n</i> which divide evenly into <i>n</i>).<br>
If d(<i>a</i>) = <i>b</i> and d(<i>b</i>) = <i>a</i>, where <i>a</i> ≠ <i>b</i>, then <i>a</i> and <i>b</i> are an amicable pair and each of <i>a</i> and <i>b</i> are called amicable numbers.</br></p>
<p>For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220.</p>
<p>Evaluate the sum of all the amicable numbers under 10000.</p>
</div>
<h2 style="color: #6b4e3d;">Names scores</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 22</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>Using <a href="project/resources/p022_names.txt">names.txt</a> (right click and 'Save Link/Target As...'), a 46K text file containing over five-thousand first names, begin by sorting it into alphabetical order. Then working out the alphabetical value for each name, multiply this value by its alphabetical position in the list to obtain a name score.</p>
<p>For example, when the list is sorted into alphabetical order, COLIN, which is worth 3 + 15 + 12 + 9 + 14 = 53, is the 938th name in the list. So, COLIN would obtain a score of 938 × 53 = 49714.</p>
<p>What is the total of all the name scores in the file?</p>
</div>
<h2 style="color: #6b4e3d;">Non-abundant sums</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 23</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>A perfect number is a number for which the sum of its proper divisors is exactly equal to the number. For example, the sum of the proper divisors of 28 would be 1 + 2 + 4 + 7 + 14 = 28, which means that 28 is a perfect number.</p>
<p>A number <var>n</var> is called deficient if the sum of its proper divisors is less than <var>n</var> and it is called abundant if this sum exceeds <var>n</var>.</p>
<p>As 12 is the smallest abundant number, 1 + 2 + 3 + 4 + 6 = 16, the smallest number that can be written as the sum of two abundant numbers is 24. By mathematical analysis, it can be shown that all integers greater than 28123 can be written as the sum of two abundant numbers. However, this upper limit cannot be reduced any further by analysis even though it is known that the greatest number that cannot be expressed as the sum of two abundant numbers is less than this limit.</p>
<p>Find the sum of all the positive integers which cannot be written as the sum of two abundant numbers.</p>
</div>
<h2 style="color: #6b4e3d;">Lexicographic permutations</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 24</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>A permutation is an ordered arrangement of objects. For example, 3124 is one possible permutation of the digits 1, 2, 3 and 4. If all of the permutations are listed numerically or alphabetically, we call it lexicographic order. The lexicographic permutations of 0, 1 and 2 are:</p>
<p style="text-align:center;">012 021 102 120 201 210</p>
<p>What is the millionth lexicographic permutation of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9?</p>
</div>
<h2 style="color: #6b4e3d;">1000-digit Fibonacci number</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 25</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>The Fibonacci sequence is defined by the recurrence relation:</p>
<blockquote>F<sub><i>n</i></sub> = F<sub><i>n</i>−1</sub> + F<sub><i>n</i>−2</sub>, where F<sub>1</sub> = 1 and F<sub>2</sub> = 1.</blockquote>
<p>Hence the first 12 terms will be:</p>
<blockquote>F<sub>1</sub> = 1<br>
F<sub>2</sub> = 1<br/>
F<sub>3</sub> = 2<br/>
F<sub>4</sub> = 3<br/>
F<sub>5</sub> = 5<br/>
F<sub>6</sub> = 8<br/>
F<sub>7</sub> = 13<br/>
F<sub>8</sub> = 21<br/>
F<sub>9</sub> = 34<br/>
F<sub>10</sub> = 55<br/>
F<sub>11</sub> = 89<br/>
F<sub>12</sub> = 144</br></blockquote>
<p>The 12th term, F<sub>12</sub>, is the first term to contain three digits.</p>
<p>What is the index of the first term in the Fibonacci sequence to contain 1000 digits?</p>
</div>
<h2 style="color: #6b4e3d;">Reciprocal cycles</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 26</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>A unit fraction contains 1 in the numerator. The decimal representation of the unit fractions with denominators 2 to 10 are given:</p>
<blockquote>
<table><tr><td><sup>1</sup>/<sub>2</sub></td><td>= </td><td>0.5</td>
</tr><tr><td><sup>1</sup>/<sub>3</sub></td><td>= </td><td>0.(3)</td>
</tr><tr><td><sup>1</sup>/<sub>4</sub></td><td>= </td><td>0.25</td>
</tr><tr><td><sup>1</sup>/<sub>5</sub></td><td>= </td><td>0.2</td>
</tr><tr><td><sup>1</sup>/<sub>6</sub></td><td>= </td><td>0.1(6)</td>
</tr><tr><td><sup>1</sup>/<sub>7</sub></td><td>= </td><td>0.(142857)</td>
</tr><tr><td><sup>1</sup>/<sub>8</sub></td><td>= </td><td>0.125</td>
</tr><tr><td><sup>1</sup>/<sub>9</sub></td><td>= </td><td>0.(1)</td>
</tr><tr><td><sup>1</sup>/<sub>10</sub></td><td>= </td><td>0.1</td>
</tr></table></blockquote>
<p>Where 0.1(6) means 0.166666..., and has a 1-digit recurring cycle. It can be seen that <sup>1</sup>/<sub>7</sub> has a 6-digit recurring cycle.</p>
<p>Find the value of <i>d</i> < 1000 for which <sup>1</sup>/<sub><i>d</i></sub> contains the longest recurring cycle in its decimal fraction part.</p>
</div>
<h2 style="color: #6b4e3d;">Quadratic primes</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 27</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>Euler discovered the remarkable quadratic formula:</p>
<p style="text-align:center;">$n^2 + n + 41$</p>
<p>It turns out that the formula will produce 40 primes for the consecutive integer values $0 \le n \le 39$. However, when $n = 40, 40^2 + 40 + 41 = 40(40 + 1) + 41$ is divisible by 41, and certainly when $n = 41, 41^2 + 41 + 41$ is clearly divisible by 41.</p>
<p>The incredible formula $n^2 - 79n + 1601$ was discovered, which produces 80 primes for the consecutive values $0 \le n \le 79$. The product of the coefficients, −79 and 1601, is −126479.</p>
<p>Considering quadratics of the form:</p>
<blockquote>
$n^2 + an + b$, where $|a| < 1000$ and $|b| \le 1000$<br><br/><div>where $|n|$ is the modulus/absolute value of $n$<br/>e.g. $|11| = 11$ and $|-4| = 4$</div>
</br></blockquote>
<p>Find the product of the coefficients, $a$ and $b$, for the quadratic expression that produces the maximum number of primes for consecutive values of $n$, starting with $n = 0$.</p>
</div>
<h2 style="color: #6b4e3d;">Number spiral diagonals</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 28</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>Starting with the number 1 and moving to the right in a clockwise direction a 5 by 5 spiral is formed as follows:</p>
<p style="text-align:center;font-family:'courier new';"><span style="color:#ff0000;font-family:'courier new';"><b>21</b></span> 22 23 24 <span style="color:#ff0000;font-family:'courier new';"><b>25</b></span><br>
20 <span style="color:#ff0000;font-family:'courier new';"><b>7</b></span> 8 <span style="color:#ff0000;font-family:'courier new';"><b>9</b></span> 10<br/>
19 6 <span style="color:#ff0000;font-family:'courier new';"><b>1</b></span> 2 11<br/>
18 <span style="color:#ff0000;font-family:'courier new';"><b>5</b></span> 4 <span style="color:#ff0000;font-family:'courier new';"><b>3</b></span> 12<br/><span style="color:#ff0000;font-family:'courier new';"><b>17</b></span> 16 15 14 <span style="color:#ff0000;font-family:'courier new';"><b>13</b></span></br></p>
<p>It can be verified that the sum of the numbers on the diagonals is 101.</p>
<p>What is the sum of the numbers on the diagonals in a 1001 by 1001 spiral formed in the same way?</p>
</div>
<h2 style="color: #6b4e3d;">Distinct powers</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 29</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>Consider all integer combinations of <i>a</i><sup><i>b</i></sup> for 2 ≤ <i>a</i> ≤ 5 and 2 ≤ <i>b</i> ≤ 5:</p>
<blockquote>2<sup>2</sup>=4, 2<sup>3</sup>=8, 2<sup>4</sup>=16, 2<sup>5</sup>=32<br>
3<sup>2</sup>=9, 3<sup>3</sup>=27, 3<sup>4</sup>=81, 3<sup>5</sup>=243<br/>
4<sup>2</sup>=16, 4<sup>3</sup>=64, 4<sup>4</sup>=256, 4<sup>5</sup>=1024<br/>
5<sup>2</sup>=25, 5<sup>3</sup>=125, 5<sup>4</sup>=625, 5<sup>5</sup>=3125<br/></br></blockquote>
<p>If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:</p>
<p style="text-align:center;">4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125</p>
<p>How many distinct terms are in the sequence generated by <i>a</i><sup><i>b</i></sup> for 2 ≤ <i>a</i> ≤ 100 and 2 ≤ <i>b</i> ≤ 100?</p>
</div>
<h2 style="color: #6b4e3d;">Digit fifth powers</h2>
<div id="problem_info" style="font-family: Consolas;"><h3>Problem 30</h3></div>
<div class="problem_content" role="problem" style='background-color: #fff; color: #111; padding: 20px;font-family: "Segoe UI", Arial, sans-serif; font-size: 110%;border: solid 1px #bbb; box-shadow: 5px 5px 5px #bbb;'>
<p>Surprisingly there are only three numbers that can be written as the sum of fourth powers of their digits:</p>
<blockquote>1634 = 1<sup>4</sup> + 6<sup>4</sup> + 3<sup>4</sup> + 4<sup>4</sup><br>
8208 = 8<sup>4</sup> + 2<sup>4</sup> + 0<sup>4</sup> + 8<sup>4</sup><br/>
9474 = 9<sup>4</sup> + 4<sup>4</sup> + 7<sup>4</sup> + 4<sup>4</sup></br></blockquote>
<p class="info">As 1 = 1<sup>4</sup> is not a sum it is not included.</p>
<p>The sum of these numbers is 1634 + 8208 + 9474 = 19316.</p>
<p>Find the sum of all the numbers that can be written as the sum of fifth powers of their digits.</p>
</div>
| github_jupyter |
<font size=6>
<b>Curso de Programación en Python</b>
</font>
<font size=4>
Curso de formación interna, CIEMAT. <br/>
Madrid, Octubre de 2021
Antonio Delgado Peris
</font>
https://github.com/andelpe/curso-intro-python/
<br/>
# Tema 9 - El ecosistema Python: librería estándar y otros paquetes populares
## Objetivos
- Conocer algunos módulos de la librería estándar
- Interacción con el propio intérprete
- Interacción con el sistema operativo
- Gestión del sistema de ficheros
- Gestión de procesos y concurrencia
- Desarrollo, depuración y perfilado
- Números y matemáticas
- Acceso y funcionalidad de red
- Utilidades para manejo avanzado de funciones e iteradores
- Introducir el ecosistema de librerías científicas de Python
- La pila Numpy/SciPY
- Gráficos
- Matemáticas y estadística
- Aprendizaje automático
- Procesamiento del lenguaje natural
- Biología
- Física
## La librería estándar
Uno de los eslóganes de Python es _batteries included_. Se refiere a la cantidad de funcionalidad disponible en la instalación Python básica, sin necesidad de recurrir a paquetes externos.
En esta sección revisamos brevemente algunos de los módulos disponibles. Para muchas más información: https://docs.python.org/3/library/
### Interacción con el intérprete de Python: `sys`
Ofrece tanto información, como capacidad de manipular diversos aspectos del propio entorno de Python.
- `sys.argv`: Lista con los argumentos pasados al programa en ejecución.
- `sys.version`: String con la versión actual de Python.
- `sys.stdin/out/err`: Objetos fichero usados por el intérprete para entrada, salida y error.
- `sys.exit`: Función para acabar el programa.
### Interacción con el sistema operativo: `os`
Interfaz _portable_ para funcionalidad que depende del sistema operativo.
Contiene funcionalidad muy variada, a veces de muy bajo nivel.
- `os.environ`: diccionario con variables de entorno (modificable)
- `os.getuid`, `os.getgid`, `os.getpid`...: Obtener UID, GID, process ID, etc. (Unix)
- `os.uname`: información sobre el sistema operativo
- `os.getcwd`, `os.chdir`, `os.mkdir`, `os.remove`, `os.stat`...: operaciones sobre el sistema de ficheros
- `os.exec`, `os.fork`, `os.kill`... : gestión de procesos
Para algunas de estas operaciones es más conveniente utilizar módulos más específicos, o de más alto nivel.
### Operaciones sobre el sistema de ficheros
- Para manipulación de _paths_, borrado, creación de directorios, etc.: `pathlib` (moderno), o `os.path` (clásico)
- Expansión de _wildcards_ de nombres de fichero (Unix _globs_): `glob`
- Para operaciones de copia (y otros) de alto nivel: `shutil`
- Para ficheros y directorios temporales (de usar y tirar): `tempfile`
### Gestión de procesos
- `threading`: interfaz de alto nivel para gestión de _threads_.
- Padece el problema del _Global Interpreter Lock_, de Python: es un _lock_ global, que asegura que solo un thread se está ejecutando en Python en un momento dado (excepto en pausas por I/O). Impide mejorar el rendimiento con múltiples CPUs.
- `queue`: implementa colas multi-productor, multi-consumidor para un intercambio seguro de información entre múltiples _threads_.
- `multiprocessing`: interfaz que imita al the `threading`, pero utiliza multi-proceso, en lugar de threads (evita el problema del GIL). Soporta Unix y Windows. Ofrece concurrencia local y remota.
- El módulo `multiprocessing.shared_memory`: facilita la asignación y gestión de memoria compartida entre varios procesos.
- `subprocess`: Permite lanzar y gestionar subprocesos (comandos externos) desde Python.
- Para Python >= 3.5, se recomienda usar la función `run`, salvo casos complejos.
```
from subprocess import run
def showRes(res):
print('\n------- ret code:', res.returncode, '; err:', res.stderr)
if res.stdout:
print('\n'.join(res.stdout.splitlines()[:3]))
print()
print('NO SHELL')
res = run(['ls', '-l'], capture_output=True, text=True)
showRes(res)
print('WITH SHELL')
res = run('ls -l', shell=True, capture_output=True, text=True)
showRes(res)
print('NO OUTPUT')
res = run(['ls', '-l'])
showRes(res)
print('ERROR NO-CHECK')
res = run(['ls', '-l', 'XXXX'], capture_output=True, text=True)
showRes(res)
print('ERROR CHECK')
try:
res = run(['ls', '-l', 'XXXX'], capture_output=True, check=True)
showRes(res)
except Exception as ex:
print(f'--- Error of type {type(ex)}:\n {ex}\n')
print('NO OUTPUT')
res = run(['ls', '-l', 'XXXX'])
showRes(res)
```
### Números y matemáticas
- `math`: operaciones matemáticas definidas por el estándar de C (`cmath`, para números complejos)
- `random`: generadores de números pseudo-aleatorios para varias distribuciones
- `statistics`: estadísticas básicas
### Manejo avanzado de funciones e iteradores
- `itertools`: útiles para crear iteradores de forma eficiente.
- `functools`: funciones de alto nivel que manipulan otras funciones
- `operators`: funciones correspondientes a los operadores intrínsicos de Python
```
import operator
operator.add(3, 4)
```
### Red
- `socket`: operaciones de red de bajo nivel
- `asyncio`: soporte para entornos de entrada/salida asíncrona
- Existen varias librerías para interacción HTTP, pero se recomienda la librería externa `requests`.
### Desarrollo, depuración y perfilado
- `pydoc`: generación de documentación (HTML), a partir de los docstrings
- Depuración
- Muchos IDEs, y Jupyterlab, incluyen facilidades de depuración en sus entornos.
- `pdb`: _Debugger_ oficial de Python
- Correr scripts como `python3 -m pdb myscript.py`
- Introducir un _break point_ con `import pdb; pdb.set_trace()`
- `cProfile`: _Profiler_
- `timeit`: Medición de tiempos de ejecución de código/scripts
```python
$ python3 -m timeit '"-".join(str(n) for n in range(100))'
10000 loops, best of 5: 30.2 usec per loop
>>> import timeit
>>> timeit.timeit('"-".join(str(n) for n in range(100))', number=10000)
0.3018611848820001
%timeit "-".join(str(n) for n in range(100)) # Jupyter line mode
%%timeit ... # Jupyter cell mode
```
- `unittest`: creación de tests para validación de código (_test-driven programming_)
- La librería externa `pytest` simplifica algunas tareas, y es muy popular
### Números y matemáticas
- `math`: operaciones matemáticas definidas por el estándar de C (`cmath`, para números complejos)
- `random`: generadores de números pseudo-aleatorios para varias distribuciones
- `statistics`: estadísticas básicas
### Otros
- `argparse`: procesado de argumentos y opciones por línea de comando
- Mi recomendación es crearse un _esqueleto_ tipo como base para futuros scripts.
- `re`: procesado de expresiones regulares
- `time`, `datetime`: manipulación de fechas y tiempo (medición y representación del tiempo, deltas de tiempo, etc.)
## La pila NumPy/Scipy
Este conjunto de librerías de código abierto constituye la base numérica, matemática, y de visualización sobre la que se construye el universo matemático/científico en Python.
- **NumPy**: Paquete de propósito general para procesamiento de objetos _array_ (vectores y matrices), de altas prestaciones.
- Sirve de base para la mayoría de los demás paquetes matemáticos.
- Permite realizar operaciones matriciales eficientes (sin usar bucles explícitos)
- Utiliza librerías compiladas (C y Fortran), con un API Python, para conseguir mejor rendimiento.
- **SciPy**: Construida sobre NumPy, y como base de muchas de las siguientes, ofrece múltiples utilidades para integración numérica, interpolación, optimización, algebra lineal, procesado de señal y estadística.
- No confundir la _librería SciPy_, con el proyecto o pila SciPy, que se refiere a todas las de esta sección.
- **Matplotlib**: Librería de visualización (gráficos 2D) de referencia de Python.
- También sirve de base para otras librerías, como _Seaborn_ o _Pandas_.
- **Pandas**: Manipulación de datos de manera ágil y eficiente.
- Utiliza un objeto _DataFrame_, que representa la información en columnas etiquetadas e indexadas.
- Ofrece funcionalidades para buscar, filtrar, ordenar, transformar o extraer información.
- **SymPy**: Librería de matemáticas simbólicas (al estilo de _Mathematica_)
## Gráficos
- **Seaborn**: Construida sobre Matplotlib ofrece un interfaz de alto nivel, para construir, de forma sencilla, gráficos avanzados para modelos estadísticos.
- **Bokeh**: Librería para visualización interactiva de gráficos en web, o en Jupyter notebooks.
- **Plotly**: Gráficos interactivos para web. Es parte de un proyecto mayor **_Dash_**, un entorno para construir aplicaciones web para análisis de datos en Python (sin escribir _javascript_).
- **Scikit-image**: Algoritmos para _procesado_ de imágenes (diferente propósito que los anteriores).
- Otras: **ggplot2/plotnine** (basadas en la librería _ggplot2_ de R), **Altair** (librería declarativa, basada en _Vega-Lite_), `Geoplotlib` y `Folium` (para construir mapas).
## Matemáticas y estadística
- **Statsmodel**: Estimación de modelos estadísticos, realización de tests y exploración de datos estadísticos.
- **PyStan**: Inferencia Bayesiana.
- **NetworkX**: Creación, manipulación y análisis de redes y grafos.
## Machine Learning
- **Scikit-learn**: Librería de aprendizaje automático de propósito general, construida sobre NumPy. Ofrece múltiples algoritmos de ML, como _support vector machines_, o _random forests_, así como muchas utilidades para pre- y postprocesado de datos.
- **TensorFlow** y **PyTorch**: son dos librerías para programación de redes neuronales, incluyendo optimización para GPUs, muy extendidas.
- **Keras**: Es un interfaz simplificado (de alto nivel) para el uso de TensorFlow.
## Otros
### Procesamiento del Lenguaje Natural
Las siguientes librerías ofrecen funcionalidades de análisis sintáctico y semántico de textos libres:
- **GenSim**
- **SpaCy**
- **NLTK**
### Biología
- **Scikit-bio**: Estructuras de datos, algoritmos y recursos educativos para bioinformática.
- **BioPython**: Herramientas para computación biológica.
- **PyEnsembl**: Interfaz Python a Ensembl, base de datos de genómica.
### Física
- Astronomía: **Astropy**, y **PyFITS**
- Física de altas energías:
- **PyROOT**: interfaz Python a ROOT, entorno con ambición generalista, que ofrece muchas utilidades para análisis y almacenamiento de datos, estadística y visualización.
- **Scikit-HEP**: colección de librerías que pretenden trabajar con datos ROOT utilizando código exclusivamente Python (integrado con Numpy), sin usar PyROOT. Algunas son **uproot**, **awkward array**, **coffea**.
### Datos HDF5
- **h5py**: Interfaz a datos HDF5 que trata de ofrecer toda la funcionalidad del interfaz C de HDF5 en Python, integrado con el los objetos y tipos NumPy, por lo que puede usarse en código Python de manera sencilla.
- **pytables**: Otro interfaz a datos HDF5 con un interfaz a más alto nivel que `h5py`, y que ofrece funcionalidades adicionales al estilo de una base de datos (consultas complejas, indexado avanzado, optimización de computación con datos HDF5, etc.)
| github_jupyter |
# Acknowledgement
**Origine:** This notebook is downloaded at https://github.com/justmarkham/scikit-learn-videos.
Some modifications are done.
## Agenda
1. K-nearest neighbors (KNN) classification
2. Logistic Regression
3. Review of model evaluation
4. Classification accuracy
5. Confusion matrix
6. Adjusting the classification threshold
## 1. K-nearest neighbors (KNN) classification
1. Pick a value for K.
2. Search for the K observations in the training data that are "nearest" to the measurements of the unknown point.
3. Use the most popular response value from the K nearest neighbors as the predicted response value for the unknown point.
### Example training data

### KNN classification map (K=1)

### KNN classification map (K=5)

*Image Credits: [Data3classes](http://commons.wikimedia.org/wiki/File:Data3classes.png#/media/File:Data3classes.png), [Map1NN](http://commons.wikimedia.org/wiki/File:Map1NN.png#/media/File:Map1NN.png), [Map5NN](http://commons.wikimedia.org/wiki/File:Map5NN.png#/media/File:Map5NN.png) by Agor153. Licensed under CC BY-SA 3.0*
## 2. Logistic Regression
* Linear Model of classification, assumes linear relationship between feature & target
* Returns class probabilities
* Hyperparameter : C - regularization coef
* Fundamentally suited for bi-class classification
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import make_blobs
X,y = make_blobs(n_features=2, n_samples=1000, cluster_std=2,centers=2)
plt.scatter(X[:,0],X[:,1],c=y,s=10)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(random_state=0, solver='lbfgs')
lr.fit(X,y)
h = .02
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
plt.scatter(X[:,0],X[:,1],c=y,s=10)
```
## 3. Review of model evaluation
- Need a way to choose between models: different model types, tuning parameters, and features
- Use a **model evaluation procedure** to estimate how well a model will generalize to out-of-sample data
- Requires a **model evaluation metric** to quantify the model performance
## 4. Classification accuracy
[Pima Indians Diabetes dataset](https://www.kaggle.com/uciml/pima-indians-diabetes-database) originally from the UCI Machine Learning Repository
```
# read the data into a pandas DataFrame
path = 'pima-indians-diabetes.data'
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(path, header=None, names=col_names)
# print the first 5 rows of data
pima.head()
```
**Question:** Can we predict the diabetes status of a patient given their health measurements?
```
# define X and y
feature_cols = ['pregnant', 'insulin', 'bmi', 'age']
X = pima[feature_cols]
y = pima.label
# split X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# train a logistic regression model on the training set
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(random_state=0, solver='lbfgs')
logreg.fit(X_train, y_train)
# make class predictions for the testing set
y_pred_class = logreg.predict(X_test)
```
**Classification accuracy:** percentage of correct predictions
```
# calculate accuracy
from sklearn import metrics
print(metrics.accuracy_score(y_test, y_pred_class))
```
**Null accuracy:** accuracy that could be achieved by always predicting the most frequent class
```
# examine the class distribution of the testing set (using a Pandas Series method)
y_test.value_counts()
# calculate the percentage of ones
y_test.mean()
# calculate the percentage of zeros
1 - y_test.mean()
# calculate null accuracy (for binary classification problems coded as 0/1)
max(y_test.mean(), 1 - y_test.mean())
# calculate null accuracy (for multi-class classification problems)
y_test.value_counts().head(1) / len(y_test)
```
Comparing the **true** and **predicted** response values
```
# print the first 25 true and predicted responses
print('True:', y_test.values[0:25])
print('Pred:', y_pred_class[0:25])
```
**Conclusion:**
- Classification accuracy is the **easiest classification metric to understand**
- But, it does not tell you the **underlying distribution** of response values
- And, it does not tell you what **"types" of errors** your classifier is making
## 5. Confusion matrix
Table that describes the performance of a classification model
```
# IMPORTANT: first argument is true values, second argument is predicted values
print(metrics.confusion_matrix(y_test, y_pred_class))
```

- Every observation in the testing set is represented in **exactly one box**
- It's a 2x2 matrix because there are **2 response classes**
- The format shown here is **not** universal
**Basic terminology**
- **True Positives (TP):** we *correctly* predicted that they *do* have diabetes
- **True Negatives (TN):** we *correctly* predicted that they *don't* have diabetes
- **False Positives (FP):** we *incorrectly* predicted that they *do* have diabetes (a "Type I error")
- **False Negatives (FN):** we *incorrectly* predicted that they *don't* have diabetes (a "Type II error")
```
# print the first 25 true and predicted responses
print('True:', y_test.values[0:25])
print('Pred:', y_pred_class[0:25])
# save confusion matrix and slice into four pieces
confusion = metrics.confusion_matrix(y_test, y_pred_class)
TP = confusion[1, 1]
TN = confusion[0, 0]
FP = confusion[0, 1]
FN = confusion[1, 0]
```

## Metrics computed from a confusion matrix
**Classification Accuracy:** Overall, how often is the classifier correct?
```
print((TP + TN) / float(TP + TN + FP + FN))
print(metrics.accuracy_score(y_test, y_pred_class))
```
**Classification Error:** Overall, how often is the classifier incorrect?
- Also known as "Misclassification Rate"
```
print((FP + FN) / float(TP + TN + FP + FN))
print(1 - metrics.accuracy_score(y_test, y_pred_class))
```
**Sensitivity:** When the actual value is positive, how often is the prediction correct?
- How "sensitive" is the classifier to detecting positive instances?
- Also known as "True Positive Rate" or "Recall"
```
print(TP / float(TP + FN))
print(metrics.recall_score(y_test, y_pred_class))
```
**Specificity:** When the actual value is negative, how often is the prediction correct?
- How "specific" (or "selective") is the classifier in predicting positive instances?
```
print(TN / float(TN + FP))
```
**False Positive Rate:** When the actual value is negative, how often is the prediction incorrect?
```
print(FP / float(TN + FP))
```
**Precision:** When a positive value is predicted, how often is the prediction correct?
- How "precise" is the classifier when predicting positive instances?
```
print(TP / float(TP + FP))
print(metrics.precision_score(y_test, y_pred_class))
```
Many other metrics can be computed: F1 score, Matthews correlation coefficient, etc.
**Conclusion:**
- Confusion matrix gives you a **more complete picture** of how your classifier is performing
- Also allows you to compute various **classification metrics**, and these metrics can guide your model selection
**Which metrics should you focus on?**
- Choice of metric depends on your **business objective**
- **Spam filter** (positive class is "spam"): Optimize for **precision or specificity** because false negatives (spam goes to the inbox) are more acceptable than false positives (non-spam is caught by the spam filter)
- **Fraudulent transaction detector** (positive class is "fraud"): Optimize for **sensitivity** because false positives (normal transactions that are flagged as possible fraud) are more acceptable than false negatives (fraudulent transactions that are not detected)
## 6. Adjusting the classification threshold
```
# print the first 10 predicted responses
logreg.predict(X_test)[0:10]
# print the first 10 predicted probabilities of class membership
logreg.predict_proba(X_test)[0:10, :]
# print the first 10 predicted probabilities for class 1
logreg.predict_proba(X_test)[0:10, 1]
# store the predicted probabilities for class 1
y_pred_prob = logreg.predict_proba(X_test)[:, 1]
# allow plots to appear in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
# histogram of predicted probabilities
plt.hist(y_pred_prob, bins=8)
plt.xlim(0, 1)
plt.title('Histogram of predicted probabilities')
plt.xlabel('Predicted probability of diabetes')
plt.ylabel('Frequency')
```
**Decrease the threshold** for predicting diabetes in order to **increase the sensitivity** of the classifier
```
# predict diabetes if the predicted probability is greater than 0.3
from sklearn.preprocessing import binarize
y_pred_class = binarize([y_pred_prob], 0.3)[0]
# print the first 10 predicted probabilities
y_pred_prob[0:10]
# print the first 10 predicted classes with the lower threshold
y_pred_class[0:10]
# previous confusion matrix (default threshold of 0.5)
print(confusion)
# new confusion matrix (threshold of 0.3)
print(metrics.confusion_matrix(y_test, y_pred_class))
# sensitivity has increased (used to be 0.24)
print(46 / float(46 + 16))
# specificity has decreased (used to be 0.91)
print(80 / float(80 + 50))
```
**Conclusion:**
- **Threshold of 0.5** is used by default (for binary problems) to convert predicted probabilities into class predictions
- Threshold can be **adjusted** to increase sensitivity or specificity
- Sensitivity and specificity have an **inverse relationship**
| github_jupyter |
<a href="https://colab.research.google.com/github/google/evojax/blob/main/examples/notebooks/TutorialTaskImplementation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Tutorial: Creating Tasks
## Pre-requisite
Before we start, we need to install EvoJAX and import some libraries.
**Note** In our [paper](https://arxiv.org/abs/2202.05008), we ran the experiments on NVIDIA V100 GPU(s). Your results can be different from ours.
```
from IPython.display import clear_output, Image
!pip install evojax
!pip install torchvision # We use torchvision.datasets.MNIST in this tutorial.
clear_output()
import os
import numpy as np
import jax
import jax.numpy as jnp
from evojax.task.cartpole import CartPoleSwingUp
from evojax.policy.mlp import MLPPolicy
from evojax.algo import PGPE
from evojax import Trainer
from evojax.util import create_logger
# Let's create a directory to save logs and models.
log_dir = './log'
logger = create_logger(name='EvoJAX', log_dir=log_dir)
logger.info('Welcome to the tutorial on Task creation!')
logger.info('Jax backend: {}'.format(jax.local_devices()))
!nvidia-smi --query-gpu=name --format=csv,noheader
```
## Introduction
EvoJAX has three major components: the *task*, the *policy network* and the *neuroevolution algorithm*. Once these components are implemented and instantiated, we can use a trainer to start the training process. The following code snippet provides an example of how we use EvoJAX.
```
seed = 42 # Wish me luck!
# We use the classic cart-pole swing up as our tasks, see
# https://github.com/google/evojax/tree/main/evojax/task for more example tasks.
# The test flag provides the opportunity for a user to
# 1. Return different signals as rewards. For example, in our MNIST example,
# we use negative cross-entropy loss as the reward in training tasks, and the
# classification accuracy as the reward in test tasks.
# 2. Perform reward shaping. It is common for RL practitioners to modify the
# rewards during training so that the agent learns more efficiently. But this
# modification should not be allowed in tests for fair evaluations.
hard = False
train_task = CartPoleSwingUp(harder=hard, test=False)
test_task = CartPoleSwingUp(harder=hard, test=True)
# We use a feedforward network as our policy.
# By default, MLPPolicy uses "tanh" as its activation function for the output.
policy = MLPPolicy(
input_dim=train_task.obs_shape[0],
hidden_dims=[64, 64],
output_dim=train_task.act_shape[0],
logger=logger,
)
# We use PGPE as our evolution algorithm.
# If you want to know more about the algorithm, please take a look at the paper:
# https://people.idsia.ch/~juergen/nn2010.pdf
solver = PGPE(
pop_size=64,
param_size=policy.num_params,
optimizer='adam',
center_learning_rate=0.05,
seed=seed,
)
# Now that we have all the three components instantiated, we can create a
# trainer and start the training process.
trainer = Trainer(
policy=policy,
solver=solver,
train_task=train_task,
test_task=test_task,
max_iter=600,
log_interval=100,
test_interval=200,
n_repeats=5,
n_evaluations=128,
seed=seed,
log_dir=log_dir,
logger=logger,
)
_ = trainer.run()
# Let's visualize the learned policy.
def render(task, algo, policy):
"""Render the learned policy."""
task_reset_fn = jax.jit(test_task.reset)
policy_reset_fn = jax.jit(policy.reset)
step_fn = jax.jit(test_task.step)
act_fn = jax.jit(policy.get_actions)
params = algo.best_params[None, :]
task_s = task_reset_fn(jax.random.PRNGKey(seed=seed)[None, :])
policy_s = policy_reset_fn(task_s)
images = [CartPoleSwingUp.render(task_s, 0)]
done = False
step = 0
reward = 0
while not done:
act, policy_s = act_fn(task_s, params, policy_s)
task_s, r, d = step_fn(task_s, act)
step += 1
reward = reward + r
done = bool(d[0])
if step % 3 == 0:
images.append(CartPoleSwingUp.render(task_s, 0))
print('reward={}'.format(reward))
return images
imgs = render(test_task, solver, policy)
gif_file = os.path.join(log_dir, 'cartpole.gif')
imgs[0].save(
gif_file, save_all=True, append_images=imgs[1:], duration=40, loop=0)
Image(open(gif_file,'rb').read())
```
Including the three major components, EvoJAX implements the entire training pipeline in JAX. In the first release, we have created several [demo tasks](https://github.com/google/evojax/tree/main/evojax/task) to showcase EvoJAX's capacity. And we encourage the users to bring their own tasks. To this end, we will walk you through the process of creating EvoJAX tasks in this tutorial.
To contribute a task implementation to EvoJAX, all you need to do is to implement the `VectorizedTask` interface.
The interface is defined as the following and you can see the related Python file [here](https://github.com/google/evojax/blob/main/evojax/task/base.py):
```python
class TaskState(ABC):
"""A template of the task state."""
obs: jnp.ndarray
class VectorizedTask(ABC):
"""Interface for all the EvoJAX tasks."""
max_steps: int
obs_shape: Tuple
act_shape: Tuple
test: bool
multi_agent_training: bool = False
@abstractmethod
def reset(self, key: jnp.array) -> TaskState:
"""This resets the vectorized task.
Args:
key - A jax random key.
Returns:
TaskState. Initial task state.
"""
raise NotImplementedError()
@abstractmethod
def step(self,
state: TaskState,
action: jnp.ndarray) -> Tuple[TaskState, jnp.ndarray, jnp.ndarray]:
"""This steps once the simulation.
Args:
state - System internal states of shape (num_tasks, *).
action - Vectorized actions of shape (num_tasks, action_size).
Returns:
TaskState. Task states.
jnp.ndarray. Reward.
jnp.ndarray. Task termination flag: 1 for done, 0 otherwise.
"""
raise NotImplementedError()
```
## MNIST classification
While one would obviously use gradient descent for MNIST in practice, the point is to show that neuroevolution can also solve them to some degree of accuracy within a short amount of time, which will be useful when these models are adapted within a more complicated task where gradient-based approaches may not work.
The following code snippet shows how we wrap the dataset and treat it as a one-step `VectorizedTask`.
```
from torchvision import datasets
from flax.struct import dataclass
from evojax.task.base import TaskState
from evojax.task.base import VectorizedTask
# This state contains the information we wish to carry over to the next step.
# The state will be used in `VectorizedTask.step` method.
# In supervised learning tasks, we want to store the data and the labels so that
# we can calculate the loss or the accuracy and use that as the reward signal.
@dataclass
class State(TaskState):
obs: jnp.ndarray
labels: jnp.ndarray
def sample_batch(key, data, labels, batch_size):
ix = jax.random.choice(
key=key, a=data.shape[0], shape=(batch_size,), replace=False)
return (jnp.take(data, indices=ix, axis=0),
jnp.take(labels, indices=ix, axis=0))
def loss(prediction, target):
target = jax.nn.one_hot(target, 10)
return -jnp.mean(jnp.sum(prediction * target, axis=1))
def accuracy(prediction, target):
predicted_class = jnp.argmax(prediction, axis=1)
return jnp.mean(predicted_class == target)
class MNIST(VectorizedTask):
"""MNIST classification task.
We model the classification as an one-step task, i.e.,
`MNIST.reset` returns a batch of data to the agent, the agent outputs
predictions, `MNIST.step` returns the reward (loss or accuracy) and
terminates the rollout.
"""
def __init__(self, batch_size, test):
self.max_steps = 1
# These are similar to OpenAI Gym environment's
# observation_space and action_space.
# They are helpful for initializing the policy networks.
self.obs_shape = tuple([28, 28, 1])
self.act_shape = tuple([10, ])
# We download the dataset and normalize the value.
dataset = datasets.MNIST('./data', train=not test, download=True)
data = np.expand_dims(dataset.data.numpy() / 255., axis=-1)
labels = dataset.targets.numpy()
def reset_fn(key):
if test:
# In the test mode, we want to test on the entire test set.
batch_data, batch_labels = data, labels
else:
# In the training mode, we only sample a batch of training data.
batch_data, batch_labels = sample_batch(
key, data, labels, batch_size)
return State(obs=batch_data, labels=batch_labels)
# We use jax.vmap for auto-vectorization.
self._reset_fn = jax.jit(jax.vmap(reset_fn))
def step_fn(state, action):
if test:
# In the test mode, we report the classification accuracy.
reward = accuracy(action, state.labels)
else:
# In the training mode, we return the negative loss as the
# reward signal. It is legitimate to return accuracy as the
# reward signal in training too, but we find the performance is
# not as good as when we use the negative loss.
reward = -loss(action, state.labels)
# This is an one-step task, so that last return value (the `done`
# flag) is one.
return state, reward, jnp.ones(())
# We use jax.vmap for auto-vectorization.
self._step_fn = jax.jit(jax.vmap(step_fn))
def reset(self, key):
return self._reset_fn(key)
def step(self, state, action):
return self._step_fn(state, action)
# Okay, let's test out the task with a ConvNet policy.
from evojax.policy.convnet import ConvNetPolicy
batch_size = 1024
train_task = MNIST(batch_size=batch_size, test=False)
test_task = MNIST(batch_size=batch_size, test=True)
policy = ConvNetPolicy(logger=logger)
solver = PGPE(
pop_size=64,
param_size=policy.num_params,
optimizer='adam',
center_learning_rate=0.006,
stdev_learning_rate=0.09,
init_stdev=0.04,
logger=logger,
seed=seed,
)
trainer = Trainer(
policy=policy,
solver=solver,
train_task=train_task,
test_task=test_task,
max_iter=5000,
log_interval=100,
test_interval=1000,
n_repeats=1,
n_evaluations=1,
seed=seed,
log_dir=log_dir,
logger=logger,
)
_ = trainer.run()
```
Okay! Our implementation of the classification task is successful and EvoJAX achieved $>98\%$ test accuracy within 5 min on a V100 GPU.
As mentioned before, MNIST is a simple one-step task, we want to get you familiar with the interfaces.
Next, we will build the classic cart-pole task from scratch.
## Cart-pole swing up
In our cart-pole swing up task, the agent applies an action $a \in [-1, 1]$ on the cart, and we maintain 4 states:
1. cart position $x$
2. cart velocity $\dot{x}$
3. the angle between the cart and the pole $\theta$
4. the pole's angular velocity $\dot{\theta}$
We randomly sample the initial states and will use the forward Euler integration to update them:
$\mathbf{x}(t + \Delta t) = \mathbf{x}(t) + \Delta t \mathbf{v}(t)$ and
$\mathbf{v}(t + \Delta t) = \mathbf{v}(t) + \Delta t f(a, \mathbf{x}(t), \mathbf{v}(t))$
where $\mathbf{x}(t) = [x, \theta]^{\intercal}$, $\mathbf{v}(t) = [\dot{x}, \dot{\theta}]^{\intercal}$ and $f(\cdot)$ is a function that represents the physical model.
Thanks to `jax.vmap`, we are able to write the task as if it is designed to deal with non-batch inputs though in the training process JAX will automatically vectorize the task for us.
```
from evojax.task.base import TaskState
from evojax.task.base import VectorizedTask
import PIL
# Define some physics metrics.
GRAVITY = 9.82
CART_MASS = 0.5
POLE_MASS = 0.5
POLE_LEN = 0.6
FRICTION = 0.1
FORCE_SCALING = 10.0
DELTA_T = 0.01
CART_X_LIMIT = 2.4
# Define some constants for visualization.
SCREEN_W = 600
SCREEN_H = 600
CART_W = 40
CART_H = 20
VIZ_SCALE = 100
WHEEL_RAD = 5
@dataclass
class State(TaskState):
obs: jnp.ndarray # This is the tuple (x, x_dot, theta, theta_dot)
state: jnp.ndarray # This maintains the system's state.
steps: jnp.int32 # This tracks the rollout length.
key: jnp.ndarray # This serves as a random seed.
class CartPole(VectorizedTask):
"""A quick implementation of the cart-pole task."""
def __init__(self, max_steps=1000, test=False):
self.max_steps = max_steps
self.obs_shape = tuple([4, ])
self.act_shape = tuple([1, ])
def sample_init_state(sample_key):
return (
jax.random.normal(sample_key, shape=(4,)) * 0.2 +
jnp.array([0, 0, jnp.pi, 0])
)
def get_reward(x, x_dot, theta, theta_dot):
# We encourage
# the pole to be held upward (i.e., theta is close to 0) and
# the cart to be at the origin (i.e., x is close to 0).
reward_theta = (jnp.cos(theta) + 1.0) / 2.0
reward_x = jnp.cos((x / CART_X_LIMIT) * (jnp.pi / 2.0))
return reward_theta * reward_x
def update_state(action, x, x_dot, theta, theta_dot):
action = jnp.clip(action, -1.0, 1.0)[0] * FORCE_SCALING
s = jnp.sin(theta)
c = jnp.cos(theta)
total_m = CART_MASS + POLE_MASS
m_p_l = POLE_MASS * POLE_LEN
# This is the physical model: f-function.
x_dot_update = (
(-2 * m_p_l * (theta_dot ** 2) * s +
3 * POLE_MASS * GRAVITY * s * c +
4 * action - 4 * FRICTION * x_dot) /
(4 * total_m - 3 * POLE_MASS * c ** 2)
)
theta_dot_update = (
(-3 * m_p_l * (theta_dot ** 2) * s * c +
6 * total_m * GRAVITY * s +
6 * (action - FRICTION * x_dot) * c) /
(4 * POLE_LEN * total_m - 3 * m_p_l * c ** 2)
)
# This is the forward Euler integration.
x = x + x_dot * DELTA_T
theta = theta + theta_dot * DELTA_T
x_dot = x_dot + x_dot_update * DELTA_T
theta_dot = theta_dot + theta_dot_update * DELTA_T
return jnp.array([x, x_dot, theta, theta_dot])
def out_of_screen(x):
"""We terminate the rollout if the cart is out of the screen."""
beyond_boundary_l = jnp.where(x < -CART_X_LIMIT, 1, 0)
beyond_boundary_r = jnp.where(x > CART_X_LIMIT, 1, 0)
return jnp.bitwise_or(beyond_boundary_l, beyond_boundary_r)
def reset_fn(key):
next_key, key = jax.random.split(key)
state = sample_init_state(key)
return State(
obs=state, # We make the task fully-observable.
state=state,
steps=jnp.zeros((), dtype=int),
key=next_key,
)
self._reset_fn = jax.jit(jax.vmap(reset_fn))
def step_fn(state, action):
current_state = update_state(action, *state.state)
reward = get_reward(*current_state)
steps = state.steps + 1
done = jnp.bitwise_or(
out_of_screen(current_state[0]), steps >= max_steps)
# We reset the step counter to zero if the rollout has ended.
steps = jnp.where(done, jnp.zeros((), jnp.int32), steps)
# We automatically reset the states if the rollout has ended.
next_key, key = jax.random.split(state.key)
# current_state = jnp.where(
# done, sample_init_state(key), current_state)
return State(
state=current_state,
obs=current_state,
steps=steps,
key=next_key), reward, done
self._step_fn = jax.jit(jax.vmap(step_fn))
def reset(self, key):
return self._reset_fn(key)
def step(self, state, action):
return self._step_fn(state, action)
# Optinally, we can implement a render method to visualize the task.
@staticmethod
def render(state, task_id):
"""Render a specified task."""
img = PIL.Image.new('RGB', (SCREEN_W, SCREEN_H), (255, 255, 255))
draw = PIL.ImageDraw.Draw(img)
x, _, theta, _ = np.array(state.state[task_id])
cart_y = SCREEN_H // 2 + 100
cart_x = x * VIZ_SCALE + SCREEN_W // 2
# Draw the horizon.
draw.line(
(0, cart_y + CART_H // 2 + WHEEL_RAD,
SCREEN_W, cart_y + CART_H // 2 + WHEEL_RAD),
fill=(0, 0, 0), width=1)
# Draw the cart.
draw.rectangle(
(cart_x - CART_W // 2, cart_y - CART_H // 2,
cart_x + CART_W // 2, cart_y + CART_H // 2),
fill=(255, 0, 0), outline=(0, 0, 0))
# Draw the wheels.
draw.ellipse(
(cart_x - CART_W // 2 - WHEEL_RAD,
cart_y + CART_H // 2 - WHEEL_RAD,
cart_x - CART_W // 2 + WHEEL_RAD,
cart_y + CART_H // 2 + WHEEL_RAD),
fill=(220, 220, 220), outline=(0, 0, 0))
draw.ellipse(
(cart_x + CART_W // 2 - WHEEL_RAD,
cart_y + CART_H // 2 - WHEEL_RAD,
cart_x + CART_W // 2 + WHEEL_RAD,
cart_y + CART_H // 2 + WHEEL_RAD),
fill=(220, 220, 220), outline=(0, 0, 0))
# Draw the pole.
draw.line(
(cart_x, cart_y,
cart_x + POLE_LEN * VIZ_SCALE * np.cos(theta - np.pi / 2),
cart_y + POLE_LEN * VIZ_SCALE * np.sin(theta - np.pi / 2)),
fill=(0, 0, 255), width=6)
return img
# Okay, let's test this simple cart-pole implementation.
rollout_key = jax.random.PRNGKey(seed=seed)
reset_key, rollout_key = jax.random.split(rollout_key, 2)
reset_key = reset_key[None, :] # Expand dim, the leading is the batch dim.
# Initialize the task.
cart_pole_task = CartPole()
t_state = cart_pole_task.reset(reset_key)
task_screens = [CartPole.render(t_state, 0)]
# Rollout with random actions.
done = False
step_cnt = 0
total_reward = 0
while not done:
action_key, rollout_key = jax.random.split(rollout_key, 2)
action = jax.random.uniform(
action_key, shape=(1, 1), minval=-1., maxval=1.)
t_state, reward, done = cart_pole_task.step(t_state, action)
total_reward = total_reward + reward
step_cnt += 1
if step_cnt % 4 == 0:
task_screens.append(CartPole.render(t_state, 0))
print('reward={}, steps={}'.format(total_reward, step_cnt))
# Visualze the rollout.
gif_file = os.path.join(log_dir, 'rand_cartpole.gif')
task_screens[0].save(
gif_file, save_all=True, append_images=task_screens[1:], loop=0)
Image(open(gif_file,'rb').read())
```
The random policy does not solve the cart-pole task, but our implementation seems to be correct. Let's now plug in this task to EvoJAX.
```
train_task = CartPole(test=False)
test_task = CartPole(test=True)
# We use the same policy and solver to solve this "new" task.
policy = MLPPolicy(
input_dim=train_task.obs_shape[0],
hidden_dims=[64, 64],
output_dim=train_task.act_shape[0],
logger=logger,
)
solver = PGPE(
pop_size=64,
param_size=policy.num_params,
optimizer='adam',
center_learning_rate=0.05,
seed=seed,
)
trainer = Trainer(
policy=policy,
solver=solver,
train_task=train_task,
test_task=test_task,
max_iter=600,
log_interval=100,
test_interval=200,
n_repeats=5,
n_evaluations=128,
seed=seed,
log_dir=log_dir,
logger=logger,
)
_ = trainer.run()
# Let's visualize the learned policy.
def render(task, algo, policy):
"""Render the learned policy."""
task_reset_fn = jax.jit(test_task.reset)
policy_reset_fn = jax.jit(policy.reset)
step_fn = jax.jit(test_task.step)
act_fn = jax.jit(policy.get_actions)
params = algo.best_params[None, :]
task_s = task_reset_fn(jax.random.PRNGKey(seed=seed)[None, :])
policy_s = policy_reset_fn(task_s)
images = [CartPole.render(task_s, 0)]
done = False
step = 0
reward = 0
while not done:
act, policy_s = act_fn(task_s, params, policy_s)
task_s, r, d = step_fn(task_s, act)
step += 1
reward = reward + r
done = bool(d[0])
if step % 3 == 0:
images.append(CartPole.render(task_s, 0))
print('reward={}'.format(reward))
return images
imgs = render(test_task, solver, policy)
gif_file = os.path.join(log_dir, 'trained_cartpole.gif')
imgs[0].save(
gif_file, save_all=True, append_images=imgs[1:], duration=40, loop=0)
Image(open(gif_file,'rb').read())
```
Nice! EvoJAX is able to solve the new cart-pole task within a minute.
In this tutorial, we walked you through the process of creating tasks from scratch. The two examples we used are simple and are supposed to help you understand the interfaces. If you are interested in learning more, please check out our GitHub [repo](https://github.com/google/evojax/tree/main/evojax/task).
Please let us ([email protected]) know if you have any problems or suggestions, thanks!
```
```
| github_jupyter |
# Categorical encoders
Examples of how to use the different categorical encoders using the Titanic dataset.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from feature_engine import categorical_encoders as ce
from feature_engine.missing_data_imputers import CategoricalVariableImputer
pd.set_option('display.max_columns', None)
# Load titanic dataset from OpenML
def load_titanic():
data = pd.read_csv('https://www.openml.org/data/get_csv/16826755/phpMYEkMl')
data = data.replace('?', np.nan)
data['cabin'] = data['cabin'].astype(str).str[0]
data['pclass'] = data['pclass'].astype('O')
data['age'] = data['age'].astype('float')
data['fare'] = data['fare'].astype('float')
data['embarked'].fillna('C', inplace=True)
data.drop(labels=['boat', 'body', 'home.dest'], axis=1, inplace=True)
return data
# load data
data = load_titanic()
data.head()
data.isnull().sum()
# we will encode the below variables, they have no missing values
data[['cabin', 'pclass', 'embarked']].isnull().sum()
data[['cabin', 'pclass', 'embarked']].dtypes
data[['cabin', 'pclass', 'embarked']].dtypes
# let's separate into training and testing set
X_train, X_test, y_train, y_test = train_test_split(
data.drop(['survived', 'name', 'ticket'], axis=1), data['survived'], test_size=0.3, random_state=0)
X_train.shape, X_test.shape
```
## CountFrequencyCategoricalEncoder
The CountFrequencyCategoricalEncoder, replaces the categories by the count or frequency of the observations in the train set for that category.
If we select "count" in the encoding_method, then for the variable colour, if there are 10 observations in the train set that show colour blue, blue will be replaced by 10. Alternatively, if we select "frequency" in the encoding_method, if 10% of the observations in the train set show blue colour, then blue will be replaced by 0.1.
### Frequency
Labels are replaced by the percentage of the observations that show that label in the train set.
```
count_enc = ce.CountFrequencyCategoricalEncoder(
encoding_method='frequency', variables=['cabin', 'pclass', 'embarked'])
count_enc.fit(X_train)
# we can explore the encoder_dict_ to find out the category replacements.
count_enc.encoder_dict_
# transform the data: see the change in the head view
train_t = count_enc.transform(X_train)
test_t = count_enc.transform(X_test)
test_t.head()
test_t['pclass'].value_counts().plot.bar()
```
### Count
Labels are replaced by the number of the observations that show that label in the train set.
```
# this time we encode only 1 variable
count_enc = ce.CountFrequencyCategoricalEncoder(encoding_method='count',
variables='cabin')
count_enc.fit(X_train)
# we can find the mappings in the encoder_dict_ attribute.
count_enc.encoder_dict_
# transform the data: see the change in the head view for Cabin
train_t = count_enc.transform(X_train)
test_t = count_enc.transform(X_test)
test_t.head()
test_t['pclass'].value_counts().plot.bar()
```
### Select categorical variables automatically
If we don't indicate which variables we want to encode, the encoder will find all categorical variables
```
# this time we ommit the argument for variable
count_enc = ce.CountFrequencyCategoricalEncoder(encoding_method = 'count')
count_enc.fit(X_train)
# we can see that the encoder selected automatically all the categorical variables
count_enc.variables
# transform the data: see the change in the head view
train_t = count_enc.transform(X_train)
test_t = count_enc.transform(X_test)
test_t.head()
```
Note that if there are labels in the test set that were not present in the train set, the transformer will introduce NaN, and raise a warning.
## MeanCategoricalEncoder
The MeanCategoricalEncoder replaces the labels of the variables by the mean value of the target for that label. For example, in the variable colour, if the mean value of the binary target is 0.5 for the label blue, then blue is replaced by 0.5
```
# we will transform 3 variables
mean_enc = ce.MeanCategoricalEncoder(variables=['cabin', 'pclass', 'embarked'])
# Note: the MeanCategoricalEncoder needs the target to fit
mean_enc.fit(X_train, y_train)
# see the dictionary with the mappings per variable
mean_enc.encoder_dict_
mean_enc.variables
# we can see the transformed variables in the head view
train_t = count_enc.transform(X_train)
test_t = count_enc.transform(X_test)
test_t.head()
```
### Automatically select the variables
This encoder will select all categorical variables to encode, when no variables are specified when calling the encoder
```
mean_enc = ce.MeanCategoricalEncoder()
mean_enc.fit(X_train, y_train)
mean_enc.variables
# we can see the transformed variables in the head view
train_t = count_enc.transform(X_train)
test_t = count_enc.transform(X_test)
test_t.head()
```
## WoERatioCategoricalEncoder
This encoder replaces the labels by the weight of evidence or the ratio of probabilities. It only works for binary classification.
The weight of evidence is given by: np.log( p(1) / p(0) )
The target probability ratio is given by: p(1) / p(0)
### Weight of evidence
```
## Rare value encoder first to reduce the cardinality
# see below for more details on this encoder
rare_encoder = ce.RareLabelCategoricalEncoder(
tol=0.03, n_categories=2, variables=['cabin', 'pclass', 'embarked'])
rare_encoder.fit(X_train)
# transform
train_t = rare_encoder.transform(X_train)
test_t = rare_encoder.transform(X_test)
woe_enc = ce.WoERatioCategoricalEncoder(
encoding_method='woe', variables=['cabin', 'pclass', 'embarked'])
# to fit you need to pass the target y
woe_enc.fit(train_t, y_train)
woe_enc.encoder_dict_
# transform and visualise the data
train_t = woe_enc.transform(train_t)
test_t = woe_enc.transform(test_t)
test_t.head()
```
### Ratio
Similarly, it is recommended to remove rare labels and high cardinality before using this encoder.
```
# rare label encoder first: transform
train_t = rare_encoder.transform(X_train)
test_t = rare_encoder.transform(X_test)
ratio_enc = ce.WoERatioCategoricalEncoder(
encoding_method='ratio', variables=['cabin', 'pclass', 'embarked'])
# to fit we need to pass the target y
ratio_enc.fit(train_t, y_train)
ratio_enc.encoder_dict_
# transform and visualise the data
train_t = woe_enc.transform(train_t)
test_t = woe_enc.transform(test_t)
test_t.head()
```
## OrdinalCategoricalEncoder
The OrdinalCategoricalEncoder will replace the variable labels by digits, from 1 to the number of different labels. If we select "arbitrary", then the encoder will assign numbers as the labels appear in the variable (first come first served). If we select "ordered", the encoder will assign numbers following the mean of the target value for that label. So labels for which the mean of the target is higher will get the number 1, and those where the mean of the target is smallest will get the number n.
### Ordered
```
# we will encode 3 variables:
ordinal_enc = ce.OrdinalCategoricalEncoder(
encoding_method='ordered', variables=['pclass', 'cabin', 'embarked'])
# for this encoder, we need to pass the target as argument
# if encoding_method='ordered'
ordinal_enc.fit(X_train, y_train)
# here we can see the mappings
ordinal_enc.encoder_dict_
# transform and visualise the data
train_t = ordinal_enc.transform(X_train)
test_t = ordinal_enc.transform(X_test)
test_t.head()
```
### Arbitrary
```
ordinal_enc = ce.OrdinalCategoricalEncoder(encoding_method='arbitrary',
variables='cabin')
# for this encoder we don't need to add the target. You can leave it or remove it.
ordinal_enc.fit(X_train, y_train)
ordinal_enc.encoder_dict_
```
Note that the ordering of the different labels is not the same when we select "arbitrary" or "ordered"
```
# transform: see the numerical values in the former categorical variables
train_t = ordinal_enc.transform(X_train)
test_t = ordinal_enc.transform(X_test)
test_t.head()
```
### Automatically select categorical variables
These encoder as well selects all the categorical variables, if None is passed to the variable argument when calling the enconder.
```
ordinal_enc = ce.OrdinalCategoricalEncoder(encoding_method = 'arbitrary')
# for this encoder we don't need to add the target. You can leave it or remove it.
ordinal_enc.fit(X_train)
ordinal_enc.variables
# transform: see the numerical values in the former categorical variables
train_t = ordinal_enc.transform(X_train)
test_t = ordinal_enc.transform(X_test)
test_t.head()
```
## OneHotCategoricalEncoder
Performs One Hot Encoding. The encoder can select how many different labels per variable to encode into binaries. When top_categories is set to None, all the categories will be transformed in binary variables. However, when top_categories is set to an integer, for example 10, then only the 10 most popular categories will be transformed into binary, and the rest will be discarded.
The encoder has also the possibility to create binary variables from all categories (drop_last = False), or remove the binary for the last category (drop_last = True), for use in linear models.
### All binary, no top_categories
```
ohe_enc = ce.OneHotCategoricalEncoder(
top_categories=None,
variables=['pclass', 'cabin', 'embarked'],
drop_last=False)
ohe_enc.fit(X_train)
ohe_enc.drop_last
ohe_enc.encoder_dict_
train_t = ohe_enc.transform(X_train)
test_t = ohe_enc.transform(X_train)
test_t.head()
```
### Dropping the last category for linear models
```
ohe_enc = ce.OneHotCategoricalEncoder(
top_categories=None,
variables=['pclass', 'cabin', 'embarked'],
drop_last=True)
ohe_enc.fit(X_train)
ohe_enc.encoder_dict_
train_t = ohe_enc.transform(X_train)
test_t = ohe_enc.transform(X_train)
test_t.head()
```
### Selecting top_categories to encode
```
ohe_enc = ce.OneHotCategoricalEncoder(
top_categories=2,
variables=['pclass', 'cabin', 'embarked'],
drop_last=False)
ohe_enc.fit(X_train)
ohe_enc.encoder_dict_
train_t = ohe_enc.transform(X_train)
test_t = ohe_enc.transform(X_train)
test_t.head()
```
## RareLabelCategoricalEncoder
The RareLabelCategoricalEncoder groups labels that show a small number of observations in the dataset into a new category called 'Rare'. This helps to avoid overfitting.
The argument tol indicates the percentage of observations that the label needs to have in order not to be re-grouped into the "Rare" label. The argument n_categories indicates the minimum number of distinct categories that a variable needs to have for any of the labels to be re-grouped into rare. If the number of labels is smaller than n_categories, then the encoder will not group the labels for that variable.
```
## Rare value encoder
rare_encoder = ce.RareLabelCategoricalEncoder(
tol=0.03, n_categories=5, variables=['cabin', 'pclass', 'embarked'])
rare_encoder.fit(X_train)
# the encoder_dict_ contains a dictionary of the {variable: frequent labels} pair
rare_encoder.encoder_dict_
train_t = rare_encoder.transform(X_train)
test_t = rare_encoder.transform(X_train)
test_t.head()
```
### Automatically select all categorical variables
If no variable list is passed as argument, it selects all the categorical variables.
```
## Rare value encoder
rare_encoder = ce.RareLabelCategoricalEncoder(tol = 0.03, n_categories=5)
rare_encoder.fit(X_train)
rare_encoder.encoder_dict_
train_t = rare_encoder.transform(X_train)
test_t = rare_encoder.transform(X_train)
test_t.head()
```
| github_jupyter |
```
__author__ = 'Mike Fitzpatrick <[email protected]>, Robert Nikutta <[email protected]>'
__version__ = '20211130'
__datasets__ = []
__keywords__ = []
```
## How to use the Data Lab *Store Client* Service
This notebook documents how to use the Data Lab virtual storage system via the store client service. This can be done either from a Python script (e.g. within this notebook) or from the command line using the <i>datalab</i> command.
### The storage manager service interface
The store client service simplifies access to the Data Lab virtual storage system. This section describes the store client service interface in case we want to write our own code against that rather than using one of the provided tools. The store client service accepts an HTTP GET call to the appropriate endpoint for the particular operation:
| Endpoint | Description | Req'd Parameters |
|----------|-------------|------------|
| /get | Retrieve a file | name |
| /put | Upload a file | name |
| /load | Load a file to vospace | name, endpoint |
| /cp | Copy a file/directory | from, to |
| /ln | Link a file/directory | from, to |
| /lock | Lock a node from write updates | name |
| /ls | Get a file/directory listing | name |
| /access | Determine file accessability | name |
| /stat | File status info | name,verbose |
| /mkdir | Create a directory | name |
| /mv | Move/rename a file/directory | from, to |
| /rm | Delete a file | name |
| /rmdir | Delete a directory | name |
| /tag | Annotate a file/directory | name, tag |
For example, a call to <i>http://datalab.noirlab.edu/storage/get?name=vos://mag.csv</i> will retrieve the file '_mag.csv_' from the root directory of the user's virtual storage. Likewise, a python call using the _storeClient_ interface such as "_storeClient.get('vos://mag.csv')_" would get the same file.
#### Virtual storage identifiers
Files in the virtual storage are usually identified via the prefix "_vos://_". This shorthand identifier is resolved to a user's home directory of the storage space in the service. As a convenience, the prefix may optionally be omitted when the parameter refers to a node in the virtual storage. Navigation above a user's home directory is not supported, however, subdirectories within the space may be created and used as needed.
#### Authentication
The storage manager service requires a DataLab security token. This needs to be passed as the value of the header keyword "X-DL-AuthToken" in any HTTP GET call to the service. If the token is not supplied anonymous access is assumed but provides access only to public storage spaces.
### From Python code
The store client service can be called from Python code using the <i>datalab</i> module. This provides methods to access the various functions in the <i>storeClient</i> subpackage.
#### Initialization
This is the setup that is required to use the store client. The first thing to do is import the relevant Python modules and also retrieve our DataLab security token.
```
# Standard notebook imports
from getpass import getpass
from dl import authClient, storeClient
```
Comment out and run the cell below if you need to login to Data Lab:
```
## Get the authentication token for the user
#token = authClient.login(input("Enter user name: (+ENTER) "),getpass("Enter password: (+ENTER) "))
#if not authClient.isValidToken(token):
# raise Exception('Token is not valid. Please check your usename/password and execute this cell again.')
```
#### Listing a file/directory
We can see all the files that are in a specific directory or get a full listing for a specific file. In this case, we'll list the default virtual storage directory to use as a basis for changes we'll make below.
```
listing = storeClient.ls (name = 'vos://')
print (listing)
```
The *public* directory shown here is visible to all Data Lab users and provides a means of sharing data without having to setup special access. Similarly, the *tmp* directory is read-protected and provides a convenient temporary directory to be used in a workflow.
#### File Existence and Info
Aside from simply listing files, it's possible to test whether a named file already exists or to determine more information about it.
```
# A simple file existence test:
if storeClient.access ('vos://public'):
print ('User "public" directory exists')
if storeClient.access ('vos://public', mode='w'):
print ('User "public" directory is group/world writable')
else:
print ('User "public" directory is not group/world writable')
if storeClient.access ('vos://tmp'):
print ('User "tmp" directory exists')
if storeClient.access ('vos://tmp', mode='w'):
print ('User "tmp" directory is group/world writable')
else:
print ('User "tmp" directory is not group/world writable')
```
#### Uploading a file
Now we want to upload a new data file from our local disk to the virtual storage:
```
storeClient.put (to = 'vos://newmags.csv', fr = './newmags.csv')
print(storeClient.ls (name='vos://'))
```
#### Downloading a file
Let's say we want to download a file from our virtual storage space, in this case a query result that we saved to it in the "How to use the Data Lab query manager service" notebook:
```
storeClient.get (fr = 'vos://newmags.csv', to = './mymags.csv')
```
It is also possible to get the contents of a remote file directly into your notebook by specifying the location as an empty string:
```
data = storeClient.get (fr = 'vos://newmags.csv', to = '')
print (data)
```
#### Loading a file from a remote URL
It is possible to load a file directly to virtual storage from a remote URL )e.g. an "accessURL" for an image cutout, a remote data file, etc) using the "storeClient.load()" method:
```
url = "http://datalab.noirlab.edu/svc/cutout?col=&siaRef=c4d_161005_022804_ooi_g_v1.fits.fz&extn=31&POS=335.0,0.0&SIZE=0.1"
storeClient.load('vos://cutout.fits',url)
```
#### Creating a directory
We can create a directory on the remote storage to be used for saving data later:
```
storeClient.mkdir ('vos://results')
```
#### Copying a file/directory
We want to put a copy of the file in a remote work directory:
```
storeClient.mkdir ('vos://temp')
print ("Before: " + storeClient.ls (name='vos://temp/'))
storeClient.cp (fr = 'vos://newmags.csv', to = 'vos://temp/newmags.csv',verbose=True)
print ("After: " + storeClient.ls (name='vos://temp/'))
print(storeClient.ls('vos://',format='long'))
```
Notice that in the *ls()* call we append the directory name with a trailing '/' to list the contents of the directory rather than the directory itself.
#### Linking to a file/directory
**WARNING**: Linking is currently **not** working in the Data Lab storage manager. This notebook will be updated when the problem has been resolved.
Sometimes we want to create a link to a file or directory. In this case, the link named by the *'fr'* parameter is created and points to the file/container named by the *'target'* parameter.
```
storeClient.ln ('vos://mags.csv', 'vos://temp/newmags.csv')
print ("Root dir: " + storeClient.ls (name='vos://'))
print ("Temp dir: " + storeClient.ls (name='vos://temp/'))
```
#### Moving/renaming a file/directory
We can move a file or directory:
```
storeClient.mv(fr = 'vos://temp/newmags.csv', to = 'vos://results')
print ("Results dir: " + storeClient.ls (name='vos://results/'))
```
#### Deleting a file
We can delete a file:
```
print ("Before: " + storeClient.ls (name='vos://'))
storeClient.rm (name = 'vos://mags.csv')
print ("After: " + storeClient.ls (name='vos://'))
```
#### Deleting a directory
We can also delete a directory, doing so also deletes the contents of that directory:
```
storeClient.rmdir(name = 'vos://temp')
```
#### Tagging a file/directory
**Warning**: Tagging is currently **not** working in the Data Lab storage manager. This notebook will be updated when the problem has been resolved.
We can tag any file or directory with arbitrary metadata:
```
storeClient.tag('vos://results', 'The results from my analysis')
```
#### Cleanup the demo directory of remaining files
```
storeClient.rm (name = 'vos://newmags.csv')
storeClient.rm (name = 'vos://results')
storeClient.ls (name = 'vos://')
```
### Using the datalab command
The <i>datalab</i> command provides an alternate command line way to work with the query manager through the <i>query</i> subcommands, which is especially useful if you want to interact with the query manager from your local computer. Please have the `datalab` command line utility installed first (for install instructions see https://github.com/astro-datalab/datalab ).
The cells below are commented out. Copy and paste any of them (without the comment sign) and run locally.
#### Log in once
```
#!datalab login
```
and enter the credentials as prompted.
#### Downloading a file
Let's say we want to download a file from our virtual storage space:
```
#!datalab get fr="vos://mags.csv" to="./mags.csv"
```
#### Uploading a file
Now we want to upload a new data file from our local disk:
```
#!datalab put fr="./newmags.csv" to="vos://newmags.csv"
```
#### Copying a file/directory
We want to put a copy of the file in a remote work directory:
```
#!datalab cp fr="vos://newmags.csv" to="vos://temp/newmags.csv"
```
#### Linking to a file/directory
Sometimes we want to create a link to a file or directory:
```
#!datalab ln fr="vos://temp/mags.csv" to="vos://mags.csv"
```
#### Listing a file/directory
We can see all the files that are in a specific directory or get a full listing for a specific file:
```
#!datalab ls name="vos://temp"
```
#### Creating a directory
We can create a directory:
```
#!datalab mkdir name="vos://results"
```
#### Moving/renaming a file/directory
We can move a file or directory:
```
#!datalab mv fr="vos://temp/newmags.csv" to="vos://results"
```
#### Deleting a file
We can delete a file:
```
#!datalab rm name="vos://temp/mags.csv"
```
#### Deleting a directory
We can also delete a directory:
```
#!datalab rmdir name="vos://temp"
```
#### Tagging a file/directory
We can tag any file or directory with arbitrary metadata:
```
#!datalab tag name="vos://results" tag="The results from my analysis"
```
| github_jupyter |
# *Bosonic statistics and the Bose-Einstein condensation*
`Doruk Efe Gökmen -- 30/08/2018 -- Ankara`
## Non-interacting ideal bosons
Non-interacting bosons is the only system in physics that can undergo a phase transition without mutual interactions between its components.
Let us enumerate the energy eigenstates of a single 3D boson in an harmonic trap by the following program.
```
Emax = 30
States = []
for E_x in range(Emax):
for E_y in range(Emax):
for E_z in range(Emax):
States.append(((E_x + E_y + E_z), (E_x, E_y, E_z)))
States.sort()
for k in range(Emax):
print '%3d' % k, States[k][0], States[k][1]
```
Here it can be perceived that the degeneracy at an energy level $E_n$, which we denote by $\mathcal{N}(E_n)$, is $\frac{(n+1)(n+2)}{2}$. Alternatively, we may use a more systematic approach. We can calculate the number of states at the $n$th energy level as $\mathcal{N}(E_n)=\sum_{E_x=0}^{E_n}\sum_{E_y=0}^{E_n}\sum_{E_z=0}^{E_n}\delta_{(E_x+E_y+E_z),E_n}$, where $\delta_{j,k}$ is the Kronecker delta. In the continuous limit we have the Dirac delta function
$\delta_{j,k}\rightarrow\delta(j-k) =\int_{-\pi}^\pi \frac{\text{d}\lambda}{2\pi}e^{i(j-k)\lambda}$. (1)
If we insert this function into above expression, we get $\mathcal{N}(E_n)=\int_{-\pi}^\pi \frac{\text{d}\lambda}{2\pi}e^{-iE_n\lambda}\left(\sum_{E_x=0}^{E_n}e^{iE_x\lambda}\right)^3$. The geometric sum can be evaluated, hence we have the integral $\mathcal{N}(E_n)=\int_{-\pi}^\pi \frac{\text{d}\lambda}{2\pi}e^{-iE_n\lambda}\left[\frac{1-e^{i\lambda (n+1)}}{1-e^{i\lambda}}\right]^3$. The integration range corresponds to a circular contour $\mathcal{C}$ of radius 1 centered at 0 at the complex plane. If we define $z=e^{i\lambda}$, the integral transforms into $\mathcal{N}(E_n)=\frac{1}{2\pi i}\oint_{\mathcal{C}}\frac{\text{d}z}{z^{n+1}}\left[\frac{1-z^{n+1}}{1-z}\right]^3$. Using the residue theorem, this integral can be evaluated by determining the coefficient of the $z^{-1}$ term in the Laurent series of $\frac{1}{z^{n+1}}\left[\frac{1-z^{n+1}}{1-z}\right]^3$, which is $(n+1)(n+1)/2$. Hence we recover the previous result.
##### Five boson bounded trap model
Consider 5 bosons in the harmonic trap, but with a cutoff on the single-particle energies: $E_\sigma\leq 4$. There are $34$ possible single-particles energy states. For this model, the above naive enumeration of these energy states still works. We can label the state of each 5 particle by $\sigma_i$, so that $\{\text{5-particle state}\}=\{\sigma_1,\cdots,\sigma_5\}$. The partititon function for this system is given by $Z(\beta)=\sum_{0\leq\sigma_1\leq\cdots\leq\sigma_5\leq 34}e^{-\beta E(\sigma_1,\cdots,\sigma_5)}$. In the following program, the average occupation number of the ground state per particle is calculated at different temperatures (corresponds to the condensate). However, due to the nested for loops, this method is very inconvenient for higher number of particles.
```
%pylab inline
import math, numpy as np, pylab as plt
#calculate the partition function for 5 bosons by stacking the bosons in one of the N_states
#number of possible states and counting only a specific order of them (they are indistinguishable)
def bosons_bounded_harmonic(beta, N):
Energy = [] #initialise the vector that the energy values are saved with enumeration
n_states_1p = 0 #initialise the total number of single trapped boson states
for n in range(N + 1):
degeneracy = (n + 1) * (n + 2) / 2 #degeneracy in the 3D harmonic oscillator
Energy += [float(n)] * degeneracy
n_states_1p += degeneracy
n_states_5p = 0 #initialise the total number states of 5 trapped bosons
Z = 0.0 #initialise the partition function
N0_mean = 0.0
E_mean = 0.0
for s_0 in range(n_states_1p):
for s_1 in range(s_0, n_states_1p): #consider the order s_0<s_1... to avoid overcounting
for s_2 in range(s_1, n_states_1p):
for s_3 in range(s_2, n_states_1p):
for s_4 in range(s_3, n_states_1p):
n_states_5p += 1
state = [s_0, s_1, s_2, s_3, s_4] #construct the state of each 5 boson
E = sum(Energy[s] for s in state) #calculate the total energy by above enumeration
Z += math.exp(-beta * E) #canonical partition function
E_mean += E * math.exp(-beta * E) #avg. total energy
N0_mean += state.count(0) * math.exp(-beta * E) #avg. ground level occupation number
return n_states_5p, Z, E_mean, N0_mean
N = 4 #the energy cutoff for each boson
beta = 1.0 #inverse temperature
n_states_5p, Z, E_mean, N0_mean = bosons_bounded_harmonic(beta, N)
print 'Temperature:', 1 / beta, 'Total number of possible states:', n_states_5p, '| Partition function:', Z,\
'| Average energy per particle:', E_mean / Z / 5.0,\
'| Condensate fraction (ground state occupation per particle):', N0_mean / Z / 5.0
cond_frac = []
temperature = []
for T in np.linspace(0.1, 1.0, 10):
n_states_5p, Z, E_mean, N0_mean = bosons_bounded_harmonic(1.0 / T, N)
cond_frac.append(N0_mean / Z / 5.0)
temperature.append(T)
plt.plot(temperature, cond_frac)
plt.title('Condensate? fraction for the $N=5$ bosons bounded trap model ($N_{bound}=%i$)' % N, fontsize = 14)
plt.xlabel('$T$', fontsize = 14)
plt.ylabel('$\\langle N_0 \\rangle$ / N', fontsize = 14)
plt.grid()
```
Here we see that all particles are in the ground states at very low temperatures this is a simple consequence of Boltzmann statistics. At zero temperature all the particles populate the ground state. Bose-Einstein condensation is something else, it means that a finite fraction of the system is in the ground-state for temperatures which are much higher than the gap between the gap between the ground-state and the first excited state, which is one, in our system. Bose-Einstein condensation occurs when all of a sudden a finite fraction of particles populate the single-particle ground state. In a trap, this happens at higher and higher temperatures as we increase the particle number.
Alternatively, we can characterise any single particle state $\sigma=0,\cdots,34$ by an occupation number $n_\sigma$. Using this occupation number representation, the energy is given by $E=n_0E_0+\cdots + n_{34}E_{34}$, and the partition function is $Z(\beta)=\sum^{N=5}_{n_0=0}\cdots\sum^{N=5}_{n_{34}=0}e^{-\beta(n_0E_0+\cdots + n_{34}E_{34})}\delta_{(n_0+\cdots + n_{34}),N=5}$. Using the integral representation of the Kronecker delta given in (1), and evaluating the resulting sums, we have
$Z(\beta)=\int_{-\pi}^\pi\frac{\text{d}\lambda}{2\pi}e^{-iN\lambda}\Pi_{E=0}^{E_\text{max}}[f_E(\beta,\lambda)]^{\mathcal{N}(E)}$. (2)
### The bosonic density matrix
**Distinguishable particles:** The partition function of $N$ distinguishable particles is given by $Z^D(\beta)=\int \text{d}\mathbf{x}\rho(\mathbf{x},\mathbf{x},\beta)$, where $\mathbf{x}=\{0,\cdots,N-1\}$, i.e. the positions of the $i$th particle; and $\rho$ is the $N$ distinguishable particle density matrix. If the particles are non-interacting (ideal), then the density matrix can simply be decomposed into $N$ single particle density matrices as
$\rho^{D,\text{ideal}}(\mathbf{x},\mathbf{x}',\beta)=\Pi_{i=0}^{N-1}\rho(x_i,x_i',\beta)$, (3)
with the single particle density matrix $\rho(x_i,x_i',\beta)=\sum_{\lambda_i=0}^{\infty}\psi_{\lambda_i}(x_i)\psi_{\lambda_i}^{*}(x'_i)e^{-\beta E_{\lambda_i}}$, where $\lambda_i$ is the energy eigenstate of the $i$th particle. That means that the quantum statistical paths of the two particles are independent. More generally, the interacting many distinguishable particle density matrix is
$\rho^{D}(\mathbf{x},\mathbf{x}',\beta)=\sum_{\sigma}\Psi_{\sigma}(\mathbf{x})\Psi_{\sigma}^{*}(\mathbf{x}')e^{-\beta E_{\sigma}}$, (4)
where the sum is done over the all possible $N$ particle states $\sigma=\{\lambda_0,\cdots,\lambda_{N-1}\}$. The interacting paths are described by the paths whose weight are modified through Trotter decomposition, which *correlates* those paths.
**Indistinguishable particles:** The particles $\{0,\cdots,N-1\}$ are indistinguishable if and only if
$\Psi_{\sigma_\text{id}}(\mathbf{x})=\xi^\mathcal{P}\Psi_{\sigma_\text{id}}(\mathcal{P}\mathbf{x})$ $\forall \sigma$, (5)
where they are in an indistinguishable state ${\sigma_\text{id}}$, $\mathcal{P}$ is any $N$ particle permutation and the *species factor* $\xi$ is $-1$ (antisymmetric) for fermions, and $1$ (symmetric) for bosons. Here we focus on the bosonic case. Since there are $N!$ such permutations, if the particles are indistinguishable bosons, using (5) we get $\frac{1}{N!}\sum_{\mathcal{P}}\Psi_\sigma(\mathcal{P}x)=\Psi_\sigma(\mathbf{x})$, i.e. $\Psi_\sigma(x)=\Psi_{\sigma_\text{id}}(x)$. Furthermore, from a group theory argument it follows that $\frac{1}{N!}\sum_{\mathcal{P}}\Psi_\sigma(\mathcal{P}x)=0$ otherwise (fermionic or distinguishable). This can be expressed in a more compact form as
$\frac{1}{N!}\sum_{\mathcal{P}}\Psi_\sigma(\mathcal{P}x)=\delta_{{\sigma_\text{id}},\sigma}\Psi_\sigma(x)$. (6)
By definition, the bosonic density matrix should be $\rho^\text{bose}(\mathbf{x},\mathbf{x}',\beta)=\sum_{\sigma=\{\sigma_\text{id}\}}\Psi_\sigma(\mathbf{x})\Psi^{*}_\sigma(\mathbf{x}')e^{-\beta E_\sigma}=\sum_{\sigma}\delta_{{\sigma_\text{id}},\sigma}\Psi_\sigma(\mathbf{x})\Psi^{*}_\sigma(\mathbf{x}')e^{-\beta E_\sigma}$, i.e. a sum over all $N$ particle states which are symmetric. If we insert Eqn. (6) here in the latter equality, we get $\rho^\text{bose}(\mathbf{x},\mathbf{x}',\beta)=\frac{1}{N!}\sum_\sigma\Psi_\sigma(\mathbf{x})\sum_\mathcal{P}\Psi^{*}_\sigma(\mathcal{P}\mathbf{x}')e^{-\beta E_\sigma}$. Exchanging the sums, we get $\rho^\text{bose}(\mathbf{x},\mathbf{x}',\beta)=\frac{1}{N!}\sum_\mathcal{P}\sum_\sigma\Psi_\sigma(\mathbf{x})\Psi^{*}_\sigma(\mathcal{P}\mathbf{x}')e^{-\beta E_\sigma}$. In other words, we simply have
$\boxed{\rho^\text{bose}(\mathbf{x},\mathbf{x}',\beta)=\frac{1}{N!}\sum_\mathcal{P}\rho^D(\mathbf{x},\mathcal{P}\mathbf{x}',\beta)}$, (7)
that is the average of the distinguishable density matrices over all permutations of $N$ particles.
For ideal bosons, we have $\boxed{\rho^\text{bose, ideal}(\mathbf{x},\mathbf{x}',\beta)=\frac{1}{N!}\sum_\mathcal{P}\rho(x_0,\mathcal{P}x_0',\beta)\rho(x_1,\mathcal{P}x_1',\beta)\cdots\rho(x_{N-1},\mathcal{P}x_{N-1}',\beta)}$. (8)
The partition function is therefore
$Z^\text{bose}(\beta)=\frac{1}{N!}\int \text{d}x_0\cdots\text{d}x_{N-1}\sum_\mathcal{P}\rho^D(\mathbf{x},\mathcal{P}\mathbf{x},\beta)=\frac{1}{N!}\sum_\mathcal{P}Z_\mathcal{P}$, (9)
i.e. an integral over paths and an average over all permutations. We should therefore sample both positions and permutations.
For fermions, the sum over permutations $\mathcal{P}$ involve a weighting with factor $(-1)^{\mathcal{P}}$:
$\rho^\text{fermi}(\mathbf{x},\mathbf{x}',\beta)=\frac{1}{N!}\sum_\mathcal{P}(-1)^\mathcal{P}\rho^D(\mathbf{x},\mathcal{P}\mathbf{x}',\beta)$
Therefore for fermions corresponding path integrals are nontrivial, and they involve Grassmann variables (see e.g. Negele, Orland https://www.amazon.com/Quantum-Many-particle-Systems-Advanced-Classics/dp/0738200522 ).
#### Sampling permutations
The following Markov-chain algorithm samples permutations of $N$ elements on a list $L$. The permutation function for the uniformly distributed $\mathcal{P}$ is $Y_N=\sum_\mathcal{P}1=N!$.
```
import random
N = 3 #length of the list
statistics = {}
L = range(N) #initialise the list
nsteps = 10
for step in range(nsteps):
i = random.randint(0, N - 1) #pick two random indices i and j from the list L
j = random.randint(0, N - 1)
L[i], L[j] = L[j], L[i] #exchange the i'th and j'th elements
if tuple(L) in statistics:
statistics[tuple(L)] += 1 #if a certain configuration appears again, add 1 to its count
else:
statistics[tuple(L)] = 1 #if a certain configuration for the first time, give it a count of 1
print L
print range(N)
print
for item in statistics:
print item, statistics[item]
```
Let us look at the permutation cycles and their frequency of occurrence:
```
import random
N = 20 #length of the list
stats = [0] * (N + 1) #initialise the "stats" vector
L = range(N) #initialise the list
nsteps = 1000000 #number of steps
for step in range(nsteps):
i = random.randint(0, N - 1) #pick two random indices i and j from the list L
j = random.randint(0, N - 1)
L[i], L[j] = L[j], L[i] #exchange the i'th and j'th elements in the list L
#Calculate the lengths of the permutation cycles in list L
if step % 100 == 0: #i.e. at each 100 steps
cycle_dict = {} #initialise the permutation cycle dictionary
for k in range(N): #loop over the list length,where keys (k) represent the particles
cycle_dict[k] = L[k] #and the values (L) are for the successors of the particles in the perm. cycle
while cycle_dict != {}: #i.e. when the cycle dictionary is not empty?
starting_element = cycle_dict.keys()[0] #save the first (0th) element in the cycle as the starting element
cycle_length = 0 #initialise the cycle length
old_element = starting_element #ancillary variable
while True:
cycle_length += 1 #increase the cycle length while...
new_element = cycle_dict.pop(old_element) #get the successor of the old element in the perm. cycle
if new_element == starting_element: break #the new element is the same as the first one (cycle complete)
else: old_element = new_element #move on to the next successor in the perm. cycle
stats[cycle_length] += 1 #increase the number of occurrences of a cycle of that length by 1
for k in range(1, N + 1): #print the cycle lengths and their number of occurrences
print k, stats[k]
```
The partition function of permutations $\mathcal{P}$ on a list of lentgth $N$ is $Y_N=\sum_\mathcal{P}\text{weight}(\mathcal{P})$. Let $z_n$ be the weight of a permutation cycle of length $n$. Then, the permutation $[0,1,2,3]\rightarrow[0,1,2,3]$, which can be represented as $(0)(1)(2)(3)$, has the weight $z_1^4$; similarly, $(0)(12)(3)$ would have $z_1^2z_2$, etc.
Generally, the cycle $\{n_1,\cdots,n_{k-1},\text{last element}\}$, i.e. the cycle containing the last element, has a length $k$, with the weight $z_k$. The remaining $N-k$ elements have the partition function $Y_{(N-k)}$. Hence, the total partition function is given by $Y_N=\sum_{k=1}^Nz_k\{\text{# of choices for} \{n_1,\cdots,n_{k-1}\}\}\{\text{# of cycles with} \{n_1,\cdots,n_{k}\}\}Y_{N-k}$
$\implies Y_N=\sum_{k=1}^N z_k{{N-1}\choose{k-1}}(k-1)!Y_{N-k}$ which leads to the following recursion formula
$\boxed{Y_N=\frac{1}{N}\sum_{k=1}^N z_k\frac{N!}{(N-k)!}Y_{N-k}, (\text{with }Y_0=1)}$. (10)
***Using the convolution property, we can regard the $l+1$ bosons in a permutation cycle of length $l$ at temperatyre $1/\beta$ as a single boson at a temperature $1/(l\beta)$.***
*Example 1:* Consider the permutation $[0,3,1,2]\rightarrow[0,1,2,3]$ consists of the following permutation cycle $1\rightarrow 2 \rightarrow 3 \rightarrow 1$ of length 3 ($\mathcal{P}=(132)$). This corresponds to the partition function $Z^\text{bose}_{(0)(132)}(\beta)=\int \text{d}x_0\rho(x_0,x_0,\beta)\int\text{d}x_1\int\text{d}x_2\int\text{d}x_3\rho(x_1,x_3,\beta)\rho(x_3,x_2,\beta)\rho(x_2,x_1,\beta)$. Using the convolution property, we have: $\int\text{d}x_3\rho(x_1,x_3,\beta)\rho(x_3,x_2,\beta)=\rho(x_1,x_2,2\beta)\implies\int\text{d}x_2\rho(x_1,x_2,2\beta)\rho(x_2,x_1,\beta)=\rho(x_1,x_1,3\beta)$. The single particle partition function is defined as $z(\beta)=\int\text{d}\mathbf{x}\rho(\mathbf{x},\mathbf{x},\beta) =\left[ \int\text{d}x\rho(x,x,\beta)\right]^3$.
$\implies Z^\text{bose}_{(0)(132)}(\beta)=\int \text{d}x_0\rho(x_0,x_0,\beta)\int\text{d}x_1\rho(x_1,x_1,3\beta)=z(\beta)z(3\beta)$.
*Example 2:* $Z^\text{bose}_{(0)(1)(2)(3)}(\beta)=z(\beta)^4$.
Simulation of bosons in a harmonic trap: (Carefully note that here are no intermediate slices in the sampled paths, since the paths are sampled from the exact distribution.)
```
import random, math, pylab, mpl_toolkits.mplot3d
#3 dimensional Levy algorithm, used for resampling the positions of entire permutation cycles of bosons
#to sample positions
def levy_harmonic_path(k, beta):
#direct sample (rejection-free) three coordinate values, use diagonal density matrix
#k corresponds to the length of the permutation cycle
xk = tuple([random.gauss(0.0, 1.0 / math.sqrt(2.0 *
math.tanh(k * beta / 2.0))) for d in range(3)])
x = [xk] #save the 3 coordinate values xk into a 3d vector x (final point)
for j in range(1, k): #loop runs through the permutation cycle
#Levy sampling (sample a point given the latest sample and the final point)
Upsilon_1 = (1.0 / math.tanh(beta) +
1.0 / math.tanh((k - j) * beta))
Upsilon_2 = [x[j - 1][d] / math.sinh(beta) + xk[d] /
math.sinh((k - j) * beta) for d in range(3)]
x_mean = [Upsilon_2[d] / Upsilon_1 for d in range(3)]
sigma = 1.0 / math.sqrt(Upsilon_1)
dummy = [random.gauss(x_mean[d], sigma) for d in range(3)] #direct sample the j'th point
x.append(tuple(dummy)) #construct the 3d path (permutation cycle) by appending tuples
return x
#(Non-diagonal) harmonic oscillator density matrix, used for organising the exchange of two elements
#to sample permutations
def rho_harm(x, xp, beta):
Upsilon_1 = sum((x[d] + xp[d]) ** 2 / 4.0 *
math.tanh(beta / 2.0) for d in range(3))
Upsilon_2 = sum((x[d] - xp[d]) ** 2 / 4.0 /
math.tanh(beta / 2.0) for d in range(3))
return math.exp(- Upsilon_1 - Upsilon_2)
N = 256 #number of bosons
T_star = 0.3
beta = 1.0 / (T_star * N ** (1.0 / 3.0)) #??
nsteps = 1000000
positions = {} #initial position dictionary
for j in range(N): #loop over all particles, initial permutation is identity (k=1)
a = levy_harmonic_path(1, beta) #initial positions (outputs a single 3d point)
positions[a[0]] = a[0] #positions of particles are keys for themselves in the initial position dict.
for step in range(nsteps):
boson_a = random.choice(positions.keys()) #randomly pick the position of boson "a" from the dict.
perm_cycle = [] #initialise the permutation cycle
while True: #compute the permutation cycle of the boson "a":
perm_cycle.append(boson_a) #construct the permutation cycle by appending the updated position of boson "a"
boson_b = positions.pop(boson_a) #remove and return (pop) the position of "a", save it as a temp. var.
if boson_b == perm_cycle[0]: break #if the cycle is completed, break the while loop
else: boson_a = boson_b #move boson "a" to position of "b" and continue permuting
k = len(perm_cycle) #length of the permutation cycle
#SAMPLE POSITIONS:
perm_cycle = levy_harmonic_path(k, beta) #resample the particle positions in the current permutation cycle
positions[perm_cycle[-1]] = perm_cycle[0] #assures that the new path is a "cycle" (last term maps to the first term)
for j in range(len(perm_cycle) - 1): #update the positions of bosons
positions[perm_cycle[j]] = perm_cycle[j + 1] #construct the "cycle": j -> j+1
#SAMPLE PERMUTATION CYCLES by exchanges:
#Pick two particles and attempt an exchange to sample permutations (with Metropolis acceptance rate):
a_1 = random.choice(positions.keys()) #pick the first random particle
b_1 = positions.pop(a_1) #save the random particle to a temporary variable
a_2 = random.choice(positions.keys()) #pick the second random particle
b_2 = positions.pop(a_2) #save the random particle to a temporary variable
weight_new = rho_harm(a_1, b_2, beta) * rho_harm(a_2, b_1, beta) #the new Metropolis acceptance rate
weight_old = rho_harm(a_1, b_1, beta) * rho_harm(a_2, b_2, beta) #the old Metropolis acceptance rate
if random.uniform(0.0, 1.0) < weight_new / weight_old:
positions[a_1] = b_2 #accept
positions[a_2] = b_1
else:
positions[a_1] = b_1 #reject
positions[a_2] = b_2
#Figure output:
fig = pylab.figure()
ax = mpl_toolkits.mplot3d.axes3d.Axes3D(fig)
ax.set_aspect('equal')
list_colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k']
n_colors = len(list_colors)
dict_colors = {}
i_color = 0
# find and plot permutation cycles:
while positions:
x, y, z = [], [], []
starting_boson = positions.keys()[0]
boson_old = starting_boson
while True:
x.append(boson_old[0])
y.append(boson_old[1])
z.append(boson_old[2])
boson_new = positions.pop(boson_old)
if boson_new == starting_boson: break
else: boson_old = boson_new
len_cycle = len(x)
if len_cycle > 2:
x.append(x[0])
y.append(y[0])
z.append(z[0])
if len_cycle in dict_colors:
color = dict_colors[len_cycle]
ax.plot(x, y, z, color + '+-', lw=0.75)
else:
color = list_colors[i_color]
i_color = (i_color + 1) % n_colors
dict_colors[len_cycle] = color
ax.plot(x, y, z, color + '+-', label='k=%i' % len_cycle, lw=0.75)
# finalize plot
pylab.title('$N=%i$, $T^*=%s$' % (N, T_star))
pylab.legend()
ax.set_xlabel('$x$', fontsize=16)
ax.set_ylabel('$y$', fontsize=16)
ax.set_zlabel('$z$', fontsize=16)
ax.set_xlim3d([-8, 8])
ax.set_ylim3d([-8, 8])
ax.set_zlim3d([-8, 8])
pylab.savefig('snapshot_bosons_3d_N%04i_Tstar%04.2f.png' % (N, T_star))
pylab.show()
```

But we do know that for the harmonic trap, the single 3-dimensional particle partition function is given by $z(\beta)=\left(\frac{1}{1-e^{-\beta}}\right)^3$. The permutation cycle of length $k$ corresponds to $z_k=z(k\beta)=\left(\frac{1}{1-e^{-k\beta}}\right)^3$. Hence, using (9) and (10), we have that
$Z^\text{bose}_N=Y_N/{N!}=\frac{1}{N}\sum_{k=1}^N z_k Z^\text{bose}_{N-k}, (\text{with }Z^\text{bose}_0=1)$. (11)
(Due to Landsberg, 1961 http://store.doverpublications.com/0486664937.html)
This recursion relation relates the partition function of a system of $N$ ideal bosons to the partition function of a single particle and the partition functions of systems with fewer particles.
```
import math, pylab
def z(k, beta):
return 1.0 / (1.0 - math.exp(- k * beta)) ** 3 #partition function of a single particle in a harmonic trap
def canonic_recursion(N, beta): #Landsberg recursion relations for the partition function of N bosons
Z = [1.0] #Z_0 = 1
for M in range(1, N + 1):
Z.append(sum(Z[k] * z(M - k, beta) \
for k in range(M)) / M)
return Z #list of partition functions for boson numbers up to N
N = 256 #number of bosons
T_star = 0.5 #temperature
beta = 1.0 / N ** (1.0 / 3.0) / T_star
Z = canonic_recursion(N, beta) #partition function
pi_k = [(z(k, beta) * Z[N - k] / Z[-1]) / float(N) for k in range(1, N + 1)] #probability of a cycle of length k
# graphics output
pylab.plot(range(1, N + 1), pi_k, 'b-', lw=2.5)
pylab.ylim(0.0, 0.01)
pylab.xlabel('cycle length $k$', fontsize=16)
pylab.ylabel('cycle probability $\pi_k$', fontsize=16)
pylab.title('Cycle length distribution ($N=%i$, $T^*=%s$)' % (N, T_star), fontsize=16)
pylab.savefig('plot-prob_cycle_length.png')
phase = [pi[k+1] - pi[k] for k in range(1, N+1)]
# graphics output
pylab.plot(range(1, N + 1), pi_k, 'b-', lw=2.5)
pylab.ylim(0.0, 0.01)
pylab.xlabel('cycle length $k$', fontsize=16)
pylab.ylabel('cycle probability $\pi_k$', fontsize=16)
pylab.title('Cycle length distribution ($N=%i$, $T^*=%s$)' % (N, T_star), fontsize=16)
pylab.savefig('plot-prob_cycle_length.png')
```
Since we have an analytical solution to the problem, we can now implement a rejection-free direct sampling algorithm for the permutations.
```
import math, random
def z(k, beta): #partition function of a single particle in a harmonic trap
return (1.0 - math.exp(- k * beta)) ** (-3)
def canonic_recursion(N, beta): #Landsberg recursion relation for the partition function of N bosons in a harmonic trap
Z = [1.0]
for M in range(1, N + 1):
Z.append(sum(Z[k] * z(M - k, beta) for k in range(M)) / M)
return Z
def make_pi_list(Z, M): #the probability for a boson to be in a permutation length of length up to M?
pi_list = [0.0] + [z(k, beta) * Z[M - k] / Z[M] / M for k in range(1, M + 1)]
pi_cumulative = [0.0]
for k in range(1, M + 1):
pi_cumulative.append(pi_cumulative[k - 1] + pi_list[k])
return pi_cumulative
def naive_tower_sample(pi_cumulative):
eta = random.uniform(0.0, 1.0)
for k in range(len(pi_cumulative)):
if eta < pi_cumulative[k]: break
return k
def levy_harmonic_path(dtau, N): #path sampling (to sample permutation positions)
beta = N * dtau
x_N = random.gauss(0.0, 1.0 / math.sqrt(2.0 * math.tanh(beta / 2.0)))
x = [x_N]
for k in range(1, N):
dtau_prime = (N - k) * dtau
Upsilon_1 = 1.0 / math.tanh(dtau) + 1.0 / math.tanh(dtau_prime)
Upsilon_2 = x[k - 1] / math.sinh(dtau) + x_N / math.sinh(dtau_prime)
x_mean = Upsilon_2 / Upsilon_1
sigma = 1.0 / math.sqrt(Upsilon_1)
x.append(random.gauss(x_mean, sigma))
return x
### main program starts here ###
N = 8 #number of bosons
T_star = 0.1 #temperature
beta = 1.0 / N ** (1.0 / 3.0) / T_star
n_steps = 1000
Z = canonic_recursion(N, beta) #{N} boson partition function
for step in range(n_steps):
N_tmp = N #ancillary
x_config, y_config, z_config = [], [], [] #initialise the configurations in each 3 directions
while N_tmp > 0: #iterate through all particles
pi_sum = make_pi_list(Z, N_tmp)
k = naive_tower_sample(pi_sum)
x_config += levy_harmonic_path(beta, k)
y_config += levy_harmonic_path(beta, k)
z_config += levy_harmonic_path(beta, k)
N_tmp -= k #reduce the number of particles that are in the permutation cycle of length k
```
### Physical properties of the 1-dimensional classical and bosonic systems
* Consider 2 non-interacting **distinguishable particles** in a 1-dimensional harmonic trap:
```
import random, math, pylab
#There are only two possible cases: For k=1, we sample a single position (cycle of length 1),
#for k=2, we sample two positions (a cycle of length two).
def levy_harmonic_path(k):
x = [random.gauss(0.0, 1.0 / math.sqrt(2.0 * math.tanh(k * beta / 2.0)))] #direct-sample the first position
if k == 2:
Ups1 = 2.0 / math.tanh(beta)
Ups2 = 2.0 * x[0] / math.sinh(beta)
x.append(random.gauss(Ups2 / Ups1, 1.0 / math.sqrt(Ups1)))
return x[:]
def pi_x(x, beta):
sigma = 1.0 / math.sqrt(2.0 * math.tanh(beta / 2.0))
return math.exp(-x ** 2 / (2.0 * sigma ** 2)) / math.sqrt(2.0 * math.pi) / sigma
beta = 2.0
nsteps = 1000000
#initial sample has identity permutation
low = levy_harmonic_path(2) #tau=0
high = low[:] #tau=beta
data = []
for step in xrange(nsteps):
k = random.choice([0, 1])
low[k] = levy_harmonic_path(1)[0]
high[k] = low[k]
data.append(high[k])
list_x = [0.1 * a for a in range (-30, 31)]
y = [pi_x(a, beta) for a in list_x]
pylab.plot(list_x, y, linewidth=2.0, label='Exact distribution')
pylab.hist(data, normed=True, bins=80, label='QMC', alpha=0.5, color='green')
pylab.legend()
pylab.xlabel('$x$',fontsize=14)
pylab.ylabel('$\\pi(x)$',fontsize=14)
pylab.title('2 non-interacting distinguishable 1-d particles',fontsize=14)
pylab.xlim(-3, 3)
pylab.savefig('plot_A1_beta%s.png' % beta)
```
* Consider two non-interacting **indistinguishable bosonic** quantum particles in a one-dimensional harmonic trap:
```
import math, random, pylab, numpy as np
def z(beta):
return 1.0 / (1.0 - math.exp(- beta))
def pi_two_bosons(x, beta): #exact two boson position distribution
pi_x_1 = math.sqrt(math.tanh(beta / 2.0)) / math.sqrt(math.pi) * math.exp(-x ** 2 * math.tanh(beta / 2.0))
pi_x_2 = math.sqrt(math.tanh(beta)) / math.sqrt(math.pi) * math.exp(-x ** 2 * math.tanh(beta))
weight_1 = z(beta) ** 2 / (z(beta) ** 2 + z(2.0 * beta))
weight_2 = z(2.0 * beta) / (z(beta) ** 2 + z(2.0 * beta))
pi_x = pi_x_1 * weight_1 + pi_x_2 * weight_2
return pi_x
def levy_harmonic_path(k):
x = [random.gauss(0.0, 1.0 / math.sqrt(2.0 * math.tanh(k * beta / 2.0)))]
if k == 2:
Ups1 = 2.0 / math.tanh(beta)
Ups2 = 2.0 * x[0] / math.sinh(beta)
x.append(random.gauss(Ups2 / Ups1, 1.0 / math.sqrt(Ups1)))
return x[:]
def rho_harm_1d(x, xp, beta):
Upsilon_1 = (x + xp) ** 2 / 4.0 * math.tanh(beta / 2.0)
Upsilon_2 = (x - xp) ** 2 / 4.0 / math.tanh(beta / 2.0)
return math.exp(- Upsilon_1 - Upsilon_2)
beta = 2.0
list_beta = np.linspace(0.1, 5.0)
nsteps = 10000
low = levy_harmonic_path(2)
high = low[:]
fract_one_cycle_dat, fract_two_cycles_dat = [], []
for beta in list_beta:
one_cycle_dat = 0.0 #initialise the permutation fractions for each temperature
data = []
for step in xrange(nsteps):
# move 1 (direct-sample the positions)
if low[0] == high[0]: #if the cycle is of length 1
k = random.choice([0, 1])
low[k] = levy_harmonic_path(1)[0]
high[k] = low[k] #assures the cycle
else: #if the cycle is of length 2s
low[0], low[1] = levy_harmonic_path(2)
high[1] = low[0] #assures the cycle
high[0] = low[1]
one_cycle_dat += 1.0 / float(nsteps) #calculate the fraction of the single cycle cases
data += low[:] #save the position histogram data
# move 2 (Metropolis for sampling the permutations)
weight_old = (rho_harm_1d(low[0], high[0], beta) * rho_harm_1d(low[1], high[1], beta))
weight_new = (rho_harm_1d(low[0], high[1], beta) * rho_harm_1d(low[1], high[0], beta))
if random.uniform(0.0, 1.0) < weight_new / weight_old:
high[0], high[1] = high[1], high[0]
fract_one_cycle_dat.append(one_cycle_dat)
fract_two_cycles_dat.append(1.0 - one_cycle_dat) #save the fraction of the two cycles cases
#Exact permutation distributions for all temperatures
fract_two_cycles = [z(beta) ** 2 / (z(beta) ** 2 + z(2.0 * beta)) for beta in list_beta]
fract_one_cycle = [z(2.0 * beta) / (z(beta) ** 2 + z(2.0 * beta)) for beta in list_beta]
#Graphics output:
list_x = [0.1 * a for a in range (-30, 31)]
y = [pi_two_bosons(a, beta) for a in list_x]
pylab.plot(list_x, y, linewidth=2.0, label='Exact distribution')
pylab.hist(data, normed=True, bins=80, label='QMC', alpha=0.5, color='green')
pylab.legend()
pylab.xlabel('$x$',fontsize=14)
pylab.ylabel('$\\pi(x)$',fontsize=14)
pylab.title('2 non-interacting bosonic 1-d particles',fontsize=14)
pylab.xlim(-3, 3)
pylab.savefig('plot_A2_beta%s.png' % beta)
pylab.show()
pylab.clf()
fig = pylab.figure(figsize=(10, 5))
ax = fig.add_subplot(1, 2, 1)
ax.plot(list_beta, fract_one_cycle_dat, linewidth=4, label='QMC')
ax.plot(list_beta, fract_one_cycle, linewidth=2, label='exact')
ax.legend()
ax.set_xlabel('$\\beta$',fontsize=14)
ax.set_ylabel('$\\pi_2(\\beta)$',fontsize=14)
ax.set_title('Fraction of cycles of length 2',fontsize=14)
ax = fig.add_subplot(1, 2, 2)
ax.plot(list_beta, fract_two_cycles_dat, linewidth=4, label='QMC')
ax.plot(list_beta, fract_two_cycles, linewidth=2,label='exact')
ax.legend()
ax.set_xlabel('$\\beta$',fontsize=14)
ax.set_ylabel('$\\pi_1(\\beta)$',fontsize=14)
ax.set_title('Fraction of cycles of length 1',fontsize=14)
pylab.savefig('plot_A2.png')
pylab.show()
pylab.clf()
```
We can use dictionaries instead of lists. The implementation is in the following program.
Here we also calculate the correlation between the two particles, i.e. sample of the absolute distance $r$ between the two bosons. The comparison between the resulting distribution and the distribution for the distinguishable case corresponds to boson bunching (high weight for small distances between the bosons).
```
import math, random, pylab
def prob_r_distinguishable(r, beta): #the exact correlation function for two particles
sigma = math.sqrt(2.0) / math.sqrt(2.0 * math.tanh(beta / 2.0))
prob = (math.sqrt(2.0 / math.pi) / sigma) * math.exp(- r ** 2 / 2.0 / sigma ** 2)
return prob
def levy_harmonic_path(k):
x = [random.gauss(0.0, 1.0 / math.sqrt(2.0 * math.tanh(k * beta / 2.0)))]
if k == 2:
Ups1 = 2.0 / math.tanh(beta)
Ups2 = 2.0 * x[0] / math.sinh(beta)
x.append(random.gauss(Ups2 / Ups1, 1.0 / math.sqrt(Ups1)))
return x[:]
def rho_harm_1d(x, xp, beta):
Upsilon_1 = (x + xp) ** 2 / 4.0 * math.tanh(beta / 2.0)
Upsilon_2 = (x - xp) ** 2 / 4.0 / math.tanh(beta / 2.0)
return math.exp(- Upsilon_1 - Upsilon_2)
beta = 0.1
nsteps = 1000000
low_1, low_2 = levy_harmonic_path(2)
x = {low_1:low_1, low_2:low_2}
data_corr = []
for step in xrange(nsteps):
# move 1
a = random.choice(x.keys())
if a == x[a]:
dummy = x.pop(a)
a_new = levy_harmonic_path(1)[0]
x[a_new] = a_new
else:
a_new, b_new = levy_harmonic_path(2)
x = {a_new:b_new, b_new:a_new}
r = abs(x.keys()[1] - x.keys()[0])
data_corr.append(r)
# move 2
(low1, high1), (low2, high2) = x.items()
weight_old = rho_harm_1d(low1, high1, beta) * rho_harm_1d(low2, high2, beta)
weight_new = rho_harm_1d(low1, high2, beta) * rho_harm_1d(low2, high1, beta)
if random.uniform(0.0, 1.0) < weight_new / weight_old:
x = {low1:high2, low2:high1}
#Graphics output:
list_x = [0.1 * a for a in range (0, 100)]
y = [prob_r_distinguishable(a, beta) for a in list_x]
pylab.plot(list_x, y, linewidth=2.0, label='Exact distinguishable distribution')
pylab.hist(data_corr, normed=True, bins=120, label='Indistinguishable QMC', alpha=0.5, color='green')
pylab.legend()
pylab.xlabel('$r$',fontsize=14)
pylab.ylabel('$\\pi_{corr}(r)$',fontsize=14)
pylab.title('Correlation function of non-interacting 1-d bosons',fontsize=14)
pylab.xlim(0, 10)
pylab.savefig('plot_A3_beta%s.png' % beta)
pylab.show()
pylab.clf()
```
### 3-dimensional bosons
#### Isotropic trap
```
import random, math, numpy, sys, os
import matplotlib.pyplot as plt
def harmonic_ground_state(x):
return math.exp(-x ** 2)/math.sqrt(math.pi)
def levy_harmonic_path_3d(k):
x0 = tuple([random.gauss(0.0, 1.0 / math.sqrt(2.0 *
math.tanh(k * beta / 2.0))) for d in range(3)])
x = [x0]
for j in range(1, k):
Upsilon_1 = 1.0 / math.tanh(beta) + 1.0 / \
math.tanh((k - j) * beta)
Upsilon_2 = [x[j - 1][d] / math.sinh(beta) + x[0][d] /
math.sinh((k - j) * beta) for d in range(3)]
x_mean = [Upsilon_2[d] / Upsilon_1 for d in range(3)]
sigma = 1.0 / math.sqrt(Upsilon_1)
dummy = [random.gauss(x_mean[d], sigma) for d in range(3)]
x.append(tuple(dummy))
return x
def rho_harm_3d(x, xp):
Upsilon_1 = sum((x[d] + xp[d]) ** 2 / 4.0 *
math.tanh(beta / 2.0) for d in range(3))
Upsilon_2 = sum((x[d] - xp[d]) ** 2 / 4.0 /
math.tanh(beta / 2.0) for d in range(3))
return math.exp(- Upsilon_1 - Upsilon_2)
N = 512
T_star = 0.8
list_T = numpy.linspace(0.8,0.1,5)
beta = 1.0 / (T_star * N ** (1.0 / 3.0))
cycle_min = 10
nsteps = 50000
data_x, data_y, data_x_l, data_y_l = [], [], [], []
for T_star in list_T:
# Initial condition
filename = 'data_boson_configuration_N%i_T%.1f.txt' % (N,T_star)
positions = {}
if os.path.isfile(filename):
f = open(filename, 'r')
for line in f:
a = line.split()
positions[tuple([float(a[0]), float(a[1]), float(a[2])])] = \
tuple([float(a[3]), float(a[4]), float(a[5])])
f.close()
if len(positions) != N:
sys.exit('ERROR in the input file.')
print 'starting from file', filename
else:
for k in range(N):
a = levy_harmonic_path_3d_anisotropic(1)
positions[a[0]] = a[0]
print 'Starting from a new configuration'
# Monte Carlo loop
for step in range(nsteps):
# move 1: resample one permutation cycle
boson_a = random.choice(positions.keys())
perm_cycle = []
while True:
perm_cycle.append(boson_a)
boson_b = positions.pop(boson_a)
if boson_b == perm_cycle[0]:
break
else:
boson_a = boson_b
k = len(perm_cycle)
data_x.append(boson_a[0])
data_y.append(boson_a[1])
if k > cycle_min:
data_x_l.append(boson_a[0])
data_y_l.append(boson_a[1])
perm_cycle = levy_harmonic_path_3d(k)
positions[perm_cycle[-1]] = perm_cycle[0]
for k in range(len(perm_cycle) - 1):
positions[perm_cycle[k]] = perm_cycle[k + 1]
# move 2: exchange
a_1 = random.choice(positions.keys())
b_1 = positions.pop(a_1)
a_2 = random.choice(positions.keys())
b_2 = positions.pop(a_2)
weight_new = rho_harm_3d(a_1, b_2) * rho_harm_3d(a_2, b_1)
weight_old = rho_harm_3d(a_1, b_1) * rho_harm_3d(a_2, b_2)
if random.uniform(0.0, 1.0) < weight_new / weight_old:
positions[a_1] = b_2
positions[a_2] = b_1
else:
positions[a_1] = b_1
positions[a_2] = b_2
f = open(filename, 'w')
for a in positions:
b = positions[a]
f.write(str(a[0]) + ' ' + str(a[1]) + ' ' + str(a[2]) + ' ' +
str(b[0]) + ' ' + str(b[1]) + ' ' + str(b[2]) + '\n')
f.close()
# Analyze cycles, do 3d plot
import pylab, mpl_toolkits.mplot3d
fig = pylab.figure()
ax = mpl_toolkits.mplot3d.axes3d.Axes3D(fig)
ax.set_aspect('equal')
n_colors = 10
list_colors = pylab.cm.rainbow(numpy.linspace(0, 1, n_colors))[::-1]
dict_colors = {}
i_color = 0
positions_copy = positions.copy()
while positions_copy:
x, y, z = [], [], []
starting_boson = positions_copy.keys()[0]
boson_old = starting_boson
while True:
x.append(boson_old[0])
y.append(boson_old[1])
z.append(boson_old[2])
boson_new = positions_copy.pop(boson_old)
if boson_new == starting_boson: break
else: boson_old = boson_new
len_cycle = len(x)
if len_cycle > 2:
x.append(x[0])
y.append(y[0])
z.append(z[0])
if len_cycle in dict_colors:
color = dict_colors[len_cycle]
ax.plot(x, y, z, '+-', c=color, lw=0.75)
else:
color = list_colors[i_color]
i_color = (i_color + 1) % n_colors
dict_colors[len_cycle] = color
ax.plot(x, y, z, '+-', c=color, label='k=%i' % len_cycle, lw=0.75)
pylab.title(str(N) + ' bosons at T* = ' + str(T_star))
pylab.legend()
ax.set_xlabel('$x$', fontsize=16)
ax.set_ylabel('$y$', fontsize=16)
ax.set_zlabel('$z$', fontsize=16)
xmax = 6.0
ax.set_xlim3d([-xmax, xmax])
ax.set_ylim3d([-xmax, xmax])
ax.set_zlim3d([-xmax, xmax])
pylab.savefig('plot_boson_configuration_N%i_T%.1f.png' %(N,T_star))
pylab.show()
pylab.clf()
#Plot the histograms
list_x = [0.1 * a for a in range (-50, 51)]
y = [harmonic_ground_state(a) for a in list_x]
pylab.plot(list_x, y, linewidth=2.0, label='Ground state')
pylab.hist(data_x, normed=True, bins=120, alpha = 0.5, label='All bosons')
pylab.hist(data_x_l, normed=True, bins=120, alpha = 0.5, label='Bosons in longer cycle')
pylab.xlim(-3.0, 3.0)
pylab.xlabel('$x$',fontsize=14)
pylab.ylabel('$\pi(x)$',fontsize=14)
pylab.title('3-d non-interacting bosons $x$ distribution $N= %i$, $T= %.1f$' %(N,T_star))
pylab.legend()
pylab.savefig('position_distribution_N%i_T%.1f.png' %(N,T_star))
pylab.show()
pylab.clf()
plt.hist2d(data_x_l, data_y_l, bins=40, normed=True)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.title('The distribution of the $x$ and $y$ positions')
plt.colorbar()
plt.xlim(-3.0, 3.0)
plt.ylim(-3.0, 3.0)
plt.show()
```
#### Anisotropic trap
We can imitate the experiments that imitate 1-d bosons in *cigar shaped* anisotropic harmonic traps, and 2-d bosons in *pancake shaped* anisotropic harmonic traps.
```
%pylab inline
import random, math, numpy, os, sys
def levy_harmonic_path_3d_anisotropic(k, omega):
sigma = [1.0 / math.sqrt(2.0 * omega[d] *
math.tanh(0.5 * k * beta * omega[d])) for d in xrange(3)]
xk = tuple([random.gauss(0.0, sigma[d]) for d in xrange(3)])
x = [xk]
for j in range(1, k):
Upsilon_1 = [1.0 / math.tanh(beta * omega[d]) +
1.0 / math.tanh((k - j) * beta * omega[d]) for d in range(3)]
Upsilon_2 = [x[j - 1][d] / math.sinh(beta * omega[d]) + \
xk[d] / math.sinh((k - j) * beta * omega[d]) for d in range(3)]
x_mean = [Upsilon_2[d] / Upsilon_1[d] for d in range(3)]
sigma = [1.0 / math.sqrt(Upsilon_1[d] * omega[d]) for d in range(3)]
dummy = [random.gauss(x_mean[d], sigma[d]) for d in range(3)]
x.append(tuple(dummy))
return x
def rho_harm_3d_anisotropic(x, xp, beta, omega):
Upsilon_1 = sum(omega[d] * (x[d] + xp[d]) ** 2 / 4.0 *
math.tanh(beta * omega[d] / 2.0) for d in range(3))
Upsilon_2 = sum(omega[d] * (x[d] - xp[d]) ** 2 / 4.0 /
math.tanh(beta * omega[d] / 2.0) for d in range(3))
return math.exp(- Upsilon_1 - Upsilon_2)
omegas = numpy.array([[4.0, 4.0, 1.0], [1.0, 5.0, 1.0]])
for i in range(len(omegas[:,1])):
N = 512
nsteps = 100000
omega_harm = 1.0
omega = omegas[i,:]
for d in range(3):
omega_harm *= omega[d] ** (1.0 / 3.0)
T_star = 0.5
T = T_star * omega_harm * N ** (1.0 / 3.0)
beta = 1.0 / T
print 'omega: ', omega
# Initial condition
if i == 0:
filename = 'data_boson_configuration_anisotropic_N%i_T%.1f_cigar.txt' % (N,T_star)
elif i == 1:
filename = 'data_boson_configuration_anisotropic_N%i_T%.1f_pancake.txt' % (N,T_star)
positions = {}
if os.path.isfile(filename):
f = open(filename, 'r')
for line in f:
a = line.split()
positions[tuple([float(a[0]), float(a[1]), float(a[2])])] = \
tuple([float(a[3]), float(a[4]), float(a[5])])
f.close()
if len(positions) != N:
sys.exit('ERROR in the input file.')
print 'starting from file', filename
else:
for k in range(N):
a = levy_harmonic_path_3d_anisotropic(1,omega)
positions[a[0]] = a[0]
print 'Starting from a new configuration'
for step in range(nsteps):
boson_a = random.choice(positions.keys())
perm_cycle = []
while True:
perm_cycle.append(boson_a)
boson_b = positions.pop(boson_a)
if boson_b == perm_cycle[0]: break
else: boson_a = boson_b
k = len(perm_cycle)
perm_cycle = levy_harmonic_path_3d_anisotropic(k,omega)
positions[perm_cycle[-1]] = perm_cycle[0]
for j in range(len(perm_cycle) - 1):
positions[perm_cycle[j]] = perm_cycle[j + 1]
a_1 = random.choice(positions.keys())
b_1 = positions.pop(a_1)
a_2 = random.choice(positions.keys())
b_2 = positions.pop(a_2)
weight_new = (rho_harm_3d_anisotropic(a_1, b_2, beta, omega) *
rho_harm_3d_anisotropic(a_2, b_1, beta, omega))
weight_old = (rho_harm_3d_anisotropic(a_1, b_1, beta, omega) *
rho_harm_3d_anisotropic(a_2, b_2, beta, omega))
if random.uniform(0.0, 1.0) < weight_new / weight_old:
positions[a_1], positions[a_2] = b_2, b_1
else:
positions[a_1], positions[a_2] = b_1, b_2
f = open(filename, 'w')
for a in positions:
b = positions[a]
f.write(str(a[0]) + ' ' + str(a[1]) + ' ' + str(a[2]) + ' ' +
str(b[0]) + ' ' + str(b[1]) + ' ' + str(b[2]) + '\n')
f.close()
import pylab, mpl_toolkits.mplot3d
fig = pylab.figure()
ax = mpl_toolkits.mplot3d.axes3d.Axes3D(fig)
ax.set_aspect('equal')
n_colors = 10
list_colors = pylab.cm.rainbow(numpy.linspace(0, 1, n_colors))[::-1]
dict_colors = {}
i_color = 0
positions_copy = positions.copy()
while positions_copy:
x, y, z = [], [], []
starting_boson = positions_copy.keys()[0]
boson_old = starting_boson
while True:
x.append(boson_old[0])
y.append(boson_old[1])
z.append(boson_old[2])
boson_new = positions_copy.pop(boson_old)
if boson_new == starting_boson: break
else: boson_old = boson_new
len_cycle = len(x)
if len_cycle > 2:
x.append(x[0])
y.append(y[0])
z.append(z[0])
if len_cycle in dict_colors:
color = dict_colors[len_cycle]
ax.plot(x, y, z, '+-', c=color, lw=0.75)
else:
color = list_colors[i_color]
i_color = (i_color + 1) % n_colors
dict_colors[len_cycle] = color
ax.plot(x, y, z, '+-', c=color, label='k=%i' % len_cycle, lw=0.75)
pylab.legend()
ax.set_xlabel('$x$', fontsize=16)
ax.set_ylabel('$y$', fontsize=16)
ax.set_zlabel('$z$', fontsize=16)
xmax = 8.0
ax.set_xlim3d([-xmax, xmax])
ax.set_ylim3d([-xmax, xmax])
ax.set_zlim3d([-xmax, xmax])
if i == 0:
pylab.title(str(N) + ' bosons at T* = ' + str(T_star) + ' cigar potential')
pylab.savefig('position_distribution_N%i_T%.1f_cigar.png' %(N,T_star))
elif i == 1:
pylab.title(str(N) + ' bosons at T* = ' + str(T_star) + ' pancake potential')
pylab.savefig('position_distribution_N%i_T%.1f_pancake.png' %(N,T_star))
pylab.show()
```
There it is found that the critical temperature for Bose-Einstein condensation is around $T^*\sim 0.9$.
## To do:
* Calculate the pair correlation function
| github_jupyter |
# Working with 3D city models in Python
**Balázs Dukai** [*@BalazsDukai*](https://twitter.com/balazsdukai), **FOSS4G 2019**
Tweet <span style="color:blue">#CityJSON</span>
[3D geoinformation research group, TU Delft, Netherlands](https://3d.bk.tudelft.nl/)

Repo of this talk: [https://github.com/balazsdukai/foss4g2019](https://github.com/balazsdukai/foss4g2019)
# 3D + city + model ?

Probably the most well known 3d city model is what we see in Google Earth. And it is a very nice model to look at and it is improving continuously. However, certain applications require more information than what is stored in such a mesh model. They need to know what does an object in the model represent in the real world.
# Semantic models

That is why we have semantic models, where for each object in the model we store a label of is meaning.
Once we have labels on the object and on their parts, data preparation becomes more simple. An important property for analytical applications, such as wind flow simulations.
# Useful for urban analysis

García-Sánchez, C., van Beeck, J., Gorlé, C., Predictive Large Eddy Simulations for Urban Flows: Challenges and Opportunities, Building and Environment, 139, 146-156, 2018.
But we can do much more with 3d city models. We can use them to better estimate the energy consumption in buildings, simulate noise in cities or analyse views and shadows. In the Netherlands sunshine is precious commodity, so we like to get as much as we can.
# And many more...

There are many open 3d city models available. They come in different formats and quality. However, at our group we are still waiting for the "year of the 3d city model" to come. We don't really see mainstream use, apart of visualisation. Which is nice, I belive they can provide much more value than having a nice thing to simply look at.
# ...mostly just production of the models
many available, but who **uses** them? **For more than visualisation?**

# In truth, 3D CMs are a bit difficult to work with
### Our built environment is complex, and the objects are complex too

### Software are lagging behind
+ not many software supports 3D city models
+ if they do, mostly propietary data model and format
+ large, *"eterprise"*-type applications (think Esri, FME, Bentley ... )
+ few tools accessible for the individual developer / hobbyist
2. GML doesn't help ( *[GML madness](http://erouault.blogspot.com/2014/04/gml-madness.html) by Even Rouault* )
That is why we are developing CityJSON, which is a data format for 3d city models. Essentially, it aims to increase the value of 3d city models by making it more simple to work with them and lower the entry for a wider audience than cadastral organisations.

## Key concepts of CityJSON
+ *simple*, as in easy to implement
+ designed with programmers in mind
+ fully developed in the open
+ flattened hierarchy of objects
+ <span style="color:red">implementation first</span>

CityJSON implements the data model of CityGML. CityGML is an international standard for 3d city models and it is coupled with its GML-based encoding.
We don't really like GML, because it's verbose, files are deeply nested and large (often several GB). And there are many different ways to do one thing.
Also, I'm not a web-developer, but I would be surprised if anyone prefers GML over JSON for sending stuff around the web.
# JSON-based encoding of the CityGML data model

<blockquote class="twitter-tweet"><p lang="en" dir="ltr">I just got sent a CityGML file. <a href="https://t.co/jnTVoRnVLS">pic.twitter.com/jnTVoRnVLS</a></p>— James Fee (@jamesmfee) <a href="https://twitter.com/jamesmfee/status/748270105319006208?ref_src=twsrc%5Etfw">June 29, 2016</a></blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script>
+ files are deeply nested, and large
+ many "points of entry"
+ many diff ways to do one thing (GML doesn't help, *[GML madness](http://erouault.blogspot.com/2014/04/gml-madness.html) by Even Rouault* )
## The CityGML data model

## Compression ~6x over CityGML

## Compression
| file | CityGML size (original) | CityGML size (w/o spaces) | textures | CityJSON | compression |
| -------- | ----------------------- | ----------------------------- |--------- | ------------ | --------------- |
| [CityGML demo "GeoRes"](https://www.citygml.org/samplefiles/) | 4.3MB | 4.1MB | yes | 524KB | 8.0 |
| [CityGML v2 demo "Railway"](https://www.citygml.org/samplefiles/) | 45MB | 34MB | yes | 4.3MB | 8.1 |
| [Den Haag "tile 01"](https://data.overheid.nl/data/dataset/ngr-3d-model-den-haag) | 23MB | 18MB | no, material | 2.9MB | 6.2 |
| [Montréal VM05](http://donnees.ville.montreal.qc.ca/dataset/maquette-numerique-batiments-citygml-lod2-avec-textures/resource/36047113-aa19-4462-854a-cdcd6281a5af) | 56MB | 42MB | yes | 5.4MB | 7.8 |
| [New York LoD2 (DA13)](https://www1.nyc.gov/site/doitt/initiatives/3d-building.page) | 590MB | 574MB | no | 105MB | 5.5 |
| [Rotterdam Delfshaven](http://rotterdamopendata.nl/dataset/rotterdam-3d-bestanden/resource/edacea54-76ce-41c7-a0cc-2ebe5750ac18) | 16MB | 15MB | yes | 2.6MB | 5.8 |
| [Vienna (the demo file)](https://www.data.gv.at/katalog/dataset/86d88cae-ad97-4476-bae5-73488a12776d) | 37MB | 36MB | no | 5.3MB | 6.8 |
| [Zürich LoD2](https://www.data.gv.at/katalog/dataset/86d88cae-ad97-4476-bae5-73488a12776d) | 3.03GB | 2.07GB | no | 292MB | 7.1 |
If you are interested in a more detailed comparison between CityGML and CityJSON you can read our article, its open access.

And yes, we are guilty of charge.

[https://xkcd.com/927/](https://xkcd.com/927/)
# Let's have a look-see, shall we?

Now let's take a peek under the hood, what's going on in a CityJSON file.
## An empty CityJSON file

In a city model we represent the real-world objects such as buildings, bridges, trees as different types of CityObjects. Each CityObject has its
+ unique ID,
+ attributes,
+ geometry,
+ and it can have children objects or it can be part of a parent object.
Note however, that CityObject are not nested. Each of them is stored at root and the hierachy represented by linking to object IDs.
## A CityObject

Each CityObject has a geometry representation. This geometry is composed of *boundaries* and *semantics*.
## Geometry
+ **boundaries** definition uses vertex indices (inspired by Wavefront OBJ)
+ We have a vertex list at the root of the document
+ Vertices are not repeated (unlike Simple Features)
+ **semantics** are linked to the boundary surfaces

This `MulitSurface` has
5 surfaces
```json
[[0, 3, 2, 1]], [[4, 5, 6, 7]], [[0, 1, 5, 4]], [[0, 2, 3, 8]], [[10, 12, 23, 48]]
```
each surface has only an exterior ring (the first array)
```json
[ [0, 3, 2, 1] ]
```
The semantic surfaces in the `semantics` json-object are linked to the boundary surfaces. The integers in the `values` property of `surfaces` are the 0-based indices of the surfaces of the boundary.
```
import json
import os
path = os.path.join('data', 'rotterdam_subset.json')
with open(path) as fin:
cm = json.loads(fin.read())
print(f"There are {len(cm['CityObjects'])} CityObjects")
# list all IDs
for id in cm['CityObjects']:
print(id, "\t")
```
+ Working with a CityJSON file is straightforward. One can open it with the standard library and get going.
+ But you need to know the schema well.
+ And you need to write everything from scratch.
That is why we are developing **cjio**.
**cjio** is how *we eat what we cook*
Aims to help to actually work with and analyse 3D city models, and extract more value from them. Instead of letting them gather dust in some governmental repository.

## `cjio` has a (quite) stable CLI
```bash
$ cjio city_model.json reproject 2056 export --format glb /out/model.glb
```
## and an experimental API
```python
from cjio import cityjson
cm = cityjson.load('city_model.json')
cm.get_cityobjects(type='building')
```
**`pip install cjio`**
This notebook is based on the develop branch.
**`pip install git+https://github.com/tudelft3d/cjio@develop`**
# `cjio`'s CLI
```
! cjio --help
! cjio data/rotterdam_subset.json info
! cjio data/rotterdam_subset.json validate
! cjio data/rotterdam_subset.json \
subset --exclude --id "{CD98680D-A8DD-4106-A18E-15EE2A908D75}" \
merge data/rotterdam_one.json \
reproject 2056 \
save data/test_rotterdam.json
```
+ The CLI was first, no plans for API
+ **Works with whole city model only**
+ Functions for the CLI work with the JSON directly, passing it along
+ Simple and effective architecture
# `cjio`'s API
Allow *read* --> *explore* --> *modify* --> *write* iteration
Work with CityObjects and their parts
Functions for common operations
Inspired by the *tidyverse* from the R ecosystem
```
import os
from copy import deepcopy
from cjio import cityjson
from shapely.geometry import Polygon
import matplotlib.pyplot as plt
plt.close('all')
from sklearn.preprocessing import FunctionTransformer
from sklearn import cluster
import numpy as np
```
In the following we work with a subset of the 3D city model of Rotterdam

## Load a CityJSON
The `load()` method loads a CityJSON file into a CityJSON object.
```
path = os.path.join('data', 'rotterdam_subset.json')
cm = cityjson.load(path)
print(type(cm))
```
## Using the CLI commands in the API
You can use any of the CLI commands on a CityJSON object
*However,* not all CLI commands are mapped 1-to-1 to `CityJSON` methods
And we haven't harmonized the CLI and the API yet.
```
cm.validate()
```
## Explore the city model
Print the basic information about the city model. Note that `print()` returns the same information as the `info` command in the CLI.
```
print(cm)
```
## Getting objects from the model
Get CityObjects by their *type*, or a list of types. Also by their IDs.
Note that `get_cityobjects()` == `cm.cityobjects`
```
buildings = cm.get_cityobjects(type='building')
# both Building and BuildingPart objects
buildings_parts = cm.get_cityobjects(type=['building', 'buildingpart'])
r_ids = ['{C9D4A5CF-094A-47DA-97E4-4A3BFD75D3AE}',
'{6271F75F-E8D8-4EE4-AC46-9DB02771A031}']
buildings_ids = cm.get_cityobjects(id=r_ids)
```
## Properties and geometry of objects
```
b01 = buildings_ids['{C9D4A5CF-094A-47DA-97E4-4A3BFD75D3AE}']
print(b01)
b01.attributes
```
CityObjects can have *children* and *parents*
```
b01.children is None and b01.parents is None
```
CityObject geometry is a list of `Geometry` objects. That is because a CityObject can have multiple geometry representations in different levels of detail, eg. a geometry in LoD1 and a second geometry in LoD2.
```
b01.geometry
geom = b01.geometry[0]
print("{}, lod {}".format(geom.type, geom.lod))
```
### Geometry boundaries and Semantic Surfaces
On the contrary to a CityJSON file, the geometry boundaries are dereferenced when working with the API. This means that the vertex coordinates are included in the boundary definition, not only the vertex indices.
`cjio` doesn't provide specific geometry classes (yet), eg. MultiSurface or Solid class. If you are working with the geometry boundaries, you need to the geometric operations yourself, or cast the boundary to a geometry-class of some other library. For example `shapely` if 2D is enough.
Vertex coordinates are kept 'as is' on loading the geometry. CityJSON files are often compressed and coordinates are shifted and transformed into integers so probably you'll want to transform them back. Otherwise geometry operations won't make sense.
```
transformation_object = cm.transform
geom_transformed = geom.transform(transformation_object)
geom_transformed.boundaries[0][0]
```
But it might be easier to transform (decompress) the whole model on load.
```
cm_transformed = cityjson.load(path, transform=True)
print(cm_transformed)
```
Semantic Surfaces are stored in a similar fashion as in a CityJSON file, in the `surfaces` attribute of a Geometry object.
```
geom.surfaces
```
`surfaces` does not store geometry boundaries, just references (`surface_idx`). Use the `get_surface_boundaries()` method to obtain the boundary-parts connected to the semantic surface.
```
roofs = geom.get_surfaces(type='roofsurface')
roofs
roof_boundaries = []
for r in roofs.values():
roof_boundaries.append(geom.get_surface_boundaries(r))
roof_boundaries
```
### Assigning attributes to Semantic Surfaces
1. extract the surfaces,
2. make the changes on the surface,
3. overwrite the CityObjects with the changes.
```
cm_copy = deepcopy(cm)
new_cos = {}
for co_id, co in cm.cityobjects.items():
new_geoms = []
for geom in co.geometry:
# Only LoD >= 2 models have semantic surfaces
if geom.lod >= 2.0:
# Extract the surfaces
roofsurfaces = geom.get_surfaces('roofsurface')
for i, rsrf in roofsurfaces.items():
# Change the attributes
if 'attributes' in rsrf.keys():
rsrf['attributes']['cladding'] = 'tiles'
else:
rsrf['attributes'] = {}
rsrf['attributes']['cladding'] = 'tiles'
geom.surfaces[i] = rsrf
new_geoms.append(geom)
else:
# Use the unchanged geometry
new_geoms.append(geom)
co.geometry = new_geoms
new_cos[co_id] = co
cm_copy.cityobjects = new_cos
print(cm_copy.cityobjects['{C9D4A5CF-094A-47DA-97E4-4A3BFD75D3AE}'])
```
### Create new Semantic Surfaces
The process is similar as previously. However, in this example we create new SemanticSurfaces that hold the values which we compute from the geometry. The input city model has a single semantic "WallSurface", without attributes, for all the walls of a building. The snippet below illustrates how to separate surfaces and assign the semantics to them.
```
new_cos = {}
for co_id, co in cm_copy.cityobjects.items():
new_geoms = []
for geom in co.geometry:
if geom.lod >= 2.0:
max_id = max(geom.surfaces.keys())
old_ids = []
for w_i, wsrf in geom.get_surfaces('wallsurface').items():
old_ids.append(w_i)
del geom.surfaces[w_i]
boundaries = geom.get_surface_boundaries(wsrf)
for j, boundary_geometry in enumerate(boundaries):
# The original geometry has the same Semantic for all wall,
# but we want to divide the wall surfaces by their orientation,
# thus we need to have the correct surface index
surface_index = wsrf['surface_idx'][j]
new_srf = {
'type': wsrf['type'],
'surface_idx': surface_index
}
for multisurface in boundary_geometry:
# Do any operation here
x, y, z = multisurface[0]
if j % 2 > 0:
orientation = 'north'
else:
orientation = 'south'
# Add the new attribute to the surface
if 'attributes' in wsrf.keys():
wsrf['attributes']['orientation'] = orientation
else:
wsrf['attributes'] = {}
wsrf['attributes']['orientation'] = orientation
new_srf['attributes'] = wsrf['attributes']
# if w_i in geom.surfaces.keys():
# del geom.surfaces[w_i]
max_id = max_id + 1
geom.surfaces[max_id] = new_srf
new_geoms.append(geom)
else:
# If LoD1, just add the geometry unchanged
new_geoms.append(geom)
co.geometry = new_geoms
new_cos[co_id] = co
cm_copy.cityobjects = new_cos
```
# Analysing CityModels

In the following I show how to compute some attributes from CityObject geometry and use these attributes as input for machine learning. For this we use the LoD2 model of Zürich.
Download the Zürich data set from https://3d.bk.tudelft.nl/opendata/cityjson/1.0/Zurich_Building_LoD2_V10.json
```
path = os.path.join('data', 'zurich.json')
zurich = cityjson.load(path, transform=True)
```
## A simple geometry function
Here is a simple geometry function that computes the area of the groundsurface (footprint) of buildings in the model. It also show how to cast surfaces, in this case the ground surface, to Shapely Polygons.
```
def compute_footprint_area(co):
"""Compute the area of the footprint"""
footprint_area = 0
for geom in co.geometry:
# only LoD2 (or higher) objects have semantic surfaces
if geom.lod >= 2.0:
footprints = geom.get_surfaces(type='groundsurface')
# there can be many surfaces with label 'groundsurface'
for i,f in footprints.items():
for multisurface in geom.get_surface_boundaries(f):
for surface in multisurface:
# cast to Shapely polygon
shapely_poly = Polygon(surface)
footprint_area += shapely_poly.area
return footprint_area
```
## Compute new attributes
Then we need to loop through the CityObjects and update add the new attributes. Note that the `attributes` CityObject attribute is just a dictionary.
Thus we compute the number of vertices of the CityObject and the area of is footprint. Then we going to cluster these two variables. This is completely arbitrary excercise which is simply meant to illustrate how to transform a city model into machine-learnable features.
```
for co_id, co in zurich.cityobjects.items():
co.attributes['nr_vertices'] = len(co.get_vertices())
co.attributes['fp_area'] = compute_footprint_area(co)
zurich.cityobjects[co_id] = co
```
It is possible to export the city model into a pandas DataFrame. Note that only the CityObject attributes are exported into the dataframe, with CityObject IDs as the index of the dataframe. Thus if you want to export the attributes of SemanticSurfaces for example, then you need to add them as CityObject attributes.
The function below illustrates this operation.
```
def assign_cityobject_attribute(cm):
"""Copy the semantic surface attributes to CityObject attributes.
Returns a copy of the citymodel.
"""
new_cos = {}
cm_copy = deepcopy(cm)
for co_id, co in cm.cityobjects.items():
for geom in co.geometry:
for srf in geom.surfaces.values():
if 'attributes' in srf:
for attr,a_v in srf['attributes'].items():
if (attr not in co.attributes) or (co.attributes[attr] is None):
co.attributes[attr] = [a_v]
else:
co.attributes[attr].append(a_v)
new_cos[co_id] = co
cm_copy.cityobjects = new_cos
return cm_copy
df = zurich.to_dataframe()
df.head()
```
In order to have a nicer distribution of the data, we remove the missing values and apply a log-transform on the two variables. Note that the `FuntionTransformer.transform` transforms a DataFrame to a numpy array that is ready to be used in `scikit-learn`. The details of a machine learning workflow is beyond the scope of this tutorial however.
```
df_subset = df[df['Geomtype'].notnull() & df['fp_area'] > 0.0].loc[:, ['nr_vertices', 'fp_area']]
transformer = FunctionTransformer(np.log, validate=True)
df_logtransform = transformer.transform(df_subset)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(df_logtransform[:,0], df_logtransform[:,1], alpha=0.3, s=1.0)
plt.show()
def plot_model_results(model, data):
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
colormap = np.array(['lightblue', 'red', 'lime', 'blue','black'])
ax.scatter(data[:,0], data[:,1], c=colormap[model.labels_], s=10, alpha=0.5)
ax.set_xlabel('Number of vertices [log]')
ax.set_ylabel('Footprint area [log]')
plt.title(f"DBSCAN clustering with estimated {len(set(model.labels_))} clusters")
plt.show()
```
Since we transformed our DataFrame, we can fit any model in `scikit-learn`. I use DBSCAN because I wanted to find the data points on the fringes of the central cluster.
```
%matplotlib notebook
model = cluster.DBSCAN(eps=0.2).fit(df_logtransform)
plot_model_results(model, df_logtransform)
# merge the cluster labels back to the data frame
df_subset['dbscan'] = model.labels_
```
## Save the results back to CityJSON
And merge the DataFrame with cluster labels back to the city model.
```
for co_id, co in zurich.cityobjects.items():
if co_id in df_subset.index:
ml_results = dict(df_subset.loc[co_id])
else:
ml_results = {'nr_vertices': 'nan', 'fp_area': 'nan', 'dbscan': 'nan'}
new_attrs = {**co.attributes, **ml_results}
co.attributes = new_attrs
zurich.cityobjects[co_id] = co
```
At the end, the `save()` method saves the edited city model into a CityJSON file.
```
path_out = os.path.join('data', 'zurich_output.json')
cityjson.save(zurich, path_out)
```
## And view the results in QGIS again

However, you'll need to set up the styling based on the cluster labels by hand.
# Other software
## Online CityJSON viewer

## QGIS plugin

## Azul

# Full conversion CityGML <--> CityJSON

# Thank you!
Balázs Dukai
[email protected]
@BalazsDukai
## A few links
Repo of this talk: [https://github.com/balazsdukai/foss4g2019](https://github.com/balazsdukai/foss4g2019)
[cityjson.org](cityjson.org)
[viewer.cityjson.org](viewer.cityjson.org)
QGIS plugin: [github.com/tudelft3d/cityjson-qgis-plugin](github.com/tudelft3d/cityjson-qgis-plugin)
Azul – CityJSON viewer on Mac – check the [AppStore](https://apps.apple.com/nl/app/azul/id1173239678?mt=12)
cjio: [github.com/tudelft3d/cjio](github.com/tudelft3d/cjio) & [tudelft3d.github.io/cjio/](tudelft3d.github.io/cjio/)
| github_jupyter |
# Working With TileMatrixSets (other than WebMercator)
[](https://mybinder.org/v2/gh/developmentseed/titiler/master?filepath=docs%2Fexamples%2FWorking_with_nonWebMercatorTMS.ipynb)
TiTiler has builtin support for serving tiles in multiple Projections by using [rio-tiler](https://github.com/cogeotiff/rio-tiler) and [morecantile](https://github.com/developmentseed/morecantile).
The default `cog` and `stac` endpoint (`titiler.endpoints.cog`and `titiler.endoints.stac`) are built with Mutli TMS support using the default grids provided by morecantile:
```python
from fastapi import FastAPI
from titiler.endpoints.factory import TilerFactory
# Create a Multi TMS Tiler using `TilerFactory` Factory
cog = TilerFactory(router_prefix="cog")
app = FastAPI()
app.include_router(cog.router, prefix="/cog", tags=["Cloud Optimized GeoTIFF"])
```
This Notebook shows how to use and display tiles with non-webmercator TileMatrixSet
#### Requirements
- ipyleaflet
- requests
```
# Uncomment if you need to install those module within the notebook
# !pip install ipyleaflet requests
import json
import requests
from ipyleaflet import (
Map,
basemaps,
basemap_to_tiles,
TileLayer,
WMSLayer,
GeoJSON,
projections
)
titiler_endpoint = "https://api.cogeo.xyz" # Devseed Custom TiTiler endpoint
url = "https://s3.amazonaws.com/opendata.remotepixel.ca/cogs/natural_earth/world.tif" # Natural Earth WORLD tif
```
### List Supported TileMatrixSets
```
r = requests.get("https://api.cogeo.xyz/tileMatrixSets").json()
print("Supported TMS:")
for tms in r["tileMatrixSets"]:
print("-", tms["id"])
```
## WGS 84 -- WGS84 - World Geodetic System 1984 - EPSG:4326
https://epsg.io/4326
```
r = requests.get(
"https://api.cogeo.xyz/cog/WorldCRS84Quad/tilejson.json", params = {"url": url}
).json()
m = Map(center=(45, 0), zoom=4, basemap={}, crs=projections.EPSG4326)
layer = TileLayer(url=r["tiles"][0], opacity=1)
m.add_layer(layer)
m
```
## WGS 84 / NSIDC Sea Ice Polar Stereographic North - EPSG:3413
https://epsg.io/3413
```
r = requests.get(
"https://api.cogeo.xyz/cog/EPSG3413/tilejson.json", params = {"url": url}
).json()
m = Map(center=(70, 0), zoom=1, basemap={}, crs=projections.EPSG3413)
layer = TileLayer(url=r["tiles"][0], opacity=1)
m.add_layer(layer)
m
```
## ETRS89-extended / LAEA Europe - EPSG:3035
https://epsg.io/3035
```
r = requests.get(
"https://api.cogeo.xyz/cog/EuropeanETRS89_LAEAQuad/tilejson.json", params = {"url": url}
).json()
my_projection = {
'name': 'EPSG:3035',
'custom': True, #This is important, it tells ipyleaflet that this projection is not on the predefined ones.
'proj4def': '+proj=laea +lat_0=52 +lon_0=10 +x_0=4321000 +y_0=3210000 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs',
'origin': [6500000.0, 5500000.0],
'resolutions': [
8192.0,
4096.0,
2048.0,
1024.0,
512.0,
256.0
]
}
m = Map(center=(50, 65), zoom=1, basemap={}, crs=my_projection)
layer = TileLayer(url=r["tiles"][0], opacity=1)
m.add_layer(layer)
m
```
| github_jupyter |
# 100 pandas puzzles
Inspired by [100 Numpy exerises](https://github.com/rougier/numpy-100), here are 100* short puzzles for testing your knowledge of [pandas'](http://pandas.pydata.org/) power.
Since pandas is a large library with many different specialist features and functions, these excercises focus mainly on the fundamentals of manipulating data (indexing, grouping, aggregating, cleaning), making use of the core DataFrame and Series objects.
Many of the excerises here are stright-forward in that the solutions require no more than a few lines of code (in pandas or NumPy... don't go using pure Python or Cython!). Choosing the right methods and following best practices is the underlying goal.
The exercises are loosely divided in sections. Each section has a difficulty rating; these ratings are subjective, of course, but should be a seen as a rough guide as to how inventive the required solution is.
If you're just starting out with pandas and you are looking for some other resources, the official documentation is very extensive. In particular, some good places get a broader overview of pandas are...
- [10 minutes to pandas](http://pandas.pydata.org/pandas-docs/stable/10min.html)
- [pandas basics](http://pandas.pydata.org/pandas-docs/stable/basics.html)
- [tutorials](http://pandas.pydata.org/pandas-docs/stable/tutorials.html)
- [cookbook and idioms](http://pandas.pydata.org/pandas-docs/stable/cookbook.html#cookbook)
Enjoy the puzzles!
\* *the list of exercises is not yet complete! Pull requests or suggestions for additional exercises, corrections and improvements are welcomed.*
## Importing pandas
### Getting started and checking your pandas setup
Difficulty: *easy*
**1.** Import pandas under the alias `pd`.
**2.** Print the version of pandas that has been imported.
**3.** Print out all the *version* information of the libraries that are required by the pandas library.
## DataFrame basics
### A few of the fundamental routines for selecting, sorting, adding and aggregating data in DataFrames
Difficulty: *easy*
Note: remember to import numpy using:
```python
import numpy as np
```
Consider the following Python dictionary `data` and Python list `labels`:
``` python
data = {'animal': ['cat', 'cat', 'snake', 'dog', 'dog', 'cat', 'snake', 'cat', 'dog', 'dog'],
'age': [2.5, 3, 0.5, np.nan, 5, 2, 4.5, np.nan, 7, 3],
'visits': [1, 3, 2, 3, 2, 3, 1, 1, 2, 1],
'priority': ['yes', 'yes', 'no', 'yes', 'no', 'no', 'no', 'yes', 'no', 'no']}
labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
```
(This is just some meaningless data I made up with the theme of animals and trips to a vet.)
**4.** Create a DataFrame `df` from this dictionary `data` which has the index `labels`.
```
import numpy as np
data = {'animal': ['cat', 'cat', 'snake', 'dog', 'dog', 'cat', 'snake', 'cat', 'dog', 'dog'],
'age': [2.5, 3, 0.5, np.nan, 5, 2, 4.5, np.nan, 7, 3],
'visits': [1, 3, 2, 3, 2, 3, 1, 1, 2, 1],
'priority': ['yes', 'yes', 'no', 'yes', 'no', 'no', 'no', 'yes', 'no', 'no']}
labels = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j']
df = # (complete this line of code)
```
**5.** Display a summary of the basic information about this DataFrame and its data (*hint: there is a single method that can be called on the DataFrame*).
**6.** Return the first 3 rows of the DataFrame `df`.
**7.** Select just the 'animal' and 'age' columns from the DataFrame `df`.
**8.** Select the data in rows `[3, 4, 8]` *and* in columns `['animal', 'age']`.
**9.** Select only the rows where the number of visits is greater than 3.
**10.** Select the rows where the age is missing, i.e. it is `NaN`.
**11.** Select the rows where the animal is a cat *and* the age is less than 3.
**12.** Select the rows the age is between 2 and 4 (inclusive).
**13.** Change the age in row 'f' to 1.5.
**14.** Calculate the sum of all visits in `df` (i.e. find the total number of visits).
**15.** Calculate the mean age for each different animal in `df`.
**16.** Append a new row 'k' to `df` with your choice of values for each column. Then delete that row to return the original DataFrame.
**17.** Count the number of each type of animal in `df`.
**18.** Sort `df` first by the values in the 'age' in *decending* order, then by the value in the 'visit' column in *ascending* order (so row `i` should be first, and row `d` should be last).
**19.** The 'priority' column contains the values 'yes' and 'no'. Replace this column with a column of boolean values: 'yes' should be `True` and 'no' should be `False`.
**20.** In the 'animal' column, change the 'snake' entries to 'python'.
**21.** For each animal type and each number of visits, find the mean age. In other words, each row is an animal, each column is a number of visits and the values are the mean ages (*hint: use a pivot table*).
## DataFrames: beyond the basics
### Slightly trickier: you may need to combine two or more methods to get the right answer
Difficulty: *medium*
The previous section was tour through some basic but essential DataFrame operations. Below are some ways that you might need to cut your data, but for which there is no single "out of the box" method.
**22.** You have a DataFrame `df` with a column 'A' of integers. For example:
```python
df = pd.DataFrame({'A': [1, 2, 2, 3, 4, 5, 5, 5, 6, 7, 7]})
```
How do you filter out rows which contain the same integer as the row immediately above?
You should be left with a column containing the following values:
```python
1, 2, 3, 4, 5, 6, 7
```
**23.** Given a DataFrame of numeric values, say
```python
df = pd.DataFrame(np.random.random(size=(5, 3))) # a 5x3 frame of float values
```
how do you subtract the row mean from each element in the row?
**24.** Suppose you have DataFrame with 10 columns of real numbers, for example:
```python
df = pd.DataFrame(np.random.random(size=(5, 10)), columns=list('abcdefghij'))
```
Which column of numbers has the smallest sum? Return that column's label.
**25.** How do you count how many unique rows a DataFrame has (i.e. ignore all rows that are duplicates)? As input, use a DataFrame of zeros and ones with 10 rows and 3 columns.
```python
df = pd.DataFrame(np.random.randint(0, 2, size=(10, 3)))
```
The next three puzzles are slightly harder.
**26.** In the cell below, you have a DataFrame `df` that consists of 10 columns of floating-point numbers. Exactly 5 entries in each row are NaN values.
For each row of the DataFrame, find the *column* which contains the *third* NaN value.
You should return a Series of column labels: `e, c, d, h, d`
```
nan = np.nan
data = [[0.04, nan, nan, 0.25, nan, 0.43, 0.71, 0.51, nan, nan],
[ nan, nan, nan, 0.04, 0.76, nan, nan, 0.67, 0.76, 0.16],
[ nan, nan, 0.5 , nan, 0.31, 0.4 , nan, nan, 0.24, 0.01],
[0.49, nan, nan, 0.62, 0.73, 0.26, 0.85, nan, nan, nan],
[ nan, nan, 0.41, nan, 0.05, nan, 0.61, nan, 0.48, 0.68]]
columns = list('abcdefghij')
df = pd.DataFrame(data, columns=columns)
# write a solution to the question here
```
**27.** A DataFrame has a column of groups 'grps' and and column of integer values 'vals':
```python
df = pd.DataFrame({'grps': list('aaabbcaabcccbbc'),
'vals': [12,345,3,1,45,14,4,52,54,23,235,21,57,3,87]})
```
For each *group*, find the sum of the three greatest values. You should end up with the answer as follows:
```
grps
a 409
b 156
c 345
```
```
df = pd.DataFrame({'grps': list('aaabbcaabcccbbc'),
'vals': [12,345,3,1,45,14,4,52,54,23,235,21,57,3,87]})
# write a solution to the question here
```
**28.** The DataFrame `df` constructed below has two integer columns 'A' and 'B'. The values in 'A' are between 1 and 100 (inclusive).
For each group of 10 consecutive integers in 'A' (i.e. `(0, 10]`, `(10, 20]`, ...), calculate the sum of the corresponding values in column 'B'.
The answer should be a Series as follows:
```
A
(0, 10] 635
(10, 20] 360
(20, 30] 315
(30, 40] 306
(40, 50] 750
(50, 60] 284
(60, 70] 424
(70, 80] 526
(80, 90] 835
(90, 100] 852
```
```
df = pd.DataFrame(np.random.RandomState(8765).randint(1, 101, size=(100, 2)), columns = ["A", "B"])
# write a solution to the question here
```
## DataFrames: harder problems
### These might require a bit of thinking outside the box...
...but all are solvable using just the usual pandas/NumPy methods (and so avoid using explicit `for` loops).
Difficulty: *hard*
**29.** Consider a DataFrame `df` where there is an integer column 'X':
```python
df = pd.DataFrame({'X': [7, 2, 0, 3, 4, 2, 5, 0, 3, 4]})
```
For each value, count the difference back to the previous zero (or the start of the Series, whichever is closer). These values should therefore be
```
[1, 2, 0, 1, 2, 3, 4, 0, 1, 2]
```
Make this a new column 'Y'.
**30.** Consider the DataFrame constructed below which contains rows and columns of numerical data.
Create a list of the column-row index locations of the 3 largest values in this DataFrame. In this case, the answer should be:
```
[(5, 7), (6, 4), (2, 5)]
```
```
df = pd.DataFrame(np.random.RandomState(30).randint(1, 101, size=(8, 8)))
```
**31.** You are given the DataFrame below with a column of group IDs, 'grps', and a column of corresponding integer values, 'vals'.
```python
df = pd.DataFrame({"vals": np.random.RandomState(31).randint(-30, 30, size=15),
"grps": np.random.RandomState(31).choice(["A", "B"], 15)})
```
Create a new column 'patched_values' which contains the same values as the 'vals' any negative values in 'vals' with the group mean:
```
vals grps patched_vals
0 -12 A 13.6
1 -7 B 28.0
2 -14 A 13.6
3 4 A 4.0
4 -7 A 13.6
5 28 B 28.0
6 -2 A 13.6
7 -1 A 13.6
8 8 A 8.0
9 -2 B 28.0
10 28 A 28.0
11 12 A 12.0
12 16 A 16.0
13 -24 A 13.6
14 -12 A 13.6
```
**32.** Implement a rolling mean over groups with window size 3, which ignores NaN value. For example consider the following DataFrame:
```python
>>> df = pd.DataFrame({'group': list('aabbabbbabab'),
'value': [1, 2, 3, np.nan, 2, 3, np.nan, 1, 7, 3, np.nan, 8]})
>>> df
group value
0 a 1.0
1 a 2.0
2 b 3.0
3 b NaN
4 a 2.0
5 b 3.0
6 b NaN
7 b 1.0
8 a 7.0
9 b 3.0
10 a NaN
11 b 8.0
```
The goal is to compute the Series:
```
0 1.000000
1 1.500000
2 3.000000
3 3.000000
4 1.666667
5 3.000000
6 3.000000
7 2.000000
8 3.666667
9 2.000000
10 4.500000
11 4.000000
```
E.g. the first window of size three for group 'b' has values 3.0, NaN and 3.0 and occurs at row index 5. Instead of being NaN the value in the new column at this row index should be 3.0 (just the two non-NaN values are used to compute the mean (3+3)/2)
## Series and DatetimeIndex
### Exercises for creating and manipulating Series with datetime data
Difficulty: *easy/medium*
pandas is fantastic for working with dates and times. These puzzles explore some of this functionality.
**33.** Create a DatetimeIndex that contains each business day of 2015 and use it to index a Series of random numbers. Let's call this Series `s`.
**34.** Find the sum of the values in `s` for every Wednesday.
**35.** For each calendar month in `s`, find the mean of values.
**36.** For each group of four consecutive calendar months in `s`, find the date on which the highest value occurred.
**37.** Create a DateTimeIndex consisting of the third Thursday in each month for the years 2015 and 2016.
## Cleaning Data
### Making a DataFrame easier to work with
Difficulty: *easy/medium*
It happens all the time: someone gives you data containing malformed strings, Python, lists and missing data. How do you tidy it up so you can get on with the analysis?
Take this monstrosity as the DataFrame to use in the following puzzles:
```python
df = pd.DataFrame({'From_To': ['LoNDon_paris', 'MAdrid_miLAN', 'londON_StockhOlm',
'Budapest_PaRis', 'Brussels_londOn'],
'FlightNumber': [10045, np.nan, 10065, np.nan, 10085],
'RecentDelays': [[23, 47], [], [24, 43, 87], [13], [67, 32]],
'Airline': ['KLM(!)', '<Air France> (12)', '(British Airways. )',
'12. Air France', '"Swiss Air"']})
```
Formatted, it looks like this:
```
From_To FlightNumber RecentDelays Airline
0 LoNDon_paris 10045.0 [23, 47] KLM(!)
1 MAdrid_miLAN NaN [] <Air France> (12)
2 londON_StockhOlm 10065.0 [24, 43, 87] (British Airways. )
3 Budapest_PaRis NaN [13] 12. Air France
4 Brussels_londOn 10085.0 [67, 32] "Swiss Air"
```
(It's some flight data I made up; it's not meant to be accurate in any way.)
**38.** Some values in the the **FlightNumber** column are missing (they are `NaN`). These numbers are meant to increase by 10 with each row so 10055 and 10075 need to be put in place. Modify `df` to fill in these missing numbers and make the column an integer column (instead of a float column).
**39.** The **From\_To** column would be better as two separate columns! Split each string on the underscore delimiter `_` to give a new temporary DataFrame called 'temp' with the correct values. Assign the correct column names 'From' and 'To' to this temporary DataFrame.
**40.** Notice how the capitalisation of the city names is all mixed up in this temporary DataFrame 'temp'. Standardise the strings so that only the first letter is uppercase (e.g. "londON" should become "London".)
**41.** Delete the **From_To** column from `df` and attach the temporary DataFrame 'temp' from the previous questions.
**42**. In the **Airline** column, you can see some extra puctuation and symbols have appeared around the airline names. Pull out just the airline name. E.g. `'(British Airways. )'` should become `'British Airways'`.
**43**. In the RecentDelays column, the values have been entered into the DataFrame as a list. We would like each first value in its own column, each second value in its own column, and so on. If there isn't an Nth value, the value should be NaN.
Expand the Series of lists into a DataFrame named `delays`, rename the columns `delay_1`, `delay_2`, etc. and replace the unwanted RecentDelays column in `df` with `delays`.
The DataFrame should look much better now.
```
FlightNumber Airline From To delay_1 delay_2 delay_3
0 10045 KLM London Paris 23.0 47.0 NaN
1 10055 Air France Madrid Milan NaN NaN NaN
2 10065 British Airways London Stockholm 24.0 43.0 87.0
3 10075 Air France Budapest Paris 13.0 NaN NaN
4 10085 Swiss Air Brussels London 67.0 32.0 NaN
```
## Using MultiIndexes
### Go beyond flat DataFrames with additional index levels
Difficulty: *medium*
Previous exercises have seen us analysing data from DataFrames equipped with a single index level. However, pandas also gives you the possibilty of indexing your data using *multiple* levels. This is very much like adding new dimensions to a Series or a DataFrame. For example, a Series is 1D, but by using a MultiIndex with 2 levels we gain of much the same functionality as a 2D DataFrame.
The set of puzzles below explores how you might use multiple index levels to enhance data analysis.
To warm up, we'll look make a Series with two index levels.
**44**. Given the lists `letters = ['A', 'B', 'C']` and `numbers = list(range(10))`, construct a MultiIndex object from the product of the two lists. Use it to index a Series of random numbers. Call this Series `s`.
**45.** Check the index of `s` is lexicographically sorted (this is a necessary proprty for indexing to work correctly with a MultiIndex).
**46**. Select the labels `1`, `3` and `6` from the second level of the MultiIndexed Series.
**47**. Slice the Series `s`; slice up to label 'B' for the first level and from label 5 onwards for the second level.
**48**. Sum the values in `s` for each label in the first level (you should have Series giving you a total for labels A, B and C).
**49**. Suppose that `sum()` (and other methods) did not accept a `level` keyword argument. How else could you perform the equivalent of `s.sum(level=1)`?
**50**. Exchange the levels of the MultiIndex so we have an index of the form (letters, numbers). Is this new Series properly lexsorted? If not, sort it.
## Minesweeper
### Generate the numbers for safe squares in a Minesweeper grid
Difficulty: *medium* to *hard*
If you've ever used an older version of Windows, there's a good chance you've played with Minesweeper:
- https://en.wikipedia.org/wiki/Minesweeper_(video_game)
If you're not familiar with the game, imagine a grid of squares: some of these squares conceal a mine. If you click on a mine, you lose instantly. If you click on a safe square, you reveal a number telling you how many mines are found in the squares that are immediately adjacent. The aim of the game is to uncover all squares in the grid that do not contain a mine.
In this section, we'll make a DataFrame that contains the necessary data for a game of Minesweeper: coordinates of the squares, whether the square contains a mine and the number of mines found on adjacent squares.
**51**. Let's suppose we're playing Minesweeper on a 5 by 4 grid, i.e.
```
X = 5
Y = 4
```
To begin, generate a DataFrame `df` with two columns, `'x'` and `'y'` containing every coordinate for this grid. That is, the DataFrame should start:
```
x y
0 0 0
1 0 1
2 0 2
```
**52**. For this DataFrame `df`, create a new column of zeros (safe) and ones (mine). The probability of a mine occuring at each location should be 0.4.
**53**. Now create a new column for this DataFrame called `'adjacent'`. This column should contain the number of mines found on adjacent squares in the grid.
(E.g. for the first row, which is the entry for the coordinate `(0, 0)`, count how many mines are found on the coordinates `(0, 1)`, `(1, 0)` and `(1, 1)`.)
**54**. For rows of the DataFrame that contain a mine, set the value in the `'adjacent'` column to NaN.
**55**. Finally, convert the DataFrame to grid of the adjacent mine counts: columns are the `x` coordinate, rows are the `y` coordinate.
## Plotting
### Visualize trends and patterns in data
Difficulty: *medium*
To really get a good understanding of the data contained in your DataFrame, it is often essential to create plots: if you're lucky, trends and anomalies will jump right out at you. This functionality is baked into pandas and the puzzles below explore some of what's possible with the library.
**56.** Pandas is highly integrated with the plotting library matplotlib, and makes plotting DataFrames very user-friendly! Plotting in a notebook environment usually makes use of the following boilerplate:
```python
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')
```
matplotlib is the plotting library which pandas' plotting functionality is built upon, and it is usually aliased to ```plt```.
```%matplotlib inline``` tells the notebook to show plots inline, instead of creating them in a separate window.
```plt.style.use('ggplot')``` is a style theme that most people find agreeable, based upon the styling of R's ggplot package.
For starters, make a scatter plot of this random data, but use black X's instead of the default markers.
```df = pd.DataFrame({"xs":[1,5,2,8,1], "ys":[4,2,1,9,6]})```
Consult the [documentation](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.plot.html) if you get stuck!
**57.** Columns in your DataFrame can also be used to modify colors and sizes. Bill has been keeping track of his performance at work over time, as well as how good he was feeling that day, and whether he had a cup of coffee in the morning. Make a plot which incorporates all four features of this DataFrame.
(Hint: If you're having trouble seeing the plot, try multiplying the Series which you choose to represent size by 10 or more)
*The chart doesn't have to be pretty: this isn't a course in data viz!*
```
df = pd.DataFrame({"productivity":[5,2,3,1,4,5,6,7,8,3,4,8,9],
"hours_in" :[1,9,6,5,3,9,2,9,1,7,4,2,2],
"happiness" :[2,1,3,2,3,1,2,3,1,2,2,1,3],
"caffienated" :[0,0,1,1,0,0,0,0,1,1,0,1,0]})
```
**58.** What if we want to plot multiple things? Pandas allows you to pass in a matplotlib *Axis* object for plots, and plots will also return an Axis object.
Make a bar plot of monthly revenue with a line plot of monthly advertising spending (numbers in millions)
```
df = pd.DataFrame({"revenue":[57,68,63,71,72,90,80,62,59,51,47,52],
"advertising":[2.1,1.9,2.7,3.0,3.6,3.2,2.7,2.4,1.8,1.6,1.3,1.9],
"month":range(12)
})
```
Now we're finally ready to create a candlestick chart, which is a very common tool used to analyze stock price data. A candlestick chart shows the opening, closing, highest, and lowest price for a stock during a time window. The color of the "candle" (the thick part of the bar) is green if the stock closed above its opening price, or red if below.

This was initially designed to be a pandas plotting challenge, but it just so happens that this type of plot is just not feasible using pandas' methods. If you are unfamiliar with matplotlib, we have provided a function that will plot the chart for you so long as you can use pandas to get the data into the correct format.
Your first step should be to get the data in the correct format using pandas' time-series grouping function. We would like each candle to represent an hour's worth of data. You can write your own aggregation function which returns the open/high/low/close, but pandas has a built-in which also does this.
The below cell contains helper functions. Call ```day_stock_data()``` to generate a DataFrame containing the prices a hypothetical stock sold for, and the time the sale occurred. Call ```plot_candlestick(df)``` on your properly aggregated and formatted stock data to print the candlestick chart.
```
import numpy as np
def float_to_time(x):
return str(int(x)) + ":" + str(int(x%1 * 60)).zfill(2) + ":" + str(int(x*60 % 1 * 60)).zfill(2)
def day_stock_data():
#NYSE is open from 9:30 to 4:00
time = 9.5
price = 100
results = [(float_to_time(time), price)]
while time < 16:
elapsed = np.random.exponential(.001)
time += elapsed
if time > 16:
break
price_diff = np.random.uniform(.999, 1.001)
price *= price_diff
results.append((float_to_time(time), price))
df = pd.DataFrame(results, columns = ['time','price'])
df.time = pd.to_datetime(df.time)
return df
#Don't read me unless you get stuck!
def plot_candlestick(agg):
"""
agg is a DataFrame which has a DatetimeIndex and five columns: ["open","high","low","close","color"]
"""
fig, ax = plt.subplots()
for time in agg.index:
ax.plot([time.hour] * 2, agg.loc[time, ["high","low"]].values, color = "black")
ax.plot([time.hour] * 2, agg.loc[time, ["open","close"]].values, color = agg.loc[time, "color"], linewidth = 10)
ax.set_xlim((8,16))
ax.set_ylabel("Price")
ax.set_xlabel("Hour")
ax.set_title("OHLC of Stock Value During Trading Day")
plt.show()
```
**59.** Generate a day's worth of random stock data, and aggregate / reformat it so that it has hourly summaries of the opening, highest, lowest, and closing prices
**60.** Now that you have your properly-formatted data, try to plot it yourself as a candlestick chart. Use the ```plot_candlestick(df)``` function above, or matplotlib's [```plot``` documentation](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.plot.html) if you get stuck.
*More exercises to follow soon...*
| github_jupyter |
<a href="https://colab.research.google.com/github/rjrahul24/ai-with-python-series/blob/main/01.%20Getting%20Started%20with%20Python/Python_Revision_and_Statistical_Methods.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
**Inheritence in Python**
Object Oriented Programming is a coding paradigm that revolves around creating modular code and stopping mulitple uses of the same structure. It is aimed at increasing stability and usability of code. It consists of some well-known concepts stated below:
1. Classes: These often show a collection of functions and attributes that are fastened to a precise name and represent an abstract container.
2. Attributes: Generally, the data that is associated with each class. Examples are variables declared during creation of the class.
3. Objects: An instance generated from the class. There can be multiple objects of a class and every individual object takes on the properties of the class.
```
# Implementation of Classes in Python
# Creating a Class Math with 2 functions
class Math:
def subtract (self, i, j):
return i-j
def add (self, x, y):
return x+y
# Creating an object of the class Math
math_child = Math()
test_int_A = 10
test_int_B = 20
print(math_child.subtract(test_int_B, test_int_A))
# Creating a Class Person with an attribute and an initialization function
class Person:
name = 'George'
def __init__ (self):
self.age = 34
# Creating an object of the class and printing its attributes
p1 = Person()
print (p1.name)
print (p1.age)
```
**Constructors and Inheritance**
The constructor is an initialization function that is always called when a class’s instance is created. The constructor is named __init__() in Python and defines the specifics of instantiating a class and its attributes.
Class inheritance is a concept of taking values of a class from its origin and giving the same properties to a child class. It creates relationship models like “Class A is a Class B”, like a triangle (child class) is a shape (parent class). All the functions and attributes of a superclass are inherited by the subclass.
1. Overriding: During the inheritance, the behavior of the child class or the subclass can be modified. Doing this modification on functions is class “overriding” and is achieved by declaring functions in the subclass with the same name. Functions created in the subclass will take precedence over those in the parent class.
2. Composition: Classes can also be built from other smaller classes that support relationship models like “Class A has a Class B”, like a Department has Students.
3. Polymorphism: The functionality of similar looking functions can be changed in run-time, during their implementation. This is achieved using Polymorphism, that includes two objects of different parent class but having the same set of functions. The outward look of these functions is the same, but implementations differ.
```
# Creating a class and instantiating variables
class Animal_Dog:
species = "Canis"
def __init__(self, name, age):
self.name = name
self.age = age
# Instance method
def description(self):
return f"{self.name} is {self.age} years old"
# Another instance method
def animal_sound(self, sound):
return f"{self.name} says {sound}"
# Check the object’s type
Animal_Dog("Bunny", 7)
# Even though a and b are both instances of the Dog class, they represent two distinct objects in memory.
a = Animal_Dog("Fog", 6)
b = Animal_Dog("Bunny", 7)
a == b
# Instantiating objects with the class’s constructor arguments
fog = Animal_Dog("Fog", 6)
bunny = Animal_Dog("Bunny", 7)
print (bunny.name)
print (bunny.age)
# Accessing attributes directly
print (bunny.species)
# Creating a new Object to access through instance functions
fog = Animal_Dog("Fog", 6)
fog.description()
fog.animal_sound("Whoof Whoof")
fog.animal_sound("Bhoof Whoof")
# Inheriting the Class
class GoldRet(Animal_Dog):
def speak(self, sound="Warf"):
return f"{self.name} says {sound}"
bunny = GoldRet("Bunny", 5)
bunny.speak()
bunny.speak("Grrr Grrr")
# Code Snippet 3: Variables and data types
int_var = 100 # Integer variable
float_var = 1000.0 # Float value
string_var = "John" # String variable
print (int_var)
print (float_var)
print (string_var)
```
Variables and Data Types in Python
Variables are reserved locations in the computer’s memory that store values defined within them. Whenever a variable is created, a piece of the computer’s memory is allocated to it. Based on the data type of this declared variable, the interpreter allocates varied chunks of memory. Therefore, basis the assignment of variables as integer, float, strings, etc. different sizes of memory allocations are invoked.
• Declaration: Variables in Python do not need explicit declaration to reserve memory space. This happens automatically when a value is assigned. The (=) sign is used to assign values to variables.
• Multiple Assignment: Python allows for multiple variables to hold a single value and this declaration can be done together for all variables.
• Deleting References: Memory reference once created can also be deleted. The 'del' statement is used to delete the reference to a number object. Multiple object deletion is also supported by the 'del' statement.
• Strings: Strings are a set of characters, that Python allows representation through single or double quotes. String subsets can be formed using the slice operator ([ ] and [:] ) where indexing starts from 0 on the left and -1 on the right. The (+) sign is the string concatenation operator and the (*) sign is the repetition operator.
Datatype Conversion
Function Description
int(x [,base]) Converts given input to integer. Base is used for string conversions.
long(x [,base] ) Converts given input to a long integer
float(x) Follows conversion to floating-point number.
complex(real [,imag]) Used for creating a complex number.
str(x) Converts any given object to a string
eval(str) Evaluates given string and returns an object.
tuple(s) Conversion to tuple
list(s) List conversion of given input
set(s) Converts the given value to a set
unichr(x) Conversion from an integer to Unicode character.
Looking at Variables and Datatypes
Data stored as Python’s variables is abstracted as objects. Data is represented by objects or through relations between individual objects. Therefore, every variable and its corresponding values are an object of a class, depending on the stored data.
```
# Multiple Assignment: All are assigned to the same memory location
a = b = c = 1
# Assigning multiple variables with multiple values
a,b,c = 1,2,"jacob"
# Assigning and deleting variable references
var1 = 1
var2 = 10
del var1 # Removes the reference of var1
del var2
# Basic String Operations in Python
str = 'Hello World!'
print (str)
# Print the first character of string variable
print (str[0])
# Prints characters from 3rd to 5th positions
print (str[2:5])
# Print the string twice
print (str * 2)
# Concatenate the string and print
print (str + "TEST")
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import dask.array as da
import dask.dataframe as dd
import time
import math
from netCDF4 import Dataset
import os,datetime,sys,fnmatch
import h5py
from dask.distributed import Client, LocalCluster
cluster = LocalCluster()
client = Client(cluster)
client
%%time
def read_filelist(loc_dir,prefix,unie,fileformat):
# Read the filelist in the specific directory
str = os.popen("ls "+ loc_dir + prefix + unie + "*."+fileformat).read()
fname = np.array(str.split("\n"))
fname = np.delete(fname,len(fname)-1)
return fname
def read_MODIS(fname1,fname2,verbose=False): # READ THE HDF FILE
# Read the cloud mask from MYD06_L2 product')
ncfile=Dataset(fname1,'r')
CM1km = np.array(ncfile.variables['Cloud_Mask_1km'])
CM = (np.array(CM1km[:,:,0],dtype='byte') & 0b00000110) >>1
#ncfile = Dataset(fname1, "r")
#CM = myd06.variables["Cloud_Mask_1km"][:,:,:] # Reading Specific Variable 'Cloud_Mask_1km'.
#CM = (np.array(CM[:,:,0],dtype='byte') & 0b00000110) >>1
ncfile.close()
ncfile=Dataset(fname2,'r')
lat = np.array(ncfile.variables['Latitude'])
lon = np.array(ncfile.variables['Longitude'])
#ncfile = Dataset(MOD03_files, "r")
#latitude = myd03.variables["Latitude"][:,:] # Reading Specific Variable 'Latitude'.
#latitude = np.array(latitude).byteswap().newbyteorder() # Addressing Byteswap For Big Endian Error.
#longitude = myd03.variables["Longitude"][:,:] # Reading Specific Variable 'Longitude'.
attr_lat = ncfile.variables['Latitude']._FillValue
attr_lon = ncfile.variables['Longitude']._FillValue
return lat,lon,CM
def countzero(x, axis=1):
#print(x)
count0 = 0
count1 = 0
for i in x:
if i <= 1:
count0 +=1
#print(count0/len(x))
return count0/len(x)
satellite = 'Aqua'
MYD06_dir= '/Users/dprakas1/Desktop/modis_files/'
MYD06_prefix = 'MYD06_L2.A2008'
MYD03_dir= '/Users/dprakas1/Desktop/modis_files/'
MYD03_prefix = 'MYD03.A2008'
fileformat = 'hdf'
fname1,fname2 = [],[]
days = np.arange(1,31,dtype=np.int)
for day in days:
dc ='%03i' % day
fname_tmp1 = read_filelist(MYD06_dir,MYD06_prefix,dc,fileformat)
fname_tmp2 = read_filelist(MYD03_dir,MYD03_prefix,dc,fileformat)
fname1 = np.append(fname1,fname_tmp1)
fname2 = np.append(fname2,fname_tmp2)
# Initiate the number of day and total cloud fraction
files = np.arange(len(fname1))
for j in range(0,1):#hdfs:
print('steps: ',j+1,'/ ',(fname1))
# Read Level-2 MODIS data
lat,lon,CM = read_MODIS(fname1[j],fname2[j])
print((fname1))
print((fname2))
#rint(CM)
#lat = lat.ravel()
#lon = lon.ravel()
#CM = CM.ravel()
CM.shape
cm = np.zeros((2030,1354), dtype=np.float32)
for MOD06_file in fname1:
#print(MOD06_file)
myd06 = Dataset(MOD06_file, "r")
CM = myd06.variables["Cloud_Mask_1km"][:,:,0]# Reading Specific Variable 'Cloud_Mask_1km'.
CM = (np.array(CM,dtype='byte') & 0b00000110) >>1
CM = np.array(CM).byteswap().newbyteorder()
#cm = da.from_array(CM, chunks =(2030,1354))
#print(CM.shape)
#cm = np.concatenate((cm,CM))
cm = da.concatenate((cm,CM),axis=0)
#bit0 = np.dstack((bit0,bit0r))
#bit12 = np.dstack((bit12,bit12r))
print('The Cloud Mask Array Shape Is: ',cm.shape)
lat = np.zeros((2030,1354), dtype=np.float32)
lon = np.zeros((2030,1354), dtype=np.float32)
for MOD03_file in fname2:
#print(MOD03_file)
myd03 = Dataset(MOD03_file, "r")
latitude = myd03.variables["Latitude"][:,:]# Reading Specific Variable 'Latitude'.
#lat = da.from_array(latitude, chunks =(2030,1354))
lat = da.concatenate((lat,latitude),axis=0)
longitude = myd03.variables["Longitude"][:,:] # Reading Specific Variable 'Longitude'.
#lon = da.from_array(longitude, chunks =(2030,1354))
lon = da.concatenate((lon,longitude),axis=0)
print('Longitude Shape Is: ',lon.shape)
print('Latitude Shape Is: ',lat.shape)
cm=da.ravel(cm)
lat=da.ravel(lat)
lon=da.ravel(lon)
lon=lon.astype(int)
lat=lat.astype(int)
cm=cm.astype(int)
Lat=lat.to_dask_dataframe()
Lon=lon.to_dask_dataframe()
CM=cm.to_dask_dataframe()
df=dd.concat([Lat,Lon,CM],axis=1,interleave_partitions=False)
cols = {0:'Latitude',1:'Longitude',2:'CM'}
df = df.rename(columns=cols)
#df.compute()
df2=df.groupby(['Longitude','Latitude']).CM.apply(countzero).reset_index()
df3=df2.compute(num_workers=4)
combs=[]
for x in range(-89,91):
for y in range(-179,181):
combs.append((x, y))
df_1=pd.DataFrame(combs)
df_1.columns=['Latitude','Longitude']
df_2=dd.from_pandas(df_1,npartitions=1)
df4=pd.merge(df_1, df3,on=('Longitude','Latitude'), how='left')
df5=df4['CM'].values
b=df5.reshape(180,360)
print(b)
%%time
import pandas as pd
import numpy as np
import dask.array as da
import dask.dataframe as dd
import dask.delayed as delayed
import time
import math
#import graphviz
from netCDF4 import Dataset
import os,datetime,sys,fnmatch
import h5py
import dask
def read_filelist(loc_dir,prefix,unie,fileformat):
# Read the filelist in the specific directory
str = os.popen("ls "+ loc_dir + prefix + unie + "*."+fileformat).read()
fname = np.array(str.split("\n"))
fname = np.delete(fname,len(fname)-1)
return fname
def read_MODIS(fname1,fname2,verbose=False): # READ THE HDF FILE
# Read the cloud mask from MYD06_L2 product')
ncfile=Dataset(fname1,'r')
CM1km = np.array(ncfile.variables['Cloud_Mask_1km'])
CM = (np.array(CM1km[:,:,0],dtype='byte') & 0b00000110) >>1
#ncfile = Dataset(fname1, "r")
#CM = myd06.variables["Cloud_Mask_1km"][:,:,:] # Reading Specific Variable 'Cloud_Mask_1km'.
#CM = (np.array(CM[:,:,0],dtype='byte') & 0b00000110) >>1
CM=delayed(CM)
ncfile.close()
ncfile=Dataset(fname2,'r')
lat = np.array(ncfile.variables['Latitude'])
lon = np.array(ncfile.variables['Longitude'])
#ncfile = Dataset(MOD03_files, "r")
#latitude = myd03.variables["Latitude"][:,:] # Reading Specific Variable 'Latitude'.
#latitude = np.array(latitude).byteswap().newbyteorder() # Addressing Byteswap For Big Endian Error.
#longitude = myd03.variables["Longitude"][:,:] # Reading Specific Variable 'Longitude'.
attr_lat = ncfile.variables['Latitude']._FillValue
attr_lon = ncfile.variables['Longitude']._FillValue
lat=delayed(lat)
lon=delayed(lon)
return lat,lon,CM
def countzero(x, axis=1):
#print(x)
count0 = 0
count1 = 0
for i in x:
if i <= 1:
count0 +=1
#print(count0/len(x))
return (count0/len(x))
MYD06_dir= '/Users/dprakas1/Desktop/modis_files/'
MYD06_prefix = 'MYD06_L2.A2008'
MYD03_dir= '/Users/dprakas1/Desktop/modis_files/'
MYD03_prefix = 'MYD03.A2008'
fileformat = 'hdf'
fname1,fname2 = [],[]
days = np.arange(1,31,dtype=np.int)
for day in days:
dc ='%03i' % day
fname_tmp1 = read_filelist(MYD06_dir,MYD06_prefix,dc,fileformat)
fname_tmp2 = read_filelist(MYD03_dir,MYD03_prefix,dc,fileformat)
fname1 = np.append(fname1,fname_tmp1)
fname2 = np.append(fname2,fname_tmp2)
# Initiate the number of day and total cloud fraction
files = np.arange(len(fname1))
for j in range(0,1):#hdfs:
('steps: ',j+1,'/ ',(fname1))
# Read Level-2 MODIS data
lat,lon,CM = read_MODIS(fname1[j],fname2[j])
#rint(CM)
lat = lat.compute()
lon = lon.compute()
CM = CM.compute()
cloud_pix = np.zeros((180, 360))
delayed_b1=[]
def aggregateOneFileData(M06_file, M03_file):
cm = np.zeros((2030,1354), dtype=np.float32)
lat = np.zeros((2030,1354), dtype=np.float32)
lon = np.zeros((2030,1354), dtype=np.float32)
print(x,y)
myd06 = Dataset(M06_file, "r")
CM = myd06.variables["Cloud_Mask_1km"][:,:,0]# Reading Specific Variable 'Cloud_Mask_1km'.
CM = (np.array(CM,dtype='byte') & 0b00000110) >>1
CM = np.array(CM).byteswap().newbyteorder()
print("CM intial shape:",CM.shape)
cm = da.concatenate((cm,CM),axis=0)
#print("CM shape after con:",cm.shape)
cm=da.ravel(cm)
print("cm shape after ravel:",cm.shape)
myd03 = Dataset(M03_file, "r")
latitude = myd03.variables["Latitude"][:,:]
longitude = myd03.variables["Longitude"][:,:]
print("Lat intial shape:",latitude.shape)
print("lon intial shape:",longitude.shape)
lat = da.concatenate((lat,latitude),axis=0)
lon = da.concatenate((lon,longitude),axis=0)
print("lat shape after con:",lat.shape)
print("lon shape after con:",lon.shape)
lat=da.ravel(lat)
lon=da.ravel(lon)
print("lat shape after ravel:",lat.shape)
print("lon shape after ravel:",lon.shape)
cm=cm.astype(int)
lon=lon.astype(int)
lat=lat.astype(int)
Lat=(lat.to_dask_dataframe())
Lon=(lon.to_dask_dataframe())
CM=(cm.to_dask_dataframe())
df=(dd.concat([Lat,Lon,CM],axis=1,interleave_partitions=False))
print(type(df))
cols = {0:'Latitude',1:'Longitude',2:'CM'}
df = df.rename(columns=cols)
df2=delayed(df.groupby(['Longitude','Latitude']).CM.apply(countzero).reset_index())
print(type(df2))
df3=df2.compute()
print(type(df3))
df4=[df2['Longitude'].values,df2['Latitude'].values,df2['CM'].values]
print(type(df4))
delayed_b1.append(df4)
return delayed_b1
for x,y in zip(fname1,fname2):
results = aggregateOneFileData(x,y)
print(results)
cf = np.zeros((180,360))
cf[:]=np.nan
for i in range(len(delayed_b1)):
cf[(delayed_b1[i][1].compute()-90),(180+delayed_b1[i][0].compute())] = delayed_b1[i][2].compute()
print(cf)
client.close()
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("white")
#x_size, y_size = 12,8
plt.rcParams.update({'font.size': 12})
df = pd.read_csv("regression_results.csv")
f = open("data\\counters_per_route.txt", encoding="utf8")
routes = []
for l in f:
if l.startswith("#") or (l == "\n"):
continue
ss = l.strip().split(";")
route_id = ss[0]
routes.append(route_id)
#route_id = int(route_id)
routes
# feature_labels
def set_feature_labels(features, sep="\n"):
features=features.replace("'","").replace("[","").replace("]","").replace('"','')
features=features.replace("workday, weather, time_x, time_y", "basic")
features=features.replace("900000","")
features=features.replace(" ","")
features=features.replace(",",sep)
return features
df['feature_labels'] = df['features'].map(set_feature_labels)
```
### Models and features
```
#for route in df.route.unique():
for route in routes:
try:
df2 = df[df['route'] == route]
sns.barplot(data=df2, x="model", y="R2_test", hue="feature_labels")
y1,y2 = plt.ylim()
plt.ylim((max(0,y1),y2))
plt.title(route)
plt.ylabel("$R^2$(test)")
f = plt.gcf()
f.set_size_inches(15, 10)
plt.savefig(f"figs\\models\\models_{route}.pdf", bbox_inches="tight")
plt.savefig(f"figs\\models\\models_{route}.png", bbox_inches="tight")
plt.show()
except:
pass
#df[(df['route']=='Dunajska1') & (df['feature_labels']=="0655-1")]
```
### Best features
```
fig, axs = plt.subplots(4, 2, sharey=False)
#for i, (route,ax) in enumerate(zip(df.route.unique(), axs.flatten())):
for i, (route,ax) in enumerate(zip(routes, axs.flatten())):
try:
df2 = df[df['route'] == route]
df3 = pd.DataFrame()
for features in df2.feature_labels.unique():
df_features = df2[df2['feature_labels'] == features]
df_best_model = df_features[df_features['R2_test'] == df_features['R2_test'].max()]
df3 = df3.append(df_best_model, ignore_index=True)
#print(df_best_model.model)
sns.barplot(data=df3, x="feature_labels", y="R2_test", ax=ax)
#fig = plt.gcf()
#fig.setsiz
y1,y2 = ax.get_ylim()
ax.set_ylim((max(0,y1),y2))
ax.set_title(route)
ax.set_ylabel("$R^2$(test)")
if i < 6:
ax.set_xlabel("")
else:
ax.set_xlabel("features")
except:
pass
fig.set_size_inches(15, 20)
plt.savefig("figs\\models\\features.pdf", bbox_inches="tight")
plt.savefig("figs\\models\\features.png", bbox_inches="tight")
plt.show()
fig, axs = plt.subplots(4, 2, sharey=False)
#for i, (route,ax) in enumerate(zip(df.route.unique(), axs.flatten())):
for i, (route,ax) in enumerate(zip(routes, axs.flatten())):
try:
df2 = df[df['route'] == route]
df3 = pd.DataFrame()
for features in df2.feature_labels.unique():
df_features = df2[df2['feature_labels'] == features]
df_best_model = df_features[df_features['R2_train'] == df_features['R2_train'].max()]
df3 = df3.append(df_best_model, ignore_index=True)
#print(df_best_model.model)
sns.barplot(data=df3, x="feature_labels", y="R2_train", ax=ax)
#fig = plt.gcf()
#fig.setsiz
y1,y2 = ax.get_ylim()
ax.set_ylim((max(0,y1),y2))
ax.set_title(route)
ax.set_ylabel("$R^2$(train)")
if i < 6:
ax.set_xlabel("")
else:
ax.set_xlabel("features")
except:
pass
fig.set_size_inches(15, 20)
plt.savefig("figs\\models\\features_train.pdf", bbox_inches="tight")
plt.savefig("figs\\models\\features_train.png", bbox_inches="tight")
plt.show()
```
### Best models
```
#for features in df.features.unique():
fig, axs = plt.subplots(4, 2, sharey=False)
#for i, (route,ax) in enumerate(zip(df.route.unique(), axs.flatten())):
for i, (route,ax) in enumerate(zip(routes, axs.flatten())):
try:
df2 = df[df['route'] == route]
df3 = pd.DataFrame()
#features = df2.features.unique()
#max_feature = sorted(features, key=len, reverse=True)[0]
#df2 = df2[df2['features']==max_feature]
for model in df2.model.unique():
df_model = df2[df2['model'] == model]
df_best_model = df_model[df_model['R2_test'] == df_model['R2_test'].max()]
df3 = df3.append(df_best_model, ignore_index=True)
#print(df_best_model.feature_labels)
sns.barplot(data=df3, x="model", y="R2_test", ax=ax)
ax.set_title(route)
ax.set_ylabel("$R^2$(test)")
if i < 6:
ax.set_xlabel("")
else:
ax.set_xlabel("models")
except:
pass
fig.set_size_inches(15, 20)
plt.savefig("figs\\models\\models.pdf", bbox_inches="tight")
plt.savefig("figs\\models\\models.png", bbox_inches="tight")
plt.show()
#for features in df.features.unique():
fig, axs = plt.subplots(4, 2, sharey=False)
#for i, (route,ax) in enumerate(zip(df.route.unique(), axs.flatten())):
for i, (route,ax) in enumerate(zip(routes, axs.flatten())):
try:
df2 = df[df['route'] == route]
df3 = pd.DataFrame()
#features = df2.features.unique()
#max_feature = sorted(features, key=len, reverse=True)[0]
#df2 = df2[df2['features']==max_feature]
for model in df2.model.unique():
df_model = df2[df2['model'] == model]
df_best_model = df_model[df_model['R2_train'] == df_model['R2_train'].max()]
df3 = df3.append(df_best_model, ignore_index=True)
#print(df_best_model.feature_labels)
sns.barplot(data=df3, x="model", y="R2_train", ax=ax)
ax.set_title(route)
ax.set_ylabel("$R^2$(train)")
if i < 6:
ax.set_xlabel("")
else:
ax.set_xlabel("models")
except:
pass
fig.set_size_inches(15, 20)
plt.savefig("figs\\models\\models_train.pdf", bbox_inches="tight")
plt.savefig("figs\\models\\models_train.png", bbox_inches="tight")
plt.show()
```
### Best results
```
df_best = pd.read_csv("regression_results_best.csv")
df_best['feature_labels'] = df_best['features'].map(lambda x: set_feature_labels(x, sep=", "))
df_best['R2_test'] = round(df_best['R2_test'],3)
df_best['R2_train'] = round(df_best['R2_train'],3)
df_best = df_best[['route', 'feature_labels','model', 'R2_train','R2_test']]
df_best.columns = ['segment', 'features', 'best model', 'R2(train)', 'R2(test)']
f = open("best_results.txt", "w")
print(df_best.to_latex(index=False), file=f)
f.close()
df_best
```
| github_jupyter |
# Sentiment Analysis
## Using XGBoost in SageMaker
_Deep Learning Nanodegree Program | Deployment_
---
In this example of using Amazon's SageMaker service we will construct a random tree model to predict the sentiment of a movie review. You may have seen a version of this example in a pervious lesson although it would have been done using the sklearn package. Instead, we will be using the XGBoost package as it is provided to us by Amazon.
## Instructions
Some template code has already been provided for you, and you will need to implement additional functionality to successfully complete this notebook. You will not need to modify the included code beyond what is requested. Sections that begin with '**TODO**' in the header indicate that you need to complete or implement some portion within them. Instructions will be provided for each section and the specifics of the implementation are marked in the code block with a `# TODO: ...` comment. Please be sure to read the instructions carefully!
In addition to implementing code, there will be questions for you to answer which relate to the task and your implementation. Each section where you will answer a question is preceded by a '**Question:**' header. Carefully read each question and provide your answer below the '**Answer:**' header by editing the Markdown cell.
> **Note**: Code and Markdown cells can be executed using the **Shift+Enter** keyboard shortcut. In addition, a cell can be edited by typically clicking it (double-click for Markdown cells) or by pressing **Enter** while it is highlighted.
## Step 1: Downloading the data
The dataset we are going to use is very popular among researchers in Natural Language Processing, usually referred to as the [IMDb dataset](http://ai.stanford.edu/~amaas/data/sentiment/). It consists of movie reviews from the website [imdb.com](http://www.imdb.com/), each labeled as either '**pos**itive', if the reviewer enjoyed the film, or '**neg**ative' otherwise.
> Maas, Andrew L., et al. [Learning Word Vectors for Sentiment Analysis](http://ai.stanford.edu/~amaas/data/sentiment/). In _Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies_. Association for Computational Linguistics, 2011.
We begin by using some Jupyter Notebook magic to download and extract the dataset.
```
%mkdir ../data
!wget -O ../data/aclImdb_v1.tar.gz http://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz
!tar -zxf ../data/aclImdb_v1.tar.gz -C ../data
```
## Step 2: Preparing the data
The data we have downloaded is split into various files, each of which contains a single review. It will be much easier going forward if we combine these individual files into two large files, one for training and one for testing.
```
import os
import glob
def read_imdb_data(data_dir='../data/aclImdb'):
data = {}
labels = {}
for data_type in ['train', 'test']:
data[data_type] = {}
labels[data_type] = {}
for sentiment in ['pos', 'neg']:
data[data_type][sentiment] = []
labels[data_type][sentiment] = []
path = os.path.join(data_dir, data_type, sentiment, '*.txt')
files = glob.glob(path)
for f in files:
with open(f) as review:
data[data_type][sentiment].append(review.read())
# Here we represent a positive review by '1' and a negative review by '0'
labels[data_type][sentiment].append(1 if sentiment == 'pos' else 0)
assert len(data[data_type][sentiment]) == len(labels[data_type][sentiment]), \
"{}/{} data size does not match labels size".format(data_type, sentiment)
return data, labels
data, labels = read_imdb_data()
print("IMDB reviews: train = {} pos / {} neg, test = {} pos / {} neg".format(
len(data['train']['pos']), len(data['train']['neg']),
len(data['test']['pos']), len(data['test']['neg'])))
from sklearn.utils import shuffle
def prepare_imdb_data(data, labels):
"""Prepare training and test sets from IMDb movie reviews."""
#Combine positive and negative reviews and labels
data_train = data['train']['pos'] + data['train']['neg']
data_test = data['test']['pos'] + data['test']['neg']
labels_train = labels['train']['pos'] + labels['train']['neg']
labels_test = labels['test']['pos'] + labels['test']['neg']
#Shuffle reviews and corresponding labels within training and test sets
data_train, labels_train = shuffle(data_train, labels_train)
data_test, labels_test = shuffle(data_test, labels_test)
# Return a unified training data, test data, training labels, test labets
return data_train, data_test, labels_train, labels_test
train_X, test_X, train_y, test_y = prepare_imdb_data(data, labels)
print("IMDb reviews (combined): train = {}, test = {}".format(len(train_X), len(test_X)))
train_X[100]
```
## Step 3: Processing the data
Now that we have our training and testing datasets merged and ready to use, we need to start processing the raw data into something that will be useable by our machine learning algorithm. To begin with, we remove any html formatting that may appear in the reviews and perform some standard natural language processing in order to homogenize the data.
```
import nltk
nltk.download("stopwords")
from nltk.corpus import stopwords
from nltk.stem.porter import *
stemmer = PorterStemmer()
import re
from bs4 import BeautifulSoup
def review_to_words(review):
text = BeautifulSoup(review, "html.parser").get_text() # Remove HTML tags
text = re.sub(r"[^a-zA-Z0-9]", " ", text.lower()) # Convert to lower case
words = text.split() # Split string into words
words = [w for w in words if w not in stopwords.words("english")] # Remove stopwords
words = [PorterStemmer().stem(w) for w in words] # stem
return words
import pickle
cache_dir = os.path.join("../cache", "sentiment_analysis") # where to store cache files
os.makedirs(cache_dir, exist_ok=True) # ensure cache directory exists
def preprocess_data(data_train, data_test, labels_train, labels_test,
cache_dir=cache_dir, cache_file="preprocessed_data.pkl"):
"""Convert each review to words; read from cache if available."""
# If cache_file is not None, try to read from it first
cache_data = None
if cache_file is not None:
try:
with open(os.path.join(cache_dir, cache_file), "rb") as f:
cache_data = pickle.load(f)
print("Read preprocessed data from cache file:", cache_file)
except:
pass # unable to read from cache, but that's okay
# If cache is missing, then do the heavy lifting
if cache_data is None:
# Preprocess training and test data to obtain words for each review
#words_train = list(map(review_to_words, data_train))
#words_test = list(map(review_to_words, data_test))
words_train = [review_to_words(review) for review in data_train]
words_test = [review_to_words(review) for review in data_test]
# Write to cache file for future runs
if cache_file is not None:
cache_data = dict(words_train=words_train, words_test=words_test,
labels_train=labels_train, labels_test=labels_test)
with open(os.path.join(cache_dir, cache_file), "wb") as f:
pickle.dump(cache_data, f)
print("Wrote preprocessed data to cache file:", cache_file)
else:
# Unpack data loaded from cache file
words_train, words_test, labels_train, labels_test = (cache_data['words_train'],
cache_data['words_test'], cache_data['labels_train'], cache_data['labels_test'])
return words_train, words_test, labels_train, labels_test
# Preprocess data
train_X, test_X, train_y, test_y = preprocess_data(train_X, test_X, train_y, test_y)
```
### Extract Bag-of-Words features
For the model we will be implementing, rather than using the reviews directly, we are going to transform each review into a Bag-of-Words feature representation. Keep in mind that 'in the wild' we will only have access to the training set so our transformer can only use the training set to construct a representation.
```
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
import joblib
# joblib is an enhanced version of pickle that is more efficient for storing NumPy arrays
def extract_BoW_features(words_train, words_test, vocabulary_size=5000,
cache_dir=cache_dir, cache_file="bow_features.pkl"):
"""Extract Bag-of-Words for a given set of documents, already preprocessed into words."""
# If cache_file is not None, try to read from it first
cache_data = None
if cache_file is not None:
try:
with open(os.path.join(cache_dir, cache_file), "rb") as f:
cache_data = joblib.load(f)
print("Read features from cache file:", cache_file)
except:
pass # unable to read from cache, but that's okay
# If cache is missing, then do the heavy lifting
if cache_data is None:
# Fit a vectorizer to training documents and use it to transform them
# NOTE: Training documents have already been preprocessed and tokenized into words;
# pass in dummy functions to skip those steps, e.g. preprocessor=lambda x: x
vectorizer = CountVectorizer(max_features=vocabulary_size,
preprocessor=lambda x: x, tokenizer=lambda x: x) # already preprocessed
features_train = vectorizer.fit_transform(words_train).toarray()
# Apply the same vectorizer to transform the test documents (ignore unknown words)
features_test = vectorizer.transform(words_test).toarray()
# NOTE: Remember to convert the features using .toarray() for a compact representation
# Write to cache file for future runs (store vocabulary as well)
if cache_file is not None:
vocabulary = vectorizer.vocabulary_
cache_data = dict(features_train=features_train, features_test=features_test,
vocabulary=vocabulary)
with open(os.path.join(cache_dir, cache_file), "wb") as f:
joblib.dump(cache_data, f)
print("Wrote features to cache file:", cache_file)
else:
# Unpack data loaded from cache file
features_train, features_test, vocabulary = (cache_data['features_train'],
cache_data['features_test'], cache_data['vocabulary'])
# Return both the extracted features as well as the vocabulary
return features_train, features_test, vocabulary
# Extract Bag of Words features for both training and test datasets
train_X, test_X, vocabulary = extract_BoW_features(train_X, test_X)
```
## Step 4: Classification using XGBoost
Now that we have created the feature representation of our training (and testing) data, it is time to start setting up and using the XGBoost classifier provided by SageMaker.
### Writing the dataset
The XGBoost classifier that we will be using requires the dataset to be written to a file and stored using Amazon S3. To do this, we will start by splitting the training dataset into two parts, the data we will train the model with and a validation set. Then, we will write those datasets to a file and upload the files to S3. In addition, we will write the test set input to a file and upload the file to S3. This is so that we can use SageMakers Batch Transform functionality to test our model once we've fit it.
```
import pandas as pd
val_X = pd.DataFrame(train_X[:10000])
train_X = pd.DataFrame(train_X[10000:])
val_y = pd.DataFrame(train_y[:10000])
train_y = pd.DataFrame(train_y[10000:])
test_y = pd.DataFrame(test_y)
test_X = pd.DataFrame(test_X)
```
The documentation for the XGBoost algorithm in SageMaker requires that the saved datasets should contain no headers or index and that for the training and validation data, the label should occur first for each sample.
For more information about this and other algorithms, the SageMaker developer documentation can be found on __[Amazon's website.](https://docs.aws.amazon.com/sagemaker/latest/dg/)__
```
# First we make sure that the local directory in which we'd like to store the training and validation csv files exists.
data_dir = '../data/xgboost'
if not os.path.exists(data_dir):
os.makedirs(data_dir)
# First, save the test data to test.csv in the data_dir directory. Note that we do not save the associated ground truth
# labels, instead we will use them later to compare with our model output.
pd.DataFrame(test_X).to_csv(os.path.join(data_dir, 'test.csv'), header=False, index=False)
pd.concat([val_y, val_X], axis=1).to_csv(os.path.join(data_dir, 'validation.csv'), header=False, index=False)
pd.concat([train_y, train_X], axis=1).to_csv(os.path.join(data_dir, 'train.csv'), header=False, index=False)
# To save a bit of memory we can set text_X, train_X, val_X, train_y and val_y to None.
train_X = val_X = train_y = val_y = None
```
### Uploading Training / Validation files to S3
Amazon's S3 service allows us to store files that can be access by both the built-in training models such as the XGBoost model we will be using as well as custom models such as the one we will see a little later.
For this, and most other tasks we will be doing using SageMaker, there are two methods we could use. The first is to use the low level functionality of SageMaker which requires knowing each of the objects involved in the SageMaker environment. The second is to use the high level functionality in which certain choices have been made on the user's behalf. The low level approach benefits from allowing the user a great deal of flexibility while the high level approach makes development much quicker. For our purposes we will opt to use the high level approach although using the low-level approach is certainly an option.
Recall the method `upload_data()` which is a member of object representing our current SageMaker session. What this method does is upload the data to the default bucket (which is created if it does not exist) into the path described by the key_prefix variable. To see this for yourself, once you have uploaded the data files, go to the S3 console and look to see where the files have been uploaded.
For additional resources, see the __[SageMaker API documentation](http://sagemaker.readthedocs.io/en/latest/)__ and in addition the __[SageMaker Developer Guide.](https://docs.aws.amazon.com/sagemaker/latest/dg/)__
```
import sagemaker
session = sagemaker.Session() # Store the current SageMaker session
# S3 prefix (which folder will we use)
prefix = 'sentiment-xgboost'
test_location = session.upload_data(os.path.join(data_dir, 'test.csv'), key_prefix=prefix)
val_location = session.upload_data(os.path.join(data_dir, 'validation.csv'), key_prefix=prefix)
train_location = session.upload_data(os.path.join(data_dir, 'train.csv'), key_prefix=prefix)
```
### (TODO) Creating a hypertuned XGBoost model
Now that the data has been uploaded it is time to create the XGBoost model. As in the Boston Housing notebook, the first step is to create an estimator object which will be used as the *base* of your hyperparameter tuning job.
```
from sagemaker import get_execution_role
# Our current execution role is require when creating the model as the training
# and inference code will need to access the model artifacts.
role = get_execution_role()
# We need to retrieve the location of the container which is provided by Amazon for using XGBoost.
# As a matter of convenience, the training and inference code both use the same container.
from sagemaker.amazon.amazon_estimator import get_image_uri
container = get_image_uri(session.boto_region_name, 'xgboost')
# TODO: Create a SageMaker estimator using the container location determined in the previous cell.
# It is recommended that you use a single training instance of type ml.m4.xlarge. It is also
# recommended that you use 's3://{}/{}/output'.format(session.default_bucket(), prefix) as the
# output path.
xgb = sagemaker.estimator.Estimator(container,
role,
train_instance_count=1,
train_instance_type='ml.m4.xlarge',
output_path='s3://{}/{}/output'.format(session.default_bucket(), prefix),
sagemaker_session=session)
# TODO: Set the XGBoost hyperparameters in the xgb object. Don't forget that in this case we have a binary
# label so we should be using the 'binary:logistic' objective.
xgb.set_hyperparameters(max_depth=5,
eta=0.2,
gamma=5,
min_child_weight=6,
subsample=0.8,
objective='binary:logistic',
early_stopping=10,
num_round=300)
```
### (TODO) Create the hyperparameter tuner
Now that the base estimator has been set up we need to construct a hyperparameter tuner object which we will use to request SageMaker construct a hyperparameter tuning job.
**Note:** Training a single sentiment analysis XGBoost model takes longer than training a Boston Housing XGBoost model so if you don't want the hyperparameter tuning job to take too long, make sure to not set the total number of models (jobs) too high.
```
# First, make sure to import the relevant objects used to construct the tuner
from sagemaker.tuner import IntegerParameter, ContinuousParameter, HyperparameterTuner
# TODO: Create the hyperparameter tuner object
xgb_hyperparameter_tuner = HyperparameterTuner(estimator=xgb,
objective_metric_name='validation:rmse',
objective_type='Minimize',
max_jobs=6,
max_parallel_jobs=3,
hyperparameter_ranges={
'max_depth': IntegerParameter(3,6),
'eta': ContinuousParameter(0.05, 0.5),
'gamma': IntegerParameter(2,8),
'min_child_weight': IntegerParameter(3,8),
'subsample': ContinuousParameter(0.5, 0.9)
})
```
### Fit the hyperparameter tuner
Now that the hyperparameter tuner object has been constructed, it is time to fit the various models and find the best performing model.
```
s3_input_train = sagemaker.s3_input(s3_data=train_location, content_type='csv')
s3_input_validation = sagemaker.s3_input(s3_data=val_location, content_type='csv')
xgb_hyperparameter_tuner.fit({'train': s3_input_train, 'validation': s3_input_validation})
```
Remember that the tuning job is constructed and run in the background so if we want to see the progress of our training job we need to call the `wait()` method.
```
xgb_hyperparameter_tuner.wait()
```
### (TODO) Testing the model
Now that we've run our hyperparameter tuning job, it's time to see how well the best performing model actually performs. To do this we will use SageMaker's Batch Transform functionality. Batch Transform is a convenient way to perform inference on a large dataset in a way that is not realtime. That is, we don't necessarily need to use our model's results immediately and instead we can peform inference on a large number of samples. An example of this in industry might be peforming an end of month report. This method of inference can also be useful to us as it means to can perform inference on our entire test set.
Remember that in order to create a transformer object to perform the batch transform job, we need a trained estimator object. We can do that using the `attach()` method, creating an estimator object which is attached to the best trained job.
```
# TODO: Create a new estimator object attached to the best training job found during hyperparameter tuning
xgb_attached = sagemaker.estimator.Estimator.attach(xgb_hyperparameter_tuner.best_training_job())
```
Now that we have an estimator object attached to the correct training job, we can proceed as we normally would and create a transformer object.
```
# TODO: Create a transformer object from the attached estimator. Using an instance count of 1 and an instance type of ml.m4.xlarge
# should be more than enough.
xgb_transformer = xgb_attached.transformer(instance_count=1, instance_type='ml.m4.xlarge')
```
Next we actually perform the transform job. When doing so we need to make sure to specify the type of data we are sending so that it is serialized correctly in the background. In our case we are providing our model with csv data so we specify `text/csv`. Also, if the test data that we have provided is too large to process all at once then we need to specify how the data file should be split up. Since each line is a single entry in our data set we tell SageMaker that it can split the input on each line.
```
# TODO: Start the transform job. Make sure to specify the content type and the split type of the test data.
xgb_transformer.transform(test_location, content_type='text/csv', split_type='Line')
```
Currently the transform job is running but it is doing so in the background. Since we wish to wait until the transform job is done and we would like a bit of feedback we can run the `wait()` method.
```
xgb_transformer.wait()
```
Now the transform job has executed and the result, the estimated sentiment of each review, has been saved on S3. Since we would rather work on this file locally we can perform a bit of notebook magic to copy the file to the `data_dir`.
```
!aws s3 cp --recursive $xgb_transformer.output_path $data_dir
```
The last step is now to read in the output from our model, convert the output to something a little more usable, in this case we want the sentiment to be either `1` (positive) or `0` (negative), and then compare to the ground truth labels.
```
predictions = pd.read_csv(os.path.join(data_dir, 'test.csv.out'), header=None)
predictions = [round(num) for num in predictions.squeeze().values]
from sklearn.metrics import accuracy_score
accuracy_score(test_y, predictions)
```
## Optional: Clean up
The default notebook instance on SageMaker doesn't have a lot of excess disk space available. As you continue to complete and execute notebooks you will eventually fill up this disk space, leading to errors which can be difficult to diagnose. Once you are completely finished using a notebook it is a good idea to remove the files that you created along the way. Of course, you can do this from the terminal or from the notebook hub if you would like. The cell below contains some commands to clean up the created files from within the notebook.
```
# First we will remove all of the files contained in the data_dir directory
!rm $data_dir/*
# And then we delete the directory itself
!rmdir $data_dir
# Similarly we will remove the files in the cache_dir directory and the directory itself
!rm $cache_dir/*
!rmdir $cache_dir
```
| github_jupyter |
```
import numpy as np
numbers=np.array([4,6,9.5])
numbers
conda install -c plotly plotly
numbers2=np.array([[1,2,3],[4,5,6]])
numbers2
numbers3=np.array([[2,'d',4],[4,'g',6]])
numbers3
evens=np.array([2*i for i in range(1,11)])
evens
evens = np.array([x for x in range(2,21,2)])
evens
three = np.array([[x for x in range(2,11,2)],[y for y in range(1,10,2)]])
three
three.ndim
three.shape
three.size
three.itemsize
for rows in three:
for number in rows:
print(number, end=' ')
print()
for item in three.flat:
print(item, end=' ')
np.zeros(5, dtype=int)
np.ones(3)
np.full((2,3), 6, dtype=float)
test1=np.array([1,2,3.])
test1
test1.dtype
test2=np.arange(5,10,2)
test2
test3=np.linspace(0,1)
test3
test4=np.linspace(0,1,num=3)
test4
test4=np.arange(0,20000).reshape(20,1000)
test4
test5=np.arange(2,41,2).reshape(4,5)
test5
import random
%timeit die1=[random.randrange(1,7) for i in range(0,6_000_000)]
%timeit die2=np.random.randint(1,7,6_000_000)
sum([i for i in range (0,10_000_000)])
import numpy as np
w= np.arange(10_000_000)
w
w.sum()
w=2147483647+1
w
w=2147483647^2
w
w=2147483647**2
w
w=2147483647
w
s=0
for i in range(10_000_000):
s+=i
s
a=np.arange(5)
a
a**2
a*2
b=np.random.randint(1,7,5)
b
c=np.full((2,3), 4)
d=np.full((1,2),5)
c-d
numbers=np.arange(5)
numbers
numbers2=np.linspace(1.1,5.5, 5)
numbers2
numbers+numbers2
numbers >=numbers2
grades=np.random.randint(60,100, 20)
grades
type(grades)
grades.dtype
grades=np.random.randint(60,100, 20)
grades.sum()
import numpy as np
array=np.random.randint(60,101, 12).reshape((3,4))
print(array)
print(array.mean())
print('row mean is ', np.mean(array,axis=1))
print('column mean is ', np.mean(array,axis=0))
a=np.arange(1,6,1)
a
b=np.power(a,3)
b
if 1:
print('hi')
import numpy as np
a=np.arange(1,16).reshape(3,5)
a
a[[0,2]]
a[:,0]
a[:,1:4]
a=np.array([1,2,3])
a
b=a
b
a=np.array([4,5])
b, a
b=a.view()
b
a=np.array([1,2,3])
a
b
a=np.arange(1,6)
a
b=a.view()
b
a[1] *= 20
a
b
a[3] +=4
a, b
a=np.arange(1,7)
a
a.reshape(2,3)
a
a.resize(2,3)
a
a= np.arange(1,7)
b=a.reshape(2,3)
a,b
b[1,1]=500
b
a
a = np.array([[1,2,3],[4,5,6]])
a.reshape (1,6)
b = a.copy()
a, b
a[0,1]=30000
b,a
b
c=np.array([2,3,4,5])
c
d=c
c,d
c=np.array([1,20])
d,c
jasdhg
pip install autopep8
import numpy as np
a=np.arange(60_000_000)
a
import numpy as np
grade1=np.arange(1,7).reshape(2,3)
grade1
grade2=np.hstack((grade1,grade1))
grade3=np.vstack((grade2,grade2))
grade3
import pandas as pd
test=pd.Series([2,3,4.])
test[2]
import numpy as np
import pandas as pd
test=pd.Series(10.1, [2,3,4])
test
import pandas as pd
test=pd.Series((5,7, 10))
test
import pandas as pd
test=pd.Series([5,7, 10])
test
import pandas as pd
test=pd.Series(2.5, index = range(4))
test
import pandas as pd
student_grades = pd.Series([85, 95, 90, 100], index = ['Anna', 'John', 'Milo', 'Yasmin'])
student_grades
import pandas as pd
studentGrades = pd.Series([85, 95, 90, 100], index = ['Anna', 'John', 'Milo', 'Yasmin'])
studentGrades.values
import pandas as pd
studentGrades = pd.Series([85, 95, 90, 100], index = ['Anna', 'John', 'Milo', 'Yasmin'])
studentGrades.index
import pandas as pd
studentGrades = pd.Series([85, 95, 90, 100], index = ['Anna', 'John', 'Milo', 'Yasmin'])
studentGrades.index
import pandas as pd
studentGrades = pd.Series([85, 95, 90, 100], index = ['Anna', 'John', 'Milo', 'Yasmin'])
studentGrades.values
import pandas as pd
studentGrades = pd.Series([85, 95, 90, 100], index = ['Anna', 'John', 'Milo', 'Yasmin'])
studentGrades['Milo']
d = {'Anna':85, 'John':95, 'Milo':90, 'Yasmin':100}
studentGrades = pd.Series(d)
studentGrades
x=10
y=20
sum = x + y
average = sum / 2
print(sum)
grade = float(input('Enter a grade'))
print('Pass') if grade >= 70 else print('fail')
import numpy as np
import pandas as pd
%load_ext lab_black
2 + 3
2+3
```
| github_jupyter |
# Continuous Control
---
In this notebook, you will learn how to use the Unity ML-Agents environment for the second project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893) program.
### 1. Start the Environment
We begin by importing the necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
```
import numpy as np
import torch
import matplotlib.pyplot as plt
import time
from unityagents import UnityEnvironment
from collections import deque
from itertools import count
import datetime
from ddpg import DDPG, ReplayBuffer
%matplotlib inline
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Reacher.app"`
- **Windows** (x86): `"path/to/Reacher_Windows_x86/Reacher.exe"`
- **Windows** (x86_64): `"path/to/Reacher_Windows_x86_64/Reacher.exe"`
- **Linux** (x86): `"path/to/Reacher_Linux/Reacher.x86"`
- **Linux** (x86_64): `"path/to/Reacher_Linux/Reacher.x86_64"`
- **Linux** (x86, headless): `"path/to/Reacher_Linux_NoVis/Reacher.x86"`
- **Linux** (x86_64, headless): `"path/to/Reacher_Linux_NoVis/Reacher.x86_64"`
For instance, if you are using a Mac, then you downloaded `Reacher.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Reacher.app")
```
```
#env = UnityEnvironment(file_name='envs/Reacher_Linux_NoVis_20/Reacher.x86_64') # Headless
env = UnityEnvironment(file_name='envs/Reacher_Linux_20/Reacher.x86_64') # Visual
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
In this environment, a double-jointed arm can move to target locations. A reward of `+0.1` is provided for each step that the agent's hand is in the goal location. Thus, the goal of your agent is to maintain its position at the target location for as many time steps as possible.
The observation space consists of `33` variables corresponding to position, rotation, velocity, and angular velocities of the arm. Each action is a vector with four numbers, corresponding to torque applicable to two joints. Every entry in the action vector must be a number between `-1` and `1`.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents
num_agents = len(env_info.agents)
print('Number of agents:', num_agents)
# size of each action
action_size = brain.vector_action_space_size
print('Size of each action:', action_size)
# examine the state space
states = env_info.vector_observations
state_size = states.shape[1]
print('There are {} agents. Each observes a state with length: {}'.format(states.shape[0], state_size))
print('The state for the first agent looks like:', states[0])
```
### 3. Take Random Actions in the Environment
In the next code cell, you will learn how to use the Python API to control the agent and receive feedback from the environment.
Once this cell is executed, you will watch the agent's performance, if it selects an action at random with each time step. A window should pop up that allows you to observe the agent, as it moves through the environment.
Of course, as part of the project, you'll have to change the code so that the agent is able to use its experience to gradually choose better actions when interacting with the environment!
```
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
states = env_info.vector_observations # get the current state (for each agent)
scores = np.zeros(num_agents) # initialize the score (for each agent)
while True:
actions = np.random.randn(num_agents, action_size) # select an action (for each agent)
actions = np.clip(actions, -1, 1) # all actions between -1 and 1
env_info = env.step(actions)[brain_name] # send all actions to tne environment
next_states = env_info.vector_observations # get next state (for each agent)
rewards = env_info.rewards # get reward (for each agent)
dones = env_info.local_done # see if episode finished
scores += env_info.rewards # update the score (for each agent)
states = next_states # roll over states to next time step
if np.any(dones): # exit loop if episode finished
break
break
print('Total score (averaged over agents) this episode: {}'.format(np.mean(scores)))
```
When finished, you can close the environment.
### 4. It's Your Turn!
Now it's your turn to train your own agent to solve the environment! When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
```python
env_info = env.reset(train_mode=True)[brain_name]
```
```
BUFFER_SIZE = int(5e5) # replay buffer size
CACHE_SIZE = int(6e4)
BATCH_SIZE = 256 # minibatch size
GAMMA = 0.99 # discount factor
TAU = 1e-3 # for soft update of target parameters
LR_ACTOR = 1e-3 # learning rate of the actor
LR_CRITIC = 1e-3 # learning rate of the critic
WEIGHT_DECAY = 0 # L2 weight decay
UPDATE_EVERY = 20 # timesteps between updates
NUM_UPDATES = 15 # num of update passes when updating
EPSILON = 1.0 # epsilon for the noise process added to the actions
EPSILON_DECAY = 1e-6 # decay for epsilon above
NOISE_SIGMA = 0.05
# 96 Neurons solves the environment consistently and usually fastest
fc1_units=96
fc2_units=96
random_seed=23
def store(buffers, states, actions, rewards, next_states, dones, timestep):
memory, cache = buffers
for state, action, reward, next_state, done in zip(states, actions, rewards, next_states, dones):
memory.add(state, action, reward, next_state, done)
cache.add(state, action, reward, next_state, done)
store
def learn(agent, buffers, timestep):
memory, cache = buffers
if len(memory) > BATCH_SIZE and timestep % UPDATE_EVERY == 0:
for _ in range(NUM_UPDATES):
experiences = memory.sample()
agent.learn(experiences, GAMMA)
for _ in range(3):
experiences = cache.sample()
agent.learn(experiences, GAMMA)
learn
avg_over = 100
print_every = 10
def ddpg(agent, buffers, n_episodes=200, stopOnSolved=True):
print('Start: ',datetime.datetime.now())
scores_deque = deque(maxlen=avg_over)
scores_global = []
average_global = []
min_global = []
max_global = []
best_avg = -np.inf
tic = time.time()
print('\rEpis,EpAvg,GlAvg, Max, Min, Time')
for i_episode in range(1, n_episodes+1):
env_info = env.reset(train_mode=True)[brain_name] # reset the environment
states = env_info.vector_observations # get the current state (for each agent)
scores = np.zeros(num_agents) # initialize the score (for each agent)
agent.reset()
score_average = 0
timestep = time.time()
for t in count():
actions = agent.act(states, add_noise=True)
env_info = env.step(actions)[brain_name] # send all actions to tne environment
next_states = env_info.vector_observations # get next state (for each agent)
rewards = env_info.rewards # get reward (for each agent)
dones = env_info.local_done # see if episode finished
store(buffers, states, actions, rewards, next_states, dones, t)
learn(agent, buffers, t)
states = next_states # roll over states to next time step
scores += rewards # update the score (for each agent)
if np.any(dones): # exit loop if episode finished
break
score = np.mean(scores)
scores_deque.append(score)
score_average = np.mean(scores_deque)
scores_global.append(score)
average_global.append(score_average)
min_global.append(np.min(scores))
max_global.append(np.max(scores))
print('\r {}, {:.2f}, {:.2f}, {:.2f}, {:.2f}, {:.2f}'\
.format(str(i_episode).zfill(3), score, score_average, np.max(scores),
np.min(scores), time.time() - timestep), end="\n")
if i_episode % print_every == 0:
agent.save('./')
if stopOnSolved and score_average >= 30.0:
toc = time.time()
print('\nSolved in {:d} episodes!\tAvg Score: {:.2f}, time: {}'.format(i_episode, score_average, toc-tic))
agent.save('./'+str(i_episode)+'_')
break
print('End: ',datetime.datetime.now())
return scores_global, average_global, max_global, min_global
ddpg
# Create new empty buffers to start training from scratch
buffers = [ReplayBuffer(action_size, BUFFER_SIZE, BATCH_SIZE, random_seed),
ReplayBuffer(action_size, CACHE_SIZE, BATCH_SIZE, random_seed)]
agent = DDPG(state_size=state_size, action_size=action_size, random_seed=23,
fc1_units=96, fc2_units=96)
scores, averages, maxima, minima = ddpg(agent, buffers, n_episodes=130)
plt.plot(np.arange(1, len(scores)+1), scores)
plt.plot(np.arange(1, len(averages)+1), averages)
plt.plot(np.arange(1, len(maxima)+1), maxima)
plt.plot(np.arange(1, len(minima)+1), minima)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.legend(['EpAvg', 'GlAvg', 'Max', 'Min'], loc='upper left')
plt.show()
# Smaller agent learning this task from larger agent experiences
agent = DDPG(state_size=state_size, action_size=action_size, random_seed=23,
fc1_units=48, fc2_units=48)
scores, averages, maxima, minima = ddpg(agent, buffers, n_episodes=200)
plt.plot(np.arange(1, len(scores)+1), scores)
plt.plot(np.arange(1, len(averages)+1), averages)
plt.plot(np.arange(1, len(maxima)+1), maxima)
plt.plot(np.arange(1, len(minima)+1), minima)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.legend(['EpAvg', 'GlAvg', 'Max', 'Min'], loc='lower center')
plt.show()
```
Saves experiences for training future agents. Warning file is quite large.
```
memory, cache = buffers
memory.save('experiences.pkl')
#env.close()
```
### 5. See the pre-trained agent in action
```
agent = DDPG(state_size=state_size, action_size=action_size, random_seed=23,
fc1_units=96, fc2_units=96)
agent.load('./saves/96_96_108_actor.pth', './saves/96_96_108_critic.pth')
def play(agent, episodes=3):
for i_episode in range(episodes):
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
states = env_info.vector_observations # get the current state (for each agent)
scores = np.zeros(num_agents) # initialize the score (for each agent)
while True:
actions = np.random.randn(num_agents, action_size) # select an action (for each agent)
actions = agent.act(states, add_noise=False) # all actions between -1 and 1
env_info = env.step(actions)[brain_name] # send all actions to tne environment
next_states = env_info.vector_observations # get next state (for each agent)
rewards = env_info.rewards # get reward (for each agent)
dones = env_info.local_done # see if episode finished
scores += env_info.rewards # update the score (for each agent)
states = next_states # roll over states to next time step
if np.any(dones): # exit loop if episode finished
break
#break
print('Ep No: {} Total score (averaged over agents): {}'.format(i_episode, np.mean(scores)))
play(agent, 10)
```
### 6. Experiences
Experiences from the Replay Buffer could be saved and loaded for training different agents.
As an example I've provided `experiences.pkl.7z` which you should unpack with your favorite archiver.
Create new ReplayBuffer and load saved experiences
```
savedBuffer = ReplayBuffer(action_size, BUFFER_SIZE, BATCH_SIZE, random_seed)
savedBuffer.load('experiences.pkl')
```
Afterward you can use it to train your agent
```
savedBuffer.sample()
```
| github_jupyter |
```
def download(url, params={}, retries=3):
resp = None
header = {"user-agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/74.0.3729.108 Safari/537.36"}
try:
resp = requests.get(url, params=params, headers = header)
resp.raise_for_status()
except requests.exceptions.HTTPError as e:
if 500 <= e.response.status_code < 600 and retries > 0:
print(retries)
resp = download(url, params, retries - 1)
else:
print(e.response.status_code)
print(e.response.reason)
print(e.request.headers)
return resp
from bs4 import BeautifulSoup
import requests
html = download("https://media.daum.net/breakingnews/society")
daumnews = BeautifulSoup(html.text, "lxml")
daumnewstitellists = daumnews.select("strong > a")
output_file_name = "DaumNews_Urls.txt"
output_file = open(output_file_name, "w", encoding="utf-8")
for links in daumnewstitellists:
#print(links.text)
links.get('href')
print()
output_file_name = "DaumNews_Urls.txt"
output_file = open(output_file_name, "w", encoding="utf-8")
page_num = 1
max_page_num = 2
user_agent = "'Mozilla/5.0"
headers ={"User-Agent" : user_agent}
while page_num<=max_page_num:
page_url = "https://media.daum.net/breakingnews/society"
response = requests.get(page_url, headers=headers)
html = response.text
"""
주어진 HTML에서 기사 URL을 추출한다.
"""
url_frags = re.findall('<a href="(.*?)"',html)
urls = []
for url_frag in url_frags:
urls.append(url_frag)
for url in urls:
print(url, file=output_file)
time.sleep(2)
page_num+=1
output_file.close()
html = download('http://v.media.daum.net/v/20190512030900250')
daumnews = BeautifulSoup(html.text, "lxml")
import json
daumnewstitellists = daumnews.select("p")
print(daumnewstitellists)
for links in daumnewstitellists:
a = links.text
print(a)
with open('사회-2019051101.txt', 'w+', encoding='utf-8') as json_file:
json.dump(a, json_file, ensure_ascii=False, indent='\n', sort_keys=True)
import requests
from bs4 import BeautifulSoup
import re
import ast
base_url = 'https://media.daum.net/society/'
req = requests.get(base_url)
html = req.content
soup = BeautifulSoup(html, 'lxml')
newslist = soup.find(name="div", attrs={"class":"section_cate section_headline"})
newslist_atag = newslist.find_all('a')
#print(newslist_atag)
url_list = []
for a in newslist_atag:
url_list.append(a.get('href'))
print(url_list)
#print(url_list)
# 각 기사에서 텍스트만 정제하여 추출
req = requests.get(url_list[0])
#print(req)
html = req.content
#print(html)
soup = BeautifulSoup(html, 'lxml')
text = ''
doc = None
for item in soup.find_all('div', id='mArticle'):
text = text + str(item.find_all(text=True))
text = ast.literal_eval(text)
print(text)
print(url_list[3])
req = requests.get(url_list[3])
#print(req)
html = req.content
#print(html)
soup = BeautifulSoup(html, 'lxml')
text = ''
doc = None
for item in soup.find_all('div', id='mArticle'):
text = text + str(item.find_all(text=True))
text = ast.literal_eval(text)
print(text)
from selenium import webdriver
import json
driver = webdriver.Chrome()
driver.get('https://media.daum.net/society/')
driver.find_element_by_xpath('//*[@id="cSub"]/div/div[1]/div[1]/div/strong/a').click()
driver.implicitly_wait(5)
html = driver.page_source
daumnews = BeautifulSoup(html, "lxml")
lists = daumnews.select("p")
data = {}
for contents in lists:
a = contents.text
print(a)
with open('daumnews-society.json', 'w+') as json_file:
json.dump(data, json_file)
#ensure_ascii=False, indent='\t'
# encoding='utf-8'
#driver.close()
driver.close()
from bs4 import BeautifulSoup
import requests
html = download("https://media.daum.net/society/")
daumnews = BeautifulSoup(html.text, "lxml")
req = requests.get(daumnews)
html = req.content
soup = BeautifulSoup(html, 'lxml')
#!/usr/bin/env python3
#-*- coding: utf-8 -*
"""
네이버 경제 뉴스 중 증권관련 뉴스의 기사 URL을 수집합니다. 최근 10개의 페이지만 가져오겠습니다.
"""
import time
import re
import requests
eval_d = "20190511"
output_file_name = "DaumNews_Urls.txt"
output_file = open(output_file_name, "w", encoding="utf-8")
page_num = 1
max_page_num = 2
user_agent = "'Mozilla/5.0"
headers ={"User-Agent" : user_agent}
while page_num<=max_page_num:
page_url = "https://media.daum.net/breakingnews/society"
response = requests.get(page_url, headers=headers)
html = response.text
"""
주어진 HTML에서 기사 URL을 추출한다.
"""
url_frags = re.findall('<a href="(.*?)"',html)
urls = []
for url_frag in url_frags:
urls.append(url_frag)
for url in urls:
print(url, file=output_file)
time.sleep(2)
page_num+=1
output_file.close()
#[출처] 증권뉴스 데이터 수집(1/3)|작성자 엉드루
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
네이버 뉴스 기사를 수집한다.
"""
import time
import requests
import os
def get_url_file_name() :
"""
url 파일 이름을 받아 돌려준다.
:return:
"""
url_file_name = input("Enter url file name : ")
return url_file_name
def get_output_file_name():
"""
철력 파일의 이름을 입력받아 돌려준다.
:return:
"""
output_file_name = input("Enter output file name : ")
return output_file_name
def open_url_file(url_file_name):
"""
URL 파일을 연다.
:param url_file_name:
:return:
"""
url_file = open(url_file_name, "r", encoding ="utf-8")
return url_file
def create_output_file(output_file_name):
"""
출력 파일을 생성한다.
:param output_file_name:
:return:
"""
output_file = open(output_file_name, "w", encoding='utf-8')
return output_file
def gen_print_url(url_line):
"""
주어진 기사 링크 URL로 부터 인쇄용 URL을 만들어 돌려준다.
:param url_line:
:return:
"""
article_id = url_line[(len(url_line)-24):len(url_line)]
print_url = "https://media.daum.net/breakingnews/society" + article_id
return print_url
def get_html(print_url) :
"""
주어진 인쇄용 URL에 접근하여 HTML을 읽어서 돌려준다.
:param print_url:
:return:
"""
user_agent = "'Mozilla/5.0"
headers ={"User-Agent" : user_agent}
response = requests.get(print_url, headers=headers)
html = response.text
return html
def write_html(output_file, html):
"""
주어진 HTML 텍스트를 출력 파일에 쓴다.
:param output_file:
:param html:
:return:
"""
output_file.write("{}\n".format(html))
output_file.write("@@@@@ ARTICLE DELMITER @@@@\n")
def pause():
"""
3초동안 쉰다.
:return:
"""
time.sleep(3)
def close_output_file(output_file):
"""
출력 파일을 닫는다.
:param output_file:
:return:
"""
output_file.close()
def close_url_file(url_file):
"""
URL 파일을 닫는다.
:param url_file:
:return:
"""
url_file.close()
def main():
"""
네이버 뉴스기사를 수집한다.
:return:
"""
url_file_name = get_url_file_name()
output_file_name = get_output_file_name()
url_file = open_url_file(url_file_name)
output_file = create_output_file(output_file_name)
for line in url_file:
print_url = gen_print_url(line)
html = get_html(print_url)
write_html(output_file,html)
close_output_file(output_file)
close_url_file(url_file)
main()
#[출처] 증권뉴스데이터 수집(2/3편)|작성자 엉드루
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
네이버 뉴스 기사 HTML에서 순수 텍스트 기사를 추출한다.
"""
import bs4
import time
import requests
import os
ARTICLE_DELIMITER = "@@@@@ ARTICLE DELMITER @@@@\n"
TITLE_START_PAT = '<h3 class="tit_view" data-translation="">'
TITLE_END_PAT = '</h3>'
DATE_TIME_START_PAT = '<span class="txt_info">입력 </span>'
BODY_START_PAT = '<p dmcf-pid="" dmcf-ptype="">'
BODY_END_PAT = '</p>'
TIDYUP_START_PAT = '<div class="foot_view">'
def get_html_file_name():
"""
사용자로 부터 HTML 파일 이름을 입력받아 돌려준다.
:return:
"""
html_file_name = input("Enter HTML File name : ")
return html_file_name
def get_text_file_name():
"""
사용자로부터 텍스트 파일 이름을 입력받아 돌려준다.
:return:
"""
text_file_name = input("Enter text file name : ")
return text_file_name
def open_html_file(html_file_name):
"""
HTML 기사 파일을 열어서 파일 객체를 돌려준다.
:param html_file_name:
:return:
"""
html_file = open(html_file_name, "r", encoding="utf-8")
return html_file
def create_text_file(text_file_name):
"""
텍스트 기사 파일을 만들어 파일 객체를 돌려준다.
:param text_file_name:
:return:
"""
text_file = open(text_file_name, "w", encoding="utf-8")
return text_file
def read_html_article(html_file):
"""
HTML 파일에서 기사 하나를 읽어서 돌려준다.
:param html_file:
:return:
"""
lines = []
for line in html_file:
if line.startswith(ARTICLE_DELIMITER):
html_text = "".join(lines).strip()
return html_text
lines.append(line)
return None
def ext_title(html_text):
"""
HTML 기사에서 제목을 추출하여 돌려준다.
:param html_text:
:return:
"""
p = html_text.find(TITLE_START_PAT)
q = html_text.find(TITLE_END_PAT)
title = html_text[p + len(TITLE_START_PAT):q]
title = title.strip()
return title
def ext_date_time(html_text):
"""
HTML 기사에서 날짜와 시간을 추출하여 돌려준다.
:param html_text:
:return:
"""
start_p = html_text.find(DATE_TIME_START_PAT)+len(DATE_TIME_START_PAT)
end_p = start_p + 10
date_time = html_text[start_p:end_p]
date_time = date_time.strip()
return date_time
def strip_html(html_body):
"""
HTML 본문에서 HTML 태그를 제거하고 돌려준다.
:param html_body:
:return:
"""
page = bs4.BeautifulSoup(html_body, "html.parser")
body = page.text
return body
def tidyup(body):
"""
본문에서 필요없는 부분을 자르고 돌려준다.
:param body:
:return:
"""
p = body.find(TIDYUP_START_PAT)
body = body[:p]
body = body.strip()
return body
def ext_body(html_text):
"""
HTML 기사에서 본문을 추출하여 돌려준다.
:param html_text:
:return:
"""
p = html_text.find(BODY_START_PAT)
q = html_text.find(BODY_END_PAT)
html_body = html_text[p + len(BODY_START_PAT):q]
html_body = html_body.replace("<br />","\n")
html_body = html_body.strip()
body = strip_html(html_body)
body = tidyup(body)
return body
def write_article(text_file, title, date_time, body):
"""
텍스트 파일에 항목이 구분된 기사를 출력한다.
:param text_file:
:param title:
:param date_time:
:param body:
:return:
"""
text_file.write("{}\n".format(title))
text_file.write("{}\n".format(date_time))
text_file.write("{}\n".format(body))
text_file.write("{}\n".format(ARTICLE_DELIMITER))
def main():{
"cells": [
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"^C\n"
]
}
],
"source": [
"!pip install newspaper3k"
]
},
{
"cell_type": "code",
"execution_count": 112,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"[포토] G2 '밀키' 미하엘, \"이제 IG만 남았어요\"\n",
"13일 오후 베트남 하노이 국립 컨벤션센터에서 열린 MSI 그룹 스테이지 4일차 G2 e스포츠와 플래시 울브즈의 경기서 승리한 G2 '밀키' 미하엘 메흘레가 베트남어 방송 인터뷰를 하고 있다.\n",
"\n",
"하노이(베트남) ㅣ 김용우 기자 [email protected]\n",
"\n",
"포모스와 함께 즐기는 e스포츠, 게임 그 이상을 향해!\n",
"\n",
"Copyrights ⓒ FOMOS(http://www.fomos.kr) 무단 전재 및 재배포 금지\n"
]
}
],
"source": [
"from newspaper import Article\n",
"\n",
"'''\n",
"http://v.media.daum.net/v/20190513202543774\n",
"http://v.media.daum.net/v/20190513202526771\n",
"http://v.media.daum.net/v/20190513202442768\n",
"http://v.media.daum.net/v/20190513202100733\n",
"http://v.media.daum.net/v/20190513201951713\n",
"http://v.media.daum.net/v/20190513201912711\n",
"http://v.media.daum.net/v/20190513201708688\n",
"http://v.media.daum.net/v/20190513201646686\n",
"http://v.media.daum.net/v/20190513201515670\n",
"http://v.media.daum.net/v/20190513201343654\n",
"http://v.media.daum.net/v/20190513201042627\n",
"http://v.media.daum.net/v/20190513200900613\n",
"http://v.media.daum.net/v/20190513200731602\n",
"http://v.media.daum.net/v/20190513200601595\n",
"http://v.media.daum.net/v/20190513200601594\n",
"http://v.media.daum.net/v/20190513201012624\n",
"http://v.media.daum.net/v/20190513200300564\n",
"'''\n",
"\n",
"url = 'http://v.media.daum.net/v/20190513202526771'\n",
"a = Article(url, language='ko')\n",
"a.download()\n",
"a.parse()\n",
"print(a.title)\n",
"print(a.text)\n",
"\n",
"with open(\"F:/daumnews/sports/02.txt\", \"w\") as f:\n",
" f.write(a.text)\n",
"f.close()"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [],
"source": [
"from newspaper import Article"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {},
"outputs": [],
"source": [
"from bs4 import BeautifulSoup\n",
"import requests\n",
"\n",
"html = download(\"https://media.daum.net/breakingnews/culture\")\n",
"daumnews = BeautifulSoup(html.text, \"lxml\")"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {},
"outputs": [],
"source": [
"daumnewstitellists = daumnews.select(\"div > strong > a\")\n",
"k = []\n",
"\n",
"t = 18\n",
"\n",
"for links in daumnewstitellists:\n",
" l = links.get('href')\n",
" k.append(l)\n",
"\n",
"for i in range(0,17):\n",
" url = k[i]\n",
" a = Article(url, language='ko')\n",
" a.download()\n",
" a.parse()\n",
" with open(\"F:/daumnews/culture/%d.txt\" % int(i+t), \"w\", encoding=\"utf-8\") as f:\n",
" f.write(a.title)\n",
" f.write(a.text)\n",
" f.close()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"from bs4 import BeautifulSoup\n",
"import requests\n",
"\n",
"html = download(\"https://media.daum.net/breakingnews/sports\")\n",
"daumnews = BeautifulSoup(html.text, \"lxml\")\n",
"\n",
"daumnewstitellists = daumnews.select(\"div > strong > a\")\n",
"\n",
"for links in daumnewstitellists:\n",
" #print(links.text)\n",
" print(links.get('href'))\n",
" #print()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
"def download(url, params={}, retries=3):\n",
" resp = None\n",
" \n",
" header = {\"user-agent\": \"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/74.0.3729.108 Safari/537.36\"}\n",
" \n",
" try:\n",
" resp = requests.get(url, params=params, headers = header)\n",
" resp.raise_for_status()\n",
" except requests.exceptions.HTTPError as e:\n",
" if 500 <= e.response.status_code < 600 and retries > 0:\n",
" print(retries)\n",
" resp = download(url, params, retries - 1)\n",
" else:\n",
" print(e.response.status_code)\n",
" print(e.response.reason)\n",
" print(e.request.headers)\n",
"\n",
" return resp"
]
},
{
"cell_type": "code",
"execution_count": 117,
"metadata": {},
"outputs": [],
"source": [
"from newspaper import Article\n",
"from bs4 import BeautifulSoup\n",
"import requests\n",
"\n",
"html = download(\"https://media.daum.net/breakingnews/sports\")\n",
"daumnews = BeautifulSoup(html.text, \"lxml\")"
]
},
{
"cell_type": "code",
"execution_count": 139,
"metadata": {},
"outputs": [],
"source": [
"daumnewstitellists = daumnews.select(\"div > strong > a\")\n",
"\n",
"for links in daumnewstitellists:\n",
" b = links.get('href')\n",
" a = Article(b, language='ko')\n",
" a.download()\n",
" a.parse() \n",
" with open(\"F:/daumnews/sports/01.txt\", \"w\") as f:\n",
" f.write(a.text)\n",
" f.close()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": []
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.3"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"""
네이트 뉴스 기사 HTML에서 순수 텍스트 기사를 추출한다.
:return:
"""
html_file_name = get_html_file_name()
text_file_name = get_text_file_name()
html_file = open_html_file(html_file_name)
text_file = create_text_file(text_file_name)
while True:
html_text = read_html_article(html_file)
if not html_text:
break
title = ext_title(html_text)
date_time = ext_date_time(html_text)
body = ext_body(html_text)
write_article(text_file, title, date_time, body)
html_file.close()
text_file.close()
main()
```
| github_jupyter |
```
%matplotlib inline
```
# Species distribution modeling
Modeling species' geographic distributions is an important
problem in conservation biology. In this example we
model the geographic distribution of two south american
mammals given past observations and 14 environmental
variables. Since we have only positive examples (there are
no unsuccessful observations), we cast this problem as a
density estimation problem and use the :class:`sklearn.svm.OneClassSVM`
as our modeling tool. The dataset is provided by Phillips et. al. (2006).
If available, the example uses
`basemap <https://matplotlib.org/basemap/>`_
to plot the coast lines and national boundaries of South America.
The two species are:
- `"Bradypus variegatus"
<http://www.iucnredlist.org/details/3038/0>`_ ,
the Brown-throated Sloth.
- `"Microryzomys minutus"
<http://www.iucnredlist.org/details/13408/0>`_ ,
also known as the Forest Small Rice Rat, a rodent that lives in Peru,
Colombia, Ecuador, Peru, and Venezuela.
References
----------
* `"Maximum entropy modeling of species geographic distributions"
<http://rob.schapire.net/papers/ecolmod.pdf>`_
S. J. Phillips, R. P. Anderson, R. E. Schapire - Ecological Modelling,
190:231-259, 2006.
```
# Authors: Peter Prettenhofer <[email protected]>
# Jake Vanderplas <[email protected]>
#
# License: BSD 3 clause
from time import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.utils import Bunch
from sklearn.datasets import fetch_species_distributions
from sklearn import svm, metrics
# if basemap is available, we'll use it.
# otherwise, we'll improvise later...
try:
from mpl_toolkits.basemap import Basemap
basemap = True
except ImportError:
basemap = False
print(__doc__)
def construct_grids(batch):
"""Construct the map grid from the batch object
Parameters
----------
batch : Batch object
The object returned by :func:`fetch_species_distributions`
Returns
-------
(xgrid, ygrid) : 1-D arrays
The grid corresponding to the values in batch.coverages
"""
# x,y coordinates for corner cells
xmin = batch.x_left_lower_corner + batch.grid_size
xmax = xmin + (batch.Nx * batch.grid_size)
ymin = batch.y_left_lower_corner + batch.grid_size
ymax = ymin + (batch.Ny * batch.grid_size)
# x coordinates of the grid cells
xgrid = np.arange(xmin, xmax, batch.grid_size)
# y coordinates of the grid cells
ygrid = np.arange(ymin, ymax, batch.grid_size)
return (xgrid, ygrid)
def create_species_bunch(species_name, train, test, coverages, xgrid, ygrid):
"""Create a bunch with information about a particular organism
This will use the test/train record arrays to extract the
data specific to the given species name.
"""
bunch = Bunch(name=' '.join(species_name.split("_")[:2]))
species_name = species_name.encode('ascii')
points = dict(test=test, train=train)
for label, pts in points.items():
# choose points associated with the desired species
pts = pts[pts['species'] == species_name]
bunch['pts_%s' % label] = pts
# determine coverage values for each of the training & testing points
ix = np.searchsorted(xgrid, pts['dd long'])
iy = np.searchsorted(ygrid, pts['dd lat'])
bunch['cov_%s' % label] = coverages[:, -iy, ix].T
return bunch
def plot_species_distribution(species=("bradypus_variegatus_0",
"microryzomys_minutus_0")):
"""
Plot the species distribution.
"""
if len(species) > 2:
print("Note: when more than two species are provided,"
" only the first two will be used")
t0 = time()
# Load the compressed data
data = fetch_species_distributions()
# Set up the data grid
xgrid, ygrid = construct_grids(data)
# The grid in x,y coordinates
X, Y = np.meshgrid(xgrid, ygrid[::-1])
# create a bunch for each species
BV_bunch = create_species_bunch(species[0],
data.train, data.test,
data.coverages, xgrid, ygrid)
MM_bunch = create_species_bunch(species[1],
data.train, data.test,
data.coverages, xgrid, ygrid)
# background points (grid coordinates) for evaluation
np.random.seed(13)
background_points = np.c_[np.random.randint(low=0, high=data.Ny,
size=10000),
np.random.randint(low=0, high=data.Nx,
size=10000)].T
# We'll make use of the fact that coverages[6] has measurements at all
# land points. This will help us decide between land and water.
land_reference = data.coverages[6]
# Fit, predict, and plot for each species.
for i, species in enumerate([BV_bunch, MM_bunch]):
print("_" * 80)
print("Modeling distribution of species '%s'" % species.name)
# Standardize features
mean = species.cov_train.mean(axis=0)
std = species.cov_train.std(axis=0)
train_cover_std = (species.cov_train - mean) / std
# Fit OneClassSVM
print(" - fit OneClassSVM ... ", end='')
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.5)
clf.fit(train_cover_std)
print("done.")
# Plot map of South America
plt.subplot(1, 2, i + 1)
if basemap:
print(" - plot coastlines using basemap")
m = Basemap(projection='cyl', llcrnrlat=Y.min(),
urcrnrlat=Y.max(), llcrnrlon=X.min(),
urcrnrlon=X.max(), resolution='c')
m.drawcoastlines()
m.drawcountries()
else:
print(" - plot coastlines from coverage")
plt.contour(X, Y, land_reference,
levels=[-9998], colors="k",
linestyles="solid")
plt.xticks([])
plt.yticks([])
print(" - predict species distribution")
# Predict species distribution using the training data
Z = np.ones((data.Ny, data.Nx), dtype=np.float64)
# We'll predict only for the land points.
idx = np.where(land_reference > -9999)
coverages_land = data.coverages[:, idx[0], idx[1]].T
pred = clf.decision_function((coverages_land - mean) / std)
Z *= pred.min()
Z[idx[0], idx[1]] = pred
levels = np.linspace(Z.min(), Z.max(), 25)
Z[land_reference == -9999] = -9999
# plot contours of the prediction
plt.contourf(X, Y, Z, levels=levels, cmap=plt.cm.Reds)
plt.colorbar(format='%.2f')
# scatter training/testing points
plt.scatter(species.pts_train['dd long'], species.pts_train['dd lat'],
s=2 ** 2, c='black',
marker='^', label='train')
plt.scatter(species.pts_test['dd long'], species.pts_test['dd lat'],
s=2 ** 2, c='black',
marker='x', label='test')
plt.legend()
plt.title(species.name)
plt.axis('equal')
# Compute AUC with regards to background points
pred_background = Z[background_points[0], background_points[1]]
pred_test = clf.decision_function((species.cov_test - mean) / std)
scores = np.r_[pred_test, pred_background]
y = np.r_[np.ones(pred_test.shape), np.zeros(pred_background.shape)]
fpr, tpr, thresholds = metrics.roc_curve(y, scores)
roc_auc = metrics.auc(fpr, tpr)
plt.text(-35, -70, "AUC: %.3f" % roc_auc, ha="right")
print("\n Area under the ROC curve : %f" % roc_auc)
print("\ntime elapsed: %.2fs" % (time() - t0))
plot_species_distribution()
plt.show()
```
| github_jupyter |
```
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon
import matplotlib.cm as cm
import matplotlib
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
%matplotlib inline
import numpy as np
from sklearn.neighbors import KDTree
```
First create some random 3d data points
```
N = 10 # The number of points
points = np.random.rand(N, 3)
```
Now create KDTree from these so that we can look for the neighbours. TBH we don't really need KDTree. We can do this probably better and easier with a distance matrix but this will do for now.
```
kdt = KDTree(points)
```
Test by looking for the two neighbours of the first point
```
kdt.query([points[0]], 3, False)
```
So the neighbous of 0 are point 2 and 4. ok.
Let's plot the 3d points and see them
```
x = [p[0] for p in points]
y = [p[1] for p in points]
z = [p[2] for p in points]
fig = plt.figure(figsize=(8, 8), constrained_layout=True)
ax = fig.add_subplot(projection='3d')
ax.scatter(points[0][0],points[0][1],points[0][2], c='yellow',s=75)
ax.scatter(x[1:],y[1:],z[1:],c='blue',s=45)
for i, p in enumerate(points):
ax.text(p[0], p[1], p[2], str(i), fontsize=14)
plt.show()
```
Now we will look at the the algo and if it works...
```
def gen_tris(points):
processed_points = set()
points_to_do = set(range(len(points)))
tris = []
# pick the first three points
start = 0
nns = kdt.query([points[start]], N, False)
work_pts = nns[0][:3]
tris.append(Poly3DCollection([[points[i] for i in work_pts]], edgecolors='black', facecolors='w', linewidths=1, alpha=0.8))
for p in work_pts:
processed_points.add(p)
print(f'added tri [{work_pts[0]}, {work_pts[1]}, {work_pts[2]}]')
start = work_pts[1]
while True:
nns = kdt.query([points[start]], N, False)
for p in nns[0]:
if p in processed_points:
continue
nns2 = kdt.query([points[p]], N, False)
for p2 in nns2[0]:
if p2 in processed_points and p2 != start:
break
print(f'added tri [{start}, {p}, {p2}]')
tris.append(Poly3DCollection([[points[start], points[p], points[p2]]],edgecolors='black',facecolors='w', linewidths=1, alpha=0.8))
processed_points.add(p)
start = p
break
if len(processed_points) == len(points):
break
return tris
tris = gen_tris(points)
# and show the points and the triangles
fig = plt.figure(figsize=(10, 10), constrained_layout=True)
# ax = Axes3D(fig, auto_add_to_figure=False)
ax = fig.add_subplot(111, projection='3d')
fig.add_axes(ax)
ax.scatter(points[0][0],points[0][1],points[0][2], c='yellow',s=75)
ax.scatter(x[1:],y[1:],z[1:],c='blue',s=45)
for p in tris:
ax.add_collection3d(p)
for i, p in enumerate(points):
ax.text(p[0], p[1], p[2], str(i), fontsize=16)
plt.show()
```
It does. Sort of...
| github_jupyter |
```
%pushd ../../
%env CUDA_VISIBLE_DEVICES=3
import json
import os
import sys
import tempfile
from tqdm.auto import tqdm
import torch
import torchvision
from torchvision import transforms
from PIL import Image
import numpy as np
torch.cuda.set_device(0)
from netdissect import setting
segopts = 'netpqc'
segmodel, seglabels, _ = setting.load_segmenter(segopts)
segmodel.get_label_and_category_names()
!ls notebooks/stats/churches
import glob
ns = []
for f in glob.glob('/data/vision/torralba/ganprojects/placesgan/tracer/utils/samples/domes/*.png'):
ns.append(int(os.path.split(f)[1][6:][:-4]))
ns = sorted(ns)
label2idx = {l: i for i, l in enumerate(seglabels)}
label2idx['dome']
label2idx['building']
label2idx['tree']
class Dataset():
def __init__(self, before, before_prefix, after, after_prefix, device='cpu'):
self.before = before
self.before_prefix = before_prefix
self.after = after
self.after_prefix = after_prefix
self.device = device
def __getitem__(self, key):
before_seg = torch.load(os.path.join(self.before, f'{self.before_prefix}{key}.pth'), map_location=self.device)
after_seg = torch.load(os.path.join(self.after, f'{self.after_prefix}{key}.pth'), map_location=self.device)
mapped = after_seg.permute(1, 2, 0)[(before_seg == 1708).sum(0).nonzero(as_tuple=True)]
assert mapped.shape[1] == 6
return (mapped == 5).sum(), mapped.shape[0]
class Sampler(torch.utils.data.Sampler):
def __init__(self, indices):
self.indices = indices
def __len__(self):
return len(self.indices)
def __iter__(self):
yield from self.indices
def compute(before, before_pref, after, after_pref, tgt=5, tgtc=0, src=1708, srcc=2, ns=ns):
total = 0
count = 0
import time
for subn in tqdm(torch.as_tensor(ns).split(100)):
t0 = time.time()
before_segs = [
torch.load(os.path.join(before, f'{before_pref}{n}.pth'), map_location='cpu') for n in subn]
after_segs = [
torch.load(os.path.join(after, f'{after_pref}{n}.pth'), map_location='cpu') for n in subn]
t1 = time.time()
before_segs = torch.stack(before_segs).cuda()
after_segs = torch.stack(after_segs).cuda()
mapped = after_segs[:, tgtc][before_segs[:, srcc] == src]
t2 = time.time()
total += (mapped == tgt).sum()
count += mapped.shape[0]
print(total, count, t1-t0,t2-t1)
return total.item(), count
before = 'notebooks/stats/churches/domes'
before_pref = 'domes_'
after = 'notebooks/stats/churches/dome2tree/ours'
after_pref = 'dome2tree_'
dome2tree_ours = compute(before, before_pref, after, after_pref, tgt=4)
before = 'notebooks/stats/churches/domes'
before_pref = 'domes_'
after = 'notebooks/stats/churches/dome2tree/overfit'
after_pref = 'image_'
dome2tree_overfit = compute(before, before_pref, after, after_pref, tgt=4)
before = 'notebooks/stats/churches/church'
before_pref = 'church_'
after = 'notebooks/stats/churches/dome2tree_all/ours'
after_pref = 'dome2tree_all_'
dome2tree_all_ours = compute(before, before_pref, after, after_pref, ns=torch.arange(10000))
dome2tree_all_overfit[0] / dome2tree_all_overfit[1]
!ls /data/vision/torralba/ganprojects/placesgan/tracer/results/ablations/stylegan-church-dome2tree-8-1-2001-0.0001-overfit
Image.open('/data/vision/torralba/ganprojects/placesgan/tracer/utils/samples/church/church_1.png')
Image.open('/data/vision/torralba/ganprojects/placesgan/tracer/utils/samples/dome2spire_all/dome2spire_all_1.png')
Image.open('/data/vision/torralba/distillation/gan_rewriting/results/ablations/stylegan-church-dome2spire-8-10-2001-0.05-ours-10-stdcovariance/images/image_0.png')
before = 'notebooks/stats/churches/church'
before_pref = 'church_'
after = 'notebooks/stats/churches/dome2tree_all/overfit'
after_pref = 'image_'
dome2tree_all_overfit = compute(before, before_pref, after, after_pref, ns=torch.arange(10000), tgt=4)
before = 'notebooks/stats/churches/domes'
before_pref = 'domes_'
after = 'notebooks/stats/churches/dome2spire/ours'
after_pref = 'dome2spire_'
all_mapped = []
total = 0
count = 0
import time
for subn in tqdm(torch.as_tensor(ns).split(100)):
t0 = time.time()
before_segs = [
torch.load(os.path.join(before, f'{before_pref}{n}.pth'), map_location='cpu') for n in subn]
after_segs = [
torch.load(os.path.join(after, f'{after_pref}{n}.pth'), map_location='cpu') for n in subn]
t1 = time.time()
before_segs = torch.stack(before_segs).cuda()
after_segs = torch.stack(after_segs).cuda()
# mapped = after_segs.permute(0, 2, 3, 1)[before_segs[:, 2] == 1708]
mapped = after_segs[:, 0][before_segs[:, 2] == 1708]
# all_mapped.append()
t2 = time.time()
total += (mapped == 5).sum()
count += mapped.shape[0]
print(total, count, t1-t0,t2-t1)
before = 'notebooks/stats/churches/domes'
before_pref = 'domes_'
after = 'notebooks/stats/churches/dome2spire/ours'
after_pref = 'dome2spire_'
dataset = Dataset(before, before_pref, after, after_pref)
def wif(*args):
torch.set_num_threads(8)
def cfn(l):
return torch.stack([p[0] for p in l]).sum(), sum(p[1] for p in l)
loader = torch.utils.data.DataLoader(dataset, num_workers=10, batch_size=50, sampler=Sampler(ns), collate_fn=cfn, worker_init_fn=wif)
all_mapped = []
for mapped in tqdm(loader):
all_mapped.append(mapped)
after_seg.permute(1, 2, 0)[(before_seg == 1708).to(torch.int64).sum(0).nonzero(as_tuple=True)].shape
!ls notebooks/stats/churches/dome2spire/ours
class UnsupervisedImageFolder(torchvision.datasets.ImageFolder):
def __init__(self, root, transform=None, max_size=None, get_path=False):
self.temp_dir = tempfile.TemporaryDirectory()
os.symlink(root, os.path.join(self.temp_dir.name, 'dummy'))
root = self.temp_dir.name
super().__init__(root, transform=transform)
self.get_path = get_path
self.perm = None
if max_size is not None:
actual_size = super().__len__()
if actual_size > max_size:
self.perm = torch.randperm(actual_size)[:max_size].clone()
logging.info(f"{root} has {actual_size} images, downsample to {max_size}")
else:
logging.info(f"{root} has {actual_size} images <= max_size={max_size}")
def _find_classes(self, dir):
return ['./dummy'], {'./dummy': 0}
def __getitem__(self, key):
if self.perm is not None:
key = self.perm[key].item()
sample = super().__getitem__(key)[0]
if self.get_path:
path, _ = self.samples[key]
return sample, path
else:
return sample
def __len__(self):
if self.perm is not None:
return self.perm.size(0)
else:
return super().__len__()
len(seglabels)
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
])
def process(img_path, seg_path, device='cuda', batch_size=128, **kwargs):
os.makedirs(seg_path, exist_ok=True)
dataset = UnsupervisedImageFolder(img_path, transform=transform, get_path=True)
loader = torch.utils.data.DataLoader(dataset, num_workers=24, batch_size=batch_size, pin_memory=True)
with torch.no_grad():
for x, paths in tqdm(loader):
segs = segmodel.segment_batch(x.to(device), **kwargs).detach().cpu()
for path, seg in zip(paths, segs):
k = os.path.splitext(os.path.basename(path))[0]
torch.save(seg, os.path.join(seg_path, k + '.pth'))
del segs
import glob
torch.backends.cudnn.benchmark=True
process(
'/data/vision/torralba/ganprojects/placesgan/tracer/utils/samples/domes',
'churches/domes',
batch_size=12)
process(
'/data/vision/torralba/ganprojects/placesgan/tracer/utils/samples/dome2tree',
'churches/dome2tree/ours',
batch_size=8)
process(
'/data/vision/torralba/ganprojects/placesgan/tracer/utils/samples/dome2spire',
'churches/dome2spire/ours',
batch_size=8)
```
| github_jupyter |
# Introduction to the Python language
**Note**: This notebooks is not really a ready-to-use tutorial but rather serves as a table of contents that we will fill during the short course. It might later be useful as a memo, but it clearly lacks important notes and explanations.
There are lots of tutorials that you can find online, though. A useful ressource is for example the [The Python Tutorial](https://docs.python.org/3/tutorial/).
Topics covered:
- Primitives (use Python as a calculator)
- Control flows (for, while, if...)
- Containers (tuple, list, dict)
- Some Python specifics!
- Immutable vs. mutable
- Variables: names bound to objects
- Typing
- List comprehensions
- Functions
- Modules
- Basic (text) File IO
## Comments
```
# this is a comment
```
## Using Python as a calculator
```
2 / 2
```
Automatic type casting for int and float (more on that later)
```
2 + 2.
```
Automatic float conversion for division (only in Python 3 !!!)
```
2 / 3
```
**Tip**: if you don't want integer division, use float explicitly (works with both Python 2 and 3)
```
2. / 3
```
Integer division (in Python: returns floor)
```
2 // 3
```
Import math module for built-in math functions (more on how to import modules later)
```
import math
math.sin(math.pi / 2)
math.log(2.)
```
**Tip**: to get help interactively for a function, press shift-tab when the cursor is on the function, or alternatively use `?` or `help()`
```
math.log?
help(math.log)
```
Complex numbers built in the language
```
0+1j**2
(3+4j).real
(3+4j).imag
```
Create variables, or rather bound values (objects) to identifiers (more on that later)
```
earth_radius = 6.371e6
earth_radius * 2
```
*Note*: Python instructions are usually separated by new line characters
```
a = 1
a + 2
```
It is possible to write several instructions on a single line using semi-colons, but it is strongly discouraged
```
a = 1; a + 1
A
```
In a notebook, only the output of the last line executed in the cell is shown
```
a = 10
2 + 2
a
2 + 2
2 + 1
```
To show intermediate results, you need to use the `print()` built-in function, or write code in separate notebook cells
```
print(2 + 2)
print(2 + 1)
```
### Strings
String are created using single or double quotes
```
food = "bradwurst"
dessert = 'cake'
```
You may need to include a single (double) quote in a string
```
s = 'you\'ll need the \\ character'
s
```
We still see two "\". Why??? This is actually what you want when printing the string
```
print(s)
```
Other special characters (e.g., line return)
```
two_lines = "frist_line\n\tsecond_line"
two_lines
print(two_lines)
```
Long strings
```
lunch = """
Menu
Main courses
"""
lunch
print(lunch)
```
Concatenate strings using the `+` operator
```
food + ' and ' + dessert
```
Concatenate strings using `join()`
```
s = ' '.join([food, 'and', dessert, 'coffee'])
s
s = '\n'.join([food, 'and', dessert, 'coffee'])
print(s)
```
Some useful string manipulation (see https://docs.python.org/3/library/stdtypes.html#string-methods)
```
food = ' bradwurst '
food.strip()
```
Format strings
For more info, see this very nice user guide: https://pyformat.info/
```
nb = 2
"{} bradwursts bitte!".format(nb)
"{number} bradwursts bitte!".format(number=nb)
```
## Control flow
Example of an if/else statement
```
x = -1
if x < 0:
print("negative")
```
Indentation is important!
```
x = 1
if x < 0:
print("negative")
print(x)
print(x)
```
**Warning**: don't mix tabs and space!!! visually it may look as properly indented but for Python tab and space are different.
A more complete example:
if elif else example + comparison operators (==, !=, <, >, ) + logical operators (and, or, not)
```
x = -1
if x < 0:
x = 0
print("negative and changed to zero")
elif x == 0:
print("zero")
elif x == 1:
print("Single")
else:
print("More")
True and False
```
The `range()` function, used in a `for` loop
```
for i in range(10):
print(i)
```
*Note*: by default, range starts from 0 (this is consistent with other behavior that we'll see later). Also, its stops just before the given value.
Range can be used with more parameters (see help). For example: start, stop, step:
```
for i in range(1, 11, 2):
print(i)
```
A loop can also be used to iterate through values other than incrementing numbers (more on how to create iterables later).
```
words = ['cat', 'open', 'window', 'floor 20', 'be careful']
for w in words:
print(w)
```
Control the loop: the continue statement
```
for w in words:
if w == 'open':
continue
print(w)
```
More possibilities, e.g., a `while` loop and the `break` statement
```
i = 0
while True:
i = i + 1
print(i)
if i > 9:
break
```
## Containers
### Lists
```
a = [1, 2, 3, 4]
a
```
Lists may contain different types of values
```
a = [1, "2", 3., 4+0j]
a
```
Lists may contain lists (nested)
```
c = [1, [2, 3], 4]
c
```
"Indexing": retrieve elements of a list by location
**Warning**: Unlike Fortran and Matlab, position start at zero!!
```
c[0]
```
Negative position is for starting the search at the end of the list
```
a = [1, 2, 3, 4]
a[-1]
```
"Slicing": extract a sublist
```
a
list(range(4))
```
$$[0, 4[$$
Iterate through a list
```
for i in a:
print(i)
```
# Tuples
very similar to lists
```
t = (1, 2, 3, 4)
t
```
*Note*: the brackets are optional
```
t = 1, 2, 3, 4
t
```
"Unpacking": as with lists (or any iterable), it is possible to extract values in a tuple and assign them to new variables
```
t[1:3]
second_item, third_item = t[1], t[2]
print(second_item)
print(third_item)
```
**Tip**: unpack undefined number of items
```
second_item, *greater_items = t[1:]
second_item
greater_items
```
### Dictionnaries
Map keys to values
```
d = {'key1': 0, 'key2': 1}
d
```
Keys must be unique.
But be careful: no error is raised if you provide multiple, identical keys!
```
d = {'key1': 0, 'key2': 1, 'key1': 3}
d
```
Indexing dictionnaries by key
```
d['key1']
```
Keys are not limited to strings, they can be many things (but not anything, we'll see later)
```
d = {'key1': 0, 2: 1, 3.: 3}
d[2]
```
Get keys or values
```
d.keys()
d.values()
a[d['key1']]
d = {
'benoit': {
'age': 33,
'section':'5.5'
}
}
d['benoit']['age']
```
## Mutable vs. immutable
We can change the value of a variable in place (after we create the variable) or we can't.
For example, lists are mutable.
```
a = [1, 2, 3, 4]
a
```
Change the value of one item in place
```
a[0] = 'one'
a
```
Append one item at the end of the list
```
a.append(5)
a
```
Insert one item at a given position
```
a.insert(0, 'zero')
a
```
Extract and remove the last item
```
a.pop()
a
```
Dictionnaries are mutable
(note the order of the keys in the printed dict)
```
d = {'key1': 0, 'key2': 1, 'key3': 2}
d['key4'] = 4
d
```
Pop an item of given key
```
d.pop('key1')
d
```
Tuples are immutable!
```
t = (1, 2, 3, 4)
t.append(5)
```
Strings are immutable!
```
food = "bradwurst"
food[0:4] = "cury"
```
But is easy and efficient to create new strings
```
food = "curry" + food[-5:]
food
```
A reason why strings are immutable?
The keys of a dictionnary cannot be mutable, e.g., we cannot not use a list
```
d = {[1, 3]: 0}
```
The keys of a dictionnary cannot be mutable, for a quite obvious reason that it is used as indexes, like in a database. If we allow changing the indexes, it can be a real mess!
If strings were mutable, then we could'nt use it as keys in dictionnaries.
*Note*: more precisely, keys of a dictionnary must be "hashable".
## Variables or identifiers?
What's happening here?
```
a = [1, 2, 3]
b = a
b[0] = 'one'
a
```
Explanation: the concept of variable is different in Python than in, e.g., C or Fortran
`a = [1, 2, 3]` means we create a list object and we bind this object to a name (label or identifier) "a"
`b = a` means we bind the same object to a new name "b"
You can find more details and good illustrations here: https://nedbatchelder.com/text/names1.html
`id()` returns the (unique) identifiant of the value (object) bound to a given identifier
```
id(a)
id(b)
```
`is` : check whether two identifiers are bound to the same value (object)
```
a is b
```
OK, but how do you explain this?
```
a = 1
b = a
b = 2
a
a is b
id(a)
id(b)
```
Can you explain what's going on here?
```
a = 1
b = 2
b = a + b
b
```
Where does go the value "2" that was initially bounded to "b"?
OK, now what about this? Very confusing!
```
a = 1
b = 1
a is b
a = 1.
b = 1.
a is b
```
## Dynamic, strong, duck typing
Dynamic typing: no need to explicitly declare a type of an object/variable before using it. This is done automatically depending on the given object/value.
```
a = 1
type(a)
```
Strong typing: Converting from one type to another must be explicit, i.e., a value of a given type cannot be magically converted into another type
```
a + '1'
a + int('1')
eval('1 + 2 * 3')
```
An exception: integer to float casting
```
a + 1.
```
Duck typing: The type of an object doesn't really matter. What an object can or cannot do is more important.
> "If it walks like a duck and it quacks like a duck, then it must be a duck"
For example, we can show that iterating trough list, string or dict can be done using the exact same loop
```
var = [1, 2, 3, 4]
for i in var:
print(i)
var = 'abcd'
for i in var:
print(i)
var = {'key1': 1, 'key2': 2}
for i in var:
print(i)
```
In the last case, iterating a dictionnary uses the keys.
It is possible to iterate the values:
```
for v in var.values():
print(v)
```
Or more useful, iterate trough both keys and values
```
for k, v in var.items():
print(k, v)
t = ('key1', 1)
k, v = t
var.items()
```
Arithmetic operators can be obviously applied on integer, float...
```
1 + 1
1 + 2.
```
...but also on strings and lists (in this case it does concatenation)
```
[1, 2, 3] + ['a', 'b', 'c']
'other' + 'one'
```
... and also mixing the types, e.g., repeat sequence x times
```
[1, 2, 3] * 3
'one' * 3
```
...although, everything is not possible
```
[1, 2, 3] * 3.5
```
Boolean: what is True and what is False
```
print(True)
print(False)
print(bool(0))
print(bool(-1))
a = 1.7
if a:
print('non zero')
print(bool(''))
print(bool('no empty'))
print(bool([]))
print(bool([1, 2]))
print(bool({}))
print(bool({'key1': 1}))
d = {}
if not d:
print('there is no item')
```
## list comprehension
Example: we create a list from another one using a `for` loop
```
ints = [1, 3, 5, 0, 2, 0]
true_or_false = []
for i in ints:
true_or_false.append(bool(i))
true_or_false
```
But there is a much more succint way to do it. It is still (and maybe even more) readable
```
true_or_false = [bool(i) for i in ints]
true_or_false
```
More complex example, with conditions
```
float_no3 = [float(i) for i in ints if i != 3]
float_no3
```
Other kinds of conditions
(It starts to be less readable -> don't abuse list comprehension)
```
float_str3 = [float(i) if i != 3 else str(i) for i in ints]
float_str3
```
Dict comprehensions
```
int2float_map = {i: float(i) for i in ints}
int2float_map
```
## Functions
A function take value(s) as input and (optionally) return value(s) as output
inputs = arguments
```
def add(a, b):
"""Add two things."""
return a + b
def print_the_argument(arg):
print(arg)
print_the_argument('a string')
```
We can call it several times with different values
```
add(1, 3)
help(add)
```
Nested calls
```
add(add(1, 2), 3)
```
Duck typing is really useful! A single function for doing many things (write less code)
```
add(1., 2.)
add('one', 'two')
add([1, 2, 3], [1, 2, 3])
```
Functions have a scope that is local
```
a = 1
def func():
a = 2
a
func()
a
```
Call by value?
```
def func(j):
j = j + 1
print('inside: ', j)
return j
i = 1
print('before:', i)
i = func(i)
print('after:', i)
```
Not really...
```
def func(li):
li[0] = 1000
print('inside: ', li[0])
li = [1]
print('before:', li[0])
func(li)
print('after:', li[0])
```
Composing functions (start to look like functional programming)
```
C2K_OFFSET = 273.15
def fahr_to_kelvin(temp):
"""convert temp from fahrenheit to kelvin"""
return ((temp - 32) * (5/9)) + C2K_OFFSET
def kelvin_to_celsius(temp_k):
# convert temperature from kevin to celsius
return temp_k - C2K_OFFSET
def fahr_to_celsius(temp_f):
temp_k = fahr_to_kelvin(temp_f)
temp_c = kelvin_to_celsius(temp_k)
return temp_c
fahr_to_kelvin(50)
fahr_to_celsius(50)
```
Function docstring (help)
Default argument values (keyword arguments)
```
def display(a=1, b=2, c=3):
print(a, b, c)
display(b=4)
```
When calling a function, the order of the keyword arguments doesn't matter
But the order matters for positional arguments!!
```
display(c=5, a=1)
display(3)
```
Mix positional and keyword arguments: positional arguments must be added before keyword arguments
```
def display(c, a=1, b=2):
print(a, b, c)
display(1000)
```
What's going on here?
```
def add_to_list(li=[], value=1):
li.append(value)
return li
add_to_list()
add_to_list()
add_to_list()
```
Try running again the cell that defines the function, and then the cells that call the function
This is sooo confusing!
So you shouldn't use mutable objects as default values
Workaround:
```
def add_to_list(li=None, value=1):
if li is None:
li = []
li.append(value)
return li
add_to_list()
add_to_list()
```
Arbitrary number of arguments
```
def display_args(*args):
print(args)
nb_args = len(args)
print(nb_args)
print(*args)
display_args('one')
display_args(1, '2', 'bradwurst')
```
Arbitrary number of keyword arguments
```
def display_args_kwargs(*args, **kwargs):
print(*args)
print(kwargs)
display_args_kwargs('one', 2, three=3.)
```
Return more than one value (tuple)
```
def spherical_coords(x, y, z):
# convert
return r, theta, phi
```
## Modules
Modules are Python code in (`.py`) files that can be imported from within Python.
Like functions, it allows to reusing the code in different contexts.
Write a module with the temperature conversion functions above
(note: the `%%writefile` is a magic cell command in the notebook that writes the content of the cell in a file)
```
%%writefile temp_converter.py
C2K_OFFSET = 273.15
def fahr_to_kelvin(temp):
"""convert temp from fahrenheit to kelvin"""
return ((temp - 32) * (5/9)) + C2K_OFFSET
def kelvin_to_celsius(temp_k):
# convert temperature from kevin to celsius
return temp_k - C2K_OFFSET
def fahr_to_celsius(temp_f):
temp_k = fahr_to_kelvin(temp_f)
temp_c = kelvin_to_celsius(temp_k)
return temp_c
```
Import a module
```
import temp_converter
```
Access the functions imported with the module using the module name as a "namespace"
**Tip**: imported module + dot + <tab> for autocompletion
```
temp_converter.fahr_to_celsius(100.)
```
Import the module with a (short) alias for the namespace
```
import temp_converter as tc
tc.fahr_to_celsius(100.)
```
Import just a function from the module
```
from temp_converter import fahr_to_celsius
fahr_to_celsius(100.)
```
Import everything in the module (without using a namespace)
Strongly discouraged!! Name conflicts!
```
from temp_converter import *
kelvin_to_celsius(270)
```
## (Text) file IO
Let's create a small file with some data
```
%%writefile data.csv
"depth", "some_variable"
200, 2.4e2
400, 5.6e2
600, 2.6e8
```
Open the file using Python:
```
f = open("data.csv", "r")
f
```
Read the content
```
raw_data = f.readlines()
raw_data
```
What happens here?
```
f.readlines()
f.seek(0)
f.readlines()
```
Close the file
```
f.close()
```
It is safer to use the `with` statement (contexts)
```
with open("data.csv") as f:
raw_data = f.readlines()
raw_data
f.closed
```
We don't need to close the file, it is done automatically after executing the block of instructions under the `with` statement
It is safer because if an error happens within the block of instructions, the file is closed anyway.
Note here how we can explicitly raise an Error. There are many kinds of exceptions, see: https://docs.python.org/3/library/exceptions.html#bltin-exceptions
```
with open("data.csv") as f:
raw_data = f.readlines()
raise ValueError("something wrong happened")
raw_data
f.closed
```
*Note*: there are much more efficient ways to import data from a csv file!!! We'll see that later using scientific libraries.
| github_jupyter |
# 14 - Introduction to Deep Learning
by [Alejandro Correa Bahnsen](albahnsen.com/)
version 0.1, May 2016
## Part of the class [Machine Learning Applied to Risk Management](https://github.com/albahnsen/ML_RiskManagement)
This notebook is licensed under a [Creative Commons Attribution-ShareAlike 3.0 Unported License](http://creativecommons.org/licenses/by-sa/3.0/deed.en_US)
Based on the slides and presentation by [Alec Radford](https://www.youtube.com/watch?v=S75EdAcXHKk) [github](https://github.com/Newmu/Theano-Tutorials/)
For this class you must install theno
```pip instal theano```
# Motivation
How do we program a computer to recognize a picture of a
handwritten digit as a 0-9?

### What if we have 60,000 of these images and their label?
```
import numpy as np
from load import mnist
X_train, X_test, y_train2, y_test2 = mnist(onehot=True)
y_train = np.argmax(y_train2, axis=1)
y_test = np.argmax(y_test2, axis=1)
X_train[1].reshape((28, 28)).round(0).astype(int)[:, 4:26].tolist()
from pylab import imshow, show, cm
import matplotlib.pylab as plt
%matplotlib inline
def view_image(image, label="", predicted='', size=4):
"""View a single image."""
plt.figure(figsize = (size, size))
plt.imshow(image.reshape((28, 28)), cmap=cm.gray, )
plt.tick_params(axis='x',which='both', bottom='off',top='off', labelbottom='off')
plt.tick_params(axis='y',which='both', left='off',top='off', labelleft='off')
show()
if predicted == '':
print("Label: %s" % label)
else:
print('Label: ', str(label), 'Predicted: ', str(predicted))
view_image(X_train[1], y_train[1])
view_image(X_train[40000], y_train[40000])
```
# Naive model
For each image, find the “most similar” image and guess
that as the label
```
def similarity(image, images):
similarities = []
image = image.reshape((28, 28))
images = images.reshape((-1, 28, 28))
for i in range(images.shape[0]):
distance = np.sqrt(np.sum(image - images[i]) ** 2)
sim = 1 / distance
similarities.append(sim)
return similarities
np.random.seed(52)
small_train = np.random.choice(X_train.shape[0], 100)
view_image(X_test[0])
similarities = similarity(X_test[0], X_train[small_train])
view_image(X_train[small_train[np.argmax(similarities)]])
```
Lets try an other example
```
view_image(X_test[200])
similarities = similarity(X_test[200], X_train[small_train])
view_image(X_train[small_train[np.argmax(similarities)]])
```
# Logistic Regression
Logistic regression is a probabilistic, linear classifier. It is parametrized
by a weight matrix $W$ and a bias vector $b$ Classification is
done by projecting data points onto a set of hyperplanes, the distance to
which is used to determine a class membership probability.
Mathematically, this can be written as:
$$
P(Y=i\vert x, W,b) = softmax_i(W x + b)
$$
$$
P(Y=i|x, W,b) = \frac {e^{W_i x + b_i}} {\sum_j e^{W_j x + b_j}}
$$
The output of the model or prediction is then done by taking the argmax of
the vector whose i'th element is $P(Y=i|x)$.
$$
y_{pred} = argmax_i P(Y=i|x,W,b)
$$

```
import theano
from theano import tensor as T
import numpy as np
import datetime as dt
theano.config.floatX = 'float32'
```
```
Theano is a Python library that lets you to define, optimize, and evaluate mathematical expressions, especially ones with multi-dimensional arrays (numpy.ndarray). Using Theano it is possible to attain speeds rivaling hand-crafted C implementations for problems involving large amounts of data. It can also surpass C on a CPU by many orders of magnitude by taking advantage of recent GPUs.
Theano combines aspects of a computer algebra system (CAS) with aspects of an optimizing compiler. It can also generate customized C code for many mathematical operations. This combination of CAS with optimizing compilation is particularly useful for tasks in which complicated mathematical expressions are evaluated repeatedly and evaluation speed is critical. For situations where many different expressions are each evaluated once Theano can minimize the amount of compilation/analysis overhead, but still provide symbolic features such as automatic differentiation.
```
```
def floatX(X):
# return np.asarray(X, dtype='float32')
return np.asarray(X, dtype=theano.config.floatX)
def init_weights(shape):
return theano.shared(floatX(np.random.randn(*shape) * 0.01))
def model(X, w):
return T.nnet.softmax(T.dot(X, w))
X = T.fmatrix()
Y = T.fmatrix()
w = init_weights((784, 10))
w.get_value()
```
initialize model
```
py_x = model(X, w)
y_pred = T.argmax(py_x, axis=1)
cost = T.mean(T.nnet.categorical_crossentropy(py_x, Y))
gradient = T.grad(cost=cost, wrt=w)
update = [[w, w - gradient * 0.05]]
train = theano.function(inputs=[X, Y], outputs=cost, updates=update, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_pred, allow_input_downcast=True)
```
One iteration
```
for start, end in zip(range(0, X_train.shape[0], 128), range(128, X_train.shape[0], 128)):
cost = train(X_train[start:end], y_train2[start:end])
errors = [(np.mean(y_train != predict(X_train)),
np.mean(y_test != predict(X_test)))]
errors
```
Now for 100 epochs
```
t0 = dt.datetime.now()
for i in range(100):
for start, end in zip(range(0, X_train.shape[0], 128),
range(128, X_train.shape[0], 128)):
cost = train(X_train[start:end], y_train2[start:end])
errors.append((np.mean(y_train != predict(X_train)),
np.mean(y_test != predict(X_test))))
print(i, errors[-1])
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
res = np.array(errors)
plt.plot(np.arange(res.shape[0]), res[:, 0], label='train error')
plt.plot(np.arange(res.shape[0]), res[:, 1], label='test error')
plt.legend()
```
### Checking the results
```
y_pred = predict(X_test)
np.random.seed(2)
small_test = np.random.choice(X_test.shape[0], 10)
for i in small_test:
view_image(X_test[i], label=y_test[i], predicted=y_pred[i], size=1)
```
# Simple Neural Net
Add a hidden layer with a sigmoid activation function

```
def sgd(cost, params, lr=0.05):
grads = T.grad(cost=cost, wrt=params)
updates = []
for p, g in zip(params, grads):
updates.append([p, p - g * lr])
return updates
def model(X, w_h, w_o):
h = T.nnet.sigmoid(T.dot(X, w_h))
pyx = T.nnet.softmax(T.dot(h, w_o))
return pyx
w_h = init_weights((784, 625))
w_o = init_weights((625, 10))
py_x = model(X, w_h, w_o)
y_x = T.argmax(py_x, axis=1)
cost = T.mean(T.nnet.categorical_crossentropy(py_x, Y))
params = [w_h, w_o]
updates = sgd(cost, params)
train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_x, allow_input_downcast=True)
t0 = dt.datetime.now()
errors = []
for i in range(100):
for start, end in zip(range(0, X_train.shape[0], 128),
range(128, X_train.shape[0], 128)):
cost = train(X_train[start:end], y_train2[start:end])
errors.append((np.mean(y_train != predict(X_train)),
np.mean(y_test != predict(X_test))))
print(i, errors[-1])
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
res = np.array(errors)
plt.plot(np.arange(res.shape[0]), res[:, 0], label='train error')
plt.plot(np.arange(res.shape[0]), res[:, 1], label='test error')
plt.legend()
```
# Complex Neural Net
Two hidden layers with dropout

```
from theano.sandbox.rng_mrg import MRG_RandomStreams as RandomStreams
srng = RandomStreams()
def rectify(X):
return T.maximum(X, 0.)
```
### Understanding rectifier units

```
def RMSprop(cost, params, lr=0.001, rho=0.9, epsilon=1e-6):
grads = T.grad(cost=cost, wrt=params)
updates = []
for p, g in zip(params, grads):
acc = theano.shared(p.get_value() * 0.)
acc_new = rho * acc + (1 - rho) * g ** 2
gradient_scaling = T.sqrt(acc_new + epsilon)
g = g / gradient_scaling
updates.append((acc, acc_new))
updates.append((p, p - lr * g))
return updates
```
### RMSprop
RMSprop is an unpublished, adaptive learning rate method proposed by Geoff Hinton in
[Lecture 6e of his Coursera Class](http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf)
RMSprop and Adadelta have both been developed independently around the same time stemming from the need to resolve Adagrad's radically diminishing learning rates. RMSprop in fact is identical to the first update vector of Adadelta that we derived above:
$$ E[g^2]_t = 0.9 E[g^2]_{t-1} + 0.1 g^2_t. $$
$$\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}.$$
RMSprop as well divides the learning rate by an exponentially decaying average of squared gradients. Hinton suggests $\gamma$ to be set to 0.9, while a good default value for the learning rate $\eta$ is 0.001.
```
def dropout(X, p=0.):
if p > 0:
retain_prob = 1 - p
X *= srng.binomial(X.shape, p=retain_prob, dtype=theano.config.floatX)
X /= retain_prob
return X
def model(X, w_h, w_h2, w_o, p_drop_input, p_drop_hidden):
X = dropout(X, p_drop_input)
h = rectify(T.dot(X, w_h))
h = dropout(h, p_drop_hidden)
h2 = rectify(T.dot(h, w_h2))
h2 = dropout(h2, p_drop_hidden)
py_x = softmax(T.dot(h2, w_o))
return h, h2, py_x
def softmax(X):
e_x = T.exp(X - X.max(axis=1).dimshuffle(0, 'x'))
return e_x / e_x.sum(axis=1).dimshuffle(0, 'x')
w_h = init_weights((784, 625))
w_h2 = init_weights((625, 625))
w_o = init_weights((625, 10))
noise_h, noise_h2, noise_py_x = model(X, w_h, w_h2, w_o, 0.2, 0.5)
h, h2, py_x = model(X, w_h, w_h2, w_o, 0., 0.)
y_x = T.argmax(py_x, axis=1)
cost = T.mean(T.nnet.categorical_crossentropy(noise_py_x, Y))
params = [w_h, w_h2, w_o]
updates = RMSprop(cost, params, lr=0.001)
train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_x, allow_input_downcast=True)
t0 = dt.datetime.now()
errors = []
for i in range(100):
for start, end in zip(range(0, X_train.shape[0], 128),
range(128, X_train.shape[0], 128)):
cost = train(X_train[start:end], y_train2[start:end])
errors.append((np.mean(y_train != predict(X_train)),
np.mean(y_test != predict(X_test))))
print(i, errors[-1])
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
res = np.array(errors)
plt.plot(np.arange(res.shape[0]), res[:, 0], label='train error')
plt.plot(np.arange(res.shape[0]), res[:, 1], label='test error')
plt.legend()
```
# Convolutional Neural Network
In machine learning, a convolutional neural network (CNN, or ConvNet) is a type of feed-forward artificial neural network in which the connectivity pattern between its neurons is inspired by the organization of the animal visual cortex, whose individual neurons are arranged in such a way that they respond to overlapping regions tiling the visual field. Convolutional networks were inspired by biological processes and are variations of multilayer perceptrons designed to use minimal amounts of preprocessing. (Wikipedia)

### Motivation
Convolutional Neural Networks (CNN) are biologically-inspired variants of MLPs.
From Hubel and Wiesel's early work on the cat's visual cortex, we
know the visual cortex contains a complex arrangement of cells. These cells are
sensitive to small sub-regions of the visual field, called a *receptive
field*. The sub-regions are tiled to cover the entire visual field. These
cells act as local filters over the input space and are well-suited to exploit
the strong spatially local correlation present in natural images.
Additionally, two basic cell types have been identified: Simple cells respond
maximally to specific edge-like patterns within their receptive field. Complex
cells have larger receptive fields and are locally invariant to the exact
position of the pattern.
The animal visual cortex being the most powerful visual processing system in
existence, it seems natural to emulate its behavior. Hence, many
neurally-inspired models can be found in the literature.
### Sparse Connectivity
CNNs exploit spatially-local correlation by enforcing a local connectivity
pattern between neurons of adjacent layers. In other words, the inputs of
hidden units in layer **m** are from a subset of units in layer **m-1**, units
that have spatially contiguous receptive fields. We can illustrate this
graphically as follows:

Imagine that layer **m-1** is the input retina. In the above figure, units in
layer **m** have receptive fields of width 3 in the input retina and are thus
only connected to 3 adjacent neurons in the retina layer. Units in layer
**m+1** have a similar connectivity with the layer below. We say that their
receptive field with respect to the layer below is also 3, but their receptive
field with respect to the input is larger (5). Each unit is unresponsive to
variations outside of its receptive field with respect to the retina. The
architecture thus ensures that the learnt "filters" produce the strongest
response to a spatially local input pattern.
However, as shown above, stacking many such layers leads to (non-linear)
"filters" that become increasingly "global" (i.e. responsive to a larger region
of pixel space). For example, the unit in hidden layer **m+1** can encode a
non-linear feature of width 5 (in terms of pixel space).
### Shared Weights
In addition, in CNNs, each filter $h_i$ is replicated across the entire
visual field. These replicated units share the same parameterization (weight
vector and bias) and form a *feature map*.

In the above figure, we show 3 hidden units belonging to the same feature map.
Weights of the same color are shared---constrained to be identical. Gradient
descent can still be used to learn such shared parameters, with only a small
change to the original algorithm. The gradient of a shared weight is simply the
sum of the gradients of the parameters being shared.
Replicating units in this way allows for features to be detected *regardless
of their position in the visual field.* Additionally, weight sharing increases
learning efficiency by greatly reducing the number of free parameters being
learnt. The constraints on the model enable CNNs to achieve better
generalization on vision problems.
### Details and Notation
A feature map is obtained by repeated application of a function across
sub-regions of the entire image, in other words, by *convolution* of the
input image with a linear filter, adding a bias term and then applying a
non-linear function. If we denote the k-th feature map at a given layer as
$h^k$, whose filters are determined by the weights $W^k$ and bias
$b_k$, then the feature map $h^k$ is obtained as follows (for
$tanh$ non-linearities):
$$
h^k_{ij} = \tanh ( (W^k * x)_{ij} + b_k ).
$$
Note
* Recall the following definition of convolution for a 1D signal.
$$ o[n] = f[n]*g[n] = \sum_{u=-\infty}^{\infty} f[u] g[n-u] = \sum_{u=-\infty}^{\infty} f[n-u] g[u]`.
$$
* This can be extended to 2D as follows:
$$o[m,n] = f[m,n]*g[m,n] = \sum_{u=-\infty}^{\infty} \sum_{v=-\infty}^{\infty} f[u,v] g[m-u,n-v]`.
$$
To form a richer representation of the data, each hidden layer is composed of
*multiple* feature maps, $\{h^{(k)}, k=0..K\}$. The weights $W$ of
a hidden layer can be represented in a 4D tensor containing elements for every
combination of destination feature map, source feature map, source vertical
position, and source horizontal position. The biases $b$ can be
represented as a vector containing one element for every destination feature
map. We illustrate this graphically as follows:
**Figure 1**: example of a convolutional layer

The figure shows two layers of a CNN. **Layer m-1** contains four feature maps.
**Hidden layer m** contains two feature maps ($h^0$ and $h^1$).
Pixels (neuron outputs) in $h^0$ and $h^1$ (outlined as blue and
red squares) are computed from pixels of layer (m-1) which fall within their
2x2 receptive field in the layer below (shown as colored rectangles). Notice
how the receptive field spans all four input feature maps. The weights
$W^0$ and $W^1$ of $h^0$ and $h^1$ are thus 3D weight
tensors. The leading dimension indexes the input feature maps, while the other
two refer to the pixel coordinates.
Putting it all together, $W^{kl}_{ij}$ denotes the weight connecting
each pixel of the k-th feature map at layer m, with the pixel at coordinates
(i,j) of the l-th feature map of layer (m-1).
### The Convolution Operator
ConvOp is the main workhorse for implementing a convolutional layer in Theano.
ConvOp is used by ``theano.tensor.signal.conv2d``, which takes two symbolic inputs:
* a 4D tensor corresponding to a mini-batch of input images. The shape of the
tensor is as follows: [mini-batch size, number of input feature maps, image
height, image width].
* a 4D tensor corresponding to the weight matrix $W$. The shape of the
tensor is: [number of feature maps at layer m, number of feature maps at
layer m-1, filter height, filter width]
### MaxPooling
Another important concept of CNNs is *max-pooling,* which is a form of
non-linear down-sampling. Max-pooling partitions the input image into
a set of non-overlapping rectangles and, for each such sub-region, outputs the
maximum value.
Max-pooling is useful in vision for two reasons:
* By eliminating non-maximal values, it reduces computation for upper layers.
* It provides a form of translation invariance. Imagine
cascading a max-pooling layer with a convolutional layer. There are 8
directions in which one can translate the input image by a single pixel.
If max-pooling is done over a 2x2 region, 3 out of these 8 possible
configurations will produce exactly the same output at the convolutional
layer. For max-pooling over a 3x3 window, this jumps to 5/8.
Since it provides additional robustness to position, max-pooling is a
"smart" way of reducing the dimensionality of intermediate representations.
Max-pooling is done in Theano by way of
``theano.tensor.signal.downsample.max_pool_2d``. This function takes as input
an N dimensional tensor (where N >= 2) and a downscaling factor and performs
max-pooling over the 2 trailing dimensions of the tensor.
### The Full Model: CovNet
Sparse, convolutional layers and max-pooling are at the heart of the LeNet
family of models. While the exact details of the model will vary greatly,
the figure below shows a graphical depiction of a LeNet model.

The lower-layers are composed to alternating convolution and max-pooling
layers. The upper-layers however are fully-connected and correspond to a
traditional MLP (hidden layer + logistic regression). The input to the
first fully-connected layer is the set of all features maps at the layer
below.
From an implementation point of view, this means lower-layers operate on 4D
tensors. These are then flattened to a 2D matrix of rasterized feature maps,
to be compatible with our previous MLP implementation.
```
# from theano.tensor.nnet.conv import conv2d
from theano.tensor.nnet import conv2d
from theano.tensor.signal.downsample import max_pool_2d
```
Modify dropout function
```
def model(X, w, w2, w3, w4, w_o, p_drop_conv, p_drop_hidden):
l1a = rectify(conv2d(X, w, border_mode='full'))
l1 = max_pool_2d(l1a, (2, 2))
l1 = dropout(l1, p_drop_conv)
l2a = rectify(conv2d(l1, w2))
l2 = max_pool_2d(l2a, (2, 2))
l2 = dropout(l2, p_drop_conv)
l3a = rectify(conv2d(l2, w3))
l3b = max_pool_2d(l3a, (2, 2))
# convert from 4tensor to normal matrix
l3 = T.flatten(l3b, outdim=2)
l3 = dropout(l3, p_drop_conv)
l4 = rectify(T.dot(l3, w4))
l4 = dropout(l4, p_drop_hidden)
pyx = softmax(T.dot(l4, w_o))
return l1, l2, l3, l4, pyx
```
reshape into conv 4tensor (b, c, 0, 1) format
```
X_train2 = X_train.reshape(-1, 1, 28, 28)
X_test2 = X_test.reshape(-1, 1, 28, 28)
# now 4tensor for conv instead of matrix
X = T.ftensor4()
Y = T.fmatrix()
w = init_weights((32, 1, 3, 3))
w2 = init_weights((64, 32, 3, 3))
w3 = init_weights((128, 64, 3, 3))
w4 = init_weights((128 * 3 * 3, 625))
w_o = init_weights((625, 10))
noise_l1, noise_l2, noise_l3, noise_l4, noise_py_x = model(X, w, w2, w3, w4, w_o, 0.2, 0.5)
l1, l2, l3, l4, py_x = model(X, w, w2, w3, w4, w_o, 0., 0.)
y_x = T.argmax(py_x, axis=1)
cost = T.mean(T.nnet.categorical_crossentropy(noise_py_x, Y))
params = [w, w2, w3, w4, w_o]
updates = RMSprop(cost, params, lr=0.001)
train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
predict = theano.function(inputs=[X], outputs=y_x, allow_input_downcast=True)
t0 = dt.datetime.now()
errors = []
for i in range(100):
t1 = dt.datetime.now()
for start, end in zip(range(0, X_train.shape[0], 128),
range(128, X_train.shape[0], 128)):
cost = train(X_train2[start:end], y_train2[start:end])
errors.append((np.mean(y_train != predict(X_train2)),
np.mean(y_test != predict(X_test2))))
print(i, errors[-1])
print('Current iter time: ', (dt.datetime.now()-t1).seconds / 60.)
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
print('Total time: ', (dt.datetime.now()-t0).seconds / 60.)
res = np.array(errors)
plt.plot(np.arange(res.shape[0]), res[:, 0], label='train error')
plt.plot(np.arange(res.shape[0]), res[:, 1], label='test error')
plt.legend()
```
# Even more complex networks
## GoogLeNet

[examples](http://www.csc.kth.se/~roelof/deepdream/bvlc_googlenet.html)
| github_jupyter |
```
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.preprocessing import image
import numpy as np
import tensorflow as tf
from tensorflow import keras
import warnings;
warnings.filterwarnings('ignore')
```
# Predict batches of images
```
tf.compat.v1.enable_v2_behavior()
label = ['3_24+10', '3_24+30', '3_24+5', '3_24+60', '3_24+70', '3_24+90', '3_24+110', '3_24+20', '3_24+40', '3_24+50', '3_24+80', '1_12_1', '1_12_2', '1_13', '1_14', '1_19', '1_24', '1_26', '1_27', '3_21', '3_31', '3_33', '4_4_1', '4_4_2', '4_5_2', '4_5_4', '4_5_5', '4_8_5', '4_8_6', '5_17', '6_2+50', '6_2+70', '6_2+30', '6_2+40', '6_2+60', '6_2+80', '6_7', '7_1', '7_11', '7_13', '7_14', '7_2', '7_4', '7_7', '7_9', 'smoke', 'unknown', '1_11_1', '1_11_2', '1_15', '1_16', '1_18', '1_20_1', '1_22', '1_25', '1_28', '1_29', '1_30', '1_8', '2_3_1', '2_3_L', '2_3_R', '2_6', '2_7', '3_15', '3_17', '3_20', '3_25+70', '3_25+20', '3_25+30', '3_25+40', '3_25+50', '3_25+5', '3_25+60', '3_6', '4_1_6', '4_2_1', '4_2_2', '5_15_5', '6_3_1', '7_3', '7_6', '1_17', '3_16', '5_15_3', '5_20', '7_12', '1_31', '3_10', '3_19', '3_2', '3_5', '3_7', '3_9', '4_1_2_1', '4_1_3_1', '4_5_1', '4_5_6', '4_8_1', '4_8_2', '4_8_3', '5_1', '5_11_1', '5_12_1', '5_13_1', '5_13_2', '5_14_1', '5_14_2', '5_14_3', '5_2', '5_23_2', '5_24_2', '5_3', '5_4', '5_8', '7_5', '3_32', '7_18', '1_2', '1_33', '1_7', '2_4', '3_18_1', '3_18_2', '3_8', '4_1_2', '4_1_3', '5_14', '6_15_2', '6_15_3', '6_6', '6_8_1', '1_1', '1_20_2', '1_20_3', '1_21', '1_23', '1_5', '2_1', '2_2', '2_5', '3_1', '3_26', '3_27', '3_28', '3_29', '3_30', '4_1_1', '4_1_4', '4_1_5', '4_2_3', '4_3', '4_8_4', '5_16', '5_18', '5_19', '5_21', '5_22', '5_5', '5_6', '5_7_1', '5_7_2', '5_9', '6_15_1', '6_16', '6_4', '6_8_2', '6_8_3', '5_29', '5_31+10', '5_31+20', '5_31+30', '5_31+40', '5_31+5', '5_31+50', '5_32', '5_33', '1_6', '5_15_2+2', '5_15_2+1', '5_15_2+3', '5_15_2+5']
autoencoder = keras.models.load_model("../input/aaaaaaaaaa/autoencoder.h5") # load pre_trained auto encoder model
model_1= keras.models.load_model("../input/aaaaaaaaaa/VGG19_2.h5")
model_2= keras.models.load_model("../input/aaaaaaaaaa/InceptionResNetV2_2.h5")
model_3 = keras.models.load_model('../input/aaaaaaaaaa/denset201_2.h5')
root_dir = '../input/aiijc-final-dcm/AIJ_2gis_data/'
def load_and_change_img(img):
img = image.img_to_array(img)
img = img/255.
result= autoencoder.predict(img[None])
new_arr = ((result - result.min()) * (1/(result.max() - result.min()) * 255)).astype('uint8')
img_new = np.zeros(shape=(80,80,3), dtype= np.int16)
img_new[..., 0] = new_arr[...,2]
img_new[...,1]=new_arr[...,1]
img_new[..., 2] = new_arr[...,0]
return img_new/255.
df = pd.read_csv("../input/aiijc-final-dcm/AIJ_2gis_data/sample_submission.csv")
df_a=df[0:100000]
train_datagen = tf.keras.preprocessing.image.ImageDataGenerator(preprocessing_function=load_and_change_img)
test_set =train_datagen.flow_from_dataframe(directory = root_dir,
dataframe=df_a,
x_col = 'filename',
y_col='label',
classes=None,
class_model=None,
shuffle=False,
batch_size=256,
target_size=(80,80))
outputs=[]
y_pred_1=model_1.predict(test_set, batch_size=256,verbose=1)
y_pred_2=model_2.predict(test_set, batch_size=256,verbose=1)
y_pred_3=model_3.predict(test_set, batch_size=256, verbose=1)
y_pred=y_pred_1*0.2 + y_pred_2*0.4 + y_pred_3*0.4
del y_pred_1
del y_pred_2
del y_pred_3
for i in range(len(np.argmax(y_pred, axis=1))):
outputs.append(label[np.argmax(y_pred[i], axis=0)])
df_new=pd.DataFrame({'filename': df_a['filename'], 'label': outputs})
df_new.to_csv('predict.csv')
```
# Predict single image
```
model1= keras.models.load_model("../input/aaaaaaaaaa/VGG19_2.h5")
model2= keras.models.load_model("../input/aaaaaaaaaa/InceptionResNetV2_2.h5")
model3 = keras.models.load_model('../input/aaaaaaaaaa/denset201_2.h5')
def auto_encoder(img_path):
img = image.load_img(img_path, target_size=(80,80,3))
img = image.img_to_array(img)
img = img/255.
result= autoencoder.predict(img[None])
new_arr = ((result - result.min()) * (1/(result.max() - result.min()) * 255)).astype('uint8')
img_new = np.zeros(shape=(80,80,3), dtype=np.int16)
img_new[..., 0] = new_arr[...,2]
img_new[...,1]=new_arr[...,1]
img_new[..., 2] = new_arr[...,0]
return img_new/255.
labels=[]
img_path=""
def predict(img_path):
img = auto_encoder(img_path)
y_pred1=model1.predict(np.expand_dims(img, axis=0)*1/255.0)
y_pred2=model2.predict(np.expand_dims(img, axis=0)*1/255.0)
y_pred3=model3.predict(np.expand_dims(img, axis=0)*1/255.0)
y_pred=y_pred1*0.2 + y_pred2*0.4 + y_pred3*0.4
print(label[np.argmax(y_pred)])
```
| github_jupyter |
# ML Project 6033657523 - Feedforward neural network
## Importing the libraries
```
from sklearn.metrics import mean_absolute_error
from sklearn.svm import SVR
from sklearn.model_selection import KFold, train_test_split
from math import sqrt
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error, mean_absolute_error
import matplotlib.pyplot as plt
```
## Importing the cleaned dataset
```
dataset = pd.read_csv('cleanData_Final.csv')
X = dataset[['PrevAVGCost', 'PrevAssignedCost', 'AVGCost', 'LatestDateCost', 'A', 'B', 'C', 'D', 'E', 'F', 'G']]
y = dataset['GenPrice']
X
```
## Splitting the dataset into the Training set and Test set
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
```
## Feedforward neural network
### Fitting Feedforward neural network to the Training Set
```
from sklearn.neural_network import MLPRegressor
regressor = MLPRegressor(hidden_layer_sizes = (200, 200, 200, 200, 200), activation = 'relu', solver = 'adam', max_iter = 500, learning_rate = 'adaptive')
regressor.fit(X_train, y_train)
trainSet = pd.concat([X_train, y_train], axis = 1)
trainSet.head()
```
## Evaluate model accuracy
```
y_pred = regressor.predict(X_test)
y_pred
testSet = pd.concat([X_test, y_test], axis = 1)
testSet.head()
```
Compare GenPrice with PredictedGenPrice
```
datasetPredict = pd.concat([testSet.reset_index(), pd.Series(y_pred, name = 'PredictedGenPrice')], axis = 1).round(2)
datasetPredict.head(10)
datasetPredict.corr()
print("Training set accuracy = " + str(regressor.score(X_train, y_train)))
print("Test set accuracy = " + str(regressor.score(X_test, y_test)))
```
Training set accuracy = 0.9885445650077587<br>
Test set accuracy = 0.9829187423043221
### MSE
```
from sklearn import metrics
print('MSE:', metrics.mean_squared_error(y_test, y_pred))
```
MSE v1: 177.15763887557458<br>
MSE v2: 165.73161615532584<br>
MSE v3: 172.98494783761967
### MAPE
```
def mean_absolute_percentage_error(y_test, y_pred):
y_test, y_pred = np.array(y_test), np.array(y_pred)
return np.mean(np.abs((y_test - y_pred)/y_test)) * 100
print('MAPE:', mean_absolute_percentage_error(y_test, y_pred))
```
MAPE v1: 6.706572320387714<br>
MAPE v2: 6.926678067146115<br>
MAPE v3: 7.34081953098462
### Visualize
```
import matplotlib.pyplot as plt
plt.plot([i for i in range(len(y_pred))], y_pred, color = 'r')
plt.scatter([i for i in range(len(y_pred))], y_test, color = 'b')
plt.ylabel('Price')
plt.xlabel('Index')
plt.legend(['Predict', 'True'], loc = 'best')
plt.show()
```
| github_jupyter |
# Transfer Learning
Most of the time you won't want to train a whole convolutional network yourself. Modern ConvNets training on huge datasets like ImageNet take weeks on multiple GPUs. Instead, most people use a pretrained network either as a fixed feature extractor, or as an initial network to fine tune. In this notebook, you'll be using [VGGNet](https://arxiv.org/pdf/1409.1556.pdf) trained on the [ImageNet dataset](http://www.image-net.org/) as a feature extractor. Below is a diagram of the VGGNet architecture.
<img src="assets/cnnarchitecture.jpg" width=700px>
VGGNet is great because it's simple and has great performance, coming in second in the ImageNet competition. The idea here is that we keep all the convolutional layers, but replace the final fully connected layers with our own classifier. This way we can use VGGNet as a feature extractor for our images then easily train a simple classifier on top of that. What we'll do is take the first fully connected layer with 4096 units, including thresholding with ReLUs. We can use those values as a code for each image, then build a classifier on top of those codes.
You can read more about transfer learning from [the CS231n course notes](http://cs231n.github.io/transfer-learning/#tf).
## Pretrained VGGNet
We'll be using a pretrained network from https://github.com/machrisaa/tensorflow-vgg. This code is already included in 'tensorflow_vgg' directory, sdo you don't have to clone it.
This is a really nice implementation of VGGNet, quite easy to work with. The network has already been trained and the parameters are available from this link. **You'll need to clone the repo into the folder containing this notebook.** Then download the parameter file using the next cell.
```
from urllib.request import urlretrieve
from os.path import isfile, isdir
from tqdm import tqdm
vgg_dir = 'tensorflow_vgg/'
# Make sure vgg exists
if not isdir(vgg_dir):
raise Exception("VGG directory doesn't exist!")
class DLProgress(tqdm):
last_block = 0
def hook(self, block_num=1, block_size=1, total_size=None):
self.total = total_size
self.update((block_num - self.last_block) * block_size)
self.last_block = block_num
if not isfile(vgg_dir + "vgg16.npy"):
with DLProgress(unit='B', unit_scale=True, miniters=1, desc='VGG16 Parameters') as pbar:
urlretrieve(
'https://s3.amazonaws.com/content.udacity-data.com/nd101/vgg16.npy',
vgg_dir + 'vgg16.npy',
pbar.hook)
else:
print("Parameter file already exists!")
```
## Flower power
Here we'll be using VGGNet to classify images of flowers. To get the flower dataset, run the cell below. This dataset comes from the [TensorFlow inception tutorial](https://www.tensorflow.org/tutorials/image_retraining).
```
import tarfile
dataset_folder_path = 'flower_photos'
class DLProgress(tqdm):
last_block = 0
def hook(self, block_num=1, block_size=1, total_size=None):
self.total = total_size
self.update((block_num - self.last_block) * block_size)
self.last_block = block_num
if not isfile('flower_photos.tar.gz'):
with DLProgress(unit='B', unit_scale=True, miniters=1, desc='Flowers Dataset') as pbar:
urlretrieve(
'http://download.tensorflow.org/example_images/flower_photos.tgz',
'flower_photos.tar.gz',
pbar.hook)
if not isdir(dataset_folder_path):
with tarfile.open('flower_photos.tar.gz') as tar:
tar.extractall()
tar.close()
```
## ConvNet Codes
Below, we'll run through all the images in our dataset and get codes for each of them. That is, we'll run the images through the VGGNet convolutional layers and record the values of the first fully connected layer. We can then write these to a file for later when we build our own classifier.
Here we're using the `vgg16` module from `tensorflow_vgg`. The network takes images of size $224 \times 224 \times 3$ as input. Then it has 5 sets of convolutional layers. The network implemented here has this structure (copied from [the source code](https://github.com/machrisaa/tensorflow-vgg/blob/master/vgg16.py)):
```
self.conv1_1 = self.conv_layer(bgr, "conv1_1")
self.conv1_2 = self.conv_layer(self.conv1_1, "conv1_2")
self.pool1 = self.max_pool(self.conv1_2, 'pool1')
self.conv2_1 = self.conv_layer(self.pool1, "conv2_1")
self.conv2_2 = self.conv_layer(self.conv2_1, "conv2_2")
self.pool2 = self.max_pool(self.conv2_2, 'pool2')
self.conv3_1 = self.conv_layer(self.pool2, "conv3_1")
self.conv3_2 = self.conv_layer(self.conv3_1, "conv3_2")
self.conv3_3 = self.conv_layer(self.conv3_2, "conv3_3")
self.pool3 = self.max_pool(self.conv3_3, 'pool3')
self.conv4_1 = self.conv_layer(self.pool3, "conv4_1")
self.conv4_2 = self.conv_layer(self.conv4_1, "conv4_2")
self.conv4_3 = self.conv_layer(self.conv4_2, "conv4_3")
self.pool4 = self.max_pool(self.conv4_3, 'pool4')
self.conv5_1 = self.conv_layer(self.pool4, "conv5_1")
self.conv5_2 = self.conv_layer(self.conv5_1, "conv5_2")
self.conv5_3 = self.conv_layer(self.conv5_2, "conv5_3")
self.pool5 = self.max_pool(self.conv5_3, 'pool5')
self.fc6 = self.fc_layer(self.pool5, "fc6")
self.relu6 = tf.nn.relu(self.fc6)
```
So what we want are the values of the first fully connected layer, after being ReLUd (`self.relu6`). To build the network, we use
```
with tf.Session() as sess:
vgg = vgg16.Vgg16()
input_ = tf.placeholder(tf.float32, [None, 224, 224, 3])
with tf.name_scope("content_vgg"):
vgg.build(input_)
```
This creates the `vgg` object, then builds the graph with `vgg.build(input_)`. Then to get the values from the layer,
```
feed_dict = {input_: images}
codes = sess.run(vgg.relu6, feed_dict=feed_dict)
```
```
import os
import numpy as np
import tensorflow as tf
from tensorflow_vgg import vgg16
from tensorflow_vgg import utils
data_dir = 'flower_photos/'
contents = os.listdir(data_dir)
classes = [each for each in contents if os.path.isdir(data_dir + each)]
```
Below I'm running images through the VGG network in batches.
> **Exercise:** Below, build the VGG network. Also get the codes from the first fully connected layer (make sure you get the ReLUd values).
```
# Set the batch size higher if you can fit in in your GPU memory
batch_size = 10
codes_list = []
labels = []
batch = []
codes = None
with tf.Session() as sess:
# TODO: Build the vgg network here
vgg = vgg16.Vgg16()
input_ = tf.placeholder(tf.float32, [None,224,224,3])
with tf.name_scope("content_vgg"):
vgg.build(input_)
for each in classes:
print("Starting {} images".format(each))
class_path = data_dir + each
files = os.listdir(class_path)
for ii, file in enumerate(files, 1):
# Add images to the current batch
# utils.load_image crops the input images for us, from the center
img = utils.load_image(os.path.join(class_path, file))
batch.append(img.reshape((1, 224, 224, 3)))
labels.append(each)
# Running the batch through the network to get the codes
if ii % batch_size == 0 or ii == len(files):
# Image batch to pass to VGG network
images = np.concatenate(batch)
# TODO: Get the values from the relu6 layer of the VGG network
feed_dict = {input_: images}
codes_batch = sess.run(vgg.relu6, feed_dict=feed_dict)
# Here I'm building an array of the codes
if codes is None:
codes = codes_batch
else:
codes = np.concatenate((codes, codes_batch))
# Reset to start building the next batch
batch = []
print('{} images processed'.format(ii))
# write codes to file
with open('codes', 'w') as f:
codes.tofile(f)
# write labels to file
import csv
with open('labels', 'w') as f:
writer = csv.writer(f, delimiter='\n')
writer.writerow(labels)
```
## Building the Classifier
Now that we have codes for all the images, we can build a simple classifier on top of them. The codes behave just like normal input into a simple neural network. Below I'm going to have you do most of the work.
```
# read codes and labels from file
import csv
with open('labels') as f:
reader = csv.reader(f, delimiter='\n')
labels = np.array([each for each in reader if len(each) > 0]).squeeze()
with open('codes') as f:
codes = np.fromfile(f, dtype=np.float32)
codes = codes.reshape((len(labels), -1))
```
### Data prep
As usual, now we need to one-hot encode our labels and create validation/test sets. First up, creating our labels!
> **Exercise:** From scikit-learn, use [LabelBinarizer](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelBinarizer.html) to create one-hot encoded vectors from the labels.
```
from sklearn.preprocessing import LabelBinarizer
lb = LabelBinarizer()
lb.fit(labels)
labels_vecs = lb.transform(labels)
```
Now you'll want to create your training, validation, and test sets. An important thing to note here is that our labels and data aren't randomized yet. We'll want to shuffle our data so the validation and test sets contain data from all classes. Otherwise, you could end up with testing sets that are all one class. Typically, you'll also want to make sure that each smaller set has the same the distribution of classes as it is for the whole data set. The easiest way to accomplish both these goals is to use [`StratifiedShuffleSplit`](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.StratifiedShuffleSplit.html) from scikit-learn.
You can create the splitter like so:
```
ss = StratifiedShuffleSplit(n_splits=1, test_size=0.2)
```
Then split the data with
```
splitter = ss.split(x, y)
```
`ss.split` returns a generator of indices. You can pass the indices into the arrays to get the split sets. The fact that it's a generator means you either need to iterate over it, or use `next(splitter)` to get the indices. Be sure to read the [documentation](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.StratifiedShuffleSplit.html) and the [user guide](http://scikit-learn.org/stable/modules/cross_validation.html#random-permutations-cross-validation-a-k-a-shuffle-split).
> **Exercise:** Use StratifiedShuffleSplit to split the codes and labels into training, validation, and test sets.
```
from sklearn.model_selection import StratifiedShuffleSplit
ss = StratifiedShuffleSplit(n_splits=1, test_size=0.2)
X = codes
y = labels_vecs
for train_index, test_index in ss.split(X, y):
train_x, train_y = X[train_index], y[train_index]
test_x, test_y = X[test_index], y[test_index]
ss = StratifiedShuffleSplit(n_splits=1, test_size=0.5)
X = test_x
y = test_y
for train_index, test_index in ss.split(X, y):
test_x, test_y = X[train_index], y[train_index]
val_x, val_y = X[test_index], y[test_index]
print("Train shapes (x, y):", train_x.shape, train_y.shape)
print("Validation shapes (x, y):", val_x.shape, val_y.shape)
print("Test shapes (x, y):", test_x.shape, test_y.shape)
```
If you did it right, you should see these sizes for the training sets:
```
Train shapes (x, y): (2936, 4096) (2936, 5)
Validation shapes (x, y): (367, 4096) (367, 5)
Test shapes (x, y): (367, 4096) (367, 5)
```
### Classifier layers
Once you have the convolutional codes, you just need to build a classfier from some fully connected layers. You use the codes as the inputs and the image labels as targets. Otherwise the classifier is a typical neural network.
> **Exercise:** With the codes and labels loaded, build the classifier. Consider the codes as your inputs, each of them are 4096D vectors. You'll want to use a hidden layer and an output layer as your classifier. Remember that the output layer needs to have one unit for each class and a softmax activation function. Use the cross entropy to calculate the cost.
```
inputs_ = tf.placeholder(tf.float32, shape=[None, codes.shape[1]])
labels_ = tf.placeholder(tf.int64, shape=[None, labels_vecs.shape[1]])
print(labels_vecs.shape)
# TODO: Classifier layers and operations
fc = tf.contrib.layers.fully_connected(inputs_, 256)
logits = tf.contrib.layers.fully_connected(fc, labels_vecs.shape[1], activation_fn=None)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=labels_, logits=logits)
cost = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer().minimize(cost)
# Operations for validation/test accuracy
predicted = tf.nn.softmax(logits)
correct_pred = tf.equal(tf.argmax(predicted, 1), tf.argmax(labels_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
```
### Batches!
Here is just a simple way to do batches. I've written it so that it includes all the data. Sometimes you'll throw out some data at the end to make sure you have full batches. Here I just extend the last batch to include the remaining data.
```
def get_batches(x, y, n_batches=10):
""" Return a generator that yields batches from arrays x and y. """
batch_size = len(x)//n_batches
for ii in range(0, n_batches*batch_size, batch_size):
# If we're not on the last batch, grab data with size batch_size
if ii != (n_batches-1)*batch_size:
X, Y = x[ii: ii+batch_size], y[ii: ii+batch_size]
# On the last batch, grab the rest of the data
else:
X, Y = x[ii:], y[ii:]
# I love generators
yield X, Y
```
### Training
Here, we'll train the network.
> **Exercise:** So far we've been providing the training code for you. Here, I'm going to give you a bit more of a challenge and have you write the code to train the network. Of course, you'll be able to see my solution if you need help. Use the `get_batches` function I wrote before to get your batches like `for x, y in get_batches(train_x, train_y)`. Or write your own!
```
saver = tf.train.Saver()
epochs = 10
iteration = 0
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for x, y in get_batches(train_x, train_y):
feed = {inputs_: x,
labels_: y}
loss, _ = sess.run([cost, optimizer], feed_dict=feed)
print("Epoch: {}/{}".format(e+1, epochs),
"Iteration: {}".format(iteration),
"Training loss: {:.5f}".format(loss))
iteration += 1
if iteration % 5 == 0:
feed = {inputs_: val_x,
labels_: val_y}
val_acc = sess.run(accuracy, feed_dict=feed)
print("Epoch: {}/{}".format(e, epochs),
"Iteration: {}".format(iteration),
"Validation Acc: {:.4f}".format(val_acc))
saver.save(sess, "checkpoints/flowers.ckpt")
```
### Testing
Below you see the test accuracy. You can also see the predictions returned for images.
```
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))
feed = {inputs_: test_x,
labels_: test_y}
test_acc = sess.run(accuracy, feed_dict=feed)
print("Test accuracy: {:.4f}".format(test_acc))
%matplotlib inline
import matplotlib.pyplot as plt
from scipy.ndimage import imread
```
Below, feel free to choose images and see how the trained classifier predicts the flowers in them.
```
test_img_path = 'flower_photos/roses/10894627425_ec76bbc757_n.jpg'
test_img = imread(test_img_path)
plt.imshow(test_img)
# Run this cell if you don't have a vgg graph built
if 'vgg' in globals():
print('"vgg" object already exists. Will not create again.')
else:
#create vgg
with tf.Session() as sess:
input_ = tf.placeholder(tf.float32, [None, 224, 224, 3])
vgg = vgg16.Vgg16()
vgg.build(input_)
with tf.Session() as sess:
img = utils.load_image(test_img_path)
img = img.reshape((1, 224, 224, 3))
feed_dict = {input_: img}
code = sess.run(vgg.relu6, feed_dict=feed_dict)
saver = tf.train.Saver()
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))
feed = {inputs_: code}
prediction = sess.run(predicted, feed_dict=feed).squeeze()
plt.imshow(test_img)
plt.barh(np.arange(5), prediction)
_ = plt.yticks(np.arange(5), lb.classes_)
```
| github_jupyter |
```
import tensorflow as tf
from keras.applications.resnet50 import ResNet50
from keras.preprocessing import image
from keras.applications.resnet50 import preprocess_input
from keras.models import Model
import numpy as np
base_model=ResNet50(weights="imagenet")
model=Model(inputs=base_model.input, outputs=base_model.get_layer(base_model.layers[-2].name).output)
img_path="cnn_img/rabbit.jpg"
img=image.load_img(img_path, target_size=(224, 224))
x=image.img_to_array(img)
x=np.expand_dims(x, axis=0)
x=preprocess_input(x)
features=model.predict(x)
print(features.shape)
feature_layer_size=features.shape[1];
f16_dir="plane/f16/"
spitfire_dir="plane/spitfire/"
def create_numbered_paths(home_dir, n):
return [home_dir+str(i)+".jpg" for i in range(n)]
def create_paired_numbered_paths(first_home_dir, second_home_dir, n):
image_paths=[]
for p in zip(create_numbered_paths(first_home_dir, n), create_numbered_paths(second_home_dir, n)):
image_paths.extend(p)
return image_paths
def create_features(paths, verbose=True):
n=len(paths)
features=np.zeros((n, feature_layer_size))
for i in range(n):
if (verbose==True):
print("\t%2d / %2d"%(i+1, n))
img=image.load_img(paths[i], target_size=(224, 224))
img=image.img_to_array(img)
img=np.expand_dims(img, axis=0)
features[i, :]=preprocess_input(model.predict(img))
return features
individual_n=30
image_paths=create_paired_numbered_paths(f16_dir, spitfire_dir, individual_n)
image_classes=[]
for i in range(individual_n):
#0 stands for the pincer image and 0 stands for the scissors image
image_classes.extend((0, 1))
#number of all images
n=60
#number of training images
n_train=30
#number of test images
n_test=n-n_train
print("Creating training features...")
#here we will store the features of training images
x_train=create_features(image_paths[:n_train])
#train classes
y_train=np.array(image_classes[:n_train])
print("Creating test features...")
#here we will store the features of test images
x_test=create_features(image_paths[n_train:])
#train classes
y_test=np.array(image_classes[n_train:])
print (np.shape(x_train))
print (y_train)
print (np.shape(x_test))
print (y_test)
from sklearn import svm
def create_svm_classifier(x, y):
#we will use linear SVM
C=1.0
classifier=svm.SVC(kernel="rbf", C=C);
classifier.fit(x, y)
return classifier
def calculate_accuracy(classifier, x, y):
predicted=classifier.predict(x)
return np.sum(y==predicted)/y.size
#training the model
classifier=create_svm_classifier(x_train, y_train)
#checking the model's accuracy
print("Accuracy: %.2lf%%"%(100*calculate_accuracy(classifier, x_test, y_test)))
for i in range(60):
test_example_1 = np.zeros((1, feature_layer_size))
img=image.load_img("plane/f16/"+str(i)+".jpg", target_size=(224, 224))
img=image.img_to_array(img)
img=np.expand_dims(img, axis=0)
test_example_1[0,:]=preprocess_input(model.predict(img))
print("example num "+str(i)+" " + str(classifier.predict(test_example_1)))
for i in range(60):
test_example_2 = np.zeros((1,feature_layer_size))
img = image.load_img("plane/spitfire/"+str(i)+".jpg",target_size=(224,224))
img = image.img_to_array(img)
img = np.expand_dims(img,axis=0)
test_example_2[0,:] = preprocess_input(model.predict(img))
print("example num "+str(i)+" " + str(classifier.predict(test_example_2)))
```
| github_jupyter |
# Introduction to Programming
Topics for today will include:
- Mozilla Developer Network [(MDN)](https://developer.mozilla.org/en-US/)
- Python Documentation [(Official Documentation)](https://docs.python.org/3/)
- Importance of Design
- Functions
- Built in Functions
## Mozilla Developer Network [(MDN)](https://developer.mozilla.org/en-US/)
---
The Mozilla Developer Network is a great resource for all things web dev. This site is good for trying to learn about standards as well as finding out quick information about something that you're trying to do Web Dev Wise
This will be a major resource going forward when it comes to doing things with HTML and CSS
You'll often find that you're not the first to try and do something. That being said you need to start to get comfortable looking for information on your own when things go wrong.
## Python Documentation [(Official Documentation)](https://docs.python.org/3/)
---
This section is similar to the one above. Python has a lot of resources out there that we can utilize when we're stuck or need some help with something that we may not have encountered before.
Since this is the official documentation page for the language you may often be given too much information or something that you wanted but in the wrong form or for the wrong version of the language. It is up to you to learn how to utilize these things and use them to your advantage.
## Importance of Design
---
So this is a topic that i didn't learn the importance of until I was in the work force. Design is a major influence in the way that code is build and in a major capacity and significant effect on the industry.
Let's pretend we have a client that wants us to do the following:
- Write a function which will count the number of times any one character appears in a string of characters.
- Write a main function which takes the character to be counted from the user and calls the function, outputting the result to the user.
For example, are you like Android and take the latest and greatest and put them into phones in an unregulated hardware market. Thus leaving great variability in the market for your brand? Are you an Apple where you control the full stack. Your hardware and software may not be bleeding edge but it's seamless and uniform.
What does the market want? What are you good at? Do you have people around you that can fill your gaps?
Here's a blurb from a friend about the matter:
>Design, often paired with the phrase "design thinking", is an approach and method of problem solving that builds empathy for user(s) of a product, resulting in the creation of a seamless and delightful user experience tailored to the user's needs.
>Design thinks holistically about the experience that a user would go through when encountering and interacting with a product or technology. Design understands the user and their needs in great detail so that the product team can build the product and experience that fits what the user is looking for. We don't want to create products for the sake of creating them, we want to ensure that there is a need for it by a user.
>Design not only focuses on the actual interface design of a product, but can also ensure the actual technology has a seamless experience as well. Anything that blocks potential users from wanting to buy a product or prohibits current users from utilizing the product successfully, design wants to investigate. We ensure all pieces fit together from the user's standpoint, and we work to build a bridge between the technology and the user, who doesn't need to understand the technical depths of the product.
### Sorting Example [(Toptal Sorting Algorithms)](https://www.toptal.com/developers/sorting-algorithms)
---
Hypothetical, a client comes to you and they want you sort a list of numbers how do you optimally sort a list? `[2, 5, 6, 1, 4, 3]`
### Design Thinking [(IBM Design Thinking)](https://www.ibm.com/design/thinking/)
---
As this idea starts to grow you come to realize that different companies have different design methodologies. IBM has it's own version of Design Thinking. You can find more information about that at the site linked in the title. IBM is very focused on being exactly like its customers in most aspects.
What we're mostly going to take from this is that there are entire careers birthed from thinking before you act. That being said we're going to harp on a couple parts of this.
### Knowing what your requirements are
---
One of the most common scenarios to come across is a product that is annouced that's going to change everything. In the planning phase everyone agrees that the idea is amazing and going to solve all of our problems.
We get down the line and things start to fall apart, we run out of time. Things ran late, or didn't come in in time pushing everything out.
Scope creep ensued.
This is typically the result of not agreeing on what our requirements are. Something as basic as agreeing on what needs to be done needs to be discussed and checked on thouroughly. We do this because often two people rarely are thinking exactly the same thing.
You need to be on the same page as your client and your fellow developers as well. If you don't know ask.
### Planning Things Out
---
We have an idea on what we want to do. So now we just write it? No, not quite. We need to have a rough plan on how we're going to do things. Do we want to use functions, do we need a quick solution, is this going to be verbose and complex?
It's important to look at what we can set up for ourselves. We don't need to make things difficult by planning things out poorly. This means allotting time for things like getting stuck and brainstorming.
### Breaking things down
---
Personally I like to take my problem and scale it down into an easy example so in the case of our problem. The client may want to process a text like Moby Dick. We can start with a sentence and work our way up!
Taking the time to break things in to multiple pieces and figure out what goes where is an art in itself.
```
def char_finder(character, string):
total = 0
for char in string:
if char == character:
total += 1
return total
if __name__ == "__main__":
output = char_finder('z', 'Quick brown fox jumped over the lazy dog')
print(output)
```
## Functions
---
This is a intergral piece of how we do things in any programming language. This allows us to repeat instances of code that we've seen and use them at our preferance.
We'll often be using functions similar to how we use variables and our data types.
### Making Our Own Functions
---
So to make a functions we'll be using the `def` keyword followed by a name and then parameters. We've seen this a couple times now in code examples.
```
def exampleName(exampleParameter1, exampleParameter2):
print(exampleParameter1, exampleParameter2)
```
There are many ways to write functions, we can say that we're going return a specific type of data type.
```
def exampleName(exampleParameter1, exampleParameter2) -> any:
print(exampleParameter1, exampleParameter2)
```
We can also specify the types that the parameters are going to be.
```
def exampleName(exampleParameter1: any, exampleParameter2: any) -> any:
print(exampleParameter1, exampleParameter2)
```
Writing functions is only one part of the fun. We still have to be able to use them.
```
def exampleName(exampleParameter1: any, exampleParameter2: any) -> any:
print(exampleParameter1, exampleParameter2)
exampleName("Hello", 5)
```
### Using functions
---
Using functions is fairly simple. To use a function all we have to do is give the function name followed by parenthesis. This should seem familiar.
### Functions In Classes
---
Now we've mentioned classes before, classes can have functions but they're used a little differently. Functions that stem from classes are used often with a dot notation.
```
class Person:
def __init__(self, weight: int, height: int, name: str):
self.weight = weight
self.height = height
self.name = name
def who_is_this(self):
print("This person's name is " + self.name)
print("This person's weight is " + str(self.weight) + " pounds")
print("This person's height is " + str(self.height) + " inches")
if __name__ == "__main__":
Kipp = Person(225, 70, "Aaron Kippins")
Kipp.who_is_this()
```
## Built in Functions and Modules
---
With the talk of dot notation those are often used with built in functions. Built in function are functions that come along with the language. These tend to be very useful because as we start to visit more complex issues they allow us to do complexs thing with ease in some cases.
We have functions that belong to particular classes or special things that can be done with things of a certain class type.
Along side those we can also have Modules. Modules are classes or functions that other people wrote that we can import into our code to use.
### Substrings
---
```
string = "I want to go home!"
print(string[0:12], "to Cancun!")
# print(string[0:1])
```
### toUpper toLower
---
```
alpha_sentence = 'Quick brown fox jumped over the lazy dog'
print(alpha_sentence.title())
print(alpha_sentence.upper())
print(alpha_sentence.lower())
if alpha_sentence.lower().islower():
print("sentence is all lowercase")
```
### Exponents
---
```
print(2 ** 3)
```
### math.sqrt()
---
```
import math
math.sqrt(4)
```
### Integer Division vs Float Division
---
```
print(4//2)
print(4/2)
```
### Abs()
---
```
abs(-10)
```
### String Manipulation
---
```
dummy_string = "Hey there I'm just a string for the example about to happen."
print(dummy_string.center(70, "-"))
print(dummy_string.partition(" "))
print(dummy_string.swapcase())
print(dummy_string.split(" "))
```
### Array Manipulation
---
```
arr = [2, 5, 6, 1, 4, 3]
arr.sort()
print(arr)
print(arr[3])
# sorted(arr)
print(arr[1:3])
```
### Insert and Pop, Append and Remove
---
```
arr.append(7)
print(arr)
arr.pop()
print(arr)
```
| github_jupyter |
```
!conda info
```
# Variables
```
x = 2
y = '3'
print(x+int(y))
z = [1, 2, 3] #List
w = (2, 3, 4) #Tuple
import numpy as np
q = np.array([1, 2, 3]) #numpy.ndarray
type(q)
```
# Console input and output
```
MyName = input('My name is: ')
print('Hello, '+MyName)
```
# File input and output
```
fid = open('msg.txt','w')
fid.write('demo of writing.\n')
fid.write('Second line')
fid.close()
fid = open('msg.txt','r')
msg = fid.readline()
print(msg)
msg = fid.readline()
print(msg)
fid.close()
fid = open('msg.txt','r')
msg = fid.readlines()
print(msg)
fid = open('msg.txt','r')
msg = fid.read()
print(msg)
import numpy as np
x = np.linspace(0, 2*np.pi,4)
y = np.cos(x)
#Stack arrays in sequence vertically (row wise).
data = np.vstack((x,y)) #上下對隊齊好
dataT = data.T #Transpose
np.savetxt('data.txt', data, delimiter=',')
z = np.loadtxt('data.txt', delimiter=',')
print(x)
print(y)
print(data)
print(dataT)
print(z)
import numpy as np
x = np.linspace(0, 2*np.pi,20)
y = np.cos(x)
z = np.sin(x)
%matplotlib inline
import matplotlib.pyplot as plt
#使用 help(plt.plot) 可以看到所有畫圖玩法
plt.plot(x,y,'b')
plt.plot(x,y,'go', label = 'cos(x)')
plt.plot(x,z,'r')
plt.plot(x,z,'go', label = 'sin(x)')
plt.legend(loc='best') # 放到最好的位置
plt.xlim([0, 2*np.pi])
import numpy as np
x = np.linspace(0, 2*np.pi,20)
y = np.cos(x)
z = np.sin(x)
%matplotlib inline
import matplotlib.pyplot as plt
#使用 help(plt.plot) 可以看到所有畫圖玩法
plt.subplot(2,1,1) #分成兩張圖 形式是(row, column, order)
plt.plot(x,y,'b')
plt.plot(x,y,'go', label = 'cos(x)')
plt.legend(loc='best') #放到最好的位置
plt.subplot(2,1,2) #分成兩張圖
plt.plot(x,z,'r')
plt.plot(x,z,'go', label = 'sin(x)')
plt.legend(loc='best') #放到最好的位置
plt.xlim([0, 2*np.pi])
```
# Functions, Conditions, Loop
```
import numpy as np
def f(x):
return x**2
x = np.linspace(0,5,10)
y = f(x)
print(y)
import numpy as np
def f(x): #這是個奇怪的練習用函數
res = x
if res < 3:
res = np.nan #<3就傳 Not a Number
elif res < 15:
res = x**3
else:
res = x**4
return res
x = np.linspace(0,10,20)
y = np.empty_like(x)
#Return a new array with the same shape and type as a given array.
#傳一個跟x一樣的array回來
i = 0
for xi in x:
y[i] = f(xi)
i = i + 1
print(y)
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(x,y,'bp')
plt.xlim([0,11])
```
# Matrices, linear equations
```
A = np.array([[1,2],[3,2]])
B = np.array([1,0])
# x = A^-1 * b
sol1 = np.dot(np.linalg.inv(A),B)
print(sol1)
sol2 = np.linalg.solve(A,B)
print(sol2)
import sympy as sym
sym.init_printing()
#This will automatically enable the best printer available in your environment.
x,y = sym.symbols('x y')
z = sym.linsolve([3*x+2*y-1,x+2*y],(x,y))
z
#sym.pprint(z) The ASCII pretty printer
```
# Non-linear equation
```
from scipy.optimize import fsolve
def f(z): #用z參數來表示x和y,做函數運算
x = z[0]
y = z[1]
return [x+2*y, x**2+y**2-1]
z0 = [0,1]
z = fsolve(f,z0)
print(z)
print(f(z))
```
# Integration
```
from scipy.integrate import quad
def f(x):
return x**2
quad(f,0,2) #計算積分值
import sympy as sym
sym.init_printing()
x = sym.Symbol('x')
f = sym.integrate(x**2,x)
f.subs(x,2) #將值帶入函數中
f
```
# Derivative
```
from scipy.misc import derivative
def f(x):
return x**2
print(derivative(f,2,dx=0.01)) #dx表示精確程度
import sympy as sym
sym.init_printing()
x = sym.Symbol('x')
f = sym.diff(x**3,x)
f.subs(x,2) #將值帶入函數中,得解
f
```
# Interpolation
```
from scipy.interpolate import interp1d #中間的字是1不是L喔!!!
x = np.arange(0,6,1)
y = np.array([0.2,0.3,0.5,1.0,0.9,1.1])
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(x,y,'bo')
xp = np.linspace(0,5,100) #為了顯示差別把點增加
y1 = interp1d(x,y,kind='linear') #一階
plt.plot(xp,y1(xp),'r-')
y2 = interp1d(x,y,kind='quadratic') #二階
plt.plot(xp,y2(xp),'k--')
y3 = interp1d(x,y,kind='cubic') #三階
plt.plot(xp,y3(xp),'g--')
```
# Linear regression
```
import numpy as np
x = np.array([0,1,2,3,4,5])
y = np.array([0.1,0.2,0.3,0.5,0.8,2.0 ])
#多項式逼近法,選擇階層
p1 = np.polyfit(x,y,1)
print(p1)
p2 = np.polyfit(x,y,2)
print(p2)
p3 = np.polyfit(x,y,3)
print(p3)
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(x,y,'ro')
# np.polyval表示多項式的值,把係數p_帶入多項式x求出來的值
xp = np.linspace(0,5,100)
plt.plot(xp, np.polyval(p1,xp), 'b-', label='linear') #這個字是polyvaL喔!!
plt.plot(xp, np.polyval(p2,xp), 'g--', label='quadratic')
plt.plot(xp, np.polyval(p3,xp), 'k:', label='cubic')
plt.legend(loc='best')
```
# Nonlinear regression
```
import numpy as np
from scipy.optimize import curve_fit
x = np.array([0,1,2,3,4,5])
y = np.array([0.1,0.2,0.3,0.5,0.8,2.0 ])
#多項式逼近法,選擇階層
p1 = np.polyfit(x,y,1)
print(p1)
p2 = np.polyfit(x,y,2)
print(p2)
p3 = np.polyfit(x,y,3)
print(p3)
#使用指數對數
def f(x,a):
return 0.1 * np.exp(a*x)
a = curve_fit(f,x,y)[0] #非線性回歸,Use non-linear least squares to fit a function,取第0項
print('a='+str(a))
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(x,y,'ro')
# np.polyval表示多項式的值,把係數p_帶入多項式x求出來的值
xp = np.linspace(0,5,100)
plt.plot(xp, np.polyval(p1,xp), 'b-', label='linear') #這個字是polyvaL喔!!
plt.plot(xp, np.polyval(p2,xp), 'g--', label='quadratic')
plt.plot(xp, np.polyval(p3,xp), 'k:', label='cubic')
plt.plot(xp, f(xp,a), 'c', label='nonlinear')
plt.legend(loc='best')
```
# Differential equation
```
from scipy.integrate import odeint
def dydt(y,t,a):
return -a * y
a = 0.5
t = np.linspace(0,20)
y0 = 5.0
y = odeint(dydt,y0,t,args=(a,))
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(t,y)
plt.xlabel('time')
plt.ylabel('y')
```
# Nonlinear optimization
```
#概念:要有Objective、Constraint,然後初始猜想值
import numpy as np
from scipy.optimize import minimize
def objective(x): #此函數求最小值
x1 = x[0]
x2 = x[1]
x3 = x[2]
x4 = x[3]
return x1*x4*(x1+x2+x3)+x3
#用減法做比較
def constraint1(x):
return x[0]*x[1]*x[2]*x[3] - 25.0
#用減法做比較
def constraint2(x):
sum_sq = 40.0
for i in range(0,4):
sum_sq = sum_sq - x[i]**2
return sum_sq
#初始猜想值
x0 = [1,5,5,1]
print(objective(x0))
#設定值域
b = (1.0,5.0) #x的值域
bnds = (b,b,b,b) #四個值域都一樣b
con1 = {'type':'ineq','fun': constraint1} #第一個是不等式
con2 = {'type':'eq','fun': constraint2} #第二個需要等式
cons = [con1,con2] #cons合成一個list
sol = minimize(objective,x0,method='SLSQP',\
bounds = bnds, constraints = cons)
print(sol)
print(sol.fun)
print(sol.x)
```
| github_jupyter |
# PyFunc Model + Transformer Example
This notebook demonstrates how to deploy a Python function based model and a custom transformer. This type of model is useful as user would be able to define their own logic inside the model as long as it satisfy contract given in `merlin.PyFuncModel`. If the pre/post-processing steps could be implemented in Python, it's encouraged to write them in the PyFunc model code instead of separating them into another transformer.
The model we are going to develop and deploy is a cifar10 model accepts a tensor input. The transformer has preprocessing step that allows the user to send a raw image data and convert it to a tensor input.
## Requirements
- Authenticated to gcloud (```gcloud auth application-default login```)
```
!pip install --upgrade -r requirements.txt > /dev/null
import warnings
warnings.filterwarnings('ignore')
```
## 1. Initialize Merlin
### 1.1 Set Merlin Server
```
import merlin
MERLIN_URL = "<MERLIN_HOST>/api/merlin"
merlin.set_url(MERLIN_URL)
```
### 1.2 Set Active Project
`project` represent a project in real life. You may have multiple model within a project.
`merlin.set_project(<project-name>)` will set the active project into the name matched by argument. You can only set it to an existing project. If you would like to create a new project, please do so from the MLP UI.
```
PROJECT_NAME = "sample"
merlin.set_project(PROJECT_NAME)
```
### 1.3 Set Active Model
`model` represents an abstract ML model. Conceptually, `model` in Merlin is similar to a class in programming language. To instantiate a `model` you'll have to create a `model_version`.
Each `model` has a type, currently model type supported by Merlin are: sklearn, xgboost, tensorflow, pytorch, and user defined model (i.e. pyfunc model).
`model_version` represents a snapshot of particular `model` iteration. You'll be able to attach information such as metrics and tag to a given `model_version` as well as deploy it as a model service.
`merlin.set_model(<model_name>, <model_type>)` will set the active model to the name given by parameter, if the model with given name is not found, a new model will be created.
```
from merlin.model import ModelType
MODEL_NAME = "transformer-pyfunc"
merlin.set_model(MODEL_NAME, ModelType.PYFUNC)
```
## 2. Train Model
In this step, we are going to train a cifar10 model using PyToch and create PyFunc model class that does the prediction using trained PyTorch model.
### 2.1 Prepare Training Data
```
import torch
import torchvision
import torchvision.transforms as transforms
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
```
### 2.2 Create PyTorch Model
```
import torch.nn as nn
import torch.nn.functional as F
class PyTorchModel(nn.Module):
def __init__(self):
super(PyTorchModel, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
```
### 2.3 Train Model
```
import torch.optim as optim
net = PyTorchModel()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs; data is a list of [inputs, labels]
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
```
### 2.4 Check Prediction
```
dataiter = iter(trainloader)
inputs, labels = dataiter.next()
predict_out = net(inputs[0:1])
predict_out
```
### 2.5 Serialize Model
```
import os
model_dir = "pytorch-model"
model_path = os.path.join(model_dir, "model.pt")
model_class_path = os.path.join(model_dir, "model.py")
torch.save(net.state_dict(), model_path)
```
### 2.6 Save PyTorchModel Class
We also need to save the PyTorchModel class and upload it to Merlin alongside the serialized trained model. The next cell will write the PyTorchModel we defined above to `pytorch-model/model.py` file.
```
%%file pytorch-model/model.py
import torch.nn as nn
import torch.nn.functional as F
class PyTorchModel(nn.Module):
def __init__(self):
super(PyTorchModel, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
```
## 3. Create PyFunc Model
To create a PyFunc model you'll have to extend `merlin.PyFuncModel` class and implement its `initialize` and `infer` method.
`initialize` will be called once during model initialization. The argument to `initialize` is a dictionary containing a key value pair of artifact name and its URL. The artifact's keys are the same value as received by `log_pyfunc_model`.
`infer` method is the prediction method that is need to be implemented. It accept a dictionary type argument which represent incoming request body. `infer` should return a dictionary object which correspond to response body of prediction result.
In following example we are creating PyFunc model called `CifarModel`. In its `initialize` method we expect 2 artifacts called `model_path` and `model_class_path`, those 2 artifacts would point to the serialized model and the PyTorch model class file. The `infer` method will simply does prediction for the model and return the result.
```
import importlib
import sys
from merlin.model import PyFuncModel
MODEL_CLASS_NAME="PyTorchModel"
class CifarModel(PyFuncModel):
def initialize(self, artifacts):
model_path = artifacts["model_path"]
model_class_path = artifacts["model_class_path"]
# Load the python class into memory
sys.path.append(os.path.dirname(model_class_path))
modulename = os.path.basename(model_class_path).split('.')[0].replace('-', '_')
model_class = getattr(importlib.import_module(modulename), MODEL_CLASS_NAME)
# Make sure the model weight is transform with the right device in this machine
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
self._pytorch = model_class().to(device)
self._pytorch.load_state_dict(torch.load(model_path, map_location=device))
self._pytorch.eval()
def infer(self, request, **kwargs):
inputs = torch.tensor(request["instances"])
result = self._pytorch(inputs)
return {"predictions": result.tolist()}
```
Now, let's test it locally.
```
import json
with open(os.path.join("input-tensor.json"), "r") as f:
tensor_req = json.load(f)
m = CifarModel()
m.initialize({"model_path": model_path, "model_class_path": model_class_path})
m.infer(tensor_req)
```
## 4. Deploy Model
To deploy the model, we will have to create an iteration of the model (by create a `model_version`), upload the serialized model to MLP, and then deploy.
### 4.1 Create Model Version and Upload
`merlin.new_model_version()` is a convenient method to create a model version and start its development process. It is equal to following codes:
```
v = model.new_model_version()
v.start()
v.log_pyfunc_model(model_instance=EnsembleModel(),
conda_env="env.yaml",
artifacts={"xgb_model": model_1_path, "sklearn_model": model_2_path})
v.finish()
```
To upload PyFunc model you have to provide following arguments:
1. `model_instance` is the instance of PyFunc model, the model has to extend `merlin.PyFuncModel`
2. `conda_env` is path to conda environment yaml file. The environment yaml file must contain all dependency required by the PyFunc model.
3. (Optional) `artifacts` is additional artifact that you want to include in the model
4. (Optional) `code_path` is a list of directory containing python code that will be loaded during model initialization, this is required when `model_instance` depend on local python package
```
with merlin.new_model_version() as v:
merlin.log_pyfunc_model(model_instance=CifarModel(),
conda_env="env.yaml",
artifacts={"model_path": model_path, "model_class_path": model_class_path})
```
### 4.2 Deploy Model and Transformer
To deploy a model and its transformer, you must pass a `transformer` object to `deploy()` function. Each of deployed model version will have its own generated url.
```
from merlin.resource_request import ResourceRequest
from merlin.transformer import Transformer
# Create a transformer object and its resources requests
resource_request = ResourceRequest(min_replica=1, max_replica=1,
cpu_request="100m", memory_request="200Mi")
transformer = Transformer("gcr.io/kubeflow-ci/kfserving/image-transformer:latest",
resource_request=resource_request)
endpoint = merlin.deploy(v, transformer=transformer)
```
### 4.3 Send Test Request
```
import json
import requests
with open(os.path.join("input-raw-image.json"), "r") as f:
req = json.load(f)
resp = requests.post(endpoint.url, json=req)
resp.text
```
## 4. Clean Up
## 4.1 Delete Deployment
```
merlin.undeploy(v)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/mghendi/smartphonepriceclassifier/blob/main/CCI_501_ML_Project.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## CCI501 - Machine Learning Project
### Name: Samuel Mwamburi Mghendi
### Admission Number: P52/37621/2020
### Email: [email protected]
### Course: Machine Learning – CCI 501
### Applying Logistic Regression to Establish a Good Pricing Model for Mobile Phone Manufacturers in the Current Market Landscape using Technical Specifications and User Preference.
#### This report is organised as follows.
1. Problem Statement
2. Data Description
* Data Loading and Preparation
* Exploratory Data Analysis
3. Data Preprocessing
4. Data Modelling
5. Performance Evaluation
6. Conclusion
### 1. Problem Statement
#### To determine the price of a mobile phone in the current market using specifications i.e. screen size, screen and camera resolution, internal storage and battery capacity and user preference.
Traditionally, and rightfully so, consumers have been forced to part with a premium to own a mobile phone with top-of-the-line features and specifications. Some smartphone manufacturers in 2020 still charge upwards of KES 100,000 for a mobile phone that has a large screen, good battery, fast processor and sufficient storage capacity. However, according to a December article on Android Central, mobile phones with great features are getting significantly affordable. (Johnson, 2020)
A phone’s specifications is a logical way of determining which class it falls under, with the emergence of cheaper manufacturing techniques and parts however, phone pricing models have become more blurry and it is possible for consumers to purchase more powerful smartphones at cheaper prices.
This study intends to explore this hypothesis and predict the relationship between these features and the price of a mobile phone in the current landscape using phone specification, product rating and prices data scraped from a Kenyan e-commerce site.
#### Why Logistic Regression?
A supervised learning approach would be useful for this experiment since the data being explored has price labels and categories. Logistic regression is used to classify data by considering outcome variables on extreme ends and consequently forms a line to distinguish them.
### 2. Data Description
#### Data Loading and Preparation
#### Initialization
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
from tqdm import trange
```
#### Import Data
```
df = pd.read_csv("productdata.csv")
df
from sklearn import preprocessing
```
#### Exploratory Data Analysis
Gathering more information about the dataset in order to better understand it.
The relationship and distribution between screen size, screen resolution, camera resolution, storage space, memory, rating and likes against the resultant price charged for each phone sold was plotted and analyzed.
```
df.describe()
df.info()
```
The feature OS has missing values.
```
# check shape
df.shape
```
The dataset has 1,148 records and 12 features.
```
# remove duplicates, if any
df.drop_duplicates(inplace = True)
df.shape
```
No duplicate records available in the dataset.
#### Mobile Phones by Screen Size Contrasted by User Rating
```
# previewing distribution of screen size by rating
df['Round Rating'] = df['Rating'].round(decimals=0)
plt.figure(figsize = (20, 6))
ax = sns.histplot(df, x="Screen (inches)", stat="count", hue="Round Rating", multiple="dodge", shrink=0.8)
for p in ax.patches:# histogram bar label
h = p.get_height()
if (h != 0): ax.text(x = p.get_x()+(p.get_width()/2), y = h+1, s = "{:.0f}".format(h),ha = "center")
plt.xlabel('Screen Size (inches)')
plt.title("Screen Size of Mobile Phones contrasted by User Rating", fontsize=12, fontweight="bold");
plt.show()
print("Screen Size: values count=" + str(df['Screen (inches)'].count()) + ", min=" + str(df['Screen (inches)'].min()) + ", max=" + str(df['Screen (inches)'].max()) + ", mean=" + str(df['Screen (inches)'].mean()))
```
The chart can be used to deduce a high-level inference on the phone industry consumer purchase preference. Phones with a larger screen size, which are inherently larger in size, between 5 to 7 inches are seen to be rated higher.
```
# changing the datatype of the 'OS' variable
df['OS'] = df['OS'].astype('str')
```
#### Mobile Phones by Camera Resolution contrasted by User Rating
```
# previewing distribution of camera resolution by rating
plt.figure(figsize = (20, 6))
ax = sns.histplot(df, x="Camera (MP)", hue="Round Rating", multiple="dodge", shrink=0.8)
for p in ax.patches:# label each bar in histogram
h = p.get_height()
if (h != 0): ax.text(x = p.get_x()+(p.get_width()/2), y = h+1, s = "{:.0f}".format(h),ha = "center")
plt.xlabel('Camera (MP)')
plt.title("Distribution of Camera Resolution by User Rating", fontsize=12, fontweight="bold");
plt.show()
print("Camera (MP): values count=" + str(df['Camera (MP)'].count()) + ", min=" + str(df['Camera (MP)'].min()) + ", max=" + str(df['Camera (MP)'].max()) + ", mean=" + str(df['Camera (MP)'].mean()))
```
Mobile phones with cameras sporting high resolutions,15 and 32 Megapixels , based on the current offering in the market have significantly better relative ratings than mid-tier models between 20 to 30 Megapixels and low-tier models less than 5 megapixels.
```
# previewing distribution of Storage Capacity by rating
plt.figure(figsize = (20, 6))
ax = sns.histplot(df, x="Storage (GB)", hue="Round Rating", multiple="dodge", shrink=0.8)
for p in ax.patches:# label each bar in histogram
h = p.get_height()
if (h != 0): ax.text(x = p.get_x()+(p.get_width()/2), y = h+1, s = "{:.0f}".format(h),ha = "center")
plt.xlabel('Storage (GB)')
plt.title("Distribution of Storage Capacity by User Rating", fontsize=12, fontweight="bold");
plt.show()
print("Storage (GB): values count=" + str(df['Storage (GB)'].count()) + ", min=" + str(df['Storage (GB)'].min()) + ", max=" + str(df['Storage (GB)'].max()) + ", mean=" + str(df['Storage (GB)'].mean()))
```
As anticipated, mobile phones with higher internal storage capacities, greater than or equal to 256 Gigabytes, recieve significantly better relative ratings than models with less than 128 gigabytes. Additionally, there are very few purchases of mobile phones equal to or greater than 512 gigabytes of storage.
#### Mobile Phones Specifications by User Preference(Likes)
In the E-Commerce store from which the data was retrieved, users are also capable of adding a product to their wishlist after a high level assessment of the product features and pricing. The number of likes a product has recieved refers to the number of users who have added the given product to their wishlist.
```
#pairplot to investigate the relationship between all the variables
sns.pairplot(df)
plt.show()
```
In reference to the pair plot above, mid-tier phone models are significantly better rated and well recieved as compared to their much more expensive and budget counterparts in the local current market.
Phones with mid-tier features such as an average storage capacity, such as a large display 5 to 7 inches, storage of between 128 Gigabytes of storage, 4 Gigabytes of RAM, 3000 to 5000 milliampere hours battery capacity and 10 to 30 Megapixel Camera Resolution are well recieve more likes.
There appears to be a direct correlation between the number of likes a product recieves before-hand and the user ratings after purchase. Mobile phones that recieved an average rating of 4 had roughly 300 likes from users based on the specifications and price point provided.
This also implies that the likes a product recieved directly translates to an purchase of the product in the long term.
### 3. Data Preprocessing
#### Converting Text to Numerical Vector
The features Price Category and Battery Type contain important dependent and independent values respectively key in the experiment. These values would need to be converted into numerical values in order to be applied in the algorithm.
```
# creating categorigal variables for the battery type feature
df["Battery Type"].replace({"Li-Po": "0", "Li-Ion": "1"}, inplace=True)
print(df)
# creating categorigal variables for the battery type feature
df["Price Category"].replace({"Budget": "0", "Mid-Tier": "1", "Flagship": "2"}, inplace=True)
print(df)
df["Price Category"].value_counts(normalize= True)
import nltk
import string
import math
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import SGDClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn import metrics
import re
import string
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(min_df=0, lowercase=False)
vectorizer.fit(df["OS"])
vectorizer.vocabulary_
vectorizer = CountVectorizer(min_df=0, lowercase=False)
vectorizer.fit(df["Resolution (pixels)"])
vectorizer.vocabulary_
```
#### Creating Bag of Words models
```
df["OS"] = vectorizer.transform(df["OS"]).toarray()
print(df)
df["Resolution (pixels)"] = vectorizer.transform(df["Resolution (pixels)"]).toarray()
print (df)
```
### 4. Data Modelling
### Data Modelling for Logistic Regression
#### Feature Selection
For this experiment, the mobile phone's technical specifications will be used as the independent variables. The ratings and likes which are subjective assessments will be dropped.
Variables such as the Phone Name are not important in price point predictability for this particular endevour and will therefore be dropped.
```
X = df.drop(columns = ['Phone','Price(Kshs)', 'Rating', 'Likes', 'OS', 'Battery Type', 'Resolution (pixels)', 'Round Rating']).values
y = df['Price Category'].values
```
#### Splitting Data
```
# splitting into 75% training and 25% test sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=1000)
```
#### Feature Scaling
```
scaler = preprocessing.StandardScaler().fit(X_train)
scaler
scaler.mean_
scaler.scale_
X_scaled = scaler.transform(X_train)
X_scaled
X_scaled.mean(axis=0)
X_scaled.std(axis=0)
```
#### Logistic Regression
```
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
X, y = make_classification(random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
pipe = make_pipeline(StandardScaler(), LogisticRegression())
pipe.fit(X_train, y_train) # apply scaling on training data
# apply scaling on testing data, without leaking training data.
pipe.score(X_test, y_test)
classifier = LogisticRegression()
classifier.fit(X_train, y_train)
score = classifier.score(X_test, y_test)
```
### 5. Performance Evaluation
```
print("Accuracy:", (score)*100, "%")
```
### 6. Conclusion
Logistic regression provides great efficiency, works well in the segmentation and categorization of a small number of categorical variables, in this case, price category.
It allows the evaluation of multiple explanatory variables and is relatively fast compared to other supervised classification techniques applied in this experiment such as SVM.
It is, however, not accurate enough for complex relationships between variables denoted by the exclusion of multiple features.
This algorithm seems to have performed well in the creation of this model because the decision boundary was rather linear as observed during the exploratory analysis between the various technical specifications against the pricing model.
| github_jupyter |
# PROYECTO CIFAR-10
## CARLOS CABAÑÓ
## 1. Librerias
Descargamos la librería para los arrays en preprocesamiento de Keras
```
from tensorflow import keras as ks
from matplotlib import pyplot as plt
import numpy as np
import time
import datetime
import random
from sklearn.preprocessing import LabelEncoder
from tensorflow.keras.regularizers import l2
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.preprocessing.image import ImageDataGenerator
```
## 2. Arquitectura de red del modelo
Adoptamos la arquitectura del modelo 11 con los ajustes en Batch Normalization, Kernel Regularizer y Kernel Initializer. Añadimos Batch normalization a las capas de convolución.
```
model = ks.Sequential()
model.add(ks.layers.Conv2D(64, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same', input_shape=(32,32,3)))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Conv2D(64, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.MaxPooling2D((2, 2)))
model.add(ks.layers.Dropout(0.2))
model.add(ks.layers.Conv2D(128, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Conv2D(128, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(ks.layers.Dropout(0.2))
model.add(ks.layers.Conv2D(256, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Conv2D(256, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Conv2D(256, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(ks.layers.Dropout(0.2))
model.add(ks.layers.Conv2D(512, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Conv2D(512, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Conv2D(512, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Conv2D(512, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(ks.layers.Conv2D(512, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Conv2D(512, (3, 3), strides=1, activation='relu', kernel_regularizer=l2(0.0005), kernel_initializer="he_uniform", padding='same'))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Dropout(0.3))
model.add(ks.layers.Flatten())
model.add(ks.layers.Dense(512, activation='relu', kernel_regularizer=l2(0.001), kernel_initializer="he_uniform"))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Dropout(0.4))
model.add(ks.layers.Dense(512, activation='relu', kernel_regularizer=l2(0.001), kernel_initializer="he_uniform"))
model.add(ks.layers.BatchNormalization())
model.add(ks.layers.Dropout(0.5))
model.add(ks.layers.Dense(10, activation='softmax'))
model.summary()
```
## 3. Optimizador, función error
Añadimos el learning rate al optimizador
```
from keras.optimizers import SGD
model.compile(optimizer=SGD(lr=0.001, momentum=0.9),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
```
## 4. Preparamos los datos
```
cifar10 = ks.datasets.cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
cifar10_labels = [
'airplane', # id 0
'automobile',
'bird',
'cat',
'deer',
'dog',
'frog',
'horse',
'ship',
'truck',
]
print('Number of labels: %s' % len(cifar10_labels))
```
Pintemos una muestra de las imagenes del dataset CIFAR10:
```
# Pintemos una muestra de las las imagenes del dataset MNIST
print('Train: X=%s, y=%s' % (x_train.shape, y_train.shape))
print('Test: X=%s, y=%s' % (x_test.shape, y_test.shape))
for i in range(9):
plt.subplot(330 + 1 + i)
plt.imshow(x_train[i], cmap=plt.get_cmap('gray'))
plt.title(cifar10_labels[y_train[i,0]])
plt.subplots_adjust(hspace = 1)
plt.show()
```
Hacemos la validación al mismo tiempo que el entrenamiento:
```
x_val = x_train[-10000:]
y_val = y_train[-10000:]
x_train = x_train[:-10000]
y_train = y_train[:-10000]
```
Hacemos el OHE para la clasificación
```
le = LabelEncoder()
le.fit(y_train.ravel())
y_train_encoded = le.transform(y_train.ravel())
y_val_encoded = le.transform(y_val.ravel())
y_test_encoded = le.transform(y_test.ravel())
```
## 5. Ajustes: Early Stopping
Definimos un early stopping con base en el loss de validación y con el parámetro de "patience" a 10, para tener algo de margen. Con el Early Stopping lograremos parar el entrenamiento en el momento óptimo para evitar que siga entrenando a partir del overfitting.
```
callback_val_loss = EarlyStopping(monitor="val_loss", patience=5)
callback_val_accuracy = EarlyStopping(monitor="val_accuracy", patience=10)
```
## 6. Transformador de imágenes
### 6.1 Imágenes de entrenamiento
```
train_datagen = ImageDataGenerator(
horizontal_flip=True,
width_shift_range=0.2,
height_shift_range=0.2,
)
train_generator = train_datagen.flow(
x_train,
y_train_encoded,
batch_size=64
)
```
### 6.2 Imágenes de validación y testeo
```
validation_datagen = ImageDataGenerator(
horizontal_flip=True,
width_shift_range=0.2,
height_shift_range=0.2,
)
validation_generator = validation_datagen.flow(
x_val,
y_val_encoded,
batch_size=64
)
test_datagen = ImageDataGenerator(
horizontal_flip=True,
width_shift_range=0.2,
height_shift_range=0.2,
)
test_generator = test_datagen.flow(
x_test,
y_test_encoded,
batch_size=64
)
```
### 6.3 Generador de datos
```
sample = random.choice(range(0,1457))
image = x_train[sample]
plt.imshow(image, cmap=plt.cm.binary)
sample = random.choice(range(0,1457))
example_generator = train_datagen.flow(
x_train[sample:sample+1],
y_train_encoded[sample:sample+1],
batch_size=64
)
plt.figure(figsize=(12, 12))
for i in range(0, 15):
plt.subplot(5, 3, i+1)
for X, Y in example_generator:
image = X[0]
plt.imshow(image)
break
plt.tight_layout()
plt.show()
```
## 7. Entrenamiento
```
t = time.perf_counter()
steps=int(x_train.shape[0]/64)
history = model.fit(train_generator, epochs=100, use_multiprocessing=False, batch_size= 64, validation_data=validation_generator, steps_per_epoch=steps, callbacks=[callback_val_loss, callback_val_accuracy])
elapsed_time = datetime.timedelta(seconds=(time.perf_counter() - t))
print('Tiempo de entrenamiento:', elapsed_time)
```
## 8. Evaluamos los resultados
```
_, acc = model.evaluate(x_test, y_test_encoded, verbose=0)
print('> %.3f' % (acc * 100.0))
plt.title('Cross Entropy Loss')
plt.plot(history.history['loss'], color='blue', label='train')
plt.plot(history.history['val_loss'], color='orange', label='test')
plt.show()
plt.title('Classification Accuracy')
plt.plot(history.history['accuracy'], color='blue', label='train')
plt.plot(history.history['val_accuracy'], color='orange', label='test')
plt.show()
predictions = model.predict(x_test)
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array, true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(predicted_label,
100*np.max(predictions_array),
true_label[0]),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array, true_label[i]
plt.grid(False)
plt.xticks(range(10))
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[predicted_label].set_color('red')
thisplot[true_label[0]].set_color('blue')
```
Dibujamos las primeras imágenes:
```
i = 0
for l in cifar10_labels:
print(i, l)
i += 1
num_rows = 5
num_cols = 4
start = 650
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i+start, predictions[i+start], y_test, x_test)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i+start, predictions[i+start], y_test)
plt.tight_layout()
plt.show()
```
| github_jupyter |
```
__author__ = "Jithin Pradeep"
__copyright__ = "Copyright (C) 2018 Jithin Pradeep"
__license__ = "MIT License"
__version__ = "1.0"
```
# Summary
## About the Dataset
The data files train.csv and test.csv contain gray-scale images of hand-drawn digits, from zero through nine.
Each image is 28 pixels in height and 28 pixels in width, for a total of 784 pixels in total. Each pixel has a single pixel-value associated with it, indicating the lightness or darkness of that pixel, with higher numbers meaning darker. This pixel-value is an integer between 0 and 255, inclusive.
The training data set, (train.csv), has 785 columns. The first column, called "label", is the digit that was drawn by the user. The rest of the columns contain the pixel-values of the associated image.
Each pixel column in the training set has a name like pixelx, where x is an integer between 0 and 783, inclusive. To locate this pixel on the image, suppose that we have decomposed x as x = i * 28 + j, where i and j are integers between 0 and 27, inclusive. Then pixelx is located on row i and column j of a 28 x 28 matrix, (indexing by zero).
For example, pixel31 indicates the pixel that is in the fourth column from the left, and the second row from the top, as in the ascii-diagram below.
Visually, the pixels make up the image like this:
000 001 002 003 ... 026 027
028 029 030 031 ... 054 055
056 057 058 059 ... 082 083
| | | | ... | |
728 729 730 731 ... 754 755
756 757 758 759 ... 782 783
The test data set, (test.csv), is the same as the training set, except that it does not contain the "label" column.
[More about MNIST Dataset can be found here](http://yann.lecun.com/exdb/mnist/)
[Wiki Link](https://en.wikipedia.org/wiki/MNIST_database)
## Method
In this post I will be describing my solution to classify handwritten digits(MNIST Dataset). Below is a deep neural network(Convolution neural network) consisting of convolution and fully connected layers.

Go ahead and use the tensorboard for deatiled visualization saved from the model.
```
import numpy as np
import pandas as pd
import tensorflow as tf
import keras.preprocessing.image
import sklearn.preprocessing
import sklearn.model_selection
import sklearn.metrics
import sklearn.linear_model
import sklearn.naive_bayes
import sklearn.tree
import sklearn.ensemble
import os;
import datetime
import cv2
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.cm as cm
%matplotlib inline
import platform
print("Platform deatils {0} \nPython version {1}".format(
platform.platform(), platform.python_version()))
```
Additional info: I am going to use the Kaggle csv based data set but MNIST Data set can also be downloaded and extracted using the below functions.
#### Function to downlaod and Extract MNIST Dataset
```
url = 'http://commondatastorage.googleapis.com/books1000/'
last_percent_reported = None
def download_progress_hook(count, blockSize, totalSize):
"""A hook to report the progress of a download. This is mostly intended for users with
slow internet connections. Reports every 1% change in download progress.
"""
global last_percent_reported
percent = int(count * blockSize * 100 / totalSize)
if last_percent_reported != percent:
if percent % 5 == 0:
sys.stdout.write("%s%%" % percent)
sys.stdout.flush()
else:
sys.stdout.write(".")
sys.stdout.flush()
last_percent_reported = percent
def maybe_download(filename, expected_bytes, force=False):
"""Download a file if not present, and make sure it's the right size."""
if force or not os.path.exists(filename):
print('Attempting to download:', filename)
filename, _ = urlretrieve(url + filename, filename, reporthook=download_progress_hook)
print('\nDownload Complete!')
statinfo = os.stat(filename)
if statinfo.st_size == expected_bytes:
print('Found and verified', filename)
else:
raise Exception(
'Failed to verify ' + filename + '. Can you get to it with a browser?')
return filename
train_filename = maybe_download('notMNIST_large.tar.gz', 247336696)
test_filename = maybe_download('notMNIST_small.tar.gz', 8458043)
num_classes = 10
np.random.seed(133)
def maybe_extract(filename, force=False):
root = os.path.splitext(os.path.splitext(filename)[0])[0] # remove .tar.gz
if os.path.isdir(root) and not force:
# You may override by setting force=True.
print('%s already present - Skipping extraction of %s.' % (root, filename))
else:
print('Extracting data for %s. This may take a while. Please wait.' % root)
tar = tarfile.open(filename)
sys.stdout.flush()
tar.extractall()
tar.close()
data_folders = [
os.path.join(root, d) for d in sorted(os.listdir(root))
if os.path.isdir(os.path.join(root, d))]
if len(data_folders) != num_classes:
raise Exception(
'Expected %d folders, one per class. Found %d instead.' % (
num_classes, len(data_folders)))
print(data_folders)
return data_folders
train_folders = maybe_extract(train_filename)
test_folders = maybe_extract(test_filename)
#Load the input file from the folder
if os.path.isfile('MNISTdatacsv/train.csv'):
data_df = pd.read_csv('MNISTdatacsv/train.csv')
print('train.csv loaded: data_df({0[0]},{0[1]})'.format(data_df.shape))
else:
print('Error: train.csv not found')
## read test data
# read test data from CSV file
if os.path.isfile('MNISTdatacsv/test.csv'):
test_df = pd.read_csv('MNISTdatacsv/test.csv')
print('test.csv loaded: test_df{0}'.format(test_df.shape))
else:
print('Error: test.csv not found')
# transforma and normalize test data
x_test = test_df.iloc[:,0:].values.reshape(-1,28,28,1) # (28000,28,28,1) array
x_test = x_test.astype(np.float)
x_test = normalize_data(x_test)
print('x_test.shape = ', x_test.shape)
# for saving results
y_test_pred = {}
y_test_pred_labels = {}
```
### Preprocessing
#### Normalize data and split into training and validation sets
- In order to scale feature that robust to outlier you can use sklearn.preprocessing.RobustScaler()
- rtoo = sklearn.preprocessing.RobustScaler()
- rtoo.fit(data)
- data = rtoo.transform(data)
- or you can do standraization by using mean and std dev
- data = (data-data.mean())/(data.std()) (Try different normalization techniques
- to understand more about normalization, these are just few)
- Another idea might be is to convert the rgb range to -1 to 1 from 255 to 0
- data = ((data / 255.)-0.5)*2.
- I am converting the range to 0 to 1
[One hot encoding my notes](http://jp.jithinjp.in/2018/Representing-Categorical-values-in-Machine-learning)
```
# function to normalize data
def normalize_data(data):
data = data / data.max() # convert from [0:255] to [0.:1.]
return data
# class labels to one-hot vectors e.g. 1 => [0 1 0 0 0 0 0 0 0 0]
def dense_to_one_hot(labels_dense, num_classes):
num_labels = labels_dense.shape[0]
index_offset = np.arange(num_labels) * num_classes
labels_one_hot = np.zeros((num_labels, num_classes))
labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1
return labels_one_hot
# one-hot encodings into labels
def one_hot_to_dense(labels_one_hot):
return np.argmax(labels_one_hot,1)
# accuracy o
def accuracy_from_dense_labels(y_target, y_pred):
y_target = y_target.reshape(-1,)
y_pred = y_pred.reshape(-1,)
return np.mean(y_target == y_pred)
# accuracy of one-hot encoded predictions
def accuracy_from_one_hot_labels(y_target, y_pred):
y_target = one_hot_to_dense(y_target).reshape(-1,)
y_pred = one_hot_to_dense(y_pred).reshape(-1,)
return np.mean(y_target == y_pred)
# extract and normalize images
x_train_valid = data_df.iloc[:,1:].values.reshape(-1,28,28,1) # (42000,28,28,1) array
x_train_valid = x_train_valid.astype(np.float) # convert from int64 to float32
x_train_valid = normalize_data(x_train_valid)
image_width = image_height = 28
image_size = 784
# extract image labels
y_train_valid_labels = data_df.iloc[:,0].values # (42000,1) array
labels_count = np.unique(y_train_valid_labels).shape[0]; # number of different labels = 10
#plot some images and labels
plt.figure(figsize=(15,9))
for i in range(50):
plt.subplot(5,10,1+i)
plt.title(y_train_valid_labels[i])
plt.imshow(x_train_valid[i].reshape(28,28), cmap=cm.inferno)
# labels in one hot representation
y_train_valid = dense_to_one_hot(y_train_valid_labels, labels_count).astype(np.uint8)
# dictionaries for saving results
y_valid_pred = {}
y_train_pred = {}
y_test_pred = {}
train_loss, valid_loss = {}, {}
train_acc, valid_acc = {}, {}
print('x_train_valid.shape = ', x_train_valid.shape)
print('y_train_valid_labels.shape = ', y_train_valid_labels.shape)
print('image_size = ', image_size )
print('image_width = ', image_width)
print('image_height = ', image_height)
print('labels_count = ', labels_count)
```
#### Data augmenttaion
lets stick to basics like rotations, translations, zoom using keras
```
def generate_images(imgs):
# rotations, translations, zoom
image_generator = keras.preprocessing.image.ImageDataGenerator(
rotation_range = 10, width_shift_range = 0.1 , height_shift_range = 0.1,
zoom_range = 0.1)
# get transformed images
imgs = image_generator.flow(imgs.copy(), np.zeros(len(imgs)),
batch_size=len(imgs), shuffle = False).next()
return imgs[0]
# Visulizing the image augmnettaion
fig,axs = plt.subplots(5,10, figsize=(15,9))
for i in range(5):
n = np.random.randint(0,x_train_valid.shape[0]-2)
axs[i,0].imshow(x_train_valid[n:n+1].reshape(28,28),cmap=cm.inferno)
for j in range(1,10):
axs[i,j].imshow(generate_images(x_train_valid[n:n+1]).reshape(28,28), cmap=cm.inferno)
```
### Benchmarking on some basic ML models
As we have our training data ready lets run couple of basic machine elarning model, I would consider these models to kind of create a baseline which would help me later own to generlize the performance of my model. In simple word these would give me datapoints to compare the performance across models.
lets use Logistic regression, Extra tress regressor and Random forest model along with cross validation for benmarking.
```
logistic_regression = sklearn.linear_model.LogisticRegression(verbose=0, solver='lbfgs',multi_class='multinomial')
extra_trees = sklearn.ensemble.ExtraTreesClassifier(verbose=0)
random_forest = sklearn.ensemble.RandomForestClassifier(verbose=0)
bench_markingDict = {'logistic_regression': logistic_regression,
'extra_trees': extra_trees,
'random_forest': random_forest }
bench_marking = ['logistic_regression', 'extra_trees','random_forest']
for bm_model in bench_marking:
train_acc[bm_model] = []
valid_acc[bm_model] = []
cv_num = 10 # cross validations default = 20 => 5% validation set
kfold = sklearn.model_selection.KFold(cv_num, shuffle=True, random_state=123)
for i,(train_index, valid_index) in enumerate(kfold.split(x_train_valid)):
# start timer
start = datetime.datetime.now();
# train and validation data of original images
x_train = x_train_valid[train_index].reshape(-1,784)
y_train = y_train_valid[train_index]
x_valid = x_train_valid[valid_index].reshape(-1,784)
y_valid = y_train_valid[valid_index]
for bm_model in bench_marking:
# create cloned model from base models
model = sklearn.base.clone(bench_markingDict[bm_model])
model.fit(x_train, one_hot_to_dense(y_train))
# predictions
y_train_pred[bm_model] = model.predict_proba(x_train)
y_valid_pred[bm_model] = model.predict_proba(x_valid)
train_acc[bm_model].append(accuracy_from_one_hot_labels(y_train_pred[bm_model], y_train))
valid_acc[bm_model].append(accuracy_from_one_hot_labels(y_valid_pred[bm_model], y_valid))
print(i+1,': '+bm_model+' train/valid accuracy = %.3f/%.3f'%(train_acc[bm_model][-1],
valid_acc[bm_model][-1]))
# only one iteration
if False:
break;
print(bm_model+': averaged train/valid accuracy = %.3f/%.3f'%(np.mean(train_acc[bm_model]),
np.mean(valid_acc[bm_model])))
```
### Neural network -
Lets get to the fun part Neural network
```
class nn_class:
# class that implements the neural network
# constructor
def __init__(self, nn_name = 'nn_1'):
# hyperparameters
self.s_f_conv1 = 3; # filter size of first convolution layer (default = 3)
self.n_f_conv1 = 36; # number of features of first convolution layer (default = 36)
self.s_f_conv2 = 3; # filter size of second convolution layer (default = 3)
self.n_f_conv2 = 36; # number of features of second convolution layer (default = 36)
self.s_f_conv3 = 3; # filter size of third convolution layer (default = 3)
self.n_f_conv3 = 36; # number of features of third convolution layer (default = 36)
self.n_n_fc1 = 576; # number of neurons of first fully connected layer (default = 576)
# hyperparameters for training
self.mb_size = 50 # mini batch size
self.keep_prob = 0.33 # keeping probability with dropout regularization
self.learn_rate_array = [10*1e-4, 7.5*1e-4, 5*1e-4, 2.5*1e-4, 1*1e-4, 1*1e-4,
1*1e-4,0.75*1e-4, 0.5*1e-4, 0.25*1e-4, 0.1*1e-4,
0.1*1e-4, 0.075*1e-4,0.050*1e-4, 0.025*1e-4, 0.01*1e-4,
0.0075*1e-4, 0.0050*1e-4,0.0025*1e-4,0.001*1e-4]
self.learn_rate_step_size = 3 # in terms of epochs
# parameters
self.learn_rate = self.learn_rate_array[0]
self.learn_rate_pos = 0 # current position pointing to current learning rate
self.index_in_epoch = 0
self.current_epoch = 0
self.log_step = 0.2 # log results in terms of epochs
self.n_log_step = 0 # counting current number of mini batches trained on
self.use_tb_summary = False # True = use tensorboard visualization
self.use_tf_saver = False # True = use saver to save the model
self.nn_name = nn_name # name of the neural network
# permutation array
self.perm_array = np.array([])
# get the next mini batch
def next_mini_batch(self):
start = self.index_in_epoch
self.index_in_epoch += self.mb_size
self.current_epoch += self.mb_size/len(self.x_train)
# adapt length of permutation array
if not len(self.perm_array) == len(self.x_train):
self.perm_array = np.arange(len(self.x_train))
# shuffle once at the start of epoch
if start == 0:
np.random.shuffle(self.perm_array)
# at the end of the epoch
if self.index_in_epoch > self.x_train.shape[0]:
np.random.shuffle(self.perm_array) # shuffle data
start = 0 # start next epoch
self.index_in_epoch = self.mb_size # set index to mini batch size
if self.train_on_augmented_data:
# use augmented data for the next epoch
self.x_train_aug = normalize_data(self.generate_images(self.x_train))
self.y_train_aug = self.y_train
end = self.index_in_epoch
if self.train_on_augmented_data:
# use augmented data
x_tr = self.x_train_aug[self.perm_array[start:end]]
y_tr = self.y_train_aug[self.perm_array[start:end]]
else:
# use original data
x_tr = self.x_train[self.perm_array[start:end]]
y_tr = self.y_train[self.perm_array[start:end]]
return x_tr, y_tr
# generate new images via rotations, translations, zoom using keras
def generate_images(self, imgs):
print('generate new set of images')
# rotations, translations, zoom
image_generator = keras.preprocessing.image.ImageDataGenerator(
rotation_range = 10, width_shift_range = 0.1 , height_shift_range = 0.1,
zoom_range = 0.1)
# get transformed images
imgs = image_generator.flow(imgs.copy(), np.zeros(len(imgs)),
batch_size=len(imgs), shuffle = False).next()
return imgs[0]
# weight initialization
def weight_variable(self, shape, name = None):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial, name = name)
# bias initialization
def bias_variable(self, shape, name = None):
initial = tf.constant(0.1, shape=shape) # positive bias
return tf.Variable(initial, name = name)
# 2D convolution
def conv2d(self, x, W, name = None):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME', name = name)
# max pooling
def max_pool_2x2(self, x, name = None):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1],
padding='SAME', name = name)
# attach summaries to a tensor for TensorBoard visualization
def summary_variable(self, var, var_name):
with tf.name_scope(var_name):
mean = tf.reduce_mean(var)
stddev = tf.sqrt(tf.reduce_mean(tf.square(var - mean)))
tf.summary.scalar('mean', mean)
tf.summary.scalar('stddev', stddev)
tf.summary.scalar('max', tf.reduce_max(var))
tf.summary.scalar('min', tf.reduce_min(var))
tf.summary.histogram('histogram', var)
# function to create the graph
def create_graph(self):
# reset default graph
tf.reset_default_graph()
# variables for input and output
self.x_data_tf = tf.placeholder(dtype=tf.float32, shape=[None,28,28,1],
name='x_data_tf')
self.y_data_tf = tf.placeholder(dtype=tf.float32, shape=[None,10], name='y_data_tf')
# 1.layer: convolution + max pooling
self.W_conv1_tf = self.weight_variable([self.s_f_conv1, self.s_f_conv1, 1,
self.n_f_conv1],
name = 'W_conv1_tf') # (5,5,1,32)
self.b_conv1_tf = self.bias_variable([self.n_f_conv1], name = 'b_conv1_tf') # (32)
self.h_conv1_tf = tf.nn.relu(self.conv2d(self.x_data_tf,
self.W_conv1_tf) + self.b_conv1_tf,
name = 'h_conv1_tf') # (.,28,28,32)
self.h_pool1_tf = self.max_pool_2x2(self.h_conv1_tf,
name = 'h_pool1_tf') # (.,14,14,32)
# 2.layer: convolution + max pooling
self.W_conv2_tf = self.weight_variable([self.s_f_conv2, self.s_f_conv2,
self.n_f_conv1, self.n_f_conv2],
name = 'W_conv2_tf')
self.b_conv2_tf = self.bias_variable([self.n_f_conv2], name = 'b_conv2_tf')
self.h_conv2_tf = tf.nn.relu(self.conv2d(self.h_pool1_tf,
self.W_conv2_tf) + self.b_conv2_tf,
name ='h_conv2_tf') #(.,14,14,32)
self.h_pool2_tf = self.max_pool_2x2(self.h_conv2_tf, name = 'h_pool2_tf') #(.,7,7,32)
# 3.layer: convolution + max pooling
self.W_conv3_tf = self.weight_variable([self.s_f_conv3, self.s_f_conv3,
self.n_f_conv2, self.n_f_conv3],
name = 'W_conv3_tf')
self.b_conv3_tf = self.bias_variable([self.n_f_conv3], name = 'b_conv3_tf')
self.h_conv3_tf = tf.nn.relu(self.conv2d(self.h_pool2_tf,
self.W_conv3_tf) + self.b_conv3_tf,
name = 'h_conv3_tf') #(.,7,7,32)
self.h_pool3_tf = self.max_pool_2x2(self.h_conv3_tf,
name = 'h_pool3_tf') # (.,4,4,32)
# 4.layer: fully connected
self.W_fc1_tf = self.weight_variable([4*4*self.n_f_conv3,self.n_n_fc1],
name = 'W_fc1_tf') # (4*4*32, 1024)
self.b_fc1_tf = self.bias_variable([self.n_n_fc1], name = 'b_fc1_tf') # (1024)
self.h_pool3_flat_tf = tf.reshape(self.h_pool3_tf, [-1,4*4*self.n_f_conv3],
name = 'h_pool3_flat_tf') # (.,1024)
self.h_fc1_tf = tf.nn.relu(tf.matmul(self.h_pool3_flat_tf,
self.W_fc1_tf) + self.b_fc1_tf,
name = 'h_fc1_tf') # (.,1024)
# add dropout
self.keep_prob_tf = tf.placeholder(dtype=tf.float32, name = 'keep_prob_tf')
self.h_fc1_drop_tf = tf.nn.dropout(self.h_fc1_tf, self.keep_prob_tf,
name = 'h_fc1_drop_tf')
# 5.layer: fully connected
self.W_fc2_tf = self.weight_variable([self.n_n_fc1, 10], name = 'W_fc2_tf')
self.b_fc2_tf = self.bias_variable([10], name = 'b_fc2_tf')
self.z_pred_tf = tf.add(tf.matmul(self.h_fc1_drop_tf, self.W_fc2_tf),
self.b_fc2_tf, name = 'z_pred_tf')# => (.,10)
# cost function
self.cross_entropy_tf = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(
labels=self.y_data_tf, logits=self.z_pred_tf), name = 'cross_entropy_tf')
# optimisation function
self.learn_rate_tf = tf.placeholder(dtype=tf.float32, name="learn_rate_tf")
self.train_step_tf = tf.train.AdamOptimizer(self.learn_rate_tf).minimize(
self.cross_entropy_tf, name = 'train_step_tf')
# predicted probabilities in one-hot encoding
self.y_pred_proba_tf = tf.nn.softmax(self.z_pred_tf, name='y_pred_proba_tf')
# tensor of correct predictions
self.y_pred_correct_tf = tf.equal(tf.argmax(self.y_pred_proba_tf, 1),
tf.argmax(self.y_data_tf, 1),
name = 'y_pred_correct_tf')
# accuracy
self.accuracy_tf = tf.reduce_mean(tf.cast(self.y_pred_correct_tf, dtype=tf.float32),
name = 'accuracy_tf')
# tensors to save intermediate accuracies and losses during training
self.train_loss_tf = tf.Variable(np.array([]), dtype=tf.float32,
name='train_loss_tf', validate_shape = False)
self.valid_loss_tf = tf.Variable(np.array([]), dtype=tf.float32,
name='valid_loss_tf', validate_shape = False)
self.train_acc_tf = tf.Variable(np.array([]), dtype=tf.float32,
name='train_acc_tf', validate_shape = False)
self.valid_acc_tf = tf.Variable(np.array([]), dtype=tf.float32,
name='valid_acc_tf', validate_shape = False)
# number of weights and biases
num_weights = (self.s_f_conv1**2*self.n_f_conv1
+ self.s_f_conv2**2*self.n_f_conv1*self.n_f_conv2
+ self.s_f_conv3**2*self.n_f_conv2*self.n_f_conv3
+ 4*4*self.n_f_conv3*self.n_n_fc1 + self.n_n_fc1*10)
num_biases = self.n_f_conv1 + self.n_f_conv2 + self.n_f_conv3 + self.n_n_fc1
print('num_weights =', num_weights)
print('num_biases =', num_biases)
return None
def attach_summary(self, sess):
# create summary tensors for tensorboard
self.use_tb_summary = True
self.summary_variable(self.W_conv1_tf, 'W_conv1_tf')
self.summary_variable(self.b_conv1_tf, 'b_conv1_tf')
self.summary_variable(self.W_conv2_tf, 'W_conv2_tf')
self.summary_variable(self.b_conv2_tf, 'b_conv2_tf')
self.summary_variable(self.W_conv3_tf, 'W_conv3_tf')
self.summary_variable(self.b_conv3_tf, 'b_conv3_tf')
self.summary_variable(self.W_fc1_tf, 'W_fc1_tf')
self.summary_variable(self.b_fc1_tf, 'b_fc1_tf')
self.summary_variable(self.W_fc2_tf, 'W_fc2_tf')
self.summary_variable(self.b_fc2_tf, 'b_fc2_tf')
tf.summary.scalar('cross_entropy_tf', self.cross_entropy_tf)
tf.summary.scalar('accuracy_tf', self.accuracy_tf)
# merge all summaries for tensorboard
self.merged = tf.summary.merge_all()
# initialize summary writer
timestamp = datetime.datetime.now().strftime('%d-%m-%Y_%H-%M-%S')
filepath = os.path.join(os.getcwd(), 'logs', (self.nn_name+'_'+timestamp))
self.train_writer = tf.summary.FileWriter(os.path.join(filepath,'train'), sess.graph)
self.valid_writer = tf.summary.FileWriter(os.path.join(filepath,'valid'), sess.graph)
def attach_saver(self):
# initialize tensorflow saver
self.use_tf_saver = True
self.saver_tf = tf.train.Saver()
# train
def train_graph(self, sess, x_train, y_train, x_valid, y_valid, n_epoch = 1,
train_on_augmented_data = False):
# train on original or augmented data
self.train_on_augmented_data = train_on_augmented_data
# training and validation data
self.x_train = x_train
self.y_train = y_train
self.x_valid = x_valid
self.y_valid = y_valid
# use augmented data
if self.train_on_augmented_data:
print('generate new set of images')
self.x_train_aug = normalize_data(self.generate_images(self.x_train))
self.y_train_aug = self.y_train
# parameters
mb_per_epoch = self.x_train.shape[0]/self.mb_size
train_loss, train_acc, valid_loss, valid_acc = [],[],[],[]
# start timer
start = datetime.datetime.now();
print(datetime.datetime.now().strftime('%d-%m-%Y %H:%M:%S'),': start training')
print('learnrate = ',self.learn_rate,', n_epoch = ', n_epoch,
', mb_size = ', self.mb_size)
# looping over mini batches
for i in range(int(n_epoch*mb_per_epoch)+1):
# adapt learn_rate
self.learn_rate_pos = int(self.current_epoch // self.learn_rate_step_size)
if not self.learn_rate == self.learn_rate_array[self.learn_rate_pos]:
self.learn_rate = self.learn_rate_array[self.learn_rate_pos]
print(datetime.datetime.now()-start,': set learn rate to %.6f'%self.learn_rate)
# get new batch
x_batch, y_batch = self.next_mini_batch()
# run the graph
sess.run(self.train_step_tf, feed_dict={self.x_data_tf: x_batch,
self.y_data_tf: y_batch,
self.keep_prob_tf: self.keep_prob,
self.learn_rate_tf: self.learn_rate})
# store losses and accuracies
if i%int(self.log_step*mb_per_epoch) == 0 or i == int(n_epoch*mb_per_epoch):
self.n_log_step += 1 # for logging the results
feed_dict_train = {
self.x_data_tf: self.x_train[self.perm_array[:len(self.x_valid)]],
self.y_data_tf: self.y_train[self.perm_array[:len(self.y_valid)]],
self.keep_prob_tf: 1.0}
feed_dict_valid = {self.x_data_tf: self.x_valid,
self.y_data_tf: self.y_valid,
self.keep_prob_tf: 1.0}
# summary for tensorboard
if self.use_tb_summary:
train_summary = sess.run(self.merged, feed_dict = feed_dict_train)
valid_summary = sess.run(self.merged, feed_dict = feed_dict_valid)
self.train_writer.add_summary(train_summary, self.n_log_step)
self.valid_writer.add_summary(valid_summary, self.n_log_step)
train_loss.append(sess.run(self.cross_entropy_tf,
feed_dict = feed_dict_train))
train_acc.append(self.accuracy_tf.eval(session = sess,
feed_dict = feed_dict_train))
valid_loss.append(sess.run(self.cross_entropy_tf,
feed_dict = feed_dict_valid))
valid_acc.append(self.accuracy_tf.eval(session = sess,
feed_dict = feed_dict_valid))
print('%.2f epoch: train/val loss = %.4f/%.4f, train/val acc = %.4f/%.4f'%(
self.current_epoch, train_loss[-1], valid_loss[-1],
train_acc[-1], valid_acc[-1]))
# concatenate losses and accuracies and assign to tensor variables
tl_c = np.concatenate([self.train_loss_tf.eval(session=sess), train_loss], axis = 0)
vl_c = np.concatenate([self.valid_loss_tf.eval(session=sess), valid_loss], axis = 0)
ta_c = np.concatenate([self.train_acc_tf.eval(session=sess), train_acc], axis = 0)
va_c = np.concatenate([self.valid_acc_tf.eval(session=sess), valid_acc], axis = 0)
sess.run(tf.assign(self.train_loss_tf, tl_c, validate_shape = False))
sess.run(tf.assign(self.valid_loss_tf, vl_c , validate_shape = False))
sess.run(tf.assign(self.train_acc_tf, ta_c , validate_shape = False))
sess.run(tf.assign(self.valid_acc_tf, va_c , validate_shape = False))
print('running time for training: ', datetime.datetime.now() - start)
return None
# save summaries
def save_model(self, sess):
# tf saver
if self.use_tf_saver:
#filepath = os.path.join(os.getcwd(), 'logs' , self.nn_name)
filepath = os.path.join(os.getcwd(), self.nn_name)
self.saver_tf.save(sess, filepath)
# tb summary
if self.use_tb_summary:
self.train_writer.close()
self.valid_writer.close()
return None
# prediction
def forward(self, sess, x_data):
y_pred_proba = self.y_pred_proba_tf.eval(session = sess,
feed_dict = {self.x_data_tf: x_data,
self.keep_prob_tf: 1.0})
return y_pred_proba
# load tensors from a saved graph
def load_tensors(self, graph):
# input tensors
self.x_data_tf = graph.get_tensor_by_name("x_data_tf:0")
self.y_data_tf = graph.get_tensor_by_name("y_data_tf:0")
# weights and bias tensors
self.W_conv1_tf = graph.get_tensor_by_name("W_conv1_tf:0")
self.W_conv2_tf = graph.get_tensor_by_name("W_conv2_tf:0")
self.W_conv3_tf = graph.get_tensor_by_name("W_conv3_tf:0")
self.W_fc1_tf = graph.get_tensor_by_name("W_fc1_tf:0")
self.W_fc2_tf = graph.get_tensor_by_name("W_fc2_tf:0")
self.b_conv1_tf = graph.get_tensor_by_name("b_conv1_tf:0")
self.b_conv2_tf = graph.get_tensor_by_name("b_conv2_tf:0")
self.b_conv3_tf = graph.get_tensor_by_name("b_conv3_tf:0")
self.b_fc1_tf = graph.get_tensor_by_name("b_fc1_tf:0")
self.b_fc2_tf = graph.get_tensor_by_name("b_fc2_tf:0")
# activation tensors
self.h_conv1_tf = graph.get_tensor_by_name('h_conv1_tf:0')
self.h_pool1_tf = graph.get_tensor_by_name('h_pool1_tf:0')
self.h_conv2_tf = graph.get_tensor_by_name('h_conv2_tf:0')
self.h_pool2_tf = graph.get_tensor_by_name('h_pool2_tf:0')
self.h_conv3_tf = graph.get_tensor_by_name('h_conv3_tf:0')
self.h_pool3_tf = graph.get_tensor_by_name('h_pool3_tf:0')
self.h_fc1_tf = graph.get_tensor_by_name('h_fc1_tf:0')
self.z_pred_tf = graph.get_tensor_by_name('z_pred_tf:0')
# training and prediction tensors
self.learn_rate_tf = graph.get_tensor_by_name("learn_rate_tf:0")
self.keep_prob_tf = graph.get_tensor_by_name("keep_prob_tf:0")
self.cross_entropy_tf = graph.get_tensor_by_name('cross_entropy_tf:0')
self.train_step_tf = graph.get_operation_by_name('train_step_tf')
self.z_pred_tf = graph.get_tensor_by_name('z_pred_tf:0')
self.y_pred_proba_tf = graph.get_tensor_by_name("y_pred_proba_tf:0")
self.y_pred_correct_tf = graph.get_tensor_by_name('y_pred_correct_tf:0')
self.accuracy_tf = graph.get_tensor_by_name('accuracy_tf:0')
# tensor of stored losses and accuricies during training
self.train_loss_tf = graph.get_tensor_by_name("train_loss_tf:0")
self.train_acc_tf = graph.get_tensor_by_name("train_acc_tf:0")
self.valid_loss_tf = graph.get_tensor_by_name("valid_loss_tf:0")
self.valid_acc_tf = graph.get_tensor_by_name("valid_acc_tf:0")
return None
# get losses of training and validation sets
def get_loss(self, sess):
train_loss = self.train_loss_tf.eval(session = sess)
valid_loss = self.valid_loss_tf.eval(session = sess)
return train_loss, valid_loss
# get accuracies of training and validation sets
def get_accuracy(self, sess):
train_acc = self.train_acc_tf.eval(session = sess)
valid_acc = self.valid_acc_tf.eval(session = sess)
return train_acc, valid_acc
# get weights
def get_weights(self, sess):
W_conv1 = self.W_conv1_tf.eval(session = sess)
W_conv2 = self.W_conv2_tf.eval(session = sess)
W_conv3 = self.W_conv3_tf.eval(session = sess)
W_fc1_tf = self.W_fc1_tf.eval(session = sess)
W_fc2_tf = self.W_fc2_tf.eval(session = sess)
return W_conv1, W_conv2, W_conv3, W_fc1_tf, W_fc2_tf
# get biases
def get_biases(self, sess):
b_conv1 = self.b_conv1_tf.eval(session = sess)
b_conv2 = self.b_conv2_tf.eval(session = sess)
b_conv3 = self.b_conv3_tf.eval(session = sess)
b_fc1_tf = self.b_fc1_tf.eval(session = sess)
b_fc2_tf = self.b_fc2_tf.eval(session = sess)
return b_conv1, b_conv2, b_conv3, b_fc1_tf, b_fc2_tf
# load session from file, restore graph, and load tensors
def load_session_from_file(self, filename):
tf.reset_default_graph()
filepath = os.path.join(os.getcwd(), filename + '.meta')
#filepath = os.path.join(os.getcwd(),'logs', filename + '.meta')
saver = tf.train.import_meta_graph(filepath)
print(filepath)
sess = tf.Session()
saver.restore(sess, instance)
graph = tf.get_default_graph()
self.load_tensors(graph)
return sess
# receive activations given the input
def get_activations(self, sess, x_data):
feed_dict = {self.x_data_tf: x_data, self.keep_prob_tf: 1.0}
h_conv1 = self.h_conv1_tf.eval(session = sess, feed_dict = feed_dict)
h_pool1 = self.h_pool1_tf.eval(session = sess, feed_dict = feed_dict)
h_conv2 = self.h_conv2_tf.eval(session = sess, feed_dict = feed_dict)
h_pool2 = self.h_pool2_tf.eval(session = sess, feed_dict = feed_dict)
h_conv3 = self.h_conv3_tf.eval(session = sess, feed_dict = feed_dict)
h_pool3 = self.h_pool3_tf.eval(session = sess, feed_dict = feed_dict)
h_fc1 = self.h_fc1_tf.eval(session = sess, feed_dict = feed_dict)
h_fc2 = self.z_pred_tf.eval(session = sess, feed_dict = feed_dict)
return h_conv1,h_pool1,h_conv2,h_pool2,h_conv3,h_pool3,h_fc1,h_fc2
## train the neural network graph
Model_instance_list = ['CNN1'] # use full when you would want to run diffrent
#instamnce of same model with diffrent parameter
# we wont be doing it but you can try, we just ahve one
# cross validations
cv_num = 10 # cross validations default = 20 => 5% validation set
kfold = sklearn.model_selection.KFold(cv_num, shuffle=True, random_state=123)
for i,(train_index, valid_index) in enumerate(kfold.split(x_train_valid)):
# start timer
start = datetime.datetime.now();
# train and validation data of original images
x_train = x_train_valid[train_index]
y_train = y_train_valid[train_index]
x_valid = x_train_valid[valid_index]
y_valid = y_train_valid[valid_index]
# create neural network graph
nn_graph = nn_class(nn_name = Model_instance_list[i]) # instance of nn_class
nn_graph.create_graph() # create graph
nn_graph.attach_saver() # attach saver tensors
# start tensorflow session
with tf.Session() as sess:
# attach summaries
nn_graph.attach_summary(sess)
# variable initialization of the default graph
sess.run(tf.global_variables_initializer())
# training on original data
nn_graph.train_graph(sess, x_train, y_train, x_valid, y_valid, n_epoch = 1.0)
# training on augmented data
nn_graph.train_graph(sess, x_train, y_train, x_valid, y_valid, n_epoch = 14.0,
train_on_augmented_data = True)
# save tensors and summaries of model
nn_graph.save_model(sess)
# only one iteration
if True:
break;
print('total running time for training: ', datetime.datetime.now() - start)
instance = Model_instance_list[0]
nn_graph = nn_class()
sess = nn_graph.load_session_from_file(instance)
y_valid_pred[instance] = nn_graph.forward(sess, x_valid)
sess.close()
cnf_matrix = sklearn.metrics.confusion_matrix(
one_hot_to_dense(y_valid_pred[instance]), one_hot_to_dense(y_valid)).astype(np.float32)
labels_array = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
fig, ax = plt.subplots(1,figsize=(10,10))
ax = sns.heatmap(cnf_matrix, ax=ax, cmap=plt.cm.PuBuGn, annot=True)
ax.set_xticklabels(labels_array)
ax.set_yticklabels(labels_array)
plt.title('Confusion matrix of validation set')
plt.ylabel('True digit')
plt.xlabel('Predicted digit')
plt.show();
## loss and accuracy curves
nn_graph = nn_class()
sess = nn_graph.load_session_from_file(instance)
train_loss[instance], valid_loss[instance] = nn_graph.get_loss(sess)
train_acc[instance], valid_acc[instance] = nn_graph.get_accuracy(sess)
sess.close()
print('final train/valid loss = %.4f/%.4f, train/valid accuracy = %.4f/%.4f'%(
train_loss[instance][-1], valid_loss[instance][-1], train_acc[instance][-1], valid_acc[instance][-1]))
plt.figure(figsize=(10, 5));
plt.subplot(1,2,1);
plt.plot(np.arange(0,len(train_acc[instance])), train_acc[instance],'-b', label='Training')
plt.plot(np.arange(0,len(valid_acc[instance])), valid_acc[instance],'-g', label='Validation')
plt.legend(loc='lower right', frameon=False)
plt.ylim(ymax = 1.1, ymin = 0.0)
plt.ylabel('accuracy')
plt.xlabel('log steps');
plt.subplot(1,2,2)
plt.plot(np.arange(0,len(train_loss[instance])), train_loss[instance],'-b', label='Training')
plt.plot(np.arange(0,len(valid_loss[instance])), valid_loss[instance],'-g', label='Validation')
plt.legend(loc='lower right', frameon=False)
plt.ylim(ymax = 3.0, ymin = 0.0)
plt.ylabel('loss')
plt.xlabel('log steps');
## visualize weights
nn_graph = nn_class()
sess = nn_graph.load_session_from_file(instance)
W_conv1, W_conv2, W_conv3, _, _ = nn_graph.get_weights(sess)
sess.close()
print('W_conv1: min = ' + str(np.min(W_conv1)) + ' max = ' + str(np.max(W_conv1))
+ ' mean = ' + str(np.mean(W_conv1)) + ' std = ' + str(np.std(W_conv1)))
print('W_conv2: min = ' + str(np.min(W_conv2)) + ' max = ' + str(np.max(W_conv2))
+ ' mean = ' + str(np.mean(W_conv2)) + ' std = ' + str(np.std(W_conv2)))
print('W_conv3: min = ' + str(np.min(W_conv3)) + ' max = ' + str(np.max(W_conv3))
+ ' mean = ' + str(np.mean(W_conv3)) + ' std = ' + str(np.std(W_conv3)))
s_f_conv1 = nn_graph.s_f_conv1
s_f_conv2 = nn_graph.s_f_conv2
s_f_conv3 = nn_graph.s_f_conv3
W_conv1 = np.reshape(W_conv1,(s_f_conv1,s_f_conv1,1,6,6))
W_conv1 = np.transpose(W_conv1,(3,0,4,1,2))
W_conv1 = np.reshape(W_conv1,(s_f_conv1*6,s_f_conv1*6,1))
W_conv2 = np.reshape(W_conv2,(s_f_conv2,s_f_conv2,6,6,36))
W_conv2 = np.transpose(W_conv2,(2,0,3,1,4))
W_conv2 = np.reshape(W_conv2,(6*s_f_conv2,6*s_f_conv2,6,6))
W_conv2 = np.transpose(W_conv2,(2,0,3,1))
W_conv2 = np.reshape(W_conv2,(6*6*s_f_conv2,6*6*s_f_conv2))
W_conv3 = np.reshape(W_conv3,(s_f_conv3,s_f_conv3,6,6,36))
W_conv3 = np.transpose(W_conv3,(2,0,3,1,4))
W_conv3 = np.reshape(W_conv3,(6*s_f_conv3,6*s_f_conv3,6,6))
W_conv3 = np.transpose(W_conv3,(2,0,3,1))
W_conv3 = np.reshape(W_conv3,(6*6*s_f_conv3,6*6*s_f_conv3))
plt.figure(figsize=(15,5))
plt.subplot(1,3,1)
plt.gca().set_xticks(np.arange(-0.5, s_f_conv1*6, s_f_conv1), minor = False);
plt.gca().set_yticks(np.arange(-0.5, s_f_conv1*6, s_f_conv1), minor = False);
plt.grid(which = 'minor', color='b', linestyle='-', linewidth=1)
plt.title('W_conv1 ' + str(W_conv1.shape))
plt.colorbar(plt.imshow(W_conv1[:,:,0], cmap=cm.inferno));
plt.subplot(1,3,2)
plt.gca().set_xticks(np.arange(-0.5, 6*6*s_f_conv2, 6*s_f_conv2), minor = False);
plt.gca().set_yticks(np.arange(-0.5, 6*6*s_f_conv2, 6*s_f_conv2), minor = False);
plt.grid(which = 'minor', color='b', linestyle='-', linewidth=1)
plt.title('W_conv2 ' + str(W_conv2.shape))
plt.colorbar(plt.imshow(W_conv2[:,:], cmap=cm.inferno));
plt.subplot(1,3,3)
plt.gca().set_xticks(np.arange(-0.5, 6*6*s_f_conv3, 6*s_f_conv3), minor = False);
plt.gca().set_yticks(np.arange(-0.5, 6*6*s_f_conv3, 6*s_f_conv3), minor = False);
plt.grid(which = 'minor', color='b', linestyle='-', linewidth=1)
plt.title('W_conv3 ' + str(W_conv3.shape))
plt.colorbar(plt.imshow(W_conv3[:,:], cmap=cm.inferno));
## visualize activations
img_no = 143;
nn_graph = nn_class()
sess = nn_graph.load_session_from_file(instance)
(h_conv1, h_pool1, h_conv2, h_pool2,h_conv3, h_pool3, h_fc1,
h_fc2) = nn_graph.get_activations(sess, x_train_valid[img_no:img_no+1])
sess.close()
# original image
plt.figure(figsize=(15,9))
plt.subplot(2,4,1)
plt.imshow(x_train_valid[img_no].reshape(28,28),cmap=cm.inferno);
# 1. convolution
plt.subplot(2,4,2)
plt.title('h_conv1 ' + str(h_conv1.shape))
h_conv1 = np.reshape(h_conv1,(-1,28,28,6,6))
h_conv1 = np.transpose(h_conv1,(0,3,1,4,2))
h_conv1 = np.reshape(h_conv1,(-1,6*28,6*28))
plt.imshow(h_conv1[0], cmap=cm.inferno);
# 1. max pooling
plt.subplot(2,4,3)
plt.title('h_pool1 ' + str(h_pool1.shape))
h_pool1 = np.reshape(h_pool1,(-1,14,14,6,6))
h_pool1 = np.transpose(h_pool1,(0,3,1,4,2))
h_pool1 = np.reshape(h_pool1,(-1,6*14,6*14))
plt.imshow(h_pool1[0], cmap=cm.inferno);
# 2. convolution
plt.subplot(2,4,4)
plt.title('h_conv2 ' + str(h_conv2.shape))
h_conv2 = np.reshape(h_conv2,(-1,14,14,6,6))
h_conv2 = np.transpose(h_conv2,(0,3,1,4,2))
h_conv2 = np.reshape(h_conv2,(-1,6*14,6*14))
plt.imshow(h_conv2[0], cmap=cm.inferno);
# 2. max pooling
plt.subplot(2,4,5)
plt.title('h_pool2 ' + str(h_pool2.shape))
h_pool2 = np.reshape(h_pool2,(-1,7,7,6,6))
h_pool2 = np.transpose(h_pool2,(0,3,1,4,2))
h_pool2 = np.reshape(h_pool2,(-1,6*7,6*7))
plt.imshow(h_pool2[0], cmap=cm.inferno);
# 3. convolution
plt.subplot(2,4,6)
plt.title('h_conv3 ' + str(h_conv3.shape))
h_conv3 = np.reshape(h_conv3,(-1,7,7,6,6))
h_conv3 = np.transpose(h_conv3,(0,3,1,4,2))
h_conv3 = np.reshape(h_conv3,(-1,6*7,6*7))
plt.imshow(h_conv3[0], cmap=cm.inferno);
# 3. max pooling
plt.subplot(2,4,7)
plt.title('h_pool2 ' + str(h_pool3.shape))
h_pool3 = np.reshape(h_pool3,(-1,4,4,6,6))
h_pool3 = np.transpose(h_pool3,(0,3,1,4,2))
h_pool3 = np.reshape(h_pool3,(-1,6*4,6*4))
plt.imshow(h_pool3[0], cmap=cm.inferno);
# 4. FC layer
plt.subplot(2,4,8)
plt.title('h_fc1 ' + str(h_fc1.shape))
h_fc1 = np.reshape(h_fc1,(-1,24,24))
plt.imshow(h_fc1[0], cmap=cm.inferno);
# 5. FC layer
np.set_printoptions(precision=2)
print('h_fc2 = ', h_fc2)
## show misclassified images
nn_graph = nn_class()
sess = nn_graph.load_session_from_file(instance)
y_valid_pred[instance] = nn_graph.forward(sess, x_valid)
sess.close()
y_valid_pred_label = one_hot_to_dense(y_valid_pred[instance])
y_valid_label = one_hot_to_dense(y_valid)
y_val_false_index = []
for i in range(y_valid_label.shape[0]):
if y_valid_pred_label[i] != y_valid_label[i]:
y_val_false_index.append(i)
print('# false predictions: ', len(y_val_false_index),'out of', len(y_valid))
plt.figure(figsize=(10,15))
for j in range(0,5):
for i in range(0,10):
if j*10+i<len(y_val_false_index):
plt.subplot(10,10,j*10+i+1)
plt.title('%d/%d'%(y_valid_label[y_val_false_index[j*10+i]],
y_valid_pred_label[y_val_false_index[j*10+i]]))
plt.imshow(x_valid[y_val_false_index[j*10+i]].reshape(28,28),cmap=cm.inferno)
nn_graph = nn_class() # create instance
sess = nn_graph.load_session_from_file(instance) # receive session
y_test_pred = {}
y_test_pred_labels = {}
# split evaluation of test predictions into batches
kfold = sklearn.model_selection.KFold(40, shuffle=False)
for i,(train_index, valid_index) in enumerate(kfold.split(x_test)):
if i==0:
y_test_pred[instance] = nn_graph.forward(sess, x_test[valid_index])
else:
y_test_pred[instance] = np.concatenate([y_test_pred[instance],
nn_graph.forward(sess, x_test[valid_index])])
sess.close()
y_test_pred_labels[instance] = one_hot_to_dense(y_test_pred[instance])
print(instance +': y_test_pred_labels[instance].shape = ', y_test_pred_labels[instance].shape)
unique, counts = np.unique(y_test_pred_labels[instance], return_counts=True)
print(dict(zip(unique, counts)))
plt.figure(figsize=(10,15))
for j in range(0,5):
for i in range(0,10):
plt.subplot(10,10,j*10+i+1)
plt.title('%d'%y_test_pred_labels[instance][j*10+i])
plt.imshow(x_test[j*10+i].reshape(28,28), cmap=cm.inferno)
# Suppose I have 4 models, how would I stack them up
Model_instance_list = ['CNN1', 'CNN2', 'CNN3', 'CNN4']
# cross validations
# choose the same seed as was done for training the neural nets
kfold = sklearn.model_selection.KFold(len(Model_instance_list), shuffle=True, random_state = 123)
# train and test data for meta model
x_train_meta = np.array([]).reshape(-1,10)
y_train_meta = np.array([]).reshape(-1,10)
x_test_meta = np.zeros((x_test.shape[0], 10))
print('Out-of-folds predictions:')
# make out-of-folds predictions from base models
for i,(train_index, valid_index) in enumerate(kfold.split(x_train_valid)):
# training and validation data
x_train = x_train_valid[train_index]
y_train = y_train_valid[train_index]
x_valid = x_train_valid[valid_index]
y_valid = y_train_valid[valid_index]
# load neural network and make predictions
instance = Model_instance_list[i]
nn_graph = nn_class()
sess = nn_graph.load_session_from_file(instance)
y_train_pred[instance] = nn_graph.forward(sess, x_train[:len(x_valid)])
y_valid_pred[instance] = nn_graph.forward(sess, x_valid)
y_test_pred[instance] = nn_graph.forward(sess, x_test)
sess.close()
# collect train and test data for meta model
x_train_meta = np.concatenate([x_train_meta, y_valid_pred[instance]])
y_train_meta = np.concatenate([y_train_meta, y_valid])
x_test_meta += y_test_pred[instance]
print(take_models[i],': train/valid accuracy = %.4f/%.4f'%(
accuracy_from_one_hot_labels(y_train_pred[instance], y_train[:len(x_valid)]),
accuracy_from_one_hot_labels(y_valid_pred[instance], y_valid)))
if False:
break;
# take average of test predictions
x_test_meta = x_test_meta/(i+1)
y_test_pred['stacked_models'] = x_test_meta
print('Stacked models: valid accuracy = %.4f'%accuracy_from_one_hot_labels(x_train_meta,
y_train_meta))
```
| github_jupyter |
## plan_pole_transect
Visualize pole locations on Pea Island beach transect.
Profiles were extracted from SfM maps by Jenna on 31 August 2021 - Provisional Data.
#### Read in profiles
Use pandas to read profiles; pull out arrays of x, y (UTM meters, same for all profiles) and z (m NAVD88).
Calculate distance along profile from arbitrary starting point.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
fnames = ['crossShore_profile_2019_preDorian.xyz', 'crossShore_profile_2019_postDorian.xyz',
'crossShore_profile_2020_Sep.xyz', 'crossShore_profile_2021_Apr.xyz']
df0 = pd.read_csv(fnames[0],skiprows=1,sep=',',header=None,names=['x','y','z'])
df1 = pd.read_csv(fnames[1],skiprows=1,sep=',',header=None,names=['x','y','z'])
df2 = pd.read_csv(fnames[2],skiprows=1,sep=',',header=None,names=['x','y','z'])
df3 = pd.read_csv(fnames[3],skiprows=1,sep=',',header=None,names=['x','y','z'])
df0.describe()
x = df0['x'].values
y = df0['y'].values
z0 = df0['z'].values
z1 = df1['z'].values
z2 = df2['z'].values
z3 = df3['z'].values
dist = np.sqrt((x - x[0])**2+(y-y[0])**2)
```
#### Use Stockdon equation to calculate runup for slope on upper beach and offshore waves
```
def calcR2(H,T,slope,igflag=0):
"""
%
% [R2,S,setup, Sinc, SIG, ir] = calcR2(H,T,slope,igflag);
%
% Calculated 2% runup (R2), swash (S), setup (setup), incident swash (Sinc)
% and infragravity swash (SIG) elevations based on parameterizations from runup paper
% also Iribarren (ir)
% August 2010 - Included 15% runup (R16) statistic that, for a Guassian distribution,
% represents mean+sigma. It is calculated as R16 = setup + swash/4.
% In a wave tank, Palmsten et al (2010) found this statistic represented initiation of dune erosion.
%
%
% H = significant wave height, reverse shoaled to deep water
% T = deep-water peak wave period
% slope = radians
% igflag = 0 (default)use full equation for all data
% = 1 use dissipative-specific calculations when dissipative conditions exist (Iribarren < 0.3)
% = 2 use dissipative-specific (IG energy) calculation for all data
%
% based on:
% Stockdon, H. F., R. A. Holman, P. A. Howd, and J. Sallenger A. H. (2006),
% Empirical parameterization of setup, swash, and runup,
% Coastal Engineering, 53, 573-588.
% author: [email protected]
# Converted to Python by [email protected]
"""
g = 9.81
# make slopes positive!
slope = np.abs(slope)
# compute wavelength and Iribarren
L = (g*T**2) / (2.*np.pi)
sqHL = np.sqrt(H*L)
ir = slope/np.sqrt(H/L)
if igflag == 2: # use dissipative equations (IG) for ALL data
R2 = 1.1*(0.039 * sqHL)
S = 0.046*sqHL
setup = 0.016*sqHL
elif igflag == 1 and ir < 0.3: # if dissipative site use diss equations
R2 = 1.1*(0.039 * sqHL)
S = 0.046*sqHL
setup = 0.016*sqHL
else: # if int/ref site, use full equations
setup = 0.35*slope*sqHL
Sinc = 0.75*slope*sqHL
SIG = 0.06*sqHL
S = np.sqrt(Sinc**2 + SIG**2)
R2 = 1.1*(setup + S/2.)
R16 = 1.1*(setup + S/4.)
return R2, S, setup, Sinc, SIG, ir, R16
H = 2.
T = 17.
slp = .05
R2, S, setup, Sinc, SIG, ir, R16 = calcR2(H,T,slp,igflag=0)
mllw = -0.6 #NAVD88
high_water = 1.6 + mllw # high water estimates from Duck and Jenettes
maxHW = R2 + high_water
print('R2: {:.2f}, max HW: {:.2f}'.format(R2, maxHW))
```
#### Plot profiles and pole locations
Apply arbitrary vertical offset to profiles to collapse them. The range of these offsets suggests fairly big uncertainty in the elevation data.
Define a function to plot pole at ground level with 2 m embedded and 3 m above ground.
Make plot with vertical exaggeration of 2.1 bazillion.
`edist` - Horizontal retreat of hypothetical eroded profile.
`pole_locations` - Locations of the pole along the transect...fiddle with this.
`polz` - Function to plot the poles at the specified locations, with 2 m buried below local ground elev. and 3 m proud.
```
# eyeball offsets to make plot easier to interpret (note this elevates May profile)
ioff1 = -.25
ioff2 = +.3
ioff3 = +.25
mhw = 0.77 # estimated from VDatum
edist = -5 # distance to offset eroded profile
#pole_locations = [96, 89, 82, 75, 68, 55, 42] # Chris's original
pole_locations = [104, 95, 84, 76, 68, 55, 42] # Katherine's idea to stretch the array seaward; less overlap
lidar_res_left = 6 # m, depends on orientation
lidar_res_right = 4 # m, depends on orientation
# function to plot pole at ground level, given a distance (pdist) along a profile (dist and z)
def polz(pdist,dist,z,x,y):
idx = (dist>=pdist).argmax()
plt.plot([dist[idx],dist[idx]],[z[idx]-2.,z[idx]+3],'-',c='gray',linewidth=3)
print('dist, z: {:.1f}, {:.1f} utmx, utmy: {:.1f}, {:.1f}'.format(dist[idx],z[idx],x[idx],y[idx]))
plt.hlines(np.min(z), pz-lidar_res_left, pz+lidar_res_right, alpha=0.5)
plt.figure(figsize=(12,3))
plt.plot([dist[0],dist[-1]],[mhw,mhw],'--k',alpha=0.3,label='MHW')
plt.plot([dist[0],dist[-1]],[maxHW,maxHW],'--r',alpha=0.3,label='Max HW')
plt.plot(dist,z0,alpha=0.3,label='pre Dorian')
plt.plot(dist,z1+ioff1,alpha=0.3,label='Post Dorian')
plt.plot(dist,z2+ioff2,alpha=0.3,label='Sep 2020')
plt.plot(dist,z3+ioff3,'-k',linewidth=2,label='May 2021')
plt.plot(dist[500:]+edist,z3[500:]+ioff3,'--r',linewidth=2,label='Eroded')
for pz in pole_locations:
polz(pz,dist,z3+ioff3,x,y)
plt.grid()
plt.legend()
plt.ylabel('Elevation (m NAVD88)')
_ = plt.xlabel('Distance along transect (m)')
```
**Comments from Katherine here:**
How much overlap do we really need? Why is this important? Are there severe edge effects?
It seems to me that we should either 1) try to cover as much of the profile as we can with the LiDARs since you're interested in runup (i.e., minimal to no overlap) or 2) cluster poles in areas where we expect high gradients in bed-level changes or impacts (i.e., where interpolations in bed-level change between sensors may be a bad assumption: around the "dune toe"(100 m?) and near the dune face). The whole profile looks steeper right now than pre-Dorian, so maybe we'll get more erosion/collision at the dune?
I plotted the horizontal lidar resolution because I was having a hard time visualizing.
```
# plot beach slope
slope = np.diff(z3)/np.diff(dist)
plt.plot(dist,0.1*(z3+ioff3),'-k',linewidth=2,label='May 2021')
plt.plot(dist[1:],slope)
plt.ylim((-.5,.5))
# plot smoothed slope v. index
def running_mean(x, N):
return np.convolve(x, np.ones((N,))/N)[(N-1):]
N = int(2/.12478)
print(N)
sslope = running_mean(slope,N)
plt.plot(0.1*(z3+ioff3),'-k',linewidth=2,label='May 2021')
plt.plot(sslope)
print(np.median(sslope[690:700]))
print(np.std(sslope[690:700]))
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
sns.set(style='white', color_codes=True)
dataset = pd.read_csv("/content/drive/MyDrive/Colab Notebooks/ortho_knnnb.csv")
dataset.head()
print("Dimension of dataset:", dataset.shape)
print("Number of rows in the dataset:", dataset.shape[0])
print("Number of columns in the dataset:", dataset.shape[1])
print("Column Names:",dataset.columns.values)
```
We are trying to predict weather the classification is normal or abnormal.
```
dataset.info()
dataset.describe()
import seaborn as sns
sns.set_style("whitegrid");
sns.FacetGrid(dataset, hue="class", size=5.5) \
.map(plt.scatter, "pelvic_incidence", "pelvic_tilt numeric") \
.add_legend();
plt.show();
sns.set_style("whitegrid");
sns.pairplot(dataset, hue="class", size=3);
plt.show()
for name in dataset.columns.values[:-1]:
sns.FacetGrid(dataset, hue="class", size=5).map(sns.distplot, name).add_legend()
plt.show()
X = dataset.iloc[:, :-1]
display(X)
Y = dataset.iloc[:, -1]
display(Y)
symptom_class = ['Abnormal:1', 'Normal:0']
dataset['symptom_class']
dataset.head()
from sklearn import preprocessing
label_encoder=preprocessing.LabelEncoder()
dataset['symptom_class']=label_encoder.fit_transform(dataset['class'])
dataset.head()
dataset= dataset.drop('class', axis=1)
dataset.head()
from sklearn.model_selection import train_test_split
train, test = train_test_split(dataset, test_size=0.20,random_state = 1)
train_x = train.drop(['symptom_class'], axis = 1)
train_y = train['symptom_class']
test_x = test.drop(['symptom_class'],axis = 1)
test_y = test['symptom_class']
print('Dimension of train_x :',train_x.shape)
print('Dimension of train_y :',train_y.shape)
print('Dimension of test_x :',test_x.shape)
print('Dimension of test_y :',test_y.shape)
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier(n_neighbors=3)
KNN.fit(train_x, train_y)
pred = KNN.predict(test_x)
pred
from sklearn.metrics import accuracy_score
print('The accuracy of the KNN with K=3 is {}%'.format(round(accuracy_score(pred,test_y)*100,2)))
from sklearn.metrics import accuracy_score
print('The accuracy of the KNN with K=5 is {}%'.format(round(accuracy_score(pred,test_y)*100,2)))
train_accuracy =[]
test_accuracy = []
for k in range(1,15):
KNN = KNeighborsClassifier(n_neighbors=k)
KNN.fit(train_x, train_y)
train_pred = KNN.predict(train_x)
train_score = accuracy_score(train_pred, train_y)
train_accuracy.append(train_score)
test_pred = KNN.predict(test_x)
test_score = accuracy_score(test_pred, test_y)
test_accuracy.append(test_score)
print("Best accuracy is {} with K = {}".format(max(test_accuracy),1+test_accuracy.index(max(test_accuracy))))
plt.figure(figsize=[8,5]) #Accuracy Plot
plt.plot(range(1,15), test_accuracy, label = 'Testing Accuracy')
plt.plot(range(1,15), train_accuracy, label = 'Training Accuracy')
plt.legend()
plt.title('\nTrain Accuracy Vs Test Accuracy\n',fontsize=15)
plt.xlabel('Value of K',fontsize=15)
plt.ylabel('Accuracy',fontsize=15)
plt.xticks(range(1,15))
plt.grid()
plt.show()
from sklearn.model_selection import GridSearchCV
knn_params = {"n_neighbors": list(range(1,15,1)), 'metric': ['euclidean','manhattan']}
grid_knn = GridSearchCV(KNeighborsClassifier(), knn_params, cv=5)
grid_knn.fit(train_x, train_y)
knn_besthypr = grid_knn.best_estimator_ #KNN best estimator
knn_besthypr
print("Tuned hyperparameter: {}".format(grid_knn.best_params_))
print("Best score: {}".format(grid_knn.best_score_))
knn = knn_besthypr.fit(train_x,train_y) #Using best hyperparameter
y_pred = knn.predict(test_x)
acc = accuracy_score(y_pred,test_y)
print('The accuracy of the KNN with K = {} is {}%'.format(knn_besthypr.n_neighbors,round(acc*100,2)))
test = test.reset_index(drop = True) #actual value and predicted value
test["pred_value"] = y_pred
test
from sklearn.naive_bayes import GaussianNB
nvclassifier = GaussianNB()
nvclassifier.fit(train_x, train_y)
y_pred = nvclassifier.predict(test_x)
print(y_pred)
test = test.reset_index(drop = True)
test["pred_value"] = y_pred
test.head()
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(test_y, y_pred)
plt.figure(figsize=(6,5))
sns.heatmap(cm, annot=True)
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
a = cm.shape
corrPred = 0
falsePred = 0
for row in range(a[0]):
for c in range(a[1]):
if row == c:
corrPred += cm[row,c]
else:
falsePred += cm[row,c]
print("*"*70)
print('Correct predictions: ', corrPred)
print('False predictions', falsePred)
print("*"*70)
acc = corrPred/cm.sum()
print ('Accuracy of the Naive Bayes Clasification is {}% '.format(round(acc*100,2)))
print("*"*70)
from sklearn.metrics import accuracy_score
print('The accuracy of the NB is {}%'.format(round(accuracy_score(y_pred,test_y)*100,2)))
nvclassifier.predict_proba(test_x)[:10]
```
I will recommend KNN than NB because it has a high accuracy than NB.
| github_jupyter |
# Analysis of how mentions of a stock on WSB relates to stock prices
WallStreetBets is a popular forum on reddit known for going to the moon, apes and stonks. Jokes aside, despite all of the ridiculous bad trades, undecipherable jargon and love for memes, it's effect on the stock market is undeniable. Therefore in this project, we want to investigate how the reaction of reddit users on the forum relate to actual changes in the stock market.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
import os
import tensorflow as tf
from datetime import datetime
warnings.filterwarnings('ignore')
from google.colab import drive
drive.mount('/content/drive')
```
### Reddit Post Data
Source: https://huggingface.co/datasets/SocialGrep/reddit-wallstreetbets-aug-2021
```
# TODO: add shortcut from shared drive for:
# wsb-aug-2021-comments.csv
def load_data(filename, path="/content/drive/MyDrive/"):
# read csv file and drop indices
df = pd.read_csv(os.path.join(path, filename))
df = df.dropna(axis=0)
# convert utc to datetime format
df["date"] = pd.to_datetime(df["created_utc"],unit="s").dt.date
return df
filename = "wsb-aug-2021-comments.csv"
df = load_data(filename)
```
#### Overal Sentiment on the Subreddit
```
def sentiment_bins(df):
# extract sentiment
sent_df = df[["date","sentiment"]]
bins = {}
bins["positive"] = sent_df.loc[sent_df["sentiment"] > 0.25,:]
bins["negative"] = sent_df.loc[sent_df["sentiment"] < -0.25,:]
bins["neutral"] = sent_df.loc[sent_df["sentiment"].between(-0.25,0.25),:]
# count the posts in each bin for each day
for name in bins:
bins[name] = bins[name].groupby(['date']).count()
counts = sent_df.groupby(['date']).count()
return bins, counts
def plot_sentiment(df,normalize=True, title=None):
# collect sentiment into three bins
bins, counts = sentiment_bins(df)
# plot counts of each bin every day
colours = ["lightgreen", "coral", "grey"]
for i, name in enumerate(["positive", "negative", "neutral"]):
dates = bins[name].index
total_counts = counts.loc[dates,:].values.reshape(-1)
bin_counts = bins[name]["sentiment"].values
if not normalize:
total_counts = 1
plt.plot(dates, bin_counts / total_counts,
alpha=0.7, c=colours[i])
plt.legend(["positive", "negative", "neutral"])
if title:
plt.title(title)
plt.xticks(rotation=20)
plt.show()
plot_sentiment(df,normalize=False, title="overall-unnormalized")
plot_sentiment(df,normalize=True, title="overall-normalized")
# distribution of sentiment of the posts
plt.hist(df["sentiment"], color="coral",
alpha=0.5)
plt.show()
```
#### Sentiment for individual stocks
```
stocks = ["GME", "AMC", "AMD","AMZN", "PLTR", "NVDA"]
for stock in stocks:
gme_posts = df.loc[df["body"].str.contains(stock),:]
plot_sentiment(gme_posts,title=f"{stock}-normalized", normalize=True)
plot_sentiment(gme_posts,title=f"{stock}-unnormalized", normalize=False)
```
### Analyzing Stock Data
```
def get_daily_sentiment(df, stock):
# intialize df with all dates in august
datelist = pd.date_range(datetime(2021,8,1), periods=31).tolist()
sentiment_df = pd.DataFrame({"date":datelist})
sentiment_df = sentiment_df.set_index("date")
# get all posts mentioning stock
posts = df.loc[df["body"].str.contains(stock),:]
bins, counts = sentiment_bins(posts)
# get number of posts in each bin
for name,values in bins.items():
values = values
values.index = pd.to_datetime(values.index)
values = values.rename(columns={"sentiment":name})
sentiment_df = sentiment_df.join(values)
# get the total number of posts for each day
counts.index = pd.to_datetime(counts.index)
counts = counts.rename(columns={"sentiment":"count"})
sentiment_df = sentiment_df.join(counts)
sentiment_df = sentiment_df.fillna(0)
return sentiment_df
def load_stocks(filename="drive/MyDrive/Stock Prices.csv"):
stonks = pd.read_csv(filename)
# add missing dates to df
stonks.Date = pd.to_datetime(stonks.Date)
datelist = pd.date_range(datetime(2021,8,1), periods=31).tolist()
dates = pd.DataFrame({"Date":datelist})
stonks_df = pd.merge(dates, stonks, on="Date", how="left")
# fill the null values using closest date
stonks_df = stonks_df.interpolate(method='nearest')
stonks_df = stonks_df.set_index('Date')
return stonks_df
# we identified the forum's favourite stocks
stocks = ["GME", "AMC", "AMD","AMZN", "PLTR", "NVDA"]
# retrieve the sentiment informationn for each stock
sentiment_df = {stock: get_daily_sentiment(df, stock) for stock in stocks}
stonks_df = load_stocks()
```
#### visualize stock prices
```
def scale(x):
minx = np.min(x); maxx = np.max(x)
return (x-minx) / (maxx-minx)
for stock in stocks:
# plot scaled price against the number of posts
price = stonks_df.dropna(axis=0)[[stock]]
num_posts = sentiment_df[stock]["count"].loc[price.index,].values
plt.plot(price.index, scale(price), alpha=0.7)
plt.plot(price.index, scale(num_posts), alpha=0.7)
plt.xticks(rotation=20)
plt.title(f"{stock}: scaled stock price vs number of posts")
plt.legend(["stock price", "posts count"])
plt.show()
stonks_log = np.log(stonks_df)
for stock in stocks:
returns = stonks_df.diff().dropna(axis=0)[[stock]]
log_returns = stonks_log.diff().dropna(axis=0)[[stock]]
num_posts = sentiment_df[stock]["count"].loc[returns.index,].values
plt.plot(returns.index, scale(returns), alpha=0.7)
plt.plot(returns.index, scale(log_returns),alpha=0.7)
plt.plot(returns.index, scale(num_posts),alpha=0.7)
plt.xticks(rotation=20)
plt.title(f"{stock}: returns vs number of posts, scaled")
plt.legend(["returns", "log returns", "posts count"])
plt.show()
```
#### sentiment vs stock prices
```
# from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
for stock in stocks:
# get stock prices
y = stonks_df.dropna(axis=0)[[stock]]
print("="*50)
print(f'name: {stock}, total:{sum(sentiment_df[stock]["count"])}')
print("="*50)
for col in sentiment_df[stock].columns:
# fit a linear model using the number of posts in each bin
X = sentiment_df[stock][col].loc[y.index,].values
X = sm.add_constant(X)
mod = sm.OLS(y,X)
res = mod.fit()
print(f'{col}: {res.rsquared:.3f}, pval: {res.pvalues.x1:.3f}')
norm_df = {}
for stock in sentiment_df:
norm_df[stock] = sentiment_df[stock].copy()
for col in norm_df[stock].columns:
if col != "count":
norm_df[stock][col] = norm_df[stock][col]/ norm_df[stock]["count"]
import statsmodels.api as sm
names = ["intercept"] + list(norm_df["GME"].columns)
for stock in stocks:
# get stock prices
y = stonks_df.dropna(axis=0)[[stock]]
print("="*50)
print(f'name: {stock}, total:{sum(sentiment_df[stock]["count"])}')
print("="*50)
# fit a linear model using the number of posts in each bin
X = norm_df[stock].loc[y.index,:].values
X = sm.add_constant(X)
mod = sm.OLS(y,X)
res = mod.fit()
print(f'{"rsquared"}: {res.rsquared:.3f}')
for name, pval in zip(names, res.pvalues):
print(f'{name}: {pval:.3f}')
```
#### sentiment vs stock direction
```
from sklearn.metrics import roc_auc_score
stonks_diff = stonks_df.diff()
for stock in stocks:
# check if stock increased
y = (stonks_diff.dropna(axis=0)[[stock]] > 0) * 1
print("="*50)
print(f'name: {stock}, total:{sum(sentiment_df[stock]["count"])}')
print("="*50)
for col in sentiment_df[stock].columns:
# fit a linear model using the number of posts in each bin
X = sentiment_df[stock][col].loc[y.index,].values
X = sm.add_constant(X)
log_reg = sm.Logit(y, X).fit(disp=False)
ypred = log_reg.predict(X)
score = roc_auc_score(y.values, ypred)
acc = np.mean((ypred > 0.5) == y.values)
print(f'{col}: auc:{score:.3f}, acc:{acc:.3f}')
from sklearn.metrics import roc_auc_score
names = ["intercept"] + list(norm_df["GME"].columns)
stonks_diff = stonks_df.diff()
for stock in stocks:
# get stock prices
y = (stonks_diff.dropna(axis=0)[[stock]] > 0) * 1
print("="*50)
print(f'name: {stock}, total:{sum(sentiment_df[stock]["count"])}')
print("="*50)
# fit a linear model using the number of posts in each bin
X = norm_df[stock].loc[y.index,:].values
X = sm.add_constant(X)
log_reg = sm.Logit(y, X).fit(disp=False)
ypred = log_reg.predict(X)
score = roc_auc_score(y.values, ypred)
acc = np.mean((ypred > 0.5) == y.values)
print(f'{col}: auc:{score:.3f}, acc:{acc:.3f}')
```
#### sentiment vs returns
```
stonks_diff = stonks_df.diff()
for stock in stocks:
y = stonks_diff.dropna(axis=0)[[stock]]
print("="*50)
print(f'name: {stock}')
print("="*50)
for col in sentiment_df[stock].columns:
X = sentiment_df[stock][col].loc[y.index,].values
X = sm.add_constant(X)
mod = sm.OLS(y,X)
res = mod.fit()
print(f'{col}: {res.rsquared:.3f}, pval: {res.pvalues.x1:.3f}')
# incorporate the sentiment for each day as well
names = ["intercept"] + list(norm_df["GME"].columns)
stonks_diff = stonks_df.diff()
for stock in stocks:
# get stock prices
y = stonks_diff.dropna(axis=0)[[stock]]
print("="*50)
print(f'name: {stock}, total:{sum(sentiment_df[stock]["count"])}')
print("="*50)
# fit a linear model using the number of posts in each bin
X = norm_df[stock].loc[y.index,:].values
X = sm.add_constant(X)
mod = sm.OLS(y,X)
res = mod.fit()
print(f'{"rsquared"}: {res.rsquared:.3f}')
for name, pval in zip(names, res.pvalues):
print(f'{name}: {pval:.3f}')
```
#### sentiment vs log returns
```
stonks_log = np.log(stonks_df)
for stock in stocks:
y = stonks_log.diff().dropna(axis=0)[[stock]]
print("="*50)
print(f'name: {stock}')
print("="*50)
for col in sentiment_df[stock].columns:
X = sentiment_df[stock][col].loc[y.index,].values
X = sm.add_constant(X)
mod = sm.OLS(y,X)
res = mod.fit()
print(f'{col}: {res.rsquared:.3f}, pval: {res.pvalues.x1:.3f}')
```
The
```
```
### Further Areas of Interest
| github_jupyter |
# NumPy arrays
Nikolay Koldunov
[email protected]
This is part of [**Python for Geosciences**](https://github.com/koldunovn/python_for_geosciences) notes.
================
<img height="100" src="files/numpy.png" >
- a powerful N-dimensional array object
- sophisticated (broadcasting) functions
- tools for integrating C/C++ and Fortran code
- useful linear algebra, Fourier transform, and random number capabilities
```
#allow graphics inline
%matplotlib inline
import matplotlib.pylab as plt #import plotting library
import numpy as np #import numpy library
np.set_printoptions(precision=3) # this is just to make the output look better
```
## Load data
I am going to use some real data as an example of array manipulations. This will be the AO index downloaded by wget through a system call (you have to be on Linux of course):
```
!wget www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/monthly.ao.index.b50.current.ascii
```
This is how data in the file look like (we again use system call for *head* command):
```
!head monthly.ao.index.b50.current.ascii
```
Load data in to a variable:
```
ao = np.loadtxt('monthly.ao.index.b50.current.ascii')
ao
ao.shape
```
So it's a *row-major* order. Matlab and Fortran use *column-major* order for arrays.
```
type(ao)
```
Numpy arrays are statically typed, which allow faster operations
```
ao.dtype
```
You can't assign value of different type to element of the numpy array:
```
ao[0,0] = 'Year'
```
Slicing works similarly to Matlab:
```
ao[0:5,:]
```
One can look at the data. This is done by matplotlib.pylab module that we have imported in the beggining as `plt`. We will plot only first 780 poins:
```
plt.plot(ao[:780,2])
```
## Index slicing
In general it is similar to Matlab
First 12 elements of **second** column (months). Remember that indexing starts with 0:
```
ao[0:12,1]
```
First raw:
```
ao[0,:]
```
We can create mask, selecting all raws where values in second raw (months) equals 10 (October):
```
mask = (ao[:,1]==10)
```
Here we apply this mask and show only first 5 rowd of the array:
```
ao[mask][:5,:]
```
You don't have to create separate variable for mask, but apply it directly. Here instead of first five rows I show five last rows:
```
ao[ao[:,1]==10][-5:,:]
```
You can combine conditions. In this case we select October-December data (only first 10 elements are shown):
```
ao[(ao[:,1]>=10)&(ao[:,1]<=12)][0:10,:]
```
You can assighn values to subset of values (*thi expression fixes the problem with very small value at 2015-04*)
```
ao[ao<-10]=0
```
## Basic operations
Create example array from first 12 values of second column and perform some basic operations:
```
months = ao[0:12,1]
months
months+10
months*20
months*months
```
## Basic statistics
Create *ao_values* that will contain onlu data values:
```
ao_values = ao[:,2]
```
Simple statistics:
```
ao_values.min()
ao_values.max()
ao_values.mean()
ao_values.std()
ao_values.sum()
```
You can also use *np.sum* function:
```
np.sum(ao_values)
```
One can make operations on the subsets:
```
np.mean(ao[ao[:,1]==1,2]) # January monthly mean
```
Result will be the same if we use method on our selected data:
```
ao[ao[:,1]==1,2].mean()
```
## Saving data
You can save your data as a text file
```
np.savetxt('ao_only_values.csv',ao[:, 2], fmt='%.4f')
```
Head of resulting file:
```
!head ao_only_values.csv
```
You can also save it as binary:
```
f=open('ao_only_values.bin', 'w')
ao[:,2].tofile(f)
f.close()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/moonryul/course-v3/blob/master/MidTermPart2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Creating your own dataset from Google Images
*by: Francisco Ingham and Jeremy Howard. Inspired by [Adrian Rosebrock](https://www.pyimagesearch.com/2017/12/04/how-to-create-a-deep-learning-dataset-using-google-images/)*
In this tutorial we will see how to easily create an image dataset through Google Images. **Note**: You will have to repeat these steps for any new category you want to Google (e.g once for dogs and once for cats).
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
# You need to mount your google drive to the /content/gdrive folder of your virtual computer
# located in the colab server
from google.colab import drive
drive.mount("/content/gdrive")
#drive.mount("/content/gdrive", force_remount=True)
from fastai.vision import *
```
## Get a list of URLs
### Search and scroll
Question 1: (1.1) Please download 3 categories of animal images from google. Download about 100 images for each category.
Go to [Google Images](http://images.google.com) and search for the images you are interested in. The more specific you are in your Google Search, the better the results and the less manual pruning you will have to do.
Scroll down until you've seen all the images you want to download, or until you see a button that says 'Show more results'. All the images you scrolled past are now available to download. To get more, click on the button, and continue scrolling. The maximum number of images Google Images shows is 700.
It is a good idea to put things you want to exclude into the search query, for instance if you are searching for the Eurasian wolf, "canis lupus lupus", it might be a good idea to exclude other variants:
"canis lupus lupus" -dog -arctos -familiaris -baileyi -occidentalis
You can also limit your results to show only photos by clicking on Tools and selecting Photos from the Type dropdown.
### Download into file
Question 1 (1.2) Move the downloaded files to your google dirve and make the names of the files in the form of *.csv.
Now you must run some Javascript code in your browser which will save the URLs of all the images you want for you dataset.
In Google Chrome press <kbd>Ctrl</kbd><kbd>+Shift</kbd><kbd>+j</kbd> on Windows/Linux and <kbd>Cmd</kbd><kbd>Opt</kbd><kbd>j</kbd> on macOS, and a small window the javascript 'Console' will appear. In Firefox press <kbd>Ctrl</kbd><kbd>Shift</kbd><kbd>k</kbd> on Windows/Linux or <kbd>Cmd</kbd><kbd>Opt</kbd><kbd>k</kbd> on macOS. That is where you will paste the JavaScript commands.
You will need to get the urls of each of the images. Before running the following commands, you may want to disable ad blocking extensions (uBlock, AdBlockPlus etc.) in Chrome. Otherwise the window.open() command doesn't work. Then you can run the following commands:
```javascript
urls=Array.from(document.querySelectorAll('.rg_i')).map(el=> el.hasAttribute('data-src')?el.getAttribute('data-src'):el.getAttribute('data-iurl'));
window.open('data:text/csv;charset=utf-8,' + escape(urls.join('\n')));
```
### upload urls file into /content folder
You will need to run this cell once per each category. The following is an illustration.
```
path = Path('gdrive/My Drive/fastai-v3/data/bears')
```
## Download images
Now you will need to download your images from their respective urls.
fast.ai has a function that allows you to do just that. You just have to specify the urls filename as well as the destination folder and this function will download and save all images that can be opened. If they have some problem in being opened, they will not be saved.
Let's download our images! Notice you can choose a maximum number of images to be downloaded. In this case we will not download all the urls.
You will need to run this line once for every category. The following is an illustration.
```
classes = ['teddys','grizzly','black']
# For example, Do this when download "urls_black.csv' file:
folder = 'teddys'
dest = path/folder
file = 'urls_teddy.csv'
download_images(dest/file, dest, max_pics=100)
# Question 2: Explain what happens when you execute download_images() statement.
for c in classes:
print(c)
verify_images(path/c, delete=True, max_size=500)
```
## View data
```
np.random.seed(42)
data = ImageDataBunch.from_folder(path, train=".", valid_pct=0.2,
ds_tfms=get_transforms(), size=224, num_workers=4).normalize(imagenet_stats
# Question 3: Explain how the categories of the images are extracted when you execute the above statement.
```
Good! Let's take a look at some of our pictures then.
## Train model
```
learn = cnn_learner(data, models.resnet34, metrics=error_rate)
# Question 4: 4.1) cnn_learner() has input paramters other than the shown above.
# One of them is pretrained, which is True by default when you do not specify it.
# What happens when you specify pretrained=True as in
# learn = cnn_learner(data, models.resnet34, metrics=error_rate, pretrained=False)
interp = ClassificationInterpretation.from_learner(learn)
interp.plot_confusion_matrix()
# Question 5: What does your confusion matrix tell you about the prediction capability of your neural network?
# Explain in a conscise manner but do not omit important points.
#Question 6: use interp.plot_top_losses() to find out the prediction capability of your neural network?
# Explain in a conscise manner but do not omit important points.
```
| github_jupyter |
<img src="http://hilpisch.com/tpq_logo.png" alt="The Python Quants" width="35%" align="right" border="0"><br>
# Python for Finance (2nd ed.)
**Mastering Data-Driven Finance**
© Dr. Yves J. Hilpisch | The Python Quants GmbH
<img src="http://hilpisch.com/images/py4fi_2nd_shadow.png" width="300px" align="left">
# Data Analysis with pandas
## pandas Basics
### First Steps with DataFrame Class
```
import pandas as pd
df = pd.DataFrame([10, 20, 30, 40],
columns=['numbers'],
index=['a', 'b', 'c', 'd'])
df
df.index
df.columns
df.loc['c']
df.loc[['a', 'd']]
df.iloc[1:3]
df.sum()
df.apply(lambda x: x ** 2)
df ** 2
df['floats'] = (1.5, 2.5, 3.5, 4.5)
df
df['floats']
df['names'] = pd.DataFrame(['Yves', 'Sandra', 'Lilli', 'Henry'],
index=['d', 'a', 'b', 'c'])
df
df.append({'numbers': 100, 'floats': 5.75, 'names': 'Jil'},
ignore_index=True)
df = df.append(pd.DataFrame({'numbers': 100, 'floats': 5.75,
'names': 'Jil'}, index=['y',]))
df
df = df.append(pd.DataFrame({'names': 'Liz'}, index=['z',]), sort=False)
df
df.dtypes
df[['numbers', 'floats']].mean()
df[['numbers', 'floats']].std()
```
### Second Steps with DataFrame Class
```
import numpy as np
np.random.seed(100)
a = np.random.standard_normal((9, 4))
a
df = pd.DataFrame(a)
df
df.columns = ['No1', 'No2', 'No3', 'No4']
df
df['No2'].mean()
dates = pd.date_range('2019-1-1', periods=9, freq='M')
dates
df.index = dates
df
df.values
np.array(df)
```
## Basic Analytics
```
df.info()
df.describe()
df.sum()
df.mean()
df.mean(axis=0)
df.mean(axis=1)
df.cumsum()
np.mean(df)
# raises warning
np.log(df)
np.sqrt(abs(df))
np.sqrt(abs(df)).sum()
100 * df + 100
```
## Basic Visualization
```
from pylab import plt, mpl
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
%matplotlib inline
df.cumsum().plot(lw=2.0, figsize=(10, 6));
# plt.savefig('../../images/ch05/pd_plot_01.png')
df.plot.bar(figsize=(10, 6), rot=30);
# df.plot(kind='bar', figsize=(10, 6))
# plt.savefig('../../images/ch05/pd_plot_02.png')
```
## Series Class
```
type(df)
S = pd.Series(np.linspace(0, 15, 7), name='series')
S
type(S)
s = df['No1']
s
type(s)
s.mean()
s.plot(lw=2.0, figsize=(10, 6));
# plt.savefig('../../images/ch05/pd_plot_03.png')
```
## GroupBy Operations
```
df['Quarter'] = ['Q1', 'Q1', 'Q1', 'Q2', 'Q2',
'Q2', 'Q3', 'Q3', 'Q3']
df
groups = df.groupby('Quarter')
groups.size()
groups.mean()
groups.max()
groups.aggregate([min, max]).round(2)
df['Odd_Even'] = ['Odd', 'Even', 'Odd', 'Even', 'Odd', 'Even',
'Odd', 'Even', 'Odd']
groups = df.groupby(['Quarter', 'Odd_Even'])
groups.size()
groups[['No1', 'No4']].aggregate([sum, np.mean])
```
## Complex Selection
```
data = np.random.standard_normal((10, 2))
df = pd.DataFrame(data, columns=['x', 'y'])
df.info()
df.head()
df.tail()
df['x'] > 0.5
(df['x'] > 0) & (df['y'] < 0)
(df['x'] > 0) | (df['y'] < 0)
df[df['x'] > 0]
df.query('x > 0')
df[(df['x'] > 0) & (df['y'] < 0)]
df.query('x > 0 & y < 0')
df[(df.x > 0) | (df.y < 0)]
df > 0
df[df > 0]
```
## Concatenation, Joining and Merging
```
df1 = pd.DataFrame(['100', '200', '300', '400'],
index=['a', 'b', 'c', 'd'],
columns=['A',])
df1
df2 = pd.DataFrame(['200', '150', '50'],
index=['f', 'b', 'd'],
columns=['B',])
df2
```
#### Concatenation
```
df1.append(df2, sort=False)
df1.append(df2, ignore_index=True, sort=False)
pd.concat((df1, df2), sort=False)
pd.concat((df1, df2), ignore_index=True, sort=False)
```
#### Joining
```
df1.join(df2)
df2.join(df1)
df1.join(df2, how='left')
df1.join(df2, how='right')
df1.join(df2, how='inner')
df1.join(df2, how='outer')
df = pd.DataFrame()
df['A'] = df1['A']
df
df['B'] = df2
df
df = pd.DataFrame({'A': df1['A'], 'B': df2['B']})
df
```
#### Merging
```
c = pd.Series([250, 150, 50], index=['b', 'd', 'c'])
df1['C'] = c
df2['C'] = c
df1
df2
pd.merge(df1, df2)
pd.merge(df1, df2, on='C')
pd.merge(df1, df2, how='outer')
pd.merge(df1, df2, left_on='A', right_on='B')
pd.merge(df1, df2, left_on='A', right_on='B', how='outer')
pd.merge(df1, df2, left_index=True, right_index=True)
pd.merge(df1, df2, on='C', left_index=True)
pd.merge(df1, df2, on='C', right_index=True)
pd.merge(df1, df2, on='C', left_index=True, right_index=True)
```
## Performance Aspects
```
data = np.random.standard_normal((1000000, 2))
data.nbytes
df = pd.DataFrame(data, columns=['x', 'y'])
df.info()
%time res = df['x'] + df['y']
res[:3]
%time res = df.sum(axis=1)
res[:3]
%time res = df.values.sum(axis=1)
res[:3]
%time res = np.sum(df, axis=1)
res[:3]
%time res = np.sum(df.values, axis=1)
res[:3]
%time res = df.eval('x + y')
res[:3]
%time res = df.apply(lambda row: row['x'] + row['y'], axis=1)
res[:3]
```
<img src="http://hilpisch.com/tpq_logo.png" alt="The Python Quants" width="35%" align="right" border="0"><br>
<a href="http://tpq.io" target="_blank">http://tpq.io</a> | <a href="http://twitter.com/dyjh" target="_blank">@dyjh</a> | <a href="mailto:[email protected]">[email protected]</a>
| github_jupyter |
## RAC/DVR step 1: diagonalize **H**($\lambda$)
```
import numpy as np
import sys
import matplotlib.pyplot as plt
%matplotlib qt5
import pandas as pd
#
# extend path by location of the dvr package
#
sys.path.append('../../Python_libs')
import dvr
import jolanta
amu_to_au=1822.888486192
au2cm=219474.63068
au2eV=27.211386027
Angs2Bohr=1.8897259886
#
# Jolanata-3D parameters a, b, c: (0.028, 1.0, 0.028)
#
# CS-DVR:
# bound state: -7.17051 eV
# resonance (3.1729556 - 0.16085j) eV
#
jparam=(0.028, 1.0, 0.028)
#
# compute DVR of T and V
# then show the density of states
# in a potential + energy-levels plot
# the standard 3D-Jolanta is used (resonance at 1.75 -0.2i eV)
#
rmin=0
rmax=12 # grid from 0 to rmax
thresh = 8 # maximum energy for plot
ppB = 15 # grid points per Bohr
nGrid=int((rmax-rmin)*ppB)
rs = dvr.DVRGrid(rmin, rmax, nGrid)
Vs = jolanta.Jolanta_3D(rs, jparam)
Ts = dvr.KineticEnergy(1, rmin, rmax, nGrid)
[energy, wf] = dvr.DVRDiag2(nGrid, Ts, Vs, wf=True)
n_ene=0
for i in range(nGrid):
print("%3d %12.8f au = %12.5f eV" % (i+1, energy[i], energy[i]*au2eV))
n_ene += 1
if energy[i]*au2eV > thresh:
break
# "DVR normalization", sum(wf[:,0]**2)
# this is correct for plotting
c=["orange", "blue"]
#h=float(xmax) / (nGrid+1.0)
scale=3*au2eV
plt.cla()
plt.plot(rs,Vs*au2eV, '-', color="black")
for i in range(n_ene):
plt.plot(rs, scale*wf[:,i]**2+energy[i]*au2eV, '-', color=c[i%len(c)])
plt.ylim(-8, 1.5*thresh)
plt.xlabel('$r$ [Bohr]')
plt.ylabel('$E$ [eV]')
plt.show()
```
## RAC by increasing $b$
The last energy needs to be about $7E_r \approx 22$eV
```
#
# show the potential
#
a_ref, b_ref, c_ref = jparam
plt.cla()
for b_curr in [1.1, 1.3, 1.5, 1.7]:
param = [a_ref, b_curr, c_ref]
plt.plot(rs, jolanta.Jolanta_3D(rs, param)*au2eV)
plt.ylim(-30, 10)
plt.show()
a_ref, b_ref, c_ref = jparam
b_min=b_ref
b_max=2.5
nEs_keep=4 # how many energies are kept
n_b=101
bs=np.linspace(b_min, b_max, num=n_b, endpoint=True)
run_data = np.zeros((n_b, nEs_keep+1)) # array used to collect all eta-run data
run_data[:,0]=bs
for l, b_curr in enumerate(bs):
param = [a_ref, b_curr, c_ref]
Vs = jolanta.Jolanta_3D(rs, param)
energy = dvr.DVRDiag2(nGrid, Ts, Vs)
run_data[l,1:] = au2eV*energy[0:nEs_keep]
print(l+1, end=" ")
if (l+1)%10==0:
print()
print(run_data[-1,:])
plt.cla()
for i in range(0, nEs_keep):
plt.plot(bs, run_data[:,i+1], 'o-')
plt.ylim(-25,5)
plt.show()
cols = ['z']
for i in range(nEs_keep):
cols.append('E'+str(i+1))
df = pd.DataFrame(run_data, columns=cols)
df.to_csv('rac_DVR_3D_b-scale_rmax_12.csv', index=False)
df.head(5)
```
## RAC with Coulomb potential
```
#
# show the potential
#
def coulomb(r, lbd=1.0):
""" attractive Coulomb potential with strength lbd = lamda """
return -lbd/r
plt.cla()
for l_curr in [0, 0.5, 1.0, 1.5, 2.0]:
plt.plot(rs, (jolanta.Jolanta_3D(rs, jparam)+coulomb(rs, lbd=l_curr))*au2eV)
#plt.xlim(0,15)
plt.ylim(-30, 10)
plt.show()
l_min=0.0
l_max=2.6
nEs_keep=4 # how many energies are kept
npts=101
ls=np.linspace(l_min, l_max, num=npts, endpoint=True)
run_data = np.zeros((npts, nEs_keep+1)) # array used to collect all eta-run data
run_data[:,0]=ls
VJs = jolanta.Jolanta_3D(rs, jparam)
Ws = coulomb(rs, lbd=1.0)
for j, l_curr in enumerate(ls):
Vs = VJs + l_curr*Ws
energy = dvr.DVRDiag2(nGrid, Ts, Vs)
run_data[j,1:] = au2eV*energy[0:nEs_keep]
print(j+1, end=" ")
if (j+1)%10==0:
print()
print(run_data[-1,:])
plt.cla()
for i in range(0, nEs_keep):
plt.plot(ls, run_data[:,i+1], 'o-')
plt.ylim(-25,5)
plt.show()
cols = ['z']
for i in range(nEs_keep):
cols.append('E'+str(i+1))
df = pd.DataFrame(run_data, columns=cols)
df.to_csv('rac_DVR_3D_coulomb_rmax_12.csv', index=False)
df.head(5)
```
## RAC with soft-box
```
#
# show the box potential
#
def softbox(r, rcut=1.0, lbd=1.0):
"""
Softbox:
-1 at the origin, rises at r0 softly to asymptotic 0
based on Gaussian with inverted scale
"""
return lbd*(np.exp(-(2*rcut)**2/r**2) - 1)
plt.cla()
for l_curr in [0.1, 0.2, 0.3, 0.4, 0.5]:
Vs = jolanta.Jolanta_3D(rs, jparam)
Ws = softbox(rs, rcut=5.0, lbd=l_curr)
plt.plot(rs, Ws*au2eV)
plt.xlim(0,20)
plt.ylim(-15, 0)
plt.show()
#
# show the full potential
#
plt.cla()
for l_curr in [0.1, 0.2, 0.3, 0.4, 0.5]:
Vs = jolanta.Jolanta_3D(rs, jparam)
Ws = softbox(rs, rcut=3.0, lbd=l_curr)
plt.plot(rs, (Vs+Ws)*au2eV)
#plt.xlim(0,20)
plt.ylim(-30, 8)
plt.show()
l_min=0.0
l_max=1.2
nEs_keep=4 # how many energies are kept
npts=101
ls=np.linspace(l_min, l_max, num=npts, endpoint=True)
run_data = np.zeros((npts, nEs_keep+1)) # array used to collect all eta-run data
run_data[:,0]=ls
VJs = jolanta.Jolanta_3D(rs, jparam)
Ws = softbox(rs, rcut=3.0, lbd=1.0)
for j, l_curr in enumerate(ls):
Vs = VJs + l_curr*Ws
energy = dvr.DVRDiag2(nGrid, Ts, Vs)
run_data[j,1:] = au2eV*energy[0:nEs_keep]
print(j+1, end=" ")
if (j+1)%10==0:
print()
print(run_data[-1,:])
plt.cla()
for i in range(0, nEs_keep):
plt.plot(ls, run_data[:,i+1], 'o-')
plt.ylim(-25,5)
plt.show()
cols = ['z']
for i in range(nEs_keep):
cols.append('E'+str(i+1))
df = pd.DataFrame(run_data, columns=cols)
df.to_csv('rac_DVR_3D_softbox_rmax_12.csv', index=False)
df.head(5)
```
| github_jupyter |
Deep Learning
=============
Assignment 4
------------
Previously in `2_fullyconnected.ipynb` and `3_regularization.ipynb`, we trained fully connected networks to classify [notMNIST](http://yaroslavvb.blogspot.com/2011/09/notmnist-dataset.html) characters.
The goal of this assignment is make the neural network convolutional.
```
# These are all the modules we'll be using later. Make sure you can import them
# before proceeding further.
from __future__ import print_function
import time
import numpy as np
import tensorflow as tf
from six.moves import cPickle as pickle
from six.moves import range
pickle_file = 'notMNIST.pickle'
with open(pickle_file, 'rb') as f:
save = pickle.load(f)
train_dataset = save['train_dataset']
train_labels = save['train_labels']
valid_dataset = save['valid_dataset']
valid_labels = save['valid_labels']
test_dataset = save['test_dataset']
test_labels = save['test_labels']
del save # hint to help gc free up memory
print('Training set', train_dataset.shape, train_labels.shape)
print('Validation set', valid_dataset.shape, valid_labels.shape)
print('Test set', test_dataset.shape, test_labels.shape)
```
Reformat into a TensorFlow-friendly shape:
- convolutions need the image data formatted as a cube (width by height by #channels)
- labels as float 1-hot encodings.
```
image_size = 28
num_labels = 10
num_channels = 1 # grayscale
import numpy as np
def reformat(dataset, labels):
dataset = dataset.reshape(
(-1, image_size, image_size, num_channels)).astype(np.float32)
labels = (np.arange(num_labels) == labels[:,None]).astype(np.float32)
return dataset, labels
train_dataset, train_labels = reformat(train_dataset, train_labels)
valid_dataset, valid_labels = reformat(valid_dataset, valid_labels)
test_dataset, test_labels = reformat(test_dataset, test_labels)
print('Training set', train_dataset.shape, train_labels.shape)
print('Validation set', valid_dataset.shape, valid_labels.shape)
print('Test set', test_dataset.shape, test_labels.shape)
def accuracy(predictions, labels):
return (100.0 * np.sum(np.argmax(predictions, 1) == np.argmax(labels, 1))
/ predictions.shape[0])
```
Let's build a small network with two convolutional layers, followed by one fully connected layer. Convolutional networks are more expensive computationally, so we'll limit its depth and number of fully connected nodes.
```
batch_size = 16
patch_size = 5
depth = 16
num_hidden = 64
graph = tf.Graph()
with graph.as_default():
# Input data.
tf_train_dataset = tf.placeholder(
tf.float32, shape=(batch_size, image_size, image_size, num_channels))
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels))
tf_valid_dataset = tf.constant(valid_dataset)
tf_test_dataset = tf.constant(test_dataset)
# Variables.
layer1_weights = tf.Variable(tf.truncated_normal(
[patch_size, patch_size, num_channels, depth], stddev=0.1))
layer1_biases = tf.Variable(tf.zeros([depth]))
layer2_weights = tf.Variable(tf.truncated_normal(
[patch_size, patch_size, depth, depth], stddev=0.1))
layer2_biases = tf.Variable(tf.constant(1.0, shape=[depth]))
layer3_weights = tf.Variable(tf.truncated_normal(
[image_size // 4 * image_size // 4 * depth, num_hidden], stddev=0.1))
layer3_biases = tf.Variable(tf.constant(1.0, shape=[num_hidden]))
layer4_weights = tf.Variable(tf.truncated_normal(
[num_hidden, num_labels], stddev=0.1))
layer4_biases = tf.Variable(tf.constant(1.0, shape=[num_labels]))
# Model.
def model(data):
conv = tf.nn.conv2d(data, layer1_weights, [1, 2, 2, 1], padding='SAME')
hidden = tf.nn.relu(conv + layer1_biases)
conv = tf.nn.conv2d(hidden, layer2_weights, [1, 2, 2, 1], padding='SAME')
hidden = tf.nn.relu(conv + layer2_biases)
shape = hidden.get_shape().as_list()
reshape = tf.reshape(hidden, [shape[0], shape[1] * shape[2] * shape[3]])
hidden = tf.nn.relu(tf.matmul(reshape, layer3_weights) + layer3_biases)
return tf.matmul(hidden, layer4_weights) + layer4_biases
# Training computation.
logits = model(tf_train_dataset)
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels))
# Optimizer.
optimizer = tf.train.GradientDescentOptimizer(0.05).minimize(loss)
# Predictions for the training, validation, and test data.
train_prediction = tf.nn.softmax(logits)
valid_prediction = tf.nn.softmax(model(tf_valid_dataset))
test_prediction = tf.nn.softmax(model(tf_test_dataset))
num_steps = 1001
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print('Initialized')
for step in range(num_steps):
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
batch_data = train_dataset[offset:(offset + batch_size), :, :, :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset : batch_data, tf_train_labels : batch_labels}
_, l, predictions = session.run(
[optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 50 == 0):
print('Minibatch loss at step %d: %f' % (step, l))
print('Minibatch accuracy: %.1f%%' % accuracy(predictions, batch_labels))
print('Validation accuracy: %.1f%%' % accuracy(
valid_prediction.eval(), valid_labels))
print('Test accuracy: %.1f%%' % accuracy(test_prediction.eval(), test_labels))
```
---
Problem 1
---------
The convolutional model above uses convolutions with stride 2 to reduce the dimensionality. Replace the strides by a max pooling operation (`nn.max_pool()`) of stride 2 and kernel size 2.
---
```
# TODO
```
---
Problem 2
---------
Try to get the best performance you can using a convolutional net. Look for example at the classic [LeNet5](http://yann.lecun.com/exdb/lenet/) architecture, adding Dropout, and/or adding learning rate decay.
---
```
batch_size = 16
patch_size = 3
depth = 16
num_hidden = 705
num_hidden_last = 205
graph = tf.Graph()
with graph.as_default():
# Input data.
tf_train_dataset = tf.placeholder(
tf.float32, shape=(batch_size, image_size, image_size, num_channels))
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels))
tf_valid_dataset = tf.constant(valid_dataset)
tf_test_dataset = tf.constant(test_dataset)
# Variables.
layerconv1_weights = tf.Variable(tf.truncated_normal(
[patch_size, patch_size, num_channels, depth], stddev=0.1))
layerconv1_biases = tf.Variable(tf.zeros([depth]))
layerconv2_weights = tf.Variable(tf.truncated_normal(
[patch_size, patch_size, depth, depth * 2], stddev=0.1))
layerconv2_biases = tf.Variable(tf.zeros([depth * 2]))
layerconv3_weights = tf.Variable(tf.truncated_normal(
[patch_size, patch_size, depth * 2, depth * 4], stddev=0.03))
layerconv3_biases = tf.Variable(tf.zeros([depth * 4]))
layerconv4_weights = tf.Variable(tf.truncated_normal(
[patch_size, patch_size, depth * 4, depth * 4], stddev=0.03))
layerconv4_biases = tf.Variable(tf.zeros([depth * 4]))
layerconv5_weights = tf.Variable(tf.truncated_normal(
[patch_size, patch_size, depth * 4, depth * 16], stddev=0.03))
layerconv5_biases = tf.Variable(tf.zeros([depth * 16]))
layer3_weights = tf.Variable(tf.truncated_normal(
[image_size / 7 * image_size / 7 * (depth * 4), num_hidden], stddev=0.03))
layer3_biases = tf.Variable(tf.zeros([num_hidden]))
layer4_weights = tf.Variable(tf.truncated_normal(
[num_hidden, num_hidden_last], stddev=0.0532))
layer4_biases = tf.Variable(tf.zeros([num_hidden_last]))
layer5_weights = tf.Variable(tf.truncated_normal(
[num_hidden_last, num_labels], stddev=0.1))
layer5_biases = tf.Variable(tf.zeros([num_labels]))
# Model.
def model(data, use_dropout=False):
conv = tf.nn.conv2d(data, layerconv1_weights, [1, 1, 1, 1], padding='SAME')
hidden = tf.nn.elu(conv + layerconv1_biases)
pool = tf.nn.max_pool(hidden, [1, 2, 2, 1], [1, 2, 2, 1], padding='SAME')
conv = tf.nn.conv2d(pool, layerconv2_weights, [1, 1, 1, 1], padding='SAME')
hidden = tf.nn.elu(conv + layerconv2_biases)
#pool = tf.nn.max_pool(hidden, [1, 2, 2, 1], [1, 2, 2, 1], padding='SAME')
conv = tf.nn.conv2d(hidden, layerconv3_weights, [1, 1, 1, 1], padding='SAME')
hidden = tf.nn.elu(conv + layerconv3_biases)
pool = tf.nn.max_pool(hidden, [1, 2, 2, 1], [1, 2, 2, 1], padding='SAME')
# norm1
# norm1 = tf.nn.lrn(pool, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)
conv = tf.nn.conv2d(pool, layerconv4_weights, [1, 1, 1, 1], padding='SAME')
hidden = tf.nn.elu(conv + layerconv4_biases)
pool = tf.nn.max_pool(hidden, [1, 2, 2, 1], [1, 2, 2, 1], padding='SAME')
# norm1 = tf.nn.lrn(pool, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)
conv = tf.nn.conv2d(pool, layerconv5_weights, [1, 1, 1, 1], padding='SAME')
hidden = tf.nn.elu(conv + layerconv5_biases)
pool = tf.nn.max_pool(hidden, [1, 2, 2, 1], [1, 2, 2, 1], padding='SAME')
# norm1 = tf.nn.lrn(pool, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75)
shape = pool.get_shape().as_list()
#print(shape)
reshape = tf.reshape(pool, [shape[0], shape[1] * shape[2] * shape[3]])
hidden = tf.nn.elu(tf.matmul(reshape, layer3_weights) + layer3_biases)
if use_dropout:
hidden = tf.nn.dropout(hidden, 0.75)
nn_hidden_layer = tf.matmul(hidden, layer4_weights) + layer4_biases
hidden = tf.nn.elu(nn_hidden_layer)
if use_dropout:
hidden = tf.nn.dropout(hidden, 0.75)
return tf.matmul(hidden, layer5_weights) + layer5_biases
# Training computation.
logits = model(tf_train_dataset, True)
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels))
global_step = tf.Variable(0) # count the number of steps taken.
learning_rate = tf.train.exponential_decay(0.1, global_step, 3000, 0.86, staircase=True)
# Optimizer.
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
# Predictions for the training, validation, and test data.
train_prediction = tf.nn.softmax(logits)
valid_prediction = tf.nn.softmax(model(tf_valid_dataset))
test_prediction = tf.nn.softmax(model(tf_test_dataset))
num_steps = 45001
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
for step in xrange(num_steps):
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
batch_data = train_dataset[offset:(offset + batch_size), :, :, :]
batch_labels = train_labels[offset:(offset + batch_size), :]
feed_dict = {tf_train_dataset : batch_data, tf_train_labels : batch_labels}
_, l, predictions = session.run(
[optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 500 == 0):
print("Minibatch loss at step", step, ":", l)
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(
valid_prediction.eval(), valid_labels))
print(time.ctime())
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
```
| github_jupyter |
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# You can write up to 20GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
# Read in data
df=pd.read_csv("../input/all-labelled/all_labelled.tsv", delimiter="\t")
!pip install -q ktrain
df['text']=df['abstract']
df['label']=df['class']
df.drop(['abstract', 'journal', 'title', 'uid', 'class'], axis=1, inplace=True)
df.dropna(inplace=True)
df=df.drop_duplicates()
import tensorflow as tf
import ktrain
from ktrain import text
from sklearn.model_selection import train_test_split
# Enable AMP
from tensorflow.keras.mixed_precision import experimental as mixed_precision
policy = mixed_precision.Policy('mixed_float16')
mixed_precision.set_policy(policy)
df.dropna(inplace=True)
X = df['text'].tolist()
y = df['label'].tolist()
pos = y.count(1)
neg=y.count(0)
total=len(y)
print(pos)
print(neg)
print(total)
t_mod = text.Transformer('microsoft/BiomedNLP-PubMedBERT-base-uncased-abstract-fulltext', maxlen=500, class_names = [0,1])
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
import copy
#weight_for_0 = (1 / y.count(0)) * (len(y) / 2.0)
#weight_for_1 = (1 / y.count(1)) * (len(y) / 2.0)
#class_weight = {0: weight_for_0, 1: weight_for_1}
kf = StratifiedKFold(n_splits=5, shuffle=True, random_state=10)
y=np.asarray(y)
X=np.asarray(X)
# Re-run cell if one of the classifiers predicts all 0s
# Initialize empty array for prediction probabilities/confidence
psx = np.zeros((len(y), 2))
# Fill in this array using k fold cross validation
for k, (cv_train_idx, cv_holdout_idx) in enumerate(kf.split(X, y)):
t_mod = text.Transformer('microsoft/BiomedNLP-PubMedBERT-base-uncased-abstract-fulltext', maxlen=500, class_names = [0,1])
# Select the training and holdout cross-validated sets.
X_train_cv, X_holdout_cv = X[cv_train_idx], X[cv_holdout_idx]
y_train_cv, y_holdout_cv = y[cv_train_idx], y[cv_holdout_idx]
# Preprocess train
data= t_mod.preprocess_train(X_train_cv,y_train_cv)
# Get new classifier for each iteration
model = t_mod.get_classifier()
# Fit model
learner = ktrain.get_learner(model, train_data=data, batch_size=16)
learning_rate= 5e-5
epochs=3
learner.fit_onecycle(learning_rate, epochs)
predictor=ktrain.get_predictor(learner.model, preproc=t_mod)
# Check performance of model
predictions=predictor.predict((X_holdout_cv))
print(accuracy_score((y_holdout_cv), predictions))
print(classification_report((y_holdout_cv), predictions))
# Get probabilities
psx_cv = predictor.predict_proba(X_holdout_cv) # P(s = k|x) # [:,1]
psx[cv_holdout_idx] = psx_cv
!pip install -q cleanlab
from cleanlab.pruning import get_noise_indices
ordered_label_errors = get_noise_indices(
s=y,
psx=psx,
sorted_index_method='normalized_margin', # Orders label errors
)
print(len(ordered_label_errors))
print(ordered_label_errors)
list_abs=[]
for i in ordered_label_errors:
list_abs.append(X[i])
print(len(list_abs))
df_o=pd.read_csv("../input/all-labelled/all_labelled.tsv", delimiter="\t")
df_o.dropna(inplace=True)
df_o=df_o.drop_duplicates()
df_top_errors= df_o[df_o['abstract'].isin(list_abs)]
print(len(df_top_errors))
print(df_top_errors)
df_top_errors.to_csv('top_losses_cl.tsv', sep= "\t", index=False)
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
import ipdb
import dan_utils
warnings.filterwarnings("ignore")
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.arima_model import ARIMA
def base_arima(data, pre_step):
# data should be 1-D DataFrame
D_data=data.diff(periods=1).dropna()
data = np.array(data)
model=ARIMA(data,(1,1,1)).fit()
forecast=model.forecast(pre_step)
return (forecast[0])
randseed = 25
dan_utils.setup_seed(randseed)
res = 11
v = pd.read_csv('../data/q_20_aggragated.csv')
v = v.rename(columns={'Unnamed: 0': 'id'})
det_with_class = pd.read_csv('../res/%i_res%i_id_402_withclass.csv'%(randseed, res), index_col=0)
v['class_i'] = ''
for i in range(len(v)):
v.loc[i, 'class_i'] = det_with_class[det_with_class['id']==v.loc[i, 'id']].iloc[0, 5] # 5 stands for 'class_i'
num_class = det_with_class['class_i'].drop_duplicates().size
v_class = []
for i in range(num_class):
v_class.append(v[v['class_i']==i])
print('There are %i class(es)'%num_class)
dist_mat = pd.read_csv('../data/dist_mat.csv', index_col=0)
id_info = pd.read_csv('../data/id2000.csv', index_col=0)
dist_mat.index = id_info['id2']
dist_mat.columns = id_info['id2']
for i in range(len(dist_mat)):
for j in range(len(dist_mat)):
if i==j:
dist_mat.iloc[i, j] = 0
near_id = pd.DataFrame(np.argsort(np.array(dist_mat)), index = id_info['id2'], columns = id_info['id2'])
seg = pd.read_csv('../data/segement.csv', header=None)
num_dets = 25
det_list_class = []
for i in range(num_class):
det_list_class_temp, v_class_temp = dan_utils.get_class_with_node(seg, v_class[i])
det_list_class.append(det_list_class_temp)
v_class_temp = v_class_temp[v_class_temp['id'].isin(det_list_class_temp[:num_dets])]
v_class[i] = v_class_temp
near_road_set = []
for i in range(num_class):
near_road_set.append(dan_utils.rds_mat(dist_mat, det_list_class[i][:num_dets], seg))
# ind, class
# 0 , blue
# 1 , green
# 2 , yellow <--
# 3 , black <--
# 4 , red <--
class_color_set = ['b', 'g', 'y', 'black', 'r']
class_i = 4
# v_class[4].iloc[:, 2:-1]
data = np.array(v_class[4].iloc[:, 2:-1])
window = 100
pred_num = 6
pred_mat_all = []
label_mat_all = []
for i in range(data.shape[0]): # iterate over detectors
pred_mat = []
label_mat = []
for j in range(data.shape[1] - window - pred_num):
data_temp = data[i, j:j+window]
label = data[i, j:j+window+pred_num]
pred = base_arima(pd.DataFrame(data_temp), pred_num)
pred_mat.append(pred)
label_mat.append(label)
pred_mat_all.append(np.array(pred_mat))
label_mat_all.append(np.array(label_mat))
```
| github_jupyter |
# STEP 4 - Making DRL PySC2 Agent
```
%load_ext autoreload
%autoreload 2
import sys; sys.path.append('..')
### unfortunately, PySC2 uses Abseil, which treats python code as if its run like an app
# This does not play well with jupyter notebook
# So we will need to monkeypatch sys.argv
import sys
#sys.argv = ["python", "--map", "AbyssalReef"]
sys.argv = ["python", "--map", "Simple64"]
```
## 0. Runnning 'Agent code' on jupyter notebook
```
# Copyright 2017 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS-IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
"""Run an agent."""
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import importlib
import threading
from absl import app
from absl import flags
from future.builtins import range # pylint: disable=redefined-builtin
from pysc2 import maps
from pysc2.env import available_actions_printer
from pysc2.env import run_loop
from pysc2.env import sc2_env
from pysc2.lib import point_flag
from pysc2.lib import stopwatch
from pysc2.lib import actions
FLAGS = flags.FLAGS
# because of Abseil's horrible design for running code underneath Colabs
# We have to pull out this ugly hack from the hat
if "flags_defined" not in globals():
flags.DEFINE_bool("render", False, "Whether to render with pygame.")
point_flag.DEFINE_point("feature_screen_size", "84",
"Resolution for screen feature layers.")
point_flag.DEFINE_point("feature_minimap_size", "64",
"Resolution for minimap feature layers.")
point_flag.DEFINE_point("rgb_screen_size", None,
"Resolution for rendered screen.")
point_flag.DEFINE_point("rgb_minimap_size", None,
"Resolution for rendered minimap.")
flags.DEFINE_enum("action_space", "RAW", sc2_env.ActionSpace._member_names_, # pylint: disable=protected-access
"Which action space to use. Needed if you take both feature "
"and rgb observations.")
flags.DEFINE_bool("use_feature_units", False,
"Whether to include feature units.")
flags.DEFINE_bool("use_raw_units", True,
"Whether to include raw units.")
flags.DEFINE_integer("raw_resolution", 64, "Raw Resolution.")
flags.DEFINE_bool("disable_fog", True, "Whether to disable Fog of War.")
flags.DEFINE_integer("max_agent_steps", 0, "Total agent steps.")
flags.DEFINE_integer("game_steps_per_episode", None, "Game steps per episode.")
flags.DEFINE_integer("max_episodes", 0, "Total episodes.")
flags.DEFINE_integer("step_mul", 8, "Game steps per agent step.")
flags.DEFINE_float("fps", 22.4, "Frames per second to run the game.")
#flags.DEFINE_string("agent", "sc2.agent.BasicAgent.ZergBasicAgent",
# "Which agent to run, as a python path to an Agent class.")
#flags.DEFINE_enum("agent_race", "zerg", sc2_env.Race._member_names_, # pylint: disable=protected-access
# "Agent 1's race.")
flags.DEFINE_string("agent", "TerranRLAgentWithRawActsAndRawObs",
"Which agent to run, as a python path to an Agent class.")
flags.DEFINE_enum("agent_race", "terran", sc2_env.Race._member_names_, # pylint: disable=protected-access
"Agent 1's race.")
flags.DEFINE_string("agent2", "Bot", "Second agent, either Bot or agent class.")
flags.DEFINE_enum("agent2_race", "random", sc2_env.Race._member_names_, # pylint: disable=protected-access
"Agent 2's race.")
flags.DEFINE_enum("difficulty", "hard", sc2_env.Difficulty._member_names_, # pylint: disable=protected-access
"If agent2 is a built-in Bot, it's strength.")
flags.DEFINE_bool("profile", False, "Whether to turn on code profiling.")
flags.DEFINE_bool("trace", False, "Whether to trace the code execution.")
flags.DEFINE_integer("parallel", 1, "How many instances to run in parallel.")
flags.DEFINE_bool("save_replay", True, "Whether to save a replay at the end.")
flags.DEFINE_string("map", None, "Name of a map to use.")
flags.mark_flag_as_required("map")
flags_defined = True
def run_thread(agent_classes, players, map_name, visualize):
"""Run one thread worth of the environment with agents."""
with sc2_env.SC2Env(
map_name=map_name,
players=players,
agent_interface_format=sc2_env.parse_agent_interface_format(
feature_screen=FLAGS.feature_screen_size,
feature_minimap=FLAGS.feature_minimap_size,
rgb_screen=FLAGS.rgb_screen_size,
rgb_minimap=FLAGS.rgb_minimap_size,
action_space=FLAGS.action_space,
use_raw_units=FLAGS.use_raw_units,
raw_resolution=FLAGS.raw_resolution),
step_mul=FLAGS.step_mul,
game_steps_per_episode=FLAGS.game_steps_per_episode,
disable_fog=FLAGS.disable_fog,
visualize=visualize) as env:
#env = available_actions_printer.AvailableActionsPrinter(env)
agents = [agent_cls() for agent_cls in agent_classes]
run_loop.run_loop(agents, env, FLAGS.max_agent_steps, FLAGS.max_episodes)
if FLAGS.save_replay:
env.save_replay(agent_classes[0].__name__)
def main(unused_argv):
"""Run an agent."""
#stopwatch.sw.enabled = FLAGS.profile or FLAGS.trace
#stopwatch.sw.trace = FLAGS.trace
map_inst = maps.get(FLAGS.map)
agent_classes = []
players = []
#agent_module, agent_name = FLAGS.agent.rsplit(".", 1)
#agent_cls = getattr(importlib.import_module(agent_module), agent_name)
#agent_classes.append(agent_cls)
agent_classes.append(TerranRLAgentWithRawActsAndRawObs)
players.append(sc2_env.Agent(sc2_env.Race[FLAGS.agent_race]))
if map_inst.players >= 2:
if FLAGS.agent2 == "Bot":
players.append(sc2_env.Bot(sc2_env.Race[FLAGS.agent2_race],
sc2_env.Difficulty[FLAGS.difficulty]))
else:
#agent_module, agent_name = FLAGS.agent2.rsplit(".", 1)
#agent_cls = getattr(importlib.import_module(agent_module), agent_name)
agent_classes.append(TerranRandomAgent)
players.append(sc2_env.Agent(sc2_env.Race[FLAGS.agent2_race]))
threads = []
for _ in range(FLAGS.parallel - 1):
t = threading.Thread(target=run_thread,
args=(agent_classes, players, FLAGS.map, False))
threads.append(t)
t.start()
run_thread(agent_classes, players, FLAGS.map, FLAGS.render)
for t in threads:
t.join()
if FLAGS.profile:
pass
#print(stopwatch.sw)
```
## 1. Creating a PySC2 Agent with Raw Actions & Observations

ref : https://on-demand.gputechconf.com/gtc/2018/presentation/s8739-machine-learning-with-starcraft-II.pdf
### < PySC2 Interfaces 3가지 종류 >
### 1st, Rendered
* Decomposed :
- Screen, minimap, resources, available actions
* Same control as humans :
- Pixel coordinates
- Move camera
- Select unit/rectangle
* Great for Deep Learning, but hard
### 2nd, Feature Layer
* Same actions : still in pixel space
* Same decomposed observations, but more abstract
- Orthogonal camera
* Layers:
- unit type
- unit owner
- selection
- health
- unit density
- etc
### 3rd, Raw
* List of units and state
* Control each unit individually in world coordinates
* Gives all observable state (no camera)
* Great for scripted agents and programmatic replay analysis
### < Raw Actions & Observations 을 사용하는 이유>
* Raw Actions & Observations 은 world cordinates를 사용하므로 전체 Map을 한번에 관찰하고 Camera를 이동하지 않고도 Map 상의 어느 곳에서도 Action을 취할 수 있는 새로운 형태의 Feature 이다.
* 이번 과정에 SL(Supervised Learning, 지도학습)을 활용한 학습은 없지만 스타크래프트 2 리플레이를 활용한 SL은 Raw Actions & Observations를 활용한 "programmatic replay analysis"가 필요하다.
* 인간 플레이어를 이긴 DeepMind의 AlphaStar의 주요 변경사항 중의 하나는 Raw Actions & Observations 의 활용이다.
### DRL 모델의 성능 추이를 보기위해 Reward의 평균 추이를 이용한다. 이때 단순이동평균 보다는 지수이동평균이 적절하다.
### 지수이동평균(EMA:Exponential Moving Average) 란?
지수이동평균(Exponential Moving Average)은 과거의 모든 기간을 계산대상으로 하며 최근의 데이타에 더 높은 가중치를 두는 일종의 가중이동평균법이다.
단순이동평균의 계산법에 비하여 원리가 복잡해 보이지만 실제로 이동평균을 산출하는 방법은 Previous Step의 지수이동평균값과 평활계수(smoothing constant) 그리고 당일의 가격만으로 구할 수 있으므로 Previous Step의 지수이동평균값만 구해진다면 오히려 간단한 편이다.
따라서 지수이동평균은 단순이동평균에 비해 몇가지 중요한 강점을 가진다.
첫째는 가장 최근의 Step에 가장 큰 가중치를 둠으로 해서 최근의 Episode들을 잘 반영한다는 점이고, 둘째는 단순이동평균에서와 같이 오래된 데이타를 갑자기 제외하지 않고 천천히 그 영향력을 사라지게 한다는 점이다.
또한 전 기간의 데이타를 분석대상으로 함으로써 가중이동평균에서 문제되는 특정 기간의 데이타만을 분석대상으로 한다는 단점도 보완하고 있다.
### 지수이동평균(EMA:Exponential Moving Average) 계산
지수이동평균은 가장 최근의 값에 많은 가중치를 부여하고 오래 된 값에는 적은 가중치를 부여한다. 비록 오래 된 값이라고 할지라도 완전히 무시하지는 않고 적게나마 반영시켜 계산한다는 장점이 있다. 단기 변동성을 포착하려는 것이 목적이다.
EMA=Previous Step 지수이동평균+(k∗(Current Step Reward − Previous Step 지수이동평균))
## 3. Applying Vanilla DQN to a PySC2 Agent
구현된 기능
- Implementing 'Experience Replay' :
- 'Maximization Bias' 문제를 발생시키는 원인 중 하나인 'Sample간의 시간적 연관성'을 해결하기 위한 방법
- Online Learning 에서 Batch Learning 으로 학습방법 바뀜 : Online update 는 Batch update 보다 일반적으로 Validation loss 가 더 높게 나타남.
- Reinforcement Learning for Robots. Using Neural Networks. Long -Ji Lin. January 6, 1993. 논문에서 최초로 연구됨 http://isl.anthropomatik.kit.edu/pdf/Lin1993.pdf
- Implementing 'Fixed Q-Target' :
- 'Moving Q-Target' 문제 해결하기 위한 방법
- 2015년 Nature 버전 DQN 논문에서 처음 제안됨. https://deepmind.com/research/publications/human-level-control-through-deep-reinforcement-learning
구현되지 않은 기능
- Implementing 'Sensory Input Feature-Extraction' :
- 게임의 Raw Image 를 Neural Net에 넣기 위한 Preprocessing(전처리) 과정
- Raw Image 의 Sequence중 '최근 4개의 이미지'(과거 정보)를 하나의 새로운 State로 정의하여 non-MDP를 MDP 문제로 바꾸는 Preprocessing 과정
- CNN(합성곱 신경망)을 활용한 '차원의 저주' 극복
```
import random
import time
import math
import os.path
import numpy as np
import pandas as pd
from collections import deque
import pickle
from pysc2.agents import base_agent
from pysc2.env import sc2_env
from pysc2.lib import actions, features, units, upgrades
from absl import app
import torch
from torch.utils.tensorboard import SummaryWriter
from skdrl.pytorch.model.mlp import NaiveMultiLayerPerceptron
from skdrl.common.memory.memory import ExperienceReplayMemory
DATA_FILE_QNET = 'rlagent_with_vanilla_dqn_qnet'
DATA_FILE_QNET_TARGET = 'rlagent_with_vanilla_dqn_qnet_target'
SCORE_FILE = 'rlagent_with_vanilla_dqn_score'
scores = [] # list containing scores from each episode
scores_window = deque(maxlen=100) # last 100 scores
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
writer = SummaryWriter()
import torch
import torch.nn as nn
class NaiveMultiLayerPerceptron(nn.Module):
def __init__(self,
input_dim: int,
output_dim: int,
num_neurons: list = [64, 32],
hidden_act_func: str = 'ReLU',
out_act_func: str = 'Identity'):
super(NaiveMultiLayerPerceptron, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.num_neurons = num_neurons
self.hidden_act_func = getattr(nn, hidden_act_func)()
self.out_act_func = getattr(nn, out_act_func)()
input_dims = [input_dim] + num_neurons
output_dims = num_neurons + [output_dim]
self.layers = nn.ModuleList()
for i, (in_dim, out_dim) in enumerate(zip(input_dims, output_dims)):
is_last = True if i == len(input_dims) - 1 else False
self.layers.append(nn.Linear(in_dim, out_dim))
if is_last:
self.layers.append(self.out_act_func)
else:
self.layers.append(self.hidden_act_func)
def forward(self, xs):
for layer in self.layers:
xs = layer(xs)
return xs
if __name__ == '__main__':
net = NaiveMultiLayerPerceptron(10, 1, [20, 12], 'ReLU', 'Identity')
print(net)
xs = torch.randn(size=(12, 10))
ys = net(xs)
print(ys)
```
### Q-update 공식
#### 1. Online Q-learning

#### 2. Online Q-learning with Function Approximation

#### 3. Batch Q-learning with Function Approximation & Experience Replay

```
from random import sample
class ExperienceReplayMemory:
def __init__(self, max_size):
# deque object that we've used for 'episodic_memory' is not suitable for random sampling
# here, we instead use a fix-size array to implement 'buffer'
self.buffer = [None] * max_size
self.max_size = max_size
self.index = 0
self.size = 0
def push(self, obj):
self.buffer[self.index] = obj
self.size = min(self.size + 1, self.max_size)
self.index = (self.index + 1) % self.max_size
def sample(self, batch_size):
indices = sample(range(self.size), batch_size)
return [self.buffer[index] for index in indices]
def __len__(self):
return self.size
```
### Moving target problem
#### 1. Function Approximation을 사용하지 않는 Q-learning 의 경우 : 특정한 Q(s,a) update가 다른 Q(s,a)에 영향을 주지 않는다.

#### 2. Function Approximation을 사용하는 Q-learnig 의 경우 : 특정한 Q(s,a) update가 다른 Q(s,a)에 영향을 준다.

### Moving target 문제는 Deep Neural Network를 사용하는 Function Approximation 기법인 경우 심해지는 경향성이 있음.
image ref : Fast Campus RL online courese
### `nn.SmoothL1Loss()` = Huber loss 란?
Mean-squared Error (MSE) Loss 는 데이터의 outlier에 매우 취약하다.
어떤 이유로 타겟하는 레이블 y (이 경우는 q-learning target)이 noisy 할때를 가정하면, 잘못된 y 값을 맞추기 위해 파라미터들이 너무 sensitive 하게 움직이게 된다.
이런 현상은 q-learning 의 학습초기에 매우 빈번해 나타난다. 이러한 문제를 조금이라도 완화하기 위해서 outlier에 덜 민감한 Huber loss 함수를 사용한다.
### SmoothL1Loss (aka Huber loss)
$$loss(x,y) = \frac{1}{n}\sum_i z_i$$
$|x_i - y_i| <1$ 일때,
$$z_i = 0.5(x_i - y_i)^2$$
$|x_i - y_i| \geq1$ 일때,
$$z_i = |x_i - y_i|-0.5$$
ref : https://pytorch.org/docs/master/generated/torch.nn.SmoothL1Loss.html
```
import torch
import torch.nn as nn
import numpy as np
import random
class DQN(nn.Module):
def __init__(self,
state_dim: int,
action_dim: int,
qnet: nn.Module,
qnet_target: nn.Module,
lr: float,
gamma: float,
epsilon: float):
"""
:param state_dim: input state dimension
:param action_dim: action dimension
:param qnet: main q network
:param qnet_target: target q network
:param lr: learning rate
:param gamma: discount factor of MDP
:param epsilon: E-greedy factor
"""
super(DQN, self).__init__()
self.state_dim = state_dim
self.action_dim = action_dim
self.qnet = qnet
self.lr = lr
self.gamma = gamma
self.opt = torch.optim.Adam(params=self.qnet.parameters(), lr=lr)
self.register_buffer('epsilon', torch.ones(1) * epsilon)
# target network related
qnet_target.load_state_dict(qnet.state_dict())
self.qnet_target = qnet_target
self.criteria = nn.SmoothL1Loss()
def choose_action(self, state):
qs = self.qnet(state)
#prob = np.random.uniform(0.0, 1.0, 1)
#if torch.from_numpy(prob).float() <= self.epsilon: # random
if random.random() <= self.epsilon: # random
action = np.random.choice(range(self.action_dim))
else: # greedy
action = qs.argmax(dim=-1)
return int(action)
def learn(self, state, action, reward, next_state, done):
s, a, r, ns = state, action, reward, next_state
# print("state: ", s)
# print("action: ", a)
# print("reward: ", reward)
# print("next_state: ", ns)
# compute Q-Learning target with 'target network'
with torch.no_grad():
q_max, _ = self.qnet_target(ns).max(dim=-1, keepdims=True)
q_target = r + self.gamma * q_max * (1 - done)
q_val = self.qnet(s).gather(1, a)
loss = self.criteria(q_val, q_target)
self.opt.zero_grad()
loss.backward()
self.opt.step()
def prepare_training_inputs(sampled_exps, device='cpu'):
states = []
actions = []
rewards = []
next_states = []
dones = []
for sampled_exp in sampled_exps:
states.append(sampled_exp[0])
actions.append(sampled_exp[1])
rewards.append(sampled_exp[2])
next_states.append(sampled_exp[3])
dones.append(sampled_exp[4])
states = torch.cat(states, dim=0).float().to(device)
actions = torch.cat(actions, dim=0).to(device)
rewards = torch.cat(rewards, dim=0).float().to(device)
next_states = torch.cat(next_states, dim=0).float().to(device)
dones = torch.cat(dones, dim=0).float().to(device)
return states, actions, rewards, next_states, dones
```
# Action 함수 정의
```
class TerranAgentWithRawActsAndRawObs(base_agent.BaseAgent):
# actions 추가 및 함수 정의(hirerachy하게)
actions = ("do_nothing",
"train_scv",
"harvest_minerals",
"harvest_gas",
"build_commandcenter",
"build_refinery",
"build_supply_depot",
"build_barracks",
"train_marine",
"build_factorys",
"build_techlab_factorys",
"train_tank",
"build_armorys",
"build_starports",
"build_techlab_starports",
"train_banshee",
"attack",
"attack_all",
"tank_control"
)
def unit_type_is_selected(self, obs, unit_type):
if (len(obs.observation.single_select) > 0 and
obs.observation.single_select[0].unit_type == unit_type):
return True
if (len(obs.observation.multi_select) > 0 and
obs.observation.multi_select[0].unit_type == unit_type):
return True
return False
def get_my_units_by_type(self, obs, unit_type):
if unit_type == units.Neutral.VespeneGeyser: # 가스 일 때만
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type]
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type
and unit.alliance == features.PlayerRelative.SELF]
def get_enemy_units_by_type(self, obs, unit_type):
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type
and unit.alliance == features.PlayerRelative.ENEMY]
def get_my_completed_units_by_type(self, obs, unit_type):
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type
and unit.build_progress == 100
and unit.alliance == features.PlayerRelative.SELF]
def get_enemy_completed_units_by_type(self, obs, unit_type):
return [unit for unit in obs.observation.raw_units
if unit.unit_type == unit_type
and unit.build_progress == 100
and unit.alliance == features.PlayerRelative.ENEMY]
def get_distances(self, obs, units, xy):
units_xy = [(unit.x, unit.y) for unit in units]
return np.linalg.norm(np.array(units_xy) - np.array(xy), axis=1)
def step(self, obs):
super(TerranAgentWithRawActsAndRawObs, self).step(obs)
if obs.first():
command_center = self.get_my_units_by_type(
obs, units.Terran.CommandCenter)[0]
self.base_top_left = (command_center.x < 32)
self.top_left_gas_xy = [(14, 25), (21,19), (46,23), (39,16)]
self.bottom_right_gas_xy = [(44, 43), (37,50), (12,46), (19,53)]
self.cloaking_flag = 1
self.TerranVehicleWeaponsLevel1 = False
self.TerranVehicleWeaponsLevel2 = False
self.TerranVehicleWeaponsLevel3 = False
def do_nothing(self, obs):
return actions.RAW_FUNCTIONS.no_op()
def train_scv(self, obs):
completed_commandcenterses = self.get_my_completed_units_by_type(
obs, units.Terran.CommandCenter)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (len(completed_commandcenterses) > 0 and obs.observation.player.minerals >= 100
and len(scvs) < 35):
commandcenters = self.get_my_units_by_type(obs, units.Terran.CommandCenter)
ccs =[commandcenter for commandcenter in commandcenters if commandcenter.assigned_harvesters < 18]
if ccs:
ccs = ccs[0]
if ccs.order_length < 5:
return actions.RAW_FUNCTIONS.Train_SCV_quick("now", ccs.tag)
return actions.RAW_FUNCTIONS.no_op()
def harvest_minerals(self, obs):
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
commandcenters = self.get_my_units_by_type(obs,units.Terran.CommandCenter) # 최적 자원 할당 유닛 구현
cc = [commandcenter for commandcenter in commandcenters if commandcenter.assigned_harvesters < 18]
if cc:
cc = cc[0]
idle_scvs = [scv for scv in scvs if scv.order_length == 0]
if len(idle_scvs) > 0 and cc.assigned_harvesters < 18:
mineral_patches = [unit for unit in obs.observation.raw_units
if unit.unit_type in [
units.Neutral.BattleStationMineralField,
units.Neutral.BattleStationMineralField750,
units.Neutral.LabMineralField,
units.Neutral.LabMineralField750,
units.Neutral.MineralField,
units.Neutral.MineralField750,
units.Neutral.PurifierMineralField,
units.Neutral.PurifierMineralField750,
units.Neutral.PurifierRichMineralField,
units.Neutral.PurifierRichMineralField750,
units.Neutral.RichMineralField,
units.Neutral.RichMineralField750
]]
scv = random.choice(idle_scvs)
distances = self.get_distances(obs, mineral_patches, (scv.x, scv.y))
mineral_patch = mineral_patches[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Harvest_Gather_unit(
"now", scv.tag, mineral_patch.tag)
return actions.RAW_FUNCTIONS.no_op()
def harvest_gas(self, obs):
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
refs = self.get_my_units_by_type(obs, units.Terran.Refinery)
refs = [refinery for refinery in refs if refinery.assigned_harvesters < 3]
if refs:
ref = refs[0]
if len(scvs) > 0 and ref.ideal_harvesters:
scv = random.choice(scvs)
distances = self.get_distances(obs, refs, (scv.x, scv.y))
ref = refs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Harvest_Gather_unit(
"now", scv.tag, ref.tag)
return actions.RAW_FUNCTIONS.no_op()
def build_commandcenter(self,obs):
commandcenters = self.get_my_units_by_type(obs,units.Terran.CommandCenter)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if len(commandcenters) == 0 and obs.observation.player.minerals >= 400 and len(scvs) > 0:
# 본진 commandcenter가 파괴된 경우
ccs_xy = (19, 23) if self.base_top_left else (39,45)
distances = self.get_distances(obs, scvs, ccs_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_CommandCenter_pt(
"now", scv.tag, ccs_xy)
if ( len(commandcenters) < 2 and obs.observation.player.minerals >= 400 and
len(scvs) > 0):
ccs_xy = (41, 21) if self.base_top_left else (17, 48)
if len(commandcenters) == 1 and ( (commandcenters[0].x,commandcenters[0].y) == (41,21) or
(commandcenters[0].x,commandcenters[0].y) == (17,48)):
# 본진 commandcenter가 파괴된 경우
ccs_xy = (19, 23) if self.base_top_left else (39,45)
distances = self.get_distances(obs, scvs, ccs_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_CommandCenter_pt(
"now", scv.tag, ccs_xy)
return actions.RAW_FUNCTIONS.no_op()
################################################################################################
####################################### refinery ###############################################
def build_refinery(self,obs):
refinerys = self.get_my_units_by_type(obs,units.Terran.Refinery)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (obs.observation.player.minerals >= 100 and
len(scvs) > 0):
gas = self.get_my_units_by_type(obs, units.Neutral.VespeneGeyser)[0]
if self.base_top_left:
gases = self.top_left_gas_xy
else:
gases = self.bottom_right_gas_xy
rc = np.random.choice([0,1,2,3])
gas_xy = gases[rc]
if (gas.x, gas.y) == gas_xy:
distances = self.get_distances(obs, scvs, gas_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_Refinery_pt(
"now", scv.tag, gas.tag)
return actions.RAW_FUNCTIONS.no_op()
def build_supply_depot(self, obs):
supply_depots = self.get_my_units_by_type(obs, units.Terran.SupplyDepot)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
free_supply = (obs.observation.player.food_cap -
obs.observation.player.food_used)
if (obs.observation.player.minerals >= 100 and
len(scvs) > 0 and free_supply < 8):
ccs = self.get_my_units_by_type(obs, units.Terran.CommandCenter)
if ccs:
for cc in ccs:
cc_x, cc_y = cc.x, cc.y
rand1,rand2 = random.randint(0,10),random.randint(-10,0)
supply_depot_xy = (cc_x + rand1, cc_y + rand2) if self.base_top_left else (cc_x - rand1, cc_y - rand2)
if 0 < supply_depot_xy[0] < 64 and 0 < supply_depot_xy[1] < 64:
pass
else:
return actions.RAW_FUNCTIONS.no_op()
distances = self.get_distances(obs, scvs, supply_depot_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_SupplyDepot_pt(
"now", scv.tag, supply_depot_xy)
return actions.RAW_FUNCTIONS.no_op()
def build_barracks(self, obs):
completed_supply_depots = self.get_my_completed_units_by_type(
obs, units.Terran.SupplyDepot)
barrackses = self.get_my_units_by_type(obs, units.Terran.Barracks)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (len(completed_supply_depots) > 0 and
obs.observation.player.minerals >= 150 and len(scvs) > 0 and
len(barrackses)< 3):
brks = self.get_my_units_by_type(obs, units.Terran.SupplyDepot)
completed_command_center = self.get_my_completed_units_by_type(
obs, units.Terran.CommandCenter)
if len(barrackses) >= 1 and len(completed_command_center) == 1:
# double commands
commandcenters = self.get_my_units_by_type(obs,units.Terran.CommandCenter)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if ( len(commandcenters) < 2 and obs.observation.player.minerals >= 400 and
len(scvs) > 0):
ccs_xy = (41, 21) if self.base_top_left else (17, 48)
distances = self.get_distances(obs, scvs, ccs_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_CommandCenter_pt(
"now", scv.tag, ccs_xy)
if brks:
for brk in brks:
brk_x,brk_y = brk.x, brk.y
rand1, rand2 = random.randint(1,3),random.randint(1,3)
barracks_xy = (brk_x + rand1, brk_y + rand2) if self.base_top_left else (brk_x - rand1, brk_y - rand2)
if 0 < barracks_xy[0] < 64 and 0 < barracks_xy[1] < 64:
pass
else:
return actions.RAW_FUNCTIONS.no_op()
distances = self.get_distances(obs, scvs, barracks_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_Barracks_pt(
"now", scv.tag, barracks_xy)
return actions.RAW_FUNCTIONS.no_op()
def train_marine(self, obs):
################# 아머리가 완성된 후 부터 토르생산 ######################
completed_barrackses = self.get_my_completed_units_by_type(
obs, units.Terran.Barracks)
completed_factorys = self.get_my_completed_units_by_type(
obs, units.Terran.Factory)
completed_armorys = self.get_my_completed_units_by_type(
obs, units.Terran.Armory)
marines = self.get_my_units_by_type(obs, units.Terran.Marine)
free_supply = (obs.observation.player.food_cap -
obs.observation.player.food_used)
if (len(completed_barrackses) > 0 and obs.observation.player.minerals >= 100
and free_supply > 0 and len(completed_armorys) == 0):
barracks = self.get_my_units_by_type(obs, units.Terran.Barracks)[0]
if barracks.order_length < 5:
return actions.RAW_FUNCTIONS.Train_Marine_quick("now", barracks.tag)
elif free_supply > 0 and len(completed_factorys) > 0 and len(completed_armorys) > 0:
factory = completed_factorys[0]
if factory.order_length < 5:
return actions.RAW_FUNCTIONS.Train_Thor_quick("now", factory.tag)
return actions.RAW_FUNCTIONS.no_op()
###############################################################################################
###################################### Factorys ###############################################
###############################################################################################
def build_factorys(self, obs):
completed_barrackses = self.get_my_completed_units_by_type(
obs, units.Terran.Barracks)
factorys = self.get_my_units_by_type(obs, units.Terran.Factory)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
ref = self.get_my_completed_units_by_type(obs,units.Terran.Refinery)
# print("gas: ", obs.observation.player.minerals)
# print("gas: ", obs.observation.player.gas)
if (len(completed_barrackses) > 0 and
obs.observation.player.minerals >= 200 and
len(factorys) < 3 and
len(scvs) > 0):
if len(factorys) >= 1 and len(ref) < 4: # 가스부족시 가스 건설
refinerys = self.get_my_units_by_type(obs,units.Terran.Refinery)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (obs.observation.player.minerals >= 100 and
len(scvs) > 0):
gas = self.get_my_units_by_type(obs, units.Neutral.VespeneGeyser)[0]
if self.base_top_left:
gases = self.top_left_gas_xy
else:
gases = self.bottom_right_gas_xy
rc = np.random.choice([0,1,2,3])
gas_xy = gases[rc]
if (gas.x, gas.y) == gas_xy:
distances = self.get_distances(obs, scvs, gas_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_Refinery_pt(
"now", scv.tag, gas.tag)
if len(factorys) >= 1:
rand1 = random.randint(-5,5)
fx, fy = factorys[0].x, factorys[0].y
factorys_xy = (fx + rand1, fy + rand1) if self.base_top_left else (fx - rand1, fy - rand1)
else:
rand1, rand2 = random.randint(-2,2), random.randint(-2,2) # x, y
factorys_xy = (39 + rand1, 25 + rand2) if self.base_top_left else (17 - rand1, 40 - rand2)
if 0 < factorys_xy[0] < 64 and 0 < factorys_xy[1] < 64 and factorys_xy != (17,48) and factorys_xy != (41,21):
pass
else:
return actions.RAW_FUNCTIONS.no_op()
distances = self.get_distances(obs, scvs, factorys_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_Factory_pt(
"now", scv.tag, factorys_xy)
return actions.RAW_FUNCTIONS.no_op()
def build_techlab_factorys(self, obs):
completed_factorys = self.get_my_completed_units_by_type(
obs, units.Terran.Factory)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (len(completed_factorys) > 0 and
obs.observation.player.minerals >= 200):
ftrs = self.get_my_units_by_type(obs, units.Terran.Factory)
if ftrs:
for ftr in ftrs:
ftr_x,ftr_y = ftr.x, ftr.y
factorys_xy = (ftr_x,ftr_y)
if 0 < factorys_xy[0] < 64 and 0 < factorys_xy[1] < 64:
pass
else:
return actions.RAW_FUNCTIONS.no_op()
return actions.RAW_FUNCTIONS.Build_TechLab_Factory_pt(
"now", ftr.tag, factorys_xy)
return actions.RAW_FUNCTIONS.no_op()
def train_tank(self, obs):
completed_factorytechlab = self.get_my_completed_units_by_type(
obs, units.Terran.FactoryTechLab)
free_supply = (obs.observation.player.food_cap -
obs.observation.player.food_used)
if (len(completed_factorytechlab) > 0 and obs.observation.player.minerals >= 200):
factorys = self.get_my_units_by_type(obs, units.Terran.Factory)[0]
if factorys.order_length < 5:
return actions.RAW_FUNCTIONS.Train_SiegeTank_quick("now", factorys.tag)
return actions.RAW_FUNCTIONS.no_op()
###############################################################################
############################ Build Armory ##################################
def build_armorys(self, obs):
completed_factory = self.get_my_completed_units_by_type(
obs, units.Terran.Factory)
armorys = self.get_my_units_by_type(obs, units.Terran.Armory)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (len(completed_factory) > 0 and
obs.observation.player.minerals >= 200 and
len(armorys) < 2 and
len(scvs) > 0):
rand1, rand2 = random.randint(-2,2),random.randint(-2,2)
armorys_xy = (36 + rand1, 20 + rand2) if self.base_top_left else ( 20 - rand1, 50 - rand2)
if 0 < armorys_xy[0] < 64 and 0 < armorys_xy[1] < 64:
pass
else:
return actions.RAW_FUNCTIONS.no_op()
distances = self.get_distances(obs, scvs, armorys_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_Armory_pt(
"now", scv.tag, armorys_xy)
elif (len(completed_factory) > 0 and
obs.observation.player.minerals >= 200 and
1 <= len(armorys) and
len(scvs) > 0):
# armory upgrade 추가
armory = armorys[0]
armory_xy = (armory.x, armory.y)
#cloak_field = self.get_my_units_by_type(obs, upgrades.Upgrades.CloakingField)[0]
if self.TerranVehicleWeaponsLevel1 == False:
self.TerranVehicleWeaponsLevel1 = True
return actions.RAW_FUNCTIONS.Research_TerranVehicleWeapons_quick("now", armory.tag)
elif self.TerranVehicleWeaponsLevel1 == True and self.TerranVehicleWeaponsLevel2 == False:
self.TerranVehicleWeaponsLevel2 = True
return actions.RAW_FUNCTIONS.Research_TerranVehicleWeaponsLevel2_quick("now", armory.tag)
elif self.TerranVehicleWeaponsLevel1 == True and self.TerranVehicleWeaponsLevel2 == True and self.TerranVehicleWeaponsLevel3 == False:
self.TerranVehicleWeaponsLevel3 = True
return actions.RAW_FUNCTIONS.Research_TerranVehicleWeaponsLevel3_quick("now", armory.tag)
return actions.RAW_FUNCTIONS.no_op()
############################################################################################
#################################### StarPort ##############################################
def build_starports(self, obs):
completed_factorys = self.get_my_completed_units_by_type(
obs, units.Terran.Factory)
starports = self.get_my_units_by_type(obs, units.Terran.Starport)
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
if (len(completed_factorys) > 0 and
obs.observation.player.minerals >= 200 and
len(starports) < 1 and
len(scvs) > 0):
# stp_x,stp_y = (22,22), (36,46) # minerals기준 중앙부쪽 좌표
if len(starports) >= 1:
rand1 = random.randint(-5,5)
sx, sy = starports[0].x, starports[0].y
starport_xy = (sx + rand1, sy + rand1) if self.base_top_left else (sx - rand1, sy - rand1)
else:
rand1, rand2 = random.randint(-5,5),random.randint(-5,5)
starport_xy = (22 + rand1, 22 + rand2) if self.base_top_left else (36 - rand1, 46 - rand2)
if 0 < starport_xy[0] < 64 and 0 < starport_xy[1] < 64:
pass
else:
return actions.RAW_FUNCTIONS.no_op()
distances = self.get_distances(obs, scvs, starport_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_Starport_pt(
"now", scv.tag, starport_xy)
####################### 스타포트 건설 후 팩토리 증설 #########################
elif (len(starports) >= 1 and obs.observation.player.minerals >= 200 and
len(completed_factorys) < 4 and len(scvs) > 0):
if len(starports) >= 1:
rand1 = random.randint(-5,5)
sx, sy = starports[0].x, starports[0].y
factory_xy = (sx + rand1, sy + rand1) if self.base_top_left else (sx - rand1, sy - rand1)
else:
rand1, rand2 = random.randint(-5,5),random.randint(-5,5)
factory_xy = (22 + rand1, 22 + rand2) if self.base_top_left else (36 - rand1, 46 - rand2)
if 0 < factory_xy[0] < 64 and 0 < factory_xy[1] < 64:
pass
else:
return actions.RAW_FUNCTIONS.no_op()
distances = self.get_distances(obs, scvs, factory_xy)
scv = scvs[np.argmin(distances)]
return actions.RAW_FUNCTIONS.Build_Factory_pt(
"now", scv.tag, factory_xy)
else:
completed_barrackses = self.get_my_completed_units_by_type(
obs, units.Terran.Barracks)
marines = self.get_my_units_by_type(obs, units.Terran.Marine)
free_supply = (obs.observation.player.food_cap -
obs.observation.player.food_used)
if (len(completed_barrackses) > 0 and obs.observation.player.minerals >= 100
and free_supply > 0):
barracks = self.get_my_units_by_type(obs, units.Terran.Barracks)[0]
if barracks.order_length < 5:
return actions.RAW_FUNCTIONS.Train_Marine_quick("now", barracks.tag)
return actions.RAW_FUNCTIONS.no_op()
def build_techlab_starports(self, obs):
completed_starports = self.get_my_completed_units_by_type(
obs, units.Terran.Starport)
completed_starport_techlab = self.get_my_completed_units_by_type(
obs, units.Terran.StarportTechLab)
if (len(completed_starports) < 3 and
obs.observation.player.minerals >= 200):
stps = self.get_my_units_by_type(obs, units.Terran.Starport)
if stps:
for stp in stps:
stp_x,stp_y = stp.x, stp.y
starport_xy = (stp_x,stp_y)
return actions.RAW_FUNCTIONS.Build_TechLab_Starport_pt(
"now", stp.tag, starport_xy)
############ Cloak upgrade #########################
if len(completed_starport_techlab) > 0 and self.cloaking_flag:
# self.cloaking_flag = 0
cloaking = upgrades.Upgrades.CloakingField
stp_techlab = self.get_my_units_by_type(obs, units.Terran.StarportTechLab)
if stp_techlab:
stp_tech_xy = (stp_techlab[0].x, stp_techlab[0].y)
cloak_field = self.get_my_units_by_type(obs, upgrades.Upgrades.CloakingField)[0]
# print("stp_tech_xy: ", stp_tech_xy)
# print("cloaking upgrade: ",cloak_field.tag)
return actions.FUNCTIONS.Research_BansheeCloakingField_quick("now", cloaking )
return actions.RAW_FUNCTIONS.no_op()
def train_banshee(self, obs):
completed_starporttechlab = self.get_my_completed_units_by_type(
obs, units.Terran.StarportTechLab)
ravens = self.get_my_units_by_type(obs, units.Terran.Raven)
free_supply = (obs.observation.player.food_cap -
obs.observation.player.food_used)
if (len(completed_starporttechlab) > 0 and obs.observation.player.minerals >= 200
and free_supply > 3):
starports = self.get_my_units_by_type(obs, units.Terran.Starport)[0]
############################### cloaking detecting을 위한 Raven 생산 #######################
if starports.order_length < 2 and len(ravens) < 3 :
return actions.RAW_FUNCTIONS.Train_Raven_quick("now", starports.tag)
#########################################################################################
if starports.order_length < 5:
return actions.RAW_FUNCTIONS.Train_Banshee_quick("now", starports.tag)
return actions.RAW_FUNCTIONS.no_op()
############################################################################################
def attack(self, obs):
marines = self.get_my_units_by_type(obs, units.Terran.Marine)
if 20 < len(marines):
flag = random.randint(0,2)
if flag == 1:
attack_xy = (38, 44) if self.base_top_left else (19, 23)
else:
attack_xy = (16, 45) if self.base_top_left else (42, 19)
distances = self.get_distances(obs, marines, attack_xy)
marine = marines[np.argmax(distances)]
#marine = marines
x_offset = random.randint(-5, 5)
y_offset = random.randint(-5, 5)
return actions.RAW_FUNCTIONS.Attack_pt(
"now", marine.tag, (attack_xy[0] + x_offset, attack_xy[1] + y_offset))
else:
barracks = self.get_my_units_by_type(obs, units.Terran.Barracks)
if len(barracks) > 0:
barracks = barracks[0]
if barracks.order_length < 5:
return actions.RAW_FUNCTIONS.Train_Marine_quick("now", barracks.tag)
return actions.RAW_FUNCTIONS.no_op()
def attack_all(self,obs):
# 추가 유닛 생길 때 마다 추가
marines = self.get_my_units_by_type(obs, units.Terran.Marine)
tanks = self.get_my_units_by_type(obs, units.Terran.SiegeTank)
banshees = self.get_my_units_by_type(obs, units.Terran.Banshee)
raven = self.get_my_units_by_type(obs, units.Terran.Raven)
thor = self.get_my_units_by_type(obs, units.Terran.Thor)
sieged_tanks = self.get_my_units_by_type(obs, units.Terran.SiegeTankSieged)
total_tanks = tanks + sieged_tanks
all_units = marines + total_tanks + banshees + raven + thor
if 25 < len(all_units):
flag = random.randint(0,1000)
if flag%4 == 0:
attack_xy = (39, 45) if self.base_top_left else (19, 23)
elif flag%4 == 1:
attack_xy = (39, 45) if self.base_top_left else (19, 23)
if len(tanks) > 0:
distances = self.get_distances(obs, tanks, attack_xy)
tank = tanks[np.argmax(distances)]
x_offset = random.randint(-1, 1)
y_offset = random.randint(-1, 1)
return actions.RAW_FUNCTIONS.Morph_SiegeMode_quick(
"now", tank.tag, (attack_xy[0] + x_offset, attack_xy[1] + y_offset))
elif flag%4 == 2:
attack_xy = (39, 45) if self.base_top_left else (19, 23)
#### siegeMode 제거 ####
if len(total_tanks) > 0:
all_tanks_tag = [tank.tag for tank in total_tanks]
return actions.RAW_FUNCTIONS.Morph_Unsiege_quick(
"now", all_tanks_tag)
else:
attack_xy = (17, 48) if self.base_top_left else (41, 21)
x_offset = random.randint(-5, 5)
y_offset = random.randint(-5, 5)
all_tag = [unit.tag for unit in all_units]
return actions.RAW_FUNCTIONS.Attack_pt(
"now", all_tag, (attack_xy[0] + x_offset, attack_xy[1] + y_offset))
else:
flag = random.randint(0,1000)
if flag%4 == 0:
attack_xy = (35, 25) if self.base_top_left else (25, 40)
elif flag%4 == 1:
attack_xy = (35, 25) if self.base_top_left else (25, 40)
if len(tanks) > 0:
tanks_tag = [tank.tag for tank in tanks]
x_offset = random.randint(-1, 1)
y_offset = random.randint(-1, 1)
return actions.RAW_FUNCTIONS.Morph_SiegeMode_quick(
"now", tanks_tag, (attack_xy[0] + x_offset, attack_xy[1] + y_offset))
elif flag%4 == 2:
attack_xy = (35, 25) if self.base_top_left else (25, 40)
else:
attack_xy = (30, 25) if self.base_top_left else (33, 40)
x_offset = random.randint(-1, 1)
y_offset = random.randint(-1, 1)
all_units = marines + banshees + raven + thor
all_tag = [unit.tag for unit in all_units]
if all_tag:
return actions.RAW_FUNCTIONS.Attack_pt(
"now", all_tag, (attack_xy[0] + x_offset, attack_xy[1] + y_offset))
return actions.RAW_FUNCTIONS.no_op()
###################################################################################
############################### Unit Controls #####################################
def tank_control(self, obs):
tanks = self.get_my_units_by_type(obs, units.Terran.SiegeTank)
sieged_tanks = self.get_my_units_by_type(obs, units.Terran.SiegeTankSieged)
total_tanks = tanks + sieged_tanks
if len(total_tanks) < 8:
if tanks:
attack_xy = (40, 25) if self.base_top_left else (25, 40)
distances = self.get_distances(obs, tanks, attack_xy)
distances.sort()
tank_tag = [t.tag for t in tanks[:4]]
x_offset = random.randint(-5, 5)
y_offset = random.randint(-5, 5)
return actions.RAW_FUNCTIONS.Morph_SiegeMode_quick(
"now", tank_tag, (attack_xy[0] + x_offset, attack_xy[1] + y_offset))
else:
#### siegeMode 제거 ####
all_tanks_tag = [tank.tag for tank in total_tanks]
return actions.RAW_FUNCTIONS.Morph_Unsiege_quick(
"now", all_tanks_tag)
return actions.RAW_FUNCTIONS.no_op()
class TerranRandomAgent(TerranAgentWithRawActsAndRawObs):
def step(self, obs):
super(TerranRandomAgent, self).step(obs)
action = random.choice(self.actions)
return getattr(self, action)(obs)
```
### Hyperparameter
하이퍼파라미터는 심층강화학습 알고리즘에서 성능에 매우 큰 영향을 미칩니다.
이 실험에 쓰인 하이퍼파라미터는 https://github.com/chucnorrisful/dqn 실험에서 제안된 값들을 참고하였습니다.
- self.s_dim = 21
- self.a_dim = 6
- self.lr = 1e-4 * 1
- self.batch_size = 32
- self.gamma = 0.99
- self.memory_size = 200000
- self.eps_max = 1.0
- self.eps_min = 0.01
- self.epsilon = 1.0
- self.init_sampling = 4000
- self.target_update_interval = 10
- self.epsilon = max(self.eps_min, self.eps_max - self.eps_min * (self.episode_count / 50))

```
class TerranRLAgentWithRawActsAndRawObs(TerranAgentWithRawActsAndRawObs):
def __init__(self):
super(TerranRLAgentWithRawActsAndRawObs, self).__init__()
self.s_dim = 21
self.a_dim = 19
self.lr = 1e-4 * 1
self.batch_size = 32
self.gamma = 0.99
self.memory_size = 200000
self.eps_max = 1.0
self.eps_min = 0.01
self.epsilon = 1.0
self.init_sampling = 4000
self.target_update_interval = 10
self.data_file_qnet = DATA_FILE_QNET
self.data_file_qnet_target = DATA_FILE_QNET_TARGET
self.score_file = SCORE_FILE
self.qnetwork = NaiveMultiLayerPerceptron(input_dim=self.s_dim,
output_dim=self.a_dim,
num_neurons=[128],
hidden_act_func='ReLU',
out_act_func='Identity').to(device)
self.qnetwork_target = NaiveMultiLayerPerceptron(input_dim=self.s_dim,
output_dim=self.a_dim,
num_neurons=[128],
hidden_act_func='ReLU',
out_act_func='Identity').to(device)
############################################ qnet 로드하면 이전 모델이라 학습모델 인풋 아웃풋차원이 바뀜 #########
if os.path.isfile(self.data_file_qnet + '.pt'):
self.qnetwork.load_state_dict(torch.load(self.data_file_qnet + '.pt'))
if os.path.isfile(self.data_file_qnet_target + '.pt'):
self.qnetwork_target.load_state_dict(torch.load(self.data_file_qnet_target + '.pt'))
# initialize target network same as the main network.
self.qnetwork_target.load_state_dict(self.qnetwork.state_dict())
self.dqn = DQN(state_dim=self.s_dim,
action_dim=self.a_dim,
qnet=self.qnetwork,
qnet_target=self.qnetwork_target,
lr=self.lr,
gamma=self.gamma,
epsilon=self.epsilon).to(device)
self.memory = ExperienceReplayMemory(self.memory_size)
self.print_every = 1
self.cum_reward = 0
self.cum_loss = 0
self.episode_count = 0
self.new_game()
def reset(self):
super(TerranRLAgentWithRawActsAndRawObs, self).reset()
self.new_game()
def new_game(self):
self.base_top_left = None
self.previous_state = None
self.previous_action = None
self.cum_reward = 0
self.cum_loss = 0
# epsilon scheduling
# slowly decaying_epsilon
self.epsilon = max(self.eps_min, self.eps_max - self.eps_min * (self.episode_count / 50))
self.dqn.epsilon = torch.tensor(self.epsilon).to(device)
def get_state(self, obs):
scvs = self.get_my_units_by_type(obs, units.Terran.SCV)
idle_scvs = [scv for scv in scvs if scv.order_length == 0]
command_centers = self.get_my_units_by_type(obs, units.Terran.CommandCenter)
supply_depots = self.get_my_units_by_type(obs, units.Terran.SupplyDepot)
completed_supply_depots = self.get_my_completed_units_by_type(
obs, units.Terran.SupplyDepot)
barrackses = self.get_my_units_by_type(obs, units.Terran.Barracks)
completed_barrackses = self.get_my_completed_units_by_type(
obs, units.Terran.Barracks)
marines = self.get_my_units_by_type(obs, units.Terran.Marine)
queued_marines = (completed_barrackses[0].order_length
if len(completed_barrackses) > 0 else 0)
free_supply = (obs.observation.player.food_cap -
obs.observation.player.food_used)
can_afford_supply_depot = obs.observation.player.minerals >= 100
can_afford_barracks = obs.observation.player.minerals >= 150
can_afford_marine = obs.observation.player.minerals >= 100
enemy_scvs = self.get_enemy_units_by_type(obs, units.Terran.SCV)
enemy_idle_scvs = [scv for scv in enemy_scvs if scv.order_length == 0]
enemy_command_centers = self.get_enemy_units_by_type(
obs, units.Terran.CommandCenter)
enemy_supply_depots = self.get_enemy_units_by_type(
obs, units.Terran.SupplyDepot)
enemy_completed_supply_depots = self.get_enemy_completed_units_by_type(
obs, units.Terran.SupplyDepot)
enemy_barrackses = self.get_enemy_units_by_type(obs, units.Terran.Barracks)
enemy_completed_barrackses = self.get_enemy_completed_units_by_type(
obs, units.Terran.Barracks)
enemy_marines = self.get_enemy_units_by_type(obs, units.Terran.Marine)
return (len(command_centers),
len(scvs),
len(idle_scvs),
len(supply_depots),
len(completed_supply_depots),
len(barrackses),
len(completed_barrackses),
len(marines),
queued_marines,
free_supply,
can_afford_supply_depot,
can_afford_barracks,
can_afford_marine,
len(enemy_command_centers),
len(enemy_scvs),
len(enemy_idle_scvs),
len(enemy_supply_depots),
len(enemy_completed_supply_depots),
len(enemy_barrackses),
len(enemy_completed_barrackses),
len(enemy_marines))
def step(self, obs):
super(TerranRLAgentWithRawActsAndRawObs, self).step(obs)
#time.sleep(0.5)
state = self.get_state(obs)
state = torch.tensor(state).float().view(1, self.s_dim).to(device)
action_idx = self.dqn.choose_action(state)
action = self.actions[action_idx]
done = True if obs.last() else False
if self.previous_action is not None:
experience = (self.previous_state.to(device),
torch.tensor(self.previous_action).view(1, 1).to(device),
torch.tensor(obs.reward).view(1, 1).to(device),
state.to(device),
torch.tensor(done).view(1, 1).to(device))
self.memory.push(experience)
self.cum_reward += obs.reward
self.previous_state = state
self.previous_action = action_idx
if obs.last():
self.episode_count = self.episode_count + 1
if len(self.memory) >= self.init_sampling:
# training dqn
sampled_exps = self.memory.sample(self.batch_size)
sampled_exps = prepare_training_inputs(sampled_exps, device)
self.dqn.learn(*sampled_exps)
if self.episode_count % self.target_update_interval == 0:
self.dqn.qnet_target.load_state_dict(self.dqn.qnet.state_dict())
if self.episode_count % self.print_every == 0:
msg = (self.episode_count, self.cum_reward, self.epsilon)
print("Episode : {:4.0f} | Cumulative Reward : {:4.0f} | Epsilon : {:.3f}".format(*msg))
torch.save(self.dqn.qnet.state_dict(), self.data_file_qnet + '.pt')
torch.save(self.dqn.qnet_target.state_dict(), self.data_file_qnet_target + '.pt')
scores_window.append(obs.reward) # save most recent reward
win_rate = scores_window.count(1)/len(scores_window)*100
tie_rate = scores_window.count(0)/len(scores_window)*100
lost_rate = scores_window.count(-1)/len(scores_window)*100
scores.append([win_rate, tie_rate, lost_rate]) # save most recent score(win_rate, tie_rate, lost_rate)
with open(self.score_file + '.txt', "wb") as fp:
pickle.dump(scores, fp)
#writer.add_scalar("Loss/train", self.cum_loss/obs.observation.game_loop, self.episode_count)
writer.add_scalar("Score", self.cum_reward, self.episode_count)
return getattr(self, action)(obs)
if __name__ == "__main__":
app.run(main)
```
### [Winning rate graph]
```
!pip install matplotlib
import pickle
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
SCORE_FILE = 'rlagent_with_vanilla_dqn_score'
with open(SCORE_FILE + '.txt', "rb") as fp:
scores = pickle.load(fp)
np_scores = np.array(scores)
np_scores
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(np_scores)), np_scores.T[0], color='r', label='win rate')
plt.plot(np.arange(len(np_scores)), np_scores.T[1], color='g', label='tie rate')
plt.plot(np.arange(len(np_scores)), np_scores.T[2], color='b', label='lose rate')
plt.ylabel('Score %')
plt.xlabel('Episode #')
plt.legend(loc='best')
plt.show()
f = file.open()
```
| github_jupyter |
```
# HIDDEN
from datascience import *
from prob140 import *
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
import math
from scipy import stats
```
## MGFs, the Normal, and the CLT ##
Let $Z$ be standard normal. Then the mgf of $Z$ is given by
$$
M_Z(t) ~ = ~ e^{t^2/2} ~~~ \text{for all } t
$$
To see this, just work out the integral:
\begin{align*}
M_Z(t) ~ &= ~ \int_{-\infty}^\infty e^{tz} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}z^2} dz \\ \\
&= ~ \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}(z^2 - 2tz)} dz \\ \\
&= ~ e^{t^2/2} \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}(z^2 - 2tz + t^2)} dz \\ \\
&= ~ e^{t^2/2} \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}(z- t)^2} dz \\ \\
&= ~ e^{t^2/2}
\end{align*}
because the integral is 1. It is the normal $(t, 1)$ density integrated over the whole real line.
### Normal $(\mu, \sigma^2)$ ###
It's a good idea to first note that moment generating functions behave well under linear transformations.
$$
M_{aX+b}(t) ~ = ~ E(e^{t(aX + b)}) ~ = ~ e^{bt}E(e^{atX}) ~ = ~ e^{bt}M_X(at)
$$
Since a normal $(\mu, \sigma^2)$ variable can be written as $\sigma Z + \mu$ where $Z$ is standard normal, its m.g.f. is
$$
M_{\sigma Z + \mu} (t) ~ = ~ e^{\mu t}M_Z(\sigma t) ~ = ~ e^{\mu t +\sigma^2 t^2/2}
$$
Details aside, what this formula is saying is that if a moment generating function is $\exp(c_1t + c_2t^2)$ for any constant $c_1$ and any positive constant $c_2$, then it is the moment generating function of a normally distributed random variable.
### Sums of Independent Normal Variables ###
We can now show that sums of independent normal variables are normal.
Let $X$ have normal $(\mu_X, \sigma_X^2)$ distribution, and let $Y$ independent of $X$ have normal $(\mu_Y, \sigma_Y^2)$ distribution. Then
$$
M_{X+Y} (t) ~ = ~ e^{\mu_X t + \sigma_X^2 t^2/2} \cdot e^{\mu_Y t + \sigma_Y^2 t^2/2} ~ = ~ e^{(\mu_X + \mu_Y)t + (\sigma_X^2 + \sigma_Y^2)t^2/2}
$$
That's the m.g.f. of the normal distribution with mean $\mu_X + \mu_Y$ and variance $\sigma_X^2 + \sigma_Y^2$.
### "Proof" of the Central Limit Theorem ###
Another important reason for studying mgf's is that they can help us identify the limit of a sequence of distributions.
The main example of convergence that we have seen is the Central Limit Theorem. Now we can indicate a proof.
Let $X_1, X_2, \ldots$ be i.i.d. random variables with expectation $\mu$ and SD $\sigma$. For every $n \ge 1$ let $S_n = X_1 + X_2 + \cdots + X_n$.
The Central Limit Theorem says that for large $n$, the distribution of the standardized sum
$$
S_n^* ~ = ~ \frac{S_n - n\mu}{\sqrt{n}\sigma}
$$
is approximately standard normal.
To show this, we will assume a major result whose proof is well beyond the scope of this class. Suppose $Y_1, Y_2, \ldots $ are random variables and we want to show that the the distribution of the $Y_n$'s converges to the distribution of some random variable $Y$. The result says that it is enough to show that the mgf's of the $Y_n$'s converge to the mgf of $Y$.
The result requires a careful statement and the proof requires considerable attention to detail. We won't go into that in this course. Instead we'll just point out that it should seem reasonable. Since mgf's determine distributions, it's not difficult to accept that if two mgf's are close to each other then the corresponding distributions should also be close to each other.
Let's use this result to "prove" the CLT. The quotes are because we will use the above result without proof, and also because the argument below involves some hand-waving about approximations.
First, write the standardized sum in terms of the standardized $X$'s.
$$
S_n^* ~ = ~ \frac{S_n - n\mu}{\sqrt{n}\sigma} ~ = ~ \sum_{i=1}^n \frac{1}{\sqrt{n}} \big{(} \frac{X_i - \mu}{\sigma} \big{)} ~ = ~ \sum_{i=1}^n \frac{1}{\sqrt{n}} X_i^*
$$
where for each $i$, the random variable $X_i^*$ is $X_i$ in standard units.
The random variables $X_i^*$ are i.i.d., so let $M_{X^*}$ denote the mgf of any one of them. By the linear transformation property proved above, the mgf of each $\frac{1}{\sqrt{n}}X_i^*$ is given by
$$
M_{\frac{1}{\sqrt{n}}X_i^*} (t) ~ = ~ M_{X^*} (t/\sqrt{n})
$$
Therefore
\begin{align*}
M_{S_n^*} (t) ~ &= ~ \big{(} M_{X^*}(t/\sqrt{n}) \big{)}^n \\ \\
&= ~ \Big{(} 1 ~ + ~ \frac{t}{\sqrt{n}} \cdot \frac{E(X^*)}{1!} ~ + ~ \frac{t^2}{n} \cdot \frac{E({X^*}^2)}{2!} ~ + ~ \frac{t^3}{n^{3/2}} \cdot \frac{E({X^*}^3)}{3!} ~ + ~ \cdots \Big{)}^n \\ \\
&\approx ~ \Big{(} 1 ~ + ~ \frac{t^2}{2n}\Big{)}^n ~~~ \text{for large } n\\ \\
\end{align*}
by ignoring small terms and using the fact that for any standardized random variable $X^*$ we have $E(X^*) = 0$ and $E({X^*}^2) = 1$.
Thus for large $n$,
$$
M_{S_n^*} (t) ~ \approx ~ \Big{(} 1 ~ + ~ \frac{t^2}{2n}\Big{)}^n
~ \to ~ e^{\frac{t^2}{2}} ~~ \text{as } n \to \infty
$$
The limit is the moment generating function of the standard normal distribution.
| github_jupyter |
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Custom training: basics
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r1/tutorials/eager/custom_training.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r1/tutorials/eager/custom_training.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
In the previous tutorial we covered the TensorFlow APIs for automatic differentiation, a basic building block for machine learning.
In this tutorial we will use the TensorFlow primitives introduced in the prior tutorials to do some simple machine learning.
TensorFlow also includes a higher-level neural networks API (`tf.keras`) which provides useful abstractions to reduce boilerplate. We strongly recommend those higher level APIs for people working with neural networks. However, in this short tutorial we cover neural network training from first principles to establish a strong foundation.
## Setup
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow.compat.v1 as tf
```
## Variables
Tensors in TensorFlow are immutable stateless objects. Machine learning models, however, need to have changing state: as your model trains, the same code to compute predictions should behave differently over time (hopefully with a lower loss!). To represent this state which needs to change over the course of your computation, you can choose to rely on the fact that Python is a stateful programming language:
```
# Using python state
x = tf.zeros([10, 10])
x += 2 # This is equivalent to x = x + 2, which does not mutate the original
# value of x
print(x)
```
TensorFlow, however, has stateful operations built in, and these are often more pleasant to use than low-level Python representations of your state. To represent weights in a model, for example, it's often convenient and efficient to use TensorFlow variables.
A Variable is an object which stores a value and, when used in a TensorFlow computation, will implicitly read from this stored value. There are operations (`tf.assign_sub`, `tf.scatter_update`, etc) which manipulate the value stored in a TensorFlow variable.
```
v = tf.Variable(1.0)
assert v.numpy() == 1.0
# Re-assign the value
v.assign(3.0)
assert v.numpy() == 3.0
# Use `v` in a TensorFlow operation like tf.square() and reassign
v.assign(tf.square(v))
assert v.numpy() == 9.0
```
Computations using Variables are automatically traced when computing gradients. For Variables representing embeddings TensorFlow will do sparse updates by default, which are more computation and memory efficient.
Using Variables is also a way to quickly let a reader of your code know that this piece of state is mutable.
## Example: Fitting a linear model
Let's now put the few concepts we have so far ---`Tensor`, `GradientTape`, `Variable` --- to build and train a simple model. This typically involves a few steps:
1. Define the model.
2. Define a loss function.
3. Obtain training data.
4. Run through the training data and use an "optimizer" to adjust the variables to fit the data.
In this tutorial, we'll walk through a trivial example of a simple linear model: `f(x) = x * W + b`, which has two variables - `W` and `b`. Furthermore, we'll synthesize data such that a well trained model would have `W = 3.0` and `b = 2.0`.
### Define the model
Let's define a simple class to encapsulate the variables and the computation.
```
class Model(object):
def __init__(self):
# Initialize variable to (5.0, 0.0)
# In practice, these should be initialized to random values.
self.W = tf.Variable(5.0)
self.b = tf.Variable(0.0)
def __call__(self, x):
return self.W * x + self.b
model = Model()
assert model(3.0).numpy() == 15.0
```
### Define a loss function
A loss function measures how well the output of a model for a given input matches the desired output. Let's use the standard L2 loss.
```
def loss(predicted_y, desired_y):
return tf.reduce_mean(tf.square(predicted_y - desired_y))
```
### Obtain training data
Let's synthesize the training data with some noise.
```
TRUE_W = 3.0
TRUE_b = 2.0
NUM_EXAMPLES = 1000
inputs = tf.random_normal(shape=[NUM_EXAMPLES])
noise = tf.random_normal(shape=[NUM_EXAMPLES])
outputs = inputs * TRUE_W + TRUE_b + noise
```
Before we train the model let's visualize where the model stands right now. We'll plot the model's predictions in red and the training data in blue.
```
import matplotlib.pyplot as plt
plt.scatter(inputs, outputs, c='b')
plt.scatter(inputs, model(inputs), c='r')
plt.show()
print('Current loss: '),
print(loss(model(inputs), outputs).numpy())
```
### Define a training loop
We now have our network and our training data. Let's train it, i.e., use the training data to update the model's variables (`W` and `b`) so that the loss goes down using [gradient descent](https://en.wikipedia.org/wiki/Gradient_descent). There are many variants of the gradient descent scheme that are captured in `tf.train.Optimizer` implementations. We'd highly recommend using those implementations, but in the spirit of building from first principles, in this particular example we will implement the basic math ourselves.
```
def train(model, inputs, outputs, learning_rate):
with tf.GradientTape() as t:
current_loss = loss(model(inputs), outputs)
dW, db = t.gradient(current_loss, [model.W, model.b])
model.W.assign_sub(learning_rate * dW)
model.b.assign_sub(learning_rate * db)
```
Finally, let's repeatedly run through the training data and see how `W` and `b` evolve.
```
model = Model()
# Collect the history of W-values and b-values to plot later
Ws, bs = [], []
epochs = range(10)
for epoch in epochs:
Ws.append(model.W.numpy())
bs.append(model.b.numpy())
current_loss = loss(model(inputs), outputs)
train(model, inputs, outputs, learning_rate=0.1)
print('Epoch %2d: W=%1.2f b=%1.2f, loss=%2.5f' %
(epoch, Ws[-1], bs[-1], current_loss))
# Let's plot it all
plt.plot(epochs, Ws, 'r',
epochs, bs, 'b')
plt.plot([TRUE_W] * len(epochs), 'r--',
[TRUE_b] * len(epochs), 'b--')
plt.legend(['W', 'b', 'true W', 'true_b'])
plt.show()
```
## Next Steps
In this tutorial we covered `Variable`s and built and trained a simple linear model using the TensorFlow primitives discussed so far.
In theory, this is pretty much all you need to use TensorFlow for your machine learning research.
In practice, particularly for neural networks, the higher level APIs like `tf.keras` will be much more convenient since it provides higher level building blocks (called "layers"), utilities to save and restore state, a suite of loss functions, a suite of optimization strategies etc.
| github_jupyter |
# ENGR 1330 Exam 1 Sec 003/004 Fall 2020
Take Home Portion of Exam 1
<hr>
## Full name
## R#:
## HEX:
## ENGR 1330 Exam 1 Sec 003/004
## Date:
<hr>
## Question 1 (1 pts):
Run the cell below, and leave the results in your notebook (Windows users may get an error, leave the error in place)
```
#### RUN! the Cell ####
import sys
! hostname
! whoami
print(sys.executable) # OK if generates an exception message on Windows machines
```
<hr>
## Question 2 (9 pts):
- __When it is 8:00 in Lubbock,__
- __It is 9:00 in New York__
- __It is 14:00 in London__
- __It is 15:00 in Cairo__
- __It is 16:00 in Istanbul__
- __It is 19:00 in Hyderabad__
- __It is 22:00 in Tokyo__ <br>
__Write a function that reports the time in New York, London, Cairo, Istanbul, Hyderabad, and Tokyo based on the time in Lubbock. Use a 24-hour time format. Include error trapping that:__<br>
1- Issues a message like "Please Enter A Number from 00 to 23" if the first input is numeric but outside the range of [0,23].<br>
2- Takes any numeric input for "Lubbock time" selection , and forces it into an integer.<br>
3- Issues an appropriate message if the user's selection is non-numeric.<br>
__Check your function for these times:__
- 8:00
- 17:00
- 0:00
```
def LBBtime():
try:
LBK = int(input('What hour is it in Lubbock?- Please enter a number from 0 to 23'))
if LBK>23:
print('Please Enter A Number from 00 to 23')
if LBK<23 and LBK>=0:
if LBK+1>23:
print("Time in New York is",(LBK+1)-24,":00")
else:
print("Time in New York is",(LBK+1),":00")
if LBK+6>23:
print("Time in London is",(LBK+6)-24,":00")
else:
print("Time in London is",(LBK+6),":00")
if LBK+7>23:
print("Time in Cairo is",(LBK+7)-24,":00")
else:
print("Time in Cairo is",(LBK+7),":00")
if LBK+8>23:
print("Time in Istanbul is",(LBK+8)-24,":00")
else:
print("Time in Istanbul is",(LBK+8),":00")
if LBK+11>23:
print("Time in Hyderabad is",(LBK+11)-24,":00")
else:
print("Time in Hyderabad is",(LBK+11),":00")
if LBK+14>23:
print("Time in Tokyo is",(LBK+14)-24,":00")
else:
print("Time in Tokyo is",(LBK+14),":00")
return #null return
except:
print("Please Enter an Appropriate Input")
LBBtime()
LBBtime()
LBBtime()
```
<hr>
## Question 3 (28 pts):
Follow the steps below. Add comments to your script and signify when each step and each task is done. *hint: For this problem you will need the numpy and pandas libraries.
- __STEP1: There are 8 digits in your R#. Define a 2x4 array with these 8 digits, name it "Rarray", and print it__
- __STEP2: Find the maximum value of the "Rarray" and its position__
- __STEP3: Sort the "Rarray" along the rows, store it in a new array named "Rarraysort", and print the new array out__
- __STEP4: Define and print a 4x4 array that has the "Rarray" as its two first rows, and "Rarraysort" as its next rows. Name this new array "DoubleRarray"__
- __STEP5: Slice and print a 4x3 array from the "DoubleRarray" that contains the last three columns of it. Name this new array "SliceRarray".__
- __STEP6: Define the "SliceRarray" as a panda dataframe:__
- name it "Rdataframe",
- name the rows as "Row A","Row B","Row C", and "Row D"
- name the columns as "Column 1", "Column 2", and "Column 3"
- __STEP7: Print the first few rows of the "Rdataframe".__
- __STEP8: Create a new dataframe object ("R2dataframe") by adding a column to the "Rdataframe", name it "Column X" and fill it with "None" values. Then, use the appropriate descriptor function and print the data model (data column count, names, data types) of the "R2dataframe"__
- __STEP9: Replace the **'None'** in the "R2dataframe" with 0. Then, print the summary statistics of each numeric column in the data frame.__
- __STEP10: Define a function based on the equation below, apply on the entire "R2dataframe", store the results in a new dataframe ("R3dataframe"), and print the results and the summary statistics again.__
$$ y = x^2 - 5x +7 $$
- __STEP11: Print the number of occurrences of each unique value in "Column 3"__
- __STEP12: Sort the data frame with respect to "Column 1" with a descending order and print it__
- __STEP13: Write the final format of the "R3dataframe" on a CSV file, named "Rfile.csv"__
- __STEP14: Read the "Rfile.csv" and print its content.__<br>
** __Make sure to attach the "Rfile.csv" file to your midterm exam submission.__
```
# Code and Run your solution here:
print('#Step0: Install Dependencies')
import numpy as np
import pandas as pd
print('#Step1: Create the array')
Rarray = np.array([[1,6,7,4],[5,2,3,8]]) #Define Rarray
print(Rarray)
print('#Step2: find max and its position ')
print(np.max(Rarray)) #Find the maximum Value
print(np.argmax(Rarray)) #Find the posirtion of the maximum value
print('#Step3: Sort the array')
Rarraysort = np.sort(Rarray,axis = 1) #Sort Rarray along the rows and define a new array
print(Rarraysort)
print('#Step4: Create the double array - manual entry')
DoubleRarray = np.array([[1,6,7,4],[5,2,3,8],[1,4,6,7],[2,3,5,8]]) #Define DoubleRarray
print(DoubleRarray)
print('#Step5: Slice the array')
SliceRarray = DoubleRarray[0:4,1:4] #Slice DoubleRarray and Define SliceRarray
print(SliceRarray)
print('#Step6: Make a dataframey')
myrowname = ["Row A","Row B","Row C","Row D"]
mycolname = ["Column 1", "Column 2","Column 3"]
Rdataframe = pd.DataFrame(SliceRarray,myrowname,mycolname) #Define Rdataframe
print('#Step7: head method on dataframe')
print(Rdataframe.head()) #Print the first few rows of the Rdataframe
print('#Step8: add column to a dataframe')
Rdataframe['Column X']= None #Add a new column, "Column X"
R2dataframe = Rdataframe #Define R2dataframe
print(R2dataframe.info()) #Get the info
print('#Step9: Replace NA')
R2dataframe = R2dataframe.fillna(0) #Replace NAs with 0
print(R2dataframe.describe()) #Get the summary statistics
print('#Step10: Define a function, apply to a dataframe')
def myfunc(x): # A user-built function
y = (x**2) - (10*x) +7
return(y)
R3dataframe = R2dataframe.apply(myfunc) #Apply the function on the entire R2dataframe
print(R3dataframe)
print(R3dataframe.describe())
print('#Step11: Descriptors')
print(R3dataframe['Column 3'].value_counts()) #Returns the number of occurences of each unique value in Column 3
print('#Step12: Sort on values')
print(R3dataframe.sort_values('Column 1', ascending = False)) #Sorting based on Column 1
print('#Step13: Write to an external file')
R3dataframe.to_csv('Rfile.csv') #Write R3dataframe on a CSV file
print('#Step14: Verify the write')
readfilecsv = pd.read_csv('Rfile.csv') #Read the Rfile.csv
print(readfilecsv) #Print the contents of the Rfile.csv
```
<hr>
## Problem 4 (32 pts)
Graphing Functions Special Functions
Consider the two functions listed below:
\begin{equation}
f(x) = e^{-\alpha x}
\label{eqn:fofx}
\end{equation}
\begin{equation}
g(x) = \gamma sin(\beta x)
\label{eqn:gofx}
\end{equation}
Prepare a plot of the two functions on the same graph.
Use the values in Table below for $\alpha$, $\beta$, and $\gamma$.
|Parameter|Value|
|:---|---:|
|$\alpha$|0.50|
|$\beta$|3.00|
|$\gamma$|$\frac{\pi}{2}$|
The plot should have $x$ values ranging from $0$ to $10$ (inclusive) in sufficiently small increments to see curvature in the two functions as well as to identify the number and approximate locations of intersections. In this problem, intersections are locations in the $x-y$ plane where the two "curves" cross one another of the two plots.
#### By-hand evaluate f(x) for x=1, alpha = 1/2 (Simply enter your answer from a calculator)
f(x) = 0.61
#### By-hand evaluate g(x) for x=3.14, beta = 1/2, gamma = 2 (Simply enter your answer from a calculator)
g(x) = 1.99
```
# Define the first function f(x,alpha), test the function using your by hand answer
# Define the first function f(x,alpha), test the function using your by hand answer
def f(x,alpha):
import math
f = math.exp(-1.0*alpha*x)
return f
f(1,0.5)
# Define the second function g(x,beta,gamma), test the function using your by hand answer
def g(x,beta,gamma):
import math
f = gamma*math.sin(beta*x)
return f
g(3.14,0.5,2.0)
# Built a list for x that ranges from 0 to 10, inclusive, with adjustable step sizes for plotting later on
howMany = 100
scale = 10.0/howMany
xvector = []
for i in range(0,howMany+1):
xvector.append(scale*i)
#xvector # activate to display
# xvector
# Build a plotting function that plots both functions on the same chart
# Build a plotting function that plots both functions on the same chart
import mplcursors
alpha = 0.5
beta = 3.0
gamma = 1.57
yf = []
yg = []
for i in range(0,howMany+1):
yf.append(f(xvector[i],alpha))
yg.append(g(xvector[i],beta,gamma))
def plot2lines(list11,list21,list12,list22,strx,stry,strtitle): # plot list1 on x, list2 on y, xlabel, ylabel, title
from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
plt.plot( list11, list21, color ='green', marker ='s', linestyle ='dashdot' , label = "Observed" ) # create a line chart, years on x-axis, gdp on y-axis
plt.plot( list12, list22, color ='red', marker ='o', linestyle ='solid' , label = "Model") # create a line chart, years on x-axis, gdp on y-axis
plt.legend()
plt.title(strtitle)# add a title
plt.ylabel(stry)# add a label to the x and y-axes
plt.xlabel(strx)
mplcursors.cursor()
plt.show() # display the plot
return #null return
plot2lines(xvector,yf,xvector,yg,'x-value','y-value','plot of f and g')
# Using the plot as a guide, find the approximate values of x where the two curves intercept (i.e. f(x) = g(x))
# You can either use interactive input, or direct specify x values, but need to show results
# Using the plot as a guide, find the values of x where the two curves intercept (i.e. f(x) = g(x))
#xguess = float(input('my guess for x')) # ~0.7, and 6.25
alpha = 0.5
beta = 0.5
gamma = 2.0
xguess = 1
result = f(xguess,alpha) - g(xguess,beta,gamma)
print('f(x) - g(x) =', result,' at x = ', xguess)
xguess = 2
result = f(xguess,alpha) - g(xguess,beta,gamma)
print('f(x) - g(x) =', result,' at x = ', xguess)
```
<hr>
## Bonus Problem 1. Extra Credit (You must complete the regular problems)!
__create a class to compute the average grade (out of 10) of the students based on their grades in Quiz1, Quiz2, the Mid-term, Quiz3, and the Final exam.__
| Student Name | Quiz 1 | Quiz 2 | Mid-term | Quiz 3 | Final Exam |
| ------------- | -----------| -----------| -------------| -----------| -------------|
| Harry | 8 | 9 | 8 | 10 | 9 |
| Ron | 7 | 8 | 8 | 7 | 9 |
| Hermione | 10 | 10 | 9 | 10 | 10 |
| Draco | 8 | 7 | 9 | 8 | 9 |
| Luna | 9 | 8 | 7 | 6 | 5 |
1. __Use docstrings to describe the purpose of the class.__
2. __Create an object for each car brand and display the output as shown below.__
"Student Name": **Average Grade**
3. __Create and print out a dictionary with the student names as keys and their average grades as data.__
```
#Code and run your solution here:
#Suggested Solution:
class Hogwarts:
"""This class calculates the average grade of the students"""
def __init__(self, Name,Quiz1,Quiz2,MidTerm,Quiz3,Final):
self.Name = Name
self.Quiz1 = Quiz1
self.Quiz2 = Quiz2
self.MidTerm = MidTerm
self.Quiz3 = Quiz3
self.Final= Final
def average(self):
return (self.Quiz1 + self.Quiz2 + self.MidTerm + self.Quiz3 + self.Final) /5
S1 = Hogwarts('Harry',8,9,8,10,9) #Fill the instances
S2 = Hogwarts('Ron',7,8,8,7,9)
S3 = Hogwarts('Hermione',10,10,9,10,10)
S4 = Hogwarts('Draco',8,7,9,8,9)
S5 = Hogwarts('Luna',9,8,7,6,5)
print("Harry", S1.average())
print("Ron", S2.average())
print("Hermione", S3.average())
print("Draco", S4.average())
print("Luna", S5.average())
GradeDict = {"Harry":S1.average(),"Ron":S2.average(),"Hermione":S3.average(),"Draco":S4.average(),"Luna":S5.average()}
print(GradeDict)
```
<hr>
## Bonus 2 Extra credit (You must complete the regular problems)!
#### Write the VOLUME Function to compute the volume of Cylinders, Spheres, Cones, and Rectangular Boxes. This function should:
- First, ask the user about __the shape of the object__ of interest using this statement:<br>
**"Please choose the shape of the object. Enter 1 for "Cylinder", 2 for "Sphere", 3 for "Cone", or 4 for "Rectangular Box""**<br>
- Second, based on user's choice in the previous step, __ask for the right inputs__.
- Third, print out an statement with __the input values and the calculated volumes__.
#### Include error trapping that:
1. Issues a message that **"The object should be either a Cylinder, a Sphere, a Cone, or a Rectangular Box. Please Enter A Number from 1,2,3, and 4!"** if the first input is non-numeric.
2. Takes any numeric input for the initial selection , and force it into an integer.
4. Issues an appropriate message if the user's selection is numeric but outside the range of [1,4]
3. Takes any numeric input for the shape characteristics , and force it into a float.
4. Issues an appropriate message if the object characteristics are as non-numerics.
#### Test the script for:
1. __Sphere, r=10__
2. __r=10 , Sphere__
3. __Rectangular Box, w=5, h=10, l=0.5__
- <font color=orange>__Volume of a Cylinder = πr²h__</font>
- <font color=orange>__Volume of a Sphere = 4(πr3)/3__</font>
- <font color=orange>__Volume of a Cone = (πr²h)/3__</font>
- <font color=orange>__Volume of a Rectangular Box = whl__</font>
```
#Code and Run your solution here
#Suggested Solution:
import numpy as np # import NumPy: for large, multi-dimensional arrays and matrices, along with high-level mathematical functions to operate on these arrays.
pi = np.pi #pi value from the np package
def VOLUME():
try:
UI = input('Please choose the shape of the object. Enter 1 for "Cylinder", 2 for "Sphere", 3 for "Cone", or 4 for "Rectangular Box"')
UI =int(UI)
if UI==1:
try:
UI2 = input('Please enter the radius of the Cylinder')
r= float(UI2)
UI3 = input('Please enter the height of the Cylinder')
h= float(UI3)
V= pi*h*r**2
print("The volume of the Cylinder with the radius of ",r," and the height of ",h," is equal to", V)
except:
print("The radius and height of the Cylinder must be numerics. Please Try Again!")
elif UI==2:
try:
UI2 = input('Please enter the radius of the Sphere')
r= float(UI2)
V= (4*pi*r**3)/3
print("The volume of the Sphere with the radius of ",r," is equal to", V)
except:
print("The radius of the Sphere must be numeric. Please Try Again!")
elif UI==3:
try:
UI2 = input('Please enter the radius of the Cone')
r= float(UI2)
UI3 = input('Please enter the height of the Cone')
h= float(UI3)
V= (pi*h*r**2)/3
print("The volume of the Cone with the radius of ",r," and the height of ",h," is equal to", V)
except:
print("The radius and height of the Cone must be numerics. Please Try Again!")
elif UI==4:
try:
UI2 = input('Please enter the width of the Rectangular Box')
w= float(UI2)
UI3 = input('Please enter the height of the Rectangular Box')
h= float(UI3)
UI4 = input('Please enter the length of the Rectangular Box')
l= float(UI4)
V= w*h*l
print("The volume of the Rectangular Box with the width of ",w," and the height of ",h," and the length of ",l," is equal to", V)
except:
print("The width, height, and length of the Rectangular Box must be numerics. Please Try Again!")
else:
print("Please Enter A Number from 1,2,3, and 4!")
except:
print("The object should be either a Cylinder, a Sphere, a Cone, or a Rectangular Box. Please Enter A Number from 1,2,3, and 4!")
VOLUME()
```
| github_jupyter |
# 转置卷积
:label:`sec_transposed_conv`
到目前为止,我们所见到的卷积神经网络层,例如卷积层( :numref:`sec_conv_layer`)和汇聚层( :numref:`sec_pooling`),通常会减少下采样输入图像的空间维度(高和宽)。
然而如果输入和输出图像的空间维度相同,在以像素级分类的语义分割中将会很方便。
例如,输出像素所处的通道维可以保有输入像素在同一位置上的分类结果。
为了实现这一点,尤其是在空间维度被卷积神经网络层缩小后,我们可以使用另一种类型的卷积神经网络层,它可以增加上采样中间层特征图的空间维度。
在本节中,我们将介绍
*转置卷积*(transposed convolution) :cite:`Dumoulin.Visin.2016`,
用于逆转下采样导致的空间尺寸减小。
```
from mxnet import init, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l
npx.set_np()
```
## 基本操作
让我们暂时忽略通道,从基本的转置卷积开始,设步幅为1且没有填充。
假设我们有一个$n_h \times n_w$的输入张量和一个$k_h \times k_w$的卷积核。
以步幅为1滑动卷积核窗口,每行$n_w$次,每列$n_h$次,共产生$n_h n_w$个中间结果。
每个中间结果都是一个$(n_h + k_h - 1) \times (n_w + k_w - 1)$的张量,初始化为0。
为了计算每个中间张量,输入张量中的每个元素都要乘以卷积核,从而使所得的$k_h \times k_w$张量替换中间张量的一部分。
请注意,每个中间张量被替换部分的位置与输入张量中元素的位置相对应。
最后,所有中间结果相加以获得最终结果。
例如, :numref:`fig_trans_conv`解释了如何为$2\times 2$的输入张量计算卷积核为$2\times 2$的转置卷积。

:label:`fig_trans_conv`
我们可以对输入矩阵`X`和卷积核矩阵`K`(**实现基本的转置卷积运算**)`trans_conv`。
```
def trans_conv(X, K):
h, w = K.shape
Y = np.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Y[i: i + h, j: j + w] += X[i, j] * K
return Y
```
与通过卷积核“减少”输入元素的常规卷积(在 :numref:`sec_conv_layer`中)相比,转置卷积通过卷积核“广播”输入元素,从而产生大于输入的输出。
我们可以通过 :numref:`fig_trans_conv`来构建输入张量`X`和卷积核张量`K`从而[**验证上述实现输出**]。
此实现是基本的二维转置卷积运算。
```
X = np.array([[0.0, 1.0], [2.0, 3.0]])
K = np.array([[0.0, 1.0], [2.0, 3.0]])
trans_conv(X, K)
```
或者,当输入`X`和卷积核`K`都是四维张量时,我们可以[**使用高级API获得相同的结果**]。
```
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.Conv2DTranspose(1, kernel_size=2)
tconv.initialize(init.Constant(K))
tconv(X)
```
## [**填充、步幅和多通道**]
与常规卷积不同,在转置卷积中,填充被应用于的输出(常规卷积将填充应用于输入)。
例如,当将高和宽两侧的填充数指定为1时,转置卷积的输出中将删除第一和最后的行与列。
```
tconv = nn.Conv2DTranspose(1, kernel_size=2, padding=1)
tconv.initialize(init.Constant(K))
tconv(X)
```
在转置卷积中,步幅被指定为中间结果(输出),而不是输入。
使用 :numref:`fig_trans_conv`中相同输入和卷积核张量,将步幅从1更改为2会增加中间张量的高和权重,因此输出张量在 :numref:`fig_trans_conv_stride2`中。

:label:`fig_trans_conv_stride2`
以下代码可以验证 :numref:`fig_trans_conv_stride2`中步幅为2的转置卷积的输出。
```
tconv = nn.Conv2DTranspose(1, kernel_size=2, strides=2)
tconv.initialize(init.Constant(K))
tconv(X)
```
对于多个输入和输出通道,转置卷积与常规卷积以相同方式运作。
假设输入有$c_i$个通道,且转置卷积为每个输入通道分配了一个$k_h\times k_w$的卷积核张量。
当指定多个输出通道时,每个输出通道将有一个$c_i\times k_h\times k_w$的卷积核。
同样,如果我们将$\mathsf{X}$代入卷积层$f$来输出$\mathsf{Y}=f(\mathsf{X})$,并创建一个与$f$具有相同的超参数、但输出通道数量是$\mathsf{X}$中通道数的转置卷积层$g$,那么$g(Y)$的形状将与$\mathsf{X}$相同。
下面的示例可以解释这一点。
```
X = np.random.uniform(size=(1, 10, 16, 16))
conv = nn.Conv2D(20, kernel_size=5, padding=2, strides=3)
tconv = nn.Conv2DTranspose(10, kernel_size=5, padding=2, strides=3)
conv.initialize()
tconv.initialize()
tconv(conv(X)).shape == X.shape
```
## [**与矩阵变换的联系**]
:label:`subsec-connection-to-mat-transposition`
转置卷积为何以矩阵变换命名呢?
让我们首先看看如何使用矩阵乘法来实现卷积。
在下面的示例中,我们定义了一个$3\times 3$的输入`X`和$2\times 2$卷积核`K`,然后使用`corr2d`函数计算卷积输出`Y`。
```
X = np.arange(9.0).reshape(3, 3)
K = np.array([[1.0, 2.0], [3.0, 4.0]])
Y = d2l.corr2d(X, K)
Y
```
接下来,我们将卷积核`K`重写为包含大量0的稀疏权重矩阵`W`。
权重矩阵的形状是($4$,$9$),其中非0元素来自卷积核`K`。
```
def kernel2matrix(K):
k, W = np.zeros(5), np.zeros((4, 9))
k[:2], k[3:5] = K[0, :], K[1, :]
W[0, :5], W[1, 1:6], W[2, 3:8], W[3, 4:] = k, k, k, k
return W
W = kernel2matrix(K)
W
```
逐行连结输入`X`,获得了一个长度为9的矢量。
然后,`W`的矩阵乘法和向量化的`X`给出了一个长度为4的向量。
重塑它之后,可以获得与上面的原始卷积操作所得相同的结果`Y`:我们刚刚使用矩阵乘法实现了卷积。
```
Y == np.dot(W, X.reshape(-1)).reshape(2, 2)
```
同样,我们可以使用矩阵乘法来实现转置卷积。
在下面的示例中,我们将上面的常规卷积$2 \times 2$的输出`Y`作为转置卷积的输入。
想要通过矩阵相乘来实现它,我们只需要将权重矩阵`W`的形状转置为$(9, 4)$。
```
Z = trans_conv(Y, K)
Z == np.dot(W.T, Y.reshape(-1)).reshape(3, 3)
```
抽象来看,给定输入向量$\mathbf{x}$和权重矩阵$\mathbf{W}$,卷积的前向传播函数可以通过将其输入与权重矩阵相乘并输出向量$\mathbf{y}=\mathbf{W}\mathbf{x}$来实现。
由于反向传播遵循链式法则和$\nabla_{\mathbf{x}}\mathbf{y}=\mathbf{W}^\top$,卷积的反向传播函数可以通过将其输入与转置的权重矩阵$\mathbf{W}^\top$相乘来实现。
因此,转置卷积层能够交换卷积层的正向传播函数和反向传播函数:它的正向传播和反向传播函数将输入向量分别与$\mathbf{W}^\top$和$\mathbf{W}$相乘。
## 小结
* 与通过卷积核减少输入元素的常规卷积相反,转置卷积通过卷积核广播输入元素,从而产生形状大于输入的输出。
* 如果我们将$\mathsf{X}$输入卷积层$f$来获得输出$\mathsf{Y}=f(\mathsf{X})$并创造一个与$f$有相同的超参数、但输出通道数是$\mathsf{X}$中通道数的转置卷积层$g$,那么$g(Y)$的形状将与$\mathsf{X}$相同。
* 我们可以使用矩阵乘法来实现卷积。转置卷积层能够交换卷积层的正向传播函数和反向传播函数。
## 练习
1. 在 :numref:`subsec-connection-to-mat-transposition`中,卷积输入`X`和转置的卷积输出`Z`具有相同的形状。他们的数值也相同吗?为什么?
1. 使用矩阵乘法来实现卷积是否有效率?为什么?
[Discussions](https://discuss.d2l.ai/t/3301)
| github_jupyter |
# **LSTM - Time Series Prediction**
## **Importing libraries**
```
import pandas
import matplotlib.pyplot as plt
import numpy
import math
from tqdm import tqdm
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# fix random seed for reproducibility
numpy.random.seed(7)
```
## **Load the data**
```
! rm /content/airline-passengers.csv
! wget https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv
dataset = pandas.read_csv('airline-passengers.csv', usecols=[1], engine='python')
plt.plot(dataset)
plt.show()
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return numpy.array(dataX), numpy.array(dataY)
```
## **LSTM Network for Regression**
```
# load the dataset
dataframe = pandas.read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
print(len(train), len(test))
# reshape into X=t and Y=t+1
look_back = 1
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = numpy.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = numpy.reshape(testX, (testX.shape[0], 1, testX.shape[1]))
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(4, input_shape=(1, look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=0)
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
```
## **LSTM for Regression Using the Window Method**
```
# load the dataset
dataframe = pandas.read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = numpy.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = numpy.reshape(testX, (testX.shape[0], 1, testX.shape[1]))
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(4, input_shape=(1, look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=0)
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
```
## **LSTM for Regression with Time Steps**
```
# load the dataset
dataframe = pandas.read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))
# create and fit the LSTM network
model = Sequential()
model.add(LSTM(4, input_shape=(look_back, 1)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=0)
# make predictions
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
```
## **LSTM with Memory Between Batches**
```
# load the dataset
dataframe = pandas.read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))
# create and fit the LSTM network
batch_size = 1
model = Sequential()
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
for i in range(100):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
model.reset_states()
# make predictions
trainPredict = model.predict(trainX, batch_size=batch_size)
model.reset_states()
testPredict = model.predict(testX, batch_size=batch_size)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
```
## **Stacked LSTMs with Memory Between Batches**
```
# load the dataset
dataframe = pandas.read_csv('airline-passengers.csv', usecols=[1], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))
# create and fit the LSTM network
batch_size = 1
model = Sequential()
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True, return_sequences=True))
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
for i in tqdm(range(100)):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
model.reset_states()
# make predictions
trainPredict = model.predict(trainX, batch_size=batch_size)
model.reset_states()
testPredict = model.predict(testX, batch_size=batch_size)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
```
## **Time series prediction of TESLA closing stock price**
```
# Importing libraries
import numpy
import matplotlib.pyplot as plt
from pandas import read_csv
import math
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
! pip install nsepy
from nsepy import get_history
from datetime import date
from tqdm import tqdm
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
a = dataset[i:(i+look_back), 0]
dataX.append(a)
dataY.append(dataset[i + look_back, 0])
return numpy.array(dataX), numpy.array(dataY)
# load the dataset
dataframe = pandas.read_csv('TSLA.csv', usecols=[4], engine='python')
dataset = dataframe.values
dataset = dataset.astype('float32')
# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
# split into train and test sets
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
# reshape into X=t and Y=t+1
look_back = 3
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# reshape input to be [samples, time steps, features]
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))
# create and fit the LSTM network
batch_size = 1
model = Sequential()
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True, return_sequences=True))
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
for i in tqdm(range(300)):
model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
model.reset_states()
# make predictions
trainPredict = model.predict(trainX, batch_size=batch_size)
model.reset_states()
testPredict = model.predict(testX, batch_size=batch_size)
# invert predictions
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
# shift train predictions for plotting
trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
# shift test predictions for plotting
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
# plot baseline and predictions
plt.plot(scaler.inverse_transform(dataset))
plt.plot(trainPredictPlot)
plt.plot(testPredictPlot)
plt.show()
```
| github_jupyter |
```
from tensorflow import keras
from tensorflow.keras import *
from tensorflow.keras.models import *
from tensorflow.keras.layers import *
from tensorflow.keras.regularizers import l2#正则化L2
import tensorflow as tf
import numpy as np
import pandas as pd
normal = np.loadtxt(r'F:\张老师课题学习内容\code\数据集\试验数据(包括压力脉动和振动)\2013.9.12-未发生缠绕前\2013-9.12振动\2013-9-12振动-1450rmin-mat\1450r_normalvibx.txt', delimiter=',')
chanrao = np.loadtxt(r'F:\张老师课题学习内容\code\数据集\试验数据(包括压力脉动和振动)\2013.9.17-发生缠绕后\振动\9-17下午振动1450rmin-mat\1450r_chanraovibx.txt', delimiter=',')
print(normal.shape,chanrao.shape,"***************************************************")
data_normal=normal[16:18] #提取前两行
data_chanrao=chanrao[16:18] #提取前两行
print(data_normal.shape,data_chanrao.shape)
print(data_normal,"\r\n",data_chanrao,"***************************************************")
data_normal=data_normal.reshape(1,-1)
data_chanrao=data_chanrao.reshape(1,-1)
print(data_normal.shape,data_chanrao.shape)
print(data_normal,"\r\n",data_chanrao,"***************************************************")
#水泵的两种故障类型信号normal正常,chanrao故障
data_normal=data_normal.reshape(-1, 512)#(65536,1)-(128, 515)
data_chanrao=data_chanrao.reshape(-1,512)
print(data_normal.shape,data_chanrao.shape)
import numpy as np
def yuchuli(data,label):#(4:1)(51:13)
#打乱数据顺序
np.random.shuffle(data)
train = data[0:102,:]
test = data[102:128,:]
label_train = np.array([label for i in range(0,102)])
label_test =np.array([label for i in range(0,26)])
return train,test ,label_train ,label_test
def stackkk(a,b,c,d,e,f,g,h):
aa = np.vstack((a, e))
bb = np.vstack((b, f))
cc = np.hstack((c, g))
dd = np.hstack((d, h))
return aa,bb,cc,dd
x_tra0,x_tes0,y_tra0,y_tes0 = yuchuli(data_normal,0)
x_tra1,x_tes1,y_tra1,y_tes1 = yuchuli(data_chanrao,1)
tr1,te1,yr1,ye1=stackkk(x_tra0,x_tes0,y_tra0,y_tes0 ,x_tra1,x_tes1,y_tra1,y_tes1)
x_train=tr1
x_test=te1
y_train = yr1
y_test = ye1
#打乱数据
state = np.random.get_state()
np.random.shuffle(x_train)
np.random.set_state(state)
np.random.shuffle(y_train)
state = np.random.get_state()
np.random.shuffle(x_test)
np.random.set_state(state)
np.random.shuffle(y_test)
#对训练集和测试集标准化
def ZscoreNormalization(x):
"""Z-score normaliaztion"""
x = (x - np.mean(x)) / np.std(x)
return x
x_train=ZscoreNormalization(x_train)
x_test=ZscoreNormalization(x_test)
# print(x_test[0])
#转化为一维序列
x_train = x_train.reshape(-1,512,1)
x_test = x_test.reshape(-1,512,1)
print(x_train.shape,x_test.shape)
def to_one_hot(labels,dimension=2):
results = np.zeros((len(labels),dimension))
for i,label in enumerate(labels):
results[i,label] = 1
return results
one_hot_train_labels = to_one_hot(y_train)
one_hot_test_labels = to_one_hot(y_test)
x = layers.Input(shape=[512,1,1])
Flatten=layers.Flatten()(x)
Dense1=layers.Dense(12, activation='relu')(Flatten)
Dense2=layers.Dense(6, activation='relu')(Dense1)
Dense3=layers.Dense(2, activation='softmax')(Dense2)
model = keras.Model(x, Dense3)
model.summary()
#定义优化
model.compile(loss='categorical_crossentropy',
optimizer='adam',metrics=['accuracy'])
import time
time_begin = time.time()
history = model.fit(x_train,one_hot_train_labels,
validation_split=0.1,
epochs=50,batch_size=10,
shuffle=True)
time_end = time.time()
time = time_end - time_begin
print('time:', time)
import time
time_begin = time.time()
score = model.evaluate(x_test,one_hot_test_labels, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
time_end = time.time()
time = time_end - time_begin
print('time:', time)
#绘制acc-loss曲线
import matplotlib.pyplot as plt
plt.plot(history.history['loss'],color='r')
plt.plot(history.history['val_loss'],color='g')
plt.plot(history.history['accuracy'],color='b')
plt.plot(history.history['val_accuracy'],color='k')
plt.title('model loss and acc')
plt.ylabel('Accuracy')
plt.xlabel('epoch')
plt.legend(['train_loss', 'test_loss','train_acc', 'test_acc'], loc='center right')
# plt.legend(['train_loss','train_acc'], loc='upper left')
#plt.savefig('1.png')
plt.show()
import matplotlib.pyplot as plt
plt.plot(history.history['loss'],color='r')
plt.plot(history.history['accuracy'],color='b')
plt.title('model loss and sccuracy ')
plt.ylabel('loss/sccuracy')
plt.xlabel('epoch')
plt.legend(['train_loss', 'train_sccuracy'], loc='center right')
plt.show()
```
| github_jupyter |
# The YUSAG Football Model
by Matt Robinson, [email protected], Yale Undergraduate Sports Analytics Group
This notebook introduces the model we at the Yale Undergraduate Sports Analytics Group (YUSAG) use for our college football rankings. This specific notebook details our FBS rankings at the beginning of the 2017 season.
```
import numpy as np
import pandas as pd
import math
```
Let's start by reading in the NCAA FBS football data from 2013-2016:
```
df_1 = pd.read_csv('NCAA_FBS_Results_2013_.csv')
df_2 = pd.read_csv('NCAA_FBS_Results_2014_.csv')
df_3 = pd.read_csv('NCAA_FBS_Results_2015_.csv')
df_4 = pd.read_csv('NCAA_FBS_Results_2016_.csv')
df = pd.concat([df_1,df_2,df_3,df_4],ignore_index=True)
df.head()
```
As you can see, the `OT` column has some `NaN` values that we will replace with 0.
```
# fill missing data with 0
df = df.fillna(0)
df.head()
```
I'm also going to make some weights for when we run our linear regression. I have found that using the factorial of the difference between the year and 2012 seems to work decently well. Clearly, the most recent seasons are weighted quite heavily in this scheme.
```
# update the weights based on a factorial scheme
df['weights'] = (df['year']-2012)
df['weights'] = df['weights'].apply(lambda x: math.factorial(x))
```
And now, we also are going to make a `scorediff` column that we can use in our linear regression.
```
df['scorediff'] = (df['teamscore']-df['oppscore'])
df.head()
```
Since we need numerical values for the linear regression algorithm, I am going to replace the locations with what seem like reasonable numbers:
* Visiting = -1
* Neutral = 0
* Home = 1
The reason we picked these exact numbers will become clearer in a little bit.
```
df['location'] = df['location'].replace('V',-1)
df['location'] = df['location'].replace('N',0)
df['location'] = df['location'].replace('H',1)
df.head()
```
The way our linear regression model works is a little tricky to code up in scikit-learn. It's much easier to do in R, but then you don't have a full understanding of what's happening when we make the model.
In simplest terms, our model predicts the score differential (`scorediff`) of each game based on three things: the strength of the `team`, the strength of the `opponent`, and the `location`.
You'll notice that the `team` and `opponent` features are categorical, and thus are not curretnly ripe for use with linear regression. However, we can use what is called 'one hot encoding' in order to transform these features into a usable form. One hot encoding works by taking the `team` feature, for example, and transforming it into many features such as `team_Yale` and `team_Harvard`. This `team_Yale` feature will usally equal zero, except when the team is actually Yale, then `team_Yale` will equal 1. In this way, it's a binary encoding (which is actually very useful for us as we'll see later).
One can use `sklearn.preprocessing.OneHotEncoder` for this task, but I am going to use Pandas instead:
```
# create dummy variables, need to do this in python b/c does not handle automatically like R
team_dummies = pd.get_dummies(df.team, prefix='team')
opponent_dummies = pd.get_dummies(df.opponent, prefix='opponent')
df = pd.concat([df, team_dummies, opponent_dummies], axis=1)
df.head()
```
Now let's make our training data, so that we can construct the model. At this point, I am going to use all the avaiable data to train the model, using our predetermined hyperparameters. This way, the model is ready to make predictions for the 2017 season.
```
# make the training data
X = df.drop(['year','month','day','team','opponent','teamscore','oppscore','D1','OT','weights','scorediff'], axis=1)
y = df['scorediff']
weights = df['weights']
X.head()
y.head()
weights.head()
```
Now let's train the linear regression model. You'll notice that I'm actually using ridge regression (adds an l2 penalty with alpha = 1.0) because that prevents the model from overfitting and also limits the values of the coefficients to be more interpretable. If I did not add this penalty, the coefficients would be huge.
```
from sklearn.linear_model import Ridge
ridge_reg = Ridge()
ridge_reg.fit(X, y, sample_weight=weights)
# get the R^2 value
r_squared = ridge_reg.score(X, y, sample_weight=weights)
print('R^2 on the training data:')
print(r_squared)
```
Now that the model is trained, we can use it to provide our rankings. Note that in this model, a team's ranking is simply defined as its linear regression coefficient, which we call the YUSAG coefficient.
When predicting a game's score differential on a neutral field, the predicted score differential (`scorediff`) is just the difference in YUSAG coefficients. The reason this works is the binary encoding we did earlier.
#### More details below on how it actually works
Ok, so you may have noticed that every game in our dataframe is actually duplicated, just with the `team` and `opponent` variables switched. This may have seemed like a mistake but it is actually useful for making the model more interpretable.
When we run the model, we get a coefficient for the `team_Yale` variable, which we call the YUSAG coefficient, and a coefficient for the `opponent_Yale` variable. Since we allow every game to be repeated, these variables end up just being negatives of each other.
So let's think about what we are doing when we predict the score differential for the Harvard-Penn game with `team` = Harvard and `opponent` = Penn.
In our model, the coefficients are as follows:
- team_Harvard_coef = 7.78
- opponent_Harvard_coef = -7.78
- team_Penn_coef = 6.68
- opponent_Penn_coef = -6.68
when we go to use the model for this game, it looks like this:
`scorediff` = (location_coef $*$ `location`) + (team_Harvard_coef $*$ `team_Harvard`) + (opponent_Harvard_coef $*$ `opponent_Harvard`) + (team_Penn_coef $*$ `team_Penn`) + (opponent_Penn_coef $*$ `opponent_Penn`) + (team_Yale_coef $*$ `team_Yale`) + (opponent_Yale_coef $*$ `opponent_Yale`) + $\cdots$
where the $\cdots$ represent data for many other teams, which will all just equal $0$.
To put numbers in for the variables, the model looks like this:
`scorediff` = (location_coef $*$ $0$) + (team_Harvard_coef $*$ $1$) + (opponent_Harvard_coef $*$ $0$) + (team_Penn_coef $*$ $0$) + (opponent_Penn_coef $*$ $1$) + (team_Yale_coef $*$ $0$) + (opponent_Yale_coef $*$ $0$) + $\cdots$
Which is just:
`scorediff` = (location_coef $*$ $0$) + (7.78 $*$ $1$) + (-6.68 $*$ $1$) = $7.78 - 6.68$ = Harvard_YUSAG_coef - Penn_YUSAG_coef
Thus showing how the difference in YUSAG coefficients is the same as the predicted score differential. Furthermore, the higher YUSAG coefficient a team has, the better they are.
Lastly, if the Harvard-Penn game was to be home at Harvard, we would just add the location_coef:
`scorediff` = (location_coef $*$ $1$) + (team_Harvard_coef $*$ $1$) + (opponent_Penn_coef $*$ $1$) = $1.77 + 7.78 - 6.68$ = Location_coef + Harvard_YUSAG_coef - Penn_YUSAG_coef
```
# get the coefficients for each feature
coef_data = list(zip(X.columns,ridge_reg.coef_))
coef_df = pd.DataFrame(coef_data,columns=['feature','feature_coef'])
coef_df.head()
```
Let's get only the team variables, so that it is a proper ranking
```
# first get rid of opponent_ variables
team_df = coef_df[~coef_df['feature'].str.contains("opponent")]
# get rid of the location variable
team_df = team_df.iloc[1:]
team_df.head()
# rank them by coef, not alphabetical order
ranked_team_df = team_df.sort_values(['feature_coef'],ascending=False)
# reset the indices at 0
ranked_team_df = ranked_team_df.reset_index(drop=True);
ranked_team_df.head()
```
I'm goint to change the name of the columns and remove the 'team_' part of every string:
```
ranked_team_df.rename(columns={'feature':'team', 'feature_coef':'YUSAG_coef'}, inplace=True)
ranked_team_df['team'] = ranked_team_df['team'].str.replace('team_', '')
ranked_team_df.head()
```
Lastly, I'm just going to shift the index to start at 1, so that it corresponds to the ranking.
```
ranked_team_df.index = ranked_team_df.index + 1
ranked_team_df.to_csv("FBS_power_rankings.csv")
```
## Additional stuff: Testing the model
This section is mostly about how own could test the performance of the model or how one could choose appropriate hyperparamters.
#### Creating a new dataframe
First let's take the original dataframe and sort it by date, so that the order of games in the dataframe matches the order the games were played.
```
# sort by date and reset the indices to 0
df_dated = df.sort_values(['year', 'month','day'], ascending=[True, True, True])
df_dated = df_dated.reset_index(drop=True)
df_dated.head()
```
Let's first make a dataframe with training data (the first three years of results)
```
thirteen_df = df_dated.loc[df_dated['year']==2013]
fourteen_df = df_dated.loc[df_dated['year']==2014]
fifteen_df = df_dated.loc[df_dated['year']==2015]
train_df = pd.concat([thirteen_df,fourteen_df,fifteen_df], ignore_index=True)
```
Now let's make an initial testing dataframe with the data from this past year.
```
sixteen_df = df_dated.loc[df_dated['year']==2016]
seventeen_df = df_dated.loc[df_dated['year']==2017]
test_df = pd.concat([sixteen_df,seventeen_df], ignore_index=True)
```
I am now going to set up a testing/validation scheme for the model. It works like this:
First I start off where my training data is all games from 2012-2015. Using the model trained on this data, I then predict games from the first week of the 2016 season and look at the results.
Next, I add that first week's worth of games to the training data, and now I train on all 2012-2015 results plus the first week from 2016. After training the model on this data, I then test on the second week of games. I then add that week's games to the training data and repeat the same procedure week after week.
In this way, I am never testing on a result that I have trained on. Though, it should be noted that I have also used this as a validation scheme, so I have technically done some sloppy 'data snooping' and this is not a great predictor of my generalization error.
```
def train_test_model(train_df, test_df):
# make the training data
X_train = train_df.drop(['year','month','day','team','opponent','teamscore','oppscore','D1','OT','weights','scorediff'], axis=1)
y_train = train_df['scorediff']
weights_train = train_df['weights']
# train the model
ridge_reg = Ridge()
ridge_reg.fit(X_train, y_train, weights_train)
fit = ridge_reg.score(X_train,y_train,sample_weight=weights_train)
print('R^2 on the training data:')
print(fit)
# get the test data
X_test = test_df.drop(['year','month','day','team','opponent','teamscore','oppscore','D1','OT','weights','scorediff'], axis=1)
y_test = test_df['scorediff']
# get the metrics
compare_data = list(zip(ridge_reg.predict(X_test),y_test))
right_count = 0
for tpl in compare_data:
if tpl[0] >= 0 and tpl[1] >=0:
right_count = right_count + 1
elif tpl[0] <= 0 and tpl[1] <=0:
right_count = right_count + 1
accuracy = right_count/len(compare_data)
print('accuracy on this weeks games')
print(right_count/len(compare_data))
total_squared_error = 0.0
for tpl in compare_data:
total_squared_error = total_squared_error + (tpl[0]-tpl[1])**2
RMSE = (total_squared_error / float(len(compare_data)))**(0.5)
print('RMSE on this weeks games:')
print(RMSE)
return fit, accuracy, RMSE, right_count, total_squared_error
#Now the code for running the week by week testing.
base_df = train_df
new_indices = []
# this is the hash for the first date
last_date_hash = 2018
fit_list = []
accuracy_list = []
RMSE_list = []
total_squared_error = 0
total_right_count = 0
for index, row in test_df.iterrows():
year = row['year']
month = row['month']
day = row['day']
date_hash = year+month+day
if date_hash != last_date_hash:
last_date_hash = date_hash
test_week = test_df.iloc[new_indices]
fit, accuracy, RMSE, correct_calls, squared_error = train_test_model(base_df,test_week)
fit_list.append(fit)
accuracy_list.append(accuracy)
RMSE_list.append(RMSE)
total_squared_error = total_squared_error + squared_error
total_right_count = total_right_count + correct_calls
base_df = pd.concat([base_df,test_week],ignore_index=True)
new_indices = [index]
else:
new_indices.append(index)
# get the number of games it called correctly in 2016
total_accuracy = total_right_count/test_df.shape[0]
total_accuracy
# get the Root Mean Squared Error
overall_RMSE = (total_squared_error/test_df.shape[0])**(0.5)
overall_RMSE
```
| github_jupyter |
### Using fmriprep
[fmriprep](https://fmriprep.readthedocs.io/en/stable/) is a package developed by the Poldrack lab to do the minimal preprocessing of fMRI data required. It covers brain extraction, motion correction, field unwarping, and registration. It uses a combination of well-known software packages (e.g., FSL, SPM, ANTS, AFNI) and selects the 'best' implementation of each preprocessing step.
Once installed, `fmriprep` can be invoked from the command line. We can even run it inside this notebook! The following command should work after you remove the 'hashtag' `#`.
However, running fmriprep takes quite some time (we included the hashtag to prevent you from accidentally running it). You'll most likely want to run it in parallel on a computing cluster.
```
#!fmriprep \
# --ignore slicetiming \
# --ignore fieldmaps \
# --output-space template \
# --template MNI152NLin2009cAsym \
# --template-resampling-grid 2mm \
# --fs-no-reconall \
# --fs-license-file \
# ../license.txt \
# ../data/ds000030 ../data/ds000030/derivatives/fmriprep participant
```
The command above consists of the following parts:
- \"fmriprep\" calls fmriprep
- `--ignore slicetiming` tells fmriprep to _not_ perform slice timing correction
- `--ignore fieldmaps` tells fmriprep to _not_ perform distortion correction (unfortunately, there are no field maps available in this data set)
- `--output-space template` tells fmriprep to normalize (register) data to a template
- `--template MNI152NLin2009cAsym` tells fmriprep that the template should be MNI152 version 6 (2009c)
- `--template-resampling-grid 2mm` tells fmriprep to resample the output images to 2mm isotropic resolution
- `--fs-license-file ../../license.txt` tells fmriprep where to find the license.txt-file for freesurfer - you can ignore this
- `bids` is the name of the folder containing the data in bids format
- `output_folder` is the name of the folder where we want the preprocessed data to be stored,
- `participant` tells fmriprep to run only at the participant level (and not, for example, at the group level - you can forget about this)
The [official documentation](http://fmriprep.readthedocs.io/) contains all possible arguments you can pass.
### Using nipype
fmriprep makes use of [Nipype](https://nipype.readthedocs.io/en/latest/), a pipelining tool for preprocessing neuroimaging data. Nipype makes it easy to share and document pipelines and run them in parallel on a computing cluster. If you would like to build your own preprocessing pipelines, a good resource to get started is [this tutorial](https://miykael.github.io/nipype_tutorial/).
| github_jupyter |
Скачайте данные в формате csv, выберите из таблицы данные по России, начиная с 3 марта 2020 г. (в этот момент впервые стало больше 2 заболевших). В качестве целевой переменной возьмём число случаев заболевания (столбцы total_cases и new_cases); для упрощения обработки можно заменить в столбце new_cases все нули на единицы. Для единообразия давайте зафиксируем тренировочный набор в виде первых 50 отсчётов (дней), начиная с 3 марта; остальные данные можно использовать в качестве тестового набора (и он даже будет увеличиваться по мере выполнения задания).
- Постройте графики целевых переменных. Вы увидите, что число заболевших растёт очень быстро, на первый взгляд экспоненциально. Для первого подхода к снаряду давайте это и используем.
- Используя линейную регрессию, обучите модель с экспоненциальным ростом числа заболевших: y ~ exp(линейная функция от x), где x — номер текущего дня.
- Найдите апостериорное распределение параметров этой модели для достаточно широкого априорного распределения. Требующееся для этого значение дисперсии шума в данных оцените, исходя из вашей же максимальной апостериорной модели (это фактически первый шаг эмпирического Байеса).
- Посэмплируйте много разных экспонент, постройте графики. Сколько, исходя из этих сэмплов, предсказывается случаев коронавируса в России к 1 мая? к 1 июня? к 1 сентября? Постройте предсказательные распределения (можно эмпирически, исходя из данных сэмплирования).
Предсказания экспоненциальной модели наверняка получились грустными. Но это, конечно, чересчур пессимистично — экспоненциальный рост в природе никак не может продолжаться вечно. Кривая общего числа заболевших во время эпидемии в реальности имеет сигмоидальный вид: после начальной фазы экспоненциального роста неизбежно происходит насыщение. В качестве конкретной формы такой сигмоиды давайте возьмём форму функции распределения для гауссиана. Естественно, в нашем случае сигмоида стремится не к единице, т.е. константа перед интегралом может быть произвольной (и её можно внести в экспоненту), а в экспоненте под интегралом может быть произвольная квадратичная функция от t.
- Предложите способ обучать параметры такой сигмоидальной функции при помощи линейной регрессии.
- Обучите эти параметры на датасете случаев коронавируса в России. Найдите апостериорное распределение параметров этой модели для достаточно широкого априорного распределения. Требующееся для этого значение дисперсии шума в данных оцените, исходя из вашей же максимальной апостериорной модели.
- Посэмплируйте много разных сигмоид из апостериорного распределения, постройте графики. Сколько, исходя из этих сэмплов, будет всего случаев коронавируса в России? Постройте эмпирическое предсказательное распределение, нарисуйте графики. Каков ваш прогноз числа случаев коронавируса в пессимистичном сценарии (90-й процентиль в выборке числа случаев)? В оптимистичном сценарии (10-й процентиль)?
Бонус: проведите такой же анализ для других стран (здесь придётся руками подобрать дни начала моделирования — коронавирус приходил в разные страны в разное время). Насколько разные параметры получаются? Можно ли разделить страны на кластеры (хотя бы чисто визуально) в зависимости от этих параметров?
[Эта часть задания не оценивается, здесь нет правильных и неправильных ответов, но буду рад узнать, что вы думаете]
Что вы поняли из этого упражнения? Что можно сказать про коронавирус по итогам такого моделирования? Как принять решение, например, о том, нужно ли вводить карантин?
```
from datetime import datetime
import pandas as pd
import numpy as np
import scipy
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = 16, 6
```
### Загрузка и предобработка данных
```
# загрузим данные
df = pd.read_csv('full_data.csv')
df = df[(df['location'] == 'Russia') & (df['date'] >= '2020-03-03')].reset_index(drop=True)
df.loc[df['new_cases'] == 0, 'new_cases'] = 1
df['day'] = df.index
start_day = datetime.strptime('2020-03-03', '%Y-%m-%d')
may_first = datetime.strptime('2020-05-01', '%Y-%m-%d')
june_first = datetime.strptime('2020-06-01', '%Y-%m-%d')
sept_first = datetime.strptime('2020-09-01', '%Y-%m-%d')
year_end = datetime.strptime('2020-12-31', '%Y-%m-%d')
till_may = (may_first - start_day).days
till_june = (june_first - start_day).days
till_sept = (sept_first - start_day).days
till_year_end = (year_end - start_day).days
```
### Разделим на трейн и тест
```
# разделим на трейн и тест. Возьмем 60! дней, т.к. результаты получаются более адекватные
TRAIN_DAYS = 60
train = df[:TRAIN_DAYS]
test = df[TRAIN_DAYS:]
```
### Код для байесовской регрессии
```
class BayesLR(BaseEstimator, TransformerMixin):
def __init__(self, mu, sigma, noise=None):
self.mu = mu
self.sigma = sigma
self.noise = None
def _estimate_noise(self, X, y):
return np.std(y - X.dot(np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y))) # linear regression
def _add_intercept(self, X):
return np.hstack((np.ones((len(X), 1)), X))
def fit(self, X, y):
"""
X: (n_samples, n_features)
y: (n_samples, )
"""
X = self._add_intercept(X)
if self.noise is None:
self.noise = self._estimate_noise(X, y)
beta = 1 / self.noise ** 2
mu_prev = self.mu
sigma_prev = self.sigma
self.sigma = np.linalg.inv(np.linalg.inv(sigma_prev) + beta * np.dot(X.T, X))
self.mu = np.dot(self.sigma, np.dot(np.linalg.inv(sigma_prev), mu_prev) + beta * np.dot(X.T, y))
return self
def predict(self, X):
X = self._add_intercept(X)
return X.dot(self.mu)
def sample_w(self, n_samples=1000):
return np.random.multivariate_normal(self.mu, self.sigma, n_samples)
def sample(self, X, n_samples=1000):
X = self._add_intercept(X)
w = self.sample_w(n_samples)
return X.dot(w.T)
def plot_sampled(sampled, true=None):
for i in range(sampled.shape[1]):
plt.plot(sampled[:, i], 'k-', lw=.4)
```
## Часть 1: моделирование экспонентной
### 1.1 Графики
```
plt.plot(train['total_cases'], label='общее число зараженных')
plt.plot(train['new_cases'], label='количество новых случаев за день')
plt.title('Графики целевых переменных')
plt.legend();
```
### 1.2 Линейная регрессия y ~ exp(wX)
Чтобы построить линейную регрессию для такого случая, прологарифмируем целевую переменную (общее количество зараженных).
```
X_tr = train[['day']].values
y_tr = np.log(train['total_cases'].values)
X_te = test[['day']].values
y_te = np.log(test['total_cases'].values)
X_full = np.arange(till_year_end + 1).reshape(-1, 1) # до конца года
# Выберем uninformative prior
mu_prior = np.array([0, 0])
sigma_prior = 100 * np.array([[1, 0],
[0, 1]])
bayes_lr = BayesLR(mu_prior, sigma_prior)
bayes_lr.fit(X_tr, y_tr)
print(bayes_lr.mu)
print(bayes_lr.sigma)
# Семплируем параметры модели
w = bayes_lr.sample_w(n_samples=10000)
fig, ax = plt.subplots(1, 2)
ax[0].hist(w[:, 0], bins=100)
ax[0].set_title('Распределение свободного члена')
ax[1].hist(w[:, 1], bins=100)
ax[1].set_title('Распределение коэффициента наклона')
plt.show()
```
### 1.3 Предсказания
```
# Семплируем экспоненты для трейна
sampled_train = np.exp(bayes_lr.sample(X_tr))
plot_sampled(sampled_train)
plt.plot(np.exp(y_tr), color='red', label='Реальное число зараженных')
plt.legend()
plt.title('Предсказания для трейна');
# Посемплируем экспоненты для теста
sampled_test = np.exp(bayes_lr.sample(X_te, n_samples=10000))
# Делаем предсказания
preds_full = np.exp(bayes_lr.predict(X_full))
plot_sampled(sampled_test)
plt.plot(np.exp(y_te), color='red', label='Реальное число зараженных')
plt.legend()
plt.title('Предсказания для теста');
print(f'1 мая: {preds_full[till_may] / 1_000_000:.4f} млн зараженных')
print(f'1 июня: {preds_full[till_june] / 1_000_000:.4f} млн зараженных')
print(f'1 сентября: {preds_full[till_sept] / 1_000_000:.4f} млн зараженных')
```
Получается, что к 1 июня 2/3 России вымрет, не очень реалистично.
```
# Посемплируем экспоненты на будущее
sampled_full = np.exp(bayes_lr.sample(X_full, n_samples=10000))
fig, ax = plt.subplots(2, 2, figsize=(16, 10))
ax[0][0].hist(sampled_full[till_may], bins=50)
ax[0][0].set_title('Предсказательное распределение количества зараженных к маю')
ax[0][1].hist(sampled_full[till_june], bins=50)
ax[0][1].set_title('Предсказательное распределение количества зараженных к июню')
ax[1][0].hist(sampled_full[till_sept], bins=50)
ax[1][0].set_title('Предсказательное распределение количества зараженных к сентябрю')
ax[1][1].hist(sampled_test.mean(0), bins=30)
ax[1][1].set_title('Распределение среднего числа зараженных для тестовой выборки')
plt.show()
```
Вывод: моделирование экспонентой - это шляпа =)
## Часть 2: моделирование сигмоидой
### 2.1 Как такое обучать
Справа у нас интеграл - можем взять производную, а затем прологарифмировать, в итоге получим:
$ln$($\Delta$y) = w_2 * x^2 + w_1 * x + w_0
Другими словами, мы можем замоделировать количество новых случаев заражения с помощью плотности нормального распределения. В качестве функции в экспоненте возьмет квадратичную функцию от дня.
### 2.2 Обучаем
```
# Функция для приведения наших предсказаний приростов к общему числу зараженных
def to_total(preds):
return 2 + np.cumsum(np.exp(preds), axis=0)
X_tr = np.hstack([X_tr, X_tr ** 2])
y_tr = np.log(train['new_cases'].values)
X_te = np.hstack([X_te, X_te ** 2])
y_te = np.log(test['new_cases'].values)
X_full = np.hstack([X_full, X_full ** 2])
# Выберем uninformative prior
mu_prior = np.array([0, 0, 0])
sigma_prior = 1000 * np.array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]])
bayes_lr = BayesLR(mu_prior, sigma_prior)
bayes_lr.fit(X_tr, y_tr)
print(bayes_lr.mu)
print(bayes_lr.sigma)
# Семплируем параметры модели
w = bayes_lr.sample_w(n_samples=10000)
fig, ax = plt.subplots(1, 3)
ax[0].hist(w[:, 0], bins=100)
ax[0].set_title('Распределение свободного члена')
ax[1].hist(w[:, 1], bins=100)
ax[1].set_title('Распределение коэффициента при X')
ax[2].hist(w[:, 2], bins=100)
ax[2].set_title('Распределение коэффициента при X^2')
plt.show()
```
### 2.3 Предсказываем
```
# Семплируем сигмоиды для трейна
sampled_train = to_total(bayes_lr.sample(X_tr))
plot_sampled(sampled_train)
plt.plot(to_total(y_tr), color='red', label='Реальное число зараженных')
plt.legend()
plt.title('Предсказания для трейна');
# Посемплируем сигмоиды для теста
sampled_test = to_total(bayes_lr.sample(X_te))
# Делаем предсказания
preds_full = to_total(bayes_lr.predict(X_full))
plt.plot(preds_full)
plt.plot(to_total(np.hstack([y_tr, y_te])), color='red', label='Реальное известное число зараженных')
plt.legend()
plt.title('Среднее наших предсказаний по числу зараженных до конца года');
plot_sampled(sampled_test)
plt.plot(to_total(y_te), color='red', label='Реальное число зараженных')
plt.legend()
plt.title('Предсказания для теста');
print(f'1 мая: {preds_full[till_may] / 1_000_000:.4f} млн зараженных')
print(f'1 июня: {preds_full[till_june] / 1_000_000:.4f} млн зараженных')
print(f'1 сентября: {preds_full[till_sept] / 1_000_000:.4f} млн зараженных')
# Посемплируем сигмоиды на будущее
sampled_full = to_total(bayes_lr.sample(X_full, n_samples=100))
plot_sampled(sampled_full)
plt.ylim(0, 1_000_000)
plt.title('Предсказания до конца года');
# Посемплируем больше сигмоид на будущее
sampled_full = to_total(bayes_lr.sample(X_full, n_samples=10000))
fig, ax = plt.subplots(3, 2, figsize=(16, 16))
SHOW_THR = 3_000_000
ax[0][0].hist(sampled_full[till_may], bins=50)
ax[0][0].set_title('Предсказательное распределение количества зараженных к маю')
ax[0][1].hist(sampled_full[till_june][sampled_full[till_june] < SHOW_THR], bins=50)
ax[0][1].set_title('Предсказательное распределение количества зараженных к июню')
ax[1][0].hist(sampled_full[till_sept][sampled_full[till_sept] < SHOW_THR], bins=50)
ax[1][0].set_title('Предсказательное распределение количества зараженных к сентябрю')
ax[1][1].hist(sampled_full[-1][sampled_full[-1] < SHOW_THR], bins=50)
ax[1][1].set_title('Предсказательное распределение количества зараженных к концу года')
ax[2][0].hist(sampled_test.mean(0), bins=30)
ax[2][0].set_title('Распределение среднего числа зараженных для тестовой выборки')
ax[2][1].hist(sampled_full.mean(0)[sampled_full.mean(0) < SHOW_THR], bins=30)
ax[2][1].set_title('Распределение среднего числа зараженных до конца года')
plt.show()
print(f'Оптимистичный прогноз к концу года: {int(np.quantile(sampled_full[-1], 0.1)) / 1_000_000:.4f} млн человек')
print(f'Пессимистичный прогноз к концу года: {int(np.quantile(sampled_full[-1], 0.9)) / 1_000_000:.4f} млн человек')
```
Если смотреть на пессимистичный прогноз, то он кажется уже чуть более реальным.
#### Что я понял
- Разобрался с байесовским выводом, понял (надеюсь), как обучать сигмоиды
- Параметры априорных распределений не играют большой роли, когда имеется уже 50 точек
- Моделировать экспонентой - шляпа, сигмоидой получше, хотя такие модели кажутся здесь все равно слишком неточными, и почти все зависит от выбора точки начала и конца моделирования
- Решение вводить или не вводить карантин, наверное, можно принять, оценив результат от его введения (быстрее ли затухает сигмоида) в других странах
| github_jupyter |
SVM
```
import pandas as pd
from sklearn import svm, metrics
from sklearn.model_selection import train_test_split
wesad_eda = pd.read_csv('D:\data\wesad-chest-combined-classification-eda.csv') # need to adjust a path of dataset
wesad_eda.columns
original_column_list = ['MEAN', 'MAX', 'MIN', 'RANGE', 'KURT', 'SKEW', 'MEAN_1ST_GRAD',
'STD_1ST_GRAD', 'MEAN_2ND_GRAD', 'STD_2ND_GRAD', 'ALSC', 'INSC', 'APSC',
'RMSC', 'subject id', 'MEAN_LOG', 'INSC_LOG', 'APSC_LOG', 'RMSC_LOG',
'RANGE_LOG', 'ALSC_LOG', 'MIN_LOG', 'MEAN_1ST_GRAD_LOG',
'MEAN_2ND_GRAD_LOG', 'MIN_LOG_LOG', 'MEAN_1ST_GRAD_LOG_LOG',
'MEAN_2ND_GRAD_LOG_LOG', 'APSC_LOG_LOG', 'ALSC_LOG_LOG', 'APSC_BOXCOX',
'RMSC_BOXCOX', 'RANGE_BOXCOX', 'MEAN_YEO_JONSON', 'SKEW_YEO_JONSON',
'KURT_YEO_JONSON', 'APSC_YEO_JONSON', 'MIN_YEO_JONSON',
'MAX_YEO_JONSON', 'MEAN_1ST_GRAD_YEO_JONSON', 'RMSC_YEO_JONSON',
'STD_1ST_GRAD_YEO_JONSON', 'RANGE_SQRT', 'RMSC_SQUARED',
'MEAN_2ND_GRAD_CUBE', 'INSC_APSC', 'condition', 'SSSQ class',
'SSSQ Label', 'condition label']
original_column_list_withoutString = ['MEAN', 'MAX', 'MIN', 'RANGE', 'KURT', 'SKEW', 'MEAN_1ST_GRAD',
'STD_1ST_GRAD', 'MEAN_2ND_GRAD', 'STD_2ND_GRAD', 'ALSC', 'INSC', 'APSC',
'RMSC', 'MEAN_LOG', 'INSC_LOG', 'APSC_LOG', 'RMSC_LOG',
'RANGE_LOG', 'ALSC_LOG', 'MIN_LOG', 'MEAN_1ST_GRAD_LOG',
'MEAN_2ND_GRAD_LOG', 'MIN_LOG_LOG', 'MEAN_1ST_GRAD_LOG_LOG',
'MEAN_2ND_GRAD_LOG_LOG', 'APSC_LOG_LOG', 'ALSC_LOG_LOG', 'APSC_BOXCOX',
'RMSC_BOXCOX', 'RANGE_BOXCOX', 'MEAN_YEO_JONSON', 'SKEW_YEO_JONSON',
'KURT_YEO_JONSON', 'APSC_YEO_JONSON', 'MIN_YEO_JONSON',
'MAX_YEO_JONSON', 'MEAN_1ST_GRAD_YEO_JONSON', 'RMSC_YEO_JONSON',
'STD_1ST_GRAD_YEO_JONSON', 'RANGE_SQRT', 'RMSC_SQUARED',
'MEAN_2ND_GRAD_CUBE', 'INSC_APSC']
selected_colum_list = ['MEAN', 'MAX', 'MIN', 'RANGE', 'KURT', 'SKEW', 'MEAN_1ST_GRAD',
'STD_1ST_GRAD', 'MEAN_2ND_GRAD', 'STD_2ND_GRAD', 'ALSC', 'INSC', 'APSC',
'RMSC', 'subject id', 'MEAN_LOG', 'INSC_LOG', 'APSC_LOG', 'RMSC_LOG',
'RANGE_LOG', 'ALSC_LOG', 'MIN_LOG']
stress_data = wesad_eda[original_column_list_withoutString]
stress_label = wesad_eda['condition label']
stress_data
train_data, test_data, train_label, test_label = train_test_split(stress_data, stress_label)
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(train_data)
X_t_train = pca.transform(train_data)
X_t_test = pca.transform(test_data)
model = svm.SVC()
model.fit(X_t_train, train_label)
predict = model.predict(X_t_test)
acc_score = metrics.accuracy_score(test_label, predict)
print(acc_score)
import pickle
from sklearn.externals import joblib
saved_model = pickle.dumps(model)
joblib.dump(model, 'SVMmodel1.pkl')
model_from_pickle = joblib.load('SVMmodel1.pkl')
predict = model_from_pickle.predict(test_data)
acc_score = metrics.accuracy_score(test_label, predict)
print(acc_score)
```
| github_jupyter |
# Time series analysis on AWS
*Chapter 1 - Time series analysis overview*
## Initializations
---
```
!pip install --quiet tqdm kaggle tsia ruptures
```
### Imports
```
import matplotlib.colors as mpl_colors
import matplotlib.dates as mdates
import matplotlib.ticker as ticker
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import ruptures as rpt
import sys
import tsia
import warnings
import zipfile
from matplotlib import gridspec
from sklearn.preprocessing import normalize
from tqdm import tqdm
from urllib.request import urlretrieve
```
### Parameters
```
RAW_DATA = os.path.join('..', 'Data', 'raw')
DATA = os.path.join('..', 'Data')
warnings.filterwarnings("ignore")
os.makedirs(RAW_DATA, exist_ok=True)
%matplotlib inline
# plt.style.use('Solarize_Light2')
plt.style.use('fivethirtyeight')
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
plt.rcParams['figure.dpi'] = 300
plt.rcParams['lines.linewidth'] = 0.3
plt.rcParams['axes.titlesize'] = 6
plt.rcParams['axes.labelsize'] = 6
plt.rcParams['xtick.labelsize'] = 4.5
plt.rcParams['ytick.labelsize'] = 4.5
plt.rcParams['grid.linewidth'] = 0.2
plt.rcParams['legend.fontsize'] = 5
```
### Helper functions
```
def progress_report_hook(count, block_size, total_size):
mb = int(count * block_size // 1048576)
if count % 500 == 0:
sys.stdout.write("\r{} MB downloaded".format(mb))
sys.stdout.flush()
```
### Downloading datasets
#### **Dataset 1:** Household energy consumption
```
ORIGINAL_DATA = 'https://archive.ics.uci.edu/ml/machine-learning-databases/00321/LD2011_2014.txt.zip'
ARCHIVE_PATH = os.path.join(RAW_DATA, 'energy-consumption.zip')
FILE_NAME = 'energy-consumption.csv'
FILE_PATH = os.path.join(DATA, 'energy', FILE_NAME)
FILE_DIR = os.path.dirname(FILE_PATH)
if not os.path.isfile(FILE_PATH):
print("Downloading dataset (258MB), can take a few minutes depending on your connection")
urlretrieve(ORIGINAL_DATA, ARCHIVE_PATH, reporthook=progress_report_hook)
os.makedirs(os.path.join(DATA, 'energy'), exist_ok=True)
print("\nExtracting data archive")
zip_ref = zipfile.ZipFile(ARCHIVE_PATH, 'r')
zip_ref.extractall(FILE_DIR + '/')
zip_ref.close()
!rm -Rf $FILE_DIR/__MACOSX
!mv $FILE_DIR/LD2011_2014.txt $FILE_PATH
else:
print("File found, skipping download")
```
#### **Dataset 2:** Nasa Turbofan remaining useful lifetime
```
ok = True
ok = ok and os.path.exists(os.path.join(DATA, 'turbofan', 'train_FD001.txt'))
ok = ok and os.path.exists(os.path.join(DATA, 'turbofan', 'test_FD001.txt'))
ok = ok and os.path.exists(os.path.join(DATA, 'turbofan', 'RUL_FD001.txt'))
if (ok):
print("File found, skipping download")
else:
print('Some datasets are missing, create working directories and download original dataset from the NASA repository.')
# Making sure the directory already exists:
os.makedirs(os.path.join(DATA, 'turbofan'), exist_ok=True)
# Download the dataset from the NASA repository, unzip it and set
# aside the first training file to work on:
!wget https://ti.arc.nasa.gov/c/6/ --output-document=$RAW_DATA/CMAPSSData.zip
!unzip $RAW_DATA/CMAPSSData.zip -d $RAW_DATA
!cp $RAW_DATA/train_FD001.txt $DATA/turbofan/train_FD001.txt
!cp $RAW_DATA/test_FD001.txt $DATA/turbofan/test_FD001.txt
!cp $RAW_DATA/RUL_FD001.txt $DATA/turbofan/RUL_FD001.txt
```
#### **Dataset 3:** Human heartbeat
```
ECG_DATA_SOURCE = 'http://www.timeseriesclassification.com/Downloads/ECG200.zip'
ARCHIVE_PATH = os.path.join(RAW_DATA, 'ECG200.zip')
FILE_NAME = 'ecg.csv'
FILE_PATH = os.path.join(DATA, 'ecg', FILE_NAME)
FILE_DIR = os.path.dirname(FILE_PATH)
if not os.path.isfile(FILE_PATH):
urlretrieve(ECG_DATA_SOURCE, ARCHIVE_PATH)
os.makedirs(os.path.join(DATA, 'ecg'), exist_ok=True)
print("\nExtracting data archive")
zip_ref = zipfile.ZipFile(ARCHIVE_PATH, 'r')
zip_ref.extractall(FILE_DIR + '/')
zip_ref.close()
!mv $DATA/ecg/ECG200_TRAIN.txt $FILE_PATH
else:
print("File found, skipping download")
```
#### **Dataset 4:** Industrial pump data
To download this dataset from Kaggle, you will need to have an account and create a token that you install on your machine. You can follow [**this link**](https://www.kaggle.com/docs/api) to get started with the Kaggle API. Once generated, make sure your Kaggle token is stored in the `~/.kaggle/kaggle.json` file, or the next cells will issue an error. In some cases, you may still have an error while using this location. Try moving your token in this location instead: `~/kaggle/kaggle.json` (not the absence of the `.` in the folder name).
To get a Kaggle token, go to kaggle.com and create an account. Then navigate to **My account** and scroll down to the API section. There, click the **Create new API token** button:
<img src="../Assets/kaggle_api.png" />
```
FILE_NAME = 'pump-sensor-data.zip'
ARCHIVE_PATH = os.path.join(RAW_DATA, FILE_NAME)
FILE_PATH = os.path.join(DATA, 'pump', 'sensor.csv')
FILE_DIR = os.path.dirname(FILE_PATH)
if not os.path.isfile(FILE_PATH):
if not os.path.exists('/home/ec2-user/.kaggle/kaggle.json'):
os.makedirs('/home/ec2-user/.kaggle/', exist_ok=True)
raise Exception('The kaggle.json token was not found.\nCreating the /home/ec2-user/.kaggle/ directory: put your kaggle.json file there once you have generated it from the Kaggle website')
else:
print('The kaggle.json token file was found: making sure it is not readable by other users on this system.')
!chmod 600 /home/ec2-user/.kaggle/kaggle.json
os.makedirs(os.path.join(DATA, 'pump'), exist_ok=True)
!kaggle datasets download -d nphantawee/pump-sensor-data -p $RAW_DATA
print("\nExtracting data archive")
zip_ref = zipfile.ZipFile(ARCHIVE_PATH, 'r')
zip_ref.extractall(FILE_DIR + '/')
zip_ref.close()
else:
print("File found, skipping download")
```
#### **Dataset 5:** London household energy consumption with weather data
```
FILE_NAME = 'smart-meters-in-london.zip'
ARCHIVE_PATH = os.path.join(RAW_DATA, FILE_NAME)
FILE_PATH = os.path.join(DATA, 'energy-london', 'smart-meters-in-london.zip')
FILE_DIR = os.path.dirname(FILE_PATH)
# Checks if the data were already downloaded:
if os.path.exists(os.path.join(DATA, 'energy-london', 'acorn_details.csv')):
print("File found, skipping download")
else:
# Downloading and unzipping datasets from Kaggle:
print("Downloading dataset (2.26G), can take a few minutes depending on your connection")
os.makedirs(os.path.join(DATA, 'energy-london'), exist_ok=True)
!kaggle datasets download -d jeanmidev/smart-meters-in-london -p $RAW_DATA
print('Unzipping files...')
zip_ref = zipfile.ZipFile(ARCHIVE_PATH, 'r')
zip_ref.extractall(FILE_DIR + '/')
zip_ref.close()
!rm $DATA/energy-london/*zip
!rm $DATA/energy-london/*gz
!mv $DATA/energy-london/halfhourly_dataset/halfhourly_dataset/* $DATA/energy-london/halfhourly_dataset
!rm -Rf $DATA/energy-london/halfhourly_dataset/halfhourly_dataset
!mv $DATA/energy-london/daily_dataset/daily_dataset/* $DATA/energy-london/daily_dataset
!rm -Rf $DATA/energy-london/daily_dataset/daily_dataset
```
## Dataset visualization
---
### **1.** Household energy consumption
```
%%time
FILE_PATH = os.path.join(DATA, 'energy', 'energy-consumption.csv')
energy_df = pd.read_csv(FILE_PATH, sep=';', decimal=',')
energy_df = energy_df.rename(columns={'Unnamed: 0': 'Timestamp'})
energy_df['Timestamp'] = pd.to_datetime(energy_df['Timestamp'])
energy_df = energy_df.set_index('Timestamp')
energy_df.iloc[100000:, 1:5].head()
fig = plt.figure(figsize=(5, 1.876))
plt.plot(energy_df['MT_002'])
plt.title('Energy consumption for household MT_002')
plt.show()
```
### **2.** NASA Turbofan data
```
FILE_PATH = os.path.join(DATA, 'turbofan', 'train_FD001.txt')
turbofan_df = pd.read_csv(FILE_PATH, header=None, sep=' ')
turbofan_df.dropna(axis='columns', how='all', inplace=True)
print('Shape:', turbofan_df.shape)
turbofan_df.head(5)
columns = [
'unit_number',
'cycle',
'setting_1',
'setting_2',
'setting_3',
] + ['sensor_{}'.format(s) for s in range(1,22)]
turbofan_df.columns = columns
turbofan_df.head()
# Add a RUL column and group the data by unit_number:
turbofan_df['rul'] = 0
grouped_data = turbofan_df.groupby(by='unit_number')
# Loops through each unit number to get the lifecycle counts:
for unit, rul in enumerate(grouped_data.count()['cycle']):
current_df = turbofan_df[turbofan_df['unit_number'] == (unit+1)].copy()
current_df['rul'] = rul - current_df['cycle']
turbofan_df[turbofan_df['unit_number'] == (unit+1)] = current_df
df = turbofan_df.iloc[:, [0,1,2,3,4,5,6,25,26]].copy()
df = df[df['unit_number'] == 1]
def highlight_cols(s):
return f'background-color: rgba(0, 143, 213, 0.3)'
df.head(10).style.applymap(highlight_cols, subset=['rul'])
```
### **3.** ECG Data
```
FILE_PATH = os.path.join(DATA, 'ecg', 'ecg.csv')
ecg_df = pd.read_csv(FILE_PATH, header=None, sep=' ')
print('Shape:', ecg_df.shape)
ecg_df.head()
plt.rcParams['lines.linewidth'] = 0.7
fig = plt.figure(figsize=(5,2))
label_normal = False
label_ischemia = False
for i in range(0,100):
label = ecg_df.iloc[i, 0]
if (label == -1):
color = colors[1]
if label_ischemia:
plt.plot(ecg_df.iloc[i,1:96], color=color, alpha=0.5, linestyle='--', linewidth=0.5)
else:
plt.plot(ecg_df.iloc[i,1:96], color=color, alpha=0.5, label='Ischemia', linestyle='--')
label_ischemia = True
else:
color = colors[0]
if label_normal:
plt.plot(ecg_df.iloc[i,1:96], color=color, alpha=0.5)
else:
plt.plot(ecg_df.iloc[i,1:96], color=color, alpha=0.5, label='Normal')
label_normal = True
plt.title('Human heartbeat activity')
plt.legend(loc='upper right', ncol=2)
plt.show()
```
### **4.** Industrial pump data
```
FILE_PATH = os.path.join(DATA, 'pump', 'sensor.csv')
pump_df = pd.read_csv(FILE_PATH, sep=',')
pump_df.drop(columns={'Unnamed: 0'}, inplace=True)
pump_df['timestamp'] = pd.to_datetime(pump_df['timestamp'], format='%Y-%m-%d %H:%M:%S')
pump_df = pump_df.set_index('timestamp')
pump_df['machine_status'].replace(to_replace='NORMAL', value=np.nan, inplace=True)
pump_df['machine_status'].replace(to_replace='BROKEN', value=1, inplace=True)
pump_df['machine_status'].replace(to_replace='RECOVERING', value=1, inplace=True)
print('Shape:', pump_df.shape)
pump_df.head()
file_structure_df = pump_df.iloc[:, 0:10].resample('5D').mean()
plt.rcParams['hatch.linewidth'] = 0.5
plt.rcParams['lines.linewidth'] = 0.5
fig = plt.figure(figsize=(5,1))
ax1 = fig.add_subplot(1,1,1)
plot1 = ax1.plot(pump_df['sensor_00'], label='Healthy pump')
ax2 = ax1.twinx()
plot2 = ax2.fill_between(
x=pump_df.index,
y1=0.0,
y2=pump_df['machine_status'],
color=colors[1],
linewidth=0.0,
edgecolor='#000000',
alpha=0.5,
hatch="//////",
label='Broken pump'
)
ax2.grid(False)
ax2.set_yticks([])
labels = [plot1[0].get_label(), plot2.get_label()]
plt.legend(handles=[plot1[0], plot2], labels=labels, loc='lower center', ncol=2, bbox_to_anchor=(0.5, -.4))
plt.title('Industrial pump sensor data')
plt.show()
```
### **5.** London household energy consumption with weather data
We want to filter out households that are are subject to the dToU tariff and keep only the ones with a known ACORN (i.e. not in the ACORN-U group): this will allow us to better model future analysis by adding the Acorn detail informations (which by definitions, won't be available for the ACORN-U group).
```
household_filename = os.path.join(DATA, 'energy-london', 'informations_households.csv')
household_df = pd.read_csv(household_filename)
household_df = household_df[(household_df['stdorToU'] == 'Std') & (household_df['Acorn'] == 'ACORN-E')]
print(household_df.shape)
household_df.head()
```
#### Associating households with they energy consumption data
Each household (with an ID starting by `MACxxxxx` in the table above) has its consumption data stored in a block file name `block_xx`. This file is also available from the `informations_household.csv` file extracted above. We have the association between `household_id` and `block_file`: we can open each of them and keep the consumption for the households of interest. All these data will be concatenated into an `energy_df` dataframe:
```
%%time
household_ids = household_df['LCLid'].tolist()
consumption_file = os.path.join(DATA, 'energy-london', 'hourly_consumption.csv')
min_data_points = ((pd.to_datetime('2020-12-31') - pd.to_datetime('2020-01-01')).days + 1)*24*2
if os.path.exists(consumption_file):
print('Half-hourly consumption file already exists, loading from disk...')
energy_df = pd.read_csv(consumption_file)
energy_df['timestamp'] = pd.to_datetime(energy_df['timestamp'], format='%Y-%m-%d %H:%M:%S.%f')
print('Done.')
else:
print('Half-hourly consumption file not found. We need to generate it.')
# We know have the block number we can use to open the right file:
energy_df = pd.DataFrame()
target_block_files = household_df['file'].unique().tolist()
print('- {} block files to process: '.format(len(target_block_files)), end='')
df_list = []
for block_file in tqdm(target_block_files):
# Reads the current block file:
current_filename = os.path.join(DATA, 'energy-london', 'halfhourly_dataset', '{}.csv'.format(block_file))
df = pd.read_csv(current_filename)
# Set readable column names and adjust data types:
df.columns = ['household_id', 'timestamp', 'energy']
df = df.replace(to_replace='Null', value=0.0)
df['energy'] = df['energy'].astype(np.float64)
df['timestamp'] = pd.to_datetime(df['timestamp'], format='%Y-%m-%d %H:%M:%S.%f')
# We filter on the households sampled earlier:
df_list.append(df[df['household_id'].isin(household_ids)].reset_index(drop=True))
# Concatenate with the main dataframe:
energy_df = pd.concat(df_list, axis='index', ignore_index=True)
datapoints = energy_df.groupby(by='household_id').count()
datapoints = datapoints[datapoints['timestamp'] < min_data_points]
hhid_to_remove = datapoints.index.tolist()
energy_df = energy_df[~energy_df['household_id'].isin(hhid_to_remove)]
# Let's save this dataset to disk, we will use it from now on:
print('Saving file to disk... ', end='')
energy_df.to_csv(consumption_file, index=False)
print('Done.')
start = np.min(energy_df['timestamp'])
end = np.max(energy_df['timestamp'])
weather_filename = os.path.join(DATA, 'energy-london', 'weather_hourly_darksky.csv')
weather_df = pd.read_csv(weather_filename)
weather_df['time'] = pd.to_datetime(weather_df['time'], format='%Y-%m-%d %H:%M:%S')
weather_df = weather_df.drop(columns=['precipType', 'icon', 'summary'])
weather_df = weather_df.sort_values(by='time')
weather_df = weather_df.set_index('time')
weather_df = weather_df[start:end]
# Let's make sure we have one datapoint per hour to match
# the frequency used for the household energy consumption data:
weather_df = weather_df.resample(rule='1H').mean() # This will generate NaN values timestamp missing data
weather_df = weather_df.interpolate(method='linear') # This will fill the missing values with the average
print(weather_df.shape)
weather_df
energy_df = energy_df.set_index(['household_id', 'timestamp'])
energy_df
hhid = household_ids[2]
hh_energy = energy_df.loc[hhid, :]
start = '2012-07-01'
end = '2012-07-15'
fig = plt.figure(figsize=(5,1))
ax1 = fig.add_subplot(1,1,1)
plot2 = ax1.fill_between(
x=weather_df.loc[start:end, 'temperature'].index,
y1=0.0,
y2=weather_df.loc[start:end, 'temperature'],
color=colors[1],
linewidth=0.0,
edgecolor='#000000',
alpha=0.25,
hatch="//////",
label='Temperature'
)
ax1.set_ylim((0,40))
ax1.grid(False)
ax2 = ax1.twinx()
ax2.plot(hh_energy[start:end], label='Energy consumption', linewidth=2, color='#FFFFFF', alpha=0.5)
plot1 = ax2.plot(hh_energy[start:end], label='Energy consumption', linewidth=0.7)
ax2.set_title(f'Energy consumption for household {hhid}')
labels = [plot1[0].get_label(), plot2.get_label()]
plt.legend(handles=[plot1[0], plot2], labels=labels, loc='upper left', fontsize=3, ncol=2)
plt.show()
acorn_filename = os.path.join(DATA, 'energy-london', 'acorn_details.csv')
acorn_df = pd.read_csv(acorn_filename, encoding='ISO-8859-1')
acorn_df = acorn_df.sample(10).loc[:, ['MAIN CATEGORIES', 'CATEGORIES', 'REFERENCE', 'ACORN-A', 'ACORN-B', 'ACORN-E']]
acorn_df
```
## File structure exploration
---
```
from IPython.display import display_html
def display_multiple_dataframe(*args, max_rows=None, max_cols=None):
html_str = ''
for df in args:
html_str += df.to_html(max_cols=max_cols, max_rows=max_rows)
display_html(html_str.replace('table','table style="display:inline"'), raw=True)
display_multiple_dataframe(
file_structure_df[['sensor_00']],
file_structure_df[['sensor_01']],
file_structure_df[['sensor_03']],
max_rows=10, max_cols=None
)
display_multiple_dataframe(
file_structure_df.loc['2018-04', :].head(6),
file_structure_df.loc['2018-05', :].head(6),
file_structure_df.loc['2018-06', :].head(6),
max_rows=None, max_cols=2
)
display_multiple_dataframe(
file_structure_df.loc['2018-04', ['sensor_00']].head(6),
file_structure_df.loc['2018-05', ['sensor_00']].head(6),
file_structure_df.loc['2018-06', ['sensor_00']].head(6),
max_rows=10, max_cols=None
)
display_multiple_dataframe(
file_structure_df.loc['2018-04', ['sensor_01']].head(6),
file_structure_df.loc['2018-05', ['sensor_01']].head(6),
file_structure_df.loc['2018-06', ['sensor_01']].head(6),
max_rows=10, max_cols=None
)
print('.\n.\n.')
display_multiple_dataframe(
file_structure_df.loc['2018-04', ['sensor_09']].head(6),
file_structure_df.loc['2018-05', ['sensor_09']].head(6),
file_structure_df.loc['2018-06', ['sensor_09']].head(6),
max_rows=10, max_cols=None
)
df1 = pump_df.iloc[:, [0]].resample('5D').mean()
df2 = pump_df.iloc[:, [1]].resample('2D').mean()
df3 = pump_df.iloc[:, [2]].resample('7D').mean()
display_multiple_dataframe(
df1.head(10), df2.head(10), df3.head(10),
pd.merge(pd.merge(df1, df2, left_index=True, right_index=True, how='outer'), df3, left_index=True, right_index=True, how='outer').head(10),
max_rows=None, max_cols=None
)
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 10)
pd.merge(pd.merge(df1, df2, left_index=True, right_index=True, how='outer'), df3, left_index=True, right_index=True, how='outer').head(10)
plt.figure(figsize=(5,1))
for i in range(len(colors)):
plt.plot(file_structure_df[f'sensor_0{i}'], linewidth=2, alpha=0.5, label=colors[i])
plt.legend()
plt.show()
```
## Visualization
---
```
fig = plt.figure(figsize=(5,1))
ax1 = fig.add_subplot(1,1,1)
ax2 = ax1.twinx()
plot_sensor_0 = ax1.plot(pump_df['sensor_00'], label='Sensor 0', color=colors[0], linewidth=1, alpha=0.8)
plot_sensor_1 = ax2.plot(pump_df['sensor_01'], label='Sensor 1', color=colors[1], linewidth=1, alpha=0.8)
ax2.grid(False)
plt.title('Pump sensor values (2 sensors)')
plt.legend(handles=[plot_sensor_0[0], plot_sensor_1[0]], ncol=2, loc='lower right')
plt.show()
reduced_pump_df = pump_df.loc[:, 'sensor_00':'sensor_14']
reduced_pump_df = reduced_pump_df.replace([np.inf, -np.inf], np.nan)
reduced_pump_df = reduced_pump_df.fillna(0.0)
reduced_pump_df = reduced_pump_df.astype(np.float32)
scaled_pump_df = pd.DataFrame(normalize(reduced_pump_df), index=reduced_pump_df.index, columns=reduced_pump_df.columns)
scaled_pump_df
fig = plt.figure(figsize=(5,1))
for i in range(0,15):
plt.plot(scaled_pump_df.iloc[:, i], alpha=0.6)
plt.title('Pump sensor values (15 sensors)')
plt.show()
pump_df2 = pump_df.copy()
pump_df2 = pump_df2.replace([np.inf, -np.inf], np.nan)
pump_df2 = pump_df2.fillna(0.0)
pump_df2 = pump_df2.astype(np.float32)
pump_description = pump_df2.describe().T
constant_signals = pump_description[pump_description['min'] == pump_description['max']].index.tolist()
pump_df2 = pump_df2.drop(columns=constant_signals)
features = pump_df2.columns.tolist()
def hex_to_rgb(hex_color):
"""
Converts a color string in hexadecimal format to RGB format.
PARAMS
======
hex_color: string
A string describing the color to convert from hexadecimal. It can
include the leading # character or not
RETURNS
=======
rgb_color: tuple
Each color component of the returned tuple will be a float value
between 0.0 and 1.0
"""
hex_color = hex_color.lstrip('#')
rgb_color = tuple(int(hex_color[i:i+2], base=16) / 255.0 for i in [0, 2, 4])
return rgb_color
def plot_timeseries_strip_chart(binned_timeseries, signal_list, fig_width=12, signal_height=0.15, dates=None, day_interval=7):
# Build a suitable colormap:
colors_list = [
hex_to_rgb('#DC322F'),
hex_to_rgb('#B58900'),
hex_to_rgb('#2AA198')
]
cm = mpl_colors.LinearSegmentedColormap.from_list('RdAmGr', colors_list, N=len(colors_list))
fig = plt.figure(figsize=(fig_width, signal_height * binned_timeseries.shape[0]))
ax = fig.add_subplot(1,1,1)
# Devising the extent of the actual plot:
if dates is not None:
dnum = mdates.date2num(dates)
start = dnum[0] - (dnum[1]-dnum[0])/2.
stop = dnum[-1] + (dnum[1]-dnum[0])/2.
extent = [start, stop, 0, signal_height * (binned_timeseries.shape[0])]
else:
extent = None
# Plot the matrix:
im = ax.imshow(binned_timeseries,
extent=extent,
aspect="auto",
cmap=cm,
origin='lower')
# Adjusting the x-axis if we provide dates:
if dates is not None:
ax.xaxis.set_major_locator(mdates.MonthLocator())
ax.xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m-%d'))
for tick in ax.xaxis.get_major_ticks():
tick.label.set_fontsize(4)
tick.label.set_rotation(60)
tick.label.set_fontweight('bold')
ax.tick_params(axis='x', which='major', pad=7, labelcolor='#000000')
plt.xticks(ha='right')
# Adjusting the y-axis:
ax.yaxis.set_major_locator(ticker.MultipleLocator(signal_height))
ax.set_yticklabels(signal_list, verticalalignment='bottom', fontsize=4)
ax.set_yticks(np.arange(len(signal_list)) * signal_height)
plt.grid()
return ax
from IPython.display import display, Markdown, Latex
# Build a list of dataframes, one per sensor:
df_list = []
for f in features[:1]:
df_list.append(pump_df2[[f]])
# Discretize each signal in 3 bins:
array = tsia.markov.discretize_multivariate(df_list)
fig = plt.figure(figsize=(5.5, 0.6))
plt.plot(pump_df2['sensor_00'], linewidth=0.7, alpha=0.6)
plt.title('Line plot of the pump sensor 0')
plt.show()
display(Markdown('<img src="arrow.png" align="left" style="padding-left: 730px"/>'))
# Plot the strip chart:
ax = plot_timeseries_strip_chart(
array,
signal_list=features[:1],
fig_width=5.21,
signal_height=0.2,
dates=df_list[0].index.to_pydatetime(),
day_interval=2
)
ax.set_title('Strip chart of the pump sensor 0');
# Build a list of dataframes, one per sensor:
df_list = []
for f in features:
df_list.append(pump_df2[[f]])
# Discretize each signal in 3 bins:
array = tsia.markov.discretize_multivariate(df_list)
# Plot the strip chart:
fig = plot_timeseries_strip_chart(
array,
signal_list=features,
fig_width=5.5,
signal_height=0.1,
dates=df_list[0].index.to_pydatetime(),
day_interval=2
)
```
### Recurrence plot
```
from pyts.image import RecurrencePlot
from pyts.image import GramianAngularField
from pyts.image import MarkovTransitionField
hhid = household_ids[2]
hh_energy = energy_df.loc[hhid, :]
pump_extract_df = pump_df.iloc[:800, 0].copy()
rp = RecurrencePlot(threshold='point', percentage=30)
weather_rp = rp.fit_transform(weather_df.loc['2013-01-01':'2013-01-31']['temperature'].values.reshape(1, -1))
energy_rp = rp.fit_transform(hh_energy['2012-07-01':'2012-07-15'].values.reshape(1, -1))
pump_rp = rp.fit_transform(pump_extract_df.values.reshape(1, -1))
fig = plt.figure(figsize=(5.5, 2.4))
gs = gridspec.GridSpec(nrows=3, ncols=2, width_ratios=[3,1], hspace=0.8, wspace=0.0)
# Pump sensor 0:
ax = fig.add_subplot(gs[0])
ax.plot(pump_extract_df, label='Pump sensor 0')
ax.set_title(f'Pump sensor 0')
ax = fig.add_subplot(gs[1])
ax.imshow(pump_rp[0], cmap='binary', origin='lower')
ax.axis('off')
# Energy consumption line plot and recurrence plot:
ax = fig.add_subplot(gs[2])
plot1 = ax.plot(hh_energy['2012-07-01':'2012-07-15'], color=colors[1])
ax.set_title(f'Energy consumption for household {hhid}')
ax = fig.add_subplot(gs[3])
ax.imshow(energy_rp[0], cmap='binary', origin='lower')
ax.axis('off')
# Daily temperature line plot and recurrence plot:
ax = fig.add_subplot(gs[4])
start = '2012-07-01'
end = '2012-07-15'
ax.plot(weather_df.loc['2013-01-01':'2013-01-31']['temperature'], color=colors[2])
ax.set_title(f'Daily temperature')
ax = fig.add_subplot(gs[5])
ax.imshow(weather_rp[0], cmap='binary', origin='lower')
ax.axis('off')
plt.show()
hhid = household_ids[2]
hh_energy = energy_df.loc[hhid, :]
pump_extract_df = pump_df.iloc[:800, 0].copy()
gaf = GramianAngularField(image_size=48, method='summation')
weather_gasf = gaf.fit_transform(weather_df.loc['2013-01-01':'2013-01-31']['temperature'].values.reshape(1, -1))
energy_gasf = gaf.fit_transform(hh_energy['2012-07-01':'2012-07-15'].values.reshape(1, -1))
pump_gasf = gaf.fit_transform(pump_extract_df.values.reshape(1, -1))
fig = plt.figure(figsize=(5.5, 2.4))
gs = gridspec.GridSpec(nrows=3, ncols=2, width_ratios=[3,1], hspace=0.8, wspace=0.0)
# Pump sensor 0:
ax = fig.add_subplot(gs[0])
ax.plot(pump_extract_df, label='Pump sensor 0')
ax.set_title(f'Pump sensor 0')
ax = fig.add_subplot(gs[1])
ax.imshow(pump_gasf[0], cmap='RdBu_r', origin='lower')
ax.axis('off')
# Energy consumption line plot and recurrence plot:
ax = fig.add_subplot(gs[2])
plot1 = ax.plot(hh_energy['2012-07-01':'2012-07-15'], color=colors[1])
ax.set_title(f'Energy consumption for household {hhid}')
ax = fig.add_subplot(gs[3])
ax.imshow(energy_gasf[0], cmap='RdBu_r', origin='lower')
ax.axis('off')
# Daily temperature line plot and recurrence plot:
ax = fig.add_subplot(gs[4])
start = '2012-07-01'
end = '2012-07-15'
ax.plot(weather_df.loc['2013-01-01':'2013-01-31']['temperature'], color=colors[2])
ax.set_title(f'Daily temperature')
ax = fig.add_subplot(gs[5])
ax.imshow(weather_gasf[0], cmap='RdBu_r', origin='lower')
ax.axis('off')
plt.show()
mtf = MarkovTransitionField(image_size=48)
weather_mtf = mtf.fit_transform(weather_df.loc['2013-01-01':'2013-01-31']['temperature'].values.reshape(1, -1))
energy_mtf = mtf.fit_transform(hh_energy['2012-07-01':'2012-07-15'].values.reshape(1, -1))
pump_mtf = mtf.fit_transform(pump_extract_df.values.reshape(1, -1))
fig = plt.figure(figsize=(5.5, 2.4))
gs = gridspec.GridSpec(nrows=3, ncols=2, width_ratios=[3,1], hspace=0.8, wspace=0.0)
# Pump sensor 0:
ax = fig.add_subplot(gs[0])
ax.plot(pump_extract_df, label='Pump sensor 0')
ax.set_title(f'Pump sensor 0')
ax = fig.add_subplot(gs[1])
ax.imshow(pump_mtf[0], cmap='RdBu_r', origin='lower')
ax.axis('off')
# Energy consumption line plot and recurrence plot:
ax = fig.add_subplot(gs[2])
plot1 = ax.plot(hh_energy['2012-07-01':'2012-07-15'], color=colors[1])
ax.set_title(f'Energy consumption for household {hhid}')
ax = fig.add_subplot(gs[3])
ax.imshow(energy_mtf[0], cmap='RdBu_r', origin='lower')
ax.axis('off')
# Daily temperature line plot and recurrence plot:
ax = fig.add_subplot(gs[4])
start = '2012-07-01'
end = '2012-07-15'
ax.plot(weather_df.loc['2013-01-01':'2013-01-31']['temperature'], color=colors[2])
ax.set_title(f'Daily temperature')
ax = fig.add_subplot(gs[5])
ax.imshow(weather_mtf[0], cmap='RdBu_r', origin='lower')
ax.axis('off')
plt.show()
import matplotlib
import matplotlib.cm as cm
import networkx as nx
import community
def compute_network_graph(markov_field):
G = nx.from_numpy_matrix(markov_field[0])
# Uncover the communities in the current graph:
communities = community.best_partition(G)
nb_communities = len(pd.Series(communities).unique())
cmap = 'autumn'
# Compute node colors and edges colors for the modularity encoding:
edge_colors = [matplotlib.colors.to_hex(cm.get_cmap(cmap)(communities.get(v)/(nb_communities - 1))) for u,v in G.edges()]
node_colors = [communities.get(node) for node in G.nodes()]
node_size = [nx.average_clustering(G, [node])*90 for node in G.nodes()]
# Builds the options set to draw the network graph in the "modularity" configuration:
options = {
'node_size': 10,
'edge_color': edge_colors,
'node_color': node_colors,
'linewidths': 0,
'width': 0.1,
'alpha': 0.6,
'with_labels': False,
'cmap': cmap
}
return G, options
fig = plt.figure(figsize=(5.5, 2.4))
gs = gridspec.GridSpec(nrows=3, ncols=2, width_ratios=[3,1], hspace=0.8, wspace=0.0)
# Pump sensor 0:
ax = fig.add_subplot(gs[0])
ax.plot(pump_extract_df, label='Pump sensor 0')
ax.set_title(f'Pump sensor 0')
ax = fig.add_subplot(gs[1])
G, options = compute_network_graph(weather_mtf)
nx.draw_networkx(G, **options, pos=nx.spring_layout(G), ax=ax)
ax.axis('off')
# Energy consumption line plot and recurrence plot:
ax = fig.add_subplot(gs[2])
plot1 = ax.plot(hh_energy['2012-07-01':'2012-07-15'], color=colors[1])
ax.set_title(f'Energy consumption for household {hhid}')
ax = fig.add_subplot(gs[3])
G, options = compute_network_graph(energy_mtf)
nx.draw_networkx(G, **options, pos=nx.spring_layout(G), ax=ax)
ax.axis('off')
# Daily temperature line plot and recurrence plot:
ax = fig.add_subplot(gs[4])
start = '2012-07-01'
end = '2012-07-15'
ax.plot(weather_df.loc['2013-01-01':'2013-01-31']['temperature'], color=colors[2])
ax.set_title(f'Daily temperature')
ax = fig.add_subplot(gs[5])
G, options = compute_network_graph(weather_mtf)
nx.draw_networkx(G, **options, pos=nx.spring_layout(G), ax=ax)
ax.axis('off')
plt.show()
```
## Symbolic representation
---
```
from pyts.bag_of_words import BagOfWords
window_size, word_size = 30, 5
bow = BagOfWords(window_size=window_size, word_size=word_size, window_step=window_size, numerosity_reduction=False)
X = weather_df.loc['2013-01-01':'2013-01-31']['temperature'].values.reshape(1, -1)
X_bow = bow.transform(X)
time_index = weather_df.loc['2013-01-01':'2013-01-31']['temperature'].index
len(X_bow[0].replace(' ', ''))
# Plot the considered subseries
plt.figure(figsize=(5, 2))
splits_series = np.linspace(0, X.shape[1], 1 + X.shape[1] // window_size, dtype='int64')
for start, end in zip(splits_series[:-1], np.clip(splits_series[1:] + 1, 0, X.shape[1])):
plt.plot(np.arange(start, end), X[0, start:end], 'o-', linewidth=0.5, ms=0.1)
# Plot the corresponding letters
splits_letters = np.linspace(0, X.shape[1], 1 + word_size * X.shape[1] // window_size)
splits_letters = ((splits_letters[:-1] + splits_letters[1:]) / 2)
splits_letters = splits_letters.astype('int64')
for i, (x, text) in enumerate(zip(splits_letters, X_bow[0].replace(' ', ''))):
t = plt.text(x, X[0, x], text, color="C{}".format(i // 5), fontsize=3.5)
t.set_bbox(dict(facecolor='#FFFFFF', alpha=0.5, edgecolor="C{}".format(i // 5), boxstyle='round4'))
plt.title('Bag-of-words representation for weather temperature')
plt.tight_layout()
plt.show()
from pyts.transformation import WEASEL
from sklearn.preprocessing import LabelEncoder
X_train = ecg_df.iloc[:, 1:].values
y_train = ecg_df.iloc[:, 0]
y_train = LabelEncoder().fit_transform(y_train)
weasel = WEASEL(word_size=3, n_bins=3, window_sizes=[10, 25], sparse=False)
X_weasel = weasel.fit_transform(X_train, y_train)
vocabulary_length = len(weasel.vocabulary_)
plt.figure(figsize=(5,1.5))
width = 0.4
x = np.arange(vocabulary_length) - width / 2
for i in range(len(X_weasel[y_train == 0])):
if i == 0:
plt.bar(x, X_weasel[y_train == 0][i], width=width, alpha=0.25, color=colors[1], label='Time series for Ischemia')
else:
plt.bar(x, X_weasel[y_train == 0][i], width=width, alpha=0.25, color=colors[1])
for i in range(len(X_weasel[y_train == 1])):
if i == 0:
plt.bar(x+width, X_weasel[y_train == 1][i], width=width, alpha=0.25, color=colors[0], label='Time series for Normal heartbeat')
else:
plt.bar(x+width, X_weasel[y_train == 1][i], width=width, alpha=0.25, color=colors[0])
plt.xticks(
np.arange(vocabulary_length),
np.vectorize(weasel.vocabulary_.get)(np.arange(X_weasel[0].size)),
fontsize=2,
rotation=60
)
plt.legend(loc='upper right')
plt.show()
```
## Statistics
---
```
plt.rcParams['xtick.labelsize'] = 3
import statsmodels.api as sm
fig = plt.figure(figsize=(5.5, 3))
gs = gridspec.GridSpec(nrows=3, ncols=2, width_ratios=[1,1], hspace=0.8)
# Pump
ax = fig.add_subplot(gs[0])
ax.plot(pump_extract_df, label='Pump sensor 0')
ax.set_title(f'Pump sensor 0')
ax.tick_params(axis='x', which='both', labelbottom=False)
ax = fig.add_subplot(gs[1])
sm.graphics.tsa.plot_acf(pump_extract_df.values.squeeze(), ax=ax, markersize=1, title='')
ax.set_ylim(-1.2, 1.2)
ax.tick_params(axis='x', which='major', labelsize=4)
# Energy consumption
ax = fig.add_subplot(gs[2])
ax.plot(hh_energy['2012-07-01':'2012-07-15'], color=colors[1])
ax.set_title(f'Energy consumption for household {hhid}')
ax.tick_params(axis='x', which='both', labelbottom=False)
ax = fig.add_subplot(gs[3])
sm.graphics.tsa.plot_acf(hh_energy['2012-07-01':'2012-07-15'].values.squeeze(), ax=ax, markersize=1, title='')
ax.set_ylim(-0.3, 0.3)
ax.tick_params(axis='x', which='major', labelsize=4)
# Daily temperature:
ax = fig.add_subplot(gs[4])
start = '2012-07-01'
end = '2012-07-15'
ax.plot(weather_df.loc['2013-01-01':'2013-01-31']['temperature'], color=colors[2])
ax.set_title(f'Daily temperature')
ax.tick_params(axis='x', which='both', labelbottom=False)
ax = fig.add_subplot(gs[5])
sm.graphics.tsa.plot_acf(weather_df.loc['2013-01-01':'2013-01-31']['temperature'].values.squeeze(), ax=ax, markersize=1, title='')
ax.set_ylim(-1.2, 1.2)
ax.tick_params(axis='x', which='major', labelsize=4)
plt.show()
from statsmodels.tsa.seasonal import STL
endog = endog.resample('30T').mean()
plt.rcParams['lines.markersize'] = 1
title = f'Energy consumption for household {hhid}'
endog = hh_energy['2012-07-01':'2012-07-15']
endog.columns = [title]
endog = endog[title]
stl = STL(endog, period=48)
res = stl.fit()
fig = res.plot()
fig = plt.gcf()
fig.set_size_inches(5.5, 4)
plt.show()
```
## Binary segmentation
---
```
signal = weather_df.loc['2013-01-01':'2013-01-31']['temperature'].values.squeeze()
algo = rpt.Binseg(model='l2').fit(signal)
my_bkps = algo.predict(n_bkps=3)
my_bkps = [0] + my_bkps
my_bkps
fig = plt.figure(figsize=(5.5,1))
start = '2012-07-01'
end = '2012-07-15'
plt.plot(weather_df.loc['2013-01-01':'2013-01-31']['temperature'], color='#FFFFFF', linewidth=1.2, alpha=0.8)
plt.plot(weather_df.loc['2013-01-01':'2013-01-31']['temperature'], color=colors[2], linewidth=0.7)
plt.title(f'Daily temperature')
plt.xticks(rotation=60, fontsize=4)
weather_index = weather_df.loc['2013-01-01':'2013-01-31']['temperature'].index
for index, bkps in enumerate(my_bkps[:-1]):
x1 = weather_index[my_bkps[index]]
x2 = weather_index[np.clip(my_bkps[index+1], 0, len(weather_index)-1)]
plt.axvspan(x1, x2, color=colors[index % 5], alpha=0.2)
plt.title('Daily temperature segmentation')
plt.show()
```
| github_jupyter |
# MOHID visualisation tools
```
from IPython.display import HTML
HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide();
} else {
$('div.input').show();
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
<form action="javascript:code_toggle()"><input type="submit" value="Click here to toggle on/off the raw code."></form>''')
import matplotlib.pyplot as plt
import xarray as xr
import numpy as np
import cmocean
%matplotlib inline
```
## How to Parse time into datetime64 string format
```
from datetime import datetime, timedelta
from dateutil.parser import parse
def to_datetime64(time):
"""Convert string to string in datetime64[s] format
:arg time: string
:return datetime64: str in datetime64[s] format
"""
time = parse(time) # parse to datetime format
# now just take care of formatting
year, month, day, hour, minute, second = str(time.year), str(time.month), str(time.day), str(time.hour), str(time.minute), str(time.second)
if len(month) < 2:
month = '0' + month
if len(day) < 2:
day = '0' + day
if len(hour) < 2:
hour = '0' + hour
if len(minute) < 2:
minute = '0' + minute
if len(second) < 2:
second = '0' + second
datetime64 = '{}-{}-{}T{}:{}:{}'.format(year, month, day, hour, minute, second)
return datetime64
```
### Usage:
```
to_datetime64('1 Jan 2016')
```
<h2>Generate heat maps of vertical velocities</h2>
<h3>Getting depth slices</h3>
```
# load a profile
sog2015 = xr.open_dataset('Vertical_velocity_profiles/sog2015.nc')
sog2015
# slice by layer index
sog2015.vovecrtz.isel(depthw = slice(0,11))
# slice explicitly by layer depth
# print depth with corresponding index
for i in zip(range(40), sog2015.depthw.values):
print(i)
sog2015.vovecrtz.sel(depthw = slice(0.0, 10.003407))
```
### Getting time slices using parsing
```
# this is where to_datetime64 comes in handy
# getting the first week in january
sog2015.sel(time_counter = slice(to_datetime64('1 jan 2015'), to_datetime64('7 jan 2015')))
```
### Slicing by time and depth at the same time
```
slice_example = sog2015.vovecrtz.sel(time_counter = slice(to_datetime64('1 jan 2015'), to_datetime64('7 jan 2015'))).isel(depthw = slice(0,11))
slice_example
```
### Plotting the slice
```
slice_example.T.plot(cmap = 'RdBu') # transposed to have depth on y axis. cmap specified as RdBu.
plt.gca().invert_yaxis()
```
<h3>Extracting the data you just visualised</h3>
```
a_slice.data()
```
## Plotting the trend of the depth of maximum vertical change
```
def find_bottom(array):
"""Find the bottom depth layer index
:arg array: one dimesional array (profile at giventime stamp)
:returns bottom: int, 1 + index of sea floor layer
"""
i=-1
for value in np.flip(array):
if value != 0:
bottom = 39-i
return bottom
else:
i=i+1
def max_delta(depths, truncated_array):
"""return raw plot data for depth of maximum delta
"""
# time is axis 0, depth is axis 1
difference = np.abs(np.diff(truncated_array, axis=1))
data = (depths[np.argmax(difference, axis=1)])
return data, difference
depths = sog2015.depthw.values
array = sog2015.vovecrtz.sel(time_counter = slice(convert_timestamp('1 Jan 2015'), convert_timestamp('7 Jan 2015')))
bottom_index = find_bottom(array[0].values)
truncated_array = array.isel(depthw = slice(0,bottom_index)).values
times = array.time_counter.values
delta, difference = max_delta(depths,truncated_array)
fig = plt.figure(figsize=(10,5))
plt.plot(times, delta)
plt.xlim(times[0], times[-1])
plt.ylim(depths[0], depths[-1])
plt.hlines(depths[bottom_index-1], times[0], times[-1], label = 'sea floor')
plt.hlines(depths[0:bottom_index], times[0], times[-1], linewidth = 0.25, label='layer depths')
plt.gca().invert_yaxis()
plt.ylabel('layer depth (m)')
plt.title('Timeseries of depth of maximum chnage in vertical velocity')
plt.legend()
```
## Salinity profiles with shaded range region
```
import seaborn as sns
palette = sns.color_palette("Reds", n_colors = 14)
sal_sog2015 = xr.open_dataset('salinity_profiles/salinity_sog2015.nc')
A = sal_sog2015.sel(time_counter = slice(to_datetime64('1 Jan 2015'),to_datetime64('8 Jan 2015')))
fig = plt.figure(figsize = (10,10))
ax = plt.subplot(111)
depths = A.deptht.values.T
#bottom = find_bottom(A.isel(time_counter= 0).vosaline.values)
bottom = 11
try:
for i in range(14):
plt.plot(A.vosaline.isel(time_counter = 12*i).values[0: bottom],depths[0: bottom], label = A.time_counter.values[12*i], color = palette[i])
except IndexError:
pass
# find the fill_between values
low, high = np.min(A.vosaline.values,axis = 0)[0: bottom], np.max(A.vosaline.values, axis=0)[0:bottom]
mean = np.average(A.vosaline.values,axis = 0)[0: bottom]
stddev = np.std(A.vosaline.values,axis = 0)[0: bottom]
plt.plot(mean,depths[0: bottom], 'k--',label = 'Average Salinity')
plt.fill_betweenx(depths[0:bottom],low, high, facecolor = 'lightgray', label = 'Range')
plt.fill_betweenx(depths[0:bottom], mean-stddev, mean+stddev,facecolor = 'deepskyblue', label = '1 Std. Dev')
ax.set_ylim(depths[0], depths[bottom-1])
plt.gca().invert_yaxis()
plt.legend(loc='lower left')
plt.ylabel('Ocean Depth [m]')
plt.xlabel('Salinity [g kg-1]')
plt.title('Salinity profiles over a week, showing profile every 12th hour')
```
<h2>Heat maps of Salinity</h2>
```
salinity_slice = sal_sog2015.sel(time_counter=slice(to_datetime64('1 Jan 2015'), to_datetime64('7 jan 2015')))
salinity_slice.vosaline.T.plot(cmap = cmocean.cm.haline)
plt.gca().invert_yaxis()
```
## Difference between surface and botttom salinity
```
salinity_slice = sal_sog2015.sel(time_counter=slice(to_datetime64('1 Jan 2015'), to_datetime64('7 jan 2015')))
bottom = find_bottom(sal_sog2015.vosaline.isel(time_counter=0).values)
# plot the difference between the surface and bottom salinity
diff = salinity_slice.isel(deptht = 0) - salinity_slice.isel(deptht = bottom-1)
diff.vosaline.plot()
plt.title('(Surface Salinity - Bottom Salinity) [g.cm-3]')
plt.ylabel('(Surface - Bottom Salinity) [g kg-1]')
depths = sal_sog2015.deptht.values
array = sal_sog2015.vosaline.sel(time_counter = slice(convert_timestamp('1 Jan 2015'), convert_timestamp('7 Jan 2015')))
bottom_index = find_bottom(array[0].values)
truncated_array = array.isel(deptht = slice(0,bottom_index)).values
times = array.time_counter.values
delta, difference = max_delta(depths,truncated_array)
fig = plt.figure(figsize=(10,5))
plt.plot(times, delta)
plt.xlim(times[0], times[-1])
plt.ylim(depths[0], depths[-1])
plt.hlines(depths[bottom_index-1], times[0], times[-1], label = 'sea floor')
plt.hlines(depths[0:bottom_index], times[0], times[-1], linewidth = 0.25, label='layer depths')
plt.gca().invert_yaxis()
plt.ylabel('layer depth (m)')
plt.title('Timeseries of Halocline depth')
plt.legend()
```
| github_jupyter |
## ML Lab 3
### Neural Networks
In the following exercise class we explore how to design and train neural networks in various ways.
#### Prerequisites:
In order to follow the exercises you need to:
1. Activate your conda environment from last week via: `source activate <env-name>`
2. Install tensorflow (https://www.tensorflow.org) via: `pip install tensorflow` (CPU-only)
3. Install keras (provides high level wrapper for tensorflow) (https://keras.io) via: `pip install keras`
## Exercise 1: Create a 2 layer network that acts as an XOR gate using numpy.
XOR is a fundamental logic gate that outputs a one whenever there is an odd parity of ones in its input and zero otherwise. For two inputs this can be thought of as an exclusive or operation and the associated boolean function is fully characterized by the following truth table.
| X | Y | XOR(X,Y) |
|---|---|----------|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The function of an XOR gate can also be understood as a classification problem on $v \in \{0,1\}^2$ and we can think about designing a classifier acting as an XOR gate. It turns out that this problem is not solvable by any single layer perceptron (https://en.wikipedia.org/wiki/Perceptron) because the set of points $\{(0,0), (0,1), (1,0), (1,1)\}$ is not linearly seperable.
**Design a two layer perceptron using basic numpy matrix operations that implements an XOR Gate on two inputs. Think about the flow of information and accordingly set the weight values by hand.**
### Data
```
import numpy as np
def generate_xor_data():
X = [(i,j) for i in [0,1] for j in [0,1]]
y = [int(np.logical_xor(x[0], x[1])) for x in X]
return X, y
print(generate_xor_data())
```
### Hints
A single layer in a multilayer perceptron can be described by the equation $y = f(\vec{b} + W\vec{x})$ with $f$ the logistic function, a smooth and differentiable version of the step function, and defined as $f(z) = \frac{1}{1+e^{-z}}$. $\vec{b}$ is the so called bias, a constant offset vector and $W$ is the weight matrix. However, since we set the weights by hand feel free to use hard thresholding instead of using the logistic function. Write down the equation for a two layer MLP and implement it with numpy. For documentation see https://docs.scipy.org/doc/numpy-1.13.0/reference/
```
"""
Implement your solution here.
"""
```
### Solution
| X | Y | AND(NOT X, Y) | AND(X,NOT Y) | OR[AND(NOT X, Y), AND(X, NOT Y)]| XOR(X,Y) |
|---|---|---------------|--------------|---------------------------------|----------|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
Implement XOR as a combination of 2 AND Gates and 1 OR gate where each neuron in the network acts as one of these gates.
```
"""
Definitions:
Input = np.array([X,Y])
0 if value < 0.5
1 if value >= 0.5
"""
def threshold(vector):
return (vector>=0.5).astype(float)
def mlp(x, W0, W1, b0, b1, f):
x0 = f(np.dot(W0, x) + b0)
x1 = f(np.dot(W1, x0) + b1)
return x1
# AND(NOT X, Y)
w_andnotxy = np.array([-1.0, 1.0])
# AND(X, NOT Y)
w_andxnoty = np.array([1.0, -1.0])
# W0 weight matrix:
W0 = np.vstack([w_andnotxy, w_andxnoty])
# OR(X,Y)
w_or = np.array([1., 1.])
W1 = w_or
# No biases needed
b0 = np.array([0.0,0.0])
b1 = 0.0
print("Input", "Output", "XOR")
xx,yy = generate_xor_data()
for x,y in zip(xx, yy):
print(x, int(mlp(x, W0, W1, b0, b1, threshold))," ", y)
```
## Exercise 2: Use Keras to design, train and evaluate a neural network that can classify points on a 2D plane.
### Data generator
```
import numpy as np
import matplotlib.pyplot as plt
def generate_spiral_data(n_points, noise=1.0):
n = np.sqrt(np.random.rand(n_points,1)) * 780 * (2*np.pi)/360
d1x = -np.cos(n)*n + np.random.rand(n_points,1) * noise
d1y = np.sin(n)*n + np.random.rand(n_points,1) * noise
return (np.vstack((np.hstack((d1x,d1y)),np.hstack((-d1x,-d1y)))),
np.hstack((np.zeros(n_points),np.ones(n_points))))
```
### Training data
```
X_train, y_train = generate_spiral_data(1000)
plt.title('Training set')
plt.plot(X_train[y_train==0,0], X_train[y_train==0,1], '.', label='Class 1')
plt.plot(X_train[y_train==1,0], X_train[y_train==1,1], '.', label='Class 2')
plt.legend()
plt.show()
```
### Test data
```
X_test, y_test = generate_spiral_data(1000)
plt.title('Test set')
plt.plot(X_test[y_test==0,0], X_test[y_test==0,1], '.', label='Class 1')
plt.plot(X_test[y_test==1,0], X_test[y_test==1,1], '.', label='Class 2')
plt.legend()
plt.show()
```
### 2.1. Design and train your model
The current model performs badly, try to find a more advanced architecture that is able to solve the classification problem. Read the following code snippet and understand the involved functions. Vary width and depth of the network and play around with activation functions, loss functions and optimizers to achieve a better result. Read up on parameters and functions for sequential models at https://keras.io/getting-started/sequential-model-guide/.
```
from keras.models import Sequential
from keras.layers import Dense
"""
Replace the following model with yours and try to achieve better classification performance
"""
bad_model = Sequential()
bad_model.add(Dense(12, input_dim=2, activation='tanh'))
bad_model.add(Dense(1, activation='sigmoid'))
bad_model.compile(loss='mean_squared_error',
optimizer='SGD', # SGD = Stochastic Gradient Descent
metrics=['accuracy'])
# Train the model
bad_model.fit(X_train, y_train, epochs=150, batch_size=10, verbose=0)
```
### Predict
```
bad_prediction = np.round(bad_model.predict(X_test).T[0])
```
### Visualize
```
plt.subplot(1,2,1)
plt.title('Test set')
plt.plot(X_test[y_test==0,0], X_test[y_test==0,1], '.')
plt.plot(X_test[y_test==1,0], X_test[y_test==1,1], '.')
plt.subplot(1,2,2)
plt.title('Bad model classification')
plt.plot(X_test[bad_prediction==0,0], X_test[bad_prediction==0,1], '.')
plt.plot(X_test[bad_prediction==1,0], X_test[bad_prediction==1,1], '.')
plt.show()
```
### 2.2. Visualize the decision boundary of your model.
```
"""
Implement your solution here.
"""
```
## Solution
### Model design and training
```
from keras.layers import Dense, Dropout
good_model = Sequential()
good_model.add(Dense(64, input_dim=2, activation='relu'))
good_model.add(Dense(64, activation='relu'))
good_model.add(Dense(64, activation='relu'))
good_model.add(Dense(1, activation='sigmoid'))
good_model.compile(loss='binary_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
good_model.fit(X_train, y_train, epochs=150, batch_size=10, verbose=0)
```
### Prediction
```
good_prediction = np.round(good_model.predict(X_test).T[0])
```
### Visualization
#### Performance
```
plt.subplot(1,2,1)
plt.title('Test set')
plt.plot(X_test[y_test==0,0], X_test[y_test==0,1], '.')
plt.plot(X_test[y_test==1,0], X_test[y_test==1,1], '.')
plt.subplot(1,2,2)
plt.title('Good model classification')
plt.plot(X_test[good_prediction==0,0], X_test[good_prediction==0,1], '.')
plt.plot(X_test[good_prediction==1,0], X_test[good_prediction==1,1], '.')
plt.show()
```
#### Decision boundary
```
# Generate grid:
line = np.linspace(-15,15)
xx, yy = np.meshgrid(line,line)
grid = np.stack((xx,yy))
# Reshape to fit model input size:
grid = grid.T.reshape(-1,2)
# Predict:
good_prediction = good_model.predict(grid)
bad_prediction = bad_model.predict(grid)
# Reshape to grid for visualization:
plt.title("Good Decision Boundary")
good_prediction = good_prediction.T[0].reshape(len(line),len(line))
plt.contourf(xx,yy,good_prediction)
plt.show()
plt.title("Bad Decision Boundary")
bad_prediction = bad_prediction.T[0].reshape(len(line),len(line))
plt.contourf(xx,yy,bad_prediction)
plt.show()
```
## Design, train and test a neural network that is able to classify MNIST digits using Keras.
### Data
```
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
"""
Returns:
2 tuples:
x_train, x_test: uint8 array of grayscale image data with shape (num_samples, 28, 28).
y_train, y_test: uint8 array of digit labels (integers in range 0-9) with shape (num_samples,).
"""
# Show example data
plt.subplot(1,4,1)
plt.imshow(x_train[0], cmap=plt.get_cmap('gray'))
plt.subplot(1,4,2)
plt.imshow(x_train[1], cmap=plt.get_cmap('gray'))
plt.subplot(1,4,3)
plt.imshow(x_train[2], cmap=plt.get_cmap('gray'))
plt.subplot(1,4,4)
plt.imshow(x_train[3], cmap=plt.get_cmap('gray'))
plt.show()
"""
Implement your solution here.
"""
```
### Solution
```
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense, Flatten, Dropout, Conv2D, MaxPooling2D
"""
We need to add a channel dimension
to the image input.
"""
x_train = x_train.reshape(x_train.shape[0],
x_train.shape[1],
x_train.shape[2],
1)
x_test = x_test.reshape(x_test.shape[0],
x_test.shape[1],
x_test.shape[2],
1)
"""
Train the image using 32-bit floats normalized
between 0 and 1 for numerical stability.
"""
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
input_shape = (x_train.shape[1], x_train.shape[2], 1)
"""
Output should be a 10 dimensional 1-hot vector,
not just an integer denoting the digit.
This is due to our use of softmax to "squish" network
output for classification.
"""
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)
"""
We construct a CNN with 2 convolution layers
and use max-pooling between each convolution layer;
we finish with two dense layers for classification.
"""
cnn_model = Sequential()
cnn_model.add(Conv2D(filters=32,
kernel_size=(3,3),
activation='relu',
input_shape=input_shape))
cnn_model.add(MaxPooling2D(pool_size=(2, 2)))
cnn_model.add(Conv2D(filters=32,
kernel_size=(3, 3),
activation='relu'))
cnn_model.add(MaxPooling2D(pool_size=(2, 2)))
cnn_model.add(Flatten())
cnn_model.add(Dense(64, activation='relu'))
cnn_model.add(Dense(10, activation='softmax')) # softmax for classification
cnn_model.compile(loss='categorical_crossentropy',
optimizer='adagrad', # adaptive optimizer (still similar to SGD)
metrics=['accuracy'])
"""Train the CNN model and evaluate test accuracy."""
cnn_model.fit(x_train,
y_train,
batch_size=128,
epochs=10,
verbose=1,
validation_data=(x_test, y_test)) # never actually validate using test data!
score = cnn_model.evaluate(x_test, y_test, verbose=0)
print('MNIST test set accuracy:', score[1])
"""Visualize some test data and network output."""
y_predict = cnn_model.predict(x_test, verbose=0)
y_predict_digits = [np.argmax(y_predict[i]) for i in range(y_predict.shape[0])]
plt.subplot(1,4,1)
plt.imshow(x_test[0,:,:,0], cmap=plt.get_cmap('gray'))
plt.subplot(1,4,2)
plt.imshow(x_test[1,:,:,0], cmap=plt.get_cmap('gray'))
plt.subplot(1,4,3)
plt.imshow(x_test[2,:,:,0], cmap=plt.get_cmap('gray'))
plt.subplot(1,4,4)
plt.imshow(x_test[3,:,:,0], cmap=plt.get_cmap('gray'))
plt.show()
print("CNN predictions: {0}, {1}, {2}, {3}".format(y_predict_digits[0],
y_predict_digits[1],
y_predict_digits[2],
y_predict_digits[3]))
```
| github_jupyter |
# data acquisition / processing homework 2
> I pledge my Honor that I have abided by the Stevens Honor System. - Joshua Schmidt 2/27/21
## Problem 1
a. For a stationary AR(1) time series x(t), x(t) is uncorrelated to x(t-l) for l>=2.
This is false. For AR(1), $x(t) = a_0 + a_1 \cdot x(t - 1) + \epsilon_t$. In this expression, $x(t)$ is correlated to $x(t - 1)$, with a value of $a_1$. $x(t - 1)$ can be expanded to $a_0 + a_1 \cdot x(t - 2) + \epsilon_{t - 1}$, with a correlation of $a_1^2$. Subsequent members or the series can be expanded, for any value of l. Therefore, for all values of l>=2, $x(t)$ is correlated to $x(t-l)$.
b. For a stationary MA(1) time series x(t), you will observe a coefficient cliff after time lag l>=1 in the ACF plot.
This is true. In the ACF plot, there is decrease in the coefficients when lagging the time by 1>=1 in the plot. This is because noise is uncorrelated, and contains no information. ACF(K) = 0.
## Problem 2
Find the best predictive model for each of the time series, using the techniques in the lecture.
```
# imports
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
q2_data = pd.read_csv('./q2.csv', header=None)
print('question 2 samples:')
q2_data.head()
q2_plot = sns.lineplot(data=q2_data)
q2_plot.set_title('q2 data')
q2_plot.set(xlabel='count', ylabel='value')
plt.show()
# graph looks stationary, not much variance
plot_acf(q2_data, title='q2 acf')
plt.show()
plot_pacf(q2_data, title='q2 pacf', zero=False)
plt.show()
```
Looking at these plots, the acf quickly converges towards 0 (like a cliff), but the pacf takes a lag of 9 before finally converging towards 0 (it is gradual). Therefore, the best predictive model of this time series is most likely an MA model, maybe moving average of 2.
```
q2_model = ARIMA(q2_data, order=(0, 0, 4))
q2_model_fit = q2_model.fit()
q2_model_fit.summary()
q2_residuals = pd.DataFrame(q2_model_fit.resid)
plot_acf(q2_residuals, title='q2 residuals acf')
plt.show()
plot_pacf(q2_residuals, title='q2 residuals pacf', zero=False)
plt.show()
q3_data = pd.read_csv('./q3.csv', header=None)
print('question 3 samples:')
q3_data.head()
q3_plot = sns.lineplot(data=q3_data)
q3_plot.set_title('q3 data')
q3_plot.set(xlabel='count', ylabel='value')
plt.show()
# graph does not look stationary
plot_acf(q3_data, title='q3 acf')
plt.show()
plot_pacf(q3_data, title='q3 pacf', zero=False)
plt.show()
```
Looking at these plots, the acf does not converge to 0, but instead slowly decreases in value while the pacf quickly converges towards 0 (like a cliff). This suggests that there are correlation values, and it is not a statistical fluke.
```
q3_model = ARIMA(q3_data, order=(3, 1, 2))
q3_model_fit = q3_model.fit()
q3_model_fit.summary()
q3_residuals = pd.DataFrame(q3_model_fit.resid)
plot_acf(q3_residuals, title='q3 residuals acf')
plt.show()
plot_pacf(q3_residuals, title='q3 residuals pacf', zero=False)
plt.show()
```
| github_jupyter |
## Initiate the vissim instance
```
# COM-Server
import win32com.client as com
import igraph
import qgrid
from VISSIM_helpers import VissimRoadNet
from os.path import abspath, join, exists
import os
from shutil import copyfile
import pandas as pd
import math
from pythoncom import com_error
```
Add autocompletion for VISSIM COM Object
```
from IPython.utils.generics import complete_object
@complete_object.register(com.DispatchBaseClass)
def complete_dispatch_base_class(obj, prev_completions):
try:
ole_props = set(obj._prop_map_get_).union(set(obj._prop_map_put_))
return list(ole_props) + prev_completions
except AttributeError:
pass
```
Start Vissim and load constants
```
Vissim = com.gencache.EnsureDispatch("Vissim.Vissim")
from win32com.client import constants as c
```
Setting the parameters used for simulation
```
DTA_Parameters = dict(
# DTA Parameters
EvalInt = 600, # seconds
ScaleTotVol = False,
ScaleTotVolPerc = 1,
CostFile = 'costs.bew',
ChkEdgOnReadingCostFile = True,
PathFile = 'paths.weg',
ChkEdgOnReadingPathFile = True,
CreateArchiveFiles = True,
VehClasses = '',
)
# Simulation parameters
Sim_Parameters = dict(
NumRuns = 1,
RandSeedIncr = 0,
UseMaxSimSpeed = True,
SimBreakAt = 600,
NumCores = 8,
)
FileName = abspath(r"..\SO sim files\Vol100per.inpx")
WorkingFolder = abspath(r"..\SO sim files")
def current_period():
return int(math.ceil(Vissim.Simulation.SimulationSecond / DTA_Parameters['EvalInt']))
```
Resetting edge and path cost files
```
default_cost_file = abspath('..\SO sim files\costs_020.bew')
defualt_path_file = abspath('..\SO sim files\paths_020.weg')
current_cost_file = abspath(join(WorkingFolder, DTA_Parameters['CostFile']))
if exists(current_cost_file):
os.remove(current_cost_file)
copyfile(default_cost_file, current_cost_file)
current_path_file = abspath(join(WorkingFolder, DTA_Parameters['PathFile']))
if exists(current_path_file):
os.remove(current_path_file)
copyfile(defualt_path_file, current_path_file)
```
Load the test network
```
Vissim.LoadNet(FileName)
```
Read dynamic assignment network
```
vis_net = Vissim.Net
vis_net.Paths.ReadDynAssignPathFile()
network_graph = VissimRoadNet(vis_net)
```
Check if dynamic assignment graph has changed
```
ref_edge_list = pd.read_pickle("edges_attr.pkl.gz")
assert (network_graph.visedges['ToNode'] == ref_edge_list['ToNode']).all()
network_graph.save(join(WorkingFolder, "network_graph.pkl.gz"), format="picklez")
```
We start by opening the network to be tested and adjust its settings
```
DynamicAssignment = Vissim.Net.DynamicAssignment
for attname, attvalue in DTA_Parameters.items():
DynamicAssignment.SetAttValue(attname, attvalue)
Simulation = Vissim.Net.Simulation
for attname, attvalue in Sim_Parameters.items():
Simulation.SetAttValue(attname, attvalue)
```
Run first DTA period as usual
```
Vissim.Graphics.CurrentNetworkWindow.SetAttValue("QuickMode", 1)
Simulation.RunSingleStep()
while current_period() < 2:
network_graph.update_volume(vis_net)
Simulation.RunSingleStep()
```
Run simulation with custom route assignment
```
bad_paths = []
while True:
network_graph.update_weights(vis_net)
new_vehs = vis_net.Vehicles.GetDeparted()
for veh in new_vehs:
origin_lot = int(veh.AttValue('OrigParkLot'))
destination_lot = int(veh.AttValue('DestParkLot'))
node_paths, edge_paths = network_graph.parking_lot_routes(origin_lot, destination_lot)
try:
vis_path = vis_net.Paths.AddPath(origin_lot, destination_lot, [str(node) for node in node_paths[0]])
veh.AssignPath(vis_path)
except com_error:
bad_paths.append((node_paths[0], edge_paths[0]))
network_graph.update_volume(vis_net)
if Vissim.Simulation.SimulationSecond > 4499:
break
Vissim.Simulation.RunSingleStep()
Vissim.Simulation.RunContinuous()
vis_net.Paths.AddPath(origin_lot, destination_lot, [str(node) for node in node_paths[0]])
veh.AttValue('No')
from pythoncom import com_error
node_paths[0]
edge_weights = network_graph.es[[ed - 1 for ed in edge_paths[0]]]['weight']
print(sum(edge_weights))
pd.DataFrame(list(zip(edge_paths[0], edge_weights)), columns=['edge', 'edge_weights'])
edges = [int(ed) for ed in veh.Path.AttValue('EdgeSeq').split(',')]
edge_weights = network_graph.es[[ed - 1 for ed in edges]]['weight']
print(sum(edge_weights))
pd.DataFrame(list(zip(edges, edge_weights)), columns=['edge', 'edge_weights'])
Vissim.Simulation.RunContinuous()
Vissim.Exit()
```
| github_jupyter |
## Some more on ```spaCy``` and ```pandas```
First we want to import some of the packages we need.
```
import os
import spacy
# Remember we need to initialise spaCy
nlp = spacy.load("en_core_web_sm")
```
We can inspect this object and see that it's what we've been called a ```spaCy``` object.
```
type(nlp)
```
We use this ```spaCy``` object to create annotated outputs, what we call a ```Doc``` object.
```
example = "This is a sentence written in English"
doc = nlp(example)
type(doc)
```
```Doc``` objects are sequences of tokens, meaning we can iterate over the tokens and output specific annotations that we want such as POS tag or lemma.
```
for token in doc:
print(token.text, token.pos_, token.tag_, token.lemma_)
```
__Reading data with ```pandas```__
```pandas``` is the main library in Python for working with DataFrames. These are tabular objects of mixed data types, comprising rows and columns.
In ```pandas``` vocabulary, a column is called a ```Series```, which is like a sophisticated list. I'll be using the names ```Series``` and column pretty interchangably.
```
import pandas as pd
in_file = os.path.join("..", "data", "labelled_data", "fake_or_real_news.csv")
data = pd.read_csv(in_file)
```
We can use ```.sample()``` to take random samples of the dataframe.
```
data.sample(5)
```
To delete unwanted columns, we can do the following:
```
del data["Unnamed: 0"]
type(data["label"])
```
We can count the distribution of possible values in our data using ```.value_counts()``` - e.g. how many REAL and FAKE news entries do we have in our DataFrame?
```
data["label"].value_counts()
```
__Filter on columns__
To filter on columns, we define a condition on which we want to filter and use that to filer our DataFrame. We use the square-bracket syntax, just as if we were slicing a list or string.
```
data["label"]=="FAKE"
data["label"]=="REAL"
```
Here we create two new dataframes, one with only fake news text, and one with only real news text.
```
fake_news_df = data[data["label"]=="FAKE"]
real_news_df = data[data["label"]=="REAL"]
fake_news_df["label"].value_counts()
real_news_df["label"].value_counts()
```
__Counters__
In the following cell, you can see how to use a 'counter' to count how many entries are in a list.
The += operator adds 1 to the variable ```counter``` for every entry in the list.
```
counter = 0
test_list = range(0,100)
for entry in test_list:
counter += 1
```
__Counting features in data__
Using the same logic, we can count how often adjectives (```JJ```) appear in our data.
This is useful from a lingustic perspective; we could now, for example, figure out how many of each part of speech can be found in our data.
```
# create counters
adj_count = 0
# process texts in batch
for doc in nlp.pipe(fake_news_df["title"], batch_size=500):
for token in doc:
if token.tag_ == "JJ":
adj_count += 1
```
In this case, we're using ```nlp.pipe``` from ```spaCy``` to group the entries together into batches of 500 at a time.
Why?
Everytime we execute ```nlp(text)``` it incurs a small computational overhead which means that scaling becomes an issue. An overhead of 0.01s per document becomes an issue when dealing with 1,000,000 or 10,000,000 or 100,000,000...
If we batch, we can therefore be a bit more efficient. It also allows us to keep our ```spaCy``` logic compact and together, which becomes useful for more complex tasks.
```
print(adj_count)
```
## Sentiment with ```spaCy```
To work with spaCyTextBlob, we need to make sure that we are working with ```spacy==2.3.5```.
Follow the separate instructions posted to Slack to make this work.
```
import os
import pandas as pd
import matplotlib.pyplot as plt
import spacy
from spacytextblob.spacytextblob import SpacyTextBlob
# initialise spacy
nlp = spacy.load("en_core_web_sm")
```
Here, we initialise spaCyTextBlob and add it as a new component to our ```spaCy``` nlp pipeline.
```
spacy_text_blob = SpacyTextBlob()
nlp.add_pipe(spacy_text_blob)
```
Let's test spaCyTextBlob on a single text, specifically Virgian Woolf's _To The Lighthouse_, published in 1927.
```
text_file = os.path.join("..", "data", "100_english_novels", "corpus", "Woolf_Lighthouse_1927.txt")
with open(text_file, "r", encoding="utf-8") as file:
text = file.read()
print(text[:1000])
```
We use ```spaCy``` to create a ```Doc``` object for the entire text (how might you do this in batch?)
```
doc = nlp(text)
```
We can extract the polarity for each sentence in the novel and create list of scores per sentence.
```
polarity = []
for sentence in doc.sents:
score = sentence._.sentiment.polarity
polarity.append(score)
polarity[:10]
```
We can create a quick and cheap plot using matplotlib - this is only fine in Jupyter Notebooks, don't do this in the wild!
```
plt.plot(polarity)
```
We can the use some fancy methods from ```pandas``` to calculate a rolling mean over a certain window length.
For example, we group together our polarity scores into a window of 100 sentences at a time and calculate an average on that window.
```
smoothed_sentiment = pd.Series(polarity).rolling(100).mean()
```
This plot with a rolling average shows us a 'smoothed' output showing the rolling average over time, helping to cut through the noise.
```
plt.plot(smoothed_sentiment)
```
| github_jupyter |
# #05 - Exploring Utils
Falar sobre para se trabalhar com trajetórias pode ser necessária algumas c onversões envolvendo tempo e data, distância e etc, fora outros utilitários.
Falar dos módulos presentes no pacote utils
- constants
- conversions
- datetime
- distances
- math
- mem
- trajectories
- transformations
---
### Imports
```
import pymove.utils as utils
import pymove
from pymove import MoveDataFrame
```
---
### Load data
```
move_data = pymove.read_csv("geolife_sample.csv")
```
---
### Conversions
To transform latitude degree to meters, you can use function **lat_meters**. For example, you can convert Fortaleza's latitude -3.8162973555:
```
utils.conversions.lat_meters(-3.8162973555)
```
To concatenates list elements, joining them by the separator specified by the parameter "delimiter", you can use **list_to_str**
```
utils.conversions.list_to_str(["a", "b", "c", "d"], "-")
```
To concatenates the elements of the list, joining them by ",", , you can use **list_to_csv_str**
```
utils.conversions.list_to_csv_str(["a", "b", "c", "d"])
```
To concatenates list elements in consecutive element pairs, you can use **list_to_svm_line**
```
utils.conversions.list_to_svm_line(["a", "b", "c", "d"])
```
To convert longitude to X EPSG:3857 WGS 84/Pseudo-Mercator, you can use **lon_to_x_spherical**
```
utils.conversions.lon_to_x_spherical(-38.501597)
```
To convert latitude to Y EPSG:3857 WGS 84/Pseudo-Mercator, you can use **lat_to_y_spherical**
```
utils.conversions.lat_to_y_spherical(-3.797864)
```
To convert X EPSG:3857 WGS 84/Pseudo-Mercator to longitude, you can use **x_to_lon_spherical**
```
utils.conversions.x_to_lon_spherical(-4285978.172767829)
```
To convert Y EPSG:3857 WGS 84/Pseudo-Mercator to latitude, you can use **y_to_lat_spherical**
```
utils.conversions.y_to_lat_spherical(-423086.2213610324)
```
To convert values, in ms, in label_speed column to kmh, you can use **ms_to_kmh**
```
utils.conversions.ms_to_kmh(move_data)
```
To convert values, in kmh, in label_speed column to ms, you can use **kmh_to_ms**
```
utils.conversions.kmh_to_ms(move_data)
```
To convert values, in meters, in label_distance column to kilometer, you can use **meters_to_kilometers**
```
utils.conversions.meters_to_kilometers(move_data)
```
To convert values, in kilometers, in label_distance column to meters, you can use **kilometers_to_meters**
```
utils.conversions.kilometers_to_meters(move_data)
```
To convert values, in seconds, in label_distance column to minutes, you can use **seconds_to_minutes**
```
utils.conversions.seconds_to_minutes(move_data)
```
To convert values, in minutes, in label_distance column to seconds, you can use **minute_to_seconds**
```
utils.conversions.minute_to_seconds(move_data)
```
To convert in minutes, in label_distance column to hours, you can use **minute_to_hours**
```
utils.conversions.minute_to_hours(move_data)
```
To convert in hours, in label_distance column to minute, you can use **hours_to_minute**
```
utils.conversions.hours_to_minute(move_data)
```
To convert in seconds, in label_distance column to hours, you can use **seconds_to_hours**
```
utils.conversions.seconds_to_hours(move_data)
```
To convert in seconds, in label_distance column to hours, you can use **hours_to_seconds**
```
utils.conversions.hours_to_seconds(move_data)
```
---
## Datetime
To converts a datetime in string"s format "%Y-%m-%d" or "%Y-%m-%d %H:%M:%S" to datetime"s format, you can use **str_to_datetime**.
```
utils.datetime.str_to_datetime('2018-06-29 08:15:27')
```
To get date, in string's format, from timestamp, you can use **date_to_str**.
```
utils.datetime.date_to_str(utils.datetime.str_to_datetime('2018-06-29 08:15:27'))
```
To converts a date in datetime's format to string's format, you can use **to_str**.
```
import datetime
utils.datetime.to_str(datetime.datetime(2018, 6, 29, 8, 15, 27))
```
To converts a datetime to an int representation in minutes, you can use **to_min**.
```
utils.datetime.to_min(datetime.datetime(2018, 6, 29, 8, 15, 27))
```
To do the reverse use: **min_to_datetime**
```
utils.datetime.min_to_datetime(25504335)
```
To get day of week of a date, you can use **to_day_of_week_int**, where 0 represents Monday and 6 is Sunday.
```
utils.datetime.to_day_of_week_int(datetime.datetime(2018, 6, 29, 8, 15, 27))
```
To indices if a day specified by the user is a working day, you can use **working_day**.
```
utils.datetime.working_day(datetime.datetime(2018, 6, 29, 8, 15, 27), country='BR')
utils.datetime.working_day(datetime.datetime(2018, 4, 21, 8, 15, 27), country='BR')
```
To get datetime of now, you can use **now_str**.
```
utils.datetime.now_str()
```
To convert time in a format appropriate of time, you can use **deltatime_str**.
```
utils.datetime.deltatime_str(1082.7180936336517)
```
To converts a local datetime to a POSIX timestamp in milliseconds, you can use **timestamp_to_millis**.
```
utils.datetime.timestamp_to_millis("2015-12-12 08:00:00.123000")
```
To converts milliseconds to timestamp, you can use **millis_to_timestamp**.
```
utils.datetime.millis_to_timestamp(1449907200123)
```
To get time, in string's format, from timestamp, you can use **time_to_str**.
```
utils.datetime.time_to_str(datetime.datetime(2018, 6, 29, 8, 15, 27))
```
To converts a time in string's format "%H:%M:%S" to datetime's format, you can use **str_to_time**.
```
utils.datetime.str_to_time("08:00:00")
```
To computes the elapsed time from a specific start time to the moment the function is called, you can use **elapsed_time_dt**.
```
utils.datetime.elapsed_time_dt(utils.datetime.str_to_time("08:00:00"))
```
To computes the elapsed time from the start time to the end time specifed by the user, you can use **diff_time**.
```
utils.datetime.diff_time(utils.datetime.str_to_time("08:00:00"), utils.datetime.str_to_time("12:00:00"))
```
---
## Distances
To calculate the great circle distance between two points on the earth, you can use **haversine**.
```
utils.distances.haversine(-3.797864,-38.501597,-3.797890, -38.501681)
```
---
<!-- Ver com a arina se é válido fazer a doc dessas 2 -->
<!-- ## Trajectories -->
<!-- ## Transformations -->
## Math
To compute standard deviation, you can use **std**.
```
utils.math.std(600, 20, 5)
```
To compute the average of standard deviation, you can use **avg_std**.
```
# utils.math.avg_std(600, 600, 20)
```
To compute the standard deviation of sample, you can use **std_sample**.
```
utils.math.std_sample(600, 20, 5)
```
To compute the average of standard deviation of sample, you can use **avg_std_sample**.
```
# utils.math.avg_std_sample(600, 20, 5)
```
To computes the sum of the elements of the array, you can use **array_sum**.
```
utils.math.array_sum([600, 20, 5])
```
To computes the sum of all the elements in the array, the sum of the square of each element and the number of elements of the array, you can use **array_stats**.
```
utils.math.array_stats([600, 20, 5])
```
To perfomers interpolation and extrapolation, you can use **interpolation**.
```
utils.math.interpolation(15, 20, 65, 86, 5)
```
| github_jupyter |
# Initial Modelling notebook
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
import bay12_solution_eposts as solution
```
## Load data
```
post, thread = solution.prepare.load_dfs('train')
post.head(2)
thread.head(2)
```
I will set the thread number to be the index, to simplify matching in the future:
```
thread = thread.set_index('thread_num')
thread.head(2)
```
We'll load the label map as well, which tells us which index goes to which label
```
label_map = solution.prepare.load_label_map()
label_map
```
## Create features from thread dataframe
We will fit a CountVectorizer, which is a simple transformation that counts the number of times the word was found.
The parameter `min_df` sets the minimum number of occurances in our set that will allow a word to join our vocabulary.
```
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer(ngram_range=(1, 1), min_df=3)
word_vectors_raw = cv.fit_transform(thread['thread_name'])
```
To save space, this outputs a sparse matrix:
```
word_vectors_raw
```
However, since we'll be using it with a DataFrame, we need to convert it into a Pandas DataFrame:
```
word_df = pd.DataFrame(word_vectors_raw.toarray(), columns=cv.get_feature_names(), index=thread.index)
word_df.head()
```
The only other feature we have from our thread data is the number of replies. Let's add one to get the number of replies. Also, let's use the logarithm of post count as well, just for fun.
We'll concatenate those into our X dataframe (Note that I'm renaming the columns, to keep track more easily):
```
X = pd.concat([
(thread['thread_replies'] + 1).rename('posts'),
np.log(thread['thread_replies'] + 1).rename('log_posts'),
word_df,
], axis='columns')
X.head()
```
Our target is the category number. Remember that this isn't a regression task - there is no actual order between these categories! Also, our Y is one-dimensional, so we'll keep it as a Series (even though it prints less prettily).
```
y = thread['thread_label_id']
y.head()
```
## Split dataset into "training" and "validation"
In order to check the quality of our model in a more realistic setting, we will split all our input (training) data into a "training set" (which our model will see and learn from) and a "validation set" (where we see how well our model generalized). [Relevant link](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html).
```
from sklearn.model_selection import train_test_split
# NOTE: setting the `random_state` lets you get the same results with the pseudo-random generator
validation_pct = 0.25
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=validation_pct, random_state=99)
X_train.shape, y_train.shape
X_val.shape, y_val.shape
```
## Fit a model
Since we are fitting a multiclass model, [this scikit-learn link](https://scikit-learn.org/stable/modules/multiclass.html) is very relevant. To simplify things, we will be using an algorithm that is inherently multi-class.
```
from sklearn.tree import DecisionTreeClassifier
# Just using default parameters... what can do wrong?
cls = DecisionTreeClassifier(random_state=1337)
# Fit
cls.fit(X_train, y_train)
# In-sample and out-of-sample predictions
# NOTE: we
y_train_pred = pd.Series(
cls.predict(X_train),
index=X_train.index,
)
y_val_pred = pd.Series(
cls.predict(X_val),
index=X_val.index,
)
y_val_pred.head()
```
## Score the model
To find out how well the model did, we'll use the [model evaluation functionality of sklearn](https://scikit-learn.org/stable/modules/model_evaluation.html); specifically, the [multiclass classification metrics](https://scikit-learn.org/stable/modules/model_evaluation.html#classification-metrics).
```
from sklearn.metrics import confusion_matrix, accuracy_score, classification_report
```
The [confusion matrix](https://en.wikipedia.org/wiki/Confusion_matrix) shows how our predictions differ from the actual values.
It's important to note how strongly our in-sample (training) and out-of-sample (validation/test) metrics differ.
```
def confusion_df(y_actual, y_pred):
res = pd.DataFrame(
confusion_matrix(y_actual, y_pred, labels=label_map.values),
index=label_map.index.rename('predicted'),
columns=label_map.index.rename('actual'),
)
return res
confusion_df(y_train, y_train_pred).style.highlight_max()
confusion_df(y_val, y_val_pred).style.highlight_max()
```
Oh boy. That's pretty bad - we didn't predict anything for several columns!
Let's look at the metrics to confirm that it is indeed bad.
```
print("Test accuracy:", accuracy_score(y_train, y_train_pred))
print("Validation accuracy:", accuracy_score(y_val, y_val_pred))
report = classification_report(y_val, y_val_pred, labels=label_map.values, target_names=label_map.index)
print(report)
```
Well, that's pretty bad. We seriously overfit our training set... which is sort-of what I expected. Oh well.
By the way, the warnings at the bottom say that we have no real Precision or F-score to use, with no predictions for some classes.
# Predict with the model
Here, we will predict on the test set (predicitions to send in), then save the results and the model.
**IMPORTANT NOTE**: In reality, you need to re-train your same model on the entire set to predict! However, I'm just using the same model as before, as it will bad anyways. ;)
```
post_test, thread_test = solution.prepare.load_dfs('test')
thread_test = thread_test.set_index('thread_num')
thread_test.head(2)
```
We need to attach a `thread_label_id` column, as given in the training set:
```
thread.head(2)
```
Use the fitted CountVectorizer and other features to make our X dataframe:
```
word_vectors_raw_test = cv.transform(thread_test['thread_name'])
word_df_test = pd.DataFrame(word_vectors_raw_test.toarray(), columns=cv.get_feature_names(), index=thread_test.index)
word_df_test.head()
X_test = pd.concat([
(thread_test['thread_replies'] + 1).rename('posts'),
np.log(thread_test['thread_replies'] + 1).rename('log_posts'),
word_df_test,
], axis='columns')
X_test.head()
```
Now we predict with our model, then paste it to a copy of `thread_test` as column `thread_label_id`.
```
y_test_pred = pd.Series(
cls.predict(X_test),
index=X_test.index,
)
y_test_pred.head()
result = thread_test.copy()
result['thread_label_id'] = y_test_pred
result.head()
```
We need to reshape to conform to the submission format specified [here](https://www.kaggle.com/c/ni-mafia-gametype#evaluation).
```
result = result.reset_index()[['thread_num', 'thread_label_id']]
result.head()
```
# Export predictions, model
Our model consists of the text vectorizer `cv` and classifier `cls`. We already formatted our results, we just need to make sure not to write an extra index column.
```
# NOTE: Exporting next to the notebooks - the files are small, but usually you don't want to do this.
out_dir = os.path.abspath('1_output')
os.makedirs(out_dir, exist_ok=True)
result.to_csv(
os.path.join(out_dir, 'baseline_predict.csv'),
index=False, header=True, encoding='utf-8',
)
import joblib
joblib.dump(cv, os.path.join(out_dir, 'cv.joblib'))
joblib.dump(cls, os.path.join(out_dir, 'cls.joblib'))
print("Done. :)")
```
# Final Remarks
I'd like to mention that the above notebook is here JUST TO GET YOU STARTED. Feel free to change anything or everything above.
It may be a good idea to keep a piece of paper with you, and draw out your entire pipeline there, to keep organized.
This model is severely overfit because of a huge number of features from the names. Some ways to combat this are PCA and lowering dimensionality, increasing regularization, using a more feature-limited classifier, etc. You can also split this into two sub-problems: a classifier to tell whether it is a game or `"other"`, then classify game type if it's a game.
| github_jupyter |
```
import numpy as np
import pandas as pd
import pydicom
import os
import random
import matplotlib.pyplot as plt
from tqdm import tqdm
from PIL import Image
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import KFold
import warnings
warnings.filterwarnings("ignore")
import torch.nn as nn
import torch
from torch.utils.data.dataset import Dataset
from torch.utils.data import DataLoader
def seed_everything(seed=2020):
random.seed(seed)
os.environ["PYTHONHASHSEED"] = str(seed)
np.random.seed(seed)
torch.manual_seed(seed)
if torch.cuda.is_available():
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)#set all gpus seed
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False#if input data type and channels' changes arent' large use it improve train efficient
torch.backends.cudnn.enabled = True
seed_everything(42)
class cfgOsic:
ROOT = "../data/"
device = torch.device('cuda')
tr = pd.read_csv(f"{cfgOsic.ROOT}/train.csv")
tr.drop_duplicates(keep=False, inplace=True, subset=['Patient','Weeks'])
chunk = pd.read_csv(f"{cfgOsic.ROOT}/test.csv")
print("add infos")
sub = pd.read_csv(f"{cfgOsic.ROOT}/sample_submission.csv")
sub['Patient'] = sub['Patient_Week'].apply(lambda x:x.split('_')[0])
sub['Weeks'] = sub['Patient_Week'].apply(lambda x: int(x.split('_')[-1]))
sub = sub[['Patient','Weeks','Confidence','Patient_Week']]
sub = sub.merge(chunk.drop('Weeks', axis=1), on="Patient")
tr['WHERE'] = 'train'
chunk['WHERE'] = 'val'
sub['WHERE'] = 'test'
data = tr.append([chunk, sub])
data['min_week'] = data['Weeks']
data.loc[data.WHERE=='test','min_week'] = np.nan
data['min_week'] = data.groupby('Patient')['min_week'].transform('min')
base = data.loc[data.Weeks == data.min_week]
base = base[['Patient','FVC']].copy()
base.columns = ['Patient','min_FVC']
base['nb'] = 1
base['nb'] = base.groupby('Patient')['nb'].transform('cumsum')
base = base[base.nb==1]
base.drop('nb', axis=1, inplace=True)
data = data.merge(base, on='Patient', how='left')
data['base_week'] = data['Weeks'] - data['min_week']
del base
#aggiunta altezza
def calculate_height(row):
if row['Sex'] == 'Male':
return row['min_FVC'] / (27.63 - 0.112 * row['Age'])
else:
return row['min_FVC'] / (21.78 - 0.101 * row['Age'])
data['Height'] = data.apply(calculate_height, axis=1)
data['WeeksPassed'] = data['Weeks'] - data['min_week']
COLS = ['Sex','SmokingStatus'] #,'Age'
FE = []
for col in COLS:
for mod in data[col].unique():
FE.append(mod)
data[mod] = (data[col] == mod).astype(int)
def scale_feature(series):
return (series - series.min()) / (series.max() - series.min())
data['age'] = scale_feature(data['Age'])
data['BASE'] = scale_feature(data['min_FVC'])
data['week'] = scale_feature(data['base_week'])
data['percent'] = scale_feature(data['Percent'])
data['height'] = scale_feature(data['Height'])
data['week_passed'] = scale_feature(data['WeeksPassed'])
FE += ['age','percent','week','BASE', 'height', 'week_passed']
data
tr = data.loc[data.WHERE=='train']
chunk = data.loc[data.WHERE=='val']
sub = data.loc[data.WHERE=='test']
del data
```
| github_jupyter |
```
# Import Dependencies
import os
import csv
# Establish filepath
budget_csv = os.path.join(".", "resources", "budget_data.csv")
output_file = os.path.join(".", "financial_analysis.txt")
# Index Reference for the Profit and Loss List
# Track Financial Parameters
# Open and read csv file
with open(budget_csv, newline='') as csvfile:
csvreader = csv.reader(csvfile, delimiter=',')
# Captures and removes the header row (list) into csvheader
csvheader = next(csvreader)
# Set up Counter, had to circle back to adjust bc of using next(csvreader) twice
total_months = 0
total_months = total_months + 1
# Setup for change analysis and calculations
financial_data = [867884]
# Calculating the "Average of Changes" and Tracking the Month
netchange_list = []
month_of_change_list = []
# Greatest Increase / Decrease- use list, save spot for Period and Value
# counter intuitive
greatest_increase = ["", 0]
greatest_decrease = ["", 999999]
# Captures and removes the next row into first_row (Python knows to go to the next line / list down in the csvreader)
first_row = next(csvreader) # first whole row is a list month & value
# Isolate the first value of "Profit/Losses"
# Note: the first_row[0] is Jan-10
prev_net = int(first_row[1])
for row in csvreader:
#print(f"{row[0]} , {row[1]}")
# Loop Thru and count the total number of months included in the dataset
total_months += 1
# The net total amount of “Profit/Losses” over the entire period
financial_data.append(int(row[1]))
# Average of the changes in “Profit/Losses” over the entire period
#Part one: "Numberator" Net Change
# Track the net change
# This calculates Month to Month (differences) aka changes
net_change = int(row[1]) - int(prev_net) # @ this point prev_net = first value
# This appends those changes to the list
netchange_list.append(net_change) #- JG initial thought
prev_net = int(row[1])
#netchange_list.append(net_change) # solution. test after
# Track month of change as well
#month_of_change_list = month_of_change_list + [row[0]] # concatenate row[0] to the list
month_of_change_list.append(row[0]) # add the month of change to list
# will not need this for calculations
# Greatest increase and decrease in the dataset caculations
if net_change > greatest_increase[1]:
greatest_increase[1] = net_change
greatest_increase[0] = row[0] #capture the month
if net_change < greatest_decrease[1]:
greatest_decrease[1] = net_change
greatest_decrease[0] = row[0]
net = sum(financial_data)
print(f"Financial Analysis")
print("="*60)
print(f"Total Months: {total_months}")
print(f"Total: ${net}")
print(f"Average Change: {sum(netchange_list)/len(netchange_list)}")
print(f"Greatest Increase in Profits: {greatest_increase[0]} '({greatest_increase[1]})'")
print(f"Greatest Decrease in Profits: {greatest_decrease[0]} '({greatest_decrease[1]})'")
print("="*60)
output = (
f"\nFinancial Analysis\n"
f"----------------------------\n"
f"Total Months: {total_months}\n"
f"Total: ${net}\n"
f"Average Change: {sum(netchange_list)/len(netchange_list)}\n"
f"Greatest Increase in Profits: {greatest_increase[0]} '({greatest_increase[1]})'\n"
f"Greatest Decrease in Profits: {greatest_decrease[0]} '({greatest_decrease[1]})'\n"
)
with open ("financial_analysis.txt", 'w') as txt_file:
txt_file.write(output)
# Test Cells
with open(budget_csv, newline='') as csvfile:
csvreader = csv.reader(csvfile, delimiter=',')
csvheader = next(csvreader)
total_months = 0
financial_data = []
rolling_average = []
first_row = next(csvreader)
print(first_row[1])
# test cells below.
```
| github_jupyter |
```
import numpy as np
import pandas as pd
```
# Pandas Metodları ve Özellikleri
### Veri Analizi için Önemli Konular
#### Eksik Veriler (Missing Value)
```
data = {'Istanbul':[30,29,np.nan],'Ankara':[20,np.nan,25],'Izmir':[40,39,38],'Antalya':[40,np.nan,np.nan]}
weather = pd.DataFrame(data,index=['pzt','sali','car'])
weather
```
Satırında değer olmayan satırları veya sütunları silmek için **dropna** fonksiyonu kullanılır.
```
weather.dropna()
weather.dropna(axis=1)
# sütunda 2 veya daha fazla nan var ise siler.
weather.dropna(axis=1, thresh=2)
```
Boş olan değerleri doldurmak için **fillna** fonksiyonunu kullanırız.
```
weather.fillna(22)
```
#### Gruplama (Group By)
```
data = {'Departman':['Yazılım','Pazarlama','Yazılım','Pazarlama','Hukuk','Hukuk'],
'Calisanlar':['Ahmet','Mehmet','Enes','Burak','Zeynep','Fatma'],
'Maas':[150,100,200,300,400,500]}
workers = pd.DataFrame(data)
workers
groupbyobje = workers.groupby('Departman')
groupbyobje.count()
groupbyobje.mean()
groupbyobje.min()
groupbyobje.max()
groupbyobje.describe()
```
#### Concatenation
```
data1 = {'Isim':['Ahmet','Mehmet','Zeynep','Enes'],
'Spor':['Koşu','Yüzme','Koşu','Basketbol'],
'Kalori':[100,200,300,400]}
data2 = {'Isim':['Osman','Levent','Atlas','Fatma'],
'Spor':['Koşu','Yüzme','Koşu','Basketbol'],
'Kalori':[200,200,30,400]}
data3 = {'Isim':['Ayse','Mahmut','Duygu','Nur'],
'Spor':['Koşu','Yüzme','Badminton','Tenis'],
'Kalori':[150,200,350,400]}
df1 = pd.DataFrame(data1)
df2 = pd.DataFrame(data2)
df3 = pd.DataFrame(data3)
pd.concat([df1,df2,df3], ignore_index=True, axis=0)
```
#### Merging
```
mdata1 = {'Isim':['Ahmet','Mehmet','Zeynep','Enes'],
'Spor':['Koşu','Yüzme','Koşu','Basketbol']}
mdata2 = {'Isim':['Ahmet','Mehmet','Zeynep','Enes'],
'Kalori':[100,200,300,400]}
mdf1 = pd.DataFrame(mdata1)
mdf1
mdf2 = pd.DataFrame(mdata2)
mdf2
pd.merge(mdf1,mdf2,on='Isim')
```
### Önemli Metodlar ve Özellikleri
```
data = {'Departman' : ['Yazılım','Pazarlama','Yazılım','Pazarlama','Hukuk','Hukuk'],
'Isim' : ['Ahmet','Mehmet','Enes','Burak','Zeynep','Fatma'],
'Maas' : [150,100,200,300,400,500]}
workerdf = pd.DataFrame(data)
workerdf
```
#### Unique Değerleri Listeleme ve Sayısını Bulma
```
workerdf['Departman'].unique()
workerdf['Departman'].nunique()
```
#### Sütundaki Değerlerden Toplamda Kaçar Adet Var?
```
workerdf['Departman'].value_counts()
```
#### Değerler Üzerinde Fonksiyon Yardımı ile İşlemler Yapmak
```
workerdf['Maas'].apply(lambda maas : maas*0.66)
```
#### Dataframe'de Null Değer Var mı?
```
workerdf.isnull()
```
#### Pivot Table
```
characters = {'Karakter Sınıfı':['South Park','South Park','Simpson','Simpson','Simpson'],
'Karakter Ismi':['Cartman','Kenny','Homer','Bart','Bart'],
'Puan':[9,10,50,20,10]}
dfcharacters = pd.DataFrame(characters)
dfcharacters
dfcharacters.pivot_table(values='Puan',index=['Karakter Sınıfı','Karakter Ismi'],aggfunc=np.sum)
```
#### Belli Bir Sütuna Göre Değerleri Sıralama (Sorting)
```
workerdf.sort_values(by='Maas', ascending=False)
```
#### Duplicate Veriler
```
employees = [('Stuti', 28, 'Varanasi'),
('Saumya', 32, 'Delhi'),
('Aaditya', 25, 'Mumbai'),
('Saumya', 32, 'Delhi'),
('Saumya', 32, 'Delhi'),
('Saumya', 32, 'Mumbai'),
('Aaditya', 40, 'Dehradun'),
('Seema', 32, 'Delhi')]
df = pd.DataFrame(employees, columns = ['Name', 'Age', 'City'])
duplicate = df[df.duplicated()]
print("Duplicate Rows :")
duplicate
duplicate = df[df.duplicated('City')]
print("Duplicate Rows based on City :")
duplicate
df.drop_duplicates()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/keivanipchihagh/Intro_To_MachineLearning/blob/master/Models/Newswires_Classification_with_Reuters.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Newswires Classification with Reuters
##### Imports
```
import numpy as np # Numpy
from matplotlib import pyplot as plt # Matplotlib
import keras # Keras
import pandas as pd # Pandas
from keras.datasets import reuters # Reuters Dataset
from keras.utils.np_utils import to_categorical # Categirical Classifier
import random # Random
```
##### Load dataset
```
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words = 10000)
print('Size:', len(train_data))
print('Training Data:', train_data[0])
```
##### Get the feel of data
```
def decode(index): # Decoding the sequential integers into the corresponding words
word_index = reuters.get_word_index()
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
decoded_newswire = ' '.join([reverse_word_index.get(i - 3, '?') for i in test_data[0]])
return decoded_newswire
print("Decoded test data sample [0]: ", decode(0))
```
##### Data Prep (One-Hot Encoding)
```
def vectorize_sequences(sequences, dimension = 10000): # Encoding the integer sequences into a binary matrix
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1.
return results
train_data = vectorize_sequences(train_data)
test_data = vectorize_sequences(test_data)
train_labels = to_categorical(train_labels)
test_labels = to_categorical(test_labels)
```
##### Building the model
```
model = keras.models.Sequential()
model.add(keras.layers.Dense(units = 64, activation = 'relu', input_shape = (10000,)))
model.add(keras.layers.Dense(units = 64, activation = 'relu'))
model.add(keras.layers.Dense(units = 46, activation = 'softmax'))
model.compile( optimizer = 'rmsprop', loss = 'categorical_crossentropy', metrics = ['accuracy'])
model.summary()
```
##### Training the model
```
x_val = train_data[:1000]
train_data = train_data[1000:]
y_val = train_labels[:1000]
train_labels = train_labels[1000:]
history = model.fit(train_data, train_labels, batch_size = 512, epochs = 10, validation_data = (x_val, y_val), verbose = False)
```
##### Evaluating the model
```
result = model.evaluate(train_data, train_labels)
print('Loss:', result[0])
print('Accuracy:', result[1] * 100)
```
##### Statistics
```
epochs = range(1, len(history.history['loss']) + 1)
plt.plot(epochs, history.history['loss'], 'b', label = 'Training Loss')
plt.plot(epochs, history.history['val_loss'], 'r', label = 'Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf()
plt.plot(epochs, history.history['accuracy'], 'b', label = 'Training Accuracy')
plt.plot(epochs, history.history['val_accuracy'], 'r', label = 'Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
```
##### Making predictions
```
prediction_index = random.randint(0, len(test_data))
prediction_data = test_data[prediction_index]
decoded_prediction_data = decode(prediction_index)
# Info
print('Random prediction index:', prediction_index)
print('Original prediction Data:', prediction_data)
print('Decoded prediction Data:', decoded_prediction_data)
print('Expected prediction label:', np.argmax(test_labels[prediction_index]))
# Prediction
predictions = model.predict(test_data)
print('Prediction index: ', np.argmax(predictions[prediction_index]))
```
| github_jupyter |
# Interpreting text models: IMDB sentiment analysis
This notebook loads pretrained CNN model for sentiment analysis on IMDB dataset. It makes predictions on test samples and interprets those predictions using integrated gradients method.
The model was trained using an open source sentiment analysis tutorials described in: https://github.com/bentrevett/pytorch-sentiment-analysis/blob/master/4%20-%20Convolutional%20Sentiment%20Analysis.ipynb
**Note:** Before running this tutorial, please install:
- spacy package, and its NLP modules for English language (https://spacy.io/usage)
- sentencpiece (https://pypi.org/project/sentencepiece/)
```
import spacy
import torch
import torchtext
import torchtext.data
import torch.nn as nn
import torch.nn.functional as F
from torchtext.vocab import Vocab
from captum.attr import LayerIntegratedGradients, TokenReferenceBase, visualization
nlp = spacy.load('en')
device = torch.device("cuda:5" if torch.cuda.is_available() else "cpu")
```
The dataset used for training this model can be found in: https://ai.stanford.edu/~amaas/data/sentiment/
Redefining the model in order to be able to load it.
```
class CNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, n_filters, filter_sizes, output_dim,
dropout, pad_idx):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim, padding_idx = pad_idx)
self.convs = nn.ModuleList([
nn.Conv2d(in_channels = 1,
out_channels = n_filters,
kernel_size = (fs, embedding_dim))
for fs in filter_sizes
])
self.fc = nn.Linear(len(filter_sizes) * n_filters, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, text):
#text = [sent len, batch size]
#text = text.permute(1, 0)
#text = [batch size, sent len]
embedded = self.embedding(text)
#embedded = [batch size, sent len, emb dim]
embedded = embedded.unsqueeze(1)
#embedded = [batch size, 1, sent len, emb dim]
conved = [F.relu(conv(embedded)).squeeze(3) for conv in self.convs]
#conved_n = [batch size, n_filters, sent len - filter_sizes[n] + 1]
pooled = [F.max_pool1d(conv, conv.shape[2]).squeeze(2) for conv in conved]
#pooled_n = [batch size, n_filters]
cat = self.dropout(torch.cat(pooled, dim = 1))
#cat = [batch size, n_filters * len(filter_sizes)]
return self.fc(cat)
```
Loads pretrained model and sets the model to eval mode. The model is already in the provided in the 'models' folder.
Download source: https://github.com/pytorch/captum/blob/master/tutorials/models/imdb-model-cnn.pt
```
model = torch.load('models/imdb-model-cnn.pt')
model.eval()
model = model.to(device)
```
Load a small subset of test data using torchtext from IMDB dataset.
```
TEXT = torchtext.data.Field(lower=True, tokenize='spacy')
Label = torchtext.data.LabelField(dtype = torch.float)
```
Download IMDB file 'aclImdb_v1.tar.gz' from https://ai.stanford.edu/~amaas/data/sentiment/ in a 'data' subfolder where this notebook is saved.
Then unpack file using 'tar -xzf aclImdb_v1.tar.gz'
```
train, test = torchtext.datasets.IMDB.splits(text_field=TEXT,
label_field=Label,
train='train',
test='test',
path='data/aclImdb')
test, _ = test.split(split_ratio = 0.04)
len(test.examples)
# expected result: 1000
```
Loading and setting up vocabulary for word embeddings using torchtext.
```
from torchtext import vocab
loaded_vectors = vocab.GloVe(name='6B', dim=50)
# If you prefer to use pre-downloaded glove vectors, you can load them with the following two command line
# loaded_vectors = torchtext.vocab.Vectors('data/glove.6B.50d.txt')
# source for downloading: https://github.com/uclnlp/inferbeddings/tree/master/data/glove
TEXT.build_vocab(train, vectors=loaded_vectors, max_size=len(loaded_vectors.stoi))
TEXT.vocab.set_vectors(stoi=loaded_vectors.stoi, vectors=loaded_vectors.vectors, dim=loaded_vectors.dim)
Label.build_vocab(train)
print('Vocabulary Size: ', len(TEXT.vocab))
# expected result: 101982
```
Define the padding token. The padding token will also serve as the reference/baseline token used for the application of the Integrated Gradients. The padding token is used for this since it is one of the most commonly used references for tokens.
This is then used with the Captum helper class `TokenReferenceBase` further down to generate a reference for each input text using the number of tokens in the text and a reference token index.
```
PAD = 'pad'
PAD_INDEX = TEXT.vocab.stoi[PAD]
print(PAD, PAD_INDEX)
```
Let's create an instance of `LayerIntegratedGradients` using forward function of our model and the embedding layer.
This instance of layer integrated gradients will be used to interpret movie rating review.
Layer Integrated Gradients will allow us to assign an attribution score to each word/token embedding tensor in the movie review text. We will ultimately sum the attribution scores across all embedding dimensions for each word/token in order to attain a word/token level attribution score.
Note that we can also use `IntegratedGradients` class instead, however in that case we need to precompute the embeddings and wrap Embedding layer with `InterpretableEmbeddingBase` module. This is necessary because we cannot perform input scaling and subtraction on the level of word/token indices and need access to the embedding layer.
```
lig = LayerIntegratedGradients(model, model.embedding)
```
In the cell below, we define a generic function that generates attributions for each movie rating and stores them in a list using `VisualizationDataRecord` class. This will ultimately be used for visualization purposes.
```
def interpret_sentence(model, sentence, min_len = 7, label = 0):
# create input tensor from sentence
text_list = sentence_to_wordlist(sentence, min_len)
text_tensor, reference_tensor = wordlist_to_tensors(text_list)
# apply model forward function with sigmoid
model.zero_grad()
pred = torch.sigmoid(model(text_tensor)).item()
pred_ind = round(pred)
# compute attributions and approximation delta using layer integrated gradients
attributions, delta = lig.attribute(text_tensor, reference_tensor, \
n_steps=500, return_convergence_delta = True)
print('pred: ', Label.vocab.itos[pred_ind], '(', '%.2f'%pred, ')', ', delta: ', abs(delta))
attributions = attributions.sum(dim=2).squeeze(0)
attributions = attributions / torch.norm(attributions)
attributions = attributions.cpu().detach().numpy()
# create and return data visualization record
return visualization.VisualizationDataRecord(
attributions,
pred,
Label.vocab.itos[pred_ind],
Label.vocab.itos[label],
Label.vocab.itos[1],
attributions.sum(),
text_list,
delta)
# add_attributions_to_visualizer(attributions, text_list, pred, pred_ind, label, delta, vis_data_records_ig)
def sentence_to_wordlist(sentence, min_len = 7):
# convert sentence into list of word/tokens (using spacy tokenizer)
text = [tok.text for tok in nlp.tokenizer(sentence)]
# fill text up with 'pad' tokens
if len(text) < min_len:
text += [PAD] * (min_len - len(text))
return text
def wordlist_to_tensors(text):
# get list of token/word indices using the vocabulary
sentence_indices = [TEXT.vocab.stoi[t] for t in text]
# transform token indices list into torch tensor
sentence_tensor = torch.tensor(sentence_indices, device=device)
sentence_tensor = sentence_tensor.unsqueeze(0)
# create reference tensor using the padding token (one of the most frequently used tokens)
token_reference = TokenReferenceBase(reference_token_idx = PAD_INDEX)
reference_tensor = token_reference.generate_reference(len(text), device=device).unsqueeze(0)
return sentence_tensor, reference_tensor
```
Below cells call `interpret_sentence` to interpret a couple handcrafted review phrases.
```
# reset accumulated data
vis_records = []
vis_records.append(interpret_sentence(model, 'It was a fantastic performance !', label=1))
vis_records.append(interpret_sentence(model, 'Best film ever', label=1))
vis_records.append(interpret_sentence(model, 'Such a great show!', label=1))
vis_records.append(interpret_sentence(model, 'I\'ve never watched something as bad', label=0))
vis_records.append(interpret_sentence(model, 'It is a disgusting movie!', label=0))
vis_records.append(interpret_sentence(model, 'Makes a poorly convincing argument', label=0))
vis_records.append(interpret_sentence(model, 'Makes a fairly convincing argument', label=1))
vis_records.append(interpret_sentence(model, 'Skyfall is one of the best action film in recent years but is just too long', min_len=18, label=1))
```
Below is an example of how we can visualize attributions for the text tokens. Feel free to visualize it differently if you choose to have a different visualization method.
```
vis_example = vis_records[-1]
# print(dir(vis_example))
print('raw input: ', vis_example.raw_input)
print('true class: ', vis_example.true_class)
print('pred class (prob): ', vis_example.pred_class, '(', vis_example.pred_prob, ')')
print('attr score (sum over word attributions): ', vis_example.attr_score)
print('word attributions\n', vis_example.word_attributions)
print('Visualize attributions based on Integrated Gradients')
visualization.visualize_text(vis_records)
```
Above cell generates an output similar to this:
```
from IPython.display import Image
Image(filename='img/sentiment_analysis.png')
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
%config InlineBackend.figure_format='svg'
df=pd.read_csv('train_Data.csv')
df.columns
df_min=df[df['4']==1]
df_min.to_csv('iris0_minority_train.csv',index=False)
df_min=pd.read_csv('iris0_minority_train.csv')
df_majority=df[df['4']==0]
df_majority.to_csv('iris0_majority_train.csv',index=False)
df_majority=pd.read_csv('iris0_majority_train.csv')
%matplotlib inline
sns.countplot(x='4',data=df)
def create_dataset(dataset,look_back=1):
datax,datay=[],[]
for i in range(len(dataset)-look_back-1):
a=dataset[i:(i+look_back),:]
datax.append(a)
datay.append(dataset[i+look_back,:])
return np.array(datax),np.array(datay)
df_minor=np.array(df_min)
scaler=MinMaxScaler(feature_range=(0,1))
df_minor=scaler.fit_transform(df_min)
x,y=create_dataset(df_minor,5)#5
print(x.shape)
print(y.shape)
Xtrain,xtest,Ytrain,ytest=train_test_split(x,y,test_size=0.40,random_state=60)
model=Sequential()
model.add(LSTM(20,input_shape=(Xtrain.shape[1],Xtrain.shape[2])))#5
model.add(Dense(5))
print(model.summary())
model.compile(loss='mse',optimizer='adam')
history=model.fit(Xtrain,Ytrain,epochs=500,verbose=1)
model.save('7-24-2019-iris0-v1.h5')
Xtrain.shape
plt.plot(history.history['loss'],label='train')
#plt.plot(history.history['val_loss'],label='test')
plt.xlabel('number of epochs')
plt.ylabel('val_loss')
plt.legend()
#pyplot.savefig('LSTM training.png',dpi=300)
plt.show()
prediction=model.predict(xtest)
def draw_prediction(ytest,d,columns):
_,axes=plt.subplots(len(columns),1,figsize=(10,20))
for i,cols in enumerate(columns):
axes[i].plot(ytest[:,i],label='real',color='blue')
axes[i].plot(d[:,i],label='prediction',color='orange')
#axes[i].set_xlabel='index'
#axes[i].set_ylabel=cols
axes[i].xlabel='index'
axes[i].ylabel=cols
clmns=df.columns
draw_prediction(ytest,prediction,clmns)
prediction
prediction2=scaler.inverse_transform(prediction)
ytest2=scaler.inverse_transform(ytest)
draw_prediction(ytest2,prediction2,clmns)
prediction
new_data=pd.DataFrame(prediction2)
new_data.to_csv('new_corrected_data-v1-7-24-2019.csv',index=False)
```
| github_jupyter |
# autotimeseries
> Nixtla SDK. Time Series Forecasting pipeline at scale.
[](https://github.com/Nixtla/nixtla/actions/workflows/python-sdk.yml)
[](https://pypi.org/project/autotimeseries/)
[](https://pypi.org/project/autotimeseries/)
[](https://github.com/Nixtla/nixtla/blob/main/sdk/python-autotimeseries/LICENSE)
**autotimeseries** is a python SDK to consume the APIs developed in https://github.com/Nixtla/nixtla.
## Install
### PyPI
`pip install autotimeseries`
## How to use
Check the following examples for a full pipeline:
- [M5 state-of-the-art reproduction](https://github.com/Nixtla/autotimeseries/tree/main/examples/m5).
- [M5 state-of-the-art reproduction in Colab](https://colab.research.google.com/drive/1pmp4rqiwiPL-ambxTrJGBiNMS-7vm3v6?ts=616700c4)
### Basic usage
```python
import os
from autotimeseries.core import AutoTS
autotimeseries = AutoTS(bucket_name=os.environ['BUCKET_NAME'],
api_id=os.environ['API_ID'],
api_key=os.environ['API_KEY'],
aws_access_key_id=os.environ['AWS_ACCESS_KEY_ID'],
aws_secret_access_key=os.environ['AWS_SECRET_ACCESS_KEY'])
```
#### Upload dataset to S3
```python
train_dir = '../data/m5/parquet/train'
# File with target variables
filename_target = autotimeseries.upload_to_s3(f'{train_dir}/target.parquet')
# File with static variables
filename_static = autotimeseries.upload_to_s3(f'{train_dir}/static.parquet')
# File with temporal variables
filename_temporal = autotimeseries.upload_to_s3(f'{train_dir}/temporal.parquet')
```
Each time series of the uploaded datasets is defined by the column `item_id`. Meanwhile the time column is defined by `timestamp` and the target column by `demand`. We need to pass this arguments to each call.
```python
columns = dict(unique_id_column='item_id',
ds_column='timestamp',
y_column='demand')
```
#### Send the job to make forecasts
```python
response_forecast = autotimeseries.tsforecast(filename_target=filename_target,
freq='D',
horizon=28,
filename_static=filename_static,
filename_temporal=filename_temporal,
objective='tweedie',
metric='rmse',
n_estimators=170,
**columns)
```
#### Download forecasts
```python
autotimeseries.download_from_s3(filename='forecasts_2021-10-12_19-04-32.csv', filename_output='../data/forecasts.csv')
```
| github_jupyter |
```
#!/usr/bin/env python
# encoding: utf-8
"""
@Author: yangwenhao
@Contact: [email protected]
@Software: PyCharm
@File: cam_2.py
@Time: 2021/4/12 21:47
@Overview:
Created on 2019/8/4 上午9:37
@author: mick.yi
"""
import os
import pdb
import numpy as np
import torch
from torch.nn.parallel.distributed import DistributedDataParallel
from Define_Model.ResNet import ThinResNet
os.environ['CUDA_VISIBLE_DEVICES'] = "0,1"
torch.distributed.init_process_group(backend="nccl", init_method='tcp://localhost:12556', rank=0,
world_size=1)
class GradCAM(object):
"""
1: 网络不更新梯度,输入需要梯度更新
2: 使用目标类别的得分做反向传播
"""
def __init__(self, net, layer_name):
self.net = net
self.layer_name = layer_name
self.feature = {}
self.gradient = {}
self.net.eval()
self.handlers = []
self._register_hook()
def _get_features_hook(self, module, input, output):
print(type(module))
if isinstance(self.net, DistributedDataParallel):
self.feature[input[0].device] = output[0]
else:
self.feature = output[0]
# print("Device {}, forward out feature shape:{}".format(input[0].device, output[0].size()))
def _get_grads_hook(self, module, input_grad, output_grad):
"""
:param input_grad: tuple, input_grad[0]: None
input_grad[1]: weight
input_grad[2]: bias
:param output_grad:tuple,长度为1
:return:
"""
if isinstance(self.net, DistributedDataParallel):
if input_grad[0].device not in self.gradient:
self.gradient[input_grad[0].device] = output_grad[0]
else:
self.gradient[input_grad[0].device] += output_grad[0]
else:
self.gradient += output_grad[0]
# print(output_grad[0])
# print("Device {}, backward out gradient shape:{}".format(input_grad[0].device, output_grad[0].size()))
def _register_hook(self):
if isinstance(self.net, DistributedDataParallel):
modules = self.net.module.named_modules()
else:
modules = self.net.named_modules()
for (name, module) in modules:
if name == self.layer_name:
self.handlers.append(module.register_backward_hook(self._get_features_hook))
self.handlers.append(module.register_backward_hook(self._get_grads_hook))
def remove_handlers(self):
for handle in self.handlers:
handle.remove()
def __call__(self, inputs, index):
"""
:param inputs: [1,3,H,W]
:param index: class id
:return:
"""
# self.net.zero_grad()
output, _ = self.net(inputs) # [1,num_classes]
pdb.set_trace()
if index is None:
index = torch.argmax(output)
target = output.gather(1, index)# .mean()
# target = output[0][index]
for i in target:
i.backward(retain_graph=True)
if isinstance(self.net, DistributedDataParallel):
feature = []
gradient = []
for d in self.gradient:
feature.append(self.feature[d])
gradient.append(self.gradient[d])
feature = torch.cat(feature, dim=0)
gradient = torch.cat(gradient, dim=0)
else:
feature = self.feature
gradient = self.gradient
return feature, gradient
# gradient = self.gradient[0].cpu().data.numpy() # [C,H,W]
# weight = np.mean(gradient, axis=(1, 2)) # [C]
# feature = self.feature[0].cpu().data.numpy() # [C,H,W]
# cam = feature * weight[:, np.newaxis, np.newaxis] # [C,H,W]
# cam = np.sum(cam, axis=0) # [H,W]
# cam = np.maximum(cam, 0) # ReLU
#
# # 数值归一化
# cam -= np.min(cam)
# cam /= np.max(cam)
# # resize to 224*224
# cam = cv2.resize(cam, (224, 224))
# return cam
# print("gradient shape: ", gradient.shape)
# print("feature shape: ", feature.shape)
class Sum_GradCAM(object):
"""
1: 网络不更新梯度,输入需要梯度更新
2: 使用目标类别的得分做反向传播
"""
def __init__(self, net, layer_name):
self.net = net
self.layer_name = layer_name
self.feature = {}
self.gradient = {}
self.net.eval()
self.handlers = []
self._register_hook()
def _get_features_hook(self, module, input, output):
if isinstance(self.net, DistributedDataParallel):
self.feature[input[0].device] = output[0]
else:
self.feature = output[0]
# print("Device {}, forward out feature shape:{}".format(input[0].device, output[0].size()))
def _get_grads_hook(self, module, input_grad, output_grad):
"""
:param input_grad: tuple, input_grad[0]: None
input_grad[1]: weight
input_grad[2]: bias
:param output_grad:tuple,长度为1
:return:
"""
if isinstance(self.net, DistributedDataParallel):
if input_grad[0].device not in self.gradient:
self.gradient[input_grad[0].device] = output_grad[0]
else:
self.gradient[input_grad[0].device] += output_grad[0]
else:
self.gradient = output_grad[0]
# print(output_grad[0])
# print("Device {}, backward out gradient shape:{}".format(input_grad[0].device, output_grad[0].size()))
def _register_hook(self):
if isinstance(self.net, DistributedDataParallel):
modules = self.net.module.named_modules()
else:
modules = self.net.named_modules()
for (name, module) in modules:
if name == self.layer_name:
self.handlers.append(module.register_backward_hook(self._get_features_hook))
self.handlers.append(module.register_backward_hook(self._get_grads_hook))
def remove_handlers(self):
for handle in self.handlers:
handle.remove()
def __call__(self, inputs, index):
"""
:param inputs: [1,3,H,W]
:param index: class id
:return:
"""
# self.net.zero_grad()
output, _ = self.net(inputs) # [1,num_classes]
pdb.set_trace()
if index is None:
index = torch.argmax(output)
target = output.gather(1, index).mean()
target.backward(retain_graph=True)
if isinstance(self.net, DistributedDataParallel):
feature = []
gradient = []
for d in self.gradient:
feature.append(self.feature[d])
gradient.append(self.gradient[d])
feature = torch.cat(feature, dim=0)
gradient = torch.cat(gradient, dim=0)
else:
feature = self.feature
gradient = self.gradient
return feature, gradient
# print("gradient shape: ", gradient.shape)
# print("feature shape: ", feature.shape)
model = ThinResNet()
model = model.cuda()
model = DistributedDataParallel(model)
gc = GradCAM(model, 'layer4')
x = torch.randn((20, 1, 224, 224)).cuda() # *1.2 +1.
l = torch.range(0, 19).long().unsqueeze(1).cuda()
y = model(x)
#
cam = gc(x, l)
# print(cam.shape)
```
| github_jupyter |
# The Structure and Geometry of the Human Brain
[Noah C. Benson](https://nben.net/) <[[email protected]](mailto:[email protected])>
[eScience Institute](https://escience.washingtonn.edu/)
[University of Washington](https://www.washington.edu/)
[Seattle, WA 98195](https://seattle.gov/)
## Introduction
This notebook is designed to accompany the lecture "Introduction to the Strugure and Geometry of the Human Brain" as part of the Neurohackademt 2020 curriculum. It can be run either in Neurohackademy's Jupyterhub environment, or using the `docker-compose.yml` file (see the `README.md` file for instructions).
In this notebook we will examine various structural and geometric data used commonly in neuroscience. These demos will primarily use [FreeSurfer](http://surfer.nmr.mgh.harvard.edu/) subjects. In the lecture and the Neurohackademy Jupyterhub environment, we will look primarily at a subject named `nben`; however, you can alternately use the subject `bert`, which is an example subject that comes with FreeSurfer. Optionally, this notebook can be used with subject from the [Human Connectome Project (HCP)](https://db.humanconnectome.org/)--see the `README.md` file for instructions on getting credentials for use with the HCP.
We will look at these data using both the [`nibabel`](https://nipy.org/nibabel/), which is an excellent core library for importing various kinds of neuroimaging data, as well as [`neuropythy`](https://github.com/noahbenson/neuropythy), which builds on `nibabel` to provide a user-friendly API for interacting with subjects. At its core, `neuropythy` is a library for interacting with neuroscientific data in the context of brain structure.
This notebook itself consists of this introduction as well as four sections that follow the topic areas in the slide-deck from the lecture. These sections are intended to be explored in order.
### Libraries
Before running any of the code in this notebook, we need to start by importing a few libraries and making sure we have configured those that need to be configured (mainly, `matplotlib`).
```
# We will need os for paths:
import os
# Numpy, Scipy, and Matplotlib are effectively standard libraries.
import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.pyplot as plt
# Ipyvolume is a 3D plotting library that is used by neuropythy.
import ipyvolume as ipv
# Nibabel is the library that understands various neuroimaging file
# formats; it is also used by neuropythy.
import nibabel as nib
# Neuropythy is the main library we will be using in this notebook.
import neuropythy as ny
%matplotlib inline
```
## MRI and Volumetric Data
The first section of this notebook will deal with MR images and volumetric data. We will start by loading in an MRImage. We will use the same image that was visualized in the lecture (if you are not using the Jupyterhub, you won't have access to this subject, but you can use the subject `'bert'` instead).
---
### Load a subject.
---
For starters, we will load the subject.
```
subject_id = 'nben'
subject = ny.freesurfer_subject(subject_id)
# If you have configured the HCP credentials and wish to use an HCP
# subject instead of nben:
#
#subject_id = 111312
#subject = ny.hcp_subject(subject_id)
```
The `freesurfer_subject` function returns a `neuropythy` `Subject` object.
```
subject
```
---
### Load an MRImage file.
---
Let's load in an image file. FreeSurfer directories contain a subdirectory `mri/` that contains all of the volumetric/image data for the subject. This includes images that have been preprocessed as well as copies of the original T1-weighted image. We will load an image called `T1.mgz`.
```
# This function will load data from a subject's directory using neuropythy's
# builtin ny.load() function; in most cases, this calls down to nibabel's own
# nib.load() function.
im = subject.load('mri/T1.mgz')
# For an HCP subject, use this file instead:
#im = subject.load("T1w/T1w_acpc_dc.nii.gz")
# The return value should be a nibabel image object.
im
# In fact, we could just as easily have loaded the same object using nibabel:
im_from_nibabel = nib.load(subject.path + '/mri/T1.mgz')
print('From neuropythy: ', im.get_filename())
print('From nibabel: ', im_from_nibabel.get_filename())
# And neuropythy manages this image as part of the subject-data. Neuropythy's
# name for it is 'intensity_normalized', which is due to its position as an
# output in FreeSurfer's processing pipeline.
ny_im = subject.images['intensity_normalized']
(ny_im.dataobj == im.dataobj).all()
```
---
### Visualize some slices of the image.
---
Next, we will make 2D plots of some of the image slices. Feel free to change which slices you visualize; I have just chosen some defaults.
```
# What axis do we want to plot slices along? 0, 1, or 2 (for the first, second,
# or third 3D image axis).
axis = 2
# Which slices along this axis should we plot? These must be at least 0 and at
# most 255 (There are 256 slices in each dimension of these images).
slices = [75, 125, 175]
# Make a figure and axes using matplotlib.pyplot:
(fig, axes) = plt.subplots(1, len(slices), figsize=(5, 5/len(slices)), dpi=144)
# Plot each of the slices:
for (ax, slice_num) in zip(axes, slices):
# Get the slice:
if axis == 0:
imslice = im.dataobj[slice_num,:,:]
elif axis == 1:
imslice = im.dataobj[:,slice_num,:]
else:
imslice = im.dataobj[:,:,slice_num]
ax.imshow(imslice, cmap='gray')
# Turn off labels:
ax.axis('off')
```
---
### Visualize the 3D Image as a whole.
---
Next we will use `ipyvolume` to render a 3D View of the volume. The volume plotting function is part of `ipyvolume` and has a variety of options that are beyond the scope of this demo.
```
# Note that this will generate a warning, which can be safely ignored.
fig = ipv.figure()
ipv.quickvolshow(subject.images['intensity_normalized'].dataobj)
ipv.show()
```
---
### Load and visualize anatomical segments.
---
FreeSurfer creates a segmentation image file called `aseg.mgz`, which we can load and use to identify ROIs. First, we will load this file and plot some slices from it.
```
# First load the file; any of these lines will work:
#aseg = subject.load('mri/aseg.mgz')
#aseg = nib.load(subject.path + '/mri/aseg.mgz')
aseg = subject.images['segmentation']
```
We can plot this as-is, but we don't know what the values in the numbers correspond to. Nonetheless, let's go ahead. This code block is the same as the block we used to plot slices above except that it uses the new image `aseg` we just loaded.
```
# What axis do we want to plot slices along? 0, 1, or 2 (for the first, second,
# or third 3D image axis).
axis = 2
# Which slices along this axis should we plot? These must be at least 0 and at
# most 255 (There are 256 slices in each dimension of these images).
slices = [75, 125, 175]
# Make a figure and axes using matplotlib.pyplot:
(fig, axes) = plt.subplots(1, len(slices), figsize=(5, 5/len(slices)), dpi=144)
# Plot each of the slices:
for (ax, slice_num) in zip(axes, slices):
# Get the slice:
if axis == 0:
imslice = aseg.dataobj[slice_num,:,:]
elif axis == 1:
imslice = aseg.dataobj[:,slice_num,:]
else:
imslice = aseg.dataobj[:,:,slice_num]
ax.imshow(imslice, cmap='gray')
# Turn off labels:
ax.axis('off')
```
Clearly, the balues in the plots above are discretized, but it's not clear what they correspond to. The map of numbers to characters and colors can be found in the various FreeSurfer color LUT files. These are all located in the FreeSurfer home directory and end with `LUT.txt`. They are essentially spreadsheets and are loaded by `neuropythy` as `pandas.DataFrame` objects. In `neuropythy`, the LUT objects are associated with the `'freesurfer_home'` configuration variable. This has been setup automatically in the course and the `neuropythy` docker-image.
```
ny.config['freesurfer_home'].luts['aseg']
```
So suppose we want to look at left cerebral cortex. In the table, this has value 3. We can find this value in the images we are plotting and plot only it to see the ROI in each the slices we plot.
```
# We want to plot left cerebral cortex (label ID = 3, per the LUT)
label = 3
(fig, axes) = plt.subplots(1, len(slices), figsize=(5, 5/len(slices)), dpi=144)
# Plot each of the slices:
for (ax, slice_num) in zip(axes, slices):
# Get the slice:
if axis == 0:
imslice = aseg.dataobj[slice_num,:,:]
elif axis == 1:
imslice = aseg.dataobj[:,slice_num,:]
else:
imslice = aseg.dataobj[:,:,slice_num]
# Plot only the values that are equal to the label ID.
imslice = (imslice == label)
ax.imshow(imslice, cmap='gray')
# Turn off labels:
ax.axis('off')
```
By plotting the LH cortex specifically, we can see that LEFT is in the direction of increasing rows (down the image slices, if you used `axis = 2`), thus RIGHT must be in the direction of decreasing rows in the image.
Let's also make some images from these slices in which we replace each of the pixels in each slice with the color recommended by the color LUT.
```
# We are using this color LUT:
lut = ny.config['freesurfer_home'].luts['aseg']
# The axis:
axis = 2
(fig, axes) = plt.subplots(1, len(slices), figsize=(5, 5/len(slices)), dpi=144)
# Plot each of the slices:
for (ax, slice_num) in zip(axes, slices):
# Get the slice:
if axis == 0:
imslice = aseg.dataobj[slice_num,:,:]
elif axis == 1:
imslice = aseg.dataobj[:,slice_num,:]
else:
imslice = aseg.dataobj[:,:,slice_num]
# Convert the slice into an RGBA image using the color LUT:
rgba_im = np.zeros(imslice.shape + (4,))
for (label_id, row) in lut.iterrows():
rgba_im[imslice == label_id,:] = row['color']
ax.imshow(rgba_im)
# Turn off labels:
ax.axis('off')
```
## Cortical Surface Data
Cortical surface data is handled and represented much differently than volumetric data. This section demonstrates how to interact with cortical surface data in a Jupyter notebook, primarily using `neuropythy`.
To start off, however, we will just load a surface file using `nibabel` to see what one contains.
---
### Load a Surface-Geometry File Using `nibabel`
---
```
# Each subject has a number of surface files; we will look at the
# left hemisphere, white surface.
hemi = 'lh'
surf = 'white'
# Feel free to change hemi to 'rh' for the RH and surf to 'pial'
# or 'inflated'.
# We load the surface from the subject's 'surf' directory in FreeSurfer.
# Nibabel refers to these files as "geometry" files.
filename = subject.path + f'/surf/{hemi}.{surf}'
# If you are using an HCP subject, you should instead load from this path:
#relpath = f'T1w/{subject.name}/surf/{hemi}.{surf}'
#filename = subject.pseudo_path.local_path(relpath)
# Read the file, using nibabel.
surface_data = nib.freesurfer.read_geometry(filename)
# What does this return?
surface_data
```
So when `nibabel` reads in one of these surface files, what we get back is an `n x 3` matrix of real numbers (coordiantes) and an `m x 3` matrix of integers (triangle indices).
The `ipyvolume` module has support for plotting triangle meshes--let's see how it works.
```
# Extract the coordinates and triangle-faces.
(coords, faces) = surface_data
# And get the (x,y,z) from coordinates.
(x, y, z) = coords.T
# Now, plot the triangle mesh.
fig = ipv.figure()
ipv.plot_trisurf(x, y, z, triangles=faces)
# Adjust the plot limits (making them equal makes the plot look good).
ipv.pylab.xlim(-100,100)
ipv.pylab.ylim(-100,100)
ipv.pylab.zlim(-100,100)
# Generally, one must call show() with ipyvolume.
ipv.show()
```
---
### Hemisphere (`neuropythy.mri.Cortex`) objects
---
Although one can load and plot cortical surfaces with `nibabel`, `neuropythy` builds on `nibabel` by providing a framework around which the cortical surface can be represented. It includes a number of utilities related specifically to cortical surface analysis, and allows much of the power of FreeSurfer to be leveraged through simple Python data structures.
To start with, we will look at our subject's hemispheres (`neuropythy.mri.Cortex` objects) and how they represent surfaces.
```
# Grab the hemisphere for our subject.
cortex = subject.hemis[hemi]
# Note that `cortex = subject.lh` and `cortex = subject.rh` are equivalent
# to `cortex = subject.hemis['lh']` and `cortex = subject.hemis['rh']`.
# What is cortex?
cortex
```
From this we can see which hemisphere we have selected, the number of triangle faces that it has, and the number of vertices that it has. Let's look at a few of its' properties.
#### Surfaces
Each hemisphere has a number of surfaces; we can view them through the `cortex.surfaces` dictionary.
```
cortex.surfaces.keys()
cortex.surfaces['white_smooth']
```
The `'white_smooth'` mesh is a well-processed mesh of the white surface that has been well-smoothed. You might notice that there is a `'midgray'` surface, even though FreeSurfer does not include a mid-gray mesh file. The `'midgray'` mesh, however, can be made by averaging the white and pial mesh vertices.
Recall that all surfaces of a hemisphere have equivalent vertices and identical triangles. We can test that here.
```
np.array_equal(cortex.surfaces['white'].tess.faces,
cortex.surfaces['pial'].tess.faces)
```
Surfaces track a large amount of data about their meshes and vertices and inherit most of the properties of hemispheres that are discussed below. In addition, surfaces uniquely carry data about cortical distances and surface areas. For example:
```
# The area of each of the triangle-faces in nthe white surface mesh, in mm^2.
cortex.surfaces['white'].face_areas
# The length of each edge in the white surface mesh, in mm.
cortex.surfaces['white'].edge_lengths
# And the edges themselves, as indices like the faces.
cortex.surfaces['white'].tess.edges
```
#### Vertex Properties
Properties arre values assigned to each surface vertex. They can include anatomical or geometric properties, such as ROI labels (i.e., a vector of values for each vertex: `True` if the vertex is in the ROI and `False` if not), cortical thickness (in mm), the vertex surface-area (in square mm), the curvature, or data from other functional measurements, such as BOLD-time-series data or source-localized MEG data.
The properties of a hemisphere are stored in the `properties` value. `Cortex.properties` is a kind of dictionary object and can generally be treated as a dictionary. One can also access property vectors via `cortex.prop(property_name)` rather than `cortex.properties[property_name]`; the former is largely short-hand for the latter.
```
sorted(cortex.properties.keys())
```
A few thigs worth noting: First, not all FreeSurfer subjects will have all of the properties listed. This is because different versions of FreeSurfer include different files, and sometimes subjects are distributed without their full set of files (e.g., to save storage space). However, rather than go and try to load all of these files right away, `neuropythy` makes place-holders for them and loads them only when first requested (this saves on loading time drastically). Accordingly, if you try to use a property whose file doesn't exist, an nexception will be raised.
Additionally, notice that the first several properties are for Brodmann Area labels. The ones ending in `_label` are `True` / `False` boolean labels indicating whether the vertex is in the given ROI (according to an estimation based on anatomy). The subject we are using in the Jupyterhub environment does not actually have these files included, but they do have, for example `BA1_weight` files. The weights represent the probability that a vertex is in the associated ROI, so we can make a label from this.
```
ba1_label = cortex.prop('BA1_weight') >= 0.5
```
We can now plot this property using `neuropythy`'s `cortex_plot()` function.
```
ny.cortex_plot(cortex.surfaces['white'], color=ba1_label)
```
**Improving this plot.** While this plot shows us where the ROI is, it's rather hard to interpret. Rather, we would prefer to plot the ROI in red and the rest of the brain using a binarized curvature map. `neuropythy` supports this kind of binarized curvature map as a default underlay, so, in fact, the easiest way to accomplish this is to tell `cortex_plot` to color the surface red, but to add a vertex mask that instructs the function to *only* color the ROI vertices.
Additionally, it is easier to see the inflated surface, so we will switch to that.
```
ny.cortex_plot(cortex.surfaces['inflated'], color='r', mask=ba1_label)
```
We can optionally make this red ROI plot a little bit transparent as well.
```
ny.cortex_plot(cortex.surfaces['inflated'], color='r', mask=ba1_label, alpha=0.4)
```
**Plotting the weight instead of the label.** Alternately, we might have wanted to plot the weight / probability of the ROI. Continuous properties like probability can be plotted using color-maps, similar to how they are plotted in `matplotlib`.
```
ny.cortex_plot(cortex.surfaces['inflated'], color='BA1_weight',
cmap='hot', vmin=0, vmax=1, alpha=0.6)
```
**Another property.** Other properties can be very informative. For example, the cortical thickness property, which is stored in mm. This can tell us the parts of the brain that are thick or not thick.
```
ny.cortex_plot(cortex.surfaces['inflated'], color='thickness',
cmap='hot', vmin=1, vmax=6)
```
---
### Interpolation (Surface to Image and Image to Surface)
---
Hemisphere/Cortex objects also manage interpolation, both to/from image volumes as well as to/from the cortical surfaces of other subjects (we will demo interpolation between subjects in the last section). Here we will focus on the former: interpolation to and from images.
**Cortex to Image Interpolation.**
Because our subjects only have structural data and do not have functional data, we do not have anything handy to interpolate out of a volume onto a surface. So instead, we will start by innterpolating from the cortex into the volume. A good property for this is the subject's cortical thickness. Thickness is difficult to calculate in the volume, so if one wants thickness data in a volume, it would typically be calculated using surface meshes then projected back into the volume. We will do that now.
Note that in order to create a new image, we have to provide the interpolation method with some information about how the image is oriented and shaped. This includes two critical pieces of information: the `'image_shape'` (i.e., the `numpy.shape` of the image's array) and the `'affine'`, which is simply the affine-transformation that aligns the image with the subject. Usually, it is easiest to provide this information in the form of a template image. For all kinds of subjects (HCP and FreeSurfer), an image is correctly aligned with a subject and thus the subject's cortical surfaces if its affine transfomation correctly aligns it with `subject.images['brain']`.
```
# We need a template image; the new image will have the same shape,
# affine, image type, and hader as the template image.
template_im = subject.images['brain']
# We can use just the template's header for this.
template = template_im.header
# We can alternately just provide information about the image geometry:
#template = {'image_shape': (256,256,256), 'affine': template_im.affine}
# Alternately, we can provide an actual image into which the data will
# be inserted. In this case, we would want to make a cleared-duplicate
# of the brain image (i.e. all voxels set to 0)
#template = ny.image_clear(template_im)
# All of the above templates should provide the same result.
# We are going to save the property from both hemispheres into an image.
lh_prop = subject.lh.prop('thickness')
rh_prop = subject.rh.prop('thickness')
# This may be either 'linear' or 'nearest'; for thickness 'linear'
# is probably best, but the difference will be small.
method = 'linear'
# Do the interpolation. This may take a few minutes the first time it is run.
new_im = subject.cortex_to_image((lh_prop, rh_prop), template, method=method,
# The template is integer, so we override it.
dtype='float')
```
Now that we have made this new image, let's take a look at it by plotting some slices from it, once again.
```
# What axis do we want to plot slices along? 0, 1, or 2 (for the first, second,
# or third 3D image axis).
axis = 2
# Which slices along this axis should we plot? These must be at least 0 and at
# most 255 (There are 256 slices in each dimension of these images).
slices = [75, 125, 175]
# Make a figure and axes using matplotlib.pyplot:
(fig, axes) = plt.subplots(1, len(slices), figsize=(5, 5/len(slices)), dpi=144)
# Plot each of the slices:
for (ax, slice_num) in zip(axes, slices):
# Get the slice:
if axis == 0:
imslice = new_im.dataobj[slice_num,:,:]
elif axis == 1:
imslice = new_im.dataobj[:,slice_num,:]
else:
imslice = new_im.dataobj[:,:,slice_num]
ax.imshow(imslice, cmap='hot', vmin=0, vmax=6)
# Turn off labels:
ax.axis('off')
```
**Image to Cortex Interpolation.** A good test of our interpolation methods is now to ensure that, when we interpolate data from the image we just created back to the cortex, we get approximately the same values. The values we interpolate back out of the volume will not be identical to the volumes we started with because the resolution of the image is finite, but they should be close.
The `image_to_cortex()` method of the `Subject` class is capable of interpolating from an image to the cortical surface(s), based on the alignment of the image with the cortex.
```
(lh_prop_interp, rh_prop_interp) = subject.image_to_cortex(new_im, method=method)
```
We can plot the hemispheres together to visualize the difference between the original thickenss and the thickness that was interpolated into an image then back onto the cortex.
```
fig = ny.cortex_plot(subject.lh, surface='midgray',
color=(lh_prop_interp - lh_prop)**2,
cmap='hot', vmin=0, vmax=2)
fig = ny.cortex_plot(subject.rh, surface='midgray',
color=(rh_prop_interp - rh_prop)**2,
cmap='hot', vmin=0, vmax=2,
figure=fig)
ipv.show()
```
## Intersubject Surface Alignment
Comparison between multiple subjects is usually accomplished by first aligning each subject's cortical surface with that of a template surface (*fsaverage* in FreeSurfer, *fs_LR* in the HCP), then interpolating between vertices in the aligned arrangements. The alignment to the template are calculated and saved by FreeSurfer, the HCPpipelines, and various other utilities, but as of when this tutorial was written, `neuropythy` only supports these first two formats. Alignments are calculated by warping the vertices of the subject's spherical (fully inflated) hemisphere in a diffeomorphic fashion with the goal of minimizing the difference between the sulcal topology (curvature and depth) of the subject's vertices and that of the nearby *fsaverage* vertices. The process involves a number of steps, and any who are interested should follow up with the various documentations and papers published by the [FreeSurfer group](https://surfer.nmr.mgh.harvard.edu/).
For practical purposes, it is not necessary to understand the details of this algorithm--FreeSurfer is a large complex collection of software that has been under development for decades. However, to better understand what is produced by FreeSurfer's alignment procedure, let us start by looking at its outputs.
---
### Compare Subject Registrations
---
To better understand the various spherical surfaces produced by FreeSurfer, let's start by plotting three spherical surfaces in 3D. The first will be the subject's "native" inflated spherical surface. The next will be the subjects "fsaverage"-aligned sphere. The last will be The *fsaverage* subject's native sphere.
These spheres are accessed not through the `subject.surfaces` dictionary but through the `subject.registrations` dictionary. This is simply a design decision--registrations and surfaces are not fundamentally different except that registrations can be used for interpolation between subjects (more below).
Note that you may need to zoom out once the plot has been made.
```
# Get the fsaverage subject.
fsaverage = ny.freesurfer_subject('fsaverage')
# Get the hemispheres we will be examining.
fsa_hemi = fsaverage.hemis[hemi]
sub_hemi = subject.hemis[hemi]
# Next, get the three registrations we want to plot.
sub_native_reg = sub_hemi.registrations['native']
sub_fsaverage_reg = sub_hemi.registrations['fsaverage']
fsa_native_reg = fsa_hemi.registrations['native']
# We want to plot them all three together in one scene, so to do this
# we need to translate two of them a bit along the x-axis.
sub_native_reg = sub_native_reg.translate([-225,0,0])
fsa_native_reg = fsa_native_reg.translate([ 225,0,0])
# Now plot them all.
fig = ipv.figure(width=900, height=300)
ny.cortex_plot(sub_native_reg, figure=fig)
ny.cortex_plot(fsa_native_reg, figure=fig)
ny.cortex_plot(sub_fsaverage_reg, figure=fig)
ipv.show()
```
---
### Interpolate Between Subjects
---
Interpolation between subjects requires interpolating between a shared registration. For a subject and the *fsaverage*, this is the subject's *fsaverage*-aligned registration and *fsaverage*'s native. However, for two non-meta subjects, the *fsaverage*-aligned registration of both subjects are used.
We will first show how to interpolate from a subject over to the **fsaverage**. This is a very valuable operation to be able to do as it allows you to compute statistics across subejcts of cortical surface data (such as BOLD activation data or source-localized MEG data).
```
# The property we're going to interpolate over to fsaverage:
sub_prop = sub_hemi.prop('thickness')
# The method we use ('nearest' or 'linear'):
method = 'linear'
# Interpolate the subject's thickness onto the fsaverage surface.
fsa_prop = sub_hemi.interpolate(fsa_hemi, sub_prop, method=method)
# Let's make a plot of this:
ny.cortex_plot(fsa_hemi, surface='inflated',
color=fsa_prop, cmap='hot', vmin=0, vmax=6)
```
Okay, for our last exercise, let's interpolate back from the *fsaverage* subject to our subject. It is occasionally nice to be able to plot the *fsaverage*'s average curvature map as an underlay, so let's do that.
```
# This time we are going to interpolate curvature from the fsaverage
# back to the subject. When the property we are interpolating is a
# named property of the hemisphere, we can actually just specify it
# by name in the interpolation call.
fsa_curv_on_sub = fsa_hemi.interpolate(sub_hemi, 'curvature')
# We can make a duplicate subject hemisphere with this new property
# so that it's easy to plot this curvature map.
sub_hemi_fsacurv = sub_hemi.with_prop(curvature=fsa_curv_on_sub)
# Great, let's see what this looks like:
ny.cortex_plot(sub_hemi_fsacurv, surface='inflated')
```
| github_jupyter |
# Baye's Theorem
### Introduction
Befor starting with *Bayes Theorem* we can have a look at some definitions.
**Conditional Probability :**
Conditional Probability is the Probability of one event occuring with some Relationship to one or more events.
Let A and B be the two interdependent event,where A has already occured then the probabilty of B will be
$$ P(B|A) = P(A \cap B)|P(A) $$
**Joint Probability :**
Joint Probability is a Statistical measure that Calculates the Likehood of two events occuring together and at the same point in time.
$$ P(A \cap B) = P(A|B) * P(B) $$
### Bayes Theorem
Bayes Theorem was named after **Thomas Bayes**,who discovered it in **1763** and worked in the field of Decision Theory.
Bayes Theorem is a mathematical formula used to determine the **Conditional Probability** of events without the **Joint Probability**.
**Statement**
If B$_{1}$, B$_{2}$, B$_{3}$,.....,B$_{n}$ are Mutually exclusive event with P(B$_{i}$) $\not=$ 0 ,( i=1,2,3,...,n) of Random Experiment then for any Arbitrary event A of the Sample Space of the above Experiment with P(A)>0,we have
$$ P(B_{i}|A) = P(B_{i})P(A|B_{i})/ \sum\limits_{i=1}^{n} P(B_{i})P(A|B_{i}) $$
**Proof**
Let S be the Sample Space of the Random Experiment.The Event B$_{1}$, B$_{2}$, B$_{3}$,.....,B$_{n}$ being Exhaustive
$$ S = (B_{1} \cup B_{2} \cup ...\cup B_{n}) \hspace{1cm} \hspace{0.1cm} [\therefore A \subset S] $$
$$ A = A \cap S = A \cap ( B_{1} \cup B_{2} \cup B_{3},.....,\cup B_{n}) $$
$$ = (A \cap B_{1}) \cup (A \cap B_{2}) \cup ... \cup (A \cap B_{n}) $$
$$ P(A) = P(A \cap B_{1}) + P (A \cap B_{2}) + ...+ P(A \cap B_{n}) $$
$$ \hspace{3cm} \hspace{0.1cm} = P(B_{1})P(A|B_{1}) + P(B_{2})P(A|B_{2}) + ... +P(B_{n})P(A|B_{n}) $$
$$ = \sum\limits_{i=1}^{n} P(B_{i})P(A|B_{i}) $$
Now,
$$ P(A \cap B_{i}) = P(A)P(B_{i}|A) $$
$$ P(B_{i}|A) = P(A \cap B_{i})/P(A) = P(B_{i})P(A|B_{i})/\sum\limits_{i=1}^{n} P(B_{i})P(A|B_{i}) $$
**P(B)** is the Probability of occurence **B**.If we know that the event **A** has already occured.On knowing about the event **A**,**P(B)** is changed to **P(B|A)**.With the help of **Bayes Theorem we can Calculate P(B|A)**.
**Naming Conventions :**
<br>
P(A/B) : Posterior Probability
<br>
P(A) : Prior Probability
<br>
P(B/A) : Likelihood
<br>
P(B) : Evidence
<br>
So, Bayes Theorem can be Restated as :
$$ Posterior = Likelihood * Prior / Evidence $$
Now we will be looking at some problem examples on Bayes Theorem.
**Example 1** :Suppose that the reliability of a Covid-19 test is specified as follows:
<br>
Of Population having Covid-19 , 90% of the test detect the desire but 10% go undetected.Of Population free of Covid-19 , 99% of the test are judged Covid-19 -tive but 1% are diagnosed showing Covid-19 +tive.From a large population of which only 0.1% have Covid-19,one person is selected at Random,given the Covid-19 test,and the pathologist Report him/her as Covid-19 positive.What is the Probability that the person actually have Covid-19?
**Solution**<br>
Let, <br>
B$_{1}$ = The Person Selected is Actually having Covid-19.<br>
B$_{2}$ = The Person Selected is not having Covid-19.<br>
A = The Person Covid-19 Test is Diagnosed as Positive.<br>
P(B$_{1}$) = 0.1% = 0.1/100 = 0.001<br>
P(B$_{2}$) = 1-P(B$_{1}$) = 1-0.001 = 0.999<br>
P(A|B$_{1}$) = Probability that the person tested Covid-19 +tive given that he / she is actually having Covid-19.= 90/100 = 0.9 <br>
P(A|B$_{2}$) = Probability that the person tested Covid-19 +tive given that he / she is actually not having Covid-19.= 1/100 = 0.01 <br>
Required Probability = P(B$_{1}$|A) = P(B$_{1}$) * P(A|B$_{1}$)/ (((P(B$_{1}$) * P(A|B$_{1}$))+((P(B$_{2}$) * P(A|B$_{2}$)))<br>
= (0.001 * 0.9)/(0.001 * 0.9+0.999 * 0.01) = 90/1089 =0.08264
We will Now use Python to calculate the same.
```
#calculate P(B1|A) given P(B1),P(A|B1),P(A|B2),P(B2)
def bayes_theorem(p_b1,p_a_given_b1,p_a_given_b2,p_b2):
p_b1_given_a=(p_b1*p_a_given_b1)/((p_b1*p_a_given_b1)+(p_b2*p_a_given_b2))
return p_b1_given_a
#P(B1)
p_b1=0.001
#P(B2)
p_b2=0.999
#P(A|B1)
p_a_given_b1=0.9
#P(A|B2)
p_a_given_b2=0.01
result=bayes_theorem(p_b1,p_a_given_b1,p_a_given_b2,p_b2)
print('P(B1|A)=% .3f %%'%(result*100))
```
**Example 2 :** In a Quiz,a contestant either guesses or cheat or knows the answer to a multiple choice question with four choices.The Probability that he/she makes a guess is 1/3 and the Probability that he /she cheats the answer is 1/6.The Probability that his answer is correct,given that he cheated it,is 1/8.Find the Probability that he knows the answer to the question,given that he/she correctly answered it.
**Solution**<br>
Let, <br>
B$_{1}$ = Contestant guesses the answer.<br>
B$_{2}$ = Contestant cheated the answer.<br>
B$_{3}$ = Contestant knows the answer.<br>
A = Contestant answer correctly.<br>
clearly,<br>
P(B$_{1}$) = 1/3 , P(B$_{2}$) =1/6<br>
Since B$_{1}$ ,B$_{2}$, B$_{3}$ are mutually exclusive and exhaustive event.
P(B$_{1}$) + P(B$_{2}$) + P(B$_{3}$) = 1 => P(B$_{3}$) = 1 - (P(B$_{1}$) + P(B$_{2}$))
=1-1/3-1/6=1/2
If B$_{1}$ has already occured,the contestant guesses,the there are four choices out of which only one is correct.<br>
$\therefore$ the Probability that he answers correctly given that he/she has made a guess is 1/4 i.e. **P(A|B$-{1}$) = 1/4**<br>
It is given that he knew the answer = 1<br>
By Bayes Theorem,<br>
Required Probability = P(B$_{3}$|A)<br>
= P(B$_{3}$)P(A|B$_{3}$)/(P(B$_{1}$)P(A|B$_{1}$)+P(B$_{2}$)P(A|B$_{2}$)+P(B$_{3}$)P(A|B$_{3}$))
= (1/2 * 1) / ((1/3 * 1/4) + (1/6 * 1/8) + (1/2 * 1))=24/29
```
#calculate P(B1|A) given P(B1),P(A|B1),P(A|B2),P(B2),P(B3),P(A|B3)
def bayes_theorem(p_b1,p_a_given_b1,p_a_given_b2,p_b2,p_b3,p_a_given_b3):
p_b3_given_a=(p_b3*p_a_given_b3)/((p_b1*p_a_given_b1)+(p_b2*p_a_given_b2)+(p_b3*p_a_given_b3))
return p_b3_given_a
#P(B1)
p_b1=1/3
#P(B2)
p_b2=1/6
#P(B3)
p_b3=1/2
#P(A|B1)
p_a_given_b1=1/4
#P(A|B2)
p_a_given_b2=1/8
#P(A|B3)
p_a_given_b3=1
result=bayes_theorem(p_b1,p_a_given_b1,p_a_given_b2,p_b2,p_b3,p_a_given_b3)
print('P(B3|A)=% .3f %%'%(result*100))
```
| github_jupyter |
[learning-python3.ipynb]: https://gist.githubusercontent.com/kenjyco/69eeb503125035f21a9d/raw/learning-python3.ipynb
Right-click -> "save link as" [https://gist.githubusercontent.com/kenjyco/69eeb503125035f21a9d/raw/learning-python3.ipynb][learning-python3.ipynb] to get most up-to-date version of this notebook file.
## Quick note about Jupyter cells
When you are editing a cell in Jupyter notebook, you need to re-run the cell by pressing **`<Shift> + <Enter>`**. This will allow changes you made to be available to other cells.
Use **`<Enter>`** to make new lines inside a cell you are editing.
#### Code cells
Re-running will execute any statements you have written. To edit an existing code cell, click on it.
#### Markdown cells
Re-running will render the markdown text. To edit an existing markdown cell, double-click on it.
<hr>
## Common Jupyter operations
Near the top of the https://try.jupyter.org page, Jupyter provides a row of menu options (`File`, `Edit`, `View`, `Insert`, ...) and a row of tool bar icons (disk, plus sign, scissors, 2 files, clipboard and file, up arrow, ...).
#### Inserting and removing cells
- Use the "plus sign" icon to insert a cell below the currently selected cell
- Use "Insert" -> "Insert Cell Above" from the menu to insert above
#### Clear the output of all cells
- Use "Kernel" -> "Restart" from the menu to restart the kernel
- click on "clear all outputs & restart" to have all the output cleared
#### Save your notebook file locally
- Clear the output of all cells
- Use "File" -> "Download as" -> "IPython Notebook (.ipynb)" to download a notebook file representing your https://try.jupyter.org session
#### Load your notebook file in try.jupyter.org
1. Visit https://try.jupyter.org
2. Click the "Upload" button near the upper right corner
3. Navigate your filesystem to find your `*.ipynb` file and click "open"
4. Click the new "upload" button that appears next to your file name
5. Click on your uploaded notebook file
<hr>
## References
- https://try.jupyter.org
- https://docs.python.org/3/tutorial/index.html
- https://docs.python.org/3/tutorial/introduction.html
- https://daringfireball.net/projects/markdown/syntax
<hr>
## Python objects, basic types, and variables
Everything in Python is an **object** and every object in Python has a **type**. Some of the basic types include:
- **`int`** (integer; a whole number with no decimal place)
- `10`
- `-3`
- **`float`** (float; a number that has a decimal place)
- `7.41`
- `-0.006`
- **`str`** (string; a sequence of characters enclosed in single quotes, double quotes, or triple quotes)
- `'this is a string using single quotes'`
- `"this is a string using double quotes"`
- `'''this is a triple quoted string using single quotes'''`
- `"""this is a triple quoted string using double quotes"""`
- **`bool`** (boolean; a binary value that is either true or false)
- `True`
- `False`
- **`NoneType`** (a special type representing the absence of a value)
- `None`
In Python, a **variable** is a name you specify in your code that maps to a particular **object**, object **instance**, or value.
By defining variables, we can refer to things by names that make sense to us. Names for variables can only contain letters, underscores (`_`), or numbers (no spaces, dashes, or other characters). Variable names must start with a letter or underscore.
<hr>
## Basic operators
In Python, there are different types of **operators** (special symbols) that operate on different values. Some of the basic operators include:
- arithmetic operators
- **`+`** (addition)
- **`-`** (subtraction)
- **`*`** (multiplication)
- **`/`** (division)
- __`**`__ (exponent)
- assignment operators
- **`=`** (assign a value)
- **`+=`** (add and re-assign; increment)
- **`-=`** (subtract and re-assign; decrement)
- **`*=`** (multiply and re-assign)
- comparison operators (return either `True` or `False`)
- **`==`** (equal to)
- **`!=`** (not equal to)
- **`<`** (less than)
- **`<=`** (less than or equal to)
- **`>`** (greater than)
- **`>=`** (greater than or equal to)
When multiple operators are used in a single expression, **operator precedence** determines which parts of the expression are evaluated in which order. Operators with higher precedence are evaluated first (like PEMDAS in math). Operators with the same precedence are evaluated from left to right.
- `()` parentheses, for grouping
- `**` exponent
- `*`, `/` multiplication and division
- `+`, `-` addition and subtraction
- `==`, `!=`, `<`, `<=`, `>`, `>=` comparisons
> See https://docs.python.org/3/reference/expressions.html#operator-precedence
```
# Assigning some numbers to different variables
num1 = 10
num2 = -3
num3 = 7.41
num4 = -.6
num5 = 7
num6 = 3
num7 = 11.11
# Addition
num1 + num2
# Subtraction
num2 - num3
# Multiplication
num3 * num4
# Division
num4 / num5
# Exponent
num5 ** num6
# Increment existing variable
num7 += 4
num7
# Decrement existing variable
num6 -= 2
num6
# Multiply & re-assign
num3 *= 5
num3
# Assign the value of an expression to a variable
num8 = num1 + num2 * num3
num8
# Are these two expressions equal to each other?
num1 + num2 == num5
# Are these two expressions not equal to each other?
num3 != num4
# Is the first expression less than the second expression?
num5 < num6
# Is this expression True?
5 > 3 > 1
# Is this expression True?
5 > 3 < 4 == 3 + 1
# Assign some strings to different variables
simple_string1 = 'an example'
simple_string2 = "oranges "
# Addition
simple_string1 + ' of using the + operator'
# Notice that the string was not modified
simple_string1
# Multiplication
simple_string2 * 4
# This string wasn't modified either
simple_string2
# Are these two expressions equal to each other?
simple_string1 == simple_string2
# Are these two expressions equal to each other?
simple_string1 == 'an example'
# Add and re-assign
simple_string1 += ' that re-assigned the original string'
simple_string1
# Multiply and re-assign
simple_string2 *= 3
simple_string2
# Note: Subtraction, division, and decrement operators do not apply to strings.
```
## Basic containers
> Note: **mutable** objects can be modified after creation and **immutable** objects cannot.
Containers are objects that can be used to group other objects together. The basic container types include:
- **`str`** (string: immutable; indexed by integers; items are stored in the order they were added)
- **`list`** (list: mutable; indexed by integers; items are stored in the order they were added)
- `[3, 5, 6, 3, 'dog', 'cat', False]`
- **`tuple`** (tuple: immutable; indexed by integers; items are stored in the order they were added)
- `(3, 5, 6, 3, 'dog', 'cat', False)`
- **`set`** (set: mutable; not indexed at all; items are NOT stored in the order they were added; can only contain immutable objects; does NOT contain duplicate objects)
- `{3, 5, 6, 3, 'dog', 'cat', False}`
- **`dict`** (dictionary: mutable; key-value pairs are indexed by immutable keys; items are NOT stored in the order they were added)
- `{'name': 'Jane', 'age': 23, 'fav_foods': ['pizza', 'fruit', 'fish']}`
When defining lists, tuples, or sets, use commas (,) to separate the individual items. When defining dicts, use a colon (:) to separate keys from values and commas (,) to separate the key-value pairs.
Strings, lists, and tuples are all **sequence types** that can use the `+`, `*`, `+=`, and `*=` operators.
```
# Assign some containers to different variables
list1 = [3, 5, 6, 3, 'dog', 'cat', False]
tuple1 = (3, 5, 6, 3, 'dog', 'cat', False)
set1 = {3, 5, 6, 3, 'dog', 'cat', False}
dict1 = {'name': 'Jane', 'age': 23, 'fav_foods': ['pizza', 'fruit', 'fish']}
# Items in the list object are stored in the order they were added
list1
# Items in the tuple object are stored in the order they were added
tuple1
# Items in the set object are not stored in the order they were added
# Also, notice that the value 3 only appears once in this set object
set1
# Items in the dict object are not stored in the order they were added
dict1
# Add and re-assign
list1 += [5, 'grapes']
list1
# Add and re-assign
tuple1 += (5, 'grapes')
tuple1
# Multiply
[1, 2, 3, 4] * 2
# Multiply
(1, 2, 3, 4) * 3
```
## Accessing data in containers
For strings, lists, tuples, and dicts, we can use **subscript notation** (square brackets) to access data at an index.
- strings, lists, and tuples are indexed by integers, **starting at 0** for first item
- these sequence types also support accesing a range of items, known as **slicing**
- use **negative indexing** to start at the back of the sequence
- dicts are indexed by their keys
> Note: sets are not indexed, so we cannot use subscript notation to access data elements.
```
# Access the first item in a sequence
list1[0]
# Access the last item in a sequence
tuple1[-1]
# Access a range of items in a sequence
simple_string1[3:8]
# Access a range of items in a sequence
tuple1[:-3]
# Access a range of items in a sequence
list1[4:]
# Access an item in a dictionary
dict1['name']
# Access an element of a sequence in a dictionary
dict1['fav_foods'][2]
```
## Python built-in functions and callables
A **function** is a Python object that you can "call" to **perform an action** or compute and **return another object**. You call a function by placing parentheses to the right of the function name. Some functions allow you to pass **arguments** inside the parentheses (separating multiple arguments with a comma). Internal to the function, these arguments are treated like variables.
Python has several useful built-in functions to help you work with different objects and/or your environment. Here is a small sample of them:
- **`type(obj)`** to determine the type of an object
- **`len(container)`** to determine how many items are in a container
- **`callable(obj)`** to determine if an object is callable
- **`sorted(container)`** to return a new list from a container, with the items sorted
- **`sum(container)`** to compute the sum of a container of numbers
- **`min(container)`** to determine the smallest item in a container
- **`max(container)`** to determine the largest item in a container
- **`abs(number)`** to determine the absolute value of a number
- **`repr(obj)`** to return a string representation of an object
> Complete list of built-in functions: https://docs.python.org/3/library/functions.html
There are also different ways of defining your own functions and callable objects that we will explore later.
```
# Use the type() function to determine the type of an object
type(simple_string1)
# Use the len() function to determine how many items are in a container
len(dict1)
# Use the len() function to determine how many items are in a container
len(simple_string2)
# Use the callable() function to determine if an object is callable
callable(len)
# Use the callable() function to determine if an object is callable
callable(dict1)
# Use the sorted() function to return a new list from a container, with the items sorted
sorted([10, 1, 3.6, 7, 5, 2, -3])
# Use the sorted() function to return a new list from a container, with the items sorted
# - notice that capitalized strings come first
sorted(['dogs', 'cats', 'zebras', 'Chicago', 'California', 'ants', 'mice'])
# Use the sum() function to compute the sum of a container of numbers
sum([10, 1, 3.6, 7, 5, 2, -3])
# Use the min() function to determine the smallest item in a container
min([10, 1, 3.6, 7, 5, 2, -3])
# Use the min() function to determine the smallest item in a container
min(['g', 'z', 'a', 'y'])
# Use the max() function to determine the largest item in a container
max([10, 1, 3.6, 7, 5, 2, -3])
# Use the max() function to determine the largest item in a container
max('gibberish')
# Use the abs() function to determine the absolute value of a number
abs(10)
# Use the abs() function to determine the absolute value of a number
abs(-12)
# Use the repr() function to return a string representation of an object
repr(set1)
```
## Python object attributes (methods and properties)
Different types of objects in Python have different **attributes** that can be referred to by name (similar to a variable). To access an attribute of an object, use a dot (`.`) after the object, then specify the attribute (i.e. `obj.attribute`)
When an attribute of an object is a callable, that attribute is called a **method**. It is the same as a function, only this function is bound to a particular object.
When an attribute of an object is not a callable, that attribute is called a **property**. It is just a piece of data about the object, that is itself another object.
The built-in `dir()` function can be used to return a list of an object's attributes.
<hr>
## Some methods on string objects
- **`.capitalize()`** to return a capitalized version of the string (only first char uppercase)
- **`.upper()`** to return an uppercase version of the string (all chars uppercase)
- **`.lower()`** to return an lowercase version of the string (all chars lowercase)
- **`.count(substring)`** to return the number of occurences of the substring in the string
- **`.startswith(substring)`** to determine if the string starts with the substring
- **`.endswith(substring)`** to determine if the string ends with the substring
- **`.replace(old, new)`** to return a copy of the string with occurences of the "old" replaced by "new"
```
# Assign a string to a variable
a_string = 'tHis is a sTriNg'
# Return a capitalized version of the string
a_string.capitalize()
# Return an uppercase version of the string
a_string.upper()
# Return a lowercase version of the string
a_string.lower()
# Notice that the methods called have not actually modified the string
a_string
# Count number of occurences of a substring in the string
a_string.count('i')
# Count number of occurences of a substring in the string after a certain position
a_string.count('i', 7)
# Count number of occurences of a substring in the string
a_string.count('is')
# Does the string start with 'this'?
a_string.startswith('this')
# Does the lowercase string start with 'this'?
a_string.lower().startswith('this')
# Does the string end with 'Ng'?
a_string.endswith('Ng')
# Return a version of the string with a substring replaced with something else
a_string.replace('is', 'XYZ')
# Return a version of the string with a substring replaced with something else
a_string.replace('i', '!')
# Return a version of the string with the first 2 occurences a substring replaced with something else
a_string.replace('i', '!', 2)
```
## Some methods on list objects
- **`.append(item)`** to add a single item to the list
- **`.extend([item1, item2, ...])`** to add multiple items to the list
- **`.remove(item)`** to remove a single item from the list
- **`.pop()`** to remove and return the item at the end of the list
- **`.pop(index)`** to remove and return an item at an index
## Some methods on set objects
- **`.add(item)`** to add a single item to the set
- **`.update([item1, item2, ...])`** to add multiple items to the set
- **`.update(set2, set3, ...)`** to add items from all provided sets to the set
- **`.remove(item)`** to remove a single item from the set
- **`.pop()`** to remove and return a random item from the set
- **`.difference(set2)`** to return items in the set that are not in another set
- **`.intersection(set2)`** to return items in both sets
- **`.union(set2)`** to return items that are in either set
- **`.symmetric_difference(set2)`** to return items that are only in one set (not both)
- **`.issuperset(set2)`** does the set contain everything in the other set?
- **`.issubset(set2)`** is the set contained in the other set?
## Some methods on dict objects
- **`.update([(key1, val1), (key2, val2), ...])`** to add multiple key-value pairs to the dict
- **`.update(dict2)`** to add all keys and values from another dict to the dict
- **`.pop(key)`** to remove key and return its value from the dict (error if key not found)
- **`.pop(key, default_val)`** to remove key and return its value from the dict (or return default_val if key not found)
- **`.get(key)`** to return the value at a specified key in the dict (or None if key not found)
- **`.get(key, default_val)`** to return the value at a specified key in the dict (or default_val if key not found)
- **`.keys()`** to return a list of keys in the dict
- **`.values()`** to return a list of values in the dict
- **`.items()`** to return a list of key-value pairs (tuples) in the dict
## Positional arguments and keyword arguments to callables
You can call a function/method in a number of different ways:
- `func()`: Call `func` with no arguments
- `func(arg)`: Call `func` with one positional argument
- `func(arg1, arg2)`: Call `func` with two positional arguments
- `func(arg1, arg2, ..., argn)`: Call `func` with many positional arguments
- `func(kwarg=value)`: Call `func` with one keyword argument
- `func(kwarg1=value1, kwarg2=value2)`: Call `func` with two keyword arguments
- `func(kwarg1=value1, kwarg2=value2, ..., kwargn=valuen)`: Call `func` with many keyword arguments
- `func(arg1, arg2, kwarg1=value1, kwarg2=value2)`: Call `func` with positonal arguments and keyword arguments
- `obj.method()`: Same for `func`.. and every other `func` example
When using **positional arguments**, you must provide them in the order that the function defined them (the function's **signature**).
When using **keyword arguments**, you can provide the arguments you want, in any order you want, as long as you specify each argument's name.
When using positional and keyword arguments, positional arguments must come first.
## Formatting strings and using placeholders
## Python "for loops"
It is easy to **iterate** over a collection of items using a **for loop**. The strings, lists, tuples, sets, and dictionaries we defined are all **iterable** containers.
The for loop will go through the specified container, one item at a time, and provide a temporary variable for the current item. You can use this temporary variable like a normal variable.
## Python "if statements" and "while loops"
Conditional expressions can be used with these two **conditional statements**.
The **if statement** allows you to test a condition and perform some actions if the condition evaluates to `True`. You can also provide `elif` and/or `else` clauses to an if statement to take alternative actions if the condition evaluates to `False`.
The **while loop** will keep looping until its conditional expression evaluates to `False`.
> Note: It is possible to "loop forever" when using a while loop with a conditional expression that never evaluates to `False`.
>
> Note: Since the **for loop** will iterate over a container of items until there are no more, there is no need to specify a "stop looping" condition.
## List, set, and dict comprehensions
## Creating objects from arguments or other objects
The basic types and containers we have used so far all provide **type constructors**:
- `int()`
- `float()`
- `str()`
- `list()`
- `tuple()`
- `set()`
- `dict()`
Up to this point, we have been defining objects of these built-in types using some syntactic shortcuts, since they are so common.
Sometimes, you will have an object of one type that you need to convert to another type. Use the **type constructor** for the type of object you want to have, and pass in the object you currently have.
## Importing modules
## Exceptions
## Classes: Creating your own objects
```
# Define a new class called `Thing` that is derived from the base Python object
class Thing(object):
my_property = 'I am a "Thing"'
# Define a new class called `DictThing` that is derived from the `dict` type
class DictThing(dict):
my_property = 'I am a "DictThing"'
print(Thing)
print(type(Thing))
print(DictThing)
print(type(DictThing))
print(issubclass(DictThing, dict))
print(issubclass(DictThing, object))
# Create "instances" of our new classes
t = Thing()
d = DictThing()
print(t)
print(type(t))
print(d)
print(type(d))
# Interact with a DictThing instance just as you would a normal dictionary
d['name'] = 'Sally'
print(d)
d.update({
'age': 13,
'fav_foods': ['pizza', 'sushi', 'pad thai', 'waffles'],
'fav_color': 'green',
})
print(d)
print(d.my_property)
```
## Defining functions and methods
## Creating an initializer method for your classes
## Other "magic methods"
## Context managers and the "with statement"
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.