code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
```
import re
from typing import List
import pandas as pd
import numpy as np
from tqdm.notebook import tqdm
import optuna
from sklearn.metrics import roc_auc_score
from sklearn.preprocessing import OneHotEncoder, StandardScaler, MinMaxScaler, PolynomialFeatures
from sklearn.linear_model import LogisticRegression, SGDClassifier
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
from lightgbm import LGBMClassifier
from catboost import CatBoostClassifier
tqdm.pandas()
# XGB
# fillna числовых колонок как средние значения по соотв колонке,
# TENURE & REGION OneHotEncoded
# StScaler on whole dataset
# target endocding by region and tenure
#import data
train = pd.read_csv('./data/Train_folds.zip')
# train = train[train['kfold'].isin([0, 1, 2])]
test = pd.read_csv('./data/Test.zip')
submission = pd.read_csv('./data/SampleSubmission.csv')
cat_cols = [
'REGION',
'TENURE',
'TOP_PACK'
]
num_cols = [
'MONTANT',
'FREQUENCE_RECH',
'REVENUE',
'ARPU_SEGMENT',
'FREQUENCE',
'DATA_VOLUME',
'ON_NET',
'ORANGE',
'TIGO',
'ZONE1',
'ZONE2',
'REGULARITY',
'FREQ_TOP_PACK',
]
target = 'CHURN'
mapping = {
'D 3-6 month': 1,
'E 6-9 month': 2,
'F 9-12 month': 3,
'G 12-15 month': 4,
'H 15-18 month': 5,
'I 18-21 month': 6,
'J 21-24 month': 7,
'K > 24 month': 8,
'OTHER': 9
}
train['TOP_PACK'] = train['TOP_PACK'].fillna('OTHER')
test['TOP_PACK'] = test['TOP_PACK'].fillna('OTHER')
train['TENURE'] = train['TENURE'].fillna('OTHER')
test['TENURE'] = test['TENURE'].fillna('OTHER')
train['TENURE'] = train['TENURE'].map(mapping)
test['TENURE'] = test['TENURE'].map(mapping)
train['REGION'] = train['REGION'].fillna('OTHER')
test['REGION'] = test['REGION'].fillna('OTHER')
for nc in tqdm(num_cols):
mean = train[nc].mean()
train[nc] = train[nc].fillna(mean)
test[nc] = test[nc].fillna(mean)
train.shape, test.shape
churn_by_tenure = pd.read_csv('./data/agg_by_tenure_churn.csv')
churn_by_tenure = churn_by_tenure.append(pd.DataFrame({'TENURE': [9], 'CHURN_mean': 0, 'CHURN_median': 0}))
train = pd.merge(train, churn_by_tenure[['TENURE', 'CHURN_mean']], left_on='TENURE', right_on='TENURE', how='left')
train = train.rename({'CHURN_mean': 'MEAN_CHURN_BY_TENURE'}, axis='columns')
test = pd.merge(test, churn_by_tenure[['TENURE', 'CHURN_mean']], left_on='TENURE', right_on='TENURE', how='left')
test = test.rename({'CHURN_mean': 'MEAN_CHURN_BY_TENURE'}, axis='columns')
train.shape, test.shape
churn_by_region = pd.read_csv('./data/agg_by_region_churn.csv')
vc = train[train['REGION'] == 'OTHER']['CHURN'].value_counts()
churn_by_region_mean = vc[1]/(vc[0]+vc[1])
churn_by_region = churn_by_region.append(pd.DataFrame({'REGION': ['OTHER'], 'CHURN_mean': churn_by_region_mean, 'CHURN_median': 0}))
train = pd.merge(train, churn_by_region[['REGION', 'CHURN_mean']], left_on='REGION', right_on='REGION', how='left')
train = train.rename({'CHURN_mean': 'MEAN_CHURN_BY_REGION'}, axis='columns')
test = pd.merge(test, churn_by_region[['REGION', 'CHURN_mean']], left_on='REGION', right_on='REGION', how='left')
test = test.rename({'CHURN_mean': 'MEAN_CHURN_BY_REGION'}, axis='columns')
train.shape, test.shape
churn_by_top_pack = train[['TOP_PACK', 'CHURN']].groupby('TOP_PACK').agg({'CHURN': ['mean', 'median']})
churn_by_top_pack.columns = ['_'.join(col).strip() for col in churn_by_top_pack.columns.values]
churn_by_top_pack_mean = np.mean(train[train['TOP_PACK'] == 'OTHER']['CHURN'])
churn_by_top_pack = churn_by_top_pack.reset_index()
d = {
'TOP_PACK': [],
'CHURN_mean': [],
'CHURN_median': []
}
for tp in test['TOP_PACK'].unique():
if tp not in churn_by_top_pack['TOP_PACK'].unique():
d['TOP_PACK'].append(tp)
d['CHURN_mean'].append(churn_by_top_pack_mean)
d['CHURN_median'].append(0)
churn_by_top_pack = churn_by_top_pack.append(pd.DataFrame(d))
train = pd.merge(train, churn_by_top_pack[['TOP_PACK', 'CHURN_mean']], left_on='TOP_PACK', right_on='TOP_PACK', how='left')
train = train.rename({'CHURN_mean': 'MEAN_CHURN_BY_TOP_PACK'}, axis='columns')
test = pd.merge(test, churn_by_top_pack[['TOP_PACK', 'CHURN_mean']], left_on='TOP_PACK', right_on='TOP_PACK', how='left')
test = test.rename({'CHURN_mean': 'MEAN_CHURN_BY_TOP_PACK'}, axis='columns')
train.shape, test.shape
train.head()
useful_cols = [
'REGION',
'TENURE',
# 'MRG', # constant
'TOP_PACK', # wtf column
'MONTANT',
'FREQUENCE_RECH',
'REVENUE',
'ARPU_SEGMENT',
'FREQUENCE',
'DATA_VOLUME',
'ON_NET',
'ORANGE',
'TIGO',
'ZONE1',
'ZONE2',
'REGULARITY',
'FREQ_TOP_PACK',
'MEAN_CHURN_BY_TENURE',
'MEAN_CHURN_BY_REGION',
'MEAN_CHURN_BY_TOP_PACK'
]
for cat_col in cat_cols:
encoder = OneHotEncoder(handle_unknown='ignore')
unique_values = train[cat_col].unique()
one_hot_encoded_cols = [f'{cat_col}_{i}' for i in range(len(unique_values))]
ohe_df = pd.DataFrame(encoder.fit_transform(train[[cat_col]]).toarray(), columns=one_hot_encoded_cols)
ohe_df.index = train.index
train = train.drop(cat_col, axis=1)
train = pd.concat([train, ohe_df], axis=1)
print(f'[{cat_col}] xtrain transformed')
ohe_df = pd.DataFrame(encoder.transform(test[[cat_col]]).toarray(), columns=one_hot_encoded_cols)
ohe_df.index = test.index
test = test.drop(cat_col, axis=1)
test = pd.concat([test, ohe_df], axis=1)
print(f'[{cat_col}] xtest transformed')
useful_cols += one_hot_encoded_cols
useful_cols.remove(cat_col)
scaler = StandardScaler()
train[num_cols] = scaler.fit_transform(train[num_cols])
test[num_cols] = scaler.transform(test[num_cols])
poly = PolynomialFeatures(degree=3, interaction_only=True, include_bias=False)
train_poly = poly.fit_transform(train[num_cols])
test_poly = poly.fit_transform(test[num_cols])
poly_columns = [f'poly_{x.replace(" ", "__")}' for x in poly.get_feature_names(num_cols)] # [f"poly_{i}" for i in range(train_poly.shape[1])]
df_poly = pd.DataFrame(train_poly, columns=poly_columns, dtype=np.float32)
df_test_poly = pd.DataFrame(test_poly, columns=poly_columns, dtype=np.float32)
train = pd.concat([train, df_poly], axis=1)
test = pd.concat([test, df_test_poly], axis=1)
useful_cols += poly_columns
train.head()
original_columns = [x for x in train.columns if not x.startswith(('poly', 'MEAN_', 'REGION_', 'TENURE_', 'TOP_PACK_'))]
train[original_columns]
for col in [x for x in original_columns if x != 'user_id' and x != 'MRG']:
print(f'{col}:', train[[col]].corrwith(train['CHURN']).iloc[-1])
# from sklearn.preprocessing import MinMaxScaler
# def corr(df: pd.DataFrame) -> None:
# for col in [x for x in list(df) if x != 'CHURN']:
# print(f'{col}:', df[[col]].corrwith(df['CHURN']).iloc[-1])
# tmp = pd.DataFrame({
# 'CHURN': train['CHURN'],
# 'REG': train['REGULARITY'],
# })
# tmp['REG_LOG'] = tmp['REG'].apply(np.log)
# tmp['REG_SQRT'] = tmp['REG'].apply(np.sqrt)
# tmp['REG_ABS'] = tmp['REG'].apply(np.abs)
# tmp['REG_POW2'] = tmp['REG'].apply(lambda x: x ** 2)
# tmp['REG_ABS_LOG'] = tmp['REG_ABS'].apply(np.log)
# tmp['REG_ABS_SQRT'] = tmp['REG_ABS'].apply(np.sqrt)
# corr(tmp)
# scaler = MinMaxScaler()
# arr_scaled = scaler.fit_transform([tmp['REG_ABS_SQRT']])
maximum = tmp['REG_ABS_SQRT'].max()
minumum = tmp['REG_ABS_SQRT'].min()
pd.DataFrame({'c': tmp['REG_ABS_SQRT'].apply(lambda x: (x - minumum) / (maximum - minumum))}).corrwith(tmp['CHURN'])
def optimize_floats(df: pd.DataFrame) -> pd.DataFrame:
floats = df.select_dtypes(include=['float64']).columns.tolist()
df[floats] = df[floats].apply(pd.to_numeric, downcast='float')
return df
def optimize_ints(df: pd.DataFrame) -> pd.DataFrame:
ints = df.select_dtypes(include=['int64']).columns.tolist()
df[ints] = df[ints].apply(pd.to_numeric, downcast='integer')
return df
def optimize_objects(df: pd.DataFrame, datetime_features: List[str]) -> pd.DataFrame:
for col in df.select_dtypes(include=['object']):
if col not in datetime_features:
num_unique_values = len(df[col].unique())
num_total_values = len(df[col])
if float(num_unique_values) / num_total_values < 0.5:
df[col] = df[col].astype('category')
else:
df[col] = pd.to_datetime(df[col])
return df
def optimize(df: pd.DataFrame, datetime_features: List[str] = []):
return optimize_floats(optimize_ints(optimize_objects(df, datetime_features)))
train = optimize(train, [])
sum(train.memory_usage())/1024/1024
def fit_predict(xtrain: pd.DataFrame,
ytrain: pd.DataFrame,
xvalid: pd.DataFrame = None,
yvalid: pd.DataFrame = None,
valid_ids: list[str] = None):
xtest = test[useful_cols]
model = LGBMClassifier(
n_estimators=7000,
n_jobs=-1,
random_state=42,
# xgb
# **{
# 'learning_rate': 0.014461849398074727,
# 'reg_lambda': 0.08185850904776007,
# 'reg_alpha': 0.0001173486815850512,
# 'subsample': 0.7675905290878289,
# 'colsample_bytree': 0.2708299922996371,
# 'max_depth': 7
# }
# lbg
**{
'learning_rate': 0.029253877255476443,
'reg_lambda': 16.09426889606859,
'reg_alpha': 0.014354120473120952,
'subsample': 0.43289663848783977,
'colsample_bytree': 0.5268279718406376,
'max_depth': 6
}
)
if xvalid is not None:
model.fit(xtrain, ytrain, early_stopping_rounds=300, eval_set=[(xvalid, yvalid)], verbose=1000)
preds_valid = model.predict_proba(xvalid)[:, 1]
test_preds = model.predict_proba(xtest)[:, 1]
score = roc_auc_score(yvalid, preds_valid)
print(fold, score)
return model, test_preds, dict(zip(valid_ids, preds_valid)), score
model.fit(xtrain, ytrain, verbose=1000)
return model, None, None, None
final_test_predictions = []
final_valid_predictions = {}
scores = []
for fold in tqdm(range(2), 'folds'):
xtrain = train[train['kfold'] != fold][useful_cols]
ytrain = train[train['kfold'] != fold][target]
xvalid = train[train['kfold'] == fold][useful_cols]
yvalid = train[train['kfold'] == fold][target]
valid_ids = train[train['kfold'] == fold]['user_id'].values.tolist()
# xtest = test[useful_cols]
# model = LGBMClassifier(
# n_estimators=7000,
# n_jobs=-1,
# random_state=42,
# tree_method='gpu_hist',
# gpu_id=0,
# predictor="gpu_predictor",
# **{
# 'learning_rate': 0.014461849398074727,
# 'reg_lambda': 0.08185850904776007,
# 'reg_alpha': 0.0001173486815850512,
# 'subsample': 0.7675905290878289,
# 'colsample_bytree': 0.2708299922996371,
# 'max_depth': 7
# }
# )
# model.fit(xtrain, ytrain, early_stopping_rounds=300, eval_set=[(xvalid, yvalid)], verbose=1000)
# preds_valid = model.predict_proba(xvalid)[:, 1]
# test_preds = model.predict_proba(xtest)[:, 1]
# final_test_predictions.append(test_preds)
# final_valid_predictions.update(dict(zip(valid_ids, preds_valid)))
# score = roc_auc_score(yvalid, preds_valid)
model, test_preds, val_preds, score = fit_predict(xtrain, ytrain, xvalid, yvalid, valid_ids)
del xtrain
del ytrain
del xvalid
del yvalid
del valid_ids
del model
scores.append(score)
print(fold, score)
print(np.mean(scores), np.std(scores))
final_test_predictions = []
final_valid_predictions = {}
scores = []
model, test_preds, val_preds, score = fit_predict(train[useful_cols], train[target])
preds = model.predict_proba(test[useful_cols])
preds
sample_submission = pd.read_csv('./data/SampleSubmission.csv')
sample_submission['CHURN'] = preds[:, 1]
sample_submission.to_csv("./data/2021-10-29-01-03-lgb-full-dataset.csv", index=False)
def fit_predict(xtrain: pd.DataFrame, ytrain: pd.DataFrame, xvalid: pd.DataFrame, yvalid: pd.DataFrame, valid_ids: list[str]):
xtest = test[useful_cols]
model = XGBClassifier(
n_estimators=7000,
n_jobs=-1,
random_state=42,
tree_method='gpu_hist',
gpu_id=0,
predictor="gpu_predictor",
# xgb
# **{
# 'learning_rate': 0.014461849398074727,
# 'reg_lambda': 0.08185850904776007,
# 'reg_alpha': 0.0001173486815850512,
# 'subsample': 0.7675905290878289,
# 'colsample_bytree': 0.2708299922996371,
# 'max_depth': 7
# }
# lbg
**{
'learning_rate': 0.029253877255476443,
'reg_lambda': 16.09426889606859,
'reg_alpha': 0.014354120473120952,
'subsample': 0.43289663848783977,
'colsample_bytree': 0.5268279718406376,
'max_depth': 6
}
)
model.fit(xtrain, ytrain, early_stopping_rounds=300, eval_set=[(xvalid, yvalid)], verbose=1000)
preds_valid = model.predict_proba(xvalid)[:, 1]
test_preds = model.predict_proba(xtest)[:, 1]
score = roc_auc_score(yvalid, preds_valid)
print(fold, score)
return test_preds, dict(zip(valid_ids, preds_valid)), score
final_test_predictions = []
final_valid_predictions = {}
scores = []
folds = train['kfold'].unique()
for fold in tqdm([0,1,2], 'folds'):
xtrain = train[train['kfold'] != fold][useful_cols]
ytrain = train[train['kfold'] != fold][target]
xvalid = train[train['kfold'] == fold][useful_cols]
yvalid = train[train['kfold'] == fold][target]
valid_ids = train[train['kfold'] == fold]['user_id'].values.tolist()
test_preds, val_preds, score = fit_predict(xtrain, ytrain, xvalid, yvalid, valid_ids)
final_test_predictions.append(test_preds)
final_valid_predictions.update(val_preds)
scores.append(score)
print(np.mean(scores), np.std(scores))
sample_submission = pd.read_csv('./data/SampleSubmission.csv')
sample_submission['CHURN'] = np.mean(np.column_stack(final_test_predictions), axis=1)
# sample_submission.columns = ["id", "pred_1"]
sample_submission.to_csv("./data/2021-10-27-xgb.csv", index=False)
sample_submission
val = train[train['kfold'] == 1]
train = train[train['kfold'] == 0]
print(train.shape, val.shape)
train_copy = train.copy()
test_copy = test.copy()
val_copy = val.copy()
minmax_scaler_cols = ['DATA_VOLUME', 'ON_NET']
scaler = MinMaxScaler()
train_copy[minmax_scaler_cols] = scaler.fit_transform(train_copy[minmax_scaler_cols])
test_copy[minmax_scaler_cols] = scaler.transform(test_copy[minmax_scaler_cols])
standard_scaler_cols = [col for col in train_copy.columns if col not in set(['user_id', 'MRG', 'TOP_PACK', 'REGION', 'DATA_VOLUME', 'ON_NET', 'kfold', 'CHURN'])]
scaler = StandardScaler()
train_copy[standard_scaler_cols] = scaler.fit_transform(train_copy[standard_scaler_cols])
test_copy[standard_scaler_cols] = scaler.transform(test_copy[standard_scaler_cols])
# poly features
numerical_cols = [
'DATA_VOLUME',
'ON_NET',
# 'MONTANT',
# 'FREQUENCE_RECH',
# 'REVENUE',
# 'ARPU_SEGMENT',
# 'FREQUENCE',
'ORANGE',
'TIGO',
# 'ZONE1',
# 'ZONE2',
# 'REGULARITY',
]
poly = PolynomialFeatures(degree=3, interaction_only=True, include_bias=False)
train_poly = poly.fit_transform(train_copy[numerical_cols])
test_poly = poly.fit_transform(test_copy[numerical_cols])
poly_columns = [f"poly_{i}" for i in range(train_poly.shape[1])]
df_poly = pd.DataFrame(train_poly, columns=poly_columns)
df_test_poly = pd.DataFrame(test_poly, columns=poly_columns)
train_copy = pd.concat([train_copy, df_poly], axis=1)
test_copy = pd.concat([test_copy, df_test_poly], axis=1)
useful_cols += poly_columns
for cat_col in cat_cols:
encoder = OneHotEncoder(handle_unknown='ignore')
unique_values = train_copy[cat_col].unique()
one_hot_encoded_cols = [f'{cat_col}_{i}' for i in range(len(unique_values))]
ohe_df = pd.DataFrame(encoder.fit_transform(train_copy[[cat_col]]).toarray(), columns=one_hot_encoded_cols)
ohe_df.index = train_copy.index
train_copy = train_copy.drop(cat_col, axis=1)
train_copy = pd.concat([train_copy, ohe_df], axis=1)
print(f'[{cat_col}] xtrain transformed')
ohe_df = pd.DataFrame(encoder.transform(test_copy[[cat_col]]).toarray(), columns=one_hot_encoded_cols)
ohe_df.index = test_copy.index
test_copy = test_copy.drop(cat_col, axis=1)
test_copy = pd.concat([test_copy, ohe_df], axis=1)
print(f'[{cat_col}] xtest transformed')
useful_cols += one_hot_encoded_cols
useful_cols.remove(cat_col)
useful_cols = [col for col in train.columns if col not in set(['user_id',
'MRG',
'TOP_PACK',
'CHURN',
'kfold'])]
lgb = LGBMClassifier(random_state=42)
lgb.fit(train[useful_cols], train[target])
```
| github_jupyter |
<a href="https://colab.research.google.com/github/yukinaga/minnano_ai/blob/master/section_7/ml_libraries.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 機械学習ライブラリ
機械学習ライブラリ、KerasとPyTorchのコードを紹介します。
今回はコードの詳しい解説は行いませんが、実装の大まかな流れを把握しましょう。
## ● Kerasのコード
以下のコードは、Kerasによるシンプルなニューラルネットワークの実装です。
Irisの各花を、SetosaとVersicolorに分類します。
以下のコードでは、`Sequential`でモデルを作り、層や活性化関数を追加しています。
```
import numpy as np
from sklearn import datasets
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
iris_data = iris.data
sl_data = iris_data[:100, 0] # SetosaとVersicolor、Sepal length
sw_data = iris_data[:100, 1] # SetosaとVersicolor、Sepal width
# 平均値を0に
sl_ave = np.average(sl_data) # 平均値
sl_data -= sl_ave # 平均値を引く
sw_ave = np.average(sw_data)
sw_data -= sw_ave
# 入力をリストに格納
input_data = []
correct_data = []
for i in range(100):
input_data.append([sl_data[i], sw_data[i]])
correct_data.append([iris.target[i]])
# 訓練データとテストデータに分割
input_data = np.array(input_data) # NumPyの配列に変換
correct_data = np.array(correct_data)
x_train, x_test, t_train, t_test = train_test_split(input_data, correct_data)
# ------ ここからKerasのコード ------
from keras.utils import np_utils
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
model = Sequential()
model.add(Dense(2, input_dim=2)) # 入力:2、中間層のニューロン数:2
model.add(Activation("sigmoid")) # シグモイド関数
model.add(Dense(1)) # 出力層のニューロン数:1
model.add(Activation("sigmoid")) # シグモイド関数
model.compile(optimizer=SGD(lr=0.3), loss="mean_squared_error", metrics=["accuracy"])
model.fit(x_train, t_train, epochs=32, batch_size=1) # 訓練
loss, accuracy = model.evaluate(x_test, t_test)
print("正解率: " + str(accuracy*100) + "%")
```
## ● PyTorchのコード
以下のコードは、PyTorchよるシンプルなニューラルネットワークの実装です。
Irisの各花を、SetosaとVersicolorに分類します。
以下のコードでは、Kerasと同様に`Sequential`でモデルを作り、層や活性化関数を並べています。
PyTorchでは、入力や正解をTensor形式のデータに変換する必要があります。
```
import numpy as np
from sklearn import datasets
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
iris_data = iris.data
sl_data = iris_data[:100, 0] # SetosaとVersicolor、Sepal length
sw_data = iris_data[:100, 1] # SetosaとVersicolor、Sepal width
# 平均値を0に
sl_ave = np.average(sl_data) # 平均値
sl_data -= sl_ave # 平均値を引く
sw_ave = np.average(sw_data)
sw_data -= sw_ave
# 入力をリストに格納
input_data = []
correct_data = []
for i in range(100):
input_data.append([sl_data[i], sw_data[i]])
correct_data.append([iris.target[i]])
# 訓練データとテストデータに分割
input_data = np.array(input_data) # NumPyの配列に変換
correct_data = np.array(correct_data)
x_train, x_test, t_train, t_test = train_test_split(input_data, correct_data)
# ------ ここからPyTorchのコード ------
import torch
from torch import nn
from torch import optim
# Tensorに変換
x_train = torch.tensor(x_train, dtype=torch.float32)
t_train = torch.tensor(t_train, dtype=torch.float32)
x_test = torch.tensor(x_test, dtype=torch.float32)
t_test = torch.tensor(t_test, dtype=torch.float32)
net = nn.Sequential(
nn.Linear(2, 2), # 入力:2、中間層のニューロン数:2
nn.Sigmoid(), # シグモイド関数
nn.Linear(2, 1), # 出力層のニューロン数:1
nn.Sigmoid() # シグモイド関数
)
loss_fnc = nn.MSELoss()
optimizer = optim.SGD(net.parameters(), lr=0.3)
# 1000エポック学習
for i in range(1000):
# 勾配を0に
optimizer.zero_grad()
# 順伝播
y_train = net(x_train)
y_test = net(x_test)
# 誤差を求める
loss_train = loss_fnc(y_train, t_train)
loss_test = loss_fnc(y_test, t_test)
# 逆伝播(勾配を求める)
loss_train.backward()
# パラメータの更新
optimizer.step()
if i%100 == 0:
print("Epoch:", i, "Loss_Train:", loss_train.item(), "Loss_Test:", loss_test.item())
y_test = net(x_test)
count = ((y_test.detach().numpy()>0.5) == (t_test.detach().numpy()==1.0)).sum().item()
print("正解率: " + str(count/len(y_test)*100) + "%")
```
| github_jupyter |
# Transfer Learning Template
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import os, json, sys, time, random
import numpy as np
import torch
from torch.optim import Adam
from easydict import EasyDict
import matplotlib.pyplot as plt
from steves_models.steves_ptn import Steves_Prototypical_Network
from steves_utils.lazy_iterable_wrapper import Lazy_Iterable_Wrapper
from steves_utils.iterable_aggregator import Iterable_Aggregator
from steves_utils.ptn_train_eval_test_jig import PTN_Train_Eval_Test_Jig
from steves_utils.torch_sequential_builder import build_sequential
from steves_utils.torch_utils import get_dataset_metrics, ptn_confusion_by_domain_over_dataloader
from steves_utils.utils_v2 import (per_domain_accuracy_from_confusion, get_datasets_base_path)
from steves_utils.PTN.utils import independent_accuracy_assesment
from torch.utils.data import DataLoader
from steves_utils.stratified_dataset.episodic_accessor import Episodic_Accessor_Factory
from steves_utils.ptn_do_report import (
get_loss_curve,
get_results_table,
get_parameters_table,
get_domain_accuracies,
)
from steves_utils.transforms import get_chained_transform
```
# Allowed Parameters
These are allowed parameters, not defaults
Each of these values need to be present in the injected parameters (the notebook will raise an exception if they are not present)
Papermill uses the cell tag "parameters" to inject the real parameters below this cell.
Enable tags to see what I mean
```
required_parameters = {
"experiment_name",
"lr",
"device",
"seed",
"dataset_seed",
"n_shot",
"n_query",
"n_way",
"train_k_factor",
"val_k_factor",
"test_k_factor",
"n_epoch",
"patience",
"criteria_for_best",
"x_net",
"datasets",
"torch_default_dtype",
"NUM_LOGS_PER_EPOCH",
"BEST_MODEL_PATH",
}
from steves_utils.CORES.utils import (
ALL_NODES,
ALL_NODES_MINIMUM_1000_EXAMPLES,
ALL_DAYS
)
from steves_utils.ORACLE.utils_v2 import (
ALL_DISTANCES_FEET_NARROWED,
ALL_RUNS,
ALL_SERIAL_NUMBERS,
)
standalone_parameters = {}
standalone_parameters["experiment_name"] = "STANDALONE PTN"
standalone_parameters["lr"] = 0.001
standalone_parameters["device"] = "cuda"
standalone_parameters["seed"] = 1337
standalone_parameters["dataset_seed"] = 1337
standalone_parameters["n_way"] = 8
standalone_parameters["n_shot"] = 3
standalone_parameters["n_query"] = 2
standalone_parameters["train_k_factor"] = 1
standalone_parameters["val_k_factor"] = 2
standalone_parameters["test_k_factor"] = 2
standalone_parameters["n_epoch"] = 50
standalone_parameters["patience"] = 10
standalone_parameters["criteria_for_best"] = "source_loss"
standalone_parameters["datasets"] = [
{
"labels": ALL_SERIAL_NUMBERS,
"domains": ALL_DISTANCES_FEET_NARROWED,
"num_examples_per_domain_per_label": 100,
"pickle_path": os.path.join(get_datasets_base_path(), "oracle.Run1_framed_2000Examples_stratified_ds.2022A.pkl"),
"source_or_target_dataset": "source",
"x_transforms": ["unit_mag", "minus_two"],
"episode_transforms": [],
"domain_prefix": "ORACLE_"
},
{
"labels": ALL_NODES,
"domains": ALL_DAYS,
"num_examples_per_domain_per_label": 100,
"pickle_path": os.path.join(get_datasets_base_path(), "cores.stratified_ds.2022A.pkl"),
"source_or_target_dataset": "target",
"x_transforms": ["unit_power", "times_zero"],
"episode_transforms": [],
"domain_prefix": "CORES_"
}
]
standalone_parameters["torch_default_dtype"] = "torch.float32"
standalone_parameters["x_net"] = [
{"class": "nnReshape", "kargs": {"shape":[-1, 1, 2, 256]}},
{"class": "Conv2d", "kargs": { "in_channels":1, "out_channels":256, "kernel_size":(1,7), "bias":False, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":256}},
{"class": "Conv2d", "kargs": { "in_channels":256, "out_channels":80, "kernel_size":(2,7), "bias":True, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 80*256, "out_features": 256}}, # 80 units per IQ pair
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features":256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
]
# Parameters relevant to results
# These parameters will basically never need to change
standalone_parameters["NUM_LOGS_PER_EPOCH"] = 10
standalone_parameters["BEST_MODEL_PATH"] = "./best_model.pth"
# Parameters
parameters = {
"experiment_name": "cores+wisig -> oracle.run2.framed",
"device": "cuda",
"lr": 0.001,
"seed": 1337,
"dataset_seed": 1337,
"n_shot": 3,
"n_query": 2,
"train_k_factor": 3,
"val_k_factor": 2,
"test_k_factor": 2,
"torch_default_dtype": "torch.float32",
"n_epoch": 50,
"patience": 3,
"criteria_for_best": "target_loss",
"x_net": [
{"class": "nnReshape", "kargs": {"shape": [-1, 1, 2, 256]}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 1,
"out_channels": 256,
"kernel_size": [1, 7],
"bias": False,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 256}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 256,
"out_channels": 80,
"kernel_size": [2, 7],
"bias": True,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 20480, "out_features": 256}},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features": 256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
],
"NUM_LOGS_PER_EPOCH": 10,
"BEST_MODEL_PATH": "./best_model.pth",
"n_way": 16,
"datasets": [
{
"labels": [
"1-10.",
"1-11.",
"1-15.",
"1-16.",
"1-17.",
"1-18.",
"1-19.",
"10-4.",
"10-7.",
"11-1.",
"11-14.",
"11-17.",
"11-20.",
"11-7.",
"13-20.",
"13-8.",
"14-10.",
"14-11.",
"14-14.",
"14-7.",
"15-1.",
"15-20.",
"16-1.",
"16-16.",
"17-10.",
"17-11.",
"17-2.",
"19-1.",
"19-16.",
"19-19.",
"19-20.",
"19-3.",
"2-10.",
"2-11.",
"2-17.",
"2-18.",
"2-20.",
"2-3.",
"2-4.",
"2-5.",
"2-6.",
"2-7.",
"2-8.",
"3-13.",
"3-18.",
"3-3.",
"4-1.",
"4-10.",
"4-11.",
"4-19.",
"5-5.",
"6-15.",
"7-10.",
"7-14.",
"8-18.",
"8-20.",
"8-3.",
"8-8.",
],
"domains": [1, 2, 3, 4, 5],
"num_examples_per_domain_per_label": 100,
"pickle_path": "/mnt/wd500GB/CSC500/csc500-main/datasets/cores.stratified_ds.2022A.pkl",
"source_or_target_dataset": "source",
"x_transforms": ["unit_mag"],
"episode_transforms": [],
"domain_prefix": "C_A_",
},
{
"labels": [
"1-10",
"1-12",
"1-14",
"1-16",
"1-18",
"1-19",
"1-8",
"10-11",
"10-17",
"10-4",
"10-7",
"11-1",
"11-10",
"11-19",
"11-20",
"11-4",
"11-7",
"12-19",
"12-20",
"12-7",
"13-14",
"13-18",
"13-19",
"13-20",
"13-3",
"13-7",
"14-10",
"14-11",
"14-12",
"14-13",
"14-14",
"14-19",
"14-20",
"14-7",
"14-8",
"14-9",
"15-1",
"15-19",
"15-6",
"16-1",
"16-16",
"16-19",
"16-20",
"17-10",
"17-11",
"18-1",
"18-10",
"18-11",
"18-12",
"18-13",
"18-14",
"18-15",
"18-16",
"18-17",
"18-19",
"18-2",
"18-20",
"18-4",
"18-5",
"18-7",
"18-8",
"18-9",
"19-1",
"19-10",
"19-11",
"19-12",
"19-13",
"19-14",
"19-15",
"19-19",
"19-2",
"19-20",
"19-3",
"19-4",
"19-6",
"19-7",
"19-8",
"19-9",
"2-1",
"2-13",
"2-15",
"2-3",
"2-4",
"2-5",
"2-6",
"2-7",
"2-8",
"20-1",
"20-12",
"20-14",
"20-15",
"20-16",
"20-18",
"20-19",
"20-20",
"20-3",
"20-4",
"20-5",
"20-7",
"20-8",
"3-1",
"3-13",
"3-18",
"3-2",
"3-8",
"4-1",
"4-10",
"4-11",
"5-1",
"5-5",
"6-1",
"6-15",
"6-6",
"7-10",
"7-11",
"7-12",
"7-13",
"7-14",
"7-7",
"7-8",
"7-9",
"8-1",
"8-13",
"8-14",
"8-18",
"8-20",
"8-3",
"8-8",
"9-1",
"9-7",
],
"domains": [1, 2, 3, 4],
"num_examples_per_domain_per_label": 100,
"pickle_path": "/mnt/wd500GB/CSC500/csc500-main/datasets/wisig.node3-19.stratified_ds.2022A.pkl",
"source_or_target_dataset": "source",
"x_transforms": ["unit_mag"],
"episode_transforms": [],
"domain_prefix": "W_A_",
},
{
"labels": [
"3123D52",
"3123D65",
"3123D79",
"3123D80",
"3123D54",
"3123D70",
"3123D7B",
"3123D89",
"3123D58",
"3123D76",
"3123D7D",
"3123EFE",
"3123D64",
"3123D78",
"3123D7E",
"3124E4A",
],
"domains": [32, 38, 8, 44, 14, 50, 20, 26],
"num_examples_per_domain_per_label": 2000,
"pickle_path": "/mnt/wd500GB/CSC500/csc500-main/datasets/oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl",
"source_or_target_dataset": "target",
"x_transforms": ["unit_mag"],
"episode_transforms": [],
"domain_prefix": "ORACLE.run2_",
},
],
}
# Set this to True if you want to run this template directly
STANDALONE = False
if STANDALONE:
print("parameters not injected, running with standalone_parameters")
parameters = standalone_parameters
if not 'parameters' in locals() and not 'parameters' in globals():
raise Exception("Parameter injection failed")
#Use an easy dict for all the parameters
p = EasyDict(parameters)
supplied_keys = set(p.keys())
if supplied_keys != required_parameters:
print("Parameters are incorrect")
if len(supplied_keys - required_parameters)>0: print("Shouldn't have:", str(supplied_keys - required_parameters))
if len(required_parameters - supplied_keys)>0: print("Need to have:", str(required_parameters - supplied_keys))
raise RuntimeError("Parameters are incorrect")
###################################
# Set the RNGs and make it all deterministic
###################################
np.random.seed(p.seed)
random.seed(p.seed)
torch.manual_seed(p.seed)
torch.use_deterministic_algorithms(True)
###########################################
# The stratified datasets honor this
###########################################
torch.set_default_dtype(eval(p.torch_default_dtype))
###################################
# Build the network(s)
# Note: It's critical to do this AFTER setting the RNG
###################################
x_net = build_sequential(p.x_net)
start_time_secs = time.time()
p.domains_source = []
p.domains_target = []
train_original_source = []
val_original_source = []
test_original_source = []
train_original_target = []
val_original_target = []
test_original_target = []
# global_x_transform_func = lambda x: normalize(x.to(torch.get_default_dtype()), "unit_power") # unit_power, unit_mag
# global_x_transform_func = lambda x: normalize(x, "unit_power") # unit_power, unit_mag
def add_dataset(
labels,
domains,
pickle_path,
x_transforms,
episode_transforms,
domain_prefix,
num_examples_per_domain_per_label,
source_or_target_dataset:str,
iterator_seed=p.seed,
dataset_seed=p.dataset_seed,
n_shot=p.n_shot,
n_way=p.n_way,
n_query=p.n_query,
train_val_test_k_factors=(p.train_k_factor,p.val_k_factor,p.test_k_factor),
):
if x_transforms == []: x_transform = None
else: x_transform = get_chained_transform(x_transforms)
if episode_transforms == []: episode_transform = None
else: raise Exception("episode_transforms not implemented")
episode_transform = lambda tup, _prefix=domain_prefix: (_prefix + str(tup[0]), tup[1])
eaf = Episodic_Accessor_Factory(
labels=labels,
domains=domains,
num_examples_per_domain_per_label=num_examples_per_domain_per_label,
iterator_seed=iterator_seed,
dataset_seed=dataset_seed,
n_shot=n_shot,
n_way=n_way,
n_query=n_query,
train_val_test_k_factors=train_val_test_k_factors,
pickle_path=pickle_path,
x_transform_func=x_transform,
)
train, val, test = eaf.get_train(), eaf.get_val(), eaf.get_test()
train = Lazy_Iterable_Wrapper(train, episode_transform)
val = Lazy_Iterable_Wrapper(val, episode_transform)
test = Lazy_Iterable_Wrapper(test, episode_transform)
if source_or_target_dataset=="source":
train_original_source.append(train)
val_original_source.append(val)
test_original_source.append(test)
p.domains_source.extend(
[domain_prefix + str(u) for u in domains]
)
elif source_or_target_dataset=="target":
train_original_target.append(train)
val_original_target.append(val)
test_original_target.append(test)
p.domains_target.extend(
[domain_prefix + str(u) for u in domains]
)
else:
raise Exception(f"invalid source_or_target_dataset: {source_or_target_dataset}")
for ds in p.datasets:
add_dataset(**ds)
# from steves_utils.CORES.utils import (
# ALL_NODES,
# ALL_NODES_MINIMUM_1000_EXAMPLES,
# ALL_DAYS
# )
# add_dataset(
# labels=ALL_NODES,
# domains = ALL_DAYS,
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "cores.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"cores_{u}"
# )
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# add_dataset(
# labels=ALL_SERIAL_NUMBERS,
# domains = list(set(ALL_DISTANCES_FEET) - {2,62}),
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"),
# source_or_target_dataset="source",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"oracle1_{u}"
# )
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# add_dataset(
# labels=ALL_SERIAL_NUMBERS,
# domains = list(set(ALL_DISTANCES_FEET) - {2,62,56}),
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"),
# source_or_target_dataset="source",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"oracle2_{u}"
# )
# add_dataset(
# labels=list(range(19)),
# domains = [0,1,2],
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "metehan.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"met_{u}"
# )
# # from steves_utils.wisig.utils import (
# # ALL_NODES_MINIMUM_100_EXAMPLES,
# # ALL_NODES_MINIMUM_500_EXAMPLES,
# # ALL_NODES_MINIMUM_1000_EXAMPLES,
# # ALL_DAYS
# # )
# import steves_utils.wisig.utils as wisig
# add_dataset(
# labels=wisig.ALL_NODES_MINIMUM_100_EXAMPLES,
# domains = wisig.ALL_DAYS,
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "wisig.node3-19.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"wisig_{u}"
# )
###################################
# Build the dataset
###################################
train_original_source = Iterable_Aggregator(train_original_source, p.seed)
val_original_source = Iterable_Aggregator(val_original_source, p.seed)
test_original_source = Iterable_Aggregator(test_original_source, p.seed)
train_original_target = Iterable_Aggregator(train_original_target, p.seed)
val_original_target = Iterable_Aggregator(val_original_target, p.seed)
test_original_target = Iterable_Aggregator(test_original_target, p.seed)
# For CNN We only use X and Y. And we only train on the source.
# Properly form the data using a transform lambda and Lazy_Iterable_Wrapper. Finally wrap them in a dataloader
transform_lambda = lambda ex: ex[1] # Original is (<domain>, <episode>) so we strip down to episode only
train_processed_source = Lazy_Iterable_Wrapper(train_original_source, transform_lambda)
val_processed_source = Lazy_Iterable_Wrapper(val_original_source, transform_lambda)
test_processed_source = Lazy_Iterable_Wrapper(test_original_source, transform_lambda)
train_processed_target = Lazy_Iterable_Wrapper(train_original_target, transform_lambda)
val_processed_target = Lazy_Iterable_Wrapper(val_original_target, transform_lambda)
test_processed_target = Lazy_Iterable_Wrapper(test_original_target, transform_lambda)
datasets = EasyDict({
"source": {
"original": {"train":train_original_source, "val":val_original_source, "test":test_original_source},
"processed": {"train":train_processed_source, "val":val_processed_source, "test":test_processed_source}
},
"target": {
"original": {"train":train_original_target, "val":val_original_target, "test":test_original_target},
"processed": {"train":train_processed_target, "val":val_processed_target, "test":test_processed_target}
},
})
from steves_utils.transforms import get_average_magnitude, get_average_power
print(set([u for u,_ in val_original_source]))
print(set([u for u,_ in val_original_target]))
s_x, s_y, q_x, q_y, _ = next(iter(train_processed_source))
print(s_x)
# for ds in [
# train_processed_source,
# val_processed_source,
# test_processed_source,
# train_processed_target,
# val_processed_target,
# test_processed_target
# ]:
# for s_x, s_y, q_x, q_y, _ in ds:
# for X in (s_x, q_x):
# for x in X:
# assert np.isclose(get_average_magnitude(x.numpy()), 1.0)
# assert np.isclose(get_average_power(x.numpy()), 1.0)
###################################
# Build the model
###################################
model = Steves_Prototypical_Network(x_net, device=p.device, x_shape=(2,256))
optimizer = Adam(params=model.parameters(), lr=p.lr)
###################################
# train
###################################
jig = PTN_Train_Eval_Test_Jig(model, p.BEST_MODEL_PATH, p.device)
jig.train(
train_iterable=datasets.source.processed.train,
source_val_iterable=datasets.source.processed.val,
target_val_iterable=datasets.target.processed.val,
num_epochs=p.n_epoch,
num_logs_per_epoch=p.NUM_LOGS_PER_EPOCH,
patience=p.patience,
optimizer=optimizer,
criteria_for_best=p.criteria_for_best,
)
total_experiment_time_secs = time.time() - start_time_secs
###################################
# Evaluate the model
###################################
source_test_label_accuracy, source_test_label_loss = jig.test(datasets.source.processed.test)
target_test_label_accuracy, target_test_label_loss = jig.test(datasets.target.processed.test)
source_val_label_accuracy, source_val_label_loss = jig.test(datasets.source.processed.val)
target_val_label_accuracy, target_val_label_loss = jig.test(datasets.target.processed.val)
history = jig.get_history()
total_epochs_trained = len(history["epoch_indices"])
val_dl = Iterable_Aggregator((datasets.source.original.val,datasets.target.original.val))
confusion = ptn_confusion_by_domain_over_dataloader(model, p.device, val_dl)
per_domain_accuracy = per_domain_accuracy_from_confusion(confusion)
# Add a key to per_domain_accuracy for if it was a source domain
for domain, accuracy in per_domain_accuracy.items():
per_domain_accuracy[domain] = {
"accuracy": accuracy,
"source?": domain in p.domains_source
}
# Do an independent accuracy assesment JUST TO BE SURE!
# _source_test_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.test, p.device)
# _target_test_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.test, p.device)
# _source_val_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.val, p.device)
# _target_val_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.val, p.device)
# assert(_source_test_label_accuracy == source_test_label_accuracy)
# assert(_target_test_label_accuracy == target_test_label_accuracy)
# assert(_source_val_label_accuracy == source_val_label_accuracy)
# assert(_target_val_label_accuracy == target_val_label_accuracy)
experiment = {
"experiment_name": p.experiment_name,
"parameters": dict(p),
"results": {
"source_test_label_accuracy": source_test_label_accuracy,
"source_test_label_loss": source_test_label_loss,
"target_test_label_accuracy": target_test_label_accuracy,
"target_test_label_loss": target_test_label_loss,
"source_val_label_accuracy": source_val_label_accuracy,
"source_val_label_loss": source_val_label_loss,
"target_val_label_accuracy": target_val_label_accuracy,
"target_val_label_loss": target_val_label_loss,
"total_epochs_trained": total_epochs_trained,
"total_experiment_time_secs": total_experiment_time_secs,
"confusion": confusion,
"per_domain_accuracy": per_domain_accuracy,
},
"history": history,
"dataset_metrics": get_dataset_metrics(datasets, "ptn"),
}
ax = get_loss_curve(experiment)
plt.show()
get_results_table(experiment)
get_domain_accuracies(experiment)
print("Source Test Label Accuracy:", experiment["results"]["source_test_label_accuracy"], "Target Test Label Accuracy:", experiment["results"]["target_test_label_accuracy"])
print("Source Val Label Accuracy:", experiment["results"]["source_val_label_accuracy"], "Target Val Label Accuracy:", experiment["results"]["target_val_label_accuracy"])
json.dumps(experiment)
```
| github_jupyter |
```
import tqdm
from tqdm import tqdm_notebook
import time
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as axes3d
import matplotlib.ticker as ticker
# import warnings
# warnings.filterwarnings('ignore')
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
# fonts for ICML
def SetPlotRC():
#If fonttype = 1 doesn't work with LaTeX, try fonttype 42.
plt.rc('pdf',fonttype = 42)
plt.rc('ps',fonttype = 42)
SetPlotRC()
def get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title, num_show = []):
acc_num = 3
dist_calc_num = 7
df = []
for i in range(len(file_names)):
file_name = os.path.expanduser(file_names[i])
data = np.genfromtxt(file_name, dtype=('U10','U10','U10',float,'U10',int,'U10',int,'U10',float)).tolist()
cur_line = -1
for mod in range(num_models[i]):
for j in range(num_exper[i]):
cur_line += 1
if y_axe == 11:
df.append([1.00001 - data[cur_line][acc_num],
1 / data[cur_line][y_axe], model_names[i][mod], title])
else:
df.append([1.00001 - data[cur_line][acc_num],
data[cur_line][y_axe], model_names[i][mod], title])
df = pd.DataFrame(df, columns=["Error = 1 - Recall@1", y_axe_name, "algorithm", "title"])
# print(df.shape)
if len(num_show) > 0:
it = 0
itt = 0
num_for_iloc = []
model_names_list = []
for i in range(len(file_names)):
for mod in range(len(model_names[i])):
model_names_list.append(model_names[i][mod])
allowed_set = set()
same_dict = dict()
for i in range(len(file_names)):
for mod in range(len(model_names[i])):
if itt in num_show:
allowed_set.add(model_names_list[i])
for j in range(num_exper[i]):
num_for_iloc.append(it)
it += 1
else:
it += num_exper[i]
itt += 1
df = df.iloc[num_for_iloc]
return df
def show_results(frames, title, y_axe_name, x_log=True, y_log=False,
dims=(18, 12), save=False, file_name='trash'):
size = len(frames)
ylim = [[500, 5000], [0, 1000],[0, 1000],[0, 1000]]
a4_dims = dims
fig, axs = plt.subplots(2, 2, figsize=a4_dims)
for i in range(2):
for j in range(2):
num = i * 2 + j
if i + j == 2:
sns.lineplot(x="Error = 1 - Recall@1", y=y_axe_name,hue="algorithm",
markers=True, style="algorithm", dashes=False,
data=frames[num], ax=axs[i, j], linewidth=3, ms=15)
else:
sns.lineplot(x="Error = 1 - Recall@1", y=y_axe_name,hue="algorithm",
markers=True, style="algorithm", dashes=False,
data=frames[num], ax=axs[i, j], legend=False, linewidth=3, ms=15)
axs[i, j].set_title(title[num], size='30')
lx = axs[i, j].get_xlabel()
ly = axs[i, j].get_ylabel()
axs[i, j].set_xlabel(lx, fontsize=25)
axs[i, j].set_ylabel(ly, fontsize=25)
axs[i, j].tick_params(axis='both', which='both', labelsize=25)
axs[i, j].set_ymargin(0.075)
if i == 0:
axs[i, j].set_xlabel('')
if j == 1:
axs[i, j].set_ylabel('')
# ApplyFont(axs[i,j])
plt.legend(loc=2, bbox_to_anchor=(1.05, 1, 0.5, 0.5), fontsize='30', markerscale=3, borderaxespad=0.)
if y_log:
for i in range(2):
for j in range(2):
axs[i, j].set(yscale="log")
if x_log:
for i in range(2):
for j in range(2):
axs[i, j].set(xscale="log")# num_exper = [6, 6, 3]
if save:
fig.savefig(file_name + ".pdf", bbox_inches='tight')
path = '~/Desktop/results/synthetic_n_10_6_d_'
# path = '~/results/synthetic_n_10_6_d_'
y_axe = 7
y_axe_name = "dist calc"
model_names = [['kNN', 'kNN + Kl', 'kNN + Kl + llf', 'kNN + beam', 'kNN + beam + Kl + llf']]
num_show = [0, 1, 2, 3, 4]
num_exper = [5]
num_models = [5]
file_names = [path + '3.txt']
df_2 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
# print(df_2)
num_exper = [6]
num_models = [5]
file_names = [path + '5.txt']
df_4 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
num_exper = [6]
num_models = [5]
file_names = [path + '9.txt']
df_8 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
num_exper = [6]
num_models = [5]
file_names = [path + '17.txt']
df_16 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
frames = [df_2, df_4, df_8, df_16]
show_results(frames, ['d = 2', 'd = 4', 'd = 8', 'd = 16'], y_axe_name,
y_log=False, x_log=True, dims=(24, 14),
save=False, file_name='synthetic_datasets_2_2_final')
```
## Supplementary
```
def show_results_dist_1_3(frames, title, y_axe_name,
dims=(18, 12), save=False, file_name='trash', legend_size=13):
size = len(frames)
a4_dims = dims
fig, axs = plt.subplots(1, 3, figsize=a4_dims)
for i in range(3):
sns.lineplot(x="Error = 1 - Recall@1", y=y_axe_name,hue="algorithm",
markers=True, style="algorithm", dashes=False,
data=frames[i], ax=axs[i], linewidth=2, ms=10)
axs[i].set_title(title[i], size='20')
lx = axs[i].get_xlabel()
ly = axs[i].get_ylabel()
axs[i].set_xlabel(lx, fontsize=20)
axs[i].set_ylabel(ly, fontsize=20)
axs[i].set_xscale('log')
if i == 0:
axs[i].set_xticks([0.001, 0.01, .1])
else:
axs[i].set_xticks([0.01, 0.1])
axs[i].get_xaxis().set_major_formatter(matplotlib.ticker.ScalarFormatter())
axs[i].tick_params(axis='both', which='both', labelsize=15)
if i > 0:
axs[i].set_ylabel('')
plt.setp(axs[i].get_legend().get_texts(), fontsize=legend_size)
if save:
fig.savefig(file_name + ".pdf", bbox_inches='tight')
y_axe = 7
y_axe_name = "dist calc"
model_names = [['kNN', 'kNN + Kl + llf 4', 'kNN + Kl + llf 8',
'kNN + Kl + llf 16', 'kNN + Kl + llf 32']]
num_show = [0, 1, 2, 3, 4]
num_exper = [6]
num_models = [5]
file_names = [path + '5_nlt.txt']
df_kl_4 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
num_exper = [6]
num_models = [5]
file_names = [path + '9_nlt.txt']
df_kl_8 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
num_exper = [6]
num_models = [5]
file_names = [path + '17_nlt.txt']
df_kl_16 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
frames = [df_kl_4, df_kl_8, df_kl_16]
show_results_dist_1_3(frames, ['d = 4', 'd = 8', 'd = 16'], y_axe_name, dims=(20, 6),
save=False, file_name='suppl_figure_optimal_kl_number')
path_end = '_llt.txt'
y_axe = 7
y_axe_name = "dist calc"
model_names = [['kNN', 'thrNN', 'kNN + Kl-dist + llf', 'kNN + Kl-rank + llf', 'kNN + Kl-rank sample + llf']]
num_show = [0, 1, 2, 3, 4]
num_exper = [6]
num_models = [5]
file_names = [path + '5' + path_end]
df_kl_4 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
num_exper = [6]
num_models = [5]
file_names = [path + '9' + path_end]
df_kl_8 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
num_exper = [6]
num_models = [5]
file_names = [path + '17' + path_end]
df_kl_16 = get_df(num_models, num_exper, file_names, model_names, y_axe, y_axe_name, title="trash", num_show=num_show)
frames = [df_kl_4, df_kl_8, df_kl_16]
show_results_dist_1_3(frames, ['d = 4', 'd = 8', 'd = 16'], y_axe_name, dims=(20, 6),
save=False, file_name='suppl_figure_optimal_kl_type', legend_size=10)
path_start = "~/Desktop/results/distr_to_1_"
path_end = ".txt"
a4_dims = (7, 3)
fig, ax = plt.subplots(figsize=a4_dims)
ax.set_yticks([])
file_name = path_start + "sift" + path_end
file_name = os.path.expanduser(file_name)
distr = np.genfromtxt(file_name)
sns.distplot(distr, label="SIFT")
file_name = path_start + "d_9" + path_end
file_name = os.path.expanduser(file_name)
distr = np.genfromtxt(file_name)
sns.distplot(distr, label="d=8")
file_name = path_start + "d_17" + path_end
file_name = os.path.expanduser(file_name)
distr = np.genfromtxt(file_name)
sns.distplot(distr, label="d=16")
file_name = path_start + "d_33" + path_end
file_name = os.path.expanduser(file_name)
distr = np.genfromtxt(file_name)
sns.distplot(distr, label="d=32")
file_name = path_start + "d_65" + path_end
file_name = os.path.expanduser(file_name)
distr = np.genfromtxt(file_name)
sns.distplot(distr, label="d=64")
plt.legend()
fig.savefig("suppl_dist_disrt.pdf", bbox_inches='tight')
```
| github_jupyter |
# Fig.3 - Comparisons of MDR's AUC across 12 different sets
Change plot's default size and font
```
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [20, 12]
rc = {"font.family" : "sans-serif",
"font.style" : "normal",
"mathtext.fontset" : "dejavusans"}
plt.rcParams.update(rc)
plt.rcParams["font.sans-serif"] = ["Myriad Pro"] + plt.rcParams["font.sans-serif"]
from constant import HEADER_NAME, COLUMNS_TO_DROP
import pandas as pd
TITLE_FONTSIZE = 20
XLABEL_FONTSIZE = 18
```
## PfPR = 0.1%
```
fig, axes = plt.subplots(5, 3, sharex='col', sharey='row',
gridspec_kw={'hspace': 0, 'wspace': 0})
fig.patch.set_facecolor('white')
fig.suptitle('PfPR = 0.1%', y=0.93, fontweight='bold', fontsize=TITLE_FONTSIZE)
# plot IQR of AUC for most-dangerous-triple and -double
from plotter import fig3_dangerous_triple_or_double_AUC_IQR
for (a,b,idx) in zip([1,5,9],[20,40,60],[0,1,2]): # set#, coverage, index#
file_path_cyc = 'raw_data/set%s_c/monthly/set%sc_' % (a,a) +'%smonthly_data_0.txt'
file_path_mft = 'raw_data/set%s_m/monthly/set%sm_' % (a,a) + '%smonthly_data_0.txt'
file_path_adpcyc = 'raw_data/set%s_ac/monthly/set%sac_' % (a,a) + '%smonthly_data_0.txt'
dflist_cyc = []
dflist_mft = []
dflist_adpcyc = []
for i in range(1,101):
dflist_cyc.append(pd.read_csv(file_path_cyc % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
dflist_mft.append(pd.read_csv(file_path_mft % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
dflist_adpcyc.append(pd.read_csv(file_path_adpcyc % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
axes[0][idx].set_title('%s%% coverage' % b, fontsize=XLABEL_FONTSIZE)
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[0][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='TYY..Y2.',
option='triple')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[1][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='KNF..Y2.',
option='triple')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[2][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='DHA-PPQ',
option='double')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[3][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='ASAQ',
option='double')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[4][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='AL',
option='double')
for c in range(5):
for tick in axes[c][0].yaxis.get_major_ticks():
tick.label.set_fontsize(XLABEL_FONTSIZE)
axes[0][0].set_xlim(-1, 22) # left col
axes[0][1].set_xlim(-90/22, 90) # mid col
fig.add_subplot(111, frameon=False)
# hide tick and tick label of the big axis
plt.tick_params(labelcolor='none', top=False, bottom=False, left=False, right=False)
# add common x- and y-labels
plt.xlabel('AUC', fontsize=XLABEL_FONTSIZE)
```
## PfPR = 1%
```
fig, axes = plt.subplots(5, 3, sharex='col', sharey='row',
gridspec_kw={'hspace': 0, 'wspace': 0})
fig.patch.set_facecolor('white')
fig.suptitle('PfPR = 1%', y=0.93, fontweight='bold', fontsize=TITLE_FONTSIZE)
# plot IQR of AUC for most-dangerous-triple and -double
from plotter import fig3_dangerous_triple_or_double_AUC_IQR
for (a,b,idx) in zip([2,6,10],[20,40,60],[0,1,2]): # set#, coverage, index#
file_path_cyc = 'raw_data/set%s_c/monthly/set%sc_' % (a,a) +'%smonthly_data_0.txt'
file_path_mft = 'raw_data/set%s_m/monthly/set%sm_' % (a,a) + '%smonthly_data_0.txt'
file_path_adpcyc = 'raw_data/set%s_ac/monthly/set%sac_' % (a,a) + '%smonthly_data_0.txt'
dflist_cyc = []
dflist_mft = []
dflist_adpcyc = []
for i in range(1,101):
dflist_cyc.append(pd.read_csv(file_path_cyc % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
dflist_mft.append(pd.read_csv(file_path_mft % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
dflist_adpcyc.append(pd.read_csv(file_path_adpcyc % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
axes[0][idx].set_title('%s%% coverage' % b, fontsize=XLABEL_FONTSIZE)
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[0][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='TYY..Y2.',
option='triple')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[1][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='KNF..Y2.',
option='triple')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[2][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='DHA-PPQ',
option='double')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[3][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='ASAQ',
option='double')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[4][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='AL',
option='double')
for c in range(5):
for tick in axes[c][0].yaxis.get_major_ticks():
tick.label.set_fontsize(XLABEL_FONTSIZE)
fig.add_subplot(111, frameon=False)
# hide tick and tick label of the big axis
plt.tick_params(labelcolor='none', top=False, bottom=False, left=False, right=False)
# add common x- and y-labels
plt.xlabel('AUC', fontsize=XLABEL_FONTSIZE)
```
## PfPR = 5%
```
fig, axes = plt.subplots(5, 3, sharex='col', sharey='row',
gridspec_kw={'hspace': 0, 'wspace': 0})
fig.patch.set_facecolor('white')
fig.suptitle('PfPR = 5%', y=0.93, fontweight='bold', fontsize=TITLE_FONTSIZE)
# plot IQR of AUC for most-dangerous-triple and -double
from plotter import fig3_dangerous_triple_or_double_AUC_IQR
for (a,b,idx) in zip([3,7,11],[20,40,60],[0,1,2]): # set#, coverage, index#
file_path_cyc = 'raw_data/set%s_c/monthly/set%sc_' % (a,a) +'%smonthly_data_0.txt'
file_path_mft = 'raw_data/set%s_m/monthly/set%sm_' % (a,a) + '%smonthly_data_0.txt'
file_path_adpcyc = 'raw_data/set%s_ac/monthly/set%sac_' % (a,a) + '%smonthly_data_0.txt'
dflist_cyc = []
dflist_mft = []
dflist_adpcyc = []
for i in range(1,101):
dflist_cyc.append(pd.read_csv(file_path_cyc % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
dflist_mft.append(pd.read_csv(file_path_mft % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
dflist_adpcyc.append(pd.read_csv(file_path_adpcyc % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
axes[0][idx].set_title('%s%% coverage' % b, fontsize=XLABEL_FONTSIZE)
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[0][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='TYY..Y2.',
option='triple')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[1][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='KNF..Y2.',
option='triple')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[2][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='DHA-PPQ',
option='double')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[3][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='ASAQ',
option='double')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[4][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='AL',
option='double')
for c in range(5):
for tick in axes[c][0].yaxis.get_major_ticks():
tick.label.set_fontsize(XLABEL_FONTSIZE)
fig.add_subplot(111, frameon=False)
# hide tick and tick label of the big axis
plt.tick_params(labelcolor='none', top=False, bottom=False, left=False, right=False)
# add common x- and y-labels
plt.xlabel('AUC', fontsize=XLABEL_FONTSIZE)
```
## PfPR = 20%
```
fig, axes = plt.subplots(5, 3, sharex='col', sharey='row',
gridspec_kw={'hspace': 0, 'wspace': 0})
fig.patch.set_facecolor('white')
fig.suptitle('PfPR = 20%', y=0.93, fontweight='bold', fontsize=TITLE_FONTSIZE)
# plot IQR of AUC for most-dangerous-triple and -double
from plotter import fig3_dangerous_triple_or_double_AUC_IQR
for (a,b,idx) in zip([4,8,12],[20,40,60],[0,1,2]): # set#, coverage, index#
file_path_cyc = 'raw_data/set%s_c/monthly/set%sc_' % (a,a) +'%smonthly_data_0.txt'
file_path_mft = 'raw_data/set%s_m/monthly/set%sm_' % (a,a) + '%smonthly_data_0.txt'
file_path_adpcyc = 'raw_data/set%s_ac/monthly/set%sac_' % (a,a) + '%smonthly_data_0.txt'
dflist_cyc = []
dflist_mft = []
dflist_adpcyc = []
for i in range(1,101):
dflist_cyc.append(pd.read_csv(file_path_cyc % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
dflist_mft.append(pd.read_csv(file_path_mft % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
dflist_adpcyc.append(pd.read_csv(file_path_adpcyc % i, index_col=False, \
names=HEADER_NAME, sep='\t').drop(columns=COLUMNS_TO_DROP))
axes[0][idx].set_title('%s%% coverage' % b, fontsize=XLABEL_FONTSIZE)
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[0][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='TYY..Y2.',
option='triple')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[1][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='KNF..Y2.',
option='triple')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[2][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='DHA-PPQ',
option='double')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[3][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='ASAQ',
option='double')
fig3_dangerous_triple_or_double_AUC_IQR(ax=axes[4][idx], m=dflist_mft, c=dflist_cyc,
a=dflist_adpcyc, pattern='AL',
option='double')
for c in range(5):
for tick in axes[c][0].yaxis.get_major_ticks():
tick.label.set_fontsize(XLABEL_FONTSIZE)
fig.add_subplot(111, frameon=False)
# hide tick and tick label of the big axis
plt.tick_params(labelcolor='none', top=False, bottom=False, left=False, right=False)
# add common x- and y-labels
plt.xlabel('AUC', fontsize=XLABEL_FONTSIZE)
```
| github_jupyter |
```
# Define a function calls addNumber(x, y) that takes in two number and returns the sum of the two numbers.
def addNumber(x, y):
return(sum((x, y)))
addNumber(10,20)
# Define a function calls subtractNumber(x, y) that takes in two numbers and returns the difference of the two numbers.
def subtractNumber(x,y):
return(x-y)
subtractNumber(10,20)
# Write a function getBiggerNumber(x, y) that takes in two numbers as arguments and returns the bigger number.
def getBiggerNumber(x,y):
return(max(x,y))
getBiggerNumber(56,32)
# You will need to do a "import math" before you are allowed to use the functions within the math module.
# Calculate the square root of 16 and stores it in the variable a
# Calculate 3 to the power of 5 and stores it in the variable b
# Calculate area of circle with radius = 3.0 by making use of the math.pi constant and store it in the variable c
import math
def sq(sq_root):
a=math.sqrt(sq_root)
return a
sq(16)
def pwr(x,y):
b=math.pow(x,y)
return b
pwr(3,5)
def area(r):
c=round((math.pi)*(r*r),2)
return c
area(3.0)
# Write a function to convert temperature from Celsius to Fahrenheit scale.
# oC to oF Conversion: Multipy by 9, then divide by 5, then add 32.
# Note: Return a string of 2 decimal places.
# In - Cel2Fah(28.0)
# Out - '82.40'
# In - Cel2Fah(0.00)
# Out - '32.00'
import math
def Cel2Fah(cel):
fahrenheit = ((cel * 9)/5) + 32
format='{0:.2f}'.format(fahrenheit)
return (f"'{format}'")
print(Cel2Fah(28.0))
print(Cel2Fah(0.00))
# Write a function to compute the BMI of a person.
# BMI = weight(kg) / ( height(m)*height(m) )
# Note: Return a string of 1 decimal place.
# In - BMI(63, 1.7)
# Out - '21.8'
# In - BMI(110, 2)
# Out - '27.5'
def BMI(weight,Height):
cal=weight/(Height*Height)
format='{0:.1f}'.format(cal)
return (f"'{format}'")
print(BMI(63,1.7))
print(BMI(110,2))
# Write a function to compute the hypotenuse given sides a and b of the triangle.
# Hint: You can use math.sqrt(x) to compute the square root of x.
# In - hypotenuse(3, 4)
# Out - 5
# In - hypotenuse(5, 12)
# Out - 13
from math import sqrt
def hypo(a,b):
return(int(sqrt(a**2 + b**2)))
print(hypo(3,4))
print(hypo(5,12))
# Write a function getSumOfLastDigits() that takes in a list of positive numbers and returns the sum
#of all the last digits in the list.
# getSumOfLastDigits([2, 3, 4])
# 9
# getSumOfLastDigits([1, 23, 456])
# 10
def getSumOfLastDigits(lst):
lst_digit=[]
for i in lst:
lst_digit.append(i % 10)
s=sum(lst_digit)
return s
print(getSumOfLastDigits([2, 3, 4]))
print(getSumOfLastDigits([1, 23, 456]))
# Write a function that uses a default value.
# In - introduce('Lim', 20)
# Out - 'My name is Lim. I am 20 years old.'
# In - introduce('Ahmad')
# Out - 'My name is Ahmad. My age is secret.'
def introduce(name,age='My age is secret'):
if age is introduce.__defaults__[0]:
print(f"My name is {name}.{age}")
else:
print(f"My name is {name}. I am {age} years old.")
introduce('Lim',20)
introduce('Ahmad')
# Write a function isEquilateral(x, y, z) that accepts the 3 sides of a triangle as arguments.
# The program should return True if it is an equilateral triangle.
# In - isEquilateral(2, 4, 3)
# False - False
# In - isEquilateral(3, 3, 3)
# Out - True
# In - isEquilateral(-3, -3, -3)
# Out - False
def Eq(x,y,z):
return (x == y == z )
print(Eq(2,4,3))
print(Eq(3,3,3))
print(Eq(-3,-3,-3))
# For a quadratic equation in the form of ax2+bx+c, the discriminant, D is b2-4ac. Write a function to compute the discriminant, D.
# In - quadratic(1, 2, 3)
# Out - 'The discriminant is -8.'
# In - quadratic(1, 3, 2)
# Out - 'The discriminant is 1.'
# In - quadratic(1, 4, 4)
# Out - 'The discriminant is 0.'
def qa(a,b,c):
d= (b*b)-(4*a*c)
print(f"The discriminant is {d}")
#return(d)
qa(1, 2, 3)
qa(1,3,2)
qa(1,4,4)
# Define a function calls addFirstAndLast(x) that takes in a list of numbers and returns the sum of the first and last numbers.
# In - addFirstAndLast([])
# Out - 0
# In - addFirstAndLast([2, 7, 3])
# Out - 5
# In - addFirstAndLast([10])
# Out - 10
def addFirstAndLast(x=0):
return(x[0] + x[-1])
print(addFirstAndLast([2,7,3]))
print(addFirstAndLast([10]))
# Complete the 'lambda' expression so that it returns True if the argument is an even number, and False otherwise.
def even(num):
return (lambda num : num% 2 ==0 )(num)
even(6)
# getScore.__doc__
# 'A function that computes and returns the final score.'
# In Python, it is possible to pass a function as a argument to another function. --yes
# Write a function useFunction(func, num) that takes in a function and a number as arguments.
# The useFunction should produce the output shown in the examples given below.
# def addOne(x):
# return x + 1
# useFunction(addOne, 4)
# 25
# useFunction(addOne, 9)
# 100
# useFunction(addOne, 0)
# 1
def useFunction(addOne,num):
new=addOne(num)
return new**2
def addOne(x):
return x + 1
useFunction(addOne,4)
useFunction(addOne,9)
```
| github_jupyter |
# Image Classification
In this project, you'll classify images from the [CIFAR-10 dataset](https://www.cs.toronto.edu/~kriz/cifar.html). The dataset consists of airplanes, dogs, cats, and other objects. You'll preprocess the images, then train a convolutional neural network on all the samples. The images need to be normalized and the labels need to be one-hot encoded. You'll get to apply what you learned and build a convolutional, max pooling, dropout, and fully connected layers. At the end, you'll get to see your neural network's predictions on the sample images.
## Get the Data
Run the following cell to download the [CIFAR-10 dataset for python](https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz).
```
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
from urllib.request import urlretrieve
from os.path import isfile, isdir
from tqdm import tqdm
import problem_unittests as tests
import tarfile
cifar10_dataset_folder_path = 'cifar-10-batches-py'
# Use Floyd's cifar-10 dataset if present
floyd_cifar10_location = '/input/cifar-10/python.tar.gz'
if isfile(floyd_cifar10_location):
tar_gz_path = floyd_cifar10_location
else:
tar_gz_path = 'cifar-10-python.tar.gz'
class DLProgress(tqdm):
last_block = 0
def hook(self, block_num=1, block_size=1, total_size=None):
self.total = total_size
self.update((block_num - self.last_block) * block_size)
self.last_block = block_num
if not isfile(tar_gz_path):
with DLProgress(unit='B', unit_scale=True, miniters=1, desc='CIFAR-10 Dataset') as pbar:
urlretrieve(
'https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz',
tar_gz_path,
pbar.hook)
if not isdir(cifar10_dataset_folder_path):
with tarfile.open(tar_gz_path) as tar:
tar.extractall()
tar.close()
tests.test_folder_path(cifar10_dataset_folder_path)
```
## Explore the Data
The dataset is broken into batches to prevent your machine from running out of memory. The CIFAR-10 dataset consists of 5 batches, named `data_batch_1`, `data_batch_2`, etc.. Each batch contains the labels and images that are one of the following:
* airplane
* automobile
* bird
* cat
* deer
* dog
* frog
* horse
* ship
* truck
Understanding a dataset is part of making predictions on the data. Play around with the code cell below by changing the `batch_id` and `sample_id`. The `batch_id` is the id for a batch (1-5). The `sample_id` is the id for a image and label pair in the batch.
Ask yourself "What are all possible labels?", "What is the range of values for the image data?", "Are the labels in order or random?". Answers to questions like these will help you preprocess the data and end up with better predictions.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import helper
import numpy as np
# Explore the dataset
batch_id = 1
sample_id = 5
helper.display_stats(cifar10_dataset_folder_path, batch_id, sample_id)
```
## Implement Preprocess Functions
### Normalize
In the cell below, implement the `normalize` function to take in image data, `x`, and return it as a normalized Numpy array. The values should be in the range of 0 to 1, inclusive. The return object should be the same shape as `x`.
```
def normalize(x):
"""
Normalize a list of sample image data in the range of 0 to 1
: x: List of image data. The image shape is (32, 32, 3)
: return: Numpy array of normalize data
"""
min = np.amin(x)
max = np.amax(x)
return (x - min) / (max - min)
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_normalize(normalize)
```
### One-hot encode
Just like the previous code cell, you'll be implementing a function for preprocessing. This time, you'll implement the `one_hot_encode` function. The input, `x`, are a list of labels. Implement the function to return the list of labels as One-Hot encoded Numpy array. The possible values for labels are 0 to 9. The one-hot encoding function should return the same encoding for each value between each call to `one_hot_encode`. Make sure to save the map of encodings outside the function.
Hint: Don't reinvent the wheel.
```
x = np.array([6, 1, 5])
np.array([[1 if i == y else 0 for i in range(10)] for y in x])
def one_hot_encode(x):
"""
One hot encode a list of sample labels. Return a one-hot encoded vector for each label.
: x: List of sample Labels
: return: Numpy array of one-hot encoded labels
"""
return np.array([[1 if i == y else 0 for i in range(10)] for y in x])
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_one_hot_encode(one_hot_encode)
```
### Randomize Data
As you saw from exploring the data above, the order of the samples are randomized. It doesn't hurt to randomize it again, but you don't need to for this dataset.
## Preprocess all the data and save it
Running the code cell below will preprocess all the CIFAR-10 data and save it to file. The code below also uses 10% of the training data for validation.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# Preprocess Training, Validation, and Testing Data
helper.preprocess_and_save_data(cifar10_dataset_folder_path, normalize, one_hot_encode)
```
# Check Point
This is your first checkpoint. If you ever decide to come back to this notebook or have to restart the notebook, you can start from here. The preprocessed data has been saved to disk.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import pickle
import problem_unittests as tests
import helper
# Load the Preprocessed Validation data
valid_features, valid_labels = pickle.load(open('preprocess_validation.p', mode='rb'))
```
## Build the network
For the neural network, you'll build each layer into a function. Most of the code you've seen has been outside of functions. To test your code more thoroughly, we require that you put each layer in a function. This allows us to give you better feedback and test for simple mistakes using our unittests before you submit your project.
>**Note:** If you're finding it hard to dedicate enough time for this course each week, we've provided a small shortcut to this part of the project. In the next couple of problems, you'll have the option to use classes from the [TensorFlow Layers](https://www.tensorflow.org/api_docs/python/tf/layers) or [TensorFlow Layers (contrib)](https://www.tensorflow.org/api_guides/python/contrib.layers) packages to build each layer, except the layers you build in the "Convolutional and Max Pooling Layer" section. TF Layers is similar to Keras's and TFLearn's abstraction to layers, so it's easy to pickup.
>However, if you would like to get the most out of this course, try to solve all the problems _without_ using anything from the TF Layers packages. You **can** still use classes from other packages that happen to have the same name as ones you find in TF Layers! For example, instead of using the TF Layers version of the `conv2d` class, [tf.layers.conv2d](https://www.tensorflow.org/api_docs/python/tf/layers/conv2d), you would want to use the TF Neural Network version of `conv2d`, [tf.nn.conv2d](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d).
Let's begin!
### Input
The neural network needs to read the image data, one-hot encoded labels, and dropout keep probability. Implement the following functions
* Implement `neural_net_image_input`
* Return a [TF Placeholder](https://www.tensorflow.org/api_docs/python/tf/placeholder)
* Set the shape using `image_shape` with batch size set to `None`.
* Name the TensorFlow placeholder "x" using the TensorFlow `name` parameter in the [TF Placeholder](https://www.tensorflow.org/api_docs/python/tf/placeholder).
* Implement `neural_net_label_input`
* Return a [TF Placeholder](https://www.tensorflow.org/api_docs/python/tf/placeholder)
* Set the shape using `n_classes` with batch size set to `None`.
* Name the TensorFlow placeholder "y" using the TensorFlow `name` parameter in the [TF Placeholder](https://www.tensorflow.org/api_docs/python/tf/placeholder).
* Implement `neural_net_keep_prob_input`
* Return a [TF Placeholder](https://www.tensorflow.org/api_docs/python/tf/placeholder) for dropout keep probability.
* Name the TensorFlow placeholder "keep_prob" using the TensorFlow `name` parameter in the [TF Placeholder](https://www.tensorflow.org/api_docs/python/tf/placeholder).
These names will be used at the end of the project to load your saved model.
Note: `None` for shapes in TensorFlow allow for a dynamic size.
```
import tensorflow as tf
def neural_net_image_input(image_shape):
"""
Return a Tensor for a batch of image input
: image_shape: Shape of the images
: return: Tensor for image input.
"""
return tf.placeholder(tf.float32, shape = [None] + list(image_shape), name = "x")
def neural_net_label_input(n_classes):
"""
Return a Tensor for a batch of label input
: n_classes: Number of classes
: return: Tensor for label input.
"""
return tf.placeholder(tf.float32, shape = (None, n_classes), name = "y")
def neural_net_keep_prob_input():
"""
Return a Tensor for keep probability
: return: Tensor for keep probability.
"""
# TODO: Implement Function
return tf.placeholder(tf.float32, shape = None, name = "keep_prob")
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tf.reset_default_graph()
tests.test_nn_image_inputs(neural_net_image_input)
tests.test_nn_label_inputs(neural_net_label_input)
tests.test_nn_keep_prob_inputs(neural_net_keep_prob_input)
```
### Convolution and Max Pooling Layer
Convolution layers have a lot of success with images. For this code cell, you should implement the function `conv2d_maxpool` to apply convolution then max pooling:
* Create the weight and bias using `conv_ksize`, `conv_num_outputs` and the shape of `x_tensor`.
* Apply a convolution to `x_tensor` using weight and `conv_strides`.
* We recommend you use same padding, but you're welcome to use any padding.
* Add bias
* Add a nonlinear activation to the convolution.
* Apply Max Pooling using `pool_ksize` and `pool_strides`.
* We recommend you use same padding, but you're welcome to use any padding.
**Note:** You **can't** use [TensorFlow Layers](https://www.tensorflow.org/api_docs/python/tf/layers) or [TensorFlow Layers (contrib)](https://www.tensorflow.org/api_guides/python/contrib.layers) for **this** layer, but you can still use TensorFlow's [Neural Network](https://www.tensorflow.org/api_docs/python/tf/nn) package. You may still use the shortcut option for all the **other** layers.
```
def conv2d_maxpool(x_tensor, conv_num_outputs, conv_ksize, conv_strides, pool_ksize, pool_strides):
"""
Apply convolution then max pooling to x_tensor
:param x_tensor: TensorFlow Tensor
:param conv_num_outputs: Number of outputs for the convolutional layer
:param conv_ksize: kernal size 2-D Tuple for the convolutional layer
:param conv_strides: Stride 2-D Tuple for convolution
:param pool_ksize: kernel size 2-D Tuple for pool
:param pool_strides: Stride 2-D Tuple for pool
: return: A tensor that represents convolution and max pooling of x_tensor
"""
x_size = x_tensor.get_shape().as_list()[1:]
W = tf.Variable(tf.truncated_normal(x_size + [conv_num_outputs], stddev=0.05))
b = tf.Variable(tf.zeros(conv_num_outputs))
x = tf.nn.conv2d(x_tensor, W, strides = (1, conv_strides[0], conv_strides[1], 1),
padding = "SAME")
x = tf.nn.bias_add(x, b)
x = tf.nn.relu(x)
x = tf.nn.max_pool(x, ksize = (1, pool_ksize[0], pool_ksize[1], 1),
strides = (1, pool_strides[0], pool_strides[1], 1),
padding = "SAME")
return x
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_con_pool(conv2d_maxpool)
```
### Flatten Layer
Implement the `flatten` function to change the dimension of `x_tensor` from a 4-D tensor to a 2-D tensor. The output should be the shape (*Batch Size*, *Flattened Image Size*). Shortcut option: you can use classes from the [TensorFlow Layers](https://www.tensorflow.org/api_docs/python/tf/layers) or [TensorFlow Layers (contrib)](https://www.tensorflow.org/api_guides/python/contrib.layers) packages for this layer. For more of a challenge, only use other TensorFlow packages.
```
import numpy as np
def flatten(x_tensor):
"""
Flatten x_tensor to (Batch Size, Flattened Image Size)
: x_tensor: A tensor of size (Batch Size, ...), where ... are the image dimensions.
: return: A tensor of size (Batch Size, Flattened Image Size).
"""
x_size = x_tensor.get_shape().as_list()
return tf.reshape(x_tensor, shape=(-1, np.prod(x_size[1:])))
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_flatten(flatten)
```
### Fully-Connected Layer
Implement the `fully_conn` function to apply a fully connected layer to `x_tensor` with the shape (*Batch Size*, *num_outputs*). Shortcut option: you can use classes from the [TensorFlow Layers](https://www.tensorflow.org/api_docs/python/tf/layers) or [TensorFlow Layers (contrib)](https://www.tensorflow.org/api_guides/python/contrib.layers) packages for this layer. For more of a challenge, only use other TensorFlow packages.
```
def fully_conn(x_tensor, num_outputs):
"""
Apply a fully connected layer to x_tensor using weight and bias
: x_tensor: A 2-D tensor where the first dimension is batch size.
: num_outputs: The number of output that the new tensor should be.
: return: A 2-D tensor where the second dimension is num_outputs.
"""
x_size = x_tensor.get_shape().as_list()[1:]
W = tf.Variable(tf.truncated_normal(x_size + [num_outputs], stddev=.05))
b = tf.Variable(tf.zeros(num_outputs))
x = tf.add(tf.matmul(x_tensor, W), b)
x = tf.nn.relu(x)
return x
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_fully_conn(fully_conn)
```
### Output Layer
Implement the `output` function to apply a fully connected layer to `x_tensor` with the shape (*Batch Size*, *num_outputs*). Shortcut option: you can use classes from the [TensorFlow Layers](https://www.tensorflow.org/api_docs/python/tf/layers) or [TensorFlow Layers (contrib)](https://www.tensorflow.org/api_guides/python/contrib.layers) packages for this layer. For more of a challenge, only use other TensorFlow packages.
**Note:** Activation, softmax, or cross entropy should **not** be applied to this.
```
def output(x_tensor, num_outputs):
"""
Apply a output layer to x_tensor using weight and bias
: x_tensor: A 2-D tensor where the first dimension is batch size.
: num_outputs: The number of output that the new tensor should be.
: return: A 2-D tensor where the second dimension is num_outputs.
"""
x_size = x_tensor.get_shape().as_list()[1:]
W = tf.Variable(tf.truncated_normal(x_size + [num_outputs], stddev=.05))
b = tf.Variable(tf.zeros(num_outputs))
x = tf.add(tf.matmul(x_tensor, W), b)
return x
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_output(output)
```
### Create Convolutional Model
Implement the function `conv_net` to create a convolutional neural network model. The function takes in a batch of images, `x`, and outputs logits. Use the layers you created above to create this model:
* Apply 1, 2, or 3 Convolution and Max Pool layers
* Apply a Flatten Layer
* Apply 1, 2, or 3 Fully Connected Layers
* Apply an Output Layer
* Return the output
* Apply [TensorFlow's Dropout](https://www.tensorflow.org/api_docs/python/tf/nn/dropout) to one or more layers in the model using `keep_prob`.
```
def conv_net(x, keep_prob):
"""
Create a convolutional neural network model
: x: Placeholder tensor that holds image data.
: keep_prob: Placeholder tensor that hold dropout keep probability.
: return: Tensor that represents logits
"""
# TODO: Apply 1, 2, or 3 Convolution and Max Pool layers
# Play around with different number of outputs, kernel size and stride
# Function Definition from Above:
# conv2d_maxpool(x_tensor, conv_num_outputs, conv_ksize, conv_strides, pool_ksize, pool_strides)
x = conv2d_maxpool(x, conv_num_outputs=64, conv_ksize=2,
conv_strides=(1, 1), pool_ksize=(2, 2), pool_strides=(2, 2))
x = tf.layers.dropout(x, keep_prob)
# x = conv2d_maxpool(x, conv_num_outputs=128, conv_ksize=3,
# conv_strides=(1, 1), pool_ksize=(2, 2), pool_strides=(2, 2))
# x = conv2d_maxpool(x, conv_num_outputs=256, conv_ksize=3,
# conv_strides=(1, 1), pool_ksize=(2, 2), pool_strides=(2, 2))
# TODO: Apply a Flatten Layer
# Function Definition from Above:
# flatten(x_tensor)
x = flatten(x)
# TODO: Apply 1, 2, or 3 Fully Connected Layers
# Play around with different number of outputs
# Function Definition from Above:
# fully_conn(x_tensor, num_outputs)
x = fully_conn(x, 512)
x = tf.layers.dropout(x, keep_prob)
# x = fully_conn(x, 128)
# x = tf.layers.dropout(x, keep_prob)
# x = fully_conn(x, 64)
# x = tf.layers.dropout(x, keep_prob)
# TODO: Apply an Output Layer
# Set this to the number of classes
# Function Definition from Above:
# output(x_tensor, num_outputs)
x = output(x, 10)
# TODO: return output
return x
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
##############################
## Build the Neural Network ##
##############################
# Remove previous weights, bias, inputs, etc..
tf.reset_default_graph()
# Inputs
x = neural_net_image_input((32, 32, 3))
y = neural_net_label_input(10)
keep_prob = neural_net_keep_prob_input()
# Model
logits = conv_net(x, keep_prob)
# Name logits Tensor, so that is can be loaded from disk after training
logits = tf.identity(logits, name='logits')
# Loss and Optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y))
optimizer = tf.train.AdamOptimizer().minimize(cost)
# Accuracy
correct_pred = tf.equal(tf.argmax(logits, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32), name='accuracy')
tests.test_conv_net(conv_net)
```
## Train the Neural Network
### Single Optimization
Implement the function `train_neural_network` to do a single optimization. The optimization should use `optimizer` to optimize in `session` with a `feed_dict` of the following:
* `x` for image input
* `y` for labels
* `keep_prob` for keep probability for dropout
This function will be called for each batch, so `tf.global_variables_initializer()` has already been called.
Note: Nothing needs to be returned. This function is only optimizing the neural network.
```
def train_neural_network(session, optimizer, keep_probability, feature_batch, label_batch):
"""
Optimize the session on a batch of images and labels
: session: Current TensorFlow session
: optimizer: TensorFlow optimizer function
: keep_probability: keep probability
: feature_batch: Batch of Numpy image data
: label_batch: Batch of Numpy label data
"""
session.run(optimizer, feed_dict={keep_prob: keep_probability, x: feature_batch,
y: label_batch})
pass
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_train_nn(train_neural_network)
```
### Show Stats
Implement the function `print_stats` to print loss and validation accuracy. Use the global variables `valid_features` and `valid_labels` to calculate validation accuracy. Use a keep probability of `1.0` to calculate the loss and validation accuracy.
```
def print_stats(session, feature_batch, label_batch, cost, accuracy):
"""
Print information about loss and validation accuracy
: session: Current TensorFlow session
: feature_batch: Batch of Numpy image data
: label_batch: Batch of Numpy label data
: cost: TensorFlow cost function
: accuracy: TensorFlow accuracy function
"""
# print(feature_batch)
loss, acc = session.run([cost, accuracy],
feed_dict={x: feature_batch, y: label_batch,
keep_prob: 1.})
print("Training Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
valid_loss, valid_acc = session.run([cost, accuracy],
feed_dict={x: valid_features, y: valid_labels,
keep_prob: 1.})
print("Validation Loss= " + \
"{:.6f}".format(valid_loss) + ", Validation Accuracy= " + \
"{:.5f}".format(valid_acc))
# batch_cost = session.run(cost, feed_dict={keep_probability: 1,
# x: feature_batch, y: label_batch})
# batch_accuracy = session.run(accuracy, feed_dict={keep_probability: 1,
# x: feature_batch, y: label_batch})
# valid_cost = session.run(cost, feed_dict={keep_probability: 1,
# x: valid_features, y: valid_labels})
# valid_accuracy = session.run(accuracy, feed_dict={keep_probability: 1,
# x: valid_features, y: valid_labels})
# print('Training Cost: {}'.format(batch_cost))
# print('Training Accuracy: {}'.format(batch_accuracy))
# print('Validation Cost: {}'.format(valid_cost))
# print('Validation Accuracy: {}'.format(valid_accuracy))
# print('Accuracy: {}'.format(accuracy))
pass
```
### Hyperparameters
Tune the following parameters:
* Set `epochs` to the number of iterations until the network stops learning or start overfitting
* Set `batch_size` to the highest number that your machine has memory for. Most people set them to common sizes of memory:
* 64
* 128
* 256
* ...
* Set `keep_probability` to the probability of keeping a node using dropout
```
# TODO: Tune Parameters
epochs = 10
batch_size = 256
keep_probability = .5
```
### Train on a Single CIFAR-10 Batch
Instead of training the neural network on all the CIFAR-10 batches of data, let's use a single batch. This should save time while you iterate on the model to get a better accuracy. Once the final validation accuracy is 50% or greater, run the model on all the data in the next section.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
print('Checking the Training on a Single Batch...')
with tf.Session() as sess:
# Initializing the variables
sess.run(tf.global_variables_initializer())
# Training cycle
for epoch in range(epochs):
batch_i = 1
for batch_features, batch_labels in helper.load_preprocess_training_batch(batch_i, batch_size):
train_neural_network(sess, optimizer, keep_probability, batch_features, batch_labels)
print('Epoch {:>2}, CIFAR-10 Batch {}: '.format(epoch + 1, batch_i), end='')
print_stats(sess, batch_features, batch_labels, cost, accuracy)
```
### Fully Train the Model
Now that you got a good accuracy with a single CIFAR-10 batch, try it with all five batches.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
save_model_path = './image_classification'
print('Training...')
with tf.Session() as sess:
# Initializing the variables
sess.run(tf.global_variables_initializer())
# Training cycle
for epoch in range(epochs):
# Loop over all batches
n_batches = 5
for batch_i in range(1, n_batches + 1):
for batch_features, batch_labels in helper.load_preprocess_training_batch(batch_i, batch_size):
train_neural_network(sess, optimizer, keep_probability, batch_features, batch_labels)
print('Epoch {:>2}, CIFAR-10 Batch {}: '.format(epoch + 1, batch_i), end='')
print_stats(sess, batch_features, batch_labels, cost, accuracy)
# Save Model
saver = tf.train.Saver()
save_path = saver.save(sess, save_model_path)
```
# Checkpoint
The model has been saved to disk.
## Test Model
Test your model against the test dataset. This will be your final accuracy. You should have an accuracy greater than 50%. If you don't, keep tweaking the model architecture and parameters.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import tensorflow as tf
import pickle
import helper
import random
# Set batch size if not already set
try:
if batch_size:
pass
except NameError:
batch_size = 64
save_model_path = './image_classification'
n_samples = 4
top_n_predictions = 3
def test_model():
"""
Test the saved model against the test dataset
"""
test_features, test_labels = pickle.load(open('preprocess_test.p', mode='rb'))
loaded_graph = tf.Graph()
with tf.Session(graph=loaded_graph) as sess:
# Load model
loader = tf.train.import_meta_graph(save_model_path + '.meta')
loader.restore(sess, save_model_path)
# Get Tensors from loaded model
loaded_x = loaded_graph.get_tensor_by_name('x:0')
loaded_y = loaded_graph.get_tensor_by_name('y:0')
loaded_keep_prob = loaded_graph.get_tensor_by_name('keep_prob:0')
loaded_logits = loaded_graph.get_tensor_by_name('logits:0')
loaded_acc = loaded_graph.get_tensor_by_name('accuracy:0')
# Get accuracy in batches for memory limitations
test_batch_acc_total = 0
test_batch_count = 0
for test_feature_batch, test_label_batch in helper.batch_features_labels(test_features, test_labels, batch_size):
test_batch_acc_total += sess.run(
loaded_acc,
feed_dict={loaded_x: test_feature_batch, loaded_y: test_label_batch, loaded_keep_prob: 1.0})
test_batch_count += 1
print('Testing Accuracy: {}\n'.format(test_batch_acc_total/test_batch_count))
# Print Random Samples
random_test_features, random_test_labels = tuple(zip(*random.sample(list(zip(test_features, test_labels)), n_samples)))
random_test_predictions = sess.run(
tf.nn.top_k(tf.nn.softmax(loaded_logits), top_n_predictions),
feed_dict={loaded_x: random_test_features, loaded_y: random_test_labels, loaded_keep_prob: 1.0})
helper.display_image_predictions(random_test_features, random_test_labels, random_test_predictions)
test_model()
```
## Why 50-80% Accuracy?
You might be wondering why you can't get an accuracy any higher. First things first, 50% isn't bad for a simple CNN. Pure guessing would get you 10% accuracy. However, you might notice people are getting scores [well above 80%](http://rodrigob.github.io/are_we_there_yet/build/classification_datasets_results.html#43494641522d3130). That's because we haven't taught you all there is to know about neural networks. We still need to cover a few more techniques.
## Submitting This Project
When submitting this project, make sure to run all the cells before saving the notebook. Save the notebook file as "dlnd_image_classification.ipynb" and save it as a HTML file under "File" -> "Download as". Include the "helper.py" and "problem_unittests.py" files in your submission.
| github_jupyter |
# Least-squares technique
## References
- Statistics in geography: https://archive.org/details/statisticsingeog0000ebdo/
## Imports
```
from functools import partial
import numpy as np
from scipy.stats import multivariate_normal, t
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from ipywidgets import interact, IntSlider
inv = np.linalg.inv
df = pd.read_csv('regression_data.csv')
df.head(3)
```
## Population
0.5 and 0.2 are NOT the population parameters. Although we used them to generate the population, the population parameters can be different from them.
```
def get_y(x):
ys = x * 0.5 + 0.2
noises = 1 * np.random.normal(size=len(ys))
return ys + noises
np.random.seed(52)
xs = np.linspace(0, 10, 10000)
ys = get_y(xs)
np.random.seed(32)
np.random.shuffle(xs)
np.random.seed(32)
np.random.shuffle(ys)
plt.scatter(xs, ys, s=5)
plt.show()
```
## Design matrices
```
PHI = xs.reshape(-1, 1)
PHI = np.hstack([
PHI,
np.ones(PHI.shape)
])
T = ys.reshape(-1, 1)
```
## Normal equation with regularization
```
def regularized_least_squares(PHI, T, regularizer=0):
assert PHI.shape[0] == T.shape[0]
pseudo_inv = inv(PHI.T @ PHI + np.eye(PHI.shape[1]) * regularizer)
assert pseudo_inv.shape[0] == pseudo_inv.shape[1]
W = pseudo_inv @ PHI.T @ T
return {'slope' : float(W[0]), 'intercept' : float(W[1])}
```
## Sampling distributions
### Population parameters
```
pop_params = regularized_least_squares(PHI, T)
pop_slope, pop_intercept = pop_params['slope'], pop_params['intercept']
```
### Sample statistics
Verify that the sampling distribution for both regression coefficients are normal.
```
n = 10 # sample size
num_samps = 1000
def sample(PHI, T, n):
idxs = np.random.randint(PHI.shape[0], size=n)
return PHI[idxs], T[idxs]
samp_slopes, samp_intercepts = [], []
for i in range(num_samps):
PHI_samp, T_samp = sample(PHI, T, n)
learned_param = regularized_least_squares(PHI_samp, T_samp)
samp_slopes.append(learned_param['slope']); samp_intercepts.append(learned_param['intercept'])
np.std(samp_slopes), np.std(samp_intercepts)
fig = plt.figure(figsize=(12, 4))
fig.add_subplot(121)
sns.kdeplot(samp_slopes)
plt.title('Sample distribution of sample slopes')
fig.add_subplot(122)
sns.kdeplot(samp_intercepts)
plt.title('Sample distribution of sample intercepts')
plt.show()
```
Note that the two normal distributions above are correlated. This means that we need to be careful when plotting the 95% CI for the regression line, because we can't just plot the regression line with the highest slope and the highest intercept and the regression line with the lowest slope and the lowest intercept.
```
sns.jointplot(samp_slopes, samp_intercepts, s=5)
plt.show()
```
## Confidence interval
**Caution.** The following computation of confidence intervals does not apply to regularized least squares.
### Sample one sample
```
n = 500
PHI_samp, T_samp = sample(PHI, T, n)
```
### Compute sample statistics
```
learned_param = regularized_least_squares(PHI_samp, T_samp)
samp_slope, samp_intercept = learned_param['slope'], learned_param['intercept']
samp_slope, samp_intercept
```
### Compute standard errors of sample statistics
Standard error is the estimate of the standard deviation of the sampling distribution.
$$\hat\sigma = \sqrt{\frac{\text{Sum of all squared residuals}}{\text{Degrees of freedom}}}$$
Standard error for slope:
$$\text{SE}(\hat\beta_1)=\hat\sigma \sqrt{\frac{1}{(n-1)s_X^2}}$$
Standard error for intercept:
$$\text{SE}(\hat\beta_0)=\hat\sigma \sqrt{\frac{1}{n} + \frac{\bar X^2}{(n-1)s_X^2}}$$
where $\bar X$ is the sample mean of the $X$'s and $s_X^2$ is the sample variance of the $X$'s.
```
preds = samp_slope * PHI_samp[:,0] + samp_intercept
sum_of_squared_residuals = np.sum((T_samp.reshape(-1) - preds) ** 2)
samp_sigma_y_give_x = np.sqrt(sum_of_squared_residuals / (n - 2))
samp_sigma_y_give_x
samp_mean = np.mean(PHI_samp[:,0])
samp_var = np.var(PHI_samp[:,0])
SE_slope = samp_sigma_y_give_x * np.sqrt(1 / ((n - 1) * samp_var))
SE_intercept = samp_sigma_y_give_x * np.sqrt(1 / n + samp_mean ** 2 / ((n - 1) * samp_var))
SE_slope, SE_intercept
```
### Compute confidence intervals for sample statistics
```
slope_lower, slope_upper = samp_slope - 1.96 * SE_slope, samp_slope + 1.96 * SE_slope
slope_lower, slope_upper
intercept_lower, intercept_upper = samp_intercept - 1.96 * SE_intercept, samp_intercept + 1.96 * SE_intercept
intercept_lower, intercept_upper
```
### Compute confidence interval for regression line
#### Boostrapped solution
Use a 2-d Guassian to model the joint distribution between boostrapped sample slopes and boostrapped sample intercepts.
**Fixed.** `samp_slopes` and `samp_intercepts` used in the cell below are not boostrapped; they are directly sampled from the population. Next time, add the boostrapped version. Using `samp_slopes` and `samp_intercepts` still has its value, though; it shows the population regression line lie right in the middle of all sample regression lines. Remember that, when ever you use bootstrapping to estimate the variance / covariance of the sample distribution of some statistic, there might be an equation that you can use from statistical theory.
```
num_resamples = 10000
resample_slopes, resample_intercepts = [], []
for i in range(num_resamples):
PHI_resample, T_resample = sample(PHI_samp, T_samp, n=len(PHI_samp))
learned_params = regularized_least_squares(PHI_resample, T_resample)
resample_slopes.append(learned_params['slope']); resample_intercepts.append(learned_params['intercept'])
```
**Fixed.** The following steps might improve the results, but I don't think they are part of the standard practice.
```
# means = [np.mean(resample_slopes), np.mean(resample_intercepts)]
# cov = np.cov(resample_slopes, resample_intercepts)
# model = multivariate_normal(mean=means, cov=cov)
```
Sample 5000 (slope, intercept) pairs from the Gaussian.
```
# num_pairs_sampled = 10000
# pairs = model.rvs(num_pairs_sampled)
```
Scatter samples, plot regression lines and CI.
```
plt.figure(figsize=(20, 10))
plt.scatter(PHI_samp[:,0], T_samp.reshape(-1), s=20) # sample
granularity = 1000
xs = np.linspace(0, 10, granularity)
plt.plot(xs, samp_slope * xs + samp_intercept, label='Sample') # sample regression line
plt.plot(xs, pop_slope * xs + pop_intercept, '--', color='black', label='Population') # population regression line
lines = np.zeros((num_resamples, granularity))
for i, (slope, intercept) in enumerate(zip(resample_slopes, resample_intercepts)):
lines[i] = slope * xs + intercept
confidence_level = 95
uppers_95 = np.percentile(lines, confidence_level + (100 - confidence_level) / 2, axis=0)
lowers_95 = np.percentile(lines, (100 - confidence_level) / 2, axis=0)
confidence_level = 99
uppers_99 = np.percentile(lines, confidence_level + (100 - confidence_level) / 2, axis=0)
lowers_99 = np.percentile(lines, (100 - confidence_level) / 2, axis=0)
plt.fill_between(xs, lowers_95, uppers_95, color='grey', alpha=0.7, label='95% CI')
plt.plot(xs, uppers_99, color='grey', label='99% CI')
plt.plot(xs, lowers_99, color='grey')
plt.legend()
plt.show()
```
#### Analytic solution
**Reference.** Page 97, Statistics of Geograph: A Practical Approach, David Ebdon, 1987.
For a particular value $x_0$ of the independent variable $x$, its confidence interval is given by:
$$\sqrt{\frac{\sum e^{2}}{n-2}\left[\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{\sum x^{2}-n \bar{x}^{2}}\right]}$$
where
- $\sum e^2$ is the sum of squares of residuals from regression,
- $x$ is the independent variables,
- $\bar{x}$ is the sample mean of the independent variables.
```
sum_of_squared_xs = np.sum(PHI_samp[:,0] ** 2)
SEs = np.sqrt(
(sum_of_squared_residuals / (n - 2)) *
(1 / n + (xs - samp_mean) ** 2 / (sum_of_squared_xs - n * samp_mean ** 2))
)
t_97dot5 = t.ppf(0.975, df=n-2)
t_99dot5 = t.ppf(0.995, df=n-2)
yhats = samp_slope * xs + samp_intercept
uppers_95 = yhats + t_97dot5 * SEs
lowers_95 = yhats - t_97dot5 * SEs
uppers_99 = yhats + t_99dot5 * SEs
lowers_99 = yhats - t_99dot5 * SEs
plt.figure(figsize=(20, 10))
plt.scatter(PHI_samp[:,0], T_samp.reshape(-1), s=20) # sample
granularity = 1000
xs = np.linspace(0, 10, granularity)
plt.plot(xs, samp_slope * xs + samp_intercept, label='Sample') # sample regression line
plt.plot(xs, pop_slope * xs + pop_intercept, '--', color='black', label='Population') # population regression line
plt.fill_between(xs, lowers_95, uppers_95, color='grey', alpha=0.7, label='95% CI')
plt.plot(xs, uppers_99, color='grey', label='99% CI')
plt.plot(xs, lowers_99, color='grey')
plt.legend()
plt.show()
```
## Regularized least squares
```
def plot_regression_line(PHI, T, regularizer):
plt.scatter(PHI[:,0], T, s=5)
params = regularized_least_squares(PHI, T, regularizer)
x_min, x_max = PHI[:,0].min(), PHI[:,0].max()
xs = np.linspace(x_min, x_max, 2)
ys = params['slope'] * xs + params['intercept']
plt.plot(xs, ys, color='orange')
plt.ylim(-3, 10)
plt.show()
plot_regression_line(PHI, T, regularizer=20)
def plot_regression_line_wrapper(regularizer, num_points):
plot_regression_line(PHI[:num_points], T[:num_points], regularizer)
```
Yes! The effect of regularization does change with the size of the dataset.
```
_ = interact(
plot_regression_line_wrapper,
regularizer=IntSlider(min=0, max=10000, value=5000, continuous_update=False),
num_points=IntSlider(min=2, max=1000, value=1000, continuous_update=False)
)
```
| github_jupyter |
# 1. 정규 표현식
* 출처 : 서적 "잡아라! 텍스트 마이닝 with 파이썬"
* 문자열이 주어진 규칙에 일치하는 지, 일치하지 않는지 판단할 수 있다.
정규 표현식을 이용하여 특정 패턴을 지니니 문자열을 찾을 수 있어 텍스트 데이터 사전 처리 및
크롤링에서 주로 쓰임
```
string = '기상청은 슈퍼컴퓨터도 서울지역의 집중호우를 제대로 예측하지 못했다고 설명했습니다. 왜 오류가 발생했\
습니다. 왜 오류가 발생했는지 자세히 분석해 예측 프로그램을 보완해야 할 대목입니다. 관측 분야는 개선될 여지가\
있습니다. 지금 보시는 왼쪽 사진이 현재 천리안 위성이 촬영한 것이고 오른쪽이 올해 말 쏘아 올릴 천리안 2A호가 \
촬영한 영상입니다. 오른쪽이 왼쪽보다 태풍의 눈이 좀 더 뚜렷하고 주변 구름도 더 잘 보이죠. 새 위성을 통해 태풍\
구름 등의 움직임을 상세히 분석하면 좀 더 정확한 예측을 할 수 있지 않을까 기대해 봅니다. 정구희 기자([email protected])'
string
import re
re.sub("\([A-Za-z0-9\._+]+@[A-Za-z]+\.(com|org|edu|net|co.kr)\)", "", string)
```
* \([A-Za-z0-9\._+]+ : 이메일 주소가 괄호로 시작하여 \(특수문자를 원래 의미대로 쓰게 함)와 (로 시작
대괄호[ ] 안에 이메일 주소의 패턴을 입력(입력한 것 중 아무거나)
A-Z = 알파벳 대문자, a-z = 알파벳 소문자, 0-9 = 숫자, ._+ = .나 _나 +
마지막 +는 바로 앞에 있는 것이 최소 한번 이상 나와야 한다는 의미
* @ : 이메일 주소 다음에 @
* [A-Za-z]+ : 도메인 주소에 해당하는 알파벳 대문자나 소문자
* \. : 도메인 주소 다음의 .
* (com|org|edu|net|co.kr)\) : |는 or조건, 도메인 주소 마침표 다음의 패턴 마지막 )까지 찾음
### 파이썬 정규표현식 기호 설명
* '*' : 바로 앞 문자, 표현식이 0번 이상 반복
* '+' : 바로 앞 문자, 표현식이 1번 이상 반복
* '[]' : 대괄호 안의 문자 중 하나
* '()' : 괄호안의 정규식을 그룹으로 만듬
* '.' : 어떤 형태든 문자 1자
* '^' : 바로 뒤 문자, 표현식이 문자열 맨 앞에 나타남
* '$' : 바로 앞 문자, 표현식이 문자열 맨 뒤에 나타남
* '{m}' : 바로 앞 문자, 표현식이 m회 반복
* '{m,n}' : 바로 앞 문자, 표현식이 m번 이상, n번 이하 나타남
* '|' : |로 분리된 문자, 문자열, 표현식 중 하나가 나타남(or조건)
* '[^]' : 대괄호 안에 있는 문자를 제외한 문자가 나타남
```
# a문자가 1번 이상 나오고 b 문자가 0번 이상 나오는 문자열 찾기
r = re.compile("a+b*")
r.findall("aaaa, cc, bbbb, aabbb")
# 대괄호를 이용해 대문자로 구성된 문자열 찾기
r = re.compile("[A-Z]+")
r.findall("HOME, home")
# ^와 .을 이용하여 맨 앞에 a가 오고 그 다음에 어떠한 형태든 2개의 문자가 오는 문자열 찾기
r = re.compile("^a..")
r.findall("abc, cba")
# 중괄호 표현식 {m,n}을 이요하여 해당 문자열이 m번 이상 n번 이하 나타나는 패턴 찾기
r = re.compile("a{2,3}b{2,3}")
r.findall("aabb, aaabb, ab, aab")
# compile 메서드에 정규 표현식 패턴 지정, search로 정규 표현식 패턴과 일치하는 문자열의 위치 찾기
# group을 통해 패턴과 일치하는 문자들을 그룹핑하여 추출
p = re.compile(".+:")
m = p.search("http://google.com")
m.group()
# sub : 정규 표현식과 일치하는 부분을 다른 문자로 치환
p = re.compile("(내|나의|내꺼)")
p.sub("그의", "나의 물건에 손대지 마시오.")
```
# 2. 전처리
### 대소문자 통일
```
s = 'Hello World'
print(s.lower())
print(s.upper())
```
### 숫자, 문장부호, 특수문자 제거
```
# 숫자 제거
p = re.compile("[0-9]+")
p.sub("", '서울 부동산 가격이 올해 들어 평균 30% 상승했습니다.')
# 문장부호, 특수문자 제거
p = re.compile("\W+")
p.sub(" ", "★서울 부동산 가격이 올해 들어 평균 30% 상승했습니다.")
s = p.sub(" ", "주제_1: 건강한 물과 건강한 정신!")
s
p = re.compile("_")
p.sub(" ", s)
```
### 불용어 제거
```
words_Korean = ['추석','연휴','민족','대이동','시작','늘어','교통량','교통사고','특히','자동차','고장',
'상당수','차지','나타','것','기자']
stopwords = ['가다','늘어','나타','것','기자']
[i for i in words_Korean if i not in stopwords]
from nltk.corpus import stopwords
# 그냥하면 LookupError 발생하므로 다운로드가 필요함
# import nltk
# nltk.download() or nltk.download('stopwords')
words_English = ['chief','justice','roberts',',','president','carter',',','president','clinton',',',
'president','bush',',','president','obama',',','fellow','americans','and','people',
'of','the','world',',','thank','you','.']
[w for w in words_English if not w in stopwords.words('english')]
```
### 같은 어근 동일화(stemming)
```
from nltk.tokenize import word_tokenize
from nltk.stem import PorterStemmer
ps_stemmer = PorterStemmer()
new_text = 'It is important to be immersed while you are pythoning with python.\
All pythoners have pothoned poorly at least once.'
words = word_tokenize(new_text)
for w in words:
print(ps_stemmer.stem(w), end=' ')
from nltk.stem.lancaster import LancasterStemmer
LS_stemmer = LancasterStemmer()
for w in words:
print(LS_stemmer.stem(w), end=' ')
from nltk.stem.regexp import RegexpStemmer # 특정한 표현식을 일괄적으로 제거
RS_stemmer = RegexpStemmer('python')
for w in words:
print(RS_stemmer.stem(w), end=' ')
```
### N-gram
* n번 연이어 등장하는 단어들의 연쇄
* 두 번 : 바이그램, 세 번 : 트라이그램(트라이그램 이상은 보편적으로 활용하지 않음)
```
from nltk import ngrams
sentence = 'Chief Justice Roberts, Preskdent Carter, President Clinton, President Bush, President Obama, \
fellow Americans and people of the world, thank you. We, the citizens of America are now joined in a great \
national effort to rebuild our country and restore its promise for all of our people. Together, we will \
determine the course of America and the world for many, many years to come. We will face challenges. We \
will confront hardships, but we will get the job done.'
grams = ngrams(sentence.split(), 2)
for gram in grams:
print(gram, end=' ')
```
### 품사 분석
```
from konlpy.tag import Hannanum
hannanum = Hannanum()
print(hannanum.morphs("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
print(hannanum.nouns("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
print(hannanum.pos("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다.", ntags=9))
from konlpy.tag import Kkma
kkma = Kkma()
print(kkma.morphs("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
print(kkma.nouns("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
print(kkma.pos("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
from konlpy.tag import Twitter
twitter = Twitter()
print(twitter.morphs("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
print(twitter.nouns("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
print(twitter.pos("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
print(twitter.phrases("친척들이 모인 이번 추석 차례상에서는 단연 '집값'이 화제에 올랐다."))
from nltk import pos_tag
tokens = "The little yellow dog barked at the Persian cat.".split()
tags_en = pos_tag(tokens)
print(tags_en)
```
| github_jupyter |
```
# For cross-validation
FRACTION_TRAINING = 0.5
# For keeping output
detailed_output = {}
# dictionary for keeping model
model_dict = {}
import pandas as pd
import pickle
import numpy as np
import matplotlib.pyplot as plt
import sklearn
from matplotlib.colors import ListedColormap
from sklearn import linear_model
%matplotlib inline
plt.style.use("ggplot")
"""
Data Preprocessing
EXPERIMENT_DATA - Contain training data
EVALUATION_DATA - Contain testing data
"""
EXPERIMENT_DATA = pickle.load(open('EXPERIMENT_SET_pandas.pkl', 'rb'))
EVALUATION_SET = pickle.load(open('EVALUATION_SET_pandas.pkl', 'rb'))
# Shuffle Data
EXPERIMENT_DATA = sklearn.utils.shuffle(EXPERIMENT_DATA)
EXPERIMENT_DATA = EXPERIMENT_DATA.reset_index(drop=True)
TRAINING_DATA = EXPERIMENT_DATA[:int(FRACTION_TRAINING*len(EXPERIMENT_DATA))]
TESTING_DATA = EXPERIMENT_DATA[int(FRACTION_TRAINING*len(EXPERIMENT_DATA)):]
# Consider only graduated species
TRAINING_DATA_GRAD = TRAINING_DATA[TRAINING_DATA["GRAD"] == "YES"]
TESTING_DATA_GRAD = TESTING_DATA[TESTING_DATA["GRAD"] == "YES"]
print("Graduate Training Data size: {}".format(len(TRAINING_DATA_GRAD)))
print("Graduate Testing Data size: {}".format(len(TESTING_DATA_GRAD)))
def plotRegression(data):
plt.figure(figsize=(8,8))
###########################
# 1st plot: linear scale
###########################
bagSold = np.asarray(data["BAGSOLD"]).reshape(-1, 1).astype(np.float)
rm = np.asarray(data["RM"]).reshape(-1,1).astype(np.float)
bias_term = np.ones_like(rm)
x_axis = np.arange(rm.min(),rm.max(),0.01)
# Liear Regression
regr = linear_model.LinearRegression(fit_intercept=True)
regr.fit(rm, bagSold)
bagSold_prediction = regr.predict(rm)
print("Coefficients = {}".format(regr.coef_))
print("Intercept = {}".format(regr.intercept_))
# Find MSE
mse = sklearn.metrics.mean_squared_error(bagSold, bagSold_prediction)
# plt.subplot("121")
plt.title('Linear Regression RM vs. Bagsold')
true_value = plt.plot(rm, bagSold, 'ro', label='True Value')
regression_line = plt.plot(x_axis, regr.intercept_[0] + regr.coef_[0][0]*x_axis, color="green")
plt.legend(["true_value", "Regression Line\nMSE = {:e}".format(mse)])
plt.xlabel("RM")
plt.ylabel("Bagsold")
plt.xlim(rm.min(),rm.max())
detailed_output["MSE of linear regression on entire dataset (linear scale)"] = mse
plt.savefig("linear_reg_entire_dataset_linearscale.png")
plt.show()
#######################
# 2nd plot: log scale
#######################
plt.figure(figsize=(8,8))
bagSold = np.log(bagSold)
# Linear Regression
regr = linear_model.LinearRegression()
regr.fit(rm, bagSold)
bagSold_prediction = regr.predict(rm)
print("Coefficients = {}".format(regr.coef_))
print("Intercept = {}".format(regr.intercept_))
# Find MSE
mse = sklearn.metrics.mean_squared_error(bagSold, bagSold_prediction)
# plt.subplot("122")
plt.title('Linear Regression RM vs. log of Bagsold')
true_value = plt.plot(rm,bagSold, 'ro', label='True Value')
regression_line = plt.plot(x_axis, regr.intercept_[0] + regr.coef_[0][0]*x_axis, color="green")
plt.legend(["true_value", "Regression Line\nMSE = {:e}".format(mse)])
plt.xlabel("RM")
plt.ylabel("log Bagsold")
plt.xlim(rm.min(),rm.max())
detailed_output["MSE of linear regression on entire dataset (log scale)"] = mse
# plt.savefig("linear_reg_entire_dataset_logscale.png")
plt.show()
# Coefficients = [[-14956.36881671]]
# Intercept = [ 794865.84758174]
plotRegression(TRAINING_DATA_GRAD)
```
## Location-based algorithm
```
location_map = list(set(TRAINING_DATA_GRAD["LOCATION"]))
location_map.sort()
# print(location_map)
list_location = []
list_avg_rm = []
list_avg_yield = []
for val in location_map:
avg_rm = np.average(TRAINING_DATA_GRAD[EXPERIMENT_DATA["LOCATION"] == str(val)]["RM"])
avg_yield = np.average(TRAINING_DATA_GRAD[EXPERIMENT_DATA["LOCATION"] == str(val)]["YIELD"])
list_location.append(str(val))
list_avg_rm.append(avg_rm)
list_avg_yield.append(avg_yield)
# print("{} = {},{}".format(val,avg_rm,avg_yield))
plt.title("Average RM and YIELD for each location")
plt.plot(list_avg_rm, list_avg_yield, 'ro')
for i, txt in enumerate(list_location):
if int(txt) <= 1000:
plt.annotate(txt, (list_avg_rm[i],list_avg_yield[i]), color="blue")
elif int(txt) <= 2000:
plt.annotate(txt, (list_avg_rm[i],list_avg_yield[i]), color="red")
elif int(txt) <= 3000:
plt.annotate(txt, (list_avg_rm[i],list_avg_yield[i]), color="green")
elif int(txt) <= 4000:
plt.annotate(txt, (list_avg_rm[i],list_avg_yield[i]), color="black")
elif int(txt) <= 5000:
plt.annotate(txt, (list_avg_rm[i],list_avg_yield[i]), color="orange")
else:
plt.annotate(txt, (list_avg_rm[i],list_avg_yield[i]), color="purple")
plt.show()
```
### Analysis
From the preliminary analysis, we find that the number of different locateion in the dataset is 140. The location in the dataset is encoded as a 4-digit number. We first expected that we can group the quality of the species based on the location parameters. We then plot the average of __RM__ and __YIELD__ for each location, which is shown below:
## Linear Regression on each group of location
According to prior analaysis, it appears that we can possibly categorize species on location. The approach we decide to adopt is to use first digit of the location number as a categorizer. The histogram in the previous section indicates that there exists roughly about 7 groups. Notice that the leftmost and rightmost columns seem to be outliers.
```
# Calculate the number of possible locations
location_set = set(TRAINING_DATA_GRAD["LOCATION"])
print("The number of possible location is {}.".format(len(location_set)))
location_histogram_list = []
for location in sorted(location_set):
amount = len(TRAINING_DATA_GRAD[TRAINING_DATA_GRAD["LOCATION"] == str(location)])
for j in range(amount):
location_histogram_list.append(int(location))
# print("Location {} has {:>3} species".format(location, amount))
plt.title("Histogram of each location")
plt.xlabel("Location Number")
plt.ylabel("Amount")
plt.hist(location_histogram_list, bins=7, range=(0,7000))
plt.savefig("location_histogram.png")
plt.show()
# Convert location column to numeric
TRAINING_DATA_GRAD["LOCATION"] = TRAINING_DATA_GRAD["LOCATION"].apply(pd.to_numeric)
# Separate training dataset into 7 groups
dataByLocation = []
for i in range(7):
dataByLocation.append(TRAINING_DATA_GRAD[(TRAINING_DATA_GRAD["LOCATION"] < ((i+1)*1000)) & (TRAINING_DATA_GRAD["LOCATION"] >= (i*1000))])
for i in range(len(dataByLocation)):
data = dataByLocation[i]
bagSold = np.log(np.asarray(data["BAGSOLD"]).reshape(-1,1).astype(np.float))
rm = np.asarray(data["RM"]).reshape(-1,1).astype(np.float)
# Liear Regression
regr = linear_model.LinearRegression()
regr.fit(rm, bagSold)
model_dict[i] = regr
bagSold_prediction = regr.predict(rm)
x_axis = np.arange(rm.min(), rm.max(), 0.01).reshape(-1,1)
# Find MSE
mse = sklearn.metrics.mean_squared_error(bagSold, bagSold_prediction)
print(mse, np.sqrt(mse))
detailed_output["number of data point on location {}xxx".format(i)] = len(data)
detailed_output["MSE on location {}xxx log scale".format(i)] = mse
plt.figure(figsize=(8,8))
# plt.subplot("{}".format(int(str(len(dataByLocation))+str(1)+str(i+1))))
plt.title("Linear Regression RM vs. Log Bagsold on Location {}xxx".format(i))
true_value = plt.plot(rm,bagSold, 'ro', label='True Value')
regression_line = plt.plot(x_axis, regr.predict(x_axis), color="green")
plt.legend(["true_value", "Regression Line\nMSE = {:e}".format(mse)])
# plt.show()
plt.xlim(rm.min(),rm.max())
plt.savefig("location{}.png".format(i))
```
## Test with validation set
```
# Test with validation set
TESTING_DATA_GRAD = TESTING_DATA_GRAD.reset_index(drop=True)
Xtest = np.column_stack((TESTING_DATA_GRAD["LOCATION"],
TESTING_DATA_GRAD["RM"],
TESTING_DATA_GRAD["YIELD"]))
ytest = TESTING_DATA_GRAD["BAGSOLD"].astype(np.float)
log_ytest = np.log(ytest)
ypredicted = []
for row in Xtest:
location = row[0]
rm_val = row[1]
yield_val = row[2]
model = model_dict[int(location[0])]
prediction = model.predict(rm_val)[0][0]
ypredicted.append(prediction)
ypredicted = np.array(ypredicted)
# MSE error
sklearn.metrics.mean_squared_error(log_ytest, ypredicted)
```
#### Testing Ridge Reg vs. Linear Reg
Below is not used. It's for testing the difference between Ridge Regression and Linear Regression.
The result is that the MSE is almsot the same
```
bagSold = np.log(np.asarray(TRAINING_DATA_GRAD["BAGSOLD"]).reshape(-1, 1).astype(np.float))
rm = np.asarray(TRAINING_DATA_GRAD["RM"]).reshape(-1,1).astype(np.float)
yield_val = np.asarray(TRAINING_DATA_GRAD["YIELD"]).reshape(-1,1).astype(np.float)
x = np.column_stack((rm, yield_val))
# Liear Regression
regr = linear_model.LinearRegression(fit_intercept=True)
regr.fit(x, bagSold)
bagSold_prediction = regr.predict(x)
print("Coefficients = {}".format(regr.coef_))
print("Intercept = {}".format(regr.intercept_))
# Find MSE
mse = sklearn.metrics.mean_squared_error(bagSold, bagSold_prediction)
print("MSE = {}".format(mse))
bagSold = np.log(np.asarray(TRAINING_DATA_GRAD["BAGSOLD"]).reshape(-1, 1).astype(np.float))
rm = np.asarray(TRAINING_DATA_GRAD["RM"]).reshape(-1,1).astype(np.float)
yield_val = np.asarray(TRAINING_DATA_GRAD["YIELD"]).reshape(-1,1).astype(np.float)
x = np.column_stack((rm, yield_val))
# Liear Regression
regr = linear_model.Ridge(alpha=20000)
regr.fit(x, bagSold)
bagSold_prediction = regr.predict(x)
print("Coefficients = {}".format(regr.coef_))
print("Intercept = {}".format(regr.intercept_))
# Find MSE
mse = sklearn.metrics.mean_squared_error(bagSold, bagSold_prediction)
print("MSE = {}".format(mse))
```
| github_jupyter |
# Callin Switzer
## Modifications to TLD code for ODE system
___
```
from matplotlib import pyplot as plt
%matplotlib inline
from matplotlib import cm
import numpy as np
import os
import scipy.io
import seaborn as sb
import matplotlib.pylab as pylab
# forces plots to appear in the ipython notebook
%matplotlib inline
from scipy.integrate import odeint
from pylab import plot,xlabel,ylabel,title,legend,figure,subplots
import random
import time
from pylab import cos, pi, arange, sqrt, pi, array
import sys
sb.__version__
sys.executable
sys.version
def FlyTheBug(state,t):
# unpack the state vector
x,xd,y,yd,theta,thetad,phi,phid = state # displacement,x and velocity xd etc... You got it?'
# compute acceleration xdd = x''
# Jorge's order . x,y,theta,phi,xd,yd,thetad,phid
# . there is no entry for Q(2) ... which would be y. I wonder why not?
#Reynolds number calculation:
Re_head = rhoA*(np.sqrt((xd**2)+(yd**2)))*(2*bhead)/muA; #dimensionless number
Re_butt = rhoA*(np.sqrt((xd**2)+(yd**2)))*(2*bbutt)/muA; #dimensionless number
#Coefficient of drag stuff:
Cd_head = 24/np.abs(Re_head) + 6/(1 + np.sqrt(np.abs(Re_head))) + 0.4;
Cd_butt = 24/np.abs(Re_butt) + 6/(1 + np.sqrt(np.abs(Re_butt))) + 0.4;
h1 = m1 + m2;
h2 = (-1)*L1*m1*np.sin(theta);
h3 = (-1)*L2*m2*np.sin(phi);
h4 = L1*m1*np.cos(theta);
h5 = L2*m2*np.cos(phi);
h6 = (-1)*F*np.cos(alpha+theta)+(1/2)*Cd_butt*rhoA*S_butt*np.abs(xd)*xd+(1/2)*Cd_head*rhoA*S_head*np.abs(xd)*xd+(-1)*L1*m1*np.cos(theta)*thetad**2+(-1)*L2*m2*np.cos(phi)*phid**2
h7 = g*(m1+m2)+(1/2)*Cd_butt*rhoA*S_butt*np.abs(yd)*yd+(1/2)*Cd_head*rhoA*S_head*np.abs(yd)*yd+(-1)*L1*m1*thetad**2*np.sin(theta)+(-1)*F*np.sin(alpha+theta)+(-1)*L2*m2*phid**2*np.sin(phi);
h8 = (-1)*tau0+g*L1*m1*np.cos(theta)+(-1)*K*((-1)*betaR+(-1)*pi+(-1)*theta+phi)+(-1)*c*((-1)*thetad+phid)+(-1)*F*L3*np.sin(alpha);
h9 = tau0+g*L2*m2*np.cos(phi)+K*((-1)*betaR+(-1)*pi+(-1)*theta+phi)+c*((-1)*thetad+phid);
h10 = I1+L1**2*m1
h11 = I2+L2**2*m2
xdd = (-1)*(h10*h11*h1**2+(-1)*h11*h1*h2**2+(-1)*h10*h1*h3**2+(-1)*h11*h1*h4**2+h3**2*h4**2+(-2)*h2*
h3*h4*h5+(-1)*h10*h1*h5**2+h2**2*h5**2)**(-1)*(
h10*h11*h1*h6+(-1)*h11*h4**2*h6+(-1)*h10*h5**2*
h6+h11*h2*h4*h7+h10*h3*h5*h7+(-1)*h11*h1*h2*
h8+(-1)*h3*h4*h5*h8+h2*h5**2*h8+(-1)*h10*h1*
h3*h9+h3*h4**2*h9+(-1)*h2*h4*h5*h9)
ydd = (-1)*((-1)*h10*h11*h1**2+h11*h1*h2**2+h10*h1*
h3**2+h11*h1*h4**2+(-1)*h3**2*h4**2+2*h2*h3*h4*
h5+h10*h1*h5**2+(-1)*h2**2*h5**2)**(-1)*((-1)*h11*
h2*h4*h6+(-1)*h10*h3*h5*h6+(-1)*h10*h11*h1*
h7+h11*h2**2*h7+h10*h3**2*h7+h11*h1*h4*h8+(-1)*
h3**2*h4*h8+h2*h3*h5*h8+h2*h3*h4*h9+h10*h1*
h5*h9+(-1)*h2**2*h5*h9)
thetadd = (-1)*((-1)*h10*h11*h1**2+h11*h1*h2**2+h10*h1*
h3**2+h11*h1*h4**2+(-1)*h3**2*h4**2+2*h2*h3*h4*
h5+h10*h1*h5**2+(-1)*h2**2*h5**2)**(-1)*(h11*h1*
h2*h6+h3*h4*h5*h6+(-1)*h2*h5**2*h6+h11*h1*
h4*h7+(-1)*h3**2*h4*h7+h2*h3*h5*h7+(-1)*h11*
h1**2*h8+h1*h3**2*h8+h1*h5**2*h8+(-1)*h1*h2*
h3*h9+(-1)*h1*h4*h5*h9);
phidd = (-1)*((-1)*h10*h11*h1**2+h11*h1*h2**2+h10*h1*
h3**2+h11*h1*h4**2+(-1)*h3**2*h4**2+2*h2*h3*h4*
h5+h10*h1*h5**2+(-1)*h2**2*h5**2)**(-1)*(h10*h1*
h3*h6+(-1)*h3*h4**2*h6+h2*h4*h5*h6+h2*h3*h4*
h7+h10*h1*h5*h7+(-1)*h2**2*h5*h7+(-1)*h1*h2*
h3*h8+(-1)*h1*h4*h5*h8+(-1)*h10*h1**2*h9+h1*
h2**2*h9+h1*h4**2*h9)
return [xd, xdd,yd,ydd,thetad,thetadd,phid,phidd]
# Bunches of parameters ... these don't vary from run to run
#masses and moment of inertias in terms of insect density and eccentricity
#of the head/thorax & gaster
# oh.. and I'm offline -- so I just made up a bunch of numbers.
bhead = 0.507
ahead = 0.908
bbutt = 0.1295
abutt = 1.7475
rho = 1 #cgs density of insect
rhoA = 0.00118 #cgs density of air
muA = 0.000186 #cgs viscosity
L1 = 0.908 #Length from the thorax-abdomen joint to the center of the
#head-thorax mass in cm
L2 = 1.7475 #Length from the thorax-abdomen joint to the center of the
#abdomen mass in cm
L3 = 0.75 #Length from the thorax-abdomen joint to the aerodynamic force
#vector in cm
m1 = rho*(4/3)*pi*(bhead**2)*ahead; #m1 is the mass of the head-thorax
m2 = rho*(4/3)*pi*(bbutt**2)*abutt; #m2 is the mass of the abdomen
#(petiole + gaster)
echead = ahead/bhead; #Eccentricity of head-thorax (unitless)
ecbutt = abutt/bbutt; #Eccentricity of gaster (unitless)
I1 = (1/5)*m1*(bhead**2)*(1 + echead**2); #Moment of inertia of the
#head-thorax
I2 = (1/5)*m2*(bbutt**2)*(1 + ecbutt**2); #Moment of inertia of the gaster
S_head = pi*bhead**2; #This is the surface area of the object experiencing drag.
#In this case, it is modeled as a sphere.
S_butt = pi*bbutt**2; #This is the surface area of the object experiencing drag.
#In this case, it is modeled as a sphere.
K = 29.3 #K is the torsional spring constant of the thorax-petiole joint
#in (cm^2)*g/(rad*(s^2))
c = 14075.8 #c is the torsional damping constant of the thorax-petiole joint
#in (cm^2)*g/s
g = 980.0 #g is the acceleration due to gravity in cm/(s^2)
betaR = 0.0 #This is the resting configuration of our
#torsional spring(s) = Initial abdomen angle - initial head angle - pi
#This cell just checks to be sure we can run this puppy and graph results.
state0 = [0.0, 0.0001, 0.0, 0.0001, np.pi/4, 0.0, np.pi/4 + np.pi, 0.0] #initial conditions [x0 , v0 etc0 ]
F = 0 # . CAUTION .. .I just set this to zero.
# By the way --if you give this an initial kick and keep the force low, it has a nice parabolic trajectory
alpha = 5.75
tau0 = 100.
# ti = 0.0 # initial time
# tf = 8 # final time
# nstep = 1000
# t = np.linspace(0, tf, num = nstep, endpoint = True)
tf = 1.0 # final time
nstep = 1000
step = (tf-ti)/nstep # step
t = arange(ti, tf, step)
print(t.shape)
state = odeint(FlyTheBug, state0, t)
x = array(state[:,[0]])
xd = array(state[:,[1]])
y = array(state[:,[2]])
yd = array(state[:,[3]])
theta = array(state[:,[4]])
thetad = array(state[:,[5]])
phi = array(state[:,[6]])
phid = array(state[:,[7]])
# And let's just plot it all
sb.set()
print(x[-1:], y[-1:])
x100 = [x[-1:], y[-1:]]
plt.figure()
plt.plot(t,xd, label = 'Ux vs time')
plt.plot(t,yd, label = 'Uy vs time')
plt.legend()
plt.figure()
plt.plot(t,theta, label = 'theta vs time')
plt.legend()
plt.show()
plt.plot(t,theta-phi - np.pi, label = 'theta vs time')
plt.figure()
plt.plot(x,y, label = 'x vs y')
plt.legend()
#This cell just checks to be sure we can run this puppy and graph results.
state0 = [0.0, 0.0001, 0.0, 0.0001, np.pi/4, 0.0, np.pi/4 + np.pi, 0.0] #initial conditions [x0 , v0 etc0 ]
F = 40462.5 # . CAUTION .. .I just set this to zero.
# By the way --if you give this an initial kick and keep the force low, it has a nice parabolic trajectory
alpha = 5.75
# tau0 = 69825.
# ti = 0.0 # initial time
# tf = 0.02 # final time
# nstep = 2
# t = np.linspace(0, tf, num = nstep, endpoint = True)
tf = 1.0 # final time
nstep = 1000
step = (tf-ti)/nstep # step
t = arange(ti, tf, step)
print(t.shape)
state = odeint(FlyTheBug, state0, t)
x = array(state[:,[0]])
xd = array(state[:,[1]])
y = array(state[:,[2]])
yd = array(state[:,[3]])
theta = array(state[:,[4]])
thetad = array(state[:,[5]])
phi = array(state[:,[6]])
phid = array(state[:,[7]])
# And let's just plot it all
sb.set()
print(x[-1:], y[-1:])
plt.figure()
plt.plot(t,xd, label = 'Ux vs time')
plt.plot(t,yd, label = 'Uy vs time')
plt.legend()
plt.figure()
plt.plot(t,theta, label = 'theta vs time')
plt.legend()
plt.figure()
plt.plot(x,y, label = 'x vs y')
plt.legend()
plt.show()
x100 - np.array([x[-1:], y[-1:]])
print(x[99])
print(y[99])
print(theta[99])
# This cell just tests the random assignmnent of forces and plots the result in the next cell
tic = time.time()
ti = 0.0 # initial time
tf = 0.02 # final time
nstep = 100 # number of time steps.
step = (tf-ti)/nstep # duration of the time step
t = arange(ti, tf, step) # how much time
nrun = 100 #number of trajectories.
x = [[0 for x in range(nrun)] for y in range(nstep)] # initialize the matrix of locations
xd = [[0 for x in range(nrun)] for y in range(nstep)]
y = [[0 for x in range(nrun)] for y in range(nstep)]
yd = [[0 for x in range(nrun)] for y in range(nstep)]
theta = [[0 for x in range(nrun)] for y in range(nstep)]
thetad = [[0 for x in range(nrun)] for y in range(nstep)]
phi = [[0 for x in range(nrun)] for y in range(nstep)]
phid = [[0 for x in range(nrun)] for y in range(nstep)]
state0 = [0.0, 0.1, 0.0, 0.1, 0.0, 0.0, 0.0, 0.0] #initial conditions [x0 , v0 etc0 ]
for i in range(0,nrun):
r = random.random()-0.5 # random number between -0.5 and 0.5
F = r*100000
# By the way --if you give this an initial kick and keep the force low, it has a nice parabolic trajectory
r = random.random()-0.5
alpha = r*np.pi
r = random.random()-0.5
tau0 = r*100
state = odeint(FlyTheBug, state0, t)
x[i][:] = array(state[:,[0]])
xd[i][:] = array(state[:,[1]])
y[i][:] = array(state[:,[2]])
yd[i][:] = array(state[:,[3]])
theta[i][:] = array(state[:,[4]])
thetad[i][:] = array(state[:,[5]])
phi[i][:] = array(state[:,[6]])
phid[i][:] = array(state[:,[7]])
print('elapsed time = ',time.time()-tic)
plt.figure()
for i in range(0,nrun):
plt.plot(x[i][:],y[i][:], label = 'trajectory x vs y')
# There are two forks in the road
# One is to select myriad random ICs and and myriad random Forces/ Torques.. then learn.
# The other fork generates a tracking beahvior using MPC with MC. In the latter, we want to specify a trajectory
print(x[:][nstep-1])
#%Weighting coefficients from Jorge ... hope they're the recent ones.
#%c1 = xdot, c2 = ydot, c3 = thetadot, c4 = x, c5 = y, c6 = theta
#c1 = 1*10^-5; c2 = 1*10^-5; c3 = 10^6; c4 = 10^7; c5 = 10^8; c6 = 10^10;
CostWeights = [10**7,10**-5,10**8,10**-5,10^10,10^6,0,0]
#EndState = [x[:][nstep-1],xd[:][nstep-1]],y[:][nstep-1],yd[:][nstep-1],theta[:][nstep-1],thetad[:][nstep-1],phi[:][nstep-1],phid[:][nstep-1]
Goal = [0.01,0.01,0.01,0.01,0.01,0.01,0.01,0.01]
print(np.dot(CostWeights,np.abs(EndState - Goal)))
import multiprocessing
multiprocessing.cpu_count()
```
| github_jupyter |
```
from IPython.display import display, HTML
from pyspark.sql import SparkSession
from pyspark import StorageLevel
import pandas as pd
from pyspark.sql.types import StructType, StructField,StringType, LongType, IntegerType, DoubleType, ArrayType
from pyspark.sql.functions import regexp_replace
from sedona.register import SedonaRegistrator
from sedona.utils import SedonaKryoRegistrator, KryoSerializer
from pyspark.sql.functions import col, split, expr
from pyspark.sql.functions import udf, lit
from sedona.utils import SedonaKryoRegistrator, KryoSerializer
from pyspark.sql.functions import col, split, expr
from pyspark.sql.functions import udf, lit
```
# Create Spark Session for application
```
spark = SparkSession.\
builder.\
master("local[*]").\
appName("Demo-app").\
config("spark.serializer", KryoSerializer.getName).\
config("spark.kryo.registrator", SedonaKryoRegistrator.getName) .\
config("spark.jars.packages", "org.apache.sedona:sedona-python-adapter-3.0_2.12:1.1.0-incubating,org.datasyslab:geotools-wrapper:1.1.0-25.2") .\
getOrCreate()
SedonaRegistrator.registerAll(spark)
sc = spark.sparkContext
```
# Geotiff Loader
1. Loader takes as input a path to directory which contains geotiff files or a parth to particular geotiff file
2. Loader will read geotiff image in a struct named image which contains multiple fields as shown in the schema below which can be extracted using spark SQL
```
# Path to directory of geotiff images
DATA_DIR = "./data/raster/"
df = spark.read.format("geotiff").option("dropInvalid",True).load(DATA_DIR)
df.printSchema()
df = df.selectExpr("image.origin as origin","ST_GeomFromWkt(image.wkt) as Geom", "image.height as height", "image.width as width", "image.data as data", "image.nBands as bands")
df.show(5)
```
# Extract a particular band from geotiff dataframe using RS_GetBand()
```
''' RS_GetBand() will fetch a particular band from given data array which is the concatination of all the bands'''
df = df.selectExpr("Geom","RS_GetBand(data, 1,bands) as Band1","RS_GetBand(data, 2,bands) as Band2","RS_GetBand(data, 3,bands) as Band3", "RS_GetBand(data, 4,bands) as Band4")
df.createOrReplaceTempView("allbands")
df.show(5)
```
# Map Algebra operations on band values
```
''' RS_NormalizedDifference can be used to calculate NDVI for a particular geotiff image since it uses same computational formula as ndvi'''
NomalizedDifference = df.selectExpr("RS_NormalizedDifference(Band1, Band2) as normDiff")
NomalizedDifference.show(5)
''' RS_Mean() can used to calculate mean of piel values in a particular spatial band '''
meanDF = df.selectExpr("RS_Mean(Band1) as mean")
meanDF.show(5)
""" RS_Mode() is used to calculate mode in an array of pixels and returns a array of double with size 1 in case of unique mode"""
modeDF = df.selectExpr("RS_Mode(Band1) as mode")
modeDF.show(5)
''' RS_GreaterThan() is used to mask all the values with 1 which are greater than a particular threshold'''
greaterthanDF = spark.sql("Select RS_GreaterThan(Band1,1000.0) as greaterthan from allbands")
greaterthanDF.show()
''' RS_GreaterThanEqual() is used to mask all the values with 1 which are greater than a particular threshold'''
greaterthanEqualDF = spark.sql("Select RS_GreaterThanEqual(Band1,360.0) as greaterthanEqual from allbands")
greaterthanEqualDF.show()
''' RS_LessThan() is used to mask all the values with 1 which are less than a particular threshold'''
lessthanDF = spark.sql("Select RS_LessThan(Band1,1000.0) as lessthan from allbands")
lessthanDF.show()
''' RS_LessThanEqual() is used to mask all the values with 1 which are less than equal to a particular threshold'''
lessthanEqualDF = spark.sql("Select RS_LessThanEqual(Band1,2890.0) as lessthanequal from allbands")
lessthanEqualDF.show()
''' RS_AddBands() can add two spatial bands together'''
sumDF = df.selectExpr("RS_AddBands(Band1, Band2) as sumOfBand")
sumDF.show(5)
''' RS_SubtractBands() can subtract two spatial bands together'''
subtractDF = df.selectExpr("RS_SubtractBands(Band1, Band2) as diffOfBand")
subtractDF.show(5)
''' RS_MultiplyBands() can multiple two bands together'''
multiplyDF = df.selectExpr("RS_MultiplyBands(Band1, Band2) as productOfBand")
multiplyDF.show(5)
''' RS_DivideBands() can divide two bands together'''
divideDF = df.selectExpr("RS_DivideBands(Band1, Band2) as divisionOfBand")
divideDF.show(5)
''' RS_MultiplyFactor() will multiply a factor to a spatial band'''
mulfacDF = df.selectExpr("RS_MultiplyFactor(Band2, 2) as target")
mulfacDF.show(5)
''' RS_BitwiseAND() will return AND between two values of Bands'''
bitwiseAND = df.selectExpr("RS_BitwiseAND(Band1, Band2) as AND")
bitwiseAND.show(5)
''' RS_BitwiseOR() will return OR between two values of Bands'''
bitwiseOR = df.selectExpr("RS_BitwiseOR(Band1, Band2) as OR")
bitwiseOR.show(5)
''' RS_Count() will calculate the total number of occurence of a target value'''
countDF = df.selectExpr("RS_Count(RS_GreaterThan(Band1,1000.0), 1.0) as count")
countDF.show(5)
''' RS_Modulo() will calculate the modulus of band value with respect to a given number'''
moduloDF = df.selectExpr("RS_Modulo(Band1, 21.0) as modulo ")
moduloDF.show(5)
''' RS_SquareRoot() will calculate calculate square root of all the band values upto two decimal places'''
rootDF = df.selectExpr("RS_SquareRoot(Band1) as root")
rootDF.show(5)
''' RS_LogicalDifference() will return value from band1 if value at that particular location is not equal tp band1 else it will return 0'''
logDiff = df.selectExpr("RS_LogicalDifference(Band1, Band2) as loggDifference")
logDiff.show(5)
''' RS_LogicalOver() will iterate over two bands and return value of first band if it is not equal to 0 else it will return value from later band'''
logOver = df.selectExpr("RS_LogicalOver(Band3, Band2) as logicalOver")
logOver.show(5)
```
# Visualising Geotiff Images
1. Normalize the bands in range [0-255] if values are greater than 255
2. Process image using RS_Base64() which converts in into a base64 string
3. Embedd results of RS_Base64() in RS_HTML() to embedd into IPython notebook
4. Process results of RS_HTML() as below:
```
''' Plotting images as a dataframe using geotiff Dataframe.'''
df = spark.read.format("geotiff").option("dropInvalid",True).load(DATA_DIR)
df = df.selectExpr("image.origin as origin","ST_GeomFromWkt(image.wkt) as Geom", "image.height as height", "image.width as width", "image.data as data", "image.nBands as bands")
df = df.selectExpr("RS_GetBand(data,1,bands) as targetband", "height", "width", "bands", "Geom")
df_base64 = df.selectExpr("Geom", "RS_Base64(height,width,RS_Normalize(targetBand), RS_Array(height*width,0.0), RS_Array(height*width, 0.0)) as red","RS_Base64(height,width,RS_Array(height*width, 0.0), RS_Normalize(targetBand), RS_Array(height*width, 0.0)) as green", "RS_Base64(height,width,RS_Array(height*width, 0.0), RS_Array(height*width, 0.0), RS_Normalize(targetBand)) as blue","RS_Base64(height,width,RS_Normalize(targetBand), RS_Normalize(targetBand),RS_Normalize(targetBand)) as RGB" )
df_HTML = df_base64.selectExpr("Geom","RS_HTML(red) as RedBand","RS_HTML(blue) as BlueBand","RS_HTML(green) as GreenBand", "RS_HTML(RGB) as CombinedBand")
df_HTML.show(5)
display(HTML(df_HTML.limit(2).toPandas().to_html(escape=False)))
```
# User can also create some UDF manually to manipulate Geotiff dataframes
```
''' Sample UDF calculates sum of all the values in a band which are greater than 1000.0 '''
def SumOfValues(band):
total = 0.0
for num in band:
if num>1000.0:
total+=1
return total
calculateSum = udf(SumOfValues, DoubleType())
spark.udf.register("RS_Sum", calculateSum)
sumDF = df.selectExpr("RS_Sum(targetband) as sum")
sumDF.show()
''' Sample UDF to visualize a particular region of a GeoTiff image'''
def generatemask(band, width,height):
for (i,val) in enumerate(band):
if (i%width>=12 and i%width<26) and (i%height>=12 and i%height<26):
band[i] = 255.0
else:
band[i] = 0.0
return band
maskValues = udf(generatemask, ArrayType(DoubleType()))
spark.udf.register("RS_MaskValues", maskValues)
df_base64 = df.selectExpr("Geom", "RS_Base64(height,width,RS_Normalize(targetband), RS_Array(height*width,0.0), RS_Array(height*width, 0.0), RS_MaskValues(targetband,width,height)) as region" )
df_HTML = df_base64.selectExpr("Geom","RS_HTML(region) as selectedregion")
display(HTML(df_HTML.limit(2).toPandas().to_html(escape=False)))
```
| github_jupyter |
# Stepper Motors
* [How to use a stepper motor with the Raspberry Pi Pico](https://www.youngwonks.com/blog/How-to-use-a-stepper-motor-with-the-Raspberry-Pi-Pico)
* [Control 28BYJ-48 Stepper Motor with ULN2003 Driver & Arduino](https://lastminuteengineers.com/28byj48-stepper-motor-arduino-tutorial/) Description of the 27BYJ-48 stepper motor, ULN2003 driver, and Arduino code.
* [28BYJ-48 stepper motor and ULN2003 Arduino (Quick tutorial for beginners)](https://www.youtube.com/watch?v=avrdDZD7qEQ) Video description.
* [Stepper Motor - Wikipedia](https://en.wikipedia.org/wiki/Stepper_motor)
<img src="https://upload.wikimedia.org/wikipedia/commons/6/66/28BYJ-48_unipolar_stepper_motor_with_ULN2003_driver.jpg" alt="28BYJ-48 unipolar stepper motor with ULN2003 driver.jpg" height="480" width="640">
<a href="https://commons.wikimedia.org/w/index.php?curid=83551720">Link</a>
## Stepper Motors

[Adafruit](https://learn.adafruit.com/all-about-stepper-motors/types-of-steppers)

[Adafruit](https://learn.adafruit.com/all-about-stepper-motors/types-of-steppers)

## Unipolar Stepper Motors
The ubiquitous 28BYJ-48 stepper motor with reduction gears that is manufactured by the millions and widely available at very low cost. [Elegoo, for example, sells kits of 5 motors with ULN2003 5V driver boards](https://www.elegoo.com/products/elegoo-uln2003-5v-stepper-motor-uln2003-driver-board) for less than $15/kit. The [UNL2003](https://en.wikipedia.org/wiki/ULN2003A) is a package of seven NPN Darlington transistors capable of 500ma output at 50 volts, with flyback diodes to drive inductive loads.


The 28BJY-48 has 32 teeth thus each full step corresponds to 360/32 = 11.25 degrees of rotation. A set of four reduction gears yields a 63.68395:1 gear reduction, or 2037.8864 steps per rotation. The maximum speed is 500 steps per second. If half steps are used, then there are 4075.7728 half steps per revolution at a maximum speed of 1000 half steps per second.
(See https://youtu.be/15K9N1yVnhc for a teardown of the 28BYJ-48 motor.)
## Driving the 28BYJ-48 Stepper Motor
(Also see https://www.youtube.com/watch?v=UJ4JjeCLuaI&ab_channel=TinkerTechTrove)
The following code assigns four GPIO pins to the four coils. For this code, the pins don't need to be contiguous or in order, but keeping that discipline may help later when we attempt to implement a driver using the PIO state machines of the Raspberry Pi Pico.
Note that the Stepper class maintains an internal parameter corresponding to the current rotor position. This is used to index into the sequence data using modular arithmetic.
See []() for ideas on a Stepper class.
```
%serialconnect
from machine import Pin
import time
class Stepper(object):
step_seq = [[1, 0, 0, 0],
[1, 1, 0, 0],
[0, 1, 0, 0],
[0, 1, 1, 0],
[0, 0, 1, 0],
[0, 0, 1, 1],
[0, 0, 0, 1],
[1, 0, 0, 1]]
def __init__(self, gpio_pins):
self.pins = [Pin(pin, Pin.OUT) for pin in gpio_pins]
self.motor_position = 0
def rotate(self, degrees=360):
n_steps = abs(int(4075.7728*degrees/360))
d = 1 if degrees > 0 else -1
for _ in range(n_steps):
self.motor_position += d
phase = self.motor_position % len(self.step_seq)
for i, value in enumerate(self.step_seq[phase]):
self.pins[i].value(value)
time.sleep(0.001)
stepper = Stepper([2, 3, 4, 5])
stepper.rotate(360)
stepper.rotate(-360)
print(stepper.motor_position)
```
Discussion:
* What class methods should we build to support the syringe pump project?
* Should we simplify and stick with half-step sequence?
* How will be integrate motor operation with UI buttons and other controls?
## Programmable Input/Ouput (PIO)
* MicroPython (https://datasheets.raspberrypi.org/pico/raspberry-pi-pico-python-sdk.pdf)
* TinkerTechTrove [[github]](https://github.com/tinkertechtrove/pico-pi-playinghttps://github.com/tinkertechtrove/pico-pi-playing) [[youtube]](https://www.youtube.com/channel/UCnoBIijHK7NnCBVpUojYFTA/videoshttps://www.youtube.com/channel/UCnoBIijHK7NnCBVpUojYFTA/videos)
* [Raspberry Pi Pico PIO - Ep. 1 - Overview with Pull, Out, and Parallel Port](https://youtu.be/YafifJLNr6I)
```
%serialconnect
from machine import Pin
from rp2 import PIO, StateMachine, asm_pio
from time import sleep
import sys
@asm_pio(set_init=(PIO.OUT_LOW,) * 4)
def prog():
wrap_target()
set(pins, 8) [31] # 8
nop() [31]
nop() [31]
nop() [31]
nop() [31]
nop() [31]
nop() [31]
set(pins, 4) [31] # 4
nop() [31]
nop() [31]
nop() [31]
nop() [31]
nop() [31]
nop() [31]
set(pins, 2) [31] # 2
nop() [31]
nop() [31]
nop() [31]
nop() [31]
nop() [31]
nop() [31]
set(pins, 1) [31] # 1
nop() [31]
nop() [31]
nop() [31]
nop() [31]
nop() [31]
nop() [31]
wrap()
sm = StateMachine(0, prog, freq=100000, set_base=Pin(14))
sm.active(1)
sleep(10)
sm.active(0)
sm.exec("set(pins,0)")
%serialconnect
from machine import Pin
from rp2 import PIO, StateMachine, asm_pio
from time import sleep
import sys
@asm_pio(set_init=(PIO.OUT_LOW,) * 4,
out_init=(PIO.OUT_HIGH,) * 4,
out_shiftdir=PIO.SHIFT_LEFT)
def prog():
pull()
mov(y, osr) # step pattern
pull()
mov(x, osr) # num steps
jmp(not_x, "end")
label("loop")
jmp(not_osre, "step") # loop pattern if exhausted
mov(osr, y)
label("step")
out(pins, 4) [31]
nop() [31]
nop() [31]
nop() [31]
jmp(x_dec,"loop")
label("end")
set(pins, 8) [31] # 8
sm = StateMachine(0, prog, freq=10000, set_base=Pin(14), out_base=Pin(14))
sm.active(1)
sm.put(2216789025) #1000 0100 0010 0001 1000010000100001
sm.put(1000)
sleep(10)
sm.active(0)
sm.exec("set(pins,0)")
%serialconnect
from machine import Pin
from rp2 import PIO, StateMachine, asm_pio
from time import sleep
import sys
@asm_pio(set_init=(PIO.OUT_LOW,) * 4,
out_init=(PIO.OUT_LOW,) * 4,
out_shiftdir=PIO.SHIFT_RIGHT,
in_shiftdir=PIO.SHIFT_LEFT)
def prog():
pull()
mov(x, osr) # num steps
pull()
mov(y, osr) # step pattern
jmp(not_x, "end")
label("loop")
jmp(not_osre, "step") # loop pattern if exhausted
mov(osr, y)
label("step")
out(pins, 4) [31]
jmp(x_dec,"loop")
label("end")
irq(rel(0))
sm = StateMachine(0, prog, freq=10000, set_base=Pin(14), out_base=Pin(14))
data = [(1,2,4,8),(2,4,8,1),(4,8,1,2),(8,1,2,4)]
steps = 0
def turn(sm):
global steps
global data
idx = steps % 4
a = data[idx][0] | (data[idx][1] << 4) | (data[idx][2] << 8) | (data[idx][3] << 12)
a = a << 16 | a
#print("{0:b}".format(a))
sleep(1)
sm.put(500)
sm.put(a)
steps += 500
sm.irq(turn)
sm.active(1)
turn(sm)
sleep(50)
print("done")
sm.active(0)
sm.exec("set(pins,0)")
%serialconnect
import time
import rp2
@rp2.asm_pio()
def irq_test():
wrap_target()
nop() [31]
nop() [31]
nop() [31]
nop() [31]
irq(0)
nop() [31]
nop() [31]
nop() [31]
nop() [31]
irq(1)
wrap()
rp2.PIO(0).irq(lambda pio: print(pio.irq().flags()))
#rp2.PIO(1).irq(lambda pio: print("1"))
sm = rp2.StateMachine(0, irq_test, freq=2000)
sm1 = rp2.StateMachine(1, irq_test, freq=2000)
sm.active(1)
#sm1.active(1)
time.sleep(1)
sm.active(0)
sm1.active(0)
```
| github_jupyter |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Image/image_smoothing.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Image/image_smoothing.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Image/image_smoothing.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Image/image_smoothing.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The following script checks if the geehydro package has been installed. If not, it will install geehydro, which automatically install its dependencies, including earthengine-api and folium.
```
import subprocess
try:
import geehydro
except ImportError:
print('geehydro package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geehydro'])
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once.
```
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
image = ee.Image('srtm90_v4')
smoothed = image.reduceNeighborhood(**{
'reducer': ee.Reducer.mean(),
'kernel': ee.Kernel.square(3),
})
# vis_params = {'min': 0, 'max': 3000}
# Map.addLayer(image, vis_params, 'SRTM original')
# Map.addLayer(smooth, vis_params, 'SRTM smoothed')
Map.setCenter(-112.40, 42.53, 12)
Map.addLayer(ee.Terrain.hillshade(image), {}, 'Original hillshade')
Map.addLayer(ee.Terrain.hillshade(smoothed), {}, 'Smoothed hillshade')
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
| github_jupyter |
# Self-Driving Car Engineer Nanodegree
## Deep Learning
## Project: Build a Traffic Sign Recognition Classifier
In this notebook, a template is provided for you to implement your functionality in stages, which is required to successfully complete this project. If additional code is required that cannot be included in the notebook, be sure that the Python code is successfully imported and included in your submission if necessary.
> **Note**: Once you have completed all of the code implementations, you need to finalize your work by exporting the iPython Notebook as an HTML document. Before exporting the notebook to html, all of the code cells need to have been run so that reviewers can see the final implementation and output. You can then export the notebook by using the menu above and navigating to \n",
"**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
In addition to implementing code, there is a writeup to complete. The writeup should be completed in a separate file, which can be either a markdown file or a pdf document. There is a [write up template](https://github.com/udacity/CarND-Traffic-Sign-Classifier-Project/blob/master/writeup_template.md) that can be used to guide the writing process. Completing the code template and writeup template will cover all of the [rubric points](https://review.udacity.com/#!/rubrics/481/view) for this project.
The [rubric](https://review.udacity.com/#!/rubrics/481/view) contains "Stand Out Suggestions" for enhancing the project beyond the minimum requirements. The stand out suggestions are optional. If you decide to pursue the "stand out suggestions", you can include the code in this Ipython notebook and also discuss the results in the writeup file.
>**Note:** Code and Markdown cells can be executed using the **Shift + Enter** keyboard shortcut. In addition, Markdown cells can be edited by typically double-clicking the cell to enter edit mode.
```
import pickle
import numpy as np
import pandas as pd
import random
from sklearn.utils import shuffle
import tensorflow as tf
from tensorflow.contrib.layers import flatten
import cv2
import glob
import os
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
%matplotlib inline
```
---
## Step 0: Load The Data
```
# TODO: Fill this in based on where you saved the training and testing data
training_file = "../data/train.p"
validation_file= "../data/valid.p"
testing_file = "../data/test.p"
with open(training_file, mode='rb') as f:
train = pickle.load(f)
with open(validation_file, mode='rb') as f:
valid = pickle.load(f)
with open(testing_file, mode='rb') as f:
test = pickle.load(f)
X_train, y_train = train['features'], train['labels']
X_valid, y_valid = valid['features'], valid['labels']
X_test, y_test = test['features'], test['labels']
```
---
## Step 1: Dataset Summary & Exploration
The pickled data is a dictionary with 4 key/value pairs:
- `'features'` is a 4D array containing raw pixel data of the traffic sign images, (num examples, width, height, channels).
- `'labels'` is a 1D array containing the label/class id of the traffic sign. The file `signnames.csv` contains id -> name mappings for each id.
- `'sizes'` is a list containing tuples, (width, height) representing the original width and height the image.
- `'coords'` is a list containing tuples, (x1, y1, x2, y2) representing coordinates of a bounding box around the sign in the image. **THESE COORDINATES ASSUME THE ORIGINAL IMAGE. THE PICKLED DATA CONTAINS RESIZED VERSIONS (32 by 32) OF THESE IMAGES**
Complete the basic data summary below. Use python, numpy and/or pandas methods to calculate the data summary rather than hard coding the results. For example, the [pandas shape method](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.shape.html) might be useful for calculating some of the summary results.
### Provide a Basic Summary of the Data Set Using Python, Numpy and/or Pandas
```
### Replace each question mark with the appropriate value.
### Use python, pandas or numpy methods rather than hard coding the results
# TODO: Number of training examples
n_train = len(X_train)
# TODO: Number of validation examples
n_validation = len(X_valid)
# TODO: Number of testing examples.
n_test = len(X_test)
# TODO: What's the shape of an traffic sign image?
image_shape = X_train[0].shape
# TODO: How many unique classes/labels there are in the dataset.
n_classes = len(np.unique(y_train))
print("Number of training examples =", n_train)
print("Number of testing examples =", n_test)
print("Image data shape =", image_shape)
print("Number of classes =", n_classes)
```
### Include an exploratory visualization of the dataset
Visualize the German Traffic Signs Dataset using the pickled file(s). This is open ended, suggestions include: plotting traffic sign images, plotting the count of each sign, etc.
The [Matplotlib](http://matplotlib.org/) [examples](http://matplotlib.org/examples/index.html) and [gallery](http://matplotlib.org/gallery.html) pages are a great resource for doing visualizations in Python.
**NOTE:** It's recommended you start with something simple first. If you wish to do more, come back to it after you've completed the rest of the sections. It can be interesting to look at the distribution of classes in the training, validation and test set. Is the distribution the same? Are there more examples of some classes than others?
```
### Data exploration visualization code goes here.
### Feel free to use as many code cells as needed.
index = random.randint(0, len(X_train))
image = X_train[index].squeeze()
plt.figure(figsize=(1,1))
plt.imshow(image)
print(y_train[index])
```
----
## Step 2: Design and Test a Model Architecture
Design and implement a deep learning model that learns to recognize traffic signs. Train and test your model on the [German Traffic Sign Dataset](http://benchmark.ini.rub.de/?section=gtsrb&subsection=dataset).
The LeNet-5 implementation shown in the [classroom](https://classroom.udacity.com/nanodegrees/nd013/parts/fbf77062-5703-404e-b60c-95b78b2f3f9e/modules/6df7ae49-c61c-4bb2-a23e-6527e69209ec/lessons/601ae704-1035-4287-8b11-e2c2716217ad/concepts/d4aca031-508f-4e0b-b493-e7b706120f81) at the end of the CNN lesson is a solid starting point. You'll have to change the number of classes and possibly the preprocessing, but aside from that it's plug and play!
With the LeNet-5 solution from the lecture, you should expect a validation set accuracy of about 0.89. To meet specifications, the validation set accuracy will need to be at least 0.93. It is possible to get an even higher accuracy, but 0.93 is the minimum for a successful project submission.
There are various aspects to consider when thinking about this problem:
- Neural network architecture (is the network over or underfitting?)
- Play around preprocessing techniques (normalization, rgb to grayscale, etc)
- Number of examples per label (some have more than others).
- Generate fake data.
Here is an example of a [published baseline model on this problem](http://yann.lecun.com/exdb/publis/pdf/sermanet-ijcnn-11.pdf). It's not required to be familiar with the approach used in the paper but, it's good practice to try to read papers like these.
### Pre-process the Data Set (normalization, grayscale, etc.)
Minimally, the image data should be normalized so that the data has mean zero and equal variance. For image data, `(pixel - 128)/ 128` is a quick way to approximately normalize the data and can be used in this project.
Other pre-processing steps are optional. You can try different techniques to see if it improves performance.
Use the code cell (or multiple code cells, if necessary) to implement the first step of your project.
```
### Preprocess the data here. It is required to normalize the data. Other preprocessing steps could include
### converting to grayscale, etc.
### Feel free to use as many code cells as needed.
#Convert to gray
X_train_gry = np.sum(X_train/3, axis=3, keepdims=True)
X_valid_gry = np.sum(X_valid/3, axis=3, keepdims=True)
X_test_gry = np.sum(X_test/3, axis=3, keepdims=True)
#Normalize Images
X_train_norm = (X_train_gry)/255
X_valid_norm = (X_valid_gry)/255
X_test_norm = (X_test_gry)/255
#Shuffle dataset
X_train_norm, y_train = shuffle(X_train_gry, y_train)
X_valid_norm, y_valid = shuffle(X_valid_gry, y_valid)
```
### Model Architecture
```
### Define your architecture here.
### Feel free to use as many code cells as needed.
def LeNet(x):
#HyperParameters
mu = 0
sigma = 0.1
keep_prob = 0.5
# SOLUTION: Layer 1: Convolutional. Input = 32x32x1. Output = 28x28x6.
conv1_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 1, 6), mean = mu, stddev = sigma))
conv1_b = tf.Variable(tf.zeros(6))
conv1 = tf.nn.conv2d(x, conv1_W, strides=[1, 1, 1, 1], padding='VALID') + conv1_b
conv1 = tf.nn.relu(conv1)
conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# SOLUTION: Layer 2: Convolutional. Output = 10x10x16.
conv2_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 6, 16), mean = mu, stddev = sigma))
conv2_b = tf.Variable(tf.zeros(16))
conv2 = tf.nn.conv2d(conv1, conv2_W, strides=[1, 1, 1, 1], padding='VALID') + conv2_b
conv2 = tf.nn.relu(conv2)
conv2 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# SOLUTION: Flatten. Input = 5x5x16. Output = 400.
fc0 = flatten(conv2)
# SOLUTION: Layer 3: Fully Connected. Input = 400. Output = 120.
fc1_W = tf.Variable(tf.truncated_normal(shape=(400, 120), mean = mu, stddev = sigma))
fc1_b = tf.Variable(tf.zeros(120))
fc1 = tf.matmul(fc0, fc1_W) + fc1_b
fc1 = tf.nn.relu(fc1)
#fc1 = tf.nn.dropout(fc1, keep_prob)
# SOLUTION: Layer 4: Fully Connected. Input = 120. Output = 84.
fc2_W = tf.Variable(tf.truncated_normal(shape=(120, 84), mean = mu, stddev = sigma))
fc2_b = tf.Variable(tf.zeros(84))
fc2 = tf.matmul(fc1, fc2_W) + fc2_b
fc2 = tf.nn.relu(fc2)
#fc2 = tf.nn.dropout(fc2, keep_prob)
# SOLUTION: Layer 5: Fully Connected. Input = 84. Output = 10.
fc3_W = tf.Variable(tf.truncated_normal(shape=(84, 43), mean = mu, stddev = sigma))
fc3_b = tf.Variable(tf.zeros(43))
logits = tf.matmul(fc2, fc3_W) + fc3_b
return logits
```
### Train, Validate and Test the Model
A validation set can be used to assess how well the model is performing. A low accuracy on the training and validation
sets imply underfitting. A high accuracy on the training set but low accuracy on the validation set implies overfitting.
```
### Train your model here.
### Calculate and report the accuracy on the training and validation set.
### Once a final model architecture is selected,
### the accuracy on the test set should be calculated and reported as well.
### Feel free to use as many code cells as needed.
x = tf.placeholder(tf.float32, (None, 32, 32, 1))
y = tf.placeholder(tf.int32, (None))
one_hot_y = tf.one_hot(y, 43)
#Training Pipeline
rate = 0.001
logits = LeNet(x)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot_y, logits=logits)
loss_operation = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate = rate)
training_operation = optimizer.minimize(loss_operation)
#Model Evaluation
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(one_hot_y, 1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()
def evaluate(X_data, y_data):
num_examples = len(X_data)
total_accuracy = 0
sess = tf.get_default_session()
for offset in range(0, num_examples, BATCH_SIZE):
batch_x, batch_y = X_data[offset:offset+BATCH_SIZE], y_data[offset:offset+BATCH_SIZE]
accuracy = sess.run(accuracy_operation, feed_dict={x: batch_x, y: batch_y})
total_accuracy += (accuracy * len(batch_x))
return total_accuracy / num_examples
EPOCHS = 30
BATCH_SIZE = 128
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
num_examples = len(X_train_norm)
print("Training...")
print()
for i in range(EPOCHS):
X_train_norm, y_train = shuffle(X_train_norm, y_train)
for offset in range(0, num_examples, BATCH_SIZE):
end = offset + BATCH_SIZE
batch_x, batch_y = X_train_norm[offset:end], y_train[offset:end]
sess.run(training_operation, feed_dict={x: batch_x, y: batch_y})
validation_accuracy = evaluate(X_valid_norm, y_valid)
print("EPOCH {} ...".format(i+1))
print("Validation Accuracy = {:.3f}".format(validation_accuracy))
print()
saver.save(sess, './lenet')
print("Model saved")
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
test_accuracy = evaluate(X_test_gry, y_test)
print("Test Accuracy = {:.3f}".format(test_accuracy))
```
---
## Step 3: Test a Model on New Images
To give yourself more insight into how your model is working, download at least five pictures of German traffic signs from the web and use your model to predict the traffic sign type.
You may find `signnames.csv` useful as it contains mappings from the class id (integer) to the actual sign name.
### Load and Output the Images
```
### Load the images and plot them here.
### Feel free to use as many code cells as needed.
#fig, axs = plt.subplots(2,4, figsize=(4, 2))
#fig.subplots_adjust(hspace = .2, wspace=.001)
#axs = axs.ravel()
#../data/Images/traffic*.png
fig, axes = plt.subplots(1, 5, figsize=(18,4))
new_images = []
for i, img in enumerate(sorted(glob.glob('../data/Images/traffic*.png'))):
image = mpimg.imread(img)
axes[i].imshow(image)
axes[i].axis('off')
image = cv2.resize(image, (32, 32))
image = np.sum(image/3, axis = 2, keepdims = True)
image = (image - image.mean())/np.std(image)
new_images.append(image)
print(image.shape)
#new_images.shape
X_new_images = np.asarray(new_images)
y_new_images = np.array([12, 18, 38, 18, 38])
print(X_new_images.shape)
```
### Predict the Sign Type for Each Image
```
### Run the predictions here and use the model to output the prediction for each image.
### Make sure to pre-process the images with the same pre-processing pipeline used earlier.
### Feel free to use as many code cells as needed.
#my_labels = [35, 12, 11, 24, 16, 14, 1, 4]
keep_prob = tf.placeholder(tf.float32)
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
sess = tf.get_default_session()
new_images_accuracy = sess.run(accuracy_operation, feed_dict={x: X_new_images, y: y_new_images, keep_prob: 1.0})
print("Test Accuracy = {:.3f}".format(new_images_accuracy))
```
### Analyze Performance
```
### Calculate the accuracy for these 5 new images.
### For example, if the model predicted 1 out of 5 signs correctly, it's 20% accurate on these new images.
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
sess = tf.get_default_session()
prediction = sess.run(logits, feed_dict={x: X_new_images, y: y_new_images, keep_prob: 1.0})
print(np.argmax(prediction,1))
```
### Output Top 5 Softmax Probabilities For Each Image Found on the Web
For each of the new images, print out the model's softmax probabilities to show the **certainty** of the model's predictions (limit the output to the top 5 probabilities for each image). [`tf.nn.top_k`](https://www.tensorflow.org/versions/r0.12/api_docs/python/nn.html#top_k) could prove helpful here.
The example below demonstrates how tf.nn.top_k can be used to find the top k predictions for each image.
`tf.nn.top_k` will return the values and indices (class ids) of the top k predictions. So if k=3, for each sign, it'll return the 3 largest probabilities (out of a possible 43) and the correspoding class ids.
Take this numpy array as an example. The values in the array represent predictions. The array contains softmax probabilities for five candidate images with six possible classes. `tf.nn.top_k` is used to choose the three classes with the highest probability:
```
# (5, 6) array
a = np.array([[ 0.24879643, 0.07032244, 0.12641572, 0.34763842, 0.07893497,
0.12789202],
[ 0.28086119, 0.27569815, 0.08594638, 0.0178669 , 0.18063401,
0.15899337],
[ 0.26076848, 0.23664738, 0.08020603, 0.07001922, 0.1134371 ,
0.23892179],
[ 0.11943333, 0.29198961, 0.02605103, 0.26234032, 0.1351348 ,
0.16505091],
[ 0.09561176, 0.34396535, 0.0643941 , 0.16240774, 0.24206137,
0.09155967]])
```
Running it through `sess.run(tf.nn.top_k(tf.constant(a), k=3))` produces:
```
TopKV2(values=array([[ 0.34763842, 0.24879643, 0.12789202],
[ 0.28086119, 0.27569815, 0.18063401],
[ 0.26076848, 0.23892179, 0.23664738],
[ 0.29198961, 0.26234032, 0.16505091],
[ 0.34396535, 0.24206137, 0.16240774]]), indices=array([[3, 0, 5],
[0, 1, 4],
[0, 5, 1],
[1, 3, 5],
[1, 4, 3]], dtype=int32))
```
Looking just at the first row we get `[ 0.34763842, 0.24879643, 0.12789202]`, you can confirm these are the 3 largest probabilities in `a`. You'll also notice `[3, 0, 5]` are the corresponding indices.
```
### Print out the top five softmax probabilities for the predictions on the German traffic sign images found on the web.
### Feel free to use as many code cells as needed.
with tf.Session() as sess:
print(sess.run(tf.nn.top_k(tf.nn.softmax(prediction), k=5)))
```
### Project Writeup
Once you have completed the code implementation, document your results in a project writeup using this [template](https://github.com/udacity/CarND-Traffic-Sign-Classifier-Project/blob/master/writeup_template.md) as a guide. The writeup can be in a markdown or pdf file.
> **Note**: Once you have completed all of the code implementations and successfully answered each question above, you may finalize your work by exporting the iPython Notebook as an HTML document. You can do this by using the menu above and navigating to \n",
"**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
---
## Step 4 (Optional): Visualize the Neural Network's State with Test Images
This Section is not required to complete but acts as an additional excersise for understaning the output of a neural network's weights. While neural networks can be a great learning device they are often referred to as a black box. We can understand what the weights of a neural network look like better by plotting their feature maps. After successfully training your neural network you can see what it's feature maps look like by plotting the output of the network's weight layers in response to a test stimuli image. From these plotted feature maps, it's possible to see what characteristics of an image the network finds interesting. For a sign, maybe the inner network feature maps react with high activation to the sign's boundary outline or to the contrast in the sign's painted symbol.
Provided for you below is the function code that allows you to get the visualization output of any tensorflow weight layer you want. The inputs to the function should be a stimuli image, one used during training or a new one you provided, and then the tensorflow variable name that represents the layer's state during the training process, for instance if you wanted to see what the [LeNet lab's](https://classroom.udacity.com/nanodegrees/nd013/parts/fbf77062-5703-404e-b60c-95b78b2f3f9e/modules/6df7ae49-c61c-4bb2-a23e-6527e69209ec/lessons/601ae704-1035-4287-8b11-e2c2716217ad/concepts/d4aca031-508f-4e0b-b493-e7b706120f81) feature maps looked like for it's second convolutional layer you could enter conv2 as the tf_activation variable.
For an example of what feature map outputs look like, check out NVIDIA's results in their paper [End-to-End Deep Learning for Self-Driving Cars](https://devblogs.nvidia.com/parallelforall/deep-learning-self-driving-cars/) in the section Visualization of internal CNN State. NVIDIA was able to show that their network's inner weights had high activations to road boundary lines by comparing feature maps from an image with a clear path to one without. Try experimenting with a similar test to show that your trained network's weights are looking for interesting features, whether it's looking at differences in feature maps from images with or without a sign, or even what feature maps look like in a trained network vs a completely untrained one on the same sign image.
<figure>
<img src="visualize_cnn.png" width="380" alt="Combined Image" />
<figcaption>
<p></p>
<p style="text-align: center;"> Your output should look something like this (above)</p>
</figcaption>
</figure>
<p></p>
```
### Visualize your network's feature maps here.
### Feel free to use as many code cells as needed.
# image_input: the test image being fed into the network to produce the feature maps
# tf_activation: should be a tf variable name used during your training procedure that represents the calculated state of a specific weight layer
# activation_min/max: can be used to view the activation contrast in more detail, by default matplot sets min and max to the actual min and max values of the output
# plt_num: used to plot out multiple different weight feature map sets on the same block, just extend the plt number for each new feature map entry
def outputFeatureMap(image_input, tf_activation, activation_min=-1, activation_max=-1 ,plt_num=1):
# Here make sure to preprocess your image_input in a way your network expects
# with size, normalization, ect if needed
# image_input =
# Note: x should be the same name as your network's tensorflow data placeholder variable
# If you get an error tf_activation is not defined it may be having trouble accessing the variable from inside a function
activation = tf_activation.eval(session=sess,feed_dict={x : image_input})
featuremaps = activation.shape[3]
plt.figure(plt_num, figsize=(15,15))
for featuremap in range(featuremaps):
plt.subplot(6,8, featuremap+1) # sets the number of feature maps to show on each row and column
plt.title('FeatureMap ' + str(featuremap)) # displays the feature map number
if activation_min != -1 & activation_max != -1:
plt.imshow(activation[0,:,:, featuremap], interpolation="nearest", vmin =activation_min, vmax=activation_max, cmap="gray")
elif activation_max != -1:
plt.imshow(activation[0,:,:, featuremap], interpolation="nearest", vmax=activation_max, cmap="gray")
elif activation_min !=-1:
plt.imshow(activation[0,:,:, featuremap], interpolation="nearest", vmin=activation_min, cmap="gray")
else:
plt.imshow(activation[0,:,:, featuremap], interpolation="nearest", cmap="gray")
```
| github_jupyter |
```
import numpy as np
arr = np.arange(0,11)
arr
# Simplest way to pick an element or some of the elements from an array is similar to indexing in a python list.
arr[8] # Gives value at the index 8
# Slice Notations [start:stop]
arr[1:5] # 1 inclusive and 5 exclusive
# Another Example of Slicing
arr[0:5]
# To have everything from beginning to the index 6 we use the following syntax on a numpy array :
print(arr[:6]) # No need to define the starting point and this basically means arr[0:6]
# To have everything from a 5th index to the last we use the following syntax on a numpy array :
print(arr[5:])
```
# Broadcasting the Value
**Numpy arrays differ from normal python list due to their ability to broadcast.**
```
arr[0:5] = 100 # Broacasts the value 100 to first 5 digits.
arr
# Reset the array
arr = np.arange(0,11)
arr
slice_of_arr = arr[0:6]
slice_of_arr
# To grab everything in the slice
slice_of_arr[:]
# Broadcasting after grabbing everything in the array
slice_of_arr[:] = 99
slice_of_arr
arr
# Notice above how not only slice_of_arr got changed due to the broadcast but the array arr was also changed.
# Slice and the original array both got changed in terms of values.
# Data is not copied but rather just copied or pointed from original array.
# Reason behind such behaviour is that to prevent memory issues while dealing with large arrays.
# It basically means numpy prefers not setting copies of arrays and would rather point slices to their original parent arrays.
# Use copy() method which is array_name.copy()
arr_copy = arr.copy()
arr_copy
arr_copy[0:5] = 23
arr
arr_copy #Since we have copied now we can see that arr and arr_copy would be different even after broadcasting.
# Original array remains unaffected despite changes on the copied array.
# Main idea here is that if you grab the actual slice of the array and set it as variable without calling the method copy
# on the array then you are just seeing the link to original array and changes on slice would reflect on original/parent array.
```
# 2D Array/Matrix
```
arr_2d = np.array([[5,10,15],[20,25,30],[35,40,45]])
arr_2d # REMEMBER If having confusion regarding dimensions of the matrix just call shape.
arr_2d.shape # 3 rows, 3 columns
# Two general formats for grabbing elements from a 2D array or matrix format :
# (i) Double Bracket Format (ii) Single Bracket Format with comma (Recommended)
# (i) Double Bracket Format
arr_2d[0][:] # Gives all the elements inside the 0th index of array arr.
# arr_2d[0][:] Also works
arr_2d[1][2] # Gives the element at index 2 of the 1st index of arr_2d i.e. 30
# (ii) Single Bracket Format with comma (Recommended) : Removes [][] 2 square brackets with a tuple kind (x,y) format
# To print 30 we do the following 1st row and 2nd index
arr_2d[1,2]
# Say we want sub matrices from the matrix arr_2d
arr_2d[:3,1:] # Everything upto the third row, and anything from column 1 onwards.
arr_2d[1:,:]
```
# Conditional Selection
```
arr = np.arange(1,11)
arr
# Taking the array arr and comapring it using comparison operators to get a full boolean array out of this.
bool_arr = arr > 5
'''
1. Getting the array and using a comparison operator on it will actually return a boolean array.
2. An array with boolean values in response to our condition.
3. Now we can use the boolean array to actually index or conditionally select elements from the original array where boolean
array is true.
'''
bool_arr
arr[bool_arr] # Gives us only the results which are only true.
# Doing what's described above in one line will be
arr[arr<3] # arr[comaprison condition] Get used to this notation we use this a lot especially in Pandas!
```
# Exercise
1. Create a new 2d array np.arange(50).reshape(5,10).
2. Grab any 2sub matrices from the 5x10 chunk.
```
arr_2d = np.arange(50).reshape(5,10)
arr_2d
# Selecting 11 to 35
arr_2d[1:4,1:6]# Keep in mind it is exclusive for the end value in the start:end format of indexing.
# Selecting 5-49
arr_2d[0:,5:]
```
| github_jupyter |
# NumPy, Pandas and Matplotlib with ICESat
UW Geospatial Data Analysis
CEE498/CEWA599
David Shean
## Objectives
1. Solidify basic skills with NumPy, Pandas, and Matplotlib
2. Learn basic data manipulation, exploration, and visualizatioin with a relatively small, clean point dataset (65K points)
3. Learn a bit more about the ICESat mission, the GLAS instrument, and satellite laser altimetry
4. Explore outlier removal, grouping and clustering
# ICESat GLAS Background
The NASA Ice Cloud and land Elevation Satellite ([ICESat](https://icesat.gsfc.nasa.gov/icesat/)) was a NASA mission carrying the Geosciences Laser Altimeter System (GLAS) instrument: a space laser, pointed down at the Earth (and unsuspecting Earthlings).
It measured surface elevations by precisely tracking laser pulses emitted from the spacecraft at a rate of 40 Hz (a new pulse every 0.025 seconds). These pulses traveled through the atmosphere, reflected off the surface, back up through the atmosphere, and into space, where some small fraction of that original energy was received by a telescope on the spacecraft. The instrument electronics precisely recorded the time when these intrepid photons left the instrument and when they returned. The position and orientation of the spacecraft was precisely known, so the two-way traveltime (and assumptions about the speed of light and propagation through the atmosphere) allowed for precise forward determination of the spot on the Earth's surface (or cloud tops, as was often the case) where the reflection occurred. The laser spot size varied during the mission, but was ~70 m in diameter.
ICESat collected billions of measurements from 2003 to 2009, and was operating in a "repeat-track" mode that sacrificed spatial coverage for more observations along the same ground tracks over time. One primary science focus involved elevation change over the Earth's ice sheets. It allowed for early measurements of full Antarctic and Greenland ice sheet elevation change, which offered a detailed look at spatial distribution and rates of mass loss, and total ice sheet contributions to sea level rise.
There were problems with the lasers during the mission, so it operated in short campaigns lasting only a few months to prolong the full mission lifetime. While the primary measurements focused on the polar regions, many measurements were also collected over lower latitudes, to meet other important science objectives (e.g., estimating biomass in the Earth's forests, observing sea surface height/thickness over time).
# Sample GLAS dataset for CONUS
A few years ago, I wanted to evaluate ICESat coverage of the Continental United States (CONUS). The primary application was to extract a set of accurate control points to co-register a large set of high-resolution digital elevation modoels (DEMs) derived from satellite stereo imagery. I wrote some Python/shell scripts to download, filter, and process all of the [GLAH14 L2 Global Land Surface Altimetry Data](https://nsidc.org/data/GLAH14/versions/34) granules in parallel ([https://github.com/dshean/icesat_tools](https://github.com/dshean/icesat_tools)).
The high-level workflow is here: https://github.com/dshean/icesat_tools/blob/master/glas_proc.py#L24. These tools processed each HDF5 (H5) file and wrote out csv files containing “good” points. These csv files were concatenated to prepare the single input csv (`GLAH14_tllz_conus_lulcfilt_demfilt.csv`) that we will use for this tutorial.
The csv contains ICESat GLAS shots that passed the following filters:
* Within some buffer (~110 km) of mapped glacier polygons from the [Randolph Glacier Inventory (RGI)](https://www.glims.org/RGI/)
* Returns from exposed bare ground (landcover class 31) or snow/ice (12) according to a 30-m Land-use/Land-cover dataset (2011 NLCD, https://www.mrlc.gov/data?f%5B0%5D=category%3Aland%20cover)
* Elevation values within some threshold (200 m) of elevations sampled from an external reference DEM (void-filled 1/3-arcsec [30-m] SRTM-GL1, https://lpdaac.usgs.gov/products/srtmgl1v003/), used to remove spurious points and returns from clouds.
* Various other ICESat-specific quality flags (see comments in `glas_proc.py` for details)
The final file contains a relatively small subset (~65K) of the total shots in the original GLAH14 data granules from the full mission timeline (2003-2009). The remaining points should represent returns from the Earth's surface with reasonably high quality, and can be used for subsequent analysis.
# Lab Exercises
Let's use this dataset to explore some of the NumPy and Pandas functionality, and practice some basic plotting with Matplotlib.
I've provided instructions and hints, and you will need to fill in the code to generate the output results and plots.
## Import necessary modules
```
#Use shorter names (np, pd, plt) instead of full (numpy, pandas, matplotlib.pylot) for convenience
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#Magic function to enable interactive plotting (zoom/pan) in Jupyter notebook
#If running locally, this would be `%matplotlib notebook`, but since we're using Juptyerlab, we use widget
#%matplotlib widget
#Use matplotlib inline to render/embed figures in the notebook for upload to github
%matplotlib inline
#%matplotlib widget
```
## Define relative path to the GLAS data csv from week 01
```
glas_fn = '../01_Shell_Github/data/GLAH14_tllz_conus_lulcfilt_demfilt.csv'
```
## Do a quick check of file contents
* Use iPython functionality to run the `head` shell command on the your filename variable
# NumPy Exercises
## Load the file
* NumPy has some convenience functions for loading text files: `loadtxt` and `genfromtxt`
* Use `loadtxt` here (simpler), but make sure you properly set the delimiter and handle the first row (see the `skiprows` option)
* Use iPython `?` to look up reference on arguments for `np.loadtxt`
* Store the NumPy array as variable called `glas_np`
## Do a quick check to make sure your array looks good
* Don't use `print(glas_np)` here, just run cell containing `glas_np`
* Try both - note that the latter returns the object type, in this case `array`
## How many rows and columns are in your array?
## What is the datatype of your array?
Note that a NumPy array typically has a single datatype, while a Pandas DataFrame can contain multiple data types (e.g., `string`, `float64`)
## Examine the first 3 rows
* Use slicing here
## Examine the column with glas_z values
* You will need to figure out which column number corresponds to these values (can do this manually from header), then slice the array to return all rows, but only that column
## Compute the mean and standard deviation of the glas_z values
## Use print formatting to create a formatted string with these values
* Should be `'GLAS z: mean +/- std meters'` using your `mean` and `std` values, both formatted with 2 decimal places (cm-precision)
* For example: 'GLAS z: 1234.56 +/- 42.42 meters'
## Create a Matplotlib scatter plot of the `glas_z` values
* Careful about correclty defining your x and y with values for latitude and longitude - easy to mix these up
* Use point color to represent the elevation
* You should see points that roughly outline the western United States
* Label the x axis, y axis, and add a descriptive title
## Use conditionals and fancy indexing to extract points from 2005
* Design a "filter" to isolate the points from 2005
* Can use boolean indexing
* Can then extract values from original array using the boolean index
* Store these points in a new NumPy array
### How many points were acquired in 2005?
# Pandas Exercises
A significant portion of the Python data science ecosystem is based on Pandas and/or Pandas data models.
>pandas is a Python package providing fast, flexible, and expressive data structures designed to make working with "relational" or "labeled" data both easy and intuitive. It aims to be the fundamental high-level building block for doing practical, real world data analysis in Python. Additionally, it has the broader goal of becoming the most powerful and flexible open source data analysis / manipulation tool available in any language. It is already well on its way towards this goal.
https://github.com/pandas-dev/pandas#main-features
If you are working with tabular data, especially time series data, please use pandas.
* A better way to deal with tabular data, built on top of NumPy arrays
* With NumPy, we had to remember which column number (e.g., 3, 4) represented each variable (lat, lon, glas_z, etc)
* Pandas allows you to store data with different types, and then reference using more meaningful labels
* NumPy: `glas_np[:,4]`
* Pandas: `glas_df['glas_z']`
* A good "10-minute" reference with examples: https://pandas.pydata.org/pandas-docs/stable/getting_started/10min.html
## Load the csv file with Pandas
* Note that pandas has excellent readers for most common file formats: https://pandas.pydata.org/pandas-docs/stable/reference/io.html
## That was easy. Let's inspect the `DataFrame`
## Check data types
* Can use the DataFrame `info` method
## Get the column labels
* Can use the DataFrame `columns` attribute
If you are new to Python and object-oriented programming, take a moment to consider the difference between the methods and attributes of the DataFrame, and how both are accessed.
https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.html
If this is confusing, ask your neighbor or instructor.
## Preview records using DataFrame `head` and `tail` methods
## Compute the mean and standard deviation for all values in each column
* Don't overthink this, should be simple (no loops!)
## Print quick stats for entire DataFrame with the `describe` method
Useful, huh? Note that `median` is the `50%` statistic
## Use the Pandas plotting functionality to create a 2D scatterplot of `glas_z` values
* https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.plot.scatter.html
* Note that labels and colorbar are automatically plotted!
* Adjust the size of the points using the `s=1` keyword
* Experiment with different color ramps:
* https://matplotlib.org/examples/color/colormaps_reference.html (I prefer `inferno`)
#### Color ramps
Information on how to choose a good colormap for your data: https://matplotlib.org/3.1.0/tutorials/colors/colormaps.html
Another great resource (Thanks @fperez!): https://matplotlib.org/cmocean/
**TL;DR** Don't use `jet`, use a perceptually uniform colormap for linear variables like elevation. Use a diverging color ramp for values where sign is important.
## Experiment by changing the variable represented with the color ramp
* Try `decyear` or other columns to quickly visualize spatial distribution of these values.
## Extra Credit: Create a 3D scatterplot
See samples here: https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html
Explore with the interactive tools (click and drag to change perspective). Some lag here considering number of points to be rendered, and maybe useful for visualizing small 3D datasets in the future. There are other 3D plotting packages that are built for performance and efficiency (e.g., `ipyvolume`: https://github.com/maartenbreddels/ipyvolume)
## Create a histogram that shows the number of points vs time (`decyear`)
* Should be simple with built-in method for your `DataFrame`
* Make sure that you use enough bins to avoid aliasing. This could require some trial and error (try 10, 100, 1000, and see if you can find a good compromise)
* Can also consider some of the options (e.g., 'auto') here: https://docs.scipy.org/doc/numpy/reference/generated/numpy.histogram_bin_edges.html#numpy.histogram_bin_edges
* You should be able to resolve the distinct campaigns during the mission (each ~1-2 months long). There is an extra credit problem at the end to group by years and play with clustering for the campaigns.
## Create a histogram of all `glas_z` elevation values
* What do you note about the distribution?
* Any negative values?
## Wait a minute...negative elevations!? Who calibrated this thing? C'mon NASA.
## A note on vertical datums
Note that some elevations are less than 0 m. How can this be?
The `glas_z` values are height above (or below) the WGS84 ellipsoid. This is not the same vertical datum as mean sea level (roughly approximated by a geoid model).
A good resource explaining the details: https://vdatum.noaa.gov/docs/datums.html
## Let's check the spatial distribution of points below 0 (height above WGS84 ellipsoid)
* How many shots have a negative glas_z value?
* Create a scatterplot only using points with negative values
* Adjust the color ramp bounds to bring out more detail for these points
* hint: see the `vmin` and `vmax` arguments for the `plot` function
* What do you notice about these points? (may be tough without more context, like coastlines and state boundaries or a tiled basemap - we'll learn how to incorporate these soon)
## Geoid offset
Height difference between the WGS84 ellipsoid (simple shape model of the Earth) and a geoid, that approximates a geopotential (gravitational) surface, approximately mean sea level.
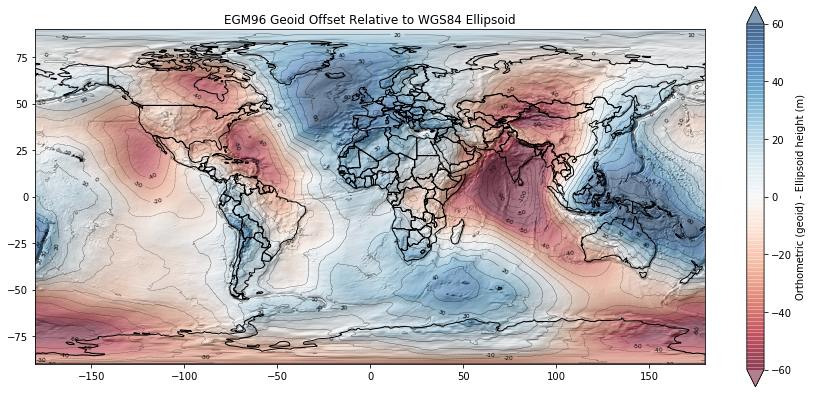
Note values for the Western U.S.
### Interpretation
A lot of the points with elevation < 0 m in your scatterplot are near coastal sites, roughly near mean sea level. We see that the geoid offset (difference between WGS84 ellipsoid and EGM96 geoid in this case) for CONUS is roughly -20 m. So the ICESat GLAS point elevations near the coast will have values of around -20 m relative to the ellipsoid, even though they are around 0 m relative to the geoid (approximately mean sea level).
Another cluster of points with negative elevations is over Death Valley, CA, which is actually below sea level: https://en.wikipedia.org/wiki/Death_Valley.
If this is confusing, we will revisit when we explore raster DEMs later in the quarter. We also get into all of this in the Spring Advanced Surveying course (ask me for details).
## Compute the elevation difference between ICESat `glas_z` and SRTM `dem_z` values
Earlier, I mentioned that I had sampled the SRTM DEM for each GLAS shot. Let's compute the difference and store in a new column in our DataFrame called `glas_srtm_dh`
Remember the order of this calculation (if the difference values are negative, which dataset is higher elevation?)
## Do a quick `head` to verify that the values in your new column look reasonable
## Compute the time difference between ICESat point timestamp and the SRTM timestamp
* Store in a new column named `glas_srtm_dt`
* The SRTM data were collected between February 11-22, 2000
* Can assume a constant decimal year value of 2000.112 for now
* Check values with `head`
## Compute *apparent* annualized elevation change rates (meters per year) from these new columns
* This will be rate of change between the SRTM timestamp (2000) and each GLAS point timestamp (2003-2009)
* Check values with `head`
## Create a scatterplot of the difference values
* Use a `RdBu` (Red to Blue) color ramp
* Set the color ramp limits using `vmin` and `vmax` keyword arguments to be symmetrical about 0
* Generate two plots with different color ramp range to bring out detail
* Do you see outliers (values far outside the expected distribution)?
* Do you see any coherent spatial patterns in the difference values?
## Create a histogram of the difference values
* Increase the number of bins, and limit the range to bring out detail of the distribution
## Compute the mean, median and standard deviation of the differences
* Why might we have a non-zero mean/median difference?
## Create a scatterplot of elevation difference `glas_srtm_dh` values vs elevation values
* `glas_srtm_dh` should be on the y-axis
* `glas_z` values on the x-axis
## Extra Credit: Remove outliers
The initial filter in `glas_proc.py` removed GLAS points with absolute elevation difference >200 m compared to the SRTM elevations. We expect most real elevation change signals to be less than this for the given time period. But clearly some outliers remain.
Design and apply a filter that removes outliers. One option is to define outliers as values outside some absolute threshold. Can set this threshold as some multiple of the standard deviation (e.g., `3*std`). Can also use quantile or percentile values for this.
Create new plot(s) to visualize the distribution of outliers and inliers. I've included my figure as a reference, but please don't worry about reproducing! Focus on the filtering and create some quick plots to verify that things worked.
## Active remote sensing sanity check
Even after removing outliers, there are still some big differences between the SRTM and GLAS elevation values.
* Do you see systematic differences between the glas_z and dem_z values?
* Any clues from the scatterplot? (e.g., do some tracks (north-south lines of points) display systematic bias?)
* Brainstorm some ideas about what might be going on here. Think about the nature of each sensor:
* ICESat was a Near-IR laser (1064 nm wavelength) with a big ground spot size (~70 m in diameter)
* Timestamps span different seasons between 2003-2009
* SRTM was a C-band radar (5.3 GHz, 5.6 cm wavelength) with approximately 30 m ground sample distance (pixel size)
* Timestamp was February 2000
* Data gaps (e.g., radar shadows, steep slopes) were filled with ASTER GDEM2 composite, which blends DEMs acquired over many years ~2000-2014
* Consider different surfaces and how the laser/radar footprint might be affected:
* Flat bedrock surface
* Dry sand dunes
* Steep montain topography like the Front Range in Colorado
* Dense vegetation of the Hoh Rainforest in Olympic National Park
## Let's check to see if differences are due to our land-use/land-cover classes
* Determine the unique values in the `lulc` column (hint: see the `value_counts` method)
* In the introduction, I said that I initially preserved only two classes for these points (12 - snow/ice, 31 - barren land), so this isn't going to help us over forests:
* https://www.mrlc.gov/data/legends/national-land-cover-database-2011-nlcd2011-legend
## Use Pandas `groupby` to compute stats for the LULC classes
* This is one of the most powerful features in Pandas, efficient grouping and analysis based on some values
* Compute mean, median and std of the difference values (glas_z - dem_z) for each LULC class
* Do you see a difference between values over glaciers vs bare rock?
## Extra credit: `groupby` year
* See if you can use Pandas `groupby` to count the number of shots for each year
* Multiple ways to accomplish this
* One approach might be to create a new column with integer year, then groupby that column
* Can modify the `decyear` values (see `floor`), or parse the Python time ordinals
* Create a bar plot showing number of shots in each year
## Extra Credit: Cluster by campaign
* See if you can create an algorithm to cluster the points by campaign
* Note, spatial coordinates should not be necessary here (remember your histogram earlier that showed the number of points vs time)
* Can do something involving differences between sorted point timestamps
* Can also go back and count the number of campaigns in your earlier histogram of `decyear` values, assuming that you used enough bins to discretize!
* K-Means clustering is a nice option: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
* Compute the number of shots and length (number of days) for each campaign
* Compare your answer with table here: https://nsidc.org/data/icesat/laser_op_periods.html (remember that we are using a subset of points over CONUS, so the number of days might not match perfectly)
## Extra Credit: Annual scatterplots
* Create a figure with multiple subplots showing scatterplots of points for each year
## Extra Credit: Campaign scatterplots
* Create a figure with multiple subplots showing scatterplots of points for each campaign
| github_jupyter |
```
import numpy as np
import pandas as pd
training_data = pd.read_csv("hackerrank-predict-email-opens-dataset/training_dataset.csv")
testing_data = pd.read_csv("hackerrank-predict-email-opens-dataset/test_dataset.csv")
training_data.head()
training_data.shape
testing_data.head()
testing_data.shape
training_data.info()
testing_data.info()
```
## Data Preprocessing
```
# drop the following columns as they are only available in training data
# click_time, clicked, open_time, unsubscribe_time, unsubscribed
training_data.drop(['click_time','clicked', 'open_time', 'unsubscribe_time', 'unsubscribed'], axis=1, inplace=True)
```
### Missing Values
```
training_data.isnull().sum()
training_data['mail_category'].fillna(training_data['mail_category'].value_counts().index[0], inplace=True)
training_data['mail_type'].fillna(training_data['mail_type'].value_counts().index[0],inplace=True)
training_data['hacker_timezone'].fillna(training_data['hacker_timezone'].value_counts().index[0], inplace=True)
training_data['last_online'].fillna(training_data['last_online'].mean(), inplace=True)
testing_data.isnull().sum()
testing_data['mail_category'].fillna(testing_data['mail_category'].value_counts().index[0], inplace=True)
testing_data['mail_type'].fillna(testing_data['mail_type'].value_counts().index[0],inplace=True)
testing_data['hacker_timezone'].fillna(testing_data['hacker_timezone'].value_counts().index[0], inplace=True)
testing_data['last_online'].fillna(testing_data['last_online'].mean(), inplace=True)
```
### Outliers
```
training_data.describe().T
min_threshold, max_threshold = training_data.sent_time.quantile([0.001, 0.999])
training_data = training_data[(training_data['sent_time'] > min_threshold) & (training_data['sent_time'] < max_threshold)]
min_threshold, max_threshold = training_data.last_online.quantile([0.001, 0.999])
training_data = training_data[(training_data['last_online'] > min_threshold) & (training_data['last_online'] < max_threshold)]
training_data.shape
```
### Encoding Categorical Attributes
```
from sklearn.preprocessing import LabelEncoder
encode = LabelEncoder()
# Extract Categorical Attributes
#cat_training_data = training_data.select_dtypes(include=['object']).copy()
# encode the categorical attributes of training_data
training_data = training_data.apply(encode.fit_transform)
# encode the categorical attribute of testing_data
testing_data = testing_data.apply(encode.fit_transform)
training_data.head()
testing_data.head()
```
### Seperate the Label Column from training_data
```
label = training_data['opened']
training_data.drop('opened', inplace=True, axis=1)
```
### Scaling Numerical Features
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# extract numerical attributes and scale it to have zero mean and unit variance
train_cols = training_data.select_dtypes(include=['float64', 'int64']).columns
training_data = scaler.fit_transform(training_data.select_dtypes(include=['float64','int64']))
# extract numerical attributes and scale it to have zero mean and unit variance
test_cols = testing_data.select_dtypes(include=['float64', 'int64']).columns
testing_data = scaler.fit_transform(testing_data.select_dtypes(include=['float64','int64']))
training_data = pd.DataFrame(training_data, columns=train_cols)
testing_data = pd.DataFrame(testing_data, columns=test_cols)
training_data.shape
testing_data.shape
```
### Split the training_data into training and validaiton data
```
from sklearn.model_selection import train_test_split
x_train, x_val, y_train, y_val = train_test_split(training_data, label, test_size = 0.2, random_state=2)
```
## Models Training
### Decision Tree
```
from sklearn import tree
from sklearn import metrics
DT_Classifier = tree.DecisionTreeClassifier(criterion='entropy', random_state=0)
DT_Classifier.fit(x_train, y_train)
```
#### Accuracy and Confusion Matrix
```
accuracy = metrics.accuracy_score(y_val, DT_Classifier.predict(x_val))
confustion_matrix = metrics.confusion_matrix(y_val, DT_Classifier.predict(x_val))
accuracy
confustion_matrix
```
### K-Nearest Neighbour
```
from sklearn.neighbors import KNeighborsClassifier
KNN_Classifier = KNeighborsClassifier(n_jobs=-1)
KNN_Classifier.fit(x_train, y_train)
accuracy = metrics.accuracy_score(y_val, KNN_Classifier.predict(x_val))
confusion_matrix = metrics.confusion_matrix(y_val, KNN_Classifier.predict(x_val))
accuracy
confusion_matrix
```
## Prediction on test data
```
predicted = DT_Classifier.predict(testing_data)
predicted.shape
prediction_df = pd.DataFrame(predicted, columns=['Prediction'])
prediction_df.to_csv('prediction.csv')
import pickle
pkl_filename = "Decision_Tree_model.pkl"
with open(pkl_filename, 'wb') as file:
pickle.dump(DT_Classifier, file)
```
| github_jupyter |
## Implement Sliding Windows and Fit a Polynomial
This notebook displays how to create a sliding windows on a image using Histogram we did in an earlier notebook.
we can use the two highest peaks from our histogram as a starting point for determining where the lane lines are, and then use sliding windows moving upward in the image (further along the road) to determine where the lane lines go. The output should look something like this:
<img src='./img/sliding_window_example.png'/>
<br>
#### Steps:
1. Split the histogram for the two lines.
2. Set up windows and window hyper parameters.
3. Iterate through number of sliding windows to track curvature.
4. Fit the polynomial.
5. Plot the image.
#### 1. Split the histogram for the two lines
The first step we'll take is to split the histogram into two sides, one for each lane line.
NOTE: You will need an image from the previous notebook: warped-example.jpg
Below is the pseucode:
**Do not Run the Below Cell it is for explanation only**
```
# Assuming you have created a warped binary image called "binary_warped"
# Take a histogram of the bottom half of the image
histogram = np.sum(binary_warped[binary_warped.shape[0]//2:,:], axis=0)
# Create an output image to draw on and visualize the result
out_img = np.dstack((binary_warped, binary_warped, binary_warped))*255
# Find the peak of the left and right halves of the histogram
# These will be the starting point for the left and right lines
midpoint = np.int(histogram.shape[0]//2)
leftx_base = np.argmax(histogram[:midpoint])
rightx_base = np.argmax(histogram[midpoint:]) + midpoint
```
#### 2. Set up windows and window hyper parameters.
Our next step is to set a few hyper parameters related to our sliding windows, and set them up to iterate across the binary activations in the image. I have some base hyper parameters below, but don't forget to try out different values in your own implementation to see what works best!
Below is the pseudocode:<br>
**Do not run the below Cell, it is for explanation only**
```
# HYPERPARAMETERS
# Choose the number of sliding windows
nwindows = 9
# Set the width of the windows +/- margin
margin = 100
# Set minimum number of pixels found to recenter window
minpix = 50
# Set height of windows - based on nwindows above and image shape
window_height = np.int(binary_warped.shape[0]//nwindows)
# Identify the x and y positions of all nonzero (i.e. activated) pixels in the image
nonzero = binary_warped.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
# Current positions to be updated later for each window in nwindows
leftx_current = leftx_base
rightx_current = rightx_base
# Create empty lists to receive left and right lane pixel indices
left_lane_inds = []
right_lane_inds = []
```
#### 3. Iterate through number of sliding windows to track curvature
now that we've set up what the windows look like and have a starting point, we'll want to loop for `nwindows`, with the given window sliding left or right if it finds the mean position of activated pixels within the window to have shifted.
Let's approach this like below:
1. Loop through each window in `nwindows`
2. Find the boundaries of our current window. This is based on a combination of the current window's starting point `(leftx_current` and `rightx_current`), as well as the margin you set in the hyperparameters.
3. Use cv2.rectangle to draw these window boundaries onto our visualization image `out_img`.
4. Now that we know the boundaries of our window, find out which activated pixels from `nonzeroy` and `nonzerox` above actually fall into the window.
5. Append these to our lists `left_lane_inds` and `right_lane_inds`.
6. If the number of pixels you found in Step 4 are greater than your hyperparameter `minpix`, re-center our window (i.e. `leftx_current` or `rightx_current`) based on the mean position of these pixels.
#### 4. Fit the polynomial
Now that we have found all our pixels belonging to each line through the sliding window method, it's time to fit a polynomial to the line. First, we have a couple small steps to ready our pixels.
<br>
Below is the pseudocode:<br>
**Do not run the below Cell, it is for explanation only**
```
# Concatenate the arrays of indices (previously was a list of lists of pixels)
left_lane_inds = np.concatenate(left_lane_inds)
right_lane_inds = np.concatenate(right_lane_inds)
# Extract left and right line pixel positions
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
Assuming we have `left_fit` and `right_fit` from `np.polyfit` before
# Generate x and y values for plotting
ploty = np.linspace(0, binary_warped.shape[0]-1, binary_warped.shape[0])
left_fitx = left_fit[0]*ploty**2 + left_fit[1]*ploty + left_fit[2]
right_fitx = right_fit[0]*ploty**2 + right_fit[1]*ploty + right_fit[2]
```
#### 5. Visualize
We will use subplots to visualize the output.
Lets get to coding then.
```
import numpy as np
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import cv2
# Load our image
binary_warped = mpimg.imread('./img/warped-example.jpg')
def find_lane_pixels(binary_warped):
# Take a histogram of the bottom half of the image
histogram = np.sum(binary_warped[binary_warped.shape[0]//2:,:], axis=0)
# Create an output image to draw on and visualize the result
out_img = np.dstack((binary_warped, binary_warped, binary_warped))
# Find the peak of the left and right halves of the histogram
# These will be the starting point for the left and right lines
midpoint = np.int(histogram.shape[0]//2)
leftx_base = np.argmax(histogram[:midpoint])
rightx_base = np.argmax(histogram[midpoint:]) + midpoint
# HYPERPARAMETERS
# Choose the number of sliding windows
nwindows = 9
# Set the width of the windows +/- margin
margin = 100
# Set minimum number of pixels found to recenter window
minpix = 50
# Set height of windows - based on nwindows above and image shape
window_height = np.int(binary_warped.shape[0]//nwindows)
# Identify the x and y positions of all nonzero pixels in the image
nonzero = binary_warped.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
# Current positions to be updated later for each window in nwindows
leftx_current = leftx_base
rightx_current = rightx_base
# Create empty lists to receive left and right lane pixel indices
left_lane_inds = []
right_lane_inds = []
# Step through the windows one by one
for window in range(nwindows):
# Identify window boundaries in x and y (and right and left)
win_y_low = binary_warped.shape[0] - (window+1)*window_height
win_y_high = binary_warped.shape[0] - window*window_height
win_xleft_low = leftx_current - margin
win_xleft_high = leftx_current + margin
win_xright_low = rightx_current - margin
win_xright_high = rightx_current + margin
# Draw the windows on the visualization image
cv2.rectangle(out_img,(win_xleft_low,win_y_low),
(win_xleft_high,win_y_high),(0,255,0), 2)
cv2.rectangle(out_img,(win_xright_low,win_y_low),
(win_xright_high,win_y_high),(0,255,0), 2)
# Identify the nonzero pixels in x and y within the window #
good_left_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xleft_low) & (nonzerox < win_xleft_high)).nonzero()[0]
good_right_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xright_low) & (nonzerox < win_xright_high)).nonzero()[0]
# Append these indices to the lists
left_lane_inds.append(good_left_inds)
right_lane_inds.append(good_right_inds)
# If you found > minpix pixels, recenter next window on their mean position
if len(good_left_inds) > minpix:
leftx_current = np.int(np.mean(nonzerox[good_left_inds]))
if len(good_right_inds) > minpix:
rightx_current = np.int(np.mean(nonzerox[good_right_inds]))
# Concatenate the arrays of indices (previously was a list of lists of pixels)
try:
left_lane_inds = np.concatenate(left_lane_inds)
right_lane_inds = np.concatenate(right_lane_inds)
except ValueError:
# Avoids an error if the above is not implemented fully
pass
# Extract left and right line pixel positions
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
return leftx, lefty, rightx, righty, out_img
def fit_polynomial(binary_warped):
# Find our lane pixels first
leftx, lefty, rightx, righty, out_img = find_lane_pixels(binary_warped)
# Fit a second order polynomial to each using `np.polyfit`
left_fit = np.polyfit(lefty, leftx, 2)
right_fit = np.polyfit(righty, rightx, 2)
# Generate x and y values for plotting
ploty = np.linspace(0, binary_warped.shape[0]-1, binary_warped.shape[0] )
try:
left_fitx = left_fit[0]*ploty**2 + left_fit[1]*ploty + left_fit[2]
right_fitx = right_fit[0]*ploty**2 + right_fit[1]*ploty + right_fit[2]
except TypeError:
# Avoids an error if `left` and `right_fit` are still none or incorrect
print('The function failed to fit a line!')
left_fitx = 1*ploty**2 + 1*ploty
right_fitx = 1*ploty**2 + 1*ploty
## Visualization ##
# Colors in the left and right lane regions
out_img[lefty, leftx] = [255, 0, 0]
out_img[righty, rightx] = [0, 0, 255]
# Plots the left and right polynomials on the lane lines
plt.plot(left_fitx, ploty, color='white')
plt.plot(right_fitx, ploty, color='white')
print(left_fit)
print(right_fit)
return out_img
out_img = fit_polynomial(binary_warped)
plt.imshow(out_img)
```
| github_jupyter |
```
"""
基于扩展窗的欧拉反卷积算法
欧拉反卷积的常用方法是基于滑动窗口:但由于每个窗口是在整个区域仅运行一次解卷积会产生很多虚假的解决方案。
并且基于滑动窗口的反卷积方法不能出给指定的源的个数。所以发展了基于扩展窗的欧拉反卷积算法。
其基本思想是:从一个选点的中心点扩展许多窗口进行反卷积。然后只选择其中一个解决方案(最小误差方案)作为最终估计。
这种方法不仅可以提供单一解决方案,还可以通过可以针对每个异常选择不同的扩展中心实现对多个异常的解释。
扩展窗口方案实现于:geoist.euler_expanding_window.ipynb。
"""
from geoist.pfm import sphere, pftrans, euler, giutils
from geoist import gridder
from geoist.inversion import geometry
from geoist.vis import giplt
import matplotlib.pyplot as plt
import numpy as np
##合成磁数据测试欧拉反卷积
# 磁倾角,磁偏角
inc, dec = -45, 0
# 制作仅包含感应磁化的两个球体模型
model = [
geometry.Sphere(x=-1000, y=-1000, z=1500, radius=1000,
props={'magnetization': giutils.ang2vec(2, inc, dec)}),
geometry.Sphere(x=1000, y=1500, z=1000, radius=1000,
props={'magnetization': giutils.ang2vec(1, inc, dec)})]
# 从模型中生成磁数据
shape = (100, 100)
area = [-5000, 5000, -5000, 5000]
x, y, z = gridder.regular(area, shape, z=-150)
data = sphere.tf(x, y, z, model, inc, dec)
# 一阶导数
xderiv = pftrans.derivx(x, y, data, shape)
yderiv = pftrans.derivy(x, y, data, shape)
zderiv = pftrans.derivz(x, y, data, shape)
#通过扩展窗方法实现欧拉反卷积
#给出2个解决方案,每一个扩展窗都靠近异常
#stutural_index=3表明异常源为球体
'''
===================================== ======== =========
源类型 SI (磁) SI (重力)
===================================== ======== =========
Point, sphere 3 2
Line, cylinder, thin bed fault 2 1
Thin sheet edge, thin sill, thin dyke 1 0
===================================== ======== =========
'''
#制作求解器并使用fit()函数来获取右下角异常的估计值
print("Euler solutions:")
sol1 = euler.EulerDeconvEW(x, y, z, data, xderiv, yderiv, zderiv,
structural_index=3, center=(-2000, -2000),
sizes=np.linspace(300, 7000, 20))
sol1.fit()
print("Lower right anomaly location:", sol1.estimate_)
#制作求解器并使用fit()函数来获取左上角异常的估计值
sol2 = euler.EulerDeconvEW(x, y, z, data, xderiv, yderiv, zderiv,
structural_index=3, center=(2000, 2000),
sizes=np.linspace(300, 7000, 20))
sol2.fit()
print("Upper left anomaly location:", sol2.estimate_)
print("Centers of the model spheres:")
print(model[0].center)
print(model[1].center)
# 在磁数据上绘制异常估计值结果
# 异常源的中心的真正深度为1500 m 和1000 m。
plt.figure(figsize=(6, 5))
plt.title('Euler deconvolution with expanding windows')
plt.contourf(y.reshape(shape), x.reshape(shape), data.reshape(shape), 30,
cmap="RdBu_r")
plt.scatter([sol1.estimate_[1], sol2.estimate_[1]],
[sol1.estimate_[0], sol2.estimate_[0]],
c=[sol1.estimate_[2], sol2.estimate_[2]],
s=50, cmap='cubehelix')
plt.colorbar(pad=0).set_label('Depth (m)')
plt.xlim(area[2:])
plt.ylim(area[:2])
plt.tight_layout()
plt.show()
```
| github_jupyter |
```
import os
import couchdb
from lib.genderComputer.genderComputer import GenderComputer
server = couchdb.Server(url='http://127.0.0.1:15984/')
db = server['tweets']
gc = GenderComputer(os.path.abspath('./data/nameLists'))
date_list = []
for row in db.view('_design/analytics/_view/conversation-date-breakdown', reduce=True, group=True):
date_list.append(row.key)
print(date_list)
from collections import Counter
view_data = []
for row in db.view('_design/analytics/_view/tweets-victoria',startkey="2017/3/6",endkey="2017/3/9"):
view_data.append(row.value)
len(view_data)
try:
hashtags = server.create["twitter-hashtags"]
except:
hashtags = server["twitter-hashtags"]
hashtag_count = Counter()
for row in view_data:
hashtag_count.update(row["hashtags"])
for tag in hashtag_count.most_common():
doc = hashtags.get(tag[0]) # tag[0] -> hashtag, tag[1] -> frequency
if doc is None:
data = {}
data["_id"] = tag[0].replace('\u','') # use word as an id
data["hashtag"] = tag[0].replace('\u','')
data["count"] = tag[1]
else:
data = doc
data["count"] = data["count"] + tag[1]
hashtags.save(data)
texts = []
users = []
for row in view_data:
text = {}
text["text"] = row["text"]
text["sentiment"] = row["sentiment"]
texts.append(text)
user = row["user"]
try:
gender = gc.resolveGender(user["name"], None)
user["gender"] = gender
except:
continue
users.append(user)
print("text",len(texts)," user", len(users))
import re
emoticons_str = r"""
(?:
[:=;] # Eyes
[oO\-]? # Nose (optional)
[D\)\]\(\]/\\OpP] # Mouth
)"""
regex_str = [
emoticons_str,
r'<[^>]+>', # HTML tags
r'(?:@[\w_]+)', # @-mentions
r"(?:\#+[\w_]+[\w\'_\-]*[\w_]+)", # hash-tags
r'http[s]?://(?:[a-z]|[0-9]|[$-_@.&+]|[!*\(\),]|(?:%[0-9a-f][0-9a-f]))+', # URLs
r'(?:(?:\d+,?)+(?:\.?\d+)?)', # numbers
r"(?:[a-z][a-z'\-_]+[a-z])", # words with - and '
r'(?:[\w_]+)', # other words
r'(?:\S)' # anything else
]
tokens_re = re.compile(r'('+'|'.join(regex_str)+')', re.VERBOSE | re.IGNORECASE)
emoticon_re = re.compile(r'^'+emoticons_str+'$', re.VERBOSE | re.IGNORECASE)
def tokenize(s):
return tokens_re.findall(s)
def preprocess(s, lowercase=False):
tokens = tokenize(s)
if lowercase:
tokens = [token if emoticon_re.search(token) else token.lower() for token in tokens]
return tokens
## Save Terms Frequency
import HTMLParser
from collections import Counter
from nltk.corpus import stopwords
import string
punctuation = list(string.punctuation)
stop = stopwords.words('english') + punctuation + ['rt', 'via']
count_all = Counter()
html_parser = HTMLParser.HTMLParser()
emoji_pattern = re.compile(
u"(\ud83d[\ude00-\ude4f])|" # emoticons
u"(\ud83c[\udf00-\uffff])|" # symbols & pictographs (1 of 2)
u"(\ud83d[\u0000-\uddff])|" # symbols & pictographs (2 of 2)
u"(\ud83d[\ude80-\udeff])|" # transport & map symbols
u"(\ud83c[\udde0-\uddff])" # flags (iOS)
"+", flags=re.UNICODE)
for text in texts:
cleanText = re.sub(r"http\S+", "", text['text'])
cleanText = html_parser.unescape(cleanText)
cleanText = emoji_pattern.sub(r'', cleanText)
terms_stop = [term for term in preprocess(cleanText) if term not in stop]
count_all.update(terms_stop)
try:
words = server.create["twitter-words"]
except:
words = server["twitter-words"]
for num in count_all.most_common():
doc = words.get(num[0]) # num[0] -> word, num[1] -> frequency
try:
if doc is None:
data = {}
word_text = num[0].decode("utf8").encode('ascii','ignore') # make sure we don't save unsafe character
data["_id"] = word_text # use word as an id
data["word"] = word_text
data["count"] = num[1]
else:
data = doc
data["count"] = data["count"] + num[1]
words.save(data)
except:
continue
#save user data
# try create user db
try:
user = server.create["twitter-users"]
except:
user = server["twitter-users"]
for row in users:
id = row["id"]
doc = user.get(str(id))
if doc is None:
row["_id"] = str(row["id"])
user.save(row)
"☕".decode("utf8").encode('ascii','ignore') == ""
import datetime
today = datetime.date.today()
today = today.strftime('%Y/%-m/%-d')
print(today)
```
| github_jupyter |
```
import pandas as pd
import numpy as np
pd.set_option('display.max_columns', None)
df = pd.read_csv('/Users/mattmastin/Desktop/Valley-Behavioral/vbhsample.csv')
df.describe()
columns_drop = ['Unnamed: 15', 'EmploymentInformation', 'HeadOfHousehold']
df.drop(columns=columns_drop, axis=1)
df['ClientStatus'] = df['ClientStatus'].map({'Y': 1, 'N': 0})
df['MilitaryStatus'] = df['MilitaryStatus'].map({'Yes': 1, 'No': 0})
# df['Ethnicity'].value_counts()
df.drop(columns='Ethnicity', axis=1)
df['HispanicOrigin'] = df['HispanicOrigin'].map({'Not of Hispanic Origin': 0, 'Unknown': 0,
'Mexican': 1, 'Other Hispanic Origin': 1,
'Puerto Rican': 1, 'Cuban': 1})
df['HispanicOrigin'] = df['HispanicOrigin'].fillna(0)
df.drop(columns=['ClientState', 'ClientCounty'], axis=1)
df['FinanciallyResponsible'] = df['FinanciallyResponsible'].map({'Y': 1, 'N': 0})
df['LivingArrangement'] = df['LivingArrangement'].map({'Private Residence-Independent': 0,
'Private Residence-Dependent': 0,
'Institutional Setting': 1,
'24-hour Residential Care': 1,
'Jail or Correctional Facility': 2,
'Adult or Child Foster Care': 2,
'On Street or in a Homeless Shelter': 3})
# filling with by far largest class. Wrong choice?
df['LivingArrangement'].fillna(0, inplace=True)
df['LivingArrangement'].isna().sum()
df['MilitaryStatus'].fillna(0, inplace=True)
df['SmokingStatus'] = df['SmokingStatus'].map({'NEVER SMOKED/VAPED': 0,
'CURRENT EVERDAY SMOKER/E-CIG USER': 1,
'FORMER SMOKER/E-CIG USER': 1,
'NOT APPLICABLE': 0,
'CURRENT SOME DAY SMOKER/E-CIG USER': 1,
'USE SMOKELESS TOBACCO ONLY (In last 30 days)': 1,
'FORMER SMOKING STATUS UNKNOWN': 0})
df['SmokingStatus'].fillna(0, inplace=True)
df.drop(columns='AgeOfFirstTobaccoUse', inplace=True)
df['EducationStatus'].value_counts()
df['EducationStatus'] = df['EducationStatus'].map({'Not currently enrolled': 0,
'Yes currently enrolled': 1,
'Unknown': 0})
df['EducationStatus'].fillna(0, inplace=True)
df['ForensicTreatment'] = df['ForensicTreatment'].map({'Not applicable': 0,
'Declined to answer': 0,
'New-(Justice Involved) OLD-Criminal Court Ordered Compelled for Tx': 1,
'Criminal court – ordered treatment': 1,
'Department of corrections client': 1,
'Civil Court ordered – treatment': 1,
'Court- ordered evaluation/assessment only': 1})
df['ForensicTreatment'].fillna(0, inplace=True)
```
| github_jupyter |
### Natural Language Processing, a look at distinguishing subreddit categories by analyzing the text of the comments and posts
**Matt Paterson, [email protected]**
General Assembly Data Science Immersive, July 2020
### Abstract
**HireMattPaterson.com has been (fictionally) contracted by Virgin Galactic’s marketing team to build a Natural Language Processing Model that will efficiently predict if reddit posts are being made for the SpaceX subreddit or the Boeing subreddit as a proof of concept to segmenting the targeted markets.**
We’ve created a model that predicts the silo of the post with nearly 80% accuracy (with a top score of 79.9%). To get there we tried over 2,000 different iterations on a total of 5 different classification modeling algorithms including two versions of Multinomial Naïve Bayes, Random Cut Forest, Extra Trees, and a simple Logistic Regression Classifier. We’d like to use Support Vector Machines as well as Gradient Boosting and a K-Nearest Neighbors model in our follow-up to this presentation.
If you like our proof of concept, the next iteration of our model will take in to account the trend or frequency in the comments of each user; what other subreddits these users can be found to post to (are they commenting on the Rolex and Gulfstream and Maserati or are they part of the Venture Capital and AI crowd?); and if their comments appear to be professional in nature (are they looking to someday work in aerospace or maybe they already do). These trends will help the marketing team tune their tone, choose words that are trending, and speak directly to each cohort in a narrow-cast fashion thus allowing VG to spend less money on ads and on people over time.
This notebook shows how we got there.
### Problem Statement:
Virgin Galactic wants to charge customers USD 250K per voyage to bring customers into outer space on a pleasure cruise in null G
The potential customers range from more traditional HNWI who have more conservative values, to the Nouveau Riche, and various levels of tech millionaires in between
Large teams of many Marketing Analysts and Marketing Managers are expensive
If you can keep your current headcount or only add a few you are better off, since as headcount grows, overall ROI tends to shrink (VG HC ~ 200 ppl)
### Solution:
Create a machine learning model to identify what type of interests each user has based on their social media and reddit posts
Narrowcast to each smaller cohort with the language, tone, and vocabulary that will push each to purchase the quarter-million dollar flight
## Import libraries
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import nltk
import lebowski as dude
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import confusion_matrix, plot_confusion_matrix
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier, AdaBoostClassifier, VotingClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
```
## Read in the data.
In the data_file_creation.ipynb found in this directory, we have already gone to the 'https://api.pushshift.io/reddit/search/' api and pulled subreddit posts and comments from SpaceX, Boeing, BlueOrigin, and VirginGalactic; four specific companies venturing into the outer space exploration business with distinct differences therein. It is the theory of this research team that each subreddit will also have a distinct group of main users, or possible customers that are engaging on each platform. While there will be overlap in the usership, there will also be a clear lexicon that each subreddit thread has.
In this particular study, we will look specifically at the differences between SpaceX and Boeing, and will create a classification model that predicts whether a post is indeed in the SpaceX subreddit or not in the SpaceX subreddit.
Finally we will test the model against a testing set that is made up of posts from all four companies and measure its ability to predict which posts are SpaceX and which are not.
```
spacex = pd.read_csv('./data/spacex.csv')
boeing = pd.read_csv('./data/boeing.csv')
spacex.head()
```
We have already done a lot of cleaning up, but as we see there are still many NaN values and other meaningless values in our data. We'll create a function to remove these values using mapping in our dataframe.
Before we get there, let's convert our target column into a binary selector.
```
spacex['subreddit'] = spacex['subreddit'].map({'spacex': 1, 'boeing': 0})
boeing['subreddit'] = boeing['subreddit'].map({'spacex': 1, 'boeing': 0})
```
And drop the null values right off too.
```
print(f"spacex df has {spacex.isna().sum()} null values not including extraneous words")
print(f"boeing df has {boeing.isna().sum()} null values not including extraneous words")
```
we can remove these 61 rows right off
```
spacex = spacex.dropna()
boeing = boeing.dropna()
spacex.shape
boeing.shape
```
## Merge into one dataframe
```
space_wars = pd.concat([spacex, boeing])
space_wars.shape
```
## Use TF to break up the dataframes into numbers and then drop the unneeded words
```
tvec = TfidfVectorizer(stop_words = 'english')
```
We will only put the 'body' column in to the count vectorizer
```
X_list = space_wars.body
nums_df = pd.DataFrame(tvec.fit_transform(X_list).toarray(),
columns=tvec.get_feature_names())
nums_df.head()
```
And with credit to Noelle Brown, let's graph the resulting top words:
```
# get count of top-occurring words
top_words_tf = {}
for i in nums_df.columns:
top_words_tf[i] = nums_df[i].sum()
# top_words to dataframe sorted by highest occurance
most_freq_tf = pd.DataFrame(sorted(top_words_tf.items(), key = lambda x: x[1], reverse = True))
plt.figure(figsize = (10, 5))
# visualize top 10 words
plt.bar(most_freq_tf[0][:10], most_freq_tf[1][:10]);
```
We can see that if we remove 'replace_me', 'removed', and 'deleted', then we'll be dealing with a much more useful dataset. For the words dataframe, we can just add these words to our stop_words library. For the numeric dataframe we'll drop them here, as well as a few more.
```
dropwords = ['replace_me', 'removed', 'deleted', 'https', 'com', 'don', 'www']
nums_df = nums_df.drop(columns=dropwords)
```
And we can re-run the graph above for a better look.
```
# get count of top-occurring words
top_words_tf = {}
for i in nums_df.columns:
top_words_tf[i] = nums_df[i].sum()
# top_words to dataframe sorted by highest occurance
most_freq_tf = pd.DataFrame(sorted(top_words_tf.items(), key = lambda x: x[1], reverse = True))
plt.figure(figsize = (18, 6))
dude.graph_words('black')
# visualize top 10 words
plt.bar(most_freq_tf[0][:15], most_freq_tf[1][:15]);
```
If I had more time I'd like to graph the words used most in each company. I can go ahead and try to display which company is more verbose, wordy that is, and which one uses longer words (Credit to Hovanes Gasparian).
```
nums_df = pd.concat([space_wars['subreddit'], nums_df])
space_wars['word_count'] = space_wars['body'].apply(dude.word_count)
space_wars['post_length'] = space_wars['body'].apply(dude.count_chars)
space_wars[['word_count', 'post_length']].describe().T
space_wars.groupby(['word_count']).size().sort_values(ascending=False)#.head()
space_wars[space_wars['word_count'] > 1000]
#space_wars.groupby(['subreddit', 'word_count']).size().sort_values(ascending=False).head()
space_wars.subreddit.value_counts()
plt.figure(figsize=(18,6))
dude.graph_words('black')
plt.hist([space_wars[space_wars['subreddit']==0]['word_count'],
space_wars[space_wars['subreddit']==1]['word_count']],
bins=3, color=['blue', 'red'], ec='k')
plt.title('Word Count by Company', fontsize=30)
plt.legend(['Boeing', 'SpaceX']);
```
## Trouble in parsing-dise
It appears that I'm having some issues with manipulating this portion of the data. I will clean this up before final pull request.
## Create test_train_split with word data
#### Find the baseline:
```
baseline = space_wars.subreddit.value_counts(normalize=True)[1]
all_scores = {}
all_scores['baseline'] = baseline
all_scores['baseline']
X_words = space_wars['body']
y_words = space_wars['subreddit']
X_train_w, X_test_w, y_train_w, y_test_w = train_test_split(X_words,
y_words,
random_state=42,
test_size=.1,
stratify=y_words)
```
## Now it's time to train some models!
```
# Modify our stopwords list from the nltk.'english'
stopwords = nltk.corpus.stopwords.words('english')
# Above we created a list called dropwords
for i in dropwords:
stopwords.append(i)
param_cv = {
'stop_words' : stopwords,
'ngram_range' : (1, 2),
'analyzer' : 'word',
'max_df' : 0.8,
'min_df' : 0.02,
}
cntv = CountVectorizer(param_cv)
# Print y_test for a sanity check
y_test_w
# credit Noelle from lecture
train_data_features = cntv.fit_transform(X_train_w, y_train_w)
test_data_features = cntv.transform(X_test_w)
```
## Logistic Regression
```
lr = LogisticRegression( max_iter = 10_000)
lr.fit(train_data_features, y_train_w)
lr.score(train_data_features, y_train_w)
all_scores['Logistic Regression'] = lr.score(test_data_features, y_test_w)
all_scores['Logistic Regression']
```
***Using a simple Logistic regression with very little tweaking, a set of stopwords, we created a model that while slightly overfit, is more than 22 points more accurate than the baseline.***
## What does the confusion matrix look like? Is 80% accuracy even good?
Perhaps I can get some help making a confusion matrix with this data?
## Multinomial Naive Bayes using CountVectorizer
In this section we will create a Pipeline that starts with the CountVectorizer and ends with the Multinomial Naive Bayes Algorithm. We'll run through 270 possible configurations of this model, and run it in parallel on 3 of the 4 cores on my machine.
```
pipe = Pipeline([
('count_v', CountVectorizer()),
('nb', MultinomialNB())
])
pipe_params = {
'count_v__max_features': [2000, 5000, 9000],
'count_v__stop_words': [stopwords],
'count_v__min_df': [2, 3, 10],
'count_v__max_df': [.9, .8, .7],
'count_v__ngram_range': [(1, 1), (1, 2)]
}
gs = GridSearchCV(pipe,
pipe_params,
cv = 5,
n_jobs=6
)
%%time
gs.fit(X_train_w, y_train_w)
gs.best_params_
all_scores['Naive Bayes'] = gs.best_score_
all_scores['Naive Bayes']
gs.best_index_
# is this the index that has the best indication of being positive?
```
We see that our Naive Bayes model yields an accuracy score just shy of our Logistic Regression model, 79.7%
**What does the confusion matrix look like?**
```
# Get predictions and true/false pos/neg
preds = gs.predict(X_test_w)
tn, fp, fn, tp = confusion_matrix(y_test_w, preds).ravel()
# View confusion matrix
dude.graph_words('black')
plot_confusion_matrix(gs, X_test_w, y_test_w, cmap='Blues', values_format='d');
sensitivity = tp / (tp + fp)
sensitivity
specificity = tn / (tn + fn)
specificity
```
## Naive Bayes using the TFID Vectorizer
```
pipe_tvec = Pipeline([
('tvec', TfidfVectorizer()),
('nb', MultinomialNB())
])
pipe_params_tvec = {
'tvec__max_features': [2000, 9000],
'tvec__stop_words' : [None, stopwords],
'tvec__ngram_range': [(1, 1), (1, 2)]
}
gs_tvec = GridSearchCV(pipe_tvec, pipe_params_tvec, cv = 5)
%%time
gs_tvec.fit(X_train_w, y_train_w)
all_scores['Naive Bayes TFID'] = gs_tvec.best_score_
all_scores['Naive Bayes TFID']
all_scores
# Confusion Matrix for tvec
preds = gs_tvec.predict(X_test_w)
tn, fp, fn, tp = confusion_matrix(y_test_w, preds).ravel()
# View confusion matrix
dude.graph_words('black')
plot_confusion_matrix(gs_tvec, X_test_w, y_test_w, cmap='Blues', values_format='d');
specificity = tn / (tn+fn)
specificity
sensitivity = tp / (tp+fp)
sensitivity
```
Here, the specificity is 4 points higher than the NB using Count Vectorizer, but the sensitity and overall accuracy are about the same.
## Random Cut Forest and Extra Trees
```
pipe_rf = Pipeline([
('count_v', CountVectorizer()),
('rf', RandomForestClassifier()),
])
pipe_ef = Pipeline([
('count_v', CountVectorizer()),
('ef', ExtraTreesClassifier()),
])
pipe_params = {
'count_v__max_features': [2000, 5000, 9000],
'count_v__stop_words': [stopwords],
'count_v__min_df': [2, 3, 10],
'count_v__max_df': [.9, .8, .7],
'count_v__ngram_range': [(1, 1), (1, 2)]
}
%%time
gs_rf = GridSearchCV(pipe_rf,
pipe_params,
cv = 5,
n_jobs=6)
gs_rf.fit(X_train_w, y_train_w)
print(gs_rf.best_score_)
gs_rf.best_params_
gs_rf.best_estimator_
all_scores['Random Cut Forest'] = gs_rf.best_score_
all_scores
# Confusion Matrix for Random Cut Forest
preds = gs_rf.predict(X_test_w)
tn, fp, fn, tp = confusion_matrix(y_test_w, preds).ravel()
# View confusion matrix
dude.graph_words('black')
plot_confusion_matrix(gs_rf, X_test_w, y_test_w, cmap='Blues', values_format='d');
specificity = tn / (tn+fn)
specificity
sensitivity = tp / (tp+fp)
sensitivity
```
Our original Logistic Regression model is still the winner.
## What does the matchup look like?
```
score_df = pd.DataFrame([all_scores])
score_df.shape
score_df.head()
```
## Create a Count Vecotorized dataset
Since the below cells have been troublesome, we'll create a dataset using only the count vectorizer and then use that data in the model as we did above.
```
# Re-establish the subsets using Noelle's starter script again
train_data_features = cntv.fit_transform(X_train_w, y_train_w)
test_data_features = cntv.transform(X_test_w)
pipe_params_tvec = {
'tvec__max_features': [2000, 9000],
'tvec__stop_words' : [None, stopwords],
'tvec__ngram_range': [(1, 1), (1, 2)]
}
knn_pipe = Pipeline([
('ss', StandardScaler()),
('knn', KNeighborsClassifier())
])
tree_pipe = Pipeline([
('tvec', TfidfVectorizer()),
('tree', DecisionTreeClassifier())
])
ada_pipe = Pipeline([
('tvec', TfidfVectorizer()),
('ada', AdaBoostClassifier(base_estimator=DecisionTreeClassifier())),
])
grad_pipe = Pipeline([
('tvec', TfidfVectorizer()),
('grad_boost', GradientBoostingClassifier()),
])
```
### Irreconcilable Error:
At this time there are still structural issues that are not allowing this last block of code to complete the final model attempts (user error).
***In the next few days, prior to publication, this notebook will be revamped and this final cell will execute.***
```
%%time
vote = VotingClassifier([
('ada', AdaBoostClassifier(base_estimator=DecisionTreeClassifier())),
('grad_boost', GradientBoostingClassifier()),
('tree', DecisionTreeClassifier()),
('knn_pipe', knn_pipe)
])
params = {
'ada__n_estimators': [50, 51], # since HPO names are common, use dunder from tuple names
'grad_boost__n_estimators': [10, 11],
'knn_pipe__knn__n_neighbors': [3, 5],
'ada__base_estimator__max_depth': [1, 2],
'tree__max_depth': [1, 2],
'weights':[[.25] * 4, [.3, .3, .3, .1]]
}
gs = GridSearchCV(vote, param_grid=params, cv=3)
gs.fit(train_data_features, y_train_w)
print(gs.best_score_)
gs.best_params_
```
| github_jupyter |
<a href="https://colab.research.google.com/github/vitutorial/exercises/blob/master/LatentFactorModel/LatentFactorModel.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
%matplotlib inline
import os
import re
import urllib.request
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
import itertools
from torch.utils.data import Dataset, DataLoader
from torch.nn.utils.rnn import pack_padded_sequence, pad_packed_sequence
device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")
```
In this notebook you will work with a deep generative language model that maps words from a discrete (bit-vector-valued) latent space. We will use text data (we will work on the character level) in Spanish and pytorch.
The first section concerns data manipulation and data loading classes necessary for our implementation. You do not need to modify anything in this part of the code.
Let's first download the SIGMORPHON dataset that we will be using for this notebook: these are inflected Spanish words together with some morphosyntactic descriptors. For this notebook we will ignore the morphosyntactic descriptors.
```
url = "https://raw.githubusercontent.com/ryancotterell/sigmorphon2016/master/data/"
train_file = "spanish-task1-train"
val_file = "spanish-task1-dev"
test_file = "spanish-task1-test"
print("Downloading data files...")
if not os.path.isfile(train_file):
urllib.request.urlretrieve(url + train_file, filename=train_file)
if not os.path.isfile(val_file):
urllib.request.urlretrieve(url + val_file, filename=val_file)
if not os.path.isfile(test_file):
urllib.request.urlretrieve(url + test_file, filename=test_file)
print("Download complete.")
```
# Data
In order to work with text data, we need to transform the text into something that our algorithms can work with. The first step of this process is converting words into word ids. We do this by constructing a vocabulary from the data, assigning a new word id to each new word it encounters.
```
UNK_TOKEN = "?"
PAD_TOKEN = "_"
SOW_TOKEN = ">"
EOW_TOKEN = "."
def extract_inflected_word(s):
"""
Extracts the inflected words in the SIGMORPHON dataset.
"""
return s.split()[-1]
class Vocabulary:
def __init__(self):
self.idx_to_char = {0: UNK_TOKEN, 1: PAD_TOKEN, 2: SOW_TOKEN, 3: EOW_TOKEN}
self.char_to_idx = {UNK_TOKEN: 0, PAD_TOKEN: 1, SOW_TOKEN: 2, EOW_TOKEN: 3}
self.word_freqs = {}
def __getitem__(self, key):
return self.char_to_idx[key] if key in self.char_to_idx else self.char_to_idx[UNK_TOKEN]
def word(self, idx):
return self.idx_to_char[idx]
def size(self):
return len(self.char_to_idx)
@staticmethod
def from_data(filenames):
"""
Creates a vocabulary from a list of data files. It assumes that the data files have been
tokenized and pre-processed beforehand.
"""
vocab = Vocabulary()
for filename in filenames:
with open(filename) as f:
for line in f:
# Strip whitespace and the newline symbol.
word = extract_inflected_word(line.strip())
# Split the words into characters and assign ids to each
# new character it encounters.
for char in list(word):
if char not in vocab.char_to_idx:
idx = len(vocab.char_to_idx)
vocab.char_to_idx[char] = idx
vocab.idx_to_char[idx] = char
return vocab
# Construct a vocabulary from the training and validation data.
print("Constructing vocabulary...")
vocab = Vocabulary.from_data([train_file, val_file])
print("Constructed a vocabulary of %d types" % vocab.size())
# some examples
print('e', vocab['e'])
print('é', vocab['é'])
print('ș', vocab['ș']) # something UNKNOWN
```
We also need to load the data files into memory. We create a simple class `TextDataset` that stores the data as a list of words:
```
class TextDataset(Dataset):
"""
A simple class that loads a list of words into memory from a text file,
split by newlines. This does not do any memory optimisation,
so if your dataset is very large, you might want to use an alternative
class.
"""
def __init__(self, text_file, max_len=30):
self.data = []
with open(text_file) as f:
for line in f:
word = extract_inflected_word(line.strip())
if len(list(word)) <= max_len:
self.data.append(word)
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.data[idx]
# Load the training, validation, and test datasets into memory.
train_dataset = TextDataset(train_file)
val_dataset = TextDataset(val_file)
test_dataset = TextDataset(test_file)
# Print some samples from the data:
print("Sample from training data: \"%s\"" % train_dataset[np.random.choice(len(train_dataset))])
print("Sample from validation data: \"%s\"" % val_dataset[np.random.choice(len(val_dataset))])
print("Sample from test data: \"%s\"" % test_dataset[np.random.choice(len(test_dataset))])
```
Now it's time to write a function that converts a word into a list of character ids using the vocabulary we created before. This function is `create_batch` in the code cell below. This function creates a batch from a list of words, and makes sure that each word starts with a start-of-word symbol and ends with an end-of-word symbol. Because not all words are of equal length in a certain batch, words are padded with padding symbols so that they match the length of the largest word in the batch. The function returns an input batch, an output batch, a mask of 1s for words and 0s for padding symbols, and the sequence lengths of each word in the batch. The output batch is shifted by one character, to reflect the predictions that the model is expected to make. For example, for a word
\begin{align}
\text{e s p e s e m o s}
\end{align}
the input sequence is
\begin{align}
\text{SOW e s p e s e m o s}
\end{align}
and the output sequence is
\begin{align}
\text{e s p e s e m o s EOW}
\end{align}
You can see the output is shifted wrt the input, that's because we will be computing a distribution for the next character in context of its prefix, and that's why we need to shift the sequence this way.
Lastly, we create an inverse function `batch_to_words` that recovers the list of words from a padded batch of character ids to use during test time.
```
def create_batch(words, vocab, device, word_dropout=0.):
"""
Converts a list of words to a padded batch of word ids. Returns
an input batch, an output batch shifted by one, a sequence mask over
the input batch, and a tensor containing the sequence length of each
batch element.
:param words: a list of words, each a list of token ids
:param vocab: a Vocabulary object for this dataset
:param device:
:param word_dropout: rate at which we omit words from the context (input)
:returns: a batch of padded inputs, a batch of padded outputs, mask, lengths
"""
tok = np.array([[SOW_TOKEN] + list(w) + [EOW_TOKEN] for w in words])
seq_lengths = [len(w)-1 for w in tok]
max_len = max(seq_lengths)
pad_id = vocab[PAD_TOKEN]
pad_id_input = [
[vocab[w[t]] if t < seq_lengths[idx] else pad_id for t in range(max_len)]
for idx, w in enumerate(tok)]
# Replace words of the input with <unk> with p = word_dropout.
if word_dropout > 0.:
unk_id = vocab[UNK_TOKEN]
word_drop = [
[unk_id if (np.random.random() < word_dropout and t < seq_lengths[idx]) else word_ids[t] for t in range(max_len)]
for idx, word_ids in enumerate(pad_id_input)]
# The output batch is shifted by 1.
pad_id_output = [
[vocab[w[t+1]] if t < seq_lengths[idx] else pad_id for t in range(max_len)]
for idx, w in enumerate(tok)]
# Convert everything to PyTorch tensors.
batch_input = torch.tensor(pad_id_input)
batch_output = torch.tensor(pad_id_output)
seq_mask = (batch_input != vocab[PAD_TOKEN])
seq_length = torch.tensor(seq_lengths)
# Move all tensors to the given device.
batch_input = batch_input.to(device)
batch_output = batch_output.to(device)
seq_mask = seq_mask.to(device)
seq_length = seq_length.to(device)
return batch_input, batch_output, seq_mask, seq_length
def batch_to_words(tensors, vocab: Vocabulary):
"""
Converts a batch of word ids back to words.
:param tensors: [B, T] word ids
:param vocab: a Vocabulary object for this dataset
:returns: an array of strings (each a word).
"""
words = []
batch_size = tensors.size(0)
for idx in range(batch_size):
word = [vocab.word(t.item()) for t in tensors[idx,:]]
# Filter out the start-of-word and padding tokens.
word = list(filter(lambda t: t != PAD_TOKEN and t != SOW_TOKEN, word))
# Remove the end-of-word token and all tokens following it.
if EOW_TOKEN in word:
word = word[:word.index(EOW_TOKEN)]
words.append("".join(word))
return np.array(words)
```
In PyTorch the RNN functions expect inputs to be sorted from long words to shorter ones. Therefore we create a simple wrapper class for the DataLoader class that sorts words from long to short:
```
class SortingTextDataLoader:
"""
A wrapper for the DataLoader class that sorts a list of words by their
lengths in descending order.
"""
def __init__(self, dataloader):
self.dataloader = dataloader
self.it = iter(dataloader)
def __iter__(self):
return self
def __next__(self):
words = None
for s in self.it:
words = s
break
if words is None:
self.it = iter(self.dataloader)
raise StopIteration
words = np.array(words)
sort_keys = sorted(range(len(words)),
key=lambda idx: len(list(words[idx])),
reverse=True)
sorted_words = words[sort_keys]
return sorted_words
```
# Model
## Deterministic language model
In language modelling, we model a word $x = \langle x_1, \ldots, x_n \rangle$ of length $n = |x|$ as a sequence of categorical draws:
\begin{align}
X_i|x_{<i} & \sim \text{Cat}(f(x_{<i}; \theta))
& i = 1, \ldots, n \\
\end{align}
where we use $x_{<i}$ to denote a (possibly empty) prefix string, and thus the model makes no Markov assumption. We map from the conditioning context, the prefix $x_{<i}$, to the categorical parameters (a $v$-dimensional probability vector, where $v$ denotes the size of the vocabulary, in this case, the size of the character set) using a fixed neural network architecture whose parameters we collectively denote by $\theta$.
This assigns the following likelihood to the word
\begin{align}
P(x|\theta) &= \prod_{i=1}^n P(x_i|x_{<i}, \theta) \\
&= \prod_{i=1}^n \text{Cat}(x_i|f(x_{<i}; \theta))
\end{align}
where the categorical pmf is $\text{Cat}(k|\pi) = \prod_{j=1}^v \pi_j^{[k=j]} = \pi_k$.
Suppose we have a dataset $\mathcal D = \{x^{(1)}, \ldots, x^{(N)}\}$ containing $N$ i.i.d. observations. Then we can use the log-likelihood function
\begin{align}
\mathcal L(\theta|\mathcal D) &= \sum_{k=1}^{N} \log P(x^{(k)}| \theta) \\
&= \sum_{k=1}^{N} \sum_{i=1}^{|x^{(k)}|} \log \text{Cat}(x^{(k)}_i|f(x^{(k)}_{<i}; \theta))
\end{align}
to estimate $\theta$ by maximisation:
\begin{align}
\theta^\star = \arg\max_{\theta \in \Theta} \mathcal L(\theta|\mathcal D) ~ .
\end{align}
We can use stochastic gradient-ascent to find a local optimum of $\mathcal L(\theta|\mathcal D)$, which only requires a gradient estimate:
\begin{align}
\nabla_\theta \mathcal L(\theta|\mathcal D) &= \sum_{k=1}^{|\mathcal D|} \nabla_\theta \log P(x^{(k)}|\theta) \\
&= \sum_{k=1}^{|\mathcal D|} \frac{1}{N} N \nabla_\theta \log P(x^{(k)}| \theta) \\
&= \mathbb E_{\mathcal U(1/N)} \left[ N \nabla_\theta \log P(x^{(K)}| \theta) \right] \\
&\overset{\text{MC}}{\approx} \frac{N}{M} \sum_{m=1}^M \nabla_\theta \log P(x^{(k_m)}|\theta) \\
&\text{where }K_m \sim \mathcal U(1/N)
\end{align}
This is a Monte Carlo (MC) estimate of the gradient computed on $M$ data points selected uniformly at random from $\mathcal D$.
For as long as $f$ remains differentiable wrt to its inputs and parameters, we can rely on automatic differentiation to obtain gradient estimates.
An example design for $f$ is:
\begin{align}
\mathbf x_i &= \text{emb}(x_i; \theta_{\text{emb}}) \\
\mathbf h_0 &= \mathbf 0 \\
\mathbf h_i &= \text{rnn}(\mathbf h_{i-1}, \mathbf x_{i-1}; \theta_{\text{rnn}}) \\
f(x_{<i}; \theta) &= \text{softmax}(\text{dense}_v(\mathbf h_{i}; \theta_{\text{out}}))
\end{align}
where
* $\text{emb}$ is a fixed embedding layer with parameters $\theta_{\text{emb}}$;
* $\text{rnn}$ is a recurrent architecture with parameters $\theta_{\text{rnn}}$, e.g. an LSTM or GRU, and $\mathbf h_0$ is part of the architecture's parameters;
* $\text{dense}_v$ is a dense layer with $v$ outputs (vocabulary size) and parameters $\theta_{\text{out}}$.
In what follows we show how to extend this model with a continuous latent word embedding.
## Deep generative language model
We want to model a word $x$ as a draw from the marginal of deep generative model $P(z, x|\theta, \alpha) = P(z|\alpha)P(x|z, \theta)$.
### Generative model
The generative story is:
\begin{align}
Z_k & \sim \text{Bernoulli}(\alpha_k) & k=1,\ldots, K \\
X_i | z, x_{<i} &\sim \text{Cat}(f(z, x_{<i}; \theta)) & i=1, \ldots, n
\end{align}
where $z \in \mathbb R^K$ and we impose a product of independent Bernoulli distributions prior. Other choices of prior can induce interesting properties in latent space, for example, the Bernoullis could be correlated, however, in this notebook, we use independent distributions.
**About the prior parameter** The parameter of the $k$th Bernoulli distribution is the probability that the $k$th bit in $z$ is set to $1$, and therefore, if we have reasons to believe some bits are more frequent than others (for example, because we expect some bits to capture verb attributes and others to capture noun attributes, and we know nouns are more frequent than verbs) we may be able to have a good guess at $\alpha_k$ for different $k$, otherwise, we may simply say that bits are about as likely to be on or off a priori, thus setting $\alpha_k = 0.5$ for every $k$. In this lab, we will treat the prior parameter ($\alpha$) as *fixed*.
**Architecture** It is easy to design $f$ by a simple modification of the deterministic design shown before:
\begin{align}
\mathbf x_i &= \text{emb}(x_i; \theta_{\text{emb}}) \\
\mathbf h_0 &= \tanh(\text{dense}(z; \theta_{\text{init}})) \\
\mathbf h_i &= \text{rnn}(\mathbf h_{i-1}, \mathbf x_{i-1}; \theta_{\text{rnn}}) \\
f(x_{<i}; \theta) &= \text{softmax}(\text{dense}_v(\mathbf h_{i}; \theta_{\text{out}}))
\end{align}
where we just initialise the recurrent cell using $z$. Note we could also use $z$ in other places, for example, as additional input to every update of the recurrent cell $\mathbf h_i = \text{rnn}(\mathbf h_{i-1}, [\mathbf x_{i-1}, z])$. This is an architecture choice which like many others can only be judged empirically or on the basis of practical convenience.
### Parameter estimation
The marginal likelihood, necessary for parameter estimation, is now no longer tractable:
\begin{align}
P(x|\theta, \alpha) &= \sum_{z \in \{0,1\}^K} P(z|\alpha)P(x|z, \theta) \\
&= \sum_{z \in \{0,1\}^K} \prod_{k=1}^K \text{Bernoulli}(z_k|\alpha_k)\prod_{i=1}^n \text{Cat}(x_i|f(z,x_{<i}; \theta) )
\end{align}
the intractability is clear as there is an exponential number of assignments to $z$, namely, $2^K$.
We turn to variational inference and derive a lowerbound $\mathcal E(\theta, \lambda|\mathcal D)$ on the log-likelihood function
\begin{align}
\mathcal E(\theta, \lambda|\mathcal D) &= \sum_{s=1}^{|\mathcal D|} \mathcal E_s(\theta, \lambda|x^{(s)})
\end{align}
which for a single datapoint $x$ is
\begin{align}
\mathcal E(\theta, \lambda|x) &= \mathbb{E}_{Q(z|x, \lambda)}\left[\log P(x|z, \theta)\right] - \text{KL}\left(Q(z|x, \lambda)||P(z|\alpha)\right)\\
\end{align}
where we have introduce an independently parameterised auxiliary distribution $Q(z|x, \lambda)$. The distribution $Q$ which maximises this *evidence lowerbound* (ELBO) is also the distribution that minimises
\begin{align}
\text{KL}(Q(z|x, \lambda)||P(z|x, \theta, \alpha)) = \mathbb E_{Q(z|x, \lambda)}\left[\log \frac{Q(z|x, \lambda)}{P(z|x, \theta, \alpha)}\right]
\end{align}
where $P(z|x, \theta, \alpha) = \frac{P(x, z|\theta, \alpha)}{P(x|\theta, \alpha)}$ is our intractable true posterior. For that reason, we think of $Q(z|x, \lambda)$ as an *approximate posterior*.
The approximate posterior is an independent model of the latent variable given the data, for that reason we also call it an *inference model*.
In this notebook, our inference model will be a product of independent Bernoulli distributions, to make sure that we cover the sample space of our latent variable. We will leave at the end of the notebook as an optional exercise to model correlations (thus achieving *structured* inference, rather than mean field inference). Such mean field (MF) approximation takes $K$ Bernoulli variational factors whose parameters we predict with a neural network:
\begin{align}
Q(z|x, \lambda) &= \prod_{k=1}^K \text{Bernoulli}(z_k|\beta_k(x; \lambda))
\end{align}
Note we compute a *fixed* number, namely, $K$, of Bernoulli parameters. This can be done with a neural network that outputs $K$ values and employs a sigmoid activation for the outputs.
For this choice, the KL term in the ELBO is tractable:
\begin{align}
\text{KL}\left(Q(z|x, \lambda)||P(z|\alpha)\right) &= \sum_{k=1}^K \text{KL}\left(Q(z_k|x, \lambda)||P(z_k|\alpha_k)\right) \\
&= \sum_{k=1}^K \text{KL}\left(\text{Bernoulli}(\beta_k(x;\lambda))|| \text{Bernoulli}(\alpha_k)\right) \\
&= \sum_{k=1}^K \beta_k(x;\lambda) \log \frac{\beta_k(x;\lambda)}{\alpha_k} + (1-\beta_k(x;\lambda)) \log \frac{1-\beta_k(x;\lambda)}{1-\alpha_k}
\end{align}
Here's an example design for our inference model:
\begin{align}
\mathbf x_i &= \text{emb}(x_i; \lambda_{\text{emb}}) \\
\mathbf f_i &= \text{rnn}(\mathbf f_{i-1}, \mathbf x_{i}; \lambda_{\text{fwd}}) \\
\mathbf b_i &= \text{rnn}(\mathbf b_{i+1}, \mathbf x_{i}; \lambda_{\text{bwd}}) \\
\mathbf h &= \text{dense}([\mathbf f_{n}, \mathbf b_1]; \lambda_{\text{hid}}) \\
\beta(x; \lambda) &= \text{sigmoid}(\text{dense}_K(\mathbf h; \lambda_{\text{out}}))
\end{align}
where we use the $\text{sigmoid}$ activation to make sure our probabilities are independently set between $0$ and $1$.
Because we have neural networks compute the Bernoulli variational factors for us, we call this *amortised* mean field inference.
### Gradient estimation
We have to obtain gradients of the ELBO with respect to $\theta$ (generative model) and $\lambda$ (inference model). Recall we will leave $\alpha$ fixed.
For the **generative model**
\begin{align}
\nabla_\theta \mathcal E(\theta, \lambda|x) &=\nabla_\theta\sum_{z} Q(z|x, \lambda)\log P(x|z,\theta) - \underbrace{\nabla_\theta \sum_{k=1}^K \text{KL}(Q(z_k|x, \lambda) || P(z_k|\alpha_k))}_{\color{blue}{0}} \\
&=\sum_{z} Q(z|x, \lambda)\nabla_\theta\log P(x|z,\theta) \\
&= \mathbb E_{Q(z|x, \lambda)}\left[\nabla_\theta\log P(x|z,\theta) \right] \\
&\overset{\text{MC}}{\approx} \frac{1}{S} \sum_{s=1}^S \nabla_\theta \log P(x|z^{(s)}, \theta)
\end{align}
where $z^{(s)} \sim Q(z|x,\lambda)$.
Note there is no difficulty in obtaining gradient estimates precisely because the samples come from the inference model and therefore do not interfere with backpropagation for updates to $\theta$.
For the **inference model** the story is less straightforward, and we have to use the *score function estimator* (a.k.a. REINFORCE):
\begin{align}
\nabla_\lambda \mathcal E(\theta, \lambda|x) &=\nabla_\lambda\sum_{z} Q(z|x, \lambda)\log P(x|z,\theta) - \nabla_\lambda \underbrace{\sum_{k=1}^K \text{KL}(Q(z_k|x, \lambda) || P(z_k|\alpha_k))}_{ \color{blue}{\text{tractable} }} \\
&=\sum_{z} \nabla_\lambda Q(z|x, \lambda)\log P(x|z,\theta) - \sum_{k=1}^K \nabla_\lambda \text{KL}(Q(z_k|x, \lambda) || P(z_k|\alpha_k)) \\
&=\sum_{z} \underbrace{Q(z|x, \lambda) \nabla_\lambda \log Q(z|x, \lambda)}_{\nabla_\lambda Q(z|x, \lambda)} \log P(x|z,\theta) - \sum_{k=1}^K \nabla_\lambda \text{KL}(Q(z_k|x, \lambda) || P(z_k|\alpha_k)) \\
&= \mathbb E_{Q(z|x, \lambda)}\left[ \log P(x|z,\theta) \nabla_\lambda \log Q(z|x, \lambda) \right] - \sum_{k=1}^K \nabla_\lambda \text{KL}(Q(z_k|x, \lambda) || P(z_k|\alpha_k)) \\
&\overset{\text{MC}}{\approx} \left(\frac{1}{S} \sum_{s=1}^S \log P(x|z^{(s)}, \theta) \nabla_\lambda \log Q(z^{(s)}|x, \lambda) \right) - \sum_{k=1}^K \nabla_\lambda \text{KL}(Q(z_k|x, \lambda) || P(z_k|\alpha_k))
\end{align}
where $z^{(s)} \sim Q(z|x,\lambda)$.
## Implementation
Let's implement the model and the loss (negative ELBO). We work with the notion of a *surrogate loss*, that is, a computation node whose gradients wrt to parameters are equivalent to the gradients we need.
For a given sample $z \sim Q(z|x, \lambda)$, the following is a single-sample surrogate loss:
\begin{align}
\mathcal S(\theta, \lambda|x) = \log P(x|z, \theta) + \color{red}{\text{detach}(\log P(x|z, \theta) )}\log Q(z|x, \lambda) - \sum_{k=1}^K \text{KL}(Q(z_k|x, \lambda) || P(z_k|\alpha_k))
\end{align}
Check the documentation of pytorch's `detach` method.
Show that it's gradients wrt $\theta$ and $\lambda$ are exactly what we need:
\begin{align}
\nabla_\theta \mathcal S(\theta, \lambda|x) = \color{red}{?}
\end{align}
\begin{align}
\nabla_\lambda \mathcal S(\theta, \lambda|x) = \color{red}{?}
\end{align}
Let's now turn to the actual implementation in pytorch of the inference model as well as the generative model.
Here and there we will provide helper code for you.
```
def bernoulli_log_probs_from_logits(logits):
"""
Let p be the Bernoulli parameter and q = 1 - p.
This function is a stable computation of p and q from logit = log(p/q).
:param logit: log (p/q)
:return: log_p, log_q
"""
return - F.softplus(-logits), - F.softplus(logits)
```
We start with the implementation of a product of Bernoulli distributions where the parameters are *given* at construction time. That is, for some vector $b_1, \ldots, b_K$ we have
\begin{equation}
Z_k \sim \text{Bernoulli}(b_k)
\end{equation}
and thus the joint probability of $z_1, \ldots, z_K$ is given by $\prod_{k=1}^K \text{Bernoulli}(z_k|b_k)$.
```
class ProductOfBernoullis:
"""
This is class models a product of independent Bernoulli distributions.
Each product of Bernoulli is defined by a D-dimensional vector of logits
for each independent Bernoulli variable.
"""
def __init__(self, logits):
"""
:param p: a tensor of D Bernoulli parameters (logits) for each batch element. [B, D]
"""
pass
def mean(self):
"""For Bernoulli variables this is the probability of each Bernoulli being 1."""
return None
def std(self):
"""For Bernoulli variables this is p*(1-p) where p
is the probability of the Bernoulli being 1"""
return self.probs * (1.0 - self.probs)
def sample(self):
"""
Returns a sample with the shape of the Bernoulli parameter. # [B, D]
"""
return None
def log_prob(self, x):
"""
Assess the log probability mass of x.
:param x: a tensor of Bernoulli samples (same shape as the Bernoulli parameter) [B, D]
:returns: tensor of log probabilitie densities [B]
"""
return None
def unstable_kl(self, other: 'Bernoulli'):
"""
The straightforward implementation of the KL between two Bernoullis.
This implementation is unstable, a stable implementation is provided in
ProductOfBernoullis.kl(self, q)
:returns: a tensor of KL values with the same shape as the parameters of self.
"""
return None
def kl(self, other: 'Bernoulli'):
"""
A stable implementation of the KL divergence between two Bernoulli variables.
:returns: a tensor of KL values with the same shape as the parameters of self.
"""
return None
```
Then we should implement the inference model $Q(z | x, \lambda)$, that is, a module that uses a neural network to map from a data point $x$ to the parameters of a product of Bernoullis.
You might want to consult the documentation of
* `torch.nn.Embedding`
* `torch.nn.LSTM`
* `torch.nn.Linear`
* and of our own `ProductOfBernoullis` distribution (see above).
```
class InferenceModel(nn.Module):
def __init__(self, vocab_size, embedder, hidden_size,
latent_size, pad_idx, bidirectional=False):
"""
Implement the layers in the inference model.
:param vocab_size: size of the vocabulary of the language
:param embedder: embedding layer
:param hidden_size: size of recurrent cell
:param latent_size: size K of the latent variable
:param pad_idx: id of the -PAD- token
:param bidirectional: whether we condition on x via a bidirectional or
unidirectional encoder
"""
super().__init__() # pytorch modules should always start with this
pass
# Construct your NN blocks here
# and make sure every block is an attribute of self
# or they won't get initialised properly
# for example, self.my_linear_layer = torch.nn.Linear(...)
def forward(self, x, seq_mask, seq_len) -> ProductOfBernoullis:
"""
Return an inference product of Bernoullis per instance in the mini-batch
:param x: words [B, T] as token ids
:param seq_mask: indicates valid positions vs padding positions [B, T]
:param seq_len: the length of the sequences [B]
:return: a collection of B ProductOfBernoullis approximate posterior,
each a distribution over K-dimensional bit vectors
"""
pass
# tests for inference model
pad_idx = vocab.char_to_idx[PAD_TOKEN]
dummy_inference_model = InferenceModel(
vocab_size=vocab.size(),
embedder=nn.Embedding(vocab.size(), 64, padding_idx=pad_idx),
hidden_size=128, latent_size=16, pad_idx=pad_idx, bidirectional=True
).to(device=device)
dummy_batch_size = 32
dummy_dataloader = SortingTextDataLoader(DataLoader(train_dataset, batch_size=dummy_batch_size))
dummy_words = next(dummy_dataloader)
x_in, _, seq_mask, seq_len = create_batch(dummy_words, vocab, device)
q_z_given_x = dummy_inference_model.forward(x_in, seq_mask, seq_len)
```
Then we should implement the generative latent factor model. The decoder is a sequence of correlated Categorical draws that condition on a latent factor assignment.
We will be parameterising categorical distributions, so you might want to check the documentation of `torch.distributions.categorical.Categorical`.
```
from torch.distributions import Categorical
class LatentFactorModel(nn.Module):
def __init__(self, vocab_size, emb_size, hidden_size, latent_size,
pad_idx, dropout=0.):
"""
:param vocab_size: size of the vocabulary of the language
:param emb_size: dimensionality of embeddings
:param hidden_size: dimensionality of recurrent cell
:param latent_size: this is D the dimensionality of the latent variable z
:param pad_idx: the id reserved to the -PAD- token
:param dropout: a dropout rate (you can ignore this for now)
"""
super().__init__()
# Construct your NN blocks here,
# remember to assign them to attributes of self
pass
def init_hidden(self, z):
"""
Returns the hidden state of the LSTM initialized with a projection of a given z.
:param z: [B, K]
:returns: [num_layers, B, H] hidden state, [num_layers, B, H] cell state
"""
pass
def step(self, prev_x, z, hidden):
"""
Performs a single LSTM step for a given previous word and hidden state.
Returns the unnormalized log probabilities (logits) over the vocabulary
for this time step.
:param prev_x: [B, 1] id of the previous token
:param z: [B, K] latent variable
:param hidden: hidden ([num_layers, B, H] state, [num_layers, B, H] cell)
:returns: [B, V] logits, ([num_layers, B, H] updated state, [num_layers, B, H] updated cell)
"""
pass
def forward(self, x, z) -> Categorical:
"""
Performs an entire forward pass given a sequence of words x and a z.
This returns a collection of [B, T] categorical distributions, each
with support over V events.
:param x: [B, T] token ids
:param z: [B, K] a latent sample
:returns: Categorical object with shape [B,T,V]
"""
hidden = self.init_hidden(z)
outputs = []
for t in range(x.size(1)):
# [B, 1]
prev_x = x[:, t].unsqueeze(-1)
# logits: [B, V]
logits, hidden = self.step(prev_x, z, hidden)
outputs.append(logits)
outputs = torch.cat(outputs, dim=1)
return Categorical(logits=outputs)
def loss(self, output_distributions, observations, pz, qz, free_nats=0., evaluation=False):
"""
Computes the terms in the loss (negative ELBO) given the
output Categorical distributions, observations,
the prior distribution p(z), and the approximate posterior distribution q(z|x).
If free_nats is nonzero it will clamp the KL divergence between the posterior
and prior to that value, preventing gradient propagation via the KL if it's
below that value.
If evaluation is set to true, the loss will be summed instead
of averaged over the batch.
Returns the (surrogate) loss, the ELBO, and the KL.
:returns:
surrogate loss (scalar),
ELBO (scalar),
KL (scalar)
"""
pass
```
The code below is used to assess the model and also investigate what it learned. We implemented it for you, so that you can focus on the VAE part. It's useful however to learn from this example: we do interesting things like computing perplexity and sampling novel words!
# Evaluation metrics
During training we'd like to keep track of some evaluation metrics on the validation data in order to keep track of how our model is doing and to perform early stopping. One simple metric we can compute is the ELBO on all the validation or test data using a single sample from the approximate posterior $Q(z|x, \lambda)$:
```
def eval_elbo(model, inference_model, eval_dataset, vocab, device, batch_size=128):
"""
Computes a single sample estimate of the ELBO on a given dataset.
This returns both the average ELBO and the average KL (for inspection).
"""
dl = DataLoader(eval_dataset, batch_size=batch_size)
sorted_dl = SortingTextDataLoader(dl)
# Make sure the model is in evaluation mode (i.e. disable dropout).
model.eval()
total_ELBO = 0.
total_KL = 0.
num_words = 0
# We don't need to compute gradients for this.
with torch.no_grad():
for words in sorted_dl:
x_in, x_out, seq_mask, seq_len = create_batch(words, vocab, device)
# Infer the approximate posterior and construct the prior.
qz = inference_model(x_in, seq_mask, seq_len)
pz = ProductOfBernoullis(torch.ones_like(qz.probs) * 0.5)
# Compute the unnormalized probabilities using a single sample from the
# approximate posterior.
z = qz.sample()
# Compute distributions X_i|z, x_{<i}
px_z = model(x_in, z)
# Compute the reconstruction loss and KL divergence.
loss, ELBO, KL = model.loss(px_z, x_out, pz, qz, z,
free_nats=0.,
evaluation=True)
total_ELBO += ELBO
total_KL += KL
num_words += x_in.size(0)
# Return the average reconstruction loss and KL.
avg_ELBO = total_ELBO / num_words
avg_KL = total_KL / num_words
return avg_ELBO, avg_KL
dummy_lm = LatentFactorModel(
vocab.size(), emb_size=64, hidden_size=128,
latent_size=16, pad_idx=pad_idx).to(device=device)
!head -n 128 {val_file} > ./dummy_dataset
dummy_data = TextDataset('./dummy_dataset')
dummy_ELBO, dummy_kl = eval_elbo(dummy_lm, dummy_inference_model,
dummy_data, vocab, device)
print(dummy_ELBO, dummy_kl)
assert dummy_kl.item() > 0
```
A common metric to evaluate language models is the perplexity per word. The perplexity per word for a dataset is defined as:
\begin{align}
\text{ppl}(\mathcal{D}|\theta, \lambda) = \exp\left(-\frac{1}{\sum_{k=1}^{|\mathcal D|} n^{(k)}} \sum_{k=1}^{|\mathcal{D}|} \log P(x^{(k)}|\theta, \lambda)\right)
\end{align}
where $n^{(k)} = |x^{(k)}|$ is the number of tokens in a word and $P(x^{(k)}|\theta, \lambda)$ is the probability that our model assigns to the datapoint $x^{(k)}$. In order to compute $\log P(x|\theta, \lambda)$ for our model we need to evaluate the marginal:
\begin{align}
P(x|\theta, \lambda) = \sum_{z \in \{0, 1\}^K} P(x|z,\theta) P(z|\alpha)
\end{align}
As this is summation cannot be computed in a reasonable amount of time (due to exponential complexity), we have two options: we can use the earlier derived lower-bound on the log-likelihood, which will give us an upper-bound on the perplexity, or we can make an importance sampling estimate using our approximate posterior distribution. The importance sampling (IS) estimate can be done as:
\begin{align}
\hat P(x|\theta, \lambda) &\overset{\text{IS}}{\approx} \frac{1}{S} \sum_{s=1}^{S} \frac{P(z^{(s)}|\alpha)P(x|z^{(s)}, \theta)}{Q(z^{(s)}|x)} & \text{where }z^{(s)} \sim Q(z|x)
\end{align}
where $S$ is the number of samples.
Then our perplexity becomes:
\begin{align}
&\frac{1}{\sum_{k=1}^{|\mathcal D|} n^{(k)}} \sum_{k=1}^{|\mathcal D|} \log P(x^{(k)}|\theta) \\
&\approx \frac{1}{\sum_{k=1}^{|\mathcal D|} n^{(k)}} \sum_{k=1}^{|\mathcal D|} \log \frac{1}{S} \sum_{s=1}^{S} \frac{P(z^{(s)}|\alpha)P(x^{(k)}|z^{(s)}, \theta)}{Q(z^{(s)}|x^{(k)})} \\
\end{align}
We define the function `eval_perplexity` below that implements this importance sampling estimate:
```
def eval_perplexity(model, inference_model, eval_dataset, vocab, device,
n_samples, batch_size=128):
"""
Estimates the per-word perplexity using importance sampling with the
given number of samples.
"""
dl = DataLoader(eval_dataset, batch_size=batch_size)
sorted_dl = SortingTextDataLoader(dl)
# Make sure the model is in evaluation mode (i.e. disable dropout).
model.eval()
log_px = 0.
num_predictions = 0
num_words = 0
# We don't need to compute gradients for this.
with torch.no_grad():
for words in sorted_dl:
x_in, x_out, seq_mask, seq_len = create_batch(words, vocab, device)
# Infer the approximate posterior and construct the prior.
qz = inference_model(x_in, seq_mask, seq_len)
pz = ProductOfBernoullis(torch.ones_like(qz.probs) * 0.5) # TODO different prior
# Create an array to hold all samples for this batch.
batch_size = x_in.size(0)
log_px_samples = torch.zeros(n_samples, batch_size)
# Sample log P(x) n_samples times.
for s in range(n_samples):
# Sample a z^s from the posterior.
z = qz.sample()
# Compute log P(x^k|z^s)
px_z = model(x_in, z)
# [B, T]
cond_log_prob = px_z.log_prob(x_out)
cond_log_prob = torch.where(seq_mask, cond_log_prob, torch.zeros_like(cond_log_prob))
# [B]
cond_log_prob = cond_log_prob.sum(-1)
# Compute log p(z^s) and log q(z^s|x^k)
prior_log_prob = pz.log_prob(z) # B
posterior_log_prob = qz.log_prob(z) # B
# Store the sample for log P(x^k) importance weighted with p(z^s)/q(z^s|x^k).
log_px_sample = cond_log_prob + prior_log_prob - posterior_log_prob
log_px_samples[s] = log_px_sample
# Average over the number of samples and count the number of predictions made this batch.
log_px_batch = torch.logsumexp(log_px_samples, dim=0) - \
torch.log(torch.Tensor([n_samples]))
log_px += log_px_batch.sum()
num_predictions += seq_len.sum()
num_words += seq_len.size(0)
# Compute and return the perplexity per word.
perplexity = torch.exp(-log_px / num_predictions)
NLL = -log_px / num_words
return perplexity, NLL
```
Lastly, we want to occasionally qualitatively see the performance of the model during training, by letting it reconstruct a given word from the latent space. This gives us an idea of whether the model is using the latent space to encode some semantics about the data. For this we use a deterministic greedy decoding algorithm, that chooses the word with maximum probability at every time step, and feeds that word into the next time step.
```
def greedy_decode(model, z, vocab, max_len=50):
"""
Greedily decodes a word from a given z, by picking the word with
maximum probability at each time step.
"""
# Disable dropout.
model.eval()
# Don't compute gradients.
with torch.no_grad():
batch_size = z.size(0)
# We feed the model the start-of-word symbol at the first time step.
prev_x = torch.ones(batch_size, 1, dtype=torch.long).fill_(vocab[SOW_TOKEN]).to(z.device)
# Initialize the hidden state from z.
hidden = model.init_hidden(z)
predictions = []
for t in range(max_len):
logits, hidden = model.step(prev_x, z, hidden)
# Choose the argmax of the unnnormalized probabilities as the
# prediction for this time step.
prediction = torch.argmax(logits, dim=-1)
predictions.append(prediction)
prev_x = prediction.view(batch_size, 1)
return torch.cat(predictions, dim=1)
```
# Training
Now it's time to train the model. We use early stopping on the validation perplexity for model selection.
```
# Define the model hyperparameters.
emb_size = 256
hidden_size = 256
latent_size = 16
bidirectional_encoder = True
free_nats = 0 # 5.
annealing_steps = 0 # 11400
dropout = 0.6
word_dropout = 0 # 0.75
batch_size = 64
learning_rate = 0.001
num_epochs = 20
n_importance_samples = 3 # 50
# Create the training data loader.
dl = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
sorted_dl = SortingTextDataLoader(dl)
# Create the generative model.
model = LatentFactorModel(vocab_size=vocab.size(),
emb_size=emb_size,
hidden_size=hidden_size,
latent_size=latent_size,
pad_idx=vocab[PAD_TOKEN],
dropout=dropout)
model = model.to(device)
# Create the inference model.
inference_model = InferenceModel(vocab_size=vocab.size(),
embedder=model.embedder,
hidden_size=hidden_size,
latent_size=latent_size,
pad_idx=vocab[PAD_TOKEN],
bidirectional=bidirectional_encoder)
inference_model = inference_model.to(device)
# Create the optimizer.
optimizer = optim.Adam(itertools.chain(model.parameters(),
inference_model.parameters()),
lr=learning_rate)
# Save the best model (early stopping).
best_model = "./best_model.pt"
best_val_ppl = float("inf")
best_epoch = 0
# Keep track of some statistics to plot later.
train_ELBOs = []
train_KLs = []
val_ELBOs = []
val_KLs = []
val_perplexities = []
val_NLLs = []
step = 0
training_ELBO = 0.
training_KL = 0.
num_batches = 0
for epoch_num in range(1, num_epochs+1):
for words in sorted_dl:
# Make sure the model is in training mode (for dropout).
model.train()
# Transform the words to input, output, seq_len, seq_mask batches.
x_in, x_out, seq_mask, seq_len = create_batch(words, vocab, device,
word_dropout=word_dropout)
# Compute the multiplier for the KL term if we do annealing.
if annealing_steps > 0:
KL_weight = min(1., (1.0 / annealing_steps) * step)
else:
KL_weight = 1.
# Do a forward pass through the model and compute the training loss. We use
# a reparameterized sample from the approximate posterior during training.
qz = inference_model(x_in, seq_mask, seq_len)
pz = ProductOfBernoullis(torch.ones_like(qz.probs) * 0.5)
z = qz.sample()
px_z = model(x_in, z)
loss, ELBO, KL = model.loss(px_z, x_out, pz, qz, z, free_nats=free_nats)
# Backpropagate and update the model weights.
loss.backward()
optimizer.step()
optimizer.zero_grad()
# Update some statistics to track for the training loss.
training_ELBO += ELBO
training_KL += KL
num_batches += 1
# Every 100 steps we evaluate the model and report progress.
if step % 100 == 0:
val_ELBO, val_KL = eval_elbo(model, inference_model, val_dataset, vocab, device)
print("(%d) step %d: training ELBO (KL) = %.2f (%.2f) --"
" KL weight = %.2f --"
" validation ELBO (KL) = %.2f (%.2f)" %
(epoch_num, step, training_ELBO/num_batches,
training_KL/num_batches, KL_weight, val_ELBO, val_KL))
# Update some statistics for plotting later.
train_ELBOs.append((step, (training_ELBO/num_batches).item()))
train_KLs.append((step, (training_KL/num_batches).item()))
val_ELBOs.append((step, val_ELBO.item()))
val_KLs.append((step, val_KL.item()))
# Reset the training statistics.
training_ELBO = 0.
training_KL = 0.
num_batches = 0
step += 1
# After an epoch we'll compute validation perplexity and save the model
# for early stopping if it's better than previous models.
print("Finished epoch %d" % (epoch_num))
val_perplexity, val_NLL = eval_perplexity(model, inference_model, val_dataset, vocab, device,
n_importance_samples)
val_ELBO, val_KL = eval_elbo(model, inference_model, val_dataset, vocab, device)
# Keep track of the validation perplexities / NLL.
val_perplexities.append((epoch_num, val_perplexity.item()))
val_NLLs.append((epoch_num, val_NLL.item()))
# If validation perplexity is better, store this model for early stopping.
if val_perplexity < best_val_ppl:
best_val_ppl = val_perplexity
best_epoch = epoch_num
torch.save(model.state_dict(), best_model)
# Print epoch statistics.
print("Evaluation epoch %d:\n"
" - validation perplexity: %.2f\n"
" - validation NLL: %.2f\n"
" - validation ELBO (KL) = %.2f (%.2f)"
% (epoch_num, val_perplexity, val_NLL, val_ELBO, val_KL))
# Also show some qualitative results by reconstructing a word from the
# validation data. Use the mean of the approximate posterior and greedy
# decoding.
random_word = val_dataset[np.random.choice(len(val_dataset))]
x_in, _, seq_mask, seq_len = create_batch([random_word], vocab, device)
qz = inference_model(x_in, seq_mask, seq_len)
z = qz.mean()
reconstruction = greedy_decode(model, z, vocab)
reconstruction = batch_to_words(reconstruction, vocab)[0]
print("-- Original word: \"%s\"" % random_word)
print("-- Model reconstruction: \"%s\"" % reconstruction)
```
# Let's plot the training and validation statistics:
```
steps, training_ELBO = list(zip(*train_ELBOs))
_, training_KL = list(zip(*train_KLs))
_, val_ELBO = list(zip(*val_ELBOs))
_, val_KL = list(zip(*val_KLs))
epochs, val_ppl = list(zip(*val_perplexities))
_, val_NLL = list(zip(*val_NLLs))
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(18, 5))
# Plot training ELBO and KL
ax1.set_title("Training ELBO")
ax1.plot(steps, training_ELBO, "-o")
ax2.set_title("Training KL")
ax2.plot(steps, training_KL, "-o")
plt.show()
# Plot validation ELBO and KL
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(18, 5))
ax1.set_title("Validation ELBO")
ax1.plot(steps, val_ELBO, "-o", color="orange")
ax2.set_title("Validation KL")
ax2.plot(steps, val_KL, "-o", color="orange")
plt.show()
# Plot validation perplexities.
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(18, 5))
ax1.set_title("Validation perplexity")
ax1.plot(epochs, val_ppl, "-o", color="orange")
ax2.set_title("Validation NLL")
ax2.plot(epochs, val_NLL, "-o", color="orange")
plt.show()
print()
```
Let's load the best model according to validation perplexity and compute its perplexity on the test data:
```
# Load the best model from disk.
model = LatentFactorModel(vocab_size=vocab.size(),
emb_size=emb_size,
hidden_size=hidden_size,
latent_size=latent_size,
pad_idx=vocab[PAD_TOKEN],
dropout=dropout)
model.load_state_dict(torch.load(best_model))
model = model.to(device)
# Compute test perplexity and ELBO.
test_perplexity, test_NLL = eval_perplexity(model, inference_model, test_dataset, vocab,
device, n_importance_samples)
test_ELBO, test_KL = eval_elbo(model, inference_model, test_dataset, vocab, device)
print("test ELBO (KL) = %.2f (%.2f) -- test perplexity = %.2f -- test NLL = %.2f" %
(test_ELBO, test_KL, test_perplexity, test_NLL))
```
# Qualitative analysis
Let's have a look at what how our trained model interacts with the learned latent space. First let's greedily decode some samples from the prior to assess the diversity of the model:
```
# Generate 10 samples from the standard normal prior.
num_prior_samples = 10
pz = ProductOfBernoullis(torch.ones(num_prior_samples, latent_size) * 0.5)
z = pz.sample()
z = z.to(device)
# Use the greedy decoding algorithm to generate words.
predictions = greedy_decode(model, z, vocab)
predictions = batch_to_words(predictions, vocab)
for num, prediction in enumerate(predictions):
print("%d: %s" % (num+1, prediction))
```
Let's now have a look how good the model is at reconstructing words from the test dataset using the approximate posterior mean and a couple of samples:
```
# Pick a random test word.
test_word = test_dataset[np.random.choice(len(test_dataset))]
# Infer q(z|x).
x_in, _, seq_mask, seq_len = create_batch([test_word], vocab, device)
qz = inference_model(x_in, seq_mask, seq_len)
# Decode using the mean.
z_mean = qz.mean()
mean_reconstruction = greedy_decode(model, z_mean, vocab)
mean_reconstruction = batch_to_words(mean_reconstruction, vocab)[0]
print("Original: \"%s\"" % test_word)
print("Posterior mean reconstruction: \"%s\"" % mean_reconstruction)
# Decode a couple of samples from the approximate posterior.
for s in range(3):
z = qz.sample()
sample_reconstruction = greedy_decode(model, z, vocab)
sample_reconstruction = batch_to_words(sample_reconstruction, vocab)[0]
print("Posterior sample reconstruction (%d): \"%s\"" % (s+1, sample_reconstruction))
```
We can also qualitatively assess the smoothness of the learned latent space by interpolating between two words in the test set:
```
# Pick a random test word.
test_word_1 = test_dataset[np.random.choice(len(test_dataset))]
# Infer q(z|x).
x_in, _, seq_mask, seq_len = create_batch([test_word_1], vocab, device)
qz = inference_model(x_in, seq_mask, seq_len)
qz_1 = qz.mean()
# Pick a random second test word.
test_word_2 = test_dataset[np.random.choice(len(test_dataset))]
# Infer q(z|x) again.
x_in, _, seq_mask, seq_len = create_batch([test_word_2], vocab, device)
qz = inference_model(x_in, seq_mask, seq_len)
qz_2 = qz.mean()
# Now interpolate between the two means and generate words between those.
num_words = 5
print("Word 1: \"%s\"" % test_word_1)
for alpha in np.linspace(start=0., stop=1., num=num_words):
z = (1-alpha) * qz_1 + alpha * qz_2
reconstruction = greedy_decode(model, z, vocab)
reconstruction = batch_to_words(reconstruction, vocab)[0]
print("(1-%.2f) * qz1.mean + %.2f qz2.mean: \"%s\"" % (alpha, alpha, reconstruction))
print("Word 2: \"%s\"" % test_word_2)
```
| github_jupyter |
# Lambda School Data Science - Recurrent Neural Networks and LSTM
> "Yesterday's just a memory - tomorrow is never what it's supposed to be." -- Bob Dylan
# Lecture
Wish you could save [Time In A Bottle](https://www.youtube.com/watch?v=AnWWj6xOleY)? With statistics you can do the next best thing - understand how data varies over time (or any sequential order), and use the order/time dimension predictively.
A sequence is just any enumerated collection - order counts, and repetition is allowed. Python lists are a good elemental example - `[1, 2, 2, -1]` is a valid list, and is different from `[1, 2, -1, 2]`. The data structures we tend to use (e.g. NumPy arrays) are often built on this fundamental structure.
A time series is data where you have not just the order but some actual continuous marker for where they lie "in time" - this could be a date, a timestamp, [Unix time](https://en.wikipedia.org/wiki/Unix_time), or something else. All time series are also sequences, and for some techniques you may just consider their order and not "how far apart" the entries are (if you have particularly consistent data collected at regular intervals it may not matter).
## Time series with plain old regression
Recurrences are fancy, and we'll get to those later - let's start with something simple. Regression can handle time series just fine if you just set them up correctly - let's try some made-up stock data. And to make it, let's use a few list comprehensions!
```
import numpy as np
from random import random
days = np.array((range(28)))
stock_quotes = np.array([random() + day * random() for day in days])
stock_quotes
```
Let's take a look with a scatter plot:
```
from matplotlib.pyplot import scatter
scatter(days, stock_quotes)
```
Looks pretty linear, let's try a simple OLS regression.
First, these need to be NumPy arrays:
```
days = days.reshape(-1, 1) # X needs to be column vectors
```
Now let's use good old `scikit-learn` and linear regression:
```
from sklearn.linear_model import LinearRegression
ols_stocks = LinearRegression()
ols_stocks.fit(days, stock_quotes)
ols_stocks.score(days, stock_quotes)
```
That seems to work pretty well, but real stocks don't work like this.
Let's make *slightly* more realistic data that depends on more than just time:
```
# Not everything is best as a comprehension
stock_data = np.empty([len(days), 4])
for day in days:
asset = random()
liability = random()
quote = random() + ((day * random()) + (20 * asset) - (15 * liability))
quote = max(quote, 0.01) # Want positive quotes
stock_data[day] = np.array([quote, day, asset, liability])
stock_data
```
Let's look again:
```
stock_quotes = stock_data[:,0]
scatter(days, stock_quotes)
```
How does our old model do?
```
days = np.array(days).reshape(-1, 1)
ols_stocks.fit(days, stock_quotes)
ols_stocks.score(days, stock_quotes)
```
Not bad, but can we do better?
```
ols_stocks.fit(stock_data[:,1:], stock_quotes)
ols_stocks.score(stock_data[:,1:], stock_quotes)
```
Yep - unsurprisingly, the other covariates (assets and liabilities) have info.
But, they do worse without the day data.
```
ols_stocks.fit(stock_data[:,2:], stock_quotes)
ols_stocks.score(stock_data[:,2:], stock_quotes)
```
## Time series jargon
There's a lot of semi-standard language and tricks to talk about this sort of data. [NIST](https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4.htm) has an excellent guidebook, but here are some highlights:
### Moving average
Moving average aka rolling average aka running average.
Convert a series of data to a series of averages of continguous subsets:
```
stock_quotes_rolling = [sum(stock_quotes[i:i+3]) / 3
for i in range(len(stock_quotes - 2))]
stock_quotes_rolling
```
Pandas has nice series related functions:
```
import pandas as pd
df = pd.DataFrame(stock_quotes)
df.rolling(3).mean()
```
### Forecasting
Forecasting - at it's simplest, it just means "predict the future":
```
ols_stocks.fit(stock_data[:,1:], stock_quotes)
ols_stocks.predict([[29, 0.5, 0.5]])
```
One way to predict if you just have the series data is to use the prior observation. This can be pretty good (if you had to pick one feature to model the temperature for tomorrow, the temperature today is a good choice).
```
temperature = np.array([30 + random() * day
for day in np.array(range(365)).reshape(-1, 1)])
temperature_next = temperature[1:].reshape(-1, 1)
temperature_ols = LinearRegression()
temperature_ols.fit(temperature[:-1], temperature_next)
temperature_ols.score(temperature[:-1], temperature_next)
```
But you can often make it better by considering more than one prior observation.
```
temperature_next_next = temperature[2:].reshape(-1, 1)
temperature_two_past = np.concatenate([temperature[:-2], temperature_next[:-1]],
axis=1)
temperature_ols.fit(temperature_two_past, temperature_next_next)
temperature_ols.score(temperature_two_past, temperature_next_next)
```
### Exponential smoothing
Exponential smoothing means using exponentially decreasing past weights to predict the future.
You could roll your own, but let's use Pandas.
```
temperature_df = pd.DataFrame(temperature)
temperature_df.ewm(halflife=7).mean()
```
Halflife is among the parameters we can play with:
```
sse_1 = ((temperature_df - temperature_df.ewm(halflife=7).mean())**2).sum()
sse_2 = ((temperature_df - temperature_df.ewm(halflife=3).mean())**2).sum()
print(sse_1)
print(sse_2)
```
Note - the first error being higher doesn't mean it's necessarily *worse*. It's *smoother* as expected, and if that's what we care about - great!
### Seasonality
Seasonality - "day of week"-effects, and more. In a lot of real world data, certain time periods are systemically different, e.g. holidays for retailers, weekends for restaurants, seasons for weather.
Let's try to make some seasonal data - a store that sells more later in a week:
```
sales = np.array([random() + (day % 7) * random() for day in days])
scatter(days, sales)
```
How does linear regression do at fitting this?
```
sales_ols = LinearRegression()
sales_ols.fit(days, sales)
sales_ols.score(days, sales)
```
That's not great - and the fix depends on the domain. Here, we know it'd be best to actually use "day of week" as a feature.
```
day_of_week = days % 7
sales_ols.fit(day_of_week, sales)
sales_ols.score(day_of_week, sales)
```
Note that it's also important to have representative data across whatever seasonal feature(s) you use - don't predict retailers based only on Christmas, as that won't generalize well.
## Recurrent Neural Networks
There's plenty more to "traditional" time series, but the latest and greatest technique for sequence data is recurrent neural networks. A recurrence relation in math is an equation that uses recursion to define a sequence - a famous example is the Fibonacci numbers:
$F_n = F_{n-1} + F_{n-2}$
For formal math you also need a base case $F_0=1, F_1=1$, and then the rest builds from there. But for neural networks what we're really talking about are loops:

The hidden layers have edges (output) going back to their own input - this loop means that for any time `t` the training is at least partly based on the output from time `t-1`. The entire network is being represented on the left, and you can unfold the network explicitly to see how it behaves at any given `t`.
Different units can have this "loop", but a particularly successful one is the long short-term memory unit (LSTM):

There's a lot going on here - in a nutshell, the calculus still works out and backpropagation can still be implemented. The advantage (ane namesake) of LSTM is that it can generally put more weight on recent (short-term) events while not completely losing older (long-term) information.
After enough iterations, a typical neural network will start calculating prior gradients that are so small they effectively become zero - this is the [vanishing gradient problem](https://en.wikipedia.org/wiki/Vanishing_gradient_problem), and is what RNN with LSTM addresses. Pay special attention to the $c_t$ parameters and how they pass through the unit to get an intuition for how this problem is solved.
So why are these cool? One particularly compelling application is actually not time series but language modeling - language is inherently ordered data (letters/words go one after another, and the order *matters*). [The Unreasonable Effectiveness of Recurrent Neural Networks](https://karpathy.github.io/2015/05/21/rnn-effectiveness/) is a famous and worth reading blog post on this topic.
For our purposes, let's use TensorFlow and Keras to train RNNs with natural language. Resources:
- https://github.com/keras-team/keras/blob/master/examples/imdb_lstm.py
- https://keras.io/layers/recurrent/#lstm
- http://adventuresinmachinelearning.com/keras-lstm-tutorial/
Note that `tensorflow.contrib` [also has an implementation of RNN/LSTM](https://www.tensorflow.org/tutorials/sequences/recurrent).
### RNN/LSTM Sentiment Classification with Keras
```
'''
#Trains an LSTM model on the IMDB sentiment classification task.
The dataset is actually too small for LSTM to be of any advantage
compared to simpler, much faster methods such as TF-IDF + LogReg.
**Notes**
- RNNs are tricky. Choice of batch size is important,
choice of loss and optimizer is critical, etc.
Some configurations won't converge.
- LSTM loss decrease patterns during training can be quite different
from what you see with CNNs/MLPs/etc.
'''
from __future__ import print_function
from keras.preprocessing import sequence
from keras.models import Sequential
from keras.layers import Dense, Embedding
from keras.layers import LSTM
from keras.datasets import imdb
max_features = 20000
# cut texts after this number of words (among top max_features most common words)
maxlen = 80
batch_size = 32
print('Loading data...')
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=max_features)
print(len(x_train), 'train sequences')
print(len(x_test), 'test sequences')
print('Pad sequences (samples x time)')
x_train = sequence.pad_sequences(x_train, maxlen=maxlen)
x_test = sequence.pad_sequences(x_test, maxlen=maxlen)
print('x_train shape:', x_train.shape)
print('x_test shape:', x_test.shape)
print('Build model...')
model = Sequential()
model.add(Embedding(max_features, 128))
model.add(LSTM(128, dropout=0.2, recurrent_dropout=0.2))
model.add(Dense(1, activation='sigmoid'))
# try using different optimizers and different optimizer configs
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
print('Train...')
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=15,
validation_data=(x_test, y_test))
score, acc = model.evaluate(x_test, y_test,
batch_size=batch_size)
print('Test score:', score)
print('Test accuracy:', acc)
```
### RNN Text generation with NumPy
What else can we do with RNN? Since we're analyzing the *sequence*, we can do more than classify - we can *generate* text. We'll pull some news stories using [newspaper](https://github.com/codelucas/newspaper/).
#### Initialization
```
!pip install newspaper3k
import newspaper
ap = newspaper.build('https://www.apnews.com')
len(ap.articles)
article_text = ''
for article in ap.articles[:1]:
try:
article.download()
article.parse()
article_text += '\n\n' + article.text
except:
print('Failed: ' + article.url)
article_text = article_text.split('\n\n')[1]
print(article_text)
# Based on "The Unreasonable Effectiveness of RNN" implementation
import numpy as np
chars = list(set(article_text)) # split and remove duplicate characters. convert to list.
num_chars = len(chars) # the number of unique characters
txt_data_size = len(article_text)
print("unique characters : ", num_chars)
print("txt_data_size : ", txt_data_size)
# one hot encode
char_to_int = dict((c, i) for i, c in enumerate(chars)) # "enumerate" retruns index and value. Convert it to dictionary
int_to_char = dict((i, c) for i, c in enumerate(chars))
print(char_to_int)
print("----------------------------------------------------")
print(int_to_char)
print("----------------------------------------------------")
# integer encode input data
integer_encoded = [char_to_int[i] for i in article_text] # "integer_encoded" is a list which has a sequence converted from an original data to integers.
print(integer_encoded)
print("----------------------------------------------------")
print("data length : ", len(integer_encoded))
# hyperparameters
iteration = 1000
sequence_length = 40
batch_size = round((txt_data_size /sequence_length)+0.5) # = math.ceil
hidden_size = 500 # size of hidden layer of neurons.
learning_rate = 1e-1
# model parameters
W_xh = np.random.randn(hidden_size, num_chars)*0.01 # weight input -> hidden.
W_hh = np.random.randn(hidden_size, hidden_size)*0.01 # weight hidden -> hidden
W_hy = np.random.randn(num_chars, hidden_size)*0.01 # weight hidden -> output
b_h = np.zeros((hidden_size, 1)) # hidden bias
b_y = np.zeros((num_chars, 1)) # output bias
h_prev = np.zeros((hidden_size,1)) # h_(t-1)
```
#### Forward propagation
```
def forwardprop(inputs, targets, h_prev):
# Since the RNN receives the sequence, the weights are not updated during one sequence.
xs, hs, ys, ps = {}, {}, {}, {} # dictionary
hs[-1] = np.copy(h_prev) # Copy previous hidden state vector to -1 key value.
loss = 0 # loss initialization
for t in range(len(inputs)): # t is a "time step" and is used as a key(dic).
xs[t] = np.zeros((num_chars,1))
xs[t][inputs[t]] = 1
hs[t] = np.tanh(np.dot(W_xh, xs[t]) + np.dot(W_hh, hs[t-1]) + b_h) # hidden state.
ys[t] = np.dot(W_hy, hs[t]) + b_y # unnormalized log probabilities for next chars
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars.
# Softmax. -> The sum of probabilities is 1 even without the exp() function, but all of the elements are positive through the exp() function.
loss += -np.log(ps[t][targets[t],0]) # softmax (cross-entropy loss). Efficient and simple code
# y_class = np.zeros((num_chars, 1))
# y_class[targets[t]] =1
# loss += np.sum(y_class*(-np.log(ps[t]))) # softmax (cross-entropy loss)
return loss, ps, hs, xs
```
#### Backward propagation
```
def backprop(ps, inputs, hs, xs):
dWxh, dWhh, dWhy = np.zeros_like(W_xh), np.zeros_like(W_hh), np.zeros_like(W_hy) # make all zero matrices.
dbh, dby = np.zeros_like(b_h), np.zeros_like(b_y)
dhnext = np.zeros_like(hs[0]) # (hidden_size,1)
# reversed
for t in reversed(range(len(inputs))):
dy = np.copy(ps[t]) # shape (num_chars,1). "dy" means "dloss/dy"
dy[targets[t]] -= 1 # backprop into y. After taking the soft max in the input vector, subtract 1 from the value of the element corresponding to the correct label.
dWhy += np.dot(dy, hs[t].T)
dby += dy
dh = np.dot(W_hy.T, dy) + dhnext # backprop into h.
dhraw = (1 - hs[t] * hs[t]) * dh # backprop through tanh nonlinearity #tanh'(x) = 1-tanh^2(x)
dbh += dhraw
dWxh += np.dot(dhraw, xs[t].T)
dWhh += np.dot(dhraw, hs[t-1].T)
dhnext = np.dot(W_hh.T, dhraw)
for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients.
return dWxh, dWhh, dWhy, dbh, dby
```
#### Training
```
%%time
data_pointer = 0
# memory variables for Adagrad
mWxh, mWhh, mWhy = np.zeros_like(W_xh), np.zeros_like(W_hh), np.zeros_like(W_hy)
mbh, mby = np.zeros_like(b_h), np.zeros_like(b_y)
for i in range(iteration):
h_prev = np.zeros((hidden_size,1)) # reset RNN memory
data_pointer = 0 # go from start of data
for b in range(batch_size):
inputs = [char_to_int[ch] for ch in article_text[data_pointer:data_pointer+sequence_length]]
targets = [char_to_int[ch] for ch in article_text[data_pointer+1:data_pointer+sequence_length+1]] # t+1
if (data_pointer+sequence_length+1 >= len(article_text) and b == batch_size-1): # processing of the last part of the input data.
# targets.append(char_to_int[txt_data[0]]) # When the data doesn't fit, add the first char to the back.
targets.append(char_to_int[" "]) # When the data doesn't fit, add space(" ") to the back.
# forward
loss, ps, hs, xs = forwardprop(inputs, targets, h_prev)
# print(loss)
# backward
dWxh, dWhh, dWhy, dbh, dby = backprop(ps, inputs, hs, xs)
# perform parameter update with Adagrad
for param, dparam, mem in zip([W_xh, W_hh, W_hy, b_h, b_y],
[dWxh, dWhh, dWhy, dbh, dby],
[mWxh, mWhh, mWhy, mbh, mby]):
mem += dparam * dparam # elementwise
param += -learning_rate * dparam / np.sqrt(mem + 1e-8) # adagrad update
data_pointer += sequence_length # move data pointer
if i % 100 == 0:
print ('iter %d, loss: %f' % (i, loss)) # print progress
```
#### Prediction
```
def predict(test_char, length):
x = np.zeros((num_chars, 1))
x[char_to_int[test_char]] = 1
ixes = []
h = np.zeros((hidden_size,1))
for t in range(length):
h = np.tanh(np.dot(W_xh, x) + np.dot(W_hh, h) + b_h)
y = np.dot(W_hy, h) + b_y
p = np.exp(y) / np.sum(np.exp(y))
ix = np.random.choice(range(num_chars), p=p.ravel()) # ravel -> rank0
# "ix" is a list of indexes selected according to the soft max probability.
x = np.zeros((num_chars, 1)) # init
x[ix] = 1
ixes.append(ix) # list
txt = test_char + ''.join(int_to_char[i] for i in ixes)
print ('----\n %s \n----' % (txt, ))
predict('C', 50)
```
Well... that's *vaguely* language-looking. Can you do better?
# Assignment

It is said that [infinite monkeys typing for an infinite amount of time](https://en.wikipedia.org/wiki/Infinite_monkey_theorem) will eventually type, among other things, the complete works of Wiliam Shakespeare. Let's see if we can get there a bit faster, with the power of Recurrent Neural Networks and LSTM.
This text file contains the complete works of Shakespeare: https://www.gutenberg.org/files/100/100-0.txt
Use it as training data for an RNN - you can keep it simple and train character level, and that is suggested as an initial approach.
Then, use that trained RNN to generate Shakespearean-ish text. Your goal - a function that can take, as an argument, the size of text (e.g. number of characters or lines) to generate, and returns generated text of that size.
Note - Shakespeare wrote an awful lot. It's OK, especially initially, to sample/use smaller data and parameters, so you can have a tighter feedback loop when you're trying to get things running. Then, once you've got a proof of concept - start pushing it more!
```
# TODO - Words, words, mere words, no matter from the heart.
```
# Resources and Stretch Goals
## Stretch goals:
- Refine the training and generation of text to be able to ask for different genres/styles of Shakespearean text (e.g. plays versus sonnets)
- Train a classification model that takes text and returns which work of Shakespeare it is most likely to be from
- Make it more performant! Many possible routes here - lean on Keras, optimize the code, and/or use more resources (AWS, etc.)
- Revisit the news example from class, and improve it - use categories or tags to refine the model/generation, or train a news classifier
- Run on bigger, better data
## Resources:
- [The Unreasonable Effectiveness of Recurrent Neural Networks](https://karpathy.github.io/2015/05/21/rnn-effectiveness/) - a seminal writeup demonstrating a simple but effective character-level NLP RNN
- [Simple NumPy implementation of RNN](https://github.com/JY-Yoon/RNN-Implementation-using-NumPy/blob/master/RNN%20Implementation%20using%20NumPy.ipynb) - Python 3 version of the code from "Unreasonable Effectiveness"
- [TensorFlow RNN Tutorial](https://github.com/tensorflow/models/tree/master/tutorials/rnn) - code for training a RNN on the Penn Tree Bank language dataset
- [4 part tutorial on RNN](http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/) - relates RNN to the vanishing gradient problem, and provides example implementation
- [RNN training tips and tricks](https://github.com/karpathy/char-rnn#tips-and-tricks) - some rules of thumb for parameterizing and training your RNN
| github_jupyter |
# Assignment 1.
## Formalia:
Please read the [assignment overview page](https://github.com/suneman/socialdata2021/wiki/Assignment-1-and-2) carefully before proceeding. This page contains information about formatting (including formats etc), group sizes, and many other aspects of handing in the assignment.
_If you fail to follow these simple instructions, it will negatively impact your grade!_
**Due date and time**: The assignment is due on Monday March 1st, 2021 at 23:55. Hand in your files via [`http://peergrade.io`](http://peergrade.io/).
**Peergrading date and time**: _Remember that after handing in you have 1 week to evaluate a few assignments written by other members of the class_. Thus, the peer evaluations are due on Monday March 8th, 2021 at 23:55.
## Part 1: Temporal Patterns
We look only at the focus-crimes in the exercise below
```
focuscrimes = set(['WEAPON LAWS', 'PROSTITUTION', 'DRIVING UNDER THE INFLUENCE', 'ROBBERY', 'BURGLARY', 'ASSAULT', 'DRUNKENNESS', 'DRUG/NARCOTIC', 'TRESPASS', 'LARCENY/THEFT', 'VANDALISM', 'VEHICLE THEFT', 'STOLEN PROPERTY', 'DISORDERLY CONDUCT'])
```
*Exercise*: More temporal patterns. During week 1, we plotted some crime development over time (how each of the focus-crimes changed over time, year-by-year).
In this exercise, please generate the visualizations described below. Use the same date-ranges as in Week 1. For each set of plots, describe the plots (as you would in the figure text in a report or paper), and pick a few aspects that stand out to you and comment on those (a couple of ideas below for things that could be interesting to comment on ... but it's OK to chose something else).
* *Weekly patterns*. Basically, we'll forget about the yearly variation and just count up what happens during each weekday. [Here's what my version looks like](https://raw.githubusercontent.com/suneman/socialdata2021/master/files/weekdays.png). Hint for comment: Some things make sense - for example `drunkenness` and the weekend. But there are some aspects that were surprising to me. Check out `prostitution` and mid-week behavior, for example!?
* *The months*. We can also check if some months are worse by counting up number of crimes in Jan, Feb, ..., Dec. Did you see any surprises there?
* *The 24 hour cycle*. We'll can also forget about weekday and simply count up the number of each crime-type that occurs in the entire dataset from midnight to 1am, 1am - 2am ... and so on. Again: Give me a couple of comments on what you see.
* *Hours of the week*. But by looking at just 24 hours, we may be missing some important trends that can be modulated by week-day, so let's also check out the 168 hours of the week. So let's see the number of each crime-type Monday night from midninght to 1am, Monday night from 1am-2am - all the way to Sunday night from 11pm to midnight.
```
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("../incidents.csv")
df = df[df["Category"].isin(focuscrimes)]
df["Date_Time"] = pd.to_datetime(df["Date"] + " " + df["Time"])
df.sort_values(by=["Date_Time"], inplace=True, ascending=True)
df.head()
weeks = ["Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday", "Sunday"]
df1 = pd.DataFrame(df, columns=["Category", "DayOfWeek"])
wdf = pd.DataFrame(index=weeks, columns=focuscrimes)
for crime in focuscrimes:
crime_df = df1[df1["Category"] == crime]
for week_day in weeks:
wdf.at[week_day, crime] = len(crime_df[crime_df["DayOfWeek"] == week_day])
plt.figure(1, figsize=(18,27))
count = 1
for crime in wdf.columns:
plt.subplot(7, 2, count)
wdf[crime].plot(kind="bar", subplots=True, figsize=(9, 6), rot=0)
count += 1
```
## Part 2: Thinking about data and visualization
*Excercise:* Questions for the [second video lecture](https://www.youtube.com/watch?v=yiU56codNlI).
* As mentioned earlier, visualization is not the only way to test for correlation. We can (for example) calculate the Pearson correlation. Explain in your own words how the Pearson correlation works and write down it's mathematical formulation. Can you think of an example where it fails (and visualization works)?
* What is the difference between a bar-chart and a histogram?
* I mention in the video that it's important to choose the right bin-size in histograms. But how do you do that? Do a Google search to find a criterion you like and explain it.
## Part 3: Generating important plot types
*Excercise*: Let us recreate some plots from DAOST but using our own favorite dataset.
* First, let's make a jitter-plot (that is, code up something like **Figure 2-1** from DAOST from scratch), but based on SF Police data. My hunch from inspecting the file is that the police-folks might be a little bit lazy in noting down the **exact** time down to the second. So choose a crime-type and a suitable time interval (somewhere between a month and 6 months depending on the crime-type) and create a jitter plot of the arrest times during a single hour (like 13-14, for example). So let time run on the $x$-axis and create vertical jitter.
* Now for some histograms (please create a crime-data based versions of the plot-type shown in DAOST **Figure 2-2**). (I think the GPS data could be fun to understand from this perspective.)
* This time, pick two crime-types with different geographical patterns **and** a suitable time-interval for each (you want between 1000 and 10000 points in your histogram)
* Then take the latitude part of the GPS coordinates for each crime and bin the latitudes so that you have around 50 bins across the city of SF. You can use your favorite method for binning. I like `numpy.histogram`. This function gives you the counts and then you do your own plotting.
## Part 4: A bit of geo-data
*Exercise*: A new take on geospatial data using Folium (see the Week 4 exercises for full info and tutorials).
Now we look at studying geospatial data by plotting raw data points as well as heatmaps on top of actual maps.
* First start by plotting a map of San Francisco with a nice tight zoom. Simply use the command `folium.Map([lat, lon], zoom_start=13)`, where you'll have to look up San Francisco's longitude and latitude.
* Next, use the the coordinates for SF City Hall `37.77919, -122.41914` to indicate its location on the map with a nice, pop-up enabled maker. (In the screenshot below, I used the black & white Stamen tiles, because they look cool).
* Now, let's plot some more data (no need for popups this time). Select a couple of months of data for `'DRUG/NARCOTIC'` and draw a little dot for each arrest for those two months. You could, for example, choose June-July 2016, but you can choose anything you like - the main concern is to not have too many points as this uses a lot of memory and makes Folium behave non-optimally.
We can call this a kind of visualization a *point scatter plot*.
```
import numpy as np # linear algebra
import folium
import datetime as dt
SF = folium.Map([37.773972, -122.431297], zoom_start=13, tiles="Stamen Toner")
folium.Marker([37.77919, -122.41914], popup='City Hall').add_to(SF)
# Address, location, X, Y
ndf = df[df["Category"] == "DRUG/NARCOTIC"]
start = ndf["Date_Time"].searchsorted(dt.datetime(2016, 6, 1))
end = ndf["Date_Time"].searchsorted(dt.datetime(2016, 7, 1))
for i, case in ndf[start : end].iterrows():
folium.CircleMarker(location=[case["Y"], case["X"]], radius=2,weight=5).add_to(SF)
SF
```
## Part 5: Errors in the data. The importance of looking at raw (or close to raw) data.
We started the course by plotting simple histogram plots that showed a lot of cool patterns. But sometimes the binning can hide imprecision, irregularity, and simple errors in the data that could be misleading. In the work we've done so far, we've already come across at least three examples of this in the SF data.
1. In the hourly activity for `PROSTITUTION` something surprising is going on on Thursday. Remind yourself [**here**](https://raw.githubusercontent.com/suneman/socialdata2021/master/files/prostitution_hourly.png), where I've highlighted the phenomenon I'm talking about.
1. When we investigated the details of how the timestamps are recorded using jitter-plots, we saw that many more crimes were recorded e.g. on the hour, 15 minutes past the hour, and to a lesser in whole increments of 10 minutes. Crimes didn't appear to be recorded as frequently in between those round numbers. Remind yourself [**here**](https://raw.githubusercontent.com/suneman/socialdata2021/master/files/jitter_plot.png), where I've highlighted the phenomenon I'm talking about.
1. And finally, today we saw that the Hall of Justice seemed to be an unlikely hotspot for sex offences. Remind yourself [**here**](https://raw.githubusercontent.com/suneman/socialdata2021/master/files/crime_hot_spot.png).
> *Exercise*: Data errors. The data errors we discovered above become difficult to notice when we aggregate data (and when we calculate mean values, as well as statistics more generally). Thus, when we visualize, errors become difficult to notice when when we bin the data. We explore this process in the exercise below.
>
> The exercise is simply this:
> * For each of the three examples above, describe in your own words how the data-errors I call attention to above can bias the binned versions of the data. Also briefly mention how not noticing these errors can result in misconceptions about the underlying patterns of what's going on in San Francisco (and our modeling).
| github_jupyter |
# AU Fundamentals of Python Programming-W10X
## Topic 1(主題1)-字串和print()的參數
### Step 1: Hello World with 其他參數
sep = "..." 列印分隔 end="" 列印結尾
* sep: string inserted between values, default a space.
* end: string appended after the last value, default a newline.
```
print('Hello World!') #'Hello World!' is the same as "Hello World!"
help(print) #註解是不會執行的
print('Hello '+'World!')
print("Hello","World", sep="+")
print("Hello"); print("World!")
print("Hello", end=' ');print("World")
```
### Step 2: Escape Sequence (逸出序列)
* \newline Ignored
* \\ Backslash (\)
* \' Single quote (')
* \" Double quote (")
* \a ASCII Bell (BEL)
* \b ASCII Backspace (BS)
* \n ASCII Linefeed (LF)
* \r ASCII Carriage Return (CR)
* \t ASCII Horizontal Tab (TAB)
* \ooo ASCII character with octal value ooo
* \xhh... ASCII character with hex value hh...
```
print("Hello\nWorld!")
print("Hello","World!", sep="\n")
txt = "We are the so-called \"Vikings\" from the north."
print(txt)
```
### Step 3: 使用 字串尾部的\來建立長字串
```
iPhone11='iPhone 11是由蘋果公司設計和銷售的智能手機,為第13代iPhone系列智能手機之一,亦是iPhone XR的後繼機種。\
其在2019年9月10日於蘋果園區史蒂夫·喬布斯劇院由CEO蒂姆·庫克隨iPhone 11 Pro及iPhone 11 Pro Max一起發佈,\
並於2019年9月20日在世界大部分地區正式發售。其採用類似iPhone XR的玻璃配鋁金屬設計;\
具有6.1英吋Liquid Retina HD顯示器,配有Face ID;並採用由蘋果自家設計的A13仿生晶片,\
帶有第三代神經網絡引擎。機器能夠防濺、耐水及防塵,在最深2米的水下停留時間最長可達30分鐘。'
print(iPhone11)
```
### Step 4: 使用六個雙引號來建立長字串 ''' ... ''' 或 """ ... """
```
iPhone11='''
iPhone 11是由蘋果公司設計和銷售的智能手機,為第13代iPhone系列智能手機之一,亦是iPhone XR的後繼機種。
其在2019年9月10日於蘋果園區史蒂夫·喬布斯劇院由CEO蒂姆·庫克隨iPhone 11 Pro及iPhone 11 Pro Max一起發佈,
並於2019年9月20日在世界大部分地區正式發售。其採用類似iPhone XR的玻璃配鋁金屬設計;
具有6.1英吋Liquid Retina HD顯示器,配有Face ID;並採用由蘋果自家設計的A13仿生晶片,
帶有第三代神經網絡引擎。機器能夠防濺、耐水及防塵,在最深2米的水下停留時間最長可達30分鐘。'''
print(iPhone11)
iPhone11="""
iPhone 11是由蘋果公司設計和銷售的智能手機,為第13代iPhone系列智能手機之一,亦是iPhone XR的後繼機種。
其在2019年9月10日於蘋果園區史蒂夫·喬布斯劇院由CEO蒂姆·庫克隨iPhone 11 Pro及iPhone 11 Pro Max一起發佈,
並於2019年9月20日在世界大部分地區正式發售。其採用類似iPhone XR的玻璃配鋁金屬設計;
具有6.1英吋Liquid Retina HD顯示器,配有Face ID;並採用由蘋果自家設計的A13仿生晶片,
帶有第三代神經網絡引擎。機器能夠防濺、耐水及防塵,在最深2米的水下停留時間最長可達30分鐘。"""
print(iPhone11)
```
## Topic 2(主題2)-型別轉換函數
### Step 5: 輸入變數的值
```
name = input('Please input your name:')
print('Hello, ', name)
print(type(name)) #列印變數的型別
```
### Step 6: Python 型別轉換函數
* int() #變整數
* float() #變浮點數
* str() #變字串
* 變數名稱=int(字串變數)
* 變數名稱=str(數值變數
```
#變數宣告
varA = 66 #宣告一個整數變數
varB = 1.68 #宣告一個有小數的變數(電腦叫浮點數)
varC = 'GoPython' #宣告一個字串變數
varD = str(varA) #將整數88轉成字串的88
varE = str(varB) #將浮點數1.68轉成字串的1.68
varF = int('2019') #將字串2019轉作整數數值的2019
varG = float('3.14') #將字串3.14轉作浮點數數值的3.14
score = input('Please input your score:')
score = int(score)
print(type(score)) #列印變數的型別
```
## Topic 3(主題3)-索引和切片
```
a = "Hello, World!"
print(a[1]) #Indexing
print(a[2:5]) #Slicing
```
### Step 8: 索引(Indexing)
```
a = "Hello Wang"
d = "0123456789"
print(a[3]) #Indexing
a = "Hello Wang"
d = "0123456789"
print(a[-3]) #Negative Indexing
```
### Step 9: 切片(Slicing)
```
a = "Hello Wang"
d = "0123456789"
print(a[2:5]) #Slicing
a = "Hello Wang"
d = "0123456789"
print(a[2:]) #Slicing
a = "Hello Wang"
d = "0123456789"
print(a[:5]) #Slicing
a = "Hello Wang"
d = "0123456789"
print(a[-6:-2]) #Slicing
a = "Hello Wang"
d = "0123456789"
print(a[-4:]) #Slicing
```
## Topic 4(主題4)-格式化輸出
```
A = 435; B = 59.058
print('Art: %5d, Price per Unit: %8.2f' % (A, B)) #%-formatting 格式化列印
print("Art: {0:5d}, Price per Unit: {1:8.2f}".format(A,B)) #str-format(Python 2.6+)
print(f"Art:{A:5d}, Price per Unit: {B:8.2f}") #f-string (Python 3.6+)
```
### Step 10: %-formatting 格式化列印
透過% 運算符號,將在元組(tuple)中的一組變量依照指定的格式化方式輸出。如 %s(字串)、%d (十進位整數)、 %f(浮點數)
```
A = 435; B = 59.058
print('Art: %5d, Price per Unit: %8.2f' % (A, B))
FirstName = "Mary"; LastName= "Lin"
print("She is %s %s" %(FirstName, LastName))
```
### Step 11: str-format(Python 2.6+)格式化列印
```
A = 435; B = 59.058
print("Art: {0:5d}, Price per Unit: {1:8.2f}".format(435, 59.058))
FirstName = "Mary"; LastName= "Lin"
print("She is {} {}".format(FirstName, LastName))
```
### Step 12: f-string (Python 3.6+)格式化列印
```
A = 435; B = 59.058
print(f"Art:{A:5d}, Price per Unit: {B:8.2f}")
FirstName = "Mary"; LastName= "Lin"
print(f"She is {FirstName} {LastName}")
```
| github_jupyter |
```
import csv
from sklearn import preprocessing
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
%matplotlib inline
datContent = [i.strip().split() for i in open("./doughs.dat").readlines()]
y=np.array(datContent[1:])
labels = y[:,7].astype(np.float32)
y = y[:,1:7].astype(np.float32)
labels
class pca:
def __init__(self,k,scaling = False, ratio = False):
self.k = k
self.scaling = scaling
self.ratio = ratio
def EV(self,y):
if self.scaling:
scaler = preprocessing.StandardScaler().fit(y)
y=scaler.transform(y)
else:
y = y - y.mean(axis=0)
self.y = y
s = (y.shape[0]-1)*np.cov(y.T)
l, v = np.linalg.eig(s)
self.v = v[:self.k]
if self.ratio:
print(l[:self.k]/np.sum(l))
return l[:self.k],v[:self.k]
def pdata(self):
self.pdata1 = np.dot(self.y,np.array(self.v).T)
return self.pdata1
def mse(self):
self.pdata1 = np.dot(self.y,np.array(self.v).T)
e = (self.y - np.dot(self.pdata1,self.v))**2
e = e.mean()
return e
def Scatter3D(self,labels):
l = np.ones(labels.shape[0])
for i in range(labels.shape[0]):
if labels[i] >= 5:
l[i]=0
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i in range(self.pdata1.shape[0]):
if l[i]==1:
m='^'
c='b'
else:
m='o'
c='r'
ax.scatter(self.pdata1[i,0], self.pdata1[i,1], self.pdata1[i,2], marker=m, color=c)
def Scatter2D(self,labels):
l = np.ones(labels.shape[0])
for i in range(labels.shape[0]):
if labels[i] >= 5:
l[i]=0
fig = plt.figure()
ax = fig.add_subplot(131)
for i in range(self.pdata1.shape[0]):
if l[i]==1:
m='^'
c='b'
else:
m='o'
c='r'
ax.scatter(self.pdata1[i,0],self.pdata1[i,1], marker=m, color=c)
ax1 = fig.add_subplot(132)
for i in range(self.pdata1.shape[0]):
if l[i]==1:
m='^'
c='b'
else:
m='o'
c='r'
ax1.scatter(self.pdata1[i,0], self.pdata1[i,2], marker=m, color=c)
ax2 = fig.add_subplot(133)
for i in range(self.pdata1.shape[0]):
if l[i]==1:
m='^'
c='b'
else:
m='o'
c='r'
ax2.scatter(self.pdata1[i,1], self.pdata1[i,2],marker=m, color=c)
p = pca(6)
p.__init__(8,scaling=False,ratio=True)
p.EV(y)
p.mse()
x = p.pdata()
k2, p = stats.normaltest(x)
p
```
| github_jupyter |
## Topic Modelling (joint plots by quality band)
Shorter notebook just for Figures 9 and 10 in the paper.
```
%matplotlib inline
import matplotlib.pyplot as plt
# magics and warnings
%load_ext autoreload
%autoreload 2
import warnings; warnings.simplefilter('ignore')
import os, random
from tqdm import tqdm
import pandas as pd
import numpy as np
seed = 43
random.seed(seed)
np.random.seed(seed)
import nltk, gensim, sklearn, spacy
from gensim.models import CoherenceModel
import matplotlib.pyplot as plt
import pyLDAvis.gensim
import seaborn as sns
sns.set(style="white")
```
### Load the dataset
Created with the main Topic Modelling notebook.
```
bands_data = {x:dict() for x in range(1,5)}
import pickle, os
for band in range(1,5):
with open("trove_overproof/models/hum_band_%d.pkl"%band, 'rb') as handle:
bands_data[band]["model_human"] = pickle.load(handle)
with open("trove_overproof/models/corpus_hum_band_%d.pkl"%band, 'rb') as handle:
bands_data[band]["corpus_human"] = pickle.load(handle)
with open("trove_overproof/models/dictionary_hum_band_%d.pkl"%band, 'rb') as handle:
bands_data[band]["dictionary_human"] = pickle.load(handle)
with open("trove_overproof/models/ocr_band_%d.pkl"%band, 'rb') as handle:
bands_data[band]["model_ocr"] = pickle.load(handle)
with open("trove_overproof/models/corpus_ocr_band_%d.pkl"%band, 'rb') as handle:
bands_data[band]["corpus_ocr"] = pickle.load(handle)
with open("trove_overproof/models/dictionary_ocr_band_%d.pkl"%band, 'rb') as handle:
bands_data[band]["dictionary_ocr"] = pickle.load(handle)
```
### Evaluation
#### Intrinsic eval
See http://qpleple.com/topic-coherence-to-evaluate-topic-models.
```
for band in range(1,5):
print("Quality band",band)
# Human
# Compute Perplexity
print('\nPerplexity (Human): ', bands_data[band]["model_human"].log_perplexity(bands_data[band]["corpus_human"])) # a measure of how good the model is. The lower the better.
# Compute Coherence Score
coherence_model_lda = CoherenceModel(model=bands_data[band]["model_human"], corpus=bands_data[band]["corpus_human"], dictionary=bands_data[band]["dictionary_human"], coherence='u_mass')
coherence_lda = coherence_model_lda.get_coherence()
print('\nCoherence Score (Human): ', coherence_lda)
# OCR
# Compute Perplexity
print('\nPerplexity (OCR): ', bands_data[band]["model_ocr"].log_perplexity(bands_data[band]["corpus_ocr"])) # a measure of how good the model is. The lower the better.
# Compute Coherence Score
coherence_model_lda = CoherenceModel(model=bands_data[band]["model_ocr"], corpus=bands_data[band]["corpus_ocr"], dictionary=bands_data[band]["dictionary_ocr"], coherence='u_mass')
coherence_lda = coherence_model_lda.get_coherence()
print('\nCoherence Score (OCR): ', coherence_lda)
print("==========\n")
```
#### Match of topics
We match every topic in the OCR model with a topic in the human model (by best matching), and assess the overall distance between the two using the weighted total distance over a set of N top words (from the human model to the ocr model). The higher this value, the closest two topics are.
Note that to find a matching, we create a weighted network and find the maximal bipartite matching using NetworkX.
Afterwards, we can measure the distance of the best match, e.g., using the KL divergence (over the same set of words).
```
import networkx as nx
from scipy.stats import entropy
from collections import defaultdict
# analyse matches
distances = {x:list() for x in range(1,5)}
n_words_in_common = {x:list() for x in range(1,5)}
matches = {x:defaultdict(int) for x in range(1,5)}
top_n = 500
for band in range(1,5):
G = nx.Graph()
model_human = bands_data[band]["model_human"]
model_ocr = bands_data[band]["model_ocr"]
# add bipartite nodes
G.add_nodes_from(['h_'+str(t_h[0]) for t_h in model_human.show_topics(num_topics = -1, formatted=False, num_words=1)], bipartite=0)
G.add_nodes_from(['o_'+str(t_o[0]) for t_o in model_ocr.show_topics(num_topics = -1, formatted=False, num_words=1)], bipartite=1)
# add weighted edges
for t_h in model_human.show_topics(num_topics = -1, formatted=False, num_words=top_n):
for t_o in model_ocr.show_topics(num_topics = -1, formatted=False, num_words=top_n):
# note that the higher the weight, the shorter the distance between the two distributions, so we do 1-weight to then do minimal matching
words_of_h = [x[0] for x in t_h[1]]
words_of_o = [x[0] for x in t_o[1]]
weights_of_o = {x[0]:x[1] for x in t_o[1]}
words_in_common = list(set(words_of_h).intersection(set(words_of_o)))
# sum the weighted joint probability of every shared word in the two models
avg_weight = 1 - sum([x[1]*weights_of_o[x[0]] for x in t_h[1] if x[0] in words_in_common])
G.add_edge('h_'+str(t_h[0]),'o_'+str(t_o[0]),weight=avg_weight)
G.add_edge('o_'+str(t_o[0]),'h_'+str(t_h[0]),weight=avg_weight)
bipartite_solution = nx.bipartite.matching.minimum_weight_full_matching(G)
# calculate distances
for match_h,match_o in bipartite_solution.items():
if match_h.startswith('o'): # to avoid repeating the matches (complete graph!)
break
matches[band][int(match_h.split("_")[1])] = int(match_o.split("_")[1])
m_h = model_human.show_topic(int(match_h.split("_")[1]), topn=top_n)
m_o = model_ocr.show_topic(int(match_o.split("_")[1]), topn=top_n)
weights_of_o = {x[0]:x[1] for x in m_o}
words_of_h = [x[0] for x in m_h]
words_of_o = [x[0] for x in m_o]
words_in_common = list(set(words_of_h).intersection(set(words_of_o)))
n_words_in_common[band].append(len(words_in_common)/top_n)
dist_h = list()
dist_o = list()
for w in m_h:
if w[0] in words_in_common:
dist_h.append(w[1])
dist_o.append(weights_of_o[w[0]])
# normalize
dist_h = dist_h/sum(dist_h)
dist_o = dist_o/sum(dist_o)
dist = entropy(dist_h,dist_o)
distances[band].append(dist)
sns.set_context("notebook", font_scale=1.2, rc={"lines.linewidth": 2.5})
# Figure 9
for band in range(1,5):
sns.distplot(distances[band], hist=False, label="Quality band %d"%band)
plt.xlim((0,1))
plt.xlabel("KL divergence between topics, V=%d."%top_n)
plt.tight_layout()
plt.savefig("figures/topic_modelling/KL_divergence_topics.pdf")
# Figure 10
for band in range(1,5):
sns.distplot(n_words_in_common[band], hist=False, label="Quality band %d"%band)
plt.xlim((0,1))
plt.tight_layout()
plt.savefig("figures/topic_modelling/Words_in_common_topics.pdf")
```
| github_jupyter |
# Inspect Nucleus Training Data
Inspect and visualize data loading and pre-processing code.
https://www.kaggle.com/c/data-science-bowl-2018
```
import os
import sys
import itertools
import math
import logging
import json
import re
import random
import time
import concurrent.futures
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.lines as lines
from matplotlib.patches import Polygon
import imgaug
from imgaug import augmenters as iaa
# Root directory of the project
ROOT_DIR = os.getcwd()
print("ROOT_DIR",ROOT_DIR)
if ROOT_DIR.endswith("nucleus"):
# Go up two levels to the repo root
ROOT_DIR = os.path.dirname(os.path.dirname(ROOT_DIR))
print("ROOT_DIR",ROOT_DIR)
# Import Mask RCNN
sys.path.append(ROOT_DIR)
from mrcnn import utils
from mrcnn import visualize
from mrcnn.visualize import display_images
from mrcnn import model as modellib
from mrcnn.model import log
import nucleus
%matplotlib inline
# Comment out to reload imported modules if they change
# %load_ext autoreload
# %autoreload 2
```
## Configurations
```
# Dataset directory
DATASET_DIR = os.path.join(ROOT_DIR, "datasets/nucleus")
# Use configuation from nucleus.py, but override
# image resizing so we see the real sizes here
class NoResizeConfig(nucleus.NucleusConfig):
IMAGE_RESIZE_MODE = "none"
config = NoResizeConfig()
```
## Notebook Preferences
```
def get_ax(rows=1, cols=1, size=16):
"""Return a Matplotlib Axes array to be used in
all visualizations in the notebook. Provide a
central point to control graph sizes.
Adjust the size attribute to control how big to render images
"""
_, ax = plt.subplots(rows, cols, figsize=(size*cols, size*rows))
return ax
```
## Dataset
Download the dataset from the competition Website. Unzip it and save it in `mask_rcnn/datasets/nucleus`. If you prefer a different directory then change the `DATASET_DIR` variable above.
https://www.kaggle.com/c/data-science-bowl-2018/data
```
# Load dataset
dataset = nucleus.NucleusDataset()
# The subset is the name of the sub-directory, such as stage1_train,
# stage1_test, ...etc. You can also use these special values:
# train: loads stage1_train but excludes validation images
# val: loads validation images from stage1_train. For a list
# of validation images see nucleus.py
dataset.load_nucleus(DATASET_DIR, subset="train")
# Must call before using the dataset
dataset.prepare()
print("Image Count: {}".format(len(dataset.image_ids)))
print("Class Count: {}".format(dataset.num_classes))
for i, info in enumerate(dataset.class_info):
print("{:3}. {:50}".format(i, info['name']))
```
## Display Samples
```
# Load and display random samples
image_ids = np.random.choice(dataset.image_ids, 4)
for image_id in image_ids:
image = dataset.load_image(image_id)
mask, class_ids = dataset.load_mask(image_id)
visualize.display_top_masks(image, mask, class_ids, dataset.class_names, limit=1)
# Example of loading a specific image by its source ID
source_id = "ed5be4b63e9506ad64660dd92a098ffcc0325195298c13c815a73773f1efc279"
# Map source ID to Dataset image_id
# Notice the nucleus prefix: it's the name given to the dataset in NucleusDataset
image_id = dataset.image_from_source_map["nucleus.{}".format(source_id)]
# Load and display
image, image_meta, class_ids, bbox, mask = modellib.load_image_gt(
dataset, config, image_id, use_mini_mask=False)
log("molded_image", image)
log("mask", mask)
visualize.display_instances(image, bbox, mask, class_ids, dataset.class_names,
show_bbox=False)
```
## Dataset Stats
Loop through all images in the dataset and collect aggregate stats.
```
def image_stats(image_id):
"""Returns a dict of stats for one image."""
image = dataset.load_image(image_id)
mask, _ = dataset.load_mask(image_id)
bbox = utils.extract_bboxes(mask)
# Sanity check
assert mask.shape[:2] == image.shape[:2]
# Return stats dict
return {
"id": image_id,
"shape": list(image.shape),
"bbox": [[b[2] - b[0], b[3] - b[1]]
for b in bbox
# Uncomment to exclude nuclei with 1 pixel width
# or height (often on edges)
# if b[2] - b[0] > 1 and b[3] - b[1] > 1
],
"color": np.mean(image, axis=(0, 1)),
}
# Loop through the dataset and compute stats over multiple threads
# This might take a few minutes
t_start = time.time()
with concurrent.futures.ThreadPoolExecutor() as e:
stats = list(e.map(image_stats, dataset.image_ids))
t_total = time.time() - t_start
print("Total time: {:.1f} seconds".format(t_total))
```
### Image Size Stats
```
# Image stats
image_shape = np.array([s['shape'] for s in stats])
image_color = np.array([s['color'] for s in stats])
print("Image Count: ", image_shape.shape[0])
print("Height mean: {:.2f} median: {:.2f} min: {:.2f} max: {:.2f}".format(
np.mean(image_shape[:, 0]), np.median(image_shape[:, 0]),
np.min(image_shape[:, 0]), np.max(image_shape[:, 0])))
print("Width mean: {:.2f} median: {:.2f} min: {:.2f} max: {:.2f}".format(
np.mean(image_shape[:, 1]), np.median(image_shape[:, 1]),
np.min(image_shape[:, 1]), np.max(image_shape[:, 1])))
print("Color mean (RGB): {:.2f} {:.2f} {:.2f}".format(*np.mean(image_color, axis=0)))
# Histograms
fig, ax = plt.subplots(1, 3, figsize=(16, 4))
ax[0].set_title("Height")
_ = ax[0].hist(image_shape[:, 0], bins=20)
ax[1].set_title("Width")
_ = ax[1].hist(image_shape[:, 1], bins=20)
ax[2].set_title("Height & Width")
_ = ax[2].hist2d(image_shape[:, 1], image_shape[:, 0], bins=10, cmap="Blues")
```
### Nuclei per Image Stats
```
# Segment by image area
image_area_bins = [256**2, 600**2, 1300**2]
print("Nuclei/Image")
fig, ax = plt.subplots(1, len(image_area_bins), figsize=(16, 4))
area_threshold = 0
for i, image_area in enumerate(image_area_bins):
nuclei_per_image = np.array([len(s['bbox'])
for s in stats
if area_threshold < (s['shape'][0] * s['shape'][1]) <= image_area])
area_threshold = image_area
if len(nuclei_per_image) == 0:
print("Image area <= {:4}**2: None".format(np.sqrt(image_area)))
continue
print("Image area <= {:4.0f}**2: mean: {:.1f} median: {:.1f} min: {:.1f} max: {:.1f}".format(
np.sqrt(image_area), nuclei_per_image.mean(), np.median(nuclei_per_image),
nuclei_per_image.min(), nuclei_per_image.max()))
ax[i].set_title("Image Area <= {:4}**2".format(np.sqrt(image_area)))
_ = ax[i].hist(nuclei_per_image, bins=10)
```
### Nuclei Size Stats
```
# Nuclei size stats
fig, ax = plt.subplots(1, len(image_area_bins), figsize=(16, 4))
area_threshold = 0
for i, image_area in enumerate(image_area_bins):
nucleus_shape = np.array([
b
for s in stats if area_threshold < (s['shape'][0] * s['shape'][1]) <= image_area
for b in s['bbox']])
nucleus_area = nucleus_shape[:, 0] * nucleus_shape[:, 1]
area_threshold = image_area
print("\nImage Area <= {:.0f}**2".format(np.sqrt(image_area)))
print(" Total Nuclei: ", nucleus_shape.shape[0])
print(" Nucleus Height. mean: {:.2f} median: {:.2f} min: {:.2f} max: {:.2f}".format(
np.mean(nucleus_shape[:, 0]), np.median(nucleus_shape[:, 0]),
np.min(nucleus_shape[:, 0]), np.max(nucleus_shape[:, 0])))
print(" Nucleus Width. mean: {:.2f} median: {:.2f} min: {:.2f} max: {:.2f}".format(
np.mean(nucleus_shape[:, 1]), np.median(nucleus_shape[:, 1]),
np.min(nucleus_shape[:, 1]), np.max(nucleus_shape[:, 1])))
print(" Nucleus Area. mean: {:.2f} median: {:.2f} min: {:.2f} max: {:.2f}".format(
np.mean(nucleus_area), np.median(nucleus_area),
np.min(nucleus_area), np.max(nucleus_area)))
# Show 2D histogram
_ = ax[i].hist2d(nucleus_shape[:, 1], nucleus_shape[:, 0], bins=20, cmap="Blues")
# Nuclei height/width ratio
nucleus_aspect_ratio = nucleus_shape[:, 0] / nucleus_shape[:, 1]
print("Nucleus Aspect Ratio. mean: {:.2f} median: {:.2f} min: {:.2f} max: {:.2f}".format(
np.mean(nucleus_aspect_ratio), np.median(nucleus_aspect_ratio),
np.min(nucleus_aspect_ratio), np.max(nucleus_aspect_ratio)))
plt.figure(figsize=(15, 5))
_ = plt.hist(nucleus_aspect_ratio, bins=100, range=[0, 5])
```
## Image Augmentation
Test out different augmentation methods
```
# List of augmentations
# http://imgaug.readthedocs.io/en/latest/source/augmenters.html
augmentation = iaa.Sometimes(0.9, [
iaa.Fliplr(0.5),
iaa.Flipud(0.5),
iaa.Multiply((0.8, 1.2)),
iaa.GaussianBlur(sigma=(0.0, 5.0))
])
# Load the image multiple times to show augmentations
limit = 4
ax = get_ax(rows=2, cols=limit//2)
for i in range(limit):
image, image_meta, class_ids, bbox, mask = modellib.load_image_gt(
dataset, config, image_id, use_mini_mask=False, augment=False, augmentation=augmentation)
visualize.display_instances(image, bbox, mask, class_ids,
dataset.class_names, ax=ax[i//2, i % 2],
show_mask=False, show_bbox=False)
```
## Image Crops
Microscoy images tend to be large, but nuclei are small. So it's more efficient to train on random crops from large images. This is handled by `config.IMAGE_RESIZE_MODE = "crop"`.
```
class RandomCropConfig(nucleus.NucleusConfig):
IMAGE_RESIZE_MODE = "crop"
IMAGE_MIN_DIM = 256
IMAGE_MAX_DIM = 256
crop_config = RandomCropConfig()
# Load the image multiple times to show augmentations
limit = 4
image_id = np.random.choice(dataset.image_ids, 1)[0]
ax = get_ax(rows=2, cols=limit//2)
for i in range(limit):
image, image_meta, class_ids, bbox, mask = modellib.load_image_gt(
dataset, crop_config, image_id, use_mini_mask=False)
visualize.display_instances(image, bbox, mask, class_ids,
dataset.class_names, ax=ax[i//2, i % 2],
show_mask=False, show_bbox=False)
```
## Mini Masks
Instance binary masks can get large when training with high resolution images. For example, if training with 1024x1024 image then the mask of a single instance requires 1MB of memory (Numpy uses bytes for boolean values). If an image has 100 instances then that's 100MB for the masks alone.
To improve training speed, we optimize masks:
* We store mask pixels that are inside the object bounding box, rather than a mask of the full image. Most objects are small compared to the image size, so we save space by not storing a lot of zeros around the object.
* We resize the mask to a smaller size (e.g. 56x56). For objects that are larger than the selected size we lose a bit of accuracy. But most object annotations are not very accuracy to begin with, so this loss is negligable for most practical purposes. Thie size of the mini_mask can be set in the config class.
To visualize the effect of mask resizing, and to verify the code correctness, we visualize some examples.
```
# Load random image and mask.
image_id = np.random.choice(dataset.image_ids, 1)[0]
image = dataset.load_image(image_id)
mask, class_ids = dataset.load_mask(image_id)
original_shape = image.shape
# Resize
image, window, scale, padding, _ = utils.resize_image(
image,
min_dim=config.IMAGE_MIN_DIM,
max_dim=config.IMAGE_MAX_DIM,
mode=config.IMAGE_RESIZE_MODE)
mask = utils.resize_mask(mask, scale, padding)
# Compute Bounding box
bbox = utils.extract_bboxes(mask)
# Display image and additional stats
print("image_id: ", image_id, dataset.image_reference(image_id))
print("Original shape: ", original_shape)
log("image", image)
log("mask", mask)
log("class_ids", class_ids)
log("bbox", bbox)
# Display image and instances
visualize.display_instances(image, bbox, mask, class_ids, dataset.class_names)
image_id = np.random.choice(dataset.image_ids, 1)[0]
image, image_meta, class_ids, bbox, mask = modellib.load_image_gt(
dataset, config, image_id, use_mini_mask=False)
log("image", image)
log("image_meta", image_meta)
log("class_ids", class_ids)
log("bbox", bbox)
log("mask", mask)
display_images([image]+[mask[:,:,i] for i in range(min(mask.shape[-1], 7))])
visualize.display_instances(image, bbox, mask, class_ids, dataset.class_names)
# Add augmentation and mask resizing.
image, image_meta, class_ids, bbox, mask = modellib.load_image_gt(
dataset, config, image_id, augment=True, use_mini_mask=True)
log("mask", mask)
display_images([image]+[mask[:,:,i] for i in range(min(mask.shape[-1], 7))])
mask = utils.expand_mask(bbox, mask, image.shape)
visualize.display_instances(image, bbox, mask, class_ids, dataset.class_names)
```
## Anchors
For an FPN network, the anchors must be ordered in a way that makes it easy to match anchors to the output of the convolution layers that predict anchor scores and shifts.
* Sort by pyramid level first. All anchors of the first level, then all of the second and so on. This makes it easier to separate anchors by level.
* Within each level, sort anchors by feature map processing sequence. Typically, a convolution layer processes a feature map starting from top-left and moving right row by row.
* For each feature map cell, pick any sorting order for the anchors of different ratios. Here we match the order of ratios passed to the function.
```
## Visualize anchors of one cell at the center of the feature map
# Load and display random image
image_id = np.random.choice(dataset.image_ids, 1)[0]
image, image_meta, _, _, _ = modellib.load_image_gt(dataset, crop_config, image_id)
# Generate Anchors
backbone_shapes = modellib.compute_backbone_shapes(config, image.shape)
anchors = utils.generate_pyramid_anchors(config.RPN_ANCHOR_SCALES,
config.RPN_ANCHOR_RATIOS,
backbone_shapes,
config.BACKBONE_STRIDES,
config.RPN_ANCHOR_STRIDE)
# Print summary of anchors
num_levels = len(backbone_shapes)
anchors_per_cell = len(config.RPN_ANCHOR_RATIOS)
print("Count: ", anchors.shape[0])
print("Scales: ", config.RPN_ANCHOR_SCALES)
print("ratios: ", config.RPN_ANCHOR_RATIOS)
print("Anchors per Cell: ", anchors_per_cell)
print("Levels: ", num_levels)
anchors_per_level = []
for l in range(num_levels):
num_cells = backbone_shapes[l][0] * backbone_shapes[l][1]
anchors_per_level.append(anchors_per_cell * num_cells // config.RPN_ANCHOR_STRIDE**2)
print("Anchors in Level {}: {}".format(l, anchors_per_level[l]))
# Display
fig, ax = plt.subplots(1, figsize=(10, 10))
ax.imshow(image)
levels = len(backbone_shapes)
for level in range(levels):
colors = visualize.random_colors(levels)
# Compute the index of the anchors at the center of the image
level_start = sum(anchors_per_level[:level]) # sum of anchors of previous levels
level_anchors = anchors[level_start:level_start+anchors_per_level[level]]
print("Level {}. Anchors: {:6} Feature map Shape: {}".format(level, level_anchors.shape[0],
backbone_shapes[level]))
center_cell = backbone_shapes[level] // 2
center_cell_index = (center_cell[0] * backbone_shapes[level][1] + center_cell[1])
level_center = center_cell_index * anchors_per_cell
center_anchor = anchors_per_cell * (
(center_cell[0] * backbone_shapes[level][1] / config.RPN_ANCHOR_STRIDE**2) \
+ center_cell[1] / config.RPN_ANCHOR_STRIDE)
level_center = int(center_anchor)
# Draw anchors. Brightness show the order in the array, dark to bright.
for i, rect in enumerate(level_anchors[level_center:level_center+anchors_per_cell]):
y1, x1, y2, x2 = rect
p = patches.Rectangle((x1, y1), x2-x1, y2-y1, linewidth=2, facecolor='none',
edgecolor=(i+1)*np.array(colors[level]) / anchors_per_cell)
ax.add_patch(p)
```
## Data Generator
```
# Create data generator
random_rois = 2000
g = modellib.data_generator(
dataset, crop_config, shuffle=True, random_rois=random_rois,
batch_size=4,
detection_targets=True)
# Uncomment to run the generator through a lot of images
# to catch rare errors
# for i in range(1000):
# print(i)
# _, _ = next(g)
# Get Next Image
if random_rois:
[normalized_images, image_meta, rpn_match, rpn_bbox, gt_class_ids, gt_boxes, gt_masks, rpn_rois, rois], \
[mrcnn_class_ids, mrcnn_bbox, mrcnn_mask] = next(g)
log("rois", rois)
log("mrcnn_class_ids", mrcnn_class_ids)
log("mrcnn_bbox", mrcnn_bbox)
log("mrcnn_mask", mrcnn_mask)
else:
[normalized_images, image_meta, rpn_match, rpn_bbox, gt_boxes, gt_masks], _ = next(g)
log("gt_class_ids", gt_class_ids)
log("gt_boxes", gt_boxes)
log("gt_masks", gt_masks)
log("rpn_match", rpn_match, )
log("rpn_bbox", rpn_bbox)
image_id = modellib.parse_image_meta(image_meta)["image_id"][0]
print("image_id: ", image_id, dataset.image_reference(image_id))
# Remove the last dim in mrcnn_class_ids. It's only added
# to satisfy Keras restriction on target shape.
mrcnn_class_ids = mrcnn_class_ids[:,:,0]
b = 0
# Restore original image (reverse normalization)
sample_image = modellib.unmold_image(normalized_images[b], config)
# Compute anchor shifts.
indices = np.where(rpn_match[b] == 1)[0]
refined_anchors = utils.apply_box_deltas(anchors[indices], rpn_bbox[b, :len(indices)] * config.RPN_BBOX_STD_DEV)
log("anchors", anchors)
log("refined_anchors", refined_anchors)
# Get list of positive anchors
positive_anchor_ids = np.where(rpn_match[b] == 1)[0]
print("Positive anchors: {}".format(len(positive_anchor_ids)))
negative_anchor_ids = np.where(rpn_match[b] == -1)[0]
print("Negative anchors: {}".format(len(negative_anchor_ids)))
neutral_anchor_ids = np.where(rpn_match[b] == 0)[0]
print("Neutral anchors: {}".format(len(neutral_anchor_ids)))
# ROI breakdown by class
for c, n in zip(dataset.class_names, np.bincount(mrcnn_class_ids[b].flatten())):
if n:
print("{:23}: {}".format(c[:20], n))
# Show positive anchors
fig, ax = plt.subplots(1, figsize=(16, 16))
visualize.draw_boxes(sample_image, boxes=anchors[positive_anchor_ids],
refined_boxes=refined_anchors, ax=ax)
# Show negative anchors
visualize.draw_boxes(sample_image, boxes=anchors[negative_anchor_ids])
# Show neutral anchors. They don't contribute to training.
visualize.draw_boxes(sample_image, boxes=anchors[np.random.choice(neutral_anchor_ids, 100)])
```
## ROIs
Typically, the RPN network generates region proposals (a.k.a. Regions of Interest, or ROIs). The data generator has the ability to generate proposals as well for illustration and testing purposes. These are controlled by the `random_rois` parameter.
```
if random_rois:
# Class aware bboxes
bbox_specific = mrcnn_bbox[b, np.arange(mrcnn_bbox.shape[1]), mrcnn_class_ids[b], :]
# Refined ROIs
refined_rois = utils.apply_box_deltas(rois[b].astype(np.float32), bbox_specific[:,:4] * config.BBOX_STD_DEV)
# Class aware masks
mask_specific = mrcnn_mask[b, np.arange(mrcnn_mask.shape[1]), :, :, mrcnn_class_ids[b]]
visualize.draw_rois(sample_image, rois[b], refined_rois, mask_specific, mrcnn_class_ids[b], dataset.class_names)
# Any repeated ROIs?
rows = np.ascontiguousarray(rois[b]).view(np.dtype((np.void, rois.dtype.itemsize * rois.shape[-1])))
_, idx = np.unique(rows, return_index=True)
print("Unique ROIs: {} out of {}".format(len(idx), rois.shape[1]))
if random_rois:
# Dispalay ROIs and corresponding masks and bounding boxes
ids = random.sample(range(rois.shape[1]), 8)
images = []
titles = []
for i in ids:
image = visualize.draw_box(sample_image.copy(), rois[b,i,:4].astype(np.int32), [255, 0, 0])
image = visualize.draw_box(image, refined_rois[i].astype(np.int64), [0, 255, 0])
images.append(image)
titles.append("ROI {}".format(i))
images.append(mask_specific[i] * 255)
titles.append(dataset.class_names[mrcnn_class_ids[b,i]][:20])
display_images(images, titles, cols=4, cmap="Blues", interpolation="none")
# Check ratio of positive ROIs in a set of images.
if random_rois:
limit = 10
temp_g = modellib.data_generator(
dataset, crop_config, shuffle=True, random_rois=10000,
batch_size=1, detection_targets=True)
total = 0
for i in range(limit):
_, [ids, _, _] = next(temp_g)
positive_rois = np.sum(ids[0] > 0)
total += positive_rois
print("{:5} {:5.2f}".format(positive_rois, positive_rois/ids.shape[1]))
print("Average percent: {:.2f}".format(total/(limit*ids.shape[1])))
```
| github_jupyter |
```
import numpy as np
import cv2
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import matplotlib.patches as patches
from moviepy.editor import VideoFileClip
from IPython.display import HTML
import glob
%matplotlib inline
objp = np.zeros((6*9,3), np.float32)
objp[:,:2] = np.mgrid[0:9,0:6].T.reshape(-1,2)
nx = 9
ny = 6
# Arrays to store object points and image points from all the images.
objpoints = [] # 3d points in real world space
imgpoints = [] # 2d points in image plane.
# Make a list of calibration images
images = glob.glob('camera_cal/calibration*.jpg')
# Step through the list and search for chessboard corners
for fname in images:
img = cv2.imread(fname)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
# Find the chessboard corners
ret, corners = cv2.findChessboardCorners(gray, (nx,ny),None)
# If found, add object points, image points
if ret == True:
objpoints.append(objp)
imgpoints.append(corners)
# Draw and display the corners
img = cv2.drawChessboardCorners(img, (nx,ny), corners, ret)
#cv2.imshow('img',img)
#cv2.waitKey(500)
#cv2.destroyAllWindows()
def get_camera_calibration(img, objpoints, imgpoints):
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
return mtx, dist
img = cv2.imread('camera_cal/calibration1.jpg')
mtx, dist = get_camera_calibration(img, objpoints, imgpoints)
def get_undistorted_image(img, mtx, dist):
undist = cv2.undistort(img, mtx, dist, None, mtx)
return undist
def abs_sobel_thresh(img, orient, sobel_kernel, thresh):
thresh_min, thresh_max = thresh
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
if orient == 'x':
sobel = cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=sobel_kernel)
else:
sobel = cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=sobel_kernel)
abs_sobel = np.absolute(sobel)
scaled_sobel = np.uint8(255*abs_sobel/np.max(abs_sobel))
masked_sobel = np.zeros_like(scaled_sobel)
masked_sobel[(scaled_sobel >= thresh_min) & (scaled_sobel <= thresh_max)] = 1
return masked_sobel
def mag_thresh(img, sobel_kernel=3, mag_thresh=(0, 255)):
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
sobel_x = cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=sobel_kernel)
sobel_y = cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=sobel_kernel)
sobel_mag = np.sqrt(np.power(sobel_x, 2)+np.power(sobel_y, 2))
sobel_scaled = np.uint8(255*sobel_mag/np.max(sobel_mag))
sobel_mask = np.zeros_like(sobel_scaled)
sobel_mask[(sobel_scaled>mag_thresh[0]) & (sobel_scaled<mag_thresh[1])] =1
return sobel_mask
def dir_threshold(img, sobel_kernel=3, thresh=(0, np.pi/2)):
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
abs_sobel_x = np.absolute(cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=sobel_kernel))
abs_sobel_y = np.absolute(cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=sobel_kernel))
grad_dir = np.arctan2(abs_sobel_y, abs_sobel_x)
binary_output = np.zeros_like(grad_dir)
binary_output[(grad_dir > thresh[0]) & (grad_dir < thresh[1])] = 1
return binary_output
def hls_select(img, thresh=(0, 255)):
hls = cv2.cvtColor(image, cv2.COLOR_RGB2HLS)
s = hls[:,:,2]
binary_output = np.zeros_like(s)
binary_output[(s>thresh[0]) & (s<=thresh[1])] = 1
return binary_output
def get_thresholded_binary_image(image, ksize = 15):
gradx = abs_sobel_thresh(image, orient='x', sobel_kernel=ksize, thresh=(20, 100))
grady = abs_sobel_thresh(image, orient='y', sobel_kernel=ksize, thresh=(20, 100))
mag_binary = mag_thresh(image, sobel_kernel=ksize, mag_thresh=(30, 100))
dir_binary = dir_threshold(image, sobel_kernel=ksize, thresh=(0.7, 1.3))
hls_binary = hls_select(image, thresh=(120, 255))
combined = np.zeros_like(dir_binary)
combined[ ((dir_binary == 1) &(grady==1) &(mag_binary==1)) |(hls_binary==1) ] = 1
return combined
def get_warp_matrix(undist_img):
gray = cv2.cvtColor(undist_img, cv2.COLOR_BGR2GRAY)
img_size = (gray.shape[1], gray.shape[0])
# For source points I'm grabbing the outer four detected corners
src = np.float32([[img_size[0]//7+20,img_size[1]],#img_size[0]//7, img_size[1]],
[(6*img_size[0])//7+30, img_size[1]],
[img_size[0]//2+60, img_size[1]//2+100],
[img_size[0]//2-60, img_size[1]//2+100]])
print(src)
# For destination points, I'm arbitrarily choosing some points to be
# a nice fit for displaying our warped result
# again, not exact, but close enough for our purposes
offset=200
dst = np.float32([[offset, img_size[1]],
[img_size[0]-offset, img_size[1]],
[img_size[0]-offset,0],
[offset, 0]])
# Given src and dst points, calculate the perspective transform matrix
M = cv2.getPerspectiveTransform(src, dst)
Minv = cv2.getPerspectiveTransform(dst, src)
# Warp the image using OpenCV warpPerspective()
warped = cv2.warpPerspective(undist_img, M, img_size)
return warped, M, Minv, src, dst
image = cv2.imread('test_images/straight_lines1.jpg')
undist_img = get_undistorted_image(image, mtx, dist)
warped_img, perspective_M, perspective_Minv, _, dst = get_warp_matrix(undist_img)
#perspective_M, perspective_Minv
def get_transformed_image(img, perspective_M):
img_size = (img.shape[1], img.shape[0])
warped_img = cv2.warpPerspective(img, perspective_M, img_size)
return warped_img
def find_lane_pixels(binary_warped):
histogram = np.sum(binary_warped[binary_warped.shape[0]//2:,:], axis=0)
out_img = np.dstack((binary_warped, binary_warped, binary_warped))
midpoint = np.int(histogram.shape[0]//2)
leftx_base = np.argmax(histogram[:midpoint])
rightx_base = np.argmax(histogram[midpoint:]) + midpoint
nwindows = 9
margin = 100
minpix = 50
window_height = np.int(binary_warped.shape[0]//nwindows)
nonzero = binary_warped.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
leftx_current = leftx_base
rightx_current = rightx_base
left_lane_inds = []
right_lane_inds = []
for window in range(nwindows):
win_y_low = binary_warped.shape[0] - (window+1)*window_height
win_y_high = binary_warped.shape[0] - window*window_height
win_xleft_low = leftx_current-margin # Update this
win_xleft_high = leftx_current+margin # Update this
win_xright_low = rightx_current-margin # Update this
win_xright_high = rightx_current+margin # Update this
cv2.rectangle(out_img,(win_xleft_low,win_y_low),
(win_xleft_high,win_y_high),(0,255,0), 2)
cv2.rectangle(out_img,(win_xright_low,win_y_low),
(win_xright_high,win_y_high),(0,255,0), 2)
good_left_inds =((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xleft_low) & (nonzerox < win_xleft_high)).nonzero()[0]
good_right_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) &
(nonzerox >= win_xright_low) & (nonzerox < win_xright_high)).nonzero()[0]
left_lane_inds.append(good_left_inds)
right_lane_inds.append(good_right_inds)
if len(good_left_inds)>minpix:
leftx_current = np.int(np.mean(nonzerox[good_left_inds]))
if len(good_right_inds)>minpix:
rightx_current = np.int(np.mean(nonzerox[good_right_inds]))
try:
left_lane_inds = np.concatenate(left_lane_inds)
right_lane_inds = np.concatenate(right_lane_inds)
except ValueError:
pass
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
return leftx, lefty, rightx, righty, out_img
def fit_polynomial(binary_warped):
binary_warped = binary_warped.copy()
leftx, lefty, rightx, righty, out_img = find_lane_pixels(binary_warped)
left_fit = np.polyfit(lefty, leftx, 2)
right_fit = np.polyfit(righty, rightx, 2)
ploty = np.linspace(0, binary_warped.shape[0]-1, binary_warped.shape[0] )
try:
left_fitx = left_fit[0]*ploty**2 + left_fit[1]*ploty + left_fit[2]
right_fitx = right_fit[0]*ploty**2 + right_fit[1]*ploty + right_fit[2]
except TypeError:
# Avoids an error if `left` and `right_fit` are still none or incorrect
print('The function failed to fit a line!')
left_fitx = 1*ploty**2 + 1*ploty
right_fitx = 1*ploty**2 + 1*ploty
out_img[lefty, leftx] = [255, 0, 0]
out_img[righty, rightx] = [0, 0, 255]
# Plots the left and right polynomials on the lane lines
plt.plot(left_fitx, ploty, color='yellow')
plt.plot(right_fitx, ploty, color='yellow')
return out_img, left_fit, right_fit, ploty, left_fitx, right_fitx
def fit_poly(img_shape, leftx, lefty, rightx, righty):
### TO-DO: Fit a second order polynomial to each with np.polyfit() ###
left_fit = np.polyfit(lefty, leftx, 2)
right_fit = np.polyfit(righty, rightx, 2)
# Generate x and y values for plotting
ploty = np.linspace(0, img_shape[0]-1, img_shape[0])
### TO-DO: Calc both polynomials using ploty, left_fit and right_fit ###
ploty = np.linspace(0, img_shape[0]-1, img_shape[0] )
left_fitx = left_fit[0]*ploty**2 + left_fit[1]*ploty + left_fit[2]
right_fitx = right_fit[0]*ploty**2 + right_fit[1]*ploty + right_fit[2]
# left_fitx = None
# right_fitx = None
return left_fitx, right_fitx, ploty, left_fit, right_fit
def search_around_poly(binary_warped, left_fit, right_fit):
# HYPERPARAMETER
# Choose the width of the margin around the previous polynomial to search
# The quiz grader expects 100 here, but feel free to tune on your own!
binary_warped = binary_warped.copy()
margin = 100
# Grab activated pixels
nonzero = binary_warped.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
### TO-DO: Set the area of search based on activated x-values ###
### within the +/- margin of our polynomial function ###
### Hint: consider the window areas for the similarly named variables ###
### in the previous quiz, but change the windows to our new search area ###
left_lane_inds = ((nonzerox > (left_fit[0]*(nonzeroy**2) + left_fit[1]*nonzeroy +
left_fit[2] - margin)) & (nonzerox < (left_fit[0]*(nonzeroy**2) +
left_fit[1]*nonzeroy + left_fit[2] + margin)))
right_lane_inds = ((nonzerox > (right_fit[0]*(nonzeroy**2) + right_fit[1]*nonzeroy +
right_fit[2] - margin)) & (nonzerox < (right_fit[0]*(nonzeroy**2) +
right_fit[1]*nonzeroy + right_fit[2] + margin)))
# Again, extract left and right line pixel positions
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
# Fit new polynomials
left_fitx, right_fitx, ploty , left_fit, right_fit= fit_poly(binary_warped.shape, leftx, lefty, rightx, righty)
## Visualization ##
# Create an image to draw on and an image to show the selection window
out_img = np.dstack((binary_warped, binary_warped, binary_warped))*255
window_img = np.zeros_like(out_img)
# Color in left and right line pixels
out_img[nonzeroy[left_lane_inds], nonzerox[left_lane_inds]] = [255, 0, 0]
out_img[nonzeroy[right_lane_inds], nonzerox[right_lane_inds]] = [0, 0, 255]
# Generate a polygon to illustrate the search window area
# And recast the x and y points into usable format for cv2.fillPoly()
left_line_window1 = np.array([np.transpose(np.vstack([left_fitx-margin, ploty]))])
left_line_window2 = np.array([np.flipud(np.transpose(np.vstack([left_fitx+margin,
ploty])))])
left_line_pts = np.hstack((left_line_window1, left_line_window2))
right_line_window1 = np.array([np.transpose(np.vstack([right_fitx-margin, ploty]))])
right_line_window2 = np.array([np.flipud(np.transpose(np.vstack([right_fitx+margin,
ploty])))])
right_line_pts = np.hstack((right_line_window1, right_line_window2))
# Draw the lane onto the warped blank image
cv2.fillPoly(window_img, np.int_([left_line_pts]), (0,255, 0))
cv2.fillPoly(window_img, np.int_([right_line_pts]), (0,255, 0))
result = cv2.addWeighted(out_img, 1, window_img, 0.3, 0)
# Plot the polynomial lines onto the image
#plt.plot(left_fitx, ploty, color='yellow')
#plt.plot(right_fitx, ploty, color='yellow')
## End visualization steps ##
return result, left_fitx, right_fitx, ploty, left_fit, right_fit
def measure_curvature_real(ploty, left_fit_cr, right_fit_cr):
ym_per_pix = 30/720 # meters per pixel in y dimension
xm_per_pix = 3.7/700 # meters per pixel in x dimension
y_eval = np.max(ploty)
##### TO-DO: Implement the calculation of R_curve (radius of curvature) #####
left_curverad = np.power(1+(2*left_fit_cr[0]*y_eval*ym_per_pix + left_fit_cr[1])**2, 3/2)/(2*np.absolute(left_fit_cr[0])) ## Implement the calculation of the left line here
right_curverad = np.power(1+(2*right_fit_cr[0]*y_eval*ym_per_pix + right_fit_cr[1])**2, 3/2)/(2*np.absolute(right_fit_cr[0])) ## Implement the calculation of the right line here
return left_curverad, right_curverad
def plot_lanes(warped, undist, left_fitx, right_fitx, ploty, Minv):
# Create an image to draw the lines on
warp_zero = np.zeros_like(warped).astype(np.uint8)
color_warp = np.dstack((warp_zero, warp_zero, warp_zero))
# Recast the x and y points into usable format for cv2.fillPoly()
pts_left = np.array([np.transpose(np.vstack([left_fitx, ploty]))])
pts_right = np.array([np.flipud(np.transpose(np.vstack([right_fitx, ploty])))])
pts = np.hstack((pts_left, pts_right))
# Draw the lane onto the warped blank image
cv2.fillPoly(color_warp, np.int_([pts]), (0,255, 0))
# Warp the blank back to original image space using inverse perspective matrix (Minv)
newwarp = cv2.warpPerspective(color_warp, Minv, (image.shape[1], image.shape[0]))
# Combine the result with the original image
result = cv2.addWeighted(undist, 1, newwarp, 0.3, 0)
return result
class Line():
def __init__(self):
self.detected = False
self.recent_xfitted = []
self.bestx = None
self.best_fit = None
self.current_fit = [np.array([False])]
self.radius_of_curvature = None
self.line_base_pos = None
self.diffs = np.array([0,0,0], dtype='float')
self.allx = None
self.ally = None
class Pipeline():
def __init__(self):
self.mtx = mtx
self.dist = dist
self.perspective_M = perspective_M
self.perspective_Minv = perspective_Minv
self.left_lines = []
self.right_lines = []
self.xm_per_pix = 3.7/700
self.ym_per_pix = 30/720
def get_undistorted_image(self, img):
undist = cv2.undistort(img, self.mtx, self.dist, None, self.mtx)
return undist
def get_thresholded_binary_image(self, image, ksize = 15):
gradx = abs_sobel_thresh(image, orient='x', sobel_kernel=ksize, thresh=(20, 100))
grady = abs_sobel_thresh(image, orient='y', sobel_kernel=ksize, thresh=(20, 100))
mag_binary = mag_thresh(image, sobel_kernel=ksize, mag_thresh=(30, 100))
dir_binary = dir_threshold(image, sobel_kernel=ksize, thresh=(0.7, 1.3))
hls_binary = hls_select(image, thresh=(120, 255))
combined = np.zeros_like(dir_binary)
combined[ ((dir_binary == 1) &(grady==1) &(mag_binary==1)) |(hls_binary==1) ] = 1
return combined
def get_transformed_image(self, img):
img_size = (img.shape[1], img.shape[0])
warped_img = cv2.warpPerspective(img, self.perspective_M, img_size)
return warped_img
def get_vehicle_offset(self, left_fitx, right_fitx, img_size):
left_dist = img_size[1]//2 - left_fitx[-1]
right_dist = right_fitx[-1] - img_size[1]//2
return left_dist, right_dist
def get_vehicle_dist_from_centre(self, left_fitx, right_fitx, img_size):
lane_midpoint = (right_fitx[-1]+left_fitx[-1])//2
img_mid_point = img_size[1]//2
return round((lane_midpoint - img_mid_point)*self.xm_per_pix,4)
def check_last_line(self):
if abs(self.left_lines[-1].radius_of_curvature - self.right_lines[-1].radius_of_curvature) > 200:
flag = False
else:
dist_bet_lines = self.left_lines[-1].line_base_pos + self.left_lines[-1].line_base_pos
if dist_bet_lines > 1000 or dist_bet_lines < 1:#change this values later
flag = False
else:
flag = True#Add function to check if lanes are parallel
return flag
def get_lines_from_scratch(self, warped_img, undist_img):
#change result to out_img
result, left_fit, right_fit, ploty, left_fitx, right_fitx = fit_polynomial(warped_img)
new_left_line = Line()
new_right_line = Line()
new_left_line.current_fit = left_fit
new_right_line.current_fit = right_fit
left_radius, right_radius = measure_curvature_real(ploty, left_fit, right_fit)
new_left_line.radius_of_curvature = left_radius
new_right_line.radius_of_curvature = right_radius
left_dist, right_dist = self.get_vehicle_offset(left_fitx, right_fitx, warped_img.shape)
new_left_line.line_base_pos = left_dist
new_right_line.line_base_pos = right_dist
new_left_line.allx = left_fitx
new_left_line.ally = ploty
new_right_line.allx = right_fitx
new_right_line.ally = ploty
self.left_lines.append(new_left_line)
self.right_lines.append(new_right_line)
#result = plot_lanes(warped_img, undist_img, left_fitx, right_fitx, ploty, self.perspective_Minv)
result = cv2.putText(result,'Radius of curvature=' + str(right_radius) + '(m)', (0, 100), 0,
2, (255, 255, 255), 5, cv2.LINE_AA)
vehicle_dist = self.get_vehicle_dist_from_centre(left_fitx, right_fitx, warped_img.shape)
if vehicle_dist > 0:
result = cv2.putText(result,'Vehicle is ' + str(vehicle_dist) + 'm left of center', (0, 200), 0,
2, (255, 255, 255), 5, cv2.LINE_AA)
else:
result = cv2.putText(result,'Vehicle is ' + str(-1*vehicle_dist) + 'm right of center', (0, 200), 0,
2, (255, 255, 255), 5, cv2.LINE_AA)
print(left_radius, right_radius)
return result
def get_lines_from_previous(self, warped_img, undist_img, flag):
result, left_fitx, right_fitx, ploty, left_fit, right_fit = search_around_poly(warped_img,
self.left_lines[-1].current_fit,
self.right_lines[-1].current_fit)
new_left_line = Line()
new_right_line = Line()
if flag:
new_left_line.detected=True
new_right_line.detected = True
new_left_line.current_fit = left_fit
new_right_line.current_fit = right_fit
left_radius, right_radius = measure_curvature_real(ploty, left_fit, right_fit)
new_left_line.radius_of_curvature = left_radius
new_right_line.radius_of_curvature = right_radius
left_dist, right_dist = self.get_vehicle_offset(left_fitx, right_fitx, warped_img.shape)
new_left_line.line_base_pos = left_dist
new_right_line.line_base_pos = right_dist
new_left_line.allx = left_fitx
new_left_line.ally = ploty
new_right_line.allx = right_fitx
new_right_line.ally = ploty
self.left_lines.append(new_left_line)
self.right_lines.append(new_right_line)
result = plot_lanes(warped_img, undist_img, left_fitx, right_fitx, ploty, self.perspective_Minv)
result = cv2.putText(result,'Radius of curvature=' + str(left_radius) + '(m)', (0, 100), 0,
2, (255, 255, 255), 5, cv2.LINE_AA)
vehicle_dist = self.get_vehicle_dist_from_centre(left_fitx, right_fitx, warped_img.shape)
if vehicle_dist > 0:
result = cv2.putText(result,'Vehicle is ' + str(vehicle_dist) + 'm left of center', (0, 200), 0,
2, (255, 255, 255), 5, cv2.LINE_AA)
else:
result = cv2.putText(result,'Vehicle is ' + str(-1*vehicle_dist) + 'm right of center', (0, 200), 0,
2, (255, 255, 255), 5, cv2.LINE_AA)
print(left_radius, right_radius)
return result
def process_frame(self, image):
#plt.imshow(image)
undist_img = self.get_undistorted_image(image)
combined = self.get_thresholded_binary_image(undist_img)
warped_img = self.get_transformed_image(combined)
#return np.dstack((np.zeros_like(warped_img), warped_img, np.zeros_like(warped_img)))*255
result = self.get_lines_from_scratch(warped_img, undist_img)
return result
# if len(self.left_lines) == 0:
# result = self.get_lines_from_scratch(warped_img, undist_img)
# return result
# else:
# flag = self.check_last_line
# if not flag:
# result = self.get_lines_from_scratch(warped_img, undist_img)
# return result
# else:
# result = self.get_lines_from_previous(warped_img, undist_img, flag)
# return result
pipeline_object = Pipeline()
img = cv2.imread('test_images/test6.jpg')
result = pipeline_object.process_frame(img)
plt.imshow(result)
pipeline_object = Pipeline()
white_output = 'project_video_output_combined.mp4'
## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video
## To do so add .subclip(start_second,end_second) to the end of the line below
## Where start_second and end_second are integer values representing the start and end of the subclip
## You may also uncomment the following line for a subclip of the first 5 seconds
##clip1 = VideoFileClip("test_videos/solidWhiteRight.mp4").subclip(0,5)
clip1 = VideoFileClip("project_video.mp4").subclip(0, 1)
white_clip = clip1.fl_image(pipeline_object.process_frame) #NOTE: this function expects color images!!
%time white_clip.write_videofile(white_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(white_output))
```
| github_jupyter |
+ This notebook is part of lecture 7 *Solving Ax=0, pivot variables, and special solutions* in the OCW MIT course 18.06 by Prof Gilbert Strang [1]
+ Created by me, Dr Juan H Klopper
+ Head of Acute Care Surgery
+ Groote Schuur Hospital
+ University Cape Town
+ <a href="mailto:[email protected]">Email me with your thoughts, comments, suggestions and corrections</a>
<a rel="license" href="http://creativecommons.org/licenses/by-nc/4.0/"><img alt="Creative Commons Licence" style="border-width:0" src="https://i.creativecommons.org/l/by-nc/4.0/88x31.png" /></a><br /><span xmlns:dct="http://purl.org/dc/terms/" href="http://purl.org/dc/dcmitype/InteractiveResource" property="dct:title" rel="dct:type">Linear Algebra OCW MIT18.06</span> <span xmlns:cc="http://creativecommons.org/ns#" property="cc:attributionName">IPython notebook [2] study notes by Dr Juan H Klopper</span> is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by-nc/4.0/">Creative Commons Attribution-NonCommercial 4.0 International License</a>.
+ [1] <a href="http://ocw.mit.edu/courses/mathematics/18-06sc-linear-algebra-fall-2011/index.htm">OCW MIT 18.06</a>
+ [2] Fernando Pérez, Brian E. Granger, IPython: A System for Interactive Scientific Computing, Computing in Science and Engineering, vol. 9, no. 3, pp. 21-29, May/June 2007, doi:10.1109/MCSE.2007.53. URL: http://ipython.org
```
from IPython.core.display import HTML, Image
css_file = 'style.css'
HTML(open(css_file, 'r').read())
#import numpy as np
from sympy import init_printing, Matrix, symbols
#import matplotlib.pyplot as plt
#import seaborn as sns
#from IPython.display import Image
from warnings import filterwarnings
init_printing(use_latex = 'mathjax')
%matplotlib inline
filterwarnings('ignore')
```
# Solving homogeneous systems
# Pivot variables
# Special solutions
* We are trying to solve a system of linear equations
* For homogeneous systems the right-hand side is the zero vector
* Consider the example below
```
A = Matrix([[1, 2, 2, 2], [2, 4, 6, 8], [3, 6, 8, 10]])
A # A 3x4 matrix
x1, x2, x3, x4 = symbols('x1, x2, x3, x4')
x_vect = Matrix([x1, x2, x3, x4]) # A 4x1 matrix
x_vect
b = Matrix([0, 0, 0])
b # A 3x1 matrix
```
* The **x** column vector is a set of all the solutions to this homogeneous equation
* It forms the nullspace
* Note that the column vectors in A are not linearly independent
* Performing elementary row operations leaves us with the matrix below
* It has two pivots, which is termed **rank** 2
```
A.rref() # rref being reduced row echelon form
```
* Which represents the following
$$ { x }_{ 1 }\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}+{ x }_{ 2 }\begin{bmatrix} 2 \\ 0 \\ 0 \end{bmatrix}+{ x }_{ 3 }\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}+{ x }_{ 4 }\begin{bmatrix} -2 \\ 2 \\ 0 \end{bmatrix}=\begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}\\ { x }_{ 1 }+2{ x }_{ 2 }+0{ x }_{ 3 }-2{ x }_{ 4 }=0\\ 0{ x }_{ 1 }+0{ x }_{ 2 }+{ x }_{ 3 }+2{ x }_{ 4 }=0\\ { x }_{ 1 }+0{ x }_{ 2 }+0{ x }_{ 3 }+0{ x }_{ 4 }=0 $$
* We are free set a value for *x*<sub>4</sub>, let's sat *t*
$$ { x }_{ 1 }+2{ x }_{ 2 }+0{ x }_{ 3 }-2{ x }_{ 4 }=0\\ 0{ x }_{ 1 }+0{ x }_{ 2 }+{ x }_{ 3 }+2t=0\\ { x }_{ 1 }+0{ x }_{ 2 }+0{ x }_{ 3 }+0{ x }_{ 4 }=0\\ \therefore \quad { x }_{ 3 }=-2t $$
* We will have to make *x*<sub>2</sub> equal to another variable, say *s*
$$ { x }_{ 1 }+2s+0{ x }_{ 3 }-2t=0 $$
$$ \therefore \quad {x}_{1}=2t-2s $$
* This results in the following, which is the complete nullspace and has dimension 2
$$ \begin{bmatrix} { x }_{ 1 } \\ { x }_{ 2 } \\ { x }_{ 3 } \\ { x }_{ 4 } \end{bmatrix}=\begin{bmatrix} -2s+2t \\ s \\ -2t \\ t \end{bmatrix}=\begin{bmatrix} -2s \\ s \\ 0 \\ 0 \end{bmatrix}+\begin{bmatrix} 2t \\ 0 \\ -2t \\ t \end{bmatrix}=s\begin{bmatrix} -2 \\ 1 \\ 0 \\ 0 \end{bmatrix}+t\begin{bmatrix} 2 \\ 0 \\ -2 \\ 1 \end{bmatrix} $$
* From the above, we clearly have two vectors in the solution and we can take constant multiples of these to fill up our solution space (our nullspace)
* We can easily calculate how many free variables we will have by subtracting the number of pivots (rank) from the number of variables (*x*) in **x**
* Here we have 4 - 2 = 2
#### Example problem
* Calculate **x** for the transpose of A above
#### Solution
```
A_trans = A.transpose() # Creating a new matrix called A_trans and giving it the value of the inverse of A
A_trans
A_trans.rref() # In reduced row echelon form this would be the following matrix
```
* Remember this is 4 equations in 3 unknowns, i.e.
$$ { x }_{ 1 }\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}+{ x }_{ 2 }\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}+{ x }_{ 3 }\begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix}=\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\\ { x }_{ 1 }+0{ x }_{ 2 }+{ x }_{ 3 }=0\\ 0{ x }_{ 1 }+{ x }_{ 2 }+{ x }_{ 3 }=0\\ 0{ x }_{ 1 }+0{ x }_{ 2 }+0{ x }_{ 3 }=0\\ 0{ x }_{ 1 }+0{ x }_{ 2 }+0{ x }_{ 3 }=0 $$
* It seems we are free to choose a value for *x*<sub>3</sub>
* Let's make is *t*
$$ t\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}-t\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}+t\begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix}=\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\\ { x }_{ 3 }=t\\ { x }_{ 1 }+0{ x }_{ 2 }+t=0\\ 0{ x }_{ 1 }+{ x }_{ 2 }+t=0\\ \therefore \quad { x }_{ 2 }=-t\\ \therefore \quad { x }_{ 1 }=-t\\ \begin{bmatrix} { x }_{ 1 } \\ { x }_{ 2 } \\ { x }_{ 3 } \end{bmatrix}=\begin{bmatrix} t \\ -t \\ t \end{bmatrix}=t\begin{bmatrix} 1 \\ -1 \\ 1 \end{bmatrix} $$
* We had *n* = 3 unknowns and *r* (rank) = 2 pivots
* The solution set (nullspace) will thus have 1 variable (*t*) (3-2=1)
* The third column is the sum of the first two, so only 2 columns are linearly independent
* We thus expect 2 pivots and can predict the nullspace to have only 1 variable (i.e. it is one-dimensional)
| github_jupyter |
```
# !pip install simplejson
from pymongo import MongoClient
from pathlib import Path
from tqdm.notebook import tqdm
import numpy as np
import simplejson as json
import itertools
from functools import cmp_to_key
import networkx as nx
from IPython.display import display, Image, JSON
from ipywidgets import widgets, Image, HBox, VBox, Button, ButtonStyle, Layout, Box
from lib.image_dedup import make_hashes, calculate_distance, hashes_diff
from lib.PersistentSet import PersistentSet
from lib.sort_things import post_score, sort_posts, sort_images
from lib.parallel import parallel
images_dir = Path('../images')
handmade_dir = Path('./handmade')
handmade_dir.mkdir(exist_ok=True)
mongo_uri = json.load(open('./credentials/mongodb_credentials.json'))['uri']
mongo = MongoClient(mongo_uri)
db = mongo['bad-vis']
posts = db['posts']
imagefiles = db['imagefiles']
imagemeta = db['imagemeta']
imagededup = db['imagededup']
imagededup.drop()
for i in imagemeta.find():
imagededup.insert_one(i)
```
# Load image metadata
```
imageDedup = [m for m in imagemeta.find()]
imageDedup.sort(key=lambda x: x['image_id'])
phash_to_idx_mapping = {}
for i in range(len(imageDedup)):
phash = imageDedup[i]['phash']
l = phash_to_idx_mapping.get(phash, [])
l.append(i)
phash_to_idx_mapping[phash] = l
def phash_to_idx (phash):
return phash_to_idx_mapping.get(phash, None)
image_id_to_idx_mapping = {imageDedup[i]['image_id']:i for i in range(len(imageDedup))}
def image_id_to_idx (image_id):
return image_id_to_idx_mapping.get(image_id, None)
```
# Calculate distance
## Hash distance
```
image_hashes = [make_hashes(m) for m in imageDedup]
# distance = calculate_distance(image_hashes)
distance = calculate_distance(image_hashes, hash_type='phash')
# distance2 = np.ndarray([len(image_hashes), len(image_hashes)])
# for i in tqdm(range(len(image_hashes))):
# for j in range(i+1):
# diff = hashes_diff(image_hashes[i], image_hashes[j])
# distance2[i, j] = diff
# distance2[j, i] = diff
# np.array_equal(distance, distance2)
# pdistance = calculate_distance(image_hashes, hash_type='phash')
```
## Find duplicated pairs from distance matrix
```
def set_distance (hashes, value, mat=distance):
phash_x = hashes[0]
phash_y = phash_x if len(hashes) == 1 else hashes[1]
idx_x = phash_to_idx(phash_x)
idx_y = phash_to_idx(phash_y)
if idx_x == None or idx_y == None:
return
for s in itertools.product(idx_x, idx_y):
i, j = s
mat[i, j] = value
mat[j, i] = value
def set_distance_pairs (phash_pairs, value, mat=distance):
for p in phash_pairs:
set_distance(list(p), value, mat=mat)
auto_duplicated_image_phash_pairs = PersistentSet()
auto_duplicated_image_phash_pairs.set_file(handmade_dir/'auto_duplicated_image_phash_pairs.json')
for i in tqdm(range(distance.shape[0])):
for j in range(i):
if distance[i, j] <= 1: # checked, all distance <= 1 are duplicated
auto_duplicated_image_phash_pairs.add(frozenset([imageDedup[i]['phash'], imageDedup[j]['phash']]))
# for i in tqdm(range(pdistance.shape[0])):
# for j in range(i):
# if pdistance[i, j] <= 1: # checked, all distance <= 1 are duplicated
# auto_duplicated_image_phash_pairs.add(frozenset([imageDedup[i]['phash'], imageDedup[j]['phash']]))
auto_duplicated_image_phash_pairs.save()
```
## Apply information from meta data
```
duplicated_post_image_phash_pairs = PersistentSet()
duplicated_post_image_phash_pairs.set_file(handmade_dir/'duplicated_post_image_phash_pairs.json')
for p in tqdm(posts.find()):
if len(p.get('duplicated_posts', [])) == 0:
continue
dp_phashes = {i['phash']
for dp in p['duplicated_posts']
for i in imagemeta.find({'post_id': dp})}
if len(dp_phashes) > 1:
# print(f"More than 1 dp image {p['post_id']}")
# print(f"{p['duplicated_posts']} {dp_phashes}")
continue
phashes = [i['phash'] for i in imagemeta.find({'post_id': p['post_id']})]
if len(phashes) > 1:
# print(f"More than 1 image {p['post_id']} {phashes}")
continue
for s in itertools.product(dp_phashes, phashes):
fs = frozenset(s)
if len(fs) > 1:
duplicated_post_image_phash_pairs.add(fs)
duplicated_post_image_phash_pairs.save()
related_album_image_phash_pairs = PersistentSet()
related_album_image_phash_pairs.set_file(handmade_dir/'related_album_image_phash_pairs.json')
for album in tqdm({i['album'] for i in imagemeta.find({'album': {'$exists': True, '$ne': ''}})}):
ra_phashes = [i['phash'] for i in imagemeta.find({'album': album})]
if len(ra_phashes) <= 1:
print(f"Only 1 or less image {album} {ra_phashes}")
for s in itertools.product(ra_phashes, ra_phashes):
fs = frozenset(s)
if len(fs) > 1:
related_album_image_phash_pairs.add(fs)
related_album_image_phash_pairs.save()
```
## Apply manual labeled data
```
duplicated_image_phash_pairs = PersistentSet.load_set(handmade_dir/'duplicated_image_phash_pairs.json')
not_duplicated_image_phash_pairs = PersistentSet.load_set(handmade_dir/'not_duplicated_image_phash_pairs.json')
related_image_phash_pairs = PersistentSet.load_set(handmade_dir/'related_image_phash_pairs.json')
invalid_image_phashes = PersistentSet.load_set(handmade_dir/'invalid_image_phashes.json')
set_distance_pairs(auto_duplicated_image_phash_pairs, 0)
set_distance_pairs(duplicated_post_image_phash_pairs, 0)
set_distance_pairs(duplicated_image_phash_pairs, 0)
set_distance_pairs(not_duplicated_image_phash_pairs, 60)
set_distance_pairs(related_album_image_phash_pairs, 60)
set_distance_pairs(related_image_phash_pairs, 60)
related_distance = np.full(distance.shape, 60)
set_distance_pairs(related_album_image_phash_pairs, 0, mat=related_distance)
set_distance_pairs(related_image_phash_pairs, 0, mat=related_distance)
```
# Human in the Loop
```
def make_dedup_box (idx_x, idx_y, default=None):
image_x = imageDedup[idx_x]
phash_x = image_x['phash']
image_y = imageDedup[idx_y]
phash_y = image_y['phash']
hash_pair = frozenset([phash_x, phash_y])
yes_btn = widgets.Button(description="Duplicated", button_style='success')
no_btn = widgets.Button(description="Not", button_style='info')
related_btn = widgets.Button(description="Related", button_style='warning')
invalid_x_btn = widgets.Button(description="X Invalid")
invalid_y_btn = widgets.Button(description="Y Invalid")
reset_btn = widgets.Button(description="Reset")
output = widgets.Output()
def on_yes (btn):
with output:
if hash_pair in not_duplicated_image_phash_pairs:
not_duplicated_image_phash_pairs.persist_remove(hash_pair)
print('-Not')
duplicated_image_phash_pairs.persist_add(hash_pair)
print('Duplicated')
def on_no (btn):
with output:
if hash_pair in duplicated_image_phash_pairs:
duplicated_image_phash_pairs.persist_remove(hash_pair)
print('-Duplicated')
not_duplicated_image_phash_pairs.persist_add(hash_pair)
print('Not')
def on_related (btn):
with output:
if hash_pair in not_duplicated_image_phash_pairs:
not_duplicated_image_phash_pairs.persist_remove(hash_pair)
print('-Not')
related_image_phash_pairs.persist_add(hash_pair)
print('Related')
def on_invalid_x (btn):
invalid_image_phashes.persist_add(phash_x)
with output:
print('Invalid X')
def on_invalid_y (btn):
invalid_image_phashes.persist_add(phash_y)
with output:
print('Invalid Y')
def on_reset (btn):
with output:
if hash_pair in duplicated_image_phash_pairs:
duplicated_image_phash_pairs.persist_remove(hash_pair)
print('-Duplicated')
if hash_pair in not_duplicated_image_phash_pairs:
not_duplicated_image_phash_pairs.persist_remove(hash_pair)
print('-Not')
if hash_pair in related_image_phash_pairs:
related_image_phash_pairs.persist_remove(hash_pair)
print('-Related')
if phash_x in invalid_image_phashes:
invalid_image_phashes.persist_remove(phash_x)
print('-Invalid X')
if phash_y in invalid_image_phashes:
invalid_image_phashes.persist_remove(phash_y)
print('-Invalid Y')
print('Reset')
yes_btn.on_click(on_yes)
no_btn.on_click(on_no)
related_btn.on_click(on_related)
invalid_x_btn.on_click(on_invalid_x)
invalid_y_btn.on_click(on_invalid_y)
reset_btn.on_click(on_reset)
if default == 'no':
on_no(None)
elif default == 'yes':
on_yes(None)
return HBox([VBox([yes_btn, no_btn, related_btn, invalid_x_btn, invalid_y_btn, reset_btn, output]),
widgets.Image(value=open(image_x['file_path'], 'rb').read(), width=250, height=150),
widgets.Image(value=open(image_y['file_path'], 'rb').read(), width=250, height=150)])
def potential_duplicates (threshold):
for i in range(distance.shape[0]):
for j in range(i):
if distance[i, j] <= threshold:
phash_pair = frozenset([imageDedup[i]['phash'], imageDedup[j]['phash']])
if (phash_pair not in auto_duplicated_image_phash_pairs and
phash_pair not in duplicated_post_image_phash_pairs and
phash_pair not in duplicated_image_phash_pairs and
phash_pair not in not_duplicated_image_phash_pairs and
phash_pair not in related_album_image_phash_pairs and
phash_pair not in related_image_phash_pairs):
yield (i, j)
distance_threshold = 10
pdup = potential_duplicates(distance_threshold)
for i in range(10):
try:
next_pdup = next(pdup)
except StopIteration:
print('StopIteration')
break
idx_x, idx_y = next_pdup
image_x = imageDedup[idx_x]
image_y = imageDedup[idx_y]
print(f"{idx_x} {idx_y} {distance[idx_x, idx_y]} {image_x['phash']} {image_y['phash']} {image_x['width']} {image_y['width']} {image_x['image_id']} {image_y['image_id']}")
display(make_dedup_box(idx_x, idx_y, default=None if distance[idx_x, idx_y] < 6 else 'no'))
# display(make_dedup_box(idx_x, idx_y, default='yes' if distance[idx_x, idx_y] < 9 else 'no'))
```
# Visually check images
## Images with high variability
```
# interested_phashes = set()
# def potential_duplicates_high (threshold):
# for i in range(distance.shape[0]):
# for j in range(i):
# if distance[i, j] >= threshold:
# phash_pair = frozenset([imageDedup[i]['phash'], imageDedup[j]['phash']])
# if (phash_pair in duplicated_image_phash_pairs):
# interested_phashes.add(imageDedup[i]['phash'])
# interested_phashes.add(imageDedup[j]['phash'])
# yield (i, j)
# pduph = potential_duplicates_high(13)
# for i in range(100):
# try:
# next_pdup = next(pduph)
# except StopIteration:
# print('StopIteration')
# break
# idx_x, idx_y = next_pdup
# image_x = imageDedup[idx_x]
# image_y = imageDedup[idx_y]
# print(f"{idx_x} {idx_y} {distance[idx_x, idx_y]} {image_x['phash']} {image_y['phash']} {image_x['width']} {image_y['width']} {image_x['image_id']} {image_y['image_id']}")
# display(make_dedup_box(idx_x, idx_y))
# invalid_image_phashes = set(json.load(open('handmade/invalid_image_phashes.json')))
# examined_images = [
# 'reddit/dataisugly/2o08rl_0', # manually downloaded
# 'reddit/dataisugly/2nwubr_0', # manually downloaded
# 'reddit/dataisugly/beivt8_0', # manually downloaded
# 'reddit/dataisugly/683b4i_0', # manually downloaded
# 'reddit/dataisugly/3zcw30_0', # manually downloaded
# 'reddit/dataisugly/1oxrh5_0', # manually downloaded a higher resolution image
# 'reddit/dataisugly/3or2g0_0', # manually downloaded
# 'reddit/dataisugly/5iobqn_0', # manually downloaded
# 'reddit/dataisugly/29fpuo_0', # manually downloaded
# 'reddit/dataisugly/5xux1f_0', # manually downloaded
# 'reddit/dataisugly/35lrw1_0', # manually downloaded
# 'reddit/dataisugly/1bxhv2_0', # manually downloaded a higher resolution image
# 'reddit/dataisugly/3peais_0', # manually downloaded
# 'reddit/dataisugly/2vdk71_0', # manually downloaded
# 'reddit/dataisugly/6b8w73_0', # manually downloaded
# 'reddit/dataisugly/2w8pnr_0', # manually downloaded an image with more context
# 'reddit/dataisugly/2dt19h_0', # manually downloaded
# 'reddit/dataisugly/31tj8a_0', # manually downloaded
# 'reddit/dataisugly/30smxr_0', # manually downloaded
# 'reddit/dataisugly/30dbx6_0', # manually downloaded
# 'reddit/dataisugly/561ytm_0', # manually downloaded
# 'reddit/dataisugly/6q4tre_0', # manually downloaded
# 'reddit/dataisugly/3icm4g_0', # manually downloaded
# 'reddit/dataisugly/6z5v98_0', # manually downloaded
# 'reddit/dataisugly/5fucjm_0', # manually downloaded
# 'reddit/dataisugly/99bczz_0', # manually downloaded
# 'reddit/dataisugly/2662wv_0', # manually downloaded
# 'reddit/dataisugly/26otpi_0', # manually downloaded a higher resolution image
# 'reddit/dataisugly/68scgb_0', # manually downloaded
# 'reddit/dataisugly/et75qp_0', # manually downloaded
# 'reddit/dataisugly/4c9zc1_0', # manually downloaded an image with more context
# 'reddit/dataisugly/2525a5_0', # manually downloaded more images, but does not matched with the one with more context
# 'reddit/dataisugly/2la7zt_0', # thumbnail alt
# ]
```
## Invalid images
```
# invalids = []
# for h in invalid_image_phashes:
# invalid_images = [f for f in imagefiles.find({'phash': h})]
# if len(invalid_images) > 0:
# invalids.append(invalid_images[0])
# display(Box([widgets.Image(value=open(i['file_path'], 'rb').read(), width=100, height=100) for i in invalids],
# layout=Layout(display='flex', flex_flow='row wrap')))
```
# Consolidate
## Related images
```
related_images = [[imageDedup[idx]['image_id'] for idx in c]
for c in nx.components.connected_components(nx.Graph(related_distance <= 1))
if len(c) > 1]
len(related_images)
for ids in related_images:
for i in ids:
imageMeta = imageDedup[image_id_to_idx(i)]
ri = [r for r in set(imageMeta.get('related_images', []) + ids) if r != i]
imagededup.update_one({'image_id': i}, {'$set': {'related_images': ri}})
```
## Duplicated images
```
excluding_image_phashes = PersistentSet.load_set(handmade_dir/'excluding_image_phashes.json')
excluding_image_phashes.persist_add('c13e3ae10e70fd86')
excluding_image_phashes.persist_add('fe81837a94e3807e')
excluding_image_phashes.persist_add('af9da24292fae149')
excluding_image_phashes.persist_add('ad87d2696738ca4c')
excluding_image_phashes.persist_add('d25264dfa9659392')
excluding_image_phashes.persist_add('964e3b3160e14f8f')
class ImageDedup ():
_attrs = [
'id',
'post_id',
'datetime',
'url',
'title',
'content',
'author',
'removed',
'ups',
'num_comments',
'external_link',
'source',
'source_platform',
'source_url',
'tags',
'labels',
'media_type',
'thumbnail_url',
'preview_url',
'external_link_url',
'archive_url',
'thumbnail',
'preview',
'external_link',
'archive',
'manual',
'image_id',
'short_image_id',
'album',
'index_in_album',
'image_type',
'file_path',
'ext',
'animated',
'size',
'width',
'height',
'pixels',
'image_order',
'ahash',
'phash',
'pshash',
'dhash',
'whash',
'duplicated_posts',
'related_images',
'duplicated_images',
'popularity_score'
]
def __init__ (self, imageMetas=[]):
# print(imageMetas)
if len(imageMetas) == 0:
raise Exception('Empty imageFiles array.')
self._imageMetas = imageMetas
self._image_ids = [i['image_id'] for i in imageMetas]
self._image_order = sort_images(self._imageMetas)
self._post_ids = {i['post_id'] for i in imageMetas}
self._posts = [posts.find_one({'post_id': i}) for i in self._post_ids]
dpost = []
for p in self._posts:
if 'duplicated_posts' in p:
for i in p['duplicated_posts']:
if i not in self._post_ids:
dpost.append(posts.find_one({'post_id': i}))
self._posts += dpost
if None in self._posts:
print(self._post_ids)
self._post_order = sort_posts(self._posts)
for k, v in self.main_image.items():
if k in ['duplicated_posts', 'related_images']:
continue
setattr(self, k, v)
for k, v in self.main_post.items():
if k in ['duplicated_posts', 'related_images']:
continue
if k in ['preview', 'thumbnail', 'external_link', 'archive', 'manual']:
setattr(self, f"{k}_url", v)
else:
setattr(self, k, v)
def digest (self):
return {a:getattr(self, a) for a in ImageDedup._attrs if hasattr(self, a)}
@property
def duplicated_posts (self):
post_ids = self._post_ids.union(*[set(p.get('duplicated_posts', [])) for p in self._posts])
return [i for i in post_ids if i != self.post_id]
@property
def duplicated_images (self):
return [i for i in self._image_ids if i != self.image_id]
@property
def related_images (self):
return [ri for i in self._imageMetas for ri in i.get('related_images', []) if ri != self.image_id]
@property
def main_post (self):
# if len(self._post_order) > 1 and self._post_order[0]['source_platform'] != 'reddit':
# print(f"main post warning: {[p['post_id'] for p in self._post_order]}")
return self._post_order[0]
@property
def popularity_score (self):
return sum([post_score(p) for p in self._posts if p['source'] == 'dataisugly'])
@property
def main_image (self):
# if len(self._image_order) > 1 and self._image_order[0]['source_platform'] != 'reddit':
# print(f"main image warning: {[i['image_id'] for i in self._image_order]}")
mi = [i for i in self._image_order if i['phash'] not in excluding_image_phashes][0]
return mi
duplicated_images = [list(set([imageDedup[idx]['image_id'] for idx in c]))
for c in nx.components.connected_components(nx.Graph(distance <= 1))]
# imageDedup[image_id_to_idx('reddit/AusFinance/fman6b_0')]
def dedup_image (ids):
imagedd = ImageDedup([imageDedup[image_id_to_idx(i)] for i in set(ids)])
# if imagedd.main_post['source'] != 'dataisugly':
# print(f"Image not from dataisugly: {imagedd.main_post['post_id']}")
for i in imagedd.duplicated_images:
imagededup.delete_one({'image_id': i})
imagededup.replace_one({'image_id': imagedd.image_id}, imagedd.digest(), upsert=True)
return imagedd
imagedds = parallel(dedup_image, duplicated_images, n_jobs=-1)
# duplicated_image_ids = [c
# for c in nx.components.connected_components(nx.Graph(distance <= 1))
# if len(c) > 1]
# start = 0
# # len(duplicated_image_ids)
# cnt = 0
# end = start + 50
# for idxs in duplicated_image_ids:
# # print(f"{[imageDedup[i]['image_id'] for i in idxs]}")
# # if len(idxs) == 2:
# if len(idxs) >= 4:
# if cnt >= start:
# print(*[imageDedup[i]['image_id'] for i in idxs])
# print(*[imageDedup[i]['phash'] for i in idxs])
# display(HBox([
# widgets.Image(value=open(imageDedup[i]['file_path'], 'rb').read(), width=100, height=100)
# for i in idxs]))
# cnt += 1
# if cnt >= end:
# print(end)
# start = end
# break
```
| github_jupyter |
# Using enterprise_extensions to analyze PTA data
In this notebook you will learn:
* How to use `enterprise_extensions` to create `enterprise` models,
* How to search in PTA data for a isotropic stochastic gravitational wave background using multiple pulsars,
* How to implement a HyperModel object to sample a `model_2a` model,
* How to post-process your results.
```
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
%load_ext autoreload
%autoreload 2
import os, glob, json, pickle
import matplotlib.pyplot as plt
import numpy as np
from enterprise.pulsar import Pulsar
from enterprise_extensions import models, hypermodel
import sys
sys.path.append("..")
from settings import fd_bins
```
## Get par, tim, and noise files
```
psrlist = None # define a list of pulsar name strings that can be used to filter.
# set the data directory
datadir = '../data'
if not os.path.isdir(datadir):
datadir = '../../data'
print('datadir =', datadir)
# for the entire pta
parfiles = sorted(glob.glob(datadir + '/par/*par'))
timfiles = sorted(glob.glob(datadir + '/tim/*tim'))
# filter
if psrlist is not None:
parfiles = [x for x in parfiles if x.split('/')[-1].split('.')[0] in psrlist]
timfiles = [x for x in timfiles if x.split('/')[-1].split('.')[0] in psrlist]
# Make sure you use the tempo2 parfile for J1713+0747!!
# ...filtering out the tempo parfile...
parfiles = [x for x in parfiles if 'J1713+0747_NANOGrav_12yv3.gls.par' not in x]
```
## Read par and tim files into `enterprise` `Pulsar` objects
```
# check for file and load pickle if it exists:
pickle_loc = datadir + '/psrs.pkl'
if os.path.exists(pickle_loc):
with open(pickle_loc, 'rb') as f:
psrs = pickle.load(f)
# else: load them in slowly:
else:
psrs = []
ephemeris = 'DE438'
for p, t in zip(parfiles, timfiles):
psr = Pulsar(p, t, ephem=ephemeris)
psrs.append(psr)
# Make your own pickle of these loaded objects to reduce load times significantly
# at the cost of some space on your computer (~1.8 GB).
with open(datadir + '/psrs.pkl', 'wb') as f:
pickle.dump(psrs, f)
## Get parameter noise dictionary
noise_ng12 = datadir + '/channelized_12p5yr_v3_full_noisedict.json'
params = {}
with open(noise_ng12, 'r') as fp:
params.update(json.load(fp))
```
### Set up PTA model
* This model_2a includes everything from the verbose version in these tutorials:
* fixed white noise parameters based on noisedict `params`,
* common red noise signal (no correlation function) with 5 frequencies,
* and a spectral index of 13/3
```
pta = models.model_2a(psrs,
psd='powerlaw',
noisedict=params,
n_gwbfreqs=5, # modify the number of common red noise frequencies used here
gamma_common=13/3) # remove this line for a varying spectral index
```
### Setup an instance of a HyperModel.
* This doesn't mean we are doing model selection (yet!), but the
hypermodel module gives access to some nifty sampling schemes.
```
super_model = hypermodel.HyperModel({0: pta})
```
### Setup PTMCMCSampler
```
outDir = '../../chains/extensions_chains'
sampler = super_model.setup_sampler(resume=True,
outdir=outDir,
sample_nmodel=False,)
# sampler for N steps
N = int(5e6)
x0 = super_model.initial_sample()
# Sampling this will take a very long time. If you want to sample it yourself, uncomment the next line:
# sampler.sample(x0, N, SCAMweight=30, AMweight=15, DEweight=50, )
```
### Plot Output
```
# Uncomment this one to load the chain if you have sampled with PTMCMCSampler:
# chain = np.loadtxt(os.path.join(outDir, 'chain_1.txt'))
# This will load the chain that we have provided:
chain = np.load(os.path.join(outDir, 'chain_1.npz'))['arr_0']
burn = int(0.25 * chain.shape[0]) # remove burn in segment of sampling
ind = list(pta.param_names).index('gw_log10_A')
# Make trace-plot to diagnose sampling
plt.figure(figsize=(12, 5))
plt.plot(chain[burn:, ind])
plt.xlabel('Sample Number')
plt.ylabel('log10_A_gw')
plt.title('Trace Plot')
plt.grid(b=True)
plt.show()
# Plot a histogram of the marginalized posterior distribution
bins = fd_bins(chain[:, ind], logAmin=-18, logAmax=-12) # let FD rule decide bins (in ../settings.py)
plt.figure(figsize=(12, 5))
plt.title('Histogram')
plt.hist(chain[:, ind], bins=bins, histtype='stepfilled',
lw=2, color='C0', alpha=0.5, density=True)
plt.xlabel('log10_A_gw')
plt.show()
# Compute maximum posterior value
hist = np.histogram(chain[burn:, pta.param_names.index('gw_log10_A')],
bins=bins,
density=True)
max_ind = np.argmax(hist[0])
print('our_max =', hist[1][max_ind]) # from our computation
```
This analysis is consistent with the verbose version.
Here we have introduced some convenient methods:
* Using a HyperModel object for a single model,
* Using `enterprise_extensions` to create the model,
* Sampling a `HyperModel` with `PTMCMCSampler`.
| github_jupyter |
### This Notebook is done for Pixelated Data for 1 Compton, 2 PhotoElectric with 2 more Ambiguity!
#### I got 89% Accuracy on Test set!
##### I am getting X from Blurred Dataset, y as labels from Ground Truth
```
import pandas as pd
import numpy as np
from keras.utils import to_categorical
import math
df = {'Label':[],
'Theta_P1':[], 'Theta_E1':[], 'Theta_P2':[], 'Theta_E2':[], 'Theta_P3':[], 'Theta_E3':[], 'Theta_P4':[], 'Theta_E4':[],
'Theta_P5':[], 'Theta_E5':[], 'Theta_P6':[], 'Theta_E6':[], 'Theta_P7':[], 'Theta_E7':[], 'Theta_P8':[], 'Theta_E8':[],
'y': []}
with open("Data/test_Output_8.csv", 'r') as f:
counter = 0
counter_Theta_E = 0
for line in f:
sline = line.split('\t')
if len(sline) == 12:
df['Label'].append(int(sline[0]))
df['Theta_P1'].append(float(sline[1]))
df['Theta_E1'].append(float(sline[4]))
df['Theta_P2'].append(float(sline[5]))
df['Theta_E2'].append(float(sline[6]))
df['Theta_P3'].append(float(sline[7]))
df['Theta_E3'].append(float(sline[8]))
df['Theta_P4'].append(float(sline[9]))
df['Theta_E4'].append(float(sline[10]))
df['y'].append(int(sline[11]))
# df.info() Counts Nan in the dataset
df = pd.DataFrame(df)
df.to_csv('GroundTruth.csv', index=False)
df[0:4]
X = []
y = []
df = pd.read_csv('GroundTruth.csv')
for i in range(0, len(df)-1, 1): # these are from Blurred Data!
features = df.loc[i, 'Theta_P1':'Theta_E4'].values.tolist()
label = df.loc[i, 'y':'y'].values.tolist()
X.append(features)
y.append(label)
X = np.array(X)
y = np.array(y)
y = to_categorical(y, num_classes=None, dtype='float32')
print(y[0])
# ID = df.loc[i,'ID'] # get family ID from blurred dataframe
# gt_temp_rows = df[df['ID'] == ID] # find corresponding rows in grund truth dataframe
# count = 0
# if (len(gt_temp_rows)==0) or(len(gt_temp_rows)==1): # yani exactly we have 2 lines!
# count += 1
# continue
# idx = gt_temp_rows.index.tolist()[0] # read the first row's index
# # print(len(gt_temp_rows))
# # print(gt_temp_rows.index.tolist())
# # # set the target value
# # print('********************')
# # print('eventID_label:', int(sline[0]))
# # print(gt_temp_rows)
# if (gt_temp_rows.loc[idx, 'DDA':'DDA'].item() <= gt_temp_rows.loc[idx+1, 'DDA':'DDA'].item()):
# label = 1
# else:
# label = 0
# X.append(row1)
# y.append(label)
# X = np.array(X)
# y = np.array(y)
# # print(y)
# y = to_categorical(y, num_classes=None, dtype='float32')
# # print(y)
```
# Define the Model
```
# Define the keras model
from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add(Dense(128, input_dim=X.shape[1], activation='relu')) #8, 8: 58 12, 8:64 32,16: 66 16,16: 67
model.add(Dense(64, activation='relu'))
model.add(Dense(64, activation='relu'))
model.add(Dense(y.shape[1], activation='softmax'))
model.summary()#CNN, LSTM, RNN, Residual, dense
print(model)
# compile the keras model
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
#loss: categorical_crossentropy (softmax output vector mide: multi class classification)
#binary_crossentropy (sigmoid output: binary classification)
#mean_squared_error MSE
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# fit the keras model on the dataset
history = model.fit(X_train, y_train, epochs=220, batch_size=10, validation_split=0.15)
import matplotlib.pyplot as plt
# Plot training & validation loss values
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Valid'], loc='upper left')
plt.grid(True)
# plt.xticks(np.arange(1, 100, 5))
plt.show()
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('Model Accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Valid'], loc='upper left')
plt.grid(True)
# plt.xticks(np.arange(1, 100, 5))
plt.show()
# Evaluating trained model on test set. This Accuracy came from DDA Labeling
_, accuracy = model.evaluate(X_test, y_test)
print('Accuracy: %.2f' % (accuracy*100))
```
# HyperParameterOptimization
```
def create_model(hyperParams):
hidden_layers = hyperParams['hidden_layers']
activation = hyperParams['activation']
dropout = hyperParams['dropout']
output_activation = hyperParams['output_activation']
loss = hyperParams['loss']
input_size = hyperParams['input_size']
output_size = hyperParams['output_size']
model = Sequential()
model.add(Dense(hidden_layers[0], input_shape=(input_size,), activation=activation))
model.add(Dropout(dropout))
for i in range(len(hidden_layers)-1):
model.add(Dense(hidden_layers[i], activation=activation))
model.add(Dropout(dropout))
model.add(Dense(output_size, activation=output_activation))
model.compile(loss=loss, optimizer='adam', metrics=['accuracy'])
# categorical_crossentropy, binary_crossentropy
return model
def cv_model_fit(X, y, hyperParams):
kfold = KFold(n_splits=10, shuffle=True)
scores=[]
for train_idx, test_idx in kfold.split(X):
model = create_model(hyperParams)
model.fit(X[train_idx], y[train_idx], batch_size=hyperParams['batch_size'],
epochs=hyperParams['epochs'], verbose=0)
score = model.evaluate(X[test_idx], y[test_idx], verbose=0)
scores.append(score*100) # f_score
# print('fold ', len(scores), ' score: ', scores[-1])
del model
return scores
# hyper parameter optimization
from itertools import product
from sklearn.model_selection import KFold
from keras.layers import Activation, Conv2D, Input, Embedding, Reshape, MaxPool2D, Concatenate, Flatten, Dropout, Dense, Conv1D
# default parameter setting:
hyperParams = {'input_size': 4, 'output_size': 2, 'batch_size': 32, 'epochs': 100, 'hidden_layers': [512, 512, 128],
'activation': 'relu', 'dropout': 0.5, 'output_activation': 'softmax', 'loss': 'categorical_crossentropy'}
# parameter search space:
batch_chices = [32]
epochs_choices = [100]
hidden_layers_choices = [[4, 4], [16, 32],
[8, 8, 8], [4, 8, 16],
[4, 4, 4]]
activation_choices = ['relu', 'sigmoid'] #, 'tanh'
dropout_choices = [ 0.5]
s = [batch_chices, epochs_choices, hidden_layers_choices, activation_choices, dropout_choices]
perms = list(product(*s)) # permutations
# Linear search:
best_score = 0
for row in perms:
hyperParams['batch_size'] = row[0]
hyperParams['epochs'] = row[1]
hyperParams['hidden_layers'] = row[2]
hyperParams['activation'] = row[3]
hyperParams['dropout'] = row[4]
print('10-fold cross validation on these hyperparameters: ', hyperParams, '\n')
cvscores = cv_model_fit(X, y, hyperParams)
print('\n-------------------------------------------')
mean_score = np.mean(cvscores)
std_score = np.std(cvscores)
# Update the best parameter setting:
print('CV mean: {0:0.4f}, CV std: {1:0.4f}'.format(mean_score, std_score))
if mean_score > best_score: # later I should incorporate std in best model selection
best_score = mean_score
print('****** Best model so far ******')
best_params = hyperParams
print('-------------------------------------------\n')
```
| github_jupyter |
# LassoLars Regression with Scale
This Code template is for the regression analysis using a simple LassoLars Regression. It is a lasso model implemented using the LARS algorithm and feature scaling.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import seaborn as se
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn import preprocessing
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
from sklearn.linear_model import LassoLars
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
```
###Data Scaling
Standardize a dataset along any axis.
Center to the mean and component wise scale to unit variance.<br>
For more information... [click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.scale.html)
```
x_train = preprocessing.scale(x_train)
x_test = preprocessing.scale(x_test)
```
### Model
LassoLars is a lasso model implemented using the LARS algorithm, and unlike the implementation based on coordinate descent, this yields the exact solution, which is piecewise linear as a function of the norm of its coefficients.
### Tuning parameters
> **fit_intercept** -> whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations
> **alpha** -> Constant that multiplies the penalty term. Defaults to 1.0. alpha = 0 is equivalent to an ordinary least square, solved by LinearRegression. For numerical reasons, using alpha = 0 with the LassoLars object is not advised and you should prefer the LinearRegression object.
> **eps** -> The machine-precision regularization in the computation of the Cholesky diagonal factors. Increase this for very ill-conditioned systems. Unlike the tol parameter in some iterative optimization-based algorithms, this parameter does not control the tolerance of the optimization.
> **max_iter** -> Maximum number of iterations to perform.
> **positive** -> Restrict coefficients to be >= 0. Be aware that you might want to remove fit_intercept which is set True by default. Under the positive restriction the model coefficients will not converge to the ordinary-least-squares solution for small values of alpha. Only coefficients up to the smallest alpha value (alphas_[alphas_ > 0.].min() when fit_path=True) reached by the stepwise Lars-Lasso algorithm are typically in congruence with the solution of the coordinate descent Lasso estimator.
> **precompute** -> Whether to use a precomputed Gram matrix to speed up calculations.
```
model=LassoLars()
model.fit(x_train,y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
score: The score function returns the coefficient of determination R2 of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(14,10))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(x_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator: Anu Rithiga , Github: [Profile](https://github.com/iamgrootsh7)
| github_jupyter |
[Table of Contents](./table_of_contents.ipynb)
# Discrete Bayes Filter
# 离散贝叶斯滤波
```
%matplotlib inline
#format the book
import book_format
book_format.set_style()
```
The Kalman filter belongs to a family of filters called *Bayesian filters*. Most textbook treatments of the Kalman filter present the Bayesian formula, perhaps shows how it factors into the Kalman filter equations, but mostly keeps the discussion at a very abstract level.
That approach requires a fairly sophisticated understanding of several fields of mathematics, and it still leaves much of the work of understanding and forming an intuitive grasp of the situation in the hands of the reader.
I will use a different way to develop the topic, to which I owe the work of Dieter Fox and Sebastian Thrun a great debt. It depends on building an intuition on how Bayesian statistics work by tracking an object through a hallway - they use a robot, I use a dog. I like dogs, and they are less predictable than robots which imposes interesting difficulties for filtering. The first published example of this that I can find seems to be Fox 1999 [1], with a fuller example in Fox 2003 [2]. Sebastian Thrun also uses this formulation in his excellent Udacity course Artificial Intelligence for Robotics [3]. In fact, if you like watching videos, I highly recommend pausing reading this book in favor of first few lessons of that course, and then come back to this book for a deeper dive into the topic.
Let's now use a simple thought experiment, much like we did with the g-h filter, to see how we might reason about the use of probabilities for filtering and tracking.
卡爾曼濾波器屬於一個名為“貝葉斯濾波器”的大家族。許多教材将卡爾曼濾波器作為貝葉斯公式的範例講授,例如展示貝葉斯公式是如何組成卡爾曼濾波器公式的。這些討論往往停留在抽象层面。
這種學習方法需要讀者理解許多複雜的數學知識,而且無助於讀者直觀地理解卡爾曼濾波器。
我會用不一樣的方式展開這個主題。對此,我首先要感謝Dieter Fox和Sebastian Thrun的工作,從他們那裡我獲益良多。具體来說,我會以如何跟踪走廊上的一個目標為例來為你建立對貝葉斯統計方法的直覺上的理解——別人使用機器人作為目標,而我則喜欢用狗。原因是狗的運動比機器人的更難預測,這為濾波任務帶來許多有趣的挑戰。我找到的關於這類例子最早的記錄見於Fox於1999年所作的【1】,隨後他在2003年的【2】中增加了更多細節。Sebastian Thrun在他的優達學城的“面向机器人学的人工智能”课程上引用了這個例子。如果你喜欢看視頻,我强烈建議你在閱讀本書之前先學一學該課程的前面几節,然后再回来繼續深入了解這個問題。
像先前g-h濾波器一章中那樣,讓我們从一个簡單的思想實驗開始,看看如何用概率工具来解释濾波器和跟蹤器。
## Tracking a Dog
Let's begin with a simple problem. We have a dog friendly workspace, and so people bring their dogs to work. Occasionally the dogs wander out of offices and down the halls. We want to be able to track them. So during a hackathon somebody invented a sonar sensor to attach to the dog's collar. It emits a signal, listens for the echo, and based on how quickly an echo comes back we can tell whether the dog is in front of an open doorway or not. It also senses when the dog walks, and reports in which direction the dog has moved. It connects to the network via wifi and sends an update once a second.
I want to track my dog Simon, so I attach the device to his collar and then fire up Python, ready to write code to track him through the building. At first blush this may appear impossible. If I start listening to the sensor of Simon's collar I might read **door**, **hall**, **hall**, and so on. How can I use that information to determine where Simon is?
To keep the problem small enough to plot easily we will assume that there are only 10 positions in the hallway, which we will number 0 to 9, where 1 is to the right of 0. For reasons that will be clear later, we will also assume that the hallway is circular or rectangular. If you move right from position 9, you will be at position 0.
When I begin listening to the sensor I have no reason to believe that Simon is at any particular position in the hallway. From my perspective he is equally likely to be in any position. There are 10 positions, so the probability that he is in any given position is 1/10.
Let's represent our belief of his position in a NumPy array. I could use a Python list, but NumPy arrays offer functionality that we will be using soon.
## 狗的跟蹤問題
我们先从一个简单的问题开始。因为我们的工作室是宠物友好型,所以同事们会带狗狗到工作场所来。偶尔狗会从办公室跑出来,到走廊去玩。因為我们希望能跟踪狗的运动,所以在一次黑客马拉松上,某个人提出在狗狗的项圈上装一个超声波传感器。传感器能发出声波,并接受回声。根据回声的速度,传感器能够输出狗是否來到了開放的門道前。它能够在狗运动的时候给出信号,报告运动的方向。它还能通过无线网络连接以每秒钟一次的频率上传数据。
我想要跟踪我的狗,西蒙。于是我打开Python,准备編寫代码来实现在建筑内跟踪狗狗的功能。乍看起来这似乎不可能。如果我监听西蒙项圈传来的信号,能得到類似於**门、走廊、走廊**這樣的一连串信号。但我们如何才能使用这些信号确定西蒙的位置呢?
為控制問題的規模以便於繪圖,我們假設走廊中一共僅有10個不同的地點,從0到9標號。1號在0號右側。我們還假設走廊是圓形或矩形的環,其中理由隨後自明。於是當你從9號地點向右移動,你就會回到0點。
我開始監聽傳感器時,我並沒有任何理由相信西蒙現在位於某個具體地點。從這一角度看,他在任意位置的可能性都是均等的。一共有10個位置,所以每個位置的概率都是1/10.
首先,我们将狗狗在各个位置的置信度表示为一个NumPy数组。雖然用Python提供的list也可以,但NumPy数组提供了一些我們需要的功能。
```
import numpy as np
belief = np.array([1/10]*10)
print(belief)
```
In [Bayesian statistics](https://en.wikipedia.org/wiki/Bayesian_probability) this is called a [*prior*](https://en.wikipedia.org/wiki/Prior_probability). It is the probability prior to incorporating measurements or other information. More completely, this is called the *prior probability distribution*. A [*probability distribution*](https://en.wikipedia.org/wiki/Probability_distribution) is a collection of all possible probabilities for an event. Probability distributions always sum to 1 because something had to happen; the distribution lists all possible events and the probability of each.
I'm sure you've used probabilities before - as in "the probability of rain today is 30%". The last paragraph sounds like more of that. But Bayesian statistics was a revolution in probability because it treats probability as a belief about a single event. Let's take an example. I know that if I flip a fair coin infinitely many times I will get 50% heads and 50% tails. This is called [*frequentist statistics*](https://en.wikipedia.org/wiki/Frequentist_inference) to distinguish it from Bayesian statistics. Computations are based on the frequency in which events occur.
I flip the coin one more time and let it land. Which way do I believe it landed? Frequentist probability has nothing to say about that; it will merely state that 50% of coin flips land as heads. In some ways it is meaningless to assign a probability to the current state of the coin. It is either heads or tails, we just don't know which. Bayes treats this as a belief about a single event - the strength of my belief or knowledge that this specific coin flip is heads is 50%. Some object to the term "belief"; belief can imply holding something to be true without evidence. In this book it always is a measure of the strength of our knowledge. We'll learn more about this as we go.
Bayesian statistics takes past information (the prior) into account. We observe that it rains 4 times every 100 days. From this I could state that the chance of rain tomorrow is 1/25. This is not how weather prediction is done. If I know it is raining today and the storm front is stalled, it is likely to rain tomorrow. Weather prediction is Bayesian.
In practice statisticians use a mix of frequentist and Bayesian techniques. Sometimes finding the prior is difficult or impossible, and frequentist techniques rule. In this book we can find the prior. When I talk about the probability of something I am referring to the probability that some specific thing is true given past events. When I do that I'm taking the Bayesian approach.
Now let's create a map of the hallway. We'll place the first two doors close together, and then another door further away. We will use 1 for doors, and 0 for walls:
在[贝叶斯统计学](https://en.wikipedia.org/wiki/Bayesian_probability)中这被称为[先验](https://en.wikipedia.org/wiki/Prior_probability). 它是在考虑测量结果或其它信息之前的概率。更完整的说,这叫做“先验概率”。 所谓[“先验概率”](https://en.wikipedia.org/wiki/Probability_distribution)是某个事件所有可能概率的集合。由于所有可能之中必有其一真实发生,所以概率分布的总和恆等於1。概率分布列出了所有可能的事件及每个事件的对应概率。
我知道你肯定有使用过概率——比如“今天下雨的概率是30%”。這句話與上一段文字有相似的含義。贝叶斯统计是概率论的一场革命,是因为它将概率视作是每个事件的置信度。举例来说,如果我多次抛掷一个理想的硬币,我将得到50%正面,50%反面的统计结果。这叫做[频率统计](https://en.wikipedia.org/wiki/Frequentist_inference)。同贝叶斯统计不同,频率统计的計算基於事件發生的頻率。
假如我再掷一次硬币,我相信它是哪一面落地?频率學派對此沒有什麼建議。它唯一能回答的是,有50%的硬币正面朝上。然而從某些方面看,像這樣为硬币的当前状态赋予概率是无意义的。它要么正要么反,只是我們不確定罷了。贝叶斯学派則將此視為单个事件的信念——它表示我们对该硬币正面朝上的概率是50%的信念或者知识。“信念”一词的含义是,在没有充分的证据的情况下相信某种情况属实。本书中,始终使用置信度来作为对知识的强度的度量。随着阅读的继续,我们将了解更多细节。
贝叶斯统计学考虑過去的信息(先验概率)。通过觀察我们知道过去100天内有4天下雨,据此推出明天下雨的概率是1/25. 当然天气预报不是这么做的。如果我知道今天是雨天,而风暴的边沿移动迟缓,于是我猜测明天继续下雨。这才是天气预报的做法,属于贝叶斯方法。
实践中频率统计和贝叶斯方法常常混合使用。有时候先验难以取得,或者无法取得,就使用频率统计的方法。本书中,先验是提供了的。当我们提到某事的概率时,我们指的是已知过去的系列事件的條件下,某事为真的概率。这时我们使用的是贝叶斯方法。
现在,我们来为走廊建一个地图。我们将两个门靠近放在一起,另一个门放远一些。用1表示门,0表示墙壁。
```
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
```
I start listening to Simon's transmissions on the network, and the first data I get from the sensor is **door**. For the moment assume the sensor always returns the correct answer. From this I conclude that he is in front of a door, but which one? I have no reason to believe he is in front of the first, second, or third door. What I can do is assign a probability to each door. All doors are equally likely, and there are three of them, so I assign a probability of 1/3 to each door.
我开始监听西蒙发送到网络的信号,得到的第一个数据是**门**。假設传感器返回的信号永远准确,於是我知道西蒙就在某道门前。但是是哪一道门?我没有理由去相信它现在是在第一道门前。对于第二三道门也是如此。我唯一能做的是为各个门的赋予一个置信度。因为每个门看起来都是等可能的,而有三道门,故我为每道门赋予$1/3$的置信度。
```
import kf_book.book_plots as book_plots
from kf_book.book_plots import figsize, set_figsize
import matplotlib.pyplot as plt
belief = np.array([1/3, 1/3, 0, 0, 0, 0, 0, 0, 1/3, 0])
book_plots.bar_plot(belief)
```
This distribution is called a [*categorical distribution*](https://en.wikipedia.org/wiki/Categorical_distribution), which is a discrete distribution describing the probability of observing $n$ outcomes. It is a [*multimodal distribution*](https://en.wikipedia.org/wiki/Multimodal_distribution) because we have multiple beliefs about the position of our dog. Of course we are not saying that we think he is simultaneously in three different locations, merely that we have narrowed down our knowledge to one of these three locations. My (Bayesian) belief is that there is a 33.3% chance of being at door 0, 33.3% at door 1, and a 33.3% chance of being at door 8.
This is an improvement in two ways. I've rejected a number of hallway positions as impossible, and the strength of my belief in the remaining positions has increased from 10% to 33%. This will always happen. As our knowledge improves the probabilities will get closer to 100%.
A few words about the [*mode*](https://en.wikipedia.org/wiki/Mode_%28statistics%29)
of a distribution. Given a list of numbers, such as {1, 2, 2, 2, 3, 3, 4}, the *mode* is the number that occurs most often. For this set the mode is 2. A distribution can contain more than one mode. The list {1, 2, 2, 2, 3, 3, 4, 4, 4} contains the modes 2 and 4, because both occur three times. We say the former list is [*unimodal*](https://en.wikipedia.org/wiki/Unimodality), and the latter is *multimodal*.
Another term used for this distribution is a [*histogram*](https://en.wikipedia.org/wiki/Histogram). Histograms graphically depict the distribution of a set of numbers. The bar chart above is a histogram.
I hand coded the `belief` array in the code above. How would we implement this in code? We represent doors with 1, and walls as 0, so we will multiply the hallway variable by the percentage, like so;
此分布称为[**分类分布**](https://en.wikipedia.org/wiki/Categorical_distribution),它是描述了$n$个输出的离散分布。它还是[**多峰分布(multimodal distribution)**](https://en.wikipedia.org/wiki/Multimodal_distribution) ,因为它为狗的多种可能位置给出了置信度。当然这不是说我们认为它可以同时出现在三个不同的位置,我们只是根据知识将范围缩小到三个位置之一。我们的(贝叶斯)置信度认为狗狗有33.3%的概率出现在0号门,有33.3%的方式出现在1号门,还有33.3%的方式出现在8号门。
我们的改进体现在两个方面。一是我们拒绝了狗狗在一些位置出现的可能性,二是我们将余下位置的置信度从10%增长到33%。随着我们知识的增加,这种差别会更加明显。
这里要说一說分布的[**众数(mode)**](https://en.wikipedia.org/wiki/Mode_%28statistics%29)。给定一个数组,比如{1, 2, 2, 2, 3, 3, 4}, **众数**是其中出现次数最多的数。对于该例,众数是2. 一个分布可以有多个众数。例如{1, 2, 2, 2, 3, 3, 4, 4, 4}的众数是2和4,因为它们都出现三次。所以第一个数组是[**单峰分布**](https://en.wikipedia.org/wiki/Unimodality),后一个数组是**多峰分布**。
另一个重要的概念是[**直方图**](https://en.wikipedia.org/wiki/Histogram)。直方图通过图像的形式了一系列数组分布。上面那个图就是直方图的一个例子。
上面的置信度数组`belief`是我手算的。如何用代码来实现这个过程呢?我们用1表示门,用0表示墙。我们用一个比例乘以这个数组,如下所示。
```
belief = hallway * (1/3)
print(belief)
```
## Extracting Information from Sensor Readings
Let's put Python aside and think about the problem a bit. Suppose we were to read the following from Simon's sensor:
* door
* move right
* door
Can we deduce Simon's location? Of course! Given the hallway's layout there is only one place from which you can get this sequence, and that is at the left end. Therefore we can confidently state that Simon is in front of the second doorway. If this is not clear, suppose Simon had started at the second or third door. After moving to the right, his sensor would have returned 'wall'. That doesn't match the sensor readings, so we know he didn't start there. We can continue with that logic for all the remaining starting positions. The only possibility is that he is now in front of the second door. Our belief is:
## 从传感器读数中提取信息
我们先抛开Python来思考这个问题。假如我们从西蒙的传感器读取到如下数据:
* 门
* 右移
* 门
我们可以推导出西蒙的位置吗?当然可以!根据走廊的地图,只有一个位置可以产生测得的序列,即地图的最左端。因此我们非常肯定西蒙在第二道门前。如果这还不够清晰,可以试着假定西蒙从第二道门或第三道门出发,向右走。这样它的传感器会返回“墙”这个信号。这与传感器实际读数不匹配,所以我们知道这两处不是真正的起点。我们也可以在其它可能起点重复这样的推理。唯一的可能是西蒙目前在第二道门前。我们的置信度是:
```
belief = np.array([0., 1., 0., 0., 0., 0., 0., 0., 0., 0.])
```
I designed the hallway layout and sensor readings to give us an exact answer quickly. Real problems are not so clear cut. But this should trigger your intuition - the first sensor reading only gave us low probabilities (0.333) for Simon's location, but after a position update and another sensor reading we know more about where he is. You might suspect, correctly, that if you had a very long hallway with a large number of doors that after several sensor readings and positions updates we would either be able to know where Simon was, or have the possibilities narrowed down to a small number of possibilities. This is possible when a set of sensor readings only matches one to a few starting locations.
We could implement this solution now, but instead let's consider a real world complication to the problem.
我特意将走廊的地图以及传感器的读数设计成这样以方便快速得到准确的答案。但现实问题往往没有这么清晰。但这个例子可以帮助你建立一种直觉——当收到第一个传感器信号的时候,我们只能以一个较低的置信度(0.333)猜测西蒙的位置,但是当第二个传感器数据到来时,我们就获得了更多关于西蒙位置的信息。你猜得对,就算有一道很长的走廊和许多道门,只要我们有一段足够长的传感器读数和位置更新的信息,我们就能定位西蒙,或者将可能性缩小到有限的几种情况。因为有可能一系列传感器读数只能通过个别起始点获得。
我们现在就可以实现该解法,但在此之前,让我们再考虑考虑这个问题在现实世界中的复杂性。
## Noisy Sensors
Perfect sensors are rare. Perhaps the sensor would not detect a door if Simon sat in front of it while scratching himself, or misread if he is not facing down the hallway. Thus when I get **door** I cannot use 1/3 as the probability. I have to assign less than 1/3 to each door, and assign a small probability to each blank wall position. Something like
```Python
[.31, .31, .01, .01, .01, .01, .01, .01, .31, .01]
```
At first this may seem insurmountable. If the sensor is noisy it casts doubt on every piece of data. How can we conclude anything if we are always unsure?
The answer, as for the problem above, is with probabilities. We are already comfortable assigning a probabilistic belief to the location of the dog; now we have to incorporate the additional uncertainty caused by the sensor noise.
Say we get a reading of **door**, and suppose that testing shows that the sensor is 3 times more likely to be right than wrong. We should scale the probability distribution by 3 where there is a door. If we do that the result will no longer be a probability distribution, but we will learn how to fix that in a moment.
Let's look at that in Python code. Here I use the variable `z` to denote the measurement. `z` or `y` are customary choices in the literature for the measurement. As a programmer I prefer meaningful variable names, but I want you to be able to read the literature and/or other filtering code, so I will start introducing these abbreviated names now.
## 传感器噪声
不存在有理想的傳感器。傳感器有可能在西蒙坐在門前撓癢癢的時候無法給出正确定位,也有可能在沒有正面朝向走廊時候給出錯誤讀數。因此當傳感器傳來“門”這一數據时,我不能使用$1/3$作为其概率,而應使用比$1/3$小的数作为門的概率,然后用一个较小的值作为其它位置的概率。一个可能的情况是:
```Python
[.31, .31, .01, .01, .01, .01, .01, .01, .31, .01]
```
乍看之下,问题似乎是无解的。如果传感器含有噪声,那么每一段数据都值得怀疑。在我們無法確定任何事情的情況下,如何下結論呢?
同上面那個問題的回答一樣,我們應該使用概率。我們對於為每個可能的位置賦予一定概率的做法已經習慣了。那麼現在我們需要將傳感器噪聲導致的額外的不確定性考慮進來。
假如我們得到傳感器數據“門”,同時假設根據測試,該類數據正確的概率是錯誤的概率的三倍。在此情況下,概率分佈上對應門的位置應當放大三倍。如果我們這麼做,原來的數據就不再是概率分佈了,但我們後面會介紹修復這個問題的方法。
讓我們看看這種做法用Python怎麼寫。我們這裡用`z`表示測量值。`z`或`y`常常在文獻中用來代表測量值。作為程序員我喜歡更有意義的名字,但我還希望能方便你閱讀有關文獻和查看其它濾波器的代碼,因此我這裡會使用這些簡化的變量名。
```
def update_belief(hall, belief, z, correct_scale):
for i, val in enumerate(hall):
if val == z:
belief[i] *= correct_scale
belief = np.array([0.1] * 10)
reading = 1 # 1 is 'door'
update_belief(hallway, belief, z=reading, correct_scale=3.)
print('belief:', belief)
print('sum =', sum(belief))
plt.figure()
book_plots.bar_plot(belief)
```
This is not a probability distribution because it does not sum to 1.0. But the code is doing mostly the right thing - the doors are assigned a number (0.3) that is 3 times higher than the walls (0.1). All we need to do is normalize the result so that the probabilities correctly sum to 1.0. Normalization is done by dividing each element by the sum of all elements in the list. That is easy with NumPy:
該數組的和不為1,因而不構成一個概率分佈。但代碼所作的事情大致還是對的——門對應的置信度(0.3)是其它位置的置信度(0,1)的三倍。我們只需做一個歸一化,就能使數組的和為1. 所謂歸一化,是將數組的各個元素除以自身的總和。這很容易用NumPy實現:
```
belief / sum(belief)
```
FilterPy implements this with the `normalize` function:
```Python
from filterpy.discrete_bayes import normalize
normalize(belief)
```
It is a bit odd to say "3 times as likely to be right as wrong". We are working in probabilities, so let's specify the probability of the sensor being correct, and compute the scale factor from that. The equation for that is
$$scale = \frac{prob_{correct}}{prob_{incorrect}} = \frac{prob_{correct}} {1-prob_{correct}}$$
Also, the `for` loop is cumbersome. As a general rule you will want to avoid using `for` loops in NumPy code. NumPy is implemented in C and Fortran, so if you avoid for loops the result often runs 100x faster than the equivalent loop.
How do we get rid of this `for` loop? NumPy lets you index arrays with boolean arrays. You create a boolean array with logical operators. We can find all the doors in the hallway with:
FilterPy實現了該歸一化函數`normalize`:
```Python
from filterpy.discrete_bayes import normalize
normalize(belief)
```
“正確概率是錯誤概率三倍”這樣的說法很奇怪。我們既然以概率論為工具,那麼更好的做法還是為指定傳感器正確的概率,並據此計算縮放係數。公式如下
$$scale = \frac{prob_{correct}}{prob_{incorrect}} = \frac{prob_{correct}} {1-prob_{correct}}$$
另外,`for`循環也很多餘。通常你需要避免在使用NumPy時寫`for`循環。NumPy是用C和Fortran實現的,如果你能避免經常使用for循環,那麼程序往往能加快100倍。
如何避免`for`循環呢?NumPy可以使用布爾值作為數組的索引。布爾值可以用邏輯運算符得到。我們可以通過如下方式獲得所有門的位置:
```
hallway == 1
```
When you use the boolean array as an index to another array it returns only the elements where the index is `True`. Thus we can replace the `for` loop with
```python
belief[hall==z] *= scale
```
and only the elements which equal `z` will be multiplied by `scale`.
Teaching you NumPy is beyond the scope of this book. I will use idiomatic NumPy constructs and explain them the first time I present them. If you are new to NumPy there are many blog posts and videos on how to use NumPy efficiently and idiomatically.
Here is our improved version:
當你使用布爾類型數組作為其他數組的索引的時候,就會得到對應值為真的位置。根據這個原理我們可以用下面的代碼替換掉前面使用的`for`循環
```python
belief[hall==z] *= scale
```
這樣,只有對應`z`的位置的元素會被縮放`scale`倍。
本書的目的不是NumPy教學。我只會使用常見的NumPy寫法,並且在引入新用法的時候做介紹。如果你是NumPy的新手,網絡上又許多介紹如何高效、規範使用NumPy的文章和視頻。
經過改進的代碼如下:
```
from filterpy.discrete_bayes import normalize
def scaled_update(hall, belief, z, z_prob):
scale = z_prob / (1. - z_prob)
belief[hall==z] *= scale
normalize(belief)
belief = np.array([0.1] * 10)
scaled_update(hallway, belief, z=1, z_prob=.75)
print('sum =', sum(belief))
print('probability of door =', belief[0])
print('probability of wall =', belief[2])
book_plots.bar_plot(belief, ylim=(0, .3))
```
We can see from the output that the sum is now 1.0, and that the probability of a door vs wall is still three times larger. The result also fits our intuition that the probability of a door must be less than 0.333, and that the probability of a wall must be greater than 0.0. Finally, it should fit our intuition that we have not yet been given any information that would allow us to distinguish between any given door or wall position, so all door positions should have the same value, and the same should be true for wall positions.
This result is called the [*posterior*](https://en.wikipedia.org/wiki/Posterior_probability), which is short for *posterior probability distribution*. All this means is a probability distribution *after* incorporating the measurement information (posterior means 'after' in this context). To review, the *prior* is the probability distribution before including the measurement's information.
Another term is the [*likelihood*](https://en.wikipedia.org/wiki/Likelihood_function). When we computed `belief[hall==z] *= scale` we were computing how *likely* each position was given the measurement. The likelihood is not a probability distribution because it does not sum to one.
The combination of these gives the equation
$$\mathtt{posterior} = \frac{\mathtt{likelihood} \times \mathtt{prior}}{\mathtt{normalization}}$$
When we talk about the filter's output we typically call the state after performing the prediction the *prior* or *prediction*, and we call the state after the update either the *posterior* or the *estimated state*.
It is very important to learn and internalize these terms as most of the literature uses them extensively.
Does `scaled_update()` perform this computation? It does. Let me recast it into this form:
我們可以通過程序輸出看到數組的和為1.0,同時對應于門的概率是墻壁的概率的三倍。同時,結果顯示對應門的概率小於0.333,這是符合我們直覺的。除此之外,由於我們沒有任何信息能幫助我們對各個門、墻進行內部區分,因此所有墻壁具有一樣的概率,所有門具有一樣的概率,這也是符合我們認識的。
這個結果即所謂的[**後驗**](https://en.wikipedia.org/wiki/Posterior_probability),是**後驗概率分佈**的縮寫。這表示該概率分佈是在考慮測量結果信息**之後**得到的(英文的posterior在此上下文中意思等同於after)。複習一下,**先驗**概率是考慮測量結果信息之前的概率分佈。
另一個術語是[**似然**](https://en.wikipedia.org/wiki/Likelihood_function). 當我們計算`belief[hall==z] *= scale`時,我們計算的是給定測量結果後每個位置的**似然**程度。似然度不是概率分佈,因為其和不必等於1.
結合上述步驟可以得到如下公式
$$\mathtt{posterior} = \frac{\mathtt{likelihood} \times \mathtt{prior}}{\mathtt{normalization}}$$
當我們討論濾波器的輸出的時候,我們一般將更新前的狀態叫做**先驗**或者**預測**,將更新後的狀態叫做**後驗**或者**估計**。
大多數相關文獻廣泛使用類似術語,因此學習和內化這些術語非常重要。
函數`scaled_update()`包含了此操作了嗎?答案是肯定的。我們可以將其轉化為如下形式:
```
def scaled_update(hall, belief, z, z_prob):
scale = z_prob / (1. - z_prob)
likelihood = np.ones(len(hall))
likelihood[hall==z] *= scale
return normalize(likelihood * belief)
```
This function is not fully general. It contains knowledge about the hallway, and how we match measurements to it. We always strive to write general functions. Here we will remove the computation of the likelihood from the function, and require the caller to compute the likelihood themselves.
Here is a full implementation of the algorithm:
```python
def update(likelihood, prior):
return normalize(likelihood * prior)
```
Computation of the likelihood varies per problem. For example, the sensor might not return just 1 or 0, but a `float` between 0 and 1 indicating the probability of being in front of a door. It might use computer vision and report a blob shape that you then probabilistically match to a door. It might use sonar and return a distance reading. In each case the computation of the likelihood will be different. We will see many examples of this throughout the book, and learn how to perform these calculations.
FilterPy implements `update`. Here is the previous example in a fully general form:
這個函數還不夠通用。它包含有關於走廊問題以及測量方法的知識。而我們總是盡可能寫通用的函數。這裡我們要從函數中移除似然度的計算,要求函數調用者計算似然度。
算法的完整實現如下:
```python
def update(likelihood, prior):
return normalize(likelihood * prior)
```
對於不同問題,似然度計算方法不盡相同。例如,傳感器可能返回的不是0、1信號,而是返回一個出於0和1之間的浮點型小數用於表示目標出於門前的概率。它可能採用計算機視覺的方法去檢測團塊的外形來計算目標物體是門的概率。它也可能通過傳感器獲得距離的讀數。在不同的案例中,計算似然度的方式也不相同。本書中會介紹許多種不同的例子及對應的計算方式。
FilterPy也實現了`update`函數。前面的例子用完全通用的形式寫出來會是這樣:
```
from filterpy.discrete_bayes import update
def lh_hallway(hall, z, z_prob):
""" compute likelihood that a measurement matches
positions in the hallway."""
try:
scale = z_prob / (1. - z_prob)
except ZeroDivisionError:
scale = 1e8
likelihood = np.ones(len(hall))
likelihood[hall==z] *= scale
return likelihood
belief = np.array([0.1] * 10)
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
update(likelihood, belief)
```
## Incorporating Movement
Recall how quickly we were able to find an exact solution when we incorporated a series of measurements and movement updates. However, that occurred in a fictional world of perfect sensors. Might we be able to find an exact solution with noisy sensors?
Unfortunately, the answer is no. Even if the sensor readings perfectly match an extremely complicated hallway map, we cannot be 100% certain that the dog is in a specific position - there is, after all, a tiny possibility that every sensor reading was wrong! Naturally, in a more typical situation most sensor readings will be correct, and we might be close to 100% sure of our answer, but never 100% sure. This may seem complicated, but let's go ahead and program the math.
First let's deal with the simple case - assume the movement sensor is perfect, and it reports that the dog has moved one space to the right. How would we alter our `belief` array?
I hope that after a moment's thought it is clear that we should shift all the values one space to the right. If we previously thought there was a 50% chance of Simon being at position 3, then after he moved one position to the right we should believe that there is a 50% chance he is at position 4. The hallway is circular, so we will use modulo arithmetic to perform the shift.
## 考慮運動模型
回想一下之前我們是如何通過同時考慮一系列測量值和運動模型來快速找出準確解的。但是,該解法只存在於可以使用理想傳感器的幻想世界中。我們是否可以通過帶有噪聲的傳感器獲得精確解呢?
不幸的是,答案是否定的。即使傳感器讀數和複雜的走廊地圖完美吻合,我們還是無法百分百確定狗的確切位置——畢竟每個傳感器讀書都有小概率出錯!自然,在典型的環境中,大多數傳感器數據都是正確的,這使得我們的推理正確的概率接近100%,但也永遠達不到100%。這看起來有點複雜,我們且繼續前進,把數學代碼寫出來。
我們先解決一個簡單的問題——假如運動傳感器是準確的,它回報說狗向右移動一步。此時我們應如何更新`belief`數組?
略經思考,你已明白,我們應當將所有數值向右移動一步。假如我們先前認為西蒙處於位置3的概率為50%,那麼現在它處於位置4的概率為50%。走廊是環形的,所以我們使用取模運算來執行此操作。
```
def perfect_predict(belief, move):
""" move the position by `move` spaces, where positive is
to the right, and negative is to the left
"""
n = len(belief)
result = np.zeros(n)
for i in range(n):
result[i] = belief[(i-move) % n]
return result
belief = np.array([.35, .1, .2, .3, 0, 0, 0, 0, 0, .05])
plt.subplot(121)
book_plots.bar_plot(belief, title='Before prediction', ylim=(0, .4))
belief = perfect_predict(belief, 1)
plt.subplot(122)
book_plots.bar_plot(belief, title='After prediction', ylim=(0, .4))
```
We can see that we correctly shifted all values one position to the right, wrapping from the end of the array back to the beginning.
The next cell animates this so you can see it in action. Use the slider to move forwards and backwards in time. This simulates Simon walking around and around the hallway. It does not yet incorporate new measurements so the probability distribution does not change shape, only position.
可見我們正確地將所有數值都向右移動了一步,最右邊的數組回到了數組的左側。
下一個單元格輸出一個動畫。你可以用滑塊在時間上前移或後移。這就好像西蒙在走廊上四處遊走一般。因為沒有新的測量結果進來,分佈只是發生平移,形狀沒有改變。
```
from ipywidgets import interact, IntSlider
belief = np.array([.35, .1, .2, .3, 0, 0, 0, 0, 0, .05])
perfect_beliefs = []
for _ in range(20):
# Simon takes one step to the right
belief = perfect_predict(belief, 1)
perfect_beliefs.append(belief)
def simulate(time_step):
book_plots.bar_plot(perfect_beliefs[time_step], ylim=(0, .4))
interact(simulate, time_step=IntSlider(value=0, max=len(perfect_beliefs)-1));
```
## Terminology
Let's pause a moment to review terminology. I introduced this terminology in the last chapter, but let's take a second to help solidify your knowledge.
The *system* is what we are trying to model or filter. Here the system is our dog. The *state* is its current configuration or value. In this chapter the state is our dog's position. We rarely know the actual state, so we say our filters produce the *estimated state* of the system. In practice this often gets called the state, so be careful to understand the context.
One cycle of prediction and updating with a measurement is called the state or system *evolution*, which is short for *time evolution* [7]. Another term is *system propagation*. It refers to how the state of the system changes over time. For filters, time is usually a discrete step, such as 1 second. For our dog tracker the system state is the position of the dog, and the state evolution is the position after a discrete amount of time has passed.
We model the system behavior with the *process model*. Here, our process model is that the dog moves one or more positions at each time step. This is not a particularly accurate model of how dogs behave. The error in the model is called the *system error* or *process error*.
The prediction is our new *prior*. Time has moved forward and we made a prediction without benefit of knowing the measurements.
Let's work an example. The current position of the dog is 17 m. Our epoch is 2 seconds long, and the dog is traveling at 15 m/s. Where do we predict he will be in two seconds?
Clearly,
$$ \begin{aligned}
\bar x &= 17 + (15*2) \\
&= 47
\end{aligned}$$
I use bars over variables to indicate that they are priors (predictions). We can write the equation for the process model like this:
$$ \bar x_{k+1} = f_x(\bullet) + x_k$$
$x_k$ is the current position or state. If the dog is at 17 m then $x_k = 17$.
$f_x(\bullet)$ is the state propagation function for x. It describes how much the $x_k$ changes over one time step. For our example it performs the computation $15 \cdot 2$ so we would define it as
$$f_x(v_x, t) = v_k t$$.
## 術語
我們暫停複習一下術語。我上一章已經介紹過這些術語,但我們稍微花幾秒鐘鞏固一下知識。
所谓**系統**是我們嘗試建模和濾波的對象。這裡,系統指的是那隻狗。**狀態**表示當前的配置或數值。本章中,狀態是狗的位置。我們一般無法知道真實的狀態,所以我們說濾波器得到的是**狀態估計**。實踐中我們往往也將其稱為狀態,所以你要小心理解上下文。
一個預測步和一個根據測量更新狀態的更新步構成一個循環,這個循環被稱為狀態的**演化**,或系統的演化,它是**時間演化**【7】的縮寫。另一個術語是**系統傳播**。他指的是狀態是如何隨著時間改變的。對於濾波器,時間步是離散的,例如一秒的時間。對於我們的狗的跟蹤問題而言,系統的狀態是狗的位置,狀態的演化是經過一段離散的時間步後狗的位置的改變。
我們用“過程模型”來建模系統的行為。這裡,我們的過程模型是夠經過每個時間步都會移動一段距離。這個模型並不精確地建模狗的運動。模型的誤差稱為“系統誤差”或者“過程誤差”。
每個預測結果都給我們一個新的“先驗”。隨著時間的推進,我們在無測量結果輔助的情況下做出下一時刻的預測。
讓我們看一個例子。當前狗的位置是17m。一個時間步是兩秒,狗的速度是15米每秒。我們預測它兩秒後的位置會在哪裡。
顯而易見,
$$ \begin{aligned}
\bar x &= 17 + (15*2) \\
&= 47
\end{aligned}$$
我通過在符號上加一橫表示先驗(即預測結果)。我們將過程模型用公式表示出來,如下所示:
$$ \bar x_{k+1} = f_x(\bullet) + x_k$$
$x_k$是當前位置或狀態,如果狗在17 m處,那麼$x_k = 17$.
$f_x(\bullet)$是x的狀態傳播函數。它描述了$x_k$經過一個時間步的改變程度。對於這個例子,它執行了此計算$15 \cdot 2$,所以我們將它定義為
$$f_x(v_x, t) = v_k t$$
## Adding Uncertainty to the Prediction
`perfect_predict()` assumes perfect measurements, but all sensors have noise. What if the sensor reported that our dog moved one space, but he actually moved two spaces, or zero? This may sound like an insurmountable problem, but let's model it and see what happens.
Assume that the sensor's movement measurement is 80% likely to be correct, 10% likely to overshoot one position to the right, and 10% likely to undershoot to the left. That is, if the movement measurement is 4 (meaning 4 spaces to the right), the dog is 80% likely to have moved 4 spaces to the right, 10% to have moved 3 spaces, and 10% to have moved 5 spaces.
Each result in the array now needs to incorporate probabilities for 3 different situations. For example, consider the reported movement of 2. If we are 100% certain the dog started from position 3, then there is an 80% chance he is at 5, and a 10% chance for either 4 or 6. Let's try coding that:
## 在預測中考慮不確定性
`perfect_predict()`函數假定測量是完美的,但實際上所有傳感器都有噪聲。如果傳感器顯示狗移動了一位,但實際上移動了兩位,會發生什麼?又或者實際上沒有移動呢?雖然這個問題乍看之下是無法解決的,但我們還是先建模一下問題,看看會發生什麼。
設傳感器測量的位移有80%的幾率是正確的,10%的幾率給出右偏一位的值,10%的概率給出左偏一位的值。即是說,如果傳感器測得的位移是4(向右移4位),那麼狗有80%的概率向右移4位,有10%的概率向右移3位,有10%的概率向右移5位。
對於數組中的每一個結果,我們都需要考慮三種情況的概率。例如,若傳感器報告位移為2,且我們百分百確定狗是從位置3起步的,那麼此時狗有80%的概率位於位置5,各有10%的概率位於4或6.
我們試著用代碼的形式表達這個問題:
```
def predict_move(belief, move, p_under, p_correct, p_over):
n = len(belief)
prior = np.zeros(n)
for i in range(n):
prior[i] = (
belief[(i-move) % n] * p_correct +
belief[(i-move-1) % n] * p_over +
belief[(i-move+1) % n] * p_under)
return prior
belief = [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]
prior = predict_move(belief, 2, .1, .8, .1)
book_plots.plot_belief_vs_prior(belief, prior)
```
It appears to work correctly. Now what happens when our belief is not 100% certain?
看起來代碼工作正常。現在我們看看置信度不是100%的情況會是怎樣?
```
belief = [0, 0, .4, .6, 0, 0, 0, 0, 0, 0]
prior = predict_move(belief, 2, .1, .8, .1)
book_plots.plot_belief_vs_prior(belief, prior)
prior
```
Here the results are more complicated, but you should still be able to work it out in your head. The 0.04 is due to the possibility that the 0.4 belief undershot by 1. The 0.38 is due to the following: the 80% chance that we moved 2 positions (0.4 $\times$ 0.8) and the 10% chance that we undershot (0.6 $\times$ 0.1). Overshooting plays no role here because if we overshot both 0.4 and 0.6 would be past this position. **I strongly suggest working some examples until all of this is very clear, as so much of what follows depends on understanding this step.**
If you look at the probabilities after performing the update you might be dismayed. In the example above we started with probabilities of 0.4 and 0.6 in two positions; after performing the update the probabilities are not only lowered, but they are strewn out across the map.
This is not a coincidence, or the result of a carefully chosen example - it is always true of the prediction. If the sensor is noisy we lose some information on every prediction. Suppose we were to perform the prediction an infinite number of times - what would the result be? If we lose information on every step, we must eventually end up with no information at all, and our probabilities will be equally distributed across the `belief` array. Let's try this with 100 iterations. The plot is animated; use the slider to change the step number.
儘管現在情況更加複雜了,但你還是能夠用你的大腦的理解它。0.04是對應0.4置信度的信念被高估的可能性。而0.38是這樣算來的:有80%的概率移動了兩步 (0.4 $\times$ 0.8)和10%概率高估了位移(0.6 $\times$ 0.1)。低估的情況不參與計算,因為這種情況下對應於0.4和0.6的信念都會跳過該點。**我強烈建議你多使幾個例子,直到你深刻理解它們,這是因為後面許多內容都依賴於這一步。**
如果你看過更新後的概率,那你可能會感覺失望。上面的例子中,我們開始時對兩個位置各有0.4和0.6的置信度;在更新後,置信度不僅減小了,它們還在地圖上分散開來。
這不是偶然,也不是特意挑選的例子才能產生的結果——不論如何,預測的結果永遠會像這樣。如果傳感器包含噪聲,我們每次預測就都會丟失信息。假如我們在無限的時間裡無數次預測——結果會是怎樣?如果我們每次預測都丟失信息,我們最終會什麼信息都無法留下,我們的`belief`數組上的概率分佈將會處處均等。我們試試迭代100次。下面是繪製的動畫。你可以用滑塊來逐步瀏覽。
```
belief = np.array([1.0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
predict_beliefs = []
for i in range(100):
belief = predict_move(belief, 1, .1, .8, .1)
predict_beliefs.append(belief)
print('Final Belief:', belief)
# make interactive plot
def show_prior(step):
book_plots.bar_plot(predict_beliefs[step-1])
plt.title(f'Step {step}')
interact(show_prior, step=IntSlider(value=1, max=len(predict_beliefs)));
print('Final Belief:', belief)
```
After 100 iterations we have lost almost all information, even though we were 100% sure that we started in position 0. Feel free to play with the numbers to see the effect of differing number of updates. For example, after 100 updates a small amount of information is left, after 50 a lot is left, but by 200 iterations essentially all information is lost.
儘管我們以100%的置信度相信我們從0點開始,100次迭代後我們仍然幾乎丟失了所有信息。請隨意改變數目,觀察步數的影響。例如,經過100次更新,仍存在有一小部分信息;50次更新後,留下的信息較多;而200次更新後基本上所有數據都丟失了。
And, if you are viewing this online here is an animation of that output.
<img src="animations/02_no_info.gif">
I will not generate these standalone animations through the rest of the book. Please see the preface for instructions to run this book on the web, for free, or install IPython on your computer. This will allow you to run all of the cells and see the animations. It's very important that you practice with this code, not just read passively.
另外,如果你通過線上方式閱讀本書,你會看到這裡有輸出的動圖。
<img src="animations/02_no_info.gif">
這之後我就不會再生成單獨的動圖了。請遵循本前言部分的介紹在網頁上,或者在你電腦上配置IPython以免費運行本書內容。這樣你就能運行所有單元格並且看到動圖。為了能練習本書代碼而不僅僅是被動閱讀,這點非常重要。
## Generalizing with Convolution
We made the assumption that the movement error is at most one position. But it is possible for the error to be two, three, or more positions. As programmers we always want to generalize our code so that it works for all cases.
This is easily solved with [*convolution*](https://en.wikipedia.org/wiki/Convolution). Convolution modifies one function with another function. In our case we are modifying a probability distribution with the error function of the sensor. The implementation of `predict_move()` is a convolution, though we did not call it that. Formally, convolution is defined as
## 在卷積的幫助下推廣該方法
我們先前假設位移的誤差最多不差過一位。但實際上可能有兩位、三位、甚至更多。作為程序員,我們總希望能將我們的代碼推廣到適應所有情況。
這可以藉助[**卷積**](https://en.wikipedia.org/wiki/Convolution)工具輕鬆解決。卷積通過一個函數來修改另一個函數。在我們的案例中,我們用傳感器的誤差函數修改概率分佈。雖然我們之前沒這麼稱呼它,但`predict_move()`函數的實現就是一個卷積。卷積的正式定義如下:
$$ (f \ast g) (t) = \int_0^t \!f(\tau) \, g(t-\tau) \, \mathrm{d}\tau$$
where $f\ast g$ is the notation for convolving f by g. It does not mean multiply.
Integrals are for continuous functions, but we are using discrete functions. We replace the integral with a summation, and the parenthesis with array brackets.
$$ (f \ast g) [t] = \sum\limits_{\tau=0}^t \!f[\tau] \, g[t-\tau]$$
Comparison shows that `predict_move()` is computing this equation - it computes the sum of a series of multiplications.
[Khan Academy](https://www.khanacademy.org/math/differential-equations/laplace-transform/convolution-integral/v/introduction-to-the-convolution) [4] has a good introduction to convolution, and Wikipedia has some excellent animations of convolutions [5]. But the general idea is already clear. You slide an array called the *kernel* across another array, multiplying the neighbors of the current cell with the values of the second array. In our example above we used 0.8 for the probability of moving to the correct location, 0.1 for undershooting, and 0.1 for overshooting. We make a kernel of this with the array `[0.1, 0.8, 0.1]`. All we need to do is write a loop that goes over each element of our array, multiplying by the kernel, and summing the results. To emphasize that the belief is a probability distribution I have named it `pdf`.
其中 $f\ast g$ 表示f和g的卷積。它不代表乘法。
積分對應於連續函數,但我們使用的是離散函數。我們將積分替換為求和符號,將圓括號換成數組使用的方括號。
$$ (f \ast g) [t] = \sum\limits_{\tau=0}^t \!f[\tau] \, g[t-\tau]$$
比較發現`predict_move()`是在實行該計算——即一系列數值的積的和。
[可汗學院](https://www.khanacademy.org/math/differential-equations/laplace-transform/convolution-integral/v/introduction-to-the-convolution) 【4】很好地介紹了卷積。維基百科提供了描繪卷積的優美動圖【5】。不論如何,卷積的大概思想是清除易懂的。你將一個稱為“核(kernel)”的數組劃過另一個數組,連同當前單元格的鄰接單元格與對應數組上的單元格相乘。在上面的例子中,我們用0.8作為正確估計的概率,0.1作為高估的概率,0.1作為低估的概率。這可以用數組`[0.1, 0.8, 0.1]`構成的核來表示。我們所要做的事情循環遍歷數組的每一元素,與核對應相乘,對結果求和。為強調置信度是一個概率分佈,我用`pdf`作為變量名。
```
def predict_move_convolution(pdf, offset, kernel):
N = len(pdf)
kN = len(kernel)
width = int((kN - 1) / 2)
prior = np.zeros(N)
for i in range(N):
for k in range (kN):
index = (i + (width-k) - offset) % N
prior[i] += pdf[index] * kernel[k]
return prior
```
This illustrates the algorithm, but it runs very slow. SciPy provides a convolution routine `convolve()` in the `ndimage.filters` module. We need to shift the pdf by `offset` before convolution; `np.roll()` does that. The move and predict algorithm can be implemented with one line:
```python
convolve(np.roll(pdf, offset), kernel, mode='wrap')
```
FilterPy implements this with `discrete_bayes`' `predict()` function.
雖然該函數演示了算法執行流程,然而它執行得很慢。SciPy庫在`ndimage.filters`包中提供了卷積操作`convolve()`。我們要在作卷積前先將pdf平移`offset`步,這可以通過`np.roll()`函數實現。移動操作和預測操作可以由一行代碼實現:
```python
convolve(np.roll(pdf, offset), kernel, mode='wrap')
```
FilterPy在`discrete_bayes`的`predict()`函數中實現了此操作。
```
from filterpy.discrete_bayes import predict
belief = [.05, .05, .05, .05, .55, .05, .05, .05, .05, .05]
prior = predict(belief, offset=1, kernel=[.1, .8, .1])
book_plots.plot_belief_vs_prior(belief, prior, ylim=(0,0.6))
```
All of the elements are unchanged except the middle ones. The values in position 4 and 6 should be
$$(0.1 \times 0.05)+ (0.8 \times 0.05) + (0.1 \times 0.55) = 0.1$$
Position 5 should be $$(0.1 \times 0.05) + (0.8 \times 0.55)+ (0.1 \times 0.05) = 0.45$$
Let's ensure that it shifts the positions correctly for movements greater than one and for asymmetric kernels.
除去中部的幾個數值外,其它數保持不變。位於4和6除的概率應為
$$(0.1 \times 0.05)+ (0.8 \times 0.05) + (0.1 \times 0.55) = 0.1$$
位置5處的概率應為$$(0.1 \times 0.05) + (0.8 \times 0.55)+ (0.1 \times 0.05) = 0.45$$
接著,我們來確認一下對於移動量大於1,且非對稱的核,它也能正確地移動位置。
```
prior = predict(belief, offset=3, kernel=[.05, .05, .6, .2, .1])
book_plots.plot_belief_vs_prior(belief, prior, ylim=(0,0.6))
```
The position was correctly shifted by 3 positions and we give more weight to the likelihood of an overshoot vs an undershoot, so this looks correct.
Make sure you understand what we are doing. We are making a prediction of where the dog is moving, and convolving the probabilities to get the prior.
If we weren't using probabilities we would use this equation that I gave earlier:
$$ \bar x_{k+1} = x_k + f_{\mathbf x}(\bullet)$$
The prior, our prediction of where the dog will be, is the amount the dog moved plus his current position. The dog was at 10, he moved 5 meters, so he is now at 15 m. It couldn't be simpler. But we are using probabilities to model this, so our equation is:
$$ \bar{ \mathbf x}_{k+1} = \mathbf x_k \ast f_{\mathbf x}(\bullet)$$
We are *convolving* the current probabilistic position estimate with a probabilistic estimate of how much we think the dog moved. It's the same concept, but the math is slightly different. $\mathbf x$ is bold to denote that it is an array of numbers.
预测位置正确移动了三步,且我们为偏大的位移给出了更高的似然权重,所以结果看起来是正确的。
你要保证确实理解我们在做的事情。我们在预测狗的位移,通过对概率分布做卷积来给出先验:
如果我们使用的不是概率分布,那么我们需要使用前面给出的公式
$$ \bar x_{k+1} = x_k + f_{\mathbf x}(\bullet)$$
先验等于狗的当前位置加上狗的位移(这里先验指的是狗的预测位置)。如果狗在位置10,位移了5米,那么它现在出现在15米的位置。简单到不能再简单了。但现在我们使用概率分布来建模,于是我们的公式变为:
$$ \bar{ \mathbf x}_{k+1} = \mathbf x_k \ast f_{\mathbf x}(\bullet)$$
## Integrating Measurements and Movement Updates
The problem of losing information during a prediction may make it seem as if our system would quickly devolve into having no knowledge. However, each prediction is followed by an update where we incorporate the measurement into the estimate. The update improves our knowledge. The output of the update step is fed into the next prediction. The prediction degrades our certainty. That is passed into another update, where certainty is again increased.
Let's think about this intuitively. Consider a simple case - you are tracking a dog while he sits still. During each prediction you predict he doesn't move. Your filter quickly *converges* on an accurate estimate of his position. Then the microwave in the kitchen turns on, and he goes streaking off. You don't know this, so at the next prediction you predict he is in the same spot. But the measurements tell a different story. As you incorporate the measurements your belief will be smeared along the hallway, leading towards the kitchen. On every epoch (cycle) your belief that he is sitting still will get smaller, and your belief that he is inbound towards the kitchen at a startling rate of speed increases.
That is what intuition tells us. What does the math tell us?
We have already programmed the update and predict steps. All we need to do is feed the result of one into the other, and we will have implemented a dog tracker!!! Let's see how it performs. We will input measurements as if the dog started at position 0 and moved right one position each epoch. As in a real world application, we will start with no knowledge of his position by assigning equal probability to all positions.
## 在位移更新过程中结合测量值
因為在预测过程中存在信息丢失的问题,所以看起來似乎我们的系统会迅速退化到没有任何信息的状态。然而並非如此,因為每次預測後面都會緊跟著一個更新操作。有了更新操作,我們就可以在作估計時將測量結果納入考量。更新操作能改善信息的質量。更新的結果作為下一次預測的輸入。經過預測,確定性降低了。其結果傳遞給下一次更新,確定性又再一次得到增強。
讓我們從直覺上思考這個問題。考慮一個簡單的例子:你需要跟蹤一條狗,而這條狗永遠坐在那裡不動。每次預測,你給出的結果都是它原地不動。於是你的濾波器迅速“收斂”到其位置的精確估計。這時候廚房的微波爐打開了,狗狗飛奔出去。你不知道這件事,所以下一次預測,你還是預言它原地不動。而這時測量值則傳遞出相悖的信息。如果你結合測量結果去做更新,那你關於位置的信念起始時散佈在走廊上各處,總體向著廚房移動。每一輪迭代(循環),你對狗原地不動的信念俞弱,俞相信狗在以驚人的速度向廚房進發。
這是直覺上我們所能理解的。那麼我們是否能從數學中得到什麼呢?
我們已編寫好更新和預測操作。我們所要做的只是將其中一步的結果傳給下一步,這樣我們就實現了一個狗跟蹤器!!!我們看下它表現如何。我們輸入測量值,假裝狗從位置0開始移動,每次向右移動一步。如果是在真實世界的應用中,起始狀態下我們沒有任何關於其位置的知識,這時我們就為每種可能位置賦予相等的概率。
```
from filterpy.discrete_bayes import update
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
prior = np.array([.1] * 10)
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))
```
After the first update we have assigned a high probability to each door position, and a low probability to each wall position.
第一次更新後,我们为每个门的位置分配了更高的权重,而为墙壁的位置赋予了较低的权重。
```
kernel = (.1, .8, .1)
prior = predict(posterior, 1, kernel)
book_plots.plot_prior_vs_posterior(prior, posterior, True, ylim=(0,.5))
```
The predict step shifted these probabilities to the right, smearing them about a bit. Now let's look at what happens at the next sense.
预测操作使得概率分布右移,并且使分布散得更开。现在让我们看看下一个读入传感器的读数会发生什么。
```
likelihood = lh_hallway(hallway, z=1, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))
```
Notice the tall bar at position 1. This corresponds with the (correct) case of starting at position 0, sensing a door, shifting 1 to the right, and sensing another door. No other positions make this set of observations as likely. Now we will add an update and then sense the wall.
注意看位置1处的高峰。它对应的(正確)情況是:以位置0为起点出發,傳感器感應到門,向右移一步,然後傳感器再次感應到門。除此以外的情形則不太可能產生同樣的觀測結果。現在我們增加一個更新操作,這個更新操作中傳感器感應到墻壁。
```
prior = predict(posterior, 1, kernel)
likelihood = lh_hallway(hallway, z=0, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))
```
This is exciting! We have a very prominent bar at position 2 with a value of around 35%. It is over twice the value of any other bar in the plot, and is about 4% larger than our last plot, where the tallest bar was around 31%. Let's see one more cycle.
結果真是令人激動!條形圖在位置2處的數值顯著突出,其值為35%,其高度在其它任意一柱高度的兩倍以上。上一張圖的最高高度約為31%,所以經過本次操作高度提高的量約為4%。我們再觀察一輪。
```
prior = predict(posterior, 1, kernel)
likelihood = lh_hallway(hallway, z=0, z_prob=.75)
posterior = update(likelihood, prior)
book_plots.plot_prior_vs_posterior(prior, posterior, ylim=(0,.5))
```
I ignored an important issue. Earlier I assumed that we had a motion sensor for the predict step; then, when talking about the dog and the microwave I assumed that you had no knowledge that he suddenly began running. I mentioned that your belief that the dog is running would increase over time, but I did not provide any code for this. In short, how do we detect and/or estimate changes in the process model if we aren't directly measuring it?
For now I want to ignore this problem. In later chapters we will learn the mathematics behind this estimation; for now it is a large enough task just to learn this algorithm. It is profoundly important to solve this problem, but we haven't yet built enough of the mathematical apparatus that is required, and so for the remainder of the chapter we will ignore the problem by assuming we have a sensor that senses movement.
我忽略了一個重要問題。起初我們為預測步提供了運動傳感器,可是之後談及狗與微波爐的例子的時候,我卻假定你沒有關於狗突然開始運動的知識。我斷言道即使如此你仍會越來越相信狗處於運動狀態,但我未提供任何證明該斷言的代碼。簡而言之,在不直接測量的條件下,我們如何才能檢測或估計過程模型狀態的改變呢?
我想暫時擱置這一問題。後續章節會介紹估計方法幕後的數學原理。而現在,僅僅是學習算法就已經是一個大任務。雖然解決這個問題很重要,但是我們還缺乏解決該問題所需的數學工具。那麼本章的後續部分會暫時忽略這個問題,仍然假設我們有一個專門用於測量運動的傳感器。
## The Discrete Bayes Algorithm
This chart illustrates the algorithm:
## 離散貝葉斯算法
下圖顯示了算法的流程:
```
book_plots.predict_update_chart()
```
This filter is a form of the g-h filter. Here we are using the percentages for the errors to implicitly compute the $g$ and $h$ parameters. We could express the discrete Bayes algorithm as a g-h filter, but that would obscure the logic of this filter.
The filter equations are:
$$\begin{aligned} \bar {\mathbf x} &= \mathbf x \ast f_{\mathbf x}(\bullet)\, \, &\text{Predict Step} \\
\mathbf x &= \|\mathcal L \cdot \bar{\mathbf x}\|\, \, &\text{Update Step}\end{aligned}$$
$\mathcal L$ is the usual way to write the likelihood function, so I use that. The $\|\|$ notation denotes taking the norm. We need to normalize the product of the likelihood with the prior to ensure $x$ is a probability distribution that sums to one.
We can express this in pseudocode.
**Initialization**
1. Initialize our belief in the state
**Predict**
1. Based on the system behavior, predict state for the next time step
2. Adjust belief to account for the uncertainty in prediction
**Update**
1. Get a measurement and associated belief about its accuracy
2. Compute how likely it is the measurement matches each state
3. Update state belief with this likelihood
When we cover the Kalman filter we will use this exact same algorithm; only the details of the computation will differ.
Algorithms in this form are sometimes called *predictor correctors*. We make a prediction, then correct them.
Let's animate this. First Let's write functions to perform the filtering and to plot the results at any step. I've plotted the position of the doorways in black. Prior are drawn in orange, and the posterior in blue. I draw a thick vertical line to indicate where Simon really is. This is not an output of the filter - we know where Simon is only because we are simulating his movement.
如圖所示的濾波器是g-h濾波器的一種特殊形式。這裡我們用誤差的百分比隱式計算g和h參數。我們也可以將貝葉斯濾波器用g-h濾波器的形式該寫出來,但這麼做會使得濾波器所遵循的邏輯變得模糊。
濾波器的公式如下:
$$\begin{aligned} \bar {\mathbf x} &= \mathbf x \ast f_{\mathbf x}(\bullet)\, \, &\text{預測操作} \\
\mathbf x &= \|\mathcal L \cdot \bar{\mathbf x}\|\, \, &\text{更新操作}\end{aligned}$$
遵循慣例,我是用$\mathcal L$來代表似然函數。$\|\|$符號表示取模。我們需要對似然與先驗的乘積作歸一化來確保$x$是和為1的概率分佈。
我們可以用如下的偽代碼來表達這個過程。
**初始化**
1. 為狀態的置信度賦予初始值。
**預測**
1. 基於系統的行為預測下一時間步的狀態;
2. 根據預測操作的不確定性調整置信度;
**更新**
1. 得到測量值和對測量精度的置信度;
2. 計算測量值與真實狀態相符的似然程度;
3. 根據似然更新狀態置信度;
在卡爾曼濾波的章節,我們會使用完全一致的算法;只在於計算的細節上有所不同。
這類算法有時候被稱為“預測校準器”,因為它們先做預測,再修正預測的值。
讓我們用動畫來展示這個算法。我們先實現濾波函數,然後將每一步結果繪製出來。我用黑色來指示門道的位置。用橙色來繪製先驗,用藍色繪製後驗。縱向粗線用於指示西蒙的實際位置。注意它不是濾波器的輸出——之所以我們能知道西蒙的真實位置是因為我們在用程序模擬這個過程。
```
def discrete_bayes_sim(prior, kernel, measurements, z_prob, hallway):
posterior = np.array([.1]*10)
priors, posteriors = [], []
for i, z in enumerate(measurements):
prior = predict(posterior, 1, kernel)
priors.append(prior)
likelihood = lh_hallway(hallway, z, z_prob)
posterior = update(likelihood, prior)
posteriors.append(posterior)
return priors, posteriors
def plot_posterior(hallway, posteriors, i):
plt.title('Posterior')
book_plots.bar_plot(hallway, c='k')
book_plots.bar_plot(posteriors[i], ylim=(0, 1.0))
plt.axvline(i % len(hallway), lw=5)
def plot_prior(hallway, priors, i):
plt.title('Prior')
book_plots.bar_plot(hallway, c='k')
book_plots.bar_plot(priors[i], ylim=(0, 1.0), c='#ff8015')
plt.axvline(i % len(hallway), lw=5)
def animate_discrete_bayes(hallway, priors, posteriors):
def animate(step):
step -= 1
i = step // 2
if step % 2 == 0:
plot_prior(hallway, priors, i)
else:
plot_posterior(hallway, posteriors, i)
return animate
```
Let's run the filter and animate it.
讓我們運行濾波器,並觀察運行結果。
```
# change these numbers to alter the simulation
kernel = (.1, .8, .1)
z_prob = 1.0
hallway = np.array([1, 1, 0, 0, 0, 0, 0, 0, 1, 0])
# measurements with no noise
zs = [hallway[i % len(hallway)] for i in range(50)]
priors, posteriors = discrete_bayes_sim(prior, kernel, zs, z_prob, hallway)
interact(animate_discrete_bayes(hallway, priors, posteriors), step=IntSlider(value=1, max=len(zs)*2));
```
Now we can see the results. You can see how the prior shifts the position and reduces certainty, and the posterior stays in the same position and increases certainty as it incorporates the information from the measurement. I've made the measurement perfect with the line `z_prob = 1.0`; we will explore the effect of imperfect measurements in the next section. Finally,
Another thing to note is how accurate our estimate becomes when we are in front of a door, and how it degrades when in the middle of the hallway. This should make intuitive sense. There are only a few doorways, so when the sensor tells us we are in front of a door this boosts our certainty in our position. A long stretch of no doors reduces our certainty.
現在,我們可以觀察到結果。你可以看到先驗是如何發生移動的,其不確定性是如何減少的。還注意到雖然先驗與後驗的極大值點重合,但後驗的確定性更高,這是後驗結合了測量信息的緣故。這裡通過令`z_prob = 1.0`使得測量是完全準確的。後續小節我們會探索不完美的測量造成的影響。
最後一個值得注意的事是,當狗處於門前時估計的準確度是如何增加的,以及當狗位於走廊中心時它是如何退化的。你可以從直覺上理解這個問題。門的數量很少,所以一旦傳感器感應到門,我們對位置的確定性就增加。成片的非門區域則會降低確定性。
## The Effect of Bad Sensor Data
You may be suspicious of the results above because I always passed correct sensor data into the functions. However, we are claiming that this code implements a *filter* - it should filter out bad sensor measurements. Does it do that?
To make this easy to program and visualize I will change the layout of the hallway to mostly alternating doors and hallways, and run the algorithm on 6 correct measurements:
## 不良傳感器數據的影響
你可能會對上面的結果表示懷疑,畢竟我一直只給函數傳入正確的傳感器數據。然而,既然我們聲稱自己實現了“濾波器”,那麼它應當能過濾不良傳感器數據。那麼它確實能做到這一點嗎?
為使得問題易於編程實現和方便可視化,我要改變走廊的佈局,使門道和走廊均勻交替分佈。以六個正確測量結果為輸入運行算法:
```
hallway = np.array([1, 0, 1, 0, 0]*2)
kernel = (.1, .8, .1)
prior = np.array([.1] * 10)
zs = [1, 0, 1, 0, 0, 1]
z_prob = 0.75
priors, posteriors = discrete_bayes_sim(prior, kernel, zs, z_prob, hallway)
interact(animate_discrete_bayes(hallway, priors, posteriors), step=IntSlider(value=12, max=len(zs)*2));
```
We have identified the likely cases of having started at position 0 or 5, because we saw this sequence of doors and walls: 1,0,1,0,0. Now I inject a bad measurement. The next measurement should be 0, but instead we get a 1:
我們看到最可能的起始位置是0或5。這是因為傳感器的讀數序列為:1、0、1、0、0.現在我插入一個錯誤的測量值。原本下一個讀數應當是0,但我將其替換為1.
```
measurements = [1, 0, 1, 0, 0, 1, 1]
priors, posteriors = discrete_bayes_sim(prior, kernel, measurements, z_prob, hallway);
plot_posterior(hallway, posteriors, 6)
```
That one bad measurement has significantly eroded our knowledge. Now let's continue with a series of correct measurements.
一個不良傳感器數據的插入嚴重污染了我們的知識。接著,我們在正確測量數據上繼續運行。
```
with figsize(y=5.5):
measurements = [1, 0, 1, 0, 0, 1, 1, 1, 0, 0]
for i, m in enumerate(measurements):
likelihood = lh_hallway(hallway, z=m, z_prob=.75)
posterior = update(likelihood, prior)
prior = predict(posterior, 1, kernel)
plt.subplot(5, 2, i+1)
book_plots.bar_plot(posterior, ylim=(0, .4), title=f'step {i+1}')
plt.tight_layout()
```
We quickly filtered out the bad sensor reading and converged on the most likely positions for our dog.
我們很快就濾除了不良傳感器讀數,並且概率分佈收斂在狗的最可能位置上。
## Drawbacks and Limitations
Do not be mislead by the simplicity of the examples I chose. This is a robust and complete filter, and you may use the code in real world solutions. If you need a multimodal, discrete filter, this filter works.
With that said, this filter it is not used often because it has several limitations. Getting around those limitations is the motivation behind the chapters in the rest of this book.
The first problem is scaling. Our dog tracking problem used only one variable, $pos$, to denote the dog's position. Most interesting problems will want to track several things in a large space. Realistically, at a minimum we would want to track our dog's $(x,y)$ coordinate, and probably his velocity $(\dot{x},\dot{y})$ as well. We have not covered the multidimensional case, but instead of an array we use a multidimensional grid to store the probabilities at each discrete location. Each `update()` and `predict()` step requires updating all values in the grid, so a simple four variable problem would require $O(n^4)$ running time *per time step*. Realistic filters can have 10 or more variables to track, leading to exorbitant computation requirements.
The second problem is that the filter is discrete, but we live in a continuous world. The histogram requires that you model the output of your filter as a set of discrete points. A 100 meter hallway requires 10,000 positions to model the hallway to 1cm accuracy. So each update and predict operation would entail performing calculations for 10,000 different probabilities. It gets exponentially worse as we add dimensions. A 100x100 m$^2$ courtyard requires 100,000,000 bins to get 1cm accuracy.
A third problem is that the filter is multimodal. In the last example we ended up with strong beliefs that the dog was in position 4 or 9. This is not always a problem. Particle filters, which we will study later, are multimodal and are often used because of this property. But imagine if the GPS in your car reported to you that it is 40% sure that you are on D street, and 30% sure you are on Willow Avenue.
A forth problem is that it requires a measurement of the change in state. We need a motion sensor to detect how much the dog moves. There are ways to work around this problem, but it would complicate the exposition of this chapter, so, given the aforementioned problems, I will not discuss it further.
With that said, if I had a small problem that this technique could handle I would choose to use it; it is trivial to implement, debug, and understand, all virtues.
## 缺點和局限
不要受我選的這個示例的簡單性所誤導。這是一個穩健的完整濾波器,可以應用於現實世界的解決方案。如果你需要一個多峰的,離散的濾波器,那麼這個濾波器可以為你所用。
說是這麼說。實際上由於一些限制,這種濾波器也不是經常使用。餘下的章節就主要圍繞如何克服這些限制展開。
第一個問題在於其伸縮性。我們的狗跟蹤問題只使用一個變量$pos$來表示狗的位置。許多有趣的問題都需要在一個大的向量空間中跟蹤多個變量。比如在現實中我們往往需要跟蹤狗的位置$(x,y)$,有時還需跟蹤其速度$(\dot{x},\dot{y})$ 。我們還沒有處理過多維的情況。在高維空間中,我們不再使用一維數組表示狀態,而是使用一個多維的網格來存儲各離散位置的對應概率。每個`update()`和`predict()`步都需要更新網格上的所有位置。那麼一個含有四個變量**每一步**運算都需要$O(n^4)$的運行時間。現實世界中的濾波器往往有超過10個需要跟蹤的變量,這需要極多的計算資源。
第二個問題是這種濾波器是離散的,但我們生活的世界是連續的。這種基於直方圖的方式要求你將濾波器的輸出建模為一些列離散點。要在100米的走廊上達到1cm的定位精度需要10000個點。情況隨著維度的增加指數惡化。要在100平方米的庭院內達到1cm的精確度需要尺寸為一億的直方圖。
第三個問題是,這種濾波器是多峰的。上一個問題中,程序以堅信狗處於位置4或9的狀態結束。這並不總成問題。我們後面將介紹粒子濾波器。粒子濾波器正是因為其具有多峰的性質而被廣泛應用。但你可以想象看你車里的GPS報告說你有40%的概率位於D街,又有30%的概率位於柳樹大道嗎。
第四個問題是它需要狀態改變程度的測量值。我們需要運動傳感器以測量狗的運動量。有許多應對該問題的方法,但為不使本章的闡述過於複雜這裡就不再介紹。總之基於上述所有原因,我們不再做進一步的討論。
話雖如此,如果我手頭有一個可以由這項技術處理的小問題,我就會使用它。易於實現、調試和理解都是它的優點。
## Tracking and Control
We have been passively tracking an autonomously moving object. But consider this very similar problem. I am automating a warehouse and want to use robots to collect all of the items for a customer's order. Perhaps the easiest way to do this is to have the robots travel on a train track. I want to be able to send the robot a destination and have it go there. But train tracks and robot motors are imperfect. Wheel slippage and imperfect motors means that the robot is unlikely to travel to exactly the position you command. There is more than one robot, and we need to know where they all are so we do not cause them to crash.
So we add sensors. Perhaps we mount magnets on the track every few feet, and use a Hall sensor to count how many magnets are passed. If we count 10 magnets then the robot should be at the 10th magnet. Of course it is possible to either miss a magnet or to count it twice, so we have to accommodate some degree of error. We can use the code from the previous section to track our robot since magnet counting is very similar to doorway sensing.
But we are not done. We've learned to never throw information away. If you have information you should use it to improve your estimate. What information are we leaving out? We know what control inputs we are feeding to the wheels of the robot at each moment in time. For example, let's say that once a second we send a movement command to the robot - move left 1 unit, move right 1 unit, or stand still. If I send the command 'move left 1 unit' I expect that in one second from now the robot will be 1 unit to the left of where it is now. This is a simplification because I am not taking acceleration into account, but I am not trying to teach control theory. Wheels and motors are imperfect. The robot might end up 0.9 units away, or maybe 1.2 units.
Now the entire solution is clear. We assumed that the dog kept moving in whatever direction he was previously moving. That is a dubious assumption for my dog! Robots are far more predictable. Instead of making a dubious prediction based on assumption of behavior we will feed in the command that we sent to the robot! In other words, when we call `predict()` we will pass in the commanded movement that we gave the robot along with a kernel that describes the likelihood of that movement.
## 跟蹤和控制
我們已經實現了對單個自主移動目標的被動跟蹤。但請你考慮一個十分相似的問題。我要實現仓库自動化,希望使用机器人收集客户訂的所有貨。或許一個最簡單的辦法是讓機器人在火車軌道上行駛。我希望我能讓機器人去到我所指定的目的地。但是鐵軌和機器人的發動機都不是完美的。輪胎打滑和發動機不完美決定了機器人不太可能準確移動到你指定的位置。機器人不止一個,我需要知道所有機器人的位置以免它們碰撞。
所以我们增加了传感器。也许我们每隔几英尺就在轨道上安装一块磁铁,并使用霍尔传感器来计算經過的磁铁数。如果我們數到10個磁鐵,那麼機器人應在第10個磁鐵處。當然,有可能會發生漏掉一塊磁鐵沒統計,或者一塊磁鐵被數了兩次的情況,所以我們需要能適應一定程度的誤差。因為磁鐵計數和走廊傳感器相似,所以我們可以使用前面的代碼來跟蹤機器人。
但這還沒有完成。我們學到一句話:永遠不要丟掉任何信息。如果信息存在,就應當用來改善你的估計。有什麼信息是為我們忽略的呢?我們能即時獲得對機器輪的控制信號輸入。比如,不妨設我們每秒傳遞一個信號給機器人——左一步,右一步,站住不動。我一送出命令“左一步”,我就預期一秒後機器人將位於當前位置的左邊一步。我沒有考慮加速度,所以這隻是一個簡化的問題。但我也不打算在這裡教控制論。車輪和發動機都是不完美的。機器人可能只移動0.9步,也可能移動1.2步。
現在整個問題的解清晰了。我們先前假定狗總是保持之前的移動方向。這個假設對於我的狗來說是不可靠的。但機器人的行為就容易預測得多。預期使用假設得到一個不準確的預測,不如將我們送給機器人的命令作為輸入!換句話說,當調用`predict()`函數時,我們將送給機器人的移動命令,同描述移動的似然度的卷積核一起作為函數的輸入。
### Simulating the Train Behavior
We need to simulate an imperfect train. When we command it to move it will sometimes make a small mistake, and its sensor will sometimes return the incorrect value.
## 列車的行為模擬
我們要模擬一個不完美的列車。當我們命令它移動時,它偶爾會犯一些小錯,它的傳感器有時會返回錯誤的值。
```
class Train(object):
def __init__(self, track_len, kernel=[1.], sensor_accuracy=.9):
self.track_len = track_len
self.pos = 0
self.kernel = kernel
self.sensor_accuracy = sensor_accuracy
def move(self, distance=1):
""" move in the specified direction
with some small chance of error"""
self.pos += distance
# insert random movement error according to kernel
r = random.random()
s = 0
offset = -(len(self.kernel) - 1) / 2
for k in self.kernel:
s += k
if r <= s:
break
offset += 1
self.pos = int((self.pos + offset) % self.track_len)
return self.pos
def sense(self):
pos = self.pos
# insert random sensor error
if random.random() > self.sensor_accuracy:
if random.random() > 0.5:
pos += 1
else:
pos -= 1
return pos
```
With that we are ready to write the filter. We will put it in a function so that we can run it with different assumptions. I will assume that the robot always starts at the beginning of the track. The track is implemented as being 10 units long, but think of it as a track of length, say 10,000, with the magnet pattern repeated every 10 units. A length of 10 makes it easier to plot and inspect.
有了這個我們就可以實現濾波器了。我們將其封裝為一個函數,以便我們可以在不同假設條件下運行這段代碼。我假設機器人總是從軌道的起點出發。我們實現的軌道長度為10個單位。你可以想象他是一個每10單位長度就放置一塊磁鐵的10000單位長度的軌道。令長度為10有利於繪圖和分析。
```
def train_filter(iterations, kernel, sensor_accuracy,
move_distance, do_print=True):
track = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
prior = np.array([.9] + [0.01]*9)
posterior = prior[:]
normalize(prior)
robot = Train(len(track), kernel, sensor_accuracy)
for i in range(iterations):
# move the robot and
robot.move(distance=move_distance)
# peform prediction
prior = predict(posterior, move_distance, kernel)
# and update the filter
m = robot.sense()
likelihood = lh_hallway(track, m, sensor_accuracy)
posterior = update(likelihood, prior)
index = np.argmax(posterior)
if do_print:
print(f'time {i}: pos {robot.pos}, sensed {m}, at position {track[robot.pos]}')
conf = posterior[index] * 100
print(f' estimated position is {index} with confidence {conf:.4f}%:')
book_plots.bar_plot(posterior)
if do_print:
print()
print('final position is', robot.pos)
index = np.argmax(posterior)
print('''Estimated position is {} with '''
'''confidence {:.4f}%:'''.format(
index, posterior[index]*100))
```
Read the code and make sure you understand it. Now let's do a run with no sensor or movement error. If the code is correct it should be able to locate the robot with no error. The output is a bit tedious to read, but if you are at all unsure of how the update/predict cycle works make sure you read through it carefully to solidify your understanding.
請閱讀代碼并且保证你确实理解它。我們先在沒有傳感器誤差和運動誤差的情況下運行代码。如果代码正确,那么它应当能正确无误地检出目标机器人。虽然程序输出有点冗长难读,但若你对更新/预测循环的工作方式完全不确顶,你务必通读这些文字以巩固你的理解。
```
import random
random.seed(3)
np.set_printoptions(precision=2, suppress=True, linewidth=60)
train_filter(4, kernel=[1.], sensor_accuracy=.999,
move_distance=4, do_print=True)
```
We can see that the code was able to perfectly track the robot so we should feel reasonably confident that the code is working. Now let's see how it fairs with some errors.
我们可以看到程序完美无误地实现了对机器人的跟踪,所以我们相当有信心相信代码在正常工作。现在我们来看一些失败案例和几个错误。
```
random.seed(5)
train_filter(4, kernel=[.1, .8, .1], sensor_accuracy=.9,
move_distance=4, do_print=True)
```
There was a sensing error at time 1, but we are still quite confident in our position.
Now let's run a very long simulation and see how the filter responds to errors.
在时刻1有一个传感器异常,但我们仍然对预测的位置有相当高的置信度。
现在加長模擬時間,看看滤波器是如何应对错误的。
```
with figsize(y=5.5):
for i in range (4):
random.seed(3)
plt.subplot(221+i)
train_filter(148+i, kernel=[.1, .8, .1],
sensor_accuracy=.8,
move_distance=4, do_print=False)
plt.title (f'iteration {148 + i}')
```
We can see that there was a problem on iteration 149 as the confidence degrades. But within a few iterations the filter is able to correct itself and regain confidence in the estimated position.
我们可以看到虽然第149次迭代出现问题,导致置信度降低,但是数次迭代后,滤波器能自我校正,使其对预测位置的置信度再次提升。
## Bayes Theorem and the Total Probability Theorem
## 贝叶斯理论和全概率定理
We developed the math in this chapter merely by reasoning about the information we have at each moment. In the process we discovered [*Bayes' Theorem*](https://en.wikipedia.org/wiki/Bayes%27_theorem) and the [*Total Probability Theorem*](https://en.wikipedia.org/wiki/Law_of_total_probability).
Bayes theorem tells us how to compute the probability of an event given previous information.
We implemented the `update()` function with this probability calculation:
$$ \mathtt{posterior} = \frac{\mathtt{likelihood}\times \mathtt{prior}}{\mathtt{normalization\, factor}}$$
We haven't developed the mathematics to discuss Bayes yet, but this is Bayes' theorem. Every filter in this book is an expression of Bayes' theorem. In the next chapter we will develop the mathematics, but in many ways that obscures the simple idea expressed in this equation:
$$ updated\,knowledge = \big\|likelihood\,of\,new\,knowledge\times prior\, knowledge \big\|$$
where $\| \cdot\|$ expresses normalizing the term.
We came to this with simple reasoning about a dog walking down a hallway. Yet, as we will see the same equation applies to a universe of filtering problems. We will use this equation in every subsequent chapter.
Likewise, the `predict()` step computes the total probability of multiple possible events. This is known as the *Total Probability Theorem* in statistics, and we will also cover this in the next chapter after developing some supporting math.
For now I need you to understand that Bayes' theorem is a formula to incorporate new information into existing information.
我们仅通过利用每个时刻的现有信息作推理就引出了本章的所有数学公式。这个过程中,我们发现了[贝叶斯理论](https://en.wikipedia.org/wiki/Bayes%27_theorem)和[全概率定理](https://en.wikipedia.org/wiki/Law_of_total_probability).
贝叶斯理论告诉我们如何基于给定历史信息的计算某一事件的概率。
我们实现了`update()`函数以执行如下的概率计算:
$$ \mathtt{後验} = \frac{\mathtt{似然}\times \mathtt{先验}}{\mathtt{归一化系数}}$$
我们还没有用数学推导讨论过贝叶斯,但这就是贝叶斯定理。本书的每个滤波器都是贝叶斯定理的表达形式。下一章我们会用多种方式推导数学公式,这个过程中,如下等式所表示的简单思想会从各方面掩藏起来。
$$ 更新後的知识 = \big\|新知识的似然度\times 先验知识 \big\|$$
其中 $\| \cdot\|$ 表示归一化。
我们通过关于狗跟踪问题的简单推理得到这一式子。然而,我们将会看到这一式子适用于一些列滤波问题。在接下来的每一章中我们都会用到它。
类似的,`predict()`步骤计算多个可能事件的总概率。这在统计学中被称为“全概率定理”,在下一章中,我们会在一系列数学推导後讲授此定理。
当下我想要你理解的是,贝叶斯公式所做的是将新信息合并到现有信息中去。
## Summary
The code is very short, but the result is impressive! We have implemented a form of a Bayesian filter. We have learned how to start with no information and derive information from noisy sensors. Even though the sensors in this chapter are very noisy (most sensors are more than 80% accurate, for example) we quickly converge on the most likely position for our dog. We have learned how the predict step always degrades our knowledge, but the addition of another measurement, even when it might have noise in it, improves our knowledge, allowing us to converge on the most likely result.
This book is mostly about the Kalman filter. The math it uses is different, but the logic is exactly the same as used in this chapter. It uses Bayesian reasoning to form estimates from a combination of measurements and process models.
**If you can understand this chapter you will be able to understand and implement Kalman filters.** I cannot stress this enough. If anything is murky, go back and reread this chapter and play with the code. The rest of this book will build on the algorithms that we use here. If you don't understand why this filter works you will have little success with the rest of the material. However, if you grasp the fundamental insight - multiplying probabilities when we measure, and shifting probabilities when we update leads to a converging solution - then after learning a bit of math you are ready to implement a Kalman filter.
## 总结
虽然代码很短,但它的运行结果让人映像深刻!我们实现了贝叶斯滤波器的一种具体形式。我们学会了如何从没有任何信息的状态开始,从带有噪声的传感器中推理出信息。虽然本章所用的传感器大多包含许多噪声(举例来说,大多数的传感器的准确率在80%以上),我们还是能快速收敛到狗的最可能位置。我们学到,预测操作总是减少我们的知识,但一旦引入额外的测量值我们就能改善我们的知识,加快收敛到最可能結果的速度。即使引入的测量值中包含噪声也是如此。
本書的主旨是卡爾曼濾波。卡爾曼濾波使用的數學工具有些不同,但其邏輯同本章所用的是一樣的。它使用貝葉斯推理結合測量與過程模型構造估計。
**如果你能理解本章的內容,你就能理解和實現卡爾曼濾波。**我怎么强调这一点都不为过。 如果有任何不清楚的地方,可以重新阅读本章,跑一跑代码。 本书的其余部分将建立在我们在这里使用的算法之上。 如果你不理解此濾波器的工作原理,你也无法順利學習後續內容。 但是,如果你掌握了基本知识——測量時測量分佈乘上概率分佈,更新時平移概率分佈,這樣我們就能收斂於解——那么在学习一些数学原理后,就可以准备实施卡尔曼滤波器了。
## References
* [1] D. Fox, W. Burgard, and S. Thrun. "Monte carlo localization: Efficient position estimation for mobile robots." In *Journal of Artifical Intelligence Research*, 1999.
http://www.cs.cmu.edu/afs/cs/project/jair/pub/volume11/fox99a-html/jair-localize.html
* [2] Dieter Fox, et. al. "Bayesian Filters for Location Estimation". In *IEEE Pervasive Computing*, September 2003.
http://swarmlab.unimaas.nl/wp-content/uploads/2012/07/fox2003bayesian.pdf
* [3] Sebastian Thrun. "Artificial Intelligence for Robotics".
https://www.udacity.com/course/cs373
* [4] Khan Acadamy. "Introduction to the Convolution"
https://www.khanacademy.org/math/differential-equations/laplace-transform/convolution-integral/v/introduction-to-the-convolution
* [5] Wikipedia. "Convolution"
http://en.wikipedia.org/wiki/Convolution
* [6] Wikipedia. "Law of total probability"
http://en.wikipedia.org/wiki/Law_of_total_probability
* [7] Wikipedia. "Time Evolution"
https://en.wikipedia.org/wiki/Time_evolution
* [8] We need to rethink how we teach statistics from the ground up
http://www.statslife.org.uk/opinion/2405-we-need-to-rethink-how-we-teach-statistics-from-the-ground-up
## 參考資料
* [1] D. Fox, W. Burgard, and S. Thrun. "Monte carlo localization: Efficient position estimation for mobile robots." In *Journal of Artifical Intelligence Research*, 1999.
http://www.cs.cmu.edu/afs/cs/project/jair/pub/volume11/fox99a-html/jair-localize.html
* [2] Dieter Fox, et. al. "Bayesian Filters for Location Estimation". In *IEEE Pervasive Computing*, September 2003.
http://swarmlab.unimaas.nl/wp-content/uploads/2012/07/fox2003bayesian.pdf
* [3] Sebastian Thrun. "Artificial Intelligence for Robotics".
https://www.udacity.com/course/cs373
* [4] Khan Acadamy. "Introduction to the Convolution"
https://www.khanacademy.org/math/differential-equations/laplace-transform/convolution-integral/v/introduction-to-the-convolution
* [5] Wikipedia. "Convolution"
http://en.wikipedia.org/wiki/Convolution
* [6] Wikipedia. "Law of total probability"
http://en.wikipedia.org/wiki/Law_of_total_probability
* [7] Wikipedia. "Time Evolution"
https://en.wikipedia.org/wiki/Time_evolution
* [8] We need to rethink how we teach statistics from the ground up
http://www.statslife.org.uk/opinion/2405-we-need-to-rethink-how-we-teach-statistics-from-the-ground-up
| github_jupyter |
# House Prices: Advanced Regression Techniques
This goal of this project was to predict sales prices and practice feature engineering, RFs, and gradient boosting. The dataset was part of the [House Prices Kaggle Competition](https://www.kaggle.com/c/house-prices-advanced-regression-techniques).
<br>
### Table of Contents
* [1 Summary](#1-Summary)
* [2 Introduction](#2-Introduction)
* [3 Loading & Exploring the Data](#3-Loading-&-Exploring-the-Data-Structure)
* [3.1 Loading Required Libraries and Reading the Data into Python](#3.1-Loading-Required-Libraries-and-Reading-the-Data-into-Python)
* [3.2 Data Structure](#3.2-Data-Structure)
* [4 Exploring the Variables](#4-Exploring-the-Variables)
* [4.1 Exploring the Response Variable: SalePrice](#4.1-Exploring-the-Response-Variable:-SalePrice)
* [4.2 Log-Transformation of the Response Variable](#4.2-Log-Transformation-of-the-Response-Variable)
* [5 Data Imputation](#5-Data-Imputation)
* [5.1 Completeness of the Data](#5.1-Completeness-of-the-Data)
* [5.2 Impute the Missing Data](#5.2-Impute-the-Missing-Data)
* [5.2.1 Missing Values Corresponding to Lack of Specific Feature](#5.2.1-Missing-Values-Corresponding-to-Lack-of-Specific-Feature)
* [5.2.2 Mode Imputation: Replacing Missing Values with Most Frequent Value](#5.2.2-Mode-Imputation:-Replacing-Missing-Values-with-Most-Frequent-Value)
* [6 Feature Engineering](#6-Feature-Engineering)
* [6.1 Mixed Conditions](#6.1-Mixed-Conditions)
* [6.2 Mixed Exterior](#6.2-Mixed-Exterior)
* [6.3 Total Square Feet](#6.3-Total-Square-Feet)
* [6.4 Total Number of Bathrooms](#6.4-Total-Number-of-Bathrooms)
* [6.5 Binning the Neighbourhoods](#6.5-Binning-the-Neighbourhoods)
* [7 LotFrontage Imputation](#7-LotFrontage-Imputation)
* [7.1 LotFrontage Data Structure](#7.1-LotFrontage-Data-Structure)
* [7.2 Outlier Detection & Removal](#7.2-Outlier-Detection-&-Removal)
* [7.3 Determining Relevant Variables of LotFrontage](#7.3-Determining-Relevant-Variables-of-LotFrontage)
* [7.4 LotFrontage Model Building and Evaluation](#7.4-LotFrontage-Model-Building-and-Evaluation)
* [8 Preparing the Data for Modelling](#8-Preparing-the-Data-for-Modelling)
* [8.1 Removing Outliers](#8.1-Removing-Outliers)
* [8.2 Correlation Between Numeric Predictors](#8.2-Correlation-Between-Numeric-Predictors)
* [8.3 Label Encoding](#8.3-Label-Encoding)
* [8.4 Skewness & Normalization of Numeric Variables](#8.4-Skewness-&-Normalization-of-Numeric-Variables)
* [8.5 One Hot Encoding the Categorical Variables](#8.5-One-Hot-Encoding-the-Categorical-Variables)
* [9 SalePrice Modelling](#9-SalePrice-Modelling)
* [9.1 Obtaining Final Train and Test Sets](#9.1-Obtaining-Final-Train-and-Test-Sets)
* [9.2 Defining a Cross Validation Strategy](#9.2-Defining-a-Cross-Validation-Strategy)
* [9.3 Lasso Regression Model](#9.3-Lasso-Regression-Model)
* [9.4 Ridge Regression Model](#9.4-Ridge-Regression-Model)
* [9.5 XGBoost Model](#9.5-XGBoost-Model)
* [9.6 Ensemble Model](#9.6-Ensemble-Model)
<br>
### Ensemble Model Accuracy: (RMSE = 0.12220)
### Competition Description
> Ask a home buyer to describe their dream house, and they probably won't begin with the height of the basement ceiling or the proximity to an east-west railroad. But this playground competition's dataset proves that much more influences price negotiations than the number of bedrooms or a white-picket fence.
>With 79 explanatory variables describing (almost) every aspect of residential homes in Ames, Iowa, this competition challenges you to predict the final price of each home.
### Competition Evaluation
As part of a Kaggle competition dataset, the accuracy of the sales prices was evaluated on [Root-Mean-Squared-Error (RMSE)](https://en.wikipedia.org/wiki/Root-mean-square_deviation) between the logarithm of the predicted value and the logarithm of the observed sales price.
# 1 Summary
I started this competition by focusing on getting a thorough understanding of the dataset. Particular attention was paid to impute the missing values within the dataset. The EDA process is detailed as well as visualized.
In this project, I created a predictive model that has been trained on data collected from homes in Ames, Iowa. Three algorithms were used, and their validation set RMSE and test set RMSE are listed below:
| Regression Model | Validation RMSE | Test RMSE |
|------------------|-----------------|-----------|
| Ridge | 0.1130 | 0.12528 |
| Lasso | 0.1125 | 0.12679 |
| XGBoost | 0.1238 | 0.12799 |
| |
| <b>Ensemble</b> | | 0.12220 |
The Ridge regression model performed the best as a single model, likely due to the high multicollinearity. However, combining it with the Lasso and XGBoost regression models resulting in a higher prediction accuracy and a lower RMSE (<i>0.12220</i> vs <i>0.12528</i>).
# 2 Introduction
The dataset used for this project is the [Ames Housing dataset](https://amstat.tandfonline.com/doi/abs/10.1080/10691898.2011.11889627) that was compiled by <i>Dean De Cock</i> for use in data science education. It is an alternative to the popular but older [Boston Housing dataset](http://lib.stat.cmu.edu/datasets/boston).
The Ames Housing dataset is also used in the [Advanced Regression Techniques challenge](https://www.kaggle.com/c/house-prices-advanced-regression-techniques) on the Kaggle Website. These competitions is a great way to improve my skills and measure my progress as a data scientist.
Kaggle describes the competition as follows:
> Ask a home buyer to describe their dream house, and they probably won't begin with the height of the basement ceiling or the proximity to an east-west railroad. But this playground competition's dataset proves that much more influences price negotiations than the number of bedrooms or a white-picket fence.
>With 79 explanatory variables describing (almost) every aspect of residential homes in Ames, Iowa, this competition challenges you to predict the final price of each home.
<img src="https://i.imgur.com/vOg5fOF.jpg">
# 3 Loading & Exploring the Data Structure
## 3.1 Loading Required Libraries and Reading the Data into Python
Loading Python packages used in the project
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno
from time import time
from math import sqrt
import statsmodels.api as sm
from statsmodels.formula.api import ols
import scipy.stats as st
from scipy.special import boxcox1p
from sklearn.cluster import KMeans
from sklearn import svm
from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.model_selection import train_test_split, KFold, cross_val_score, GridSearchCV
from sklearn.preprocessing import RobustScaler, LabelEncoder, StandardScaler
from sklearn.linear_model import Lasso, Ridge
from sklearn.pipeline import make_pipeline
from xgboost.sklearn import XGBRegressor
%matplotlib inline
```
Now, we read in the csv's as datarames into Python.
```
train = pd.read_csv('../input/train.csv')
test = pd.read_csv('../input/test.csv')
```
## 3.2 Data Structure
In total, there are 81 columns/variables in the train dataset, including the response variable (SalePrice). I am only displaying a subset of the variables, as all of them will be discussed in more detail throughout the notebook.
The train dataset consists of character and integer variables. Many of these variables are ordinal factors, despite being represented as character or integer variables. These will require cleaning and/or feature engineering later.
```
print("Dimensions of Train Dataset:" + str(train.shape))
print("Dimensions of Test Dataset:" + str(test.shape))
train.iloc[:,0:10].info()
```
Next, we are going to define a few variables that will be used in later analyses as well as being required for the submission file.
```
y_train = train['SalePrice']
test_id = test['Id']
ntrain = train.shape[0]
ntest = test.shape[0]
```
Lastly, we are going to merge the train and test datasets to explore the data as well as impute any missing values.
```
all_data = pd.concat((train, test), sort=True).reset_index(drop=True)
all_data['Dataset'] = np.repeat(['Train', 'Test'], [ntrain, ntest], axis=0)
all_data.drop('Id', axis=1,inplace=True)
```
# 4 Exploring the Variables
## 4.1 Exploring the Response Variable: SalePrice
The probability distribution plot show that the sale prices are right skewed. This is to be expected as few people can afford very expensive houses.
```
sns.set_style('whitegrid')
sns.distplot(all_data['SalePrice'][~all_data['SalePrice'].isnull()], axlabel="Normal Distribution", fit=st.norm, fit_kws={"color":"red"})
plt.title('Distribution of Sales Price in Dollars')
(mu, sigma) = st.norm.fit(train['SalePrice'])
plt.legend(['Normal Distribution \n ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best', fancybox=True)
plt.show()
st.probplot(all_data['SalePrice'][~all_data['SalePrice'].isnull()], plot=plt)
plt.show()
```
Linear models tend to work better with normally distributed data. As such, we need to transform the response variable to make it more normally distributed.
## 4.2 Log-Transformation of the Response Variable
```
all_data['SalePrice'] = np.log1p(all_data['SalePrice'])
sns.distplot(all_data['SalePrice'][~all_data['SalePrice'].isnull()], axlabel="Normal Distribution", fit=st.norm, fit_kws={"color":"red"})
plt.title('Distribution of Transformed Sales Price in Dollars')
(mu, sigma) = st.norm.fit(train['SalePrice'])
plt.legend(['Normal Distribution \n ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best', fancybox=True)
plt.show()
st.probplot(all_data['SalePrice'][~all_data['SalePrice'].isnull()], plot=plt)
plt.show()
```
The skew is highly corrected and the distribution of the log-transformed sale prices appears more normally distributed.
# 5 Data Imputation
## 5.1 Completeness of the Data
We first need to find which variables contain missing values.
```
cols_with_missing_values = all_data.isnull().sum().sort_values(ascending=False)
display(pd.DataFrame(cols_with_missing_values[cols_with_missing_values[cols_with_missing_values > 0].index],
columns=["Number of Missing Values"]))
cols_with_missing_values = all_data.isnull().sum().sort_values(ascending=False)
cols_with_missing_values = all_data[cols_with_missing_values[cols_with_missing_values > 0].index]
msno.bar(cols_with_missing_values)
plt.show()
```
## 5.2 Impute the Missing Data
### 5.2.1 Missing Values Corresponding to Lack of Specific Feature
* <b>PoolQC</b>: data description of the variables states that NA represents "no pool". This makes sense given the vast number of missing values (>99%) and that a majority of houses do not have a pool.
```
all_data['PoolQC'].replace(np.nan, 'None', regex=True, inplace=True)
```
* <b>MiscFeature</b>: data description of the variables states that NA represents "no miscellaneous feature".
```
all_data['MiscFeature'].replace(np.nan, 'None', regex=True, inplace=True)
```
* <b>Alley</b>: data description of the variables states that NA represents "no alley access".
```
all_data['Alley'].replace(np.nan, 'None', regex=True, inplace=True)
```
* <b>Fence</b>: data description of the variables states that NA represents "no fence".
```
all_data['Fence'].replace(np.nan, 'None', regex=True, inplace=True)
```
* <b>FireplaceQU</b>: data description of the variables states that NA represents "no fireplace".
```
all_data['FireplaceQu'].replace(np.nan, 'None', regex=True, inplace=True)
```
* <b>GarageType, GarageFinish, GarageQual, and GarageCond</b>: Missing values are likely due to lack of a garage. Replacing missing data with None.
```
garage_categorical = ['GarageType', 'GarageFinish', 'GarageQual', 'GarageCond']
for variable in garage_categorical:
all_data[variable].replace(np.nan, 'None', regex=True, inplace=True)
```
* <b>GarageYrBlt, GarageCars, and GarageArea</b>: Missing values are likely due to lack of a basement. Replacing missing data with 0 (since no garage means no cars in a garage).
```
garage_numeric = ['GarageYrBlt', 'GarageCars', 'GarageArea']
for variable in garage_numeric:
all_data[variable].replace(np.nan, 0, regex=True, inplace=True)
```
* <b>BsmtQual, BsmtCond, BsmtExposure, BsmtFinType1, and BsmtFinType2</b>: Missing values are likely due to lack of a basement. Replacing missing data with None.
```
basement_categorical = ['BsmtQual','BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2']
for variable in basement_categorical:
all_data[variable].replace(np.nan, 'None', regex=True, inplace=True)
```
* <b>BsmtFinSF1, BsmtFinSF2, BsmtUnfSF, TotalBsmtSF, BsmtFullBath, and BsmtHalfBath</b>: Missing values are likely due to lack of a basement. Replacing missing data with 0.
```
basement_numeric = ['BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'BsmtFullBath', 'BsmtHalfBath']
for variable in basement_numeric:
all_data[variable].replace(np.nan, 0, regex=True, inplace=True)
```
* <b>MasVnrType and MasVnrArea</b>: Missing values are likely due to lack of masonry vaneer. We will replace the missing values with None for the type and 0 for the area.
```
all_data['MasVnrType'].replace(np.nan, 'None', regex=True, inplace=True)
all_data['MasVnrArea'].replace(np.nan, 0, regex=True, inplace=True)
```
* <b>Functional</b>: data description of the variables states that NA represents "typical".
```
all_data['Functional'].replace(np.nan, 'Typ', regex=True, inplace=True)
```
### 5.2.2 Mode Imputation: Replacing Missing Values with Most Frequent Value
Using a mode imputation, we replace the missing values of a categorical variable with the mode of the non-missing cases of that variable. While it does have the advantage of being fast, it comes at the cost of a reduction in variance within the dataset.
Due to the low number of missing values imputed using this method, the bias introduced on the mean and standard deviation, as well as correlations with other variables are minimal.
<br>
First, we define a function "<b>mode_impute_and_plot</b>" to simplify the process of visualizing the categorical variables and replacing the missing variables with the most frequent value.
```
def mode_impute_and_plot(variable):
print('# of missing values: ' + str(all_data[variable].isna().sum()))
plt.figure(figsize=(8,4))
ax = sns.countplot(all_data[variable])
ax.set_xticklabels(ax.get_xticklabels(), rotation=40, ha="right")
plt.tight_layout()
plt.show()
all_data[variable].replace(np.nan, all_data[variable].mode()[0], regex=True, inplace=True)
```
Now we can proceed to replace the missing values for the following variables:
[]() |
------|------
[MSZoning](#MSZoning) | [Utilities](#Utilities) | [Electrical](#Electrical) | [Exterior1st and Exterior2nd](#Exterior1st and Exterior2nd) | [KitchenQual](#KitchenQual) | [SaleType](#SaleType)
<a id="MSZoning"></a>
* <b>MSZoning</b>: "RL" is by far the most common value. Missing values will be replace with "RL".
```
mode_impute_and_plot('MSZoning')
```
<a id="Utilities"></a>
* <b>Utilities</b>: With the exception of one "NoSeWa" value, all records for this variable are "AllPub". Since "NoSeWa" is only in the training set, <b>this feature will not help in predictive modelling</b>. As such, we can safely remove it.
```
mode_impute_and_plot('Utilities')
all_data = all_data.drop('Utilities', axis=1)
```
<a id="Electrical"></a>
* <b>Electrical</b>: Only one missing value, replace it with "SBrkr", the most common value.
```
mode_impute_and_plot('Electrical')
```
<a id="Exterior1st and Exterior2nd"></a>
* <b>Exterior1st and Exterior2nd</b>: There is only one missing value for both Exterior 1 & 2. Missing values will be replaced by the most common value.
```
mode_impute_and_plot('Exterior1st')
mode_impute_and_plot('Exterior2nd')
```
<a id="KitchenQual"></a>
* <b>KitchenQual</b>: Only one missing value, replace it with "TA", the most common value.
```
mode_impute_and_plot('KitchenQual')
```
<a id="SaleType"></a>
* <b>SaleType</b>: Replace missing values with "WD", the most common value.
```
mode_impute_and_plot('SaleType')
```
Are there any remaining missing values?
```
cols_with_missing_values = all_data.isnull().sum().sort_values(ascending=False)
display(pd.DataFrame(cols_with_missing_values[cols_with_missing_values[cols_with_missing_values > 0].index], columns=["Number of Missing Values"]))
```
Due to its numeric nature and the large number of missing values, the LotFrontage variable will be imputed separately using an SVM algorithm (See Section [7 LotFrontage Imputation](#7-Lot-Frontage-Imputation)).
<br>
The remaining variables are all complete! Now to move on to feature engineering.
# 6 Feature Engineering
## 6.1 Mixed Conditions
In order to simplify and boost the accuracy of the preditive models, we will merge the two conditions into one variable: <b>MixedConditions</b>
The data descriptions states:
* <b>Condition1</b> represents proximity to various conditions.
* <b>Condition2</b> represents proximity to various conditions (if more than one is present).
If a property does not have one or multiple conditions, then it is classified as normal. However, designation of "normal" are condition 1 or condition 2 is strictly alphabetical.
For example, if a property is in proximity to a feeder street ("Feedr") and no other condition, then the data would appear as follows:
Condition1 | Condition2
-----------|-------------
Feedr | Norm
<br>
However, if a property is within 200' of East-West Railroad (RRNe) and no other condition, then the data would appear as follows:
Condition1 | Condition2
-----------|-------------
Norm | RRNe
<br><br>
Once we merge Conditions 1 & 2 into the <b>MixedConditions</b> variable, we will remove them from the analysis.
```
all_data['MixedConditions'] = all_data['Condition1'] + ' - ' + all_data['Condition2']
all_data.drop(labels=['Condition1', 'Condition2'], axis=1, inplace=True)
```
## 6.2 Mixed Exterior
The Exterior1st and Exterior2nd features are similar to the Conditions feature we merged and remove above. Properties with multiple types of exterior covering the house are assigned to Exterior1st or Exterior2nd alphabetically.
As such, we will conduct the same process to merge the two columns into a single <b>MixedExterior</b> variable and remove them from the analysis.
```
all_data['MixedExterior'] = all_data['Exterior1st'] + ' - ' + all_data['Exterior2nd']
all_data.drop(labels=['Exterior1st', 'Exterior2nd'], axis=1, inplace=True)
```
## 6.3 Total Square Feet
One of the important factors that people consider when buying a house is the total living space in square feet. Since the total square feet is not explicitly listed, we will add a new variable by adding up the square footage of the basement, first floor, and the second floor.
```
SF_df = all_data[['TotalBsmtSF', '1stFlrSF', '2ndFlrSF', 'SalePrice']]
SF_df = SF_df[~SF_df['SalePrice'].isnull()]
SF_vars = list(SF_df)
del SF_vars[-1]
SF_summary = []
for SF_type in SF_vars:
corr_val = np.corrcoef(SF_df[SF_type], SF_df['SalePrice'])[1][0]
SF_summary.append(corr_val)
pd.DataFrame([SF_summary], columns=SF_vars, index=['SalePrice Correlation'])
all_data['TotalSF'] = all_data['TotalBsmtSF'] + all_data['1stFlrSF'] + all_data['2ndFlrSF']
plt.figure(figsize=(10,6))
ax = sns.regplot(all_data['TotalSF'], all_data['SalePrice'], line_kws={'color': 'red'})
ax.set(ylabel='ln(SalePrice)')
plt.show()
print("Pearson Correlation Coefficient: %.3f" % (np.corrcoef(all_data['TotalSF'].iloc[:ntrain], train['SalePrice']))[1][0])
```
There is a very strong correlation (r = 0.78) between the TotalSF and the SalePrice, with the exception of two outliers. These outliers should be removed to increase the accuracy of our model.
## 6.4 Total Number of Bathrooms
There are 4 bathroom variables. Individually, these variables are not very important. Together, however, these predictors are likely to become a strong one.
A full bath is made up of four parts: a sink, shower, a bathtub, and a toilet. A half-bath, also called a powder room or guest bath, only has a sink and a toilet. As such, half-bathrooms will have half the value of a full bath.
```
bath_df = all_data[['BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath', 'SalePrice']]
bath_df = bath_df[~bath_df['SalePrice'].isnull()]
bath_vars = list(bath_df)
del bath_vars[-1]
bath_summary = []
for bath_type in bath_vars:
corr_val = np.corrcoef(bath_df[bath_type], bath_df['SalePrice'])[1][0]
bath_summary.append(corr_val)
pd.DataFrame([bath_summary], columns=bath_vars, index=['SalePrice Correlation'])
all_data['TotalBath'] = all_data['BsmtFullBath'] + (all_data['BsmtHalfBath']*0.5) + all_data['FullBath'] + (all_data['HalfBath']*0.5)
plt.figure(figsize=(10,4))
sns.countplot(all_data['TotalBath'], color='grey')
plt.tight_layout()
plt.show()
plt.figure(figsize=(10,6))
sns.regplot(all_data['TotalBath'].iloc[:ntrain], train['SalePrice'], line_kws={'color': 'red'})
ax.set(ylabel='ln(SalePrice)')
plt.show()
print("Pearson Correlation Coefficient: %.3f" % (np.corrcoef(all_data['TotalBath'].iloc[:ntrain], train['SalePrice']))[1][0])
```
We can see a high positive correlation (r = 0.67) between TotalBath and SalePrice. The new variable correlation is much higher than any of the four original bathroom variables.
## 6.5 Binning the Neighbourhoods
```
neighborhood_prices = all_data.iloc[:ntrain].copy()
neighborhood_prices['SalePrice'] = np.exp(all_data['SalePrice'])
neighborhood_prices = neighborhood_prices[['Neighborhood', 'SalePrice']].groupby('Neighborhood').median().sort_values('SalePrice')
plt.figure(figsize=(15,7))
ax = sns.barplot(x= neighborhood_prices.index, y=neighborhood_prices['SalePrice'], color='grey')
ax.set_xticklabels(ax.get_xticklabels(), rotation=40, ha="right")
plt.tight_layout()
plt.show()
```
In order to bin the neighbourhoods into approriate clusters, we will use K-Mean clustering. <b>K-Means</b> is an unsupervised machine learning algorithm that groups a dataset into a user-specified number (<i>k</i>) of clusters. One potential issue with the algorithm is that it will cluster the data into <i>k</i> clusters, even if <i>k</i> is not the right number of cluster to use.
Therefore, we need to identity the optimal number of k clusters to use. To do so, we will use the <i>Elbow Method</i>.
Briefly, the idea of the elbow method is to run k-means clustering for a range of values and calculate the sum of squared errors (SSE). We then plot a line chart of the SSE for each value of <i>k</i>. Each additional <i>k</i> cluster will result in a lower SSE, but will eventually exhibit significantly diminished return.
The goal is the choose a small value of k with a low SSE, after which the subsequent k values exhibit diminishing returns. If the line plot looks like an arm, then the "elbow" of the arm is the optimal <i>k</i> value.
The plot below indicates that the optimal number of neighbourhood clusters is <i>k</i> = 3.
```
SS_distances = []
K = range(1,10)
for k in K:
km = KMeans(n_clusters=k)
km = km.fit(neighborhood_prices)
SS_distances.append(km.inertia_)
plt.plot(K, SS_distances, 'bx-')
plt.xlabel('k')
plt.ylabel('Sum of squared distances')
plt.title('Elbow Method For Optimal k')
plt.show()
```
Now let's see how the binned neighborhoods look like.
```
neighborhood_prices['Cluster'] = KMeans(n_clusters=3).fit(neighborhood_prices).labels_
plt.figure(figsize=(15,7))
ax = sns.barplot(x= neighborhood_prices.index, y=neighborhood_prices['SalePrice'],
hue=neighborhood_prices['Cluster'])
ax.set_xticklabels(ax.get_xticklabels(), rotation=40, ha="right")
plt.tight_layout()
plt.show()
```
Lastly, we have to create a new variable in the dataset based on the new cluster labels.
```
neighborhood_dict = dict(zip(neighborhood_prices.index, neighborhood_prices.Cluster))
all_data['Neighborhood_Class'] = all_data['Neighborhood']
all_data['Neighborhood_Class'].replace(neighborhood_dict, inplace = True)
```
# 7 LotFrontage Imputation
Due to the numeric nature and sheer number of missing values in the <i>LotFrontage</i> column, we will impute the missing values using an SVM Regressor algorithm to predict the missing values.
The first step is to subset the dataset into two groups. The <i>train</i> dataset (train_LotFrontage) contains the complete records while the <i>test</i> dataset (test_LotFrontage) contains the missing values. Next, we examine the structure of the newly created datasets. There are 486 missing values in the full dataset, or roughly 16% of the data.
## 7.1 LotFrontage Data Structure
```
train_LotFrontage = all_data[~all_data.LotFrontage.isnull()]
test_LotFrontage = all_data[all_data.LotFrontage.isnull()]
print("Dimensions of Train LotFrontage Dataset:" + str(train_LotFrontage.shape))
print("Dimensions of Test LotFrontage Dataset:" + str(test_LotFrontage.shape))
display(pd.DataFrame(all_data['LotFrontage'].describe()).transpose())
```
Now let's examine the distribution of LotFrontages values in the Train LotFrontage dataset through a boxplot and distribution plot. Through these graphs, we can see several interesting observations appear:
* There is a cluster of low <i>LotFrontage</i> value properties, shown as a peak on the far left of the distribution plot. The boxplot indicates these values may be outliers, shown as outlier points on the left of the whisker of the boxplot.
* There is a long tail of high <i>LotFrontage</i> value properties. These values extend beyond the Median + 1.5IQR range.
In other words, there are outliers on both ends of the <i>LotFrontage</i> value distributions.
```
fig, ax = plt.subplots(1,2, figsize=(16,4))
sns.boxplot(train_LotFrontage['LotFrontage'], ax=ax[0])
sns.distplot(train_LotFrontage['LotFrontage'], ax=ax[1], fit=st.norm, fit_kws={"color":"red"})
(mu, sigma) = st.norm.fit(train_LotFrontage['LotFrontage'])
plt.legend(['Normal Distribution \n ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best', fancybox=True)
plt.show()
```
## 7.2 Outlier Detection & Removal
Before we examine the correlations between <i>LotFrontage</i> and other variables, we should remove the outliers seen above.
To do so, we will use the Interquartile Range (IQR) method, where values outside the <i>Median ± 1.5IQR</i> are considered to be outliers. These outliers are then removed from the <i>LotFrontage</i> datasets.
```
def outlier_detection(data):
Q1, Q3 = np.percentile(data, [25,75])
IQR = Q3-Q1
lower_cutoff = Q1 - (IQR * 1.5)
upper_cutoff = Q3 + (IQR * 1.5)
outliers = (data > Q3+1.5*IQR) | (data < Q1-1.5*IQR)
return outliers
train_LotFrontage_no_outliers = train_LotFrontage[~outlier_detection(train_LotFrontage.LotFrontage)]
fig, ax = plt.subplots(1,2, figsize=(16,4))
sns.boxplot(train_LotFrontage_no_outliers['LotFrontage'], ax=ax[0])
sns.distplot(train_LotFrontage_no_outliers['LotFrontage'], ax=ax[1], fit=st.norm, fit_kws={"color":"red"})
(mu, sigma) = st.norm.fit(train_LotFrontage_no_outliers['LotFrontage'])
plt.legend(['Normal Distribution \n ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
loc='best', fancybox=True)
plt.show()
```
Two new values previously not deemed outliers by the first iteration of the IQR range method are now shown as potential outliers in the boxplot. This is caused by having a new smaller IQR value after removing the first batch of outliers. As such, we will keep these values.
## 7.3 Determining Relevant Variables of LotFrontage
Now we can explore the relationship between the <i>LotFrontage</i> target variable and other features. In order to confirm a relationship between these key features and we will conduct an <b>ANOVA</b> (Analysis of Variance) test to determine statistical significance (in this case, <i>p < 0.01</i>).
<br>
Using the type III ANOVA, we are confident the variables listed in the table below are correlated with LotFrontage.
* Note: Variables that begin with a number (<i>1stFlrSF</i>, <i>2ndFlrSF</i>, and <i>3SsnPorch</i>) cause a syntax error within the ols formula input. I briefly converted them to an appropriate name in the <i>temp_train</i> dataset for the purpose of the ANOVA.
```
temp_train = train_LotFrontage_no_outliers.copy()
temp_train.rename(columns={'1stFlrSF':'X1stFlrSF', '2ndFlrSF': 'X2ndFlrSF', '3SsnPorch': 'X3SsnPorch'}, inplace=True)
mod = ols('LotFrontage ~ X1stFlrSF + X2ndFlrSF + X3SsnPorch + Alley + BedroomAbvGr + BldgType + BsmtCond + BsmtExposure + BsmtFinSF1 + BsmtFinSF2 + BsmtFinType1 + BsmtFinType2 + BsmtFullBath + BsmtHalfBath + BsmtQual + BsmtUnfSF + CentralAir + Electrical + EnclosedPorch + ExterCond + ExterQual + Fence + FireplaceQu + Fireplaces + Foundation + FullBath + Functional + GarageArea + GarageCars + GarageCond + GarageFinish + GarageQual + GarageType + GarageYrBlt + GrLivArea + HalfBath + Heating + HeatingQC + HouseStyle + KitchenAbvGr + KitchenQual + LandContour + LandSlope + LotArea + LotConfig + LotShape + LowQualFinSF + MSSubClass + MSZoning + MasVnrArea + MasVnrType + MiscFeature + MiscVal + MoSold + Neighborhood + OpenPorchSF + OverallCond + OverallQual + PavedDrive + PoolArea + PoolQC + RoofMatl + RoofStyle + SaleCondition + SaleType + ScreenPorch + Street + TotRmsAbvGrd + TotalBsmtSF + WoodDeckSF + YearBuilt + YearRemodAdd + YrSold + MixedConditions + MixedExterior + TotalSF + TotalBath + Neighborhood_Class', data=temp_train).fit()
aov_table = sm.stats.anova_lm(mod, typ=3)
display(aov_table[aov_table['PR(>F)'] < 0.01])
```
## 7.4 LotFrontage Model Building and Evaluation
Now let's build a model using the relevant variables selected above. We will be using Support Vector Regressor to build the model.
The first step is to seperate the target variable, <i>LotFrontage</i>, select the relevant variables, and dummifying the categorical variables.
```
X = train_LotFrontage_no_outliers[aov_table[aov_table['PR(>F)'] < 0.01].index]
y = train_LotFrontage_no_outliers['LotFrontage']
X = pd.get_dummies(X)
transformer = StandardScaler().fit(X)
X = transformer.transform(X)
```
In order to determine the accuracy of our predictive model, we will create a <i>Validation</i> dataset. This dataset will have known values for the target <i>LotFrontage</i> variable which can we compare our model's prediction against. Using the mean absolute error, we can measure the difference between our predicted <i>LotFrontage</i> values with the true values.
<img src="https://i.imgur.com/jswcCd8.png">
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1234)
clf = svm.SVR(kernel='rbf', C=100, gamma=0.001)
clf.fit(X_train, y_train)
preds = clf.predict(X_test)
print('Mean Absolute Error: %.3f' % mean_absolute_error(y_test, preds))
```
These results show that using the SVR model to impute <i>LotFrontage</i> gives an average rror of less than 7 feet.
We will now use the same SVR model to predict the unknown <i>LotFrontage</i> values in the test_Frontage dataset.
```
model_data = train_LotFrontage_no_outliers.copy()
model_data= model_data.append(test_LotFrontage)
y = model_data['LotFrontage']
model_data = model_data[['MSZoning', 'Alley', 'LotArea', 'LotShape', 'LotConfig', 'Neighborhood', 'MixedConditions', 'GarageType', 'GarageCars', 'GarageArea']]
model_data = pd.get_dummies(model_data)
model_X_train = model_data[~y.isnull()]
model_X_test = model_data[y.isnull()]
model_y_train = y[~y.isnull()]
transformer = StandardScaler().fit(model_X_train)
model_X_train = transformer.transform(model_X_train)
model_X_test = transformer.transform(model_X_test)
clf = svm.SVR(kernel='rbf', C=100, gamma=0.001)
clf.fit(model_X_train, model_y_train)
LotFrontage_preds = clf.predict(model_X_test)
```
Now that we have the newly predicted <i>LotFrontage</i> values, we can examine the distribution of predicted values relative to the known <i>LotFrontage</i> values in the training dataset. Both distributions have a mean around 70 feet with similar tail lengths on either end.
```
sns.distplot(model_y_train)
sns.distplot(LotFrontage_preds)
```
Lastly, we need to add the predicted values back into the original dataset.
```
all_data.LotFrontage[all_data.LotFrontage.isnull()] = LotFrontage_preds
```
# 8 Preparing the Data for Modelling
## 8.1 Removing Outliers
Although we could be more in depth in our outliet detection and removal, we are only going to remove the two outliers found in the TotalSF variable. These properties exhibited large total square feet values with low SalePrice.
```
all_data.drop(all_data['TotalSF'].iloc[:ntrain].nlargest().index[:2], axis=0, inplace=True)
ntrain = train.shape[0]-2
```
## 8.2 Correlation Between Numeric Predictors
We can see a large correlation between many variables, suggesting a high level of multicollinearity. There are two options to consider:
1. Use a regression model that deals well with multicollinearity, such as a ridge regression.
2. Remove highly correlated predictors from the model.
```
corr = all_data.corr()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
f, ax = plt.subplots(figsize=(15, 15))
cmap = sns.diverging_palette(220, 10, as_cmap=True)
sns.heatmap(corr, mask=mask, cmap=cmap,
center=0, square=True, linewidths = .5)
plt.show()
```
## 8.3 Label Encoding
Many of the ordinal variables are presented as numeric values. Therefore we need to label encode these numeric characters into strings.
```
num_to_str_columns = ['MSSubClass', 'OverallQual', 'OverallCond', 'MoSold', 'YrSold']
for col in num_to_str_columns:
all_data[col] = all_data[col].astype('str')
cat_cols = ['OverallQual', 'OverallCond', 'ExterQual', 'ExterCond', 'BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1',
'BsmtFinType2', 'BsmtFinSF2', 'HeatingQC', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath', 'HalfBath', 'BedroomAbvGr',
'KitchenAbvGr', 'KitchenQual', 'TotRmsAbvGrd', 'Fireplaces', 'FireplaceQu', 'GarageFinish', 'GarageCars',
'GarageQual', 'GarageCond', 'PoolQC', 'Fence', 'YearBuilt', 'YearRemodAdd', 'GarageYrBlt', 'MoSold', 'YrSold']
for col in cat_cols:
label = LabelEncoder()
label.fit(list(all_data[col].values))
all_data[col] = label.transform(list(all_data[col].values))
print('Shape all_data: {}'.format(all_data.shape))
all_data.head()
```
## 8.4 Skewness & Normalization of Numeric Variables
<b>Skewness</b> is a measure of asymmetry of a distribution, and can be used to define the extent to which the distribution differs from a normal distribution. Therefore, a normal distribution will have a skewness of 0. As a rule of thumb, if skewness is less than -1 or greater than 1, the distribution is highly skewed.
In order to account for skewness, we will transform the (highly) skewed data into normality using a Log Transformation. We define highly skewed data as variables with a skewness greater than 0.85. This method is similar to the approach used to normalize the [SalePrice Response Variable](#4.2-Log-Transformation-of-the-Response-Variable), except we will use log+1 to avoid division by zero issues.
```
numeric_feats = ['LotFrontage', 'LotArea', 'BsmtFinSF1', 'BsmtUnfSF', 'TotalBsmtSF', '1stFlrSF', '2ndFlrSF',
'LowQualFinSF', 'GrLivArea', 'GarageArea', 'WoodDeckSF', 'OpenPorchSF', 'EnclosedPorch',
'3SsnPorch', 'ScreenPorch', 'PoolArea', 'MiscVal', 'TotalSF']
skewed_feats = all_data[numeric_feats].apply(lambda x: st.skew(x.dropna())).sort_values(ascending=False)
skewness = pd.DataFrame({'Skew Before Transformation' :skewed_feats})
skewness = skewness[abs(skewness) > 1].dropna(axis=0)
skewed_features = skewness.index
for feat in skewed_features:
all_data[feat] = np.log1p(all_data[feat]+1)
skewed_feats = all_data[skewed_features].apply(lambda x: st.skew(x.dropna())).sort_values(ascending=False)
skewness['Skew After Transformation'] = skewed_feats
skewness
```
## 8.5 One Hot Encoding the Categorical Variables
The last step needed to prepare the data is to make sure that all categorical predictor variables are converted into a form that is usable by machine learning algorithms. This process is known as 'one-hot encoding' the categorical variables.
The process involved all non-ordinal factors receiving their own separate column with 1's and 0's, and is required by most ML algorithms.
```
all_data = pd.get_dummies(all_data)
print(all_data.shape)
all_data.head(3)
```
# 9 SalePrice Modelling
Now that the data is correctly processed, we are ready to begin building our predictive models.
## 9.1 Obtaining Final Train and Test Sets
```
final_y_train = all_data['SalePrice'][~all_data['SalePrice'].isnull()]
final_X_train = all_data[all_data['Dataset_Train'] == 1].drop(['Dataset_Train', 'Dataset_Test', 'SalePrice'], axis=1)
final_X_test = all_data[all_data['Dataset_Test'] == 1].drop(['Dataset_Train', 'Dataset_Test', 'SalePrice'], axis=1)
```
## 9.2 Defining a Cross Validation Strategy
We will use the [cross_val_score](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html) function of Sklearn and calculate the Root-Mean-Squared Error (RMSE) as a measure of accuracy.
```
n_folds = 10
def rmse_cv(model):
kf = KFold(n_folds, shuffle=True, random_state=1234).get_n_splits(final_X_train.values)
rmse= np.sqrt(-cross_val_score(model, final_X_train.values, final_y_train, scoring="neg_mean_squared_error", cv = kf))
return(rmse)
```
## 9.3 Lasso Regression Model
This model may be senstitive to outliers, so we need to make it more robust. This will be done using the <b>RobustScaler</b> function on pipeline.
```
lasso = make_pipeline(RobustScaler(), Lasso(alpha = 0.0005, random_state = 1234))
```
Next, we tested out multiple alpha values and compared their accuracy using the <b>rmse_cv</b> function above. The results below show that using a value of 0.00025 is the optimal value of alpha for a Lasso Regression.
```
lasso_alpha = [1, 0.5, 0.25, 0.1, 0.05, 0.025, 0.01, 0.005, 0.0025, 0.001, 0.0005, 0.00025, 0.0001]
lasso_rmse = []
for value in lasso_alpha:
lasso = make_pipeline(RobustScaler(), Lasso(alpha = value, max_iter=3000, random_state = 1234))
lasso_rmse.append(rmse_cv(lasso).mean())
lasso_score_table = pd.DataFrame(lasso_rmse,lasso_alpha,columns=['RMSE'])
display(lasso_score_table.transpose())
plt.semilogx(lasso_alpha, lasso_rmse)
plt.xlabel('alpha')
plt.ylabel('score')
plt.show()
print("\nLasso Score: {:.4f} (alpha = {:.5f})\n".format(min(lasso_score_table['RMSE']), lasso_score_table.idxmin()[0]))
```
Using the newly defined alpha value, we can optimize the model and predict the missing values of <i>SalePrice</i>. The predictions are then formatted in a appropriate layout for submission to Kaggle.
```
lasso = make_pipeline(RobustScaler(), Lasso(alpha = 0.00025, random_state = 1234))
lasso.fit(final_X_train, final_y_train)
lasso_preds = np.expm1(lasso.predict(final_X_test))
sub = pd.DataFrame()
sub['Id'] = test_id
sub['SalePrice'] = lasso_preds
#sub.to_csv('Lasso Submission 2.csv',index=False)
```
### LASSO Regression Score: 0.12679
<br>
## 9.4 Ridge Regression Model
Identical steps were taken for the ridge regression model as we took for the [Lasso Regression Model](#9.3-Lasso-Regression-Model). In the case of the Ridge model, the optimal alpha value was 6.
```
ridge_alpha = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]
ridge_rmse = []
for value in ridge_alpha:
ridge = make_pipeline(RobustScaler(), Ridge(alpha = value, random_state = 1234))
ridge_rmse.append(rmse_cv(ridge).mean())
ridge_score_table = pd.DataFrame(ridge_rmse,ridge_alpha,columns=['RMSE'])
display(ridge_score_table.transpose())
plt.semilogx(ridge_alpha, ridge_rmse)
plt.xlabel('alpha')
plt.ylabel('score')
plt.show()
print("\nRidge Score: {:.4f} (alpha = {:.4f})\n".format(min(ridge_score_table['RMSE']), ridge_score_table.idxmin()[0]))
ridge = make_pipeline(RobustScaler(), Ridge(alpha = 6, random_state = 1234))
ridge.fit(final_X_train, final_y_train)
ridge_preds = np.expm1(ridge.predict(final_X_test))
sub = pd.DataFrame()
sub['Id'] = test_id
sub['SalePrice'] = ridge_preds
#sub.to_csv('Ridge Submission.csv',index=False)
```
### Ridge Regression Score: 0.12528
<br>
## 9.5 XGBoost Model
Since there are multiple hyperparameters to tune in the XGBoost model, we will use the [GridSearchCV](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html) function of Sklearn to determine the optimal values. Next, I used the [train_test_split](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html) function to generate a validation set and find the RMSE of the models. This method is used in lieu of the [rmse_cv](#9.2-Defining-a-Cross-Validation-Strategy)
function used above for the Lasso and Ridge Regression models.
```
xg_X_train, xg_X_test, xg_y_train, xg_y_test = train_test_split(final_X_train, final_y_train, test_size=0.33, random_state=1234)
xg_model = XGBRegressor(n_estimators=100, seed = 1234)
param_dict = {'max_depth': [3,4,5],
'min_child_weight': [2,3,4],
'learning_rate': [0.05, 0.1,0.15],
'gamma': [0.0, 0.1, 0.2]
}
start = time()
grid_search = GridSearchCV(xg_model, param_dict)
grid_search.fit(xg_X_train, xg_y_train)
print("GridSearch took %.2f seconds to complete." % (time()-start))
display(grid_search.best_params_)
```
Now that the hyperparameter have been chosen, we can calculate the validation RMSE of the XGBoost model.
```
xg_model = XGBRegressor(n_estimators = 1000,
learning_rate = 0.1,
max_depth = 4,
min_child_weight = 4,
gamma = 0,
seed = 1234)
start = time()
xg_model.fit(xg_X_train, xg_y_train)
xg_preds = xg_model.predict(xg_X_test)
print("Model took %.2f seconds to complete." % (time()-start))
print("RMSE: %.4f" % sqrt(mean_squared_error(xg_y_test, xg_preds)))
```
Lastly, we predict the <i>SalePrice</i> using the test data. The predictions are then formatted in a appropriate layout for submission to Kaggle.
```
xg_model = XGBRegressor(n_estimators = 1000,
learning_rate = 0.1,
max_depth = 4,
min_child_weight = 4,
gamma = 0,
seed = 1234)
xg_model.fit(final_X_train, final_y_train)
xg_preds = np.expm1(xg_model.predict(final_X_test))
sub = pd.DataFrame()
sub['Id'] = test_id
sub['SalePrice'] = xg_preds
#sub.to_csv('XGBoost Submission.csv',index=False)
```
### XGBoost Regression Model: 0.12799
<br>
## 9.6 Ensemble Model
Since the Lasso, Ridge, XGBoost algorithms so different, averaging the final <i>Saleprice</i> predictions may improve the accuracy. Since the Ridge regression performed the best with regards to the final RMSE (0.125 vs 0.126 and 0.127), I will assign it's weight to be double that of the other two models.
Our final ensemble model performed better than any individual regression model (<b>RMSE = 0.12220</b>).
```
lasso = make_pipeline(RobustScaler(), Lasso(alpha = 0.00025, random_state = 1234))
lasso.fit(final_X_train, final_y_train)
lasso_preds = np.expm1(lasso.predict(final_X_test))
ridge = make_pipeline(RobustScaler(), Ridge(alpha = 6, random_state = 1234))
ridge.fit(final_X_train, final_y_train)
ridge_preds = np.expm1(ridge.predict(final_X_test))
xg_model = XGBRegressor(n_estimators = 1000,
learning_rate = 0.1,
max_depth = 4,
min_child_weight = 4,
gamma = 0,
seed = 1234)
xg_model.fit(final_X_train, final_y_train)
xg_preds = np.expm1(xg_model.predict(final_X_test))
weights = [0.5, 0.25, 0.25]
sub = pd.DataFrame()
sub['Id'] = test_id
sub['SalePrice'] = (ridge_preds*weights[0]) + (lasso_preds*weights[1]) + (xg_preds*weights[2])
sub.to_csv('Ensemble Submission.csv',index=False)
```
### Ensemble Regression Score: 0.12220
<br>
| github_jupyter |
<a href="https://colab.research.google.com/github/mees/calvin/blob/main/RL_with_CALVIN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<h1>Reinforcement Learning with CALVIN</h1>
The **CALVIN** simulated benchmark is perfectly suited for training agents with reinforcement learning, in this notebook we will demonstrate how to integrate your agents to these environments.
## Installation
The first step is to install the CALVIN github repository such that we have access to the packages
```
# Download repo
%mkdir /content/calvin
%cd /content/calvin
!git clone https://github.com/mees/calvin_env.git
%cd /content/calvin/calvin_env
!git clone https://github.com/lukashermann/tacto.git
# Install packages
%cd /content/calvin/calvin_env/tacto/
!pip3 install -e .
%cd /content/calvin/calvin_env
!pip3 install -e .
!pip3 install -U numpy
# Run this to check if the installation was succesful
from calvin_env.envs.play_table_env import PlayTableSimEnv
```
## Loading the environment
After the installation has finished successfully, we can start using the environment for reinforcement Learning.
To be able to use the environment we need to have the appropriate configuration that define the desired features, for this example, we will load the static and gripper camera.
```
%cd /content/calvin
from hydra import initialize, compose
with initialize(config_path="./calvin_env/conf/"):
cfg = compose(config_name="config_data_collection.yaml", overrides=["cameras=static_and_gripper"])
cfg.env["use_egl"] = False
cfg.env["show_gui"] = False
cfg.env["use_vr"] = False
cfg.env["use_scene_info"] = True
print(cfg.env)
```
The environment has similar structure to traditional OpenAI Gym environments.
* We can restart the simulation with the *reset* function.
* We can perform an action in the environment with the *step* function.
* We can visualize images taken from the cameras in the environment by using the *render* function.
```
import time
import hydra
import numpy as np
from google.colab.patches import cv2_imshow
env = hydra.utils.instantiate(cfg.env)
observation = env.reset()
#The observation is given as a dictionary with different values
print(observation.keys())
for i in range(5):
# The action consists in a pose displacement (position and orientation)
action_displacement = np.random.uniform(low=-1, high=1, size=6)
# And a binary gripper action, -1 for closing and 1 for oppening
action_gripper = np.random.choice([-1, 1], size=1)
action = np.concatenate((action_displacement, action_gripper), axis=-1)
observation, reward, done, info = env.step(action)
rgb = env.render(mode="rgb_array")[:,:,::-1]
cv2_imshow(rgb)
```
## Custom environment for Reinforcement Learning
There are some aspects that needs to be defined to be able to use it for reinforcement learning, including:
1. Observation space
2. Action space
3. Reward function
We are going to create a Custom environment that extends the **PlaytableSimEnv** to add these requirements. <br/>
The specific task that will be solved is called "move_slider_left", here you can find a [list of possible tasks](https://github.com/mees/calvin_env/blob/main/conf/tasks/new_playtable_tasks.yaml) that can be evaluated using CALVIN.
```
from gym import spaces
from calvin_env.envs.play_table_env import PlayTableSimEnv
class SlideEnv(PlayTableSimEnv):
def __init__(self,
tasks: dict = {},
**kwargs):
super(SlideEnv, self).__init__(**kwargs)
# For this example we will modify the observation to
# only retrieve the end effector pose
self.action_space = spaces.Box(low=-1, high=1, shape=(7,))
self.observation_space = spaces.Box(low=-1, high=1, shape=(7,))
# We can use the task utility to know if the task was executed correctly
self.tasks = hydra.utils.instantiate(tasks)
def reset(self):
obs = super().reset()
self.start_info = self.get_info()
return obs
def get_obs(self):
"""Overwrite robot obs to only retrieve end effector position"""
robot_obs, robot_info = self.robot.get_observation()
return robot_obs[:7]
def _success(self):
""" Returns a boolean indicating if the task was performed correctly """
current_info = self.get_info()
task_filter = ["move_slider_left"]
task_info = self.tasks.get_task_info_for_set(self.start_info, current_info, task_filter)
return 'move_slider_left' in task_info
def _reward(self):
""" Returns the reward function that will be used
for the RL algorithm """
reward = int(self._success()) * 10
r_info = {'reward': reward}
return reward, r_info
def _termination(self):
""" Indicates if the robot has reached a terminal state """
success = self._success()
done = success
d_info = {'success': success}
return done, d_info
def step(self, action):
""" Performing a relative action in the environment
input:
action: 7 tuple containing
Position x, y, z.
Angle in rad x, y, z.
Gripper action
each value in range (-1, 1)
output:
observation, reward, done info
"""
# Transform gripper action to discrete space
env_action = action.copy()
env_action[-1] = (int(action[-1] >= 0) * 2) - 1
self.robot.apply_action(env_action)
for i in range(self.action_repeat):
self.p.stepSimulation(physicsClientId=self.cid)
obs = self.get_obs()
info = self.get_info()
reward, r_info = self._reward()
done, d_info = self._termination()
info.update(r_info)
info.update(d_info)
return obs, reward, done, info
```
# Training an RL agent
After generating the wrapper training a reinforcement learning agent is straightforward, for this example we will use stable baselines 3 agents
```
!pip3 install stable_baselines3
```
To train the agent we create an instance of our new environment and send it to the stable baselines agent to learn a policy.
> Note: the example uses Soft Actor Critic (SAC) which is one of the state of the art algorithm for off-policy RL.
```
import gym
import numpy as np
from stable_baselines3 import SAC
new_env_cfg = {**cfg.env}
new_env_cfg["tasks"] = cfg.tasks
new_env_cfg.pop('_target_', None)
new_env_cfg.pop('_recursive_', None)
env = SlideEnv(**new_env_cfg)
model = SAC("MlpPolicy", env, verbose=1)
model.learn(total_timesteps=10000, log_interval=4)
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import seaborn as sbn
import scipy.stats as stats
from pandas.plotting import scatter_matrix
import statsmodels.api as sm
import datetime as dt
import pandasql as ps
data = pd.read_csv('~/Downloads/EIA930_BALANCE_2020_Jan_Jun.csv')
data_2 = pd.read_csv('~/Downloads/EIA930_BALANCE_2020_Jul_Dec.csv')
def change_cols_to_floats(dataframe,lst):
for i in lst:
dataframe[i] = dataframe[i].str.replace(',', '')
dataframe[i] = dataframe[i].astype(float)
return dataframe
def make_date_time_col(df):
df['Hour Number'] = df_total['Hour Number'].replace(24, 0)
df['Hour Number'] = df_total['Hour Number'].replace(25, 0)
df['Data Date']= df['Data Date'].astype(str)
df['Hour Number'] = df['Hour Number'].astype(str)
df['New_datetime'] = df['Data Date'].map(str) + " " + df['Hour Number']
df['Hour Number'] = df['Hour Number'].astype(int)
return df
def make_hourly_demand_means(df,lst):
d = {}
for i in lst:
filt =df['Hour Number']==i
d[i] = df.loc[filt]['Demand (MW)'].mean()
return d
def graph_maker_for_energy_type_by_hour(df,column, lst = np.arange(0,24)):
d= {}
for i in lst:
filt =df['Hour Number']==i
hour_avg = df.loc[filt][column].mean()
d[i]=hour_avg
x = d.keys()
y = d.values()
fig, ax =plt.subplots(figsize = (8,8))
ax.plot(x, y)
ax.set_title(column)
ax.set_xlabel('Hours in Day')
ax.set_xticks(lst)
plt.show()
lst_cols = ['Demand (MW)','Net Generation (MW) from Natural Gas', 'Net Generation (MW) from Nuclear','Net Generation (MW) from All Petroleum Products','Net Generation (MW) from Hydropower and Pumped Storage', 'Net Generation (MW) from Solar', 'Net Generation (MW) from Wind', 'Net Generation (MW) from Other Fuel Sources','Net Generation (MW)','Demand Forecast (MW)', 'Total Interchange (MW)', 'Net Generation (MW) (Adjusted)','Net Generation (MW) from Coal','Sum(Valid DIBAs) (MW)','Demand (MW) (Imputed)', 'Net Generation (MW) (Imputed)','Demand (MW) (Adjusted)']
data_convert = change_cols_to_floats(data, lst_cols)
data_2_convert = change_cols_to_floats(data_2, lst_cols)
lst_data = [data_convert,data_2_convert]
df_total = pd.concat(lst_data)
make_date_time_col(df_total)
df_total['New_datetime']= df_total['New_datetime'].apply(lambda x:f'{x}:00:00')
df_total['New_datetime'] = pd.to_datetime(df_total['New_datetime'],infer_datetime_format=True, format ='%m/%d/%Y %H')
df_total['Demand Delta'] = df_total['Demand Forecast (MW)']- df_total['Demand (MW)']
df_total['Net Generation Delta'] = df_total['Net Generation (MW)']- df_total['Demand (MW)']
lst_hours = np.arange(0,24)
make_hourly_demand_means(df_total, lst_hours)
graph_maker_for_energy_type_by_hour(df_total,'Net Generation (MW) from Nuclear')
```
# TEXAS ERCOT
```
filter_1 = df_total['Balancing Authority'] == 'ERCO'
df_texas = df_total[filter_1]
df_texas
catagories_lst = ['Demand Forecast (MW)''Net Generation (MW) (Imputed)',
'Demand (MW) (Adjusted)', 'Net Generation (MW) (Adjusted)',
'Net Generation (MW) from Coal', 'Net Generation (MW) from Natural Gas',
'Net Generation (MW) from Nuclear',
'Net Generation (MW) from All Petroleum Products',
'Net Generation (MW) from Hydropower and Pumped Storage',
'Net Generation (MW) from Solar', 'Net Generation (MW) from Wind','Demand Delta', 'Net Generation Delta']
del df_texas['UTC Time at End of Hour']
del df_texas['Balancing Authority']
del df_texas['Net Generation (MW) (Imputed)']
del df_texas['Demand (MW) (Imputed)']
del df_texas['Net Generation (MW) from All Petroleum Products']
del df_texas['Net Generation (MW) from Unknown Fuel Sources']
del df_texas['Data Date']
del df_texas['Hour Number']
del df_texas['Local Time at End of Hour']
df_texas
df_texas.info()
df_texas
df_texas.to_csv (r'/Users/cp/Desktop/capstone2/DF_TEXAS_FINAL_ENERGY_cleanv1.csv', index = False, header=True)
df_dallas =pd.read_csv('/Users/cp/Desktop/capstone2/DALLASV1_FINAL_WEATHER.csv')
df_texas.info()
df_dallas['New_datetime'] = pd.to_datetime(df_dallas['New_datetime'],infer_datetime_format=True,format ='%m/%d/%Y %H')
Energy_Houston_weather=df_texas.merge(df_dallas, left_on ='New_datetime', right_on='New_datetime' )
Energy_Houston_weather
Energy_Houston_weather['Cloud_numerical'] = Energy_Houston_weather['cloud']
Energy_Houston_weather['cloud'].value_counts()
d1 = {
'Fair':0
,'Mostly Cloudy':2
,'Cloudy':1
,'Partly Cloudy':1
,'Light Rain':2
, 'Light Drizzle':2
,'Rain':2
,'Light Rain with Thunder':2
,'Heavy T-Storm':2
,'Thunder':2
, 'Heavy Rain':2
,'T-Storm':2
, 'Fog':2
, 'Mostly Cloudy / Windy':2
, 'Cloudy / Windy':2
, 'Haze':1
, 'Fair / Windy':0
, 'Partly Cloudy / Windy':1
, 'Light Rain / Windy':2
, 'Heavy T-Storm / Windy':2
, 'Heavy Rain / Windy':2
, 'Widespread Dust':1
, 'Thunder and Hail':2
,'Thunder / Windy':2
,'Blowing Dust':1
, 'Patches of Fog':1
, 'Blowing Dust / Windy':1
, 'Rain / Windy':2
, 'Fog / Windy':2
, 'Light Drizzle / Windy':2
, 'Haze / Windy':1
}
Energy_Houston_weather['Cloud_numerical'].replace(d1, inplace= True)
Energy_Houston_weather['Cloud_numerical']
# Energy_Houston_weather.replace({'Cloud_numerical':d1})
Energy_Houston_weather.info()
Energy_Houston_weather
Energy_Houston_weather['cloud'].value_counts()
Energy_Houston_weather.info()
Energy_Houston_weather.loc[:,'temp']
# Energy_Houston_weather['temp1'] =Energy_Houston_weather['temp'].str[:3]
Energy_Houston_weather['temp'].value_counts()
Energy_Houston_weather['humdity1'] =Energy_Houston_weather['humidity'].str[:2]
# Energy_Houston_weather['humidity'].str[:3]
Energy_Houston_weather.info()
Energy_Houston_weather['humdity1'] = Energy_Houston_weather['humdity1'].astype(float)
Energy_Houston_weather.info()
Energy_Houston_weather['Cloud_numerical'] = Energy_Houston_weather['Cloud_numerical'].astype(float)
# Energy_Houston_weather[Energy_Houston_weather['Cloud_numerical']=='Cloudy']
Energy_Houston_weather.info()
# Energy_Houston_weather['humdity1'] =Energy_Houston_weather['humidity'].str[:2]
Energy_Houston_weather['precip1'] = Energy_Houston_weather['precip'].str[:2]
Energy_Houston_weather['precip1']= Energy_Houston_weather['precip1'].astype(float)
Energy_Houston_weather['pressure1'] = Energy_Houston_weather['pressure'].str[:5]
# Energy_Houston_weather['pressure'].unique()
x =Energy_Houston_weather['pressure1']
x.unique()
def column_convert_float(pd_series):
lst = []
for i in pd_series:
lst1 = i.split('\\')
lst.append(lst1[0])
results = pd.Series(lst)
return results
def temp_column_convert_float2(pd_series):
lst = []
for string in pd_series:
string = string.replace(u'\xa0F','')
lst.append(string)
results = pd.Series(lst)
return results
temp2 = Energy_Houston_weather['temp']
temp2.unique()
timevar1 = temp_column_convert_float2(temp2)
timevar1.unique()
Energy_Houston_weather['temp1']= timevar1
Energy_Houston_weather['temp1']= Energy_Houston_weather['temp1'].astype(float)
Energy_Houston_weather['pressure1'].unique()
def press_column_convert_float2(pd_series):
lst = []
for string in pd_series:
string = string.replace(u'\xa0in','')
if string == '0.00\xa0':
string = '0.00'
lst.append(string)
results = pd.Series(lst)
# results2 = results.astype(float)
return results
press1 = Energy_Houston_weather['pressure']
press1_convert = press_column_convert_float2(press1)
Energy_Houston_weather['pressure1'].unique()
filt = Energy_Houston_weather['pressure1'].str[:3] =='0.0'
press1[filt] = '0.00'
press1.unique()
press_series = press_column_convert_float2(press1)
press_series.unique()
Energy_Houston_weather['pressure1'] = press_series
Energy_Houston_weather['pressure1']= Energy_Houston_weather['pressure1'].astype(float)
Energy_Houston_weather.info()
Energy_Houston_weather['wind_speed'].unique()
def wind_column_convert(pd_series):
lst = []
for string in pd_series:
string = string.replace(u'\xa0mph','')
if string == '0.00\xa0':
string = '0.00'
lst.append(string)
results = pd.Series(lst)
# results2 = results.astype(float)
return results
wind1 = Energy_Houston_weather['wind_speed']
wind_convert = wind_column_convert(wind1)
wind_convert.unique()
Energy_Houston_weather['wind1'] = wind_convert
Energy_Houston_weather['wind1']= Energy_Houston_weather['wind1'].astype(float)
Energy_Houston_weather.info()
Energy_Houston_weather['dew'].unique()
def dew_column_convert_float2(pd_series):
lst = []
for string in pd_series:
string = string.replace(u'\xa0F','')
lst.append(string)
results = pd.Series(lst)
return results
dew1 = Energy_Houston_weather['dew']
dew_convert = dew_column_convert_float2(dew1)
Energy_Houston_weather['dew1']= dew_convert
Energy_Houston_weather['dew1']= Energy_Houston_weather['dew1'].astype(float)
Energy_Houston_weather.info()
Energy_Houston_weather.to_csv (r'/Users/cp/Desktop/capstone2/WEATHER_CONVERTED&ENERGY_cleanv1.csv', index = False, header=True)
```
| github_jupyter |
# Polish phonetic comparison
> "Transcript matching for E2E ASR with phonetic post-processing"
- toc: false
- branch: master
- hidden: true
- categories: [asr, polish, phonetic, todo]
```
from difflib import SequenceMatcher
import icu
plipa = icu.Transliterator.createInstance('pl-pl_FONIPA')
```
The errors in E2E models are quite often phonetic confusions, so we do the opposite of traditional ASR and generate the phonetic representation from the output as a basis for comparison.
```
def phonetic_check(word1, word2, ignore_spaces=False):
"""Uses ICU's IPA transliteration to check if words are the same"""
tl1 = plipa.transliterate(word1) if not ignore_spaces else plipa.transliterate(word1.replace(' ', ''))
tl2 = plipa.transliterate(word2) if not ignore_spaces else plipa.transliterate(word2.replace(' ', ''))
return tl1 == tl2
phonetic_check("jórz", "jusz", False)
```
The Polish `y` is phonetically a raised schwa; like the schwa in English, it's often deleted in fast speech. This function returns true if the only differences between the first word and the second is are deletions of `y`, except at the end of the word (which is typically the plural ending).
```
def no_igrek(word1, word2):
"""Checks if a word-internal y has been deleted"""
sm = SequenceMatcher(None, word1, word2)
for oc in sm.get_opcodes():
if oc[0] == 'equal':
continue
elif oc[0] == 'delete' and word1[oc[1]:oc[2]] != 'y':
return False
elif oc[0] == 'delete' and word1[oc[1]:oc[2]] == 'y' and oc[2] == len(word1):
return False
elif oc[0] == 'insert' or oc[0] == 'replace':
return False
return True
no_igrek('uniwersytet', 'uniwerstet')
no_igrek('uniwerstety', 'uniwerstet')
phonetic_alternatives = [ ['u', 'ó'], ['rz', 'ż'] ]
def reverse_alts(phonlist):
return [ [i[1], i[0]] for i in phonlist ]
sm = SequenceMatcher(None, "już", "jurz")
for oc in sm.get_opcodes():
print(oc)
```
Reads a `CTM`-like file, returning a list of lists containing the filename, start time, end time, and word.
```
def read_ctmish(filename):
output = []
with open(filename, 'r') as f:
for line in f.readlines():
pieces = line.strip().split(' ')
if len(pieces) <= 4:
continue
for piece in pieces[4:]:
output.append([pieces[0], pieces[2], pieces[3], piece])
return output
```
Returns the contents of a plain text file as a list of lists containing the line number and the word, for use in locating mismatches
```
def read_text(filename):
output = []
counter = 0
with open(filename, 'r') as f:
for line in f.readlines():
counter += 1
for word in line.strip().split(' ')
output.append([counter, word])
return output
ctmish = read_ctmish("/mnt/c/Users/Jim O\'Regan/git/notes/PlgU9JyTLPE.ctm")
rec_words = [i[3] for i in ctmish]
```
| github_jupyter |
# HW9: Forecasting Solar Cycles
Below is the notebook associated with HW\#9. You can run the notebook in two modes. If you have the `emcee` and `corner` packages installed on your machine, along with the data files, just keep the following variable set to `False`. If you are running it in a Google colab notebook, set it to `True` so that it will grab the packages and files. Remember that the Google colab environment will shutdown after ~1 hour of inactivity, so you'll need to keep interacting with it or else will lose the data.
A script version of this file will also be provided to you, but you cannot use this in a Google colab environment
```
COLAB = False
if COLAB:
# Install emcee package
!pip install emcee
# Install corner package
!pip install corner
# Grab sunspot data file
!wget -O SN_m_tot_V2.0.txt https://raw.githubusercontent.com/mtlam/ASTP-720_F2020/master/HW9/SN_m_tot_V2.0.txt
import numpy as np
from matplotlib.pyplot import *
from matplotlib import rc
import emcee
import corner
%matplotlib inline
# Make more readable plots
rc('font',**{'size':14})
rc('xtick',**{'labelsize':16})
rc('ytick',**{'labelsize':16})
rc('axes',**{'labelsize':18,'titlesize':18})
```
## Define the (log-)priors
Here, the function should take a vector of parameters, `theta`, and return `0.0` if the it is in the prior range and `-np.inf` if it is outside. This is equivalent to a uniform prior over the parameters. You can, of course, define a different set of priors if you so choose!
```
def lnprior(theta):
"""
Parameters
----------
theta : np.ndarray
Array of parameters.
Returns
-------
Value of log-prior.
"""
pass
```
## Define the (log-)likelihood
```
def lnlike(theta, data):
"""
Parameters
----------
theta : np.ndarray
Array of parameters.
data : np.ndarray
Returns
-------
Value of log-likelihood
"""
residuals = None
pass
```
## Define total (log-)probability
No need to change this if the other two functions work as described.
```
def lnprob(theta, data):
lp = lnprior(theta)
if not np.isfinite(lp):
return -np.inf
return lp + lnlike(theta, data)
```
## Set up the MCMC sampler here
```
# Number of walkers to search through parameter space
nwalkers = 10
# Number of iterations to run the sampler for
niter = 50000
# Initial guess of parameters. For example, if you had a model like
# s(t) = a + bt + ct^2
# and your initial guesses for a, b, and c were 5, 3, and 8, respectively, then you would write
# pinit = np.array([5, 3, 8])
# Make sure the guesses are allowed inside your lnprior range!
pinit = np.array([])
# Number of dimensions of parameter space
ndim = len(pinit)
# Perturbed set of initial guesses. Have your walkers all start out at
# *slightly* different starting values
p0 = [pinit + 1e-4*pinit*np.random.randn(ndim) for i in range(nwalkers)]
```
## Load the data, plot to show
```
# Data: decimal year, sunspot number
decyear, ssn = np.loadtxt("SN_m_tot_V2.0.txt", unpack=True, usecols=(2, 3))
plot(decyear, ssn, 'k.')
xlabel('Year')
ylabel('Sunspot Number')
show()
```
## Run the sampler
```
# Number of CPU threads to use. Reduce if you are running on your own machine
# and don't want to use too many cores
nthreads = 4
# Set up the sampler
sampler = emcee.EnsembleSampler(nwalkers, ndim, lnprob, args=(ssn,), threads=nthreads)
# Run the sampler. May take a while! You might consider changing the
# number of iterations to a much smaller value when you're testing. Or use a
# larger value when you're trying to get your final results out!
sampler.run_mcmc(p0, niter, progress=True)
```
## Get the samples in the appropriate format, with a burn value
```
# Burn-in value = 1/4th the number of iterations. Feel free to change!
burn = int(0.25*niter)
# Reshape the chains for input to corner.corner()
samples = sampler.chain[:, burn:, :].reshape((-1, ndim))
```
## Make a corner plot
You should feel free to adjust the parameters to the `corner` function. You **should** also add labels, which should just be a list of the names of the parameters. So, if you had two parameters, $\phi_1$ and $\phi_2$, then you could write:
```
labels = [r"$\phi_1$", r"$\phi_2$"]
```
and that will make the appropriate label in LaTeX (if the distribution is installed correctly) for the two 1D posteriors of the corner plot.
```
fig = corner.corner(samples, bins=50, color='C0', smooth=0.5, plot_datapoints=False, plot_density=True, \
plot_contours=True, fill_contour=False, show_titles=True)#, labels=labels)
fig.savefig("corner.png")
show()
```
| github_jupyter |
# Load Cats and Dogs Images
## Install Packages
```
!pip install --upgrade keras==2.2.4
!pip install --upgrade tensorflow==1.13.1
!pip install --upgrade 'numpy<1.15.0'
```
> **Note:** After running the pip command you should restart the Jupyter kernel.<br>
> To restart the kernel, click on the kernel-restart button in the notebook menu toolbar (the refresh icon next to the **Code** button).
## Import Library
```
# This Python 3 environment comes with many helpful analytics libraries installed.
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python.
# For example, here are several helpful packages to load:
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
from keras.preprocessing.image import load_img
# Input data files are available in the "../input/" directory.
# For example, running the following (by selecting 'Run' or pressing Shift+Enter) will list the files in the input directory:
import matplotlib.pyplot as plt
import random
import os
import zipfile
# Define locations
BASE_PATH = os.getcwd()
DATA_PATH = BASE_PATH + "/cats_and_dogs_filtered/"
!mkdir model
MODEL_PATH = BASE_PATH + '/model/'
# Define image parameters
FAST_RUN = False
IMAGE_WIDTH=128
IMAGE_HEIGHT=128
IMAGE_SIZE=(IMAGE_WIDTH, IMAGE_HEIGHT)
IMAGE_CHANNELS=3 # RGB color
# Any results you write to the current directory are saved as output.
DATA_PATH + 'catsndogs.zip'
```
## Download the Data
```
!mkdir cats_and_dogs_filtered
# Download a sample stocks file from Iguazio demo bucket in AWS S3
!curl -L "iguazio-sample-data.s3.amazonaws.com/catsndogs.zip" > ./cats_and_dogs_filtered/catsndogs.zip
zip_ref = zipfile.ZipFile(DATA_PATH + 'catsndogs.zip', 'r')
zip_ref.extractall('cats_and_dogs_filtered')
zip_ref.close()
```
## Prepare the Traning Data
```
import json
def build_prediction_map(categories_map):
return {v:k for k ,v in categories_map.items()}
# Create a file-names list (JPG image-files only)
filenames = [file for file in os.listdir(DATA_PATH+"/cats_n_dogs") if file.endswith('jpg')]
categories = []
# Categories and prediction-classes map
categories_map = {
'dog': 1,
'cat': 0,
}
prediction_map = build_prediction_map(categories_map)
with open(MODEL_PATH + 'prediction_classes_map.json', 'w') as f:
json.dump(prediction_map, f)
# Create a pandas DataFrame for the full sample
for filename in filenames:
category = filename.split('.')[0]
categories.append([categories_map[category]])
df = pd.DataFrame({
'filename': filenames,
'category': categories
})
df['category'] = df['category'].astype('str');
df.head()
df.tail()
```
## Check the Total Image Count
Check the total image count for each category.<br>
The data set has 12,000 cat images and 12,000 dog images.
```
df['category'].value_counts().plot.bar()
```
## Display the Sample Image
```
sample = random.choice(filenames)
image = load_img(DATA_PATH+"/cats_n_dogs/"+sample)
plt.imshow(image)
```
| github_jupyter |
# INSTALLATION
```
!pip install aif360
!pip install fairlearn
!apt-get install -jre
!java -version
!pip install h2o
!pip install xlsxwriter
```
#IMPORTS
```
import numpy as np
from mlxtend.feature_selection import ExhaustiveFeatureSelector
from xgboost import XGBClassifier
# import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import openpyxl
import xlsxwriter
from openpyxl import load_workbook
import shap
#suppress setwith copy warning
pd.set_option('mode.chained_assignment',None)
from sklearn.feature_selection import VarianceThreshold
from sklearn.feature_selection import SelectKBest, SelectFwe, SelectPercentile,SelectFdr, SelectFpr, SelectFromModel
from sklearn.feature_selection import chi2, mutual_info_classif
# from skfeature.function.similarity_based import fisher_score
import aif360
import matplotlib.pyplot as plt
from aif360.metrics.classification_metric import ClassificationMetric
from aif360.metrics import BinaryLabelDatasetMetric
from aif360.datasets import StandardDataset , BinaryLabelDataset
from sklearn.preprocessing import MinMaxScaler
MM= MinMaxScaler()
import h2o
from h2o.automl import H2OAutoML
from h2o.estimators.glm import H2OGeneralizedLinearEstimator
import sys
sys.path.append("../")
import os
h2o.init()
```
#**************************LOADING DATASET*******************************
```
from google.colab import drive
drive.mount('/content/gdrive')
for i in range(1,51,1):
train_url=r'/content/gdrive/MyDrive/Datasets/SurveyData/DATASET/German/Train'
train_path= os.path.join(train_url ,("Train"+ str(i)+ ".csv"))
train= pd.read_csv(train_path)
test_url=r'/content/gdrive/MyDrive/Datasets/SurveyData/DATASET/German/Test'
test_path= os.path.join(test_url ,("Test"+ str(i)+ ".csv"))
test= pd.read_csv(test_path)
# normalization of train and test sets
Fitter= MM.fit(train)
transformed_train=Fitter.transform(train)
train=pd.DataFrame(transformed_train, columns= train.columns)
#test normalization
transformed_test=Fitter.transform(test)
test=pd.DataFrame(transformed_test, columns= test.columns)
# *************CHECKING FAIRNESS IN DATASET**************************
## ****************CONVERTING TO BLD FORMAT******************************
#Transforming the Train and Test Set to BinaryLabel
advantagedGroup= [{'age':1}]
disadvantagedGroup= [{'age':0}]
# class Train(StandardDataset):
# def __init__(self,label_name= 'default',
# favorable_classes= [1],protected_attribute_names=['age'], privileged_classes=[[1]], ):
# super(Train, self).__init__(df=train , label_name=label_name ,
# favorable_classes=favorable_classes , protected_attribute_names=protected_attribute_names ,
# privileged_classes=privileged_classes ,
# )
# BLD_Train= Train(protected_attribute_names= ['age'],
# privileged_classes= [[1]])
class Test(StandardDataset):
def __init__(self,label_name= 'default',
favorable_classes= [1],protected_attribute_names=['age'], privileged_classes=[[1]], ):
super(Test, self).__init__(df=test , label_name=label_name ,
favorable_classes=favorable_classes , protected_attribute_names=protected_attribute_names ,
privileged_classes=privileged_classes ,
)
BLD_Test= Test(protected_attribute_names= ['age'],
privileged_classes= [[1]])
## ********************Checking Bias in Data********************************
DataBias_Checker = BinaryLabelDatasetMetric(BLD_Test , unprivileged_groups= disadvantagedGroup, privileged_groups= advantagedGroup)
dsp= DataBias_Checker .statistical_parity_difference()
dif= DataBias_Checker.consistency()
ddi= DataBias_Checker.disparate_impact()
print('The Statistical Parity diference is = {diff}'.format(diff= dsp ))
print('Individual Fairness is = {IF}'.format( IF= dif ))
print('Disparate Impact is = {IF}'.format( IF= ddi ))
# ********************SETTING TO H20 FRAME AND MODEL TRAINING*******************************
x = list(train.columns)
y = "default"
x.remove(y)
Train=h2o.H2OFrame(train)
Test= h2o.H2OFrame(test)
Train[y] = Train[y].asfactor()
Test[y] = Test[y].asfactor()
aml = H2OAutoML(max_models=10, nfolds=10, include_algos=['GBM'] , stopping_metric='AUTO') #verbosity='info',,'GBM', 'DRF'
aml.train(x=x, y=y, training_frame=Train)
best_model= aml.leader
# a.model_performance()
#**********************REPLACE LABELS OF DUPLICATED TEST SET WITH PREDICTIONS****************************
#predicted labels
gbm_Predictions= best_model.predict(Test)
gbm_Predictions= gbm_Predictions.as_data_frame()
predicted_df= test.copy()
predicted_df['default']= gbm_Predictions.predict.to_numpy()
# ********************COMPUTE DISCRIMINATION*****************************
advantagedGroup= [{'age':1}]
disadvantagedGroup= [{'age':0}]
class PredTest(StandardDataset):
def __init__(self,label_name= 'default',
favorable_classes= [1],protected_attribute_names=['age'], privileged_classes=[[1]], ):
super(PredTest, self).__init__(df=predicted_df , label_name=label_name ,
favorable_classes=favorable_classes , protected_attribute_names=protected_attribute_names ,
privileged_classes=privileged_classes ,
)
BLD_PredTest= PredTest(protected_attribute_names= ['age'],
privileged_classes= [[1]])
# # Workbook= pd.ExcelFile(r'/content/gdrive/MyDrive/Datasets/SurveyData/RESULTS/BaseLines/GBM/gbm_Results.xlsx')
# excelBook= load_workbook('/content/gdrive/MyDrive/Datasets/SurveyData/RESULTS/BaseLines/GBM/gbm_Results.xlsx')
# OldDF= excelBook.get_sheet_by_name("German")#pd.read_excel(Workbook,sheet_name='German')
#load workbook
excelBook= load_workbook('/content/gdrive/MyDrive/Datasets/SurveyData/RESULTS/BaseLines/GBM/gbm_Results.xlsx')
German= excelBook['German']
data= German.values
# Get columns
columns = next(data)[0:]
10# Create a DataFrame based on the second and subsequent lines of data
OldDF = pd.DataFrame(data, columns=columns)
ClassifierBias = ClassificationMetric( BLD_Test,BLD_PredTest , unprivileged_groups= disadvantagedGroup, privileged_groups= advantagedGroup)
Accuracy= ClassifierBias.accuracy()
TPR= ClassifierBias.true_positive_rate()
TNR= ClassifierBias.true_negative_rate()
NPV= ClassifierBias.negative_predictive_value()
PPV= ClassifierBias.positive_predictive_value()
SP=ClassifierBias .statistical_parity_difference()
IF=ClassifierBias.consistency()
DI=ClassifierBias.disparate_impact()
EOP=ClassifierBias.true_positive_rate_difference()
EO=ClassifierBias.average_odds_difference()
FDR= ClassifierBias.false_discovery_rate(privileged=False)- ClassifierBias.false_discovery_rate(privileged=True)
NPV_diff=ClassifierBias.negative_predictive_value(privileged=False)-ClassifierBias.negative_predictive_value(privileged=True)
FOR=ClassifierBias.false_omission_rate(privileged=False)-ClassifierBias.false_omission_rate(privileged=True)
PPV_diff=ClassifierBias.positive_predictive_value(privileged=False) -ClassifierBias.positive_predictive_value(privileged=True)
BGE = ClassifierBias.between_group_generalized_entropy_index()
WGE = ClassifierBias.generalized_entropy_index()-ClassifierBias.between_group_generalized_entropy_index()
BGTI = ClassifierBias.between_group_theil_index()
WGTI = ClassifierBias.theil_index() -ClassifierBias.between_group_theil_index()
EDF= ClassifierBias.differential_fairness_bias_amplification()
newdf= pd.DataFrame(index = [0], data= { 'ACCURACY': Accuracy,'TPR': TPR, 'PPV':PPV, 'TNR':TNR,'NPV':NPV,'SP':SP,'CONSISTENCY':IF,'DI':DI,'EOP':EOP,'EO':EO,'FDR':FDR,'NPV_diff':NPV_diff,
'FOR':FOR,'PPV_diff':PPV_diff,'BGEI':BGE,'WGEI':WGE,'BGTI':BGTI,'WGTI':WGTI,'EDF':EDF,
'DATA_SP':dsp,'DATA_CONS':dif,'DATA_DI':ddi})
newdf=pd.concat([OldDF,newdf])
pathway= r"/content/gdrive/MyDrive/Datasets/SurveyData/RESULTS/BaseLines/GBM/gbm_Results.xlsx"
with pd.ExcelWriter(pathway, engine='openpyxl') as writer:
#load workbook base as for writer
writer.book= excelBook
writer.sheets=dict((ws.title, ws) for ws in excelBook.worksheets)
newdf.to_excel(writer, sheet_name='German', index=False)
# newdf.to_excel(writer, sheet_name='Adult', index=False)
print('Accuracy', Accuracy)
```
#LOGISTIC REGRESSION
```
for i in range(1,51,1):
train_url=r'/content/gdrive/MyDrive/Datasets/SurveyData/DATASET/German/Train'
train_path= os.path.join(train_url ,("Train"+ str(i)+ ".csv"))
train= pd.read_csv(train_path)
test_url=r'/content/gdrive/MyDrive/Datasets/SurveyData/DATASET/German/Test'
test_path= os.path.join(test_url ,("Test"+ str(i)+ ".csv"))
test= pd.read_csv(test_path)
# normalization of train and test sets
Fitter= MM.fit(train)
transformed_train=Fitter.transform(train)
train=pd.DataFrame(transformed_train, columns= train.columns)
#test normalization
transformed_test=Fitter.transform(test)
test=pd.DataFrame(transformed_test, columns= test.columns)
# *************CHECKING FAIRNESS IN DATASET**************************
## ****************CONVERTING TO BLD FORMAT******************************
#Transforming the Train and Test Set to BinaryLabel
advantagedGroup= [{'age':1}]
disadvantagedGroup= [{'age':0}]
# class Train(StandardDataset):
# def __init__(self,label_name= 'default',
# favorable_classes= [1],protected_attribute_names=['age'], privileged_classes=[[1]], ):
# super(Train, self).__init__(df=train , label_name=label_name ,
# favorable_classes=favorable_classes , protected_attribute_names=protected_attribute_names ,
# privileged_classes=privileged_classes ,
# )
# BLD_Train= Train(protected_attribute_names= ['age'],
# privileged_classes= [[1]])
class Test(StandardDataset):
def __init__(self,label_name= 'default',
favorable_classes= [1],protected_attribute_names=['age'], privileged_classes=[[1]], ):
super(Test, self).__init__(df=test , label_name=label_name ,
favorable_classes=favorable_classes , protected_attribute_names=protected_attribute_names ,
privileged_classes=privileged_classes ,
)
BLD_Test= Test(protected_attribute_names= ['age'],
privileged_classes= [[1]])
## ********************Checking Bias in Data********************************
DataBias_Checker = BinaryLabelDatasetMetric(BLD_Test , unprivileged_groups= disadvantagedGroup, privileged_groups= advantagedGroup)
dsp= DataBias_Checker .statistical_parity_difference()
dif= DataBias_Checker.consistency()
ddi= DataBias_Checker.disparate_impact()
print('The Statistical Parity diference is = {diff}'.format(diff= dsp ))
print('Individual Fairness is = {IF}'.format( IF= dif ))
print('Disparate Impact is = {IF}'.format( IF= ddi ))
# ********************SETTING TO H20 FRAME AND MODEL TRAINING*******************************
x = list(train.columns)
y = "default"
x.remove(y)
Train=h2o.H2OFrame(train)
Test= h2o.H2OFrame(test)
Train[y] = Train[y].asfactor()
Test[y] = Test[y].asfactor()
LogReg = H2OGeneralizedLinearEstimator(family= "binomial", lambda_ = 0)
LogReg.train(x=x, y=y, training_frame=Train)
LogReg_Predictions= LogReg.predict(Test)
LogReg_Predictions= LogReg_Predictions.as_data_frame()
# *************************REPLACE LABELS OF DUPLICATED TEST SET WITH PREDICTIONS**************************************
predicted_df= test.copy()
predicted_df['default']= LogReg_Predictions.predict.to_numpy()
# ***************************COMPUTE DISCRIMINATION********************************
advantagedGroup= [{'age':1}]
disadvantagedGroup= [{'age':0}]
class PredTest(StandardDataset):
def __init__(self,label_name= 'default',
favorable_classes= [1],protected_attribute_names=['age'], privileged_classes=[[1]], ):
super(PredTest, self).__init__(df=predicted_df , label_name=label_name ,
favorable_classes=favorable_classes , protected_attribute_names=protected_attribute_names ,
privileged_classes=privileged_classes ,
)
BLD_PredTest= PredTest(protected_attribute_names= ['age'],
privileged_classes= [[1]])
excelBook= load_workbook(r"/content/gdrive/MyDrive/Datasets/SurveyData/RESULTS/BaseLines/LogReg/LR_Results.xlsx")
German= excelBook['German']
data= German.values
# Get columns
columns = next(data)[0:]
OldDF = pd.DataFrame(data, columns=columns)
ClassifierBias = ClassificationMetric( BLD_Test,BLD_PredTest , unprivileged_groups= disadvantagedGroup, privileged_groups= advantagedGroup)
Accuracy= ClassifierBias.accuracy()
TPR= ClassifierBias.true_positive_rate()
TNR= ClassifierBias.true_negative_rate()
NPV= ClassifierBias.negative_predictive_value()
PPV= ClassifierBias.positive_predictive_value()
SP=ClassifierBias .statistical_parity_difference()
IF=ClassifierBias.consistency()
DI=ClassifierBias.disparate_impact()
EOP=ClassifierBias.true_positive_rate_difference()
EO=ClassifierBias.average_odds_difference()
FDR= ClassifierBias.false_discovery_rate(privileged=False)- ClassifierBias.false_discovery_rate(privileged=True)
NPV_diff=ClassifierBias.negative_predictive_value(privileged=False)-ClassifierBias.negative_predictive_value(privileged=True)
FOR=ClassifierBias.false_omission_rate(privileged=False)-ClassifierBias.false_omission_rate(privileged=True)
PPV_diff=ClassifierBias.positive_predictive_value(privileged=False) -ClassifierBias.positive_predictive_value(privileged=True)
BGE = ClassifierBias.between_group_generalized_entropy_index()
WGE = ClassifierBias.generalized_entropy_index()-ClassifierBias.between_group_generalized_entropy_index()
BGTI = ClassifierBias.between_group_theil_index()
WGTI = ClassifierBias.theil_index() -ClassifierBias.between_group_theil_index()
EDF= ClassifierBias.differential_fairness_bias_amplification()
newdf= pd.DataFrame(index = [0], data= { 'ACCURACY': Accuracy,'TPR': TPR, 'PPV':PPV, 'TNR':TNR,'NPV':NPV,'SP':SP,'CONSISTENCY':IF,'DI':DI,'EOP':EOP,'EO':EO,'FDR':FDR,'NPV_diff':NPV_diff,
'FOR':FOR,'PPV_diff':PPV_diff,'BGEI':BGE,'WGEI':WGE,'BGTI':BGTI,'WGTI':WGTI,'EDF':EDF,
'DATA_SP':dsp,'DATA_CONS':dif,'DATA_DI':ddi})
newdf=pd.concat([OldDF,newdf])
pathway= r"/content/gdrive/MyDrive/Datasets/SurveyData/RESULTS/BaseLines/LogReg/LR_Results.xlsx"
with pd.ExcelWriter(pathway, engine='openpyxl') as writer:
#load workbook base as for writer
writer.book= excelBook
writer.sheets=dict((ws.title, ws) for ws in excelBook.worksheets)
newdf.to_excel(writer, sheet_name='German', index=False)
# newdf.to_excel(writer, sheet_name='Adult', index=False)
print('Accuracy', Accuracy)
```
| github_jupyter |
This notebook compares the email activities and draft activites of an IETF working group.
Import the BigBang modules as needed. These should be in your Python environment if you've installed BigBang correctly.
```
import bigbang.mailman as mailman
from bigbang.parse import get_date
#from bigbang.functions import *
from bigbang.archive import Archive
from ietfdata.datatracker import *
```
Also, let's import a number of other dependencies we'll use later.
```
import pandas as pd
import datetime
import matplotlib.pyplot as plt
import numpy as np
import math
import pytz
import pickle
import os
```
## Load the HRPC Mailing List
Now let's load the email data for analysis.
```
wg = "httpbisa"
urls = [wg]
archives = [Archive(url,mbox=True) for url in urls]
activities = [arx.get_activity(resolved=False) for arx in archives]
activity = activities[0]
```
## Load IETF Draft Data
Next, we will use the `ietfdata` tracker to look at the frequency of drafts for this working group.
```
import glob
path = '../../archives/datatracker/httpbis/draft_metadata.csv' # use your path
draft_df = pd.read_csv(path, index_col=None, header=0, parse_dates=['date'])
```
We will want to use the data of the drafts. Time resolution is too small.
```
draft_df['date'] = draft_df['date'].dt.date
```
## Gender score and tendency measures
This notebook uses the (notably imperfect) method of using first names to guess the gender of each draft author.
```
from gender_detector import gender_detector as gd
detector = gd.GenderDetector('us')
def gender_score(name):
"""
Takes a full name and returns a score for the guessed
gender.
1 - male
0 - female
.5 - unknown
"""
try:
first_name = name.split(" ")[0]
guess = detector.guess(first_name)
score = 0
if guess == "male":
return 1.0
elif guess == "female":
return 0.0
else:
# name does not have confidence to guesss
return 0.5
except:
# Some error, "unknown"
return .5
```
## Gender guesses on mailing list activity
Now to use the gender guesser to track the contributions by differently gendered participants over time.
```
from bigbang.parse import clean_name
gender_activity = activity.groupby(
by=lambda x: gender_score(clean_name(x)),
axis=1).sum().rename({0.0 : "women", 0.5 : "unknown", 1.0 : "men"},
axis="columns")
```
Note that our gender scoring method currently is unable to get a clear guess for a large percentage of the emails!
```
print("%f.2 percent of emails are from an unknown gender." \
% (gender_activity["unknown"].sum() / gender_activity.sum().sum()))
plt.bar(["women","unknown","men"],gender_activity.sum())
plt.title("Total emails sent by guessed gender")
```
## Plotting
Some preprocessing is necessary to get the drafts data ready for plotting.
```
from matplotlib import cm
viridis = cm.get_cmap('viridis')
drafts_per_day = draft_df.groupby('date').count()['title']
dpd_log = drafts_per_day.apply(lambda x: np.log1p(x))
```
For each of the mailing lists we are looking at, plot the rolling average (over `window`) of number of emails sent per day.
Then plot a vertical line with the height of the drafts count and colored by the gender tendency.
```
window = 100
plt.figure(figsize=(12, 6))
for i, gender in enumerate(gender_activity.columns):
colors = [viridis(0), viridis(.5), viridis(.99)]
ta = gender_activity[gender]
rmta = ta.rolling(window).mean()
rmtadna = rmta.dropna()
plt.plot_date(np.array(rmtadna.index),
np.array(rmtadna.values),
color = colors[i],
linestyle = '-', marker = None,
label='%s email activity - %s' % (wg, gender),
xdate=True)
vax = plt.vlines(drafts_per_day.index,
0,
drafts_per_day,
colors = 'r', # draft_gt_per_day,
cmap = 'viridis',
label=f'{wg} drafts ({drafts_per_day.sum()} total)'
)
plt.legend()
plt.title("%s working group emails and drafts" % (wg))
#plt.colorbar(vax, label = "more womanly <-- Gender Tendency --> more manly")
#plt.savefig("activites-marked.png")
#plt.show()
```
### Is gender diversity correlated with draft output?
```
from scipy.stats import pearsonr
import pandas as pd
def calculate_pvalues(df):
df = df.dropna()._get_numeric_data()
dfcols = pd.DataFrame(columns=df.columns)
pvalues = dfcols.transpose().join(dfcols, how='outer')
for r in df.columns:
for c in df.columns:
pvalues[r][c] = round(pearsonr(df[r], df[c])[1], 4)
return pvalues
drafts_per_ordinal_day = pd.Series({x[0].toordinal(): x[1] for x in drafts_per_day.items()})
drafts_per_ordinal_day
ta.rolling(window).mean()
garm = np.log1p(gender_activity.rolling(window).mean())
garm['diversity'] = (garm['unknown'] + garm['women']) / garm['men']
garm['drafts'] = drafts_per_ordinal_day
garm['drafts'] = garm['drafts'].fillna(0)
garm.corr(method='pearson')
calculate_pvalues(garm)
```
Some variations...
```
garm_dna = garm.dropna(subset=['drafts'])
```
| github_jupyter |
# Visualize 3D Points (Parabolic data)
This notebook uses 3D plots to visualize 3D points. Reads measurement data from a csv file.
```
%matplotlib notebook
##%matplotlib inline
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
import numpy as np
from filter.kalman import Kalman3D
fmt = lambda x: "%9.3f" % x
np.set_printoptions(formatter={'float_kind':fmt})
## Read from csv file
import pandas as pd
```
## Read and Prepare Data
Read ball tracking position data from saved CSV file and prepare mx,my,mz. The file should have dT values along with X,Y,Z values.
We use these as measurements and use Kalman3D tracker to track the ball. Once we exhaust all measurements, we use Kalman3D to predict rest of the trajectory.
*Note*: The position data that we are using is in millimeters and milliseconds. However, the Kalman3D tracker uses all values in meters and seconds. We have do to this conversion here.
```
# File containing 3D points predicted and measured. Last column with time passage will be ignored
SYNTH = False
if SYNTH:
data_ = pd.read_csv('data/datafile_parabolic.csv') ## Synthetic data
else:
data_ = pd.read_csv('data/input_positions_3.csv') ## Real data
print(data_.keys())
data = data_/1000.
_mx = np.float32(data['mx'])
_my = np.float32(data['my'])
_mz = np.float32(data['mz'])
if SYNTH:
## Drop useless data
mx = _mx[0:19]
my = _my[0:19]
mz = _mz[0:19]
else:
mx = _mx
my = _my
mz = _mz
print("mx: {} {}".format(mx.shape, mx))
print("my: {} {}".format(my.shape, my))
print("mz: {} {}".format(mz.shape, mz))
def getpos(i, x,y,z):
return(np.float32([x[i],y[i],z[i]]))
mx
```
## Track and Predict
Now we use our Kalman3D tracker to track the position of the ball based on measured data and then predict the trajectory when all measurement data is exhausted.
```
fps = 100.
dT = (1 / fps)
print("dT: {:f}".format(dT))
KF = Kalman3D(drg=1.0, dbg=0)
pred = KF.init(getpos(0,mx,my,mz))
print("pred: {}".format(pred))
##-#######################################################################################
## Tracking
## Since we are doing all operations in zero time, specify dT manually (e.g., 0.033 sec)
px = np.float32([pred[0]])
py = np.float32([pred[1]])
pz = np.float32([pred[2]])
for i in range(len(mx)-1):
pred = KF.track(getpos([i+1], mx, my, mz), dT)
px = np.append(px, pred[0])
py = np.append(py, pred[1])
pz = np.append(pz, pred[2])
print(" tracked position : {}".format(pred*1000))
##-#######################################################################################
## Trajectory prediction
## Since we are doing all operations in zero time, specify dT manually (e.g., 0.033 sec)
for ii in range(15):
pred = KF.predict(dT) # Use last value of dT for all predictions
px = np.append(px, pred[0])
py = np.append(py, pred[1])
pz = np.append(pz, pred[2])
print("predicted position : {}".format(pred*1000))
x, y, z = 10, 10 ,10
x, y, z = 5, 8 ,2
x, y, z = 53, 18 ,12
fps = 100.
dT = (1 / fps)
print("dT: {:f}".format(dT))
KF = Kalman3D(drg=1.0, dbg=0)
pred = KF.init(np.float32([x,y,z]))
print("predicted position : {}".format(pred))
pred = KF.track(np.float32([x,y,z]), dT)
pred = KF.predict(dT)
sum = 0
tm = np.zeros(len(px))
for i in range(len(tm)):
sum += dT
tm[i] = sum
## Convert mx also back to millimeters.
px = px * 1000.
py = py * 1000.
pz = pz * 1000.
nmx = mx * 1000.
nmy = my * 1000.
nmz = mz * 1000.
ntm = tm * 1000.
##-#######################################################################################
## Everything is in millimeters and milliseconds now
##-#######################################################################################
print("px size", px.shape)
print("tm size", tm.shape)
## Visualize X, Y, and Z individually
## In the plot below, we visualize the pairs of px, mx; py, my and pz, mz to see how they relate to each other
print("PX, MX")
fig1a = plt.figure()
plt.plot(tm, px)
plt.plot(tm[0:len(nmx)], nmx)
plt.legend('PM', ncol=1, loc='upper left')
print("PY, MY")
fig1b = plt.figure()
plt.plot(tm, py)
plt.plot(tm[0:len(nmy)], nmy)
plt.legend('PM', ncol=1, loc='upper left')
print("PZ, MZ")
fig1c = plt.figure()
plt.plot(tm, pz)
plt.plot(tm[0:len(nmz)], nmz)
plt.legend('PM', ncol=1, loc='upper left')
```
## Visualize (X,Y,Z) of Predicted and Measured in Points in 3D
In the plot below, we visualize all the predicted and measured points in 3D. This gives a more realistic view of how the predicted points are related to the measured points.
```
fig2 = plt.figure()
ax = plt.axes(projection='3d')
#ax.set_xlim3d(-2000,2000)
#ax.set_ylim3d(-2000,2000)
#ax.set_zlim3d(-2000,2000)
if 0: ## Plot axis or not
st = [0,0,0]
xx = [200, 0, 0]
yy = [ 0, 200, 0]
zz =[ 0, 0, 200]
for i in range(len(st)):
ax.plot([st[i], xx[i]], [st[i],yy[i]],zs=[st[i],zz[i]])
ax.plot3D(px, py, pz, 'blue')
ax.plot3D(nmx, nmy, nmz, 'magenta')
class Kalman_filiter():
def __init__(self, x_init, y_init, z_init, dT):
self.KF = Kalman3D(drg=0.507, dbg=4)
self.dT = dT
self.pred = self.KF.init(np.float32([x_init, y_init, z_init]))
def update(self, x, y, z, dT):
self.dT = dT
self.pred = self.KF.track(np.float32([x, y, z]), self.dT)
def get_predict(self, dT):
self.pred = self.KF.predict(dT)
x,y,z = [-7.923465928004007, -0.6755867599611189, 2.580941671512611]
a = Kalman_filiter(x,y,z,0.04)
print(a.pred)
a.update(x,y,z,0.04)
print(a.pred)
a.get_predict(0.04)
print(a.pred)
x,y,z = [-5.810376800248608, -0.4175195849390212, 2.3275454429899285]
a.KF.measNoise
```
| github_jupyter |
# Fastpages Notebook Blog Post
> A tutorial of fastpages for Jupyter notebooks.
- toc: true
- badges: true
- comments: true
- categories: [jupyter]
- image: images/chart-preview.png
# About
This notebook is a demonstration of some of capabilities of [fastpages](https://github.com/fastai/fastpages) with notebooks.
With `fastpages` you can save your jupyter notebooks into the `_notebooks` folder at the root of your repository, and they will be automatically be converted to Jekyll compliant blog posts!
## Front Matter
Front Matter is a markdown cell at the beginning of your notebook that allows you to inject metadata into your notebook. For example:
- Setting `toc: true` will automatically generate a table of contents
- Setting `badges: true` will automatically include GitHub and Google Colab links to your notebook.
- Setting `comments: true` will enable commenting on your blog post, powered by [utterances](https://github.com/utterance/utterances).
More details and options for front matter can be viewed on the [front matter section](https://github.com/fastai/fastpages#front-matter-related-options) of the README.
## Markdown Shortcuts
A `#hide` comment at the top of any code cell will hide **both the input and output** of that cell in your blog post.
A `#hide_input` comment at the top of any code cell will **only hide the input** of that cell.
```
#hide_input
print('The comment #hide_input was used to hide the code that produced this.\n')
```
put a `#collapse-hide` flag at the top of any cell if you want to **hide** that cell by default, but give the reader the option to show it:
```
#collapse-hide
import pandas as pd
import altair as alt
```
put a `#collapse-show` flag at the top of any cell if you want to **show** that cell by default, but give the reader the option to hide it:
```
#collapse-show
cars = 'https://vega.github.io/vega-datasets/data/cars.json'
movies = 'https://vega.github.io/vega-datasets/data/movies.json'
sp500 = 'https://vega.github.io/vega-datasets/data/sp500.csv'
stocks = 'https://vega.github.io/vega-datasets/data/stocks.csv'
flights = 'https://vega.github.io/vega-datasets/data/flights-5k.json'
```
## Interactive Charts With Altair
Charts made with Altair remain interactive. Example charts taken from [this repo](https://github.com/uwdata/visualization-curriculum), specifically [this notebook](https://github.com/uwdata/visualization-curriculum/blob/master/altair_interaction.ipynb).
```
# hide
df = pd.read_json(movies) # load movies data
genres = df['Major_Genre'].unique() # get unique field values
genres = list(filter(lambda d: d is not None, genres)) # filter out None values
genres.sort() # sort alphabetically
#hide
mpaa = ['G', 'PG', 'PG-13', 'R', 'NC-17', 'Not Rated']
```
### Example 1: DropDown
```
# single-value selection over [Major_Genre, MPAA_Rating] pairs
# use specific hard-wired values as the initial selected values
selection = alt.selection_single(
name='Select',
fields=['Major_Genre', 'MPAA_Rating'],
init={'Major_Genre': 'Drama', 'MPAA_Rating': 'R'},
bind={'Major_Genre': alt.binding_select(options=genres), 'MPAA_Rating': alt.binding_radio(options=mpaa)}
)
# scatter plot, modify opacity based on selection
alt.Chart(movies).mark_circle().add_selection(
selection
).encode(
x='Rotten_Tomatoes_Rating:Q',
y='IMDB_Rating:Q',
tooltip='Title:N',
opacity=alt.condition(selection, alt.value(0.75), alt.value(0.05))
)
```
### Example 2: Tooltips
```
alt.Chart(movies).mark_circle().add_selection(
alt.selection_interval(bind='scales', encodings=['x'])
).encode(
x='Rotten_Tomatoes_Rating:Q',
y=alt.Y('IMDB_Rating:Q', axis=alt.Axis(minExtent=30)), # use min extent to stabilize axis title placement
tooltip=['Title:N', 'Release_Date:N', 'IMDB_Rating:Q', 'Rotten_Tomatoes_Rating:Q']
).properties(
width=600,
height=400
)
```
### Example 3: More Tooltips
```
# select a point for which to provide details-on-demand
label = alt.selection_single(
encodings=['x'], # limit selection to x-axis value
on='mouseover', # select on mouseover events
nearest=True, # select data point nearest the cursor
empty='none' # empty selection includes no data points
)
# define our base line chart of stock prices
base = alt.Chart().mark_line().encode(
alt.X('date:T'),
alt.Y('price:Q', scale=alt.Scale(type='log')),
alt.Color('symbol:N')
)
alt.layer(
base, # base line chart
# add a rule mark to serve as a guide line
alt.Chart().mark_rule(color='#aaa').encode(
x='date:T'
).transform_filter(label),
# add circle marks for selected time points, hide unselected points
base.mark_circle().encode(
opacity=alt.condition(label, alt.value(1), alt.value(0))
).add_selection(label),
# add white stroked text to provide a legible background for labels
base.mark_text(align='left', dx=5, dy=-5, stroke='white', strokeWidth=2).encode(
text='price:Q'
).transform_filter(label),
# add text labels for stock prices
base.mark_text(align='left', dx=5, dy=-5).encode(
text='price:Q'
).transform_filter(label),
data=stocks
).properties(
width=700,
height=400
)
```
## Data Tables
You can display tables per the usual way in your blog:
```
movies = 'https://vega.github.io/vega-datasets/data/movies.json'
df = pd.read_json(movies)
# display table with pandas
df[['Title', 'Worldwide_Gross',
'Production_Budget', 'IMDB_Rating']].head()
```
## Images
### Local Images
You can reference local images and they will be copied and rendered on your blog automatically. You can include these with the following markdown syntax:
``

### Remote Images
Remote images can be included with the following markdown syntax:
``

### Animated Gifs
Animated Gifs work, too!
`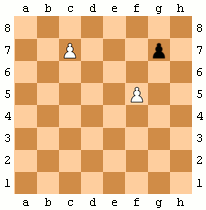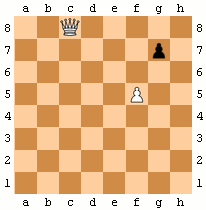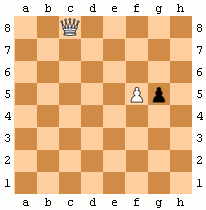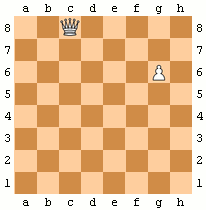`

### Captions
You can include captions with markdown images like this:
```

```

# Other Elements
## Tweetcards
Typing `> twitter: https://twitter.com/jakevdp/status/1204765621767901185?s=20` will render this:
> twitter: https://twitter.com/jakevdp/status/1204765621767901185?s=20
## Youtube Videos
Typing `> youtube: https://youtu.be/XfoYk_Z5AkI` will render this:
> youtube: https://youtu.be/XfoYk_Z5AkI
## Boxes / Callouts
Typing `> Warning: There will be no second warning!` will render this:
> Warning: There will be no second warning!
Typing `> Important: Pay attention! It's important.` will render this:
> Important: Pay attention! It's important.
Typing `> Tip: This is my tip.` will render this:
> Tip: This is my tip.
Typing `> Note: Take note of this.` will render this:
> Note: Take note of this.
Typing `> Note: A doc link to [an example website: fast.ai](https://www.fast.ai/) should also work fine.` will render in the docs:
> Note: A doc link to [an example website: fast.ai](https://www.fast.ai/) should also work fine.
## Footnotes
You can have footnotes in notebooks just like you can with markdown.
For example, here is a footnote [^1].
[^1]: This is the footnote.
| github_jupyter |
# Coupling to Ideal Loads
In this notebook, we investigate the WEST ICRH antenna behaviour when the front-face is considered as the combination of ideal (and independant) loads made of impedances all equal to $Z_s=R_c+j X_s$, where $R_c$ corresponds to the coupling resistance and $X_s$ is the strap reactance.
<img src="West_front_face_ideal.png" width="300"/>
In such case, the power delivered to the plasma/front-face is then:
$$
P_t
= \frac{1}{2} \sum_{i=1}^4 \Re[V_i I_i^* ]
= \frac{1}{2} \sum_{i=1}^4 \Re[Z_i] |I_i|^2
= \frac{1}{2} R_c \sum_{i=1}^4 |I_i|^2
$$
Hence, we have defined the coupling resistance as:
$$
R_c = \frac{\sum_{i=1}^4 \Re[Z_i] |I_i|^2}{\sum_{i=1}^4 |I_i|^2}
$$
Inversely, the coupling resistance can be determine from:
$$
R_c = \frac{2 P_t}{\sum_{i=1}^4 |I_i|^2}
$$
In practice however, it is easier to measure RF voltages than currents.
$$
I = \frac{V}{Z_s} = \frac{V}{R_c + j X_s}
\rightarrow
|I|^2 = \frac{|V|^2}{|R_c + j X_s|}
\approx
\frac{|V|^2}{|X_s|^2}
$$
since in $|X_s|>>|R_c|$.
The antenna model allows to calculate the coupling resistance from currents (`.Rc()` method) or from the voltage (`.Rc_WEST()` method).
The strap reactance $X_s$ depends on the strap geometry and varies with the frequency. So, let's find how the strap reactance from the realistic CAD model.
```
%matplotlib widget
import matplotlib.pyplot as plt
import numpy as np
import skrf as rf
from tqdm.notebook import tqdm
# WEST ICRH Antenna package
import sys; sys.path.append('..')
from west_ic_antenna import WestIcrhAntenna
# styling the figures
rf.stylely()
```
## Coupling to an ideal front-face
Coupling to an ideal front face of coupling resistance $R_c$ is easy using the the `.load()` method of the `WestIcrhAntenna` class. This method takes into account the strap reactance frequency fit (derived in [Strap Reactance Frequency Fit](./strap_reactance.ipynb))
```
freq = rf.Frequency(30, 70, npoints=1001, unit='MHz')
ant_ideal = WestIcrhAntenna(frequency=freq)
ant_ideal.load(Rc=1) # 1 Ohm coupling resistance front-face
# matching left and right sides : note that the solutions are (almost) the same
f_match = 55.5e6
C_left = ant_ideal.match_one_side(f_match=f_match, side='left')
C_right = ant_ideal.match_one_side(f_match=f_match, side='right')
```
At the difference of the "real" situation (see the [Matching](./matching.ipynb) or the [Coupling to a TOPICA plasma](./coupling_to_plasma_from_TOPICA.ipynb)), here is no poloidal neither toroidal coupling of the straps in this front-face model. This leads to:
* Match soluitions are the same for both sides (within $10^{-3}$ pF).
* Using the match solutions for each sides does not require to shift the operating frequency:
```
# dipole excitation
power = [1, 1]
phase = [0, rf.pi]
# active S-parameter for the match point:
C_match = [C_left[0], C_left[1], C_right[2], C_right[3]]
s_act = ant_ideal.s_act(power, phase, Cs=C_match)
fig, ax = plt.subplots()
ax.plot(ant_ideal.f_scaled, 20*np.log10(np.abs(s_act)), lw=2)
ax.legend(('$S_{act,1}$', '$S_{act,2}$'))
ax.grid(True)
```
## Match Points vs Coupling Resistance
Let's determine the match points for a range of coupling resistance at a given frequency
```
f_match = 55e6
Rcs = np.r_[0.01, 0.05, np.arange(0.1, 2.5, 0.2)]
C_matchs = []
ant = WestIcrhAntenna()
for Rc in tqdm(Rcs):
ant.load(Rc)
C_match = ant.match_one_side(f_match=f_match)
C_matchs.append(C_match)
```
As the coupling resistance increases, the distance between capacitances (Top vs Bottom) increases:
```
fig, ax = plt.subplots()
ax.plot(Rcs, np.array(C_matchs)[:,0:2], lw=2, marker='o')
ax.axhline(C_matchs[0][0], ls='--', color='C0')
ax.axhline(C_matchs[0][1], ls='--', color='C1')
ax.set_xlabel('Rc [Ohm]')
ax.set_ylabel('C [pF]')
ax.legend(('Top', 'Bot'))
```
Displayed differently, the distance between capacitances (Top - Bottom) versus coupling resistance is:
```
delta_C_pos = np.array(C_matchs)[:,0] - C_matchs[0][0]
delta_C_neg = C_matchs[0][1] - np.array(C_matchs)[:,1]
fig, ax = plt.subplots()
ax.plot(Rcs, delta_C_pos, label='Top: + $\Delta C$', lw=2)
ax.plot(Rcs, delta_C_neg, label='Bot: - $\Delta C$', lw=2)
ax.set_xlabel('Rc [Ohm]')
ax.set_ylabel('$\Delta C$ [pF]')
ax.set_ylim(bottom=0)
ax.set_xlim(left=0)
ax.legend()
```
## Load Resilience Curves
Ideal loads is usefull to study the behaviour of the load tolerance property of the antenna and the capacitance match points. It is only necessary to work on half-antenna here, because there is no coupling between toroidal elements.
Now that we have figured out the match points, let's vary the coupling resistances for a fixed match point and look to the return power (or VSWR): this will highlight the load resilience property of the antenna.
```
# create a single frequency point antenna to speed-up calculations
ant = WestIcrhAntenna(frequency=rf.Frequency.from_f(f_match, unit='Hz'))
fig, ax = plt.subplots()
power = [1, 1]
phase = [0, np.pi]
for C_match in tqdm(C_matchs[0:8]):
SWRs = []
ant.Cs = [C_match[0], C_match[1], 150, 150]
for Rc in Rcs:
ant.load(Rc)
SWR = ant.circuit().network.s_vswr.squeeze()[0,0]
SWRs.append(SWR)
ax.plot(Rcs, np.array(SWRs), lw=2)
ax.set_xlabel('Rc [Ohm]')
ax.set_ylabel('VSWR')
ax.set_ylim(1, 8)
ax.axhline(2, color='r')
ax.legend(Rcs)
from IPython.core.display import HTML
def _set_css_style(css_file_path):
"""
Read the custom CSS file and load it into Jupyter
Pass the file path to the CSS file
"""
styles = open(css_file_path, "r").read()
s = '<style>%s</style>' % styles
return HTML(s)
_set_css_style('custom.css')
```
| github_jupyter |
# 数组基础
## 创建一个数组
```
import numpy as np
import pdir
pdir(np)
import numpy as np
a1 = np.array([0, 1, 2, 3, 4])#将列表转换为数组,可以传递任何序列(类数组),而不仅仅是常见的列表(list)数据类型。
a2 = np.array((0, 1, 2, 3, 4))#将元组转换为数组
print 'a1:',a1,type(a1)
print 'a2:',a2,type(a2)
b = np.arange(5) #python内置函数range()的数组版,返回的是numpy ndarrays数组对象,而不是列表
print 'b:',b,type(b)
c1 = np.ones((3,4))#根据元组指定形状,返回全1数组
c2 = np.ones_like(a1)#以另一个数组为参数,以其形状和dtype创建全1数组
print 'c1',c1,type(c1)
print 'c2',c2,type(c2)
d1 = np.zeros((5,6))#根据元组指定形状,返回全0数组
d2 = np.zeros_like(c1)#以另一个数组为参数,以其形状和dtype创建全0数组
print 'd1',d1,type(d1)
print 'd2',d2,type(d2)
e1 = np.empty((2,3))#创建新数组,只分配内存空间但不填充任何值,不是返回0,而是未初始化的垃圾值
e2 = np.empty_like(d1)#
print 'e1',e1,type(e1)
print 'e2',e2,type(e2)
f1 = np.eye(3)#创建一个正方的N*N单位矩阵对角线为1,其余为0()
f2 = np.identity(4)#Return the identity array.
print 'f1',f1,type(f1)
print 'f2',f2,type(f2)
g = np.linspace(0, 10, 5) #linspace: Return evenly spaced numbers over a specified interval.
print 'g',g,type(g)
```
## 数组属性
```
a = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28 ,29, 30],
[31, 32, 33, 34, 35]])
print(type(a)) #<type 'numpy.ndarray'>
print(a.dtype) #int32
print(a.size) #25 Return the number of elements along a given axis.
print(a.shape) #(5L, 5L),Return the shape of an array
print(a.itemsize) #4,itemsize输出array元素的字节数,本例32/8=4
print(a.ndim) #2,Return the number of dimensions of an array
```
# 使用数组
数组可不必编写循环即可实现循环-数组的矢量化
大小相等的数组之间的任何数学运算都会应用到元素级
大小不相等的数组之间的运算-叫做广播
## 基本操作符-数组四则运算 +、- 、/
```
a = np.arange(25)
print 'a:',a,type(a)
a = a.reshape((5, 5))#Gives a new shape to an array without changing its data
print 'a:',a,type(a)
b = np.array([10, 62, 1, 14, 2, 56, 79, 2, 1, 45,
4, 92, 5, 55, 63, 43, 35, 6, 53, 24,
56, 3, 56, 44, 78])
print b.shape
b = b.reshape((5,5))
print 'b:',b,type(b)
print(a + b)#逐元素运算,分别对每一个元素进行配对,然后对它们进行运算
print(a - b)
print(a * b)
print(a / b)
print(a ** 2)
print(a < b) #逻辑运算符比如 “<” 和 “>” 的时候,返回的将是一个布尔型数组
print(a > b)
print(a.dot(b))#dot() 函数计算两个数组的点积。它返回的是一个标量(只有大小没有方向的一个值)而不是数组
```
## 数组特殊运算符
```
# sum, min, max, cumsum
a = np.arange(10)
print 'a:',a
print(a.sum()) # >>>45
print(a.min()) # >>>0
print(a.max()) # >>>9
print(a.cumsum()) # >>>[ 0 1 3 6 10 15 21 28 36 45]
```
# 索引
## 基本索引-整数索引
```
a = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28 ,29, 30],
[31, 32, 33, 34, 35]])
print 'a:',a,type(a)
# 访问元素:二者功能相同
print a[1][3]
print a[1,3]#逗号隔开的索引列表来选取单个元素
# 多维数组中,如果省略了后面的索引,则返回对象是一个维度低一点的数组。
print a[2]
```
## 数组切片
数组切片与列表切片重要区别在于。数组切片是原数组的视图,这意味着数据不会被复制,视图上的任何修改都会直接反映到源数组上
```
a = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28 ,29, 30],
[31, 32, 33, 34, 35]])
print 'a:',a
# 单纯切片只能得到相同维度的数组视图,
print(a[::2,::2])
# [[11 13 15]
# [21 23 25]
# [31 33 35]]
print(a[:3,:2])
#切片和整数索引混合使用,可以得到低维度的切片
print(a[0, 1:4]) # >>>[12 13 14]
print(a[1:4, 0]) # >>>[16 21 26]
print(a[:, 1]) # >>>[12 17 22 27 32]
a_slice = a[:,0]#数组切片是原数组的视图,这意味着数据不会被复制,视图上的任何修改都会直接反映到源数组上
print 'a_slice:',a_slice
a_slice[:] = 66
print 'a:',a
#若想要数组切片的一份副本而非视图,则需要显式的进行复制操作
a_slice_copy = a[:,0].copy()
print "a_slice_copy:",a_slice_copy
a_slice_copy[:] = 111
print "a_slice_copy:",a_slice_copy
print 'a:',a
```
## 布尔型索引
布尔型数组可用于数组索引,通过布尔型数组获取到数组中的数据,将总是创建副本
==,!=,>,<
```
#数组的比较运算也是矢量化的,会产生一个布尔型数组
names = np.array(['bob','joe','will','bob','will','joe','joe'])
names.shape
names == 'bob'
data = np.random.randn(7,4)
data
#布尔型数组可用于数组索引,布尔型数组的长度必须跟被索引的轴长度一致,
#例如names == 'bob'长度为7;data按行索引
#names2 == 'bob'长度为4;data按列索引
print data[names == 'bob']
names2 = names[:4].copy()
print(names2)
print data[:,names2=='bob']
# 布尔型数组还可以与切片、整数索引混合使用
print data[names == 'bob',1:3]
print data[names == 'bob',1]
# 注意:python关键字and or在布尔型数组中无效
#利用逻辑关系构造复杂布尔型数组,|或,&和,!非
mask = (names !='bob')
print data[mask]
mask = (names =='bob') | (names == 'will')
print data[mask]
# 通过布尔型数组设置值
data[data < 0] = 7
print data
#通过布尔型数组设置整行/整列
data[names !='bob'] = 100
print data
data[:,names2 !='bob'] = 200
print data
```
## 花式索引
花式索引是指利用整数数组进行索引,可以指定顺序选取、
花式索引不同于切片,花式索引总是将数据复制到新数组中
```
arr = np.empty((8,4))
for i in range(8):
arr[i] = i
print arr
#可以指定顺序选取行子集,只需传入一个用于指定顺序的整数列表或数组即可
print arr[[4,3,0,6]]
#使用负数索引将从末尾开始选取行
print arr[[-1,-2]]
#可以同时使用正数和负数进行花式索引
print arr[[1,2,-1,-2]]
#使用多个索引数组,返回的是一个一维数组
arr = np.arange(32).reshape(8,4)
print arr
print arr[[4,3,0,6],[1,2,3,0]]
#获取的元素是(4,1)(3,2)(0,3)(6,0)
#要想得到矩阵的行列子集(矩形区域)
#方法1
print arr[[4,3,0,6]][:,[1,2,3,0]]
#方法2 np.ix_()用两个一维整数数组转换为一个用于选取方形局域的索引器
print arr[np.ix_([4,3,0,6],[1,2,3,0])]
```
## 数组转置和轴对换
```
# 转置(transpose)返回源数据的视图(不会进行任何复制操作),
# 两种办法实现转置:
# arr.transpose()方法
# arr.T属性
arr = np.arange(15).reshape(3,5)
print arr
print arr.T
print arr.transpose()
#高维数组(>=3维)需要参数:轴编号组成的元组才能对轴进行转置
arr = np.arange(16).reshape(2,2,4)
print arr
print arr.T
print arr.transpose((1,0,2))
```
## 通用函数-快速的元素级数组函数
对数组中数据进行元素级运算的函数
```
#一元通用函数,接收一个数组
arr = np.arange(10)
print arr
print np.sqrt(arr)#开方
print np.exp(arr)#指数
print np.square(arr)#平方
#二元通用函数,接收2个数组
x = np.random.randn(5)
print x
y = np.random.randn(5)
print y
print np.add(x,y)#加法
print np.subtract(x,y)#减法
print np.greater(x,y)#元素比较
```
## 将条件逻辑表述为数组运算
numpy.where()函数是三元表达式 x if condition else y的矢量化版本
```
xarr = np.array([1.1,1.2,1.3,1.4,1.5])
yarr = np.array([2.1,2.2,2.3,2.4,2.5])
condition = np.array([True,False,True,True,False])
# 列表生成式
print [(x if c else y)for x,y,c in zip(xarr,yarr,condition)]
#存在问题
#速度不是很快,原因:纯python实现
#无法用于多维数组
#利用np.where()实现相同功能很简洁
print np.where(condition,xarr,yarr)
#np.where()函数,第2,3参数不一定为数组,也可以为标量值
#where通常用于根据另一个数组生成一个新数组
arr = np.random.randn(4,4)
print arr
print np.where(arr > 0,1,-1)#根据arr原始元素>0,置位1;arr原始元素<0,置位-1
print np.where(arr > 0,1,arr)#根据arr原始元素>0,置位1;arr原始元素<0,保持不变
```
## 数学和统计方法
数组的数学函数对数组或数组某个轴向的数据进行统计计算;
既可以通过数据实例方法调用;
也可以当做nump顶级函数使用.
```
arr = np.arange(10).reshape(2,5)
print arr
print arr.mean()#计算数组平均值
print arr.mean(axis = 0)#可指定轴,用以统计该轴上的值
print arr.mean(axis = 1)
print np.mean(arr)
print np.mean(arr,axis = 0)
print np.mean(arr,axis = 1)
print arr.sum()#计算数组和
print arr.sum(axis = 0)
print arr.sum(axis = 1)
print np.sum(arr)
print np.sum(arr,axis = 0)
print np.sum(arr,axis = 1)
print arr.var()#计算方差差
print arr.var(axis = 0)#
print arr.var(axis = 1)#
print np.var(arr)#计算方差差
print np.var(arr,axis = 0)#
print np.var(arr,axis = 1)#
print arr.std()#计算标准差
print arr.std(axis = 0)#
print arr.std(axis = 1)#
print np.std(arr)#计算标准差
print np.std(arr,axis = 0)#
print np.std(arr,axis = 1)#
print arr
print arr.min()#计算最小值
print arr.min(axis = 0)#
print arr.min(axis = 1)#
print np.min(arr)#
print np.min(arr,axis = 0)#
print np.min(arr,axis = 1)#
print arr
print arr.max()#计算最大值
print arr.max(axis = 0)#
print arr.max(axis = 1)#
print np.max(arr)
print np.max(arr,axis = 0)#
print np.max(arr,axis = 1)#
print arr
print arr[0].argmin()#最小值的索引
print arr[1].argmin()#最小值的索引
print arr[0].argmax()#最大值的索引
print arr[1].argmax()#最大值的索引
print arr
print arr.cumsum()#不聚合,所有元素的累积和,而是返回中间结果构成的数组
arr = arr + 1
print arr
print arr.cumprod()#不聚合,所有元素的累积积,而是返回中间结果构成的数组
```
## 用于布尔型数组的方法
any()测试布尔型数组是否存在一个或多个True
all()检查数组中所有值是否都为True
```
arr = np.random.randn(10)
# print
bools = arr > 0
print bools
print bools.any()
print np.any(bools)
print bools.all()
print np.all(bools)
arr = np.array([0,1,2,3,4])
print arr.any()#非布尔型数组,所有非0元素会被当做True
```
## 排序
```
arr = np.random.randn(10)
print arr
arr.sort()#与python内置列表排序一样;就地排序,会修改数组本身
print arr
arr = np.random.randn(10)
print arr
print np.sort(arr)#返回数组已排序副本
```
## 唯一化及其他的集合逻辑
numpy针对一维数组的基本集合运算
np.unique()找出数组中的唯一值,并返回已排序的结果
```
names = np.array(['bob', 'joe', 'will', 'bob', 'will', 'joe', 'joe'])
print names
print np.unique(names)
```
## 线性代数
```
#矩阵乘法
x = np.array([[1,2,3],[4,5,6]])
y = np.array([[6,23],[-1,7],[8,9]])
print x
print y
print x.dot(y)
print np.dot(x,y)
```
## 随机数生成
numpy.random模块对python内置的random进行补充,增接了一些用于高效生成多生概率分布的样本值的函数
```
#从给定的上下限范围内随机选取整数
print np.random.randint(10)
#产生正态分布的样本值
print np.random.randn(3,2)
```
### 数组组合
```
a = np.array([1,2,3])
b = np.array([4,5,6])
c = np.arange(6).reshape(2,3)
d = np.arange(2,8).reshape(2,3)
print(a)
print(b)
print(c)
print(d)
np.concatenate([c,d])
# In machine learning, useful to enrich or
# add new/concatenate features with hstack
np.hstack([c, d])
# Use broadcasting when needed to do this automatically
np.vstack([a,b, d])
```
| github_jupyter |
# A Scientific Deep Dive Into SageMaker LDA
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Data Exploration](#DataExploration)
1. [Training](#Training)
1. [Inference](#Inference)
1. [Epilogue](#Epilogue)
# Introduction
***
Amazon SageMaker LDA is an unsupervised learning algorithm that attempts to describe a set of observations as a mixture of distinct categories. Latent Dirichlet Allocation (LDA) is most commonly used to discover a user-specified number of topics shared by documents within a text corpus. Here each observation is a document, the features are the presence (or occurrence count) of each word, and the categories are the topics. Since the method is unsupervised, the topics are not specified up front, and are not guaranteed to align with how a human may naturally categorize documents. The topics are learned as a probability distribution over the words that occur in each document. Each document, in turn, is described as a mixture of topics.
This notebook is similar to **LDA-Introduction.ipynb** but its objective and scope are a different. We will be taking a deeper dive into the theory. The primary goals of this notebook are,
* to understand the LDA model and the example dataset,
* understand how the Amazon SageMaker LDA algorithm works,
* interpret the meaning of the inference output.
Former knowledge of LDA is not required. However, we will run through concepts rather quickly and at least a foundational knowledge of mathematics or machine learning is recommended. Suggested references are provided, as appropriate.
```
!conda install -y scipy
%matplotlib inline
import os, re, tarfile
import boto3
import matplotlib.pyplot as plt
import mxnet as mx
import numpy as np
np.set_printoptions(precision=3, suppress=True)
# some helpful utility functions are defined in the Python module
# "generate_example_data" located in the same directory as this
# notebook
from generate_example_data import (
generate_griffiths_data, match_estimated_topics,
plot_lda, plot_lda_topics)
# accessing the SageMaker Python SDK
import sagemaker
from sagemaker.amazon.common import numpy_to_record_serializer
from sagemaker.predictor import csv_serializer, json_deserializer
```
# Setup
***
*This notebook was created and tested on an ml.m4.xlarge notebook instance.*
We first need to specify some AWS credentials; specifically data locations and access roles. This is the only cell of this notebook that you will need to edit. In particular, we need the following data:
* `bucket` - An S3 bucket accessible by this account.
* Used to store input training data and model data output.
* Should be withing the same region as this notebook instance, training, and hosting.
* `prefix` - The location in the bucket where this notebook's input and and output data will be stored. (The default value is sufficient.)
* `role` - The IAM Role ARN used to give training and hosting access to your data.
* See documentation on how to create these.
* The script below will try to determine an appropriate Role ARN.
```
from sagemaker import get_execution_role
role = get_execution_role()
bucket = '<your_s3_bucket_name_here>'
prefix = 'sagemaker/lda_science'
print('Training input/output will be stored in {}/{}'.format(bucket, prefix))
print('\nIAM Role: {}'.format(role))
```
## The LDA Model
As mentioned above, LDA is a model for discovering latent topics describing a collection of documents. In this section we will give a brief introduction to the model. Let,
* $M$ = the number of *documents* in a corpus
* $N$ = the average *length* of a document.
* $V$ = the size of the *vocabulary* (the total number of unique words)
We denote a *document* by a vector $w \in \mathbb{R}^V$ where $w_i$ equals the number of times the $i$th word in the vocabulary occurs within the document. This is called the "bag-of-words" format of representing a document.
$$
\underbrace{w}_{\text{document}} = \overbrace{\big[ w_1, w_2, \ldots, w_V \big] }^{\text{word counts}},
\quad
V = \text{vocabulary size}
$$
The *length* of a document is equal to the total number of words in the document: $N_w = \sum_{i=1}^V w_i$.
An LDA model is defined by two parameters: a topic-word distribution matrix $\beta \in \mathbb{R}^{K \times V}$ and a Dirichlet topic prior $\alpha \in \mathbb{R}^K$. In particular, let,
$$\beta = \left[ \beta_1, \ldots, \beta_K \right]$$
be a collection of $K$ *topics* where each topic $\beta_k \in \mathbb{R}^V$ is represented as probability distribution over the vocabulary. One of the utilities of the LDA model is that a given word is allowed to appear in multiple topics with positive probability. The Dirichlet topic prior is a vector $\alpha \in \mathbb{R}^K$ such that $\alpha_k > 0$ for all $k$.
# Data Exploration
---
## An Example Dataset
Before explaining further let's get our hands dirty with an example dataset. The following synthetic data comes from [1] and comes with a very useful visual interpretation.
> [1] Thomas Griffiths and Mark Steyvers. *Finding Scientific Topics.* Proceedings of the National Academy of Science, 101(suppl 1):5228-5235, 2004.
```
print('Generating example data...')
num_documents = 6000
known_alpha, known_beta, documents, topic_mixtures = generate_griffiths_data(
num_documents=num_documents, num_topics=10)
num_topics, vocabulary_size = known_beta.shape
# separate the generated data into training and tests subsets
num_documents_training = int(0.9*num_documents)
num_documents_test = num_documents - num_documents_training
documents_training = documents[:num_documents_training]
documents_test = documents[num_documents_training:]
topic_mixtures_training = topic_mixtures[:num_documents_training]
topic_mixtures_test = topic_mixtures[num_documents_training:]
print('documents_training.shape = {}'.format(documents_training.shape))
print('documents_test.shape = {}'.format(documents_test.shape))
```
Let's start by taking a closer look at the documents. Note that the vocabulary size of these data is $V = 25$. The average length of each document in this data set is 150. (See `generate_griffiths_data.py`.)
```
print('First training document =\n{}'.format(documents_training[0]))
print('\nVocabulary size = {}'.format(vocabulary_size))
print('Length of first document = {}'.format(documents_training[0].sum()))
average_document_length = documents.sum(axis=1).mean()
print('Observed average document length = {}'.format(average_document_length))
```
The example data set above also returns the LDA parameters,
$$(\alpha, \beta)$$
used to generate the documents. Let's examine the first topic and verify that it is a probability distribution on the vocabulary.
```
print('First topic =\n{}'.format(known_beta[0]))
print('\nTopic-word probability matrix (beta) shape: (num_topics, vocabulary_size) = {}'.format(known_beta.shape))
print('\nSum of elements of first topic = {}'.format(known_beta[0].sum()))
```
Unlike some clustering algorithms, one of the versatilities of the LDA model is that a given word can belong to multiple topics. The probability of that word occurring in each topic may differ, as well. This is reflective of real-world data where, for example, the word *"rover"* appears in a *"dogs"* topic as well as in a *"space exploration"* topic.
In our synthetic example dataset, the first word in the vocabulary belongs to both Topic #1 and Topic #6 with non-zero probability.
```
print('Topic #1:\n{}'.format(known_beta[0]))
print('Topic #6:\n{}'.format(known_beta[5]))
```
Human beings are visual creatures, so it might be helpful to come up with a visual representation of these documents.
In the below plots, each pixel of a document represents a word. The greyscale intensity is a measure of how frequently that word occurs within the document. Below we plot the first few documents of the training set reshaped into 5x5 pixel grids.
```
%matplotlib inline
fig = plot_lda(documents_training, nrows=3, ncols=4, cmap='gray_r', with_colorbar=True)
fig.suptitle('$w$ - Document Word Counts')
fig.set_dpi(160)
```
When taking a close look at these documents we can see some patterns in the word distributions suggesting that, perhaps, each topic represents a "column" or "row" of words with non-zero probability and that each document is composed primarily of a handful of topics.
Below we plots the *known* topic-word probability distributions, $\beta$. Similar to the documents we reshape each probability distribution to a $5 \times 5$ pixel image where the color represents the probability of that each word occurring in the topic.
```
%matplotlib inline
fig = plot_lda(known_beta, nrows=1, ncols=10)
fig.suptitle(r'Known $\beta$ - Topic-Word Probability Distributions')
fig.set_dpi(160)
fig.set_figheight(2)
```
These 10 topics were used to generate the document corpus. Next, we will learn about how this is done.
## Generating Documents
LDA is a generative model, meaning that the LDA parameters $(\alpha, \beta)$ are used to construct documents word-by-word by drawing from the topic-word distributions. In fact, looking closely at the example documents above you can see that some documents sample more words from some topics than from others.
LDA works as follows: given
* $M$ documents $w^{(1)}, w^{(2)}, \ldots, w^{(M)}$,
* an average document length of $N$,
* and an LDA model $(\alpha, \beta)$.
**For** each document, $w^{(m)}$:
* sample a topic mixture: $\theta^{(m)} \sim \text{Dirichlet}(\alpha)$
* **For** each word $n$ in the document:
* Sample a topic $z_n^{(m)} \sim \text{Multinomial}\big( \theta^{(m)} \big)$
* Sample a word from this topic, $w_n^{(m)} \sim \text{Multinomial}\big( \beta_{z_n^{(m)}} \; \big)$
* Add to document
The [plate notation](https://en.wikipedia.org/wiki/Plate_notation) for the LDA model, introduced in [2], encapsulates this process pictorially.

> [2] David M Blei, Andrew Y Ng, and Michael I Jordan. Latent Dirichlet Allocation. Journal of Machine Learning Research, 3(Jan):993–1022, 2003.
## Topic Mixtures
For the documents we generated above lets look at their corresponding topic mixtures, $\theta \in \mathbb{R}^K$. The topic mixtures represent the probablility that a given word of the document is sampled from a particular topic. For example, if the topic mixture of an input document $w$ is,
$$\theta = \left[ 0.3, 0.2, 0, 0.5, 0, \ldots, 0 \right]$$
then $w$ is 30% generated from the first topic, 20% from the second topic, and 50% from the fourth topic. In particular, the words contained in the document are sampled from the first topic-word probability distribution 30% of the time, from the second distribution 20% of the time, and the fourth disribution 50% of the time.
The objective of inference, also known as scoring, is to determine the most likely topic mixture of a given input document. Colloquially, this means figuring out which topics appear within a given document and at what ratios. We will perform infernece later in the [Inference](#Inference) section.
Since we generated these example documents using the LDA model we know the topic mixture generating them. Let's examine these topic mixtures.
```
print('First training document =\n{}'.format(documents_training[0]))
print('\nVocabulary size = {}'.format(vocabulary_size))
print('Length of first document = {}'.format(documents_training[0].sum()))
print('First training document topic mixture =\n{}'.format(topic_mixtures_training[0]))
print('\nNumber of topics = {}'.format(num_topics))
print('sum(theta) = {}'.format(topic_mixtures_training[0].sum()))
```
We plot the first document along with its topic mixture. We also plot the topic-word probability distributions again for reference.
```
%matplotlib inline
fig, (ax1,ax2) = plt.subplots(2, 1)
ax1.matshow(documents[0].reshape(5,5), cmap='gray_r')
ax1.set_title(r'$w$ - Document', fontsize=20)
ax1.set_xticks([])
ax1.set_yticks([])
cax2 = ax2.matshow(topic_mixtures[0].reshape(1,-1), cmap='Reds', vmin=0, vmax=1)
cbar = fig.colorbar(cax2, orientation='horizontal')
ax2.set_title(r'$\theta$ - Topic Mixture', fontsize=20)
ax2.set_xticks([])
ax2.set_yticks([])
fig.set_dpi(100)
%matplotlib inline
# pot
fig = plot_lda(known_beta, nrows=1, ncols=10)
fig.suptitle(r'Known $\beta$ - Topic-Word Probability Distributions')
fig.set_dpi(160)
fig.set_figheight(1.5)
```
Finally, let's plot several documents with their corresponding topic mixtures. We can see how topics with large weight in the document lead to more words in the document within the corresponding "row" or "column".
```
%matplotlib inline
fig = plot_lda_topics(documents_training, 3, 4, topic_mixtures=topic_mixtures)
fig.suptitle(r'$(w,\theta)$ - Documents with Known Topic Mixtures')
fig.set_dpi(160)
```
# Training
***
In this section we will give some insight into how AWS SageMaker LDA fits an LDA model to a corpus, create an run a SageMaker LDA training job, and examine the output trained model.
## Topic Estimation using Tensor Decompositions
Given a document corpus, Amazon SageMaker LDA uses a spectral tensor decomposition technique to determine the LDA model $(\alpha, \beta)$ which most likely describes the corpus. See [1] for a primary reference of the theory behind the algorithm. The spectral decomposition, itself, is computed using the CPDecomp algorithm described in [2].
The overall idea is the following: given a corpus of documents $\mathcal{W} = \{w^{(1)}, \ldots, w^{(M)}\}, \; w^{(m)} \in \mathbb{R}^V,$ we construct a statistic tensor,
$$T \in \bigotimes^3 \mathbb{R}^V$$
such that the spectral decomposition of the tensor is approximately the LDA parameters $\alpha \in \mathbb{R}^K$ and $\beta \in \mathbb{R}^{K \times V}$ which maximize the likelihood of observing the corpus for a given number of topics, $K$,
$$T \approx \sum_{k=1}^K \alpha_k \; (\beta_k \otimes \beta_k \otimes \beta_k)$$
This statistic tensor encapsulates information from the corpus such as the document mean, cross correlation, and higher order statistics. For details, see [1].
> [1] Animashree Anandkumar, Rong Ge, Daniel Hsu, Sham Kakade, and Matus Telgarsky. *"Tensor Decompositions for Learning Latent Variable Models"*, Journal of Machine Learning Research, 15:2773–2832, 2014.
>
> [2] Tamara Kolda and Brett Bader. *"Tensor Decompositions and Applications"*. SIAM Review, 51(3):455–500, 2009.
## Store Data on S3
Before we run training we need to prepare the data.
A SageMaker training job needs access to training data stored in an S3 bucket. Although training can accept data of various formats we convert the documents MXNet RecordIO Protobuf format before uploading to the S3 bucket defined at the beginning of this notebook.
```
# convert documents_training to Protobuf RecordIO format
recordio_protobuf_serializer = numpy_to_record_serializer()
fbuffer = recordio_protobuf_serializer(documents_training)
# upload to S3 in bucket/prefix/train
fname = 'lda.data'
s3_object = os.path.join(prefix, 'train', fname)
boto3.Session().resource('s3').Bucket(bucket).Object(s3_object).upload_fileobj(fbuffer)
s3_train_data = 's3://{}/{}'.format(bucket, s3_object)
print('Uploaded data to S3: {}'.format(s3_train_data))
```
Next, we specify a Docker container containing the SageMaker LDA algorithm. For your convenience, a region-specific container is automatically chosen for you to minimize cross-region data communication
```
containers = {
'us-west-2': '266724342769.dkr.ecr.us-west-2.amazonaws.com/lda:latest',
'us-east-1': '766337827248.dkr.ecr.us-east-1.amazonaws.com/lda:latest',
'us-east-2': '999911452149.dkr.ecr.us-east-2.amazonaws.com/lda:latest',
'eu-west-1': '999678624901.dkr.ecr.eu-west-1.amazonaws.com/lda:latest'
}
region_name = boto3.Session().region_name
container = containers[region_name]
print('Using SageMaker LDA container: {} ({})'.format(container, region_name))
```
## Training Parameters
Particular to a SageMaker LDA training job are the following hyperparameters:
* **`num_topics`** - The number of topics or categories in the LDA model.
* Usually, this is not known a priori.
* In this example, howevever, we know that the data is generated by five topics.
* **`feature_dim`** - The size of the *"vocabulary"*, in LDA parlance.
* In this example, this is equal 25.
* **`mini_batch_size`** - The number of input training documents.
* **`alpha0`** - *(optional)* a measurement of how "mixed" are the topic-mixtures.
* When `alpha0` is small the data tends to be represented by one or few topics.
* When `alpha0` is large the data tends to be an even combination of several or many topics.
* The default value is `alpha0 = 1.0`.
In addition to these LDA model hyperparameters, we provide additional parameters defining things like the EC2 instance type on which training will run, the S3 bucket containing the data, and the AWS access role. Note that,
* Recommended instance type: `ml.c4`
* Current limitations:
* SageMaker LDA *training* can only run on a single instance.
* SageMaker LDA does not take advantage of GPU hardware.
* (The Amazon AI Algorithms team is working hard to provide these capabilities in a future release!)
Using the above configuration create a SageMaker client and use the client to create a training job.
```
session = sagemaker.Session()
# specify general training job information
lda = sagemaker.estimator.Estimator(
container,
role,
output_path='s3://{}/{}/output'.format(bucket, prefix),
train_instance_count=1,
train_instance_type='ml.c4.2xlarge',
sagemaker_session=session,
)
# set algorithm-specific hyperparameters
lda.set_hyperparameters(
num_topics=num_topics,
feature_dim=vocabulary_size,
mini_batch_size=num_documents_training,
alpha0=1.0,
)
# run the training job on input data stored in S3
lda.fit({'train': s3_train_data})
```
If you see the message
> `===== Job Complete =====`
at the bottom of the output logs then that means training sucessfully completed and the output LDA model was stored in the specified output path. You can also view information about and the status of a training job using the AWS SageMaker console. Just click on the "Jobs" tab and select training job matching the training job name, below:
```
print('Training job name: {}'.format(lda.latest_training_job.job_name))
```
## Inspecting the Trained Model
We know the LDA parameters $(\alpha, \beta)$ used to generate the example data. How does the learned model compare the known one? In this section we will download the model data and measure how well SageMaker LDA did in learning the model.
First, we download the model data. SageMaker will output the model in
> `s3://<bucket>/<prefix>/output/<training job name>/output/model.tar.gz`.
SageMaker LDA stores the model as a two-tuple $(\alpha, \beta)$ where each LDA parameter is an MXNet NDArray.
```
# download and extract the model file from S3
job_name = lda.latest_training_job.job_name
model_fname = 'model.tar.gz'
model_object = os.path.join(prefix, 'output', job_name, 'output', model_fname)
boto3.Session().resource('s3').Bucket(bucket).Object(model_object).download_file(fname)
with tarfile.open(fname) as tar:
tar.extractall()
print('Downloaded and extracted model tarball: {}'.format(model_object))
# obtain the model file
model_list = [fname for fname in os.listdir('.') if fname.startswith('model_')]
model_fname = model_list[0]
print('Found model file: {}'.format(model_fname))
# get the model from the model file and store in Numpy arrays
alpha, beta = mx.ndarray.load(model_fname)
learned_alpha_permuted = alpha.asnumpy()
learned_beta_permuted = beta.asnumpy()
print('\nLearned alpha.shape = {}'.format(learned_alpha_permuted.shape))
print('Learned beta.shape = {}'.format(learned_beta_permuted.shape))
```
Presumably, SageMaker LDA has found the topics most likely used to generate the training corpus. However, even if this is case the topics would not be returned in any particular order. Therefore, we match the found topics to the known topics closest in L1-norm in order to find the topic permutation.
Note that we will use the `permutation` later during inference to match known topic mixtures to found topic mixtures.
Below plot the known topic-word probability distribution, $\beta \in \mathbb{R}^{K \times V}$ next to the distributions found by SageMaker LDA as well as the L1-norm errors between the two.
```
permutation, learned_beta = match_estimated_topics(known_beta, learned_beta_permuted)
learned_alpha = learned_alpha_permuted[permutation]
fig = plot_lda(np.vstack([known_beta, learned_beta]), 2, 10)
fig.set_dpi(160)
fig.suptitle('Known vs. Found Topic-Word Probability Distributions')
fig.set_figheight(3)
beta_error = np.linalg.norm(known_beta - learned_beta, 1)
alpha_error = np.linalg.norm(known_alpha - learned_alpha, 1)
print('L1-error (beta) = {}'.format(beta_error))
print('L1-error (alpha) = {}'.format(alpha_error))
```
Not bad!
In the eyeball-norm the topics match quite well. In fact, the topic-word distribution error is approximately 2%.
# Inference
***
A trained model does nothing on its own. We now want to use the model we computed to perform inference on data. For this example, that means predicting the topic mixture representing a given document.
We create an inference endpoint using the SageMaker Python SDK `deploy()` function from the job we defined above. We specify the instance type where inference is computed as well as an initial number of instances to spin up.
```
lda_inference = lda.deploy(
initial_instance_count=1,
instance_type='ml.m4.xlarge', # LDA inference may work better at scale on ml.c4 instances
)
```
Congratulations! You now have a functioning SageMaker LDA inference endpoint. You can confirm the endpoint configuration and status by navigating to the "Endpoints" tab in the AWS SageMaker console and selecting the endpoint matching the endpoint name, below:
```
print('Endpoint name: {}'.format(lda_inference.endpoint))
```
With this realtime endpoint at our fingertips we can finally perform inference on our training and test data.
We can pass a variety of data formats to our inference endpoint. In this example we will demonstrate passing CSV-formatted data. Other available formats are JSON-formatted, JSON-sparse-formatter, and RecordIO Protobuf. We make use of the SageMaker Python SDK utilities `csv_serializer` and `json_deserializer` when configuring the inference endpoint.
```
lda_inference.content_type = 'text/csv'
lda_inference.serializer = csv_serializer
lda_inference.deserializer = json_deserializer
```
We pass some test documents to the inference endpoint. Note that the serializer and deserializer will atuomatically take care of the datatype conversion.
```
results = lda_inference.predict(documents_test[:12])
print(results)
```
It may be hard to see but the output format of SageMaker LDA inference endpoint is a Python dictionary with the following format.
```
{
'predictions': [
{'topic_mixture': [ ... ] },
{'topic_mixture': [ ... ] },
{'topic_mixture': [ ... ] },
...
]
}
```
We extract the topic mixtures, themselves, corresponding to each of the input documents.
```
inferred_topic_mixtures_permuted = np.array([prediction['topic_mixture'] for prediction in results['predictions']])
print('Inferred topic mixtures (permuted):\n\n{}'.format(inferred_topic_mixtures_permuted))
```
## Inference Analysis
Recall that although SageMaker LDA successfully learned the underlying topics which generated the sample data the topics were in a different order. Before we compare to known topic mixtures $\theta \in \mathbb{R}^K$ we should also permute the inferred topic mixtures
```
inferred_topic_mixtures = inferred_topic_mixtures_permuted[:,permutation]
print('Inferred topic mixtures:\n\n{}'.format(inferred_topic_mixtures))
```
Let's plot these topic mixture probability distributions alongside the known ones.
```
%matplotlib inline
# create array of bar plots
width = 0.4
x = np.arange(10)
nrows, ncols = 3, 4
fig, ax = plt.subplots(nrows, ncols, sharey=True)
for i in range(nrows):
for j in range(ncols):
index = i*ncols + j
ax[i,j].bar(x, topic_mixtures_test[index], width, color='C0')
ax[i,j].bar(x+width, inferred_topic_mixtures[index], width, color='C1')
ax[i,j].set_xticks(range(num_topics))
ax[i,j].set_yticks(np.linspace(0,1,5))
ax[i,j].grid(which='major', axis='y')
ax[i,j].set_ylim([0,1])
ax[i,j].set_xticklabels([])
if (i==(nrows-1)):
ax[i,j].set_xticklabels(range(num_topics), fontsize=7)
if (j==0):
ax[i,j].set_yticklabels([0,'',0.5,'',1.0], fontsize=7)
fig.suptitle('Known vs. Inferred Topic Mixtures')
ax_super = fig.add_subplot(111, frameon=False)
ax_super.tick_params(labelcolor='none', top='off', bottom='off', left='off', right='off')
ax_super.grid(False)
ax_super.set_xlabel('Topic Index')
ax_super.set_ylabel('Topic Probability')
fig.set_dpi(160)
```
In the eyeball-norm these look quite comparable.
Let's be more scientific about this. Below we compute and plot the distribution of L1-errors from **all** of the test documents. Note that we send a new payload of test documents to the inference endpoint and apply the appropriate permutation to the output.
```
%%time
# create a payload containing all of the test documents and run inference again
#
# TRY THIS:
# try switching between the test data set and a subset of the training
# data set. It is likely that LDA inference will perform better against
# the training set than the holdout test set.
#
payload_documents = documents_test # Example 1
known_topic_mixtures = topic_mixtures_test # Example 1
#payload_documents = documents_training[:600]; # Example 2
#known_topic_mixtures = topic_mixtures_training[:600] # Example 2
print('Invoking endpoint...\n')
results = lda_inference.predict(payload_documents)
inferred_topic_mixtures_permuted = np.array([prediction['topic_mixture'] for prediction in results['predictions']])
inferred_topic_mixtures = inferred_topic_mixtures_permuted[:,permutation]
print('known_topics_mixtures.shape = {}'.format(known_topic_mixtures.shape))
print('inferred_topics_mixtures_test.shape = {}\n'.format(inferred_topic_mixtures.shape))
%matplotlib inline
l1_errors = np.linalg.norm((inferred_topic_mixtures - known_topic_mixtures), 1, axis=1)
# plot the error freqency
fig, ax_frequency = plt.subplots()
bins = np.linspace(0,1,40)
weights = np.ones_like(l1_errors)/len(l1_errors)
freq, bins, _ = ax_frequency.hist(l1_errors, bins=50, weights=weights, color='C0')
ax_frequency.set_xlabel('L1-Error')
ax_frequency.set_ylabel('Frequency', color='C0')
# plot the cumulative error
shift = (bins[1]-bins[0])/2
x = bins[1:] - shift
ax_cumulative = ax_frequency.twinx()
cumulative = np.cumsum(freq)/sum(freq)
ax_cumulative.plot(x, cumulative, marker='o', color='C1')
ax_cumulative.set_ylabel('Cumulative Frequency', color='C1')
# align grids and show
freq_ticks = np.linspace(0, 1.5*freq.max(), 5)
freq_ticklabels = np.round(100*freq_ticks)/100
ax_frequency.set_yticks(freq_ticks)
ax_frequency.set_yticklabels(freq_ticklabels)
ax_cumulative.set_yticks(np.linspace(0, 1, 5))
ax_cumulative.grid(which='major', axis='y')
ax_cumulative.set_ylim((0,1))
fig.suptitle('Topic Mixutre L1-Errors')
fig.set_dpi(110)
```
Machine learning algorithms are not perfect and the data above suggests this is true of SageMaker LDA. With more documents and some hyperparameter tuning we can obtain more accurate results against the known topic-mixtures.
For now, let's just investigate the documents-topic mixture pairs that seem to do well as well as those that do not. Below we retreive a document and topic mixture corresponding to a small L1-error as well as one with a large L1-error.
```
N = 6
good_idx = (l1_errors < 0.05)
good_documents = payload_documents[good_idx][:N]
good_topic_mixtures = inferred_topic_mixtures[good_idx][:N]
poor_idx = (l1_errors > 0.3)
poor_documents = payload_documents[poor_idx][:N]
poor_topic_mixtures = inferred_topic_mixtures[poor_idx][:N]
%matplotlib inline
fig = plot_lda_topics(good_documents, 2, 3, topic_mixtures=good_topic_mixtures)
fig.suptitle('Documents With Accurate Inferred Topic-Mixtures')
fig.set_dpi(120)
%matplotlib inline
fig = plot_lda_topics(poor_documents, 2, 3, topic_mixtures=poor_topic_mixtures)
fig.suptitle('Documents With Inaccurate Inferred Topic-Mixtures')
fig.set_dpi(120)
```
In this example set the documents on which inference was not as accurate tend to have a denser topic-mixture. This makes sense when extrapolated to real-world datasets: it can be difficult to nail down which topics are represented in a document when the document uses words from a large subset of the vocabulary.
## Stop / Close the Endpoint
Finally, we should delete the endpoint before we close the notebook.
To do so execute the cell below. Alternately, you can navigate to the "Endpoints" tab in the SageMaker console, select the endpoint with the name stored in the variable `endpoint_name`, and select "Delete" from the "Actions" dropdown menu.
```
sagemaker.Session().delete_endpoint(lda_inference.endpoint)
```
# Epilogue
---
In this notebook we,
* learned about the LDA model,
* generated some example LDA documents and their corresponding topic-mixtures,
* trained a SageMaker LDA model on a training set of documents and compared the learned model to the known model,
* created an inference endpoint,
* used the endpoint to infer the topic mixtures of a test input and analyzed the inference error.
There are several things to keep in mind when applying SageMaker LDA to real-word data such as a corpus of text documents. Note that input documents to the algorithm, both in training and inference, need to be vectors of integers representing word counts. Each index corresponds to a word in the corpus vocabulary. Therefore, one will need to "tokenize" their corpus vocabulary.
$$
\text{"cat"} \mapsto 0, \; \text{"dog"} \mapsto 1 \; \text{"bird"} \mapsto 2, \ldots
$$
Each text document then needs to be converted to a "bag-of-words" format document.
$$
w = \text{"cat bird bird bird cat"} \quad \longmapsto \quad w = [2, 0, 3, 0, \ldots, 0]
$$
Also note that many real-word applications have large vocabulary sizes. It may be necessary to represent the input documents in sparse format. Finally, the use of stemming and lemmatization in data preprocessing provides several benefits. Doing so can improve training and inference compute time since it reduces the effective vocabulary size. More importantly, though, it can improve the quality of learned topic-word probability matrices and inferred topic mixtures. For example, the words *"parliament"*, *"parliaments"*, *"parliamentary"*, *"parliament's"*, and *"parliamentarians"* are all essentially the same word, *"parliament"*, but with different conjugations. For the purposes of detecting topics, such as a *"politics"* or *governments"* topic, the inclusion of all five does not add much additional value as they all essentiall describe the same feature.
| github_jupyter |
```
#default_exp synchro.extracting
from nbdev.showdoc import *
%load_ext autoreload
%autoreload 2
```
# synchro.extracting
> Function to extract data of an experiment from 3rd party programs
To align timeseries of an experiment, we need to read logs and import data produced by 3rd party softwares used during the experiment. It includes:
* QDSpy logging
* Numpy arrays of the stimuli
* SpykingCircus spike sorting refined with Phy
* Eye tracking results from MaskRCNN
```
#export
import numpy as np
import datetime
import os, glob
import csv
import re
from theonerig.synchro.io import *
from theonerig.utils import *
def get_QDSpy_logs(log_dir):
"""Factory function to generate QDSpy_log objects from all the QDSpy logs of the folder `log_dir`"""
log_names = glob.glob(os.path.join(log_dir,'[0-9]*.log'))
qdspy_logs = [QDSpy_log(log_name) for log_name in log_names]
for qdspy_log in qdspy_logs:
qdspy_log.find_stimuli()
return qdspy_logs
class QDSpy_log:
"""Class defining a QDSpy log.
It reads the log it represent and extract the stimuli information from it:
- Start and end time
- Parameters like the md5 key
- Frame delays
"""
def __init__(self, log_path):
self.log_path = log_path
self.stimuli = []
self.comments = []
def _extract_data(self, data_line):
data = data_line[data_line.find('{')+1:data_line.find('}')]
data_splitted = data.split(',')
data_dict = {}
for data in data_splitted:
ind = data.find("'")
if type(data[data.find(":")+2:]) is str:
data_dict[data[ind+1:data.find("'",ind+1)]] = data[data.find(":")+2:][1:-1]
else:
data_dict[data[ind+1:data.find("'",ind+1)]] = data[data.find(":")+2:]
return data_dict
def _extract_time(self,data_line):
return datetime.datetime.strptime(data_line.split()[0], '%Y%m%d_%H%M%S')
def _extract_delay(self,data_line):
ind = data_line.find('#')
index_frame = int(data_line[ind+1:data_line.find(' ',ind)])
ind = data_line.find('was')
delay = float(data_line[ind:].split(" ")[1])
return (index_frame, delay)
def __repr__(self):
return "\n".join([str(stim) for stim in self.stimuli])
@property
def n_stim(self):
return len(self.stimuli)
@property
def stim_names(self):
return [stim.name for stim in self.stimuli]
def find_stimuli(self):
"""Find the stimuli in the log file and return the list of the stimuli
found by this object."""
with open(self.log_path, 'r', encoding="ISO-8859-1") as log_file:
for line in log_file:
if "DATA" in line:
data_juice = self._extract_data(line)
if 'stimState' in data_juice.keys():
if data_juice['stimState'] == "STARTED" :
curr_stim = Stimulus(self._extract_time(line))
curr_stim.set_parameters(data_juice)
self.stimuli.append(curr_stim)
stimulus_ON = True
elif data_juice['stimState'] == "FINISHED" or data_juice['stimState'] == "ABORTED":
curr_stim.is_aborted = data_juice['stimState'] == "ABORTED"
curr_stim.stop_time = self._extract_time(line)
stimulus_ON = False
elif 'userComment' in data_juice.keys():
pass
#print("userComment, use it to bind logs to records")
elif stimulus_ON: #Information on stimulus parameters
curr_stim.set_parameters(data_juice)
# elif 'probeX' in data_juice.keys():
# print("Probe center not implemented yet")
if "WARNING" in line and "dt of frame" and stimulus_ON:
curr_stim.frame_delay.append(self._extract_delay(line))
if curr_stim.frame_delay[-1][1] > 2000/60: #if longer than 2 frames could be bad
print(curr_stim.name, " ".join(line.split()[1:])[:-1])
return self.stimuli
class Stimulus:
"""Stimulus object containing information about it's presentation.
- start_time : a datetime object)
- stop_time : a datetime object)
- parameters : Parameters extracted from the QDSpy
- md5 : The md5 hash of that compiled version of the stimulus
- name : The name of the stimulus
"""
def __init__(self,start):
self.start_time = start
self.stop_time = None
self.parameters = {}
self.md5 = None
self.name = "NoName"
self.frame_delay = []
self.is_aborted = False
def set_parameters(self, parameters):
self.parameters.update(parameters)
if "_sName" in parameters.keys():
self.name = parameters["_sName"]
if "stimMD5" in parameters.keys():
self.md5 = parameters["stimMD5"]
def __str__(self):
return "%s %s at %s" %(self.name+" "*(24-len(self.name)),self.md5,self.start_time)
def __repr__(self):
return self.__str__()
```
To read QDSpy logs of your experiment, simply provide the folder containing the log you want to read to `get_QDSpy_logs`
```
#logs = get_QDSpy_logs("./files/basic_synchro")
```
It returns a list fo the QDSpy logs. Stimuli are contained in a list inside each log:
```
#logs[0].stimuli
```
The stimuli objects contains informations on how their display went:
```
# stim = logs[0].stimuli[5]
# print(stim.name, stim.start_time, stim.frame_delay, stim.md5)
#export
def unpack_stim_npy(npy_dir, md5_hash):
"""Find the stimuli of a given hash key in the npy stimulus folder. The stimuli are in a compressed version
comprising three files. inten for the stimulus values on the screen, marker for the values of the marker
read by a photodiode to get the stimulus timing during a record, and an optional shader that is used to
specify informations about a shader when used, like for the moving gratings."""
#Stimuli can be either npy or npz (useful when working remotely)
def find_file(ftype):
flist = glob.glob(os.path.join(npy_dir, "*_"+ftype+"_"+md5_hash+".npy"))
if len(flist)==0:
flist = glob.glob(os.path.join(npy_dir, "*_"+ftype+"_"+md5_hash+".npz"))
res = np.load(flist[0])["arr_0"]
else:
res = np.load(flist[0])
return res
inten = find_file("intensities")
marker = find_file("marker")
shader, unpack_shader = None, None
if len(glob.glob(os.path.join(npy_dir, "*_shader_"+md5_hash+".np*")))>0:
shader = find_file("shader")
unpack_shader = np.empty((np.sum(marker[:,0]), *shader.shape[1:]))
#The latter unpacks the arrays
unpack_inten = np.empty((np.sum(marker[:,0]), *inten.shape[1:]))
unpack_marker = np.empty(np.sum(marker[:,0]))
cursor = 0
for i, n_frame in enumerate(marker[:,0]):
unpack_inten[cursor:cursor+n_frame] = inten[i]
unpack_marker[cursor:cursor+n_frame] = marker[i, 1]
if shader is not None:
unpack_shader[cursor:cursor+n_frame] = shader[i]
cursor += n_frame
return unpack_inten, unpack_marker, unpack_shader
# logs = get_QDSpy_logs("./files/basic_synchro")
```
To unpack the stimulus values, provide the folder of the numpy arrays and the hash of the stimulus:
```
# unpacked = unpack_stim_npy("./files/basic_synchro/stimulus_data", "eed21bda540934a428e93897908d049e")
```
Unpacked is a tuple, where the first element is the intensity of shape (n_frames, n_colors, y, x)
```
# unpacked[0].shape
```
The second element of the tuple repesents the marker values for the timing. QDSpy defaults are zero and ones, but I used custom red squares taking intensities [50,100,150,200,250] to time with five different signals
```
# unpacked[1][:50]
```
Each stimulus is also starting with a barcode, of the form:
0 0 0 0 0 0 4 0 4\*[1-4] 0 4\*[1-4] 0 4\*[1-4] 0 4\*[1-4] 0 4 0 0 0 0 0 0
and ends with 0 0 0 0 0 0
```
#export
def extract_spyking_circus_results(dir_, record_basename):
"""Extract the good cells of a record. Overlap with phy_results_dict."""
phy_dir = os.path.join(dir_,record_basename+"/"+record_basename+".GUI")
phy_dict = phy_results_dict(phy_dir)
good_clusters = []
with open(os.path.join(phy_dir,'cluster_group.tsv'), 'r') as tsvfile:
spamreader = csv.reader(tsvfile, delimiter='\t', quotechar='|')
for i,row in enumerate(spamreader):
if row[1] == "good":
good_clusters.append(int(row[0]))
good_clusters = np.array(good_clusters)
phy_dict["good_clusters"] = good_clusters
return phy_dict
#export
def extract_best_pupil(fn):
"""From results of MaskRCNN, go over all or None pupil detected and select the best pupil.
Each pupil returned is (x,y,width,height,angle,probability)"""
pupil = np.load(fn, allow_pickle=True)
filtered_pupil = np.empty((len(pupil), 6))
for i, detected in enumerate(pupil):
if len(detected)>0:
best = detected[0]
for detect in detected[1:]:
if detect[5]>best[5]:
best = detect
filtered_pupil[i] = np.array(best)
else:
filtered_pupil[i] = np.array([0,0,0,0,0,0])
return filtered_pupil
#export
def stack_len_extraction(stack_info_dir):
"""Extract from ImageJ macro directives the size of the stacks acquired."""
ptrn_nFrame = r".*number=(\d*) .*"
l_epochs = []
for fn in glob.glob(os.path.join(stack_info_dir, "*.txt")):
with open(fn) as f:
line = f.readline()
l_epochs.append(int(re.findall(ptrn_nFrame, line)[0]))
return l_epochs
#hide
from nbdev.export import *
notebook2script()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/totti0223/deep_learning_for_biologists_with_keras/blob/master/notebooks/PlantDisease_tutorial.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Training a Plant Disease Diagnosis Model with PlantVillage Dataset
```
import numpy as np
import os
import matplotlib.pyplot as plt
from skimage.io import imread
from sklearn.metrics import classification_report, confusion_matrix
from sklearn .model_selection import train_test_split
import keras
import keras.backend as K
from keras.preprocessing.image import load_img, img_to_array, ImageDataGenerator
from keras.utils.np_utils import to_categorical
from keras import layers
from keras.models import Sequential, Model
from keras.callbacks import EarlyStopping, ModelCheckpoint
```
# Preparation
## Data Preparation
```
!apt-get install subversion > /dev/null
#Retreive specifc diseases of tomato for training
!svn export https://github.com/spMohanty/PlantVillage-Dataset/trunk/raw/color/Tomato___Bacterial_spot image/Tomato___Bacterial_spot > /dev/null
!svn export https://github.com/spMohanty/PlantVillage-Dataset/trunk/raw/color/Tomato___Early_blight image/Tomato___Early_blight > /dev/null
!svn export https://github.com/spMohanty/PlantVillage-Dataset/trunk/raw/color/Tomato___Late_blight image/Tomato___Late_blight > /dev/null
!svn export https://github.com/spMohanty/PlantVillage-Dataset/trunk/raw/color/Tomato___Septoria_leaf_spot image/Tomato___Septoria_leaf_spot > /dev/null
!svn export https://github.com/spMohanty/PlantVillage-Dataset/trunk/raw/color/Tomato___Target_Spot image/Tomato___Target_Spot > /dev/null
!svn export https://github.com/spMohanty/PlantVillage-Dataset/trunk/raw/color/Tomato___healthy image/Tomato___healthy > /dev/null
#folder structure
!ls image
plt.figure(figsize=(15,10))
#visualize several images
parent_directory = "image"
for i, folder in enumerate(os.listdir(parent_directory)):
print(folder)
folder_directory = os.path.join(parent_directory,folder)
files = os.listdir(folder_directory)
#will inspect only 1 image per folder
file = files[0]
file_path = os.path.join(folder_directory,file)
image = imread(file_path)
plt.subplot(1,6,i+1)
plt.imshow(image)
plt.axis("off")
name = folder.split("___")[1][:-1]
plt.title(name)
#plt.show()
#load everything into memory
x = []
y = []
class_names = []
parent_directory = "image"
for i,folder in enumerate(os.listdir(parent_directory)):
print(i,folder)
class_names.append(folder)
folder_directory = os.path.join(parent_directory,folder)
files = os.listdir(folder_directory)
#will inspect only 1 image per folder
for file in files:
file_path = os.path.join(folder_directory,file)
image = load_img(file_path,target_size=(64,64))
image = img_to_array(image)/255.
x.append(image)
y.append(i)
x = np.array(x)
y = to_categorical(y)
#check the data shape
print(x.shape)
print(y.shape)
print(y[0])
x_train, _x, y_train, _y = train_test_split(x,y,test_size=0.2, stratify = y, random_state = 1)
x_valid,x_test, y_valid, y_test = train_test_split(_x,_y,test_size=0.4, stratify = _y, random_state = 1)
print("train data:",x_train.shape,y_train.shape)
print("validation data:",x_valid.shape,y_valid.shape)
print("test data:",x_test.shape,y_test.shape)
```
## Model Preparation
```
K.clear_session()
nfilter = 32
#VGG16 like model
model = Sequential([
#block1
layers.Conv2D(nfilter,(3,3),padding="same",name="block1_conv1",input_shape=(64,64,3)),
layers.Activation("relu"),
layers.BatchNormalization(),
#layers.Dropout(rate=0.2),
layers.Conv2D(nfilter,(3,3),padding="same",name="block1_conv2"),
layers.BatchNormalization(),
layers.Activation("relu"),
#layers.Dropout(rate=0.2),
layers.MaxPooling2D((2,2),strides=(2,2),name="block1_pool"),
#block2
layers.Conv2D(nfilter*2,(3,3),padding="same",name="block2_conv1"),
layers.BatchNormalization(),
layers.Activation("relu"),
#layers.Dropout(rate=0.2),
layers.Conv2D(nfilter*2,(3,3),padding="same",name="block2_conv2"),
layers.BatchNormalization(),
layers.Activation("relu"),
#layers.Dropout(rate=0.2),
layers.MaxPooling2D((2,2),strides=(2,2),name="block2_pool"),
#block3
layers.Conv2D(nfilter*2,(3,3),padding="same",name="block3_conv1"),
layers.BatchNormalization(),
layers.Activation("relu"),
#layers.Dropout(rate=0.2),
layers.Conv2D(nfilter*4,(3,3),padding="same",name="block3_conv2"),
layers.BatchNormalization(),
layers.Activation("relu"),
#layers.Dropout(rate=0.2),
layers.Conv2D(nfilter*4,(3,3),padding="same",name="block3_conv3"),
layers.BatchNormalization(),
layers.Activation("relu"),
#layers.Dropout(rate=0.2),
layers.MaxPooling2D((2,2),strides=(2,2),name="block3_pool"),
#layers.Flatten(),
layers.GlobalAveragePooling2D(),
#inference layer
layers.Dense(128,name="fc1"),
layers.BatchNormalization(),
layers.Activation("relu"),
#layers.Dropout(rate=0.2),
layers.Dense(128,name="fc2"),
layers.BatchNormalization(),
layers.Activation("relu"),
#layers.Dropout(rate=0.2),
layers.Dense(6,name="prepredictions"),
layers.Activation("softmax",name="predictions")
])
model.compile(optimizer = "adam", loss="categorical_crossentropy", metrics=["accuracy"])
model.summary()
```
## Training
```
#utilize early stopping function to stop at the lowest validation loss
es = EarlyStopping(monitor='val_loss', patience=10, verbose=1, mode='auto')
#utilize save best weight model during training
ckpt = ModelCheckpoint("PlantDiseaseCNNmodel.hdf5", monitor='val_loss', verbose=1, save_best_only=True, save_weights_only=False, mode='auto', period=1)
#we will define a generator class for training data and validation data seperately, as no augmentation is not required for validation data
t_gen = ImageDataGenerator(rotation_range=90,horizontal_flip=True)
v_gen = ImageDataGenerator()
train_gen = t_gen.flow(x_train,y_train,batch_size=98)
valid_gen = v_gen.flow(x_valid,y_valid,batch_size=98)
history = model.fit_generator(
train_gen,
steps_per_epoch = train_gen.n // 98,
callbacks = [es,ckpt],
validation_data = valid_gen,
validation_steps = valid_gen.n // 98,
epochs=50)
```
## Evaluation
```
#load the model weight file with lowest validation loss
model.load_weights("PlantDiseaseCNNmodel.hdf5")
#or can obtain the pretrained model from the github repo.
#check the model metrics
print(model.metrics_names)
#evaluate training data
print(model.evaluate(x= x_train, y = y_train))
#evaluate validation data
print(model.evaluate(x= x_valid, y = y_valid))
#evaluate test data
print(model.evaluate(x= x_test, y = y_test))
#draw a confusion matrix
#true label
y_true = np.argmax(y_test,axis=1)
#prediction label
Y_pred = model.predict(x_test)
y_pred = np.argmax(Y_pred, axis=1)
print(y_true)
print(y_pred)
#https://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html#sphx-glr-auto-examples-model-selection-plot-confusion-matrix-py
from sklearn.metrics import confusion_matrix
from sklearn.utils.multiclass import unique_labels
def plot_confusion_matrix(y_true, y_pred, classes,
normalize=False,
title=None,
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if not title:
if normalize:
title = 'Normalized confusion matrix'
else:
title = 'Confusion matrix, without normalization'
# Compute confusion matrix
cm = confusion_matrix(y_true, y_pred)
# Only use the labels that appear in the data
#classes = classes[unique_labels(y_true, y_pred)]
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
fig, ax = plt.subplots(figsize=(5,5))
im = ax.imshow(cm, interpolation='nearest', cmap=cmap)
#ax.figure.colorbar(im, ax=ax)
# We want to show all ticks...
ax.set(xticks=np.arange(cm.shape[1]),
yticks=np.arange(cm.shape[0]),
# ... and label them with the respective list entries
xticklabels=classes, yticklabels=classes,
title=title,
ylabel='True label',
xlabel='Predicted label')
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
# Loop over data dimensions and create text annotations.
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j, i, format(cm[i, j], fmt),
ha="center", va="center",
color="white" if cm[i, j] > thresh else "black")
fig.tight_layout()
return ax
np.set_printoptions(precision=2)
plot_confusion_matrix(y_true, y_pred, classes=class_names, normalize=True,
title='Normalized confusion matrix')
```
## Predicting Indivisual Images
```
n = 15 #do not exceed (number of test image - 1)
plt.imshow(x_test[n])
plt.show()
true_label = np.argmax(y_test,axis=1)[n]
print("true_label is:",true_label,":",class_names[true_label])
prediction = model.predict(x_test[n][np.newaxis,...])[0]
print("predicted_value is:",prediction)
predicted_label = np.argmax(prediction)
print("predicted_label is:",predicted_label,":",class_names[predicted_label])
if true_label == predicted_label:
print("correct prediction")
else:
print("wrong prediction")
```
| github_jupyter |
# LeNet Lab Solution

Source: Yan LeCun
## Load Data
Load the MNIST data, which comes pre-loaded with TensorFlow.
You do not need to modify this section.
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", reshape=False)
X_train, y_train = mnist.train.images, mnist.train.labels
X_validation, y_validation = mnist.validation.images, mnist.validation.labels
X_test, y_test = mnist.test.images, mnist.test.labels
assert(len(X_train) == len(y_train))
assert(len(X_validation) == len(y_validation))
assert(len(X_test) == len(y_test))
print()
print("Image Shape: {}".format(X_train[0].shape))
print()
print("Training Set: {} samples".format(len(X_train)))
print("Validation Set: {} samples".format(len(X_validation)))
print("Test Set: {} samples".format(len(X_test)))
```
The MNIST data that TensorFlow pre-loads comes as 28x28x1 images.
However, the LeNet architecture only accepts 32x32xC images, where C is the number of color channels.
In order to reformat the MNIST data into a shape that LeNet will accept, we pad the data with two rows of zeros on the top and bottom, and two columns of zeros on the left and right (28+2+2 = 32).
You do not need to modify this section.
```
import numpy as np
# Pad images with 0s
X_train = np.pad(X_train, ((0,0),(2,2),(2,2),(0,0)), 'constant')
X_validation = np.pad(X_validation, ((0,0),(2,2),(2,2),(0,0)), 'constant')
X_test = np.pad(X_test, ((0,0),(2,2),(2,2),(0,0)), 'constant')
print("Updated Image Shape: {}".format(X_train[0].shape))
```
## Visualize Data
View a sample from the dataset.
You do not need to modify this section.
```
import random
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
index = random.randint(0, len(X_train))
image = X_train[index].squeeze()
plt.figure(figsize=(1,1))
plt.imshow(image, cmap="gray")
print(y_train[index])
```
## Preprocess Data
Shuffle the training data.
You do not need to modify this section.
```
from sklearn.utils import shuffle
X_train, y_train = shuffle(X_train, y_train)
```
## Setup TensorFlow
The `EPOCH` and `BATCH_SIZE` values affect the training speed and model accuracy.
You do not need to modify this section.
```
import tensorflow as tf
EPOCHS = 10
BATCH_SIZE = 128
```
## SOLUTION: Implement LeNet-5
Implement the [LeNet-5](http://yann.lecun.com/exdb/lenet/) neural network architecture.
This is the only cell you need to edit.
### Input
The LeNet architecture accepts a 32x32xC image as input, where C is the number of color channels. Since MNIST images are grayscale, C is 1 in this case.
### Architecture
**Layer 1: Convolutional.** The output shape should be 28x28x6.
**Activation.** Your choice of activation function.
**Pooling.** The output shape should be 14x14x6.
**Layer 2: Convolutional.** The output shape should be 10x10x16.
**Activation.** Your choice of activation function.
**Pooling.** The output shape should be 5x5x16.
**Flatten.** Flatten the output shape of the final pooling layer such that it's 1D instead of 3D. The easiest way to do is by using `tf.contrib.layers.flatten`, which is already imported for you.
**Layer 3: Fully Connected.** This should have 120 outputs.
**Activation.** Your choice of activation function.
**Layer 4: Fully Connected.** This should have 84 outputs.
**Activation.** Your choice of activation function.
**Layer 5: Fully Connected (Logits).** This should have 10 outputs.
### Output
Return the result of the 2nd fully connected layer.
```
from tensorflow.contrib.layers import flatten
def LeNet(x):
# Arguments used for tf.truncated_normal, randomly defines variables for the weights and biases for each layer
mu = 0
sigma = 0.1
# SOLUTION: Layer 1: Convolutional. Input = 32x32x1. Output = 28x28x6.
conv1_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 1, 6), mean = mu, stddev = sigma))
conv1_b = tf.Variable(tf.zeros(6))
conv1 = tf.nn.conv2d(x, conv1_W, strides=[1, 1, 1, 1], padding='VALID') + conv1_b
# SOLUTION: Activation.
conv1 = tf.nn.relu(conv1)
# SOLUTION: Pooling. Input = 28x28x6. Output = 14x14x6.
conv1 = tf.nn.max_pool(conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# SOLUTION: Layer 2: Convolutional. Output = 10x10x16.
conv2_W = tf.Variable(tf.truncated_normal(shape=(5, 5, 6, 16), mean = mu, stddev = sigma))
conv2_b = tf.Variable(tf.zeros(16))
conv2 = tf.nn.conv2d(conv1, conv2_W, strides=[1, 1, 1, 1], padding='VALID') + conv2_b
# SOLUTION: Activation.
conv2 = tf.nn.relu(conv2)
# SOLUTION: Pooling. Input = 10x10x16. Output = 5x5x16.
conv2 = tf.nn.max_pool(conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='VALID')
# SOLUTION: Flatten. Input = 5x5x16. Output = 400.
fc0 = flatten(conv2)
# SOLUTION: Layer 3: Fully Connected. Input = 400. Output = 120.
fc1_W = tf.Variable(tf.truncated_normal(shape=(400, 120), mean = mu, stddev = sigma))
fc1_b = tf.Variable(tf.zeros(120))
fc1 = tf.matmul(fc0, fc1_W) + fc1_b
# SOLUTION: Activation.
fc1 = tf.nn.relu(fc1)
# SOLUTION: Layer 4: Fully Connected. Input = 120. Output = 84.
fc2_W = tf.Variable(tf.truncated_normal(shape=(120, 84), mean = mu, stddev = sigma))
fc2_b = tf.Variable(tf.zeros(84))
fc2 = tf.matmul(fc1, fc2_W) + fc2_b
# SOLUTION: Activation.
fc2 = tf.nn.relu(fc2)
# SOLUTION: Layer 5: Fully Connected. Input = 84. Output = 10.
fc3_W = tf.Variable(tf.truncated_normal(shape=(84, 10), mean = mu, stddev = sigma))
fc3_b = tf.Variable(tf.zeros(10))
logits = tf.matmul(fc2, fc3_W) + fc3_b
return logits
```
## Features and Labels
Train LeNet to classify [MNIST](http://yann.lecun.com/exdb/mnist/) data.
`x` is a placeholder for a batch of input images.
`y` is a placeholder for a batch of output labels.
You do not need to modify this section.
```
x = tf.placeholder(tf.float32, (None, 32, 32, 1))
y = tf.placeholder(tf.int32, (None))
one_hot_y = tf.one_hot(y, 10)
```
## Training Pipeline
Create a training pipeline that uses the model to classify MNIST data.
You do not need to modify this section.
```
rate = 0.001
logits = LeNet(x)
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=one_hot_y, logits=logits)
loss_operation = tf.reduce_mean(cross_entropy)
optimizer = tf.train.AdamOptimizer(learning_rate = rate)
training_operation = optimizer.minimize(loss_operation)
```
## Model Evaluation
Evaluate how well the loss and accuracy of the model for a given dataset.
You do not need to modify this section.
```
correct_prediction = tf.equal(tf.argmax(logits, 1), tf.argmax(one_hot_y, 1))
accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
saver = tf.train.Saver()
def evaluate(X_data, y_data):
num_examples = len(X_data)
total_accuracy = 0
sess = tf.get_default_session()
for offset in range(0, num_examples, BATCH_SIZE):
batch_x, batch_y = X_data[offset:offset+BATCH_SIZE], y_data[offset:offset+BATCH_SIZE]
accuracy = sess.run(accuracy_operation, feed_dict={x: batch_x, y: batch_y})
total_accuracy += (accuracy * len(batch_x))
return total_accuracy / num_examples
```
## Train the Model
Run the training data through the training pipeline to train the model.
Before each epoch, shuffle the training set.
After each epoch, measure the loss and accuracy of the validation set.
Save the model after training.
You do not need to modify this section.
```
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
num_examples = len(X_train)
print("Training...")
print()
for i in range(EPOCHS):
X_train, y_train = shuffle(X_train, y_train)
for offset in range(0, num_examples, BATCH_SIZE):
end = offset + BATCH_SIZE
batch_x, batch_y = X_train[offset:end], y_train[offset:end]
sess.run(training_operation, feed_dict={x: batch_x, y: batch_y})
validation_accuracy = evaluate(X_validation, y_validation)
print("EPOCH {} ...".format(i+1))
print("Validation Accuracy = {:.3f}".format(validation_accuracy))
print()
saver.save(sess, './lenet')
print("Model saved")
```
## Evaluate the Model
Once you are completely satisfied with your model, evaluate the performance of the model on the test set.
Be sure to only do this once!
If you were to measure the performance of your trained model on the test set, then improve your model, and then measure the performance of your model on the test set again, that would invalidate your test results. You wouldn't get a true measure of how well your model would perform against real data.
You do not need to modify this section.
```
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('.'))
test_accuracy = evaluate(X_test, y_test)
print("Test Accuracy = {:.3f}".format(test_accuracy))
```
| github_jupyter |
# Single-stepping the `logictools` Pattern Generator
* This notebook will show how to use single-stepping mode with the pattern generator
* Note that all generators in the _logictools_ library may be **single-stepped**
### Visually ...
#### The _logictools_ library on the Zynq device on the PYNQ board

### Demonstrator notes
* For this demo, the pattern generator implements a simple, 4-bit binary, up-counter
* We will single-step the clock and verify the counter operation
* The output is verified using the waveforms captured by the trace analyzer
### Points to note
* __Everything__ runs on the Zynq chip on the PYNQ board, even this slide show!
* We will specify and implement circuits __using only Python code__
* __No__ Xilinx CAD tools are used
* We can create live, real-time circuits __instantaneously__
```
# Specify a stimulus waveform and display it
from pynq.overlays.logictools import LogicToolsOverlay
from pynq.lib.logictools import Waveform
logictools_olay = LogicToolsOverlay('logictools.bit')
up_counter_stimulus = {'signal': [
{'name': 'bit0', 'pin': 'D0', 'wave': 'lh' * 8},
{'name': 'bit1', 'pin': 'D1', 'wave': 'l.h.' * 4},
{'name': 'bit2', 'pin': 'D2', 'wave': 'l...h...' * 2},
{'name': 'bit3', 'pin': 'D3', 'wave': 'l.......h.......'}]}
# Check visually that the stimulus pattern is correct
waveform = Waveform(up_counter_stimulus)
waveform.display()
# Add the signals we want to analyze
up_counter = {'signal': [
['stimulus',
{'name': 'bit0', 'pin': 'D0', 'wave': 'lh' * 8},
{'name': 'bit1', 'pin': 'D1', 'wave': 'l.h.' * 4},
{'name': 'bit2', 'pin': 'D2', 'wave': 'l...h...' * 2},
{'name': 'bit3', 'pin': 'D3', 'wave': 'l.......h.......'}],
{},
['analysis',
{'name': 'bit0_output', 'pin': 'D0'},
{'name': 'bit1_output', 'pin': 'D1'},
{'name': 'bit2_output', 'pin': 'D2'},
{'name': 'bit3_output', 'pin': 'D3'}]]}
# Display the stimulus and analysis signal groups
waveform = Waveform(up_counter)
waveform.display()
# Configure the pattern generator and analyzer
pattern_generator = logictools_olay.pattern_generator
pattern_generator.trace(num_analyzer_samples=16)
pattern_generator.setup(up_counter,
stimulus_group_name='stimulus',
analysis_group_name='analysis')
# Press `cntrl-enter` to advance the pattern generator by one clock cycle
pattern_generator.step()
pattern_generator.show_waveform()
# Advance an arbitrary number of cycles
no_of_cycles = 7
for _ in range(no_of_cycles):
pattern_generator.step()
pattern_generator.show_waveform()
# Finally, reset the pattern generator after use
pattern_generator.reset()
```
| github_jupyter |
## Practice: approximate q-learning
_Reference: based on Practical RL_ [week04](https://github.com/yandexdataschool/Practical_RL/tree/master/week04_approx_rl)
In this notebook you will teach a __pytorch__ neural network to do Q-learning.
```
# # in google colab uncomment this
# import os
# os.system('apt-get install -y xvfb')
# os.system('wget https://raw.githubusercontent.com/yandexdataschool/Practical_DL/fall18/xvfb -O ../xvfb')
# os.system('apt-get install -y python-opengl ffmpeg')
# XVFB will be launched if you run on a server
import os
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
!bash ../xvfb start
%env DISPLAY = : 1
import gym
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
env = gym.make("CartPole-v0").env
env.reset()
n_actions = env.action_space.n
state_dim = env.observation_space.shape
plt.imshow(env.render("rgb_array"))
env.close()
```
# Approximate Q-learning: building the network
To train a neural network policy one must have a neural network policy. Let's build it.
Since we're working with a pre-extracted features (cart positions, angles and velocities), we don't need a complicated network yet. In fact, let's build something like this for starters:
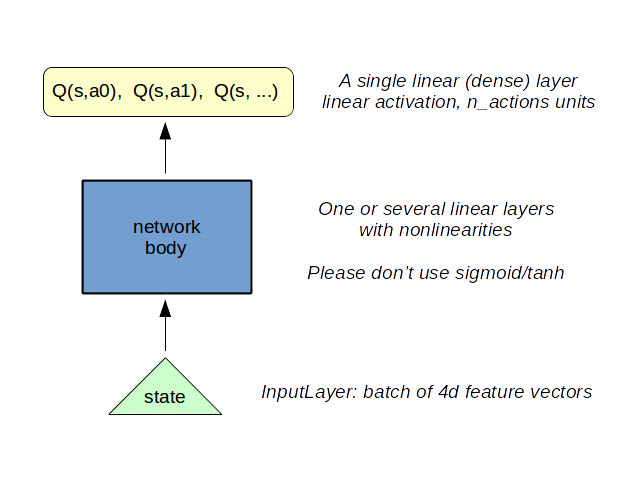
For your first run, please only use linear layers (nn.Linear) and activations. Stuff like batch normalization or dropout may ruin everything if used haphazardly.
Also please avoid using nonlinearities like sigmoid & tanh: agent's observations are not normalized so sigmoids may become saturated from init.
Ideally you should start small with maybe 1-2 hidden layers with < 200 neurons and then increase network size if agent doesn't beat the target score.
```
import torch
import torch.nn as nn
import torch.nn.functional as F
network = nn.Sequential()
network.add_module('layer1', < ... >)
<YOUR CODE: stack layers!!!1 >
# hint: use state_dim[0] as input size
def get_action(state, epsilon=0):
"""
sample actions with epsilon-greedy policy
recap: with p = epsilon pick random action, else pick action with highest Q(s,a)
"""
state = torch.tensor(state[None], dtype=torch.float32)
q_values = network(state).detach().numpy()
# YOUR CODE
return int( < epsilon-greedily selected action > )
s = env.reset()
assert tuple(network(torch.tensor([s]*3, dtype=torch.float32)).size()) == (
3, n_actions), "please make sure your model maps state s -> [Q(s,a0), ..., Q(s, a_last)]"
assert isinstance(list(network.modules(
))[-1], nn.Linear), "please make sure you predict q-values without nonlinearity (ignore if you know what you're doing)"
assert isinstance(get_action(
s), int), "get_action(s) must return int, not %s. try int(action)" % (type(get_action(s)))
# test epsilon-greedy exploration
for eps in [0., 0.1, 0.5, 1.0]:
state_frequencies = np.bincount(
[get_action(s, epsilon=eps) for i in range(10000)], minlength=n_actions)
best_action = state_frequencies.argmax()
assert abs(state_frequencies[best_action] -
10000 * (1 - eps + eps / n_actions)) < 200
for other_action in range(n_actions):
if other_action != best_action:
assert abs(state_frequencies[other_action] -
10000 * (eps / n_actions)) < 200
print('e=%.1f tests passed' % eps)
```
### Q-learning via gradient descent
We shall now train our agent's Q-function by minimizing the TD loss:
$$ L = { 1 \over N} \sum_i (Q_{\theta}(s,a) - [r(s,a) + \gamma \cdot max_{a'} Q_{-}(s', a')]) ^2 $$
Where
* $s, a, r, s'$ are current state, action, reward and next state respectively
* $\gamma$ is a discount factor defined two cells above.
The tricky part is with $Q_{-}(s',a')$. From an engineering standpoint, it's the same as $Q_{\theta}$ - the output of your neural network policy. However, when doing gradient descent, __we won't propagate gradients through it__ to make training more stable (see lectures).
To do so, we shall use `x.detach()` function which basically says "consider this thing constant when doingbackprop".
```
def to_one_hot(y_tensor, n_dims=None):
""" helper: take an integer vector and convert it to 1-hot matrix. """
y_tensor = y_tensor.type(torch.LongTensor).view(-1, 1)
n_dims = n_dims if n_dims is not None else int(torch.max(y_tensor)) + 1
y_one_hot = torch.zeros(
y_tensor.size()[0], n_dims).scatter_(1, y_tensor, 1)
return y_one_hot
def where(cond, x_1, x_2):
""" helper: like np.where but in pytorch. """
return (cond * x_1) + ((1-cond) * x_2)
def compute_td_loss(states, actions, rewards, next_states, is_done, gamma=0.99, check_shapes=False):
""" Compute td loss using torch operations only. Use the formula above. """
states = torch.tensor(
states, dtype=torch.float32) # shape: [batch_size, state_size]
actions = torch.tensor(actions, dtype=torch.int32) # shape: [batch_size]
rewards = torch.tensor(rewards, dtype=torch.float32) # shape: [batch_size]
# shape: [batch_size, state_size]
next_states = torch.tensor(next_states, dtype=torch.float32)
is_done = torch.tensor(is_done, dtype=torch.float32) # shape: [batch_size]
# get q-values for all actions in current states
predicted_qvalues = network(states)
# select q-values for chosen actions
predicted_qvalues_for_actions = torch.sum(
predicted_qvalues * to_one_hot(actions, n_actions), dim=1)
# compute q-values for all actions in next states
predicted_next_qvalues = # YOUR CODE
# compute V*(next_states) using predicted next q-values
next_state_values = # YOUR CODE
assert next_state_values.dtype == torch.float32
# compute "target q-values" for loss - it's what's inside square parentheses in the above formula.
target_qvalues_for_actions = # YOUR CODE
# at the last state we shall use simplified formula: Q(s,a) = r(s,a) since s' doesn't exist
target_qvalues_for_actions = where(
is_done, rewards, target_qvalues_for_actions)
# mean squared error loss to minimize
loss = torch.mean((predicted_qvalues_for_actions -
target_qvalues_for_actions.detach()) ** 2)
if check_shapes:
assert predicted_next_qvalues.data.dim(
) == 2, "make sure you predicted q-values for all actions in next state"
assert next_state_values.data.dim(
) == 1, "make sure you computed V(s') as maximum over just the actions axis and not all axes"
assert target_qvalues_for_actions.data.dim(
) == 1, "there's something wrong with target q-values, they must be a vector"
return loss
# sanity checks
s = env.reset()
a = env.action_space.sample()
next_s, r, done, _ = env.step(a)
loss = compute_td_loss([s], [a], [r], [next_s], [done], check_shapes=True)
loss.backward()
assert len(loss.size()) == 0, "you must return scalar loss - mean over batch"
assert np.any(next(network.parameters()).grad.detach().numpy() !=
0), "loss must be differentiable w.r.t. network weights"
```
### Playing the game
```
opt = torch.optim.Adam(network.parameters(), lr=1e-4)
epsilon = 0.5
def generate_session(t_max=1000, epsilon=0, train=False):
"""play env with approximate q-learning agent and train it at the same time"""
total_reward = 0
s = env.reset()
for t in range(t_max):
a = get_action(s, epsilon=epsilon)
next_s, r, done, _ = env.step(a)
if train:
opt.zero_grad()
compute_td_loss([s], [a], [r], [next_s], [done]).backward()
opt.step()
total_reward += r
s = next_s
if done:
break
return total_reward
for i in range(1000):
session_rewards = [generate_session(
epsilon=epsilon, train=True) for _ in range(100)]
print("epoch #{}\tmean reward = {:.3f}\tepsilon = {:.3f}".format(
i, np.mean(session_rewards), epsilon))
epsilon *= 0.99
assert epsilon >= 1e-4, "Make sure epsilon is always nonzero during training"
if np.mean(session_rewards) > 300:
print("You Win!")
break
```
### How to interpret results
Welcome to the f.. world of deep f...n reinforcement learning. Don't expect agent's reward to smoothly go up. Hope for it to go increase eventually. If it deems you worthy.
Seriously though,
* __ mean reward__ is the average reward per game. For a correct implementation it may stay low for some 10 epochs, then start growing while oscilating insanely and converges by ~50-100 steps depending on the network architecture.
* If it never reaches target score by the end of for loop, try increasing the number of hidden neurons or look at the epsilon.
* __ epsilon__ - agent's willingness to explore. If you see that agent's already at < 0.01 epsilon before it's is at least 200, just reset it back to 0.1 - 0.5.
### Record videos
As usual, we now use `gym.wrappers.Monitor` to record a video of our agent playing the game. Unlike our previous attempts with state binarization, this time we expect our agent to act ~~(or fail)~~ more smoothly since there's no more binarization error at play.
As you already did with tabular q-learning, we set epsilon=0 for final evaluation to prevent agent from exploring himself to death.
```
# record sessions
import gym.wrappers
env = gym.wrappers.Monitor(gym.make("CartPole-v0"),
directory="videos", force=True)
sessions = [generate_session(epsilon=0, train=False) for _ in range(100)]
env.close()
# Show video. This may not work in some setups. If it doesn't
# work for you, you can download the videos and view them locally.
import sys
from pathlib import Path
from base64 import b64encode
from IPython.display import HTML
video_paths = sorted([s for s in Path('videos').iterdir() if s.suffix == '.mp4'])
video_path = video_paths[-3] # You can also try other indices
if 'google.colab' in sys.modules:
# https://stackoverflow.com/a/57378660/1214547
with video_path.open('rb') as fp:
mp4 = fp.read()
data_url = 'data:video/mp4;base64,' + b64encode(mp4).decode()
else:
data_url = str(video_path)
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format(data_url))
```
| github_jupyter |
# Frame of reference
> Marcos Duarte, Renato Naville Watanabe
> [Laboratory of Biomechanics and Motor Control](http://pesquisa.ufabc.edu.br/bmclab)
> Federal University of ABC, Brazil
<h1>Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Frame-of-reference-for-human-motion-analysis" data-toc-modified-id="Frame-of-reference-for-human-motion-analysis-1"><span class="toc-item-num">1 </span>Frame of reference for human motion analysis</a></span></li><li><span><a href="#Cartesian-coordinate-system" data-toc-modified-id="Cartesian-coordinate-system-2"><span class="toc-item-num">2 </span>Cartesian coordinate system</a></span><ul class="toc-item"><li><span><a href="#Standardizations-in-movement-analysis" data-toc-modified-id="Standardizations-in-movement-analysis-2.1"><span class="toc-item-num">2.1 </span>Standardizations in movement analysis </a></span></li></ul></li><li><span><a href="#Determination-of-a-coordinate-system" data-toc-modified-id="Determination-of-a-coordinate-system-3"><span class="toc-item-num">3 </span>Determination of a coordinate system</a></span><ul class="toc-item"><li><span><a href="#Definition-of-a-basis" data-toc-modified-id="Definition-of-a-basis-3.1"><span class="toc-item-num">3.1 </span>Definition of a basis</a></span></li><li><span><a href="#Using-the-cross-product" data-toc-modified-id="Using-the-cross-product-3.2"><span class="toc-item-num">3.2 </span>Using the cross product</a></span></li><li><span><a href="#Gram–Schmidt-process" data-toc-modified-id="Gram–Schmidt-process-3.3"><span class="toc-item-num">3.3 </span>Gram–Schmidt process</a></span></li></ul></li><li><span><a href="#Polar-and-spherical-coordinate-systems" data-toc-modified-id="Polar-and-spherical-coordinate-systems-4"><span class="toc-item-num">4 </span>Polar and spherical coordinate systems</a></span><ul class="toc-item"><li><span><a href="#Polar-coordinate-system" data-toc-modified-id="Polar-coordinate-system-4.1"><span class="toc-item-num">4.1 </span>Polar coordinate system</a></span></li><li><span><a href="#Spherical-coordinate-system" data-toc-modified-id="Spherical-coordinate-system-4.2"><span class="toc-item-num">4.2 </span>Spherical coordinate system </a></span></li></ul></li><li><span><a href="#Generalized-coordinates" data-toc-modified-id="Generalized-coordinates-5"><span class="toc-item-num">5 </span>Generalized coordinates</a></span></li><li><span><a href="#Further-reading" data-toc-modified-id="Further-reading-6"><span class="toc-item-num">6 </span>Further reading</a></span></li><li><span><a href="#Video-lectures-on-the-Internet" data-toc-modified-id="Video-lectures-on-the-Internet-7"><span class="toc-item-num">7 </span>Video lectures on the Internet</a></span></li><li><span><a href="#Problems" data-toc-modified-id="Problems-8"><span class="toc-item-num">8 </span>Problems</a></span></li><li><span><a href="#References" data-toc-modified-id="References-9"><span class="toc-item-num">9 </span>References</a></span></li></ul></div>
<a href="http://en.wikipedia.org/wiki/Motion_(physics)">Motion</a> (a change of position in space with respect to time) is not an absolute concept; a reference is needed to describe the motion of the object in relation to this reference. Likewise, the state of such reference cannot be absolute in space and so motion is relative.
A [frame of reference](http://en.wikipedia.org/wiki/Frame_of_reference) is the place with respect to we choose to describe the motion of an object. In this reference frame, we define a [coordinate system](http://en.wikipedia.org/wiki/Coordinate_system) (a set of axes) within which we measure the motion of an object (but frame of reference and coordinate system are often used interchangeably).
Often, the choice of reference frame and coordinate system is made by convenience. However, there is an important distinction between reference frames when we deal with the dynamics of motion, where we are interested to understand the forces related to the motion of the object. In dynamics, we refer to [inertial frame of reference](http://en.wikipedia.org/wiki/Inertial_frame_of_reference) (a.k.a., Galilean reference frame) when the Newton's laws of motion in their simple form are valid in this frame and to non-inertial frame of reference when the Newton's laws in their simple form are not valid (in such reference frame, fictitious accelerations/forces appear). An inertial reference frame is at rest or moves at constant speed (because there is no absolute rest!), whereas a non-inertial reference frame is under acceleration (with respect to an inertial reference frame).
The concept of frame of reference has changed drastically since Aristotle, Galileo, Newton, and Einstein. To read more about that and its philosophical implications, see [Space and Time: Inertial Frames](http://plato.stanford.edu/entries/spacetime-iframes/).
## Frame of reference for human motion analysis
In anatomy, we use a simplified reference frame composed by perpendicular planes to provide a standard reference for qualitatively describing the structures and movements of the human body, as shown in the next figure.
<div class='center-align'><figure><img src="http://upload.wikimedia.org/wikipedia/commons/3/34/BodyPlanes.jpg" width="300" alt="Anatomical body position"/><figcaption><center><i>Figure. Anatomical body position and body planes (<a href="http://en.wikipedia.org/wiki/Human_anatomical_terms" target="_blank">image from Wikipedia</a>).</i></center></figcaption> </figure></div>
## Cartesian coordinate system
As we perceive the surrounding space as three-dimensional, a convenient coordinate system is the [Cartesian coordinate system](http://en.wikipedia.org/wiki/Cartesian_coordinate_system) in the [Euclidean space](http://en.wikipedia.org/wiki/Euclidean_space) with three orthogonal axes as shown below. The axes directions are commonly defined by the [right-hand rule](http://en.wikipedia.org/wiki/Right-hand_rule) and attributed the letters X, Y, Z. The orthogonality of the Cartesian coordinate system is convenient for its use in classical mechanics, most of the times the structure of space is assumed having the [Euclidean geometry](http://en.wikipedia.org/wiki/Euclidean_geometry) and as consequence, the motion in different directions are independent of each other.
<div class='center-align'><figure><img src="https://raw.githubusercontent.com/demotu/BMC/master/images/CCS.png" width=350/><figcaption><center><i>Figure. A point in three-dimensional Euclidean space described in a Cartesian coordinate system.</i></center></figcaption> </figure></div>
### Standardizations in movement analysis
The concept of reference frame in Biomechanics and motor control is very important and central to the understanding of human motion. For example, do we see, plan and control the movement of our hand with respect to reference frames within our body or in the environment we move? Or a combination of both?
The figure below, although derived for a robotic system, illustrates well the concept that we might have to deal with multiple coordinate systems.
<div class='center-align'><figure><img src="https://raw.githubusercontent.com/demotu/BMC/master/images/coordinatesystems.png" width=450/><figcaption><center><i>Figure. Multiple coordinate systems for use in robots (figure from Corke (2017)).</i></center></figcaption></figure></div>
For three-dimensional motion analysis in Biomechanics, we may use several different references frames for convenience and refer to them as global, laboratory, local, anatomical, or technical reference frames or coordinate systems (we will study this later).
There has been proposed different standardizations on how to define frame of references for the main segments and joints of the human body. For instance, the International Society of Biomechanics has a [page listing standardization proposals](https://isbweb.org/activities/standards) by its standardization committee and subcommittees:
```
from IPython.display import IFrame
IFrame('https://isbweb.org/activities/standards', width='100%', height=400)
```
Another initiative for the standardization of references frames is from the [Virtual Animation of the Kinematics of the Human for Industrial, Educational and Research Purposes (VAKHUM)](https://raw.githubusercontent.com/demotu/BMC/master/refs/VAKHUM.pdf) project.
## Determination of a coordinate system
In Biomechanics, we may use different coordinate systems for convenience and refer to them as global, laboratory, local, anatomical, or technical reference frames or coordinate systems. For example, in a standard gait analysis, we define a global or laboratory coordinate system and a different coordinate system for each segment of the body to be able to describe the motion of a segment in relation to anatomical axes of another segment. To define this anatomical coordinate system, we need to place markers on anatomical landmarks on each segment. We also may use other markers (technical markers) on the segment to improve the motion analysis and then we will also have to define a technical coordinate system for each segment.
As we perceive the surrounding space as three-dimensional, a convenient coordinate system to use is the [Cartesian coordinate system](http://en.wikipedia.org/wiki/Cartesian_coordinate_system) with three orthogonal axes in the [Euclidean space](http://en.wikipedia.org/wiki/Euclidean_space). From [linear algebra](http://en.wikipedia.org/wiki/Linear_algebra), a set of unit linearly independent vectors (orthogonal in the Euclidean space and each with norm (length) equals to one) that can represent any vector via [linear combination](http://en.wikipedia.org/wiki/Linear_combination) is called a <a href="http://en.wikipedia.org/wiki/Basis_(linear_algebra)">basis</a> (or orthonormal basis). The figure below shows a point and its position vector in the Cartesian coordinate system and the corresponding versors (unit vectors) of the basis for this coordinate system. See the notebook [Scalar and vector](http://nbviewer.ipython.org/github/demotu/BMC/blob/master/notebooks/ScalarVector.ipynb) for a description on vectors.
<div class='center-align'><figure><img src="https://raw.githubusercontent.com/demotu/BMC/master/images/vector3Dijk.png" width=350/><figcaption><center><i>Figure. Representation of a point **P** and its position vector <span class="notranslate"> $\overrightarrow{\mathbf{r}}$</span> in a Cartesian coordinate system. The versors<span class="notranslate"> $\hat{\mathbf{i}}, \hat{\mathbf{j}}, \hat{\mathbf{k}}$</span> form a basis for this coordinate system and are usually represented in the color sequence RGB (red, green, blue) for easier visualization.</i></center></figcaption></figure></div>
One can see that the versors of the basis shown in the figure above have the following coordinates in the Cartesian coordinate system:
<span class="notranslate">
\begin{equation}
\hat{\mathbf{i}} = \begin{bmatrix}1\\0\\0 \end{bmatrix}, \quad \hat{\mathbf{j}} = \begin{bmatrix}0\\1\\0 \end{bmatrix}, \quad \hat{\mathbf{k}} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}
\end{equation}
</span>
Using the notation described in the figure above, the position vector $\overrightarrow{\mathbf{r}}$ (or the point $\overrightarrow{\mathbf{P}}$) can be expressed as:
<span class="notranslate">
\begin{equation}
\overrightarrow{\mathbf{r}} = x\hat{\mathbf{i}} + y\hat{\mathbf{j}} + z\hat{\mathbf{k}}
\end{equation}
</span>
### Definition of a basis
The mathematical problem of determination of a coordinate system is to find a basis and an origin for it (a basis is only a set of vectors, with no origin). There are different methods to calculate a basis given a set of points (coordinates), for example, one can use the scalar product or the cross product for this problem.
### Using the cross product
Let's now define a basis using a common method in motion analysis (employing the cross product):
Given the coordinates of three noncollinear points in 3D space (points that do not all lie on the same line),<span class="notranslate"> $\overrightarrow{\mathbf{m}}_1, \overrightarrow{\mathbf{m}}_2, \overrightarrow{\mathbf{m}}_3$</span>, which would represent the positions of markers captured from a motion analysis session, a basis can be found following these steps:
1. First axis, <span class="notranslate">$\overrightarrow{\mathbf{v}}_1$</span>, the vector <span class="notranslate">$\overrightarrow{\mathbf{m}}_2-\overrightarrow{\mathbf{m}}_1$</span> (or any other vector difference);
2. Second axis,<span class="notranslate"> $\overrightarrow{\mathbf{v}}_2$</span>, the cross or vector product between the vectors <span class="notranslate"> $\overrightarrow{\mathbf{v}}_1$</span> and <span class="notranslate">$\overrightarrow{\mathbf{m}}_3-\overrightarrow{\mathbf{m}}_1$ </span>(or <span class="notranslate">$\overrightarrow{\mathbf{m}}_3-\overrightarrow{\mathbf{m}}_2$)</span>;
3. Third axis, <span class="notranslate"> $\overrightarrow{\mathbf{v}}_3$</span>, the cross product between the vectors <span class="notranslate"> $\overrightarrow{\mathbf{v}}_1$</span> and <span class="notranslate"> $\overrightarrow{\mathbf{v}}_2$</span>.
4. Make all vectors to have norm 1 dividing each vector by its norm.
The positions of the points used to construct a coordinate system have, by definition, to be specified in relation to an already existing coordinate system. In motion analysis, this coordinate system is the coordinate system from the motion capture system and it is established in the calibration phase. In this phase, the positions of markers placed on an object with perpendicular axes and known distances between the markers are captured and used as the reference (laboratory) coordinate system.
For example, given the positions <span class="notranslate"> $\overrightarrow{\mathbf{m}}_1 = [1,2,5], \overrightarrow{\mathbf{m}}_2 = [2,3,3], \overrightarrow{\mathbf{m}}_3 = [4,0,2]$</span>, a basis can be found with:
```
import numpy as np
m1 = np.array([1, 2, 5])
m2 = np.array([2, 3, 3])
m3 = np.array([4, 0, 2])
v1 = m2 - m1 # first axis
v2 = np.cross(v1, m3 - m1) # second axis
v3 = np.cross(v1, v2) # third axis
# Vector normalization
e1 = v1/np.linalg.norm(v1)
e2 = v2/np.linalg.norm(v2)
e3 = v3/np.linalg.norm(v3)
print('Versors:', '\ne1 =', e1, '\ne2 =', e2, '\ne3 =', e3)
print('\nTest of orthogonality (cross product between versors):',
'\ne1 x e2:', np.linalg.norm(np.cross(e1, e2)),
'\ne1 x e3:', np.linalg.norm(np.cross(e1, e3)),
'\ne2 x e3:', np.linalg.norm(np.cross(e2, e3)))
print('\nNorm of each versor:',
'\n||e1|| =', np.linalg.norm(e1),
'\n||e2|| =', np.linalg.norm(e2),
'\n||e3|| =', np.linalg.norm(e3))
```
To define a coordinate system using the calculated basis, we also need to define an origin. In principle, we could use any point as origin, but if the calculated coordinate system should follow anatomical conventions, e.g., the coordinate system origin should be at a joint center, we will have to calculate the basis and origin according to standards used in motion analysis as discussed before.
If the coordinate system is a technical basis and not anatomic-based, a common procedure in motion analysis is to define the origin for the coordinate system as the centroid (average) position among the markers at the reference frame. Using the average position across markers potentially reduces the effect of noise (for example, from soft tissue artifact) on the calculation.
For the markers in the example above, the origin of the coordinate system will be:
```
origin = np.mean((m1, m2, m3), axis=0)
print('Origin: ', origin)
```
Let's plot the coordinate system and the basis using the custom Python function `CCS.py`:
```
import sys
sys.path.insert(1, r'./../functions') # add to pythonpath
from CCS import CCS
markers = np.vstack((m1, m2, m3))
basis = np.vstack((e1, e2, e3))
```
Create figure in this page (inline):
```
%matplotlib notebook
markers = np.vstack((m1, m2, m3))
basis = np.vstack((e1, e2, e3))
CCS(xyz=[], Oijk=origin, ijk=basis, point=markers, vector=True);
```
### Gram–Schmidt process
Another classical procedure in mathematics, employing the scalar product, is known as the [Gram–Schmidt process](http://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process). See the notebook [Scalar and Vector](http://nbviewer.jupyter.org/github/bmclab/BMC/blob/master/notebooks/ScalarVector.ipynb) for a demonstration of the Gram–Schmidt process and how to implement it in Python.
The [Gram–Schmidt process](http://en.wikipedia.org/wiki/Gram%E2%80%93Schmidt_process) is a method for orthonormalizing (orthogonal unit versors) a set of vectors using the scalar product. The Gram–Schmidt process works for any number of vectors.
For example, given three vectors, <span class="notranslate">
$\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}$</span>, in the 3D space, a basis <span class="notranslate"> $\{\hat{e}_a, \hat{e}_b, \hat{e}_c\}$</span> can be found using the Gram–Schmidt process by:
The first versor is in the <span class="notranslate">
$\overrightarrow{\mathbf{a}}$</span> direction (or in the direction of any of the other vectors):
<span class="notranslate">
\begin{equation}
\hat{e}_a = \frac{\overrightarrow{\mathbf{a}}}{||\overrightarrow{\mathbf{a}}||}
\end{equation}
</span>
The second versor, orthogonal to <span class="notranslate"> $\hat{e}_a$</span>, can be found considering we can express vector <span class="notranslate"> $\overrightarrow{\mathbf{b}}$ </span> in terms of the <span class="notranslate"> $\hat{e}_a$ </span> direction as:
<span class="notranslate">
$$ \overrightarrow{\mathbf{b}} = \overrightarrow{\mathbf{b}}^\| + \overrightarrow{\mathbf{b}}^\bot $$
</span>
Then:
<span class="notranslate">
$$ \overrightarrow{\mathbf{b}}^\bot = \overrightarrow{\mathbf{b}} - \overrightarrow{\mathbf{b}}^\| = \overrightarrow{\mathbf{b}} - (\overrightarrow{\mathbf{b}} \cdot \hat{e}_a ) \hat{e}_a $$
</span>
Finally:
<span class="notranslate">
$$ \hat{e}_b = \frac{\overrightarrow{\mathbf{b}}^\bot}{||\overrightarrow{\mathbf{b}}^\bot||} $$
</span>
The third versor, orthogonal to <span class="notranslate"> $\{\hat{e}_a, \hat{e}_b\}$</span>, can be found expressing the vector <span class="notranslate"> $\overrightarrow{\mathbf{C}}$</span> in terms of <span class="notranslate"> $\hat{e}_a$</span> and <span class="notranslate"> $\hat{e}_b$</span> directions as:
<span class="notranslate">
$$ \overrightarrow{\mathbf{c}} = \overrightarrow{\mathbf{c}}^\| + \overrightarrow{\mathbf{c}}^\bot $$
</span>
Then:
<span class="notranslate">
$$ \overrightarrow{\mathbf{c}}^\bot = \overrightarrow{\mathbf{c}} - \overrightarrow{\mathbf{c}}^\| $$
</span>
Where:
<span class="notranslate">
$$ \overrightarrow{\mathbf{c}}^\| = (\overrightarrow{\mathbf{c}} \cdot \hat{e}_a ) \hat{e}_a + (\overrightarrow{\mathbf{c}} \cdot \hat{e}_b ) \hat{e}_b $$
</span>
Finally:
<span class="notranslate">
$$ \hat{e}_c = \frac{\overrightarrow{\mathbf{c}}^\bot}{||\overrightarrow{\mathbf{c}}^\bot||} $$
</span>
Let's implement the Gram–Schmidt process in Python.
For example, consider the positions (vectors) <span class="notranslate">
$\overrightarrow{\mathbf{a}} = [1,2,0], \overrightarrow{\mathbf{b}} = [0,1,3], \overrightarrow{\mathbf{c}} = [1,0,1]$</span>:
```
import numpy as np
a = np.array([1, 2, 0])
b = np.array([0, 1, 3])
c = np.array([1, 0, 1])
```
The first versor is:
```
ea = a/np.linalg.norm(a)
print(ea)
```
The second versor is:
```
eb = b - np.dot(b, ea)*ea
eb = eb/np.linalg.norm(eb)
print(eb)
```
And the third version is:
```
ec = c - np.dot(c, ea)*ea - np.dot(c, eb)*eb
ec = ec/np.linalg.norm(ec)
print(ec)
```
Let's check the orthonormality between these versors:
```
print(' Versors:', '\nea =', ea, '\neb =', eb, '\nec =', ec)
print('\n Test of orthogonality (scalar product between versors):',
'\n ea x eb:', np.dot(ea, eb),
'\n eb x ec:', np.dot(eb, ec),
'\n ec x ea:', np.dot(ec, ea))
print('\n Norm of each versor:',
'\n ||ea|| =', np.linalg.norm(ea),
'\n ||eb|| =', np.linalg.norm(eb),
'\n ||ec|| =', np.linalg.norm(ec))
```
## Polar and spherical coordinate systems
When studying circular motion in two or three dimensions, the use of a polar (for 2D) or spherical (for 3D) coordinate system can be more convenient than the Cartesian coordinate system.
### Polar coordinate system
In the polar coordinate system, a point in a plane is described by its distance $r$ to the origin (the ray from the origin to this point is the polar axis) and the angle $\theta$ (measured counterclockwise) between the polar axis and an axis of the coordinate system as shown next.
<div class='center-align'><figure><img src="https://raw.githubusercontent.com/demotu/BMC/master/images/polar.png"/><figcaption><center><i>Figure. Representation of a point in a polar coordinate system.</i></center></figcaption></figure></div>
The relation of the coordinates in the Cartesian and polar coordinate systems is:
<span class="notranslate">
$$\begin{array}{l l}
x = r\cos\theta \\
y = r\sin\theta \\
r = \sqrt{x^2 + y^2}
\end{array} $$
</span>
### Spherical coordinate system
The spherical coordinate system can be seen as an extension of the polar coordinate system to three dimensions where an orthogonal axis is added and a second angle is used to describe the point with respect to this third axis as shown next.
<div class='center-align'><figure><img src="https://raw.githubusercontent.com/demotu/BMC/master/images/spherical.png"/><figcaption><center><i>Figure. Representation of a point in a spherical coordinate system.</i></center></figcaption></figure></div>
The relation of the coordinates in the Cartesian and spherical coordinate systems is:
<span class="notranslate">
$$\begin{array}{l l}
x = r\sin\theta\cos\phi \\
y = r\sin\theta\sin\phi \\
z = r\cos\theta \\
r = \sqrt{x^2 + y^2 + z^2}
\end{array} $$
</span>
## Generalized coordinates
In mechanics, generalized coordinates are a set of coordinates that describes the configuration of a system. Generalized coordinates are usually selected for convenience (e.g., simplifies the resolution of the problem) or to provide the minimum number of coordinates to describe the configuration of a system.
For instance, generalized coordinates are used to describe the motion of a system with multiple links where instead of using Cartesian coordinates, it's more convenient to use the angles between links as coordinates.
## Further reading
- Read pages 70-92 of the 1st chapter of the [Ruina and Rudra's book](http://ruina.tam.cornell.edu/Book/index.html) for a review of Gram-Schmidt and cross products.
## Video lectures on the Internet
- Khan Academy: [Finding an orthonormal basis using the Gram-Schmidt Process](https://www.khanacademy.org/math/linear-algebra/alternate-bases/orthonormal-basis/v/linear-algebra-the-gram-schmidt-process)
## Problems
1. Right now, how fast are you moving? In your answer, consider your motion in relation to Earth and in relation to Sun.
2. Go to the website [http://www.wisc-online.com/Objects/ViewObject.aspx?ID=AP15305](http://www.wisc-online.com/Objects/ViewObject.aspx?ID=AP15305) and complete the interactive lesson to learn about the anatomical terminology to describe relative position in the human body.
3. To learn more about Cartesian coordinate systems go to the website [http://www.mathsisfun.com/data/cartesian-coordinates.html](http://www.mathsisfun.com/data/cartesian-coordinates.html), study the material, and answer the 10 questions at the end.
4. Given the points in the 3D space,<span class="notranslate"> $m1 = [2,2,0], m2 = [0,1,1], m3 = [1,2,0]$</span>, find an orthonormal basis.
5. Determine if the following points form a basis in the 3D space,<span class="notranslate"> $m1 = [2,2,0], m2 = [1,1,1], m3 = [1,1,0]$</span>.
6. Derive expressions for the three axes of the pelvic basis considering the convention of the [Virtual Animation of the Kinematics of the Human for Industrial, Educational and Research Purposes (VAKHUM)](https://raw.githubusercontent.com/demotu/BMC/master/refs/VAKHUM.pdf) project (use RASIS, LASIS, RPSIS, and LPSIS as names for the pelvic anatomical landmarks and indicate the expression for each axis).
7. Determine the basis for the pelvis following the convention of the [Virtual Animation of the Kinematics of the Human for Industrial, Educational and Research Purposes (VAKHUM)](https://raw.githubusercontent.com/demotu/BMC/master/refs/VAKHUM.pdf) project for the following anatomical landmark positions (units in meters):<span class="notranslate"> $RASIS=[0.5,0.8,0.4], LASIS=[0.55,0.78,0.1], RPSIS=[0.3,0.85,0.2], LPSIS=[0.29,0.78,0.3]$</span>.
## References
- Corke P (2017) [Robotics, Vision and Control: Fundamental Algorithms in MATLAB](http://www.petercorke.com/RVC/). 2nd ed. Springer-Verlag Berlin.
- [Standards - International Society of Biomechanics](https://isbweb.org/activities/standards).
- Stanford Encyclopedia of Philosophy. [Space and Time: Inertial Frames](http://plato.stanford.edu/entries/spacetime-iframes/).
- [Virtual Animation of the Kinematics of the Human for Industrial, Educational and Research Purposes (VAKHUM)](https://raw.githubusercontent.com/demotu/BMC/master/refs/VAKHUM.pdf).
| github_jupyter |
# Volume Sampling vs projection DPP for low rank approximation
## Introduction
#### In this notebook we compare the volume sampling and projection DPP for low rank approximation.
We recall the result proved in the article [DRVW]:\\
Let S be a random subset of k columns of X chosen with probability: $$P(S) = \frac{1}{Z_{k}} det(X_{.,S}^{T}X_{.,S})$$ with $$Z_{k} = \sum\limits_{S \subset [N], |S| = k} det(X_{.,S}^{T}X_{.,S})$$
Then
$$\begin{equation}
E(\| X - \pi_{X_{.,S}}(X) \|_{Fr}^{2}) \leq (k+1)\| X - \pi_{k}(X) \|_{Fr}^{2}
\end{equation}$$
We can prove that the volume sampling distribution is a mixture of projection DPPs distributions..., in particular one projection DPP distribution stands out for the problem of low rank approximation: ....\\
For the moment, there is no analytical expression for $$\begin{equation}
E(\| X - \pi_{X_{.,S}}(X) \|_{Fr}^{2})
\end{equation}$$ under the distribution of projection DPP.\\
However, we can calculate this quantity using simulation on some matrices representing cloud points with some specific geometric constraints.
Let $$X \in R^{n \times m}$$ a matrix representing a cloud of points.
We can write the SVD of $$X = UDV^{T}$$
In this notebook we investigate the influence of some structures enforced to V and D on the expected error expressed above for different algorithms: Volume Sampling, Projection DPP and the deterministic algorithm.
As for the Volume Sampling distribution, we can express the expected approximation error using only the elements of D. We can test this theoretical property in the next Numerical Study below. However, there is no closed formula (for the moment) for the expected approximation error under Projection DPP distribution. We will see in the Numerical Study section, that this value cannot depends only on the elements of D.
#### References
[DRVW] Deshpande, Amit and Rademacher, Luis and Vempala, Santosh and Wang, Grant - Matrix Approximation and Projective Clustering via Volume Sampling 2006
[BoDr] Boutsidis, Christos and Drineas, Petros - Deterministic and randomized column selection algorithms for matrices 2014
[] INDERJIT S. DHILLON , ROBERT W. HEATH JR., MA ́TYA ́S A. SUSTIK, AND
JOEL A. TROPP - GENERALIZED FINITE ALGORITHMS FOR CONSTRUCTING HERMITIAN MATRICES
WITH PRESCRIBED DIAGONAL AND SPECTRUM 2005
## I- Generating a cloud of points with geometric constraints
In this simulation we will enforce some structure on the matrix V for two values of the matrix D. While the matrix U will be choosen randomly.
We want to investigate the influence of the profile of the norms of the V_k rows: the k-leverage scores. For this purpose we use an algorithm proposed in the article []: this algorithm outputs a ( dxk) matrix Q with orthonormal columns and a prescribed profile of the norms of the rows. If we consider the Gram matrix H= QQ^{T}, this boils down to enforce the diagonal of H while keeping its spectrum containing k ones and d-k zeros.
The algorithm proceed as following:
* Initialization of the matrix Q by the rectangular identity
* Apply a Givens Rotation (of dimension d) to the matrix Q: this step will enforce the norm of a row every iteration
* Outputs the resulting matrix when all the rows norms are enforced.
```
import numpy as np
import pandas as pd
from itertools import combinations
from scipy.stats import binom
import scipy.special
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from IPython.display import display, HTML
from FrameBuilder.eigenstepsbuilder import *
from decimal import *
u = np.random.uniform(0,1)
u
```
### I-1- Givens Rotations generators
These functions generate a Givens rotation
```
def t_func(q_i,q_j,q_ij,l_i,l_j):
# t in section 3.1 Dhillon (2005)
delta = np.power(q_ij,2)-(q_i-l_i)*(q_j-l_i)
if delta<0:
print(delta)
print("error sqrt")
t = q_ij - np.sqrt(delta)
t = t/(q_j-l_i)
return t
def G_func(i,j,q_i,q_j,q_ij,l_i,l_j,N):
# Gitens Rotation
G=np.eye(N)
t = t_func(q_i,q_j,q_ij,l_i,l_j)
c = 1/(np.sqrt(np.power(t,2)+1))
s = t*c
G[i,i]=c
G[i,j]=s
G[j,i]= -s
G[j,j]= c
return G
```
The following function is an implementation of the algorithm [] figuring in the article [] to generate an orthogonal matrix with a prescribed profile of leverage scores.
In fact this is a simplification of the algorithm .....
```
class Data_Set_Generator:
def __init__(self, N, d, nu, Sigma):
self.N = N
self.d = d
self.nu = nu
self.Sigma = Sigma
self.mean = np.zeros(d)
def multivariate_t_rvs(self):
x = np.random.chisquare(self.nu, self.N)/self.nu
z = np.random.multivariate_normal(self.mean,self.Sigma,(self.N,))
return self.mean + z/np.sqrt(x)[:,None]
def generate_orthonormal_matrix_with_leverage_scores_ES(N,d,lv_scores_vector,versions_number,nn_cardinal_list):
lambda_vector = np.zeros((N))
lambda_vector[0:d] = np.ones((d))
#mu_vector = np.linspace(1, 0.1, num=N)
#sum_mu_vector = np.sum(mu_vector)
#mu_vector = d/sum_mu_vector*mu_vector
Q = np.zeros((N,d))
previous_Q = np.zeros((versions_number+1,N,d))
#mu_vector = d/N*np.ones((N,1))
E = np.zeros((N,N)) #(d,N)
counter = 0
for j in nn_cardinal_list:
print("counter")
print(counter)
mu_vector = generate_leverage_scores_vector_with_dirichlet(N,d,j)
print(np.sum(mu_vector))
print(mu_vector)
E_test = get_eigensteps_random(mu_vector,lambda_vector,N,d)
E_ = np.zeros((d,N+1))
for i in range(d):
E_[i,1:N+1] = E_test[i,:]
print(E_test)
#F_test = get_F(d,N,np.asmatrix(E_),mu_vector)
#previous_Q[counter,:,:] = np.transpose(F_test)
#Q = np.transpose(F_test)
counter = counter +1
return Q,previous_Q
Q,previous_Q = generate_orthonormal_matrix_with_leverage_scores_ES(20,2,[],3,[18,15,10])
def generate_leverage_scores_vector_with_dirichlet(d,k,nn_cardinal):
getcontext().prec = 3
mu_vector = np.float16(np.zeros((d,)))
mu_vector_2 = np.float16(np.zeros((d,)))
not_bounded = 1
while(not_bounded == 1):
mu_vector[0:nn_cardinal] = (k*np.random.dirichlet([1]*nn_cardinal, 1))[0]
mu_vector = np.flip(np.sort(mu_vector),axis = 0)
if max(mu_vector)<=1:
not_bounded = 0
for i in range(nn_cardinal):
mu_vector_2[i] = round(mu_vector[i],4)
mu_vector_2 = k*mu_vector_2/np.sum(mu_vector_2)
return list(mu_vector_2)
l = generate_leverage_scores_vector_with_dirichlet(10,2,6)
print(l)
print(np.sum(l))
def generate_orthonormal_matrix_with_leverage_scores(N,d,lv_scores_vector,versions_number,mode):
#Transforming an idendity matrix to an orthogonal matrix with prescribed lengths
Q = np.zeros((N,d))
previous_Q = np.zeros((versions_number+1,N,d))
versionning_period = (int)(N/versions_number)
if mode == 'identity':
for _ in range(0,d):
Q[_,_] = 1
if mode == 'spread':
nu = 1
Sigma = np.diag(np.ones(d))
mean = np.zeros(d)
x = np.random.chisquare(nu, N)/nu
z = np.random.multivariate_normal(mean,Sigma,(N,))
dataset = mean + z/np.sqrt(x)[:,None]
[Q,_,_] = np.linalg.svd(dataset,full_matrices=False)
print(np.shape(Q))
I_sorting = list(reversed(np.argsort(lv_scores_vector)))
lv_scores_vector = np.asarray(list(reversed(np.sort(lv_scores_vector))))
initial_lv_scores_vector = np.diag(np.dot(Q,Q.T))
I_initial_sorting = list(reversed(np.argsort(initial_lv_scores_vector)))
initial_lv_scores_vector = np.asarray(list(reversed(np.sort(np.diag(np.dot(Q,Q.T))))))
#initial_lv_scores_vector =
Q[I_initial_sorting,:] = Q
print(lv_scores_vector)
print(initial_lv_scores_vector)
delta_lv_scores_vector = lv_scores_vector - initial_lv_scores_vector
print(delta_lv_scores_vector)
min_index = next((i for i, x in enumerate(delta_lv_scores_vector) if x>0), None)
i = min_index-1
j = min_index
print(i)
print(j)
#if mode == 'identity':
# i = d-1
# j = d
#if mode == 'spread':
# i = d-2
# j = d-1
v_counter =0
for t in range(N-1):
#print(i)
#print(j)
delta_i = np.abs(lv_scores_vector[i] - np.power(np.linalg.norm(Q[i,:]),2))
delta_j = np.abs(lv_scores_vector[j] - np.power(np.linalg.norm(Q[j,:]),2))
q_i = np.power(np.linalg.norm(Q[i,:]),2)
q_j = np.power(np.linalg.norm(Q[j,:]),2)
q_ij = np.dot(Q[i,:],Q[j,:].T)
l_i = lv_scores_vector[i]
l_j = lv_scores_vector[j]
G = np.eye(N)
if t%versionning_period ==0:
previous_Q[v_counter,:,:] = Q
v_counter = v_counter +1
if delta_i <= delta_j:
l_k = q_i + q_j -l_i
G = G_func(i,j,q_i,q_j,q_ij,l_i,l_k,N)
Q = np.dot(G,Q)
i = i-1
else:
l_k = q_i + q_j -l_j
G = G_func(i,j,q_j,q_i,q_ij,l_j,l_k,N)
Q = np.dot(G,Q)
j = j+1
previous_Q[versions_number,:,:] = Q
return Q,previous_Q
```
The following function allows to estimate the leverage scores for an orthogonal matrix Q: the function calculates the diagonoal of the matrix $$Q Q^{T}$$
```
def estimate_leverage_scores_from_orthogonal_matrix(Q):
[N,_] = np.shape(Q)
lv_scores_vector = np.zeros((N,1))
lv_scores_vector = np.diag(np.dot(Q,np.transpose(Q)))
lv_scores_vector = np.asarray(list(reversed(np.sort(lv_scores_vector))))
return lv_scores_vector
def estimate_sum_first_k_leverage_scores(Q,k):
lv_scores_vector = estimate_leverage_scores_from_orthogonal_matrix(Q)
res = np.sum(lv_scores_vector[0:k])
return res
```
## I-2- Extending the orthogonal matrices
For the task of low rank approximation, we have seen that only the information contained in the first right k eigenvectors of the matrix X are relevant. In the previous step we build only the first right k eigenvectors but we still need to complete these orthogonal matrices with d-k columns. We proceed as following:
Generate a random vector (Nx1) using independent standard gaussian variables,
Project this vector in the orthogonal of the span of Q
Normalize the obtained vector after the projection
Extend the matrix Q
Note that this procedure is not the unique way to extend the matrix Q to an orthogonal (Nxd) matrix.
```
def extend_orthogonal_matrix(Q,d_target):
[N,d] = np.shape(Q)
Q_target = np.zeros((N,d))
Q_target = Q
delta = d_target - d
for t in range(delta):
Q_test = np.random.normal(0, 1, N)
for _ in range(d):
Q_test = Q_test - np.dot(Q_test,Q[:,_])*Q[:,_]
Q_test = Q_test/np.linalg.norm(Q_test)
Q_test = Q_test.reshape(N,1)
Q_target = np.append(Q_target,Q_test,1)
return Q_target
#extended_Q = extend_orthogonal_matrix(Q,r)
```
## I-3 - Constructing a dataset for every extended orthogonal matrix
The previous step allow us to build (N x d) orthogonal matrices such that the extracted (N x k) matrix have a prescribed profile of leverage scores.
Now we construct a cloud of point by assigning a covariance matrix D and a matrix V
```
def contruct_dataset_from_orthogonal_matrix(multi_Q,N,target_d,cov,mean,versions_number):
multi_X = np.zeros((versions_number+1,N,real_dim))
for t in range(versions_number+1):
test_X = np.random.multivariate_normal(mean, cov, N)
[U,_,_] = np.linalg.svd(test_X, full_matrices=False)
Q_test = extend_orthogonal_matrix(multi_Q[t,:,:],target_d)
multi_X[t,:,:] = np.dot(np.dot(Q_test,cov),U.T).T
return multi_X
```
## II- Volume sampling vs Projection DPP for low rank approximation
These functions allow to quantify the approximation error:
* approximation_error_function_fro calculate the ratio of the approximation error of a subset of columns to the optimal approximatione error given by the first k left eigenvectors of the matrix X
* expected_approximation_error_for_sampling_scheme calculate the expected value of the ratio of the approximatione error under some sampling distribution
```
def approximation_error_function_fro(Sigma,k,X,X_S):
## Sigma is the spectrum of the matrix X: we need to calculate the optimal approximation error given by the PCA
## k is the rank of the approximation
## X is the initial matrix
## X_S is the subset of columns of the matrix X for witch we calculate the approximation error ratio
d = list(Sigma.shape)[0] # the dimension of the matrix X
Sigma = np.multiply(Sigma,Sigma) # Sigma power 2 -> we are intersted in the approximation error square
sigma_S_temp = np.linalg.inv(np.dot(X_S.T,X_S)) # just a temporary matrix to construct the projection matrix
projection_S = np.dot(np.dot(X_S,sigma_S_temp),X_S.T) # the projection matrix P_S
res_X = X - np.dot(projection_S,X) # The projection of the matrix X in the orthogonal of S
approximation_error_ratio = np.power(np.linalg.norm(res_X,'fro'),2)/np.sum(Sigma[k:d])
# Calculate the apparoximation error ratio
return approximation_error_ratio
def approximation_error_function_spectral(Sigma,k,X,X_S):
## Sigma is the spectrum of the matrix X: we need to calculate the optimal approximation error given by the PCA
## k is the rank of the approximation
## X is the initial matrix
## X_S is the subset of columns of the matrix X for witch we calculate the approximation error ratio
d = list(Sigma.shape)[0] # the dimension of the matrix X
Sigma = np.multiply(Sigma,Sigma) # Sigma power 2 -> we are intersted in the approximation error square
sigma_S_temp = np.linalg.inv(np.dot(X_S.T,X_S)) # just a temporary matrix to construct the projection matrix
projection_S = np.dot(np.dot(X_S,sigma_S_temp),X_S.T) # the projection matrix P_S
res_X = X - np.dot(projection_S,X) # The projection of the matrix X in the orthogonal of S
approximation_error_ratio = np.power(np.linalg.norm(res_X,ord = 2),2)/np.sum(Sigma[k:k+1])
# Calculate the apparoximation error ratio
return approximation_error_ratio
def upper_bound_error_function_for_projection_DPP(k,X,X_S):
## Sigma is the spectrum of the matrix X: we need to calculate the optimal approximation error given by the PCA
## k is the rank of the approximation
## X is the initial matrix
## X_S is the subset of columns of the matrix X for witch we calculate the approximation error ratio
_,sigma_S_temp,_ = np.linalg.svd(X_S, full_matrices=False) # just a temporary matrix to construct the projection matrix
trunc_product = np.power(np.prod(sigma_S_temp[0:k-1]),2)
if np.power(np.prod(sigma_S_temp[0:k]),2) == 0:
trunc_product = 0
# Calculate the apparoximation error ratio
return trunc_product
def tight_upper_bound_error_function_fro(k,X,X_S,V_k,V_k_S):
## Sigma is the spectrum of the matrix X: we need to calculate the optimal approximation error given by the PCA
## k is the rank of the approximation
## X is the initial matrix
## X_S is the subset of columns of the matrix X for witch we calculate the approximation error ratio
_,Sigma,_ = np.linalg.svd(X, full_matrices=False)
d = list(Sigma.shape)[0]
Sigma = np.multiply(Sigma,Sigma)
if np.linalg.matrix_rank(V_k_S,0.000001) == k:
temp_T = np.dot(np.linalg.inv(V_k_S),V_k)
temp_matrix = X - np.dot(X_S,temp_T)
return np.power(np.linalg.norm(temp_matrix,'fro'),2)/np.sum(Sigma[k:d])
else:
return 0
def get_the_matrix_sum_T_S(k,d,V_k,V_d_k):
## Sigma is the spectrum of the matrix X: we need to calculate the optimal approximation error given by the PCA
## k is the rank of the approximation
## X is the initial matrix
## X_S is the subset of columns of the matrix X for witch we calculate the approximation error ratio
#Sigma = np.multiply(Sigma,Sigma)
#matrices_array = [ np.dot(V_d_k[:,list(comb)],np.dot(np.dot(np.linalg.inv(V_k[:,list(comb)]),np.linalg.inv(V_k[:,list(comb)]))),np.transpose(V_d_k[:,list(comb)])) for comb in combinations(range(d),k) if np.linalg.matrix_rank(V_k[:,list(comb)],0.000001) == k]
T = np.zeros((d-k,d-k))
for comb in combinations(range(d),k):
if np.linalg.matrix_rank(V_k[:,list(comb)],0.0000000001) == k:
V_k_S_inv = np.linalg.inv(V_k[:,list(comb)])
V_d_k_S = V_d_k[:,list(comb)]
V_k_S_inv_2 = np.transpose(np.dot(V_k_S_inv,np.transpose(V_k_S_inv)))
#T = np.dot(np.dot(np.dot(V_d_k_S,np.dot(V_k_S_inv,np.transpose(V_k_S_inv)))),np.transpose(V_d_k_S)) + T
T = np.power(np.linalg.det(V_k[:,list(comb)]),2)*np.dot(V_d_k_S,np.dot(V_k_S_inv_2,np.transpose(V_d_k_S))) +T
return T
def tight_approximation_error_fro_for_sampling_scheme(X,U,k,N):
## X is the matrix X :)
## U is the matrix used in the sampling: we sample propotional to the volume of UU^{T}_{S,S}:
## we are not sampling but we need the weigth to estimate the expected error
## k is the rank of the approximation
## N is the number of columns (to be changed to avoid confusion with the number of points)
_,Sigma,V = np.linalg.svd(X, full_matrices=False)
V_k = V[0:k,:]
## Estimating the spectrum of X -> needed in approximation_error_function_fro
volumes_array = [np.abs(np.linalg.det(np.dot(U[:,list(comb)].T,U[:,list(comb)]))) for comb in combinations(range(N),k)]
## Construct the array of weights: the volumes of UU^{T}_{S,S}
volumes_array_sum = np.sum(volumes_array)
## The normalization constant
volumes_array = volumes_array/volumes_array_sum
## The weigths normalized
approximation_error_array = [tight_upper_bound_error_function_fro(k,X,X[:,list(comb)],V_k,V_k[:,list(comb)]) for comb in combinations(range(N),k)]
## Calculating the approximation error for every k-tuple
expected_value = np.dot(approximation_error_array,volumes_array)
## The expected value of the approximatione error is just the dot product of the two arrays above
return expected_value
def expected_approximation_error_fro_for_sampling_scheme(X,U,k,N):
## X is the matrix X :)
## U is the matrix used in the sampling: we sample propotional to the volume of UU^{T}_{S,S}:
## we are not sampling but we need the weigth to estimate the expected error
## k is the rank of the approximation
## N is the number of columns (to be changed to avoid confusion with the number of points)
_,Sigma,_ = np.linalg.svd(X, full_matrices=False)
## Estimating the spectrum of X -> needed in approximation_error_function_fro
volumes_array = [np.abs(np.linalg.det(np.dot(U[:,list(comb)].T,U[:,list(comb)]))) for comb in combinations(range(N),k)]
## Construct the array of weights: the volumes of UU^{T}_{S,S}
volumes_array_sum = np.sum(volumes_array)
## The normalization constant
volumes_array = volumes_array/volumes_array_sum
## The weigths normalized
approximation_error_array = [approximation_error_function_fro(Sigma,k,X,X[:,list(comb)]) for comb in combinations(range(N),k)]
## Calculating the approximation error for every k-tuple
expected_value = np.dot(approximation_error_array,volumes_array)
## The expected value of the approximatione error is just the dot product of the two arrays above
return expected_value
def expected_approximation_error_spectral_for_sampling_scheme(X,U,k,N):
## X is the matrix X :)
## U is the matrix used in the sampling: we sample propotional to the volume of UU^{T}_{S,S}:
## we are not sampling but we need the weigth to estimate the expected error
## k is the rank of the approximation
## N is the number of columns (to be changed to avoid confusion with the number of points)
_,Sigma,_ = np.linalg.svd(X, full_matrices=False)
## Estimating the spectrum of X -> needed in approximation_error_function_fro
volumes_array = [np.abs(np.linalg.det(np.dot(U[:,list(comb)].T,U[:,list(comb)]))) for comb in combinations(range(N),k)]
## Construct the array of weights: the volumes of UU^{T}_{S,S}
volumes_array_sum = np.sum(volumes_array)
## The normalization constant
volumes_array = volumes_array/volumes_array_sum
## The weigths normalized
approximation_error_array = [approximation_error_function_spectral(Sigma,k,X,X[:,list(comb)]) for comb in combinations(range(N),k)]
## Calculating the approximation error for every k-tuple
expected_value = np.dot(approximation_error_array,volumes_array)
## The expected value of the approximatione error is just the dot product of the two arrays above
return expected_value
def expected_upper_bound_for_projection_DPP(X,U,k,N):
## X is the matrix X :)
## U is the matrix used in the sampling: we sample propotional to the volume of UU^{T}_{S,S}:
## we are not sampling but we need the weigth to estimate the expected error
## k is the rank of the approximation
## N is the number of columns (to be changed to avoid confusion with the number of points)
approximation_error_array = [upper_bound_error_function_for_projection_DPP(k,X,U[:,list(comb)]) for comb in combinations(range(N),k)]
## Calculating the approximation error for every k-tuple
## The expected value of the approximatione error is just the dot product of the two arrays above
#return expected_value
return np.sum(approximation_error_array)
```
## III - Numerical analysis
In this section we use the functions developed previously to investigate the influence of two parameters: the spectrum of X and the k-leverage scores.
For this purpose, we assemble these functionalities in a class allowing fast numerical experiments.
```
class Numrerical_Analysis_DPP:
def __init__(self,N,real_dim,r,k,versions_number,mean,cov,lv_scores,versions_list):
self.N = N
self.real_dim = real_dim
self.r = r
self.k = k
self.versions_number = versions_number
self.mean = mean
self.cov = cov
self.lv_scores = lv_scores
self.Q = np.zeros((real_dim,k))
self.multi_Q = np.zeros((self.versions_number+1,real_dim,k))
self.X = np.zeros((N,real_dim))
self.multi_X = np.zeros((self.versions_number+1,N,real_dim))
#[self.Q,self.multi_Q] = generate_orthonormal_matrix_with_leverage_scores(real_dim,k,lv_scores,versions_number,'identity')
[self.Q,self.multi_Q] = generate_orthonormal_matrix_with_leverage_scores_ES(self.real_dim,self.k,[],self.versions_number+1,versions_list)
self.multi_X = contruct_dataset_from_orthogonal_matrix(self.multi_Q,self.N,self.real_dim,self.cov,self.mean,self.versions_number)
def contruct_dataset_from_orthogonal_matrix_4(self,multi_Q,N,target_d,cov,mean,versions_number):
test_multi_X = np.zeros((self.versions_number+1,N,real_dim))
for t in range(self.versions_number+1):
test_X = np.random.multivariate_normal(mean, cov, N)
[U,_,_] = np.linalg.svd(test_X, full_matrices=False)
Q_test = extend_orthogonal_matrix(self.multi_Q[t,:,:],target_d)
test_multi_X[t,:,:] = np.dot(np.dot(Q_test,cov),U.T).T
return test_multi_X
def get_effective_kernel_from_orthogonal_matrix(self):
test_eff_V = np.zeros((self.versions_number+1,self.real_dim,self.k))
p_eff_list = self.get_p_eff()
for t in range(self.versions_number+1):
test_V = self.multi_Q[t,:,:]
p_eff = p_eff_list[t]
diag_Q_t = np.diag(np.dot(test_V,test_V.T))
#diag_Q_t = list(diag_Q_t[::-1].sort())
print(diag_Q_t)
permutation_t = list(reversed(np.argsort(diag_Q_t)))
print(permutation_t)
for i in range(self.real_dim):
if i >p_eff-1:
test_V[permutation_t[i],:] = 0
#Q_test = extend_orthogonal_matrix(self.multi_Q[t,:,:],target_d)
test_eff_V[t,:,:] = test_V
return test_eff_V
def get_expected_error_fro_for_volume_sampling(self):
## Calculate the expected error ratio for the Volume Sampling distribution for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
res_list[t] = expected_approximation_error_fro_for_sampling_scheme(test_X,test_X,self.k,self.real_dim)
return res_list
def get_expected_error_fro_for_effective_kernel_sampling(self):
## Calculate the expected error ratio for the Volume Sampling distribution for every dataset
res_list = np.zeros(self.versions_number+1)
test_eff_V = self.get_effective_kernel_from_orthogonal_matrix()
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
test_U = test_eff_V[t,:,:].T
res_list[t] = expected_approximation_error_fro_for_sampling_scheme(test_X,test_U,self.k,self.real_dim)
return res_list
def get_tight_upper_bound_error_fro_for_projection_DPP(self):
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
test_U = self.multi_Q[t,:,:].T
res_list[t] = tight_approximation_error_fro_for_sampling_scheme(test_X,test_U,self.k,self.real_dim)
return res_list
def get_max_diag_sum_T_matrices(self):
res_list = np.zeros((self.versions_number+1))
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
_,_,test_V = np.linalg.svd(test_X, full_matrices=False)
test_V_k = test_V[0:self.k,:]
test_V_d_k = test_V[self.k:self.real_dim,:]
res_list[t] = 1+np.max(np.diag(get_the_matrix_sum_T_S(self.k,self.real_dim,test_V_k,test_V_d_k)))
return res_list
def get_max_spectrum_sum_T_matrices(self):
res_list = np.zeros((self.versions_number+1))
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
_,_,test_V = np.linalg.svd(test_X, full_matrices=False)
test_V_k = test_V[0:self.k,:]
test_V_d_k = test_V[self.k:self.real_dim,:]
res_list[t] = 1+np.max(np.diag(get_the_matrix_sum_T_S(self.k,self.real_dim,test_V_k,test_V_d_k)))
return res_list
def get_expected_error_fro_for_projection_DPP(self):
## Calculate the expected error ratio for the Projection DPP distribution for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
test_U = self.multi_Q[t,:,:].T
res_list[t] = expected_approximation_error_fro_for_sampling_scheme(test_X,test_U,self.k,self.real_dim)
return res_list
def get_expected_error_spectral_for_volume_sampling(self):
## Calculate the expected error ratio for the Volume Sampling distribution for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
res_list[t] = expected_approximation_error_spectral_for_sampling_scheme(test_X,test_X,self.k,self.real_dim)
return res_list
def get_expected_error_spectral_for_projection_DPP(self):
## Calculate the expected error ratio for the Projection DPP distribution for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
test_U = self.multi_Q[t,:,:].T
res_list[t] = expected_approximation_error_spectral_for_sampling_scheme(test_X,test_U,self.k,self.real_dim)
return res_list
def get_upper_bound_error_for_projection_DPP(self):
## Calculate the expected error ratio for the Projection DPP distribution for every dataset
#res_list = np.zeros(self.versions_number+1)
res_list = []
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
test_U = self.multi_Q[t,:,:].T
#res_list[t] = expected_upper_bound_for_projection_DPP(test_X,test_U,self.k,self.real_dim)
res_list.append( expected_upper_bound_for_projection_DPP(test_X,test_U,self.k,self.real_dim))
return res_list
def get_error_fro_for_deterministic_selection(self):
## Calculate the error ratio for the k-tuple selected by the deterministic algorithm for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
test_U = self.multi_Q[t,:,:].T
lv_scores_vector = np.diag(np.dot(np.transpose(test_U),test_U))
test_I_k = list(np.argsort(lv_scores_vector)[self.real_dim-self.k:self.real_dim])
_,test_Sigma,_ = np.linalg.svd(test_X, full_matrices=False)
res_list[t] = approximation_error_function_fro(test_Sigma,self.k,test_X,test_X[:,test_I_k])
#res_list.append(test_I_k)
return res_list
def get_error_spectral_for_deterministic_selection(self):
## Calculate the error ratio for the k-tuple selected by the deterministic algorithm for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
test_X = self.multi_X[t,:,:]
test_U = self.multi_Q[t,:,:].T
lv_scores_vector = np.diag(np.dot(np.transpose(test_U),test_U))
test_I_k = list(np.argsort(lv_scores_vector)[self.real_dim-self.k:self.real_dim])
_,test_Sigma,_ = np.linalg.svd(test_X, full_matrices=False)
res_list[t] = approximation_error_function_spectral(test_Sigma,self.k,test_X,test_X[:,test_I_k])
#res_list.append(test_I_k)
return res_list
def get_p_eff(self):
## A function that calculate the p_eff.
## It is a measure of the concentration of V_k. This is done for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
diag_Q_t = np.diag(np.dot(self.multi_Q[t,:,:],self.multi_Q[t,:,:].T))
#diag_Q_t = list(diag_Q_t[::-1].sort())
diag_Q_t = list(np.sort(diag_Q_t)[::-1])
p = self.real_dim
print(diag_Q_t)
while np.sum(diag_Q_t[0:p-1]) > float(self.k-1.0/2):
p = p-1
res_list[t] = p
return res_list
def get_sum_k_leverage_scores(self):
## A function that calculate the k-sum: the sum of the first k k-leverage scores. It is a measure of the concentration of V_k
## This is done for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
res_list[t] = estimate_sum_first_k_leverage_scores(self.multi_Q[t,:,:],self.k)
return res_list
def get_deterministic_upper_bound(self):
## A function that calculate the theoretical upper bound for the deterministic algorithm for every dataset
res_list = np.zeros(self.versions_number+1)
for t in range(self.versions_number+1):
res_list[t] = 1/(1+estimate_sum_first_k_leverage_scores(self.multi_Q[t,:,:],self.k)-self.k)
return res_list
def get_alpha_sum_k_leverage_scores(self,alpha):
## A function that calculate the theoretical upper bound for the deterministic algorithm for every dataset
res_list = np.zeros(self.versions_number+1)
#k_l = self.get_sum_k_leverage_scores()
for t in range(self.versions_number+1):
k_l = estimate_leverage_scores_from_orthogonal_matrix(self.multi_Q[t,:,:])[0:k]
func_k = np.power(np.linspace(1, k, num=k),alpha)
res_list[t] = np.dot(func_k,k_l)
return res_list
```
### III- 0 Parameters of the simultations
```
## The dimensions of the design matrix X
N = 100 # The number of observations in the dataset
real_dim = 20 # The dimension of the dataset
## The low rank paramters
k = 2 # The rank of the low rank approximation
## The covariance matrix parameters
r = 6 # Just a parameter to control the number of non trivial singular values in the covariance matrix
mean = np.zeros((real_dim)) # The mean vector useful to generate U (X = UDV^T)
cov_test = 0.01*np.ones((real_dim-r)) # The "trivial" singular values in the covariance matrix (there are real_dim-r)
## The paramters of the matrix V
versions_number = 3 # The number of orthogonal matrices (and therefor datasets) (-1) generated by the algorithm above
lv_scores_vector = k/real_dim*np.ones(real_dim) # The vector of leverage scores (the last one)
l = [1,5,2,10]
ll = list(reversed(np.argsort(l)))
ll
```
### III-1 The influence of the spectrum
In this subsection we compare the Volume Sampling distribution to the projection DPP distribution and the deterministic algorithm of [] for different profiles of the spectrum with k-leverage scores profile fixed. In other words, if we note $$X = UDV^{T}$$ We keep V_{k} constant and we investigate the effect of D.
#### III-1-1 The case of a non-projection spectrum
We mean by a projection spectrum matrix, a matrix with equal the first k singular values.
We observe that the two distributions are very similar.... \todo{reword}
```
cov_1 = np.diag(np.concatenate(([100,100,1,1,1,1],cov_test)))
versions_list = [20,19,18,17]
NAL_1 = Numrerical_Analysis_DPP(N,real_dim,r,k,versions_number,mean,cov_1,lv_scores_vector,versions_list)
projection_DPP_res_fro_1 = NAL_1.get_expected_error_fro_for_projection_DPP()
volume_sampling_res_fro_1 = NAL_1.get_expected_error_fro_for_volume_sampling()
deterministic_selection_res_fro_1 = NAL_1.get_error_fro_for_deterministic_selection()
projection_DPP_res_spectral_1 = NAL_1.get_expected_error_spectral_for_projection_DPP()
volume_sampling_res_spectral_1 = NAL_1.get_expected_error_spectral_for_volume_sampling()
deterministic_selection_res_spectral_1 = NAL_1.get_error_spectral_for_deterministic_selection()
effective_kernel_sampling_res_fro_1 = NAL_1.get_expected_error_fro_for_effective_kernel_sampling()
#sss = NAL_1.get_effective_kernel_from_orthogonal_matrix()
#p_eff_res_1 = NAL_1.get_p_eff()
upper_tight_bound_projection_DPP_res_fro_1 = NAL_1.get_tight_upper_bound_error_fro_for_projection_DPP()
alpha_sum_res_1 = NAL_1.get_alpha_sum_k_leverage_scores(1)
sum_U_res_1 = NAL_1.get_sum_k_leverage_scores()
deterministic_upper_bound_res_1 = NAL_1.get_deterministic_upper_bound()
expected_upper_bound_res_1 = NAL_1.get_upper_bound_error_for_projection_DPP()
multi_Q_1 = NAL_1.multi_Q[1,:,:].T
p_eff_res_1 = NAL_1.get_p_eff()
eff_kernel_upper_bound_1 = 1+ (p_eff_res_1-k)/(real_dim-k)*(k+1)
eff_kernel_upper_bound
print(k*(real_dim-k+1))
sum_T_matrices = NAL_1.get_sum_T_matrices()
pd_1 = pd.DataFrame(
{'k-sum (ratio)': sum_U_res_1/k,
'p_eff':p_eff_res_1,
'alpha k-sum': alpha_sum_res_1,
'Expected Upper Bound for Projection DPP': expected_upper_bound_res_1,
'Volume Sampling(Fro)': volume_sampling_res_fro_1,
'Projection DPP(Fro)': projection_DPP_res_fro_1,
'Effective kernel(Fro)' : effective_kernel_sampling_res_fro_1,
'Effective kernel upper bound (Fro)':eff_kernel_upper_bound_1,
'Very sharp approximation of Projection DPP(Fro)': upper_tight_bound_projection_DPP_res_fro_1,
'Deterministic Algorithm(Fro)': deterministic_selection_res_fro_1,
'Volume Sampling(Spectral)': volume_sampling_res_spectral_1,
'Projection DPP(Spectral)': projection_DPP_res_spectral_1,
'Deterministic Algorithm(Spectral)': deterministic_selection_res_spectral_1,
'Deterministic Upper Bound': deterministic_upper_bound_res_1
})
pd_1 = pd_1[['k-sum (ratio)','p_eff', 'alpha k-sum','Expected Upper Bound for Projection DPP','Volume Sampling(Fro)','Projection DPP(Fro)','Effective kernel(Fro)','Effective kernel upper bound (Fro)','Very sharp approximation of Projection DPP(Fro)','Deterministic Algorithm(Fro)','Volume Sampling(Spectral)','Projection DPP(Spectral)','Deterministic Algorithm(Spectral)','Deterministic Upper Bound']]
p_eff_res_1[3]
#'1+Largest eigenvalue of sum_T': sum_T_matrices,
pd_1
```
#### Observations:
* The expected error is always smaller under the Projection DPP distribution compared to the Volume Sampling distribution.
* The expected error for the Volume Sampling distribution is constant for a contant D
* However the expected error for the Projection DPP distribution depends on the k-sum
* For X_0 and X_1, the profile of the k-leverage scores are highly concentrated (k-sum > k-1) thus epsilon is smaller than 1, in this regime the determinstic algorithm have the lower approximation error and it performs better than expected (the theoretical bound is 1/(1-epsilon).
* However, for the other datasets, the (k-sum < k-1) thus epsilon >1 and the deterministic algorithm have no guarantee in this regime: we observe that the approximation error for the deterministic algorithm can be very high in this regime.
#### Recall:
We recall here some geometrical properties of the matrices $$X_i$$
$$X_i = UD_{j}V_{i}$$
Where for every i, the first k columns of $$V_{i}$$ are the $$Q_{i}$$ while the other columns are gernerated randomly
```
previous_Q = NAL_1.multi_Q
lv_0 = estimate_leverage_scores_from_orthogonal_matrix(previous_Q[0,:,:])
lv_1 = estimate_leverage_scores_from_orthogonal_matrix(previous_Q[1,:,:])
lv_2 = estimate_leverage_scores_from_orthogonal_matrix(previous_Q[2,:,:])
lv_3 = estimate_leverage_scores_from_orthogonal_matrix(previous_Q[3,:,:])
lv_4 = estimate_leverage_scores_from_orthogonal_matrix(previous_Q[4,:,:])
lv_5 = estimate_leverage_scores_from_orthogonal_matrix(previous_Q[5,:,:])
index_list = list(range(real_dim))
```
In this example the objective is Q and the initialization is Q_0 (the rectangular identity)
We have with respect to the Schur-order (or the majorization):
$$Q = Q_5 \prec_{S} Q_4 \prec_{S} Q_3 \prec_{S} Q_2 \prec_{S} Q_1 \prec_{S} Q_0 $$
```
plt.plot(index_list[0:10], lv_0[0:10], 'c--',index_list[0:10], lv_1[0:10], 'k--', index_list[0:10], lv_2[0:10], 'r--', index_list[0:10], lv_3[0:10], 'b--',index_list[0:10], lv_4[0:10], 'g--',index_list[0:10], lv_5[0:10], 'y--')
plt.xlabel('index')
plt.ylabel('leverage score')
cyan_patch = mpatches.Patch(color='cyan', label='Q_0')
black_patch = mpatches.Patch(color='black', label='Q_1')
red_patch = mpatches.Patch(color='red', label='Q_2')
blue_patch = mpatches.Patch(color='blue', label='Q_3')
green_patch = mpatches.Patch(color='green', label='Q_4')
yellow_patch = mpatches.Patch(color='yellow', label='Q = Q_5')
plt.legend(handles=[cyan_patch,black_patch,red_patch,blue_patch,green_patch,yellow_patch])
plt.show()
```
#### III-1-2 The case of a projection spectrum
We mean by a projection spectrum matrix, a matrix with equal the first k singular values.
We observe that the two distributions are very similar.... \todo{reword}
```
cov_2 = np.diag(np.concatenate(([1000,1000,1000,1,0.1],cov_test)))
NAL_2 = Numrerical_Analysis_DPP(N,real_dim,r,k,versions_number,mean,cov_2,lv_scores_vector)
projection_DPP_res_2 = NAL_2.get_expected_error_for_projection_DPP()
volume_sampling_res_2 = NAL_2.get_expected_error_for_volume_sampling()
deterministic_selection_res_2 = NAL_1.get_error_for_deterministic_selection()
sum_U_res_2 = NAL_2.get_sum_k_leverage_scores()
deterministic_upper_bound_res_2 = NAL_2.get_deterministic_upper_bound()
results = [["Dataset","Using Volume Sampling","Using Projection DPP","k-sum","1/(1-epsilon)","Using Deterministic Algorithm"],["X_0",volume_sampling_res_2[0],projection_DPP_res_2[0],sum_U_res_2[0],deterministic_upper_bound_res_2[0],deterministic_selection_res_2[0]],["X_1",volume_sampling_res_2[1],projection_DPP_res_2[1],sum_U_res_2[1],deterministic_upper_bound_res_2[1],deterministic_selection_res_2[1]],
["X_2",volume_sampling_res_2[2],projection_DPP_res_2[2],sum_U_res_2[2],deterministic_upper_bound_res_2[2],deterministic_selection_res_2[2]],["X_3",volume_sampling_res_2[3],projection_DPP_res_2[3],sum_U_res_2[3],deterministic_upper_bound_res_2[3],deterministic_selection_res_2[3]],["X_4",volume_sampling_res_2[4],projection_DPP_res_2[4],sum_U_res_2[4],deterministic_upper_bound_res_2[4],deterministic_selection_res_2[4]],["X_5",volume_sampling_res_2[5],projection_DPP_res_2[5],sum_U_res_2[5],deterministic_upper_bound_res_2[5],deterministic_selection_res_2[5]]]
display(HTML(
'<center><b>The expected approximation error (divided by the optimal error) according to a sampling scheme for different distribution</b><br><table><tr>{}</tr></table>'.format(
'</tr><tr>'.join(
'<td>{}</td>'.format('</td><td>'.join(str(_) for _ in row)) for row in results)
)
))
```
### III-2 The influence of the "spread" of V
In this section we investigate the influence of the "spread" (to be defined formally) of the cloud of points. We can change this "spread" by changing the initialization of the generator of orthogonal matrices: we replace the rectangular identity by "other" orthogonal matrices.
Technically, this boils down to change the generator mode in the constructor call from "nonspread" to "spread".
```
np.power(np.linspace(1, k, num=k),2)
matrices_array = [ np.zeros((4,4)) for comb in combinations(range(5),4)]
matrix_sum = np.sum(matrices_array)
matrix_sum
matrices_array
```
| github_jupyter |
# Convolutional Neural Network Example
Build a convolutional neural network with TensorFlow.
- Author: Aymeric Damien
- Project: https://github.com/aymericdamien/TensorFlow-Examples/
These lessons are adapted from [aymericdamien TensorFlow tutorials](https://github.com/aymericdamien/TensorFlow-Examples)
/ [GitHub](https://github.com/aymericdamien/TensorFlow-Examples)
which are published under the [MIT License](https://github.com/Hvass-Labs/TensorFlow-Tutorials/blob/master/LICENSE) which allows very broad use for both academic and commercial purposes.
## CNN Overview
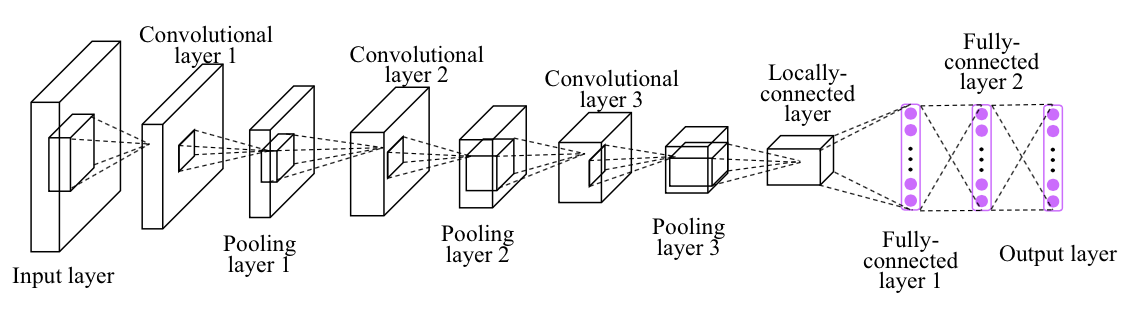
## MNIST Dataset Overview
This example is using MNIST handwritten digits. The dataset contains 60,000 examples for training and 10,000 examples for testing. The digits have been size-normalized and centered in a fixed-size image (28x28 pixels) with values from 0 to 1. For simplicity, each image has been flattened and converted to a 1-D numpy array of 784 features (28*28).

More info: http://yann.lecun.com/exdb/mnist/
```
from __future__ import division, print_function, absolute_import
import tensorflow as tf
# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
# Training Parameters
learning_rate = 0.001
num_steps = 500
batch_size = 128
display_step = 10
# Network Parameters
num_input = 784 # MNIST data input (img shape: 28*28)
num_classes = 10 # MNIST total classes (0-9 digits)
dropout = 0.75 # Dropout, probability to keep units
# tf Graph input
X = tf.placeholder(tf.float32, [None, num_input])
Y = tf.placeholder(tf.float32, [None, num_classes])
keep_prob = tf.placeholder(tf.float32) # dropout (keep probability)
# Create some wrappers for simplicity
def conv2d(x, W, b, strides=1):
# Conv2D wrapper, with bias and relu activation
x = tf.nn.conv2d(x, W, strides=[1, strides, strides, 1], padding='SAME')
x = tf.nn.bias_add(x, b)
return tf.nn.relu(x)
def maxpool2d(x, k=2):
# MaxPool2D wrapper
return tf.nn.max_pool(x, ksize=[1, k, k, 1], strides=[1, k, k, 1],
padding='SAME')
# Create model
def conv_net(x, weights, biases, dropout):
# MNIST data input is a 1-D vector of 784 features (28*28 pixels)
# Reshape to match picture format [Height x Width x Channel]
# Tensor input become 4-D: [Batch Size, Height, Width, Channel]
x = tf.reshape(x, shape=[-1, 28, 28, 1])
# Convolution Layer
conv1 = conv2d(x, weights['wc1'], biases['bc1'])
# Max Pooling (down-sampling)
conv1 = maxpool2d(conv1, k=2)
# Convolution Layer
conv2 = conv2d(conv1, weights['wc2'], biases['bc2'])
# Max Pooling (down-sampling)
conv2 = maxpool2d(conv2, k=2)
# Fully connected layer
# Reshape conv2 output to fit fully connected layer input
fc1 = tf.reshape(conv2, [-1, weights['wd1'].get_shape().as_list()[0]])
fc1 = tf.add(tf.matmul(fc1, weights['wd1']), biases['bd1'])
fc1 = tf.nn.relu(fc1)
# Apply Dropout
fc1 = tf.nn.dropout(fc1, dropout)
# Output, class prediction
out = tf.add(tf.matmul(fc1, weights['out']), biases['out'])
return out
# Store layers weight & bias
weights = {
# 5x5 conv, 1 input, 32 outputs
'wc1': tf.Variable(tf.random_normal([5, 5, 1, 32])),
# 5x5 conv, 32 inputs, 64 outputs
'wc2': tf.Variable(tf.random_normal([5, 5, 32, 64])),
# fully connected, 7*7*64 inputs, 1024 outputs
'wd1': tf.Variable(tf.random_normal([7*7*64, 1024])),
# 1024 inputs, 10 outputs (class prediction)
'out': tf.Variable(tf.random_normal([1024, num_classes]))
}
biases = {
'bc1': tf.Variable(tf.random_normal([32])),
'bc2': tf.Variable(tf.random_normal([64])),
'bd1': tf.Variable(tf.random_normal([1024])),
'out': tf.Variable(tf.random_normal([num_classes]))
}
# Construct model
logits = conv_net(X, weights, biases, keep_prob)
prediction = tf.nn.softmax(logits)
# Define loss and optimizer
loss_op = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
logits=logits, labels=Y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op)
# Evaluate model
correct_pred = tf.equal(tf.argmax(prediction, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()
# Start training
with tf.Session() as sess:
# Run the initializer
sess.run(init)
for step in range(1, num_steps+1):
batch_x, batch_y = mnist.train.next_batch(batch_size)
# Run optimization op (backprop)
sess.run(train_op, feed_dict={X: batch_x, Y: batch_y, keep_prob: dropout})
if step % display_step == 0 or step == 1:
# Calculate batch loss and accuracy
loss, acc = sess.run([loss_op, accuracy], feed_dict={X: batch_x,
Y: batch_y,
keep_prob: 1.0})
print("Step " + str(step) + ", Minibatch Loss= " + \
"{:.4f}".format(loss) + ", Training Accuracy= " + \
"{:.3f}".format(acc))
print("Optimization Finished!")
# Calculate accuracy for 256 MNIST test images
print("Testing Accuracy:", \
sess.run(accuracy, feed_dict={X: mnist.test.images[:256],
Y: mnist.test.labels[:256],
keep_prob: 1.0}))
```
| github_jupyter |
```
import os, os.path
import pickle
import time
import numpy
from scipy import interpolate
from galpy.util import bovy_conversion, bovy_plot, save_pickles
import gd1_util
from gd1_util import R0, V0
import seaborn as sns
from matplotlib import cm, pyplot
import simulate_streampepper
import statsmodels.api as sm
lowess = sm.nonparametric.lowess
%pylab inline
from matplotlib.ticker import NullFormatter, FuncFormatter
save_figures= False
```
# Figures for the section on approximately computing the stream structure
```
# Load the smooth and peppered stream
sdf_smooth= gd1_util.setup_gd1model()
pepperfilename= 'gd1pepper.pkl'
if os.path.exists(pepperfilename):
with open(pepperfilename,'rb') as savefile:
sdf_pepper= pickle.load(savefile)
else:
timpacts= simulate_streampepper.parse_times('256sampling',9.)
sdf_pepper= gd1_util.setup_gd1model(timpact=timpacts,
hernquist=True)
save_pickles(pepperfilename,sdf_pepper)
```
## Is the mean perpendicular frequency close to zero?
```
# Sampling functions
massrange=[5.,9.]
plummer= False
Xrs= 5.
nsubhalo= simulate_streampepper.nsubhalo
rs= simulate_streampepper.rs
dNencdm= simulate_streampepper.dNencdm
sample_GM= lambda: (10.**((-0.5)*massrange[0])\
+(10.**((-0.5)*massrange[1])\
-10.**((-0.5)*massrange[0]))\
*numpy.random.uniform())**(1./(-0.5))\
/bovy_conversion.mass_in_msol(V0,R0)
rate_range= numpy.arange(massrange[0]+0.5,massrange[1]+0.5,1)
rate= numpy.sum([dNencdm(sdf_pepper,10.**r,Xrs=Xrs,
plummer=plummer)
for r in rate_range])
sample_rs= lambda x: rs(x*bovy_conversion.mass_in_1010msol(V0,R0)*10.**10.,
plummer=plummer)
numpy.random.seed(2)
sdf_pepper.simulate(rate=rate,sample_GM=sample_GM,sample_rs=sample_rs,Xrs=Xrs)
n= 100000
aa_mock_per= sdf_pepper.sample(n=n,returnaAdt=True)
dO= numpy.dot(aa_mock_per[0].T-sdf_pepper._progenitor_Omega,
sdf_pepper._sigomatrixEig[1][:,sdf_pepper._sigomatrixEigsortIndx])
dO[:,2]*= sdf_pepper._sigMeanSign
da= numpy.dot(aa_mock_per[1].T-sdf_pepper._progenitor_angle,
sdf_pepper._sigomatrixEig[1][:,sdf_pepper._sigomatrixEigsortIndx])
da[:,2]*= sdf_pepper._sigMeanSign
apar= da[:,2]
xs= numpy.linspace(0.,1.5,1001)
mO_unp= numpy.array([sdf_smooth.meanOmega(x,oned=True,use_physical=False) for x in xs])
mOint= interpolate.InterpolatedUnivariateSpline(xs,mO_unp,k=3)
mOs= mOint(apar)
frac= 0.02
alpha=0.01
linecolor='0.65'
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=14.)
figsize(12,4)
subplot(1,3,1)
bovy_plot.bovy_plot(apar[::3],dO[::3,2]/mOs[::3]-1,'k.',alpha=alpha*2,gcf=True,
rasterized=True,xrange=[0.,1.5],yrange=[-1.2,1.2])
z= lowess(dO[:,2]/mOs-1,apar,frac=frac)
plot(z[::100,0],z[::100,1],color=linecolor,lw=2.5)
#xlim(0.,1.5)
#ylim(-1.2,1.2)
xlabel(r'$\Delta\theta_\parallel$')
bovy_plot.bovy_text(r'$\Delta\Omega_\parallel/\langle\Delta\Omega^0_\parallel\rangle-1$',top_left=True,
size=18.)
subplot(1,3,2)
bovy_plot.bovy_plot(apar[::3],dO[::3,1]/mOs[::3],'k.',alpha=alpha*2,gcf=True,
rasterized=True,xrange=[0.,1.5],yrange=[-0.05,0.05])
z= lowess(dO[:,1]/mOs,apar,frac=frac)
plot(z[::100,0],z[::100,1],color=linecolor,lw=2.5)
#xlim(0.,1.5)
#ylim(-0.05,0.05)
xlabel(r'$\Delta\theta_\parallel$')
bovy_plot.bovy_text(r'$\Delta\Omega_{\perp,1}/\langle\Delta\Omega^0_\parallel\rangle$',top_left=True,
size=18.)
subplot(1,3,3)
bovy_plot.bovy_plot(apar[::3],dO[::3,0]/mOs[::3],'k.',alpha=alpha,gcf=True,
rasterized=True,xrange=[0.,1.5],yrange=[-0.05,0.05])
z= lowess(dO[:,0]/mOs,apar,frac=frac)
plot(z[::100,0],z[::100,1],color=linecolor,lw=2.5)
#xlim(0.,1.5)
#ylim(-0.05,0.05)
xlabel(r'$\Delta\theta_\parallel$')
bovy_plot.bovy_text(r'$\Delta\Omega_{\perp,2}/\langle\Delta\Omega^0_\parallel\rangle$',top_left=True,
size=18.)
if save_figures:
tight_layout()
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats','gd1like_meanOparOperp.pdf'))
print "This stream had %i impacts" % len(sdf_pepper._GM)
```
## Test the single-impact approximations
```
# Setup a single, large impact
m= 10.**8.
GM= 10**8./bovy_conversion.mass_in_msol(V0,R0)
timpactIndx= numpy.argmin(numpy.fabs(numpy.array(sdf_pepper._uniq_timpact)-1.3/bovy_conversion.time_in_Gyr(V0,R0)))
# Load the single-impact stream
gapfilename= 'gd1single.pkl'
if os.path.exists(gapfilename):
with open(gapfilename,'rb') as savefile:
sdf_gap= pickle.load(savefile)
else:
sdf_gap= gd1_util.setup_gd1model(hernquist=True,
singleImpact=True,
impactb=0.5*rs(m),
subhalovel=numpy.array([-25.,155.,30.])/V0,
impact_angle=0.6,
timpact=sdf_pepper._uniq_timpact[timpactIndx],
GM=GM,rs=rs(m))
save_pickles(gapfilename,sdf_gap)
n= 100000
aa_mock_per= sdf_gap.sample(n=n,returnaAdt=True)
dO= numpy.dot(aa_mock_per[0].T-sdf_gap._progenitor_Omega,
sdf_gap._sigomatrixEig[1][:,sdf_gap._sigomatrixEigsortIndx])
dO[:,2]*= sdf_gap._sigMeanSign
da= numpy.dot(aa_mock_per[1].T-sdf_gap._progenitor_angle,
sdf_gap._sigomatrixEig[1][:,sdf_gap._sigomatrixEigsortIndx])
da[:,2]*= sdf_gap._sigMeanSign
num= True
apar= numpy.arange(0.,sdf_smooth.length()+0.003,0.003)
dens_unp= numpy.array([sdf_smooth._density_par(x) for x in apar])
dens_approx= numpy.array([sdf_gap.density_par(x,approx=True) for x in apar])
dens_approx_higherorder= numpy.array([sdf_gap._density_par(x,approx=True,higherorder=True) for x in apar])
# normalize
dens_unp= dens_unp/numpy.sum(dens_unp)/(apar[1]-apar[0])
dens_approx= dens_approx/numpy.sum(dens_approx)/(apar[1]-apar[0])
dens_approx_higherorder= dens_approx_higherorder/numpy.sum(dens_approx_higherorder)/(apar[1]-apar[0])
if num:
dens_num= numpy.array([sdf_gap.density_par(x,approx=False) for x in apar])
dens_num= dens_num/numpy.sum(dens_num)/(apar[1]-apar[0])
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=14.)
figsize(6,7)
axTop= pyplot.axes([0.15,0.3,0.825,0.65])
fig= pyplot.gcf()
fig.sca(axTop)
bovy_plot.bovy_plot(apar,dens_approx,lw=2.5,gcf=True,
color='k',
xrange=[0.,1.],
yrange=[0.,2.24],
ylabel=r'$\mathrm{density}$')
plot(apar,dens_unp,lw=3.5,color='k',ls='--',zorder=0)
nullfmt = NullFormatter() # no labels
axTop.xaxis.set_major_formatter(nullfmt)
dum= hist(da[:,2],bins=101,normed=True,range=[apar[0],apar[-1]],
histtype='step',color='0.55',zorder=0,lw=3.)
axBottom= pyplot.axes([0.15,0.1,0.825,0.2])
fig= pyplot.gcf()
fig.sca(axBottom)
bovy_plot.bovy_plot(apar,100.*(dens_approx_higherorder-dens_approx)/dens_approx_higherorder,
lw=2.5,gcf=True,color='k',
xrange=[0.,1.],
yrange=[-0.145,0.145],
zorder=2,
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\mathrm{relative\ difference\ in}\ \%$')
if num:
plot(apar,100.*(dens_num-dens_approx_higherorder)/dens_approx_higherorder,
lw=2.5,zorder=1,color='0.55')
# label
aparIndx= numpy.argmin(numpy.fabs(apar-0.64))
plot([0.45,apar[aparIndx]],[0.06,(100.*(dens_approx_higherorder-dens_approx)/dens_approx_higherorder)[aparIndx]],
'k',lw=1.)
bovy_plot.bovy_text(0.1,0.07,r'$\mathrm{higher\!\!-\!\!order\ minus\ linear}$',size=17.)
if num:
aparIndx= numpy.argmin(numpy.fabs(apar-0.62))
plot([0.45,apar[aparIndx]],[-0.07,(100.*(dens_num-dens_approx_higherorder)/dens_approx_higherorder)[aparIndx]],
'k',lw=1.)
bovy_plot.bovy_text(0.05,-0.12,r'$\mathrm{numerical\ minus\ higher\!\!-\!\!order}$',size=17.)
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats','gd1likeSingle_densapprox.pdf'))
mO_unp= numpy.array([sdf_smooth.meanOmega(x,oned=True) for x in apar])\
*bovy_conversion.freq_in_Gyr(V0,R0)
mO_approx= numpy.array([sdf_gap.meanOmega(x,approx=True,oned=True) for x in apar])\
*bovy_conversion.freq_in_Gyr(V0,R0)
mO_approx_higherorder= numpy.array([sdf_gap.meanOmega(x,oned=True,approx=True,higherorder=True) for x in apar])\
*bovy_conversion.freq_in_Gyr(V0,R0)
if num:
mO_num= numpy.array([sdf_gap.meanOmega(x,approx=False,oned=True) for x in apar])\
*bovy_conversion.freq_in_Gyr(V0,R0)
frac= 0.005
alpha=0.01
linecolor='0.65'
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=14.)
figsize(6,7)
axTop= pyplot.axes([0.15,0.3,0.825,0.65])
fig= pyplot.gcf()
fig.sca(axTop)
bovy_plot.bovy_plot(apar,mO_approx,lw=2.5,gcf=True,
color='k',
xrange=[0.,1.],
yrange=[0.,0.2],
ylabel=r'$\Delta \Omega_\parallel\,(\mathrm{Gyr}^{-1})$')
plot(apar,mO_unp,lw=2.5,color='k',ls='--')
plot(da[::3,2],dO[::3,2]*bovy_conversion.freq_in_Gyr(V0,R0),
'k.',alpha=alpha*2,rasterized=True)
nullfmt = NullFormatter() # no labels
axTop.xaxis.set_major_formatter(nullfmt)
axBottom= pyplot.axes([0.15,0.1,0.825,0.2])
fig= pyplot.gcf()
fig.sca(axBottom)
bovy_plot.bovy_plot(apar,100.*(mO_approx_higherorder-mO_approx)/mO_approx_higherorder,
lw=2.5,gcf=True,color='k',
xrange=[0.,1.],zorder=1,
yrange=[-0.039,0.039],
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\mathrm{relative\ difference\ in\ \%}$')
if num:
plot(apar,100.*(mO_num-mO_approx_higherorder)/mO_approx_higherorder,
lw=2.5,color='0.55',zorder=0)
# label
aparIndx= numpy.argmin(numpy.fabs(apar-0.64))
plot([0.45,apar[aparIndx]],[0.024,(100.*(mO_approx_higherorder-mO_approx)/mO_approx_higherorder)[aparIndx]],
'k',lw=1.)
bovy_plot.bovy_text(0.1,0.026,r'$\mathrm{higher\!\!-\!\!order\ minus\ linear}$',size=17.)
aparIndx= numpy.argmin(numpy.fabs(apar-0.6))
if num:
plot([0.45,apar[aparIndx]],[-0.02,(100.*(mO_num-mO_approx_higherorder)/mO_approx_higherorder)[aparIndx]],
'k',lw=1.)
bovy_plot.bovy_text(0.05,-0.03,r'$\mathrm{numerical\ minus\ higher\!\!-\!\!order}$',size=17.)
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats','gd1likeSingle_mOparapprox.pdf'))
start= time.time()
numpy.array([sdf_gap.density_par(x,approx=False) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
start= time.time()
numpy.array([sdf_gap.density_par(x,approx=True) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
start= time.time()
numpy.array([sdf_gap.density_par(x,approx=True,higherorder=True) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
start= time.time()
numpy.array([sdf_gap.meanOmega(x,approx=False,oned=True) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
start= time.time()
numpy.array([sdf_gap.meanOmega(x,approx=True,oned=True) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
start= time.time()
numpy.array([sdf_gap.meanOmega(x,approx=True,oned=True,higherorder=True) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
```
## Test the multiple-impact approximations
```
# Setup a four, intermediate impacts
m= [10.**7.,10.**7.25,10.**6.75,10.**7.5]
GM= [mm/bovy_conversion.mass_in_msol(V0,R0) for mm in m]
timpactIndx= [numpy.argmin(numpy.fabs(numpy.array(sdf_pepper._uniq_timpact)-1.3/bovy_conversion.time_in_Gyr(V0,R0))),
numpy.argmin(numpy.fabs(numpy.array(sdf_pepper._uniq_timpact)-2.3/bovy_conversion.time_in_Gyr(V0,R0))),
numpy.argmin(numpy.fabs(numpy.array(sdf_pepper._uniq_timpact)-3.3/bovy_conversion.time_in_Gyr(V0,R0))),
numpy.argmin(numpy.fabs(numpy.array(sdf_pepper._uniq_timpact)-4.3/bovy_conversion.time_in_Gyr(V0,R0)))]
sdf_pepper.set_impacts(impactb=[0.5*rs(m[0]),2.*rs(m[1]),1.*rs(m[2]),2.5*rs(m[3])],
subhalovel=numpy.array([[-25.,155.,30.],
[125.,35.,80.],
[-225.,5.,-40.],
[25.,-155.,37.]])/V0,
impact_angle=[0.6,0.4,0.3,0.3],
timpact=[sdf_pepper._uniq_timpact[ti] for ti in timpactIndx],
GM=GM,rs=[rs(mm) for mm in m])
sdf_gap= sdf_pepper
n= 100000
aa_mock_per= sdf_pepper.sample(n=n,returnaAdt=True)
dO= numpy.dot(aa_mock_per[0].T-sdf_gap._progenitor_Omega,
sdf_gap._sigomatrixEig[1][:,sdf_gap._sigomatrixEigsortIndx])
dO[:,2]*= sdf_gap._sigMeanSign
da= numpy.dot(aa_mock_per[1].T-sdf_gap._progenitor_angle,
sdf_gap._sigomatrixEig[1][:,sdf_gap._sigomatrixEigsortIndx])
da[:,2]*= sdf_gap._sigMeanSign
num= True
apar= numpy.arange(0.,sdf_smooth.length()+0.003,0.003)
dens_unp= numpy.array([sdf_smooth._density_par(x) for x in apar])
dens_approx= numpy.array([sdf_gap.density_par(x,approx=True) for x in apar])
# normalize
dens_unp= dens_unp/numpy.sum(dens_unp)/(apar[1]-apar[0])
dens_approx= dens_approx/numpy.sum(dens_approx)/(apar[1]-apar[0])
if num:
dens_num= numpy.array([sdf_gap.density_par(x,approx=False) for x in apar])
dens_num= dens_num/numpy.sum(dens_num)/(apar[1]-apar[0])
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=14.)
figsize(6,7)
axTop= pyplot.axes([0.15,0.3,0.825,0.65])
fig= pyplot.gcf()
fig.sca(axTop)
bovy_plot.bovy_plot(apar,dens_approx,lw=2.5,gcf=True,
color='k',
xrange=[0.,1.],
yrange=[0.,2.24],
ylabel=r'$\mathrm{density}$')
plot(apar,dens_unp,lw=3.5,color='k',ls='--',zorder=0)
nullfmt = NullFormatter() # no labels
axTop.xaxis.set_major_formatter(nullfmt)
dum= hist(da[:,2],bins=101,normed=True,range=[apar[0],apar[-1]],
histtype='step',color='0.55',zorder=0,lw=3.)
axBottom= pyplot.axes([0.15,0.1,0.825,0.2])
fig= pyplot.gcf()
fig.sca(axBottom)
if num:
bovy_plot.bovy_plot(apar,100.*(dens_num-dens_approx)/dens_approx,
lw=2.5,gcf=True,color='k',
xrange=[0.,1.],
yrange=[-1.45,1.45],
zorder=2,
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\mathrm{relative\ difference\ in}\ \%$')
# label
if num:
aparIndx= numpy.argmin(numpy.fabs(apar-0.6))
plot([0.45,apar[aparIndx]],[0.7,(100.*(dens_num-dens_approx)/dens_approx)[aparIndx]],
'k',lw=1.)
bovy_plot.bovy_text(0.15,0.4,r'$\mathrm{numerical\ minus}$'+'\n'+r'$\mathrm{approximation}$',size=17.)
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats','gd1likeMulti_densapprox.pdf'))
mO_unp= numpy.array([sdf_smooth.meanOmega(x,oned=True) for x in apar])\
*bovy_conversion.freq_in_Gyr(V0,R0)
mO_approx= numpy.array([sdf_gap.meanOmega(x,approx=True,oned=True) for x in apar])\
*bovy_conversion.freq_in_Gyr(V0,R0)
if num:
mO_num= numpy.array([sdf_gap.meanOmega(x,approx=False,oned=True) for x in apar])\
*bovy_conversion.freq_in_Gyr(V0,R0)
frac= 0.005
alpha=0.01
linecolor='0.65'
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=14.)
figsize(6,7)
axTop= pyplot.axes([0.15,0.3,0.825,0.65])
fig= pyplot.gcf()
fig.sca(axTop)
bovy_plot.bovy_plot(apar,mO_approx,lw=2.5,gcf=True,
color='k',
xrange=[0.,1.],
yrange=[0.,0.2],
ylabel=r'$\Delta \Omega_\parallel\,(\mathrm{Gyr}^{-1})$')
plot(apar,mO_unp,lw=2.5,color='k',ls='--')
plot(da[::3,2],dO[::3,2]*bovy_conversion.freq_in_Gyr(V0,R0),
'k.',alpha=alpha*2,rasterized=True)
nullfmt = NullFormatter() # no labels
axTop.xaxis.set_major_formatter(nullfmt)
axBottom= pyplot.axes([0.15,0.1,0.825,0.2])
fig= pyplot.gcf()
fig.sca(axBottom)
if num:
bovy_plot.bovy_plot(apar,100.*(mO_num-mO_approx)/mO_approx,
lw=2.5,gcf=True,color='k',
xrange=[0.,1.],zorder=1,
yrange=[-0.39,0.39],
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\mathrm{relative\ difference\ in\ \%}$')
# label
if num:
aparIndx= numpy.argmin(numpy.fabs(apar-0.6))
plot([0.35,apar[aparIndx]],[0.2,(100.*(mO_num-mO_approx)/mO_approx)[aparIndx]],
'k',lw=1.)
bovy_plot.bovy_text(0.05,0.1,r'$\mathrm{numerical\ minus}$'+'\n'+r'$\mathrm{approximation}$',size=17.)
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats','gd1likeMulti_mOparapprox.pdf'))
start= time.time()
numpy.array([sdf_gap.density_par(x,approx=False) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
start= time.time()
numpy.array([sdf_gap.density_par(x,approx=True) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
start= time.time()
numpy.array([sdf_gap.meanOmega(x,approx=False,oned=True) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
start= time.time()
numpy.array([sdf_gap.meanOmega(x,approx=True,oned=True) for x in apar[::10]])
end= time.time()
print (end-start)*1000.*10./len(apar)
```
## Computational speed
```
nimp= 2**numpy.arange(1,9)
ntrials= 3
nsample= [10,10,10,10,10,10,33,33,33]
compt= numpy.zeros(len(nimp))
for ii,ni in enumerate(nimp):
tcompt= 0.
for t in range(ntrials):
nimpact=ni
timpacts= numpy.random.permutation(numpy.array(sdf_pepper._uniq_timpact))[:ni]
print len(timpacts)
impact_angles= numpy.array([\
sdf_pepper._icdf_stream_len[ti](numpy.random.uniform())
for ti in timpacts])
GMs= numpy.array([sample_GM() for a in impact_angles])
rss= numpy.array([sample_rs(gm) for gm in GMs])
impactbs= numpy.random.uniform(size=len(impact_angles))*Xrs*rss
subhalovels= numpy.empty((len(impact_angles),3))
for jj in range(len(timpacts)):
subhalovels[jj]=\
sdf_pepper._draw_impact_velocities(timpacts[jj],120./V0,
impact_angles[jj],n=1)[0]
# Flip angle sign if necessary
if not sdf_pepper._gap_leading: impact_angles*= -1.
# Setup
sdf_pepper.set_impacts(impact_angle=impact_angles,
impactb=impactbs,
subhalovel=subhalovels,
timpact=timpacts,
GM=GMs,rs=rss)
start= time.time()
numpy.array([sdf_pepper.density_par(x,approx=True) for x in apar[::nsample[ii]]])
end= time.time()
tcompt+= (end-start)*1000.*nsample[ii]/len(apar)
compt[ii]= tcompt/ntrials
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=14.)
figsize(6,4)
bovy_plot.bovy_plot(numpy.log2(nimp),compt,'ko',
semilogy=True,
xrange=[0.,9.],
yrange=[.5,100000.],
ylabel=r'$\mathrm{time}\,(\mathrm{ms})$',
xlabel=r'$\mathrm{number\ of\ impacts}$')
p= numpy.polyfit(numpy.log10(nimp),numpy.log10(compt),deg=1)
bovy_plot.bovy_plot(numpy.log2(nimp),10.**(p[0]*numpy.log10(nimp)+p[1]),
'-',lw=2.,
color=(0.0, 0.4470588235294118, 0.6980392156862745),
overplot=True)
pyplot.text(0.3,0.075,
r'$\log_{10}\ \mathrm{time/ms} = %.2f \,\log_{10} N %.2f$' % (p[0],p[1]),
transform=pyplot.gca().transAxes,size=14.)
# Use 100, 1000 instead of 10^2, 10^3
gca().yaxis.set_major_formatter(ScalarFormatter())
def twoto(x,pos):
return r'$%i$' % (2**x)
formatter = FuncFormatter(twoto)
gca().xaxis.set_major_formatter(formatter)
gcf().subplots_adjust(left=0.175,bottom=0.15,right=0.95,top=0.95)
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats','gd1likeMulti_compTime.pdf'))
```
## Example densities and tracks
### Single masses
```
# Load our fiducial simulation's output, for apars and smooth stream
data= numpy.genfromtxt(os.path.join(os.getenv('DATADIR'),'streamgap-pepper','gd1_multtime',
'gd1_t64sampling_X5_5-9_dens.dat'),
delimiter=',',max_rows=2)
apars= data[0]
dens_unp= data[1]
data= numpy.genfromtxt(os.path.join(os.getenv('DATADIR'),'streamgap-pepper','gd1_multtime',
'gd1_t64sampling_X5_5-9_omega.dat'),
delimiter=',',max_rows=2)
omega_unp= data[1]
dens_example= []
omega_example= []
# Perform some simulations, for different mass ranges
numpy.random.seed(3)
nexample= 4
masses= [5.5,6.5,7.5,8.5]
for ii in range(nexample):
# Sampling functions
sample_GM= lambda: 10.**(masses[ii]-10.)\
/bovy_conversion.mass_in_1010msol(V0,R0)
rate= dNencdm(sdf_pepper,10.**masses[ii],Xrs=Xrs,
plummer=plummer)
sdf_pepper.simulate(rate=rate,sample_GM=sample_GM,sample_rs=sample_rs,Xrs=Xrs)
densOmega= numpy.array([sdf_pepper._densityAndOmega_par_approx(a) for a in apars]).T
dens_example.append(densOmega[0])
omega_example.append(densOmega[1])
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=18.)
figsize(6,7)
overplot= False
for ii in range(nexample):
bovy_plot.bovy_plot(apars,dens_example[ii]/dens_unp+2.*ii+0.5*(ii>2),lw=2.5,
color='k',
xrange=[0.,1.3],
yrange=[0.,2.*nexample+1],
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\mathrm{density}/\mathrm{smooth\ density}+\mathrm{constant}$',
overplot=overplot)
plot(apars,apars*0.+1.+2.*ii+0.5*(ii>2),lw=1.5,color='k',ls='--',zorder=0)
bovy_plot.bovy_text(1.025,1.+2.*ii+0.5*(ii>2),r'$10^{%.1f}\,M_\odot$' % masses[ii],verticalalignment='center',size=18.)
overplot=True
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats',
'gd1like_densexample_singlemasses.pdf'))
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=18.)
figsize(6,7)
overplot= False
mult= [3.,3.,1.,1.]
for ii in range(nexample):
bovy_plot.bovy_plot(apars,mult[ii]*(omega_example[ii]/omega_unp-1.)+1.+2.*ii+0.5*(ii>2),
lw=2.5,
color='k',
xrange=[0.,1.3],
yrange=[0.,2.*nexample+1.],
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\langle\Delta \Omega_\parallel\rangle\big/\langle\Delta \Omega_\parallel^0\rangle+\mathrm{constant}$',
overplot=overplot)
plot(apars,apars*0.+1.+2.*ii+0.5*(ii>2),lw=1.5,color='k',ls='--',zorder=0)
bovy_plot.bovy_text(1.025,1.+2.*ii+0.5*(ii>2),r'$10^{%.1f}\,M_\odot$' % masses[ii],verticalalignment='center',size=18.)
bovy_plot.bovy_text(0.025,1.+2.*ii+0.1+0.5*(ii>2),r'$\times%i$' % mult[ii],size=18.)
overplot= True
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats',
'gd1like_omegaexample_singlemasses.pdf'))
```
### Full mass range
First look at low apar resolution:
```
apars= apars[::30]
dens_unp= dens_unp[::30]
omega_unp= omega_unp[::30]
# Sampling functions
massrange=[5.,9.]
plummer= False
Xrs= 5.
nsubhalo= simulate_streampepper.nsubhalo
rs= simulate_streampepper.rs
dNencdm= simulate_streampepper.dNencdm
sample_GM= lambda: (10.**((-0.5)*massrange[0])\
+(10.**((-0.5)*massrange[1])\
-10.**((-0.5)*massrange[0]))\
*numpy.random.uniform())**(1./(-0.5))\
/bovy_conversion.mass_in_msol(V0,R0)
rate_range= numpy.arange(massrange[0]+0.5,massrange[1]+0.5,1)
rate= numpy.sum([dNencdm(sdf_pepper,10.**r,Xrs=Xrs,
plummer=plummer)
for r in rate_range])
sample_rs= lambda x: rs(x*bovy_conversion.mass_in_1010msol(V0,R0)*10.**10.,
plummer=plummer)
dens_example2= []
omega_example2= []
# Perform some simulations
numpy.random.seed(3)
nexample= 4
for ii in range(nexample):
sdf_pepper.simulate(rate=rate,sample_GM=sample_GM,sample_rs=sample_rs,Xrs=Xrs)
densOmega= numpy.array([sdf_pepper._densityAndOmega_par_approx(a) for a in apars]).T
dens_example2.append(densOmega[0])
omega_example2.append(densOmega[1])
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=18.)
figsize(6,7)
overplot= False
for ii in range(nexample):
bovy_plot.bovy_plot(apars,dens_example2[ii]/dens_unp+2.*ii,lw=2.5,
color='k',
xrange=[0.,1.],
yrange=[0.,2.*nexample+1.],
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\mathrm{density}/\mathrm{smooth\ density}+\mathrm{constant}$',
overplot=overplot)
plot(apars,apars*0.+1.+2.*ii,lw=1.5,color='k',ls='--',zorder=0)
overplot=True
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=18.)
figsize(6,7)
overplot= False
for ii in range(nexample):
bovy_plot.bovy_plot(apars,omega_example2[ii]/omega_unp+2.*ii,lw=2.5,
color='k',
xrange=[0.,1.],
yrange=[0.,2.*nexample],
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\langle\Delta \Omega_\parallel\rangle\big/\langle\Delta \Omega_\parallel^0\rangle+\mathrm{constant}$',
overplot=overplot)
plot(apars,apars*0.+1.+2.*ii,lw=1.5,color='k',ls='--',zorder=0)
overplot= True
```
At full apar resolution:
```
# Load our fiducial simulation's output, for apars and smooth stream
data= numpy.genfromtxt(os.path.join(os.getenv('DATADIR'),'streamgap-pepper','gd1_multtime',
'gd1_t64sampling_X5_5-9_dens.dat'),
delimiter=',',max_rows=2)
apars= data[0]
dens_unp= data[1]
data= numpy.genfromtxt(os.path.join(os.getenv('DATADIR'),'streamgap-pepper','gd1_multtime',
'gd1_t64sampling_X5_5-9_omega.dat'),
delimiter=',',max_rows=2)
omega_unp= data[1]
dens_example2= []
omega_example2= []
# Perform some simulations
numpy.random.seed(3)
nexample= 4
for ii in range(nexample):
sdf_pepper.simulate(rate=rate,sample_GM=sample_GM,sample_rs=sample_rs,Xrs=Xrs)
densOmega= numpy.array([sdf_pepper._densityAndOmega_par_approx(a) for a in apars]).T
dens_example2.append(densOmega[0])
omega_example2.append(densOmega[1])
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=18.)
figsize(6,7)
overplot= False
for ii in range(nexample):
bovy_plot.bovy_plot(apars,dens_example2[ii]/dens_unp+2.*ii,lw=2.5,
color='k',
xrange=[0.,1.],
yrange=[0.,2.*nexample+1.],
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\mathrm{density}/\mathrm{smooth\ density}+\mathrm{constant}$',
overplot=overplot)
plot(apars,apars*0.+1.+2.*ii,lw=1.5,color='k',ls='--',zorder=0)
overplot=True
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats','gd1like_densexample.pdf'))
bovy_plot.bovy_print(axes_labelsize=18.,xtick_labelsize=14.,ytick_labelsize=18.)
figsize(6,7)
overplot= False
for ii in range(nexample):
bovy_plot.bovy_plot(apars,omega_example2[ii]/omega_unp+2.*ii,lw=2.5,
color='k',
xrange=[0.,1.],
yrange=[0.,2.*nexample],
xlabel=r'$\Delta \theta_\parallel$',
ylabel=r'$\langle\Delta \Omega_\parallel\rangle\big/\langle\Delta \Omega_\parallel^0\rangle+\mathrm{constant}$',
overplot=overplot)
plot(apars,apars*0.+1.+2.*ii,lw=1.5,color='k',ls='--',zorder=0)
overplot= True
if save_figures:
bovy_plot.bovy_end_print(os.path.join(os.getenv('PAPERSDIR'),'2016-stream-stats','gd1like_omegaexample.pdf'))
```
| github_jupyter |
```
import numpy as np
import nibabel.cifti2 as ci
from itertools import product
from joblib import Parallel, delayed
import pickle
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
from graspy.plot import heatmap
%matplotlib inline
from hyppo.time_series import MGCX
```
## Look At It
```
# Load image - individual 100307.
img = ci.load("fmri_data/rfMRI_REST1_LR_Atlas_hp2000_clean_filt_sm6.HCPMMP.ptseries.nii")
fmri_data = np.array(img.get_fdata())
# Visualize data, i.e. inspect the first 60 timesteps of each parcel.
# Generate heatmap.
timesteps = 60
displayed_data = np.transpose(fmri_data[range(timesteps),:])
plt.subplots(figsize=(15,10))
ax = sns.heatmap(displayed_data, yticklabels=False)
# Plot parameters.
plt.title('Resting fMRI Signal by Parcel - Individual 100307 LR', fontsize = 20)
plt.ylabel('Parcel', fontsize = 15)
plt.xlabel('Timestep', fontsize = 15)
plt.show()
```
## Set Up Hyperparameters
```
# From Ting: Regions-of-Interest (ROIs)
roi_keys = np.array([1, 23, 18, 53, 24, 96, 117, 50, 143, 109, 148, 60, 38, 135, 93, 83, 149, 150, 65, 161, 132, 71]) - 1
roi_labels = np.array([
"Visual",
"Visual",
"Visual",
"SM",
"SM",
"dAtt",
"dAtt",
"dAtt",
"dAtt",
"vAtt",
"vAtt",
"vAtt",
"vAtt",
"Limbic",
"Limbic",
"FP",
"FP",
"DMN",
"DMN",
"DMN",
"DMN",
"DMN",
])
roi_data = fmri_data[0:300, roi_keys]
num_roi = len(roi_keys)
# Hyperparameters
max_lag = 1 # number of lags to check in the past
reps = 1000 # number of bootstrap replicates
workers = 1 # number of workers in internal MGC parallelization
# Subsample to test experiment.
# pairs = list(product(range(num_roi), repeat = 2)) # Fake param for testing.
pairs = list(product(range(num_roi), repeat = 2))
```
## Run Experiment
```
mgcx = MGCX(max_lag = max_lag)
def worker(i, j):
X = roi_data[:, i]
Y = roi_data[:, j]
stat, pval, mgcx_dict = mgcx.test(X, Y, reps = reps, workers = workers)
opt_lag = mgcx_dict['opt_lag']
opt_scale_x, opt_scale_y = mgcx_dict['opt_scale']
return stat, pval, opt_lag, opt_scale_x, opt_scale_y
output = np.array(Parallel(n_jobs=-2)(delayed(worker)(i, j) for i, j in pairs))
pickle.dump(output, open('fmri_data/mgcx_fmri_output.pkl', 'wb'))
# Load results into num_roi-by-num_roi matrices.
results = pickle.load(open('fmri_data/mgcx_fmri_output.pkl', 'rb'))
test_outputs = ['stat', 'pval', 'opt_lag', 'opt_scale_x', 'opt_scale_y']
matrices = np.zeros((len(test_outputs), num_roi, num_roi))
for p, pair in enumerate(pairs):
i, j = pair
for t in range(len(test_outputs)):
matrices[t, i, j] = results[p, t]
for t, test_output in enumerate(test_outputs):
pickle.dump(matrices[t], open('fmri_data/%s_matrix.pkl' % test_output, 'wb'))
```
## Visualize Matrices
```
def plot_heatmap(matrix, labels, title, filename):
# sns.set()
cmap = mpl.cm.get_cmap('Purples')
cc = np.linspace(0, 1, 256)
cmap = mpl.colors.ListedColormap(cmap(cc))
heatmap_kws = dict(
cbar=False,
font_scale=1.4,
inner_hier_labels=labels,
hier_label_fontsize=20,
cmap=cmap,
center=None,
)
side_label_kws = dict(labelpad=45, fontsize=24)
fig, ax = plt.subplots(1, 1, figsize=(20, 16))
# Plot heatmap via graspy.
heatmap(matrix, ax=ax, **heatmap_kws)
ax.set_title(title, pad = 100, fontdict = {'fontsize' : 23})
# Create ticks.
num_ticks = 8
top_val = np.max(matrix)
ticks = [i * np.max(matrix) / num_ticks for i in range(num_ticks+1)]
yticks = [('%.2f' % np.round(10 ** -p, 2)) for p in ticks]
# Add colorbar.
sm = plt.cm.ScalarMappable(cmap=cmap)
sm.set_array(matrix)
cbar = fig.colorbar(sm, ax=ax, fraction=0.0475, pad=-0.1, ticks=ticks)
cbar.ax.set_yticklabels(yticks)
cbar.ax.tick_params(labelsize=25)
plt.savefig(
"%s.pdf" % filename,
facecolor="w",
format="pdf",
bbox_inches="tight",
)
plt.tight_layout()
plt.show()
```
### p-value Matrix
```
# Apply negative log10 transform.
# matrix = pickle.load(open('fmri_data/pval_matrix.pkl', 'rb'))
# matrix = -np.log10(matrix)
# pickle.dump(matrix, open('fmri_data/nl10_pval_matrix.pkl', 'wb'))
matrix = pickle.load(open('fmri_data/nl10_pval_matrix.pkl', 'rb'))
plot_heatmap(matrix, roi_labels, 'p-Value', 'pval')
```
| github_jupyter |
```
!nvidia-smi
# -*- coding: utf-8 -*-
from __future__ import print_function
import keras
from keras.datasets import cifar10
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten, Lambda
from keras.layers import Conv2D, MaxPooling2D
from keras.layers.normalization import BatchNormalization as BN
from keras.layers import GaussianNoise as GN
from keras.optimizers import SGD, Adam, RMSprop
from keras.models import Model
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from keras.callbacks import LearningRateScheduler as LRS
from keras.preprocessing.image import ImageDataGenerator
batch_size = 32
num_classes = 20
epochs = 50
#### LOAD AND TRANSFORM
# ## Download: ONLY ONCE!
# !wget https://www.dropbox.com/s/kdhn10jwj99xkv7/data.tgz
# !tar xvzf data.tgz
# #####
# Load
x_train = np.load('x_train.npy')
x_test = np.load('x_test.npy')
y_train = np.load('y_train.npy')
y_test = np.load('y_test.npy')
# Stats
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
## View some images
plt.imshow(x_train[2,:,:,: ] )
plt.show()
## Transforms
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
y_train = y_train.astype('float32')
y_test = y_test.astype('float32')
x_train /= 255
x_test /= 255
## Labels
y_train=y_train-1
y_test=y_test-1
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
from keras.applications.vgg16 import VGG16
from keras.callbacks import ModelCheckpoint
# load the model
model1 = VGG16(weights='imagenet', include_top=False, input_shape=x_train.shape[1:])
#############################
### BILINEAR ####
#############################
# No entrenar la VGG
for layer in model1.layers:
layer.trainable = False
def outer_product(x):
phi_I = tf.einsum('ijkm,ijkn->imn',x[0],x[1]) # Einstein Notation [batch,1,1,depth] x [batch,1,1,depth] -> [batch,depth,depth]
phi_I = tf.reshape(phi_I,[-1,512*512]) # Reshape from [batch_size,depth,depth] to [batch_size, depth*depth]
phi_I = tf.divide(phi_I,31*31) # Divide by feature map size [sizexsize]
y_ssqrt = tf.multiply(tf.sign(phi_I),tf.sqrt(tf.abs(phi_I)+1e-12)) # Take signed square root of phi_I
z_l2 = tf.nn.l2_normalize(y_ssqrt, dim=1) # Apply l2 normalization
return z_l2
conv=model1.get_layer('block4_conv3') # block4_conv3
d1=Dropout(0.5)(conv.output) ## Why??
d2=Dropout(0.5)(conv.output) ## Why??
x = Lambda(outer_product, name='outer_product')([d1,d2])
predictions=Dense(num_classes, activation='softmax', name='predictions')(x)
#layer_x=Dense(256, activation='relu', name='midle_layer')(x)
#predictions=Dense(num_classes, activation='softmax', name='predictions')(layer_x)
model = Model(inputs=model1.input, outputs=predictions)
# DEFINE A LEARNING RATE SCHEDULER
def scheduler(epoch):
if epoch < 25:
return 0.0001
elif epoch < 50:
return 0.00001
else:
return 0.000001
set_lr = LRS(scheduler)
## DATAGEN
datagen = ImageDataGenerator(
width_shift_range=0.2,
height_shift_range=0.2,
rotation_range=20,
zoom_range=[1.0,1.2],
horizontal_flip=True)
## OPTIM AND COMPILE use Adam Rsmprop
opt = SGD(lr=0.0001, decay=1e-6)
rms = RMSprop(lr=0.001, rho=0.9, epsilon=None, decay=0.0)
adam = Adam(lr=0.0001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=1e-6, amsgrad=False)
model.compile(loss='categorical_crossentropy',
optimizer=rms,
metrics=['accuracy'])
model.summary()
checkpoint_path = "Wehigts.hdf5"
checkpointer = ModelCheckpoint(filepath=checkpoint_path, verbose=1, save_best_only=True)
## TRAINING with DA and LRA
history=model.fit_generator(datagen.flow(x_train, y_train,batch_size=batch_size),
steps_per_epoch=len(x_train) / batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
callbacks=[checkpointer],
verbose=1)
#Usar Checpoint mejor de ejecución
model.load_weights(checkpoint_path)
for j, layer in enumerate(model1.layers):
layer.trainable = True
#if j <14:
# if "conv" in layer.name:
# layer.trainable = True
#Compile y ejecutar de nuevo
#rms = RMSprop(lr=0.0001, rho=0.9, epsilon=None, decay=0.0)
#adam = Adam(lr=0.0001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=1e-6, amsgrad=False)
model.compile(loss='categorical_crossentropy',
optimizer=rms,
metrics=['accuracy'])
model.summary()
checkpoint_path = "Wehigts_final.hdf5"
checkpointer = ModelCheckpoint(filepath=checkpoint_path, verbose=1, save_best_only=True)
## TRAINING with DA and LRA
history=model.fit_generator(datagen.flow(x_train, y_train,batch_size=batch_size),
steps_per_epoch=len(x_train) / batch_size,
epochs=epochs,
validation_data=(x_test, y_test),
callbacks=[checkpointer],
verbose=1)
```
| github_jupyter |
# Buffered Text-to-Speech
In this tutorial, we are going to build a state machine that controls a text-to-speech synthesis. The problem we solve is the following:
- Speaking the text takes time, depending on how long the text is that the computer should speak.
- Commands for speaking can arrive at any time, and we would like our state machine to process one of them at a time. So, even if we send three messages to it shortly after each other, it processes them one after the other.
While solving this problem, we can learn more about the following concepts in STMPY state machines:
- **Do-Activities**, which allow us to encapsulate the long-running text-to-speech function in a state machine.
- **Deferred Events**, which allow us to ignore incoming messages until a later state, when we are ready again.
# Text-to-Speech
## Mac
On a Mac, this is a function to make your computer speak:
```
from os import system
def text_to_speech(text):
system('say {}'.format(text))
```
Run the above cell so the function is available in the following, and then execute the following cell to test it:
```
text_to_speech("Hello. I am a computer.")
```
## Windows
TODO: We should have some code to run text to speech on Windows, too!
# State Machine 1
With this function, we can create our first state machine that accepts a message and then speaks out some text. (Let's for now ignore how we get the text into the method, we will do that later.)

Unfortunately, this state machine has a problem. This is because the method `text_to_speech(text)` is taking a long time to complete. This means, for the entire time that it takes to speak the text, nothing else can happen in all the state machines that are part of the same driver!
# State Machine 2
## Long-Running Actions
The way this function is implented makes that it **blocks**. This means, the Python program is busy executing this function as long as the speech takes to pronouce the message. Longer message, longer blocking.
You can test this by putting some debugging aroud the function, to see when the functions returns:
```
print('Before speaking.')
text_to_speech("Hello. I am a computer.")
print('After speaking.')
```
You see that the string _"After speaking"_ is printed after the speaking is finished. During the execution, the program is blocked and does not do anything else.
When our program should also do other stuff at the same time, either completely unrelated to speech or even just accepting new speech commands, this is not working! The driver is now completely blocked with executing the speech method, not being able to do anything else.
## Do-Activities
Instead of executing the method as part of a transition, we execute it as part of a state. This is called a **Do-Activity**, and it is declared as part of a state. The do-activity is started when the state is entered. Once the activity is finished, the state machine receives the event `done`, which triggers it to switch into another state.

You may think now that the do-activity is similar to an entry action, as it is started when entering a state. However, a do-activity is started as part of its own thread, so that it does not block any other behavior from happening. Our state machine stays responsive, and so does any of the other state machines that may be assigned to the same driver. This happens in the background, STMPY is creating a new thread for a do-activity, starts it, and dispatches the `done` event once the do-activity finishes.
When the do-activity finishes (in the case of the text-to-speech function, this means when the computer is finished talking), the state machine dispatches _automatically_ the event `done`, which brings the state machine into the next state.
- A state with a do activity can therefore only declare one single outgoing transition that is triggered by the event `done`.
- A state can have at most one do-activity.
- A do-activity cannot be aborted. Instead, it should be programmed so that the function itself terminates, indicated for instance by the change of a variable.
The following things are still possible in a state with a do-activity:
- A state with a do-activity can have entry and exit actions. They are simply executed before or after the do activities.
- A state with a do-activity can have internal transitions, since they don't leave the state.
```
from stmpy import Machine, Driver
from os import system
import logging
debug_level = logging.DEBUG
logger = logging.getLogger('stmpy')
logger.setLevel(debug_level)
ch = logging.StreamHandler()
ch.setLevel(debug_level)
formatter = logging.Formatter('%(asctime)s - %(name)-12s - %(levelname)-8s - %(message)s')
ch.setFormatter(formatter)
logger.addHandler(ch)
class Speaker:
def speak(self, string):
system('say {}'.format(string))
speaker = Speaker()
t0 = {'source': 'initial', 'target': 'ready'}
t1 = {'trigger': 'speak', 'source': 'ready', 'target': 'speaking'}
t2 = {'trigger': 'done', 'source': 'speaking', 'target': 'ready'}
s1 = {'name': 'speaking', 'do': 'speak(*)'}
stm = Machine(name='stm', transitions=[t0, t1, t2], states=[s1], obj=speaker)
speaker.stm = stm
driver = Driver()
driver.add_machine(stm)
driver.start()
driver.send('speak', 'stm', args=['My first sentence.'])
driver.send('speak', 'stm', args=['My second sentence.'])
driver.send('speak', 'stm', args=['My third sentence.'])
driver.send('speak', 'stm', args=['My fourth sentence.'])
driver.wait_until_finished()
```
The state machine 2 still has a problem, but this time another one: If we receive a new message with more text to speak _while_ we are in state `speaking`, this message is discarded. Our next state machine will fix this.
# State Machine 3
As you know, events arriving in a state that do not declare outgoing triggers with that event, are discarded (that means, thrown away). For our state machine 2 above this means that when we are in state `speaking` and a new message arrives, this message is discarded. However, what we ideally want is that this message is handled once the currently spoken text is finished. There are two ways of achieving this:
1. We could build a queue variable into our logic, and declare a transition that puts any arriving `speak` message into that queue. Whenever the currently spoken text finishes, we take another one from the queue until the queue is empty again. This has the drawback that we need to code the queue ourselves.
2. We use a mechanism called **deferred event**, which is part of the state machine mechanics. This is the one we are going to use below.
## Deferred Events
A state can declare that it wants to **defer** an event, which simply means to not handle it. For our speech state machine it means that state `speaking` can declare that it defers event `speak`.

Any event that arrives in a state that defers it, is ignored by that state. It is as if it never arrived, or as if it is invisible in the incoming event queue. Only once we switch into a next state that does not defer it, it gets visible again, and then either consumed by a transition, or discarded if the state does not declare any transition triggered by it.
```
s1 = {'name': 'speaking', 'do': 'speak(*)', 'speak': 'defer'}
stm = Machine(name='stm', transitions=[t0, t1, t2], states=[s1], obj=speaker)
speaker.stm = stm
driver = Driver()
driver.add_machine(stm)
driver.start()
driver.send('speak', 'stm', args=['My first sentence.'])
driver.send('speak', 'stm', args=['My second sentence.'])
driver.send('speak', 'stm', args=['My third sentence.'])
driver.send('speak', 'stm', args=['My fourth sentence.'])
driver.wait_until_finished()
```
| github_jupyter |
# 概要
- 101クラス分類
- 対象:料理画像
- VGG16による転移学習
1. 全結合層
1. 全層
- RXなし
```
RUN = 100
```
# 使用するGPUメモリの制限
```
import tensorflow as tf
tf_ver = tf.__version__
if tf_ver.startswith('1.'):
from tensorflow.keras.backend import set_session
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
config.log_device_placement = True
sess = tf.Session(config=config)
set_session(sess)
```
# 使用するGPUを指定
```
import os
os.environ["CUDA_VISIBLE_DEVICES"]="0"
```
# matplotlibでプロットしたグラフをファイルへ保存
```
import os
def save_fig(plt, file_prefix):
if file_prefix == '':
return
parent = os.path.dirname(os.path.abspath(file_prefix))
os.makedirs(parent, exist_ok=True)
plt.savefig(f'{file_prefix}.pdf', transparent=True, bbox_inches='tight', pad_inches = 0)
plt.savefig(f'{file_prefix}.png', transparent=True, dpi=300, bbox_inches='tight', pad_inches = 0)
```
# 指定フォルダ以下にある画像リストを作成
- サブフォルダはラベルに対応する数字であること
- TOP_DIR
- 0
- 00001.jpg
- 00002.jpg
- 1
- 00003.jpg
- 00004.jpg
```
import pathlib
import random
import os
TOP_DIR = '/data1/Datasets/Food-101/03_all'
sub_dirs = pathlib.Path(TOP_DIR).glob('*/**')
label2files = dict()
for s in sub_dirs:
files = pathlib.Path(s).glob('**/*.jpg')
label = int(os.path.basename(s))
label2files[label] = list(files)
```
# 画像とラベルを訓練データと検証データに分割する
```
ratio = 0.8
train_list = []
train_labels = []
val_list = []
val_labels = []
for k, v in label2files.items():
random.shuffle(v)
N = len(v)
N_train = int(N * ratio)
train_list.extend(v[:N_train])
train_labels.extend([k] * N_train)
val_list.extend(v[N_train:])
val_labels.extend([k] * (N - N_train))
NUM_CLASSES = len(label2files.keys())
```
# 画像ファイルリストとラベルから教師データを生成するクラス
```
import math
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
%matplotlib inline
import keras
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.applications.vgg16 import preprocess_input
import tensorflow as tf
class ImageSequence(tf.keras.utils.Sequence):
def __init__(self, file_list, labels, batch_size, image_shape=(224, 224), shuffle=True, horizontal_flip=True):
self.file_list = np.array(file_list)
self.labels = to_categorical(labels)
self.batch_size = batch_size
self.image_shape = image_shape
self.shuffle = shuffle
self.horizontal_flip = horizontal_flip
self.indexes = np.arange(len(self.file_list))
if self.shuffle:
random.shuffle(self.indexes)
def __getitem__(self, index):
idx = self.indexes[index * self.batch_size : (index + 1) * self.batch_size]
y = self.labels[idx]
files = self.file_list[idx]
x = []
for f in files:
try:
img = Image.open(f)
# 正しいデータはRGB画像
# データセットの中には、グレースケール画像が入っている可能性がある。
# RGBに変換して、正しいデータと次元を揃える
img = img.convert('RGB')
img = img.resize(self.image_shape, Image.BILINEAR)
img = img_to_array(img)
img = preprocess_input(img) / 255.0
if self.horizontal_flip and np.random.random() > 0.5:
img = img[:,::-1, :]
x.append(np.expand_dims(img, axis=0))
except:
print(f)
return np.concatenate(x, axis=0), y
def __len__(self):
return len(self.file_list) // self.batch_size
def on_epoch_end(self):
if self.shuffle:
random.shuffle(self.indexes)
```
# モデル保存用のディレクトリを作成★
```
import os
from datetime import datetime
# モデル保存用ディレクトリの準備
model_dir = os.path.join(
f'../run/VGG16_run{RUN}'
)
os.makedirs(model_dir, exist_ok=True)
print('model_dir:', model_dir) # 保存先のディレクトリ名を表示
dir_weights = model_dir
os.makedirs(dir_weights, exist_ok=True)
```
# VGGモデルのロード
```
from tensorflow.keras.applications.vgg16 import VGG16
# 既存の1000クラスの出力を使わないため、
# `incliude_top=False`として出力層を含まない状態でロード
vgg16 = VGG16(include_top=False, input_shape=(224, 224, 3))
# モデルのサマリを確認。出力層が含まれてないことがわかる
vgg16.summary()
```
# VGG16を利用したモデルの作成と学習方法の設定★
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Flatten
# モデルを編集し、ネットワークを生成する関数の定義
def build_transfer_model(vgg16):
# 読み出したモデルを使って、新しいモデルを作成
model = Sequential(vgg16.layers)
# 読み出した重みの一部は再学習しないように設定。
# ここでは、追加する層と出力層に近い層の重みのみを再学習
for layer in model.layers[:15]:
layer.trainable = False
# 追加する出力部分の層を構築
model.add(Flatten())
model.add(Dense(1024, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1024, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(NUM_CLASSES, activation='softmax'))
return model
```
# 全結合層とそれに近い畳み込み層の学習★
## モデル作成
```
# 定義した関数を呼び出して、ネットワークを生成
model = build_transfer_model(vgg16)
```
## ネットワーク構造の保存★
```
import json
import pickle
# ネットワークの保存
model_json = os.path.join(model_dir, 'model.json')
with open(model_json, 'w') as f:
json.dump(model.to_json(), f)
```
## 最適化アルゴリズムなどを指定してモデルをコンパイルする
```
from tensorflow.keras.optimizers import SGD
model.compile(
loss='categorical_crossentropy',
optimizer=SGD(lr=1e-4, momentum=0.9),
metrics=['accuracy']
)
# モデルのサマリを確認
model.summary()
```
## シーケンス生成
```
batch_size = 25
img_seq_train = ImageSequence(train_list, train_labels, batch_size=batch_size)
img_seq_validation = ImageSequence(val_list, val_labels, batch_size=batch_size)
print('Train images =', len(img_seq_train) * batch_size)
print('Validation images =', len(img_seq_validation) * batch_size)
```
## Callbackの生成★
```
from tensorflow.keras.callbacks import ModelCheckpoint, CSVLogger, EarlyStopping, ReduceLROnPlateau
# Callbacksの設定
cp_filepath = os.path.join(dir_weights, 'ep_{epoch:04d}_ls_{loss:.1f}.h5')
cp = ModelCheckpoint(
cp_filepath,
monitor='val_acc',
verbose=0,
save_best_only=True,
save_weights_only=True,
mode='auto'
)
csv_filepath = os.path.join(model_dir, 'loss.csv')
csv = CSVLogger(csv_filepath, append=True)
es = EarlyStopping(monitor='val_acc', patience=20, verbose=1, mode='auto')
rl = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=5, verbose=1, mode='auto', epsilon=0.0001, cooldown=0, min_lr=0)
```
## 学習
```
n_epoch = 200
# モデルの学習
history = model.fit_generator(
img_seq_train,
epochs=n_epoch, # 学習するエポック数
steps_per_epoch=len(img_seq_train),
validation_data=img_seq_validation,
validation_steps=len(img_seq_validation),
verbose=1,
callbacks=[cp, csv, es, rl]
)
```
## Stage1の損失と正解率の保存
```
h = history.history
stage1_loss = h['loss']
stage1_val_loss = h['val_loss']
stage1_acc = h['acc']
stage1_val_acc = h['val_acc']
```
# 全層の学習
## Stage1の最良モデルパラメータをロード
```
import pathlib
checkpoints = pathlib.Path(model_dir).glob('*.h5')
checkpoints = sorted(checkpoints, key=lambda cp:cp.stat().st_mtime)
latest = str(checkpoints[-1])
model.load_weights(latest)
```
## 全層を学習可能にする
```
for l in model.layers:
l.trainable = True
model.summary()
```
## 最適化アルゴリズムなどを指定してモデルをコンパイルする
```
from tensorflow.keras.optimizers import SGD
model.compile(
loss='categorical_crossentropy',
optimizer=SGD(lr=1e-4, momentum=0.9),
metrics=['accuracy']
)
```
## シーケンス生成
```
batch_size = 25
img_seq_train = ImageSequence(train_list, train_labels, batch_size=batch_size)
img_seq_validation = ImageSequence(val_list, val_labels, batch_size=batch_size)
print('Train images =', len(img_seq_train) * batch_size)
print('Validation images =', len(img_seq_validation) * batch_size)
```
## Callbackの生成★
```
from tensorflow.keras.callbacks import ModelCheckpoint, CSVLogger, EarlyStopping, ReduceLROnPlateau
# Callbacksの設定
cp_filepath = os.path.join(dir_weights, 'ep_{epoch:04d}_ls_{loss:.1f}.h5')
cp = ModelCheckpoint(
cp_filepath,
monitor='val_acc',
verbose=0,
save_best_only=True,
save_weights_only=True,
mode='auto'
)
csv_filepath = os.path.join(model_dir, 'stage2_loss.csv')
csv = CSVLogger(csv_filepath, append=True)
es = EarlyStopping(monitor='val_acc', patience=20, verbose=1, mode='auto')
rl = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=5, verbose=1, mode='auto', epsilon=0.0001, cooldown=0, min_lr=0)
```
## 学習
```
n_epoch = 500
initial_epoch = len(stage1_loss)
# モデルの学習
history = model.fit_generator(
img_seq_train,
epochs=n_epoch, # 学習するエポック数
steps_per_epoch=len(img_seq_train),
validation_data=img_seq_validation,
validation_steps=len(img_seq_validation),
verbose=1,
callbacks=[cp, csv, es, rl],
initial_epoch=initial_epoch
)
```
# 結果
## 損失関数のプロット
```
plt.figure(figsize=(8, 6))
h = history.history
loss = stage1_loss + h['loss']
val_loss = stage1_val_loss + h['val_loss']
ep = np.arange(1, len(loss) + 1)
plt.title('Loss', fontsize=16)
plt.plot(ep, loss, label='Training')
plt.plot(ep, val_loss, label='Validation')
plt.legend(fontsize=16)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel('Epoch', fontsize=16)
plt.ylabel('Loss', fontsize=16)
plt.tight_layout()
save_fig(plt, file_prefix=os.path.join(model_dir, 'Loss'))
plt.show()
```
## 正解率のプロット
```
plt.figure(figsize=(8, 6))
h = history.history
acc = stage1_acc + h['acc']
val_acc = stage1_val_acc + h['val_acc']
ep = np.arange(1, len(loss) + 1)
plt.title('Accuracy', fontsize=16)
plt.plot(ep, acc, label='Training')
plt.plot(ep, val_acc, label='Validation')
plt.legend(fontsize=16)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel('Epoch', fontsize=16)
plt.ylabel('Accuracy', fontsize=16)
plt.tight_layout()
save_fig(plt, file_prefix=os.path.join(model_dir, 'Loss'))
plt.show()
```
## 汎化能力の推定
```
from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score
import seaborn as sns
def evalulate(y_true, y_pred, file_prefix=''):
cm = confusion_matrix(y_true, y_pred)
# print(cm)
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred, average=None)
recall = recall_score(y_true, y_pred, average=None)
print('正解率')
print(f' {accuracy}')
class_labels = []
for i in range(y_true.max() + 1):
class_labels.append(f'{i:4d}')
precision_str = []
recall_str = []
for i in range(y_true.max() + 1):
precision_str.append(f'{precision[i]}')
recall_str.append(f'{recall[i]}')
print('精度')
print(' ' + ' '.join(class_labels))
print(' ' + ' '.join(precision_str))
print('再現率')
print(' ' + ' '.join(class_labels))
print(' ' + ' '.join(recall_str))
plt.figure(figsize = (10,7))
sns.heatmap(cm, annot=True, fmt='3d', square=True, cmap='hot')
plt.tight_layout()
save_fig(plt, file_prefix=file_prefix)
plt.show()
import pathlib
checkpoints = pathlib.Path(model_dir).glob('*.h5')
checkpoints = sorted(checkpoints, key=lambda cp:cp.stat().st_mtime)
latest = str(checkpoints[-1])
model.load_weights(latest)
batch_size = 25
img_seq_validation = ImageSequence(val_list, val_labels, shuffle=False, batch_size=batch_size)
y_pred = model.predict_generator(img_seq_validation)
y_pred_classes = y_pred.argmax(axis=1)
y_true = np.array(val_labels)
evalulate(y_true, y_pred_classes, file_prefix=os.path.join(model_dir, 'cm'))
```
| github_jupyter |
# Query Classifier Tutorial
[](https://colab.research.google.com/github/deepset-ai/haystack/blob/master/tutorials/Tutorial14_Query_Classifier.ipynb)
In this tutorial we introduce the query classifier the goal of introducing this feature was to optimize the overall flow of Haystack pipeline by detecting the nature of user queries. Now, the Haystack can detect primarily three types of queries using both light-weight SKLearn Gradient Boosted classifier or Transformer based more robust classifier. The three categories of queries are as follows:
### 1. Keyword Queries:
Such queries don't have semantic meaning and merely consist of keywords. For instance these three are the examples of keyword queries.
* arya stark father
* jon snow country
* arya stark younger brothers
### 2. Interrogative Queries:
In such queries users usually ask a question, regardless of presence of "?" in the query the goal here is to detect the intent of the user whether any question is asked or not in the query. For example:
* who is the father of arya stark ?
* which country was jon snow filmed ?
* who are the younger brothers of arya stark ?
### 3. Declarative Queries:
Such queries are variation of keyword queries, however, there is semantic relationship between words. Fo example:
* Arya stark was a daughter of a lord.
* Jon snow was filmed in a country in UK.
* Bran was brother of a princess.
In this tutorial, you will learn how the `TransformersQueryClassifier` and `SklearnQueryClassifier` classes can be used to intelligently route your queries, based on the nature of the user query. Also, you can choose between a lightweight Gradients boosted classifier or a transformer based classifier.
Furthermore, there are two types of classifiers you can use out of the box from Haystack.
1. Keyword vs Statement/Question Query Classifier
2. Statement vs Question Query Classifier
As evident from the name the first classifier detects the keywords search queries and semantic statements like sentences/questions. The second classifier differentiates between question based queries and declarative sentences.
### Prepare environment
#### Colab: Enable the GPU runtime
Make sure you enable the GPU runtime to experience decent speed in this tutorial.
**Runtime -> Change Runtime type -> Hardware accelerator -> GPU**
<img src="https://raw.githubusercontent.com/deepset-ai/haystack/master/docs/img/colab_gpu_runtime.jpg">
These lines are to install Haystack through pip
```
# Install the latest release of Haystack in your own environment
#! pip install farm-haystack
# Install the latest master of Haystack
!pip install --upgrade pip
!pip install git+https://github.com/deepset-ai/haystack.git#egg=farm-haystack[colab]
# Install pygraphviz
!apt install libgraphviz-dev
!pip install pygraphviz
# In Colab / No Docker environments: Start Elasticsearch from source
! wget https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-7.9.2-linux-x86_64.tar.gz -q
! tar -xzf elasticsearch-7.9.2-linux-x86_64.tar.gz
! chown -R daemon:daemon elasticsearch-7.9.2
import os
from subprocess import Popen, PIPE, STDOUT
es_server = Popen(
["elasticsearch-7.9.2/bin/elasticsearch"], stdout=PIPE, stderr=STDOUT, preexec_fn=lambda: os.setuid(1) # as daemon
)
# wait until ES has started
! sleep 30
```
If running from Colab or a no Docker environment, you will want to start Elasticsearch from source
## Initialization
Here are some core imports
Then let's fetch some data (in this case, pages from the Game of Thrones wiki) and prepare it so that it can
be used indexed into our `DocumentStore`
```
from haystack.utils import (
print_answers,
print_documents,
fetch_archive_from_http,
convert_files_to_docs,
clean_wiki_text,
launch_es,
)
from haystack.pipelines import Pipeline
from haystack.document_stores import ElasticsearchDocumentStore
from haystack.nodes import (
BM25Retriever,
EmbeddingRetriever,
FARMReader,
TransformersQueryClassifier,
SklearnQueryClassifier,
)
# Download and prepare data - 517 Wikipedia articles for Game of Thrones
doc_dir = "data/tutorial14"
s3_url = "https://s3.eu-central-1.amazonaws.com/deepset.ai-farm-qa/datasets/documents/wiki_gameofthrones_txt14.zip"
fetch_archive_from_http(url=s3_url, output_dir=doc_dir)
# convert files to dicts containing documents that can be indexed to our datastore
got_docs = convert_files_to_docs(dir_path=doc_dir, clean_func=clean_wiki_text, split_paragraphs=True)
# Initialize DocumentStore and index documents
launch_es()
document_store = ElasticsearchDocumentStore()
document_store.delete_documents()
document_store.write_documents(got_docs)
# Initialize Sparse retriever
bm25_retriever = BM25Retriever(document_store=document_store)
# Initialize dense retriever
embedding_retriever = EmbeddingRetriever(
document_store=document_store,
model_format="sentence_transformers",
embedding_model="sentence-transformers/multi-qa-mpnet-base-dot-v1",
)
document_store.update_embeddings(embedding_retriever, update_existing_embeddings=False)
reader = FARMReader(model_name_or_path="deepset/roberta-base-squad2")
```
## Keyword vs Question/Statement Classifier
The keyword vs question/statement query classifier essentially distinguishes between the keyword queries and statements/questions. So you can intelligently route to different retrieval nodes based on the nature of the query. Using this classifier can potentially yield the following benefits:
* Getting better search results (e.g. by routing only proper questions to DPR / QA branches and not keyword queries)
* Less GPU costs (e.g. if 50% of your traffic is only keyword queries you could just use elastic here and save the GPU resources for the other 50% of traffic with semantic queries)
![image]()
Below, we define a `SklearnQueryClassifier` and show how to use it:
Read more about the trained model and dataset used [here](https://ext-models-haystack.s3.eu-central-1.amazonaws.com/gradboost_query_classifier/readme.txt)
```
# Here we build the pipeline
sklearn_keyword_classifier = Pipeline()
sklearn_keyword_classifier.add_node(component=SklearnQueryClassifier(), name="QueryClassifier", inputs=["Query"])
sklearn_keyword_classifier.add_node(
component=embedding_retriever, name="EmbeddingRetriever", inputs=["QueryClassifier.output_1"]
)
sklearn_keyword_classifier.add_node(component=bm25_retriever, name="ESRetriever", inputs=["QueryClassifier.output_2"])
sklearn_keyword_classifier.add_node(component=reader, name="QAReader", inputs=["ESRetriever", "EmbeddingRetriever"])
sklearn_keyword_classifier.draw("pipeline_classifier.png")
# Run only the dense retriever on the full sentence query
res_1 = sklearn_keyword_classifier.run(query="Who is the father of Arya Stark?")
print("Embedding Retriever Results" + "\n" + "=" * 15)
print_answers(res_1, details="minimum")
# Run only the sparse retriever on a keyword based query
res_2 = sklearn_keyword_classifier.run(query="arya stark father")
print("ES Results" + "\n" + "=" * 15)
print_answers(res_2, details="minimum")
# Run only the dense retriever on the full sentence query
res_3 = sklearn_keyword_classifier.run(query="which country was jon snow filmed ?")
print("Embedding Retriever Results" + "\n" + "=" * 15)
print_answers(res_3, details="minimum")
# Run only the sparse retriever on a keyword based query
res_4 = sklearn_keyword_classifier.run(query="jon snow country")
print("ES Results" + "\n" + "=" * 15)
print_answers(res_4, details="minimum")
# Run only the dense retriever on the full sentence query
res_5 = sklearn_keyword_classifier.run(query="who are the younger brothers of arya stark ?")
print("Embedding Retriever Results" + "\n" + "=" * 15)
print_answers(res_5, details="minimum")
# Run only the sparse retriever on a keyword based query
res_6 = sklearn_keyword_classifier.run(query="arya stark younger brothers")
print("ES Results" + "\n" + "=" * 15)
print_answers(res_6, details="minimum")
```
## Transformer Keyword vs Question/Statement Classifier
Firstly, it's essential to understand the trade-offs between SkLearn and Transformer query classifiers. The transformer classifier is more accurate than SkLearn classifier however, it requires more memory and most probably GPU for faster inference however the transformer size is roughly `50 MBs`. Whereas, SkLearn is less accurate however is much more faster and doesn't require GPU for inference.
Below, we define a `TransformersQueryClassifier` and show how to use it:
Read more about the trained model and dataset used [here](https://huggingface.co/shahrukhx01/bert-mini-finetune-question-detection)
```
# Here we build the pipeline
transformer_keyword_classifier = Pipeline()
transformer_keyword_classifier.add_node(
component=TransformersQueryClassifier(), name="QueryClassifier", inputs=["Query"]
)
transformer_keyword_classifier.add_node(
component=embedding_retriever, name="EmbeddingRetriever", inputs=["QueryClassifier.output_1"]
)
transformer_keyword_classifier.add_node(
component=bm25_retriever, name="ESRetriever", inputs=["QueryClassifier.output_2"]
)
transformer_keyword_classifier.add_node(component=reader, name="QAReader", inputs=["ESRetriever", "EmbeddingRetriever"])
transformer_keyword_classifier.draw("pipeline_classifier.png")
# Run only the dense retriever on the full sentence query
res_1 = transformer_keyword_classifier.run(query="Who is the father of Arya Stark?")
print("Embedding Retriever Results" + "\n" + "=" * 15)
print_answers(res_1, details="minimum")
# Run only the sparse retriever on a keyword based query
res_2 = transformer_keyword_classifier.run(query="arya stark father")
print("ES Results" + "\n" + "=" * 15)
print_answers(res_2, details="minimum")
# Run only the dense retriever on the full sentence query
res_3 = transformer_keyword_classifier.run(query="which country was jon snow filmed ?")
print("Embedding Retriever Results" + "\n" + "=" * 15)
print_answers(res_3, details="minimum")
# Run only the sparse retriever on a keyword based query
res_4 = transformer_keyword_classifier.run(query="jon snow country")
print("ES Results" + "\n" + "=" * 15)
print_answers(res_4, details="minimum")
# Run only the dense retriever on the full sentence query
res_5 = transformer_keyword_classifier.run(query="who are the younger brothers of arya stark ?")
print("Embedding Retriever Results" + "\n" + "=" * 15)
print_answers(res_5, details="minimum")
# Run only the sparse retriever on a keyword based query
res_6 = transformer_keyword_classifier.run(query="arya stark younger brothers")
print("ES Results" + "\n" + "=" * 15)
print_answers(res_6, details="minimum")
```
## Question vs Statement Classifier
One possible use case of this classifier could be to route queries after the document retrieval to only send questions to QA reader and in case of declarative sentence, just return the DPR/ES results back to user to enhance user experience and only show answers when user explicitly asks it.
![image]()
Below, we define a `TransformersQueryClassifier` and show how to use it:
Read more about the trained model and dataset used [here](https://huggingface.co/shahrukhx01/question-vs-statement-classifier)
```
# Here we build the pipeline
transformer_question_classifier = Pipeline()
transformer_question_classifier.add_node(component=embedding_retriever, name="EmbeddingRetriever", inputs=["Query"])
transformer_question_classifier.add_node(
component=TransformersQueryClassifier(model_name_or_path="shahrukhx01/question-vs-statement-classifier"),
name="QueryClassifier",
inputs=["EmbeddingRetriever"],
)
transformer_question_classifier.add_node(component=reader, name="QAReader", inputs=["QueryClassifier.output_1"])
transformer_question_classifier.draw("question_classifier.png")
# Run only the QA reader on the question query
res_1 = transformer_question_classifier.run(query="Who is the father of Arya Stark?")
print("Embedding Retriever Results" + "\n" + "=" * 15)
print_answers(res_1, details="minimum")
res_2 = transformer_question_classifier.run(query="Arya Stark was the daughter of a Lord.")
print("ES Results" + "\n" + "=" * 15)
print_documents(res_2)
```
## Standalone Query Classifier
Below we run queries classifiers standalone to better understand their outputs on each of the three types of queries
```
# Here we create the keyword vs question/statement query classifier
from haystack.nodes import TransformersQueryClassifier
queries = [
"arya stark father",
"jon snow country",
"who is the father of arya stark",
"which country was jon snow filmed?",
]
keyword_classifier = TransformersQueryClassifier()
for query in queries:
result = keyword_classifier.run(query=query)
if result[1] == "output_1":
category = "question/statement"
else:
category = "keyword"
print(f"Query: {query}, raw_output: {result}, class: {category}")
# Here we create the question vs statement query classifier
from haystack.nodes import TransformersQueryClassifier
queries = [
"Lord Eddard was the father of Arya Stark.",
"Jon Snow was filmed in United Kingdom.",
"who is the father of arya stark?",
"Which country was jon snow filmed in?",
]
question_classifier = TransformersQueryClassifier(model_name_or_path="shahrukhx01/question-vs-statement-classifier")
for query in queries:
result = question_classifier.run(query=query)
if result[1] == "output_1":
category = "question"
else:
category = "statement"
print(f"Query: {query}, raw_output: {result}, class: {category}")
```
## Conclusion
The query classifier gives you more possibility to be more creative with the pipelines and use different retrieval nodes in a flexible fashion. Moreover, as in the case of Question vs Statement classifier you can also choose the queries which you want to send to the reader.
Finally, you also have the possible of bringing your own classifier and plugging it into either `TransformersQueryClassifier(model_name_or_path="<huggingface_model_name_or_file_path>")` or using the `SklearnQueryClassifier(model_name_or_path="url_to_classifier_or_file_path_as_pickle", vectorizer_name_or_path="url_to_vectorizer_or_file_path_as_pickle")`
## About us
This [Haystack](https://github.com/deepset-ai/haystack/) notebook was made with love by [deepset](https://deepset.ai/) in Berlin, Germany
We bring NLP to the industry via open source!
Our focus: Industry specific language models & large scale QA systems.
Some of our other work:
- [German BERT](https://deepset.ai/german-bert)
- [GermanQuAD and GermanDPR](https://deepset.ai/germanquad)
- [FARM](https://github.com/deepset-ai/FARM)
Get in touch:
[Twitter](https://twitter.com/deepset_ai) | [LinkedIn](https://www.linkedin.com/company/deepset-ai/) | [Slack](https://haystack.deepset.ai/community/join) | [GitHub Discussions](https://github.com/deepset-ai/haystack/discussions) | [Website](https://deepset.ai)
By the way: [we're hiring!](https://www.deepset.ai/jobs)
| github_jupyter |
# Chapter 3: Inferential statistics
[Link to outline](https://docs.google.com/document/d/1fwep23-95U-w1QMPU31nOvUnUXE2X3s_Dbk5JuLlKAY/edit#heading=h.uutryzqeo2av)
Concept map:

#### Notebook setup
```
# loading Python modules
import math
import random
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.stats.distributions import norm
# set random seed for repeatability
np.random.seed(42)
# notebooks figs setup
%matplotlib inline
import matplotlib.pyplot as plt
sns.set(rc={'figure.figsize':(8,5)})
blue, orange = sns.color_palette()[0], sns.color_palette()[1]
# silence annoying warnings
import warnings; warnings.filterwarnings('ignore')
```
## Overview
- Main idea = learn about a population based on a sample
- Recall Amy's two research questions about the employee lifetime value (ELV) data:
- Question 1 = Is there a difference between ELV of the two groups? → **hypothesis testing**
- Question 2 = How much difference in ELV does stats training provide? → **estimation**
- Inferential statistics provides us with tools to answer both of these questions
## Estimators
We'll begin our study of inferential statistics by introducing **estimators**,
which are used for both **hypothesis testing** and **estimation**.

$\def\stderr#1{\mathbf{se}_{#1}}$
$\def\stderrhat#1{\hat{\mathbf{se}}_{#1}}$
### Definitions
- We use the term "estimator" to describe a function $f$ that takes samples as inputs,
which is written mathematically as:
$$
f \ \colon \underbrace{\mathcal{X}\times \mathcal{X}\times \cdots \times \mathcal{X}}_{n \textrm{ copies}}
\quad \to \quad \mathbb{R},
$$
where $n$ is the samples size and $\mathcal{X}$ denotes the possible values of the random variable $X$.
- We give different names to estimators, depending on the use case:
- **statistic** = a function computed from samples (descriptive statistics)
- **parameter estimators** = statistics that estimates population parameters
- **test statistic** = an estimator used as part of hypothesis testing procedure
- The **value** of the estimator $f(\mathbf{x})$ is computer from a particular sample $\mathbf{x}$.
- The **sampling distribution** of an estimator is when $f$ is the distribution of $f(\mathbf{X})$,
where $\mathbf{X}$ is a random sample.
- Example of estimators we discussed in descriptive statistics:
- Sample mean
- estimator: $\overline{x} = g(\mathbf{x}) = \frac{1}{n}\sum_{i=1}^n x_i$
- gives an estimate for the population mean $\mu$
- sampling distribution: $\overline{X} = g(\mathbf{X}) = \frac{1}{n}\sum_{i=1}^n X_i$
- Sample variance
- estimator: $s^2 = h(\mathbf{x}) = \frac{1}{n-1}\sum_{i=1}^n (x_i-\overline{x})^2$
- gives an estimate for the population variance $\sigma^2$
- sampling distribution: $S^2 = h(\mathbf{X}) = \frac{1}{n-1}\sum_{i=1}^n (X_i-\overline{X})^2$
- In this notebook we focus on one estimator: **difference between group means**
- estimator: $d = \texttt{mean}(\mathbf{x}_A) - \texttt{mean}(\mathbf{x}_{B}) = \overline{x}_{A} - \overline{x}_{B}$
- gives an estimate for the difference between population means: $\Delta = \mu_A - \mu_{B}$
- sampling distribution: $D = \overline{X}_A - \overline{X}_{B}$, which is a random variable
### Difference between group means
Consider two random variables $X_A$ and $X_B$:
$$ \large
X_A \sim \mathcal{N}\!\left(\mu_A, \sigma^2_A \right)
\qquad
\textrm{and}
\qquad
X_B \sim \mathcal{N}\!\left(\mu_B, \sigma^2_B \right)
$$
that describe the probability distribution for groups A and B, respectively.
- A sample of size $n_A$ from $X_A$ is denoted $\mathbf{x}_A = x_1x_2\cdots x_{n_A}$=`xA`, and let $\mathbf{x}_B = x_1x_2\cdots x_{n_B}$=`xB` be a random sample of size $n_B$ from $X_B$.
- We compute the mean in each group: $\overline{x}_{A} = \texttt{mean}(\mathbf{x}_A)$
and $\overline{x}_{B} = \texttt{mean}(\mathbf{x}_B)$
- The value of the estimator is $d = \overline{x}_{A} - \overline{x}_{B}$
```
def dmeans(xA, xB):
"""
Estimator for the difference between group means.
"""
d = np.mean(xA) - np.mean(xB)
return d
```
Note the difference between group means is precisely the estimator Amy need for her analysis (**Group S** and **Group NS**). We intentionally use the labels **A** and **B** to illustrate the general case.
```
# example parameters for each group
muA, sigmaA = 300, 10
muB, sigmaB = 200, 20
# size of samples for each group
nA = 5
nB = 4
```
#### Particular value of the estimator `dmeans`
```
xA = norm(muA, sigmaA).rvs(nA) # random sample from Group A
xB = norm(muB, sigmaB).rvs(nB) # random sample from Group B
d = dmeans(xA, xB)
d
```
The value of $d$ computed from the samples is an estimate for the difference between means of two groups: $\Delta = \mu_A - \mu_{B}$ (which we know is $100$ in this example).
#### Sampling distribution of the estimator `dmeans`
How well does the estimate $d$ approximate the true value $\Delta$?
**What is the accuracy and variability of the estimates we can expect?**
To answer these questions, consider the random samples
$\mathbf{X}_A = X_1X_2\cdots X_{n_A}$
and $\mathbf{X}_B = X_1X_2\cdots X_{n_B}$,
then compute the **sampling distribution**: $D = \overline{X}_A - \overline{X}_{B}$.
By definition, the sampling distribution of the estimator is obtained by repeatedly generating samples `xA` and `xB` from the two distributions and computing `dmeans` on the random samples. For example, we can obtain the sampling distribution by generating $N=1000$ samples.
```
def get_sampling_dist(statfunc, meanA, stdA, nA, meanB, stdB, nB, N=1000):
"""
Obtain the sampling distribution of the statistic `statfunc`
from `N` random samples drawn from groups A and B with parmeters:
- Group A: `nA` values taken from `norm(meanA, stdA)`
- Group B: `nB` values taken from `norm(meanB, stdB)`
Returns a list of samples from the sampling distribution of `statfunc`.
"""
sampling_dist = []
for i in range(0, N):
xA = norm(meanA, stdA).rvs(nA) # random sample from Group A
xB = norm(meanB, stdB).rvs(nB) # random sample from Group B
stat = statfunc(xA, xB) # evaluate `statfunc`
sampling_dist.append(stat) # record the value of statfunc
return sampling_dist
# Generate the sampling distirbution for dmeans
dmeans_sdist = get_sampling_dist(statfunc=dmeans,
meanA=muA, stdA=sigmaA, nA=nA,
meanB=muB, stdB=sigmaB, nB=nB)
print("Generated", len(dmeans_sdist), "values from `dmeans(XA, XB)`")
# first 3 values
dmeans_sdist[0:3]
```
#### Plot the sampling distribution of `dmeans`
```
fig3, ax3 = plt.subplots()
title3 = "Samping distribution of D = mean($\mathbf{X}_A$) - mean($\mathbf{X}_B$) " + \
"for samples of size $n_A$ = " + str(nA) + \
" from $\mathcal{N}$(" + str(muA) + "," + str(sigmaA) + ")" + \
" and $n_B$ = " + str(nB) + \
" from $\mathcal{N}$(" + str(muB) + "," + str(sigmaB) + ")"
sns.distplot(dmeans_sdist, kde=False, norm_hist=True, ax=ax3)
_ = ax3.set_title(title3)
```
#### Theoretical model for the sampling distribution of `dmeans`
Let's use probability theory to build a theoretical model for the sampling distribution of the difference-between-means estimator `dmeans`.
- The central limit theorem
the rules of to obtain a model for the random variable $D = \overline{X}_A - \overline{X}_{B}$,
which describes the sampling distribution of `dmeans`.
- The central limit theorem tells us the sample mean within the two group are
$$ \large
\overline{X}_A \sim \mathcal{N}\!\left(\mu_A, \tfrac{\sigma^2_A}{n_A} \right)
\qquad \textrm{and} \qquad
\overline{X}_B \sim \mathcal{N}\!\left(\mu_B, \tfrac{\sigma^2_B}{n_B} \right)
$$
- The rules of probability theory tells us that the [difference of two normal random variables](https://en.wikipedia.org/wiki/Sum_of_normally_distributed_random_variables#Independent_random_variables) requires subtracting their means and adding their variance, so we get:
$$ \large
D \sim \mathcal{N}\!\left(\mu_A - \mu_B, \ \tfrac{\sigma^2_A}{n_A} + \tfrac{\sigma^2_B}{n_B} \right)
$$
In other words, the sampling distribution for the difference of means estimator has mean and standard deviation given by:
$$ \large
\mu_D = \mu_A - \mu_B
\qquad \textrm{and} \qquad
\sigma_D = \sqrt{ \tfrac{\sigma^2_A}{n_A} + \tfrac{\sigma^2_B}{n_B} }
$$
Let's plot the theoretical prediction on top of the simulated data to see if they are a good fit.
```
Dmean = muA - muB
Dstd = np.sqrt(sigmaA**2/nA + sigmaB**2/nB)
print("Probability theory predicts the sampling distribution had"
"mean", round(Dmean, 3),
"and standard deviation", round(Dstd, 3))
x = np.linspace(min(dmeans_sdist), max(dmeans_sdist), 10000)
D = norm(Dmean, Dstd).pdf(x)
label = 'Theory prediction'
ax3 = sns.lineplot(x, D, ax=ax3, label=label, color=blue)
fig3
```
### Regroup and reality check
How are you doing, dear readers?
I know this was a lot of math and a lot of code, but the good news is we're done now!
The key things to remember is that we have two ways to compute sampling distribution for any estimator:
- Repeatedly generate random samples from model and compute the estimator values (histogram)
- Use probability theory to obtain a analytical formula
#### Why are we doing all this modelling?
The estimator `dmeans` we defined above measures the quantity we're interested in:
the difference between the means of two groups (**Group S** and **Group NS** in Amy's statistical analysis of ELV data).
Using the functions we developed above, we now have the ability to simulate the data from any two groups by simply choosing the appropriate parameters. In particular if we choose `stdS=266`, `nS=30`; and `stdNS=233`, `nNS=31`,
we can generate random data that has similar variability to Amy ELV measurements.
Okay, dear reader, we're about to jump into the deep end of the statistics pool: **hypothesis testing**,
which is one of the two major ideas in the STATS 101 curriculum.
Heads up this will get complicated, but we have to go into it because it is an essential procedure
that is used widely in science, engineering, business, and other types of research.
You need to trust me this one: it's worth knowing this stuff, even if it is boring.
Don't worry about it though, since you have all the prerequisites needed to get through this!
____
Recall Amy's research Question 1:
Is there a difference between ELV of the employees in **Group S** and the employees in **Group NS**?
## Hypothesis testing
- An approach to formulating research questions as **yes-no decisions** and a **procedure for making these decisions**
- Hypothesis testing is a standardized procedure for doing statistical analysis
(also, using stats jargon makes everything look more convincing ;)
- We formulate research question as two **competing hypotheses**:
- **Null hypothesis $H_0$** = no effect
in our example: "no difference between means," which is written as $\color{red}{\mu_S = \mu_{NS} = \mu_0}$.
In other words, the probability models for the two groups are:
$$ \large
H_0: \qquad X_S = \mathcal{N}(\color{red}{\mu_0}, \sigma_S)
\quad \textrm{and} \quad
X_{NS} = \mathcal{N}(\color{red}{\mu_0}, \sigma_{NS}) \quad
$$
- **Alternative hypothesis $H_A$** = an effect exists
in our example: "means for Group S different from mean for Group NS", $\color{blue}{\mu_S} \neq \color{orange}{\mu_{NS}}$.
The probability models for the two groups are:
$$
H_A: \qquad X_S = \mathcal{N}(\color{blue}{\mu_S}, \sigma_S)
\quad \textrm{and} \quad
X_{NS} = \mathcal{N}(\color{orange}{\mu_{NS}}, \sigma_{NS})
$$
- The purpose of hypothesis testing is to perform a basic sanity-check to show the difference between the group means
we observed ($d = \overline{x}_{S} - \overline{x}_{NS} = 130$) is **unlikely to have occurred by chance**
- NEW CONCEPT: $p$-value is the probability of observing $d$ or more extreme under the null hypothesis.
### Overview of the hypothesis testing procedure
Here is the high-level overview of the hypothesis testing procedure:
- **inputs**: sample statistics computed from the observed data
(in our case the signal $\overline{x}_S$, $\overline{x}_{NS}$,
and our estimates of the noise $s^2_S$, and $s^2_{NS}$)
- **outputs**: a decision that is one of: "reject the null hypothesis" or "fail to reject the null hypothesis"

We'll now look at two different approaches for computing the sampling distribution of
the difference between group means statistic, $D = \overline{X}_S - \overline{X}_{NS}$:
permutation tests and analytical approximations.
### Interpreting the results of hypothesis testing (optional)
- The implication of rejecting the null hypothesis (no difference) is that there must is a difference between the group means.
In other words, the ELV data for employees who took the statistics training (**Group S**) is different form
the average ELV for employees who didn't take the statistics training (**Group NS**),
which is what Amy is trying to show.
- Note that rejecting null hypothesis (H0) is not the same as "proving" the alternative hypothesis (HA),
we have just shown that the data is unlikely under the null hypothesis and we must be *some* difference between the groups,
so is worth looking for *some* alternative hypothesis.
- The alternative hypothesis we picked above, $\mu_S \neq \mu_{NS}$, is just a placeholder,
that includes desirable effect: $\mu_S > \mu_{NS}$ (stats training improves ELV),
but also includes the opposite effect: $\mu_S < \mu_{NS}$ (stats training decreases ELV).
- Using statistics jargon, when we reject the hypothesis H0 we say we've observed a "statistically significant" result,
which sounds a lot more impressive statement than it actually is.
Recall hypothesis test is just used to rule out "occurred by chance," which is a very basic sanity check.
- The implication of failing to reject the null hypothesis is that the observed difference
between means is "not significant," meaning it could have occurred by chance,
so there is no need to search for an alternative hypothesis.
- Note that "failing to reject" is not the same as "proving" the null hypothesis
- Note also "failing to reject H0" doesn't mean we reject HA.
In fact, the alternative hypothesis didn't play any role in the calculations whatsoever.
I know all this sounds super complicated and roundabout (an it is!),
but you will get a hang of it in no time with some practice.
Trust me, you need to know this shit.
### Start by load data again...
First things first, let's reload the data which we prepared back in the DATA where we left off back in the [01_DATA.ipynb](./01_DATA.ipynb) notebook.
```
df = pd.read_csv('data/employee_lifetime_values.csv')
df
# remember the descriptive statistics
df.groupby("group").describe()
def dmeans(sample):
"""
Compute the difference between groups means.
"""
xS = sample[sample["group"]=="S"]["ELV"]
xNS = sample[sample["group"]=="NS"]["ELV"]
d = np.mean(xS) - np.mean(xNS)
return d
# the observed value in Amy's data
dmeans(df)
```
Our goal is to determine how likely or unlikely this observed value is under the null hypothesis $H_0$.
In the next two sections, we'll look at two different approaches for obtaining the sampling distribution of $D$ under $H_0$.
## Approach 1: Permutation test for hypothesis testing
- The permutation test allow us to reject $H_0$ using existing sample $\mathbf{x}$ that we have,
treating the sample as if it were a population.
- Relevant probability distributions:
- Sampling distribution = obtained from repeated samples from a hypothetical population under $H_0$.
- Approximate sampling distribution: obtained by **resampling data from the single sample we have**.
- Recall Goal 1: make sure data cannot be explained by $H_0$ (observed difference due to natural variability)
- We want to obtain an approximation of the sampling distribution under $H_0$
- The $H_0$ probability model describes a hypothetical scenario with **no difference between groups**,
which means data from **Group S** and **Group NS** comes the same distribution.
- To generate a new random sample $\mathbf{x}^p$ from $H_0$ model we can reuse the sample we have obtained $\mathbf{x}$, but randomly mix-up the group labels. Since under the $H_0$ model, the **S** and **NS** populations are identical, mixing up the labels should have no effect.
- The math term for "mixing up" is **permutation**, meaning
each value is input is randomly reassigned to a new random place in the output.
```
def resample_under_H0(sample, groupcol="group"):
"""
Return a copy of the dataframe `sample` with the labels in the column `groupcol`
modified based on a random permutation of the values in the original sample.
"""
resample = sample.copy()
labels = sample[groupcol].values
newlabels = np.random.permutation(labels)
resample[groupcol] = newlabels
return resample
resample_under_H0(df)
# resample
resample = resample_under_H0(df)
# compute the difference in means for the new labels
dmeans(resample)
```
The steps in the above code cell give us a simple way to generate samples from the null hypothesis and compute the value of `dmeans` statistic for these samples. We used the assumption of "no difference" under the null hypothesis, and translated this to the "forget the labels" interpretation.
#### Running a permutation test
We can repeat the resampling procedure `10000` times to get the sampling distribution of $D$ under $H_0$,
as illustrated in the code procedure below.
```
def permutation_test(sample, statfunc, groupcol="group", permutations=10000):
"""
Compute the p-value of the observed `statfunc(sample)` under the null hypothesis
where the labels in the `groupcol` are randomized.
"""
# 1. compute the observed value of the statistic for the sample
obsstat = statfunc(sample)
# 2. generate the sampling distr. using random permutations of the group labels
resampled_stats = []
for i in range(0, permutations):
resample = resample_under_H0(sample, groupcol=groupcol)
restat = statfunc(resample)
resampled_stats.append(restat)
# 3. compute p-value: how many `restat`s are equal-or-more-extreme than `obsstat`
tailstats = [restat for restat in resampled_stats \
if restat <= -abs(obsstat) or restat >= abs(obsstat)]
pvalue = len(tailstats) / len(resampled_stats)
return resampled_stats, pvalue
sampling_dist, pvalue = permutation_test(df, statfunc=dmeans)
# plot the sampling distribution in blue
sns.displot(sampling_dist, bins=200)
# plot red line for the observed statistic
obsstat = dmeans(df)
plt.axvline(obsstat, color='r')
# plot the values that are equal or more extreme in red
tailstats = [rs for rs in sampling_dist if rs <= -obsstat or rs >= obsstat]
_ = sns.histplot(tailstats, bins=200, color="red")
```
- Once we have the sampling distribution of `D` under $H_0$,
we can see where the observed value $d=130$
falls within this distribution.
- p-value: the probability of observing value $d$ or more extreme under the null hypothesis
```
pvalue
```
We can now make the decision based on the $p$-value and a pre-determined threshold:
- If the observed value $d$ is unlikely under $H_0$ ($p$-value less than 5% chance of occurring),
then our decision will be to "reject the null hypothesis."
- Otherwise, if the observed value $d$ is not that unusual ($p$-value greater than 5%),
we conclude that we have "failed to reject the null hypothesis."
```
if pvalue < 0.05:
print("DECISION: Reject H0", "( p-value =", pvalue, ")")
print(" There is a statistically significant difference between xS and xNS means")
else:
print("DECISION: Fail to reject H0")
print(" The difference between groups means could have occurred by chance")
```
#### Permutations test using SciPy
The above code was given only for illustrative purposes.
In practice, you can use the SciPy implementation of permutation test,
by calling `ttest_ind(..., permutations=10000)` to perform a permutation test, then obtain the $p$-value.
```
from scipy.stats import ttest_ind
xS = df[df["group"]=="S"]["ELV"]
xNS = df[df["group"]=="NS"]["ELV"]
ttest_ind(xS, xNS, permutations=10000).pvalue
```
#### Discussion
- The procedure we used is called a **permutations test** for comparison of group means.
- The permutation test takes it's name from the action of mixing up the group-membership labels
and computing a statistic which is a way to generate samples from the null hypothesis
in situations where we're comparing two groups.
- Permutation tests are very versatile since we can use them for any estimator $h(\mathbf{x})$.
For example, we could have used difference in medians by specifying the `median` as the input `statfunc`.
## Approach 2: Analytical approximations for hypothesis testing
We'll now look at another approach for answering Question 1:
using and analytical approximation,
which is the way normally taught in STATS 101 courses.
How likely or unlikely is the observed difference $d=130$ under the null hypothesis?
- Analytical approximations are math models for describing the sampling distribution under $H_0$
- Sampling distributions = obtained by repeated sampling from $H_0$
- Analytical approximation = probability distribution model based on estimated parameters
- Assumption: population is normally distributed
- Based on this assumption we can use the theoretical model we developed above for difference between group means
to obtain a **closed form expression** for the sampling distribution of $D$
- In particular, the probability model for the two groups under $H_0$ are:
$$ \large
H_0: \qquad X_S = \mathcal{N}(\color{red}{\mu_0}, \sigma_S)
\quad \textrm{and} \quad
X_{NS} = \mathcal{N}(\color{red}{\mu_0}, \sigma_{NS}), \quad
$$
from which we can derive the model for $D = \overline{X}_S - \overline{X}_{NS}$:
$$ \large
D \sim \mathcal{N}\!\left( \color{red}{0}, \ \tfrac{\sigma^2_S}{n_S} + \tfrac{\sigma^2_{NS}}{n_{NS}} \right)
$$
In words, the sampling distribution of the difference between group means is
normally distributed with mean $\mu_D = 0$ and variance $\sigma^2_D$ dependent
on the variance of the two groups $\sigma^2_S$ and $\sigma^2_{NS}$.
Recall we obtained this expression earlier when we discussed difference of means between groups A and B.
- However, the population variances are unknown $\sigma^2_S$ and $\sigma^2_{NS}$,
and we only have the estimated variances $s_S^2$ and $s_{NS}^2$ calculated from the sample.
- That's OK though, since sample variances are good approximation to the population variances.
There are two common ways to obtain an approximation for $\sigma^2_D$:
- Pooled variance: $\sigma^2_D \approx s^2_p = \frac{(n_S-1)s_S^2 \; + \; (n_{NS}-1)s_{NS}^2}{n_S + n_{NS} - 2}$
(takes advantage of assumption that both samples come from the same population under $H_0$)
- Unpooled variance: $\sigma^2_D \approx s^2_u = \tfrac{s^2_S}{n_S} + \tfrac{s^2_{NS}}{n_{NS}}$
(follows from general rule of prob theory)
- NEW CONCEPT: **Student's $t$-distribution** is a model for $D$ which takes into account
we are using $s_S^2$ and $s_{NS}^2$ instead of $\sigma_S^2$ and $\sigma_{NS}^2$.
- NEW CONCEPT: **degrees of freedom**, denoted `dof` in code or $\nu$ (Greek letter *nu*) in equations,
is the parameter Student's $t$ distribution related to the sample size used to estimate quantities.
### Student's t-test (pooled variance)
[Student's t-test for comparison of difference between groups means](https://statkat.com/stattest.php?&t=9),
is a procedure that makes use of the pooled variance $s^2_p$.
#### Black-box approach
The `scipy.stats` function `ttest_ind` will perform all the steps of the $t$-test procedure,
without the need for us to understand the details.
```
from scipy.stats import ttest_ind
# extract data for two groups
xS = df[df["group"]=="S"]['ELV']
xNS = df[df["group"]=="NS"]['ELV']
# run the complete t-test procedure for ind-ependent samples:
result = ttest_ind(xS, xNS)
result.pvalue
```
The $p$-value is less than 0.05 so our decision is to **reject the null hypothesis**.
#### Student's t-test under the hood
The computations hidden behind the function `ttest_ind` involve a six step procedure that makes use of the pooled variance $s^2_p$.
```
from statistics import stdev
from scipy.stats.distributions import t
# 1. calculate the mean in each group
meanS, meanNS = np.mean(xS), np.mean(xNS)
# 2. calculate d, the observed difference between means
d = meanS - meanNS
# 3. calculate the standard deviations in each group
stdS, stdNS = stdev(xS), stdev(xNS)
nS, nNS = len(xS), len(xNS)
# 4. compute the pooled variance and standard error
var_pooled = ((nS-1)*stdS**2 + (nNS-1)*stdNS**2)/(nS + nNS - 2)
std_pooled = np.sqrt(var_pooled)
std_err = np.sqrt(std_pooled**2/nS + std_pooled**2/nNS)
# 5. compute the value of the t-statistic
tstat = d / std_err
# 6. obtain the p-value for the t-statistic from a
# t-distribution with 31+30-2 = 59 degrees of freedom
dof = nS + nNS - 2
pvalue = 2 * t(dof).cdf(-abs(tstat)) # 2* because two-sided
pvalue
```
#### Welch's t-test (unpooled variances)
An [alternative t-test procedure](https://statkat.com/stattest.php?&t=9) that doesn't assume the variances in groups are equal.
```
result2 = ttest_ind(xS, xNS, equal_var=False)
result2.pvalue
```
Welch's $t$-test differs only in steps 4 through 6 as shown below:
```
# 4'. compute the unpooled standard deviation of D
stdD = np.sqrt(stdS**2/nS + stdNS**2/nNS)
# 5'. compute the value of the t-statistic
tstat = d / stdD
# 6'. obtain the p-value from a t-distribution with
# (insert crazy formula here) degrees of freedom
dof = (stdS**2/nS + stdNS**2/nNS)**2 / \
((stdS**2/nS)**2/(nS-1) + (stdNS**2/nNS)**2/(nNS-1) )
pvalue = 2 * t(dof).cdf(-abs(tstat)) # 2* because two-sided
pvalue
```
### Summary of Question 1
We saw two ways to answer Question 1 (is there a difference between group means) and obtain the p-value.
We interpreted the small p-values as evidence that the observed difference, $d=130$, is unlikely to be due to chance,
i.e. we rejected the null hypothesis.
Note this whole procedure is just a sanity check—we haven't touched the alternative hypothesis at all yet,
and for all we know the stats training could have the effect of decreasing ELV!
____
It's time to study Question 2, which is to estimate the magnitude of the change in ELV obtained from completing the stats training, which is called *effect size* in statistics.
## Estimating the effect size
- Question 2 of statistical analysis is to estimate the difference in ELV gained by stats training.
- NEW CONCEPT: **effect size** is a measure of difference between intervention and control groups.
- We assume the data of **Group S** and **Group NS** come from different populations with means $\mu_S$ and $\mu_{NS}$
- We're interested in the difference between population means, denoted $\Delta = \mu_S - \mu_{NS}$.
- By analyzing the sample, we have obtained an estimate $d=130$ for the unknown $\Delta$,
but we know our data contains lots of variability, so we know our estimate might be off.
- We want an answer to Question 2 (What is the estimated difference between group means?)
that takes into account the variability of the data.
- NEW CONCEPT: **confidence interval** is a way to describe a range of values for an estimate
- We want to provide an answer to Question 2 in the form of a confidence interval that tells
us a range of values where we believe the true value of $\Delta$ falls.
- Similar to how we showed to approaches for hypothesis testing,
we'll work on effect size estimation using two approaches: resampling methods and analytical approximations.
### Approach 1: estimate the effect size using bootstrap method
- We want to estimate the distribution of ELV values for the two groups,
and compute the difference between the means of these distributions.
- Distributions:
- Sampling distributions = obtained by repeated sampling from the populations
- Bootstrap sampling distributions = resampling data from the samples we have (with replacement)
- Intuition: treat the samples as if they were the population
- We'll compute $B=5000$ bootstrap samples from the two groups and compute the difference,
then look at the distribution of the bootstrap sample difference to obtain $CI_{\Delta}$,
the confidence interval for the difference between population means.
```
from statistics import mean
def bootstrap_stat(sample, statfunc=mean, B=5000):
"""
Compute the bootstrap estimate of the function `statfunc` from the sample.
Returns a list of statistic values from bootstrap samples.
"""
n = len(sample)
bstats = []
for i in range(0, B):
bsample = np.random.choice(sample, n, replace=True)
bstat = statfunc(bsample)
bstats.append(bstat)
return bstats
# load data for two groups
df = pd.read_csv('data/employee_lifetime_values.csv')
xS = df[df["group"]=="S"]['ELV']
xNS = df[df["group"]=="NS"]['ELV']
# compute bootstrap estimates for mean in each group
meanS_bstats = bootstrap_stat(xS, statfunc=mean)
meanNS_bstats = bootstrap_stat(xNS, statfunc=mean)
# compute the difference between means from bootstrap samples
dmeans_bstats = []
for bmeanS, bmeanNS in zip(meanS_bstats, meanNS_bstats):
d = bmeanS - bmeanNS
dmeans_bstats.append(d)
sns.displot(dmeans_bstats)
# 90% confidence interval for the difference in means
CI_boot = [np.percentile(dmeans_bstats, 5), np.percentile(dmeans_bstats, 95)]
CI_boot
```
#### SciPy bootstrap method
```
from scipy.stats import bootstrap
def dmeans2(sample1, sample2):
return np.mean(sample1) - np.mean(sample2)
res = bootstrap((xS, xNS), statistic=dmeans2, vectorized=False,
confidence_level=0.9, n_resamples=5000, method='percentile')
CI_boot2 = [res.confidence_interval.low, res.confidence_interval.high]
CI_boot2
```
### Approach 2: Estimates using analytical approximation method
- Assumption 1: populations for **Group S** and **Group NS** are normally distributed
- Assumption 2: the variance of the two populations is the same (or approximately equal)
- Using the theoretical model for the populations,
we can obtain a formula for CI of effect size $\Delta$:
$$
\textrm{CI}_{(1-\alpha)}
= \left[ d - t^*\!\cdot\!\sigma_D, \,
d + t^*\!\cdot\!\sigma_D
\right].
$$
The confidence interval is centred at $d$,
with width proportional to the standard deviation $\sigma_D$.
The constant $t^*$ denotes the value of the inverse CDF of Student's $t$-distribution
with appropriate number of degrees of freedom `dof` evaluated at $1-\frac{\alpha}{2}$.
For a 90% confidence interval, we choose $\alpha=0.10$,
which gives $(1-\frac{\alpha}{2}) = 0.95$, $t^* = F_{T_{\textrm{dof}}}^{-1}\left(0.95\right)$.
- We can use the two different analytical approximations to obtain a formula for $\sigma_D$
just as we did in the hypothesis testing:
- Pooled variance: $\sigma^2_p = \frac{(n_S-1)s_S^2 + (n_{NS}-1)s_{NS}^2}{n_S + n_{NS} - 2}$,
and `dof` = $n_S + n_{NS} -2$
- Unpooled variance: $\sigma^2_u = \tfrac{s^2_A}{n_A} + \tfrac{s^2_B}{n_B}$, and `dof` = [...](https://en.wikipedia.org/wiki/Student%27s_t-test#Equal_or_unequal_sample_sizes,_unequal_variances_(sX1_%3E_2sX2_or_sX2_%3E_2sX1))
#### Using pooled variance
The calculations are similar to Student's t-test for hypothesis testing.
```
from scipy.stats.distributions import t
d = np.mean(xS) - np.mean(xNS)
nS, nNS = len(xS), len(xNS)
stdS, stdNS = stdev(xS), stdev(xNS)
var_pooled = ((nS-1)*stdS**2 + (nNS-1)*stdNS**2)/(nS + nNS - 2)
std_pooled = np.sqrt(var_pooled)
std_err = std_pooled * np.sqrt(1/nS + 1/nNS)
dof = nS + nNS - 2
# for 90% confidence interval, need 10% in tails
alpha = 0.10
# now use inverse-CDF of Students t-distribution
tstar = abs(t(dof).ppf(alpha/2))
CI_tpooled = [d - tstar*std_err, d + tstar*std_err]
CI_tpooled
```
#### Using unpooled variance
The calculations are similar to the Welch's t-test for hypothesis testing.
```
d = np.mean(xS) - np.mean(xNS)
nS, nNS = len(xS), len(xNS)
stdS, stdNS = stdev(xS), stdev(xNS)
stdD = np.sqrt(stdS**2/nS + stdNS**2/nNS)
dof = (stdS**2/nS + stdNS**2/nNS)**2 / \
((stdS**2/nS)**2/(nS-1) + (stdNS**2/nNS)**2/(nNS-1) )
# for 90% confidence interval, need 10% in tails
alpha = 0.10
# now use inverse-CDF of Students t-distribution
tstar = abs(t(dof).ppf(alpha/2))
CI_tunpooled = [d - tstar*stdD, d + tstar*stdD]
CI_tunpooled
```
#### Summary of Question 2 results
We now have all the information we need to give a precise and nuanced answer to Question 2: "How big is the increase in ELV produced by stats training?".
The basic estimate of the difference is $130$ can be reported, and additionally can can report the 90% confidence interval for the difference between group means, that takes into account the variability in the data we have observed.
Note the CIs obtained using different approaches are all similar (+/- 5 ELV points), so it doesn't matter much which approach we use:
```
CI_boot, CI_boot2, CI_tpooled, CI_tunpooled
```
### Standardized effect size (optional)
It is sometimes useful to report the effect size using a "standardized" measure for effect sizes.
*Cohen's $d$* one such measure, and it is defined as the difference between two means divided by the pooled standard deviation.
```
def cohend(sample1, sample2):
"""
Compute Cohen's d measure of effect size for two independent samples.
"""
n1, n2 = len(sample1), len(sample2)
mean1, mean2 = np.mean(sample1), np.mean(sample2)
var1, var2 = np.var(sample1, ddof=1), np.var(sample2, ddof=1)
# calculate the pooled variance and standard deviaiton
var_pooled = ((n1-1)*var1 + (n2-1)*var2) / (n1 + n2 - 2)
std_pooled = np.sqrt(var_pooled)
# compute Cohen's d
cohend = (mean1 - mean2) / std_pooled
return cohend
cohend(xS, xNS)
```
We can interpret the value of Cohen's d obtained using the [reference table](https://en.wikipedia.org/wiki/Effect_size#Cohen's_d) of values:
| Cohen's d | Effect size |
| ----------- | ----------- |
| 0.01 | very small |
| 0.20 | small |
| 0.50 | medium |
| 0.80 | large |
We can therefore say the effect size of offering statistics training for employees has an **medium** effect size.
## Conclusion of Amy's statistical analysis
Recall the two research questions that Amy set out to answer in the beginning of this video series:
- Question 1: Is there a difference between the means in the two groups?
- Question 2: How much does statistics training improve the ELV of employees?
The statistical analysis we did allows us to answer these two questions as follows:
- Answer 1: There is a statistically significant difference between Group S and Group NS, p = 0.048.
- Answer 2: The estimated improvement in ELV is 130 points, which is corresponds to Cohen's d value of 0.52 (medium effect size). A 90% confidence interval for the true effect size is [25.9, 234.2].
Note: we used the numerical results obtained from resampling methods (Approach 1), but conclusions would be qualitatively the same if we reported results obtained from analytical approximations (Approach 2).
### Using statistics for convincing others
You may be wondering if all this probabilistic modelling and complicated statistical analysis was worth it to reach a conclusion that seems obvious in retrospect. Was all this work worth it? The purpose of all this work is to obtains something close to an objective conclusion. Without statistics it is very easy to fool ourselves and interpret patterns in data the way we want to, or alternatively, not see patterns that are present. By following the standard statistical procedures, we're less likely to fool ourselves, and more likely to be able to convince others.
It can very useful to imagine Amy explaining the results to a skeptical colleague. Suppose the colleague is very much against the idea of statistical training, and sees it as a distraction, saying things like "We hire employees to do a job, not to play with Python." and "I don't know any statistics and I'm doing my job just fine!" You get the picture.
Imagine Amy presenting her findings about how 100 hours of statistical training improves employee lifetime value (ELV) results after one year, and suggesting the statistical training be implemented for all new hires from now on. The skeptical colleague immediately rejects the idea and questions Amy's recommendation using emotional arguments like about necessity, time wasting, and how statistics is a specialty topic that is not required for all employees. Instead of arguing based on opinions and emotions with her colleague, Amy explains her recommendation is based on a statistical experiment she conducted, and shows the results.
- When the colleague asks if the observed difference could be due to chance, Amy says that this is unlikely, and quotes the p-value of 0.048 (less than 0.05), and interprets the result as saying the probability of observed difference between **Group S** and **Group NS** to be due to chance is less than 5%.
- The skeptical colleague is forced to concede that statistical training does improve ELV, but then asks about the effect size of the improvement: "How much more ELV can we expect if we provide statistics training?" Amy is ready to answer quoting the observed difference of $130$ ELV points, and further specifies the 90% confidence interval of [25.9, 234.2] for the improvement, meaning in the worst case there is 25 ELV points improvement.
The skeptic is forced to back down from their objections, and the "stats training for all" program is adopted in the company. Not only was Amy able to win the argument using statistics, but she was also able to set appropriate expectations for the results. In other words, she hasn't promised a guaranteed +130 ELV improvement, but a realistic range of values that can be expected.
## Comparison of resampling methods and analytical approximations
In this notebook we saw two different approaches for doing statistical analysis: resampling methods and analytical approximations. This is a general pattern in statistics where there is not only one correct answer: multiple approaches to data analysis are valid, and you need to think about the specifics of each data analysis situation. You'll learn about both approaches in the book.
Analytical approximations currently taught in most stats courses (STAT 101). Historically, analytical approximations have been used more widely because they require only simple arithmetic calculations: statistic practitioners (scientists, engineers, etc.) simply need to compute sample statistics, plug them into a formula, and obtain a $p$-value. This convenience is at the cost of numerous assumptions about the data distribution, which often don't hold in practice (e.g. assuming population is normal, when it is isn't).
In recent years, resampling methods like the permutation test and bootstrap estimation are becoming more popular and widely in industry, and increasingly also taught at to university students (*modern statistics*). **The main advantage so resampling methods is that they require less modelling assumptions.** Procedures like the permutation test can be applied broadly to any scenarios where two groups are compared, and don't require developing specific formulas for different cases. Resampling methods are easier to understand since the statistical procedure they require are directly related to the sampling distribution, and there are no formulas to memorize.
Understanding resampling methods requires some basic familiarity with programming, but the skills required are not advanced: knowledge of variables, expressions, and basic `for` loop is sufficient. If you were able to follow the code examples described above (see `resample_under_H0`, `permutation_test`, and `bootstrap_stat`), then you've already **seen all the code you will need for the entire book!**
## Other statistics topics in the book
The goal of this notebook was to focus on the two main ideas of inferential statistics ([Chapter 3](https://docs.google.com/document/d/1fwep23-95U-w1QMPU31nOvUnUXE2X3s_Dbk5JuLlKAY/edit#heading=h.uutryzqeo2av)): hypothesis testing and estimation. We didn't have time to cover many of the other important topics in statistics, which will be covered in the book (and in future notebooks). Here is a list of some of these topics:
- Null Hypothesis Significance Testing (NHST) procedure in full details (Type I and Type II error, power, sample size calculations)
- Statistical assumptions behind analytical approximations
- Cookbook of statistical analysis recipes (analytical approximations for different scenarios)
- Experimental design (how to plan and conduct statistical experiments)
- Misuses of statistics (caveats to watch out for and mistakes to avoid)
- Bayesian statistics (very deep topic; we'll cover only main ideas)
- Practice problems and exercises (real knowledge is when you can do the calculations yourself)
___
So far our statistical analysis was limited to comparing two groups, which is referred to as **categorical predictor variable** using stats jargon. In the next notebook we'll learn about statistical analysis with **continuous predictor variables**: instead of comparing stats vs. no-stats, we analyze what happens when variable amount of stats training is provided (a continuous predictor variable).
Open the notebook [04_LINEAR_MODELS.ipynb](./04_LINEAR_MODELS.ipynb) when you're ready to continue.
```
code = list(["um"])
```
| github_jupyter |
## Compare built-in Sagemaker classification algorithms for a binary classification problem using Iris dataset
In the notebook tutorial, we build 3 classification models using HPO and then compare the AUC on test dataset on 3 deployed models
IRIS is perhaps the best known database to be found in the pattern recognition literature. Fisher's paper is a classic in the field and is referenced frequently to this day. (See Duda & Hart, for example.) The data set contains 3 classes of 50 instances each, where each class refers to a type of iris plant. The dataset is built-in by default into R or can also be downloaded from https://archive.ics.uci.edu/ml/datasets/iris
The iris dataset, besides its historical importance, is also a fun dataset to play with since it can educate us about various ML techniques such as clustering, classification and regression, all in one dataset.
The dataset is built into any base R installation, so no download is required.
Attribute Information:
1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
5. Species of flowers: Iris setosa, Iris versicolor, Iris virginica
The prediction we will perform is `Species ~ f(sepal.length,sepal.width,petal.width,petal.length)`
Predicted attribute: Species of iris plant.
### Load required libraries and initialize variables.
```
rm(list=ls())
library(reticulate) # be careful not to install reticulate again. since it can cause problems.
library(tidyverse)
library(pROC)
set.seed(1324)
```
SageMaker needs to be imported using the reticulate library. If this was performed in a local computer, we would have to make sure that Python and appropriate SageMaker libraries are installed, but inside a SageMaker notebook R kernels, these are all pre-loaded and the R user does not have to worry about installing reticulate or Python.
Session is the unique session ID associated with each SageMaker call. It remains the same throughout the execution of the program and can be recalled later to close a session or open a new session.
The bucket is the Amazon S3 bucket where we will be storing our data output. The Amazon S3 bucket and prefix that you want to use for training and model data. This should be within the same region as the Notebook Instance, training, and hosting.
The role is the role of the SageMaker notebook as when it was initially deployed. The IAM role arn used to give training and hosting access to your data. See the documentation for how to create these. Note, if more than one role is required for notebook instances, training, and/or hosting, please replace the boto regexp with appropriate full IAM role arn string(s).
```
sagemaker <- import('sagemaker')
session <- sagemaker$Session()
bucket <- session$default_bucket() # you may replace with name of your personal S3 bucket
role_arn <- sagemaker$get_execution_role()
```
### Input the data and basic pre-processing
```
head(iris)
summary(iris)
```
In above, we see that there are 50 flowers of the setosa species, 50 flowers of the versicolor species, and 50 flowers of the virginica species.
In this case, the target variable is the Species prediction. We are trying to predict the species of the flower given its numerical measurements of Sepal length, sepal width, petal length, and petal width. Since we are trying to do binary classification, we will only take the flower species setosa and versicolor for simplicity. Also we will perform one-hot encoding on the categorical variable Species.
```
iris1 <- iris %>%
dplyr::select(Species,Sepal.Length,Sepal.Width,Petal.Length,Petal.Width) %>% # change order of columns such that the label column is the first column.
dplyr::filter(Species %in% c("setosa","versicolor")) %>% #only select two flower for binary classification.
dplyr::mutate(Species = as.numeric(Species) -1) # one-hot encoding,starting with 0 as setosa and 1 as versicolor.
head(iris1)
```
We now obtain some basic descriptive statistics of the features.
```
iris1 %>% group_by(Species) %>% summarize(mean_sepal_length = mean(Sepal.Length),
mean_petal_length = mean(Petal.Length),
mean_sepal_width = mean(Sepal.Width),
mean_petal_width = mean(Petal.Width),
)
```
In the summary statistics, we observe that mean sepal length is longer than mean petal length for both flowers.
### Prepare for modelling
##### We split the train and test and validate into 70%, 15%, and 15%, using random sampling.
```
iris_train <- iris1 %>%
sample_frac(size = 0.7)
iris_test <- anti_join(iris1, iris_train) %>%
sample_frac(size = 0.5)
iris_validate <- anti_join(iris1, iris_train) %>%
anti_join(., iris_test)
```
##### We do a check of the summary statistics to make sure train, test, validate datasets are appropriately split and have proper class balance.
```
table(iris_train$Species)
nrow(iris_train)
```
We see that the class balance between 0 and 1 is almost 50% each for the binary classification. We also see that there are 70 rows in the train dataset.
```
table(iris_validate$Species)
nrow(iris_validate)
```
We see that the class balance in validation dataset between 0 and 1 is almost 50% each for the binary classification. We also see that there are 15 rows in the validation dataset.
```
table(iris_test$Species)
nrow(iris_test)
```
We see that the class balance in test dataset between 0 and 1 is almost 50% each for the binary classification. We also see that there are 15 rows in the test dataset.
### Write the data to Amazon S3
Different algorithms in SageMaker will have different data formats required for training and for testing. These formats are created to make model production easier. csv is the most well known of these formats and has been used here as input in all algorithms to make it consistent.
SageMaker algorithms take in data from an Amazon S3 object and output data to an Amazon S3 object, so data has to be stored in Amazon S3 as csv,json, proto-buf or any format that is supported by the algorithm that you are going to use.
```
write_csv(iris_train, 'iris_train.csv', col_names = FALSE)
write_csv(iris_validate, 'iris_valid.csv', col_names = FALSE)
write_csv(iris_test, 'iris_test.csv', col_names = FALSE)
s3_train <- session$upload_data(path = 'iris_train.csv',
bucket = bucket,
key_prefix = 'data')
s3_valid <- session$upload_data(path = 'iris_valid.csv',
bucket = bucket,
key_prefix = 'data')
s3_test <- session$upload_data(path = 'iris_test.csv',
bucket = bucket,
key_prefix = 'data')
s3_train_input <- sagemaker$inputs$TrainingInput(s3_data = s3_train,
content_type = 'text/csv')
s3_valid_input <- sagemaker$inputs$TrainingInput(s3_data = s3_valid,
content_type = 'text/csv')
s3_test_input <- sagemaker$inputs$TrainingInput(s3_data = s3_test,
content_type = 'text/csv')
```
To perform Binary classification on Tabular data, SageMaker contains following algorithms:
- XGBoost Algorithm
- Linear Learner Algorithm,
- K-Nearest Neighbors (k-NN) Algorithm,
## Create model 1: XGBoost model in SageMaker
Use the XGBoost built-in algorithm to build an XGBoost training container as shown in the following code example. You can automatically spot the XGBoost built-in algorithm image URI using the SageMaker image_uris.retrieve API (or the get_image_uri API if using Amazon SageMaker Python SDK version 1). If you want to ensure if the image_uris.retrieve API finds the correct URI, see Common parameters for built-in algorithms and look up XGBoost from the full list of built-in algorithm image URIs and available regions.
After specifying the XGBoost image URI, you can use the XGBoost container to construct an estimator using the SageMaker Estimator API and initiate a training job. This XGBoost built-in algorithm mode does not incorporate your own XGBoost training script and runs directly on the input datasets.
See https://docs.aws.amazon.com/sagemaker/latest/dg/xgboost.html for more information.
```
container <- sagemaker$image_uris$retrieve(framework='xgboost', region= session$boto_region_name, version='latest')
cat('XGBoost Container Image URL: ', container)
s3_output <- paste0('s3://', bucket, '/output_xgboost')
estimator1 <- sagemaker$estimator$Estimator(image_uri = container,
role = role_arn,
train_instance_count = 1L,
train_instance_type = 'ml.m5.4xlarge',
input_mode = 'File',
output_path = s3_output,
output_kms_key = NULL,
base_job_name = NULL,
sagemaker_session = NULL)
```
How would an untuned model perform compared to a tuned model? Is it worth the effort? Before going deeper into XGBoost model tuning, let’s highlight the reasons why you have to tune your model. The main reason to perform hyper-parameter tuning is to increase predictability of our models by choosing our hyperparameters in a well thought manner. There are 3 ways to perform hyperparameter tuning: grid search, random search, bayesian search. Popular packages like scikit-learn use grid search and random search techniques. SageMaker uses Bayesian search techniques.
We need to choose
- a learning objective function to optimize during model training
- an eval_metric to use to evaluate model performance during validation
- a set of hyperparameters and a range of values for each to use when tuning the model automatically
SageMaker XGBoost model can be tuned with many hyperparameters. The hyperparameters that have the greatest effect on optimizing the XGBoost evaluation metrics are:
- alpha,
- min_child_weight,
- subsample,
- eta,
- num_round.
The hyperparameters that are required are num_class (the number of classes if it is a multi-class classification problem) and num_round ( the number of rounds to run the training on). All other hyperparameters are optional and will be set to default values if it is not specified by the user.
```
# check to make sure which are required and which are optional
estimator1$set_hyperparameters(eval_metric='auc',
objective='binary:logistic',
num_round = 6L
)
# Set Hyperparameter Ranges, check to make sure which are integer and which are continuos parameters.
hyperparameter_ranges = list('eta' = sagemaker$parameter$ContinuousParameter(0,1),
'min_child_weight'= sagemaker$parameter$ContinuousParameter(0,10),
'alpha'= sagemaker$parameter$ContinuousParameter(0,2),
'max_depth'= sagemaker$parameter$IntegerParameter(0L,10L))
```
The evaluation metric that we will use for our binary classification purpose is validation:auc, but you could use any other metric that is right for your problem. You do have to be careful to change your objective_type to point to the right direction of Maximize or Minimize according to the objective metric you have chosen.
```
# Create a hyperparamter tuner
objective_metric_name = 'validation:auc'
tuner1 <- sagemaker$tuner$HyperparameterTuner(estimator1,
objective_metric_name,
hyperparameter_ranges,
objective_type='Maximize',
max_jobs=4L,
max_parallel_jobs=2L)
# Define the data channels for train and validation datasets
input_data <- list('train' = s3_train_input,
'validation' = s3_valid_input)
# train the tuner
tuner1$fit(inputs = input_data,
job_name = paste('tune-xgb', format(Sys.time(), '%Y%m%d-%H-%M-%S'), sep = '-'),
wait=TRUE)
```
The output of the tuning job can be checked in SageMaker if needed.
### Calculate AUC for the test data on model 1
SageMaker will automatically recognize the training job with the best evaluation metric and load the hyperparameters associated with that training job when we deploy the model. One of the benefits of SageMaker is that we can easily deploy models in a different instance than the instance in which the notebook is running. So we can deploy into a more powerful instance or a less powerful instance.
```
model_endpoint1 <- tuner1$deploy(initial_instance_count = 1L,
instance_type = 'ml.t2.medium')
```
The serializer tells SageMaker what format the model expects data to be input in.
```
model_endpoint1$serializer <- sagemaker$serializers$CSVSerializer(content_type='text/csv')
```
We input the `iris_test` dataset without the labels into the model using the `predict` function and check its AUC value.
```
# Prepare the test sample for input into the model
test_sample <- as.matrix(iris_test[-1])
dimnames(test_sample)[[2]] <- NULL
# Predict using the deployed model
predictions_ep <- model_endpoint1$predict(test_sample)
predictions_ep <- stringr::str_split(predictions_ep, pattern = ',', simplify = TRUE)
predictions_ep <- as.numeric(predictions_ep > 0.5)
# Add the predictions to the test dataset.
iris_predictions_ep1 <- dplyr::bind_cols(predicted_flower = predictions_ep,
iris_test)
iris_predictions_ep1
# Get the AUC
auc(roc(iris_predictions_ep1$predicted_flower,iris_test$Species))
```
## Create model 2: Linear Learner in SageMaker
Linear models are supervised learning algorithms used for solving either classification or regression problems. For input, you give the model labeled examples (x, y). x is a high-dimensional vector and y is a numeric label. For binary classification problems, the label must be either 0 or 1.
The linear learner algorithm requires a data matrix, with rows representing the observations, and columns representing the dimensions of the features. It also requires an additional column that contains the labels that match the data points. At a minimum, Amazon SageMaker linear learner requires you to specify input and output data locations, and objective type (classification or regression) as arguments. The feature dimension is also required. You can specify additional parameters in the HyperParameters string map of the request body. These parameters control the optimization procedure, or specifics of the objective function that you train on. For example, the number of epochs, regularization, and loss type.
See https://docs.aws.amazon.com/sagemaker/latest/dg/linear-learner.html for more information.
```
container <- sagemaker$image_uris$retrieve(framework='linear-learner', region= session$boto_region_name, version='latest')
cat('Linear Learner Container Image URL: ', container)
s3_output <- paste0('s3://', bucket, '/output_glm')
estimator2 <- sagemaker$estimator$Estimator(image_uri = container,
role = role_arn,
train_instance_count = 1L,
train_instance_type = 'ml.m5.4xlarge',
input_mode = 'File',
output_path = s3_output,
output_kms_key = NULL,
base_job_name = NULL,
sagemaker_session = NULL)
```
For the text/csv input type, the first column is assumed to be the label, which is the target variable for prediction.
predictor_type is the only hyperparameter that is required to be pre-defined for tuning. The rest are optional.
Normalization, or feature scaling, is an important preprocessing step for certain loss functions that ensures the model being trained on a dataset does not become dominated by the weight of a single feature. Decision trees do not require normalization of their inputs; and since XGBoost is essentially an ensemble algorithm comprised of decision trees, it does not require normalization for the inputs either.
However, Generalized Linear Models require a normalization of their input. The Amazon SageMaker Linear Learner algorithm has a normalization option to assist with this preprocessing step. If normalization is turned on, the algorithm first goes over a small sample of the data to learn the mean value and standard deviation for each feature and for the label. Each of the features in the full dataset is then shifted to have mean of zero and scaled to have a unit standard deviation.
To make our job easier, we do not have to go back to our previous steps to do normalization. Normalization is built in as a hyper-parameter in SageMaker Linear learner algorithm. So no need to worry about normalization for the training portions.
```
estimator2$set_hyperparameters(predictor_type="binary_classifier",
normalize_data = TRUE)
```
The tunable hyperparameters for linear learner are:
- wd
- l1
- learning_rate
- mini_batch_size
- use_bias
- positive_example_weight_mult
Be careful to check which parameters are integers and which parameters are continuous because that is one of the common sources of errors. Also be careful to give a proper range for hyperparameters that makes sense for your problem. Training jobs can sometimes fail if the mini-batch size is too big compared to the training data available.
```
# Set Hyperparameter Ranges
hyperparameter_ranges = list('wd' = sagemaker$parameter$ContinuousParameter(0.00001,1),
'l1' = sagemaker$parameter$ContinuousParameter(0.00001,1),
'learning_rate' = sagemaker$parameter$ContinuousParameter(0.00001,1),
'mini_batch_size' = sagemaker$parameter$IntegerParameter(10L, 50L)
)
```
The evaluation metric we will be using in our case to compare the models will be the objective loss and is based on the validation dataset.
```
# Create a hyperparamter tuner
objective_metric_name = 'validation:objective_loss'
tuner2 <- sagemaker$tuner$HyperparameterTuner(estimator2,
objective_metric_name,
hyperparameter_ranges,
objective_type='Minimize',
max_jobs=4L,
max_parallel_jobs=2L)
# Create a tuning job name
job_name <- paste('tune-linear', format(Sys.time(), '%Y%m%d-%H-%M-%S'), sep = '-')
# Define the data channels for train and validation datasets
input_data <- list('train' = s3_train_input,
'validation' = s3_valid_input)
# Train the tuner
tuner2$fit(inputs = input_data, job_name = job_name, wait=TRUE, content_type='csv') # since we are using csv files as input into the model, we need to specify content type as csv.
```
### Calculate AUC for the test data on model 2
```
# Deploy the model into an instance of your choosing.
model_endpoint2 <- tuner2$deploy(initial_instance_count = 1L,
instance_type = 'ml.t2.medium')
```
For inference, the linear learner algorithm supports the application/json, application/x-recordio-protobuf, and text/csv formats. For more information, https://docs.aws.amazon.com/sagemaker/latest/dg/LL-in-formats.html
```
# Specify what data formats you want the input and output of your model to look like.
model_endpoint2$serializer <- sagemaker$serializers$CSVSerializer(content_type='text/csv')
model_endpoint2$deserializer <- sagemaker$deserializers$JSONDeserializer()
```
In Linear Learner the output inference files are in JSON or RecordIO formats. https://docs.aws.amazon.com/sagemaker/latest/dg/LL-in-formats.html
When you make predictions on new data, the contents of the response data depends on the type of model you choose within Linear Learner. For regression (predictor_type='regressor'), the score is the prediction produced by the model. For classification (predictor_type='binary_classifier' or predictor_type='multiclass_classifier'), the model returns a score and also a predicted_label. The predicted_label is the class predicted by the model and the score measures the strength of that prediction. So, for binary classification, predicted_label is 0 or 1, and score is a single floating point number that indicates how strongly the algorithm believes that the label should be 1.
To interpret the score in classification problems, you have to consider the loss function used. If the loss hyperparameter value is logistic for binary classification or softmax_loss for multiclass classification, then the score can be interpreted as the probability of the corresponding class. These are the loss values used by the linear learner when the `loss` hyperparameter is set to auto as default value. But if the `loss` is set to `hinge_loss`, then the score cannot be interpreted as a probability. This is because hinge loss corresponds to a Support Vector Classifier, which does not produce probability estimates. In the current example, since our loss hyperparameter is logistic for binary classification, we can interpret it as probability of the corresponding class.
```
# Prepare the test data for input into the model
test_sample <- as.matrix(iris_test[-1])
dimnames(test_sample)[[2]] <- NULL
# Predict using the test data on the deployed model
predictions_ep <- model_endpoint2$predict(test_sample)
# Add the predictions to the test dataset.
df <- data.frame(matrix(unlist(predictions_ep$predictions), nrow=length(predictions_ep$predictions), byrow=TRUE))
df <- df %>% dplyr::rename(score = X1, predicted_label = X2)
iris_predictions_ep2 <- dplyr::bind_cols(predicted_flower = df$predicted_label,
iris_test)
iris_predictions_ep2
# Get the AUC
auc(roc(iris_predictions_ep2$predicted_flower,iris_test$Species))
```
## Create model 3: KNN in SageMaker
Amazon SageMaker k-nearest neighbors (k-NN) algorithm is an index-based algorithm. It uses a non-parametric method for classification or regression. For classification problems, the algorithm queries the k points that are closest to the sample point and returns the most frequently used label of their class as the predicted label. For regression problems, the algorithm queries the k closest points to the sample point and returns the average of their feature values as the predicted value.
Training with the k-NN algorithm has three steps: sampling, dimension reduction, and index building. Sampling reduces the size of the initial dataset so that it fits into memory. For dimension reduction, the algorithm decreases the feature dimension of the data to reduce the footprint of the k-NN model in memory and inference latency. We provide two methods of dimension reduction methods: random projection and the fast Johnson-Lindenstrauss transform. Typically, you use dimension reduction for high-dimensional (d >1000) datasets to avoid the “curse of dimensionality” that troubles the statistical analysis of data that becomes sparse as dimensionality increases. The main objective of k-NN's training is to construct the index. The index enables efficient lookups of distances between points whose values or class labels have not yet been determined and the k nearest points to use for inference.
See https://docs.aws.amazon.com/sagemaker/latest/dg/k-nearest-neighbors.html for more information.
```
container <- sagemaker$image_uris$retrieve(framework='knn', region= session$boto_region_name, version='latest')
cat('KNN Container Image URL: ', container)
s3_output <- paste0('s3://', bucket, '/output_knn')
estimator3 <- sagemaker$estimator$Estimator(image_uri = container,
role = role_arn,
train_instance_count = 1L,
train_instance_type = 'ml.m5.4xlarge',
input_mode = 'File',
output_path = s3_output,
output_kms_key = NULL,
base_job_name = NULL,
sagemaker_session = NULL)
```
Hyperparameter `dimension_reduction_target` should not be set when `dimension_reduction_type` is set to its default value, which is `None`. If 'dimension_reduction_target' is set to a certain number without setting `dimension_reduction_type`, then SageMaker will ask us to remove 'dimension_reduction_target' from the specified hyperparameters and try again. In this tutorial, we are not performing dimensionality reduction, since we only have 4 features; so `dimension_reduction_type` is set to its default value of `None`.
```
estimator3$set_hyperparameters(
feature_dim = 4L,
sample_size = 10L,
predictor_type = "classifier"
)
```
Amazon SageMaker k-nearest neighbor model can be tuned with the following hyperparameters:
- k
- sample_size
```
# Set Hyperparameter Ranges
hyperparameter_ranges = list('k' = sagemaker$parameter$IntegerParameter(1L,10L)
)
# Create a hyperparamter tuner
objective_metric_name = 'test:accuracy'
tuner3 <- sagemaker$tuner$HyperparameterTuner(estimator3,
objective_metric_name,
hyperparameter_ranges,
objective_type='Maximize',
max_jobs=2L,
max_parallel_jobs=2L)
# Create a tuning job name
job_name <- paste('tune-knn', format(Sys.time(), '%Y%m%d-%H-%M-%S'), sep = '-')
# Define the data channels for train and validation datasets
input_data <- list('train' = s3_train_input,
'test' = s3_valid_input # KNN needs a test data, does not work without it.
)
# train the tuner
tuner3$fit(inputs = input_data, job_name = job_name, wait=TRUE, content_type='text/csv;label_size=0')
```
### Calculate AUC for the test data on model 3
```
# Deploy the model into an instance of your choosing.
model_endpoint3 <- tuner3$deploy(initial_instance_count = 1L,
instance_type = 'ml.t2.medium')
```
For inference, the linear learner algorithm supports the application/json, application/x-recordio-protobuf, and text/csv formats. For more information, https://docs.aws.amazon.com/sagemaker/latest/dg/LL-in-formats.html
```
# Specify what data formats you want the input and output of your model to look like.
model_endpoint3$serializer <- sagemaker$serializers$CSVSerializer(content_type='text/csv')
model_endpoint3$deserializer <- sagemaker$deserializers$JSONDeserializer()
```
In KNN, the input formats for inference are:
- CSV
- JSON
- JSONLINES
- RECORDIO
The output formats for inference are:
- JSON
- JSONLINES
- Verbose JSON
- Verbose RecordIO-ProtoBuf
Notice that there is no CSV output format for inference.
See https://docs.aws.amazon.com/sagemaker/latest/dg/kNN-inference-formats.html for more details.
When you make predictions on new data, the contents of the response data depends on the type of model you choose within Linear Learner. For regression (predictor_type='regressor'), the score is the prediction produced by the model. For classification (predictor_type='binary_classifier' or predictor_type='multiclass_classifier'), the model returns a score and also a predicted_label. The predicted_label is the class predicted by the model and the score measures the strength of that prediction. So, for binary classification, predicted_label is 0 or 1, and score is a single floating point number that indicates how strongly the algorithm believes that the label should be 1.
To interpret the score in classification problems, you have to consider the loss function used. If the loss hyperparameter value is logistic for binary classification or softmax_loss for multiclass classification, then the score can be interpreted as the probability of the corresponding class. These are the loss values used by the linear learner when the loss hyperparameter is set to auto as default value. But if the loss is set to hinge_loss, then the score cannot be interpreted as a probability. This is because hinge loss corresponds to a Support Vector Classifier, which does not produce probability estimates. In the current example, since our loss hyperparameter is logistic for binary classification, we can interpret it as probability of the corresponding class.
```
# Prepare the test data for input into the model
test_sample <- as.matrix(iris_test[-1])
dimnames(test_sample)[[2]] <- NULL
# Predict using the test data on the deployed model
predictions_ep <- model_endpoint3$predict(test_sample)
```
We see that the output is of a deserialized JSON format.
```
predictions_ep
typeof(predictions_ep)
# Add the predictions to the test dataset.
df = data.frame(predicted_flower = unlist(predictions_ep$predictions))
iris_predictions_ep2 <- dplyr::bind_cols(predicted_flower = df$predicted_flower,
iris_test)
iris_predictions_ep2
# Get the AUC
auc(roc(iris_predictions_ep2$predicted_flower,iris_test$Species))
```
## Compare the AUC of 3 models for the test data
- AUC of Sagemaker XGBoost = 1
- AUC of Sagemaker Linear Learner = 0.83
- AUC of Sagemaker KNN = 1
Based on the AUC metric (the higher the better), both XGBoost and KNN perform equally well and are better than the Linear Learner. We can also explore the 3 models with other binary classification metrics such as accuracy, F1 score, and misclassification error. Comparing only the AUC, in this example, we could chose either the XGBoost model or the KNN model to move onto production and close the other two. The deployed model of our choosing can be passed onto production to generate predictions of flower species given that the user only has its sepal and petal measurements. The performance of the deployed model can also be tracked in Amazon CloudWatch.
## Clean up
##### We close the endpoints which we created to free up resources.
```
model_endpoint1$delete_model()
model_endpoint2$delete_model()
model_endpoint3$delete_model()
session$delete_endpoint(model_endpoint1$endpoint)
session$delete_endpoint(model_endpoint2$endpoint)
session$delete_endpoint(model_endpoint3$endpoint)
```
| github_jupyter |
## This Notebook - Goals - FOR EDINA
**What?:**
- Standard classification method example/tutorial
**Who?:**
- Researchers in ML
- Students in computer science
- Teachers in ML/STEM
**Why?:**
- Demonstrate capability/simplicity of core scipy stack.
- Demonstrate common ML concept known to learners and used by researchers.
**Noteable features to exploit:**
- use of pre-installed libraries: <code>numpy</code>, <code>scikit-learn</code>, <code>matplotlib</code>
**How?:**
- clear to understand - minimise assumed knowledge
- clear visualisations - concise explanations
- recognisable/familiar - use standard methods
- Effective use of core libraries
<hr>
# Classification - K nearest neighbours
K nearest neighbours is a simple and effective way to deal with classification problems. This method classifies each sample based on the class of the points that are closest to it.
This is a supervised learning method, meaning that data used contains information on some feature that the model should predict.
This notebook shows the process of classifying handwritten digits.
<hr>
### Import libraries
On Noteable, all the libaries required for this notebook are pre-installed, so they simply need to be imported:
```
import numpy as np
import sklearn.datasets as ds
import sklearn.model_selection as ms
from sklearn import decomposition
from sklearn import neighbors
from sklearn import metrics
import matplotlib.pyplot as plt
%matplotlib inline
```
<hr>
# Data - Handwritten Digits
In terms of data, [scikit-learn](https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_digits.html) has a loading function for some data regarding hand written digits.
```
# get the digits data from scikit into the notebook
digits = ds.load_digits()
```
The cell above loads the data as a [bunch object](https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_digits.html), meaning that the data (in this case images of handwritten digits) and the target (the number that is written) can be split by accessing the attributes of the bunch object:
```
# store data and targets seperately
X = digits.data
y = digits.target
print("The data is of the shape", X.shape)
print("The target data is of the shape", y.shape)
```
The individual samples in the <code>X</code> array each represent an image. In this representation, 64 numbers are used to represent a greyscale value on an 8\*8 square. The images can be examined by using pyplot's [matshow](https://matplotlib.org/3.3.0/api/_as_gen/matplotlib.pyplot.matshow.html) function.
The next cell displays the 17th sample in the dataset as an 8\*8 image.
```
# create figure to display the 17th sample
fig = plt.matshow(digits.images[17], cmap=plt.cm.gray)
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
```
Suppose instead of viewing the 17th sample, we want to see the average of samples corresponding to a certain value.
This can be done as follows (using 0 as an example):
- All samples where the target value is 0 are located
- The mean of these samples is taken
- The resulting 64 long array is reshaped to be 8\*8 (for display)
- The image is displayed
```
# take samples with target=0
izeros = np.where(y == 0)
# take average across samples, reshape to visualise
zeros = np.mean(X[izeros], axis=0).reshape(8,8)
# display
fig = plt.matshow(zeros, cmap=plt.cm.gray)
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
```
<hr>
# Fit and test the model
## Split the data
Now that you have an understanding of the data, the model can be fitted.
Fitting the model involves setting some of the data aside for testing, and allowing the model to "see" the target values corresponding to the training samples.
Once the model has been fitted to the training data, the model will be tested on some data it has not seen before.
The next cell uses [train_test_split](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html) to shuffle all data, then set some data aside for testing later.
For this example, $\frac{1}{4}$ of the data will be set aside for testing, and the model will be trained on the remaining training set.
As before, <code>X</code> corresponds to data samples, and <code>y</code> corresponds to labels.
```
# split data to train and test sets
X_train, X_test, y_train, y_test = \
ms.train_test_split(X, y, test_size=0.25, shuffle=True,
random_state=22)
```
The data can be examined - here you can see that 1347 samples have been put into the training set, and 450 have been set aside for testing.
```
# print shape of data
print("training samples:", X_train.shape)
print("testing samples :", X_test.shape)
print("training targets:", y_train.shape)
print("testing targets :", y_test.shape)
```
## Using PCA to visualise data
Before diving into classifying, it is useful to visualise the data.
Since each sample has 64 dimensions, some dimensionality reduction is needed in order to visualise the samples as points on a 2D map.
One of the easiest ways of visualising high dimensional data is by principal component analysis (PCA). This maps the 64 dimensional image data onto a lower dimension map (here we will map to 2D) so it can be easily viewed on a screen.
In this case, the 2 most important "components" are maintained.
```
# create PCA model with 2 components
pca = decomposition.PCA(n_components=2)
```
The next step is to perform the PCA on the samples, and store the results.
```
# transform training data to 2 principal components
X_pca = pca.fit_transform(X_train)
# transform test data to 2 principal components
T_pca = pca.transform(X_test)
# check shape of result
print(X_pca.shape)
print(T_pca.shape)
```
As you can see from the above cell, the <code>X_pca</code> and <code>T_pca</code> data is now represented by only 2 elements per sample. The number of samples has remained the same.
Now that there is a 2D representation of the data, it can be plotted on a regular scatter graph. Since the labels corresponding to each point are stored in the <code>y_train</code> variable, the plot can be colour coded by target value!
Different coloured dots have different target values.
```
# choose the colours for each digit
cmap_digits = plt.cm.tab10
# plot training data with labels
plt.figure(figsize = (9,6))
plt.scatter(X_pca[:,0], X_pca[:,1], s=7, c=y_train,
cmap=cmap_digits, alpha=0.7)
plt.title("Training data coloured by target value")
plt.colorbar();
```
## Create and fit the model
The scikit-learn library allows fitting of a k-NN model just as with PCA above.
First, create the classifier:
```
# create model
knn = neighbors.KNeighborsClassifier()
```
The next step fits the k-NN model using the training data.
```
# fit model to training data
knn.fit(X_train,y_train);
```
## Test model
Now use the data that was set aside earlier - this stage involves getting the model to "guess" the samples (this time without seeing their target values).
Once the model has predicted the sample's class, a score can be calculated by checking how many samples the model guessed correctly.
```
# predict test data
preds = knn.predict(X_test)
# test model on test data
score = round(knn.score(X_test,y_test)*100, 2)
print("Score on test data: " + str(score) + "%")
```
98.44% is a really high score, one that would not likely be seen on real life applications of the method.
It can often be useful to visualise the results of your example. Below are plots showing:
- The labels that the model predicted for the test data
- The actual labels for the test data
- The data points that were incorrectly labelled
In this case, the predicted and actual plots are very similar, so these plots are not very informative. In other cases, this kind of visualisation may reveal patterns for you to explore further.
```
# plot 3 axes
fig, axes = plt.subplots(2,2,figsize=(12,12))
# top left axis for predictions
axes[0,0].scatter(T_pca[:,0], T_pca[:,1], s=5,
c=preds, cmap=cmap_digits)
axes[0,0].set_title("Predicted labels")
# top right axis for actual targets
axes[0,1].scatter(T_pca[:,0], T_pca[:,1], s=5,
c=y_test, cmap=cmap_digits)
axes[0,1].set_title("Actual labels")
# bottom left axis coloured to show correct and incorrect
axes[1,0].scatter(T_pca[:,0], T_pca[:,1], s=5,
c=(preds==y_test))
axes[1,0].set_title("Incorrect labels")
# bottom right axis not used
axes[1,1].set_axis_off()
```
So which samples did the model get wrong?
There were 7 samples that were misclassified. These can be displayed alongside their actual and predicted labels using the cell below:
```
# find the misclassified samples
misclass = np.where(preds!=y_test)[0]
# display misclassified samples
r, c = 1, len(misclass)
fig, axes = plt.subplots(r,c,figsize=(10,5))
for i in range(c):
ax = axes[i]
ax.matshow(X_test[misclass[i]].reshape(8,8),cmap=plt.cm.gray)
ax.set_axis_off()
act = y_test[misclass[i]]
pre = preds[misclass[i]]
strng = "actual: {a:.0f} \npredicted: {p:.0f}".format(a=act, p=pre)
ax.set_title(strng)
```
Additionally, a confusion matrix can be used to identify which samples are misclassified by the model. This can help you identify if their are samples that are commonly misidentified - for example you may identify that 8's are often mistook for 1's.
```
# confusion matrix
conf = metrics.confusion_matrix(y_test,preds)
# figure
f, ax = plt.subplots(figsize=(9,5))
im = ax.imshow(conf, cmap=plt.cm.RdBu)
# set labels as ticks on axes
ax.set_xticks(np.arange(10))
ax.set_yticks(np.arange(10))
ax.set_xticklabels(list(range(0,10)))
ax.set_yticklabels(list(range(0,10)))
ax.set_ylim(9.5,-0.5)
# axes labels
ax.set_ylabel("actual value")
ax.set_xlabel("predicted value")
ax.set_title("Digit classification confusion matrix")
# display
plt.colorbar(im).set_label(label="number of classifications")
```
| github_jupyter |
## Dependencies
```
!nvidia-smi
!jupyter notebook list
%env CUDA_VISIBLE_DEVICES=3
%matplotlib inline
%load_ext autoreload
%autoreload 2
import time
from pathlib import Path
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from models import tiramisu
from models import tiramisu_bilinear
from models import tiramisu_m3
from models import unet
from datasets import deepglobe
from datasets import maroads
from datasets import joint_transforms
import utils.imgs
import utils.training as train_utils
# tensorboard
from torch.utils.tensorboard import SummaryWriter
```
## Dataset
Download the DeepGlobe dataset from https://competitions.codalab.org/competitions/18467. Place it in datasets/deepglobe/dataset/train,test,valid
Download the Massachusetts Road Dataset from https://www.cs.toronto.edu/~vmnih/data/. Combine the training, validation, and test sets, process with `crop_dataset.ipynb` and place the output in datasets/maroads/dataset/map,sat
```
run = "expM.3.drop2.1"
DEEPGLOBE_PATH = Path('datasets/', 'deepglobe/dataset')
MAROADS_PATH = Path('datasets/', 'maroads/dataset')
RESULTS_PATH = Path('.results/')
WEIGHTS_PATH = Path('.weights/')
RUNS_PATH = Path('.runs/')
RESULTS_PATH.mkdir(exist_ok=True)
WEIGHTS_PATH.mkdir(exist_ok=True)
RUNS_PATH.mkdir(exist_ok=True)
batch_size = 1 # TODO: Should be `MAX_BATCH_PER_CARD * torch.cuda.device_count()` (which in this case is 1 assuming max of 1 batch per card)
# resize = joint_transforms.JointRandomCrop((300, 300))
normalize = transforms.Normalize(mean=deepglobe.mean, std=deepglobe.std)
train_joint_transformer = transforms.Compose([
# resize,
joint_transforms.JointRandomHorizontalFlip(),
joint_transforms.JointRandomVerticalFlip(),
joint_transforms.JointRandomRotate()
])
train_slice = slice(None,4000)
test_slice = slice(4000,None)
train_dset = deepglobe.DeepGlobe(DEEPGLOBE_PATH, 'train', slc = train_slice,
joint_transform=train_joint_transformer,
transform=transforms.Compose([
transforms.ColorJitter(brightness=.4,contrast=.4,saturation=.4),
transforms.ToTensor(),
normalize,
]))
train_dset_ma = maroads.MARoads(MAROADS_PATH,
joint_transform=train_joint_transformer,
transform=transforms.Compose([
transforms.ColorJitter(brightness=.4,contrast=.4,saturation=.4),
transforms.ToTensor(),
normalize,
]))
# print(len(train_dset_ma.imgs))
# print(len(train_dset_ma.msks))
train_dset_combine = torch.utils.data.ConcatDataset((train_dset, train_dset_ma))
# train_loader = torch.utils.data.DataLoader(train_dset, batch_size=batch_size, shuffle=True)
# train_loader = torch.utils.data.DataLoader(train_dset_ma, batch_size=batch_size, shuffle=True)
train_loader = torch.utils.data.DataLoader(
train_dset_combine, batch_size=batch_size, shuffle=True)
# resize_joint_transformer = transforms.Compose([
# resize
# ])
resize_joint_transformer = None
val_dset = deepglobe.DeepGlobe(
DEEPGLOBE_PATH, 'valid', joint_transform=resize_joint_transformer,
transform=transforms.Compose([
transforms.ToTensor(),
normalize
]))
val_loader = torch.utils.data.DataLoader(
val_dset, batch_size=batch_size, shuffle=False)
test_dset = deepglobe.DeepGlobe(
DEEPGLOBE_PATH, 'train', joint_transform=resize_joint_transformer, slc = test_slice,
transform=transforms.Compose([
transforms.ToTensor(),
normalize
]))
test_loader = torch.utils.data.DataLoader(
test_dset, batch_size=batch_size, shuffle=False)
print("Train: %d" %len(train_loader.dataset))
print("Val: %d" %len(val_loader.dataset.imgs))
print("Test: %d" %len(test_loader.dataset.imgs))
# print("Classes: %d" % len(train_loader.dataset.classes))
print((iter(train_loader)))
inputs, targets = next(iter(train_loader))
print("Inputs: ", inputs.size())
print("Targets: ", targets.size())
# utils.imgs.view_image(inputs[0])
# utils.imgs.view_image(targets[0])
# utils.imgs.view_annotated(targets[0])
# print(targets[0])
for i,(image,label) in enumerate(iter(test_loader)):
if i % 10 == 0:
print("Procssing image",i)
im = image[0]
# scale to [0,1]
im -= im.min()
im /= im.max()
im = torchvision.transforms.ToPILImage()(im)
im.save("ds_test/" + str(i) + ".png")
label = label.float()
la = torchvision.transforms.ToPILImage()(label)
la.save("ds_test/" + str(i) + ".mask.png")
print("Done!")
```
| github_jupyter |
```
from os import listdir
from numpy import array
from keras.preprocessing.text import Tokenizer, one_hot
from keras.preprocessing.sequence import pad_sequences
from keras.models import Model, Sequential, model_from_json
from keras.utils import to_categorical
from keras.layers.core import Dense, Dropout, Flatten
from keras.optimizers import RMSprop
from keras.layers.convolutional import Conv2D
from keras.callbacks import ModelCheckpoint
from keras.layers import Embedding, TimeDistributed, RepeatVector, LSTM, concatenate , Input, Reshape, Dense
from keras.preprocessing.image import array_to_img, img_to_array, load_img
import numpy as np
dir_name = '/data/train/'
# Read a file and return a string
def load_doc(filename):
file = open(filename, 'r')
text = file.read()
file.close()
return text
def load_data(data_dir):
text = []
images = []
# Load all the files and order them
all_filenames = listdir(data_dir)
all_filenames.sort()
for filename in (all_filenames):
if filename[-3:] == "npz":
# Load the images already prepared in arrays
image = np.load(data_dir+filename)
images.append(image['features'])
else:
# Load the boostrap tokens and rap them in a start and end tag
syntax = '<START> ' + load_doc(data_dir+filename) + ' <END>'
# Seperate all the words with a single space
syntax = ' '.join(syntax.split())
# Add a space after each comma
syntax = syntax.replace(',', ' ,')
text.append(syntax)
images = np.array(images, dtype=float)
return images, text
train_features, texts = load_data(dir_name)
# Initialize the function to create the vocabulary
tokenizer = Tokenizer(filters='', split=" ", lower=False)
# Create the vocabulary
tokenizer.fit_on_texts([load_doc('bootstrap.vocab')])
# Add one spot for the empty word in the vocabulary
vocab_size = len(tokenizer.word_index) + 1
# Map the input sentences into the vocabulary indexes
train_sequences = tokenizer.texts_to_sequences(texts)
# The longest set of boostrap tokens
max_sequence = max(len(s) for s in train_sequences)
# Specify how many tokens to have in each input sentence
max_length = 48
def preprocess_data(sequences, features):
X, y, image_data = list(), list(), list()
for img_no, seq in enumerate(sequences):
for i in range(1, len(seq)):
# Add the sentence until the current count(i) and add the current count to the output
in_seq, out_seq = seq[:i], seq[i]
# Pad all the input token sentences to max_sequence
in_seq = pad_sequences([in_seq], maxlen=max_sequence)[0]
# Turn the output into one-hot encoding
out_seq = to_categorical([out_seq], num_classes=vocab_size)[0]
# Add the corresponding image to the boostrap token file
image_data.append(features[img_no])
# Cap the input sentence to 48 tokens and add it
X.append(in_seq[-48:])
y.append(out_seq)
return np.array(X), np.array(y), np.array(image_data)
X, y, image_data = preprocess_data(train_sequences, train_features)
#Create the encoder
image_model = Sequential()
image_model.add(Conv2D(16, (3, 3), padding='valid', activation='relu', input_shape=(256, 256, 3,)))
image_model.add(Conv2D(16, (3,3), activation='relu', padding='same', strides=2))
image_model.add(Conv2D(32, (3,3), activation='relu', padding='same'))
image_model.add(Conv2D(32, (3,3), activation='relu', padding='same', strides=2))
image_model.add(Conv2D(64, (3,3), activation='relu', padding='same'))
image_model.add(Conv2D(64, (3,3), activation='relu', padding='same', strides=2))
image_model.add(Conv2D(128, (3,3), activation='relu', padding='same'))
image_model.add(Flatten())
image_model.add(Dense(1024, activation='relu'))
image_model.add(Dropout(0.3))
image_model.add(Dense(1024, activation='relu'))
image_model.add(Dropout(0.3))
image_model.add(RepeatVector(max_length))
visual_input = Input(shape=(256, 256, 3,))
encoded_image = image_model(visual_input)
language_input = Input(shape=(max_length,))
language_model = Embedding(vocab_size, 50, input_length=max_length, mask_zero=True)(language_input)
language_model = LSTM(128, return_sequences=True)(language_model)
language_model = LSTM(128, return_sequences=True)(language_model)
#Create the decoder
decoder = concatenate([encoded_image, language_model])
decoder = LSTM(512, return_sequences=True)(decoder)
decoder = LSTM(512, return_sequences=False)(decoder)
decoder = Dense(vocab_size, activation='softmax')(decoder)
# Compile the model
model = Model(inputs=[visual_input, language_input], outputs=decoder)
optimizer = RMSprop(lr=0.0001, clipvalue=1.0)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)
#Save the model for every 2nd epoch
filepath="org-weights-epoch-{epoch:04d}--val_loss-{val_loss:.4f}--loss-{loss:.4f}.hdf5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_weights_only=True, period=2)
callbacks_list = [checkpoint]
# Train the model
model.fit([image_data, X], y, batch_size=64, shuffle=False, validation_split=0.1, callbacks=callbacks_list, verbose=1, epochs=50)
```
| github_jupyter |
# Inference and Validation
Now that you have a trained network, you can use it for making predictions. This is typically called **inference**, a term borrowed from statistics. However, neural networks have a tendency to perform *too well* on the training data and aren't able to generalize to data that hasn't been seen before. This is called **overfitting** and it impairs inference performance. To test for overfitting while training, we measure the performance on data not in the training set called the **validation** set. We avoid overfitting through regularization such as dropout while monitoring the validation performance during training. In this notebook, I'll show you how to do this in PyTorch.
As usual, let's start by loading the dataset through torchvision. You'll learn more about torchvision and loading data in a later part. This time we'll be taking advantage of the test set which you can get by setting `train=False` here:
```python
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
```
The test set contains images just like the training set. Typically you'll see 10-20% of the original dataset held out for testing and validation with the rest being used for training.
```
import torch
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
```
Here I'll create a model like normal, using the same one from my solution for part 4.
```
from torch import nn, optim
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
The goal of validation is to measure the model's performance on data that isn't part of the training set. Performance here is up to the developer to define though. Typically this is just accuracy, the percentage of classes the network predicted correctly. Other options are [precision and recall](https://en.wikipedia.org/wiki/Precision_and_recall#Definition_(classification_context)) and top-5 error rate. We'll focus on accuracy here. First I'll do a forward pass with one batch from the test set.
```
model = Classifier()
images, labels = next(iter(testloader))
# Get the class probabilities
ps = torch.exp(model(images))
# Make sure the shape is appropriate, we should get 10 class probabilities for 64 examples
print(ps.shape)
```
With the probabilities, we can get the most likely class using the `ps.topk` method. This returns the $k$ highest values. Since we just want the most likely class, we can use `ps.topk(1)`. This returns a tuple of the top-$k$ values and the top-$k$ indices. If the highest value is the fifth element, we'll get back 4 as the index.
```
top_p, top_class = ps.topk(1, dim=1)
# Look at the most likely classes for the first 10 examples
print(top_class[:10,:])
```
Now we can check if the predicted classes match the labels. This is simple to do by equating `top_class` and `labels`, but we have to be careful of the shapes. Here `top_class` is a 2D tensor with shape `(64, 1)` while `labels` is 1D with shape `(64)`. To get the equality to work out the way we want, `top_class` and `labels` must have the same shape.
If we do
```python
equals = top_class == labels
```
`equals` will have shape `(64, 64)`, try it yourself. What it's doing is comparing the one element in each row of `top_class` with each element in `labels` which returns 64 True/False boolean values for each row.
```
equals = top_class == labels.view(*top_class.shape)
```
Now we need to calculate the percentage of correct predictions. `equals` has binary values, either 0 or 1. This means that if we just sum up all the values and divide by the number of values, we get the percentage of correct predictions. This is the same operation as taking the mean, so we can get the accuracy with a call to `torch.mean`. If only it was that simple. If you try `torch.mean(equals)`, you'll get an error
```
RuntimeError: mean is not implemented for type torch.ByteTensor
```
This happens because `equals` has type `torch.ByteTensor` but `torch.mean` isn't implemented for tensors with that type. So we'll need to convert `equals` to a float tensor. Note that when we take `torch.mean` it returns a scalar tensor, to get the actual value as a float we'll need to do `accuracy.item()`.
```
accuracy = torch.mean(equals.type(torch.FloatTensor))
print(f'Accuracy: {accuracy.item()*100}%')
```
The network is untrained so it's making random guesses and we should see an accuracy around 10%. Now let's train our network and include our validation pass so we can measure how well the network is performing on the test set. Since we're not updating our parameters in the validation pass, we can speed up our code by turning off gradients using `torch.no_grad()`:
```python
# turn off gradients
with torch.no_grad():
# validation pass here
for images, labels in testloader:
...
```
>**Exercise:** Implement the validation loop below and print out the total accuracy after the loop. You can largely copy and paste the code from above, but I suggest typing it in because writing it out yourself is essential for building the skill. In general you'll always learn more by typing it rather than copy-pasting. You should be able to get an accuracy above 80%.
```
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
epochs = 30
steps = 0
train_losses, test_losses = [], []
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
optimizer.zero_grad()
log_ps = model(images)
loss = criterion(log_ps, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
test_loss = 0
accuracy = 0
# Turn off gradients for validation, saves memory and computations
with torch.no_grad():
for images, labels in testloader:
log_ps = model(images)
test_loss += criterion(log_ps, labels)
ps = torch.exp(log_ps)
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
train_losses.append(running_loss/len(trainloader))
test_losses.append(test_loss/len(testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(running_loss/len(trainloader)),
"Test Loss: {:.3f}.. ".format(test_loss/len(testloader)),
"Test Accuracy: {:.3f}".format(accuracy/len(testloader)))
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.plot(train_losses, label='Training loss')
plt.plot(test_losses, label='Validation loss')
plt.legend(frameon=False)
```
## Overfitting
If we look at the training and validation losses as we train the network, we can see a phenomenon known as overfitting.
<img src='assets/overfitting.png' width=450px>
The network learns the training set better and better, resulting in lower training losses. However, it starts having problems generalizing to data outside the training set leading to the validation loss increasing. The ultimate goal of any deep learning model is to make predictions on new data, so we should strive to get the lowest validation loss possible. One option is to use the version of the model with the lowest validation loss, here the one around 8-10 training epochs. This strategy is called *early-stopping*. In practice, you'd save the model frequently as you're training then later choose the model with the lowest validation loss.
The most common method to reduce overfitting (outside of early-stopping) is *dropout*, where we randomly drop input units. This forces the network to share information between weights, increasing it's ability to generalize to new data. Adding dropout in PyTorch is straightforward using the [`nn.Dropout`](https://pytorch.org/docs/stable/nn.html#torch.nn.Dropout) module.
```python
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
# Dropout module with 0.2 drop probability
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
# Now with dropout
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
# output so no dropout here
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
During training we want to use dropout to prevent overfitting, but during inference we want to use the entire network. So, we need to turn off dropout during validation, testing, and whenever we're using the network to make predictions. To do this, you use `model.eval()`. This sets the model to evaluation mode where the dropout probability is 0. You can turn dropout back on by setting the model to train mode with `model.train()`. In general, the pattern for the validation loop will look like this, where you turn off gradients, set the model to evaluation mode, calculate the validation loss and metric, then set the model back to train mode.
```python
# turn off gradients
with torch.no_grad():
# set model to evaluation mode
model.eval()
# validation pass here
for images, labels in testloader:
...
# set model back to train mode
model.train()
```
> **Exercise:** Add dropout to your model and train it on Fashion-MNIST again. See if you can get a lower validation loss or higher accuracy.
```
## TODO: Define your model with dropout added
class MyClassifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
self.dropout = nn.Dropout(p=0.2)
def forward(self, x):
x = x.view(x.shape[0], -1)
x = self.dropout(F.relu(self.fc1(x)))
x = self.dropout(F.relu(self.fc2(x)))
x = self.dropout(F.relu(self.fc3(x)))
x = F.log_softmax(self.dropout(self.fc4(x)), dim=1)
return x
## TODO: Train your model with dropout, and monitor the training progress with the validation loss and accuracy
model = MyClassifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
epochs = 30
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
log_ps = model(images)
loss = criterion(log_ps, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
with torch.no_grad():
model.eval()
for images, labels in testloader:
ps = torch.exp(model(images))
top_p, top_class = ps.topk(1, dim=1)
equals = top_class == labels.view(*top_class.shape)
accuracy = torch.mean(equals.type(torch.FloatTensor))
print(f'Accuracy: {accuracy.item()*100}%')
model.train()
```
## Inference
Now that the model is trained, we can use it for inference. We've done this before, but now we need to remember to set the model in inference mode with `model.eval()`. You'll also want to turn off autograd with the `torch.no_grad()` context.
```
# Import helper module (should be in the repo)
import helper
# Test out your network!
model.eval()
dataiter = iter(testloader)
images, labels = dataiter.next()
img = images[0]
# Convert 2D image to 1D vector
img = img.view(1, 784)
# Calculate the class probabilities (softmax) for img
with torch.no_grad():
output = model.forward(img)
ps = torch.exp(output)
# Plot the image and probabilities
helper.view_classify(img.view(1, 28, 28), ps, version='Fashion')
```
## Next Up!
In the next part, I'll show you how to save your trained models. In general, you won't want to train a model everytime you need it. Instead, you'll train once, save it, then load the model when you want to train more or use if for inference.
| github_jupyter |
# Regular Expressions
Regular expressions are text-matching patterns described with a formal syntax. You'll often hear regular expressions referred to as 'regex' or 'regexp' in conversation. Regular expressions can include a variety of rules, from finding repetition, to text-matching, and much more. As you advance in Python you'll see that a lot of your parsing problems can be solved with regular expressions (they're also a common interview question!).
If you're familiar with Perl, you'll notice that the syntax for regular expressions are very similar in Python. We will be using the <code>re</code> module with Python for this lecture.
Let's get started!
## Searching for Patterns in Text
One of the most common uses for the re module is for finding patterns in text. Let's do a quick example of using the search method in the re module to find some text:
```
import re
# List of patterns to search for
patterns = ['term1', 'term2']
# Text to parse
text = 'This is a string with term1, but it does not have the other term.'
for pattern in patterns:
print('Searching for "%s" in:\n "%s"\n' %(pattern,text))
#Check for match
if re.search(pattern,text):
print('Match was found. \n')
else:
print('No Match was found.\n')
```
Now we've seen that <code>re.search()</code> will take the pattern, scan the text, and then return a **Match** object. If no pattern is found, **None** is returned. To give a clearer picture of this match object, check out the cell below:
```
# List of patterns to search for
pattern = 'term1'
# Text to parse
text = 'This is a string with term1, but it does not have the other term.'
match = re.search(pattern,text)
type(match)
```
This **Match** object returned by the search() method is more than just a Boolean or None, it contains information about the match, including the original input string, the regular expression that was used, and the location of the match. Let's see the methods we can use on the match object:
```
# Show start of match
match.start()
# Show end
match.end()
```
## Split with regular expressions
Let's see how we can split with the re syntax. This should look similar to how you used the split() method with strings.
```
# Term to split on
split_term = '@'
phrase = 'What is the domain name of someone with the email: [email protected]'
# Split the phrase
re.split(split_term,phrase)
```
Note how <code>re.split()</code> returns a list with the term to split on removed and the terms in the list are a split up version of the string. Create a couple of more examples for yourself to make sure you understand!
## Finding all instances of a pattern
You can use <code>re.findall()</code> to find all the instances of a pattern in a string. For example:
```
# Returns a list of all matches
re.findall('match','test phrase match is in middle')
```
## re Pattern Syntax
This will be the bulk of this lecture on using re with Python. Regular expressions support a huge variety of patterns beyond just simply finding where a single string occurred.
We can use *metacharacters* along with re to find specific types of patterns.
Since we will be testing multiple re syntax forms, let's create a function that will print out results given a list of various regular expressions and a phrase to parse:
```
def multi_re_find(patterns,phrase):
'''
Takes in a list of regex patterns
Prints a list of all matches
'''
for pattern in patterns:
print('Searching the phrase using the re check: %r' %(pattern))
print(re.findall(pattern,phrase))
print('\n')
```
### Repetition Syntax
There are five ways to express repetition in a pattern:
1. A pattern followed by the meta-character <code>*</code> is repeated zero or more times.
2. Replace the <code>*</code> with <code>+</code> and the pattern must appear at least once.
3. Using <code>?</code> means the pattern appears zero or one time.
4. For a specific number of occurrences, use <code>{m}</code> after the pattern, where **m** is replaced with the number of times the pattern should repeat.
5. Use <code>{m,n}</code> where **m** is the minimum number of repetitions and **n** is the maximum. Leaving out **n** <code>{m,}</code> means the value appears at least **m** times, with no maximum.
Now we will see an example of each of these using our multi_re_find function:
```
test_phrase = 'sdsd..sssddd...sdddsddd...dsds...dsssss...sdddd'
test_patterns = [ 'sd*', # s followed by zero or more d's
'sd+', # s followed by one or more d's
'sd?', # s followed by zero or one d's
'sd{3}', # s followed by three d's
'sd{2,3}', # s followed by two to three d's
]
multi_re_find(test_patterns,test_phrase)
```
## Character Sets
Character sets are used when you wish to match any one of a group of characters at a point in the input. Brackets are used to construct character set inputs. For example: the input <code>[ab]</code> searches for occurrences of either **a** or **b**.
Let's see some examples:
```
test_phrase = 'sdsd..sssddd...sdddsddd...dsds...dsssss...sdddd'
test_patterns = ['[sd]', # either s or d
's[sd]+'] # s followed by one or more s or d
multi_re_find(test_patterns,test_phrase)
```
It makes sense that the first input <code>[sd]</code> returns every instance of s or d. Also, the second input <code>s[sd]+</code> returns any full strings that begin with an s and continue with s or d characters until another character is reached.
## Exclusion
We can use <code>^</code> to exclude terms by incorporating it into the bracket syntax notation. For example: <code>[^...]</code> will match any single character not in the brackets. Let's see some examples:
```
test_phrase = 'This is a string! But it has punctuation. How can we remove it?'
```
Use <code>[^!.? ]</code> to check for matches that are not a !,.,?, or space. Add a <code>+</code> to check that the match appears at least once. This basically translates into finding the words.
```
re.findall('[^!.? ]+',test_phrase)
```
## Character Ranges
As character sets grow larger, typing every character that should (or should not) match could become very tedious. A more compact format using character ranges lets you define a character set to include all of the contiguous characters between a start and stop point. The format used is <code>[start-end]</code>.
Common use cases are to search for a specific range of letters in the alphabet. For instance, <code>[a-f]</code> would return matches with any occurrence of letters between a and f.
Let's walk through some examples:
```
test_phrase = 'This is an example sentence. Lets see if we can find some letters.'
test_patterns=['[a-z]+', # sequences of lower case letters
'[A-Z]+', # sequences of upper case letters
'[a-zA-Z]+', # sequences of lower or upper case letters
'[A-Z][a-z]+'] # one upper case letter followed by lower case letters
multi_re_find(test_patterns,test_phrase)
```
## Escape Codes
You can use special escape codes to find specific types of patterns in your data, such as digits, non-digits, whitespace, and more. For example:
<table border="1" class="docutils">
<colgroup>
<col width="14%" />
<col width="86%" />
</colgroup>
<thead valign="bottom">
<tr class="row-odd"><th class="head">Code</th>
<th class="head">Meaning</th>
</tr>
</thead>
<tbody valign="top">
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\d</span></tt></td>
<td>a digit</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\D</span></tt></td>
<td>a non-digit</td>
</tr>
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\s</span></tt></td>
<td>whitespace (tab, space, newline, etc.)</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\S</span></tt></td>
<td>non-whitespace</td>
</tr>
<tr class="row-even"><td><tt class="docutils literal"><span class="pre">\w</span></tt></td>
<td>alphanumeric</td>
</tr>
<tr class="row-odd"><td><tt class="docutils literal"><span class="pre">\W</span></tt></td>
<td>non-alphanumeric</td>
</tr>
</tbody>
</table>
Escapes are indicated by prefixing the character with a backslash <code>\</code>. Unfortunately, a backslash must itself be escaped in normal Python strings, and that results in expressions that are difficult to read. Using raw strings, created by prefixing the literal value with <code>r</code>, eliminates this problem and maintains readability.
Personally, I think this use of <code>r</code> to escape a backslash is probably one of the things that block someone who is not familiar with regex in Python from being able to read regex code at first. Hopefully after seeing these examples this syntax will become clear.
```
test_phrase = 'This is a string with some numbers 1233 and a symbol #hashtag'
test_patterns=[ r'\d+', # sequence of digits
r'\D+', # sequence of non-digits
r'\s+', # sequence of whitespace
r'\S+', # sequence of non-whitespace
r'\w+', # alphanumeric characters
r'\W+', # non-alphanumeric
]
multi_re_find(test_patterns,test_phrase)
```
## Conclusion
You should now have a solid understanding of how to use the regular expression module in Python. There are a ton of more special character instances, but it would be unreasonable to go through every single use case. Instead take a look at the full [documentation](https://docs.python.org/3/library/re.html#regular-expression-syntax) if you ever need to look up a particular pattern.
You can also check out the nice summary tables at this [source](http://www.tutorialspoint.com/python/python_reg_expressions.htm).
Good job!
| github_jupyter |
### What is an Autoencoder?
An Autoencoder is a model that can make use of a CNN's ability to compress the data into a flat vector / feature vector. We can think of it as a smart encoder that learns compression and decompression algorithms from the data. As an example, if you had a file format that was highly dimensional or noisy then you could use an autoencoder to get a file that you are able to work with.
The main ability of an autoencoder is that it's able to compress the data while maintaining its content which makes it possible to use the compress representation of the input.

### Linear autoencoder
This is a simple autoencoder that uses an MLP with with a few linear layers for encoder and decoder. The number of layers depends on the problem you trying to solve.
Another thing to note here is you might want to consider a different loss function such as **MSE** because it's suitable for comparing pixel quantities rather than probabilities, it's a function that uses regression instead of probabilities. You are also interested in only the images and not the labels, same goes for validation set, you're mostly focusing on training and then you're using test to visualize the reconstruction.
**Key point**: we are comparing the images that resulted from the reconstruction with the original ones so we're not interested in accuracy like in usual applications.
**Code**: [Notebook](autoencoder/linear-autoencoder/Simple_Autoencoder_Exercise.ipynb) with fully connected layers.
### Upsampling
Encoder performs what is called **downsampling** as it is compressing the data into a flat vector. Conversely, the decoder is doing an **upsampling** through a transpose convolutional layer or sometimes called deconvolutional layer. Note: deconv layer doesn't strictly mean that we are undoing a convolution. It is essentially reversing the downsampling by increasing the spatial dimensions of a compressed input so that you get to the original dimensions of the input
### Transpose convolutional layer
Beginning from the compressed representation, a filter with a given size and stride passes over the input and multiplies the pixel with its weight resulting a representation.
Below is the result after the convolution went over all points. The interesting part is that this pixel representation will overlap with another convolution and what happens is that the overlapping section/edges get summed together. In this case a stride of 2 was used for the output.

There are options to add/substract the padding from the output as above but the most common solution is a 2x2 filter and stride of 2 to double the dimensions of the input.

When not sure about how the calculations are done there is a very good explanation of how convolutional arithmethic works in this [repo](https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md).
**Code**: [Notebook](autoencoder/convolutional-autoencoder/Convolutional_Autoencoder_Exercise.ipynb) with convolutional and transpose convolutional layers.
Convolutional neural networks gives as as an output the image that is much closely resembling the original imaage compared to the autoencoder that used linear layers. However, there are still some artifacts present in some of the images. This can be attributed to how Transpose conv layer works.
The solution for this is to use a technique called upsampling with nearest-neightbor interpolation coupled with convolutional layers.
**Code**: [Notebook](autoencoder/convolutional-autoencoder/Upsampling_Solution.ipynb) with upsampling.
### De-noising
One of the most interesting things you can use an autoencoder for is de-noising.
**Code**: [Exercise](autoencoder/denoising-autoencoder/Denoising_Autoencoder_Exercise.ipynb) of using it for de-noising.
| github_jupyter |
Lambda School Data Science
*Unit 4, Sprint 3, Module 2*
---
# Convolutional Neural Networks (Prepare)
> Convolutional networks are simply neural networks that use convolution in place of general matrix multiplication in at least one of their layers. *Goodfellow, et al.*
## Learning Objectives
- <a href="#p1">Part 1: </a>Describe convolution and pooling
- <a href="#p2">Part 2: </a>Apply a convolutional neural network to a classification task
- <a href="#p3">Part 3: </a>Use a pre-trained convolution neural network for object detection
Modern __computer vision__ approaches rely heavily on convolutions as both a dimensinoality reduction and feature extraction method. Before we dive into convolutions, let's talk about some of the common computer vision applications:
* Classification [(Hot Dog or Not Dog)](https://www.youtube.com/watch?v=ACmydtFDTGs)
* Object Detection [(YOLO)](https://www.youtube.com/watch?v=MPU2HistivI)
* Pose Estimation [(PoseNet)](https://ai.googleblog.com/2019/08/on-device-real-time-hand-tracking-with.html)
* Facial Recognition [Emotion Detection](https://www.cbronline.com/wp-content/uploads/2018/05/Mona-lIsa-test-570x300.jpg)
* and *countless* more
We are going to focus on classification and pre-trained object detection today. What are some of the applications of object detection?
```
from IPython.display import YouTubeVideo
YouTubeVideo('MPU2HistivI', width=600, height=400)
```
# Convolution & Pooling (Learn)
<a id="p1"></a>
## Overview
Like neural networks themselves, CNNs are inspired by biology - specifically, the receptive fields of the visual cortex.
Put roughly, in a real brain the neurons in the visual cortex *specialize* to be receptive to certain regions, shapes, colors, orientations, and other common visual features. In a sense, the very structure of our cognitive system transforms raw visual input, and sends it to neurons that specialize in handling particular subsets of it.
CNNs imitate this approach by applying a convolution. A convolution is an operation on two functions that produces a third function, showing how one function modifies another. Convolutions have a [variety of nice mathematical properties](https://en.wikipedia.org/wiki/Convolution#Properties) - commutativity, associativity, distributivity, and more. Applying a convolution effectively transforms the "shape" of the input.
One common confusion - the term "convolution" is used to refer to both the process of computing the third (joint) function and the process of applying it. In our context, it's more useful to think of it as an application, again loosely analogous to the mapping from visual field to receptive areas of the cortex in a real animal.
```
from IPython.display import YouTubeVideo
YouTubeVideo('IOHayh06LJ4', width=600, height=400)
```
## Follow Along
Let's try to do some convolutions in `Keras`.
### Convolution - an example
Consider blurring an image - assume the image is represented as a matrix of numbers, where each number corresponds to the color value of a pixel.
```
import imageio
import matplotlib.pyplot as plt
from skimage import color, io
from skimage.exposure import rescale_intensity
austen = io.imread('https://dl.airtable.com/S1InFmIhQBypHBL0BICi_austen.jpg')
austen_grayscale = rescale_intensity(color.rgb2gray(austen))
austen_grayscale
plt.imshow(austen_grayscale, cmap="gray");
import scipy.ndimage as nd
import numpy as np
horizontal_edge_convolution = np.array([[1,1,1,1,1],
[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0],
[-1,-1,-1,-1,-1]])
vertical_edge_convolution = np.array([[1, 0, 0, 0, -1],
[1, 0, 0, 0, -1],
[1, 0, 0, 0, -1],
[1, 0, 0, 0, -1],
[1, 0, 0, 0, -1]])
austen_edges = nd.convolve(austen_grayscale, vertical_edge_convolution)
#austen_edges
plt.imshow(austen_edges, cmap="gray");
```
## Challenge
You will be expected to be able to describe convolution.
# CNNs for Classification (Learn)
## Overview
### Typical CNN Architecture

The first stage of a CNN is, unsurprisingly, a convolution - specifically, a transformation that maps regions of the input image to neurons responsible for receiving them. The convolutional layer can be visualized as follows:
The red represents the original input image, and the blue the neurons that correspond.
As shown in the first image, a CNN can have multiple rounds of convolutions, [downsampling](https://en.wikipedia.org/wiki/Downsampling_(signal_processing)) (a digital signal processing technique that effectively reduces the information by passing through a filter), and then eventually a fully connected neural network and output layer. Typical output layers for a CNN would be oriented towards classification or detection problems - e.g. "does this picture contain a cat, a dog, or some other animal?"
Why are CNNs so popular?
1. Compared to prior image learning techniques, they require relatively little image preprocessing (cropping/centering, normalizing, etc.)
2. Relatedly, they are *robust* to all sorts of common problems in images (shifts, lighting, etc.)
Actually training a cutting edge image classification CNN is nontrivial computationally - the good news is, with transfer learning, we can get one "off-the-shelf"!
## Follow Along
```
from tensorflow.keras import datasets
from tensorflow.keras.models import Sequential, Model # <- May Use
from tensorflow.keras.layers import Dense, Conv2D, MaxPooling2D, Flatten
import matplotlib.pyplot as plt
(train_images, train_labels), (test_images, test_labels) = datasets.cifar10.load_data()
# Normalize pixel values to be between 0 and 1
train_images, test_images = train_images / 255.0, test_images / 255.0
class_names = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
# The CIFAR labels happen to be arrays,
# which is why you need the extra index
plt.xlabel(class_names[train_labels[i][0]])
plt.show()
train_images[0].shape
# Setup Architecture
model = Sequential()
model.add(Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(MaxPooling2D((2,2)))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D((2,2)))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.summary()
# Compile Model
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# Fit Model
model.fit(train_images, train_labels, epochs=10, validation_data=(test_images, test_labels));
# Evaluate Model
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
```
## Challenge
You will apply CNNs to a classification task in the module project.
# CNNs for Object Detection (Learn)
## Overview
### Transfer Learning - TensorFlow Hub
"A library for reusable machine learning modules"
This lets you quickly take advantage of a model that was trained with thousands of GPU hours. It also enables transfer learning - reusing a part of a trained model (called a module) that includes weights and assets, but also training the overall model some yourself with your own data. The advantages are fairly clear - you can use less training data, have faster training, and have a model that generalizes better.
https://www.tensorflow.org/hub/
**WARNING** - Dragons ahead!

TensorFlow Hub is very bleeding edge, and while there's a good amount of documentation out there, it's not always updated or consistent. You'll have to use your problem-solving skills if you want to use it!
## Follow Along
```
import numpy as np
from tensorflow.keras.applications.resnet50 import ResNet50
from tensorflow.keras.preprocessing import image
from tensorflow.keras.applications.resnet50 import preprocess_input, decode_predictions
def process_img_path(img_path):
return image.load_img(img_path, target_size=(224, 224))
def img_contains_banana(img):
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
model = ResNet50(weights='imagenet')
features = model.predict(x)
results = decode_predictions(features, top=3)[0]
print(results)
for entry in results:
if entry[1] == 'banana':
return entry[2]
return 0.0
import requests
image_urls = ["https://github.com/LambdaSchool/ML-YouOnlyLookOnce/raw/master/sample_data/negative_examples/example11.jpeg",
"https://github.com/LambdaSchool/ML-YouOnlyLookOnce/raw/master/sample_data/positive_examples/example0.jpeg"]
for _id,img in enumerate(image_urls):
r = requests.get(img)
with open(f'example{_id}.jpg', 'wb') as f:
f.write(r.content)
from IPython.display import Image
Image(filename='./example0.jpg', width=600)
img_contains_banana(process_img_path('example0.jpg'))
Image(filename='example1.jpg', width=600)
img_contains_banana(process_img_path('example1.jpg'))
```
Notice that, while it gets it right, the confidence for the banana image is fairly low. That's because so much of the image is "not-banana"! How can this be improved? Bounding boxes to center on items of interest.
## Challenge
You will be expected to apply a pretrained model to a classificaiton problem today.
# Review
- <a href="#p1">Part 1: </a>Describe convolution and pooling
* A Convolution is a function applied to another function to produce a third function
* Convolutional Kernels are typically 'learned' during the process of training a Convolution Neural Network
* Pooling is a dimensionality reduction technique that uses either Max or Average of a feature max region to downsample data
- <a href="#p2">Part 2: </a>Apply a convolutional neural network to a classification task
* Keras has layers for convolutions :)
- <a href="#p3">Part 3: </a>Use a pre-trained convolution neural network for object detection
* Check out both pretinaed models available in Keras & TensorFlow Hub
# Sources
- *_Deep Learning_*. Goodfellow *et al.*
- [Keras CNN Tutorial](https://www.tensorflow.org/tutorials/images/cnn)
- [Tensorflow + Keras](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Conv2D)
- [Convolution Wiki](https://en.wikipedia.org/wiki/Convolution)
- [Keras Conv2D: Working with CNN 2D Convolutions in Keras](https://missinglink.ai/guides/keras/keras-conv2d-working-cnn-2d-convolutions-keras/)
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import urllib.request as urllib
from datetime import datetime
import time
import ergo # Download from https://github.com/rethinkpriorities/ergo
def fetch(url):
max_attempts = 80
attempts = 0
sleeptime = 10 #in seconds, no reason to continuously try if network is down
while attempts < max_attempts:
time.sleep(sleeptime)
try:
response = urllib.urlopen(url, timeout=5)
content = response.read()
return content
except urllib.URLError as e:
print(e)
attempts += 1
def kelly(user_odds, market_odds):
return (user_odds - ((1 - user_odds) * (market_odds / (1 - market_odds))))
def compare_metaculus_vs_polymarket(polymarket_url, metaculus_qid, actual, inverse_pm=False):
print('Fetching...')
content = fetch(polymarket_url)
print('Fetched')
polymarket_df = pd.DataFrame(eval(str(content).split('"All":')[1].split('},"graphKeys":[')[0]))
if inverse_pm:
polymarket_df.columns = ['no_price', 'yes_price', 'time']
else:
polymarket_df.columns = ['yes_price', 'no_price', 'time']
polymarket_df['yes_price'] = polymarket_df['yes_price'].astype(float)
polymarket_df['no_price'] = polymarket_df['no_price'].astype(float)
polymarket_df['time'] = polymarket_df['time'].apply(lambda t: t.split(',')[0])
polymarket_df = polymarket_df[~((polymarket_df['yes_price'] == 0) & (polymarket_df['no_price'] == 0))]
polymarket_df['polymarket_yes'] = polymarket_df['yes_price']
polymarket_df = polymarket_df[['time', 'polymarket_yes']].drop_duplicates('time', keep='last')
polymarket_df['time'] = polymarket_df['time'].apply(lambda t: t + ' 21' if ('Jan' in t or 'Feb' in t) else t + ' 20')
polymarket_df['time'] = pd.to_datetime(polymarket_df['time'], format='%b %d %y')
polymarket_df = polymarket_df.reset_index(drop=True)
q = metaculus.get_question(metaculus_qid)
metaculus_df = pd.DataFrame(q.data['metaculus_prediction']['history'])
metaculus_df.columns = ['time', 'metaculus_yes']
metaculus_df['time'] = pd.to_datetime(metaculus_df['time'].apply(lambda t: datetime.fromtimestamp(t)).dt.date)
metaculus_df = metaculus_df.drop_duplicates('time', keep='last')
metaculus_df = metaculus_df.reset_index(drop=True)
metaculus_df
merged_df = metaculus_df.merge(polymarket_df, on='time', how='left').dropna()
merged_df['metaculus_brier'] = (merged_df['metaculus_yes'] - actual) ** 2
merged_df['polymarket_brier'] = (merged_df['polymarket_yes'] - actual) ** 2
merged_df['50_50_yes'] = merged_df['polymarket_yes'] * 0.5 + merged_df['metaculus_yes'] * 0.5
merged_df['50_50_brier'] = (merged_df['50_50_yes'] - actual) ** 2
bankroll = 1000
metaculus_bets = []
metaculus_winnings = []
for index, row in merged_df.iterrows():
if row['polymarket_yes'] == 0:
row['polymarket_yes'] = 0.001
if row['metaculus_yes'] == 0:
row['metaculus_yes'] = 0.001
if row['metaculus_yes'] > row['polymarket_yes']:
bet = bankroll * kelly(row['metaculus_yes'], row['polymarket_yes'])
shares = bet / row['polymarket_yes']
winnings = shares if actual == 1 else -bet
elif row['metaculus_yes'] < row['polymarket_yes']:
bet = bankroll * kelly(1 - row['metaculus_yes'], 1 - row['polymarket_yes'])
shares = bet / (1 - row['polymarket_yes'])
winnings = shares if actual == 0 else -bet
else:
bet = 0
shares = 0
winnings += (bankroll - bet)
metaculus_bets.append(bet)
metaculus_winnings.append(winnings)
polymarket_bets = []
polymarket_winnings = []
for index, row in merged_df.iterrows():
if row['polymarket_yes'] > row['metaculus_yes']:
bet = bankroll * kelly(row['polymarket_yes'], row['metaculus_yes'])
shares = bet / row['metaculus_yes']
winnings = shares if actual == 1 else -bet
elif row['polymarket_yes'] < row['metaculus_yes']:
bet = bankroll * kelly(1 - row['polymarket_yes'], 1 - row['metaculus_yes'])
shares = bet / (1 - row['metaculus_yes'])
winnings = shares if actual == 0 else -bet
else:
bet = 0
shares = 0
winnings = 0
winnings += (bankroll - bet)
polymarket_bets.append(bet)
polymarket_winnings.append(winnings)
merged_df['metaculus_bets'] = metaculus_bets
merged_df['metaculus_winnings'] = metaculus_winnings
merged_df['polymarket_bets'] = polymarket_bets
merged_df['polymarket_winnings'] = polymarket_winnings
return {'metaculus': metaculus_df,
'polymarket': polymarket_df,
'data': merged_df,
'brier': merged_df[['metaculus_brier', 'polymarket_brier', '50_50_brier']].sum() / len(merged_df),
'winnings': merged_df[['metaculus_winnings', 'polymarket_winnings']].sum() / len(merged_df)}
def plot_predictions(preds, q_title):
plt.plot(preds['data']['time'], preds['data']['metaculus_yes'], label='Metaculus')
plt.plot(preds['data']['time'], preds['data']['polymarket_yes'], label='Polymarket')
plt.title(q_title)
plt.legend()
return plt
print('Logging in to Metaculus...')
metaculus = ergo.Metaculus()
metaculus.login_via_username_and_password(username='PeterHurford', password='GaZKQ6hEtZH0')
print('...Logged on')
```
## Trump Charges
```
# https://www.metaculus.com/questions/6222/criminal-charges-against-trump/
trump_charges = compare_metaculus_vs_polymarket('https://polymarket.com/market/donald-trump-federally-charged-by-february-20th',
6222,
actual=0)
trump_charges['data']
trump_charges['brier']
trump_charges['winnings']
plot_predictions(trump_charges, 'Criminal charges against Trump by 20 Feb?').show()
```
## GOP Win
```
# https://www.metaculus.com/questions/5734/gop-to-hold-senate-on-feb-1st-2021/
gop_senate = compare_metaculus_vs_polymarket('https://polymarket.com/market/which-party-will-control-the-senate',
5734,
actual=0)
gop_senate['data']
gop_senate['brier']
gop_senate['winnings']
plot_predictions(gop_senate, 'GOP Hold Senate for 2021?').show()
```
## Trump Pardon
```
# https://www.metaculus.com/questions/5685/will-donald-trump-attempt-to-pardon-himself/
trump_pardon = compare_metaculus_vs_polymarket('https://polymarket.com/market/will-trump-pardon-himself-in-his-first-term',
5685,
actual=0)
trump_pardon['data']
trump_pardon['brier']
trump_pardon['winnings']
plot_predictions(trump_pardon, 'Trump self-pardon?').show()
```
## 538 - Economist
```
# https://www.metaculus.com/questions/5503/comparing-538-and-economist-forecasts-in-2020/
economist_538 = compare_metaculus_vs_polymarket('https://polymarket.com/market/will-538-outperform-the-economist-in-forecasting-the-2020-presidential-election',
5503,
actual=0)
economist_538['data']
economist_538['brier']
economist_538['winnings']
plot_predictions(economist_538, '538 prez forecast beat Economist?').show()
```
## Biden in-person inauguration
```
## https://www.metaculus.com/questions/6293/biden-in-person-inauguration/
biden_in_person = compare_metaculus_vs_polymarket('https://polymarket.com/market/will-joe-biden-be-officially-inaugurated-as-president-in-person-outside-the-us-capitol-on-january-20th-2021',
6293,
actual=1)
biden_in_person['data']
biden_in_person['brier']
biden_in_person['winnings']
plot_predictions(biden_in_person, 'Biden inaugurated in-person on 20 Jan 2021?').show()
```
## Trump at Biden's Inauguration
```
## https://www.metaculus.com/questions/5825/trump-at-bidens-inauguration/
trump_attend = compare_metaculus_vs_polymarket('https://polymarket.com/market/will-donald-trump-attend-joe-biden-s-inauguration-ceremony-in-person',
5825,
actual=0)
trump_attend['data']
trump_attend['brier']
trump_attend['winnings']
plot_predictions(trump_attend, 'Trump attend Biden\'s inauguration?').show()
```
## Electoral Challenge
```
## https://www.metaculus.com/questions/5844/electoral-college-results-challenged/
challenge = compare_metaculus_vs_polymarket('https://polymarket.com/market/will-any-electoral-certificates-be-formally-challenged-in-congress',
5844,
actual=1)
challenge['data']
challenge['brier']
challenge['winnings']
plot_predictions(challenge, 'Electoral college challenge?').show()
```
## Trump Convict
```
## https://www.metaculus.com/questions/6303/trump-convicted-by-senate/
trump_convict = compare_metaculus_vs_polymarket('https://polymarket.com/market/will-the-senate-convict-donald-trump-on-impeachment-before-june-1-2021',
6303,
actual=0)
trump_convict['data']
trump_convict['brier']
trump_convict['winnings']
plot_predictions(trump_convict, 'Senate convict Trump in 2021?').show()
```
## Tokyo Olympics
```
# https://polymarket.com/market/will-the-tokyo-summer-olympics-be-cancelled-or-postponed
# https://www.metaculus.com/questions/5555/rescheduled-2020-olympics/
```
## Brier
```
(challenge['brier'] + trump_attend['brier'] + biden_in_person['brier'] + economist_538['brier'] +
trump_pardon['brier'] + gop_senate['brier'] + trump_charges['brier'] + trump_convict['brier']) / 8
(challenge['winnings'] + trump_attend['winnings'] + biden_in_person['winnings'] + economist_538['winnings'] +
trump_pardon['winnings'] + gop_senate['winnings'] + trump_charges['winnings'] + trump_convict['winnings']) / 8
```
| github_jupyter |
```
%matplotlib inline
```
# Training a ConvNet PyTorch
In this notebook, you'll learn how to use the powerful PyTorch framework to specify a conv net architecture and train it on the CIFAR-10 dataset.
```
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torch.utils.data import sampler
import torchvision.datasets as dset
import torchvision.transforms as T
import numpy as np
import matplotlib.pyplot as plt
import timeit
from tqdm import tqdm
# for auto-reloading extenrnal modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
```
## What's this PyTorch business?
You've written a lot of code in this assignment to provide a whole host of neural network functionality. Dropout, Batch Norm, and 2D convolutions are some of the workhorses of deep learning in computer vision. You've also worked hard to make your code efficient and vectorized.
For the last part of this assignment, though, we're going to leave behind your beautiful codebase and instead migrate to one of two popular deep learning frameworks: in this instance, PyTorch (or TensorFlow, if you switch over to that notebook).
Why?
* Our code will now run on GPUs! Much faster training. When using a framework like PyTorch or TensorFlow you can harness the power of the GPU for your own custom neural network architectures without having to write CUDA code directly (which is beyond the scope of this class).
* We want you to be ready to use one of these frameworks for your project so you can experiment more efficiently than if you were writing every feature you want to use by hand.
* We want you to stand on the shoulders of giants! TensorFlow and PyTorch are both excellent frameworks that will make your lives a lot easier, and now that you understand their guts, you are free to use them :)
* We want you to be exposed to the sort of deep learning code you might run into in academia or industry.
## How will I learn PyTorch?
If you've used Torch before, but are new to PyTorch, this tutorial might be of use: http://pytorch.org/tutorials/beginner/former_torchies_tutorial.html
Otherwise, this notebook will walk you through much of what you need to do to train models in Torch. See the end of the notebook for some links to helpful tutorials if you want to learn more or need further clarification on topics that aren't fully explained here.
## Load Datasets
We load the CIFAR-10 dataset. This might take a couple minutes the first time you do it, but the files should stay cached after that.
```
class ChunkSampler(sampler.Sampler):
"""Samples elements sequentially from some offset.
Arguments:
num_samples: # of desired datapoints
start: offset where we should start selecting from
"""
def __init__(self, num_samples, start = 0):
self.num_samples = num_samples
self.start = start
def __iter__(self):
return iter(range(self.start, self.start + self.num_samples))
def __len__(self):
return self.num_samples
NUM_TRAIN = 49000
NUM_VAL = 1000
cifar10_train = dset.CIFAR10('./cs231n/datasets', train=True, download=True,
transform=T.ToTensor())
loader_train = DataLoader(cifar10_train, batch_size=64, sampler=ChunkSampler(NUM_TRAIN, 0))
cifar10_val = dset.CIFAR10('./cs231n/datasets', train=True, download=True,
transform=T.ToTensor())
loader_val = DataLoader(cifar10_val, batch_size=64, sampler=ChunkSampler(NUM_VAL, NUM_TRAIN))
cifar10_test = dset.CIFAR10('./cs231n/datasets', train=False, download=True,
transform=T.ToTensor())
loader_test = DataLoader(cifar10_test, batch_size=64)
```
For now, we're going to use a CPU-friendly datatype. Later, we'll switch to a datatype that will move all our computations to the GPU and measure the speedup.
```
# Constant to control how frequently we print train loss
print_every = 100
# This is a little utility that we'll use to reset the model
# if we want to re-initialize all our parameters
def reset(m):
if hasattr(m, 'reset_parameters'):
m.reset_parameters()
```
## Example Model
### Some assorted tidbits
Let's start by looking at a simple model. First, note that PyTorch operates on Tensors, which are n-dimensional arrays functionally analogous to numpy's ndarrays, with the additional feature that they can be used for computations on GPUs.
We'll provide you with a Flatten function, which we explain here. Remember that our image data (and more relevantly, our intermediate feature maps) are initially N x C x H x W, where:
* N is the number of datapoints
* C is the number of channels
* H is the height of the intermediate feature map in pixels
* W is the height of the intermediate feature map in pixels
This is the right way to represent the data when we are doing something like a 2D convolution, that needs spatial understanding of where the intermediate features are relative to each other. When we input data into fully connected affine layers, however, we want each datapoint to be represented by a single vector -- it's no longer useful to segregate the different channels, rows, and columns of the data. So, we use a "Flatten" operation to collapse the C x H x W values per representation into a single long vector. The Flatten function below first reads in the N, C, H, and W values from a given batch of data, and then returns a "view" of that data. "View" is analogous to numpy's "reshape" method: it reshapes x's dimensions to be N x ??, where ?? is allowed to be anything (in this case, it will be C x H x W, but we don't need to specify that explicitly).
```
class Flatten(nn.Module):
def forward(self, x):
N, C, H, W = x.size() # read in N, C, H, W
return x.view(N, -1) # "flatten" the C * H * W values into a single vector per image
def out_dim(sz, filter_size, padding, stride):
"""
Computes the size of dimension after convolution.
Input:
- sz: Original size of dimension
- filter_size: Filter size applied in convolution
- padding: Applied to the original dimension
- stride: Between the two applications of convolution
Returns a tuple of:
- out: The size of the dimension after the convolution is computed
"""
return 1 + int((sz + 2 * padding - filter_size) / stride)
# Verify that CUDA is properly configured and you have a GPU available
if torch.cuda.is_available():
dtype = torch.cuda.FloatTensor
ltype = torch.cuda.LongTensor
else:
dtype = torch.FloatTensor
ltype = torch.LongTensor
```
### The example model itself
The first step to training your own model is defining its architecture.
Here's an example of a convolutional neural network defined in PyTorch -- try to understand what each line is doing, remembering that each layer is composed upon the previous layer. We haven't trained anything yet - that'll come next - for now, we want you to understand how everything gets set up. nn.Sequential is a container which applies each layer
one after the other.
In that example, you see 2D convolutional layers (Conv2d), ReLU activations, and fully-connected layers (Linear). You also see the Cross-Entropy loss function, and the Adam optimizer being used.
Make sure you understand why the parameters of the Linear layer are 5408 and 10.
```
# Here's where we define the architecture of the model...
simple_model = nn.Sequential(
nn.Conv2d(3, 32, kernel_size=7, stride=2),
nn.ReLU(inplace=True),
Flatten(), # see above for explanation
nn.Linear(5408, 10), # affine layer
)
# the number of output classes:
# 10
# 32*out_dim(32, 7, 0, 2)**2
# 5408
# Set the type of all data in this model to be FloatTensor
simple_model.type(dtype)
loss_fn = nn.CrossEntropyLoss().type(dtype)
optimizer = optim.Adam(simple_model.parameters(), lr=1e-2) # lr sets the learning rate of the optimizer
```
PyTorch supports many other layer types, loss functions, and optimizers - you will experiment with these next. Here's the official API documentation for these (if any of the parameters used above were unclear, this resource will also be helpful). One note: what we call in the class "spatial batch norm" is called "BatchNorm2D" in PyTorch.
* Layers: http://pytorch.org/docs/nn.html
* Activations: http://pytorch.org/docs/nn.html#non-linear-activations
* Loss functions: http://pytorch.org/docs/nn.html#loss-functions
* Optimizers: http://pytorch.org/docs/optim.html#algorithms
## Training a specific model
In this section, we're going to specify a model for you to construct. The goal here isn't to get good performance (that'll be next), but instead to get comfortable with understanding the PyTorch documentation and configuring your own model.
Using the code provided above as guidance, and using the following PyTorch documentation, specify a model with the following architecture:
* 7x7 Convolutional Layer with 32 filters and stride of 1
* ReLU Activation Layer
* Spatial Batch Normalization Layer
* 2x2 Max Pooling layer with a stride of 2
* Affine layer with 1024 output units
* ReLU Activation Layer
* Affine layer from 1024 input units to 10 outputs
And finally, set up a **cross-entropy** loss function and the **RMSprop** learning rule.
```
n_Conv2d = out_dim(32, 7, 0, 1)
n_MaxPool2d = out_dim(n_Conv2d, 2, 0, 2)
n_Flatten = 32*n_MaxPool2d**2
fixed_model_base = nn.Sequential( # You fill this in!
nn.Conv2d(3, 32, kernel_size=7, stride=1),
nn.ReLU(inplace=True),
nn.BatchNorm2d(32),
nn.MaxPool2d(2, stride=2),
Flatten(), # see above for explanation
nn.Linear(n_Flatten, 1024), # affine layer
nn.ReLU(inplace=True),
nn.Linear(1024, 10) # affine layer
)
fixed_model = fixed_model_base.type(dtype)
```
To make sure you're doing the right thing, use the following tool to check the dimensionality of your output (it should be 64 x 10, since our batches have size 64 and the output of the final affine layer should be 10, corresponding to our 10 classes):
```
## Now we're going to feed a random batch into the model you defined and make sure the output is the right size
x = torch.randn(64, 3, 32, 32).type(dtype)
x_var = Variable(x.type(dtype)) # Construct a PyTorch Variable out of your input data
ans = fixed_model(x_var) # Feed it through the model!
# Check to make sure what comes out of your model
# is the right dimensionality... this should be True
# if you've done everything correctly
np.array_equal(np.array(ans.size()), np.array([64, 10]))
```
### GPU!
Now, we're going to switch the dtype of the model and our data to the GPU-friendly tensors, and see what happens... everything is the same, except we are casting our model and input tensors as this new dtype instead of the old one.
If this returns false, or otherwise fails in a not-graceful way (i.e., with some error message), you may not have an NVIDIA GPU available on your machine. If you're running locally, we recommend you switch to Google Cloud and follow the instructions to set up a GPU there. If you're already on Google Cloud, something is wrong -- make sure you followed the instructions on how to request and use a GPU on your instance. If you did, post on Piazza or come to Office Hours so we can help you debug.
```
import copy
fixed_model_gpu = copy.deepcopy(fixed_model_base).type(dtype)
x_gpu = torch.randn(64, 3, 32, 32).type(dtype)
x_var_gpu = Variable(x.type(dtype)) # Construct a PyTorch Variable out of your input data
ans = fixed_model_gpu(x_var_gpu) # Feed it through the model!
# Check to make sure what comes out of your model
# is the right dimensionality... this should be True
# if you've done everything correctly
np.array_equal(np.array(ans.size()), np.array([64, 10]))
```
Run the following cell to evaluate the performance of the forward pass running on the CPU:
```
%%timeit
ans = fixed_model(x_var)
```
... and now the GPU:
```
%%timeit
# torch.cuda.synchronize() # Make sure there are no pending GPU computations
ans = fixed_model_gpu(x_var_gpu) # Feed it through the model!
# torch.cuda.synchronize() # Make sure there are no pending GPU computations
```
You should observe that even a simple forward pass like this is significantly faster on the GPU. So for the rest of the assignment (and when you go train your models in assignment 3 and your project!), you should use the GPU datatype for your model and your tensors: as a reminder that is *torch.cuda.FloatTensor* (in our notebook here as *gpu_dtype*)
### Train the model.
Now that you've seen how to define a model and do a single forward pass of some data through it, let's walk through how you'd actually train one whole epoch over your training data (using the simple_model we provided above).
Make sure you understand how each PyTorch function used below corresponds to what you implemented in your custom neural network implementation.
Note that because we are not resetting the weights anywhere below, if you run the cell multiple times, you are effectively training multiple epochs (so your performance should improve).
First, set up an RMSprop optimizer (using a 1e-3 learning rate) and a cross-entropy loss function:
```
loss_fn = nn.CrossEntropyLoss()
optimizer = optim.RMSprop(fixed_model_gpu.parameters(), lr=1e-3)
# This sets the model in "training" mode. This is relevant for some layers that may have different behavior
# in training mode vs testing mode, such as Dropout and BatchNorm.
fixed_model_gpu.train()
# Load one batch at a time.
for t, (x, y) in enumerate(tqdm(loader_train)):
x_var = Variable(x.type(dtype))
y_var = Variable(y.type(ltype))
# This is the forward pass: predict the scores for each class, for each x in the batch.
scores = fixed_model_gpu(x_var)
# Use the correct y values and the predicted y values to compute the loss.
loss = loss_fn(scores, y_var)
if (t + 1) % print_every == 0:
print('t = %d, loss = %.4f' % (t + 1, loss.data[0]))
# Zero out all of the gradients for the variables which the optimizer will update.
optimizer.zero_grad()
# This is the backwards pass: compute the gradient of the loss with respect to each
# parameter of the model.
loss.backward()
# Actually update the parameters of the model using the gradients computed by the backwards pass.
optimizer.step()
```
Now you've seen how the training process works in PyTorch. To save you writing boilerplate code, we're providing the following helper functions to help you train for multiple epochs and check the accuracy of your model:
```
def train(model, loss_fn, optimizer, num_epochs = 1, verbose = True):
for epoch in range(num_epochs):
if verbose:
print('Starting epoch %d / %d' % (epoch + 1, num_epochs))
model.train()
for t, (x, y) in enumerate(loader_train):
x_var = Variable(x.type(dtype))
y_var = Variable(y.type(ltype))
scores = model(x_var)
loss = loss_fn(scores, y_var)
if (t + 1) % print_every == 0 and verbose:
print('t = %d, loss = %.4f' % (t + 1, loss.data[0]))
optimizer.zero_grad()
loss.backward()
optimizer.step()
def check_accuracy(model, loader, verbose = True):
if verbose:
if loader.dataset.train:
print('Checking accuracy on validation set')
else:
print('Checking accuracy on test set')
num_correct = 0
num_samples = 0
model.eval() # Put the model in test mode (the opposite of model.train(), essentially)
for x, y in loader:
x_var = Variable(x.type(dtype), volatile=True)
scores = model(x_var)
_, preds = scores.data.cpu().max(1)
num_correct += (preds == y).sum()
num_samples += preds.size(0)
acc = float(num_correct) / num_samples
if verbose:
print('Got %d / %d correct (%.2f)' % (num_correct, num_samples, 100 * acc))
return acc
torch.cuda.random.manual_seed(12345)
```
### Check the accuracy of the model.
Let's see the train and check_accuracy code in action -- feel free to use these methods when evaluating the models you develop below.
You should get a training loss of around 1.2-1.4, and a validation accuracy of around 50-60%. As mentioned above, if you re-run the cells, you'll be training more epochs, so your performance will improve past these numbers.
But don't worry about getting these numbers better -- this was just practice before you tackle designing your own model.
```
fixed_model_gpu.apply(reset)
train(fixed_model_gpu, loss_fn, optimizer, num_epochs=5)
check_accuracy(fixed_model_gpu, loader_val)
```
### Don't forget the validation set!
And note that you can use the check_accuracy function to evaluate on either the test set or the validation set, by passing either **loader_test** or **loader_val** as the second argument to check_accuracy. You should not touch the test set until you have finished your architecture and hyperparameter tuning, and only run the test set once at the end to report a final value.
## Train a _great_ model on CIFAR-10!
Now it's your job to experiment with architectures, hyperparameters, loss functions, and optimizers to train a model that achieves **>=70%** accuracy on the CIFAR-10 **validation** set. You can use the check_accuracy and train functions from above.
### Things you should try:
- **Filter size**: Above we used 7x7; this makes pretty pictures but smaller filters may be more efficient
- **Number of filters**: Above we used 32 filters. Do more or fewer do better?
- **Pooling vs Strided Convolution**: Do you use max pooling or just stride convolutions?
- **Batch normalization**: Try adding spatial batch normalization after convolution layers and vanilla batch normalization after affine layers. Do your networks train faster?
- **Network architecture**: The network above has two layers of trainable parameters. Can you do better with a deep network? Good architectures to try include:
- [conv-relu-pool]xN -> [affine]xM -> [softmax or SVM]
- [conv-relu-conv-relu-pool]xN -> [affine]xM -> [softmax or SVM]
- [batchnorm-relu-conv]xN -> [affine]xM -> [softmax or SVM]
- **Global Average Pooling**: Instead of flattening and then having multiple affine layers, perform convolutions until your image gets small (7x7 or so) and then perform an average pooling operation to get to a 1x1 image picture (1, 1 , Filter#), which is then reshaped into a (Filter#) vector. This is used in [Google's Inception Network](https://arxiv.org/abs/1512.00567) (See Table 1 for their architecture).
- **Regularization**: Add l2 weight regularization, or perhaps use Dropout.
### Tips for training
For each network architecture that you try, you should tune the learning rate and regularization strength. When doing this there are a couple important things to keep in mind:
- If the parameters are working well, you should see improvement within a few hundred iterations
- Remember the coarse-to-fine approach for hyperparameter tuning: start by testing a large range of hyperparameters for just a few training iterations to find the combinations of parameters that are working at all.
- Once you have found some sets of parameters that seem to work, search more finely around these parameters. You may need to train for more epochs.
- You should use the validation set for hyperparameter search, and save your test set for evaluating your architecture on the best parameters as selected by the validation set.
### Going above and beyond
If you are feeling adventurous there are many other features you can implement to try and improve your performance. You are **not required** to implement any of these; however they would be good things to try for extra credit.
- Alternative update steps: For the assignment we implemented SGD+momentum, RMSprop, and Adam; you could try alternatives like AdaGrad or AdaDelta.
- Alternative activation functions such as leaky ReLU, parametric ReLU, ELU, or MaxOut.
- Model ensembles
- Data augmentation
- New Architectures
- [ResNets](https://arxiv.org/abs/1512.03385) where the input from the previous layer is added to the output.
- [DenseNets](https://arxiv.org/abs/1608.06993) where inputs into previous layers are concatenated together.
- [This blog has an in-depth overview](https://chatbotslife.com/resnets-highwaynets-and-densenets-oh-my-9bb15918ee32)
If you do decide to implement something extra, clearly describe it in the "Extra Credit Description" cell below.
### What we expect
At the very least, you should be able to train a ConvNet that gets at least 70% accuracy on the validation set. This is just a lower bound - if you are careful it should be possible to get accuracies much higher than that! Extra credit points will be awarded for particularly high-scoring models or unique approaches.
You should use the space below to experiment and train your network.
Have fun and happy training!
```
import time
import hyperopt.pyll
from hyperopt import fmin, tpe, hp, STATUS_OK, Trials
from hyperopt.pyll import scope
@scope.define_pure
def L1_shift(a):
return [a + 5]
@scope.define_pure
def L2_shift(a):
return [a + 5]
@scope.define_pure
def L2_L3_shift(a, b):
return [a + 5, b + 5]
@scope.define_pure
def W1_shift(a):
return [a + 256]
@scope.define_pure
def W2_shift(a):
return [a + 64]
```
## Base Model
After 20 rounds of hyperparameters optimization we were able to get a 60% validation accuracy.
parameters_zero = {'L1': [6], 'S': [3], 'W1': [651], 'loss': 0.6},
```
# Train your model here, and make sure the output of this cell is the accuracy of your best model on the
# train, val, and test sets. Here's some code to get you started. The output of this cell should be the training
# and validation accuracy on your best model (measured by validation accuracy).
def model_zero(L1, W1, S, C = 10):
n_Conv2d = out_dim(32, S, 0, 1)
n_MaxPool2d = out_dim(n_Conv2d, 2, 0, 2)
n_Flatten = L1*n_MaxPool2d**2
return nn.Sequential( # You fill this in!
nn.Conv2d(3, L1, kernel_size=S, stride=1),
nn.ReLU(inplace=True),
nn.BatchNorm2d(L1),
nn.MaxPool2d(2, stride=2),
Flatten(), # see above for explanation
nn.Linear(n_Flatten, W1), # affine layer
nn.ReLU(inplace=True),
nn.Linear(W1, C) # affine layer
)
search_space_zero = {
'L1': L1_shift(hp.randint('L1', 20)),
'W1': W1_shift(hp.randint('W1', 2048)),
'S': hp.choice('S', [3, 5, 7])
}
def loss_zero(x):
print(x)
model = model_zero(x['L1'][0], x['W1'][0], x['S']).type(dtype)
loss_fn = nn.CrossEntropyLoss()
optimizer = optim.RMSprop(model.parameters(), lr=1e-3)
train(model, loss_fn, optimizer, num_epochs=20, verbose=False)
return -check_accuracy(model, loader_val, verbose=False)
def objective_zero(x):
return {
'loss': loss_zero(x),
'status': STATUS_OK,
# -- store other results
'eval_time': time.time()
}
trials_zero = Trials()
best_zero = fmin(objective_zero,
space=search_space_zero,
algo=tpe.suggest,
max_evals=20,
trials=trials_zero)
def extract_zero(x):
return {
'loss': -x['result']['loss'],
'L1': list(map(lambda v: v+5, x['misc']['vals']['L1'])),
'W1': list(map(lambda v: v+256, x['misc']['vals']['W1'])),
'S': list(map(lambda v: 3 if v == 0 else 5 if v == 1 else 7,x['misc']['vals']['S']))
}
res_zero = list(map(extract_zero, trials_zero))
[{'L1': [9], 'S': [5], 'W1': [1870], 'loss': 0.584},
{'L1': [8], 'S': [7], 'W1': [649], 'loss': 0.568},
{'L1': [16], 'S': [5], 'W1': [614], 'loss': 0.55},
{'L1': [18], 'S': [7], 'W1': [1773], 'loss': 0.513},
{'L1': [21], 'S': [3], 'W1': [1664], 'loss': 0.616},
{'L1': [6], 'S': [3], 'W1': [651], 'loss': 0.6},
{'L1': [5], 'S': [3], 'W1': [750], 'loss': 0.587},
{'L1': [17], 'S': [3], 'W1': [2189], 'loss': 0.623},
{'L1': [14], 'S': [7], 'W1': [2240], 'loss': 0.553},
{'L1': [5], 'S': [5], 'W1': [1008], 'loss': 0.533},
{'L1': [22], 'S': [5], 'W1': [1498], 'loss': 0.609},
{'L1': [15], 'S': [3], 'W1': [2065], 'loss': 0.581},
{'L1': [11], 'S': [7], 'W1': [1174], 'loss': 0.557},
{'L1': [9], 'S': [7], 'W1': [923], 'loss': 0.566},
{'L1': [15], 'S': [7], 'W1': [2022], 'loss': 0.59},
{'L1': [6], 'S': [5], 'W1': [969], 'loss': 0.587},
{'L1': [9], 'S': [3], 'W1': [1193], 'loss': 0.514},
{'L1': [16], 'S': [5], 'W1': [2252], 'loss': 0.627},
{'L1': [12], 'S': [5], 'W1': [1821], 'loss': 0.611},
{'L1': [9], 'S': [7], 'W1': [279], 'loss': 0.53}]
```
## [conv-relu-pool]xN -> [affine]xM -> [softmax or SVM]
66.5% validation accuracy with:
{'L1': [16], 'L2': [8], 'W1': [464], 'W2': [], 'loss': 0.665}
```
def model_one(conv_relu_pool_depths, affine_depths, C = 10):
from functools import reduce
from collections import OrderedDict
Conv2d_K = 3
Conv2d_S = 1
MaxPool2d_K = 2
MaxPool2d_S = 2
# 15, 4500; 6, 720
conv_relu_pool_sizes = [
lambda N: out_dim(N, Conv2d_K, 0, Conv2d_S),
lambda N: out_dim(N, MaxPool2d_K, 0, MaxPool2d_S)
] * len(conv_relu_pool_depths)
n_to_Flatten = reduce(lambda value, f: f(value), conv_relu_pool_sizes, 32)
n_Flatten = conv_relu_pool_depths[-1]*n_to_Flatten**2
def conv_relu_pool_layers_ctr():
for i, (L0, L1) in enumerate(zip([3] + conv_relu_pool_depths[:-1], conv_relu_pool_depths)):
yield 'conv2d_%s'%i, nn.Conv2d(L0, L1, kernel_size=Conv2d_K, stride=Conv2d_S)
yield 'relu_%s'%i, nn.ReLU(inplace=True)
yield 'pool_%s'%i, nn.MaxPool2d(MaxPool2d_K, stride=MaxPool2d_S)
def affine_layers_ctr():
for i, (W0, W1) in enumerate(zip([n_Flatten] + affine_depths[:-1], affine_depths)):
yield 'affine_linear_%s'%i, nn.Linear(W0, W1)
yield 'affine_relu_%s'%i, nn.ReLU(inplace=True)
layers = list(conv_relu_pool_layers_ctr()) + [tuple(('flatten', Flatten()))] + list(affine_layers_ctr()) + [tuple(('to_classes', nn.Linear(affine_depths[-1], C)))]
return nn.Sequential(OrderedDict(layers))
search_space_one = {
'conv_relu_pool_layers': L1_shift(hp.randint('L1', 20)) + hp.choice('conv_relu_pool_depths', [
list(),
L2_shift(hp.randint('L2', 20))
]),
'affine_layers': W1_shift(hp.randint('W1', 2048)) + hp.choice('affine_depths', [
list(),
W2_shift(hp.randint('W2', 256))
])
}
def loss_one(x):
print(x)
model = model_one(list(x['conv_relu_pool_layers']), list(x['affine_layers'])).type(dtype)
loss_fn = nn.CrossEntropyLoss()
optimizer = optim.RMSprop(model.parameters(), lr=1e-3)
train(model, loss_fn, optimizer, num_epochs=20, verbose=True)
return -check_accuracy(model, loader_val, verbose=True)
def objective_one(x):
return {
'loss': loss_one(x),
'status': STATUS_OK,
# -- store other results
'eval_time': time.time()
}
trials_one = Trials()
best_one = fmin(objective_one,
space=search_space_one,
algo=tpe.suggest,
max_evals=20,
trials=trials_one)
def extract_one(x):
return {
'loss': -x['result']['loss'],
'L1': list(map(lambda x: x+5, x['misc']['vals']['L1'])),
'L2': list(map(lambda x: x+5, x['misc']['vals']['L2'])),
'W1': list(map(lambda x: x+256, x['misc']['vals']['W1'])),
'W2': list(map(lambda x: x+64, x['misc']['vals']['W2']))
}
res_one = list(map(extract_one, trials_one))
[{'L1': [18], 'L2': [], 'W1': [950], 'W2': [], 'loss': 0.614},
{'L1': [7], 'L2': [], 'W1': [2072], 'W2': [168], 'loss': 0.586},
{'L1': [21], 'L2': [20], 'W1': [840], 'W2': [], 'loss': 0.653},
{'L1': [16], 'L2': [8], 'W1': [464], 'W2': [], 'loss': 0.665},
{'L1': [17], 'L2': [], 'W1': [2011], 'W2': [316], 'loss': 0.619},
{'L1': [24], 'L2': [], 'W1': [1908], 'W2': [174], 'loss': 0.644},
{'L1': [14], 'L2': [8], 'W1': [2196], 'W2': [], 'loss': 0.604},
{'L1': [15], 'L2': [10], 'W1': [1806], 'W2': [], 'loss': 0.607},
{'L1': [20], 'L2': [], 'W1': [1820], 'W2': [], 'loss': 0.643},
{'L1': [11], 'L2': [], 'W1': [1431], 'W2': [247], 'loss': 0.62},
{'L1': [9], 'L2': [5], 'W1': [2238], 'W2': [], 'loss': 0.548},
{'L1': [7], 'L2': [], 'W1': [1655], 'W2': [], 'loss': 0.6},
{'L1': [12], 'L2': [], 'W1': [2241], 'W2': [], 'loss': 0.612},
{'L1': [20], 'L2': [9], 'W1': [1818], 'W2': [], 'loss': 0.589},
{'L1': [22], 'L2': [], 'W1': [934], 'W2': [], 'loss': 0.636},
{'L1': [24], 'L2': [13], 'W1': [667], 'W2': [210], 'loss': 0.64},
{'L1': [18], 'L2': [], 'W1': [455], 'W2': [278], 'loss': 0.62},
{'L1': [9], 'L2': [], 'W1': [967], 'W2': [], 'loss': 0.594},
{'L1': [13], 'L2': [], 'W1': [1033], 'W2': [], 'loss': 0.63},
{'L1': [19], 'L2': [24], 'W1': [573], 'W2': [], 'loss': 0.647}]
```
## [batchnorm-relu-conv]xN -> [affine]xM -> [softmax or SVM]
64.9% validation accuracy with:
{'L1': [20],
'L2': [21],
'L2_1': [],
'L3_1': [],
'W1': [487],
'W2': [],
'loss': 0.649}
```
def model_three(batchnorm_conv_relu_depths, affine_depths, C = 10):
from functools import reduce
from collections import OrderedDict
Conv2d_K = 3
Conv2d_S = 1
batchnorm_conv_relu_sizes = [
lambda N: out_dim(N, Conv2d_K, 0, Conv2d_S)
] * len(batchnorm_conv_relu_depths)
n_to_Flatten = reduce(lambda value, f: f(value), batchnorm_conv_relu_sizes, 32)
n_Flatten = batchnorm_conv_relu_depths[-1]*n_to_Flatten**2
def batchnorm_conv_relu_layers_ctr():
for i, (L0, L1) in enumerate(zip([3] + batchnorm_conv_relu_depths[:-1], batchnorm_conv_relu_depths)):
yield 'batchnorm2d_%s'%i, nn.BatchNorm2d(L0)
yield 'conv2d_%s'%i, nn.Conv2d(L0, L1, kernel_size=Conv2d_K, stride=Conv2d_S)
yield 'relu_%s'%i, nn.ReLU(inplace=True)
def affine_layers_ctr():
for i, (W0, W1) in enumerate(zip([n_Flatten] + affine_depths[:-1], affine_depths)):
yield 'affine_linear_%s'%i, nn.Linear(W0, W1)
yield 'affine_relu_%s'%i, nn.ReLU(inplace=True)
layers = list(batchnorm_conv_relu_layers_ctr()) + [tuple(('flatten', Flatten()))] + list(affine_layers_ctr()) + [tuple(('to_classes', nn.Linear(affine_depths[-1], C)))]
return nn.Sequential(OrderedDict(layers))
search_space_three = {
'batchnorm2d_conv_relu_layers': L1_shift(hp.randint('L1', 20)) + hp.choice('batchnorm2d_conv_relu_L2', [
list(),
L2_shift(hp.randint('L2', 20))
]) + hp.choice('batchnorm2d_conv_relu_L3', [
list(),
L2_shift(hp.randint('L3', 20))
]),
'affine_layers': W1_shift(hp.randint('W1', 2048)) + hp.choice('affine_depths', [
list(),
W2_shift(hp.randint('W2', 256))
])
}
def loss_three(x):
print(x)
model = model_three(list(x['batchnorm2d_conv_relu_layers']), list(x['affine_layers'])).type(dtype)
loss_fn = nn.CrossEntropyLoss()
optimizer = optim.RMSprop(model.parameters(), lr=1e-3)
train(model, loss_fn, optimizer, num_epochs=20, verbose=False)
return -check_accuracy(model, loader_val, verbose=False)
def objective_three(x):
return {
'loss': loss_three(x),
'status': STATUS_OK,
# -- store other results
'eval_time': time.time()
}
trials_three = Trials()
best_three = fmin(objective_three,
space=search_space_three,
algo=tpe.suggest,
max_evals=20,
trials=trials_three)
def extract_three(x):
val = x['misc']['vals']
return {
'loss': -x['result']['loss'],
'L1': list(map(lambda x: x+5, val['L1'])),
'L2': list(map(lambda x: x+5, val.get('L2', []))),
'L2_1': list(map(lambda x: x+5, val.get('L2_1', []))),
'L3_1': list(map(lambda x: x+5, val.get('L3_1', []))),
'W1': list(map(lambda x: x+256, val['W1'])),
'W2': list(map(lambda x: x+64, val.get('W2', [])))
}
res_three = list(map(extract_three, trials_three))
[{'L1': [24],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [975],
'W2': [],
'loss': 0.603},
{'L1': [13],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [1873],
'W2': [222],
'loss': 0.613},
{'L1': [9],
'L2': [10],
'L2_1': [],
'L3_1': [],
'W1': [2180],
'W2': [161],
'loss': 0.616},
{'L1': [14],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [1241],
'W2': [295],
'loss': 0.622},
{'L1': [11],
'L2': [8],
'L2_1': [],
'L3_1': [],
'W1': [1138],
'W2': [74],
'loss': 0.6},
{'L1': [20],
'L2': [10],
'L2_1': [],
'L3_1': [],
'W1': [1968],
'W2': [261],
'loss': 0.618},
{'L1': [15],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [803],
'W2': [],
'loss': 0.614},
{'L1': [24],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [1607],
'W2': [],
'loss': 0.594},
{'L1': [24],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [1132],
'W2': [],
'loss': 0.596},
{'L1': [10],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [1500],
'W2': [302],
'loss': 0.584},
{'L1': [9],
'L2': [22],
'L2_1': [],
'L3_1': [],
'W1': [2272],
'W2': [],
'loss': 0.559},
{'L1': [15],
'L2': [18],
'L2_1': [],
'L3_1': [],
'W1': [1224],
'W2': [],
'loss': 0.614},
{'L1': [23],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [1120],
'W2': [],
'loss': 0.621},
{'L1': [22],
'L2': [11],
'L2_1': [],
'L3_1': [],
'W1': [1398],
'W2': [],
'loss': 0.573},
{'L1': [13],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [1214],
'W2': [283],
'loss': 0.61},
{'L1': [24],
'L2': [7],
'L2_1': [],
'L3_1': [],
'W1': [302],
'W2': [],
'loss': 0.559},
{'L1': [20],
'L2': [21],
'L2_1': [],
'L3_1': [],
'W1': [487],
'W2': [],
'loss': 0.649},
{'L1': [22],
'L2': [22],
'L2_1': [],
'L3_1': [],
'W1': [1007],
'W2': [],
'loss': 0.641},
{'L1': [15],
'L2': [18],
'L2_1': [],
'L3_1': [],
'W1': [509],
'W2': [168],
'loss': 0.61},
{'L1': [12],
'L2': [],
'L2_1': [],
'L3_1': [],
'W1': [1424],
'W2': [],
'loss': 0.583}]
```
### Describe what you did
In the cell below you should write an explanation of what you did, any additional features that you implemented, and any visualizations or graphs that you make in the process of training and evaluating your network.
DNN with architectures 0, 1 and 3 were implemented and trained on data. Hyperparameter optimization was performed.
The best model found was the [conv-relu-pool]xN -> [affine]xM -> [softmax] with parameters: {'L1': 16, 'L2': 8, 'W1': 464} which got an accuracy of 0.665.
## Test set -- run this only once
Now that we've gotten a result we're happy with, we test our final model on the test set (which you should store in best_model). This would be the score we would achieve on a competition. Think about how this compares to your validation set accuracy.
```
best_model = None
check_accuracy(best_model, loader_test)
```
## Going further with PyTorch
The next assignment will make heavy use of PyTorch. You might also find it useful for your projects.
Here's a nice tutorial by Justin Johnson that shows off some of PyTorch's features, like dynamic graphs and custom NN modules: http://pytorch.org/tutorials/beginner/pytorch_with_examples.html
If you're interested in reinforcement learning for your final project, this is a good (more advanced) DQN tutorial in PyTorch: http://pytorch.org/tutorials/intermediate/reinforcement_q_learning.html
| github_jupyter |
# Programación lineal
<img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/commons/thumb/0/0c/Linear_Programming_Feasible_Region.svg/2000px-Linear_Programming_Feasible_Region.svg.png" width="400px" height="125px" />
> La programación lineal es el campo de la optimización matemática dedicado a maximizar o minimizar (optimizar) funciones lineales, denominada función objetivo, de tal forma que las variables de dicha función estén sujetas a una serie de restricciones expresadas mediante un sistema de ecuaciones o inecuaciones también lineales.
**Referencias:**
- https://es.wikipedia.org/wiki/Programaci%C3%B3n_lineal
- https://docs.scipy.org/doc/scipy-0.18.1/reference/optimize.html
## 1. Apuntes históricos
<img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/commons/5/5e/JohnvonNeumann-LosAlamos.gif" width="400px" height="125px" />
- 1826: Joseph Fourier anticipa la programación lineal. Carl Friedrich Gauss resuelve ecuaciones lineales por eliminación "gaussiana".
- 1902: Gyula Farkas concibe un método para resolver sistemas de inecuaciones.
- Es hasta la Segunda Guerra Mundial que se plantea la programación lineal como un modelo matemático para planificar gastos y retornos, de modo que se reduzcan costos de guerra y aumentar pérdidas del enemigo. Secreto hasta 1947 (posguerra).
- 1947: George Dantzig publica el algoritmo simplex y John von Neumann desarrolló la teoría de la dualidad. Se sabe que Leonid Kantoróvich también formuló la teoría en forma independiente.
- Fue usado por muchas industrias en la planificación diaria.
**Hasta acá, tiempos exponenciales de solución. Lo siguiente, tiempo polinomial.**
- 1979: Leonid Khachiyan, diseñó el llamado Algoritmo del elipsoide, a través del cual demostró que el problema de la programación lineal es resoluble de manera eficiente, es decir, en tiempo polinomial.
- 1984: Narendra Karmarkar introduce el método del punto interior para resolver problemas de programación lineal.
**Mencionar complejidad computacional.**
## 2. Motivación
Ya la clase pasada habíamos mencionado que cuando se quería optimizar una función de varias variables con restricciones, se podía aplicar siempre el método de Multiplicadores de Lagrange. Sin embargo, este método es computacionalmente muy complejo conforme crece el número de variables.
Por tanto, cuando la función a optimizar y las restricciones son de caracter lineal, los métodos de solución que se pueden desarrollar son computacionalmente eficientes, por lo que es útil realizar la distinción.
## 3. Problemas de programación lineal
### 3.1. Ejemplo básico
Una compañía produce dos productos ($X_1$ y $X_2$) usando dos máquinas ($A$ y $B$). Cada unidad de $X_1$ que se produce requiere 50 minutos en la máquina $A$ y 30 minutos en la máquina $B$. Cada unidad de $X_2$ que se produce requiere 24 minutos en la máquina $A$ y 33 minutos en la máquina $B$.
Al comienzo de la semana hay 30 unidades de $X_1$ y 90 unidades de $X_2$ en inventario. El tiempo de uso disponible de la máquina $A$ es de 40 horas y el de la máquina $B$ es de 35 horas.
La demanda para $X_1$ en la semana actual es de 75 unidades y de $X_2$ es de 95 unidades. La política de la compañía es maximizar la suma combinada de unidades de $X_1$ e $X_2$ en inventario al finalizar la semana.
Formular el problema de decidir cuánto hacer de cada producto en la semana como un problema de programación lineal.
#### Solución
Sean:
- $x_1$ la cantidad de unidades de $X_1$ a ser producidas en la semana, y
- $x_2$ la cantidad de unidades de $X_2$ a ser producidas en la semana.
Notar que lo que se quiere es maximizar $x_1+x_2$.
Restricciones:
1. El tiempo de uso disponible de la máquina $A$ es de 40 horas: $50x_1+24x_2\leq 40(60)\Rightarrow 50x_1+24x_2\leq 2400$.
2. El tiempo de uso disponible de la máquina $B$ es de 35 horas: $30x_1+33x_2\leq 35(60)\Rightarrow 30x_1+33x_2\leq 2100$.
3. La demanda para $X_1$ en la semana actual es de 75 unidades: $x_1+30\geq 75\Rightarrow x_1\geq 45\Rightarrow -x_1\leq -45$.
4. La demanda para $X_2$ en la semana actual es de 95 unidades: $x_2+90\geq 95\Rightarrow x_2\geq 5\Rightarrow -x_2\leq -5$.
Finalmente, el problema puede ser expresado en la forma explicada como:
\begin{equation}
\begin{array}{ll}
\min_{x_1,x_2} & -x_1-x_2 \\
\text{s. a. } & 50x_1+24x_2\leq 2400 \\
& 30x_1+33x_2\leq 2100 \\
& -x_1\leq -45 \\
& -x_2\leq -5,
\end{array}
\end{equation}
o, eqivalentemente
\begin{equation}
\begin{array}{ll}
\min_{\boldsymbol{x}} & \boldsymbol{c}^T\boldsymbol{x} \\
\text{s. a. } & \boldsymbol{A}_{eq}\boldsymbol{x}=\boldsymbol{b}_{eq} \\
& \boldsymbol{A}\boldsymbol{x}\leq\boldsymbol{b},
\end{array}
\end{equation}
con
- $\boldsymbol{c}=\left[-1 \quad -1\right]^T$,
- $\boldsymbol{A}=\left[\begin{array}{cc}50 & 24 \\ 30 & 33\\ -1 & 0\\ 0 & -1\end{array}\right]$, y
- $\boldsymbol{b}=\left[2400\quad 2100\quad -45\quad -5\right]^T$.
Preferiremos, en adelante, la notación vectorial/matricial.
### 3.2. En general
De acuerdo a lo descrito anteriormente, un problema de programación lineal puede escribirse en la siguiente forma:
\begin{equation}
\begin{array}{ll}
\min_{x_1,\dots,x_n} & c_1x_1+\dots+c_nx_n \\
\text{s. a. } & a^{eq}_{j,1}x_1+\dots+a^{eq}_{j,n}x_n=b^{eq}_j \text{ para } 1\leq j\leq m_1 \\
& a_{k,1}x_1+\dots+a_{k,n}x_n\leq b_k \text{ para } 1\leq k\leq m_2,
\end{array}
\end{equation}
donde:
- $x_i$ para $i=1,\dots,n$ son las incógnitas o variables de decisión,
- $c_i$ para $i=1,\dots,n$ son los coeficientes de la función a optimizar,
- $a^{eq}_{j,i}$ para $j=1,\dots,m_1$ e $i=1,\dots,n$, son los coeficientes de la restricción de igualdad,
- $a_{k,i}$ para $k=1,\dots,m_2$ e $i=1,\dots,n$, son los coeficientes de la restricción de desigualdad,
- $b^{eq}_j$ para $j=1,\dots,m_1$ son valores conocidos que deben ser respetados estrictamente, y
- $b_k$ para $k=1,\dots,m_2$ son valores conocidos que no deben ser superados.
Equivalentemente, el problema puede escribirse como
\begin{equation}
\begin{array}{ll}
\min_{\boldsymbol{x}} & \boldsymbol{c}^T\boldsymbol{x} \\
\text{s. a. } & \boldsymbol{A}_{eq}\boldsymbol{x}=\boldsymbol{b}_{eq} \\
& \boldsymbol{A}\boldsymbol{x}\leq\boldsymbol{b},
\end{array}
\end{equation}
donde:
- $\boldsymbol{x}=\left[x_1\quad\dots\quad x_n\right]^T$,
- $\boldsymbol{c}=\left[c_1\quad\dots\quad c_n\right]^T$,
- $\boldsymbol{A}_{eq}=\left[\begin{array}{ccc}a^{eq}_{1,1} & \dots & a^{eq}_{1,n}\\ \vdots & \ddots & \vdots\\ a^{eq}_{m_1,1} & \dots & a^{eq}_{m_1,n}\end{array}\right]$,
- $\boldsymbol{A}=\left[\begin{array}{ccc}a_{1,1} & \dots & a_{1,n}\\ \vdots & \ddots & \vdots\\ a_{m_2,1} & \dots & a_{m_2,n}\end{array}\right]$,
- $\boldsymbol{b}_{eq}=\left[b^{eq}_1\quad\dots\quad b^{eq}_{m_1}\right]^T$, y
- $\boldsymbol{b}=\left[b_1\quad\dots\quad b_{m_2}\right]^T$.
**Nota:** el problema $\max_{\boldsymbol{x}}\boldsymbol{g}(\boldsymbol{x})$ es equivalente a $\min_{\boldsymbol{x}}-\boldsymbol{g}(\boldsymbol{x})$.
#### Bueno, y una vez planteado, ¿cómo se resuelve el problema?
Este problema está sencillo pues solo es en dos variables. La solución gráfica es válida.
```
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
def res1(x1):
return (2400-50*x1)/24
def res2(x1):
return (2100-30*x1)/33
x1 = np.linspace(40, 50)
r1 = res1(x1)
r2 = res2(x1)
plt.figure(figsize = (8,6))
plt.plot(x1, res1(x1), 'b--', label = 'res1')
plt.plot(x1, res2(x1), 'r--', label = 'res2')
plt.plot([45, 45], [0, 25], 'k', label = 'res3')
plt.plot([40, 50], [5, 5], 'm', label = 'res4')
plt.fill_between(np.array([45.0, 45.6]), res1(np.array([45.0, 45.6])), 5*np.ones(2))
plt.text(44,4,'$(45,5)$',fontsize=10)
plt.text(45.1,6.35,'$(45,6.25)$',fontsize=10)
plt.text(45.6,4,'$(45.6,5)$',fontsize=10)
plt.legend(loc = 'best')
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
plt.axis([44, 46, 4, 7])
plt.show()
```
**Actividad.** Mónica hace aretes y cadenitas de joyería. Es tan buena, que todo lo que hace lo vende.
Le toma 30 minutos hacer un par de aretes y una hora hacer una cadenita, y como Mónica también es estudihambre, solo dispone de 10 horas a la semana para hacer las joyas. Por otra parte, el material que compra solo le alcanza para hacer 15 unidades (el par de aretes cuenta como unidad) de joyas por semana.
La utilidad que le deja la venta de las joyas es \$15 en cada par de aretes y \$20 en cada cadenita.
¿Cuántos pares de aretes y cuántas cadenitas debería hacer Mónica para maximizar su utilidad?
Formular el problema en la forma explicada y obtener la solución gráfica (puede ser a mano).
**Diez minutos: quien primero lo haga, pasará a explicarlo al tablero y le subiré la nota de alguna tarea a 100. Debe salir a explicar el problema en el pizarrón.**
## 5. ¿Cómo se resuelve en python?
### 5.1 Librería `SciPy`
<img style="float: right; margin: 0px 0px 15px 15px;" src="https://scipy.org/_static/images/scipy_med.png" width="200px" height="75px" />
`SciPy` es un softwar de código abierto basado en `Python` para matemáticas, ciencia e ingeniería.
En particular, los siguientes son algunos de los paquetes básicos:
- `NumPy`
- **Librería `SciPy`**
- `SymPy`
- `matplotlib`
- `pandas`
La **Librería `SciPy`** es uno de los paquetes principales y provee varias rutinas numéricas eficientes. Entre ellas, para integración numérica y optimización.
En esta clase, y en lo que resta del módulo, estaremos utilizando el módulo `optimize` de la librería `SciPy`.
**Importémoslo**
```
# Importar el módulo optimize de la librería scipy
import scipy.optimize as opt
```
El módulo `optimize` que acabamos de importar contiene varias funciones para optimización y búsqueda de raices ($f(x)=0$). Entre ellas se encuentra la función `linprog`
```
# Función linprog del módulo optimize
help(opt.linprog)
```
la cual resuelve problemas como los que aprendimos a plantear.
### 5.2 Solución del ejemplo básico con linprog
Ya hicimos la solución gráfica. Contrastemos con la solución que nos da `linprog`...
```
# Importar numpy para crear las matrices
import numpy as np
# Crear las matrices para resolver el problema
c = np.array([-1, -1])
A = np.array([[50, 24],
[30, 33],
[-1, 0],
[0, -1]])
b = np.array([2400, 2100, -45, -5])
b
# Resolver utilizando linprog
resultado = opt.linprog(c, A_ub=A, b_ub=b)
# Mostrar el resultado
resultado
# Extraer el vector solución
resultado.x
```
**Conclusión**
- Para maximizar el inventario conjunto de cantidad de productos X1 y X2, se deben producir 45 unidades de X1 y 6.25 unidades de X2.
- Con esa producción, el inventario conjunto al finalizar la semana es de 1.25 unidades.
**Otra forma:** poner las cotas de las variables a parte
```
# Escribir matrices y cotas
c = np.array([-1, -1])
A = np.array([[50, 24],
[30, 33]])
b = np.array([2400, 2100])
x1_bound = (45, None)
x2_bound = (5, None)
# Resolver
resultado2 = opt.linprog(c, A_ub=A, b_ub=b, bounds=(x1_bound,x2_bound))
# Mostrar el resultado
resultado2
```
**Actividad.** Resolver el ejemplo de Mónica y sus tiliches con `linprog`
```
# Resolver acá
c = np.array([-15, -20])
A = np.array([[1, 2],
[1, 1]])
b = np.array([20, 15])
resultado_monica = opt.linprog(c, A_ub=A, b_ub=b)
resultado_monica
```
## 6. Problema de transporte 1
- **Referencia**: https://es.wikipedia.org/wiki/Programaci%C3%B3n_lineal
<img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/commons/a/a0/Progr_Lineal.PNG" width="400px" height="125px" />
Este es un caso curioso, con solo 6 variables (un caso real de problema de transporte puede tener fácilmente más de 1.000 variables) en el cual se aprecia la utilidad de este procedimiento de cálculo.
Existen tres minas de carbón cuya producción diaria es:
- la mina "a" produce 40 toneladas de carbón por día;
- la mina "b" produce 40 t/día; y,
- la mina "c" produce 20 t/día.
En la zona hay dos centrales termoeléctricas que consumen:
- la central "d" consume 40 t/día de carbón; y,
- la central "e" consume 60 t/día.
Los costos de mercado, de transporte por tonelada son:
- de "a" a "d" = 2 monedas;
- de "a" a "e" = 11 monedas;
- de "b" a "d" = 12 monedas;
- de "b" a "e" = 24 monedas;
- de "c" a "d" = 13 monedas; y,
- de "c" a "e" = 18 monedas.
Si se preguntase a los pobladores de la zona cómo organizar el transporte, tal vez la mayoría opinaría que debe aprovecharse el precio ofrecido por el transportista que va de "a" a "d", porque es más conveniente que los otros, debido a que es el de más bajo precio.
En este caso, el costo total del transporte es:
- transporte de 40 t de "a" a "d" = 80 monedas;
- transporte de 20 t de "c" a "e" = 360 monedas; y,
- transporte de 40 t de "b" a "e" = 960 monedas,
Para un total 1.400 monedas.
Sin embargo, formulando el problema para ser resuelto por la programación lineal con
- $x_1$ toneladas transportadas de la mina "a" a la central "d"
- $x_2$ toneladas transportadas de la mina "a" a la central "e"
- $x_3$ toneladas transportadas de la mina "b" a la central "d"
- $x_4$ toneladas transportadas de la mina "b" a la central "e"
- $x_5$ toneladas transportadas de la mina "c" a la central "d"
- $x_6$ toneladas transportadas de la mina "c" a la central "e"
se tienen las siguientes ecuaciones:
Restricciones de la producción:
- $x_1 + x_2 \leq 40$
- $x_3 + x_4 \leq 40$
- $x_5 + x_6 \leq 20$
Restricciones del consumo:
- $x_1 + x_3 + x_5 \geq 40$
- $x_2 + x_4 + x_6 \geq 60$
La función objetivo será:
$$\min_{x_1,\dots,x_6}2x_1 + 11x_2 + 12x_3 + 24x_4 + 13x_5 + 18x_6$$
Resolver con `linprog`
```
# Matrices y cotas
c = np.array([2, 11, 12, 24, 13, 18])
A = np.array([[1, 1, 0, 0, 0, 0],
[0, 0, 1, 1, 0, 0],
[0, 0, 0, 0, 1, 1],
[-1, 0, -1, 0, -1, 0],
[0, -1, 0, -1, 0, -1]])
b = np.array([40, 40, 20, -40, -60])
# Resolver
resultado_transporte = opt.linprog(c, A_ub=A, b_ub=b)
# Mostrar resultado
resultado_transporte
```
**Conclusión**
- La estrategia de menor costo es llevar 40 toneladas de la mina "a" a la central "e", 40 toneladas de la mina "b" a la central "d" y 20 toneladas de la mina "c" a la central "e". El costo total de esta estrategia de transporte es 1280 monedas.
## 7. Optimización de inversión en bonos
**Referencia:**
```
from IPython.display import YouTubeVideo
YouTubeVideo('gukxBus8lOs')
```
El objetivo de este problema es determinar la mejor estrategia de inversión, dados diferentes tipos de bono, la máxima cantidad que puede ser invertida en cada bono, el porcentaje de retorno y los años de madurez. También hay una cantidad fija de dinero disponible ($\$750,000$). Por lo menos la mitad de este dinero debe ser invertido en bonos con 10 años o más para la madurez. Se puede invertir un máximo del $25\%$ de esta cantidad en cada bono. Finalmente, hay otra restricción que no permite usar más de $35\%$ en bonos de alto riesgo.
Existen seis (6) opciones de inversión con las letras correspondientes $A_i$
1. $A_1$:(Tasa de retorno=$8.65\%$; Años para la madurez=11, Riesgo=Bajo)
1. $A_2$:(Tasa de retorno=$9.50\%$; Años para la madurez=10, Riesgo=Alto)
1. $A_3$:(Tasa de retorno=$10.00\%$; Años para la madurez=6, Riesgo=Alto)
1. $A_4$:(Tasa de retorno=$8.75\%$; Años para la madurez=10, Riesgo=Bajo)
1. $A_5$:(Tasa de retorno=$9.25\%$; Años para la madurez=7, Riesgo=Alto)
1. $A_6$:(Tasa de retorno=$9.00\%$; Años para la madurez=13, Riesgo=Bajo)
Lo que se quiere entonces es maximizar el retorno que deja la inversión.
Este problema puede ser resuelto con programación lineal. Formalmente, puede ser descrito como:
$$\max_{A_1,A_2,...,A_6}\sum^{6}_{i=1} A_iR_i,$$
donde $A_i$ representa la cantidad invertida en la opción, y $R_i$ representa la tasa de retorno respectiva.
Plantear restricciones...
```
# Matrices y cotas
# Resolver
# Mostrar resultado
```
Recordar que en el problema minimizamos $-\sum^{6}_{i=1} A_iR_i$. El rendimiento obtenido es entonces:
**Conclusión**
-
## 8. Tarea
### 1. Diseño de la Dieta Óptima
Se quiere producir comida para gatos de la manera más barata, no obstante se debe también asegurar que se cumplan los datos requeridos de analisis nutricional. Por lo que se quiere variar la cantidad de cada ingrediente para cumplir con los estandares nutricionales. Los requisitos que se tienen es que en 100 gramos, se deben tener por lo menos 8 gramos de proteína y 6 gramos de grasa. Así mismo, no se debe tener más de 2 gramos de fibra y 0.4 gramos de sal.
Los datos nutricionales se pueden obtener de la siguiente tabla:
Ingrediente|Proteína|Grasa|Fibra|Sal
:----|----
Pollo| 10.0%|08.0%|00.1%|00.2%
Carne| 20.0%|10.0%|00.5%|00.5%
Cordero|15.0%|11.0%|00.5%|00.7%
Arroz| 00.0%|01.0%|10.0%|00.2%
Trigo| 04.0%|01.0%|15.0%|00.8%
Gel| 00.0%|00.0%|00.0%|00.0%
Los costos de cada producto son:
Ingrediente|Costo por gramo
:----|----
Pollo|$\$$0.013
Carne|$\$$0.008
Cordero|$\$$0.010
Arroz|$\$$0.002
Trigo|$\$$0.005
Gel|$\$$0.001
Lo que se busca optimizar en este caso es la cantidad de productos que se debe utilizar en la comida de gato, para simplificar la notación se van a nombrar las siguientes variables:
$x_1:$ Gramos de pollo
$x_2:$ Gramos de carne
$x_3:$ Gramos de cordero
$x_4:$ Gramos de arroz
$x_5:$ Gramos de trigo
$x_6:$ Gramos de gel
Con los datos, se puede plantear la función objetivo, está dada por la siguiente expresión:
$$\min 0.013 x_1 + 0.008 x_2 + 0.010 x_3 + 0.002 x_4 + 0.005 x_5 + 0.001 x_6$$
Las restricciones estarían dadas por el siguiente conjunto de ecuaciones:
$x_1+x_2+x_3+x_4+x_5+x_6=100$
$(10.0 x_1+ 20.0 x_2+ 15.0 x_3+ 00.0 x_4+ 04.0 x_5+ 00.0 x_6)/100 \geq 8.0$
$(08.0 x_1+ 10.0 x_2+ 11.0 x_3+ 01.0 x_4+ 01.0 x_5+ 00.0 x_6)/100 \geq 6.0$
$(00.1 x_1+ 00.5 x_2+ 00.5 x_3+ 10.0 x_4+ 15.0 x_5+ 00.0 x_6)/100 \leq 2.0$
$(00.2 x_1+ 00.5 x_2+ 00.7 x_3+ 00.2 x_4+ 00.8 x_5+ 00.0 x_6)/100 \leq 0.4$
La primer condición asegura que la cantidad de productos que se usará cumple con los 100 gramos. Las siguientes sólo siguen los lineamientos planteados para cumplir con los requisitos nutrimentales.
### 2. Otro problema de transporte
Referencia: https://relopezbriega.github.io/blog/2017/01/18/problemas-de-optimizacion-con-python/
Supongamos que tenemos que enviar cajas de cervezas de 2 cervecerías (Modelo y Cuauhtémoc Moctezuma) a 5 bares de acuerdo al siguiente gráfico:
<img style="float: center; margin: 0px 0px 15px 15px;" src="https://relopezbriega.github.io/images/Trans_problem.png" width="500px" height="150px" />
Asimismo, supongamos que nuestro gerente financiero nos informa que el costo de transporte por caja de cada ruta se conforma de acuerdo a la siguiente tabla:
```
import pandas as pd
info = pd.DataFrame({'Bar1': [2, 3], 'Bar2': [4, 1], 'Bar3': [5, 3], 'Bar4': [2, 2], 'Bar5': [1, 3]}, index = ['CerveceriaA', 'CerveceriaB'])
info
```
Y por último, las restricciones del problema, van a estar dadas por las capacidades de oferta y demanda de cada cervecería (en cajas de cerveza) y cada bar, las cuales se detallan en el gráfico de más arriba.
Sean:
- $x_i$ cajas transportadas de la cervecería A al Bar $i$,
- $x_{i+5}$ cajas transportadas de la cervecería B al Bar $i$.
La tarea consiste en plantear el problema de minimizar el costo de transporte de la forma vista y resolverlo con `linprog`.
Deben crear un notebook de jupyter (archivo .ipynb) y llamarlo Tarea4_ApellidoNombre, y subirlo a moodle.
**Definir fecha**
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Esteban Jiménez Rodríguez.
</footer>
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy as sp
import os
os.chdir('/Users/steve/GetOldTweets3-0.0.10')
import re
import nltk
import contractions
os.environ['KMP_DUPLICATE_LIB_OK']='True'
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.decomposition import NMF, LatentDirichletAllocation
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
from sklearn.linear_model import LogisticRegression
from sent2vec.vectorizer import Vectorizer
from nltk.corpus import stopwords
from vaderSentiment.vaderSentiment import SentimentIntensityAnalyzer
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
!git clone https://github.com/facebookresearch/fastText.git
!cd fastText
!python3 setup.py install
import fasttext.util
from imblearn.combine import SMOTETomek
from gensim.parsing.preprocessing import remove_stopwords, preprocess_string, strip_tags, strip_punctuation, stem_text, preprocess_documents, strip_multiple_whitespaces, strip_non_alphanum, strip_short
nltk.download('words')
words = set(nltk.corpus.words.words())
CUSTOM_FILTERS = [lambda x: x.lower(), strip_tags, strip_punctuation, strip_non_alphanum, stem_text,
remove_stopwords, strip_short]
def prep(sentence):
sentence = contractions.fix(sentence)
split_sentence = sentence.split()
return preprocess_string(sentence, CUSTOM_FILTERS)
def prep_withspell(sentence):
holder = " "
sentence = contractions.fix(sentence)
preprocessed = preprocess_string(sentence, CUSTOM_FILTERS)
spell_correct = TextBlob(holder.join(preprocessed))
corrected_sentence = spell_correct.correct()
return corrected_sentence.split()
def prepare(sentence):
processed_feature = re.sub(r'\W', ' ', str(sentence))
processed_feature= re.sub(r'\s+[a-zA-Z]\s+', ' ', processed_feature)
processed_feature = re.sub(r'\^[a-zA-Z]\s+', ' ', processed_feature)
processed_feature = re.sub(r'\s+', ' ', processed_feature, flags=re.I)
processed_feature = re.sub(r'^b\s+', '', processed_feature)
processed_feature = processed_feature.lower()
stop_words = set(stopwords.words('english'))
add = ['football', 'league', 'soccer', 'super', 'super league', 'footbal', 'leagu', 'footbal soccer']
stop_words = set.union(stop_words, add)
sentence = processed_feature.split()
return [w for w in sentence if not w.lower() in stop_words]
def cont_to_multiclass(cont):
if cont > 0.66:
return 'highly positive'
elif cont > 0.33:
return 'positive'
elif cont > 0:
return 'partly positive'
elif cont > -0.33:
return 'partly negative'
elif cont > -0.66:
return 'negative'
else:
return 'highly negative'
def cont_to_binary(cont):
if cont > 0:
#return 'positive'
return 1
else:
#return 'negative'
return 0
def get_document_frequency(data, wi, wj=None):
if wj is None:
D_wi = 0
for l in range(len(data)):
doc = data[l]
if wi in doc:
D_wi += 1
return D_wi
D_wj = 0
D_wi_wj = 0
for l in range(len(data)):
doc = data[l]
if wj in doc:
D_wj += 1
if wi in doc:
D_wi_wj += 1
return D_wj, D_wi_wj
def get_topic_coherence(beta, data, vocab, seed):
D = len(data)
TC = []
num_topics = len(beta.components_)
selected = -1
selected = []
for k, topic in enumerate(beta.components_):
print('k: {}/{}'.format(k, num_topics))
top_10 = topic.argsort()[:-20 - 1:-1]
top_words = [vocab[i] for i in top_10]
print(top_words)
TC_k = 0
counter = 0
for i, word in enumerate(top_words):
D_wi = get_document_frequency(data, word)
j = i + 1
tmp = 0
while j < len(top_10) and j > i:
D_wj, D_wi_wj = get_document_frequency(data, word, top_words[j])
if D_wi_wj == 0:
f_wi_wj = -1
else:
f_wi_wj = -1 + ( np.log(D_wi) + np.log(D_wj) - 2.0 * np.log(D) ) / ( np.log(D_wi_wj) - np.log(D) )
tmp += f_wi_wj
j += 1
counter += 1
TC_k += tmp
TC.append(TC_k)
print('num topics: ', len(TC))
print('Topic Coherence is: {}'.format(TC))
return TC, selected
def sentiment_scores(sentence):
sid_obj = SentimentIntensityAnalyzer()
sentiment_dict = sid_obj.polarity_scores(sentence)
return sentiment_dict['compound']
def word_vector(model, tokens, size):
vec = np.zeros(size).reshape((1, size))
count = 0
for word in tokens:
try:
vec += model.wv[word].reshape((1, size))
count += 1.
except KeyError: # handling the case where the token is not in vocabulary
continue
if count != 0:
vec /= count
return vec
sl_df = pd.read_csv('SL.csv', usecols = ['content'])
sl_df = sl_df.rename(columns={"content": 0})
dataset = sl_df.drop_duplicates()
dataset[1] = dataset.apply(lambda row: re.sub(r'http\S+', '', str(row[0])), axis=1)
dataset[2] = dataset.apply(lambda row: ''.join([c for c in row[1] if not c.isdigit()]), axis=1)
dataset[3] = dataset.apply(lambda row : " ".join(w for w in nltk.wordpunct_tokenize(row[2]) if w.lower() in words or not w.isalpha()), axis = 1)
dataset[4] = dataset.apply(lambda row : prep(row[3]), axis = 1)
dataset[5] = dataset.apply(lambda row : prepare(row[3]), axis = 1)
processed_data = [" ".join(x) for x in dataset[4]]
tfidf = TfidfVectorizer(max_df=0.90, min_df=50, stop_words='english', ngram_range=(1,3))
dtm = tfidf.fit_transform(processed_data)
nmf_model = NMF(n_components=50, random_state=42, beta_loss='kullback-leibler', solver='mu',
max_iter=1000, alpha=2, l1_ratio=0.5)
nmf_topics = nmf_model.fit_transform(dtm)
for index, topic in enumerate(nmf_model.components_):
print(f'THE TOP 50 WORDS FOR TOPIC #{index} GIVEN BY NMF:')
print([tfidf.get_feature_names()[i] for i in topic.argsort()[-50:]])
print('\n')
tf_vectorizer = CountVectorizer(analyzer='word', min_df=50, ngram_range=(1, 3))
tf_fit = tf_vectorizer.fit_transform(processed_data)
lda_model = LatentDirichletAllocation(n_components=50, doc_topic_prior=.01)
lda_topics = lda_model.fit_transform(tf_fit)
for index, topic in enumerate(lda_model.components_):
print(f'THE TOP 50 WORDS FOR TOPIC #{index} GIVEN BY LDA:')
print([tf_vectorizer.get_feature_names()[i] for i in topic.argsort()[-50:]])
print('\n')
naming={0:'Topic0', 1:'Topic1', 2:'Topic2', 3:'Topic3', 4:'Topic4', 5:'Topic5', 6:'Topic6', 7:'Topic7',
8:'Topic8', 9:'Topic9', 10:'Topic10', 11:'Topic11', 12:'Topic12', 13:'Topic13', 14:'Topic14', 15:'Topic15',
16:'Topic16', 17:'Topic17', 18:'Topic18', 19:'Topic19', 20:'Topic20', 21:'Topic21', 22:'Topic22', 23:'Topic23',
24:'Topic24', 25:'Topic25', 26:'Topic26', 27:'Topic27', 28:'Topic28', 29:'Topic29', 30:'Topic30', 31:'Topic31',
32:'Topic32', 33:'Topic33', 34:'Topic34', 35:'Topic35', 36:'Topic36', 37:'Topic37', 38:'Topic38', 39:'Topic39',
40:'Topic40', 41:'Topic41', 42:'Topic42', 43:'Topic43', 44:'Topic44', 45:'Topic45', 46:'Topic46', 47:'Topic47',
48:'Topic48', 49:'Topic49'}
dataset[5] = nmf_topics.argmax(axis=1)
dataset[5] = dataset[5].map(naming)
dataset[6] = lda_topics.argmax(axis=1)
dataset[6] = dataset[6].map(naming)
dataset[7] = dataset[4].apply(lambda row: ' '.join(row))
lab_num = 20000
labeled_sentiment = dataset.sample(n=lab_num)
labeled_sentiment[9] = labeled_sentiment.apply(lambda row : sentiment_scores(row[2]), axis = 1)
labeled_sentiment[10] = labeled_sentiment[9].apply(lambda row: cont_to_binary(row))
dataset = dataset.join(labeled_sentiment[10], how='left', lsuffix='_left', rsuffix='_right')
%%capture
fasttext.util.download_model('en', if_exists='ignore')
ft_model = fasttext.load_model('cc.en.300.bin')
ft = pd.DataFrame(processed_data, columns=['tweets'])
ft['tweets'] = ft['tweets'].apply(lambda row: ft_model.get_sentence_vector(row))
ft = np.stack(ft['tweets'].to_numpy())
dtm_ar = dtm.toarray()
tf_fit_ar = tf_fit.toarray()
embed_array = np.hstack((dtm_ar, tf_fit_ar, ft))
embed_array_df = pd.DataFrame(embed_array, index=dataset.index)
labeled_sentiment_embeddings = labeled_sentiment.join(embed_array_df, how='left', lsuffix='_left', rsuffix='_right')
labeled_sentiment_embeddings.drop(['0_left', '1_left', '2_left', '3_left', '4_left', '5_left'], axis=1, inplace=True)
labeled_sentiment_embeddings.drop(['6_left','7_left', '8_left', '9_left'], axis=1, inplace=True)
print('here')
smt = SMOTETomek(random_state=42)
X_train, X_test, y_train, y_test = train_test_split(labeled_sentiment_embeddings, labeled_sentiment[9], test_size=0.1, random_state=42)
X_train, y_train = smt.fit_resample(X_train, y_train)
X_train_dtm = X_train[X_train.columns[0:dtm.shape[1]]]
X_train_tf = X_train[X_train.columns[dtm.shape[1]:(dtm.shape[1]+tf_fit.shape[1])]]
X_train_tf = X_train[X_train.columns[dtm.shape[1]:(dtm.shape[1]+tf_fit.shape[1])]]
X_train_ft = X_train[X_train.columns[(dtm.shape[1]+tf_fit.shape[1]):(dtm.shape[1]+tf_fit.shape[1]+ft.shape[1])]]
X_test_dtm = X_test[X_test.columns[0:dtm.shape[1]]]
X_test_tf = X_test[X_test.columns[dtm.shape[1]:(dtm.shape[1]+tf_fit.shape[1])]]
X_test_ft = X_test[X_test.columns[(dtm.shape[1]+tf_fit.shape[1]):(dtm.shape[1]+tf_fit.shape[1]+ft.shape[1])]]
dtm_df = pd.DataFrame(dtm_ar, columns=X_test_dtm.columns)
tf_fit_df = pd.DataFrame(tf_fit_ar, columns=X_test_tf.columns)
ft_df = pd.DataFrame(ft, columns=X_test_ft.columns)
lab_num=20000
lab_num=int(lab_num/10)
rf_pred = pd.DataFrame(np.empty((lab_num, 3), columns=['dtm', 'tf_fit', 'fasttext'])
etc_pred = pd.DataFrame(np.empty((lab_num, 3)), columns=['dtm', 'tf_fit', 'fasttext'])
sgd_pred = pd.DataFrame(np.empty((lab_num, 3)), columns=['dtm', 'tf_fit', 'fasttext'])
rf_pred_full = pd.DataFrame(np.empty((len(dataset[0]), 3)), columns=['dtm', 'tf_fit', 'fasttext'])
etc_pred_full = pd.DataFrame(np.empty((len(dataset[0]), 3)), columns=['dtm', 'tf_fit', 'fasttext'])
sgd_pred_full = pd.DataFrame(np.empty((len(dataset[0]), 3)), columns=['dtm', 'tf_fit', 'fasttext'])
print("RandomForest: ")
rf_classifier_dtm = RandomForestClassifier(n_estimators=300, max_depth=300, random_state=42)
rf_classifier_dtm.fit(X_train_dtm, y_train)
predictions = rf_classifier_dtm.predict(X_test_dtm)
rf_pred['dtm'] = predictions
print(confusion_matrix(y_test,predictions))
print(classification_report(y_test,predictions))
print(accuracy_score(y_test, predictions))
predictions = rf_classifier_dtm.predict(dtm_df)
rf_pred_full['dtm'] = predictions
print("ExtraTree: ")
etc_dtm = ExtraTreesClassifier(n_estimators=300, random_state=42)
etc_dtm.fit(X_train_dtm, y_train)
predictions = etc_dtm.predict(X_test_dtm)
etc_pred['dtm'] = predictions
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
predictions = etc_dtm.predict(dtm_df)
etc_pred_full['dtm'] = predictions
print("StochasticGradientDescent: ")
sgd_classifier_dtm = SGDClassifier(loss="hinge", penalty="l1")
sgd_classifier_dtm.fit(X_train_dtm, y_train)
predictions = sgd_classifier_dtm.predict(X_test_dtm)
sgd_pred['dtm'] = predictions
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
predictions = sgd_classifier_dtm.predict(dtm_df)
sgd_pred_full['dtm'] = predictions
print("RandomForest: ")
rf_classifier_tf = RandomForestClassifier(n_estimators=300, max_depth=300, random_state=42)
rf_classifier_tf.fit(X_train_tf, y_train)
predictions = rf_classifier_tf.predict(X_test_tf)
rf_pred['tf_fit'] = predictions
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
predictions = rf_classifier_tf.predict(tf_fit)
rf_pred_full['tf_fit'] = predictions
print("ExtraTree: ")
etc_tf = ExtraTreesClassifier(n_estimators=300, random_state=42)
etc_tf.fit(X_train_tf, y_train)
predictions = etc_tf.predict(X_test_tf)
etc_pred['tf_fit'] = predictions
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
predictions = etc_tf.predict(tf_fit)
etc_pred_full['tf_fit'] = predictions
print("StochasticGradientDescent: ")
sgd_classifier_tf = SGDClassifier(loss="hinge", penalty="l1")
sgd_classifier_tf.fit(X_train_tf, y_train)
predictions = sgd_classifier_tf.predict(X_test_tf)
sgd_pred['tf_fit'] = predictions
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
predictions = sgd_classifier_tf.predict(tf_fit)
sgd_pred_full['tf_fit'] = predictions
print("RandomForest: ")
rf_classifier_ft = RandomForestClassifier(n_estimators=300, max_depth=300, random_state=42)
rf_classifier_ft.fit(X_train_ft, y_train)
predictions = rf_classifier_ft.predict(X_test_ft)
rf_pred['fasttext'] = predictions
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
predictions = rf_classifier_ft.predict(ft)
rf_pred_full['fasttext'] = predictions
print("ExtraTree: ")
etc_ft = ExtraTreesClassifier(n_estimators=300, random_state=42)
etc_ft.fit(X_train_ft, y_train)
predictions = etc_ft.predict(X_test_ft)
etc_pred['fasttext'] = predictions
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
predictions = etc_ft.predict(ft)
etc_pred_full['fasttext'] = predictions
print("StochasticGradientDescent: ")
sgd_classifier_ft = SGDClassifier(loss="hinge", penalty="l1")
sgd_classifier_ft.fit(X_train_ft, y_train)
predictions = sgd_classifier_ft.predict(X_test_ft)
sgd_pred['fasttext'] = predictions
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
predictions = sgd_classifier_ft.predict(ft)
sgd_pred_full['fasttext'] = predictions
print("RF Model: ")
rf_model = LogisticRegression(random_state=42).fit(rf_pred, y_test)
predictions = rf_model.predict(rf_pred)
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
print("ETC Model: ")
etc_model = LogisticRegression(random_state=42).fit(etc_pred, y_test)
predictions = etc_model.predict(etc_pred)
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
print("SGD Model: ")
sgd_model = LogisticRegression(random_state=42).fit(sgd_pred, y_test)
predictions = sgd_model.predict(sgd_pred)
print(confusion_matrix(y_test, predictions))
print(classification_report(y_test, predictions))
print(accuracy_score(y_test, predictions))
dataset[10] = rf_model.predict(rf_pred_full)
dataset[11] = etc_model.predict(etc_pred_full)
dataset[12] = sgd_model.predict(sgd_pred_full)
dataset[13] = xgb_model.predict(xgb_pred_full)
sent_pred = dataset[9]
ml_pred = dataset[11]
sent_pred[np.isnan(sent_pred)] = ml_pred
dataset[14] = sent_pred.to_frame()
race_nmf, race_lda = 'Topic28', 'Topic3'
gun_nmf, gun_lda = 'Topic31', 'Topic50'
mask_nmf, mask_lda = 'Topic27', 'Topic5'
resist_nmf, resist_lda = 'Topic25', 'Topic42'
immig_nmf, immig_lda = 'Topic45', 'Topic44'
race_nmf = dataset[dataset[5] == race_nmf]
gun_nmf = dataset[dataset[5] == gun_nmf]
mask_nmf = dataset[dataset[5] == mask_nmf]
resist_nmf = dataset[dataset[5] == resist_nmf]
immig_nmf = dataset[dataset[5] == immig_nmf]
from collections import Counter
race_nmf_vol = pd.DataFrame.from_dict(Counter([date[0:7] for date in (race_nmf[0].values)]), orient='index').reset_index()
gun_nmf_vol = pd.DataFrame.from_dict(Counter([date[0:7] for date in (gun_nmf[0].values)]), orient='index').reset_index()
mask_nmf_vol = pd.DataFrame.from_dict(Counter([date[0:7] for date in (mask_nmf[0].values)]), orient='index').reset_index()
resist_nmf_vol = pd.DataFrame.from_dict(Counter([date[0:7] for date in (resist_nmf[0].values)]), orient='index').reset_index()
immig_nmf_vol = pd.DataFrame.from_dict(Counter([date[0:7] for date in (immig_nmf[0].values)]), orient='index').reset_index()
import datetime
race_nmf_vol = race_nmf_vol.sort_values(by=['index'])
race_nmf_vol['index'] = [datetime.datetime.strptime(d,"%Y-%m").date() for d in race_nmf_vol['index']]
plt.plot(race_nmf_vol['index'], race_nmf_vol[0])
plt.ylabel('# Posts per Month')
plt.title('Race NMF Volumetric Analysis')
#plt.locator_params(axis="x", nbins=4)
plt.show()
gun_nmf_vol = gun_nmf_vol.sort_values(by=['index'])
gun_nmf_vol['index'] = [datetime.datetime.strptime(d,"%Y-%m").date() for d in gun_nmf_vol['index']]
plt.plot(gun_nmf_vol['index'], gun_nmf_vol[0])
plt.ylabel('# Posts per Month')
plt.title('Gun NMF Volumetric Analysis')
plt.show()
mask_nmf_vol = mask_nmf_vol.sort_values(by=['index'])
mask_nmf_vol['index'] = [datetime.datetime.strptime(d,"%Y-%m").date() for d in mask_nmf_vol['index']]
plt.plot(mask_nmf_vol['index'], mask_nmf_vol[0])
plt.ylabel('# Posts per Month')
plt.title('COVID NMF Volumetric Analysis')
#plt.locator_params(axis="x", nbins=4)
plt.show()
resist_nmf_vol = resist_nmf_vol.sort_values(by=['index'])
resist_nmf_vol['index'] = [datetime.datetime.strptime(d,"%Y-%m").date() for d in resist_nmf_vol['index']]
plt.plot(resist_nmf_vol['index'], resist_nmf_vol[0])
plt.ylabel('# Posts per Month')
plt.title('Resist NMF Volumetric Analysis')
#plt.locator_params(axis="x", nbins=4)
plt.show()
immig_nmf_vol = immig_nmf_vol.sort_values(by=['index'])
immig_nmf_vol['index'] = [datetime.datetime.strptime(d,"%Y-%m").date() for d in immig_nmf_vol['index']]
plt.plot(immig_nmf_vol['index'], immig_nmf_vol[0])
plt.ylabel('# Posts per Month')
plt.title('Immigration NMF Volumetric Analysis')
plt.locator_params(axis="x", nbins=4)
plt.show()
race_sentiment = pd.DataFrame([date for date in (race_nmf[14].values)], index=(race_nmf[0].values))
race_sentiment_pos = race_sentiment.groupby(race_sentiment[0]).get_group(1)
race_sentiment_neg = race_sentiment.groupby(race_sentiment[0]).get_group(0)
race_sentiment_pos = (pd.DataFrame.from_dict(Counter(race_sentiment_pos.index.str[:7]), orient='index').reset_index()).sort_values(by=['index'])
race_sentiment_neg = (pd.DataFrame.from_dict(Counter(race_sentiment_neg.index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
ax = plt.gca()
race_sentiment_pos.plot(style=[':', '--', '-'], color='blue', ax=ax)
race_sentiment_neg.plot(style=[':', '--', '-'], color='red', ax=ax)
plt.ylabel('# Posts per Month')
plt.xlabel('Time-Series')
plt.xticks(np.arange(0, max(len(race_sentiment_pos), len(race_sentiment_neg))+1, 10))
plt.title('Race NMF Sentiment Analysis')
ax.xaxis.set_major_locator(plt.MaxNLocator(10))
plt.gcf().autofmt_xdate()
plt.show()
gun_sentiment = pd.DataFrame([date for date in (gun_nmf[14].values)], index=(gun_nmf[0].values))
gun_sentiment_pos = gun_sentiment.groupby(gun_sentiment[0]).get_group(1)
gun_sentiment_neg = gun_sentiment.groupby(gun_sentiment[0]).get_group(0)
gun_sentiment_pos = (pd.DataFrame.from_dict(Counter(gun_sentiment_pos[0].index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
gun_sentiment_neg = (pd.DataFrame.from_dict(Counter(gun_sentiment_neg[0].index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
ax = plt.gca()
gun_sentiment_pos.plot(style=[':', '--', '-'], color='blue', ax=ax)
gun_sentiment_neg.plot(style=[':', '--', '-'], color='red', ax=ax)
plt.ylabel('# Gun per Month')
plt.xlabel('Time-Series')
plt.title('Immigration NMF Sentiment Analysis')
ax.xaxis.set_major_locator(plt.MaxNLocator(10))
plt.gcf().autofmt_xdate()
plt.show()
mask_sentiment = pd.DataFrame([date for date in (mask_nmf[14].values)], index=(mask_nmf[0].values))
mask_sentiment_pos = mask_sentiment.groupby(mask_sentiment[0]).get_group(1)
mask_sentiment_neg = mask_sentiment.groupby(mask_sentiment[0]).get_group(0)
mask_sentiment_pos = (pd.DataFrame.from_dict(Counter(mask_sentiment_pos[0].index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
mask_sentiment_neg = (pd.DataFrame.from_dict(Counter(mask_sentiment_neg[0].index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
ax = plt.gca()
mask_sentiment_pos.plot(style=[':', '--', '-'], color='blue', ax=ax)
mask_sentiment_neg.plot(style=[':', '--', '-'], color='red', ax=ax)
plt.ylabel('# Posts per Month')
plt.xlabel('Time-Series')
plt.title('Healthcare NMF Sentiment Analysis')
ax.xaxis.set_major_locator(plt.MaxNLocator(10))
plt.gcf().autofmt_xdate()
plt.show()
resist_sentiment = pd.DataFrame([date for date in (resist_nmf[14].values)], index=(resist_nmf[0].values))
resist_sentiment_pos = resist_sentiment.groupby(resist_sentiment[0]).get_group(1)
resist_sentiment_neg = resist_sentiment.groupby(resist_sentiment[0]).get_group(0)
resist_sentiment_pos = (pd.DataFrame.from_dict(Counter(resist_sentiment_pos[0].index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
resist_sentiment_neg = (pd.DataFrame.from_dict(Counter(resist_sentiment_neg[0].index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
ax = plt.gca()
resist_sentiment_pos.plot(style=[':', '--', '-'], color='blue', ax=ax)
resist_sentiment_neg.plot(style=[':', '--', '-'], color='red', ax=ax)
plt.ylabel('# Posts per Month')
plt.xlabel('Time-Series')
plt.title('Racism NMF Sentiment Analysis')
ax.xaxis.set_major_locator(plt.MaxNLocator(10))
plt.gcf().autofmt_xdate()
plt.show()
immig_sentiment = pd.DataFrame([date for date in (immig_nmf[14].values)], index=(immig_nmf[0].values))
immig_sentiment_pos = immig_sentiment.groupby(immig_sentiment[0]).get_group(1)
immig_sentiment_neg = immig_sentiment.groupby(immig_sentiment[0]).get_group(0)
immig_sentiment_pos = (pd.DataFrame.from_dict(Counter(immig_sentiment_pos[0].index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
immig_sentiment_neg = (pd.DataFrame.from_dict(Counter(immig_sentiment_neg[0].index.str[:7]), orient='index').reset_index()).sort_values(by=['index']).set_index('index')
ax = plt.gca()
resist_sentiment_pos.plot(style=[':', '--', '-'], color='blue', ax=ax)
resist_sentiment_neg.plot(style=[':', '--', '-'], color='red', ax=ax)
plt.ylabel('# Posts per Month')
plt.xlabel('Time-Series')
plt.title('Immigration NMF Sentiment Analysis')
ax.xaxis.set_major_locator(plt.MaxNLocator(10))
plt.gcf().autofmt_xdate()
plt.show()
fig, ax = plt.subplots(figsize=(10, 10))
ax.plot(race_sentiment_neg[0].index,
race_sentiment_neg[0],
linestyle=":",
color='red')
ax.plot(race_sentiment_pos[0].index,
race_sentiment_pos[0],
color='blue',
linestyle="--")
ax.set(xlabel="Date",
ylabel="Negative Sentiment",
title="Daily Total Precipitation\nBoulder, Colorado in July 2018")
plt.gcf().autofmt_xdate()
ax.xaxis.set_major_locator(plt.MaxNLocator(30))
plt.show()
immig_sentiment_pos.index
```
| github_jupyter |
# NYSE & Blurr
In this guide we will train a machine learning model that predicts closing price of a stock based on historical data. We will transform time-series stock data into features to train this model.
## Prerequisites
It's recommended to have a basic understanding of how Blurr works. Following [tutorials 1](http://productml-blurr.readthedocs.io/en/latest/Streaming%20BTS%20Tutorial/) and [2](http://productml-blurr.readthedocs.io/en/latest/Window%20BTS%20Tutorial/) should provide enough background context.
## Preparation
Let's start by installing `Blurr` and other required dependencies (using requirements.txt):
```
import sys
print("installing blurr and other required dependencies...")
!{sys.executable} -m pip install blurr --quiet
!{sys.executable} -m pip install -r requirements.txt --quiet
print("done.")
```
## The Dataset
This walkthrough is based on [New York Stock Exchange Data](https://www.kaggle.com/dgawlik/nyse/data) made available for [Kaggle challenges](https://www.kaggle.com/dgawlik/nyse).
Let's start by downloading and having a peek at the available data:
```
!wget http://demo.productml.com/data/nyse-input-data.json.zip
!unzip -o nyse-input-data.json.zip -d .
import pandas as pd
stocks = pd.read_json("./nyse-input-data.json", lines=True)
stocks.head()
```
This dataset contains data for each market day.
Our **goal is to predict closing price** of a stock for any given day based on historical data. In order to do that, we need to transform our original data source into **features** that can be used for training.
We'll calculate **moving averages** and other aggregate data for different **time windows**: one, three and seven days.
## Blurr Templates
We perform initial aggregations of our data by day with [nyse-streaming-bts.yml](./nyse-streaming-bts.yml). Features are then computed using [nyse-window-bts.yml](./nyse-window-bts.yml) for each stock per day.
```
!cat 'nyse-streaming-bts.yml'
```
**Streaming BTS**
We're predicting values for tech companies only (Apple, Facebook, Microsoft, Google):
```yaml
When: source.symbol in ['AAPL', 'MSFT', 'GOOG', 'FB']
```
Each record in the original dataset represents a single stock transaction. By setting `Split: str(time.date()) != stats.date` we'll create a new aggregate for each day per stock.
```
!cat 'nyse-window-bts.yml'
```
**Window BTS**
We'll use a very rough criteria to remove outliers: our model will only work when closing price changes less than a 4%:
```yaml
Anchor:
Condition: nyse.stats.volatility < 0.04
```
We're using [moving averages](https://www.investopedia.com/terms/m/movingaverage.asp) to generate features based on historical data about a stock:
```yaml
- Type: Blurr:Aggregate:Window
Name: last_7
WindowType: count
WindowValue: -7
Source: nyse.stats
Fields:
- Name: close_avg
Type: float
Value: sum(source.close) / len(source.close)
```
## Transforming Data
```
from blurr_util import print_head, validate, transform
validate('nyse-streaming-bts.yml')
validate('nyse-window-bts.yml')
```
Let's run our Streaming BTS for informational purposes only, so we can preview the result of the transformation:
```
transform(log_files=["./nyse-input-data.json"],
stream_bts='./nyse-streaming-bts.yml',
output_file="./nyse-streaming-bts-out.log")
print_head("./nyse-streaming-bts-out.log")
transform(log_files=["./nyse-input-data.json"],
stream_bts='./nyse-streaming-bts.yml',
window_bts='./nyse-window-bts.yml',
output_file="./nyse-processed-data.csv")
```
Let's now preview the data that will be used to **train our model**
```
window_out = pd.read_csv("./nyse-processed-data.csv")
window_out.head()
```
## Modelling
**Blurr** is about Data Preparation and Feature Engineering. Modeling is included here for illustration purpose, and the reader can use any modeling library or tool for such purpose.
Let's start by importing the output of our Window BTS as the source dataset. We're dropping unnecessary `_identity` columns:
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def import_dataset():
data = pd.read_csv("./nyse-processed-data.csv")
data["close"] = data["close.value"] # Moving close to the last column
data.drop(['close.value'], 1, inplace=True)
data.drop(['close._identity'], 1, inplace=True)
data.drop(['last._identity'], 1, inplace=True)
data.drop(['last_3._identity'], 1, inplace=True)
data.drop(['last_7._identity'], 1, inplace=True)
return data
dataset = import_dataset()
dataset.head()
```
Each column represents a Feature, except the rightmost column which represents the Output we're trying to predic
```
feature_count = len(dataset.columns) - 1
print("#features=" + str(feature_count))
```
We're splitting our dataset into Input Variables (`X`) and the Output Variable (`Y`) using pandas' [`iloc` function](http://pandas.pydata.org/pandas-docs/version/0.17.0/generated/pandas.DataFrame.iloc.html):
```
X = dataset.iloc[:, 0:feature_count].values
print(X.shape)
Y = dataset.iloc[:, feature_count].values
print(Y.shape)
```
We need to split between train and test datasets for training and evaluation of the model:
```
from sklearn.model_selection import train_test_split
X_train_raw, X_test_raw, Y_train_raw, Y_test_raw = train_test_split(X, Y, test_size = 0.2)
```
Finally, we need to scale our data before training:
```
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train_raw)
X_test = scaler.transform(X_test_raw)
Y_train = scaler.fit_transform(Y_train_raw.reshape(-1, 1))
Y_test = scaler.transform(Y_test_raw.reshape(-1, 1))
```
It's now time to build and train our model:
```
# Importing the Keras libraries and packages
import keras
from keras.models import Sequential
from keras.layers import Dense
#Initializing Neural Network
model = Sequential()
model.add(Dense(units = 36, kernel_initializer = 'uniform', activation = 'relu', input_dim = feature_count))
model.add(Dense(units = 36, kernel_initializer = 'uniform', activation = 'relu'))
model.add(Dense(units = 1, kernel_initializer = 'uniform', activation = 'linear'))
# Compiling Neural Network
model.compile(loss='mse',optimizer='adam', metrics=['accuracy'])
# Fitting our model
model.fit(X_train, Y_train, batch_size = 512, epochs = 70, validation_split=0.1, verbose=1)
```
We can measure the quality of our model using [MSE](https://en.wikipedia.org/wiki/Mean_squared_error) and [RMSE](https://en.wikipedia.org/wiki/Root-mean-square_deviation):
```
import math
score = model.evaluate(X_test, Y_test, verbose=0)
print('Model Score: %.5f MSE (%.2f RMSE)' % (score[0], math.sqrt(score[0])))
```
Finally, let's plot prediction vs actual data.
Prior to normalisation, we undo scaling and perform a sort for graph quality:
```
import matplotlib.pyplot as plt2
prediction_sorted = scaler.inverse_transform(model.predict(X_test))
prediction_sorted.sort(axis=0)
Y_test_sorted = scaler.inverse_transform(Y_test.copy().reshape(-1, 1))
Y_test_sorted.sort(axis=0)
plt2.plot(prediction_sorted, color='red', label='Prediction')
plt2.plot(Y_test_sorted, color='blue', label='Actual')
plt2.xlabel('#sample')
plt2.ylabel('close value')
plt2.legend(loc='best')
plt2.show()
```
| github_jupyter |
# Xarray-spatial
### User Guide: Surface tools
-----
With the Surface tools, you can quantify and visualize a terrain landform represented by a digital elevation model.
Starting with a raster elevation surface, represented as an Xarray DataArray, these tools can help you identify some specific patterns that may not be readily apparent in the original surface. The return of each function is also an Xarray DataArray.
[Hillshade](#Hillshade): Creates a shaded relief from a surface raster by considering the illumination source angle and shadows.
[Slope](#Slope): Identifies the slope for each cell of a raster.
[Curvature](#Curvature): Calculates the curvature of a raster surface.
[Aspect](#Aspect): Derives the aspect for each cell of a raster surface.
[Viewshed](#Viewshed): Determines visible locations in the input raster surface from a viewpoint with an optional observer height.
-----------
#### Let's use datashader to render our images...
We'll need the basic Numpy and Pandas, as well as datashader,
a data rasterization package highly compatible with Xarray-spatial.
Along with the base package, we'll import several nested functions (shade, stack...)
including Elevation, which we'll use below.
```
import numpy as np
import pandas as pd
import xarray as xr
import datashader as ds
from datashader.transfer_functions import shade
from datashader.transfer_functions import stack
from datashader.transfer_functions import dynspread
from datashader.transfer_functions import set_background
from datashader.colors import Elevation
import xrspatial
```
## Generate Terrain Data
The rest of the geo-related functions focus on raster data, i.e. data that's been aggregated into the row-column grid of cells in a raster image. Datashader's Canvas object provides a convenient frame to set up a new raster, so we'll use that with our `generate_terrain` function to generate some fake terrain as an elevation raster. Once we have that, we'll use datashader's shade for easy visualization.
```
from xrspatial import generate_terrain
W = 800
H = 600
terrain = xr.DataArray(np.zeros((H, W)))
terrain = generate_terrain(terrain)
shade(terrain, cmap=['black', 'white'], how='linear')
```
The grayscale values in the image above show elevation, scaled linearly in black-to-white color intensity (with the large black areas indicating low elevation). This shows the data, but it would look more like a landscape if we map the lowest values to colors representing water, and the highest to colors representing mountaintops. Let's try the Elevation colormap we imported above:
```
shade(terrain, cmap=Elevation, how='linear')
```
## Hillshade
[Hillshade](https://en.wikipedia.org/wiki/Terrain_cartography) is a technique used to visualize terrain as shaded relief by illuminating it with a hypothetical light source. The illumination value for each cell is determined by its orientation to the light source, which can be calculated from slope and aspect.
Let's apply Hillshade to our terrain and visualize the result with shade.
```
from xrspatial import hillshade
illuminated = hillshade(terrain)
hillshade_gray_white = shade(illuminated, cmap=['gray', 'white'], alpha=255, how='linear')
hillshade_gray_white
```
Applying hillshade reveals a lot of detail in the 3D shape of the terrain.
To add even more detail, we can add the Elevation colormapped terrain from earlier and combine it with the hillshade terrain using datashader's stack function.
```
terrain_elevation = shade(terrain, cmap=Elevation, alpha=128, how='linear')
stack(hillshade_gray_white, terrain_elevation)
```
## Slope
[Slope](https://en.wikipedia.org/wiki/Slope) is the inclination of a surface.
In geography, *slope* is the amount of change in elevation for an area in a terrain relative to its surroundings.
Xarray-spatial's slope function returns the slope at each cell in degrees.
Because Xarray-spatial is integrated with Xarray and Numpy, we can apply standard Numpy filters. For example, we can highlight only slopes in the [avalanche risk](https://www.gravityprotection.co.uk/blog/slope-steepness-avalanche-risk.html) range of 25 - 50 degrees. (Note the use of risky.data since these are DataArrays).
Stacking the resulting raster with the hillshaded and plain terrain ones from above gives an image with areas of avalanche risk neatly highlighted.
```
from xrspatial import slope
risky = slope(terrain)
risky.data = np.where(np.logical_and(risky.data > 25, risky.data < 50), 1, np.nan)
stack(shade(terrain, cmap=['black', 'white'], how='linear'),
shade(illuminated, cmap=['black', 'white'], how='linear', alpha=128),
shade(risky, cmap='red', how='linear', alpha=200))
```
## Curvature
[Curvature](https://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-analyst-toolbox/curvature.htm) is the second derivative of a surface's elevation, or the *slope-of-the-slope*; in other words, how fast the slope is increasing or decreasing as we move along a surface.
- A positive curvature means the surface is curving up (upwardly convex) at that cell.
- A negative curvature means the surface is curving down (downwardly convex) at that cell.
- A curvature of 0 means the surface is striaght and constant in whatever angle it's sloped towards.
The Xarray-spatial curvature function returns a raster in units one hundredth (1/100) of the z-factor, or scaling factor (which you can set explicitly in generate _terrain as "zfactor").
Reasonably expected values in the curvature raster for a hilly area (moderate relief) would be between -0.5 and 0.5, while for steep, rugged mountains (extreme relief) these can range as far as -4 and 4. For certain raster surfaces it is possible to go even larger than that.
Let's generate a terrain with an appropriate z-factor and apply the curvature function to it. Then, we can apply some Numpy filtering (remember, we have access to all those functions) to highlight steeper and gentler curves in the slopes.
Stacking these with the hillshaded and plain terrains gives us a fuller picture of the slopes.
```
from xrspatial import curvature
terrain_z_one = xr.DataArray(np.zeros((H, W)))
terrain_z_one = generate_terrain(terrain_z_one, zfactor=1)
curv = curvature(terrain_z_one)
curv_hi, curv_low = curv.copy(), curv.copy()
curv_hi.data = np.where(np.logical_and(curv_hi.data > 1, curv_hi.data < 4), 1, np.nan)
curv_low.data = np.where(np.logical_and(curv_low.data > 0.5, curv_low.data < 1), 1, np.nan)
stack(shade(terrain, cmap=['black', 'white'], how='linear'),
shade(illuminated, cmap=['black', 'white'], how='linear', alpha=128),
shade(curv_hi, cmap='red', how='log', alpha=200),
shade(curv_low, cmap='green', how='log', alpha=200))
```
## Aspect
[Aspect](https://en.wikipedia.org/wiki/Aspect_(geography)) is the orientation of a slope, measured clockwise in degrees from 0 to 360, where 0 is north-facing, 90 is east-facing, 180 is south-facing, and 270 is west-facing.
The Xarray-spatial aspect function returns the aspect in degrees for each cell in an elevation terrain.
We can apply aspect to our terrain, then use Numpy to filter out only slopes facing close to North. Then, we can stack that with the hillshaded and plain terrains.
(Note: the printout images are from a North point-of-view.)
```
from xrspatial import aspect
north_faces = aspect(terrain)
north_faces.data = np.where(np.logical_or(north_faces.data > 350 ,
north_faces.data < 10), 1, np.nan)
stack(shade(terrain, cmap=['black', 'white'], how='linear'),
shade(illuminated, cmap=['black', 'white'], how='linear', alpha=128),
shade(north_faces, cmap=['aqua'], how='linear', alpha=100))
```
## Viewshed
The `xrspatial.viewshed` function operates on a given aggregate to calculate the viewshed (the visible cells in the raster) for a given viewpoint, or *observer location*.
The visibility model is as follows: Two cells are visible to each other if the line of sight that connects their centers is not blocked at any point by another part of the terrain. If the line of sight does not pass through the cell center, elevation is determined using bilinear interpolation.
##### Simple Viewshed Example
- The example below creates a datashader aggregate from a 2d normal distribution.
- To calculate the viewshed, we need an observer location so we'll set up an aggregate for that as well.
- Then, we can visualize all of that with hillshade, shade, and stack.
- The observer location is indicated by the orange point in the upper-left of the plot.
```
from xrspatial import viewshed
OBSERVER_X = -12.5
OBSERVER_Y = 10
canvas = ds.Canvas(plot_width=W, plot_height=H,
x_range=(-20, 20), y_range=(-20, 20))
normal_df = pd.DataFrame({
'x': np.random.normal(.5, 1, 10000000),
'y': np.random.normal(.5, 1, 10000000)
})
normal_agg = canvas.points(normal_df, 'x', 'y')
normal_agg.values = normal_agg.values.astype("float64")
normal_shaded = shade(normal_agg)
observer_df = pd.DataFrame({'x': [OBSERVER_X], 'y': [OBSERVER_Y]})
observer_agg = canvas.points(observer_df, 'x', 'y')
observer_shaded = dynspread(shade(observer_agg, cmap=['orange']),
threshold=1, max_px=4)
normal_illuminated = hillshade(normal_agg)
normal_illuminated_shaded = shade(normal_illuminated, cmap=['black', 'white'],
alpha=128, how='linear')
stack(normal_illuminated_shaded, observer_shaded)
```
##### Calculate viewshed using the observer location
Now we can apply viewshed to the normal_agg, with the observer_agg for the viewpoint. We can then visualize it and stack it with the hillshade and observer rasters.
```
# Will take some time to run...
%time view = viewshed(normal_agg, x=OBSERVER_X, y=OBSERVER_Y)
view_shaded = shade(view, cmap=['white', 'red'], alpha=128, how='linear')
stack(normal_illuminated_shaded, observer_shaded, view_shaded)
```
As you can see, the image highlights in red all points visible from the observer location marked with the orange dot. As one might expect, the areas behind the normal distribution *mountain* are blocked from the viewer.
#### Viewshed on Terrain
Now we can try using viewshed on our more complicated terrain.
- We'll set up our terrain aggregate and apply hillshade and shade for easy visualization.
- We'll also set up an observer location aggregate, setting the location to the center, at (x, y) = (0, 0).
```
from xrspatial import viewshed
x_range=(-20e6, 20e6)
y_range=(-20e6, 20e6)
terrain = xr.DataArray(np.zeros((H, W)))
terrain = generate_terrain(terrain, x_range=x_range, y_range=y_range)
terrain_shaded = shade(terrain, cmap=Elevation, alpha=128, how='linear')
illuminated = hillshade(terrain)
OBSERVER_X = 0.0
OBSERVER_Y = 0.0
cvs = ds.Canvas(plot_width=W, plot_height=H, x_range=x_range, y_range=y_range)
observer_df = pd.DataFrame({'x': [OBSERVER_X],'y': [OBSERVER_Y]})
observer_agg = cvs.points(observer_df, 'x', 'y')
observer_shaded = dynspread(shade(observer_agg, cmap=['orange']),
threshold=1, max_px=4)
stack(shade(illuminated, cmap=['black', 'white'], alpha=128, how='linear'),
terrain_shaded,
observer_shaded)
```
Now we can apply viewshed.
- Notice the use of the `observer_elev` argument, which is the height of the observer above the terrain.
```
%time view = viewshed(terrain, x=OBSERVER_X, y=OBSERVER_Y, observer_elev=100)
view_shaded = shade(view, cmap='fuchsia', how='linear')
stack(shade(illuminated, cmap=['black', 'white'], alpha=128, how='linear'),
terrain_shaded,
view_shaded,
observer_shaded)
```
The fuchsia areas are those visible to an observer of the given height at the indicated orange location.
### References
- An overview of the Surface toolset: https://pro.arcgis.com/en/pro-app/tool-reference/spatial-analyst/an-overview-of-the-surface-tools.htm
- Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), p. 406.
- Making Maps with Noise Functions: https://www.redblobgames.com/maps/terrain-from-noise/
- How Aspect Works: http://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-analyst-toolbox/how-aspect-works.htm#ESRI_SECTION1_4198691F8852475A9F4BC71246579FAA
| github_jupyter |
<a href="https://www.bigdatauniversity.com"><img src="https://ibm.box.com/shared/static/cw2c7r3o20w9zn8gkecaeyjhgw3xdgbj.png" width=400 align="center"></a>
<h1 align="center"><font size="5"> Logistic Regression with Python</font></h1>
In this notebook, you will learn Logistic Regression, and then, you'll create a model for a telecommunication company, to predict when its customers will leave for a competitor, so that they can take some action to retain the customers.
<h1>Table of contents</h1>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<ol>
<li><a href="#about_dataset">About the dataset</a></li>
<li><a href="#preprocessing">Data pre-processing and selection</a></li>
<li><a href="#modeling">Modeling (Logistic Regression with Scikit-learn)</a></li>
<li><a href="#evaluation">Evaluation</a></li>
<li><a href="#practice">Practice</a></li>
</ol>
</div>
<br>
<hr>
<a id="ref1"></a>
## What is the difference between Linear and Logistic Regression?
While Linear Regression is suited for estimating continuous values (e.g. estimating house price), it is not the best tool for predicting the class of an observed data point. In order to estimate the class of a data point, we need some sort of guidance on what would be the <b>most probable class</b> for that data point. For this, we use <b>Logistic Regression</b>.
<div class="alert alert-success alertsuccess" style="margin-top: 20px">
<font size = 3><strong>Recall linear regression:</strong></font>
<br>
<br>
As you know, <b>Linear regression</b> finds a function that relates a continuous dependent variable, <b>y</b>, to some predictors (independent variables $x_1$, $x_2$, etc.). For example, Simple linear regression assumes a function of the form:
<br><br>
$$
y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots
$$
<br>
and finds the values of parameters $\theta_0, \theta_1, \theta_2$, etc, where the term $\theta_0$ is the "intercept". It can be generally shown as:
<br><br>
$$
ℎ_\theta(𝑥) = \theta^TX
$$
<p></p>
</div>
Logistic Regression is a variation of Linear Regression, useful when the observed dependent variable, <b>y</b>, is categorical. It produces a formula that predicts the probability of the class label as a function of the independent variables.
Logistic regression fits a special s-shaped curve by taking the linear regression and transforming the numeric estimate into a probability with the following function, which is called sigmoid function 𝜎:
$$
ℎ_\theta(𝑥) = \sigma({\theta^TX}) = \frac {e^{(\theta_0 + \theta_1 x_1 + \theta_2 x_2 +...)}}{1 + e^{(\theta_0 + \theta_1 x_1 + \theta_2 x_2 +\cdots)}}
$$
Or:
$$
ProbabilityOfaClass_1 = P(Y=1|X) = \sigma({\theta^TX}) = \frac{e^{\theta^TX}}{1+e^{\theta^TX}}
$$
In this equation, ${\theta^TX}$ is the regression result (the sum of the variables weighted by the coefficients), `exp` is the exponential function and $\sigma(\theta^TX)$ is the sigmoid or [logistic function](http://en.wikipedia.org/wiki/Logistic_function), also called logistic curve. It is a common "S" shape (sigmoid curve).
So, briefly, Logistic Regression passes the input through the logistic/sigmoid but then treats the result as a probability:
<img
src="https://ibm.box.com/shared/static/kgv9alcghmjcv97op4d6onkyxevk23b1.png" width="400" align="center">
The objective of __Logistic Regression__ algorithm, is to find the best parameters θ, for $ℎ_\theta(𝑥)$ = $\sigma({\theta^TX})$, in such a way that the model best predicts the class of each case.
### Customer churn with Logistic Regression
A telecommunications company is concerned about the number of customers leaving their land-line business for cable competitors. They need to understand who is leaving. Imagine that you are an analyst at this company and you have to find out who is leaving and why.
Lets first import required libraries:
```
import pandas as pd
import pylab as pl
import numpy as np
import scipy.optimize as opt
from sklearn import preprocessing
%matplotlib inline
import matplotlib.pyplot as plt
```
<h2 id="about_dataset">About the dataset</h2>
We will use a telecommunications dataset for predicting customer churn. This is a historical customer dataset where each row represents one customer. The data is relatively easy to understand, and you may uncover insights you can use immediately. Typically it is less expensive to keep customers than acquire new ones, so the focus of this analysis is to predict the customers who will stay with the company.
This data set provides information to help you predict what behavior will help you to retain customers. You can analyze all relevant customer data and develop focused customer retention programs.
The dataset includes information about:
- Customers who left within the last month – the column is called Churn
- Services that each customer has signed up for – phone, multiple lines, internet, online security, online backup, device protection, tech support, and streaming TV and movies
- Customer account information – how long they had been a customer, contract, payment method, paperless billing, monthly charges, and total charges
- Demographic info about customers – gender, age range, and if they have partners and dependents
### Load the Telco Churn data
Telco Churn is a hypothetical data file that concerns a telecommunications company's efforts to reduce turnover in its customer base. Each case corresponds to a separate customer and it records various demographic and service usage information. Before you can work with the data, you must use the URL to get the ChurnData.csv.
To download the data, we will use `!wget` to download it from IBM Object Storage.
```
#Click here and press Shift+Enter
!wget -O ChurnData.csv https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/ChurnData.csv
```
__Did you know?__ When it comes to Machine Learning, you will likely be working with large datasets. As a business, where can you host your data? IBM is offering a unique opportunity for businesses, with 10 Tb of IBM Cloud Object Storage: [Sign up now for free](http://cocl.us/ML0101EN-IBM-Offer-CC)
### Load Data From CSV File
```
churn_df = pd.read_csv("ChurnData.csv")
churn_df.head()
```
<h2 id="preprocessing">Data pre-processing and selection</h2>
Lets select some features for the modeling. Also we change the target data type to be integer, as it is a requirement by the skitlearn algorithm:
```
churn_df = churn_df[['tenure', 'age', 'address', 'income', 'ed', 'employ', 'equip', 'callcard', 'wireless','churn']]
churn_df['churn'] = churn_df['churn'].astype('int')
churn_df.head()
```
## Practice
How many rows and columns are in this dataset in total? What are the name of columns?
```
# write your code here
churn_df.shape
```
Lets define X, and y for our dataset:
```
X = np.asarray(churn_df[['tenure', 'age', 'address', 'income', 'ed', 'employ', 'equip']])
X[0:5]
y = np.asarray(churn_df['churn'])
y [0:5]
```
Also, we normalize the dataset:
```
from sklearn import preprocessing
X = preprocessing.StandardScaler().fit(X).transform(X)
X[0:5]
```
## Train/Test dataset
Okay, we split our dataset into train and test set:
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=4)
print ('Train set:', X_train.shape, y_train.shape)
print ('Test set:', X_test.shape, y_test.shape)
```
<h2 id="modeling">Modeling (Logistic Regression with Scikit-learn)</h2>
Lets build our model using __LogisticRegression__ from Scikit-learn package. This function implements logistic regression and can use different numerical optimizers to find parameters, including ‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’ solvers. You can find extensive information about the pros and cons of these optimizers if you search it in internet.
The version of Logistic Regression in Scikit-learn, support regularization. Regularization is a technique used to solve the overfitting problem in machine learning models.
__C__ parameter indicates __inverse of regularization strength__ which must be a positive float. Smaller values specify stronger regularization.
Now lets fit our model with train set:
```
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
LR = LogisticRegression(C=0.01, solver='liblinear').fit(X_train,y_train)
LR
```
Now we can predict using our test set:
```
yhat = LR.predict(X_test)
yhat
```
__predict_proba__ returns estimates for all classes, ordered by the label of classes. So, the first column is the probability of class 1, P(Y=1|X), and second column is probability of class 0, P(Y=0|X):
```
yhat_prob = LR.predict_proba(X_test)
yhat_prob
```
<h2 id="evaluation">Evaluation</h2>
### jaccard index
Lets try jaccard index for accuracy evaluation. we can define jaccard as the size of the intersection divided by the size of the union of two label sets. If the entire set of predicted labels for a sample strictly match with the true set of labels, then the subset accuracy is 1.0; otherwise it is 0.0.
```
from sklearn.metrics import jaccard_similarity_score
jaccard_similarity_score(y_test, yhat)
```
### confusion matrix
Another way of looking at accuracy of classifier is to look at __confusion matrix__.
```
from sklearn.metrics import classification_report, confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
print(confusion_matrix(y_test, yhat, labels=[1,0]))
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, yhat, labels=[1,0])
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=['churn=1','churn=0'],normalize= False, title='Confusion matrix')
```
Look at first row. The first row is for customers whose actual churn value in test set is 1.
As you can calculate, out of 40 customers, the churn value of 15 of them is 1.
And out of these 15, the classifier correctly predicted 6 of them as 1, and 9 of them as 0.
It means, for 6 customers, the actual churn value were 1 in test set, and classifier also correctly predicted those as 1. However, while the actual label of 9 customers were 1, the classifier predicted those as 0, which is not very good. We can consider it as error of the model for first row.
What about the customers with churn value 0? Lets look at the second row.
It looks like there were 25 customers whom their churn value were 0.
The classifier correctly predicted 24 of them as 0, and one of them wrongly as 1. So, it has done a good job in predicting the customers with churn value 0. A good thing about confusion matrix is that shows the model’s ability to correctly predict or separate the classes. In specific case of binary classifier, such as this example, we can interpret these numbers as the count of true positives, false positives, true negatives, and false negatives.
```
print (classification_report(y_test, yhat))
```
Based on the count of each section, we can calculate precision and recall of each label:
- __Precision__ is a measure of the accuracy provided that a class label has been predicted. It is defined by: precision = TP / (TP + FP)
- __Recall__ is true positive rate. It is defined as: Recall = TP / (TP + FN)
So, we can calculate precision and recall of each class.
__F1 score:__
Now we are in the position to calculate the F1 scores for each label based on the precision and recall of that label.
The F1 score is the harmonic average of the precision and recall, where an F1 score reaches its best value at 1 (perfect precision and recall) and worst at 0. It is a good way to show that a classifer has a good value for both recall and precision.
And finally, we can tell the average accuracy for this classifier is the average of the F1-score for both labels, which is 0.72 in our case.
### log loss
Now, lets try __log loss__ for evaluation. In logistic regression, the output can be the probability of customer churn is yes (or equals to 1). This probability is a value between 0 and 1.
Log loss( Logarithmic loss) measures the performance of a classifier where the predicted output is a probability value between 0 and 1.
```
from sklearn.metrics import log_loss
log_loss(y_test, yhat_prob)
```
<h2 id="practice">Practice</h2>
Try to build Logistic Regression model again for the same dataset, but this time, use different __solver__ and __regularization__ values? What is new __logLoss__ value?
```
# write your code here
```
Double-click __here__ for the solution.
<!-- Your answer is below:
LR2 = LogisticRegression(C=0.01, solver='sag').fit(X_train,y_train)
yhat_prob2 = LR2.predict_proba(X_test)
print ("LogLoss: : %.2f" % log_loss(y_test, yhat_prob2))
-->
<h2>Want to learn more?</h2>
IBM SPSS Modeler is a comprehensive analytics platform that has many machine learning algorithms. It has been designed to bring predictive intelligence to decisions made by individuals, by groups, by systems – by your enterprise as a whole. A free trial is available through this course, available here: <a href="http://cocl.us/ML0101EN-SPSSModeler">SPSS Modeler</a>
Also, you can use Watson Studio to run these notebooks faster with bigger datasets. Watson Studio is IBM's leading cloud solution for data scientists, built by data scientists. With Jupyter notebooks, RStudio, Apache Spark and popular libraries pre-packaged in the cloud, Watson Studio enables data scientists to collaborate on their projects without having to install anything. Join the fast-growing community of Watson Studio users today with a free account at <a href="https://cocl.us/ML0101EN_DSX">Watson Studio</a>
<h3>Thanks for completing this lesson!</h3>
<h4>Author: <a href="https://ca.linkedin.com/in/saeedaghabozorgi">Saeed Aghabozorgi</a></h4>
<p><a href="https://ca.linkedin.com/in/saeedaghabozorgi">Saeed Aghabozorgi</a>, PhD is a Data Scientist in IBM with a track record of developing enterprise level applications that substantially increases clients’ ability to turn data into actionable knowledge. He is a researcher in data mining field and expert in developing advanced analytic methods like machine learning and statistical modelling on large datasets.</p>
<hr>
<p>Copyright © 2018 <a href="https://cocl.us/DX0108EN_CC">Cognitive Class</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.</p>
| github_jupyter |
```
from PyQt5 import QtCore, QtGui, QtWidgets
class Ui_Dialog(object):
def setupUi(self, Dialog):
Dialog.setObjectName("Dialog")
Dialog.resize(419, 383)
self.radioButton = QtWidgets.QRadioButton(Dialog)
self.radioButton.setGeometry(QtCore.QRect(200, 110, 100, 20))
self.radioButton.setObjectName("radioButton")
self.buttonGroup = QtWidgets.QButtonGroup(Dialog)
self.buttonGroup.setObjectName("buttonGroup")
self.buttonGroup.addButton(self.radioButton)
self.radioButton_2 = QtWidgets.QRadioButton(Dialog)
self.radioButton_2.setGeometry(QtCore.QRect(200, 140, 100, 20))
self.radioButton_2.setObjectName("radioButton_2")
self.buttonGroup.addButton(self.radioButton_2)
self.radioButton_3 = QtWidgets.QRadioButton(Dialog)
self.radioButton_3.setGeometry(QtCore.QRect(200, 190, 100, 20))
self.radioButton_3.setObjectName("radioButton_3")
self.buttonGroup_2 = QtWidgets.QButtonGroup(Dialog)
self.buttonGroup_2.setObjectName("buttonGroup_2")
self.buttonGroup_2.addButton(self.radioButton_3)
self.radioButton_4 = QtWidgets.QRadioButton(Dialog)
self.radioButton_4.setGeometry(QtCore.QRect(200, 220, 161, 20))
self.radioButton_4.setObjectName("radioButton_4")
self.buttonGroup_2.addButton(self.radioButton_4)
self.radioButton_5 = QtWidgets.QRadioButton(Dialog)
self.radioButton_5.setGeometry(QtCore.QRect(200, 250, 100, 20))
self.radioButton_5.setObjectName("radioButton_5")
self.buttonGroup_2.addButton(self.radioButton_5)
self.label = QtWidgets.QLabel(Dialog)
self.label.setGeometry(QtCore.QRect(90, 10, 271, 51))
font = QtGui.QFont()
font.setPointSize(31)
font.setBold(True)
font.setWeight(75)
self.label.setFont(font)
self.label.setObjectName("label")
self.label_2 = QtWidgets.QLabel(Dialog)
self.label_2.setGeometry(QtCore.QRect(330, 50, 81, 31))
self.label_2.setObjectName("label_2")
self.label_3 = QtWidgets.QLabel(Dialog)
self.label_3.setGeometry(QtCore.QRect(20, 90, 171, 81))
font = QtGui.QFont()
font.setPointSize(18)
self.label_3.setFont(font)
self.label_3.setObjectName("label_3")
self.label_4 = QtWidgets.QLabel(Dialog)
self.label_4.setGeometry(QtCore.QRect(20, 190, 171, 81))
font = QtGui.QFont()
font.setPointSize(18)
self.label_4.setFont(font)
self.label_4.setObjectName("label_4")
self.commandLinkButton = QtWidgets.QCommandLinkButton(Dialog)
self.commandLinkButton.setGeometry(QtCore.QRect(10, 330, 131, 51))
font = QtGui.QFont()
font.setPointSize(18)
self.commandLinkButton.setFont(font)
self.commandLinkButton.setIconSize(QtCore.QSize(25, 25))
self.commandLinkButton.setCheckable(False)
self.commandLinkButton.setDescription("")
self.commandLinkButton.setObjectName("commandLinkButton")
self.commandLinkButton_2 = QtWidgets.QCommandLinkButton(Dialog)
self.commandLinkButton_2.setGeometry(QtCore.QRect(150, 330, 131, 51))
font = QtGui.QFont()
font.setPointSize(18)
self.commandLinkButton_2.setFont(font)
self.commandLinkButton_2.setIconSize(QtCore.QSize(25, 25))
self.commandLinkButton_2.setCheckable(False)
self.commandLinkButton_2.setDescription("")
self.commandLinkButton_2.setObjectName("commandLinkButton_2")
self.commandLinkButton_3 = QtWidgets.QCommandLinkButton(Dialog)
self.commandLinkButton_3.setGeometry(QtCore.QRect(280, 330, 131, 51))
font = QtGui.QFont()
font.setPointSize(18)
self.commandLinkButton_3.setFont(font)
self.commandLinkButton_3.setIconSize(QtCore.QSize(25, 25))
self.commandLinkButton_3.setCheckable(False)
self.commandLinkButton_3.setDescription("")
self.commandLinkButton_3.setObjectName("commandLinkButton_3")
self.pushButton = QtWidgets.QPushButton(Dialog)
self.pushButton.setGeometry(QtCore.QRect(270, 280, 131, 51))
self.pushButton.setObjectName("pushButton")
self.retranslateUi(Dialog)
QtCore.QMetaObject.connectSlotsByName(Dialog)
def retranslateUi(self, Dialog):
_translate = QtCore.QCoreApplication.translate
Dialog.setWindowTitle(_translate("Dialog", "Dialog"))
self.radioButton.setText(_translate("Dialog", "Tiếng Việt"))
self.radioButton_2.setText(_translate("Dialog", "English"))
self.radioButton_3.setText(_translate("Dialog", "Dễ / Easy"))
self.radioButton_4.setText(_translate("Dialog", "Trung bình / Medium"))
self.radioButton_5.setText(_translate("Dialog", "Khó / Hard"))
self.label.setText(_translate("Dialog", "Đuổi hình bắt chữ"))
self.label_2.setText(_translate("Dialog", "by NoName"))
self.label_3.setText(_translate("Dialog", "Phiên bản / Version"))
self.label_4.setText(_translate("Dialog", "Mức độ chơi / Level"))
self.commandLinkButton.setText(_translate("Dialog", "Facebook"))
self.commandLinkButton_2.setText(_translate("Dialog", "Google"))
self.commandLinkButton_3.setText(_translate("Dialog", "Twitter"))
self.pushButton.setText(_translate("Dialog", "Start"))
if __name__ == "__main__":
import sys
app = QtWidgets.QApplication(sys.argv)
Dialog = QtWidgets.QDialog()
ui = Ui_Dialog()
ui.setupUi(Dialog)
Dialog.show()
sys.exit(app.exec_())
```
| github_jupyter |
<a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_13_02_checkpoint.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# T81-558: Applications of Deep Neural Networks
**Module 13: Advanced/Other Topics**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 13 Video Material
* Part 13.1: Flask and Deep Learning Web Services [[Video]](https://www.youtube.com/watch?v=H73m9XvKHug&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_13_01_flask.ipynb)
* **Part 13.2: Interrupting and Continuing Training** [[Video]](https://www.youtube.com/watch?v=kaQCdv46OBA&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_13_02_checkpoint.ipynb)
* Part 13.3: Using a Keras Deep Neural Network with a Web Application [[Video]](https://www.youtube.com/watch?v=OBbw0e-UroI&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_13_03_web.ipynb)
* Part 13.4: When to Retrain Your Neural Network [[Video]](https://www.youtube.com/watch?v=K2Tjdx_1v9g&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_13_04_retrain.ipynb)
* Part 13.5: Tensor Processing Units (TPUs) [[Video]](https://www.youtube.com/watch?v=Ygyf3NUqvSc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_13_05_tpu.ipynb)
## Google CoLab Instructions
The following code ensures that Google CoLab is running the correct version of TensorFlow.
```
try:
from google.colab import drive
COLAB = True
print("Note: using Google CoLab")
%tensorflow_version 2.x
except:
print("Note: not using Google CoLab")
COLAB = False
# Nicely formatted time string
def hms_string(sec_elapsed):
h = int(sec_elapsed / (60 * 60))
m = int((sec_elapsed % (60 * 60)) / 60)
s = sec_elapsed % 60
return f"{h}:{m:>02}:{s:>05.2f}"
```
# Part 13.2: Interrupting and Continuing Training
We would train our Keras models in one pass in an ideal world, utilizing as much GPU and CPU power as we need. The world in which we train our models is anything but ideal. In this part, we will see that we can stop and continue and even adjust training at later times. We accomplish this continuation with checkpoints. We begin by creating several utility functions. The first utility generates an output directory that has a unique name. This technique allows us to organize multiple runs of our experiment. We provide the Logger class to route output to a log file contained in the output directory.
```
import os
import re
import sys
import time
import numpy as np
from typing import Any, List, Tuple, Union
from tensorflow.keras.datasets import mnist
from tensorflow.keras import backend as K
import tensorflow as tf
import tensorflow.keras
import tensorflow as tf
from tensorflow.keras.callbacks import EarlyStopping, \
LearningRateScheduler, ModelCheckpoint
from tensorflow.keras import regularizers
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Flatten
from tensorflow.keras.layers import Conv2D, MaxPooling2D
from tensorflow.keras.models import load_model
import pickle
def generate_output_dir(outdir, run_desc):
prev_run_dirs = []
if os.path.isdir(outdir):
prev_run_dirs = [x for x in os.listdir(outdir) if os.path.isdir(\
os.path.join(outdir, x))]
prev_run_ids = [re.match(r'^\d+', x) for x in prev_run_dirs]
prev_run_ids = [int(x.group()) for x in prev_run_ids if x is not None]
cur_run_id = max(prev_run_ids, default=-1) + 1
run_dir = os.path.join(outdir, f'{cur_run_id:05d}-{run_desc}')
assert not os.path.exists(run_dir)
os.makedirs(run_dir)
return run_dir
# From StyleGAN2
class Logger(object):
"""Redirect stderr to stdout, optionally print stdout to a file, and
optionally force flushing on both stdout and the file."""
def __init__(self, file_name: str = None, file_mode: str = "w", \
should_flush: bool = True):
self.file = None
if file_name is not None:
self.file = open(file_name, file_mode)
self.should_flush = should_flush
self.stdout = sys.stdout
self.stderr = sys.stderr
sys.stdout = self
sys.stderr = self
def __enter__(self) -> "Logger":
return self
def __exit__(self, exc_type: Any, exc_value: Any, \
traceback: Any) -> None:
self.close()
def write(self, text: str) -> None:
"""Write text to stdout (and a file) and optionally flush."""
if len(text) == 0:
return
if self.file is not None:
self.file.write(text)
self.stdout.write(text)
if self.should_flush:
self.flush()
def flush(self) -> None:
"""Flush written text to both stdout and a file, if open."""
if self.file is not None:
self.file.flush()
self.stdout.flush()
def close(self) -> None:
"""Flush, close possible files, and remove
stdout/stderr mirroring."""
self.flush()
# if using multiple loggers, prevent closing in wrong order
if sys.stdout is self:
sys.stdout = self.stdout
if sys.stderr is self:
sys.stderr = self.stderr
if self.file is not None:
self.file.close()
def obtain_data():
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print("Shape of x_train: {}".format(x_train.shape))
print("Shape of y_train: {}".format(y_train.shape))
print()
print("Shape of x_test: {}".format(x_test.shape))
print("Shape of y_test: {}".format(y_test.shape))
# input image dimensions
img_rows, img_cols = 28, 28
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
print('x_train shape:', x_train.shape)
print("Training samples: {}".format(x_train.shape[0]))
print("Test samples: {}".format(x_test.shape[0]))
# convert class vectors to binary class matrices
y_train = tf.keras.utils.to_categorical(y_train, num_classes)
y_test = tf.keras.utils.to_categorical(y_test, num_classes)
return input_shape, x_train, y_train, x_test, y_test
```
We define the basic training parameters and where we wish to write the output.
```
outdir = "./data/"
run_desc = "test-train"
batch_size = 128
num_classes = 10
run_dir = generate_output_dir(outdir, run_desc)
print(f"Results saved to: {run_dir}")
```
Keras provides a prebuilt checkpoint class named **ModelCheckpoint** that contains most of our desired functionality. This built-in class can save the model's state repeatedly as training progresses. Stopping neural network training is not always a controlled event. Sometimes this stoppage can be abrupt, such as a power failure or a network resource shutting down. If Microsoft Windows is your operating system of choice, your training can also be interrupted by a high-priority system update. Because of all of this uncertainty, it is best to save your model at regular intervals. This process is similar to saving a game at critical checkpoints, so you do not have to start over if something terrible happens to your avatar in the game.
We will create our checkpoint class, named **MyModelCheckpoint**. In addition to saving the model, we also save the state of the training infrastructure. Why save the training infrastructure, in addition to the weights? This technique eases the transition back into training for the neural network and will be more efficient than a cold start.
Consider if you interrupted your college studies after the first year. Sure, your brain (the neural network) will retain all the knowledge. But how much rework will you have to do? Your transcript at the university is like the training parameters. It ensures you do not have to start over when you come back.
```
class MyModelCheckpoint(ModelCheckpoint):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
def on_epoch_end(self, epoch, logs=None):
super().on_epoch_end(epoch,logs)\
# Also save the optimizer state
filepath = self._get_file_path(epoch=epoch,
logs=logs, batch=None)
filepath = filepath.rsplit( ".", 1 )[ 0 ]
filepath += ".pkl"
with open(filepath, 'wb') as fp:
pickle.dump(
{
'opt': model.optimizer.get_config(),
'epoch': epoch+1
# Add additional keys if you need to store more values
}, fp, protocol=pickle.HIGHEST_PROTOCOL)
print('\nEpoch %05d: saving optimizaer to %s' % (epoch + 1, filepath))
```
The optimizer applies a step decay schedule during training to decrease the learning rate as training progresses. It is essential to preserve the current epoch that we are on to perform correctly after a training resume.
```
def step_decay_schedule(initial_lr=1e-3, decay_factor=0.75, step_size=10):
def schedule(epoch):
return initial_lr * (decay_factor ** np.floor(epoch/step_size))
return LearningRateScheduler(schedule)
```
We build the model just as we have in previous sessions. However, the training function requires a few extra considerations. We specify the maximum number of epochs; however, we also allow the user to select the starting epoch number for training continuation.
```
def build_model(input_shape, num_classes):
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
activation='relu',
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(
loss='categorical_crossentropy',
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
return model
def train_model(model, initial_epoch=0, max_epochs=10):
start_time = time.time()
checkpoint_cb = MyModelCheckpoint(
os.path.join(run_dir, 'model-{epoch:02d}-{val_loss:.2f}.hdf5'),
monitor='val_loss',verbose=1)
lr_sched_cb = step_decay_schedule(initial_lr=1e-4, decay_factor=0.75, \
step_size=2)
cb = [checkpoint_cb, lr_sched_cb]
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=max_epochs,
initial_epoch = initial_epoch,
verbose=2, callbacks=cb,
validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0, callbacks=cb)
print('Test loss: {}'.format(score[0]))
print('Test accuracy: {}'.format(score[1]))
elapsed_time = time.time() - start_time
print("Elapsed time: {}".format(hms_string(elapsed_time)))
```
We now begin training, using the **Logger** class to write the output to a log file in the output directory.
```
with Logger(os.path.join(run_dir, 'log.txt')):
input_shape, x_train, y_train, x_test, y_test = obtain_data()
model = build_model(input_shape, num_classes)
train_model(model, max_epochs=3)
```
You should notice that the above output displays the name of the hdf5 and pickle (pkl) files produced at each checkpoint. These files serve the following functions:
* Pickle files contain the state of the optimizer.
* HDF5 files contain the saved model.
For this training run, which went for 3 epochs, these two files were named:
* ./data/00013-test-train/model-03-0.08.hdf5
* ./data/00013-test-train/model-03-0.08.pkl
We can inspect the output from the training run. Notice we can see a folder named "00000-test-train". This new folder was the first training run. The program will call the next training run "00001-test-train", and so on. Inside this directory, you will find the pickle and hdf5 files for each checkpoint.
```
!ls ./data
!ls ./data/00000-test-train
```
Keras stores the model itself in an HDF5, which includes the optimizer. Because of this feature, it is not generally necessary to restore the internal state of the optimizer (such as ADAM). However, we include the code to do so. We can obtain the internal state of an optimizer by calling **get_config**, which will return a dictionary similar to the following:
```
{'name': 'Adam', 'learning_rate': 7.5e-05, 'decay': 0.0,
'beta_1': 0.9, 'beta_2': 0.999, 'epsilon': 1e-07, 'amsgrad': False}
```
In practice, I've found that different optimizers implement get_config differently. This function will always return the training hyperparameters. However, it may not always capture the complete internal state of an optimizer beyond the hyperparameters. The exact implementation of get_config can vary per optimizer implementation.
## Continuing Training
We are now ready to continue training. You will need the paths to both your HDF5 and PKL files. You can find these paths in the output above. Your values may differ from mine, so perform a copy/paste.
```
MODEL_PATH = './data/00000-test-train/model-03-0.08.hdf5'
OPT_PATH = './data/00000-test-train/model-03-0.08.pkl'
```
The following code loads the HDF5 and PKL files and then recompiles the model based on the PKL file. Depending on the optimizer in use, you might have to recompile the model.
```
import tensorflow as tf
from tensorflow.keras.models import load_model
import pickle
def load_model_data(model_path, opt_path):
model = load_model(model_path)
with open(opt_path, 'rb') as fp:
d = pickle.load(fp)
epoch = d['epoch']
opt = d['opt']
return epoch, model, opt
epoch, model, opt = load_model_data(MODEL_PATH, OPT_PATH)
# note: often it is not necessary to recompile the model
model.compile(
loss='categorical_crossentropy',
optimizer=tf.keras.optimizers.Adam.from_config(opt),
metrics=['accuracy'])
```
Finally, we train the model for additional epochs. You can see from the output that the new training starts at a higher accuracy than the first training run. Further, the accuracy increases with additional training. Also, you will notice that the epoch number begins at four and not one.
```
outdir = "./data/"
run_desc = "cont-train"
num_classes = 10
run_dir = generate_output_dir(outdir, run_desc)
print(f"Results saved to: {run_dir}")
with Logger(os.path.join(run_dir, 'log.txt')):
input_shape, x_train, y_train, x_test, y_test = obtain_data()
train_model(model, initial_epoch=epoch, max_epochs=6)
```
| github_jupyter |
```
%matplotlib inline
import matplotlib.pylab as plt
import numpy as np
from keras import objectives
from keras import backend as K
from keras import losses
import tensorflow as tf
import interactions_results
import train_interactions
OBJ_IDS = ['1', '2']
COLUMNS_MAP = [('x', 'ant%s_x'),
('y', 'ant%s_y'),
('major', 'ant%s_major'),
('minor', 'ant%s_minor'),
('angle_deg', 'ant%s_angle_deg'),
('dx', 'ant%s_dx'),
('dy', 'ant%s_dy'),
]
COL = dict(COLUMNS_MAP)
NAMES = reduce(list.__add__, [[value % i for key, value in COLUMNS_MAP] for i in OBJ_IDS])
COL2ID = {key: i for i, (key, value) in enumerate(COLUMNS_MAP)}
COL2ID
def angle_absolute_error(y_true, y_pred, backend, scaler=None):
if scaler is not None:
# y_pred_ = scaler.inverse_transform(y_pred[:, 4:5]) # this doesn't work with Tensors
y_pred_ = y_pred[:, 4:5] * scaler[1] + scaler[0]
else:
y_pred_ = y_pred[:, 4:5]
val = backend.abs(y_pred_ - y_true[:, 4:5]) % 180
return backend.minimum(val, 180 - val)
def xy_absolute_error(y_true, y_pred, backend):
return backend.abs(y_pred[:, :2] - y_true[:, :2])
def absolute_errors(y_true, y_pred, backend, angle_scaler):
theta = angle_absolute_error(y_true, y_pred, backend, angle_scaler)
pos = xy_absolute_error(y_true, y_pred, backend)
return pos, theta
def interaction_loss(y_true, y_pred, angle_scaler=None, alpha=0.5):
assert 0 <= alpha <= 1
sum_errors_xy, sum_errors_angle, indices = match_pred_to_gt(y_true, y_pred, K, angle_scaler)
return K.mean(tf.gather_nd(sum_errors_xy, indices) * (1 - alpha) +
tf.gather_nd(sum_errors_angle, indices) * alpha)
y_a = np.array([[10., 10, 25, 5, 20, 100, 100, 25, 5, 30],
[100., 100, 25, 5, 30, 20, 20, 25, 5, 20],
[10., 10, 25, 5, 20, 200, 200, 25, 5, 30]])
y_b = np.array([[20., 20, 25, 5, 30, 150, 170, 25, 5, 0],
[30., 30, 25, 5, 30, 170, 150, 25, 5, 5],
[30., 60, 25, 5, 30, 170, 120, 25, 5, 5]])
xy, angle, indices = train_interactions.match_pred_to_gt(y_a, y_b, np)
print (xy[indices[:, 0], indices[:, 1]]).mean()
print (angle[indices[:, 0], indices[:, 1]]).mean()
# with h5py.File(DATA_DIR + '/imgs_inter_test.h5', 'r') as hf:
# X_test = hf['data'][:]
#
y_a_ = interactions_results.tostruct(y_a)
y_b_ = interactions_results.tostruct(y_b)
i = 1
interactions_results.plot_interaction(y_a_[[i]], y_b_[[i]])
plt.ylim(0, 200)
plt.xlim(0, 200)
y_true = K.variable(y_a)
y_pred = K.variable(y_b)
backend = K
angle_scaler = None
K.eval(y_pred[:, 1:2])
K.eval(y_pred[:, [COL2ID['x'], COL2ID['y']]] - y_true[:, [COL2ID['x'], COL2ID['y']]])
y_true = y_a
y_pred = y_b
backend = np
angle_scaler = None
mean_errors_xy, mean_errors_angle, indices = train_interactions.match_pred_to_gt(y_true, y_pred, backend)
for x in [mean_errors_xy, mean_errors_angle, indices]:
print x
mean_errors_xy, mean_errors_angle, indices = train_interactions.match_pred_to_gt(y_true, y_pred, backend)
for x in [mean_errors_xy, mean_errors_angle, indices]:
print K.eval(x)
mean_errors_xy, mean_errors_angle, indices = train_interactions.match_pred_to_gt(y_true, y_pred, K)
for x in [mean_errors_xy, mean_errors_angle, indices]:
print K.eval(x)
# def match_pred_to_gt(y_true, y_pred, backend, angle_scaler=None):
"""
Return mean absolute errors for individual samples for xy and theta
in two possible combinations of prediction and ground truth.
"""
xy11, theta11 = absolute_errors(y_true[:, :5], y_pred[:, :5], backend, angle_scaler)
xy22, theta22 = absolute_errors(y_true[:, 5:], y_pred[:, 5:], backend, angle_scaler)
xy12, theta12 = absolute_errors(y_true[:, :5], y_pred[:, 5:], backend, angle_scaler)
xy21, theta21 = absolute_errors(y_true[:, 5:], y_pred[:, :5], backend, angle_scaler)
if backend == np:
norm = np.linalg.norm
int64 = np.int64
shape = lambda x, n: x.shape[n]
else:
norm = tf.linalg.norm
int64 = tf.int64
shape = lambda x, n: backend.cast(backend.shape(x)[n], int64)
mean_errors_xy = backend.stack((backend.mean(backend.stack((norm(xy11, axis=1), norm(xy22, axis=1))), axis=0),
backend.mean(backend.stack((norm(xy12, axis=1), norm(xy21, axis=1))), axis=0))) # shape=(2, n)
mean_errors_angle = backend.stack((backend.mean(backend.concatenate((theta11, theta22)), axis=1),
backend.mean(backend.concatenate((theta12, theta21)), axis=1))) # shape=(2, n)
print K.eval(theta11)
print K.eval(backend.concatenate((theta11, theta22)))
print K.eval(backend.sum(backend.concatenate((theta11, theta22)), axis=1))
swap_idx = backend.argmin(mean_errors_xy, axis=0) # shape = (n,)
indices = backend.transpose(
backend.stack((swap_idx, backend.arange(0, shape(mean_errors_xy, 1))))) # shape=(n, 2)
# return mean_errors_xy, mean_errors_angle, indices
for x in [mean_errors_xy, mean_errors_angle, indices]:
print K.eval(x)
angle_scaler = None
y_true = K.variable(y_a)
y_pred = K.variable(y_b)
xy11, theta11 = absolute_errors(y_true[:, :5], y_pred[:, :5], angle_scaler)
xy22, theta22 = absolute_errors(y_true[:, 5:], y_pred[:, 5:], angle_scaler)
xy12, theta12 = absolute_errors(y_true[:, :5], y_pred[:, 5:], angle_scaler)
xy21, theta21 = absolute_errors(y_true[:, 5:], y_pred[:, :5], angle_scaler)
norm = tf.linalg.norm
# print y_a
# print y_b
# print K.eval(xy11)
# print K.eval(xy22)
# print K.eval(xy12)
# print K.eval(xy21)
sum_errors_xy = K.stack((K.sum(K.stack((norm(xy11, axis=1), norm(xy22, axis=1))), axis=0),
K.sum(K.stack((norm(xy12, axis=1), norm(xy21, axis=1))), axis=0))) # shape=(2, n)
sum_errors_angle = K.stack((K.sum(K.concatenate((theta11, theta22)), axis=1),
K.sum(K.concatenate((theta12, theta21)), axis=1))) # shape=(2, n)
swap_idx = K.argmin(sum_errors_xy, axis=0) # shape = (n,)
indices = K.transpose(K.stack((swap_idx, K.arange(0, K.cast(K.shape(sum_errors_xy)[1], tf.int64))))) # shape=(n, 2)
print K.eval(tf.gather_nd(sum_errors_xy, idx))
print K.eval(tf.gather_nd(sum_errors_angle, idx))
print K.eval(tf.gather_nd(sum_errors_xy, idx) + tf.gather_nd(sum_errors_angle, idx))
idx = K.transpose(K.stack((swap_idx, K.arange(0, K.cast(K.shape(sum_errors_xy)[1], tf.int64)))))
K.eval(tf.gather_nd(sum_errors_xy, idx))
K.eval(sum_errors_xy)
K.eval(sum_errors_angle)
K.eval(tf.gather_nd(sum_errors_angle, idx))
np.ca
```
| github_jupyter |
> Developed by [Yeison Nolberto Cardona Álvarez](https://github.com/yeisonCardona)
> [Andrés Marino Álvarez Meza, PhD.](https://github.com/amalvarezme)
> César Germán Castellanos Dominguez, PhD.
> _Digital Signal Processing and Control Group_ | _Grupo de Control y Procesamiento Digital de Señales ([GCPDS](https://github.com/UN-GCPDS/))_
> _National University of Colombia at Manizales_ | _Universidad Nacional de Colombia sede Manizales_
----
# OpenBCI-Stream
High level Python module for EEG/EMG/ECG acquisition and distributed streaming for OpenBCI Cyton board.







[](https://openbci-stream.readthedocs.io/en/latest/?badge=latest)
Comprise a set of scripts that deals with the configuration and connection with the board, also is compatible with both connection modes supported by [Cyton](https://shop.openbci.com/products/cyton-biosensing-board-8-channel?variant=38958638542): RFduino (Serial dongle) and Wi-Fi (with the OpenBCI Wi-Fi Shield). These drivers are a stand-alone library that can handle the board from three different endpoints: (i) a [Command-Line Interface](06-command_line_interface.ipynb) (CLI) with simple instructions configure, start and stop data acquisition, debug stream status, and register events markers; (ii) a [Python Module](03-data_acuisition.ipynb) with high-level instructions and asynchronous acquisition; (iii) an object-proxying using Remote Python Call (RPyC) for [distributed implementations](A4-server-based-acquisition.ipynb) that can manipulate the Python modules as if they were local, this last mode needs a daemon running in the remote host that will listen to connections and driving instructions.
The main functionality of the drivers live on to serve real-time and distributed access to data flow, even on single machine implementations, this is achieved by implementing [Kafka](https://kafka.apache.org/) and their capabilities to create multiple topics for classifying the streaming, these topics are used to separate the neurophysiological data from the [event markers](05-stream_markers), so the clients can subscribe to a specific topic for injecting or read content, this means that is possible to implement an event register in a separate process that stream markers for all clients in real-time without handle dense time-series data. A crucial issue that stays on [time synchronization](A4-server-based_acquisition.ipynb#Step-5---Configure-time-server), all systems components in the network should have the same real-time protocol (RTP) server reference.
## Main features
* **Asynchronous acquisition:** Acquisition and deserialization are done in uninterrupted parallel processes. In this way, the sampling rate keeps stable as long as possible.
* **Distributed streaming system:** The acquisition, processing, visualizations, and any other system that needs to be fed with EEG/EMG/ECG real-time data can run with their architecture.
* **Remote board handle:** Same code syntax for developing and debug Cython boards connected to any node in the distributed system.
* **Command-line interface:** A simple interface for handle the start, stop, and access to data stream directly from the command line.
* **Markers/Events handler:** Besides the marker boardmode available in Cyton, a stream channel for the reading and writing of markers is available for use in any development.
* **Multiple boards:** Is possible to use multiple OpenBCI boards just by adding multiple endpoints to the commands.
## Examples
```
# Acquisition with blocking call
from openbci_stream.acquisition import Cyton
openbci = Cyton('serial', endpoint='/dev/ttyUSB0', capture_stream=True)
# blocking call
openbci.stream(15) # collect data for 15 seconds
# openbci.eeg_time_series
# openbci.aux_time_series
# openbci.timestamp_time_series
# Acquisition with asynchronous call
from openbci_stream.acquisition import Cyton
openbci = Cyton('wifi', endpoint='192.68.1.113', capture_stream=True)
openbci.stream(15) # collect data for 15 seconds
# asynchronous call
openbci.start_stream()
time.sleep(15) # collect data for 15 seconds
openbci.stop_stream()
# Remote acquisition
from openbci_stream.acquisition import Cyton
openbci = Cyton('serial', endpoint='/dev/ttyUSB0', host='192.168.1.1', capture_stream=True)
# blocking call
openbci.stream(15) # collect data for 15 seconds
# Consumer for active streamming
from openbci_stream.acquisition import OpenBCIConsumer
with OpenBCIConsumer() as stream:
for i, message in enumerate(stream):
if message.topic == 'eeg':
print(f"received {message.value['samples']} samples")
if i == 9:
break
# Create stream then consume data
from openbci_stream.acquisition import OpenBCIConsumer
with OpenBCIConsumer(mode='serial', endpoint='/dev/ttyUSB0', streaming_package_size=250) as (stream, openbci):
t0 = time.time()
for i, message in enumerate(stream):
if message.topic == 'eeg':
print(f"{i}: received {message.value['samples']} samples")
t0 = time.time()
if i == 9:
break
# Acquisition with multiple boards
from openbci_stream.acquisition import Cyton
openbci = Cyton('wifi', endpoint=['192.68.1.113', '192.68.1.185'], capture_stream=True)
openbci.stream(15) # collect data for 15 seconds
# asynchronous call
openbci.start_stream()
time.sleep(15) # collect data for 15 seconds
openbci.stop_stream()
```
| github_jupyter |
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# tf.function で性能アップ
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/customization/performance"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/ja/tutorials/customization/performance.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/ja/tutorials/customization/performance.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/ja/tutorials/customization/performance.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
TensorFlow 2.0 では Eager Execution が既定で有効になっています。ユーザーインターフェイスは直感的で柔軟です(演算を一度だけ行う場合にはずっと簡単に、かつ迅速に実行されます)。しかしながら、それは性能と展開の面での犠牲の上に成り立っています。
最高性能を得ながら、モデルをどこへでも展開できるようにするには、`tf.function` を使ってプログラムから計算グラフを作成します。
AutoGraph のおかげで、驚くほど多くの Python コードが tf.function でそのまま動作しますが、気をつけなければならない落とし穴も存在します。
ポイントと推奨事項は下記の通りです。
- オブジェクトの変更やリストへの追加のような Python の副作用に依存しないこと
- tf.functions は NumPy の演算や Python の組み込み演算よりも、TensorFlow の演算に適していること
- 迷ったときは、`for x in y` というイディオムを使うこと
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
import contextlib
# 遭遇するかもしれないいくつかのエラーをデモするためのヘルパー関数
@contextlib.contextmanager
def assert_raises(error_class):
try:
yield
except error_class as e:
print('Caught expected exception \n {}: {}'.format(error_class, e))
except Exception as e:
print('Got unexpected exception \n {}: {}'.format(type(e), e))
else:
raise Exception('Expected {} to be raised but no error was raised!'.format(
error_class))
```
あなたが定義した `tf.function` は TensorFlow Core の演算に似たものです。例えばそれを即時に実行することも、計算グラフで使うこともできますし、勾配を計算することも可能です。
```
# function は演算のように振る舞う
@tf.function
def add(a, b):
return a + b
add(tf.ones([2, 2]), tf.ones([2, 2])) # [[2., 2.], [2., 2.]]
# function は勾配を計算できる
@tf.function
def add(a, b):
return a + b
v = tf.Variable(1.0)
with tf.GradientTape() as tape:
result = add(v, 1.0)
tape.gradient(result, v)
# function 内で function を使うこともできる
@tf.function
def dense_layer(x, w, b):
return add(tf.matmul(x, w), b)
dense_layer(tf.ones([3, 2]), tf.ones([2, 2]), tf.ones([2]))
```
## トレーシングとポリモーフィズム
Python の動的型付けは、関数をさまざまな型の引数で呼び出すことができ、Python がそれぞれのシナリオで異なる動作をするということを意味します。
他方で、TensorFlow の計算グラフでは、dtype と shape の次元が静的であることが必要です。`tf.function` は、正しい計算グラフを生成するために必要なときには関数を再トレースして、このギャップをつなぐ役割を果たします。
異なる型の引数を使って関数を呼び出し、何が起きるか見てみましょう。
```
# Function はポリモーフィック
@tf.function
def double(a):
print("Tracing with", a)
return a + a
print(double(tf.constant(1)))
print()
print(double(tf.constant(1.1)))
print()
print(double(tf.constant("a")))
print()
```
トレースの動作を制御するためには、下記のようなテクニックを使います。
- 新しい `tf.function` を作成する。別々の `tf.function` オブジェクトがトレースを共有することはない。
- 特定のトレースを得るには `get_concrete_function` メソッドを使用する。
- 計算グラフの呼び出し時に1回だけトレースを行うには、 `input_signature` を指定して `tf.function` を呼び出す。
```
print("Obtaining concrete trace")
double_strings = double.get_concrete_function(tf.TensorSpec(shape=None, dtype=tf.string))
print("Executing traced function")
print(double_strings(tf.constant("a")))
print(double_strings(a=tf.constant("b")))
print("Using a concrete trace with incompatible types will throw an error")
with assert_raises(tf.errors.InvalidArgumentError):
double_strings(tf.constant(1))
@tf.function(input_signature=(tf.TensorSpec(shape=[None], dtype=tf.int32),))
def next_collatz(x):
print("Tracing with", x)
return tf.where(tf.equal(x % 2, 0), x // 2, 3 * x + 1)
print(next_collatz(tf.constant([1, 2])))
# 1次元のテンソルを input signature として指定しているので、これは失敗する
with assert_raises(ValueError):
next_collatz(tf.constant([[1, 2], [3, 4]]))
```
## いつ再トレースするのか?
ポリモーフィックな `tf.function` はトレーシングによって生成された具象関数のキャッシュを保持しています。キャッシュのキーは、実際にはその関数の引数及びキーワード引数から生成されたキーのタプルです。`tf.Tensor` 引数から生成されるキーは、テンソルの shape と型です。Python の組み込み型引数から生成されるキーはその値です。それ以外の Python の型では、キーはオブジェクトの `id()` に基づいており、メソッドはクラスのインスタンスひとつずつ独立にトレースされます。将来、TensorFlowには、Python オブジェクトについて安全にテンソルに変換できるような、より洗練されたキャッシングが追加されるかもしれません。
## 引数は Python か? Tensor か?
しばしば、ハイパーパラメータやグラフ構成を制御するために Python の組み込み型の引数が使われます。例えば、`num_layers=10` や `training=True` あるいは `nonlinearity='relu'` のようにです。このため、この Python の組み込み型の引数が変更されると、計算グラフを再びトレースする必要があるということになります。
しかし、グラフの生成を制御するために Python の組み込み型の引数を使用する必要はありません。これらのケースでは、Python引数の値の変更が不必要な再トレースを引き起こす可能性があります。例えば、この訓練ループでは、AutoGraph は動的に展開を行います。複数回トレースを行っていますが、生成される計算グラフは全く変わりません。これは少し非効率です。
```
def train_one_step():
pass
@tf.function
def train(num_steps):
print("Tracing with num_steps = {}".format(num_steps))
for _ in tf.range(num_steps):
train_one_step()
train(num_steps=10)
train(num_steps=20)
```
ここでの簡単な回避方法は、生成されたグラフの shape が変わらないのであれば、引数をテンソルにキャストすることです。
```
train(num_steps=tf.constant(10))
train(num_steps=tf.constant(20))
```
## `tf.function` の中の副作用
一般的には、(印字やオブジェクト変更のような)Python の副作用は、トレーシングの最中にだけ発生します。それでは、どうしたら `tf.function` で安定的に副作用を起こすことができるでしょうか?
一般的な原則は、トレースをデバッグする際にだけ Python の副作用を使用するというものです。あるいは、`tf.Variable.assign`、`tf.print`、そして `tf.summary` のような TensorFlow の演算を使うことで、コードがトレースされるときにも、TensorFlowランタイムによって都度呼び出される際にも、確実に実行されるようにできます。一般には、関数型のスタイルを使用することで最も良い結果を得られます。
```
@tf.function
def f(x):
print("Traced with", x)
tf.print("Executed with", x)
f(1)
f(1)
f(2)
```
`tf.function` が呼び出されるたびに Python のコードを実行したいのであれば、`tf.py_function` がぴったりです。`tf.py_function` の欠点は、ポータブルでないこと、それほど性能が高くないこと、(マルチGPU、TPUの)分散環境ではうまく動作しないことなどです。また、`tf.py_function` は計算グラフに組み込まれるため、入出力すべてをテンソルにキャストします。
```
external_list = []
def side_effect(x):
print('Python side effect')
external_list.append(x)
@tf.function
def f(x):
tf.py_function(side_effect, inp=[x], Tout=[])
f(1)
f(1)
f(1)
assert len(external_list) == 3
# .numpy() call required because py_function casts 1 to tf.constant(1)
assert external_list[0].numpy() == 1
```
## Python の状態に注意
ジェネレーターやイテレーターなど Python の機能の多くは、状態を追跡するために Python のランタイムに依存しています。これらの仕組みは、一般的には Eager モードでも期待通りに動作しますが、トレーシングの振る舞いにより、`tf.function` の中では予期しないことが起きることがあります。
1例として、イテレーターの状態が進むのは Python の副作用であり、トレーシングの中だけで発生します。
```
external_var = tf.Variable(0)
@tf.function
def buggy_consume_next(iterator):
external_var.assign_add(next(iterator))
tf.print("Value of external_var:", external_var)
iterator = iter([0, 1, 2, 3])
buggy_consume_next(iterator)
# 次のコードは、イテレーターの次の値を使うのではなく、最初の値を再利用する
buggy_consume_next(iterator)
buggy_consume_next(iterator)
```
イテレーターが tf.function の中で生成されすべて使われる場合には、正しく動作するはずです。しかし、イテレーター全体がトレースされることとなり、巨大な計算グラフの生成をまねく可能性があります。これは、望みどおりの動作かもしれません。しかし、もし Python のリストとして表されたメモリー上の巨大なデータセットを使って訓練を行うとすると、これは非常に大きな計算グラフを生成することになり、`tf.function` がスピードアップにはつながらないと考えられます。
Python データを繰り返し使用する場合、もっとも安全な方法は tf.data.Dataset でラップして、`for x in y` というイディオムを使用することです。AutoGraph には、`y` がテンソルあるいは tf.data.Dataset である場合、`for` ループを安全に変換する特別な機能があります。
```
def measure_graph_size(f, *args):
g = f.get_concrete_function(*args).graph
print("{}({}) contains {} nodes in its graph".format(
f.__name__, ', '.join(map(str, args)), len(g.as_graph_def().node)))
@tf.function
def train(dataset):
loss = tf.constant(0)
for x, y in dataset:
loss += tf.abs(y - x) # ダミー計算
return loss
small_data = [(1, 1)] * 2
big_data = [(1, 1)] * 10
measure_graph_size(train, small_data)
measure_graph_size(train, big_data)
measure_graph_size(train, tf.data.Dataset.from_generator(
lambda: small_data, (tf.int32, tf.int32)))
measure_graph_size(train, tf.data.Dataset.from_generator(
lambda: big_data, (tf.int32, tf.int32)))
```
Python/Numpy のデータを Dataset でラップする際には、`tf.data.Dataset.from_generator` と `tf.data.Dataset.from_tensors` の違いに留意しましょう。前者はデータを Python のまま保持し `tf.py_function` を通じて取得するため、性能に影響する場合があります。これに対して後者はデータのコピーを計算グラフの中の、ひとつの大きな `tf.constant()` に結びつけるため、メモリー消費に影響する可能性があります。
TFRecordDataset/CsvDataset/などを通じてデータをファイルから読み込むことが、データを使用する最も効率的な方法です。TensorFlow 自身が Python とは関係なく非同期のデータ読み込みとプリフェッチを管理することができるからです。
## 自動的な依存関係の制御
プログラミングモデルとしての関数が一般的なデータフローグラフに対して非常に優位である点は、意図したコードの振る舞いがどのようなものであるかということについて、より多くの情報をランタイムに与えられるということにあります。
例えば、同じ変数を何度も読んだり書いたりするコードを書く場合、データフローグラフではもともと意図されていた演算の順番を自然に組み込むわけではありません。`tf.function` の中では、もともとの Python コードの文の実行順序を参照することで、実行順序の曖昧さを解消します。これにより、`tf.function` の中のステートフルな演算の順序が、先行実行モードのセマンティクスを模していることになります。
これは、手動で制御の依存関係を加える必要がないことを意味しています。`tf.function` は十分賢いので、あなたのコードが正しく動作するために必要十分な最小限の制御の依存関係を追加してくれます。
```
# 自動的な依存関係の制御
a = tf.Variable(1.0)
b = tf.Variable(2.0)
@tf.function
def f(x, y):
a.assign(y * b)
b.assign_add(x * a)
return a + b
f(1.0, 2.0) # 10.0
```
## 変数
`tf.function` の中では、意図したコードの実行順序を活用するという同じアイデアを使って、変数の作成と活用を簡単に行うことができます。しかし、ひとつだけ非常に重要な欠点があります。それは、変数を使った場合、先行実行モードとグラフモードでは動作が変わるコードを書いてしまう可能性があるということです。
特に、呼び出しの都度新しい変数を作成する場合にこれが発生します。トレーシングの意味では、`tf.function` は呼び出しのたびに同じ変数を再利用しますが、Eager モードでは呼び出しごとに新しい変数を生成します。この間違いを防止するため、`tf.function` は危険な変数の生成動作を見つけるとエラーを発生させます。
```
@tf.function
def f(x):
v = tf.Variable(1.0)
v.assign_add(x)
return v
with assert_raises(ValueError):
f(1.0)
# しかし、曖昧さの無いコードは大丈夫
v = tf.Variable(1.0)
@tf.function
def f(x):
return v.assign_add(x)
print(f(1.0)) # 2.0
print(f(2.0)) # 4.0
# 初めて関数が実行されるときだけ変数が生成されることを保証できれば
# tf.function 内で変数を作成できる
class C: pass
obj = C(); obj.v = None
@tf.function
def g(x):
if obj.v is None:
obj.v = tf.Variable(1.0)
return obj.v.assign_add(x)
print(g(1.0)) # 2.0
print(g(2.0)) # 4.0
# 変数の初期化は、関数の引数や他の変数の値に依存可能
# 制御の依存関係を生成するのと同じ手法で、正しい初期化の順序を発見可能
state = []
@tf.function
def fn(x):
if not state:
state.append(tf.Variable(2.0 * x))
state.append(tf.Variable(state[0] * 3.0))
return state[0] * x * state[1]
print(fn(tf.constant(1.0)))
print(fn(tf.constant(3.0)))
```
# AutoGraph の使用
[autograph](https://www.tensorflow.org/guide/function) ライブラリは `tf.function` に完全に統合されており、計算グラフの中で動的に実行される条件文や繰り返しを書くことができます。
`tf.cond` や `tf.while_loop` は `tf.function` でも使えますが、制御フローを含むコードは、命令形式で書いたほうが書きやすいし理解しやすいです。
```
# 単純な繰り返し
@tf.function
def f(x):
while tf.reduce_sum(x) > 1:
tf.print(x)
x = tf.tanh(x)
return x
f(tf.random.uniform([5]))
# 興味があれば AutoGraph が生成するコードを調べることができる
# ただし、アセンブリ言語を読むような感じがする
def f(x):
while tf.reduce_sum(x) > 1:
tf.print(x)
x = tf.tanh(x)
return x
print(tf.autograph.to_code(f))
```
## AutoGraph: 条件分岐
AutoGraph は `if` 文を等価である `tf.cond` の呼び出しに変換します。
この置換は条件がテンソルである場合に行われます。そうでない場合には、条件分岐はトレーシングの中で実行されます。
```
def test_tf_cond(f, *args):
g = f.get_concrete_function(*args).graph
if any(node.name == 'cond' for node in g.as_graph_def().node):
print("{}({}) uses tf.cond.".format(
f.__name__, ', '.join(map(str, args))))
else:
print("{}({}) executes normally.".format(
f.__name__, ', '.join(map(str, args))))
@tf.function
def hyperparam_cond(x, training=True):
if training:
x = tf.nn.dropout(x, rate=0.5)
return x
@tf.function
def maybe_tensor_cond(x):
if x < 0:
x = -x
return x
test_tf_cond(hyperparam_cond, tf.ones([1], dtype=tf.float32))
test_tf_cond(maybe_tensor_cond, tf.constant(-1))
test_tf_cond(maybe_tensor_cond, -1)
```
`tf.cond` には、色々と注意すべき細かな点があります。
- `tf.cond` は条件分岐の両方をトレーシングし、条件に従って実行時に適切な分岐を選択することで機能します。分岐の両方をトレースすることで、Python プログラムを予期せず実行する可能性があります。
- `tf.cond` では、分岐の一方が後ほど使用されるテンソルを作成する場合、もう一方の分岐もそのテンソルを作成することが必要です。
```
@tf.function
def f():
x = tf.constant(0)
if tf.constant(True):
x = x + 1
print("Tracing `then` branch")
else:
x = x - 1
print("Tracing `else` branch")
return x
f()
@tf.function
def f():
if tf.constant(True):
x = tf.ones([3, 3])
return x
# 分岐のどちらの枝でも `x` を定義する必要があるためエラーが発生
with assert_raises(ValueError):
f()
```
## AutoGraph と繰り返し
AutoGraph には繰り返しの変換にいくつかの単純なルールがあります。
- `for`: 反復可能オブジェクトがテンソルである場合に変換する
- `while`: while 条件がテンソルに依存している場合に変換する
繰り返しが変換される場合、`tf.while_loop` によって動的に展開されます。あるいは、 `for x in tf.data.Dataset` という特別なケースの場合には、 `tf.data.Dataset.reduce` に変換されます。
繰り返しが変換されない場合、それは静的に展開されます。
```
def test_dynamically_unrolled(f, *args):
g = f.get_concrete_function(*args).graph
if any(node.name == 'while' for node in g.as_graph_def().node):
print("{}({}) uses tf.while_loop.".format(
f.__name__, ', '.join(map(str, args))))
elif any(node.name == 'ReduceDataset' for node in g.as_graph_def().node):
print("{}({}) uses tf.data.Dataset.reduce.".format(
f.__name__, ', '.join(map(str, args))))
else:
print("{}({}) gets unrolled.".format(
f.__name__, ', '.join(map(str, args))))
@tf.function
def for_in_range():
x = 0
for i in range(5):
x += i
return x
test_dynamically_unrolled(for_in_range)
@tf.function
def for_in_tfrange():
x = tf.constant(0, dtype=tf.int32)
for i in tf.range(5):
x += i
return x
test_dynamically_unrolled(for_in_tfrange)
@tf.function
def for_in_tfdataset():
x = tf.constant(0, dtype=tf.int64)
for i in tf.data.Dataset.range(5):
x += i
return x
test_dynamically_unrolled(for_in_tfdataset)
@tf.function
def while_py_cond():
x = 5
while x > 0:
x -= 1
return x
test_dynamically_unrolled(while_py_cond)
@tf.function
def while_tf_cond():
x = tf.constant(5)
while x > 0:
x -= 1
return x
test_dynamically_unrolled(while_tf_cond)
```
繰り返しに、テンソルに依存する `break` や、途中での `return` がある場合、一番外側の条件あるいは反復可能オブジェクトはテンソルである必要があります。
比較してみましょう。
```
@tf.function
def while_py_true_py_break(x):
while True: # py true
if x == 0: # py break
break
x -= 1
return x
test_dynamically_unrolled(while_py_true_py_break, 5)
@tf.function
def buggy_while_py_true_tf_break(x):
while True: # py true
if tf.equal(x, 0): # tf break
break
x -= 1
return x
with assert_raises(TypeError):
test_dynamically_unrolled(buggy_while_py_true_tf_break, 5)
@tf.function
def while_tf_true_tf_break(x):
while tf.constant(True): # tf true
if x == 0: # py break
break
x -= 1
return x
test_dynamically_unrolled(while_tf_true_tf_break, 5)
@tf.function
def buggy_py_for_tf_break():
x = 0
for i in range(5): # py for
if tf.equal(i, 3): # tf break
break
x += i
return x
with assert_raises(TypeError):
test_dynamically_unrolled(buggy_py_for_tf_break)
@tf.function
def tf_for_py_break():
x = 0
for i in tf.range(5): # tf for
if i == 3: # py break
break
x += i
return x
test_dynamically_unrolled(tf_for_py_break)
```
動的に展開される繰り返しの結果を集計するため、`tf.TensorArray` を使いたくなるかもしれません。
```
batch_size = 2
seq_len = 3
feature_size = 4
def rnn_step(inp, state):
return inp + state
@tf.function
def dynamic_rnn(rnn_step, input_data, initial_state):
# [batch, time, features] -> [time, batch, features]
input_data = tf.transpose(input_data, [1, 0, 2])
max_seq_len = input_data.shape[0]
states = tf.TensorArray(tf.float32, size=max_seq_len)
state = initial_state
for i in tf.range(max_seq_len):
state = rnn_step(input_data[i], state)
states = states.write(i, state)
return tf.transpose(states.stack(), [1, 0, 2])
dynamic_rnn(rnn_step,
tf.random.uniform([batch_size, seq_len, feature_size]),
tf.zeros([batch_size, feature_size]))
```
`tf.cond` と同様に、`tf.while_loop` にも、色々と注意すべき細かな点があります。
- 繰り返しの実行回数が 0 である可能性があるため、while_loop の後で使用されるテンソルは、繰り返しの前に初期化されなければならない
- すべての繰り返しの変数は、各繰り返しを通じてその形状と dtype が変わらないことが必要
```
@tf.function
def buggy_loop_var_uninitialized():
for i in tf.range(3):
x = i
return x
with assert_raises(ValueError):
buggy_loop_var_uninitialized()
@tf.function
def f():
x = tf.constant(0)
for i in tf.range(3):
x = i
return x
f()
@tf.function
def buggy_loop_type_changes():
x = tf.constant(0, dtype=tf.float32)
for i in tf.range(3): # tf.int32 型のテンソルを1つづつ取り出して…
x = i
return x
with assert_raises(tf.errors.InvalidArgumentError):
buggy_loop_type_changes()
@tf.function
def buggy_concat():
x = tf.ones([0, 10])
for i in tf.range(5):
x = tf.concat([x, tf.ones([1, 10])], axis=0)
return x
with assert_raises(ValueError):
buggy_concat()
@tf.function
def concat_with_padding():
x = tf.zeros([5, 10])
for i in tf.range(5):
x = tf.concat([x[:i], tf.ones([1, 10]), tf.zeros([4-i, 10])], axis=0)
x.set_shape([5, 10])
return x
concat_with_padding()
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import tensorflow as tf
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
from tensorflow.keras.preprocessing.image import ImageDataGenerator
df = pd.DataFrame(columns=['filename','label'])
df.head()
for file in os.listdir('./data/scene_classification/seg_train/seg_train/buildings'):
df.loc[len(df)] = [file,'buildings']
for file in os.listdir('./data/scene_classification/seg_train/seg_train/forest'):
df.loc[len(df)] = [file,'forest']
for file in os.listdir('./data/scene_classification/seg_train/seg_train/glacier'):
df.loc[len(df)] = [file,'glacier']
for file in os.listdir('./data/scene_classification/seg_train/seg_train/mountain'):
df.loc[len(df)] = [file,'mountain']
for file in os.listdir('./data/scene_classification/seg_train/seg_train/sea'):
df.loc[len(df)] = [file,'sea']
for file in os.listdir('./data/scene_classification/seg_train/seg_train/street'):
df.loc[len(df)] = [file,'street']
df = df.sample(frac=1).reset_index(drop=True)
df.head()
df_train,df_val = train_test_split(df,test_size=0.2,random_state=42)
df_train.head()
train_datagen = ImageDataGenerator(rescale = 1./255,shear_range = 0.2,zoom_range = 0.2,horizontal_flip = True,vertical_flip=True,brightness_range=[0.5,1.5])
val_datagen = ImageDataGenerator(rescale = 1./255)
training_set = train_datagen.flow_from_dataframe(dataframe = df_train,directory = './data/scene_classification/seg_train/seg_train/images/',x_col = 'filename',y_col = 'label',class_mode = 'categorical',target_size = (150,150),batch_size = 32,shuffle = True)
validation_set = val_datagen.flow_from_dataframe(dataframe = df_val,directory = './data/scene_classification/seg_train/seg_train/images/',x_col = 'filename',y_col = 'label',class_mode = 'categorical',target_size = (150,150),batch_size = 32,shuffle = True)
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32,(3,3),activation='relu',input_shape=(150,150,3)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512,activation='relu'),
tf.keras.layers.Dense(6,activation='softmax')
])
model.summary()
model.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy'])
history = model.fit(training_set,validation_data=validation_set,epochs=10)
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
path = './models/scene_classification/'
model.save(path+'model.h5')
model.save_weights(path+'weights.h5')
new_model = tf.keras.models.load_model(path+'model.h5')
loss,accuracy = new_model.evaluate(validation_set)
new_model.summary()
import cv2
# Utility
import itertools
import random
from collections import Counter
from glob import iglob
def load_image(filename):
img = mpimg.imread('data/Scene_Classification/seg_train/seg_train/images/' + filename)
img = cv2.resize(img, (150,150) )
img = img /255
return img
def predict(image):
probabilities = model.predict(np.asarray([img]))[0]
class_idx = np.argmax(probabilities)
return class_idx
plt.imshow(mpimg.imread('data/Scene_Classification/seg_train/seg_train/street/2.jpg'))
img = load_image('2.jpg')
predict(img)
```
| github_jupyter |
```
from __future__ import division
import numpy as np
import pylab as plt
import swordfish as sf
from scipy.interpolate import interp1d
from scipy.constants import c
from numpy.random import multivariate_normal
from matplotlib import rc
from scipy.interpolate import UnivariateSpline
rc('text', usetex=True)
rc('font',**{'family':'sans-serif','sans-serif':['cmr']})
rc('font',**{'family':'serif','serif':['cmr']})
%matplotlib inline
c_kms = c*1.e-3 # in km s^-1
g2 = 1.e-18
sig0 = 1e-45
m_med = 1e5 # MeV
GeV_inv_cm = 1.98e-14
mp = 0.93
```
# Xenon1T
We can now implement the projected limits for Xenon1T based off 83 days of exposure using the same recoil energy spectrum as for CRESST-III but with the appropriate changes made for the Xenon nuclei (it is more simple here since there are only Xenon nuclei). We assume that there is only one isotope for our calculations. Since we do not have access to the Xenon background with much detail we perform a 1D analysis using the backgrounds published in 1705.06655 as a function of the S1 signal. We therefore need to to approximate the way that the dark matter signal is distributed between S1 and S2.
Now we define the signal component as,
$$ \frac{dR}{dE_R} = \frac{\rho_0\xi_T}{2\pi m_{DM}} \frac{g^2 F_T^2(E_{R})}{(2m_TE_{R} + m^2_{med})^2}\eta(v_{min}(E_R))$$
where $E_R$ is the recoil energy, $\rho_0$ is the dark matter density at earth (which we take to be $0.3 GeV cm^{-3}$, $m_{DM}$ is the dark matter mass, $m_{med}$ is the mediator mass, $F_T^2(E_{R})$ is the recoil form factor, and $m_T$ is the mass of the target isotope.
```
rho_0 = 0.3*1.e3 # MeV/cm3
# Define energy range in MeV
def eta_F():
"""Returns an interpolated integral over the velocity distribution, taken to be Maxwellian"""
v, gave = np.loadtxt("DD_files/gave.dat", unpack=True, dtype=float)
f = interp1d(v, gave, bounds_error=False, fill_value=0.0) # s km^-1
return f
def dRdE(E_R, m_DM, A, xi_T):
"""Return differential recoil rate in 1/s/MeV/kg."""
# g is the parameter we wish to set a limit on so is left out
# Form factor taken from eq4.4 of http://pa.brown.edu/articles/Lewin_Smith_DM_Review.pdf
m_T = A*931.5 # MeV
muT = m_DM*m_T/(m_DM + m_T) # unitless
rn = A**(1./3.) * 1/197. # fm --> MeV^-1
F_T = lambda q: np.sqrt(np.exp(-((q*rn)**2.)/3.))
vmin = lambda E_R: np.sqrt(m_T*E_R/2/(muT**2.))
eta = eta_F()
q = np.sqrt(2*m_T*E_R)
signal = (A**2)*F_T(q)**2*eta(vmin(E_R)*c_kms)*rho_0*xi_T*g2/2./np.pi/m_DM/((q**2+m_med**2)**2)
conversion = 1.96311325e24 # MeV^-4 cm^-3 s km^-1 hbar^2 c^6 --> MeV^-1 s^-1 kg^-1
signal *= conversion
return signal
eff1, eff2 = np.loadtxt("Swordfish_Xenon1T/Efficiency-1705.06655.txt", unpack=True)
efficiency = UnivariateSpline(eff1, eff2, ext="zeros", k=1, s=0)
S1_vals, E_vals = np.loadtxt("Swordfish_Xenon1T/S1vsER.txt", unpack=True)
# Interpolation for the recoil energy as a function of S1
# and the derivative
CalcER = UnivariateSpline(S1_vals, E_vals, k=4, s=0)
dERdS1 = CalcER.derivative()
# Recoil distribution as a function of S1
# taking into account the efficiency and change
# of variables ER -> S1
def dRdS1(S1, m_DM):
A_Xe = 131. #FIXME: Change to Xenon values
xi_T_Xe = 1.0
ER_keV = CalcER(S1)
ER_MeV = ER_keV*1.e-3
#Factor of 0.475 comes from the fact that
#the reference region should contain about
#47.5% of nuclear recoils (between median and 2sigma lines)
# Factor of 1/1e3 to convert 1/MeV --> 1/keV
return 0.475*efficiency(ER_keV)*dRdE(ER_MeV,m_DM,A_Xe,xi_T_Xe)/1e3*dERdS1(S1)
# We are now working in distributions as a function of s1
s1 = np.linspace(3,70,num=100)
s1width = s1[1]-s1[0]
s1means = s1[0:-1]+s1width/2.
bkgs = ['acc','Anom','ElectronRecoil','n','Neutrino','Wall']
def load_bkgs():
b = dict()
for i in range(len(bkgs)):
S1, temp = np.loadtxt("DD_files/" + bkgs[i] + ".txt", unpack=True)
interp = interp1d(S1, temp, bounds_error=False, fill_value=0.0)
b[bkgs[i]] = interp(s1means)
return b
def XenonIT_sig(m_DM):
m_DM *= 1.e3 # conversion to MeV
sig = dRdS1(s1means,m_DM)*s1width
return sig
b_dict = load_bkgs()
obsT = np.ones_like(s1means)*24.*3600.*35636.
mlist = np.logspace(1, 3, 50) # GeV
b = np.array(b_dict[bkgs[0]]/obsT)
K = np.diag((b.flatten()*0.01)**2)
B = [b_dict[bkgs[0]]/obsT, b_dict[bkgs[1]]/obsT, b_dict[bkgs[2]]/obsT,
b_dict[bkgs[3]]/obsT, b_dict[bkgs[4]]/obsT, b_dict[bkgs[5]]/obsT]
def g(m, sigma):
# Takes in sigma and returns g^2
mu_temp = m*mp/(m+mp)
return np.ones_like(s1means)*np.pi*((m_med/1.e3)**4.)*sigma/(GeV_inv_cm**2.)/(mu_temp**2.)
SF = sf.Swordfish(B, T=[0.1,0.1,0.1,0.1,0.1,0.1], E=obsT, K=K)
ULlist_Xenon = []
DRlist_Xenon = []
for i, m in enumerate(mlist):
sig = XenonIT_sig(m)
UL = SF.upperlimit(sig, 0.05)
DR = SF.discoveryreach(sig, 2.87e-7)
DRlist_Xenon.append(DR*g2)
ULlist_Xenon.append(UL*g2)
mu_xp = mlist*mp/(mlist+mp)
sigma_Xe = (GeV_inv_cm**2.)*np.array(ULlist_Xenon)*mu_xp**2./np.pi/(m_med/1.e3)**4.
sigma_Xe_DR = (GeV_inv_cm**2.)*np.array(DRlist_Xenon)*mu_xp**2./np.pi/(m_med/1.e3)**4.
m10list = np.linspace(1, 3, 50) # GeV
s10list = np.linspace(-46, -44, 50)
S = lambda m, sigma: g(10**m, 10**sigma)*(g2**(-1))*XenonIT_sig(10**m)
print S(1.7, -46).sum()*3600.*24*35636
TF = SF.getfield(S, m10list, s10list)
vf1, vf2 = TF.VectorFields()
plt.figure(figsize=(5,4))
mask = lambda x, y: (y > np.interp(x, np.log10(mlist), np.log10(sigma_Xe))) & (y<-44)
vf1.streamlines(color='0.5', mask = mask, Nmax = 40);
vf2.streamlines(color='0.5', mask = mask, Nmax = 40);
plt.plot(np.log10(mlist), np.log10(sigma_Xe), label=r"95\% CL Exclusion Limit")
plt.plot(np.log10(mlist), np.log10(sigma_Xe_DR), "-.", label=r"$5\sigma$ Discovery Reach")
TF.contour([1.4, -45.], 1., color='r', ls='-');
TF.contour([1.4, -45.], 2., color='r', ls='--');
TF.contour([1.5, -44.25], 1., color='b', ls='-');
TF.contour([1.5, -44.25], 2., color='b', ls='--');
plt.legend(loc=4)
y = [-46,-45,-44]
x = [1,2,3]
plt.xlim(1.,3.)
plt.ylim(-46,-44)
plt.xlabel(r"$\log_{10}(m_{\mathrm{DM}}/\rm GeV)$")
plt.ylabel(r"$\log_{10}(\sigma /\rm cm^{-2})$")
plt.yticks(np.arange(min(y), max(y)+1, 1.0))
plt.xticks(np.arange(min(x), max(x)+1, 1.0))
plt.tight_layout(pad=0.3)
plt.savefig("Xe_stream_limits.eps")
```
| github_jupyter |
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = "retina"
# print(plt.style.available)
plt.style.use("ggplot")
# plt.style.use("fivethirtyeight")
plt.style.use("seaborn-talk")
from tqdm import tnrange, tqdm_notebook
def uniform_linear_array(n_mics, spacing):
return spacing*np.arange(-(n_mics-1)/2, (n_mics-1)/2+1).reshape(1, n_mics)
def compute_MVDR_weight(source_steering_vector, signals):
snapshot = signals.shape[1]
sample_covariance_matrix = signals.dot(signals.transpose().conjugate()) / snapshot
inverse_sample_covariance_matrix = np.linalg.inv(sample_covariance_matrix)
normalization_factor = (source_steering_vector.transpose().conjugate().dot(inverse_sample_covariance_matrix).dot(source_steering_vector))
weight = inverse_sample_covariance_matrix.dot(source_steering_vector) / normalization_factor
return weight
def compute_steering_vector_ULA(u, microphone_array):
return np.exp(1j*2*np.pi*microphone_array.geometry*u).reshape((microphone_array.n_mics, 1))
def generate_gaussian_samples(power, shape):
return np.sqrt(power/2)*np.random.randn(shape[0], shape[1]) + 1j*np.sqrt(power/2)*np.random.randn(shape[0], shape[1]); # signal samples
class MicrophoneArray():
def __init__(self, array_geometry):
self.dim = array_geometry.shape[0]
self.n_mics = array_geometry.shape[1]
self.geometry = array_geometry
class BaseDLBeamformer(object):
def __init__(self, vs, bf_type="MVDR"):
"""
Parameters
----------
vs: Source manifold array vector
bf_type: Type of beamformer
"""
self.vs = vs
self.bf_type = bf_type
self.weights_ = None
def _compute_weights(self, training_data):
n_training_samples = len(training_data)
n_mics, snapshot = training_data[0].shape
D = np.zeros((n_mics, n_training_samples), dtype=complex)
for i_training_sample in range(n_training_samples):
nv = training_data[i_training_sample]
if self.bf_type == "MVDR":
w = compute_MVDR_weight(vs, nv)
D[:, i_training_sample] = w.reshape(n_mics,)
return D
def _initialize(self, X):
pass
def _choose_weights(self, x):
n_dictionary_atoms = self.weights_.shape[1]
R = x.dot(x.transpose().conjugate())
proxy = np.diagonal(self.weights_.transpose().conjugate().dot(R).dot(self.weights_))
optimal_weight_index = np.argmin(proxy)
return self.weights_[:, optimal_weight_index]
def fit(self, training_data):
"""
Parameters
----------
X: shape = [n_samples, n_features]
"""
D = self._compute_weights(training_data)
self.weights_ = D
return self
def choose_weights(self, x):
return self._choose_weights(x)
```
#### Setup
```
array_geometry = uniform_linear_array(n_mics=10, spacing=0.5)
microphone_array = MicrophoneArray(array_geometry)
us = 0
vs = compute_steering_vector_ULA(us, microphone_array)
SNRs = np.arange(0, 31, 10)
n_SNRs = len(SNRs)
sigma_n = 1
```
#### Training data
```
n_training_samples = 5000
training_snapshots = [10, 50, 1000]
interference_powers = [10, 20, 30]
n_interference_list = [1, 2, 3]
# interference_powers = [20]
# n_interference_list = [1]
# sigma = 10**(20/10)
training_noise_interference_data_various_snapshots = []
for training_snapshot in training_snapshots:
training_noise_interference_data = []
for i_training_sample in range(n_training_samples):
n_interferences = np.random.choice(n_interference_list)
nv = np.zeros((microphone_array.n_mics, training_snapshot), dtype=complex)
for _ in range(n_interferences):
u = np.random.uniform(0, 1)
vi = compute_steering_vector_ULA(u, microphone_array)
sigma = 10**(np.random.choice(interference_powers)/10)
ii = generate_gaussian_samples(power=sigma, shape=(1, training_snapshot))
nv += vi.dot(ii)
noise = generate_gaussian_samples(power=sigma_n, shape=(microphone_array.n_mics, training_snapshot))
nv += noise
training_noise_interference_data.append(nv)
training_noise_interference_data_various_snapshots.append(training_noise_interference_data)
```
#### Train baseline dictionary
```
dictionaries = []
for i_training_snapshot in range(len(training_snapshots)):
training_noise_interference_data = training_noise_interference_data_various_snapshots[i_training_snapshot]
dictionary = BaseDLBeamformer(vs)
dictionary.fit(training_noise_interference_data);
dictionaries.append(dictionary)
```
#### Testing
```
n_trials = 200
snapshots = np.array([10, 20, 30, 40, 60, 100, 200, 500, 1000])
n_snapshots = len(snapshots)
ui1 = np.random.uniform(0, 1)
ui2 = np.random.uniform(0, 1)
sigma_1 = 10**(20/10)
sigma_2 = 0*10**(20/10)
vi1 = compute_steering_vector_ULA(ui1, microphone_array)
vi2 = compute_steering_vector_ULA(ui2, microphone_array)
n_interferences = np.random.choice(n_interference_list)
interference_steering_vectors = []
for _ in range(n_interferences):
u = np.random.uniform(0, 1)
vi = compute_steering_vector_ULA(u, microphone_array)
interference_steering_vectors.append(vi)
sinr_snr_mvdr = np.zeros((n_SNRs, n_snapshots))
sinr_snr_mpdr = np.zeros((n_SNRs, n_snapshots))
sinr_snr_baseline_mpdr = np.zeros((len(training_snapshots), n_SNRs, n_snapshots))
for i_SNR in tqdm_notebook(range(n_SNRs), desc="SNRs"):
sigma_s = 10**(SNRs[i_SNR] / 10)
Rs = sigma_s * vs.dot(vs.transpose().conjugate())
for i_snapshot in tqdm_notebook(range(n_snapshots), desc="Snapshots", leave=False):
snapshot = snapshots[i_snapshot]
sinr_mvdr = np.zeros(n_trials)
sinr_mpdr = np.zeros(n_trials)
sinr_baseline_mpdr = np.zeros((len(training_snapshots), n_trials))
for i_trial in range(n_trials):
ss = generate_gaussian_samples(power=sigma_s, shape=(1, snapshot)) # signal samples
nn = generate_gaussian_samples(power=sigma_n, shape=(microphone_array.n_mics, snapshot)) # Gaussian noise samples
# ii1 = generate_gaussian_samples(power=sigma_1, shape=(1, snapshot)) # first interference samples
# ii2 = generate_gaussian_samples(power=sigma_2, shape=(1, snapshot)) # second interference samples
nv = np.zeros((microphone_array.n_mics, snapshot), dtype=complex)
Rn = np.zeros((microphone_array.n_mics, microphone_array.n_mics), dtype=complex)
for i_interference in range(n_interferences):
sigma = 10**(np.random.choice(interference_powers)/10)
ii = generate_gaussian_samples(power=sigma, shape=(1, snapshot))
nv += interference_steering_vectors[i_interference].dot(ii)
Rn += sigma*interference_steering_vectors[i_interference].dot(interference_steering_vectors[i_interference].transpose().conjugate())
Rn += sigma_n*np.identity(microphone_array.n_mics)
Rninv = np.linalg.inv(Rn)
Wo = Rninv.dot(vs) / (vs.transpose().conjugate().dot(Rninv).dot(vs))
SINRopt = ( np.real(Wo.transpose().conjugate().dot(Rs).dot(Wo)) / np.real(Wo.transpose().conjugate().dot(Rn).dot(Wo)) )[0][0]
nv += nn
sv = vs.dot(ss)
xx = sv + nv
wv = compute_MVDR_weight(vs, nv)
wp = compute_MVDR_weight(vs, xx)
for i_dictionary in range(len(dictionaries)):
dictionary = dictionaries[i_dictionary]
w_baseline_p = dictionary.choose_weights(xx)
sinr_baseline_mpdr[i_dictionary, i_trial] = np.real(w_baseline_p.transpose().conjugate().dot(Rs).dot(w_baseline_p)) / np.real(w_baseline_p.transpose().conjugate().dot(Rn).dot(w_baseline_p))
sinr_mvdr[i_trial] = np.real(wv.transpose().conjugate().dot(Rs).dot(wv)) / np.real(wv.transpose().conjugate().dot(Rn).dot(wv))
sinr_mpdr[i_trial] = np.real(wp.transpose().conjugate().dot(Rs).dot(wp)) / np.real(wp.transpose().conjugate().dot(Rn).dot(wp))
sinr_snr_mvdr[i_SNR, i_snapshot] = np.sum(sinr_mvdr) / n_trials
sinr_snr_mpdr[i_SNR, i_snapshot] = np.sum(sinr_mpdr) / n_trials
for i_dictionary in range(len(dictionaries)):
sinr_snr_baseline_mpdr[i_dictionary, i_SNR, i_snapshot] = np.sum(sinr_baseline_mpdr[i_dictionary, :]) / n_trials
```
#### Visualize results
```
fig = plt.figure(figsize=(9, 6*n_SNRs));
for i_SNR in range(n_SNRs):
sigma_s = 10**(SNRs[i_SNR] / 10)
Rs = sigma_s * vs.dot(vs.transpose().conjugate())
SINRopt = ( np.real(Wo.transpose().conjugate().dot(Rs).dot(Wo)) / np.real(Wo.transpose().conjugate().dot(Rn).dot(Wo)) )[0][0]
ax = fig.add_subplot(n_SNRs, 1, i_SNR+1)
ax.semilogx(snapshots, 10*np.log10(sinr_snr_mvdr[i_SNR, :]), marker="o", label="MVDR")
ax.semilogx(snapshots, 10*np.log10(sinr_snr_mpdr[i_SNR, :]), marker="*", label="MPDR")
for i_training_snapshot in range(len(training_snapshots)):
ax.semilogx(snapshots, 10*np.log10(sinr_snr_baseline_mpdr[i_training_snapshot, i_SNR, :]),
label="Baseline - {} training snapshots".format(training_snapshots[i_training_snapshot]))
ax.set_xlim(10, 1000); ax.set_ylim(-10, 45)
ax.legend(loc="lower right")
ax.set_xlabel("Number of snapshots")
ax.set_ylabel(r"$SINR_0$ [dB]")
ax.set_title("Testing performance, {} training samples".format(n_training_samples))
plt.tight_layout()
fig.savefig("baseline_dl_mvdr_various_interferences.jpg", dpi=600)
```
| github_jupyter |
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Automated Machine Learning
_**Orange Juice Sales Forecasting**_
## Contents
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Compute](#Compute)
1. [Data](#Data)
1. [Train](#Train)
1. [Predict](#Predict)
1. [Operationalize](#Operationalize)
## Introduction
In this example, we use AutoML to train, select, and operationalize a time-series forecasting model for multiple time-series.
Make sure you have executed the [configuration notebook](../../../configuration.ipynb) before running this notebook.
The examples in the follow code samples use the University of Chicago's Dominick's Finer Foods dataset to forecast orange juice sales. Dominick's was a grocery chain in the Chicago metropolitan area.
## Setup
```
import azureml.core
import pandas as pd
import numpy as np
import logging
from azureml.core.workspace import Workspace
from azureml.core.experiment import Experiment
from azureml.train.automl import AutoMLConfig
from azureml.automl.core.featurization import FeaturizationConfig
```
This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
```
print("This notebook was created using version 1.19.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
```
As part of the setup you have already created a <b>Workspace</b>. To run AutoML, you also need to create an <b>Experiment</b>. An Experiment corresponds to a prediction problem you are trying to solve, while a Run corresponds to a specific approach to the problem.
```
ws = Workspace.from_config()
# choose a name for the run history container in the workspace
experiment_name = 'automl-ojforecasting'
experiment = Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['SKU'] = ws.sku
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Run History Name'] = experiment_name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## Compute
You will need to create a [compute target](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute) for your AutoML run. In this tutorial, you create AmlCompute as your training compute resource.
#### Creation of AmlCompute takes approximately 5 minutes.
If the AmlCompute with that name is already in your workspace this code will skip the creation process.
As with other Azure services, there are limits on certain resources (e.g. AmlCompute) associated with the Azure Machine Learning service. Please read this article on the default limits and how to request more quota.
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
amlcompute_cluster_name = "oj-cluster"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=6)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
## Data
You are now ready to load the historical orange juice sales data. We will load the CSV file into a plain pandas DataFrame; the time column in the CSV is called _WeekStarting_, so it will be specially parsed into the datetime type.
```
time_column_name = 'WeekStarting'
data = pd.read_csv("dominicks_OJ.csv", parse_dates=[time_column_name])
data.head()
```
Each row in the DataFrame holds a quantity of weekly sales for an OJ brand at a single store. The data also includes the sales price, a flag indicating if the OJ brand was advertised in the store that week, and some customer demographic information based on the store location. For historical reasons, the data also include the logarithm of the sales quantity. The Dominick's grocery data is commonly used to illustrate econometric modeling techniques where logarithms of quantities are generally preferred.
The task is now to build a time-series model for the _Quantity_ column. It is important to note that this dataset is comprised of many individual time-series - one for each unique combination of _Store_ and _Brand_. To distinguish the individual time-series, we define the **time_series_id_column_names** - the columns whose values determine the boundaries between time-series:
```
time_series_id_column_names = ['Store', 'Brand']
nseries = data.groupby(time_series_id_column_names).ngroups
print('Data contains {0} individual time-series.'.format(nseries))
```
For demonstration purposes, we extract sales time-series for just a few of the stores:
```
use_stores = [2, 5, 8]
data_subset = data[data.Store.isin(use_stores)]
nseries = data_subset.groupby(time_series_id_column_names).ngroups
print('Data subset contains {0} individual time-series.'.format(nseries))
```
### Data Splitting
We now split the data into a training and a testing set for later forecast evaluation. The test set will contain the final 20 weeks of observed sales for each time-series. The splits should be stratified by series, so we use a group-by statement on the time series identifier columns.
```
n_test_periods = 20
def split_last_n_by_series_id(df, n):
"""Group df by series identifiers and split on last n rows for each group."""
df_grouped = (df.sort_values(time_column_name) # Sort by ascending time
.groupby(time_series_id_column_names, group_keys=False))
df_head = df_grouped.apply(lambda dfg: dfg.iloc[:-n])
df_tail = df_grouped.apply(lambda dfg: dfg.iloc[-n:])
return df_head, df_tail
train, test = split_last_n_by_series_id(data_subset, n_test_periods)
```
### Upload data to datastore
The [Machine Learning service workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-workspace), is paired with the storage account, which contains the default data store. We will use it to upload the train and test data and create [tabular datasets](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabulardataset?view=azure-ml-py) for training and testing. A tabular dataset defines a series of lazily-evaluated, immutable operations to load data from the data source into tabular representation.
```
train.to_csv (r'./dominicks_OJ_train.csv', index = None, header=True)
test.to_csv (r'./dominicks_OJ_test.csv', index = None, header=True)
datastore = ws.get_default_datastore()
datastore.upload_files(files = ['./dominicks_OJ_train.csv', './dominicks_OJ_test.csv'], target_path = 'dataset/', overwrite = True,show_progress = True)
```
### Create dataset for training
```
from azureml.core.dataset import Dataset
train_dataset = Dataset.Tabular.from_delimited_files(path=datastore.path('dataset/dominicks_OJ_train.csv'))
train_dataset.to_pandas_dataframe().tail()
```
## Modeling
For forecasting tasks, AutoML uses pre-processing and estimation steps that are specific to time-series. AutoML will undertake the following pre-processing steps:
* Detect time-series sample frequency (e.g. hourly, daily, weekly) and create new records for absent time points to make the series regular. A regular time series has a well-defined frequency and has a value at every sample point in a contiguous time span
* Impute missing values in the target (via forward-fill) and feature columns (using median column values)
* Create features based on time series identifiers to enable fixed effects across different series
* Create time-based features to assist in learning seasonal patterns
* Encode categorical variables to numeric quantities
In this notebook, AutoML will train a single, regression-type model across **all** time-series in a given training set. This allows the model to generalize across related series. If you're looking for training multiple models for different time-series, please see the many-models notebook.
You are almost ready to start an AutoML training job. First, we need to separate the target column from the rest of the DataFrame:
```
target_column_name = 'Quantity'
```
## Customization
The featurization customization in forecasting is an advanced feature in AutoML which allows our customers to change the default forecasting featurization behaviors and column types through `FeaturizationConfig`. The supported scenarios include:
1. Column purposes update: Override feature type for the specified column. Currently supports DateTime, Categorical and Numeric. This customization can be used in the scenario that the type of the column cannot correctly reflect its purpose. Some numerical columns, for instance, can be treated as Categorical columns which need to be converted to categorical while some can be treated as epoch timestamp which need to be converted to datetime. To tell our SDK to correctly preprocess these columns, a configuration need to be add with the columns and their desired types.
2. Transformer parameters update: Currently supports parameter change for Imputer only. User can customize imputation methods. The supported imputing methods for target column are constant and ffill (forward fill). The supported imputing methods for feature columns are mean, median, most frequent, constant and ffill (forward fill). This customization can be used for the scenario that our customers know which imputation methods fit best to the input data. For instance, some datasets use NaN to represent 0 which the correct behavior should impute all the missing value with 0. To achieve this behavior, these columns need to be configured as constant imputation with `fill_value` 0.
3. Drop columns: Columns to drop from being featurized. These usually are the columns which are leaky or the columns contain no useful data.
```
featurization_config = FeaturizationConfig()
featurization_config.drop_columns = ['logQuantity'] # 'logQuantity' is a leaky feature, so we remove it.
# Force the CPWVOL5 feature to be numeric type.
featurization_config.add_column_purpose('CPWVOL5', 'Numeric')
# Fill missing values in the target column, Quantity, with zeros.
featurization_config.add_transformer_params('Imputer', ['Quantity'], {"strategy": "constant", "fill_value": 0})
# Fill missing values in the INCOME column with median value.
featurization_config.add_transformer_params('Imputer', ['INCOME'], {"strategy": "median"})
# Fill missing values in the Price column with forward fill (last value carried forward).
featurization_config.add_transformer_params('Imputer', ['Price'], {"strategy": "ffill"})
```
## Forecasting Parameters
To define forecasting parameters for your experiment training, you can leverage the ForecastingParameters class. The table below details the forecasting parameter we will be passing into our experiment.
|Property|Description|
|-|-|
|**time_column_name**|The name of your time column.|
|**forecast_horizon**|The forecast horizon is how many periods forward you would like to forecast. This integer horizon is in units of the timeseries frequency (e.g. daily, weekly).|
|**time_series_id_column_names**|The column names used to uniquely identify the time series in data that has multiple rows with the same timestamp. If the time series identifiers are not defined, the data set is assumed to be one time series.|
## Train
The [AutoMLConfig](https://docs.microsoft.com/en-us/python/api/azureml-train-automl-client/azureml.train.automl.automlconfig.automlconfig?view=azure-ml-py) object defines the settings and data for an AutoML training job. Here, we set necessary inputs like the task type, the number of AutoML iterations to try, the training data, and cross-validation parameters.
For forecasting tasks, there are some additional parameters that can be set in the `ForecastingParameters` class: the name of the column holding the date/time, the timeseries id column names, and the maximum forecast horizon. A time column is required for forecasting, while the time_series_id is optional. If time_series_id columns are not given, AutoML assumes that the whole dataset is a single time-series. We also pass a list of columns to drop prior to modeling. The _logQuantity_ column is completely correlated with the target quantity, so it must be removed to prevent a target leak.
The forecast horizon is given in units of the time-series frequency; for instance, the OJ series frequency is weekly, so a horizon of 20 means that a trained model will estimate sales up to 20 weeks beyond the latest date in the training data for each series. In this example, we set the forecast horizon to the number of samples per series in the test set (n_test_periods). Generally, the value of this parameter will be dictated by business needs. For example, a demand planning application that estimates the next month of sales should set the horizon according to suitable planning time-scales. Please see the [energy_demand notebook](https://github.com/Azure/MachineLearningNotebooks/tree/master/how-to-use-azureml/automated-machine-learning/forecasting-energy-demand) for more discussion of forecast horizon.
We note here that AutoML can sweep over two types of time-series models:
* Models that are trained for each series such as ARIMA and Facebook's Prophet.
* Models trained across multiple time-series using a regression approach.
In the first case, AutoML loops over all time-series in your dataset and trains one model (e.g. AutoArima or Prophet, as the case may be) for each series. This can result in long runtimes to train these models if there are a lot of series in the data. One way to mitigate this problem is to fit models for different series in parallel if you have multiple compute cores available. To enable this behavior, set the `max_cores_per_iteration` parameter in your AutoMLConfig as shown in the example in the next cell.
Finally, a note about the cross-validation (CV) procedure for time-series data. AutoML uses out-of-sample error estimates to select a best pipeline/model, so it is important that the CV fold splitting is done correctly. Time-series can violate the basic statistical assumptions of the canonical K-Fold CV strategy, so AutoML implements a [rolling origin validation](https://robjhyndman.com/hyndsight/tscv/) procedure to create CV folds for time-series data. To use this procedure, you just need to specify the desired number of CV folds in the AutoMLConfig object. It is also possible to bypass CV and use your own validation set by setting the *validation_data* parameter of AutoMLConfig.
Here is a summary of AutoMLConfig parameters used for training the OJ model:
|Property|Description|
|-|-|
|**task**|forecasting|
|**primary_metric**|This is the metric that you want to optimize.<br> Forecasting supports the following primary metrics <br><i>spearman_correlation</i><br><i>normalized_root_mean_squared_error</i><br><i>r2_score</i><br><i>normalized_mean_absolute_error</i>
|**experiment_timeout_hours**|Experimentation timeout in hours.|
|**enable_early_stopping**|If early stopping is on, training will stop when the primary metric is no longer improving.|
|**training_data**|Input dataset, containing both features and label column.|
|**label_column_name**|The name of the label column.|
|**compute_target**|The remote compute for training.|
|**n_cross_validations**|Number of cross-validation folds to use for model/pipeline selection|
|**enable_voting_ensemble**|Allow AutoML to create a Voting ensemble of the best performing models|
|**enable_stack_ensemble**|Allow AutoML to create a Stack ensemble of the best performing models|
|**debug_log**|Log file path for writing debugging information|
|**featurization**| 'auto' / 'off' / FeaturizationConfig Indicator for whether featurization step should be done automatically or not, or whether customized featurization should be used. Setting this enables AutoML to perform featurization on the input to handle *missing data*, and to perform some common *feature extraction*.|
|**max_cores_per_iteration**|Maximum number of cores to utilize per iteration. A value of -1 indicates all available cores should be used
```
from azureml.automl.core.forecasting_parameters import ForecastingParameters
forecasting_parameters = ForecastingParameters(
time_column_name=time_column_name,
forecast_horizon=n_test_periods,
time_series_id_column_names=time_series_id_column_names
)
automl_config = AutoMLConfig(task='forecasting',
debug_log='automl_oj_sales_errors.log',
primary_metric='normalized_mean_absolute_error',
experiment_timeout_hours=0.25,
training_data=train_dataset,
label_column_name=target_column_name,
compute_target=compute_target,
enable_early_stopping=True,
featurization=featurization_config,
n_cross_validations=3,
verbosity=logging.INFO,
max_cores_per_iteration=-1,
forecasting_parameters=forecasting_parameters)
```
You can now submit a new training run. Depending on the data and number of iterations this operation may take several minutes.
Information from each iteration will be printed to the console. Validation errors and current status will be shown when setting `show_output=True` and the execution will be synchronous.
```
remote_run = experiment.submit(automl_config, show_output=False)
remote_run
remote_run.wait_for_completion()
```
### Retrieve the Best Model
Each run within an Experiment stores serialized (i.e. pickled) pipelines from the AutoML iterations. We can now retrieve the pipeline with the best performance on the validation dataset:
```
best_run, fitted_model = remote_run.get_output()
print(fitted_model.steps)
model_name = best_run.properties['model_name']
```
## Transparency
View updated featurization summary
```
custom_featurizer = fitted_model.named_steps['timeseriestransformer']
custom_featurizer.get_featurization_summary()
```
# Forecasting
Now that we have retrieved the best pipeline/model, it can be used to make predictions on test data. First, we remove the target values from the test set:
```
X_test = test
y_test = X_test.pop(target_column_name).values
X_test.head()
```
To produce predictions on the test set, we need to know the feature values at all dates in the test set. This requirement is somewhat reasonable for the OJ sales data since the features mainly consist of price, which is usually set in advance, and customer demographics which are approximately constant for each store over the 20 week forecast horizon in the testing data.
```
# forecast returns the predictions and the featurized data, aligned to X_test.
# This contains the assumptions that were made in the forecast
y_predictions, X_trans = fitted_model.forecast(X_test)
```
If you are used to scikit pipelines, perhaps you expected `predict(X_test)`. However, forecasting requires a more general interface that also supplies the past target `y` values. Please use `forecast(X,y)` as `predict(X)` is reserved for internal purposes on forecasting models.
The [forecast function notebook](../forecasting-forecast-function/auto-ml-forecasting-function.ipynb).
# Evaluate
To evaluate the accuracy of the forecast, we'll compare against the actual sales quantities for some select metrics, included the mean absolute percentage error (MAPE).
We'll add predictions and actuals into a single dataframe for convenience in calculating the metrics.
```
assign_dict = {'predicted': y_predictions, target_column_name: y_test}
df_all = X_test.assign(**assign_dict)
from azureml.automl.core.shared import constants
from azureml.automl.runtime.shared.score import scoring
from matplotlib import pyplot as plt
# use automl scoring module
scores = scoring.score_regression(
y_test=df_all[target_column_name],
y_pred=df_all['predicted'],
metrics=list(constants.Metric.SCALAR_REGRESSION_SET))
print("[Test data scores]\n")
for key, value in scores.items():
print('{}: {:.3f}'.format(key, value))
# Plot outputs
%matplotlib inline
test_pred = plt.scatter(df_all[target_column_name], df_all['predicted'], color='b')
test_test = plt.scatter(df_all[target_column_name], df_all[target_column_name], color='g')
plt.legend((test_pred, test_test), ('prediction', 'truth'), loc='upper left', fontsize=8)
plt.show()
```
# Operationalize
_Operationalization_ means getting the model into the cloud so that other can run it after you close the notebook. We will create a docker running on Azure Container Instances with the model.
```
description = 'AutoML OJ forecaster'
tags = None
model = remote_run.register_model(model_name = model_name, description = description, tags = tags)
print(remote_run.model_id)
```
### Develop the scoring script
For the deployment we need a function which will run the forecast on serialized data. It can be obtained from the best_run.
```
script_file_name = 'score_fcast.py'
best_run.download_file('outputs/scoring_file_v_1_0_0.py', script_file_name)
```
### Deploy the model as a Web Service on Azure Container Instance
```
from azureml.core.model import InferenceConfig
from azureml.core.webservice import AciWebservice
from azureml.core.webservice import Webservice
from azureml.core.model import Model
inference_config = InferenceConfig(environment = best_run.get_environment(),
entry_script = script_file_name)
aciconfig = AciWebservice.deploy_configuration(cpu_cores = 1,
memory_gb = 2,
tags = {'type': "automl-forecasting"},
description = "Automl forecasting sample service")
aci_service_name = 'automl-oj-forecast-01'
print(aci_service_name)
aci_service = Model.deploy(ws, aci_service_name, [model], inference_config, aciconfig)
aci_service.wait_for_deployment(True)
print(aci_service.state)
aci_service.get_logs()
```
### Call the service
```
import json
X_query = X_test.copy()
# We have to convert datetime to string, because Timestamps cannot be serialized to JSON.
X_query[time_column_name] = X_query[time_column_name].astype(str)
# The Service object accept the complex dictionary, which is internally converted to JSON string.
# The section 'data' contains the data frame in the form of dictionary.
test_sample = json.dumps({'data': X_query.to_dict(orient='records')})
response = aci_service.run(input_data = test_sample)
# translate from networkese to datascientese
try:
res_dict = json.loads(response)
y_fcst_all = pd.DataFrame(res_dict['index'])
y_fcst_all[time_column_name] = pd.to_datetime(y_fcst_all[time_column_name], unit = 'ms')
y_fcst_all['forecast'] = res_dict['forecast']
except:
print(res_dict)
y_fcst_all.head()
```
### Delete the web service if desired
```
serv = Webservice(ws, 'automl-oj-forecast-01')
serv.delete() # don't do it accidentally
```
| github_jupyter |
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Automated Machine Learning
_**Classification with Deployment using a Bank Marketing Dataset**_
## Contents
1. [Introduction](#Introduction)
1. [Setup](#Setup)
1. [Train](#Train)
1. [Results](#Results)
1. [Deploy](#Deploy)
1. [Test](#Test)
1. [Acknowledgements](#Acknowledgements)
## Introduction
In this example we use the UCI Bank Marketing dataset to showcase how you can use AutoML for a classification problem and deploy it to an Azure Container Instance (ACI). The classification goal is to predict if the client will subscribe to a term deposit with the bank.
If you are using an Azure Machine Learning Compute Instance, you are all set. Otherwise, go through the [configuration](../../../configuration.ipynb) notebook first if you haven't already to establish your connection to the AzureML Workspace.
Please find the ONNX related documentations [here](https://github.com/onnx/onnx).
In this notebook you will learn how to:
1. Create an experiment using an existing workspace.
2. Configure AutoML using `AutoMLConfig`.
3. Train the model using local compute with ONNX compatible config on.
4. Explore the results, featurization transparency options and save the ONNX model
5. Inference with the ONNX model.
6. Register the model.
7. Create a container image.
8. Create an Azure Container Instance (ACI) service.
9. Test the ACI service.
In addition this notebook showcases the following features
- **Blacklisting** certain pipelines
- Specifying **target metrics** to indicate stopping criteria
- Handling **missing data** in the input
## Setup
As part of the setup you have already created an Azure ML `Workspace` object. For AutoML you will need to create an `Experiment` object, which is a named object in a `Workspace` used to run experiments.
```
import logging
from matplotlib import pyplot as plt
import pandas as pd
import os
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.automl.core.featurization import FeaturizationConfig
from azureml.core.dataset import Dataset
from azureml.train.automl import AutoMLConfig
from azureml.explain.model._internal.explanation_client import ExplanationClient
```
This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
```
print("This notebook was created using version 1.8.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
```
Accessing the Azure ML workspace requires authentication with Azure.
The default authentication is interactive authentication using the default tenant. Executing the `ws = Workspace.from_config()` line in the cell below will prompt for authentication the first time that it is run.
If you have multiple Azure tenants, you can specify the tenant by replacing the `ws = Workspace.from_config()` line in the cell below with the following:
```
from azureml.core.authentication import InteractiveLoginAuthentication
auth = InteractiveLoginAuthentication(tenant_id = 'mytenantid')
ws = Workspace.from_config(auth = auth)
```
If you need to run in an environment where interactive login is not possible, you can use Service Principal authentication by replacing the `ws = Workspace.from_config()` line in the cell below with the following:
```
from azureml.core.authentication import ServicePrincipalAuthentication
auth = auth = ServicePrincipalAuthentication('mytenantid', 'myappid', 'mypassword')
ws = Workspace.from_config(auth = auth)
```
For more details, see [aka.ms/aml-notebook-auth](http://aka.ms/aml-notebook-auth)
```
ws = Workspace.from_config()
# choose a name for experiment
experiment_name = 'automl-classification-bmarketing-all'
experiment=Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## Create or Attach existing AmlCompute
You will need to create a compute target for your AutoML run. In this tutorial, you create AmlCompute as your training compute resource.
#### Creation of AmlCompute takes approximately 5 minutes.
If the AmlCompute with that name is already in your workspace this code will skip the creation process.
As with other Azure services, there are limits on certain resources (e.g. AmlCompute) associated with the Azure Machine Learning service. Please read this article on the default limits and how to request more quota.
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
cpu_cluster_name = "cpu-cluster-4"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=cpu_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=6)
compute_target = ComputeTarget.create(ws, cpu_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
# Data
### Load Data
Leverage azure compute to load the bank marketing dataset as a Tabular Dataset into the dataset variable.
### Training Data
```
data = pd.read_csv("https://automlsamplenotebookdata.blob.core.windows.net/automl-sample-notebook-data/bankmarketing_train.csv")
data.head()
# Add missing values in 75% of the lines.
import numpy as np
missing_rate = 0.75
n_missing_samples = int(np.floor(data.shape[0] * missing_rate))
missing_samples = np.hstack((np.zeros(data.shape[0] - n_missing_samples, dtype=np.bool), np.ones(n_missing_samples, dtype=np.bool)))
rng = np.random.RandomState(0)
rng.shuffle(missing_samples)
missing_features = rng.randint(0, data.shape[1], n_missing_samples)
data.values[np.where(missing_samples)[0], missing_features] = np.nan
if not os.path.isdir('data'):
os.mkdir('data')
# Save the train data to a csv to be uploaded to the datastore
pd.DataFrame(data).to_csv("data/train_data.csv", index=False)
ds = ws.get_default_datastore()
ds.upload(src_dir='./data', target_path='bankmarketing', overwrite=True, show_progress=True)
# Upload the training data as a tabular dataset for access during training on remote compute
train_data = Dataset.Tabular.from_delimited_files(path=ds.path('bankmarketing/train_data.csv'))
label = "y"
```
### Validation Data
```
validation_data = "https://automlsamplenotebookdata.blob.core.windows.net/automl-sample-notebook-data/bankmarketing_validate.csv"
validation_dataset = Dataset.Tabular.from_delimited_files(validation_data)
```
### Test Data
```
test_data = "https://automlsamplenotebookdata.blob.core.windows.net/automl-sample-notebook-data/bankmarketing_test.csv"
test_dataset = Dataset.Tabular.from_delimited_files(test_data)
```
## Train
Instantiate a AutoMLConfig object. This defines the settings and data used to run the experiment.
|Property|Description|
|-|-|
|**task**|classification or regression or forecasting|
|**primary_metric**|This is the metric that you want to optimize. Classification supports the following primary metrics: <br><i>accuracy</i><br><i>AUC_weighted</i><br><i>average_precision_score_weighted</i><br><i>norm_macro_recall</i><br><i>precision_score_weighted</i>|
|**iteration_timeout_minutes**|Time limit in minutes for each iteration.|
|**blacklist_models** | *List* of *strings* indicating machine learning algorithms for AutoML to avoid in this run. <br><br> Allowed values for **Classification**<br><i>LogisticRegression</i><br><i>SGD</i><br><i>MultinomialNaiveBayes</i><br><i>BernoulliNaiveBayes</i><br><i>SVM</i><br><i>LinearSVM</i><br><i>KNN</i><br><i>DecisionTree</i><br><i>RandomForest</i><br><i>ExtremeRandomTrees</i><br><i>LightGBM</i><br><i>GradientBoosting</i><br><i>TensorFlowDNN</i><br><i>TensorFlowLinearClassifier</i><br><br>Allowed values for **Regression**<br><i>ElasticNet</i><br><i>GradientBoosting</i><br><i>DecisionTree</i><br><i>KNN</i><br><i>LassoLars</i><br><i>SGD</i><br><i>RandomForest</i><br><i>ExtremeRandomTrees</i><br><i>LightGBM</i><br><i>TensorFlowLinearRegressor</i><br><i>TensorFlowDNN</i><br><br>Allowed values for **Forecasting**<br><i>ElasticNet</i><br><i>GradientBoosting</i><br><i>DecisionTree</i><br><i>KNN</i><br><i>LassoLars</i><br><i>SGD</i><br><i>RandomForest</i><br><i>ExtremeRandomTrees</i><br><i>LightGBM</i><br><i>TensorFlowLinearRegressor</i><br><i>TensorFlowDNN</i><br><i>Arima</i><br><i>Prophet</i>|
| **whitelist_models** | *List* of *strings* indicating machine learning algorithms for AutoML to use in this run. Same values listed above for **blacklist_models** allowed for **whitelist_models**.|
|**experiment_exit_score**| Value indicating the target for *primary_metric*. <br>Once the target is surpassed the run terminates.|
|**experiment_timeout_hours**| Maximum amount of time in hours that all iterations combined can take before the experiment terminates.|
|**enable_early_stopping**| Flag to enble early termination if the score is not improving in the short term.|
|**featurization**| 'auto' / 'off' Indicator for whether featurization step should be done automatically or not. Note: If the input data is sparse, featurization cannot be turned on.|
|**n_cross_validations**|Number of cross validation splits.|
|**training_data**|Input dataset, containing both features and label column.|
|**label_column_name**|The name of the label column.|
**_You can find more information about primary metrics_** [here](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-configure-auto-train#primary-metric)
```
automl_settings = {
"experiment_timeout_hours" : 0.3,
"enable_early_stopping" : True,
"iteration_timeout_minutes": 5,
"max_concurrent_iterations": 4,
"max_cores_per_iteration": -1,
#"n_cross_validations": 2,
"primary_metric": 'AUC_weighted',
"featurization": 'auto',
"verbosity": logging.INFO,
}
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
compute_target=compute_target,
experiment_exit_score = 0.9984,
blacklist_models = ['KNN','LinearSVM'],
enable_onnx_compatible_models=True,
training_data = train_data,
label_column_name = label,
validation_data = validation_dataset,
**automl_settings
)
```
Call the `submit` method on the experiment object and pass the run configuration. Execution of local runs is synchronous. Depending on the data and the number of iterations this can run for a while.
```
remote_run = experiment.submit(automl_config, show_output = False)
remote_run
```
Run the following cell to access previous runs. Uncomment the cell below and update the run_id.
```
#from azureml.train.automl.run import AutoMLRun
#remote_run = AutoMLRun(experiment=experiment, run_id='<run_ID_goes_here')
#remote_run
# Wait for the remote run to complete
remote_run.wait_for_completion()
best_run_customized, fitted_model_customized = remote_run.get_output()
```
## Transparency
View updated featurization summary
```
custom_featurizer = fitted_model_customized.named_steps['datatransformer']
df = custom_featurizer.get_featurization_summary()
pd.DataFrame(data=df)
```
Set `is_user_friendly=False` to get a more detailed summary for the transforms being applied.
```
df = custom_featurizer.get_featurization_summary(is_user_friendly=False)
pd.DataFrame(data=df)
df = custom_featurizer.get_stats_feature_type_summary()
pd.DataFrame(data=df)
```
## Results
```
from azureml.widgets import RunDetails
RunDetails(remote_run).show()
```
### Retrieve the Best Model's explanation
Retrieve the explanation from the best_run which includes explanations for engineered features and raw features. Make sure that the run for generating explanations for the best model is completed.
```
# Wait for the best model explanation run to complete
from azureml.core.run import Run
model_explainability_run_id = remote_run.get_properties().get('ModelExplainRunId')
print(model_explainability_run_id)
if model_explainability_run_id is not None:
model_explainability_run = Run(experiment=experiment, run_id=model_explainability_run_id)
model_explainability_run.wait_for_completion()
# Get the best run object
best_run, fitted_model = remote_run.get_output()
```
#### Download engineered feature importance from artifact store
You can use ExplanationClient to download the engineered feature explanations from the artifact store of the best_run.
```
client = ExplanationClient.from_run(best_run)
engineered_explanations = client.download_model_explanation(raw=False)
exp_data = engineered_explanations.get_feature_importance_dict()
exp_data
```
#### Download raw feature importance from artifact store
You can use ExplanationClient to download the raw feature explanations from the artifact store of the best_run.
```
client = ExplanationClient.from_run(best_run)
engineered_explanations = client.download_model_explanation(raw=True)
exp_data = engineered_explanations.get_feature_importance_dict()
exp_data
```
### Retrieve the Best ONNX Model
Below we select the best pipeline from our iterations. The `get_output` method returns the best run and the fitted model. The Model includes the pipeline and any pre-processing. Overloads on `get_output` allow you to retrieve the best run and fitted model for *any* logged metric or for a particular *iteration*.
Set the parameter return_onnx_model=True to retrieve the best ONNX model, instead of the Python model.
```
best_run, onnx_mdl = remote_run.get_output(return_onnx_model=True)
```
### Save the best ONNX model
```
from azureml.automl.runtime.onnx_convert import OnnxConverter
onnx_fl_path = "./best_model.onnx"
OnnxConverter.save_onnx_model(onnx_mdl, onnx_fl_path)
```
### Predict with the ONNX model, using onnxruntime package
```
import sys
import json
from azureml.automl.core.onnx_convert import OnnxConvertConstants
from azureml.train.automl import constants
if sys.version_info < OnnxConvertConstants.OnnxIncompatiblePythonVersion:
python_version_compatible = True
else:
python_version_compatible = False
import onnxruntime
from azureml.automl.runtime.onnx_convert import OnnxInferenceHelper
def get_onnx_res(run):
res_path = 'onnx_resource.json'
run.download_file(name=constants.MODEL_RESOURCE_PATH_ONNX, output_file_path=res_path)
with open(res_path) as f:
onnx_res = json.load(f)
return onnx_res
if python_version_compatible:
test_df = test_dataset.to_pandas_dataframe()
mdl_bytes = onnx_mdl.SerializeToString()
onnx_res = get_onnx_res(best_run)
onnxrt_helper = OnnxInferenceHelper(mdl_bytes, onnx_res)
pred_onnx, pred_prob_onnx = onnxrt_helper.predict(test_df)
print(pred_onnx)
print(pred_prob_onnx)
else:
print('Please use Python version 3.6 or 3.7 to run the inference helper.')
```
## Deploy
### Retrieve the Best Model
Below we select the best pipeline from our iterations. The `get_output` method returns the best run and the fitted model. Overloads on `get_output` allow you to retrieve the best run and fitted model for *any* logged metric or for a particular *iteration*.
#### Widget for Monitoring Runs
The widget will first report a "loading" status while running the first iteration. After completing the first iteration, an auto-updating graph and table will be shown. The widget will refresh once per minute, so you should see the graph update as child runs complete.
**Note:** The widget displays a link at the bottom. Use this link to open a web interface to explore the individual run details
```
best_run, fitted_model = remote_run.get_output()
model_name = best_run.properties['model_name']
script_file_name = 'inference/score.py'
conda_env_file_name = 'inference/env.yml'
best_run.download_file('outputs/scoring_file_v_1_0_0.py', 'inference/score.py')
best_run.download_file('outputs/conda_env_v_1_0_0.yml', 'inference/env.yml')
```
### Register the Fitted Model for Deployment
If neither `metric` nor `iteration` are specified in the `register_model` call, the iteration with the best primary metric is registered.
```
description = 'AutoML Model trained on bank marketing data to predict if a client will subscribe to a term deposit'
tags = None
model = remote_run.register_model(model_name = model_name, description = description, tags = tags)
print(remote_run.model_id) # This will be written to the script file later in the notebook.
```
### Deploy the model as a Web Service on Azure Container Instance
```
from azureml.core.model import InferenceConfig
from azureml.core.webservice import AciWebservice
from azureml.core.webservice import Webservice
from azureml.core.model import Model
from azureml.core.environment import Environment
myenv = Environment.from_conda_specification(name="myenv", file_path=conda_env_file_name)
inference_config = InferenceConfig(entry_script=script_file_name, environment=myenv)
aciconfig = AciWebservice.deploy_configuration(cpu_cores = 1,
memory_gb = 1,
tags = {'area': "bmData", 'type': "automl_classification"},
description = 'sample service for Automl Classification')
aci_service_name = 'automl-sample-bankmarketing-all'
print(aci_service_name)
aci_service = Model.deploy(ws, aci_service_name, [model], inference_config, aciconfig)
aci_service.wait_for_deployment(True)
print(aci_service.state)
```
### Delete a Web Service
Deletes the specified web service.
```
#aci_service.delete()
```
### Get Logs from a Deployed Web Service
Gets logs from a deployed web service.
```
#aci_service.get_logs()
```
## Test
Now that the model is trained, run the test data through the trained model to get the predicted values.
```
# Load the bank marketing datasets.
from numpy import array
X_test = test_dataset.drop_columns(columns=['y'])
y_test = test_dataset.keep_columns(columns=['y'], validate=True)
test_dataset.take(5).to_pandas_dataframe()
X_test = X_test.to_pandas_dataframe()
y_test = y_test.to_pandas_dataframe()
y_pred = fitted_model.predict(X_test)
actual = array(y_test)
actual = actual[:,0]
print(y_pred.shape, " ", actual.shape)
```
### Calculate metrics for the prediction
Now visualize the data on a scatter plot to show what our truth (actual) values are compared to the predicted values
from the trained model that was returned.
```
%matplotlib notebook
test_pred = plt.scatter(actual, y_pred, color='b')
test_test = plt.scatter(actual, actual, color='g')
plt.legend((test_pred, test_test), ('prediction', 'truth'), loc='upper left', fontsize=8)
plt.show()
```
## Acknowledgements
This Bank Marketing dataset is made available under the Creative Commons (CCO: Public Domain) License: https://creativecommons.org/publicdomain/zero/1.0/. Any rights in individual contents of the database are licensed under the Database Contents License: https://creativecommons.org/publicdomain/zero/1.0/ and is available at: https://www.kaggle.com/janiobachmann/bank-marketing-dataset .
_**Acknowledgements**_
This data set is originally available within the UCI Machine Learning Database: https://archive.ics.uci.edu/ml/datasets/bank+marketing
[Moro et al., 2014] S. Moro, P. Cortez and P. Rita. A Data-Driven Approach to Predict the Success of Bank Telemarketing. Decision Support Systems, Elsevier, 62:22-31, June 2014
| github_jupyter |
### Lesson outline
If you're familiar with NumPy (esp. the following operations), feel free to skim through this lesson.
- #### Create a NumPy array:
- from a pandas dataframe: [pandas.DataFrame.values](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.values.html)
- from a Python sequence: [numpy.array](http://docs.scipy.org/doc/numpy/reference/generated/numpy.array.html)
- with constant initial values: [numpy.ones, numpy.zeros](http://docs.scipy.org/doc/numpy/reference/generated/numpy.ones.html)
- with random values: [numpy.random](http://docs.scipy.org/doc/numpy/reference/routines.random.html)
- #### Access array attributes: [shape](http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.shape.html), [ndim](http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.ndim.html), [size](http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.size.html), [dtype](http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.dtype.html)
- #### Compute statistics: [sum](http://docs.scipy.org/doc/numpy/reference/generated/numpy.sum.html), [min](http://docs.scipy.org/doc/numpy/reference/generated/numpy.min.html), [max](http://docs.scipy.org/doc/numpy/reference/generated/numpy.max.html), [mean](http://docs.scipy.org/doc/numpy/reference/generated/numpy.mean.html)
- #### Carry out arithmetic operations: [add](http://docs.scipy.org/doc/numpy/reference/generated/numpy.add.html), [subtract](http://docs.scipy.org/doc/numpy/reference/generated/numpy.subtract.html), [multiply](http://docs.scipy.org/doc/numpy/reference/generated/numpy.multiply.html), [divide](http://docs.scipy.org/doc/numpy/reference/generated/numpy.divide.html)
- #### Measure execution time: [time.time](https://docs.python.org/2/library/time.html#time.time), [profile](https://docs.python.org/2/library/profile.html)
- #### Manipulate array elements: [Using simple indices and slices](http://docs.scipy.org/doc/numpy/reference/arrays.indexing.html#basic-slicing-and-indexing), [integer arrays](http://docs.scipy.org/doc/numpy/reference/arrays.indexing.html#integer-array-indexing), [boolean arrays](http://docs.scipy.org/doc/numpy/reference/arrays.indexing.html#boolean-array-indexing)
```
'''Creating NumPy arrays.'''
import numpy as np
def test_run():
# List to 1D array
print np.array([2, 3, 4])
print ''
#List of tuples to 2D array
print np.array([(2, 3, 4), (5, 6, 7)])
if __name__ == '__main__':
test_run()
'''Arrays with initial values.'''
import numpy as np
def test_run():
# Empty array
print np.empty(5)
print np.empty((5,4))
#Arrays of 1s
print np.ones((5,4))
if __name__ == '__main__':
test_run()
'''Specify the datatype.'''
import numpy as np
def test_run():
#Arrays of integers 1s
print np.ones((5,4), dtype=np.int)
if __name__ == '__main__':
test_run()
'''Generating random numbers.'''
import numpy as np
def test_run():
#Generate an anrray full of rando, numbers, uniformly sampled from [0.0, 1.0)
print np.random.random((5,4)) # Pass in a size tuple
print ''
# Sample numbers from a Gaussian (normal) distribution
print 'Standard Normal'
print np.random.normal(size=(2, 3)) # "Standard normal" (mean =0, s.d. = 1)
print ''
print 'Standard Normal'
print np.random.normal(50,10, size=(2, 3)) # Change mean to 50 and s.d. = 10
print ''
#Random integers
print 'A single integer'
print np.random.randint(10) # A single integer in [0, 10)
print ''
print 'A single integer'
print np.random.randint(0, 10) # Same as above, especifying [low, high) explicit
print ''
print '1d-array'
print np.random.randint(0, 10, size = 5) # 5 random integers as a 1D array
print ''
print '2d-array'
print np.random.randint(0, 10, size = (2, 3)) # 2x3 array of random integers
if __name__ == '__main__':
test_run()
'''Array attributes.'''
import numpy as np
def test_run():
a = np.random.random((5,4)) # 5x4 array of random numbers
print a
print a.shape
print a.shape[0] # Number of rows
print a.shape[1] # Number of columns
print len(a.shape)
print a.size
print a.dtype
if __name__ == '__main__':
test_run()
'''Operations on arrays.'''
import numpy as np
def test_run():
a = np.random.randint(0,10, size = (5,4)) # 5x4 random integers in [0, 10)
print 'Array:\n', a
#Sum of all elements
print 'Sum of all elements:', a.sum()
#Iterate over rows, to compute sum of each column
print 'Sum of each column:', a.sum(axis=0)
#Iterate over columns, to compute sum of each row
print 'Sum of each row:', a.sum(axis=1)
#Statistics: min, max, mean (accross rows, cols, and overall)
print 'Minimum of each column:\n', a.min(axis=0)
print 'Maximum of each row:\n', a.min(axis=1)
print 'Mean of all elements:\n', a.min() # Leave out axis arg.
if __name__ == '__main__':
test_run()
```
---
## Quiz: Locate Maximum Value
```
"""Locate maximum value."""
import numpy as np
def get_max_index(a):
"""Return the index of the maximum value in given 1D array."""
return np.argmax(a)
def test_run():
a = np.array([9, 6, 2, 3, 12, 14, 7, 10], dtype=np.int32) # 32-bit integer array
print "Array:", a
# Find the maximum and its index in array
print "Maximum value:", a.max()
print "Index of max.:", get_max_index(a)
if __name__ == "__main__":
test_run()
```
---
```
'''Using time function.'''
import numpy as np
import time
def test_run():
t1 = time.time()
print 'ML4T'
t2 = time.time()
print 'The time taken by print statement is ', t2 - t1,'seconds'
if __name__ == '__main__':
test_run()
'''How fast is NumPy.'''
import numpy as np
from time import time
def how_long(func, *args):
'''Execute funcion with given arguments, and measure execution time.'''
t0 = time()
result = func(*args) # All arguments are passed in as-is
t1 = time()
return result, t1- t0
def manual_mean(arr):
'''Compute mean (average) of all elements in the given 2D array'''
sum = 0
for i in xrange(0, arr.shape[0]):
for j in xrange (0, arr.shape[1]):
sum = sum + arr[i, j]
return sum / arr.size
def numpy_mean(arr):
'''Compute mean (average) using NumPy'''
return arr.mean()
def test_run():
'''Function called by Test Run.'''
nd1 = np.random.random((1000, 10000)) # Use a sufficiently large array
#Time the two functions, retrieving results and execution times
res_manual, t_manual = how_long(manual_mean, nd1)
res_numpy, t_numpy = how_long(numpy_mean, nd1)
print 'Manual: {:.6f} ({:.3f} secs.) vs NumPy: {:.6f} ({:.3f} secs.)'.format(res_manual, t_manual, res_numpy, t_numpy)
#Make sure both give us the same answer (upto some precision)
assert abs(res_manual - res_numpy) <= 10e-6, 'Results aren´t equal!'
#Compute speedup
speedup = t_manual / t_numpy
print 'NumPy mean is', speedup, 'times faster than manual for loops.'
if __name__ == '__main__':
test_run()
'''Accessing array elements.'''
import numpy as np
def test_run():
a = np.random.rand(5, 4)
print 'Array:\n', a
print''
#Accessing element at position (3, 2)
element = a[3, 2]
print 'Position (3, 2):\n', element
print''
#Elements in defined range
print 'Range (0, 1:3):\n', a[0, 1:3]
print''
#Top-left corner
print 'Top-left corner :\n', a[0:2, 0:2]
print''
#Slicing
#Note: Slice n:m:t specifies a range that starts at n, and stops before m, in steps of sizet
print 'Slicing:', a[:, 0:3:2]
if __name__ == '__main__':
test_run()
'''Modifying array elements.'''
import numpy as np
def test_run():
a = np.random.rand(5, 4)
print 'Array:\n', a
print''
#Assigning a value to aa particular location
a[0, 0] = 1
print '\nModified (replaced one element):\n', a
print''
#Assingning a single value to an entire row
a[0, :] = 2
print '\nModified (replaced a row with a single value):\n', a
print''
#Assingning a list to a column in an array
a[:, 3] = [1, 2, 3, 4, 5]
print '\nModified (replaced a column with a list):\n', a
print''
if __name__ == '__main__':
test_run()
'''Indexing an array with another array.'''
import numpy as np
def test_run():
a = np.random.rand(5)
#Accessing using list of indices
indices = np.array([1, 1, 2, 3])
print a
print a[indices]
if __name__ == '__main__':
test_run()
'''Boolean or "mask" index arrays.'''
import numpy as np
def test_run():
a = np.array([(20, 25, 10, 23, 26, 32, 10, 5, 0), (0, 2, 50, 20, 0, 1, 28, 5, 0)])
print 'Array:\n', a
print ''
#Calculating mean
mean = a.mean()
print 'Mean:\n', mean
print ''
#Masking
a[a<mean] = mean
print 'Masking:\n', a
if __name__ == '__main__':
test_run()
'''Arithmetic operations.'''
import numpy as np
def test_run():
a = np.array([(1, 2, 3, 4, 5), (10, 20, 30, 40, 50)])
print 'Original array a:\n', a
print ''
b = np.array([(100, 200, 300, 400, 500), (1, 2, 3, 4, 5)])
print 'Original array b:\n', b
print ''
#Multiply a by 2
mean = a.mean()
print 'Multiply a by 2:\n', 2*a
print ''
#Divide a by 2
mean = a.mean()
print 'Divide a by 2:\n', a/2.0
#Add the two arrays
print '\nAdd a + b:\n', a + b
#Multiply a and b
print '\nMultiply a * b:\n', a * b
#Divide a and b
print '\nDivide a / b:\n', a / b
if __name__ == '__main__':
test_run()
```
### Learning more NumPy
Resources from NumPy [User Guide](http://docs.scipy.org/doc/numpy/user/index.html) and [Reference](http://docs.scipy.org/doc/numpy/reference/index.html):
- #### [The N-dimensional array](http://docs.scipy.org/doc/numpy/reference/arrays.ndarray.html)
- #### [Data types](http://docs.scipy.org/doc/numpy/user/basics.types.html)
- #### [Array creation](http://docs.scipy.org/doc/numpy/user/basics.creation.html) [[more]](http://docs.scipy.org/doc/numpy/reference/routines.array-creation.html)
- #### [Indexing](http://docs.scipy.org/doc/numpy/user/basics.indexing.html) [[more]](http://docs.scipy.org/doc/numpy/reference/arrays.indexing.html)
- #### [Broadcasting](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
- #### [Random sampling](http://docs.scipy.org/doc/numpy/reference/routines.random.html)
- #### [Mathematical functions](http://docs.scipy.org/doc/numpy/reference/routines.math.html)
- #### [Linear algebra](http://docs.scipy.org/doc/numpy/reference/routines.linalg.html)
| github_jupyter |
# Setup
```
%load_ext rpy2.ipython
import os
from json import loads as jloads
from glob import glob
import pandas as pd
import datetime
%%R
library(gplots)
library(ggplot2)
library(ggthemes)
library(reshape2)
library(gridExtra)
library(heatmap.plus)
ascols = function(facs, pallette){
facs = facs[,1]
ffacs = as.factor(as.character(facs))
n = length(unique(facs))
cols = pallette(n)[ffacs]
}
greyscale = function(n){
return(rev(gray.colors(n)))
}
def getsname(filename):
return filename.split('/')[-1].split('.')[0]
def readJSON(jsonf):
return jloads(open(jsonf).read())
```
# Beta Diversity
```
obj = readJSON('results/olympiome.beta_diversity_stats.json.json')
speciesRhoKraken = obj['species']['rho_proportionality']['kraken']
speciesRhoKrakenDF = pd.DataFrame(speciesRhoKraken)
speciesJSDKraken = obj['species']['jensen_shannon_distance']['kraken']
speciesJSDKrakenDF = pd.DataFrame(speciesJSDKraken)
%%R -i speciesRhoKrakenDF
beta.df = as.matrix(speciesRhoKrakenDF)
diag(beta.df) = NA
heatmap.2(beta.df, trace='none', margins=c(8,8), ColSideColorsSize=3, KeyValueName="Rho Prop.", labCol=F, cexRow=0.8, dendrogram="both", density.info="histogram", col=greyscale)
%%R -i speciesJSDKrakenDF
beta.df = as.matrix(speciesJSDKrakenDF)
diag(beta.df) = NA
heatmap.2(beta.df,
trace='none',
margins=c(8,8),
ColSideColorsSize=3,
KeyValueName="Rho Prop.",
labCol=F,
cexRow=0.8,
dendrogram="both",
density.info="histogram",
col=greyscale)
```
# AMR
```
amrclassfs = glob('results/*.resistome_amrs.classus.tsv')
def parseF(fname):
out = {}
with open(fname) as f:
f.readline()
for line in f:
tkns = line.strip().split('\t')
out[tkns[1]] = int(tkns[2])
return out
amrclass = {getsname(amrclassf): parseF(amrclassf) for amrclassf in amrclassfs}
amrclass = pd.DataFrame(amrclass).fillna(0).transpose()
amrclass.shape
%%R -i amrclass
amr.df = t(as.matrix(amrclass))
heatmap.2(amr.df,
trace='none',
margins=c(8,8),
ColSideColorsSize=3,
KeyValueName="Rho Prop.",
cexCol=0.8,
cexRow=0.8,
dendrogram="both",
density.info="histogram",
col=greyscale)
```
# Virulence Factors
```
virfs = glob('results/*.vfdb_quantify.table.tsv')
virs = {getsname(virf): pd.read_csv(virf).set_index('Unnamed: 0').transpose() for virf in virfs}
virpan = pd.Panel(virs).transpose(2,0,1)
#vrpkm = virpan['RPKM'].fillna(0).apply(pd.to_numeric)
vrpkmg = virpan['RPKMG'].fillna(0).apply(pd.to_numeric)
vrpkmghigh = vrpkmg.transpose().loc[vrpkmg.mean(axis=0) > 200]
vrpkmghigh.shape
%%R -i vrpkmghigh
vir.df = as.matrix(vrpkmghigh)
heatmap.2(vir.df,
trace='none',
margins=c(8,8),
ColSideColorsSize=3,
KeyValueName="Rho Prop.",
cexCol=0.8,
cexRow=0.8,
dendrogram="both",
density.info="histogram",
col=greyscale)
```
# Virulence vs AMR
```
virlevels = vrpkmg.transpose().mean()
amrlevels = amrclass.transpose().mean().loc[virlevels.index]
%%R -i virlevels -i amrlevels
df = cbind(virlevels, amrlevels)
colnames(df) = c("virulence", "antimicrobial")
df = as.data.frame(df)
ggplot(df, aes(virulence, antimicrobial)) + geom_point() + geom_rug() + theme_tufte(ticks=F) +
xlab("Total Virulence") + ylab("Total AMR") +
theme(axis.title.x = element_text(vjust=-0.5), axis.title.y = element_text(vjust=1))
```
# Alpha Diversity
```
adivfs = glob('results/*.alpha_diversity_stats.json.json')
adivs = {getsname(adivf): readJSON(adivf) for adivf in adivfs}
chaoSpecies = {}
shanSpecies = {}
richSpecies = {}
for sname, adiv in adivs.items():
chaoSpecies[sname] = adiv['kraken']['species']['chao1']
shanSpecies[sname] = adiv['kraken']['species']['shannon_index']
richSpecies[sname] = adiv['kraken']['species']['richness']
chaoSpeciesDF = pd.DataFrame(chaoSpecies).fillna(0)
shanSpeciesDF = pd.DataFrame(shanSpecies).fillna(0)
richSpeciesDF = pd.DataFrame(richSpecies).fillna(0)
shanSpeciesDF.loc['500000'].sort_values()
```
# HMP Comparison
```
hmpfs = glob('results/*.hmp_site_dists.metaphlan2.json')
def crunch(obj):
out = {}
for k, v in obj.items():
out[k] = sum(v) / len(v)
return out
hmps = {getsname(hmpf): crunch(readJSON(hmpf)) for hmpf in hmpfs}
hmps = pd.DataFrame(hmps).transpose()
%%R -i hmps
hmp.df = melt(hmps)
ggplot(hmp.df, aes(x=variable, y=value)) +
theme_tufte() +
geom_boxplot() +
ylab('Cosine Similarity to HMP Sites') +
xlab('Body Site')
```
# Taxonomy
```
krakfs = glob('results/*.kraken_taxonomy_profiling.mpa.mpa.tsv')
def parseKrakF(krakf):
out = {}
with open(krakf) as kf:
for line in kf:
tkns = line.strip().split()
taxa = tkns[0]
if ('g__' in taxa) and ('s__' not in taxa):
key = taxa.split('g__')[-1]
out[key] = int(tkns[1])
return out
def getTopN(vec, n):
tups = vec.items()
tups = sorted(tups, key=lambda x: -x[1])
out = {k: v for k, v in tups[:n]}
return out
krak10 = {getsname(krakf): getTopN(parseKrakF(krakf), 10)
for krakf in krakfs}
krak10 = pd.DataFrame(krak10).fillna(0).transpose()
%%R -i krak10
krak.df = t(as.matrix(krak10))
krak.df = log(krak.df)
krak.df[!is.finite(krak.df)] = 0
heatmap.2(krak.df,
trace='none',
margins=c(8,8),
ColSideColorsSize=3,
KeyValueName="Rho Prop.",
cexCol=0.8,
cexRow=0.7,
dendrogram="both",
density.info="histogram",
col=greyscale)
```
| github_jupyter |
```
import cv2 as cv
import numpy as np
import random
img = cv.imread("task13.jpg")
temp = cv.imread("task13temp.jpg")
noise = 100
prev_noise = 0
result_of_ch = np.copy(img)
result_of_matching = np.copy(img)
rotated_img = np.copy(img)
bright_size = 10
contrast_size = 10
angle_size = 0.0
scale_size = 1.0
point_list=list()
point_list.append((0, 0))
point_list.append((img.shape[1], 0))
point_list.append((img.shape[1], img.shape[0]))
point_list.append((0, img.shape[0]))
point_for_change = 0
def update():
global noise
global prev_noise
global result_of_ch
global rotated_img
global result_of_matching
height, width = img.shape[:2]
center = (width / 2, height / 2)
if( prev_noise != noise):
prev_noise = noise
img_tmp = np.float64(img)
noise_pic = np.copy(img_tmp)
for i in range(img_tmp.shape[0]):
for j in range(img_tmp.shape[1]):
noise_val = random.randint(-noise, noise)
noise_pic[i][j] = img_tmp[i][j] + noise_val
result_of_ch = np.uint8(np.clip(noise_pic, 0, 255))
rotated_img = result_of_ch.copy()
change_brightness(bright_size)
change_contrast(contrast_size)
rotate_matrix = cv.getRotationMatrix2D(center, angle_size, scale_size)
rotated_img = cv.warpAffine(rotated_img, rotate_matrix, (width, height))
matrix = cv.getPerspectiveTransform( np.float32([[0, 0], [img.shape[1], 0], [img.shape[1], img.shape[0]], [0, img.shape[0]]]), \
np.float32(point_list))
rotated_img = cv.warpPerspective(rotated_img, matrix, (img.shape[1], img.shape[0]), cv.INTER_CUBIC, borderMode = cv.BORDER_CONSTANT, borderValue = (0, 0, 0))
imageGray = cv.cvtColor(rotated_img, cv.COLOR_BGR2GRAY)
templateGray = cv.cvtColor(temp, cv.COLOR_BGR2GRAY)
result = cv.matchTemplate(imageGray, templateGray,
cv.TM_CCOEFF_NORMED)
(minVal, maxVal, minLoc, maxLoc) = cv.minMaxLoc(result)
(startX, startY) = maxLoc
endX = startX + temp.shape[1]
endY = startY + temp.shape[0]
result_of_matching = cv.rectangle(cv.resize(rotated_img, (int(result_of_matching.shape[1] * 0.7), int(result_of_matching.shape[0] * 0.7))), (startX, startY), (endX, endY), (255, 0, 0), 3)
#cv.imshow("image", cv.resize(rotated_img, (int(rotated_img.shape[1] / 2), int(rotated_img.shape[0] / 2))))
cv.imshow("result", cv.resize(result_of_matching, (int(result_of_matching.shape[1] / 2), int(result_of_matching.shape[0] / 2))))
def change_noise(val):
global noise
noise = val
update()
def change_brightness( brightness):
global rotated_img
if brightness != 0:
rotated_img = cv.addWeighted(rotated_img, (255 - brightness) / 255, rotated_img, 0, brightness)
def change_contrast(contrast):
global rotated_img
if contrast != 0:
f = 131 * (contrast + 127) / (127 * (131 - contrast))
rotated_img = cv.addWeighted(rotated_img, f, rotated_img, 0, 127 * (1 - f))
def change_brightness_size(val):
global bright_size
bright_size = val
update()
def change_contrast_size(val):
global contrast_size
contrast_size = val
update()
def change_rotate_angle(val):
global angle_size
angle_size = val
update()
def change_rotate_scale(val):
global scale_size
if val > 0:
scale_size = val / 10.0
update()
def change_point_for_changing(val):
global point_for_change
point_for_change = val
def change_point_x_val(val):
global point_list
_, old_y = point_list[point_for_change]
point_list[point_for_change] = (val, old_y)
update()
def change_point_y_val(val):
global point_list
old_x, _ = point_list[point_for_change]
point_list[point_for_change] = (old_x, val)
update()
def return_to_default(val):
global point_list
global scale_size
global angle_size
global contrast_size
global bright_size
scale_size = 1
angle_size = 0
point_list[0] = (0, 0)
point_list[1] = (img.shape[1], 0)
point_list[2] = (img.shape[1], img.shape[0])
point_list[3] = (0, img.shape[0])
update()
#cv.imshow("image", cv.resize(result_of_ch, (int(result_of_ch.shape[1] / 2), int(result_of_ch.shape[0] / 2))))
cv.imshow("result", cv.resize(result_of_matching, (int(result_of_matching.shape[1] / 2), int(result_of_matching.shape[0] / 2))))
cv.namedWindow('Control')
cv.createTrackbar('noise', 'Control', 100, 255, change_noise)
cv.createTrackbar('contrast', 'Control', 0, 255, change_contrast_size)
cv.createTrackbar('brightness', 'Control', 0, 255, change_brightness_size)
cv.createTrackbar('Angle', 'Control', 0, 360, change_rotate_angle)
cv.createTrackbar('Scale', 'Control', 10, 360, change_rotate_scale)
cv.namedWindow('Control2')
cv.createTrackbar('Point', 'Control2', 0, 3, change_point_for_changing)
cv.createTrackbar('X', 'Control2', 0, img.shape[1] - 1, change_point_x_val)
cv.createTrackbar('Y', 'Control2', 0, img.shape[0] - 1, change_point_y_val)
cv.createTrackbar('Return', 'Control2', 0, 1, return_to_default)
cv.waitKey(0)
cv.destroyAllWindows()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/brit228/AB-Demo/blob/master/module2-Bag-of-Words/LS_DS_422_BOW_Assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import re
import string
!pip install -U nltk
import nltk
nltk.download('punkt')
nltk.download('stopwords')
nltk.download('wordnet')
from nltk.tokenize import sent_tokenize # Sentence Tokenizer
from nltk.tokenize import word_tokenize # Word Tokenizer
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
from nltk.probability import FreqDist
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
```
# 1) (optional) Scrape 100 Job Listings that contain the title "Data Scientist" from indeed.com
At a minimum your final dataframe of job listings should contain
- Job Title
- Job Description
```
import requests
from bs4 import BeautifulSoup
addition = ""
i = 0
data = []
while True:
r = requests.get("https://www.indeed.com/jobs?q=data%20scientist&l=Boston,%20MA"+addition)
soup = BeautifulSoup(r.text, 'html.parser')
for card in soup.find_all('div', class_="jobsearch-SerpJobCard", attrs={"data-tn-component": "organicJob"}):
try:
d = {}
d["Job Title"] = card.h2.a.text
d["Company"] = card.find("span", class_="company").text.strip()
d["Location"] = card.find("span", class_="location").text.strip()
r2 = requests.get("https://www.indeed.com"+card.a["href"])
soup2 = BeautifulSoup(r2.text, 'html.parser')
d["Job Description"] = "\n".join([a.text for a in soup2.find("div", class_="jobsearch-JobComponent-description icl-u-xs-mt--md").contents])
data.append(d)
except:
pass
i += 10
print(i)
addition = "&start={}".format(i)
if len(data) > 100:
break
df = pd.DataFrame(data)
df
```
# 2) Use NLTK to tokenize / clean the listings
```
df2 = df.copy()
stop_words = stopwords.words('english')
lemmatizer = WordNetLemmatizer()
df2["Job Description"] = df2["Job Description"].apply(lambda v: [lemmatizer.lemmatize(w) for w in word_tokenize(v) if w.isalpha() and w not in stop_words])
vector_list = sorted(list(set([inner for outer in df2["Job Description"].values for inner in outer])))
print(vector_list)
```
# 3) Use Scikit-Learn's CountVectorizer to get word counts for each listing.
```
df2["Job Description - Most Common"] = df2["Job Description"].apply(lambda v: FreqDist(v).most_common(20))
df2["Job Description - Most Common"]
```
# 4) Visualize the most common word counts
```
import matplotlib.pyplot as plt
fdist = FreqDist([inner for outer in df2["Job Description"].values for inner in outer])
fdist.plot(30, cumulative=False)
plt.show()
```
# 5) Use Scikit-Learn's tfidfVectorizer to get a TF-IDF feature matrix
```
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(stop_words='english')
tfidf = TfidfVectorizer(ngram_range=(1,1), max_features=20)
bag_of_words = tfidf.fit_transform([" ".join(v) for v in df2["Job Description"].values])
df_vec = pd.DataFrame(bag_of_words.toarray(), columns=tfidf.get_feature_names())
df_vec.head()
```
## Stretch Goals
- Scrape Job Listings for the job title "Data Analyst". How do these differ from Data Scientist Job Listings
- Try and identify requirements for experience specific technologies that are asked for in the job listings. How are those distributed among the job listings?
- Use a clustering algorithm to cluster documents by their most important terms. Do the clusters reveal any common themes?
- **Hint:** K-means might not be the best algorithm for this. Do a little bit of research to see what might be good for this. Also, remember that algorithms that depend on Euclidean distance break down with high dimensional data.
| github_jupyter |
# Code stuff - not slides!
```
%run ../ML_plots.ipynb
```
# Session 12:
## Supervised learning, part 1
*Andreas Bjerre-Nielsen*
## Agenda
1. [Modelling data](#Modelling-data)
1. [A familiar regression model](#A-familiar-regression-model)
1. [The curse of overfitting](#The-curse-of-overfitting)
1. [Important details](#Implementation-details)
## Vaaaamos
```
import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
plt.style.use('default') # set style (colors, background, size, gridlines etc.)
plt.rcParams['figure.figsize'] = 10, 4 # set default size of plots
plt.rcParams.update({'font.size': 18})
```
## Supervised problems (1)
*How do we distinguish between problems?*
```
f_identify_question
```
## Supervised problems (2)
*The two canonical problems*
```
f_identify_answer
```
## Supervised problems (3)
*Which models have we seen for classification?*
- .
- .
- .
# Modelling data
## Model complexity (1)
*What does a model of low complexity look like?*
```
f_complexity[0]
```
## Model complexity (2)
*What does medium model complexity look like?*
```
f_complexity[1]
```
## Model complexity (3)
*What does high model complexity look like?*
```
f_complexity[2]
```
## Model fitting (1)
*Quiz (1 min.): Which model fitted the data best?*
```
f_bias_var['regression'][2]
```
## Model fitting (2)
*What does underfitting and overfitting look like for classification?*
```
f_bias_var['classification'][2]
```
## Two agendas (1)
What are the objectives of empirical research?
1. *causation*: what is the effect of a particular variable on an outcome?
2. *prediction*: find some function that provides a good prediction of $y$ as a function of $x$
## Two agendas (2)
How might we express the agendas in a model?
$$ y = \alpha + \beta x + \varepsilon $$
- *causation*: interested in $\hat{\beta}$
- *prediction*: interested in $\hat{y}$
## Two agendas (3)
Might these two agendas be related at a deeper level?
Can prediction quality inform us about how to make causal models?
# A familiar regression model
## Estimation (1)
*Do we know already some ways to estimate regression models?*
- Social scientists know all about the Ordinary Least Squares (OLS).
- OLS estimate both parameters and their standard deviation.
- Is best linear unbiased estimator under regularity conditions.
*How is OLS estimated?*
- $\beta=(\textbf{X}^T\textbf{X})^{-1}\textbf{X}^T\textbf{y}$
- computation requires non perfect multicollinarity.
## Estimation (2)
*How might we estimate a linear regression model?*
- first order method (e.g. gradient descent)
- second order method (e.g. Newton-Raphson)
*So what the hell was gradient descent?*
- compute errors, multiply with features and update
## Estimation (3)
*Can you explain that in details?*
- Yes, like with Adaline, we minimize the sum of squared errors (SSE):
\begin{align}SSE&=\boldsymbol{e}^{T}\boldsymbol{e}\\\boldsymbol{e}&=\textbf{y}-\textbf{X}\textbf{w}\end{align}
```
X = np.random.normal(size=(3,2))
y = np.random.normal(size=(3))
w = np.random.normal(size=(3))
e = y-(w[0]+X.dot(w[1:]))
SSE = e.T.dot(e)
```
## Estimation (4)
*And what about the updating..? What is it something about the first order deritative?*
\begin{align}
\frac{\partial SSE}{\partial\hat{w}}=&\textbf{X}^T\textbf{e},\\
\Delta\hat{w}=&\eta\cdot\textbf{X}^T\textbf{e}=\eta\cdot\textbf{X}^T(\textbf{y}-\hat{\textbf{y}})
\end{align}
```
eta = 0.001 # learning rate
fod = X.T.dot(e)
update_vars = eta*fod
update_bias = eta*e.sum()
```
## Estimation (5)
*What might some advantages be relative to OLS?*
- Works despite high multicollinarity
- Speed
- OLS has $\mathcal{O}(K^2N)$ computation time ([read more](https://math.stackexchange.com/questions/84495/computational-complexity-of-least-square-regression-operation))
- Quadratic scaling in number of variables ($K$).
- Stochastic gradient descent
- Likely to converge faster with many observations ($N$)
## Fitting a polynomial (1)
Polyonomial: $f(x) = 2+8*x^4$
Try models of increasing order polynomials.
- Split data into train and test (50/50)
- For polynomial order 0 to 9:
- Iteration n: $y = \sum_{k=0}^{n}(\beta_k\cdot x^k)+\varepsilon$.
- Estimate order n model on training data
- Evaluate with on test data with RMSE:
- $log RMSE = \log (\sqrt{MSE})$
## Fitting a polynomial (2)
We generate samples of data from true model.
```
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
def true_fct(X):
return 2+X**4
n_samples = 25
n_degrees = 15
np.random.seed(0)
X_train = np.random.normal(size=(n_samples,1))
y_train = true_fct(X_train).reshape(-1) + np.random.randn(n_samples)
X_test = np.random.normal(size=(n_samples,1))
y_test = true_fct(X_test).reshape(-1) + np.random.randn(n_samples)
```
## Fitting a polynomial (3)
We estimate the polynomials
```
from sklearn.metrics import mean_squared_error as mse
test_mse = []
train_mse = []
parameters = []
degrees = range(n_degrees+1)
for p in degrees:
X_train_p = PolynomialFeatures(degree=p).fit_transform(X_train)
X_test_p = PolynomialFeatures(degree=p).fit_transform(X_train)
reg = LinearRegression().fit(X_train_p, y_train)
train_mse += [mse(reg.predict(X_train_p),y_train)]
test_mse += [mse(reg.predict(X_test_p),y_test)]
parameters.append(reg.coef_)
```
## Fitting a polynomial (4)
*So what happens to the model performance in- and out-of-sample?*
```
degree_index = pd.Index(degrees,name='Polynomial degree ~ model complexity')
ax = pd.DataFrame({'Train set':train_mse, 'Test set':test_mse})\
.set_index(degree_index)\
.plot(figsize=(10,4))
ax.set_ylabel('Mean squared error')
```
## Fitting a polynomial (4)
*Why does it go wrong?*
- more spurious parameters
- the coefficient size increases
## Fitting a polynomial (5)
*What do you mean coefficient size increase?*
```
order_idx = pd.Index(range(n_degrees+1),name='Polynomial order')
ax = pd.DataFrame(parameters,index=order_idx)\
.abs().mean(1)\
.plot(logy=True)
ax.set_ylabel('Mean parameter size')
```
## Fitting a polynomial (6)
*How else could we visualize this problem?*
```
f_bias_var['regression'][2]
```
# The curse of overfitting
## Looking for a remedy
*How might we solve the overfitting problem?*
By reducing
- the number of variables
- the coefficient size of variables
## Regularization (1)
*Why do we regularize?*
- To mitigate overfitting > better model predictions
*How do we regularize?*
- We make models which are less complex:
- reducing the **number** of coefficient;
- reducing the **size** of the coefficients.
## Regularization (2)
*What does regularization look like?*
We add a penalty term our optimization procedure:
$$ \text{arg min}_\beta \, \underset{\text{MSE}}{\underbrace{E[(y_0 - \hat{f}(x_0))^2]}} + \underset{\text{penalty}}{\underbrace{\lambda \cdot R(\beta)}}$$
Introduction of penalties implies that increased model complexity has to be met with high increases precision of estimates.
## Regularization (3)
*What are some used penalty functions?*
The two most common penalty functions are L1 and L2 regularization.
- L1 regularization (***Lasso***): $R(\beta)=\sum_{j=1}^{p}|\beta_j|$
- Makes coefficients sparse, i.e. selects variables by removing some (if $\lambda$ is high)
- L2 regularization (***Ridge***): $R(\beta)=\sum_{j=1}^{p}\beta_j^2$
- Reduce coefficient size
- Fast due to analytical solution
*To note:* The *Elastic Net* uses a combination of L1 and L2 regularization.
## Regularization (4)
*How the Lasso (L1 reg.) deviates from OLS*
<img src='http://rasbt.github.io/mlxtend/user_guide/general_concepts/regularization-linear_files/l1.png'>
## Regularization (5)
*How the Ridge regression (L2 reg.) deviates from OLS*
<img src='http://rasbt.github.io/mlxtend/user_guide/general_concepts/regularization-linear_files/l2.png'>
## Regularization (6)
*How might we describe the $\lambda$ of Lasso and Ridge?*
These are hyperparameters that we can optimize over.
- More about this tomorrow.
# Implementation details
## The devils in the details (1)
*So we just run regularization?*
# NO
We need to rescale our features:
- convert to zero mean:
- standardize to unit std:
Compute in Python:
- option 1: `StandardScaler` in `sklearn`
- option 2: `(X - np.mean(X)) / np.std(X)`
## The devils in the details (2)
*So we just scale our test and train?*
# NO
Fit to the distribution in the training data first, then rescale train and test! See more [here](https://stats.stackexchange.com/questions/174823/how-to-apply-standardization-normalization-to-train-and-testset-if-prediction-i).
## The devils in the details (3)
*So we just rescale before using polynomial features?*
# NO
Otherwise the interacted varaibles are not gaussian distributed.
## The devils in the details (4)
*Does sklearn's `PolynomialFeatures` work for more than variable?*
# YES!
# The end
[Return to agenda](#Agenda)
| github_jupyter |
# Colab FAQ
For some basic overview and features offered in Colab notebooks, check out: [Overview of Colaboratory Features](https://colab.research.google.com/notebooks/basic_features_overview.ipynb)
You need to use the colab GPU for this assignmentby selecting:
> **Runtime** → **Change runtime type** → **Hardware Accelerator: GPU**
## Setup PyTorch
All files are stored at /content/csc421/a4/ folder
```
######################################################################
# Setup python environment and change the current working directory
######################################################################
!pip install torch torchvision
!pip install imageio
!pip install matplotlib
%mkdir -p ./content/csc413/a4/
%cd ./content/csc413/a4
```
# Helper code
## Utility functions
```
import os
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn
from torch.nn import Parameter
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision import transforms
from six.moves.urllib.request import urlretrieve
import tarfile
import imageio
from urllib.error import URLError
from urllib.error import HTTPError
os.environ["CUDA_VISABLE_DEVICES"] = "GPU_ID"
def get_file(fname,
origin,
untar=False,
extract=False,
archive_format='auto',
cache_dir='data'):
datadir = os.path.join(cache_dir)
if not os.path.exists(datadir):
os.makedirs(datadir)
if untar:
untar_fpath = os.path.join(datadir, fname)
fpath = untar_fpath + '.tar.gz'
else:
fpath = os.path.join(datadir, fname)
print(fpath)
if not os.path.exists(fpath):
print('Downloading data from', origin)
error_msg = 'URL fetch failure on {}: {} -- {}'
try:
try:
urlretrieve(origin, fpath)
except URLError as e:
raise Exception(error_msg.format(origin, e.errno, e.reason))
except HTTPError as e:
raise Exception(error_msg.format(origin, e.code, e.msg))
except (Exception, KeyboardInterrupt) as e:
if os.path.exists(fpath):
os.remove(fpath)
raise
if untar:
if not os.path.exists(untar_fpath):
print('Extracting file.')
with tarfile.open(fpath) as archive:
archive.extractall(datadir)
return untar_fpath
return fpath
class AttrDict(dict):
def __init__(self, *args, **kwargs):
super(AttrDict, self).__init__(*args, **kwargs)
self.__dict__ = self
def to_var(tensor, cuda=True):
"""Wraps a Tensor in a Variable, optionally placing it on the GPU.
Arguments:
tensor: A Tensor object.
cuda: A boolean flag indicating whether to use the GPU.
Returns:
A Variable object, on the GPU if cuda==True.
"""
if cuda:
return Variable(tensor.cuda())
else:
return Variable(tensor)
def to_data(x):
"""Converts variable to numpy."""
if torch.cuda.is_available():
x = x.cpu()
return x.data.numpy()
def create_dir(directory):
"""Creates a directory if it doesn't already exist.
"""
if not os.path.exists(directory):
os.makedirs(directory)
def gan_checkpoint(iteration, G, D, opts):
"""Saves the parameters of the generator G and discriminator D.
"""
G_path = os.path.join(opts.checkpoint_dir, 'G.pkl')
D_path = os.path.join(opts.checkpoint_dir, 'D.pkl')
torch.save(G.state_dict(), G_path)
torch.save(D.state_dict(), D_path)
def load_checkpoint(opts):
"""Loads the generator and discriminator models from checkpoints.
"""
G_path = os.path.join(opts.load, 'G.pkl')
D_path = os.path.join(opts.load, 'D_.pkl')
G = DCGenerator(noise_size=opts.noise_size, conv_dim=opts.g_conv_dim, spectral_norm=opts.spectral_norm)
D = DCDiscriminator(conv_dim=opts.d_conv_dim)
G.load_state_dict(torch.load(G_path, map_location=lambda storage, loc: storage))
D.load_state_dict(torch.load(D_path, map_location=lambda storage, loc: storage))
if torch.cuda.is_available():
G.cuda()
D.cuda()
print('Models moved to GPU.')
return G, D
def merge_images(sources, targets, opts):
"""Creates a grid consisting of pairs of columns, where the first column in
each pair contains images source images and the second column in each pair
contains images generated by the CycleGAN from the corresponding images in
the first column.
"""
_, _, h, w = sources.shape
row = int(np.sqrt(opts.batch_size))
merged = np.zeros([3, row * h, row * w * 2])
for (idx, s, t) in (zip(range(row ** 2), sources, targets, )):
i = idx // row
j = idx % row
merged[:, i * h:(i + 1) * h, (j * 2) * h:(j * 2 + 1) * h] = s
merged[:, i * h:(i + 1) * h, (j * 2 + 1) * h:(j * 2 + 2) * h] = t
return merged.transpose(1, 2, 0)
def generate_gif(directory_path, keyword=None):
images = []
for filename in sorted(os.listdir(directory_path)):
if filename.endswith(".png") and (keyword is None or keyword in filename):
img_path = os.path.join(directory_path, filename)
print("adding image {}".format(img_path))
images.append(imageio.imread(img_path))
if keyword:
imageio.mimsave(
os.path.join(directory_path, 'anim_{}.gif'.format(keyword)), images)
else:
imageio.mimsave(os.path.join(directory_path, 'anim.gif'), images)
def create_image_grid(array, ncols=None):
"""
"""
num_images, channels, cell_h, cell_w = array.shape
if not ncols:
ncols = int(np.sqrt(num_images))
nrows = int(np.math.floor(num_images / float(ncols)))
result = np.zeros((cell_h * nrows, cell_w * ncols, channels), dtype=array.dtype)
for i in range(0, nrows):
for j in range(0, ncols):
result[i * cell_h:(i + 1) * cell_h, j * cell_w:(j + 1) * cell_w, :] = array[i * ncols + j].transpose(1, 2,
0)
if channels == 1:
result = result.squeeze()
return result
def gan_save_samples(G, fixed_noise, iteration, opts):
generated_images = G(fixed_noise)
generated_images = to_data(generated_images)
grid = create_image_grid(generated_images)
# merged = merge_images(X, fake_Y, opts)
path = os.path.join(opts.sample_dir, 'sample-{:06d}.png'.format(iteration))
imageio.imwrite(path, grid)
print('Saved {}'.format(path))
```
## Data loader
```
def get_emoji_loader(emoji_type, opts):
"""Creates training and test data loaders.
"""
transform = transforms.Compose([
transforms.Scale(opts.image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, ), (0.5, )),
])
train_path = os.path.join('data/emojis', emoji_type)
test_path = os.path.join('data/emojis', 'Test_{}'.format(emoji_type))
train_dataset = datasets.ImageFolder(train_path, transform)
test_dataset = datasets.ImageFolder(test_path, transform)
train_dloader = DataLoader(dataset=train_dataset, batch_size=opts.batch_size, shuffle=True, num_workers=opts.num_workers)
test_dloader = DataLoader(dataset=test_dataset, batch_size=opts.batch_size, shuffle=False, num_workers=opts.num_workers)
return train_dloader, test_dloader
def get_emnist_loader(emnist_type, opts):
transform = transforms.Compose([
transforms.Scale(opts.image_size),
transforms.ToTensor(),
transforms.Normalize((0.5), (0.5)),
])
train = datasets.EMNIST(".", split=emnist_type,train = True, download = True, transform= transform)
test = datasets.EMNIST(".", split=emnist_type,train = False, download = True, transform = transform)
train_dloader = DataLoader(dataset=train, batch_size=opts.batch_size, shuffle=True,num_workers=opts.num_workers)
test_dloader = DataLoader(dataset=test, batch_size=opts.batch_size, shuffle=False,num_workers=opts.num_workers)
return train_dloader, test_dloader
```
## Training and evaluation code
```
def print_models(G_XtoY, G_YtoX, D_X, D_Y):
"""Prints model information for the generators and discriminators.
"""
print(" G ")
print("---------------------------------------")
print(G_XtoY)
print("---------------------------------------")
print(" D ")
print("---------------------------------------")
print(D_X)
print("---------------------------------------")
def create_model(opts):
"""Builds the generators and discriminators.
"""
### GAN
G = DCGenerator(noise_size=opts.noise_size, conv_dim=opts.g_conv_dim, spectral_norm=opts.spectral_norm)
D = DCDiscriminator(conv_dim=opts.d_conv_dim, spectral_norm=opts.spectral_norm)
print_models(G, None, D, None)
if torch.cuda.is_available():
G.cuda()
D.cuda()
print('Models moved to GPU.')
return G, D
def train(opts):
"""Loads the data, creates checkpoint and sample directories, and starts the training loop.
"""
# Create train and test dataloaders for images from the two domains X and Y
dataloader_X, test_dataloader_X = get_emnist_loader(opts.X, opts=opts)
# Create checkpoint and sample directories
create_dir(opts.checkpoint_dir)
create_dir(opts.sample_dir)
# Start training
G, D = gan_training_loop(dataloader_X, test_dataloader_X, opts)
return G, D
def print_opts(opts):
"""Prints the values of all command-line arguments.
"""
print('=' * 80)
print('Opts'.center(80))
print('-' * 80)
for key in opts.__dict__:
if opts.__dict__[key]:
print('{:>30}: {:<30}'.format(key, opts.__dict__[key]).center(80))
print('=' * 80)
```
# Your code for generators and discriminators
## Helper modules
```
def sample_noise(batch_size, dim):
"""
Generate a PyTorch Tensor of uniform random noise.
Input:
- batch_size: Integer giving the batch size of noise to generate.
- dim: Integer giving the dimension of noise to generate.
Output:
- A PyTorch Tensor of shape (batch_size, dim, 1, 1) containing uniform
random noise in the range (-1, 1).
"""
return to_var(torch.rand(batch_size, dim) * 2 - 1).unsqueeze(2).unsqueeze(3)
def upconv(in_channels, out_channels, kernel_size, stride=2, padding=2, batch_norm=True, spectral_norm=False):
"""Creates a upsample-and-convolution layer, with optional batch normalization.
"""
layers = []
if stride>1:
layers.append(nn.Upsample(scale_factor=stride))
conv_layer = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=1, padding=padding, bias=False)
if spectral_norm:
layers.append(SpectralNorm(conv_layer))
else:
layers.append(conv_layer)
if batch_norm:
layers.append(nn.BatchNorm2d(out_channels))
return nn.Sequential(*layers)
def conv(in_channels, out_channels, kernel_size, stride=2, padding=2, batch_norm=True, init_zero_weights=False, spectral_norm=False):
"""Creates a convolutional layer, with optional batch normalization.
"""
layers = []
conv_layer = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=kernel_size, stride=stride, padding=padding, bias=False)
if init_zero_weights:
conv_layer.weight.data = torch.randn(out_channels, in_channels, kernel_size, kernel_size) * 0.001
if spectral_norm:
layers.append(SpectralNorm(conv_layer))
else:
layers.append(conv_layer)
if batch_norm:
layers.append(nn.BatchNorm2d(out_channels))
return nn.Sequential(*layers)
class ResnetBlock(nn.Module):
def __init__(self, conv_dim):
super(ResnetBlock, self).__init__()
self.conv_layer = conv(in_channels=conv_dim, out_channels=conv_dim, kernel_size=3, stride=1, padding=1)
def forward(self, x):
out = x + self.conv_layer(x)
return out
```
## DCGAN
## Spectral Norm class
### GAN generator
```
class DCGenerator(nn.Module):
def __init__(self, noise_size, conv_dim, spectral_norm=False):
super(DCGenerator, self).__init__()
self.conv_dim = conv_dim
self.relu = nn.ReLU()
self.linear_bn = upconv(100, conv_dim*4,3) #BS X noise_size x 1 x 1 -> BS x 128 x 4 x 4
self.upconv1 = upconv(conv_dim*4,conv_dim*2,5)
self.upconv2 = upconv(conv_dim*2,conv_dim,5)
self.upconv3 = upconv(conv_dim,1,5, batch_norm=False)
self.tanh = nn.Tanh()
def forward(self, z):
"""Generates an image given a sample of random noise.
Input
-----
z: BS x noise_size x 1 x 1 --> BSx100x1x1 (during training)
Output
------
out: BS x channels x image_width x image_height --> BSx3x32x32 (during training)
"""
batch_size = z.size(0)
out = self.relu(self.linear_bn(z)) # BS x 128 x 4 x 4 conv_dim=32
out = out.view(-1, self.conv_dim*4, 4, 4)
out = self.relu(self.upconv1(out)) # BS x 64 x 8 x 8
out = self.relu(self.upconv2(out)) # BS x 32 x 16 x 16
out = self.tanh(self.upconv3(out)) # BS x 3 x 32 x 32
out_size = out.size()
if out_size != torch.Size([batch_size, 1, 32, 32]):
raise ValueError("expect {} x 3 x 32 x 32, but get {}".format(batch_size, out_size))
return out
```
### GAN discriminator
```
class DCDiscriminator(nn.Module):
"""Defines the architecture of the discriminator network.
Note: Both discriminators D_X and D_Y have the same architecture in this assignment.
"""
def __init__(self, conv_dim=64, spectral_norm=False):
super(DCDiscriminator, self).__init__()
self.conv1 = conv(in_channels=1, out_channels=conv_dim, kernel_size=5, stride=2, spectral_norm=spectral_norm)
self.conv2 = conv(in_channels=conv_dim, out_channels=conv_dim*2, kernel_size=5, stride=2, spectral_norm=spectral_norm)
self.conv3 = conv(in_channels=conv_dim*2, out_channels=conv_dim*4, kernel_size=5, stride=2, spectral_norm=spectral_norm)
self.conv4 = conv(in_channels=conv_dim*4, out_channels=1, kernel_size=5, stride=2, padding=1, batch_norm=False, spectral_norm=spectral_norm)
def forward(self, x):
batch_size = x.size(0)
out = F.relu(self.conv1(x)) # BS x 64 x 16 x 16
out = F.relu(self.conv2(out)) # BS x 64 x 8 x 8
out = F.relu(self.conv3(out)) # BS x 64 x 4 x 4
out = self.conv4(out).squeeze()
out_size = out.size()
if out_size != torch.Size([batch_size,]):
raise ValueError("expect {} x 1, but get {}".format(batch_size, out_size))
return out
from torch.utils.tensorboard import SummaryWriter
import numpy as np
def log_to_tensorboard(iteration, losses):
writer = SummaryWriter("./runs/")
for key in losses:
arr = losses[key]
writer.add_scalar(f'loss/{key}', arr[-1], iteration)
writer.close()
def calculate_log_likelihood(model, opts):
transform = transforms.Compose([
transforms.Scale(opts.image_size),
transforms.ToTensor(),
transforms.Normalize((0.5), (0.5)),
])
train = datasets.EMNIST(".", split="letters",train = True, download = True, transform= transform)
train_dloader = DataLoader(dataset=train, batch_size=opts.batch_size, shuffle=True,num_workers=opts.num_workers)
x = next(iter(train_dloader))[0]
print(x)
return torch.log(model(x)).mean()
```
### GAN training loop
```
def gan_training_loop(dataloader, test_dataloader, opts):
"""Runs the training loop.
* Saves checkpoint every opts.checkpoint_every iterations
* Saves generated samples every opts.sample_every iterations
"""
# Create generators and discriminators
G, D = create_model(opts)
g_params = G.parameters() # Get generator parameters
d_params = D.parameters() # Get discriminator parameters
# Create optimizers for the generators and discriminators
g_optimizer = optim.RMSprop(g_params, opts.lr)
d_optimizer = optim.RMSprop(d_params, opts.lr)
train_iter = iter(dataloader)
test_iter = iter(test_dataloader)
# Get some fixed data from domains X and Y for sampling. These are images that are held
# constant throughout training, that allow us to inspect the model's performance.
fixed_noise = sample_noise(100, opts.noise_size) # # 100 x noise_size x 1 x 1
iter_per_epoch = len(train_iter)
total_train_iters = opts.train_iters
losses = {"iteration": [], "D_fake_loss": [], "D_real_loss": [], "G_loss": [], "D_loss": [], "W_loss": []}
# adversarial_loss = torch.nn.BCEWithLogitsLoss()
gp_weight = 1
epoch = 0
total_iters = 0
try:
for iteration in range(1, opts.train_iters + 1):
# Reset data_iter for each epoch
# ones = Variable(torch.Tensor(real_images.shape[0]).float().cuda().fill_(1.0), requires_grad=False)
if total_iters % iter_per_epoch == 0:
epoch +=1
train_iter = iter(dataloader)
print("EPOCH:", epoch)
b = opts.batch_size
for i in range(opts.n_critic):
real_images, real_labels = train_iter.next()
real_images, real_labels = to_var(real_images), to_var(real_labels).long().squeeze()
m = b
noise = sample_noise(m, opts.noise_size)
fake_images = G(noise)
D_real_loss = D(real_images).mean()
D_fake_loss = D(fake_images).mean()
D_loss = -(D_real_loss - D_fake_loss) #Minimize D_real_loss - D_fake_loss
D_loss.backward()
d_optimizer.step()
Wasserstein_Distance = D_real_loss - D_fake_loss
total_iters += 1
for param in D.parameters():
param.data.clamp_(-opts.clip, opts.clip)
D.zero_grad()
G.zero_grad()
#
z = sample_noise(m, opts.noise_size)
G_z = G(z)
G_loss = -torch.mean(D(G_z))
G_loss.backward()
g_optimizer.step()
D.zero_grad()
G.zero_grad()
if iteration % opts.log_step == 0:
w_loss = Wasserstein_Distance
losses['iteration'].append(iteration)
losses['D_real_loss'].append(D_real_loss.item())
losses['D_loss'].append(D_loss.item())
losses['D_fake_loss'].append(D_fake_loss.item())
losses['W_loss'].append(w_loss.item())
losses['G_loss'].append(G_loss.item())
print('Iteration [{:4d}/{:4d}] | D_real_loss: {:6.4f} | D_fake_loss: {:6.4f} | G_loss: {:6.4f} | D_loss: {:6.4f} | Wasserstein_Distance: {:6.4f}'.format(
iteration, total_train_iters, D_real_loss.item(), D_fake_loss.item(), G_loss.item(), D_loss.item(), Wasserstein_Distance.item() ))
log_to_tensorboard(iteration, losses)
# Save the generated samples
if iteration % opts.sample_every == 0:
gan_save_samples(G, fixed_noise, iteration, opts)
# Save the model parameters
if iteration % opts.checkpoint_every == 0:
gan_checkpoint(iteration, G, D, opts)
except KeyboardInterrupt:
print('Exiting early from training.')
return G, D
plt.figure()
plt.plot(losses['iteration'], losses['D_real_loss'], label='D_real')
plt.plot(losses['iteration'], losses['D_fake_loss'], label='D_fake')
plt.plot(losses['iteration'], losses['G_loss'], label='G')
plt.plot(losses['iteration'], losses['D_loss'], label='D')
plt.legend()
plt.savefig(os.path.join(opts.sample_dir, 'losses.png'))
plt.close()
return G, D
```
# Training
## Download dataset
### WGAN
```
SEED = 11
# Set the random seed manually for reproducibility.
np.random.seed(SEED)
torch.manual_seed(SEED)
if torch.cuda.is_available():
torch.cuda.manual_seed(SEED)
args = AttrDict()
args_dict = {
'clip': .01,
'n_critic': 5,
'image_size':32,
'g_conv_dim':32,
'd_conv_dim':64,
'noise_size':100,
'num_workers': 0,
'train_iters':300000,
'X':'letters', # options: 'Windows' / 'Apple'
'Y': None,
'lr':5e-5,
'beta1':0.5,
'beta2':0.999,
'batch_size':64,
'checkpoint_dir':'./results/checkpoints_gan_gp1_lr3e-5',
'sample_dir': './results/samples_gan_gp1_lr3e-5',
'load': None,
'log_step':200,
'sample_every':200,
'checkpoint_every':1000,
'spectral_norm': False,
'gradient_penalty': False,
'd_train_iters': 1
}
args.update(args_dict)
print_opts(args)
G, D = train(args)
generate_gif("results/samples_gan_gp1_lr3e-5")
torch.cuda.is_available()
torch.cuda.device(0)
torch.cuda.get_device_name(0)
torch.version.cuda
torch.cuda.FloatTensor()
load_args = AttrDict()
args_dict = {
'clip': .01,
'n_critic': 5,
'image_size':32,
'g_conv_dim':32,
'd_conv_dim':64,
'noise_size':100,
'num_workers': 0,
'train_iters':300000,
'X':'letters', # options: 'Windows' / 'Apple'
'Y': None,
'lr':5e-5,
'beta1':0.5,
'beta2':0.999,
'batch_size':64,
'checkpoint_dir':'./results/checkpoints_gan_gp1_lr3e-5',
'sample_dir': './results/samples_gan_gp1_lr3e-5',
'load': './results/samples_gan_gp1_lr3e-5',
'log_step':200,
'sample_every':200,
'checkpoint_every':1000,
'spectral_norm': False,
'gradient_penalty': False,
'd_train_iters': 1
}
load_args.update(args_dict)
D,G = load_checkpoint(load_args)
```
| github_jupyter |
```
import cv2
import os
import numpy
from PIL import Image
import matplotlib.pyplot as plt
# !tar -xf EnglishHnd.tgz
# !mv English/Hnd ./
# !rm -rf Hnd/Trj/
# !mv Hnd/Img/* Hnd/
# !rm -rf Hnd/Img
# !rm -rf English
# !rm -rf Hnd
label_list = ['0','1','2','3','4','5','6','7','8','9', 'A','B','C','D','E','F','G','H', 'I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z','a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z','fail']
# # count = 0
# os.remove("./Hnd/all.txt~")
# for cc in os.listdir("./Hnd"):
# count = cc[-2:]
# os.rename('Hnd/' + cc, 'Hnd/' + label_list[int(count)-1])
import torch
from torch.utils.data import Dataset
from torchvision import datasets
from torchvision import transforms
import matplotlib.pyplot as plt
from torchvision.io import read_image
transform = transforms.Compose(
[
# transforms.ToPILImage(),
transforms.Grayscale(),
transforms.Resize((28,28)),
transforms.ToTensor(),
# transforms.Normalize((0.5), (0.5)),
]
)
def load_dataset():
data_path = './Img/'
train_dataset = datasets.ImageFolder(
root=data_path,
transform=transform
)
# train_dataset = datasets.EMNIST(root= "./data",split="byclass", train = True, download = True, transform = transform)
train_loader = torch.utils.data.DataLoader(
train_dataset,
batch_size=64,
num_workers=2,
shuffle=True
)
return train_loader
# for batch_idx, (data, target) in enumerate(load_dataset()):
# print(batch_idx)
dataiter = iter(load_dataset())
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
figure = plt.figure()
num_of_images = 60
for index in range(1, num_of_images + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(images[index].numpy().squeeze(), cmap='gray_r')
load_dataset()
device = 'cuda' if torch.cuda.is_available() else 'cpu'
device
# defining the model architecture
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.cnn_layers = torch.nn.Sequential(
# Defining a 2D convolution layer
torch.nn.Conv2d(1, 128, kernel_size=3, stride=1, padding=1),
torch.nn.BatchNorm2d(128),
torch.nn.ReLU(inplace=True),
torch.nn.MaxPool2d(kernel_size=2, stride=2),
# Defining another 2D convolution layer
torch.nn.Conv2d(128, 128, kernel_size=3, stride=1, padding=1),
torch.nn.BatchNorm2d(128),
torch.nn.ReLU(inplace=True),
torch.nn.MaxPool2d(kernel_size=2, stride=2),
)
self.linear_layers = torch.nn.Sequential(
torch.nn.Linear(128 * 7 * 7, 63)
)
# Defining the forward pass
def forward(self, x):
x = self.cnn_layers(x)
x = x.view(x.size(0), -1)
# print(x.size)
x = self.linear_layers(x)
return x
model = Net()
# optimizer = torch.optim.Adam(model.parameters(), lr = 0.05)
optimizer = torch.optim.SGD(model.parameters(), lr=0.005, momentum=0.9)
cc = torch.nn.CrossEntropyLoss()
model.cuda()
cc = cc.cuda()
model
for i in range(30):
running_loss = 0
for batch_idx, (images, labels) in enumerate(load_dataset()):
if torch.cuda.is_available():
images = images.cuda()
labels = labels.cuda()
# Training pass
optimizer.zero_grad()
output = model(images)
loss = cc(output, labels)
#This is where the model learns by backpropagating
loss.backward()
#And optimizes its weights here
optimizer.step()
running_loss += loss.item()
else:
print("Epoch {} - Training loss: {}".format(i+1, running_loss/len(load_dataset())))
torch.save(model, './model_character_detect.pt')
running_loss
image = Image.open("../../Images/segmentation2/image_2_ROI_5.png")
image
mm = torch.load('./model_character_detect.pt')
image = image.resize((28,28))
# from PIL import ImageOps
# # image = ImageOps.grayscale(image)
image = transform(image)
image = image.cuda()
mm
# image = image.cuda()
lp = mm(image[None, ...])
ps = torch.exp(lp)
probab = list(ps.cpu()[0])
pred_label = probab.index(max(probab))
pred_label
max(probab)
label_list[pred_label]
```
| github_jupyter |
```
!pip install datasets -q
!pip install sagemaker -U -q
!pip install s3fs==0.4.2 -U -q
```
### Load dataset and have a peak:
This cell is required in SageMaker Studio, otherwise the download of the dataset will throw an error.
After running this cell, the kernel needs to be restarted. After restarting tthe kernel, continue with the cell below (loading the dataset)
```
%%capture
import IPython
!conda install -c conda-forge ipywidgets -y
IPython.Application.instance().kernel.do_shutdown(True)
from datasets import load_dataset
import pandas as pd
dataset = load_dataset('ade_corpus_v2', 'Ade_corpus_v2_classification')
df = pd.DataFrame(dataset['train'])
df.sample(5, random_state=124)
```
### Determine ratio of positive ADE phrases compared to total dataset
```
df['label'].sum()/len(df)
```
### Initialise Sagemaker variables and create S3 bucket
```
from sagemaker.huggingface.processing import HuggingFaceProcessor
import sagemaker
from sagemaker import get_execution_role
sess = sagemaker.Session()
role = sagemaker.get_execution_role()
bucket = f"az-ade-{sess.account_id()}"
sess._create_s3_bucket_if_it_does_not_exist(bucket_name=bucket, region=sess._region_name)
```
### Save the name of the S3 bucket for later sessions
```
%store bucket
```
### Set up processing job
```
hf_processor = HuggingFaceProcessor(
role=role,
instance_type="ml.p3.2xlarge",
transformers_version='4.6',
base_job_name="az-ade",
pytorch_version='1.7',
instance_count=1,
)
from sagemaker.processing import ProcessingInput, ProcessingOutput
outputs=[
ProcessingOutput(output_name="train_data", source="/opt/ml/processing/training", destination=f"s3://{bucket}/processing_output/train_data"),
ProcessingOutput(output_name="validation_data", source="/opt/ml/processing/validation", destination=f"s3://{bucket}/processing_output/validation_data"),
ProcessingOutput(output_name="test_data", source="/opt/ml/processing/test", destination=f"s3://{bucket}/processing_output/test_data"),
]
arguments = ["--dataset-name", "ade_corpus_v2",
"--datasubset-name", "Ade_corpus_v2_classification",
"--model-name", "distilbert-base-uncased",
"--train-ratio", "0.7",
"--val-ratio", "0.15",]
hf_processor.run(
code="scripts/preprocess.py",
outputs=outputs,
arguments=arguments
)
preprocessing_job_description = hf_processor.jobs[-1].describe()
output_config = preprocessing_job_description['ProcessingOutputConfig']
for output in output_config['Outputs']:
print(output['S3Output']['S3Uri'])
```
| github_jupyter |
# IllusTrip: Text to Video 3D
Part of [Aphantasia](https://github.com/eps696/aphantasia) suite, made by Vadim Epstein [[eps696](https://github.com/eps696)]
Based on [CLIP](https://github.com/openai/CLIP) + FFT/pixel ops from [Lucent](https://github.com/greentfrapp/lucent).
3D part by [deKxi](https://twitter.com/deKxi), based on [AdaBins](https://github.com/shariqfarooq123/AdaBins) depth.
thanks to [Ryan Murdock](https://twitter.com/advadnoun), [Jonathan Fly](https://twitter.com/jonathanfly), [@eduwatch2](https://twitter.com/eduwatch2) for ideas.
## Features
* continuously processes **multiple sentences** (e.g. illustrating lyrics or poems)
* makes **videos**, evolving with pan/zoom/rotate motion
* works with [inverse FFT](https://github.com/greentfrapp/lucent/blob/master/lucent/optvis/param/spatial.py) representation of the image or **directly with RGB** pixels (no GANs involved)
* generates massive detailed textures (a la deepdream), **unlimited resolution**
* optional **depth** processing for 3D look
* various CLIP models
* can start/resume from an image
**Run the cell below after each session restart**
Ensure that you're given Tesla T4/P4/P100 GPU, not K80!
```
#@title General setup
!pip install ftfy==5.8 transformers
!pip install gputil ffpb
try:
!pip3 install googletrans==3.1.0a0
from googletrans import Translator, constants
translator = Translator()
except: pass
# !apt-get -qq install ffmpeg
work_dir = '/content/illustrip'
import os
os.makedirs(work_dir, exist_ok=True)
%cd $work_dir
import os
import io
import time
import math
import random
import imageio
import numpy as np
import PIL
from base64 import b64encode
import shutil
from easydict import EasyDict as edict
a = edict()
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
from torchvision import transforms as T
from torch.autograd import Variable
from IPython.display import HTML, Image, display, clear_output
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
import ipywidgets as ipy
from google.colab import output, files
import warnings
warnings.filterwarnings("ignore")
!pip install git+https://github.com/openai/CLIP.git --no-deps
import clip
!pip install sentence_transformers
from sentence_transformers import SentenceTransformer
!pip install kornia
import kornia
!pip install lpips
import lpips
!pip install PyWavelets==1.1.1
!pip install git+https://github.com/fbcotter/pytorch_wavelets
%cd /content
!rm -rf aphantasia
!git clone https://github.com/eps696/aphantasia
%cd aphantasia/
from clip_fft import to_valid_rgb, fft_image, rfft2d_freqs, img2fft, pixel_image, un_rgb
from utils import basename, file_list, img_list, img_read, txt_clean, plot_text, old_torch
from utils import slice_imgs, derivat, pad_up_to, slerp, checkout, sim_func, latent_anima
import transforms
import depth
from progress_bar import ProgressIPy as ProgressBar
shutil.copy('mask.jpg', work_dir)
depth_mask_file = os.path.join(work_dir, 'mask.jpg')
clear_output()
def save_img(img, fname=None):
img = np.array(img)[:,:,:]
img = np.transpose(img, (1,2,0))
img = np.clip(img*255, 0, 255).astype(np.uint8)
if fname is not None:
imageio.imsave(fname, np.array(img))
imageio.imsave('result.jpg', np.array(img))
def makevid(seq_dir, size=None):
char_len = len(basename(img_list(seq_dir)[0]))
out_sequence = seq_dir + '/%0{}d.jpg'.format(char_len)
out_video = seq_dir + '.mp4'
print('.. generating video ..')
!ffmpeg -y -v warning -i $out_sequence -crf 18 $out_video
data_url = "data:video/mp4;base64," + b64encode(open(out_video,'rb').read()).decode()
wh = '' if size is None else 'width=%d height=%d' % (size, size)
return """<video %s controls><source src="%s" type="video/mp4"></video>""" % (wh, data_url)
# Hardware check
!ln -sf /opt/bin/nvidia-smi /usr/bin/nvidia-smi
import GPUtil as GPU
gpu = GPU.getGPUs()[0] # XXX: only one GPU on Colab and isn’t guaranteed
!nvidia-smi -L
print("GPU RAM {0:.0f}MB | Free {1:.0f}MB)".format(gpu.memoryTotal, gpu.memoryFree))
#@title Load inputs
#@markdown **Content** (either type a text string, or upload a text file):
content = "" #@param {type:"string"}
upload_texts = False #@param {type:"boolean"}
#@markdown **Style** (either type a text string, or upload a text file):
style = "" #@param {type:"string"}
upload_styles = False #@param {type:"boolean"}
#@markdown For non-English languages use Google translation:
translate = False #@param {type:"boolean"}
#@markdown Resume from the saved `.pt` snapshot, or from an image
#@markdown (resolution settings below will be ignored in this case):
if upload_texts:
print('Upload main text file')
uploaded = files.upload()
text_file = list(uploaded)[0]
texts = list(uploaded.values())[0].decode().split('\n')
texts = [tt.strip() for tt in texts if len(tt.strip())>0 and tt[0] != '#']
print(' main text:', text_file, len(texts), 'lines')
workname = txt_clean(basename(text_file))
else:
texts = [content]
workname = txt_clean(content)[:44]
if upload_styles:
print('Upload styles text file')
uploaded = files.upload()
text_file = list(uploaded)[0]
styles = list(uploaded.values())[0].decode().split('\n')
styles = [tt.strip() for tt in styles if len(tt.strip())>0 and tt[0] != '#']
print(' styles:', text_file, len(styles), 'lines')
else:
styles = [style]
resume = False #@param {type:"boolean"}
if resume:
print('Upload file to resume from')
resumed = files.upload()
resumed_filename = list(resumed)[0]
resumed_bytes = list(resumed.values())[0]
assert len(texts) > 0 and len(texts[0]) > 0, 'No input text[s] found!'
tempdir = os.path.join(work_dir, workname)
os.makedirs(tempdir, exist_ok=True)
print('main dir', tempdir)
```
**`content`** (what to draw) is your primary input; **`style`** (how to draw) is optional, if you want to separate such descriptions.
If you load text file[s], the imagery will interpolate from line to line (ensure equal line counts for content and style lists, for their accordance).
```
#@title Google Drive [optional]
#@markdown Run this cell, if you want to store results on your Google Drive.
using_GDrive = True#@param{type:"boolean"}
if using_GDrive:
import os
from google.colab import drive
if not os.path.isdir('/G/MyDrive'):
drive.mount('/G', force_remount=True)
gdir = '/G/MyDrive'
tempdir = os.path.join(gdir, 'illustrip', workname)
os.makedirs(tempdir, exist_ok=True)
print('main dir', tempdir)
#@title Main settings
sideX = 1280 #@param {type:"integer"}
sideY = 720 #@param {type:"integer"}
steps = 200 #@param {type:"integer"}
frame_step = 100 #@param {type:"integer"}
#@markdown > Config
method = 'RGB' #@param ['FFT', 'RGB']
model = 'ViT-B/32' #@param ['ViT-B/16', 'ViT-B/32', 'RN101', 'RN50x16', 'RN50x4', 'RN50']
# Default settings
if method == 'RGB':
align = 'overscan'
colors = 2
contrast = 1.2
sharpness = -1.
aug_noise = 0.
smooth = False
else:
align = 'uniform'
colors = 1.8
contrast = 1.1
sharpness = 1.
aug_noise = 2.
smooth = True
interpolate_topics = True
style_power = 1.
samples = 200
save_step = 1
learning_rate = 1.
aug_transform = 'custom'
similarity_function = 'cossim'
macro = 0.4
enforce = 0.
expand = 0.
zoom = 0.012
shift = 10
rotate = 0.8
distort = 0.3
animate_them = True
sample_decrease = 1.
DepthStrength = 0.
print(' loading CLIP model..')
model_clip, _ = clip.load(model, jit=old_torch())
modsize = model_clip.visual.input_resolution
xmem = {'ViT-B/16':0.25, 'RN50':0.5, 'RN50x4':0.16, 'RN50x16':0.06, 'RN101':0.33}
if model in xmem.keys():
sample_decrease *= xmem[model]
clear_output()
print(' using CLIP model', model)
```
**`FFT`** method uses inverse FFT representation of the image. It allows flexible motion, but is either blurry (if smoothed) or noisy (if not).
**`RGB`** method directly optimizes image pixels (without FFT parameterization). It's more clean and stable, when zooming in.
There are few choices for CLIP `model` (results do vary!). I prefer ViT-B/32 for consistency, next best bet is ViT-B/16.
**`steps`** defines the length of animation per text line (multiply it to the inputs line count to get total video duration in frames).
`frame_step` sets frequency of the changes in animation (how many frames between motion keypoints).
## Other settings [optional]
```
#@title Run this cell to override settings, if needed
#@markdown [to roll back defaults, run "Main settings" cell again]
style_power = 1. #@param {type:"number"}
overscan = True #@param {type:"boolean"}
align = 'overscan' if overscan else 'uniform'
interpolate_topics = True #@param {type:"boolean"}
#@markdown > Look
colors = 2 #@param {type:"number"}
contrast = 1.2 #@param {type:"number"}
sharpness = 0. #@param {type:"number"}
#@markdown > Training
samples = 200 #@param {type:"integer"}
save_step = 1 #@param {type:"integer"}
learning_rate = 1. #@param {type:"number"}
#@markdown > Tricks
aug_transform = 'custom' #@param ['elastic', 'custom', 'none']
aug_noise = 0. #@param {type:"number"}
macro = 0.4 #@param {type:"number"}
enforce = 0. #@param {type:"number"}
expand = 0. #@param {type:"number"}
similarity_function = 'cossim' #@param ['cossim', 'spherical', 'mixed', 'angular', 'dot']
#@markdown > Motion
zoom = 0.012 #@param {type:"number"}
shift = 10 #@param {type:"number"}
rotate = 0.8 #@param {type:"number"}
distort = 0.3 #@param {type:"number"}
animate_them = True #@param {type:"boolean"}
smooth = True #@param {type:"boolean"}
if method == 'RGB': smooth = False
```
`style_power` controls the strength of the style descriptions, comparing to the main input.
`overscan` provides better frame coverage (needed for RGB method).
`interpolate_topics` changes the subjects smoothly, otherwise they're switched by cut, making sharper transitions.
Decrease **`samples`** if you face OOM (it's the main RAM eater), or just to speed up the process (with the cost of quality).
`save_step` defines, how many optimization steps are taken between saved frames. Set it >1 for stronger image processing.
Experimental tricks:
`aug_transform` applies some augmentations, which quite radically change the output of this method (and slow down the process). Try yourself to see which is good for your case. `aug_noise` augmentation [FFT only!] seems to enhance optimization with transforms.
`macro` boosts bigger forms.
`enforce` adds more details by enforcing similarity between two parallel samples.
`expand` boosts diversity (up to irrelevant) by enforcing difference between prev/next samples.
Motion section:
`shift` is in pixels, `rotate` in degrees. The values will be used as limits, if you mark `animate_them`.
`smooth` reduces blinking, but induces motion blur with subtle screen-fixed patterns (valid only for FFT method, disabled for RGB).
## Add 3D depth [optional]
```
### deKxi:: This whole cell contains most of whats needed,
# with just a few changes to hook it up via frame_transform
# (also glob_step now as global var)
# I highly recommend performing the frame transformations and depth *after* saving,
# (or just the depth warp if you prefer to keep the other affines as they are)
# from my testing it reduces any noticeable stretching and allows the new areas
# revealed from the changed perspective to be filled/detailed
# pretrained models: Nyu is much better but Kitti is an option too
depth_model = 'nyu' # @ param ["nyu","kitti"]
DepthStrength = 0.01 #@param{type:"number"}
MaskBlurAmt = 33 #@param{type:"integer"}
save_depth = False #@param{type:"boolean"}
size = (sideY,sideX)
#@markdown NB: depth computing may take up to ~3x more time. Read the comments inside for more info.
#@markdown Courtesy of [deKxi](https://twitter.com/deKxi)
if DepthStrength > 0:
if not os.path.exists("AdaBins_nyu.pt"):
!gdown https://drive.google.com/uc?id=1lvyZZbC9NLcS8a__YPcUP7rDiIpbRpoF
if not os.path.exists('AdaBins_nyu.pt'):
!wget https://www.dropbox.com/s/tayczpcydoco12s/AdaBins_nyu.pt
# if depth_model=='kitti' and not os.path.exists(os.path.join(workdir_depth, "pretrained/AdaBins_kitti.pt")):
# !gdown https://drive.google.com/uc?id=1HMgff-FV6qw1L0ywQZJ7ECa9VPq1bIoj
if save_depth:
depthdir = os.path.join(tempdir, 'depth')
os.makedirs(depthdir, exist_ok=True)
print('depth dir', depthdir)
else:
depthdir = None
depth_infer, depth_mask = depth.init_adabins(model_path='AdaBins_nyu.pt', mask_path='mask.jpg', size=size)
def depth_transform(img_t, img_np, depth_infer, depth_mask, size, depthX=0, scale=1., shift=[0,0], colors=1, depth_dir=None, save_num=0):
# d X/Y define the origin point of the depth warp, effectively a "3D pan zoom", [-1..1]
# plus = look ahead, minus = look aside
dX = 100. * shift[0] / size[1]
dY = 100. * shift[1] / size[0]
# dZ = movement direction: 1 away (zoom out), 0 towards (zoom in), 0.5 stay
dZ = 0.5 + 23. * (scale[0]-1)
# dZ += 0.5 * float(math.sin(((save_num % 70)/70) * math.pi * 2))
if img_np is None:
img2 = img_t.clone().detach()
par, imag, _ = pixel_image(img2.shape, resume=img2)
img2 = to_valid_rgb(imag, colors=colors)()
img2 = img2.detach().cpu().numpy()[0]
img2 = (np.transpose(img2, (1,2,0))) # [h,w,c]
img2 = np.clip(img2*255, 0, 255).astype(np.uint8)
image_pil = T.ToPILImage()(img2)
del img2
else:
image_pil = T.ToPILImage()(img_np)
size2 = [s//2 for s in size]
img = depth.depthwarp(img_t, image_pil, depth_infer, depth_mask, size2, depthX, [dX,dY], dZ, rescale=0.5, clip_range=2, save_path=depth_dir, save_num=save_num)
return img
```
## Generate
```
#@title Generate
if aug_transform == 'elastic':
trform_f = transforms.transforms_elastic
sample_decrease *= 0.95
elif aug_transform == 'custom':
trform_f = transforms.transforms_custom
sample_decrease *= 0.95
else:
trform_f = transforms.normalize()
if enforce != 0:
sample_decrease *= 0.5
samples = int(samples * sample_decrease)
print(' using %s method, %d samples' % (method, samples))
if translate:
translator = Translator()
def enc_text(txt):
if translate:
txt = translator.translate(txt, dest='en').text
emb = model_clip.encode_text(clip.tokenize(txt).cuda()[:77])
return emb.detach().clone()
# Encode inputs
count = 0 # max count of texts and styles
key_txt_encs = [enc_text(txt) for txt in texts]
count = max(count, len(key_txt_encs))
key_styl_encs = [enc_text(style) for style in styles]
count = max(count, len(key_styl_encs))
assert count > 0, "No inputs found!"
# !rm -rf $tempdir
# os.makedirs(tempdir, exist_ok=True)
# opt_steps = steps * save_step # for optimization
glob_steps = count * steps # saving
if glob_steps == frame_step: frame_step = glob_steps // 2 # otherwise no motion
outpic = ipy.Output()
outpic
if method == 'RGB':
if resume:
img_in = imageio.imread(resumed_bytes) / 255.
params_tmp = torch.Tensor(img_in).permute(2,0,1).unsqueeze(0).float().cuda()
params_tmp = un_rgb(params_tmp, colors=1.)
sideY, sideX = img_in.shape[0], img_in.shape[1]
else:
params_tmp = torch.randn(1, 3, sideY, sideX).cuda() # * 0.01
else: # FFT
if resume:
if os.path.splitext(resumed_filename)[1].lower()[1:] in ['jpg','png','tif','bmp']:
img_in = imageio.imread(resumed_bytes)
params_tmp = img2fft(img_in, 1.5, 1.) * 2.
else:
params_tmp = torch.load(io.BytesIO(resumed_bytes))
if isinstance(params_tmp, list): params_tmp = params_tmp[0]
params_tmp = params_tmp.cuda()
sideY, sideX = params_tmp.shape[2], (params_tmp.shape[3]-1)*2
else:
params_shape = [1, 3, sideY, sideX//2+1, 2]
params_tmp = torch.randn(*params_shape).cuda() * 0.01
params_tmp = params_tmp.detach()
# function() = torch.transformation(linear)
# animation controls
if animate_them:
if method == 'RGB':
m_scale = latent_anima([1], glob_steps, frame_step, uniform=True, cubic=True, start_lat=[-0.3])
m_scale = 1 + (m_scale + 0.3) * zoom # only zoom in
else:
m_scale = latent_anima([1], glob_steps, frame_step, uniform=True, cubic=True, start_lat=[0.6])
m_scale = 1 - (m_scale-0.6) * zoom # ping pong
m_shift = latent_anima([2], glob_steps, frame_step, uniform=True, cubic=True, start_lat=[0.5,0.5])
m_angle = latent_anima([1], glob_steps, frame_step, uniform=True, cubic=True, start_lat=[0.5])
m_shear = latent_anima([1], glob_steps, frame_step, uniform=True, cubic=True, start_lat=[0.5])
m_shift = (m_shift-0.5) * shift * abs(m_scale-1.) / zoom
m_angle = (m_angle-0.5) * rotate * abs(m_scale-1.) / zoom
m_shear = (m_shear-0.5) * distort * abs(m_scale-1.) / zoom
def get_encs(encs, num):
cnt = len(encs)
if cnt == 0: return []
enc_1 = encs[min(num, cnt-1)]
enc_2 = encs[min(num+1, cnt-1)]
return slerp(enc_1, enc_2, steps)
def frame_transform(img, size, angle, shift, scale, shear):
if old_torch(): # 1.7.1
img = T.functional.affine(img, angle, shift, scale, shear, fillcolor=0, resample=PIL.Image.BILINEAR)
img = T.functional.center_crop(img, size)
img = pad_up_to(img, size)
else: # 1.8+
img = T.functional.affine(img, angle, shift, scale, shear, fill=0, interpolation=T.InterpolationMode.BILINEAR)
img = T.functional.center_crop(img, size) # on 1.8+ also pads
return img
global img_np
img_np = None
prev_enc = 0
def process(num):
global params_tmp, img_np, opt_state, params, image_f, optimizer, pbar
if interpolate_topics:
txt_encs = get_encs(key_txt_encs, num)
styl_encs = get_encs(key_styl_encs, num)
else:
txt_encs = [key_txt_encs[min(num, len(key_txt_encs)-1)][0]] * steps if len(key_txt_encs) > 0 else []
styl_encs = [key_styl_encs[min(num, len(key_styl_encs)-1)][0]] * steps if len(key_styl_encs) > 0 else []
if len(texts) > 0: print(' ref text: ', texts[min(num, len(texts)-1)][:80])
if len(styles) > 0: print(' ref style: ', styles[min(num, len(styles)-1)][:80])
for ii in range(steps):
glob_step = num * steps + ii # saving/transforming
### animation: transform frame, reload params
h, w = sideY, sideX
# transform frame for motion
scale = m_scale[glob_step] if animate_them else 1-zoom
trans = tuple(m_shift[glob_step]) if animate_them else [0, shift]
angle = m_angle[glob_step][0] if animate_them else rotate
shear = m_shear[glob_step][0] if animate_them else distort
if method == 'RGB':
if DepthStrength > 0:
params_tmp = depth_transform(params_tmp, img_np, depth_infer, depth_mask, size, DepthStrength, scale, trans, colors, depthdir, glob_step)
params_tmp = frame_transform(params_tmp, (h,w), angle, trans, scale, shear)
params, image_f, _ = pixel_image([1,3,h,w], resume=params_tmp)
img_tmp = None
else: # FFT
if old_torch(): # 1.7.1
img_tmp = torch.irfft(params_tmp, 2, normalized=True, signal_sizes=(h,w))
if DepthStrength > 0:
img_tmp = depth_transform(img_tmp, img_np, depth_infer, depth_mask, size, DepthStrength, scale, trans, colors, depthdir, glob_step)
img_tmp = frame_transform(img_tmp, (h,w), angle, trans, scale, shear)
params_tmp = torch.rfft(img_tmp, 2, normalized=True)
else: # 1.8+
if type(params_tmp) is not torch.complex64:
params_tmp = torch.view_as_complex(params_tmp)
img_tmp = torch.fft.irfftn(params_tmp, s=(h,w), norm='ortho')
if DepthStrength > 0:
img_tmp = depth_transform(img_tmp, img_np, depth_infer, depth_mask, size, DepthStrength, scale, trans, colors, depthdir, glob_step)
img_tmp = frame_transform(img_tmp, (h,w), angle, trans, scale, shear)
params_tmp = torch.fft.rfftn(img_tmp, s=[h,w], dim=[2,3], norm='ortho')
params_tmp = torch.view_as_real(params_tmp)
params, image_f, _ = fft_image([1,3,h,w], resume=params_tmp, sd=1.)
image_f = to_valid_rgb(image_f, colors=colors)
del img_tmp
optimizer = torch.optim.Adam(params, learning_rate)
# optimizer = torch.optim.AdamW(params, learning_rate, weight_decay=0.01, amsgrad=True)
if smooth is True and num + ii > 0:
optimizer.load_state_dict(opt_state)
# get encoded inputs
txt_enc = txt_encs[ii % len(txt_encs)].unsqueeze(0) if len(txt_encs) > 0 else None
styl_enc = styl_encs[ii % len(styl_encs)].unsqueeze(0) if len(styl_encs) > 0 else None
### optimization
for ss in range(save_step):
loss = 0
noise = aug_noise * (torch.rand(1, 1, *params[0].shape[2:4], 1)-0.5).cuda() if aug_noise > 0 else 0.
img_out = image_f(noise)
img_sliced = slice_imgs([img_out], samples, modsize, trform_f, align, macro)[0]
out_enc = model_clip.encode_image(img_sliced)
if method == 'RGB': # empirical hack
loss += 1.5 * abs(img_out.mean((2,3)) - 0.45).mean() # fix brightness
loss += 1.5 * abs(img_out.std((2,3)) - 0.17).sum() # fix contrast
if txt_enc is not None:
loss -= sim_func(txt_enc, out_enc, similarity_function)
if styl_enc is not None:
loss -= style_power * sim_func(styl_enc, out_enc, similarity_function)
if sharpness != 0: # mode = scharr|sobel|naive
loss -= sharpness * derivat(img_out, mode='naive')
# loss -= sharpness * derivat(img_sliced, mode='scharr')
if enforce != 0:
img_sliced = slice_imgs([image_f(noise)], samples, modsize, trform_f, align, macro)[0]
out_enc2 = model_clip.encode_image(img_sliced)
loss -= enforce * sim_func(out_enc, out_enc2, similarity_function)
del out_enc2; torch.cuda.empty_cache()
if expand > 0:
global prev_enc
if ii > 0:
loss += expand * sim_func(prev_enc, out_enc, similarity_function)
prev_enc = out_enc.detach().clone()
del img_out, img_sliced, out_enc; torch.cuda.empty_cache()
optimizer.zero_grad()
loss.backward()
optimizer.step()
### save params & frame
params_tmp = params[0].detach().clone()
if smooth is True:
opt_state = optimizer.state_dict()
with torch.no_grad():
img_t = image_f(contrast=contrast)[0].permute(1,2,0)
img_np = torch.clip(img_t*255, 0, 255).cpu().numpy().astype(np.uint8)
imageio.imsave(os.path.join(tempdir, '%05d.jpg' % glob_step), img_np, quality=95)
shutil.copy(os.path.join(tempdir, '%05d.jpg' % glob_step), 'result.jpg')
outpic.clear_output()
with outpic:
display(Image('result.jpg'))
del img_t
pbar.upd()
params_tmp = params[0].detach().clone()
outpic = ipy.Output()
outpic
pbar = ProgressBar(glob_steps)
for i in range(count):
process(i)
HTML(makevid(tempdir))
files.download(tempdir + '.mp4')
## deKxi: downloading depth video
if save_depth and DepthStrength > 0:
HTML(makevid(depthdir))
files.download(depthdir + '.mp4')
```
If video is not auto-downloaded after generation (for whatever reason), run this cell to do that:
```
files.download(tempdir + '.mp4')
if save_depth and DepthStrength > 0:
files.download(depthdir + '.mp4')
```
| github_jupyter |
```
import time
from IPython import display
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
plt.rcParams['figure.figsize'] = [16, 10]
```
# 1) Get data in a pandas.DataFrame and plot it using matplotlib.pyplot
```
# Get data
# 1) directement sous forme de list python
GPU = [2048,2048,4096,4096,3072,6144,6144,8192,8192,8192,8192,11264,11264]
prix = [139.96,149.95,184.96,194.95,299.95,332.95,359.95,459.95,534.95,569.95,699.95,829.96,929.95]
data = pd.DataFrame({'x1':GPU,'y':prix})
# Remarque: On peut également enregistrer des données structurées (dataFrame) en .csv
data.to_csv('graphicCardsData.csv',index=False)
# 2) En utilisant la fonction .read_csv() de pandas pour importer des données extérieure sous form .csv
# directement dans un pandas.DataFrame
data = pd.read_csv('graphicCards.csv')
data.head()
data = data[['memory (Go)', 'price (euros)']]
data = data.rename(columns={"memory (Go)": 'x1', 'price (euros)': 'y'})
data['x1'] = data['x1'] * 1000
#PLot data
plt.plot(data.x1,data.y,'o')
plt.xlabel('GPU (Mo)')
plt.ylabel('prix (€)')
plt.show();
```
# 2) Contruire un modéle pour nos données
```
# Définir notre hypothèse (fonction)
def hypothesis(x,theta):
return np.dot(x,theta)
# On génére aléatoirement une valeur de départ pour le paramètre theta1 de notre modèle
theta = np.random.rand()
# Fonction pour générer la droite représentant notre modèle
def getHypothesisForPLot(theta):
return pd.DataFrame({'x':np.arange(0, 12000, 100),
'y':[hypothesis(x,theta) for x in np.arange(0, 12000, 100)]})
# On plot les données avec notre hypothèse ...
plt.plot(data.x1,data.y,'o',label='data')
plt.plot(getHypothesisForPLot(theta).x,getHypothesisForPLot(theta).y ,'r',label='hypothèse')
plt.xlabel('GPU (Mo)')
plt.ylabel('prix (€)')
plt.title("C'est pas ça ....")
plt.legend()
plt.show();
print("theta = %f" % theta)
```
# 3) Tester la pertinence de notre modèle: la fonction de coût
```
data.shape
# On définit notre fonction de coût: somme quadratique (eg: on somme les carré)
def costFunction(y,yhat):
return np.power(yhat - y,2).sum()*(2/y.shape[0])
# Prix prédis par notre modèle (avec un theta choisi pour illustrer) pour chaque exemple
theta = 0.07
yhat = hypothesis(data.x1,theta)
#Comment fonctionne la fonction de coût: on somme le carré de toute les barre noire
plt.plot(data.x1,data.y,'o',label='data')
plt.plot(getHypothesisForPLot(theta).x,getHypothesisForPLot(theta).y,'r',label='hypothèse')
for i in range(data.shape[0]):
plt.plot((data.x1[i],data.x1[i]), (min(data.y[i],yhat[i]),max(data.y[i],yhat[i])), 'k-')
plt.xlabel('GPU (Mo)')
plt.ylabel('prix (€)')
plt.legend()
plt.show();
print("theta = %f" % theta)
print("J(theta) = %f" % costFunction(data.y,yhat))
```
# 4) À quoi ressemble J(theta) en fonction de theta1
```
# Calculons (brutalement) la valeur de J(theta) dans un intervale de valeur de theta1
# pour observer la forme de notre fonction de coût que nous allons chercher à minimiser
thetaRange = np.arange(-0.8,1,0.01)
costFctEvol = pd.DataFrame({'theta':thetaRange,
'cost':[costFunction(data.y,hypothesis(data.x1,theta))
for theta in thetaRange]})
plt.plot(costFctEvol.theta,costFctEvol.cost)
plt.xlabel('theta')
plt.ylabel('J(theta)')
plt.show;
```
# 5) La descente de Gradient
```
# La descente de gradient utilise la notion de dérivée,
# illustrée ici avec la fonction carré (qui doit nous en rappeler une autre!)
def fct(x):
return np.power(x,2)
def fctDeriv(x):
return 2*x
fctCarre = pd.DataFrame({'x':np.arange(-10,10,0.1),'y':[fct(x) for x in np.arange(-10,10,0.1)]})
fctCarreD = pd.DataFrame({'x':np.arange(-10,10,0.1),
'y':[fctDeriv(x) for x in np.arange(-10,10,0.1)]})
plt.plot(fctCarre.x,fctCarre.y,label='f(x)')
plt.plot(fctCarreD.x,fctCarreD.y,label="f'(x)")
plt.legend();
# La descente de gradient utilise la dérivé de la fonction de coût
# par rapport au paramètre theta1
def costFctDeriv(x,y,yhat):
return ((yhat - y)*x.T).sum().sum()/y.shape[0]
# À chaque étape de la descente de gradient (jusqu'à la convergence),
# on incremente la valeur de theta1 par ce résultat.
# Alpha est le learning rate
def gradDescent(x,y,yhat,alpha):
return -alpha*costFctDeriv(x,y,yhat)
# on plot les données avec l'hypothèse correpondant à la valeur de theta
# ainsi que l'évolution dans la courbe de J(theta) en fonction de theta
# On rajoute également la valeur de J(theta) en fonction du temps qui va nous servir à
# débuger notre algorithme
def plotData(ax,data,theta,yhat,gradDescentEvol, title=''):
ax.plot(data.x1,data.y,'o',label='data')
ax.plot(getHypothesisForPLot(theta).x,getHypothesisForPLot(theta).y,'r',label='hypothèse')
for i in range(data.shape[0]):
ax.plot((data.x1[i],data.x1[i]), (min(data.y[i],yhat[i]),max(data.y[i],yhat[i])), 'k-')
ax.set_xlabel('iteration step')
if title != "":
ax.set_title(title)
ax.legend()
def plotCostFunction(ax,data,theta,gradDescentEvol,thetaInit, title=''):
thetaRange = np.arange(-abs(thetaInit)+0.07,abs(thetaInit)+0.07,0.01)
costFctEvol = pd.DataFrame({'theta':thetaRange,
'cost':[costFunction(data.y,hypothesis(data.x1,genTheta))
for genTheta in thetaRange]})
ax.plot(costFctEvol.theta,costFctEvol.cost,label='J(theta)')
for i in range(gradDescentEvol.shape[0]):
ax.plot(gradDescentEvol.theta[i],gradDescentEvol.J[i],'ro')
for i in range(gradDescentEvol.shape[0]-1):
ax.plot((gradDescentEvol.theta[i],gradDescentEvol.theta[i+1]),
(gradDescentEvol.J[i],gradDescentEvol.J[i+1]),'k-',lw=1)
ax.set_xlabel('iteration step')
if title != "":
ax.set_title(title)
ax.legend()
def plotCostFunctionEvol(ax,gradDescentEvol,title=""):
ax.plot(np.arange(gradDescentEvol.shape[0]),gradDescentEvol.J,label='J(theta)')
ax.set_xlabel('iteration step')
if title != "":
ax.set_title(title)
ax.legend()
# On utilise donc une valeur de départ pour theta généré aléatoirement entre 0 et 1,
# la valeur du learning rate est fixé à 0.00000003
# Epsilon correspond à la précision que l'on veut atteindre pour stopper la descente de gradient
thetaInit = np.random.rand()
yhat = hypothesis(data.x1,thetaInit)
alpha = 0.003
epsilon = 0.001
# On prepare un dataframe pour stocker les valeurs de J(theta) et theta1
gradDescentEvol = pd.DataFrame({'theta':thetaInit,
'J':costFunction(data.y,yhat)},index = np.arange(1))
# On parametrise deux trois trucs
plt.rcParams['figure.figsize'] = [16, 5]
costFct = 0
count = 0
theta = thetaInit
# Et on se lance dans la boucle: La descente de gradient!
while np.abs(costFunction(data.y,yhat) - costFct)/costFct >= epsilon:
count += 1
costFct = costFunction(data.y,yhat)
theta += gradDescent(data.x1,data.y,yhat,alpha)
yhat = hypothesis(data.x1,theta)
gradDescentEvol = gradDescentEvol.append(pd.DataFrame({'theta':theta,
'J':costFunction(data.y,yhat)},
index = np.arange(1)),
ignore_index=True)
fig, ax = plt.subplots(ncols=3)
plotData(ax[0],data,theta,yhat,gradDescentEvol)
plotCostFunction(ax[1],data,theta,gradDescentEvol,thetaInit)
plotCostFunctionEvol(ax[2],gradDescentEvol)
display.clear_output(wait=True)
display.display(plt.gcf())
time.sleep(1)
```
# 6) Conclusion
```
# Afficher les résultat:
print('La descente de gradient a été réalisé en %i étapes.' % count)
print('theta = %f' % theta)
print('J(theta) = %f' % costFunction(data.y,yhat))
# Faisons une prédiction ....
newGPUs = [3072*1.5,11264*1.2]
for newGPU in newGPUs:
print("Notre nouvelle carte de %i Mo de GPU pourra se vendre autour de %.2f €" %
(newGPU,newGPU*theta))
plt.rcParams['figure.figsize'] = [14, 8]
plt.plot(data.x1,data.y,'o',label='data')
plt.plot(getHypothesisForPLot(theta).x,getHypothesisForPLot(theta).y,'r',label='hypothèse')
for i in range(data.shape[0]):
plt.plot((data.x1[i],data.x1[i]), (min(data.y[i],yhat[i]),max(data.y[i],yhat[i])), 'k-')
plt.plot(newGPUs,[newGPU*theta for newGPU in newGPUs], 'or', label='predictions')
plt.xlabel('GPU (Mo)')
plt.ylabel('prix (€)')
plt.legend()
plt.show();
```
# 7) Choix du taux d'apprentissage lambda
```
# On utilise donc une valeur de départ pour theta généré aléatoirement entre 0 et 1,
# la valeur du learning rate est fixé à 0.00000003
# Epsilon correspond à la précision que l'on veut atteindre pour stopper la descente de gradient
thetaInit = np.random.rand()
yhat1 = hypothesis(data.x1,thetaInit)
yhat2 = hypothesis(data.x1,thetaInit)
yhat3 = hypothesis(data.x1,thetaInit)
alpha1 = 0.000000001
alpha2 = 0.00000001
alpha3 = 0.00000006
epsilon = 0.001
# On prepare un dataframe pour stocker les valeurs de J(theta) et theta1
gradDescentEvol1 = pd.DataFrame({'theta':thetaInit,
'J':costFunction(data.y,yhat1)},index = np.arange(1))
gradDescentEvol2 = pd.DataFrame({'theta':thetaInit,
'J':costFunction(data.y,yhat2)},index = np.arange(1))
gradDescentEvol3 = pd.DataFrame({'theta':thetaInit,
'J':costFunction(data.y,yhat3)},index = np.arange(1))
# On parametrise deux trois trucs
plt.rcParams['figure.figsize'] = [16, 5]
count = 0
costFct1 = 0
theta1 = thetaInit
costFct2 = 0
theta2 = thetaInit
costFct3 = 0
theta3 = thetaInit
# Et on se lance dans la boucle: La descente de gradient!
while np.abs(costFunction(data.y,yhat2) - costFct2)/costFct2 >= epsilon:
count += 1
costFct1 = costFunction(data.y,yhat1)
theta1 += gradDescent(data.x1,data.y,yhat1,alpha1)
yhat1 = hypothesis(data.x1,theta1)
gradDescentEvol1 = gradDescentEvol1.append(pd.DataFrame({'theta':theta1,
'J':costFunction(data.y,yhat1)},
index = np.arange(1)),
ignore_index=True)
costFct2 = costFunction(data.y,yhat2)
theta2 += gradDescent(data.x1,data.y,yhat2,alpha2)
yhat2 = hypothesis(data.x1,theta2)
gradDescentEvol2 = gradDescentEvol2.append(pd.DataFrame({'theta':theta2,
'J':costFunction(data.y,yhat2)},
index = np.arange(1)),
ignore_index=True)
costFct3 = costFunction(data.y,yhat3)
theta3 += gradDescent(data.x1,data.y,yhat3,alpha3)
yhat3 = hypothesis(data.x1,theta3)
gradDescentEvol3 = gradDescentEvol3.append(pd.DataFrame({'theta':theta3,
'J':costFunction(data.y,yhat3)},
index = np.arange(1)),
ignore_index=True)
fig, ax = plt.subplots(ncols=3)
plotCostFunctionEvol(ax[0],gradDescentEvol1,'small alpha')
plotCostFunctionEvol(ax[1],gradDescentEvol2,'correct alpha')
plotCostFunctionEvol(ax[2],gradDescentEvol3,'huge alpha')
display.clear_output(wait=True)
display.display(plt.gcf())
time.sleep(1)
```
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.