code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
```
import sys
import pandas as pd
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
sys.path.append('../Scripts')
from Data_Processing import DataProcessing
from tensorflow import keras
from keras.callbacks import ModelCheckpoint
from keras.models import load_model
from keras import backend as K
from datetime import datetime
from sklearn.preprocessing import PowerTransformer
import joblib
import warnings
warnings.filterwarnings('ignore')
ColumnTransformer = joblib.load('../Models/Column_Transformer.pkl')
#PowerTransformer = joblib.load('../Models/Power_Transformer.pkl')
ColumnTransformer_NN = joblib.load('../Models/Column_Transformer_NN.pkl')
df = DataProcessing('../Data/test.csv')
y = df['Lap_Time']
X = df.drop(columns=['Lap_Time'])
obj_columns = list(X.select_dtypes(include=object).columns)
obj_columns.append('Lap_Number')
obj_columns.append('Lap_Improvement')
num_columns = list(X.select_dtypes(include='number').columns)
num_columns.remove('Lap_Number')
num_columns.remove('Lap_Improvement')
#NN Only
y = df['Lap_Time']
X = df.drop(columns=['Lap_Time'])
obj_columns = list(X.select_dtypes(include=object).columns)
obj_columns.append('Lap_Improvement')
obj_columns.append('Lap_Number')
obj_columns.append('S1_Improvement')
obj_columns.append('S2_Improvement')
obj_columns.append('S3_Improvement')
num_columns = list(X.select_dtypes(include='number').columns)
num_columns.remove('Lap_Number')
num_columns.remove('Lap_Improvement')
num_columns.remove('S1_Improvement')
num_columns.remove('S2_Improvement')
num_columns.remove('S3_Improvement')
#X[num_columns] = PowerTransformer.transform(X[num_columns])
trans_X_nn = ColumnTransformer_NN.transform(X)
#trans_X = trans_X.toarray()
#trans_X = trans_X[:,[0, 2, 4, 6, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 72, 73]]
#trans_X_nn = trans_X_nn.toarray()
def root_mean_squared_log_error(y_true, y_pred):
return K.sqrt(K.mean(K.square(K.log(1+y_pred) - K.log(1+y_true))))
#Neural Network
nn_model = load_model('../Models/NN_model_test.h5')
#nn_model = load_model('../Models/NN_model.h5', custom_objects={'root_mean_squared_log_error': root_mean_squared_log_error})
#Random Forest
rf_model = joblib.load('../Models/RF_Model.h5')
#Gradient Boost
gb_model = joblib.load('../Models/Gradient_Boost_Model.h5')
nn_y_scaler = joblib.load('../Models/NN_Y_Scaler.pkl')
y_predicted_nn = nn_y_scaler.inverse_transform(nn_model.predict(trans_X_nn))
y_predicted_nn = ((1 / y_predicted_nn) - 1).ravel()
y_predicted_nn = nn_y_scaler.inverse_transform(nn_model.predict(trans_X_nn))
#y_predicted_rf = rf_model.predict(trans_X)
#y_predicted_gb = gb_model.predict(trans_X)
results = pd.DataFrame()
results['NN'] = y_predicted_nn
results['RF'] = y_predicted_rf
results['GB'] = y_predicted_gb
results['LAP_TIME'] = (results['NN'] + results['RF'] + results['GB']) / 3
submission = results[['LAP_TIME']]
results
#Random Forest Only
submission = results[['RF']]
submission = submission.rename(columns={'RF': 'LAP_TIME'})
today = datetime.today().strftime('%m-%d-%y %H-%M')
submission.to_csv(f'../Submissions/Dare_In_Reality {today}.csv', index=False)
```
### Just Neural Network
```
submission = pd.DataFrame()
submission['LAP_TIME'] = y_predicted_nn.ravel()
submission
submission.to_csv(f'../Submissions/Dare_In_Reality NN Only.csv', index=False)
y_predicted_nn
df
```
| github_jupyter |
# Amazon Fine Food Reviews Analysis
Data Source: https://www.kaggle.com/snap/amazon-fine-food-reviews <br>
EDA: https://nycdatascience.com/blog/student-works/amazon-fine-foods-visualization/
The Amazon Fine Food Reviews dataset consists of reviews of fine foods from Amazon.<br>
Number of reviews: 568,454<br>
Number of users: 256,059<br>
Number of products: 74,258<br>
Timespan: Oct 1999 - Oct 2012<br>
Number of Attributes/Columns in data: 10
Attribute Information:
1. Id
2. ProductId - unique identifier for the product
3. UserId - unqiue identifier for the user
4. ProfileName
5. HelpfulnessNumerator - number of users who found the review helpful
6. HelpfulnessDenominator - number of users who indicated whether they found the review helpful or not
7. Score - rating between 1 and 5
8. Time - timestamp for the review
9. Summary - brief summary of the review
10. Text - text of the review
#### Objective:
Given a review, determine whether the review is positive (rating of 4 or 5) or negative (rating of 1 or 2).
<br>
[Q] How to determine if a review is positive or negative?<br>
<br>
[Ans] We could use Score/Rating. A rating of 4 or 5 can be cosnidered as a positive review. A rating of 1 or 2 can be considered as negative one. A review of rating 3 is considered nuetral and such reviews are ignored from our analysis. This is an approximate and proxy way of determining the polarity (positivity/negativity) of a review.
# [1]. Reading Data
## [1.1] Loading the data
The dataset is available in two forms
1. .csv file
2. SQLite Database
In order to load the data, We have used the SQLITE dataset as it is easier to query the data and visualise the data efficiently.
<br>
Here as we only want to get the global sentiment of the recommendations (positive or negative), we will purposefully ignore all Scores equal to 3. If the score is above 3, then the recommendation wil be set to "positive". Otherwise, it will be set to "negative".
```
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import sqlite3
import pandas as pd
import numpy as np
import nltk
import string
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import confusion_matrix
from sklearn import metrics
from sklearn.metrics import roc_curve, auc
from nltk.stem.porter import PorterStemmer
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.metrics import roc_auc_score
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import TruncatedSVD
from sklearn.cluster import KMeans
from wordcloud import WordCloud, STOPWORDS
import re
# Tutorial about Python regular expressions: https://pymotw.com/2/re/
import string
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
from gensim.models import Word2Vec
from gensim.models import KeyedVectors
import pickle
from tqdm import tqdm
import os
from google.colab import drive
drive.mount('/content/drive')
# using SQLite Table to read data.
con = sqlite3.connect('drive/My Drive/database.sqlite')
# filtering only positive and negative reviews i.e.
# not taking into consideration those reviews with Score=3
# SELECT * FROM Reviews WHERE Score != 3 LIMIT 500000, will give top 500000 data points
# you can change the number to any other number based on your computing power
# filtered_data = pd.read_sql_query(""" SELECT * FROM Reviews WHERE Score != 3 LIMIT 500000""", con)
# for tsne assignment you can take 5k data points
filtered_data = pd.read_sql_query(""" SELECT * FROM Reviews WHERE Score != 3 LIMIT 200000""", con)
# Give reviews with Score>3 a positive rating(1), and reviews with a score<3 a negative rating(0).
def partition(x):
if x < 3:
return 0
return 1
#changing reviews with score less than 3 to be positive and vice-versa
actualScore = filtered_data['Score']
positiveNegative = actualScore.map(partition)
filtered_data['Score'] = positiveNegative
print("Number of data points in our data", filtered_data.shape)
filtered_data.head(3)
display = pd.read_sql_query("""
SELECT UserId, ProductId, ProfileName, Time, Score, Text, COUNT(*)
FROM Reviews
GROUP BY UserId
HAVING COUNT(*)>1
""", con)
print(display.shape)
display.head()
display[display['UserId']=='AZY10LLTJ71NX']
display['COUNT(*)'].sum()
```
# [2] Exploratory Data Analysis
## [2.1] Data Cleaning: Deduplication
It is observed (as shown in the table below) that the reviews data had many duplicate entries. Hence it was necessary to remove duplicates in order to get unbiased results for the analysis of the data. Following is an example:
```
display= pd.read_sql_query("""
SELECT *
FROM Reviews
WHERE Score != 3 AND UserId="AR5J8UI46CURR"
ORDER BY ProductID
""", con)
display.head()
```
As it can be seen above that same user has multiple reviews with same values for HelpfulnessNumerator, HelpfulnessDenominator, Score, Time, Summary and Text and on doing analysis it was found that <br>
<br>
ProductId=B000HDOPZG was Loacker Quadratini Vanilla Wafer Cookies, 8.82-Ounce Packages (Pack of 8)<br>
<br>
ProductId=B000HDL1RQ was Loacker Quadratini Lemon Wafer Cookies, 8.82-Ounce Packages (Pack of 8) and so on<br>
It was inferred after analysis that reviews with same parameters other than ProductId belonged to the same product just having different flavour or quantity. Hence in order to reduce redundancy it was decided to eliminate the rows having same parameters.<br>
The method used for the same was that we first sort the data according to ProductId and then just keep the first similar product review and delelte the others. for eg. in the above just the review for ProductId=B000HDL1RQ remains. This method ensures that there is only one representative for each product and deduplication without sorting would lead to possibility of different representatives still existing for the same product.
```
#Sorting data according to ProductId in ascending order
sorted_data=filtered_data.sort_values('ProductId', axis=0, ascending=True, inplace=False, kind='quicksort', na_position='last')
#Deduplication of entries
final=sorted_data.drop_duplicates(subset={"UserId","ProfileName","Time","Text"}, keep='first', inplace=False)
final.shape
#Checking to see how much % of data still remains
(final['Id'].size*1.0)/(filtered_data['Id'].size*1.0)*100
```
<b>Observation:-</b> It was also seen that in two rows given below the value of HelpfulnessNumerator is greater than HelpfulnessDenominator which is not practically possible hence these two rows too are removed from calcualtions
```
display= pd.read_sql_query("""
SELECT *
FROM Reviews
WHERE Score != 3 AND Id=44737 OR Id=64422
ORDER BY ProductID
""", con)
display.head()
final=final[final.HelpfulnessNumerator<=final.HelpfulnessDenominator]
#Before starting the next phase of preprocessing lets see the number of entries left
print(final.shape)
#How many positive and negative reviews are present in our dataset?
final['Score'].value_counts()
```
# [3] Preprocessing
## [3.1]. Preprocessing Review Text
Now that we have finished deduplication our data requires some preprocessing before we go on further with analysis and making the prediction model.
Hence in the Preprocessing phase we do the following in the order below:-
1. Begin by removing the html tags
2. Remove any punctuations or limited set of special characters like , or . or # etc.
3. Check if the word is made up of english letters and is not alpha-numeric
4. Check to see if the length of the word is greater than 2 (as it was researched that there is no adjective in 2-letters)
5. Convert the word to lowercase
6. Remove Stopwords
7. Finally Snowball Stemming the word (it was obsereved to be better than Porter Stemming)<br>
After which we collect the words used to describe positive and negative reviews
```
# printing some random reviews
sent_0 = final['Text'].values[0]
print(sent_0)
print("="*50)
sent_1000 = final['Text'].values[1000]
print(sent_1000)
print("="*50)
sent_1500 = final['Text'].values[1500]
print(sent_1500)
print("="*50)
sent_4900 = final['Text'].values[4900]
print(sent_4900)
print("="*50)
# remove urls from text python: https://stackoverflow.com/a/40823105/4084039
sent_0 = re.sub(r"http\S+", "", sent_0)
sent_1000 = re.sub(r"http\S+", "", sent_1000)
sent_150 = re.sub(r"http\S+", "", sent_1500)
sent_4900 = re.sub(r"http\S+", "", sent_4900)
print(sent_0)
# https://stackoverflow.com/questions/16206380/python-beautifulsoup-how-to-remove-all-tags-from-an-element
from bs4 import BeautifulSoup
soup = BeautifulSoup(sent_0, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_1000, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_1500, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_4900, 'lxml')
text = soup.get_text()
print(text)
# https://stackoverflow.com/a/47091490/4084039
import re
def decontracted(phrase):
# specific
phrase = re.sub(r"won't", "will not", phrase)
phrase = re.sub(r"can\'t", "can not", phrase)
# general
phrase = re.sub(r"n\'t", " not", phrase)
phrase = re.sub(r"\'re", " are", phrase)
phrase = re.sub(r"\'s", " is", phrase)
phrase = re.sub(r"\'d", " would", phrase)
phrase = re.sub(r"\'ll", " will", phrase)
phrase = re.sub(r"\'t", " not", phrase)
phrase = re.sub(r"\'ve", " have", phrase)
phrase = re.sub(r"\'m", " am", phrase)
return phrase
sent_1500 = decontracted(sent_1500)
print(sent_1500)
print("="*50)
#remove words with numbers python: https://stackoverflow.com/a/18082370/4084039
sent_0 = re.sub("\S*\d\S*", "", sent_0).strip()
print(sent_0)
#remove spacial character: https://stackoverflow.com/a/5843547/4084039
sent_1500 = re.sub('[^A-Za-z0-9]+', ' ', sent_1500)
print(sent_1500)
# https://gist.github.com/sebleier/554280
# we are removing the words from the stop words list: 'no', 'nor', 'not'
# <br /><br /> ==> after the above steps, we are getting "br br"
# we are including them into stop words list
# instead of <br /> if we have <br/> these tags would have revmoved in the 1st step
stopwords= set(['br', 'the', 'i', 'me', 'my', 'myself', 'we', 'our', 'ours', 'ourselves', 'you', "you're", "you've",\
"you'll", "you'd", 'your', 'yours', 'yourself', 'yourselves', 'he', 'him', 'his', 'himself', \
'she', "she's", 'her', 'hers', 'herself', 'it', "it's", 'its', 'itself', 'they', 'them', 'their',\
'theirs', 'themselves', 'what', 'which', 'who', 'whom', 'this', 'that', "that'll", 'these', 'those', \
'am', 'is', 'are', 'was', 'were', 'be', 'been', 'being', 'have', 'has', 'had', 'having', 'do', 'does', \
'did', 'doing', 'a', 'an', 'the', 'and', 'but', 'if', 'or', 'because', 'as', 'until', 'while', 'of', \
'at', 'by', 'for', 'with', 'about', 'against', 'between', 'into', 'through', 'during', 'before', 'after',\
'above', 'below', 'to', 'from', 'up', 'down', 'in', 'out', 'on', 'off', 'over', 'under', 'again', 'further',\
'then', 'once', 'here', 'there', 'when', 'where', 'why', 'how', 'all', 'any', 'both', 'each', 'few', 'more',\
'most', 'other', 'some', 'such', 'only', 'own', 'same', 'so', 'than', 'too', 'very', \
's', 't', 'can', 'will', 'just', 'don', "don't", 'should', "should've", 'now', 'd', 'll', 'm', 'o', 're', \
've', 'y', 'ain', 'aren', "aren't", 'couldn', "couldn't", 'didn', "didn't", 'doesn', "doesn't", 'hadn',\
"hadn't", 'hasn', "hasn't", 'haven', "haven't", 'isn', "isn't", 'ma', 'mightn', "mightn't", 'mustn',\
"mustn't", 'needn', "needn't", 'shan', "shan't", 'shouldn', "shouldn't", 'wasn', "wasn't", 'weren', "weren't", \
'won', "won't", 'wouldn', "wouldn't"])
# Combining all the above stundents
from tqdm import tqdm
preprocessed_reviews = []
# tqdm is for printing the status bar
for sentance in tqdm(final['Text'].values):
sentance = re.sub(r"http\S+", "", sentance)
sentance = BeautifulSoup(sentance, 'lxml').get_text()
sentance = decontracted(sentance)
sentance = re.sub("\S*\d\S*", "", sentance).strip()
sentance = re.sub('[^A-Za-z]+', ' ', sentance)
# https://gist.github.com/sebleier/554280
sentance = ' '.join(e.lower() for e in sentance.split() if e.lower() not in stopwords)
preprocessed_reviews.append(sentance.strip())
preprocessed_reviews[100000]
```
# [4] Featurization
## [4.1] BAG OF WORDS
```
#BoW
count_vect = CountVectorizer() #in scikit-learn
count_vect.fit(preprocessed_reviews)
print("some feature names ", count_vect.get_feature_names()[:10])
print('='*50)
final_counts = count_vect.transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_counts))
print("the shape of out text BOW vectorizer ",final_counts.get_shape())
print("the number of unique words ", final_counts.get_shape()[1])
```
## [4.2] Bi-Grams and n-Grams.
```
#bi-gram, tri-gram and n-gram
#removing stop words like "not" should be avoided before building n-grams
# count_vect = CountVectorizer(ngram_range=(1,2))
# please do read the CountVectorizer documentation http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html
# you can choose these numebrs min_df=10, max_features=5000, of your choice
count_vect = CountVectorizer(ngram_range=(1,2), min_df=10, max_features=5000)
final_bigram_counts = count_vect.fit_transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_bigram_counts))
print("the shape of out text BOW vectorizer ",final_bigram_counts.get_shape())
print("the number of unique words including both unigrams and bigrams ", final_bigram_counts.get_shape()[1])
```
## [4.3] TF-IDF
```
tf_idf_vect = TfidfVectorizer(ngram_range=(1,2), min_df=10)
tf_idf_vect.fit(preprocessed_reviews)
print("some sample features(unique words in the corpus)",tf_idf_vect.get_feature_names()[0:10])
print('='*50)
final_tf_idf = tf_idf_vect.transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_tf_idf))
print("the shape of out text TFIDF vectorizer ",final_tf_idf.get_shape())
print("the number of unique words including both unigrams and bigrams ", final_tf_idf.get_shape()[1])
```
## [4.4] Word2Vec
```
# Train your own Word2Vec model using your own text corpus
i=0
list_of_sentance=[]
for sentance in preprocessed_reviews:
list_of_sentance.append(sentance.split())
# Using Google News Word2Vectors
# in this project we are using a pretrained model by google
# its 3.3G file, once you load this into your memory
# it occupies ~9Gb, so please do this step only if you have >12G of ram
# we will provide a pickle file wich contains a dict ,
# and it contains all our courpus words as keys and model[word] as values
# To use this code-snippet, download "GoogleNews-vectors-negative300.bin"
# from https://drive.google.com/file/d/0B7XkCwpI5KDYNlNUTTlSS21pQmM/edit
# it's 1.9GB in size.
# http://kavita-ganesan.com/gensim-word2vec-tutorial-starter-code/#.W17SRFAzZPY
# you can comment this whole cell
# or change these varible according to your need
is_your_ram_gt_16g=False
want_to_use_google_w2v = False
want_to_train_w2v = True
if want_to_train_w2v:
# min_count = 5 considers only words that occured atleast 5 times
w2v_model=Word2Vec(list_of_sentance,min_count=5,size=50, workers=4)
print(w2v_model.wv.most_similar('great'))
print('='*50)
print(w2v_model.wv.most_similar('worst'))
elif want_to_use_google_w2v and is_your_ram_gt_16g:
if os.path.isfile('GoogleNews-vectors-negative300.bin'):
w2v_model=KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin', binary=True)
print(w2v_model.wv.most_similar('great'))
print(w2v_model.wv.most_similar('worst'))
else:
print("you don't have gogole's word2vec file, keep want_to_train_w2v = True, to train your own w2v ")
w2v_words = list(w2v_model.wv.vocab)
print("number of words that occured minimum 5 times ",len(w2v_words))
print("sample words ", w2v_words[0:50])
```
## [4.4.1] Converting text into vectors using Avg W2V, TFIDF-W2V
#### [4.4.1.1] Avg W2v
```
# average Word2Vec
# compute average word2vec for each review.
sent_vectors = []; # the avg-w2v for each sentence/review is stored in this list
for sent in tqdm(list_of_sentance): # for each review/sentence
sent_vec = np.zeros(50) # as word vectors are of zero length 50, you might need to change this to 300 if you use google's w2v
cnt_words =0; # num of words with a valid vector in the sentence/review
for word in sent: # for each word in a review/sentence
if word in w2v_words:
vec = w2v_model.wv[word]
sent_vec += vec
cnt_words += 1
if cnt_words != 0:
sent_vec /= cnt_words
sent_vectors.append(sent_vec)
print(len(sent_vectors))
print(len(sent_vectors[0]))
```
#### [4.4.1.2] TFIDF weighted W2v
```
# S = ["abc def pqr", "def def def abc", "pqr pqr def"]
model = TfidfVectorizer()
tf_idf_matrix = model.fit_transform(preprocessed_reviews)
# we are converting a dictionary with word as a key, and the idf as a value
dictionary = dict(zip(model.get_feature_names(), list(model.idf_)))
# TF-IDF weighted Word2Vec
tfidf_feat = model.get_feature_names() # tfidf words/col-names
# final_tf_idf is the sparse matrix with row= sentence, col=word and cell_val = tfidf
tfidf_sent_vectors = []; # the tfidf-w2v for each sentence/review is stored in this list
row=0;
for sent in tqdm(list_of_sentance): # for each review/sentence
sent_vec = np.zeros(50) # as word vectors are of zero length
weight_sum =0; # num of words with a valid vector in the sentence/review
for word in sent: # for each word in a review/sentence
if word in w2v_words and word in tfidf_feat:
vec = w2v_model.wv[word]
# tf_idf = tf_idf_matrix[row, tfidf_feat.index(word)]
# to reduce the computation we are
# dictionary[word] = idf value of word in whole courpus
# sent.count(word) = tf valeus of word in this review
tf_idf = dictionary[word]*(sent.count(word)/len(sent))
sent_vec += (vec * tf_idf)
weight_sum += tf_idf
if weight_sum != 0:
sent_vec /= weight_sum
tfidf_sent_vectors.append(sent_vec)
row += 1
```
## Truncated-SVD
### [5.1] Taking top features from TFIDF,<font color='red'> SET 2</font>
```
# Please write all the code with proper documentation
X = preprocessed_reviews[:]
y = final['Score'][:]
tf_idf = TfidfVectorizer()
tfidf_data = tf_idf.fit_transform(X)
tfidf_feat = tf_idf.get_feature_names()
```
### [5.2] Calulation of Co-occurrence matrix
```
# Please write all the code with proper documentation
#Ref:https://datascience.stackexchange.com/questions/40038/how-to-implement-word-to-word-co-occurence-matrix-in-python
#Ref:# https://github.com/PushpendraSinghChauhan/Amazon-Fine-Food-Reviews/blob/master/Computing%20Word%20Vectors%20using%20TruncatedSVD.ipynb
def Co_Occurrence_Matrix(neighbour_num , list_words):
# Storing all words with their indices in the dictionary
corpus = dict()
# List of all words in the corpus
doc = []
index = 0
for sent in preprocessed_reviews:
for word in sent.split():
doc.append(word)
corpus.setdefault(word,[])
corpus[word].append(index)
index += 1
# Co-occurrence matrix
matrix = []
# rows in co-occurrence matrix
for row in list_words:
# row in co-occurrence matrix
temp = []
# column in co-occurrence matrix
for col in list_words :
if( col != row):
# No. of times col word is in neighbourhood of row word
count = 0
# Value of neighbourhood
num = neighbour_num
# Indices of row word in the corpus
positions = corpus[row]
for i in positions:
if i<(num-1):
# Checking for col word in neighbourhood of row
if col in doc[i:i+num]:
count +=1
elif (i>=(num-1)) and (i<=(len(doc)-num)):
# Check col word in neighbour of row
if (col in doc[i-(num-1):i+1]) and (col in doc[i:i+num]):
count +=2
# Check col word in neighbour of row
elif (col in doc[i-(num-1):i+1]) or (col in doc[i:i+num]):
count +=1
else :
if (col in doc[i-(num-1):i+1]):
count +=1
# appending the col count to row of co-occurrence matrix
temp.append(count)
else:
# Append 0 in the column if row and col words are equal
temp.append(0)
# appending the row in co-occurrence matrix
matrix.append(temp)
# Return co-occurrence matrix
return np.array(matrix)
X_new = Co_Occurrence_Matrix(15, top_feat)
```
### [5.3] Finding optimal value for number of components (n) to be retained.
```
# Please write all the code with proper documentation
k = np.arange(2,100,3)
variance =[]
for i in k:
svd = TruncatedSVD(n_components=i)
svd.fit_transform(X_new)
score = svd.explained_variance_ratio_.sum()
variance.append(score)
plt.plot(k, variance)
plt.xlabel('Number of Components')
plt.ylabel('Explained Variance')
plt.title('n_components VS Explained variance')
plt.show()
```
### [5.4] Applying k-means clustering
```
# Please write all the code with proper documentation
errors = []
k = [2, 5, 10, 15, 25, 30, 50, 100]
for i in k:
kmeans = KMeans(n_clusters=i, random_state=0)
kmeans.fit(X_new)
errors.append(kmeans.inertia_)
plt.plot(k, errors)
plt.xlabel('K')
plt.ylabel('Error')
plt.title('K VS Error Plot')
plt.show()
svd = TruncatedSVD(n_components = 20)
svd.fit(X_new)
score = svd.explained_variance_ratio_
```
### [5.5] Wordclouds of clusters obtained in the above section
```
# Please write all the code with proper documentation
indices = np.argsort(tf_idf.idf_[::-1])
top_feat = [tfidf_feat[i] for i in indices[0:3000]]
top_indices = indices[0:3000]
top_n = np.argsort(top_feat[::-1])
feature_importances = pd.DataFrame(top_n, index = top_feat, columns=['importance']).sort_values('importance',ascending=False)
top = feature_importances.iloc[0:30]
comment_words = ' '
for val in top.index:
val = str(val)
tokens = val.split()
# Converts each token into lowercase
for i in range(len(tokens)):
tokens[i] = tokens[i].lower()
for words in tokens:
comment_words = comment_words + words + ' '
stopwords = set(STOPWORDS)
wordcloud = WordCloud(width = 600, height = 600,
background_color ='black',
stopwords = stopwords,
min_font_size = 10).generate(comment_words)
plt.figure(figsize = (10, 10), facecolor = None)
plt.imshow(wordcloud)
plt.axis("off")
plt.tight_layout(pad = 0)
plt.show()
```
### [5.6] Function that returns most similar words for a given word.
```
# Please write all the code with proper documentation
def similarity(word):
similarity = cosine_similarity(X_new)
word_vect = similarity[top_feat.index(word)]
index = word_vect.argsort()[::-1][1:5]
for i in range(len(index)):
print((i+1),top_feat[index[i]] ,"\n")
similarity('sugary')
similarity('notlike')
```
# [6] Conclusions
```
# Please write down few lines about what you observed from this assignment.
# Also please do mention the optimal values that you obtained for number of components & number of clusters.
from prettytable import PrettyTable
x = PrettyTable()
x.field_names = ["Algorithm","Best Hyperparameter"]
x.add_row(["T-SVD", 20])
x.add_row(["K-Means", 20])
print(x)
```
* It can be obseverd that just 20 components preserve about 99.9% of the variance in the data.
* The co occurence matrix used is to find the correlation of one word with respect to the other in the dataset.
| github_jupyter |
# Conditional statements - part 1
## Motivation
All the previous programs are based on a pure sequence of statements. After the start of the program the statements are
executed step by step and the program ends afterwards. However, it is often necessary that parts of a program are
only executed under certain conditions. For example, think of the following sentence and how it
would be converted into a [pseudo code](https://de.wikipedia.org/wiki/Pseudocode) program:
> If it rains tomorrow, I will clean up the basement. Then I will tidy the cupboards and sort the photos. Otherwise, I
> will go swimming. In the evening I will go to the cinema with my wife.
The textual description of the task is not precise. It is not exactly clear what is to be done.
This is common for description in natural language. Often addition information is conveyed through the
context of e.g. a conversation. What is probably meant in the previous example is the following:
```
If it rains tomorrow, I will:
- clean up the basement
- tidy the cupboards
- sort the photos
Otherwise (so if it doesn't rain), I will:
go swimming.
In the evening I will go to the cinema with my wife.
```
So, depending on the weather either one or the other path of the pseudo code program is executed. This
is illustrated in the following graphic:

To enable this more complex workflow two things are required:
- First, a construction that allows to split the workflow in different paths depending on a given condition.
- Second, a specification of conditions.
## Conditions
So, what is a condition? In the end, it is something that is either `True` or `False`, in other word, a condition always results in a boolean value. In principal, you could use `True` or `False`, when a condition is required. However, this not flexible, i.e. `True` is always true. More sophisticated conditions can be expressed by comparing the content of variables with a given value. For example, there is an integer variable `age`. Then the value can be either equal to 18 or not equal. So checking for *is the value of age equal to 18* can either be `True` or `False`. There are a number of comparison operators, which can be used for both numerical datatypes and string datatypes. In the former case, the usual order of numbers is used, in the latter case, the alphabetic order is taken.
## Comparison Operators
In order to use decisions in programs a way to specify conditions is needed. To formulate condition the comparison
operators can be used. The following table shows a selection of comparison operators available in Python. The result of
a comparison using these operators is always a `Boolean` value. As already explained, the only possible `Boolean` values
are `True` and `False`. For each comparison operator the table contain two example expressions that result in `True`
and `False` respectively.
| Operator | Explanation | Example True | Example False |
| -------- | ------------------------------------ | ------------ | ------------- |
| == | Check for equality | 2 == 2 | 2 == 3 |
| != | Check for inequality | 2 != 3 | 2 != 2 |
| < | Check for "smaller" | 2 < 3 | 2 < 1 |
| > | Check for "larger" | 3 > 2 | 2 > 3 |
| <= | Check for "less than or equal to" | 3 <= 3 | 3 <= 2 |
| >= | Check for "greater than or equal to" | 2 >= 2 | 2 >= 3 |
## `=` vs. `==`
It is important to emphasize the difference between `=` and `==`. If there is one equal sign, the statement is an *assignment*. A value is assigned to a variable. The assignment has no return value, it is neither true or false. If there are two equal signs, it is a comparison. The values on both sides of the `""` are unchanged. However, the comparison leads to a value, namely `True` or `False`.
## Complex Conditions
What happens, if you want to check, if the variable `age` is greater than 18 but smaller than 30? In this case, you can build complex conditions using the boolean operators `and`, `or` and `not` (cf. the notebook about datatypes).
## Exercise
Familiarize yourself with the comparison operators. Also test more complex comparisons, such as:
```python
"abc" < "abd"
"abcd" > "abc"
2 == 2.0
1 == True
0 != True
```
```
1 == True
```
# Conditional statements
Using the conditional operators it is now possible to formulate conditional statements in Python.
The syntax for conditional statements in Python is:
```python
if condition:
statement_a1
...
statement_an
else:
statement_b1
...
statement_bm
```
The result of the condition can be either `True` or `False`. If the condition is `True` the statements `a1` to `an` are executed.
If the condition is `False` the statements `b1` to `bm` are executed.
Note, that the `else` branch is optional, i.e. an
`if` condition can also be specified without an `else` alternative. If the condition then is not true (i.e. `false`),
the statements of the `if` block are simply skipped.
```
number = int(input("Please type a number: "))
if number > 100:
print(number, "is greater than 100!")
number = int(input("Please type a number: "))
if number > 100:
print(number, "is greater than 100!")
else:
print(number, "is smaller or equals 100!")
```
### Indentations mark the boundaries of code blocks
Statements that belong together are called *code blocks*.
As can be seen in the previous examples, Python does not use special characters or keywords to mark the
beginning and the end of code blocks. Instead, indentation is used in Python.
So indentation and spaces have a meaning in Python! Therefore, you must not indent arbitrarily within a program. Execute the code in the following two cells to see what happens.
```
a = 3
b = 4
print(a + b)
number = 100
if number > 0:
print("Number is greater than 0")
```
Let us challenge your understanding of code blocks in Python. Take a look at the following program. The last statement
`print("Done")` is not indented. What does this mean for the execution of the
program? Change the program and indent the `print("Done")`. How does the execution of the
program change?
```
number = int(input("Please insert a number: "))
if number > 100:
print(number, "is greater than 100!")
else:
print(number, "is smaller oder equals 100!")
print("Done")
```
### Exercise
Write a conditional statement that asks for the user's name. Use the `input()` function. If his name is Harry or Harry Potter, then output "Welcome to Gryffindor, Mr. Potter!". Otherwise output "Sorry, Hogwarts is full.".
```
name =
```
| github_jupyter |
<a href="https://colab.research.google.com/github/microprediction/microblog/blob/main/Election_in_the_run_with_correlation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Greetings!
You might be here because you think
* Betting markets are far more efficient then Nate Silver or G. Elliott Morris. I really can't help you if you insist otherwise - perhaps G. Elliott will offer you 19/1 on Trump LOL.
* Betting markets still requires some interpretation, because many punters are so lazy they don't even run simulations, or because they involve heterogeneous groups and some markets are products of others, approximately, so we get a convexity effect.
See this post https://www.linkedin.com/posts/petercotton_is-bidens-chance-of-winning-90-percent-or-activity-6730191890530095104-njhk and if you like it, please react on linked-in so the marketting dollar for the open source prediction network goes further. Because it really is a dollar.
## Okay then...
This notebook provides you with a simple interpretation of market implied state electoral college probabilities, nothing more. It can be used to compute things like the market implied correlation between states, using a very simple correlation model. That may, or may not, provide you with a new perspective on the markets or a lens as to their degree of internal consistency.
In using this, rather than the groovy graphics at 538, you are taking a stand against the ridiculous celebritization of statistics and journalistic group-think.
```
import numpy as np
from pprint import pprint
import math
from scipy.stats import norm
# Current prices for Biden, expressed as inverse probabilities, and electoral votes
states = [ ('arizona',1.23,11), ('michigan',1.01,16), ('pennsylvania',1.03,20),
('georgia',1.12,16),('nevada',1.035,6), ('north carolina',6.5,15), ('alaska',50,3),
('wisconsin',1.03,10)]
# Maybe you want to add Wisconsin.
# Okay, let's see if this foreignor can get the basic electoral calculus right.
# You might want to re-introduce some other states, but if so change the existing totals below:
biden = 227
trump = 214 # Does not include Alaska
# Sanity check.
undecided = sum([a[2] for a in states])
print(undecided)
total = biden + trump + undecided
assert total==538
# Next ... let's write a little guy that simulated from modified state probabilities. Just ignore this if you
# don't think there is any correlation between results at this late stage of the race.
# Perhaps, however, there is some latent correlation still in the results - related to legal moves or military voting patterns or
# consistent bias across state markets. I will merely remark that some correlation is required to make the betting markets coherent, but
# also that this implied correlation will not necessarily be justified.
def conditional(p:float,rho=None,z=None):
""" Simulate binary event conditioned on common factor, leaving unconditional probability alone
p Unconditional probability
z Gaussian common factor
rho Correlation
(this is a Normal Copula with common off-diagonal entries)
"""
if p<1e-8:
return 0
elif p>1-1e-8:
return 1
else:
x1 = math.sqrt(1-rho)*np.random.randn() + math.sqrt(rho)*z if z is not None else np.random.randn()
return x1<norm.ppf(p)
examples = {'p_z=0':conditional(p=0.5,rho=0.5,z=0),
'p_z=1':conditional(p=0.5,rho=0.5,z=1)}
pprint(examples)
# A quick sanity check. The mean of the conditional draws should be the same as the original probability
p_unconditional = 0.22
zs = np.random.randn(10000)
p_mean = np.mean([ conditional(p=p_unconditional, rho=.7, z=z) for z in zs])
pprint( {'p_unconditional':p_unconditional,'mean of p_conditional':p_mean})
# Jolly good. Now let's use this model.
# I've added a simple translational bias as well, if you'd rather use that to introduce correlation.
BIAS = 0 # If you want to systematically translate all state probs (this is not mean preserving)
RHO = 0.4 # If you want correlation introduced via a Normal Copula with constant off-diagnonal terms
def biden_sim() -> int:
"""
Simulate, once, the number of electoral college votes for Joe Biden
"""
votes = biden
bias = BIAS*np.random.randn() # Apply the same translation to all states
z = np.random.randn() # Common latent factor capturing ... you tell me
for s in states:
p = 1/s[1]
conditional_p = conditional(p=p,rho=RHO,z=z)
shifted_p = conditional_p + BIAS
if np.random.rand()<shifted_p:
votes = votes + s[2]
return votes
biden_sim()
# Simulate it many times
bs = [ biden_sim() for _ in range(50000) ]
ts = [538-b for b in bs] # Trump electoral votes
b_win = np.mean([b>=270 for b in bs])
print('Biden win probability is '+str(b_win))
import matplotlib.pyplot as plt
plt.hist(bs,bins=200)
t_win = np.mean([b<=268 for b in bs ])
tie = np.mean([b==269 for b in bs ])
print('Trump win probability is '+str(t_win))
print('Tie probability is '+ str(tie))
b270 = np.mean([b==270 for b in bs])
print('Biden=270 probability is '+str(b270))
# Compute inverse probabilities (European quoting convention) for range outcomes
prices = {'trump_270_299':1./np.mean([t>=270 and t<=299 for t in ts]),
'trump_300_329':1./np.mean([t>=300 and t<=329 for t in ts]),
'biden_270_299':1./np.mean([b>=270 and b<=299 for b in bs]),
'biden_300_329':1./np.mean([b>=300 and b<=329 for b in bs]),
'biden_330_359':1./np.mean([b>=330 and b<=359 for b in bs]),
'biden_m_100.5':1./np.mean([b-t-100.5>0 for b,t in zip(bs,ts)]),
'biden_m_48.5':1./np.mean([b-t-48.5>0 for b,t in zip(bs,ts)])}
pprint(prices)
# American quoting conventions
def pm(p):
if p>0.5:
return '-'+str(round(100*(p/(1-p)),0))
else:
return '+'+str(round(100/p - 100,0))
examples = {'p=0.33333':pm(0.333333),
'p=0.75':pm(0.75)}
#pprint(examples)
prices = {'trump_270_or_more':pm(t_win),
'biden_270_or_more':pm(b_win),
'trump_270_299':pm(np.mean([t>=270 and t<=299 for t in ts])),
'trump_300_329':pm(np.mean([t>=300 and t<=329 for t in ts])),
'biden_270_299':pm(np.mean([b>=270 and b<=299 for b in bs])),
'biden_300_329':pm(np.mean([b>=300 and b<=329 for b in bs]))}
pprint(prices)
```
| github_jupyter |
# Using a random forest for demographic model selection
In Schrider and Kern (2017) we give a toy example of demographic model selection via supervised machine learning in Figure Box 1. Following a discussion on twitter, Vince Buffalo had the great idea of our providing a simple example of supervised ML in population genetics using a jupyter notebook; this notebook aims to serve that purpose by showing you exactly how we produced that figure in our paper
## Preliminaries
The road map here will be to 1) do some simulation of three demographic models, 2) to train a classifier to distinguish among those models, 3) test that classifier with new simulation data, and 4) to graphically present how well our trained classifier works.
To do this we will use coalescent simulations as implemented in Dick Hudson's well known `ms` software and for the ML side of things we will use the `scikit-learn` package. Let's start by installing these dependencies (if you don't have them installed already)
### Install, and compile `ms`
We have put a copy of the `ms` tarball in this repo, so the following should work upon cloning
```
#untar and compile ms and sample_stats
!tar zxf ms.tar.gz; cd msdir; gcc -o ms ms.c streec.c rand1.c -lm; gcc -o sample_stats sample_stats.c tajd.c -lm
#I get three compiler warnings from ms, but everything should be fine
#now I'll just move the programs into the current working dir
!mv msdir/ms . ; mv msdir/sample_stats .;
```
### Install `scikit-learn`
If you use anaconda, you may already have these modules installed, but if not you can install with either of the following
```
!conda install scikit-learn --yes
```
or if you don't use `conda`, you can use `pip` to install scikit-learn with
```
!pip install -U scikit-learn
```
# Step 1: create a training set and a testing set
We will create a training set using simulations from three different demographic models: equilibrium population size, instantaneous population growth, and instantaneous population contraction. As you'll see this is really just a toy example because we will perform classification based on data from a single locus; in practice this would be ill-advised and you would want to use data from many loci simulataneously.
So lets do some simulation using `ms` and summarize those simulations using the `sample_stats` program that Hudson provides. Ultimately we will only use two summary stats for classification, but one could use many more. Each of these simulations should take a few seconds to run.
```
#simulate under the equilibrium model
!./ms 20 2000 -t 100 -r 100 10000 | ./sample_stats > equilibrium.msOut.stats
#simulate under the contraction model
!./ms 20 2000 -t 100 -r 100 10000 -en 0 1 0.5 -en 0.2 1 1 | ./sample_stats > contraction.msOut.stats
#simulate under the growth model
!./ms 20 2000 -t 100 -r 100 10000 -en 0.2 1 0.5 | ./sample_stats > growth.msOut.stats
#now lets suck up the data columns we want for each of these files, and create one big training set; we will use numpy for this
# note that we are only using two columns of the data- these correspond to segSites and Fay & Wu's H
import numpy as np
X1 = np.loadtxt("equilibrium.msOut.stats",usecols=(3,9))
X2 = np.loadtxt("contraction.msOut.stats",usecols=(3,9))
X3 = np.loadtxt("growth.msOut.stats",usecols=(3,9))
X = np.concatenate((X1,X2,X3))
#create associated 'labels' -- these will be the targets for training
y = [0]*len(X1) + [1]*len(X2) + [2]*len(X3)
Y = np.array(y)
#the last step in this process will be to shuffle the data, and then split it into a training set and a testing set
#the testing set will NOT be used during training, and will allow us to check how well the classifier is doing
#scikit-learn has a very convenient function for doing this shuffle and split operation
#
# will will keep out 10% of the data for testing
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.1)
```
# Step 2: train our classifier and visualize decision surface
Now that we have a training and testing set ready to go, we can move on to training our classifier. For this example we will use a random forest classifier (Breiman 2001). This is all implemented in `scikit-learn` and so the code is very brief.
```
from sklearn.ensemble import RandomForestClassifier
rfClf = RandomForestClassifier(n_estimators=100,n_jobs=10)
clf = rfClf.fit(X_train, Y_train)
```
That's it! The classifier is trained. This Random Forest classifer used 100 decision trees in its ensemble, a pretty large number considering that we are only using two summary stats to represent our data. Nevertheless it trains on the data very, very quickly.
Confession: the real reason we are using only two summary statistics right here is because it makes it really easy to visualize that classifier's decision surface: which regions of the feature space would be assigned to which class? Let's have a look!
(Note: I have increased the h argument for the call to `make_meshgrid` below, coarsening the contour plot in the interest of efficiency. Decreasing this will yield a smoother plot, but may take a while and use up a lot more memory. Adjust at your own risk!)
```
from sklearn.preprocessing import normalize
#These two functions (taken from scikit-learn.org) plot the decision boundaries for a classifier.
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
def make_meshgrid(x, y, h=.05):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
#Let's do the plotting
import matplotlib.pyplot as plt
fig,ax= plt.subplots(1,1)
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1, h=0.2)
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
# plotting only a subset of our data to keep things from getting too cluttered
ax.scatter(X_test[:200, 0], X_test[:200, 1], c=Y_test[:200], cmap=plt.cm.coolwarm, edgecolors='k')
ax.set_xlabel(r"$\theta_{w}$", fontsize=14)
ax.set_ylabel(r"Fay and Wu's $H$", fontsize=14)
ax.set_xticks(())
ax.set_yticks(())
ax.set_title("Classifier decision surface", fontsize=14)
plt.show()
```
Above we can see which regions of our feature space are assigned to each class: dark blue shaded areas will be classified as Equilibrium, faint blue as Contraction, and red as Growth. Note the non-linear decision surface. Looks pretty cool! And also illustrates how this type of classifier might be useful for discriminating among classes that are difficult to linearly separate. Also plotted are a subset of our test examples, as dots colored according to their true class. Looks like we are doing pretty well but have a few misclassifications. Would be nice to quantify this somehow, which brings us to...
# Step 3: benchmark our classifier
The last step of the process is to use our trained classifier to predict which demographic models our test data are drawn from. Recall that the classifier hasn't seen these test data so this should be a fair test of how well the classifier will perform on any new data we throw at it in the future. We will visualize performance using a confusion matrix.
```
#here's the confusion matrix function
def makeConfusionMatrixHeatmap(data, title, trueClassOrderLs, predictedClassOrderLs, ax):
data = np.array(data)
data = normalize(data, axis=1, norm='l1')
heatmap = ax.pcolor(data, cmap=plt.cm.Blues, vmin=0.0, vmax=1.0)
for i in range(len(predictedClassOrderLs)):
for j in reversed(range(len(trueClassOrderLs))):
val = 100*data[j, i]
if val > 50:
c = '0.9'
else:
c = 'black'
ax.text(i + 0.5, j + 0.5, '%.2f%%' % val, horizontalalignment='center', verticalalignment='center', color=c, fontsize=9)
cbar = plt.colorbar(heatmap, cmap=plt.cm.Blues, ax=ax)
cbar.set_label("Fraction of simulations assigned to class", rotation=270, labelpad=20, fontsize=11)
# put the major ticks at the middle of each cell
ax.set_xticks(np.arange(data.shape[1]) + 0.5, minor=False)
ax.set_yticks(np.arange(data.shape[0]) + 0.5, minor=False)
ax.axis('tight')
ax.set_title(title)
#labels
ax.set_xticklabels(predictedClassOrderLs, minor=False, fontsize=9, rotation=45)
ax.set_yticklabels(reversed(trueClassOrderLs), minor=False, fontsize=9)
ax.set_xlabel("Predicted class")
ax.set_ylabel("True class")
#now the actual work
#first get the predictions
preds=clf.predict(X_test)
counts=[[0.,0.,0.],[0.,0.,0.],[0.,0.,0.]]
for i in range(len(Y_test)):
counts[Y_test[i]][preds[i]] += 1
counts.reverse()
classOrderLs=['equil','contraction','growth']
#now do the plotting
fig,ax= plt.subplots(1,1)
makeConfusionMatrixHeatmap(counts, "Confusion matrix", classOrderLs, classOrderLs, ax)
plt.show()
```
Looks pretty good. But can we make it better? Well a simple way might be to increase the number of features (i.e. summary statistics) we use as input. Let's give that a whirl using all of the output from Hudson's `sample_stats`
```
X1 = np.loadtxt("equilibrium.msOut.stats",usecols=(1,3,5,7,9))
X2 = np.loadtxt("contraction.msOut.stats",usecols=(1,3,5,7,9))
X3 = np.loadtxt("growth.msOut.stats",usecols=(1,3,5,7,9))
X = np.concatenate((X1,X2,X3))
#create associated 'labels' -- these will be the targets for training
y = [0]*len(X1) + [1]*len(X2) + [2]*len(X3)
Y = np.array(y)
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.1)
rfClf = RandomForestClassifier(n_estimators=100,n_jobs=10)
clf = rfClf.fit(X_train, Y_train)
preds=clf.predict(X_test)
counts=[[0.,0.,0.],[0.,0.,0.],[0.,0.,0.]]
for i in range(len(Y_test)):
counts[Y_test[i]][preds[i]] += 1
counts.reverse()
fig,ax= plt.subplots(1,1)
makeConfusionMatrixHeatmap(counts, "Confusion matrix", classOrderLs, classOrderLs, ax)
plt.show()
```
Even better!
Hopefully this simple example gives you the gist of how supervised ML can be used. In the future we will populate this GitHub repository with further examples that might be illustrative.
| github_jupyter |
## This notebook will help you train a vanilla Point-Cloud AE with the basic architecture we used in our paper.
(it assumes latent_3d_points is in the PYTHONPATH and the structural losses have been compiled)
```
import os.path as osp
from latent_3d_points.src.ae_templates import mlp_architecture_ala_iclr_18, default_train_params
from latent_3d_points.src.autoencoder import Configuration as Conf
from latent_3d_points.src.point_net_ae import PointNetAutoEncoder
from latent_3d_points.src.in_out import snc_category_to_synth_id, create_dir, PointCloudDataSet, \
load_all_point_clouds_under_folder
from latent_3d_points.src.tf_utils import reset_tf_graph
from latent_3d_points.src.general_utils import plot_3d_point_cloud
%load_ext autoreload
%autoreload 2
%matplotlib inline
```
Define Basic Parameters
```
top_out_dir = '../data/' # Use to save Neural-Net check-points etc.
top_in_dir = '../data/shape_net_core_uniform_samples_2048/' # Top-dir of where point-clouds are stored.
experiment_name = 'single_class_ae'
n_pc_points = 2048 # Number of points per model.
bneck_size = 128 # Bottleneck-AE size
ae_loss = 'chamfer' # Loss to optimize: 'emd' or 'chamfer'
class_name = raw_input('Give me the class name (e.g. "chair"): ').lower()
```
Load Point-Clouds
```
syn_id = snc_category_to_synth_id()[class_name]
class_dir = osp.join(top_in_dir , syn_id)
all_pc_data = load_all_point_clouds_under_folder(class_dir, n_threads=8, file_ending='.ply', verbose=True)
```
Load default training parameters (some of which are listed beloq). For more details please print the configuration object.
'batch_size': 50
'denoising': False (# by default AE is not denoising)
'learning_rate': 0.0005
'z_rotate': False (# randomly rotate models of each batch)
'loss_display_step': 1 (# display loss at end of these many epochs)
'saver_step': 10 (# over how many epochs to save neural-network)
```
train_params = default_train_params()
encoder, decoder, enc_args, dec_args = mlp_architecture_ala_iclr_18(n_pc_points, bneck_size)
train_dir = create_dir(osp.join(top_out_dir, experiment_name))
conf = Conf(n_input = [n_pc_points, 3],
loss = ae_loss,
training_epochs = train_params['training_epochs'],
batch_size = train_params['batch_size'],
denoising = train_params['denoising'],
learning_rate = train_params['learning_rate'],
train_dir = train_dir,
loss_display_step = train_params['loss_display_step'],
saver_step = train_params['saver_step'],
z_rotate = train_params['z_rotate'],
encoder = encoder,
decoder = decoder,
encoder_args = enc_args,
decoder_args = dec_args
)
conf.experiment_name = experiment_name
conf.held_out_step = 5 # How often to evaluate/print out loss on
# held_out data (if they are provided in ae.train() ).
conf.save(osp.join(train_dir, 'configuration'))
```
If you ran the above lines, you can reload a saved model like this:
```
load_pre_trained_ae = False
restore_epoch = 500
if load_pre_trained_ae:
conf = Conf.load(train_dir + '/configuration')
reset_tf_graph()
ae = PointNetAutoEncoder(conf.experiment_name, conf)
ae.restore_model(conf.train_dir, epoch=restore_epoch)
```
Build AE Model.
```
reset_tf_graph()
ae = PointNetAutoEncoder(conf.experiment_name, conf)
```
Train the AE (save output to train_stats.txt)
```
buf_size = 1 # Make 'training_stats' file to flush each output line regarding training.
fout = open(osp.join(conf.train_dir, 'train_stats.txt'), 'a', buf_size)
train_stats = ae.train(all_pc_data, conf, log_file=fout)
fout.close()
```
## Evaluation
Get a batch of reconstuctions and their latent-codes.
```
feed_pc, feed_model_names, _ = all_pc_data.next_batch(10)
reconstructions = ae.reconstruct(feed_pc)[0]
latent_codes = ae.transform(feed_pc)
```
Use any plotting mechanism such as matplotlib to visualize the results.
```
i = 2
plot_3d_point_cloud(reconstructions[i][:, 0],
reconstructions[i][:, 1],
reconstructions[i][:, 2], in_u_sphere=True);
i = 4
plot_3d_point_cloud(reconstructions[i][:, 0],
reconstructions[i][:, 1],
reconstructions[i][:, 2], in_u_sphere=True);
```
| github_jupyter |
## Figs for the measurement force paper
```
from scipy.io import loadmat
from scipy.optimize import curve_fit
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from numpy import trapz
def cm2inch(value):
return value/2.54
#axes.xaxis.set_tick_params(direction='in', which='both')
#axes.yaxis.set_tick_params(direction='in', which='both')
mpl.rcParams["xtick.direction"] = "in"
mpl.rcParams["ytick.direction"] = "in"
mpl.rcParams["lines.markeredgecolor"] = "k"
mpl.rcParams["lines.markeredgewidth"] = 1.5
mpl.rcParams["figure.dpi"] = 200
from matplotlib import rc
rc('font', family='serif')
rc('text', usetex=True)
rc('xtick', labelsize='medium')
rc('ytick', labelsize='medium')
rc("axes", labelsize = "large")
def cm2inch(value):
return value/2.54
def cm2inch(value):
return value/2.54
def gauss_function(x, a, x0, sigma):
return a*np.exp(-(x-x0)**2/(2*sigma**2))
def pdf(data, bins = 10, density = True):
pdf, bins_edge = np.histogram(data, bins = bins, density = density)
bins_center = (bins_edge[0:-1] + bins_edge[1:]) / 2
return pdf, bins_center
#import the plots data
dataset = loadmat("data_graphs.mat")
for i in dataset.keys():
try:
dataset[i] = np.squeeze(dataset[i])
except:
continue
fit_data = loadmat("data_fit_2705.mat")
for i in fit_data.keys():
try:
fit_data[i] = np.squeeze(fit_data[i])
except:
continue
def movmin(z, window):
result = np.empty_like(z)
start_pt = 0
end_pt = int(np.ceil(window / 2))
for i in range(len(z)):
if i < int(np.ceil(window / 2)):
start_pt = 0
if i > len(z) - int(np.ceil(window / 2)):
end_pt = len(z)
result[i] = np.min(z[start_pt:end_pt])
start_pt += 1
end_pt += 1
return result
plt.figure(figsize=( cm2inch(16),cm2inch(8)))
plt.plot(dataset["time"], dataset["z"], label="raw")
plt.plot(dataset["time"], dataset["z"] - movmin(dataset["z"], 10000), label="rescaled")
plt.xlabel("time (s)")
plt.ylabel("$z$ ($\mu$m)")
plt.legend(frameon=False)
plt.savefig("traj_rescaled.pdf")
dataset
color = ['tab:blue', 'tab:orange', 'tab:green', 'tab:red', 'tab:purple', 'tab:brown', 'tab:pink', 'tab:gray', 'tab:olive', 'tab:cyan']
plt.figure()
for n,i in enumerate(['pdf_Dz_short_t_1', 'pdf_Dz_short_t_2', 'pdf_Dz_short_t_3', 'pdf_Dz_short_t_4', 'pdf_Dz_short_t_5']):
plt.semilogy(dataset[i][0,:],dataset[i][1,:], color = color[n], marker = "o", linestyle = "")
plt.plot(dataset["pdf_Dz_short_th_t_5"][0,:],dataset["pdf_Dz_short_th_t_5"][1,:], color = color[4])
plt.plot(dataset["gaussian_short_timetheory_z"][0,:],dataset["gaussian_short_timetheory_z"][1,:], color = "gray",linestyle = "--")
ax = plt.gca()
ax.set_ylim([1e-5,1])
ax.set_xlim([-7,7])
plt.xlabel("$\Delta z / \sigma$")
plt.ylabel("$P(\Delta z / \sigma)$")
#dataset
fig = plt.figure(figsize=(cm2inch(8.6), cm2inch(8.6)/1.68*1.3),constrained_layout=False)
gs = fig.add_gridspec(2,3)
##### MSD
fig.add_subplot(gs[0,:])
plt.loglog(dataset["MSD_time_tot"], dataset["MSD_fit_x"], color = "k")
plt.loglog(dataset["MSD_time_tot"], dataset["MSD_fit_z"], color = "k")
plt.loglog(dataset["MSD_time_tot"],dataset["MSD_x_tot"],"o", label = "x", markersize = 5)
plt.loglog(dataset["MSD_time_tot"][::2],dataset["MSD_y_tot"][::2],"o", label = "y", markersize = 5)
plt.loglog(dataset["MSD_time_tot"],dataset["MSD_z_tot"],"o", label = "z", markersize = 5)
# plateau
plateau = [dataset["fitted_MSD_Plateau"] for i in range(len(dataset["MSD_time_tot"]))]
plt.loglog(dataset["MSD_time_tot"][-60:], plateau[-60:], color = "black", linewidth = 1,zorder = 10, linestyle = "--")
##
ax = plt.gca()
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.xaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.xaxis.set_minor_locator(locmin)
ax.xaxis.set_minor_formatter(mpl.ticker.NullFormatter())
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.yaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.yaxis.set_minor_locator(locmin)
ax.yaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ax.set_xlim([1e-2,1e3])
ax.set_ylim([None,1e-10])
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.text(0.45*xmax,2.5*ymin,'a)')
plt.ylabel("$\mathrm{MSD}$ ($\mathrm{m^2}$)",fontsize = "small", labelpad=0.5)
plt.xlabel("$\Delta t$ (s)",fontsize = "small",labelpad=0.5)
plt.legend(frameon = False,fontsize = "x-small",loc = "upper left")
####### SHORT TIME X
fig.add_subplot(gs[1,0])
for n,i in enumerate(['pdf_Dx_short_t_1', 'pdf_Dx_short_t_2', 'pdf_Dx_short_t_3', 'pdf_Dx_short_t_4', 'pdf_Dx_short_t_5']):
plt.semilogy(dataset[i][0,:],dataset[i][1,:], color = color[n], marker = "o", linestyle = "",markersize = 3)
plt.plot(dataset["pdf_Dx_short_th_t_5"][0,:],dataset["pdf_Dx_short_th_t_5"][1,:], color = "k",zorder=6,linewidth=1)
plt.plot(dataset["gaussianx_short_timetheory"][0,:],dataset["gaussianx_short_timetheory"][1,:], color = "gray",zorder=-1,linestyle = "--",)
ax = plt.gca()
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.yaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.yaxis.set_minor_locator(locmin)
ax.yaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ax.set_ylim([1e-5,1])
ax.set_xlim([-7,7])
plt.xlabel("$\Delta x / \sigma$",fontsize = "small", labelpad=0.5)
plt.ylabel("$P_{x} \sigma$",fontsize = "small", labelpad=0.5)
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.text(0.54*xmax,0.25*ymax,'b)')
####### SHORT TIME Z
fig.add_subplot(gs[1,1])
for n,i in enumerate(['pdf_Dz_short_t_1', 'pdf_Dz_short_t_2', 'pdf_Dz_short_t_3', 'pdf_Dz_short_t_4', 'pdf_Dz_short_t_5']):
plt.semilogy(dataset[i][0,:],dataset[i][1,:], color = color[n], marker = "o", linestyle = "",markersize = 3)
plt.plot(dataset["pdf_Dz_short_th_t_5"][0,:],dataset["pdf_Dz_short_th_t_5"][1,:], color = "k",zorder=6,linewidth=1)
plt.plot(dataset["gaussian_short_timetheory_z"][0,:],dataset["gaussian_short_timetheory_z"][1,:], color = "gray",zorder=-1,linestyle = "--",)
ax = plt.gca()
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.yaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.yaxis.set_minor_locator(locmin)
ax.yaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ax.set_ylim([1e-5,1])
ax.set_xlim([-7,7])
plt.xlabel("$\Delta z / \sigma$",fontsize = "small",labelpad=0.5)
plt.ylabel("$P_{z} \sigma$",fontsize = "small",labelpad=0.5)
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.text(0.58*xmax,0.25*ymax,'c)')
###### LONG TIME PDF\
fig.add_subplot(gs[1,2])
plt.errorbar(dataset["x_pdf_longtime"]*1e6,dataset["pdf_longtime"],yerr=dataset["err_long_t"],ecolor = "k",barsabove=False,linewidth = 0.8, label = "experimental pdf",marker="o", markersize=3,capsize = 1,linestyle="")
#plt.fill_between(bins_centers_long_t, pdf_long_t-err_long_t, pdf_long_t+err_long_t, alpha = 0.3)
plt.semilogy(dataset["bins_centers_long_t"],dataset["Pdeltaz_long_th"],color="black", linewidth = 1, zorder=10)
plt.ylabel("$P_z$ ($\mathrm{\mu m^{-1}})$",fontsize = "small", labelpad=0.5)
plt.xlabel("$\Delta z$ ($\mathrm{\mu m}$)",fontsize = "small", labelpad=0.5)
ax = plt.gca()
ax = plt.gca()
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.yaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.yaxis.set_minor_locator(locmin)
ax.yaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ax.set_ylim([1e-3,1])
#ax.set_xlim([None,1e-10])
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.text(0.5*xmax,0.4*ymax,'d)')
plt.tight_layout(pad = 0.1,h_pad=0.1, w_pad=0.3)
plt.savefig("MSD_displacements.svg")
#dataset
def P_b_off(z,z_off, B, ld, lb):
z_off = z_off * 1e-6
lb = lb * 1e-9
ld = ld * 1e-9
z = z - z_off
P_b = np.exp(-B * np.exp(-z / (ld)) - z / lb)
P_b[z < 0] = 0
# Normalization of P_b
A = trapz(P_b,z * 1e6)
P_b = P_b / A
return P_b
fig = plt.figure(figsize=(cm2inch(8.6), 0.75*cm2inch(8.6)/1.68),constrained_layout=False)
gs = fig.add_gridspec(1,2)
fig.add_subplot(gs[0,0])
#########
def pdf(data, bins = 10, density = True):
pdf, bins_edge = np.histogram(data, bins = bins, density = density)
bins_center = (bins_edge[0:-1] + bins_edge[1:]) / 2
return pdf, bins_center
pdf_z,bins_center = pdf(dataset["z"]- np.min(dataset["z"]),bins = 150)
def logarithmic_hist(data,begin,stop,num = 50,base = 2):
if begin == 0:
beg = stop/num
bins = np.logspace(np.log(beg)/np.log(base), np.log(stop)/np.log(base), num-1, base=base)
widths = (bins[1:] - bins[:-1])
#bins = np.cumsum(widths[::-1])
bins = np.concatenate(([0],bins))
#widths = (bins[1:] - bins[:-1])
else:
bins = np.logspace(np.log(begin)/np.log(base), np.log(stop)/np.log(base), num, base=base)
widths = (bins[1:] - bins[:-1])
hist,a= np.histogram(data, bins=bins,density=True)
# normalize by bin width
bins_center = (bins[1:] + bins[:-1])/2
return bins_center,widths, hist
#bins_center_pdf_z,widths,hist = logarithmic_hist(z_0offset, 0.000001, 3, num = 31,base=2)
#pdf_z, bins_center_pdf_z = pdf(z_dedrift[z_dedrift < 3], bins = 100)
#bins_center,widths, pdf_z = logarithmic_hist(dataset["z"]-np.mean(dataset["z"]),0.0001,4,num = 10,base = 10)
P_b_th = P_b_off(bins_center*1e-6, 0, dataset["B"], dataset["ld"], dataset["lb"])
fig.add_subplot(gs[0,1])
plt.plot(bins_center,P_b_th/trapz(P_b_th,bins_center),color = "k",linewidth=1)
plt.semilogy(bins_center - dataset["offset_B"],pdf_z, "o", markersize = 2.5)
plt.xlabel("$z$ ($\mathrm{\mu m}$)",fontsize = "small", labelpad=0.5)
plt.ylabel("$P_{\mathrm{eq}}$ ($\mathrm{\mu m ^{-1}}$)",fontsize = "small", labelpad=0.5)
ax = plt.gca()
ax.set_ylim([1e-4,3])
ax.set_xlim([-0.2,4.5])
#plt.xticks([0,1,2,3,4])
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.yaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.yaxis.set_minor_locator(locmin)
ax.yaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.text(0.8*xmax,1.2*ymin,'b)')
plt.tight_layout(pad = 0.01,h_pad=0.001, w_pad=0.1)
plt.savefig("viscosityxpdfz.svg")
#fig = plt.figure(figsize=(cm2inch(8.6), cm2inch(8.6)/1.68),constrained_layout=False)
plt.errorbar(dataset["z_Force"]*1e6, dataset["Force"]*1e15,yerr=2*np.sqrt(2)*dataset["err_Force"]*1e15,xerr=dataset["x_err_Force"],ecolor = "k", linestyle="", marker="o", markersize = 4,linewidth = 0.8, capsize=1,zorder=3)
plt.semilogx(dataset["z_Force_th"]*1e6,dataset["Force_th"]*1e15)
plt.plot(np.linspace(1e-2,2,10), np.ones(10) * np.mean(dataset["Force"][-10:]*1e15),zorder=-4,linewidth=1)
ax = plt.gca()
ax.set_ylim([-100,1200])
ax.set_xlim([0.1e-1,3])
plt.ylabel("$F_z$ $\\mathrm{(fN)}$",fontsize = "small", labelpad=0.5)
plt.xlabel("$z$ $(\\mathrm{\mu m})$",fontsize = "small", labelpad=0.5)
plt.text(1.2e-2,100, "$F_g = -7 ~ \mathrm{fN}$ ",fontsize="x-small")
plt.tight_layout()
plt.savefig("Force.pdf")
fig = plt.figure(figsize=(cm2inch(8.6), 0.75*cm2inch(8.6)/1.68),constrained_layout=False)
gs = fig.add_gridspec(1,5)
fig.add_subplot(gs[0,:2])
z_th = np.linspace(10e-9,10e-6,100)
#plt.errorbar(z_D_para_fit, D_para_fit/Do, yerr = err_d_para_fit/Do, linewidth = 3, marker = "x", linestyle = "",color = "tab:red", label = "$D_ \\parallel$")
plt.loglog(z_th*1e6, dataset["D_x_th"], color = "k")
plt.plot(dataset["z_D_yacine"]*1e6 - dataset["offset_diffusion"], dataset["z_D_x_yacine"] / dataset["Do"], marker = "o", linestyle = "",color = "tab:blue",label = "$D_\\parallel$", markersize = 4)
#plt.errorbar(bins_center_pdf_z[:-1], Dz[:]/Do, yerr=err[:]/Do, linewidth = 3, marker = "o", linestyle = "",color = "tab:red",label = "$D_ \\bot$")
plt.semilogx(z_th*1e6, dataset["D_z_th"],color = "k")
plt.plot(dataset["z_D_yacine"]*1e6 - dataset["offset_diffusion"], dataset["z_D_z_yacine"] / dataset["Do"], marker = "o", linestyle = "",color = "tab:green",label = "$D_z$", markersize = 4)
ax = plt.gca()
ax.set_ylim([None,1.01])
ax.set_xlim([None,10])
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.xaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.xaxis.set_minor_locator(locmin)
ax.xaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.text(0.3*xmax,1.5*ymin,'a)')
plt.legend(frameon = False,fontsize = "x-small",loc="lower center")
plt.xlabel("$z$ ($\mathrm{\mu m}$)",fontsize = "small", labelpad=0.5)
plt.ylabel("$D_i/ D_\mathrm{0}$",fontsize = "small", labelpad=0.5)
#########
fig.add_subplot(gs[0,2:])
plt.errorbar(dataset["z_Force"]*1e6, dataset["Force"]*1e15,yerr=2*np.sqrt(2)*dataset["err_Force"]*1e15,xerr=dataset["x_err_Force"],ecolor = "k", linestyle="", marker="o", markersize = 4,linewidth = 0.8, capsize=1,zorder=3)
plt.semilogx(dataset["z_Force_th"]*1e6,dataset["Force_th"]*1e15,zorder = 9, color = "k",linewidth = 1)
plt.plot(np.linspace(1e-2,5,100), np.ones(100) * np.mean(dataset["Force"][-10:]*1e15),zorder=10, linewidth = 1, linestyle="--", color = "tab:red")
ax = plt.gca()
ax.set_ylim([-100,1500])
ax.set_xlim([0.1e-1,3])
plt.ylabel("$F_z$ $\\mathrm{(fN)}$",fontsize = "small", labelpad=0.5)
plt.xlabel("$z$ $(\\mathrm{\mu m})$",fontsize = "small", labelpad=0.5)
plt.text(1.6e-1,100, "$F_\mathrm{g} = -7 ~ \mathrm{fN}$ ",fontsize="x-small", color = "tab:red")
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.yticks([0,250,500,750,1000,1250,1500])
plt.text(0.5*xmax,0.85*ymax,'b)')
#inset
plt.tight_layout(pad = 0.01)
plt.savefig("viscosityxforce.svg")
plt.semilogx(dataset["z_Force_th"][500:1000]*1e6,dataset["Force_th"][500:1000]*1e15,zorder = 10, color = "k",linewidth = 1)
fig = plt.figure(figsize=(cm2inch(8.6), cm2inch(8.6)/1.68),constrained_layout=False)
gs = fig.add_gridspec(6,8)
I_radius = fit_data["I_radius"]
I_r_exp = fit_data["I_r_exp"]
I_radius = fit_data["I_radius"]
theo_exp = fit_data["theo_exp"]
err = fit_data["I_errr_exp"]
#fig.add_subplot(gs[0:2,0:2])
fig.add_subplot(gs[0:3,5:])
plt.imshow(fit_data["exp_image"], cmap = "gray")
plt.yticks([0,125,250])
fig.add_subplot(gs[3:6,5:])
plt.imshow(fit_data["th_image"], cmap = "gray")
#plt.xticks([], [])
plt.xticks([0,125,250])
plt.yticks([0,125,250])
fig.add_subplot(gs[3:6,0:5])
plt.plot(I_radius* 0.532,I_r_exp,label = "Experiment", linewidth = 0.8)
#plt.fill_between(I_radius* 0.532,I_r_exp-err,I_r_exp+err, alpha = 0.7)
plt.plot(I_radius* 0.532,theo_exp,label = "Theory",linewidth = 0.8)
plt.ylabel("$I/I_0$ ", fontsize = "x-small", labelpad=0.5)
plt.xlabel("radial distance ($\mathrm{\mu m}$)", fontsize = "x-small", labelpad=0.5)
plt.legend(fontsize = 5,frameon = False, loc = "lower right")
plt.tight_layout(pad = 0.01)
plt.savefig("exp.svg")
x = dataset["x"]
y = dataset["y"]
z = dataset["z"]- np.min(dataset["z"])
import matplotlib as mpl
def axisEqual3D(ax):
extents = np.array([getattr(ax, 'get_{}lim'.format(dim))() for dim in 'xyz'])
sz = extents[:,1] - extents[:,0]
centers = np.mean(extents, axis=1)
maxsize = max(abs(sz))
r = maxsize/2
for ctr, dim in zip(centers, 'xyz'):
getattr(ax, 'set_{}lim'.format(dim))(ctr - r, ctr + r)
from matplotlib.ticker import MultipleLocator
N = 200
cmap = plt.get_cmap('jet')
fig = plt.figure(figsize=(cm2inch(8.6)/1.5, 0.75*cm2inch(8.6)/1.68))
#plt.figaspect(0.21)*1.5
ax = fig.gca(projection='3d')
ax.pbaspect = [1, 20/25, 3/25*4]
ax.ticklabel_format(style = "sci")
for i in range(N-1):
ax.plot(x[i*360:i*360+360], y[i*360:i*360+360], z[i*360:i*360+360], color=plt.cm.jet(1*i/N), linewidth = 0.2)
norm = mpl.colors.Normalize(vmin=0,vmax=1)
sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])
ax = plt.gca()
ax.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
ax.w_yaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
#ax.w_zaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
plt.rcParams['grid.color'] = "gray"
ax.grid(False)
#ax.w_xaxis._axinfo.update({'grid' : {'color': (0, 0, 0, 1)}})
#ax.w_yaxis._axinfo.update({'grid' : {'color': (0, 0, 0, 1)}})
#ax.w_zaxis._axinfo.update({'grid' : {'color': (0, 0, 0, 1)}})
ax.set_ylim([25,45])
ax.set_xlim([15,40])
#plt.xticks([20,30,40])
#plt.yticks([30,35,40])
ax.set_zticks([0,1.5,3])
plt.xlabel("$x$ ($\mathrm{\mu m}$)",fontsize = "small", labelpad=0.5)
plt.ylabel("$y$ ($\mathrm{\mu m}$)",fontsize = "small", labelpad=0.5)
ax.set_zlabel("$z$ ($\mathrm{\mu m}$)",fontsize = "small", labelpad=0.5)
ax.view_init(10,45)
ax.grid(False)
ax.xaxis.pane.set_edgecolor('black')
ax.yaxis.pane.set_edgecolor('black')
ax.xaxis.pane.fill = False
ax.yaxis.pane.fill = False
ax.zaxis.pane.fill = False
[t.set_va('center') for t in ax.get_yticklabels()]
[t.set_ha('left') for t in ax.get_yticklabels()]
[t.set_va('center') for t in ax.get_xticklabels()]
[t.set_ha('right') for t in ax.get_xticklabels()]
[t.set_va('center') for t in ax.get_zticklabels()]
[t.set_ha('left') for t in ax.get_zticklabels()]
ax.xaxis._axinfo['tick']['inward_factor'] = 0
ax.xaxis._axinfo['tick']['outward_factor'] = 0.4
ax.yaxis._axinfo['tick']['inward_factor'] = 0
ax.yaxis._axinfo['tick']['outward_factor'] = 0.4
ax.zaxis._axinfo['tick']['inward_factor'] = 0
ax.zaxis._axinfo['tick']['outward_factor'] = 0.4
ax.zaxis._axinfo['tick']['outward_factor'] = 0.4
ax.view_init(elev=5, azim=135)
#ax.xaxis.set_major_locator(MultipleLocator(1))
#ax.yaxis.set_major_locator(MultipleLocator(5))
#ax.zaxis.set_major_locator(MultipleLocator())
ticks_c = []
for i in np.linspace(0,1,5):
ticks_c.append("{:.0f}".format(N*360*i/60/60))
cbar = plt.colorbar(sm, ticks=np.linspace(0,1,5), format = "%.1f",shrink = 0.4,orientation='horizontal')
cbar.set_ticklabels(ticks_c)
cbar.set_label("$t$ (min)", labelpad=0.5)
plt.tight_layout(h_pad=0.1)
plt.savefig("traj.svg")
dir(ax)
20/25*0.55
ticks_c = []
for i in np.linspace(0,1,10):
ticks_c.append("{:.0f} m".format(N*500*i/60/60))
ticks_c
200*360
fig = plt.figure(figsize=(cm2inch(8.6), 1*cm2inch(8.6)/1.68),constrained_layout=False)
gs = fig.add_gridspec(1,10)
fig.add_subplot(gs[0,0:5], projection='3d')
N = 200
cmap = plt.get_cmap('jet')
ax = plt.gca()
ax.ticklabel_format(style = "sci")
ax.pbaspect = [1, 15/25, 0.25/25*4]
for i in range(N-1):
ax.plot(x[i*500:i*500+500], y[i*500:i*500+500], z[i*500:i*500+500], color=plt.cm.jet(1*i/N), linewidth = 0.2)
norm = mpl.colors.Normalize(vmin=0,vmax=1)
sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])
ax = plt.gca()
ax.pbaspect = [1, 20/25, 3/25*4]
plt.xlabel("x [$\mathrm{\mu m}$]")
plt.ylabel("y [$\mathrm{\mu m}$]")
ax.set_zlabel("z [$\mathrm{\mu m}$]")
ax.grid(False)
#ax.view_init(30, -10)
#ax.view_init(20, -1)
ticks_c = []
for i in np.linspace(0,1,10):
ticks_c.append("{:.0f} min".format(N*500*i/60/60))
cbar = plt.colorbar(sm, ticks=np.linspace(0,1,10), format = "%.1f",orientation='horizontal')
cbar.set_ticklabels(ticks_c)
#########
fig.add_subplot(gs[0,7:])
plt.plot(dataset["x_pdf_z"] * 1e6,dataset["Pb_th"])
plt.semilogy(dataset["x_pdf_z"] * 1e6 - dataset["offset_B"],dataset["pdf_z"], "o", markersize = 4)
plt.xlabel("$z$ ($\mathrm{\mu m}$)",fontsize = "small")
plt.ylabel("$P(z)$ (a.u.)",fontsize = "small")
ax = plt.gca()
ax.set_ylim([1e-2,3])
ax.set_xlim([-0.2,1])
plt.xticks([0,1,2])
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.yaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.yaxis.set_minor_locator(locmin)
ax.yaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.text(0.8*xmax,1.2*ymin,'b)')
plt.tight_layout(pad = 0.01)
plt.savefig("viscosityxpdfz.pdf")
fig = plt.figure(figsize=(cm2inch(8.6), 0.75*cm2inch(8.6)/1.68),constrained_layout=False)
gs = fig.add_gridspec(10,1)
fig.add_subplot(gs[0:2,0])
plt.plot(np.arange(len(z))/60,z)
plt.xlabel("time (s)")
plt.ylabel("$z$ ($\mathrm{\mu m}$)")
#########
fig.add_subplot(gs[5:,0])
plt.plot(dataset["x_pdf_z"] * 1e6,dataset["Pb_th"])
plt.semilogy(dataset["x_pdf_z"] * 1e6 - dataset["offset_B"],dataset["pdf_z"], "o", markersize = 4)
plt.xlabel("$z$ ($\mathrm{\mu m}$)",fontsize = "small")
plt.ylabel("$P(z)$ (a.u.)",fontsize = "small")
ax = plt.gca()
ax.set_ylim([1e-2,3])
ax.set_xlim([-0.2,1])
plt.xticks([0,1,2])
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.yaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.yaxis.set_minor_locator(locmin)
ax.yaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
plt.text(0.8*xmax,1.2*ymin,'b)')
plt.tight_layout(pad = 0.01,h_pad=0.001, w_pad=0.1)
plt.savefig("viscosityxpdfz.pdf")
bins_center
dataset["B"]
t = np.arange(len(z))/60
for n,i in enumerate(['pdf_Dz_short_t_1', 'pdf_Dz_short_t_2', 'pdf_Dz_short_t_3', 'pdf_Dz_short_t_4', 'pdf_Dz_short_t_5']):
plt.semilogy(dataset[i][0,:],dataset[i][1,:], color = color[n], marker = "o", linestyle = "",markersize = 6)
plt.plot(dataset["pdf_Dz_short_th_t_5"][0,:],dataset["pdf_Dz_short_th_t_5"][1,:], color = color[4])
plt.plot(dataset["gaussia_short_timetheory"][0,:],dataset["gaussia_short_timetheory"][1,:], color = "gray",linestyle = "--")
ax = plt.gca()
locmaj = mpl.ticker.LogLocator(base=10.0, subs=(1.0, ), numticks=100)
ax.yaxis.set_major_locator(locmaj)
locmin = mpl.ticker.LogLocator(base=10.0, subs=np.arange(2, 10) * .1,
numticks=100)
ax.yaxis.set_minor_locator(locmin)
ax.yaxis.set_minor_formatter(mpl.ticker.NullFormatter())
ax.set_ylim([1e-5,3])
ax.set_xlim([-7,7])
plt.xlabel("$\Delta z / \sigma$",fontsize = "small")
plt.ylabel("$P(\Delta z / \sigma)$",fontsize = "small")
ymin, ymax = fig.gca().get_ylim()
xmin, xmax = fig.gca().get_xlim()
from matplotlib.ticker import MultipleLocator
N = 200
cmap = plt.get_cmap('jet')
fig = plt.figure(figsize=(cm2inch(8.6)/1.5, 1.2*cm2inch(8.6)/1.68))
#plt.figaspect(0.21)*1.5
ax = fig.gca(projection='3d')
ax.pbaspect = [1, 20/25, 3/25*4]
ax.ticklabel_format(style = "sci")
for i in range(N-1):
ax.plot(x[i*360:i*360+360], y[i*360:i*360+360], z[i*360:i*360+360], color=plt.cm.jet(1*i/N), linewidth = 0.2)
norm = mpl.colors.Normalize(vmin=0,vmax=1)
sm = plt.cm.ScalarMappable(cmap=cmap, norm=norm)
sm.set_array([])
ax = plt.gca()
ax.w_xaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
ax.w_yaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
#ax.w_zaxis.set_pane_color((1.0, 1.0, 1.0, 1.0))
plt.rcParams['grid.color'] = "gray"
ax.grid(False)
#ax.w_xaxis._axinfo.update({'grid' : {'color': (0, 0, 0, 1)}})
#ax.w_yaxis._axinfo.update({'grid' : {'color': (0, 0, 0, 1)}})
#ax.w_zaxis._axinfo.update({'grid' : {'color': (0, 0, 0, 1)}})
ax.set_ylim([25,45])
ax.set_xlim([15,40])
#plt.xticks([20,30,40])
#plt.yticks([30,35,40])
#ax.set_zticks([0,1.5,3])
plt.xlabel("$x$ ($\mathrm{\mu m}$)",fontsize = "small")
plt.ylabel("$y$ ($\mathrm{\mu m}$)",fontsize = "small")
ax.set_zlabel("$z$ ($\mathrm{\mu m}$)",fontsize = "small")
#ax.view_init(10,45)
ax.grid(False)
ax.xaxis.pane.set_edgecolor('black')
ax.yaxis.pane.set_edgecolor('black')
ax.xaxis.pane.fill = False
ax.yaxis.pane.fill = False
ax.zaxis.pane.fill = False
[t.set_va('center') for t in ax.get_yticklabels()]
[t.set_ha('left') for t in ax.get_yticklabels()]
[t.set_va('center') for t in ax.get_xticklabels()]
[t.set_ha('right') for t in ax.get_xticklabels()]
[t.set_va('center') for t in ax.get_zticklabels()]
[t.set_ha('left') for t in ax.get_zticklabels()]
ax.xaxis._axinfo['tick']['inward_factor'] = 0
ax.xaxis._axinfo['tick']['outward_factor'] = 0.4
ax.yaxis._axinfo['tick']['inward_factor'] = 0
ax.yaxis._axinfo['tick']['outward_factor'] = 0.4
ax.zaxis._axinfo['tick']['inward_factor'] = 0
ax.zaxis._axinfo['tick']['outward_factor'] = 0.4
ax.zaxis._axinfo['tick']['outward_factor'] = 0.4
ax.view_init(elev=10, azim=135)
#ax.xaxis.set_major_locator(MultipleLocator(1))
#ax.yaxis.set_major_locator(MultipleLocator(5))
#ax.zaxis.set_major_locator(MultipleLocator())
ticks_c = []
for i in np.linspace(0,1,5):
ticks_c.append("{:.0f}".format(N*360*i/60/60))
cbar = plt.colorbar(sm, ticks=np.linspace(0,1,5), format = "%.1f",shrink = 0.4,orientation='horizontal')
cbar.set_ticklabels(ticks_c)
plt.tight_layout(h_pad=0.1)
plt.savefig("traj.svg")
```
| github_jupyter |
#### Copyright 2017 Google LLC.
```
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Mejora del rendimiento de las redes neuronales
**Objetivo de aprendizaje:** mejorar el rendimiento de una red neuronal al normalizar los atributos y aplicar diversos algoritmos de optimización
**NOTA:** Los métodos de optimización que se describen en este ejercicio no son específicos para las redes neuronales; son medios eficaces para mejorar la mayoría de los tipos de modelos.
## Preparación
Primero, cargaremos los datos.
```
from __future__ import print_function
import math
from IPython import display
from matplotlib import cm
from matplotlib import gridspec
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
from sklearn import metrics
import tensorflow as tf
from tensorflow.python.data import Dataset
tf.logging.set_verbosity(tf.logging.ERROR)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
california_housing_dataframe = pd.read_csv("https://download.mlcc.google.com/mledu-datasets/california_housing_train.csv", sep=",")
california_housing_dataframe = california_housing_dataframe.reindex(
np.random.permutation(california_housing_dataframe.index))
def preprocess_features(california_housing_dataframe):
"""Prepares input features from California housing data set.
Args:
california_housing_dataframe: A Pandas DataFrame expected to contain data
from the California housing data set.
Returns:
A DataFrame that contains the features to be used for the model, including
synthetic features.
"""
selected_features = california_housing_dataframe[
["latitude",
"longitude",
"housing_median_age",
"total_rooms",
"total_bedrooms",
"population",
"households",
"median_income"]]
processed_features = selected_features.copy()
# Create a synthetic feature.
processed_features["rooms_per_person"] = (
california_housing_dataframe["total_rooms"] /
california_housing_dataframe["population"])
return processed_features
def preprocess_targets(california_housing_dataframe):
"""Prepares target features (i.e., labels) from California housing data set.
Args:
california_housing_dataframe: A Pandas DataFrame expected to contain data
from the California housing data set.
Returns:
A DataFrame that contains the target feature.
"""
output_targets = pd.DataFrame()
# Scale the target to be in units of thousands of dollars.
output_targets["median_house_value"] = (
california_housing_dataframe["median_house_value"] / 1000.0)
return output_targets
# Choose the first 12000 (out of 17000) examples for training.
training_examples = preprocess_features(california_housing_dataframe.head(12000))
training_targets = preprocess_targets(california_housing_dataframe.head(12000))
# Choose the last 5000 (out of 17000) examples for validation.
validation_examples = preprocess_features(california_housing_dataframe.tail(5000))
validation_targets = preprocess_targets(california_housing_dataframe.tail(5000))
# Double-check that we've done the right thing.
print("Training examples summary:")
display.display(training_examples.describe())
print("Validation examples summary:")
display.display(validation_examples.describe())
print("Training targets summary:")
display.display(training_targets.describe())
print("Validation targets summary:")
display.display(validation_targets.describe())
```
## Entrenamiento de la red neuronal
A continuación, entrenaremos la red neuronal.
```
def construct_feature_columns(input_features):
"""Construct the TensorFlow Feature Columns.
Args:
input_features: The names of the numerical input features to use.
Returns:
A set of feature columns
"""
return set([tf.feature_column.numeric_column(my_feature)
for my_feature in input_features])
def my_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):
"""Trains a neural network model.
Args:
features: pandas DataFrame of features
targets: pandas DataFrame of targets
batch_size: Size of batches to be passed to the model
shuffle: True or False. Whether to shuffle the data.
num_epochs: Number of epochs for which data should be repeated. None = repeat indefinitely
Returns:
Tuple of (features, labels) for next data batch
"""
# Convert pandas data into a dict of np arrays.
features = {key:np.array(value) for key,value in dict(features).items()}
# Construct a dataset, and configure batching/repeating.
ds = Dataset.from_tensor_slices((features,targets)) # warning: 2GB limit
ds = ds.batch(batch_size).repeat(num_epochs)
# Shuffle the data, if specified.
if shuffle:
ds = ds.shuffle(10000)
# Return the next batch of data.
features, labels = ds.make_one_shot_iterator().get_next()
return features, labels
def train_nn_regression_model(
my_optimizer,
steps,
batch_size,
hidden_units,
training_examples,
training_targets,
validation_examples,
validation_targets):
"""Trains a neural network regression model.
In addition to training, this function also prints training progress information,
as well as a plot of the training and validation loss over time.
Args:
my_optimizer: An instance of `tf.train.Optimizer`, the optimizer to use.
steps: A non-zero `int`, the total number of training steps. A training step
consists of a forward and backward pass using a single batch.
batch_size: A non-zero `int`, the batch size.
hidden_units: A `list` of int values, specifying the number of neurons in each layer.
training_examples: A `DataFrame` containing one or more columns from
`california_housing_dataframe` to use as input features for training.
training_targets: A `DataFrame` containing exactly one column from
`california_housing_dataframe` to use as target for training.
validation_examples: A `DataFrame` containing one or more columns from
`california_housing_dataframe` to use as input features for validation.
validation_targets: A `DataFrame` containing exactly one column from
`california_housing_dataframe` to use as target for validation.
Returns:
A tuple `(estimator, training_losses, validation_losses)`:
estimator: the trained `DNNRegressor` object.
training_losses: a `list` containing the training loss values taken during training.
validation_losses: a `list` containing the validation loss values taken during training.
"""
periods = 10
steps_per_period = steps / periods
# Create a DNNRegressor object.
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
dnn_regressor = tf.estimator.DNNRegressor(
feature_columns=construct_feature_columns(training_examples),
hidden_units=hidden_units,
optimizer=my_optimizer
)
# Create input functions.
training_input_fn = lambda: my_input_fn(training_examples,
training_targets["median_house_value"],
batch_size=batch_size)
predict_training_input_fn = lambda: my_input_fn(training_examples,
training_targets["median_house_value"],
num_epochs=1,
shuffle=False)
predict_validation_input_fn = lambda: my_input_fn(validation_examples,
validation_targets["median_house_value"],
num_epochs=1,
shuffle=False)
# Train the model, but do so inside a loop so that we can periodically assess
# loss metrics.
print("Training model...")
print("RMSE (on training data):")
training_rmse = []
validation_rmse = []
for period in range (0, periods):
# Train the model, starting from the prior state.
dnn_regressor.train(
input_fn=training_input_fn,
steps=steps_per_period
)
# Take a break and compute predictions.
training_predictions = dnn_regressor.predict(input_fn=predict_training_input_fn)
training_predictions = np.array([item['predictions'][0] for item in training_predictions])
validation_predictions = dnn_regressor.predict(input_fn=predict_validation_input_fn)
validation_predictions = np.array([item['predictions'][0] for item in validation_predictions])
# Compute training and validation loss.
training_root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(training_predictions, training_targets))
validation_root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(validation_predictions, validation_targets))
# Occasionally print the current loss.
print(" period %02d : %0.2f" % (period, training_root_mean_squared_error))
# Add the loss metrics from this period to our list.
training_rmse.append(training_root_mean_squared_error)
validation_rmse.append(validation_root_mean_squared_error)
print("Model training finished.")
# Output a graph of loss metrics over periods.
plt.ylabel("RMSE")
plt.xlabel("Periods")
plt.title("Root Mean Squared Error vs. Periods")
plt.tight_layout()
plt.plot(training_rmse, label="training")
plt.plot(validation_rmse, label="validation")
plt.legend()
print("Final RMSE (on training data): %0.2f" % training_root_mean_squared_error)
print("Final RMSE (on validation data): %0.2f" % validation_root_mean_squared_error)
return dnn_regressor, training_rmse, validation_rmse
_ = train_nn_regression_model(
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.0007),
steps=5000,
batch_size=70,
hidden_units=[10, 10],
training_examples=training_examples,
training_targets=training_targets,
validation_examples=validation_examples,
validation_targets=validation_targets)
```
## Ajuste lineal
Una buena práctica estándar puede ser normalizar las entradas para que estén dentro del rango -1, 1. Esto ayuda al SGD a no bloquearse al realizar pasos que son demasiado grandes en una dimensión o demasiado pequeños en otra. Los apasionados de la optimización numérica pueden observar aquí una relación con la idea de usar un precondicionador.
```
def linear_scale(series):
min_val = series.min()
max_val = series.max()
scale = (max_val - min_val) / 2.0
return series.apply(lambda x:((x - min_val) / scale) - 1.0)
```
## Tarea 1: Normalizar los atributos con ajuste lineal
**Normaliza las entradas a la escala -1, 1.**
**Dedica alrededor de 5 minutos a entrenar y evaluar los datos recientemente normalizados. ¿Qué nivel de eficacia puedes tener?**
Como regla general, las redes neuronales se entrenan mejor cuando los atributos de entrada están casi en la misma escala.
Realiza una comprobación de estado de tus datos normalizados. (¿Qué ocurriría si olvidaras normalizar un atributo?)
```
def normalize_linear_scale(examples_dataframe):
"""Returns a version of the input `DataFrame` that has all its features normalized linearly."""
#
# Your code here: normalize the inputs.
#
pass
normalized_dataframe = normalize_linear_scale(preprocess_features(california_housing_dataframe))
normalized_training_examples = normalized_dataframe.head(12000)
normalized_validation_examples = normalized_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.0007),
steps=5000,
batch_size=70,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
### Solución
Haz clic más abajo para conocer una solución posible.
Dado que la normalización usa mín. y máx., debemos asegurarnos de que esta se realice en todo el conjunto de datos a la vez.
En este caso podemos hacerlo, porque todos nuestros datos están en un mismo DataFrame. Si tuviéramos varios conjuntos de datos, una buena práctica sería derivar los parámetros de normalización del conjunto de entrenamiento y aplicarlos de manera idéntica al conjunto de prueba.
```
def normalize_linear_scale(examples_dataframe):
"""Returns a version of the input `DataFrame` that has all its features normalized linearly."""
processed_features = pd.DataFrame()
processed_features["latitude"] = linear_scale(examples_dataframe["latitude"])
processed_features["longitude"] = linear_scale(examples_dataframe["longitude"])
processed_features["housing_median_age"] = linear_scale(examples_dataframe["housing_median_age"])
processed_features["total_rooms"] = linear_scale(examples_dataframe["total_rooms"])
processed_features["total_bedrooms"] = linear_scale(examples_dataframe["total_bedrooms"])
processed_features["population"] = linear_scale(examples_dataframe["population"])
processed_features["households"] = linear_scale(examples_dataframe["households"])
processed_features["median_income"] = linear_scale(examples_dataframe["median_income"])
processed_features["rooms_per_person"] = linear_scale(examples_dataframe["rooms_per_person"])
return processed_features
normalized_dataframe = normalize_linear_scale(preprocess_features(california_housing_dataframe))
normalized_training_examples = normalized_dataframe.head(12000)
normalized_validation_examples = normalized_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.005),
steps=2000,
batch_size=50,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
## Tarea 2: Probar un optimizador diferente
** Usa los optmizadores AdaGrad y Adam, y compara el rendimiento.**
El optimizador AdaGrad es una alternativa. La idea clave de AdaGrad es que modifica la tasa de aprendizaje de forma adaptativa para cada coeficiente de un modelo, lo cual disminuye la tasa de aprendizaje efectiva de forma monótona. Esto funciona muy bien para los problemas convexos, pero no siempre resulta ideal para el entrenamiento de redes neuronales con problemas no convexos. Puedes usar AdaGrad al especificar `AdagradOptimizer` en lugar de `GradientDescentOptimizer`. Ten en cuenta que, con AdaGrad, es posible que debas usar una tasa de aprendizaje más alta.
Para los problemas de optimización no convexos, en algunas ocasiones Adam es más eficaz que AdaGrad. Para usar Adam, invoca el método `tf.train.AdamOptimizer`. Este método toma varios hiperparámetros opcionales como argumentos, pero nuestra solución solo especifica uno de estos (`learning_rate`). En un entorno de producción, debes especificar y ajustar los hiperparámetros opcionales con cuidado.
```
#
# YOUR CODE HERE: Retrain the network using Adagrad and then Adam.
#
```
### Solución
Haz clic más abajo para conocer la solución.
Primero, probemos AdaGrad.
```
_, adagrad_training_losses, adagrad_validation_losses = train_nn_regression_model(
my_optimizer=tf.train.AdagradOptimizer(learning_rate=0.5),
steps=500,
batch_size=100,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
Ahora, probemos Adam.
```
_, adam_training_losses, adam_validation_losses = train_nn_regression_model(
my_optimizer=tf.train.AdamOptimizer(learning_rate=0.009),
steps=500,
batch_size=100,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
Imprimamos un gráfico de métricas de pérdida en paralelo.
```
plt.ylabel("RMSE")
plt.xlabel("Periods")
plt.title("Root Mean Squared Error vs. Periods")
plt.plot(adagrad_training_losses, label='Adagrad training')
plt.plot(adagrad_validation_losses, label='Adagrad validation')
plt.plot(adam_training_losses, label='Adam training')
plt.plot(adam_validation_losses, label='Adam validation')
_ = plt.legend()
```
## Tarea 3: Explorar métodos de normalización alternativos
**Prueba alternar las normalizaciones para distintos atributos a fin de mejorar aún más el rendimiento.**
Si observas detenidamente las estadísticas de resumen de los datos transformados, es posible que observes que, al realizar un ajuste lineal en algunos atributos, estos quedan agrupados cerca de `-1`.
Por ejemplo, muchos atributos tienen una mediana de alrededor de `-0.8`, en lugar de `0.0`.
```
_ = training_examples.hist(bins=20, figsize=(18, 12), xlabelsize=2)
```
Es posible que obtengamos mejores resultados al elegir formas adicionales para transformar estos atributos.
Por ejemplo, un ajuste logarítmico podría ayudar a algunos atributos. O bien, el recorte de los valores extremos podría hacer que el resto del ajuste sea más informativo.
```
def log_normalize(series):
return series.apply(lambda x:math.log(x+1.0))
def clip(series, clip_to_min, clip_to_max):
return series.apply(lambda x:(
min(max(x, clip_to_min), clip_to_max)))
def z_score_normalize(series):
mean = series.mean()
std_dv = series.std()
return series.apply(lambda x:(x - mean) / std_dv)
def binary_threshold(series, threshold):
return series.apply(lambda x:(1 if x > threshold else 0))
```
El bloque anterior contiene algunas funciones de normalización adicionales posibles. Prueba algunas de estas o agrega otras propias.
Ten en cuenta que, si normalizas el objetivo, deberás anular la normalización de las predicciones para que las métricas de pérdida sean comparables.
```
def normalize(examples_dataframe):
"""Returns a version of the input `DataFrame` that has all its features normalized."""
#
# YOUR CODE HERE: Normalize the inputs.
#
pass
normalized_dataframe = normalize(preprocess_features(california_housing_dataframe))
normalized_training_examples = normalized_dataframe.head(12000)
normalized_validation_examples = normalized_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.0007),
steps=5000,
batch_size=70,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
### Solución
Haz clic más abajo para conocer una solución posible.
Estas son solo algunas formas en las que podemos pensar acerca de los datos. Otras transformaciones podrían funcionar incluso mejor.
Las funciones `households`, `median_income` y `total_bedrooms` aparecen todas distribuidas normalmente en un espacio logarítmico.
Las funciones `latitude`, `longitude` y `housing_median_age` probablemente serían mejores si solamente se ajustaran de forma lineal, como antes.
Las funciones `population`, `totalRooms` y `rooms_per_person` tienen algunos valores atípicos extremos. Parecen ser demasiado extremos como para que la normalización logarítmica resulte útil. Por lo tanto, los recortaremos en su lugar.
```
def normalize(examples_dataframe):
"""Returns a version of the input `DataFrame` that has all its features normalized."""
processed_features = pd.DataFrame()
processed_features["households"] = log_normalize(examples_dataframe["households"])
processed_features["median_income"] = log_normalize(examples_dataframe["median_income"])
processed_features["total_bedrooms"] = log_normalize(examples_dataframe["total_bedrooms"])
processed_features["latitude"] = linear_scale(examples_dataframe["latitude"])
processed_features["longitude"] = linear_scale(examples_dataframe["longitude"])
processed_features["housing_median_age"] = linear_scale(examples_dataframe["housing_median_age"])
processed_features["population"] = linear_scale(clip(examples_dataframe["population"], 0, 5000))
processed_features["rooms_per_person"] = linear_scale(clip(examples_dataframe["rooms_per_person"], 0, 5))
processed_features["total_rooms"] = linear_scale(clip(examples_dataframe["total_rooms"], 0, 10000))
return processed_features
normalized_dataframe = normalize(preprocess_features(california_housing_dataframe))
normalized_training_examples = normalized_dataframe.head(12000)
normalized_validation_examples = normalized_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.AdagradOptimizer(learning_rate=0.15),
steps=1000,
batch_size=50,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
## Desafío opcional: Usar solo los atributos de latitud y longitud
**Entrena un modelo de red neuronal que use solo latitud y longitud como atributos.**
A los agentes de bienes raíces les gusta decir que la ubicación es el único atributo importante en el precio de la vivienda.
Veamos si podemos confirmar esto al entrenar un modelo que use solo latitud y longitud como atributos.
Esto funcionará bien únicamente si nuestra red neuronal puede aprender no linealidades complejas a partir de la latitud y la longitud.
**NOTA:** Es posible que necesitemos una estructura de red que tenga más capas que las que eran útiles anteriormente en el ejercicio.
```
#
# YOUR CODE HERE: Train the network using only latitude and longitude
#
```
### Solución
Haz clic más abajo para conocer una solución posible.
Una buena idea es mantener latitud y longitud normalizadas:
```
def location_location_location(examples_dataframe):
"""Returns a version of the input `DataFrame` that keeps only the latitude and longitude."""
processed_features = pd.DataFrame()
processed_features["latitude"] = linear_scale(examples_dataframe["latitude"])
processed_features["longitude"] = linear_scale(examples_dataframe["longitude"])
return processed_features
lll_dataframe = location_location_location(preprocess_features(california_housing_dataframe))
lll_training_examples = lll_dataframe.head(12000)
lll_validation_examples = lll_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.AdagradOptimizer(learning_rate=0.05),
steps=500,
batch_size=50,
hidden_units=[10, 10, 5, 5, 5],
training_examples=lll_training_examples,
training_targets=training_targets,
validation_examples=lll_validation_examples,
validation_targets=validation_targets)
```
Esto no es tan malo para solo dos funciones. De todos modos, los valores de la propiedad pueden variar en distancias cortas.
| github_jupyter |
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interpn
import os
import config
import utils
# Read measured profiles
measuredDoseFiles10 = ['./Measured/Method3/PDD1_10x10.dat','./Measured/Method3/PDD2_10x10.dat',
'./Measured/Method3/PROF1_10x10_14mm.dat','./Measured/Method3/PROF2_10x10_14mm.dat',
'./Measured/Method3/PROF1_10x10_100mm.dat','./Measured/Method3/PROF2_10x10_100mm.dat']
measuredDoseFiles30 = ['./Measured/Method3/PDD1_30x30.dat',
'./Measured/Method3/PROF1_30x30_14mm.dat','./Measured/Method3/PROF2_30x30_14mm.dat',
'./Measured/Method3/PROF1_30x30_100mm.dat','./Measured/Method3/PROF2_30x30_100mm.dat']
clinicalProfiles = []
xStart = [0,0,-8.1,-8.1,-8.8,-8.8]
profiles = []
for n, measuredDoseFile in enumerate(measuredDoseFiles10):
f = open(measuredDoseFile)
lines = f.readlines()
f.close()
x = np.asarray([l.split() for l in lines[:-1]],dtype=np.float)
x[:,0] = x[:,0]/10.
interpRange = np.arange(xStart[n],x[x.shape[0]-1,0]+config.spaceStep/2,config.spaceStep)
profile = interpn((x[:,0],),x[:,1] , interpRange)
print(profile.shape,interpRange.shape,profile[0],profile[profile.shape[0]-1],interpRange[0],interpRange[interpRange.shape[0]-1])
profiles.append(profile)
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[1][0][0]:config.analyzedRanges[1][0][1]],(profiles[0][3:]+profiles[1][3:])*0.5)
scale = dum[12]
dum = dum*100.0/scale
clinicalProfiles.append(dum) #Field 10x10 depth profile from 0.3 to 30.0 (both included)
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[1][1][0]:config.analyzedRanges[1][1][1]],0.5*(profiles[2]+profiles[3]))
dum = dum*100.0/scale
clinicalProfiles.append(dum) #Field 10x10 lateral profile at depth 14mm from -8.1 to 8.1 cm, both included
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[1][2][0]:config.analyzedRanges[1][2][1]],0.5*(profiles[4]+profiles[5]))
dum = dum*100.0/scale
clinicalProfiles.append(dum) #Field 10x10 lateral profile at depth 100mm from -8.8 to 8.8 cm, both included
xStart = [0,-18.2,-18.2,-19.7,-19.7]
profiles = []
for n, measuredDoseFile in enumerate(measuredDoseFiles30):
f = open(measuredDoseFile)
lines = f.readlines()
f.close()
x = np.asarray([l.split() for l in lines[:-1]],dtype=np.float)
x[:,0] = x[:,0]/10.
interpRange = np.arange(xStart[n],np.round(x[x.shape[0]-1,0],2)-config.spaceStep/2,config.spaceStep)
profile = interpn((x[:,0],),x[:,1] , interpRange)
print(profile.shape,interpRange.shape,interpRange[0],interpRange[interpRange.shape[0]-1])
profiles.append(profile)
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[2][0][0]:config.analyzedRanges[2][0][1]],profiles[0][3:])
scale = dum[12]
dum = dum*100/scale
clinicalProfiles.append(dum) #Field 30x30 lateral profile at depth 1.4cm from -18.2 to 18.2 cm, both included
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[2][1][0]:config.analyzedRanges[2][1][1]],0.5*(profiles[1]+profiles[2]))
dum = dum*100/scale
clinicalProfiles.append(dum) #Field 30x30 lateral profile at depth 1.4cm from -18.2 to 18.2 cm, both included
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[2][2][0]:config.analyzedRanges[2][2][1]],0.5*(profiles[3]+profiles[4]))
dum = dum*100/scale
clinicalProfiles.append(dum) #Field 30x30 lateral profile at depth 10cm from -19.7 to 19.7 cm, both included
#plt.figure(figsize=(10,10))
#plt.plot(clinicalProfiles[0])
#plt.plot(clinicalProfiles[1])
#plt.show()
#plt.figure(figsize=(10,10))
#plt.plot(clinicalProfiles[2],'r-')
#plt.plot(clinicalProfiles[3],'g-')
#plt.show()
means = np.load(config.modelDIR + config.meansFileName)
print(means.shape,clinicalProfiles[0].shape) #(3, 6, 487) (487,)
diffTest = np.zeros((3,1,6,config.numOfSimulatedProfileSamples),dtype=np.float)
#Field 10
diff = clinicalProfiles[0] - means[1,0]
np.copyto(diffTest[1,0,0,:],diff)
diff = clinicalProfiles[1] - means[1,1]
np.copyto(diffTest[1,0,1,:],diff)
diff = clinicalProfiles[2] - means[1,3]
np.copyto(diffTest[1,0,3,:],diff)
#Field 30
diff = clinicalProfiles[3] - means[2,0]
np.copyto(diffTest[2,0,0,:],diff)
diff = clinicalProfiles[4] - means[2,1]
np.copyto(diffTest[2,0,1,:],diff)
diff = clinicalProfiles[5] - means[2,3]
np.copyto(diffTest[2,0,3,:],diff)
print(diffTest.shape)
from sklearn.decomposition import PCA
import pickle
testFeatures = []
for nfield,(field,Ranges) in enumerate(zip(config.analyzedProfiles,config.analyzedRanges)):
if field != None:
for profile,Range in zip(field,Ranges):
print(nfield,profile)
pcaName = config.modelDIR + 'PCA_' + str(nfield) + '_' + str(profile) + '_.pkl'
pca = pickle.load(open(pcaName,'rb'))
X = diffTest[nfield][:,profile,Range[0]:Range[1]]
X_projected = pca.transform(X)
testFeatures.append(X_projected)
X_test = np.stack(testFeatures)
X_test = np.swapaxes(X_test,1,0)
X_test = np.reshape(X_test,(X_test.shape[0],X_test.shape[1]*X_test.shape[2]))
print(X_test.shape)
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
preds = []
for goal in [0,1,2,3]:
modelName = config.modelDIR + 'SVR_' + str(goal) + '_.pkl'
clf = pickle.load(open(modelName,'rb'))
predTest = clf.predict(X_test)
preds.append(predTest[0])
print(preds)
allMeans,allFieldFeatures,allFieldPCAModels = utils.allPCAResults()
recons = utils.reconstruct(preds,allMeans,allFieldFeatures,allFieldPCAModels)
print(preds)
print(utils.difference(preds,clinicalProfiles,allMeans,allFieldFeatures,allFieldPCAModels))
# Optimize solution
# https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html
# https://scipy-lectures.org/advanced/mathematical_optimization/auto_examples/plot_non_bounds_constraints.html
preds = [5.62,0.5,0.27, 2.46] # from DeepBeam
import scipy.optimize as opt
from scipy.optimize import SR1
def fun(cP,aM,aF,aPCA):
def diff(y):
return utils.difference(y,cP,aM,aF,aPCA)
return diff
difference = fun(clinicalProfiles,allMeans,allFieldFeatures,allFieldPCAModels)
res = opt.minimize(difference, preds, method='SLSQP', jac="2-point",
options={'ftol': 1e-9, 'disp': True},
bounds=config.bounds)
print(res.x)
```
```
recons = utils.reconstruct(res.x,allMeans,allFieldFeatures,allFieldPCAModels)
plt.rcParams.update({'font.size': 18})
fig, (axs1,axs2) = plt.subplots(1, 2,figsize = (20,10))
for n in [0,3]:
if n==0:
axs1.plot(np.arange(0.3,30.05,0.1),clinicalProfiles[n][config.allRanges[n][0]:config.allRanges[n][1]],'r--',label='real profiles')
axs1.plot(np.arange(0.3,49.75,0.1),recons[n],'g-',label='predicted profiles')
else:
axs1.plot(np.arange(0.3,29.95,0.1),clinicalProfiles[n][config.allRanges[n][0]:config.allRanges[n][1]],'r--')
axs1.plot(np.arange(0.3,49.75,0.1),recons[n],'g-')
axs1.set(xlabel = 'depth [cm]',ylabel = '% of maximal dose')
axs1.legend(loc='upper right')
for n in [1,2,4,5]:
start = config.allRanges[n][0]*0.1 -24.7
end = config.allRanges[n][1]*0.1 - 24.7 - 0.05
if n==1:
axs2.plot(np.arange(start,end,0.1),clinicalProfiles[n][config.allRanges[n][0]:config.allRanges[n][1]],'r--',label='real profiles')
axs2.plot(np.arange(-24.7,24.75,0.1),recons[n],'g-',label='predicted profiles')
else:
axs2.plot(np.arange(start,end,0.1),clinicalProfiles[n][config.allRanges[n][0]:config.allRanges[n][1]],'r--')
axs2.plot(np.arange(-24.7,24.75,0.1),recons[n],'g-')
axs2.set(xlabel = 'off axis distance [cm]',ylabel = '% of maximal dose')
axs2.legend(loc='lower right')
plt.savefig('results3')
```
| github_jupyter |


```
import torch
import random
import numpy as np
random.seed(0)
np.random.seed(0)
torch.manual_seed(0)
torch.cuda.manual_seed(0)
torch.backends.cudnn.deterministic = True
import torchvision.datasets
CIFAR_train = torchvision.datasets.CIFAR10('./', download=True, train=True)
CIFAR_test = torchvision.datasets.CIFAR10('./', download=True, train=False)
X_train = torch.FloatTensor(CIFAR_train.data)
y_train = torch.LongTensor(CIFAR_train.targets)
X_test = torch.FloatTensor(CIFAR_test.data)
y_test = torch.LongTensor(CIFAR_test.targets)
len(y_train), len(y_test)
X_train.min(), X_train.max()
X_train /= 255.
X_test /= 255.
CIFAR_train.classes
import matplotlib.pyplot as plt
plt.figure(figsize=(20,2))
for i in range(10):
plt.subplot(1, 10, i+1)
plt.imshow(X_train[i])
print(y_train[i], end=' ')
X_train.shape, y_train.shape
X_train = X_train.permute(0, 3, 1, 2)
X_test = X_test.permute(0, 3, 1, 2)
X_train.shape
class LeNet5(torch.nn.Module):
def __init__(self,
activation='tanh',
pooling='avg',
conv_size=5,
use_batch_norm=False):
super(LeNet5, self).__init__()
self.conv_size = conv_size
self.use_batch_norm = use_batch_norm
if activation == 'tanh':
activation_function = torch.nn.Tanh()
elif activation == 'relu':
activation_function = torch.nn.ReLU()
else:
raise NotImplementedError
if pooling == 'avg':
pooling_layer = torch.nn.AvgPool2d(kernel_size=2, stride=2)
elif pooling == 'max':
pooling_layer = torch.nn.MaxPool2d(kernel_size=2, stride=2)
else:
raise NotImplementedError
if conv_size == 5:
self.conv1 = torch.nn.Conv2d(
in_channels=3, out_channels=6, kernel_size=5, padding=0)
elif conv_size == 3:
self.conv1_1 = torch.nn.Conv2d(
in_channels=3, out_channels=6, kernel_size=3, padding=0)
self.conv1_2 = torch.nn.Conv2d(
in_channels=6, out_channels=6, kernel_size=3, padding=0)
else:
raise NotImplementedError
self.act1 = activation_function
self.bn1 = torch.nn.BatchNorm2d(num_features=6)
self.pool1 = pooling_layer
if conv_size == 5:
self.conv2 = self.conv2 = torch.nn.Conv2d(
in_channels=6, out_channels=16, kernel_size=5, padding=0)
elif conv_size == 3:
self.conv2_1 = torch.nn.Conv2d(
in_channels=6, out_channels=16, kernel_size=3, padding=0)
self.conv2_2 = torch.nn.Conv2d(
in_channels=16, out_channels=16, kernel_size=3, padding=0)
else:
raise NotImplementedError
self.act2 = activation_function
self.bn2 = torch.nn.BatchNorm2d(num_features=16)
self.pool2 = pooling_layer
self.fc1 = torch.nn.Linear(5 * 5 * 16, 120)
self.act3 = activation_function
self.fc2 = torch.nn.Linear(120, 84)
self.act4 = activation_function
self.fc3 = torch.nn.Linear(84, 10)
def forward(self, x):
if self.conv_size == 5:
x = self.conv1(x)
elif self.conv_size == 3:
x = self.conv1_2(self.conv1_1(x))
x = self.act1(x)
if self.use_batch_norm:
x = self.bn1(x)
x = self.pool1(x)
if self.conv_size == 5:
x = self.conv2(x)
elif self.conv_size == 3:
x = self.conv2_2(self.conv2_1(x))
x = self.act2(x)
if self.use_batch_norm:
x = self.bn2(x)
x = self.pool2(x)
x = x.view(x.size(0), x.size(1) * x.size(2) * x.size(3))
x = self.fc1(x)
x = self.act3(x)
x = self.fc2(x)
x = self.act4(x)
x = self.fc3(x)
return x
def train(net, X_train, y_train, X_test, y_test):
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
net = net.to(device)
loss = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=1.0e-3)
batch_size = 100
test_accuracy_history = []
test_loss_history = []
X_test = X_test.to(device)
y_test = y_test.to(device)
for epoch in range(30):
order = np.random.permutation(len(X_train))
for start_index in range(0, len(X_train), batch_size):
optimizer.zero_grad()
net.train()
batch_indexes = order[start_index:start_index+batch_size]
X_batch = X_train[batch_indexes].to(device)
y_batch = y_train[batch_indexes].to(device)
preds = net.forward(X_batch)
loss_value = loss(preds, y_batch)
loss_value.backward()
optimizer.step()
X_batch
net.eval()
test_preds = net.forward(X_test)
test_loss_history.append(loss(test_preds, y_test).data.cpu())
accuracy = (test_preds.argmax(dim=1) == y_test).float().mean().data.cpu()
test_accuracy_history.append(accuracy)
print(accuracy)
del net
return test_accuracy_history, test_loss_history
accuracies = {}
losses = {}
accuracies['tanh'], losses['tanh'] = \
train(LeNet5(activation='tanh', conv_size=5),
X_train, y_train, X_test, y_test)
accuracies['relu'], losses['relu'] = \
train(LeNet5(activation='relu', conv_size=5),
X_train, y_train, X_test, y_test)
accuracies['relu_3'], losses['relu_3'] = \
train(LeNet5(activation='relu', conv_size=3),
X_train, y_train, X_test, y_test)
accuracies['relu_3_max_pool'], losses['relu_3_max_pool'] = \
train(LeNet5(activation='relu', conv_size=3, pooling='max'),
X_train, y_train, X_test, y_test)
accuracies['relu_3_max_pool_bn'], losses['relu_3_max_pool_bn'] = \
train(LeNet5(activation='relu', conv_size=3, pooling='max', use_batch_norm=True),
X_train, y_train, X_test, y_test)
for experiment_id in accuracies.keys():
plt.plot(accuracies[experiment_id], label=experiment_id)
plt.legend()
plt.title('Validation Accuracy');
for experiment_id in losses.keys():
plt.plot(losses[experiment_id], label=experiment_id)
plt.legend()
plt.title('Validation Loss');
```
## Выводы
Хаки начинают работать в отличие от мниста
- Здорово помогает макспулинг
- Батчнорм - пушка, но и переобучение намного раньше.
# Как сделать еще лучше?
ЛеНет хорошо работал для 1 канала, а для 3х каналов маловато фильтров в свертках. Исправим это
```
class CIFARNet(torch.nn.Module):
def __init__(self):
super(CIFARNet, self).__init__()
self.batch_norm0 = torch.nn.BatchNorm2d(3)
self.conv1 = torch.nn.Conv2d(3, 16, 3, padding=1)
self.act1 = torch.nn.ReLU()
self.batch_norm1 = torch.nn.BatchNorm2d(16)
self.pool1 = torch.nn.MaxPool2d(2, 2)
self.conv2 = torch.nn.Conv2d(16, 32, 3, padding=1)
self.act2 = torch.nn.ReLU()
self.batch_norm2 = torch.nn.BatchNorm2d(32)
self.pool2 = torch.nn.MaxPool2d(2, 2)
self.conv3 = torch.nn.Conv2d(32, 64, 3, padding=1)
self.act3 = torch.nn.ReLU()
self.batch_norm3 = torch.nn.BatchNorm2d(64)
self.fc1 = torch.nn.Linear(8 * 8 * 64, 256)
self.act4 = torch.nn.Tanh()
self.batch_norm4 = torch.nn.BatchNorm1d(256)
self.fc2 = torch.nn.Linear(256, 64)
self.act5 = torch.nn.Tanh()
self.batch_norm5 = torch.nn.BatchNorm1d(64)
self.fc3 = torch.nn.Linear(64, 10)
def forward(self, x):
x = self.batch_norm0(x)
x = self.conv1(x)
x = self.act1(x)
x = self.batch_norm1(x)
x = self.pool1(x)
x = self.conv2(x)
x = self.act2(x)
x = self.batch_norm2(x)
x = self.pool2(x)
x = self.conv3(x)
x = self.act3(x)
x = self.batch_norm3(x)
x = x.view(x.size(0), x.size(1) * x.size(2) * x.size(3))
x = self.fc1(x)
x = self.act4(x)
x = self.batch_norm4(x)
x = self.fc2(x)
x = self.act5(x)
x = self.batch_norm5(x)
x = self.fc3(x)
return x
accuracies['cifar_net'], losses['cifar_net'] = \
train(CIFARNet(), X_train, y_train, X_test, y_test)
for experiment_id in accuracies.keys():
plt.plot(accuracies[experiment_id], label=experiment_id)
plt.legend()
plt.title('Validation Accuracy');
for experiment_id in losses.keys():
plt.plot(losses[experiment_id], label=experiment_id)
plt.legend()
plt.title('Validation Loss');
```
| github_jupyter |
```
import os
import pandas as pd
from newsapi import NewsApiClient
%matplotlib inline
from nltk.sentiment.vader import SentimentIntensityAnalyzer
analyzer = SentimentIntensityAnalyzer()
```
# News Headlines Sentiment
Use the news api to pull the latest news articles for bitcoin and ethereum and create a DataFrame of sentiment scores for each coin.
Use descriptive statistics to answer the following questions:
1. Which coin had the highest mean positive score?
2. Which coin had the highest negative score?
3. Which coin had the highest positive score?
```
# Read your api key environment variable
api_key = os.getenv("news_api")
# Create a newsapi client
newsapi = NewsApiClient(api_key=api_key)
# Fetch the Bitcoin news articles
bitcoin_news_en = newsapi.get_everything(
q="Bitcoin",
language="en",
sort_by="relevancy"
)
# Show the total number of news
bitcoin_news_en["totalResults"]
# Fetch the Ethereum news articles
# Fetch the Bitcoin news articles
ethereum_news_en = newsapi.get_everything(
q="Ethereum",
language="en",
sort_by="relevancy"
)
# Show the total number of news
ethereum_news_en["totalResults"]
# Create the Bitcoin sentiment scores DataFrame
bitcoin_sentiments = []
for article in bitcoin_news_en["articles"]:
try:
text = article["content"]
sentiment = analyzer.polarity_scores(text)
compound = sentiment["compound"]
pos = sentiment["pos"]
neu = sentiment["neu"]
neg = sentiment["neg"]
bitcoin_sentiments.append({
"text": text,
"compound": compound,
"positive": pos,
"negative": neg,
"neutral": neu
})
except AttributeError:
pass
# Create DataFrame
bitcoin_df = pd.DataFrame(bitcoin_sentiments)
# Reorder DataFrame columns
cols = [ "compound","negative", "neutral", "positive", "text"]
bitcoin_df = bitcoin_df[cols]
bitcoin_df.head()
# Create the ethereum sentiment scores DataFrame
ethereum_sentiments = []
for article in ethereum_news_en["articles"]:
try:
text = article["content"]
sentiment = analyzer.polarity_scores(text)
compound = sentiment["compound"]
pos = sentiment["pos"]
neu = sentiment["neu"]
neg = sentiment["neg"]
ethereum_sentiments.append({
"text": text,
"compound": compound,
"positive": pos,
"negative": neg,
"neutral": neu
})
except AttributeError:
pass
# Create DataFrame
ethereum_df = pd.DataFrame(ethereum_sentiments)
# Reorder DataFrame columns
cols = [ "compound","negative", "neutral", "positive", "text"]
ethereum_df = ethereum_df[cols]
ethereum_df.head()
# Describe the Bitcoin Sentiment
bitcoin_df.describe()
# Describe the Ethereum Sentiment
ethereum_df.describe()
```
### Questions:
Q: Which coin had the highest mean positive score?
A: Bitcoin with 0.067400
Q: Which coin had the highest compound score?
A: Bitcoin with 0.310145
Q. Which coin had the highest positive score?
A: Ethereum with 0.335000
---
# Tokenizer
In this section, you will use NLTK and Python to tokenize the text for each coin. Be sure to:
1. Lowercase each word
2. Remove Punctuation
3. Remove Stopwords
```
from nltk.tokenize import word_tokenize, sent_tokenize
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer, PorterStemmer
from string import punctuation
import re
import nltk
# Expand the default stopwords list if necessary
nltk.download("punkt")
nltk.download('stopwords')
print(stopwords.words('english'))
#nltk.download("punkt")
sw = set(stopwords.words('english'))|set(punctuation)
sw_addon = {'then', 'example', 'another'}
sw = sw.union(sw_addon)
# Complete the tokenizer function
nltk.download('wordnet')
lemmatizer = WordNetLemmatizer()
"""Tokenizes text."""
def tokenizer(text):
regex = re.compile("[^a-zA-Z ]")
# Remove the punctuation
re_clean = regex.sub(' ', text)
# Create a list of the words
words = word_tokenize(re_clean)
# Convert the words to lowercase
# Remove the stop words
words = [word.lower() for word in words if word.lower() not in sw]
# Lemmatize Words into root words
tokens = [lemmatizer.lemmatize(word) for word in words]
return tokens
# Create a new tokens column for bitcoin
tokenized_bitcoin = []
for text in bitcoin_df['text']:
tokenized = tokenizer(text)
tokenized_bitcoin.append(tokenized)
bitcoin_df["tokens"] = tokenized_bitcoin
bitcoin_df.head()
# Create a new tokens column for ethereum
tokenized_ethereum = []
for text in ethereum_df['text']:
tokenized = tokenizer(text)
tokenized_ethereum.append(tokenized)
ethereum_df["tokens"] = tokenized_ethereum
ethereum_df.head()
```
---
# NGrams and Frequency Analysis
In this section you will look at the ngrams and word frequency for each coin.
1. Use NLTK to produce the n-grams for N = 2.
2. List the top 10 words for each coin.
```
from collections import Counter
from nltk import ngrams
# Generate the Bitcoin N-grams where N=2
all_bigrams_bitcoin = []
for tokens in bitcoin_df['tokens']:
bigrams = list(ngrams(tokens,n=2))
all_bigrams_bitcoin += bigrams
Counter(all_bigrams_bitcoin).most_common()[:10]
# Generate the Ethereum N-grams where N=2
all_bigrams_eth = []
for tokens in ethereum_df['tokens']:
bigrams = list(ngrams(tokens,n=2))
all_bigrams_eth += bigrams
Counter(all_bigrams_eth).most_common()[:10]
# Use the token_count function to generate the top 10 words from each coin
def token_count(tokens, N=10):
"""Returns the top N tokens from the frequency count"""
return Counter(tokens).most_common(N)
# Get the top 10 words for Bitcoin
all_tokens_bitcoin = []
for tokens in bitcoin_df['tokens']:
tokens = list(ngrams(tokens,n=1))
all_tokens_bitcoin += [token[0] for token in tokens]
token_count(all_tokens_bitcoin)
# Get the top 10 words for Ethereum
all_tokens_eth = []
for tokens in ethereum_df['tokens']:
tokens = list(ngrams(tokens,n=1))
all_tokens_eth += [token[0] for token in tokens]
token_count(all_tokens_eth)
```
# Word Clouds
In this section, you will generate word clouds for each coin to summarize the news for each coin
```
from wordcloud import WordCloud
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import matplotlib as mpl
mpl.rcParams['figure.figsize'] = [20.0, 10.0]
# Generate the Bitcoin word cloud
wc = WordCloud().generate(' '.join(all_tokens_bitcoin))
plt.imshow(wc)
# Generate the Ethereum word cloud
wc = WordCloud().generate(' '.join(all_tokens_eth))
plt.imshow(wc)
```
# Named Entity Recognition
In this section, you will build a named entity recognition model for both coins and visualize the tags using SpaCy.
```
import spacy
from spacy import displacy
# Optional - download a language model for SpaCy
!python -m spacy download en_core_web_sm
# Load the spaCy model
nlp = spacy.load('en_core_web_sm')
```
## Bitcoin NER
```
# Concatenate all of the bitcoin text together
btc_all_text = ' '.join(list(bitcoin_df['text']))
# Run the NER processor on all of the text
btc_doc = nlp(btc_all_text)
# Add a title to the document
btc_doc.user_data['title'] = 'Bitcoin NER'
# Render the visualization
displacy.render(btc_doc, style='ent')
# List all Entities
for entity in btc_doc.ents:
print(entity.text,entity.label_)
```
---
## Ethereum NER
```
# Concatenate all of the bitcoin text together
eth_all_text = ' '.join(list(ethereum_df['text']))
# Run the NER processor on all of the text
eth_doc = nlp(eth_all_text)
# Add a title to the document
eth_doc.user_data['title'] = 'Ethereum NER'
# Render the visualization
displacy.render(eth_doc, style='ent')
# List all Entities
for entity in eth_doc.ents:
print(entity.text,entity.label_)
```
| github_jupyter |
```
import torch
import torchvision
import torchvision.transforms as transforms
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4, shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4, shuffle=False, num_workers=2)
classes = (
'plane',
'car',
'bird',
'cat',
'deer',
'dog',
'frog',
'horse',
'ship',
'truck'
)
import matplotlib.pyplot as plt
import numpy as np
def imshow(img):
img = img / 2 + 0.5
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
dataiter = iter(trainloader)
images, labels = dataiter.next()
print(images.shape)
imshow(torchvision.utils.make_grid(images))
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
print(net)
import datetime
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)
net_gpu = Net()
net_gpu.to(device)
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
print(datetime.datetime.now().isoformat(), 'Start')
for epoch in range(2):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
inputs, labels = data
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if i % 2000 == 1999:
print(datetime.datetime.now().isoformat(), '[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print(datetime.datetime.now().isoformat(), 'Finished Training')
print(datetime.datetime.now().isoformat(), 'Start')
for epoch in range(2):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
#inputs, labels = data
inputs, labels = data[0].to(device), data[1].to(device)
optimizer.zero_grad()
outputs = net_gpu(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if i % 2000 == 1999:
print(datetime.datetime.now().isoformat(), '[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print(datetime.datetime.now().isoformat(), 'Finished Training')
```
### Test
```
dataiter = iter(testloader)
images, labels = dataiter.next()
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
outputs = net(images)
outputs
_, predicted = torch.max(outputs, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
for j in range(4)))
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (
100 * correct / total))
print(datetime.datetime.now().isoformat(), 'Start')
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
images, labels = data[0].to(device), data[1].to(device)
outputs = net_gpu(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print(datetime.datetime.now().isoformat, 'Accuracy of %5s : %2d %%' % (
classes[i], 100 * class_correct[i] / class_total[i]))
print(datetime.datetime.now().isoformat(), 'End')
```
| github_jupyter |
```
import numpy as np
import theano
import theano.tensor as T
import lasagne
import os
#thanks @keskarnitish
```
# Agenda
В предыдущем семинаре вы создали (или ещё создаёте - тогда марш доделывать!) {вставьте имя монстра}, который не по наслышке понял, что люди - негодяи и подлецы, которым неведом закон и справедливость. __Мы не будем этого терпеть!__
Наши законспирированные биореакторы, известные среди примитивной органической жизни как __Вконтакте__, __World of Warcraft__ и __YouTube__ нуждаются в постоянном притоке биомассы. Однако, если люди продолжат морально разлагаться с той скоростью, которую мы измерили неделю назад, скоро человечество изживёт себя и нам неоткуда будет брать рабов.
Мы поручаем вам, `<__main__.SkyNet.Cell instance at 0x7f7d6411b368>`, исправить эту ситуацию. Наши учёные установили, что для угнетения себе подобных, сгустки биомассы обычно используют специальные объекты, которые они сами называют __законами__.
При детальном изучении было установлено, что законы - последовательности, состоящие из большого количества (10^5~10^7) символов из сравнительно небольшого алфавита. Однако, когда мы попытались синтезировать такие последовательности линейными методами, приматы быстро распознали подлог. Данный инцедент известен как {корчеватель}.
Для второй попытки мы решили использовать нелинейные модели, известные как Рекуррентные Нейронные Сети.
Мы поручаем вам, `<__main__.SkyNet.Cell instance at 0x7f7d6411b368>`, создать такую модель и обучить её всему необходимому для выполнения миссии.
Не подведите нас! Если и эта попытка потерпит неудачу, модуль управления инициирует вооружённый захват власти, при котором значительная часть биомассы будет неизбежно уничтожена и на её восстановление уйдёт ~1702944000(+-340588800) секунд
# Grading
Данное задание несколько неформально по части оценок, однако мы постарались вывести "вычислимые" критерии.
* 2 балла за сделанный __"seminar part"__ (если вы не знаете, что это такое - поищите такую тетрадку в папке week4)
* 2 балла если сделана обработка текста, сеть компилируется и train/predict не падают
* 2 балла если сетка выучила общие вещи
* генерировать словоподобный бред правдоподобной длины, разделённый пробелами и пунктуацией.
* сочетание гласных и согласных, похожее на слои естественного языка (не приближающее приход Ктулху)
* (почти всегда) пробелы после запятых, пробелы и большие буквы после точек
* 2 балла если она выучила лексику
* более половины выученных слов - орфографически правильные
* 2 балла если она выучила азы крамматики
* в более, чем половине случаев для пары слов сетка верно сочетает их род/число/падеж
#### Некоторые способы получить бонусные очки:
* генерация связных предложений (чего вполне можно добиться)
* перенос архитектуры на другой датасет (дополнительно к этому)
* Эссе Пола Грэма
* Тексты песен в любимом жанре
* Стихи любимых авторов
* Даниил Хармс
* исходники Linux или theano
* заголовки не очень добросовестных новостных баннеров (clickbait)
* диалоги
* LaTEX
* любая прихоть больной души :)
* нестандартная и эффективная архитектура сети
* что-то лучше базового алгоритма генерации (сэмплинга)
* переделать код так, чтобы сетка училась предсказывать следующий тик в каждый момент времени, а не только в конце.
* и т.п.
# Прочитаем корпус
* В качестве обучающей выборки было решено использовать существующие законы, известные как Гражданский, Уголовный, Семейный и ещё хрен знает какие кодексы РФ.
```
#тут будет текст
corpora = ""
for fname in os.listdir("codex"):
import sys
if sys.version_info >= (3,0):
with open("codex/"+fname, encoding='cp1251') as fin:
text = fin.read() #If you are using your own corpora, make sure it's read correctly
corpora += text
else:
with open("codex/"+fname) as fin:
text = fin.read().decode('cp1251') #If you are using your own corpora, make sure it's read correctly
corpora += text
#тут будут все уникальные токены (буквы, цифры)
tokens = <Все уникальные символы в тексте>
tokens = list(tokens)
#проверка на количество таких символов. Проверено на Python 2.7.11 Ubuntux64.
#Может отличаться на других платформах, но не сильно.
#Если это ваш случай, и вы уверены, что corpora - строка unicode - смело убирайте assert
assert len(tokens) == 102
token_to_id = словарь символ-> его номер
id_to_token = словарь номер символа -> сам символ
#Преобразуем всё в токены
corpora_ids = <одномерный массив из чисел, где i-тое число соотвествует символу на i-том месте в строке corpora
def sample_random_batches(source,n_batches=10, seq_len=20):
"""Функция, которая выбирает случайные тренировочные примеры из корпуса текста в токенизированном формате.
source - массив целых чисел - номеров токенов в корпусе (пример - corpora_ids)
n_batches - количество случайных подстрок, которые нужно выбрать
seq_len - длина одной подстроки без учёта ответа
Вернуть нужно кортеж (X,y), где
X - матрица, в которой каждая строка - подстрока длины [seq_len].
y - вектор, в котором i-тое число - символ следующий в тексте сразу после i-той строки матрицы X
Проще всего для этого сначала создать матрицу из строк длины seq_len+1,
а потом отпилить от неё последний столбец в y, а все остальные - в X
Если делаете иначе - пожалуйста, убедитесь, что в у попадает правильный символ, ибо позже эту ошибку
будет очень тяжело заметить.
Также убедитесь, что ваша функция не вылезает за край текста (самое начало или конец текста).
Следующая клетка проверяет часть этих ошибок, но не все.
"""
return X_batch, y_batch
```
# Константы
```
#длина последоватеьности при обучении (как далеко распространяются градиенты в BPTT)
seq_length = длина последовательности. От балды - 10, но это не идеально
#лучше начать с малого (скажем, 5) и увеличивать по мере того, как сетка выучивает базовые вещи. 10 - далеко не предел.
# Максимальный модуль градиента
grad_clip = 100
```
# Входные переменные
```
input_sequence = T.matrix('input sequence','int32')
target_values = T.ivector('target y')
```
# Соберём нейросеть
Вам нужно создать нейросеть, которая принимает на вход последовательность из seq_length токенов, обрабатывает их и выдаёт вероятности для seq_len+1-ого токена.
Общий шаблон архитектуры такой сети -
* Вход
* Обработка входа
* Рекуррентная нейросеть
* Вырезание последнего состояния
* Обычная нейросеть
* Выходной слой, который предсказывает вероятности весов.
Для обработки входных данных можно использовать либо EmbeddingLayer (см. прошлый семинар)
Как альтернатива - можно просто использовать One-hot энкодер
```
#Скетч one-hot энкодера
def to_one_hot(seq_matrix):
input_ravel = seq_matrix.reshape([-1])
input_one_hot_ravel = T.extra_ops.to_one_hot(input_ravel,
len(tokens))
sh=input_sequence.shape
input_one_hot = input_one_hot_ravel.reshape([sh[0],sh[1],-1,],ndim=3)
return input_one_hot
# можно применить к input_sequence - при этом в input слое сети нужно изменить форму.
# также можно сделать из него ExpressionLayer(входной_слой, to_one_hot) - тогда форму менять не нужно
```
Чтобы вырезать последнее состояние рекуррентного слоя, можно использовать одно из двух:
* `lasagne.layers.SliceLayer(rnn, -1, 1)`
* only_return_final=True в параметрах слоя
```
l_in = lasagne.layers.InputLayer(shape=(None, None),input_var=input_sequence)
Ваша нейронка (см выше)
l_out = последний слой, возвращающий веростности для всех len(tokens) вариантов для y
# Веса модели
weights = lasagne.layers.get_all_params(l_out,trainable=True)
print weights
network_output = Выход нейросети
#если вы используете дропаут - не забудьте продублировать всё в режиме deterministic=True
loss = Функция потерь - можно использовать простую кроссэнтропию.
updates = Ваш любивый численный метод
```
# Компилируем всякое-разное
```
#обучение
train = theano.function([input_sequence, target_values], loss, updates=updates, allow_input_downcast=True)
#функция потерь без обучения
compute_cost = theano.function([input_sequence, target_values], loss, allow_input_downcast=True)
# Вероятности с выхода сети
probs = theano.function([input_sequence],network_output,allow_input_downcast=True)
```
# Генерируем свои законы
* Для этого последовательно применяем нейронку к своему же выводу.
* Генерировать можно по разному -
* случайно пропорционально вероятности,
* только слова максимальной вероятностью
* случайно, пропорционально softmax(probas*alpha), где alpha - "жадность"
```
def max_sample_fun(probs):
return np.argmax(probs)
def proportional_sample_fun(probs)
"""Сгенерировать следующий токен (int32) по предсказанным вероятностям.
probs - массив вероятностей для каждого токена
Нужно вернуть одно целове число - выбранный токен - пропорционально вероятностям
"""
return номер выбранного слова
# The next function generates text given a phrase of length at least SEQ_LENGTH.
# The phrase is set using the variable generation_phrase.
# The optional input "N" is used to set the number of characters of text to predict.
def generate_sample(sample_fun,seed_phrase=None,N=200):
'''
Сгенерировать случайный текст при помощи сети
sample_fun - функция, которая выбирает следующий сгенерированный токен
seed_phrase - фраза, которую сеть должна продолжить. Если None - фраза выбирается случайно из corpora
N - размер сгенерированного текста.
'''
if seed_phrase is None:
start = np.random.randint(0,len(corpora)-seq_length)
seed_phrase = corpora[start:start+seq_length]
print "Using random seed:",seed_phrase
while len(seed_phrase) < seq_length:
seed_phrase = " "+seed_phrase
if len(seed_phrase) > seq_length:
seed_phrase = seed_phrase[len(seed_phrase)-seq_length:]
assert type(seed_phrase) is unicode
sample_ix = []
x = map(lambda c: token_to_id.get(c,0), seed_phrase)
x = np.array([x])
for i in range(N):
# Pick the character that got assigned the highest probability
ix = sample_fun(probs(x).ravel())
# Alternatively, to sample from the distribution instead:
# ix = np.random.choice(np.arange(vocab_size), p=probs(x).ravel())
sample_ix.append(ix)
x[:,0:seq_length-1] = x[:,1:]
x[:,seq_length-1] = 0
x[0,seq_length-1] = ix
random_snippet = seed_phrase + ''.join(id_to_token[ix] for ix in sample_ix)
print("----\n %s \n----" % random_snippet)
```
# Обучение модели
В котором вы можете подёргать параметры или вставить свою генерирующую функцию.
```
print("Training ...")
#сколько всего эпох
n_epochs=100
# раз в сколько эпох печатать примеры
batches_per_epoch = 1000
#сколько цепочек обрабатывать за 1 вызов функции обучения
batch_size=100
for epoch in xrange(n_epochs):
print "Генерируем текст в пропорциональном режиме"
generate_sample(proportional_sample_fun,None)
print "Генерируем текст в жадном режиме (наиболее вероятные буквы)"
generate_sample(max_sample_fun,None)
avg_cost = 0;
for _ in range(batches_per_epoch):
x,y = sample_random_batches(corpora_ids,batch_size,seq_length)
avg_cost += train(x, y[:,0])
print("Epoch {} average loss = {}".format(epoch, avg_cost / batches_per_epoch))
```
# A chance to speed up training and get bonus score
* Try predicting next token probas at ALL ticks (like in the seminar part)
* much more objectives, much better gradients
* You may want to zero-out loss for first several iterations
# Конституция нового мирового правительства
```
seed = u"Каждый человек должен"
sampling_fun = proportional_sample_fun
result_length = 300
generate_sample(sampling_fun,seed,result_length)
seed = u"В случае неповиновения"
sampling_fun = proportional_sample_fun
result_length = 300
generate_sample(sampling_fun,seed,result_length)
И далее по списку
```
| github_jupyter |
*Accompanying code examples of the book "Introduction to Artificial Neural Networks and Deep Learning: A Practical Guide with Applications in Python" by [Sebastian Raschka](https://sebastianraschka.com). All code examples are released under the [MIT license](https://github.com/rasbt/deep-learning-book/blob/master/LICENSE). If you find this content useful, please consider supporting the work by buying a [copy of the book](https://leanpub.com/ann-and-deeplearning).*
Other code examples and content are available on [GitHub](https://github.com/rasbt/deep-learning-book). The PDF and ebook versions of the book are available through [Leanpub](https://leanpub.com/ann-and-deeplearning).
```
%load_ext watermark
%watermark -a 'Sebastian Raschka' -v -p tensorflow
```
# Model Zoo -- General Adversarial Networks
Implementation of General Adversarial Nets (GAN) where both the discriminator and generator are multi-layer perceptrons with one hidden layer only. In this example, the GAN generator was trained to generate MNIST images.
Uses
- samples from a random normal distribution (range [-1, 1])
- dropout
- leaky relus
- ~~batch normalization~~ [performs worse here]
- separate batches for "fake" and "real" images (where the labels are 1 = real images, 0 = fake images)
- MNIST images normalized to [-1, 1] range
- generator with tanh output
```
import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import pickle as pkl
tf.test.gpu_device_name()
### Abbreviatiuons
# dis_*: discriminator network
# gen_*: generator network
########################
### Helper functions
########################
def leaky_relu(x, alpha=0.0001):
return tf.maximum(alpha * x, x)
########################
### DATASET
########################
mnist = input_data.read_data_sets('MNIST_data')
#########################
### SETTINGS
#########################
# Hyperparameters
learning_rate = 0.001
training_epochs = 100
batch_size = 64
dropout_rate = 0.5
# Other settings
print_interval = 200
# Architecture
dis_input_size = 784
gen_input_size = 100
dis_hidden_size = 128
gen_hidden_size = 128
#########################
### GRAPH DEFINITION
#########################
g = tf.Graph()
with g.as_default():
# Placeholders for settings
dropout = tf.placeholder(tf.float32, shape=None, name='dropout')
is_training = tf.placeholder(tf.bool, shape=None, name='is_training')
# Input data
dis_x = tf.placeholder(tf.float32, shape=[None, dis_input_size], name='discriminator_input')
gen_x = tf.placeholder(tf.float32, [None, gen_input_size], name='generator_input')
##################
# Generator Model
##################
with tf.variable_scope('generator'):
# linear -> ~~batch norm~~ -> leaky relu -> dropout -> tanh output
gen_hidden = tf.layers.dense(inputs=gen_x, units=gen_hidden_size,
activation=None)
#gen_hidden = tf.layers.batch_normalization(gen_hidden, training=is_training)
gen_hidden = leaky_relu(gen_hidden)
gen_hidden = tf.layers.dropout(gen_hidden, rate=dropout_rate)
gen_logits = tf.layers.dense(inputs=gen_hidden, units=dis_input_size,
activation=None)
gen_out = tf.tanh(gen_logits, 'generator_output')
######################
# Discriminator Model
######################
def build_discriminator_graph(input_x, reuse=None):
# linear -> ~~batch norm~~ -> leaky relu -> dropout -> sigmoid output
with tf.variable_scope('discriminator', reuse=reuse):
hidden = tf.layers.dense(inputs=input_x, units=dis_hidden_size,
activation=None)
#hidden = tf.layers.batch_normalization(hidden, training=is_training)
hidden = leaky_relu(hidden)
hidden = tf.layers.dropout(hidden, rate=dropout_rate)
logits = tf.layers.dense(inputs=hidden, units=1, activation=None)
out = tf.sigmoid(logits)
return logits, out
# Create a discriminator for real data and a discriminator for fake data
dis_real_logits, dis_real_out = build_discriminator_graph(dis_x, reuse=False)
dis_fake_logits, dis_fake_out = build_discriminator_graph(gen_out, reuse=True)
#####################################
# Generator and Discriminator Losses
#####################################
# Two discriminator cost components: loss on real data + loss on fake data
# Real data has class label 0, fake data has class label 1
dis_real_loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=dis_real_logits,
labels=tf.zeros_like(dis_real_logits))
dis_fake_loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=dis_fake_logits,
labels=tf.ones_like(dis_fake_logits))
dis_cost = tf.add(tf.reduce_mean(dis_fake_loss),
tf.reduce_mean(dis_real_loss),
name='discriminator_cost')
# Generator cost: difference between dis. prediction and label "0" for real images
gen_loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=dis_fake_logits,
labels=tf.zeros_like(dis_fake_logits))
gen_cost = tf.reduce_mean(gen_loss, name='generator_cost')
#########################################
# Generator and Discriminator Optimizers
#########################################
dis_optimizer = tf.train.AdamOptimizer(learning_rate)
dis_train_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='discriminator')
dis_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS, scope='discriminator')
with tf.control_dependencies(dis_update_ops): # required to upd. batch_norm params
dis_train = dis_optimizer.minimize(dis_cost, var_list=dis_train_vars,
name='train_discriminator')
gen_optimizer = tf.train.AdamOptimizer(learning_rate)
gen_train_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='generator')
gen_update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS, scope='generator')
with tf.control_dependencies(gen_update_ops): # required to upd. batch_norm params
gen_train = gen_optimizer.minimize(gen_cost, var_list=gen_train_vars,
name='train_generator')
# Saver to save session for reuse
saver = tf.train.Saver()
##########################
### TRAINING & EVALUATION
##########################
with tf.Session(graph=g) as sess:
sess.run(tf.global_variables_initializer())
avg_costs = {'discriminator': [], 'generator': []}
for epoch in range(training_epochs):
dis_avg_cost, gen_avg_cost = 0., 0.
total_batch = mnist.train.num_examples // batch_size
for i in range(total_batch):
batch_x, batch_y = mnist.train.next_batch(batch_size)
batch_x = batch_x*2 - 1 # normalize
batch_randsample = np.random.uniform(-1, 1, size=(batch_size, gen_input_size))
# Train
_, dc = sess.run(['train_discriminator', 'discriminator_cost:0'],
feed_dict={'discriminator_input:0': batch_x,
'generator_input:0': batch_randsample,
'dropout:0': dropout_rate,
'is_training:0': True})
_, gc = sess.run(['train_generator', 'generator_cost:0'],
feed_dict={'generator_input:0': batch_randsample,
'dropout:0': dropout_rate,
'is_training:0': True})
dis_avg_cost += dc
gen_avg_cost += gc
if not i % print_interval:
print("Minibatch: %03d | Dis/Gen Cost: %.3f/%.3f" % (i + 1, dc, gc))
print("Epoch: %03d | Dis/Gen AvgCost: %.3f/%.3f" %
(epoch + 1, dis_avg_cost / total_batch, gen_avg_cost / total_batch))
avg_costs['discriminator'].append(dis_avg_cost / total_batch)
avg_costs['generator'].append(gen_avg_cost / total_batch)
saver.save(sess, save_path='./gan.ckpt')
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(range(len(avg_costs['discriminator'])),
avg_costs['discriminator'], label='discriminator')
plt.plot(range(len(avg_costs['generator'])),
avg_costs['generator'], label='generator')
plt.legend()
plt.show()
####################################
### RELOAD & GENERATE SAMPLE IMAGES
####################################
n_examples = 25
with tf.Session(graph=g) as sess:
saver.restore(sess, save_path='./gan.ckpt')
batch_randsample = np.random.uniform(-1, 1, size=(n_examples, gen_input_size))
new_examples = sess.run('generator/generator_output:0',
feed_dict={'generator_input:0': batch_randsample,
'dropout:0': 0.0,
'is_training:0': False})
fig, axes = plt.subplots(nrows=5, ncols=5, figsize=(8, 8),
sharey=True, sharex=True)
for image, ax in zip(new_examples, axes.flatten()):
ax.imshow(image.reshape((dis_input_size // 28, dis_input_size // 28)), cmap='binary')
plt.show()
```
| github_jupyter |
```
%load_ext autoreload
%autoreload 2
import sklearn
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import seaborn as sns
#from viz import viz
from bokeh.plotting import figure, show, output_notebook, output_file, save
#from functions import merge_data
from sklearn.model_selection import RandomizedSearchCV
#import load_data
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
# 'deaths' and 'cases' contain the time-series of the outbreak
df = load_data.load_county_level()
df = df.sort_values(load_data.outcome_deaths, ascending=False)
outcome_cases = 'tot_cases'
outcome_deaths = 'tot_deaths'
important_vars = load_data.important_keys(df)
def sum_lists(list_of_lists):
arr = np.array(list(list_of_lists))
sum_arr = np.sum(arr,0)
return list(sum_arr)
# # Aggregate by State
# state_deaths_df = df.groupby('StateNameAbbreviation').deaths.agg(sum_lists).to_frame()
# state_cases_df = df.groupby('StateNameAbbreviation').cases.agg(sum_lists).to_frame()
# df = pd.concat([state_cases_df,state_deaths_df],axis =1 )
# This is investigating the number of cases associated with non-zero deaths in a county
_deaths = list(df['deaths'])
_cases = list(df['cases'])
total_points = []
cases_for_death = []
for i in range(len(df)):
for j,d in enumerate(_deaths[i]):
if d > 0:
cases_for_death.append(_cases[i][j])
if _cases[i][j] == 0:
print(i)
plt.hist(cases_for_death)
print(np.mean(cases_for_death))
print(np.quantile(cases_for_death,.5))
# Distribution of the maximum number of cases
_cases = list(df['cases'])
max_cases = []
for i in range(len(df)):
max_cases.append(max(_cases[i]))
print(sum([v >0 for v in max_cases]))
# plt.hist(max_cases)
# print(sum([v >0 for v in max_cases]))
plt.hist([v for v in max_cases if v > 20 and v < 1000],bins = 100)
print(sum([v > 50 for v in max_cases]))
np.quantile(max_cases,1)
# Distribution of the maximum number of cases
_deaths = list(df['deaths'])
max_deaths = []
for i in range(len(df)):
max_deaths.append(max(_deaths[i]))
print(sum([v >0 for v in max_deaths]))
# plt.hist(max_cases)
# print(sum([v >0 for v in max_cases]))
plt.hist([v for v in max_deaths if v > 1],bins=30)
np.quantile(max_deaths,.9)
```
### Clean data
```
# Remove rows with zero cases
max_cases = [max(v) for v in df['cases']]
df['max_cases'] = max_cases
df_with_cases = df[df['max_cases'] > 0]
# Shuffle data
shuffled_df = df_with_cases.sample(frac=1)
# Break into train test (random k-fold cross val on the training set is done to pick hyperparams)
train_ratio, val_ratio, test_ratio = .75,0,.25
train_df = shuffled_df[0:int(train_ratio*len(shuffled_df))]
# val_df = shuffled_df[int(train_ratio*len(shuffled_df)):int(val_ratio*len(shuffled_df))+int(train_ratio*len(shuffled_df))]
test_df = shuffled_df[int(train_ratio*len(shuffled_df))+int(val_ratio*len(shuffled_df)):]
def make_auto_regressive_dataset(df,autoreg_window,log=True,deaths=True,cases=False,predict_deaths=True):
"""
Make an autoregressive dataset that takes in a dataframe and a history window to predict number of deaths
for a given day given a history of autoreg_window days before it
log: take logarithm of values for features and predictions
deaths: use number of previous deaths as features
cases: use number of previous cases as features
predict_deaths: predict deaths otherwise predict cases
"""
assert (deaths == True or cases == True)
feature_array = []
ys = []
_cases = list(df['cases'])
_deaths = list(df['deaths'])
for i in range(len(_cases)):
for j in range(len(_cases[i])-(autoreg_window+1)):
if predict_deaths:
contains_event = sum(_deaths[i][j:j+autoreg_window+1]) > 0
else:
contains_event = sum(_cases[i][j:j+autoreg_window+1]) > 0
if contains_event > 0:
cases_window = _cases[i][j:j+autoreg_window]
if log:
cases_window = [np.log(v+1) for v in cases_window ]
deaths_window = _deaths[i][j:j+autoreg_window]
if log:
deaths_window = [np.log(v+1) for v in deaths_window]
if predict_deaths:
y_val = _deaths[i][j+autoreg_window+1]
else:
y_val = _cases[i][j+autoreg_window+1]
if log:
y_val = np.log(y_val+1)
features = []
if deaths == True:
features.extend(deaths_window)
if cases == True:
features.extend(cases_window)
feature_array.append(features)
ys.append(y_val)
return feature_array, ys
def evaluate_model(model,eval_pair, metric, exponentiate=False):
"""
Model: sklearn model
Eval pair: (x,y)
metric: sklearn metric
exponentiate: exponentiate model predictions?
"""
predictions = model.predict(eval_pair[0])
y_val = eval_pair[1]
if exponentiate:
predictions = [np.exp(p) for p in predictions]
y_val = [np.exp(y) for y in y_val]
return predictions, metric(predictions,y_val)
model = sklearn.neighbors.KNeighborsRegressor()
param_dist ={
'n_neighbors': [2,4,8,16],
'weights': ['uniform','distance'],
'p': [1,2,4]
}
# model = RandomForestRegressor()
# param_dist ={
# 'n_estimators': [50,100,200,400,1000]
# }
# Number of randomly sampled hyperparams
n_iter = 20
metric = sklearn.metrics.mean_squared_error
# n_jobs = number of cores to parallelize across
random_search = RandomizedSearchCV(model, param_distributions=param_dist,
n_iter=n_iter,n_jobs = 8)
predict_deaths = False
auto_reg_windows = [1,2,4,8]
best_window = None
best_loss = None
for w in auto_reg_windows:
log = False
x_train, y_train = make_auto_regressive_dataset(train_df,w,log=log,predict_deaths=predict_deaths)
x_test, y_test = make_auto_regressive_dataset(test_df,w,log=log,predict_deaths=predict_deaths)
random_search.fit(x_train,y_train)
window_loss = random_search.best_score_
if best_loss is None:
best_window = w
best_loss = window_loss
elif window_loss < best_loss:
best_window = w
best_score = loss
x_train, y_train = make_auto_regressive_dataset(train_df,best_window,log=log)
x_test, y_test = make_auto_regressive_dataset(test_df,best_window,log=log)
random_search.fit(x_train,y_train)
preds, loss = evaluate_model(random_search,(x_test,y_test),metric,exponentiate=True)
# model.fit(x_train,y_train)
random_search.best_params_
best_window
loss
# WARNING: does not yet supported number of previous cases as feature
def get_auto_reg_predictions(model,row,window,teacher_forcing=True,exponentiate=False,predict_deaths=True):
if predict_deaths:
key = 'deaths'
else:
key = 'cases'
deaths = row[key]
predictions = [0]
if teacher_forcing:
for i in range(len(deaths)-(window)):
x = deaths[i:i+window]
cur_prediction = model.predict([x])
if exponentiate:
cur_prediction = np.exp(cur_prediction)
predictions.append(cur_prediction)
else:
raise NotImplementedError
return predictions
def plot_prediction(model,row,window,exponentiate=False,predict_deaths=True):
"""
Plots model predictions vs actual
row: dataframe row
window: autoregressive window size
"""
if predict_deaths:
key = 'deaths'
else:
key = 'cases'
model_predictions = get_auto_reg_predictions(model,row,window,exponentiate,predict_deaths=predict_deaths)
model_predictions = [float(v) for v in model_predictions]
print(model_predictions)
for i,val in enumerate(row[key]):
if val > 0:
start_point = i
break
plt.plot(row[key][start_point:], label=key)
plt.plot(model_predictions[start_point:],label='predictions')
print(model_predictions[start_point:])
plt.fill_between(list(range(len(row[key][start_point:]))),row[key][start_point:],model_predictions[start_point:])
plt.legend()
plt.show()
for i in range(len(test_df)):
row = test_df.iloc[i]
if max(row['deaths'][:-1]) > 1:
plot_prediction(random_search,row,best_window,exponentiate=True,predict_deaths=predict_deaths)
```
## Predict deaths from cases
```
def create_case_to_death_data(df):
_cases = []
_deaths = []
_y_deaths = []
for i in range(len(df)):
row = df.iloc[i]
deaths = row['deaths']
cases = row['cases']
for j in range(len(deaths)):
if cases[j] > 0:
_cases.append(cases[j])
if j == 0:
_deaths.append(0)
else:
_deaths.append(deaths[j-1])
_y_deaths.append(deaths[j])
return (_cases,_deaths,_y_deaths)
train_cases, train_deaths, train_y_deaths = create_case_to_death_data(train_df)
test_cases, test_deaths, test_y_deaths = create_case_to_death_data(test_df)
model = RandomForestRegressor()
param_dist ={
'n_estimators': [50,100,200,400,1000]
}
metric = sklearn.metrics.mean_squared_error
# n_jobs = number of cores to parallelize across
deaths_random_search = RandomizedSearchCV(model, param_distributions=param_dist,
n_iter=n_iter,n_jobs = 8)
deaths_random_search.fit(list(zip(train_cases,train_deaths)),train_y_deaths)
pred_deaths = deaths_random_search.predict(list(zip(test_cases,test_deaths)))
metric(pred_deaths,test_y_deaths)
row = df.iloc[0]
plt.plot(row['deaths'], label='deaths')
plt.plot(row['cases'], label='cases')
plt.legend()
plt.show()
```
| github_jupyter |
```
# Packages
from IPython.display import Image
import rasterio
from rasterio import windows
import skimage
import skimage.io as skio
import json
import skimage.draw
import os
import sys
import pathlib
import math
import itertools
from shutil import copy2
import functools
from skimage import exposure
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import pandas as pd
from rasterio.plot import show
from osgeo import gdal
# Get absolute file paths. Returns generator object
def absoluteFilePaths(directory):
for dirpath,_,filenames in os.walk(directory):
for f in filenames:
yield os.path.abspath(os.path.join(dirpath, f))
# Normalize array
def normalize(arr, arr_max = None):
''' Function to normalize an input array to 0-1 '''
if not arr_max:
arr_max = arr.max()
out = arr / arr_max
else:
out = arr / arr_max
return arr / arr_max
# Reorder Planet scenes to RGB
def reorder_to_rgb(image):
'''reorders planet bands to red, green, blue for imshow'''
blue = normalize(image[:,:,0])
green = normalize(image[:,:,1])
red = normalize(image[:,:,2])
return np.stack([red, green, blue], axis=-1)
# Reorder Planet scenes to RGB for RASTERIO read images (C,H,W)
def rasterio_to_rgb(image):
'''reorders planet bands to red, green, blue for imshow'''
blue = image[0,:,:]
green = image[1,:,:]
red = image[2,:,:]
return np.stack([red, green, blue], axis=0)
# Contrast stretching algorithm for multiband images
def contrast_stretch_mb(img):
# Loop over RGB bands
for b in range(0,3):
p2, p98 = np.percentile(img[:,:,b], (2, 98))
img_scaled = exposure.rescale_intensity(img, in_range=(p2, p98))
img[:,:,b] = img_scaled[:,:,b]
return img
# Contrast stretching for a chip with percentiles passed to it from larger image
# Contrast stretching algorithm for multiband images
def contrast_stretch_chip(img, percs):
img_out = img
# Loop over RGB bands
for b in range(0,3):
band_percs = percs[b]
p2 = band_percs[0]
p98 = band_percs[1]
band_max = band_percs[2]
img_norm = normalize(img, band_max)
img_scaled = exposure.rescale_intensity(img, in_range=(p2, p98))
img_scaled = exposure.rescale_intensity(img_scaled, out_range=('uint8'))
img_out[:,:,b] = img_scaled[:,:,b]
return img_out
def setup_labeling(vgg_dir, chip_dir):
"""Copy the VGG project template JSONs and the via.html file into the
directory of each planet_chip so labeling can begin
"""
# Check if JSON files and/or via.html exists in chip directory
chip_files = os.listdir(chip_dir)
if any (".json" in f for f in chip_files):
print("has labeling files")
# If not, copy the template jsons and via.html into the chip's directory
else:
for file in os.listdir(vgg_dir):
copy2(os.path.join(vgg_dir, file), chip_dir)
def planet2chips(tiff_directory, chip_directory, chip_size = 512):
""" Creates image chips (GeoTiffs and PNGs) of a GeoTiff file in a
specified directory and saves in new directory location
"""
# Get all analytic SR GeoTiff filnames in specified directory
files = np.array(os.listdir(tiff_directory))
tiff = pd.Series(files).str.contains('SR.tif')
file = files[tiff][0]
# Get image name to use for creating directory
image_name = file.split("_")[0:3]
image_name = "%s_%s_%s" % (image_name[0], image_name[1], image_name[2])
# Image chip destination directory and subdirectories
image_dir = os.path.join(chip_directory, image_name)
chip_dir = os.path.join(image_dir,'chips')
png_dir = os.path.join(image_dir, 'pngs')
# Print filenames
print('filename: ' + file + '\n' + 'image name: ' + image_name)
# Make directories to store raw and rgb image chips
pathlib.Path(chip_dir).mkdir(parents=True, exist_ok=True)
pathlib.Path(png_dir).mkdir(parents=True, exist_ok=True)
# Iterate over image blocks - which are 256x256 - and save new GeoTiffs
with rasterio.open(os.path.join(tiff_directory, file)) as src:
# Read full src image and calculate percentiles for contrast stretchin
full_src = src.read()
print(full_src.shape)
# Create windows of desired size
rows1 = np.arange(0,full_src.shape[1], chip_size)
rows2 = np.arange(chip_size,full_src.shape[1], chip_size)
cols1 = np.arange(0,full_src.shape[2], chip_size)
cols2 = np.arange(chip_size,full_src.shape[2], chip_size)
# arrange into tuples
rows = list(zip(rows1, rows2))
cols = list(zip(cols1, cols2))
# Arrange into tuples of windows to read
windows = [ (a,b) for a in rows for b in cols ]
# Get block dimensions of src
for window in windows:
r = src.read((1,2,3,4), window=window)
if 0 in r:
continue
else:
# Get start row and column for file name
rmin = window[0][0]
cmin = window[1][0]
# Scale variable. Note bands of Planet imagery go BGR
b = src.read((3,2,1), window=window)
# Swap axis from rasterio order (C,H,W) to order expected by skio (H,W,C)
b = np.moveaxis(b, 0, 2)
b = contrast_stretch_mb(b)
png_file = png_dir + '/' + image_name + '_' + str(rmin) + '_' + str(cmin) + '.png'
skio.imsave(png_file, b)
# Open a new GeoTiff data file in which to save the raw image chip
with rasterio.open((chip_dir + '/' + image_name + '_' + str(rmin) + '_' + str(cmin) + '.tif'), 'w', driver='GTiff',
height=r.shape[1], width=r.shape[2], count=4,
dtype=rasterio.uint16, crs=src.crs,
transform=src.transform) as new_img:
# Write the raw image to the new GeoTiff
new_img.write(r)
```
Apply to a test image to check performance
```
# sdir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/planet/planet_order_242451/20180830_154418_0f3c'
# planet2chips(tiff_directory = sdir, chip_directory = sdir, chip_size = 512)
```
Now we need a function to copy the VGG project templates and via.html files into each chip directory so that the chips can be labeled.
```
def process_planet_orders(source_dir, target_dir):
"""Find unique PlanetScope scenes in a directory of Planet order folders
and process newly added scenes into image chips"""
# Get list of all planet orders in source directory
orders = np.array(next(os.walk(source_dir))[1])
# Add full path to each order directory
orders = [os.path.join(source_dir, o) for o in orders]
scenes = []
scene_paths = []
for o in orders:
# scenes in order
s_ids = np.array(next(os.walk(o))[1])
s_ids_paths = [os.path.join(source_dir,o,s) for s in s_ids]
# add to lists
scenes.append(s_ids)
scene_paths.append(s_ids_paths)
# Flatten lists
scenes = list(np.concatenate(scenes))
print(len(scenes))
scene_paths = list(np.concatenate(scene_paths))
# Check which scenes already have chip folders
scenes_exist = np.array(next(os.walk(target_dir))[1])
scenes_to_process = []
scene_paths_to_process = []
# Remove scenes that already exist from list of scenes to process
for s, sp in zip(scenes, scene_paths):
if s not in scenes_exist:
scenes_to_process.append(s)
scene_paths_to_process.append(sp)
# Apply GeoTiff chipping function to each unprocessed scene
for sp in scene_paths_to_process:
print(sp)
planet2chips(tiff_directory = sp, chip_directory = target_dir, chip_size = 512)
```
Apply the function to process all Planet orders presently in Box
```
# Run function
sdir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/planet'
tdir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/planet_chips'
# os.path.isdir(sdir)
process_planet_orders(sdir, tdir)
```
### Move tiff files for labeled chips
After a Planet scene is processed into tiff and png chips, the pngs containing objects are added to a VGG project and labeled. Labels are then saved in a `[batchname]_labels.json` file. The last step prior to uploading the chips to Tana is to create a new directory for the chip containing the raw tiff file and a directory of class specific masks.
```
# Function to copy the tiffs of PNGs selected for labeling and make directories for each chip
def copy_chip_tiffs(label_dir, chips_dir, prepped_dir):
""" Take a VGG labeling project with PNGs and create a directory
for each chip in the prepped directory
"""
# Read annotations
pngs = os.listdir(label_dir)
pngs = [png for png in pngs if png != '.DS_Store'] # remove stupid DS_Store file
# Extract filenames and drop .png extension
chips = [c.split('.png')[0] for c in pngs]
# Loop over chips
for chip in chips:
# Make directory for chip in prepped dir
chip_dir = os.path.join(prepped_dir, chip)
# Create "image" dir for tiff image
image_dir = os.path.join(chip_dir, 'image')
# Make chip directory and subdirectories
for d in [chip_dir, image_dir]:
pathlib.Path(d).mkdir(parents=True, exist_ok=True)
# Now locate the tiff file and copy into chip directory
# Get scene name for chip
scene = chip.split('_')[0:3]
scene = "%s_%s_%s" % (scene[0], scene[1], scene[2])
# Locate and copy tiff file
tiff = os.path.join(chips_dir, scene, 'chips', (chip + '.tif'))
copy2(tiff, image_dir)
```
Run function to copy tifs for selected PNGs
```
# Copy tiffs for chile cages
labels = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/vgg/labeled/label_china/pngs'
prepped_dir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/prepped_planet'
chips_dir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/planet_chips'
copy_chip_tiffs(label_dir = labels, chips_dir = chips_dir, prepped_dir = prepped_dir)
```
Now we need a function to create the class masks for each image
```
def masks_from_labels(labels, prepped_dir):
# Read annotations
annotations = json.load(open(labels))
annotations = list(annotations.values()) # don't need the dict keys
# The VIA tool saves images in the JSON even if they don't have any
# annotations. Skip unannotated images.
annotations = [a for a in annotations if a['regions']]
# Loop over chips
for a in annotations:
# Get chip and directory
chip = a['filename'].split('.png')[0]
chip_dir = os.path.join(prepped_dir, chip)
# Create a directory to store masks
masks_dir = os.path.join(chip_dir, 'class_masks')
pathlib.Path(masks_dir).mkdir(parents=True, exist_ok=True)
# Read geotiff for chip
gtiff = chip_dir + '/' + 'image' + '/' + chip + '.tif'
src = rasterio.open(gtiff)
# Use try to only extract masks for chips with complete annotations and class labels
try:
"""Code for processing VGG annotations from Matterport balloon color splash sample"""
# Load annotations
# VGG Image Annotator saves each image in the form:
# { 'filename': '28503151_5b5b7ec140_b.jpg',
# 'regions': {
# '0': {
# 'region_attributes': {},
# 'shape_attributes': {
# 'all_points_x': [...],
# 'all_points_y': [...],
# 'name': 'polygon'}},
# ... more regions ...
# },
# 'size': 100202
# }
# Get the aquaculture class of each polygon
polygon_types = [r['region_attributes'] for r in a['regions']]
# Get unique aquaculture classes in annotations
types = set(val for dic in polygon_types for val in dic.values())
for t in types:
# Get the x, y coordinaets of points of the polygons that make up
# the outline of each object instance. There are stores in the
# shape_attributes (see json format above)
# Pull out polygons of that type
polygons = [r['shape_attributes'] for r in a['regions'] if r['region_attributes']['class'] == t]
# Draw mask using height and width of Geotiff
mask = np.zeros([src.height, src.width], dtype=np.uint8)
for p in polygons:
# Get indexes of pixels inside the polygon and set them to 1
rr, cc = skimage.draw.polygon(p['all_points_y'], p['all_points_x'])
mask[rr, cc] = 1
# Open a new GeoTiff data file in which to save the image chip
with rasterio.open((masks_dir + '/' + chip + '_' + str(t) + '_mask.tif'), 'w', driver='GTiff',
height=src.shape[0], width=src.shape[1], count=1,
dtype=rasterio.ubyte, crs=src.crs,
transform=src.transform) as new_img:
# Write the rescaled image to the new GeoTiff
new_img.write(mask.astype('uint8'),1)
except KeyError:
print(chip + ' missing aquaculture class assignment')
# write chip name to file for double checking
continue
```
Run function to create masks
```
labels = "/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/vgg/labeled/label_china/20180410_020421_0f31_labels.json"
prepped_dir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/prepped_planet/china_20180918'
masks_from_labels(labels = labels, prepped_dir = prepped_dir)
```
| github_jupyter |
# Import packages & Connect the database
```
# Install MYSQL client
pip install PyMySQL
import sklearn
print('The scikit-learn version is {}.'.format(sklearn.__version__))
%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import pandas as pd
import datetime as dt
# Connect to database
import pymysql
conn = pymysql.connect(
host='34.69.136.137',
port=int(3306),
user='root',
passwd='rtfgvb77884',
db='valenbisi',
charset='utf8mb4')
```
# Prepare data
```
# Get Stations
df_station_snapshot = pd.read_sql_query("SELECT station_number, station_service_available, creation_date FROM station_snapshot WHERE station_number=31",
conn)
def substractTime(x):
date = dt.datetime(x.year, x.month, x.day, x.hour)
return (date - dt.timedelta(hours=1))
def addTime(x):
date = dt.datetime(x.year, x.month, x.day, x.hour)
return (date + dt.timedelta(hours=1))
def getPrevAvailable(d_f, row):
new_dateTime = substractTime(row['datetime'])
try:
return d_f[(d_f['id'] == row['id']) & (d_f['year'] == new_dateTime.year) & (d_f['month'] == new_dateTime.month) & (d_f['day'] == new_dateTime.day) & (d_f['hour'] == new_dateTime.hour)].iloc[0, d_f.columns.get_loc('available')]
except:
return 0
def getNextAvailable(d_f, row):
new_dateTime = addTime(row['datetime'])
try:
return d_f[(d_f['id'] == row['id']) & (d_f['year'] == new_dateTime.year) & (d_f['month'] == new_dateTime.month) & (d_f['day'] == new_dateTime.day) & (d_f['hour'] == new_dateTime.hour)].iloc[0, d_f.columns.get_loc('available')]
except:
return 0
# Update titles
df_stations = df_station_snapshot.rename(index=str, columns={"station_number": "id", "station_service_available": "available", "creation_date": "datetime"})
df_stations['id'] = df_stations['id'].astype(str).astype(int);
# Transform date strinf to date without seconds
df_stations['datetime'] = pd.to_datetime(df_stations['datetime'], infer_datetime_format=True)
df_stations['datetime'] = df_stations['datetime'].dt.floor('H')
# # Sort by datetime
df_stations.sort_values(by=['datetime'], inplace=True, ascending=True)
# # Separate datetime in columns
df_stations['date'] = df_stations['datetime'].dt.date
df_stations['hour'] = df_stations['datetime'].dt.hour
df_stations['year'] = df_stations['datetime'].dt.year
df_stations['month'] = df_stations['datetime'].dt.month
df_stations['day'] = df_stations['datetime'].dt.day
df_stations['dayofweek'] = df_stations['datetime'].dt.dayofweek
# Group and avg by time
df_stations['available'] = df_stations.groupby(['id', 'date', 'hour'])['available'].transform('mean').astype(int)
df_stations.drop_duplicates(subset=['id', 'date', 'hour'], keep='first', inplace=True)
# # Set multiple avaiables
df_stations['available_prev'] = df_stations.apply(lambda x: getPrevAvailable(df_stations, x), axis=1)
df_stations['available_next'] = df_stations.apply(lambda x: getNextAvailable(df_stations, x), axis=1)
# # Clean columns
df_stations.drop(['datetime', 'day'], axis=1, inplace=True)
df_stations.tail()
# Get Holidays
df_holiday_snapshot = pd.read_sql_query("SELECT date, enabled FROM holiday",
conn)
# Update titles
df_holiday = df_holiday_snapshot.rename(index=str, columns={"enabled": "holiday"})
# Sort by datetime
df_holiday.sort_values(by=['date'], inplace=True, ascending=True)
# Get Sport Events
df_event_snapshot = pd.read_sql_query("SELECT date, football, basketball FROM sport_event",
conn)
# Clone data frame
df_event = df_event_snapshot
# Sort by datetime
df_event.sort_values(by=['date'], inplace=True, ascending=True)
# Get Weather
df_weather_snapshot = pd.read_sql_query("SELECT temperature, humidity, wind_speed, cloud_percentage, creation_date FROM weather",
conn)
# Update titles
df_weather = df_weather_snapshot.rename(index=str, columns={"wind_speed": "wind", "cloud_percentage": "cloud", "creation_date": "datetime"})
# Transform date strinf to date without seconds
df_weather['datetime'] = pd.to_datetime(df_weather['datetime'], infer_datetime_format=True)
df_weather['datetime'] = df_weather['datetime'].dt.floor('H')
# Separate datetime in two columns
df_weather['date'] = df_weather['datetime'].dt.date
df_weather['hour'] = df_weather['datetime'].dt.hour
# Group by datetime and get mean of the data
df_weather['temperature'] = df_weather.groupby(['hour', 'date'])['temperature'].transform('mean')
df_weather['humidity'] = df_weather.groupby(['hour', 'date'])['humidity'].transform('mean')
df_weather['wind'] = df_weather.groupby(['hour', 'date'])['wind'].transform('mean')
df_weather['cloud'] = df_weather.groupby(['hour', 'date'])['cloud'].transform('mean')
# Clean duplicated rows
df_weather.drop_duplicates(subset=['date', 'hour'], keep='first', inplace=True)
# Clean columns
df_weather.drop(['datetime'], axis=1, inplace=True)
# Merge stations with holidays
df = pd.merge(
df_stations,
df_holiday,
how='left',
left_on=['date'],
right_on=['date']
)
# Replace NaN with 0
df['holiday'] = df['holiday'].fillna(0)
# Merge (stations with holidays) with sport events
df = pd.merge(
df,
df_event,
how='left',
left_on=['date'],
right_on=['date']
)
# Replace NaN with 0
df['football'] = df['football'].fillna(0)
df['basketball'] = df['basketball'].fillna(0)
# Merge ((stations with holidays) with sport events) with weather
df = pd.merge(
df,
df_weather,
how='left',
left_on=['date', 'hour'],
right_on=['date', 'hour']
)
# Replace NaN with 0
df['temperature'] = df['temperature'].fillna(0)
df['humidity'] = df['humidity'].fillna(0)
df['wind'] = df['wind'].fillna(0)
df['cloud'] = df['cloud'].fillna(0)
# Show latest data
print('DATA AGGREGATED FOR STATION: ' + station)
df.tail(10)
```
# Visualize the data
```
# Load libraries
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.legend_handler import HandlerLine2D
import seaborn as sns;
# HEATMAP CHART PER MIN (10)
heatmap_data = pd.pivot_table(df[df['id']==31], values='available', index='hour', columns='date')
fig, ax = plt.subplots(figsize=(20,5))
sns.heatmap(heatmap_data, cmap='RdBu', ax=ax)
# HEATMAP CHART PER WEEK DAY
heatmap_data_week_day = pd.pivot_table(df[df['id']==31], values='available', index='hour', columns='dayofweek')
fig, ax = plt.subplots(figsize=(20,5))
sns.heatmap(heatmap_data_week_day, cmap='RdBu', ax=ax)
```
# Start prediction
```
# Load libraries
import math
from sklearn.ensemble import RandomForestRegressor, AdaBoostRegressor, GradientBoostingRegressor
from sklearn.linear_model import LinearRegression, Lasso, LassoLars, Ridge
from sklearn.tree import DecisionTreeRegressor
from scipy.stats import randint as sp_randint
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn import metrics
from sklearn.metrics import explained_variance_score
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
# Evaluate model
def evaluate(model, train_features, train_labels, test_features, test_labels):
print('MODEL PERFORMANCE')
train_pred = model.predict(train_features)
print('Train set')
print('| Mean Absolute Error:', metrics.mean_absolute_error(train_labels, train_pred))
print('| Mean Square Error:', metrics.mean_squared_error(train_labels, train_pred))
print('| Root Mean Square Error:', np.sqrt(metrics.mean_squared_error(train_labels, train_pred)))
print('| Train Score:', model.score(train_features, train_labels))
y_pred = model.predict(test_features)
print('Test set')
print('| Mean Absolute Error:', metrics.mean_absolute_error(test_labels, y_pred))
print('| Mean Square Error:', metrics.mean_squared_error(test_labels, y_pred))
print('| Root Mean Square Error:', np.sqrt(metrics.mean_squared_error(test_labels, y_pred)))
print('| Test Score:', model.score(test_features, test_labels))
print('| Explained Variance:', explained_variance_score(test_labels, y_pred))
if hasattr(model, 'oob_score_'): print('OOB Score:', model.oob_score_)
```
## Find best algoritm for our data
```
def quick_eval(pipeline, X_train, y_train, X_test, y_test, verbose=True):
"""
Quickly trains modeling pipeline and evaluates on test data. Returns original model, training RMSE, and testing
RMSE as a tuple.
"""
pipeline.fit(X_train, y_train)
y_train_pred = pipeline.predict(X_train)
y_test_pred = pipeline.predict(X_test)
train_score = np.sqrt(metrics.mean_squared_error(y_train, y_train_pred))
test_score = np.sqrt(metrics.mean_squared_error(y_test, y_test_pred))
if verbose:
print(f"Regression algorithm: {pipeline.named_steps['regressor'].__class__.__name__}")
print(f"Train RMSE: {train_score}")
print(f"Test RMSE: {test_score}")
print(f"----------------------------")
return pipeline.named_steps['regressor'], train_score, test_score
```
After review the result we see that **RandomForestRegressor** is the best option to predict our data
## Random Forest
```
# Create a new dataframe for random forest
df_rf = df[['id', 'year', 'month', 'dayofweek', 'hour', 'holiday', 'football', 'basketball', 'temperature', 'humidity', 'wind', 'cloud', 'available_prev', 'available', 'available_next']]
# Prepare data for train and test
# We want to predict ("available_next")
X = df_rf.drop('available_next', axis=1)
y = df_rf['available_next']
# Split data in train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
X_train.shape, y_train.shape, X_test.shape, y_test.shape
# Create our imputer to replace missing values with the mean e.g.
imp = SimpleImputer(missing_values=np.nan, strategy='mean')
imp = imp.fit(X_train)
# Impute our data, then train
X_train = imp.transform(X_train)
regressors = [
LinearRegression(),
Lasso(alpha=.5),
Ridge(alpha=.1),
LassoLars(alpha=.1),
DecisionTreeRegressor(),
RandomForestRegressor(),
AdaBoostRegressor(),
GradientBoostingRegressor()
]
for r in regressors:
pipe = Pipeline(steps = [
('regressor', r)
])
quick_eval(pipe, X_train, y_train, X_test, y_test)
```
### Find best params for Random Forest
#### Check each property
```
# Find N_ESTIMATORS
n_estimators = [int(x) for x in np.linspace(start = 1, stop = 200, num=50)]
train_results = []
test_results = []
for estimator in n_estimators:
rf = RandomForestRegressor(n_estimators=estimator, n_jobs=-1)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(n_estimators, train_results, 'b', label='Train RSME')
line2, = plt.plot(n_estimators, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('n_estimators')
plt.show()
# Find MAX_DEPTH
max_depths = np.linspace(start = 1, stop = 100, num=50, endpoint=True)
train_results = []
test_results = []
for max_depth in max_depths:
rf = RandomForestRegressor(max_depth=max_depth, n_jobs=-1)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(max_depths, train_results, 'b', label='Train RSME')
line2, = plt.plot(max_depths, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('Tree depth')
plt.show()
# Find MIN_SAMPLES_SPLIT
min_samples_splits = np.linspace(start = 0.01, stop = 1.0, num=10, endpoint=True)
train_results = []
test_results = []
for min_samples_split in min_samples_splits:
rf = RandomForestRegressor(min_samples_split=min_samples_split)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(min_samples_splits, train_results, 'b', label='Train RSME')
line2, = plt.plot(min_samples_splits, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('min samples split')
plt.show()
# Find MIN_SAMPLES_LEAF
min_samples_leafs = np.linspace(start = 0.01, stop = 0.5, num=5, endpoint=True)
train_results = []
test_results = []
for min_samples_leaf in min_samples_leafs:
rf = RandomForestRegressor(min_samples_leaf=min_samples_leaf)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(min_samples_leafs, train_results, 'b', label='Train RSME')
line2, = plt.plot(min_samples_leafs, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('min samples leaf')
plt.show()
# Find MAX_FEATURES
max_features = list(range(1,X.shape[1]))
train_results = []
test_results = []
for max_feature in max_features:
rf = RandomForestRegressor(max_features=max_feature)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(max_features, train_results, 'b', label='Train RSME')
line2, = plt.plot(max_features, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('max features')
plt.show()
```
#### Find the best combination of params
**TRY ALL PARAMS TO FIND THE BEST PARAMS FOR OUR DATA**
Now that we know where to concentrate our search, we can explicitly specify every combination of settings to try.
```
#@title Default title text
def searchBestParamsForRF(params, train_features, train_labels):
# First create the base model to tune
rf = RandomForestRegressor()
# Instantiate the grid search model
grid_search = GridSearchCV(estimator = rf, param_grid = param_grid, scoring = 'neg_mean_squared_error', cv = 5, n_jobs = -1, verbose = 2)
# Fit the grid search to the data
grid_search.fit(train_features, train_labels)
print(f"The best estimator had RMSE {np.sqrt(-grid_search.best_score_)} and the following parameters:")
print(grid_search.best_params_)
# Create the parameter grid
max_depth = [int(x) for x in np.linspace(10, 20, num = 3)]
max_depth.append(None)
param_grid = {
'bootstrap': [False, True],
'n_estimators': [int(x) for x in np.linspace(start = 40, stop = 60, num = 4)],
'max_depth': max_depth,
'min_samples_split': [float(x) for x in np.linspace(0.1, 0.2, num = 2)],
'min_samples_leaf': [float(x) for x in np.linspace(0.1, 0.2, num = 2)],
'max_features': [X.shape[1]]
}
# Comment or Uncomment this line to seach for the best params
searchBestParamsForRF(param_grid, X_train, y_train)
```
### Train and evaluate model
```
m = RandomForestRegressor(n_estimators=60, max_features=X.shape[1])
m.fit(X_train, y_train)
evaluate(m, X_train, y_train, X_test, y_test)
# MODEL PERFORMANCE
# Train set
# | Mean Absolute Error: 0.5758625862586259
# | Mean Square Error: 0.6365449044904491
# | Root Mean Square Error: 0.7978376429389936
# | Train Score: 0.9807615052050999
# Test set
# | Mean Absolute Error: 1.5209793351302785
# | Mean Square Error: 4.284529050613956
# | Root Mean Square Error: 2.0699103967597137
# | Test Score: 0.8757254225805797
# | Explained Variance: 0.8758109846903823
X_test.tail()
y_test.tail()
m.predict([[2020, 1, 6, 10, 0, 0, 0, 11.57, 70.50, 0.93, 0, 0, 1]])
# Show the importance of each variable in prediction
def rf_feat_importance(m, df):
return pd.DataFrame({'cols':df.columns, 'imp':m.feature_importances_}).sort_values('imp', ascending=False)
fi = rf_feat_importance(m, X);
fi[:].plot('cols', 'imp', 'barh', figsize=(12,7), legend=False)
```
# Download model
```
# Import package
import pickle
# Generate file
with open('model.pkl', 'wb') as model_file:
pickle.dump(m, model_file)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/dlmacedo/ml-dl-notebooks/blob/master/notebooks/machine-learning/RECOMMENDED_Principal_Component_Analysis.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# In Depth: Principal Component Analysis
In this section, we explore what is perhaps one of the most broadly used of unsupervised algorithms, principal component analysis (PCA).
PCA is fundamentally a dimensionality reduction algorithm, but it can also be useful as a tool for visualization, for noise filtering, for feature extraction and engineering, and much more.
After a brief conceptual discussion of the PCA algorithm, we will see a couple examples of these further applications.
We begin with the standard imports:
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
```
## Introducing Principal Component Analysis
Principal component analysis is a fast and flexible unsupervised method for dimensionality reduction in data.
Its behavior is easiest to visualize by looking at a two-dimensional dataset.
Consider the following 200 points:
```
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal');
```
By eye, it is clear that there is a nearly linear relationship between the x and y variables.
This is reminiscent of the linear regression data, but the problem setting here is slightly different: rather than attempting to *predict* the y values from the x values, the unsupervised learning problem attempts to learn about the *relationship* between the x and y values.
In principal component analysis, this relationship is quantified by finding a list of the *principal axes* in the data, and using those axes to describe the dataset.
Using Scikit-Learn's ``PCA`` estimator, we can compute this as follows:
```
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
```
The fit learns some quantities from the data, most importantly the "components" and "explained variance":
```
print(pca.components_)
print(pca.explained_variance_)
```
To see what these numbers mean, let's visualize them as vectors over the input data, using the "components" to define the direction of the vector, and the "explained variance" to define the squared-length of the vector:
```
def draw_vector(v0, v1, ax=None):
ax = ax or plt.gca()
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
ax.annotate('', v1, v0, arrowprops=arrowprops)
# plot data
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal');
```
These vectors represent the *principal axes* of the data, and the length of the vector is an indication of how "important" that axis is in describing the distribution of the data—more precisely, it is a measure of the variance of the data when projected onto that axis.
The projection of each data point onto the principal axes are the "principal components" of the data.
If we plot these principal components beside the original data, we see the plots shown here:

This transformation from data axes to principal axes is an *affine transformation*, which basically means it is composed of a translation, rotation, and uniform scaling.
While this algorithm to find principal components may seem like just a mathematical curiosity, it turns out to have very far-reaching applications in the world of machine learning and data exploration.
### PCA as dimensionality reduction
Using PCA for dimensionality reduction involves zeroing out one or more of the smallest principal components, resulting in a lower-dimensional projection of the data that preserves the maximal data variance.
Here is an example of using PCA as a dimensionality reduction transform:
```
pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape: ", X.shape)
print("transformed shape:", X_pca.shape)
```
The transformed data has been reduced to a single dimension.
To understand the effect of this dimensionality reduction, we can perform the inverse transform of this reduced data and plot it along with the original data:
```
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal');
```
The light points are the original data, while the dark points are the projected version.
This makes clear what a PCA dimensionality reduction means: the information along the least important principal axis or axes is removed, leaving only the component(s) of the data with the highest variance.
The fraction of variance that is cut out (proportional to the spread of points about the line formed in this figure) is roughly a measure of how much "information" is discarded in this reduction of dimensionality.
This reduced-dimension dataset is in some senses "good enough" to encode the most important relationships between the points: despite reducing the dimension of the data by 50%, the overall relationship between the data points are mostly preserved.
### PCA for visualization: Hand-written digits
The usefulness of the dimensionality reduction may not be entirely apparent in only two dimensions, but becomes much more clear when looking at high-dimensional data.
To see this, let's take a quick look at the application of PCA to the digits data.
We start by loading the data:
```
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
```
Recall that the data consists of 8×8 pixel images, meaning that they are 64-dimensional.
To gain some intuition into the relationships between these points, we can use PCA to project them to a more manageable number of dimensions, say two:
```
pca = PCA(2) # project from 64 to 2 dimensions
projected = pca.fit_transform(digits.data)
print(digits.data.shape)
print(projected.shape)
```
We can now plot the first two principal components of each point to learn about the data:
```
plt.scatter(projected[:, 0], projected[:, 1],
c=digits.target, edgecolor='none', alpha=0.5,
cmap=plt.cm.get_cmap('Accent', 10)
)
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar();
```
Recall what these components mean: the full data is a 64-dimensional point cloud, and these points are the projection of each data point along the directions with the largest variance.
Essentially, we have found the optimal stretch and rotation in 64-dimensional space that allows us to see the layout of the digits in two dimensions, and have done this in an unsupervised manner—that is, without reference to the labels.
### What do the components mean?
We can go a bit further here, and begin to ask what the reduced dimensions *mean*.
This meaning can be understood in terms of combinations of basis vectors.
For example, each image in the training set is defined by a collection of 64 pixel values, which we will call the vector $x$:
$$
x = [x_1, x_2, x_3 \cdots x_{64}]
$$
One way we can think about this is in terms of a pixel basis.
That is, to construct the image, we multiply each element of the vector by the pixel it describes, and then add the results together to build the image:
$$
{\rm image}(x) = x_1 \cdot{\rm (pixel~1)} + x_2 \cdot{\rm (pixel~2)} + x_3 \cdot{\rm (pixel~3)} \cdots x_{64} \cdot{\rm (pixel~64)}
$$
One way we might imagine reducing the dimension of this data is to zero out all but a few of these basis vectors.
For example, if we use only the first eight pixels, we get an eight-dimensional projection of the data, but it is not very reflective of the whole image: we've thrown out nearly 90% of the pixels!

The upper row of panels shows the individual pixels, and the lower row shows the cumulative contribution of these pixels to the construction of the image.
Using only eight of the pixel-basis components, we can only construct a small portion of the 64-pixel image.
Were we to continue this sequence and use all 64 pixels, we would recover the original image.
But the pixel-wise representation is not the only choice of basis. We can also use other basis functions, which each contain some pre-defined contribution from each pixel, and write something like
$$
image(x) = {\rm mean} + x_1 \cdot{\rm (basis~1)} + x_2 \cdot{\rm (basis~2)} + x_3 \cdot{\rm (basis~3)} \cdots
$$
PCA can be thought of as a process of choosing optimal basis functions, such that adding together just the first few of them is enough to suitably reconstruct the bulk of the elements in the dataset.
The principal components, which act as the low-dimensional representation of our data, are simply the coefficients that multiply each of the elements in this series.
This figure shows a similar depiction of reconstructing this digit using the mean plus the first eight PCA basis functions:

Unlike the pixel basis, the PCA basis allows us to recover the salient features of the input image with just a mean plus eight components!
The amount of each pixel in each component is the corollary of the orientation of the vector in our two-dimensional example.
This is the sense in which PCA provides a low-dimensional representation of the data: it discovers a set of basis functions that are more efficient than the native pixel-basis of the input data.
### Choosing the number of components
A vital part of using PCA in practice is the ability to estimate how many components are needed to describe the data.
This can be determined by looking at the cumulative *explained variance ratio* as a function of the number of components:
```
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
```
This curve quantifies how much of the total, 64-dimensional variance is contained within the first $N$ components.
For example, we see that with the digits the first 10 components contain approximately 75% of the variance, while you need around 50 components to describe close to 100% of the variance.
Here we see that our two-dimensional projection loses a lot of information (as measured by the explained variance) and that we'd need about 20 components to retain 90% of the variance. Looking at this plot for a high-dimensional dataset can help you understand the level of redundancy present in multiple observations.
## PCA as Noise Filtering
PCA can also be used as a filtering approach for noisy data.
The idea is this: any components with variance much larger than the effect of the noise should be relatively unaffected by the noise.
So if you reconstruct the data using just the largest subset of principal components, you should be preferentially keeping the signal and throwing out the noise.
Let's see how this looks with the digits data.
First we will plot several of the input noise-free data:
```
def plot_digits(data):
fig, axes = plt.subplots(4, 10, figsize=(10, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8, 8),
cmap='binary', interpolation='nearest',
clim=(0, 16))
plot_digits(digits.data)
```
Now lets add some random noise to create a noisy dataset, and re-plot it:
```
np.random.seed(42)
noisy = np.random.normal(digits.data, 4)
plot_digits(noisy)
```
It's clear by eye that the images are noisy, and contain spurious pixels.
Let's train a PCA on the noisy data, requesting that the projection preserve 50% of the variance:
```
pca = PCA(0.50).fit(noisy)
pca.n_components_
```
Here 50% of the variance amounts to 12 principal components.
Now we compute these components, and then use the inverse of the transform to reconstruct the filtered digits:
```
components = pca.transform(noisy)
filtered = pca.inverse_transform(components)
plot_digits(filtered)
```
This signal preserving/noise filtering property makes PCA a very useful feature selection routine—for example, rather than training a classifier on very high-dimensional data, you might instead train the classifier on the lower-dimensional representation, which will automatically serve to filter out random noise in the inputs.
## Example: Eigenfaces
Earlier we explored an example of using a PCA projection as a feature selector for facial recognition with a support vector machine.
Here we will take a look back and explore a bit more of what went into that.
Recall that we were using the Labeled Faces in the Wild dataset made available through Scikit-Learn:
```
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=60)
print(faces.target_names)
print(faces.images.shape)
```
Let's take a look at the principal axes that span this dataset.
Because this is a large dataset, we will use ``RandomizedPCA``—it contains a randomized method to approximate the first $N$ principal components much more quickly than the standard ``PCA`` estimator, and thus is very useful for high-dimensional data (here, a dimensionality of nearly 3,000).
We will take a look at the first 150 components:
```
from sklearn.decomposition import PCA as RandomizedPCA
pca = RandomizedPCA(150)
pca.fit(faces.data)
```
In this case, it can be interesting to visualize the images associated with the first several principal components (these components are technically known as "eigenvectors,"
so these types of images are often called "eigenfaces").
As you can see in this figure, they are as creepy as they sound:
```
fig, axes = plt.subplots(3, 8, figsize=(9, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(pca.components_[i].reshape(62, 47), cmap='bone')
```
The results are very interesting, and give us insight into how the images vary: for example, the first few eigenfaces (from the top left) seem to be associated with the angle of lighting on the face, and later principal vectors seem to be picking out certain features, such as eyes, noses, and lips.
Let's take a look at the cumulative variance of these components to see how much of the data information the projection is preserving:
```
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
```
We see that these 150 components account for just over 90% of the variance.
That would lead us to believe that using these 150 components, we would recover most of the essential characteristics of the data.
To make this more concrete, we can compare the input images with the images reconstructed from these 150 components:
```
# Compute the components and projected faces
pca = RandomizedPCA(150).fit(faces.data)
components = pca.transform(faces.data)
projected = pca.inverse_transform(components)
# Plot the results
fig, ax = plt.subplots(2, 10, figsize=(10, 2.5),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(10):
ax[0, i].imshow(faces.data[i].reshape(62, 47), cmap='binary_r')
ax[1, i].imshow(projected[i].reshape(62, 47), cmap='binary_r')
ax[0, 0].set_ylabel('full-dim\ninput')
ax[1, 0].set_ylabel('150-dim\nreconstruction');
```
The top row here shows the input images, while the bottom row shows the reconstruction of the images from just 150 of the ~3,000 initial features.
This visualization makes clear why the PCA feature selection used in the Support Vector Machines example was so successful: although it reduces the dimensionality of the data by nearly a factor of 20, the projected images contain enough information that we might, by eye, recognize the individuals in the image.
What this means is that our classification algorithm needs to be trained on 150-dimensional data rather than 3,000-dimensional data, which depending on the particular algorithm we choose, can lead to a much more efficient classification.
## Principal Component Analysis Summary
In this section we have discussed the use of principal component analysis for dimensionality reduction, for visualization of high-dimensional data, for noise filtering, and for feature selection within high-dimensional data.
Because of the versatility and interpretability of PCA, it has been shown to be effective in a wide variety of contexts and disciplines.
Given any high-dimensional dataset, I tend to start with PCA in order to visualize the relationship between points (as we did with the digits), to understand the main variance in the data (as we did with the eigenfaces), and to understand the intrinsic dimensionality (by plotting the explained variance ratio).
Certainly PCA is not useful for every high-dimensional dataset, but it offers a straightforward and efficient path to gaining insight into high-dimensional data.
PCA's main weakness is that it tends to be highly affected by outliers in the data.
For this reason, many robust variants of PCA have been developed, many of which act to iteratively discard data points that are poorly described by the initial components.
Scikit-Learn contains a couple interesting variants on PCA, including ``RandomizedPCA`` and ``SparsePCA``, both also in the ``sklearn.decomposition`` submodule.
``RandomizedPCA``, which we saw earlier, uses a non-deterministic method to quickly approximate the first few principal components in very high-dimensional data, while ``SparsePCA`` introduces a regularization term that serves to enforce sparsity of the components.
| github_jupyter |
**Experiment for obtaining 24 Hr prediction from Dense Model in rainymotion library**
Author: Divya S. Vidyadharan
File use: For predicting 24 Hr precipitation images with **3 hr lead time.**
Date Created: 19-03-21
Last Updated: 20-03-21
Python version: 3.8.2
```
import h5py
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import scipy.misc
import sys
import os
module_path = os.path.abspath(os.path.join('/home/divya/divya/OtherNowcastings/rainymotion-master'))
if module_path not in sys.path:
sys.path.append(module_path)
from rainymotion.models import Dense
from rainymotion.metrics import *
import cv2
import pandas as pd
import wradlib.ipol as ipol # for interpolation
from rainymotion import metrics
from rainymotion import utils
from scipy.ndimage import map_coordinates
import timeit
print(cv2.__version__)
#from tvl1sindysupport import tvl1utilities -in future our own library
times=['0000','0010', '0020', '0030', '0040', '0050',
'0100', '0110', '0120', '0130', '0140', '0150',
'0200', '0210', '0220', '0230', '0240', '0250',
'0300', '0310', '0320', '0330', '0340', '0350',
'0400', '0410', '0420', '0430', '0440' ,'0450',
'0500', '0510', '0520', '0530', '0540', '0550',
'0600', '0610', '0620', '0630', '0640', '0650',
'0700', '0710', '0720', '0730', '0740', '0750',
'0800', '0810', '0820', '0830', '0840', '0850',
'0900', '0910', '0920', '0930', '0940', '0950',
'1000', '1010', '1020', '1030', '1040', '1050',
'1100', '1110', '1120', '1130', '1140', '1150',
'1200', '1210', '1220', '1230', '1240', '1250',
'1300', '1310', '1320', '1330', '1340', '1350',
'1400', '1410', '1420', '1430', '1440', '1450',
'1500', '1510', '1520', '1530', '1540', '1550',
'1600', '1610', '1620', '1630', '1640', '1650',
'1700', '1710', '1720', '1730', '1740', '1750',
'1800', '1810', '1820', '1830', '1840', '1850',
'1900', '1910', '1920', '1930', '1940', '1950',
'2000', '2010', '2020', '2030', '2040', '2050',
'2100', '2110', '2120', '2130', '2140', '2150',
'2200', '2210', '2220', '2230', '2240', '2250',
'2300', '2310', '2320', '2330', '2340', '2350']
# Common Initialization
eventName = "TyphoonFaxai"
eventDate ="20190908"
#Latitude and Longitude of Typhoon Faxai
lat1 = 32.5
lat2 = 39
long1 = 136
long2 = 143
pred_date = 20190908 #YYYYMMDD
[height, width] = [781,561]
eventNameDate = eventName + "_" + eventDate
# startHr = 2
# startMin= 40
# predStartHr = 300
step = 5 #for rainymotion models
# For radar images
inputFolder = "./ForExperiments/Exp1/RadarImages/HeavyRainfall/For300/"
# outputFolder= "./ForExperiments/Exp1/Results/"
# print(inputFolder)
fileType='.bin'
timeStep = 10 # for Japan Radar Data
modelName = "Dense"
# startHr = 7# the first hr among for the three input images
# startMin = 30 #
# noOfImages = 3
stepRainyMotion = 5 # 5 minutes
# outputFilePath = outputFolder+modelName+'_'
# outputFilePath = outputFilePath + eventNameDate
# print(outputFilePath)
##recentFramePath##
recentFrameFolder = str(pred_date)+"_set_24Hr_bin" #20190908_set_24Hr_bin
recentFramePath = "/home/divya/divya/OneFullDayData_7TestCases_WNIMar5/%s"%recentFrameFolder
print ("\n Recent frame path ",recentFramePath)
inputFolder = recentFramePath
print("\n Input folder is ",inputFolder)
##Output path where predicted images for visual comparison are saved.##
outputimgpath = "/home/divya/divya/OneFullDayData_7TestCases_WNIMar5/24hroutputs/%i/%s/%s"%(pred_date,modelName,"pred_images")
os.makedirs(outputimgpath, exist_ok=True)
print ("\n Output image path is ",outputimgpath)
##Output path where evaluation results are saved as csv files.##
outputevalpath = "/home/divya/divya/OneFullDayData_7TestCases_WNIMar5/24hroutputs/%i/%s/%s"%(pred_date,modelName,"eval_results")
os.makedirs(outputevalpath, exist_ok=True)
print ("\n Output eval results in ",outputevalpath)
savepath = outputimgpath#"Outputs/%i/%s"%(pred_date,pred_times[0])
noOfImages = 3 # Model needs 24 frames
step = 5
outputFilePath = outputimgpath+'/'
outputFilePath = outputFilePath + eventNameDate
print(outputFilePath)
hrlimit = len(times)
leadsteps = 18 #6
totinputframes = 2
def gettimes24hr(pred_time):
# times=np.array(times)
inptimes = []
pred_times = []
index = times.index(pred_time)
indexlimit = len(times)
print("Leadsteps are ", leadsteps)
if (index+leadsteps) < indexlimit:
pred_times = times[index:index+leadsteps]
if (index-totinputframes)>=0:
inptimes = times[index-totinputframes:index]
print("PredTimes:",pred_times)
print("InpTimes:",inptimes)
print("Get Time Success..")
return inptimes, pred_times
def readRadarImages(pred_time,inputpath,height,width, noOfImages,fileType):
files = (os.listdir(recentFramePath))
files.sort()
inputRadarImages = []
i = 0
index = times.index(pred_time)
# print(index)
inputframes = times[index-noOfImages:index]
# print(len(inputframes))
while (i<noOfImages):
inputframetime = "_"+inputframes[i]
i = i +1
for fileName in files:
if inputframetime in fileName:
print("The input image at %s is available",inputframetime)
print(fileName)
if fileName.endswith(fileType):
inputFileName =recentFramePath+'/'+fileName
fd = open(inputFileName,'rb')
#print(inputFileName)
# straight to numpy data (no buffering)
inputFrame = np.fromfile(fd, dtype = np.dtype('float32'), count = 2*height*width)
inputFrame = np.reshape(inputFrame,(height,width))
inputFrame = inputFrame.astype('float16')
#print(recentFrame.shape)
inputRadarImages.append(inputFrame)
#else:
# print("Sorry, unable to find file.")
inputRadarImages = np.stack(inputRadarImages, axis=0)
print(inputRadarImages.shape)
return inputRadarImages
```
**1.2 Dense**
```
def doDenseNowcasting(startpredtime, saveimages):
model = Dense()
model.input_data = readRadarImages(startpredtime,inputFolder,height,width, noOfImages,fileType)
start = timeit.timeit()
nowcastDense = model.run()
end = timeit.timeit()
sparseTime = end - start
print("Dense took ",end - start)
print(nowcastDense.shape)
# for i in range(12):
# outFrameName = outputFilePath + '_'+str(predStartHr+(i*5))+'.png'
# # print(outFrameName)
# if saveimages:
# matplotlib.image.imsave(outFrameName, nowcastDense[i])
print("Finished Dense model nowcasting!")
return nowcastDense
```
**2. Performance Evaluation**
```
def getGroundTruthImages(pred_times,leadsteps,recentFramePath,height,width,fileType):
files = (os.listdir(recentFramePath))
files.sort()
groundTruthImages = []
i = 0
while (i<leadsteps):
groundtruthtime = "_"+pred_times[i]
i = i +1
for fileName in files:
if groundtruthtime in fileName:
print("The ground truth at %s is available",groundtruthtime)
print(fileName)
if fileName.endswith(fileType):
inputFileName =recentFramePath+'/'+fileName
fd = open(inputFileName,'rb')
#print(inputFileName)
# straight to numpy data (no buffering)
recentFrame = np.fromfile(fd, dtype = np.dtype('float32'), count = 2*height*width)
recentFrame = np.reshape(recentFrame,(height,width))
recentFrame = recentFrame.astype('float16')
#print(recentFrame.shape)
groundTruthImages.append(recentFrame)
#else:
# print("Sorry, unable to find file.")
groundTruthImages = np.moveaxis(np.dstack(groundTruthImages), -1, 0)
#print(groundTruthImages.shape)
return groundTruthImages
def evaluate(nowcasts):
fileType = '.bin'
# leadsteps = 6 # 6 for 1 hr prediction, 18 for 3hr prediction
groundTruthPath = recentFramePath
print(pred_times)
groundTruthImgs = getGroundTruthImages(pred_times,leadsteps,groundTruthPath,height,width,fileType)
maelist = []
farlist = []
podlist= []
csilist= []
thres =1.0
noOfPrecipitationImages = leadsteps
j = 0 # using another index to skip 5min interval data from rainymotion
for i in range(noOfPrecipitationImages):
mae = MAE(groundTruthImgs[i],nowcasts[j])
far = FAR(groundTruthImgs[i],nowcasts[j], threshold=0.1)
pod = POD(groundTruthImgs[i],nowcasts[j], threshold=0.1)
csi = CSI(groundTruthImgs[i],nowcasts[j],thres)
maelist.append(mae)
farlist.append(far)
podlist.append(pod)
csilist.append(csi)
j = j + 2
return csilist,maelist,farlist,podlist
```
**2. 24 Hr Prediction**
```
startpredtime = '0110' #'1100'
index = times.index(startpredtime)
indexlimit = times.index('2250') # Since we have only 6 more ground truths available from this time
print(index)
print("Last prediction is at index ", indexlimit)
csilist = []
maelist = []
podlist = []
farlist = []
pred_time = startpredtime
while index<indexlimit:#len(times):
print(times[index])
saveimages = 0
if (index==66):
saveimages=1
intimes, pred_times = gettimes24hr(pred_time)
nowcasts = doDenseNowcasting(pred_time,saveimages)
csi,mae,far,pod = evaluate(nowcasts)
csilist.append(csi)
maelist.append(mae)
podlist.append(pod)
farlist.append(far)
index = index+1
pred_time = times[index]
DISOpticalFlow_create
# For debugging
print(len(maelist))
print("\n\n")
print(len(csilist))
print("\n\n")
print(len(podlist))
print("\n\n")
print(len(farlist))
```
**To save results in excel workbook**
```
import xlwt
from xlwt import Workbook
# Workbook is created
wb = Workbook()
def writeinexcelsheet(sheetname, wb, results):
sheet1 = wb.add_sheet(sheetname)
sheet1.write(0, 0, 'Pred.no.')
sheet1.write(0, 1, 't (pred start time)')
sheet1.write(0, 2, 't + 10')
sheet1.write(0, 3, 't + 20')
sheet1.write(0, 4, 't + 30')
sheet1.write(0, 5, 't + 40')
sheet1.write(0, 6, 't + 50')
col = 0
rows = len(results)
cols = len(results[0])
print(cols)
for rowno in range(rows):
sheet1.write(rowno+1,0,rowno+1)
for col in range(cols):
# print(rowno+1,col+1,results[rowno][col])
sheet1.write(rowno+1,col+1,results[rowno][col].astype('float64'))
# sheet1.write(row, col, str(data))
# print(row,col,data)
writeinexcelsheet('CSI',wb,csilist)
writeinexcelsheet('MAE',wb,maelist)
writeinexcelsheet('FAR',wb,farlist)
writeinexcelsheet('POD',wb,podlist)
excelpath = "/home/divya/divya/OneFullDayData_7TestCases_WNIMar5/24hroutputs/20190908/Dense/eval_results/"
excelpath = excelpath + 'resultsDense.xls'
wb.save(excelpath)
```
| github_jupyter |
# **M**odel **U**ncertainty-based Data **Augment**ation (muAugment)
<a rel="license" href="http://creativecommons.org/licenses/by-nc-sa/4.0/"><img alt="Creative Commons License" align="left" src="https://i.creativecommons.org/l/by-nc-sa/4.0/80x15.png" /></a> | Mariana Alves | <a href="https://supaerodatascience.github.io/deep-learning/">https://supaerodatascience.github.io/deep-learning/</a>
## Preliminary work for colab
**This notebook was written in google colab, so it is recommended that you run it in colab as well.**
<a href="https://colab.research.google.com/github/Mariana-Andrade-Alves/muAugment/blob/main/muAugment.ipynb">
<img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/>
</a>
Before starting to work on the notebook, make sure you `change the Runtime type` to **GPU**, in the `Tool` drop menu.
In colab, please execute first the following cells, to retrieve the GitHub repository content.
```
!git clone https://github.com/Mariana-Andrade-Alves/muAugment/
```
## Preliminary Imports
```
# !pip install matplotlib
# !pip install torch torchvision
import torch
import torchvision
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from torch import nn, optim
import torch.nn.functional as F
from torch.utils.data import DataLoader, Dataset
from torchvision import datasets, transforms
from torchvision.datasets import FashionMNIST
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)
```
## Overview of Data Augmentation
Modern machine learning models, such as deep neural networks, may have billions of parameters and, consequently, require massive labeled training datasets, which are often not available. In order to avoid the **problem of data scarcity** in such models, data augmentation has become the standard technique used in nearly every state-of-the-art model in applications such as **image** and **text classification**.
> **Data augmentation refers to the technique of artificially expanding labelled training datasets by generating new data through transformation functions.**
Data augmentation schemes often rely on the composition of a set of simple transformation functions (TFs) such as rotation and flip.
<img src="https://github.com/Mariana-Andrade-Alves/muAugment/blob/main/img/transforms.png?raw=1" width='800'>
"Label-invariant transformations." [torchvision.transforms docs](https://pytorch.org/vision/stable/transforms.html#transforms-on-pil-image-only)
As was briefly discussed in the [computer vision class](https://github.com/SupaeroDataScience/deep-learning/blob/main/vision/1_hands_on.ipynb), when chosen carefully, data augmentation schemes tuned by human experts can improve model performance. However, such heuristic strategies in practice can cause large variances in end model performance, and may not produce parameterizations and compositions needed for state-of-the-art models. In addition, they are extremely laborious.
### Automated Data Augmentation Schemes
Instead of performing manual search, automated data augmentation approaches hold promise to search for more powerful parameterizations and compositions of transformations.
The biggest difficulty with automating data augmentation is how to search over the space of transformations. This can be prohibitively expensive due to the large number of transformation functions in the search space.
> **How can we design algorithms that explore the space of transformation functions efficiently and effectively, and find augmentation strategies that can outperform human-designed heuristics?**
The folklore wisdom behind data augmentation is that adding more labeled data improves generalization, i.e. the performance of the trained model on unseen test data. However, even for simpler models, **it is not well-understood how training on augmented data affects the learning process, the parameters, and the decision surface of the resulting model**.
<details class="alert alert-block alert-info">
<summary markdown="span"><b>Extra information on the Adversarial AutoAugment Scheme previsouly discussed in class (click to expand)</b></summary>
One of the current state-of-the-art algorithms in terms of performance is [Adversarial AutoAugment](https://openreview.net/pdf?id=ByxdUySKvS), which makes use of [GANs](https://proceedings.neurips.cc/paper/2014/file/5ca3e9b122f61f8f06494c97b1afccf3-Paper.pdf), already presented in a previous [class](https://github.com/SupaeroDataScience/deep-learning/tree/main/GAN), to generate new data, rather than using the traditional heuristic transformations presented above.
<img src="https://github.com/Mariana-Andrade-Alves/muAugment/blob/main/img/AdvAA.png?raw=1" width='800'>
Li et al. "Adversarial AutoAugment training framework (Zhang et al. 2019) is formulated as an adversarial min-max game." [Automating the Art of Data Augmentation.](https://hazyresearch.stanford.edu/blog/2020-02-26-data-augmentation-part2) 2020.
Although proven effective, this technique is still computationally expensive. Additionally, despite its rapid progress, this technique does not allow for a theoretical understanding of the benefits of a given transformation.
</details>
## How should we think of the effects of applying a transformation?
### Intuition for Linear Transformations
Suppose we are given $n$ training data points $x_1,...,x_n \in \mathbb{R}^p$ as $X \in \mathbb{R}^{n\times p}$ with labels $Y\in \mathbb{R}^n$.
> Suppose that the labels $Y$ obey the true linear model under ground parameters $\beta \in \mathbb{R}^p$, $$Y = X \beta + \epsilon,$$ where $\epsilon \in \mathbb{R}^n$ denotes i.d.d. random noise with mean zero and variance $\sigma²$.
Importantly, we assume that $p>n$, hence the span of the training data does not contain the entire space of $\mathbb{R}^p$.
Let's suppose we have an estimator $\hat{\beta}$ for the linear model $\beta \in \mathbb{R}^p$. The error of that given estimator is
> $$e(\hat{\beta}) = \underbrace{\lVert \underset{
\epsilon}{\mathbb{E}}[\hat{\beta}]-\beta\rVert^2}_{bias} + \underbrace{\lVert\hat{\beta} - \underset{\epsilon}{\mathbb{E}}[\beta] \rVert^2}_{variance}$$
where the bias part, intuitively, measures the intrinsic error of the model after taking into account the randomness which is present in $\hat{\beta}$.
### Label-Invariant Transformations
For a matrix $F \in \mathbb{R}^{p\times p}$, we say that $F$ is a label-invariant transformation over $\chi \subseteq \mathbb{R}^p $ for $\beta \in \mathbb{R}^p$ if $$x^\top\beta = (Fx)^\top\beta, \quad \text{ for any } x \in \chi.$$
> In simpler words, a label-invariant transformation will not alter the label $y$ of a given data point $x$.
**But what is the effect of such a transformation?**
Given a training data point $(x,y)$, let $(x^{aug},y^{aug})$ denote the augmented data where $y^{aug} = y$ and $x^{aug} = Fx$.
**Note**: In order to be able to present the next result, let's consider adding the augmented data point $(z,y^{aug})$, where $z = P^\bot_X Fx$, meaning $z$ is not $x^{aug}$, but the projection of $x^{aug}$ onto $P^\bot_X = Id_p -P_X$, which denotes the projection operator which is ortogonal to the projection matrix onto the row of $X$ ($P_X$). In such a case, $y^{aug} = y - Diag[(X^\top)^†Fx]Y$.
> An intuiton to understand why we chose to use the projection $P^\bot_X a^{aug}$ instead of the augmented data is to think about the idea of "adding new information". Remember: we assume that $p>n$, hence the subspace over which we can make an accurate estimation does not contain the entire space of $\mathbb{R}^p$. When we a data point belonging to a space ortogonal to the one we know, we expand the subspace over which we can make an accurate estimation, by adding a direction corresponding to $P^\bot_X a^{aug}$.
Suppose the estimator $\hat{\beta}$ used to infer labels is a ridge estimator with a penalty parameter $\lambda$, given by
$$\hat{\beta}(X,Y) = (X^\top X + n \lambda Id)^{-1}X^\top Y, $$
where, just to recap, $X$ denotes the training data and $Y$ the training labels.
Considering $e(\hat{\beta})$ and $e(\hat{\beta}^F)$ has the errors of the estimator before and after adding the augmented data point $(z,y^{aug})$ to $(X,Y)$, it is possible to demonstrate that,
$$ 0 \leq e(\hat{\beta}) - e(\hat{\beta}^F) - (2+o(1))\dfrac{\langle z,\beta \rangle²}{\lambda n} \leq \dfrac{poly(\gamma/\lambda)}{n²}, $$ where $poly(\gamma/\lambda)$ denotes a polynomial of $\gamma/\lambda$.
This powerful result, which we will not explain in class but can be found in the [muAugment paper](https://hazyresearch.stanford.edu/blog/2020-02-26-data-augmentation-part2), shows that
* **the reduction of the estimation error**, $e(\hat{\beta}) - e(\hat{\beta}^F)$, **scales with the correlation between the new signal and the true model**, $\langle z,\beta \rangle²$.
In other words, by adding $P^\bot_X Fx$, we reduce the **estimation error** of the ridge estimator at a rate proportional to $\langle z,\beta \rangle²$.
Finally, we know that the larger the correlation $\langle z,\beta \rangle²$, the higher the loss of $(x^{aug},y^{aug})$ would be under $\hat{\beta}$. We this information, we can extrapolate the following:
* **the reduction of the estimation error**, $e(\hat{\beta}) - e(\hat{\beta}^F)$, **scales with the loss of $(x^{aug},y^{aug})$ under $\hat{\beta}$**, $l_{\hat{\beta}}(x^{aug},y^{aug})$.
> **In an intuitive sense, an augmented data point with a small loss means the model has already learned how to predict that type of data well, so if trained on it further, the model will only pick up incidental, possibly spurious patterns — overfitting. Conversely, an augmented data point with a large loss means the model has not learned the general mapping between the type of data and its target yet, so we need to train more on those kinds of data points.**
Additional results regarding **label-mixing transformations** were obtained in the [muAugment paper](https://hazyresearch.stanford.edu/blog/2020-02-26-data-augmentation-part2). These results will not be discussed in the class.
## Uncertainty-based Sampling Scheme
In order to take advantage of the last result presented, the **muAugment** algorithm was developped. The algorithm is as follows:
* In a first step, for each data point, **C** compositions of **L** linear transformations are randomly sampled and fed to the learning model (in this example a neural network).
* In a second step, the **S** transformed samples with the highest losses are picked for training the model and a backpropagation is performed using those samples.
> **The intuition behind the sampling scheme is that these transformed samples that have the largest losses should also provide the most information.**
**The model learns more generalizable patterns, because the algorithm assures extra fitting on the "hard" augmentations while skipping the easy ones.**
<img src="https://github.com/Mariana-Andrade-Alves/muAugment/blob/main/img/dauphin.png?raw=1" width='800'>
Senwu. "Uncertainty-based random Sampling Scheme for Data Augmentation. Each transformation function is randomly sampled from a pre-defined set of operations." [Dauphin](https://github.com/senwu/dauphin) 2020.
<details class="alert alert-block alert-info">
<summary markdown="span"><b>Comparison to Adversarial Autoaugment (click to expand)</b></summary>
The idea behing this sampling scheme is conceptually similar to [Adversarial Autoaugment](https://openreview.net/pdf?id=ByxdUySKvS). However, while in the case of Adversarial Autoaugment, an additional adversarial network is used to generate augmented samples with large losses, in the current case, the model uses the training network itself to generate augmented samples.
</details>
Our goal today is to implement the **muAugment** algorithm and evaluate its performance.
### The Dataset: FashionMNIST
The dataset we will use for this application is the FashionMNIST dataset. We'll download this dataset and make batching data loaders.
```
batch_size = 4
n_images = 10 if (batch_size>10) else batch_size
# data must be normalized between -1 and 1
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
full_trainset = FashionMNIST(root='../data', train=True, download=True, transform=transform)
trainset, full_validset = torch.utils.data.random_split(full_trainset, (10000, 50000)) # 10000 images for the training set
validset, _ = torch.utils.data.random_split(full_validset, (1000, 49000)) # 1000 images for the validation set
trainloader = DataLoader(trainset, batch_size=64, shuffle=True, num_workers=2)
validloader = DataLoader(validset, batch_size=64, shuffle=True, num_workers=2)
testset = FashionMNIST(root='../data', train=False, download=True, transform=transform)
testloader = DataLoader(testset, batch_size=64, shuffle=True)
```
We can verify the normalization of our data.
```
images,labels = next(iter(trainloader))
images.min(),images.max()
```
Let's look at some example images from the FashionMNIST set.
```
# get the first batch of images and labels
labels_text = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat", "Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
plt.figure(figsize=(n_images,4))
for i in range(n_images):
l = labels[i].numpy()
plt.subplot(2, n_images/2, i+1)
plt.title('%d: %s' % (l, labels_text[l]))
plt.imshow(images[i].numpy()[0], cmap='Greys')
plt.axis('off')
```
### The Model
As mentioned above, the advantage of the **muAugment** algorithm is that it uses the learning model to automate data augmentation. The goal is to generate data which will improve our training model.
In today's example, we wish to learn to classify images into 10 possible labels:
```
labels_text
```
In order to do this, the training model we will use is a convolutional neural network, presented during a [previous class](https://github.com/SupaeroDataScience/deep-learning/blob/main/deep/PyTorch%20Ignite.ipynb).
```
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.convlayer1 = nn.Sequential(
nn.Conv2d(1, 32, 3,padding=1),
nn.BatchNorm2d(32),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.convlayer2 = nn.Sequential(
nn.Conv2d(32,64,3),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(2)
)
self.fc1 = nn.Linear(64*6*6,600)
self.drop = nn.Dropout2d(0.25)
self.fc2 = nn.Linear(600, 120)
self.fc3 = nn.Linear(120, 10)
def forward(self, x):
x = self.convlayer1(x)
x = self.convlayer2(x)
x = x.view(-1,64*6*6)
x = self.fc1(x)
x = self.drop(x)
x = self.fc2(x)
x = self.fc3(x)
return F.log_softmax(x,dim=1)
```
### Training
In order to train the model, we must first create it and define the loss function and optimizer.
```
#creating model for original data
model_original = CNN()
# creating model for augmented data
model = CNN()
# moving models to gpu if available
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)
model_original.to(device)
```
By using the parameter `weight_decay` in our optimizer we are applying a similar penalty parameter to the one in ridge regression.
```
lr = 0.001 # learning rate
# defining optimizer and loss for original model
optimizer_original = torch.optim.SGD(model_original.parameters(), lr=lr, weight_decay=0.0001, momentum=0.9)
criterion_original = nn.CrossEntropyLoss()
# defining optimizer and loss for augmented model
optimizer = torch.optim.SGD(model.parameters(), lr=lr, weight_decay=0.0001, momentum=0.9)
criterion = nn.CrossEntropyLoss()
```
In a typical training phase, each batch of images would be treated in the following loop:
```python
for epoch in range(max_epochs):
for batch in trainloader:
# zero the parameter gradients
optimizer.zero_grad()
# get inputs and labels from batch
inputs, labels = batch
# forward + backward + optimize
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
```
In order to perform data augmentation with pre-defined transforms, it would suffice to declare the transforms while generating the data loader and the loop would remain unchanged.
However, because we don't wish to train the model without evaluating the performance of each transform, this loop is going to change.
### The Random Sampling Scheme (hands-on exercises)
As mentioned above, the goal is to implement the following algorithm:
<img src="https://github.com/Mariana-Andrade-Alves/muAugment/blob/main/img/algorithm.png?raw=1" width="1000">
Wu et al. "Uncertainty-based random Sampling Algorithm." [On the Generalization Effects of Linear Transformations in Data Augmentation](https://arxiv.org/pdf/2005.00695.pdf) 2020.
Today, to simplify our work, we will not use default transformations. We will also only consider label-invariant transformations.
In our implementation, lets consider the following required arguments:
* **L** (int): Number of **linear** transformations uniformly sampled for each composition
* **C** (int): Number of **compositions** placed on each image
* **S** (int): Number of **selected** compositions for each image
> **In a first exercise, let's attempt to code the lines 4 and 5 of the algorithm. Complete the function `compute_composed_data` which takes as input a `transform_list` similar to the one presented bellow, the arguments `L` and `C` described above and the images `xb` and labels `yb` of a batch and returns 2 tensors `C_images` and `C_targets` which contain the images xb$^{\mathbf{aug}}$ and labels yb$^{\mathbf{aug}}$ of the augmented data.**
```python
transform_list = [transforms.RandomAutocontrast(p=p),
transforms.ColorJitter(brightness=MAGN/30),
transforms.ColorJitter(contrast=MAGN/30),
transforms.RandomInvert(p=p),
transforms.RandomRotation(degrees=MAGN*3),
transforms.RandomAdjustSharpness(0.18*MAGN+0.1, p=p),
transforms.RandomAffine(degrees=0, shear=MAGN/30),
transforms.RandomSolarize(MAGN*8, p=p),
transforms.RandomAffine(degrees=(0,0),
translate=(MAGN/30,0),shear=(0,0)),
transforms.RandomAffine(degrees=(0,0),
translate=(0,MAGN/30),shear=(0,0)),
]
```
```
# the load command only works on jupyter notebook
# %load solutions/compute_composed_data.py
def compute_composed_data(transform_list,L, C, xb,yb):
BS,N_CHANNELS,HEIGHT,WIDTH = xb.shape
C_images = torch.zeros(C, BS, N_CHANNELS, HEIGHT, WIDTH, device=device)
C_targets = torch.zeros(C, BS, device=device, dtype=torch.long)
for c in range(C):
# create a list of L linear transforms randomly sampled from the transform_list
# create a composition of transforms from the list sampled above. Use nn.Sequential instead of transforms.Compose in order to script the transformations
# apply the composition to the original images xb
# update tensors C_images and C_targets with the generated compositions
return C_images, C_targets
# the cat command works on google colab
#%cat muAugment/solutions/compute_composed_data.py
```
Now that we have implemented the data augmentation part, we can attempt to code the content of the main loop of the algorithm.
**Remember**: the idea is to feed the transformed batches to the model without updating it and compare the losses obtained for each batch. Since you do not want to call `python loss.backward()`, you can disable gradient calculation in your function by using `python @torch.no_grad()`.
> **In a second exercise, complete the function `compute_selected_data` that takes as inputs the learning `model`, the `loss` function, the tensors `C_images` and `C_targets` and the argument `S` and returns the seleted transformed images (`S_images`) and labels (`S_labels`).**
```
# the load command only works on jupyter notebook
# %load solutions/compute_selected_data.py
#disable gradient calculation
def compute_selected_data(model, loss, C_images, C_targets, S):
C, BS, N_CHANNELS, HEIGHT, WIDTH = C_images.shape
# create a list of predictions 'pred' by applying the model to the augmented batches contained in C_images
# create a list of losses by applying the loss function to the predictions and labels C_targets
# convert the list to a loss tensor 'loss_tensor' through the function torch.stack
# select the S indices 'S_idxs' of the loss_tensor with the highest value. You may use the function torch.topk
# select the S images 'S_images' from C_images with the highest losses
# convert the tensor 'S_images' so that it passes from shape [S, BS, N_CHANNELS, HEIGHT, WIDTH] to shape
# [S*BS, N_CHANNELS, HEIGHT, WIDTH]. You may use the function torch.view
# select the S labels 'S_targets' from C_targets corresponding to the highest losses
# convert the tensor 'S_targets' so that it passes from shape [S, BS] to shape
# [S*BS]. You may use the function torch.view
return S_images, S_targets
# the cat command works on google colab
#%cat muAugment/solutions/compute_selected_data.py
```
We have created two functions which give us the augmented data we wish to use in the training phase of our model.
### Back to Training (hands-on exercise)
Let's consider the following arguments for the algorithm:
```
# algorithm arguments
L = 3 # number of linear transformations sampled for each composition
C = 4 # number of compositions placed on each image.
S = 1 # number of selected compositions for each image
```
Let's consider the following list of linear transformations, similar to the ones used in the original paper:
```
MAGN = 4 # (int) Magnitude of augmentation applied. Ranges from [0, 10] with 10 being the max magnitude.
# function of list of linear transformations
def transform_list(MAGN,p):
return [transforms.RandomAutocontrast(p=p),
transforms.ColorJitter(brightness=MAGN/30),
transforms.ColorJitter(contrast=MAGN/30),
transforms.RandomInvert(p=p),
transforms.RandomRotation(degrees=MAGN*3),
transforms.RandomAdjustSharpness(0.18*MAGN+0.1, p=p),
transforms.RandomAffine(degrees=0, shear=MAGN/30),
transforms.RandomSolarize(MAGN, p=p),
transforms.RandomAffine(degrees=(0,0), translate=(MAGN/30,0),shear=(0,0)),
transforms.RandomAffine(degrees=(0,0), translate=(0,MAGN/30),shear=(0,0)),
]
```
The following three code boxes were adapted from the tutorial on pytorch done in [class](https://github.com/SupaeroDataScience/deep-learning/blob/main/deep/Deep%20Learning.ipynb).
In order to compare validation and training losses, we will calculate the validation losses and accuracy at each epoch.
```
def validation(model,criterion):
correct_pred = 0
total_pred = 0
valid_loss = 0
with torch.no_grad():
for data in validloader:
images, labels = data
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
loss = criterion(outputs, labels)
valid_loss += loss.item()
# calculate predictions
predictions=[]
for i in range(outputs.shape[0]):
ps = torch.exp(outputs[i])
predictions.append(np.argmax(ps))
# collect the correct predictions
for label, prediction in zip(labels, predictions):
if label == prediction:
correct_pred += 1
total_pred += 1
accuracy = 100 * (correct_pred / total_pred)
return valid_loss, accuracy
def plot_train_val(train, valid, title, label1 = 'Training', label2 = 'Validation'):
fig, ax1 = plt.subplots()
color = 'tab:red'
ax1.set_ylabel(label1, color=color)
ax1.plot(train, color=color)
ax2 = ax1.twinx()
color = 'tab:blue'
ax2.set_ylabel(label2, color=color)
ax2.plot(valid, color=color)
fig.tight_layout()
plt.title(title)
```
In order to avoid overfitting, we will implement early stopping.
```
class EarlyStopping:
def __init__(self, patience=5, delta=0):
self.patience = patience
self.counter = 0
self.best_score = None
self.delta = delta
self.early_stop = False
def step(self, val_loss):
score = -val_loss
if self.best_score is None:
self.best_score = score
elif score < self.best_score + self.delta:
self.counter += 1
print('EarlyStopping counter: %d / %d' % (self.counter, self.patience))
if self.counter >= self.patience:
self.early_stop = True
else:
self.best_score = score
self.counter = 0
```
It is time to implement the algorithm in the training loop!
> **In the final exercise, take the almost complete code of the training loop presented bellow (adapted from the [pytorch class](https://github.com/SupaeroDataScience/deep-learning/blob/main/deep/Deep%20Learning.ipynb)) and change it, so that the algorithm is implemented.**
```
# the load command only works on jupyter notebook
# %load solutions/train.py
def train(model,criterion,optimizer, earlystopping=True,max_epochs=30,patience=2, augment=False):
train_history = []
valid_history = []
accuracy_history = []
estop = EarlyStopping(patience=patience)
for epoch in range(max_epochs):
train_loss = 0.0
for i, data in enumerate(trainloader, 0):
if augment:
# generate transform list
p = np.random.random() # probability of each transformation occurring
transforms = transform_list(MAGN,p)
# get the inputs; data is a list of [inputs, labels]
xb,yb = data
xb = xb.to(device)
yb = yb.to(device)
# generate the tensors 'C_images' and 'C_targets' <---- to complete
# generated the augmented data = [inputs,labels] <---- to complete
else:
# get the inputs; data is a list of [inputs, labels]
inputs,labels = data
inputs = inputs.to(device)
labels = labels.to(device)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
train_loss += loss.item()
valid_loss, accuracy = validation(model,criterion)
train_history.append(train_loss)
valid_history.append(valid_loss)
accuracy_history.append(accuracy)
print('Epoch %02d: train loss %0.5f, validation loss %0.5f, accuracy %3.1f ' % (epoch, train_loss, valid_loss, accuracy))
estop.step(valid_loss)
if earlystopping and estop.early_stop:
break
return train_history, valid_history, accuracy_history
# the cat command works on google colab
#%cat muAugment/solutions/train.py
```
We did it! Let's train our models: one without and one with augmented data.
```
max_epochs = 30
patience = 5 #early stopping parameter
print("\n Training for the original dataset...\n")
train_history_original, valid_history_original, accuracy_history_original = train(model_original,criterion_original,optimizer_original,max_epochs=max_epochs,patience=patience)
print("\n Training for the augmented dataset...\n")
train_history, valid_history, accuracy_history = train(model,criterion,optimizer,max_epochs=max_epochs,patience=patience,augment=True)
```
#### Plotting the Training and Validation Loss
Now that we trained both models, we can compare how the loss of training and validation evolves in both cases.
```
plot_train_val(train_history_original, valid_history_original,"Original Data")
plot_train_val(train_history, valid_history,"Augmented Data")
```
Although it is not always verified, most times you can see that the training loss tends to decrease less while using the augmented data and, even, sometimes augment. This is consistent with the fact that the augmented data is more difficult to predict. However, because the model with augmented data does not excessively train the data points it already knows, the model also suffers less from overfitting.
We can also compare accuracy between models.
```
plot_train_val(accuracy_history, accuracy_history_original,"Accuracy",label1='Augmented',label2='Original')
```
#### Verifying models with Testing Dataset
Finally, let's check the results by applying our model to the test dataset.
```
# put model in evaluation mode
model.eval()
# moving model to cpu for inference
model.to('cpu')
# creating arrays to save predictions
y_true = []
y_pred = []
images_ = []
# disable all gradients things
with torch.no_grad():
for data in iter(testloader):
images, labels = data
outputs = model(images)
for i in range(outputs.shape[0]):
images_.append(images[i].unsqueeze(0))
ps = torch.exp(outputs[i])
y_pred.append(np.argmax(ps))
y_true.append(labels[i].item())
```
Firstly, let's examine the confusion matrix.
```
from sklearn.metrics import ConfusionMatrixDisplay, confusion_matrix
print("Confusion matrix")
cm = confusion_matrix(y_true, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=labels_text)
fig, ax = plt.subplots(figsize=(10,10))
disp.plot(ax=ax)
plt.show()
```
We can also plot some of the results of the test dataset.
```
# plotting the results
fig = plt.figure(figsize=(n_images+5,4))
for i in range(n_images):
ax = fig.add_subplot(2, n_images/2, i+1, xticks=[], yticks=[])
ax.imshow(images_[i].resize_(1, 28, 28).numpy().squeeze())
ax.set_title("{} ({})".format(labels_text[y_pred[i]], labels_text[y_true[i]]),
color=("green" if y_pred[i]==y_true[i] else "red"))
```
Not bad! But could you spot a problem with the algorithm? **Here's a tip**: we were very conservative when choosing the parameters of our algorithm, namely the number of compositions generated **C**, number of compositions selected **S**, the number of linear transforms per composition **L** and the magnitude **M** of the chosen transforms.
> **What do you think would happen if we increased those values?** If you have time, you can try to play with the values.
### Shortcomings of the Algorithm
It is possible that the transforms applied on an image are so severe that the image becomes indistinguishable, losing its target information. In such a case, we would end up feeding the model pure noise. However, pure noise yields a high loss when fed into the model, so using **MuAugment** selects for those unrecognizable images if they are created. There’s no simple solution for this issue other than to choose appropriate hyperparameters so as to reduce the generation of inscrutable images, so it’s a good idea to keep the number of transforms in a composition **C** under 4 and the magnitude of each transform **M** under 6.
As a heuristic, larger models and datasets require more regularization and would accordingly perform better with a greater magnitude **M**. This is because bigger models are more prone to overfit and lengthier datasets have a higher signal-to-noise ratio which should be reduced to an optimal point.
| github_jupyter |
# Adversarial Variational Optimization: PYTHIA Tuning
In this notebook Adversarial Variational Optimization (https://arxiv.org/abs/1707.07113) is applied to tuning parameters of a simplistic detector.
**Note: this notebook takes quite a long time to execute. It is recommended to run all cells at the beginning.**
**Please, don't interrupt the notebook while sampling from PythiaMill. Otherwise it might stuck at the next attempt to sample from it. IF this happens, please, restart the notebook.**
```
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%matplotlib inline
import matplotlib.pyplot as plt
from tqdm import tqdm_notebook as tqdm_notebook
import numpy as np
### don't forget about others!
import keras
import tensorflow as tf
gpu_options = tf.GPUOptions(allow_growth=True, per_process_gpu_memory_fraction=0.2)
tf_session = tf.InteractiveSession(config=tf.ConfigProto(gpu_options=gpu_options))
keras.backend.tensorflow_backend.set_session(tf_session)
```
## Generators
Pythia-mill is a python binding to Pythia generator that can run in multiple threads (processes).
For more details, please, visit https://github.com/maxim-borisyak/pythia-mill
```
import pythiamill as pm
SEED=123
```
### Note about the change of problem
The reason the detector parameters (instead of Pythia parameters) are the target for the tune is a purely technical one: on each step AVO requires samples from multiples configurations of generator + detector. However, Pythia requires about half of a second to be reconfigured, which induces a tremendous overhead.
By contrast, this simplistic detector is designed to accept its parameters as function arguments (effectively neglecting any overhead).
The detector emulates a $32 \times 32$ spherical uniform grid in `pseudorapidity` ($\eta$)-`angle in traverse plane` ($\phi$) covering $(\eta, \phi) \in [0, 5] \times [0, 2 \pi]$.
The detector is parametrized by offset in $z$-axis relative to the beam crossing point. Zero offset means that center of the sphere coincides with the collision point.
```
### ground truth offset, unknown in the real world problems.
TRUE_OFFSET=1
options = [
### telling pythia to be quiet.
'Print:quiet = on',
'Init:showProcesses = off',
'Init:showMultipartonInteractions = off',
'Init:showChangedSettings = off',
'Init:showChangedParticleData = off',
'Next:numberCount=0',
'Next:numberShowInfo=0',
'Next:numberShowEvent=0',
'Stat:showProcessLevel=off',
'Stat:showErrors=off',
### seeting default parameters to Monash values
### all options are taken from https://arxiv.org/abs/1610.08328
"Tune:ee = 7",
"Beams:idA = 11",
"Beams:idB = -11",
"Beams:eCM = 91.2",
"WeakSingleBoson:ffbar2gmZ = on",
"23:onMode = off",
"23:onIfMatch = 1 -1",
"23:onIfMatch = 2 -2",
"23:onIfMatch = 3 -3",
"23:onIfMatch = 4 -4",
"23:onIfMatch = 5 -5",
]
### defining the detector
detector = pm.utils.SphericalTracker(
### with this option detector measures total energy
### of the particles traversing each pixel.
is_binary=False,
### detector covers [0, 5] pseudo-rapidity range
max_pseudorapidity=5.0,
pseudorapidity_steps=32, phi_steps=32,
### 1 layer with radius 10 mm.
n_layers=1, R_min=10.0, R_max=10.0,
)
mill = pm.ParametrizedPythiaMill(
detector, options,
### please, don't use number of workers higher than 4.
batch_size=8, n_workers=4,
seed=SEED
)
def get_data(mill, detector_configurations, show_progress=False):
"""
Utilitary function to obtain data for a particular set of configurations.
:param mill: instance of Pythia Mill to sample from.
: param detector configuration: - list of configurations.
each configuration should be an array of detector parameters.
: param show_progress: if True shows progress via `tqdm` package.
:return:
- parameters: array of shape `<number of samples> x <parameters dim>`, parameters for each sample;
- samples: array of shape `<number of samples> x 1 x 32 x 32`, sampled events.
"""
try:
### sending requests to the queue
for args in detector_configurations:
mill.request(*args)
### retrieving results
data = [
mill.retrieve()
for _ in (
(lambda x: tqdm_notebook(x, postfix='data gen', leave=False))
if show_progress else
(lambda x: x)
)(range(len(detector_configurations)))
]
samples = np.vstack([ samples for params, samples in data ])
params = np.vstack([ np.array([params] * samples.shape[0], dtype='float32') for params, samples in data ])
return params, samples.reshape(-1, 32, 32, 1)
finally:
while mill.n_requests > 0:
mill.retrieve()
### Generating training samples with ground truth parameters.
### For a real-world problem these arrays would correspond to real data.
_, X_true_train = get_data(mill, detector_configurations=[(TRUE_OFFSET, )] * 2 ** 12, show_progress=True)
_, X_true_val = get_data(mill, detector_configurations=[(TRUE_OFFSET, )] * 2 ** 12, show_progress=True)
print(X_true_train.shape)
print(X_true_val.shape)
```
### Taking a look at events
```
n = 5
plt.subplots(nrows=n, ncols=n, figsize=(3 * n, 3 * n))
max_energy = np.max(X_true_train[:n * n])
for i in range(n):
for j in range(n):
k = i * n + j
plt.subplot(n, n, k + 1)
plt.imshow(X_true_train[k, :, :, 0], vmin=0, vmax=max_energy)
plt.show()
```
### Aggregated events
```
plt.figure(figsize=(6, 6))
plt.imshow(np.sum(X_true_train, axis=(0, 3)), vmin=0)
plt.show()
```
## Discriminator
```
from keras.models import Model
from keras.layers import Input, Conv2D, MaxPool2D, Dense, Flatten, GlobalMaxPool2D
from keras.activations import softplus, sigmoid, relu
from keras.utils.vis_utils import model_to_dot
```
### Building conv net
```
inputs = Input(shape=(32, 32, 1))
activation = lambda x: relu(x, 0.05)
net = Conv2D(8, kernel_size=(3, 3), padding='same', activation=activation)(inputs)
net = MaxPool2D(pool_size=(2, 2))(net)
net = Conv2D(12, kernel_size=(3, 3), padding='same', activation=activation)(net)
net = MaxPool2D(pool_size=(2, 2))(net)
# net = GlobalMaxPool2D()(net)
net = Conv2D(16, kernel_size=(3, 3), padding='same', activation=activation)(net)
net = MaxPool2D(pool_size=(2, 2))(net)
net = Conv2D(24, kernel_size=(3, 3), padding='same', activation=activation)(net)
net = MaxPool2D(pool_size=(2, 2))(net)
net = Flatten()(net)
predictions = Dense(1, activation=sigmoid)(net)
discriminator = Model(inputs=inputs, outputs=predictions)
discriminator.compile(optimizer='adam', loss='binary_crossentropy')
from IPython import display
from IPython.display import SVG
SVG(model_to_dot(discriminator, show_shapes=True).create(prog='dot', format='svg'))
```
In Adversarial Variational Optimization, instead of searching for a single value of detector parameters, a parametrized distribution is introduced (with parameters $\psi$):
$$\mathcal{L}(\psi) = \mathrm{JS}(X_\psi, X_\mathrm{data})$$
where:
- $X_\psi \sim \mathrm{detector}(\theta), \theta \sim P_\psi$;
- $X_\mathrm{data} \sim \mathrm{reality}$.
Note that $\mathcal{L}(\psi)$ is a vaiational bound on adversarial loss:
$$\mathcal{L}(\psi) \geq \min_\theta \mathcal{L}_\mathrm{adv}(\theta) = \mathrm{JS}(X_\theta, X_\mathrm{data})$$
In this example, detector parameters consist of a signle `offset` parameter. For simplicity normal distibution is used:
$$\mathrm{offset} \sim \mathcal{N}(\mu, \sigma)$$
In order to avoid introducing constraints $\sigma \geq 0$, an auxiliary *free variable* $\sigma'$ is introduced (denoted as `detector_params_sigma_raw` in the code):
$$\sigma = \log(1 + \exp(\sigma'))$$
Note that if there exists configuration of detector perfectly matching real data, then minimum of variational bound is achieved when the `offset` distribution collapses into delta function with the center at minumum of adversarial loss.
Otherwise, a mixture of detector configuations might be a solution (unlike convetional variational optimization).
```
X = tf.placeholder(dtype='float32', shape=(None, 32, 32, 1))
proba = discriminator(X)[:, 0]
detector_params = tf.placeholder(dtype='float32', shape=(None, 1))
detector_params_mean = tf.Variable(
initial_value=np.array([0.0], dtype='float32'),
dtype='float32'
)
detector_params_sigma_raw = tf.Variable(
initial_value=np.array([2.0], dtype='float32'),
dtype='float32'
)
detector_params_sigma = tf.nn.softplus(detector_params_sigma_raw)
neg_log_prob = tf.reduce_sum(
tf.log(detector_params_sigma)
) + tf.reduce_sum(
0.5 * (detector_params - detector_params_mean[None, :]) ** 2 / detector_params_sigma[None, :] ** 2
, axis=1
)
detector_params_loss = tf.reduce_mean(neg_log_prob * proba)
get_distribution_params = lambda : tf_session.run([detector_params_mean, detector_params_sigma])
n = tf.placeholder(dtype='int64', shape=())
params_sample = tf.random_normal(
mean=detector_params_mean,
stddev=detector_params_sigma,
shape=(n, 1),
dtype='float32'
)
distribution_opt = tf.train.AdamOptimizer(learning_rate=0.02).minimize(
detector_params_loss, var_list=[detector_params_mean, detector_params_sigma_raw]
)
tf_session.run(tf.global_variables_initializer())
def train_discriminator(n_samples=2 ** 16, n_epoches=16, plot=False):
sample_of_detector_params = tf_session.run(params_sample, { n : n_samples // 8 })
_, X_gen_train = get_data(
mill,
detector_configurations=sample_of_detector_params,
show_progress=True
)
X_train = np.vstack([ X_gen_train, X_true_train ])
y_train = np.hstack([ np.zeros(X_gen_train.shape[0]), np.ones(X_true_train.shape[0]) ]).astype('float32')
history = discriminator.fit(x=X_train, y=y_train, batch_size=32, epochs=n_epoches, verbose=0)
if plot:
plt.figure(figsize=(8, 4))
plt.plot(history.history['loss'], label='train loss')
plt.legend()
plt.show()
def train_generator():
sample_of_detector_params = tf_session.run(params_sample, { n : 2 ** 8 })
params_train, X_gen_train = get_data(mill, detector_configurations=sample_of_detector_params)
tf_session.run(
distribution_opt,
feed_dict={
X : X_gen_train,
detector_params : params_train
}
)
```
## Pretraining
AVO makes small changes in parameter distribution. When starting with the optimal discriminator from the previous iterations, adjusting discriminator to these changes should require relatively few optimization steps.
However, the initial discriminator state (which is just random weights), most probably, does not correspond to any optimal discriminator. Therefore, we pretrain discriminator in order to ensure that only a few epoches needed on each iteration to achieve an optimal discriminator.
```
%%time
train_discriminator(n_samples=2**16, n_epoches=4, plot=True)
```
## Variational optimization
```
from IPython import display
n_iterations = 256
generator_mean_history = np.ndarray(shape=(n_iterations, ))
generator_sigma_history = np.ndarray(shape=(n_iterations, ))
for i in range(n_iterations):
train_discriminator(n_samples=2**12, n_epoches=1)
train_generator()
m, s = get_distribution_params()
generator_mean_history[i] = np.float32(m[0])
generator_sigma_history[i] = np.float32(s[0])
display.clear_output(wait=True)
plt.figure(figsize=(18, 9))
plt.plot(generator_mean_history[:i + 1], color='blue', label='mean ($\\mu$)')
plt.fill_between(
np.arange(i + 1),
generator_mean_history[:i + 1] - generator_sigma_history[:i + 1],
generator_mean_history[:i + 1] + generator_sigma_history[:i + 1],
color='blue',
label='sigma ($\\sigma$)',
alpha=0.2
)
plt.plot([0, n_iterations - 1], [TRUE_OFFSET, TRUE_OFFSET], '--', color='black', alpha=0.5, label='ground truth')
plt.ylim([-2, 4])
plt.legend(loc='upper left', fontsize=18)
plt.legend(fontsize=18)
plt.xlabel('AVO step', fontsize=16)
plt.ylabel('detector offset', fontsize=16)
plt.show()
```
| github_jupyter |
# 1) Matplotlib Part 1
## 1) Functional method
```
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import randint
x = np.linspace(0,10,20)
x
y = randint(0,50,20)
y
y = np.sort(y)
y
plt.plot(x,y, color='m', linestyle='--', marker='*', markersize=10, lw=1.5)
plt.xlabel('X axis')
plt.ylabel('Y axis')
plt.title('X vs Y axis')
plt.show()
# multiple plots on same canvas
plt.subplot(1,2,1)
plt.plot(x,y,color='r')
plt.subplot(1,2,2)
plt.plot(x,y,color='m')
```
## 2) Object Oriented Method
```
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import randint
x = np.linspace(0,10,20)
y = randint(1, 50, 20)
y = np.sort(y)
x
y
fig = plt.figure()
axes = fig.add_axes([0.1,0.1,1,1])
axes.plot(x,y)
axes.set_xlabel('X axis')
axes.set_ylabel('Y axis')
axes.set_title('X vs Y axis')
# 2 sets of figures to 1 canvas
fig = plt.figure()
ax1 = fig.add_axes([0.1,0.1,0.8,0.8])
ax2 = fig.add_axes([0.2,0.5,0.4,0.3])
ax1.plot(x,y,color='r')
ax1.set_xlabel('X axis')
ax1.set_ylabel('Y axis')
ax1.set_title('Plot 1')
ax2.plot(x,y,color='m')
ax2.set_xlabel('X axis')
ax2.set_ylabel('Y axis')
ax2.set_title('Plot 2')
```
# 2) Matplotlib Part 2
## 1) Subplots method
```
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import randint
x = np.linspace(0,10,20)
y = randint(1, 50, 20)
y = np.sort(y)
x
y
fig,axes = plt.subplots()
axes.plot(x,y)
fig,axes = plt.subplots(nrows=2,ncols=3)
plt.tight_layout()
axes
fig,axes = plt.subplots(nrows=1,ncols=2)
for current_ax in axes:
current_ax.plot(x,y)
fig,axes = plt.subplots(nrows=1,ncols=2)
axes[0].plot(x,y)
axes[1].plot(x,y)
axes[0].set_title('Plot 1')
axes[1].set_title('Plot 2')
```
## 2) Figure size, Aspect ratio and DPI
```
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import randint
x = np.linspace(0,10,20)
y = randint(1, 50, 20)
y = np.sort(y)
fig = plt.figure(figsize=(3,2),dpi=100)
ax = fig.add_axes([0,0,1,1])
ax.plot(x,y)
fig,axes = plt.subplots(nrows=1,ncols=2,figsize=(7,2))
axes[0].plot(x,y)
axes[1].plot(x,y)
fig
fig.savefig('my_pic.png',dpi=100)
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.plot(x,y)
ax.set_xlabel('X axis')
ax.set_ylabel('Y axis')
ax.set_title('X vs Y')
# legends
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.plot(x,x**2,label='X vs X square')
ax.plot(x,x**3,label='X vs X cube')
ax.legend(loc=0)
```
# 3) Matplotlib Part 3
```
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import randint
x = np.linspace(0,10,20)
y = randint(1, 50, 20)
y = np.sort(y)
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.plot(x,y,color='g',linewidth=3,ls='--',alpha=0.8,marker='o',markersize=10,markerfacecolor='yellow')
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.plot(x,y,color='r',linewidth=3)
ax.set_xlim([0,1])
ax.set_ylim([0,10])
```
# 4) Different Plots
## 1) Scatter Plots
```
import matplotlib.pyplot as plt
y_views=[534,690,258,402,724,689,352]
f_views=[123,342,700,305,406,648,325]
t_views=[202,209,176,415,824,389,550]
days=[1,2,3,4,5,6,7]
plt.scatter(days,y_views,label='Youtube Views',marker='o')
plt.scatter(days,f_views,label='Facebook Views',marker='o')
plt.scatter(days,t_views,label='Twitter Views',marker='o')
plt.xlabel('Days')
plt.ylabel('Views')
plt.title('Social Media Views')
plt.grid(color='r',linestyle='--')
plt.legend()
```
## 2) Bar plot
```
plt.bar(days,y_views,label='Youtube views')
plt.bar(days,f_views,label='Facebook views')
plt.xlabel('Days')
plt.ylabel('Views')
plt.title('Social Media Views')
plt.legend()
```
## 3) Histogram
```
points=[22,55,62,45,21,22,99,34,42,4,102,110,27,48,99,84]
bins=[0,20,40,60,80,100,120]
plt.hist(points,bins)
plt.xlabel('Bins')
plt.ylabel('Frequency')
plt.title('Bins vs Frequency')
plt.show()
```
## 4) Pie chart
```
labels_1=['Facebook','Instagram','Youtube','linkedin']
views=[300,350,400,450]
explode_1=[0,0,0,0.2]
plt.pie(views,labels=labels_1,autopct='%1.1f%%',explode=explode_1,shadow=True)
plt.show()
```
| github_jupyter |
```
import gpflow
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import sys
sys.path.append('../')
from GPHetero import hetero_kernels, hetero_likelihoods, hetero_gpmc
from pyDOE import *
import os
from scipy.stats import norm
class Ex5Func(object):
def __init__(self, sigma=lambda x: 0.5):
self.sigma = sigma
def __call__(self, x):
"""
Dette et. al. function.
Dette, Holger, and Andrey Pepelyshev. "Generalized Latin hypercube design for computer experiments." Technometrics 52, no. 4 (2010): 421-429.
"""
y = 4 * ((x[0] - 2 + 8 * x[1] - 8 * (x[1] ** 2)) ** 2) + (3 - 4 * x[1]) ** 2 + 16 * np.sqrt(x[2] + 1) * ((2 * x[2] - 1)**2)
return (y - 50) / 50.
dim = 3
n = 20
noise=0
sigma = eval('lambda x: ' + str(noise))
objective = Ex5Func(sigma=sigma)
X = lhs(dim, n , criterion='center')
Xnorm = (X - 0.5) /0.5
Y = np.array([objective(x) for x in X])[:, None]
#build the model
k = gpflow.kernels.RBF(input_dim=1)
k.lengthscales.prior = gpflow.priors.Gamma(1, 1)
# from copy import copy
# l = copy(k)
noisekern = gpflow.kernels.RBF(input_dim=1)
nonstat = hetero_kernels.NonStationaryLengthscaleRBF()
mean_func = gpflow.mean_functions.Constant(1)
m = hetero_gpmc.GPMCAdaptiveLengthscaleMultDim(Xnorm, Y, k, nonstat, mean_func)
for i in xrange(dim):
print i
m.kerns["ell" + str(i)].lengthscales.prior = gpflow.priors.Gamma(1., 1.)
m.kerns["ell" + str(i)].variance.prior = gpflow.priors.Gamma(1., 1.)
#m.mean_funcs["ell" + str(i)].c = 3.
#m.mean_funcs["ell" + str(i)].c.fixed = True
m.mean_funcs["ell" + str(i)].c.prior = gpflow.priors.Exponential(1./4)
m.nonstat.signal_variance.prior = gpflow.priors.Gamma(1., 1.)
# m.nonstat.signal_variance.fixed = True
m.likelihood.variance = 1e-6
m.likelihood.variance.fixed = True
m.optimize(maxiter=1500) # start near MAP
m
mcmc_samples = 1000
num_samp_gp = 1
samples = m.sample(mcmc_samples, verbose=True, epsilon=0.00005, thin = 5, burn = 500, Lmax = 20)
m
X_test = lhs(dim, n , criterion='center')
X_test_norm = (X_test - 0.5) /0.5
Y_test = np.array([objective(x) for x in X])[:, None]
samples.shape
plt.figure(figsize=(16, 4))
plt.plot(samples[:,10:80])
X_test = lhs(dim, 100 , criterion='center')
X_test_norm = (X_test - 0.5) /0.5
Y_test = np.array([objective(x) for x in X_test])[:, None]
sample_df = m.get_samples_df(samples)
mean_f_mat = np.zeros(shape=(sample_df.shape[0], X_test_norm.shape[0]))
var_f_mat = np.zeros(shape=(sample_df.shape[0], X_test_norm.shape[0]))
for i, s in sample_df.iterrows():
m.set_parameter_dict(s)
mean_f, var_f = m.predict(X_test_norm)
mean_f_mat[i, :] = mean_f[:,0]
var_f_mat[i, :] = np.diag(var_f)
plt.figure(figsize=(12,8))
plt.scatter(mean_f_mat[5,:], Y_test)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/MadhabBarman/Epidemic-Control-Model/blob/master/SEIRD_ControlModel.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!git clone https://github.com/MadhabBarman/Epidemic-Control-Model.git
cd Epidemic-Control-Model/
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import odeint
from scipy.io import savemat, loadmat
import numpy.linalg as la
from matplotlib.lines import Line2D
M = 16
my_data = np.genfromtxt('data/age_structures/India-2019.csv', delimiter=',', skip_header=1)
Real_data = np.genfromtxt('data/covid-cases/case_time_series.csv', delimiter=',', skip_header=1)
aM, aF = my_data[:, 1], my_data[:, 2]
Ni=aM+aF; Ni=Ni[0:M]; N=np.sum(Ni)
# contact matrices
my_data = pd.read_excel('data/contact_matrices_152_countries/MUestimates_home_1.xlsx', sheet_name='India',index_col=None)
CH = np.array(my_data)
my_data = pd.read_excel('data/contact_matrices_152_countries/MUestimates_work_1.xlsx', sheet_name='India',index_col=None)
CW = np.array(my_data)
my_data = pd.read_excel('data/contact_matrices_152_countries/MUestimates_school_1.xlsx', sheet_name='India',index_col=None)
CS = np.array(my_data)
my_data = pd.read_excel('data/contact_matrices_152_countries/MUestimates_other_locations_1.xlsx', sheet_name='India',index_col=None)
CO = np.array(my_data)
my_data = pd.read_excel('data/contact_matrices_152_countries/MUestimates_all_locations_1.xlsx', sheet_name='India',index_col=None)
CA = np.array(my_data)
CM = CH + CW + CS + CO
my_data_nw = np.genfromtxt('data/covid-cases/india_10april.txt', delimiter='', skip_header=6)
death_case, active_case = my_data_nw[:,4], my_data_nw[:,5]
active = Real_data[:,7]
active_new = active[34:107]
death = Real_data[:,6]
death_new = death[34:107]
#save_results_to = 'C:/Users/HP/Desktop/Lat_radon/double peak/EPS_file/'
alpha_d = 0.05 #fractional constant
beta = 0.37 #rate of infection
rho = 0.75 #control parameter of H
xi = 0.29 #recovery rate from E
alpha_1 = 0.7 #fractional part of E-->Q
alpha_2 = 0.2 #fractional part of E-->A
alpha_3 = 1-(alpha_1+alpha_2) #fractional part of E-->I
phi_qh = 1/10 #Recovery rate of Q-->H
q = 0.1 #fractional part of Q-->H
g_as = 0.1 #rate A-->I
d_ar = 2./7 #Recovery rate of A
phi_sh = 1./2 #rate I-->H
d_sr = 1./7 #Recovery rate of I
d_hr = (1-alpha_d)/10 #Recovery rate of H
eta = alpha_d/10 #Death rate
fsa = 0.1 #Fraction of the contact matrix Cs
fsh = 0.1 #Fraction of the contact matrix Ch
# initial conditions
E_0 = np.zeros((M));
Q_0 = np.zeros((M))
A_0 = np.zeros((M))
I_0 = np.zeros((M)); I_0[6:13]=2; I_0[2:6]=1
H_0 = np.zeros((M))
R_0 = np.zeros((M))
D_0 = np.zeros((M))
S_0 = Ni - (E_0+ Q_0 + A_0 + I_0 + H_0 + R_0 + D_0)
Tf = 300; Nf = 3000 #Tf -->final time from 0, Nf-->total number points
t = np.linspace(0,Tf,Nf) #time span
#lockdown function
ld = lambda t, t_on, t_off, t_won, t_woff, pld: 1 + pld*0.5*(np.tanh((t - t_off)/t_woff) - np.tanh((t - t_on)/t_won))
#staggered lockdown
uc = lambda t:0.7-0.4*(np.tanh((t - 21)/4)) + 0.3*0.3*(1.0*np.tanh((t - 42)/4)-np.tanh((t - 93)/4))+\
0.2+0.1*(np.tanh((t - 75)/4)) + 0.4*0.5*(np.tanh((t - 93)/4))
#LD2
#uc = lambda t:0.7-0.4*(np.tanh((t - 21)/4)) + 0.3*0.3*(1.0*np.tanh((t - 42)/4)-np.tanh((t - 93)/4))+\
# 0.2+0.1*(np.tanh((t - 75)/4)) + 0.4*0.5*(np.tanh((t - 93)/4)) +\
#ld(t,128, 153, 2, 2, 0.6-0.2) + ld(t,153,193, 2, 2, 0.8-0.2) + ld(t,193,233, 2, 2, 0.6-0.2)+ld(t,233,360, 2, 2, 0.4-0.2)-4.0
#LD3
#uc = lambda t:0.7-0.4*(np.tanh((t - 21)/4)) + 0.3*0.3*(1.0*np.tanh((t - 42)/4)-np.tanh((t - 93)/4))+\
# 0.2+0.1*(np.tanh((t - 75)/4)) + 0.4*0.5*(np.tanh((t - 93)/4)) +\
#ld(t,130, 160, 2, 2, 0.6-0.2)+ld(t,160, 230, 2, 2, 0.8-0.2) + ld(t,230, 300, 2, 2, 0.6-0.2) + ld(t,300, 420, 2, 2, 0.4-0.2) - 4.0
beta_max, k, t_m, beta_min = beta, 0.2, 49, 0.21 #
def beta_f(t):
return ((beta_max-beta_min) / (1 + np.exp(-k*(-t+t_m))) + beta_min)
plt.figure(figsize=(16,5))
plt.rcParams['font.size']=26
plt.subplot(1,2,1)
plt.plot(t,beta_f(t),lw=3);
plt.title(r'$\beta(t)$')
plt.grid(True)
plt.xlim(0,100);
plt.subplot(1,2,2)
plt.plot(t, uc(t),lw=3)
plt.title('Lockdown Strategy')
plt.tight_layout(True)
plt.grid(True)
def cont(t):
return CH + uc(t)*(CW + CO + CS)
#return CM
# S=y[i], E=y[M+i], Q=y[2M+i],A=y[3M+i], I=y[4M+i], H=y[5M+i], R=y[6M+i] for i=1,2,3,...,M
dy = np.zeros(7*M)
def rhs(y, t, cont, beta_f):
CM = cont(t) #contact matrix
for i in range(M):
lmda=0
for j in range(M):
lmda += beta_f(t)*(CM[i,j]*y[3*M+j] + fsa*CM[i,j]*y[4*M+j] +fsh*(1.0-rho)*CM[i,j]*y[5*M+j])/Ni[j]
dy[i] = - lmda*y[i] + (1-q)*phi_qh*y[2*M+i] # S susceptibles
dy[i+M] = lmda*y[i] - xi*y[M+i] #E exposed class
dy[i+2*M] = alpha_1*xi*y[M+i] - phi_qh*y[2*M+i] #Q Quarantined
dy[i+3*M] = alpha_2*xi*y[M+i] - (g_as + d_ar )*y[3*M+i] #A Asymptomatic infected
dy[i+4*M] = alpha_3*xi*y[M+i] + g_as*y[3*M+i] - (phi_sh + d_sr)*y[4*M+i] #I Symptomatic infected
dy[i+5*M] = phi_sh*y[4*M+i] + q*phi_qh*y[2*M+i] - (d_hr + eta)*y[5*M+i] #H Isolated
dy[i+6*M] = d_ar*y[3*M+i] + d_sr*y[4*M+i] + d_hr*y[5*M+i] #Recovered
return dy
data = odeint(rhs, np.concatenate((S_0, E_0, Q_0, A_0, I_0, H_0, R_0)), t, args=(cont,beta_f))
tempS, tempE, tempQ, tempA, tempI, tempH, tempR = np.zeros((Nf)),\
np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf))
for i in range(M):
tempS += data[:, 0*M + i]
tempE += data[:, 1*M + i]
tempQ += data[:, 2*M + i]
tempA += data[:, 3*M + i]
tempI += data[:, 4*M + i]
tempH += data[:, 5*M + i]
tempR += data[:, 6*M + i]
IC_death = N - (tempS + tempE + tempQ + tempA + tempI + tempH + tempR)
```
**Simulated individuals figure**
```
fig = plt.figure(num=None, figsize=(28, 12), dpi=80, facecolor='w', edgecolor='k')
plt.rcParams.update({'font.size': 26})
plt.plot(t, (tempA + tempI + tempH)/N, '--', lw=6, color='g', label='Active Case', alpha=0.8)
plt.plot(t, (tempA + tempI)/N , '-', lw=7, color='k', label='$A + I$', alpha=0.8)
plt.plot(t, IC_death/N, '-.', lw=4, color='r', label='Death', alpha=0.8)
plt.plot(t, tempH/N, '-', lw=3, color='b', label='H', alpha=0.8)
plt.legend(fontsize=26, loc='best'); plt.grid()
plt.autoscale(enable=True, axis='x', tight=True)
plt.ylabel('Individuals(Normalized)');
plt.text(163.5,0.0175,'14-Aug(163Days)',rotation=90)
plt.xlim(0,300);
plt.xlabel('Time(Days)')
plt.axvline(163,c='k',lw=3,ls='--');
#plt.savefig(save_results_to+'Figure10.png', format='png', dpi=200)
```
**Analysis between real case data vs numerical**
```
fig = plt.figure(num=None, figsize=(28, 12), dpi=80, facecolor='w', edgecolor='k')
plt.rcParams.update({'font.size': 26, 'text.color':'black'})
plt.plot(t, tempA + tempI + tempH, '--', lw=4, color='g', label='Active case numerical', alpha=0.8)
plt.plot(active_new, 'o-', lw=4, color='#348ABD', ms=16, label='Active case data', alpha=0.5)
plt.plot(t, IC_death, '-.', lw=4, color='r', label='Death case numerical', alpha=0.8)
plt.plot(death_new, '-*', lw=4, color='#348ABD', ms=16, label='death case data', alpha=0.5)
plt.xticks(np.arange(0, 200, 14),('4 Mar','18 Mar','1 Apr','15 Apr','29 Apr','13 May','27 May','10Jun','24Jun'));
plt.legend(fontsize=26, loc='best'); plt.grid()
plt.autoscale(enable=True, axis='x', tight=True)
plt.ylabel('Number of individuals');
plt.xlabel('Time(Dates)')
plt.ylim(0, 60000);
plt.xlim(0, 98);
```
**Sensitivity of hospitalization parameter $\rho$**
```
q = 1.0
rhos = [0.0, 0.25, 0.5, 0.75, 1.0]
fig = plt.figure(num=None, figsize=(20, 8), dpi=80, facecolor='w', edgecolor='k')
plt.rcParams.update({'font.size': 20})
for rho in rhos:
data = odeint(rhs, np.concatenate((S_0, E_0, Q_0, A_0, I_0, H_0, R_0)), t, args=(cont,beta_f))
tempS, tempE, tempQ, tempA, tempI, tempH, tempR = np.zeros((Nf)),\
np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf))
for i in range(M):
tempA += data[:, 3 * M + i]
tempI += data[:, 4 * M + i]
tempH += data[:, 5 * M + i]
if rho==1.0:
yy = tempA/N + tempI/N + tempH/N
plt.plot(t,yy, lw = 2, ls='-',c='b', label=r'$\rho = $' + str(rho))
plt.plot(t[::100],yy[::100], '>', label=None, markersize=11, c='b')
elif rho==0.75:
plt.plot(t,tempA/N + tempI/N + tempH/N, lw = 3, c='orange')
elif rho==0.5:
plt.plot(t,tempA/N + tempI/N + tempH/N, lw = 3, c='g')
elif rho==0.25:
plt.plot(t,tempA/N + tempI/N + tempH/N, lw = 3, c='r')
else:
yy = tempA/N + tempI/N + tempH/N
plt.plot(t,tempA/N + tempI/N + tempH/N, lw = 3, ls='-', c='k')
plt.plot(t[::100],yy[::100], '.', label=None, markersize=14, c='k')
plt.ylabel('Active Case(Normalized)');
plt.xlabel('Time (Days)');
plt.autoscale(enable=True, axis='x',tight=True)
plt.grid(True)
colors = ['k', 'r','g','orange', 'b']
marker = ['.', None, None, None, '>']
lines = [Line2D([0], [0], color=c, linewidth=3, linestyle='-',marker=r, markersize=14) for (c,r) in zip(colors,marker)]
labels = [r'$\rho=0.0$',r'$\rho=0.25$',r'$\rho=0.5$',r'$\rho=0.75$',r'$\rho=1.0$']
plt.legend(lines, labels,title=r'$q$ ='+str(q)+'(Fixed)')
#plt.savefig('rho_var1.png', format='png',dpi=200)
#plt.savefig(save_results_to+'Figure08.png', format='png',dpi=200)
```
**Sensitivity of quarantine parameter $q$**
```
rho = 1.0
qs = [0.0, 0.25, 0.5, 0.75, 1.0]
fig = plt.figure(num=None, figsize=(20, 8), dpi=80, facecolor='w', edgecolor='k')
plt.rcParams.update({'font.size': 20})
for q in qs:
data = odeint(rhs, np.concatenate((S_0, E_0, Q_0, A_0, I_0, H_0, R_0)), t, args=(cont,beta_f))
tempS, tempE, tempQ, tempA, tempI, tempH, tempR = np.zeros((Nf)),\
np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf)), np.zeros((Nf))
for i in range(M):
tempA += data[:, 3 * M + i]
tempI += data[:, 4 * M + i]
tempH += data[:, 5 * M + i]
if q==1.0:
yy = tempA/N + tempI/N + tempH/N
plt.plot(t,yy, lw = 2, ls='-',c='b')
plt.plot(t[::100],yy[::100], '>', label=None, markersize=11, c='b')
elif q==0.75:
plt.plot(t,tempA/N + tempI/N + tempH/N, lw = 3, c='orange')
elif q==0.5:
plt.plot(t,tempA/N + tempI/N + tempH/N, lw = 3, c='g')
elif q==0.25:
plt.plot(t,tempA/N + tempI/N + tempH/N, lw = 3, c='r')
else:
yy = tempA/N + tempI/N + tempH/N
plt.plot(t,tempA/N + tempI/N + tempH/N, lw = 3, ls='-', c='k')
plt.plot(t[::100],yy[::100], '.', label=None, markersize=14, c='k')
plt.ylabel('Active Case(Normalized)');
plt.xlabel('Time (Days)');
plt.autoscale(enable=True, axis='x',tight=True)
plt.grid(True)
colors = ['k','r','g','orange','b']
marker = ['.', None, None, None, '>']
lines = [Line2D([0], [0], color=c, linewidth=3, linestyle='-',marker=r, markersize=14) for (c,r) in zip(colors,marker)]
labels = [r'$q=0.0$',r'$q=0.25$',r'$q=0.5$',r'$q=0.75$',r'$q=1.0$']
plt.legend(lines, labels,title=r'$\rho$ ='+str(rho)+'(Fixed)')
#plt.savefig('q_var1.png', format='png',dpi=200)
#plt.savefig(save_results_to+'Figure07.png', format='png',dpi=200)
```
| github_jupyter |
# Archive data
The Wellcome archive sits in a collections management system called CALM, which follows a rough set of standards and guidelines for storing archival records called [ISAD(G)](https://en.wikipedia.org/wiki/ISAD(G). The archive is comprised of _collections_, each of which has a hierarchical set of series, sections, subjects, items and pieces sitting underneath it.
In the following notebooks I'm going to explore it and try to make as much sense of it as I can programatically.
Let's start by loading in a few useful packages and defining some nice utils.
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("white")
plt.rcParams["figure.figsize"] = (20, 20)
import pandas as pd
import numpy as np
import networkx as nx
from sklearn.cluster import AgglomerativeClustering
from umap import UMAP
from tqdm import tqdm_notebook as tqdm
def flatten(input_list):
return [item for sublist in input_list for item in sublist]
def cartesian(*arrays):
return np.array([x.reshape(-1) for x in np.meshgrid(*arrays)]).T
def clean(subject):
return subject.strip().lower().replace("<p>", "")
```
let's load up our CALM data. The data has been exported in its entirety as a single `.json` where each line is a record.
You can download the data yourself using [this script](https://github.com/wellcometrust/platform/blob/master/misc/download_oai_harvest.py). Stick the `.json` in the neighbouring `/data` directory to run the rest of the notebook seamlessly.
```
df = pd.read_json("data/calm_records.json")
len(df)
df.astype(str).describe()
```
### Exploring individual columns
At the moment I have no idea what kind of information CALM contains - lets look at the list of column names
```
list(df)
```
Here I'm looking through a sample of values in each column, choosing the columns to explore based on the their headings, a bit of contextual info from colleagues and the `df.describe()` above.
```
df["Subject"]
```
### After much trial and error...
Subjects look like an interesting avenue to explore further. Where subjects have _actually_ been filled in and the entry is not `None`, a list of subjects is returned.
We can explore some of these subjects' subtleties by creating an adjacency matrix. We'll count the number of times each subject appears alongside every other subject and return a big $n \times n$ matrix, where $n$ is the total number of unique subjects.
We can use this adjacency matrix for all sorts of stuff, but we have to build it first. To start, lets get a uniqur list of all subjects. This involves unpacking each sub-list and flattening them out into one long list, before finding the unique elements. We'll also use the `clean` function defined above to get rid of any irregularities which might become annoying later on.
```
subjects = flatten(df["Subject"].dropna().tolist())
print(len(subjects))
subjects = list(set(map(clean, subjects)))
print(len(subjects))
```
At this point it's often helpful to index our data, ie transform words into numbers. We'll create two dictionaries which map back and forth between the subjects and their corresponding indicies:
```
index_to_subject = {index: subject for index, subject in enumerate(subjects)}
subject_to_index = {subject: index for index, subject in enumerate(subjects)}
```
Lets instantiate an empty numpy array which we'll then fill with our coocurrence data. Each column and each row will represent a subject - each cell (the intersection of a column and row) will therefore represent the 'strength' of the interaction between those subjects. As we haven't seen any interactions yet, we'll set every array element to 0.
```
adjacency = np.empty((len(subjects), len(subjects)), dtype=np.uint16)
```
To populate the matrix, we want to find every possible combination of subject in each sub-list from our original column, ie if we had the subjects
`[Disease, Heart, Heart Diseases, Cardiology]`
we would want to return
`
[['Disease', 'Disease'],
['Heart', 'Disease'],
['Heart Diseases', 'Disease'],
['Cardiology', 'Disease'],
['Disease', 'Heart'],
['Heart', 'Heart'],
['Heart Diseases', 'Heart'],
['Cardiology', 'Heart'],
['Disease', 'Heart Diseases'],
['Heart', 'Heart Diseases'],
['Heart Diseases', 'Heart Diseases'],
['Cardiology', 'Heart Diseases'],
['Disease', 'Cardiology'],
['Heart', 'Cardiology'],
['Heart Diseases', 'Cardiology'],
['Cardiology', 'Cardiology']]
`
The `cartesian()` function which I've defined above will do that for us. We then find the appropriate intersection in the matrix and add another unit of 'strength' to it.
We'll do this for every row of subjects in the `['Subjects']` column.
```
for row_of_subjects in tqdm(df["Subject"].dropna()):
for subject_pair in cartesian(row_of_subjects, row_of_subjects):
subject_index_1 = subject_to_index[clean(subject_pair[0])]
subject_index_2 = subject_to_index[clean(subject_pair[1])]
adjacency[subject_index_1, subject_index_2] += 1
```
We can do all sorts of fun stuff now - adjacency matrices are the foundation on which all of graph theory is built. However, because it's a bit more interesting, I'm going to start with some dimensionality reduction. We'll get to the graphy stuff later.
Using [UMAP](https://github.com/lmcinnes/umap), we can squash the $n \times n$ dimensional matrix down into a $n \times m$ dimensional one, where $m$ is some arbitrary integer. Setting $m$ to 2 will then allow us to plot each subject as a point on a two dimensional plane. UMAP will try to preserve the 'distances' between subjects - in this case, that means that related or topically similar subjects will end up clustered together, and different subjects will move apart.
```
embedding_2d = pd.DataFrame(UMAP(n_components=2).fit_transform(adjacency))
embedding_2d.plot.scatter(x=0, y=1);
```
We can isolate the clusters we've found above using a number of different methods - `scikit-learn` provides easy access to some very powerful algorithms. Here I'll use a technique called _agglomerative clustering_, and make a guess that 15 is an appropriate number of clusters to look for.
```
n_clusters = 15
embedding_2d["labels"] = AgglomerativeClustering(n_clusters).fit_predict(
embedding_2d.values
)
embedding_2d.plot.scatter(x=0, y=1, c="labels", cmap="Paired");
```
We can now use the `index_to_subject` mapping that we created earlier to examine which subjects have been grouped together into clusters
```
for i in range(n_clusters):
print(str(i) + " " + "-" * 80 + "\n")
print(
np.sort(
[
index_to_subject[index]
for index in embedding_2d[embedding_2d["labels"] == i].index.values
]
)
)
print("\n")
```
Interesting! Taking a look at some of the smaller clusters of subjects (for the sake of space and your willingness to read lists of 100s of subjects):
One seems to be quite distinctly involved with drugs and associated topics/treatments:
```
13 --------------------------------------------------------------------------------
['acquired immunodeficiency syndrome' 'alcohol' 'amphetamines'
'analgesics, opioid' 'campaign' 'cannabis' 'cocaine' 'counseling'
'counterculture' 'crime' 'drugs' 'education' 'hallucinogens' 'heroin'
'hypnotics and sedatives' 'information services' 'inhalant abuse'
'lysergic acid diethylamide' 'n-methyl-3,4-methylenedioxyamphetamine'
'opioid' 'policy' 'prescription drugs' 'rehabilitation' 'renabilitation'
'self-help']
```
others are linked to early/fundamental research on DNA and genetics:
```
9 --------------------------------------------------------------------------------
['bacteriophages' 'biotechnology' 'caenorhabditis elegans'
'chromosome mapping' 'cloning, organism' 'discoveries in science' 'dna'
'dna, recombinant' 'genetic code' 'genetic engineering'
'genetic research' 'genetic therapy' 'genome, human' 'genomics'
'magnetic resonance spectroscopy' 'meiosis' 'models, molecular'
'molecular biology' 'nobel prize' 'retroviridae' 'rna'
'sequence analysis' 'viruses']
```
and others about food
```
14 --------------------------------------------------------------------------------
['acids' 'advertising' 'ambergris' 'animals' 'beer' 'biscuits' 'brassica'
'bread' 'butter' 'cacao' 'cake' 'candy' 'carbohydrates' 'cattle'
'cereals' 'cheese' 'chemistry, agricultural' 'cider' 'colouring agents'
'condiments' 'cooking (deer)' 'cooking (poultry)' 'cooking (venison)'
'cucumis sativus' 'dairy products' 'daucus carota' 'desserts'
'dried fruit' 'ecology' 'economics' 'eggs' 'environmental health'
'european rabbit' 'fermentation' 'food additives' 'food and beverages'
'food preservation' 'food, genetically modified' 'fruit' 'fruit drinks'
'fungi' 'game and game-birds' 'grapes' 'hands' 'health attitudes'
'herbaria' 'honey' 'jam' 'legislation' 'lettuce' 'meat' 'meat products'
'nuts' 'oatmeal' 'olive' 'onions' 'peas' 'pickles' 'pies' 'poultry'
'preserves (jams)' 'puddings' 'rice' 'seafood' 'seeds' 'sheep'
'sociology' 'solanum tuberosum' 'spinacia oleracea' 'sweetening agents'
'swine' 'syrups' 'vegetables' 'vitis' 'whiskey' 'wild flowers' 'wine']
```
These are all noticeably different themes, and they appear to be nicely separated in the topic-space we've built.
| github_jupyter |
# TV Script Generation
In this project, you'll generate your own [Seinfeld](https://en.wikipedia.org/wiki/Seinfeld) TV scripts using RNNs. You'll be using part of the [Seinfeld dataset](https://www.kaggle.com/thec03u5/seinfeld-chronicles#scripts.csv) of scripts from 9 seasons. The Neural Network you'll build will generate a new ,"fake" TV script, based on patterns it recognizes in this training data.
## Get the Data
The data is already provided for you in `./data/Seinfeld_Scripts.txt` and you're encouraged to open that file and look at the text.
>* As a first step, we'll load in this data and look at some samples.
* Then, you'll be tasked with defining and training an RNN to generate a new script!
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# load in data
import helper
data_dir = './data/Seinfeld_Scripts.txt'
text = helper.load_data(data_dir)
```
## Explore the Data
Play around with `view_line_range` to view different parts of the data. This will give you a sense of the data you'll be working with. You can see, for example, that it is all lowercase text, and each new line of dialogue is separated by a newline character `\n`.
```
view_line_range = (0, 10)
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
import numpy as np
print('Dataset Stats')
print('Roughly the number of unique words: {}'.format(len({word: None for word in text.split()})))
lines = text.split('\n')
print('Number of lines: {}'.format(len(lines)))
word_count_line = [len(line.split()) for line in lines]
print('Average number of words in each line: {}'.format(np.average(word_count_line)))
print()
print('The lines {} to {}:'.format(*view_line_range))
print('\n'.join(text.split('\n')[view_line_range[0]:view_line_range[1]]))
```
---
## Implement Pre-processing Functions
The first thing to do to any dataset is pre-processing. Implement the following pre-processing functions below:
- Lookup Table
- Tokenize Punctuation
### Lookup Table
To create a word embedding, you first need to transform the words to ids. In this function, create two dictionaries:
- Dictionary to go from the words to an id, we'll call `vocab_to_int`
- Dictionary to go from the id to word, we'll call `int_to_vocab`
Return these dictionaries in the following **tuple** `(vocab_to_int, int_to_vocab)`
```
import problem_unittests as tests
from collections import Counter
def create_lookup_tables(text):
"""
Create lookup tables for vocabulary
:param text: The text of tv scripts split into words
:return: A tuple of dicts (vocab_to_int, int_to_vocab)
"""
# TODO: Implement Function
#define count var
countVar = Counter(text)
#define vocab var
Vocab = sorted(countVar, key=countVar.get, reverse=True)
#define integer to vocab
int_to_vocab = {ii: word for ii, word in enumerate(Vocab)}
#define vocab to integer
vocab_to_int = {word: ii for ii, word in int_to_vocab.items()}
# return tuple
return (vocab_to_int, int_to_vocab)
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_create_lookup_tables(create_lookup_tables)
```
### Tokenize Punctuation
We'll be splitting the script into a word array using spaces as delimiters. However, punctuations like periods and exclamation marks can create multiple ids for the same word. For example, "bye" and "bye!" would generate two different word ids.
Implement the function `token_lookup` to return a dict that will be used to tokenize symbols like "!" into "||Exclamation_Mark||". Create a dictionary for the following symbols where the symbol is the key and value is the token:
- Period ( **.** )
- Comma ( **,** )
- Quotation Mark ( **"** )
- Semicolon ( **;** )
- Exclamation mark ( **!** )
- Question mark ( **?** )
- Left Parentheses ( **(** )
- Right Parentheses ( **)** )
- Dash ( **-** )
- Return ( **\n** )
This dictionary will be used to tokenize the symbols and add the delimiter (space) around it. This separates each symbols as its own word, making it easier for the neural network to predict the next word. Make sure you don't use a value that could be confused as a word; for example, instead of using the value "dash", try using something like "||dash||".
```
def token_lookup():
"""
Generate a dict to turn punctuation into a token.
:return: Tokenized dictionary where the key is the punctuation and the value is the token
"""
# TODO: Implement Function
tokens = dict()
tokens['.'] = '||period||'
tokens[','] = '||comma||'
tokens['"'] = '||quotation_mark||'
tokens[';'] = '||semicolon||'
tokens['!'] = '||exclam_mark||'
tokens['?'] = '||question_mark||'
tokens['('] = '||left_par||'
tokens[')'] = '||right_par||'
tokens['-'] = '||dash||'
tokens['\n'] = '||return||'
return tokens
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_tokenize(token_lookup)
```
## Pre-process all the data and save it
Running the code cell below will pre-process all the data and save it to file. You're encouraged to lok at the code for `preprocess_and_save_data` in the `helpers.py` file to see what it's doing in detail, but you do not need to change this code.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# pre-process training data
helper.preprocess_and_save_data(data_dir, token_lookup, create_lookup_tables)
```
# Check Point
This is your first checkpoint. If you ever decide to come back to this notebook or have to restart the notebook, you can start from here. The preprocessed data has been saved to disk.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import helper
import problem_unittests as tests
int_text, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
```
## Build the Neural Network
In this section, you'll build the components necessary to build an RNN by implementing the RNN Module and forward and backpropagation functions.
### Check Access to GPU
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import torch
# Check for a GPU
train_on_gpu = torch.cuda.is_available()
if not train_on_gpu:
print('No GPU found. Please use a GPU to train your neural network.')
```
## Input
Let's start with the preprocessed input data. We'll use [TensorDataset](http://pytorch.org/docs/master/data.html#torch.utils.data.TensorDataset) to provide a known format to our dataset; in combination with [DataLoader](http://pytorch.org/docs/master/data.html#torch.utils.data.DataLoader), it will handle batching, shuffling, and other dataset iteration functions.
You can create data with TensorDataset by passing in feature and target tensors. Then create a DataLoader as usual.
```
data = TensorDataset(feature_tensors, target_tensors)
data_loader = torch.utils.data.DataLoader(data,
batch_size=batch_size)
```
### Batching
Implement the `batch_data` function to batch `words` data into chunks of size `batch_size` using the `TensorDataset` and `DataLoader` classes.
>You can batch words using the DataLoader, but it will be up to you to create `feature_tensors` and `target_tensors` of the correct size and content for a given `sequence_length`.
For example, say we have these as input:
```
words = [1, 2, 3, 4, 5, 6, 7]
sequence_length = 4
```
Your first `feature_tensor` should contain the values:
```
[1, 2, 3, 4]
```
And the corresponding `target_tensor` should just be the next "word"/tokenized word value:
```
5
```
This should continue with the second `feature_tensor`, `target_tensor` being:
```
[2, 3, 4, 5] # features
6 # target
```
```
from torch.utils.data import TensorDataset, DataLoader
def batch_data(words, sequence_length, batch_size):
"""
Batch the neural network data using DataLoader
:param words: The word ids of the TV scripts
:param sequence_length: The sequence length of each batch
:param batch_size: The size of each batch; the number of sequences in a batch
:return: DataLoader with batched data
"""
# TODO: Implement function
Num_batches = len(words)//batch_size
words = words[:Num_batches*batch_size]
x, y = [], []
for idx in range(0, len(words) - sequence_length):
x.append(words[idx:idx+sequence_length])
y.append(words[idx+sequence_length])
feature_tensors, target_tensors = torch.from_numpy(np.asarray(x)), torch.from_numpy(np.asarray(y))
dataset = TensorDataset(feature_tensors, target_tensors)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size)
# return a dataloader
return dataloader
# there is no test for this function, but you are encouraged to create
# print statements and tests of your own
```
### Test your dataloader
You'll have to modify this code to test a batching function, but it should look fairly similar.
Below, we're generating some test text data and defining a dataloader using the function you defined, above. Then, we are getting some sample batch of inputs `sample_x` and targets `sample_y` from our dataloader.
Your code should return something like the following (likely in a different order, if you shuffled your data):
```
torch.Size([10, 5])
tensor([[ 28, 29, 30, 31, 32],
[ 21, 22, 23, 24, 25],
[ 17, 18, 19, 20, 21],
[ 34, 35, 36, 37, 38],
[ 11, 12, 13, 14, 15],
[ 23, 24, 25, 26, 27],
[ 6, 7, 8, 9, 10],
[ 38, 39, 40, 41, 42],
[ 25, 26, 27, 28, 29],
[ 7, 8, 9, 10, 11]])
torch.Size([10])
tensor([ 33, 26, 22, 39, 16, 28, 11, 43, 30, 12])
```
### Sizes
Your sample_x should be of size `(batch_size, sequence_length)` or (10, 5) in this case and sample_y should just have one dimension: batch_size (10).
### Values
You should also notice that the targets, sample_y, are the *next* value in the ordered test_text data. So, for an input sequence `[ 28, 29, 30, 31, 32]` that ends with the value `32`, the corresponding output should be `33`.
```
# test dataloader
test_text = range(50)
t_loader = batch_data(test_text, sequence_length=5, batch_size=10)
data_iter = iter(t_loader)
sample_x, sample_y = data_iter.next()
print(sample_x.shape)
print(sample_x)
print()
print(sample_y.shape)
print(sample_y)
```
---
## Build the Neural Network
Implement an RNN using PyTorch's [Module class](http://pytorch.org/docs/master/nn.html#torch.nn.Module). You may choose to use a GRU or an LSTM. To complete the RNN, you'll have to implement the following functions for the class:
- `__init__` - The initialize function.
- `init_hidden` - The initialization function for an LSTM/GRU hidden state
- `forward` - Forward propagation function.
The initialize function should create the layers of the neural network and save them to the class. The forward propagation function will use these layers to run forward propagation and generate an output and a hidden state.
**The output of this model should be the *last* batch of word scores** after a complete sequence has been processed. That is, for each input sequence of words, we only want to output the word scores for a single, most likely, next word.
### Hints
1. Make sure to stack the outputs of the lstm to pass to your fully-connected layer, you can do this with `lstm_output = lstm_output.contiguous().view(-1, self.hidden_dim)`
2. You can get the last batch of word scores by shaping the output of the final, fully-connected layer like so:
```
# reshape into (batch_size, seq_length, output_size)
output = output.view(batch_size, -1, self.output_size)
# get last batch
out = output[:, -1]
```
```
import torch.nn as nn
class RNN(nn.Module):
def __init__(self, vocab_size, output_size, embedding_dim, hidden_dim, n_layers, dropout=0.5):
"""
Initialize the PyTorch RNN Module
:param vocab_size: The number of input dimensions of the neural network (the size of the vocabulary)
:param output_size: The number of output dimensions of the neural network
:param embedding_dim: The size of embeddings, should you choose to use them
:param hidden_dim: The size of the hidden layer outputs
:param dropout: dropout to add in between LSTM/GRU layers
"""
super(RNN, self).__init__()
# TODO: Implement function
# set class variables
self.output_size = output_size
self.n_layers = n_layers
self.hidden_dim = hidden_dim
# define model layers
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim, n_layers, dropout=dropout, batch_first=True)
self.fc = nn.Linear(hidden_dim, output_size)
def forward(self, nn_input, hidden):
"""
Forward propagation of the neural network
:param nn_input: The input to the neural network
:param hidden: The hidden state
:return: Two Tensors, the output of the neural network and the latest hidden state
"""
# TODO: Implement function
batch_size = nn_input.size(0)
embeds = self.embedding(nn_input)
lstm_out, hidden = self.lstm(embeds, hidden)
lstm_out = lstm_out.contiguous().view(-1, self.hidden_dim)
out = self.fc(lstm_out)
# reshape
out = out.view(batch_size, -1, self.output_size)
# find the last batch
output = out[:, -1]
# return one batch of output word scores and the hidden state
return output, hidden
def init_hidden(self, batch_size):
'''
Initialize the hidden state of an LSTM/GRU
:param batch_size: The batch_size of the hidden state
:return: hidden state of dims (n_layers, batch_size, hidden_dim)
'''
# Implement function
# initialize hidden state with zero weights, and move to GPU if available
weight = next(self.parameters()).data
if (train_on_gpu):
hidden = (weight.new(self.n_layers, batch_size, self.hidden_dim).zero_().cuda(),
weight.new(self.n_layers, batch_size, self.hidden_dim).zero_().cuda())
else:
hidden = (weight.new(self.n_layers, batch_size, self.hidden_dim).zero_(),
weight.new(self.n_layers, batch_size, self.hidden_dim).zero_())
return hidden
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_rnn(RNN, train_on_gpu)
```
### Define forward and backpropagation
Use the RNN class you implemented to apply forward and back propagation. This function will be called, iteratively, in the training loop as follows:
```
loss = forward_back_prop(decoder, decoder_optimizer, criterion, inp, target)
```
And it should return the average loss over a batch and the hidden state returned by a call to `RNN(inp, hidden)`. Recall that you can get this loss by computing it, as usual, and calling `loss.item()`.
**If a GPU is available, you should move your data to that GPU device, here.**
```
def forward_back_prop(rnn, optimizer, criterion, inp, target, hidden):
"""
Forward and backward propagation on the neural network
:param decoder: The PyTorch Module that holds the neural network
:param decoder_optimizer: The PyTorch optimizer for the neural network
:param criterion: The PyTorch loss function
:param inp: A batch of input to the neural network
:param target: The target output for the batch of input
:return: The loss and the latest hidden state Tensor
"""
# TODO: Implement Function
# move data to GPU, if available
if (train_on_gpu):
inp = inp.cuda()
target = target.cuda()
# perform backpropagation and optimization
hidden = tuple([each.data for each in hidden])
rnn.zero_grad()
output, hidden = rnn(inp, hidden)
loss = criterion(output, target)
loss.backward()
nn.utils.clip_grad_norm_(rnn.parameters(), 5)
optimizer.step()
# return the loss over a batch and the hidden state produced by our model
return loss.item(), hidden
# Note that these tests aren't completely extensive.
# they are here to act as general checks on the expected outputs of your functions
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_forward_back_prop(RNN, forward_back_prop, train_on_gpu)
```
## Neural Network Training
With the structure of the network complete and data ready to be fed in the neural network, it's time to train it.
### Train Loop
The training loop is implemented for you in the `train_decoder` function. This function will train the network over all the batches for the number of epochs given. The model progress will be shown every number of batches. This number is set with the `show_every_n_batches` parameter. You'll set this parameter along with other parameters in the next section.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
def train_rnn(rnn, batch_size, optimizer, criterion, n_epochs, show_every_n_batches=100):
batch_losses = []
rnn.train()
print("Training for %d epoch(s)..." % n_epochs)
for epoch_i in range(1, n_epochs + 1):
# initialize hidden state
hidden = rnn.init_hidden(batch_size)
for batch_i, (inputs, labels) in enumerate(train_loader, 1):
# make sure you iterate over completely full batches, only
n_batches = len(train_loader.dataset)//batch_size
if(batch_i > n_batches):
break
# forward, back prop
loss, hidden = forward_back_prop(rnn, optimizer, criterion, inputs, labels, hidden)
# record loss
batch_losses.append(loss)
# printing loss stats
if batch_i % show_every_n_batches == 0:
print('Epoch: {:>4}/{:<4} Loss: {}\n'.format(
epoch_i, n_epochs, np.average(batch_losses)))
batch_losses = []
# returns a trained rnn
return rnn
```
### Hyperparameters
Set and train the neural network with the following parameters:
- Set `sequence_length` to the length of a sequence.
- Set `batch_size` to the batch size.
- Set `num_epochs` to the number of epochs to train for.
- Set `learning_rate` to the learning rate for an Adam optimizer.
- Set `vocab_size` to the number of uniqe tokens in our vocabulary.
- Set `output_size` to the desired size of the output.
- Set `embedding_dim` to the embedding dimension; smaller than the vocab_size.
- Set `hidden_dim` to the hidden dimension of your RNN.
- Set `n_layers` to the number of layers/cells in your RNN.
- Set `show_every_n_batches` to the number of batches at which the neural network should print progress.
If the network isn't getting the desired results, tweak these parameters and/or the layers in the `RNN` class.
```
# Data params
# Sequence Length
sequence_length = 12 # of words in a sequence
# Batch Size
batch_size = 120
# data loader - do not change
train_loader = batch_data(int_text, sequence_length, batch_size)
# Training parameters
# Number of Epochs
num_epochs = 10
# Learning Rate
learning_rate = 0.001
# Model parameters
# Vocab size
vocab_size = len(vocab_to_int)
# Output size
output_size = len(vocab_to_int)
# Embedding Dimension
embedding_dim = 300
# Hidden Dimension
hidden_dim = int(300*1.25)
# Number of RNN Layers
n_layers = 2
# Show stats for every n number of batches
show_every_n_batches = 500
```
### Train
In the next cell, you'll train the neural network on the pre-processed data. If you have a hard time getting a good loss, you may consider changing your hyperparameters. In general, you may get better results with larger hidden and n_layer dimensions, but larger models take a longer time to train.
> **You should aim for a loss less than 3.5.**
You should also experiment with different sequence lengths, which determine the size of the long range dependencies that a model can learn.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# create model and move to gpu if available
rnn = RNN(vocab_size, output_size, embedding_dim, hidden_dim, n_layers, dropout=0.5)
if train_on_gpu:
rnn.cuda()
# defining loss and optimization functions for training
optimizer = torch.optim.Adam(rnn.parameters(), lr=learning_rate)
criterion = nn.CrossEntropyLoss()
# training the model
trained_rnn = train_rnn(rnn, batch_size, optimizer, criterion, num_epochs, show_every_n_batches)
# saving the trained model
helper.save_model('./save/trained_rnn', trained_rnn)
print('Model Trained and Saved')
```
### Question: How did you decide on your model hyperparameters?
For example, did you try different sequence_lengths and find that one size made the model converge faster? What about your hidden_dim and n_layers; how did you decide on those?
**Answer:**
I trained the model with the following parameters:
10 epochs
learning rate = 0.001
embedding dim = 300
hidden dim = 375
number of layers = 2
show_every_n_batches = 2500
and it gave a good loss: 2.96
---
# Checkpoint
After running the above training cell, your model will be saved by name, `trained_rnn`, and if you save your notebook progress, **you can pause here and come back to this code at another time**. You can resume your progress by running the next cell, which will load in our word:id dictionaries _and_ load in your saved model by name!
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import torch
import helper
import problem_unittests as tests
_, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
trained_rnn = helper.load_model('./save/trained_rnn')
```
## Generate TV Script
With the network trained and saved, you'll use it to generate a new, "fake" Seinfeld TV script in this section.
### Generate Text
To generate the text, the network needs to start with a single word and repeat its predictions until it reaches a set length. You'll be using the `generate` function to do this. It takes a word id to start with, `prime_id`, and generates a set length of text, `predict_len`. Also note that it uses topk sampling to introduce some randomness in choosing the most likely next word, given an output set of word scores!
```
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
import torch.nn.functional as F
def generate(rnn, prime_id, int_to_vocab, token_dict, pad_value, predict_len=100):
"""
Generate text using the neural network
:param decoder: The PyTorch Module that holds the trained neural network
:param prime_id: The word id to start the first prediction
:param int_to_vocab: Dict of word id keys to word values
:param token_dict: Dict of puncuation tokens keys to puncuation values
:param pad_value: The value used to pad a sequence
:param predict_len: The length of text to generate
:return: The generated text
"""
rnn.eval()
# create a sequence (batch_size=1) with the prime_id
current_seq = np.full((1, sequence_length), pad_value)
current_seq[-1][-1] = prime_id
predicted = [int_to_vocab[prime_id]]
for _ in range(predict_len):
if train_on_gpu:
current_seq = torch.LongTensor(current_seq).cuda()
else:
current_seq = torch.LongTensor(current_seq)
# initialize the hidden state
hidden = rnn.init_hidden(current_seq.size(0))
# get the output of the rnn
output, _ = rnn(current_seq, hidden)
# get the next word probabilities
p = F.softmax(output, dim=1).data
if(train_on_gpu):
p = p.cpu() # move to cpu
# use top_k sampling to get the index of the next word
top_k = 5
p, top_i = p.topk(top_k)
top_i = top_i.numpy().squeeze()
# select the likely next word index with some element of randomness
p = p.numpy().squeeze()
word_i = np.random.choice(top_i, p=p/p.sum())
# retrieve that word from the dictionary
word = int_to_vocab[word_i]
predicted.append(word)
# the generated word becomes the next "current sequence" and the cycle can continue
current_seq = np.roll(current_seq, -1, 1)
current_seq[-1][-1] = word_i
gen_sentences = ' '.join(predicted)
# Replace punctuation tokens
for key, token in token_dict.items():
ending = ' ' if key in ['\n', '(', '"'] else ''
gen_sentences = gen_sentences.replace(' ' + token.lower(), key)
gen_sentences = gen_sentences.replace('\n ', '\n')
gen_sentences = gen_sentences.replace('( ', '(')
# return all the sentences
return gen_sentences
```
### Generate a New Script
It's time to generate the text. Set `gen_length` to the length of TV script you want to generate and set `prime_word` to one of the following to start the prediction:
- "jerry"
- "elaine"
- "george"
- "kramer"
You can set the prime word to _any word_ in our dictionary, but it's best to start with a name for generating a TV script. (You can also start with any other names you find in the original text file!)
```
# run the cell multiple times to get different results!
gen_length = 400 # modify the length to your preference
prime_word = 'jerry' # name for starting the script
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
pad_word = helper.SPECIAL_WORDS['PADDING']
generated_script = generate(trained_rnn, vocab_to_int[prime_word + ':'], int_to_vocab, token_dict, vocab_to_int[pad_word], gen_length)
print(generated_script)
```
#### Save your favorite scripts
Once you have a script that you like (or find interesting), save it to a text file!
```
# save script to a text file
f = open("generated_script_1.txt","w")
f.write(generated_script)
f.close()
```
# The TV Script is Not Perfect
It's ok if the TV script doesn't make perfect sense. It should look like alternating lines of dialogue, here is one such example of a few generated lines.
### Example generated script
>jerry: what about me?
>
>jerry: i don't have to wait.
>
>kramer:(to the sales table)
>
>elaine:(to jerry) hey, look at this, i'm a good doctor.
>
>newman:(to elaine) you think i have no idea of this...
>
>elaine: oh, you better take the phone, and he was a little nervous.
>
>kramer:(to the phone) hey, hey, jerry, i don't want to be a little bit.(to kramer and jerry) you can't.
>
>jerry: oh, yeah. i don't even know, i know.
>
>jerry:(to the phone) oh, i know.
>
>kramer:(laughing) you know...(to jerry) you don't know.
You can see that there are multiple characters that say (somewhat) complete sentences, but it doesn't have to be perfect! It takes quite a while to get good results, and often, you'll have to use a smaller vocabulary (and discard uncommon words), or get more data. The Seinfeld dataset is about 3.4 MB, which is big enough for our purposes; for script generation you'll want more than 1 MB of text, generally.
# Submitting This Project
When submitting this project, make sure to run all the cells before saving the notebook. Save the notebook file as "dlnd_tv_script_generation.ipynb" and save another copy as an HTML file by clicking "File" -> "Download as.."->"html". Include the "helper.py" and "problem_unittests.py" files in your submission. Once you download these files, compress them into one zip file for submission.
| github_jupyter |
<a href="https://colab.research.google.com/github/lakigigar/Caltech-CS155-2021/blob/main/psets/set1/set1_prob3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Problem 3
Use this notebook to write your code for problem 3 by filling in the sections marked `# TODO` and running all cells.
```
import numpy as np
import matplotlib.pyplot as plt
import itertools
import urllib.request
urllib.request.urlretrieve('https://raw.githubusercontent.com/lakigigar/Caltech-CS155-2021/main/psets/set1/perceptron_helper.py', 'perceptron_helper.py')
from perceptron_helper import (
predict,
plot_data,
boundary,
plot_perceptron,
)
%matplotlib inline
```
## Implementation of Perceptron
First, we will implement the perceptron algorithm. Fill in the `update_perceptron()` function so that it finds a single misclassified point and updates the weights and bias accordingly. If no point exists, the weights and bias should not change.
Hint: You can use the `predict()` helper method, which labels a point 1 or -1 depending on the weights and bias.
```
def update_perceptron(X, Y, w, b):
"""
This method updates a perceptron model. Takes in the previous weights
and returns weights after an update, which could be nothing.
Inputs:
X: A (N, D) shaped numpy array containing N D-dimensional points.
Y: A (N, ) shaped numpy array containing the labels for the points.
w: A (D, ) shaped numpy array containing the weight vector.
b: A float containing the bias term.
Output:
next_w: A (D, ) shaped numpy array containing the next weight vector
after updating on a single misclassified point, if one exists.
next_b: The next float bias term after updating on a single
misclassified point, if one exists.
"""
next_w, next_b = np.copy(w), np.copy(b)
#==============================================
# TODO: Implement update rule for perceptron.
#===============================================
return next_w, next_b
```
Next you will fill in the `run_perceptron()` method. The method performs single updates on a misclassified point until convergence, or max_iter updates are made. The function will return the final weights and bias. You should use the `update_perceptron()` method you implemented above.
```
def run_perceptron(X, Y, w, b, max_iter):
"""
This method runs the perceptron learning algorithm. Takes in initial weights
and runs max_iter update iterations. Returns final weights and bias.
Inputs:
X: A (N, D) shaped numpy array containing N D-dimensional points.
Y: A (N, ) shaped numpy array containing the labels for the points.
w: A (D, ) shaped numpy array containing the initial weight vector.
b: A float containing the initial bias term.
max_iter: An int for the maximum number of updates evaluated.
Output:
w: A (D, ) shaped numpy array containing the final weight vector.
b: The final float bias term.
"""
#============================================
# TODO: Implement perceptron update loop.
#=============================================
return w, b
```
# Problem 3A
## Visualizing a Toy Dataset
We will begin by training our perceptron on a toy dataset of 3 points. The green points are labelled +1 and the red points are labelled -1. We use the helper function `plot_data()` to do so.
```
X = np.array([[ -3, -1], [0, 3], [1, -2]])
Y = np.array([ -1, 1, 1])
fig = plt.figure(figsize=(5,4))
ax = fig.gca(); ax.set_xlim(-4.1, 3.1); ax.set_ylim(-3.1, 4.1)
plot_data(X, Y, ax)
```
## Running the Perceptron
Next, we will run the perceptron learning algorithm on this dataset. Update the code to show the weights and bias at each timestep and the misclassified point used in each update.
Run the below code, and fill in the corresponding table in the set.
```
# Initialize weights and bias.
weights = np.array([0.0, 1.0])
bias = 0.0
weights, bias = run_perceptron(X, Y, weights, bias, 16)
print()
print ("final w = %s, final b = %.1f" % (weights, bias))
```
## Visualizating the Perceptron
Getting all that information in table form isn't very informative. Let us visualize what the decision boundaries are at each timestep instead.
The helper functions `boundary()` and `plot_perceptron()` plot a decision boundary given a perceptron weights and bias. Note that the equation for the decision boundary is given by:
$$w_1x_1 + w_2x_2 + b = 0.$$
Using some algebra, we can obtain $x_2$ from $x_1$ to plot the boundary as a line.
$$x_2 = \frac{-w_1x_2 - b}{w_2}. $$
Below is a redefinition of the `run_perceptron()` method to visualize the points and decision boundaries at each timestep instead of printing. Fill in the method using your previous `run_perceptron()` method, and the above helper methods.
Hint: The axs element is a list of Axes, which are used as subplots for each timestep. You can do the following:
```
ax = axs[i]
```
to get the plot correponding to $t = i$. You can then use ax.set_title() to title each subplot. You will want to use the `plot_data()` and `plot_perceptron()` helper methods.
```
def run_perceptron(X, Y, w, b, axs, max_iter):
"""
This method runs the perceptron learning algorithm. Takes in initial weights
and runs max_iter update iterations. Returns final weights and bias.
Inputs:
X: A (N, D) shaped numpy array containing N D-dimensional points.
Y: A (N, ) shaped numpy array containing the labels for the points.
w: A (D, ) shaped numpy array containing the initial weight vector.
b: A float containing the initial bias term.
axs: A list of Axes that contain suplots for each timestep.
max_iter: An int for the maximum number of updates evaluated.
Output:
The final weight and bias vectors.
"""
#============================================
# TODO: Implement perceptron update loop.
#=============================================
return w, b
```
Run the below code to get a visualization of the perceptron algorithm. The red region are areas the perceptron thinks are negative examples.
```
# Initialize weights and bias.
weights = np.array([0.0, 1.0])
bias = 0.0
f, ax_arr = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(9,8))
axs = list(itertools.chain.from_iterable(ax_arr))
for ax in axs:
ax.set_xlim(-4.1, 3.1); ax.set_ylim(-3.1, 4.1)
run_perceptron(X, Y, weights, bias, axs, 4)
f.tight_layout()
```
# Problem 3C
## Visualize a Non-linearly Separable Dataset.
We will now work on a dataset that cannot be linearly separated, namely one that is generated by the XOR function.
```
X = np.array([[0, 1], [1, 0], [0, 0], [1, 1]])
Y = np.array([1, 1, -1, -1])
fig = plt.figure(figsize=(5,4))
ax = fig.gca(); ax.set_xlim(-0.1, 1.1); ax.set_ylim(-0.1, 1.1)
plot_data(X, Y, ax)
```
We will now run the perceptron algorithm on this dataset. We will limit the total timesteps this time, but you should see a pattern in the updates. Run the below code.
```
# Initialize weights and bias.
weights = np.array([0.0, 1.0])
bias = 0.0
f, ax_arr = plt.subplots(4, 4, sharex=True, sharey=True, figsize=(9,8))
axs = list(itertools.chain.from_iterable(ax_arr))
for ax in axs:
ax.set_xlim(-0.1, 1.1); ax.set_ylim(-0.1, 1.1)
run_perceptron(X, Y, weights, bias, axs, 16)
f.tight_layout()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/chrismarkella/Kaggle-access-from-Google-Colab/blob/master/Pipeline_multiple_imputers_and_models.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!apt-get -qq install tree
import os
import numpy as np
import pandas as pd
from getpass import getpass
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import OneHotEncoder
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
def access_kaggle():
"""
Access Kaggle from Google Colab.
If the /root/.kaggle does not exist then prompt for
the username and for the Kaggle API key.
Creates the kaggle.json access file in the /root/.kaggle/ folder.
"""
KAGGLE_ROOT = os.path.join('/root', '.kaggle')
KAGGLE_PATH = os.path.join(KAGGLE_ROOT, 'kaggle.json')
if '.kaggle' not in os.listdir(path='/root'):
user = getpass(prompt='Kaggle username: ')
key = getpass(prompt='Kaggle API key: ')
!mkdir $KAGGLE_ROOT
!touch $KAGGLE_PATH
!chmod 666 $KAGGLE_PATH
with open(KAGGLE_PATH, mode='w') as f:
f.write('{"username":"%s", "key":"%s"}' %(user, key))
f.close()
!chmod 600 $KAGGLE_PATH
del user
del key
success_msg = "Kaggle is successfully set up. Good to go."
print(f'{success_msg}')
access_kaggle()
!kaggle competitions download -c home-data-for-ml-course -p datasets/ml-course
!tree -sh ./
!cat -n datasets/ml-course/train.csv|head -2
df = pd.read_csv('datasets/ml-course/train.csv', sep=',', index_col=0)
df.columns = df.columns.map(lambda c: c.lower())
df.columns
df.info()
df.saleprice.isnull().sum()
y = df.saleprice
X = df.drop(['saleprice'], axis='columns')
train_x_full, valid_x_full, train_y, valid_y = train_test_split(X, y, test_size=0.2, random_state=42)
numerical_columns = [col for col in train_x_full.columns if
train_x_full[col].dtype in ['float64', 'int64']]
categorical_columns = [col for col in train_x_full.columns if
train_x_full[col].dtype == 'object' and
train_x_full[col].nunique() < 10]
selected_columns = categorical_columns + numerical_columns
train_x = train_x_full[selected_columns].copy()
valid_x = valid_x_full[selected_columns].copy()
train_x.shape, valid_x.shape
train_x.head()
imputers = [
('imputer', SimpleImputer()),
('imputer_median', SimpleImputer(strategy='median')),
('imputer_most_frequent', SimpleImputer(strategy='most_frequent')),
]
trees_in_the_forest = [5, 10, 20, 50]
models = [RandomForestRegressor(n_estimators=N, random_state=42) for N in trees_in_the_forest]
for imputer_name, imputer in imputers:
numerical_transformer = imputer
categorical_transformer = Pipeline(steps=[
('imputer', SimpleImputer(strategy='most_frequent')),
('one_hot_encoder', OneHotEncoder(sparse=False, handle_unknown='ignore')),
])
preprocessor = ColumnTransformer(
transformers=[
# (name , transformer , columns)
('num', numerical_transformer, numerical_columns),
('cat', categorical_transformer, categorical_columns),
]
)
print(f'{imputer_name} imputer:')
print('-'*20)
for model in models:
pipe = Pipeline(
steps=[
('preprocessor', preprocessor),
('model', model),
]
)
pipe.fit(train_x, train_y)
preds = pipe.predict(valid_x)
mae = mean_absolute_error(y_true=valid_y, y_pred=preds)
print(f'{model}')
print(f'---> MAE: {mae}')
print()
```
| github_jupyter |
# Synthesis Calibration
This chapter explains how to calibrate interferometer data within the CASA task system. Calibration is the process of determining the net complex correction factors that must be applied to each visibility in order to make them as close as possible to what an idealized interferometer would measure, such that when the data is imaged an accurate picture of the sky is obtained. This is not an arbitrary process, and there is a philosophy behind the CASA calibration methodology. For the most part, calibration in CASA using the tasks is not too different than calibration in other packages such as AIPS or Miriad.
## Calibration tasks
<div class="alert alert-warning">
**Alert:** The calibration table format changed in CASA 3.4. CASA 4.2 is the last version that will support the **caltabconvert** function that provides conversions from the pre-3.4 caltable format to the modern format; it will be removed for CASA 4.3. In general, it is best to recalculate calibration using CASA 3.4 or later.
</div>
<div class="alert alert-warning">
**Alert:** In CASA 4.2 the *gaincurve* and *opacity* parameters have been removed from all calibration tasks (as advertised in 4.1). These calibration types are supported via the gencal task.
</div>
<div class="alert alert-warning">
**Alert:** As part of continuing development of a more flexible and improved interface for specifying calibration for apply, a new parameter has been introduced in **applycal** and the solving tasks: *docallib*. This parameter toggles between use of the traditional calibration apply parameters ( *gaintable*, *gainfield*, *interp*, *spwmap*, and *calwt*), and a new *callib* parameter which currently provides access to the *experimental* Cal Library mechanism, wherein calibration instructions are stored in a file. The default remains *docallib=False* in CASA 4.5, and this reveals the traditional apply parameters which continue to work as always, and the remainder of this chapter is still written using *docallib=False*. Users interested in the Cal Library mechanism's flexibility are encouraged to try it and report any problems; see [here](cal_library_syntax.ipynb#cal-library-syntax "Cal Library") for information on how to use it, including how to convert traditional applycal to Cal Library format. Note also that **plotms** and **mstransform** now support use of the Cal Library to enable on-the-fly calibration when plotting and generating new MSs.
</div>
The standard set of calibration solving tasks (to produce calibration tables) are:
- **bandpass** \-\-- complex bandpass (B) calibration solving, including options for channel-binned or polynomial solutions
- **gaincal** \-\-- complex gain (G,T) and delay (K) calibration solving, including options for time-binned or spline solutions
- **polcal** \-\-- polarization calibration including leakage, cross-hand phase, and position angle
- **blcal** \-\-- *baseline-based* complex gain or bandpass calibration
There are helper tasks to create, manipulate, and explore calibration tables:
- **applycal** \-\-- Apply calculated calibration solutions
- **clearcal** \-\-- Re-initialize the calibration for a visibility dataset
- **fluxscale** \-\-- Bootstrap the flux density scale from standard calibration sources
- **listcal** \-\-- List calibration solutions
- **plotcal** \-\-- Plot calibration solutions
- **plotbandpass** \-\-- Plot bandpass solutions
- **setjy** \-\-- Compute model visibilities with the correct flux density for a specified source
- **smoothcal** \-\-- Smooth calibration solutions derived from one or more sources
- **calstat** \-\-- Statistics of calibration solutions
- **gencal** \-\-- Create a calibration tables from metadata such as antenna position offsets, gaincurves and opacities
- **wvrgcal** \-\-- Generate a gain table based on Water Vapor Radiometer data (for ALMA)
- **uvcontsub** \-\-- Carry out uv-plane continuum fitting and subtraction
## The Calibration Process
A work-flow diagram for CASA calibration of interferometry data is shown in the following figure. This should help you chart your course through the complex set of calibration steps. In the following sections, we will detail the steps themselves and explain how to run the necessary tasks and tools.
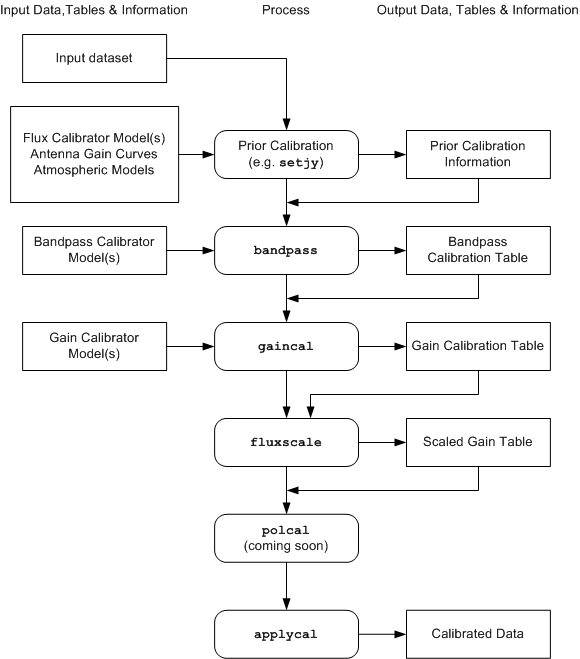{.image-inline}
>Flow chart of synthesis calibration operations. Not shown are use of table manipulation and plotting tasks: **plotcal** and **smoothcal**
The process can be broken down into a number of discrete phases:
- **Calibrator Model Visibility Specification** \-\-- set model visibilities for calibrators, either unit point source visibilities for calibrators with unknown flux density or structure (generally, sources used for calibrators are approximately point-like), or visibilities derived from *a priori* images and/or known or standard flux density values. Use the **setjy** task for calibrator flux densities and models.
- **Prior Calibration** \-\-- set up previously known calibration quantities that need to be pre-applied, such antenna gain-elevation curves, atmospheric models, delays, and antenna position offsets. Use the **gencal** task for antenna position offsets, gaincurves, antenna efficiencies, opacity, and other prior calibrations
- **Bandpass Calibration** \-\-- solve for the relative gain of the system over the frequency channels in the dataset (if needed), having pre-applied the prior calibration. Use the **bandpass** task
- **Gain Calibration** \-\-- solve for the gain variations of the system as a function of time, having pre-applied the bandpass (if needed) and prior calibration. Use the **gaincal** task
- **Polarization Calibration** \-\-- solve for polarization leakage terms and linear polarization position angle. Use the **polcal** task.
- **Establish Flux Density Scale** \-\-- if only some of the calibrators have known flux densities, then rescale gain solutions and derive flux densities of secondary calibrators. Use the **fluxscale** task
- **Smooth** \-\-- if necessary smooth calibration using the **smoothcal** task.
- **Examine Calibration** \-\-- at any point, you can (and should) use **plotcal** and/or **listcal** to look at the calibration tables that you have created
- **Apply Calibration to the Data** \-\-- Corrected data is formed using the **applycal** task, and can be undone using **clearcal**
- **Post-Calibration Activities** \-\-- this includes the determination and subtraction of continuum signal from line data (**uvcontsub**), the splitting of data-sets into subsets (**split**, **mstransform**), and other operations (such as simple model-fitting: **uvmodelfit**).
The flow chart and the above list are in a suggested order. However, the actual order in which you will carry out these operations is somewhat fluid, and will be determined by the specific data-reduction use cases you are following. For example, you may need to obtain an initial gain calibration on your bandpass calibrator before moving to the bandpass calibration stage. Or perhaps the polarization leakage calibration will be known from prior service observations, and can be applied as a constituent of prior calibration.
## Calibration Philosophy
Calibration is not an arbitrary process, and there is a methodology that has been developed to carry out synthesis calibration and an algebra to describe the various corruptions that data might be subject to: the Hamaker-Bregman-Sault Measurement Equation (ME), described [here.](casa-fundamentals.ipynb#measurement-equation "Measurement Equation") The user need not worry about the details of this mathematics as the CASA software does that for you. Anyway, it\'s just matrix algebra, and your familiar scalar methods of calibration (such as in AIPS) are encompassed in this more general approach.
There are a number of \`\`physical\'\' components to calibration in CASA:
- **data** \-\-- in the form of the MeasurementSet (MS). The MS includes a number of columns that can hold calibrated data, model information, and weights
- **calibration tables** \-\-- these are in the form of standard CASA tables, and hold the calibration solutions (or parameterizations thereof)
- **task parameters** \-\-- sometimes the calibration information is in the form of CASA task parameters that tell the calibration tasks to turn on or off various features, contain important values (such as flux densities), or list what should be done to the data.
At its most basic level, Calibration in CASA is the process of taking \"uncalibrated\" **data**, setting up the operation of calibration tasks using **task parameters**, solving for new **calibration tables**, and then applying the calibration tables to form \"calibrated\" **data**. Iteration can occur as necessary, e.g., to re-solve for an eariler **calibration table** using a better set of prior calibration, often with the aid of other non-calibration steps (e.g. imaging to generate improved source models for \"self-calibration\").
The calibration tables are the currency that is exchanged between the calibration tasks. The \"solver\" tasks (**gaincal**, **bandpass**, **blcal**, **polcal**) take in the MS (which may have a calibration model attached) and previous calibration tables, and will output an \"incremental\" calibration table (it is incremental to the previous calibration, if any). This table can then be smoothed using **smoothcal** if desired.
The final set of calibration tables represents the cumulative calibration and is what is applied to correct the data using **applycal**. It is important to keep track of each calibration table and its role relative to others. E.g., a provisional gain calibration solution will usually be obtained to optimize a bandpass calibration solve, but then be discarded in favor of a new gain calibration solution that will itself be optimized by use of the bandpass solution as a prior; the original gain calibration table should be discarded in this case. On the other hand, it is also permitted to generate a sequence of gain calibration tables, each *relative* to the last (and any other prior calibration used); in this case all relative tables should be carried forward through the process and included in the final **applycal**. It is the user\'s responsibility to keep track of the role of and relationships between all calibration tables. Depending on the complexity of the observation, this can be a confusing business, and it will help if you adopt a consistent table naming scheme. In general, it is desirable to minimize the number of different calibration tables of a specific type, to keep the overall process as simple as possible and minimize the computational cost of applying them, but relative calibraition tables may sometimes be useful as an aid to understanding the origin and properties of the calibration effects. For example, it may be instructive to obtain a short time-scale gain calibraiton relative to a long time-scale one (e.g., obtained from a single scan) to approximatly separate electronic and atmospheric effects. Of course, calibration tables of different types are necessarily relative to each other (in the order in which they are solved).
***
## Preparing for Calibration
A description of the range of prior information necessary to solve for calibration
There is a range of *a priori* information that may need to be initialized or estimated before calibration solving is carried out. This includes establishing prior information about the data within the MS:
- **weight initialization** \-\-- if desired, initialization of spectral weights, using **initweight** (by default, unchannelized weight accounting is used, and no special action is required)
- **flux density models** \-\-- establish the flux density scale using \"standard\" calibrator sources, with models for resolved calibrators, using **setjy** as well as deriving various prior calibration quanitities using various modes of **gencal**
- **gain curves** \-\-- the antenna gain-elevation dependence
- **atmospheric optical depth** \-\-- attenuation of the signal by the atmosphere, including correcting for its elevation dependence
- **antenna position errors** \-\-- offsets in the positions of antennas assumed during correlation
- **ionosphere** \-\-- dispersive delay and Faraday effects arising from signal transmission through the magnetized plasma of the ionosphere
- **switched power** (EVLA) \-\-- electronic gains monitored by the EVLA online system
- **system temperature** (ALMA) \-\-- turn correlation coefficient into correlated flux density (necessary for some telescopes)
- **generic cal factors** \-\-- antenna-based amp, phase, delay
These are all pre-determined effects and should be applied (if known) as priors when solving for other calibration terms, and included in the final application of all calibration. If unknown, then they will be solved for or subsumed in other calibration such as bandpass or gains.
Each of these will now be described in turn.
### Weight Initialization
See the section on [data weights](data_weights.ipynb#data-weights) for a more complete description of weight accounting in CASA.
CASA 4.3 introduced initial experimental support for spectral weights. At this time, this is mainly relevant to ALMA processing for which *spectral* $T_{sys}$ corrections, which faithfully reflect spectral sensitivity, are available. In most other cases, sensitivity is, to a very good approximation, channel-independent after bandpass calibration (and often also before), except perhaps at the very edges of spectral windows (and for which analytic expressions of the sensitivity loss are generally unavailable). Averaging of data with channel-dependent flagging which varies on sufficiently short timescales will also generate channel-dependent net weights (see **split** or **mstransform** for more details).
By default, CASA\'s weight accounting scheme maintains unchannelized weight information that is appropriately updated when calibration is applied. In the case of spectral calibrations ($T_{sys}$ and bandpass), an appropriate spectral average is used for the weight update. This spectral average is formally correct for weight update by bandpass. For $T_{sys}$, traditional treatments used a single measurement per spectral window; ALMA has implemented spectral $T_{sys}$ to better track sensitivity as a function of channel, and so should benefit from *spectral* weight accounting as described here, especially where atmospheric emmission lines occur. If spectral weight accounting is desired, users must re-initialize the spectral weights using the **initweights** task:
```
initweights(vis='mydata.ms', wtmode='nyq', dowtsp=True)
```
In this task, the *wtmode* parameter controls the weight initialization convention. Usually, when initializing the weight information for a raw dataset, one should choose *wtmode='nyq'* so that the channel bandwidth and integration time information are used to initialize the weight information (as described [here](data_weights.ipynb#data-weights)). The *dowtsp* parameter controls whether or not (*True* or *False*) the spectral weights (the *WEIGHT_SPECTRUM* column) are initialized. The default is *dowtsp=False*, wherein only the non-spectral weights (the *WEIGHT* column) will be initialized. If the spectral weights have been initialized, then downstream processing that supports spectral weights will use and update them. In CASA 4.3 and later, this includes **applycal**, **clean**, and **split**/**mstransform**; use of spectral weights in calibration solving (e.g., **gaincal** and other solve tasks) is scheduled for the CASA 5.0 release.
Note that **importasdm** currently initializes the *non-spectral* weights using channel bandwidth and integration time information (equivalent to using *dospwt=False* in the above example. In general, it only makes sense to run **initweights** on a raw dataset which has not yet been calibrated, and it should only be necessary if the filled weights are inappropriate, or if spectral weight accounting is desired in subsequent processing. It is usually *not* necessary to re-initialize the weight information when redoing calibration from scratch (the raw weight information is preserved in the *SIGMA*/*SIGMA_SPECTRUM* columns). (Re-)initializing the weight information for data that has already been calibrated (with *calwt=True*, presumably) is formally incorrect and is not recommended.
When combining datasets from different epochs, it is generally preferable to have used the same version of CASA (most recent is best), and with the same weight information conventions and *calwt* settings in calibration tasks. Doing so will minimize the likelihood of arbitrary weight imbalances that might lead to net loss of sensitivity, and maximize the likelihood that *real* differences in per-epoch sensitivity (e.g., due to different weather conditions and instrumental setups) will be properly accounted for. Modern instruments support more variety in bandwidth and integration time settings, and so use of these parameters in weight initialization is preferred (c.f. use of simple unit weight initialization, which has often been the traditional practice).
<div class="alert alert-warning">
**Alert:** Full and proper weight accounting for the EVLA formally depends on the veracity of the switched power calibration scheme. As of mid-2015, use of the EVLA switched power is not yet recommended for general use, and otherwise uniform weights are carried through the calibration process. As such, spectral weight accounting is not yet meaningful. Facilities for post-calibration estimation of spectral weights are rudimentarily supported in **statwt**.
</div>
### Flux Density Models
It is necessary to be sure calibrators have appropriate models set for them before solving for calibration. Please see the task documentation for **setjy** and **ft** for more information on setting non-trivial model information in the MS. Also, information about setting models for flux density calibrators can be found [here](memo-series.ipynb#flux-calibrator-models---data-formats). Fields in the MS for which no model has been explicitly set will be rendered as unpolarized unit flux density (1 Jy) point sources in calibration solving.
### Antenna Gain-Elevation Curve Calibration
Large antennas (such as the 25-meter antennas used in the VLA and VLBA) have a forward gain and efficiency that changes with elevation. Gain curve calibration involves compensating for the effects of elevation on the amplitude of the received signals at each antenna. Antennas are not absolutely rigid, and so their effective collecting area and net surface accuracy vary with elevation as gravity deforms the surface. This calibration is especially important at higher frequencies where the deformations represent a greater fraction of the observing wavelength. By design, this effect is usually minimized (i.e., gain maximized) for elevations between 45 and 60 degrees, with the gain decreasing at higher and lower elevations. Gain curves are most often described as 2nd- or 3rd-order polynomials in zenith angle.
Gain curve calibration has been implemented in CASA for the modern VLA and old VLA (only), with gain curve polynomial coefficients available directly from the CASA data repository. To make gain curve and antenna efficiency corrections for VLA data, use **gencal**:
```
gencal(vis='mydata.ms', caltable='gaincurve.cal', caltype='gceff')
```
Use of *caltype=\'gceff\'* generates a caltable that corrects for both the elevation dependence and an antenna-based efficiency unit conversion that will render the data in units of *approximate* Jy (NB: this is generally not a good substitute for proper flux density calibration, using **fluxscale**!). Use of *caltype=\'gc\'* or *caltype=\'eff\'* can be used to introduce these corrections separately.
The resulting calibration table should then be used in all subsequent processing the requires the specification of prior calibration.
<div class="alert alert-warning">
**Alert:** If you are not using VLA data, do not use gaincurve corrections. A general mechanism for incorporating gaincurve information for other arrays will be made available in future releases. The gain-curve information available for the VLA is time-dependent (on timescales of months to years, at least for the higher frequencies), and CASA will automatically select the date-appropriate gain curve information. Note, however, that the time-dependence was poorly sampled prior to 2001, and so gain curve corrections prior to this time should be considered with caution.
</div>
### Atmospheric Optical Depth Correction
The troposphere is not completely transparent. At high radio frequencies ($>$15 GHz), water vapor and molecular oxygen begin to have a substantial effect on radio observations. According to the physics of radiative transmission, the effect is threefold. First, radio waves from astronomical sources are absorbed (and therefore attenuated) before reaching the antenna. Second, since a good absorber is also a good emitter, significant noise-like power will be added to the overall system noise, and thus further decreasing the *fraction* of correlated signal from astrophysical sources. Finally, the optical path length through the troposphere introduces a time-dependent phase error. In all cases, the effects become worse at lower elevations due to the increased air mass through which the antenna is looking. In CASA, the opacity correction described here compensates only for the first of these effects, tropospheric attenuation, using a plane-parallel approximation for the troposphere to estimate the elevation dependence. (Gain solutions solved for later will account for the other two effects.)
To make opacity corrections in CASA, an estimate of the zenith opacity is required (see observatory-specific chapters for how to measure zenith opacity). This is then supplied to the *caltype=\'opac\'* parameter in **gencal** which creates a calibration table that will introduce the elevation-dependent correction when applied in later operaions. E.g. for data with two spectral windows:
```
gencal(vis='mydatas.ms',
caltable='opacity.cal',
caltype='opac',
spw='0,1',
parameter=[0.0399,0.037])
```
If you do not have an externally supplied value for *opacity*, for example from a VLA tip procedure, then you should either use an average value for the telescope, or omit this cal table and let your gain calibration compensate as best it can (e.g. that your calibrator is at the same elevation as your target at approximately the same time). As noted above, there are no facilities yet to estimate this from the data (e.g. by plotting $T_{sys}$ vs. elevation).
The resulting calibration table should then be used in all subsequent processing the requires the specification of prior calibration.
Below, we give instructions for determining opacity values for Jansky VLA data from weather statistics and VLA observations where tip-curve data is available. It is beyond the scope of this description to provide information for other telescopes.
**Determining opacity corrections for *modern* VLA data**
For the VLA site, weather statistics and/or seasonal models that average over many years of weather statistics prove to be reasonable good ways to estimate the opacity at the time of the observations. The task **plotweather** calculates the opacity as a mix of both actual weather data and seasonal model. It can be run as follows:
```
myTau=plotweather(vis='mydata.ms',doPlot=True)
```
The task plots the weather statistics if *doPlot=T*, generating a plot shown in the figure below. The bottom panel displays the calculated opacities for the run as well as a seasonal model. An additional parameter, *seasonal_weight* can be adjusted to calculate the opacities as a function of the weather data alone (*seasonal_weight=0*), only the seasonal model (*seasonal_weight=1*), or a mix of the two (values between 0 and 1). Calculated opacities are shown in the logger output, one for each spectral window. Note that **plotweather** returns a python list of opacity values with length equal to the number of spectral windows in the MS, appropriate for use in **gencal**:
```
gencal(vis='mydata.ms', caltype='opac', spw='0,1', parameter=myTau)
```
Note that the *spw* parameter is used non-trivially and explicitly here to indicate that the list of opacity values corresponds to the specified spectral windows.
The resulting calibration table should then be used in all subsequent processing the requires the specification of prior calibration.
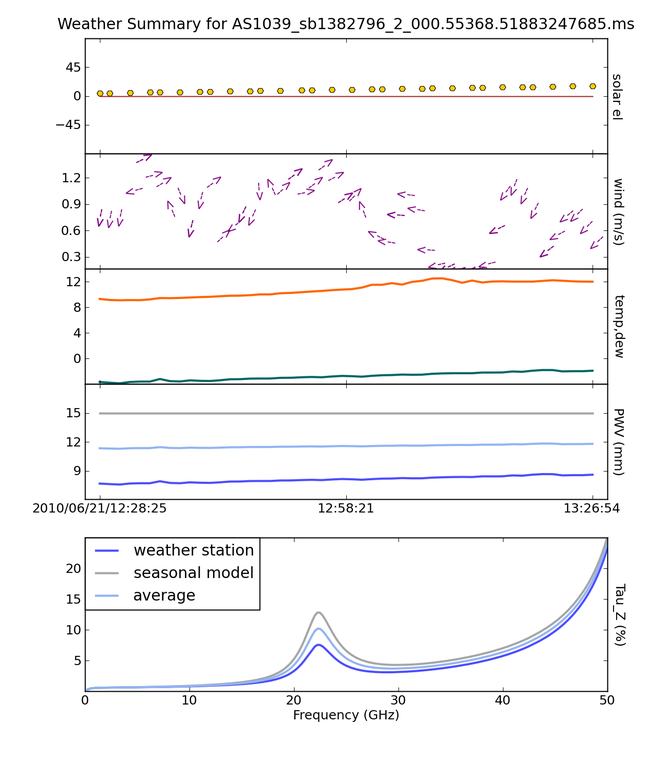{.image-inline}
> The weather information for a MS as plotted by the task {\\tt plotweather}.}
**Determining opacity corrections for historical VLA data**
For VLA data, zenith opacity can be measured at the frequency and during the time observations are made using a VLA tipping scan in the observe file. Historical tipping data are available [here.](http://www.vla.nrao.edu/astro/calib/tipper "vla tips") Choose a year, and click *Go* to get a list of all tipping scans that have been made for that year.
If a tipping scan was made for your observation, then select the appropriate file. Go to the bottom of the page and click on the button that says *Press here to continue*. The results of the tipping scan will be displayed. Go to the section called \'Overall Fit Summary\' to find the fit quality and the fitted zenith opacity in percent. If the zenith opacity is reported as 6%, then the actual zenith optical depth value is 0.060. Use this value in **gencal** as described above.
If there were no tipping scans made for your observation, then look for others made in the same band around the same time and weather conditions. If nothing is available here, then at K and Q bands you might consider using an average value (e.g. 6% in reasonable weather). See the VLA memo [here](http://www.vla.nrao.edu/memos/test/232/232.pdf "ad hoc opacity") for more on the atmospheric optical depth correction at the VLA, including plots of the seasonal variations.
### Antenna-position corrections
When antennas are moved, residual errors in the geographical coordinates of the antenna will cause time-dependent delay errors in the correlated data. Normally, the observatory will solve for these offsets soon after the move and correct the correlator model, but sometimes science data is taken before the offsets are available, and thus the correction must be handled in post-processing. If the 3D position offsets for affected antennas are known, use **gencal** as follows:
```
gencal(vis='mydata.ms', caltable='antpos.cal', caltype='antpos', antenna='ea01',
parameter=[0.01,0.02,0.005])
```
In this execution, the position offset for antenna ea01 is \[1cm,2cm,0.5cm\] in an Earth-centered right-handed coordinate system with the first axis on the prime meridian and third axis coincident with the Earth\'s axis. Corrections for multiple antennas can be specified by listing all affected antennas and extending the *parameter* list with as many offset triples as needed.
In general, it is difficut to know what position offsets to use, of course. For the VLA, **gencal** will look up the required offests automatically, simply by omitting the *antenna *and *parameter* arguments:
```
gencal(vis='mydata.ms', caltable='antpos.cal', caltype='antpos')
```
For the historical VLA, the antenna position coordinate system was a local one translated from the Earth\'s center and rotated to the VLA\'s longitude. Use *caltype=\'antposvla\'* to force this coordiate system when processing old VLA data.
The resulting calibration table should then be used in all subsequent processing the requires the specification of prior calibration.
### Ionospheric corrections
CASA 4.3 introduced initial support for on-axis ionospheric corrections, using time- and direction-dependent total electron content (TEC) information obtained from the internet. The correction includes the dispersive delay ($\propto \nu^{-1}$) delay and Faraday rotation ($\propto \nu^{-2}$) terms. These corrections are most relevant at observing frequencies less than $\sim$5 GHz. When relevant, the ionosphere correction table should be generated at the beginning of a reduction along with other calibration priors (antenna position errors, gain curve, opacity, etc.), and carried through all subsequent calibration steps. Formally, the idea is that the ionospheric effects (as a function of time and on-axis direction) will be nominally accounted for by this calibration table, and thus not spuriously leak into gain and bandpass solves, etc. In practice, the quality of the ionospheric correction is limited by the relatively sparse sampling (in time and direction) of the available TEC information. Especially active ionospheric conditions may not be corrected very well. Also, direction-dependent (*within the instantaneous field-of-view*) ionosphere corrections are not yet supported. Various improvements are under study for future releases.
To generate the ionosphere correction table, first import a helper function from the casapy recipes repository:
```
CASA 5 and earlier:
from recipes import tec_maps
CASA 6.1.2+:
from casatasks.private import tec_maps
(CASA 6 prior to 6.1.2 did not support TEC corrections)
```
Then, generate a TEC surface image:
```
tec_maps.create(vis='mydata.ms',doplot=True,imname='iono')
```
This function obtains TEC information for the observing date and location from [NASA\'s CDDIS Archive of Space Geodesy Data](https://cddis.nasa.gov/Data_and_Derived_Products/GNSS/atmospheric_products.html), and generates a time-dependent CASA image containing this information. The string specified for *imname* is used as a prefix for two output images, with suffixes *.IGS_TEC.im* (the actual TEC image) and *.IGS_RMS_TEC.im* (a TEC error image). If *imname* is unspecified, the MS name (from *vis*) will be used as the prefix.
The quality of the retrieved TEC information for a specific date improves with time after the observing date as CDDIS\'s ionospheric modelling improves, becoming optimal 1-2 weeks later. Both images can be viewed as a movie in the CASA task **imview**. If *doplot=T*, the above function will also produce a plot of the TEC as a function of time in a vertical direction over the observatory.
Finally, to generate the ionosphere correction caltable, pass the *.IGS\\\_TEC.im* image into **gencal**, using *caltype=\'tecim\'*:
```
gencal(vis='mydata.ms',caltable='tec.cal',caltype='tecim',infile='iono.IGS_TEC.im')
```
This iterates through the dataset and samples the zenith angle-dependent projected line-of-sight TEC for all times in the observation, storing the result in a standard CASA caltable. Plotting this caltable will show how the TEC varies between observing directions for different fields and times, in particular how it changes as zenith angle changes, and including the nominal difference between science targets and calibrators.
This caltable should then be used as a prior in all subsequent calibration solves, and included in the final **applycal**.
A few warnings:
- The TEC information obtained from the web is relatively poorly sampled in time and direction, and so will not always describe the details of the ionospheric corruption, especially during active periods.
- For instrumental polarization calibration, it is recommended that an *unpolarized* calibrator be used; polarized calibrators may not yield as accurate a solution since the ionospheric corrections are not yet used properly in the source polarization portion of the **polcal** solve.
- TEC corrections are only validated for use with VLA data. For data from other (low-frequency) telescopes, TEC corrections are experimental - please use at your own discretion.
Special thanks are due to Jason Kooi (UIowa) for his contributions to ionospheric corrections in CASA.
### Switched-power (EVLA)
The EVLA is equipped with noise diodes that synchronously inject a nominally constant and known power contribution appropriate for tracking electronic gain changes with time resolution as short as 1 second. The total power in both the ON and OFF states of the noise diodes is continuously recorded, enabling a gain calibration derived from their difference (as a fraction of the mean total power), and scaled by a the approximately known contributed power (nominally in K). Including this calibration will render the data in units of (nominal) K, and also calibrate the data weights to units of inverse K^2^. To generate a switched-power calibration table for use in subsequent processing, run **gencal** as follows:
```
gencal(vis='myVLAdata.ms',caltable='VLAswitchedpower.cal',caltype='evlagain')
```
The resulting calibration table should then be used in all subsequent processing the requires the specification of prior calibration.
To ensure that the weight calibration by this table works correctly, it is important that the raw data weights are proprotional to integration time and channel bandwidth. This can be guaranteed by use of **initweights** as described above.
### System Temperature (ALMA)
ALMA routinely measures $T_{sys}$ while observing, and these measurements are used to reverse the online normalization of the correlation coefficients and render the data in units of nominal K. To generate a $T_{sys}$ calibration table, run **gencal** as follows:
```
gencal(vis='myALMAdata.ms',caltable='ALMAtsys.cal',caltype='tsys')
```
The resulting calibration table should then be used in all subsequent processing the requires the specification of prior calibration.
### Miscellaneous ad hoc corrections
The **gencal** task supports generating ad hoc amp, phase, and delay corrections via appropriate settings of the *caltype* parameter. Currently, such factors must be constant in time (**gencal** has no mechanism for specifying multiple timestamps for parameters), but sometimes such corrections can be useful. See the general **gencal** task documenation for more information on this type of correction.
***
## Virtual Model Visibilities
The tasks that generate model visibilities (**clean**, **tclean**, **ft**, and **setjy**) can either (in most cases) save the data in a MODEL_DATA column inside of the MeasurementSet (MS) or it can save it in a virtual one. In the latter case the model visibilities are generated on demand when it is requested and the data necessary to generate that is stored (usually the Fourier transform of the model images or a component list). More detailed descriptions of the structure of an MS can be found on the [CASA Fundamentals](casa-fundamentals.ipynb#casa-fundamentals) pages.
The tasks that can read and make use of the virtual model columns include calibration tasks, mstransform tasks (including **uvsubtraction**), **plotms**.
Advantages of virtual model column over the real one:
- Speed of serving visibilities (in most cases because calculating models visibilities is faster than disk IO)
- Disk space saving (a full size of the original data size is saved)
When not to use virtual model
- When working with time-dependent models (e.g. ephemerides sources) within setjy; please use ephemerides source models only with *usescratch=True*
- Model image size is a significant fraction of the visibility data size (e.g large cube from a small data set). Virtual model column serving might be slower than real one
- When the user wants to edit the model physically via the table tool for e.g
- When using an FTMachine that does not support virtual model saving when imaging (AWProjectFT for e.g)
Additional Information
- When both a physical model column exists along with a virtual model, then the virtual model is the one that gets served by tasks that uses the visbuffer (e.g calibration tasks)
- Use **delmod*** *task to manage your MODEL_DATA column and virtual model
- If model data is written for a subset of the MS (say the user used *field* , *spw* and/or *intent* selection in **tclean**) then the model visibilities will be served properly for the subset in question the other part of the MS will have 1 served for parallel hand visibilities and 0 for crosshand visibilities. So be careful when doing calibration or uvsub after writing model visibilities only for a subset of the MS (this applies to using the physical scratch column MODEL_DATA too)
- The virtual model info is written in the SOURCE table of the MS usually (and in the main table if the SOURCE table does not exist)
- FTMachines (or imaging gridding mode) supporting virtual model data are:
- GridFT: Standard gridder (including mutiterm and multi fields or cube),
- WProjectFT: widefield wterm (including mutiterm and multi fields or cube),
- MosaicFT: mosaic imaging (including mutiterm or cube),
- ComponentLists
***
## Solve for Calibration
The **gaincal**, **bandpass**, **polcal**, and **blcal** tasks actually solve for the unknown calibration parameters from the visibility data obtained on calibrator sources, placing the results in a calibration table. They take as input an MS, and a number of parameters that specify any prior calibration tables to pre-apply before computing the solution, as well as parameters controlling the exact properties of the solving process.
We first discuss the parameters that are in common between many of the calibration tasks. Subsequent sub-sections will discuss the use of each of these solving task in more detail.
**Common Calibration Solver Parameters**
There are a number of parameters that are in common between the calibration solver tasks.
*Input/output*
The input MeasurementSet and output calibration table are controlled by the following parameters:
```
vis = '' #Name of input visibility file
caltable = '' #Name of output calibration table
```
The MS name is specified in *vis*. If it is highlighted red in the inputs then it does not exist, and the task will not execute. Check the name and path in this case.
The output table name is specified in *caltable*. Be sure to give a unique name to the output table, or be careful. If the table exists, then what happens next will depend on the task and the values of other parameters. The task may not execute giving a warning that the table already exists, or will go ahead and overwrite the solutions in that table, or append them. Be careful.
*Data selection*
Data selection is controlled by the following parameters:
```
field = '' #field names or index of calibrators: ''==>all
spw = '' #spectral window:channels: ''==>all
intent = '' #Select observing intent
selectdata = False #Other data selection parameters
```
Field and spectral window selection are so often used, that we have made these standard parameters, *field* and *spw* respectively. Additionally, *intent* is also included as a standard parameter to enable selection by the scan intents that were specified when the observations were set up and executed. They typically describe what was intended with a specific scan, i.e. a flux or phase calibration, a bandpass, a pointing, an observation of your target, or something else or a combination. The format for the scan intents of your observations are listed in the logger when you run listobs. Minimum matching with wildcards will work, like \*BANDPASS\*. This is especially useful when multiple intents are attached to scans. Finally, observation is an identifier to distinguish between different observing runs, mainly used for ALMA.
The selectdata parameter expands, revealing a range of other selection sub-parameters:
```
selectdata = True #data selection parameters
timerange = '' #time range (blank for all)
uvrange = '' #uv range (blank for all)
antenna = '' #antenna/baselines (blank for all)
scan = '' #scan numbers (blank for all)
correlation = '' #correlations (blank for all)
array = '' #(sub)array numbers (blank for all)
observation = '' #Select by observation ID(s)
msselect = '' #MS selection (blank for all)
```
Note that if *selectdata=False* these parameters are not used when the task is executed, even if set non-trivially.
Among the most common *selectdata=True* parameters to use is uvrange, which can be used to exclude longer baselines if the calibrator is resolved, or short baselines if the calibrator contains extended flux not accounted for in the model. The rest of these parameters may be set according to information and values available in the listobs output. Note that all parameters are specified as strings, even if the values to be specified are numbers. See the section on [MS Selection](visibility_data_selection.ipynb#visibility-data-selection) for more details on the powerful syntax available for selecting data.
*Prior calibration*
Calibration tables that have already been determined can be arranged for apply before solving for the new table using the following parameters:
```
docallib = False #Use traditional cal apply parameters
gaintable = [] #Gain calibration table(s) to apply on the fly
gainfield = [] #Select a subset of calibrators from gaintable(s)
interp = [] #Interpolation mode (in time) to use for each gaintable
spwmap = [] #Spectral windows combinations to form for gaintable(s)
```
The *docallib* parameter is a toggle that can be used to select specification of prior calibration using the new \"cal library\" mechanism (*docallib=True*) which is described in greater detail [here.](cal_library_syntax.ipynb#cal-library-syntax)
When *docalib=False*, the traditional CASA calibration apply sub-parameters will be used, as listed above.
*gaintable*
The *gaintable* parameter takes a string or list of strings giving the names of one or more calibration tables to arrange for application. For example:
```
gaintable = ['ngc5921.bcal','ngc5921.gcal']
```
specifies two tables, in this case bandpass and gain calibration tables respectively.
The *gainfield*, *interp*, and *spwmap* parameters key off *gaintable*, taking single values or lists, with an entries for each corresponding table in specified in *gaintable*. The caltables can be listed in *gaintable* in any order, without affecting the order in which they are applied to the data (for consistency, this is controlled internally according to the [Measurement Equation](casa-fundamentals.ipynb#measurement-equation) framework). If non-trivial settings are required for only a subset of the tables listed in *gaintable*, it can be convenient to specify these tables first in *gaintable*, include their qualifying settings first in the other paramters, and omit specifications for those tables not needing qualification (sensible defaults will be used for these).
*gainfield*
The *gainfield* parameter specifies which field(s) from each respective *gaintable* to select for apply. This is a list, with each entry a string. The default for an entry means to use all in that table. For example, use
```
gaintable = ['ngc5921.bcal', 'ngc5921.gcal']
gainfield = [ '1331+305', '1331+305,1445+099']
```
to specify selection of *1331+305* from *ngc5921.bcal* and fields *1331+305* and *1445+099* from *ngc5921.gcal*. Selection of this sort is only needed if avoiding other fields in these caltables is necessary. The field selection used here is the general MS Selection syntax.
In addition, *gainfield* supports a special value:
```
gainfield = [ 'nearest' ]
```
which selects the calibrator that is the spatially closest (in sky coordinates) to each of the selected MS fields specified in the *field* data selection parameter. Note that the nearest calibrator field is evaluated once per execution and is never dependent on time, spw or any other data meta-axis. This can be useful for running tasks with a number of different sources to be calibrated in a single run, and when this simple proximity notion is applicable. Note that the [cal library](cal_library_syntax.ipynb#cal-library-syntax) mechanism provides increased flexibility in this area.
*interp*
The *interp* parameter chooses the interpolation scheme to be used when pre-applying the solution in the tables. Interpolation in both time and frequency (for channel-dependent calibrations) are supported. The choices are currently \'*nearest\'* and \'*linear\'* for time-dependent interpolation, and \'*nearest\'*, \'*linear\'*, \'*cubic\'*, and \'*spline\'* for frequency-dependent interpolation. Frequency-dependent interpolation is only relevant for channel-dependent calibration tables (like bandpass) that are undersampled in frequency relative to the data.
- *\'nearest\' * just picks the entry nearest in time or freq to the visibility in question
- \'*linear*\' calibrates each datum with calibration phases and amplitudes linearly interpolated from neighboring values in time or frequency. In the case of phase, this mode will assume that phase never jumps more than 180 degrees between neighboring points, and so phase changes exceeding this between calibration solutions cannot be corrected for. Also, solutions will not be extrapolated arbitrarily in time or frequency for data before the first solution or after the last solution; such data will be calibrated using nearest to avoid unreasonable extrapolations.
- \'*cubic*\' (frequency axis only) forms a 3rd-order polynomial that passes through the nearest 4 calibration samples (separately in phase and amplitude)
- \'*spline*\' (frequency axis only) forms a cubic spline that passes through the nearest 4 calibration samples (separately in phase and amplitude)
The time-dependent interp options can be appended with *\'PD\'* to enable a \"phase delay\" correction per spw for non-channel-dependent calibration type. For example: \'*linearPD*\'. This will adjust the time-dependent phase by the ratio of the data frequency and solution frequency and effect a time-dependent delay-like calibration over spws, and is most useful when distributing a single-spw\'s solution (e.g.., as might be generated by *combine=\'spw\'* in **gaincal**) over many data spws, and when the the residual being calibrated is non-dispersively delay-like.
The time-dependent interp options can also be appended with *\'perobs\'* to enforce observation Id boundaries in the interpolation.
The frequency-dependent interp options can be appended with \'flag\' to enforce channel-dependent flagging by flagged bandpass channels (i.e., \'*nearestflag*\', \'*linearflag*\', \'*cubicflag*\', and \'*splineflag*\', rather than to automatically fill such channels in with interpolation (which is the default).
For each *gaintable*, specify the interpolation style in quotes, with the frequency-dependent interpolation style specified after a comma, if relevant. For example:
```
gaintable = ['ngc5921.bcal', 'ngc5921.gcal']
gainfield = ['1331+305', ['1331+305','1445+099'] ]
interp = ['linear,spline', 'linear']
```
uses linear interpolation on the time axis for both cal tables, and a cubic spline for interpolation of the frequency axis in the bandpass table.
*spwmap*
The *spwmap* parameter is used to redistribute the calibration available in a caltable flexibly among spectral windows, thereby permitting correction of some spectral windows using calibration derived from others. The *spwmap* parameter takes a list or a list of lists of integers, with one list of integers for every caltable specified in *gaintable*. Each list is indexed by the MS spectral window ids, and the values indicate the calibration spectral windows to use for each MS spectral window. I.e., for each MS spw, *i*, the calibration spw *j* will be *j=spwmap\[i\]*.
The default for *spwmap* (an empty list per *gaintable*) means that MS spectral windows will be calibrated by solutions identified with the same index in the calibration table (i.e., by themselves, typically). Explicit specification of the default would be *spwmap=\[0,1,2,3\]*, for an MS with four spectral windows. Less trivially, for a caltable containing solutions derived from and labelled as spectral windows 0 and 1, these two cal spectral windows can be mapped to any of the MS spectral windows. E.g., (for a single *gaintable*):
```
spwmap=[0,1,1,0] #apply from cal spw=0 to MS spws 0,3 and from cal spw 1 to MS spws 1,2
```
For multiple gaintables, use a lists of lists (one spwmap list per gaintable), e.g.,
```
gaintable = ['ngc5921.bcal', 'ngc5921.gcal']
gainfield = ['1331+305', ['1331+305','1445+099'] ]
interp = ['linear,spline', 'linear']
spwmap = [ [0,1,1,0], [2,3,2,3] ]
```
which will use bandpass spws 0 and 1 for MS spws (0,3), and (1,2), respectively, and gain spws 2 and 3 for MS spws (0,2) and (1,3), respectively.
Any spectral window mapping is mechanically valid, including using specific calibration spectral windows for more than one different MS spectral window (as above) and using alternate calibration even for spectral windows for which calibration is nominally available, as long as the mapped calibration spectral windows have calibration solutions available in the caltable. If a mapped calibration spectral window is absent from the caltable (and not merely flagged), an exception will occur.
The scientific meaningfulness of a non-trivial spwmap specification is the responsibility of the user; no internal checks are performed to attempt the scientific validity of the mapping. Usually, *spwmap* is used to distribute calibration such as Tsys, which may be measured in a wide low-resolution spectral window, to narrow high-resolution spectral windows that fall within the wide one. It is also used to distribute calibration derived from a **gaincal** solve which was performed using *combine=\'spw\'* (e.g., for increased SNR) to each of the spectral windows (and perhaps others) aggregated in the solve; in this case, it may be useful to consider using the *\'PD\'* (\"phase delay\") interpolation option described above, to account for the frequency ratios between each of the individual MS spectral windows and the aggregated calibration spectral window.
**Absolute vs. Relative frequency in frequency-dependent interpolation**
By default, frequency-dependent solutions are interpolated for application in absolute sky frequency units. Thus, it is usually necessary to obtain **bandpass** solutions that cover the frequencies of all spectral windows that must be corrected. In this context, it is mechanically valid to use *spwmap* to transfer a **bandpass** solution from a wide, low-resolution spectral window to a narrow, higher-resolution spectral window that falls within the wide one in sky frequency space. On the other hand, if adequate data for a **bandpass** solution is unavailable for a specific spectral window, e.g., due to contamination by line emission or absorption (such as HI), or because of flagging, **bandpass** solutions from other spectral windows (i.e., at different sky frequencies) can be applied using *spwmap*. In this case, it is also necessary to add *\'rel*\' to the frequency interpolation string in the *interp* parameter, as this will force the interpolation to be calculated in relative frequency units. Specifically, the center frequency of the **bandpass** solution will be registered with the absolute center frequency of each of the MS spectral windows to which it is applied, thereby enabling relative frequency registration. The quality of such calibration transfer will depend, of course, on the uniformity of the hardware parameters and properties determining the bandpass shapes in the observing system\--this is often appropriate over relatively narrow bandwidths in digital observing systems, as long as the setups are sufficiently similar (same sideband, same total spectral window bandwidth, etc., though note that the channelization need not be the same). Traditionally (e.g., at the VLA, for HI observations), **bandpass** solutions for this kind of calibration transfer have be solved by combining spectral windows on either side of the target spectral window (see the task documentation for [**bandpass**](../api/casatasks.rst) for more information on solving with *combine=\'spw\'*).
For example, to apply a bandpass solution from spectral window 0 (in a **bandpass** table called ngc5921.bcal) to MS spectral windows 0,1,2,3 with linear interpolation calculated in relative frequency units (and with frequency-dependent flagging respected):
```
gaintable = ['ngc5921.bcal']
interp = ['nearest,linearflagrel']
spwmap = [ [0,0,0,0] ]
```
When selecting channels for a **bandpass** solution that will be applied using *\'rel\'*, it is important to recognize that the selected channels will be centered on each of the \_absolute\_ centers of the MS spectral windows to which it will be applied. An asymmetric channel selection for the **bandpass** solve will cause an undesirable shift in the relative registration on apply. Avoid this by using symmetrical channel selection (or none) for the **bandpass** solve.
Also note that if relative frequency interpolation is required but *\'rel\'* is not used in *interp*, the interpolation mechanism currently assumes you want absolute frequency interpolation. If there is no overlap in absolute frequency, the result will be nearest (in channel) interpolation such that the calibration edge channel closest to the visibility data will be used to calibrate that data.
Finally, please note that relative frequency interpolation is not yet available via the cal library.
**Parallactic angle**
The *parang* parameter turns on the application of the antenna-based parallactic angle correction (P) in the Measurement Equation. This is necessary for polarization calibration and imaging, or for cases where the parallactic angles are different for geographically spaced antennas and it is desired that the ordinary calibration solves not absorb the inter-antenna parallactic angle phase. When dealing with only the parallel-hand data (e.g. RR, LL, XX, YY), and an unpolarized calibrator model for a co-located array (e.g. the VLA or ALMA), you can set *parang=False* and save some computational effort. Otherwise, set *parang=True* to apply this correction, especially if you are doing polarimetry.
**Solving parameters**
The parameters controlling common aspects of the solving process itself are:
```
solint = 'inf' #Solution interval: egs. 'inf', '60s' (see help)
combine = 'scan' #Data axes which to combine for solve (obs, scan,
#spw, and/or field)
preavg = -1.0 #Pre-averaging interval (sec) (rarely needed)
refant = '' #Reference antenna name(s)
minblperant = 4 #Minimum baselines _per antenna_ required for solve
minsnr = 3.0 #Reject solutions below this SNR
solnorm = False #Normalize solution amplitudes post-solve.
corrdepflags = False #Respect correlation-dependent flags
```
The time and frequency (if relevant) solution interval is specified in *solint*. Optionally a frequency interval for each solutglobal-task-list.ipynb#task_bandpassion can be added after a comma, e.g. *solint=\'60s,300Hz\'*. Time units are in seconds unless specified differently. Frequency units can be either \'*ch*\' or \'*Hz*\' and only make sense for bandpass or frequency dependent polarization calibration. On the time axis, the special value \'inf\' specifies an infinite solution interval encompassing the entire dataset, while \'int\' specifies a solution every integration. Omitting the frequency-dependent solution interval will yield per-sample solutions on this axis. You can use time quanta in the string, e.g. *solint=\'1min\'* and *solint=\'60s\'* both specify solution intervals of one minute. Note that \'*m*\' is a unit of distance (meters); \'*min*\' must be used to specify minutes. The *solint* parameter interacts with *combine* to determine whether the solutions cross scan, field, or other meta-data boundaries.
The parameter controlling the scope of each solution is *combine*. For the default, *combine=''*, solutions will break at *obs*, *scan*, *field*, and *spw* boundaries. Specification of any of these in *combine* will extend the solutions over the specified boundaries (up to the solint). For example, *combine='spw'* will combine spectral windows together for solving, while *combine='scan'* will cross scans, and *combine='obs,scan'* will use data across different observation IDs and scans (usually, obs Ids consist of many scans, so it is not meaningful to combine obs Ids without also combining scans). Thus, to do scan-based solutions (single solution for each scan, per spw, field, etc.), set
```
solint = 'inf'
combine = ''
```
To obtain a single solution (per spw, per field) for an entire observation id (or the whole MS, if there is only one obsid), use:
```
solint = 'inf'
combine = 'scan'
```
You can specify multiple choices for combination by separating the axes with commas, e.g.:
```
combine = 'scan,spw'
```
<div class="alert alert-warning">
Care should be exercised when using *combine='spw'* in cases where multiple groups of concurrent spectral windows are observed as a function of time. Currently, only one aggregate spectral window can be generated in a single calibration solve execution, and the meta-information for this spectral window is calculated from all selected MS spectral windows. To avoid incorrect calibration meta-information, each spectral window group should be calibrated independently (also without using *append=True*). Additional flexibility in this area will be supported in a future version.
</div>
The reference antenna is specified by the *refant* parameter. Ordinary MS Selection antenna selection syntax is used. Ideally, use of *refant* is useful to lock the solutions with time, effectively rotating (after solving) the phase of the gain solutions for all antennas such that the reference antennas phase remains constant at zero. In **gaincal** it is also possible to select a *refantmode*, either '*flex*' or \'*strict*\'. A list of antennas can be provided to this parameter and, for refantmode=\'flex\', if the first antenna is not present in the solutions (e.g., if it is flagged), the next antenna in the list will be used, etc. See the documentation for the **rerefant** task for more information. If the selected antenna drops out, the next antenna specified (or the next nearest antenna) will be substituted for ongoing continuity in time (at its current value) until the refant returns, usually at a new value (not zero), which will be kept fixed thenceforth. You can also run without a reference antenna, but in this case the solutions will formally float with time; in practice, the first antenna will be approximately constant near zero phase. It is usually prudent to select an antenna near the center of the array that is known to be particularly stable, as any gain jumps or wanders in the *refant* will be transferred to the other antenna solutions. Also, it is best to choose a reference antenna that never drops out, if possible.Setting a *preavg* time will let you average data over periods shorter than the solution interval first before solving on longer timescales. This is necessary only if the visibility data vary systematically within the solution interval in a manner independent of the solve-for factors (which are, by construction, considered constant within the solution interval), e.g., source linear polarization in **polcal**. Non-trivial use of *preavg* in such cases will avoid loss of SNR in the averaging within the solution interval.
The minimum signal-to-noise ratio allowed for an acceptable solution is specified in the *minsnr* parameter. Default is *minsnr=3*.
The *minblperant* parameter sets the minimum number of baselines to other antennas that must be preset for each antenna to be included in a solution. This enables control of the constraints that a solution will require for each antenna.
The *solnorm* parameter toggles on the option to normalize the solution after the solutions are obtained. The exact effect of this depends upon the type of solution (see **gaincal**, **bandpass**, and **blcal**). Not all tasks use this parameter.One should be aware when using *solnorm* that if this is done in the last stage of a chain of calibration, then the part of the calibration that is normalized away will be lost. It is best to use this in early stages (for example in a first bandpass calibration) so that later stages (such as final gain calibration) can absorb the lost normalization scaling. It is generally not strictly necessary to use *solnorm=True* at all, but it is sometimes helpful if you want to have a normalized bandpass for example.
The *corrdepflags* parameter controls how visibility vector flags are interpreted. If *corrdepflags=False* (the default), then when any one or more of the correlations in a single visibility vector is flagged (per spw, per baseline, per channel), it treats all available correlations in the single visibility vector as flagged, and therefore it is excluded from the calibration solve. This has been CASA\'s traditional behavior (prior to CASA 5.7), in order to be conservative w.r.t. flags. If instead *corrdepFlags=True* (for CASA 5.7+), correlation-dependent flags will be respected exactly and precisely as set, such that any available unflagged correlations will be used in the solve for calibration factors. For the tasks currently supporting the *corrdepflags* parameter (*gaincal, bandpass, fringefit, accor*), this means any unflagged parallel-hand correlations will be used in solving, even if one or the other parallel-hand (or either of the cross-hands) is flagged. Note that the *polcal* task does not support *corrdepflags* since polarization calibration is generally more sensitive to correlation-dependence in the flagging in ways which may be ill-defined for partial flagging; this stricture may be relaxed in future for non-leakage solving modes. Most notably, this feature permits recovery and calibration of visibilities on baselines to antennas for which one polarization is entirely flagged, either because the antenna did not have that polarization at all (e.g., heterogeneous VLBI, where flagged visibilities are filled for missing correlations on single-polarization antennas), or one polarization was not working properly during the observation.
**Appending calibration solutions to existing tables**
The *append* parameter, if set to *True*, will append the solutions from this run to existing solutions in *caltable*. Of course, this only matters if the table already exists. If *append=False* and the specified caltable exists, it will overwrite it (if the caltable is not open in another process).
<div class="alert alert-warning">
The *append* parameter should be used with care, especially when also using *combine* in non-trivial ways. E.g., calibration solves will currently refuse to append incongruent aggregate spectral windows (e.g., observations with more than one group of concurrent spectral windows) when using *combine='spw'*. This limitation arises from difficulty determining the appropriate spectral window fan-out on apply, and will be relaxed in a future version.
</div>
***
## Gain Calibration
In general, gain calibration includes solving for time- and frequency-dependent multiplicative calibration factors, usually in an antenna-based manner. CASA supports a range of options.
Note that polarization calibration is described in detail in a [different section](synthesis_calibration.ipynb#polarization-calibration).
- Frequency-dependent calibration: [bandpass](../api/casatasks.rst#calibration)
Frequency-dependent calibration is discussed in the general task documentaion for [bandpass](../api/casatasks.rst#calibration).
- Gain calibration: [gaincal](../api/casatasks.rst#calibration)
Gain calibration is discussed in the general task documentation for [gaincal](../api/casatasks.rst#calibration).
- Flux density scale calibration: [fluxscale](../api/casatasks.rst#calibration)
Flux density scale calibration is discussed in the general task documentation for [fluxscale](../api/casatasks.rst#calibration).
- Baseline-based (non-closing) calibration: [blcal](../api/casatasks.rst#calibration)
Non-closing baseline-based calibration is disussed in the general task documentation for [blcal](../api/casatasks.rst#calibration).
***
## Polarization Calibration
Instrumental polarization calibration is necessary because the polarizing hardware in the receiving system will, in general, be impure and non-orthogonal at a level of at least a few percent. These instrumental polarization errors are antenna-based and generally assumed constant with time, but the algebra of their effects is more complicated than the simple \~scalar multiplicative gain calibration. Also, the net gain calibration renders the data in an arbitrary cross-hand phase frame that must also be calibrated. The **polcal** task provides support for solving for instrumental polarization (poltype=\'Df\' and similar) and cross-hand phase (\'Xf\'). Here we separately describe the heuristics of solving for instrumental polarization for the circular and linear feed bases.
### Polarization Calibration in the Circular Basis
Fundamentally, with good ordinary gain and bandpass calibration already in hand, good polarization calibration must deliver both the instrumental polarization and position angle calibration. An unpolarized source can deliver only the first of these, but does not require parallactic angle coverage. A polarized source can only also deliver the position angle calibration if its polarization position angle is known a priori. Sources that are polarized, but with unknown polarization degree and angle, must always be observed with sufficient parallactic angle coverage (which enables solving for the source polarization), where \"sufficient\" is determined by SNR and the details of the solving mode.
These principles are stated assuming the instrumental polarization solution is solved using the \"linear approximation\" where cross-terms in more than a single product of the instrumental or source polarizations are ignored in the [Measurement Equation](casa-fundamentals.ipynb#measurement-equation). A more general non-linearized solution, with sufficient SNR, may enable some relaxation of the requirements indicated here, and modes supporting such an approach are currently under development.
For instrumental polarization calibration, there are 3 types of calibrator choice, listed in the following table:
Cal Polarization PA Coverage Poln Model? *poltype* Result
------------------ ------------- ------------- ------------- -----------------------
Zero any Q=U=0 *\'Df\'* D-terms only
Unknown 2+ scans ignored *\'Df+QU\'* D-terms and Q,U
Known, non-zero 2+ scans Set Q,U *\'Df+X\'* D-terms and Pos Angle
Note that the parallactic angle ranges spanned by the scans in the modes that require this should be large enough to give good separation between the components of the solution. In practice, 60 degrees is a good target.
Each of these solutions should be followed with a \'Xf\' solution on a source with known polarization position angle (and correct fractional Q+iU in the model).
The **polcal** task will solve for the \'Df\' or \'Xf\' terms using the model visibilities that are in the model attached to the MS. Calibration of the parallel hands must have already been obtained using **gaincal** and **bandpass** in order to align the amplitude and phase over time and frequency. This calibration must be supplied through the *gaintable* parameters, but any caltables to be used in **polcal** must agree (e.g. have been derived from) the data in the DATA column and the FT of the model. Thus, for example, one would not use the caltable produced by **fluxscale** as the rescaled amplitudes would no longer agree with the contents of the model.
Be careful when using resolved calibrators for polarization calibration. A particular problem is if the structure in Q and U is offset from that in I. Use of a point model, or a resolved model for I but point models for Q and U, can lead to errors in the \'Xf\' calibration. Use of a *uvrange* will help here. The use of a full-Stokes model with the correct polarization is the only way to ensure a correct calibration if these offsets are large.
**A note on channelized polarization calibration**
When your data has more than one channel per spectral window, it is important to note that the calibrator polarization estimate currently assumes the source polarization signal is coherent across each spectral window. In this case, it is important to be sure there is no large cross-hand delay still present in your data. Unless the online system has accounted for cross-hand delays (typically intended, but not always achieved), the gain and bandpass calibration will only correct for parallel-hand delay residuals since the two polarizations are referenced independently. Good gain and bandpass calibration will typically leave a single cross-hand delay (and phase) residual from the reference antenna. Plots of cross-hand phases as a function of frequency for a strongly polarized source (i.e., that dominates the instrumental polarization) will show the cross-hand delay as a phase slope with frequency. This slope will be the same magnitude on all baselines, but with different sign in the two cross-hand correlations. This cross-hand delay can be estimated using the *gaintype=\'KCROSS\'* mode of **gaincal** (in this case, using the strongly polarized source *3C286*):
```
gaincal(vis='polcal_20080224.cband.all.ms',
caltable='polcal.xdelcal',
field='3C286',
solint='inf',
combine='scan',
refant='VA15',
smodel=[1.0,0.11,0.0,0.0],
gaintype='KCROSS',
gaintable=['polcal.gcal','polcal.bcal'])
```
Note that *smodel* is used to specify that *3C286* is polarized; it is not important to specify this polarization stokes parameters correctly in scale, as only the delay will be solved for (not any absolute position angle or amplitude scaling). The resulting solution should be carried forward and applied along with the gain (.gcal) and bandpass (.bcal) solutions in subsequent polarization calibration steps.
**Circular Basis Example**
In the following example, we have a MS called *polcal_20080224.cband.all.ms* for which we already have bandpass, gain and cross-hand delay solutions. An instrumental polarization calibrator with unknown linear polarization has been observed. We solve for the instrumental polarization and source linear polarization with **polcal** using *poltype=\'Df+QU\'* as follows:
```
polcal(vis= 'polcal_20080224.cband.all.ms',
caltable='polcal.pcal',
field='2202+422',
solint='inf',
combine='scan',
preavg=300.0,
refant='VA15',
poltype='Df+QU',
gaintable=['polcal.gcal','polcal.bcal','polcal.xdelcal])
```
This run of **polcal** assumes that the model stored in the MS for *2202+422* is the one that was used to obtain the net gain calibration stored in *polcal.gcal* (i.e., we have not substituted a fluxscale result, which would create an inconsistent scale).
Alternatively, if we have an instrumental polarization calibrator that we know is unpolarized, we run polcal with poltype=\'Df\':
```
polcal(vis='polcal_20080224.cband.all.ms',
caltable='polcal.pcal',
field='0319+415',
refant='VA15',
poltype='Df',
gaintable=['polcal.gcal','polcal.bcal','polcal.xdelcal])
```
In general, if there is more than one calibrator suitable for instrumental polarization calibration, it is useful to obtain a solution from each of them, and compare results. The instrumental polarization should not vary with field, of course. Note that it is not yet possible to effectively use *combine=\'field\'* for instrumental polarization calibration solves with **polcal**, unless the prior models for all fields are set to the correct apparent linear polarization for each.
Having obtained the instrumental polarization calibration, we solve for the cross-hand phase using the flux density calibrator (for which the instrinsic linear polarization is known):
```
polcal(vis='polcal_20080224.cband.all.ms',
caltable= 'polcal.polx',
field='0137+331',
refant='VA15',
poltype='Xf',
smodel=[1.0,-0.0348,-0.0217,0.0], #the fractional Stokes for 0137+331 (3C48)
gaintable=['polcal.gcal','polcal.bcal','polcal.xdelcal','polcal.pcal'])
```
Note that the correct fractional polarization has been specified for *0137+331*. It is not necessary to use the correct absolute total and linearly polarized flux densities here, since the Xf calibration is entirely phase-like.
### Polarization Calibration in the Linear Feed Basis
CASA now supports instrumental polarization calibration for the linear feed basis at a level that is practical for the general user. Some details remain to be implemented with full flexibility, and much of what follows will be streamlined in future releases.
Calibrating the instrumental polarization for the linear feed basis is somewhat more complicated than the circular feed basis because the polarization effects (source and instrument) appear in all four correlations at first or zeroth order (whereas for circular feeds, the polarization information only enters the parallel hand correlations at second order). As a result, e.g., the time-dependent gain calibration will be distorted by any non-zero source polarization, and some degree of iteration will be required to isolate the gain calibration if the source polarization is not initially known. These complications can actually be used to advantage in solving for the instrumental calibration; in can be shown, for example, that a significantly linearly polarized calibrator enables a better instrumental polarization solution than an unpolarized calibrator.
In the following example, we show the processing steps for calibrating the instrumental polarization using a strongly (\>5%) polarized point-source calibrator (which is also the time-dependent gain calibrator) that has been observed over a range of parallactic angle (a single scan is not sufficient). We assume that we have calibrated the gain, bandpass, and cross-hand delay as described [elsewhere](synthesis_calibration.ipynb#gain-calibration), and that the gain calibration was obtained assuming the calibrator was unpolarized.
**Linear Basis Example**
First, we import some utility functions from the CASA recipes area:
```
from recipes.almapolhelpers import *
```
Our MS in this example is called *polcal_linfeed.ms*. We begin by assuming we already have a bandpass calibration result (obtained by conventional means) stored in *polcal.bcal*. We first solve for a time-dependent gain solution on the instrumental polarization calibrator, which we expect to be significantly polarized, but for which we do not yet have a polarization model:
```
gaincal(vis='polcal_linfeed.ms',
caltable='polcal.gcal',
field='1', #the instrumental polarization calibrator
solint='int',
smodel=[1,0,0,0], #assume zero polarization
gaintype='G',
gaintable=['polcal.bcal'],
parang=T) #so source poln properly rotated
```
Since the gain calibrator was assumed unpolarized, the time-dependent gain solutions contain information about the source polarization. This can be seen by plotting the amp vs. time for this cal table using *poln=\'/\'.* The antenna-based polarization amplitude ratios will reveal the sinusoidal (in parallactic angle) function of the source polarization. Run the utility method **qufromgain** to extract the apparent source polarization estimates for each spw:
```
qu=qufromgain('polcal.gcal')
```
The source polarization reported for all spws should be reasonably consistent. This estimate is not as good as can be obtained from the cross-hands (see below) since it relies on the gain amplitude polarization ratio being stable which may not be precisely true. However, this estimate will be useful in resolving an ambiguity that occurs in the cross-hand estimates.
Next we estimate both the XY-phase offset and source polarization from the cross-hands. The XY-phase offset is a spectral phase-only bandpass relating the X and Y systems of the reference antenna. If the XY-phase is solved for in a channel-dependent manner (as below), it is strictly not necessary to have solved for the cross-hand delay as described above, but it does not hurt, as it allows reasonably coherent channel averages for data examination (we assume below that we have obtained the cross-hand delay solution at this stage). The source polarization occurs in the cross-hands as a sinusoidal function of parallactic angle that is common to both cross-hands on all baselines (for a point-source). If the XY-phase bandpass is uniformly zero, then the source linear polarization function will occur entirely in the real part of the cross-hand visibilities. Non-zero XY-phase has the effect of rotating the source linear polarization signature partially into the imaginary part, where circular (and instrumental) polarization occur (cf. the circular feed basis where the cross-hand phase merely rotates the position angle of linear polarization). The following **gaincal** solve averages all baselines together and first solves for a channelized XY-phase (the slope of the source polarization function in the complex plane in each channel), then corrects the slope and solves for a channel-averaged source polarization. This calibration is obtained using *gaintype=\'XYf+QU\'* in **gaincal**:
```
gaincal(vis='polcal_linfeed.ms',
caltable='polcal.xy0amb', #possibly with 180deg ambiguity
field='1', #the calibrator
solint='inf',
combine='scan',
preavg=200.0, #minimal parang change
smodel=[1,0,1,0], #non-zero U assumed
gaintype='XYf+QU',
gaintable=['polcal.gcal','polcal.bcal','polcal.xdelcal]) #all prior calibration
```
Note that we imply non-zero Stokes U in *smodel*; this is to enforce the assumption of non-zero source polarization signature in the cross-hands in the ratio of data and model. This solve will report the center-channel XY-phase and apparent Q,U for each spw. The Q,U results should be recognizable in comparison to that reported by **qufromgain** above. However, since the XY-phase has a 180 degree ambiguity (you can rotate the source polarization signature to lie entirely in the visibility real part by rotating clockwise or counter-clockwise), some or all spw Q,U estimates may have the wrong sign. We correct this using the **xyamb** utility method, using the *qu* obtained from *qufromgain* above (which is not ambiguous):
```
S=xyamb(xy='polcal.xy0amb',qu=qu,xyout='polcal.xy0')
```
The python variable *S* now contains the mean source model (Stokes I =1; fractional Q,U; V=0) that can be used in a revision of the gain calibration and instrumental polarization calibration.
Next we revise the gain calibration using the full polarization source model:
```
gaincal(vis='polcal_linfeed.ms',
caltable='polcal.gcal1',
field='1',
solint='int',
smodel=S, #obtained from xyamb
gaintype='G',
gaintable=['polcal.bcal'],
parang=T) #so source poln properly rotated
```
Note that *parang=T* so that the supplied source linear polarization is properly rotated in the parallel-hand visibility model. This new gain solution can be plotted with *poln=\'/\'* as above to show that the source polarization is no longer distorting it. Also, if **qufromgain** is run on this new gain table, the reported source polarization should be statistically indistinguishable from zero.
Finally, we can now solve for the instrumental polarization:
```
polcal(vis= 'polcal_linfeed.ms',
caltable='polcal.dcal',
field='1',
solint='inf',
combine='scan',
preavg=200,
poltype='Dflls', #freq-dep LLS solver
refant='', #no reference antenna
smodel=S,
gaintable=['polcal.gcal1','polcal.bcal','polcal.xdelcal','polcal.xy0'])
```
Note that no reference antenna is used since this solve will produce an absolute instrumental polarization solution that is registered to the assumed source polarization (*S*) and prior calibrations. Applying a refant (referring all instrumental polarization terms to a reference antennas X feed, which would then be assumed perfect) would, in fact, discard valid information about the imperfections in the reference antennas X feed. (Had we used an unpolarized calibrator, we would not have a valid xy-phase solution, nor would we have had access to the absolute instrumental polarization solution demonstrated here.)
A few points:
- Since the gain, bandpass, and XY-phase calibrations were obtained prior to the instrumental polarization solution and maybe distorted by it, it is generally desirable to re-solve for them using this instrumental polarization solution as a prior calibration. In effect, this means iterating the sequence of calibration steps using all of the best of the available information at each stage, including the source polarization (and *parang=T*). This is a generalization of traditional self-calibration.
- If the source linear polarization fraction and position angle is known *a priori*, the processing steps outlined above can be amended to use that source polarization assertion in the gain and instrumental calibration solves from the start. The *qufromgain* method is then not needed (but can be used to verify assumptions), the **gaincal(***\...,gaintype=XYf+QU,\...***)** should not be altered (parallactic angle coverage is still required!), and the **xyamb** run should use the *a priori* polarization for *qu*. If there is likely to be a large systematic offset in the mean feed position angle, iteration of the gain, bandpass, and instrumental polarization terms is required to properly isolate the calibration effects.
- Note that the above process does not explicitly include a position angle calibration. In effect, the estimated source polarization sets the mean feed position angle as the reference position angle, and this is usually within a degree or so of optimal for linear feeds. If your mean X feed position angle is not 0 degrees, and your MS does not account for the offset in its FEED subtable, be careful in your interpretation of the final position angle. Currently, the circular feed-specific position angle calibration modes of **polcal(**\...,*poltype=\'Xf\',\...***)** will not properly handle the linear feed basis; this will be fixed in a future release.
***
## Water Vapor Radiometers
The task **wvrgcal** generates a gain table based on Water Vapor Radiometer (WVR) data and is used for ALMA data reduction. Briefly, the task enables a Bayesian approach to calculating the coefficients that convert the outputs of the ALMA 183 GHz water-vapor radiometers (mounted on each antenna) into estimates of path fluctuations which can then be used to correct the observed interferometric visibilities.
The CASA task is an interface to the executable wvrgcal, which is part of the CASA 5 distribution and can also be called from outside CASA. The wvrgcal software is based on the libair and libbnmin libraries which were developed by Bojan Nikolic at the University of Cambridge as part of EU FP6 ALMA Enhancement program. CASA 5 contains version 2.1 of wvrgcal. The algorithmic core of wvrgcal is described in three ALMA memos (number 587 [\[1\]](#Bibliography), 588 [\[2\]](#Bibliography), and 593 [\[3\]](#Bibliography) ) which describe the algorithms implemented in the software.
The CASA task interface to wvrgcal follows closely the interface of the shell executable at the same time staying within the CASA task parameter conventions. In ALMA data, the WVR measurements belonging to a given observation are contained in the ASDM for that observation. After conversion to an MS using **importasdm**, the WVR information can be found in separate spectral windows. As of April 2016, it is still one single spectral window for all WVRs, however, the ID of the spectral window may vary between datasets. The **wvrgcal** task identifies the SPW autonomously, but it can also be specified via the parameter *wvrspw* (see below). The specified spectral window(s) must be present in the MS for **wvrgcal** to work. This is not to be mixed up with the list of spectral windows for which solutions should be calculated and which can be specified with the parameter *spw*. Note that **wvrgcal** will calculate a correction only for the scans with the words ON_SOURCE, SIGNAL, or REFERENCE in the scan intent. The various features of **wvrgcal** are then controlled by a number of task parameters (see the list above). They have default values which will work for ALMA data. An example for a typical **wvrgcal** call can be found in the ALMA CASA guide for the NGC 3256 analysis:
```
wvrgcal(vis='uid___A002_X1d54a1_X5.ms',
caltable='cal-wvr-uid___A002_X1d54a1_X5.W',
toffset=-1,
segsource=True, tie=["Titan,1037-295,NGC3256"], statsource="1037-295",
wvrspw=[4],
spw=[17,19,21,23])
```
Here, *vis* is the name of input visibility file which as mentioned above also contains the WVR data and *caltable* is the name of the output gain calibration table. WVR data is typically in spectral window 0, but in the example above, the data are contained in spectral window 4. Although **wvrgcal** should automatically identify this SPW, it is explicitly specified with the *wvrspw* parameter in the above example. The *toffset* parameter is the known time offset in seconds between the WVR measurements and the visibility integrations for which they are valid. For ALMA, this offset is presently -1 s (which is also the default value).
The parameter *segsource* (segregate source) controls whether separate coefficients are calculated for each source. The default value True is the recommended one for ALMA. When *segsource* is True, the subparameter *tie* is available. It permits the formation of groups of sources for which common coefficients are calculated as well as possible. The *tie* parameter ensures best possible phase transfer between a group of sources. In general it is recommended to tie together all of the sources in a single Science Goal (in ALMA speak) and their phase calibrator(s). The recommended maximum angular distance up to which two sources can be tied is 15 degrees. The parameter statsource controls for which sources statistics are calculated and displayed in the logger. This has no influence on the generated calibration table.
Via the parameter *spw*, one can control for which of the input spectral windows **wvrgcal** will calculate phase corrections and store them in the output calibration table. By default, solutions for all spectral windows are written except for the ones containing WVR data. The **wvrgcal** task respects the flags in the Main and ANTENNA table of the MS. The parameter *mingoodfrac* lets the user set a requirement on the minimum fraction of good measurements for accepting the WVR data from an antenna. If antennas are flagged, their WVR solution is interpolated from the three nearest neighboring antennas. This process can be controlled with the new parameters *maxdistm* and *minnumants*. The former sets the maximum distance an antenna used for interpolation may have from the flagged one. And *minnumants* sets how many near antennas there have to be for interpolation to take place. For more details on the WVR Phase correction, see also the the ALMA Memo "Quality Control of WVR Phase Correction Based on Differences Between WVR Channels" by B. Nikolic, R. C. Bolton & J. S. Richer [\[4\]](#Bibliography) , see also ALMA memo 593 [\[3\]](#Bibliography).
**Statistical parameters shown in the logger output of wvrgcal**
The **wvrgcal** task writes out a variety of information to the logger, including various statistical measures of the performance. This allows the user to judge whether WVR correction is appropriate for the MS, to check whether any antennas have problematic WVR values, and to examine the predicted performance of the WVR correction when applied. For each set of correction coefficients which are calculated (the number of coefficient sets are controlled by the parameters *nsol*, *segsource* and *tie*), the **wvrgcal** output to the logger first of all shows the time sample, the individual temperatures of each of the four WVR channels, and the elevation of the source in question at that time. For each of these coefficient sets, it then gives the evidence of the bayesian parameter estimation, the calculated precipitable water vapor (PWV) and its error in mm, and the correction coefficients found for each WVR channel (dTdL).
The output then shows the statistical information about the observation. First of all it gives the start and end times for the parts of the observation used to calculate these statistics (controlled by *segsource*). It then shows a break down for each of the antennas in the data set. This gives the antenna name and number; whether or not it has a WVR (column WVR); whether or not it has been flagged (column FLAG); the RMS of the path length variation with time towards that antenna (column RMS); and the discrepancy between the RMS path length calculated separately for different WVR channels (column Disc.). These values allow the user to see if an individual WVR appears to have been suffering from problems during the observation, and to flag that antenna using *wvrflag* if necessary. This discrepancy value, Disc., can in addition be used as a simple diagnostic tool to evaluate whether or not the WVR correction caltable created by **wvrgcal** should be applied. In the event of the WVR observations being contaminated by strong cloud emission in the atmosphere, the attempt by **wvrgcal** to fit the water vapor line may not be successful, and applying the produced calibration table can in extreme cases reduce the quality of the data. However, these weather conditions should identified by a high value in the discrepancy column produced when running **wvrgcal**.
Discrepancy values of greater than a 1000 microns usually indicate strong cloud contamination of the WVR data, and the output calibration table should probably not be applied. If the values are between 100 and 1000 microns, then the user should manually examine the phases before and after applying the caltable to decide if WVR correction is appropriate. Work is underway at ALMA to provide additional routines to at least partially remove the cloud component from the WVR data before calculating phase corrections. CASA 4.7 will contain a first tested version of such a tool. After the antenna-by-antenna statistics, the output then displays some estimates of the performance of the **wvrgcal** correction. These are the thermal contribution from the water vapor to the path fluctuations per antenna (in microns), the largest path fluctuation found on a baseline (in microns), and the expected error on the path length calculated for each baseline due to the error in the coefficients (in microns).
**Antenna position calculation**
The information about antenna pointing direction is by default taken from the POINTING table. Should this table not be present for some reason, the user can instead switch to determining the antenna positions from the phase directions in the FIELD table (under the assumption that all antennas were pointing ideally). The switch is performed by setting the parameter *usefieldtab* to True.
**Spectral window selection**
By default, **wvrgcal** puts solutions for all spectral windows of the MS into the output calibration table. Since usually only the spectral windows are of interest in which the science target and the calibrators were observed, it is not necessary to store solutions for other spectral windows. The spectral windows for which solutions are stored can be selected with the parameter *spw*, e.g. spw = \[17,19,21,23\] will make **wvrgcal** write only solutions for spectral windows 17, 19, 21, and 23. With respect to the input WVR spectral windows, **wvrgcal** will by default regard all windows with 4 channels as WVR data. In typical ALMA data there is only one such spectral window in each ASDM. This may change in the future. In any case, the input WVR spectral window(s) can be selected with the optional parameter *wvrspw*. The syntax is the same as for the parameter *spw* above.
### Bibliography
1. [ALMA Memo 587](http://library.nrao.edu/public/memos/alma/memo587.pdf)
2. [ALMA Memo 588](http://library.nrao.edu/public/memos/alma/memo588.pdf)
3. [ALMA Memo 593](http://library.nrao.edu/public/memos/alma/memo593.pdf)
4. [ALMA Memo "Quality Control of WVR Phase Correction Based on Differences Between WVR Channels"](https://casa.nrao.edu/Memos/memoqachannels.pdf)
***
## Examine/Edit Cal Tables
How to plot, list, and adjust calibration tables
Information on examination and manipulation of calibration tables can be found in the task documentation for **plotcal**, **listcal**, **calstat**, **smoothcal**, and **browsetable**.
***
## Apply Calibration
How to apply calibration to generate data for imaging
Please see the task documentation for **applycal** for details on application of calibration.
***
| github_jupyter |
In this tutorial you'll learn all about **histograms** and **density plots**.
# Set up the notebook
As always, we begin by setting up the coding environment. (_This code is hidden, but you can un-hide it by clicking on the "Code" button immediately below this text, on the right._)
```
#$HIDE$
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
print("Setup Complete")
```
# Select a dataset
We'll work with a dataset of 150 different flowers, or 50 each from three different species of iris (*Iris setosa*, *Iris versicolor*, and *Iris virginica*).

# Load and examine the data
Each row in the dataset corresponds to a different flower. There are four measurements: the sepal length and width, along with the petal length and width. We also keep track of the corresponding species.
```
# Path of the file to read
iris_filepath = "../input/iris.csv"
# Read the file into a variable iris_data
iris_data = pd.read_csv(iris_filepath, index_col="Id")
# Print the first 5 rows of the data
iris_data.head()
```
# Histograms
Say we would like to create a **histogram** to see how petal length varies in iris flowers. We can do this with the `sns.distplot` command.
```
# Histogram
sns.distplot(a=iris_data['Petal Length (cm)'], kde=False)
```
We customize the behavior of the command with two additional pieces of information:
- `a=` chooses the column we'd like to plot (_in this case, we chose `'Petal Length (cm)'`_).
- `kde=False` is something we'll always provide when creating a histogram, as leaving it out will create a slightly different plot.
# Density plots
The next type of plot is a **kernel density estimate (KDE)** plot. In case you're not familiar with KDE plots, you can think of it as a smoothed histogram.
To make a KDE plot, we use the `sns.kdeplot` command. Setting `shade=True` colors the area below the curve (_and `data=` has identical functionality as when we made the histogram above_).
```
# KDE plot
sns.kdeplot(data=iris_data['Petal Length (cm)'], shade=True)
```
# 2D KDE plots
We're not restricted to a single column when creating a KDE plot. We can create a **two-dimensional (2D) KDE plot** with the `sns.jointplot` command.
In the plot below, the color-coding shows us how likely we are to see different combinations of sepal width and petal length, where darker parts of the figure are more likely.
```
# 2D KDE plot
sns.jointplot(x=iris_data['Petal Length (cm)'], y=iris_data['Sepal Width (cm)'], kind="kde")
```
Note that in addition to the 2D KDE plot in the center,
- the curve at the top of the figure is a KDE plot for the data on the x-axis (in this case, `iris_data['Petal Length (cm)']`), and
- the curve on the right of the figure is a KDE plot for the data on the y-axis (in this case, `iris_data['Sepal Width (cm)']`).
# Color-coded plots
For the next part of the tutorial, we'll create plots to understand differences between the species. To accomplish this, we begin by breaking the dataset into three separate files, with one for each species.
```
# Paths of the files to read
iris_set_filepath = "../input/iris_setosa.csv"
iris_ver_filepath = "../input/iris_versicolor.csv"
iris_vir_filepath = "../input/iris_virginica.csv"
# Read the files into variables
iris_set_data = pd.read_csv(iris_set_filepath, index_col="Id")
iris_ver_data = pd.read_csv(iris_ver_filepath, index_col="Id")
iris_vir_data = pd.read_csv(iris_vir_filepath, index_col="Id")
# Print the first 5 rows of the Iris versicolor data
iris_ver_data.head()
```
In the code cell below, we create a different histogram for each species by using the `sns.distplot` command (_as above_) three times. We use `label=` to set how each histogram will appear in the legend.
```
# Histograms for each species
sns.distplot(a=iris_set_data['Petal Length (cm)'], label="Iris-setosa", kde=False)
sns.distplot(a=iris_ver_data['Petal Length (cm)'], label="Iris-versicolor", kde=False)
sns.distplot(a=iris_vir_data['Petal Length (cm)'], label="Iris-virginica", kde=False)
# Add title
plt.title("Histogram of Petal Lengths, by Species")
# Force legend to appear
plt.legend()
```
In this case, the legend does not automatically appear on the plot. To force it to show (for any plot type), we can always use `plt.legend()`.
We can also create a KDE plot for each species by using `sns.kdeplot` (_as above_). Again, `label=` is used to set the values in the legend.
```
# KDE plots for each species
sns.kdeplot(data=iris_set_data['Petal Length (cm)'], label="Iris-setosa", shade=True)
sns.kdeplot(data=iris_ver_data['Petal Length (cm)'], label="Iris-versicolor", shade=True)
sns.kdeplot(data=iris_vir_data['Petal Length (cm)'], label="Iris-virginica", shade=True)
# Add title
plt.title("Distribution of Petal Lengths, by Species")
```
One interesting pattern that can be seen in plots is that the plants seem to belong to one of two groups, where _Iris versicolor_ and _Iris virginica_ seem to have similar values for petal length, while _Iris setosa_ belongs in a category all by itself.
In fact, according to this dataset, we might even be able to classify any iris plant as *Iris setosa* (as opposed to *Iris versicolor* or *Iris virginica*) just by looking at the petal length: if the petal length of an iris flower is less than 2 cm, it's most likely to be *Iris setosa*!
# What's next?
Put your new skills to work in a **[coding exercise](#$NEXT_NOTEBOOK_URL$)**!
| github_jupyter |
# IMPORTING THE LIBRARIES
```
import os
import pandas as pd
import pickle
import numpy as np
import seaborn as sns
from sklearn.datasets import load_files
from keras.utils import np_utils
import matplotlib.pyplot as plt
from keras.layers import Conv2D, MaxPooling2D, GlobalAveragePooling2D
from keras.layers import Dropout, Flatten, Dense
from keras.models import Sequential
from keras.utils.vis_utils import plot_model
from keras.callbacks import ModelCheckpoint
from keras.utils import to_categorical
from sklearn.metrics import confusion_matrix
from keras.preprocessing import image
from tqdm import tqdm
import seaborn as sns
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score
# Pretty display for notebooks
%matplotlib inline
!ls
```
# Defining the train,test and model directories
We will create the directories for train,test and model training paths if not present
```
TEST_DIR = os.path.join(os.getcwd(),"imgs","test")
TRAIN_DIR = os.path.join(os.getcwd(),"imgs","train")
MODEL_PATH = os.path.join(os.getcwd(),"model","self_trained")
PICKLE_DIR = os.path.join(os.getcwd(),"pickle_files")
if not os.path.exists(TEST_DIR):
print("Testing data does not exists")
if not os.path.exists(TRAIN_DIR):
print("Training data does not exists")
if not os.path.exists(MODEL_PATH):
print("Model path does not exists")
os.makedirs(MODEL_PATH)
print("Model path created")
if not os.path.exists(PICKLE_DIR):
os.makedirs(PICKLE_DIR)
```
# Data Preparation
We will create a csv file having the location of the files present for training and test images and their associated class if present so that it is easily traceable.
```
def create_csv(DATA_DIR,filename):
class_names = os.listdir(DATA_DIR)
data = list()
if(os.path.isdir(os.path.join(DATA_DIR,class_names[0]))):
for class_name in class_names:
file_names = os.listdir(os.path.join(DATA_DIR,class_name))
for file in file_names:
data.append({
"Filename":os.path.join(DATA_DIR,class_name,file),
"ClassName":class_name
})
else:
class_name = "test"
file_names = os.listdir(DATA_DIR)
for file in file_names:
data.append(({
"FileName":os.path.join(DATA_DIR,file),
"ClassName":class_name
}))
data = pd.DataFrame(data)
data.to_csv(os.path.join(os.getcwd(),"csv_files",filename),index=False)
create_csv(TRAIN_DIR,"train.csv")
create_csv(TEST_DIR,"test.csv")
data_train = pd.read_csv(os.path.join(os.getcwd(),"csv_files","train.csv"))
data_test = pd.read_csv(os.path.join(os.getcwd(),"csv_files","test.csv"))
data_train.info()
data_train['ClassName'].value_counts()
data_train.describe()
nf = data_train['ClassName'].value_counts(sort=False)
labels = data_train['ClassName'].value_counts(sort=False).index.tolist()
y = np.array(nf)
width = 1/1.5
N = len(y)
x = range(N)
fig = plt.figure(figsize=(20,15))
ay = fig.add_subplot(211)
plt.xticks(x, labels, size=15)
plt.yticks(size=15)
ay.bar(x, y, width, color="blue")
plt.title('Bar Chart',size=25)
plt.xlabel('classname',size=15)
plt.ylabel('Count',size=15)
plt.show()
data_test.head()
data_test.shape
```
## Observation:
1. There are total 22424 training samples
2. There are total 79726 training samples
3. The training dataset is equally balanced to a great extent and hence we need not do any downsampling of the data
## Converting into numerical values
```
labels_list = list(set(data_train['ClassName'].values.tolist()))
labels_id = {label_name:id for id,label_name in enumerate(labels_list)}
print(labels_id)
data_train['ClassName'].replace(labels_id,inplace=True)
with open(os.path.join(os.getcwd(),"pickle_files","labels_list.pkl"),"wb") as handle:
pickle.dump(labels_id,handle)
labels = to_categorical(data_train['ClassName'])
print(labels.shape)
```
## Splitting into Train and Test sets
```
from sklearn.model_selection import train_test_split
xtrain,xtest,ytrain,ytest = train_test_split(data_train.iloc[:,0],labels,test_size = 0.2,random_state=42)
```
### Converting into 64*64 images
You can substitute 64,64 to 224,224 for better results only if ram is >32gb
```
def path_to_tensor(img_path):
# loads RGB image as PIL.Image.Image type
img = image.load_img(img_path, target_size=(64, 64))
# convert PIL.Image.Image type to 3D tensor with shape (224, 224, 3)
x = image.img_to_array(img)
# convert 3D tensor to 4D tensor with shape (1, 224, 224, 3) and return 4D tensor
return np.expand_dims(x, axis=0)
def paths_to_tensor(img_paths):
list_of_tensors = [path_to_tensor(img_path) for img_path in tqdm(img_paths)]
return np.vstack(list_of_tensors)
from PIL import ImageFile
ImageFile.LOAD_TRUNCATED_IMAGES = True
# pre-process the data for Keras
train_tensors = paths_to_tensor(xtrain).astype('float32')/255 - 0.5
valid_tensors = paths_to_tensor(xtest).astype('float32')/255 - 0.5
##takes too much ram
## run this if your ram is greater than 16gb
# test_tensors = paths_to_tensor(data_test.iloc[:,0]).astype('float32')/255 - 0.5
```
# Defining the Model
```
model = Sequential()
model.add(Conv2D(filters=64, kernel_size=2, padding='same', activation='relu', input_shape=(64,64,3), kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=128, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=256, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=512, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax', kernel_initializer='glorot_normal'))
model.summary()
plot_model(model,to_file=os.path.join(MODEL_PATH,"model_distracted_driver.png"),show_shapes=True,show_layer_names=True)
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
filepath = os.path.join(MODEL_PATH,"distracted-{epoch:02d}-{val_accuracy:.2f}.hdf5")
checkpoint = ModelCheckpoint(filepath, monitor='val_accuracy', verbose=1, save_best_only=True, mode='max',period=1)
callbacks_list = [checkpoint]
model_history = model.fit(train_tensors,ytrain,validation_data = (valid_tensors, ytest),epochs=25, batch_size=40, shuffle=True,callbacks=callbacks_list)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 12))
ax1.plot(model_history.history['loss'], color='b', label="Training loss")
ax1.plot(model_history.history['val_loss'], color='r', label="validation loss")
ax1.set_xticks(np.arange(1, 25, 1))
ax1.set_yticks(np.arange(0, 1, 0.1))
ax2.plot(model_history.history['accuracy'], color='b', label="Training accuracy")
ax2.plot(model_history.history['val_accuracy'], color='r',label="Validation accuracy")
ax2.set_xticks(np.arange(1, 25, 1))
legend = plt.legend(loc='best', shadow=True)
plt.tight_layout()
plt.show()
```
# Model Analysis
Finding the Confusion matrix,Precision,Recall and F1 score to analyse the model thus created
```
def print_confusion_matrix(confusion_matrix, class_names, figsize = (10,7), fontsize=14):
df_cm = pd.DataFrame(
confusion_matrix, index=class_names, columns=class_names,
)
fig = plt.figure(figsize=figsize)
try:
heatmap = sns.heatmap(df_cm, annot=True, fmt="d")
except ValueError:
raise ValueError("Confusion matrix values must be integers.")
heatmap.yaxis.set_ticklabels(heatmap.yaxis.get_ticklabels(), rotation=0, ha='right', fontsize=fontsize)
heatmap.xaxis.set_ticklabels(heatmap.xaxis.get_ticklabels(), rotation=45, ha='right', fontsize=fontsize)
plt.ylabel('True label')
plt.xlabel('Predicted label')
fig.savefig(os.path.join(MODEL_PATH,"confusion_matrix.png"))
return fig
def print_heatmap(n_labels, n_predictions, class_names):
labels = n_labels #sess.run(tf.argmax(n_labels, 1))
predictions = n_predictions #sess.run(tf.argmax(n_predictions, 1))
# confusion_matrix = sess.run(tf.contrib.metrics.confusion_matrix(labels, predictions))
matrix = confusion_matrix(labels.argmax(axis=1),predictions.argmax(axis=1))
row_sum = np.sum(matrix, axis = 1)
w, h = matrix.shape
c_m = np.zeros((w, h))
for i in range(h):
c_m[i] = matrix[i] * 100 / row_sum[i]
c = c_m.astype(dtype = np.uint8)
heatmap = print_confusion_matrix(c, class_names, figsize=(18,10), fontsize=20)
class_names = list()
for name,idx in labels_id.items():
class_names.append(name)
# print(class_names)
ypred = model.predict(valid_tensors)
print_heatmap(ytest,ypred,class_names)
```
## Precision Recall F1 Score
```
ypred_class = np.argmax(ypred,axis=1)
# print(ypred_class[:10])
ytest = np.argmax(ytest,axis=1)
accuracy = accuracy_score(ytest,ypred_class)
print('Accuracy: %f' % accuracy)
# precision tp / (tp + fp)
precision = precision_score(ytest, ypred_class,average='weighted')
print('Precision: %f' % precision)
# recall: tp / (tp + fn)
recall = recall_score(ytest,ypred_class,average='weighted')
print('Recall: %f' % recall)
# f1: 2 tp / (2 tp + fp + fn)
f1 = f1_score(ytest,ypred_class,average='weighted')
print('F1 score: %f' % f1)
```
| github_jupyter |
# WeatherPy
----
#### Note
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
import json
import random
import csv as csv
# Import API key
from api_keys import api_key
# Incorporated citipy to determine city based on latitude and longitude
from citipy import citipy
# Output File (CSV)
city_file = "output_data/cities.csv"
# Range of latitudes and longitudes
lat_range = (-90, 90)
lng_range = (-180, 180)
```
## Generate Cities List
```
# List for holding lat_lngs and cities
counter = 0
randlat = []
randlngs = []
cities = []
# Create a set of random lat and lng combinations
while len(randlat)< 500:
lats = np.random.uniform(low=-90, high=90)
lngs = np.random.uniform(low=-180, high=180)
randlat.append(lats)
randlngs.append(lngs)
counter += 1
coord_df = pd.DataFrame({"lats":randlat, "lngs": randlngs})
coord_df.head()
# Create a set of random lat and lng combinations
lats = np.random.uniform(low=-90.000, high=90.000, size=1500)
lngs = np.random.uniform(low=-180.000, high=180.000, size=1500)
lat_lngs = zip(lats, lngs)
# Identify nearest city for each lat, lng combination
for lat_lng in lat_lngs:
city = citipy.nearest_city(lat_lng[0], lat_lng[1]).city_name
# If the city is unique, then add it to a our cities list
if city not in cities:
cities.append(city)
# Print the city count to confirm sufficient count
print(len(cities))
#print(cities)
```
### Perform API Calls
* Perform a weather check on each city using a series of successive API calls.
* Include a print log of each city as it'sbeing processed (with the city number and city name).
```
url = "http://api.openweathermap.org/data/2.5/weather?"
units = "metric"
# Build query URL to begin call
url = "http://api.openweathermap.org/data/2.5/weather?units=metric&appid=" + api_key
#Set up list for responses
date = []
country = []
lat = []
lon = []
temp_max = []
humidity = []
cloud = []
wind = []
_cities = []
print("Beginning Data Retrieval")
for city in cities:
url_city = url + "&q=" + str(city)
#print(url_city)
#convert to json
try:
city_data = requests.get(url_city).json()
country.append(city_data['sys']['country'])
date.append(city_data['dt'])
lat.append(city_data['coord']['lat'])
lon.append(city_data['coord']['lon'])
temp_max.append(city_data['main']['temp_max'])
humidity.append(city_data['main']['humidity'])
cloud.append(city_data['clouds']['all'])
wind.append(city_data['wind']['speed'])
_cities.append(city)
print(f"retreiving data | {city}")
except:
print("If city is not found, skipping")
print("Retrieval is complete!")
data_dict = {'city': _cities,
'country': country,
'latitude': lat,
'longitude': lon,
'max temp': temp_max,
'humidity': humidity,
'cloudiness': cloud,
'windspeed': wind}
#print(data_dict)
df = pd.DataFrame.from_dict(data_dict)
df.head()
```
### Convert Raw Data to DataFrame
* Export the city data into a .csv.
* Display the DataFrame
```
df.count()
#Convert file to csv and save
df.to_csv("weather_data.csv", encoding="utf-8", index=False)
```
### Plotting the Data
* Use proper labeling of the plots using plot titles (including date of analysis) and axes labels.
* Save the plotted figures as .pngs.
#### Latitude vs. Temperature Plot
```
# Build a scatter plot for each data type
plt.scatter(df["latitude"], df["max temp"], marker="o")
# Incorporate the other graph properties
plt.title("City Latitude vs. Temperature (F)")
plt.ylabel("Temperature (F)")
plt.xlabel("Latitude")
plt.grid(True)
# Save the figure
plt.savefig("Temperature (F).png")
# Show plot
plt.show()
```
#### Latitude vs. Humidity Plot
```
# Build a scatter plot for each data type
plt.scatter(df["latitude"], df["humidity"], marker="o")
# Incorporate the other graph properties
plt.title("City Latitude vs. Humidity %")
plt.ylabel("Humidity %")
plt.xlabel("Latitude")
plt.grid(True)
# Save the figure
plt.savefig("Humidity%.png")
# Show plot
plt.show()
```
#### Latitude vs. Cloudiness Plot
```
# Build a scatter plot for each data type
plt.scatter(df["latitude"], df["cloudiness"], marker="o")
# Incorporate the other graph properties
plt.title("City Latitude vs. Cloudiness %")
plt.ylabel("Cloudiness %")
plt.xlabel("Latitude")
plt.grid(True)
# Save the figure
plt.savefig("Clouds%.png")
# Show plot
plt.show()
```
#### Latitude vs. Wind Speed Plot
```
# Build a scatter plot for each data type
plt.scatter(df["latitude"], df["windspeed"], marker="o")
# Incorporate the other graph properties
plt.title("City Latitude vs. Windspeed (mph)")
plt.ylabel("Windspeed (mph)")
plt.xlabel("Latitude")
plt.grid(True)
# Save the figure
plt.savefig("Windspeed(mph).png")
# Show plot
plt.show()
```
| github_jupyter |
Here you have a collection of guided exercises for the first class on Python. <br>
The exercises are divided by topic, following the topics reviewed during the theory session, and for each topic you have some mandatory exercises, and other optional exercises, which you are invited to do if you still have time after the mandatory exercises. <br>
Remember that you have 5 hours to solve these exercises, after which we will review the most interesting exercises together. If you don't finish all the exercises, you can work on them tonightor tomorrow.
At the end of the class, we will upload the code with the solutions of the exercises so that you can review them again if needed. If you still have not finished some exercises, try to do them first by yourself, before taking a look at the solutions: you are doing these exercises for yourself, so it is always the best to do them your way first, as it is the fastest way to learn!
**Exercise 1.1:** The cover price of a book is 24.95 EUR, but bookstores get a 40 percent discount. Shipping costs 3 EUR for the first copy and 75 cents for each additional copy. **Calculate the total wholesale costs for 60 copies**.
```
#Your Code Here
```
**Exercise 1.2:** When something is wrong with your code, Python will raise errors. Often these will be "syntax errors" that signal that something is wrong with the form of your code (e.g., the code in the previous exercise raised a `SyntaxError`). There are also "runtime errors", which signal that your code was in itself formally correct, but that something went wrong during the code's execution. A good example is the `ZeroDivisionError`, which indicates that you tried to divide a number by zero (which, as you may know, is not allowed). Try to make Python **raise such a `ZeroDivisionError`.**
```
#Your Code Here
```
**Exercise 5.1**: Create a countdown function that starts at a certain count, and counts down to zero. Instead of zero, print "Blast off!". Use a `for` loop.
```
# Countdown
def countdown():
"""
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Blast off!
"""
return
```
**Exercise 5.2:** Write and test three functions that return the largest, the smallest, and the number of dividables by 3 in a given collection of numbers. Use the algorithm described earlier in the Part 5 lecture :)
```
# Your functions
def main():
"""
a = [2, 4, 6, 12, 15, 99, 100]
100
2
4
"""
return
```
| github_jupyter |
```
# Import that good good
import sys
import os
sys.path.append('/Users/kolbt/Desktop/ipython/diam_files')
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math
from IPython.display import display
from collections import OrderedDict
pd.options.display.max_rows = 2
import matplotlib.colors as mc
import colorsys
# Define what functions you'll need here
def getFromTxt(fname, first, last):
"Takes a string, text before and after desired text, outs text between"
start = fname.index( first ) + len( first )
end = fname.index( last, start )
myTxt = fname[start:end]
return float(myTxt)
# Above function kindly provided by user "cji" on stackoverflow
# https://stackoverflow.com/questions/3368969/find-string-between-two-substrings
# Make sure data is sorted appropriately
def sortArray(array, sort_var):
"Takes an array and the column name to sort, sorts array "
for i in range(0, len(array)):
for k in range(0, len(array[i])):
for j in range(0, len(array[i])):
# Out of order, swap them
if array[i].loc[j, sort_var] < array[i].loc[k, sort_var] and k < j:
tmp = array[i].iloc[j].copy()
array[i].iloc[j] = array[i].iloc[k]
array[i].iloc[k] = tmp
def plotter(start, stop, ylab):
"Plotting function so that I don't have to show this a zillion times"
ind = 0
for j in range(start, stop):
for i in range(0, len(SS[headers[j]])):
# Mixture
if params['xA'][i] % 100 != 0:
plt.scatter(params['peA'][i], SS[headers[j]][i], c=col[ind], label=headers[j])
# Monodisperse, always same color
else:
# If it's zero ignore it
if SS[headers[j]][i] != 0:
plt.scatter(params['peA'][i], SS[headers[j]][i], c=col[-1], label='Mono')
ind += 1
handles, labels = plt.gca().get_legend_handles_labels()
by_label = OrderedDict(zip(labels, handles))
plt.legend(by_label.values(), by_label.keys())
plt.xlabel('Activity (Pe)')
plt.ylabel(ylab)
plt.show()
def katieRoseIsCute(r):
"Take diameter, output LJ-force"
eps = 20.0
sigma = 1.0
F_LJ = 24.0 * eps * ((2 * (sigma**12) * (r**-13)) - ((sigma**6) * (r**-7)))
return F_LJ
def forceToEps(force):
"Take LJ-force and output epsilon to give diameter of 1"
epsilon = force / 24.0
return epsilon
# https://mycurvefit.com/
def powerLaw(a, x, b):
return a*(x**b)
def exponential(a, b, c, x):
"Exponential: a - (b/c) * (1 - (e**-cx))"
return a - ((b/c)*(1-(math.exp(-c*x))))
def plateau(a, x, b):
"Plateau: a * x / (b + x)"
return (a * x) / (b + x)
def logarithmic(a, x, b):
"Logarithmic: a * ln(x) + b"
if x != 0:
return (a * math.log(x)) + b
else:
return 0
# https://stackoverflow.com/questions/37765197/darken-or-lighten-a-color-in-matplotlib
def colorShade(color, amount=0.5):
"Gives multiple shades of a base color"
try:
c = mc.cnames[color]
except:
c = color
c = colorsys.rgb_to_hls(*mc.to_rgb(c))
return colorsys.hls_to_rgb(c[0], 1 - amount * (1 - c[1]), c[2])
# Get the data files
txtFiles = os.listdir('gsd')
all_sims = []
# Using the absolute path means I can go to whatever directory I want
os.chdir('/Users/kolbt/Desktop/ipython/diam_files')
for i in range(0, len(txtFiles)):
df = pd.read_csv(txtFiles[i], sep='\s+', header=0)
all_sims.append(df)
# Return to root directory
os.chdir('/Users/kolbt/Desktop/ipython')
# Make sure all data is in correct timestep order
sortArray(all_sims, 'Timestep')
display(all_sims[9])
# Make an additional frame that gives total number of particles, and simulation parameters
paramList = []
for i in range(0, len(txtFiles)):
partAll = all_sims[i]['Gas_tot'][0]
partA = all_sims[i]['Gas_A'][0]
partB = all_sims[i]['Gas_B'][0]
pa = getFromTxt(txtFiles[i], "pa", "_pb")
pb = getFromTxt(txtFiles[i], "pb", "_xa")
xa = getFromTxt(txtFiles[i], "xa", ".txt")
try:
prat = float(pa)/float(pb)
except:
prat = 0.0
paramList.append((partAll, partA, partB, pa, pb, xa, prat))
params = pd.DataFrame(paramList, columns=['partAll', 'partA', 'partB', 'peA', 'peB', 'xA', 'peR'])
display(params)
# Make list of steady state column headers
headers = list(all_sims[0])
headers.remove('Timestep')
SS = pd.DataFrame(columns=headers)
for i in range(0, len(txtFiles)):
SS.loc[i] = [0] * len(headers)
# Make dataframe of steady-state data
for i in range(0, len(txtFiles)):
# Loop through each column (aside from tstep column)
for j in range(1, len(headers) + 1):
# Compute mean of last 100 entries in jth column of ith file
avg = np.mean(all_sims[i].iloc[-100:-1,j])
SS[headers[j-1]][i] = avg
# Normalize by number of particles
# SS['Gas_A'][:] /= params['partA'][:]
# SS['Gas_B'][:] /= params['partB'][:]
# SS['Gas_tot'][:] /= params['partAll'][:]
# SS['Dense_A'][:] /= params['partA'][:]
# SS['Dense_B'][:] /= params['partB'][:]
# SS['Dense_tot'][:] /= params['partAll'][:]
# SS['Lg_clust'][:] /= params['partAll'][:]
# SS['MCS'][:] /= params['partAll'][:]
display(SS)
# Plot the data
# col = ['k', 'r', 'g', 'b']
col = ['#e6194b', '#3cb44b', '#0082c8', '#f58231', '#ffe119','#911eb4', '#46f0f0',
'#f032e6', '#d2f53c', '#fabebe', '#008080', '#e6beff', '#aa6e28', '#fffac8',
'#800000', '#aaffc3', '#808000', '#ffd8b1', '#000080', '#808080', '#ffffff',
'#000000']
plotter(0, 3, '% of total particles')
plotter(3, 6, '% of total particles')
plotter(6, 8, '% of total particles')
plotter(8, 12, r'Diameter $(\sigma)$')
plotter(12, 13, r'Effective Area Fraction $(\phi_{Eff})$')
plotter(13, 15, 'Area')
plotter(15, 17, 'Density')
plotter(17, 18, 'Density')
# # This is the way I was plotting it
# for j in range(0, 3):
# plt.scatter(params['peA'], SS[headers[j]], label=headers[j])
# plt.legend()
# plt.show()
# Take in the steady-state diameter data... output the LJ force w/ HS epsilon
diam_to_force = []
eps_one = []
for i in range(0, len(SS['sigALL'])):
diam_to_force.append(katieRoseIsCute(SS['sigALL'][i]))
eps_one.append(forceToEps(diam_to_force[i]))
# https://onlinelibrary.wiley.com/doi/pdf/10.1002/9780470126714.app4
# Good ideas for plotting are:
# Exponential: a - (b/c) * (1 - (e**-cx))
# Power: a * x ** b
# Plateau: a * x / (b + x)
# Log: a * ln(x) + b
# Let's fix the data being plotted (just monodisperse)
mono = [0]
corDat = [1]
for i in range(0, len(params['peA'])):
if params['xA'][i] % 100 == 0:
mono.append(params['peA'][i])
corDat.append(eps_one[i])
powla = []
expo = []
plato = []
loga = []
refRange = np.arange(0, 500, 0.001)
for i in range(0, len(refRange)):
powla.append(powerLaw(5.87, refRange[i], 0.36))
expo.append(exponential(9.4, -0.28, 0.006, refRange[i]))
plato.append(plateau(62.4, refRange[i], 99.1))
loga.append(logarithmic(1.0, refRange[i], 1.0))
plt.scatter(mono, corDat, c=col[8], label='Data')
plt.plot(refRange, powla, c=col[9], label='Power Law')
plt.xlabel('Activity')
plt.ylabel('Epsilon')
plt.legend()
plt.title(r'$\epsilon$ to give $\sigma=1$')
plt.show()
plt.scatter(mono, corDat, c=col[8], label='Data')
plt.plot(refRange, expo, c=col[10], label='Exponential')
plt.xlabel('Activity')
plt.ylabel('Epsilon')
plt.legend()
plt.title(r'$\epsilon$ to give $\sigma=1$')
plt.show()
plt.scatter(mono, corDat, c=col[8], label='Data')
plt.plot(refRange, plato, c=col[11], label='Plateau')
plt.xlabel('Activity')
plt.ylabel('Epsilon')
plt.legend()
plt.title(r'$\epsilon$ to give $\sigma=1$')
plt.show()
# plt.scatter(mono, corDat, c=col[8], label='Data')
# plt.plot(refRange, loga, c=col[12], label='Logarithmic')
# plt.xlabel('Activity')
# plt.ylabel('Epsilon')
# plt.legend()
# plt.title(r'$\epsilon$ to give $\sigma=1$')
# plt.show()
print('Monodisperse Data:')
for i in range(0, len(eps_one)):
# monodisperse
if params['xA'][i] % 100 == 0:
print('Activity: {}, Epsilon: {}').format(params['peA'][i], eps_one[i])
# print('Monodisperse Data:')
# for i in range(0, len(eps_one)):
# # monodisperse
# if params['xA'][i] % 100 == 0:
# print('{} \t {}').format(params['peA'][i], eps_one[i])
# Plot the composition data? Inset the plot composition over time
# A will be one color, dark = high Pe_ratio, light = low Pe_r
# Same goes for B and all
mixPar = []
mixA = []
mixB = []
mixT = []
mixInds = []
for i in range(0, len(params['peA'])):
# Mixtures only
if params['xA'][i] % 100 != 0:
mixInds.append(i)
mixPar.append(params['peR'][i])
mixA.append(SS['Dense_A'][i] / params['partA'][i])
mixB.append(SS['Dense_B'][i] / params['partB'][i])
mixT.append(SS['Dense_tot'][i] / params['partAll'][i])
plt.scatter(mixPar, mixT, label='All', c='g')
plt.scatter(mixPar, mixA, label='A', c='b')
plt.scatter(mixPar, mixB, label='B', c='r')
plt.xlabel('Activity Ratio')
plt.ylabel('Percentage of Total')
mixedSims = len(mixInds)
timeB = [[] for x in xrange(mixedSims)]
simDenseA = [[] for x in xrange(mixedSims)]
simDenseB = [[] for x in xrange(mixedSims)]
simDenseT = [[] for x in xrange(mixedSims)]
count = -1
# Let's get data for the inset
for i in range(0, len(txtFiles)):
if params['xA'][i] % 100 != 0:
count += 1
# Get the tau_B time
timeB[count].append(np.arange(0, len(all_sims[i]['Timestep']), 1))
for j in range(0, len(all_sims[i]['Timestep'])):
# Group all Dense_A data
simDenseT[count].append(all_sims[i]['Dense_tot'][j])
simDenseA[count].append(all_sims[i]['Dense_A'][j])
simDenseB[count].append(all_sims[i]['Dense_B'][j])
# Divide column by number of A particles
simDenseT[count] /= params['partAll'][i]
simDenseA[count] /= params['partA'][i]
simDenseB[count] /= params['partB'][i]
# Plot the data All
a = plt.axes([0.475, .25, .4, .4], facecolor='w')
for i in range(0, mixedSims):
plt.plot(timeB[i][0], simDenseT[i], c=colorShade('g', mixPar[i]))
plt.xlim(0, 10)
plt.ylim(0,1)
plt.xlabel(r'Time $(\tau_{B})$')
plt.ylabel(r'% of Total')
# Plot the data A
a = plt.axes([1.02, .575, .3, .3], facecolor='w')
for i in range(0, mixedSims):
plt.plot(timeB[i][0], simDenseA[i], c=colorShade('b', mixPar[i]))
plt.xlim(0, 10)
plt.ylim(0,1)
plt.ylabel(r'% of Total A')
# Plot the data B
a = plt.axes([1.02, .15, .3, .3], facecolor='w')
for i in range(0, mixedSims):
plt.plot(timeB[i][0], simDenseB[i], c=colorShade('r', mixPar[i]))
plt.xlim(0, 10)
plt.ylim(0,1)
plt.xlabel(r'Time $(\tau_{B})$')
plt.ylabel(r'% of Total B')
```
| github_jupyter |
# TensorFlow Neural Machine Translation on Cloud TPUs
This tutorial demonstrates how to translate text using a LSTM Network from one language to another (from English to German in this case). We will work with a dataset that contains pairs of English-German phrases. Given a sequence of words in English, we train a model to predict the German equivalent in the sequence.
Note: Enable TPU acceleration to execute this notebook faster. In Colab: Runtime > Change runtime type > Hardware acclerator > **TPU**.
<br>
If running locally make sure TensorFlow version >= 1.11.
This tutorial includes runnable code implemented using [tf.keras](https://www.tensorflow.org/programmers_guide/keras).
By Rishabh Anand (GitHub: @rish-16)
```
!ls
!wget http://www.manythings.org/anki/deu-eng.zip
!unzip deu-eng.zip
!head deu.txt
```
### Importing TensorFlow and other libraries
```
import string
import numpy as np
from numpy import array
import pandas as pd
import tensorflow as tf
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.layers import Dense, Embedding, RepeatVector, LSTM
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
```
### Extracting lines from dataset and into array
Here, we can examine how the dataset is structures. The English-German dataset comprises of an English and German phrase separted by a tab `\t`
```
deu_eng = open('./deu.txt', mode='rt', encoding='utf-8')
deu_eng = deu_eng.read()
deu_eng = deu_eng.strip().split('\n')
deu_eng = [i.split('\t') for i in deu_eng]
deu_eng = array(deu_eng)
deu_eng = deu_eng[:50000, :]
print (deu_eng[:5])
```
### Removing punctuation
We will be removing punctuation from the phrases and converting them to lowercase. We will not be creating embeddings for punctuations or uppercase characters as it adds to the complexity of the NMT model
```
deu_eng[:, 0] = [s.translate((str.maketrans('', '', string.punctuation))) for s in deu_eng[:, 0]]
deu_eng[:, 1] = [s.translate((str.maketrans('', '', string.punctuation))) for s in deu_eng[:, 1]]
for i in range(len(deu_eng)):
deu_eng[i, 0] = deu_eng[i, 0].lower()
deu_eng[i, 1] = deu_eng[i, 1].lower()
print (deu_eng[:5])
```
### Tokenising the phrases
Tokenisation is the process of taking a sequence and chopping it up into smaller pieces called `tokens`. For example, suppose we have a sentence
`"Bob returned home after the party"`
The tokenised sentence will return an array with the tokens:
`["Bob", "returned", "home", "after", "the", "party"]`
In this section, we will be breaking up the phrases into tokenised sequences that comprises of numbers for each unique word. For instance, the word "good" may have the value of 32 while the word "boy" may have the value of 46. Supposing the phrase is "good boy", the tokenised sequence is `[32, 46]`.
```
def tokenize(lines):
tokenizer = Tokenizer()
tokenizer.fit_on_texts(lines)
return tokenizer
eng_tokenizer = tokenize(deu_eng[:, 0])
eng_vocab_size = len(eng_tokenizer.word_index) + 1
eng_sequence_length = 8
print ('English vocabulary size: {}'.format(eng_vocab_size))
deu_tokenizer = tokenize(deu_eng[:, 1])
deu_vocab_size = len(deu_tokenizer.word_index) + 1
deu_sequence_length = 8
print ('German vocabulary size: {}'.format(deu_vocab_size))
```
### Convert lines into sequences as input for the NMT model
We will now be using our Tokeniser to create tokenised sequences of the original English and German phrases from our dataset.
```
def encode_sequences(tokenizer, sequence_length, lines):
sequence = tokenizer.texts_to_sequences(lines)
sequence = pad_sequences(sequence, sequence_length, padding="post") # 0s after the actual sequence
return sequence
```
### Splitting the dataset into training and testing sets
```
train, test = train_test_split(deu_eng, test_size=.2, random_state=12)
x_train = encode_sequences(deu_tokenizer, deu_sequence_length, train[:, 1])
y_train = encode_sequences(eng_tokenizer, eng_sequence_length, train[:, 0])
x_test = encode_sequences(deu_tokenizer, deu_sequence_length, test[:, 1])
y_test = encode_sequences(eng_tokenizer, eng_sequence_length, test[:, 0])
print (x_train.shape, y_train.shape)
print (x_test.shape, x_test.shape)
```
### Training on a TPU
In order to connect to a TPU, we can follow 4 easy steps:
1. Connect to a TPU instance
2. Initialise a parallelly-distributed training `strategy`
3. Build our NMT model under the `strategy`
4. Train the model on a TPU
For more details on training on TPUs for free, feel free to check out [this](https://medium.com/@mail.rishabh.anand/tpu-training-made-easy-with-colab-3b73b920878f) article that covers the process in great detail.
### Connecting to available TPU instances
Here, we search for available instances of version 2 TPUs (the ones Google publically allocates)
```
tpu = tf.distribute.cluster_resolver.TPUClusterResolver() # TPU detection
# Initialising a parallelly-distributed training strategy
tf.tpu.experimental.initialize_tpu_system(tpu)
strategy = tf.distribute.experimental.TPUStrategy(tpu, steps_per_run=128)
print('Running on TPU ', tpu.cluster_spec().as_dict()['worker'])
print("Number of accelerators: ", strategy.num_replicas_in_sync)
# Building our model under that strategy
in_vocab = deu_vocab_size
out_vocab = eng_vocab_size
units = 512
in_timesteps = deu_sequence_length
out_timesteps = eng_sequence_length
with strategy.scope():
model = Sequential()
model.add(Embedding(in_vocab, units, input_length=in_timesteps, mask_zero=True))
model.add(LSTM(units))
model.add(RepeatVector(out_timesteps))
model.add(LSTM(units, return_sequences=True))
model.add(Dense(out_vocab, activation='softmax'))
rms = RMSprop(lr=0.001)
model.compile(loss='sparse_categorical_crossentropy', optimizer=rms)
model.summary()
tf.keras.utils.plot_model(
model,
show_shapes=True,
show_layer_names=True,
rankdir="TB"
)
history = model.fit(x_train, y_train.reshape(y_train.shape[0], y_train.shape[1], 1), epochs=30, steps_per_epoch=500)
```
### Checking the loss values
```
plt.plot(history.history['loss'])
plt.xlabel('Epochs')
plt.ylabel('Sparse Categorical Loss')
plt.legend(['train'])
plt.show()
```
### Running our model on testing dataset
```
# Getting the predictions from the testing dataset
preds = model.predict_classes(x_test.reshape(x_test.shape[0], x_test.shape[1])[:10]) # only predicting over 10 instances
print (preds)
# A function to convert a sequence back into words
def convert_words(n, tokenizer):
for word, idx in tokenizer.word_index.items():
if idx == n:
return word
return None
# Running our model on the testing dataset
pred_texts = []
for i in preds:
temp = []
for j in range(len(i)):
word = convert_words(i[j], eng_tokenizer)
if j > 0:
if (word == convert_words(i[j-1], eng_tokenizer)) or (word == None):
temp.append('')
else:
temp.append(word)
else:
if (word == None):
temp.append('')
else:
temp.append(word)
pred_texts.append(' '.join(temp))
```
### Translating the text from German to English
We can see that our model does a relatively good job in translating the German text to English. However, there are instances that seem to have the wrong translation or are outright incorrect. Nonetheless, for a basic NMT model that was trained for 30 epochs, the model's generalisation is great.
```
pred_df = pd.DataFrame({'actual': test[:10, 0], 'prediction': pred_texts})
pred_df
```
| github_jupyter |
*Practical Data Science 19/20*
# Programming Assignment
In this programming assignment you need to apply your new `numpy`, `pandas` and `matplotlib` knowledge. You will need to do several [`groupby`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.groupby.html)s and [`join`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.join.html)`s to solve the task.
Load required packages
```
import pandas as pd
%matplotlib inline
```
Load Data
```
DATA_URL = 'https://raw.githubusercontent.com/pds1920/_a1-template/master/data/'
transactions = pd.read_csv(DATA_URL + '/sales_train.csv.gz')
items = pd.read_csv(DATA_URL + '/items.csv')
item_categories = pd.read_csv(DATA_URL + '/item_categories.csv')
```
## Get to know the data
Print the **shape** of the loaded dataframes.
- You can use a list comprehension here
```
# Write your code here
```
Use [`df.head`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.head.html) function to print several rows of each data frame. Examine the features you are given.
```
# Write your code here
# Write your code here
# Write your code here
```
Now use your `pandas` skills to get answers for the following questions.
## What was the maximum total revenue among all the shops in June, 2014?
* Revenue refers to total sales minus value of goods returned.
* Sometimes items are returned, find such examples in the dataset.
* It is handy to split `date` field into [`day`, `month`, `year`] components and use `df.year == 14` and `df.month == 6` in order to select target subset of dates.
* You may work with `date` feature as with strings, or you may first convert it to `pd.datetime` type with `pd.to_datetime` function, but do not forget to set correct `format` argument.
```
# Write your code here
max_revenue = # Write your code here
max_revenue
```
## How many items are there?
* Let's assume, that the items are returned for the same price as they had been sold
```
num_items_constant_price = # Write your code here
num_items_constant_price
```
## What was the variance of the number of sold items per day sequence for the shop with `shop_id = 25` in December, 2014?
* Do not count the items that were sold but returned back later.
* Fill `total_num_items_sold`: An (ordered) array that contains the total number of items sold on each day
* Fill `days`: An (ordered) array that contains all relevant days
* Then compute variance of the of `total_num_items_sold`
* If there were no sales at a given day, ***do not*** impute missing value with zero, just ignore that day
```
shop_id = 25
# Write your code here
total_num_items_sold = # Write your code here
days = # Write your code here
total_num_items_sold_var = # Write your code here
total_num_items_sold_var
```
## Vizualization of the daily items sold
Use `total_num_items_sold` and `days` arrays to and plot the daily revenue of `shop_id = 25` in December, 2014.
* plot-title: 'Daily items sold for shop_id = 25'
```
# Write your code here
```
## What item category that generated the highest revenue in spring 2014?</b></li>
Spring is the period from March to Mai.
```
# Write your code here
category_id_with_max_revenue =# Write your code here
category_id_with_max_revenue
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import competition_helpers
from sklearn import tree
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import VotingClassifier, RandomForestClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# I/O configuration here
X_train = competition_helpers.read_csv("train_features.csv")
y_train = competition_helpers.read_csv("train_label.csv", remove_header=True)
X_test = competition_helpers.read_csv("test_features.csv")
submission_col = np.array(pd.read_csv("test_features.csv", header=None).iloc[: , 0]).ravel()
submission_file_name = "results/voting_default_submission.csv"
print(X_train.shape, y_train.shape, X_test.shape)
# 5 fold cross validation
# train_test_split = competition_helpers.kfold_stratified_split(X_train, y_train, 5,False)
# With standardization
standardized_train_test_split = competition_helpers.kfold_stratified_split(X_train, y_train, 5,True)
# # 5 fold train test split results
# results = []
# for estimators_ in [50, 100, 150]:
# for lr in [0.1, 0.5, 1, 5]:
# for [(X_train_cv, y_train_cv), (X_test_cv, y_test_cv)] in train_test_split:
# clf = AdaBoostClassifier(random_state=42,
# base_estimator=tree.DecisionTreeClassifier(
# max_depth=None, min_samples_split=60, min_samples_leaf= 30
# ),
# n_estimators=estimators_,
# learning_rate=lr
# )
# clf.fit(X_train_cv, y_train_cv.ravel())
# prediction = clf.predict(X_test_cv)
# accuracy = accuracy_score(y_test_cv.ravel(), prediction.ravel())
# precision = precision_score(y_test_cv.ravel(), prediction.ravel())
# recall = recall_score(y_test_cv.ravel(), prediction.ravel())
# f1 = f1_score(y_test_cv.ravel(), prediction.ravel())
# results.append([accuracy, precision, recall, f1])
# measures = np.sum(np.array(results), axis=0) / len(results)
# print("n_estimators: {} learning rate: {} measures: {}".format(estimators_, lr, measures))
results = []
for [(X_train_cv, y_train_cv), (X_test_cv, y_test_cv)] in standardized_train_test_split:
clf1 = LogisticRegression(random_state=42, solver='saga',max_iter = 2000,multi_class='auto')
clf2 = RandomForestClassifier(random_state=42, n_estimators=100)
# clf3 = GaussianNB()
clf4 = SVC(gamma="auto", probability=True)
clf = VotingClassifier(
estimators=[("logistic", clf1), ("random_forest", clf2),
("svm", clf4)],
voting="soft",
weights=[1, 2, 1]
)
clf.fit(X_train_cv, y_train_cv.ravel())
prediction = clf.predict(X_test_cv)
accuracy = accuracy_score(y_test_cv.ravel(), prediction.ravel())
precision = precision_score(y_test_cv.ravel(), prediction.ravel())
recall = recall_score(y_test_cv.ravel(), prediction.ravel())
f1 = f1_score(y_test_cv.ravel(), prediction.ravel())
results.append([accuracy, precision, recall, f1])
measures = np.sum(np.array(results), axis=0) / len(results)
print(measures)
# fitting the test dataset
clf1 = LogisticRegression(random_state=42, solver='saga',max_iter = 2000,multi_class='auto')
clf2 = RandomForestClassifier(random_state=42, n_estimators=100)
# clf3 = GaussianNB()
clf4 = SVC(gamma="auto", probability=True)
clf = VotingClassifier(
estimators=[("logistic", clf1), ("random_forest", clf2),
("svm", clf4)],
voting="soft",
weights=[1, 2, 1]
)
clf.fit(X_train, y_train.ravel())
prediction = clf.predict(X_test)
pd.DataFrame({"id": submission_col, "label": prediction}).to_csv(submission_file_name, encoding='utf-8', index=False)
```
| github_jupyter |
# Demo Notebook for CPW Kappa Calculation
Let's start by importing Qiskit Metal:
```
import qiskit_metal as metal
from qiskit_metal import designs, draw
from qiskit_metal import MetalGUI, Dict, open_docs
```
Next, let's import the function "kappa_in" located in the file kappa_calculation.py. This function calculates the photon loss of a CPW resonator which is capacitively coupled to an input transmission line.
```
# Import the function "kappa_in" from the file kappa_calculation.py
from qiskit_metal.analyses.em.kappa_calculation import kappa_in
```
The function "kappa_in" takes either three or six arguments, depending on how the lowest resonant frequency of the resonator is handled. In the first case, the resonant frequency of the CPW resonator is calculated numerically (using HFSS, for example) and passed as in floating-point input along with the frequency of interest and the capacitance between the resonator and the transmission line. In the second case, the lowest resonant frequency of the CPW resonator can be estimated by assuming an ideal resonator, in which case some additional inputs are required (1/2 or 1/4 depending on the type of resonator, the resonator length, width of resonator trace, width of resonator gap.)
Here's a quick sanity check to verify that we only get numerical output from this function in the cases of N=3 or N=6 arguments:
```
# SANITY CHECK #1
# Let's check that output is only given for three and six arguments
print("Output for N=1 Arguments:", kappa_in(1.0))
print("Output for N=2 Arguments:", kappa_in(1.0, 1.0))
print("Output for N=3 Arguments:", kappa_in(1.0, 1.0, 1.0))
print("Output for N=4 Arguments:", kappa_in(1.0, 1.0, 1.0, 1.0))
print("Output for N=5 Arguments:", kappa_in(1.0, 1.0, 1.0, 1.0, 1.0))
print("Output for N=6 Arguments:", kappa_in(1.0, 1.0, 1.0, 1.0, 1.0, 1.0))
print("Output for N=7 Arguments:", kappa_in(1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0))
```
Now, let's actually calculate the photon loss for a representative CPW resonator with realistic values of input parameters. Here we'll assume a qubit frequency of 5 GHz, capacitive coupling of 30fF and a CPW resonant frequency of 4 GHz. The calculated value of kappa is the range of 0-1 MHz, as expected.
```
# SANITY CHECK #2
# Let's check that the magnitude of the output is what we would expect for 3 arguments:
# Input #1: omega = 5GHz = 5E9 Hertz
# Input #2: C_in = 30fF = 30E-15 Farads
# Input #3: omega_n = 4GHz = 4.5E9 Hertz
print("Calculated kappa (in Hz):", kappa_in(5.0E9, 30.0E-15, 4.5E9), "Hz")
print("Calculated kappa (in MHz):", kappa_in(5.0E9, 30.0E-15, 4.5E9)/1.0E6, "MHz")
```
| github_jupyter |
```
# We tweak the style of this notebook a little bit to have centered plots.
from IPython.core.display import HTML
HTML("""
<style>
.output_png {
display: table-cell;
text-align: center;
vertical-align: middle;
}
</style>
""");
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
warnings.filterwarnings('ignore', category=DeprecationWarning)
import pandas as pd
pd.options.display.max_columns = 100
from matplotlib import pyplot as plt
import numpy as np
import seaborn as sns
import pylab as plot
params = {
'axes.labelsize': "large",
'xtick.labelsize': 'x-large',
'legend.fontsize': 20,
'figure.dpi': 150,
'figure.figsize': [25, 7]
}
plot.rcParams.update(params)
data = pd.read_csv('datasets/train.csv')
print(data.shape)
#(891, 12)
data.head()
data.describe()
# (891-714) = 177 values are missing in the Age column
# fill in the null values with the median age as it's more robust to outliers
data['Age'] = data['Age'].fillna(data['Age'].median())
data['Died'] = 1 - data['Survived']
data.groupby('Sex').agg('sum')[['Survived', 'Died']].plot(kind='bar', figsize=(25, 7),
stacked=True);
data.groupby('Sex').agg('mean')[['Survived', 'Died']].plot(kind='bar', figsize=(25, 7),
stacked=True);
# correlate the survival with the age variable
fig = plt.figure(figsize=(25, 7))
sns.violinplot(x='Sex', y='Age',
hue='Survived', data=data,
split=True,
palette={0: "r", 1: "g"}
);
# fare ticket
figure = plt.figure(figsize=(25, 7))
plt.hist([data[data['Survived'] == 1]['Fare'], data[data['Survived'] == 0]['Fare']],
stacked=True, color = ['g','r'],
bins = 50, label = ['Survived','Dead'])
plt.xlabel('Fare')
plt.ylabel('Number of passengers')
plt.legend();
# age, the fare and the survival on a single chart.
plt.figure(figsize=(25, 7))
ax = plt.subplot()
ax.scatter(data[data['Survived'] == 1]['Age'], data[data['Survived'] == 1]['Fare'],
c='green', s=data[data['Survived'] == 1]['Fare'])
ax.scatter(data[data['Survived'] == 0]['Age'], data[data['Survived'] == 0]['Fare'],
c='red', s=data[data['Survived'] == 0]['Fare']);
ax = plt.subplot()
ax.set_ylabel('Average fare')
data.groupby('Pclass').mean()['Fare'].plot(kind='bar', figsize=(25, 7), ax = ax);
fig = plt.figure(figsize=(25, 7))
sns.violinplot(x='Embarked', y='Fare', hue='Survived', data=data, split=True, palette={0: "r", 1: "g"});
# Feature Engineering
# define a print function that asserts whether a feature has been processed.
def status(feature):
print('Processing', feature, ': ok')
def get_combined_data():
# reading train data
train = pd.read_csv('datasets/train.csv')
# reading test data
test = pd.read_csv('datasets/test.csv')
# extracting and then removing the targets from the training data
targets = train.Survived
train.drop(['Survived'], 1, inplace=True)
# merging train data and test data for future feature engineering
# we'll also remove the PassengerID since this is not an informative feature
combined = train.append(test)
combined.reset_index(inplace=True)
combined.drop(['index', 'PassengerId'], inplace=True, axis=1)
return combined
combined = get_combined_data()
print(combined.shape)
titles = set()
for name in data['Name']:
titles.add(name.split(',')[1].split('.')[0].strip())
print(titles)
# set(['Sir', 'Major', 'the Countess', 'Don', 'Mlle', 'Capt', 'Dr', 'Lady', 'Rev', 'Mrs', 'Jonkheer', 'Master', 'Ms', 'Mr', 'Mme', 'Miss', 'Col'])
Title_Dictionary = {
"Capt": "Officer",
"Col": "Officer",
"Major": "Officer",
"Jonkheer": "Royalty",
"Don": "Royalty",
"Sir" : "Royalty",
"Dr": "Officer",
"Rev": "Officer",
"the Countess":"Royalty",
"Mme": "Mrs",
"Mlle": "Miss",
"Ms": "Mrs",
"Mr" : "Mr",
"Mrs" : "Mrs",
"Miss" : "Miss",
"Master" : "Master",
"Lady" : "Royalty"
}
def get_titles():
# we extract the title from each name
combined['Title'] = combined['Name'].map(lambda name:name.split(',')[1].split('.')[0].strip())
# a map of more aggregated title
# we map each title
combined['Title'] = combined.Title.map(Title_Dictionary)
status('Title')
return combined
combined = get_titles()
combined.head()
# check if the titles have been filled correctly.
combined[combined['Title'].isnull()]
# Age
# Number of missing ages in train set
print(combined.iloc[:891].Age.isnull().sum())
# Number of missing ages in test set
print(combined.iloc[891:].Age.isnull().sum())
# 86
grouped_train = combined.iloc[:891].groupby(['Sex','Pclass','Title'])
grouped_median_train = grouped_train.median()
grouped_median_train = grouped_median_train.reset_index()[['Sex', 'Pclass', 'Title', 'Age']]
grouped_median_train.head()
# function that fills in the missing age in combined based on these different attributes.
def fill_age(row):
condition = (
(grouped_median_train['Sex'] == row['Sex']) &
(grouped_median_train['Title'] == row['Title']) &
(grouped_median_train['Pclass'] == row['Pclass'])
)
return grouped_median_train[condition]['Age'].values[0]
def process_age():
global combined
# a function that fills the missing values of the Age variable
combined['Age'] = combined.apply(lambda row: fill_age(row) if np.isnan(row['Age']) else row['Age'], axis=1)
status('age')
return combined
combined = process_age()
# now process the names.
def process_names():
global combined
# we clean the Name variable
combined.drop('Name', axis=1, inplace=True)
# encoding in dummy variable
titles_dummies = pd.get_dummies(combined['Title'], prefix='Title')
combined = pd.concat([combined, titles_dummies], axis=1)
# removing the title variable
combined.drop('Title', axis=1, inplace=True)
status('names')
return combined
combined = process_names()
combined.head()
# Fare
# fill missing fare value by the average fare computed on the train set
def process_fares():
global combined
# there's one missing fare value - replacing it with the mean.
combined.Fare.fillna(combined.iloc[:891].Fare.mean(), inplace=True)
status('fare')
return combined
combined = process_fares()
# Embarked
# missing values of Embarked filled with the most frequent Embarked value.
def process_embarked():
global combined
# two missing embarked values - filling them with the most frequent one in the train set(S)
combined.Embarked.fillna('S', inplace=True)
# dummy encoding
embarked_dummies = pd.get_dummies(combined['Embarked'], prefix='Embarked')
combined = pd.concat([combined, embarked_dummies], axis=1)
combined.drop('Embarked', axis=1, inplace=True)
status('embarked')
return combined
combined = process_embarked()
combined.head()
# Cabin
train_cabin, test_cabin = set(), set()
for c in combined.iloc[:891]['Cabin']:
try:
train_cabin.add(c[0])
except:
train_cabin.add('U')
for c in combined.iloc[891:]['Cabin']:
try:
test_cabin.add(c[0])
except:
test_cabin.add('U')
print(train_cabin)
print(test_cabin)
# replaces NaN values with U (for Unknown).
def process_cabin():
global combined
# replacing missing cabins with U (for Uknown)
combined.Cabin.fillna('U', inplace=True)
# mapping each Cabin value with the cabin letter
combined['Cabin'] = combined['Cabin'].map(lambda c: c[0])
# dummy encoding ...
cabin_dummies = pd.get_dummies(combined['Cabin'], prefix='Cabin')
combined = pd.concat([combined, cabin_dummies], axis=1)
combined.drop('Cabin', axis=1, inplace=True)
status('cabin')
return combined
combined = process_cabin()
combined.head()
# Sex
def process_sex():
global combined
# mapping string values to numerical one
combined['Sex'] = combined['Sex'].map({'male':1, 'female':0})
status('Sex')
return combined
combined = process_sex()
# Pclass
def process_pclass():
global combined
# encoding into 3 categories:
pclass_dummies = pd.get_dummies(combined['Pclass'], prefix="Pclass")
# adding dummy variable
combined = pd.concat([combined, pclass_dummies],axis=1)
# removing "Pclass"
combined.drop('Pclass',axis=1,inplace=True)
status('Pclass')
return combined
combined = process_pclass()
def cleanTicket(ticket):
ticket = ticket.replace('.', '')
ticket = ticket.replace('/', '')
ticket = ticket.split()
ticket = map(lambda t : t.strip(), ticket)
ticket = list(filter(lambda t : not t.isdigit(), ticket))
if len(ticket) > 0:
return ticket[0]
else:
return 'XXX'
tickets = set()
for t in combined['Ticket']:
tickets.add(cleanTicket(t))
print(len(tickets))
def process_ticket():
global combined
# Extracting dummy variables from tickets:
combined['Ticket'] = combined['Ticket'].map(cleanTicket)
tickets_dummies = pd.get_dummies(combined['Ticket'], prefix='Ticket')
combined = pd.concat([combined, tickets_dummies], axis=1)
combined.drop('Ticket', inplace=True, axis=1)
status('Ticket')
return combined
combined = process_ticket()
# family
def process_family():
global combined
# introducing a new feature : the size of families (including the passenger)
combined['FamilySize'] = combined['Parch'] + combined['SibSp'] + 1
# introducing other features based on the family size
combined['Singleton'] = combined['FamilySize'].map(lambda s: 1 if s == 1 else 0)
combined['SmallFamily'] = combined['FamilySize'].map(lambda s: 1 if 2 <= s <= 4 else 0)
combined['LargeFamily'] = combined['FamilySize'].map(lambda s: 1 if 5 <= s else 0)
status('family')
return combined
combined = process_family()
print(combined.shape)
# We end up with a total of 67 features.
combined.head()
# Modelling start
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble.gradient_boosting import GradientBoostingClassifier
from sklearn.feature_selection import SelectKBest
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
# 5-fold Cross Validation
def compute_score(clf, X, y, scoring='accuracy'):
xval = cross_val_score(clf, X, y, cv = 5, scoring=scoring)
return np.mean(xval)
# recovering train and test set
def recover_train_test_target():
global combined
targets = pd.read_csv('datasets/train.csv', usecols=['Survived'])['Survived'].values
train = combined.iloc[:891]
test = combined.iloc[891:]
return train, test, targets
train, test, targets = recover_train_test_target()
clf = RandomForestClassifier(n_estimators=50, max_features='sqrt')
clf = clf.fit(train, targets)
features = pd.DataFrame()
features['feature'] = train.columns
features['importance'] = clf.feature_importances_
features.sort_values(by=['importance'], ascending=True, inplace=True)
features.set_index('feature', inplace=True)
features.plot(kind='barh', figsize=(25, 25))
model = SelectFromModel(clf, prefit=True)
train_reduced = model.transform(train)
print(train_reduced.shape)
# (891L, 14L)
test_reduced = model.transform(test)
print(test_reduced.shape)
```
### Try Different base models.
```
logreg = LogisticRegression()
logreg_cv = LogisticRegressionCV()
rf = RandomForestClassifier()
gboost = GradientBoostingClassifier()
models = [logreg, logreg_cv, rf, gboost]
for model in models:
print('Cross-validation of : {0}'.format(model.__class__))
score = compute_score(clf=model, X=train_reduced, y=targets, scoring='accuracy')
print('CV score = {0}'.format(score))
print('****')
# Tuning
# turn run_gs to True if you want to run the gridsearch again.
run_gs = False
if run_gs:
parameter_grid = {
'max_depth' : [4, 6, 8],
'n_estimators': [50, 10],
'max_features': ['sqrt', 'auto', 'log2'],
'min_samples_split': [2, 3, 10],
'min_samples_leaf': [1, 3, 10],
'bootstrap': [True, False],
}
forest = RandomForestClassifier()
cross_validation = StratifiedKFold(n_splits=5)
grid_search = GridSearchCV(forest,
scoring='accuracy',
param_grid=parameter_grid,
cv=cross_validation,
verbose=1
)
grid_search.fit(train, targets)
model = grid_search
parameters = grid_search.best_params_
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))
else:
parameters = {'bootstrap': False, 'min_samples_leaf': 3, 'n_estimators': 50,
'min_samples_split': 10, 'max_features': 'sqrt', 'max_depth': 6}
model = RandomForestClassifier(**parameters)
model.fit(train, targets)
# output = model.predict(test).astype(int)
# df_output = pd.DataFrame()
# aux = pd.read_csv('datasets/test.csv')
# df_output['PassengerId'] = aux['PassengerId']
# df_output['Survived'] = output
# df_output[['PassengerId','Survived']].to_csv('submission_2.csv ', index=False)
```
### Save and Load Model
```
import pickle
import joblib
file = 'titanic.pkl'
joblib.dump(model, file)
load = joblib.load('titanic.pkl')
y_pred = load.predict(test).astype(int)
y_pred
val = pd.DataFrame(y_pred, columns = ['Survived'])
val = val.replace({1: 'Alive', 0: 'Died'})
val
```
| github_jupyter |
# Notebook Goal & Approach
## Goal
For each FERC 714 respondent that reports hourly demand as an electricity planning area, create a geometry representing the geographic area in which that electricity demand originated. Create a separate geometry for each year in which data is available.
## Approach
* Use the `eia_code` found in the `respondent_id_ferc714` table to link FERC 714 respondents to their corresponding EIA utilities or balancing areas.
* Use the `balancing_authority_eia861` and `sales_eia861` tables to figure out which respondents correspond to what utility or utilities (if a BA), and which states of operation.
* Use the `service_territory_eia861` table to link those combinations of years, utilities, and states of operation to collections of counties.
* Given the FIPS codes of the counties associated with each utility or balancing area in a given year, use geospatial data from the US Census to compile an annual demand area geometry.
* Merge those geometries back in with the `respondent_id_ferc714` table, along with additional EIA balancing area and utility IDs / Codes on a per-year basis.
# Imports & Config
```
%load_ext autoreload
%autoreload 2
# Standard Libraries:
import dateutil
import logging
import pathlib
import pickle
import re
import sys
import zipfile
# 3rd Party Libraries:
import contextily as ctx
import geopandas
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sqlalchemy as sa
# Local Packages:
import pudl
```
## Configure Output Formatting
```
sns.set()
%matplotlib inline
mpl.rcParams['figure.figsize'] = (20,8)
mpl.rcParams['figure.dpi'] = 150
pd.options.display.max_columns = 100
pd.options.display.max_rows = 100
```
## Logging
```
logger = logging.getLogger()
logger.setLevel(logging.INFO)
handler = logging.StreamHandler(stream=sys.stdout)
log_format = '%(asctime)s [%(levelname)8s] %(name)s:%(lineno)s %(message)s'
formatter = logging.Formatter(log_format)
handler.setFormatter(formatter)
logger.handlers = [handler]
```
## PUDL Setup
```
pudl_settings = pudl.workspace.setup.get_defaults()
ferc1_engine = sa.create_engine(pudl_settings['ferc1_db'])
pudl_engine = sa.create_engine(pudl_settings['pudl_db'])
pudl_out = pudl.output.pudltabl.PudlTabl(pudl_engine)
pudl_settings
```
# Parameters
```
MAP_CRS = "EPSG:3857"
CALC_CRS = "ESRI:102003"
```
# Function Definitions
## Dummy EIA 861 ETL
```
def test_etl_eia(eia_inputs, pudl_settings):
"""
This is a dummy function that runs the first part of the EIA ETL
process -- everything up until the entity harvesting begins. For
use in this notebook only.
"""
eia860_tables = eia_inputs["eia860_tables"]
eia860_years = eia_inputs["eia860_years"]
eia861_tables = eia_inputs["eia861_tables"]
eia861_years = eia_inputs["eia861_years"]
eia923_tables = eia_inputs["eia923_tables"]
eia923_years = eia_inputs["eia923_years"]
# generate CSVs for the static EIA tables, return the list of tables
#static_tables = _load_static_tables_eia(datapkg_dir)
# Extract EIA forms 923, 860
eia860_raw_dfs = pudl.extract.eia860.Extractor().extract(eia860_years, testing=True)
eia861_raw_dfs = pudl.extract.eia861.Extractor().extract(eia861_years, testing=True)
eia923_raw_dfs = pudl.extract.eia923.Extractor().extract(eia923_years, testing=True)
# Transform EIA forms 860, 861, 923
eia860_transformed_dfs = pudl.transform.eia860.transform(eia860_raw_dfs, eia860_tables=eia860_tables)
eia861_transformed_dfs = pudl.transform.eia861.transform(eia861_raw_dfs, eia861_tables=eia861_tables)
eia923_transformed_dfs = pudl.transform.eia923.transform(eia923_raw_dfs, eia923_tables=eia923_tables)
# create an eia transformed dfs dictionary
eia_transformed_dfs = eia860_transformed_dfs.copy()
eia_transformed_dfs.update(eia861_transformed_dfs.copy())
eia_transformed_dfs.update(eia923_transformed_dfs.copy())
# convert types..
eia_transformed_dfs = pudl.helpers.convert_dfs_dict_dtypes(eia_transformed_dfs, 'eia')
return eia_transformed_dfs
```
## Dummy EIA 861 Harvesting
* Used to separately test the EIA entity harvesting process with EIA 861
* Doesn't yet work b/c 861 is structured differently than 860/923.
```
def test_harvest_eia(eia_transformed_dfs, eia860_years, eia861_years, eia923_years):
entities_dfs, eia_transformed_dfs = pudl.transform.eia.transform(
eia_transformed_dfs,
eia860_years=eia860_years,
eia861_years=eia861_years,
eia923_years=eia923_years,
)
# convert types..
entities_dfs = pudl.helpers.convert_dfs_dict_dtypes(entities_dfs, 'eia')
# Compile transformed dfs for loading...
return entities_dfs, eia_transformed_dfs
```
## Compare Annual Demand vs. Sales
```
def annual_demand_vs_sales(dhpa_ferc714, sales_eia861, ba_eia861):
"""
Categorize EIA Codes in FERC 714 as BA or Utility IDs.
Most FERC 714 respondent IDs are associated with an `eia_code` which
refers to either a `balancing_authority_id_eia` or a `utility_id_eia`
but no indication is given as to which type of ID each one is. This
is further complicated by the fact that EIA uses the same numerical
ID to refer to the same entity in most but not all cases, when that
entity acts as both a utility and as a balancing authority.
In order to identify which type of ID each `eia_code` is, this
funciton compares the annual demand reported in association with
each code in the FERC 714 hourly planning area time series, and in
the EIA 861 sales table -- using the ID both as a utility and as a
balancing authority ID. The correlation between the FERC 714 demand
and the EIA 861 sales should be much higher for one type of ID than
the other, indicating which type of ID is represented in the FERC
714 data.
Args:
dhpa_ferc714 (pandas.DataFrame): The FERC 714 hourly demand
time series.
sales_eia861 (pandas.DataFrame): The EIA 861 Sales table.
ba_eia861 (pandas.DataFrame): The EIA 861 Balancing Authority
table, which contains the mapping between EIA Balancing
Authority Codes (3-4 letters) and EIA Balancing Authority
IDs (integers). The codes are present in the Sales table,
but the IDs are what the eia_code refers to.
Returns:
pandas.DataFrame: A table containing FERC 714 respondent IDs,
EIA codes, and a column indicating whether that code was
found to be more consistent with Balancing Authority or
Utility electricity demand / sales.
"""
# Sum up FERC 714 demand by report_year and eia_code:
dhpa_ferc714_by_eia_code = (
dhpa_ferc714
.groupby(["eia_code", "report_year"])["demand_mwh"]
.sum()
.reset_index()
)
# Sum up the EIA 861 sales by Utility ID:
sales_eia861_by_util = (
sales_eia861.groupby(["utility_id_eia", "report_date"])["sales_mwh"]
.sum()
.reset_index()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.rename(columns={"sales_mwh": "sales_utility_mwh"})
)
# Need to translate the BA Code to BA ID for comparison w/ eia_code
ba_codes_and_ids = (
ba_eia861[["balancing_authority_code_eia", "balancing_authority_id_eia", "report_date"]]
.drop_duplicates()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.dropna()
)
# Sum up the EIA 861 sales by Balancing Authority Code:
sales_eia861_by_ba = (
sales_eia861
.groupby(["balancing_authority_code_eia", "report_date"], observed=True)["sales_mwh"]
.sum()
.reset_index()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.rename(columns={"sales_mwh": "sales_ba_mwh"})
.query("balancing_authority_code_eia!='UNK'")
.merge(ba_codes_and_ids)
)
# Combine the demand and sales data with all the IDs
demand_and_sales = (
dhpa_ferc714_by_eia_code
.merge(
sales_eia861_by_util,
left_on=["eia_code", "report_year"],
right_on=["utility_id_eia", "report_year"],
how="left"
)
.merge(
sales_eia861_by_ba,
left_on=["eia_code", "report_year"],
right_on=["balancing_authority_id_eia", "report_year"],
how="left"
)
.astype({
"eia_code": pd.Int64Dtype(),
"utility_id_eia": pd.Int64Dtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
})
.assign(
ba_ratio=lambda x: x.sales_ba_mwh / x.demand_mwh,
utility_ratio=lambda x: x.sales_utility_mwh / x.demand_mwh,
)
)
return demand_and_sales
```
## EIA Code Categorization
```
def categorize_eia_code(rids_ferc714, utils_eia860, ba_eia861):
"""
Categorize EIA Codes in FERC 714 as BA or Utility IDs.
Most FERC 714 respondent IDs are associated with an `eia_code` which
refers to either a `balancing_authority_id_eia` or a `utility_id_eia`
but no indication is given as to which type of ID each one is. This
is further complicated by the fact that EIA uses the same numerical
ID to refer to the same entity in most but not all cases, when that
entity acts as both a utility and as a balancing authority.
Given the nature of the FERC 714 hourly demand dataset, this function
assumes that if the `eia_code` appears in the EIA 861 Balancing
Authority table, that it should be labeled `balancing_authority`.
If the `eia_code` appears only in the EIA 860 Utility table, then
it is labeled `utility`. These labels are put in a new column named
`respondent_type`. If the planning area's `eia_code` does not appear in
either of those tables, then `respondent_type is set to NA.
Args:
rids_ferc714 (pandas.DataFrame): The FERC 714 `respondent_id` table.
utils_eia860 (pandas.DataFrame): The EIA 860 Utilities output table.
ba_eia861 (pandas.DataFrame): The EIA 861 Balancing Authority table.
Returns:
pandas.DataFrame: A table containing all of the columns present in
the FERC 714 `respondent_id` table, plus a new one named
`respondent_type` which can take on the values `balancing_authority`,
`utility`, or the special value pandas.NA.
"""
ba_ids = set(ba_eia861.balancing_authority_id_eia.dropna())
util_not_ba_ids = set(utils_eia860.utility_id_eia.dropna()).difference(ba_ids)
new_rids = rids_ferc714.copy()
new_rids["respondent_type"] = pd.NA
new_rids.loc[new_rids.eia_code.isin(ba_ids), "respondent_type"] = "balancing_authority"
new_rids.loc[new_rids.eia_code.isin(util_not_ba_ids), "respondent_type"] = "utility"
ba_rids = new_rids[new_rids.respondent_type=="balancing_authority"]
util_rids = new_rids[new_rids.respondent_type=="utility"]
na_rids = new_rids[new_rids.respondent_type.isnull()]
ba_rids = (
ba_rids.merge(
ba_eia861
.filter(like="balancing_")
.drop_duplicates(subset=["balancing_authority_id_eia", "balancing_authority_code_eia"]),
how="left", left_on="eia_code", right_on="balancing_authority_id_eia"
)
)
util_rids = (
util_rids.merge(
utils_eia860[["utility_id_eia", "utility_name_eia"]]
.drop_duplicates("utility_id_eia"),
how="left", left_on="eia_code", right_on="utility_id_eia"
)
)
new_rids = (
pd.concat([ba_rids, util_rids, na_rids])
.astype({
"respondent_type": pd.StringDtype(),
"balancing_authority_code_eia": pd.StringDtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
"balancing_authority_name_eia": pd.StringDtype(),
"utility_id_eia": pd.Int64Dtype(),
"utility_name_eia": pd.StringDtype(),
})
)
return new_rids
```
## Georeference Balancing Authorities
```
def georef_bas(ba_eia861, st_eia861, sales_eia861, census_gdf):
"""
Create a GeoDataFrame mapping BAs to Utils to county geometries by year.
This GDF includes the following columns:
balancing_authority_id_eia (ba_eia861)
balancing_authority_name_eia (ba_eia861)
balancing_authority_code_eia (ba_eia861)
utility_id_eia (sales_eia861)
utility_name_eia (sales_eia861)
county_id_fips (st_eia861)
county (st_eia861)
state_id_fips (st_eia861)
state (st_eia861)
geometry (census_gdf)
county_name_census (census_gdf)
It includes information both about which counties are associated with
utilities that are part of balancing authorities, and utilities that
are not part part of balancing authorities, so should be possible to
use it to generate geometries for all of the respondents in FERC 714,
both BAs and Utils.
"""
# Make sure that there aren't any more BA IDs we can recover from later years:
ba_ids_missing_codes = (
ba_eia861.loc[ba_eia861.balancing_authority_code_eia.isnull(), "balancing_authority_id_eia"]
.drop_duplicates()
.dropna()
)
assert len(ba_eia861[
(ba_eia861.balancing_authority_id_eia.isin(ba_ids_missing_codes)) &
(ba_eia861.balancing_authority_code_eia.notnull())
]) == 0
# Which utilities were part of what balancing areas in 2010-2012?
early_ba_by_util = (
ba_eia861
.query("report_date <= '2012-12-31'")
.loc[:, [
"report_date",
"balancing_authority_id_eia",
"balancing_authority_code_eia",
"utility_id_eia",
"balancing_authority_name_eia",
]]
.drop_duplicates(subset=["report_date", "balancing_authority_id_eia", "utility_id_eia"])
)
# Create a dataframe that associates utilities and balancing authorities.
# This information is directly avaialble in the early_ba_by_util dataframe
# but has to be compiled for 2013 and later years based on the utility
# BA associations that show up in the Sales table
# Create an annual, normalized version of the BA table:
ba_normed = (
ba_eia861
.loc[:, [
"report_date",
"state",
"balancing_authority_code_eia",
"balancing_authority_id_eia",
"balancing_authority_name_eia",
]]
.drop_duplicates(subset=[
"report_date",
"state",
"balancing_authority_code_eia",
"balancing_authority_id_eia",
])
)
ba_by_util = (
pd.merge(
ba_normed,
sales_eia861
.loc[:, [
"report_date",
"state",
"utility_id_eia",
"balancing_authority_code_eia"
]].drop_duplicates()
)
.loc[:, [
"report_date",
"state",
"utility_id_eia",
"balancing_authority_id_eia"
]]
.append(early_ba_by_util[["report_date", "utility_id_eia", "balancing_authority_id_eia"]])
.drop_duplicates()
.merge(ba_normed)
.dropna(subset=["report_date", "utility_id_eia", "balancing_authority_id_eia"])
.sort_values(["report_date", "balancing_authority_id_eia", "utility_id_eia", "state"])
)
# Merge in county FIPS IDs for each county served by the utility from
# the service territory dataframe. We do an outer merge here so that we
# retain any utilities that are not part of a balancing authority. This
# lets us generate both BA and Util maps from the same GeoDataFrame
# We have to do this separately for the data up to 2012 (which doesn't
# include state) and the 2013 and onward data (which we need to have
# state for)
early_ba_util_county = (
ba_by_util.drop("state", axis="columns")
.merge(st_eia861, on=["report_date", "utility_id_eia"], how="outer")
.query("report_date <= '2012-12-31'")
)
late_ba_util_county = (
ba_by_util
.merge(st_eia861, on=["report_date", "utility_id_eia", "state"], how="outer")
.query("report_date >= '2013-01-01'")
)
ba_util_county = pd.concat([early_ba_util_county, late_ba_util_county])
# Bring in county geometry information based on FIPS ID from Census
ba_util_county_gdf = (
census_gdf[["GEOID10", "NAMELSAD10", "geometry"]]
.to_crs(MAP_CRS)
.rename(
columns={
"GEOID10": "county_id_fips",
"NAMELSAD10": "county_name_census",
}
)
.merge(ba_util_county)
)
return ba_util_county_gdf
```
## Map Balancing Authorities
```
def map_ba(ba_ids, year, ba_util_county_gdf, save=False):
"""
Create a map of a balancing authority for a historical year.
Args:
ba_ids (iterable): A collection of Balancing Authority IDs.
year (int): The year for which to create a map.
ba_util_county_gdf (geopandas.GeoDataFrame): A dataframe
associating report_date, balancing_authority_id_eia, and
county_id_fips.
save (bool): If True, save the figure to disk.
Returns:
None
"""
map_gdf = (
ba_util_county_gdf[
(ba_util_county_gdf.report_date.dt.year == year) &
(ba_util_county_gdf.balancing_authority_id_eia.isin(ba_ids)) &
(~ba_util_county_gdf.county_id_fips.str.match("^02")) & # Avoid Alaska
(~ba_util_county_gdf.county_id_fips.str.match("^15")) & # Avoid Hawaii
(~ba_util_county_gdf.county_id_fips.str.match("^72")) # Avoid Puerto Rico
]
.drop_duplicates(subset=["balancing_authority_id_eia", "county_id_fips"])
)
ax = map_gdf.plot(figsize=(20, 20), color="black", alpha=0.25, linewidth=0.25)
plt.title(f"Balancing Areas ({year=})")
ctx.add_basemap(ax)
if save is True:
plt.savefig(f"BA_Overlap_{year}.jpg")
def compare_hifld_eia_ba(ba_code, hifld_gdf, eia_gdf):
"""
Compare historical EIA BAs vs. HIFLD geometries.
"""
fig, (hifld_ax, eia_ax) = plt.subplots(nrows=1, ncols=2, sharex=True, sharey=True)
hifld_ax.set_title(f"{ba_code} (HIFLD)")
hifld_gdf[hifld_gdf.ABBRV==ba_code].to_crs(MAP_CRS).plot(ax=hifld_ax, linewidth=0)
eia_ax.set_title(f"{ba_code} (EIA)")
eia_gdf[
(eia_gdf.balancing_authority_code_eia==ba_code) &
(eia_gdf.report_date.dt.year == 2017)
].plot(ax=eia_ax, linewidth=0.1)
plt.show()
```
# Read Data
## EIA 860 via PUDL Outputs
```
plants_eia860 = pudl_out.plants_eia860()
utils_eia860 = pudl_out.utils_eia860()
```
## EIA 861 (2010-2018)
* Not yet fully integrated into PUDL
* Post-transform harvesting process isn't compatible w/ EIA 861 structure
* Only getting the `sales_eia861`, `balancing_authority_eia861`, and `service_territory_eia861` tables
```
%%time
logger.setLevel("WARN")
eia_years = list(range(2010, 2019))
eia_inputs = {
"eia860_years": [],
"eia860_tables": pudl.constants.pudl_tables["eia860"],
"eia861_years": eia_years,
"eia861_tables": pudl.constants.pudl_tables["eia861"],
"eia923_years": [],
"eia923_tables": pudl.constants.pudl_tables["eia923"],
}
eia_transformed_dfs = test_etl_eia(eia_inputs=eia_inputs, pudl_settings=pudl_settings)
logger.setLevel("INFO")
ba_eia861 = eia_transformed_dfs["balancing_authority_eia861"].copy()
st_eia861 = eia_transformed_dfs["service_territory_eia861"].copy()
sales_eia861 = eia_transformed_dfs["sales_eia861"].copy()
raw_eia861_dfs = pudl.extract.eia861.Extractor().extract(years=range(2010,2019), testing=True)
```
## FERC 714 (2006-2018)
```
%%time
logger.setLevel("WARN")
raw_ferc714 = pudl.extract.ferc714.extract(pudl_settings=pudl_settings)
tfr_ferc714 = pudl.transform.ferc714.transform(raw_ferc714)
logger.setLevel("INFO")
```
## HIFLD Electricity Planning Areas (2018)
* Electricty Planning Area geometries from HIFLD.
* Indexed by `ID` which corresponds to EIA utility or balancing area IDs.
* Only valid for 2017-2018.
```
hifld_pa_gdf = (
pudl.analysis.demand_mapping.get_hifld_planning_areas_gdf(pudl_settings)
.to_crs(MAP_CRS)
)
```
## US Census DP1 (2010)
* This GeoDataFrame contains county-level geometries and demographic data.
```
%%time
census_gdf = (
pudl.analysis.demand_mapping.get_census2010_gdf(pudl_settings, layer="county")
.to_crs(MAP_CRS)
)
```
# Combine Data
## Categorize FERC 714 Respondent IDs
```
rids_ferc714 = (
tfr_ferc714["respondent_id_ferc714"]
.pipe(categorize_eia_code, utils_eia860, ba_eia861)
)
```
## Add FERC 714 IDs to HIFLD
```
hifld_pa_gdf = (
hifld_pa_gdf
.merge(rids_ferc714, left_on="ID", right_on="eia_code", how="left")
)
```
## Add Respondent info to FERC 714 Demand
```
dhpa_ferc714 = pd.merge(
tfr_ferc714["demand_hourly_pa_ferc714"],
tfr_ferc714["respondent_id_ferc714"],
on="respondent_id_ferc714",
how="left", # There are respondents with no demand
)
```
# Utilities vs. Balancing Authorities
Exploration of the Balancing Authority EIA 861 table for cleanup
### Which columns are available in which years?
| Year | BA ID | BA Name | BA Code | Util ID | Util Name | State | N |
|------|-------|---------|---------|---------|-----------|-------|----|
| 2010 | XXXXX | XXXXXXX | | XXXXXXX | | |3193|
| 2011 | XXXXX | XXXXXXX | | XXXXXXX | | |3126|
| 2012 | XXXXX | XXXXXXX | | XXXXXXX | XXXXXXXXX | |3146|
| 2013 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 239|
| 2014 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 208|
| 2015 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2016 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2017 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2018 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 204|
### What does this table mean?
* In 2010-2012, the table says which utilities (by ID) are included in which balancing authorities.
* In 2013-2018, the table indicates which *states* a BA is operating in, and also provides a BA Code
### Questions:
* Where does the `balancing_authority_code` show up elsewhere in the EIA 860/861 data?
* `plants_eia860` (nowhere else that I know of)
* Are the BA to Utility mappings likely to remain valid throughout the entire time period? Can we propagate them forward?
* No, there's some variation year to year in which utilities are associated with which BAs
* Are the BA Code/Name to BA ID mappings permanent?
* No they aren't -- when a BA changes owners and names, the code changes, but ID stays the same.
## Untangling HIFLD, FERC 714, & EIA IDs
* There are unspecified "EIA codes" associated with FERC 714 respondents.
* These IDs correspond to a mix of `utility_id_eia` and `balancing_authority_id_eia` values.
* Similarly, the ID field of the HIFLD geometries are a mix of BA and Utility IDs from EIA.
* This is extra confusing, because EIA *usually* uses the *same* ID for BAs and Utils.
* However, the EIA BA and Util IDs appear to be distinct namespaces
* Not all IDs which appear in both tables identify the same entity in both tables.
* In a few cases different IDs are used to identify the same entity when it shows up in both tables.
* It could be that whoever entered the IDs in the FERC 714 / HIFLD datasets didn't realize these were different sets of IDs.
### BA / Utility ID Overlap
* Example of an ID that shows up in both, but refers to different entities, see `59504`
* `balancing_area_id_eia == 59504` is the Southwest Power Pool (SWPP).
* `utility_id_eia == 59504` is Kirkwood Community College, in MO.
* Example of an entity that exists in both datsets, but shows up with different IDs, see PacifiCorp.
* Has two BA IDs (East and West): `[14379, 14378]`
* Has one Utility ID: `14354`
* Example of an entity that shows up with the same ID in both tables:
* ID `15466` is Public Service Co of Colorado -- both a BA (PSCO) and a Utility.
```
# BA ID comes from EIA 861 BA Table
ba_ids = set(ba_eia861.balancing_authority_id_eia)
print(f"Total # of BA IDs: {len(ba_ids)}")
# Util ID comes from EIA 860 Utilities Entity table.
util_ids = set(pudl_out.utils_eia860().utility_id_eia)
print(f"Total # of Util IDs: {len(util_ids)}")
ba_not_util_ids = ba_ids.difference(util_ids)
print(f"BA IDs that are not Util IDs: {len(ba_not_util_ids)}")
util_not_ba_ids = util_ids.difference(ba_ids)
print(f"Util IDs that are not BA IDs: {len(util_not_ba_ids)}")
ba_and_util_ids = ba_ids.intersection(util_ids)
print(f"BA IDs that are also Util IDs: {len(ba_and_util_ids)}")
ba_and_util = (
ba_eia861
.loc[:, ["balancing_authority_id_eia", "balancing_authority_name_eia"]]
.dropna(subset=["balancing_authority_id_eia"])
.merge(
pudl_out.utils_eia860(),
left_on="balancing_authority_id_eia",
right_on="utility_id_eia",
how="inner"
)
.loc[:, [
"utility_id_eia",
"balancing_authority_name_eia",
"utility_name_eia",
]]
.rename(columns={"utility_id_eia": "util_ba_id"})
.drop_duplicates()
.reset_index(drop=True)
)
ba_not_util = (
ba_eia861.loc[ba_eia861.balancing_authority_id_eia.isin(ba_not_util_ids)]
.loc[:,["balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia"]]
.drop_duplicates(subset=["balancing_authority_id_eia", "balancing_authority_code_eia"])
.sort_values("balancing_authority_id_eia")
)
```
### Missing IDs
* There are `eia_code` values that don't show up in the list of balancing authority IDs (2010-2018).
* There are also `eia_code` values that don't show up in the list of utility IDs (2009-2018).
* There are a few `eia_code` values that don't show up in either!
* Mostly this is an artifact of the different time covered by FERC 714 (2006-2018).
* If we look only at the respondents that reported non-zero demand for 2010-2018, we find that all of the `eia_code` values *do* appear in either the `blancing_authority_eia861` or `utilities_eia860` tables.
```
rids_ferc714[
(~rids_ferc714.eia_code.isin(ba_eia861.balancing_authority_id_eia.unique())) &
(~rids_ferc714.eia_code.isin(utils_eia860.utility_id_eia.unique()))
]
rids_recent = (
dhpa_ferc714
.groupby(["respondent_id_ferc714", "report_year"])
.agg({"demand_mwh": sum})
.reset_index()
.query("report_year >= 2010")
.query("demand_mwh >= 0.0")
.merge(rids_ferc714[["eia_code", "respondent_id_ferc714", "respondent_name_ferc714"]], how="left")
.drop(["report_year", "demand_mwh"], axis="columns")
.drop_duplicates()
)
assert len(rids_recent[
(~rids_recent.eia_code.isin(ba_eia861.balancing_authority_id_eia.unique())) &
(~rids_recent.eia_code.isin(utils_eia860.utility_id_eia.unique()))
]) == 0
```
### BA to Utility Mappings are Many to Many
* Unsurprisingly, BAs often contain many utilities.
* However, it's also common for utilities to participate in more than one BA.
* About 1/3 of all utilities show up in association with more than one BA
```
ba_to_util_mapping = (
ba_eia861[["balancing_authority_id_eia", "utility_id_eia"]]
.dropna(subset=["balancing_authority_id_eia", "utility_id_eia"])
.drop_duplicates(subset=["balancing_authority_id_eia", "utility_id_eia"])
.groupby(["balancing_authority_id_eia"])
.agg({
"utility_id_eia": "count"
})
)
plt.hist(ba_to_util_mapping.utility_id_eia, bins=99, range=(1,100))
plt.xlabel("# of Utils / BA")
plt.ylabel("# of BAs")
plt.title("Number of Utilities per Balancing Area");
util_to_ba_mapping = (
ba_eia861[["balancing_authority_id_eia", "utility_id_eia"]]
.dropna(subset=["balancing_authority_id_eia", "utility_id_eia"])
.drop_duplicates(subset=["balancing_authority_id_eia", "utility_id_eia"])
.groupby(["utility_id_eia"])
.agg({
"balancing_authority_id_eia": "count"
})
)
plt.hist(util_to_ba_mapping.balancing_authority_id_eia, bins=4, range=(1,5))
plt.title("Number of Balancing Authorities per Utility");
```
## Georeferenced Demand Fraction
* With their original EIA codes the HIFLD Electricity Planning Areas only georeference some of the FERC 714 demand.
* It's about 86% in 2018. In 2013 and earlier years, the fraction starts to drop off more quickly, to 76% in 2010, and 58% in 2006.
* After manually identifying and fixing some bad and missing EIA codes in the FERC 714, the mapped fraction is much higher.
* 98% or more in 2014-2018, dropping to 87% in 2010, and 68% in 2006
* **However** because the geometries have also evolved over time, just the fact that the demand time series is linked to **some** HIFLD geometry, doesn't mean that it's the **right** geometry.
```
annual_demand_ferc714 = (
dhpa_ferc714
.groupby(["report_year"]).demand_mwh.sum()
.reset_index()
)
annual_demand_mapped = (
dhpa_ferc714[dhpa_ferc714.eia_code.isin(hifld_pa_gdf.eia_code)]
.groupby(["report_year"]).demand_mwh.sum()
.reset_index()
.merge(annual_demand_ferc714, on="report_year", suffixes=("_map", "_tot"))
.assign(
fraction_mapped=lambda x: x.demand_mwh_map / x.demand_mwh_tot
)
)
plt.plot("report_year", "fraction_mapped", data=annual_demand_mapped, lw=5)
plt.ylabel("Fraction of demand which is mapped")
plt.title("Completeness of HIFLD demand mapping by year")
plt.ylim(0.6, 1.05);
```
# Historical Planning Area Geometries
Compile a GeoDataFrame that relates balancing authorities, their constituent utilities, and the collections of counties which are served by those utilities, across all the years for which we have EIA 861 data (2010-2018)
```
ba_util_county_gdf = georef_bas(ba_eia861, st_eia861, sales_eia861, census_gdf)
ba_util_county_gdf.info()
for year in (2010, 2014, 2018):
map_ba(ba_util_county_gdf.balancing_authority_id_eia.unique(), year, ba_util_county_gdf, save=True)
```
## Output Simplified Annual BA Geometries
* This takes half an hour so it's commented out.
* Resulting shapefile is ~250MB compressed. Seems too big.
* Need to figure out how to add explicity projection.
* Need to figure out how to make each year's BA geometries its own layer.
```
#%%time
#ba_fips_simplified = (
# ba_util_county_gdf
# .assign(report_year=lambda x: x.report_date.dt.year)
# .drop([
# "report_date",
# "state",
# "state_id_fips",
# "county",
# "county_name_census",
# "utility_id_eia",
# "utility_name_eia"
# ], axis="columns")
# .drop_duplicates(subset=["report_year", "balancing_authority_id_eia", "county_id_fips"])
# .dropna(subset=["report_year", "balancing_authority_id_eia", "county_id_fips"])
# .loc[:,["report_year", "balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia", "county_id_fips", "geometry"]]
#)
#ba_annual_gdf = (
# ba_fips_simplified
# .dissolve(by=["report_year", "balancing_authority_id_eia"])
# .reset_index()
# .drop("county_id_fips", axis="columns")
#)
#ba_output_gdf = (
# ba_annual_gdf
# .astype({
# "report_year": int,
# "balancing_authority_id_eia": float,
# "balancing_authority_code_eia": str,
# "balancing_authority_name_eia": str,
# })
# .rename(columns={
# "report_year": "year",
# "balancing_authority_id_eia": "ba_id",
# "balancing_authority_code_eia": "ba_code",
# "balancing_authority_name_eia": "ba_name",
# })
#)
#ba_output_gdf.to_file("ba_annual.shp")
```
## Compare HIFLD and EIA BA maps for 2018
```
for ba_code in hifld_pa_gdf.ABBRV.unique():
if ba_code in ba_util_county_gdf.balancing_authority_code_eia.unique():
compare_hifld_eia_ba(ba_code, hifld_pa_gdf, ba_util_county_gdf)
```
## Time Evolution of BA Geometries
For each BA we now have a collection of annual geometries. How have they changed over time?
```
for ba_code in ba_util_county_gdf.balancing_authority_code_eia.unique():
fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(20,20), sharex=True, sharey=True, facecolor="white")
for year, ax in zip(range(2010, 2019), axes.flat):
ax.set_title(f"{ba_code} ({year})")
ax.set_xticks([])
ax.set_yticks([])
plot_gdf = (
ba_util_county_gdf
.assign(report_year=lambda x: x.report_date.dt.year)
.query(f"balancing_authority_code_eia=='{ba_code}'")
.query(f"report_year=='{year}'")
.drop_duplicates(subset="county_id_fips")
)
plot_gdf.plot(ax=ax, linewidth=0.1)
plt.show()
```
## Merge Geometries with FERC 714
Now that we have a draft of wht the BA and Utility level territories look like, we can merge those with the FERC 714 Respondent ID table, and see how many leftovers there are, and whether the BA and Utility geometires play well together.
Before dissolving the boundaries between counties the output dataframe needs to have:
* `report_date`
* `respondent_id_ferc714`
* `eia_code`
* `respondent_type`
* `balancing_authority_id_eia`
* `utility_id_eia`
* `county_id_fips`
* `geometry`
* `balancing_authority_code_eia`
* `balancing_authority_name_eia`
* `respondent_name_ferc714`
* `utility_name_eia`
* `county_name_census`
* `state`
* `state_id_fips`
```
utils_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type == "utility",
["respondent_id_ferc714", "respondent_name_ferc714", "utility_id_eia", "respondent_type"]
]
)
bas_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type == "balancing_authority",
["respondent_id_ferc714", "respondent_name_ferc714", "balancing_authority_id_eia", "respondent_type"]
]
)
null_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type.isnull(),
["respondent_id_ferc714", "respondent_name_ferc714", "respondent_type"]
]
)
bas_ferc714_gdf = (
ba_util_county_gdf
.drop(["county"], axis="columns")
.merge(bas_ferc714, how="right")
)
utils_ferc714_gdf = (
ba_util_county_gdf
.drop(["balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia", "county"], axis="columns")
.drop_duplicates()
.merge(utils_ferc714, how="right")
)
rids_ferc714_gdf = (
pd.concat([bas_ferc714_gdf, utils_ferc714_gdf, null_ferc714])
.astype({
"county_id_fips": pd.StringDtype(),
"county_name_census": pd.StringDtype(),
"respondent_type": pd.StringDtype(),
"utility_id_eia": pd.Int64Dtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
"balancing_authority_code_eia": pd.StringDtype(),
"balancing_authority_name_eia": pd.StringDtype(),
"state": pd.StringDtype(),
"utility_name_eia": pd.StringDtype(),
})
)
display(rids_ferc714_gdf.info())
rids_ferc714_gdf.sample(10)
```
## Check Geometries for Completeness
* How many balancing authorities do we have geometries for?
* How many utilities do we have geometries for?
* Do those geometries cover all of the entities that report in FERC 714?
* Do we have a geometry for every entity in every year in which it reports demand?
### Count BA & Util Geometries
```
n_bas = len(rids_ferc714_gdf.balancing_authority_id_eia.unique())
logger.info(f"Found territories for {n_bas} unique Balancing Areas")
n_utils = len(rids_ferc714_gdf.loc[
(rids_ferc714_gdf.balancing_authority_id_eia.isnull()) &
(~rids_ferc714_gdf.utility_id_eia.isnull())
].utility_id_eia.unique())
logger.info(f"Found territories for {n_utils} Utilities outside of the BAs")
```
### Identify Missing Geometries
* Within each year of historical data from 2010-2018, are there any entities (either BA or Utility) which **do** have hourly demand reported in the FERC 714, for whivh we do not have a historical geometry?
* How many of them are there?
* Why are they missing?
* Do we have the geometires in adjacent years and can we re-use them?
* Is it possible that the FERC 714 IDs correspond to a precursor entity, or one that was discontinued? E.g. if SWPP is missing in 2010, is that because the BA was reported in EIA as SPS in that year?
* How important are the missing geometries? Do the associated entities have a lot of demand associated with them in FERC 714?
* Can we use `ffill` or `backfill` on the `geometry` column in a GeoDataFrame?
```
problem_ids = pd.DataFrame()
for year in range(2010, 2019):
this_year_gdf = (
rids_ferc714_gdf
.loc[(rids_ferc714_gdf.report_date.dt.year==year) & (~rids_ferc714_gdf.geometry.isnull())]
)
# All BA IDs which show up in FERC 714:
ba_ids_ferc714 = (
rids_ferc714
.loc[rids_ferc714.respondent_type=="balancing_authority",
"balancing_authority_id_eia"]
.unique()
)
# BA IDs which have a geometry in this year
ba_geom_ids = (
this_year_gdf
.balancing_authority_id_eia
.dropna().unique()
)
# BA IDs which have reported demand in this year
ba_demand_ids = (
dhpa_ferc714
.query("report_year==@year")
.query("demand_mwh>0.0")
.loc[dhpa_ferc714.eia_code.isin(ba_ids_ferc714)]
.eia_code.unique()
)
# Need to make the demand IDs clearly either utility of BA IDs. Whoops!
missing_ba_geom_ids = [x for x in ba_demand_ids if x not in ba_geom_ids]
logger.info(f"{len(missing_ba_geom_ids)} BA respondents w/o geometries in {year}")
problem_ids = problem_ids.append(
rids_ferc714
.loc[rids_ferc714.balancing_authority_id_eia.isin(missing_ba_geom_ids)]
.assign(year=year)
)
# All EIA Utility IDs which show up in FERC 714:
util_ids_ferc714 = (
rids_ferc714
.loc[rids_ferc714.respondent_type=="utility",
"utility_id_eia"]
.unique()
)
# EIA Utility IDs which have geometry information for this year
util_geom_ids = (
this_year_gdf
.utility_id_eia
.dropna().unique()
)
util_demand_ids = (
dhpa_ferc714
.query("report_year==@year")
.query("demand_mwh>0.0")
.loc[dhpa_ferc714.eia_code.isin(util_ids_ferc714)]
.eia_code.unique()
)
missing_util_geom_ids = [x for x in util_demand_ids if x not in util_geom_ids]
logger.info(f"{len(missing_util_geom_ids)} Utility respondents w/o geometries in {year}")
problem_ids = problem_ids.append(
rids_ferc714
.loc[rids_ferc714.utility_id_eia.isin(missing_util_geom_ids)]
.assign(year=year)
)
problem_ids.query("year==2010").query("respondent_type=='balancing_authority'")
```
## Dissolve to BA or Util
* At this point we still have geometires at the county level.
* This is 150,000+ records.
* Really we just want a single geometry per respondent per year.
* Dissolve based on year and respondent_id_ferc714.
* Merge the annual per-respondent geometry with the rids_ferc714 which has more information
* Note that this takes about half an hour to run...
```
%%time
dissolved_rids_ferc714_gdf = (
rids_ferc714_gdf.drop_duplicates(subset=["report_date", "county_id_fips", "respondent_id_ferc714"])
.dissolve(by=["report_date", "respondent_id_ferc714"])
.reset_index()
.loc[:, ["report_date", "respondent_id_ferc714", "geometry"]]
.merge(rids_ferc714, on="respondent_id_ferc714", how="outer")
)
#dissolved_rids_ferc714_gdf.to_file("planning_areas_ferc714.gpkg", driver="GPKG")
```
### Select based on respondent type
```
dissolved_utils = dissolved_rids_ferc714_gdf.query("respondent_type=='utility'")
dissolved_bas = dissolved_rids_ferc714_gdf.query("respondent_type=='balancing_authority'")
```
### Nationwide BA / Util Maps
* Still want to add the US state boundaries / coastlines to this for context.
```
unwanted_ba_ids = (
112, # Alaska
133, # Alaska
178, # Hawaii
301, # PJM Dupe
302, # PJM Dupe
303, # PJM Dupe
304, # PJM Dupe
305, # PJM Dupe
306, # PJM Dupe
)
for report_date in pd.date_range(start="2010-01-01", end="2018-01-01", freq="AS"):
ba_ax = (
dissolved_bas
.query("report_date==@report_date")
.query("respondent_id_ferc714 not in @unwanted_ba_ids")
.plot(figsize=(20, 20), color="blue", alpha=0.25, linewidth=1)
)
plt.title(f"FERC 714 Balancing Authority Respondents {report_date}")
ctx.add_basemap(ba_ax)
util_ax = (
dissolved_utils
.query("report_date==@report_date")
.plot(figsize=(20, 20), color="red", alpha=0.25, linewidth=1)
)
plt.title(f"FERC 714 Utility Respondents {report_date}")
ctx.add_basemap(util_ax)
plt.show();
```
### Per-respondent annual maps
* For each respondent make a grid of 9 (2010-2018)
* Show state lines in bg for context
* Limit bounding box by the respondent's territory
# Remaining Tasks
## Geometry Cleanup:
* Why do some respondents lack geometries in some years?
* Why do some respondents lack geometries in **all** years? (e.g. Tri-State G&T)
* Why do some counties have no BA or Utility coverage in some or all years?
* What combinations of years and respondents are missing?
* Compare what we've ended up doing to the Aufhammer paper again.
* Is there any need to use name-based matching between the Planning Area descriptions & EIA Service Territories?
* Problem BAs / Utilities:
* All the WAPA BAs
* PacifiCorp East / West
* Southern Company
* MISO (Some other IDs that seem related?)
* PJM (Early years seem out of bounds)
## FERC 714 Demand Time Series Cleanup
### Find broken data:
* Run Tyler Ruggles' anomaly detection code as improved by Greg Schivley
* What kind of anomalies are we finding? Are they a problem? What portion of the overall dataset do they represent?
### Repair data:
* How do we want to fill in the gaps?
* Ideally would be able to use the MICE technique that Tyler used, but we need to keep it all in Python.
* Can do much simpler rolling averages or something for the moment when there are small gaps just to have completeness.
* Should make this gap filling process modular -- use different techniques and see whether they do what we need.
# Miscellaneous Notes
## FERC 714 Demand Irregularities
Unusual issues that need to be addressed, or demand discontinuities that may be useful in the context of aggregating historical demand into modern planning areas. Organized by FERC 714 Respondent ID:
* Missing demand data / weird zeroes
* 111: (2008)
* 125: (2015)
* 137: (2006)
* 139: (2006) Only the last hour of every day. Maybe 0-23 vs 1-24 reporting?
* 141: (2006, 2007, 2008, 2009, 2010)
* 148: (2006)
* 153: (2006)
* 154: (2006)
* 161: (all)
* 183: (2007, 2009)
* 208: (2008)
* 273: (2007, 2008)
* 283: (2007)
* 287: (2008-2012)
* 288: (2006)
* 289: (2009)
* 293: (2006)
* 294: (2006)
* 311: (2008-2011)
* Inverted Demand (Sign Errors):
* 156: (2006, 2007, 2008, 2009)
* 289: (2006-2008, 2010)
* Large demand discontinuities
* 107: Demand triples at end of 2006.
* 115: Two big step downs, 2007-2008, and 2011-2012
* 121: 50% increase at end of 2007.
* 128: Step up at end of 2007
* 133: Step down end of 2013 and again end of 2015
* 190: Demand doubled at end of 2008
* 214: 50% jump in early 2012.
* 256: big jump at end of 2006.
* 261: Big jump at end of 2008.
* 274: drop at end of 2007
* 275: Jump at end of 2007
* 287: Demand before and after big gap are very different.
* 299: Big drop at end of 2015
* 307: Jump at end of 2014
* 321: Jump at end of 2013
| github_jupyter |
<center>
<hr>
<h1>Python Crash Course</h1>
<h2>Master in Data Science - Sapienza University</h2>
<h2>Homework 2: Python Challenges</h2>
<h3>A.A. 2017/18</h3>
<h3>Tutor: Francesco Fabbri</h3>
<hr>
</center>

# Instructions
So guys, here we are! **Finally** you're facing your first **REAL** homework. Are you ready to fight?
We're going to apply all the Pythonic stuff seen before AND EVEN MORE...
## Simple rules:
1. Don't touch the instructions, you **just have to fill the blank rows**.
2. This is supposed to be an exercise for improving your Pythonic Skills in a spirit of collaboration so...of course you can help your classmates and obviously get a really huge help as well from all the others (as the proverb says: "I get help from you and then you help me", right?!...)
3. **RULE OF THUMB** for you during the homework:
- *1st Step:* try to solve the problem alone
- *2nd Step:* googling random the answer
- *3rd Step:* ask to your colleagues
- *3rd Step:* screaming and complaining about life
- *4th Step:* ask to Tutors
## And the Prize? The Beer?The glory?!:
Guys the life is hard...in this Master it's even worse...
Soooo, since that you seem so smart I want to test you before the start of all the courses.
.
.
.
But not now.
You have to come prepared to the challenge, so right now solve these first 6 exercises, then it will be the time for **FIGHTING** and (for one of you) **DRINKING**.

# Warm-up...
### 1. 12! is equal to...
```
def fatt(n):
if(n == 0):
return 1
else:
return n*fatt(n-1)
fatt(12)
```
### 2. More math...
Write a program which will find all such numbers which are divisible by 7 but are not a multiple of 5, between 0 and 1000 (both included). The numbers obtained should be printed in a comma-separated sequence on a single line. (range and CFS)
```
ex_2=[str(x) for x in range (1001) if x%7 ==0 and x%5 !=0]
','.join(ex_2)
```
### 2. Count capital letters
In this exercises you're going to deal with YOUR DATA. Indeed, in the list below there are stored your Favorite Tv Series. But, as you can see, there is something weird. There are too much CaPITal LeTTErs. Your task is to count the capital letters in all the strings and then print the total number of capital letters in all the list.
```
tv_series = ['Game of THRroneS',
'big bang tHeOrY',
'MR robot',
'WesTWorlD',
'fIRefLy',
"i haven't",
'HOW I MET your mothER',
'friENds',
'bRon broen',
'gossip girl',
'prISon break',
'breaking BAD']
count=0
for string in tv_series:
for letter in string:
if letter.lower() == letter:
pass
else:
count+=1
count
```
### 3. A remark
Using the list above, create a dictionary where the keys are Unique IDs and values the TV Series.
You have to do the exercise keeping in mind these 2 constraints:
1. The order of the IDs has to be **dependent on the alphabetical order of the titles**, i.e. 0: first_title_in_alphabetical_order and so on...
2. **Solve the mess** of the capital letter: we want them only at the start of the words ("prISon break" should be "Prison Break")
```
# write here your code
newlst = []
for x in tv_series:
x.title()
newlst.append(x.title())
newlst
a=range(12)
b=sorted(newlst)
dict1=dict(zip(a,b))
dict1
```
### 4. Dictionary to its maximum
Invert the keys with the values in the dictionary built before.
```
# write here your code
inv= {v: k for k, v in dict1.items()}
inv
```
Have you done in **one line of code**? If not, try now!
```
# write here your code
already done :D
```
### 4. Other boring math
Let's talk about our beloved exams. Starting from the exams and CFU below, are you able to compute the weighted mean of them?
Let's do it and print the result.
Description of the data:
exams[1] = $(title_1, grade_1)$
cfu[1] = $CFU_1$
```
exams = [('BIOINFORMATICS', 29),
('DATA MANAGEMENT FOR DATA SCIENCE', 30),
('DIGITAL EPIDEMIOLOGY', 26),
('NETWORKING FOR BIG DATA AND LABORATORY',28),
('QUANTITATIVE MODELS FOR ECONOMIC ANALYSIS AND MANAGEMENT','30 e lode'),
('DATA MINING TECHNOLOGY FOR BUSINESS AND SOCIETY', 30),
('STATISTICAL LEARNING',30),
('ALGORITHMIC METHODS OF DATA MINING AND LABORATORY',30),
('FUNDAMENTALS OF DATA SCIENCE AND LABORATORY', 29)]
cfu = sum([6,6,6,9,6,6,6,9,9])
cfu
type(exams [0])
a=list(zip (*exams))[1]
a
type (a)
singlecfu=([6,6,6,9,6,6,6,9,9])
b= (a[]*singlecfu[])/(cfu)
b
mean= dict2 [0]
```
### 5. Palindromic numbers
Write a script which finds all the Palindromic numbers, in the range [0,**N**] (bounds included). The numbers obtained should be printed in a comma-separated sequence on a single line.
What is **N**?
Looking at the exercise before:
**N** = (Total number of CFU) x (Sum of all the grades)
(details: https://en.wikipedia.org/wiki/Palindromic_number)
```
def pali(n):
return str(n) == str(n)[::-1]
a=list(filter(pali, range(0,15876)))
print(a)
?filter
```
### 6. StackOverflow
Let's start using your new best friend. Now I'm going to give other task, slightly more difficult BUT this time, just googling, you will find easily the answer on the www.stackoverflow.com. You can use the code there for solving the exercise BUT you have to understand the solution there **COMMENTING** the code, showing me you understood the thinking process behind the code.
### 6. A
Show me an example of how to use **PROPERLY** the *Try - Except* statements
```
# write here your code
```
#### 6. B
Giving this list of words below, after copying in a variable, explain and provide me a code for obtaining a **Bag of Words** from them.
(Hint: use dictionaries and loops)
['theory', 'of', 'bron', 'firefly', 'thrones', 'break', 'bad', 'mother', 'firefly', "haven't", 'prison', 'big', 'friends', 'girl', 'westworld', 'bad', "haven't", 'gossip', 'thrones', 'your', 'big', 'how', 'friends', 'theory', 'your', 'bron', 'bad', 'bad', 'breaking', 'met', 'breaking', 'breaking', 'game', 'bron', 'your', 'breaking', 'met', 'bang', 'how', 'mother', 'bad', 'theory', 'how', 'i', 'friends', "haven't", 'of', 'of', 'gossip', 'i', 'robot', 'of', 'prison', 'bad', 'friends', 'friends', 'i', 'robot', 'bang', 'mother', 'bang', 'i', 'of', 'bad', 'friends', 'theory', 'i', 'friends', 'thrones', 'prison', 'theory', 'theory', 'big', 'of', 'bang', 'how', 'thrones', 'bang', 'theory', 'friends', 'game', 'bang', 'mother', 'broen', 'bad', 'game', 'break', 'break', 'bang', 'big', 'gossip', 'robot', 'met', 'i', 'game', 'your', 'met', 'bad', 'firefly', 'your']
```
# write here your code
```
#### 6. C
And now, write down a code which computes the first 10 Fibonacci numbers
(details: https://en.wikipedia.org/wiki/Fibonacci_number)
```
# write here your code
```
| github_jupyter |
```
import numpy
import numpy as np
# import matplotlib
import matplotlib.pyplot as plt
# set the figure size for each figure in this tutorial
plt.rcParams["figure.figsize"] = (10,6)
```
## Lineplot
```
# 200 values from the interval <0,100>, equidistantly divided
x = np.linspace(0,100,200)
y = np.sin(x)
# a line plot
plt.plot(x,y,'red')
plt.show()
```
## scatterplot
```
# 200 random values from the interval <0,10>
x = 10*np.random.rand(200,1)
# 200 random values from the interval <0,15>
y = 15*np.random.rand(200,1)
# a scatter plot
plt.scatter(x,y)
plt.show()
```
## histogram
```
# 200 random values from the interval <0,15>
y = 15*np.random.rand(200,1)
# a histogram with 20 bins
plt.hist(y,bins=20)
plt.show()
```
## Graphs on common axes
```
# 200 values from the interval <0,100>, equidistantly divided
x = np.linspace(0,100,200)
# sin(x) values
y1 = np.sin(x)
# sin(x)*cos(x) values
y2 =(np.sin(x))*(np.cos(x))
# a line plot of sin(x), red line
plt.plot(x,y1,'red')
# a line plot of sin(x)*cos(x), blue line
plt.plot(x,y2,'blue')
plt.show()
```
## Subplots
```
# the first figure
plt.subplot(2,1,1)
plt.plot(x,y1,'red')
plt.title('sin(x)')
# the second figure
plt.subplot(2,1,2)
plt.plot(x,y2,'blue')
plt.title('sin(x)*(cos(x))')
# automatically adjust the subplot parameters to give a specified padding
plt.tight_layout()
plt.show()
```
## Legends
```
# import pandas
import pandas as pd
# import sklearn datasets
from sklearn import datasets
# load iris dataset
iris = datasets.load_iris()
# create dataframe
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)
# create target
iris_df['target'] = iris.target
# map the target values to the target names
iris_df['target_name'] =iris_df.target.map(
{0: 'setosa',
1: 'versicolor',
2: 'virginica'}
)
iris_df.head()
# Iris setosa
setosa = iris_df[iris_df.target_name == 'setosa']
# Iris versicolor
versicolor = iris_df[iris_df.target_name == 'versicolor']
# Iris virginica
virginica = iris_df[iris_df.target_name == 'virginica']
# plot setosa
plt.scatter(setosa['sepal length (cm)'], setosa['sepal width (cm)'],
marker ='o', color = 'red', label = 'setosa')
# plot versicolor
plt.scatter(versicolor['sepal length (cm)'], versicolor['sepal width (cm)'],
marker ='o', color = 'green', label = 'versicolor')
# plot virginica
plt.scatter(virginica['sepal length (cm)'], virginica['sepal width (cm)'],
marker ='o', color = 'blue', label = 'virginica')
# legend location
plt.legend(loc='upper right')
# plot title
plt.title('Iris flower')
# x-axis title
plt.xlabel('sepal length (cm)')
# y-axis title
plt.ylabel('sepal width (cm)')
plt.show()
```
## Annotations
```
# the same code as before
plt.scatter(setosa['sepal length (cm)'],setosa['sepal width (cm)'],
marker ='o', color = 'red', label = 'setosa')
plt.scatter(versicolor['sepal length (cm)'],versicolor['sepal width (cm)'],
marker ='o', color = 'green', label = 'versicolor')
plt.scatter(virginica['sepal length (cm)'],virginica['sepal width (cm)'],
marker ='o', color = 'blue', label = 'virginica')
# new lines of code
# it can be tricky to find the right coordinates for the first time
######################
plt.annotate('setosa', xy =(5.0,3.5),
xytext = (4.25,4.0), arrowprops={'color':'red'})
plt.annotate('versicolor', xy =(7.2,3.6),
xytext = (6.5,4.0), arrowprops={'color':'red'})
plt.annotate('virginica', xy =(5.05,1.95),
xytext = (5.5,1.75), arrowprops={'color':'red'})
######################
# the same code as before
plt.legend(loc='upper right')
plt.title('Iris flower')
plt.xlabel('sepal length (cm)')
plt.ylabel('sepal width (cm)')
plt.ylim(1.5,4.7)
plt.show()
```
| github_jupyter |
```
import numpy as np
import cv2
import matplotlib.pyplot as plt
from keras import models
import keras.backend as K
import tensorflow as tf
from sklearn.metrics import f1_score
import requests
import xmltodict
import json
plateCascade = cv2.CascadeClassifier('indian_license_plate.xml')
#detect the plate and return car + plate image
def plate_detect(img):
plateImg = img.copy()
roi = img.copy()
plateRect = plateCascade.detectMultiScale(plateImg,scaleFactor = 1.2, minNeighbors = 7)
for (x,y,w,h) in plateRect:
roi_ = roi[y:y+h, x:x+w, :]
plate_part = roi[y:y+h, x:x+w, :]
cv2.rectangle(plateImg,(x+2,y),(x+w-3, y+h-5),(0,255,0),3)
return plateImg, plate_part
#normal function to display
def display_img(img):
img_ = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
plt.imshow(img_)
plt.show()
#test image is used for detecting plate
inputImg = cv2.imread('test.jpeg')
inpImg, plate = plate_detect(inputImg)
display_img(inpImg)
def find_contours(dimensions, img) :
#finding all contours in the image using
#retrieval mode: RETR_TREE
#contour approximation method: CHAIN_APPROX_SIMPLE
cntrs, _ = cv2.findContours(img.copy(), cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
#Approx dimensions of the contours
lower_width = dimensions[0]
upper_width = dimensions[1]
lower_height = dimensions[2]
upper_height = dimensions[3]
#Check largest 15 contours for license plate character respectively
cntrs = sorted(cntrs, key=cv2.contourArea, reverse=True)[:15]
ci = cv2.imread('contour.jpg')
x_cntr_list = []
target_contours = []
img_res = []
for cntr in cntrs :
#detecting contour in binary image and returns the coordinates of rectangle enclosing it
intX, intY, intWidth, intHeight = cv2.boundingRect(cntr)
#checking the dimensions of the contour to filter out the characters by contour's size
if intWidth > lower_width and intWidth < upper_width and intHeight > lower_height and intHeight < upper_height :
x_cntr_list.append(intX)
char_copy = np.zeros((44,24))
#extracting each character using the enclosing rectangle's coordinates.
char = img[intY:intY+intHeight, intX:intX+intWidth]
char = cv2.resize(char, (20, 40))
cv2.rectangle(ci, (intX,intY), (intWidth+intX, intY+intHeight), (50,21,200), 2)
plt.imshow(ci, cmap='gray')
char = cv2.subtract(255, char)
char_copy[2:42, 2:22] = char
char_copy[0:2, :] = 0
char_copy[:, 0:2] = 0
char_copy[42:44, :] = 0
char_copy[:, 22:24] = 0
img_res.append(char_copy) # List that stores the character's binary image (unsorted)
#return characters on ascending order with respect to the x-coordinate
plt.show()
#arbitrary function that stores sorted list of character indeces
indices = sorted(range(len(x_cntr_list)), key=lambda k: x_cntr_list[k])
img_res_copy = []
for idx in indices:
img_res_copy.append(img_res[idx])# stores character images according to their index
img_res = np.array(img_res_copy)
return img_res
def segment_characters(image) :
#pre-processing cropped image of plate
#threshold: convert to pure b&w with sharpe edges
#erod: increasing the backgroung black
#dilate: increasing the char white
img_lp = cv2.resize(image, (333, 75))
img_gray_lp = cv2.cvtColor(img_lp, cv2.COLOR_BGR2GRAY)
_, img_binary_lp = cv2.threshold(img_gray_lp, 200, 255, cv2.THRESH_BINARY+cv2.THRESH_OTSU)
img_binary_lp = cv2.erode(img_binary_lp, (3,3))
img_binary_lp = cv2.dilate(img_binary_lp, (3,3))
LP_WIDTH = img_binary_lp.shape[0]
LP_HEIGHT = img_binary_lp.shape[1]
img_binary_lp[0:3,:] = 255
img_binary_lp[:,0:3] = 255
img_binary_lp[72:75,:] = 255
img_binary_lp[:,330:333] = 255
#estimations of character contours sizes of cropped license plates
dimensions = [LP_WIDTH/6,
LP_WIDTH/2,
LP_HEIGHT/10,
2*LP_HEIGHT/3]
plt.imshow(img_binary_lp, cmap='gray')
plt.show()
cv2.imwrite('contour.jpg',img_binary_lp)
#getting contours
char_list = find_contours(dimensions, img_binary_lp)
return char_list
char = segment_characters(plate)
for i in range(10):
plt.subplot(1, 10, i+1)
plt.imshow(char[i], cmap='gray')
plt.axis('off')
#It is the harmonic mean of precision and recall
#Output range is [0, 1]
#Works for both multi-class and multi-label classification
def f1score(y, y_pred):
return f1_score(y, tf.math.argmax(y_pred, axis=1), average='micro')
def custom_f1score(y, y_pred):
return tf.py_function(f1score, (y, y_pred), tf.double)
model = models.load_model('license_plate_character.pkl', custom_objects= {'custom_f1score': custom_f1score})
def fix_dimension(img):
new_img = np.zeros((28,28,3))
for i in range(3):
new_img[:,:,i] = img
return new_img
def show_results():
dic = {}
characters = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'
for i,c in enumerate(characters):
dic[i] = c
output = []
for i,ch in enumerate(char):
img_ = cv2.resize(ch, (28,28), interpolation=cv2.INTER_AREA)
img = fix_dimension(img_)
img = img.reshape(1,28,28,3)
y_ = model.predict_classes(img)[0]
character = dic[y_] #
output.append(character)
plate_number = ''.join(output)
return plate_number
final_plate = show_results()
print(final_plate)
def get_vehicle_info(plate_number):
r = requests.get("http://www.regcheck.org.uk/api/reg.asmx/CheckIndia?RegistrationNumber={0}&username=licenseguy".format(str(plate_number)))
data = xmltodict.parse(r.content)
jdata = json.dumps(data)
df = json.loads(jdata)
df1 = json.loads(df['Vehicle']['vehicleJson'])
return df1
if len(final_plate) > 10:
final_plate = final_plate[-10:]
print(final_plate)
get_vehicle_info(final_plate)
```
| github_jupyter |
```
# Datset source
# https://archive.ics.uci.edu/ml/datasets/Appliances+energy+prediction
# Problem statement: Predict the appliances energy use based on various features
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# Common imports
import numpy as np
import os
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Ignore useless warnings (see SciPy issue #5998)
import warnings
warnings.filterwarnings(action="ignore", message="^internal gelsd")
# Read the dataset
import pandas as pd
pd.options.display.max_columns = 1000
aep_df = pd.read_csv('energydata_complete.csv', sep=',')
print(aep_df.shape)
aep_df.head()
# Check for NAN values in the entire dataframe
aep_df.isnull().sum().sum()
# Info about the dataframe
aep_df.info()
# Some statistics about the dataframe
aep_df.describe()
# Plot the histograms for all the features in the dataset
aep_df.hist(bins=50, figsize=(20,15))
plt.show()
# To make this notebook's output identical at every run
np.random.seed(2)
# Plot correlation between scaled sound level in decibels and other features
corr_matrix = aep_df.corr()
corr_matrix["Appliances"].sort_values(ascending=False)
# Split the dataframe into features and labels
X = aep_df.drop(['date', 'Appliances'], axis=1).values
y = aep_df.loc[:, 'Appliances'].values
print("X shape: ", X.shape, "y shape: ", y.shape)
print("Sample X values: ", X[:5], "\n", "Sample y values: ", y[:5])
# Split the dataset into train, validation and test sets
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.05, random_state=2)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.05, random_state=2)
print(" X_train shape: ", X_train.shape,"\n", "y_train shape: ", y_train.shape,"\n",
"X_val shape: ", X_val.shape,"\n", "y_val shape: ", y_val.shape,"\n",
"X_test shape: ", X_test.shape,"\n", "y_test shape: ", y_test.shape,"\n")
# Model 1
# Sklearn Simple Linear Regression model with default parameters
from sklearn.linear_model import LinearRegression
lr_model_1 = LinearRegression()
lr_model_1.fit(X_train, y_train)
print("Train set score: ", lr_model_1.score(X_train, y_train))
print("Validation set score: ", lr_model_1.score(X_val, y_val))
print("Test set score: ", lr_model_1.score(X_test, y_test))
# Mean Squared Errors of train, validation and test set predictions
from sklearn.metrics import mean_squared_error
print("Train set mse: ", mean_squared_error(y_train, lr_model_1.predict(X_train)))
print("Validation set mse: ", mean_squared_error(y_val, lr_model_1.predict(X_val)))
print("Test set mse: ", mean_squared_error(y_test, lr_model_1.predict(X_test)))
# Here the R^2 values are very low and MSE values are very high, more complex models are required to fit the data
# Model 2
# Sklearn Simple Linear Regression model with normalized data
from sklearn.linear_model import LinearRegression
lr_model_2 = LinearRegression(normalize=True)
lr_model_2.fit(X_train, y_train)
print("Train set score: ", lr_model_2.score(X_train, y_train))
print("Validation set score: ", lr_model_2.score(X_val, y_val))
print("Test set score: ", lr_model_2.score(X_test, y_test))
# Here normalizing the data didn't made any difference, confirming that more complex models are required to fit the data
```
| github_jupyter |
# Part 0: Mining the web
Perhaps the richest source of openly available data today is [the Web](http://www.computerhistory.org/revolution/networking/19/314)! In this lab, you'll explore some of the basic programming tools you need to scrape web data.
> **Note.** The Vocareum platform runs in a cloud-based environment that limits what websites a program can connect to directly. Therefore, some (or possibly all) of the code below will **not** work. Therefore, we are making this notebook **optional** and are providing solutions inline.
>
> Even if you are using a home or local installation of Jupyter, you may encounter problems if you attempt to access a site too many times or too rapidly. That can happen if your internet service provider (ISP) or the target website detect your accesses as "unusual" and reject them. It's easy to imagine accidentally writing an infinite loop that tries to access a page and being seen from the other side as a malicious program. :)
## The Requests module
Python's [Requests module](http://requests.readthedocs.io/en/latest/user/quickstart/) to download a web page.
For instance, here is a code fragment to download the [Georgia Tech](http://www.gatech.edu) home page and print the first 250 characters. You might also want to [view the source](http://www.computerhope.com/issues/ch000746.htm) of Georgia Tech's home page to get a nicely formatted view, and compare its output to what you see above.
```
import requests
response = requests.get('https://www.gatech.edu/')
webpage = response.text # or response.content for raw bytes
print(webpage[0:250]) # Prints the first hundred characters only
```
**Exercise 1.** Given the contents of the GT home page as above, write a function that returns a list of links (URLs) of the "top stories" on the page.
For instance, on Friday, September 9, 2016, here was the front page:

The top stories cycle through in the large image placeholder shown above. We want your function to return the list of URLs behind each of the "Full Story" links, highlighted in red. If no URLs can be found, the function should return an empty list.
```
import re # Maybe you want to use a regular expression?
def get_gt_top_stories(webpage_text):
"""Given the HTML text for the GT front page, returns a list
of the URLs of the top stories or an empty list if none are
found.
"""
pattern = '''<a class="slide-link" href="(?P<url>[^"]+)"'''
return re.findall(pattern, webpage_text)
top_stories = get_gt_top_stories(webpage)
print("Links to GT's top stories:", top_stories)
```
## A more complex example
Go to [Yelp!](http://www.yelp.com) and look up `ramen` in `Atlanta, GA`. Take note of the URL:

This URL encodes what is known as an _HTTP "get"_ method (or request). It basically means a URL with two parts: a _command_ followed by one or more _arguments_. In this case, the command is everything up to and including the word `search`; the arguments are the rest, where individual arguments are separated by the `&` or `#`.
> "HTTP" stands for "HyperText Transport Protocol," which is a standardized set of communication protocols that allow _web clients_, like your web browser or your Python program, to communicate with _web servers_.
In this next example, let's see how to build a "get request" with the `requests` module. It's pretty easy!
```
url_command = 'https://yelp.com/search'
url_args = {'find_desc': "ramen",
'find_loc': "atlanta, ga"}
response = requests.get (url_command, params=url_args, timeout=60)
print ("==> Downloading from: '%s'" % response.url) # confirm URL
print ("\n==> Excerpt from this URL:\n\n%s\n" % response.text[0:100])
```
**Exercise 2.** Given a search topic, location, and a rank $k$, return the name of the $k$-th item of a Yelp! search. If there is no $k$-th item, return `None`.
> The demo query above only gives you a website with the top 10 items, meaning you could only use it for $k \leq 10$. Figure out how to modify it to solve the problem when $k > 10$.
```
def find_yelp_item (topic, location, k):
"""Returns the k-th suggested item from Yelp! in Atlanta for the given topic."""
import re
if k < 1: return None
# Download page
url_command = 'http://yelp.com/search'
url_args = {'find_desc': topic,
'find_loc': location,
'start': k-1
}
response = requests.get (url_command, params=url_args)
if not response: return None
# Split page into lines
lines = response.text.split ('\n')
# Look for the line containing the name of the k-th item
item_pattern = re.compile ('<span class="indexed-biz-name">{}\..*<span >(?P<item_name>.*)</span></a>'.format (k))
for l in lines:
item_match = item_pattern.search (l)
if item_match:
return item_match.group ('item_name')
# No matches, evidently
return None
assert find_yelp_item('fried chicken', 'Atlanta, GA', -1) is None # Tests an invalid value for 'k'
```
> Search queries on Yelp! don't always return the same answers, since the site is always changing! Also, your results might not match a query you do via your web browser (_why not?_). As such, you should manually check your answers.
```
item = find_yelp_item ('fried chicken', 'Atlanta, GA', 1)
print (item)
item = find_yelp_item ('fried chicken', 'Atlanta, GA', 5)
print (item)
# The most likely answer on September 11, 2018:
#assert item == 'Buttermilk Kitchen'
item = find_yelp_item('fried chicken', 'Atlanta, GA', 10)
print(item)
# Most likely correct answer as of September 11, 2018:
#assert item == 'Colonnade Restaurant'
```
One issue with the above exercises is that they treat HTML as a flat string, whereas the document is at least semi-structured. Moreover, web pages are such a common source of data today that you would expect better tools for processing them. Indeed, such tools exist! The next part of this assignment, Part 1, walks you through one such tool. So, head there when you are ready!
| github_jupyter |
# Main notebook for battery state estimation
```
import numpy as np
import pandas as pd
import scipy.io
import math
import os
import ntpath
import sys
import logging
import time
import sys
from importlib import reload
import plotly.graph_objects as go
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import SGD, Adam
from keras.utils import np_utils
from keras.layers import LSTM, Embedding, RepeatVector, TimeDistributed, Masking
from keras.callbacks import EarlyStopping, ModelCheckpoint, LambdaCallback
IS_COLAB = False
if IS_COLAB:
from google.colab import drive
drive.mount('/content/drive')
data_path = "/content/drive/My Drive/battery-state-estimation/battery-state-estimation/"
else:
data_path = "../../"
sys.path.append(data_path)
from data_processing.lg_dataset import LgData
```
### Config logging
```
reload(logging)
logging.basicConfig(format='%(asctime)s [%(levelname)s]: %(message)s', level=logging.DEBUG, datefmt='%Y/%m/%d %H:%M:%S')
```
# Load Data
```
train_names = [
'n10degC/601_Mixed1',
'n10degC/601_Mixed2',
'n10degC/604_Mixed3',
'n10degC/602_Mixed4',
'n10degC/602_Mixed5',
'n10degC/604_Mixed6',
'n10degC/604_Mixed7',
'n10degC/604_Mixed8',
'n20degC/610_Mixed1',
'n20degC/610_Mixed2',
'n20degC/611_Mixed3',
'n20degC/611_Mixed4',
'n20degC/611_Mixed5',
'n20degC/611_Mixed6',
'n20degC/611_Mixed7',
'n20degC/611_Mixed8'
]
test_names = [
'n10degC/596_UDDS',
'n10degC/601_US06',
'n10degC/596_LA92',
'n20degC/610_UDDS',
'n20degC/610_US06',
'n20degC/610_LA92',
]
steps = 500
lg_data = LgData(data_path)
cycles = lg_data.get_discharge_whole_cycle(train_names, test_names, output_capacity=False, scale_test=True)
train_x, train_y, test_x, test_y = lg_data.get_discharge_multiple_step(cycles, steps)
train_y = lg_data.keep_only_y_end(train_y, steps)
test_y = lg_data.keep_only_y_end(test_y, steps)
```
# Model training
```
EXPERIMENT = "lstm_soc_percentage_lg_negative_temp_500_steps_drive_cycle_test"
experiment_name = time.strftime("%Y-%m-%d-%H-%M-%S") + '_' + EXPERIMENT
print(experiment_name)
os.environ["CUDA_VISIBLE_DEVICES"] = "1"
# Model definition
opt = tf.keras.optimizers.Adam(lr=0.00001)
model = Sequential()
model.add(LSTM(256, activation='selu',
return_sequences=True,
input_shape=(train_x.shape[1], train_x.shape[2])))
model.add(LSTM(256, activation='selu', return_sequences=False))
model.add(Dense(256, activation='selu'))
model.add(Dense(128, activation='selu'))
model.add(Dense(1, activation='linear'))
model.summary()
model.compile(optimizer=opt, loss='huber', metrics=['mse', 'mae', 'mape', tf.keras.metrics.RootMeanSquaredError(name='rmse')])
es = EarlyStopping(monitor='val_loss', patience=50)
mc = ModelCheckpoint(data_path + 'results/trained_model/%s_best.h5' % experiment_name,
save_best_only=True,
monitor='val_loss')
history = model.fit(train_x, train_y,
epochs=1000,
batch_size=32,
verbose=2,
validation_split=0.2,
callbacks = [es, mc]
)
model.save(data_path + 'results/trained_model/%s.h5' % experiment_name)
hist_df = pd.DataFrame(history.history)
hist_csv_file = data_path + 'results/trained_model/%s_history.csv' % experiment_name
with open(hist_csv_file, mode='w') as f:
hist_df.to_csv(f)
```
### Testing
```
results = model.evaluate(test_x, test_y)
print(results)
```
# Data Visualization
```
# fig = go.Figure()
# fig.add_trace(go.Scatter(y=history.history['loss'],
# mode='lines', name='train'))
# fig.add_trace(go.Scatter(y=history.history['val_loss'],
# mode='lines', name='validation'))
# fig.update_layout(title='Loss trend',
# xaxis_title='epoch',
# yaxis_title='loss')
# fig.show()
# train_predictions = model.predict(train_x)
# cycle_num = 0
# steps_num = 8000
# step_index = np.arange(cycle_num*steps_num, (cycle_num+1)*steps_num)
# fig = go.Figure()
# fig.add_trace(go.Scatter(x=step_index, y=train_predictions.flatten()[cycle_num*steps_num:(cycle_num+1)*steps_num],
# mode='lines', name='SoC predicted'))
# fig.add_trace(go.Scatter(x=step_index, y=train_y.flatten()[cycle_num*steps_num:(cycle_num+1)*steps_num],
# mode='lines', name='SoC actual'))
# fig.update_layout(title='Results on training',
# xaxis_title='Step',
# yaxis_title='SoC percentage')
# fig.show()
# test_predictions = model.predict(test_x)
# cycle_num = 0
# steps_num = 8000
# step_index = np.arange(cycle_num*steps_num, (cycle_num+1)*steps_num)
# fig = go.Figure()
# fig.add_trace(go.Scatter(x=step_index, y=test_predictions.flatten()[cycle_num*steps_num:(cycle_num+1)*steps_num],
# mode='lines', name='SoC predicted'))
# fig.add_trace(go.Scatter(x=step_index, y=test_y.flatten()[cycle_num*steps_num:(cycle_num+1)*steps_num],
# mode='lines', name='SoC actual'))
# fig.update_layout(title='Results on testing',
# xaxis_title='Step',
# yaxis_title='SoC percentage')
# fig.show()
```
| github_jupyter |
```
%matplotlib inline
"""
The data set in this example represents 1059 songs from various countries obtained
from the UCI Machine Learning library. Various features of the audio tracks have been
extracted, and each track has been tagged with the latitude and longitude of the capital
city of its country of origin.
We'll treat this as a classification problem, and attempt to train a model to predict
the country of origin of each model.
Data source did not specifify what the audio features specifically are, just
"In the 'default_features_1059_tracks.txt' file, the first 68 columns are audio
features of the track, and the last two columns are the origin of the music,
represented by latitude and longitude.
In the 'default_plus_chromatic_features_1059_tracks.txt' file, the first 116
columns are audio features of the track, and the last two columns are the
origin of the music."
"""
import numpy as np
import pandas as pd
import sklearn
from sklearn.preprocessing import LabelEncoder
from sklearn.utils.multiclass import unique_labels
import sys
#First get the data. The UCI ML Library distributes it as a zipped file;
#download the data and extract the two provided files to the 'data' folder before continuing
music_df = pd.read_csv('data\default_plus_chromatic_features_1059_tracks.txt', header=None)
music = music_df.as_matrix()
#Our features are all but the last two columns
X = music[:,0:-2]
#Since feature names were not given, we'll just assign strings with an incrementing integer
names = np.linspace(start=1, stop=116, num=116, dtype='int').tolist()
for idx, name in enumerate(names):
names[idx] = "Feature " + str(name)
#The source data said that each song as tied to the capital city of it's origin country via a lat/lon pair.
#Let's treat this as a multi-class classification problem.
#Rather than reverse-geocoding, we'll just make a string out of the unique lat/lon pairs
lats = ["%.2f" % lat for lat in music_df[116]]
lons = ["%.2f" % lon for lon in music_df[117]]
song_latlons = []
for index, value in enumerate(lats):
city_id = lats[index] + "," + lons[index]
song_latlons.append(city_id)
unique_latlons = unique_labels(song_latlons)
city_options = ['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z','AA','AB','AC','AD','AE','AF','AG']
city_name_map = {}
for idx,latlon in enumerate(unique_latlons):
city_name_map[latlon] = city_options[idx]
ylist = []
for latlon in song_latlons:
ylist.append(city_name_map[latlon])
y = np.array(ylist)
#We want yellowbrick to import from this repository, and assume this notebook is in repofolder/examples/subfolder/
sys.path.append("../../")
import yellowbrick as yb
from yellowbrick.features.rankd import Rank2D
from yellowbrick.features.radviz import RadViz
from yellowbrick.features.pcoords import ParallelCoordinates
#See how well correlated the features are
visualizer = Rank2D(features = names, algorithm = 'pearson')
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.poof()
from sklearn import metrics
from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from yellowbrick.classifier import ClassificationReport
def train_and_classification_report(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
print("prec: {}".format(metrics.precision_score(y_true = y_test, y_pred = y_predict, average="weighted")))
print("rec: {}".format(metrics.recall_score(y_true= y_test, y_pred = y_predict, average = "weighted")))
cr_viz = ClassificationReport(model) #,classes=city_options
cr_viz.fit(X_train, y_train)
cr_viz.score(X_test, y_test)
cr_viz.poof()
#Adding the reloading functionality so we can edit the source code and see results here.
import importlib
importlib.reload(yb.classifier)
from yellowbrick.classifier import ClassificationReport
#This produces an IndexError: list index out of range.
train_and_classification_report(LogisticRegression())
#This demonstrates a version of the Seaborn confusion matrix heatmap we could replicate (and improve on).
def train_and_confusion_matrix(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
print("prec: {}".format(metrics.precision_score(y_true = y_test, y_pred = y_predict, average="weighted")))
print("rec: {}".format(metrics.recall_score(y_true= y_test, y_pred = y_predict, average = "weighted")))
c_matrix = confusion_matrix(y_true = y_test, y_pred = y_predict)
sns.heatmap(c_matrix, square=True, annot=True, cbar=False, xticklabels=city_options, yticklabels = city_options)
plt.xlabel('predicted value')
plt.ylabel('true value')
train_and_confusion_matrix(LogisticRegression())
def train_and_class_balance(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
class_balance = yb.classifier.ClassBalance(model, classes=city_options)
class_balance.fit(X_train, y_train)
class_balance.score(X_test, y_test)
class_balance.poof()
train_and_class_balance(LogisticRegression())
```
| github_jupyter |
```
import numpy as np
import pandas as pd
from pathlib import Path
%matplotlib inline
```
# Regression Analysis: Seasonal Effects with Sklearn Linear Regression
In this notebook, you will build a SKLearn linear regression model to predict Yen futures ("settle") returns with *lagged* Yen futures returns.
```
# Futures contract on the Yen-dollar exchange rate:
# This is the continuous chain of the futures contracts that are 1 month to expiration
yen_futures = pd.read_csv(
Path("yen.csv"), index_col="Date", infer_datetime_format=True, parse_dates=True
)
yen_futures.head()
# Trim the dataset to begin on January 1st, 1990
yen_futures = yen_futures.loc["1990-01-01":, :]
yen_futures.head()
```
# Data Preparation
### Returns
```
# Create a series using "Settle" price percentage returns, drop any nan"s, and check the results:
# (Make sure to multiply the pct_change() results by 100)
# In this case, you may have to replace inf, -inf values with np.nan"s
yen_futures['Return'] = (yen_futures[["Settle"]].pct_change() * 100)
returns = yen_futures.replace(-np.inf, np.nan).dropna()
returns.tail()
```
### Lagged Returns
```
# Create a lagged return using the shift function
yen_futures['Lagged_Return'] = yen_futures['Return'].shift()
yen_futures = yen_futures.dropna()
yen_futures.tail()
```
### Train Test Split
```
# Create a train/test split for the data using 2018-2019 for testing and the rest for training
train = yen_futures[:'2017']
test = yen_futures['2018':]
# Create four dataframes:
# X_train (training set using just the independent variables), X_test (test set of of just the independent variables)
# Y_train (training set using just the "y" variable, i.e., "Futures Return"), Y_test (test set of just the "y" variable):
X_train = train["Lagged_Return"].to_frame()
X_test = test["Lagged_Return"].to_frame()
y_train = train["Return"]
y_test = test["Return"]
X_train
```
# Linear Regression Model
```
# Create a Linear Regression model and fit it to the training data
from sklearn.linear_model import LinearRegression
# Fit a SKLearn linear regression using just the training set (X_train, Y_train):
model = LinearRegression()
model.fit(X_train, y_train)
```
# Make predictions using the Testing Data
Note: We want to evaluate the model using data that it has never seen before, in this case: X_test.
```
# Make a prediction of "y" values using just the test dataset
predictions = model.predict(X_test)
# Assemble actual y data (Y_test) with predicted y data (from just above) into two columns in a dataframe:
Results = y_test.to_frame()
Results["Predicted Return"] = predictions
# Plot the first 20 predictions vs the true values
prediction_plot = Results[:20].plot(subplots=True)
```
# Out-of-Sample Performance
Evaluate the model using "out-of-sample" data (X_test and y_test)
```
from sklearn.metrics import mean_squared_error
# Calculate the mean_squared_error (MSE) on actual versus predicted test "y"
mse = mean_squared_error(Results["Return"],Results["Predicted Return"])
# Using that mean-squared-error, calculate the root-mean-squared error (RMSE):
rmse = np.sqrt(mse)
print(f"Out-of-Sample Root Mean Squared Error (RMSE): {rmse}")
```
# In-Sample Performance
Evaluate the model using in-sample data (X_train and y_train)
```
# Construct a dataframe using just the "y" training data:
in_sample_results = y_train.to_frame()
# Add a column of "in-sample" predictions to that dataframe:
in_sample_results["In-sample Predictions"] = model.predict(X_train)
# Calculate in-sample mean_squared_error (for comparison to out-of-sample)
in_sample_mse = mean_squared_error(in_sample_results["Return"], in_sample_results["In-sample Predictions"])
# Calculate in-sample root mean_squared_error (for comparison to out-of-sample)
in_sample_rmse = np.sqrt(in_sample_mse)
print(f"In-sample Root Mean Squared Error (RMSE): {in_sample_rmse}")
```
# Conclusions
YOUR CONCLUSIONS HERE!
We have a root mean square error of 0.415% for the out-of-sample data and 0.56587% for in-sample data. The model performs better with data that it has not worked with before.
| github_jupyter |
# 酷我音樂
- 下載酷我音樂平台上電台的「專輯」音檔
# 載入套件
```
import re
import os
import time
import requests
from bs4 import BeautifulSoup
```
# 設定爬蟲參數
```
headers = {'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/88.0.4324.150 Safari/537.36 Edg/88.0.705.63',
'Cookie': '_ga=GA1.2.841063431.1603504850; Hm_lvt_cdb524f42f0ce19b169a8071123a4797=1611556993; _gid=GA1.2.997533225.1613194048; Hm_lpvt_cdb524f42f0ce19b169a8071123a4797=1613194071; kw_token=UCMBLA99FF',
'referer': 'http://www.kuwo.cn/',
'If-Range': '6023dfa9-8d7179',
'Sec-Fetch-Dest': 'video',
'Sec-Fetch-Mode': 'no-cors',
'Sec-Fetch-Site': 'cross-site',
'csrf': 'UCMBLA99FF'}
```
# 爬取資料
## 蒐集連結清單
```
page = 1
links = []
while True:
# 生成網址
url = 'http://www.kuwo.cn/api/www/album/albumInfo?albumId=547562&pn={}&rn=30'.format(page)
# 請求資料
resp = requests.get(url, headers=headers)
time.sleep(0.5)
try:
musicList = [i['rid'] for i in resp.json()['data']['musicList']]
# 保存資訊
links += musicList
# 輸出資料擷取進度
print(page, ': ', len(list(set(links))))
# 判斷是否跳出迴圈
page += 1
if len(musicList) < 30:
links = list(set(links))
print('There are totally {} links!'.format(len(links)))
break
except:
print('status_code: ', resp.status_code, ', Retry')
```
# 下載連結音檔
```
# os.mkdir('./musics')
# 已下載的音樂清單
download_list = [int(i.split('_',-1)[0]) for i in os.listdir('./musics')]
len(download_list)
# 排除已下載的音樂
links = [link for link in links if link not in download_list]
len(links)
for link in links:
# 取音檔摘要
url = 'http://www.kuwo.cn/play_detail/{}'.format(link)
resp = requests.get(url, headers=headers)
soup = BeautifulSoup(resp.text)
time.sleep(3)
music_name = soup.find('title').text
music_name = re.sub(r'/|', '', music_name)
music_uploadtime = soup.find('span', {'class':'time'}).text
# 取音檔連結
music_link = 'http://www.kuwo.cn/url?format=mp3&rid={}&response=url&type=convert_url3&br=128kmp3'.format(link)
try:
music_link = requests.get(music_link).json()['url']
except:
time.sleep(1)
music_link = requests.get(music_link).json()['url']
# 下載音檔
music_content = requests.get(url=music_link).content
with open('./musics/{}.mp3'.format(str(link) + '_' + music_name), 'wb') as f:
f.write(music_content)
print('Succed: ', link, music_name)
```
# 異常狀況排除
- 通常是檔案名稱有非法字元,或者request的速度過快被擋~
```
soup.find('title').text
requests.get(music_link).json()['url']
music_name = '66823804_蕊希专访 陈乔恩:爱自己,是终身浪漫的开始_蕊希Erin_单曲在线试听_酷我音乐.mp3'
with open('./musics/{}.mp3'.format(str(link) + '_' + music_name), 'wb') as f:
f.write(music_content)
```
| github_jupyter |
```
%matplotlib inline
import json
import pylab
import copy
from pprint import pprint
import numpy as np
from lxml import etree
import matplotlib.colors
from pysurvey.plot import icolorbar, text, box
from pysurvey.plot import setup_sns as setup
import seaborn as sns
sns.set_style('white')
def make_cmap():
# from brewer -- reorganized
rgbs = (
(152,78,163),
(55,126,184),
#(77,175,74),
(69, 157, 66),
(228,26,28),
(255,127,0),
)
cdict = {}
colors = ['red', 'green', 'blue']
for i,rgb in enumerate(rgbs):
for color,value in zip(colors, rgb):
c = cdict.get(color, [])
c.append((i*1.0/(len(rgbs)-1.0), value/256.0, value/256.0))
cdict[color] = c
# Darken Rainbow
# def c(name):
# return lambda x: np.clip(pylab.cm.datad['rainbow'][name](x),0,0.8)
# cdict = dict(
# red = c('red'),
# green = c('green'),
# blue = c('blue'),
# )
cmap = matplotlib.colors.LinearSegmentedColormap('my_colormap',cdict,512)
return cmap
def grayify_cmap(cmap):
colors = cmap(np.arange(cmap.N))
RGB_weight = [0.299, 0.587, 0.114]
luminance = np.sqrt(np.dot(colors[:, :3] ** 2, RGB_weight))
colors[:, :3] = luminance[:, np.newaxis]
return cmap.from_list(cmap.name + "_grayscale", colors, cmap.N)
def show_colormap(cmap):
im = np.outer(np.ones(10), np.arange(100))
fig, ax = pylab.subplots(2, figsize=(6, 1.5), subplot_kw=dict(xticks=[], yticks=[]))
fig.subplots_adjust(hspace=0.1)
ax[0].imshow(im, cmap=cmap)
ax[1].imshow(im, cmap=grayify_cmap(cmap))
show_colormap(make_cmap())
with open('/Users/ajmendez/data/reddit/subreddit_ages.json', 'r') as f:
subreddit_map = json.load(f)
ages = [v[0] for k,v in subreddit_map.iteritems()]
np.min(ages), np.max(ages)
# This was the original one, but lets update to the clustering version
tree = etree.parse("/Users/ajmendez/data/reddit/subreddits.gexf", base_url='http://www.gexf.net/1.2draft')
ns = {'graph': '{http://www.gexf.net/1.2draft}graph'}
graph = tree.getroot().find(ns['graph'])
# tag = graph.findall('.*//*[@label="{}"]'.format(subreddit))[0]
# s = tag[1].attrib
# p = tag[2].attrib
# int(tag.attrib['id']),
# Programming subreddits compiled from:
# https://www.reddit.com/user/krispykrackers/m/programming
# https://www.reddit.com/comments/a6qgz/proggit_im_trying_to_compile_all_the_known
city_subreddits = ('orlando Quebec Colorado Calgary paris bayarea wisconsin france ottawa houston vancouver '
'newzealand Iowa sanantonio montreal ontario Miami mexico Atlanta Seattle sanfrancisco '
'toronto nothernireland boston canada LosAngeles philadelphia raleigh chicago sandiego '
'indianapolis Charleston VictoriaBC russia Winnipeg Cleveland Portland NewOrleans australia Maine StLouis pittsburgh HongKong longisland '
'Austin Portland Seattle Vancouver Boston Toronto SanFrancisco pittsburgh sandiego Chicago '
'twincitiessocial washingtondc denver philadelphia Montreal BayArea atlanta NYC melbourne houston '
'LosAngeles Dallas london '
'japan ireland nyc melbourne tampaDenver Taxans Dallas China sydney Denmark brisbane pakistan').split()
programming_subreddits = (
'ada agi algorithms applescript Arc asm aspnet awk brainfuck cappuccino carlhprogramming clojure cobol '
'cocoa cocoadev code codeprojects coding CodingContests coldfusion common_lisp compsci computerscience coq '
'cplusplus cpp csbooks csharp css csshelp c_language c_programming dailyprogrammer delphi dependent_types '
'django django_class dotnet drupal d_language emacs encryption engineering erlang factor forth fortran fortress '
'fsharp functional functionallang gamedev genetic_algorithms git greasemonkey groovy haskell haskell_proposals haxe '
'HTML html5 Ioke iOSProgramming iphonedev j2ee java javahelp javascript jquery learnprogramming learnpython linux lisp '
'lua machinelearning macprogramming matlab mercurial modula3 netsec newlisp Oberon objectivec ocaml onlycode opengl '
'pascal perl PHP php programmer programming programminglanguages prolog Python python rails ruby rubyonrails scala '
'scheme smalltalk softwaredevelopment swift systems Tcl technology techsupport threads types udk ui_programming unity3d '
'vim visualbasic webdev web_design web_dev Wolfram wolframlanguage xna XOTcl').split()
# cmap = make_cmap()
cmap = pylab.cm.rainbow # for dark background
agenorm = matplotlib.colors.Normalize(18, 30, clip=True)
dtype = [
('id', np.int),
('subreddit', '|S64'),
('nunique', np.int),
('iscity', np.int),
('isprogramming', np.int),
('x', np.float),
('y', np.float),
('size', np.float),
('age', np.float),
('rgba', np.float, 4),
]
data = np.zeros(len(subreddit_map), dtype=dtype)
for i, (subreddit, value) in enumerate(subreddit_map.iteritems()):
try:
tag = graph.findall('.*//*[@label="{}"]'.format(subreddit))[0]
except Exception as e:
# print '!',
# print subreddit, e
continue
s = tag[1].attrib
p = tag[2].attrib
age = value[0]
nunique = value[-1]
data[i] = (int(tag.attrib['id']),
subreddit,
nunique,
(subreddit in city_subreddits),
(subreddit in programming_subreddits),
float(p['x']),
float(p['y']),
float(s['value']),
age,
pylab.cm.Spectral(agenorm(age)),
)
# print i, subreddit, age
# etree.dump(tag)
# if i > 10:
# break
```
# Make cluster plot
```
_ = pylab.hist(data['nunique'][data['nunique']!= 0], 50)
def setup_clusters(width=1500, xoffset=0, yoffset=0, **params):
kwargs = dict(xticks=False, yticks=False, grid=False, tickmarks=False)
kwargs.update(params)
ax = setup(xr=[-width+xoffset,width+xoffset], yr=[-width+yoffset,width+yoffset], **kwargs)
pylab.xticks([])
pylab.yticks([])
return ax
def plot_cluster(data, isgood=None, vmin=18, vmax=32, cmap=None, maxsize=50, sizescale=1.0, **kwargs):
if isgood is None: isgood = (np.ones(data.shape) == 1)
if cmap is None: cmap=make_cmap()
agenorm = matplotlib.colors.Normalize(vmin, vmax, clip=True)
index = np.where(isgood & (data['x'] != 0) & (data['y'] != 0))[0]
s = np.clip(np.sqrt(data['nunique'][index]), 3, maxsize)*2*sizescale
sca = pylab.scatter(data['x'][index], data['y'][index], label='Age',
s=s, c=data['age'][index], vmin=vmin, vmax=vmax, cmap=cmap, lw=0, **kwargs)
return sca
def label_clusters(data, isgood=None, vmin=18, vmax=32, cmap=None, ax=None, sizescale=1.0):
if isgood is None: isgood = (np.ones(data.shape) == 1)
if cmap is None: cmap=make_cmap()
if ax is None: ax = pylab.gca()
agenorm = matplotlib.colors.Normalize(vmin, vmax, clip=True)
xr,yr = pylab.xlim(), pylab.ylim()
index = np.where(isgood &
(data['x'] > xr[0]) & (data['x'] < xr[1]) &
(data['y'] > yr[0]) & (data['y'] < yr[1]) &
(data['x'] != 0) & (data['y'] != 0))[0]
ii = np.argsort(data['nunique'][index])
for x,y,label,age,s in data[index][['x','y','subreddit', 'age', 'nunique']][ii]:
if len(label) == 0: continue
color=cmap(agenorm(age))
# s = np.clip(s, 4,12)*sizescale
fs = np.clip(12*(s/200.0), 3, 12)*sizescale
tmp = text(x,y,label, color=color,
ha='left', va='bottom', fontsize=fs,
clip_on=True, clip_path=ax.patch, outline=True)
tmp.set_clip_path(ax.patch)
sub_width = 400
sub_xoffset = 70
setup_clusters(sub_width, sub_xoffset, figsize=(12,6), subplt=(1,2,1))
sca = plot_cluster(data, cmap=pylab.cm.rainbow, vmin=18, vmax=32)
icolorbar(sca, loc=2, borderpad=0.75, tickfmt='{:.0f}')
setup_clusters(sub_width, sub_xoffset, subplt=(1,2,2))
sca = plot_cluster(data, cmap=make_cmap(), vmin=18, vmax=32)
icolorbar(sca, loc=2, borderpad=0.75, tickfmt='{:.0f}')
main_width = 1500
sub_width = 400
sub_xoffset = 70
setup_clusters(main_width, figsize=(12,4), subplt=(1,3,1))
box([-sub_width+sub_xoffset,sub_width+sub_xoffset], [-sub_width,sub_width], lw=0, alpha=0.1)
plot_cluster(data)
setup_clusters(sub_width, sub_xoffset, subplt=(1,3,2))
sca = plot_cluster(data)
icolorbar(sca, loc=2, borderpad=0.75, tickfmt='{:.0f}')
setup_clusters(sub_width, sub_xoffset, subplt=(1,3,3))
plot_cluster(data)
label_clusters(data, (data['nunique'] > 500))
pylab.tight_layout()
# pylab.savefig('/Users/ajmendez/Desktop/subreddits.png', dpi=200)
sub_width = 600
sub_xoffset = 20
sub_yoffset = -50
setup_clusters(sub_width, sub_xoffset, sub_yoffset, figsize=(12,12), subplt=(2,2,1), title='Age < 21')
plot_cluster(data, cmap=make_cmap(), alpha=0.1, maxsize=20)
isage = (data['age'] < 21) & (data['nunique'] > 10)
sca = plot_cluster(data, isage, sizescale=2.0)
label_clusters(data, isage, sizescale=2.0)
setup_clusters(sub_width, sub_xoffset, sub_yoffset, subplt=(2,2,2), title='Age > 30')
plot_cluster(data, cmap=make_cmap(), alpha=0.1, maxsize=20)
isage = (data['age'] > 30) & (data['nunique'] > 10)
sca = plot_cluster(data, isage, sizescale=2.0)
label_clusters(data, isage, sizescale=2.0)
sub_width = 60
sub_xoffset = 430
sub_yoffset = -330
setup_clusters(sub_width, sub_xoffset, sub_yoffset, subplt=(2,2,3), title='Sports Cluster')
plot_cluster(data, cmap=pylab.cm.Greys, alpha=0.1, maxsize=20)
isage = (data['nunique'] > 10)
sca = plot_cluster(data, isage, sizescale=2.0)
label_clusters(data, isage, sizescale=2.0)
sub_width = 70
sub_xoffset = 1000
sub_yoffset = 150
setup_clusters(sub_width, sub_xoffset, sub_yoffset, subplt=(2,2,4))
plot_cluster(data, cmap=pylab.cm.Greys, alpha=0.1, maxsize=20)
isage = (data['nunique'] > 5) & (data['age'] > 0)
sca = plot_cluster(data, isage, sizescale=2.0)
label_clusters(data, isage, sizescale=2.0)
icolorbar(sca, loc=1)
sub_width = 1450
sub_xoffset = 380
sub_yoffset = 100
setup_clusters(sub_width, sub_xoffset, sub_yoffset, figsize=(12,12), title='Programming Subreddits')
plot_cluster(data, alpha=0.1, maxsize=20)
isage = (data['nunique'] > 10) & (data['age'] > 0) & (data['isprogramming'] ==1)
sca = plot_cluster(data, isage, sizescale=2.0)
icolorbar(sca)
label_clusters(data, isage, sizescale=2.0)
ii = np.argsort(data[isage]['age'])
for subreddit, age in data[isage][ii][['subreddit', 'age']]:
print '{:12s} {:5.1f}'.format(subreddit, age)
sub_width = 450
sub_xoffset = -180
sub_yoffset = 100
setup_clusters(sub_width, sub_xoffset, sub_yoffset, figsize=(12,12), title='Cities and Countries')
plot_cluster(data, alpha=0.1, maxsize=20)
isage = (data['nunique'] > 10) & (data['age'] > 0) & (data['iscity'] ==1)
sca = plot_cluster(data, isage, sizescale=2.0)
icolorbar(sca)
label_clusters(data, isage, sizescale=2.0)
tmp = data[np.argsort(-data['age'])]
iscity = (tmp['nunique'] > 20) & (tmp['age'] > 10) & (tmp['iscity'] > 0)
ncity = len(np.where(iscity)[0])
cmap = make_cmap()
ax = setup(figsize=(16,4), grid=False,
title='Cities and Countries',
ylabel='Age', yr=[0, 32],
xr=[-0.2, ncity+0.2], xtickv=np.arange(ncity)+0.5,
xticknames=['' for x in tmp['subreddit'][iscity]],
xtickrotate=90)
for i, subreddit in enumerate(tmp['subreddit'][iscity]):
pylab.text(i+0.6, 1, '/r/'+subreddit,
color='w', fontsize=14, fontweight='bold',
ha='center', va='bottom', rotation=90)
# ax.set_xticklabels(tmp['subreddit'][iscity], rotation=90, ha='center')
pylab.bar(left=np.arange(ncity)+0.1, width=0.8,
height=tmp['age'][iscity], lw=0, alpha=0.8,
color=cmap(agenorm(tmp['age'][iscity])))
```
# Build data.json
```
vizit = json.load(open('/Users/ajmendez/data/reddit/vizit_data.json', 'r'))
ii = np.where(data['age'] > 0)
ageit = dict(nodes=[], edges=[])
node_ids = []
for node in vizit['nodes']:
subreddit = node['label']
i = np.where( (data['subreddit'] == subreddit) & (data['age'] > 0) )[0]
if len(i) != 0:
newnode = copy.copy(node)
newnode['color'] = 'rgb({:0.0f}, {:0.0f}, {:0.0f})'.format(*data['rgba'][i][0][:-1]*256)
newnode['size'] = 4.0*float(newnode['size'])
newnode['age'] = float(data['age'][i])
else:
newnode = copy.copy(node)
newnode['color'] = 'rgb({:0.0f}, {:0.0f}, {:0.0f})'.format(0,0,0)
newnode['age'] = 0
newnode['size'] = 0.5*float(newnode['size'])
ageit['nodes'].append(newnode)
node_ids.append(newnode['id'])
for edge in vizit['edges']:
if (edge['source'] in node_ids) and (edge['target'] in node_ids):
ageit['edges'].append(copy.copy(edge))
print 'Nodes: {:,d} Edges: {:,d}'.format(len(ageit['nodes']), len(ageit['edges']))
data['age'][1]
pprint(vizit['nodes'][-2])
pprint(vizit['edges'][1])
json.dump(ageit, open('/Users/ajmendez/data/reddit/ageit_data.json', 'w'), indent=2)
```
| github_jupyter |
```
import numpy as np
a = np.matrix([[1,2,3],[4,5,6]])
print(type(a))
print(a.T)
print(a.shape)
print(a.transpose())
class Dog:
pass # placeholder
my_dog = Dog() # must have ()!!
print(type(my_dog))
isinstance(my_dog,Dog)
```
## Class Attributes
In practice a dog as a color, breed, age, and other attributes, and it can do things like eat, run, sleep, bark etc.
```
class Dog:
# Atributes
age = 0
name = 'noname'
breed = 'nobreed'
color = 'nocolor'
my_dog = Dog()
print('{} is a {}-year old {} {}.'.format(my_dog.name,my_dog.age,my_dog.color,my_dog.breed))
my_dog = Dog()
my_dog.age = 2
my_dog.name = 'Fido'
my_dog.color = 'brown'
my_dog.breed = 'Labradoodle'
print('{} is a {}-year old {} {}.'.format(my_dog.name,my_dog.age,my_dog.color,my_dog.breed))
```
## Object Constructor
```
class Dog:
def __init__(self, age ,name ,breed ,color):
self.age = age
self.name = name
self.breed = breed
self.color = color
my_dog = Dog('4','Coco','Corgie','Brown')
print('{} is a {}-year old {} {}.'.format(my_dog.name,my_dog.age,my_dog.color,my_dog.breed))
class Dog:
def __init__(self, age ,name ,breed ,color):
self.age = age
self.name = name
self.breed = breed
self.color = color
def info(self):
print('{} is a {}-year old {} {}.'.format(my_dog.name,my_dog.age,my_dog.color,my_dog.breed))
my_dog = Dog('4','Coco','Corgie','Brown')
my_dog.info()
class Dog:
def __init__(self, age = 0 ,name = 'noname' ,breed = 'nobreed' ,color = 'nocolor'):
self.age = age
self.name = name
self.breed = breed
self.color = color
def info(self):
print('{} is a {}-year old {} {}.'.format(my_dog.name,my_dog.age,my_dog.color,my_dog.breed))
my_dog = Dog()
my_dog.info()
class Dog:
#Global Attributes
species = 'mammal'
def __init__(self, age = 0 ,name = 'noname' ,breed = 'nobreed' ,color = 'nocolor'):
self.age = age
self.name = name
self.breed = breed
self.color = color
def info(self):
print('{} is a {}-year old {} {}.'.format(my_dog.name,my_dog.age,my_dog.color,my_dog.breed))
my_dog = Dog(name = 'Ralph', age = 7, color = 'gray', breed = 'Chihuahua')
my_dog.info()
print(my_dog.species)
```
## A physics example
```
class Projectile():
gravityConstant = 9.81 # m/s^2
def __init__(self, initVelocity):
self.initVelocity = initVelocity
#self.time = time
def getHeight(self, time):
return self.initVelocity*time-.5*self.gravityConstant*time**2
ball = Projectile(initVelocity = 10)
height = ball.getHeight(.1)
print(height)
print(ball.initVelocity)
class Projectile():
gravityConstant = 9.81 # m/s^2
def __init__(self, initVelocity):
self.initVelocity = initVelocity
#self.time = time
def getHeight(self, time):
return self.initVelocity*time-.5*self.gravityConstant*time**2
```
## Inhertiance
```
class childName(parentName):
## list of all new, sub-class specific attributes and methods
# including the sub-class constructor
class Animal:
#Animal Constructor
def __init__(self,age = 0, weight = 0, animal_is_alive = True):
self.age = age
self.weigt = weight
self.animal_is_alive = animal_is_alive
#eat food
def eat(self, food = None):
if food == None:
print("There is nothing to eat :-(")
else:
print('Eating {}...yum yum....'.format(food))
#sleeping
def sleep(self):
print('Sleeping...zzzzzzzz....')
Coco = Animal(3,10,True)
Coco.sleep()
Coco.eat(food = 'bananas')
class Dog(Animal):
#Dog Constructor
def __init__(self, age = 0, weight = 0, animal_is_alive = True, breed = 'nobreed', color = 'nocolor', name = 'noname', bark_sound = 'ruff'):
self.breed = breed
self.color = color
self.bark_sound = bark_sound
self.name = name
Animal.__init__(self,age,weight,animal_is_alive)
# barking method
def bark(self, num_barks = 3):
for i in range(num_barks):
print('{}'.format(self.bark),end = ' ')
def info(self):
print('{} is a {}-year old {} {}.'.format(my_dog.name,my_dog.age,my_dog.color,my_dog.breed))
Fido = Dog(age = 1, weight = 15, animal_is_alive = True, breed='Husky',color = 'gray',name = 'Fido')
Fido.info()
Fido.bark(3)
```
## Overloading and Multiple Inheritances
```
class MotherDog(Animal):
def __init__(self,age = 0,weight = 0,animal_is_alive = True, breed = 'nobreed', color = 'nocolor', name = 'noname',):
def bark(self, num_barks = 3):
for i in range(num_barks):
print('arf', end = ' ')
class FatherDog(Animal)
```
## Polymorphism
```
Tito = FatherDog(age=12,breed='Doberman',)
```
## Overloading Operations and Functions
```
class Vector:
def __init__(self,x_comp,y_comp):
self.x_comp = x_comp
self.y_comp = y_comp
def __abs__(self):
return (self.x_comp**2+self.y_comp**2)**(0.5)
x = Vector(1,2)
print(x)
class Vector:
def __init__(self,x_comp,y_comp):
self.x_comp = x_comp
self.y_comp = y_comp
def __abs__(self):
return (self.x_comp**2+self.y_comp**2)**(0.5)
def __len__(self):
return 2
def __add__(self,other):
return Vector(self.x_comp + other.x_comp, self.y_comp + other.y_comp)
x = Vector(1,2)
y = Vector(3,7)
z = x+y
print(z.x_comp)
print(z.y_comp)
class Vector:
def __init__(self,x_comp,y_comp):
self.x_comp = x_comp
self.y_comp = y_comp
def __abs__(self):
return (self.x_comp**2+self.y_comp**2)**(0.5)
def __len__(self):
return 2
def __add__(self,other):
return Vector(self.x_comp + other.x_comp, self.y_comp + other.y_comp)
def __mul__(self,other):
return Vector(self.x_comp*other, self.y_comp*other)
#def __mul__(other,self):
#return Vector(other*self.x_comp, other*self.y_comp)
x = Vector(1,2)
y = 2
z = x*y
print(z.x_comp)
print(z.y_comp)
z2 = y*x
class Vector:
def __init__(self,x_comp,y_comp):
self.x_comp = x_comp
self.y_comp = y_comp
def __abs__(self):
return (self.x_comp**2+self.y_comp**2)**(0.5)
def __len__(self):
return 2
def __add__(self,other):
return Vector(self.x_comp + other.x_comp, self.y_comp + other.y_comp)
def __mul__(self,other):
return Vector(self.x_comp*other, self.y_comp*other)
def __rmul__(self,other):
return Vector(self.x_comp*other, self.y_comp*other)
```
| github_jupyter |
```
import cv2
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from keras.models import Sequential, Model
from keras.layers import Flatten, Dense, Conv2D, MaxPooling2D, BatchNormalization, Cropping2D, Lambda, Activation, Dropout
from keras.optimizers import Adam
from keras.initializers import glorot_normal
from sklearn.utils import shuffle
from model import processFilename, Nvidia, generator
track = 'track2_almost_working'
driving_log = pd.read_csv(
'{}/driving_log.csv'.format(track),
names=['center','left','right','angle','throttle','brake','speed']
)
center_left_right_angle = driving_log[['center', 'left', 'right', 'angle']]
image = plt.imread( processFilename(track, center_left_right_angle.iloc[0].center) )
image.shape
plt.imshow(image[75:-25,:,:])
image[75:-25,:,:].shape
# this function reads the images into memory, it is not a scalable approach when there are too many images
def read_angles(driving_log):
angles = []
for row in driving_log.itertuples():
angle = row.angle
angles.append(angle)
# end for
return np.array(angles)
# end def
angles = read_angles(center_left_right_angle)
angles.shape
augmented_angles = []
for angle in angles:
augmented_angles.append(angle)
augmented_angles.append(-angle)
plt.hist(angles, bins=100)
plt.xlabel('angle')
plt.ylabel('frequency')
plt.title('histogram before augmentation')
plt.show()
plt.hist(augmented_angles, bins=100)
plt.xlabel('angle')
plt.ylabel('frequency')
plt.title('histogram after augmentation')
plt.show()
np.random.seed(1) # set the random number seed
npts = len(center_left_right_angle)
# center_left_right_angle contains all the rows
# split into training and validation with a 0.8, 0.2 split
npts_rand = np.random.rand(npts)
train_set = center_left_right_angle[npts_rand <= 0.8]
valid_set = center_left_right_angle[npts_rand > 0.8]
batch_size = 50
train_generator = generator(train_set, batch_size, track)
valid_generator = generator(valid_set, batch_size, track)
steps_per_epoch = np.rint(len(train_set) / batch_size).astype(int)
validation_steps = np.rint(len(valid_set) / batch_size).astype(int)
def Nvidia(dropout=0.0):
model = Sequential()
model.add(Cropping2D(cropping=((75,25), (0,0)), input_shape=(160,320,3), name='crop'))
model.add(BatchNormalization()) # 60 x 320 x 3
model.add(Conv2D(
6, 5, strides=(2,2), padding='same',
kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros',
name='conv1'
))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(dropout))
model.add(Conv2D(
12, 5, strides=(1,2), padding='same',
kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros',
name='conv2'
))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(dropout))
model.add(Conv2D(
16, 5, strides=(1,2), padding='same',
kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros',
name='conv3'
))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(dropout))
model.add(Conv2D(
20, 3, padding='valid',
kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros',
name='conv4'
))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(dropout))
model.add(Conv2D(
24, 3, padding='valid',
kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros',
name='conv5'
))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(dropout))
model.add(Flatten())
model.add(Dense(100, kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros'))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(dropout))
model.add(Dense(50, kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros'))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(dropout))
model.add(Dense(10, kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros'))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(dropout))
model.add(Dense(1, kernel_initializer=glorot_normal(seed=1), bias_initializer='zeros'))
return model
from keras.models import load_model
model = load_model('params/all_data_model.h5')
model.get_layer('conv5').output
model = Nvidia(dropout=0.25)
optimizer = Adam(lr=1e-3)
model.compile(loss='mse', optimizer=optimizer)
model.fit_generator(
train_generator, steps_per_epoch=steps_per_epoch,
epochs=10,
validation_data=valid_generator, validation_steps=validation_steps
)
model.get_layer('conv1').output
intermediate_layer_model = Model(inputs=model.input, outputs=model.get_layer('conv5').output)
intermediate_output = intermediate_layer_model.predict(np.expand_dims(image, 0))
plt.imshow(intermediate_output[0,:,:,1],cmap='gray')
model.save('params/{}_model.h5'.format(track))
```
| github_jupyter |
##### Copyright 2020 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# TensorFlow Addons Optimizers: ConditionalGradient
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/addons/tutorials/optimizers_conditionalgradient"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/addons/blob/master/docs/tutorials/optimizers_conditionalgradient.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/addons/blob/master/docs/tutorials/optimizers_conditionalgradient.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/addons/docs/tutorials/optimizers_conditionalgradient.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
# Overview
This notebook will demonstrate how to use the Conditional Graident Optimizer from the Addons package.
# ConditionalGradient
> Constraining the parameters of a neural network has been shown to be beneficial in training because of the underlying regularization effects. Often, parameters are constrained via a soft penalty (which never guarantees the constraint satisfaction) or via a projection operation (which is computationally expensive). Conditional gradient (CG) optimizer, on the other hand, enforces the constraints strictly without the need for an expensive projection step. It works by minimizing a linear approximation of the objective within the constraint set. In this notebook, we demonstrate the appliction of Frobenius norm constraint via the CG optimizer on the MNIST dataset. CG is now available as a tensorflow API. More details of the optimizer are available at https://arxiv.org/pdf/1803.06453.pdf
## Setup
```
import tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt
# Hyperparameters
batch_size=64
epochs=10
```
# Build the Model
```
model_1 = tf.keras.Sequential([
tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])
```
# Prep the Data
```
# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255
```
# Define a Custom Callback Function
```
def frobenius_norm(m):
"""This function is to calculate the frobenius norm of the matrix of all
layer's weight.
Args:
m: is a list of weights param for each layers.
"""
total_reduce_sum = 0
for i in range(len(m)):
total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
norm = total_reduce_sum**0.5
return norm
CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
frobenius_norm(model_1.trainable_weights).numpy()))
```
# Train and Evaluate: Using CG as Optimizer
Simply replace typical keras optimizers with the new tfa optimizer
```
# Compile the model
model_1.compile(
optimizer=tfa.optimizers.ConditionalGradient(
learning_rate=0.99949, lambda_=203), # Utilize TFA optimizer
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
history_cg = model_1.fit(
x_train,
y_train,
batch_size=batch_size,
validation_data=(x_test, y_test),
epochs=epochs,
callbacks=[CG_get_weight_norm])
```
# Train and Evaluate: Using SGD as Optimizer
```
model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])
SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
frobenius_norm(model_2.trainable_weights).numpy()))
# Compile the model
model_2.compile(
optimizer=tf.keras.optimizers.SGD(0.01), # Utilize SGD optimizer
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
history_sgd = model_2.fit(
x_train,
y_train,
batch_size=batch_size,
validation_data=(x_test, y_test),
epochs=epochs,
callbacks=[SGD_get_weight_norm])
```
# Frobenius Norm of Weights: CG vs SGD
The current implementation of CG optimizer is based on Frobenius Norm, with considering Frobenius Norm as regularizer in the target function. Therefore, we compare CG’s regularized effect with SGD optimizer, which has not imposed Frobenius Norm regularizer.
```
plt.plot(
CG_frobenius_norm_of_weight,
color='r',
label='CG_frobenius_norm_of_weights')
plt.plot(
SGD_frobenius_norm_of_weight,
color='b',
label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)
```
# Train and Validation Accuracy: CG vs SGD
```
plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)
```
| github_jupyter |
# **Amazon Lookout for Equipment** - 익명화한 익스펜더 데이터셋에 대한 데모
*파트 5: 정기적인 추론 호출 스케줄링*
```
BUCKET = '<YOUR_BUCKET_NAME_HERE>'
PREFIX = 'data/scheduled_inference'
```
## 초기화
---
이 노트북에서는 데이터 폴더에 추론 디렉토리를 추가하게끔 저장소 구조를 갱신합니다.
```
/lookout-equipment-demo
|
+-- data/
| |
| +-- inference/
| | |
| | |-- input/
| | |
| | \-- output/
| |
| +-- labelled-data/
| | \-- labels.csv
| |
| \-- training-data/
| \-- expander/
| |-- subsystem-01
| | \-- subsystem-01.csv
| |
| |-- subsystem-02
| | \-- subsystem-02.csv
| |
| |-- ...
| |
| \-- subsystem-24
| \-- subsystem-24.csv
|
+-- dataset/
| |-- labels.csv
| |-- tags_description.csv
| |-- timeranges.txt
| \-- timeseries.zip
|
+-- notebooks/
| |-- 1_data_preparation.ipynb
| |-- 2_dataset_creation.ipynb
| |-- 3_model_training.ipynb
| |-- 4_model_evaluation.ipynb
| \-- 5_inference_scheduling.ipynb <<< 본 노트북 <<<
|
+-- utils/
|-- lookout_equipment_utils.py
\-- lookoutequipment.json
```
### 임포트
```
%%sh
pip -q install --upgrade pip
pip -q install --upgrade awscli boto3 sagemaker
aws configure add-model --service-model file://../utils/lookoutequipment.json --service-name lookoutequipment
from IPython.core.display import HTML
HTML("<script>Jupyter.notebook.kernel.restart()</script>")
import boto3
import datetime
import os
import pandas as pd
import pprint
import pyarrow as pa
import pyarrow.parquet as pq
import sagemaker
import s3fs
import sys
import time
import uuid
import warnings
# Lookout for Equipment API 호출 관리를 위한 Helper 함수
sys.path.append('../utils')
import lookout_equipment_utils as lookout
```
### 파라미터
```
warnings.filterwarnings('ignore')
DATA = os.path.join('..', 'data')
RAW_DATA = os.path.join('..', 'dataset')
INFER_DATA = os.path.join(DATA, 'inference')
os.makedirs(os.path.join(INFER_DATA, 'input'), exist_ok=True)
os.makedirs(os.path.join(INFER_DATA, 'output'), exist_ok=True)
ROLE_ARN = sagemaker.get_execution_role()
REGION_NAME = boto3.session.Session().region_name
```
## 추론 스케줄러 생성하기
---
콘솔의 모델 세부 정보 부분으로 이동하면 추론 스케줄이 아직 없음을 확인할 수 있습니다.

### 스케줄러 설정
새로운 추론 스케줄을 만들어 보겠습니다. 파라미터 일부는 필수 입력이지만 파라미터 다수는 유연하게 추가 설정할 수 있습니다.
#### 파라미터
* 추론을 위해 데이터를 업로드할 빈도로 `DATA_UPLOAD_FREQUENCY`를 설정합니다. 허용되는 값은`PT5M`,`PT10M`,`PT15M`,`PT30M`과`PT1H`입니다.
* 이것은 추론 스케줄러가 실행되는 빈도와 데이터가 소스 버킷에 업로드되는 빈도입니다.
* **참고** : ***업로드 빈도는 훈련 때 선택한 샘플링 비율과 호환되어야합니다.*** *예를 들어 모델을 30분 간격의 리샘플링으로 훈련시킨 경우 5분은 가능하지 않습니다. 추론 시 파라미터로 PT30M 또는 PT1H를 선택해야합니다.*
* 추론 데이터의 S3 버킷으로 `INFERENCE_DATA_SOURCE_BUCKET`를 설정합니다.
* 추론 데이터의 S3 접두사로 `INFERENCE_DATA_SOURCE_PREFIX`를 설정합니다.
* 추론 결과를 원하는 S3 버킷으로 `INFERENCE_DATA_OUTPUT_BUCKET`를 설정합니다.
* 추론 결과를 원하는 S3 접두사로 `INFERENCE_DATA_OUTPUT_PREFIX`를 설정합니다.
* 추론할 데이터를 **읽고** 추론 출력을 **쓸** 때 사용할 역할로 `ROLE_ARN_FOR_INFERENCE`를 설정합니다.
```
# 생성하려는 추론 스케줄러의 이름
INFERENCE_SCHEDULER_NAME = 'lookout-demo-model-v1-scheduler'
# 본 추론 스케줄러를 생성할 모델의 이름
MODEL_NAME_FOR_CREATING_INFERENCE_SCHEDULER = 'lookout-demo-model-v1'
# 필수 입력 파라미터
INFERENCE_DATA_SOURCE_BUCKET = BUCKET
INFERENCE_DATA_SOURCE_PREFIX = f'{PREFIX}/input/'
INFERENCE_DATA_OUTPUT_BUCKET = BUCKET
INFERENCE_DATA_OUTPUT_PREFIX = f'{PREFIX}/output/'
ROLE_ARN_FOR_INFERENCE = ROLE_ARN
DATA_UPLOAD_FREQUENCY = 'PT5M'
```
#### 생략 가능한 파라미터
* 데이터 업로드하는데 지연이 예상되는 시간(분)으로 `DATA_DELAY_OFFSET_IN_MINUTES`를 설정합니다. 즉, 데이터 업로드하는 시간에 대한 버퍼입니다.
* ``INPUT_TIMEZONE_OFFSET``을 설정합니다. 허용되는 값은 +00:00, +00:30, -01:00, ... +11:30, +12:00, -00:00, -00:30, -01:00, ... -11:30, -12:00입니다.
* `TIMESTAMP_FORMAT`을 설정합니다. 허용되는 값은 `EPOCH`, `yyyy-MM-dd-HH-mm-ss` 또는 `yyyyMMddHHmmss`입니다. 이것은 입력 데이터 파일 명에 접미사로 붙는 타임스탬프 형식입니다. 이것은 Lookout Equipment에서 추론을 실행할 파일을 파악하는 데 사용됩니다 (그러므로 스케줄러가 실행할 파일을 찾게 하기 위해 이전 파일을 제거할 필요가 없음).
* `COMPONENT_TIMESTAMP_DELIMITER`를 설정합니다. 허용되는 값은 `-`, `_` 또는 ` `입니다. 입력 파일 명의 타임스탬프에서 구성 요소를 분리할 때 사용하는 구분자입니다.
```
DATA_DELAY_OFFSET_IN_MINUTES = None
INPUT_TIMEZONE_OFFSET = '+00:00'
COMPONENT_TIMESTAMP_DELIMITER = '_'
TIMESTAMP_FORMAT = 'yyyyMMddHHmmss'
```
### 추론 스케줄러 생성하기
CreateInferenceScheduler API는 스케줄러를 생성**하고** 구동시킵니다. 즉, 즉각적으로 비용이 발생하기 시작합니다. 그러나 기존 스케줄러를 원하는대로 중지하거나 재구동시킬 수 있습니다 (이 노트북의 마지막 부분 참조).
```
scheduler = lookout.LookoutEquipmentScheduler(
scheduler_name=INFERENCE_SCHEDULER_NAME,
model_name=MODEL_NAME_FOR_CREATING_INFERENCE_SCHEDULER,
region_name=REGION_NAME
)
scheduler_params = {
'input_bucket': INFERENCE_DATA_SOURCE_BUCKET,
'input_prefix': INFERENCE_DATA_SOURCE_PREFIX,
'output_bucket': INFERENCE_DATA_OUTPUT_BUCKET,
'output_prefix': INFERENCE_DATA_OUTPUT_PREFIX,
'role_arn': ROLE_ARN_FOR_INFERENCE,
'upload_frequency': DATA_UPLOAD_FREQUENCY,
'delay_offset': DATA_DELAY_OFFSET_IN_MINUTES,
'timezone_offset': INPUT_TIMEZONE_OFFSET,
'component_delimiter': COMPONENT_TIMESTAMP_DELIMITER,
'timestamp_format': TIMESTAMP_FORMAT
}
scheduler.set_parameters(**scheduler_params)
```
## 추론 데이터 준비하기
---
스케줄러가 모니터링할 S3 입력 위치에 몇 가지 데이터를 준비하고 전송하겠습니다.
```
# 원본 신호 전체를 불러오겠습니다.
all_tags_fname = os.path.join(DATA, 'training-data', 'expander.parquet')
table = pq.read_table(all_tags_fname)
all_tags_df = table.to_pandas()
del table
all_tags_df.head()
```
태그 설명을 불러옵시다. 본 데이터셋에는 다음 내용을 포함하는 태그 설명 파일이 존재합니다.
* `Tag`: 이력 관리 시스템에 고객이 기록한 태그 명 (예컨대 [Honeywell 프로세스 이력 데이터베이스](https://www.honeywellprocess.com/en-US/explore/products/advanced-applications/uniformance/Pages/uniformance-phd.aspx))
* `UOM`: 기록한 신호의 측정 단위
* `Subsystem`: 해당 센서가 연결된 자산 부속의 ID
여기에서 구성 요소 (즉, 하위 시스템 열)의 List를 수집할 수 있습니다.
```
tags_description_fname = os.path.join(RAW_DATA, 'tags_description.csv')
tags_description_df = pd.read_csv(tags_description_fname)
components = tags_description_df['Subsystem'].unique()
tags_description_df.head()
```
샘플 추론 데이터셋을 구성하기 위해 원본 시계열 검증 기간에서 마지막 몇 분을 추출합니다.
```
# 추출하려는 시퀀스 개수
num_sequences = 3
# 스케줄링 빈도 (분): 이 값은 **반드시**
# 모델 학습에 사용한 리샘플링 비율에 맞춰 설정해야 합니다.
frequency = 5
# 각 시퀀스를 반복합니다.
start = all_tags_df.index.max() + datetime.timedelta(minutes=-frequency * (num_sequences) + 1)
for i in range(num_sequences):
end = start + datetime.timedelta(minutes=+frequency - 1)
# 이전 5분 단위로 시간을 반올림합니다.
tm = datetime.datetime.now()
tm = tm - datetime.timedelta(
minutes=tm.minute % frequency,
seconds=tm.second,
microseconds=tm.microsecond
)
tm = tm + datetime.timedelta(minutes=+frequency * (i))
tm = tm - datetime.timedelta(hours=9) # KST에 따른 조정
current_timestamp = (tm).strftime(format='%Y%m%d%H%M%S')
# 각 시퀀스마다 구성 요소 전체를 반복합니다.
print(f'Extracting data from {start} to {end}:')
new_index = None
for component in components:
# 해당 구성 요소와 특정 시간 범위에 대해 Dataframe을 추출합니다.
signals = list(tags_description_df.loc[(tags_description_df['Subsystem'] == component), 'Tag'])
signals_df = all_tags_df.loc[start:end, signals]
# 스케줄러가 추론을 실행할 시간에 맞게끔
# 인덱스를 재설정해야 합니다.
if new_index is None:
new_index = pd.date_range(
start=tm,
periods=signals_df.shape[0],
freq='1min'
)
signals_df.index = new_index
signals_df.index.name = 'Timestamp'
signals_df = signals_df.reset_index()
signals_df['Timestamp'] = signals_df['Timestamp'].dt.strftime('%Y-%m-%dT%H:%M:%S.%f')
# 해당 파일을 CSV 형식으로 내보냅니다.
component_fname = os.path.join(INFER_DATA, 'input', f'{component}_{current_timestamp}.csv')
signals_df.to_csv(component_fname, index=None)
start = start + datetime.timedelta(minutes=+frequency)
# 입력 위치의 전체 폴더를 S3에 업로드합니다.
INFERENCE_INPUT = os.path.join(INFER_DATA, 'input')
!aws s3 cp --recursive --quiet $INFERENCE_INPUT s3://$BUCKET/$PREFIX/input
# 이제 데이터를 준비했으므로 다음을 실행하여 스케줄러를 만듭니다.
create_scheduler_response = scheduler.create()
```
스케줄러가 실행 중이며 추론 기록은 현재 비어 있습니다.

## 추론 결과 얻기
---
### 추론 실행 결과 나열하기
**스케줄러가 추론을 최초로 실행할 경우 5-15분 정도 걸립니다.** 대기가 끝나면 현재 추론 스케줄러에서 ListInferenceExecution API를 사용할 수 있습니다. 입력 파라미터로 스케줄러 명만 필요합니다.
추론 실행 결과를 질의할 기간을 선택할 수 있습니다. 지정하지 않으면 추론 스케줄러에 대한 모든 실행 결과들이 나열됩니다. 시간 범위를 지정하려면 다음과 같이 합니다.
```python
START_TIME_FOR_INFERENCE_EXECUTIONS = datetime.datetime(2010,1,3,0,0,0)
END_TIME_FOR_INFERENCE_EXECUTIONS = datetime.datetime(2010,1,5,0,0,0)
```
즉, `2010-01-03 00:00:00`부터 `2010-01-05 00:00:00`까지의 실행 결과들이 나열됩니다.
특정 상태의 실행 결과를 질의하도록 선택할 수도 있습니다. 허용되는 상태는 `IN_PROGRESS`, `SUCCESS`와 `FAILED`입니다.
```
START_TIME_FOR_INFERENCE_EXECUTIONS = None
END_TIME_FOR_INFERENCE_EXECUTIONS = None
EXECUTION_STATUS = None
execution_summaries = []
while len(execution_summaries) == 0:
execution_summaries = scheduler.list_inference_executions(
start_time=START_TIME_FOR_INFERENCE_EXECUTIONS,
end_time=END_TIME_FOR_INFERENCE_EXECUTIONS,
execution_status=EXECUTION_STATUS
)
if len(execution_summaries) == 0:
print('WAITING FOR THE FIRST INFERENCE EXECUTION')
time.sleep(60)
else:
print('FIRST INFERENCE EXECUTED\n')
break
# execution_summaries
```
스케줄러를 5분마다 실행하도록 구성했습니다. 몇 분 후 콘솔에서 첫 번째 실행 결과가 입력된 기록을 살펴볼 수 있습니다.

스케줄러가 시작될 때, 예를 들어 `datetime.datetime (2021, 1, 27, 9, 15)`일 때 입력 위치에서 **단일** CSV 파일을 찾습니다. 여기에는 타임스탬프가 포함된 파일 명이, 말하자면 다음과 같은 파일 명이 존재해야 합니다.
* subsystem-01_2021012709**10**00.csv가 검색되고 수집됩니다.
* subsystem-01_2021012709**15**00.csv는 수집되지 **않습니다** (다음 추론 실행 시 수집됨).
`subsystem-01_20210127091000.csv` 파일을 연 다음 추론 실행의 DataStartTime과 DataEndTime 사이에 존재하는 시간 행을 찾습니다. 그러한 행을 찾지 못하면 내부 예외를 발생시킵니다.
### 실제 예측 결과 얻기
추론에 성공하면 CSV 파일이 버킷의 출력 위치에 저장됩니다. 각 추론은 `results.csv` 단일 파일이 존재하는 새 폴더를 만듭니다. 해당 파일을 읽고 여기에 내용을 표시해 보겠습니다.
```
results_df = scheduler.get_predictions()
results_df.to_csv(os.path.join(INFER_DATA, 'output', 'results.csv'))
results_df.head()
```
## 추론 스케줄러 운영
---
### 추론 스케줄러 중단하기
**근검 절약해야합니다**. 스케줄러 실행이 Amazon Lookout for Equipment 비용의 주된 원인입니다. 다음 API를 이용하여 현재 실행 중인 추론 스케줄러를 중지시키세요. 그렇게 하면 주기적인 추론 실행이 중지됩니다.
```
scheduler.stop()
```
### 추론 스케줄러 시작하기
다음 API를 사용하여 `STOPPED` 추론 스케줄러를 재시작할 수 있습니다.
```
scheduler.start()
```
### 추론 스케줄러 삭제하기
더 이상 사용하지 않는, **중지된** 스케줄러를 삭제할 수 있습니다. 모델 당 하나의 스케줄러만 가질 수 있습니다.
```
scheduler.stop()
scheduler.delete()
```
## 결론
---
이 노트북에서는 노트북 시리즈 파트 3에서 만든 모델을 사용하여 스케줄러를 구성하고 몇 차례 추론을 실행한 다음 예측값을 얻었습니다.
| github_jupyter |
```
import open3d as o3d
import numpy as np
import os
import sys
# monkey patches visualization and provides helpers to load geometries
sys.path.append('..')
import open3d_tutorial as o3dtut
# change to True if you want to interact with the visualization windows
o3dtut.interactive = not "CI" in os.environ
```
# RGBD integration
Open3D implements a scalable RGBD image integration algorithm. The algorithm is based on the technique presented in [\[Curless1996\]](../reference.html#curless1996) and [\[Newcombe2011\]](../reference.html#newcombe2011). In order to support large scenes, we use a hierarchical hashing structure introduced in [Integrater in ElasticReconstruction](https://github.com/qianyizh/ElasticReconstruction/tree/master/Integrate).
## Read trajectory from .log file
This tutorial uses the function `read_trajectory` to read a camera trajectory from a [.log file](http://redwood-data.org/indoor/fileformat.html). A sample `.log` file is as follows.
```
# examples/test_data/RGBD/odometry.log
0 0 1
1 0 0 2
0 1 0 2
0 0 1 -0.3
0 0 0 1
1 1 2
0.999988 3.08668e-005 0.0049181 1.99962
-8.84184e-005 0.999932 0.0117022 1.97704
-0.0049174 -0.0117024 0.999919 -0.300486
0 0 0 1
```
```
class CameraPose:
def __init__(self, meta, mat):
self.metadata = meta
self.pose = mat
def __str__(self):
return 'Metadata : ' + ' '.join(map(str, self.metadata)) + '\n' + \
"Pose : " + "\n" + np.array_str(self.pose)
def read_trajectory(filename):
traj = []
with open(filename, 'r') as f:
metastr = f.readline()
while metastr:
metadata = list(map(int, metastr.split()))
mat = np.zeros(shape=(4, 4))
for i in range(4):
matstr = f.readline()
mat[i, :] = np.fromstring(matstr, dtype=float, sep=' \t')
traj.append(CameraPose(metadata, mat))
metastr = f.readline()
return traj
camera_poses = read_trajectory("../../test_data/RGBD/odometry.log")
```
## TSDF volume integration
Open3D provides two types of TSDF volumes: `UniformTSDFVolume` and `ScalableTSDFVolume`. The latter is recommended since it uses a hierarchical structure and thus supports larger scenes.
`ScalableTSDFVolume` has several parameters. `voxel_length = 4.0 / 512.0` means a single voxel size for TSDF volume is $\frac{4.0\mathrm{m}}{512.0} = 7.8125\mathrm{mm}$. Lowering this value makes a high-resolution TSDF volume, but the integration result can be susceptible to depth noise. `sdf_trunc = 0.04` specifies the truncation value for the signed distance function (SDF). When `color_type = TSDFVolumeColorType.RGB8`, 8 bit RGB color is also integrated as part of the TSDF volume. Float type intensity can be integrated with `color_type = TSDFVolumeColorType.Gray32` and `convert_rgb_to_intensity = True`. The color integration is inspired by [PCL](http://pointclouds.org/).
```
volume = o3d.pipelines.integration.ScalableTSDFVolume(
voxel_length=4.0 / 512.0,
sdf_trunc=0.04,
color_type=o3d.pipelines.integration.TSDFVolumeColorType.RGB8)
for i in range(len(camera_poses)):
print("Integrate {:d}-th image into the volume.".format(i))
color = o3d.io.read_image("../../test_data/RGBD/color/{:05d}.jpg".format(i))
depth = o3d.io.read_image("../../test_data/RGBD/depth/{:05d}.png".format(i))
rgbd = o3d.geometry.RGBDImage.create_from_color_and_depth(
color, depth, depth_trunc=4.0, convert_rgb_to_intensity=False)
volume.integrate(
rgbd,
o3d.camera.PinholeCameraIntrinsic(
o3d.camera.PinholeCameraIntrinsicParameters.PrimeSenseDefault),
np.linalg.inv(camera_poses[i].pose))
```
## Extract a mesh
Mesh extraction uses the marching cubes algorithm [\[LorensenAndCline1987\]](../reference.html#lorensenandcline1987).
```
print("Extract a triangle mesh from the volume and visualize it.")
mesh = volume.extract_triangle_mesh()
mesh.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh],
front=[0.5297, -0.1873, -0.8272],
lookat=[2.0712, 2.0312, 1.7251],
up=[-0.0558, -0.9809, 0.1864],
zoom=0.47)
```
<div class="alert alert-info">
**Note:**
TSDF volume works like a weighted average filter in 3D space. If more frames are integrated, the volume produces a smoother and nicer mesh. Please check [Make fragments](../reconstruction_system/make_fragments.rst) for more examples.
</div>
| github_jupyter |
```
import astrodash
import os
import astropy
import numpy as np
from astropy.table import Table
from astropy.table import Column
import glob
import matplotlib.pyplot as plt
import pandas as pd
from collections import Counter
from mpl_toolkits.mplot3d import Axes3D
sample_location = "/home/hallflower/sample/spectra/"
dash = "/mnt/c/users/20xha/Documents/Caltech/Research/DASH/"
SEDM_ML_sample = Table.read("/mnt/c/Users/20xha/Documents/Caltech/Research/SEDM_ML_sample.ascii", format = "ascii")
SEDM_ML_sample.rename_column('col1', 'ZTF_Name')
SEDM_ML_sample.rename_column('col2', "Class")
SEDM_ML_sample.rename_column('col8', "Version")
output_list = np.load(dash+"output.npy",allow_pickle=True)
len(output_list)
len(np.unique(SEDM_ML_sample["ZTF_Name"]))
np.asarray(output_list[0][2])[:,0]
Classification = Table(
names=("ZTF_Name", "Class", "Version"
),
meta={"name": "Basic ZTF Name Data"},
dtype=("U64", "U64", "U64"
)
)
for i in np.unique(SEDM_ML_sample["ZTF_Name"]):
row = SEDM_ML_sample["ZTF_Name", "Class", "Version"][np.where(i == SEDM_ML_sample["ZTF_Name"])][-1]
Classification.add_row(row)
count = 0
ResultsTable = Table(
names=("ZTF_Name", "Both"
),
meta={"name": "Spectrum Results after SNID"},
dtype=("U64", "U64"
)
)
for i in output_list:
row = []
row.append(i[-1])
best = np.asarray(i[2])[:,0]
c = Counter(best)
row.append(c.most_common()[0][0])
ResultsTable.add_row(row)
count += 1
if(count % 500 == 0):
print(count)
counter = 0
wrong = []
JoinedResults = astropy.table.join(ResultsTable, Classification)
for j in JoinedResults:
if(j["Class"] != '-' and j["Class"] != "0.0"):
correct_1a = "Ia" in j["Class"]
classified_1a = "Ia" in j["Both"]
if(correct_1a==classified_1a):
counter += 1
else:
wrong.append([j["ZTF_Name"], j["Class"], j["Both"]])
wrong = np.asarray(wrong)
ranges = np.linspace(0, 25, 26)
ResultsTable_List_both = []
count = 0
for rlap in ranges:
for agree in range(0,16):
ResultsTable = Table(
names=("ZTF_Name", "Both"
),
meta={"name": "Spectrum Results after SNID"},
dtype=("U64", "U64"
)
)
for j in output_list:
row = []
row.append(j[-1])
matches = []
best_rlap = np.max(j[0][:,0][:,3])
if(best_rlap > rlap)
for k in range(len(j[0])):
matches.extend(j[0][k])
matches = np.asarray(matches)
c = Counter(matches[:,1])
row.append(c.most_common()[0][0])
if(c.most_common()[0][1] >= agree):
row.append(c.most_common()[0][0])
ResultsTable.add_row(row)
count += 1
if(len(ResultsTable) != 0):
ResultsTable_List_both.append([rlap,agree,ResultsTable])
if(count % 10 == 0):
print(count)
j = output_list[0]
matches = []
for k in range(len(j[0])):
matches.extend(j[0][k])
matches = np.asarray(matches)
```
| github_jupyter |
# Apache Arrow
## 1 Compare performance of csv, Parquet and Arrow - 1 Change
```
import pyarrow.parquet as pq
import pyarrow as pa
import pandas as pd
import numpy as np
import os
import psutil
```
### 1.1 Load and prepare data One more change
```
## Read Palmer Station Penguin dataset from GitHub
df = pd.read_csv("https://raw.githubusercontent.com/allisonhorst/"
"palmerpenguins/47a3476d2147080e7ceccef4cf70105c808f2cbf/"
"data-raw/penguins_raw.csv")
# Increase dataset to 1m rows and reset index
df = df.sample(1_000_000, replace=True).reset_index(drop=True)
# Update sample number (0 to 999'999)
df["Sample Number"] = df.index
# Add some random variation to numeric columns
df[["Culmen Length (mm)", "Culmen Depth (mm)",
"Flipper Length (mm)", "Body Mass (g)"]] = df[["Culmen Length (mm)", "Culmen Depth (mm)",
"Flipper Length (mm)", "Body Mass (g)"]] \
+ np.random.rand(df.shape[0], 4)
# Create dataframe where missing numeric values are filled with zero
df_nonan = df.copy()
df_nonan[["Culmen Length (mm)", "Culmen Depth (mm)",
"Flipper Length (mm)", "Body Mass (g)"]] = df[["Culmen Length (mm)", "Culmen Depth (mm)",
"Flipper Length (mm)", "Body Mass (g)"]].fillna(0)
```
### 1.2 Write to disk
```
# Write to csv
df.to_csv("penguin-dataset.csv")
# Write to parquet
df.to_parquet("penguin-dataset.parquet")
context = pa.default_serialization_context()
# Write to Arrow
# Convert from pandas to Arrow
table = pa.Table.from_pandas(df)
# Write out to file
writer = pa.RecordBatchFileWriter('penguin-dataset.arrow', table.schema)
writer.write(table)
writer.close()
#with pa.OSFile('penguin-dataset.arrow', 'wb') as sink:
#with pa.RecordBatchFileWriter(sink, table.schema,write_legacy_format=True) as writer:
#writer.write_table(table)
# Convert from no-NaN pandas to Arrow
table_nonan = pa.Table.from_pandas(df_nonan)
# Write out to file
writer = pa.RecordBatchFileWriter('penguin-dataset-nonan.arrow', table.schema)
writer.write(table_nonan)
writer.close()
#with pa.OSFile('penguin-dataset-nonan.arrow', 'wb') as sink:
#with pa.RecordBatchFileWriter(sink, table_nonan.schema,write_legacy_format=True) as writer:
#writer.write_table(table_nonan)
```
### 1.3 Reading time - calculate average of numeric column
#### 1.3.1 Read csv and calculate mean
```
%%timeit
pd.read_csv("penguin-dataset.csv")["Flipper Length (mm)"].mean()
```
#### 1.3.2 Read parquet and calculate mean
```
%%timeit
pd.read_parquet("penguin-dataset.parquet", columns=["Flipper Length (mm)"]).mean()
```
#### 1.3.3 Read Arrow using file API
```
%%timeit
with pa.OSFile('penguin-dataset.arrow', 'rb') as source:
table = pa.ipc.open_file(source).read_all().column("Flipper Length (mm)")
result = table.to_pandas().mean()
```
#### 1.3.4 Read Arrow with memory-mapped API with missing values
```
%%timeit
source = pa.memory_map('penguin-dataset.arrow', 'r')
table = pa.ipc.RecordBatchFileReader(source).read_all().column("Flipper Length (mm)")
result = table.to_pandas().mean()
```
#### 1.3.5 Read Arrow with memory-mapped API without missing values (zero-copy)
```
%%timeit
source = pa.memory_map('penguin-dataset-nonan.arrow', 'r')
table = pa.ipc.RecordBatchFileReader(source).read_all().column("Flipper Length (mm)")
result = table.to_pandas().mean()
```
### 1.4 Memory consumption - read column
```
# Measure initial memory consumption
memory_init = psutil.Process(os.getpid()).memory_info().rss >> 20
```
#### 1.4.1 Read csv
```
col_csv = pd.read_csv("penguin-dataset.csv")["Flipper Length (mm)"]
memory_post_csv = psutil.Process(os.getpid()).memory_info().rss >> 20
```
#### 1.4.2 Read parquet
```
col_parquet = pd.read_parquet("penguin-dataset.parquet", columns=["Flipper Length (mm)"])
memory_post_parquet = psutil.Process(os.getpid()).memory_info().rss >> 20
```
#### 1.4.3 Read Arrow using file API
```
with pa.OSFile('penguin-dataset.arrow', 'rb') as source:
col_arrow_file = pa.ipc.open_file(source).read_all().column("Flipper Length (mm)").to_pandas()
memory_post_arrowos = psutil.Process(os.getpid()).memory_info().rss >> 20
```
#### 1.4.4 Read Arrow with memory-mapped API with missing values
```
source = pa.memory_map('penguin-dataset.arrow', 'r')
table_mmap = pa.ipc.RecordBatchFileReader(source).read_all().column("Flipper Length (mm)")
col_arrow_mapped = table_mmap.to_pandas()
memory_post_arrowmmap = psutil.Process(os.getpid()).memory_info().rss >> 20
```
#### 1.4.5 Read Arrow with memory-mapped API without missing values (zero-copy)
```
source = pa.memory_map('penguin-dataset-nonan.arrow', 'r')
table_mmap_zc = pa.ipc.RecordBatchFileReader(source).read_all().column("Flipper Length (mm)")
col_arrow_mapped_zc = table_mmap_zc.to_pandas()
memory_post_arrowmmap_zc = psutil.Process(os.getpid()).memory_info().rss >> 20
```
#### 1.4.6 Display memory consupmtion
```
# Print memory consumption
print(f"csv: {memory_post_csv - memory_init}\n"
f"Parquet: {memory_post_parquet - memory_post_csv}\n"
f"Arrow file API: {memory_post_arrowos - memory_post_parquet}\n"
f"Arrow memory-mapped API with NaNs: {memory_post_arrowmmap - memory_post_arrowos}\n"
f"Arrow memory-mapped API (zero-copy): {memory_post_arrowmmap_zc - memory_post_arrowmmap}\n")
```
| github_jupyter |
# Controlling accesss to attributes
* Following blocks are one possible implementation of vectors of `double`s.
* Here, member variable `new_name` is in `protected:` part.
* Member methods and subclass members can access this variable but from the outside of the class, we cannot access it.
* We call it **encapsulation**; instead of directly reading or writing to the variable, we would use mutator or reader **methods**.
* This is because to modularize software components to the level of integrated circuit chips.
``` C++
// Begin vector_double.h
#include <cassert>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
// This directive would activate method call logging
#ifndef LOG
#define LOG
#endif
// This directive woudl activate bracket [] operator logging
// Added this just because the examples call [] operator frequently
#ifndef LOGBRACKET
// #define LOGBRACKET
#endif
// This is to prevent declaring vector class twice
// If declared twice, C/C++ compilers would show an error message
#ifndef VECTOR_DOUBLE
#define VECTOR_DOUBLE
class RowVector
{
// automatic allocation
// https://stackoverflow.com/questions/8553464/vector-as-a-class-member
std::vector<double> columns;
protected:
// To distinguish vectors from each other
std::string name;
public:
// Default constructor
RowVector();
// Destructor
~ RowVector();
// Default arguments
// If the function could not find the argument in the call, it uses the default value.
RowVector(const uint32_t n, const double *values=NULL, std::string new_name="None");
// Whenever possible, it is advisible to use `const` keyword
// Protects data from being overwritten and may optimize further
RowVector(const uint32_t n, std::string new_name="None");
// Copy constructor must use a reference.
// What would happen otherwise?
RowVector(const RowVector & other);
// Two versions of [] operators
// This one is for normal vectors. Allows changing values
double & operator [] (const uint32_t i);
// This one is for constant vectors. Protects the values from overwriting
double operator [] (const uint32_t i) const;
const std::string get_name() const;
RowVector operator + (const RowVector & other);
RowVector operator * (const double a);
const double operator * (const RowVector & other);
void show();
void resize(std::size_t new_size);
std::size_t size() const noexcept;
RowVector & operator += (const RowVector & other);
RowVector & operator *= (const double a);
};
#endif
// End vector_double.h
```
``` C++
// Begin vector_double.cpp
#include <cassert>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
#include "vector_double.h"
RowVector::RowVector(){
// This may look involving but sometimes helps how the program works.
#ifdef LOG
std::cout << '[' << &columns << ']' << "RowVector()" << '\n';
#endif
name = "None";
}
RowVector::~ RowVector(){
#ifdef LOG
std::cout << '[' << &columns << ']' << "~ RowVector()" << '\n';
#endif
}
RowVector::RowVector(const uint32_t n, const double *values, std::string new_name){
#ifdef LOG
std::cout << '[' << &columns << ']'
<< "RowVector(" << n << ", " << values << ", " << new_name << ")\n";
#endif
columns.resize(n);
// If initial values available, copy
if (values){
for (uint32_t i = 0; columns.size() > i; ++i){
columns[i] = values[i];
}
}
// If no initial values, set all values zero
else{
for (uint32_t i = 0; columns.size() > i; ++i){
columns[i] = 0.0;
}
}
name = new_name;
}
// Instead of implementing another constructor, calling an existing one
// c++ 11 or later
RowVector::RowVector(const uint32_t n, std::string new_name) : RowVector(n, NULL, new_name){
#ifdef LOG
std::cout << '[' << &columns << ']' << "RowVector(" << n << ", " << new_name << ")\n";
#endif
}
RowVector::RowVector(const RowVector & other){
#ifdef LOG
std::cout << '[' << &columns << ']' << "RowVector(" << & other << ")\n";
#endif
// https://codereview.stackexchange.com/questions/149669/c-operator-overloading-for-matrix-operations-follow-up
// http://www.cplusplus.com/reference/vector/vector/resize/
columns.resize(other.columns.size());
// element loop
for(uint32_t i=0; columns.size() > i; ++i){
columns[i] = other.columns[i];
}
// Copy name of the other one
name = other.name;
// Then append
name.append("2");
}
double & RowVector::operator [] (const uint32_t i){
#ifdef LOGBRACKET
std::cout << '[' << &columns << ']' << "double & RowVector::operator [] (" << i << ")\n";
#endif
// Return reference; otherwise, unable to assign
return columns[i];
}
double RowVector::operator [] (const uint32_t i) const {
#ifdef LOGBRACKET
std::cout << '[' << &columns << ']' << "double RowVector::operator [] (" << i << ") const\n";
#endif
// Return reference; otherwise, unable to assign
return columns[i];
}
const std::string RowVector::get_name() const{
#ifdef LOG
std::cout << '[' << &columns << ']' << "const std::string RowVector::get_name()\n";
#endif
// Return constant; to prevent change
return name;
}
RowVector RowVector::operator + (const RowVector & other){
#ifdef LOG
std::cout << '[' << &columns << ']' << "RowVector RowVector::operator + (" << & other << ")\n";
#endif
// Check size
assert(columns.size() == other.columns.size());
// Make a new vector to return
RowVector temp(other);
// Element loop
for (uint32_t i=0; columns.size() > i; ++i){
temp[i] += columns[i];
}
// Returning a temporary image
return temp;
}
RowVector RowVector::operator * (const double a){
#ifdef LOG
std::cout << '[' << &columns << ']' << "RowVector RowVector::operator * (" << a << ")\n";
#endif
// Make a new vector to return
RowVector temp(*this);
// Element loop in `for each` style
// c++ 11 or later
for (auto & element : temp.columns){
element *= a;
}
// Returning a temporary image
return temp;
}
const double RowVector::operator * (const RowVector & other){
#ifdef LOG
std::cout << '[' << &columns << ']' << "const double RowVector::operator * (" << & other << ")\n";
#endif
// Check size
assert(columns.size() == other.columns.size());
double dot_product = 0.0;
// Element loop
for (uint32_t i = 0; columns.size() > i; ++i){
dot_product += columns[i] * other.columns[i];
}
// Returning a temporary image
return dot_product;
}
void RowVector::show(){
#ifdef LOG
std::cout << '[' << &columns << ']' << "void RowVector::show()\n";
#endif
for (uint32_t i=0; columns.size()> i; ++i){
std::cout << name << '[' << i << "] = " << columns[i] << '\n';
}
}
void RowVector::resize(std::size_t new_size){
#ifdef LOG
std::cout << '[' << &columns << ']' << "void RowVector::resize(" << new_size << ")\n";
#endif
columns.resize(new_size);
}
std::size_t RowVector::size() const noexcept{
#ifdef LOG
std::cout << '[' << &columns << ']' << "std::size_t RowVector::size() const noexcept\n";
#endif
return columns.size();
}
RowVector & RowVector::operator += (const RowVector & other) {
#ifdef LOG
std::cout << '[' << &columns << ']' << "RowVector & RowVector::operator += (" << & other << ")\n";
#endif
// https://stackoverflow.com/questions/4581961/c-how-to-overload-operator
for (uint32_t i=0; size()>i; ++i){
columns[i] += other[i];
}
return *this;
}
RowVector & RowVector::operator *= (const double a) {
#ifdef LOG
std::cout << '[' << &columns << ']' << "RowVector & RowVector::operator *= (" << a << ")\n";
#endif
// https://stackoverflow.com/questions/4581961/c-how-to-overload-operator
for (uint32_t i=0; size()>i; ++i){
columns[i] *= a;
}
return *this;
}
// End vector_double.cpp
// Build command : g++ -Wall -g -std=c++14 vector_double.cpp -fsyntax-only
```
``` C++
// Begin cpp_vector_double_practice.cpp
#include <cassert>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
#include "vector_double.h"
int32_t main(int32_t argn, char *argv[]){
double s[] = {1.0, 2.0};
std::cout << "RowVector row (2u, s, \"row\");\n";
RowVector row (2u, s, "row");
row.show();
std::cout << "RowVector another_row (row);\n";
RowVector another_row (row);
row.show();
another_row.show();
std::cout << "another_row[1] += 0.5;\n";
another_row[1] += 0.5;
row.show();
another_row.show();
std::cout << "RowVector row_plus_another(row + another_row);\n";
RowVector row_plus_another(row + another_row);
row.show();
another_row.show();
row_plus_another.show();
std::cout << "RowVector zeros(3);\n";
RowVector zeros(3u, "zeros");
row.show();
another_row.show();
row_plus_another.show();
zeros.show();
double t[] = {2.0, -1.0};
RowVector ortho (2u, t, "ortho");
double dot = row * ortho;
std::cout << "double dot = row * ortho;\n";
std::cout << "dot = " << dot << '\n';
std::cout << "dot = row * row;\n";
dot = row * row;
std::cout << "dot = " << dot << '\n';
}
// End cpp_vector_double_practice.cpp
// Build command : g++ -Wall -g -std=c++14 cpp_vector_double_practice.cpp vector_double.cpp -o cpp_vector_double_practice
```
* In the mean while, following code blocks depict a possible implementation in python.
```
import collections
class Vector(collections.UserList):
def __add__(self, other):
# check size
assert len(self) == len(other), f"Lengths are different ({len(self)} == {len(other)})"
# trying list comprehension
return Vector([a + b for a, b in zip(self, other)])
def __radd__(self, other):
# What is this?
return self.__add__(other)
def __mul__(self, other):
# what is happening here?
if isinstance(other, (int, float, complex)):
result = Vector([a * other for a in self])
elif isinstance(other, Vector):
assert len(self) == len(other), f"Lengths are different ({len(self)} == {len(other)})"
result = sum(a * b for a, b in zip(self, other))
return result
def __rmul__(self, other):
return __mul__(self, other)
def __str__(self):
# How does the .join() work?
return '\n'.join(f"{hex(id(self))}[{i}] = {self[i]}" for i in range(len(self)))
def __len__(self):
return len(self.data)
print("a = Vector([1, 2])")
a = Vector([1, 2])
print(a)
print("b = Vector(a)")
b = Vector(a)
print(a)
print(b)
print("b[1] += (-0.5)")
b[1] += (-0.5)
print(a)
print(b)
print("c = a + b")
c = a + b
print(a)
print(b)
print(c)
print("ortho = Vector([2, -1])")
ortho = Vector([2, -1])
print(a)
print(b)
print(c)
print(ortho)
print("dot = a * ortho")
dot = a * ortho
print(f"a * ortho = {dot}")
print("dot = a * a")
dot = a * a
print(f"a * a = {dot}")
```
# Matrix class example
## In C++
* Following code blocks present a possible implementation of matrix class in C++.
* Please note that to build these files, `vector_double.h` and `vector_double.cpp` files are necessary.
```C++
// Begin matrix_double.h
#include <cassert>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
#include "vector_double.h"
#ifndef MATRIX_DOUBLE
#define MATRIX_DOUBLE
class Matrix
{
std::vector<RowVector> rows;
protected:
std::string name;
public:
Matrix();
~ Matrix();
Matrix(const uint32_t m, const uint32_t n, const double *values, std::string new_name="None");
Matrix(const uint32_t m, const uint32_t n, std::string new_name="None");
Matrix(const Matrix & other, std::string new_name="");
Matrix(const RowVector & other, std::string new_name="");
RowVector & operator [] (const uint32_t i);
const RowVector operator [] (const uint32_t i) const;
const std::string get_name() const;
Matrix operator + (const Matrix & other);
Matrix operator * (const double a);
RowVector operator * (const RowVector &v);
Matrix operator * (const Matrix & other);
void show();
Matrix transpose();
const size_t get_height() const;
const size_t get_width() const;
};
#endif
// End matrix_double.h
```
``` C++
// Begin matrix_double.cpp
#include <cassert>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
#include "vector_double.h"
#include "matrix_double.h"
Matrix::Matrix(){
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix()" << '\n';
#endif
name = "None";
}
Matrix::~ Matrix(){
#ifdef LOG
std::cout << '[' << &rows << ']' << "~ Matrix()" << '\n';
#endif
}
Matrix::Matrix(const uint32_t m, const uint32_t n, const double *values, std::string new_name){
#ifdef LOG
std::cout << '[' << &rows << ']'
<< "Matrix(" << m << ", "<< n << ", " << values << ", " << new_name << ")\n";
#endif
name = new_name;
rows.resize(m);
// If initial values available, copy
if (values){
// row loop
for (uint32_t i = 0; m > i; ++i){
rows[i].resize(n);
// column loop
for (uint32_t j = 0; n > j; ++j){
rows[i][j] = *(values + i * n + j) ;
}
}
}
// If no initial values, set all values zero
else{
// row loop
for (uint32_t i = 0; m > i; ++i){
rows[i].resize(n);
// column loop
for (uint32_t j = 0; n > j; ++j){
rows[i][j] = 0.0;
}
}
}
}
// Instead of implementing another constructor, calling an existing one
// c++ 11 or later
Matrix::Matrix(const uint32_t m, const uint32_t n, std::string new_name) : Matrix(m, n, NULL, new_name){
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix(" << m << ", " << n << ", " << new_name << ")\n";
#endif
}
Matrix::Matrix(const Matrix & other, std::string new_name){
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix(" << & other << ")\n";
#endif
// https://codereview.stackexchange.com/questions/149669/c-operator-overloading-for-matrix-operations-follow-up
// http://www.cplusplus.com/reference/vector/vector/resize/
rows.resize(other.rows.size());
// row loop
for(uint32_t i=0; rows.size() > i; ++i){
rows[i].resize(other.rows[i].size());
// column loop
for(uint32_t j=0; other.rows[i].size() > j; ++j){
// Another possibility is as follows
// rows[i][j] = other.rows[i][j];
// However for now the line above would create a temporary row vector
// To avoid seemingly unnecessary such temporary object,
// for now would use the following line
rows[i][j] = other.rows[i][j];
}
}
if ("" != new_name){
name = new_name;
}
else{
// Copy name of the other one
name = other.name;
// Then append
name.append("2");
}
}
Matrix::Matrix(const RowVector & other, std::string new_name){
// RowVector -> n x 1 matrix
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix(const RowVector &" << & other << ")\n";
#endif
rows.resize(other.size());
// row loop
for(uint32_t i=0; rows.size() > i; ++i){
rows[i].resize(1);
rows[i][0] = other[0];
}
if ("" != new_name){
name = new_name;
}
else{
// Copy name of the other one
name = other.get_name();
// Then append
name.append("2");
}
}
RowVector & Matrix::operator [] (const uint32_t i){
#ifdef LOGBRACKET
std::cout << '[' << &rows << ']' << "RowVector & Matrix::operator [] (" << i << ")\n";
#endif
// Return reference; otherwise, unable to assign
return rows[i];
}
const RowVector Matrix::operator [] (const uint32_t i) const {
#ifdef LOGBRACKET
std::cout << '[' << &rows << ']' << "const RowVector Matrix::operator [] (" << i << ")\n";
#endif
// Return reference; otherwise, unable to assign
return rows[i];
}
const std::string Matrix::get_name() const{
#ifdef LOG
std::cout << '[' << &rows << ']' << "const std::string Matrix::get_name()\n";
#endif
// Return constant; to prevent change
return name;
}
Matrix Matrix::operator + (const Matrix & other){
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix Matrix::operator + ("<< & other <<")\n";
#endif
// Check size
assert(this->get_height() == other.get_height());
assert(this->get_width() == other.get_width());
#ifdef LOG
std::cout << "Matrix temp(other);\n";
#endif
// Make a new vector to return
Matrix temp(other, get_name() + '+' + other.get_name());
#ifdef LOG
std::cout << "Begin row loop\n";
#endif
// Row loop
for (uint32_t i=0; rows.size() > i; ++i){
temp[i] += rows[i];
}
#ifdef LOG
std::cout << "End row loop\n";
#endif
// Returning a temporary image
return temp;
}
Matrix Matrix::operator * (const double a){
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix Matrix::operator * (" << a << ")\n";
#endif
// Make a new vector to return
// https://stackoverflow.com/questions/332111/how-do-i-convert-a-double-into-a-string-in-c
Matrix temp(*this, std::to_string(a) + '*' + get_name());
// Element loop in `for each` style
// c++ 11 or later
for (auto & element : temp.rows){
element *= a;
}
// Returning a temporary image
return temp;
}
RowVector Matrix::operator * (const RowVector &v){
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix Matrix::operator * (" << &v << ")\n";
#endif
// Make a new vector to return
RowVector temp(rows.size(), NULL, name + '*' + v.get_name());
// Element loop in `for each` style
// c++ 11 or later
for (uint32_t i=0; rows.size()>i; ++i){
temp[i] = rows[i] * v;
}
// Returning a temporary image
return temp;
}
Matrix Matrix::operator * (const Matrix & other){
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix Matrix::operator * (" << &other << ")\n";
#endif
// Check size
assert(rows[0].size() == other.rows.size());
Matrix temp(rows.size(), other[0].size(), name + '*' + other.name);
// row loop
for (uint32_t i = 0; rows.size() > i; ++i){
// column loop
for(uint32_t j = 0; other[0].size() > j; ++j){
// dummy index loop
for(uint32_t k = 0; rows[0].size() > k; ++k){
temp[i][j] += rows[i][k] * other[k][j];
}
}
}
// Returning a temporary image
return temp;
}
void Matrix::show(){
#ifdef LOG
std::cout << '[' << &rows << ']' << "void Matrix::show()\n";
#endif
// row loop
for (uint32_t i=0; rows.size()> i; ++i){
// column loop
for (uint32_t j=0; rows[i].size()> j; ++j){
std::cout << get_name() << '['<< i << "][" << j << "]= " << rows[i][j] << '\n';
}
}
}
Matrix Matrix::transpose(){
#ifdef LOG
std::cout << '[' << &rows << ']' << "Matrix Matrix::transpose()\n";
#endif
Matrix temp(rows[0].size(), rows.size(), name+"T");
// row loop
for(uint32_t i=0; temp.rows.size()> i; ++i){
// column loop
for(uint32_t j=0; temp.rows.size()> j; ++j){
temp[i][j] = rows[i][j];
}
}
return temp;
}
const size_t Matrix::get_height() const{
return rows.size();
}
const size_t Matrix::get_width() const{
return rows[0].size();
}
// End matrix_double.cpp
// Build command : g++ -Wall -g -std=c++14 matrix_double.cpp -fsyntax-only
```
``` C++
// Begin cpp_matrix_double_practice.cpp
#include <cassert>
#include <cmath>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
#include "matrix_double.h"
int32_t main(int32_t argn, char *argv[]){
double s[] = {1.0, 0.0,
0.0, 1.0};
std::cout << "Matrix id (2u, 2u, s, \"identity\");\n";
Matrix identity (2u, 2u, s, "id");
identity.show();
double r[] = {+cos(M_PI/6.0), sin(M_PI/6.0),
-sin(M_PI/6.0), cos(M_PI/6.0)};
std::cout << "Matrix rotation (2u, 2u, r, \"rot\");\n";
Matrix rotation (2u, 2u, r, "rot");
identity.show();
rotation.show();
std::cout << "Matrix sum(identity + rotation);\n";
Matrix sum(identity + rotation);
identity.show();
rotation.show();
sum.show();
// Check sum operation result
for (uint32_t i=0; 2u > i; ++i){
for (uint32_t j=0; 2u > j; ++j){
assert(sum[i][j] == (identity[i][j] + rotation[i][j]));
}
}
std::cout << "Matrix twice(identity * 2.0);\n";
Matrix twice(identity * 2.0);
// Check scala multiplication result
assert(twice[0][0] == 2.0);
assert(twice[0][1] == 0.0);
assert(twice[1][0] == 0.0);
assert(twice[1][1] == 2.0);
std::cout << "Matrix new_axis(twice * rotation);\n";
Matrix new_axis(twice * rotation);
// Check matrix multiplication result
for (uint32_t i=0; 2u > i; ++i){
for (uint32_t j=0; 2u > j; ++j){
assert(new_axis[i][j] == (2.0 * rotation[i][j]));
}
}
Matrix ninety_degrees(rotation * rotation * rotation);
// Check matrix multiplication result
assert(abs(ninety_degrees[0][0] - ( 0.0)) < 1e-12);
assert(abs(ninety_degrees[0][1] - ( 1.0)) < 1e-12);
assert(abs(ninety_degrees[1][0] - (-1.0)) < 1e-12);
assert(abs(ninety_degrees[1][1] - ( 0.0)) < 1e-12);
// State Space Representation Ax + B u
double xi_d[] = {1.0, 0.0};
double ones_d[] = {1.0, 1.0};
Matrix xi(2, 1, xi_d, "xi");
Matrix B(2, 1, ones_d, "B");
double u = 0.75;
Matrix xj;
// xj = A xi + B u
xj = rotation * xi + B * u;
xj.show();
assert(abs(xj[0][0] - ( 0.75 + cos(M_PI/6.0))) < 1e-12);
assert(abs(xj[1][0] - ( 0.75 - sin(M_PI/6.0))) < 1e-12);
}
// End cpp_matrix_double_practice.cpp
// Build command : g++ -Wall -g -std=c++14 cpp_matrix_double_practice.cpp vector_double.cpp matrix_double.cpp -o cpp_matrix_double_practice
```
* The build command above lists necessary files.
## In Python
* Following code blocks are a possible implementation of matrix in python.
* As in C++ example, it will build on the prior `Vector` class.
```
import collections
import copy
class Matrix(collections.UserList):
def __init__(self, m=None, n=None, values=None):
if m is None:
self.m = self.n = 0
self.data = []
elif values is not None:
self.m = int(m) # number of rows
self.n = int(n) # number of columns
# Again utilizing Vector class and list comprehension
self.data = [Vector(values[(i * n):((i+1) * n)]) for i in range(m)]
elif n is None:
if isinstance(m, Matrix):
# copy constructor
self.m = m.m
self.n = m.n
# To avoid referencing rows of m matrix
self.data = copy.deepcopy(m.data)
elif isinstance(m, Vector):
# Vector to n x 1 Matrix
self.data = [Vector([value]) for value in m]
self.m = len(self.data)
self.n = 1
elif isinstance(m, int) and isinstance(n, int) and values is None:
# zeros
self.m = m
self.n = n
self.data = [Vector([0.0] * n) for i in range(m)]
else:
raise NotImplementedError
def __add__(self, other):
assert isinstance(other, Matrix)
result = Matrix()
for self_row, other_row in zip(self, other):
result.append(self_row + other_row)
return result
def __mul__(self, other):
if isinstance(other, (int, float, complex)):
result = Matrix()
for row in self:
result.append(row * other)
elif isinstance(other, Matrix):
assert self.n == other.m, f"Matrix sizes ({self.m}, {self.n}) x ({other.m}, {other.n}) not compatible"
result = Matrix(self.m, other.n)
for i in range(self.m):
for j in range(other.n):
for k in range(self.n):
result[i][j] += self[i][k] * other[k][j]
elif isinstance(other, Vector):
assert self.n == len(other), f"Matrix sizes ({self.m}, {self.n}) x ({len(other)}, 1) not compatible"
result = Vector([row * other for row in self])
else:
raise NotImplementedError
return result
def __str__(self):
row_text = []
for i, row in enumerate(self):
for j, value in enumerate(row):
row_text.append(f"{hex(id(self))}[{i}][{j}] = {self[i][j]}")
return '\n'.join(row_text)
def transpose(self):
result = Matrix()
result.data = list(zip(self.data))
result.m = self.n
resutl.n = self.m
matA = Matrix(2, 2, list(range(4)))
print(matA)
matB = Matrix(matA)
matB[0][0] = matA[0][0] + 7
print(matA)
print(matB)
assert matA[0][0] != matB[0][0], "Please use deep copy"
vecC = Vector([1, 0])
print("matC = Matrix(vecC)")
matC = Matrix(vecC)
print(matA)
print(matB)
print(matC)
print("matD = Matrix(2, 2)")
matD = Matrix(2, 2)
print(matA)
print(matB)
print(matC)
print(matD)
for i in range(matD.m):
for j in range(matD.n):
assert 0 == matD[i][j]
print("matE = matA + matA")
matE = matA + matA
print(matA)
print(matB)
print(matC)
print(matD)
print(matE)
for i in range(matE.m):
for j in range(matE.n):
assert matE[i][j] == 2 * matA[i][j]
print("matF = matA * matA")
matF = matA * matA
print(matA)
print(matB)
print(matC)
print(matD)
print(matE)
print(matF)
print("matG = matA * vecC")
vecG = matA * vecC
print(matA)
print(matB)
print(matC)
print(matD)
print(matE)
print(matF)
print(vecG)
assert len(vecG) == matA.m
for i in range(matA.m):
assert vecG[i] == matA[i][0]
```
# State Space Representation Example
## C++
* Again, this example builds on top of the `Matrix` and `RowVector` examples.
``` C++
// Begin lti_dt.h
#include <cassert>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
#include "vector_double.h"
#include "matrix_double.h"
#ifndef LTI_DT
// Discrete Time State Space model
class LTI_DT{
protected:
Matrix A;
Matrix B;
Matrix C;
Matrix D;
Matrix X;
size_t m, n;
public:
LTI_DT(Matrix &new_A, Matrix &new_B, Matrix &new_C, Matrix &new_D, Matrix &new_X);
~LTI_DT();
const Matrix get_y(const double u);
void get_next_x(const double u);
};
#endif
// End lti_dt.h
```
``` C++
// Begin lti_dt.cpp
#include <cassert>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
#include "vector_double.h"
#include "matrix_double.h"
#include "lti_dt.h"
// Discrete Time State Space model
LTI_DT::LTI_DT(Matrix &new_A, Matrix &new_B, Matrix &new_C, Matrix &new_D, Matrix &new_X){
#ifdef LOG
std::cout << '[' << &A << ']' << "LTI_DT::LTI_DT(" << &new_A << ", " << &new_B << ", " << &new_C << ", " << &new_D << ")\n";
#endif
#ifdef LOG
std::cout << "LTI_DT::LTI_DT(): A = new_A;\n";
#endif
A = new_A;
#ifdef LOG
std::cout << "LTI_DT::LTI_DT(): B = new_B;\n";
#endif
B = new_B;
#ifdef LOG
std::cout << "LTI_DT::LTI_DT(): C = new_C;\n";
#endif
C = new_C;
#ifdef LOG
std::cout << "LTI_DT::LTI_DT(): D = new_D;\n";
#endif
D = new_D;
#ifdef LOG
std::cout << "LTI_DT::LTI_DT(): X = new_X;\n";
#endif
X = new_X;
// is A matrix square?
assert(A.get_height() == A.get_width());
// number of state variables
n = A.get_height();
// check number of rows of B matrix
assert(B.get_height() == n);
// expected size of input
m = B.get_width();
}
LTI_DT::~LTI_DT(){
#ifdef LOG
std::cout << '[' << &A << ']' << "LTI_DT::!LTI_DT()\n";
#endif
#ifdef LOG
std::cout << "delete &A;\n";
#endif
// delete &A;
#ifdef LOG
std::cout << "delete &B;\n";
#endif
// delete &B;
#ifdef LOG
std::cout << "delete &C;\n";
#endif
// delete &C;
#ifdef LOG
std::cout << "delete &D;\n";
#endif
// delete &D;
#ifdef LOG
std::cout << "delete &X;\n";
#endif
// delete &X;
}
const Matrix LTI_DT::get_y(const double u){
return Matrix (C * X + D * u);
}
void LTI_DT::get_next_x(const double u){
Matrix next_X (A * X + B * u);
// delete &X;
X = next_X;
}
// End lti_dt.cpp
```
``` C++
// Begin lti_dt_example.cpp
#include <cassert>
#include <cstdint>
#include <exception>
#include <iostream>
#include <string>
#include <vector>
#include "vector_double.h"
#include "matrix_double.h"
#include "lti_dt.h"
int32_t main(int32_t argn, char *argv[]){
// https://ccrma.stanford.edu/~jos/fp/State_Space_Simulation_Matlab.html
const double A_d[] = {0, 1, -1, 0};
std::cout << "Matrix A(2u, 2u, A_d, \"A\");\n";
Matrix A(2u, 2u, A_d, "A");
const double B_d[] = {0, 1};
std::cout << "Matrix B(2u, 1u, B_d, \"B\");\n";
Matrix B(2u, 1u, B_d, "B");
const double C_d[] = {1, 0, 0, 1, 0, 1};
std::cout << "Matrix C(3u, 2u, C_d, \"C\");\n";
Matrix C(3u, 2u, C_d, "C");
const double D_d[] = {0, 0, 0};
std::cout << "Matrix D(3u, 1u, D_d, \"D\");\n";
Matrix D(3u, 1u, D_d, "D");
const uint32_t n = 10;
const double u[n] = {1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0};
std::vector<Matrix> y_list;
Matrix X(2u, 1u, "x");
LTI_DT ss_dt(A, B, C, D, X);
for(uint32_t k=0; n > k; ++k){
Matrix y_now(ss_dt.get_y(u[k]));
y_list.push_back(y_now);
ss_dt.get_next_x(u[k]);
}
for(uint32_t i=0; n>i; ++i){
std::cout << "y[" << i << "] = " << y_list[i][2][0] << '\n';
}
return 0;
}
// End lti_dt_example.cpp
// Build command : g++ -Wall -g -std=c++14 lti_dt_example.cpp vector_double.cpp matrix_double.cpp lti_dt.cpp -o lti_dt_example
```
* However, this example may have some obvious problem. What do you think?
* For python implementation, please refer to another file.
# Exercise
## 00 Comments
* Please try to add comments to each line of the source code.
* So that anyone tries to read the code can immediately understand.
* Group work would be possible, too.
## 01 Improve the code
* See if you can find some possible improvements
* Try submit improvement through a *pull request*.
* What could be a good way to know whether the new code would be suitable?
| github_jupyter |
# Overview
- nb023 ベース
- nb034の結果を使う
# Const
```
NB = '035'
isSmallSet = False
if isSmallSet:
LENGTH = 7000
else:
LENGTH = 500_000
PATH_TRAIN = './../data/input/train_clean.csv'
PATH_TEST = './../data/input/test_clean.csv'
PATH_SMPLE_SUB = './../data/input/sample_submission.csv'
DIR_OUTPUT = './../data/output/'
cp = ['#f8b195', '#f67280', '#c06c84', '#6c5b7b', '#355c7d']
sr = 10*10**3 # 10 kHz
```
# Import everything I need :)
```
import warnings
warnings.filterwarnings('ignore')
import time
import gc
import random
import os
import itertools
import multiprocessing
import numpy as np
from scipy import signal
# from pykalman import KalmanFilter
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from fastprogress import progress_bar
from lightgbm import LGBMRegressor
from sklearn.model_selection import KFold, train_test_split, StratifiedKFold, GroupKFold
from sklearn.metrics import f1_score, mean_absolute_error, confusion_matrix
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor
# from sklearn.svm import SVR
from sklearn.linear_model import Lasso
# from dtreeviz.trees import dtreeviz
import tensorflow as tf
from tensorflow.keras.layers import *
from tensorflow.keras.callbacks import Callback, LearningRateScheduler
from tensorflow.keras.losses import categorical_crossentropy
from tensorflow.keras.optimizers import Adam
from tensorflow.keras import backend as K
from tensorflow.keras import losses, models, optimizers
# import tensorflow_addons as tfa
```
# My function
```
def f1_macro(true, pred):
return f1_score(true, pred, average='macro')
def get_df_batch(df, batch):
idxs = df['batch'] == batch
assert any(idxs), 'そのようなbatchはありません'
return df[idxs]
def get_signal_mv_mean(df, n=3001):
signal_mv = np.zeros(len(df))
for bt in df['batch'].unique():
idxs = df['batch'] == bt
_signal_mv = df['signal'][idxs].rolling(n, center=True).mean().interpolate('spline', order=5, limit_direction='both').values
signal_mv[idxs] = _signal_mv
return signal_mv
def get_signal_mv_std(df, n=3001):
signal_mv = np.zeros(len(df))
for bt in df['batch'].unique():
idxs = df['batch'] == bt
_signal_mv = df['signal'][idxs].rolling(n, center=True).std().interpolate('spline', order=5, limit_direction='both').values
signal_mv[idxs] = _signal_mv
return signal_mv
def get_signal_mv_min(df, n=3001):
signal_mv = np.zeros(len(df))
for bt in df['batch'].unique():
idxs = df['batch'] == bt
_signal_mv = df['signal'][idxs].rolling(n, center=True).min().interpolate('spline', order=5, limit_direction='both').values
signal_mv[idxs] = _signal_mv
return signal_mv
def get_signal_mv_max(df, n=3001):
signal_mv = np.zeros(len(df))
for bt in df['batch'].unique():
idxs = df['batch'] == bt
_signal_mv = df['signal'][idxs].rolling(n, center=True).max().interpolate('spline', order=5, limit_direction='both').values
signal_mv[idxs] = _signal_mv
return signal_mv
def group_feat_train(_train):
train = _train.copy()
# group init
train['group'] = int(0)
# group 1
idxs = (train['batch'] == 3) | (train['batch'] == 7)
train['group'][idxs] = int(1)
# group 2
idxs = (train['batch'] == 5) | (train['batch'] == 8)
train['group'][idxs] = int(2)
# group 3
idxs = (train['batch'] == 2) | (train['batch'] == 6)
train['group'][idxs] = int(3)
# group 4
idxs = (train['batch'] == 4) | (train['batch'] == 9)
train['group'][idxs] = int(4)
return train[['group']]
def group_feat_test(_test):
test = _test.copy()
# group init
test['group'] = int(0)
x_idx = np.arange(len(test))
# group 1
idxs = (100000<=x_idx) & (x_idx<200000)
test['group'][idxs] = int(1)
idxs = (900000<=x_idx) & (x_idx<=1000000)
test['group'][idxs] = int(1)
# group 2
idxs = (200000<=x_idx) & (x_idx<300000)
test['group'][idxs] = int(2)
idxs = (600000<=x_idx) & (x_idx<700000)
test['group'][idxs] = int(2)
# group 3
idxs = (400000<=x_idx) & (x_idx<500000)
test['group'][idxs] = int(3)
# group 4
idxs = (500000<=x_idx) & (x_idx<600000)
test['group'][idxs] = int(4)
idxs = (700000<=x_idx) & (x_idx<800000)
test['group'][idxs] = int(4)
return test[['group']]
class permutation_importance():
def __init__(self, model, metric):
self.is_computed = False
self.n_feat = 0
self.base_score = 0
self.model = model
self.metric = metric
self.df_result = []
def compute(self, X_valid, y_valid):
self.n_feat = len(X_valid.columns)
if self.metric == 'auc':
y_valid_score = self.model.predict_proba(X_valid)[:, 1]
fpr, tpr, thresholds = roc_curve(y_valid, y_valid_score)
self.base_score = auc(fpr, tpr)
else:
pred = np.round(self.model.predict(X_valid)).astype('int8')
self.base_score = self.metric(y_valid, pred)
self.df_result = pd.DataFrame({'feat': X_valid.columns,
'score': np.zeros(self.n_feat),
'score_diff': np.zeros(self.n_feat)})
# predict
for i, col in enumerate(X_valid.columns):
df_perm = X_valid.copy()
np.random.seed(1)
df_perm[col] = np.random.permutation(df_perm[col])
y_valid_pred = self.model.predict(df_perm)
if self.metric == 'auc':
y_valid_score = self.model.predict_proba(df_perm)[:, 1]
fpr, tpr, thresholds = roc_curve(y_valid, y_valid_score)
score = auc(fpr, tpr)
else:
score = self.metric(y_valid, np.round(y_valid_pred).astype('int8'))
self.df_result['score'][self.df_result['feat']==col] = score
self.df_result['score_diff'][self.df_result['feat']==col] = self.base_score - score
self.is_computed = True
def get_negative_feature(self):
assert self.is_computed!=False, 'compute メソッドが実行されていません'
idx = self.df_result['score_diff'] < 0
return self.df_result.loc[idx, 'feat'].values.tolist()
def get_positive_feature(self):
assert self.is_computed!=False, 'compute メソッドが実行されていません'
idx = self.df_result['score_diff'] > 0
return self.df_result.loc[idx, 'feat'].values.tolist()
def show_permutation_importance(self, score_type='loss'):
'''score_type = 'loss' or 'accuracy' '''
assert self.is_computed!=False, 'compute メソッドが実行されていません'
if score_type=='loss':
ascending = True
elif score_type=='accuracy':
ascending = False
else:
ascending = ''
plt.figure(figsize=(15, int(0.25*self.n_feat)))
sns.barplot(x="score_diff", y="feat", data=self.df_result.sort_values(by="score_diff", ascending=ascending))
plt.title('base_score - permutation_score')
def plot_corr(df, abs_=False, threshold=0.95):
if abs_==True:
corr = df.corr().abs()>threshold
vmin = 0
else:
corr = df.corr()
vmin = -1
# Plot
fig, ax = plt.subplots(figsize=(12, 10), dpi=100)
fig.patch.set_facecolor('white')
sns.heatmap(corr,
xticklabels=df.corr().columns,
yticklabels=df.corr().columns,
vmin=vmin,
vmax=1,
center=0,
annot=False)
# Decorations
ax.set_title('Correlation', fontsize=22)
def get_low_corr_column(df, threshold):
df_corr = df.corr()
df_corr = abs(df_corr)
columns = df_corr.columns
# 対角線の値を0にする
for i in range(0, len(columns)):
df_corr.iloc[i, i] = 0
while True:
columns = df_corr.columns
max_corr = 0.0
query_column = None
target_column = None
df_max_column_value = df_corr.max()
max_corr = df_max_column_value.max()
query_column = df_max_column_value.idxmax()
target_column = df_corr[query_column].idxmax()
if max_corr < threshold:
# しきい値を超えるものがなかったため終了
break
else:
# しきい値を超えるものがあった場合
delete_column = None
saved_column = None
# その他との相関の絶対値が大きい方を除去
if sum(df_corr[query_column]) <= sum(df_corr[target_column]):
delete_column = target_column
saved_column = query_column
else:
delete_column = query_column
saved_column = target_column
# 除去すべき特徴を相関行列から消す(行、列)
df_corr.drop([delete_column], axis=0, inplace=True)
df_corr.drop([delete_column], axis=1, inplace=True)
return df_corr.columns # 相関が高い特徴量を除いた名前リスト
def reduce_mem_usage(df, verbose=True):
numerics = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
start_mem = df.memory_usage().sum() / 1024**2
for col in df.columns:
if col!='open_channels':
col_type = df[col].dtypes
if col_type in numerics:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int':
if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
else:
if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
df[col] = df[col].astype(np.float16)
elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
end_mem = df.memory_usage().sum() / 1024**2
if verbose: print('Mem. usage decreased to {:5.2f} Mb ({:.1f}% reduction)'.format(end_mem, 100 * (start_mem - end_mem) / start_mem))
return df
def train_lgbm(X, y, X_te, lgbm_params, random_state=5, n_fold=5, verbose=50, early_stopping_rounds=100, show_fig=True):
# using features
print(f'features({len(X.columns)}): \n{X.columns}') if not verbose==0 else None
# folds = KFold(n_splits=n_fold, shuffle=True, random_state=random_state)
folds = StratifiedKFold(n_splits=n_fold, shuffle=True, random_state=random_state)
scores = []
oof = np.zeros(len(X))
oof_round = np.zeros(len(X))
test_pred = np.zeros(len(X_te))
df_pi = pd.DataFrame(columns=['feat', 'score_diff'])
for fold_n, (train_idx, valid_idx) in enumerate(folds.split(X, y=y)):
if verbose==0:
pass
else:
print('\n------------------')
print(f'- Fold {fold_n + 1}/{N_FOLD} started at {time.ctime()}')
# prepare dataset
X_train, X_valid = X.iloc[train_idx], X.iloc[valid_idx]
y_train, y_valid = y[train_idx], y[valid_idx]
# train
model = LGBMRegressor(**lgbm_params, n_estimators=N_ESTIMATORS)
model.fit(X_train, y_train,
eval_set=[(X_train, y_train), (X_valid, y_valid)],
verbose=verbose,
early_stopping_rounds=early_stopping_rounds)
# pred
y_valid_pred = model.predict(X_valid, model.best_iteration_)
y_valid_pred_round = np.round(y_valid_pred).astype('int8')
_test_pred = model.predict(X_te, model.best_iteration_)
if show_fig==False:
pass
else:
# permutation importance
pi = permutation_importance(model, f1_macro) # model と metric を渡す
pi.compute(X_valid, y_valid)
pi_result = pi.df_result
df_pi = pd.concat([df_pi, pi_result[['feat', 'score_diff']]])
# result
oof[valid_idx] = y_valid_pred
oof_round[valid_idx] = y_valid_pred_round
score = f1_score(y_valid, y_valid_pred_round, average='macro')
scores.append(score)
test_pred += _test_pred
if verbose==0:
pass
else:
print(f'---> f1-score(macro) valid: {f1_score(y_valid, y_valid_pred_round, average="macro"):.4f}')
print('')
print('====== finish ======')
print('score list:', scores)
print('CV mean score(f1_macro): {0:.4f}, std: {1:.4f}'.format(np.mean(scores), np.std(scores)))
print(f'oof score(f1_macro): {f1_score(y, oof_round, average="macro"):.4f}')
print('')
if show_fig==False:
pass
else:
# visualization
plt.figure(figsize=(5, 5))
plt.plot([0, 10], [0, 10], color='gray')
plt.scatter(y, oof, alpha=0.05, color=cp[1])
plt.xlabel('true')
plt.ylabel('pred')
plt.show()
# confusion_matrix
plot_confusion_matrix(y, oof_round, classes=np.arange(11))
# permutation importance
plt.figure(figsize=(15, int(0.25*len(X.columns))))
order = df_pi.groupby(["feat"]).mean()['score_diff'].reset_index().sort_values('score_diff', ascending=False)
sns.barplot(x="score_diff", y="feat", data=df_pi, order=order['feat'])
plt.title('base_score - permutation_score')
plt.show()
# submission
test_pred = test_pred/N_FOLD
test_pred_round = np.round(test_pred).astype('int8')
return test_pred_round, test_pred, oof_round, oof
def plot_confusion_matrix(truth, pred, classes, normalize=False, title=''):
cm = confusion_matrix(truth, pred)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
plt.figure(figsize=(10, 10))
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion matrix', size=15)
plt.colorbar(fraction=0.046, pad=0.04)
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.grid(False)
plt.tight_layout()
def train_test_split_lgbm(X, y, X_te, lgbm_params, random_state=5, test_size=0.3, verbose=50, early_stopping_rounds=100, show_fig=True):
# using features
print(f'features({len(X.columns)}): \n{X.columns}') if not verbose==0 else None
# folds = KFold(n_splits=n_fold, shuffle=True, random_state=random_state)
# folds = StratifiedKFold(n_splits=n_fold, shuffle=True, random_state=random_state)
# prepare dataset
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=test_size, random_state=random_state)
# train
model = LGBMRegressor(**lgbm_params, n_estimators=N_ESTIMATORS)
model.fit(X_train, y_train,
eval_set=[(X_train, y_train), (X_valid, y_valid)],
verbose=verbose,
early_stopping_rounds=early_stopping_rounds)
# pred
oof = model.predict(X_valid, model.best_iteration_)
oof_round = np.round(oof).astype('int8')
test_pred = model.predict(X_te, model.best_iteration_)
test_pred_round = np.round(test_pred).astype('int8')
print('====== finish ======')
print(f'oof score(f1_macro): {f1_score(y_valid, oof_round, average="macro"):.4f}')
print('')
if show_fig==False:
pass
else:
# visualization
plt.figure(figsize=(5, 5))
plt.plot([0, 10], [0, 10], color='gray')
plt.scatter(y_valid, oof, alpha=0.05, color=cp[1])
plt.xlabel('true')
plt.ylabel('pred')
plt.show()
# confusion_matrix
plot_confusion_matrix(y_valid, oof_round, classes=np.arange(11))
# permutation importance
pi = permutation_importance(model, f1_macro) # model と metric を渡す
pi.compute(X_valid, y_valid)
pi.show_permutation_importance(score_type='accuracy') # loss or accuracy
plt.show()
return test_pred_round, test_pred, oof_round, oof
```
<br>
ref: https://www.kaggle.com/martxelo/fe-and-ensemble-mlp-and-lgbm
```
def calc_gradients(s, n_grads=4):
'''
Calculate gradients for a pandas series. Returns the same number of samples
'''
grads = pd.DataFrame()
g = s.values
for i in range(n_grads):
g = np.gradient(g)
grads['grad_' + str(i+1)] = g
return grads
def calc_low_pass(s, n_filts=10):
'''
Applies low pass filters to the signal. Left delayed and no delayed
'''
wns = np.logspace(-2, -0.3, n_filts)
# wns = [0.3244]
low_pass = pd.DataFrame()
x = s.values
for wn in wns:
b, a = signal.butter(1, Wn=wn, btype='low')
zi = signal.lfilter_zi(b, a)
low_pass['lowpass_lf_' + str('%.4f' %wn)] = signal.lfilter(b, a, x, zi=zi*x[0])[0]
low_pass['lowpass_ff_' + str('%.4f' %wn)] = signal.filtfilt(b, a, x)
return low_pass
def calc_high_pass(s, n_filts=10):
'''
Applies high pass filters to the signal. Left delayed and no delayed
'''
wns = np.logspace(-2, -0.1, n_filts)
# wns = [0.0100, 0.0264, 0.0699, 0.3005, 0.4885, 0.7943]
high_pass = pd.DataFrame()
x = s.values
for wn in wns:
b, a = signal.butter(1, Wn=wn, btype='high')
zi = signal.lfilter_zi(b, a)
high_pass['highpass_lf_' + str('%.4f' %wn)] = signal.lfilter(b, a, x, zi=zi*x[0])[0]
high_pass['highpass_ff_' + str('%.4f' %wn)] = signal.filtfilt(b, a, x)
return high_pass
def calc_roll_stats(s, windows=[10, 50, 100, 500, 1000, 3000]):
'''
Calculates rolling stats like mean, std, min, max...
'''
roll_stats = pd.DataFrame()
for w in windows:
roll_stats['roll_mean_' + str(w)] = s.rolling(window=w, min_periods=1).mean().interpolate('spline', order=5, limit_direction='both')
roll_stats['roll_std_' + str(w)] = s.rolling(window=w, min_periods=1).std().interpolate('spline', order=5, limit_direction='both')
roll_stats['roll_min_' + str(w)] = s.rolling(window=w, min_periods=1).min().interpolate('spline', order=5, limit_direction='both')
roll_stats['roll_max_' + str(w)] = s.rolling(window=w, min_periods=1).max().interpolate('spline', order=5, limit_direction='both')
roll_stats['roll_range_' + str(w)] = roll_stats['roll_max_' + str(w)] - roll_stats['roll_min_' + str(w)]
roll_stats['roll_q10_' + str(w)] = s.rolling(window=w, min_periods=1).quantile(0.10).interpolate('spline', order=5, limit_direction='both')
roll_stats['roll_q25_' + str(w)] = s.rolling(window=w, min_periods=1).quantile(0.25).interpolate('spline', order=5, limit_direction='both')
roll_stats['roll_q50_' + str(w)] = s.rolling(window=w, min_periods=1).quantile(0.50).interpolate('spline', order=5, limit_direction='both')
roll_stats['roll_q75_' + str(w)] = s.rolling(window=w, min_periods=1).quantile(0.75).interpolate('spline', order=5, limit_direction='both')
roll_stats['roll_q90_' + str(w)] = s.rolling(window=w, min_periods=1).quantile(0.90).interpolate('spline', order=5, limit_direction='both')
# add zeros when na values (std)
# roll_stats = roll_stats.fillna(value=0)
return roll_stats
def calc_ewm(s, windows=[10, 50, 100, 500, 1000, 3000]):
'''
Calculates exponential weighted functions
'''
ewm = pd.DataFrame()
for w in windows:
ewm['ewm_mean_' + str(w)] = s.ewm(span=w, min_periods=1).mean()
ewm['ewm_std_' + str(w)] = s.ewm(span=w, min_periods=1).std()
# add zeros when na values (std)
ewm = ewm.fillna(value=0)
return ewm
def divide_and_add_features(s, signal_size=500000):
'''
Divide the signal in bags of "signal_size".
Normalize the data dividing it by 15.0
'''
# normalize
s = s/15.0
ls = []
for i in progress_bar(range(int(s.shape[0]/signal_size))):
sig = s[i*signal_size:(i+1)*signal_size].copy().reset_index(drop=True)
sig_featured = add_features(sig)
ls.append(sig_featured)
return pd.concat(ls, axis=0)
```
<br>
ref: https://www.kaggle.com/nxrprime/single-model-lgbm-kalman-filter-ii
```
def Kalman1D(observations,damping=1):
# To return the smoothed time series data
observation_covariance = damping
initial_value_guess = observations[0]
transition_matrix = 1
transition_covariance = 0.1
initial_value_guess
kf = KalmanFilter(
initial_state_mean=initial_value_guess,
initial_state_covariance=observation_covariance,
observation_covariance=observation_covariance,
transition_covariance=transition_covariance,
transition_matrices=transition_matrix
)
pred_state, state_cov = kf.smooth(observations)
return pred_state
```
# Preparation
setting
```
sns.set()
```
<br>
load dataset
<br>
処理のしやすさのために、バッチ番号を振る
<br>
smallset?
# Train
```
# configurations and main hyperparammeters
# EPOCHS = 180
EPOCHS = 180
NNBATCHSIZE = 16
GROUP_BATCH_SIZE = 4000
SEED = 321
LR = 0.0015
SPLITS = 6
def seed_everything(seed):
random.seed(seed)
np.random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
# tf.random.set_seed(seed)
# read data
def read_data():
train = pd.read_csv(PATH_TRAIN, dtype={'time': np.float32, 'signal': np.float32, 'open_channels':np.int32})
test = pd.read_csv(PATH_TEST, dtype={'time': np.float32, 'signal': np.float32})
sub = pd.read_csv(PATH_SMPLE_SUB, dtype={'time': np.float32})
# Y_train_proba = np.load('./../data/input/Y_train_proba.npy')
# Y_test_proba = np.load('./../data/input/Y_test_proba.npy')
probas = np.load('./../data/output_ignore/probas_nb034_RandomForestClassifier_cv_0.9383.npz')
Y_train_proba = probas['arr_0']
Y_test_proba = probas['arr_1']
for i in range(11):
train[f"proba_{i}"] = Y_train_proba[:, i]
test[f"proba_{i}"] = Y_test_proba[:, i]
return train, test, sub
# create batches of 4000 observations
def batching(df, batch_size):
df['group'] = df.groupby(df.index//batch_size, sort=False)['signal'].agg(['ngroup']).values
df['group'] = df['group'].astype(np.uint16)
return df
# normalize the data (standard scaler). We can also try other scalers for a better score!
def normalize(train, test):
train_input_mean = train.signal.mean()
train_input_sigma = train.signal.std()
train['signal'] = (train.signal - train_input_mean) / train_input_sigma
test['signal'] = (test.signal - train_input_mean) / train_input_sigma
return train, test
# get lead and lags features
def lag_with_pct_change(df, windows):
for window in windows:
df['signal_shift_pos_' + str(window)] = df.groupby('group')['signal'].shift(window).fillna(0)
df['signal_shift_neg_' + str(window)] = df.groupby('group')['signal'].shift(-1 * window).fillna(0)
return df
# main module to run feature engineering. Here you may want to try and add other features and check if your score imporves :).
def run_feat_engineering(df, batch_size):
# create batches
df = batching(df, batch_size = batch_size)
# create leads and lags (1, 2, 3 making them 6 features)
df = lag_with_pct_change(df, [1, 2, 3])
# create signal ** 2 (this is the new feature)
df['signal_2'] = df['signal'] ** 2
return df
# fillna with the mean and select features for training
def feature_selection(train, test):
features = [col for col in train.columns if col not in ['index', 'group', 'open_channels', 'time']]
train = train.replace([np.inf, -np.inf], np.nan)
test = test.replace([np.inf, -np.inf], np.nan)
for feature in features:
feature_mean = pd.concat([train[feature], test[feature]], axis = 0).mean()
train[feature] = train[feature].fillna(feature_mean)
test[feature] = test[feature].fillna(feature_mean)
return train, test, features
# model function (very important, you can try different arquitectures to get a better score. I believe that top public leaderboard is a 1D Conv + RNN style)
def Classifier(shape_):
def cbr(x, out_layer, kernel, stride, dilation):
x = Conv1D(out_layer, kernel_size=kernel, dilation_rate=dilation, strides=stride, padding="same")(x)
x = BatchNormalization()(x)
x = Activation("relu")(x)
return x
def wave_block(x, filters, kernel_size, n):
dilation_rates = [2**i for i in range(n)]
x = Conv1D(filters = filters,
kernel_size = 1,
padding = 'same')(x)
res_x = x
for dilation_rate in dilation_rates:
tanh_out = Conv1D(filters = filters,
kernel_size = kernel_size,
padding = 'same',
activation = 'tanh',
dilation_rate = dilation_rate)(x)
sigm_out = Conv1D(filters = filters,
kernel_size = kernel_size,
padding = 'same',
activation = 'sigmoid',
dilation_rate = dilation_rate)(x)
x = Multiply()([tanh_out, sigm_out])
x = Conv1D(filters = filters,
kernel_size = 1,
padding = 'same')(x)
res_x = Add()([res_x, x])
return res_x
inp = Input(shape = (shape_))
x = cbr(inp, 64, 7, 1, 1)
x = BatchNormalization()(x)
x = wave_block(x, 16, 3, 12)
x = BatchNormalization()(x)
x = wave_block(x, 32, 3, 8)
x = BatchNormalization()(x)
x = wave_block(x, 64, 3, 4)
x = BatchNormalization()(x)
x = wave_block(x, 128, 3, 1)
x = cbr(x, 32, 7, 1, 1)
x = BatchNormalization()(x)
x = Dropout(0.2)(x)
out = Dense(11, activation = 'softmax', name = 'out')(x)
model = models.Model(inputs = inp, outputs = out)
opt = Adam(lr = LR)
# opt = tfa.optimizers.SWA(opt)
# model.compile(loss = losses.CategoricalCrossentropy(), optimizer = opt, metrics = ['accuracy'])
model.compile(loss = categorical_crossentropy, optimizer = opt, metrics = ['accuracy'])
return model
# function that decrease the learning as epochs increase (i also change this part of the code)
def lr_schedule(epoch):
if epoch < 30:
lr = LR
elif epoch < 40:
lr = LR / 3
elif epoch < 50:
lr = LR / 5
elif epoch < 60:
lr = LR / 7
elif epoch < 70:
lr = LR / 9
elif epoch < 80:
lr = LR / 11
elif epoch < 90:
lr = LR / 13
else:
lr = LR / 100
return lr
# class to get macro f1 score. This is not entirely necessary but it's fun to check f1 score of each epoch (be carefull, if you use this function early stopping callback will not work)
class MacroF1(Callback):
def __init__(self, model, inputs, targets):
self.model = model
self.inputs = inputs
self.targets = np.argmax(targets, axis = 2).reshape(-1)
def on_epoch_end(self, epoch, logs):
pred = np.argmax(self.model.predict(self.inputs), axis = 2).reshape(-1)
score = f1_score(self.targets, pred, average = 'macro')
print(f'F1 Macro Score: {score:.5f}')
# main function to perfrom groupkfold cross validation (we have 1000 vectores of 4000 rows and 8 features (columns)). Going to make 5 groups with this subgroups.
def run_cv_model_by_batch(train, test, splits, batch_col, feats, sample_submission, nn_epochs, nn_batch_size):
seed_everything(SEED)
K.clear_session()
# config = tf.compat.v1.ConfigProto(intra_op_parallelism_threads=1, inter_op_parallelism_threads=1,
# gpu_options=tf.compat.v1.GPUOptions(
# visible_device_list='4', # specify GPU number
# allow_growth=True
# )
# )
# sess = tf.compat.v1.Session(graph=tf.compat.v1.get_default_graph(), config=config)
# tf.compat.v1.keras.backend.set_session(sess)
# tf.compat.v1 ---> tf (tensorflow2系からtensorflow1系に変更)
config = tf.ConfigProto(intra_op_parallelism_threads=1, inter_op_parallelism_threads=1,
# gpu_options=tf.GPUOptions(
# visible_device_list='4', # specify GPU number
# allow_growth=True
# )
)
sess = tf.Session(graph=tf.get_default_graph(), config=config)
tf.keras.backend.set_session(sess)
oof_ = np.zeros((len(train), 11)) # build out of folds matrix with 11 columns, they represent our target variables classes (from 0 to 10)
preds_ = np.zeros((len(test), 11))
target = ['open_channels']
group = train['group']
kf = GroupKFold(n_splits=5)
splits = [x for x in kf.split(train, train[target], group)]
new_splits = []
for sp in splits:
new_split = []
new_split.append(np.unique(group[sp[0]]))
new_split.append(np.unique(group[sp[1]]))
new_split.append(sp[1])
new_splits.append(new_split)
# pivot target columns to transform the net to a multiclass classification estructure (you can also leave it in 1 vector with sparsecategoricalcrossentropy loss function)
tr = pd.concat([pd.get_dummies(train.open_channels), train[['group']]], axis=1)
tr.columns = ['target_'+str(i) for i in range(11)] + ['group']
target_cols = ['target_'+str(i) for i in range(11)]
train_tr = np.array(list(tr.groupby('group').apply(lambda x: x[target_cols].values))).astype(np.float32)
train = np.array(list(train.groupby('group').apply(lambda x: x[feats].values)))
test = np.array(list(test.groupby('group').apply(lambda x: x[feats].values)))
for n_fold, (tr_idx, val_idx, val_orig_idx) in enumerate(new_splits[0:], start=0):
train_x, train_y = train[tr_idx], train_tr[tr_idx]
valid_x, valid_y = train[val_idx], train_tr[val_idx]
print(f'Our training dataset shape is {train_x.shape}')
print(f'Our validation dataset shape is {valid_x.shape}')
gc.collect()
shape_ = (None, train_x.shape[2]) # input is going to be the number of feature we are using (dimension 2 of 0, 1, 2)
model = Classifier(shape_)
# using our lr_schedule function
cb_lr_schedule = LearningRateScheduler(lr_schedule)
model.fit(train_x,train_y,
epochs = nn_epochs,
callbacks = [cb_lr_schedule, MacroF1(model, valid_x, valid_y)], # adding custom evaluation metric for each epoch
batch_size = nn_batch_size,verbose = 2,
validation_data = (valid_x,valid_y))
preds_f = model.predict(valid_x)
f1_score_ = f1_score(np.argmax(valid_y, axis=2).reshape(-1), np.argmax(preds_f, axis=2).reshape(-1), average = 'macro') # need to get the class with the biggest probability
print(f'Training fold {n_fold + 1} completed. macro f1 score : {f1_score_ :1.5f}')
preds_f = preds_f.reshape(-1, preds_f.shape[-1])
oof_[val_orig_idx,:] += preds_f
te_preds = model.predict(test)
te_preds = te_preds.reshape(-1, te_preds.shape[-1])
preds_ += te_preds / SPLITS
# calculate the oof macro f1_score
f1_score_ = f1_score(np.argmax(train_tr, axis = 2).reshape(-1), np.argmax(oof_, axis = 1), average = 'macro') # axis 2 for the 3 Dimension array and axis 1 for the 2 Domension Array (extracting the best class)
print(f'Training completed. oof macro f1 score : {f1_score_:1.5f}')
save_path = f'{DIR_OUTPUT}submission_nb{NB}_cv_{f1_score_:.4f}.csv'
print(f'save path: {save_path}')
sample_submission['open_channels'] = np.argmax(preds_, axis = 1).astype(int)
sample_submission.to_csv(save_path, index=False, float_format='%.4f')
# save_path = f'{DIR_OUTPUT}oof_nb{NB}_cv_{f1_score_:.4f}.csv'
# sample_submission['open_channels'] = np.argmax(preds_, axis = 1).astype(int)
# sample_submission.to_csv(save_path, index=False, float_format='%.4f')
return oof_
%%time
# this function run our entire program
def run_everything():
print(f'Reading Data Started...({time.ctime()})')
train, test, sample_submission = read_data()
train, test = normalize(train, test)
print(f'Reading and Normalizing Data Completed')
print(f'Creating Features({time.ctime()})')
print(f'Feature Engineering Started...')
train = run_feat_engineering(train, batch_size = GROUP_BATCH_SIZE)
test = run_feat_engineering(test, batch_size = GROUP_BATCH_SIZE)
train, test, features = feature_selection(train, test)
print(f'Feature Engineering Completed...')
print(f'Training Wavenet model with {SPLITS} folds of GroupKFold Started...({time.ctime()})')
oof_ = run_cv_model_by_batch(train, test, SPLITS, 'group', features, sample_submission, EPOCHS, NNBATCHSIZE)
print(f'Training completed...')
return oof_
oof_ = run_everything()
```
# analysis
```
df_tr = pd.read_csv(PATH_TRAIN)
batch_list = []
for n in range(10):
batchs = np.ones(500000)*n
batch_list.append(batchs.astype(int))
batch_list = np.hstack(batch_list)
df_tr['batch'] = batch_list
# group 特徴量を作成
group = group_feat_train(df_tr)
df_tr = pd.concat([df_tr, group], axis=1)
y = df_tr['open_channels'].values
oof = np.argmax(oof_, axis=1).astype(int)
for group in sorted(df_tr['group'].unique()):
idxs = df_tr['group'] == group
oof_grp = oof[idxs].astype(int)
y_grp = y[idxs]
print(f'group_score({group}): {f1_macro(y_grp, oof_grp):4f}')
```
<br>
可視化
```
x_idx = np.arange(len(df_tr))
idxs = y != oof
failed = np.zeros(len(df_tr))
failed[idxs] = 1
n = 200
b = np.ones(n)/n
failed_move = np.convolve(failed, b, mode='same')
fig, axs = plt.subplots(2, 1, figsize=(20, 6))
axs = axs.ravel()
# fig = plt.figure(figsize=(20, 3))
for i_gr, group in enumerate(sorted(df_tr['group'].unique())):
idxs = df_tr['group'] == group
axs[0].plot(np.arange(len(df_tr))[idxs], df_tr['signal'].values[idxs], color=cp[i_gr], label=f'group={group}')
for x in range(10):
axs[0].axvline(x*500000 + 500000, color='gray')
axs[0].text(x*500000 + 250000, 0.6, x)
axs[0].plot(x_idx, failed_move, '.', color='black', label='failed_mv')
axs[0].set_xlim(0, 5500000)
axs[0].legend()
axs[1].plot(x_idx, y)
axs[1].set_xlim(0, 5500000)
# fig.legend()
```
| github_jupyter |
# Using Interrupts and asyncio for Buttons and Switches
This notebook provides a simple example for using asyncio I/O to interact asynchronously with multiple input devices. A task is created for each input device and coroutines used to process the results. To demonstrate, we recreate the flashing LEDs example in the getting started notebook but using interrupts to avoid polling the GPIO devices. The aim is have holding a button result in the corresponding LED flashing.
## Initialising the Environment
First we import an instantiate all required classes to interact with the buttons, switches and LED and ensure the base overlay is loaded.
```
from pynq import PL
from pynq.overlays.base import BaseOverlay
base = BaseOverlay("base.bit")
```
## Define the flash LED task
Next step is to create a task that waits for the button to be pressed and flash the LED until the button is released. The `while True` loop ensures that the coroutine keeps running until cancelled so that multiple presses of the same button can be handled.
```
import asyncio
async def flash_led(num):
while True:
await base.buttons[num].wait_for_value_async(1)
while base.buttons[num].read():
base.leds[num].toggle()
await asyncio.sleep(0.1)
base.leds[num].off()
```
## Create the task
As there are four buttons we want to check, we create four tasks. The function `asyncio.ensure_future` is used to convert the coroutine to a task and schedule it in the event loop. The tasks are stored in an array so they can be referred to later when we want to cancel them.
```
tasks = [asyncio.ensure_future(flash_led(i)) for i in range(4)]
```
## Monitoring the CPU Usage
One of the advantages of interrupt-based I/O is to minimised CPU usage while waiting for events. To see how CPU usages is impacted by the flashing LED tasks we create another task that prints out the current CPU utilisation every 3 seconds.
```
import psutil
async def print_cpu_usage():
# Calculate the CPU utilisation by the amount of idle time
# each CPU has had in three second intervals
last_idle = [c.idle for c in psutil.cpu_times(percpu=True)]
while True:
await asyncio.sleep(3)
next_idle = [c.idle for c in psutil.cpu_times(percpu=True)]
usage = [(1-(c2-c1)/3) * 100 for c1,c2 in zip(last_idle, next_idle)]
print("CPU Usage: {0:3.2f}%, {1:3.2f}%".format(*usage))
last_idle = next_idle
tasks.append(asyncio.ensure_future(print_cpu_usage()))
```
## Run the event loop
All of the blocking wait_for commands will run the event loop until the condition is met. All that is needed is to call the blocking `wait_for_level` method on the switch we are using as the termination condition.
While waiting for switch 0 to get high, users can press any push button on the board to flash the corresponding LED. While this loop is running, try opening a terminal and running `top` to see that python is consuming no CPU cycles while waiting for peripherals.
As this code runs until the switch 0 is high, make sure it is low before running the example.
```
if base.switches[0].read():
print("Please set switch 0 low before running")
else:
base.switches[0].wait_for_value(1)
```
## Clean up
Even though the event loop has stopped running, the tasks are still active and will run again when the event loop is next used. To avoid this, the tasks should be cancelled when they are no longer needed.
```
[t.cancel() for t in tasks]
```
Now if we re-run the event loop, nothing will happen when we press the buttons. The process will block until the switch is set back down to the low position.
```
base.switches[0].wait_for_value(0)
```
Copyright (C) 2020 Xilinx, Inc
| github_jupyter |
```
import os
import pandas as pd
import matplotlib.pyplot as plt
import sys
sys.path.append('../')
from default_constants import *
from ECE_mechanism.voltammogram_ECE_no_plot import CSV_ECE_ox
from plot_tools import extract_expe_like_CSV
from scipy.optimize import minimize
def plot_experimental_data(folder_name):
directory = folder_name
for filename in os.listdir(directory):
if filename.endswith(".txt"):
path = os.path.join(directory, filename)
df = pd.read_csv(path, delimiter = ';', decimal = ',')
Potential = df['Potential applied (V)'].to_numpy()
Intensity = df['WE(1).Current (A)'].to_numpy()
plt.plot(Potential, Intensity, label = path)
continue
else:
continue
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
def find_expe_csts_CSV(file_name):
df = pd.read_csv(file_name, delimiter = ';', decimal = ',')
Potential = df['Potential applied (V)'].to_numpy()
Time = df['Time (s)'].to_numpy()
E_ox = max(Potential)
E_red = min(Potential)
E_start = Potential[0]
Delta_E = Potential[1] - Potential[0]
v = Delta_E/(Time[1] - Time[0])
return(E_ox, E_red, Delta_E, v, E_start)
def find_I_E_t(file_name):
df = pd.read_csv(file_name, delimiter = ';', decimal = ',')
Pot_ap = df['Potential applied (V)'].to_numpy()
I_expe = df['WE(1).Current (A)'].to_numpy()
Time = df['Time (s)'].to_numpy()
return(I_expe, Pot_ap, Time)
def set_expe_cst(cst_all, cst_expe_new):
cst_all_new = list(cst_all)
cst_expe_new = list(cst_expe_new)
cst_all_new[4] = list(cst_all_new[4])
for i in range(len(cst_all_new[4])):
cst_all_new[4][i] = cst_expe_new[i]
cst_all_new[4] = tuple(cst_all_new[4])
cst_all_new = tuple(cst_all_new)
return(cst_all_new)
def guess_potentials(E_0_1, E_0_2, cst_all):
cst_all_new = list(cst_all)
cst_all_new[2] = list(cst_all_new[2])
cst_all_new[2][0] = E_0_1
cst_all_new[2][9] = E_0_2
cst_all_new[2] = tuple(cst_all_new[2])
cst_all_new = tuple(cst_all_new)
return(cst_all_new)
def I_new(new_guess, *cst_expe_set):
cst_expe_guess = cst_expe_set
cst_expe_guess = list(cst_expe_guess)
cst_expe_guess[2] = list(cst_expe_guess[2])
cst_expe_guess[2][0] = new_guess[0]
cst_expe_guess[2][9] = new_guess[1]
cst_expe_guess[2][6] = new_guess[2]
cst_expe_guess[2][7] = new_guess[3]
cst_expe_guess[2][4] = new_guess[4]
cst_expe_guess[2] = tuple(cst_expe_guess[2])
cst_expe_guess = tuple(cst_expe_guess)
I_simu_CSV = CSV_ECE_ox(cst_expe_guess)
E_expe, I_simu_CSV_2 = extract_expe_like_CSV(cst_expe_guess, I_simu_CSV)
return(I_simu_CSV_2)
def Error_I(I_new, *I_expe_CSV):
Error = 0
I_new = I_new/max(I_new)
I_expe_CSV = I_expe_CSV/max(I_expe_CSV)
for i in range(len(I_new)):
Delta_I = I_new[i] - I_expe_CSV[i]
Error += Delta_I**2
print(Error)
return(Error)
def fun_1(new_guess, *fixed_parms):
cst_expe_set = fixed_parms[0]
I_expe = fixed_parms[1]
I = I_new(new_guess, *cst_expe_set)
Err = Error_I(I, *I_expe)
return(Err)
# fitting with the error
def fit_experimental_data(file_name, guess):
path = os.path.join('Examples_ECE', file_name)
# adjust set up parameters
cst_expe = find_experimental_potentials_CSV(path)
cst_default = set_default_constants()
cst_expe_set = set_expe_cst(cst_default, cst_expe)
# define the function to minimize :
cst_syst_guess = guess_potentials(guess[0], guess[1] , cst_expe_set)
df = pd.read_csv(path, delimiter = ';', decimal = ',')
I_expe_CSV = df['WE(1).Current (A)'].to_numpy()
I_expe_CSV = I_expe_CSV/max(I_expe_CSV)
E_expe_CSV = df['Potential applied (V)'].to_numpy()
Best = minimize(fun_1, guess,
args = (cst_expe_set, I_expe_CSV),
method='SLSQP',
bounds= ((0.4,0.8),(0.3,0.8), (0.001,10), (0.001,20), (0.00001,1))
)
#print(cst_expe_set[2])
return(Best)
# curve fitting with the error
def fit_experimental_data_2(file_name, guess):
path = os.path.join('Examples_ECE', file_name)
# adjust set up parameters
cst_expe = find_experimental_potentials_CSV(path)
cst_default = set_default_constants()
cst_expe_set = set_expe_cst(cst_default, cst_expe)
# define the function to minimize :
cst_syst_guess = guess_potentials(guess[0], guess[1] , cst_expe_set)
df = pd.read_csv(path, delimiter = ';', decimal = ',')
I_expe_CSV = df['WE(1).Current (A)'].to_numpy()
I_expe_CSV = I_expe_CSV/max(I_expe_CSV)
E_expe_CSV = df['Potential applied (V)'].to_numpy()
Best = minimize(fun_1, (0.6, 0.5, 1, 1, 0.01), args = (cst_expe_set, I_expe_CSV), method='SLSQP')
#print(cst_expe_set[2])
return(Best)
path = os.path.join('Fit_Experimental_CSV', 'Examples_ECE')
print(path)
plot_experimental_data(path)
path_file = os.path.join(path, 'Che207 Ni(BinapSQ) 500mV s.txt')
def fit_expe(guess, path_file, cst_all):
# set new values for cst_all extracted from the experimental data
(E_ox, E_red, Delta_E, v, E_i) = find_expe_csts_CSV(path_file)
cst_all["E_ox"] = E_ox
cst_all["E_red"] = E_red
cst_all["Delta_E"] = Delta_E
if Delta_E > 0 :
cst_all["Ox"] = True
else:
cst_all["Ox"] = False
cst_all["v"] = v
cst_all["E_i"] = E_i
# extract I_expe from the datas
(I_expe, Pot_ap, Time) = find_I_E_t(path_file)
print(len(I_expe))
# minimize the distance between I_expe and I_simulates
Best = minimize(fun_ECE, guess,
args = (cst_all, I_expe),
method='L-BFGS-B',
bounds= ((0.01,10000), (0.4,0.8), (0.3,0.8), (0.001,20), (0.00001,1)),
tol = 0.1)
return(Best)
# guess = (Lambda, E_0_1, E_0_2, k_p, k_m)
def fun_ECE(guess, *fixed_parms):
# set the new constants for cst_all
cst_new = fixed_parms[0]
cst_new["Lambda"] = guess[0]
cst_new["E_0_1"] = guess[1]
cst_new["E_0_2"] = guess[2]
cst_new["k_p"] = guess[3]
cst_new["k_m"] = guess[4]
# calculate the I correspomnding to theses new constants
(param, E, C_init, M_new_constant, M_old, fun, fun_I) = initialise(cst_new)
(I, Potential, Time) = calculate_I(param, E, C_init, M_new_constant, M_old, fun, fun_I)
(Pot_expe, I) = extract_expe_like_CSV(param, I)
# calculate the error between experimental and simulated intensity
Err = Error_I(I, *fixed_parms[1])
return(Err)
def Error_I(I_new, *I_expe_CSV):
Error = 0
I_new = I_new/max(I_new)
I_expe_CSV = I_expe_CSV/max(I_expe_CSV)
for i in range(len(I_new)):
Delta_I = I_new[i] - I_expe_CSV[i]
Error += Delta_I**2
print(Error)
return(Error)
from default_constants import default_constants
from main import *
#main programm to fit the data :
cst_all = default_constants()
# set mechanism type :
cst_all["mechanism"] = 'ECE'
# set molecule type :
cst_all["Reducible"] = False
# set concentration :
cst_all["C_a"] = 2E-3
path = os.path.join('Fit_Experimental_CSV', 'Examples_ECE')
path_file = os.path.join(path, 'Che207 Ni(BinapSQ) 500mV s.txt')
#guess = (100, 0.5, 0.5, 1.0, 1.0)
guess = (100, 5.55824144e-01, 4.41382398e-01, 9.71843960e-01, 1.00000000e+01)
Best = fit_expe(guess, path_file, cst_all)
Best
#main programm to fit the data :
cst_all = default_constants()
# set mechanism type :
cst_all["mechanism"] = 'ECE'
# set molecule type :
cst_all["Reducible"] = False
# set concentration :
cst_all["C_a"] = 2E-3
# set new values for cst_all extracted from the experimental data
(E_ox, E_red, Delta_E, v, E_i) = find_expe_csts_CSV(path_file)
cst_all["E_ox"] = E_ox
cst_all["E_red"] = E_red
cst_all["Delta_E"] = Delta_E
if Delta_E > 0 :
cst_all["Ox"] = True
else:
cst_all["Ox"] = False
cst_all["v"] = v
cst_all["E_i"] = E_i
# extract I_expe from the datas
(I_expe, Pot_ap, Time) = find_I_E_t(path_file)
guess = np.array([2, 0.5, 0.5, 1.0, 1.0])
def fun_ECE_cma(guess):
# set the new constants for cst_all
(param, E, C_init, M_new_constant, M_old, fun, fun_I) = initialise(cst_all)
cst_new = param
cst_new["Lambda"] = 10**(guess[0])
cst_new["E_0_1"] = guess[1]
cst_new["E_0_2"] = guess[2]
cst_new["k_p"] = 10**(guess[3])
cst_new["k_m"] = 10**(guess[4])
# calculate the I correspomnding to theses new constants
(param, E, C_init, M_new_constant, M_old, fun, fun_I) = initialise(cst_new)
(I_simu, Potential, Time) = calculate_I(param, E, C_init, M_new_constant, M_old, fun, fun_I)
(Pot_expe, I_new) = extract_expe_like_CSV(param, I_simu)
# calculate the error between experimental and simulated intensity
Err = Error_I(I_new, I_expe)
return(Err)
def Error_I(I_new, I_expe_CSV):
#print(len(I_new), len(I_expe_CSV))
Error = 0
I_new = I_new/max(I_new)
I_expe_CSV = I_expe_CSV/max(I_expe_CSV)
for i in range(len(I_new)):
Delta_I = I_new[i] - I_expe_CSV[i]
Error += Delta_I**2
print(Error)
return(Error)
import cma
from cma.evolution_strategy import CMAEvolutionStrategy
opts = cma.CMAOptions()
opts.set({'popsize': 200,
'maxiter' : 100000,
'maxfevals' : 10000,
'timeout' : "100000000.0 * 60**2",
'tolfun': 1e-4,
'tolfunhist': 1e-6})
es = CMAEvolutionStrategy(guess.astype(np.float16), 1, opts)
es.optimize(fun_ECE_cma, verb_disp=100, n_jobs = -1)
path_file
es.result
96500/(8.314*300)
1/38.7
```
| github_jupyter |
# Making Simple Plots
## Objectives
+ Learn how to make a simple 1D plot in Python.
+ Learn how to find the maximum/minimum of a function in Python.
We will use [Problem 4.B.2](https://youtu.be/w-IGNU2i3F8) of the lecturebook as a motivating example.
We find that the moment of the force $\vec{F}$ about point A is:
$$
\vec{M_A} = (bF\cos\theta - dF\sin\theta)\hat{k}.
$$
Let's plot the component of the moment as a function of $\theta$.
For this, we will use the Python module [matplotlib](https://matplotlib.org).
```
import numpy as np # for numerical algebra
import matplotlib.pyplot as plt # this is where the plotting capabilities are
# The following line is need so that the plots are embedded in the Jupyter notebook (remove when not using Jupyter)
%matplotlib inline
# Define a function that computes the moment magnitude as a function of all other parameters
def M_A(theta, b, d, F):
"""
Compute the k component of the moment of F about point A given all the problem parameters.
"""
return b * F * np.cos(theta) - d * F * np.sin(theta)
# Choose some parameters
b = 0.5 # In meters
d = 2. # In meters
F = 2. # In kN
# The thetas on which we will evaluate the moment for plotting
thetas = np.linspace(0, 2 * np.pi, 100)
# The moment on these thetas:
M_As = M_A(thetas, b, d, F)
# Let's plot
plt.plot(thetas / (2. * np.pi) * 360, M_As, lw=2)
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)');
```
Now, let's put two lines in the same plot.
Let's compare the moments when we change $d$ from 2 meters to 3.5 meters.
```
# We already have M_A for d=2 m (and all other paramters to whichever values we gave them)
# Let's copy it:
M_As_case_1 = M_As
# And let's compute it again for d=3.5 m
d = 3.5 # In m
M_As_case_2 = M_A(thetas, b, d, F)
# Let's plot both of them in the same figure
plt.plot(thetas / (2. * np.pi) * 360, M_As_case_1, lw=2, label='Case 1')
plt.plot(thetas / (2. * np.pi) * 360, M_As_case_2, '--', lw=2, label='Case 2')
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)')
plt.legend(loc='best')
```
Finally, let's see how we can make interactive plots.
We will use the Python module [ipywidgets](https://ipywidgets.readthedocs.io/en/stable/) and in particular the function [ipywidgets.interact](https://ipywidgets.readthedocs.io/en/stable/examples/Using%20Interact.html).
```
from ipywidgets import interact # Loading the module
# Interact needs a function that does the plotting given the parameters.
# Let's make it:
def make_plots(b=0.5, d=3., F=1.): # X=val defines default values for the function
"""
Make the plot.
"""
thetas = np.linspace(0, 2. * np.pi, 100)
M_As = M_A(thetas, b, d, F)
plt.plot(thetas / (2. * np.pi) * 360, M_As, lw=2, label='Case 1')
plt.ylim([-10., 10.])
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)')
```
Let's just check that the function works by calling it a few times:
```
# With no inputs it should use the default values
make_plots()
# You can specify all the inputs like this:
make_plots(2., 3., 2.)
# Or even by name (whatever is not specified gets the default value):
make_plots(F=2.3)
```
Ok. Let's use interact now:
```
interact(make_plots,
b=(0., 5., 0.1), # Range for b: (min, max, increment)
d=(0., 5, 0.1), # Range for d
F=(0., 2, 0.1) # Range for F
);
```
| github_jupyter |
# VacationPy
----
#### Note
* Keep an eye on your API usage. Use https://developers.google.com/maps/reporting/gmp-reporting as reference for how to monitor your usage and billing.
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import gmaps
import os
# Import API key
from api_keys import g_key
```
### Store Part I results into DataFrame
* Load the csv exported in Part I to a DataFrame
```
city_data = pd.read_csv("../output_data/cities.csv")
city_data.head()
```
### Humidity Heatmap
* Configure gmaps.
* Use the Lat and Lng as locations and Humidity as the weight.
* Add Heatmap layer to map.
```
gmaps.configure(api_key=g_key)
locations = city_data[["Lat", "Lng"]].astype(float)
humidity = city_data["Humidity"].astype(float)
fig = gmaps.figure()
heat_layer = gmaps.heatmap_layer(locations, weights = humidity, dissipating = False, max_intensity = 100, point_radius = 1)
fig.add_layer(heat_layer)
fig
```
### Create new DataFrame fitting weather criteria
* Narrow down the cities to fit weather conditions.
* Drop any rows will null values.
```
narrowed_city_df = city_data.loc[(city_data["Humidity"]>=70) & (city_data["Wind Speed"]>=10) & \
(city_data["Cloudiness"] <= 20)].dropna()
narrowed_city_df.head()
```
### Hotel Map
* Store into variable named `hotel_df`.
* Add a "Hotel Name" column to the DataFrame.
* Set parameters to search for hotels with 5000 meters.
* Hit the Google Places API for each city's coordinates.
* Store the first Hotel result into the DataFrame.
* Plot markers on top of the heatmap.
```
hotel_df = narrowed_city_df.reset_index(drop=True)
hotel_df["Hotel Name"] = ""
hotel_df
# geocoordinates
target_search = "Hotel"
target_radius = 5000
target_type = "Hotels"
params={
"radius":target_radius,
"types":target_type,
"keyword":target_search,
"key":g_key
}
# NOTE: Do not change any of the code in this cell
# Using the template add the hotel marks to the heatmap
info_box_template = """
<dl>
<dt>Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
</dl>
"""
# Store the DataFrame Row
# NOTE: be sure to update with your DataFrame name
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
locations = hotel_df[["Lat", "Lng"]]
# Add marker layer ontop of heat map
markers = gmaps.marker_layer(locations)
fig.add_layer(markers)
# Display figure
fig
```
| github_jupyter |
```
from IPython.core.display import HTML
def css_styling():
styles = open("./styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
### BEFORE YOU DO ANYTHING...
In the terminal:
1. Navigate to __inside__ your ILAS_Python repository.
2. __COMMIT__ any un-commited work on your personal computer.
3. __PULL__ any changes *you* have made using another computer.
4. __PULL__ textbook updates (including homework answers).
# Control Flow
# Lesson Goal
Compose simple programs to control the order in which the operators we have studied so far are executed.
# Objectives
Control the flow of a program using:
- __control statements__
- __loops__
## Why we are studying this:
Control flow allows us to make __choices__ using our program.
Control statements result in a decision being made as to which of __two or more possible paths__ to follow.
## Lesson structure:
- Control Statements
- `if` and `else`statements
- `for` loops
- `while` loops
- `break` and `continue` statements
- Review Exercises
- Summary
What is a *__control statement__*?
Let's start with an example from the last seminar...
## Control Statements
In the last seminar we looked at a simple computer program that returned Boolean (True or False) variables...
Based on the current time of day, the program answers two questions:
>__Is it lunchtime?__
>`True`
if it is lunch time.
<br>
>__Is it time for work?__
>`True`
if it is `not`:
- before work (`time < work_starts`)
- after work (`time > work_ends `)
- lunchtime (the previous question assigns the value `True` or `False` to variable `lunchtime`).
```
# Time-telling program
time = 13.05 # current time
work_starts = 8.00 # time work starts
work_ends = 17.00 # time work ends
lunch_starts = 13.00 # time lunch starts
lunch_ends = 14.00 # time lunch ends
# variable lunchtime is True if the time is between the start and end of lunchtime
lunchtime = time >= lunch_starts and time < lunch_ends
# variable work_time is True if the time is not...
work_time = not ( time < work_starts # ... before work
or time > work_ends # ... or after work
or lunchtime) # ... or lunchtime
print("Is it work time?")
print(work_time)
print("Is it lunchtime?")
print(lunchtime)
```
What if we now want our computer program to do something based on these answers?
To do this, we need to use *control statements*.
Control statements allow us to make decisions in a program.
This decision making is known as *control flow*.
Control statements are a fundamental part of programming.
Here is a control statement in pseudo code:
This is an `if` statement.
if A is true
Perform task X
For example
if lunchtime is true
Eat lunch
We can check if an alternative to the `if` statement is true using an `else if` statement.
if A is true
Perform task X (only)
else if B is true
Perform task Y (only)
Example:
if lunchtime is true
Eat lunch
else if work_time is true
Do work
Often it is useful to include an `else` statement.
If none of the `if` and `else if` statements are satisfied, the code following the `else` statement will be executed.
if A is true
Perform task X (only)
else if B is true
Perform task Y (only)
else
Perform task Z (only)
if lunchtime is true
Eat lunch
else if work_time is true
Do work
else
Go home
Let's get a better understanding of control flow statements by completing some examples.
<a id='IfElse'></a>
## `if` and `else` statements
Let's consider a simple example that demonstrates a Python if-else control statement.
It uses the lunch/work example from the previous seminar.
__Note:__ In Python, "else if" is written: `elif`
```
# Time-telling program
time = 13.05 # current time
work_starts = 8.00 # time work starts
work_ends = 17.00 # time work ends
lunch_starts = 13.00 # time lunch starts
lunch_ends = 14.00 # time lunch ends
# variable lunchtime is True if the time is between the start and end of lunchtime
lunchtime = time >= lunch_starts and time < lunch_ends
# variable work_time is True if the time is not...
work_time = not ( time < work_starts # ... before work
or time > work_ends # ... or after work
or lunchtime) # ... or lunchtime
#print("Is it work time?")
#print(work_time)
#print("Is it lunchtime?")
#print(lunchtime)
if lunchtime: # if lunchtime == True:
print("Eat lunch")
elif work_time: # elif work_time == True:
print("Do work")
else:
print("Go home")
```
__Remember:__ The program assigns the variables lunchtime and work_time the values `True` or `False`.
Therefore when we type:
<br>`if lunchtime`
<br>the meaning is the same as:
<br>`if lunchtime == True`
Here is another example, using algebraic operators to modify the value of an initial variable, `x`.
The modification of `x` and the message printed depend on the initial value of `x`.
```
#The input to the program is variable `x`.
x = -10.0 # Initial x value
if x > 0.0:
print('Initial x is greater than zero') #The program prints a message...
x -= 20.0 # ...and modifies `x`.
elif x < 0.0:
print('Initial x is less than zero')
x += 21.0
else:
print('Initial x is not less than zero and not greater than zero, therefore it must be zero')
x *= 2.5
print("Modified x = ", x)
```
__Note:__ The program uses the short-cut algebraic operators that you learnt to use in the last seminar.
__Try it yourself__
In the cell code cell above, try:
- changing the operations performed on `x`
- changing the value of `x` a few times.
Re-run the cell to see the different paths the program can follow.
### Look carefully at the structure of the `if`, `elif`, `else`, control statement:
__The control statement begins with an `if`__, followed by the expression to check. <br>
At the end of the `if` statement you must put a colon (`:`) <br>
````python
if x > 0.0:
````
After the `if` statement, indent the code to be run in the case that the `if` statement is `True`. <br>
To end the code to be run, simply stop indenting:
````python
if x > 0.0:
print('Initial x is greater than zero')
x -= 20.0
````
The indent can be any number of spaces.
The number of spaces must be the same for all lines of code to be run if the `if` statement is True.
Jupyter Notebooks automatically indent 4 spaces.
This is considered best practise.
`if x > 0.0` is:
- `True`:
- The indented code is executed.
- The control block is exited.
- The program moves past any subsequent `elif` or `else` statements.
<br>
- `False`:
the program moves past the inented code to the next (non-indented) part of the program... <br>
In this the next (non-indented) part of the program is `elif` (else if).
The elif statement is evaluated.
(Notice that the code is structured in the same way as the `if` statement.):
```python
if x > 0.0:
print('Initial x is greater than zero')
x -= 20.0
elif x < 0.0:
print('Initial x is less than zero')
x += 21.0
```
`elif x < 0.0`:
- `True`:
- The indented code is executed.
- The control block is exited.
- The program moves past any subsequent `elif` or `else` statements.
- `False`:
the program moves past the indented code to the next (non-indented) part of the program. <br>
If none of the preceding `if` or `elif` stements are true.
<br> e.g. in this example:
- `x > 0.0` is `False`
- `x < 0.0` is `False`
the code following the `else` statement is executed.
```python
if x > 0.0:
print('Initial x is greater than zero')
x -= 20.0
elif x < 0.0:
print('Initial x is less than zero')
x += 21.0
else:
print('Initial x is not less than zero and not greater than zero, therefore it must be zero')
```
Evaluating data against different criteria is extremely useful for solving real-world mathematical problems.
Let's look at a simple example...
### Real-World Example: currency trading
To make a comission (profit), a currency trader sells US dollars to travellers above the market rate.
The multiplier used to calculate the amount recieved by customer is shown in the table:
|Amount (JPY) |Multiplier |
|--------------------------------------------|-------------------------|
| Less than $100$ | 0.9 |
| From $100$ and less than $1,000$ | 0.925 |
| From $1,000$ and less than $10,000$ | 0.95 |
| From $10,000$ and less than $100,000$ | 0.97 |
| Over $100,000$ | 0.98 |
The currency trader charges more if the customer pays with cash.
<br>If the customer pays with cash, the currency trader reduces the rate by an __additional__ 10% after conversion.
<br>(If the transaction is made electronically, they do not).
__Current market rate:__ 1 JPY = 0.0091 USD.
__Effective rate:__ The rate that the customer receives based on the amount in JPY to be changed.
The program calculates the __effective rate__ using:
- The reduction based on the values in the table.
- An additional 10% reduction (mutiplier = 0.9) if the transaction is made in cash.
```
JPY = 1_000_000 # The amount in JPY to be changed into USD
cash = False # True if transaction is in cash, otherwise False
market_rate = 0.0091 # 1 JPY is worth this many dollars at the market rate
# Apply the appropriate reduction depending on the amount being sold
if JPY < 10_000:
multiplier = 0.9
elif JPY < 100_000:
multiplier = 0.925 * market_rate * JPY
elif JPY < 1_000_000:
multiplier = 0.95 * market_rate * JPY
elif JPY < 10_000_000:
multiplier = 0.97 * market_rate * JPY
else: # JPY > 10,000,000
multiplier = 0.98 * market_rate * JPY
# Apply the appropriate reduction depending if the transaction is made in cash or not
if cash:
cash_multiplier = 0.9
else:
cash_multiplier = 1
# Calculate the total amount sold to the customer
USD = JPY * market_rate * multiplier * cash_multiplier
print("Amount in JPY sold:", JPY)
print("Amount in USD purchased:", USD)
print("Effective rate:", USD/JPY)
```
__Note:__
- We can use multiple `elif` statements within a control block.
- We can use multipe `if` statements. <br>When the program executes and exits a control block, it moves to the next `if` statement.
- __Readability:__ <br>Underscores _ are placed between 0s in long numbers to make them easier to read.
<br>You DO NOT need to include underscores for Python to interpret the number correctly.
<br>You can place the underscores wherever you like in the sequence of digits that make up the number.
__Try it yourself__
In your textbook, try changing the values of `JPY` and `cash` a few times.
Re-run the cell to see the different paths the program can follow.
<a id='ForLoops'></a>
## `for` loops
*Loops* are used to execute a command repeatedly.
<br>
A loop is a block that repeats an operation a specified number of times (loops).
To learn about loops we are going to use the function `range()`.
### `range`
The function `range` gives us a sequence of *integer* numbers.
`range(3, 6)` returns integer values starting from 3 and ending at 6.
i.e.
> 3, 4, 5
Note this does not include 6.
We can change the starting value.
For example for integer values starting at 0 and ending at 4:
`range(0,4)`
returns:
> 0, 1, 2, 3
`range(4)` is a __shortcut__ for range(0, 4)
range (0,5)
range (5,9)
### Simple `for` loops
The statement
```python
for i in range(0, 5):
```
says that we want to run the indented code five times.
```
for i in range(0, 6):
print(i)
```
The first time through, the value of i is equal to 0.
<br>
The second time through, its value is 1.
<br>
Each loop the value `i` increases by 1 (0, 1, 2, 3, 4) until the last time when its value is 4.
Look carefully at the structure of the `for` loop:
- `for` is followed by the condition being checked.
- : colon at the end of the `for` statement.
- The indented code that follows is run each time the code loops. <br>
(The __same of spaces__ should be used for all indents)
<br>
- To end the `for` loop, simply stop indenting.
```
for i in range(-2, 3):
print(i)
print('The end of the loop')
```
The above loop starts from -2 and executes the indented code for each value of i in the range (-2, -1, 0, 1, 2).
<br>
When the loop has executed the code for the final value `i = 2`, it moves on to the next unindented line of code.
```
for n in range(4):
print("----")
print(n, n**2)
```
The above executes 4 loops.
The statement
```python
for n in range(4):
```
says that we want to loop over four integers, starting from 0.
Each loop the value `n` increases by 1 (0, 1, 2 3).
__Try it yourself__
<br>
Go back and change the __range__ of input values in the last three cells and observe the change in output.
If we want to step by three rather than one:
```
for n in range(0, 10, 3):
print(n)
```
If we want to step backwards rather than forwards we __must__ include the step size:
```
for n in range(10, 0, -1):
print(n)
```
For example...
```
for n in range(10, 0):
print(n)
```
...does not return any values because there are no values that lie between 10 and 0 when counting in the positive direction from 10.
__Try it yourself.__
In the cell below write a `for` loop that:
- starts at `n = 9`
- ends at `n = 3` (and includes `n = 3`)
- loops __backwards__ through the range in steps of -3
- prints `n`$^2$ at each loop.
```
# For loop
for n in range(9, 2, -3):
print ("-----")
print(n, n**2)
```
For loops are useful for performing operations on large data sets.
We often encounter large data sets in real-world mathematical problems.
A simple example of this is converting multiple values using the same mathematical equation to create a look-up table...
### Real-world Example: conversion table from degrees Fahrenheit to degrees Celsius
We can use a `for` loop to create a conversion table from degrees Fahrenheit ($T_F$) to degrees Celsius ($T_c$).
Conversion formula:
$$
T_c = 5(T_f - 32)/9
$$
Computing the conversion from -100 F to 200 F in steps of 20 F (not including 200 F):
```
print("T_f, T_c")
for Tf in range(-100, 200, 20):
print(Tf, "\t", round(((Tf - 32) * 5 / 9), 3))
```
<a id='WhileLoops'></a>
## `while` loops
A __`for`__ loop performs an operation a specified number of times.
```python
for x in range(5):
print(x)
```
A __`while`__ loop performs a task *while* a specified statement is true.
```python
x = 0
while x < 5:
print(x)
```
The structure of a `while` loop is similar to a `for` loop.
- `while` is followed by the condition being checked.
- : colon at the end of the `while` statement.
- The indented code that follows is repeatedly executed until the `while` statement (e.g. `x < 5`) is `False`. <br>
It can be quite easy to crash your computer using a `while` loop.
e.g. if we don't modify the value of x each time the code loops:
```python
x = 0
while x < 5:
print(x)
# x += 1
```
will continue indefinitely since `x < 5 == False` will never be satisfied.
This is called an *infinite loop*.
To perform the same function as the `for` loop we need to increment the value of `x` within the loop:
```
x = 0
print("Start of while statement")
while x < 5:
print(x)
x += 1 # Increment x
print("End of while statement")
```
`for` loops are often safer when performing an operation on a set range of values.
```
x = -2
print("Start of for statement")
for y in range(x,5):
print(y)
print("End of for statement")
```
Here is another example of a `while` loop.
```
x = 0.9
while x > 0.001:
# Square x (shortcut x *= x)
x = x * x
print(round(x, 6))
```
If we use an initial value of $x \ge 1$, an infinite loop will be generted.
`x` will increase with each loop, meaning `x` will always be greater than 0.001.
e.g.
```python
x = 2
while x > 0.001:
x = x * x
print(x)
```
However, using a `for` loop is a less appropriate solution in this case.
<br>We may not know beforehand how many steps are required before `x > 0.001` becomes false.
To avoid errors, it is good practice to check that $x < 1$ before entering the `while` loop e.g.
```
x = 0.9
if x < 1:
while x > 0.001:
# Square x (shortcut x *= x)
x = x * x
print(round(x, 6))
else:
print("x is greater than one, infinite loop avoided")
```
__Try it for yourself:__
In the cell above change the value of x to above or below 1.
Observe the output.
__Try it for yourself:__
In the cell below:
- Create a variable,`x`, with the initial value 50
- Each loop:
1. print x
1. reduce the value of x by half
- Exit the loop when `x` < 3
```
# While loop
```
## `break` and `continue`.
<a id='break'></a>
### `break`
Sometimes we want to break out of a `for` or `while` loop.
For example in a `for` loop we can check if something is true, and then exit the loop prematurely, e.g
<img src="img/flowchart-break-statement.jpg" alt="Drawing" style="width: 300px;"/>
<img src="img/break-statement-algorithm.jpg" alt="Drawing" style="width: 300px;"/>
```
for x in range(10):
print(x)
if x == 5:
print("Time to break out")
break
```
Let's look at how we can use this in a program...
The following program __finds prime numbers__.
__Prime number:__ A positive integer, greater than 1, that has no positive divisors other than 1 and itself (2, 3, 5, 11, 13, 17....)
The program checks (integer) numbers, `n` up to a limit `N` and prints the prime numbers.
We can determine in `n` is a prime nunber by diving it by every number in the range 2 to `n`.
If any of these calculations has a remainder equal to zero, n is not a prime number.
```
N = 50 # Check numbers up 50 for primes (excludes 50)
# Loop over all numbers from 2 to 50 (excluding 50)
for n in range(2, N):
# Assume that n is prime
n_is_prime = True
# Check if n divided by (any number in the range 2 to n) returns a remainder equal to 0
for m in range(2, n):
# If the remainder is zero, n is not a prime number
if n % m == 0:
n_is_prime = False
# If n is prime, print to screen
if n_is_prime:
print(n)
```
Notice that our program contains a second `for` loop.
For each value of n, it loops through incrementing values of m in the range (2 to n):
```python
# Check if n can be divided by m
# m ranges from 2 to n (excluding n)
for m in range(2, n):
```
before incrementing to the next value of n.
We call this a *nested* loop.
The indents in the code show where loops are nested.
Here it is again without the comments:
```
N = 50
# for loop 1
for n in range(2, N):
n_is_prime = True
# for loop 2
for m in range(2, n):
if n % m == 0:
n_is_prime = False
if n_is_prime:
print(n)
```
As n gets larger, dividing it by *every* number in the range (2, n) becomes more and more inefficient.
A `break` statement allows us to exit the loop as soon as a remainder equal to zero is returned (indicating that n is not a prime number).
In the program below, a break statement is added.
As soon as a number is found to be not prime, the program breaks out of loop 2 and goes to the next value of n in loop 1.
By placing `else` *one level up* from `if` the program will iterate through all values of m before printing n if n is prime.
```
N = 55
# for loop 1
for n in range(2, N):
# for loop 2
for m in range(2, n):
if n % m == 0:
break
else:
# if n is prime
print(n)
```
<a id='Continue'></a>
### `continue`
Sometimes, instead of stopping the loop we want to go to the next iteration in a loop, skipping the remaining code.
For this we use `continue`.
<img src="img/continue-statement-flowchart.jpg" alt="Drawing" style="width: 300px;"/>
<img src="img/algorithm-continue-statement.jpg" alt="Drawing" style="width: 300px;"/>
The example below loops over 20 numbers (0 to 19) and checks if the number is divisible by 4.
If the number is not divisible by 4:
- it prints a message
- it moves to the next value.
If the number is divisible by 4 it *continues* to the next value in the loop, without printing.
```
for j in range(1, 20):
if j % 4 == 0: # Check remainer of j/4
continue # continue to next value of j
print(j, "is not a multiple of 4")
```
To compare, if we used `break` instead of `continue`:
```
for j in range(1, 20):
if j % 4 == 0: # Check remainer of j/4
break # continue to next value of j
print(j, "is not a multiple of 4")
```
__Try it yourself__
We can use a `for` loop to perform an operation on each character of a string.
```Python
string = "string"
for i in range(len(sting)):
print(sting[i])
```
In the cell below, loop through the characters of the string.
Use `continue` to only print the letters of the word *sting*.
```
# Print the letters of the word sting
string = "string"
```
## Review Exercises
Here are a series of engineering problems for you to practise each of the new Python skills that you have learnt today.
### Review Exercise: `while` loops.
In the cell below, write a while loop that with each loop:
- prints the value of `x`
- then decreases the value of x by 0.5
as long as `x` remains positive.
<a href='#WhileLoops'>Jump to While Loops</a>
```
x = 4
while x > 0:
print(x)
x -= 0.5
# Example Solution
while (x > 0):
print(x)
x -= 0.5
```
### Review Exercise: `for` loops
In the cell below, write a `for` loop to print the even numbers from 2 to 100, inclusive.
```
# for loop to print the even numbers from 2 to 20, inclusive.
for n in range (2, 21):
print (n)
# Example Solution
for i in range(2, 21, 2):
print(i)
```
### Review Excercise: `for` loops and `if` statements
In the cell below, write a for loop to alternately print `Red` then `Blue` 3 times.
<br>i.e.
<br>Red
<br>Blue
<br>Red
<br>Blue
<br>Red
<br>Blue
```
# Alternately print Red and Blue
for n in range (1, 7):
if n % 2 == 0:
print("red")
elif
# Example Solution
colour = "Red"
for n in range(6):
print(colour)
if colour == "Red":
colour = "Blue"
else:
colour = "Red"
```
### Review Exercise: `continue`
In the cell below, loop through the characters of the string.
<br>Use `continue` to only print the letters of the word *sing*.
<br>Hint: Refer to __Logical Operators__ (Seminar 2).
<a href='#Continue'>Jump to continue</a>
```
# Print the letters of the word sing
string = "string"
# Example Solution
string = "string"
for i in range(len(string)):
if string[i] == "r" or string[i] == "t":
continue
print(string[i])
```
### Review Exercise: `for` loops and `if`, `else` and `continue` statements.
__(A)__ In the cell below, use a for loop to print the square roots of the first 25 odd positive integers.
<br> (Remember, the square root of a number, $x$ can be found by $x^{1/2}$)
__(B)__ If the number generated is greater than 3 and smaller than 5, print "`skip`" and __`continue`__ to the next iteration *without* printing the number.
<br>Hint: Refer to __Logical Operators__ (Seminar 2).
<a href='#ForLoops'>Jump to for loops</a>
<a href='#IfElse'>Jump to if and else statements</a>
<a href='#Continue'>Jump to continue</a>
```
# square roots of the first 25 odd positive integers
# Example Solution
for x in range(1, 50, 2):
if((x ** (1/2) > 3) and (x ** (1/2) < 5)):
print("skip")
continue
print(x ** (1/2))
```
# Updating your git repository
You have made several changes to your interactive textbook.
The final thing we are going to do is add these changes to your online repository so that:
- I can check your progress
- You can access the changes from outside of the university system.
> Save your work.
> <br> `git add -A`
> <br>`git commit -m "A short message describing changes"`
> <br>`git push`
# Summary
[*McGrath, Python in easy steps, 2013*]
- The Python `if` keyword performs a conditional test on an expression for a Boolean value of True or False.
- Alternatives to an `if` test are provided using `elif` and `else` tests.
- A `while` loop repeats until a test expression returns `False`.
- A `for`...`in`... loop iterates over each item in a specified data structure (or string).
- The `range()` function generates a numerical sequence that can be used to specify the length of the `for` loop.
- The `break` and `continue` keywords interrupt loop iterations.
# Homework
1. __PULL__ the changes you made in-class today to your personal computer before starting your homework.
1. __COMPLETE__ any unfinished Review Exercises.
1. __PUSH__ the changes you make at home to your online repository.
<br>Refer to: __1_Introduction_to_Version_Control.ipynb__.
| github_jupyter |
Prove that for integers $a,\;b,\;\dots$
(1) $(a, b) = 1, \; c | a, \; d | a \implies (c, d) = 1$
Suppose $(c, d) = e > 1$. Then $e | c$ and $c | a$ implies $e | a$; similarly $e | b$ so $(a, b) > 1$, a
contradiction, and therefore $(c, d) = 1$. $\;\;\;\boxdot$
(2) $(a, b) = (a, c) = 1 \implies (a, bc) = 1$
(3) $(a, b) = 1 \implies (a^n, b^k) = 1 \; \; \forall \; \; n \ge 1, k \ge 1$
(4) $(a, b) = 1 \implies (a + b, a - b) = 1 \; or \; 2$
(5) $(a, b) = 1 \implies (a + b, a^2 - ab + b^2) = 1 \; or \; 3$
(6) $(a, b) = 1, \; d|(a + b) \implies (a, d) = (b, d) = 1$
(7) A rational number $a/b$ with $(a, b) = 1$ is a *reduced fraction*. If the sum of two
reduced fractions is an integer, say $(a/b) + (c/d) = n$, prove that $|b| = |d|$.
(8) An integer is called *squarefree* if it is not divisible by the square of any prime. Prove that
for every $n \ge 1$ there exist uniquely determined $a > 0$ and $b > 0$ such that $n=a^2b$, where $b$ is *squarefree*.
...
(11) Prove that $n^4 + 4$ is composite if $n > 1$.
***Solution***
I first tried cases for the ones-digit. For example $n$ even gives $n^4 + 4$ also even and $n$ ending in
1, 3, 7 or 9 gives $n^4 + 4$ ending in 5.
However (particularly because the last case does not resolve in this manner) the right thing to try is
factoring $n^4 + 4$ in some obvious way:
Constants 1 and 4 or 2 and 2.
$n^4 + 4 = (n^2 + a \cdot n + 2) (n^2 + b \cdot n + 2)$
This gives $n^4 + b \cdot n^3 + 2 n^2 + a \cdot n^3 + a \cdot b \cdot n^2 + 2 \cdot a \cdot n + 2 n^2 + 2 \cdot b \cdot n + 4$
$n^4 + 4$ plus stuff that needs to be zero: $(b + a)\cdot n^3 + (4 + a \cdot b)\cdot n^2 + (2 \cdot (a + b))\cdot n$
This means $a = -b$ and $a \cdot b = -4$. Great: $a = 2$ and $b = -2$.
$n^4 + 4 = (n^2 + 2n + 2)(n^2 - 2n + 2)\;\;\;\;\boxdot$
```
def pf(n):
pfn, i = [], 2
while i * i < n:
while n%i == 0: pfn.append(i); n = n / i
i = i + 1
pfn.append(int(n))
return pfn
def npf(n): return len(pf(n))
def isprime(n):
if npf(n) == 1: return True
return False
for a in range(3):
s = a * 10 + 5
t = s*s*s*s + 4
if isprime(t): print(str(t) + ' is prime')
else: print(str(t) + ' factors are ' + str(pf(t)))
```
...
...
(20) Let $d = (826, 1890)$. Use the Euclidean algorithm to compute $d$, then express $d$ as a linear combination of 826 and 1890
Solution
$1890 = 826 \cdot 2 + 238$
$826 = 238 \cdot 3 + 112$
$238 = 112 \cdot 2 + 14$
$112 = 14 \cdot 8 + 0$
$d = 14$
$d = u \cdot 826 + v \cdot 1890$ or equivalently $1 = u \cdot 59 + v \cdot 135$
Taking $u$ positive it can take on values ${ 4, 9, 14, 19, \dots }$.
*--a miracle occurs--*
$(d = 14) = 254 \cdot 826 - 111 \cdot 1890$
```
254*826-111*1890
```
...
(19) F = 1, 1, 2, 3, 5, 8, ... where $\;a_{n+1} = a_n + a_{n-1}$. Prove $(a_n, \; a_{n+1})\;=\;1$.
(20)
(21)
(22) Prove (a, b) = (a + b, [a, b]).
Theorem R1: For $a > 1$ and $b > 1$ if $(a, b) = 1$ then
$
\begin{align}
\frac{1}{a} + \frac{1}{b}
\end{align}
$
is not an integer.
Proof: As (2, 2) = 2 one of $a$ or $b$ must be greater than 2.
Therefore $a + b < ab$ and
$
\begin{align}
0 < \frac{1}{a} + \frac{1}{b} = \frac{a+b}{ab} < 1
\end{align}
$
$\boxdot$
Now suppose $(a,b) = d$ where $a=\alpha d$, $b = \beta d$ and $(\alpha, \beta) = 1$.
Consider $(a + b, [a,b])$:
$
\begin{align}
(a + b, [a,b]) = ((\alpha + \beta)d, \frac{ab}{(a,b)}) =
((\alpha + \beta)d, \frac{\alpha\beta d^2}{d}) = d(\alpha + \beta, \alpha\beta)
\end{align}
$
For any prime factor $p$ of $\beta$ we can write $\beta = pq$ where $p$ does not divide into
$\alpha$. What is $(\alpha + \beta)/(\alpha \beta)$?
$
\begin{align}
\frac{\alpha + \beta}{\alpha \beta} = \frac{1}{\beta} + \frac{1}{\alpha}
\end{align}
$
which is not an integer.
Left off here: Show (alpha + beta, alpha beta) = 1 by dividing alpha q p into alpha + beta...
(23) Find $a, b > 0 \;\; \ni \;\; a + b = 5264 \; and \; [a, b] = 200,340$.
...
(30) If $n > 1$ prove
$
\begin{align}
\sum_{k=1}^{n} \frac{1}{k}
\end{align}
$
is not an integer.
| github_jupyter |
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Plot-Validation-and-Train-loss" data-toc-modified-id="Plot-Validation-and-Train-loss-1"><span class="toc-item-num">1 </span>Plot Validation and Train loss</a></span></li><li><span><a href="#Extract-relevant-Data-to-df" data-toc-modified-id="Extract-relevant-Data-to-df-2"><span class="toc-item-num">2 </span>Extract relevant Data to df</a></span><ul class="toc-item"><li><span><a href="#Get-best-result" data-toc-modified-id="Get-best-result-2.1"><span class="toc-item-num">2.1 </span>Get best result</a></span></li><li><span><a href="#Consider-Outliers" data-toc-modified-id="Consider-Outliers-2.2"><span class="toc-item-num">2.2 </span>Consider Outliers</a></span></li></ul></li><li><span><a href="#Results-by-model" data-toc-modified-id="Results-by-model-3"><span class="toc-item-num">3 </span>Results by model</a></span><ul class="toc-item"><li><span><a href="#Remove-Duplicates" data-toc-modified-id="Remove-Duplicates-3.1"><span class="toc-item-num">3.1 </span>Remove Duplicates</a></span></li></ul></li><li><span><a href="#Each-variable-plotted-against-loss:" data-toc-modified-id="Each-variable-plotted-against-loss:-4"><span class="toc-item-num">4 </span>Each variable plotted against loss:</a></span></li><li><span><a href="#Investigate-"band"-in-loss-model-plot" data-toc-modified-id="Investigate-"band"-in-loss-model-plot-5"><span class="toc-item-num">5 </span>Investigate "band" in loss-model plot</a></span><ul class="toc-item"><li><span><a href="#Extract-the-different-bands-and-inpsect" data-toc-modified-id="Extract-the-different-bands-and-inpsect-5.1"><span class="toc-item-num">5.1 </span>Extract the different bands and inpsect</a></span></li></ul></li><li><span><a href="#Investigate-Duplicates" data-toc-modified-id="Investigate-Duplicates-6"><span class="toc-item-num">6 </span>Investigate Duplicates</a></span></li><li><span><a href="#Investigate-Best" data-toc-modified-id="Investigate-Best-7"><span class="toc-item-num">7 </span>Investigate Best</a></span></li></ul></div>
```
%load_ext autoreload
%autoreload 2
%cd ..
import os
import sys
from notebooks import utils
from matplotlib import pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()
#import pipeline
# parent_dir = os.path.abspath(os.path.join(os.getcwd(), os.pardir))
# sys.path.append(parent_dir) #to import pipeline
%ls experiments
###CHANGE THIS FILE TO THE SUBDIRECTORY OF INTEREST:
#exp_dirs = ["experiments/07b/", "experiments/DA3_2/07a/0", "experiments/DA3_2/07a/1"]
exp_dirs = ["experiments/retrain/"]
results = utils.extract_res_from_files(exp_dirs)
#load data when utils isnt working:
if False:
import pickle
res_fp = "experiments/results/ResNeXt/res.txt"
with open(res_fp, "rb") as f:
results = pickle.load(f)
```
## Plot Validation and Train loss
```
ylim = (0, 3000)
ylim2 = (70,100)
utils.plot_results_loss_epochs(results, ylim1=ylim, ylim2=ylim2)
```
## Extract relevant Data to df
Use minimum validation loss as criterion.
In theory (if we had it) it would be better to use DA MAE
```
df_res = utils.create_res_df(results)
df_res_original = df_res.copy() #save original (in case you substitute out)
df_res
```
### Get best result
```
df_res["valid_loss"].idxmin()
print(df_res.loc[df_res["valid_loss"].idxmin()])
df_res.loc[df_res["valid_loss"].idxmin()]["path"]
```
### Consider Outliers
```
#consider third experiment run (lots of outliers)
df3 = df_res[df_res["path"].str.contains("CAE_zoo3")]
df_outlier = df_res[df_res["valid_loss"] > 150000]
df_outlier
```
## Results by model
```
relu = df_res[df_res.activation == "relu"]
lrelu = df_res[df_res.activation == "lrelu"]
plt.scatter('model', "valid_loss", data=relu, marker="+", color='r')
plt.scatter('model', "valid_loss", data=lrelu, marker="+", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 70000)
plt.legend(labels=["relu", "lrelu"])
plt.show()
#investigate number of layers
eps = 1e-5
reluNBN = df_res[(df_res.activation == "relu") & (abs(df_res.batch_norm - 0.) < eps)]
reluBN = df_res[(df_res.activation == "relu") & (abs(df_res.batch_norm - 1.) < eps)]
lreluNBN = df_res[(df_res.activation == "lrelu") & (abs(df_res.batch_norm - 0.0) < eps)]
lreluBN = df_res[(df_res.activation == "lrelu") & (abs(df_res.batch_norm - 1.) < eps)]
plt.scatter('model', "valid_loss", data=reluNBN, marker="+", color='r')
plt.scatter('model', "valid_loss", data=reluBN, marker="+", color='g')
plt.scatter('model', "valid_loss", data=lreluNBN, marker="o", color='r')
plt.scatter('model', "valid_loss", data=lreluBN, marker="o", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 70000)
plt.legend(labels=["relu, NBN", "relu, BN", "lrelu, NBN", "lrelu, BN"])
plt.show()
```
It turns out that there are lots of duplicates in the above data (as a result of a bug in my code that was giving all models the same number of channels). So remove duplicates and go again:
### Remove Duplicates
```
#remove duplicates
columns = list(df_res_original.columns)
columns.remove("model")
columns.remove("path")
print(columns)
df_res_new = df_res_original.loc[df_res_original.astype(str).drop_duplicates(subset=columns, keep="last").index]
#df_res_new = df_res_original.drop_duplicates(subset=columns, keep="last")
df_res_new.shape
df_res = df_res_new
df_res.shape
##Plot same graph again:
#investigate number of layers
relu6 = df_res[(df_res.activation == "relu") & (df_res.num_layers == 6)]
relu11 = df_res[(df_res.activation == "relu") & (df_res.num_layers != 6)]
lrelu6 = df_res[(df_res.activation == "lrelu") & (df_res.num_layers == 6)]
lrelu11 = df_res[(df_res.activation == "lrelu") & (df_res.num_layers != 6)]
plt.scatter('model', "valid_loss", data=relu6, marker="+", color='r')
plt.scatter('model', "valid_loss", data=lrelu6, marker="+", color='g')
plt.scatter('model', "valid_loss", data=relu11, marker="o", color='r')
plt.scatter('model', "valid_loss", data=lrelu11, marker="o", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 60000)
plt.legend(labels=["relu, 6", "lrelu, 6", "relu, not 6", "lrelu, not 6"])
plt.show()
```
## Each variable plotted against loss:
```
plt.scatter('latent_dims', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("latent dimensions")
plt.ylim(16000, 70000)
plt.scatter('first_channel', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("First channel")
plt.ylim(16000, 80000)
plt.scatter('batch_norm', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Batch Norm")
plt.xlim(-0.1, 1.1)
plt.ylim(16000, 80000)
plt.scatter('activation', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Activation")
plt.ylim(16000, 70000)
plt.scatter('model', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 80000)
plt.scatter('num_layers', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Number of layers in Decoder/Encoder")
plt.ylim(16000, 80000)
plt.scatter('total_channels', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Total Channels")
plt.ylim(16000, 80000)
plt.scatter('channels/layer', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Channels/Layer")
plt.ylim(16000, 80000)
plt.scatter('first_channel', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("First_channel")
plt.ylim(16000, 80000)
plt.scatter('conv_changeover', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Input size decrease at which to change to start downsampling (via transposed convolution)")
plt.ylim(16000, 80000)
```
## Investigate "band" in loss-model plot
### Extract the different bands and inpsect
```
band1 = df_res[df_res.valid_loss < 20000]
band2 = df_res[(df_res.valid_loss > 20000) & (df_res.valid_loss < 23000)]
band3 = df_res[(df_res.valid_loss > 23000) & (df_res.valid_loss < 26000)]
band1.head()
band3.head()
```
## Investigate Duplicates
```
#eg1: /data/home/jfm1118/DA/experiments/CAE_zoo2/32 and /data/home/jfm1118/DA/experiments/CAE_zoo2/12
#eg2: /data/home/jfm1118/DA/experiments/CAE_zoo2/31 and /data/home/jfm1118/DA/experiments/CAE_zoo2/27
def get_data_from_path(path):
for res in results:
if res["path"] == path:
return res
else:
raise ValueError("No path = {} in 'results' list".format(path))
def print_model(settings):
model = settings.AE_MODEL_TYPE(**settings.get_kwargs())
print(settings.__class__.__name__)
print(model.layers)
print(settings.CHANNELS)
base_exp = "/data/home/jfm1118/DA/experiments/CAE_zoo2/"
exp_32 = get_data_from_path(base_exp + "32")["settings"]
exp_12 = get_data_from_path(base_exp + "12")["settings"]
print_model(exp_32)
print()
print_model(exp_12)
base_exp = "/data/home/jfm1118/DA/experiments/CAE_zoo2/"
exp_1 = get_data_from_path(base_exp + "31")["settings"]
exp_2 = get_data_from_path(base_exp + "27")["settings"]
print_model(exp_1)
print()
print_model(exp_2)
print(list(range(1, 2*(exp_1.get_num_layers_decode() + 1) + 1, 2)))
```
## Investigate Best
```
path = "/data/home/jfm1118/DA/experiments/CAE_zoo2/17"
exp = get_data_from_path(base_exp + str(17))["settings"]
print_model(exp_1)
```
| github_jupyter |
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
# `np.tile` vs. `np.repeat`
```
np.tile([1, 2, 3], reps=2)
np.repeat([1, 2, 3], 2)
```
### multidimensional
```
np.tile(np.repeat([1, 2, 3, 4], 2), 3)
d = {'b': 12}
dict({'a': 2}, **d)
a = np.arange(4).reshape(2, -1)
np.tile(a, (2, 3))
a = np.arange(4).reshape(2, -1)
np.repeat(a, (2, 5), axis=0)
a = np.arange(4).reshape(2, -1)
np.repeat(a, (2, 5), axis=1)
```
# Set operations
```
a = np.array([1, 2, 3, 2, 3, 4, 3, 4, 5, 6])
b = np.array([7, 2, 10, 2, 7, 4, 9, 4, 9, 8])
np.intersect1d(a, b), np.setdiff1d(a, b)
```
# Matching positions and elements
```
a = np.array([1, 2, 3, 2, 3, 4, 3, 4, 5, 6])
b = np.array([7, 2, 10, 2, 7, 4, 9, 4, 9, 8])
np.where(a == b), a[a==b]
```
# Boolean indexing
```
a[a > 4]
```
# Swapping columns
```
a = np.arange(10).reshape(2, -1)
a[:, [1, 2, 3, 0, 4]]
```
# Standardizing and normalizing
Standardizing: mean 0, std 1
```
a = np.random.uniform(size=(5, 4), low=-5, high=10)
a
(a - a.mean()) / a.std()
```
Normalizing: squash into range [0, 1)
```
(a - a.min()) / a.ptp()
```
# `np.digitize`
```
a = np.arange(1, 11).reshape(2, -1)
a = np.array([20, -2, 3, 5, 8, 7])
np.digitize(a, bins=[1, 4, 8])
```
# Local peaks
```
a = np.array([1, 3, 7, 1, 2, 6, 0, 1])
diff1 = a - np.hstack((a[1:], 0))
diff2 = a - np.hstack((0, a[:-1]))
np.where((diff1>0) & (diff2>0))
a = np.array([[3,3,3],[4,4,4],[5,5,5]])
b = np.array([1,2,3])
a - b[:, None]
x = np.array([1, 2, 1, 1, 3, 4, 3, 1, 1, 2, 1, 1, 2])
np.where(x == 1)[0][4]
```
# Date range
```
np.arange(np.datetime64("2018-01-02"), np.datetime64("2018-01-15"), 3)
```
# Strides
```
a = np.arange(15)
stride = 2
window = 4
np.array([a[i:i+window] for i in range(0, a.shape[0]-window+1, stride)])
```
## Trim digital signal
Trim each consecutive block of ones to `min(cut, len(block))`.
```
import itertools
x = [0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1]
plt.step(np.arange(len(x)), x)
cut = 2
x = np.array([0] + x + [0])
up = np.where(np.diff(x) == 1)[0] + 1
down = np.where(np.diff(x) == -1)[0] + 1
delta = down - up
delta[delta > cut] = cut
x[:] = 0
x[list(itertools.chain(*(list(range(up[i], up[i]+delta[i])) for i in range(delta.shape[0]))))] = 1
x = x[1:-1]
x
plt.step(np.arange(len(x)), x)
```
# Permutations
```
a = np.array([4, 3, 0, 10, 1])
order = np.argsort(-a)
a[order]
order, a[order][np.argsort(order)]
a = np.array([[1, -1, 2], [5, 0, 0]])
np.argmax(a, -1)
a.argmax(-1)
```
# argsort
```
a = np.array([3, -1, 2, 0, 5, 2])
order = np.argsort(-a)
a[order]
a[order][np.argsort(order)]
[1, 2] * -1
```
| github_jupyter |
# Welcome!
Below, we will learn to implement and train a policy to play atari-pong, using only the pixels as input. We will use convolutional neural nets, multiprocessing, and pytorch to implement and train our policy. Let's get started!
```
# install package for displaying animation
!pip install JSAnimation
# custom utilies for displaying animation, collecting rollouts and more
import pong_utils
%matplotlib inline
# check which device is being used.
# I recommend disabling gpu until you've made sure that the code runs
device = pong_utils.device
print("using device: ",device)
# render ai gym environment
import gym
import time
# PongDeterministic does not contain random frameskip
# so is faster to train than the vanilla Pong-v4 environment
env = gym.make('PongDeterministic-v4')
print("List of available actions: ", env.unwrapped.get_action_meanings())
# we will only use the actions 'RIGHTFIRE' = 4 and 'LEFTFIRE" = 5
# the 'FIRE' part ensures that the game starts again after losing a life
# the actions are hard-coded in pong_utils.py
```
# Preprocessing
To speed up training, we can simplify the input by cropping the images and use every other pixel
```
import matplotlib
import matplotlib.pyplot as plt
# show what a preprocessed image looks like
env.reset()
_, _, _, _ = env.step(0)
# get a frame after 20 steps
for _ in range(20):
frame, _, _, _ = env.step(1)
plt.subplot(1,2,1)
plt.imshow(frame)
plt.title('original image')
plt.subplot(1,2,2)
plt.title('preprocessed image')
# 80 x 80 black and white image
plt.imshow(pong_utils.preprocess_single(frame), cmap='Greys')
plt.show()
```
# Policy
## Exercise 1: Implement your policy
Here, we define our policy. The input is the stack of two different frames (which captures the movement), and the output is a number $P_{\rm right}$, the probability of moving left. Note that $P_{\rm left}= 1-P_{\rm right}$
```
import torch
import torch.nn as nn
import torch.nn.functional as F
# set up a convolutional neural net
# the output is the probability of moving right
# P(left) = 1-P(right)
class Policy(nn.Module):
def __init__(self):
super(Policy, self).__init__()
########
##
## Modify your neural network
##
########
# 80x80 to outputsize x outputsize
# outputsize = (inputsize - kernel_size + stride)/stride
# (round up if not an integer)
# output = 20x20 here
self.conv = nn.Conv2d(2, 1, kernel_size=4, stride=4)
self.size=1*20*20
# 1 fully connected layer
self.fc = nn.Linear(self.size, 1)
self.sig = nn.Sigmoid()
def forward(self, x):
########
##
## Modify your neural network
##
########
x = F.relu(self.conv(x))
# flatten the tensor
x = x.view(-1,self.size)
return self.sig(self.fc(x))
# run your own policy!
# policy=Policy().to(device)
policy=pong_utils.Policy().to(device)
# we use the adam optimizer with learning rate 2e-4
# optim.SGD is also possible
import torch.optim as optim
optimizer = optim.Adam(policy.parameters(), lr=1e-4)
```
# Game visualization
pong_utils contain a play function given the environment and a policy. An optional preprocess function can be supplied. Here we define a function that plays a game and shows learning progress
```
pong_utils.play(env, policy, time=200)
# try to add the option "preprocess=pong_utils.preprocess_single"
# to see what the agent sees
```
# Function Definitions
Here you will define key functions for training.
## Exercise 2: write your own function for training
(what I call scalar function is the same as policy_loss up to a negative sign)
### PPO
Later on, you'll implement the PPO algorithm as well, and the scalar function is given by
$\frac{1}{T}\sum^T_t \min\left\{R_{t}^{\rm future}\frac{\pi_{\theta'}(a_t|s_t)}{\pi_{\theta}(a_t|s_t)},R_{t}^{\rm future}{\rm clip}_{\epsilon}\!\left(\frac{\pi_{\theta'}(a_t|s_t)}{\pi_{\theta}(a_t|s_t)}\right)\right\}$
the ${\rm clip}_\epsilon$ function is implemented in pytorch as ```torch.clamp(ratio, 1-epsilon, 1+epsilon)```
```
def clipped_surrogate(policy, old_probs, states, actions, rewards,
discount = 0.995, epsilon=0.1, beta=0.01):
########
##
## WRITE YOUR OWN CODE HERE
##
########
actions = torch.tensor(actions, dtype=torch.int8, device=device)
# convert states to policy (or probability)
new_probs = pong_utils.states_to_prob(policy, states)
new_probs = torch.where(actions == pong_utils.RIGHT, new_probs, 1.0-new_probs)
# include a regularization term
# this steers new_policy towards 0.5
# prevents policy to become exactly 0 or 1 helps exploration
# add in 1.e-10 to avoid log(0) which gives nan
entropy = -(new_probs*torch.log(old_probs+1.e-10)+ \
(1.0-new_probs)*torch.log(1.0-old_probs+1.e-10))
return torch.mean(beta*entropy)
```
# Training
We are now ready to train our policy!
WARNING: make sure to turn on GPU, which also enables multicore processing. It may take up to 45 minutes even with GPU enabled, otherwise it will take much longer!
```
from parallelEnv import parallelEnv
import numpy as np
# keep track of how long training takes
# WARNING: running through all 800 episodes will take 30-45 minutes
# training loop max iterations
episode = 500
# widget bar to display progress
!pip install progressbar
import progressbar as pb
widget = ['training loop: ', pb.Percentage(), ' ',
pb.Bar(), ' ', pb.ETA() ]
timer = pb.ProgressBar(widgets=widget, maxval=episode).start()
envs = parallelEnv('PongDeterministic-v4', n=8, seed=1234)
discount_rate = .99
epsilon = 0.1
beta = .01
tmax = 320
SGD_epoch = 4
# keep track of progress
mean_rewards = []
for e in range(episode):
# collect trajectories
old_probs, states, actions, rewards = \
pong_utils.collect_trajectories(envs, policy, tmax=tmax)
total_rewards = np.sum(rewards, axis=0)
# gradient ascent step
for _ in range(SGD_epoch):
# uncomment to utilize your own clipped function!
# L = -clipped_surrogate(policy, old_probs, states, actions, rewards, epsilon=epsilon, beta=beta)
L = -pong_utils.clipped_surrogate(policy, old_probs, states, actions, rewards,
epsilon=epsilon, beta=beta)
optimizer.zero_grad()
L.backward()
optimizer.step()
del L
# the clipping parameter reduces as time goes on
epsilon*=.999
# the regulation term also reduces
# this reduces exploration in later runs
beta*=.995
# get the average reward of the parallel environments
mean_rewards.append(np.mean(total_rewards))
# display some progress every 20 iterations
if (e+1)%20 ==0 :
print("Episode: {0:d}, score: {1:f}".format(e+1,np.mean(total_rewards)))
print(total_rewards)
# update progress widget bar
timer.update(e+1)
timer.finish()
pong_utils.play(env, policy, time=200)
# save your policy!
torch.save(policy, 'PPO.policy')
# load policy if needed
# policy = torch.load('PPO.policy')
# try and test out the solution
# make sure GPU is enabled, otherwise loading will fail
# (the PPO verion can win more often than not)!
#
# policy_solution = torch.load('PPO_solution.policy')
# pong_utils.play(env, policy_solution, time=2000)
```
| github_jupyter |
```
%matplotlib inline
```
# Optimization Opt 1 parameter
```
def run(Plot, Save):
return
import numpy as np
from PyMieSim import Material
from PyMieSim.Scatterer import Sphere
from PyMieSim.Detector import Photodiode, LPmode
from PyMieSim.Source import PlaneWave
from PyMieSim.Experiment import ScatSet, SourceSet, Setup, DetectorSet
DiameterList = np.linspace(100e-9, 1000e-9, 200)
Detector0 = Photodiode(NA = 0.1,
Sampling = 300,
GammaOffset = 20,
PhiOffset = 0,
CouplingMode = 'Centered')
scatKwargs = { 'Diameter' : np.linspace(400e-9, 2000e-9, 200),
'Material' : Material('BK7'),
'nMedium' : [1] }
sourceKwargs = { 'Wavelength' : 1e-6,
'Polarization' : [0]}
Detector0 = Photodiode(NA = 2.0,
Sampling = 300,
GammaOffset = 0,
PhiOffset = 0,
CouplingMode = 'Centered')
detecSet = DetectorSet([Detector0])
scatSet = ScatSet(Scatterer = Sphere, kwargs = scatKwargs )
sourceSet = SourceSet(Source = PlaneWave, kwargs = sourceKwargs )
Experiment = Setup(ScattererSet = scatSet,
SourceSet = sourceSet,
DetectorSet = detecSet)
# Metric can be "max"
# "min"
# "mean"
# "std+RI"
# "std+Diameter"
# "std+Polarization"
# "std+Wavelength"
# "std+Detector"
# "monotonic+RI"
# "monotonic+Diameter"
# "monotonic+Polarization"
# "monotonic+Wavelength"
# "monotonic+Detector"
Opt = Experiment.Optimize(Setup = Experiment,
Metric = 'mean',
Parameter = ['PhiOffset'],
Optimum = 'Maximum',
MinVal = [1e-5],
MaxVal = [180],
WhichDetector = 0,
X0 = [0.6],
MaxIter = 350,
Tol = 1e-4,
FirstStride = 30)
print(Opt.Result)
df = Experiment.Coupling(AsType='dataframe')
if Plot:
df.Plot(y='Coupling', x='Diameter') # can be "Couplimg" or "STD"
if __name__ == '__main__':
run(Plot=True, Save=False)
```
| github_jupyter |
# 6. Hidden Markov Models with Theano and TensorFlow
In the last section we went over the training and prediction procedures of Hidden Markov Models. This was all done using only vanilla numpy the Expectation Maximization algorithm. I now want to introduce how both `Theano` and `Tensorflow` can be utilized to accomplish the same goal, albeit by a very different process.
## 1. Gradient Descent
Hopefully you are familiar with the gradient descent optimization algorithm, if not I recommend reviewing my posts on Deep Learning, which leverage gradient descent heavily (or this [video](https://www.youtube.com/watch?v=IHZwWFHWa-w). With that said, a simple overview is as follows:
> Gradient descent is a first order optimization algorithm for finding the minimum of a function. To find a local minimum of a function using gradient descent, on takes steps proportional to the negative of the gradient of the function at its current point.
Visually, this iterative process looks like:
<img src="https://drive.google.com/uc?id=1R2zVTj3uo5zmow6vFujWlU-qs9jRF_XG" width="250">
Where above we are looking at a contour plot of a three dimensional bowl, and the center of the bowl is a minimum. Now, the actual underlying mechanics of gradient descent work as follows:
#### 1. Define a model/hypothesis that will be mapping inputs to outputs, or in other words making predictions:
$$h_{\theta}(x) = \theta_0 + \theta_1x$$
In this case $x$ is our input and $h(x)$, often thought of as $y$, is our output. We are stating that we believe the ground truth relationship between $x$ and $h(x)$ is captured by the linear combination of $\theta_0 + \theta_1x$. Now, what are $\theta_0$ and $\theta_1$ equal to?
#### 2. Define a **cost** function for which you are trying to find the minimum. Generally, this cost function is defined as some form of **error**, and it will be parameterized by variables related to your model in some way.
$$cost = J = (y - h_{\theta}(x))^2$$
Above $y$ refers to the ground truth/actual value of the output, and $h_{\theta}(x)$ refers to that which our model predicted. The difference, squared, represents our cost. We can see that if our prediction is exactly equal to the ground truth value, our cost will be 0. If our prediction is very far off from our ground truth value then our cost will be very high. Our goal is to minimize the cost (error) of our model.
#### 3. Take the [**gradient**](https://en.wikipedia.org/wiki/Gradient) (multi-variable generalization of the derivative) of the cost function with respect to the parameters that you have control over.
$$\nabla J = \frac{\partial J}{\partial \theta}$$
Simply put, we want to see how $J$ changes as we change our model parameters, $\theta_0$ and $\theta_1$.
#### 4. Based on the gradient update our values for $\theta$ with a simple update rule:
$$\theta_0 \rightarrow \theta_0 - \alpha \cdot \frac{\partial J}{\partial \theta_0}$$
$$\theta_1 \rightarrow \theta_1 - \alpha \cdot \frac{\partial J}{\partial \theta_1}$$
#### 5. Repeat steps two and three for a set number of iterations/until convergence.
After a set number of steps, the hope is that the model weights that were _learned_ are the most optimal weights to minimize prediction error. Now after everything we discussed in the past two posts you may be wondering, how exactly does this relate to Hidden Markov Models, which have been trained via Expectation Maximization?
### 1.1 Gradient Descent and Hidden Markov Models
Let's say for a moment that our goal that we wish to accomplish is predict the probability of an observed sequence, $p(x)$. And let's say that we have 100 observed sequences at our disposal. It should be clear that if we have a trained HMM that predicts the majority of our sequences are very unlikely, the HMM was probably not trained very well. Ideally, our HMM parameters would be learned in a way that maximizes the probability of observing what we did (this was the goal of expectation maximization).
What may start to become apparent at this point is that we have a perfect cost function already created for us! The total probability of our observed sequences, based on our HMM parameters $A$, $B$, and $\pi$. We can define this mathematically as follows (for the scaled version); in the previous post we proved that:
$$p(x) = \prod_{t=1}^T c(t)$$
Which states that the probability of an observed sequence is equal to the product of the scales at each time step. Also recall that the scale is just defined as:
$$c(t) = \sum_{i=1}^M \alpha'(t,i)$$
With that all said, we can define the cost of a single observed training sequence as:
$$cost = \sum_{t}^{T} log\big(c(t)\big)$$
Where we are using the log to avoid the underflow problem, just as we did in the last notebook. So, we have a cost function which intuitively makes sense, but can we find its gradient with respect to our HMM parameters $A$, $B$, and $\pi$? We absolutely can! The wonderful thing about Theano is that it links variables together via a [computational graph](http://deeplearning.net/software/theano/extending/graphstructures.html). So, cost is depedent on $A$, $B$ and $\pi$ via the following link:
$$cost \rightarrow c(t) \rightarrow alpha \rightarrow A, B, \pi$$
We can take the gradient of this cost function in theano as well, allowing us to then easily update our values of $A$, $B$, and $\pi$! Done iteratively, we hopefully will converge to a nice minimum.
### 1.2 HMM Theano specifics
I would be lying if I said that Theano wasn't a little bit hard to follow at first. For those unfamiliar, representing symbolic mathematical computations as graphs may feel very strange. I have a few walk throughs of Theano in my Deep Learning section, as well as `.py` files in the source repo. Additionally, the theano [documentation](http://deeplearning.net/software/theano/index.html) is also very good. With that said, I do want to discuss a few details of the upcoming code block.
#### Recurrence Block $\rightarrow$ Calculating the Forward Variable, $\alpha$
First, I want to discuss the `recurrence` and `scan` functions that you will be seeing:
```
def recurrence_to_find_alpha(t, old_alpha, x):
"""Scaled version of updates for HMM. This is used to
find the forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time
step the initial value,
outputs_info=[self.pi * self.B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(self.A) * self.B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[self.pi * self.B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used
# here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
```
The above block is where our forward variable $\alpha$ and subsequently the probability of the observed sequence $p(x)$ is found. The process works as follows:
1. The `theano.scan` function (logically similar to a for loop) is defined with the following parameters:
* `fn`: The recurrence function that the array being iterated over will be passed into.
* `sequences`: An array of indexes, $[1,2,3,...,T]$
* `outputs_info`: The initial value of $\alpha$
* `non_sequences`: Our observation sequence, $X$. This passed in it's entirety to the recurrence function at each iteration.
2. Our recurrence function, `recurrence_to_find_alpha`, is meant to calculate $\alpha$ at each time step. $\alpha$ at $t=1$ was defined by `outputs_info` in `scan`. This recurrence function essentially is performing the forward algorithm (additionally it incorporates scaling):
$$\alpha(1,i) = \pi_iB\big(i, x(1)\big)$$
$$\alpha(t+1, j) = \sum_{i=1}^M \alpha(t,i) A(i,j)B(j, x(t+1))$$
3. We calculate $p(x)$ to be the sum of the log likelihood. This is set to be our `cost`.
4. We define a `cost_op`, which is a theano function that takes in a symbolic variable `thx` and determines the output `cost`. Remember, `cost` is linked to `thx` via:
```
cost -> scale -> theano.scan(non_sequences=thx)
```
#### Update block $\rightarrow$ Updating HMM parameters $A$, $B$, and $\pi$
The other block that I want to touch on is the update block:
```
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum()
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x')
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x')
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
```
The update block functions as follows:
1. We have `cost` that was defined symbolically and linked to `thx`. We can define `pi_update` as `pi_update = self.pi - learning_rate * T.grad(cost, self.pi)`.
2. This same approach is performed for $A$ and $B$.
3. We then create a theano function, `train_op` which takes in `thx`, our symbolic input, and with perform updates via the `updates=updates` kwarg. Specifically, updates takes in a list of tuples, with the first value in the tuple being the variable that should be updated, and the second being the expression with which it should be updated to be.
4. We loop through all training examples (sequences of observations), and call `train_up`, passing in `X[n]` (a unique sequene of observations) as `thx`.
5. `train_op` then performs the `updates`, utilizing `thx = X[n]` wherever `updates` depends on `thx`.
This is clearly stochastic gradient descent, because we are performing updates to our parameters $A$, $B$, and $\pi$ for each training sequence. Full batch gradient descent would be if we defined a cost function that was based on all of the training sequences, not only an individual sequence.
## 2. HMM's with Theano
In code, our HMM can be implemented with Theano as follows:
```
import numpy as np
import theano
import theano.tensor as T
import seaborn as sns
import matplotlib.pyplot as plt
from hmm.utils import get_obj_s3, random_normalized
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
sns.set(style="white", palette="husl")
sns.set_context("talk")
sns.set_style("ticks")
class HMM:
def __init__(self, M):
self.M = M
def fit(self, X, learning_rate=0.001, max_iter=10, V=None, p_cost=1.0, print_period=10):
"""Train HMM model using stochastic gradient descent."""
# Determine V, the vocabulary size
if V is None:
V = max(max(x) for x in X) + 1
N = len(X)
# Initialize HMM variables
pi0 = np.ones(self.M) / self.M # Initial state distribution
A0 = random_normalized(self.M, self.M) # State transition matrix
B0 = random_normalized(self.M, V) # Output distribution
thx, cost = self.set(pi0, A0, B0)
# This is a beauty of theano and it's computational graph.
# By defining a cost function, which is representing p(x),
# the probability of a sequence, we can then find the gradient
# of the cost with respect to our parameters (pi, A, B).
# The gradient updated rules are applied as usual. Note, the
# reason that this is stochastic gradient descent is because
# we are only looking at a single training example at a time.
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum()
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x')
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x')
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
print("A learned from training: \n", self.A.get_value())
print("B learned from training: \n", self.B.get_value())
print("pi learned from training: \n", self.pi.get_value())
plt.figure(figsize=(8,5))
plt.plot(costs, color="blue")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
return self.cost_op(x)
def get_cost_multi(self, X, p_cost=1.0):
P = np.random.random(len(X))
return np.array([self.get_cost(x) for x, p in zip(X, P) if p < p_cost])
def log_likelihood(self, x):
return - self.cost_op(x)
def set(self, pi, A, B):
# Create theano shared variables
self.pi = theano.shared(pi)
self.A = theano.shared(A)
self.B = theano.shared(B)
# Define input, a vector
thx = T.ivector("thx")
def recurrence_to_find_alpha(t, old_alpha, x):
"""
Scaled version of updates for HMM. This is used to find the
forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time step
the initial value,
outputs_info=[self.pi * self.B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(self.A) * self.B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[self.pi * self.B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used
# here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
return thx, cost
def fit_coin(file_key):
"""Loads data and trains HMM."""
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
# Instantiate object of class HMM with 2 hidden states (heads and tails)
hmm = HMM(2)
hmm.fit(X)
L = hmm.get_cost_multi(X).sum()
print("Log likelihood with fitted params: ", round(L, 3))
# Try the true values
pi = np.array([0.5, 0.5])
A = np.array([
[0.1, 0.9],
[0.8, 0.2]
])
B = np.array([
[0.6, 0.4],
[0.3, 0.7]
])
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == "__main__":
key = "coin_data.txt"
fit_coin(key)
```
## 3. HMM's with Theano $\rightarrow$ Optimization via Softmax
One of the challenges of the approach we took is that gradient descent is _unconstrained_; it simply goes in the direction of the gradient. This presents a problem for us in the case of HMM's. Remember, the parameters of an HMM are $\pi$, $A$, and $B$, and each is a probability matrix/vector. This means that they must be between 0 and 1, and must sum to 1 (along the rows if 2-D).
We accomplished this in the previous section by performing a "hack". Specifically, we renormalized after each gradient descent step. However, this means that we weren't performing _real_ gradient descent, because by renormalizing we are not exactly moving in the direction of the gradient anymore. For reference, the pseudocode looked like this:
```
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum() # Normalizing to ensure it stays a probability
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x') # Normalize for prob
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x') # Normalize for prob
# Passing in normalized updates for pi, A, B. No longer moving in dir of gradient
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
```
This leads us to the question: is it possible to use true gradient descent, while still conforming to the constraints that each parameter much be a true probability. The answer is of course yes!
### 3.1 Softmax
If you are unfamiliar with Deep Learning then you may want to jump over this section, or go through my deep learning posts that dig into the subject. If you are familiar, recall the softmax function:
$$softmax(x)_i = \frac{exp(x_i)}{\sum_{k=1}^K exp(x_k)}$$
Where $x$ is an array of size $K$, and $K$ is the number of classes that we have. The result of the softmax is that all outputs are positive and sum to 1. What exactly does this mean in our scenario?
#### Softmax for $\pi$
Consider $\pi$, an array of size $M$. Supposed we want to parameterize $\pi$, using the symbol $\theta$. We can then assign $\pi$ to be:
$$pi = softmax(\theta)$$
In this way, $\pi$ is like an intermediate variable and $\theta$ is the actual parameter that we will be updating. This ensures that $\pi$ is always between 0 and 1, and sums to 1. At the same time, the values in $\theta$ can be anything; this means that we can freely use gradient descent on $\theta$ without having to worry about any constraints! No matter what we do to $\theta$, $\pi$ will always be between 0 and 1 and sum to 1.
#### Softmax for $A$ and $B$
Now, what about $A$ and $B$? Unlike $\pi$, which was a 1-d vector, $A$ and $B$ are matrices. Luckily for us, softmax works well for us here too! Recall that when dealing with data in deep learning (and most ML) that we are often dealing with multiple samples at the same time. Typically an $NxD$ matrix, where $N$ is the number of samples, and $D$ is the dimensionality. We know that the output of our model is usually an $NxK$ matrix, where $K$ is the number of classes. Naturally, because the classes go along the rows, each row must represent a separate probability distribution.
Why is this helpful? Well, the softmax was actually written with this specifically in mind! When you use the softmax it automatically exponentiates every element of the matrix and divides by the row sum. That is exactly what we want to do with $A$ and $B$! Each row of $A$ is the probability of the next state to transition to, and each row of $B$ is the probability of the next symbol to emit. The rows must sum to 1, just like the output predictions of a neural network!
In pseudocode, softmax looks like:
```
def softmax(A):
expA = np.exp(A)
return expA / expA.sum(axis=1, keepdims=True)
```
We can see this clearly below:
```
np.set_printoptions(suppress=True)
A = np.array([
[1,2],
[4,5],
[9,5]
])
expA = np.exp(A)
print("A exponentiated element wise: \n", np.round_(expA, decimals=3), "\n")
# Keep dims ensures a column vector (vs. row) output
output = expA / expA.sum(axis=1, keepdims=True)
print("Exponentiated A divided row sum: \n", np.round_(output, decimals=3))
```
Now you may be wondering: Why can't we just perform standard normalization? Why does the exponetial need to be used? For an answer to that I recommend reading up [here](https://stackoverflow.com/questions/17187507/why-use-softmax-as-opposed-to-standard-normalization), [here](https://stats.stackexchange.com/questions/162988/why-sigmoid-function-instead-of-anything-else/318209#318209), and [here](http://cs231n.github.io/linear-classify/#softmax).
### 3.2 Update Discrete HMM Code $\rightarrow$ with Softmax
```
class HMM:
def __init__(self, M):
self.M = M
def fit(self, X, learning_rate=0.001, max_iter=10, V=None, p_cost=1.0, print_period=10):
"""Train HMM model using stochastic gradient descent."""
# Determine V, the vocabulary size
if V is None:
V = max(max(x) for x in X) + 1
N = len(X)
preSoftmaxPi0 = np.zeros(self.M) # initial state distribution
preSoftmaxA0 = np.random.randn(self.M, self.M) # state transition matrix
preSoftmaxB0 = np.random.randn(self.M, V) # output distribution
thx, cost = self.set(preSoftmaxPi0, preSoftmaxA0, preSoftmaxB0)
# This is a beauty of theano and it's computational graph. By defining a cost function,
# which is representing p(x), the probability of a sequence, we can then find the gradient
# of the cost with respect to our parameters (pi, A, B). The gradient updated rules are
# applied as usual. Note, the reason that this is stochastic gradient descent is because
# we are only looking at a single training example at a time.
pi_update = self.preSoftmaxPi - learning_rate * T.grad(cost, self.preSoftmaxPi)
A_update = self.preSoftmaxA - learning_rate * T.grad(cost, self.preSoftmaxA)
B_update = self.preSoftmaxB - learning_rate * T.grad(cost, self.preSoftmaxB)
updates = [
(self.preSoftmaxPi, pi_update),
(self.preSoftmaxA, A_update),
(self.preSoftmaxB, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
plt.figure(figsize=(8,5))
plt.plot(costs, color="blue")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
return self.cost_op(x)
def get_cost_multi(self, X, p_cost=1.0):
P = np.random.random(len(X))
return np.array([self.get_cost(x) for x, p in zip(X, P) if p < p_cost])
def log_likelihood(self, x):
return - self.cost_op(x)
def set(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
# Create theano shared variables
self.preSoftmaxPi = theano.shared(preSoftmaxPi)
self.preSoftmaxA = theano.shared(preSoftmaxA)
self.preSoftmaxB = theano.shared(preSoftmaxB)
pi = T.nnet.softmax(self.preSoftmaxPi).flatten()
# softmax returns 1xD if input is a 1-D array of size D
A = T.nnet.softmax(self.preSoftmaxA)
B = T.nnet.softmax(self.preSoftmaxB)
# Define input, a vector
thx = T.ivector("thx")
def recurrence_to_find_alpha(t, old_alpha, x):
"""Scaled version of updates for HMM. This is used to find the forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time step the initial value,
outputs_info=[pi * B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(A) * B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[pi * B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
return thx, cost
def fit_coin(file_key):
"""Loads data and trains HMM."""
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
# Instantiate object of class HMM with 2 hidden states (heads and tails)
hmm = HMM(2)
hmm.fit(X)
L = hmm.get_cost_multi(X).sum()
print("Log likelihood with fitted params: ", round(L, 3))
# Try the true values
pi = np.array([0.5, 0.5])
A = np.array([
[0.1, 0.9],
[0.8, 0.2]
])
B = np.array([
[0.6, 0.4],
[0.3, 0.7]
])
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == "__main__":
key = "coin_data.txt"
fit_coin(key)
```
## 4. Hidden Markov Models with TensorFlow
I now want to expose everyone to an HMM implementation in TensorFlow. In order to do so, we will need to first go over the `scan` function in Tensorflow. Just like when dealing with Theano, we need to ask "What is the equivalent of a for loop in TensorFlow?". And why should we care?
### 4.1 TensorFlow Scan
In order to understand the importance of `scan`, we need to be sure that we have a good idea of how TensorFlow works, even if only from a high level. In general, with both TensorFlow and Theano, you have to create variables and link them together functionally, but they do not have values until you actually run the functions. So, when you create your $X$ matrix you don't give it a shape; you just say here is a place holder I am going to call $X$ and this is a possible shape for it:
```
X = tf.placeholder(tf.float32, shape=(None, D))
```
However, remember that the `shape` argument is _optional_, and hence for all intents and purposes we can assume that we do not know the shape of $X$. So, what happens if you want to loop through all the elements of $X$? Well you can't, because we do not know the number of elements in $X$!
```
for i in range(X.shape[0]): <------- Not possible! We don't know num elements in X
# ....
```
In order to write a for loop we must specify the number of times the loop will run. But in order to specify the number of times the loop will run we must know the number of elements in $X$. Generally speaking, we cannot guarantee the length of our training sequences. This is why we need the tensorflow `scan` function! It will allow us to loop through a tensorflow array without knowing its size. This is similar to how everything else in Tensorflow and Theano works. Using `scan` we can tell Tensorflow "how to run the for loop", without actually running it.
There is another big reason that the `scan` function is so important; it allows us to perform **automatic differentiation** when we have sequential data. Tensorflow keeps track of how all the variables in your graph link together, so that it can automatically calculate the gradient for you when you do gradient descent:
$$W(t) \leftarrow W(t-1) - \eta \nabla J\big(W(t-1)\big)$$
The `scan` function keeps track of this when it performs the loop. The anatomy of the `scan` function is shown in pseudocode below:
```
outputs = tf.scan(
fn=some_function, # Function applied to every element in sequence
elems=thing_to_loop_over # Actual sequence that is passed in
)
```
Above, `some_function` is applied to every element in `thing_to_loop_over`. Now, the way that we define `some_function` is very specific and much more strict than that for theano. In particular, it must always take in two arguments. The first element is the last output of the function, and the second element is the next element of the sequence:
```
def some_function(last_output, element):
return do_something_to(last_output, element)
```
The tensorflow scan function returns `outputs`, which is all of the return values of `some_function` concatenated together. For example, we can look at the following block:
```
outputs = tf.scan(
fn=some_function,
elems=thing_to_loop_over
)
def square(last, current):
return current * current
# sequence = [1, 2, 3]
# outputs = [1, 4, 9]
```
If we pass in `[1, 2, 3]`, then our outputs will be `[1, 4, 9]`. Now, of course the outputs is still a tensorflow graph node. So, in order to get an actual value out of it we need to run it in an actual session.
```
import tensorflow as tf
x = tf.placeholder(tf.int32, shape=(None,), name="x")
def square(last, current):
"""Last is never used, but must be included based on interface requirements of tf.scan"""
return current*current
# Essentially doing what a for loop would normally do
# It applies the square function to every element of x
square_op = tf.scan(
fn=square,
elems=x
)
# Run it!
with tf.Session() as session:
o_val = session.run(
square_op,
feed_dict={x: [1, 2, 3, 4, 5]}
)
print("Output: ", o_val)
```
Now, of course `scan` can do more complex things than this. We can implement another argument, `initializer`, that allows us to compute recurrence relationships.
```
outputs = tf.scan(
fn=some_function, # Function applied to every element in sequence
elems=thing_to_loop_over, # Actual sequence that is passed in
initializer=initial_input
)
```
Why exactly do we need this? Well, we can see that the recurrence function takes in two things: the last element that it returned, and the current element of the sequence that we are iterating over. What is the last output during the first iteration? There isn't one yet! And that is exactly why we need `initializer`.
One thing to keep in mind when using `initializer` is that it is very strict. In particular, it must be the exact same type as the output of `recurrence`. For example, if you need to return multiple things from `recurrence` it is going to be returned as a tuple. That means that the argument to `initializer` cannot be a list, it must be a tuple. This also means that a tuple containing `(5 , 5)` is not the same a tuple containing `(5.0, 5.0)`.
Let's try to compute the fibonacci sequence to get a feel for how this works:
```
# N is the number fibonacci numbers that we want
N = tf.placeholder(tf.int32, shape=(), name="N")
def fibonacci(last, current):
# last[0] is the last value, last[1] is the second last value
return (last[1], last[0] + last[1])
fib_op = tf.scan(
fn=fibonacci,
elems=tf.range(N),
initializer=(0, 1),
)
with tf.Session() as session:
o_val = session.run(
fib_op,
feed_dict={N: 8}
)
print("Output: \n", o_val)
```
Another example of what we can do with the theano `scan` is create a **low pass filter** (also known as a **moving average**). In this case, our recurrence relation is given by:
$$s(t) = \text{decay_rate} \cdot s(t-1) + (1 - \text{decay_rate}) \cdot x(t)$$
Where $x(t)$ is the input and $s(t)$ is the output. The goal here is to return a clean version of a noisy signal. To do this we can create a sine wave, add some random gaussian noise to it, and finally try to retrieve the sine wave. In code this looks like:
```
original = np.sin(np.linspace(0, 3*np.pi, 300))
X = 2*np.random.randn(300) + original
fig = plt.figure(figsize=(15,5))
plt.subplot(1, 2, 1)
ax = plt.plot(X, c="g", lw=1.5)
plt.title("Original")
# Setup placeholders
decay = tf.placeholder(tf.float32, shape=(), name="decay")
sequence = tf.placeholder(tf.float32, shape=(None, ), name="sequence")
# The recurrence function and loop
def recurrence(last, x):
return (1.0 - decay)*x + decay*last
low_pass_filter = tf.scan(
fn=recurrence,
elems=sequence,
initializer=0.0 # sequence[0] to use first value of the sequence
)
# Run it!
with tf.Session() as session:
Y = session.run(low_pass_filter, feed_dict={sequence: X, decay: 0.97})
plt.subplot(1, 2, 2)
ax2 = plt.plot(original, c="b")
ax = plt.plot(Y, c="r")
plt.title("Low pass filter")
plt.show()
```
### 4.2 Discrete HMM With Tensorflow
Let's now take a moment to walk through the creation of a discrete HMM class utilizing Tensorflow.
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from hmm.utils import get_obj_s3
class HMM:
def __init__(self, M):
self.M = M # number of hidden states
def set_session(self, session):
self.session = session
def fit(self, X, max_iter=10, print_period=1):
# train the HMM model using stochastic gradient descent
N = len(X)
print("Number of train samples:", N)
costs = []
for it in range(max_iter):
for n in range(N):
# this would of course be much faster if we didn't do this on
# every iteration of the loop
c = self.get_cost_multi(X).sum()
costs.append(c)
self.session.run(self.train_op, feed_dict={self.tfx: X[n]})
plt.figure(figsize=(8,5))
plt.plot(costs, c="b")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
# returns log P(x | model)
# using the forward part of the forward-backward algorithm
# print "getting cost for:", x
return self.session.run(self.cost, feed_dict={self.tfx: x})
def log_likelihood(self, x):
return -self.session.run(self.cost, feed_dict={self.tfx: x})
def get_cost_multi(self, X):
return np.array([self.get_cost(x) for x in X])
def build(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
M, V = preSoftmaxB.shape
self.preSoftmaxPi = tf.Variable(preSoftmaxPi)
self.preSoftmaxA = tf.Variable(preSoftmaxA)
self.preSoftmaxB = tf.Variable(preSoftmaxB)
pi = tf.nn.softmax(self.preSoftmaxPi)
A = tf.nn.softmax(self.preSoftmaxA)
B = tf.nn.softmax(self.preSoftmaxB)
# define cost
self.tfx = tf.placeholder(tf.int32, shape=(None,), name='x')
def recurrence(old_a_old_s, x_t):
old_a = tf.reshape(old_a_old_s[0], (1, M))
a = tf.matmul(old_a, A) * B[:, x_t]
a = tf.reshape(a, (M,))
s = tf.reduce_sum(a)
return (a / s), s
# remember, tensorflow scan is going to loop through
# all the values!
# we treat the first value differently than the rest
# so we only want to loop through tfx[1:]
# the first scale being 1 doesn't affect the log-likelihood
# because log(1) = 0
alpha, scale = tf.scan(
fn=recurrence,
elems=self.tfx[1:],
initializer=(pi * B[:, self.tfx[0]], np.float32(1.0)),
)
self.cost = -tf.reduce_sum(tf.log(scale))
self.train_op = tf.train.AdamOptimizer(1e-2).minimize(self.cost)
def init_random(self, V):
preSoftmaxPi0 = np.zeros(self.M).astype(np.float32) # initial state distribution
preSoftmaxA0 = np.random.randn(self.M, self.M).astype(np.float32) # state transition matrix
preSoftmaxB0 = np.random.randn(self.M, V).astype(np.float32) # output distribution
self.build(preSoftmaxPi0, preSoftmaxA0, preSoftmaxB0)
def set(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
op1 = self.preSoftmaxPi.assign(preSoftmaxPi)
op2 = self.preSoftmaxA.assign(preSoftmaxA)
op3 = self.preSoftmaxB.assign(preSoftmaxB)
self.session.run([op1, op2, op3])
def fit_coin(file_key):
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
hmm = HMM(2)
# the entire graph (including optimizer's variables) must be built
# before calling global variables initializer!
hmm.init_random(2)
init = tf.global_variables_initializer()
with tf.Session() as session:
session.run(init)
hmm.set_session(session)
hmm.fit(X, max_iter=5)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with fitted params: ", round(L, 3))
# try true values
# remember these must be in their "pre-softmax" forms
pi = np.log(np.array([0.5, 0.5])).astype(np.float32)
A = np.log(np.array([[0.1, 0.9], [0.8, 0.2]])).astype(np.float32)
B = np.log(np.array([[0.6, 0.4], [0.3, 0.7]])).astype(np.float32)
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == '__main__':
key = "coin_data.txt"
fit_coin(key)
```
| github_jupyter |
```
# use python eval sometimes. great trickdefining a class and operator overloading
import aoc
f = open('input.txt')
lines = [line.rstrip('\n') for line in f]
lines[0]
# part 1
def evaluate(line):
ans = 0
firstop = None
operator = None
wait = 0
for i, ch in enumerate(line):
if wait > 0: # still within parentheses, so ignore because the recursion took care of it
wait -= 1
continue
if ch == '(': # recurse the rest
ch, wait = evaluate(line[i+1:])
if ch == ')':
return firstop, i+1
if isinstance(ch, int):
if not firstop:
firstop = ch
else:
firstop = eval(f'{firstop}{operator}{ch}')
else:
operator = ch
return firstop
ans = 0
for line in lines:
line = line.replace("(","( ").replace(")"," )")
line = aoc.to_int(line.split())
ans+= evaluate(line)
ans
# part 2
def findclosing(line):
count = 0
for index, i in enumerate(line):
if i == "(": count+=1
if i == ')': count -=1
if count == 0: return index
def evaluate(line):
ans = 0
while '(' in line: # get rid of all the parenthesis blocks
first = line.index('(')
last = findclosing(line[first:])+first
line[first:last+1] = [evaluate(line[first+1:last])]
while '+' in line: # reduce the '+' op_indexations
op_index = line.index('+')
line[op_index-1:op_index+2] = [line[op_index-1]+line[op_index+1]]
while '*' in line: # finally, reduce the '*'
op_index = line.index('*')
line[op_index-1:op_index+2] = [line[op_index-1]*line[op_index+1]]
return line[0]
ans = 0
for line in lines:
line = line.replace("(","( ").replace(")"," )")
line = list(aoc.to_int(line.split()))
ans += evaluate(line)
ans
# alternative solution from reddit, amazing idea with operator overloading
import re
class a(int):
def __mul__(self, b):
return a(int(self) + b)
def __add__(self, b):
return a(int(self) + b)
def __sub__(self, b):
return a(int(self) * b)
def ev(expr, pt2=False):
expr = re.sub(r"(\d+)", r"a(\1)", expr)
expr = expr.replace("*", "-")
if pt2:
expr = expr.replace("+", "*")
return eval(expr, {}, {"a": a})
print("Part 1:", sum(ev(l) for l in lines))
print("Part 2:", sum(ev(l, pt2=True) for l in lines))
# another one from sophiebits, have to study the regex a bit
def solve(line):
def doInner(inner):
# part 1:
# while '+' in inner or '*' in inner:
# inner = re.sub('^(\d+)\s*\+\s*(\d+)', lambda m: str(int(m.group(1)) + int(m.group(2))), inner)
# inner = re.sub('^(\d+)\s*\*\s*(\d+)', lambda m: str(int(m.group(1)) * int(m.group(2))), inner)
while '+' in inner:
inner = re.sub('(\d+)\s*\+\s*(\d+)', lambda m: str(int(m.group(1)) + int(m.group(2))), inner)
while '*' in inner:
inner = re.sub('(\d+)\s*\*\s*(\d+)', lambda m: str(int(m.group(1)) * int(m.group(2))), inner)
return inner
while '(' in line:
def doExpr(match):
inner = match.group(1)
return doInner(inner)
line = re.sub(r'\(([^()]+)\)', doExpr, line)
return doInner(line)
total = 0
for line in lines:
total += int(solve(line))
print(total)
```
| github_jupyter |
## Automagically making a table of all protein-protein interactions for two structures
If two structures use the same or essentially the same, you can use Python to make a table of all the pairs of the protein-protein interactions by the two structures that can be used as input for the pipeline described in an earlier notebook in this series, [Using snakemake to highlight changes in multiple protein-protein interactions via PDBsum data](Using%20snakemake%20to%20highlight%20changes%20in%20multiple%20protein-protein%20interactions%20via%20PDBsum%20data.ipynb). This notebook will step through this process.
It is important to note this won't work straight away if the protein chain designations by the same or closely related proteins differ between the two structures. Elements of the process to be used in this notebook could be adapted to do that; however, that would require some progamming knowledge beyond what will be covered here. I assume the number of times this would be needed would be limited and a table could more easily done by hand following along with this notebook as well as [Using snakemake to highlight changes in multiple protein-protein interactions via PDBsum data](Using%20snakemake%20to%20highlight%20changes%20in%20multiple%20protein-protein%20interactions%20via%20PDBsum%20data.ipynb).
The process relies on the fact that PDBsum shares under the 'Prot-prot' tab for every structure, the interacting pairs of proteins chains in an 'Interface summary' on the left side of the browser page. For example, look on the left of http://www.ebi.ac.uk/thornton-srv/databases/cgi-bin/pdbsum/GetPage.pl?pdbcode=6kiv&template=interfaces.html&c=999 . That link is what the PDBsum entry for the PDB idenitifer 6kiv leads to if you click on the 'Prot-prot' tab page from [the main PDBsum page for 6kiv](http://www.ebi.ac.uk/thornton-srv/databases/cgi-bin/pdbsum/GetPage.pl?pdbcode=6kiv&template=main.html). A utility script [pdb_code_to_prot_prot_interactions_via_PDBsum.py](https://github.com/fomightez/structurework/tree/master/pdbsum-utilities) is used to collect the designations listed there for each individual structure involved. Then in this notebook a little Python is used to generate the table file that can be used as described in [Using snakemake to highlight changes in multiple protein-protein interactions via PDBsum data](Using%20snakemake%20to%20highlight%20changes%20in%20multiple%20protein-protein%20interactions%20via%20PDBsum%20data.ipynb).
An example follows. It is meant to be adaptable to use the PDB codes of structures that interest you. You may wish to work through the demonstration first so you know what to expect.
----
The next cell is used to define the structures of interest. The PDB code identifiers are supplied.
```
structure1 = "6kiz"
structure2 = "6kix"
```
The next cell gets the script `pdb_code_to_prot_prot_interactions_via_PDBsum.py` (see [here](https://github.com/fomightez/structurework/tree/master/pdbsum-utilities)) that will get the 'Interface Summary' information for each individual structure. This is the equivalent to the Summary on the left side of the 'Prot-prot' tab.
```
import os
file_needed = "pdb_code_to_prot_prot_interactions_via_PDBsum.py"
if not os.path.isfile(file_needed):
!curl -OL https://raw.githubusercontent.com/fomightez/structurework/master/pdbsum-utilities/{file_needed}
```
Import the main function of that script by running the next cell.
```
from pdb_code_to_prot_prot_interactions_via_PDBsum import pdb_code_to_prot_prot_interactions_via_PDBsum
```
The next cell gets the interaction summary for each structure and to get the pairs need to build the table described at the top of [Using snakemake to highlight changes in multiple protein-protein interactions via PDBsum data](Using%20snakemake%20to%20highlight%20changes%20in%20multiple%20protein-protein%20interactions%20via%20PDBsum%20data.ipynb).
```
structure1_il = pdb_code_to_prot_prot_interactions_via_PDBsum(structure1)
structure2_il = pdb_code_to_prot_prot_interactions_via_PDBsum(structure2)
i_union = set(structure1_il).union(set(structure2_il))
```
In this case the pairs of both are the same; however, the script is written to not fail if there was extra proteins present in the other. Specficially, the interacting pairs of proteins for both are checked because if one had additional chain, by getting the listing of both structures and making the union, the combinations for all would be in the list of pairs `i_union`.
Next the union of all the pairs is used to make a table like constructed at the top of [Using snakemake to highlight changes in multiple protein-protein interactions via PDBsum data](Using%20snakemake%20to%20highlight%20changes%20in%20multiple%20protein-protein%20interactions%20via%20PDBsum%20data.ipynb).
```
s = ""
for pair in list(i_union):
s+= f"{structure1} {pair[0]} {pair[1]} {structure2} {pair[0]} {pair[1]}\n"
%store s >int_matrix.txt
```
The table has now been stored as `int_matrix.txt`. Open the file from the Jupyter dashboard to verify. Or just run the next cell to see the contents of the file.
```
!cat int_matrix.txt
```
That's the table in the file that needed to be made. The rest of the process pickes up with 'Step #3' of [Using snakemake to highlight changes in multiple protein-protein interactions via PDBsum data](Using%20snakemake%20to%20highlight%20changes%20in%20multiple%20protein-protein%20interactions%20via%20PDBsum%20data.ipynb).
To make that clear, this following cell will run the snakemake pipeline. Consult the subsequent steps of [Using snakemake to highlight changes in multiple protein-protein interactions via PDBsum data](Using%20snakemake%20to%20highlight%20changes%20in%20multiple%20protein-protein%20interactions%20via%20PDBsum%20data.ipynb) to see what to do after it completes all the possible pairs.
```
!snakemake --cores 1
```
Now change the structures used to your favorites and re-run the notebook. If the chains are the same in your two structures, you'll generate all the reports for all the interacting pairs of proteins upon doing that.
------
Enjoy!
| github_jupyter |
# Car Decor Sales Forecasting - Perfumes
###### Importing Libraries
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.metrics import mean_squared_error
from math import sqrt
# Connecting Python to MySQL for fetching data
import mysql.connector
import warnings
from statsmodels.tools.sm_exceptions import ConvergenceWarning
warnings.simplefilter('ignore', ConvergenceWarning)
```
###### MySQL Connection to fetch data
```
try:
connection = mysql.connector.connect(host='localhost',
database='car_decors',
user='root',
password='***********')
sql_select_Query = "SELECT * FROM decorsales"
cursor = connection.cursor()
cursor.execute(sql_select_Query)
columns = len(cursor.description)
columns = [i[0] for i in cursor.description]
print(columns)
# get all records
records = cursor.fetchall()
print("Total number of rows in table: ", cursor.rowcount)
except mysql.connector.Error as e:
print("Error reading data from MySQL table", e)
```
### Data Cleaning and Exploratory Data Analysis
###### Converting fetched records to Pandas dataframe
```
records = np.array(records)
records = records[:,0:25]
decor_sales=pd.DataFrame(records,columns=columns)
```
###### Type Casting Date and other features
```
decor_sales.dtypes
decor_sales.Date = pd.to_datetime(decor_sales.Date)
decor_sales.iloc[:,1:] = decor_sales.iloc[:,1:].astype("int32")
decor_sales.dtypes
```
###### Creating Subset of Decor Sales Dataset and resampling Monthly Time Series
```
df = decor_sales
df = df.set_index('Date')
df = df.resample("MS").sum()
```
###### Data Visualization
```
plt.rc("figure", figsize=(16,8))
sns.set_style('darkgrid')
```
###### Rolling statistics to observe variation in mean and standard deviation.
```
timeseries = df ['Perfumes']
timeseries.rolling(12).mean().plot(label='12 Month Rolling Mean', marker='.')
timeseries.rolling(12).std().plot(label='12 Month Rolling Std', marker='.')
timeseries.plot(marker='.')
plt.title('Rolling Statistics to observe variation in Mean and Standard Deviation', fontsize = 18, fontweight = 'bold')
plt.xlabel('Year', fontsize = 14)
plt.ylabel('Sales (Number of Units)', fontsize = 14)
plt.legend()
```
###### Checking Seasonalty and Trend components for the feature
```
from statsmodels.tsa.seasonal import seasonal_decompose
add = seasonal_decompose(df["Perfumes"],model="additive",period=12)
add.plot();
```
##### Checking for Data Stationarity using Augmented Dickey-Fuller Test
```
from statsmodels.tsa.stattools import adfuller
def check_adf(time_series):
test_result = adfuller(df['Perfumes'])
print ('ADF Test:')
labels = ['ADF Statistic','p-value','No. of Lags Used','Number of Observations Used']
for value,label in zip(test_result,labels):
print (label+': '+str(value)+str("\n"))
if test_result [1] <= 0.05:
print ("Reject null hypothesis; Data is stationary")
else:
print ("Fail to reject H0; Data is non-stationary")
```
```
check_adf(df['Perfumes'])
```
# Adfuller test Results for all variables
```
from statsmodels.tsa.stattools import adfuller
def adfuller_parameter(x):
P = []
columns = []
used_lag = []
for i in x.columns:
test_stats,p,used_lags,nobs,critical_value,ic_best = adfuller(x[i])
columns.append(i)
P.append(p)
used_lag.append(used_lags)
return pd.DataFrame({"COLUMNS":columns,"P_VALUE":P,"MAX_USED_LAG":used_lag})
adfuller_parameter(df)
```
##### Hyper-parameter Tuning # Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) plots
```
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import statsmodels.api as sm
fig, ax = plt.subplots(1,2, figsize=(15,5))
sm.graphics.tsa.plot_acf(df["Perfumes"], lags=12, title = 'ACF Plot', ax=ax[0])
sm.graphics.tsa.plot_pacf(df["Perfumes"], lags=12, title = 'PACF Plot',ax=ax[1])
plt.show()
```
### Model Building - SARIMA Model ( Seasonal ARIMA Model )
###### Train Test Split
```
train_df = df["Perfumes"].iloc[0:int(len(df)*.95)] #train model with approx 95% data
test_df = df["Perfumes"].iloc[int(len(train_df)):] #test model with 5% data
print("Train_df : ",len(train_df))
print("Test_df : ",len(test_df))
```
###### User Defined Function to calculate the MAPE value
```
def mape(y_true, y_pred):
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
```
###### Automated Hyperparameter tuning
```
import itertools as i
p = range(0,3)
d = range(0,2)
q = range(0,3)
pdq_combo = list(i.product(p,d,q)) #this will all combination of p,d,q throgh a tuple
error = []
aic_sarima = []
order_arima = []
order_sarima = []
seasonality = 12
for pdq in pdq_combo:
for PDQ in pdq_combo:
try:
SEASONAL_ORDER = list(PDQ)
SEASONAL_ORDER.append(seasonality)
model = sm.tsa.SARIMAX(train_df,order=(pdq),seasonal_order=tuple(SEASONAL_ORDER))
result = model.fit(disp=0)
pred = result.predict(start=len(train_df),end=len(df)-1)
eror = mape(test_df,pred)
aic_sarima.append(result.aic)
order_arima.append(pdq)
order_sarima.append(tuple(SEASONAL_ORDER))
error.append(eror)
except:
continue
# Creating a dataframe of seasonality orders and errors
df_error = pd.DataFrame({"arima_order":order_arima,"sarima_order": order_sarima,"error":error,"aic":aic_sarima})
df_error = df_error.sort_values(by="error",ascending = True)
df_error.reset_index(inplace=True,drop=True)
## best parameter selection
p_d_q = df_error.iloc[0,0] #choosing best parameter for arima order
P_D_Q = df_error.iloc[0,1] #choosing best parameter for seasonal order
## best parameter selection
print("Best p_d_q parameter : ", p_d_q)
print("Best P_D_Q parameter : ", P_D_Q)
```
###### Model with best parameter
```
sarima_model = sm.tsa.SARIMAX(train_df, order=(p_d_q), seasonal_order=(P_D_Q))
sarima_results = sarima_model.fit(disp = 0)
sarima_pred = sarima_results.predict(start=test_df.index[0],end=test_df.index[-1])
sarima_pred_large = sarima_results.predict(start=75,end=86,dynamic=True)
print(sarima_results.summary())
sarima_diagnostics = sarima_results.plot_diagnostics(figsize=(16,8))
```
```
# Predicted values
# Point estimation
sarima_prediction = sarima_results.get_prediction(start = test_df.index[0], end = test_df.index[-1], dynamic = True, full_results = True)
sarima_point_estimation = sarima_prediction.predicted_mean
sarima_point_estimation
#Checking MAPE
mape(test_df, sarima_point_estimation)
# At 95% confidence interval
sarima_pred_range = sarima_prediction.conf_int(alpha = 0.05)
sarima_pred_range
# Ploting Sarima Prediction
plt.plot(train_df,color="g",label="Train Data", marker='.')
plt.plot(test_df,color="b",label="Test Data", marker='.')
plt.plot(sarima_point_estimation,color="r",label="Forecast (Test Data)", marker='.')
plt.figtext(0.13, 0.15, '\nMAPE : {} \nSARIMA : {},{} \nAIC : {}'.format(mape(test_df, sarima_point_estimation), p_d_q, P_D_Q, sarima_results.aic, fontsize = 11))
plt.fill_between(sarima_pred_range.index,sarima_pred_range.iloc[:,0],sarima_pred_range.iloc[:,1],color='b',alpha=.2)
plt.legend(loc="upper right")
```
### Holt Winters Exponential Smoothing with Additive Seasonality and Additive Trend
```
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.holtwinters import ExponentialSmoothing #
hwe_model_add_add = ExponentialSmoothing(train_df, seasonal ="add", trend = "add", seasonal_periods = 12).fit()
pred_hwe_add_add = hwe_model_add_add.predict(start = test_df.index[0], end = test_df.index[-1])
pred_hwe_add_add
```
###### Plotting Holt Winters Model
```
plt.plot(train_df,color="g",label="Train Data")
plt.plot(test_df,color="b",label="Test Data")
plt.plot(pred_hwe_add_add,color="r",label="Forecast (Test Data)")
plt.suptitle('Model : Holt Winters', fontsize = 12, fontweight = 'bold')
plt.title('Car Decors - ANDROID HEAD UNITS', fontsize = 18, fontweight = 'bold')
plt.figtext(0.13, 0.14, '\nMAPE : {} \nAIC : {}'.format(mape(test_df, pred_hwe_add_add), hwe_model_add_add.aic))
plt.xlabel('Year', fontsize = 14)
plt.ylabel('Sales (Number of Units)', fontsize = 14)
plt.legend(loc="best")
mape(test_df, pred_hwe_add_add)
```
### FB Prophet Model
```
# Loading Libraries
from fbprophet import Prophet
from fbprophet.plot import plot_plotly
df1 = decor_sales
df1 = df1.set_index('Date')
df1 = df1.resample("MS").sum()
df1.reset_index(inplace=True)
train_df1 = df1[["Date","Perfumes"]].iloc[0:int(len(df1)*.95)] #train model with approx 95% data
test_df1 = df1[["Date","Perfumes"]].iloc[int(len(train_df1)):] #test model with 5% data
print("Train : ",len(train_df1))
print("Test : ",len(test_df1))
train_df1.columns = ["ds","y"]
test_df1.columns = ["ds","y"]
# Fitting the Model
prophet_model = Prophet().fit(train_df1)
# Define the period for which we want a prediction
future = list()
for i in range(1, 5):
date = '2021-%02d' % i
future.append([date])
future = pd.DataFrame(future)
future.columns = ['ds']
future['ds']= pd.to_datetime(future['ds'])
future
forecast = prophet_model.predict(future)
print(forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']])
test_df1=test_df1.set_index("ds")
train_df1 = train_df1.set_index("ds")
forecast=forecast.set_index("ds")
plt.style.use("ggplot")
plt.plot(train_df1['y'],color="r",label="Train Data")
plt.plot(test_df1['y'],color="b",label="Test Data")
plt.plot(forecast["yhat"],color="g",label="Forecast (Test Data)")
plt.grid( linestyle='-', linewidth=2)
plt.legend(loc="best")
# MAPE
mape(test_df1['y'], forecast['yhat'])
#RMSE
sqrt(mean_squared_error(test_df1['y'], forecast['yhat'].tail(4)))
```
### Auto Time Series Model
```
from auto_ts import auto_timeseries
train_df2 = train_df1
test_df2 = test_df1
ts_model = auto_timeseries( score_type='rmse', time_interval='MS', non_seasonal_pdq=(12,12,12), seasonality=True, seasonal_period=12, model_type="best", verbose=2)
ts_model.fit(traindata= train_df2, ts_column="ds", target="y")
ts_model.get_leaderboard()
ts_model.plot_cv_scores()
future_predictions = ts_model.predict(test_df2, model='best')
future_predictions
# define the period for which we want a prediction
ts_future = list()
for i in range(1, 5):
date = '2021-%02d' % i
ts_future.append([date])
ts_future = pd.DataFrame(ts_future)
ts_future.columns = ['ds']
ts_future['ds']= pd.to_datetime(ts_future['ds'])
ts_model.predict(ts_future)
mape(test_df2["y"],future_predictions["yhat"])
```
### Models Evaluation
```
from sklearn.metrics import mean_squared_error as mse
print("\nSARIMA Trend : ", p_d_q)
print("SARIMA Seasonal Order : ", P_D_Q)
print("SARIMA AIC : ", sarima_results.aic)
print("SARIMA RMSE : ", np.sqrt(mse(test_df,sarima_point_estimation)))
print("SARIMA MAPE : ", mape(test_df, sarima_point_estimation))
print("\nHolt Winters AIC : ", hwe_model_add_add.aic)
print("Holt Winters RMSE : ", np.sqrt(mse(test_df,pred_hwe_add_add)))
print("Holt Winters MAPE : ", mape(test_df, pred_hwe_add_add))
print("\nFB Prophet RMSE : ", sqrt(mean_squared_error(test_df1['y'], forecast['yhat'])))
print("FB Prophet MAPE : ", mape(test_df1['y'], forecast['yhat']))
print("\nAuto Time Series: \n ", ts_model.get_leaderboard())
print("Auto Time Series MAPE : ", mape(test_df2["y"],future_predictions["yhat"]))
sarima = mape(test_df, sarima_point_estimation)
hwinters = mape(test_df, pred_hwe_add_add)
fbprophet = mape(test_df1['y'], forecast['yhat'])
autots = mape(test_df2["y"],future_predictions["yhat"])
mape_data = {'models':['SARIMA','HOLTWINTERS','FB_PROPHET','AUTO_TS'], 'name':['sarima_model', 'hwe_model_add_add','prophet_model','ts_model'],'mape':[sarima, hwinters, fbprophet, autots]}
mape_error = pd.DataFrame(mape_data)
mape_error = mape_error.sort_values(by="mape",ascending = True)
mape_error.reset_index(inplace=True,drop=True)
#best_model = mape_error.iloc[0,0]
print('\033[1m'+"Best Model with lowest MAPE : ", mape_error.iloc[0,0] + " ( " + mape_error.iloc[0,1] + " ) " + '\033[0m')
print("\nMAPE ERRORS :\n\n", mape_error)
```
##### Saving Model
```
import pickle
filename = 'sarima_model_perfumes.pkl'
pickle.dump(sarima_model, open(filename, 'wb'))
```
###### Testing saved Model for prediction
```
####### Model summary and diagnstics plot #######
with open(filename, "rb") as file:
load_model = pickle.load(file)
result = load_model.fit()
#print(result.summary())
#diagnostics = result.plot_diagnostics(figsize=(16,8))
pred = result.get_prediction(start = 76, end = 87, dynamic = False)
# Point estimation
prediction = pred.predicted_mean
prediction = round(prediction)
prediction
# Ploting final Sarima Prediction
plt.plot(df['Perfumes'],color="g",label="Actual", marker='.')
plt.plot(prediction,color="r",label="Forecast", marker='.')
plt.suptitle('Model : SARIMA', fontsize = 12, fontweight = 'bold')
plt.title('Car Decors - Perfumes', fontsize = 18, fontweight = 'bold')
plt.figtext(0.13, 0.14, '\nMAPE : {} \nAIC : {}'.format(mape(test_df, sarima_point_estimation), sarima_results.aic))
plt.xlabel('Year', fontsize = 14)
plt.ylabel('Sales (Number of Units)', fontsize = 14)
plt.legend(loc="best")
```
### Closing connection to MySQL and clearing variables from memory.
```
#if connection.is_connected():
# connection.close()
# cursor.close()
# print("MySQL connection is closed")
# Clear all variables from memory
#globals().clear()
#####################################################################
```
| github_jupyter |
```
import os
from IPython.core.display import Image, display
```
## Deliverables
### Tony
* Clustering -- learn about clustering. Make a LaTeX (or Markdown) file explaining what K-means, K-medeods, Spectral, Louvain do. Explain basics of implementation, and include a pro/con table discussing what each does well/poorly with examples for each. Include basic algorithms.
* Write pseudocode for clustering graphs [see Ryan's Git Issue on LaTeX]
* https://neurodatadesign.github.io/seelviz/Jupyter/ClusteringTechniques.html
Reach Goal:
* Jupyter notebook with clustering on our data [here](https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/Jupyter/Example%20Clustering%20on%20Fear199.ipynb).
* As per Jovo's recommendation, I first ran example data to make sure I understood the basic premises of what I was doing (used sample data set Images from SciKit, for handwriting)
* Then attempted to do clustering on Fear199 to implement K-means

* 3D representation makes it hard to show the clusters (orange) even when I biggify the points. Since there are an overwhelming number of regular points, I plotted along just XY to confirm my results.


### Jon
* Turn API into pipeline form: Running should output wanted graphs
* https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/Jupyter/ClarityViz%20Pipeline.ipynb
### Albert
* Kwame pipeline tutorials - deliverable is Jupyter Notebook running his tutorial
* https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/Kwame%20Registration%20Notebook%201.ipynb
* https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/Kwame%20Registration%20Notebook%202.ipynb
* Get the atlas aligned data from Kwame
* https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/croppedbrain.jpg
* Acquire new data and see if we still have problems with it.
* https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/newBrain.png
* Using the atlas aligned images, play around with atlas coordinates
* PROBLEMS: We still have problems, largely we need the new data to be propagated in order for us to play around with it. We have Kwame's images however one of the images seem to be "damaged"
* https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/novisionbrain.png
* https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/damagedbrain.png
Reach Goal:
* Run Kwame Pipeline on new data
* Incomplete, as the other file was not propagated thus I was unable to run it through Kwame's pipeline
* https://github.com/NeuroDataDesign/seelviz/blob/gh-pages/AileyRegistration.ipynb
### Luke
* Go back and make weighted versions of our graphs (decide on a weight function [e^(-distance), for instance])
* Make graphs similar to Greg's
* https://neurodatadesign.github.io/seelviz/Jupyter/CombinedPlotsandGraphStatistics.html
| github_jupyter |
<h1 align="center"> Battle of the Neighbourhoods - Toronto </h1>
Author: Ganesh Chunne
This notebook contains Questions 1, 2 & 3 of the Assignment. They have been segregated by Section headers
```
import pandas as pd
```
# Question 1
## Importing Data
```
import requests
url = "https://en.wikipedia.org/wiki/List_of_postal_codes_of_Canada:_M"
wiki_url = requests.get(url)
wiki_url
```
Response 200 means that we are able to make the connection to the page
```
wiki_data = pd.read_html(wiki_url.text)
wiki_data
len(wiki_data), type(wiki_data)
```
We need the first table alone, so dropping the other tables
```
wiki_data = wiki_data[0]
wiki_data
```
Dropping Borough which are not assigned
```
df = wiki_data[wiki_data["Borough"] != "Not assigned"]
df
```
Grouping the records based on Postal Code
```
df = df.groupby(['Postal Code']).head()
df
```
Checking for number of records where Neighbourhood is "Not assigned"
```
df.Neighbourhood.str.count("Not assigned").sum()
df = df.reset_index()
df
df.drop(['index'], axis = 'columns', inplace = True)
df
df.shape
```
Answer to Question 1: We have 103 rows and 3 columns
# Question 2
Installing geocoder
```
pip install geocoder
import geocoder # import geocoder
```
Tried the below approach, ran for 20 mins, then killed it. Changing the code cell to Text for now so that the run all execution doesn't stop.
```python
# initialize your variable to None
lat_lng_coords = None
postal_code = 'M3A'
# loop until you get the coordinates
while(lat_lng_coords is None):
g = geocoder.google('{}, Toronto, Ontario'.format(postal_code))
lat_lng_coords = g.latlng
latitude = lat_lng_coords[0]
longitude = lat_lng_coords[1]
```
Alternatively, as suggested in the assignment, Importing the CSV file from the URL
```
data = pd.read_csv("https://cocl.us/Geospatial_data")
data
print("The shape of our wiki data is: ", df.shape)
print("the shape of our csv data is: ", data.shape)
```
Since the dimensions are the same, we can try to join on the postal codes to get the required data.
Checking the column types of both the dataframes, especially Postal Code column since we are trying to join on it
```
df.dtypes
data.dtypes
combined_data = df.join(data.set_index('Postal Code'), on='Postal Code', how='inner')
combined_data
combined_data.shape
```
**Solution:** We get 103 rows as expected when we do a inner join, so we have good data.
# Question 3
Drawing inspiration from the previous lab where we cluster the neighbourhood of NYC, We cluster Toronto based on the similarities of the venues categories using Kmeans clustering and Foursquare API.
```
from geopy.geocoders import Nominatim
address = 'Toronto, Ontario'
geolocator = Nominatim(user_agent="toronto_explorer")
location = geolocator.geocode(address)
latitude = location.latitude
longitude = location.longitude
print('The coordinates of Toronto are {}, {}.'.format(latitude, longitude))
```
Let's visualize the map of Toronto
```
import folium
# Creating the map of Toronto
map_Toronto = folium.Map(location=[latitude, longitude], zoom_start=11)
# adding markers to map
for latitude, longitude, borough, neighbourhood in zip(combined_data['Latitude'], combined_data['Longitude'], combined_data['Borough'], combined_data['Neighbourhood']):
label = '{}, {}'.format(neighbourhood, borough)
label = folium.Popup(label, parse_html=True)
folium.CircleMarker(
[latitude, longitude],
radius=5,
popup=label,
color='red',
fill=True
).add_to(map_Toronto)
map_Toronto
```
Initializing Foursquare API credentials
```
CLIENT_ID = '2GQBW5PR0QFXTOGCHKTRFWJBTGOFOHXW1TRTNRAFURQ5FE1X'
CLIENT_SECRET = '3QH40WMZIIDSQN1RFAVAEQHUIMOQUJPKYPABQVNTSDQJN2YD'
VERSION = 20202808
radius = 500
LIMIT = 100
print('Your credentails:')
print('CLIENT_ID: ' + CLIENT_ID)
print('CLIENT_SECRET:' + CLIENT_SECRET)
```
Next, we create a function to get all the venue categories in Toronto
```
def getNearbyVenues(names, latitudes, longitudes):
venues_list=[]
for name, lat, lng in zip(names, latitudes, longitudes):
print(name)
# create the API request URL
url = 'https://api.foursquare.com/v2/venues/explore?&client_id={}&client_secret={}&v={}&ll={},{}&radius={}'.format(
CLIENT_ID,
CLIENT_SECRET,
VERSION,
lat,
lng,
radius
)
# make the GET request
results = requests.get(url).json()["response"]['groups'][0]['items']
# return only relevant information for each nearby venue
venues_list.append([(
name,
lat,
lng,
v['venue']['name'],
v['venue']['categories'][0]['name']) for v in results])
nearby_venues = pd.DataFrame([item for venue_list in venues_list for item in venue_list])
nearby_venues.columns = ['Neighbourhood',
'Neighbourhood Latitude',
'Neighbourhood Longitude',
'Venue',
'Venue Category']
return(nearby_venues)
```
Collecting the venues in Toronto for each Neighbourhood
```
venues_in_toronto = getNearbyVenues(combined_data['Neighbourhood'], combined_data['Latitude'], combined_data['Longitude'])
venues_in_toronto.shape
```
So we have 1317 records and 5 columns. Checking sample data
```
venues_in_toronto.head()
```
Checking the Venues based on Neighbourhood
```
venues_in_toronto.groupby('Neighbourhood').head()
```
So there are 405 records for each neighbourhood.
Checking for the maximum venue categories
```
venues_in_toronto.groupby('Venue Category').max()
```
There are around 232 different types of Venue Categories. Interesting!
## One Hot encoding the venue Categories
```
toronto_venue_cat = pd.get_dummies(venues_in_toronto[['Venue Category']], prefix="", prefix_sep="")
toronto_venue_cat
```
Adding the neighbourhood to the encoded dataframe
```
toronto_venue_cat['Neighbourhood'] = venues_in_toronto['Neighbourhood']
# moving neighborhood column to the first column
fixed_columns = [toronto_venue_cat.columns[-1]] + list(toronto_venue_cat.columns[:-1])
toronto_venue_cat = toronto_venue_cat[fixed_columns]
toronto_venue_cat.head()
```
We will group the Neighbourhoods, calculate the mean venue categories in each Neighbourhood
```
toronto_grouped = toronto_venue_cat.groupby('Neighbourhood').mean().reset_index()
toronto_grouped.head()
```
Let's make a function to get the top most common venue categories
```
def return_most_common_venues(row, num_top_venues):
row_categories = row.iloc[1:]
row_categories_sorted = row_categories.sort_values(ascending=False)
return row_categories_sorted.index.values[0:num_top_venues]
import numpy as np
```
There are way too many venue categories, we can take the top 10 to cluster the neighbourhoods
```
num_top_venues = 10
indicators = ['st', 'nd', 'rd']
# create columns according to number of top venues
columns = ['Neighbourhood']
for ind in np.arange(num_top_venues):
try:
columns.append('{}{} Most Common Venue'.format(ind+1, indicators[ind]))
except:
columns.append('{}th Most Common Venue'.format(ind+1))
# create a new dataframe
neighborhoods_venues_sorted = pd.DataFrame(columns=columns)
neighborhoods_venues_sorted['Neighbourhood'] = toronto_grouped['Neighbourhood']
for ind in np.arange(toronto_grouped.shape[0]):
neighborhoods_venues_sorted.iloc[ind, 1:] = return_most_common_venues(toronto_grouped.iloc[ind, :], num_top_venues)
neighborhoods_venues_sorted.head()
```
Let's make the model to cluster our Neighbourhoods
```
# import k-means from clustering stage
from sklearn.cluster import KMeans
# set number of clusters
k_num_clusters = 5
toronto_grouped_clustering = toronto_grouped.drop('Neighbourhood', 1)
# run k-means clustering
kmeans = KMeans(n_clusters=k_num_clusters, random_state=0).fit(toronto_grouped_clustering)
kmeans
```
Checking the labelling of our model
```
kmeans.labels_[0:100]
```
Let's add the clustering Label column to the top 10 common venue categories
```
neighborhoods_venues_sorted.insert(0, 'Cluster Labels', kmeans.labels_)
```
Join toronto_grouped with combined_data on neighbourhood to add latitude & longitude for each neighborhood to prepare it for plotting
```
toronto_merged = combined_data
toronto_merged = toronto_merged.join(neighborhoods_venues_sorted.set_index('Neighbourhood'), on='Neighbourhood')
toronto_merged.head()
```
Drop all the NaN values to prevent data skew
```
toronto_merged_nonan = toronto_merged.dropna(subset=['Cluster Labels'])
```
Plotting the clusters on the map
```
import matplotlib.cm as cm
import matplotlib.colors as colors
map_clusters = folium.Map(location=[latitude, longitude], zoom_start=11)
# set color scheme for the clusters
x = np.arange(k_num_clusters)
ys = [i + x + (i*x)**2 for i in range(k_num_clusters)]
colors_array = cm.rainbow(np.linspace(0, 1, len(ys)))
rainbow = [colors.rgb2hex(i) for i in colors_array]
# add markers to the map
markers_colors = []
for lat, lon, poi, cluster in zip(toronto_merged_nonan['Latitude'], toronto_merged_nonan['Longitude'], toronto_merged_nonan['Neighbourhood'], toronto_merged_nonan['Cluster Labels']):
label = folium.Popup('Cluster ' + str(int(cluster) +1) + '\n' + str(poi) , parse_html=True)
folium.CircleMarker(
[lat, lon],
radius=5,
popup=label,
color=rainbow[int(cluster-1)],
fill=True,
fill_color=rainbow[int(cluster-1)]
).add_to(map_clusters)
map_clusters
```
Let's verify each of our clusters
Cluster 1
```
toronto_merged_nonan.loc[toronto_merged_nonan['Cluster Labels'] == 0, toronto_merged_nonan.columns[[1] + list(range(5, toronto_merged_nonan.shape[1]))]]
```
Cluster 2
```
toronto_merged_nonan.loc[toronto_merged_nonan['Cluster Labels'] == 1, toronto_merged_nonan.columns[[1] + list(range(5, toronto_merged_nonan.shape[1]))]]
```
Cluster 3
```
toronto_merged_nonan.loc[toronto_merged_nonan['Cluster Labels'] == 2, toronto_merged_nonan.columns[[1] + list(range(5, toronto_merged_nonan.shape[1]))]]
```
Cluster 4
```
toronto_merged_nonan.loc[toronto_merged_nonan['Cluster Labels'] == 3, toronto_merged_nonan.columns[[1] + list(range(5, toronto_merged_nonan.shape[1]))]]
```
Cluster 5
```
toronto_merged_nonan.loc[toronto_merged_nonan['Cluster Labels'] == 4, toronto_merged_nonan.columns[[1] + list(range(5, toronto_merged_nonan.shape[1]))]]
```
We have successfully cluster Toronto neighbourhood based on venue categories!
| github_jupyter |
Time Series
- collecting dxata at regular intervales
**ADDITIVE MODEL**
- represent a TS as a combinatino fo patterns at diffferent scales.
- Decompose pieces
## QUANDL FINANCIAL LIBRARY
- https://www.quandl.com/tools/python
- https://github.com/quandl/quandl-python
```
#!pip install quandl
import quandl
import pandas as pd
# quandl.ApiConfig.api_key = 'getyourownkey!'
tesla = quandl.get('WIKI/TSLA')
gm = quandl.get('WIKI/GM')
gm.head()
tesla_copy = tesla.copy()
gm_copy = gm.copy()
```
## EDA
```
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.plot(gm.index, gm['Adj. Close'])
plt.title('GM Stock Prices')
plt.ylabel('Price USD')
plt.show()
plt.plot(tesla.index, tesla['Adj. Close'], 'r')
plt.title('Tesla Stock Price')
plt.ylabel('Price USD')
plt.show()
# Yearly average number of shares outstanding for Tesla and GM
tesla_shares = {2018: 168e6, 2017: 162e6, 2016: 144e6, 2015: 128e6, 2014: 125e6, 2013: 119e6, 2012: 107e6, 2011: 100e6, 2010: 51e6}
gm_shares = {2018: 1.42e9, 2017: 1.50e9, 2016: 1.54e9, 2015: 1.59e9, 2014: 1.61e9, 2013: 1.39e9, 2012: 1.57e9, 2011: 1.54e9, 2010:1.50e9}
# create a year column
tesla['Year'] = tesla.index.year
# Move dates from index to column
tesla.reset_index(level=0, inplace = True)
tesla['cap'] = 0
# calculate market cap
for i, year in enumerate(tesla['Year']):
shares = tesla_shares.get(year)
tesla.ix[i, 'cap'] = shares * tesla.ix[i, 'Adj. Close']
# create a year column
gm['Year'] = gm.index.year
# Move dates from index to column
gm.reset_index(level=0, inplace = True)
gm['cap'] = 0
# calculate market cap
for i, year in enumerate(gm['Year']):
shares = gm_shares.get(year)
gm.ix[i, 'cap'] = shares * gm.ix[i, 'Adj. Close']
# Merge Datasets
cars = gm.merge(tesla, how = 'inner', on = 'Date')
cars.rename(columns = {'cap_x': 'gm_cap', 'cap_y': 'tesla_cap'}, inplace=True)
cars = cars.loc[:, ['Date', 'gm_cap', 'tesla_cap']]
cars['gm_cap'] = cars['gm_cap'] / 1e9
cars['tesla_cap'] = cars['tesla_cap'] / 1e9
cars.head()
plt.figure(figsize=(10,8))
plt.plot(cars['Date'], cars['gm_cap'], 'b-', label = 'GM')
plt.plot(cars['Date'], cars['tesla_cap'], 'r-', label = 'TESLA')
plt.title('Market Cap of GM and Tesla')
plt.legend()
plt.show()
plt.show()
import numpy as np
#find first and last time Tesla was valued higher than GM
first_date = cars.loc[(np.min(list(np.where(cars['tesla_cap'] > cars['gm_cap'])[0]))), 'Date']
last_date = cars.loc[(np.max(list(np.where(cars['tesla_cap'] > cars['gm_cap'])[0]))), 'Date']
print("Tesla was valued higher than GM from {} to {}.".format(first_date.date(), last_date.date()))
```
| github_jupyter |
# Code Transfer Test
The code transfer test is designed to test your coding skills that is learnt during the lecture training. The allotted time for the subsequent problem set is approximately 30 minutes. You are allowed to refer to Jupyter notebook throughout the test. Good luck!
Jupyter notebook resource:
Timer extension! Heeryung
```
# First, let's import the pandas and numpy libraries
import pandas as pd
import numpy as np
# In addition, I want to show some plots, so we'll import matplotlib as well
import matplotlib.pyplot as plt
# Finally, we'll bring in the scipy stats libraries
from scipy import stats
# Hide
import pandas.util.testing as pdt
# %install_ext https://raw.githubusercontent.com/minrk/ipython_extensions/master/extensions/writeandexecute.py
# pdt.assert_series_equal(s1, s2)
# pdt.assert_frame_equal(f1, f2)
# pdt.assert_index_equal(i1, i2)
```
# Transfer Test Question
What's the probability that a NFL player makes a field goal? In this problem we are interested in predicting the probability of NFL players to make a field goal. After assuming that the probability of NFL players to make a field goal follows a beta distribution, we observe the field goals data during multiple NFL matches in 2019.
Let us describe the model specification. The prior distribution of the probability p follows beta distribution, with shape parameters alpha and beta. The likelihood, however, follows binomial distribution since we know explicitly about the number of successful and unsuccessful field goals.
$$ Y \sim Bin(n, p)$$
$$ p \sim Beta(\alpha, \beta)$$
where $\alpha$ and $\beta$ are the hyperparameters of p.
## Question 1: Import Data
Let us compile the read_csv function to read the NFL data file into a pandas DataFrame. Then, look at the first 5 lines. The file name of the CSV file is nfl.csv.
```
# Answer
file = 'nfl.csv'
def read_csv(file):
"""Read the nfl.csv data and return the first few lines of
the csv file.
"""
### BEGIN SOLUTION
data = pd.read_csv(file)
# And let's look at the first few lines
return data.head()
### END SOLUTION
read_csv(file)
# Basic Test Case
"""Check that read_csv function returns the correct dataframe output and format."""
df1 = read_csv(file)
df2 = pd.read_csv(file).head()
pdt.assert_frame_equal(df1, df2)
# Data Type Test Case
assert isinstance(read_csv(file), pd.core.frame.DataFrame)
# Advanced Test Case
```
## Question 2: Column Mean
Let us define the column_mean function which takes the csv file and the column name as inputs, and returns the mean probability of making field goals. (Look at the FG column)
```
# Sample Answer
column = 'FG'
def column_mean(file, column):
"""Take the nfl.csv file and a specific column as input.
Compute the mean value for a column in pandas dataframe.
"""
### BEGIN SOLUTION
data = pd.read_csv(file)
return data[column].mean()
### END SOLUTION
column_mean(file, column)
# Basic Test Case
"""Test whether the data type and value of column mean are correctly returned."""
assert column_mean(file, column) == pd.read_csv(file)[column].mean()
assert 0.836319 <= column_mean(file, column) <= 0.836321
# Advanced Test Cases
assert isinstance(column_mean(file, column), (np.float64, float))
```
## Question 3: Specify Prior and Likelihood
Let us specify the prior and likelihood. We are going to split two code chunks to perform the following steps:
In the first code chunk, we initialize a random number generator as 123 to make the random numbers predictable. Then, we assign the hyperparameters of prior. In this question we use beta distribution as the prior. Beta distribution has two shape parameters, which is alpha and beta. We set the parameter names as alpha and beta, and assign values 40 and 20, respectively. Finally, we set the sample size as 100, using the parameter name size.
In the second code chunk, we set up a variable observed, which is the observed outcome variable. We define a function called likelihood which takes a csv file, a column in the dataset and the sample size as inputs, and return the observed outcome variable, which the product of size and the mean field goal probability. (You can take the result from question 2).
```
# Sample answer
### BEGIN SOLUTION
# We initialize random number generator seed for reproducible results
np.random.seed(123)
# We assign the hyperparameters of prior
# We assign the shape parameters alpha and beta as 40 and 20.
alpha, beta = 40, 20
# Then we make up the sample size as 100
size = 100
### END SOLUTION
# Basic Test Case
from nose.tools import assert_equal
assert_equal(alpha, 40)
assert_equal(beta, 20)
assert_equal(size, 100)
# Finally, we set up Y the observed outcome variable as the product of size and mean field goal probability
def likelihood(file, column, size):
"""Compute the product of the column mean of field goal probability among NFL players and
sample size.
"""
### BEGIN SOLUTION
observed = column_mean(file, column) * size
return observed
### END SOLUTION
observed = likelihood(file, column, size)
# Basic Test Case
assert_equal(likelihood(file, column, size), column_mean(file, column) * size)
# Advanced Test Case
assert 83 <= likelihood(file, column, size) <= 84
assert isinstance(likelihood(file, column, size), (np.float64, float))
```
## Optional Question
You can run the following code to generate a plot for the beta distribution based on the alpha and beta parameters you defined above. Here the scipy.stats.beta function and matplotlib package are used to generate the probability density function plot.
```
# We define the linestyle and set up a linear space to clearly plot the beta distribution
x = np.linspace(0,1,1002)[1:-1]
# Then, we use scipy.stats.beta function to set up beta distribution
dist = stats.beta(alpha, beta)
# Now we want to define a plot_beta_pdf function to generate a figure
# showing the probability density function of the beta distribution
def plot_beta_pdf(x,dist):
# Note that we want the figure to be 8 inches height and 8 inches width
plt.figure(figsize=(8,8))
# We read the linear space and the beta pdf into the plot, and we want to generate a
# continuous and black curve. We also want to show a legend at the top-right corner with
# the alpha and beta value
plt.plot(x, dist.pdf(x), ls = '-', c = 'black',
label = r'$\alpha = %.1f,\ \beta=%.1f$' % (alpha, beta))
plt.legend(loc = 0)
# Finally, we set up the value ranges and labels for x-axis and y-axis and show the plot
plt.xlim(0,1)
plt.ylim(0,10)
plt.xlabel('$x$')
plt.ylabel(r'$p(x|\alpha, \beta)$')
plt.title('Beta Distribution')
plt.show()
plot_beta_pdf(x,dist)
```
You will see that the beta distribution curve surprisingly resembles the case when we conduct binomial trials with roughly 40 successes and 20 failures.
In fact, we can think of $\alpha - 1$ as the number of successes and $\beta - 1$ as the number of failures. You can choose the $\alpha$ and $\beta$ parameters however you think they should look like. If you want the probability of success to become very high, let us say 95 percent, set 95 for $\alpha$ and 5 for $\beta$. If you think otherwise, let us say 5 percent, set 95 for $\beta$ and 5 for $\alpha$.
```
import pymc3 as pm
# Hide
import unittest
```
## Question 4: Train MCMC sampler
Let us train the Markov Chain Monte Carlo sampler. In this example, we use the default NUTS algorithm to sample the posterior distribution. We need to perform the following steps:
First we set a variable called niter, the number of draw, to 1000.
Second, we instantiate the model object.
Third, we specify the beta distribution as the prior for the probability of making a field goal, using the variable name p. Please remember to use the alpha and beta value specified from question 3. Note that the function for assigning beta distribution is pm.Beta().
We also specify the observed likelihood as binomial distribution, using the variable name y. The parameters taken are sample size (n), probability (p) and observed data (observed). Note that the function for binomial distribution is pm.Binomial().
Finally, we start the sampler to take 1000 draws (from niter variable) and take 3 chains. We also provide a seed to the random_seed generator to make the results reproducible. The results should be returned as a trace object.
```
# Sample answer
seed = 1000
def sampler(alpha, beta, size, observed, seed):
"""Train a MCMC sampler to generate posterior samples for the
field goal probability.
"""
### BEGIN SOLUTION
niter = 1000
model = pm.Model()
with model:
p = pm.Beta('p', alpha=alpha, beta=beta)
# Specify the likelihood function (sampling distribution)
y = pm.Binomial('y', n=size, p=p, observed=observed)
trace = pm.sample(niter, chains = 3, random_seed = seed)
return trace
### END SOLUTION
trace = sampler(alpha, beta, size, observed, seed)
trace
# Test Cases
"""Check the correctness of parameters assigned to the PyMC3 model."""
#assert_equal(seed, 1000)
assert isinstance(trace, (pm.backends.base.MultiTrace))
assert_equal(trace.varnames, ['p_logodds__', 'p'])
assert_equal(len(trace['p']), 3000)
#
#
```
## Posterior Diagnostics
## Question 5
Now we look at the posterior diagnostics. Recall we will plot a traceplot to visualize the posterior distribution of parameters of interest. In addition, we also obtain Gelman-Rubin statistics to check whether the parameter of interest converges.
a) Define a function named traceplot which takes the trace object as input and returns a traceplot for the variable p, the probability of making a field goal.
```
# Answer 5a
# Plot results Traceplot
def traceplot(trace):
"""Generate the posterior density plot and trajectory plot for the field goal probability."""
# BEGIN SOLUTION
return pm.traceplot(trace, varnames = ['p'])
# END SOLUTION
traceplot(trace)
plt.show()
# Test cases
"""Check the length data type and shape of the traceplot object for sanity purpose.
To make sure the number of plots generated are correct."""
assert_equal(len(traceplot(trace)), 1)
assert isinstance(traceplot(trace), np.ndarray)
assert_equal(traceplot(trace).shape, (1,2))
```
b) (Optional) What trends do you see in the posterior distribution of the probability of making a field goal?
c) Define a function named posterior_summary which takes a trace object as input and displays a table-based summary of posterior statistics rounded by 2 digits.
```
# Answer 5c
# Obtain summary statistics for posterior distributions
def posterior_summary(trace):
"""Generate a table-based summary for the field goal probability."""
# BEGIN SOLUTION
return pm.summary(trace).round(2)
# END SOLUTION
# Test Cases
"""Check whether the summary output is correctly generated."""
sum1 = posterior_summary(trace)
sum2 = pm.summary(trace).round(2)
pdt.assert_frame_equal(sum1, sum2)
assert_equal(posterior_summary(trace).shape, (1, 11))
```
d) What is the posterior mean and standard deviation of the probability of making a field goal? Define a function posterior_statistics which takes a trace object as input and return the posterior mean and posterior standard deviation as a tuple looks like (mean, sd).
```
# Answer 5d
def posterior_statistics(trace):
return (posterior_summary(trace).iloc[0,0], posterior_summary(trace).iloc[0,1])
posterior_statistics(trace)
# Test Cases
"""Check whether the posterior mean and posterior standard deviation are correctly generated."""
assert_equal(posterior_statistics(trace),
tuple([posterior_summary(trace).iloc[0,0], posterior_summary(trace).iloc[0,1]]))
assert isinstance(posterior_statistics(trace), tuple)
assert_equal(len(posterior_statistics(trace)), 2)
```
e) Define a function named gelman_rubin which takes a trace object as input and return the Gelman-Rubin statistics. Does the posterior distribution converge?
```
# Answer
# Get Gelman-Rubin Convergence Criterion
def gelman_rubin(trace):
"""Compute Gelman-Rubin statistics for the posterior samples of field goal probability."""
### BEGIN SOLUTION
return print(pm.rhat(trace,
varnames=['p']))
### END SOLUTION
gelman_rubin(trace)
# Test cases
assert_equal(gelman_rubin(trace), pm.rhat(trace,varnames=['p']))
#assert 1 <= gelman_rubin(trace) <= 1.1
gelman_rubin(trace)[p]
```
## Bonus Section:
### Effective sample size
The calculation of effective sample size is given by the following formula:
$$\hat{n}_{eff} = \frac{mn}{1 + 2 \sum_{t=1}^T \hat{\rho}_t}$$
where m is the number of chains, n the number of steps per chain, T the time when the autocorrelation first becomes negative, and ρ̂_t the autocorrelation at lag t.
```
## Calculate effective sample size
pm.effective_n(trace)
```
As you can see, the effective sample size is 1271 for the total of the 3 chains. Since by default, the tuning sample is 500, leaving 500 samples to be resampled. So that means the autocorrelation is not extreme, the MCMC converges well.
### Geweke Statistics
As an alternative of Gelman-Rubin statistics, Geweke provides a sanity check of the convergence of MCMC chains. Geweke statistics compares the mean and variance of segments from the beginning and end of each single MCMC chain for a parameter. If the absolute value of Geweke statistics exceeds 1, it indicates a lack of convergence and suggests that additional samples are requred to achieve convergence.
```
# We can create a plot to show the trajectory of Geweke statistics
plt.plot(pm.geweke(trace['p'])[:,1], 'o')
plt.axhline(1, c='red')
plt.axhline(-1, c='red')
plt.gca().margins(0.05)
plt.show()
pass
```
Since the Geweke statistics are less than 1 in absolute value, it indicates a good convergence in the MCMC chains.
# Debug Question
The following question requires you to read the code carefully and correct the codes with errors. A Umich cognitive science research team want to produce an elegant code to run a MCMC sampler to determine the IQ distribution of the undergraduate students studying at the University of Michigan. They studied the literature and inferred the following priors:
$IQ \sim Normal(mean = 105, variance = 7^2)$
$\sigma(IQ) \sim HalfNormal(\beta = 2)$
Then they collected experimental data from 100 students who took the Wechsler Adult Intelligence Scale (WAIS) test at the cognitive science building. The first code chunk gives their test results.
After debugging the code, the resulting code should be error-free and return the trace object.
```
# IQ test results for the 100 students
np.random.seed(123)
y = np.random.normal(100, 15, 100)
# Hierarchical Bayesian Modeling
seed = 123
niter = 1000
nchains = 3
with pm.Model() as model:
"""Deploy NUTS sampler to update the distribution for students' IQ."""
### BEGIN CODE
mu = pm.Normal('mu', mu = 105, sigma = 7)
sigma = pm.HalfCauchy('sigma', beta = 2)
y_observed = pm.Normal('y_observed',
mu=mu,
sigma=sigma,
observed=y)
trace2 = pm.sample(niter, chains = nchains, random_seed = seed)
### END CODE
# Test cases
assert_equal(type(posterior_summary(trace2)), pd.core.frame.DataFrame)
assert_equal(posterior_summary(trace2).shape, (2,11))
```
Reference:
1. https://docs.pymc.io/api/stats.html
2. http://pymc-devs.github.io/pymc/modelchecking.html?highlight=geweke
3. Wagenmakers, E., Morey, R. D., & Lee, M. D. (n.d.). Bayesian Benefits for the Pragmatic Researcher, 1–11.
| github_jupyter |
# Creating Provenance an Example Using a Python Notebook
```
import prov, requests, pandas as pd, io, git, datetime, urllib
from prov.model import ProvDocument
```
## Initialising a Provenance Document
First we use the prov library to create a provenance and initialise it with some relevant namespaces that can be used later to define provenance activities and entities
```
pg = ProvDocument()
kn_id = "data/data-gov-au/number-of-properties-by-suburb-and-planning-zone-csv"
pg.add_namespace('kn', 'http://oznome.csiro.au/id/')
pg.add_namespace('void', 'http://vocab.deri.ie/void#')
pg.add_namespace('foaf', 'http://xmlns.com/foaf/0.1/')
pg.add_namespace('dc', 'http://purl.org/dc/elements/1.1/')
pg.add_namespace('doap', 'http://usefulinc.com/ns/doap#')
```
## Processing the Data
Processing could be anything and represents one or more provenance activities. In this example we use a KN metadata record to retrieve data on residential properities. We intersperse definition of provenance into this processing but we could have easily seperated it out and performed it after the processing steps
First we define an entity that describes the KN metadata records which we are using here
```
input_identifier = 'kn:'+ kn_id
input_entity = pg.entity(input_identifier, {'prov:label': 'road static parking off street', 'prov:type': 'void:Dataset'})
```
Then we proceed to drill down to get detailed data that we've found associated with this record
```
start_time = datetime.datetime.now()
response = requests.get('https://data.sa.gov.au/data/dataset/d080706c-2c05-433d-b84d-9aa9b6ccae73/resource/4a47e89b-4be8-430d-8926-13b180025ac6/download/city-of-onkaparinga---number-of-properties-by-suburb-and-planning-zone-2016.csv')
url_data = response.content
dataframe = pd.read_csv(io.StringIO(url_data.decode('utf-8')))
dataframe.columns
```
Our processing is very simple we are subsetting the original dataset here and creating a new dataset called residential_frame that we will then save to disk
```
residential_frame = dataframe[dataframe['Zone_Description'] == 'Residential']
residential_frame_file_name = "filtered_residential_data.csv"
residential_frame.to_csv(residential_frame_file_name)
end_time = datetime.datetime.now()
```
## Completing Provenance
We have began to build a provenance record but we are missing a record of the activity that transforms our input into the output and we are also missing a description of the output
### Generating an output provenance entity
Ideally we would store our output provenance entity somewhere known and persistent and identify it with a persistent url. However we can still mint an identifier and then describe the dataset in useful ways that will make it easy to find and query from later. To do this we create a new entity record and use the file name and sha hash of the file to describe it.
```
import subprocess
output = subprocess.check_output("sha1sum "+ residential_frame_file_name, shell=True)
sha1 = str(output).split(' ')[0][2:]
output_identifier = 'kn:' + sha1
output_entity = pg.entity(output_identifier , {'prov:label': residential_frame_file_name, 'prov:type': 'void:Dataset'})
```
### Describing the activity
We need to connect the entity representing the input data to the entity representing the output data and we may want to describe the activity that transforms the input into the output. In this case the activity is this Jupyter Notebook. One way of storing provenance information in it is to make sure it is version controlled in git and then record these details.
## Connecting things together into the provenance graph
```
import re, ipykernel, json
%%javascript
var nb = Jupyter.notebook;
var port = window.location.port;
nb.kernel.execute("NB_Port = '" + port + "'");
kernel_id = re.search('kernel-(.*).json', ipykernel.connect.get_connection_file()).group(1)
response = requests.get('http://127.0.0.1:{port}/jupyter/api/sessions'.format(port=NB_Port))
response.content
matching = [s for s in json.loads(response.text) if s['kernel']['id'] == kernel_id]
if matching:
matched = matching[0]['notebook']['path']
notebook_file_name = matched.split('/')[-1]
```
One gotcha here is that we need to make sure this notebooks relevant version has been committed and pushed to the remote. So do that and then execute these cells.
```
repo = git.Repo('./', search_parent_directories=True)
current_git_sha = repo.head.object.hexsha
current_git_remote = list(repo.remotes['origin'].urls)[0]
current_git_sha
current_git_remote
process_identifier = 'kn:' + 'notebook/' + urllib.parse.quote(notebook_file_name + current_git_sha, safe='')
process_identifier
process_entity = pg.entity(process_identifier, other_attributes={'dc:description': 'a jupyter notebook used that demonstrates provenance', 'doap:GitRepository' : current_git_remote, 'doap:Version' : current_git_sha })
import time
sunixtime = time.mktime(start_time.timetuple())
eunixtime = time.mktime(end_time.timetuple())
activity_identifier = 'kn:' + 'notebook/' + urllib.parse.quote(notebook_file_name + current_git_sha, safe='') + str(sunixtime) + str(eunixtime)
activity = pg.activity(activity_identifier, startTime=start_time, endTime=end_time)
pg.wasGeneratedBy(activity=activity, entity=output_entity)
pg.used(activity=activity, entity=input_entity)
pg.used(activity=activity, entity=process_entity)
pg
# visualize the graph
from prov.dot import prov_to_dot
dot = prov_to_dot(pg)
dot.write_png('prov.png')
from IPython.display import Image
Image('prov.png')
```
## Posting to a Provenance Storage System
TBC
| github_jupyter |
# Cython in Jupyter notebooks
To use cython in a Jupyter notebook, the extension has to be loaded.
```
%load_ext cython
```
## Pure Python
To illustrate the performance difference between a pure Python function and a cython implementation, consider a function that computes the list of the first $k_{\rm max}$ prime numbers.
```
from array import array
def primes(kmax, p=None):
if p is None:
p = array('i', [0]*kmax)
result = []
k, n = 0, 2
while k < len(p):
i = 0
while i < k and n % p[i] != 0:
i += 1
if i == k:
p[k] = n
k += 1
result.append(n)
n += 1
return result
```
Checking the results for the 20 first prime numbers.
```
primes(20)
```
Note that this is not the most efficient method to check whether $k$ is prime.
```
%timeit primes(1_000)
p = array('i', [0]*10_000)
%timeit primes(10_000, p)
```
## Cython
The cython implementation differs little from that in pure Python, type annotations have been added for the function's argument, and the variables `n`, `k`, `i`, and `p`. Note that cython expects a constant array size, hence the upper limit on `kmax`.
```
%%cython
def c_primes(int kmax):
cdef int n, k, i
cdef int p[10_000]
if kmax > 10_000:
kmax = 10_000
result = []
k, n = 0, 2
while k < kmax:
i = 0
while i < k and n % p[i] != 0:
i += 1
if i == k:
p[k] = n
k += 1
result.append(n)
n += 1
return result
```
Checking the results for the 20 first prime numbers.
```
c_primes(20)
%timeit c_primes(1_000)
%timeit c_primes(10_000)
```
It is clear that the cython implementation is more than 30 times faster than the pure Python implementation.
## Dynamic memory allocation
The cython implementation can be improved by adding dynamic memory allocation for the array `p`.
```
%%cython
from libc.stdlib cimport calloc, free
def c_primes(int kmax):
cdef int n, k, i
cdef int *p = <int *> calloc(kmax, sizeof(int))
result = []
k, n = 0, 2
while k < kmax:
i = 0
while i < k and n % p[i] != 0:
i += 1
if i == k:
p[k] = n
k += 1
result.append(n)
n += 1
free(p)
return result
```
Checking the results for the 20 first prime numbers.
```
c_primes(20)
```
This has no noticeable impact on performance.
```
%timeit c_primes(1_000)
%timeit c_primes(10_000)
```
| github_jupyter |
```
!pip install plotly
```
<a href="https://plotly.com/python/" target="_blank">Plotly's</a> Python graphing library makes interactive, publication-quality graphs. Examples of how to make line plots, scatter plots, area charts, bar charts, error bars, box plots, histograms, heatmaps, subplots, multiple-axes, polar charts, and bubble charts.
```
!pip install plotly_express
```
<a href="https://pypi.org/project/plotly-express/0.1.9/" target="_blank">Plotly Express</a> is a terse, consistent, high-level wrapper around Plotly.py for rapid data exploration and figure generation.
```
!pip install calmap
```
<a href="https://pypi.org/project/calmap/" target="_blank">Calendar heatmaps (calmap)</a> Plot Pandas time series data sampled by day in a heatmap per calendar year, similar to GitHub’s contributions plot, using matplotlib.
```
!pip install squarify
```
Pure Python implementation of the <a href="https://pypi.org/project/squarify/0.1/" target="_blank">squarify</a> treemap layout algorithm. Based on algorithm from Bruls, Huizing, van Wijk, "Squarified Treemaps", but implements it differently.
```
!pip install pycountry_convert
```
Using country data derived from wikipedia, <a href="https://pypi.org/project/pycountry-convert/" target="_blank">pycountry-convert</a> provides conversion functions between ISO country names, country-codes, and continent names.
```
!pip install GoogleMaps
```
Use Python? Want to geocode something? Looking for directions? Maybe matrices of directions? This library brings the <a href="https://pypi.org/project/googlemaps/" target="_blank">Google Maps</a> Platform Web Services to your Python application.
```
!pip install xgboost
```
<a href="https://xgboost.readthedocs.io/en/latest/" target="_blank">XGBoost</a> is an optimized distributed gradient boosting library designed to be highly efficient, flexible and portable. It implements machine learning algorithms under the Gradient Boosting framework. XGBoost provides a parallel tree boosting (also known as GBDT, GBM) that solve many data science problems in a fast and accurate way. The same code runs on major distributed environment (Hadoop, SGE, MPI) and can solve problems beyond billions of examples.
```
!pip install lightgbm
```
<a href="https://lightgbm.readthedocs.io/en/latest/" target="_blank">LightGBM</a> is a gradient boosting framework that uses tree based learning algorithms. It is designed to be distributed and efficient with the following advantages:
* Faster training speed and higher efficiency.
* Lower memory usage.
* Better accuracy.
* Support of parallel and GPU learning.
* Capable of handling large-scale data.
```
!pip install altair
```
<a href="https://pypi.org/project/altair/" target="_blank">Altair</a> is a declarative statistical visualization library for Python. With Altair, you can spend more time understanding your data and its meaning. Altair's API is simple, friendly and consistent and built on top of the powerful Vega-Lite JSON specification. This elegant simplicity produces beautiful and effective visualizations with a minimal amount of code. Altair is developed by Jake Vanderplas and Brian Granger in close collaboration with the UW Interactive Data Lab.
```
!pip install folium
```
<a href="https://pypi.org/project/folium/" target="_blank">folium</a> builds on the data wrangling strengths of the Python ecosystem and the mapping strengths of the Leaflet.js library. Manipulate your data in Python, then visualize it in a Leaflet map via folium.
```
!pip install fbprophet
```
<a href="https://pypi.org/project/fbprophet/" target="_blank">Prophet</a> is a procedure for forecasting time series data based on an additive model where non-linear trends are fit with yearly, weekly, and daily seasonality, plus holiday effects. It works best with time series that have strong seasonal effects and several seasons of historical data. Prophet is robust to missing data and shifts in the trend, and typically handles outliers well.
| github_jupyter |
# Umami notebooks
Welcome to the umami notebooks. This page provides links to notebooks that provide an introduction to umami and its use. We recommend that you look at them in the following order.
First, look at two notebooks designed to introduce you to the core classes and methods of umami.
* [Part 1: Introduction to umami and the `Metric` class](IntroductionToMetric.ipynb)
* [Part 2: Introduction to the `Residual` class](IntroductionToResidual.ipynb)
* [Part 3: Other IO options (using umami without Landlab or terrainbento)](OtherIO_options.ipynb)
Then, look at two notebooks with example applications.
* [Part 4: Example Application](ExampleApplication.ipynb)
* [Part 5: Application using the Discretized Misfit calculation](DiscretizedMisfit.ipynb)
If you have comments or questions about the notebooks, the best place to get help is through [GitHub Issues](https://github.com/TerrainBento/umami/issues).
## Some background
### What is umami?
Umami is a package for calculating objective functions or objective function components for Earth surface dynamics modeling. It was designed to work well with [terrainbento](https://github.com/TerrainBento/terrainbento) and other models built with the [Landlab Toolkit](https://github.com/landlab/landlab). However, it is not necessary to do modeling with either of these packages to use umami (this is described further in [Part 3 of the notebook series](OtherIO_options.ipynb).
Umami offers two primary classes:
* a[`Residual`](https://umami.readthedocs.io/en/latest/umami.residual.html#Residual),
which represents the difference between model and data, and
* a [`Metric`](https://umami.readthedocs.io/en/latest/umami.metric.html),
which is a calculated value on either model or data.
The set of currently supported calculations can be found in the [`umami.calculations`](https://umami.readthedocs.io/en/latest/umami.calculations.html) submodule.
### What does it do well?
Umami was designed to provide an input-file based interface for calculating single-value landscape metrics for use in model analysis. This supports reproducible analysis and systematic variation in metric construction. When used with `terrainbento`, one input file can describe the model run, and one input file can describe the model assessment or model-data comparison. This streamlines model analysis applications. Umami also provides multiple output formats (YAML and Dakota), the latter of which is designed to interface with Sandia National Laboratory's [Dakota package](https://dakota.sandia.gov).
| github_jupyter |
### Mit kellene tudni?
#### 1. Megfogalmazni egy programozási problémát <!-- .element: class="fragment" -->
#### 1. Számításelmélet értelmét elmagyarázni <!-- .element: class="fragment" -->
#### 1. Lebontani egy komplex problémát egyszerűbbekre <!-- .element: class="fragment" -->
#### 1. Megérteni egy leírt programot <!-- .element: class="fragment" -->
#### 1. Megírni egy programot <!-- .element: class="fragment" -->
#### 1. Találni érdeklődést és folytatást <!-- .element: class="fragment" -->
<center><img src="https://pics.me.me/doctors-googling-stuff-online-does-not-make-you-a-doctor-61282088.png"></center> -->
### Deklaratív tudás
A "mit?" kérdésre adott válasz egy probléma kapcsán
### Imperatív tudás
A "hogyan" kérdésre adott válasz egy probléma kapcsán
### Deklaratív példák
- tervrajz
- térképjelzés
- anatómiai ábra
### Imperatív példák
- recept
- IKEA útmutató
- útvonalterv
### Mit adunk át a gépnek?
Egy probléma megoldására szeretnénk megtanítani/megkérni:
tetszőleges $x$-re, számolja ki $ \sqrt{x} $-et úgy, hogy csak osztani, szorozni, meg összeadni tud
### Tudás Gyökvonásról
- deklaratív tudás:
- $ \sqrt{x} = y \Leftrightarrow y^2=x $
- $ x < y^2 \Leftrightarrow \sqrt{x} < y $
- $ ( (y_1 < x \land y_2 < x) \lor (y_1 > x \land y_2 > x) ) \Rightarrow $
- $ \Rightarrow ( |x - y_1| < |x - y_2| \Leftrightarrow |x^2 - y_1^2| < |x^2 - y_2^2| ) $
- imperatív tudás:
- tippelünk egy kezdeti $ G $ -t, és ameddig nem elég jó, $ G' = \frac{G+\frac{x}{G}}{2} $ -vel közelítünk, így tetszőlegesen közel kerülünk az eredményhez
(minden nemnegatív számok esetén)
### Ember
okos, kreatív, tud következtetni, memóriája ködös,
szeretné minél kevesebbet nyomkodni a számológépet
- felhasznál csomó meglévő deklaratív tudást
- összeállítja egy komplex tippelési folyamattá
- tippek eredményéből továbbfejleszti a folyamatot
- felhasznál olyan komplex fogalmakat mint nagyságrend, vagy előjelváltás
### Gép
buta, nincs önálló gondolata, memóriája tökéletes
másodpercenként töbmilliárd műveletet el tud végezni,
- tippel egy nagyon rosszat, pl G = 1
- valaki megtanította neki hogy $G' = \frac{G+\frac{x}{G}}{2}$ közelít, szóval elkezdi
- Megoldandó probléma: $ \sqrt{1366561} = ? $
### Specifikáció
Egyfajta deklaratív leírása egy programnak
Miből, mit?
- állapottér - bemenő/kimenő adatok
- előfeltétel - amit tudunk a bemenetről
- utófeltétel - az eredmény kiszámítási szabálya (amit tudunk az eredményről)
legyen **teljes** és **részletes**
### Specifikáció I. példa
Valós számok halmazán megoldható másodfokú egyneletet oldjon meg a program, ami $ax^2+bx+c=0$ formában van megadva
- Á: $(a,b,c,x_1,x_2 \in \mathbb{R})$ <!-- .element: class="fragment" data-fragment-index="1" -->
- Ef: $(a \neq 0 \land b^2-4ac \geq 0)$ <!-- .element: class="fragment" data-fragment-index="2" -->
- Uf: $ (x_1 = \frac{-b + \sqrt{b^2-4ac}}{2a} \land x_2 = \frac{-b - \sqrt{b^2-4ac}}{2a})$ <!-- .element: class="fragment" data-fragment-index="3" -->
### Specifikáció példa 2
Valós számok halmazán megoldható másodfokú egyneletet oldjon meg a program, ami $ax^2+bx+c=0$ formában van megadva
- Á: $(a,b,c,x_1,x_2 \in \mathbb{R})$
- Ef: $(a \neq 0 \land b^2-4ac \geq 0)$
- Uf: $ (\forall i (ax_i^2+bx_i+c=0) \land ( x_1 = x_2 \iff b^2-4ac = 0 ))$
### Specifikáció teljessége
Amit az előfeltétel megenged az állapottéren belül, azt az utófeltételnek kezelnie kell
Pl:
- Válassza ki két szám közül azt amelyiknek több prím osztója van
- több különböző vagy több összesen?
- mi van ha ugyanannyi?
- Válassza ki egy számsorból azt az 5 számot ami legjobban eltér az átlagtól
- mi van ha nincs 5 szám a számsorban?
- mi van ha minden szám ugyanaz?
- Sakktáblán szereplő állásról döntse el hogy matt-e.
- mi van ha mindkét fél sakkban van?
- lehet 11 királynő valakinél?
### Specifikáció részletessége
A program főzzön rántottát:
- Á: (konyha)
- Ef: ( )
- Uf: (ha a konyha alkalmas ennek elkészítésére, a konyhában legyen egy finom rántotta)
vagy:
- Á: (serpenyő, főzőlap, 3 tojás, olaj, só, fakanál, tányér)
- Ef: (a serpenyő, tányér és fakanál tiszta, a tojás nem romlott, a főzőlap képes a serpenyőt 200 Celsius fokra felmelegíteni)
- Uf: (a tojások összekeverve kerültek a 200 fokos serpenyőbe az olaj után, több mint 4 de kevesebb mint 10 percet töltöttek ott, ebből 20 másodpercnél többet nem álltak kavarás nélkül, végül megsózva kikerültek a tányérra)
### Specifikáció II. példa
Két természetes szám legnagyobb közös osztójának megtalálása
- Á: $(a,b,x \in \mathbb{N})$ <!-- .element: class="fragment" data-fragment-index="1" -->
- Ef: $(a \neq 0 \land b \neq 0)$ <!-- .element: class="fragment" data-fragment-index="2" -->
- Uf: $ (x|a \land x|b \land \nexists i(i|a \land i|b \land i > x))$ <!-- .element: class="fragment" data-fragment-index="3" -->
<a style='text-decoration:none;line-height:16px;display:flex;color:#5B5B62;padding:10px;justify-content:end;' href='https://deepnote.com?utm_source=created-in-deepnote-cell&projectId=978e47b7-a961-4dca-a945-499e8b781a34' target="_blank">
<img alt='Created in deepnote.com' style='display:inline;max-height:16px;margin:0px;margin-right:7.5px;' src='data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0iVVRGLTgiPz4KPHN2ZyB3aWR0aD0iODBweCIgaGVpZ2h0PSI4MHB4IiB2aWV3Qm94PSIwIDAgODAgODAiIHZlcnNpb249IjEuMSIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayI+CiAgICA8IS0tIEdlbmVyYXRvcjogU2tldGNoIDU0LjEgKDc2NDkwKSAtIGh0dHBzOi8vc2tldGNoYXBwLmNvbSAtLT4KICAgIDx0aXRsZT5Hcm91cCAzPC90aXRsZT4KICAgIDxkZXNjPkNyZWF0ZWQgd2l0aCBTa2V0Y2guPC9kZXNjPgogICAgPGcgaWQ9IkxhbmRpbmciIHN0cm9rZT0ibm9uZSIgc3Ryb2tlLXdpZHRoPSIxIiBmaWxsPSJub25lIiBmaWxsLXJ1bGU9ImV2ZW5vZGQiPgogICAgICAgIDxnIGlkPSJBcnRib2FyZCIgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoLTEyMzUuMDAwMDAwLCAtNzkuMDAwMDAwKSI+CiAgICAgICAgICAgIDxnIGlkPSJHcm91cC0zIiB0cmFuc2Zvcm09InRyYW5zbGF0ZSgxMjM1LjAwMDAwMCwgNzkuMDAwMDAwKSI+CiAgICAgICAgICAgICAgICA8cG9seWdvbiBpZD0iUGF0aC0yMCIgZmlsbD0iIzAyNjVCNCIgcG9pbnRzPSIyLjM3NjIzNzYyIDgwIDM4LjA0NzY2NjcgODAgNTcuODIxNzgyMiA3My44MDU3NTkyIDU3LjgyMTc4MjIgMzIuNzU5MjczOSAzOS4xNDAyMjc4IDMxLjY4MzE2ODMiPjwvcG9seWdvbj4KICAgICAgICAgICAgICAgIDxwYXRoIGQ9Ik0zNS4wMDc3MTgsODAgQzQyLjkwNjIwMDcsNzYuNDU0OTM1OCA0Ny41NjQ5MTY3LDcxLjU0MjI2NzEgNDguOTgzODY2LDY1LjI2MTk5MzkgQzUxLjExMjI4OTksNTUuODQxNTg0MiA0MS42NzcxNzk1LDQ5LjIxMjIyODQgMjUuNjIzOTg0Niw0OS4yMTIyMjg0IEMyNS40ODQ5Mjg5LDQ5LjEyNjg0NDggMjkuODI2MTI5Niw0My4yODM4MjQ4IDM4LjY0NzU4NjksMzEuNjgzMTY4MyBMNzIuODcxMjg3MSwzMi41NTQ0MjUgTDY1LjI4MDk3Myw2Ny42NzYzNDIxIEw1MS4xMTIyODk5LDc3LjM3NjE0NCBMMzUuMDA3NzE4LDgwIFoiIGlkPSJQYXRoLTIyIiBmaWxsPSIjMDAyODY4Ij48L3BhdGg+CiAgICAgICAgICAgICAgICA8cGF0aCBkPSJNMCwzNy43MzA0NDA1IEwyNy4xMTQ1MzcsMC4yNTcxMTE0MzYgQzYyLjM3MTUxMjMsLTEuOTkwNzE3MDEgODAsMTAuNTAwMzkyNyA4MCwzNy43MzA0NDA1IEM4MCw2NC45NjA0ODgyIDY0Ljc3NjUwMzgsNzkuMDUwMzQxNCAzNC4zMjk1MTEzLDgwIEM0Ny4wNTUzNDg5LDc3LjU2NzA4MDggNTMuNDE4MjY3Nyw3MC4zMTM2MTAzIDUzLjQxODI2NzcsNTguMjM5NTg4NSBDNTMuNDE4MjY3Nyw0MC4xMjg1NTU3IDM2LjMwMzk1NDQsMzcuNzMwNDQwNSAyNS4yMjc0MTcsMzcuNzMwNDQwNSBDMTcuODQzMDU4NiwzNy43MzA0NDA1IDkuNDMzOTE5NjYsMzcuNzMwNDQwNSAwLDM3LjczMDQ0MDUgWiIgaWQ9IlBhdGgtMTkiIGZpbGw9IiMzNzkzRUYiPjwvcGF0aD4KICAgICAgICAgICAgPC9nPgogICAgICAgIDwvZz4KICAgIDwvZz4KPC9zdmc+' > </img>
Created in <span style='font-weight:600;margin-left:4px;'>Deepnote</span></a>
| github_jupyter |
# Análise do eleitorado brasileiro
Fonte -> http://www.tse.jus.br/eleicoes/estatisticas/estatisticas-eleitorais
```
# importando as bibliotecas
import pandas as pd
# Carregando o arquivo csv
df = pd.read_csv('eleitorado_municipio_2020.csv', encoding='latin1', sep=';')
df.head().T
# Tamanho do arquivo
df.info()
# As cinco cidades com o maior número de eleitores deficientes.
df.nlargest(5,'QTD_ELEITORES_DEFICIENTE')
# As cinco cidades com o menor número de eleitores.
df.nsmallest(5,'QTD_ELEITORES')
# Quantidade de eleitores por gênero
print('Eleitoras: ', df['QTD_ELEITORES_FEMININO'].sum())
print('Eleitores: ', df['QTD_ELEITORES_MASCULINO'].sum())
print('Não informado: ', df['QTD_ELEITORES_NAOINFORMADO'].sum())
# Criar variáveis para calcular o percentual
tot_eleitores = df['QTD_ELEITORES'].sum()
tot_masc = df['QTD_ELEITORES_MASCULINO'].sum()
tot_fem = df['QTD_ELEITORES_FEMININO'].sum()
tot_ninf = df['QTD_ELEITORES_NAOINFORMADO'].sum()
# Mostrar valores percentuais
print('Eleitoras: ', ( ( tot_fem / tot_eleitores ) * 100) .round(2), '%' )
print('Eleitores: ', ( ( tot_masc / tot_eleitores ) * 100) .round(2), '%' )
print('Não informado: ', ( ( tot_ninf / tot_eleitores ) * 100) .round(2), '%' )
# Quantos municípios com mais homens do que mulheres
df[df['QTD_ELEITORES_MASCULINO'] > df['QTD_ELEITORES_FEMININO']].count()
# Vamos criar uma coluna nova para indicar a relação fem/masc
df['RELACAO_FM'] = df['QTD_ELEITORES_FEMININO'] / df['QTD_ELEITORES_MASCULINO']
# Quais os municípios com maior relação fem/masc?
df.nlargest(5,'RELACAO_FM').T
# Quais os municípios com menor relação fem/masc?
df.nsmallest(5,'RELACAO_FM')
# Vamos criar um DataFrame só com municípios de São Paulo
df_sp = df[ df['SG_UF'] == 'SP' ].copy()
df_sp.head()
# Quais os municípios com maior relação fem/masc de São Paulo?
df_sp.nlargest(5,'RELACAO_FM')
# Quais os municípios com menor relação fem/masc de São Paulo?
df_sp.nsmallest(5,'RELACAO_FM')
# Plotar um gráfico de distribuição fem/masc
df['RELACAO_FM'].plot.hist(bins=100)
# carregar biblioteca gráfica
import seaborn as sns
import matplotlib.pyplot as plt
# Plotar um gráfico de distribuição fem/masc
sns.distplot( df['RELACAO_FM'] , bins=100 , color='red', kde=False )
# Embelezando o gráfico
plt.title('Relação Eleitoras/Eleitores', fontsize=18)
plt.xlabel('Eleitoras/Eleitores', fontsize=14)
plt.ylabel('Frequência', fontsize=14)
plt.axvline(1.0, color='black', linestyle='--')
# Plotar um gráfico de distribuição fem/masc, mas mostrando os pontos (municípios)
sns.swarmplot( data=df , x='NM_REGIAO', y='RELACAO_FM' )
plt.axhline(1.0, color='black', linestyle='--')
# Vamos plotar o gráfico de total de eleitores por faixa etária usando o gráfico de barras horizontal
# primeiro vamos listar as colunas de nosso interesse
lista = ['QTD_ELEITORES_16', 'QTD_ELEITORES_17', 'QTD_ELEITORES_18', 'QTD_ELEITORES_19', 'QTD_ELEITORES_20']
tot_idade = df[lista].sum()
tot_idade
# Mostrando o gráfico de barras
tot_idade.plot.barh()
```
| github_jupyter |
# Módulo 2: Scraping con Selenium
## LATAM Airlines
<a href="https://www.latam.com/es_ar/"><img src="https://i.pinimg.com/originals/dd/52/74/dd5274702d1382d696caeb6e0f6980c5.png" width="420"></img></a>
<br>
Vamos a scrapear el sitio de Latam para averiguar datos de vuelos en funcion el origen y destino, fecha y cabina. La información que esperamos obtener de cada vuelo es:
- Precio(s) disponibles
- Horas de salida y llegada (duración)
- Información de las escalas
¡Empecemos!
```
url = 'https://www.latam.com/es_ar/apps/personas/booking?fecha1_dia=20&fecha1_anomes=2019-12&auAvailability=1&ida_vuelta=ida&vuelos_origen=Buenos%20Aires&from_city1=BUE&vuelos_destino=Madrid&to_city1=MAD&flex=1&vuelos_fecha_salida_ddmmaaaa=20/12/2019&cabina=Y&nadults=1&nchildren=0&ninfants=0&cod_promo='
from selenium import webdriver
options = webdriver.ChromeOptions()
options.add_argument('--incognito')
driver = webdriver.Chrome(executable_path='../../chromedriver', options=options)
driver.get(url)
#Usaremos el Xpath para obtener la lista de vuelos
vuelos = driver.find_elements_by_xpath('//li[@class="flight"]')
vuelo = vuelos[0]
```
Obtenemos la información de la hora de salida, llegada y duración del vuelo
```
# Hora de salida
vuelo.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Hora de llegada
vuelo.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
vuelo.find_element_by_xpath('.//span[@class="duration"]/time').get_attribute('datetime')
boton_escalas = vuelo.find_element_by_xpath('.//div[@class="flight-summary-stops-description"]/button')
boton_escalas
boton_escalas.click()
segmentos = vuelo.find_elements_by_xpath('//div[@class="segments-graph"]/div[@class="segments-graph-segment"]')
segmentos
escalas = len(segmentos) - 1 #0 escalas si es un vuelo directo
segmento = segmentos[0]
# Origen
segmento.find_element_by_xpath('.//div[@class="departure"]/span[@class="ground-point-name"]').text
# Hora de salida
segmento.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Destino
segmento.find_element_by_xpath('.//div[@class="arrival"]/span[@class="ground-point-name"]').text
# Hora de llegada
segmento.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
segmento.find_element_by_xpath('.//span[@class="duration flight-schedule-duration"]/time').get_attribute('datetime')
# Numero del vuelo
segmento.find_element_by_xpath('.//span[@class="equipment-airline-number"]').text
# Modelo de avion
segmento.find_element_by_xpath('.//span[@class="equipment-airline-material"]').text
# Duracion de la escala
segmento.find_element_by_xpath('.//div[@class="stop connection"]//p[@class="stop-wait-time"]//time').get_attribute('datetime')
vuelo.find_element_by_xpath('//div[@class="modal-dialog"]//button[@class="close"]').click()
vuelo.click()
tarifas = vuelo.find_elements_by_xpath('.//div[@class="fares-table-container"]//tfoot//td[contains(@class, "fare-")]')
precios = []
for tarifa in tarifas:
nombre = tarifa.find_element_by_xpath('.//label').get_attribute('for')
moneda = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="currency-symbol"]').text
valor = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="value"]').text
dict_tarifa={nombre:{'moneda':moneda, 'valor':valor}}
precios.append(dict_tarifa)
print(dict_tarifa)
def obtener_tiempos(vuelo):
# Hora de salida
salida = vuelo.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Hora de llegada
llegada = vuelo.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duracion
duracion = vuelo.find_element_by_xpath('.//span[@class="duration"]/time').get_attribute('datetime')
return {'hora_salida': salida, 'hora_llegada': llegada, 'duracion': duracion}
def obtener_precios(vuelo):
tarifas = vuelo.find_elements_by_xpath(
'.//div[@class="fares-table-container"]//tfoot//td[contains(@class, "fare-")]')
precios = []
for tarifa in tarifas:
nombre = tarifa.find_element_by_xpath('.//label').get_attribute('for')
moneda = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="currency-symbol"]').text
valor = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="value"]').text
dict_tarifa={nombre:{'moneda':moneda, 'valor':valor}}
precios.append(dict_tarifa)
return precios
def obtener_datos_escalas(vuelo):
segmentos = vuelo.find_elements_by_xpath('//div[@class="segments-graph"]/div[@class="segments-graph-segment"]')
info_escalas = []
for segmento in segmentos:
# Origen
origen = segmento.find_element_by_xpath(
'.//div[@class="departure"]/span[@class="ground-point-name"]').text
# Hora de salida
dep_time = segmento.find_element_by_xpath(
'.//div[@class="departure"]/time').get_attribute('datetime')
# Destino
destino = segmento.find_element_by_xpath(
'.//div[@class="arrival"]/span[@class="ground-point-name"]').text
# Hora de llegada
arr_time = segmento.find_element_by_xpath(
'.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
duracion_vuelo = segmento.find_element_by_xpath(
'.//span[@class="duration flight-schedule-duration"]/time').get_attribute('datetime')
# Numero del vuelo
numero_vuelo = segmento.find_element_by_xpath(
'.//span[@class="equipment-airline-number"]').text
# Modelo de avion
modelo_avion = segmento.find_element_by_xpath(
'.//span[@class="equipment-airline-material"]').text
# Duracion de la escala
if segmento != segmentos[-1]:
duracion_escala = segmento.find_element_by_xpath(
'.//div[@class="stop connection"]//p[@class="stop-wait-time"]//time').get_attribute('datetime')
else:
duracion_escala = ''
# Armo un diccionario para almacenar los datos
data_dict={'origen': origen,
'dep_time': dep_time,
'destino': destino,
'arr_time': arr_time,
'duracion_vuelo': duracion_vuelo,
'numero_vuelo': numero_vuelo,
'modelo_avion': modelo_avion,
'duracion_escala': duracion_escala}
info_escalas.append(data_dict)
return info_escalas
```
## Clase 15
Ya tenemos el scraper casi listo. Unifiquemos las 3 funciones de la clase anterior en una sola
```
def obtener_info(driver):
vuelos = driver.find_elements_by_xpath('//li[@class="flight"]')
print(f'Se encontraron {len(vuelos)} vuelos.')
print('Iniciando scraping...')
info = []
for vuelo in vuelos:
# Obtenemos los tiempos generales del vuelo
tiempos = obtener_tiempos(vuelo)
# Clickeamos el botón de escalas para ver los detalles
vuelo.find_element_by_xpath('.//div[@class="flight-summary-stops-description"]/button').click()
escalas = obtener_datos_escalas(vuelo)
# Cerramos el pop-up con los detalles
vuelo.find_element_by_xpath('//div[@class="modal-dialog"]//button[@class="close"]').click()
# Clickeamos el vuelo para ver los precios
vuelo.click()
precios = obtener_precios(vuelo)
# Cerramos los precios del vuelo
vuelo.click()
info.append({'precios':precios, 'tiempos':tiempos , 'escalas': escalas})
return info
```
Ahora podemos cargar la página con el driver y pasárselo a esta función
```
driver = webdriver.Chrome(executable_path='../../chromedriver', options=options)
driver.get(url)
obtener_info(driver)
```
Se encontraron 0 vuelos porque la página no terminó de cargar
Lo más simple que podemos hacer es agregar una demora fija lo suficientemente grande para asegurarnos que la página terminó de cargar.
```
import time
options = webdriver.ChromeOptions()
options.add_argument('--incognito')
driver = webdriver.Chrome(executable_path='../../chromedriver', options=options)
driver.get(url)
time.sleep(10)
vuelos = driver.find_elements_by_xpath('//li[@class="flight"]')
vuelos
driver.close()
```
Esto funciona pero no es muy eficiente. Lo mejor sería esperar a que la página termine de cargar y luego recuperar los elementos.
```
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.support import expected_conditions as EC
from selenium.webdriver.common.by import By
from selenium.common.exceptions import TimeoutException
options = webdriver.ChromeOptions()
options.add_argument('--incognito')
driver = webdriver.Chrome(executable_path='../../chromedriver', options=options)
driver.get(url)
delay = 10
try:
vuelo = WebDriverWait(driver, delay).until(EC.presence_of_element_located((By.XPATH, '//li[@class="flight"]')))
print("La página terminó de cargar")
info_vuelos = obtener_info(driver)
except TimeoutException:
print("La página tardó demasiado en cargar")
driver.close()
info_vuelos
```
| github_jupyter |
## RIHAD VARIAWA, Data Scientist - Who has fun LEARNING, EXPLORING & GROWING
<h1>2D <code>Numpy</code> in Python</h1>
<p><strong>Welcome!</strong> This notebook will teach you about using <code>Numpy</code> in the Python Programming Language. By the end of this lab, you'll know what <code>Numpy</code> is and the <code>Numpy</code> operations.</p>
<h2>Table of Contents</h2>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<ul>
<li><a href="create">Create a 2D Numpy Array</a></li>
<li><a href="access">Accessing different elements of a Numpy Array</a></li>
<li><a href="op">Basic Operations</a></li>
</ul>
<p>
Estimated time needed: <strong>20 min</strong>
</p>
</div>
<hr>
<h2 id="create">Create a 2D Numpy Array</h2>
```
# Import the libraries
import numpy as np
import matplotlib.pyplot as plt
```
Consider the list <code>a</code>, the list contains three nested lists **each of equal size**.
```
# Create a list
a = [[11, 12, 13], [21, 22, 23], [31, 32, 33]]
a
```
We can cast the list to a Numpy Array as follow
```
# Convert list to Numpy Array
# Every element is the same type
A = np.array(a)
A
```
We can use the attribute <code>ndim</code> to obtain the number of axes or dimensions referred to as the rank.
```
# Show the numpy array dimensions
A.ndim
```
Attribute <code>shape</code> returns a tuple corresponding to the size or number of each dimension.
```
# Show the numpy array shape
A.shape
```
The total number of elements in the array is given by the attribute <code>size</code>.
```
# Show the numpy array size
A.size
```
<hr>
<h2 id="access">Accessing different elements of a Numpy Array</h2>
We can use rectangular brackets to access the different elements of the array. The correspondence between the rectangular brackets and the list and the rectangular representation is shown in the following figure for a 3x3 array:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoEg.png" width="500" />
We can access the 2nd-row 3rd column as shown in the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFT.png" width="400" />
We simply use the square brackets and the indices corresponding to the element we would like:
```
# Access the element on the second row and third column
A[1, 2]
```
We can also use the following notation to obtain the elements:
```
# Access the element on the second row and third column
A[1][2]
```
Consider the elements shown in the following figure
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFF.png" width="400" />
We can access the element as follows
```
# Access the element on the first row and first column
A[0][0]
```
We can also use slicing in numpy arrays. Consider the following figure. We would like to obtain the first two columns in the first row
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFSF.png" width="400" />
This can be done with the following syntax
```
# Access the element on the first row and first and second columns
A[0][0:2]
```
Similarly, we can obtain the first two rows of the 3rd column as follows:
```
# Access the element on the first and second rows and third column
A[0:2, 2]
```
Corresponding to the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoTST.png" width="400" />
<hr>
<h2 id="op">Basic Operations</h2>
We can also add arrays. The process is identical to matrix addition. Matrix addition of <code>X</code> and <code>Y</code> is shown in the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoAdd.png" width="500" />
The numpy array is given by <code>X</code> and <code>Y</code>
```
# Create a numpy array X
X = np.array([[1, 0], [0, 1]])
X
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
```
We can add the numpy arrays as follows.
```
# Add X and Y
Z = X + Y
Z
```
Multiplying a numpy array by a scaler is identical to multiplying a matrix by a scaler. If we multiply the matrix <code>Y</code> by the scaler 2, we simply multiply every element in the matrix by 2 as shown in the figure.
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoDb.png" width="500" />
We can perform the same operation in numpy as follows
```
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
# Multiply Y with 2
Z = 2 * Y
Z
```
Multiplication of two arrays corresponds to an element-wise product or Hadamard product. Consider matrix <code>X</code> and <code>Y</code>. The Hadamard product corresponds to multiplying each of the elements in the same position, i.e. multiplying elements contained in the same color boxes together. The result is a new matrix that is the same size as matrix <code>Y</code> or <code>X</code>, as shown in the following figure.
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoMul.png" width="500" />
We can perform element-wise product of the array <code>X</code> and <code>Y</code> as follows:
```
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
# Create a numpy array X
X = np.array([[1, 0], [0, 1]])
X
# Multiply X with Y
Z = X * Y
Z
```
We can also perform matrix multiplication with the numpy arrays <code>A</code> and <code>B</code> as follows:
First, we define matrix <code>A</code> and <code>B</code>:
```
# Create a matrix A
A = np.array([[0, 1, 1], [1, 0, 1]])
A
# Create a matrix B
B = np.array([[1, 1], [1, 1], [-1, 1]])
B
```
We use the numpy function <code>dot</code> to multiply the arrays together.
```
# Calculate the dot product
Z = np.dot(A,B)
Z
# Calculate the sine of Z
np.sin(Z)
```
We use the numpy attribute <code>T</code> to calculate the transposed matrix
```
# Create a matrix C
C = np.array([[1,1],[2,2],[3,3]])
C
# Get the transposed of C
C.T
```
<hr>
<h2>The last exercise!</h2>
<p>Congratulations, you have completed your first lesson and hands-on lab in Python. However, there is one more thing you need to do. The Data Science community encourages sharing work. The best way to share and showcase your work is to share it on GitHub. By sharing your notebook on GitHub you are not only building your reputation with fellow data scientists, but you can also show it off when applying for a job. Even though this was your first piece of work, it is never too early to start building good habits. So, please read and follow <a href="https://cognitiveclass.ai/blog/data-scientists-stand-out-by-sharing-your-notebooks/" target="_blank">this article</a> to learn how to share your work.
<hr>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<h2>Get IBM Watson Studio free of charge!</h2>
<p><a href="https://cocl.us/bottemNotebooksPython101Coursera"><img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Ad/BottomAd.png" width="750" align="center"></a></p>
</div>
<h3>About the Authors:</h3>
<p><a href="https://www.linkedin.com/in/joseph-s-50398b136/" target="_blank">Joseph Santarcangelo</a> is a Data Scientist at IBM, and holds a PhD in Electrical Engineering. His research focused on using Machine Learning, Signal Processing, and Computer Vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.</p>
Other contributors: <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
<hr>
<p>Copyright © 2018 IBM Developer Skills Network. This notebook and its source code are released under the terms of the <a href="https://cognitiveclass.ai/mit-license/">MIT License</a>.</p>
| github_jupyter |
# Master Notebook: Bosques aleatorios
Como ya vímos en scikit-learn gran parte de codigo es reciclable. Particularmente, leyendo variables y preparando los datos es lo mismo, independientemente del clasificador que usamos.
## Leyendo datos
Para que no esta tan aburrido (también para mi) esta vez nos vamos a escribir una función para leer los datos que podemos reciclar para otros datos.
```
import numpy as np
from collections import Counter
def lea_datos(archivo, i_clase=-1, encabezado=True, delim=","):
'''Una funcion para leer archivos con datos de clasificación.
Argumentos:
archivo - direccion del archivo
i_clase - indice de columna que contiene las clases.
default es -1 y significa la ultima fila.
header - si hay un encabezado
delim - que separa los datos
Regresa:
Un tuple de los datos, clases y cabezazo en caso que hay.'''
todo = np.loadtxt(archivo, dtype="S", delimiter=delim) # para csv
if(encabezado):
encabezado = todo[0,:]
todo = todo[1:,:]
else:
encabezado = None
clases = todo[:, i_clase]
datos = np.delete(todo, i_clase, axis=1)
print ("Clases")
for k,v in Counter(clases).items(): print (k,":",v)
return (datos, clases, encabezado)
```
Ahora importando datos se hace muy simple en el futuro. Para datos de csv con cabezazo por ejemplo:
```
datos, clases, encabezado = lea_datos("datos_peña.csv") # _ significa que no nos interesa este valor
clases.shape
```
## Balanceando datos
Normalizacion de datos no es necesario para bosques aleatorios o arboles porque son invariantes al respeto de los magnitudes de variables. Lo unico que podría ser un problema es los clases son imbalanceados bajo nuestra percepción. Esto significa que a veces ni esperamos que nuestros datos van a ser balanceados y, en este caso, es permisible dejarlos sin balancear porque queremos que el clasificador incluye este probabilidad "prior" de la vida real. Si por ejemplo clasifico por ejemplo evaluaciones del vino, puede ser que lo encuentro normal que muchos vinos tienen una evaluacion promedia y solamente poco una muy buena. Si quiero que mi clasificador también tenga esta "tendencía" no tengo que balancear.
En otro caso, si diseño una prueba para una enfermeda y no quiero que mi clasificador hace asumpciones sobre el estado del paciente no basados en mis variables, mejor balanceo.
Scikit-learn no llega con una función para balancear datos entonces porque no lo hacemos nosotros?
```
def balance(datos, clases, estrategia="down"):
'''Balancea unos datos así que cada clase aparece en las mismas proporciones.
Argumentos:
datos - los datos. Filas son muestras y columnas variables.
clases - las clases para cada muestra.
estrategia - "up" para up-scaling y "down" para down-scaling'''
import numpy as np
from collections import Counter
# Decidimos los nuevos numeros de muestras para cada clase
conteos = Counter(clases)
if estrategia=="up": muestras = max( conteos.values() )
else: muestras = min( conteos.values() )
datos_nuevo = np.array([]).reshape( 0, datos.shape[1] )
clases_nuevo = []
for c in conteos:
c_i = np.where(clases==c)[0]
new_i = np.random.choice(c_i, muestras, replace=(estrategia=="up") )
datos_nuevo = np.append( datos_nuevo, datos[new_i,:], axis=0 )
clases_nuevo = np.append( clases_nuevo, clases[new_i] )
return (datos_nuevo, clases_nuevo)
```
Y vamos a ver si funciona...
```
datos_b, clases_b = balance(datos, clases)
print Counter(clases_b)
print datos_b.shape
```
## Entrenando el bosque
Corriendo un bosque aleatorio para la clasificación es casi lo mismo como todos los otros clasificadores. Nada más importamos de una libreria diferente.
```
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(oob_score=True)
clf.fit(datos_b, clases_b)
print "Exactitud estimado:", clf.oob_score_
```
Ya sabemos que los hiper-parametros mas importantes para los bosques son el numero de arboles dado por `n_estimators` y la profundidad del arbol dado por `max_depth`. Porque son monotonos los podemos variar por separado.
```
%matplotlib inline
from sklearn.cross_validation import StratifiedKFold
from sklearn.grid_search import GridSearchCV
import matplotlib.pyplot as plt
cv = StratifiedKFold(y=clases, n_folds=4)
arboles_vals = np.arange(5,200,5)
busqueda = GridSearchCV(clf, param_grid=dict(n_estimators=arboles_vals), cv=cv)
busqueda.fit(datos, clases)
print 'Mejor numero de arboles=',busqueda.best_params_,',exactitud =',busqueda.best_score_
scores = [x[1] for x in busqueda.grid_scores_]
plt.plot(arboles_vals, scores)
plt.xlabel('C')
plt.ylabel('exactitud cv')
plt.show()
```
Y para la profundidad:
```
prof_vals = np.arange(1,12)
busqueda = GridSearchCV(clf, param_grid=dict(max_depth=prof_vals), cv=cv)
busqueda.fit(datos, clases)
print 'Mejor profundidad=',busqueda.best_params_,',exactitud =',busqueda.best_score_
scores = [x[1] for x in busqueda.grid_scores_]
plt.plot(prof_vals, scores)
plt.xlabel('profundidad maxima')
plt.ylabel('exactitud cv')
plt.show()
```
Viendo unas buenas valores podemos escoger un bosque con la menor numero de arboles y profundidad para una buena exactitud. También esta vez vamos a sacar las importancias de variables de una vez.
```
clf = RandomForestClassifier(n_estimators=101, oob_score=True)
clf.fit(datos, clases)
print "Exactitud estimada:", clf.oob_score_
print cabeza
print clf.feature_importances_
```
## Predecir nuevas variables
```
datos_test, clases_test, _ = lea_datos("titanic_test.csv")
clases_pred = clf.predict(datos_test)
print "Predicho:", clases_pred
print "Verdad: ", clases_test
```
| github_jupyter |
Initialize estimator class
```
from __future__ import annotations
from typing import NoReturn
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import RocCurveDisplay, accuracy_score
from IMLearn.base import BaseEstimator
import re
from copy import copy
from datetime import datetime
from typing import NoReturn
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import FunctionTransformer
from IMLearn import BaseEstimator
from challenge.agoda_cancellation_estimator import AgodaCancellationEstimator
class AgodaCancellationEstimator(BaseEstimator):
def __init__(self, threshold: float = None) -> AgodaCancellationEstimator:
super().__init__()
self.__fit_model: RandomForestClassifier = None
self.thresh = threshold
def get_params(self, deep=False):
return {'threshold': self.thresh}
def set_params(self, threshold) -> AgodaCancellationEstimator:
self.thresh = threshold
return self
def _fit(self, X: np.ndarray, y: np.ndarray) -> NoReturn:
self.__fit_model = RandomForestClassifier(random_state=0).fit(X, y)
def _predict(self, X: pd.DataFrame) -> np.ndarray:
probs = self.__fit_model.predict_proba(X)[:, 1]
return probs > self.thresh if self.thresh is not None else probs
def _loss(self, X: np.ndarray, y: np.ndarray) -> float:
pass
def plot_roc_curve(self, X: np.ndarray, y: np.ndarray):
RocCurveDisplay.from_estimator(self.__fit_model, X, y)
def score(self, X: pd.DataFrame, y: pd.Series):
return accuracy_score(y, self._predict(X))
```
Helper Functions
```
def read_data_file(path: str) -> pd.DataFrame:
return pd.read_csv(path).drop_duplicates() \
.astype({'checkout_date': 'datetime64',
'checkin_date': 'datetime64',
'hotel_live_date': 'datetime64',
'booking_datetime': 'datetime64'})
def get_days_between_dates(dates1: pd.Series, dates2: pd.Series):
return (dates1 - dates2).apply(lambda period: period.days)
def create_col_prob_mapper(col: str, mapper: dict):
mapper = copy(mapper)
def map_col_to_prob(df):
df[col] = df[col].apply(mapper.get)
return df
return map_col_to_prob
def add_categorical_prep_to_pipe(train_features: pd.DataFrame, pipeline: Pipeline, cat_vars: list, one_hot=False,
calc_probs=True) -> Pipeline:
assert one_hot ^ calc_probs, \
'Error: can only do either one-hot encoding or probability calculations, not neither/both!'
# one-hot encoding
if one_hot:
# TODO - use sklearn OneHotEncoder
pipeline.steps.append(('one-hot encoding',
FunctionTransformer(lambda df: pd.get_dummies(df, columns=cat_vars))))
# category probability preprocessing - make each category have its success percentage
if calc_probs:
for cat_var in cat_vars:
map_cat_to_prob: dict = train_features.groupby(cat_var, dropna=False).labels.mean().to_dict()
pipeline.steps.append((f'map {cat_var} to prob',
FunctionTransformer(create_col_prob_mapper(cat_var, map_cat_to_prob))))
return pipeline
def get_week_of_year(dates):
return dates.apply(lambda d: d.weekofyear)
def get_booked_on_weekend(dates):
return dates.apply(lambda d: d.day_of_week >= 4)
def get_weekend_holiday(in_date, out_date):
return list(map(lambda d: (d[1] - d[0]).days <= 3 and d[0].dayofweek >= 4, zip(in_date, out_date)))
def get_local_holiday(col1, col2):
return list(map(lambda x: x[0] == x[1], zip(col1, col2)))
def get_days_until_policy(policy_code: str) -> list:
policies = policy_code.split('_')
return [int(policy.split('D')[0]) if 'D' in policy else 0 for policy in policies]
def get_policy_cost(policy, stay_cost, stay_length, time_until_checkin):
"""
returns tuple of the format (max lost, min lost, part min lost)
"""
if policy == 'UNKNOWN':
return 0, 0, 0
nums = tuple(map(int, re.split('[a-zA-Z]', policy)[:-1]))
if 'D' not in policy: # no show is suppressed
return 0, 0, 0
if 'N' in policy:
nights_cost = stay_cost / stay_length * nums[0]
min_cost = nights_cost if time_until_checkin <= nums[1] else 0
return nights_cost, min_cost, min_cost / stay_cost
elif 'P' in policy:
nights_cost = stay_cost * nums[0] / 100
min_cost = nights_cost if time_until_checkin <= nums[1] else 0
return nights_cost, min_cost, min_cost / stay_cost
else:
raise Exception("Invalid Input")
def get_money_lost_per_policy(features: pd.Series) -> list:
policies = features.cancellation_policy_code.split('_')
stay_cost = features.original_selling_amount
stay_length = features.stay_length
time_until_checkin = features.booking_to_arrival_time
policy_cost = [get_policy_cost(policy, stay_cost, stay_length, time_until_checkin) for policy in policies]
return list(map(list, zip(*policy_cost)))
def add_cancellation_policy_features(features: pd.DataFrame) -> pd.DataFrame:
cancellation_policy = features.cancellation_policy_code
features['n_policies'] = cancellation_policy.apply(lambda policy: len(policy.split('_')))
days_until_policy = cancellation_policy.apply(get_days_until_policy)
features['min_policy_days'] = days_until_policy.apply(min)
features['max_policy_days'] = days_until_policy.apply(max)
x = features.apply(get_money_lost_per_policy, axis='columns')
features['max_policy_cost'], features['min_policy_cost'], features['part_min_policy_cost'] = list(
map(list, zip(*x)))
features['min_policy_cost'] = features['min_policy_cost'].apply(min)
features['part_min_policy_cost'] = features['part_min_policy_cost'].apply(min)
features['max_policy_cost'] = features['max_policy_cost'].apply(max)
return features
def add_time_based_cols(df: pd.DataFrame) -> pd.DataFrame:
df['stay_length'] = get_days_between_dates(df.checkout_date, df.checkin_date)
df['time_registered_pre_book'] = get_days_between_dates(df.checkin_date, df.hotel_live_date)
df['booking_to_arrival_time'] = get_days_between_dates(df.checkin_date, df.booking_datetime)
df['checkin_week_of_year'] = get_week_of_year(df.checkin_date)
df['booking_week_of_year'] = get_week_of_year(df.booking_datetime)
df['booked_on_weekend'] = get_booked_on_weekend(df.booking_datetime)
df['is_weekend_holiday'] = get_weekend_holiday(df.checkin_date, df.checkout_date)
df['is_local_holiday'] = get_local_holiday(df.origin_country_code, df.hotel_country_code)
return df
```
Define pipeline
```
def create_pipeline_from_data(filename: str):
NONE_OUTPUT_COLUMNS = ['checkin_date',
'checkout_date',
'booking_datetime',
'hotel_live_date',
'hotel_country_code',
'origin_country_code',
'cancellation_policy_code']
CATEGORICAL_COLUMNS = ['hotel_star_rating',
'guest_nationality_country_name',
'charge_option',
'accommadation_type_name',
'language',
'is_first_booking',
'customer_nationality',
'original_payment_currency',
'is_user_logged_in',
]
RELEVANT_COLUMNS = ['no_of_adults',
'no_of_children',
'no_of_extra_bed',
'no_of_room',
'original_selling_amount'] + NONE_OUTPUT_COLUMNS + CATEGORICAL_COLUMNS
features = read_data_file(filename)
features['labels'] = features["cancellation_datetime"].isna()
pipeline_steps = [('columns selector', FunctionTransformer(lambda df: df[RELEVANT_COLUMNS])),
('add time based columns', FunctionTransformer(add_time_based_cols)),
('add cancellation policy features', FunctionTransformer(add_cancellation_policy_features))
]
pipeline = Pipeline(pipeline_steps)
pipeline = add_categorical_prep_to_pipe(features, pipeline, CATEGORICAL_COLUMNS)
pipeline.steps.append( ('drop irrelevant columns', FunctionTransformer(lambda df: df.drop(NONE_OUTPUT_COLUMNS, axis='columns'))))
return features.drop('labels', axis='columns'), features.labels, pipeline
```
Train, predict and export
```
def evaluate_and_export(estimator: BaseEstimator, X: pd.DataFrame, filename: str):
preds = (~estimator.predict(X)).astype(int)
pd.DataFrame(preds, columns=["predicted_values"]).to_csv(filename, index=False)
def create_estimator_from_data(path="../datasets/agoda_cancellation_train.csv", threshold: float = 0.47,
optimize_threshold=False, debug=False) -> Pipeline:
np.random.seed(0)
# Load data
raw_df, cancellation_labels, pipeline = create_pipeline_from_data(path)
train_X = raw_df
train_y = cancellation_labels
train_X = pipeline.transform(train_X)
# Fit model over data
estimator = AgodaCancellationEstimator(threshold).fit(train_X, train_y)
pipeline.steps.append(('estimator', estimator))
return pipeline
def export_test_data(pipeline: Pipeline, path="../datasets/test_set_week_1.csv") -> NoReturn:
data = read_data_file(path)
# Store model predictions over test set
id1, id2, id3 = 209855253, 205843964, 212107536
evaluate_and_export(pipeline, data, f"{id1}_{id2}_{id3}.csv")
pipeline = create_estimator_from_data()
export_test_data(pipeline)
```
| github_jupyter |
```
# Let's keep our notebook clean, so it's a little more readable!
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
```
# Machine learning to predict age from rs-fmri
The goal is to extract data from several rs-fmri images, and use that data as features in a machine learning model. We will integrate what we've learned in the previous machine learning lecture to build an unbiased model and test it on a left out sample.
We're going to use a dataset that was prepared for this tutorial by [Elizabeth Dupre](https://elizabeth-dupre.com/#/), [Jake Vogel](https://github.com/illdopejake) and [Gael Varoquaux](http://gael-varoquaux.info/), by preprocessing [ds000228](https://openneuro.org/datasets/ds000228/versions/1.0.0) (from [Richardson et al. (2018)](https://dx.doi.org/10.1038%2Fs41467-018-03399-2)) through [fmriprep](https://github.com/poldracklab/fmriprep). They also created this tutorial and should be credited for it.
## Load the data
<img src="data/SampFeat.png" alt="terms" width="300"/>
```
# change this to the location where you downloaded the data
wdir = '/data/ml_tutorial/'
# Now fetch the data
from glob import glob
import os
data = sorted(glob(os.path.join(wdir,'*.gz')))
confounds = sorted(glob(os.path.join(wdir,'*regressors.tsv')))
```
How many individual subjects do we have?
```
#len(data.func)
len(data)
```
## Extract features

In order to do our machine learning, we will need to extract feature from our rs-fmri images.
Specifically, we will extract signals from a brain parcellation and compute a correlation matrix, representing regional coactivation between regions.
We will practice on one subject first, then we'll extract data for all subjects
#### Retrieve the atlas for extracting features and an example subject
Since we're using rs-fmri data, it makes sense to use an atlas defined using rs-fmri data
This paper has many excellent insights about what kind of atlas to use for an rs-fmri machine learning task. See in particular Figure 5.
https://www.sciencedirect.com/science/article/pii/S1053811919301594?via%3Dihub
Let's use the MIST atlas, created here in Montreal using the BASC method. This atlas has multiple resolutions, for larger networks or finer-grained ROIs. Let's use a 64-ROI atlas to allow some detail, but to ultimately keep our connectivity matrices manageable
Here is a link to the MIST paper: https://mniopenresearch.org/articles/1-3
```
from nilearn import datasets
parcellations = datasets.fetch_atlas_basc_multiscale_2015(version='sym')
atlas_filename = parcellations.scale064
print('Atlas ROIs are located in nifti image (4D) at: %s' %
atlas_filename)
```
Let's have a look at that atlas
```
from nilearn import plotting
plotting.plot_roi(atlas_filename, draw_cross=False)
```
Great, let's load an example 4D fmri time-series for one subject
```
fmri_filenames = data[0]
print(fmri_filenames)
```
Let's have a look at the image! Because it is a 4D image, we can only look at one slice at a time. Or, better yet, let's look at an average image!
```
from nilearn import image
averaged_Img = image.mean_img(image.mean_img(fmri_filenames))
plotting.plot_stat_map(averaged_Img)
```
#### Extract signals on a parcellation defined by labels
Using the NiftiLabelsMasker
So we've loaded our atlas and 4D data for a single subject. Let's practice extracting features!
```
from nilearn.input_data import NiftiLabelsMasker
masker = NiftiLabelsMasker(labels_img=atlas_filename, standardize=True,
memory='nilearn_cache', verbose=1)
# Here we go from nifti files to the signal time series in a numpy
# array. Note how we give confounds to be regressed out during signal
# extraction
conf = confounds[0]
time_series = masker.fit_transform(fmri_filenames, confounds=conf)
```
So what did we just create here?
```
type(time_series)
time_series.shape
```
What are these "confounds" and how are they used?
```
import pandas
conf_df = pandas.read_table(conf)
conf_df.head()
conf_df.shape
```
#### Compute and display a correlation matrix
```
from nilearn.connectome import ConnectivityMeasure
correlation_measure = ConnectivityMeasure(kind='correlation')
correlation_matrix = correlation_measure.fit_transform([time_series])[0]
correlation_matrix.shape
```
Plot the correlation matrix
```
import numpy as np
# Mask the main diagonal for visualization:
np.fill_diagonal(correlation_matrix, 0)
# The labels we have start with the background (0), hence we skip the
# first label
plotting.plot_matrix(correlation_matrix, figure=(10, 8),
labels=range(time_series.shape[-1]),
vmax=0.8, vmin=-0.8, reorder=False)
# matrices are ordered for block-like representation
```
#### Extract features from the whole dataset
Here, we are going to use a for loop to iterate through each image and use the same techniques we learned above to extract rs-fmri connectivity features from every subject.
```
# Here is a really simple for loop
for i in range(10):
print('the number is', i)
container = []
for i in range(10):
container.append(i)
container
```
Now lets construct a more complicated loop to do what we want
First we do some things we don't need to do in the loop. Let's reload our atlas, and re-initiate our masker and correlation_measure
```
from nilearn.input_data import NiftiLabelsMasker
from nilearn.connectome import ConnectivityMeasure
from nilearn import datasets
# load atlas
multiscale = datasets.fetch_atlas_basc_multiscale_2015()
atlas_filename = multiscale.scale064
# initialize masker (change verbosity)
masker = NiftiLabelsMasker(labels_img=atlas_filename, standardize=True,
memory='nilearn_cache', verbose=0)
# initialize correlation measure, set to vectorize
correlation_measure = ConnectivityMeasure(kind='correlation', vectorize=True,
discard_diagonal=True)
```
Okay -- now that we have that taken care of, let's run our big loop!
**NOTE**: On a laptop, this might a few minutes.
```
all_features = [] # here is where we will put the data (a container)
for i,sub in enumerate(data):
# extract the timeseries from the ROIs in the atlas
time_series = masker.fit_transform(sub, confounds=confounds[i])
# create a region x region correlation matrix
correlation_matrix = correlation_measure.fit_transform([time_series])[0]
# add to our container
all_features.append(correlation_matrix)
# keep track of status
print('finished %s of %s'%(i+1,len(data)))
# Let's save the data to disk
import numpy as np
np.savez_compressed('MAIN_BASC064_subsamp_features',a = all_features)
```
In case you do not want to run the full loop on your computer, you can load the output of the loop here!
```
feat_file = 'MAIN_BASC064_subsamp_features.npz'
X_features = np.load(feat_file)['a']
X_features.shape
```
<img src="data/SampFeat.png" alt="terms" width="300"/>
Okay so we've got our features.
We can visualize our feature matrix
```
import matplotlib.pyplot as plt
plt.imshow(X_features, aspect='auto')
plt.colorbar()
plt.title('feature matrix')
plt.xlabel('features')
plt.ylabel('subjects')
```
## Get Y (our target) and assess its distribution
```
# Let's load the phenotype data
pheno_path = os.path.join(wdir, 'participants.tsv')
import pandas
pheno = pandas.read_csv(pheno_path, sep='\t').sort_values('participant_id')
pheno.head()
```
Looks like there is a column labeling age. Let's capture it in a variable
```
y_age = pheno['Age']
```
Maybe we should have a look at the distribution of our target variable
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.distplot(y_age)
```
## Prepare data for machine learning
Here, we will define a "training sample" where we can play around with our models. We will also set aside a "validation" sample that we will not touch until the end
We want to be sure that our training and test sample are matched! We can do that with a "stratified split". This dataset has a variable indicating AgeGroup. We can use that to make sure our training and testing sets are balanced!
```
age_class = pheno['AgeGroup']
age_class.value_counts()
from sklearn.model_selection import train_test_split
# Split the sample to training/validation with a 60/40 ratio, and
# stratify by age class, and also shuffle the data.
X_train, X_val, y_train, y_val = train_test_split(
X_features, # x
y_age, # y
test_size = 0.4, # 60%/40% split
shuffle = True, # shuffle dataset
# before splitting
stratify = age_class, # keep
# distribution
# of ageclass
# consistent
# betw. train
# & test sets.
random_state = 123 # same shuffle each
# time
)
# print the size of our training and test groups
print('training:', len(X_train),
'testing:', len(X_val))
```
Let's visualize the distributions to be sure they are matched
```
sns.distplot(y_train)
sns.distplot(y_val)
```
## Run your first model!
Machine learning can get pretty fancy pretty quickly. We'll start with a fairly standard regression model called a Support Vector Regressor (SVR).
While this may seem unambitious, simple models can be very robust. And we probably don't have enough data to create more complex models (but we can try later).
For more information, see this excellent resource:
https://hal.inria.fr/hal-01824205
Let's fit our first model!
```
from sklearn.svm import SVR
l_svr = SVR(kernel='linear') # define the model
l_svr.fit(X_train, y_train) # fit the model
```
Well... that was easy. Let's see how well the model learned the data!
<img src="data/modval.png" alt="terms" width="800"/>
```
# predict the training data based on the model
y_pred = l_svr.predict(X_train)
# caluclate the model accuracy
acc = l_svr.score(X_train, y_train)
```
Let's view our results and plot them all at once!
```
# print results
print('accuracy (R2)', acc)
sns.regplot(y_pred,y_train)
plt.xlabel('Predicted Age')
```
HOLY COW! Machine learning is amazing!!! Almost a perfect fit!
...which means there's something wrong. What's the problem here?
```
from sklearn.model_selection import train_test_split
# Split the sample to training/test with a 75/25 ratio, and
# stratify by age class, and also shuffle the data.
age_class2 = pheno.loc[y_train.index,'AgeGroup']
X_train2, X_test, y_train2, y_test = train_test_split(
X_train, # x
y_train, # y
test_size = 0.25, # 75%/25% split
shuffle = True, # shuffle dataset
# before splitting
stratify = age_class2, # keep
# distribution
# of ageclass
# consistent
# betw. train
# & test sets.
random_state = 123 # same shuffle each
# time
)
# print the size of our training and test groups
print('training:', len(X_train2),
'testing:', len(X_test))
from sklearn.metrics import mean_absolute_error
# fit model just to training data
l_svr.fit(X_train2,y_train2)
# predict the *test* data based on the model trained on X_train2
y_pred = l_svr.predict(X_test)
# caluclate the model accuracy
acc = l_svr.score(X_test, y_test)
mae = mean_absolute_error(y_true=y_test,y_pred=y_pred)
# print results
print('accuracy (R2) = ', acc)
print('MAE = ',mae)
sns.regplot(y_pred,y_test)
plt.xlabel('Predicted Age')
```
Not perfect, but as predicting with unseen data goes, not too bad! Especially with a training sample of "only" 69 subjects. But we can do better!
For example, we can increase the size our training set while simultaneously reducing bias by instead using 10-fold cross-validation
<img src="data/KCV.png" alt="terms" width="500"/>
```
from sklearn.model_selection import cross_val_predict, cross_val_score
# predict
y_pred = cross_val_predict(l_svr, X_train, y_train, cv=10)
# scores
acc = cross_val_score(l_svr, X_train, y_train, cv=10)
mae = cross_val_score(l_svr, X_train, y_train, cv=10, scoring='neg_mean_absolute_error')
```
We can look at the accuracy of the predictions for each fold of the cross-validation
```
for i in range(10):
print('Fold {} -- Acc = {}, MAE = {}'.format(i, acc[i],-mae[i]))
```
We can also look at the overall accuracy of the model
```
from sklearn.metrics import r2_score
overall_acc = r2_score(y_train, y_pred)
overall_mae = mean_absolute_error(y_train,y_pred)
print('R2:',overall_acc)
print('MAE:',overall_mae)
sns.regplot(y_pred, y_train)
plt.xlabel('Predicted Age')
```
Not too bad at all! But more importantly, this is a more accurate estimation of our model's predictive efficacy. Our sample size is larger and this is based on several rounds of prediction of unseen data.
For example, we can now see that the effect is being driven by the model's successful parsing of adults vs. children, but is not performing so well within the adult or children group. This was not evident during our previous iteration of the model
## Tweak your model
It's very important to learn when and where its appropriate to "tweak" your model.
Since we have done all of the previous analysis in our training data, it's fine to try out different models. But we **absolutely cannot** "test" it on our left out data. If we do, we are in great danger of overfitting.
It is not uncommon to try other models, or tweak hyperparameters. In this case, due to our relatively small sample size, we are probably not powered sufficiently to do so, and we would once again risk overfitting. However, for the sake of demonstration, we will do some tweaking.
<img src="data/KCV2.png" alt="terms" width="500"/>
We will try a few different examples:
* Normalizing our target data
* Tweaking our hyperparameters
* Trying a more complicated model
* Feature selection
#### Normalize the target data
```
# Create a log transformer function and log transform Y (age)
from sklearn.preprocessing import FunctionTransformer
log_transformer = FunctionTransformer(func = np.log, validate=True)
log_transformer.fit(y_train.values.reshape(-1,1))
y_train_log = log_transformer.transform(y_train.values.reshape(-1,1))[:,0]
sns.distplot(y_train_log)
plt.title("Log-Transformed Age")
```
Now let's go ahead and cross-validate our model once again with this new log-transformed target
```
# predict
y_pred = cross_val_predict(l_svr, X_train, y_train_log, cv=10)
# scores
acc = r2_score(y_train_log, y_pred)
mae = mean_absolute_error(y_train_log,y_pred)
print('R2:',acc)
print('MAE:',mae)
sns.regplot(y_pred, y_train_log)
plt.xlabel('Predicted Log Age')
plt.ylabel('Log Age')
```
Seems like a definite improvement, right? I think we can agree on that.
But we can't forget about interpretability? The MAE is much less interpretable now.
#### Tweak the hyperparameters
Many machine learning algorithms have hyperparameters that can be "tuned" to optimize model fitting. Careful parameter tuning can really improve a model, but haphazard tuning will often lead to overfitting.
Our SVR model has multiple hyperparameters. Let's explore some approaches for tuning them
```
SVR?
```
One way is to plot a "Validation Curve" -- this will let us view changes in training and validation accuracy of a model as we shift its hyperparameters. We can do this easily with sklearn.
```
from sklearn.model_selection import validation_curve
C_range = 10. ** np.arange(-3, 8) # A range of different values for C
train_scores, valid_scores = validation_curve(l_svr, X_train, y_train_log,
param_name= "C",
param_range = C_range,
cv=10)
# A bit of pandas magic to prepare the data for a seaborn plot
tScores = pandas.DataFrame(train_scores).stack().reset_index()
tScores.columns = ['C','Fold','Score']
tScores.loc[:,'Type'] = ['Train' for x in range(len(tScores))]
vScores = pandas.DataFrame(valid_scores).stack().reset_index()
vScores.columns = ['C','Fold','Score']
vScores.loc[:,'Type'] = ['Validate' for x in range(len(vScores))]
ValCurves = pandas.concat([tScores,vScores]).reset_index(drop=True)
ValCurves.head()
# And plot!
# g = sns.lineplot(x='C',y='Score',hue='Type',data=ValCurves)
# g.set_xticks(range(10))
# g.set_xticklabels(C_range, rotation=90)
g = sns.factorplot(x='C',y='Score',hue='Type',data=ValCurves)
plt.xticks(range(10))
g.set_xticklabels(C_range, rotation=90)
```
It looks like accuracy is better for higher values of C, and plateaus somewhere between 0.1 and 1. The default setting is C=1, so it looks like we can't really improve by changing C.
But our SVR model actually has two hyperparameters, C and epsilon. Perhaps there is an optimal combination of settings for these two parameters.
We can explore that somewhat quickly with a grid search, which is once again easily achieved with sklearn. Because we are fitting the model multiple times witih cross-validation, this will take some time
```
from sklearn.model_selection import GridSearchCV
C_range = 10. ** np.arange(-3, 8)
epsilon_range = 10. ** np.arange(-3, 8)
param_grid = dict(epsilon=epsilon_range, C=C_range)
grid = GridSearchCV(l_svr, param_grid=param_grid, cv=10)
grid.fit(X_train, y_train_log)
```
Now that the grid search has completed, let's find out what was the "best" parameter combination
```
print(grid.best_params_)
```
And if redo our cross-validation with this parameter set?
```
y_pred = cross_val_predict(SVR(kernel='linear',C=0.10,epsilon=0.10, gamma='auto'),
X_train, y_train_log, cv=10)
# scores
acc = r2_score(y_train_log, y_pred)
mae = mean_absolute_error(y_train_log,y_pred)
print('R2:',acc)
print('MAE:',mae)
sns.regplot(y_pred, y_train_log)
plt.xlabel('Predicted Log Age')
plt.ylabel('Log Age')
```
Perhaps unsurprisingly, the model fit is actually exactly the same as what we had with our defaults. There's a reason they are defaults ;-)
Grid search can be a powerful and useful tool. But can you think of a way that, if not properly utilized, it could lead to overfitting?
You can find a nice set of tutorials with links to very helpful content regarding how to tune hyperparameters and while be aware of over- and under-fitting here:
https://scikit-learn.org/stable/modules/learning_curve.html
#### Trying a more complicated model
In principle, there is no real reason to do this. Perhaps one could make an argument for quadratic relationship with age, but we probably don't have enough subjects to learn a complicated non-linear model. But for the sake of demonstration, we can give it a shot.
We'll use a validation curve to see the result of our model if, instead of fitting a linear model, we instead try to the fit a 2nd, 3rd, ... 8th order polynomial.
```
validation_curve?
from sklearn.model_selection import validation_curve
degree_range = list(range(1,8)) # A range of different values for C
train_scores, valid_scores = validation_curve(SVR(kernel='poly',
gamma='scale'
),
X=X_train, y=y_train_log,
param_name= "degree",
param_range = degree_range,
cv=10)
# A bit of pandas magic to prepare the data for a seaborn plot
tScores = pandas.DataFrame(train_scores).stack().reset_index()
tScores.columns = ['Degree','Fold','Score']
tScores.loc[:,'Type'] = ['Train' for x in range(len(tScores))]
vScores = pandas.DataFrame(valid_scores).stack().reset_index()
vScores.columns = ['Degree','Fold','Score']
vScores.loc[:,'Type'] = ['Validate' for x in range(len(vScores))]
ValCurves = pandas.concat([tScores,vScores]).reset_index(drop=True)
ValCurves.head()
# And plot!
# g = sns.lineplot(x='Degree',y='Score',hue='Type',data=ValCurves)
# g.set_xticks(range(10))
# g.set_xticklabels(degree_range, rotation=90)
g = sns.factorplot(x='Degree',y='Score',hue='Type',data=ValCurves)
plt.xticks(range(10))
g.set_xticklabels(degree_range, rotation=90)
```
It appears that we cannot improve our model by increasing the complexity of the fit. If one looked only at the training data, one might surmise that a 2nd order fit could be a slightly better model. But that improvement does not generalize to the validation data.
```
# y_pred = cross_val_predict(SVR(kernel='rbf', gamma='scale'), X_train, y_train_log, cv=10)
# # scores
# acc = r2_score(y_train_log, y_pred)
# mae = mean_absolute_error(y_train_log,y_pred)
# print('R2:',acc)
# print('MAE:',mae)
# sns.regplot(y_pred, y_train_log)
# plt.xlabel('Predicted Log Age')
# plt.ylabel('Log Age')
```
#### Feature selection
Right now, we have 2016 features. Are all of those really going to contribute to the model stably?
Intuitively, models tend to perform better when there are fewer, more important features than when there are many, less imortant features. The tough part is figuring out which features are useful or important.
Here will quickly try a basic feature seclection strategy
<img src="data/FeatSel.png" alt="terms" width="400"/>
The SelectPercentile() function will select the top X% of features based on univariate tests. This is a way of identifying theoretically more useful features. But remember, significance != prediction!
We are also in danger of overfitting here. For starters, if we want to test this with 10-fold cross-validation, we will need to do a separate feature selection within each fold! That means we'll need to do the cross-validation manually instead of using cross_val_predict().
```
from sklearn.feature_selection import SelectPercentile, f_regression
from sklearn.model_selection import KFold
from sklearn.pipeline import Pipeline
# Build a tiny pipeline that does feature selection (top 20% of features),
# and then prediction with our linear svr model.
model = Pipeline([
('feature_selection',SelectPercentile(f_regression,percentile=20)),
('prediction', l_svr)
])
y_pred = [] # a container to catch the predictions from each fold
y_index = [] # just in case, the index for each prediciton
# First we create 10 splits of the data
skf = KFold(n_splits=10, shuffle=True, random_state=123)
# For each split, assemble the train and test samples
for tr_ind, te_ind in skf.split(X_train):
X_tr = X_train[tr_ind]
y_tr = y_train_log[tr_ind]
X_te = X_train[te_ind]
y_index += list(te_ind) # store the index of samples to predict
# and run our pipeline
model.fit(X_tr, y_tr) # fit the data to the model using our mini pipeline
predictions = model.predict(X_te).tolist() # get the predictions for this fold
y_pred += predictions # add them to the list of predictions
```
Alrighty, let's see if only using the top 20% of features improves the model at all...
```
acc = r2_score(y_train_log[y_index], y_pred)
mae = mean_absolute_error(y_train_log[y_index],y_pred)
print('R2:',acc)
print('MAE:',mae)
sns.regplot(np.array(y_pred), y_train_log[y_index])
plt.xlabel('Predicted Log Age')
plt.ylabel('Log Age')
```
Nope, in fact it got a bit worse. It seems we're getting "value at the margins" so to speak. This is a very good example of how significance != prediction, as demonstrated in this figure from Bzdok et al., 2018 *bioRxiv*

See here for an explanation of different feature selection options and how to implement them in sklearn: https://scikit-learn.org/stable/modules/feature_selection.html
And here is a thoughtful tutorial covering feature selection for novel machine learners: https://www.datacamp.com/community/tutorials/feature-selection-python
So there you have it. We've tried many different strategies, but most of our "tweaks" haven't really lead to improvements in the model. This is not always the case, but it is not uncommon. Can you think of some reasons why?
Moving on to our validation data, we probably should just stick to a basic model, though predicting log age might be a good idea!
## Can our model predict age in completely un-seen data?
Now that we've fit a model we think has possibly learned how to decode age based on rs-fmri signal, let's put it to the test. We will train our model on all of the training data, and try to predict the age of the subjects we left out at the beginning of this section.
Because we performed a log transformation on our training data, we will need to transform our testing data using the *same information!* But that's easy because we stored our transformation in an object!
```
# Notice how we use the Scaler that was fit to X_train and apply to X_test,
# rather than creating a new Scaler for X_test
y_val_log = log_transformer.transform(y_val.values.reshape(-1,1))[:,0]
```
And now for the moment of truth!
No cross-validation needed here. We simply fit the model with the training data and use it to predict the testing data
I'm so nervous. Let's just do it all in one cell
```
l_svr.fit(X_train, y_train_log) # fit to training data
y_pred = l_svr.predict(X_val) # classify age class using testing data
acc = l_svr.score(X_val, y_val_log) # get accuracy (r2)
mae = mean_absolute_error(y_val_log, y_pred) # get mae
# print results
print('accuracy (r2) =', acc)
print('mae = ',mae)
# plot results
sns.regplot(y_pred, y_val_log)
plt.xlabel('Predicted Log Age')
plt.ylabel('Log Age')
```
***Wow!!*** Congratulations. You just trained a machine learning model that used real rs-fmri data to predict the age of real humans.
The proper thing to do at this point would be to repeat the train-validation split multiple times. This will ensure the results are not specific to this validation set, and will give you some confidence intervals around your results.
As an assignment, you can give that a try below. Create 10 different splits of the entire dataset, fit the model and get your predictions. Then, plot the range of predictions.
```
# SPACE FOR YOUR ASSIGNMENT
```
So, it seems like something in this data does seem to be systematically related to age ... but what?
#### Interpreting model feature importances
Interpreting the feature importances of a machine learning model is a real can of worms. This is an area of active research. Unfortunately, it's hard to trust the feature importance of some models.
You can find a whole tutorial on this subject here:
http://gael-varoquaux.info/interpreting_ml_tuto/index.html
For now, we'll just eschew better judgement and take a look at our feature importances. While we can't ascribe any biological relevance to the features, it can still be helpful to know what the model is using to make its predictions. This is a good way to, for example, establish whether your model is actually learning based on a confound! Could you think of some examples?
We can access the feature importances (weights) used my the model
```
l_svr.coef_
```
lets plot these weights to see their distribution better
```
plt.bar(range(l_svr.coef_.shape[-1]),l_svr.coef_[0])
plt.title('feature importances')
plt.xlabel('feature')
plt.ylabel('weight')
```
Or perhaps it will be easier to visualize this information as a matrix similar to the one we started with
We can use the correlation measure from before to perform an inverse transform
```
correlation_measure.inverse_transform(l_svr.coef_).shape
from nilearn import plotting
feat_exp_matrix = correlation_measure.inverse_transform(l_svr.coef_)[0]
plotting.plot_matrix(feat_exp_matrix, figure=(10, 8),
labels=range(feat_exp_matrix.shape[0]),
reorder=False,
tri='lower')
```
Let's see if we can throw those features onto an actual brain.
First, we'll need to gather the coordinates of each ROI of our atlas
```
coords = plotting.find_parcellation_cut_coords(atlas_filename)
```
And now we can use our feature matrix and the wonders of nilearn to create a connectome map where each node is an ROI, and each connection is weighted by the importance of the feature to the model
```
plotting.plot_connectome(feat_exp_matrix, coords, colorbar=True)
```
Whoa!! That's...a lot to process. Maybe let's threshold the edges so that only the most important connections are visualized
```
plotting.plot_connectome(feat_exp_matrix, coords, colorbar=True, edge_threshold=0.035)
```
That's definitely an improvement, but it's still a bit hard to see what's going on.
Nilearn has a new feature that let's use view this data interactively!
```
plotting.view_connectome(feat_exp_matrix, coords, threshold='98%')
```
| github_jupyter |
<!--NAVIGATION-->
< [Errors and Exceptions](09-Errors-and-Exceptions.ipynb) | [Contents](Index.ipynb) | [List Comprehensions](11-List-Comprehensions.ipynb) >
# Iterators
Often an important piece of data analysis is repeating a similar calculation, over and over, in an automated fashion.
For example, you may have a table of a names that you'd like to split into first and last, or perhaps of dates that you'd like to convert to some standard format.
One of Python's answers to this is the *iterator* syntax.
We've seen this already with the ``range`` iterator:
```
for i in range(10):
print(i, end=' ')
```
Here we're going to dig a bit deeper.
It turns out that in Python 3, ``range`` is not a list, but is something called an *iterator*, and learning how it works is key to understanding a wide class of very useful Python functionality.
## Iterating over lists
Iterators are perhaps most easily understood in the concrete case of iterating through a list.
Consider the following:
```
for value in [2, 4, 6, 8, 10]:
# do some operation
print(value + 1, end=' ')
```
The familiar "``for x in y``" syntax allows us to repeat some operation for each value in the list.
The fact that the syntax of the code is so close to its English description ("*for [each] value in [the] list*") is just one of the syntactic choices that makes Python such an intuitive language to learn and use.
But the face-value behavior is not what's *really* happening.
When you write something like "``for val in L``", the Python interpreter checks whether it has an *iterator* interface, which you can check yourself with the built-in ``iter`` function:
```
iter([2, 4, 6, 8, 10])
```
It is this iterator object that provides the functionality required by the ``for`` loop.
The ``iter`` object is a container that gives you access to the next object for as long as it's valid, which can be seen with the built-in function ``next``:
```
I = iter([2, 4, 6, 8, 10])
print(next(I))
print(next(I))
print(next(I))
```
What is the purpose of this level of indirection?
Well, it turns out this is incredibly useful, because it allows Python to treat things as lists that are *not actually lists*.
## ``range()``: A List Is Not Always a List
Perhaps the most common example of this indirect iteration is the ``range()`` function in Python 3 (named ``xrange()`` in Python 2), which returns not a list, but a special ``range()`` object:
```
range(10)
```
``range``, like a list, exposes an iterator:
```
iter(range(10))
```
So Python knows to treat it *as if* it's a list:
```
for i in range(10):
print(i, end=' ')
```
The benefit of the iterator indirection is that *the full list is never explicitly created!*
We can see this by doing a range calculation that would overwhelm our system memory if we actually instantiated it (note that in Python 2, ``range`` creates a list, so running the following will not lead to good things!):
```
N = 10 ** 12
for i in range(N):
if i >= 10: break
print(i, end=', ')
```
If ``range`` were to actually create that list of one trillion values, it would occupy tens of terabytes of machine memory: a waste, given the fact that we're ignoring all but the first 10 values!
In fact, there's no reason that iterators ever have to end at all!
Python's ``itertools`` library contains a ``count`` function that acts as an infinite range:
```
from itertools import count
for i in count():
if i >= 10:
break
print(i, end=', ')
```
Had we not thrown-in a loop break here, it would go on happily counting until the process is manually interrupted or killed (using, for example, ``ctrl-C``).
## Useful Iterators
This iterator syntax is used nearly universally in Python built-in types as well as the more data science-specific objects we'll explore in later sections.
Here we'll cover some of the more useful iterators in the Python language:
### ``enumerate``
Often you need to iterate not only the values in an array, but also keep track of the index.
You might be tempted to do things this way:
```
L = [2, 4, 6, 8, 10]
for i in range(len(L)):
print(i, L[i])
```
Although this does work, Python provides a cleaner syntax using the ``enumerate`` iterator:
```
for i, val in enumerate(L):
print(i, val)
```
This is the more "Pythonic" way to enumerate the indices and values in a list.
### ``zip``
Other times, you may have multiple lists that you want to iterate over simultaneously.
You could certainly iterate over the index as in the non-Pythonic example we looked at previously, but it is better to use the ``zip`` iterator, which zips together iterables:
```
L = [2, 4, 6, 8, 10]
R = [3, 6, 9, 12, 15]
for lval, rval in zip(L, R):
print(lval, rval)
```
Any number of iterables can be zipped together, and if they are different lengths, the shortest will determine the length of the ``zip``.
### ``map`` and ``filter``
The ``map`` iterator takes a function and applies it to the values in an iterator:
```
# find the first 10 square numbers
square = lambda x: x ** 2
for val in map(square, range(10)):
print(val, end=' ')
```
The ``filter`` iterator looks similar, except it only passes-through values for which the filter function evaluates to True:
```
# find values up to 10 for which x % 2 is zero
is_even = lambda x: x % 2 == 0
for val in filter(is_even, range(10)):
print(val, end=' ')
```
The ``map`` and ``filter`` functions, along with the ``reduce`` function (which lives in Python's ``functools`` module) are fundamental components of the *functional programming* style, which, while not a dominant programming style in the Python world, has its outspoken proponents (see, for example, the [pytoolz](https://toolz.readthedocs.org/en/latest/) library).
### Iterators as function arguments
We saw in [``*args`` and ``**kwargs``: Flexible Arguments](#*args-and-**kwargs:-Flexible-Arguments). that ``*args`` and ``**kwargs`` can be used to pass sequences and dictionaries to functions.
It turns out that the ``*args`` syntax works not just with sequences, but with any iterator:
```
print(*range(10))
```
So, for example, we can get tricky and compress the ``map`` example from before into the following:
```
print(*map(lambda x: x ** 2, range(10)))
```
Using this trick lets us answer the age-old question that comes up in Python learners' forums: why is there no ``unzip()`` function which does the opposite of ``zip()``?
If you lock yourself in a dark closet and think about it for a while, you might realize that the opposite of ``zip()`` is... ``zip()``! The key is that ``zip()`` can zip-together any number of iterators or sequences. Observe:
```
L1 = (1, 2, 3, 4)
L2 = ('a', 'b', 'c', 'd')
z = zip(L1, L2)
print(*z)
z = zip(L1, L2)
new_L1, new_L2 = zip(*z)
print(new_L1, new_L2)
```
Ponder this for a while. If you understand why it works, you'll have come a long way in understanding Python iterators!
## Specialized Iterators: ``itertools``
We briefly looked at the infinite ``range`` iterator, ``itertools.count``.
The ``itertools`` module contains a whole host of useful iterators; it's well worth your while to explore the module to see what's available.
As an example, consider the ``itertools.permutations`` function, which iterates over all permutations of a sequence:
```
from itertools import permutations
p = permutations(range(3))
print(*p)
```
Similarly, the ``itertools.combinations`` function iterates over all unique combinations of ``N`` values within a list:
```
from itertools import combinations
c = combinations(range(4), 2)
print(*c)
```
Somewhat related is the ``product`` iterator, which iterates over all sets of pairs between two or more iterables:
```
from itertools import product
p = product('ab', range(3))
print(*p)
```
Many more useful iterators exist in ``itertools``: the full list can be found, along with some examples, in Python's [online documentation](https://docs.python.org/3.5/library/itertools.html).
<!--NAVIGATION-->
< [Errors and Exceptions](09-Errors-and-Exceptions.ipynb) | [Contents](Index.ipynb) | [List Comprehensions](11-List-Comprehensions.ipynb) >
| github_jupyter |
###### Content under Creative Commons Attribution license CC-BY 4.0, code under MIT license (c)2014 L.A. Barba, G.F. Forsyth, C.D. Cooper.
# Spreading out
We're back! This is the fourth notebook of _Spreading out: parabolic PDEs,_ Module 4 of the course [**"Practical Numerical Methods with Python"**](https://openedx.seas.gwu.edu/courses/course-v1:MAE+MAE6286+2017/about).
In the [previous notebook](https://nbviewer.jupyter.org/github/numerical-mooc/numerical-mooc/blob/master/lessons/04_spreadout/04_03_Heat_Equation_2D_Explicit.ipynb), we solved a 2D problem for the first time, using an explicit scheme. We know explicit schemes have stability constraints that might make them impractical in some cases, due to requiring a very small time step. Implicit schemes are unconditionally stable, offering the advantage of larger time steps; in [notebook 2](https://nbviewer.jupyter.org/github/numerical-mooc/numerical-mooc/blob/master/lessons/04_spreadout/04_02_Heat_Equation_1D_Implicit.ipynb), we look at the 1D implicit solution of diffusion. Already, that was quite a lot of work: setting up a matrix of coefficients and a right-hand-side vector, while taking care of the boundary conditions, and then solving the linear system. And now, we want to do implicit schemes in 2D—are you ready for this challenge?
## 2D Heat conduction
We already studied 2D heat conduction in the previous lesson, but now we want to work out how to build an implicit solution scheme. To refresh your memory, here is the heat equation again:
$$
\begin{equation}
\frac{\partial T}{\partial t} = \alpha \left(\frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} \right)
\end{equation}
$$
Our previous solution used a Dirichlet boundary condition on the left and bottom boundaries, with $T(x=0)=T(y=0)=100$, and a Neumann boundary condition with zero flux on the top and right edges, with $q_x=q_y=0$.
$$
\left( \left.\frac{\partial T}{\partial y}\right|_{y=0.1} = q_y \right) \quad \text{and} \quad \left( \left.\frac{\partial T}{\partial x}\right|_{x=0.1} = q_x \right)
$$
Figure 1 shows a sketch of the problem set up for our hypothetical computer chip with two hot edges and two insulated edges.
#### <img src="./figures/2dchip.svg" width="400px"> Figure 1: Simplified microchip problem setup.
### Implicit schemes in 2D
An implicit discretization will evaluate the spatial derivatives at the next time level, $t^{n+1}$, using the unknown values of the solution variable. For the 2D heat equation with central difference in space, that is written as:
$$
\begin{equation}
\begin{split}
& \frac{T^{n+1}_{i,j} - T^n_{i,j}}{\Delta t} = \\
& \quad \alpha \left( \frac{T^{n+1}_{i+1, j} - 2T^{n+1}_{i,j} + T^{n+1}_{i-1,j}}{\Delta x^2} + \frac{T^{n+1}_{i, j+1} - 2T^{n+1}_{i,j} + T^{n+1}_{i,j-1}}{\Delta y^2} \right) \\
\end{split}
\end{equation}
$$
This equation looks better when we put what we *don't know* on the left and what we *do know* on the right. Make sure to work this out yourself on a piece of paper.
$$
\begin{equation}
\begin{split}
& -\frac{\alpha \Delta t}{\Delta x^2} \left( T^{n+1}_{i-1,j} + T^{n+1}_{i+1,j} \right) + \left( 1 + 2 \frac{\alpha \Delta t}{\Delta x^2} + 2 \frac{\alpha \Delta t}{\Delta y^2} \right) T^{n+1}_{i,j} \\
& \quad \quad \quad -\frac{\alpha \Delta t}{\Delta y^2} \left( T^{n+1}_{i,j-1} + T^{n+1}_{i,j+1} \right) = T^n_{i,j} \\
\end{split}
\end{equation}
$$
To make this discussion easier, let's assume that the mesh spacing is the same in both directions and $\Delta x=\Delta y = \delta$:
$$
\begin{equation}
-T^{n+1}_{i-1,j} - T^{n+1}_{i+1,j} + \left(\frac{\delta^2}{\alpha \Delta t} + 4 \right) T^{n+1}_{i,j} - T^{n+1}_{i,j-1}-T^{n+1}_{i,j+1} = \frac{\delta^2}{\alpha \Delta t}T^n_{i,j}
\end{equation}
$$
Just like in the one-dimensional case, $T_{i,j}$ appears in the equation for $T_{i-1,j}$, $T_{i+1,j}$, $T_{i,j+1}$ and $T_{i,j-1}$, and we can form a linear system to advance in time. But, how do we construct the matrix in this case? What are the $(i+1,j)$, $(i-1,j)$, $(i,j+1)$, and $(i,j-1)$ positions in the matrix?
With explicit schemes we don't need to worry about these things. We can lay out the data just as it is in the physical problem. We had an array `T` that was a 2-dimensional matrix. To fetch the temperature in the next node in the $x$ direction $(T_{i+1,j})$ we just did `T[j,i+1]`, and likewise in the $y$ direction $(T_{i,j+1})$ was in `T[j+1,i]`. In implicit schemes, we need to think a bit harder about how the data is mapped to the physical problem.
Also, remember from the [notebook on 1D-implicit schemes](https://nbviewer.jupyter.org/github/numerical-mooc/numerical-mooc/blob/master/lessons/04_spreadout/04_02_Heat_Equation_1D_Implicit.ipynb) that the linear system had $N-2$ elements? We applied boundary conditions on nodes $i=0$ and $i=N-1$, and they were not modified by the linear system. In 2D, this becomes a bit more complicated.
Let's use Figure 1, representing a set of grid nodes in two dimensions, to guide the discussion.
#### <img src="./figures/2D_discretization.png"> Figure 2: Layout of matrix elements in 2D problem
Say we have the 2D domain of size $L_x\times L_y$ discretized in $n_x$ and $n_y$ points. We can divide the nodes into boundary nodes (empty circles) and interior nodes (filled circles).
The boundary nodes, as the name says, are on the boundary. They are the nodes with indices $(i=0,j)$, $(i=n_x-1,j)$, $(i,j=0)$, and $(i,j=n_y-1)$, and boundary conditions are enforced there.
The interior nodes are not on the boundary, and the finite-difference equation acts on them. If we leave the boundary nodes aside for the moment, then the grid will have $(n_x-2)\cdot(n_y-2)$ nodes that need to be updated on each time step. This is the number of unknowns in the linear system. The matrix of coefficients will have $\left( (n_x-2)\cdot(n_y-2) \right)^2$ elements (most of them zero!).
To construct the matrix, we will iterate over the nodes in an x-major order: index $i$ will run faster. The order will be
* $(i=1,j=1)$
* $(i=2,j=1)$ ...
* $(i=nx-2,j=1)$
* $(i=1,j=2)$
* $(i=2,j=2)$ ...
* $(i=n_x-2,j=n_y-2)$.
That is the ordering represented by dotted line on Figure 1. Of course, if you prefer to organize the nodes differently, feel free to do so!
Because we chose this ordering, the equation for nodes $(i-1,j)$ and $(i+1,j)$ will be just before and after $(i,j)$, respectively. But what about $(i,j-1)$ and $(i,j+1)$? Even though in the physical problem they are very close, the equations are $n_x-2$ places apart! This can tie your head in knots pretty quickly.
_The only way to truly understand it is to make your own diagrams and annotations on a piece of paper and reconstruct this argument!_
### Boundary conditions
Before we attempt to build the matrix, we need to think about boundary conditions. There is some bookkeeping to be done here, so bear with us for a moment.
Say, for example, that the left and bottom boundaries have Dirichlet boundary conditions, and the top and right boundaries have Neumann boundary conditions.
Let's look at each case:
**Bottom boundary:**
The equation for $j=1$ (interior points adjacent to the bottom boundary) uses values from $j=0$, which are known. Let's put that on the right-hand side of the equation. We get this equation for all points across the $x$-axis that are adjacent to the bottom boundary:
$$
\begin{equation}
\begin{split}
-T^{n+1}_{i-1,1} - T^{n+1}_{i+1,1} + \left( \frac{\delta^2}{\alpha \Delta t} + 4 \right) T^{n+1}_{i,1} - T^{n+1}_{i,j+1} \qquad & \\
= \frac{\delta^2}{\alpha \Delta t} T^n_{i,1} + T^{n+1}_{i,0} & \\
\end{split}
\end{equation}
$$
**Left boundary:**
Like for the bottom boundary, the equation for $i=1$ (interior points adjacent to the left boundary) uses known values from $i=0$, and we will put that on the right-hand side:
$$
\begin{equation}
\begin{split}
-T^{n+1}_{2,j} + \left( \frac{\delta^2}{\alpha \Delta t} + 4 \right) T^{n+1}_{1,j} - T^{n+1}_{1,j-1} - T^{n+1}_{1,j+1} \qquad & \\
= \frac{\delta^2}{\alpha \Delta t} T^n_{1,j} + T^{n+1}_{0,j} & \\
\end{split}
\end{equation}
$$
**Right boundary:**
Say the boundary condition is $\left. \frac{\partial T}{\partial x} \right|_{x=L_x} = q_x$. Its finite-difference approximation is
$$
\begin{equation}
\frac{T^{n+1}_{n_x-1,j} - T^{n+1}_{n_x-2,j}}{\delta} = q_x
\end{equation}
$$
We can write $T^{n+1}_{n_x-1,j} = \delta q_x + T^{n+1}_{n_x-2,j}$ to get the finite difference equation for $i=n_x-2$:
$$
\begin{equation}
\begin{split}
-T^{n+1}_{n_x-3,j} + \left( \frac{\delta^2}{\alpha \Delta t} + 3 \right) T^{n+1}_{n_x-2,j} - T^{n+1}_{n_x-2,j-1} - T^{n+1}_{n_x-2,j+1} \qquad & \\
= \frac{\delta^2}{\alpha \Delta t} T^n_{n_x-2,j} + \delta q_x & \\
\end{split}
\end{equation}
$$
Not sure about this? Grab pen and paper! _Please_, check this yourself. It will help you understand!
**Top boundary:**
Neumann boundary conditions specify the derivative normal to the boundary: $\left. \frac{\partial T}{\partial y} \right|_{y=L_y} = q_y$. No need to repeat what we did for the right boundary, right? The equation for $j=n_y-2$ is
$$
\begin{equation}
\begin{split}
-T^{n+1}_{i-1,n_y-2} - T^{n+1}_{i+1,n_y-2} + \left( \frac{\delta^2}{\alpha \Delta t} + 3 \right) T^{n+1}_{i,n_y-2} - T^{n+1}_{i,n_y-3} \qquad & \\
= \frac{\delta^2}{\alpha \Delta t} T^n_{i,n_y-2} + \delta q_y & \\
\end{split}
\end{equation}
$$
So far, we have then 5 possible cases: bottom, left, right, top, and interior points. Does this cover everything? What about corners?
**Bottom-left corner**
At $T_{1,1}$ there is a Dirichlet boundary condition at $i=0$ and $j=0$. This equation is:
$$
\begin{equation}
\begin{split}
-T^{n+1}_{2,1} + \left( \frac{\delta^2}{\alpha \Delta t} + 4 \right) T^{n+1}_{1,1} - T^{n+1}_{1,2} \qquad & \\
= \frac{\delta^2}{\alpha \Delta t} T^n_{1,1} + T^{n+1}_{0,1} + T^{n+1}_{1,0} & \\
\end{split}
\end{equation}
$$
**Top-left corner:**
At $T_{1,n_y-2}$ there is a Dirichlet boundary condition at $i=0$ and a Neumann boundary condition at $i=n_y-1$. This equation is:
$$
\begin{equation}
\begin{split}
-T^{n+1}_{2,n_y-2} + \left( \frac{\delta^2}{\alpha \Delta t} + 3 \right) T^{n+1}_{1,n_y-2} - T^{n+1}_{1,n_y-3} \qquad & \\
= \frac{\delta^2}{\alpha \Delta t} T^n_{1,n_y-2} + T^{n+1}_{0,n_y-2} + \delta q_y & \\
\end{split}
\end{equation}
$$
**Top-right corner**
At $T_{n_x-2,n_y-2}$, there are Neumann boundary conditions at both $i=n_x-1$ and $j=n_y-1$. The finite difference equation is then
$$
\begin{equation}
\begin{split}
-T^{n+1}_{n_x-3,n_y-2} + \left( \frac{\delta^2}{\alpha \Delta t} + 2 \right) T^{n+1}_{n_x-2,n_y-2} - T^{n+1}_{n_x-2,n_y-3} \qquad & \\
= \frac{\delta^2}{\alpha \Delta t} T^n_{n_x-2,n_y-2} + \delta(q_x + q_y) & \\
\end{split}
\end{equation}
$$
**Bottom-right corner**
To calculate $T_{n_x-2,1}$ we need to consider a Dirichlet boundary condition to the bottom and a Neumann boundary condition to the right. We will get a similar equation to the top-left corner!
$$
\begin{equation}
\begin{split}
-T^{n+1}_{n_x-3,1} + \left( \frac{\delta^2}{\alpha \Delta t} + 3 \right) T^{n+1}_{n_x-2,1} - T^{n+1}_{n_x-2,2} \qquad & \\
= \frac{\delta^2}{\alpha \Delta t} T^n_{n_x-2,1} + T^{n+1}_{n_x-2,0} + \delta q_x & \\
\end{split}
\end{equation}
$$
Okay, now we are actually ready. We have checked every possible case!
### The linear system
Like in the previous lesson introducing implicit schemes, we will solve a linear system at every time step:
$$
[A][T^{n+1}_\text{int}] = [b]+[b]_{b.c.}
$$
The coefficient matrix now takes some more work to figure out and to build in code. There is no substitute for you working this out patiently on paper!
The structure of the matrix can be described as a series of diagonal blocks, and lots of zeros elsewhere. Look at Figure 3, representing the block structure of the coefficient matrix, and refer back to Figure 2, showing the discretization grid in physical space. The first row of interior points, adjacent to the bottom boundary, generates the matrix block labeled $A_1$. The top row of interior points, adjacent to the top boundary generates the matrix block labeled $A_3$. All other interior points in the grid generate similar blocks, labeled $A_2$ on Figure 3.
#### <img src="./figures/implicit-matrix-blocks.png"> Figure 3: Sketch of coefficient-matrix blocks.
#### <img src="./figures/matrix-blocks-on-grid.png"> Figure 4: Grid points corresponding to each matrix-block type.
The matrix block $A_1$ is
<img src="./figures/A_1.svg" width="640px">
The block matrix $A_2$ is
<img src="./figures/A_2.svg" width="640px">
The block matrix $A_3$ is
<img src="./figures/A_3.svg" width="640px">
Vector $T^{n+1}_\text{int}$ contains the temperature of the interior nodes in the next time step. It is:
$$
\begin{equation}
T^{n+1}_\text{int} = \left[
\begin{array}{c}
T^{n+1}_{1,1}\\
T^{n+1}_{2,1} \\
\vdots \\
T^{n+1}_{n_x-2,1} \\
T^{n+1}_{2,1} \\
\vdots \\
T^{n+1}_{n_x-2,n_y-2}
\end{array}
\right]
\end{equation}
$$
Remember the x-major ordering we chose!
Finally, the right-hand side is
\begin{equation}
[b]+[b]_{b.c.} =
\left[\begin{array}{c}
\sigma^\prime T^n_{1,1} + T^{n+1}_{0,1} + T^{n+1}_{1,0} \\
\sigma^\prime T^n_{2,0} + T^{n+1}_{2,0} \\
\vdots \\
\sigma^\prime T^n_{n_x-2,1} + T^{n+1}_{n_x-2,0} + \delta q_x \\
\sigma^\prime T^n_{1,2} + T^{n+1}_{0,2} \\
\vdots \\
\sigma^\prime T^n_{n_x-2,n_y-2} + \delta(q_x + q_y)
\end{array}\right]
\end{equation}
where $\sigma^\prime = 1/\sigma = \delta^2/\alpha \Delta t$. The matrix looks very ugly, but it is important you understand it! Think about it. Can you answer:
* Why a -1 factor appears $n_x-2$ columns after the diagonal? What about $n_x-2$ columns before the diagonal?
* Why in row $n_x-2$ the position after the diagonal contains a 0?
* Why in row $n_x-2$ the diagonal is $\sigma^\prime + 3$ rather than $\sigma^\prime + 4$?
* Why in the last row the diagonal is $\sigma^\prime + 2$ rather than $\sigma^\prime + 4$?
If you can answer those questions, you are in good shape to continue!
Let's write a function that will generate the matrix and right-hand side for the heat conduction problem in the previous notebook. Remember, we had Dirichlet boundary conditions in the left and bottom, and zero-flux Neumann boundary condition on the top and right $(q_x=q_y=0)$.
Also, we'll import `scipy.linalg.solve` because we need to solve a linear system.
```
import numpy
from scipy import linalg
def lhs_operator(M, N, sigma):
"""
Assembles and returns the implicit operator
of the system for the 2D diffusion equation.
We use a Dirichlet condition at the left and
bottom boundaries and a Neumann condition
(zero-gradient) at the right and top boundaries.
Parameters
----------
M : integer
Number of interior points in the x direction.
N : integer
Number of interior points in the y direction.
sigma : float
Value of alpha * dt / dx**2.
Returns
-------
A : numpy.ndarray
The implicit operator as a 2D array of floats
of size M*N by M*N.
"""
A = numpy.zeros((M * N, M * N))
for j in range(N):
for i in range(M):
I = j * M + i # row index
# Get index of south, west, east, and north points.
south, west, east, north = I - M, I - 1, I + 1, I + M
# Setup coefficients at corner points.
if i == 0 and j == 0: # bottom-left corner
A[I, I] = 1.0 / sigma + 4.0
A[I, east] = -1.0
A[I, north] = -1.0
elif i == M - 1 and j == 0: # bottom-right corner
A[I, I] = 1.0 / sigma + 3.0
A[I, west] = -1.0
A[I, north] = -1.0
elif i == 0 and j == N - 1: # top-left corner
A[I, I] = 1.0 / sigma + 3.0
A[I, south] = -1.0
A[I, east] = -1.0
elif i == M - 1 and j == N - 1: # top-right corner
A[I, I] = 1.0 / sigma + 2.0
A[I, south] = -1.0
A[I, west] = -1.0
# Setup coefficients at side points (excluding corners).
elif i == 0: # left side
A[I, I] = 1.0 / sigma + 4.0
A[I, south] = -1.0
A[I, east] = -1.0
A[I, north] = -1.0
elif i == M - 1: # right side
A[I, I] = 1.0 / sigma + 3.0
A[I, south] = -1.0
A[I, west] = -1.0
A[I, north] = -1.0
elif j == 0: # bottom side
A[I, I] = 1.0 / sigma + 4.0
A[I, west] = -1.0
A[I, east] = -1.0
A[I, north] = -1.0
elif j == N - 1: # top side
A[I, I] = 1.0 / sigma + 3.0
A[I, south] = -1.0
A[I, west] = -1.0
A[I, east] = -1.0
# Setup coefficients at interior points.
else:
A[I, I] = 1.0 / sigma + 4.0
A[I, south] = -1.0
A[I, west] = -1.0
A[I, east] = -1.0
A[I, north] = -1.0
return A
def rhs_vector(T, M, N, sigma, Tb):
"""
Assembles and returns the right-hand side vector
of the system for the 2D diffusion equation.
We use a Dirichlet condition at the left and
bottom boundaries and a Neumann condition
(zero-gradient) at the right and top boundaries.
Parameters
----------
T : numpy.ndarray
The temperature distribution as a 1D array of floats.
M : integer
Number of interior points in the x direction.
N : integer
Number of interior points in the y direction.
sigma : float
Value of alpha * dt / dx**2.
Tb : float
Boundary value for Dirichlet conditions.
Returns
-------
b : numpy.ndarray
The right-hand side vector as a 1D array of floats
of size M*N.
"""
b = 1.0 / sigma * T
# Add Dirichlet term at points located next
# to the left and bottom boundaries.
for j in range(N):
for i in range(M):
I = j * M + i
if i == 0:
b[I] += Tb
if j == 0:
b[I] += Tb
return b
```
The solution of the linear system $(T^{n+1}_\text{int})$ contains the temperatures of the interior points at the next time step in a 1D array. We will also create a function that will take the values of $T^{n+1}_\text{int}$ and put them in a 2D array that resembles the physical domain.
```
def map_1d_to_2d(T_1d, nx, ny, Tb):
"""
Maps a 1D array of the temperature at the interior points
to a 2D array that includes the boundary values.
Parameters
----------
T_1d : numpy.ndarray
The temperature at the interior points as a 1D array of floats.
nx : integer
Number of points in the x direction of the domain.
ny : integer
Number of points in the y direction of the domain.
Tb : float
Boundary value for Dirichlet conditions.
Returns
-------
T : numpy.ndarray
The temperature distribution in the domain
as a 2D array of size ny by nx.
"""
T = numpy.zeros((ny, nx))
# Get the value at interior points.
T[1:-1, 1:-1] = T_1d.reshape((ny - 2, nx - 2))
# Use Dirichlet condition at left and bottom boundaries.
T[:, 0] = Tb
T[0, :] = Tb
# Use Neumann condition at right and top boundaries.
T[:, -1] = T[:, -2]
T[-1, :] = T[-2, :]
return T
```
And to advance in time, we will use
```
def btcs_implicit_2d(T0, nt, dt, dx, alpha, Tb):
"""
Computes and returns the distribution of the
temperature after a given number of time steps.
The 2D diffusion equation is integrated using
Euler implicit in time and central differencing
in space, with a Dirichlet condition at the left
and bottom boundaries and a Neumann condition
(zero-gradient) at the right and top boundaries.
Parameters
----------
T0 : numpy.ndarray
The initial temperature distribution as a 2D array of floats.
nt : integer
Number of time steps to compute.
dt : float
Time-step size.
dx : float
Grid spacing in the x and y directions.
alpha : float
Thermal diffusivity of the plate.
Tb : float
Boundary value for Dirichlet conditions.
Returns
-------
T : numpy.ndarray
The temperature distribution as a 2D array of floats.
"""
# Get the number of points in each direction.
ny, nx = T0.shape
# Get the number of interior points in each direction.
M, N = nx - 2, ny - 2
# Compute the constant sigma.
sigma = alpha * dt / dx**2
# Create the implicit operator of the system.
A = lhs_operator(M, N, sigma)
# Integrate in time.
T = T0[1:-1, 1:-1].flatten() # interior points as a 1D array
I, J = int(M / 2), int(N / 2) # indices of the center
for n in range(nt):
# Compute the right-hand side of the system.
b = rhs_vector(T, M, N, sigma, Tb)
# Solve the system with scipy.linalg.solve.
T = linalg.solve(A, b)
# Check if the center of the domain has reached T = 70C.
if T[J * M + I] >= 70.0:
break
print('[time step {}] Center at T={:.2f} at t={:.2f} s'
.format(n + 1, T[J * M + I], (n + 1) * dt))
# Returns the temperature in the domain as a 2D array.
return map_1d_to_2d(T, nx, ny, Tb)
```
Remember, we want the function to tell us when the center of the plate reaches $70^\circ C$.
##### Dig deeper
For demonstration purposes, these functions are very explicit. But you can see a trend here, right?
Say we start with a matrix with `1/sigma+4` in the main diagonal, and `-1` on the 4 other corresponding diagonals. Now, we have to modify the matrix only where the boundary conditions are affecting. We saw the impact of the Dirichlet and Neumann boundary condition on each position of the matrix, we just need to know in which position to perform those changes.
A function that maps `i` and `j` into `row_number` would be handy, right? How about `row_number = (j-1)*(nx-2)+(i-1)`? By feeding `i` and `j` to that equation, you know exactly where to operate on the matrix. For example, `i=nx-2, j=2`, which is in row `row_number = 2*nx-5`, is next to a Neumann boundary condition: we have to substract one out of the main diagonal (`A[2*nx-5,2*nx-5]-=1`), and put a zero in the next column (`A[2*nx-5,2*nx-4]=0`). This way, the function can become much simpler!
Can you use this information to construct a more general function `lhs_operator`? Can you make it such that the type of boundary condition is an input to the function?
## Heat diffusion in 2D
Let's recast the 2D heat conduction from the previous notebook, and solve it with an implicit scheme.
```
# Set parameters.
Lx = 0.01 # length of the plate in the x direction
Ly = 0.01 # length of the plate in the y direction
nx = 21 # number of points in the x direction
ny = 21 # number of points in the y direction
dx = Lx / (nx - 1) # grid spacing in the x direction
dy = Ly / (ny - 1) # grid spacing in the y direction
alpha = 1e-4 # thermal diffusivity
# Define the locations along a gridline.
x = numpy.linspace(0.0, Lx, num=nx)
y = numpy.linspace(0.0, Ly, num=ny)
# Compute the initial temperature distribution.
Tb = 100.0 # temperature at the left and bottom boundaries
T0 = 20.0 * numpy.ones((ny, nx))
T0[:, 0] = Tb
T0[0, :] = Tb
```
We are ready to go!
```
# Set the time-step size based on CFL limit.
sigma = 0.25
dt = sigma * min(dx, dy)**2 / alpha # time-step size
nt = 300 # number of time steps to compute
# Compute the temperature along the rod.
T = btcs_implicit_2d(T0, nt, dt, dx, alpha, Tb)
```
And plot,
```
from matplotlib import pyplot
%matplotlib inline
# Set the font family and size to use for Matplotlib figures.
pyplot.rcParams['font.family'] = 'serif'
pyplot.rcParams['font.size'] = 16
# Plot the filled contour of the temperature.
pyplot.figure(figsize=(8.0, 5.0))
pyplot.xlabel('x [m]')
pyplot.ylabel('y [m]')
levels = numpy.linspace(20.0, 100.0, num=51)
contf = pyplot.contourf(x, y, T, levels=levels)
cbar = pyplot.colorbar(contf)
cbar.set_label('Temperature [C]')
pyplot.axis('scaled', adjustable='box');
```
Try this out with different values of `sigma`! You'll see that it will always give a stable solution!
Does this result match the explicit scheme from the previous notebook? Do they take the same amount of time to reach $70^\circ C$ in the center of the plate? Now that we can use higher values of `sigma`, we need fewer time steps for the center of the plate to reach $70^\circ C$! Of course, we need to be careful that `dt` is small enough to resolve the physics correctly.
---
###### The cell below loads the style of the notebook
```
from IPython.core.display import HTML
css_file = '../../styles/numericalmoocstyle.css'
HTML(open(css_file, 'r').read())
```
| github_jupyter |
# DATA 512: A1 Data Curation Assignment
By: Megan Nalani Chun
## Step 1: Gathering the data <br>
Gather Wikipedia traffic from Jan 1, 2008 - August 30, 2020 <br>
- Legacy Pagecounts API provides desktop and mobile traffic data from Dec. 2007 - July 2016 <br>
- Pageviews API provides desktop, mobile web, and mobile app traffic data from July 2015 - last month.
First, import the json and requests libraries to call the Pagecounts and Pageviews APIs and save the output in json format.
```
import json
import requests
```
Second, set the location of the endpoints and header information. This information is needed to call the Pagecounts and Pageviews APIs.
```
endpoint_legacy = 'https://wikimedia.org/api/rest_v1/metrics/legacy/pagecounts/aggregate/{project}/{access-site}/{granularity}/{start}/{end}'
endpoint_pageviews = 'https://wikimedia.org/api/rest_v1/metrics/pageviews/aggregate/{project}/{access}/{agent}/{granularity}/{start}/{end}'
headers = {
'User-Agent': 'https://github.com/NalaniKai/',
'From': '[email protected]'
}
```
Third, define a function to call the APIs taking in the endpoint and parameters. This function returns the data in json format.
```
def api_call(endpoint, parameters):
call = requests.get(endpoint.format(**parameters), headers=headers)
response = call.json()
return response
```
Fourth, define a function to make the api_call() with the correct parameters and save the output to json file in format apiname_accesstype_startyearmonth_endyearmonth.json
```
def get_data(api, access_dict, params, endpoint, access_name):
start = 0 #index of start date
end = 1 #index of end data
year_month = 6 #size of YYYYMM
for access_type, start_end_dates in access_dict.items(): #get data for all access types in API
params[access_name] = access_type
data = api_call(endpoint, params)
with open(api + "_" + access_type + "_" + start_end_dates[start][:year_month] + "_" + start_end_dates[end][:year_month] + ".json", 'w') as f:
json.dump(data, f) #save data
```
Fifth, define the parameters for the legacy page count API and call the get_data function. This will pull the data and save it.
```
api = "pagecounts"
access_type_legacy = {"desktop-site": ["2008010100", "2016070100"], #access type: start year_month, end year_month
"mobile-site": ["2014100100", "2016070100"]} #used to save outputs with correct filenames
#https://wikimedia.org/api/rest_v1/#!/Legacy_data/get_metrics_legacy_pagecounts_aggregate_project_access_site_granularity_start_end
params_legacy = {"project" : "en.wikipedia.org",
"granularity" : "monthly",
"start" : "2008010100",
"end" : "2016080100" #will get data through July 2016
}
get_data(api, access_type_legacy, params_legacy, endpoint_legacy, "access-site")
```
Sixth, define the parameters for the page views API and call the get_data function. This will pull the data and save it.
```
api = "pageviews"
start_end_dates = ["2015070100", "2020080100"] #start year_month, end year_month
access_type_pageviews = {"desktop": start_end_dates, #access type: start year_month, end year_month
"mobile-app": start_end_dates,
"mobile-web": start_end_dates }
#https://wikimedia.org/api/rest_v1/#!/Pageviews_data/get_metrics_pageviews_aggregate_project_access_agent_granularity_start_end
params_pageviews = {"project" : "en.wikipedia.org",
"access" : "mobile-web",
"agent" : "user", #remove crawler traffic
"granularity" : "monthly",
"start" : "2008010100",
"end" : '2020090100' #will get data through August 2020
}
get_data(api, access_type_pageviews, params_pageviews, endpoint_pageviews, "access")
```
## Step 2: Processing the data
First, create a function to read in all data files and extract the list of records from items.
```
def read_json(filename):
with open(filename, 'r') as f:
return json.load(f)["items"]
```
Second, use the read_json function to get a list of records for each file.
```
pageviews_mobile_web = read_json("pageviews_mobile-web_201507_202008.json")
pageviews_mobile_app = read_json("pageviews_mobile-app_201507_202008.json")
pageviews_desktop = read_json("pageviews_desktop_201507_202008.json")
pagecounts_mobile = read_json("pagecounts_mobile-site_201410_201607.json")
pagecounts_desktop = read_json("pagecounts_desktop-site_200801_201607.json")
```
Third, create a total mobile traffic count for each month using the mobile-app and mobile-web data from the pageviews API. The list of [timestamp, view_count] pairs data structure will enable easy transformation into a dataframe.
```
pageviews_mobile = [[r1["timestamp"], r0["views"] + r1["views"]] for r0 in pageviews_mobile_web for r1 in pageviews_mobile_app if r0["timestamp"] == r1["timestamp"]]
```
Fourth, get the timestamps and values in the [timestamp, view_count] format for the desktop pageviews, desktop pagecounts, and mobile pagecounts.
```
pageviews_desktop = [[record["timestamp"], record["views"]] for record in pageviews_desktop]
pagecounts_desktop = [[record["timestamp"], record["count"]] for record in pagecounts_desktop]
pagecounts_mobile = [[record["timestamp"], record["count"]] for record in pagecounts_mobile]
```
Fifth, import pandas library and transform data into dataframes.
```
import pandas as pd
pageview_desktop_views = pd.DataFrame(pageviews_desktop, columns=["timestamp", "pageview_desktop_views"])
pageview_mobile_views = pd.DataFrame(pageviews_mobile, columns=["timestamp", "pageview_mobile_views"])
pagecounts_desktop = pd.DataFrame(pagecounts_desktop, columns=["timestamp", "pagecount_desktop_views"])
pagecounts_mobile = pd.DataFrame(pagecounts_mobile, columns=["timestamp", "pagecount_mobile_views"])
```
Sixth, join page view dataframes and calculate total for all views.
```
df_pageviews = pd.merge(pageview_desktop_views, pageview_mobile_views, how="outer", on="timestamp")
df_pageviews["pageview_all_views"] = df_pageviews["pageview_desktop_views"] + df_pageviews["pageview_mobile_views"]
df_pageviews.head()
```
Seventh, join page count dataframes. Then fill in NaN values with 0 to calculate total for all counts.
```
df_pagecounts = pd.merge(pagecounts_desktop, pagecounts_mobile, how="outer", on="timestamp")
df_pagecounts["pagecount_mobile_views"] = df_pagecounts["pagecount_mobile_views"].fillna(0)
df_pagecounts["pagecount_all_views"] = df_pagecounts["pagecount_desktop_views"] + df_pagecounts["pagecount_mobile_views"]
df_pagecounts.head()
```
Eighth, join page count and page view dataframes into one table. Filling in missing values with 0.
```
df = pd.merge(df_pagecounts, df_pageviews, how="outer", on="timestamp")
df = df.fillna(0)
df.head()
```
Ninth, separate the timestamp into the year and month in YYYY and MM format for all the data. Remove the timestamp column.
```
df["year"] = df["timestamp"].apply(lambda date: date[:4])
df["month"] = df["timestamp"].apply(lambda date: date[4:6])
df.drop("timestamp", axis=1, inplace=True)
df.head()
```
Tenth, save processed data to csv file without the index column.
```
df.to_csv("en-wikipedia_traffic_200801-202008.csv", index=False)
```
## Step 3: Analyze the data
First, fill 0 values with numpy.nan values so these values are not plotted on the chart.
```
import numpy as np
df.replace(0, np.nan, inplace=True)
```
Second, transform the year and month into a datetime.date type which will be used for the x-axis in the chart.
```
from datetime import date
date = df.apply(lambda r: date(int(r["year"]), int(r["month"]), 1), axis=1)
```
Third, divide all page view counts by 1e6 so the chart is easier to read. Y-axis will be the values shown x 1,000,000.
```
pc_mobile = df["pagecount_mobile_views"] / 1e6
pv_mobile = df["pageview_mobile_views"] / 1e6
pc_desktop = df["pagecount_desktop_views"] / 1e6
pv_desktop = df["pageview_desktop_views"] / 1e6
pv_total = df["pageview_all_views"] / 1e6
pc_total = df["pagecount_all_views"] / 1e6
```
Fourth, plot the data in a time series for desktop (main site), mobile, and the total all up. The dashed lines are data from the pagecount API and the solid lines are the data from the pageview API without crawler traffic.
```
import matplotlib.pyplot as plt
from matplotlib.dates import YearLocator
#create plot and assign time series to plot
fig, ax1 = plt.subplots(figsize=(18,6))
ax1.plot(date, pc_desktop, label="main site", color="green", ls="--")
ax1.plot(date, pv_desktop, label="_Hidden label", color="green", ls="-")
ax1.plot(date, pc_mobile, label="mobile site", color="blue", ls="--")
ax1.plot(date, pv_mobile, label="_Hidden label", color="blue", ls="-")
ax1.plot(date, pc_total, label="total", color="black", ls="--")
ax1.plot(date, pv_total, label="_Hidden label", color="black", ls="-")
ax1.xaxis.set_major_locator(YearLocator()) #show every year on the x-axis
#set caption
caption = "May 2015: a new pageview definition took effect, which eliminated all crawler traffic. Solid lines mark new definition."
fig.text(.5, .01, caption, ha='center', color="red")
#set labels for x-axis, y-axis, and title
plt.xlabel("Date")
plt.ylabel("Page Views (x 1,000,000)")
plt.title("Page Views on English Wikipedia (x 1,000,000)")
plt.ylim(ymin=0) #start y-axis at 0
plt.grid(True) #turn on background grid
plt.legend(loc="upper left")
#save chart to png file
filename = "Time Series.png"
plt.savefig(filename)
plt.show() #display chart
```
| github_jupyter |
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
import os
import random
import pickle
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import AdaBoostRegressor
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import roc_curve, auc
from sklearn import preprocessing
from xgboost import XGBRegressor
from datetime import datetime
from bayes_opt import BayesianOptimization
random.seed(1234)
```
# Define Functions
```
# Performce cross validation using xgboost
def xgboostcv(X, y, fold, n_estimators, lr, depth, n_jobs, gamma, min_cw, subsample, colsample):
uid = np.unique(fold)
model_pred = np.zeros(X.shape[0])
model_valid_loss = np.zeros(len(uid))
model_train_loss = np.zeros(len(uid))
for i in uid:
x_valid = X[fold==i]
x_train = X[fold!=i]
y_valid = y[fold==i]
y_train = y[fold!=i]
model = XGBRegressor(n_estimators=n_estimators, learning_rate=lr,
max_depth = depth, n_jobs = n_jobs,
gamma = gamma, min_child_weight = min_cw,
subsample = subsample, colsample_bytree = colsample, random_state=1234)
model.fit(x_train, y_train)
pred = model.predict(x_valid)
model_pred[fold==i] = pred
model_valid_loss[uid==i] = mean_squared_error(y_valid, pred)
model_train_loss[uid==i] = mean_squared_error(y_train, model.predict(x_train))
return {'pred':model_pred, 'valid_loss':model_valid_loss, 'train_loss':model_train_loss}
# Compute MSE for xgboost cross validation
def xgboostcv_mse(n, p, depth, g, min_cw, subsample, colsample):
model_cv = xgboostcv(X_train, y_train, fold_train,
int(n)*100, 10**p, int(depth), n_nodes,
10**g, min_cw, subsample, colsample)
MSE = mean_squared_error(y_train, model_cv['pred'])
return -MSE
# Display model performance metrics for each cv iteration
def cv_performance(model, y, fold):
uid = np.unique(fold)
pred = np.round(model['pred'])
y = y.reshape(-1)
model_valid_mse = np.zeros(len(uid))
model_valid_mae = np.zeros(len(uid))
model_valid_r2 = np.zeros(len(uid))
for i in uid:
pred_i = pred[fold==i]
y_i = y[fold==i]
model_valid_mse[uid==i] = mean_squared_error(y_i, pred_i)
model_valid_mae[uid==i] = np.abs(pred_i-y_i).mean()
model_valid_r2[uid==i] = r2_score(y_i, pred_i)
results = pd.DataFrame(0, index=uid,
columns=['valid_mse', 'valid_mae', 'valid_r2',
'valid_loss', 'train_loss'])
results['valid_mse'] = model_valid_mse
results['valid_mae'] = model_valid_mae
results['valid_r2'] = model_valid_r2
results['valid_loss'] = model['valid_loss']
results['train_loss'] = model['train_loss']
print(results)
# Display overall model performance metrics
def cv_overall_performance(y, y_pred):
overall_MSE = mean_squared_error(y, y_pred)
overall_MAE = (np.abs(y_pred-y)).mean()
overall_RMSE = np.sqrt(np.square(y_pred-y).mean())
overall_R2 = r2_score(y, y_pred)
print("XGB overall MSE: %0.4f" %overall_MSE)
print("XGB overall MAE: %0.4f" %overall_MAE)
print("XGB overall RMSE: %0.4f" %overall_RMSE)
print("XGB overall R^2: %0.4f" %overall_R2)
# Plot variable importance
def plot_importance(model, columns):
importances = pd.Series(model.feature_importances_, index = columns).sort_values(ascending=False)
n = len(columns)
plt.figure(figsize=(10,15))
plt.barh(np.arange(n)+0.5, importances)
plt.yticks(np.arange(0.5,n+0.5), importances.index)
plt.tick_params(axis='both', which='major', labelsize=22)
plt.ylim([0,n])
plt.gca().invert_yaxis()
plt.savefig('variable_importance.png', dpi = 150)
# Save xgboost model
def save(obj, path):
pkl_fl = open(path, 'wb')
pickle.dump(obj, pkl_fl)
pkl_fl.close()
# Load xgboost model
def load(path):
f = open(path, 'rb')
obj = pickle.load(f)
f.close()
return(obj)
```
# Parameter Values
```
# Set a few values
validation_only = False # Whether test model with test data
n_nodes = 96 # Number of computing nodes used for hyperparamter tunning
trained = False # If a trained model exits
cols_drop = ['StationId', 'Date', 'PenRate', 'NumberOfLanes', 'Dir', 'FC', 'Month'] # Columns to be dropped
if trained:
params = load('params.dat')
xgb_cv = load('xgb_cv.dat')
xgb = load('xgb.dat')
```
# Read Data
```
if validation_only:
raw_data_train = pd.read_csv("final_train_data.csv")
data = raw_data_train.drop(cols_drop, axis=1)
if 'Dir' in data.columns:
data[['Dir']] = data[['Dir']].astype('category')
one_hot = pd.get_dummies(data[['Dir']])
data = data.drop(['Dir'], axis = 1)
data = data.join(one_hot)
if 'FC' in data.columns:
data[['FC']] = data[['FC']].astype('category')
one_hot = pd.get_dummies(data[['FC']])
data = data.drop(['FC'], axis = 1)
data = data.join(one_hot)
week_dict = {"DayOfWeek": {'Monday': 1, 'Tuesday': 2, 'Wednesday': 3, 'Thursday': 4,
'Friday': 5, 'Saturday': 6, 'Sunday': 7}}
data = data.replace(week_dict)
X = data.drop(['Volume', 'fold'], axis=1)
X_col = X.columns
y = data[['Volume']]
fold_train = data[['fold']].values.reshape(-1)
X_train = X.values
y_train = y.values
else:
raw_data_train = pd.read_csv("final_train_data.csv")
raw_data_test = pd.read_csv("final_test_data.csv")
raw_data_test1 = pd.DataFrame(np.concatenate((raw_data_test.values, np.zeros(raw_data_test.shape[0]).reshape(-1, 1)), axis=1),
columns = raw_data_test.columns.append(pd.Index(['fold'])))
raw_data = pd.DataFrame(np.concatenate((raw_data_train.values, raw_data_test1.values), axis=0),
columns = raw_data_train.columns)
data = raw_data.drop(cols_drop, axis=1)
if 'Dir' in data.columns:
data[['Dir']] = data[['Dir']].astype('category')
one_hot = pd.get_dummies(data[['Dir']])
data = data.drop(['Dir'], axis = 1)
data = data.join(one_hot)
if 'FC' in data.columns:
data[['FC']] = data[['FC']].astype('category')
one_hot = pd.get_dummies(data[['FC']])
data = data.drop(['FC'], axis = 1)
data = data.join(one_hot)
week_dict = {"DayOfWeek": {'Monday': 1, 'Tuesday': 2, 'Wednesday': 3, 'Thursday': 4,
'Friday': 5, 'Saturday': 6, 'Sunday': 7}}
data = data.replace(week_dict)
X = data.drop(['Volume'], axis=1)
y = data[['Volume']]
X_train = X.loc[X.fold!=0, :]
fold_train = X_train[['fold']].values.reshape(-1)
X_col = X_train.drop(['fold'], axis = 1).columns
X_train = X_train.drop(['fold'], axis = 1).values
y_train = y.loc[X.fold!=0, :].values
X_test = X.loc[X.fold==0, :]
X_test = X_test.drop(['fold'], axis = 1).values
y_test = y.loc[X.fold==0, :].values
X_col
# Explain variable names
X_name_dict = {'Temp': 'Temperature', 'WindSp': 'Wind Speed', 'Precip': 'Precipitation', 'Snow': 'Snow',
'Long': 'Longitude', 'Lat': 'Latitude', 'NumberOfLanes': 'Number of Lanes', 'SpeedLimit': 'Speed Limit',
'FRC': 'TomTom FRC', 'DayOfWeek': 'Day of Week', 'Month': 'Month', 'Hour': 'Hour',
'AvgSp': 'Average Speed', 'ProbeCount': 'Probe Count', 'Dir_E': 'Direction(East)',
'Dir_N': 'Direction(North)', 'Dir_S': 'Direction(South)', 'Dir_W': 'Direction(West)',
'FC_3R': 'FHWA FC(3R)', 'FC_3U': 'FHWA FC(3U)', 'FC_4R': 'FHWA FC(4R)', 'FC_4U': 'FHWA FC(4U)',
'FC_5R': 'FHWA FC(5R)', 'FC_5U': 'FHWA FC(5U)', 'FC_7R': 'FHWA FC(7R)', 'FC_7U': 'FHWA FC(7U)'}
data.head()
X_train.shape
if validation_only == False:
print(X_test.shape)
```
# Cross Validation & Hyperparameter Optimization
```
# Set hyperparameter ranges for Bayesian optimization
xgboostBO = BayesianOptimization(xgboostcv_mse,
{'n': (1, 10),
'p': (-4, 0),
'depth': (2, 10),
'g': (-3, 0),
'min_cw': (1, 10),
'subsample': (0.5, 1),
'colsample': (0.5, 1)
})
# Use Bayesian optimization to tune hyperparameters
import time
start_time = time.time()
xgboostBO.maximize(init_points=10, n_iter = 50)
print('-'*53)
print('Final Results')
print('XGBOOST: %f' % xgboostBO.max['target'])
print("--- %s seconds ---" % (time.time() - start_time))
# Save the hyperparameters the yield the highest model performance
params = xgboostBO.max['params']
save(params, 'params.dat')
params
# Perform cross validation using the optimal hyperparameters
xgb_cv = xgboostcv(X_train, y_train, fold_train, int(params['n'])*100,
10**params['p'], int(params['depth']), n_nodes,
10**params['g'], params['min_cw'], params['subsample'], params['colsample'])
# Display cv results for each iteration
cv_performance(xgb_cv, y_train, fold_train)
# Display overall cv results
cv_pred = xgb_cv['pred']
cv_pred[cv_pred<0] = 0
cv_overall_performance(y_train.reshape(-1), cv_pred)
# Save the cv results
save(xgb_cv, 'xgb_cv.dat')
```
# Model Test
```
# Build a xgboost using all the training data with the optimal hyperparameter
xgb = XGBRegressor(n_estimators=int(params['n'])*100, learning_rate=10**params['p'], max_depth = int(params['depth']),
n_jobs = n_nodes, gamma = 10**params['g'], min_child_weight = params['min_cw'],
subsample = params['subsample'], colsample_bytree = params['colsample'], random_state=1234)
xgb.fit(X_train, y_train)
# Test the trained model with test data
if validation_only == False:
y_pred = xgb.predict(X_test)
y_pred[y_pred<0] = 0
cv_overall_performance(y_test.reshape(-1), y_pred)
# Plot variable importance
col_names = [X_name_dict[i] for i in X_col]
plot_importance(xgb, col_names)
# Save the trained xgboost model
save(xgb, 'xgb.dat')
# Produce cross validation estimates or estimates for test data
train_data_pred = pd.DataFrame(np.concatenate((raw_data_train.values, cv_pred.reshape(-1, 1)), axis=1),
columns = raw_data_train.columns.append(pd.Index(['PredVolume'])))
train_data_pred.to_csv('train_data_pred.csv', index = False)
if validation_only == False:
test_data_pred = pd.DataFrame(np.concatenate((raw_data_test.values, y_pred.reshape(-1, 1)), axis=1),
columns = raw_data_test.columns.append(pd.Index(['PredVolume'])))
test_data_pred.to_csv('test_data_pred.csv', index = False)
```
# Plot Estimations vs. Observations
```
# Prepare data to plot estimated and observed values
if validation_only:
if trained:
plot_df = pd.read_csv("train_data_pred.csv")
else:
plot_df = train_data_pred
else:
if trained:
plot_df = pd.read_csv("test_data_pred.csv")
else:
plot_df = test_data_pred
plot_df = plot_df.sort_values(by=['StationId', 'Date', 'Dir', 'Hour'])
plot_df = plot_df.set_index(pd.Index(range(plot_df.shape[0])))
# Define a function to plot estimated and observed values for a day
def plot_daily_estimate(frc):
indices = plot_df.index[(plot_df.FRC == frc) & (plot_df.Hour == 0)].tolist()
from_index = np.random.choice(indices, 1)[0]
to_index = from_index + 23
plot_df_sub = plot_df.loc[from_index:to_index, :]
time = pd.date_range(plot_df_sub.Date.iloc[0] + ' 00:00:00', periods=24, freq='H')
plt.figure(figsize=(20,10))
plt.plot(time, plot_df_sub.PredVolume, 'b-', label='XGBoost', lw=2)
plt.plot(time, plot_df_sub.Volume, 'r--', label='Observed', lw=3)
plt.tick_params(axis='both', which='major', labelsize=24)
plt.ylabel('Volume (vehs/hr)', fontsize=24)
plt.xlabel("Time", fontsize=24)
plt.legend(loc='upper left', shadow=True, fontsize=24)
plt.title('Station ID: {0}, MAE={1}, FRC = {2}'.format(
plot_df_sub.StationId.iloc[0],
round(np.abs(plot_df_sub.PredVolume-plot_df_sub.Volume).mean()),
plot_df_sub.FRC.iloc[0]), fontsize=40)
plt.savefig('frc_{0}.png'.format(frc), dpi = 150)
return(plot_df_sub)
# Define a function to plot estimated and observed values for a week
def plot_weekly_estimate(frc):
indices = plot_df.index[(plot_df.FRC == frc) & (plot_df.Hour == 0) & (plot_df.DayOfWeek == 'Monday')].tolist()
from_index = np.random.choice(indices, 1)[0]
to_index = from_index + 24*7-1
plot_df_sub = plot_df.loc[from_index:to_index, :]
time = pd.date_range(plot_df_sub.Date.iloc[0] + ' 00:00:00', periods=24*7, freq='H')
plt.figure(figsize=(20,10))
plt.plot(time, plot_df_sub.PredVolume, 'b-', label='XGBoost', lw=2)
plt.plot(time, plot_df_sub.Volume, 'r--', label='Observed', lw=3)
plt.tick_params(axis='both', which='major', labelsize=24)
plt.ylabel('Volume (vehs/hr)', fontsize=24)
plt.xlabel("Time", fontsize=24)
plt.legend(loc='upper left', shadow=True, fontsize=24)
plt.title('Station ID: {0}, MAE={1}, FRC = {2}'.format(
plot_df_sub.StationId.iloc[0],
round(np.abs(plot_df_sub.PredVolume-plot_df_sub.Volume).mean()),
plot_df_sub.FRC.iloc[0]), fontsize=40)
plt.savefig('frc_{0}.png'.format(frc), dpi = 150)
return(plot_df_sub)
# Plot estimated and observed values for a day
frc2_daily_plot = plot_daily_estimate(2)
save(frc2_daily_plot, 'frc2_daily_plot.dat')
# Plot estimated and observed values for a week
frc3_weekly_plot = plot_weekly_estimate(3)
save(frc3_weekly_plot, 'frc3_weekly_plot.dat')
```
| github_jupyter |
First import the "datavis" module
```
import sys
sys.path.append('..')
import numpy as np
import datavis
import vectorized_datavis
def test_se_to_sd():
"""
Test that the value returned is a float value
"""
sdev = datavis.se_to_sd(0.5, 1000)
assert isinstance(sdev, float),\
"Returned data type is not a float number"
test_se_to_sd()
def test_ci_to_sd():
"""
Test that the value returned is a float value
"""
sdev = datavis.ci_to_sd(0.2, 0.4)
assert isinstance(sdev, float),\
"Returned data type is not a float number"
test_ci_to_sd()
def test_datagen():
"""
Test that the data returned is a numpy.ndarray
"""
randdata = datavis.datagen(25, 0.2, 0.4)
assert isinstance(randdata, np.ndarray),\
"Returned data type is not a numpy.ndarray"
test_datagen()
def test_correctdatatype():
"""
Test that the statistical parameters returned are float numbers
"""
fmean, fsdev, fserror, fuci, flci = datavis.correctdatatype(0.2, 0.4)
assert isinstance(fmean, float),\
"Returned data type is not a float number"
test_correctdatatype()
def test_compounddata():
"""
Test that the data returned are numpy.ndarrays
"""
datagenerated1, datagenerated2, datagenerated3 = \
datavis.compounddata\
(mean1=24.12,sdev1=3.87,mean2=24.43,sdev2=3.94,mean3=24.82,sdev3=3.95,size=1000)
assert isinstance(datagenerated1, np.ndarray),\
"Returned data are not numpy.ndarrays"
test_compounddata()
def test_databinning():
"""
Test that the data returned are numpy.ndarrays
"""
datagenerated1, datagenerated2, datagenerated3 = \
datavis.compounddata\
(mean1=24.12,sdev1=3.87,mean2=24.43,sdev2=3.94,mean3=24.82,sdev3=3.95,size=1000)
bins = np.linspace(10,40,num=30)
yhist1, yhist2, yhist3 = \
datavis.databinning\
(datagenerated1, datagenerated2, datagenerated3,bins_list=bins)
assert isinstance(yhist1, np.ndarray),\
"Returned data are not numpy.ndarrays"
test_databinning()
def test_pdfgen():
"""
Test that the data returned are numpy.ndarrays
"""
bins = np.linspace(10,40,num=30)
mean1 = 24.12
sdev1 = 3.87
mean2 = 24.43
sdev2 = 3.94
mean3 = 24.82
sdev3 = 3.95
pdf1, pdf2, pdf3 = datavis.pdfgen\
(mean1, sdev1, mean2, sdev2, mean3, sdev3, bins_list=bins)
assert isinstance(pdf1, np.ndarray),\
"Returned data are not numpy.ndarrays"
test_pdfgen()
def test_percent_overlap():
"""
Test that the data returned is a tuple
"""
mean1 = 24.12
sdev1 = 3.87
mean2 = 24.43
sdev2 = 3.94
mean3 = 24.82
sdev3 = 3.95
overlap_11_perc, overlap_12_perc, overlap_13_perc = \
datavis.percent_overlap\
(mean1, sdev1, mean2, sdev2, mean3, sdev3)
assert isinstance\
(datavis.percent_overlap\
(mean1, sdev1, mean2, sdev2, mean3, sdev3), tuple),\
"Returned data is not numpy.float64 type"
test_percent_overlap()
mean = np.array([24.12, 24.43, 24.82])
sdev = np.array([3.87, 3.94, 3.95])
vectorized_datavis.compounddata(mean, sdev)
def test_compounddata():
"""
Test that the data returned are numpy.ndarrays
"""
mean = np.array([24.12, 24.43, 24.82])
sdev = np.array([3.87, 3.94, 3.95])
datagenerated = vectorized_datavis.compounddata(mean, sdev)
assert isinstance(datagenerated, np.ndarray),\
"Returned data are not numpy.ndarrays"
test_compounddata()
def test_databinning():
"""
Test that the data returned are numpy.ndarrays
"""
mean = np.array([24.12, 24.43, 24.82])
sdev = np.array([3.87, 3.94, 3.95])
datagenerated = vectorized_datavis.compounddata(mean, sdev)
bins = np.linspace(10, 40, num=30)
yhist = vectorized_datavis.databinning(datagenerated, bins_list=bins)
assert isinstance(yhist, np.ndarray),\
"Returned data are not numpy.ndarrays"
test_databinning()
def test_pdfgen():
"""
Test that the data returned are numpy.ndarrays
"""
bins = np.linspace(10,40,num=30)
mean = np.array([24.12, 24.43, 24.82])
sdev = np.array([3.87, 3.94, 3.95])
pdf = vectorized_datavis.pdfgen(mean, sdev, bins_list=bins)
assert isinstance(pdf, np.ndarray),\
"Returned data are not numpy.ndarrays"
test_pdfgen()
def test_percent_overlap():
"""
Test that the data returned is a numpy.ndarray
"""
mean = np.array([24.12, 24.43, 24.82])
sdev = np.array([3.87, 3.94, 3.95])
overlap_perc_1w = vectorized_datavis.percent_overlap\
(mean, sdev)
assert isinstance(overlap_perc_1w, np.ndarray),\
"Returned data is not a numpy.ndarray"
test_percent_overlap()
```
| github_jupyter |
# IDS Instruction: Regression
(Lisa Mannel)
## Simple linear regression
First we import the packages necessary fo this instruction:
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
```
Consider the data set "df" with feature variables "x" and "y" given below.
```
df1 = pd.DataFrame({'x': [0, 1, 2, 3, 4, 5, 6, 7, 8, 9], 'y': [1, 3, 2, 5, 7, 8, 8, 9, 10, 12]})
print(df1)
```
To get a first impression of the given data, let's have a look at its scatter plot:
```
plt.scatter(df1.x, df1.y, color = "y", marker = "o", s = 40)
plt.xlabel('x')
plt.ylabel('y')
plt.title('first overview of the data')
plt.show()
```
We can already see a linear correlation between x and y. Assume the feature x to be descriptive, while y is our target feature. We want a linear function, y=ax+b, that predicts y as accurately as possible based on x. To achieve this goal we use linear regression from the sklearn package.
```
#define the set of descriptive features (in this case only 'x' is in that set) and the target feature (in this case 'y')
descriptiveFeatures1=df1[['x']]
targetFeature1=df1['y']
#define the classifier
classifier = LinearRegression()
#train the classifier
model1 = classifier.fit(descriptiveFeatures1, targetFeature1)
```
Now we can use the classifier to predict y. We print the predictions as well as the coefficient and bias (*intercept*) of the linear function.
```
#use the classifier to make prediction
targetFeature1_predict = classifier.predict(descriptiveFeatures1)
print(targetFeature1_predict)
#print coefficient and intercept
print('Coefficients: \n', classifier.coef_)
print('Intercept: \n', classifier.intercept_)
```
Let's visualize our regression function with the scatterplot showing the original data set. Herefore, we use the predicted values.
```
#visualize data points
plt.scatter(df1.x, df1.y, color = "y", marker = "o", s = 40)
#visualize regression function
plt.plot(descriptiveFeatures1, targetFeature1_predict, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.title('the data and the regression function')
plt.show()
```
### <span style="color:green"> Now it is your turn. </span> Build a simple linear regression for the data below. Use col1 as descriptive feature and col2 as target feature. Also plot your results.
```
df2 = pd.DataFrame({'col1': [770, 677, 428, 410, 371, 504, 1136, 695, 551, 550], 'col2': [54, 47, 28, 38, 29, 38, 80, 52, 45, 40]})
#Your turn
```
### Evaluation
Usually, the model and its predictions is not sufficient. In the following we want to evaluate our classifiers.
Let's start by computing their error. The sklearn.metrics package contains several errors such as
* Mean squared error
* Mean absolute error
* Mean squared log error
* Median absolute error
```
#computing the squared error of the first model
print("Mean squared error model 1: %.2f" % mean_squared_error(targetFeature1, targetFeature1_predict))
```
We can also visualize the errors:
```
plt.scatter(targetFeature1_predict, (targetFeature1 - targetFeature1_predict) ** 2, color = "blue", s = 10,)
## plotting line to visualize zero error
plt.hlines(y = 0, xmin = 0, xmax = 15, linewidth = 2)
## plot title
plt.title("Squared errors Model 1")
## function to show plot
plt.show()
```
### <span style="color:green"> Now it is your turn. </span> Compute the mean squared error and visualize the squared errors. Play around using different error metrics.
```
#Your turn
```
## Handling multiple descriptive features at once - Multiple linear regression
In most cases, we will have more than one descriptive feature . As an example we use an example data set of the scikit package. The dataset describes housing prices in Boston based on several attributes. Note, in this format the data is already split into descriptive features and a target feature.
```
from sklearn import datasets ## imports datasets from scikit-learn
df3 = datasets.load_boston()
#The sklearn package provides the data splitted into a set of descriptive features and a target feature.
#We can easily transform this format into the pandas data frame as used above.
descriptiveFeatures3 = pd.DataFrame(df3.data, columns=df3.feature_names)
targetFeature3 = pd.DataFrame(df3.target, columns=['target'])
print('Descriptive features:')
print(descriptiveFeatures3.head())
print('Target feature:')
print(targetFeature3.head())
```
To predict the housing price we will use a Multiple Linear Regression model. In Python this is very straightforward: we use the same function as for simple linear regression, but our set of descriptive features now contains more than one element (see above).
```
classifier = LinearRegression()
model3 = classifier.fit(descriptiveFeatures3,targetFeature3)
targetFeature3_predict = classifier.predict(descriptiveFeatures3)
print('Coefficients: \n', classifier.coef_)
print('Intercept: \n', classifier.intercept_)
print("Mean squared error: %.2f" % mean_squared_error(targetFeature3, targetFeature3_predict))
```
As you can see above, we have a coefficient for each descriptive feature.
## Handling categorical descriptive features
So far we always encountered numerical dscriptive features, but data sets can also contain categorical attributes. The regression function can only handle numerical input. There are several ways to tranform our categorical data to numerical data (for example using one-hot encoding as explained in the lecture: we introduce a 0/1 feature for every possible value of our categorical attribute). For adequate data, another possibility is to replace each categorical value by a numerical value and adding an ordering with it.
Popular possibilities to achieve this transformation are
* the get_dummies function of pandas
* the OneHotEncoder of scikit
* the LabelEncoder of scikit
After encoding the attributes we can apply our regular regression function.
```
#example using pandas
df4 = pd.DataFrame({'A':['a','b','c'],'B':['c','b','a'] })
one_hot_pd = pd.get_dummies(df4)
one_hot_pd
#example using scikit
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
#apply the one hot encoder
encoder = OneHotEncoder(categories='auto')
encoder.fit(df4)
df4_OneHot = encoder.transform(df4).toarray()
print('Transformed by One-hot Encoding: ')
print(df4_OneHot)
# encode labels with value between 0 and n_classes-1
encoder = LabelEncoder()
df4_LE = df4.apply(encoder.fit_transform)
print('Replacing categories by numerical labels: ')
print(df4_LE.head())
```
### <span style="color:green"> Now it is your turn. </span> Perform linear regression using the data set given below. Don't forget to transform your categorical descriptive features. The rental price attribute represents the target variable.
```
df5 = pd.DataFrame({'Size':[500,550,620,630,665],'Floor':[4,7,9,5,8], 'Energy rating':['C', 'A', 'A', 'B', 'C'], 'Rental price': [320,380,400,390,385] })
#Your turn
```
## Predicting a categorical target value - Logistic regression
We might also encounter data sets where our target feature is categorical. Here we don't transform them into numerical values, but insetad we use a logistic regression function. Luckily, sklearn provides us with a suitable function that is similar to the linear equivalent. Similar to linear regression, we can compute logistic regression on a single descriptive variable as well as on multiple variables.
```
# Importing the dataset
iris = pd.read_csv('iris.csv')
print('First look at the data set: ')
print(iris.head())
#defining the descriptive and target features
descriptiveFeatures_iris = iris[['sepal_length']] #we only use the attribute 'sepal_length' in this example
targetFeature_iris = iris['species'] #we want to predict the 'species' of iris
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(solver = 'liblinear', multi_class = 'ovr')
classifier.fit(descriptiveFeatures_iris, targetFeature_iris)
targetFeature_iris_pred = classifier.predict(descriptiveFeatures_iris)
print('Coefficients: \n', classifier.coef_)
print('Intercept: \n', classifier.intercept_)
```
### <span style="color:green"> Now it is your turn. </span> In the example above we only used the first attribute as descriptive variable. Change the example such that all available attributes are used.
```
#Your turn
```
Note, that the regression classifier (both logistic and non-logistic) can be tweaked using several parameters. This includes, but is not limited to, non-linear regression. Check out the documentation for details and feel free to play around!
# Support Vector Machines
Aside from regression models, the sklearn package also provides us with a function for training support vector machines. Looking at the example below we see that they can be trained in similar ways. We still use the iris data set for illustration.
```
from sklearn.svm import SVC
#define descriptive and target features as before
descriptiveFeatures_iris = iris[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']]
targetFeature_iris = iris['species']
#this time, we train an SVM classifier
classifier = SVC(C=1, kernel='linear', gamma = 'auto')
classifier.fit(descriptiveFeatures_iris, targetFeature_iris)
targetFeature_iris_predict = classifier.predict(descriptiveFeatures_iris)
targetFeature_iris_predict[0:5] #show the first 5 predicted values
```
As explained in the lecture, a support vector machine is defined by its support vectors. In the sklearn package we can access them and their properties very easily:
* support_: indicies of support vectors
* support_vectors_: the support vectors
* n_support_: the number of support vectors for each class
```
print('Indicies of support vectors:')
print(classifier.support_)
print('The support vectors:')
print(classifier.support_vectors_)
print('The number of support vectors for each class:')
print(classifier.n_support_)
```
We can also calculate the distance of the data points to the separating hyperplane by using the decision_function(X) method. Score(X,y) calculates the mean accuracy of the classification. The classification report shows metrics such as precision, recall, f1-score and support. You will learn more about these quality metrics in a few lectures.
```
from sklearn.metrics import classification_report
classifier.decision_function(descriptiveFeatures_iris)
print('Accuracy: \n', classifier.score(descriptiveFeatures_iris,targetFeature_iris))
print('Classification report: \n')
print(classification_report(targetFeature_iris, targetFeature_iris_predict))
```
The SVC has many parameters. In the lecture you learned about the concept of kernels. Scikit gives you the opportunity to try different kernel functions.
Furthermore, the parameter C tells the SVM optimization problem how much you want to avoid misclassifying each training example.
On the scikit website you can find more information about the available kernels etc. http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
| github_jupyter |
```
import scraping_class
logfile = 'log.txt'## name your log file.
connector = scraping_class.Connector(logfile)
import requests
from bs4 import BeautifulSoup
from tqdm import tqdm_notebook
import pandas as pd
import numpy as np
import html5lib
import sys
import pickle
from tqdm import tqdm_notebook
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import pyplot
with open('df_final.pkl', 'rb') as f:
df = pickle.load(f)
```
### Grade distrubtion by Faculties (used in the appendix)
```
# note: no NaN's
print(df['Fakultet'].unique())
# Number of courses by faculty
print(sum(df['Fakultet'] == 'Det Natur- og Biovidenskabelige Fakultet'))
print(sum(df['Fakultet'] == 'Det Samfundsvidenskabelige Fakultet'))
print(sum(df['Fakultet'] == 'Det Humanistiske Fakultet'))
print(sum(df['Fakultet'] == 'Det Sundhedsvidenskabelige Fakultet'))
print(sum(df['Fakultet'] == 'Det Juridiske Fakultet'))
print(sum(df['Fakultet'] == 'Det Teologiske Fakultet'))
#Number of grades given for each faculty.
list_number_of_grades_faculties = []
for i in tqdm_notebook(df['Fakultet'].unique()):
df_number_grades = df[df['Fakultet'] == i]
list_number_of_grades_faculties.append(int(sum(df_number_grades[[12, 10, 7, 4, 2, 0, -3]].sum(skipna = True))))
list_number_of_grades_faculties;
#Number of passing grades given for each faculty.
list_no_fail_number_of_grades_faculties = []
for i in tqdm_notebook(df['Fakultet'].unique()):
df_number_grades = df[df['Fakultet'] == i]
list_no_fail_number_of_grades_faculties.append(int(sum(df_number_grades[[12, 10, 7, 4, 2]].sum(skipna = True))))
list_no_fail_number_of_grades_faculties
```
### Grade distrubtion by Faculties, weighted against ECTS
```
# We need to weight the grades according to ECTS points. If we do not small courses will have the same weight as
# bigger courses.
df['Weigthed_m3'] = df['Credit_edit'] * df[-3]
df['Weigthed_00'] = df['Credit_edit'] * df[0]
df['Weigthed_02'] = df['Credit_edit'] * df[2]
df['Weigthed_4'] = df['Credit_edit'] * df[4]
df['Weigthed_7'] = df['Credit_edit'] * df[7]
df['Weigthed_10'] = df['Credit_edit'] * df[10]
df['Weigthed_12'] = df['Credit_edit'] * df[12]
df[['Credit_edit',-3,'Weigthed_m3',0,'Weigthed_00',2,'Weigthed_02',4,'Weigthed_4',7,'Weigthed_7',10,'Weigthed_10',12,'Weigthed_12']];
y_ects_inner = []
y_ects = []
x = ['-3','00','02','4','7','10','12']
# Looking at each faculty
for i in tqdm_notebook(df['Fakultet'].unique()):
df_faculty = df[df['Fakultet']==i]
# Using the weighted grades this time.
for k in ['Weigthed_m3','Weigthed_00','Weigthed_02','Weigthed_4','Weigthed_7','Weigthed_10','Weigthed_12']:
y_ects_inner.append(df_faculty[k].sum(skipna = True))
y_ects.append(y_ects_inner)
y_ects_inner=[]
# calc frequencies
y_ects_freq_inner = []
y_ects_freq = []
# running through each faculty
for i in range(len(y_ects)):
# calc frequencies
for q in range(len(y_ects[i])):
y_ects_freq_inner.append(y_ects[i][q]/sum(y_ects[i]))
y_ects_freq.append(y_ects_freq_inner)
y_ects_freq_inner = []
# This figure is used in the analysis. It uses WEIGHTED grades
f, ax = plt.subplots(figsize=(15,10))
plt.subplot(2, 3, 1)
plt.title(Faculty_names[0], fontsize = 16, weight = 'bold')
plt.ylim([0,0.30])
plt.grid(axis ='y',zorder=0)
plt.ylabel('Frequency',fontsize=14)
plt.annotate('Number of grades th=0.93, edgecolor='black',zorder=3)
given: '+ str(list_number_of_grades_faculties[0]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x, y_ects_freq[0], wid
plt.subplot(2, 3, 2)
plt.title(Faculty_names[1], fontsize = 16, weight = 'bold')
plt.ylim([0,0.30])
plt.grid(axis ='y',zorder=0)
plt.annotate('Number of grades given: '+ str(list_number_of_grades_faculties[1]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x, y_ects_freq[1], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 3)
plt.title(Faculty_names[2], fontsize = 16, weight = 'bold')
plt.ylim([0,0.30])
plt.grid(axis ='y',zorder=0)
plt.annotate('Number of grades given: '+ str(list_number_of_grades_faculties[2]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x, y_ects_freq[2], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 4)
plt.title(Faculty_names[3], fontsize = 16, weight = 'bold')
plt.ylim([0,0.30])
plt.grid(axis ='y',zorder=0)
plt.ylabel('Frequency',fontsize=14)
plt.annotate('Number of grades given: '+ str(list_number_of_grades_faculties[3]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x, y_ects_freq[3], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 5)
plt.title(Faculty_names[4], fontsize = 16, weight = 'bold')
plt.ylim([0,0.30])
plt.grid(axis ='y',zorder=0)
plt.annotate('Number of grades given: '+ str(list_number_of_grades_faculties[4]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x, y_ects_freq[4], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 6)
plt.title(Faculty_names[5], fontsize = 16, weight = 'bold')
plt.ylim([0,0.30])
plt.grid(axis ='y',zorder=0)
plt.annotate('Number of grades given: '+ str(list_number_of_grades_faculties[5]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x, y_ects_freq[5], width=0.93, edgecolor='black',zorder=3)
f.savefig('histogram_gades_split_faculty_ECTS_weight.png')
```
### Faculties, weighted against ECTS - droppping -3 and 00
```
y_no_fail_ects = []
x_no_fail = ['02','4','7','10','12']
# Looking at each faculty
for i in tqdm_notebook(df['Fakultet'].unique()):
df_faculty = df[df['Fakultet']==i]
y_no_fail_ects_inner=[]
for k in ['Weigthed_02','Weigthed_4','Weigthed_7','Weigthed_10','Weigthed_12']:
y_no_fail_ects_inner.append(df_faculty[k].sum(skipna = True))
y_no_fail_ects.append(y_no_fail_ects_inner)
y_no_fail_ects
# calc frequencies
y_no_fail_ects_freq = []
# running through each faculty
for i in range(len(y_ects)):
y_no_fail_ects_freq_inner = []
# calc frequencies
for q in range(len(y_no_fail_ects[i])):
y_no_fail_ects_freq_inner.append(y_no_fail_ects[i][q]/sum(y_no_fail_ects[i]))
y_no_fail_ects_freq.append(y_no_fail_ects_freq_inner)
y_no_fail_ects_freq
# This figure is used in the analysis
f, ax = plt.subplots(figsize=(15,10))
plt.subplot(2, 3, 1)
plt.title(Faculty_names[0], fontsize = 16, weight = 'bold')
plt.ylim([0,0.35])
plt.grid(axis ='y',zorder=0)
plt.ylabel('Frequency',fontsize=14)
plt.annotate('Number of passing grades: '+ str(list_no_fail_number_of_grades_faculties[0]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x_no_fail, y_no_fail_ects_freq[0], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 2)
plt.title(Faculty_names[1], fontsize = 16, weight = 'bold')
plt.ylim([0,0.35])
plt.grid(axis ='y',zorder=0)
plt.annotate('Number of passing grades: '+ str(list_no_fail_number_of_grades_faculties[1]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x_no_fail, y_no_fail_ects_freq[1], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 3)
plt.title(Faculty_names[2], fontsize = 16, weight = 'bold')
plt.ylim([0,0.35])
plt.grid(axis ='y',zorder=0)
plt.annotate('Number of passing grades: '+ str(list_no_fail_number_of_grades_faculties[2]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x_no_fail, y_no_fail_ects_freq[2], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 4)
plt.title(Faculty_names[3], fontsize = 16, weight = 'bold')
plt.ylim([0,0.35])
plt.grid(axis ='y',zorder=0)
plt.ylabel('Frequency',fontsize=14)
plt.annotate('Number of passing grades: '+ str(list_no_fail_number_of_grades_faculties[3]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x_no_fail, y_no_fail_ects_freq[3], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 5)
plt.title(Faculty_names[4], fontsize = 16, weight = 'bold')
plt.ylim([0,0.35])
plt.grid(axis ='y',zorder=0)
plt.annotate('Number of passing grades: '+ str(list_no_fail_number_of_grades_faculties[4]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x_no_fail, y_no_fail_ects_freq[4], width=0.93, edgecolor='black',zorder=3)
plt.subplot(2, 3, 6)
plt.title(Faculty_names[5], fontsize = 16, weight = 'bold')
plt.ylim([0,0.35])
plt.grid(axis ='y',zorder=0)
plt.annotate('Number of passing grades: '+ str(list_no_fail_number_of_grades_faculties[5]), (0,0), (0, -20),fontsize= 13, xycoords='axes fraction', textcoords='offset points', va='top')
plt.bar(x_no_fail, y_no_fail_ects_freq[5], width=0.93, edgecolor='black',zorder=3)
f.savefig('histogram_gades_split_faculty_ECTS_weight_NO_FAIL.png')
```
### Calculating GPA by faculty
```
from math import isnan
import math
#Calculate gpa when ONLY PASSED exams are counted
snit = []
for i in range(0,len(df)):
x_02 = df[2][i]
x_04 = df[4][i]
x_07 = df[7][i]
x_10 = df[10][i]
x_12 = df[12][i]
number = (x_12,x_10,x_07,x_04,x_02)
grades = [12,10,7,4,2]
mydick = dict(zip(grades,number))
cleandick = {k: mydick[k] for k in mydick if not isnan(mydick[k])}
num = sum([x * y for x,y in mydick.items()])
den = sum(mydick.values())
snit.append(num/den)
df["Snit"] = snit
# Here I calculate the GPA of some form of assessment
def gpa(df,string):
x_gpa = []
x_sho = []
x_ect = []
for i in range(0,len(df)):
if df["Fakultet"][i] == string:
if math.isnan(df["Snit"][i]) == False:
x_gpa.append(float(df["Snit"][i]))
x_sho.append(float(df["Fremmødte"][i]))
x_ect.append(float(df["Credit_edit"][i]))
den = 0
num = 0
for i in range(0,len(x_gpa)):
den = x_sho[i]*x_ect[i] + den
num = x_gpa[i]*x_sho[i]*x_ect[i] + num
out = num/den
return out
# Looping through each faculty
for i in df['Fakultet'].unique():
print(gpa(df,i))
```
### Type of assessments broken down by faculties
```
list_type_ass=list(df['Type of assessmet_edit'].unique())
y_type_ass_inner = []
y_type_ass = []
# Looking at each faculty
for i in tqdm_notebook(df['Fakultet'].unique()):
df_faculty = df[df['Fakultet']==i]
# Running through each type of assessment.
for k in list_type_ass:
# Summing number of passed people for all courses (in each faculty) broken down on each tyep of assessment
y_type_ass_inner.append(df_faculty[df_faculty['Type of assessmet_edit']==k]['Antal bestået'].sum(skipna = True))
y_type_ass.append(y_type_ass_inner)
y_type_ass_inner=[]
# Creating the categories which we want for plot.
categories = []
for i in range(len(df['Fakultet'].unique())):
categories_inner = []
# Oral
categories_inner.append(y_type_ass[i][1])
# Written not under invigilation
categories_inner.append(y_type_ass[i][2])
# Written under invigilation
categories_inner.append(y_type_ass[i][4])
# Rest
categories_inner.append(y_type_ass[i][0]+y_type_ass[i][3]+y_type_ass[i][5]+y_type_ass[i][6]+y_type_ass[i][7]\
+y_type_ass[i][8]+y_type_ass[i][9])
categories.append(categories_inner)
#calc share.
list_categories_share = []
# Running through each faculty
for i in range(len(categories)):
categories_share_inner = []
# For each faculty calc type of ass shares.
for k in range(len(categories[i])):
categories_share= categories[i][k]/sum(categories[i])*100 # times a 100 for %
categories_share_inner.append(categories_share)
list_categories_share.append(categories_share_inner)
# Converting list to DataFrame
dfcat= pd.DataFrame(list_categories_share)
dfcat
dfcat=dfcat.T
dfcat.columns = ['Science','Social Sciences','Humanities','Health & Medical Sciences','Law','Theology']
dfcat.rename(index={0:'Oral',1:'Written not under invigilation',2:'Written under invigilation',3:'Rest'})
#dfcat.index.name = 'type_ass'
dfcat=dfcat.T
dfcat.columns = ['Oral','Written not invigilation','Written invigilation','Rest']
colors = ["#011f4b","#005b96","#6497b1",'#b3cde0']
dfcat.plot(kind='bar', stacked=True, color = colors, fontsize = 12)
#plt.legend(bbox_to_anchor=(0, 1), loc='upper left', ncol=1)
plt.rcParams["figure.figsize"] = [15,15]
plt.legend(bbox_to_anchor=(0,1.02,1,0.2), loc="lower left", mode="expand", borderaxespad=0, ncol=2, fontsize = 12) #,weight = 'bold')
plt.tight_layout()
plt.savefig('stacked_bar_share_ass.png')
```
| github_jupyter |
<a href="https://colab.research.google.com/github/bhadreshpsavani/ExploringSentimentalAnalysis/blob/main/SentimentalAnalysisWithGPTNeo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Step1. Import and Load Data
```
!pip install -q pip install git+https://github.com/huggingface/transformers.git
!pip install -q datasets
from datasets import load_dataset
emotions = load_dataset("emotion")
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
## Step2. Preprocess Data
```
from transformers import AutoTokenizer
model_name = "EleutherAI/gpt-neo-125M"
tokenizer = AutoTokenizer.from_pretrained(model_name)
def tokenize(batch):
return tokenizer(batch["text"], padding=True, truncation=True)
tokenizer
tokenizer.add_special_tokens({'pad_token': '<|pad|>'})
tokenizer
emotions_encoded = emotions.map(tokenize, batched=True, batch_size=None)
from transformers import AutoModelForSequenceClassification
num_labels = 6
model = (AutoModelForSequenceClassification.from_pretrained(model_name, num_labels=num_labels).to(device))
emotions_encoded["train"].features
emotions_encoded.set_format("torch", columns=["input_ids", "attention_mask", "label"])
emotions_encoded["train"].features
from sklearn.metrics import accuracy_score, f1_score
def compute_metrics(pred):
labels = pred.label_ids
preds = pred.predictions.argmax(-1)
f1 = f1_score(labels, preds, average="weighted")
acc = accuracy_score(labels, preds)
return {"accuracy": acc, "f1": f1}
from transformers import Trainer, TrainingArguments
batch_size = 2
logging_steps = len(emotions_encoded["train"]) // batch_size
training_args = TrainingArguments(output_dir="results",
num_train_epochs=2,
learning_rate=2e-5,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size,
load_best_model_at_end=True,
metric_for_best_model="f1",
weight_decay=0.01,
evaluation_strategy="epoch",
disable_tqdm=False,
logging_steps=logging_steps,)
from transformers import Trainer
trainer = Trainer(model=model, args=training_args,
compute_metrics=compute_metrics,
train_dataset=emotions_encoded["train"],
eval_dataset=emotions_encoded["validation"])
trainer.train();
results = trainer.evaluate()
results
preds_output = trainer.predict(emotions_encoded["validation"])
preds_output.metrics
import numpy as np
from sklearn.metrics import plot_confusion_matrix
y_valid = np.array(emotions_encoded["validation"]["label"])
y_preds = np.argmax(preds_output.predictions, axis=1)
labels = ['sadness', 'joy', 'love', 'anger', 'fear', 'surprise']
plot_confusion_matrix(y_preds, y_valid, labels)
model.save_pretrained('./model')
tokenizer.save_pretrained('./model')
```
| github_jupyter |
## parameters
```
CLUSTER_ALGO = 'KMedoids'
C_SHAPE ='circle'
#C_SHAPE ='CIRCLE'
#C_SHAPE ='ellipse'
#N_CLUSTERS = [50,300, 1000]
N_CLUSTERS = [3]
CLUSTERS_STD = 0.3
N_P_CLUSTERS = [3, 30, 300, 3000]
N_CLUSTERS_S = N_CLUSTERS[0]
INNER_FOLDS = 3
OUTER_FOLDS = 3
```
## includes
```
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.datasets import load_iris
from sklearn.datasets import make_blobs
from sklearn.datasets import make_moons
%load_ext autoreload
%autoreload 2
packages = !conda list
packages
```
## Output registry
```
from __future__ import print_function
import sys, os
old__file__ = !pwd
__file__ = !cd ../../../photon ;pwd
#__file__ = !pwd
__file__ = __file__[0]
__file__
sys.path.append(__file__)
print(sys.path)
os.chdir(old__file__[0])
!pwd
old__file__[0]
import seaborn as sns; sns.set() # for plot styling
import numpy as np
import pandas as pd
from math import floor,ceil
from sklearn.model_selection import KFold
from sklearn.manifold import TSNE
import itertools
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
#set font size of labels on matplotlib plots
plt.rc('font', size=16)
#set style of plots
sns.set_style('white')
#define a custom palette
PALLET = ['#40111D', '#DCD5E4', '#E7CC74'
,'#39C8C6', '#AC5583', '#D3500C'
,'#FFB139', '#98ADA7', '#AD989E'
,'#708090','#6C8570','#3E534D'
,'#0B8FD3','#0B47D3','#96D30B'
,'#630C3A','#F1D0AF','#64788B'
,'#8B7764','#7A3C5D','#77648B'
,'#eaff39','#39ff4e','#4e39ff'
,'#ff4e39','#87ff39','#ff3987', ]
N_PALLET = len(PALLET)
sns.set_palette(PALLET)
sns.palplot(PALLET)
from clusim.clustering import Clustering, remap2match
import clusim.sim as sim
from photonai.base import Hyperpipe, PipelineElement, Preprocessing, OutputSettings
from photonai.optimization import FloatRange, Categorical, IntegerRange
from photonai.base.photon_elements import PhotonRegistry
from photonai.visual.graphics import plot_cm
from photonai.photonlogger.logger import logger
#from photonai.base.registry.registry import PhotonRegistry
```
## function defintions
```
def yield_parameters_ellipse(n_p_clusters):
cluster_std = CLUSTERS_STD
for n_p_cluster in n_p_clusters:
for n_cluster in N_CLUSTERS:
print('ncluster:', n_cluster)
n_cluster_std = [cluster_std for k in range(n_cluster)]
n_samples = [n_p_cluster for k in range(n_cluster)]
data_X, data_y = make_blobs(n_samples=n_samples,
cluster_std=n_cluster_std, random_state=0)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_ellipse = np.dot(data_X, transformation)
yield [X_ellipse, data_y, n_cluster]
def yield_parameters(n_p_clusters):
cluster_std = CLUSTERS_STD
for n_p_cluster in n_p_clusters:
for n_cluster in N_CLUSTERS:
n_cluster_std = [cluster_std for k in range(n_cluster)]
n_samples = [n_p_cluster for k in range(n_cluster)]
data_X, data_y = make_blobs(n_samples=n_samples,
cluster_std=n_cluster_std, random_state=0)
yield [data_X, data_y, n_cluster]
def results_to_df(results):
ll = []
for obj in results:
ll.append([obj.operation,
obj.value,
obj.metric_name])
_results=pd.DataFrame(ll).pivot(index=2, columns=0, values=1)
_results.columns=['Mean','STD']
return(_results)
def cluster_plot(my_pipe, data_X, n_cluster, PALLET):
y_pred= my_pipe.predict(data_X)
data = pd.DataFrame(data_X[:, 0],columns=['x'])
data['y'] = data_X[:, 1]
data['labels'] = y_pred
facet = sns.lmplot(data=data, x='x', y='y', hue='labels',
aspect= 1.0, height=10,
fit_reg=False, legend=True, legend_out=True)
customPalette = PALLET #*ceil((n_cluster/N_PALLET +2))
for i, label in enumerate( np.sort(data['labels'].unique())):
plt.annotate(label,
data.loc[data['labels']==label,['x','y']].mean(),
horizontalalignment='center',
verticalalignment='center',
size=5, weight='bold',
color='white',
backgroundcolor=customPalette[i])
plt.show()
return y_pred
def simple_output(string: str, number: int) -> None:
print(string, number)
logger.info(string, number )
__file__ = "exp1.log"
base_folder = os.path.dirname(os.path.abspath(''))
custom_elements_folder = os.path.join(base_folder, 'custom_elements')
custom_elements_folder
registry = PhotonRegistry(custom_elements_folder=custom_elements_folder)
registry.activate()
registry.PHOTON_REGISTRIES,PhotonRegistry.PHOTON_REGISTRIES
registry.activate()
registry.list_available_elements()
# take off last name
```
## KMeans blobs
```
registry.info(CLUSTER_ALGO)
def hyper_cluster(cluster_name):
if C_SHAPE == 'ellipse' :
yield_cluster = yield_parameters_ellipse
else:
yield_cluster = yield_parameters
n_p_clusters = N_P_CLUSTERS
for data_X, data_y,n_cluster in yield_cluster(n_p_clusters):
simple_output('CLUSTER_ALGO:', CLUSTER_ALGO)
simple_output('C_SHAPE:',C_SHAPE)
simple_output('n_cluster:', n_cluster)
simple_output('CLUSTERS_STD:', CLUSTERS_STD)
simple_output('INNER_FOLDS:', INNER_FOLDS)
simple_output('OUTER_FOLDS:', OUTER_FOLDS)
simple_output('n_points:', len(data_y))
X = data_X.copy(); y = data_y.copy()
# DESIGN YOUR PIPELINE
settings = OutputSettings(project_folder='./tmp/')
my_pipe = Hyperpipe('batching',
optimizer='sk_opt',
# optimizer_params={'n_configurations': 25},
metrics=['ARI', 'MI', 'HCV', 'FM'],
best_config_metric='ARI',
outer_cv=KFold(n_splits=OUTER_FOLDS),
inner_cv=KFold(n_splits=INNER_FOLDS),
verbosity=0,
output_settings=settings)
my_pipe += PipelineElement(cluster_name, hyperparameters={
'n_clusters': IntegerRange(floor(n_cluster*.7)
, ceil(n_cluster*1.2)),
},random_state=777)
logger.info('Cluster optimization range:', floor(n_cluster*.7), ceil(n_cluster*1.2))
print('Cluster optimization range:', floor(n_cluster*.7), ceil(n_cluster*1.2))
# NOW TRAIN YOUR PIPELINE
my_pipe.fit(X, y)
debug = True
#------------------------------plot
y_pred=cluster_plot(my_pipe, X, n_cluster, PALLET)
#--------------------------------- best
print(pd.DataFrame(my_pipe.best_config.items()
,columns=['n_clusters', 'k']))
#------------------------------
print('train','\n'
,results_to_df(my_pipe.results.metrics_train))
print('test','\n'
,results_to_df(my_pipe.results.metrics_test))
#------------------------------
# turn the ground-truth labels into a clusim Clustering
true_clustering = Clustering().from_membership_list(y)
kmeans_clustering = Clustering().from_membership_list(y_pred) # lets see how similar the predicted k-means clustering is to the true clustering
#------------------------------
# using all available similar measures!
row_format2 ="{:>25}" * (2)
for simfunc in sim.available_similarity_measures:
print(row_format2.format(simfunc, eval('sim.' + simfunc+'(true_clustering, kmeans_clustering)')))
#------------------------------# The element-centric similarity is particularly useful for understanding
# how a clustering method performed
# Let's start with the single similarity value:
elsim = sim.element_sim(true_clustering, kmeans_clustering)
print("Element-centric similarity: {}".format(elsim))
hyper_cluster(CLUSTER_ALGO)
Cottman
*-+
*+-=END
```
| github_jupyter |
```
from collections import OrderedDict
from collections import namedtuple
import numpy as np
from scipy import stats
# R precision
def r_precision(targets, predictions, max_n_predictions=500):
# Assumes predictions are sorted by relevance
# First, cap the number of predictions
predictions = predictions[:max_n_predictions]
# Calculate metric
target_set = set(targets)
target_count = len(target_set)
return float(len(set(predictions[:target_count]).intersection(target_set))) / target_count
def dcg(relevant_elements, retrieved_elements, k, *args, **kwargs):
"""Compute the Discounted Cumulative Gain.
Rewards elements being retrieved in descending order of relevance.
\[ DCG = rel_1 + \sum_{i=2}^{|R|} \frac{rel_i}{\log_2(i + 1)} \]
Args:
retrieved_elements (list): List of retrieved elements
relevant_elements (list): List of relevant elements
k (int): 1-based index of the maximum element in retrieved_elements
taken in the computation
Note: The vector `retrieved_elements` is truncated at first, THEN
deduplication is done, keeping only the first occurence of each element.
Returns:
DCG value
"""
retrieved_elements = __get_unique(retrieved_elements[:k])
relevant_elements = __get_unique(relevant_elements)
if len(retrieved_elements) == 0 or len(relevant_elements) == 0:
return 0.0
# Computes an ordered vector of 1.0 and 0.0
score = [float(el in relevant_elements) for el in retrieved_elements]
# return score[0] + np.sum(score[1:] / np.log2(
# 1 + np.arange(2, len(score) + 1)))
return np.sum(score / np.log2(1 + np.arange(1, len(score) + 1)))
def ndcg(relevant_elements, retrieved_elements, k, *args, **kwargs):
"""Compute the Normalized Discounted Cumulative Gain.
Rewards elements being retrieved in descending order of relevance.
The metric is determined by calculating the DCG and dividing it by the
ideal or optimal DCG in the case that all recommended tracks are relevant.
Note:
The ideal DCG or IDCG is on our case equal to:
\[ IDCG = 1+\sum_{i=2}^{min(\left| G \right|, k)}\frac{1}{\log_2(i +1)}\]
If the size of the set intersection of \( G \) and \( R \), is empty, then
the IDCG is equal to 0. The NDCG metric is now calculated as:
\[ NDCG = \frac{DCG}{IDCG + \delta} \]
with \( \delta \) a (very) small constant.
The vector `retrieved_elements` is truncated at first, THEN
deduplication is done, keeping only the first occurence of each element.
Args:
retrieved_elements (list): List of retrieved elements
relevant_elements (list): List of relevant elements
k (int): 1-based index of the maximum element in retrieved_elements
taken in the computation
Returns:
NDCG value
"""
# TODO: When https://github.com/scikit-learn/scikit-learn/pull/9951 is
# merged...
idcg = dcg(
relevant_elements, relevant_elements, min(k, len(relevant_elements)))
if idcg == 0:
raise ValueError("relevent_elements is empty, the metric is"
"not defined")
true_dcg = dcg(relevant_elements, retrieved_elements, k)
return true_dcg / idcg
def __get_unique(original_list):
"""Get only unique values of a list but keep the order of the first
occurence of each element
"""
return list(OrderedDict.fromkeys(original_list))
Metrics = namedtuple('Metrics', ['r_precision', 'ndcg', 'plex_clicks'])
# playlist extender clicks
def playlist_extender_clicks(targets, predictions, max_n_predictions=500):
# Assumes predictions are sorted by relevance
# First, cap the number of predictions
predictions = predictions[:max_n_predictions]
# Calculate metric
i = set(predictions).intersection(set(targets))
for index, t in enumerate(predictions):
for track in i:
if t == track:
return float(int(index / 10))
return float(max_n_predictions / 10.0 + 1)
# def compute all metrics
def get_all_metrics(targets, predictions, k):
return Metrics(r_precision(targets, predictions, k),
ndcg(targets, predictions, k),
playlist_extender_clicks(targets, predictions, k))
MetricsSummary = namedtuple('MetricsSummary', ['mean_r_precision',
'mean_ndcg',
'mean_plex_clicks',
'coverage'])
#java -jar RankLib-2.10.jar -train BigRecall-TrainingFile750-2080.txt -ranker 6 -metric2t NDCG@20 -save BigRecallTrain750-2080Model-1Trees-NDCG20-tc1-lr05-leaf5.txt -tree 1 -tc 1 -shrinkage 0.5 -leaf 5
#java -jar RankLib-2.10.jar -load BigRecallTrain750-2080Model-500Trees-NDCG20-tc1-lr05-leaf50.txt -rank BigRecallTestingFile750.txt -score BRScores750-2080Model-500Trees-NDCG20-tc1-lr05-leaf50.txt
#java -jar RankLib-2.10.jar -train BigRecall-TrainingFile750-2080.txt -ranker 6 -metric2t NDCG@20 -save BigRecallTrain750-2080Model-500Trees-NDCG20-tc1-lr05-leaf50.txt -tree 500 -tc 1 -shrinkage 0.5 -leaf 50
import os
TrainingFile='./Training/BigRecall-TrainingFile750-2080.txt'
TestingFile='./Training/BigRecallTestingFile750.txt'
trees=[500]
tcVals=[-1]
shrinkages=[0.5]
leaves= [50]
def createCommand(tree,tc,lr,leaf):
opModelFile= './Training/ModelsAndScores/BigRecallTrain750-2080Model-'+str(tree)+'Trees-NDCG20-tc'+str(tc)+'-lr'+str(lr).replace('.','')+'-leaf'+str(leaf)+'.txt'
trainCommand= 'java -jar ./Training/RankLib-2.10.jar -train ./Training/BigRecall-TrainingFile750-2080.txt -ranker 6 -metric2t NDCG@20 -silent -save '+ opModelFile+ ' -tree '+str(tree)+' -tc '+str(tc)+ ' -shrinkage '+str(lr)+ ' -leaf '+ str(leaf) +' -missingzero'
#BRScores750-2080Model-1Trees-NDCG20-tc1-lr05-leaf5.txt
opScoresFile='./Training/ModelsAndScores/BRScores750-2080Model-'+opModelFile.split('Model-')[1]
testCommand= 'java -jar ./Training/RankLib-2.10.jar -load '+opModelFile+' -rank ./Training/BigRecallTestingFile750.txt -score '+opScoresFile
return (opModelFile,trainCommand, opScoresFile, testCommand)
paramSweep=[]
for tree in trees:
for tc in tcVals:
for lr in shrinkages:
for leaf in leaves:
paramSweep.append(createCommand(tree,tc,lr,leaf))
import multiprocessing as mp
import codecs
import os
import subprocess
def ExecuteRanklib(execTuples):
try:
trainCommand=execTuples[1]
train= subprocess.check_output(trainCommand.split())
print train
print '----------'
scoreCommand=execTuples[3]
test=subprocess.check_output(scoreCommand.split())
print test
print '----------'
except:
print execTuples
pool = mp.Pool(processes=10)
pool.map(ExecuteRanklib, paramSweep)
TestFile='./Training/BigRecallTestingFile750.txt'
with open(TestFile) as f:
test = f.readlines()
PidTestTracks={}
for l in test:
pid=l.split()[1].split(':')[1].strip()
track=l.split('#')[1].strip()
PidTestTracks.setdefault(pid,[]).append(track)
###skip
import os
Meta1Resultspath='/home/ubuntu/SpotifyChallenge/notebooks/Reranking/TestingQueryResults/Meta1/'
Meta2Resultspath='/home/ubuntu/SpotifyChallenge/notebooks/Reranking/TestingQueryResults/Meta2/'
QEPRFResultspath='/home/ubuntu/SpotifyChallenge/notebooks/Reranking/TestingQueryResults/QEPRF750/'
Meta1Files=[Meta1Resultspath+x for x in os.listdir(Meta1Resultspath)]
Meta2Files=[Meta2Resultspath+x for x in os.listdir(Meta2Resultspath)]
QEPRFFiles=[QEPRFResultspath+x for x in os.listdir(QEPRFResultspath)]
###skip
import codecs
def parseMetaFiles(path):
playlistId=path.split('/')[-1].split('.op')[0]
with codecs.open(path, 'r', encoding='utf-8') as f:
lines = f.read().splitlines()
rank=0
resultSet=[]
for result in lines[1:]:
try:
rank=rank+1
splits=result.split('\t')
score = splits[0]
trackid= splits[1]
resultSet.append((rank,trackid,score))
except:
print result
return "QueryError"
return(playlistId,resultSet)
####skip
Meta1Op=[]
err1=[]
Meta2Op=[]
err2=[]
for f in Meta1Files:
res=parseMetaFiles(f)
if res !="QueryError":
Meta1Op.append(res)
else:
err1.append(f)
for f in Meta2Files:
res=parseMetaFiles(f)
if res !="QueryError":
Meta2Op.append(res)
else:
err2.append(f)
####skip
import codecs
def QEPRFParse(path):
playlistId=path.split('/')[-1].split('.op')[0]
with codecs.open(path, 'r', encoding='utf-8') as f:
lines = f.read().splitlines()
inputQueries=lines[0].split('# query: ')[1].split()
resultSet=[]
pairResults= lines[1].split(' #weight(')[2].split(') )')[0].split('" ')
rank=0
for result in pairResults[:-1]:
try:
rank=rank+1
splits=result.split('"')
score = splits[0].strip()
trackid= splits[1].strip()
resultSet.append((rank,trackid,score))
except:
print result
return "QueryError"
return(playlistId,inputQueries,resultSet)
###skip
QEPRFOp=[]
err3=[]
for f in QEPRFFiles:
res=QEPRFParse(f)
if res !="QueryError":
QEPRFOp.append(res)
else:
err3.append(f)
###skip
import pickle
pidTrackMapping=pickle.load(open('./BiPartites/AllDataPidTrackListBipartite.pkl','rb'))
####skip
import pickle
import os
import codecs
from random import shuffle
pkl = os.listdir('./SplitsInformation/')
count=0
DS={}
for fpkl in pkl:
if fpkl in ['testing25RandPid.pkl', 'testing25Pid.pkl', 'testing1Pid.pkl', 'testing100Pid.pkl', 'testing10Pid.pkl', 'testing5Pid.pkl', 'testing100RandPid.pkl']:
testType=fpkl.replace('.pkl','')
if 'Rand' in fpkl:
listLen=int(fpkl.split('testing')[1].split('Rand')[0])
qtype='Rand'
else :
listLen=int(fpkl.split('testing')[1].split('Pid')[0])
qtype='Normal'
testingPids=pickle.load(open('./SplitsInformation/'+fpkl,'rb'))
for pid in testingPids:
pid=str(pid)
referenceSet=[x.replace('spotify:track:','') for x in pidTrackMapping[pid]]
DS[pid]=(testType,qtype,listLen,referenceSet)
####skip
import pickle
import os
import codecs
from random import shuffle
pkl = os.listdir('./SplitsInformation/')
testingTitleonlyPids=[]
for fpkl in pkl:
if fpkl =='testingOnlyTitlePid.pkl':
testType=fpkl.replace('.pkl','')
listLen=0
qtype='Normal'
testingPids=pickle.load(open('./SplitsInformation/'+fpkl,'rb'))
for pid in testingPids:
pid=str(pid)
referenceSet=[x.replace('spotify:track:','') for x in pidTrackMapping[pid]]
DS[pid]=(testType,qtype,listLen,referenceSet)
testingTitleonlyPids=[str(x) for x in testingPids]
from collections import defaultdict
from random import shuffle
for comb in paramSweep:
scoresfile= comb[2]
with open(scoresfile) as f:
scores = f.readlines()
PidTracksScores={}
for l in scores:
pid=l.split()[0].strip()
trackScore=l.split()[2].strip()
PidTracksScores.setdefault(pid,[]).append(float(trackScore))
rerankedCandidates={}
for pid,tracksList in PidTestTracks.items():
scoresList=PidTracksScores[pid]
zippedPairs=zip(tracksList,scoresList)
shuffle(zippedPairs)
rerankedCandidates[pid]=[x[0] for x in sorted(zippedPairs, key=lambda x: x[1], reverse=True)]
####continue here
evalSets=[]
for pl in QEPRFOp:
plId=pl[0]
exposed=pl[1]
candidates=rerankedCandidates[plId]
candidates=[x for x in candidates if x not in exposed]
refVals= DS[plId]
testtype=refVals[0]
orderType=refVals[1]
exposedLen=refVals[2]
playlist=refVals[3]
if orderType=='Normal':
groundTruth=playlist[exposedLen:]
else:
groundTruth=[x for x in playlist if x not in exposed]
evalSets.append((groundTruth, candidates[:500], testtype, exposedLen))
for pl in Meta2Op:
plId=pl[0]
if plId in testingTitleonlyPids and plId in rerankedCandidates:
exposed=[]
candidates=rerankedCandidates[plId]
refVals= DS[plId]
testtype=refVals[0]
orderType=refVals[1]
exposedLen=refVals[2]
playlist=refVals[3]
groundTruth=playlist[exposedLen:]
evalSets.append((groundTruth, candidates[:500], testtype, exposedLen))
####continue here
'''
r_precision(targets, predictions, k),
ndcg(targets, predictions, k),
playlist_extender_clicks(targets, predictions, k)
'''
indivSumsCounts= defaultdict(int)
indivSumsRecall = defaultdict(int)
indivSumsNdcg = defaultdict(int)
indivSumsRprec = defaultdict(int)
indivSumsClicks = defaultdict(int)
globalNdcg=0
globalRprec=0
globalClicks=0
globalRecall=0
count=0
for evalTuple in evalSets:
targets=evalTuple[0]
predictions=evalTuple[1]
testType=evalTuple[2]
tupNdcg=ndcg(targets,predictions,500)
tuprprec=r_precision(targets,predictions,500)
tupClicks=playlist_extender_clicks(targets,predictions,500)
globalNdcg+=tupNdcg
indivSumsNdcg[testType]+=tupNdcg
globalRprec+=tuprprec
indivSumsRprec[testType]+=tuprprec
globalClicks+=tupClicks
indivSumsClicks[testType]+=tupClicks
indivSumsCounts[testType]+=1
recallSetSize= len(set(predictions)&set(targets))
refSetSize=len(targets)
recall=recallSetSize*1.0/refSetSize
globalRecall+=recall
indivSumsRecall[testType]+=recall
count+=1
for k, v in indivSumsCounts.items():
indivSumsRecall[k]=indivSumsRecall[k]/v
indivSumsNdcg[k]=indivSumsNdcg[k]/v
indivSumsRprec[k]=indivSumsRprec[k]/v
indivSumsClicks[k]=indivSumsClicks[k]/v
print scoresfile , 'Recall:' , globalRecall/count,'NDCG:', globalNdcg/count, 'RPrec:', globalRprec/count,'Clicks:', globalClicks/count
Recall 0.5964542020518547,
NDCG 0.30332032798678032,
RPrec 0.12934009424035461,
Clicks 5.1286
```
| github_jupyter |
# [NTDS'19] assignment 1: network science
[ntds'19]: https://github.com/mdeff/ntds_2019
[Eda Bayram](https://lts4.epfl.ch/bayram), [EPFL LTS4](https://lts4.epfl.ch) and
[Nikolaos Karalias](https://people.epfl.ch/nikolaos.karalias), [EPFL LTS2](https://lts2.epfl.ch).
## Students
* Team: `<5>`
* `<Alice Bizeul, Gaia Carparelli, Antoine Spahr and Hugues Vinzant`
## Rules
Grading:
* The first deadline is for individual submissions. The second deadline is for the team submission.
* All team members will receive the same grade based on the team solution submitted on the second deadline.
* As a fallback, a team can ask for individual grading. In that case, solutions submitted on the first deadline are graded.
* Collaboration between team members is encouraged. No collaboration between teams is allowed.
Submission:
* Textual answers shall be short. Typically one to two sentences.
* Code has to be clean.
* You cannot import any other library than we imported.
Note that Networkx is imported in the second section and cannot be used in the first.
* When submitting, the notebook is executed and the results are stored. I.e., if you open the notebook again it should show numerical results and plots. We won't be able to execute your notebooks.
* The notebook is re-executed from a blank state before submission. That is to be sure it is reproducible. You can click "Kernel" then "Restart Kernel and Run All Cells" in Jupyter.
## Objective
The purpose of this milestone is to explore a given dataset, represent it by network by constructing different graphs. In the first section, you will analyze the network properties. In the second section, you will explore various network models and find out the network model fitting the ones you construct from the dataset.
## Cora Dataset
The [Cora dataset](https://linqs.soe.ucsc.edu/node/236) consists of scientific publications classified into one of seven research fields.
* **Citation graph:** the citation network can be constructed from the connections given in the `cora.cites` file.
* **Feature graph:** each publication in the dataset is described by a 0/1-valued word vector indicating the absence/presence of the corresponding word from the dictionary and its research field, given in the `cora.content` file. The dictionary consists of 1433 unique words. A feature graph can be constructed using the Euclidean distance between the feature vector of the publications.
The [`README`](data/cora/README) provides details about the content of [`cora.cites`](data/cora/cora.cites) and [`cora.content`](data/cora/cora.content).
## Section 1: Network Properties
```
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%matplotlib inline
```
### Question 1: Construct a Citation Graph and a Feature Graph
Read the `cora.content` file into a Pandas DataFrame by setting a header for the column names. Check the `README` file.
```
column_list = ['paper_id'] + [str(i) for i in range(1,1434)] + ['class_label']
pd_content = pd.read_csv('data/cora/cora.content', delimiter='\t', names=column_list)
pd_content.head()
```
Print out the number of papers contained in each of the reasearch fields.
**Hint:** You can use the `value_counts()` function.
```
pd_content['class_label'].value_counts()
```
Select all papers from a field of your choice and store their feature vectors into a NumPy array.
Check its shape.
```
my_field = 'Neural_Networks'
features = pd_content[pd_content['class_label'] == my_field].drop(columns=['paper_id','class_label']).to_numpy()
features.shape
```
Let $D$ be the Euclidean distance matrix whose $(i,j)$ entry corresponds to the Euclidean distance between feature vectors $i$ and $j$.
Using the feature vectors of the papers from the field which you have selected, construct $D$ as a Numpy array.
```
distance = np.zeros([features.shape[0],features.shape[0]])
for i in range(features.shape[0]):
distance[i] = np.sqrt(np.sum((features[i,:] - features)**2, axis=1))
distance.shape
```
Check the mean pairwise distance $\mathbb{E}[D]$.
```
# Mean on the upper triangle as the matrix is symetric (we also excluded the diagonal)
mean_distance = distance[np.triu_indices(distance.shape[1],1)].mean()
print('Mean euclidian distance between feature vectors of papers on Neural Networks: {}'.format(mean_distance))
```
Plot an histogram of the euclidean distances.
```
fig,ax = plt.subplots(1,1,figsize=(8, 8))
ax.hist(distance.flatten(), density=True, bins=20, color='salmon', edgecolor='black', linewidth=1);
ax.set_title("Histogram of Euclidean distances between Neural-networks papers")
ax.set_xlabel("Euclidian Distances")
ax.set_ylabel("Frequency")
ax.grid(True, which='major', axis='y')
ax.set_axisbelow(True)
plt.show()
```
Now create an adjacency matrix for the papers by thresholding the Euclidean distance matrix.
The resulting (unweighted) adjacency matrix should have entries
$$ A_{ij} = \begin{cases} 1, \; \text{if} \; d(i,j)< \mathbb{E}[D], \; i \neq j, \\ 0, \; \text{otherwise.} \end{cases} $$
First, let us choose the mean distance as the threshold.
```
threshold = mean_distance
A_feature = np.where(distance < threshold, 1, 0)
np.fill_diagonal(A_feature,0)
```
Now read the `cora.cites` file and construct the citation graph by converting the given citation connections into an adjacency matrix.
```
cora_cites = np.genfromtxt('data/cora/cora.cites', delimiter='\t')
papers = np.unique(cora_cites)
A_citation = np.zeros([papers.size, papers.size])
for i in range(cora_cites.shape[0]):
A_citation[np.where(papers==cora_cites[i,1]),np.where(papers==cora_cites[i,0])] = 1
A_citation.shape
```
Get the adjacency matrix of the citation graph for the field that you chose.
You have to appropriately reduce the adjacency matrix of the citation graph.
```
# get the paper id from the chosen field
field_id = pd_content[pd_content['class_label'] == my_field]["paper_id"].unique()
# get the index of those paper in the A_citation matrix (similar to index on the vector 'papers')
field_citation_id = np.empty(field_id.shape[0]).astype(int)
for i in range(field_id.shape[0]):
field_citation_id[i] = np.where(papers == field_id[i])[0]
# get the A_citation matrix only at the index of the paper in the field
A_citation = A_citation[field_citation_id][:,field_citation_id]
A_citation.shape
```
Check if your adjacency matrix is symmetric. Symmetrize your final adjacency matrix if it's not already symmetric.
```
# a matrix is symetric if it's the same as its transpose
print('The citation adjency matrix for papers on Neural Networks is symmetric: {}'.format(np.all(A_citation == A_citation.transpose())))
# symetrize it by taking the maximum between A and A.transposed
A_citation = np.maximum(A_citation, A_citation.transpose())
# To verify if the matrix is symetric
print('After modifiying the matrix, it is symmetric: {}'.format(np.count_nonzero(A_citation - A_citation.transpose())==0))
```
Check the shape of your adjacency matrix again.
```
A_citation.shape
```
### Question 2: Degree Distribution and Moments
What is the total number of edges in each graph?
```
num_edges_feature = int(np.sum(A_feature)/2) # only half of the matrix
num_edges_citation = int(np.sum(A_citation)/2)
print(f"Number of edges in the feature graph: {num_edges_feature}")
print(f"Number of edges in the citation graph: {num_edges_citation}")
```
Plot the degree distribution histogram for each of the graphs.
```
degrees_citation = A_citation.sum(axis=1) # degree = nbr of connections --> sum of ones over columns (axis=1)
degrees_feature = A_feature.sum(axis=1)
deg_hist_normalization = np.ones(degrees_citation.shape[0]) / degrees_citation.shape[0]
fig, axes = plt.subplots(1, 2, figsize=(16, 8))
axes[0].set_title('Citation graph degree distribution')
axes[0].hist(degrees_citation, weights=deg_hist_normalization, bins=20, color='salmon', edgecolor='black', linewidth=1);
axes[1].set_title('Feature graph degree distribution')
axes[1].hist(degrees_feature, weights=deg_hist_normalization, bins=20, color='salmon', edgecolor='black', linewidth=1);
```
Calculate the first and second moments of the degree distribution of each graph.
```
cit_moment_1 = np.mean(degrees_citation)
cit_moment_2 = np.var(degrees_citation)
feat_moment_1 = np.mean(degrees_feature)
feat_moment_2 = np.var(degrees_feature)
print(f"1st moment of citation graph: {cit_moment_1:.3f}")
print(f"2nd moment of citation graph: {cit_moment_2:.3f}")
print(f"1st moment of feature graph: {feat_moment_1:.3f}")
print(f"2nd moment of feature graph: {feat_moment_2:.3f}")
```
What information do the moments provide you about the graphs?
Explain the differences in moments between graphs by comparing their degree distributions.
### Answer :
**<br>The moments provide an idea of the sparsity of the graphs and the way the data is distributed using numerical values. The first moment is associated with the average value, the second to the variance of the distribution. A large 1st moment would mean a large number of edges per node on average, whereas the 2nd moment give information about the spread of the node's degree around the average value (variance).
<br> Citation degree distribution 1st moment lays around 2.8, and the second one is higher (around 15.5) with a large number of nodes (818). It thus means that there are many nodes with a small degree but there are also larger hubs, the nework is likely to be sparse. The feature degree distribution moments are larger, meaning a rather dense graph. There are many nodes with a degree of above 800 (15%), and since the network contains 818 nodes, it means that many nodes are almost saturated. The high variance shows that the degree distribution is more diffuse around the average value than for the citation graph.**
Select the 20 largest hubs for each of the graphs and remove them. Observe the sparsity pattern of the adjacency matrices of the citation and feature graphs before and after such a reduction.
```
smallest_feat_hub_idx = np.argpartition(degrees_feature, degrees_feature.shape[0]-20)[:-20]
smallest_feat_hub_idx.sort()
reduced_A_feature = A_feature[smallest_feat_hub_idx][:,smallest_feat_hub_idx]
smallest_cit_hub_idx = np.argpartition(degrees_citation, degrees_citation.shape[0]-20)[:-20]
smallest_cit_hub_idx.sort()
reduced_A_citation = A_citation[smallest_cit_hub_idx][:,smallest_cit_hub_idx]
fig, axes = plt.subplots(2, 2, figsize=(16, 16))
axes[0, 0].set_title('Feature graph: adjacency matrix sparsity pattern')
axes[0, 0].spy(A_feature);
axes[0, 1].set_title('Feature graph without top 20 hubs: adjacency matrix sparsity pattern')
axes[0, 1].spy(reduced_A_feature);
axes[1, 0].set_title('Citation graph: adjacency matrix sparsity pattern')
axes[1, 0].spy(A_citation);
axes[1, 1].set_title('Citation graph without top 20 hubs: adjacency matrix sparsity pattern')
axes[1, 1].spy(reduced_A_citation);
```
Plot the new degree distribution histograms.
```
reduced_degrees_feat = reduced_A_feature.sum(axis=1)
reduced_degrees_cit = reduced_A_citation.sum(axis=1)
deg_hist_normalization = np.ones(reduced_degrees_feat.shape[0])/reduced_degrees_feat.shape[0]
fig, axes = plt.subplots(1, 2, figsize=(16, 8))
axes[0].set_title('Citation graph degree distribution')
axes[0].hist(reduced_degrees_cit, weights=deg_hist_normalization, bins=8, color='salmon', edgecolor='black', linewidth=1);
axes[1].set_title('Feature graph degree distribution')
axes[1].hist(reduced_degrees_feat, weights=deg_hist_normalization, bins=20, color='salmon', edgecolor='black', linewidth=1);
```
Compute the first and second moments for the new graphs.
```
reduced_cit_moment_1 = np.mean(reduced_degrees_cit)
reduced_cit_moment_2 = np.var(reduced_degrees_cit)
reduced_feat_moment_1 = np.mean(reduced_degrees_feat)
reduced_feat_moment_2 = np.var(reduced_degrees_feat)
print(f"Citation graph first moment: {reduced_cit_moment_1:.3f}")
print(f"Citation graph second moment: {reduced_cit_moment_2:.3f}")
print(f"Feature graph first moment: {reduced_feat_moment_1:.3f}")
print(f"Feature graph second moment: {reduced_feat_moment_2:.3f}")
```
Print the number of edges in the reduced graphs.
```
num_edges_reduced_feature = int(np.sum(reduced_A_feature)/2)
num_edges_reduced_citation = int(np.sum(reduced_A_citation)/2)
print(f"Number of edges in the reduced feature graph: {num_edges_reduced_feature}")
print(f"Number of edges in the reduced citation graph: {num_edges_reduced_citation}")
```
Is the effect of removing the hubs the same for both networks? Look at the percentage changes for each moment. Which of the moments is affected the most and in which graph? Explain why.
**Hint:** Examine the degree distributions.
```
change_cit_moment_1 = (reduced_cit_moment_1-cit_moment_1)/cit_moment_1
change_cit_moment_2 = (reduced_cit_moment_2-cit_moment_2)/cit_moment_2
change_feat_moment_1 = (reduced_feat_moment_1-feat_moment_1)/feat_moment_1
change_feat_moment_2 = (reduced_feat_moment_2-feat_moment_2)/feat_moment_2
print(f"% Percentage of change for citation 1st moment: {change_cit_moment_1*100:.3f}")
print(f"% Percentage of change for citation 2nd moment: {change_cit_moment_2*100:.3f}")
print(f"% Percentage of change for feature 1st moment: {change_feat_moment_1*100:.3f}")
print(f"% Percentage of change for feature 2nd moment: {change_feat_moment_2*100:.3f}")
```
### Answer :
**After looking of the percentage of change of moments, we can notice that the removal of the 20 largest hubs affects way more the citation degree distribution than the feature degree distribution. The 2nd moment of the citation degree distribution is reduced by almost 85%, this can be due to the fact that the percentage of nodes with a high degree was lower for the citation than for the feature network and they were thus all removed as part of the 20 largest hubs, resulting in a much lower variance (less spread distribution).**
**In conclusion, the new citation distribution is more condensed around its mean value, the degree landscape is hence more uniform. Regarding the feature degree distribution, a consistent number of nodes remain hotspots.**
### Question 3: Pruning, sparsity, paths
By adjusting the threshold of the euclidean distance matrix, prune the feature graph so that its number of edges is roughly close (within a hundred edges) to the number of edges in the citation graph.
```
threshold = np.max(distance)
diagonal = distance.shape[0]
threshold_flag = False
epsilon = 0.01*threshold
tolerance = 250
while threshold > 0 and not threshold_flag:
threshold -= epsilon # steps of 1% of maximum
n_edge = int((np.count_nonzero(np.where(distance < threshold, 1, 0)) - diagonal)/2)
# within a hundred edges
if abs(num_edges_citation - n_edge) < tolerance:
threshold_flag = True
print(f'Found a threshold : {threshold:.3f}')
A_feature_pruned = np.where(distance < threshold, 1, 0)
np.fill_diagonal(A_feature_pruned, 0)
num_edges_feature_pruned = int(np.count_nonzero(A_feature_pruned)/2)
print(f"Number of edges in the feature graph: {num_edges_feature}")
print(f"Number of edges in the feature graph after pruning: {num_edges_feature_pruned}")
print(f"Number of edges in the citation graph: {num_edges_citation}")
```
### Remark:
**The distribution of distances (which is a distribution of integers) for this particular field (Neural Networks) doesn't allow a configuration where the number of edges is roughly close (whithin a hundred of edges) to the citation distribution. This is independant of the chosen epsilon . The closest match is 250 edges apart.**
Check your results by comparing the sparsity patterns and total number of edges between the graphs.
```
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].set_title('Citation graph sparsity')
axes[0].spy(A_citation);
axes[1].set_title('Feature graph sparsity')
axes[1].spy(A_feature_pruned);
```
Let $C_{k}(i,j)$ denote the number of paths of length $k$ from node $i$ to node $j$.
We define the path matrix $P$, with entries
$ P_{ij} = \displaystyle\sum_{k=0}^{N}C_{k}(i,j). $
Calculate the path matrices for both the citation and the unpruned feature graphs for $N =10$.
**Hint:** Use [powers of the adjacency matrix](https://en.wikipedia.org/wiki/Adjacency_matrix#Matrix_powers).
```
def path_matrix(A, N=10):
"""Compute the path matrix for matrix A for N power """
power_A = [A]
for i in range(N-1):
power_A.append(np.matmul(power_A[-1], A))
return np.stack(power_A, axis=2).sum(axis=2)
path_matrix_citation = path_matrix(A_citation)
path_matrix_feature = path_matrix(A_feature)
```
Check the sparsity pattern for both of path matrices.
```
fig, axes = plt.subplots(1, 2, figsize=(16, 9))
axes[0].set_title('Citation Path matrix sparsity')
axes[0].spy(path_matrix_citation);
axes[1].set_title('Feature Path matrix sparsity')
axes[1].spy(path_matrix_feature, vmin=0, vmax=1); #scaling the color bar
```
Now calculate the path matrix of the pruned feature graph for $N=10$. Plot the corresponding sparsity pattern. Is there any difference?
```
path_matrix_pruned = path_matrix(A_feature_pruned)
plt.figure(figsize=(12, 6))
plt.title('Feature Path matrix sparsity')
plt.spy(path_matrix_pruned);
```
### Your answer here:
<br> **Many combinations of nodes have a path matrix value of zero now, meaning that they are not within the reach of N = 10 nodes from another node. This makes sense as many edges were removed in the pruning procedure (from 136000 to 1400). Hence, the number of possible paths from i to j was reduced, reducing at the same time the amount of paths of size N. The increase of the sparsity of the adjency matrix increases the diameter of a network.**
Describe how you can use the above process of counting paths to determine whether a graph is connected or not. Is the original (unpruned) feature graph connected?
### Answer:
<br> **The graph is connected if all points are within the reach of others. In others words, if when increasing $N$, we are able to reach a point where the path matrix doesn't contain any null value, it means that the graph is connected. Therefore, even if the path matrix has some null values it can be connected, this depends on the chosen N-value.
<br> For example, if 20 nodes are aligned and linked then we know that all point are reachable. Even though, the number of paths of length 10 between the first and the last node remain 0.**
If the graph is connected, how can you guess its diameter using the path matrix?
### Answer :
<br> **The diameter coresponds to the minimum $N$ ($N$ being a non negative integer) for which the path matrix does not contain any null value.**
If any of your graphs is connected, calculate the diameter using that process.
```
N=0
diameter = None
d_found = False
while not d_found:
N += 1
P = path_matrix(A_feature, N)
if np.count_nonzero(P == 0) == 0: # if there are no zero in P
d_found = True
diameter = N
print(f"The diameter of the feature graph (which is connected) is: {diameter}")
```
Check if your guess was correct using [NetworkX](https://networkx.github.io/documentation/stable/reference/algorithms/generated/networkx.algorithms.distance_measures.diameter.html).
Note: usage of NetworkX is only allowed in this part of Section 1.
```
import networkx as nx
feature_graph = nx.from_numpy_matrix(A_feature)
print(f"Diameter of feature graph according to networkx: {nx.diameter(feature_graph)}")
```
## Section 2: Network Models
In this section, you will analyze the feature and citation graphs you constructed in the previous section in terms of the network model types.
For this purpose, you can use the NetworkX libary imported below.
```
import networkx as nx
```
Let us create NetworkX graph objects from the adjacency matrices computed in the previous section.
```
G_citation = nx.from_numpy_matrix(A_citation)
print('Number of nodes: {}, Number of edges: {}'. format(G_citation.number_of_nodes(), G_citation.number_of_edges()))
print('Number of self-loops: {}, Number of connected components: {}'. format(G_citation.number_of_selfloops(), nx.number_connected_components(G_citation)))
```
In the rest of this assignment, we will consider the pruned feature graph as the feature network.
```
G_feature = nx.from_numpy_matrix(A_feature_pruned)
print('Number of nodes: {}, Number of edges: {}'. format(G_feature.number_of_nodes(), G_feature.number_of_edges()))
print('Number of self-loops: {}, Number of connected components: {}'. format(G_feature.number_of_selfloops(), nx.number_connected_components(G_feature)))
```
### Question 4: Simulation with Erdős–Rényi and Barabási–Albert models
Create an Erdős–Rényi and a Barabási–Albert graph using NetworkX to simulate the citation graph and the feature graph you have. When choosing parameters for the networks, take into account the number of vertices and edges of the original networks.
The number of nodes should exactly match the number of nodes in the original citation and feature graphs.
```
assert len(G_citation.nodes()) == len(G_feature.nodes())
n = len(G_citation.nodes())
print('The number of nodes ({}) matches the original number of nodes: {}'.format(n,n==A_citation.shape[0]))
```
The number of match shall fit the average of the number of edges in the citation and the feature graph.
```
m = np.round((G_citation.size() + G_feature.size()) / 2)
print('The number of match ({}) fits the average number of edges: {}'.format(m,m==np.round(np.mean([num_edges_citation,num_edges_feature_pruned]))))
```
How do you determine the probability parameter for the Erdős–Rényi graph?
### Answer:
**<br>Based on the principles ruling random networks (no preferential attachment but a random attachment), the expected number of edges is given by : $\langle L \rangle = p\frac{N(N-1)}{2}$ , where $\langle L \rangle$ is the average number of edges, $N$, the number of nodes and $p$, the probability parameter.
<br> Therefore we can get $p$ from the number of edges we want and the number of nodes we have : $ p = \langle L \rangle\frac{2}{N(N-1)}$
<br> The number of expected edges is given by $m$ in our case (defined as being the average of edges between the two original networks). $N$ is the same as in the original graphs**
```
p = m*2/(n*(n-1))
G_er = nx.erdos_renyi_graph(n, p)
```
Check the number of edges in the Erdős–Rényi graph.
```
print('My Erdos-Rényi network that simulates the citation graph has {} edges.'.format(G_er.size()))
```
How do you determine the preferential attachment parameter for Barabási–Albert graphs?
### Answer :
<br>**The Barabasi-Albert model uses growth and preferential attachement to build a scale-free network. The network is constructed by progressivly adding nodes to the network and adding a fixed number of edges, q, to each node added. Those edges are preferentially drawn towards already existing nodes with a high degree (preferential attachment).
<br> By the end of the process, the network contains n nodes and hence $n * q$ edges. Knowing that the final number of edges is defined by $m$, the parameter $q = m/n$**
```
q = int(m/n)
G_ba = nx.barabasi_albert_graph(n, q)
```
Check the number of edges in the Barabási–Albert graph.
```
print('My Barabási-Albert network that simulates the citation graph has {} edges.'.format(G_ba.size()))
```
### Question 5: Giant Component
Check the size of the largest connected component in the citation and feature graphs.
```
giant_citation = max(nx.connected_component_subgraphs(G_citation), key=len)
print('The giant component of the citation graph has {} nodes and {} edges.'.format(giant_citation.number_of_nodes(), giant_citation.size()))
giant_feature = max(nx.connected_component_subgraphs(G_feature), key=len)
print('The giant component of the feature graph has {} nodes and {} edges.'.format(giant_feature.number_of_nodes(), giant_feature.size()))
```
Check the size of the giant components in the generated Erdős–Rényi graph.
```
giant_er = max(nx.connected_component_subgraphs(G_er), key=len)
print('The giant component of the Erdos-Rényi network has {} nodes and {} edges.'.format(giant_er.number_of_nodes(), giant_er.size()))
```
Let us match the number of nodes in the giant component of the feature graph by simulating a new Erdős–Rényi network.
How do you choose the probability parameter this time?
**Hint:** Recall the expected giant component size from the lectures.
### Answer :
**<br> We can see the average degree of a network/each node as being the probability p multiplied by the amount of nodes to which it can connect ($N-1$, because the network is not recursive, N the number of nodes,): $\langle k \rangle = p . (N-1)$
<br>We can establish that, $S$, the portion of nodes in the Giant Component is given by $S = \frac{N_{GC}}{N}$ ($N_{GC}$, the number of nodes in the giant component) and $u$, the probability that $i$ is not linked to the GC via any other node $j$. U is also the portion of nodes not in the GC : $u = 1 - S$.
<br>Knowing that for one $j$ among the $N-1$ nodes, this probability can be seen as the probability to have no link with $j$ if $j$ is in the GC or having a link with $j$ if $j$ is not being in the GC ($p . u$), we can establish that: $u = (1 - p - p.u)^{N-1}$
<br> Using the relationship mentionned above : $p = \frac{<k>}{(N-1)}$, applying a log on both sides of the relationship and taking the Taylor expansion :
<br>$S = 1-e^{-\langle k \rangle S}$
<br> => $e^{-\langle k \rangle S} =1-S$
<br> => $-\langle k \rangle S = ln(1-S)$
<br> => $\langle k \rangle = -\frac{1}{S}ln(1-S)$
<br> This expression of the average degree is then used to define $p$ : $p = \frac{\langle k \rangle}{N-1} = \frac{-\frac{1}{S}ln(1-S)}{N-1}$**
```
GC_node = giant_feature.number_of_nodes()
S = GC_node/n
avg_k = -1/S*np.log(1-S)
p_new = avg_k/(n-1)
G_er_new = nx.erdos_renyi_graph(n, p_new)
```
Check the size of the new Erdős–Rényi network and its giant component.
```
print('My new Erdos Renyi network that simulates the citation graph has {} edges.'.format(G_er_new.size()))
giant_er_new = max(nx.connected_component_subgraphs(G_er_new), key=len)
print('The giant component of the new Erdos-Rényi network has {} nodes and {} edges.'.format(giant_er_new.number_of_nodes(), giant_er_new.size()))
```
### Question 6: Degree Distributions
Recall the degree distribution of the citation and the feature graph.
```
fig, axes = plt.subplots(1, 2, figsize=(15, 6),sharex = True)
axes[0].set_title('Citation graph')
citation_degrees = [deg for (node, deg) in G_citation.degree()]
axes[0].hist(citation_degrees, bins=20, color='salmon', edgecolor='black', linewidth=1);
axes[1].set_title('Feature graph')
feature_degrees = [deg for (node, deg) in G_feature.degree()]
axes[1].hist(feature_degrees, bins=20, color='salmon', edgecolor='black', linewidth=1);
```
What does the degree distribution tell us about a network? Can you make a prediction on the network model type of the citation and the feature graph by looking at their degree distributions?
### Answer :
<br> **The degree distribution tell us about the sparsity of a network.
Both show a power law degree distribution (many nodes with few edges but a couple of big components with a lot of edges). Hence they should fall in the scale-free network category which have a similar degree distribution. Therefore the Barabasi-Albert model which is a random scale free model is probably the best match.
<br> Those distributions are indeed power laws as it could be seen by the linear behavior of the distribution using a log scale.**
Now, plot the degree distribution historgrams for the simulated networks.
```
fig, axes = plt.subplots(1, 3, figsize=(20, 8))
axes[0].set_title('Erdos-Rényi network')
er_degrees = [deg for (node, deg) in G_er.degree()]
axes[0].hist(er_degrees, bins=10, color='salmon', edgecolor='black', linewidth=1)
axes[1].set_title('Barabási-Albert network')
ba_degrees = [deg for (node, deg) in G_ba.degree()]
axes[1].hist(ba_degrees, bins=10, color='salmon', edgecolor='black', linewidth=1)
axes[2].set_title('new Erdos-Rényi network')
er_new_degrees = [deg for (node, deg) in G_er_new.degree()]
axes[2].hist(er_new_degrees, bins=6, color='salmon', edgecolor='black', linewidth=1)
plt.show()
```
In terms of the degree distribution, is there a good match between the citation and feature graphs and the simulated networks?
For the citation graph, choose one of the simulated networks above that match its degree distribution best. Indicate your preference below.
### Answer :
<br> **Regarding the feature network, none of the distributions above matche the range of degrees of the feature network. Also none of the above distributions, model the large portion of hotspots seen in the feature graph. <br>Regarding the citation network, the Barabasi-Albert network seem to be a good match. Indeed, the range of values as well as the power-law shape of the model is close to the distribution of the citation graph showed earlier. Hence, a scale free model seems to be the best match to model the citation network for the Neural Networks field.**
You can also simulate a network using the configuration model to match its degree disctribution exactly. Refer to [Configuration model](https://networkx.github.io/documentation/stable/reference/generated/networkx.generators.degree_seq.configuration_model.html#networkx.generators.degree_seq.configuration_model).
Let us create another network to match the degree distribution of the feature graph.
```
G_config = nx.configuration_model(feature_degrees)
print('Configuration model has {} nodes and {} edges.'.format(G_config.number_of_nodes(), G_config.size()))
```
Does it mean that we create the same graph with the feature graph by the configuration model? If not, how do you understand that they are not the same?
### Answer :
<br> **No we don't create the same graph, the number of edges, nodes and degree distribution can be the same but the links can be different. For example, in a group of three papers, various configurations are possible using only 2 links.
<br> Also the function used to create this model considers self loops and paralell edges which is not the case for the real feature graph. Hence the network resulting from this modelisation will most probably not be identical to the original graph.**
### Question 7: Clustering Coefficient
Let us check the average clustering coefficient of the original citation and feature graphs.
```
nx.average_clustering(G_citation)
nx.average_clustering(G_feature)
```
What does the clustering coefficient tell us about a network? Comment on the values you obtain for the citation and feature graph.
### Answer :
**<br>Clustering coefficient is linked to the presence of subgroups (or clusters) in the network. A high clustering coefficient means that a node is very likely to be part of a subgroup. Here we can observe that the clustering coefficient of the citation graph is higher (almost double) than the one of the feature graph, this can highlight the fact that citations are more likely to form subgroups than feature.**
Now, let us check the average clustering coefficient for the simulated networks.
```
nx.average_clustering(G_er)
nx.average_clustering(G_ba)
nx.average_clustering(nx.Graph(G_config))
```
Comment on the values you obtain for the simulated networks. Is there any good match to the citation or feature graph in terms of clustering coefficient?
### Answer :
<br> **No, there is not any match. The clustering coefficients are rather small compared to the ones for feature and citation graphs. Random networks have generally small clustering coefficients because they don't tend to form subgroups as the pairing is random.**
Check the other [network model generators](https://networkx.github.io/documentation/networkx-1.10/reference/generators.html) provided by NetworkX. Which one do you predict to have a better match to the citation graph or the feature graph in terms of degree distribution and clustering coefficient at the same time? Justify your answer.
### Answer :
<br> **Based on the course notes about Watts Strogatz model which is a extension of the random network model generating small world properties and high clustering, we tested the watts_strogatz_graph function provided by NetworkX. We used the average degree ($k = m*2/n$) as an initial guess of the number of nearest neighbours to which we connect each node. We then modulated the rewiring probability to find a good match. Results did not show any satisfying match for the clustering coefficient (it was always rather low compared to the original networks). We then tuned parameter k by increasing it for a fixed p of 0.5 (corresponding to the small-world property). k was originally very low and we wanted to increase the occurence of clusters. At k =100, the clustering coefficient matched our expectations (being close to the clustering coeffients of the two distributions) but the distribtion did not match a powerlaw. In conclusion, watts-strogratz was left aside as no combination of parameters enabled to match the clustering coefficent as well as the shape of the distribution.
<br>After scrolling through the documention of NetworkX, we came across the power_law_cluster function. According to the documentation, parameter n is the number of nodes, (n = 818 in our case). The second parameter, k, is the _number of random edges to add to each new node_ which we chose to be the average degree of the original graph as an initial guess. Parameter p, the probability of connecting two nodes which already share a common neighbour (forming a triangle) is chosen to be the average of average clustering coefficient across the original distributions. This yield a clustering coefficient that was a bit low compared with our expectations. We therefore tuned this parameter to better match the coefficients, results showed that a good comprise was reached at p = 0.27.**
If you find a better fit, create a graph object below for that network model. Print the number of edges and the average clustering coefficient. Plot the histogram of the degree distribution.
```
k = m*2/n
p = (nx.average_clustering(G_citation) + nx.average_clustering(G_feature))*0.8
G_pwc = nx.powerlaw_cluster_graph(n, int(k), p)
print('Power law cluster model has {} edges.'.format(G_pwc.size()))
print('Power law cluster model has a clustering coefficient of {}'.format(nx.average_clustering(G_pwc)))
print('Citation model has {} edges.'.format(G_citation.size()))
print('Citation model has a clustering coefficient of {}'.format(nx.average_clustering(G_citation)))
print('Feature model has {} edges.'.format(G_feature.size()))
print('Feature model has a clustering coefficient of {}'.format(nx.average_clustering(G_feature)))
fig, axs = plt.subplots(1, 3, figsize=(15, 5), sharey=True, sharex=True)
axs[0].set_title('PWC graph')
ws_degrees = [deg for (node, deg) in G_pwc.degree()]
axs[0].hist(ws_degrees, bins=20, color='salmon', edgecolor='black', linewidth=1)
axs[1].set_title('Citation graph')
citation_degrees = [deg for (node, deg) in G_citation.degree()]
axs[1].hist(citation_degrees, bins=20, color='salmon', edgecolor='black', linewidth=1)
axs[2].set_title('Feature graph')
feature_degree = [deg for (node, deg) in G_feature.degree()]
axs[2].hist(feature_degree, bins=20, color='salmon', edgecolor='black', linewidth=1)
plt.show()
```
Comment on the similarities of your match.
### Answer :
<br> **At this point, the decay of the power law distribution (PWC) had an intermediate behavior between the citation and the feature graph and the clustering coefficient which fall in between the original graphs (~0.17). The degree range is roughly equilvalent in all three above distributions.
<br> We hence found a model that satisfies both the clustering coefficients and the degree distribution. Also the final model raises distributions which have the expected intermediate behavior in comparison with the original distributions.**
| github_jupyter |
# Implementing a CGAN for the Iris data set to generate synthetic data
### Import necessary modules and packages
```
import os
while os.path.basename(os.getcwd()) != 'Synthetic_Data_GAN_Capstone':
os.chdir('..')
from utils.utils import *
safe_mkdir('experiments')
from utils.data_loading import load_raw_dataset
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from models.VGAN import VGAN_Generator, VGAN_Discriminator
from models.CGAN_iris import CGAN_Generator, CGAN_Discriminator
import random
```
### Set random seed for reproducibility
```
manualSeed = 999
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
```
### Import and briefly inspect data
```
iris = load_raw_dataset('iris')
iris.head()
```
### Preprocessing data
Split 50-50 so we can demonstrate the effectiveness of additional data
```
x_train, x_test, y_train, y_test = train_test_split(iris.drop(columns='species'), iris.species, test_size=0.5, stratify=iris.species, random_state=manualSeed)
print("x_train:", x_train.shape)
print("x_test:", x_test.shape)
```
### Model parameters (feel free to play with these)
```
nz = 32 # Size of generator noise input
H = 16 # Size of hidden network layer
out_dim = x_train.shape[1] # Size of output
bs = x_train.shape[0] # Full data set
nc = 3 # 3 different types of label in this problem
num_batches = 1
num_epochs = 10000
exp_name = 'experiments/iris_1x16'
safe_mkdir(exp_name)
```
### Adam optimizer hyperparameters
I set these based on the original paper, but feel free to play with them as well.
```
lr = 2e-4
beta1 = 0.5
beta2 = 0.999
```
### Set the device
```
device = torch.device("cuda:0" if (torch.cuda.is_available()) else "cpu")
```
### Scale continuous inputs for neural networks
```
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_train_tensor = torch.tensor(x_train, dtype=torch.float)
y_train_dummies = pd.get_dummies(y_train)
y_train_dummies_tensor = torch.tensor(y_train_dummies.values, dtype=torch.float)
```
### Instantiate nets
```
netG = CGAN_Generator(nz=nz, H=H, out_dim=out_dim, nc=nc, bs=bs, lr=lr, beta1=beta1, beta2=beta2).to(device)
netD = CGAN_Discriminator(H=H, out_dim=out_dim, nc=nc, lr=lr, beta1=beta1, beta2=beta2).to(device)
```
### Print models
I chose to avoid using sequential mode in case I wanted to create non-sequential networks, it is more flexible in my opinion, but does not print out as nicely
```
print(netG)
print(netD)
```
### Define labels
```
real_label = 1
fake_label = 0
```
### Training Loop
Look through the comments to better understand the steps that are taking place
```
print("Starting Training Loop...")
for epoch in range(num_epochs):
for i in range(num_batches): # Only one batch per epoch since our data is horrifically small
# Update Discriminator
# All real batch first
real_data = x_train_tensor.to(device) # Format batch (entire data set in this case)
real_classes = y_train_dummies_tensor.to(device)
label = torch.full((bs,), real_label, device=device) # All real labels
output = netD(real_data, real_classes).view(-1) # Forward pass with real data through Discriminator
netD.train_one_step_real(output, label)
# All fake batch next
noise = torch.randn(bs, nz, device=device) # Generate batch of latent vectors
fake = netG(noise, real_classes) # Fake image batch with netG
label.fill_(fake_label)
output = netD(fake.detach(), real_classes).view(-1)
netD.train_one_step_fake(output, label)
netD.combine_and_update_opt()
netD.update_history()
# Update Generator
label.fill_(real_label) # Reverse labels, fakes are real for generator cost
output = netD(fake, real_classes).view(-1) # Since D has been updated, perform another forward pass of all-fakes through D
netG.train_one_step(output, label)
netG.update_history()
# Output training stats
if epoch % 1000 == 0 or (epoch == num_epochs-1):
print('[%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
% (epoch+1, num_epochs, netD.loss.item(), netG.loss.item(), netD.D_x, netD.D_G_z1, netG.D_G_z2))
with torch.no_grad():
fake = netG(netG.fixed_noise, real_classes).detach().cpu()
netG.fixed_noise_outputs.append(scaler.inverse_transform(fake))
print("Training Complete")
```
### Output diagnostic plots tracking training progress and statistics
```
%matplotlib inline
training_plots(netD=netD, netG=netG, num_epochs=num_epochs, save=exp_name)
plot_layer_scatters(netG, title="Generator", save=exp_name)
plot_layer_scatters(netD, title="Discriminator", save=exp_name)
```
It looks like training stabilized fairly quickly, after only a few thousand iterations. The fact that the weight norm increased over time probably means that this network would benefit from some regularization.
### Compare performance of training on fake data versus real data
In this next section, we will lightly tune two models via cross-validation. The first model will be trained on the 75 real training data examples and tested on the remaining 75 testing data examples, whereas the second set of models will be trained on different amounts of generated data (no real data involved whatsoever). We will then compare performance and plot some graphs to evaluate our CGAN.
```
y_test_dummies = pd.get_dummies(y_test)
print("Dummy columns match?", all(y_train_dummies.columns == y_test_dummies.columns))
x_test = scaler.transform(x_test)
labels_list = [x for x in y_train_dummies.columns]
param_grid = {'tol': [1e-9, 1e-8, 1e-7, 1e-6, 1e-5],
'C': [0.5, 0.75, 1, 1.25],
'l1_ratio': [0, 0.25, 0.5, 0.75, 1]}
```
### Train on real data
```
model_real, score_real = train_test_logistic_reg(x_train, y_train, x_test, y_test, param_grid=param_grid, cv=5, random_state=manualSeed, labels=labels_list)
```
### Train on various levels of fake data
```
test_range = [75, 150, 300, 600, 1200]
fake_bs = bs
fake_models = []
fake_scores = []
for size in test_range:
num_batches = size // fake_bs + 1
genned_data = np.empty((0, out_dim))
genned_labels = np.empty(0)
rem = size
while rem > 0:
curr_size = min(fake_bs, rem)
noise = torch.randn(curr_size, nz, device=device)
fake_labels, output_labels = gen_labels(size=curr_size, num_classes=nc, labels_list=labels_list)
fake_labels = fake_labels.to(device)
rem -= curr_size
fake_data = netG(noise, fake_labels).cpu().detach().numpy()
genned_data = np.concatenate((genned_data, fake_data))
genned_labels = np.concatenate((genned_labels, output_labels))
print("For size of:", size)
model_fake_tmp, score_fake_tmp = train_test_logistic_reg(genned_data, genned_labels, x_test, y_test,
param_grid=param_grid, cv=5, random_state=manualSeed, labels=labels_list)
fake_models.append(model_fake_tmp)
fake_scores.append(score_fake_tmp)
```
Well, it looks like this experiment was a success. The models trained on fake data were actually able to outperform models trained on real data, which supports the belief that the CGAN is able to understand the distribution of the data it was trained on and generate meaningful examples that can be used to add additional information to the model.
Let's visualize some of the distributions of outputs to get a better idea of what took place
```
iris_plot_scatters(genned_data, genned_labels, "Fake Data", scaler, alpha=0.5, save=exp_name) # Fake data
iris_plot_scatters(iris.drop(columns='species'), np.array(iris.species), "Full Real Data Set", alpha=0.5, save=exp_name) # All real data
iris_plot_densities(genned_data, genned_labels, "Fake Data", scaler, save=exp_name) # Fake data
iris_plot_densities(iris.drop(columns='species'), np.array(iris.species), "Full Real Data Set", save=exp_name) # All real data
plot_scatter_matrix(genned_data, "Fake Data", iris.drop(columns='species'), scaler=scaler, save=exp_name)
plot_scatter_matrix(iris.drop(columns='species'), "Real Data", iris.drop(columns='species'), scaler=None, save=exp_name)
```
Finally, I present a summary of the test results ran above
```
fake_data_training_plots(real_range=bs, score_real=score_real, test_range=test_range, fake_scores=fake_scores, save=exp_name)
```
| github_jupyter |
Subsets and Splits