code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
```
import qiskit
import numpy as np, matplotlib.pyplot as plt
import sys
sys.path.insert(1, '../')
import qtm.base, qtm.constant, qtm.nqubit, qtm.onequbit, qtm.fubini_study
num_qubits = 3
num_layers = 2
psi = 2*np.random.rand(2**num_qubits)-1
psi = psi / np.linalg.norm(psi)
qc_origin = qiskit.QuantumCircuit(num_qubits, num_qubits)
qc_origin.initialize(psi, range(0, num_qubits))
thetas_origin = np.ones((num_layers*num_qubits*3))
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_sgd = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.sgd,
verbose = 1,
num_layers = num_layers
)
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_adam = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.adam,
verbose = 1,
num_layers = num_layers
)
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_qfsm = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.qng_fubini_study,
verbose = 1,
num_layers = num_layers
)
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_qfim = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.qng_qfim,
verbose = 1,
num_layers = num_layers
)
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_adam_qfim = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.qng_adam,
verbose = 1,
num_layers = num_layers
)
plt.plot(loss_values_sgd, label="SGD")
plt.plot(loss_values_adam, label="Adam")
plt.plot(loss_values_qfsm, label="QNG-QFSM")
plt.plot(loss_values_qfim, label="QNG-QFIM")
plt.plot(loss_values_adam_qfim, label="Adam QNG-QFIM")
plt.xlabel("Step")
plt.ylabel("Cost value")
plt.ylim(-0.05, 1.05)
plt.legend(prop={'size': 8}, loc=1)
plt.savefig(str(num_qubits) + '.svg', format='svg')
plt.show()
```
| github_jupyter |
# Predictive Maintenance using Machine Learning on Sagemaker
*Part 3 - Timeseries data preparation*
## Initialization
---
Directory structure to run this notebook:
```
nasa-turbofan-rul-lstm
|
+--- data
| |
| +--- interim: intermediate data we can manipulate and process
| |
| \--- raw: *immutable* data downloaded from the source website
|
+--- notebooks: all the notebooks are positionned here
|
+--- src: utility python modules are stored here
```
### Imports
```
%load_ext autoreload
import matplotlib.pyplot as plt
import sagemaker
import boto3
import os
import errno
import pandas as pd
import numpy as np
import seaborn as sns
import json
import sys
import s3fs
import mxnet as mx
import joblib
%matplotlib inline
%autoreload 2
sns.set_style('darkgrid')
sys.path.append('../src')
figures = []
INTERIM_DATA = '../data/interim'
PROCESSED_DATA = '../data/processed'
```
### Loading data from the previous notebook
```
# Load data from the notebook local storage:
%store -r reduced_train_data
%store -r reduced_test_data
# If the data are not present in the notebook local storage, we need to load them from disk:
success_msg = 'Loaded "reduced_train_data"'
if 'reduced_train_data' not in locals():
print('Nothing in notebook store, trying to load from disk.')
try:
local_path = '../data/interim'
reduced_train_data = pd.read_csv(os.path.join(local_path, 'reduced_train_data.csv'))
reduced_train_data = reduced_train_data.set_index(['unit_number', 'time'])
print(success_msg)
except Exception as e:
if (e.errno == errno.ENOENT):
print('Files not found to load train data from: you need to execute the previous notebook.')
else:
print('Train data found in notebook environment.')
print(success_msg)
success_msg = 'Loaded "reduced_test_data"'
if 'reduced_test_data' not in locals():
print('Nothing in notebook store, trying to load from disk.')
try:
local_path = '../data/interim'
reduced_test_data = pd.read_csv(os.path.join(local_path, 'reduced_test_data.csv'))
reduced_test_data = reduced_test_data.set_index(['unit_number', 'time'])
print(success_msg)
except Exception as e:
if (e.errno == errno.ENOENT):
print('Files not found to load test data from: you need to execute the previous notebook.')
else:
print('Test data found in notebook environment.')
print(success_msg)
print(reduced_train_data.shape)
reduced_train_data.head()
print(reduced_test_data.shape)
reduced_test_data.head()
```
### Study parameters
```
sequence_length = 20
```
## Normalization
---
### Normalizing the training data
First, we build some scalers based on the training data:
```
from sklearn import preprocessing
# Isolate the columns to normalize:
normalized_cols = reduced_train_data.columns.difference(['true_rul', 'piecewise_rul'])
# Build MinMax scalers for the features and the labels:
features_scaler = preprocessing.MinMaxScaler()
labels_scaler = preprocessing.MinMaxScaler()
# Normalize the operational settings and sensor measurements data (our features):
reduced_train_data['sensor_measurement_17'] = reduced_train_data['sensor_measurement_17'].astype(np.float64)
normalized_data = pd.DataFrame(
features_scaler.fit_transform(reduced_train_data[normalized_cols]),
columns=normalized_cols,
index=reduced_train_data.index
)
# Normalizing the labels data:
reduced_train_data['piecewise_rul'] = reduced_train_data['piecewise_rul'].astype(np.float64)
normalized_training_labels = pd.DataFrame(
labels_scaler.fit_transform(reduced_train_data[['piecewise_rul']]),
columns=['piecewise_rul'],
index=reduced_train_data.index
)
# Join the normalized features with the RUL (label) data:
joined_data = normalized_training_labels.join(normalized_data)
normalized_train_data = joined_data.reindex(columns=reduced_train_data.columns)
normalized_train_data['true_rul'] = reduced_train_data['true_rul']
print(normalized_train_data.shape)
normalized_train_data.head()
```
### Normalizing the testing data
Next, we apply these normalizers to the testing data:
```
normalized_test_data = pd.DataFrame(
features_scaler.transform(reduced_test_data[normalized_cols]),
columns=normalized_cols,
index=reduced_test_data.index
)
reduced_test_data['piecewise_rul'] = reduced_test_data['piecewise_rul'].astype(np.float64)
normalized_test_labels = pd.DataFrame(
labels_scaler.transform(reduced_test_data[['piecewise_rul']]),
columns=['piecewise_rul'],
index=reduced_test_data.index
)
# Join the normalize data with the RUL data:
joined_data = normalized_test_labels.join(normalized_test_data)
normalized_test_data = joined_data.reindex(columns=reduced_test_data.columns)
normalized_test_data['true_rul'] = reduced_test_data['true_rul']
print(normalized_test_data.shape)
normalized_test_data.head()
```
## Sequences generation
---
```
from lstm_utils import generate_sequences, generate_labels, generate_training_sequences, generate_testing_sequences
# Building features, target and engine unit lists:
features = normalized_train_data.columns.difference(['true_rul', 'piecewise_rul'])
target = ['piecewise_rul']
unit_list = list(set(normalized_train_data.index.get_level_values(level=0).tolist()))
# Generating features and labels for the training sequences:
train_sequences = generate_training_sequences(normalized_train_data, sequence_length, features, unit_list)
train_labels = generate_training_sequences(normalized_train_data, sequence_length, target, unit_list)
test_sequences, test_labels, unit_span = generate_testing_sequences(normalized_test_data, sequence_length, features, target, unit_list)
# Checking sequences shapes:
print('train_sequences:', train_sequences.shape)
print('train_labels:', train_labels.shape)
print('test_sequences:', test_sequences.shape)
print('test_labels:', test_labels.shape)
```
### Visualizing the sequences
Let's visualize the sequences we built for an engine (e.g. unit 3 in the example below) to understand what will be fed to the LSTM model:
```
from lstm_utils import plot_timestep, plot_text
# We use the normalized sequences for the plot but the original data for the label (RUL) for understanding purpose:
current_unit = 1
tmp_sequences = generate_training_sequences(normalized_train_data, sequence_length, features, [current_unit])
tmp_labels = generate_training_sequences(reduced_train_data, sequence_length, target, [current_unit])
# Initialize the graphics:
print('Sequences generated for unit {}:\n'.format(current_unit))
sns.set_style('white')
fig = plt.figure(figsize=(35,6))
# Initialize the loop:
nb_signals = min(12, len(tmp_sequences[0][0]))
plots_per_row = nb_signals + 3
nb_rows = 7
nb_cols = plots_per_row
current_row = 0
previous_index = -1
timesteps = [
# We will plot the first 3 sequences (first timesteps fed to the LSTM model):
0, 1, 2,
# And the last 3 ones:
len(tmp_sequences) - 3, len(tmp_sequences) - 2, len(tmp_sequences) - 1
]
# Loops through all the timesteps we want to plot:
for i in timesteps:
# We draw a vertical ellispsis for the hole in the timesteps:
if (i - previous_index > 1):
plot_text(fig, nb_rows, nb_cols, nb_signals, current_row, '. . .', 1, no_axis=True, main_title='', plots_per_row=plots_per_row, options={'fontsize': 32, 'rotation': 270})
current_row += 1
# Timestep column:
previous_index = i
plot_text(fig, nb_rows, nb_cols, nb_signals, current_row, 'T{}'.format(i), 1, no_axis=True, main_title='Timestep', plots_per_row=plots_per_row, options={'fontsize': 16})
# For a given timestep, we want to loop through all the signals to plot:
plot_timestep(nb_rows, nb_cols, nb_signals, current_row, 2, tmp_sequences[i].T, features.tolist(), plots_per_row=plots_per_row)
# Then we draw an ellipsis:
plot_text(fig, nb_rows, nb_cols, nb_signals, current_row, '. . .', nb_signals + 2, no_axis=True, main_title='', plots_per_row=plots_per_row, options={'fontsize': 32})
# Finally, we show the remaining useful life at the end of the row for this timestep:
plot_text(fig, nb_rows, nb_cols, nb_signals, current_row, int(tmp_labels[i][0]), nb_signals + 3, no_axis=False, main_title='RUL', plots_per_row=plots_per_row, options={'fontsize': 16, 'color': '#CC0000'})
current_row += 1
```
## Cleanup
---
### Storing data for the next notebook
```
%store labels_scaler
%store test_sequences
%store test_labels
%store unit_span
#columns = normalized_train_data.columns.tolist()
#%store columns
#%store train_sequences
#%store train_labels
#%store normalized_train_data
#%store normalized_test_data
#%store sequence_length
```
### Persisting these data to disk
This is useful in case you want to be able to execute each notebook independantly (from one session to another) and don't want to reexecute every notebooks whenever you want to focus on a particular step. Let's start by persisting train and test sequences and the associated labels:
```
import h5py as h5
train_data = os.path.join(PROCESSED_DATA, 'train.h5')
with h5.File(train_data, 'w') as ftrain:
ftrain.create_dataset('train_sequences', data=train_sequences)
ftrain.create_dataset('train_labels', data=train_labels)
ftrain.close()
test_data = os.path.join(PROCESSED_DATA, 'test.h5')
with h5.File(test_data, 'w') as ftest:
ftest.create_dataset('test_sequences', data=test_sequences)
ftest.create_dataset('test_labels', data=test_labels)
ftest.close()
```
Pushing these files to S3:
```
sagemaker_session = sagemaker.Session()
bucket = sagemaker_session.default_bucket()
prefix = 'nasa-rul-lstm/data'
train_data_location = 's3://{}/{}'.format(bucket, prefix)
s3_resource = boto3.Session().resource('s3')
s3_resource.Bucket(bucket).Object('{}/train/train.h5'.format(prefix)).upload_file(train_data)
s3_resource.Bucket(bucket).Object('{}/test/test.h5'.format(prefix)).upload_file(test_data)
# Build the data channel and write it to disk:
data_channels = {'train': 's3://{}/{}/train/train.h5'.format(bucket, prefix)}
with open(os.path.join(PROCESSED_DATA, 'data_channels.txt'), 'w') as f:
f.write(str(data_channels))
%store data_channels
```
Storing the other elements on disk:
```
with open(os.path.join(PROCESSED_DATA, 'unit_span.lst'), 'w') as f:
f.write(str(unit_span))
_ = joblib.dump(labels_scaler, os.path.join(PROCESSED_DATA, 'labels_scaler.joblib'))
```
### Memory cleanup
```
fig.clear()
plt.close(fig)
import gc
_ = gc.collect()
```
| github_jupyter |
# О вероятности попасть под удар фигуры, поставленной случайным образом на шахматную доску
На шахматную доску случайным образом поставлены две фигуры. С какой вероятностью первая фигура бьёт вторую? В данном ноутбуке представлен расчёт этой вероятности для каждой шахматной фигуры как функции от размера доски. Рассмотрены только квадратные доски. Фигуры полагаются поставленными одновременно (обязательно стоят на разных клетках), выбор каждого из полей равновероятен.
Степень (валентность) вершины $v$ графа $G$ - количество рёбер графа $G$, инцидентных вершине $v$.
Граф ходов шахматной фигуры (далее Граф) - граф, изображающий все возможные ходы фигуры на шахматной доске - каждая вершина соответствует клетке на доске, а рёбра соответствуют возможным ходам.
Тогда валентность вершины Графа - количество полей, которые бьёт фигура, будучи поставленной на соответствующую этой вершине клетку. В целях упрощения речи далее в тексте используется формулировка "клетка имеет валентность", однако понятно, что валентность имеет не клетка, а соответствующая ей вершина в Графе.
Если событие $X$ может произойти только при выполнении одного из событий $H_1, H_2,..., H_n$, которые образуют полную группу несовместных событий, то вероятность $P(X)$ вычисляется по формуле: $$P(X) = P(H_1) \cdot P(X|H_1) + P(H_2) \cdot P(X|H_2) + ... + P(H_n) \cdot P(X|H_n),$$ которая называется формулой полной вероятности.
Пусть событие $X_{piece}$ = «Первая *фигура (piece)* бьёт вторую на доске размера $n\times n$», $a$ - некоторое значение валентности, $b$ - количество клеток, имеющих валентность $a$, каждая из гипотез $H_i$ = «Первая фигура стоит на клетке с валентностью $a_i$». Тогда $P(H_i) = \frac{b_i}{n^{2}}$ в силу классического определения вероятности - это отношение количества исходов, благоприятствующих событию $H_i$, к количеству всех равновозможных исходов. $P(X_{piece}|H_i) = \frac{a_i}{n^{2}-1}$ по той же причине - событию $X_{piece}$ при условии $H_i$ благоприятствует $a_i$ исходов (вторая фигура стоит под ударом клетки с валентностью $a_i$),а количество всех равновозможных исходов уменьшилось на единицу, так как одна из клеток уже занята первой фигурой.
### Импорты
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from string import ascii_uppercase as alphabet
```
### Функция создания доски
Создание доски как пустого массива заданной формы. Также нам понадобится массив такой же формы для хранения цвета надписи на клетках.
Заполнение доски: 0 - чёрные клетки, 1 - белые.
```
def get_board(board_size):
x, y = np.meshgrid(range(board_size), range(board_size))
board = np.empty(shape=(board_size, board_size), dtype='uint8')
text_colors = np.empty_like(board, dtype='<U5')
# force left bottom corner cell to be black
if board_size % 2 == 0:
extra_term = 1
else:
extra_term = 0
for i, j in zip(x.flatten(), y.flatten()):
board[i, j] = (i + j + extra_term) % 2
# text color should be the opposite to a cell color
text_colors[i, j] = 'black' if board[i, j] else 'white'
return board, text_colors
def get_valencies(piece, board):
# Get valencies for the given piece on the given board
valencies = np.empty_like(board)
if piece == 'Pawn':
valencies = pawn(valencies)
elif piece == 'Knight':
valencies = knight(valencies)
elif piece == 'Rook':
valencies = rook(valencies)
elif piece == 'King':
valencies = king(valencies)
else:
valencies = bishop_or_queen(piece, valencies)
return valencies
```
### Функция рисования доски
Функция создаёт изображение шахматной доски, каждая клетка которой подписана соответствующим значением валентности.
```
def plot_board(board, text_colors, piece):
board_size = np.shape(board)[0]
x, y = np.meshgrid(range(board_size), range(board_size))
# let figure size be dependent on the board size
plt.figure(figsize=(3*board_size/4, 3*board_size/4))
ax = plt.subplot(111)
ax.imshow(board, cmap='gray', interpolation='none')
# Display valency (degree) values
val_board = get_valencies(piece, board)
for i, j, valency, text_col in zip(x.flatten(), y.flatten(),
val_board.flatten(),
text_colors.flatten()):
ax.text(i, j, str(valency), color=text_col,
va='center', ha='center', fontsize=20)
ax.set_xticks(np.arange(board_size+1)) # one tick per cell
ax.set_xticklabels(alphabet[:board_size]) # set letters as ticklabels
# one tick per cell
ax.set_yticks(np.arange(board_size+1))
# set numbers as ticklabels (upside down)
ax.set_yticklabels(np.arange(board_size, 0, -1))
ax.axis('tight') # get rid of the white spaces on the edges
ax.set_title(piece, fontsize=30)
plt.show()
```
## Пешка
### Функция, возвращающая массив валентностей пешечного Графа
Иллюстрирует изложенные ниже соображения.
```
def pawn(valencies):
valencies[0, :] = 0 # empty horizontal line
valencies[1:, 0] = valencies[1:, -1] = 1 # vertical edges
valencies[1:, 1:-1] = 2
return valencies
```
Рассмотрим несколько частных случаев в поисках закономерности.
```
def special_cases(piece, board_sizes):
''' Plot boards of every board_size,
contained in board_sizes list for given piece.
'''
for board_size in board_sizes:
board, text_colors = get_board(board_size=board_size)
plot_board(board, text_colors, piece=piece)
special_cases(piece='Pawn', board_sizes=range(4,6))
```
Закономерность очевидна - всегда присутствует горизонталь (верхняя или нижняя - в зависимости от цвета фигуры), с которой пешка не бьёт ни одну клетку - все поля этой горизонтали $0$-валентны. Их количество равно $n$.
На крайних вертикалях расположены $1$-валентные клетки, которых $2(n-1)$ штук.
Все остальные поля - $2$-валентны, и расположены они прямоугольником размера $(n-1)\times(n-2)$.
Тогда $$ P(X_{pawn}) = \frac{n\cdot 0}{n^{2}(n^{2}-1)} + \frac{2(n-1)\cdot 1}{n^{2}(n^{2}-1)} + \frac{(n-1)(n-2)\cdot 2}{n^{2}(n^{2}-1)}= \frac{2(n-1)({\color{Green}1}+n-{\color{Green}2})}{n^{2}(n^{2}-1)} = \frac{2(n-1)^{2}}{n^{2}(n^{2}-1)}. $$ Так как $(n^{2}-1) = (n+1)(n-1)$, $$ P(X_{pawn}) = \frac{2(n-1)}{n^{2}(n+1)}. $$
## Конь
### Функция, возвращающая массив валентностей Графа коня
```
def knight(valencies):
board_size = valencies.shape[0]
if board_size > 3:
# Four points in each corner are the same for any board size > 3.
# corner cells
valencies[0, 0] = valencies[0, -1] = \
valencies[-1, 0] = valencies[-1, -1] = 2
# cells horizontally/vertically adjacent to the corners
valencies[0, 1] = valencies[1, 0] = \
valencies[0, -2] = valencies[1, -1] = \
valencies[-2, 0] = valencies[-1, 1] = \
valencies[-2, -1] = valencies[-1, -2] = 3
# cells diagonally adjacent
valencies[1, 1] = valencies[1, -2] = \
valencies[-2, 1] = valencies[-2, -2] = 4
if board_size > 4:
valencies[0, 2:-2] = valencies[2:-2, 0] = \
valencies[2:-2, -1] = valencies[-1, 2:-2] = 4
valencies[1, 2:-2] = valencies[2:-2, 1] = \
valencies[2:-2, -2] = valencies[-2, 2:-2] = 6
valencies[2:-2, 2:-2] = 8
# Patholigical cases
elif board_size == 3:
valencies = 2 * np.ones((board_size, board_size), dtype='uint8')
valencies[1, 1] = 0
else:
valencies = np.zeros((board_size, board_size), dtype='uint8')
return valencies
special_cases(piece='Knight', board_sizes=[4,5,6])
```
Количество $2$- и $3$-валентных клеток фиксировано при любом $n\geq 4$. Первые расположены в углах, а вторые прилегают к ним по вертикали и горизонтали. Стало быть, количество $2$-валентных клеток равно $4$, а $3$-валентных - $8$, вдвое больше. $4$-валентные клетки образуют арифметическую прогрессию с начальным элементом $4$ и шагом $4$ для всех $n\geq 4$ (при увеличении $n$ на единицу с каждой стороны появляется одна $4$-валентная клетка). Легко видеть, что рост количества $6$-валентных клеток устроен аналогично, однако существуют они только при $n\geq 5$. Таким образом, $4$-валентных клеток $4(n-3)$, а $6$-валентных клеток - $4(n-4)$ штук. Количество $8$-валентных клеток растёт квадратично, к тому же, они существуют только при $n\geq 5$. То есть, их количество - $(n-4)^2$. Итого имеем:
$$ P(X_{knight}) = \frac{4\cdot 2}{n^{2}(n^{2}-1)} + \frac{8\cdot 3}{n^{2}(n^{2}-1)} + \frac{4(n-3)\cdot 4}{n^{2}(n^{2}-1)} +$$ $$ + \frac{4(n-4)\cdot 6}{n^{2}(n^{2}-1)} + \frac{(n-4)^2\cdot 8}{n^{2}(n^{2}-1)} = \frac{32 + 24(n-4) + 16(n-3) + 8(n-4)^{2}}{n^{2}(n^{2}-1)} = $$
$$ \frac{8(4+3(n-4)+2(n-3)+(n-4)^{2})}{n^{2}(n^{2}-1)} = \frac{8({\color{Green} 4}+{\color{Red} {3n}}-{\color{Green} {12}}+{\color{Red} {2n}} - {\color{Green} 6}+ n^{2}-{\color{Red} {8n}}+{\color{Green} {16}})}{n^{2}(n^{2}-1)} = $$
$$= \frac{8(n^{2}-3n+2)}{n^{2}(n^{2}-1)} = \frac{8(n-1)(n-2)}{n^{2}(n^{2}-1)} = \frac{8(n-2)}{n^{2}(n+1)}. $$
## Офицер
### Функция, возвращающая массив валентностей Графа офицера (и ферзя)
Расположение валентностей для офицера и ферзя практически идентично, за исключением того, что наименьшее значение валентности для ферзя в три раза превышает оное для офицера.
```
def bishop_or_queen(piece, valencies):
board_size = np.shape(valencies)[0]
if piece == 'Bishop':
smallest_val = board_size-1
else:
smallest_val = 3*(board_size-1)
# external square
valencies[0, :] = valencies[:, 0] = \
valencies[:, -1] = valencies[-1, :] = smallest_val
# internal sqares
for i in range (1, int(board_size/2)+1):
# top, left
# right, bottom
valencies[i, i:-i] = valencies[i:-i, i] = \
valencies[i:-i, -(i+1)] = valencies[-(i+1), i:-i] = \
smallest_val + 2*i
return valencies
special_cases(piece='Bishop', board_sizes=range(4,8))
```
Видно, что эквивалентные клетки располагаются по периметрам образованных клетками концентрических квадратов. Поскольку при чётных $n$ в центре доски расположены $4$ поля с максимальной валентностью, а при нечётных - одно, случаи чётных и нечётных $n$ представляется удобным рассмотреть раздельно.
### Чётные $n$
Каково количество различных значений валентности, а также их величина? Наименьшее значение равно $(n-1)$, так как это количество клеток на диагонали минус клетка, на которой стоит сама фигура. Наибольшее значение - $(n-1) + (n-2) = (2n-3)$, так как оно больше наименьшего значения на количество клеток, расположенных на диагонали квадрата со стороной $(n-1)$ минус клетка, на которой стоит сама фигура.
Пусть $s$ - количество шагов размера $2$, которое требуется совершить для перехода от значения $(n-1)$ к значению $(2n-3)$. Тогда
$$ n-1 + 2s = 2n-3, $$ $$ 2s = {\color{Red} {2n}} - {\color{Green} 3} - {\color{Red} n} + {\color{Green} 1} = n - 2 \Rightarrow s = \frac{n-2}{2}. $$
Так как $n$ - чётное, $s$ $\in \mathbb{Z}$.
Однако ввиду того, что *один* шаг совершается между *двумя* разными значениями, количество различных значений валентности на единицу больше количества шагов, требующихся для перехода от минимального до максимального. В таком случае имеем $\frac{n-2}{2} + 1 = \frac{n}{2} - {\color{Green} 1} +{\color{Green} 1} = \frac{n}{2}.$ Итого, на доске со стороной $n$ содержится $\frac{n}{2}$ клеток с различными значениями валентности - $\frac{n}{2}$ концентрических квадратов.
В каком количестве представлено каждое из значений? Количество элементов, расположенных по периметру образованного клетками квадрата со стороной $\lambda$, равно учетверённой стороне минус четыре угловые клетки, которые оказываются учтёнными дважды. Тогда количество клеток с одноимённым значением валентности равно $4\lambda-4 = 4(\lambda-1)$, где $\lambda$ изменяется с шагом $2$ в пределах от $2$ (центральный квадрат) до $n$ (внешний).
При этом от $\lambda$ зависит не только количество значений валентности, но и их величина - она равна сумме $\lambda$ и наименьшего из значений валентности, встречающихся на доске. Таким образом, имея наименьшее значение валентности, а также количество концентрических квадратов, нетрудно составить зависимую от $\lambda$ сумму $P(X^{even}_{bishop}) = \sum_{}P(H_i) \cdot P(X|H_i)$. Однако удобнее суммировать по индексу, который изменяется с шагом $1$, потому заменим $k = \frac{\lambda}{2}.$ Теперь можно записать:
$$ P(X^{even}_{bishop}) = \sum_{k = 1}^{\frac{n}{2}} \frac{4(n+1-2k)\cdot(n-3+2k)} {n^{2}(n^{2}-1)} = \frac{4}{n^{2}(n^{2}-1)} \sum_{k = 1}^{\frac{n}{2}} n^{2} - {\color{Red} {3n}} + {\color{Blue} {2kn}} + {\color{Red} {n}} - 3 + {\color{Cyan} {2k}} - {\color{Blue} {2kn}} + {\color{Cyan} {6k}} - 4k^{2} = $$
$$ =\frac{4}{n^{2}(n^{2}-1)} \sum_{k = 1}^{\frac{n}{2}} n^{2} - 2n - 3 + 8k - 4k^{2}. $$
Вынесем первые три слагаемых за знак суммы, так как они не зависят от $k$, умножив их на $\frac{n}{2}$ - количество раз, которое они встречаются в сумме:
$$ P(X^{even}_{bishop}) = \frac{4}{n^{2}(n^{2}-1)}\ [\frac{n}{2}(n^{2} - 2n - 3) + \sum_{k = 1}^{\frac{n}{2}}8k - 4k^{2}] $$
Рассмотрим отдельно выражение под знаком суммы.
$$ \sum_{k = 1}^{\frac{n}{2}}8k - 4k^{2} = 8\sum_{k = 1}^{\frac{n}{2}}k - 4\sum_{k = 1}^{\frac{n}{2}} k^{2}. $$
Обозначим $ S_1 = 8\sum_{k = 1}^{\frac{n}{2}}k$, $ S_2 = 4\sum_{k = 1}^{\frac{n}{2}} k^{2}. $
$S_1$ - это умноженная на $8$ сумма первых $\frac{n}{2}$ натуральных чисел, которая есть сумма первых $\frac{n}{2}$ членов арифметической прогрессии, поэтому
$$ S_1 = 8\frac{\frac{n}{2}(\frac{n}{2}+1)}{2} = 4\frac{n}{2}(\frac{n}{2}+1) = 2n(\frac{n}{2}+1) = \frac{2n^2}{2}+2n = n^2 + 2n = n(n+2). $$
$S_2$ - это умноженная на 4 сумма квадратов первых $\frac{n}{2}$ натуральных чисел, поэтому
$$ S_2 = 4\frac{\frac{n}{2}(\frac{n}{2}+1)(2\frac{n}{2}+1)}{6} = \frac{n(n+2)(n+1)}{6}. $$
$$ S_1 - S_2 = n(n+2) - \frac{n(n+2)(n+1)}{6} = n(n+2) (1 - \frac{(n+1)}{6}) = $$ $$ = \frac{n(n+2)({\color{Green} 6}-n-{\color{Green} 1})}{6} = \frac{n(n+2)(-n + 5)}{6} = -\frac{n(n+2)(n-5)}{6}.$$
Тогда
$$ P(X^{even}_{bishop}) = \frac{4}{n^{2}(n^{2}-1)}\ [\frac{n}{2}(n^{2} - 2n - 3) - \frac{n(n+2)(n-5)}{6} ] = $$ $$ = \frac{4}{n^{2}(n^{2}-1)}\ [\frac{n(3n^{2} - 6n - 9)}{6} - \frac{n(n+2)(n-5)}{6} ] = $$ $$ = \frac{4n}{6n^{2}(n^{2}-1)}({\color{Orange} {3n^{2}}} - {\color{Red} {6n}} - {\color{Green} 9} - {\color{Orange} {n^2}} + {\color{Red} {5n}} - {\color{Red} {2n}} + {\color{Green} {10}}) = $$ $$ =\frac{2}{3n(n^{2}-1)}(2n^2 - 3n + 1) = \frac{2(2n-1)(n-1)}{3n(n^{2}-1)} = \frac{2(2n-1)}{3n(n+1)}. $$
### Нечётные $n$
Каково количество различных значений валентности? Наименьшее значение равно $(n-1)$ из тех же рассуждений, что и для чётных $n$. Наибольшее значение, очевидно, равно удвоенному наименьшему - $(n-1) + (n-1) = 2(n-1)$.
Пусть $s$ - количество шагов размера $2$, которое требуется совершить для перехода от значения $(n-1)$ к значению $2(n-1)$. Тогда
$$n-1 + 2s = 2n-2,$$ $$2s = {\color{Red} {2n}} - {\color{Green} 2} - {\color{Red} n} + {\color{Green} 1} = n - 1 \Rightarrow s = \frac{n-1}{2}.$$
Так как $n$ - нечётное, $s$ $\in \mathbb{Z}$. Итого имеем $\frac{n-1}{2} + 1 = \frac{n}{2} - {\color{Green} {\frac{1}{2}}} +{\color{Green} 1} = \frac{n}{2} + \frac{1}{2} = \frac{n+1}{2}$ клеток с различными значениями валентности.
В каком количестве представлено каждое из значений? Рассуждения для чётных и нечётных $n$ идентичны, за исключением того, что выражение $4(\lambda-1)$ равно нулю при $\lambda = 1$ (в центральной клетке доски). По этой причине слагаемое $P(H_{\frac{n+1}{2}}) \cdot P(X|H_{\frac{n+1}{2}})$ должно быть вынесено за знак общей суммы, а индекс суммирования будет принимать на единицу меньше значений: $\frac{n+1}{2} - 1 = \frac{n}{2} + \frac{1}{2} - 1 = \frac{n}{2} + {\color{Green} {\frac{1}{2}}} - {\color{Green} 1} = \frac{n}{2} - \frac{1}{2} = \frac{n-1}{2}.$
Тогда можно записать:
$$ P(X^{odd}_{bishop}) = \frac{1\cdot 2(n-1)}{n^{2}(n^{2}-1)} + \sum_{k = 1}^{\frac{n-1}{2}} \frac{4(n+1-2k)\cdot(n-3+2k)} {n^{2}(n^{2}-1)}. $$
Легко видеть, что выражение под знаком суммы отличается от $P(X^{even}_{bishop})$ только верхней границей суммирования. Следовательно, аналогично предыдущим выкладкам можно обозначить: $ S_1 = 8\sum_{k = 1}^{\frac{n-1}{2}}k$, $ S_2 = 4\sum_{k = 1}^{\frac{n-1}{2}} k^{2}. $
$$ S_1 = 8\frac{\frac{n-1}{2}(\frac{n-1}{2}+1)}{2} = 4\frac{n-1}{2}(\frac{n+1}{2}) = (n-1)(n+1). $$
$$ S_2 = 4\frac{\frac{n-1}{2}(\frac{n-1}{2}+1)(2\frac{n-1}{2}+1)}{6} = 4\frac{\frac{n-1}{2}(\frac{n-1}{2}+1)(2\frac{n-1}{2}+1)}{6} = \frac{(n-1)(\frac{n+1}{2})n}{3} = \frac{(n-1)(n+1)n}{6}. $$
$$ S_1 - S_2 = (n-1)(n+1) - \frac{(n-1)(n+1)n}{6} = (n-1)(n+1)(1 - \frac{n}{6}) = \frac{(n-1)(n+1)(6 - n)}{6} = -\frac{(n-1)(n+1)(n-6)}{6}. $$
Тогда
$$ P(X^{odd}_{bishop}) = \frac{2(n-1)}{n^{2}(n^{2}-1)} + \frac{4}{n^{2}(n^{2}-1)}\ [\frac{n-1}{2}(n^{2} - 2n - 3) -\frac{(n-1)(n+1)(n-6)}{6}] = $$ $$ =\frac{2}{n^{2}(n+1)} + \frac{4(n-1)}{n^{2}(n^{2}-1)} [\frac{3n^2 - 6n - 9}{6} -\frac{(n+1)(n-6)}{6}] = $$ $$ =\frac{2}{n^{2}(n+1)} + \frac{4}{6n^{2}(n+1)}({\color{Orange} {3n^2}} - {\color{Red} {6n}} - {\color{Green} 9} - {\color{Orange} {n^2}} + {\color{Red} {6n}} - {\color{Red} n} + {\color{Green} 6}) = $$ $$ =\frac{2}{n^{2}(n+1)} + \frac{4}{6n^{2}(n+1)}(2n^2 - n - 3) = \frac{{\color{Green} {12}} + 8n^2 - 4n - {\color{Green} {12}}}{6n^{2}(n+1)} = \frac{4n(2n-1)}{6n^{2}(n+1)} = \frac{2(2n-1)}{3n(n+1)}. $$
Как видно, чётность доски не влияет на рассматриваемую вероятность: $P(X^{even}_{bishop}) = P(X^{odd}_{bishop}) = P(X_{bishop}) = \frac{2(2n-1)}{3n(n+1)}$.
## Ладья
### Функция, возвращающая массив валентностей ладейного Графа
```
def rook(valencies):
board_size = np.shape(valencies)[0]
x, y = np.meshgrid(range(board_size), range(board_size))
for i, j in zip(x.flatten(), y.flatten()):
valencies[i, j] = 2*(board_size-1)
return valencies
special_cases(piece='Rook', board_sizes=range(4,6))
```
Известная особенность ладьи - независимо от расположения на доске, она всегда контролирует постоянное количество полей, а именно $2(n-1)$ - это сумма полей по горизонтали и вертикали минус поле, на котором стоит сама ладья.
$$P(X_{rook}) = \frac{n^{2}\cdot 2(n-1)}{n^{2}(n^{2}-1)} = \frac{2}{(n+1)}.$$
## Ферзь
```
special_cases(piece='Queen', board_sizes=range(4,8))
```
Поскольку ферзь сочетает в себе возможности офицера и ладьи, выражение для него может быть получено как сумма выражений для этих фигур:
$$ P(X_{queen}) = \frac{2(2n-1)}{3n(n+1)} + \frac{2}{n+1} = \frac{2(2n-1) + 6n}{3n(n+1)} = \frac{{\color{Red} {4n}} - 2 + {\color{Red} {6n}}}{3n(n+1)} = \frac{10n - 2}{3n(n+1)} = \frac{2(5n-1)}{3n(n+1)}. $$
## Король
### Функция, возвращающая массив валентностей Графа короля
```
def king(valencies):
# corners : top left = top right = \
# bottom left = bottom right
valencies[0, 0] = valencies[0, -1] = \
valencies[-1, 0] = valencies[-1, -1] = 3
# edges : top, left, right, bottom
valencies[0, 1:-1] = valencies[1:-1, 0] = \
valencies[1:-1, -1] = valencies[-1, 1:-1] = 5
# center
valencies[1:-1, 1:-1] = 8
return valencies
special_cases(piece='King', board_sizes=range(4,6))
```
Видно, что края доски, за исключением $3$-валентных углов, $5$-валентны, а всё оставшееся пространство $8$-валентно. Ввиду того, что краёв $4$, а $5$-валентных клеток на одном краю $(n-2)$ штук, имеем:
$$ P(X_{king}) = \frac{4\cdot 3}{n^{2}(n^{2}-1)} +\frac{4(n-2)\cdot 5}{n^{2}(n^{2}-1)} +\frac{(n-2)^2\cdot 8}{n^{2}(n^{2}-1)} = \frac{12 + 20(n-2) + 8(n-2)^2}{n^{2}(n^{2}-1)} = $$
$$ = \frac{4(3 + 5(n-2)+2(n-2)^2)}{n^{2}(n^{2}-1)} = \frac{4(3 + 5n-10+2(n^2 - 4n + 4))}{n^{2}(n^{2}-1)} = \frac{4({\color{Green} 3} + {\color{Red} {5n}}-{\color{Green} {10}}+2n^2 - {\color{Red} {8n}} + {\color{Green} {8}} )}{n^{2}(n^{2}-1)} = $$
$$ =\frac{4(2n^2 - 3n + 1)}{n^{2}(n^{2}-1)} = \frac{4(2n-1)(n-1)}{n^{2}(n^{2}-1)} = \frac{4(2n-1)}{n^{2}(n+1)}. $$
### Функция, возвращающая значение $P(X_{piece})$
```
def get_probabilities(piece, n):
# NOTE: Results can be incorrect for large n because of dividing by
# the huge denominator!
if piece == 'Pawn':
return 2*(n-1)/((n**2)*(n+1))
elif piece == 'Knight':
return 8*(n-2)/((n**2)*(n+1))
elif piece == 'Bishop':
return 2*(2*n-1)/(3*n*(n+1))
elif piece == 'Rook':
return 2/(n+1)
elif piece == 'Queen':
return 2*(5*n-1)/(3*n*(n+1))
elif piece == 'King':
return 4*(2*n-1)/(n**2*(n+1))
```
Для проверки аналитических результатов используем метод вычисления вероятности «в лоб» - напрямую из массива валентностей.
```
def straightforward_prob(piece, board_size):
# Get probability directly from the board of valencies
board, _ = get_board(board_size)
val_board = get_valencies(piece, board)
unique, counts = np.unique(val_board, return_counts=True)
prob = np.dot(unique, counts)/((board_size)**2 * (board_size**2 - 1))
return prob
```
График, отображающий зависимость вероятности от размера доски, представлен как функция действительного переменного в целях наглядности.
```
start = 2
end = 16
step = 0.02
x = np.arange(start, end)
names_list = ['Pawn', 'Knight', 'Bishop', 'Rook', 'Queen', 'King']
# Check if analytical results match straightforward calculations
for name in names_list:
for board_size in x:
y = get_probabilities(name, board_size)
if not y == straightforward_prob(name, board_size):
print('Mistake in equation for %s' % name)
print('Analytical results approved')
# Let's expand the range from Z to R for the sake of visual clarity
x = np.arange(start, end, step)
fig, ax = plt.subplots(figsize=(10, 8))
for name in names_list:
y = get_probabilities(name, x)
plt.plot(x, y, label=name, linewidth=3.0)
legend = plt.legend(loc='upper right')
for label in legend.get_lines():
label.set_linewidth(3)
for label in legend.get_texts():
label.set_fontsize(26)
plt.xlabel("Size of a board", fontsize=20)
plt.ylabel("Probability", fontsize=20)
plt.show()
```
| github_jupyter |
# Collaborative Filtering on Google Analytics Data
### Learning objectives
1. Prepare the user-item matrix and use it with WALS.
2. Train a `WALSMatrixFactorization` within TensorFlow locally and on AI Platform.
3. Visualize the embedding vectors with principal components analysis.
## Overview
This notebook demonstrates how to implement a WALS matrix refactorization approach to do collaborative filtering.
Each learning objective will correspond to a __#TODO__ in the [student lab notebook](../labs/wals.ipynb) -- try to complete that notebook first before reviewing this solution notebook.
```
import os
PROJECT = "cloud-training-demos" # REPLACE WITH YOUR PROJECT ID
BUCKET = "cloud-training-demos-ml" # REPLACE WITH YOUR BUCKET NAME
REGION = "us-central1" # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["BUCKET"] = BUCKET
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = "1.15"
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
import tensorflow as tf
print(tf.__version__)
```
## Create raw dataset
<p>
For collaborative filtering, you don't need to know anything about either the users or the content. Essentially, all you need to know is userId, itemId, and rating that the particular user gave the particular item.
<p>
In this case, you are working with newspaper articles. The company doesn't ask their users to rate the articles. However, you can use the time-spent on the page as a proxy for rating.
<p>
Normally, you would also add a time filter to this ("latest 7 days"), but your dataset is itself limited to a few days.
```
from google.cloud import bigquery
bq = bigquery.Client(project = PROJECT)
sql = """
WITH CTE_visitor_page_content AS (
SELECT
# Schema: https://support.google.com/analytics/answer/3437719?hl=en
# For a completely unique visit-session ID, you combine combination of fullVisitorId and visitNumber:
CONCAT(fullVisitorID,'-',CAST(visitNumber AS STRING)) AS visitorId,
(SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) AS latestContentId,
(LEAD(hits.time, 1) OVER (PARTITION BY fullVisitorId ORDER BY hits.time ASC) - hits.time) AS session_duration
FROM
`cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
GROUP BY
fullVisitorId,
visitNumber,
latestContentId,
hits.time )
-- Aggregate web stats
SELECT
visitorId,
latestContentId as contentId,
SUM(session_duration) AS session_duration
FROM
CTE_visitor_page_content
WHERE
latestContentId IS NOT NULL
GROUP BY
visitorId,
latestContentId
HAVING
session_duration > 0
"""
df = bq.query(sql).to_dataframe()
df.head()
stats = df.describe()
stats
df[["session_duration"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
# The rating is the session_duration scaled to be in the range 0-1. This will help with training.
median = stats.loc["50%", "session_duration"]
df["rating"] = 0.3 * df["session_duration"] / median
df.loc[df["rating"] > 1, "rating"] = 1
df[["rating"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
del df["session_duration"]
%%bash
rm -rf data
mkdir data
# TODO 1: Write object to a comma-separated values (csv) file.
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
!head data/collab_raw.csv
```
## Create dataset for WALS
<p>
The raw dataset (above) won't work for WALS:
<ol>
<li> The userId and itemId have to be 0,1,2 ... so you need to create a mapping from visitorId (in the raw data) to userId and contentId (in the raw data) to itemId.
<li> You will need to save the above mapping to a file because at prediction time, you'll need to know how to map the contentId in the table above to the itemId.
<li> You'll need two files: a "rows" dataset where all the items for a particular user are listed; and a "columns" dataset where all the users for a particular item are listed.
</ol>
<p>
### Mapping
```
import pandas as pd
import numpy as np
def create_mapping(values, filename):
with open(filename, 'w') as ofp:
value_to_id = {value:idx for idx, value in enumerate(values.unique())}
for value, idx in value_to_id.items():
ofp.write("{},{}\n".format(value, idx))
return value_to_id
df = pd.read_csv(filepath_or_buffer = "data/collab_raw.csv",
header = None,
names = ["visitorId", "contentId", "rating"],
dtype = {"visitorId": str, "contentId": str, "rating": np.float})
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
user_mapping = create_mapping(df["visitorId"], "data/users.csv")
item_mapping = create_mapping(df["contentId"], "data/items.csv")
!head -3 data/*.csv
df["userId"] = df["visitorId"].map(user_mapping.get)
df["itemId"] = df["contentId"].map(item_mapping.get)
mapped_df = df[["userId", "itemId", "rating"]]
mapped_df.to_csv(path_or_buf = "data/collab_mapped.csv", index = False, header = False)
mapped_df.head()
```
### Creating rows and columns datasets
```
import pandas as pd
import numpy as np
mapped_df = pd.read_csv(filepath_or_buffer = "data/collab_mapped.csv", header = None, names = ["userId", "itemId", "rating"])
mapped_df.head()
NITEMS = np.max(mapped_df["itemId"]) + 1
NUSERS = np.max(mapped_df["userId"]) + 1
mapped_df["rating"] = np.round(mapped_df["rating"].values, 2)
print("{} items, {} users, {} interactions".format( NITEMS, NUSERS, len(mapped_df) ))
grouped_by_items = mapped_df.groupby("itemId")
iter = 0
for item, grouped in grouped_by_items:
print(item, grouped["userId"].values, grouped["rating"].values)
iter = iter + 1
if iter > 5:
break
import tensorflow as tf
grouped_by_items = mapped_df.groupby("itemId")
with tf.python_io.TFRecordWriter("data/users_for_item") as ofp:
for item, grouped in grouped_by_items:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [item])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["userId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
grouped_by_users = mapped_df.groupby("userId")
with tf.python_io.TFRecordWriter("data/items_for_user") as ofp:
for user, grouped in grouped_by_users:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [user])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["itemId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
!ls -lrt data
```
To summarize, you created the following data files from collab_raw.csv:
<ol>
<li> ```collab_mapped.csv``` is essentially the same data as in ```collab_raw.csv``` except that ```visitorId``` and ```contentId``` which are business-specific have been mapped to ```userId``` and ```itemId``` which are enumerated in 0,1,2,.... The mappings themselves are stored in ```items.csv``` and ```users.csv``` so that they can be used during inference.
<li> ```users_for_item``` contains all the users/ratings for each item in TFExample format
<li> ```items_for_user``` contains all the items/ratings for each user in TFExample format
</ol>
## Train with WALS
Once you have the dataset, do matrix factorization with WALS using the [WALSMatrixFactorization](https://www.tensorflow.org/versions/r1.15/api_docs/python/tf/contrib/factorization/WALSMatrixFactorization) in the contrib directory.
This is an estimator model, so it should be relatively familiar.
<p>
As usual, you write an input_fn to provide the data to the model, and then create the Estimator to do train_and_evaluate.
Because it is in contrib and hasn't moved over to tf.estimator yet, you use tf.contrib.learn.Experiment to handle the training loop.<p>
```
import os
import tensorflow as tf
from tensorflow.python.lib.io import file_io
from tensorflow.contrib.factorization import WALSMatrixFactorization
def read_dataset(mode, args):
# TODO 2: Decode the example
def decode_example(protos, vocab_size):
features = {
"key": tf.FixedLenFeature(shape = [1], dtype = tf.int64),
"indices": tf.VarLenFeature(dtype = tf.int64),
"values": tf.VarLenFeature(dtype = tf.float32)}
parsed_features = tf.parse_single_example(serialized = protos, features = features)
values = tf.sparse_merge(sp_ids = parsed_features["indices"], sp_values = parsed_features["values"], vocab_size = vocab_size)
# Save key to remap after batching
# This is a temporary workaround to assign correct row numbers in each batch.
# You can ignore details of this part and remap_keys().
key = parsed_features["key"]
decoded_sparse_tensor = tf.SparseTensor(indices = tf.concat(values = [values.indices, [key]], axis = 0),
values = tf.concat(values = [values.values, [0.0]], axis = 0),
dense_shape = values.dense_shape)
return decoded_sparse_tensor
def remap_keys(sparse_tensor):
# Current indices of your SparseTensor that you need to fix
bad_indices = sparse_tensor.indices # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Current values of your SparseTensor that you need to fix
bad_values = sparse_tensor.values # shape = (current_batch_size * (number_of_items/users[i] + 1),)
# Since batch is ordered, the last value for a batch index is the user
# Find where the batch index chages to extract the user rows
# 1 where user, else 0
user_mask = tf.concat(values = [bad_indices[1:,0] - bad_indices[:-1,0], tf.constant(value = [1], dtype = tf.int64)], axis = 0) # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Mask out the user rows from the values
good_values = tf.boolean_mask(tensor = bad_values, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
item_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
user_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 1))[:, 1] # shape = (current_batch_size,)
good_user_indices = tf.gather(params = user_indices, indices = item_indices[:,0]) # shape = (current_batch_size * number_of_items/users[i],)
# User and item indices are rank 1, need to make rank 1 to concat
good_user_indices_expanded = tf.expand_dims(input = good_user_indices, axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_item_indices_expanded = tf.expand_dims(input = item_indices[:, 1], axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_indices = tf.concat(values = [good_user_indices_expanded, good_item_indices_expanded], axis = 1) # shape = (current_batch_size * number_of_items/users[i], 2)
remapped_sparse_tensor = tf.SparseTensor(indices = good_indices, values = good_values, dense_shape = sparse_tensor.dense_shape)
return remapped_sparse_tensor
def parse_tfrecords(filename, vocab_size):
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
else:
num_epochs = 1 # end-of-input after this
files = tf.gfile.Glob(filename = os.path.join(args["input_path"], filename))
# Create dataset from file list
dataset = tf.data.TFRecordDataset(files)
dataset = dataset.map(map_func = lambda x: decode_example(x, vocab_size))
dataset = dataset.repeat(count = num_epochs)
dataset = dataset.batch(batch_size = args["batch_size"])
dataset = dataset.map(map_func = lambda x: remap_keys(x))
return dataset.make_one_shot_iterator().get_next()
def _input_fn():
features = {
WALSMatrixFactorization.INPUT_ROWS: parse_tfrecords("items_for_user", args["nitems"]),
WALSMatrixFactorization.INPUT_COLS: parse_tfrecords("users_for_item", args["nusers"]),
WALSMatrixFactorization.PROJECT_ROW: tf.constant(True)
}
return features, None
return _input_fn
```
This code is helpful in developing the input function. You don't need it in production.
```
def try_out():
with tf.Session() as sess:
fn = read_dataset(
mode = tf.estimator.ModeKeys.EVAL,
args = {"input_path": "data", "batch_size": 4, "nitems": NITEMS, "nusers": NUSERS})
feats, _ = fn()
print(feats["input_rows"].eval())
print(feats["input_rows"].eval())
try_out()
def find_top_k(user, item_factors, k):
all_items = tf.matmul(a = tf.expand_dims(input = user, axis = 0), b = tf.transpose(a = item_factors))
topk = tf.nn.top_k(input = all_items, k = k)
return tf.cast(x = topk.indices, dtype = tf.int64)
def batch_predict(args):
import numpy as np
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
# This is how you would get the row factors for out-of-vocab user data
# row_factors = list(estimator.get_projections(input_fn=read_dataset(tf.estimator.ModeKeys.EVAL, args)))
# user_factors = tf.convert_to_tensor(np.array(row_factors))
# But for in-vocab data, the row factors are already in the checkpoint
user_factors = tf.convert_to_tensor(value = estimator.get_row_factors()[0]) # (nusers, nembeds)
# In either case, you have to assume catalog doesn"t change, so col_factors are read in
item_factors = tf.convert_to_tensor(value = estimator.get_col_factors()[0])# (nitems, nembeds)
# For each user, find the top K items
topk = tf.squeeze(input = tf.map_fn(fn = lambda user: find_top_k(user, item_factors, args["topk"]), elems = user_factors, dtype = tf.int64))
with file_io.FileIO(os.path.join(args["output_dir"], "batch_pred.txt"), mode = 'w') as f:
for best_items_for_user in topk.eval():
f.write(",".join(str(x) for x in best_items_for_user) + '\n')
def train_and_evaluate(args):
train_steps = int(0.5 + (1.0 * args["num_epochs"] * args["nusers"]) / args["batch_size"])
steps_in_epoch = int(0.5 + args["nusers"] / args["batch_size"])
print("Will train for {} steps, evaluating once every {} steps".format(train_steps, steps_in_epoch))
def experiment_fn(output_dir):
return tf.contrib.learn.Experiment(
tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"]),
train_input_fn = read_dataset(tf.estimator.ModeKeys.TRAIN, args),
eval_input_fn = read_dataset(tf.estimator.ModeKeys.EVAL, args),
train_steps = train_steps,
eval_steps = 1,
min_eval_frequency = steps_in_epoch
)
from tensorflow.contrib.learn.python.learn import learn_runner
learn_runner.run(experiment_fn = experiment_fn, output_dir = args["output_dir"])
batch_predict(args)
import shutil
shutil.rmtree(path = "wals_trained", ignore_errors=True)
train_and_evaluate({
"output_dir": "wals_trained",
"input_path": "data/",
"num_epochs": 0.05,
"nitems": NITEMS,
"nusers": NUSERS,
"batch_size": 512,
"n_embeds": 10,
"topk": 3
})
!ls wals_trained
!head wals_trained/batch_pred.txt
```
## Run as a Python module
Let's run it as Python module for just a few steps.
```
os.environ["NITEMS"] = str(NITEMS)
os.environ["NUSERS"] = str(NUSERS)
%%bash
rm -rf wals.tar.gz wals_trained
gcloud ai-platform local train \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
-- \
--output_dir=${PWD}/wals_trained \
--input_path=${PWD}/data \
--num_epochs=0.01 --nitems=${NITEMS} --nusers=${NUSERS} \
--job-dir=./tmp
```
## Run on Cloud
```
%%bash
gsutil -m cp data/* gs://${BUCKET}/wals/data
%%bash
OUTDIR=gs://${BUCKET}/wals/model_trained
JOBNAME=wals_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ai-platform jobs submit training $JOBNAME \
--region=$REGION \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC_GPU \
--runtime-version=$TFVERSION \
-- \
--output_dir=$OUTDIR \
--input_path=gs://${BUCKET}/wals/data \
--num_epochs=10 --nitems=${NITEMS} --nusers=${NUSERS}
```
This will take <b>10 minutes</b> to complete. Rerun the above command until the jobs gets submitted.
## Get row and column factors
Once you have a trained WALS model, you can get row and column factors (user and item embeddings) from the checkpoint file. You'll look at how to use these in the section on building a recommendation system using deep neural networks.
```
def get_factors(args):
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
row_factors = estimator.get_row_factors()[0]
col_factors = estimator.get_col_factors()[0]
return row_factors, col_factors
args = {
"output_dir": "gs://{}/wals/model_trained".format(BUCKET),
"nitems": NITEMS,
"nusers": NUSERS,
"n_embeds": 10
}
user_embeddings, item_embeddings = get_factors(args)
print(user_embeddings[:3])
print(item_embeddings[:3])
```
You can visualize the embedding vectors using dimensional reduction techniques such as PCA.
```
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
pca = PCA(n_components = 3)
pca.fit(user_embeddings)
# TODO 3: Apply the mapping (transform) to user embeddings
user_embeddings_pca = pca.transform(user_embeddings)
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111, projection = "3d")
xs, ys, zs = user_embeddings_pca[::150].T
ax.scatter(xs, ys, zs)
```
<pre>
# Copyright 2022 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
</pre>
| github_jupyter |
```
import numpy as np
from resonance.nonlinear_systems import SingleDoFNonLinearSystem
```
To apply arbitrary forcing to a single degree of freedom linear or nonlinear system, you can do so with `SingleDoFNonLinearSystem` (`SingleDoFLinearSystem` does not support arbitrary forcing...yet).
Add constants, a generalized coordinate, and a generalized speed to the system.
```
sys = SingleDoFNonLinearSystem()
sys.constants['m'] = 100 # kg
sys.constants['c'] = 1.1*1.2*0.5/2
sys.constants['k'] = 10
sys.constants['Fo'] = 1000 # N
sys.constants['Ft'] = 100 # N/s
sys.constants['to'] = 3.0 # s
sys.coordinates['x'] = 0.0
sys.speeds['v'] = 0.0
```
Create a function that evaluates the first order form of the non-linear equations of motion. In this case:
$$
\dot{x} = v \\
m\dot{v} + c \textrm{sgn}(v)v^2 + k \textrm{sgn}(x)x^2 = F(t)
$$
Make the arbitrary forcing term, $F$, an input to this function.
```
def eval_eom(x, v, m, c, k, F):
xdot = v
vdot = (F - np.sign(v)*c*v**2 - np.sign(x)*k*x**2) / m
return xdot, vdot
```
Note that you cannot add this to the system because `F` has not been defined.
```
sys.diff_eq_func = eval_eom
```
To rememdy this, create a function that returns the input value given the appropriate constants and time.
```
def eval_step_input(Fo, to, time):
if time < to:
return 0.0
else:
return Fo
import matplotlib.pyplot as plt
%matplotlib widget
ts = np.linspace(0, 10)
plt.plot(ts, eval_step_input(5.0, 3.0, ts))
ts < 3.0
def eval_step_input(Fo, to, time):
F = np.empty_like(time)
for i, ti in enumerate(time):
if ti < to:
F[i] = 0.0
else:
F[i] = Fo
return F
plt.plot(ts, eval_step_input(5.0, 3.0, ts))
eval_step_input(5.0, 3.0, ts)
eval_step_input(5.0, 3.0, 7.0)
def eval_step_input(Fo, to, time):
if np.isscalar(time):
if time < to:
return 0.0
else:
return Fo
else:
F = np.empty_like(time)
for i, ti in enumerate(time):
if ti < to:
F[i] = 0.0
else:
F[i] = Fo
return F
eval_step_input(5.0, 3.0, 7.0)
eval_step_input(5.0, 3.0, ts)
True * 5.0
False * 5.0
(ts >= 3.0)*5.0
(5.0 >= 3.0)*5.0
def eval_step_input(Fo, to, time):
return (time >=to)*Fo
eval_step_input(5.0, 3.0, ts)
eval_step_input(5.0, 3.0, 7.0)
sys.add_measurement('F', eval_step_input)
sys.diff_eq_func = eval_eom
traj = sys.free_response(20.0)
traj.plot(subplots=True)
def eval_ramp_input(Ft, to, time):
return (time >= to)*(Ft*time - Ft*to)
del sys.measurements['F']
sys.add_measurement('F', eval_ramp_input)
sys.measurements
traj = sys.free_response(20.0)
traj.plot(subplots=True)
```
| github_jupyter |
# Fit $k_{ij}$ and $r_c^{ABij}$ interactions parameter of Ethanol and CPME
This notebook has te purpose of showing how to optimize the $k_{ij}$ and $r_c^{ABij}$ for a mixture with induced association.
First it's needed to import the necessary modules
```
import numpy as np
from sgtpy import component, mixture, saftvrmie
from sgtpy.fit import fit_cross
```
Now that the functions are available it is necessary to create the mixture.
```
ethanol = component('ethanol2C', ms = 1.7728, sigma = 3.5592 , eps = 224.50,
lambda_r = 11.319, lambda_a = 6., eAB = 3018.05, rcAB = 0.3547,
rdAB = 0.4, sites = [1,0,1], cii= 5.3141080872882285e-20)
cpme = component('cpme', ms = 2.32521144, sigma = 4.13606074, eps = 343.91193798, lambda_r = 14.15484877,
lambda_a = 6.0, npol = 1.91990385,mupol = 1.27, sites =[0,0,1], cii = 3.5213681817448466e-19)
mix = mixture(ethanol, cpme)
```
Now the experimental equilibria data is read and a tuple is created. It includes the experimental liquid composition, vapor composition, equilibrium temperature and pressure. This is done with ```datavle = (Xexp, Yexp, Texp, Pexp)```
```
# Experimental data obtained from Mejia, Cartes, J. Chem. Eng. Data, vol. 64, no. 5, pp. 1970–1977, 2019
# Experimental temperature saturation in K
Texp = np.array([355.77, 346.42, 342.82, 340.41, 338.95, 337.78, 336.95, 336.29,
335.72, 335.3 , 334.92, 334.61, 334.35, 334.09, 333.92, 333.79,
333.72, 333.72, 333.81, 334.06, 334.58])
# Experimental pressure in Pa
Pexp = np.array([50000., 50000., 50000., 50000., 50000., 50000., 50000., 50000.,
50000., 50000., 50000., 50000., 50000., 50000., 50000., 50000.,
50000., 50000., 50000., 50000., 50000.])
# Experimental liquid composition
Xexp = np.array([[0. , 0.065, 0.11 , 0.161, 0.203, 0.253, 0.301, 0.351, 0.402,
0.446, 0.497, 0.541, 0.588, 0.643, 0.689, 0.743, 0.785, 0.837,
0.893, 0.947, 1. ],
[1. , 0.935, 0.89 , 0.839, 0.797, 0.747, 0.699, 0.649, 0.598,
0.554, 0.503, 0.459, 0.412, 0.357, 0.311, 0.257, 0.215, 0.163,
0.107, 0.053, 0. ]])
# Experimental vapor composition
Yexp = np.array([[0. , 0.302, 0.411, 0.48 , 0.527, 0.567, 0.592, 0.614, 0.642,
0.657, 0.678, 0.694, 0.71 , 0.737, 0.753, 0.781, 0.801, 0.837,
0.883, 0.929, 1. ],
[1. , 0.698, 0.589, 0.52 , 0.473, 0.433, 0.408, 0.386, 0.358,
0.343, 0.322, 0.306, 0.29 , 0.263, 0.247, 0.219, 0.199, 0.163,
0.117, 0.071, 0. ]])
datavle = (Xexp, Yexp, Texp, Pexp)
```
The function ```fit_cross``` optimize the $k_{ij}$ correction and $r_c^{ABij}$ distance. An initial guess is needed, as well as the mixture object, the index of the self-associating component and the equilibria data.
```
#initial guesses for kij and rcij
x0 = [0.01015194, 2.23153033]
fit_cross(x0, mix, assoc=0, datavle=datavle)
```
For more information just run:
```fit_cross?```
| github_jupyter |
# BAYES CLASSIFIERS
For any classifier $f:{X \to Y}$, it's prediction error is:
$P(f(x) \ne Y) = \mathbb{E}[ \mathbb{1}(f(X) \ne Y)] = \mathbb{E}[\mathbb{E}[ \mathbb{1}(f(X) \ne Y)|X]]$
For each $x \in X$,
$$\mathbb{E}[ \mathbb{1}(f(X) \ne Y)|X = x] = \sum\limits_{y \in Y} P(Y = y|X = x) \cdot \mathbb{1}(f(x) \ne y)$$
The above quantity is minimized for this particular $x \in X$ when,
$$f(x) = \underset{y \in Y}{argmax} \space P(Y = y|X = x) \space \star$$
A classifier $f$ with property $ \star$ for all $x \in X$ is called the `Bayes Classifier`
Under the assumption $(X,Y) \overset{iid}{\sim} P$, the optimal classifier is:
$$f^{\star}(x) = \underset{y \in Y}{argmax} \space P(Y = y|X = x)$$
And from _Bayes Rule_ we equivalently have:
$$f^{\star}(x) = \underset{y \in Y}{argmax} \space P(Y = y) \space P(X = x|Y = y)$$
Where
- $P(Y =y)$ is called _the class prior_
- $P(X = x|Y= y)$ is called _the class conditional distribution_ of $X$
Assuming $X = \mathbb{R}, Y = \{ 0,1 \}$, and the distribution of $P \space \text{of} \space (X,Y)$ is as follows:
- _Class prior_: $P(Y = y) = \pi_y, y \in \{ 0,1 \}$
- _Class conditional density_ for class $y \in \{ 0,1 \}: p_y (x) = N(x|\mu_y,\sigma^2_y)$
$$f^{\star}(x) = \underset{y \in \{ 0,1 \}}{argmax} \space P(Y = y) \space P(X = x|Y = y) =
\begin{cases}
1 & \text{if} \space \frac{\pi_1}{\sigma_1}\space exp[- \frac{(x - \mu_1)^2}{2 \sigma^2_1}] > \frac{\pi_0}{\sigma_0}\space exp[- \frac{(x - \mu_0)^2}{2 \sigma^2_0}]\\
0 & \text{otherwise}
\end{cases}$$
### _Bayes Classifier_

The `Bayes Classifier` has the smallest prediction error of all classifiers. The problem is that we need to know the distribution of $P$ in order to construct the `Bayes Classifier`
# NAIVE BAYES CLASSIFIER
A simplifying assumtion that the features values are conditionally independent given the label, the probability of observing the conjunction $x_1, x_2, x_3, ..., x_d$ is the product of the probabilities for the individual features:
$$ p(x_1, x_2, x_3, ..., x_d|y) = \prod \limits_j \space p(x_j|y)$$
Then the `Naive Bayes Classifier` is defined as:
$$f^{\star}(x) = \underset{y \in Y}{argmax} \space p(y) \space \prod \limits_j \space p(x_j|y)$$
We can estimate these two terms based on the **frequency counts** in the dataset. If the features are real-valued, Naive Bayes can be extended assuming that features follow a Gaussian distribution. This extension is called `Gaussian Naive Bayes`. Other functions can be used to estimate the distribution but the Gaussian distribution is the easiest to work with due to we only need to estimate the mean and the standard deviation from the dataset.
Ok, let's start with the implementation of `Gaussian Naive Bayes` from scratch.
```
##IMPORTING ALL NECESSARY SUPPORT LIBRARIES
import math as mt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def separate_by_label(dataset):
separate = dict()
for i in range(len(dataset)):
row = dataset[i]
label = row[-1]
if (label not in separate):
separate[label] = list()
separate[label].append(row)
return separate
def mean(list_num):
return sum(list_num)/len(list_num)
def stdv(list_num):
mu = mean(list_num)
var = sum([(x - mu)**2 for x in list_num])/(len(list_num) - 1)
return mt.sqrt(var)
def stats_per_feature(ds):
'''
argument:
> ds: 1-D Array with the all data separated by class
returns:
> stats: 1-D Array with statistics summary for each feature
'''
stats = [(mean(col), stdv(col), len(col)) for col in zip(*ds)]
del(stats[-1])
return stats
def summary_by_class(dataset):
sep_label = separate_by_label(dataset)
summary = dict()
for label, rows in sep_label.items():
summary[label] = stats_per_feature(rows)
return summary
def gaussian_pdf(mean, stdv, x):
_exp = mt.exp(-1*((x - mean)**2/(2*stdv**2)))
return (1/(mt.sqrt(2 * mt.pi)*stdv)) * _exp
```
Now it is time to use the statistics calculated from the data to calculate probabilities for new data.
Probabilities are calculated separately for each class, so we calculate the probability that a new piece of data belongs to the first class, then calculate the probability that it belongs to the second class, and so on for all the classes.
For example, if we have two inputs $x_1 and \space x_2$ the calculation of the probability that those belong to class = _y_ is:
$$P(class = y|x_1,x_2) = P(x_1|class = y) \cdot P(x_2|class = y) \cdot P(class = y)$$
```
def class_probabilities(summary, row):
total = sum([summary[label][0][2] for label in summary])
probabilities = dict()
for class_, class_summary in summary.items():
probabilities[class_] = summary[class_][0][2]/total
for i in range(len(class_summary)):
mean, stdev, count = class_summary[i]
probabilities[class_] *= gaussian_pdf(row[i], mean, stdev)
return probabilities
def predict(summary, row):
cls_prob = class_probabilities(summary, row)
_label, _prob = None, -1.0
for class_, probability in cls_prob.items():
if _label is None or probability > _prob:
_prob = probability
_label = class_
return _label
```
In order to verify proper implementation a **toy dataset** is used to evaluate the algorithm.
```
dataset = [[3.393533211,2.331273381,0],
[3.110073483,1.781539638,0],
[1.343808831,3.368360954,0],
[3.582294042,4.67917911,0],
[2.280362439,2.866990263,0],
[7.423436942,4.696522875,1],
[5.745051997,3.533989803,1],
[9.172168622,2.511101045,1],
[7.792783481,3.424088941,1],
[7.939820817,0.791637231,1]]
summaries = summary_by_class(dataset)
for row in dataset:
y_pred = predict(summaries, row)
y_real = row[-1]
print("Expected={0}, Predicted={1}".format(y_real, y_pred))
```
# _GAUSSIAN NAIVE BAYES APPLICATION_
From the `UCI Machine Learning Repository` which contains Iris dataset, we will train our `Gaussian Naive Bayes` model. The Iris dataset is perhaps the best known database to be found in the pattern recognition literature. Fisher's paper is a classic in the field and is referenced frequently to this day.
The dataset contains 3 classes of 50 instances each, where each class refers to a type of iris plant. One class is linearly separable from the other 2; the latter are not linearly separable from each other.
The dataset have 150 instances and the following attributes:
1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
5. class:
-- Iris Setosa
-- Iris Versicolour
-- Iris Virginica
To compare the performance of our _Classifier_ on the **Iris** dataset, a Gaussian Naive Bayes model from `sklearn` will be fit on the dataset and classification report for both models is generated.
```
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import classification_report
##LOADING 'IRIS' DATASET
columns = ['sepal-len','sepal-wid','petal-len','petal-wid','class']
df = pd.read_csv('./data/Iris.csv', names = columns)
df.head()
df.info()
```
Due to the class variable type is `categorical` we need first to encode it as numeric type in order to be feed it into our models.
```
def encoder(df, class_value_pair):
for class_name, value in class_value_pair.items():
df['class'] = df['class'].replace(class_name, value)
return df
class_encoder = {'Iris-setosa':0, 'Iris-versicolor':1, 'Iris-virginica':2}
df = encoder(df, class_encoder)
df.head()
df['class'].value_counts().sort_index()
```
Once the preprocessing is complete the dataset will be split into a `Training` & `Test` dataset.
```
X_ = df.drop(['class'],axis = 1)
y = df['class']
X_train, X_test, y_train, y_test = train_test_split(X_, y, test_size = 0.30, random_state = 5)
```
Now, we can `train` our customized model. Noticed that our _Gaussian Naive Bayes_ model expects a complete dataset (attributes and labels) in order to calculate the summaries.
```
ds_train = pd.concat([X_train, y_train], axis = 1)
GNB_custom = summary_by_class(ds_train.values.tolist())
ds_test = pd.concat([X_test, y_test], axis = 1)
cust_pred = [predict(GNB_custom, row) for row in ds_test.values.tolist()]
cust_pred = np.array(cust_pred, dtype = 'int64')
cust_pred
```
Now an instance of `sklearn` _Gaussian Naive Bayes_ model is created and fit it with the training data and an array of predictions is obtained in order to get out performance comparation
```
##GET AND INSTANCE OF GAUSSIAN NAIVE BAYES MODEL
GNB_skln = GaussianNB()
GNB_skln.fit(X_train, y_train)
##CREATE SKLEARN PREDICTIONS ARRAY
sk_pred = GNB_skln.predict(X_test)
sk_pred
```
By last, a comparison on both models is performed thru a _Classification Report_
```
print("Sklearn:")
print(classification_report(y_test, sk_pred))
print("Custom:")
print(classification_report(y_test, cust_pred))
```
| github_jupyter |
# Mini Project: Temporal-Difference Methods
In this notebook, you will write your own implementations of many Temporal-Difference (TD) methods.
While we have provided some starter code, you are welcome to erase these hints and write your code from scratch.
### Part 0: Explore CliffWalkingEnv
Use the code cell below to create an instance of the [CliffWalking](https://github.com/openai/gym/blob/master/gym/envs/toy_text/cliffwalking.py) environment.
```
import gym
env = gym.make('CliffWalking-v0')
```
The agent moves through a $4\times 12$ gridworld, with states numbered as follows:
```
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]]
```
At the start of any episode, state `36` is the initial state. State `47` is the only terminal state, and the cliff corresponds to states `37` through `46`.
The agent has 4 potential actions:
```
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
```
Thus, $\mathcal{S}^+=\{0, 1, \ldots, 47\}$, and $\mathcal{A} =\{0, 1, 2, 3\}$. Verify this by running the code cell below.
```
print(env.action_space)
print(env.observation_space)
```
In this mini-project, we will build towards finding the optimal policy for the CliffWalking environment. The optimal state-value function is visualized below. Please take the time now to make sure that you understand _why_ this is the optimal state-value function.
```
import numpy as np
from plot_utils import plot_values
# define the optimal state-value function
V_opt = np.zeros((4,12))
V_opt[0:13][0] = -np.arange(3, 15)[::-1]
V_opt[0:13][1] = -np.arange(3, 15)[::-1] + 1
V_opt[0:13][2] = -np.arange(3, 15)[::-1] + 2
V_opt[3][0] = -13
plot_values(V_opt)
```
### Part 1: TD Prediction: State Values
In this section, you will write your own implementation of TD prediction (for estimating the state-value function).
We will begin by investigating a policy where the agent moves:
- `RIGHT` in states `0` through `10`, inclusive,
- `DOWN` in states `11`, `23`, and `35`, and
- `UP` in states `12` through `22`, inclusive, states `24` through `34`, inclusive, and state `36`.
The policy is specified and printed below. Note that states where the agent does not choose an action have been marked with `-1`.
```
policy = np.hstack([1*np.ones(11), 2, 0, np.zeros(10), 2, 0, np.zeros(10), 2, 0, -1*np.ones(11)])
print("\nPolicy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy.reshape(4,12))
```
Run the next cell to visualize the state-value function that corresponds to this policy. Make sure that you take the time to understand why this is the corresponding value function!
```
V_true = np.zeros((4,12))
for i in range(3):
V_true[0:12][i] = -np.arange(3, 15)[::-1] - i
V_true[1][11] = -2
V_true[2][11] = -1
V_true[3][0] = -17
plot_values(V_true)
```
The above figure is what you will try to approximate through the TD prediction algorithm.
Your algorithm for TD prediction has five arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `policy`: This is a 1D numpy array with `policy.shape` equal to the number of states (`env.nS`). `policy[s]` returns the action that the agent chooses when in state `s`.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `V`: This is a dictionary where `V[s]` is the estimated value of state `s`.
Please complete the function in the code cell below.
```
from collections import defaultdict, deque
import sys
def td_prediction(env, num_episodes, policy, alpha, gamma=1.0):
# initialize empty dictionaries of floats
V = defaultdict(float)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# begin an episode, observe S
state = env.reset()
while True:
# choose action A
action = policy[state]
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# perform updates
V[state] = V[state] + (alpha * (reward + (gamma * V[next_state]) - V[state]))
# S <- S'
state = next_state
# end episode if reached terminal state
if done:
break
return V
```
Run the code cell below to test your implementation and visualize the estimated state-value function. If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
import check_test
# evaluate the policy and reshape the state-value function
V_pred = td_prediction(env, 5000, policy, .01)
# please do not change the code below this line
V_pred_plot = np.reshape([V_pred[key] if key in V_pred else 0 for key in np.arange(48)], (4,12))
check_test.run_check('td_prediction_check', V_pred_plot)
plot_values(V_pred_plot)
```
How close is your estimated state-value function to the true state-value function corresponding to the policy?
You might notice that some of the state values are not estimated by the agent. This is because under this policy, the agent will not visit all of the states. In the TD prediction algorithm, the agent can only estimate the values corresponding to states that are visited.
### Part 2: TD Control: Sarsa
In this section, you will write your own implementation of the Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def update_Q(Qsa, Qsa_next, reward, alpha, gamma):
""" updates the action-value function estimate using the most recent time step """
return Qsa + (alpha * (reward + (gamma * Qsa_next) - Qsa))
def epsilon_greedy_probs(env, Q_s, i_episode, eps=None):
""" obtains the action probabilities corresponding to epsilon-greedy policy """
epsilon = 1.0 / i_episode
if eps is not None:
epsilon = eps
policy_s = np.ones(env.nA) * epsilon / env.nA
policy_s[np.argmax(Q_s)] = 1 - epsilon + (epsilon / env.nA)
return policy_s
import matplotlib.pyplot as plt
%matplotlib inline
def sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode, observe S
state = env.reset()
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode)
# pick action A
action = np.random.choice(np.arange(env.nA), p=policy_s)
# limit number of time steps per episode
for t_step in np.arange(300):
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
if not done:
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[next_state], i_episode)
# pick next action A'
next_action = np.random.choice(np.arange(env.nA), p=policy_s)
# update TD estimate of Q
Q[state][action] = update_Q(Q[state][action], Q[next_state][next_action],
reward, alpha, gamma)
# S <- S'
state = next_state
# A <- A'
action = next_action
if done:
# update TD estimate of Q
Q[state][action] = update_Q(Q[state][action], 0, reward, alpha, gamma)
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsa = sarsa(env, 5000, .01)
# print the estimated optimal policy
policy_sarsa = np.array([np.argmax(Q_sarsa[key]) if key in Q_sarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_sarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsa)
# plot the estimated optimal state-value function
V_sarsa = ([np.max(Q_sarsa[key]) if key in Q_sarsa else 0 for key in np.arange(48)])
plot_values(V_sarsa)
```
### Part 3: TD Control: Q-learning
In this section, you will write your own implementation of the Q-learning control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def q_learning(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode, observe S
state = env.reset()
while True:
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode)
# pick next action A
action = np.random.choice(np.arange(env.nA), p=policy_s)
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
# update Q
Q[state][action] = update_Q(Q[state][action], np.max(Q[next_state]), \
reward, alpha, gamma)
# S <- S'
state = next_state
# until S is terminal
if done:
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsamax = q_learning(env, 5000, .01)
# print the estimated optimal policy
policy_sarsamax = np.array([np.argmax(Q_sarsamax[key]) if key in Q_sarsamax else -1 for key in np.arange(48)]).reshape((4,12))
check_test.run_check('td_control_check', policy_sarsamax)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsamax)
# plot the estimated optimal state-value function
plot_values([np.max(Q_sarsamax[key]) if key in Q_sarsamax else 0 for key in np.arange(48)])
```
### Part 4: TD Control: Expected Sarsa
In this section, you will write your own implementation of the Expected Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def expected_sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode
state = env.reset()
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode, 0.005)
while True:
# pick next action
action = np.random.choice(np.arange(env.nA), p=policy_s)
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
# get epsilon-greedy action probabilities (for S')
policy_s = epsilon_greedy_probs(env, Q[next_state], i_episode, 0.005)
# update Q
Q[state][action] = update_Q(Q[state][action], np.dot(Q[next_state], policy_s), \
reward, alpha, gamma)
# S <- S'
state = next_state
# until S is terminal
if done:
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_expsarsa = expected_sarsa(env, 10000, 1)
# print the estimated optimal policy
policy_expsarsa = np.array([np.argmax(Q_expsarsa[key]) if key in Q_expsarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_expsarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_expsarsa)
# plot the estimated optimal state-value function
plot_values([np.max(Q_expsarsa[key]) if key in Q_expsarsa else 0 for key in np.arange(48)])
```
| github_jupyter |
<a href="https://colab.research.google.com/github/elizabethts/DS-Unit-1-Sprint-1-Dealing-With-Data/blob/master/LS_DS_114_Making_Data_backed_Assertions.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Lambda School Data Science - Making Data-backed Assertions
This is, for many, the main point of data science - to create and support reasoned arguments based on evidence. It's not a topic to master in a day, but it is worth some focused time thinking about and structuring your approach to it.
## Lecture - generating a confounding variable
The prewatch material told a story about a hypothetical health condition where both the drug usage and overall health outcome were related to gender - thus making gender a confounding variable, obfuscating the possible relationship between the drug and the outcome.
Let's use Python to generate data that actually behaves in this fashion!
```
import random
dir(random) # Reminding ourselves what we can do here
random.seed(10) # Sets Random Seed for Reproducibility
# Let's think of another scenario:
# We work for a company that sells accessories for mobile phones.
# They have an ecommerce site, and we are supposed to analyze logs
# to determine what sort of usage is related to purchases, and thus guide
# website development to encourage higher conversion.
# The hypothesis - users who spend longer on the site tend
# to spend more. Seems reasonable, no?
# But there's a confounding variable! If they're on a phone, they:
# a) Spend less time on the site, but
# b) Are more likely to be interested in the actual products!
# Let's use namedtuple to represent our data
from collections import namedtuple
# purchased and mobile are bools, time_on_site in seconds
User = namedtuple('User', ['purchased','time_on_site', 'mobile'])
example_user = User(False, 12, False)
print(example_user)
# And now let's generate 1000 example users
# 750 mobile, 250 not (i.e. desktop)
# A desktop user has a base conversion likelihood of 10%
# And it goes up by 1% for each 15 seconds they spend on the site
# And they spend anywhere from 10 seconds to 10 minutes on the site (uniform)
# Mobile users spend on average half as much time on the site as desktop
# But have three times as much base likelihood of buying something
users = []
for _ in range(250):
# Desktop users
time_on_site = random.uniform(10, 600)
purchased = random.random() < 0.1 + (time_on_site / 1500)
users.append(User(purchased, time_on_site, False))
for _ in range(750):
# Mobile users
time_on_site = random.uniform(5, 300)
purchased = random.random() < 0.3 + (time_on_site / 1500)
users.append(User(purchased, time_on_site, True))
random.shuffle(users)
print(users[:10])
# Let's put this in a dataframe so we can look at it more easily
import pandas as pd
user_data = pd.DataFrame(users)
user_data.head()
user_data.dtypes
user_data.isnull().sum()
user_data.describe()
import numpy as np
user_data.describe(exclude=[np.number])
# Let's use crosstabulation to try to see what's going on
pd.crosstab(user_data['purchased'], user_data['time_on_site'])
# !pip freeze # 0.24.2
!pip install pandas==0.23.4
!pip freeze
# OK, that's not quite what we want
# Time is continuous! We need to put it in discrete buckets
# Pandas calls these bins, and pandas.cut helps make them
time_bins = pd.cut(user_data['time_on_site'], 6) # 6 equal-sized bins
pd.crosstab(user_data['purchased'], time_bins)
# We can make this a bit clearer by normalizing (getting %)
pd.crosstab(user_data['purchased'], time_bins, normalize='columns')
# That seems counter to our hypothesis
# More time on the site can actually have fewer purchases
# But we know why, since we generated the data!
# Let's look at mobile and purchased
pd.crosstab(user_data['purchased'], user_data['mobile'], normalize='columns')
# Yep, mobile users are more likely to buy things
# But we're still not seeing the *whole* story until we look at all 3 at once
# Live/stretch goal - how can we do that?
ct = pd.crosstab(user_data['mobile'], [user_data['purchased'], time_bins],
rownames = ['device'],
colnames = ['purchased','time_on_site'],
normalize = 'index'
)
ct
type(ct)
pt = pd.pivot_table(user_data, values = 'purchased', index = time_bins)
pt
pt.plot.bar();
ct = pd.crosstab(time_bins, [user_data['purchased'], user_data['mobile']],
normalize = 'columns')
ct
ct_final = ct.iloc[:, [2,3]]
ct_final.plot(kind = 'bar', stacked = True);
```
## Assignment - what's going on here?
Consider the data in `persons.csv` (already prepared for you, in the repo for the week). It has four columns - a unique id, followed by age (in years), weight (in lbs), and exercise time (in minutes/week) of 1200 (hypothetical) people.
Try to figure out which variables are possibly related to each other, and which may be confounding relationships.
```
import matplotlib.pyplot as plt
# TODO - your code here
# Use what we did live in lecture as an example
# HINT - you can find the raw URL on GitHub and potentially use that
# to load the data with read_csv, or you can upload it yourself
#load data
persons_url = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-1-Sprint-1-Dealing-With-Data/master/module3-databackedassertions/persons.csv'
persons_df = pd.read_csv(persons_url)
persons_df.head()
persons_df.shape
time_range = pd.cut(persons_df['exercise_time'],30) #cut time into 5 groups
age_range = pd.cut(persons_df['age'],3) #cut time into 5 groups
weight_range = pd.cut(persons_df['weight'],30)
persons_ct = pd.crosstab(persons_df['weight'],
[age_range, persons_df['exercise_time']])
persons_ct
group1 = persons_df[persons_df.age <30]
group2 = persons_df[(persons_df.age >=30) & (persons_df.age<50)]
group3 = persons_df[persons_df.age >=50]
fig, ax1 = plt.subplots()
ax1.set_axisbelow(True)
ax1.set_xlabel('Exercise Time')
ax1.set_ylabel('Weight')
ax1.set_title('Weight vs Exercise Time (Age <30)')
plt.gca().invert_yaxis()
plt.scatter(group1.exercise_time, group1.weight, color ='red', alpha = .4)
fig, ax2 = plt.subplots()
ax2.set_axisbelow(True)
ax2.set_xlabel('Exercise Time')
ax2.set_ylabel('Weight')
ax2.set_title('Weight vs Exercise Time (Age 30-50)')
plt.gca().invert_yaxis()
plt.scatter(group2.exercise_time, group2.weight, color = 'teal', alpha = .4)
fig, ax3 = plt.subplots()
ax3.set_axisbelow(True)
ax3.set_xlabel('Exercise Time')
ax3.set_ylabel('Weight')
ax3.set_title('Weight vs Exercise Time (Age > 50)')
plt.gca().invert_yaxis()
plt.scatter(group3.exercise_time, group3.weight, color = 'yellow', alpha = 0.4);
fig, ax4 = plt.subplots()
ax4.set_axisbelow(True)
ax4.set_xlabel('Exercise Time')
ax4.set_ylabel('Weight')
ax4.set_title('Weight vs Exercise Time for All Ages')
plt.scatter(group2.exercise_time, group2.weight, color = 'teal', alpha = .6)
plt.scatter(group3.exercise_time, group3.weight,color = 'yellow', alpha = 0.6);
plt.scatter(group1.exercise_time, group1.weight, color ='red', alpha = .6)
plt.gca().invert_yaxis()
fig, ax5 = plt.subplots()
ax5.set_axisbelow(True)
ax5.set_xlabel('Exercise Time')
ax5.set_ylabel('Age')
ax5.set_title('Age vs Exercise Time (All Ages)')
plt.scatter(group2.exercise_time, group2.age, color = 'teal', alpha = .6)
plt.scatter(group3.exercise_time, group3.age,color = 'yellow', alpha = 0.6);
plt.scatter(group1.exercise_time, group1.age, color ='red', alpha = .6)
fig, ax6 = plt.subplots()
ax6.set_axisbelow(True)
ax6.set_xlabel('Weight')
ax6.set_ylabel('Age')
ax6.set_title('Age vs Weight (All Ages)')
plt.scatter(group2.weight, group2.age, color = 'teal', alpha = .6)
plt.scatter(group3.weight, group3.age,color = 'yellow', alpha = 0.6);
plt.scatter(group1.weight, group1.age, color ='red', alpha = .6);
#Conclusions:
# -People who exercise more weight less
# -The group age >=50 tends to exercise for a shorter amount of time
```
### Assignment questions
After you've worked on some code, answer the following questions in this text block:
1. What are the variable types in the data?
age - ordinal and continuous
weight - ordinal and continuous
exercise time - ordinal and continuous
2. What are the relationships between the variables?
Weight decreases as exercise time increases so they are inversely related. Weight increases as age increases so they are directly related
3. Which relationships are "real", and which spurious?
The relationship between weight and exercise time is real and the relationship between age and weight is spurious (older people tend to exercise less)
## Stretch goals and resources
Following are *optional* things for you to take a look at. Focus on the above assignment first, and make sure to commit and push your changes to GitHub.
- [Spurious Correlations](http://tylervigen.com/spurious-correlations)
- [NIH on controlling for confounding variables](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4017459/)
Stretch goals:
- Produce your own plot inspired by the Spurious Correlation visualizations (and consider writing a blog post about it - both the content and how you made it)
- Pick one of the techniques that NIH highlights for confounding variables - we'll be going into many of them later, but see if you can find which Python modules may help (hint - check scikit-learn)
| github_jupyter |
```
import numpy as np
import pandas_datareader as pdr
import datetime as dt
import pandas as pd
import matplotlib.pyplot as plt
start = dt.datetime(2012, 6, 1)
end = dt.datetime(2022, 3, 9)
stock = ['fb']
stock_data = pdr.get_data_yahoo(stock, start, end)
pair = ['snap']
pair_data = pdr.get_data_yahoo(pair, start, end)
main_df = pd.DataFrame()
pair_df = pd.DataFrame()
main_df["Close"] = stock_data[["Close"]]
main_df["Open"] = stock_data[["Open"]]
main_df["High"] = stock_data[["High"]]
main_df["Low"] = stock_data[["Low"]]
main_df["Volume"] = stock_data[["Volume"]]
main_df["stock_prev_close"] = main_df["Close"].shift(1)
main_df['Date'] = main_df.index
pair_df["Close"] = pair_data[["Close"]]
pair_df["Open"] = pair_data[["Open"]]
pair_df["High"] = pair_data[["High"]]
pair_df["Low"] = pair_data[["Low"]]
pair_df["Volume"] = pair_data[["Volume"]]
pair_df["pair_prev_close"] = pair_df["Close"].shift(1)
pair_df['Date'] = pair_df.index
merged = pd.merge(main_df.reset_index(drop=True), pair_df.reset_index(drop=True), on=["Date"], how="left")
merged
merged['ratio_spread'] = merged['Close_x'] / merged['Close_y']
merged['prev_ratio_spread'] = merged['ratio_spread'].shift(1)
merged['close_spread'] = np.log(merged['Close_x']) - np.log(merged['Close_y'])
merged['close_spread_sma20'] = merged['close_spread'].rolling(20).mean()
merged['close_spread_std20'] = merged['close_spread'].rolling(20).std()
merged['zscore'] = (merged['close_spread'] - merged['close_spread_sma20']) / merged['close_spread_std20']
merged['prev_zscore'] = merged['zscore'].shift(1)
merged['lsr'] = np.log(merged['ratio_spread']) - np.log(merged['prev_ratio_spread'])
merged['strat_return'] = merged['prev_zscore'] * -1 * (merged['lsr'] - np.log(merged['ratio_spread']))
merged
figsize=(10,5)
ax = merged.plot(x="Date", y="zscore", legend=False,figsize=figsize)
figsize=(10,5)
ax = merged.plot(x="Date", y="lsr", legend=False,figsize=figsize)
figsize=(10,5)
ax = merged.plot(x="Date", y="strat_return", legend=False,figsize=figsize)
figsize=(30,10)
ax = merged[1200:].plot(y="strat_return", legend=False,figsize=figsize)
```
# Monthly Aggregates - Work in Progress - I forgot to set price to 0 - Need to rewatch video!
```
merged['date_trunc_month'] = merged.apply(lambda x: dt.datetime.strftime(x['Date'],'%Y-%m'), axis=1)
merged['date_trunc_month']
merged['is_start_of_month'] = merged.apply(lambda x: x.name == min(merged[merged['date_trunc_month'] == x['date_trunc_month']].index), axis=1)
merged['is_end_of_month'] = merged.apply(lambda x: x.name == max(merged[merged['date_trunc_month'] == x['date_trunc_month']].index), axis=1)
merged[merged['is_start_of_month'] == True]
```
```sql
SELECT
startofmonth,
stock1,
stock2,
SUM(lsr) as lsr
FROM dailyreturns
GROUP BY
startofmonth,
stock1,
stock2
```
```
merged[(merged['is_start_of_month'] == True)][['date_trunc_month','lsr']]
merged[(merged['is_start_of_month'] == True) | (merged['is_end_of_month'] == True)][['date_trunc_month','lsr']].plot()
merged['lsr'] = merged.apply(lambda x: 0 if x['is_end_of_month'] is True else x['lsr'], axis=1)
merged[merged['is_end_of_month'] == True]
monthly_agg = merged[(merged['is_start_of_month'] == True) | (merged['is_end_of_month'] == True)].copy()
monthly_agg.reset_index(drop=True)
monthly_agg = monthly_agg.dropna()
monthly_agg
figsize=(30,10)
ax = monthly_agg.plot(y="lsr", x="date_trunc_month", legend=False,figsize=figsize)
```
| github_jupyter |
# Convolutional Neural Networks
---
In this notebook, we train a **CNN** to classify images from the CIFAR-10 database.
The images in this database are small color images that fall into one of ten classes; some example images are pictured below.
<img src='notebook_ims/cifar_data.png' width=70% height=70% />
### Test for [CUDA](http://pytorch.org/docs/stable/cuda.html)
Since these are larger (32x32x3) images, it may prove useful to speed up your training time by using a GPU. CUDA is a parallel computing platform and CUDA Tensors are the same as typical Tensors, only they utilize GPU's for computation.
```
import torch
import numpy as np
# check if CUDA is available
train_on_gpu = torch.cuda.is_available()
if not train_on_gpu:
print('CUDA is not available. Training on CPU ...')
else:
print('CUDA is available! Training on GPU ...')
```
---
## Load and Augment the [Data](http://pytorch.org/docs/stable/torchvision/datasets.html)
Downloading may take a minute. We load in the training and test data, split the training data into a training and validation set, then create DataLoaders for each of these sets of data.
#### Augmentation
In this cell, we perform some simple [data augmentation](https://medium.com/nanonets/how-to-use-deep-learning-when-you-have-limited-data-part-2-data-augmentation-c26971dc8ced) by randomly flipping and rotating the given image data. We do this by defining a torchvision `transform`, and you can learn about all the transforms that are used to pre-process and augment data, [here](https://pytorch.org/docs/stable/torchvision/transforms.html).
#### TODO: Look at the [transformation documentation](https://pytorch.org/docs/stable/torchvision/transforms.html); add more augmentation transforms, and see how your model performs.
This type of data augmentation should add some positional variety to these images, so that when we train a model on this data, it will be robust in the face of geometric changes (i.e. it will recognize a ship, no matter which direction it is facing). It's recommended that you choose one or two transforms.
```
from torchvision import datasets
import torchvision.transforms as transforms
from torch.utils.data.sampler import SubsetRandomSampler
# number of subprocesses to use for data loading
num_workers = 0
# how many samples per batch to load
batch_size = 20
# percentage of training set to use as validation
valid_size = 0.2
# convert data to a normalized torch.FloatTensor
transform = transforms.Compose([
transforms.RandomHorizontalFlip(), # randomly flip and rotate
transforms.RandomRotation(10),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
# choose the training and test datasets
train_data = datasets.CIFAR10('data', train=True,
download=True, transform=transform)
test_data = datasets.CIFAR10('data', train=False,
download=True, transform=transform)
# obtain training indices that will be used for validation
num_train = len(train_data)
indices = list(range(num_train))
np.random.shuffle(indices)
split = int(np.floor(valid_size * num_train))
train_idx, valid_idx = indices[split:], indices[:split]
# define samplers for obtaining training and validation batches
train_sampler = SubsetRandomSampler(train_idx)
valid_sampler = SubsetRandomSampler(valid_idx)
# prepare data loaders (combine dataset and sampler)
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=train_sampler, num_workers=num_workers)
valid_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=valid_sampler, num_workers=num_workers)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size,
num_workers=num_workers)
# specify the image classes
classes = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
```
### Visualize a Batch of Training Data
```
import matplotlib.pyplot as plt
%matplotlib inline
# helper function to un-normalize and display an image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
plt.imshow(np.transpose(img, (1, 2, 0))) # convert from Tensor image
# obtain one batch of training images
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy() # convert images to numpy for display
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(25, 4))
# display 20 images
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
imshow(images[idx])
ax.set_title(classes[labels[idx]])
```
### View an Image in More Detail
Here, we look at the normalized red, green, and blue (RGB) color channels as three separate, grayscale intensity images.
```
rgb_img = np.squeeze(images[3])
channels = ['red channel', 'green channel', 'blue channel']
fig = plt.figure(figsize = (36, 36))
for idx in np.arange(rgb_img.shape[0]):
ax = fig.add_subplot(1, 3, idx + 1)
img = rgb_img[idx]
ax.imshow(img, cmap='gray')
ax.set_title(channels[idx])
width, height = img.shape
thresh = img.max()/2.5
for x in range(width):
for y in range(height):
val = round(img[x][y],2) if img[x][y] !=0 else 0
ax.annotate(str(val), xy=(y,x),
horizontalalignment='center',
verticalalignment='center', size=8,
color='white' if img[x][y]<thresh else 'black')
```
---
## Define the Network [Architecture](http://pytorch.org/docs/stable/nn.html)
This time, you'll define a CNN architecture. Instead of an MLP, which used linear, fully-connected layers, you'll use the following:
* [Convolutional layers](https://pytorch.org/docs/stable/nn.html#conv2d), which can be thought of as stack of filtered images.
* [Maxpooling layers](https://pytorch.org/docs/stable/nn.html#maxpool2d), which reduce the x-y size of an input, keeping only the most _active_ pixels from the previous layer.
* The usual Linear + Dropout layers to avoid overfitting and produce a 10-dim output.
A network with 2 convolutional layers is shown in the image below and in the code, and you've been given starter code with one convolutional and one maxpooling layer.
<img src='notebook_ims/2_layer_conv.png' height=50% width=50% />
#### TODO: Define a model with multiple convolutional layers, and define the feedforward metwork behavior.
The more convolutional layers you include, the more complex patterns in color and shape a model can detect. It's suggested that your final model include 2 or 3 convolutional layers as well as linear layers + dropout in between to avoid overfitting.
It's good practice to look at existing research and implementations of related models as a starting point for defining your own models. You may find it useful to look at [this PyTorch classification example](https://github.com/pytorch/tutorials/blob/master/beginner_source/blitz/cifar10_tutorial.py) or [this, more complex Keras example](https://github.com/keras-team/keras/blob/master/examples/cifar10_cnn.py) to help decide on a final structure.
#### Output volume for a convolutional layer
To compute the output size of a given convolutional layer we can perform the following calculation (taken from [Stanford's cs231n course](http://cs231n.github.io/convolutional-networks/#layers)):
> We can compute the spatial size of the output volume as a function of the input volume size (W), the kernel/filter size (F), the stride with which they are applied (S), and the amount of zero padding used (P) on the border. The correct formula for calculating how many neurons define the output_W is given by `(W−F+2P)/S+1`.
For example for a 7x7 input and a 3x3 filter with stride 1 and pad 0 we would get a 5x5 output. With stride 2 we would get a 3x3 output.
```
import torch.nn as nn
import torch.nn.functional as F
# define the CNN architecture
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# convolutional layer (sees 32x32x3 image tensor)
self.conv1 = nn.Conv2d(3, 16, 3, padding=1)
# convolutional layer (sees 16x16x16 tensor)
self.conv2 = nn.Conv2d(16, 32, 3, padding=1)
# convolutional layer (sees 8x8x32 tensor)
self.conv3 = nn.Conv2d(32, 64, 3, padding=1)
# max pooling layer
self.pool = nn.MaxPool2d(2, 2)
# linear layer (64 * 4 * 4 -> 500)
self.fc1 = nn.Linear(64 * 4 * 4, 500)
# linear layer (500 -> 10)
self.fc2 = nn.Linear(500, 10)
# dropout layer (p=0.25)
self.dropout = nn.Dropout(0.25)
def forward(self, x):
# add sequence of convolutional and max pooling layers
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = self.pool(F.relu(self.conv3(x)))
# flatten image input
x = x.view(-1, 64 * 4 * 4)
# add dropout layer
x = self.dropout(x)
# add 1st hidden layer, with relu activation function
x = F.relu(self.fc1(x))
# add dropout layer
x = self.dropout(x)
# add 2nd hidden layer, with relu activation function
x = self.fc2(x)
return x
# create a complete CNN
model = Net()
print(model)
# move tensors to GPU if CUDA is available
if train_on_gpu:
model.cuda()
```
### Specify [Loss Function](http://pytorch.org/docs/stable/nn.html#loss-functions) and [Optimizer](http://pytorch.org/docs/stable/optim.html)
Decide on a loss and optimization function that is best suited for this classification task. The linked code examples from above, may be a good starting point; [this PyTorch classification example](https://github.com/pytorch/tutorials/blob/master/beginner_source/blitz/cifar10_tutorial.py) or [this, more complex Keras example](https://github.com/keras-team/keras/blob/master/examples/cifar10_cnn.py). Pay close attention to the value for **learning rate** as this value determines how your model converges to a small error.
#### TODO: Define the loss and optimizer and see how these choices change the loss over time.
```
import torch.optim as optim
# specify loss function (categorical cross-entropy)
criterion = nn.CrossEntropyLoss()
# specify optimizer
optimizer = optim.SGD(model.parameters(), lr=0.01)
```
---
## Train the Network
Remember to look at how the training and validation loss decreases over time; if the validation loss ever increases it indicates possible overfitting.
```
# number of epochs to train the model
n_epochs = 30
valid_loss_min = np.Inf # track change in validation loss
for epoch in range(1, n_epochs+1):
# keep track of training and validation loss
train_loss = 0.0
valid_loss = 0.0
###################
# train the model #
###################
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
# move tensors to GPU if CUDA is available
if train_on_gpu:
data, target = data.cuda(), target.cuda()
# clear the gradients of all optimized variables
optimizer.zero_grad()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the batch loss
loss = criterion(output, target)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
optimizer.step()
# update training loss
train_loss += loss.item()*data.size(0)
######################
# validate the model #
######################
model.eval()
for batch_idx, (data, target) in enumerate(valid_loader):
# move tensors to GPU if CUDA is available
if train_on_gpu:
data, target = data.cuda(), target.cuda()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the batch loss
loss = criterion(output, target)
# update average validation loss
valid_loss += loss.item()*data.size(0)
# calculate average losses
train_loss = train_loss/len(train_loader.dataset)
valid_loss = valid_loss/len(valid_loader.dataset)
# print training/validation statistics
print('Epoch: {} \tTraining Loss: {:.6f} \tValidation Loss: {:.6f}'.format(
epoch, train_loss, valid_loss))
# save model if validation loss has decreased
if valid_loss <= valid_loss_min:
print('Validation loss decreased ({:.6f} --> {:.6f}). Saving model ...'.format(
valid_loss_min,
valid_loss))
torch.save(model.state_dict(), 'model_augmented.pt')
valid_loss_min = valid_loss
```
### Load the Model with the Lowest Validation Loss
```
model.load_state_dict(torch.load('model_augmented.pt'))
```
---
## Test the Trained Network
Test your trained model on previously unseen data! A "good" result will be a CNN that gets around 70% (or more, try your best!) accuracy on these test images.
```
# track test loss
test_loss = 0.0
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
model.eval()
# iterate over test data
for batch_idx, (data, target) in enumerate(test_loader):
# move tensors to GPU if CUDA is available
if train_on_gpu:
data, target = data.cuda(), target.cuda()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the batch loss
loss = criterion(output, target)
# update test loss
test_loss += loss.item()*data.size(0)
# convert output probabilities to predicted class
_, pred = torch.max(output, 1)
# compare predictions to true label
correct_tensor = pred.eq(target.data.view_as(pred))
correct = np.squeeze(correct_tensor.numpy()) if not train_on_gpu else np.squeeze(correct_tensor.cpu().numpy())
# calculate test accuracy for each object class
for i in range(batch_size):
label = target.data[i]
class_correct[label] += correct[i].item()
class_total[label] += 1
# average test loss
test_loss = test_loss/len(test_loader.dataset)
print('Test Loss: {:.6f}\n'.format(test_loss))
for i in range(10):
if class_total[i] > 0:
print('Test Accuracy of %5s: %2d%% (%2d/%2d)' % (
classes[i], 100 * class_correct[i] / class_total[i],
np.sum(class_correct[i]), np.sum(class_total[i])))
else:
print('Test Accuracy of %5s: N/A (no training examples)' % (classes[i]))
print('\nTest Accuracy (Overall): %2d%% (%2d/%2d)' % (
100. * np.sum(class_correct) / np.sum(class_total),
np.sum(class_correct), np.sum(class_total)))
```
### Visualize Sample Test Results
```
# obtain one batch of test images
dataiter = iter(test_loader)
images, labels = dataiter.next()
images.numpy()
# move model inputs to cuda, if GPU available
if train_on_gpu:
images = images.cuda()
# get sample outputs
output = model(images)
# convert output probabilities to predicted class
_, preds_tensor = torch.max(output, 1)
preds = np.squeeze(preds_tensor.numpy()) if not train_on_gpu else np.squeeze(preds_tensor.cpu().numpy())
# plot the images in the batch, along with predicted and true labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
imshow(images[idx])
ax.set_title("{} ({})".format(classes[preds[idx]], classes[labels[idx]]),
color=("green" if preds[idx]==labels[idx].item() else "red"))
```
| github_jupyter |
```
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
#default_exp data.core
#export
from fastai.torch_basics import *
from fastai.data.load import *
#hide
from nbdev.showdoc import *
```
# Data core
> Core functionality for gathering data
The classes here provide functionality for applying a list of transforms to a set of items (`TfmdLists`, `Datasets`) or a `DataLoader` (`TfmdDl`) as well as the base class used to gather the data for model training: `DataLoaders`.
## TfmdDL -
```
#export
@typedispatch
def show_batch(x, y, samples, ctxs=None, max_n=9, **kwargs):
if ctxs is None: ctxs = Inf.nones
if hasattr(samples[0], 'show'):
ctxs = [s.show(ctx=c, **kwargs) for s,c,_ in zip(samples,ctxs,range(max_n))]
else:
for i in range_of(samples[0]):
ctxs = [b.show(ctx=c, **kwargs) for b,c,_ in zip(samples.itemgot(i),ctxs,range(max_n))]
return ctxs
```
`show_batch` is a type-dispatched function that is responsible for showing decoded `samples`. `x` and `y` are the input and the target in the batch to be shown, and are passed along to dispatch on their types. There is a different implementation of `show_batch` if `x` is a `TensorImage` or a `TensorText` for instance (see vision.core or text.data for more details). `ctxs` can be passed but the function is responsible to create them if necessary. `kwargs` depend on the specific implementation.
```
#export
@typedispatch
def show_results(x, y, samples, outs, ctxs=None, max_n=9, **kwargs):
if ctxs is None: ctxs = Inf.nones
for i in range(len(samples[0])):
ctxs = [b.show(ctx=c, **kwargs) for b,c,_ in zip(samples.itemgot(i),ctxs,range(max_n))]
for i in range(len(outs[0])):
ctxs = [b.show(ctx=c, **kwargs) for b,c,_ in zip(outs.itemgot(i),ctxs,range(max_n))]
return ctxs
```
`show_results` is a type-dispatched function that is responsible for showing decoded `samples` and their corresponding `outs`. Like in `show_batch`, `x` and `y` are the input and the target in the batch to be shown, and are passed along to dispatch on their types. `ctxs` can be passed but the function is responsible to create them if necessary. `kwargs` depend on the specific implementation.
```
#export
_all_ = ["show_batch", "show_results"]
#export
_batch_tfms = ('after_item','before_batch','after_batch')
#export
@log_args(but_as=DataLoader.__init__)
@delegates()
class TfmdDL(DataLoader):
"Transformed `DataLoader`"
def __init__(self, dataset, bs=64, shuffle=False, num_workers=None, verbose=False, do_setup=True, **kwargs):
if num_workers is None: num_workers = min(16, defaults.cpus)
for nm in _batch_tfms: kwargs[nm] = Pipeline(kwargs.get(nm,None))
super().__init__(dataset, bs=bs, shuffle=shuffle, num_workers=num_workers, **kwargs)
if do_setup:
for nm in _batch_tfms:
pv(f"Setting up {nm}: {kwargs[nm]}", verbose)
kwargs[nm].setup(self)
def _one_pass(self):
b = self.do_batch([self.do_item(0)])
if self.device is not None: b = to_device(b, self.device)
its = self.after_batch(b)
self._n_inp = 1 if not isinstance(its, (list,tuple)) or len(its)==1 else len(its)-1
self._types = explode_types(its)
def _retain_dl(self,b):
if not getattr(self, '_types', None): self._one_pass()
return retain_types(b, typs=self._types)
@delegates(DataLoader.new)
def new(self, dataset=None, cls=None, **kwargs):
res = super().new(dataset, cls, do_setup=False, **kwargs)
if not hasattr(self, '_n_inp') or not hasattr(self, '_types'):
try:
self._one_pass()
res._n_inp,res._types = self._n_inp,self._types
except: print("Could not do one pass in your dataloader, there is something wrong in it")
else: res._n_inp,res._types = self._n_inp,self._types
return res
def before_iter(self):
super().before_iter()
split_idx = getattr(self.dataset, 'split_idx', None)
for nm in _batch_tfms:
f = getattr(self,nm)
if isinstance(f,Pipeline): f.split_idx=split_idx
def decode(self, b): return self.before_batch.decode(to_cpu(self.after_batch.decode(self._retain_dl(b))))
def decode_batch(self, b, max_n=9, full=True): return self._decode_batch(self.decode(b), max_n, full)
def _decode_batch(self, b, max_n=9, full=True):
f = self.after_item.decode
f = compose(f, partial(getattr(self.dataset,'decode',noop), full = full))
return L(batch_to_samples(b, max_n=max_n)).map(f)
def _pre_show_batch(self, b, max_n=9):
"Decode `b` to be ready for `show_batch`"
b = self.decode(b)
if hasattr(b, 'show'): return b,None,None
its = self._decode_batch(b, max_n, full=False)
if not is_listy(b): b,its = [b],L((o,) for o in its)
return detuplify(b[:self.n_inp]),detuplify(b[self.n_inp:]),its
def show_batch(self, b=None, max_n=9, ctxs=None, show=True, unique=False, **kwargs):
if unique:
old_get_idxs = self.get_idxs
self.get_idxs = lambda: Inf.zeros
if b is None: b = self.one_batch()
if not show: return self._pre_show_batch(b, max_n=max_n)
show_batch(*self._pre_show_batch(b, max_n=max_n), ctxs=ctxs, max_n=max_n, **kwargs)
if unique: self.get_idxs = old_get_idxs
def show_results(self, b, out, max_n=9, ctxs=None, show=True, **kwargs):
x,y,its = self.show_batch(b, max_n=max_n, show=False)
b_out = type(b)(b[:self.n_inp] + (tuple(out) if is_listy(out) else (out,)))
x1,y1,outs = self.show_batch(b_out, max_n=max_n, show=False)
res = (x,x1,None,None) if its is None else (x, y, its, outs.itemgot(slice(self.n_inp,None)))
if not show: return res
show_results(*res, ctxs=ctxs, max_n=max_n, **kwargs)
@property
def n_inp(self):
if hasattr(self.dataset, 'n_inp'): return self.dataset.n_inp
if not hasattr(self, '_n_inp'): self._one_pass()
return self._n_inp
def to(self, device):
self.device = device
for tfm in self.after_batch.fs:
for a in L(getattr(tfm, 'parameters', None)): setattr(tfm, a, getattr(tfm, a).to(device))
return self
```
A `TfmdDL` is a `DataLoader` that creates `Pipeline` from a list of `Transform`s for the callbacks `after_item`, `before_batch` and `after_batch`. As a result, it can decode or show a processed `batch`.
```
#export
add_docs(TfmdDL,
decode="Decode `b` using `tfms`",
decode_batch="Decode `b` entirely",
new="Create a new version of self with a few changed attributes",
show_batch="Show `b` (defaults to `one_batch`), a list of lists of pipeline outputs (i.e. output of a `DataLoader`)",
show_results="Show each item of `b` and `out`",
before_iter="override",
to="Put self and its transforms state on `device`")
class _Category(int, ShowTitle): pass
#Test retain type
class NegTfm(Transform):
def encodes(self, x): return torch.neg(x)
def decodes(self, x): return torch.neg(x)
tdl = TfmdDL([(TensorImage([1]),)] * 4, after_batch=NegTfm(), bs=4, num_workers=4)
b = tdl.one_batch()
test_eq(type(b[0]), TensorImage)
b = (tensor([1.,1.,1.,1.]),)
test_eq(type(tdl.decode_batch(b)[0][0]), TensorImage)
class A(Transform):
def encodes(self, x): return x
def decodes(self, x): return TitledInt(x)
@Transform
def f(x)->None: return fastuple((x,x))
start = torch.arange(50)
test_eq_type(f(2), fastuple((2,2)))
a = A()
tdl = TfmdDL(start, after_item=lambda x: (a(x), f(x)), bs=4)
x,y = tdl.one_batch()
test_eq(type(y), fastuple)
s = tdl.decode_batch((x,y))
test_eq(type(s[0][1]), fastuple)
tdl = TfmdDL(torch.arange(0,50), after_item=A(), after_batch=NegTfm(), bs=4)
test_eq(tdl.dataset[0], start[0])
test_eq(len(tdl), (50-1)//4+1)
test_eq(tdl.bs, 4)
test_stdout(tdl.show_batch, '0\n1\n2\n3')
test_stdout(partial(tdl.show_batch, unique=True), '0\n0\n0\n0')
class B(Transform):
parameters = 'a'
def __init__(self): self.a = torch.tensor(0.)
def encodes(self, x): x
tdl = TfmdDL([(TensorImage([1]),)] * 4, after_batch=B(), bs=4)
test_eq(tdl.after_batch.fs[0].a.device, torch.device('cpu'))
tdl.to(default_device())
test_eq(tdl.after_batch.fs[0].a.device, default_device())
```
### Methods
```
show_doc(TfmdDL.one_batch)
tfm = NegTfm()
tdl = TfmdDL(start, after_batch=tfm, bs=4)
b = tdl.one_batch()
test_eq(tensor([0,-1,-2,-3]), b)
show_doc(TfmdDL.decode)
test_eq(tdl.decode(b), tensor(0,1,2,3))
show_doc(TfmdDL.decode_batch)
test_eq(tdl.decode_batch(b), [0,1,2,3])
show_doc(TfmdDL.show_batch)
show_doc(TfmdDL.to)
```
## DataLoaders -
```
# export
@docs
class DataLoaders(GetAttr):
"Basic wrapper around several `DataLoader`s."
_default='train'
def __init__(self, *loaders, path='.', device=None):
self.loaders,self.path = list(loaders),Path(path)
if device is not None or hasattr(loaders[0],'to'): self.device = device
def __getitem__(self, i): return self.loaders[i]
def new_empty(self):
loaders = [dl.new(dl.dataset.new_empty()) for dl in self.loaders]
return type(self)(*loaders, path=self.path, device=self.device)
def _set(i, self, v): self.loaders[i] = v
train ,valid = add_props(lambda i,x: x[i], _set)
train_ds,valid_ds = add_props(lambda i,x: x[i].dataset)
@property
def device(self): return self._device
@device.setter
def device(self, d):
for dl in self.loaders: dl.to(d)
self._device = d
def to(self, device):
self.device = device
return self
def cuda(self): return self.to(device=default_device())
def cpu(self): return self.to(device=torch.device('cpu'))
@classmethod
def from_dsets(cls, *ds, path='.', bs=64, device=None, dl_type=TfmdDL, **kwargs):
default = (True,) + (False,) * (len(ds)-1)
defaults = {'shuffle': default, 'drop_last': default}
for nm in _batch_tfms:
if nm in kwargs: kwargs[nm] = Pipeline(kwargs[nm])
kwargs = merge(defaults, {k: tuplify(v, match=ds) for k,v in kwargs.items()})
kwargs = [{k: v[i] for k,v in kwargs.items()} for i in range_of(ds)]
return cls(*[dl_type(d, bs=bs, **k) for d,k in zip(ds, kwargs)], path=path, device=device)
@classmethod
def from_dblock(cls, dblock, source, path='.', bs=64, val_bs=None, shuffle_train=True, device=None, **kwargs):
return dblock.dataloaders(source, path=path, bs=bs, val_bs=val_bs, shuffle_train=shuffle_train, device=device, **kwargs)
_docs=dict(__getitem__="Retrieve `DataLoader` at `i` (`0` is training, `1` is validation)",
train="Training `DataLoader`",
valid="Validation `DataLoader`",
train_ds="Training `Dataset`",
valid_ds="Validation `Dataset`",
to="Use `device`",
cuda="Use the gpu if available",
cpu="Use the cpu",
new_empty="Create a new empty version of `self` with the same transforms",
from_dblock="Create a dataloaders from a given `dblock`")
dls = DataLoaders(tdl,tdl)
x = dls.train.one_batch()
x2 = first(tdl)
test_eq(x,x2)
x2 = dls.one_batch()
test_eq(x,x2)
#hide
#test assignment works
dls.train = dls.train.new(bs=4)
```
### Methods
```
show_doc(DataLoaders.__getitem__)
x2 = dls[0].one_batch()
test_eq(x,x2)
show_doc(DataLoaders.train, name="DataLoaders.train")
show_doc(DataLoaders.valid, name="DataLoaders.valid")
show_doc(DataLoaders.train_ds, name="DataLoaders.train_ds")
show_doc(DataLoaders.valid_ds, name="DataLoaders.valid_ds")
```
## TfmdLists -
```
#export
class FilteredBase:
"Base class for lists with subsets"
_dl_type,_dbunch_type = TfmdDL,DataLoaders
def __init__(self, *args, dl_type=None, **kwargs):
if dl_type is not None: self._dl_type = dl_type
self.dataloaders = delegates(self._dl_type.__init__)(self.dataloaders)
super().__init__(*args, **kwargs)
@property
def n_subsets(self): return len(self.splits)
def _new(self, items, **kwargs): return super()._new(items, splits=self.splits, **kwargs)
def subset(self): raise NotImplemented
def dataloaders(self, bs=64, val_bs=None, shuffle_train=True, n=None, path='.', dl_type=None, dl_kwargs=None,
device=None, **kwargs):
if device is None: device=default_device()
if dl_kwargs is None: dl_kwargs = [{}] * self.n_subsets
if dl_type is None: dl_type = self._dl_type
drop_last = kwargs.pop('drop_last', shuffle_train)
dl = dl_type(self.subset(0), bs=bs, shuffle=shuffle_train, drop_last=drop_last, n=n, device=device,
**merge(kwargs, dl_kwargs[0]))
dls = [dl] + [dl.new(self.subset(i), bs=(bs if val_bs is None else val_bs), shuffle=False, drop_last=False,
n=None, **dl_kwargs[i]) for i in range(1, self.n_subsets)]
return self._dbunch_type(*dls, path=path, device=device)
FilteredBase.train,FilteredBase.valid = add_props(lambda i,x: x.subset(i))
#export
class TfmdLists(FilteredBase, L, GetAttr):
"A `Pipeline` of `tfms` applied to a collection of `items`"
_default='tfms'
def __init__(self, items, tfms, use_list=None, do_setup=True, split_idx=None, train_setup=True,
splits=None, types=None, verbose=False, dl_type=None):
super().__init__(items, use_list=use_list)
if dl_type is not None: self._dl_type = dl_type
self.splits = L([slice(None),[]] if splits is None else splits).map(mask2idxs)
if isinstance(tfms,TfmdLists): tfms = tfms.tfms
if isinstance(tfms,Pipeline): do_setup=False
self.tfms = Pipeline(tfms, split_idx=split_idx)
store_attr('types,split_idx')
if do_setup:
pv(f"Setting up {self.tfms}", verbose)
self.setup(train_setup=train_setup)
def _new(self, items, split_idx=None, **kwargs):
split_idx = ifnone(split_idx,self.split_idx)
return super()._new(items, tfms=self.tfms, do_setup=False, types=self.types, split_idx=split_idx, **kwargs)
def subset(self, i): return self._new(self._get(self.splits[i]), split_idx=i)
def _after_item(self, o): return self.tfms(o)
def __repr__(self): return f"{self.__class__.__name__}: {self.items}\ntfms - {self.tfms.fs}"
def __iter__(self): return (self[i] for i in range(len(self)))
def show(self, o, **kwargs): return self.tfms.show(o, **kwargs)
def decode(self, o, **kwargs): return self.tfms.decode(o, **kwargs)
def __call__(self, o, **kwargs): return self.tfms.__call__(o, **kwargs)
def overlapping_splits(self): return L(Counter(self.splits.concat()).values()).filter(gt(1))
def new_empty(self): return self._new([])
def setup(self, train_setup=True):
self.tfms.setup(self, train_setup)
if len(self) != 0:
x = super().__getitem__(0) if self.splits is None else super().__getitem__(self.splits[0])[0]
self.types = []
for f in self.tfms.fs:
self.types.append(getattr(f, 'input_types', type(x)))
x = f(x)
self.types.append(type(x))
types = L(t if is_listy(t) else [t] for t in self.types).concat().unique()
self.pretty_types = '\n'.join([f' - {t}' for t in types])
def infer_idx(self, x):
# TODO: check if we really need this, or can simplify
idx = 0
for t in self.types:
if isinstance(x, t): break
idx += 1
types = L(t if is_listy(t) else [t] for t in self.types).concat().unique()
pretty_types = '\n'.join([f' - {t}' for t in types])
assert idx < len(self.types), f"Expected an input of type in \n{pretty_types}\n but got {type(x)}"
return idx
def infer(self, x):
return compose_tfms(x, tfms=self.tfms.fs[self.infer_idx(x):], split_idx=self.split_idx)
def __getitem__(self, idx):
res = super().__getitem__(idx)
if self._after_item is None: return res
return self._after_item(res) if is_indexer(idx) else res.map(self._after_item)
#export
add_docs(TfmdLists,
setup="Transform setup with self",
decode="From `Pipeline`",
show="From `Pipeline`",
overlapping_splits="All splits that are in more than one split",
subset="New `TfmdLists` with same tfms that only includes items in `i`th split",
infer_idx="Finds the index where `self.tfms` can be applied to `x`, depending on the type of `x`",
infer="Apply `self.tfms` to `x` starting at the right tfm depending on the type of `x`",
new_empty="A new version of `self` but with no items")
#exports
def decode_at(o, idx):
"Decoded item at `idx`"
return o.decode(o[idx])
#exports
def show_at(o, idx, **kwargs):
"Show item at `idx`",
return o.show(o[idx], **kwargs)
```
A `TfmdLists` combines a collection of object with a `Pipeline`. `tfms` can either be a `Pipeline` or a list of transforms, in which case, it will wrap them in a `Pipeline`. `use_list` is passed along to `L` with the `items` and `split_idx` are passed to each transform of the `Pipeline`. `do_setup` indicates if the `Pipeline.setup` method should be called during initialization.
```
class _IntFloatTfm(Transform):
def encodes(self, o): return TitledInt(o)
def decodes(self, o): return TitledFloat(o)
int2f_tfm=_IntFloatTfm()
def _neg(o): return -o
neg_tfm = Transform(_neg, _neg)
items = L([1.,2.,3.]); tfms = [neg_tfm, int2f_tfm]
tl = TfmdLists(items, tfms=tfms)
test_eq_type(tl[0], TitledInt(-1))
test_eq_type(tl[1], TitledInt(-2))
test_eq_type(tl.decode(tl[2]), TitledFloat(3.))
test_stdout(lambda: show_at(tl, 2), '-3')
test_eq(tl.types, [float, float, TitledInt])
tl
# add splits to TfmdLists
splits = [[0,2],[1]]
tl = TfmdLists(items, tfms=tfms, splits=splits)
test_eq(tl.n_subsets, 2)
test_eq(tl.train, tl.subset(0))
test_eq(tl.valid, tl.subset(1))
test_eq(tl.train.items, items[splits[0]])
test_eq(tl.valid.items, items[splits[1]])
test_eq(tl.train.tfms.split_idx, 0)
test_eq(tl.valid.tfms.split_idx, 1)
test_eq(tl.train.new_empty().split_idx, 0)
test_eq(tl.valid.new_empty().split_idx, 1)
test_eq_type(tl.splits, L(splits))
assert not tl.overlapping_splits()
df = pd.DataFrame(dict(a=[1,2,3],b=[2,3,4]))
tl = TfmdLists(df, lambda o: o.a+1, splits=[[0],[1,2]])
test_eq(tl[1,2], [3,4])
tr = tl.subset(0)
test_eq(tr[:], [2])
val = tl.subset(1)
test_eq(val[:], [3,4])
class _B(Transform):
def __init__(self): self.m = 0
def encodes(self, o): return o+self.m
def decodes(self, o): return o-self.m
def setups(self, items):
print(items)
self.m = tensor(items).float().mean().item()
# test for setup, which updates `self.m`
tl = TfmdLists(items, _B())
test_eq(tl.m, 2)
```
Here's how we can use `TfmdLists.setup` to implement a simple category list, getting labels from a mock file list:
```
class _Cat(Transform):
order = 1
def encodes(self, o): return int(self.o2i[o])
def decodes(self, o): return TitledStr(self.vocab[o])
def setups(self, items): self.vocab,self.o2i = uniqueify(L(items), sort=True, bidir=True)
tcat = _Cat()
def _lbl(o): return TitledStr(o.split('_')[0])
# Check that tfms are sorted by `order` & `_lbl` is called first
fns = ['dog_0.jpg','cat_0.jpg','cat_2.jpg','cat_1.jpg','dog_1.jpg']
tl = TfmdLists(fns, [tcat,_lbl])
exp_voc = ['cat','dog']
test_eq(tcat.vocab, exp_voc)
test_eq(tl.tfms.vocab, exp_voc)
test_eq(tl.vocab, exp_voc)
test_eq(tl, (1,0,0,0,1))
test_eq([tl.decode(o) for o in tl], ('dog','cat','cat','cat','dog'))
#Check only the training set is taken into account for setup
tl = TfmdLists(fns, [tcat,_lbl], splits=[[0,4], [1,2,3]])
test_eq(tcat.vocab, ['dog'])
tfm = NegTfm(split_idx=1)
tds = TfmdLists(start, A())
tdl = TfmdDL(tds, after_batch=tfm, bs=4)
x = tdl.one_batch()
test_eq(x, torch.arange(4))
tds.split_idx = 1
x = tdl.one_batch()
test_eq(x, -torch.arange(4))
tds.split_idx = 0
x = tdl.one_batch()
test_eq(x, torch.arange(4))
tds = TfmdLists(start, A())
tdl = TfmdDL(tds, after_batch=NegTfm(), bs=4)
test_eq(tdl.dataset[0], start[0])
test_eq(len(tdl), (len(tds)-1)//4+1)
test_eq(tdl.bs, 4)
test_stdout(tdl.show_batch, '0\n1\n2\n3')
show_doc(TfmdLists.subset)
show_doc(TfmdLists.infer_idx)
show_doc(TfmdLists.infer)
def mult(x): return x*2
mult.order = 2
fns = ['dog_0.jpg','cat_0.jpg','cat_2.jpg','cat_1.jpg','dog_1.jpg']
tl = TfmdLists(fns, [_lbl,_Cat(),mult])
test_eq(tl.infer_idx('dog_45.jpg'), 0)
test_eq(tl.infer('dog_45.jpg'), 2)
test_eq(tl.infer_idx(4), 2)
test_eq(tl.infer(4), 8)
test_fail(lambda: tl.infer_idx(2.0))
test_fail(lambda: tl.infer(2.0))
#hide
#Test input_types works on a Transform
cat = _Cat()
cat.input_types = (str, float)
tl = TfmdLists(fns, [_lbl,cat,mult])
test_eq(tl.infer_idx(2.0), 1)
#Test type annotations work on a function
def mult(x:(int,float)): return x*2
mult.order = 2
tl = TfmdLists(fns, [_lbl,_Cat(),mult])
test_eq(tl.infer_idx(2.0), 2)
```
## Datasets -
```
#export
@docs
@delegates(TfmdLists)
class Datasets(FilteredBase):
"A dataset that creates a tuple from each `tfms`, passed through `item_tfms`"
def __init__(self, items=None, tfms=None, tls=None, n_inp=None, dl_type=None, **kwargs):
super().__init__(dl_type=dl_type)
self.tls = L(tls if tls else [TfmdLists(items, t, **kwargs) for t in L(ifnone(tfms,[None]))])
self.n_inp = ifnone(n_inp, max(1, len(self.tls)-1))
def __getitem__(self, it):
res = tuple([tl[it] for tl in self.tls])
return res if is_indexer(it) else list(zip(*res))
def __getattr__(self,k): return gather_attrs(self, k, 'tls')
def __dir__(self): return super().__dir__() + gather_attr_names(self, 'tls')
def __len__(self): return len(self.tls[0])
def __iter__(self): return (self[i] for i in range(len(self)))
def __repr__(self): return coll_repr(self)
def decode(self, o, full=True): return tuple(tl.decode(o_, full=full) for o_,tl in zip(o,tuplify(self.tls, match=o)))
def subset(self, i): return type(self)(tls=L(tl.subset(i) for tl in self.tls), n_inp=self.n_inp)
def _new(self, items, *args, **kwargs): return super()._new(items, tfms=self.tfms, do_setup=False, **kwargs)
def overlapping_splits(self): return self.tls[0].overlapping_splits()
def new_empty(self): return type(self)(tls=[tl.new_empty() for tl in self.tls], n_inp=self.n_inp)
@property
def splits(self): return self.tls[0].splits
@property
def split_idx(self): return self.tls[0].tfms.split_idx
@property
def items(self): return self.tls[0].items
@items.setter
def items(self, v):
for tl in self.tls: tl.items = v
def show(self, o, ctx=None, **kwargs):
for o_,tl in zip(o,self.tls): ctx = tl.show(o_, ctx=ctx, **kwargs)
return ctx
@contextmanager
def set_split_idx(self, i):
old_split_idx = self.split_idx
for tl in self.tls: tl.tfms.split_idx = i
try: yield self
finally:
for tl in self.tls: tl.tfms.split_idx = old_split_idx
_docs=dict(
decode="Compose `decode` of all `tuple_tfms` then all `tfms` on `i`",
show="Show item `o` in `ctx`",
dataloaders="Get a `DataLoaders`",
overlapping_splits="All splits that are in more than one split",
subset="New `Datasets` that only includes subset `i`",
new_empty="Create a new empty version of the `self`, keeping only the transforms",
set_split_idx="Contextmanager to use the same `Datasets` with another `split_idx`"
)
```
A `Datasets` creates a tuple from `items` (typically input,target) by applying to them each list of `Transform` (or `Pipeline`) in `tfms`. Note that if `tfms` contains only one list of `tfms`, the items given by `Datasets` will be tuples of one element.
`n_inp` is the number of elements in the tuples that should be considered part of the input and will default to 1 if `tfms` consists of one set of transforms, `len(tfms)-1` otherwise. In most cases, the number of elements in the tuples spit out by `Datasets` will be 2 (for input,target) but it can happen that there is 3 (Siamese networks or tabular data) in which case we need to be able to determine when the inputs end and the targets begin.
```
items = [1,2,3,4]
dsets = Datasets(items, [[neg_tfm,int2f_tfm], [add(1)]])
t = dsets[0]
test_eq(t, (-1,2))
test_eq(dsets[0,1,2], [(-1,2),(-2,3),(-3,4)])
test_eq(dsets.n_inp, 1)
dsets.decode(t)
class Norm(Transform):
def encodes(self, o): return (o-self.m)/self.s
def decodes(self, o): return (o*self.s)+self.m
def setups(self, items):
its = tensor(items).float()
self.m,self.s = its.mean(),its.std()
items = [1,2,3,4]
nrm = Norm()
dsets = Datasets(items, [[neg_tfm,int2f_tfm], [neg_tfm,nrm]])
x,y = zip(*dsets)
test_close(tensor(y).mean(), 0)
test_close(tensor(y).std(), 1)
test_eq(x, (-1,-2,-3,-4,))
test_eq(nrm.m, -2.5)
test_stdout(lambda:show_at(dsets, 1), '-2')
test_eq(dsets.m, nrm.m)
test_eq(dsets.norm.m, nrm.m)
test_eq(dsets.train.norm.m, nrm.m)
#hide
#Check filtering is properly applied
class B(Transform):
def encodes(self, x)->None: return int(x+1)
def decodes(self, x): return TitledInt(x-1)
add1 = B(split_idx=1)
dsets = Datasets(items, [neg_tfm, [neg_tfm,int2f_tfm,add1]], splits=[[3],[0,1,2]])
test_eq(dsets[1], [-2,-2])
test_eq(dsets.valid[1], [-2,-1])
test_eq(dsets.valid[[1,1]], [[-2,-1], [-2,-1]])
test_eq(dsets.train[0], [-4,-4])
test_fns = ['dog_0.jpg','cat_0.jpg','cat_2.jpg','cat_1.jpg','kid_1.jpg']
tcat = _Cat()
dsets = Datasets(test_fns, [[tcat,_lbl]], splits=[[0,1,2], [3,4]])
test_eq(tcat.vocab, ['cat','dog'])
test_eq(dsets.train, [(1,),(0,),(0,)])
test_eq(dsets.valid[0], (0,))
test_stdout(lambda: show_at(dsets.train, 0), "dog")
inp = [0,1,2,3,4]
dsets = Datasets(inp, tfms=[None])
test_eq(*dsets[2], 2) # Retrieve one item (subset 0 is the default)
test_eq(dsets[1,2], [(1,),(2,)]) # Retrieve two items by index
mask = [True,False,False,True,False]
test_eq(dsets[mask], [(0,),(3,)]) # Retrieve two items by mask
inp = pd.DataFrame(dict(a=[5,1,2,3,4]))
dsets = Datasets(inp, tfms=attrgetter('a')).subset(0)
test_eq(*dsets[2], 2) # Retrieve one item (subset 0 is the default)
test_eq(dsets[1,2], [(1,),(2,)]) # Retrieve two items by index
mask = [True,False,False,True,False]
test_eq(dsets[mask], [(5,),(3,)]) # Retrieve two items by mask
#test n_inp
inp = [0,1,2,3,4]
dsets = Datasets(inp, tfms=[None])
test_eq(dsets.n_inp, 1)
dsets = Datasets(inp, tfms=[[None],[None],[None]])
test_eq(dsets.n_inp, 2)
dsets = Datasets(inp, tfms=[[None],[None],[None]], n_inp=1)
test_eq(dsets.n_inp, 1)
# splits can be indices
dsets = Datasets(range(5), tfms=[None], splits=[tensor([0,2]), [1,3,4]])
test_eq(dsets.subset(0), [(0,),(2,)])
test_eq(dsets.train, [(0,),(2,)]) # Subset 0 is aliased to `train`
test_eq(dsets.subset(1), [(1,),(3,),(4,)])
test_eq(dsets.valid, [(1,),(3,),(4,)]) # Subset 1 is aliased to `valid`
test_eq(*dsets.valid[2], 4)
#assert '[(1,),(3,),(4,)]' in str(dsets) and '[(0,),(2,)]' in str(dsets)
dsets
# splits can be boolean masks (they don't have to cover all items, but must be disjoint)
splits = [[False,True,True,False,True], [True,False,False,False,False]]
dsets = Datasets(range(5), tfms=[None], splits=splits)
test_eq(dsets.train, [(1,),(2,),(4,)])
test_eq(dsets.valid, [(0,)])
# apply transforms to all items
tfm = [[lambda x: x*2,lambda x: x+1]]
splits = [[1,2],[0,3,4]]
dsets = Datasets(range(5), tfm, splits=splits)
test_eq(dsets.train,[(3,),(5,)])
test_eq(dsets.valid,[(1,),(7,),(9,)])
test_eq(dsets.train[False,True], [(5,)])
# only transform subset 1
class _Tfm(Transform):
split_idx=1
def encodes(self, x): return x*2
def decodes(self, x): return TitledStr(x//2)
dsets = Datasets(range(5), [_Tfm()], splits=[[1,2],[0,3,4]])
test_eq(dsets.train,[(1,),(2,)])
test_eq(dsets.valid,[(0,),(6,),(8,)])
test_eq(dsets.train[False,True], [(2,)])
dsets
#A context manager to change the split_idx and apply the validation transform on the training set
ds = dsets.train
with ds.set_split_idx(1):
test_eq(ds,[(2,),(4,)])
test_eq(dsets.train,[(1,),(2,)])
#hide
#Test Datasets pickles
dsrc1 = pickle.loads(pickle.dumps(dsets))
test_eq(dsets.train, dsrc1.train)
test_eq(dsets.valid, dsrc1.valid)
dsets = Datasets(range(5), [_Tfm(),noop], splits=[[1,2],[0,3,4]])
test_eq(dsets.train,[(1,1),(2,2)])
test_eq(dsets.valid,[(0,0),(6,3),(8,4)])
start = torch.arange(0,50)
tds = Datasets(start, [A()])
tdl = TfmdDL(tds, after_item=NegTfm(), bs=4)
b = tdl.one_batch()
test_eq(tdl.decode_batch(b), ((0,),(1,),(2,),(3,)))
test_stdout(tdl.show_batch, "0\n1\n2\n3")
# only transform subset 1
class _Tfm(Transform):
split_idx=1
def encodes(self, x): return x*2
dsets = Datasets(range(8), [None], splits=[[1,2,5,7],[0,3,4,6]])
# only transform subset 1
class _Tfm(Transform):
split_idx=1
def encodes(self, x): return x*2
dsets = Datasets(range(8), [None], splits=[[1,2,5,7],[0,3,4,6]])
dls = dsets.dataloaders(bs=4, after_batch=_Tfm(), shuffle_train=False, device=torch.device('cpu'))
test_eq(dls.train, [(tensor([1,2,5, 7]),)])
test_eq(dls.valid, [(tensor([0,6,8,12]),)])
test_eq(dls.n_inp, 1)
```
### Methods
```
items = [1,2,3,4]
dsets = Datasets(items, [[neg_tfm,int2f_tfm]])
#hide_input
_dsrc = Datasets([1,2])
show_doc(_dsrc.dataloaders, name="Datasets.dataloaders")
show_doc(Datasets.decode)
test_eq(*dsets[0], -1)
test_eq(*dsets.decode((-1,)), 1)
show_doc(Datasets.show)
test_stdout(lambda:dsets.show(dsets[1]), '-2')
show_doc(Datasets.new_empty)
items = [1,2,3,4]
nrm = Norm()
dsets = Datasets(items, [[neg_tfm,int2f_tfm], [neg_tfm]])
empty = dsets.new_empty()
test_eq(empty.items, [])
#hide
#test it works for dataframes too
df = pd.DataFrame({'a':[1,2,3,4,5], 'b':[6,7,8,9,10]})
dsets = Datasets(df, [[attrgetter('a')], [attrgetter('b')]])
empty = dsets.new_empty()
```
## Add test set for inference
```
# only transform subset 1
class _Tfm1(Transform):
split_idx=0
def encodes(self, x): return x*3
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
test_eq(dsets.train, [(3,),(6,),(15,),(21,)])
test_eq(dsets.valid, [(0,),(6,),(8,),(12,)])
#export
def test_set(dsets, test_items, rm_tfms=None, with_labels=False):
"Create a test set from `test_items` using validation transforms of `dsets`"
if isinstance(dsets, Datasets):
tls = dsets.tls if with_labels else dsets.tls[:dsets.n_inp]
test_tls = [tl._new(test_items, split_idx=1) for tl in tls]
if rm_tfms is None: rm_tfms = [tl.infer_idx(get_first(test_items)) for tl in test_tls]
else: rm_tfms = tuplify(rm_tfms, match=test_tls)
for i,j in enumerate(rm_tfms): test_tls[i].tfms.fs = test_tls[i].tfms.fs[j:]
return Datasets(tls=test_tls)
elif isinstance(dsets, TfmdLists):
test_tl = dsets._new(test_items, split_idx=1)
if rm_tfms is None: rm_tfms = dsets.infer_idx(get_first(test_items))
test_tl.tfms.fs = test_tl.tfms.fs[rm_tfms:]
return test_tl
else: raise Exception(f"This method requires using the fastai library to assemble your data. Expected a `Datasets` or a `TfmdLists` but got {dsets.__class__.__name__}")
class _Tfm1(Transform):
split_idx=0
def encodes(self, x): return x*3
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
test_eq(dsets.train, [(3,),(6,),(15,),(21,)])
test_eq(dsets.valid, [(0,),(6,),(8,),(12,)])
#Tranform of the validation set are applied
tst = test_set(dsets, [1,2,3])
test_eq(tst, [(2,),(4,),(6,)])
#hide
#Test with different types
tfm = _Tfm1()
tfm.split_idx,tfm.order = None,2
dsets = Datasets(['dog', 'cat', 'cat', 'dog'], [[_Cat(),tfm]])
#With strings
test_eq(test_set(dsets, ['dog', 'cat', 'cat']), [(3,), (0,), (0,)])
#With ints
test_eq(test_set(dsets, [1,2]), [(3,), (6,)])
#hide
#Test with various input lengths
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()],[_Tfm(),_Tfm1()],[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
tst = test_set(dsets, [1,2,3])
test_eq(tst, [(2,2),(4,4),(6,6)])
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()],[_Tfm(),_Tfm1()],[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]], n_inp=1)
tst = test_set(dsets, [1,2,3])
test_eq(tst, [(2,),(4,),(6,)])
#hide
#Test with rm_tfms
dsets = Datasets(range(8), [[_Tfm(),_Tfm()]], splits=[[1,2,5,7],[0,3,4,6]])
tst = test_set(dsets, [1,2,3])
test_eq(tst, [(4,),(8,),(12,)])
dsets = Datasets(range(8), [[_Tfm(),_Tfm()]], splits=[[1,2,5,7],[0,3,4,6]])
tst = test_set(dsets, [1,2,3], rm_tfms=1)
test_eq(tst, [(2,),(4,),(6,)])
dsets = Datasets(range(8), [[_Tfm(),_Tfm()], [_Tfm(),_Tfm()]], splits=[[1,2,5,7],[0,3,4,6]], n_inp=2)
tst = test_set(dsets, [1,2,3], rm_tfms=(1,0))
test_eq(tst, [(2,4),(4,8),(6,12)])
#export
@delegates(TfmdDL.__init__)
@patch
def test_dl(self:DataLoaders, test_items, rm_type_tfms=None, with_labels=False, **kwargs):
"Create a test dataloader from `test_items` using validation transforms of `dls`"
test_ds = test_set(self.valid_ds, test_items, rm_tfms=rm_type_tfms, with_labels=with_labels
) if isinstance(self.valid_ds, (Datasets, TfmdLists)) else test_items
return self.valid.new(test_ds, **kwargs)
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
dls = dsets.dataloaders(bs=4, device=torch.device('cpu'))
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
dls = dsets.dataloaders(bs=4, device=torch.device('cpu'))
tst_dl = dls.test_dl([2,3,4,5])
test_eq(tst_dl._n_inp, 1)
test_eq(list(tst_dl), [(tensor([ 4, 6, 8, 10]),)])
#Test you can change transforms
tst_dl = dls.test_dl([2,3,4,5], after_item=add1)
test_eq(list(tst_dl), [(tensor([ 5, 7, 9, 11]),)])
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| github_jupyter |
<img src="images/logo.jpg" style="display: block; margin-left: auto; margin-right: auto;" alt="לוגו של מיזם לימוד הפייתון. נחש מצויר בצבעי צהוב וכחול, הנע בין האותיות של שם הקורס: לומדים פייתון. הסלוגן המופיע מעל לשם הקורס הוא מיזם חינמי ללימוד תכנות בעברית.">
# <span style="text-align: right; direction: rtl; float: right;">התנהגות של פונקציות</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בפסקאות הקרובות נבחן פונקציות מזווית ראייה מעט שונה מהרגיל.<br>
בואו נקפוץ ישירות למים!
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">שם של פונקציה</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
תכונה מעניינת שמתקיימת בפייתון היא שפונקציה היא ערך, בדיוק כמו כל ערך אחר.<br>
נגדיר פונקציה שמעלה מספר בריבוע:
</p>
```
def square(x):
return x ** 2
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נוכל לבדוק מאיזה טיפוס הפונקציה (אנחנו לא קוראים לה עם סוגריים אחרי שמה – רק מציינים את שמה):
</p>
```
type(square)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ואפילו לבצע השמה שלה למשתנה, כך ששם המשתנה החדש יצביע עליה:
</p>
```
ribua = square
print(square(5))
print(ribua(5))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
מה מתרחש בתא למעלה?<br>
כשהגדרנו את הפונקציה <var>square</var>, יצרנו לייזר עם התווית <var>square</var> שמצביע לפונקציה שמעלה מספר בריבוע.<br>
בהשמה שביצענו בשורה הראשונה בתא שלמעלה, הלייזר שעליו מודבקת התווית <var>ribua</var> כוון אל אותה הפונקציה שעליה מצביע הלייזר <var>square</var>.<br>
כעת <var>square</var> ו־<var>ribua</var> מצביעים לאותה פונקציה. אפשר לבדוק זאת כך:
</p>
```
ribua is square
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בשלב הזה אצטרך לבקש מכם לחגור חגורות, כי זה לא הולך להיות טיול רגיל הפעם.
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות במבנים מורכבים</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אם פונקציה היא בסך הכול ערך, ואם אפשר להתייחס לשם שלה בכל מקום, אין סיבה שלא נוכל ליצור רשימה של פונקציות!<br>
ננסה לממש את הרעיון:
</p>
```
def add(num1, num2):
return num1 + num2
def subtract(num1, num2):
return num1 - num2
def multiply(num1, num2):
return num1 * num2
def divide(num1, num2):
return num1 / num2
functions = [add, subtract, multiply, divide]
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כעת יש לנו רשימה בעלת 4 איברים, שכל אחד מהם מצביע לפונקציה שונה.<br>
אם נרצה לבצע פעולת חיבור, נוכל לקרוא ישירות ל־<var>add</var> או (בשביל התרגול) לנסות לאחזר אותה מהרשימה שיצרנו:
</p>
```
# Option 1
print(add(5, 2))
# Option 2
math_function = functions[0]
print(math_function(5, 2))
# Option 3 (ugly, but works!)
print(functions[0](5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אם נרצה, נוכל אפילו לעבור על רשימת הפונקציות בעזרת לולאה ולהפעיל את כולן, זו אחר זו:
</p>
```
for function in functions:
print(function(5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בכל איטרציה של לולאת ה־<code>for</code>, המשתנה <var>function</var> עבר להצביע על הפונקציה הבאה מתוך רשימת <var>functions</var>.<br>
בשורה הבאה קראנו לאותה הפונקציה ש־<var>function</var> מצביע עליה, והדפסנו את הערך שהיא החזירה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כיוון שרשימה היא מבנה ששומר על סדר האיברים שבו, התוצאות מודפסות בסדר שבו הפונקציות שמורות ברשימה.<br>
התוצאה הראשונה שאנחנו רואים היא תוצאת פונקציית החיבור, השנייה היא תוצאת פונקציית החיסור וכן הלאה.
</p>
#### <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל ביניים: סוגרים חשבון</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>calc</var> שמקבלת כפרמטר שני מספרים וסימן של פעולה חשבונית.<br>
הסימן יכול להיות אחד מאלה: <code>+</code>, <code>-</code>, <code>*</code> או <code>/</code>.<br>
מטרת הפונקציה היא להחזיר את תוצאת הביטוי החשבוני שהופעל על שני המספרים.<br>
בפתרונכם, השתמשו בהגדרת הפונקציות מלמעלה ובמילון.
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">העברת פונקציה כפרמטר</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נמשיך ללהטט בפונקציות.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
פונקציה נקראת "<dfn>פונקציה מסדר גבוה</dfn>" (<dfn>higher order function</dfn>) אם היא מקבלת כפרמטר פונקציה.<br>
ניקח לדוגמה את הפונקציה <var>calculate</var>:
</p>
```
def calculate(function, num1, num2):
return function(num1, num2)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בקריאה ל־<var>calculate</var>, נצטרך להעביר פונקציה ושני מספרים.<br>
נעביר לדוגמה את הפונקציה <var>divide</var> שהגדרנו קודם לכן:
</p>
```
calculate(divide, 5, 2)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
מה שמתרחש במקרה הזה הוא שהעברנו את הפונקציה <var>divide</var> כארגומנט ראשון.<br>
הפרמטר <var>function</var> בפונקציה <var>calculate</var> מצביע כעת על פונקציית החילוק שהגדרנו למעלה.<br>
מכאן, שהפונקציה תחזיר את התוצאה של <code>divide(5, 2)</code> – הרי היא 2.5.
</p>
#### <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל ביניים: מפה לפה</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו generator בשם <var>apply</var> שמקבל כפרמטר ראשון פונקציה (<var>func</var>), וכפרמטר שני iterable (<var dir="rtl">iter</var>).<br>
עבור כל איבר ב־iterable, ה־generator יניב את האיבר אחרי שהופעלה עליו הפונקציה <var>func</var>, דהיינו – <code>func(item)</code>.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ודאו שהרצת התא הבא מחזירה <code>True</code> עבור הקוד שלכם:
</p>
```
def square(number):
return number ** 2
square_check = apply(square, [5, -1, 6, -8, 0])
tuple(square_check) == (25, 1, 36, 64, 0)
```
### <span style="text-align: right; direction: rtl; float: right; clear: both;">סיכום ביניים</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
וואו. זה היה די משוגע.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אז למעשה, פונקציות בפייתון הן ערך לכל דבר, כמו מחרוזות ומספרים!<br>
אפשר לאחסן אותן במשתנים, לשלוח אותן כארגומנטים ולכלול אותם בתוך מבני נתונים מורכבים יותר.<br>
אנשי התיאוריה של מדעי המחשב נתנו להתנהגות כזו שם: "<dfn>אזרח ממדרגה ראשונה</dfn>" (<dfn>first class citizen</dfn>).<br>
אם כך, אפשר להגיד על פונקציות בפייתון שהן אזרחיות ממדרגה ראשונה.
</p>
## <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות מסדר גבוה בפייתון</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
החדשות הטובות הן שכבר עשינו היכרות קלה עם המונח פונקציות מסדר גבוה.<br>
עכשיו, כשאנחנו יודעים שמדובר בפונקציות שמקבלות פונקציה כפרמטר, נתחיל ללכלך קצת את הידיים.<br>
נציג כמה פונקציות פייתוניות מעניינות שכאלו:
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">הפונקציה map</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה <var>map</var> מקבלת פונקציה כפרמטר הראשון, ו־iterable כפרמטר השני.<br>
<var>map</var> מפעילה את הפונקציה מהפרמטר הראשון על כל אחד מהאיברים שהועברו ב־iterable.<br>
היא מחזירה iterator שמורכב מהערכים שחזרו מהפעלת הפונקציה.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במילים אחרות, <var>map</var> יוצרת iterable חדש.<br>
ה־iterable כולל את הערך שהוחזר מהפונקציה עבור כל איבר ב־<code>iterable</code> שהועבר.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לדוגמה:
</p>
```
squared_items = map(square, [1, 6, -1, 8, 0, 3, -3, 9, -8, 8, -7])
print(tuple(squared_items))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה קיבלה כארגומנט ראשון את הפונקציה <var>square</var> שהגדרנו למעלה, שמטרתה העלאת מספר בריבוע.<br>
כארגומנט שני היא קיבלה את רשימת כל המספרים שאנחנו רוצים שהפונקציה תרוץ עליהם.<br>
כשהעברנו ל־<var>map</var> את הארגומנטים הללו, <var>map</var> החזירה לנו ב־iterator (מבנה שאפשר לעבור עליו איבר־איבר) את התוצאה:<br>
הריבוע, קרי החזקה השנייה, של כל אחד מהאיברים ברשימה שהועברה כארגומנט השני.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
למעשה, אפשר להגיד ש־<code>map</code> שקולה לפונקציה הבאה:
</p>
```
def my_map(function, iterable):
for item in iterable:
yield function(item)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הנה דוגמה נוספת לשימוש ב־<var>map</var>:
</p>
```
numbers = [(2, 4), (1, 4, 2), (1, 3, 5, 6, 2), (3, )]
sums = map(sum, numbers)
print(tuple(sums))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במקרה הזה, בכל מעבר, קיבלה הפונקציה <var>sum</var> איבר אחד מתוך הרשימה – tuple.<br>
היא סכמה את האיברים של כל tuple שקיבלה, וכך החזירה לנו את הסכומים של כל ה־tuple־ים – זה אחרי זה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ודוגמה אחרונה:
</p>
```
def add_one(number):
return number + 1
incremented = map(add_one, (1, 2, 3))
print(tuple(incremented))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בדוגמה הזו יצרנו פונקציה משל עצמנו, ואותה העברנו ל־map.<br>
מטרת דוגמה זו היא להדגיש שאין שוני בין העברת פונקציה שקיימת בפייתון לבין פונקציה שאנחנו יצרנו.
</p>
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה שמקבלת רשימת מחרוזות של שתי מילים: שם פרטי ושם משפחה.<br>
הפונקציה תשתמש ב־map כדי להחזיר מכולן רק את השם הפרטי.
</p>
</div>
<div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
<p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
<strong>חשוב!</strong><br>
פתרו לפני שתמשיכו!
</p>
</div>
</div>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">הפונקציה filter</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה <var>filter</var> מקבלת פונקציה כפרמטר ראשון, ו־iterable כפרמטר שני.<br>
<var>filter</var> מפעילה על כל אחד מאיברי ה־iterable את הפונקציה, ומחזירה את האיבר אך ורק אם הערך שחזר מהפונקציה שקול ל־<code>True</code>.<br>
אם ערך ההחזרה שקול ל־<code>False</code> – הערך "יבלע" ב־<var>filter</var> ולא יחזור ממנה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במילים אחרות, <var>filter</var> יוצרת iterable חדש ומחזירה אותו.<br>
ה־iterable כולל רק את האיברים שעבורם הפונקציה שהועברה החזירה ערך השקול ל־<code>True</code>.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נבנה, לדוגמה, פונקציה שמחזירה אם אדם הוא בגיר.<br>
הפונקציה תקבל כפרמטר גיל, ותחזיר <code>True</code> כאשר הגיל שהועבר לה הוא לפחות 18, ו־<code>False</code> אחרת.
</p>
```
def is_mature(age):
return age >= 18
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נגדיר רשימת גילים, ונבקש מ־<var>filter</var> לסנן אותם לפי הפונקציה שהגדרנו:
</p>
```
ages = [0, 1, 4, 10, 20, 35, 56, 84, 120]
mature_ages = filter(is_mature, ages)
print(tuple(mature_ages))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כפי שלמדנו, <var>filter</var> מחזירה לנו רק גילים השווים ל־18 או גדולים ממנו.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נחדד שהפונקציה שאנחנו מעבירים ל־<var>filter</var> לא חייבת להחזיר בהכרח <code>True</code> או <code>False</code>.<br>
הערך 0, לדוגמה, שקול ל־<code>False</code>, ולכן <var>filter</var> תסנן כל ערך שעבורו הפונקציה תחזיר 0:
</p>
```
to_sum = [(1, -1), (2, 5), (5, -3, -2), (1, 2, 3)]
sum_is_not_zero = filter(sum, to_sum)
print(tuple(sum_is_not_zero))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בתא האחרון העברנו ל־<var>filter</var> את sum כפונקציה שאותה אנחנו רוצים להפעיל, ואת <var>to_sum</var> כאיברים שעליהם אנחנו רוצים לפעול.<br>
ה־tuple־ים שסכום איבריהם היה 0 סוננו, וקיבלנו חזרה iterator שהאיברים בו הם אך ורק אלו שסכומם שונה מ־0.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כטריק אחרון, נלמד ש־<var>filter</var> יכולה לקבל גם <code>None</code> בתור הפרמטר הראשון, במקום פונקציה.<br>
זה יגרום ל־<var>filter</var> לא להפעיל פונקציה על האיברים שהועברו, כלומר לסנן אותם כמו שהם.<br>
איברים השקולים ל־<code>True</code> יוחזרו, ואיברים השקולים ל־<code>False</code> לא יוחזרו:
</p>
```
to_sum = [0, "", None, 0.0, True, False, "Hello"]
equivalent_to_true = filter(None, to_sum)
print(tuple(equivalent_to_true))
```
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה שמקבלת רשימת מחרוזות, ומחזירה רק את המחרוזות הפלינדרומיות שבה.<br>
מחרוזת נחשבת פלינדרום אם קריאתה מימין לשמאל ומשמאל לימין יוצרת אותו ביטוי.<br>
השתמשו ב־<var>filter</var>.
</p>
</div>
<div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
<p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
<strong>חשוב!</strong><br>
פתרו לפני שתמשיכו!
</p>
</div>
</div>
## <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות אנונימיות</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
תעלול נוסף שנוסיף לארגז הכלים שלנו הוא <dfn>פונקציות אנונימיות</dfn> (<dfn>anonymous functions</dfn>).<br>
אל תיבהלו מהשם המאיים – בסך הכול פירושו הוא "פונקציות שאין להן שם".<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לפני שאתם מרימים גבה ושואלים את עצמכם למה הן שימושיות, בואו נבחן כמה דוגמאות.<br>
ניזכר בהגדרת פונקציית החיבור שיצרנו לא מזמן:
</p>
```
def add(num1, num2):
return num1 + num2
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ונגדיר את אותה הפונקציה בדיוק בצורה אנונימית:
</p>
```
add = lambda num1, num2: num1 + num2
print(add(5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לפני שנסביר איפה החלק של ה"פונקציה בלי שם" נתמקד בצד ימין של ההשמה.<br>
כיצד מנוסחת הגדרת פונקציה אנונימית?
</p>
<ol style="text-align: right; direction: rtl; float: right; clear: both;">
<li>הצהרנו שברצוננו ליצור פונקציה אנונימית בעזרת מילת המפתח <code>lambda</code>.</li>
<li>מייד אחריה, ציינו את שמות כל הפרמטרים שהפונקציה תקבל, כשהם מופרדים בפסיק זה מזה.</li>
<li>כדי להפריד בין רשימת הפרמטרים לערך ההחזרה של הפונקציה, השתמשנו בנקודתיים.</li>
<li>אחרי הנקודתיים, כתבנו את הביטוי שאנחנו רוצים שהפונקציה תחזיר.</li>
</ol>
<figure>
<img src="images/lambda.png" style="max-width: 500px; margin-right: auto; margin-left: auto; text-align: center;" alt="בתמונה מופיעה הגדרת ה־lambda שביצענו קודם לכן. מעל המילה lambda המודגשת בירוק ישנו פס מקווקו, ומעליו רשום 'הצהרה'. מימין למילה lambda כתוב num1 (פסיק) num2, מעליהם קו מקווקו ומעליו המילה 'פרמטרים'. מימין לפרמטרים יש נקודתיים, ואז num1 (הסימן פלוס) num2. מעליהם קו מקווקו, ומעליו המילה 'ערך החזרה'."/>
<figcaption style="margin-top: 2rem; text-align: center; direction: rtl;">חלקי ההגדרה של פונקציה אנונימית בעזרת מילת המפתח <code>lambda</code><br><span style="color: white;">A girl has no name</span></figcaption>
</figure>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במה שונה ההגדרה של פונקציה זו מההגדרה של פונקציה רגילה?<br>
היא לא באמת שונה.<br>
המטרה היא לאפשר תחביר שיקל על חיינו כשאנחנו רוצים לכתוב פונקציה קצרצרה שאורכה שורה אחת.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נראה, לדוגמה, שימוש ב־<var>filter</var> כדי לסנן את כל האיברים שאינם חיוביים:
</p>
```
def is_positive(number):
return number > 0
numbers = [-2, -1, 0, 1, 2]
positive_numbers = filter(is_positive, numbers)
print(tuple(positive_numbers))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במקום להגדיר פונקציה חדשה שנקראת <var>is_positive</var>, נוכל להשתמש בפונקציה אנונימית:
</p>
```
numbers = [-2, -1, 0, 1, 2]
positive_numbers = filter(lambda n: n > 0, numbers)
print(tuple(positive_numbers))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
איך זה עובד?<br>
במקום להעביר ל־<var>filter</var> פונקציה שיצרנו מבעוד מועד, השתמשנו ב־<code>lambda</code> כדי ליצור פונקציה ממש באותה השורה.<br>
הפונקציה שהגדרנו מקבלת מספר (<var>n</var>), ומחזירה <code>True</code> אם הוא חיובי, או <code>False</code> אחרת.<br>
שימו לב שבצורה זו באמת לא היינו צריכים לתת שם לפונקציה שהגדרנו.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
השימוש בפונקציות אנונימיות לא מוגבל ל־<var>map</var> ול־<var>filter</var>, כמובן.<br>
מקובל להשתמש ב־<code>lambda</code> גם עבור פונקציות כמו <var>sorted</var>, שמקבלות פונקציה בתור ארגומנט.
</p>
<div class="align-center" style="display: flex; text-align: right; direction: rtl;">
<div style="display: flex; width: 10%; float: right; ">
<img src="images/recall.svg" style="height: 50px !important;" alt="תזכורת" title="תזכורת">
</div>
<div style="width: 90%">
<p style="text-align: right; direction: rtl;">
הפונקציה <code>sorted</code> מאפשרת לנו לסדר ערכים, ואפילו להגדיר עבורה לפי מה לסדר אותם.<br>
לרענון בנוגע לשימוש בפונקציה גשו למחברת בנושא פונקציות מובנות בשבוע 4.
</p>
</div>
</div>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נסדר, למשל, את הדמויות ברשימה הבאה, לפי תאריך הולדתן:
</p>
```
closet = [
{'name': 'Peter', 'year_of_birth': 1927, 'gender': 'Male'},
{'name': 'Edmund', 'year_of_birth': 1930, 'gender': 'Male'},
{'name': 'Lucy', 'year_of_birth': 1932, 'gender': 'Female'},
{'name': 'Susan', 'year_of_birth': 1928, 'gender': 'Female'},
{'name': 'Jadis', 'year_of_birth': 0, 'gender': 'Female'},
]
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נרצה שסידור הרשימה יתבצע לפי המפתח <var>year_of_birth</var>.<br>
כלומר, בהינתן מילון שמייצג דמות בשם <var>d</var>, יש להשיג את <code dir="ltr">d['year_of_birth']</code>, ולפיו לבצע את סידור הרשימה.<br>
ניגש למלאכה:
</p>
```
sorted(closet, key=lambda d: d['year_of_birth'])
```
<div class="align-center" style="display: flex; text-align: right; direction: rtl;">
<div style="display: flex; width: 10%; float: right; ">
<img src="images/warning.png" style="height: 50px !important;" alt="אזהרה!">
</div>
<div style="width: 90%">
<p style="text-align: right; direction: rtl;">
פונקציות אנונימיות הן יכולת חביבה שאמורה לסייע לכם לכתוב קוד נאה וקריא.<br>
כלל אצבע טוב לחיים הוא להימנע משימוש בהן כאשר הן מסרבלות את הקוד.
</p>
</div>
</div>
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגיל" title="תרגיל">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
סדרו את הדמויות ב־<var>closet</var> לפי האות האחרונה בשמם.
</p>
</div>
</div>
## <span style="align: right; direction: rtl; float: right; clear: both;">מונחים</span>
<dl style="text-align: right; direction: rtl; float: right; clear: both;">
<dt>פונקציה מסדר גבוה</dt>
<dd>פונקציה שמקבלת פונקציה כאחד הארגומנטים, או שמחזירה פונקציה כערך ההחזרה שלה.</dd>
<dt>אזרח ממדרגה ראשונה</dt>
<dd>ישות תכנותית המתנהגת בשפת התכנות כערך לכל דבר. בפייתון, פונקציות הן אזרחיות ממדרגה ראשונה.<dd>
<dt>פונקציה אנונימית, פונקציית <code>lambda</code></dt>
<dd>פונקציה ללא שם המיועדת להגדרת פונקציה בשורה אחת, לרוב לשימוש חד־פעמי. בעברית: פונקציית למדא.</dd>
</dl>
## <span style="align: right; direction: rtl; float: right; clear: both;">תרגילים</span>
### <span style="align: right; direction: rtl; float: right; clear: both;">פילטר מותאם אישית</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>my_filter</var> שמתנהגת בדיוק כמו הפונקציה <var>filter</var>.<br>
בפתירת התרגיל, המנעו משימוש ב־<var>filter</var> או במודולים.
</p>
### <span style="align: right; direction: rtl; float: right; clear: both;">נשאר? חיובי</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>get_positive_numbers</var> שמקבלת מהמשתמש קלט בעזרת <var>input</var>.<br>
המשתמש יתבקש להזין סדרה של מספרים המופרדים בפסיק זה מזה.<br>
הפונקציה תחזיר את כל המספרים החיוביים שהמשתמש הזין, כרשימה של מספרים מסוג <code>int</code>.<br>
אפשר להניח שהקלט מהמשתמש תקין.
</p>
### <span style="align: right; direction: rtl; float: right; clear: both;">ריצת 2,000</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>timer</var> שמקבלת כפרמטר פונקציה (נקרא לה <var>f</var>) ופרמטרים נוספים.<br>
הפונקציה <var>timer</var> תמדוד כמה זמן רצה פונקציה <var>f</var> כשמועברים אליה אותם פרמטרים. <br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לדוגמה:
</p>
<ol style="text-align: right; direction: rtl; float: right; clear: both;">
<li>עבור הקריאה <code dir="ltr">timer(print, "Hello")</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">print("Hello")</code>.</li>
<li>עבור הקריאה <code dir="ltr">timer(zip, [1, 2, 3], [4, 5, 6])</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">zip([1, 2, 3], [4, 5, 6])</code>.</li>
<li>עבור הקריאה <code dir="ltr">timer("Hi {name}".format, name="Bug")</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">"Hi {name}".format(name="Bug")</code></li>
</ol>
| github_jupyter |
```
import os
import json
import pickle
import random
from collections import defaultdict, Counter
from indra.literature.adeft_tools import universal_extract_text
from indra.databases.hgnc_client import get_hgnc_name, get_hgnc_id
from adeft.discover import AdeftMiner
from adeft.gui import ground_with_gui
from adeft.modeling.label import AdeftLabeler
from adeft.modeling.classify import AdeftClassifier
from adeft.disambiguate import AdeftDisambiguator, load_disambiguator
from adeft_indra.ground.ground import AdeftGrounder
from adeft_indra.model_building.s3 import model_to_s3
from adeft_indra.model_building.escape import escape_filename
from adeft_indra.db.content import get_pmids_for_agent_text, get_pmids_for_entity, \
get_plaintexts_for_pmids
adeft_grounder = AdeftGrounder()
shortforms = ['UBC']
model_name = ':'.join(sorted(escape_filename(shortform) for shortform in shortforms))
results_path = os.path.abspath(os.path.join('../..', 'results', model_name))
miners = dict()
all_texts = {}
for shortform in shortforms:
pmids = get_pmids_for_agent_text(shortform)
text_dict = get_plaintexts_for_pmids(pmids, contains=shortforms)
text_dict = {pmid: text for pmid, text in text_dict.items() if len(text) > 5}
miners[shortform] = AdeftMiner(shortform)
miners[shortform].process_texts(text_dict.values())
all_texts.update(text_dict)
longform_dict = {}
for shortform in shortforms:
longforms = miners[shortform].get_longforms()
longforms = [(longform, count, score) for longform, count, score in longforms
if count*score > 2]
longform_dict[shortform] = longforms
combined_longforms = Counter()
for longform_rows in longform_dict.values():
combined_longforms.update({longform: count for longform, count, score
in longform_rows})
grounding_map = {}
names = {}
for longform in combined_longforms:
groundings = adeft_grounder.ground(longform)
if groundings:
grounding = groundings[0]['grounding']
grounding_map[longform] = grounding
names[grounding] = groundings[0]['name']
longforms, counts = zip(*combined_longforms.most_common())
pos_labels = []
list(zip(longforms, counts))
try:
disamb = load_disambiguator(shortforms[0])
for shortform, gm in disamb.grounding_dict.items():
for longform, grounding in gm.items():
grounding_map[longform] = grounding
for grounding, name in disamb.names.items():
names[grounding] = name
pos_labels = disamb.pos_labels
except Exception:
pass
names
grounding_map, names, pos_labels = ground_with_gui(longforms, counts,
grounding_map=grounding_map,
names=names, pos_labels=pos_labels, no_browser=True, port=8891)
result = [grounding_map, names, pos_labels]
result
grounding_map, names, pos_labels = [{'ubiquitin c': 'HGNC:12468',
'ubiquitin conjugating': 'FPLX:UBE2',
'ubiquitin conjugating enzyme': 'FPLX:UBE2',
'unipolar brush cells': 'ungrounded',
'urinary bladder cancer': 'MESH:D001749',
'urothelial bladder cancer': 'MESH:D001749',
'urothelial bladder carcinoma': 'MESH:D001749'},
{'HGNC:12468': 'UBC',
'FPLX:UBE2': 'UBE2',
'MESH:D001749': 'Urinary Bladder Neoplasms'},
['FPLX:UBE2', 'HGNC:12468', 'MESH:D001749']]
excluded_longforms = []
grounding_dict = {shortform: {longform: grounding_map[longform]
for longform, _, _ in longforms if longform in grounding_map
and longform not in excluded_longforms}
for shortform, longforms in longform_dict.items()}
result = [grounding_dict, names, pos_labels]
if not os.path.exists(results_path):
os.mkdir(results_path)
with open(os.path.join(results_path, f'{model_name}_preliminary_grounding_info.json'), 'w') as f:
json.dump(result, f)
additional_entities = {}
unambiguous_agent_texts = {}
labeler = AdeftLabeler(grounding_dict)
corpus = labeler.build_from_texts((text, pmid) for pmid, text in all_texts.items())
agent_text_pmid_map = defaultdict(list)
for text, label, id_ in corpus:
agent_text_pmid_map[label].append(id_)
entity_pmid_map = {entity: set(get_pmids_for_entity(*entity.split(':', maxsplit=1),
major_topic=True))for entity in additional_entities}
intersection1 = []
for entity1, pmids1 in entity_pmid_map.items():
for entity2, pmids2 in entity_pmid_map.items():
intersection1.append((entity1, entity2, len(pmids1 & pmids2)))
intersection2 = []
for entity1, pmids1 in agent_text_pmid_map.items():
for entity2, pmids2 in entity_pmid_map.items():
intersection2.append((entity1, entity2, len(set(pmids1) & pmids2)))
intersection1
intersection2
all_used_pmids = set()
for entity, agent_texts in unambiguous_agent_texts.items():
used_pmids = set()
for agent_text in agent_texts[1]:
pmids = set(get_pmids_for_agent_text(agent_text))
new_pmids = list(pmids - all_texts.keys() - used_pmids)
text_dict = get_plaintexts_for_pmids(new_pmids, contains=agent_texts)
corpus.extend([(text, entity, pmid) for pmid, text in text_dict.items() if len(text) >= 5])
used_pmids.update(new_pmids)
all_used_pmids.update(used_pmids)
for entity, pmids in entity_pmid_map.items():
new_pmids = list(set(pmids) - all_texts.keys() - all_used_pmids)
if len(new_pmids) > 10000:
new_pmids = random.choices(new_pmids, k=10000)
_, contains = additional_entities[entity]
text_dict = get_plaintexts_for_pmids(new_pmids, contains=contains)
corpus.extend([(text, entity, pmid) for pmid, text in text_dict.items() if len(text) >= 5])
names.update({key: value[0] for key, value in additional_entities.items()})
names.update({key: value[0] for key, value in unambiguous_agent_texts.items()})
pos_labels = list(set(pos_labels) | additional_entities.keys() |
unambiguous_agent_texts.keys())
%%capture
classifier = AdeftClassifier(shortforms, pos_labels=pos_labels, random_state=1729)
param_grid = {'C': [100.0], 'max_features': [10000]}
texts, labels, pmids = zip(*corpus)
classifier.cv(texts, labels, param_grid, cv=5, n_jobs=5)
classifier.stats
disamb = AdeftDisambiguator(classifier, grounding_dict, names)
disamb.dump(model_name, results_path)
print(disamb.info())
model_to_s3(disamb)
preds = [disamb.disambiguate(text) for text in all_texts.values()]
texts = [text for pred, text in zip(preds, all_texts.values()) if pred[0] == 'HGNC:10967']
texts[3]
```
| github_jupyter |
# Identificar Perfil de Consumo de Clientes de uma Instituição Financeira
## Uma breve introdução
Uma Instituição Financeira X tem o interesse em identificar o perfil de gastos dos seus clientes. Identificando os clientes certos, eles podem melhorar a comunicação dos ativos promocionais, utilizar com mais eficiência os canais de comunicação e aumentar o engajamento dos clientes com o uso do seu produto.
## Sobre o estudo
Os dados estão anonimizados por questões de segurança. No dataset, temos o valor gasto de 121818 clientes, no ano de 2019, em cada ramo de atividade. A base já está limpa. O intuito aqui é apresentar uma possibilidade de fazer a clusterização de clientes com base em seu consumo. Os dados são de 1 ano a fim de diminuir o efeito da sazonalidade.
## Importando a biblioteca
Será necessário instalar o pacote kmodes, caso não tenha.
```
# pip install --upgrade kmodes
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import os
import random
import plotly.express as px
# pacote do modelo
from kmodes.kmodes import KModes
# from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings("ignore")
random.seed(2020)
pd.options.display.float_format = '{:,.2f}'.format
```
## Leitura dos dados
```
# Carregar os dados
dados = pd.read_csv('../../dados_gasto_rmat.csv', sep=',')
dados.head(10)
print('O arquivo possui ' + str(dados.shape[0]) + ' linhas e ' + str(dados.shape[1]) + ' colunas.')
# Tipos dos dados
dados.dtypes
# Verificando valores nulos
dados.isnull().values.any()
```
A base não possui valores nulos.
## Visualização dos dados
```
# Total de clientes
len(dados['CLIENTE'].unique())
```
Soma do valor gasto em cada ramo de atividade.
```
# Dados agregados por RMAT e o percentual gasto
dados_agreg = dados.groupby(['RMAT'])['VALOR_GASTO'].sum().reset_index()
dados_agreg['percentual'] = round(dados_agreg['VALOR_GASTO']/sum(dados_agreg['VALOR_GASTO'])*100,2)
dados_agreg.head()
# Traz o 30 RMATs que tiveram maior gasto dos clientes
top_rotulos = dados_agreg.sort_values(by = 'percentual', ascending = False)[:30]
# Gráfico dos RMATs
ax = top_rotulos.plot.barh(x='RMAT', y='percentual', rot=0, figsize = (20, 15), fontsize=20, color='violet')
plt.title('Percentual do valor gasto por Ramo de Atividade', fontsize=22)
plt.xlabel('')
plt.ylabel('')
plt.show()
```
Supermercados, postos de combustível e drogarias são os ramos com maior consumo dos clientes, representando 13.48%, 7.07% e 5.75%, respectivamente.
### Construção da base para o modelo
Vamos construir uma base que seja a nível cliente e as colunas serão os percentuais de consumo em cada ramo de atividade. Aqui, temos muitos percentuais 0 em determinados ramos de atividade e isso tem impacto negativo na construção do modelo. Portanto, iremos categorizar as variáveis de acordo com a variação do percentual para cada atributo.
```
dados.head()
```
A função pivot faz a transposição dos dados, transformando o valor de "RMAT" em colunas.
```
# Inverter o data frame (colocar nos rmats como coluna)
cli_pivot = dados.pivot(index='CLIENTE', columns='RMAT', values='VALOR_GASTO')
cli_pivot.fillna(0, inplace = True)
# Calcular o percentual de volume transacionado de cada cliente por rmat
cli_pivot = cli_pivot.apply(lambda x: x.apply(lambda y: 100*y/sum(x)),axis = 1)
cli_pivot.head()
```
Abaixo, uma função que quebra os valores de cada coluna em quantidade de categorias escolhido. Nesse caso, utilizamos 8 quebras.
```
# Funnção para fazer categorização das variaveis
def hcut(df, colunas, nlevs, prefixo=''):
x = df.copy()
for c in colunas:
x[prefixo+c] = pd.cut(x[c] , bins=nlevs, include_lowest = False, precision=0)
return x
base_cluster = hcut(cli_pivot, cli_pivot
.columns, 8, 'esc_')
base_cluster.head()
```
Agora, filtraremos as variáveis necessárias para a modelagem.
```
# Selecionar somentes as colunas categorizadas que serão utilizadas no modelo
filter_col = [col for col in base_cluster if
col.startswith('esc_')]
df1 = base_cluster.loc[:,filter_col].reset_index()
df1.head()
```
### Criação do modelo
Para nosso caso, utilizaremos o método de clusterização chamado K-modes. Esse método é uma extensão do K-means. Em vez de distâncias, ele usa dissimilaridade (isto é, quantificação das incompatibilidades totais entre dois objetos: quanto menor esse número, masi semelhantes são os dois objetos). Além disso, ele utiliza modas. Cada vetor de elementos é criado de forma a minimizar as diferenças entre o próprio vetor e cada objetos dos dados. Assim, teremos tantos vetores de modas quanto o número de clusters necessários, pois eles atuam como centróides.
Aqui, iremos fazer a divisão dos clientes em 7 clusters.
```
km_huang = KModes(n_clusters=7, init = "Huang", n_init = 5, verbose=1, random_state=2020)
fitClusters = km_huang.fit_predict(df1)
# Adiciona os clusters na base
df1['cluster'] = fitClusters
base_cluster['cluster'] = fitClusters
```
#### Percentual de clientes por cluster.
```
df1['cluster'].value_counts()/len(df1)*100
df2 = base_cluster.drop(columns=filter_col)
df2.head()
# Para visualização dos clusters
# from sklearn.decomposition import PCA
# pca_2 = PCA(2)
# plot_columns = pca_2.fit_transform(base_cluster.iloc[:,0:65])
# plt.scatter(x=plot_columns[:,0], y=plot_columns[:,1], c=fitClusters,)
# plt.show()
```
| github_jupyter |
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
#Improving Computer Vision Accuracy using Convolutions
In the previous lessons you saw how to do fashion recognition using a Deep Neural Network (DNN) containing three layers -- the input layer (in the shape of the data), the output layer (in the shape of the desired output) and a hidden layer. You experimented with the impact of different sizes of hidden layer, number of training epochs etc on the final accuracy.
For convenience, here's the entire code again. Run it and take a note of the test accuracy that is printed out at the end.
```
import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images / 255.0
test_images=test_images / 255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
test_loss = model.evaluate(test_images, test_labels)
```
Your accuracy is probably about 89% on training and 87% on validation...not bad...But how do you make that even better? One way is to use something called Convolutions. I'm not going to details on Convolutions here, but the ultimate concept is that they narrow down the content of the image to focus on specific, distinct, details.
If you've ever done image processing using a filter (like this: https://en.wikipedia.org/wiki/Kernel_(image_processing)) then convolutions will look very familiar.
In short, you take an array (usually 3x3 or 5x5) and pass it over the image. By changing the underlying pixels based on the formula within that matrix, you can do things like edge detection. So, for example, if you look at the above link, you'll see a 3x3 that is defined for edge detection where the middle cell is 8, and all of its neighbors are -1. In this case, for each pixel, you would multiply its value by 8, then subtract the value of each neighbor. Do this for every pixel, and you'll end up with a new image that has the edges enhanced.
This is perfect for computer vision, because often it's features that can get highlighted like this that distinguish one item for another, and the amount of information needed is then much less...because you'll just train on the highlighted features.
That's the concept of Convolutional Neural Networks. Add some layers to do convolution before you have the dense layers, and then the information going to the dense layers is more focussed, and possibly more accurate.
Run the below code -- this is the same neural network as earlier, but this time with Convolutional layers added first. It will take longer, but look at the impact on the accuracy:
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
# Reshaping the images to tell the convolutional layers that the images are in greyscale by adding an extra dimension of 1
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
model = tf.keras.models.Sequential([
# Mind it, Convolutions and MaxPooling are always applied before the Deep Neural Network Layers
# Why 2D? because, applied convolutions and maxpoolings are 2D array in nature (having rows and columns)
# Here 64 is the total number of convolutional filters of size (3, 3) applied
### Be careful about the shapes!!! You obviously need to mention the input_shape at the first Conv2D(), otherwise it will turn
### into an error!!!
tf.keras.layers.Conv2D(64, (3, 3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# Mind it, model.summary() is a way of cross-verification that the DNN with Convolutions is applied correctly with accurate
# shape retention
model.summary()
model.fit(training_images, training_labels, epochs=5)
test_loss = model.evaluate(test_images, test_labels)
```
It's likely gone up to about 93% on the training data and 91% on the validation data.
That's significant, and a step in the right direction!
Try running it for more epochs -- say about 20, and explore the results! But while the results might seem really good, the validation results may actually go down, due to something called 'overfitting' which will be discussed later.
(In a nutshell, 'overfitting' occurs when the network learns the data from the training set really well, but it's too specialised to only that data, and as a result is less effective at seeing *other* data. For example, if all your life you only saw red shoes, then when you see a red shoe you would be very good at identifying it, but blue suade shoes might confuse you...and you know you should never mess with my blue suede shoes.)
Then, look at the code again, and see, step by step how the Convolutions were built:
Step 1 is to gather the data. You'll notice that there's a bit of a change here in that the training data needed to be reshaped. That's because the first convolution expects a single tensor containing everything, so instead of 60,000 28x28x1 items in a list, we have a single 4D list that is 60,000x28x28x1, and the same for the test images. If you don't do this, you'll get an error when training as the Convolutions do not recognize the shape.
```
import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
```
Next is to define your model. Now instead of the input layer at the top, you're going to add a Convolution. The parameters are:
1. The number of convolutions you want to generate. Purely arbitrary, but good to start with something in the order of 32
2. The size of the Convolution, in this case a 3x3 grid
3. The activation function to use -- in this case we'll use relu, which you might recall is the equivalent of returning x when x>0, else returning 0
4. In the first layer, the shape of the input data.
You'll follow the Convolution with a MaxPooling layer which is then designed to compress the image, while maintaining the content of the features that were highlighted by the convlution. By specifying (2,2) for the MaxPooling, the effect is to quarter the size of the image. Without going into too much detail here, the idea is that it creates a 2x2 array of pixels, and picks the biggest one, thus turning 4 pixels into 1. It repeats this across the image, and in so doing halves the number of horizontal, and halves the number of vertical pixels, effectively reducing the image by 25%.
You can call model.summary() to see the size and shape of the network, and you'll notice that after every MaxPooling layer, the image size is reduced in this way.
```
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
```
Add another convolution
```
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2)
```
Now flatten the output. After this you'll just have the same DNN structure as the non convolutional version
```
tf.keras.layers.Flatten(),
```
The same 128 dense layers, and 10 output layers as in the pre-convolution example:
```
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
```
Now compile the model, call the fit method to do the training, and evaluate the loss and accuracy from the test set.
```
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(test_acc)
```
# Visualizing the Convolutions and Pooling
This code will show us the convolutions graphically. The print (test_labels[;100]) shows us the first 100 labels in the test set, and you can see that the ones at index 0, index 23 and index 28 are all the same value (9). They're all shoes. Let's take a look at the result of running the convolution on each, and you'll begin to see common features between them emerge. Now, when the DNN is training on that data, it's working with a lot less, and it's perhaps finding a commonality between shoes based on this convolution/pooling combination.
```
print(test_labels[:100])
import matplotlib.pyplot as plt
f, axarr = plt.subplots(3,4)
FIRST_IMAGE=0
SECOND_IMAGE=7
THIRD_IMAGE=26
CONVOLUTION_NUMBER = 1
from tensorflow.keras import models
layer_outputs = [layer.output for layer in model.layers]
activation_model = tf.keras.models.Model(inputs = model.input, outputs = layer_outputs)
for x in range(0,4):
f1 = activation_model.predict(test_images[FIRST_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[0,x].imshow(f1[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[0,x].grid(False)
f2 = activation_model.predict(test_images[SECOND_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[1,x].imshow(f2[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[1,x].grid(False)
f3 = activation_model.predict(test_images[THIRD_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[2,x].imshow(f3[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[2,x].grid(False)
```
EXERCISES
1. Try editing the convolutions. Change the 32s to either 16 or 64. What impact will this have on accuracy and/or training time.
2. Remove the final Convolution. What impact will this have on accuracy or training time?
3. How about adding more Convolutions? What impact do you think this will have? Experiment with it.
4. Remove all Convolutions but the first. What impact do you think this will have? Experiment with it.
5. In the previous lesson you implemented a callback to check on the loss function and to cancel training once it hit a certain amount. See if you can implement that here!
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=10)
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(test_acc)
```
| github_jupyter |
## Fundamentals, introduction to machine learning
The purpose of these guides is to go a bit deeper into the details behind common machine learning methods, assuming little math background, and teach you how to use popular machine learning Python packages. In particular, we'll focus on the Numpy and PyTorch libraries.
I'll assume you have some experience programming with Python -- if not, check out the initial [fundamentals of Python guide](https://github.com/ml4a/ml4a-guides/blob/master/notebooks/intro_python.ipynb) or for a longer, more comprehensive resource: [Learn Python the Hard Way](http://learnpythonthehardway.org/book/). It will really help to illustrate the concepts introduced here.
Numpy underlies most Python machine learning packages and is great for performing quick sketches or working through calculations. PyTorch rivals alternative libraries, such as TensorFlow, for its flexibility and ease of use. Despite the high level appearance of PyTorch, it can be quite low-level, which is great for experimenting with novel algorithms. PyTorch can seamlessly be integrated with distributed computation libraries, like Ray, to make the Kessel Run in less than 12 parsecs (citation needed).
These guides will present the formal math for concepts alongside Python code examples since this often (for me at least) is a lot easier to develop an intuition for. Each guide is also available as an iPython notebook for your own experimentation.
The guides are not meant to exhaustively cover the field of machine learning but I hope they will instill you with the confidence and knowledge to explore further on your own.
If you do want more details, you might enjoy my [artificial intelligence notes](http://frnsys.com/ai_notes).
### Modeling the world
You've probably seen various machine learning algorithms pop up -- linear regression, SVMs, neural networks, random forests, etc. How are they all related? What do they have in common? What is machine learning for anyways?
First, let's consider the general, fundamental problem all machine learning is concerned with, leaving aside the algorithm name soup for now. The primary concern of machine learning is _modeling the world_.
We can model phenomena or systems -- both natural and artificial, if you want to make that distinction -- with mathematical functions. We see something out in the world and want to describe it in some way, we want to formalize how two or more things are related, and we can do that with a function. The problem is, for a given phenomenon, how do we figure out what function to use? There are infinitely many to choose from!
Before this gets too abstract, let's use an example to make things more concrete.
Say we have a bunch of data about the heights and weights of a species of deer. We want to understand how these two variables are related -- in particular, given the weight of a deer, can we predict its height?
You might see where this is going. The data looks like a line, and lines in general are described by functions of the form $y = mx + b$.
Remember that lines vary depending on what the values of $m$ and $b$ are:

Thus $m$ and $b$ uniquely define a function -- thus they are called the _parameters_ of the function -- and when it comes to machine learning, these parameters are what we ultimately want to learn. So when I say there are infinitely many functions to choose from, it is because $m$ and $b$ can pretty much take on any value. Machine learning techniques essentially search through these possible functions to find parameters that best fit the data you have. One way machine learning algorithms are differentiated is by how exactly they conduct this search (i.e. how they learn parameters).
In this case we've (reasonably) assumed the function takes the form $y = mx + b$, but conceivably you may have data that doesn't take the form of a line. Real world data is typically a lot more convoluted-looking. Maybe the true function has a $sin$ in it, for example.
This is where another main distinction between machine learning algorithms comes in -- certain algorithms can model only certain forms of functions. _Linear regression_, for example, can only model linear functions, as indicated by its name. Neural networks, on the other hand, are _universal function approximators_, which mean they can (in theory) approximate _any_ function, no matter how exotic. This doesn't necessarily make them a better method, just better suited for certain circumstances (there are many other considerations when choosing an algorithm).
For now, let's return to the line function. Now that we've looked at the $m$ and $b$ variables, let's consider the input variable $x$. A function takes a numerical input; that is $x$ must be a number of some kind. That's pretty straightforward here since the deer weights are already numbers. But this is not always the case! What if we want to predict the sales price of a house. A house is not a number. We have to find a way to _represent_ it as a number (or as several numbers, i.e. a vector, which will be detailed in a moment), e.g. by its square footage. This challenge of representation is a major part of machine learning; the practice of building representations is known as _feature engineering_ since each variable (e.g. square footage or zip code) used for the representation is called a _feature_.
If you think about it, representation is a practice we regularly engage in. The word "house" is not a house any more than an image of a house is -- there is no true "house" anyways, it is always a constellation of various physical and nonphysical components.
That's about it -- broadly speaking, machine learning is basically a bunch of algorithms that learn you a function, which is to say they learn the parameters that uniquely define a function.
### Vectors
In the line example before I mentioned that we might have multiple numbers representing an input. For example, a house probably can't be solely represented by its square footage -- perhaps we also want to consider how many bedrooms it has, or how high the ceilings are, or its distance from local transportation. How do we group these numbers together?
That's what _vectors_ are for (they come up for many other reasons too, but we'll focus on representation for now). Vectors, along with matrices and other tensors (which will be explained a bit further down), could be considered the "primitives" of machine learning.
The Numpy library is best for dealing with vectors (and other tensors) in Python. A more complete introduction to Numpy is provided in the [numpy and basic mathematics guide](https://github.com/ml4a/ml4a-guides/blob/master/notebooks/math_review_numpy.ipynb).
Let's import `numpy` with the alias `nf`:
```
import numpy as np
```
You may have encountered vectors before in high school or college -- to use Python terms, a vector is like a list of numbers. The mathematical notation is quite similar to Python code, e.g. `[5,4]`, but `numpy` has its own way of instantiating a vector:
```
v = np.array([5, 4])
```
$$
v = \begin{bmatrix} 5 \\ 4 \end{bmatrix}
$$
Vectors are usually represented with lowercase variables.
Note that we never specified how _many_ numbers (also called _components_) a vector has - because it can have any amount. The amount of components a vector has is called its _dimensionality_. The example vector above has two dimensions. The vector `x = [8,1,3]` has three dimensions, and so on. Components are usually indicated by their index (usually using 1-indexing), e.g. in the previous vector, $x_1$ refers to the value $8$.
"Dimensions" in the context of vectors is just like the spatial dimensions you spend every day in. These dimensions define a __space__, so a two-dimensional vector, e.g. `[5,4]`, can describe a point in 2D space and a three-dimensional vector, e.g. `[8,1,3]`, can describe a point in 3D space. As mentioned before, there is no limit to the amount of dimensions a vector may have (technically, there must be one or more dimensions), so we could conceivably have space consisting of thousands or tens of thousands of dimensions. At that point we can't rely on the same human intuitions about space as we could when working with just two or three dimensions. In practice, most interesting applications of machine learning deal with many, many dimensions.
We can get a better sense of this by plotting a vector out. For instance, a 2D vector `[5,0]` would look like:

So in a sense vectors can be thought of lines that "point" to the position they specify - here the vector is a line "pointing" to `[5,0]`. If the vector were 3D, e.g. `[8,1,3]`, then we would have to visualize it in 3D space, and so on.
So vectors are great - they allow us to form logical groupings of numbers. For instance, if we're talking about cities on a map we would want to group their latitude and longitude together. We'd represent Lagos with `[6.455027, 3.384082]` and Beijing separately with `[39.9042, 116.4074]`. If we have an inventory of books for sale, we could represent each book with its own vector consisting of its price, number of pages, and remaining stock.
To use vectors in functions, there are a few mathematical operations you need to know.
### Basic vector operations
Vectors can be added (and subtracted) easily:
```
np.array([6, 2]) + np.array([-4, 4])
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} + \begin{bmatrix} -4 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 + -4 \\ 2 + 4 \end{bmatrix} = \begin{bmatrix} 2 \\ 6 \end{bmatrix}
$$
However, when it comes to vector multiplication there are many different kinds.
The simplest is _vector-scalar_ multiplication:
```
3 * np.array([2, 1])
```
$$
3\begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \times 2 \\ 3 \times 1
\end{bmatrix} = \begin{bmatrix} 6 \\ 3 \end{bmatrix}
$$
But when you multiply two vectors together you have a few options. I'll cover the two most important ones here.
The one you might have thought of is the _element-wise product_, also called the _pointwise product_, _component-wise product_, or the _Hadamard product_, typically notated with $\odot$. This just involves multiplying the corresponding elements of each vector together, resulting in another vector:
```
np.array([6, 2]) * np.array([-4, 4])
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} \odot \begin{bmatrix} -4 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 \times -4 \\ 2 \times 4 \end{bmatrix} = \begin{bmatrix} -24 \\ 8 \end{bmatrix}
$$
The other vector product, which you'll encounter a lot, is the _dot product_, also called _inner product_, usually notated with $\cdot$ (though when vectors are placed side-by-side this often implies dot multiplication). This involves multiplying corresponding elements of each vector and then summing the resulting vector's components (so this results in a scalar rather than another vector).
```
np.dot(np.array([6, 2]), np.array([-4, 4]))
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} \cdot \begin{bmatrix} -4 \\ 4 \end{bmatrix} = (6 \times -4) + (2 \times 4) = -16
$$
The more general formulation is:
```
# a slow pure-Python dot product
def dot(a, b):
assert len(a) == len(b)
return sum(a_i * b_i for a_i, b_i in zip(a,b))
```
$$
\begin{aligned}
\vec{a} \cdot \vec{b} &= \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} = a_1b_1 + a_2b_2 + \dots + a_nb_n \\
&= \sum^n_{i=1} a_i b_i
\end{aligned}
$$
Note that the vectors in these operations must have the same dimensions!
Perhaps the most important vector operation mentioned here is the dot product. We'll return to the house example to see why. Let's say want to represent a house with three variables: square footage, number of bedrooms, and the number of bathrooms. For convenience we'll notate the variables $x_1, x_2, x_3$, respectively. We're working in three dimensions now so instead of learning a line we're learning a _hyperplane_ (if we were working with two dimensions we'd be learning a plane, "hyperplane" is the term for the equivalent of a plane in higher dimensions).
Aside from the different name, the function we're learning is essentially of the same form as before, just with more variables and thus more parameters. We'll notate each parameter as $\theta_i$ as is the convention (you may see $\beta_i$ used elsewhere), and for the intercept (what was the $b$ term in the original line), we'll add in a dummy variable $x_0 = 1$ as is the typical practice (thus $\theta_0$ is equivalent to $b$):
```
# this is so clumsy in python;
# this will become more concise in a bit
def f(x0, x1, x2, x3, theta0, theta1, theta2, theta3):
return theta0 * x0\
+ theta1 * x1\
+ theta2 * x2\
+ theta3 * x3
```
$$
y = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3
$$
This kind of looks like the dot product, doesn't it? In fact, we can re-write this entire function as a dot product. We define our feature vector $x = [x_0, x_1, x_2, x_3]$ and our parameter vector $\theta = [\theta_0, \theta_1, \theta_2, \theta_3]$, then re-write the function:
```
def f(x, theta):
return x.dot(theta)
```
$$
y = \theta x
$$
So that's how we incorporate multiple features in a representation.
There's a whole lot more to vectors than what's presented here, but this is the ground-level knowledge you should have of them. Other aspects of vectors will be explained as they come up.
## Learning
So machine learning algorithms learn parameters - how do they do it?
Here we're focusing on the most common kind of machine learning - _supervised_ learning. In supervised learning, the algorithm learns parameters from data which includes both the inputs and the true outputs. This data is called _training_ data.
Although they vary on specifics, there is a general approach that supervised machine learning algorithms use to learn parameters. The idea is that the algorithm takes an input example, inputs it into the current guess at the function (called the _hypothesis_, notate $h_{\theta}$), and then checks how wrong its output is against the true output. The algorithm then updates its hypothesis (that is, its guesses for the parameters), accordingly.
"How wrong" an algorithm is, can vary depending on the _loss function_ it is using. The loss function takes the algorithm's current guess for the output, $\hat y$, and the true output, $y$, and returns some value quantifying its wrongness. Certain loss functions are more appropriate for certain tasks, which we'll get into later.
We'll get into the specifies of how the algorithm determines what kind of update to perform (i.e. how much each parameter changes), but before we do that we should consider how we manage batches of training examples (i.e. multiple training vectors) simultaneously.
## Matrices
__Matrices__ are in a sense a "vector" of vectors. That is, where a vector can be thought of as a logical grouping of numbers, a matrix can be thought of as a logical grouping of vectors. So if a vector represents a book in our catalog (id, price, number in stock), a matrix could represent the entire catalog (each row refers to a book). Or if we want to represent a grayscale image, the matrix can represent the brightness values of the pixels in the image.
```
A = np.array([
[6, 8, 0],
[8, 2, 7],
[3, 3, 9],
[3, 8, 6]
])
```
$$
\mathbf A =
\begin{bmatrix}
6 & 8 & 0 \\
8 & 2 & 7 \\
3 & 3 & 9 \\
3 & 8 & 6
\end{bmatrix}
$$
Matrices are usually represented with uppercase variables.
Note that the "vectors" in the matrix must have the same dimension. The matrix's dimensions are expressed in the form $m \times n$, meaning that there are $m$ rows and $n$ columns. So the example matrix has dimensions of $4 \times 3$. Numpy calls these dimensions a matrix's "shape".
We can access a particular element, $A_{i,j}$, in a matrix by its indices. Say we want to refer to the element in the 2nd row and the 3rd column (remember that python uses 0-indexing):
```
A[1,2]
```
### Basic matrix operations
Like vectors, matrix addition and subtraction is straightforward (again, they must be of the same dimensions):
```
B = np.array([
[8, 3, 7],
[2, 9, 6],
[2, 5, 6],
[5, 0, 6]
])
A + B
```
$$
\begin{aligned}
\mathbf B &=
\begin{bmatrix}
8 & 3 & 7 \\
2 & 9 & 6 \\
2 & 5 & 6 \\
5 & 0 & 6
\end{bmatrix} \\
A + B &=
\begin{bmatrix}
8+6 & 3+8 & 7+0 \\
2+8 & 9+2 & 6+7 \\
2+3 & 5+3 & 6+9 \\
5+3 & 0+8 & 6+6
\end{bmatrix} \\
&=
\begin{bmatrix}
14 & 11 & 7 \\
10 & 11 & 13 \\
5 & 8 & 15 \\
8 & 8 & 12
\end{bmatrix} \\
\end{aligned}
$$
Matrices also have a few different multiplication operations, like vectors.
_Matrix-scalar multiplication_ is similar to vector-scalar multiplication - you just distribute the scalar, multiplying it with each element in the matrix.
_Matrix-vector products_ require that the vector has the same dimension as the matrix has columns, i.e. for an $m \times n$ matrix, the vector must be $n$-dimensional. The operation basically involves taking the dot product of each matrix row with the vector:
```
# a slow pure-Python matrix-vector product,
# using our previous dot product implementation
def matrix_vector_product(M, v):
return [np.dot(row, v) for row in M]
# or, with numpy, you could use np.matmul(A,v)
```
$$
\mathbf M v =
\begin{bmatrix}
M_{1} \cdot v \\
\vdots \\
M_{m} \cdot v \\
\end{bmatrix}
$$
We have a few options when it comes to multiplying matrices with matrices.
However, before we go any further we should talk about the _tranpose_ operation - this just involves switching the columns and rows of a matrix. The transpose of a matrix $A$ is notated $A^T$:
```
A = np.array([
[1,2,3],
[4,5,6]
])
np.transpose(A)
```
$$
\begin{aligned}
\mathbf A &=
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6
\end{bmatrix} \\
\mathbf A^T &=
\begin{bmatrix}
1 & 4 \\
2 & 5 \\
3 & 6
\end{bmatrix}
\end{aligned}
$$
For matrix-matrix products, the matrix on the lefthand must have the same number of columns as the righthand's rows. To be more concrete, we'll represent a matrix-matrix product as $A B$ and we'll say that $A$ has $m \times n$ dimensions. For this operation to work, $B$ must have $n \times p$ dimensions. The resulting product will have $m \times p$ dimensions.
```
# a slow pure-Python matrix Hadamard product
def matrix_matrix_product(A, B):
_, a_cols = np.shape(A)
b_rows, _ = np.shape(B)
assert a_cols == b_rows
result = []
# tranpose B so we can iterate over its columns
for col in np.tranpose(B):
# using our previous implementation
result.append(
matrix_vector_product(A, col))
return np.transpose(result)
```
$$
\mathbf AB =
\begin{bmatrix}
A B^T_1 \\
\vdots \\
A B^T_p
\end{bmatrix}^T
$$
Finally, like with vectors, we also have Hadamard (element-wise) products:
```
# a slow pure-Python matrix-matrix product
# or, with numpy, you can use A * B
def matrix_matrix_hadamard(A, B):
result = []
for a_row, b_row in zip(A, B):
result.append(
zip(a_i * b_i for a_i, b_i in zip(a_row, b_row)))
```
$$
\mathbf A \odot B =
\begin{bmatrix}
A_{1,1} B_{1,1} & \dots & A_{1,n} B_{1,n} \\
\vdots & \dots & \vdots \\
A_{m,1} B_{m,1} & \dots & A_{m,n} B_{m,n}
\end{bmatrix}
$$
Like vector Hadamard products, this requires that the two matrices share the same dimensions.
## Tensors
We've seen vectors, which is like a list of numbers, and matrices, which is like a list of a list of numbers. We can generalize this concept even further, for instance, with a list of a list of a list of numbers and so on. What all of these structures are called are _tensors_ (i.e. the "tensor" in "TensorFlow"). They are distinguished by their _rank_, which, if you're thinking in the "list of lists" way, refers to the number of nestings. So a vector has a rank of one (just a list of numbers) and a matrix has a rank of two (a list of a list of numbers).
Another way to think of rank is by number of indices necessary to access an element in the tensor. An element in a vector is accessed by one index, e.g. `v[i]`, so it is of rank one. An element in a matrix is accessed by two indices, e.g. `M[i,j]`, so it is of rank two.
Why is the concept of a tensor useful? Before we referred to vectors as a logical grouping of numbers and matrices as a logical grouping of vectors. What if we need a logical grouping of matrices? That's what 3rd-rank tensors are! A matrix can represent a grayscale image, but what about a color image with three color channels (red, green, blue)? With a 3rd-rank tensor, we could represent each channel as its own matrix and group them together.
## Learning continued
When the current hypothesis is wrong, how does the algorithm know how to adjust the parameters?
Let's take a step back and look at it another way. The loss function measures the wrongness of the hypothesis $h_{\theta}$ - another way of saying this is the loss function is a function of the parameters $\theta$. So we could notate it as $L(\theta)$.
The minimum of $L(\theta)$ is the point where the parameters guess $\theta$ is least wrong (at best, $L(\theta) = 0$, i.e. a perfect score, though this is not always good, as will be explained later); i.e. the best guess for the parameters.
So the algorithm learns the best-fitting function by minimizing its loss function. That is, we can frame this as an optimization problem.
There are many techniques to solve an optimization problem - sometimes they can be solved analytically (i.e. by moving around variables and isolating the one you want to solve for), but more often than not we must solve them numerically, i.e. by guessing a lot of different values - but not randomly!
The prevailing technique now is called _gradient descent_, and to understand how it works, we have to understand derivatives.
## Derivatives
Derivatives are everywhere in machine learning, so it's worthwhile become a bit familiar with them. I won't go into specifics on differentiation (how to calculate derivatives) because now we're spoiled with automatic differentiation, but it's still good to have a solid intuition about derivatives themselves.
A derivative expresses a rate of (instantaneous) change - they are always about how one variable quantity changes with respect to another variable quantity. That's basically all there is to it. For instance, velocity is a derivative which expresses how position changes with respect to time. Another interpretation, which is more relevant to machine learning, is that a derivative tells us how to change one variable to achieve a desired change in the other variable. Velocity, for instance, tells us how to change position by "changing" time.
To get a better understanding of _instantaneous_ change, consider a cyclist, cycling on a line. We have data about their position over time. We could calculate an average velocity over the data's entire time period, but we typically prefer to know the velocity at any given _moment_ (i.e. at any _instant_).
Let's get more concrete first. Let's say we have data for $n$ seconds, i.e. from $t_0$ to $t_n$ seconds, and the position at any given second $i$ is $p_i$. If we wanted to get the rate of change in position over the entire time interval, we'd just do:
```
positions = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, # moving forward
9, 9, 9, 9, 9, 9, 9, 9, 9, 9, # pausing
9, 8, 7, 6, 5, 4, 3, 2, 1, 0] # moving backwards
t_0 = 0
t_n = 29
(positions[t_n] - positions[t_0])/t_n
```
$$
v = \frac{p_n - p_0}{n}
$$
This kind of makes it look like the cyclist didn't move at all. It would probably be more useful to identify the velocity at a given second $t$. Thus we want to come up with some function $v(t)$ which gives us the velocity at some second $t$. We can apply the same approach we just used to get the velocity over the entire time interval, but we focus on a shorter time interval instead. To get the _instantaneous_ change at $t$ we just keep reducing the interval we look at until it is basically 0.
Derivatives have a special notation. A derivative of a function $f(x)$ with respect to a variable $x$ is notated:
$$
\frac{\delta f(x)}{\delta x}
$$
So if position is a function of time, e.g. $p = f(t)$, then velocity can be represented as $\frac{\delta p}{\delta t}$. To drive the point home, this derivative is also a function of time (derivatives are functions of what their "with respect to" variable is).
Since we are often computing derivatives of a function with respect to its input, a shorthand for the derivative of a function $f(x)$ with respect to $x$ can also be notated $f'(x)$.
### The Chain Rule
A very important property of derivatives is the _chain rule_ (there are other "chain rules" throughout mathematics, if we want to be specific, this is the "chain rule of derivatives"). The chain rule is important because it allows us to take complicated nested functions and more manageably differentiate them.
Let's look at an example to make this concrete:
```
def g(x):
return x**2
def h(x):
return x**3
def f(x):
return g(h(x))
# derivatives
def g_(x):
return 2*x
def h_(x):
return 3*(x**2)
```
$$
\begin{aligned}
g(x) &= x^2 \\
h(x) &= x^3 \\
f(x) &= g(h(x)) \\
g'(x) &= 2x \\
h'(x) &= 3x^2
\end{aligned}
$$
We're interested in understanding how $f(x)$ changes with respect to $x$, so we want to compute the derivative of $f(x)$. The chain rule allows us to individually differentiate the component functions of $f(x)$ and multiply those to get $f'(x)$:
```
def f_(x):
return g_(x) * h_(x)
```
$$
\frac{df}{dx} = \frac{dg}{dh} \frac{dh}{dx}
$$
This example is a bit contrived (there is a very easy way to differentiate this particular example that doesn't involve the chain rule) but if $g(x)$ and $h(x)$ were really nasty functions, the chain rule makes them quite a lot easier to deal with.
The chain rule can be applied to nested functions ad nauseaum! You can apply it to something crazy like $f(g(h(u(q(p(x))))))$. In fact, with deep neural networks, you are typically dealing with function compositions even more gnarly than this, so the chain rule is cornerstone there.
### Partial derivatives and gradients
The functions we've looked at so far just have a single input, but you can imagine many scenarios where you'd want to work with functions with some arbitrary number of inputs (i.e. a _multivariable_ function), like $f(x,y,z)$.
Here's where _partial deriatives_ come into play. Partial derivatives are just like regular derivatives except we use them for multivariable functions; it just means we only differentiate with respect to one variable at a time. So for $f(x,y,z)$, we'd have a partial derivative with respect to $x$, i.e. $\frac{\partial f}{\partial x}$ (note the slightly different notation), one with respect to $y$, i.e. $\frac{\partial f}{\partial y}$, and one with respect to $z$, i.e. $\frac{\partial f}{\partial z}$.
That's pretty simple! But it would be useful to group these partial derivatives together in some way. If we put these partial derivatives together in a vector, the resulting vector is the _gradient_ of $f$, notated $\nabla f$ (the symbol is called "nabla").
### Higher-order derivatives
We saw that velocity is the derivative of position because it describes how position changes over time. Acceleration similarly describes how _velocity_ changes over time, so we'd say that acceleration is the derivative of velocity. We can also say that acceleration is the _second-order_ derivative of position (that is, it is the derivative of its derivative).
This is the general idea behind higher-order derivatives.
## Gradient descent
Once you understand derivatives, gradient descent is really, really simple. The basic idea is that we use the derivative of the loss $L(\theta)$ with respect to $\theta$ and figure out which way the loss is decreasing, then "move" the parameter guess in that direction.
| github_jupyter |
# Check Environment
This notebook checks that you have correctly created the environment and that all packages needed are installed.
## Environment
The next command should return a line like (Mac/Linux):
/<YOUR-HOME-FOLDER>/anaconda/envs/ztdl/bin/python
or like (Windows 10):
C:\\<YOUR-HOME-FOLDER>\\Anaconda3\\envs\\ztdl\\python.exe
In particular you should make sure that you are using the python executable from within the course environment.
If that's not the case do this:
1. close this notebook
2. go to the terminal and stop jupyer notebook
3. make sure that you have activated the environment, you should see a prompt like:
(ztdl) $
4. (optional) if you don't see that prompt activate the environment:
- mac/linux:
conda activate ztdl
- windows:
activate ztdl
5. restart jupyter notebook
```
import os
import sys
sys.executable
```
## Python 3.6
The next line should say that you're using Python 3.6.x from Continuum Analytics. At the time of publication it looks like this (Mac/Linux):
Python 3.6.7 |Anaconda, Inc.| (default, Oct 23 2018, 14:01:38)
[GCC 4.2.1 Compatible Clang 4.0.1 (tags/RELEASE_401/final)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
or like this (Windows 10):
Python 3.6.7 |Anaconda, Inc.| (default, Oct 28 2018, 19:44:12) [MSC v.1915 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
but date and exact version of GCC may change in the future.
If you see a different version of python, go back to the previous step and make sure you created and activated the environment correctly.
```
import sys
sys.version
```
## Jupyter
Check that Jupyter is running from within the environment. The next line should look like (Mac/Linux):
/<YOUR-HOME-FOLDER>/anaconda/envs/ztdl/lib/python3.6/site-packages/jupyter.py'
or like this (Windows 10):
C:\\Users\\paperspace\\Anaconda3\\envs\\ztdl\\lib\\site-packages\\jupyter.py
```
import jupyter
jupyter.__file__
```
## Other packages
Here we will check that all the packages are installed and have the correct versions. If everything is ok you should see:
Using TensorFlow backend.
Houston we are go!
If there's any issue here please make sure you have checked the previous steps and if it's all good please send us a question in the Q&A forum.
```
import pip
import numpy
import jupyter
import matplotlib
import sklearn
import scipy
import pandas
import PIL
import seaborn
import h5py
import tensorflow
import keras
def check_version(pkg, version):
actual = pkg.__version__.split('.')
if len(actual) == 3:
actual_major = '.'.join(actual[:2])
elif len(actual) == 2:
actual_major = '.'.join(actual)
else:
raise NotImplementedError(pkg.__name__ +
"actual version :"+
pkg.__version__)
try:
assert(actual_major == version)
except Exception as ex:
print("{} {}\t=> {}".format(pkg.__name__,
version,
pkg.__version__))
raise ex
check_version(pip, '10.0')
check_version(numpy, '1.15')
check_version(matplotlib, '3.0')
check_version(sklearn, '0.20')
check_version(scipy, '1.1')
check_version(pandas, '0.23')
check_version(PIL, '5.3')
check_version(seaborn, '0.9')
check_version(h5py, '2.8')
check_version(tensorflow, '1.11')
check_version(keras, '2.2')
print("Houston we are go!")
```
| github_jupyter |
## Preprocessing
```
# Import our dependencies
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import pandas as pd
import tensorflow as tf
# Import and read the charity_data.csv.
import pandas as pd
application_df = pd.read_csv("charity_data.csv")
application_df.head()
# Drop the non-beneficial ID columns, 'EIN' and 'NAME'.
application_df = application_df.drop(['EIN', 'NAME'], axis=1)
# Determine the number of unique values in each column.
application_df.nunique()
# Look at APPLICATION_TYPE value counts for binning
val_count = application_df['APPLICATION_TYPE'].value_counts()
val_count
# Choose a cutoff value and create a list of application types to be replaced
# use the variable name `application_types_to_replace`
application_types_to_replace = list(val_count[val_count<200].index)
# Replace in dataframe
for app in application_types_to_replace:
application_df['APPLICATION_TYPE'] = application_df['APPLICATION_TYPE'].replace(app,"Other")
# Check to make sure binning was successful
application_df['APPLICATION_TYPE'].value_counts()
# Look at CLASSIFICATION value counts for binning
class_val_count = application_df['CLASSIFICATION'].value_counts()
class_val_count
# You may find it helpful to look at CLASSIFICATION value counts >1
class_val_count2 = class_val_count[class_val_count>1]
class_val_count2
# Choose a cutoff value and create a list of classifications to be replaced
# use the variable name `classifications_to_replace`
classifications_to_replace =class_val_count.loc[class_val_count<1000].index
# Replace in dataframe
for cls in classifications_to_replace:
application_df['CLASSIFICATION'] = application_df['CLASSIFICATION'].replace(cls,"Other")
# Check to make sure binning was successful
application_df['CLASSIFICATION'].value_counts()
# Convert categorical data to numeric with `pd.get_dummies`
dummies_df = pd.get_dummies(application_df)
dummies_df
# Split our preprocessed data into our features and target arrays
X = dummies_df.drop(['IS_SUCCESSFUL'],1).values
y = dummies_df['IS_SUCCESSFUL'].values
# Split the preprocessed data into a training and testing dataset
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state= 42)
print(X.shape)
print(y.shape)
# Create a StandardScaler instances
scaler = StandardScaler()
# Fit the StandardScaler
X_scaler = scaler.fit(X_train)
# Scale the data
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
```
## Compile, Train and Evaluate the Model
```
# Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
input_features = len(X_train_scaled[0])
hidden_nodes_layer1 = 80
hidden_nodes_layer2 = 30
#hidden_nodes_layer3 = 60
nn = tf.keras.models.Sequential()
# First hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer1, input_dim=input_features, activation='relu'))
# Second hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer2, activation='relu'))
# Third hidden layer
#nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer3, activation='relu'))
# Output layer
nn.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))
# Check the structure of the model
nn.summary()
# Compile the model
nn.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
# Train the model
fit_model = nn.fit(X_train_scaled, y_train, epochs=100)
# Evaluate the model using the test data
model_loss, model_accuracy = nn.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Export our model to HDF5 file
nn.save("AlphabetSoupCharity.h5")
```
**Optimization 1**
```
# Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
input_features = len(X_train_scaled[0])
hidden_nodes_layer1 = 43
hidden_nodes_layer2 = 25
#hidden_nodes_layer3 = 15
nn2 = tf.keras.models.Sequential()
# First hidden layer
nn2.add(tf.keras.layers.Dense(units=hidden_nodes_layer1, input_dim=input_features, activation='relu'))
# Second hidden layer
nn2.add(tf.keras.layers.Dense(units=hidden_nodes_layer2, activation='relu'))
# Third hidden layer
#nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer3, activation='relu'))
# Output layer
nn2.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))
# Check the structure of the model
nn2.summary()
# Compile the model
nn2.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
# Train the model
fit_model = nn2.fit(X_train_scaled, y_train, epochs=200)
# Evaluate the model using the test data
model_loss, model_accuracy = nn2.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Export our model to HDF5 file
nn2.save("AlphabetSoupCharity_optimize_1.h5")
```
**Optimization 2**
```
# Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
input_features = len(X_train_scaled[0])
hidden_nodes_layer1 = 20
hidden_nodes_layer2 = 40
hidden_nodes_layer3 = 80
nn3 = tf.keras.models.Sequential()
# First hidden layer
nn3.add(tf.keras.layers.Dense(units=hidden_nodes_layer1, input_dim=input_features, activation='relu'))
# Second hidden layer
nn3.add(tf.keras.layers.Dense(units=hidden_nodes_layer2, activation='relu'))
# Third hidden layer
nn3.add(tf.keras.layers.Dense(units=hidden_nodes_layer3, activation='relu'))
# Output layer
nn3.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))
# Check the structure of the model
nn3.summary()
# Compile the model
nn3.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
# Train the model
fit_model = nn3.fit(X_train_scaled, y_train, epochs=200)
# Evaluate the model using the test data
model_loss, model_accuracy = nn3.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Export our model to HDF5 file
nn3.save("AlphabetSoupCharity_optimize_2.h5")
# Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
input_features = len(X_train_scaled[0])
hidden_nodes_layer1 = 60
hidden_nodes_layer2 = 60
hidden_nodes_layer3 = 40
hidden_nodes_layer4 = 20
nn4 = tf.keras.models.Sequential()
# First hidden layer
nn4.add(tf.keras.layers.Dense(units=hidden_nodes_layer1, input_dim=input_features, activation='relu'))
# Second hidden layer
nn4.add(tf.keras.layers.Dense(units=hidden_nodes_layer2, activation='relu'))
# Third hidden layer
nn4.add(tf.keras.layers.Dense(units=hidden_nodes_layer3, activation='relu'))
# Forth hidden layer
nn4.add(tf.keras.layers.Dense(units=hidden_nodes_layer4, activation='relu'))
# Output layer
nn4.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))
# Check the structure of the model
nn4.summary()
# Compile the model
nn4.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
# Train the model
fit_model = nn4.fit(X_train_scaled, y_train, epochs=200)
# Evaluate the model using the test data
model_loss, model_accuracy = nn4.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Export our model to HDF5 file
nn4.save("AlphabetSoupCharity_optimize_3.h5")
```
| github_jupyter |
# The Graph Data Access
In this notebook, we read in the data that was generated and saved as a csv from the [TheGraphDataSetCreation](TheGraphDataSetCreation.ipynb) notebook.
Goals of this notebook are to obtain:
* Signals, states, event and sequences
* Volatility metrics
* ID perceived shocks (correlated with announcements)
* Signal for target price
* Signal for market price
* Error plot
As a starting point for moving to a decision support system.
```
# import libraries
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy as sp
from statsmodels.distributions.empirical_distribution import ECDF
import scipy.stats as stats
```
## Import data and add additional attributes
```
graphData = pd.read_csv('saved_results/RaiLiveGraphData.csv')
del graphData['Unnamed: 0']
graphData.head()
graphData.describe()
graphData.plot(x='blockNumber',y='redemptionPriceActual',kind='line',title='redemptionPriceActual')
graphData.plot(x='blockNumber',y='redemptionRateActual',kind='line',title='redemptionRateActual')
graphData['error'] = graphData['redemptionPriceActual'] - graphData['marketPriceUsd']
graphData['error_integral'] = graphData['error'].cumsum()
graphData.plot(x='blockNumber',y='error',kind='line',title='error')
graphData.plot(x='blockNumber',y='error_integral',kind='line',title='Steady state error')
```
## Error experimentation
#### Note: not taking into account control period
```
kp = 2e-7
#ki = (-kp * error)/(integral_error)
# computing at each time, what would the value of ki need to be such that the redemption price would be constant
graphData['equilibriation_ki'] = (-kp * graphData.error)/graphData.error_integral
# todo iterate through labels and append negative
graphData['equilibriation_ki'].apply(lambda x: -x).plot(logy = True,title='Actual equilibriation_ki - flipped sign for log plotting')
plt.hlines(5e-9, 0, 450, linestyles='solid', label='Recommended ki - flipped sign', color='r')
plt.hlines(-(graphData['equilibriation_ki'].median()), 0, 450, linestyles='solid', label='median actual ki - flipped', color='g')
locs,labels = plt.yticks() # Get the current locations and labelsyticks
new_locs = []
for i in locs:
new_locs.append('-'+str(i))
plt.yticks(locs, new_locs)
plt.legend(loc="upper right")
graphData['equilibriation_ki'].median()
```
### Counterfactual if intergral control rate had been median the whole time
```
graphData['counterfactual_redemption_rate'] = (kp * graphData['error'] + graphData['equilibriation_ki'].median())/ graphData['error_integral']
subsetGraph = graphData.iloc[50:]
sns.lineplot(data=subsetGraph,x="blockNumber", y="counterfactual_redemption_rate",label='Counterfactual')
ax2 = plt.twinx()
# let reflexer know this is wrong
sns.lineplot(data=subsetGraph,x="blockNumber", y="redemptionRateActual",ax=ax2,color='r',label='Actual')
plt.title('Actual redemption rate vs counterfactual')
plt.legend(loc="upper left")
```
## Goodness of fit tests
Whether or not counterfactual is far enough from actual to reject null that they are from the same distributions.
```
# fit a cdf
ecdf = ECDF(subsetGraph.redemptionRateActual.values)
ecdf2 = ECDF(subsetGraph.counterfactual_redemption_rate.values)
plt.plot(ecdf.x,ecdf.y,color='r')
plt.title('redemptionRateActual ECDF')
plt.show()
plt.plot(ecdf2.x,ecdf2.y,color='b')
plt.title('counterfactual_redemption_rate ECDF')
plt.show()
alpha = 0.05
statistic, p_value = stats.ks_2samp(subsetGraph.redemptionRateActual.values, subsetGraph.counterfactual_redemption_rate.values) # two sided
if p_value > alpha:
decision = "Sample is from the distribution"
elif p_value <= alpha:
decision = "Sample is not from the distribution"
print(p_value)
print(decision)
```
Based on our analysis using the Kolmogorov-Smirnov Goodness-of-Fit Test, the distributions are very different. As can be seen above from their EDCF plots, you can see a different in their distributions, however pay close attention to the x axis and you can see the distribution difference is significant.
```
# scatterplot of linear regressoin residuals
sns.residplot(x='blockNumber', y='redemptionRateActual', data=subsetGraph, label='redemptionRateActual')
plt.title('redemptionRateActual regression residuals')
sns.residplot(x='blockNumber', y='counterfactual_redemption_rate', data=subsetGraph,label='counterfactual_redemption_rate')
plt.title('counterfactual_redemption_rate regression residuals')
graphData.plot(x='blockNumber',y='globalDebt',kind='line',title='globalDebt')
graphData.plot(x='blockNumber',y='erc20CoinTotalSupply',kind='line',title='erc20CoinTotalSupply')
graphData.plot(x='blockNumber',y='marketPriceEth',kind='line',title='marketPriceEth')
graphData.plot(x='blockNumber',y='marketPriceUsd',kind='line',title='marketPriceUsd')
```
## Conclusion
Using The Graph, a lot of data about the Rai system can be obtained for analyzing the health of the system. With some data manipulation, these data streams could be intergrated into the Rai cadCAD model to turn it into a true decision support system.
| github_jupyter |
```
import pandas as pd
import numpy as np
import pickle
BASEDIR_MIMIC = '/Volumes/MyData/MIMIC_data/mimiciii/1.4'
def get_note_events():
n_rows = 100000
icd9_code = pd.read_csv(f"{BASEDIR_MIMIC}/DIAGNOSES_ICD.csv", index_col = None)
# create the iterator
noteevents_iterator = pd.read_csv(
f"{BASEDIR_MIMIC}/NOTEEVENTS.csv",
iterator=True,
chunksize=n_rows)
events_list = ['Discharge summary',
'Echo',
'ECG',
'Nursing',
'Physician ',
'Rehab Services',
'Case Management ',
'Respiratory ',
'Nutrition',
'General',
'Social Work',
'Pharmacy',
'Consult',
'Radiology',
'Nursing/other']
# concatenate according to a filter to get our noteevents data
noteevents = pd.concat(
[noteevents_chunk[
np.logical_and(
noteevents_chunk.CATEGORY.isin(events_list[1:]),
noteevents_chunk.DESCRIPTION.isin(["Report"])
)
]
for noteevents_chunk in noteevents_iterator])
# drop all nan in column HADM_ID
noteevents = noteevents.dropna(subset=["HADM_ID"])
noteevents.HADM_ID = noteevents.HADM_ID.astype(int)
try:
assert len(noteevents.drop_duplicates(["SUBJECT_ID","HADM_ID"])) == len(noteevents)
except AssertionError as e:
print("There are duplicates on Primary Key Set")
noteevents.CHARTDATE = pd.to_datetime(noteevents.CHARTDATE , format = '%Y-%m-%d %H:%M:%S', errors = 'coerce')
pd.set_option('display.max_colwidth',50)
noteevents.sort_values(["SUBJECT_ID","HADM_ID","CHARTDATE"], inplace =True)
#noteevents.drop_duplicates(["SUBJECT_ID","HADM_ID"], inplace = True)
noteevents.reset_index(drop = True, inplace = True)
top_values = (icd9_code.groupby('ICD9_CODE').
agg({"SUBJECT_ID": "nunique"}).
reset_index().sort_values(['SUBJECT_ID'], ascending = False).ICD9_CODE.tolist()[:15])
# icd9_code = icd9_code[icd9_code.ICD9_CODE.isin(top_values)]
icd9_code = icd9_code[icd9_code.ICD9_CODE.isin(top_values)]
import re
import itertools
def clean_text(text):
return [x for x in list(itertools.chain.from_iterable([t.split("<>") for t in text.replace("\n"," ").split(" ")])) if len(x) > 0]
# irrelevant_tags = ["Admission Date:", "Date of Birth:", "Service:", "Attending:", "Facility:", "Medications on Admission:", "Discharge Medications:", "Completed by:",
# "Dictated By:" , "Department:" , "Provider:"]
updated_text = ["<>".join([" ".join(re.split("\n\d|\n\s+",re.sub("^(.*?):","",x).strip()))
for x in text.split("\n\n")]) for text in noteevents.TEXT]
updated_text = [re.sub("(\[.*?\])", "", text) for text in updated_text]
updated_text = [" ".join(clean_text(x)) for x in updated_text]
noteevents["CLEAN_TEXT"] = updated_text
return noteevents
noteevents = get_note_events()
def mapNotes(dataset):
print(f"Mapping notes on {dataset}.")
df = pickle.load(open(f'../data/mimic3/train_data_mimic3/{dataset}', 'rb'))
BASEDIR_MIMIC = '/Volumes/MyData/MIMIC_data/mimiciii/1.4'
icustays = pd.read_csv(f"{BASEDIR_MIMIC}/ICUSTAYS.csv", index_col = None)
# SUBJECT_ID "_" ICUSTAY_ID "_episode" episode "_timeseries_readmission.csv"
import re
episodes = df['names']
regex = r"(\d+)_(\d+)_episode(\d+)_timeseries_readmission\.csv"
sid = []
hadmids = []
icustayid = [] # ICUSTAYS.csv ICUSTAY_ID
episode = []
notestexts = []
notextepis = []
for epi in episodes:
match = re.findall(regex, epi) #, re.MULTILINE)
sid.append(int(match[0][0]))
icustayid.append(int(match[0][1]))
episode.append(int(match[0][2]))
hadmid = icustays[icustays['ICUSTAY_ID']==int(match[0][1])]['HADM_ID']
hadmids.append(int(hadmid))
try:
#text = noteevents[noteevents['HADM_ID']==int(hadmid)]['TEXT'].iloc[0]
#text = noteevents[noteevents['HADM_ID']==int(hadmid)]['CLEAN_TEXT'].iloc[0]
text = "\n\n".join([t for t in noteevents[noteevents['HADM_ID']==int(hadmid)]['CLEAN_TEXT']])
except:
notextepis.append(int(hadmid))
text = ''
notestexts.append(text)
print(len(episodes), len(notextepis), len(set(notextepis)))
print(len(sid), len(hadmids), len(df['names']))
notesfull = pd.DataFrame({'SUBJECT_ID':sid, 'HADM_ID':hadmids, 'ICUSTAY_ID':icustayid, 'EPISODE':episode, 'CLEAN_TEXT':notestexts})
# save full data
filename = f'./events_notes_{dataset}'
with open(filename + '.pickle', 'wb') as handle:
pickle.dump(notesfull, handle, protocol=pickle.HIGHEST_PROTOCOL)
print(f"Finished mapping notes on {dataset}.\n")
def combineData(dataset):
print(f"Combining data for all {dataset}.")
df = pickle.load(open(f'../data/mimic3/train_data_mimic3/{dataset}', 'rb'))
print(df.keys(), len(df['data']),len(df['names']), df['data'][0].shape, len(df['data'][1]), len(df['names']))
notes = pickle.load(open(f'clinical_notes_{dataset}.pickle', 'rb'))
eventsnotes = pickle.load(open(f'events_notes_{dataset}.pickle', 'rb'))
# how many empty text rows
# np.where(notes.applymap(lambda x: x == ''))
# how many empty text rows
print(f"There are {len(list(notes[notes['CLEAN_TEXT'] == ''].index))} empty rows in notes.")
print(f"There are {len(list(eventsnotes[eventsnotes['CLEAN_TEXT'] == ''].index))} empty rows in eventsnotes.")
X = df['data'][0]
y = np.array(df['data'][1])
N = list(notes.CLEAN_TEXT)
EN = list(eventsnotes.CLEAN_TEXT)
# check if all three data sets have the same size/length
assert len(X) == len(y) == len(N) == len(EN)
empty_ind_N = list(notes[notes['CLEAN_TEXT'] == ''].index)
empty_ind_EN = list(notes[eventsnotes['CLEAN_TEXT'] == ''].index)
N_ = np.array(N)
EN_ = np.array(EN)
mask = np.ones(len(notes), np.bool)
mask[empty_ind_N] = 0
mask[empty_ind_EN] = 0
good_notes = N_[mask]
good_eventsnotes = EN_[mask]
good_X = X[mask]
good_y = y[mask]
print(f"Final shapes = {good_X.shape, good_y.shape, good_notes.shape}")
data = {'inputs': good_X,
'labels': good_y,
'eventsnotes': good_eventsnotes,
'notes': good_notes}
# save full data
filename = f'./new_{dataset}_CNEP'
#full_data.to_csv(filename + '.csv', index = None)
with open(filename + '.pickle', 'wb') as handle:
pickle.dump(data, handle, protocol=pickle.HIGHEST_PROTOCOL)
print("finished.\n")
all_datasets = ['train_data', 'test_data', 'val_data']
for dataset in all_datasets:
print(f"\n\nProcessing dataset {dataset}.")
mapNotes(dataset)
combineData(dataset)
```
| github_jupyter |
# Recurrent Neural Networks
```
import pandas as pd
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
```
## Time series forecasting
```
df = pd.read_csv('../data/cansim-0800020-eng-6674700030567901031.csv',
skiprows=6, skipfooter=9,
engine='python')
df.head()
from pandas.tseries.offsets import MonthEnd
df['Adjustments'] = pd.to_datetime(df['Adjustments']) + MonthEnd(1)
df = df.set_index('Adjustments')
df.head()
df.plot()
split_date = pd.Timestamp('01-01-2011')
train = df.loc[:split_date, ['Unadjusted']]
test = df.loc[split_date:, ['Unadjusted']]
ax = train.plot()
test.plot(ax=ax)
plt.legend(['train', 'test'])
from sklearn.preprocessing import MinMaxScaler
sc = MinMaxScaler()
#not fitting our test (important)
train_sc = sc.fit_transform(train)
test_sc = sc.transform(test)
train_sc[:4]
#model learn from previous value such as 0. will learn from 0.01402033
X_train = train_sc[:-1]
y_train = train_sc[1:]
X_test = test_sc[:-1]
y_test = test_sc[1:]
```
### Fully connected predictor
```
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import tensorflow.keras.backend as K
from tensorflow.keras.callbacks import EarlyStopping
K.clear_session()
model = Sequential()
model.add(Dense(12, #12 nodes
input_dim=1, #one input
activation='relu'))
model.add(Dense(1)) #one output ,no activation function this is regression problem
model.compile(loss='mean_squared_error', optimizer='adam')
model.summary()
early_stop = EarlyStopping(monitor='loss', patience=1, verbose=1)
model.fit(X_train, y_train, epochs=200,
batch_size=2, verbose=1,
callbacks=[early_stop])
y_pred = model.predict(X_test)
plt.plot(y_test)
plt.plot(y_pred)
#fully connected
#very bad performance , our model just learnt to mirroring
```
### Recurrent predictor
```
from tensorflow.keras.layers import LSTM
X_train.shape
#3D tensor with shape (batch_size, timesteps, input_dim)
X_train[:, None].shape
X_train_t = X_train[:, None]
X_test_t = X_test[:, None]
K.clear_session()
model = Sequential()
model.add(LSTM(6,
input_shape=(1, 1)#1 timestep ,1 number
))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(X_train_t, y_train,
epochs=100,
batch_size=1 #training each data point
, verbose=1,
callbacks=[early_stop])
y_pred = model.predict(X_test_t)
plt.plot(y_test)
plt.plot(y_pred)
#unfortunately LSTM didnt improve model performance
#now we try Windows
```
## Windows
```
train_sc.shape
train_sc_df = pd.DataFrame(train_sc, columns=['Scaled'], index=train.index)
test_sc_df = pd.DataFrame(test_sc, columns=['Scaled'], index=test.index)
train_sc_df.head()
#12 months back shifts
for s in range(1, 13):
train_sc_df['shift_{}'.format(s)] = train_sc_df['Scaled'].shift(s)
test_sc_df['shift_{}'.format(s)] = test_sc_df['Scaled'].shift(s)
train_sc_df.head(13)
#drop null data which mean drop first year
X_train = train_sc_df.dropna().drop('Scaled', axis=1)
y_train = train_sc_df.dropna()[['Scaled']]
X_test = test_sc_df.dropna().drop('Scaled', axis=1)
y_test = test_sc_df.dropna()[['Scaled']]
X_train.head()
X_train.shape
X_train = X_train.values
X_test= X_test.values
y_train = y_train.values
y_test = y_test.values
```
### Fully Connected on Windows
```
K.clear_session()
model = Sequential()
model.add(Dense(12, input_dim=12, activation='relu'))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.summary()
model.fit(X_train, y_train, epochs=200,
batch_size=1, verbose=1, callbacks=[early_stop])
y_pred = model.predict(X_test)
plt.plot(y_test)
plt.plot(y_pred)
#this model way more better than precious models
#our expectataion lines overlapping
```
### LSTM on Windows
```
X_train_t = X_train.reshape(X_train.shape[0], 1, 12)
X_test_t = X_test.reshape(X_test.shape[0], 1, 12)
X_train_t.shape #one time instance with 12 vector coordinates
K.clear_session()
model = Sequential()
model.add(LSTM(6, input_shape=(1, 12)#our shaped dimensions,parameter 6*12*3?
))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.summary()
model.fit(X_train_t, y_train, epochs=100,
batch_size=1, verbose=1, callbacks=[early_stop])
y_pred = model.predict(X_test_t)
plt.plot(y_test)
plt.plot(y_pred)
#best model
```
## Exercise 1
In the model above we reshaped the input shape to: `(num_samples, 1, 12)`, i.e. we treated a window of 12 months as a vector of 12 coordinates that we simultaneously passed to all the LSTM nodes. An alternative way to look at the problem is to reshape the input to `(num_samples, 12, 1)`. This means we consider each input window as a sequence of 12 values that we will pass in sequence to the LSTM. In principle this looks like a more accurate description of our situation. But does it yield better predictions? Let's check it.
- Reshape `X_train` and `X_test` so that they represent a set of univariate sequences
- retrain the same LSTM(6) model, you'll have to adapt the `input_shape`
- check the performance of this new model, is it better at predicting the test data?
## Exercise 2
RNN models can be applied to images too. In general we can apply them to any data where there's a connnection between nearby units. Let's see how we can easily build a model that works with images.
- Load the MNIST data, by now you should be able to do it blindfolded :)
- reshape it so that an image looks like a long sequence of pixels
- create a recurrent model and train it on the training data
- how does it perform compared to a fully connected? How does it compare to Convolutional Neural Networks?
(feel free to run this exercise on a cloud GPU if it's too slow on your laptop)
| github_jupyter |
# Handwritten Digits Classifier with Improved Accuracy using Data Augmentation
In previous steps, we trained a model that could recognize handwritten digits using the MNIST dataset. We were able to achieve above 98% accuracy on our validation dataset. However, when you deploy the model in an Android app and test it, you probably noticed some accuracy issue. Although the app was able to recognize digits that you drew, the accuracy is probably way lower than 98%.
In this notebook we will explore the couse of the accuracy drop and use data augmentation to improve deployment accuracy.
## Preparation
Let's start by importing TensorFlow and other supporting libraries that are used for data processing and visualization.
```
import tensorflow as tf
from tensorflow import keras
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import random
print(tf.__version__)
```
Import the MNIST dataset
```
mnist = keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# Normalize the input image so that each pixel value is between 0 to 1.
train_images = train_images / 255.0
test_images = test_images / 255.0
# Add a color dimension to the images in "train" and "validate" dataset to
# leverage Keras's data augmentation utilities later.
train_images = np.expand_dims(train_images, axis=3)
test_images = np.expand_dims(test_images, axis=3)
```
Define an utility function so that we can create quickly create multiple models with the same model architecture for comparison.
```
def create_model():
model = keras.Sequential(
[
keras.layers.InputLayer(input_shape=(28,28,1)),
keras.layers.Conv2D(filters=32, kernel_size=(3,3), activation=tf.nn.relu),
keras.layers.Conv2D(filters=64, kernel_size=(3,3), activation=tf.nn.relu),
keras.layers.MaxPooling2D(pool_size=(2,2)),
keras.layers.Dropout(0.25),
keras.layers.Flatten(),
keras.layers.Dense(10, activation=tf.nn.softmax)
]
)
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
return model
```
Confirm that our model can achieve above 98% accuracy on MNIST Dataset.
```
base_model = create_model()
base_model.fit(
train_images,
train_labels,
epochs=5,
validation_data=(test_images, test_labels)
)
```
## Troubleshoot the accuracy drop
Let's see the digit images in MNIST again and guess the cause of the accuracy drop we experienced in deployment.
```
# Show the first 25 images in the training dataset.
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(np.squeeze(train_images[i], axis=2), cmap=plt.cm.gray)
plt.xlabel(train_labels[i])
plt.show()
```
We can see from the 25 images above that the digits are about the same size, and they are in the center of the images. Let's verify if this assumption is true across the MNIST dataset.
```
# An utility function that returns where the digit is in the image.
def digit_area(mnist_image):
# Remove the color axes
mnist_image = np.squeeze(mnist_image, axis=2)
# Extract the list of columns that contain at least 1 pixel from the digit
x_nonzero = np.nonzero(np.amax(mnist_image, 0))
x_min = np.min(x_nonzero)
x_max = np.max(x_nonzero)
# Extract the list of rows that contain at least 1 pixel from the digit
y_nonzero = np.nonzero(np.amax(mnist_image, 1))
y_min = np.min(y_nonzero)
y_max = np.max(y_nonzero)
return [x_min, x_max, y_min, y_max]
# Calculate the area containing the digit across MNIST dataset
digit_area_rows = []
for image in train_images:
digit_area_row = digit_area(image)
digit_area_rows.append(digit_area_row)
digit_area_df = pd.DataFrame(
digit_area_rows,
columns=['x_min', 'x_max', 'y_min', 'y_max']
)
digit_area_df.hist()
```
Now for the histogram, you can confirm that the digit in MNIST images are fitted nicely in an certain area at the center of the images.
[MNIST Range](https://download.tensorflow.org/models/tflite/digit_classifier/mnist_range.png)
However, when you wrote digits in your Android app, you probably did not pay attention to make sure your digit fit in the virtual area that the digits appear in MNIST dataset. The Machine Learning Model have not seen such data before so it performed poorly, especially when you wrote a a digit that was off the center of the drawing pad.
Let's add some data augmentation to the MNIST dataset to verify if our assumption is true. We will distort our MNIST dataset by adding:
* Rotation
* Width and height shift
* Shear
* Zoom
```
# Define data augmentation
datagen = keras.preprocessing.image.ImageDataGenerator(
rotation_range=30,
width_shift_range=0.25,
height_shift_range=0.25,
shear_range=0.25,
zoom_range=0.2
)
# Generate augmented data from MNIST dataset
train_generator = datagen.flow(train_images, train_labels)
test_generator = datagen.flow(test_images, test_labels)
```
Let's see what our digit images look like after augmentation. You can see that we now clearly have much more variation on how the digits are placed in the images.
```
augmented_images, augmented_labels = next(train_generator)
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5, 5, i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(np.squeeze(augmented_images[i], axis=2), cmap=plt.cm.gray)
plt.xlabel('Label: %d' % augmented_labels[i])
plt.show()
```
Let's evaluate the digit classifier model that we trained earlier on this augmented test dataset and see if it makes accuracy drop.
```
base_model.evaluate(test_generator)
```
You can see that accuracy significantly dropped to below 40% in augmented test dataset.
## Improve accuracy with data augmentation
Now let's train our model using augmented dataset to make it perform better in deployment.
```
improved_model = create_model()
improved_model.fit(train_generator, epochs=5, validation_data=test_generator)
```
We can see that as the models saw more distorted digit images during training, its accuracy evaluated distorted test digit images were significantly improved to about 90%.
## Convert to TensorFlow Lite
Let's convert the improved model to TensorFlow Lite and redeploy the Android app.
```
# Convert Keras model to TF Lite format and quantize.
converter = tf.lite.TFLiteConverter.from_keras_model(improved_model)
converter.optimizations = [tf.lite.Optimize.DEFAULT]
tflite_quantized_model = converter.convert()
# Save the Quantized Model to file to the Downloads Directory
f = open('mnist-improved.tflite', "wb")
f.write(tflite_quantized_model)
f.close()
# Download the digit classification model
from google.colab import files
files.download('mnist-improved.tflite')
```
| github_jupyter |
<a href="https://colab.research.google.com/github/ilexistools/ebralc2021/blob/main/nltk_treinar_etiquetador.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
```
# Treinar um etiquetador morfossintático
Para realizar a etiquetagem morfossintática de textos, é preciso obter um etiquetador. O NLTK possui diversas opções para a criação de classificadores e etiquetadores de palavras: DefaultTagger, RegexpTagger, UnigramTagger, BigramTagger, TrigramTagger, BrillTagger, além de outros classificadores.
A criação de etiquetadores requer dados de treinamento, textos previamente etiquetados, no formato de sentenças etiquetadas, especificamente em listas de tuplas para o NLTK. A partir dos dados e algoritmos de treinamento, cria-se um objeto (etiquetador) que pode ser armazenado para usos futuros, uma vez que o treinamento leva um tempo considerável.
# Recursos
Para realizar o teste de utilização, precisamos carregar o corpus mc-morpho e o tokenizador 'punkt' da biblioteca do nltk:
```
import nltk
nltk.download('mac_morpho')
nltk.download('punkt')
import nltk
import pickle
from nltk.corpus import mac_morpho
# prepara dados de treinamento e teste
sents = mac_morpho.tagged_sents()
trein = sents[0:30000]
teste = sents[13000:]
# treina um etiquetador sequencial
etq1 = nltk.DefaultTagger('N')
etq2 = nltk.UnigramTagger(trein,backoff=etq1)
etq3 = nltk.BigramTagger(trein,backoff=etq2)
# imprime a acurácia dos etiquetadores
print('DefaultTagger', etq1.evaluate(teste))
print('UnigramTagger', etq2.evaluate(teste))
print('BigramTagger', etq3.evaluate(teste))
# armazena o etiquetador treinado
with open('etq.pickle','wb') as fh:
pickle.dump(etq3,fh)
```
No exemplo, carregamos os dados etiquetados para treinamento e teste do etiquetador. Separamos uma quantidade maior de sentenças para treino (70%) e outra menor para teste (30%).
Em seguida, iniciamos o processo de treinamento de um etiquetador sequencial a partir de três modelos diferentes combinados. O etiquetador 'DefaultTagger' atribui uma etiqueta padrão ('N') para todas as palavras. O etiquetador 'UnigramTagger', treinado com as sentenças, atribui a etiqueta mais provável para a palavra a partir de um dicionário criado internamente. O etiquetador 'BigramTagger', também treinado com as sentenças etiquetadas, atribui a etiqueta mais provável para a palavra com base na etiqueta anterior (hipótese de Markov). A combinação dos etiquetadores é feita sequencialmente por meio do argumento 'backoff''.
Tendo realizado o treinamento do etiquetador, avaliamos a precisão de cada etapa por meio da função ‘evaluate()’, passando como argumento a variável ‘teste’, que armazena parte das sentenças etiquetadas do corpus MacMorpho. No processo, obtemos a impressão do desempenho de cada um dos etiquetadores em separado. O etiquetador final, resultado da combinação de todos, obtém uma precisão de 84% com os dados de teste.
Por fim, armazenamos o etiquetador treinado para usos posteriores por meio da função ‘dump’, do módulo ‘pickle’.
Para verificar a funcionalidade do etiquetador, realizamos o seguinte teste:
```
import nltk
import pickle
# carrega o etiquetador treinado
with open('etq.pickle','rb') as fh:
etiquetador = pickle.load(fh)
# armazena um texto a ser etiquetado como teste
texto = 'Estamos realizando um teste agora.'
# itemiza o texto
itens = nltk.word_tokenize(texto,language='portuguese')
# etiqueta os itens
itens_etiquetados = etiquetador.tag(itens)
# imprime o resultado
print(itens_etiquetados)
```
| github_jupyter |
# An example of an optimal pruning based routing algorithm
- based on a simple graph and Dijkstra's algorithm with concave cost function
- Create a simple graph with multiple edge's attributes¶
- weight = w_ij
- concave = c_ij where i,j is nodes
```
import networkx as nx
import matplotlib.pyplot as plt
```
## Define functions
```
def add_multi_link_attributes(G,attr1,attr2):
"""
This funtion is to add the multiple link attributes to graph G
input: G : graph
attr1 : link attribute 1
attr2 : link attribute 2
output : G
"""
i = 0
for (u, v) in G.edges():
G.add_edge(u,v,w=attr1[i],c=attr2[i])
i = i+1
return G
def draw_graph(G,pos):
"""
This function is to draw a graph with the fixed position
input : G : graph
pos: postions of all nodes with the dictionary of coordinates (x,y)
"""
edge_labels = {} ## add edge lables from edge attribute
for u, v, data in G.edges(data=True):
edge_labels[u, v] = data
nx.draw_networkx(G,pos)
nx.draw_networkx_edge_labels(G,pos,edge_labels=edge_labels)
def remove_Edge(G,rm_edge_list):
"""
This function is to remove edges in the rm_edge_list from G
"""
G.remove_edges_from(rm_edge_list)
G.edges()
return G
def compare_path(path1,path2):
if collections.Counter(path1) == collections.Counter(path2):
print ("The lists l1 and l2 are the same")
flag = True
else:
print ("The lists l1 and l2 are not the same")
flag = False
return flag
def additive_path_cost(G, path, attr):
"""
This function is to find the path cost based on the additive costs
: Path_Cost = sum_{edges in the path}attr[edge]
Input : G : graph
path : path is a list of nodes in the path
attr : attribute of edges
output : path_cost
"""
return sum([G[path[i]][path[i+1]][attr] for i in range(len(path)-1)])
## Calculate concave path cost from attr
def max_path_cost(G, path, attr):
"""
This function is to find the path cost based on the Concave costs
: Path_Cost = max{edges in the path}attr[edge]
Input : G : graph
path : path is a list of nodes in the path
attr : attribute of edges
output : path_cost
"""
return max([G[path[i]][path[i+1]][attr] for i in range(len(path)-1)])
def rm_edge_constraint(G,Cons):
rm_edge_list = []
for u, v, data in G.edges(data=True):
e = (u,v)
cost = G.get_edge_data(*e)
print(cost)
if cost['c'] >= Cons:
rm_edge_list.append(e)
print(rm_edge_list)
remove_Edge(G,rm_edge_list)
return G
def has_path(G, source, target):
"""Return True if G has a path from source to target, False otherwise.
Parameters
----------
G : NetworkX graph
source : node
Starting node for path
target : node
Ending node for path
"""
try:
sp = nx.shortest_path(G,source, target)
except nx.NetworkXNoPath:
return False
return True
def Optimum_prun_based_routing(G,S,D,L):
"""
This function is to find the optimal path from S to D with constraint L
Input : G : graph
S : Source
D : Destination
L : constraint
"""
if has_path(G, S, D):
Shortest_path = nx.dijkstra_path(G, S, D, weight='w')
Opt_path = Shortest_path
while len(Shortest_path) != 0:
path_cost = additive_path_cost(G, Shortest_path, 'w')
print(path_cost)
if path_cost <= L:
"""go to concave cost"""
PathConcave_cost = max_path_cost(G, Shortest_path, 'c')
G = rm_edge_constraint(G,PathConcave_cost) # remove all links where the concave link is greater than PathConcave_cost
Opt_path = Shortest_path
if has_path(G, S, D):
Shortest_path = nx.dijkstra_path(G, S, D, weight='w')
else:
Shortest_path = []
else:
pass
else:
print('No path from', S, ' to ', D)
Opt_path = []
return Opt_path
```
## Create a graph
```
G = nx.Graph()
edge_list = [('S', 'B'), ('S', 'A'), ('S','E'), ('B','A'), ('B','D'), ('A','D'), ('E','D')]
Weight_edge_list = [2, 2, 3, 2, 1, 2, 2]
Concave_edge_list = [1, 3, 3, 1, 4, 3, 1]
pos = { 'S': (0,50), 'B': (50, 100), 'A': (50, 50), 'E': (50, 0), 'D': (100, 50)} # draw by position
G.add_edges_from(edge_list)
G = add_multi_link_attributes(G,Weight_edge_list,Concave_edge_list)
draw_graph(G,pos)
```
## Run the optimum-pruning-based-routing algorithm
```
Optimum_prun_based_routing(G,'S','D',5)
```
| github_jupyter |
# Machine Learning Engineer Nanodegree
## Introduction and Foundations
## Project: Titanic Survival Exploration
In 1912, the ship RMS Titanic struck an iceberg on its maiden voyage and sank, resulting in the deaths of most of its passengers and crew. In this introductory project, we will explore a subset of the RMS Titanic passenger manifest to determine which features best predict whether someone survived or did not survive. To complete this project, you will need to implement several conditional predictions and answer the questions below. Your project submission will be evaluated based on the completion of the code and your responses to the questions.
> **Tip:** Quoted sections like this will provide helpful instructions on how to navigate and use an iPython notebook.
# Getting Started
To begin working with the RMS Titanic passenger data, we'll first need to `import` the functionality we need, and load our data into a `pandas` DataFrame.
Run the code cell below to load our data and display the first few entries (passengers) for examination using the `.head()` function.
> **Tip:** You can run a code cell by clicking on the cell and using the keyboard shortcut **Shift + Enter** or **Shift + Return**. Alternatively, a code cell can be executed using the **Play** button in the hotbar after selecting it. Markdown cells (text cells like this one) can be edited by double-clicking, and saved using these same shortcuts. [Markdown](http://daringfireball.net/projects/markdown/syntax) allows you to write easy-to-read plain text that can be converted to HTML.
```
# Import libraries necessary for this project
import numpy as np
import pandas as pd
from IPython.display import display # Allows the use of display() for DataFrames
# Import supplementary visualizations code visuals.py
import visuals as vs
# Pretty display for notebooks
%matplotlib inline
# Load the dataset
in_file = 'titanic_data.csv'
full_data = pd.read_csv(in_file)
# Print the first few entries of the RMS Titanic data
display(full_data.head())
```
From a sample of the RMS Titanic data, we can see the various features present for each passenger on the ship:
- **Survived**: Outcome of survival (0 = No; 1 = Yes)
- **Pclass**: Socio-economic class (1 = Upper class; 2 = Middle class; 3 = Lower class)
- **Name**: Name of passenger
- **Sex**: Sex of the passenger
- **Age**: Age of the passenger (Some entries contain `NaN`)
- **SibSp**: Number of siblings and spouses of the passenger aboard
- **Parch**: Number of parents and children of the passenger aboard
- **Ticket**: Ticket number of the passenger
- **Fare**: Fare paid by the passenger
- **Cabin** Cabin number of the passenger (Some entries contain `NaN`)
- **Embarked**: Port of embarkation of the passenger (C = Cherbourg; Q = Queenstown; S = Southampton)
Since we're interested in the outcome of survival for each passenger or crew member, we can remove the **Survived** feature from this dataset and store it as its own separate variable `outcomes`. We will use these outcomes as our prediction targets.
Run the code cell below to remove **Survived** as a feature of the dataset and store it in `outcomes`.
```
# Store the 'Survived' feature in a new variable and remove it from the dataset
outcomes = full_data['Survived']
data = full_data.drop('Survived', axis = 1)
# Show the new dataset with 'Survived' removed
display(data.head())
```
The very same sample of the RMS Titanic data now shows the **Survived** feature removed from the DataFrame. Note that `data` (the passenger data) and `outcomes` (the outcomes of survival) are now *paired*. That means for any passenger `data.loc[i]`, they have the survival outcome `outcomes[i]`.
To measure the performance of our predictions, we need a metric to score our predictions against the true outcomes of survival. Since we are interested in how *accurate* our predictions are, we will calculate the proportion of passengers where our prediction of their survival is correct. Run the code cell below to create our `accuracy_score` function and test a prediction on the first five passengers.
**Think:** *Out of the first five passengers, if we predict that all of them survived, what would you expect the accuracy of our predictions to be?*
```
def accuracy_score(truth, pred):
""" Returns accuracy score for input truth and predictions. """
# Ensure that the number of predictions matches number of outcomes
if len(truth) == len(pred):
# Calculate and return the accuracy as a percent
return "Predictions have an accuracy of {:.2f}%.".format((truth == pred).mean()*100)
else:
return "Number of predictions does not match number of outcomes!"
# Test the 'accuracy_score' function
predictions = pd.Series(np.ones(5, dtype = int))
print accuracy_score(outcomes[:5], predictions)
```
> **Tip:** If you save an iPython Notebook, the output from running code blocks will also be saved. However, the state of your workspace will be reset once a new session is started. Make sure that you run all of the code blocks from your previous session to reestablish variables and functions before picking up where you last left off.
# Making Predictions
If we were asked to make a prediction about any passenger aboard the RMS Titanic whom we knew nothing about, then the best prediction we could make would be that they did not survive. This is because we can assume that a majority of the passengers (more than 50%) did not survive the ship sinking.
The `predictions_0` function below will always predict that a passenger did not survive.
```
def predictions_0(data):
""" Model with no features. Always predicts a passenger did not survive. """
predictions = []
for _, passenger in data.iterrows():
# Predict the survival of 'passenger'
predictions.append(0)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_0(data)
```
### Question 1
*Using the RMS Titanic data, how accurate would a prediction be that none of the passengers survived?*
**Hint:** Run the code cell below to see the accuracy of this prediction.
```
print accuracy_score(outcomes, predictions)
```
**Answer:** 61.62%
***
Let's take a look at whether the feature **Sex** has any indication of survival rates among passengers using the `survival_stats` function. This function is defined in the `visuals.py` Python script included with this project. The first two parameters passed to the function are the RMS Titanic data and passenger survival outcomes, respectively. The third parameter indicates which feature we want to plot survival statistics across.
Run the code cell below to plot the survival outcomes of passengers based on their sex.
```
vs.survival_stats(data, outcomes, 'Sex')
```
Examining the survival statistics, a large majority of males did not survive the ship sinking. However, a majority of females *did* survive the ship sinking. Let's build on our previous prediction: If a passenger was female, then we will predict that they survived. Otherwise, we will predict the passenger did not survive.
Fill in the missing code below so that the function will make this prediction.
**Hint:** You can access the values of each feature for a passenger like a dictionary. For example, `passenger['Sex']` is the sex of the passenger.
```
def predictions_1(data):
""" Model with one feature:
- Predict a passenger survived if they are female. """
predictions = []
for _, passenger in data.iterrows():
if passenger['Sex'] == 'female':
predictions.append(1)
else:
predictions.append(0)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_1(data)
```
### Question 2
*How accurate would a prediction be that all female passengers survived and the remaining passengers did not survive?*
**Hint:** Run the code cell below to see the accuracy of this prediction.
```
print accuracy_score(outcomes, predictions)
```
**Answer**: 78.68%
***
Using just the **Sex** feature for each passenger, we are able to increase the accuracy of our predictions by a significant margin. Now, let's consider using an additional feature to see if we can further improve our predictions. For example, consider all of the male passengers aboard the RMS Titanic: Can we find a subset of those passengers that had a higher rate of survival? Let's start by looking at the **Age** of each male, by again using the `survival_stats` function. This time, we'll use a fourth parameter to filter out the data so that only passengers with the **Sex** 'male' will be included.
Run the code cell below to plot the survival outcomes of male passengers based on their age.
```
vs.survival_stats(data, outcomes, 'Age', ["Sex == 'male'"])
```
Examining the survival statistics, the majority of males younger than 10 survived the ship sinking, whereas most males age 10 or older *did not survive* the ship sinking. Let's continue to build on our previous prediction: If a passenger was female, then we will predict they survive. If a passenger was male and younger than 10, then we will also predict they survive. Otherwise, we will predict they do not survive.
Fill in the missing code below so that the function will make this prediction.
**Hint:** You can start your implementation of this function using the prediction code you wrote earlier from `predictions_1`.
```
def predictions_2(data):
""" Model with two features:
- Predict a passenger survived if they are female.
- Predict a passenger survived if they are male and younger than 10. """
predictions = []
for _, passenger in data.iterrows():
if passenger['Sex'] == 'female':
predictions.append(1)
elif passenger['Sex'] == 'male' and passenger['Age'] < 10:
predictions.append(1)
else:
predictions.append(0)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_2(data)
```
### Question 3
*How accurate would a prediction be that all female passengers and all male passengers younger than 10 survived?*
**Hint:** Run the code cell below to see the accuracy of this prediction.
```
print accuracy_score(outcomes, predictions)
```
**Answer**: 79.35%
***
Adding the feature **Age** as a condition in conjunction with **Sex** improves the accuracy by a small margin more than with simply using the feature **Sex** alone. Now it's your turn: Find a series of features and conditions to split the data on to obtain an outcome prediction accuracy of at least 80%. This may require multiple features and multiple levels of conditional statements to succeed. You can use the same feature multiple times with different conditions.
**Pclass**, **Sex**, **Age**, **SibSp**, and **Parch** are some suggested features to try.
Use the `survival_stats` function below to to examine various survival statistics.
**Hint:** To use mulitple filter conditions, put each condition in the list passed as the last argument. Example: `["Sex == 'male'", "Age < 18"]`
```
vs.survival_stats(data, outcomes, 'SibSp', ["Sex == 'female'"])
```
Adding number of siblings and spouses of the passenger for females increased accuracy. Having less than 3 siblings and spouses increasing chance of survive, 3 or 4 siblings and spouses reduce survive and there is no survival chance for females who had more than 4 siblings and spouses.
```
vs.survival_stats(data, outcomes, 'Age', ["Sex == 'male'", "Pclass == 1"])
```
For male who was in first class with the age between 30 and 40 has high chance of survive.
After exploring the survival statistics visualization, fill in the missing code below so that the function will make your prediction.
Make sure to keep track of the various features and conditions you tried before arriving at your final prediction model.
**Hint:** You can start your implementation of this function using the prediction code you wrote earlier from `predictions_2`.
```
def predictions_3(data):
""" Model with multiple features. Makes a prediction with an accuracy of at least 80%. """
predictions = []
for _, passenger in data.iterrows():
if passenger['Sex'] == 'female' and passenger['SibSp'] < 3:
predictions.append(1)
elif passenger['Sex'] == 'female' and passenger['SibSp'] < 5:
predictions.append(0)
elif passenger['Sex'] == 'female' and passenger['SibSp'] >=5 :
predictions.append(0)
# code above incrased the accuracy up to 80.36%
elif passenger['Sex'] == 'male' and passenger['Age'] < 10:
predictions.append(1)
#vs.survival_stats(data, outcomes, 'Age', ["Sex == 'male'", "Pclass == 1"])
#elif statement below increases accuracy to 80.58
elif passenger['Sex'] == 'male' and passenger['Age'] < 40 and passenger['Age'] > 30 and passenger['Pclass'] == 1:
predictions.append(1)
else:
predictions.append(0)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_3(data)
```
### Question 4
*Describe the steps you took to implement the final prediction model so that it got an accuracy of at least 80%. What features did you look at? Were certain features more informative than others? Which conditions did you use to split the survival outcomes in the data? How accurate are your predictions?*
**Hint:** Run the code cell below to see the accuracy of your predictions.
```
print accuracy_score(outcomes, predictions)
```
**Answer**: 80.58%
# Conclusion
After several iterations of exploring and conditioning on the data, you have built a useful algorithm for predicting the survival of each passenger aboard the RMS Titanic. The technique applied in this project is a manual implementation of a simple machine learning model, the *decision tree*. A decision tree splits a set of data into smaller and smaller groups (called *nodes*), by one feature at a time. Each time a subset of the data is split, our predictions become more accurate if each of the resulting subgroups are more homogeneous (contain similar labels) than before. The advantage of having a computer do things for us is that it will be more exhaustive and more precise than our manual exploration above. [This link](http://www.r2d3.us/visual-intro-to-machine-learning-part-1/) provides another introduction into machine learning using a decision tree.
A decision tree is just one of many models that come from *supervised learning*. In supervised learning, we attempt to use features of the data to predict or model things with objective outcome labels. That is to say, each of our data points has a known outcome value, such as a categorical, discrete label like `'Survived'`, or a numerical, continuous value like predicting the price of a house.
### Question 5
*Think of a real-world scenario where supervised learning could be applied. What would be the outcome variable that you are trying to predict? Name two features about the data used in this scenario that might be helpful for making the predictions.*
**Answer**: Weather forecast would be a good example. We could predict the next days temperature based on previous years data. In this case, Humidity, wind could be the features and temparature would be the target.
> **Note**: Once you have completed all of the code implementations and successfully answered each question above, you may finalize your work by exporting the iPython Notebook as an HTML document. You can do this by using the menu above and navigating to
**File -> Download as -> HTML (.html)**. Include the finished document along with this notebook as your submission.
| github_jupyter |
# Make Corner Plots of Posterior Distributions
This file allows me to quickly and repeatedly make the cornor plot to examin the results of the MCMC analsys
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import pandas as pd
from astropy.table import Table
import corner
# import seaborn
matplotlib.rcParams.update({'font.size': 11})
```
This function is the general function that is repeated called throught the file. One benifite to this system, is that I only need to update to higher quality labels in one place.
```
def corner_plot(file_, saved_file, truths=None, third=0):
data = Table.read(file_, format='ascii.commented_header', delimiter='\t')
if third !=0:
size = len(data)
data = data[(third-1)*size//3:(third)*size//3]
data = data.to_pandas()
data.dropna(inplace=True)
# look at corner.hist2d(levels) to not have too many conturs on a plot
# http://corner.readthedocs.io/en/latest/api.html
fig = corner.corner(data, show_titles=True, use_math_text=True,
bins=25, quantiles=[0.16, 0.84], smooth=1,
plot_datapoints=False,
labels=[r"$\log(z/z_{\odot})$", r"$\tau_2$", r"$\tau$",
r"$t_{0}$", r"$t_{i}$", r'$\phi$',
'$\delta$', 'age'],
truths=truths, range=[0.99]*8
)
fig.savefig(saved_file)
```
## One Object
```
#run one object
SN = 16185
file_ = f'../resources/SN{SN}_campbell_chain.tsv'
saved_file = f'SN{SN}-mcmc-2018-12-21.pdf'
corner_plot(file_, saved_file)
```
## Messier Objects
```
# run all Messier objects
for id in [63, 82, 87, 89, 91, 101, 105, 108]:
file_ = f'../resources/SN{id}_messier_chain.tsv'
saved_file = f'messierTests/12-29-M{id}.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file)
# One Messier Object
ID = 63
file_ = f'../resources/SN{ID}_messier_chain.tsv'
saved_file = f'messierTests/12-22-M{ID}.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file)
```
## Circle Test -- old
```
# run on circle test
for id in [1, 2, 3, 4, 5, 6, 7]:
file_ = f'../resources/SN{id}_chain.tsv'
saved_file = f'circleTests/12-19-C{id}.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file)
# run on circle test 3 with truths
file_ = f'../resources/SN3_chain.tsv'
saved_file = f'circleTests/07-31-C3-truths.pdf'
data = Table.read(file_, format='ascii.commented_header', delimiter='\t')
data = data.to_pandas()
data.dropna(inplace=True)
fig = corner.corner(data, show_titles=True, use_math_text=True,
quantiles=[0.16, 0.5, 0.84], smooth=0.5,
plot_datapoints=False,
labels=["$logZ_{sol}$", "$dust_2$", r"$\tau$",
"$t_{start}$", "$t_{trans}$", 'sf slope',
'c', 'Age'],
truths=[-0.5, 0.1, 7.0, 3.0, 10, 15.0, -25, None]
)
fig.savefig(saved_file)
# run on circle test 1 with truths
file_ = f'../resources/SN1_chain_2017-09-11.tsv'
saved_file = f'circleTests/09-11-C1-truths.pdf'
truths=[-0.5, 0.1, 0.5, 1.5, 9.0, -1.0, -25, None]
corner_plot(file_, saved_file, truths)
# data = Table.read(file_, format='ascii.commented_header', delimiter='\t')
# data = data.to_pandas()
# data.dropna(inplace=True)
#
# fig = corner.corner(data, show_titles=True, use_math_text=True,
# quantiles=[0.16, 0.5, 0.84], smooth=0.5,
# plot_datapoints=False,
# labels=["$logZ_{sol}$", "$dust_2$", r"$\tau$",
# "$t_{start}$", "$t_{trans}$", 'sf slope',
# 'c', 'Age'],
# truths=[-0.5, 0.1, 0.5, 1.5, 9.0, -1.0, -25, None]
# )
# fig.savefig(saved_file)
```
## Test all Circle Tests
```
# for slope
# truths = {
# 1 : [-0.5, 0.1, 0.5, 1.5, 9.0, -1.0, -25, 10.68],
# 2 : [-0.5, 0.1, 0.5, 1.5, 9.0, 15.0, -25, 1.41],
# 3 : [-0.5, 0.1, 7.0, 3.0, 10, 15.0, -25, 1.75],
# 4 : [-0.5, 0.1, 7.0, 3.0, 13.0, 0.0, -25, 4.28],
# 5 : [-1.5, 0.1, 0.5, 1.5, 9.0, -1.0, -25, 10.68],
# 6 : [-0.5, 0.8, 7.0, 3.0, 10.0, 15.0, -25, 1.75],
# 7 : [-0.5, 0.1, 0.5, 1.5, 6.0, 15.0, -25, ]
# }
# for phi
truths = {
1 : [-0.5, 0.1, 0.5, 1.5, 9.0, -0.785, -25, 10.68],
2 : [-0.5, 0.1, 0.5, 1.5, 9.0, 1.504, -25, 1.41],
3 : [-0.5, 0.1, 7.0, 3.0, 10, 1.504, -25, 1.75],
4 : [-0.5, 0.1, 7.0, 3.0, 13.0, 0.0, -25, 4.28],
5 : [-1.5, 0.1, 0.5, 1.5, 9.0, -0.785, -25, 10.68],
6 : [-0.5, 0.8, 7.0, 3.0, 10.0, 1.504, -25, 1.75],
7 : [-0.5, 0.1, 0.5, 1.5, 6.0, 1.504, -25, 2.40],
8 : [-0.5, 0.1, 0.1, 8.0, 12.0, 1.52, -25, 0.437]
}
for id_ in np.arange(8) + 1:
file_ = f'../resources/SN{id_}_circle_chain.tsv'
saved_file = f'circleTests/C{id_}-truths-0717.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file, truths[id_])
# just one cirlce test
id_ = 8
file_ = f'../resources/SN{id_}_circle_chain.tsv'
saved_file = f'circleTests/C{id_}-truths-0717_1.pdf'
corner_plot(file_, saved_file, truths[id_])
```
# Check sections of chain
```
file_ = f'../resources/SN2_chain.tsv'
saved_file = f'circleTests/C2-3.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file, truths[2], third=3)
```
| github_jupyter |
```
import pandas as pd
import sqlite3
conn = sqlite3.connect('database.sqlite')
query = "SELECT * FROM sqlite_master"
df_schema = pd.read_sql_query(query, conn)
df_schema.tbl_name.unique()
df_schema.head(20)
cur = conn.cursor()
cur.execute('''SELECT * from pragma_table_info("Player_Attributes")''' )
rows = cur.fetchall()
for row in rows[:]:
print(row)
#df_schema.to_csv("soccer_schema.csv")
cur = conn.cursor()
cur.execute('''SELECT * from pragma_table_info("Player")''' )
rows = cur.fetchall()
for row in rows[:]:
print(row)
cur = conn.cursor()
cur.execute('''SELECT * from pragma_table_info("Match")''' )
rows = cur.fetchall()
for row in rows[:]:
print(row)
cur = conn.cursor()
cur.execute('''SELECT * from pragma_table_info("League")''' )
rows = cur.fetchall()
for row in rows[:]:
print(row)
cur = conn.cursor()
cur.execute('''SELECT * from pragma_table_info("Country")''' )
rows = cur.fetchall()
for row in rows[:]:
print(row)
cur = conn.cursor()
cur.execute('''SELECT * from pragma_table_info("Team")''' )
rows = cur.fetchall()
for row in rows[:]:
print(row)
cur = conn.cursor()
cur.execute('''SELECT * from pragma_table_info("Team_Attributes")''' )
rows = cur.fetchall()
for row in rows[:]:
print(row)
```
## Question 1: Which team scored the most points when playing at home?
```
cur = conn.cursor()
cur.execute("SELECT sum(a.home_team_goal) as sum_goals, b.team_api_id, b.team_long_name FROM match a, team b WHERE a.home_team_api_id = b.team_api_id group by b.team_api_id order by sum_goals desc limit 1" )
rows = cur.fetchall()
for row in rows[:]:
print(row)
```
## Question 2: Did this team also score the most points when playing away?
```
cur = conn.cursor()
cur.execute("SELECT sum(a.away_team_goal) as sum_goals, b.team_api_id, b.team_long_name FROM match a, team b WHERE a.away_team_api_id = b.team_api_id group by b.team_api_id order by sum_goals desc limit 1" )
rows = cur.fetchall()
for row in rows[:]:
print(row)
```
## Question 3: How many matches resulted in a tie?
```
cur = conn.cursor()
cur.execute("SELECT count(match_api_id) FROM match where home_team_goal = away_team_goal" )
rows = cur.fetchall()
for row in rows[:]:
print(row)
```
## Question 4: How many players have Smith for their last name? How many have 'smith' anywhere in their name?
```
cur = conn.cursor()
cur.execute("SELECT COUNT(player_name) FROM Player where player_name LIKE '% smith' " )
rows = cur.fetchall()
for row in rows[:]:
print(row)
cur = conn.cursor()
cur.execute("SELECT COUNT(player_name) FROM Player where player_name LIKE '%smith%' " )
rows = cur.fetchall()
for row in rows[:]:
print(row)
```
## Question 5: What was the median tie score? Use the value determined in the previous question for the number of tie games. Hint: PostgreSQL does not have a median function. Instead, think about the steps required to calculate a median and use the WITH command to store stepwise results as a table and then operate on these results.
```
cur = conn.cursor()
#cur.execute("WITH goal_list AS (SELECT home_team_goal FROM match where home_team_goal = away_team_goal order \
# by home_team_goal desc) select home_team_goal from goal_list limit 1 offset 6596/2" )
cur.execute("WITH goal_list AS (SELECT home_team_goal FROM match where home_team_goal = away_team_goal order \
by home_team_goal desc) select home_team_goal from goal_list limit 1 offset (select count(*) from goal_list)/2" )
rows = cur.fetchall()
for row in rows[:20]:
print(row)
```
## Question 6: What percentage of players prefer their left or right foot? Hint: Calculate either the right or left foot, whichever is easier based on how you setup the problem.
```
cur = conn.cursor()
cur.execute("SELECT (COUNT(DISTINCT(player_api_id)) * 100.0 / (SELECT COUNT(DISTINCT(player_api_id)) FROM Player_Attributes)) \
FROM Player_Attributes WHERE preferred_foot LIKE '%right%' " )
rows = cur.fetchall()
for row in rows[:20]:
print(row)
#SELECT (COUNT(DISTINCT(player_api_id)) * 100.0 / (SELECT COUNT(DISTINCT(player_api_id)) FROM Player_Attributes)) as percentage
#FROM Player_Attributes
#WHERE preferred_foot LIKE '%left%'
```
| github_jupyter |
# Importing the libraries
```
%pip install tensorflow
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import seaborn as sns
```
# Importing The Dataset
```
dataset = pd.read_csv("../input/framingham-heart-study-dataset/framingham.csv")
```
# Analysing The Data
```
dataset.shape
dataset.dtypes
dataset.info
```
# Visualizing the data
```
fig = plt.figure(figsize = (8,8))
ax = fig.gca()
dataset.hist(ax=ax)
plt.show()
fig, ax = plt.subplots()
ax.hist(dataset["TenYearCHD"],color = "yellow")
ax.set_title(' To predict heart disease')
ax.set_xlabel('TenYearCHD')
ax.set_ylabel('Frequency')
data = np.random.random([100,4])
sns.violinplot(data=data, palette=['r','g','b','m'])
```
# Separating the dependent and independent variables
```
X = dataset.iloc[:,:-1].values
y = dataset.iloc[:,-1].values
np.isnan(X).sum()
np.isnan(y).sum()
```
# Taking Care of Missing Values
```
from sklearn.impute import SimpleImputer
si = SimpleImputer(missing_values = np.nan, strategy = 'mean')
X = si.fit_transform(X)
y.shape
np.isnan(X).sum()
np.isnan(y).sum()
dataset.isna().sum()
```
# Splitting into Training and test Data
```
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.3,random_state = 0)
```
# Normalising The data
```
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
X_train
y_train
np.isnan(X_train).sum()
np.isnan(y_train).sum()
```
# Preparing ANN Model with two layers
```
ann = tf.keras.models.Sequential()
ann.add(tf.keras.layers.Dense(units = 6, activation = 'relu'))
ann.add(tf.keras.layers.Dense(units = 6, activation='relu'))
ann.add(tf.keras.layers.Dense(units = 1,activation='sigmoid'))
ann.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])
model = ann.fit(X_train,y_train,validation_data=(X_test,y_test), batch_size = 32,epochs=100)
y_pred = ann.predict(X_test)
y_pred = (y_pred > 0.5)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
from sklearn.metrics import confusion_matrix, accuracy_score, classification_report
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
```
# Model Accuracy Visualisation
```
plt.plot(model.history['accuracy'])
plt.plot(model.history['val_accuracy'])
plt.title('Model Accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='lower right')
plt.show()
```
# Model Loss Visualisation
```
plt.plot(model.history['loss'])
plt.plot(model.history['val_loss'])
plt.title('Model Loss')
plt.ylabel('loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Validation'], loc='upper right')
plt.show()
```
# Calculating Different Metrics
```
print(classification_report(y_test, y_pred))
```
# Using MLP Classifier for Prediction
```
from sklearn.neural_network import MLPClassifier
classifier = MLPClassifier(hidden_layer_sizes=(150,100,50), max_iter=300,activation = 'relu',solver='adam',random_state=1)
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
y_pred = (y_pred > 0.5)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
from sklearn.metrics import confusion_matrix, accuracy_score, classification_report
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
print(classification_report(y_test, y_pred))
```
# Visualising The MLP Model After Applying the PCA method
```
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
classifier.fit(X_train, y_train)
def visualization_train(model):
sns.set_context(context='notebook',font_scale=2)
plt.figure(figsize=(16,9))
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.6, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title("%s Model on training data" %(model))
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend()
def visualization_test(model):
sns.set_context(context='notebook',font_scale=2)
plt.figure(figsize=(16,9))
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.6, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title("%s Test Set" %(model))
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend()
visualization_train(model= 'MLP')
```
# Saving a machine learning Model
```
#import joblib
#joblib.dump(ann, 'ann_model.pkl')
#joblib.dump(sc, 'sc_model.pkl')
#knn_from_joblib = joblib.load('mlp_model.pkl')
#sc_model = joblib.load('sc_model.pkl')
```
# Saving a tensorflow model
```
#!pip install h5py
#ann.save('ann_model.h5')
#model = tf.keras.models.load_model('ann_model.h5')
```
| github_jupyter |
# Reinforcement Learning
page 441<br>
For details, see
- https://github.com/ageron/handson-ml/blob/master/16_reinforcement_learning.ipynb,
- https://gym.openai.com,
- http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html,
- https://www.jstor.org/stable/24900506?seq=1#metadata_info_tab_contents,
- http://book.pythontips.com/en/latest/enumerate.html, and
- https://docs.python.org/2.3/whatsnew/section-slices.html (on slices).
Reinforcement Learning is one of the most excititng fields of Machine Learning today. It has been around since the 1950s but flying below the radar most of the time. In 2013, *DeepMind* (at that time still an independent start-up in London) produced a reinforcement learning algorithm that could achieve superhuman performance of playing about any Atari game without having prior domain knowledge. Notably, *AlphaGo*, also a reinforcement learning algorithm by Deepmind, beat world champion *Lee Sedol* in the board game *Go* in March 2016. This has become possible by applying the power of Deep Learning to the field of Reinforcement Learning.<br><br>
Two very important concepts for Reinforcement Learning are **policy gradients** and **deep Q-networks** (DQN).
## Learning to Optimize Rewards
page 442<br>
Reinforcement learning utilizes a software **agent** that makes **observations** and takes **actions** in an **environment** by which it can earn **rewards**. Its objective is to learn to act in a way that is expected to maximise long-term rewards. This can be linked to human behaviour as humans seem to try to minimize pain (negative reward / penalty) and maximise pleasure (positive reward). The setting of Reinforcement Learning is quite broad. The following list shows some typical applications.
- The agent can be the program controlling a walking robot. In this case, the environment is the real world, the agent obersrves the environment through a set of *sensors* such as cameras and touch sensors, and its actions consist of sending signals to activate motors. It may be programmed to get positive rewards whenever it approaches the target destination, and negative rewards whenever it wastes time, goes in the wrong direction, or falls down.
- The agent can be the program controlling Ms. Pac-Man. In this case, the environment is a simulation of the Atari game, the actions are the nine possible joystick positions (upper left, down, center, and so on), the observations are screenshots, and the rewards are just the game points.
- Similarly, the agent can be the program playing a board game such as the game of *Go*.
- The agent does not have to control a physically (or virtually ) moving thing. For example, it can be a smart thermostat, getting rewards whenever it is close to the target temperature and saves energy, and negative rewards when humans need to tweak the temperature, so the agent must learn to anticipate human needs.
- The agent can observe stock market prices and decide how much to buy or sell every second. Rewards are obviously the monetary gains and losses.
Note that it is not necessary to have both positive and negative rewards. For example, using only negative rewards can be useful when a task shall be finished as soon as possible. There are many more applications of Reinforcement Learning, e.g., self-driving cars or placing ads on a webpage (maximizing clicks and/or buys).
## Policy Search
page 444<br>
The algorithm that the software agent uses to determine its action is called its **policy**. For example, the policy could be a neural network taking inputs (observations) and producing outputs (actions). The policy can be pretty much any algorithm. If that algorithm is not deterministic, it is called a *stochastic policy*.<br><br>
A simple, stochastic policy for a vacuum cleaner could be to go straight for a specified time and then turn with probability $p$ by a random angle $r$. In that example, the algorithm's *policy parameters* are $p$ and $r$. One example of *policy search* would be to try out all possible parameter values and then settle for those values that perform best (e.g., most dust picked up per time). However, if the *policy space* is too large, as is often the case, a near-optimal policy will likely be missed by such brute force approach.<br><br>
*Genetic algorithms* are another way to explore the policy space. For example, one may randomly create 100 policies, rank their performance on the task, and then filter out the bad performers. This could be done by strictly filtering out the 80 lowest performers, or filter out a policy with a probability that is high if the performance is low (this works often better). To restore the population of 100 policies, each of the 20 survivors may produce 4 offsprings, i.e., copies of the survivor[s] (parent algorithm[s]) with slight random modifications of its [their] policy parameters. With a single parent [two or more parents], this is referred to as asexual [sexual] reproduction. The surviving policies together with their offsprins constitute the next generation. This scheme can be continued until a satisfactory policy is found.<br><br>
Yet another approach is to use optimization techniques, e.g., *gradient ascent* (similar to gradient descent) to maximise the reward (similar to minimising the cost).
## Introduction to OpenAI Gym
page 445<br>
In order to train an agent, that agent needs an *environment* to operate in. The environment evolves subject to the agent's actions and the agent observes the environment. For example, an Atari game simulator is the environment for an agent that tries to learn to play an Atari game. If the agent tries to learn how to walk a humanoid robot in the real world, then the real world is the environment. Yet, the real world may have limitations when compared to software environments: if the real-world robot gets damaged, just clicking "undo" or "restart" will not suffice. It is also not possible to speed up training by having the time run faster (which would be the equivalent of increasing the clock rate or using a faster processor). And having thousands or millions of real-world robots train in parallel will be much more expensive than running simulations in parallel.<br><br>
In short, one generally wants to use a *simulated environment* at least for getting started. Here, we use the *OpenAI gym* (link at the top). A minimal installation only requires to run "pip3 install --upgrade gym" in a terminal. We shall try it out!
```
import gym # import gym from OpenAI
env = gym.make("CartPole-v0") # make CartPole environment
print(env) # print the cartpole environment
obs = env.reset() # reset observations (in case this is necessary)
print(obs) # print the observations
```
The "make()" function creates an environment (here, the CartPole environment). After creation, the environment must be reset via the "reset()" method. This returns the first observation, in the form of four floats in a $1\times4$ NumPy array: (i) the horizontal position (0=center), (ii) the velocity, (iii) the angle of the pole (0=vertical), and (iv) its angular velocity.
<br>
So far so good. Some environments including the CartPole environment demand access to the screen to visualize the environment. As explained in the Github link (linked above), this may be problematic when Jupyter is used. However, one can work around this issue by using the following function (taken from the Github link) that will render the CartPole environment within a Jupyter notebook.
```
# further imports and plot specifications (taken from Github link above)
import numpy as np
%matplotlib nbagg
import matplotlib
import matplotlib.animation as animation
import matplotlib.pyplot as plt
plt.rcParams["axes.labelsize"] = 14
plt.rcParams["xtick.labelsize"] = 12
plt.rcParams["ytick.labelsize"] = 12
# functions for rendering of the CartPole environment within the Jupyter notebook (taken from Github-link)
from PIL import Image, ImageDraw
try:
from pyglet.gl import gl_info
openai_cart_pole_rendering = True
except Exception:
openai_cart_pole_rendering = False
def render_cart_pole(env, obs):
if openai_cart_pole_rendering:
return env.render(mode="rgb_array")
else:
img_w = 600
img_h = 400
cart_w = img_w // 12
cart_h = img_h // 15
pole_len = img_h // 3.5
pole_w = img_w // 80 + 1
x_width = 2
max_ang = 0.2
bg_col = (255, 255, 255)
cart_col = 0x000000
pole_col = 0x669acc
pos, vel, ang, ang_vel = obs
img = Image.new("RGB", (img_w, img_h), bg_col)
draw = ImageDraw.Draw(img)
cart_x = pos * img_w // x_width + img_w // x_width
cart_y = img_h * 95 // 100
top_pole_x = cart_x + pole_len * np.sin(ang)
top_pole_y = cart_y - cart_h // 2 - pole_len * np.cos(ang)
draw.line((0, cart_y, img_w, cart_y), fill=0)
draw.rectangle((cart_x - cart_w // 2, cart_y - cart_h // 2,
cart_x + cart_w // 2, cart_y + cart_h // 2), fill=cart_col)
draw.line((cart_x, cart_y - cart_h // 2, top_pole_x, top_pole_y), fill=pole_col, width=pole_w)
return np.array(img)
def plot_cart_pole(env, obs):
plt.close()
img = render_cart_pole(env, obs)
plt.imshow(img)
plt.axis("off")
plt.show()
# now, employ the above code
openai_cart_pole_rendering = False # here, we do not even try to display the CartPole environment outside Jupyter
plot_cart_pole(env, obs)
```
Nice. So this is a visualization OpenAI's CartPole environment. After the visualization is finished (it may be a movie), it is best to "close" the visualization by tapping the off-button at its top-right corner.<br><br>
**Suggestion or Tip**<br>
Unfortunately, the CartPole (and a few other environments) renders the image to the screen even if you set the mode to "rgb_array". The only way to avoid this is to use a fake X server such as Xvfb or Xdummy. For example, you can install Xvfb and start Python using the following [shell] command: 'xcfb-run -s "-screen 0 1400x900x24" python'. Or use the xvfb wrapper package (https://goo.gl/wR1oJl). [With the code from the Github link, we do not have to bother about all this.]<br><br>
To continue, we ought to know what actions are possible. This can be checked via the environment's "action_space" method.
```
env.action_space # check what actions are possible
```
There are two possible actions: accelerating left (represented by the integer 0) or right (integer 1). Other environments are going to have other action spaces. We accelerate the cart in the direction that it is leaning.
```
obs = env.reset() # reset again to get different first observations when rerunning this cell
print(obs)
angle = obs[2] # get the angle
print(angle)
action = int((1 + np.sign(angle)) / 2) # compute the action
print(action)
obs, reward, done, info = env.step(action) # submit the action to the environment so the environment can evlolve
print(obs, reward, done, info)
```
The "step()" method executes the chosen action and returns 4 values:
1. "obs"<br>
This is the next observation.
2. "reward"<br>
This environment gives a reward for every time step (not more and not less). The only goal is to keep balancing the cart as long as possble.
3. "done"<br>
The value of this dictionary is "False" while the episode is running and "True" when the episode is finished. It will be finished when the cart moves out of its boundaries or the pole tilts too much.
4. info<br>
This dictionary may provide extra useful information (but not in the CartPole environment). This information can be useful for understanding the problem but shall not be used for adapting the policy. That would be cheating.
We now hardcode a simple policy that always accelerates the cart in the direction it is leaning.
```
# define a basic policy
def basic_policy(obs):
angle = obs[2] # angle
return 0 if angle < 0 else 1 # return action
totals = [] # container for total rewards of different episodes
# run 500 episodes of up to 1000 steps each
for episode in range(500): # run 500 episodes
episode_rewards = 0 # for each episode, start with 0 rewards ...
obs = env.reset() # ... and initialize the environment
for step in range(1000): # attempt 1000 steps for each episode (the policy might fail way before)
action = basic_policy(obs) # use our basic policy to infer the action from the observation
obs, reward, done, info = env.step(action) # apply the action and make a step in the environment
episode_rewards += reward # add the earned reward
if done: # if the environment says that it has finished ...
break # ... this shall be the final step within the current episode
totals.append(episode_rewards) # put the final episode rewards into the container for all the total rewards
# print statistics on the earned rewards
print("mean:", np.mean(totals),", std:", np.std(totals),", min:", np.min(totals),", max:", np.max(totals))
```
Even for 500 episodes, this policy did not manage to reach only 100 steps, not to speak of 1000. As can be seen from the additional code shown under the above Github link, the reason for this is that the pole quickly begins strongly oscillating back and forth. Certainly, the policy is just too simple: also taking the angular velocity of the pole into account should help avoiding wild angular oscillations. A more sophisticated policy might employ a neural network.
## Neural Network Policies
page 448<br>
Let's not just talk the talk but also walk the walk by actually implementing a neural network policy for the CartPole environment. This environment accepts only 2 possible actions: 0 (left) and 1 (right). So one output layer will be sufficient: it returns a value $p$ between 0 and 1. We will accelerate right with probability $p$ and – obviously – left with probability $1-p$.<br>
Why do we not go right with probability ${\rm heaviside}(p-0.5)$? This would hamper the algorithm from exploring further, i.e., it would slow down (or even stop) the learning progress, as can be illustrated with the following analogue. Consider going to a foreign restaurant for the first time. All items on the menu seem equally OK. You choose absolutely randomly one dish. If you happen to like it, you might from now on order this dish every time you visit the restaurant. Fair enough. But there might be even better dishes that you will never find out about if you stick to that policy. By just choosing this menu with a probability in the interval $(0.5,1)$, you will continue to explore the menu, and develop a better understanding of what menu is the best.<br><br>
Note that the CartPole environment returns on every instance the complete necessary information: (i) it contains the velocities (position and angle), so previous observations are not necessary to deduce them, and (ii) it is noise free, so previous observations are not necessary to deduce the actual values from an average. In that sense, the CartPole environment is really as simple as can be.<br><br>
The environment returns 4 observations so we will employ 4 input neurons. We have already mentioned that we only need one single output neuron. To keep things simple, this shall be it: 4 input neurons in the input and in the only hidden layer and 1 output neuron in the output layer. Now, let's cast this in code!
```
# code partially taken from Github link above
import tensorflow as tf
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
reset_graph()
# 1. specify the neural network architecture
n_inputs = 4
n_hidden = 4
n_outputs = 1
initializer = tf.variance_scaling_initializer()
# 2. build the neural network
X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden = tf.layers.dense(X, n_hidden, activation=tf.nn.elu, kernel_initializer=initializer)
logits = tf.layers.dense(hidden, n_outputs, kernel_initializer=initializer)
outputs = tf.nn.sigmoid(logits)
# 3. select a random action based on the estimated probabilities
p_left_and_right = tf.concat(axis=1, values=[outputs, 1 - outputs])
action = tf.multinomial(tf.log(p_left_and_right), num_samples=1)
init = tf.global_variables_initializer()
# maximal number of steps and container for video frames
n_max_steps = 1000
frames = []
# start a session, run the graph, and close the environment (see Github link)
with tf.Session() as sess:
init.run()
obs = env.reset()
for step in range(n_max_steps):
img = render_cart_pole(env, obs)
frames.append(img)
action_val = action.eval(feed_dict={X: obs.reshape(1, n_inputs)})
obs, reward, done, info = env.step(action_val[0][0])
if done:
break
env.close()
# use the below functions and commands to show an animation of the frames
def update_scene(num, frames, patch):
patch.set_data(frames[num])
return patch,
def plot_animation(frames, repeat=False, interval=40):
plt.close()
fig = plt.figure()
patch = plt.imshow(frames[0])
plt.axis("off")
return animation.FuncAnimation(fig, update_scene, fargs=(frames, patch),
frames=len(frames), repeat=repeat, interval=interval)
video = plot_animation(frames)
plt.show()
```
Above, the numbered comments indicate what is happening in the subsequent code. Here are some details.
1. Definition of the Neural Network architecture (c.f. Figure 16-5 on page 449 of the book).
2. Building the Neural Network. Obviously, it is a vanilla (most basic) version. Via the sigmoid activation function, the output lies in the interval [0,1]. If more than two actions were possible, this scheme should use one output neuron per action and a softmax activation function instead of a sigmoid (refer to Chapter 4).
3. Use a multinomial probability distribution to map the probability to one single action. See https://en.wikipedia.org/wiki/Multinomial_distribution and the book for details.
## Evaluating Actions: The Credit Assignment Problem
page 451<br>
If we knew the optimal (target) probability for taking a certain action, we could just do regular machine learning by trying to minimize the cross entropy between that target probability and the estimated probability that we obtain from our policy (see above and below "Neural Network Policies"). However, we do not know the optimal probability for taking a certain action in a certain situation. We have to guess it based on subsequent rewards and penalties (negative rewards). However, rewards are often rare and usually delayed. So it is not clear which previous actions have contributed to earning the subsequent reward. This is the *Credit Assignment Problem*.<br>
One way to tackle the Credit Assignment Problem is to introduce a *discount rate* $r\in[0,1]$. A reward $x$ that occurs $n$ steps after an action - with $n=0$ if the reward is earned directly after the action - adds a score of $r^nx$ to the rewards assigned to that action. For exmaple, if $r=0.8$ and an action is immediately followed by a reward of $+10$, then $0$ after the next action, and $-50$ after the second next action, then that initial action is assigned a score of
$$+10+0-50\times 0.8^2=10-50\times0.64=10-32=-22\,.$$
Typical discount rates are 0.95 and 0.99. When actions have rather immediate consequences, $r=0.95$ is expected to be more suitable than $r=0.99$.<br>
Of course it can happen that in one specific run of the program, a good action happens to be followed by an observation with negative reward. However, on average, a good action will be followed by positive rewards (otherwise it is not a good action). So we need to make many runs to smoothen out the effect of untypical evolutions. Then the scores need to be normalized. In the CartPole environment for example, one could discretize the continuous observations into a finite number of intervals, such that different observations may lie within the same (or different) margins. Then, the scores within one interval should be added up and divided by the number of times the according action was taken, thus giving a representative score. Such scores shall be calculated for all possible actions given that observation. The mean score over all actions needs to be subtracted from each action's score. The resulting number should probably be normalized by the standard deviation and then mapped to probabilities assigned to taking these actions.
## Policy Gradients
page 452<br>
The training procedure that has been outlined above shall now be implemented using TensorFlow.
- First, let the neural network policy play the game several times and **at each step compute the gradients** that would make the chosen action even more likely, but don't apply thes gradients yet. Note that **the gradients involve the observation / state** of the system!
- Once you have **run several episodes (to reduce noise from odd evolutions)**, compute each action's score (using the method described in the previous paragraph).
- If an action's score is positive, it means that the action was good and you want to apply the grdients computed earler to make the action even more likel to be chosen in the future. However, if the score is negative, it means the action was bad and you want to apply the opposite gradients to make this action slightly *less* likely in the future. The solution is simply to **multiply each gradient vector by the corresponding action's score**.
- Finally, compute the mean of all the resulting gradient vectors, and us it to perform a **Gradient Descent** step.
We start with two functions. The first function calculated receives a list of rewards corresponding that occur one step after another and returns a list of accumulated and discounted rewards. The second function receives a list of such lists as well as a discount rate and returns the centered (subtraction of the total mean) and normalized (division by the total standard deviation) lists of rewards. Both functions are tested with simple inputs.
```
# build a function that calculates the accumulated and discounted rewards for all steps
def discount_rewards(rewards, discount_rate):
discounted_rewards = np.empty(len(rewards))
cumulative_rewards = 0
for step in reversed(range(len(rewards))): # go from end to start
cumulative_rewards = rewards[step] + cumulative_rewards * discount_rate # the current reward has no discount
discounted_rewards[step] = cumulative_rewards
return discounted_rewards
# after rewards from 10 episodes, center and normalize the rewards in order to calculate the gradient (below)
def discount_and_normalize_rewards(all_rewards, discount_rate):
all_discounted_rewards = [discount_rewards(rewards, discount_rate) # make a list of the lists with ...
for rewards in all_rewards] # ... the rewards (i.e., a matrix)
flat_rewards = np.concatenate(all_discounted_rewards) # flatten this list to calculate ...
reward_mean = flat_rewards.mean() # ... the mean and ...
reward_std = flat_rewards.std() # ... the standard deviation
return [(discounted_rewards - reward_mean)/reward_std # return a list of centered and normalized ...
for discounted_rewards in all_discounted_rewards] # ... lists of rewards
# check whether these functions work
discount_rewards([10,0,-50], 0.8)
discount_and_normalize_rewards([[10, 0, -50], [10, 20]], 0.8)
```
The following cell is a combination of code from the book and from the github link above. It implements the entire algorithm so it is a bit complicated. Comments shall assist in understanding the code. The default value of "n_iterations" ("n_max_steps") ["discount_rate"] is 250 (1000) [0.95] but can be increased for better performance.
```
# see also "Visualizing the Graph and Training Curves Using TensorBoard" in chapter / notebook 9 to review ...
# ... how to save a graph and display it in tensorboard; important ingredients: ...
# ... (i) reset_graph(), (ii) file_writer, and (iii) file_writer.close(); possible the "saver" is also important
# create a directory with a time stamp
from datetime import datetime # import datetime
now = datetime.utcnow().strftime("%Y%m%d%H%M%S") # get current UTC time as a string with specified format
root_logdir = "./tf_logs/16_RL/Cartpole" # directory in the same folder as this .ipynb notebook
logdir = "{}/policy_gradients-{}/".format(root_logdir, now) # folder with timestamp (inside the folder "tf_logs")
print(logdir) # print the total path relative to this notebook
# reset the graph and setup the environment (cartpole)
reset_graph()
env = gym.make("CartPole-v0")
# 1. specify the neural network architecture
n_inputs = 4
n_hidden = 4
n_outputs = 1
initializer = tf.contrib.layers.variance_scaling_initializer()
learning_rate = 0.01
# 2. build the neural network
X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden = tf.layers.dense(X, n_hidden, activation=tf.nn.elu, kernel_initializer=initializer)
logits = tf.layers.dense(hidden, n_outputs, kernel_initializer=initializer)
outputs = tf.nn.sigmoid(logits)
p_left_and_right = tf.concat(axis=1, values=[outputs, 1 - outputs])
action = tf.multinomial(tf.log(p_left_and_right), num_samples=1)
y = 1. - tf.to_float(action)
# 3. cost function (cross entropy), optimizer, and calculation of gradients
cross_entropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=logits)
optimizer = tf.train.AdamOptimizer(learning_rate)
grads_and_vars = optimizer.compute_gradients(cross_entropy)
# 4. rearrange gradients and variables
gradients = [grad for grad, variable in grads_and_vars]
gradient_placeholders = []
grads_and_vars_feed = []
for grad, variable in grads_and_vars:
gradient_placeholder = tf.placeholder(tf.float32, shape=grad.get_shape())
gradient_placeholders.append(gradient_placeholder)
grads_and_vars_feed.append((gradient_placeholder, variable))
training_op = optimizer.apply_gradients(grads_and_vars_feed)
# 5. file writer, global initializer, and saver
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph()) # save the graph graph under "logdir"
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# 6. details for the iterations that will be run below
n_iterations = 250 # default is 250
n_max_steps = 1000 # default is 1000
n_games_per_update = 10
save_iterations = 10
discount_rate = 0.95 # default is 0.95
# 7. start a session and run it
with tf.Session() as sess:
init.run()
# 7.1. loop through iterations
for iteration in range(n_iterations):
all_rewards = [] # container for rewards lists
all_gradients = [] # container for gradients lists
# 7.2. loop through games
for game in range(n_games_per_update):
current_rewards = [] # container for unnormalized rewards from current episode
current_gradients = [] # container for gradients from current episode
obs = env.reset() # get first observation
# 7.3 make steps in the current game
for step in range(n_max_steps):
action_val, gradients_val = sess.run([action, gradients], # feed the observation to the model and ...
feed_dict={X: obs.reshape(1, n_inputs)}) # ... receive the ...
# ... action and the gradient (see 4. above)
obs, reward, done, info = env.step(action_val[0][0]) # feed action and receive next observation
current_rewards.append(reward) # store reward in container
current_gradients.append(gradients_val) # store gradients in container
if done: # stop when done
break
all_rewards.append(current_rewards) # update list of rewards
all_gradients.append(current_gradients) # update list of gradients
# 7.4. we have now run the current policy for "n_games_per_update" times and it shall be updated
all_rewards = discount_and_normalize_rewards(all_rewards, discount_rate) # use the function(s) defined above
# 7.5. fill place holders with actual values
feed_dict = {}
for var_index, grad_placeholder in enumerate(gradient_placeholders): # loop through placeholders
mean_gradients = np.mean([reward * all_gradients[game_index][step][var_index] # calculate ...
for game_index, rewards in enumerate(all_rewards) # ... the ...
for step, reward in enumerate(rewards)], # ... mean ...
axis=0) # ... gradients and ...
feed_dict[grad_placeholder] = mean_gradients # ... feed them
# 7.6. run the training operation
sess.run(training_op, feed_dict=feed_dict)
# 7.7. save every now and then
if iteration % save_iterations == 0:
saver.save(sess, "./tf_logs/16_RL/Cartpole/my_policy_net_pg.ckpt")
# 8. close the file writer and the environment (cartpole)
file_writer.close()
env.close()
```
Using another function from the github link, we apply the trained model and visualize the performance of the agent in its environment. The performance differs from run to run, presumably due to random initialization of the environment.
```
# use code from the github link above to apply the trained model to the cartpole environment and show the results
model = 1
def render_policy_net(model_path, action, X, n_max_steps = 1000):
frames = []
env = gym.make("CartPole-v0")
obs = env.reset()
with tf.Session() as sess:
saver.restore(sess, model_path)
for step in range(n_max_steps):
img = render_cart_pole(env, obs)
frames.append(img)
action_val = action.eval(feed_dict={X: obs.reshape(1, n_inputs)})
obs, reward, done, info = env.step(action_val[0][0])
if done:
break
env.close()
return frames
if model == 1:
frames = render_policy_net("./tf_logs/16_RL/Cartpole/my_policy_net_pg.ckpt", action, X, n_max_steps=1000)
else:
frames = render_policy_net("./tf_logs/16_RL/Cartpole/my_good_policy_net_pg.ckpt",
action, X, n_max_steps=1000)
video = plot_animation(frames)
plt.show()
```
This looks much better than without updating the gradients. Almost skillful, at least witn "n_iterations = 1000", "n_max_steps = 1000", and "discount_rate = 0.999". The according model is saved under "./tf_logs/Cartpole/my_1000_1000_0999_policy_net_pg.ckpt". In fact, **this algorithm is really powerful**. It can be used for much harder problems. **AlphaGo** was also based on it (and on *Monte Carlo Tree Search*, which is beyond the scope of this book).<br><br>
**Suggestion or Tip**<br>
Researchers try to find algorithms that work well even when the agent initially knows nothing about the environment. However, unless you are writing a paper, you should inject as much prior knowledge as possible into the agent, as it will speed up training dramatically. For example, you could add negative rewards proportional to the distance from the center of the screen, and to the pole's angle. Also, if you already have a reasonably good policy (e.g., hardcoded), you may want to train the nerual network to imitate it before using policy gradients to imporve it.<br><br>
But next, we go a different path: the agent shall calculate what future rewards (possibly discounted) it expects after an action in a certain situation. The action shall be chosen based on that expectation. To this end, some more theory is necessary.
## Markov Decision Processes
page 457<br>
A *Markov chain* is a stochastic process where a system changes between a finite number of states and the probability to transition from state $s$ to state $s'$ is only determined by the pair $(s,s')$, not on previous states (the system has no memory). Andrey Markov studied these processes in the early 20th century. If the transition $(s,s)$ has probability $1$, then the state $s$ is a *terminal state*: the system cannot leave it (see also Figure 16-7 on page 458 of the book). There can be any integer $n\geq0$ number of terminal states. Markov chains are heavily used in thermodynamics, chemistry, statistics, and much more.<br>
Markov decision processes were first decribed by Richard Bellmann in the 1950s (see the jstor-link above). They are Markov chains where at each state $s$, there is one or more action $a$ that an *agent* can choose from and the transition probilitiy between state $s$ and $s'$ depends on action $a$. Moreover, some transitions $(s,a,s')$ return a reward (positive or negative). The agent's goal is to find a policy that maximizes rewards over time (see also Figure 16-8 on page 459).<br><br>
If an agent acts optimally, then the *Bellman Optimality Equation* applies. This recursive equation states that the optimal value of the current state is equal to the reward it will get on average after taking one optimal action, plus the expected optimal vlaue of all possible next states that this action can lead to:<br><br>
$$V^*(s)={\rm max}_a\sum_{s'}T(s,a,s')[R(s,a,s')+\gamma*V^*(s')]\quad\text{for all $s$.}$$
Here,
- $V^*(s)$ is the *optimal state value* of state $s$,
- $T(s,a,s')$ is the transition probability from state $s$ to state $s'$, given that the agent chose action $a$,
- $R(s,a,s')$ is the reward that the agent gets when it goes from state $s$ to state$s'$, given that the agent chose action $a$, and
- $\gamma$ is the discount rate.
The **Value Iteration** algorithm will have the values $V(s)$ - initialized to 0 - converge towards their optima $V^*(s)$ by iteratively updating them:<br><br>
$$V_{k+1}(s)\leftarrow{\rm max}_a\sum_{s'}T(s,a,s')[R(s,a,s')+\gamma V_k(s')]\quad\text{for all $s$.}$$
Here, $V_k(s)$ is the estimated value of state $s$ in the $k$-th iteration and $\lim_{k\to\infty}V_k(s)=V^*(s)$.
<br><br>
**General note**<br>
This algorithm is an example of *Dynamic Programming*, which breaks down a complex problem (in this case estimating a potentially infinite sum of discounted future rewards) into tractable sub-problems that can be tackled iteratively (in this case finding the action that maximizes the average reward plus the discounted next state value).<br><br>
Yet even when $V^*(s)$ is known, it is still unclear what the agent shall do. Bellman thus extended the concept of state values $V(s)$ to *state-action values*, called *Q-values*. The optimal Q-value of the state-action pair $(s,a)$, noted $Q^*(s,a)$, is the sum of discounted future rewards the agent will earn on average when it applies to correct policy, i.e., choosing the right action $a$ when in state $s$. The according **Q-value iteration** algorithm is<br><br>
$$Q_{k+1}(s,a)\leftarrow\sum_{s'}T(s,a,s')[R(s,a,s')+\gamma\,{\rm max}_{a'}Q_k(s',a')],\quad\text{for all $(s,a)$.}$$<br>
This is very similar to the value iteration algorithm. Now, the optimal policy $\pi^*(s)$ is clear: when in state $s$, apply that action $a$ for which the Q-value is highest: $\pi^*(s)={\rm argmax}_aQ^*(s,a)$. We will practice this on the Markov decision process shown in Figure 16-8 on page 459 of the book.
```
nan = np.nan # for transitions that do not exist (and thus have probability 0 but shall not be updated)
# transition probabilities
T = np.array([
[[0.7, 0.3, 0.0], [1.0, 0.0, 0.0], [0.8, 0.2, 0.0]], # at state s_0: actions a_0, a_1, a_2 to states s_0, s_1, s_2
[[0.0, 1.0, 0.0], [nan, nan, nan], [0.0, 0.0, 1.0]], # at state s_1
[[nan, nan, nan], [0.8, 0.1, 0.1], [nan, nan, nan]] # at state s_2
])
# rewards associated with the transitions above
R = np.array([
[[10., 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]],
[[10., 0.0, 0.0], [nan, nan, nan], [0.0, 0.0, -50]],
[[nan, nan, nan], [40., 0.0, 0.0], [nan, nan, nan]]
])
# possible actions
possible_actions = [
[0, 1, 2], # in state s0
[0, 2], # in state s1
[1]] # in state s2
# Q value initialization
Q = np.full((3, 3), -np.inf) # -infinity for impossible actions
for state, actions in enumerate(possible_actions):
print(state, actions)
Q[state, actions] = 0.0 # 0.0 for possible actions
print(Q)
```
Above, we have specified the model (lists of transition probabilities T, rewards R, and possible actions) and initialized the Q-values. Using $-\infty$ for impossible actions ensures that those actions will not be chosen by the policy. The enumerate command can be quite helpful and is therefore shortly introduced below.
```
# see the python tips link above
for counter, value in enumerate(["apple", "banana", "grapes", "pear"]):
print(counter, value)
print()
for counter, value in enumerate(["apple", "banana", "grapes", "pear"], 1):
print(counter, value)
print()
counter_list = list(enumerate(["apple", "banana", "grapes", "pear"], 1))
print(counter_list)
```
Now, define residual parameters and run the Q-value iteration algorithm. The results are very similar to the ones in the book.
```
# learning parameters
learning_rate = 0.01
discount_rate = 0.95 # try 0.95 and 0.9 (they give different results)
n_iterations = 100
# Q-value iteration
for iteration in range(n_iterations): # loop over iterations
Q_prev = Q.copy() # previous Q
for s in range(3): # loop over states s
for a in possible_actions[s]: # loop over available actions a
# update Q[s, a]
Q[s, a] = np.sum([T[s, a, sp] * (R[s, a, sp] + # transition probability to sp times ...
discount_rate*np.max(Q_prev[sp])) # ... ( reward + max Q(sp) )
for sp in range(3)]) # sum over sp (sp = s prime)
print(Q) # print final Q
np.argmax(Q, axis=1) # best action for a given state (i.e., in a given row)
```
The Q-value iteration algorithm gives different results for different discount rates $\gamma$. For $\gamma=0.95$, the optimal policy is to choose action 0 (2) [1] in state 0 (1) [2]. But this changes to actions 0 (0) [1] if $\gamma=0.9$. And it makes sense: when someone appreciates the present more than possible future rewards, there is less motivation to go through the fire.
## Temporal Difference Learning and Q-Learning
page 461<br>
Reinforcement Learning problems can often be modelled with Markov Decision Processes, yet initially, there is no knowledge on transition probabilities $T(s,a,s')$ and rewards $R(s,a,s')$. The algorithm must experience every connection at least once to obtain the rewards and multiple times to get a glimplse of the probabilities.<br>
**Temporal Difference Learning** (TD Learning) is similar to *Value Iteration* (see above) but adapted to the fact that the agent has only partial knowledge of the MDP. In fact, it often only knows the possible states and actions and thus must *explore* the MDP via an *exploration policy* in order to recursively update the estimates for the state values based on observed transitions and rewards. This is achieved via the **Temporal Difference Learning algorithm** (Equation 16-4 in the book),
$$V_{k+1}\leftarrow(1-\alpha)V_k(s)+\alpha(r+\gamma V_k(s'))\,,$$
where $\alpha$ is the learning rate (e.g., 0.01).<br>
For each state $s$, this algorithm simply keeps track of a running average of the next reward (for the transition to the state it will end up at next) and future rewards (via the state value of the next state, since the agent is assumed to act optimally). This algorithm is stochastic: the next state $s'$ and the reward gained by going to it are not known at state $s$: this transition only happens with a certain probability and thus will – in general – be different from time to time.<br><br>
**Suggestion or Tip**<br>
TD Learning has many similarities with Stochasitc Gradient Descent, in particular the fact that it handles one sample at a time. Just like SGD, it can only truly converge if you gradually reduce the learning rate (otherwise it will keep bouncing around the optimum).<br><br>
The **Q-Learning algorithm** resembles the *Temporal Difference Learning algorithm* just like the *Q-Value Iteration algorithm* resembles the *Value Iteration algorithm* (see Equation 16-5 in the book):
$$Q_{k+1}(s,a)\leftarrow(1-\alpha)Q_k(s,a)+\alpha(r+\gamma\,{\rm max}_{a'}Q_k(s',a'))\,.$$
<br>
In comparison with the *TD Learning algorithm* above, there is another degree of freedom: the action $a$. It is assumed that the agent will act optimally. As a consequence, the maximum (w.r.t. actions a') Q-Value is chosen for the next state-action pair. Now to the implementation!
```
n_states = 3 # number of MDP states
n_actions = 3 # number of actions
n_steps = 20000 # number of steps (=iterations)
alpha = 0.01 # learning rate
gamma = 0.99 # discount rate
# class for a Markov Decision Process (taken from the github link above)
class MDPEnvironment(object):
def __init__(self, start_state=0): # necessary __init__
self.start_state=start_state
self.reset()
def reset(self): # reset the environment
self.total_rewards = 0
self.state = self.start_state
def step(self, action): # make a step
next_state =np.random.choice(range(3), # use the transition probabilities T above and the ...
p=T[self.state][action]) # ... state and action to infer the next state
reward = R[self.state][action][next_state] # in this fashion, also calculate the obtained reward
self.state = next_state # update the state ...
self.total_rewards += reward # ... and the total rewards
return self.state, reward
# function that returns a random action that is in line the given state (taken from github link above)
def policy_random(state):
return np.random.choice(possible_actions[state]) # see definition of "possible_actions" above
exploration_policy = policy_random # use that function as an exploration policy
# reinitialize the Q values (they had been updated above)
Q = np.full((3, 3), -np.inf) # -infinity for impossible actions
for state, actions in enumerate(possible_actions): # see (unchanged) defintion of possible_actions above
Q[state, actions] = 0.0 # 0.0 for possible actions
print(Q)
# use the class defined above
env = MDPEnvironment()
# loop through all steps (=iterations)
for step in range(n_steps):
action = exploration_policy(env.state) # give our "exploration_policy = policy_random" the ...
# ... current state and obtain an action in return
state = env.state # obtain the state from the environment
next_state, reward = env.step(action) # apply the action to obtain the next state and reward
next_value = np.max(Q[next_state]) # assuming optimal behavior, use the highest Q-value ...
# ... that is in line with the next state (maximise ...
# ... w.r.t. the actions)
Q[state, action] = (1-alpha)*Q[state, action] + alpha*(reward + gamma * next_value) # update Q value
Q # return the final Q values
```
The above implementation is different from the book (where prior knowledge on the transition probabilities is used). Accordingly, the resulting Q-values are different from those in the book and closer to the ones listed in the github link above.<br>
With enough iterations, this algorithm will converge towards theo optimal Q-values. It is called an **off-policy** algorithm since the policy that is used for training is different from the one that will be applied. Surprisingly, this algorithm converges towards the optimal policy by stumbling around: it's a stochastic process. So although this works, there should be a more promising approach. This shall be studied next.
### Exploration Policies
page 463<br>
Above, the transitions probabilites $T(s,a,s')$ are used to explore the MDP and obtain a policy. However, this might take a long time. An alternative approach is to use an **$\epsilon$-greedy policy** (greedy = gierig): in each state, it chooses the state-action value Q(s,a) with the highest score with probability $1-\epsilon$ or a random action (i.e., Q(s,...)) with probability $\epsilon$. This way, the policy will explorte the interesting parts of the network more intensely while still getting in touch (eventually) with all other parts. It is common to start with $\epsilon=1$ (totally random) and transition to $\epsilon=0.05$ (choose highest Q-value most of the time).<br>
Another way to incite the agent to explore the entire network is to artificially increase the value of state action pairs that have not been visited frequently. This can be done like so (Equation 16-6 in the book):<br><br>
$$Q(s,a)\leftarrow(1-\alpha)Q(s,a)+\alpha\left(r+\gamma\,{\rm max}_{\alpha'}f(Q(s',a'),N(s',a')\right)\,,$$<br>
where $\alpha$ is the learning rate, $\gamma$ is the discount rate, and $f(q,n)$ is a function of the Q-value $q$ and the additional reward $n$, e.g. $f(q,n)=q+K/(1+n)$, where $K$ is a **curiosity hyperparameter** and $n$ is the number of times the Q-value $q$ has been visited.
### Approximate Q-Learning
page 464<br>
Unfortunately, Q-Learning as described above dose not scale well. For example, in Ms. Pac-Man there exist more than 250 pellets that can be already eaten or not. This alone gives rise to $2^{250}\approx10^{75}$ states, i.e., more than the number of atoms in the universe. And this is just the pellets! There is no way, a policy could completely explore the according MDP.<br>
The solution is **Approximate Q-Learning** where estimates for the Q-values are inferred from a managable number of parameters. For a long time, the way to go had been to hand-craft features, e.g., the distances between Ms. Pac-Man and the ghosts. But DeepMind showed that deep neural networks can perform much better. On top, they do not require feature engineering. A DNN that is used to estimate Q-Values is called a **Deep Q-Network (DQN)**, and using a DQN for Approximate Q-Learning (and subsequently inferring a policy from the Q-Values) is called **Deep Q-Learning**.
The rest of this chapter is about using Deep Q-Learning to train a computer on Ms. Pac-Man, much like DeepMind did in 2013. This code is quite versatile. It works for many Atari games but tends to have problems with games with long-running storylines.
## Learning to Play Ms. Pac-Man Using Deep Q-Learning
page 464<br>
Some installations shall be made:
- Homebrew (see http://brew.sh/). For macOS, run '/usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)"' in the terminal and for Ubuntu, use 'apg-get install -y python3-numpy python3-dev cmake zlib1g-dev libjpeg-dev\xvfb libav-tools xorg-dev python3-opengl libboost-all-dev libsdl2-dev swig'.
- Extra python modules for the gym of OpenAI, via "pip3 install --upgrade 'gym[all]'".
With these, we should manage to create a Ms. Pac-Man environment.
```
env = gym.make("MsPacman-v0")
obs = env.reset()
print(obs.shape) # [height, width, channels]
print(env.action_space) # possible actions
```
So the agent observes a picture (screenshot) of 210 pixels height and 160 pixels width, with each pixel having three color values: the intensity of red, green, and blue. The agent may react by returning an action to the environment. There are nine discrete actions, corresponding to the nine joystick positions ([up, middle, down]x[left, middle, right]). The screenshots are a bit too large and grayscale should suffice. So we preprocess the data by cropping the image to the relevant part and converting the color image to grayscale. This will speed up training.
```
# see https://docs.python.org/2.3/whatsnew/section-slices.html for details on slices
trial_list = [[0.0,0.1,0.2,0.3,0.4],
[0,1,2,3,4],
[0,10,20,30,40]]
print(trial_list[:2]) # print list elements until before element 2, i.e., 0 and 1
print(trial_list[::2]) # print all list elements that are reached by step size 2, i.e., 0 and 2, not 1
print(trial_list[:3]) # print list elements until before element 3, i.e., 0, 1, and 2 (this means all, here)
print(trial_list[::3]) # print all list elements that are reached by step size 3, i.e., only 0, not 1 and 2
# back to the book
mspacman_color = np.array([210, 164, 74]).mean()
def preprocess_observation(obs):
img = obs[1:176:2, ::2] # use only every second line from line 1 to line 176 (top towards bottom) and in ...
# ... each line, use only every second row
img = img.mean(axis=2) # go to grayscale by replacing the 3 rgb values by their average
img[img==mspacman_color] = 0 # draw Ms. Pac-Man in black
img = (img-128)/128 - 1 # normalize grayscale
return img.reshape(88, 80, 1) # reshape to 88 rows and 80 columns; each scalar entry is the color in grayscale ...
# ... and thus is a bit different from the book
#print(preprocess_observation(obs))
print(preprocess_observation(obs).shape)
# slightly modified from the github link above
plt.figure(figsize=(9, 5))
plt.subplot(121)
plt.title("Original observation (160×210 RGB)")
plt.imshow(obs)
plt.axis("off")
plt.subplot(122)
plt.title("Preprocessed observation (88×80 greyscale)")
# the output of "preprocess_observation()" is reshaped as to be in line with the placeholder "X_state", to which ...
# ... it will be fed; below, another reshape operation is appropriate to conform the (possbily updated w.r.t. the ...
# ... book) "plt.imshow()" command, https://matplotlib.org/api/_as_gen/matplotlib.pyplot.imshow.html
plt.imshow(preprocess_observation(obs).reshape(88,80), interpolation="nearest", cmap="gray")
plt.axis("off")
plt.show()
```
The next task will be to build the DQN (*Deep Q-Network*). In principle, one could just feed it a state-action pair (s, a) and have it estimate the Q-Value Q(s, a). But since the actions are discrete and only 9 actions are possible, one can also feed the DQN the state s and have it estimate Q(s, a) for all 9 possible actions. The DQN shall have 3 convolutional layers followed by 2 fully connected layers, the last of which is the output layer. An actor-critic approach is used. They share the same architecture but have different tasks: the actor plays and the critic watches the play and tries to identify and fix shortcomings. After each few iterations, the critic network is copied to the actor network. So while they share the same architecture their parameters are different. Next, we define a function to build these DQNs.
```
### construction phase
# resetting the graph seems to always be a good idea
reset_graph()
# DQN architecture / hyperparameters
input_height = 88
input_width = 80
input_channels = 1
conv_n_maps = [32, 64, 64]
conv_kernel_sizes = [(8,8), (4,4), (3,3)]
conv_strides = [4, 2, 1]
conv_paddings = ["SAME"] * 3
conv_activation =[tf.nn.relu] * 3
n_hidden_in = 64 * 11 * 10 # conv3 has 64 maps of 11x10 each
n_hidden = 512
hidden_activation = tf.nn.relu # corrected from "[tf.nn.relu]*3", according to the code on github (see link above)
n_outputs = env.action_space.n # 9 discrete actions are available
initializer = tf.contrib.layers.variance_scaling_initializer()
# function to build networks with the above architecture; the function receives a state (observation) and a name
def q_network(X_state, name):
prev_layer = X_state # input from the input layer
conv_layers = [] # container for all the layers of the convolutional network (input layer is not part of that)
with tf.variable_scope(name) as scope:
# loop through tuples, see "https://docs.python.org/3.3/library/functions.html#zip" for details;
# in the first (second) [next] step take the first (second) [next] elements of the lists conv_n_maps, ...
# ... conv_kernel_sizes, etc.; this continues until one of these lists has arrived at the end;
# here, all these lists have length 3 (see above)
for n_maps, kernel_size, stride, padding, activation in zip(conv_n_maps, conv_kernel_sizes, conv_strides,
conv_paddings, conv_activation):
# in the next step (of the for-loop), this layer will be the "previous" one
# ["stride" -> "strides", see https://www.tensorflow.org/api_docs/python/tf/layers/conv2d]
prev_layer = tf.layers.conv2d(prev_layer, filters=n_maps, kernel_size=kernel_size, strides=stride,
padding=padding, activation=activation, kernel_initializer=initializer)
# put the current layer into the container for all the layers of the convolutional neural network
conv_layers.append(prev_layer)
# make the last output a vector so it it can be passed easily to the upcoming fully connected layer
last_conv_layer_flat = tf.reshape(prev_layer, shape=[-1, n_hidden_in])
# first hidden layer
hidden = tf.layers.dense(last_conv_layer_flat, n_hidden, activation=hidden_activation,
kernel_initializer=initializer)
# second hidden layer = output layer (these are the results!)
outputs = tf.layers.dense(hidden, n_outputs, kernel_initializer=initializer)
# let tensorflow figure out what variables shall be trained ...
trainable_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope=scope.name)
# ... and give these variables names so they can be distinguished in the graph
trainable_vars_by_name = {var.name[len(scope.name):]: var for var in trainable_vars}
return outputs, trainable_vars_by_name # return the outputs and the dictionary of trainable variables
# input, actor, critic, and model copying
X_state = tf.placeholder(tf.float32, shape=[None, input_height, input_width, input_channels]) # input placeholder
actor_q_values, actor_vars = q_network(X_state, name="q_networks/actor") # actor model
#q_values = actor_q_values.eval(feed_dict={X_state: [state]})
critic_q_values, critic_vars = q_network(X_state, name="q_networks/critic") # critic model
copy_ops = [actor_var.assign(critic_vars[var_name]) for var_name, actor_var in actor_vars.items()] # copy critic ...
copy_critic_to_actor = tf.group(*copy_ops) # ... to actor
# some more theory is due
print("next, some text...")
```
The somehow initialized Q-values will have the actor network play the game (initially somehow random), update the encountered Q-values (via the default discounted rewards), and leave the remaining Q-values unchanged. Every now and then, the critic network is tasked with predicting all Q-values by fitting the weights and biases. The Q-values resulting from the fitted weights and biases will be slightly different. This is supervised learning. The cost function that the critic network shall minimize is<br><br>
$$J(\theta_{\rm critic})=\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}-Q(s^{(i)},a^{(i)},\theta_{\rm critic})\right)^2{\rm , with }\quad y^{(i)}=r^{(i)}+\gamma {\rm max}_{a'}Q\left(s'^{(i)},a^{(i)},\theta_{\rm actor}\right)\,,$$
where
- $s^{(i)},\,a^{(i)},\,r^{(i)},\,s'^{(i)}$ are respectively the state, action, reward, and the next state of the $i^{\rm th}$ memory sampled from the replay memory,
- $m$ is the size of the memory batch,
- $\theta_{\rm critic}$ and $\theta_{\rm actor}$ are the critic and the actor's parameters,
- $Q(s^{(i)},a^{(i)},\theta_{\rm critic})$ is the critic DQN's prediction of the $i^{\rm th}$ memorized state-action's Q-value,
- $Q(s^{(i)},a^{(i)},\theta_{\rm actor})$ is the actor DQN's prediction of Q-value it can expect from the next state $s'^{\rm(i)}$ if it chooses action $a'$,
- $y^{(i)}$ is the target Q-value for the $i^{\rm th}$ memory. Note that it is equal to the reward actually observed by the actor, plus the actor's *prediction* of what future rewards it should expect if it were to play optimally (as far as it knows), and
- $J(\theta_{\rm critic})$ is the cost function used to train the critic DQN. As you can see, it is just the mean squared error between the target Q-values $y^{(i)}$ as estimated by the actor DQN, and the critic DQN's prediction of these Q-values.
**General note**<br>
The replay memory [see code and/or text in the book] is optional but highly recommended. Without it , you would train the critic DQN using consecutive experiences that may be very correlated. This would introduce a lot of bias and slow down the training algorithm's convergence. By using a replay memory, we ensure that the memories fed to the training algorithm can be fairly uncorrelated.
```
# the actor DQN computes 9 Q-values: 1 for each possible action; use one-hot encoding to select only the one that ...
# ... is actually chosen (https://www.tensorflow.org/api_docs/python/tf/one_hot)
X_action = tf.placeholder(tf.int32, shape=[None])
q_value = tf.reduce_sum(critic_q_values * tf.one_hot(X_action, n_outputs), axis=1, keep_dims=True)
# feed the Q-values for the critic network through a placeholder y and do all the rest for training operations
y = tf.placeholder(tf.float32, shape=[None, 1])
cost = tf.reduce_mean(tf.square(y - q_value))
global_step = tf.Variable(0, trainable=False, name="global_step")
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(cost, global_step=global_step)
# initializer and saver nodes
init = tf.global_variables_initializer()
saver = tf.train.Saver()
```
For the execution phase, we will need the following tools.
```
# time keeping; for details, see the contribution of user "daviewales" on ...
# ... https://codereview.stackexchange.com/questions/26534/is-there-a-better-way-to-count-seconds-in-python
import time
time_start = time.time()
# another import, see https://docs.python.org/3/library/collections.html#collections.deque
from collections import deque # deque or "double-ended queue" is similar to a python list but more performant
replay_memory_size = 10000 # name says it
replay_memory = deque([], maxlen=replay_memory_size) # deque container for the replay memory
# function that samples random memories
def sample_memories(batch_size):
# use "np.rand" instead of "rnd", see ...
# ... "https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.random.permutation.html"
indices = np.random.permutation(len(replay_memory))[:batch_size] # take "batch_size" random indices
cols = [[], [], [], [], []] # state, action, reward, next_state, continue
# loop over indices
for idx in indices:
memory = replay_memory[idx] # specifice memory
for col, value in zip(cols, memory): # fancy way of moving the values in the ...
col.append(value) # ... memory into col
cols = [np.array(col) for col in cols] # make entries numpy arrays
return (cols[0], cols[1], cols[2].reshape(-1,1), cols[3], cols[4].reshape(-1,1))
# use an epsilon-greedy policy
eps_min = 0.05 # next action is random with probability of 5%
eps_max = 1.0 # next action will be random for sure
eps_decay_steps = 50000 # decay schedule for epsilon
# receive the Q values for the current state and the current step
def epsilon_greedy(q_values, step):
epsilon = max(eps_min, eps_max - (eps_max-eps_min) * step/eps_decay_steps) # calculate the current epsilon
if np.random.rand() < epsilon: # choice of random or optimal action
return np.random.randint(n_outputs) # random action
else:
return np.argmax(q_values) # optimal action
### execution phase
n_steps = 10 # total number of training steps (default: 100000)
training_start = 1000 # start training after 1000 game iterations
training_interval = 3 # run a training step every few game iterations (default: 3)
save_steps = 50 # save the model every 50 training steps
copy_steps = 25 # copy the critic to the actor every few training steps (default: 25)
discount_rate = 0.95 # discount rate (default: 0.95)
skip_start = 90 # skip the start of every game (it's just waiting time)
batch_size = 50 # batch size (default: 50)
iteration = 0 # initialize the game iterations counter
checkpoint_path = "./tf_logs/16_RL/MsPacMan/my_dqn.ckpt" # checkpoint path
done = True # env needs to be reset
# remaining import
import os
# start the session
with tf.Session() as sess:
# restore a session if one has been stored
if os.path.isfile(checkpoint_path):
saver.restore(sess, checkpoint_path)
# otherwise start from scratch
else:
init.run()
while True: # continue training ...
step = global_step.eval() # ... until step ...
if step >= n_steps: # ... has reached n_steps ...
break # ... (stop in that latter case)
iteration += 1 # count the iterations
if done: # game over: start again ...
# restart 1/3
obs = env.reset() # ... and reset the environment
# restart 2/3
for skip in range(skip_start): # skip the start of each game
obs, reward, done, info = env.step(0) # get data from environment (Ms. Pacman)
# restart 3/3
state = preprocess_observation(obs) # preprocess the state of the game (screenshot)
# actor evaluates what to do
q_values = actor_q_values.eval(feed_dict={X_state: [state]}) # get available Q-values for the current state
action = epsilon_greedy(q_values, step) # apply the epsilon-greedy policy
# actor plays
obs, reward, done, info = env.step(action) # apply the action and get new data from env
next_state = preprocess_observation(obs) # preprocess the next state (screenshot)
# let's memorize what just happened
replay_memory.append((state, action, reward, next_state, 1.0 - done))
state = next_state
# go to the next iteration of the while loop (i) before training starts and (ii) if learning is not scheduled
if iteration < training_start or iteration % training_interval != 0:
continue
# if learning is scheduled for the current iteration, get samples from the memory, update the Q-values ...
# ... that the actor learned as well as the rewards, and run a training operation
X_state_val, X_action_val, rewards, X_next_state_val, continues = (sample_memories(batch_size))
next_q_values = actor_q_values.eval(feed_dict={X_state: X_next_state_val})
max_next_q_values = np.max(next_q_values, axis=1, keepdims=True)
y_val = rewards + continues * discount_rate * max_next_q_values
training_op.run(feed_dict={X_state: X_state_val, X_action: X_action_val, y: y_val})
# regularly copy critic to actor and ...
if step % copy_steps == 0:
copy_critic_to_actor.run()
# ... save the session so it could be restored
if step % save_steps == 0:
saver.save(sess, checkpoint_path)
# the output of this time keeping (see top of this cell) will be in seconds
time_finish = time.time()
print(time_finish - time_start)
```
With a function from the github link above, we can visualize the play of the trained model.
```
frames = []
n_max_steps = 10000
with tf.Session() as sess:
saver.restore(sess, checkpoint_path)
obs = env.reset()
for step in range(n_max_steps):
state = preprocess_observation(obs)
q_values = actor_q_values.eval(feed_dict={X_state: [state]}) # from "online_q_values" to "actor_q_values"
action = np.argmax(q_values)
obs, reward, done, info = env.step(action)
img = env.render(mode="rgb_array")
frames.append(img)
if done:
break
plot_animation(frames)
```
**Suggestion or Tip**<br>
Unfortunately, training is very slow: if you use your laptop for training, it will take days before Ms. Pac-Man gets any good, and if you look at the learning curve, measuring the average rewards per episode, you will notice that it is extremely noisy. At some points there may be no apparent progress for a very long time until suddenly the agent learns to survive a reasonable amount of time. As mentioned earlier, one solution is to inject as much prior knowledge as possible into the model (e.g., through preprocessing, rewards, and so on), and you can also try to bootstrap the model by first training it to imitate a basic strategy. In any case, RL still requires quite a lot of patience and tweaking but the end result is very exciting.
## Exercises
page 473<br>
### 1.-7.
Solutions are shown in Appendix A of the book and in the separate notebook *ExercisesWithoutCode*.
### 8.
Use Deep Q-Learning to tackle OpenAI gym's "BypedalWalker-v2". The Q-networks do not need to be very deep for this task.
```
# everything below is mainly from the github link above
# the rendering command (see github link) does not work here; the according code is adapted; frames are not ...
# ... displayed, here
env = gym.make("BipedalWalker-v2")
print(env)
obs = env.reset()
print(obs)
print(env.action_space)
print(env.action_space.low)
print(env.action_space.high)
```
Build all possible combinations of actions (cf. above).
```
# see https://docs.python.org/3.7/library/itertools.html#itertools.product
from itertools import product
possible_torques = np.array([-1.0, 0.0, 1.0])
possible_actions = np.array(list(product(possible_torques, repeat=4)))
possible_actions.shape
print(possible_actions)
```
Build a network and see how it performs.
```
tf.reset_default_graph()
# 1. Specify the network architecture
n_inputs = env.observation_space.shape[0] # == 24
n_hidden = 10
n_outputs = len(possible_actions) # == 625
initializer = tf.variance_scaling_initializer()
# 2. Build the neural network
X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden = tf.layers.dense(X, n_hidden, activation=tf.nn.selu, kernel_initializer=initializer)
logits = tf.layers.dense(hidden, n_outputs, kernel_initializer=initializer)
outputs = tf.nn.softmax(logits)
# 3. Select a random action based on the estimated probabilities
action_index = tf.squeeze(tf.multinomial(logits, num_samples=1), axis=-1)
# 4. Training
learning_rate = 0.01
y = tf.one_hot(action_index, depth=len(possible_actions))
cross_entropy = tf.nn.softmax_cross_entropy_with_logits_v2(labels=y, logits=logits)
optimizer = tf.train.AdamOptimizer(learning_rate)
grads_and_vars = optimizer.compute_gradients(cross_entropy)
gradients = [grad for grad, variable in grads_and_vars]
gradient_placeholders = []
grads_and_vars_feed = []
for grad, variable in grads_and_vars:
gradient_placeholder = tf.placeholder(tf.float32, shape=grad.get_shape())
gradient_placeholders.append(gradient_placeholder)
grads_and_vars_feed.append((gradient_placeholder, variable))
training_op = optimizer.apply_gradients(grads_and_vars_feed)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
# 5. execute it, count the rewards, and show them
def run_bipedal_walker(model_path=None, n_max_steps =1000): # function from github but adapted to counting rewards ...
env = gym.make("BipedalWalker-v2") # ... and showing them instead of showing rendered frames
with tf.Session() as sess:
if model_path is None:
init.run()
else:
saver.restore(sess, model_path)
obs = env.reset()
rewards = 0
for step in range(n_max_steps):
action_index_val = action_index.eval(feed_dict={X: obs.reshape(1, n_inputs)})
action = possible_actions[action_index_val]
obs, reward, done, info = env.step(action[0])
rewards += reward
if done:
break
env.close()
return rewards
run_bipedal_walker()
```
The model does not perform well because it has not been trained, yet. This shall be done!
```
n_games_per_update = 10 # default is 10
n_max_steps = 10 # default is 1000
n_iterations = 100 # default is 1000
save_iterations = 10 # default is 10
discount_rate = 0.95 # default is 0.95
with tf.Session() as sess:
init.run()
for iteration in range(n_iterations):
print("\rIteration: {}/{}".format(iteration + 1, n_iterations), end="")
all_rewards = []
all_gradients = []
for game in range(n_games_per_update):
current_rewards = []
current_gradients = []
obs = env.reset()
for step in range(n_max_steps):
action_index_val, gradients_val = sess.run([action_index, gradients],
feed_dict={X: obs.reshape(1, n_inputs)})
action = possible_actions[action_index_val]
obs, reward, done, info = env.step(action[0])
current_rewards.append(reward)
current_gradients.append(gradients_val)
if done:
break
all_rewards.append(current_rewards)
all_gradients.append(current_gradients)
all_rewards = discount_and_normalize_rewards(all_rewards, discount_rate=discount_rate)
feed_dict = {}
for var_index, gradient_placeholder in enumerate(gradient_placeholders):
mean_gradients = np.mean([reward * all_gradients[game_index][step][var_index]
for game_index, rewards in enumerate(all_rewards)
for step, reward in enumerate(rewards)], axis=0)
feed_dict[gradient_placeholder] = mean_gradients
sess.run(training_op, feed_dict=feed_dict)
if iteration % save_iterations == 0:
saver.save(sess, "./tf_logs/16_RL/BiPedal/my_bipedal_walker_pg.ckpt")
run_bipedal_walker("./tf_logs/16_RL/BiPedal/my_bipedal_walker_pg.ckpt")
```
With enough training, the network does indeed better.
### 9. Use policy gradients to train an agent to play *Pong*, the famous Atari game ("Pong-v0" in the OpenAI gym). Beware: an individual observation is insufficient to tell the direction and speed of the ball. One solution is to pass two observations at a time to the neural network policy. To reduce dimensionality and speed up training, you should definitely preprocess these images (crop, resize, and convert them to black and white), and possibly merge them into a single image (e.g., by overlaying them).
A solution may follow later.
### 10. If you have about \$100 to spare, you can purchase a Raspberry Pi 3 plus some cheap robotics components, install TensorFlow on the Pi, and go wild! For an example, check out this fun post (https://goo.gl/Eu5u28) by Lukas Biewald, or take a look at GoPiGo or BrickPi. Why not try to build a real-life cartpole by training the robot using policy gradients? Or build a robotic spider that learns to walk; give it rewards any time it gets closer to some objective (you will need sensors to measure the distance to the objective). The only limit is your imagination.
A solution for this may follow even later.
| github_jupyter |
# Dynamic Recurrent Neural Network.
TensorFlow implementation of a Recurrent Neural Network (LSTM) that performs dynamic computation over sequences with variable length. This example is using a toy dataset to classify linear sequences. The generated sequences have variable length.
## RNN Overview
<img src="http://colah.github.io/posts/2015-08-Understanding-LSTMs/img/RNN-unrolled.png" alt="nn" style="width: 600px;"/>
References:
- [Long Short Term Memory](http://deeplearning.cs.cmu.edu/pdfs/Hochreiter97_lstm.pdf), Sepp Hochreiter & Jurgen Schmidhuber, Neural Computation 9(8): 1735-1780, 1997.
```
from __future__ import print_function
import tensorflow as tf
import random
# ====================
# TOY DATA GENERATOR
# ====================
class ToySequenceData(object):
""" Generate sequence of data with dynamic length.
This class generate samples for training:
- Class 0: linear sequences (i.e. [0, 1, 2, 3,...])
- Class 1: random sequences (i.e. [1, 3, 10, 7,...])
NOTICE:
We have to pad each sequence to reach 'max_seq_len' for TensorFlow
consistency (we cannot feed a numpy array with inconsistent
dimensions). The dynamic calculation will then be perform thanks to
'seqlen' attribute that records every actual sequence length.
"""
def __init__(self, n_samples=1000, max_seq_len=20, min_seq_len=3,
max_value=1000):
self.data = []
self.labels = []
self.seqlen = []
for i in range(n_samples):
# Random sequence length
len = random.randint(min_seq_len, max_seq_len)
# Monitor sequence length for TensorFlow dynamic calculation
self.seqlen.append(len)
# Add a random or linear int sequence (50% prob)
if random.random() < .5:
# Generate a linear sequence
rand_start = random.randint(0, max_value - len)
s = [[float(i)/max_value] for i in
range(rand_start, rand_start + len)]
# Pad sequence for dimension consistency
s += [[0.] for i in range(max_seq_len - len)]
self.data.append(s)
self.labels.append([1., 0.])
else:
# Generate a random sequence
s = [[float(random.randint(0, max_value))/max_value]
for i in range(len)]
# Pad sequence for dimension consistency
s += [[0.] for i in range(max_seq_len - len)]
self.data.append(s)
self.labels.append([0., 1.])
self.batch_id = 0
def next(self, batch_size):
""" Return a batch of data. When dataset end is reached, start over.
"""
if self.batch_id == len(self.data):
self.batch_id = 0
batch_data = (self.data[self.batch_id:min(self.batch_id +
batch_size, len(self.data))])
batch_labels = (self.labels[self.batch_id:min(self.batch_id +
batch_size, len(self.data))])
batch_seqlen = (self.seqlen[self.batch_id:min(self.batch_id +
batch_size, len(self.data))])
self.batch_id = min(self.batch_id + batch_size, len(self.data))
return batch_data, batch_labels, batch_seqlen
# ==========
# MODEL
# ==========
# Parameters
learning_rate = 0.01
training_steps = 10000
batch_size = 128
display_step = 200
# Network Parameters
seq_max_len = 20 # Sequence max length
n_hidden = 64 # hidden layer num of features
n_classes = 2 # linear sequence or not
trainset = ToySequenceData(n_samples=1000, max_seq_len=seq_max_len)
testset = ToySequenceData(n_samples=500, max_seq_len=seq_max_len)
# tf Graph input
x = tf.placeholder("float", [None, seq_max_len, 1])
y = tf.placeholder("float", [None, n_classes])
# A placeholder for indicating each sequence length
seqlen = tf.placeholder(tf.int32, [None])
# Define weights
weights = {
'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([n_classes]))
}
def dynamicRNN(x, seqlen, weights, biases):
# Prepare data shape to match `rnn` function requirements
# Current data input shape: (batch_size, n_steps, n_input)
# Required shape: 'n_steps' tensors list of shape (batch_size, n_input)
# Unstack to get a list of 'n_steps' tensors of shape (batch_size, n_input)
x = tf.unstack(x, seq_max_len, 1)
# Define a lstm cell with tensorflow
lstm_cell = tf.contrib.rnn.BasicLSTMCell(n_hidden)
# Get lstm cell output, providing 'sequence_length' will perform dynamic
# calculation.
outputs, states = tf.contrib.rnn.static_rnn(lstm_cell, x, dtype=tf.float32,
sequence_length=seqlen)
# When performing dynamic calculation, we must retrieve the last
# dynamically computed output, i.e., if a sequence length is 10, we need
# to retrieve the 10th output.
# However TensorFlow doesn't support advanced indexing yet, so we build
# a custom op that for each sample in batch size, get its length and
# get the corresponding relevant output.
# 'outputs' is a list of output at every timestep, we pack them in a Tensor
# and change back dimension to [batch_size, n_step, n_input]
outputs = tf.stack(outputs)
outputs = tf.transpose(outputs, [1, 0, 2])
# Hack to build the indexing and retrieve the right output.
batch_size = tf.shape(outputs)[0]
# Start indices for each sample
index = tf.range(0, batch_size) * seq_max_len + (seqlen - 1)
# Indexing
outputs = tf.gather(tf.reshape(outputs, [-1, n_hidden]), index)
# Linear activation, using outputs computed above
return tf.matmul(outputs, weights['out']) + biases['out']
pred = dynamicRNN(x, seqlen, weights, biases)
# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()
# Start training
with tf.Session() as sess:
# Run the initializer
sess.run(init)
for step in range(1, training_steps+1):
batch_x, batch_y, batch_seqlen = trainset.next(batch_size)
# Run optimization op (backprop)
sess.run(optimizer, feed_dict={x: batch_x, y: batch_y,
seqlen: batch_seqlen})
if step % display_step == 0 or step == 1:
# Calculate batch accuracy & loss
acc, loss = sess.run([accuracy, cost], feed_dict={x: batch_x, y: batch_y,
seqlen: batch_seqlen})
print("Step " + str(step) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
print("Optimization Finished!")
# Calculate accuracy
test_data = testset.data
test_label = testset.labels
test_seqlen = testset.seqlen
print("Testing Accuracy:", \
sess.run(accuracy, feed_dict={x: test_data, y: test_label,
seqlen: test_seqlen}))
```
| github_jupyter |
```
import sys, os
sys.path.append(os.path.abspath('../..'))
from tqdm.notebook import tqdm
import math
import gym
import torch
import torch.optim as optim
from torch.utils.tensorboard import SummaryWriter
from collections import deque
from networks.dqn_atari import MC_DQN
from utils.memory import RankedReplayMemory, LabeledReplayMemory
from utils.optimization import AMN_perc_optimization, AMN_optimization_epochs
from environments.atari_wrappers import make_atari, wrap_deepmind
from utils.atari_utils import fp, ActionSelector, evaluate
from utils.acquisition_functions import mc_random
import imageio
from utils.visualization import visualize_AMN
env_name = 'Breakout'
env_raw = make_atari('{}NoFrameskip-v4'.format(env_name))
env = wrap_deepmind(env_raw, frame_stack=False, episode_life=False, clip_rewards=True)
c,h,w = c,h,w = fp(env.reset()).shape
n_actions = env.action_space.n
BATCH_SIZE = 128
LR = 0.0000625
GAMMA = 0.99
EPS = 0.05
NUM_STEPS = 10000000
NOT_LABELLED_CAPACITY = 10000
LABELLED_CAPACITY = 100000
INITIAL_STEPS=NOT_LABELLED_CAPACITY
EPOCHS=20
PERCENTAGE = 0.01
NAME = 'mc_random_1_large_buffer_many_epochs'
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # if gpu is to be used
AMN_net = MC_DQN(n_actions).to(device)
# AMN_net = ENS_DQN(n_actions).to(device)
expert_net = torch.load("models/dqn_expert_breakout_model").to(device)
AMN_net.apply(AMN_net.init_weights)
expert_net.eval()
optimizer = optim.Adam(AMN_net.parameters(), lr=LR, eps=1.5e-4)
# optimizer = optim.Adam(AMN_net.parameters(), lr=LR, eps=1.5e-4)
memory = LabeledReplayMemory(NOT_LABELLED_CAPACITY, LABELLED_CAPACITY, [5,h,w], n_actions, mc_random, AMN_net, device=device)
action_selector = ActionSelector(EPS, EPS, AMN_net, 1, n_actions, device)
steps_done = 0
writer = SummaryWriter(f'runs/{NAME}')
q = deque(maxlen=5)
done=True
eps = 0
episode_len = 0
num_labels = 0
progressive = tqdm(range(NUM_STEPS), total=NUM_STEPS, ncols=400, leave=False, unit='b')
for step in progressive:
if done:
env.reset()
sum_reward = 0
episode_len = 0
img, _, _, _ = env.step(1) # BREAKOUT specific !!!
for i in range(10): # no-op
n_frame, _, _, _ = env.step(0)
n_frame = fp(n_frame)
q.append(n_frame)
# Select and perform an action
state = torch.cat(list(q))[1:].unsqueeze(0)
action, eps = action_selector.select_action(state)
n_frame, reward, done, info = env.step(action)
n_frame = fp(n_frame)
# 5 frame as memory
q.append(n_frame)
memory.push(torch.cat(list(q)).unsqueeze(0), action, reward, done) # here the n_frame means next frame from the previous time step
episode_len += 1
# Perform one step of the optimization (on the target network)
if step % NOT_LABELLED_CAPACITY == 0 and step > INITIAL_STEPS:
num_labels += memory.label_sample(percentage=PERCENTAGE)
loss = AMN_optimization_epochs(AMN_net, expert_net, optimizer, memory, EPOCHS,
batch_size=BATCH_SIZE, device=device)
if loss is not None:
writer.add_scalar('loss_vs_#labels', loss, num_labels)
evaluated_reward = evaluate(step, AMN_net, device, env_raw, n_actions, eps=0.05, num_episode=15)
writer.add_scalar('reward_vs_#labels', evaluated_reward, num_labels)
```
| github_jupyter |
# **Exploratory Analysis**
First of all, let's import some useful libraries that will be used in the analysis.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
Now, the dataset stored in drive needs to be retieved. I am using google colab for this exploration with TPU hardware accelerator for faster computation. To get the data from drive the drive needs to be mounted first.
```
from google.colab import drive
drive.mount('/content/drive/')
```
Once the drive is successfully mounted, I fetched the data and stored it in a pandas dataframe.
```
dataset = pd.read_csv("/content/drive/My Drive/Colab Notebooks/DOB_Permit_Issuance.csv")
```
To get the gist of the dataset, I used pandas describe function that gives a very broad understanding of the data.
```
pd.set_option('display.max_colwidth', 1000)
pd.set_option('display.max_rows', 1000)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 1000)
dataset.describe()
```
From the describe function, we now know that the dataset has almost 3.5 M data. Let's take a look at the dataset now.
```
dataset.head()
```
I can see there are lot's of NaNs in many columns. To better analyse the data, the NaNs needs to be removed or dealt with. But first, let's see hoe many NaNs are there is each column.
```
dataset.isna().sum()
```
---
The information above is very useful in feature selection. Observing the columns with very high number of NaNs, such as :
Column | NaNs
------------|--------
Special District 1 | 3121182
Special District 2 | 3439516
Permittee's Other Title | 3236862
HIC License | 3477843
Site Safety Mgr's Last Name | 3481861
Site Safety Mgr's First Name | 3481885
Site Safety Mgr Business Name |3490529
Residential | 2139591
Superintendent First & Last Name | 1814931
Superintendent Business Name | 1847714
Self_Cert | 1274022
Permit Subtype | 1393411
Oil Gas | 3470104
---
From the column_info sheet of file 'DD_DOB_Permit_Issuance_2018_11_02', I know that some of the column has a meaning related to blanks. For example, for the Residential column, there are either 'Yes' or 'Blanks'. So it's safe to assume that the blanks are associated with 'No'.
Similarly, to fill the blanks based on relevant information from column_info, I am using below mappings for some columns:
* Residential : No
* Site Fill : None
* Oil Gas : None
* Self_Cert : N
* Act as Superintendent : N
* Non-Profit : N
```
values = {'Residential': 'No','Site Fill':'NONE', 'Oil Gas':'None', 'Self_Cert':'N', 'Act as Superintendent':'N',
'Non-Profit':'N' }
dataset = dataset.fillna(value= values)
```
Since there are many columns with blank spaces and we cannot fill the blanks with appropriate information, it's better to drop these column as they do not add value to the analysis.
I will drop the following columns :
* Special District 1
* Special District 2
* Work Type
* Permit Subtype
* Permittee's First Name
* Permittee's Last Name
* Permittee's Business Name
* Permittee's Phone #
* Permittee's Other Title
* HIC License
* Site Safety Mgr's First Name
* Site Safety Mgr's Last Name
* Site Safety Mgr Business Name
* Superintendent First & Last Name
* Superintendent Business Name
* Owner's Business Name
* Owner's First Name
* Owner's Last Name
* Owner's House #
* Owner's House Street Name
* Owner's Phone #
* DOBRunDate
```
dataset.drop("Special District 1", axis=1, inplace=True)
dataset.drop("Special District 2", axis=1, inplace=True)
dataset.drop("Work Type", axis=1, inplace=True) #since work type and permit type give same information
dataset.drop("Permit Subtype", axis=1, inplace=True)
dataset.drop("Permittee's First Name", axis=1, inplace=True)
dataset.drop("Permittee's Last Name", axis=1, inplace=True)
dataset.drop("Permittee's Business Name", axis=1, inplace=True)
dataset.drop("Permittee's Phone #", axis=1, inplace=True)
dataset.drop("Permittee's Other Title", axis=1, inplace=True) #Permit Subtype
dataset.drop("HIC License", axis=1, inplace=True)
dataset.drop("Site Safety Mgr's First Name", axis=1, inplace=True)
dataset.drop("Site Safety Mgr's Last Name", axis=1, inplace=True)
dataset.drop("Site Safety Mgr Business Name", axis=1, inplace=True)
dataset.drop("Superintendent First & Last Name", axis=1, inplace=True)
dataset.drop("Superintendent Business Name", axis=1, inplace=True)
dataset.drop("Owner's Business Name", axis=1, inplace=True)
dataset.drop("Owner's First Name", axis=1, inplace=True)
dataset.drop("Owner's Last Name", axis=1, inplace=True)
dataset.drop("Owner's House #", axis=1, inplace=True)
dataset.drop("Owner's House Street Name", axis=1, inplace=True)
dataset.drop("Owner's Phone #", axis=1, inplace=True)
dataset.drop("DOBRunDate", axis=1, inplace=True)
```
Let's take a look at the remaining columns and their number of blanks again.
```
dataset.isna().sum()
```
We still have blanks in few columns left. One way to deal with them is to replace them with mean of that column or the most frequent entry of that column. Mean can onlly be applied to numerical columns and even for numerical columns such as Longitude and Lattitude, this mean might not be right to replace all the missing value with single longitude or lattitude. This will skew the column and would not result in fair analysis of data.
Similarly, if we use the most frequently used entry to replace all the blanks in that column, it will either skew the matrix or the data itself would not make sense. For example, the for a particular location, there is a state, city, zip code and street name associated with it. If we replace the missing entries in zip code with most frequent entry, then it might result in a data that is having a different state, city and a zip code of another location.
Therefore, to clean the data I will drop the rows with NaNs. We will still have enough data for exploration.
```
dataset.dropna(inplace=True)
dataset.isna().sum()
```
---
Now the dataset looks clean and we can proceed with analysis. I will try find the correlation between columns using the correlation matrix.
```
# Correlation matrix
def plotCorrelationMatrix(df, graphWidth):
filename = 'DOB_Permit_Issuance.csv'
df = df[[col for col in df if df[col].nunique() > 1]] # keep columns where there are more than 1 unique values
corr = df.corr()
plt.figure(num=None, figsize=(graphWidth, graphWidth), dpi=80, facecolor='w', edgecolor='k')
corrMat = plt.matshow(corr, fignum = 1)
plt.xticks(range(len(corr.columns)), corr.columns, rotation=90)
plt.yticks(range(len(corr.columns)), corr.columns)
plt.gca().xaxis.tick_bottom()
plt.colorbar(corrMat)
plt.title(f'Correlation Matrix for {filename}', fontsize=15)
plt.show()
plotCorrelationMatrix(dataset, 15)
```
We can see that there is strong positive relationship between :
* Zip Code and Job #
* Job # and Council_District
* Zip Code and Council_District
---
To get more insight of the data and its column-wise data distribution, I will plot the columns using bar graphs. For displaying purposes, I will pick columns that have between 1 and 50 unique values.
```
def plotColumns(dataframe, nGraphShown, nGraphPerRow):
nunique = dataframe.nunique()
dataframe = dataframe[[col for col in dataframe if nunique[col] > 1 and nunique[col] < 50]]
nRow, nCol = dataframe.shape
columnNames = list(dataframe)
nGraphRow = (nCol + nGraphPerRow - 1) / nGraphPerRow
plt.figure(num = None, figsize = (6 * nGraphPerRow, 8 * nGraphRow), dpi = 80, facecolor = 'w', edgecolor = 'k')
for i in range(min(nCol, nGraphShown)):
plt.subplot(nGraphRow, nGraphPerRow, i + 1)
columndataframe = dataframe.iloc[:, i]
if (not np.issubdtype(type(columndataframe.iloc[0]), np.number)):
valueCounts = columndataframe.value_counts()
valueCounts.plot.bar()
else:
columndataframe.hist()
plt.ylabel('counts')
plt.xticks(rotation = 90)
plt.title(f'{columnNames[i]} (column {i})')
plt.tight_layout(pad = 1.0, w_pad = 1.0, h_pad = 1.0)
plt.show()
plotColumns(dataset, 38, 3)
```
From the Borough graph, it's evident that the Manhattan has highest number of filing for the permit. Then the second popuar borough after manhattan is Brooklyn with huge margin. Then comes the Queens with almost same number of permits as Brooklyn. We see another plunge in permit numbers with Bronx and Staten Island.
---
Job Document number is the number of documents that were added with the file during the application. Mostly all the filings required a single document. There are some permits that had two documents and then higher number of documents are negligible.
---
There is a pattern in Job Type as well. We can see that the most populat Job Type or Work Type is A2 with more than 1.75 M permits. The second most popular work type is NB (new building) with around 400,000 permits. The number of permits decreases with A3, A1, DM and SG where DM and SG are significantly less than other types.
---
Self_Cert indicates whether or not the application was submitted as Professionally Certified. A Professional Engineer (PE) or Registered Architect (RA) can certify compliance with applicable laws and codes on applications filed by him/her as applicant. Plot shows mostly were not filed by Professional Engineer or Registered Architect.
---
Bldg Type indicates legal occupancy classification. The most popular type of building type is '2' with more than 2M permits.
---
Most of the buildings are non Residential and only about 1.3M buildinngs were residential.
---
Permit Status indicates the current status of the permit application. Corresponding plot for the column suggests that most of the permits are 'Issued' and very small number were 'Reissued'. The 'In-Progress' and 'Revoked' are negligible.
---
Filing Status indicates if this is the first time the permit is being applied for or if the permit is being renewed. A large amount of permits were in 'Initial' status and less than half of that were in 'Renewal' state.
---
Permit Type The specific type of work covered by the permit. This is a two character code to indicate the type of work. There are 7 types of permits where EW has the highest number. The number indicates decreasing trend with PL, EQ, AL, NB, SG, and FO.
---
A sequential number assigned to each issuance of the particular permit from initial issuance to each subsequent renewal. Every initial permit should have a 01 sequence number. Every additional renewal receives a number that increases by 1 (ex: 02, 03, 04). Most of the permits have less than 5 sequence number.
---
If the permit is for work on fuel burning equipment, this indicates whether it burns oil or gas. Most of the permits are for neither Oil nor Gas. A very small fraction of permits is for Oil and there is negligible number of permits for Gas.
---
Site Fill indicates the source of any fill dirt that will be used on the construction site. When over 300 cubic yards of fill is being used, the Department is required to inform Sanitation of where the fill is coming from and the amount. About 1.1M entries didn't mention any Site Fill type indicating that the less than 300 cubic yards of fill is being used. Almost permits are not applicable. About 300,000 permits were for on-site fill and less than 100,000 were for off-site.
---
Professional license type of the person that the permit was issued to. In most of the cases the person was holding GC type. Then the number showcased a decreasing trend with MP, FS, OB, SI, NW, OW, PE, RA, and HI where NW, OW, PE, RA, and HI are negligible in number.
---
Act as Superintendent indicates if the permittee acts as the Construction Superintendent for the work site. Only about 1.1M people responded 'Yes' to this and majority respondded with 'No'
---
Owner's Business Type indicates the type of entity that owns the building where the work will be performed. Mostly the entities owning the builing were 'Corporations'. With slightly less than 'Corporation', 'Individual' type stands at the second position and 'Partnership' holds the third position. Other business types like are less significant in number.
---
Non-Profit indicates if the building is owned by a non-profit. Less than 250,000 buildings were owned by 'Non-Profit' and more than 2.75M were not 'Non-Profit'.
# Borough-wise analysis
Let's now dive deeper in the data and take a closer look. Is the trend we see above is same across all Boroughs ?. Does every borough have same type of building? Is 'EW' the most popular permit type across all cities? What about the 'owner's business type' and 'Job Type' ? I will try to find the answers to all these by exploring the pattern in each bouough.
### Bldg Type in each borough
```
manhattan_bldg_type = dataset[dataset.BOROUGH == 'MANHATTAN'][['Bldg Type']]
manhattan_bldg_type.reset_index(drop=True, inplace=True)
brooklyn_bldg_type = dataset[dataset.BOROUGH == 'BROOKLYN'][['Bldg Type']]
brooklyn_bldg_type.reset_index(drop=True, inplace=True)
bronx_bldg_type = dataset[dataset.BOROUGH == 'BRONX'][['Bldg Type']]
bronx_bldg_type.reset_index(drop=True, inplace=True)
queens_bldg_type = dataset[dataset.BOROUGH == 'QUEENS'][['Bldg Type']]
queens_bldg_type.reset_index(drop=True, inplace=True)
staten_island_bldg_type = dataset[dataset.BOROUGH == 'STATEN ISLAND'][['Bldg Type']]
staten_island_bldg_type.reset_index(drop=True, inplace=True)
building_type = pd.DataFrame()
building_type['manhattan_bldg_type'] = manhattan_bldg_type #brooklyn_bldg_type
building_type['brooklyn_bldg_type'] = brooklyn_bldg_type
building_type['bronx_bldg_type'] = bronx_bldg_type
building_type['queens_bldg_type'] = queens_bldg_type
building_type['staten_island_bldg_type'] = staten_island_bldg_type
plotColumns(building_type, 5, 3)
```
**Analysis**
The builing type is either '1' or '2' and we earlier discovered that type '2' were significantly popular as compared to type '1'. However, this is not true for all the Boroughs. For manhattan, this trend still holds true. But for other locations, the type '1' buildings are comparable in number with that of type '2'. More interestingly, in case of Staten Island, the type '1' is significantly popular beating type '2' with a good margin.
### Permit Type in Each Borough
```
manhattan_permit_type = dataset[dataset.BOROUGH == 'MANHATTAN'][['Permit Type']]
manhattan_permit_type.reset_index(drop=True, inplace=True)
brooklyn_permit_type = dataset[dataset.BOROUGH == 'BROOKLYN'][['Permit Type']]
brooklyn_permit_type.reset_index(drop=True, inplace=True)
bronx_permit_type = dataset[dataset.BOROUGH == 'BRONX'][['Permit Type']]
bronx_permit_type.reset_index(drop=True, inplace=True)
queens_permit_type = dataset[dataset.BOROUGH == 'QUEENS'][['Permit Type']]
queens_permit_type.reset_index(drop=True, inplace=True)
staten_island_permit_type = dataset[dataset.BOROUGH == 'STATEN ISLAND'][['Permit Type']]
staten_island_permit_type.reset_index(drop=True, inplace=True)
permit_type = pd.DataFrame()
permit_type['manhattan_permit_type'] = manhattan_permit_type #brooklyn_permit_type
permit_type['brooklyn_permit_type'] = brooklyn_permit_type
permit_type['bronx_permit_type'] = bronx_permit_type
permit_type['queens_permit_type'] = queens_permit_type
permit_type['staten_island_permit_type'] = staten_island_permit_type
plotColumns(permit_type, 5, 3)
```
**Analysis**
In Permit Type we earlier discovered that type 'EW' was the most popular and significantly higher in number as compared to other types. However, this is true for most of the Boroughs except Staten Island. However, other types of Permit are shuffled in each Borough. Below is the type of permits in decreasing order for each borough.
Manhattan | Brooklyn | Queens |Bronx | Staten Island
------------|--------|--------------|-------------
EW | EW | EW| EW | PL
PL | PL | PL | PL |NB
EQ | EQ | EQ |EQ |EW
AL | AL | NB | AL | EQ
SQ | NB | AL | SQ | AL
NB| FO| SG |FO | DM
FO|DM|FO| DM| SG
DM|SG|DM|SG|FO
### Owner's Business Type in Each Borough
```
manhattan_owners_business_type = dataset[dataset.BOROUGH == 'MANHATTAN'][['Owner\'s Business Type']]
manhattan_owners_business_type.reset_index(drop=True, inplace=True)
brooklyn_owners_business_type = dataset[dataset.BOROUGH == 'BROOKLYN'][['Owner\'s Business Type']]
brooklyn_owners_business_type.reset_index(drop=True, inplace=True)
bronx_owners_business_type = dataset[dataset.BOROUGH == 'BRONX'][['Owner\'s Business Type']]
bronx_owners_business_type.reset_index(drop=True, inplace=True)
queens_owners_business_type = dataset[dataset.BOROUGH == 'QUEENS'][['Owner\'s Business Type']]
queens_owners_business_type.reset_index(drop=True, inplace=True)
staten_island_owners_business_type = dataset[dataset.BOROUGH == 'STATEN ISLAND'][['Owner\'s Business Type']]
staten_island_owners_business_type.reset_index(drop=True, inplace=True)
owners_business_type = pd.DataFrame()
owners_business_type['manhattan_owners_business_type'] = manhattan_owners_business_type #brooklyn_owners_business_type
owners_business_type['brooklyn_owners_business_type'] = brooklyn_owners_business_type
owners_business_type['bronx_owners_business_type'] = bronx_owners_business_type
owners_business_type['queens_owners_business_type'] = queens_owners_business_type
owners_business_type['staten_island_owners_business_type'] = staten_island_owners_business_type
plotColumns(owners_business_type, 5, 3)
```
**Analysis**
We earlier discovered that the 'Corporation' was the most popular 'Owner's Business type' and 'Individual' type was closely competing with it. Taking a closer look at each borough reveals that the trend highly varies in all the Boroughs. In Manhattan, the 'Corporation' is still the highest but the 'Individual' is substituted by 'Partnership'. In Brooklyn, 'Individual' holds the top place and 'Corporation' and 'Partnership' are on second and third place respectively.
In Bronx, the 'Corporation' and 'Individual' are closely competing while 'Corporation' holds the highest number and 'Partnership' is on third place.
For Queens and Staten Island, the 'Individual' holds the top place and 'Corporation' and 'Partnership' are on second and third place respectively. This is consistent with the trend observed in 'Brooklyn'.
### Job Type in Each Borough
```
manhattan_job_type = dataset[dataset.BOROUGH == 'MANHATTAN'][['Job Type']]
manhattan_job_type.reset_index(drop=True, inplace=True)
brooklyn_job_type = dataset[dataset.BOROUGH == 'BROOKLYN'][['Job Type']]
brooklyn_job_type.reset_index(drop=True, inplace=True)
bronx_job_type = dataset[dataset.BOROUGH == 'BRONX'][['Job Type']]
bronx_job_type.reset_index(drop=True, inplace=True)
queens_job_type = dataset[dataset.BOROUGH == 'QUEENS'][['Job Type']]
queens_job_type.reset_index(drop=True, inplace=True)
staten_island_job_type = dataset[dataset.BOROUGH == 'STATEN ISLAND'][['Job Type']]
staten_island_job_type.reset_index(drop=True, inplace=True)
job_type = pd.DataFrame()
job_type['manhattan_job_type'] = manhattan_job_type #brooklyn_job_type
job_type['brooklyn_job_type'] = brooklyn_job_type
job_type['bronx_job_type'] = bronx_job_type
job_type['queens_job_type'] = queens_job_type
job_type['staten_island_job_type'] = staten_island_job_type
plotColumns(job_type, 5, 3)
```
**Analysis**
We earlier discovered that the 'A2' was the most popular 'Job type' and numbers showed a decreasing trend with 'NB', 'A3', 'A1', 'DM', and 'SG'. Taking a closer look at each borough revealsa slightly different trend. For example, in Manhattan, the 'A2' is still the highest but the 'NB' is pushed beyond 'A1' to the fourth place while in Staten Island 'NB' holds the first place. Below is the type of Jobs in decreasing order for each borough.
Overall | Manhattan | Brooklyn | Queens |Bronx | Staten Island
------------|--------|--------------|-------------
A2|A2|A2|A2|A2|NB
NB|A3|NB|NB|NB|A2
A3|A1|A1|A3|A1|A1
A1|NB|A3|A1|A3|A3
DM|SG|DM|SG|DM|DM
SG|DM|SG|DM|SG|SG
# Permits Per Years
### Is there is trend in the number of permits issued each year? Let's find out!
First, the date format of 'Issuance Date' needs to be converted to python Datetime format and then only the year needs to be extracted from the date.
```
dataset['Issuance Date'] = pd.to_datetime(dataset['Issuance Date'])
dataset['Issuance Date'] =dataset['Issuance Date'].dt.year
```
Once the dates are replaced by the corresponding years, we can plot the graph.
```
timeline = dataset['Issuance Date'].value_counts(ascending=True)
timeline = timeline.sort_index()
timeline.to_frame()
timeline.plot.bar()
```
**Analysis**
We can observe that the number of permits has been consistently increasing each year. The number got stagnant from 1993 to 1996 and then it increased exponentially from 1997 until 2007. The applications decreasedfor a couple of years and then rose exponentially from 2010 to 2017.
### Borough-Wise Analysis of Timeline
Whether the trend is consistent across all borough? Is there a time when construction slowed down in a city and surged in other ?
```
manhattan_permits_issued = dataset[dataset.BOROUGH == 'MANHATTAN'][['Issuance Date']]
manhattan_permits_issued.reset_index(drop=True, inplace=True)
brooklyn_permits_issued = dataset[dataset.BOROUGH == 'BROOKLYN'][['Issuance Date']]
brooklyn_permits_issued.reset_index(drop=True, inplace=True)
bronx_permits_issued = dataset[dataset.BOROUGH == 'BRONX'][['Issuance Date']]
bronx_permits_issued.reset_index(drop=True, inplace=True)
queens_permits_issued = dataset[dataset.BOROUGH == 'QUEENS'][['Issuance Date']]
queens_permits_issued.reset_index(drop=True, inplace=True)
staten_island_permits_issued = dataset[dataset.BOROUGH == 'STATEN ISLAND'][['Issuance Date']]
staten_island_permits_issued.reset_index(drop=True, inplace=True)
permits_issued = pd.DataFrame()
permits_issued['manhattan_permits_issued'] = manhattan_permits_issued #brooklyn_permits_issued
permits_issued['brooklyn_permits_issued'] = brooklyn_permits_issued
permits_issued['bronx_permits_issued'] = bronx_permits_issued
permits_issued['queens_permits_issued'] = queens_permits_issued
permits_issued['staten_island_permits_issued'] = staten_island_permits_issued
plotColumns(permits_issued, 5, 3)
```
In Manhattan and Brooklyn, most number of applications were filed during 2010 and 2015 period.
Bronx and Queens observed the highest number of filings in recent years from 2015 to 2019.
Staten Island had most applications during 2000 to 2015 and then there is again a surge in applications around 2015 but the number of applications is very less compared to its counterparts.
# Permits per month
### Is there is trend in the number of permits filed every month? Let's explore!
First, the date format of 'Filing Date' needs to be converted to python Datetime format and then only the month needs to be extracted from the date.
```
dataset['Filing Date'] = pd.to_datetime(dataset['Filing Date'])
dataset['Filing Date'] =dataset['Filing Date'].dt.month
months = dataset['Filing Date'].value_counts()
months.to_frame()
months = months.sort_index()
plotColumns(months, 1, 1)
```
Mostly all the months gets equal number of permit applications. February has less days, so that justifies the less number.
Overall, Month of 'March' has highest permit filings.
| github_jupyter |
# Laboratorio 7
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import altair as alt
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
alt.themes.enable('opaque')
%matplotlib inline
```
En este laboratorio utilizaremos los mismos datos de diabetes vistos en la clase
```
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True, as_frame=True)
diabetes = pd.concat([diabetes_X, diabetes_y], axis=1)
diabetes.head()
```
## Pregunta 1
(1 pto)
* ¿Por qué la columna de sexo tiene esos valores?
* ¿Cuál es la columna a predecir?
* ¿Crees que es necesario escalar o transformar los datos antes de comenzar el modelamiento?
__Respuesta:__
* Porque los valores se encuentran escalados y centrados por su desviación estandar multiplicada por la cantidad de muestras, entonces tienen una norma unitaria.
* La columna `target`
* Sí, para que el algoritmo los pueda reconocer más fácil y el usuario pueda comparar de manera más simple, ya que los datos vienen con escalas y magnitudes distintas.
## Pregunta 2
(1 pto)
Realiza dos regresiones lineales con todas las _features_, el primer caso incluyendo intercepto y el segundo sin intercepto. Luego obtén la predicción para así calcular el error cuadrático medio y coeficiente de determinación de cada uno de ellos.
```
regr_with_incerpet = linear_model.LinearRegression(fit_intercept=True)
regr_with_incerpet.fit(diabetes_X, diabetes_y)
diabetes_y_pred_with_intercept = regr_with_incerpet.predict(diabetes_X)
# Coeficientes
print(f"Coefficients: \n{regr_with_incerpet.coef_}\n")
# Intercepto
print(f"Intercept: \n{regr_with_incerpet.intercept_}\n")
# Error cuadrático medio
print(f"Mean squared error: {mean_squared_error(diabetes_y, diabetes_y_pred_with_intercept):.2f}\n")
# Coeficiente de determinación
print(f"Coefficient of determination: {r2_score(diabetes_y, diabetes_y_pred_with_intercept):.2f}")
regr_without_incerpet = linear_model.LinearRegression(fit_intercept=False)
regr_without_incerpet.fit(diabetes_X, diabetes_y)
diabetes_y_pred_without_intercept = regr_without_incerpet.predict(diabetes_X)
# Coeficientes
print(f"Coefficients: \n{regr_without_incerpet.coef_}\n")
# Error cuadrático medio
print(f"Mean squared error: {mean_squared_error(diabetes_y, diabetes_y_pred_without_intercept):.2f}\n")
# Coeficiente de determinación
print(f"Coefficient of determination: {r2_score(diabetes_y, diabetes_y_pred_without_intercept):.2f}")
```
**Pregunta: ¿Qué tan bueno fue el ajuste del modelo?**
__Respuesta:__
No es muy bueno, ya que el coeficiente de determinación es 0.52 para el caso con intercepto, y para que sea una buena aproximación debería ser cercano a 1. Para el caso sin intercepto el R2 es negativo por lo que es mejor utilizar el promedio de los datos, ya que estos entregarían un mejor ajuste, además se debe considerar que el error es mucho mayor que para el caso con intercepto, entonces tampoco es un buen ajuste.
## Pregunta 3
(1 pto)
Realizar multiples regresiones lineales utilizando una sola _feature_ a la vez.
En cada iteración:
- Crea un arreglo `X`con solo una feature filtrando `X`.
- Crea un modelo de regresión lineal con intercepto.
- Ajusta el modelo anterior.
- Genera una predicción con el modelo.
- Calcula e imprime las métricas de la pregunta anterior.
```
for col in diabetes_X.columns:
X_i = diabetes_X[col].to_frame()
regr_i = linear_model.LinearRegression(fit_intercept=True)
regr_i.fit(X_i,diabetes_y)
diabetes_y_pred_i = regr_i.predict(X_i)
print(f"Feature: {col}")
print(f"\tCoefficients: {regr_i.coef_}")
print(f"\tIntercept: {regr_i.intercept_}")
print(f"\tMean squared error: {mean_squared_error(diabetes_y, diabetes_y_pred_i):.2f}")
print(f"\tCoefficient of determination: {r2_score(diabetes_y, diabetes_y_pred_i):.2f}\n")
```
**Pregunta: Si tuvieras que escoger una sola _feauture_, ¿Cuál sería? ¿Por qué?**
**Respuesta:** Escogería la Feature bmi, porque es la que tiene le menor error y el coeficiente de determinación más cercano a 1.
## Ejercicio 4
(1 pto)
Con la feature escogida en el ejercicio 3 realiza el siguiente gráfico:
- Scatter Plot
- Eje X: Valores de la feature escogida.
- Eje Y: Valores de la columna a predecir (target).
- En color rojo dibuja la recta correspondiente a la regresión lineal (utilizando `intercept_`y `coefs_`).
- Coloca un título adecuado, nombre de los ejes, etc.
Puedes utilizar `matplotlib` o `altair`, el que prefieras.
```
regr = linear_model.LinearRegression(fit_intercept=True).fit(diabetes_X['bmi'].to_frame(), diabetes_y)
diabetes_y_pred_bmi = regr.predict(diabetes_X['bmi'].to_frame())
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 16
x = diabetes_X['bmi'].values
y = diabetes_y
x_reg = np.arange(-0.1, 0.2, 0.01)
y_reg = regr.intercept_ + regr.coef_ * x_reg
fig = plt.figure(figsize=(20,8))
fig.suptitle('Regresión lineal body mass index (bmi) versus progresión de la enfermedad (target)')
ax = fig.add_subplot()
ax.figsize=(20,8)
ax.scatter(x,y,c='k');
ax.plot(x_reg,y_reg,c='r');
ax.legend(["Regresión", "Datos "]);
ax.set_xlabel('Body Mass Index')
ax.set_ylabel('target');
```
| github_jupyter |
```
import radical.analytics as ra
import radical.pilot as rp
import radical.utils as ru
import radical.entk as re
import os
from glob import glob
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import cm
import csv
import pandas as pd
import json
import matplotlib as mpl
mpl.rcParams['text.usetex'] = True
mpl.rcParams['text.latex.unicode'] = True
blues = cm.get_cmap(plt.get_cmap('Blues'))
greens = cm.get_cmap(plt.get_cmap('Greens'))
reds = cm.get_cmap(plt.get_cmap('Reds'))
oranges = cm.get_cmap(plt.get_cmap('Oranges'))
purples = cm.get_cmap(plt.get_cmap('Purples'))
greys = cm.get_cmap(plt.get_cmap('Greys'))
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
import warnings
warnings.filterwarnings('ignore')
!radical-stack
```
## Design 1
```
!tar -xzvf ../Data/Design1/entk.session-design1-54875/entk.session-design1-54875.tar.gz -C ../Data/Design1/entk.session-design1-54875/
!tar -xzvf ../Data/Design1/entk.session-design1-54875/entk_workflow.tar.gz -C ../Data/Design1/entk.session-design1-54875/
des1DF = pd.DataFrame(columns=['TTX','AgentOverhead','ClientOverhead','EnTKOverhead'])
work_file = open('../Data/Design1/entk.session-design1-54875/entk_workflow.json')
work_json = json.load(work_file)
work_file.close()
workflow = work_json['workflows'][1]
unit_ids = list()
for pipe in workflow['pipes']:
unit_path = pipe['stages'][1]['tasks'][0]['path']
unit_id = unit_path.split('/')[-2]
if unit_id != 'unit.000000':
unit_ids.append(unit_id)
sids=['entk.session-design1-54875']
for sid in sids:
re_session = ra.Session(stype='radical.entk',src='../Data/Design1',sid=sid)
rp_session = ra.Session(stype='radical.pilot',src='../Data/Design1/'+sid)
units = rp_session.filter(etype='unit', inplace=False, uid=unit_ids)
pilot = rp_session.filter(etype='pilot', inplace=False)
units_duration = units.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}])
units_agent = units.duration (event=[{ru.EVENT: 'state',ru.STATE: rp.AGENT_STAGING_INPUT},{ru.EVENT: 'staging_uprof_stop'}])
all_units = rp_session.filter(etype='unit', inplace=False)
disc_unit = rp_session.filter(etype='unit', inplace=False, uid='unit.000000')
disc_time = disc_unit.duration([rp.NEW, rp.DONE])
units_client = units.duration([rp.NEW, rp.DONE])
appmanager = re_session.filter(etype='appmanager',inplace=False)
t_p2 = pilot.duration(event=[{ru.EVENT: 'bootstrap_0_start'}, {ru.EVENT: 'cmd'}])
resource_manager = re_session.filter(etype='resource_manager',inplace=False)
app_duration = appmanager.duration(event=[{ru.EVENT:"amgr run started"},{ru.EVENT:"termination done"}])
res_duration = resource_manager.duration(event=[{ru.EVENT:"rreq submitted"},{ru.EVENT:"resource active"}])
ttx = units_duration
agent_overhead = abs(units_agent - units_duration)
client_overhead = units_client - units_agent
entk_overhead = app_duration - units_client - res_duration - all_units.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}]) + ttx
des1DF.loc[len(des1DF)] = [ttx, agent_overhead, client_overhead, entk_overhead]
print(des1DF)
```
## Design 2
```
des2DF = pd.DataFrame(columns=['TTX','SetupOverhead','SetupOverhead2','AgentOverhead','ClientOverhead'])
sids = ['design2_11K_run5']
for sid in sids:
Node1 = pd.DataFrame(columns=['Start','End','Type'])
Node1Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000002/geolocate1.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Geo1']
Node1Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000002/geolocate2.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Geo2']
Node1Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000002/ransac1.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Ransac1']
Node2 = pd.DataFrame(columns=['Start','End','Type'])
Node2Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000003/geolocate3.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Geo3']
Node2Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000003/geolocate4.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Geo4']
Node2Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000003/ransac2.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Ransac2']
Node3 = pd.DataFrame(columns=['Start','End','Type'])
Node3Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000004/geolocate5.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Geo5']
Node3Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000004/geolocate6.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Geo6']
Node3Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000004/ransac3.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Ransac3']
Node4 = pd.DataFrame(columns=['Start','End','Type'])
Node4Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000005/geolocate7.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Geo7']
Node4Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000005/geolocate8.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Geo8']
Node4Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000005/ransac4.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Ransac4']
AllNodes = pd.DataFrame(columns=['Start','End','Type'])
AllNodes = AllNodes.append(Node1)
AllNodes = AllNodes.append(Node2)
AllNodes = AllNodes.append(Node3)
AllNodes = AllNodes.append(Node4)
AllNodes.reset_index(inplace=True,drop='index')
rp_sessionDes2 = ra.Session(stype='radical.pilot',src='../Data/Design2/'+sid)
unitsDes2 = rp_sessionDes2.filter(etype='unit', inplace=False)
execUnits = unitsDes2.filter(uid=['unit.000002','unit.000003','unit.000004','unit.000005'],inplace=False)
exec_units_setup_des2 = execUnits.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}])
exec_units_agent_des2 = execUnits.duration([rp.AGENT_STAGING_INPUT, rp.UMGR_STAGING_OUTPUT_PENDING])
exec_units_clientDes2 = execUnits.duration([rp.NEW, rp.DONE])
SetupUnit = unitsDes2.filter(uid=['unit.000000'],inplace=False)
setup_units_clientDes2 = SetupUnit.duration(event=[{ru.STATE: rp.NEW},{ru.EVENT: 'exec_start'}])
pilotDes2 = rp_sessionDes2.filter(etype='pilot', inplace=False)
pilot_duration = pilotDes2.duration([rp.PMGR_ACTIVE,rp.FINAL])
des2_duration = AllNodes['End'].max() - AllNodes['Start'].min()
setupDes2_overhead = exec_units_setup_des2 - des2_duration
agentDes2_overhead = exec_units_agent_des2 - exec_units_setup_des2
clientDes2_overhead = exec_units_clientDes2 - exec_units_agent_des2
des2DF.loc[len(des2DF)] = [des2_duration, setup_units_clientDes2, setupDes2_overhead, agentDes2_overhead, clientDes2_overhead]
print(des2DF)
```
## Design 2A
```
sid='../Data/Design2a/design2a_11k_test5/'
rp_sessionDes2 = ra.Session(stype='radical.pilot',src=sid)
unitsDes2 = rp_sessionDes2.filter(etype='unit', inplace=False)
execUnits = unitsDes2.filter(uid=['unit.000002','unit.000003','unit.000004','unit.000001'],inplace=False)
exec_units_setup_des2 = execUnits.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}])
exec_units_agent_des2 = execUnits.duration([rp.AGENT_STAGING_INPUT, rp.UMGR_STAGING_OUTPUT_PENDING])
exec_units_clientDes2 = execUnits.duration([rp.NEW, rp.DONE])
SetupUnit = unitsDes2.filter(uid=['unit.000000'],inplace=False)
setup_units_clientDes2 = SetupUnit.duration(event=[{ru.STATE: rp.NEW},{ru.EVENT: 'exec_start'}])
pilotDes2 = rp_sessionDes2.filter(etype='pilot', inplace=False)
Node1 = pd.DataFrame(columns=['Start','End','Type'])
Node1Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000000/geolocate1.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Geo1']
Node1Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000000/geolocate2.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Geo2']
Node1Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000000/ransac1.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Ransac1']
Node2 = pd.DataFrame(columns=['Start','End','Type'])
Node2Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000001/geolocate3.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Geo3']
Node2Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000001/geolocate4.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Geo4']
Node2Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000001/ransac2.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Ransac2']
Node3 = pd.DataFrame(columns=['Start','End','Type'])
Node3Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000002/geolocate5.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Geo5']
Node3Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000002/geolocate6.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Geo6']
Node3Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000002/ransac3.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Ransac3']
Node4 = pd.DataFrame(columns=['Start','End','Type'])
Node4Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000003/geolocate7.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Geo7']
Node4Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000003/geolocate8.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Geo8']
Node4Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000003/ransac4.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Ransac4']
des2ADF = pd.DataFrame(columns=['TTX','SetupOverhead','AgentOverhead','ClientOverhead'])
AllNodes = pd.DataFrame(columns=['Start','End','Type'])
AllNodes = AllNodes.append(Node1)
AllNodes = AllNodes.append(Node2)
AllNodes = AllNodes.append(Node3)
AllNodes = AllNodes.append(Node4)
AllNodes.reset_index(inplace=True,drop='index')
rp_sessionDes2 = ra.Session(stype='radical.pilot',src=sid)
unitsDes2 = rp_sessionDes2.filter(etype='unit', inplace=False)
execUnits = unitsDes2.filter(uid=['unit.000000','unit.000001','unit.000002','unit.000003'],inplace=False)
exec_units_setup_des2 = unitsDes2.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}])
exec_units_agent_des2 = unitsDes2.duration([rp.AGENT_STAGING_INPUT, rp.UMGR_STAGING_OUTPUT_PENDING])
exec_units_clientDes2 = execUnits.duration([rp.NEW, rp.DONE])
pilotDes2 = rp_sessionDes2.filter(etype='pilot', inplace=False)
pilot_duration = pilotDes2.duration([rp.PMGR_ACTIVE,rp.FINAL])
des2_duration = AllNodes['End'].max() - AllNodes['Start'].min()
setupDes2_overhead = exec_units_setup_des2 - des2_duration
agentDes2_overhead = exec_units_agent_des2 - exec_units_setup_des2
clientDes2_overhead = exec_units_clientDes2 - exec_units_agent_des2
queue_time = max(pilotDes2.timestamps(event=[{ru.STATE: rp.PMGR_ACTIVE}]))- max(execUnits.timestamps(event=[{ru.STATE: rp.AGENT_STAGING_INPUT_PENDING}]))
des2ADF.loc[len(des2ADF)] = [des2_duration, setupDes2_overhead, agentDes2_overhead, clientDes2_overhead-queue_time]
print(des2ADF)
fig, axis = plt.subplots(nrows=1,ncols=1, figsize=(15,7.5))
x1 = np.arange(3)
_ = axis.bar(x1[0], des1DF['TTX'].mean(), width=0.5, color=blues(300), label='Design 1 TTX')
_ = axis.bar(x1[1], des2DF['TTX'].mean(), width=0.5, color=blues(200), label='Design 2 TTX')
_ = axis.bar(x1[2], des2ADF['TTX'].mean(), width=0.5, color=blues(100), label='Design 2A TTX')
_ = axis.set_xticks([0,1,2])
_ = axis.grid(which='both', linestyle=':', linewidth=1)
_ = axis.set_xticklabels(['Design 1', 'Design 2','Design 2A'], fontsize=36)
_ = axis.set_ylabel('Time in seconds', fontsize=26)
_ = axis.set_yticklabels(axis.get_yticks().astype('int').tolist(),fontsize=24)
#fig.savefig('geo_ttx.pdf',dpi=800,bbox='tight')
dist_overhead = np.load('../Data/dist_dataset.npy')
DiscDurations = [1861.404363739,
1872.631383787,
1870.355146581,
1852.347904858,
1857.771844937,
1868.644424397,
1873.176510421,
1851.527881958,
1870.128898667,
1856.676059379]
fig, axis = plt.subplots(nrows=1, ncols=1, figsize=(9,7.5))
x1 = np.arange(3)
_ = axis.bar(x1[0], des1DF['AgentOverhead'].mean(),width=0.5, color=reds(200),label='RP Agent Overhead Design 1')
_ = axis.bar(x1[0], des1DF['ClientOverhead'].mean(), bottom=des1DF['AgentOverhead'].mean(),width=0.5, color=reds(150),label='RP Client Overhead Design 1')
_ = axis.bar(x1[0], des1DF['EnTKOverhead'].mean(),bottom=des1DF['ClientOverhead'].mean()+des1DF['AgentOverhead'].mean(),width=0.5, color=reds(100),label='EnTK Overheads Design 1')
_ = axis.bar(x1[0], np.mean(DiscDurations), yerr=np.std(DiscDurations), bottom=des1DF['ClientOverhead'].mean()+des1DF['AgentOverhead'].mean() + des1DF['EnTKOverhead'].mean(),
width=0.5, color=reds(50),label='Design 1 Dataset Discovery')
_ = axis.bar(x1[1],des2DF['AgentOverhead'].mean(),width=0.5, color=greens(200),label='RP Agent Overhead Design 2')
_ = axis.bar(x1[1],des2DF['ClientOverhead'].mean(),bottom=des2DF['AgentOverhead'].mean(),width=0.5, color=greens(150),label='RP Client Overhead Design 2')
_ = axis.bar(x1[1],(des2DF['SetupOverhead'] + des2DF['SetupOverhead2']).mean(),bottom=des2DF['ClientOverhead'].mean()+des2DF['AgentOverhead'].mean(),width=0.5, color=greens(100),label='Design 2 Setup Overhead')
_ = axis.bar(x1[1],np.mean(DiscDurations), yerr=np.std(DiscDurations), bottom=des2DF['ClientOverhead'].mean()+des2DF['AgentOverhead'].mean() + (des2DF['SetupOverhead']+des2DF['SetupOverhead2']).mean(),
width=0.5, color=greens(50),label='Design 2 Dataset Discovery')
_ = axis.bar(x1[2],des2ADF['AgentOverhead'].mean(),#yerr=des2ADF['AgentOverhead'].std(),
width=0.5, color=purples(250),label='RP Agent Overhead Design 2A',log=1)
_ = axis.bar(x1[2],des2ADF['ClientOverhead'].mean(),#yerr=des2ADF['ClientOverhead'].std(),
bottom=des2ADF['AgentOverhead'].mean(),width=0.5, color=purples(200),label='RP Client Overhead Design 2A')
_ = axis.bar(x1[2],des2ADF['SetupOverhead'].mean(),#yerr=des2ADF['SetupOverhead'].std(),
bottom=des2ADF['ClientOverhead'].mean()+des2ADF['AgentOverhead'].mean(),width=0.5, color=purples(150),label='Design 2A Setup Overhead')
_ = axis.bar(x1[2],dist_overhead.mean(),yerr=dist_overhead.std(),
bottom=des2ADF['ClientOverhead'].mean()+des2ADF['AgentOverhead'].mean()+des2ADF['SetupOverhead'].mean(),width=0.5, color=purples(100),label='Design 2A Distributing Overhead')
_ = axis.bar(x1[2],np.mean(DiscDurations), yerr=np.std(DiscDurations),
bottom=des2ADF['ClientOverhead'].mean()+des2ADF['AgentOverhead'].mean()+des2ADF['SetupOverhead'].mean() + dist_overhead.mean(),
width=0.5, color=purples(50),label='Design 2A Dataset Discovery')
_ = axis.set_xticks([0,1,2])
_ = axis.grid(which='both', linestyle=':', linewidth=1)
_ = axis.set_ylabel('Time in seconds', fontsize=26)
_ = axis.set_xticklabels(['Design 1', 'Design 2','Design 2A'], fontsize=26)
_ = axis.set_yticks([1,10,100,1000,10000,100000])
_ = axis.set_yticklabels(axis.get_yticks().astype('int').tolist(),fontsize=24)
#_ = axis.legend(fontsize=22,loc = 'lower center', bbox_to_anchor = (0,-.55,1,1), ncol=2)
#_ = fig.subplots_adjust(bottom=.205)
fig.savefig('geo_overheads.pdf',dpi=800,pad_inches=0)
```
| github_jupyter |
# Running, Debugging, Testing & Packaging
```
!code ./1-helloconnectedworld
```
Let's look at the key parts of our app:
**package.json**
This defines all contributions: commands, context menus, UI, everything!
```json
"activationEvents": [
// Use "*" to start on application start. If contributing commands, only start on command to speed up user experience
"onCommand:extension.showCurrentConnection"
],
"main": "./out/extension",
"contributes": {
"commands": [
{
"command": "extension.showCurrentConnection",
"title": "Show Current Connection"
}
]
},
```
**extension.ts** is our extension control center. Your extension always starts here by registering your extension points, and using built-in APIs to query connections, show messages, and much more
```ts
context.subscriptions.push(vscode.commands.registerCommand('extension.showCurrentConnection', () => {
sqlops.connection.getCurrentConnection().then(connection => {
let connectionId = connection ? connection.connectionId : 'No connection found!';
vscode.window.showInformationMessage(connectionId);
}, error => {
console.info(error);
});
}));
```
### VSCode APIs
All* VSCode APIs are defined in Azure Data Studio meaning VSCode extensions just work. These include common workspace, window and language services features
> *Debugger APIs are defined but the debugger is not implemented
### sqlops / azdata APIs**
Azure Data Studio APIs are in the sqlops namespace. These cover Connection, Query, advanced UI (dialogs, wizards, and other standardized UI controls]), and the Data Management Protocol (DMP).
> These are moving to a new **azdata** namespace. We will cover the types of changes being made to simplify development as part of this demo
# Run your code
* In VSCode, you should have the "Azure Data Studio Debug" extension installed

* Hit F5 or go to the debugger section and click the Run button
* Azure Data Studio will launch
* Hit `Ctrl+Shift+P` and choose **Show Current Connection**
* It will show **No Connection Found**. How do we find out what's wrong? Let's go and debug it!
# Debug your code
* As for any app, click inside the code and set a breakdpoint on the line
```
let connectionId = connection ? connection.connectionId : 'No connection found!';
```
* Run the command again
* We will see that the connection is not getting returned. Why might that be? It's because nobody connected to one!
* Open a connection and try again. This time you will see all the available information about this connection.
# Testing your code
If you like to write tests, you have a template built-into your extension. You can even debug using the **Extension Tests** option in the debugger dropdown. This uses standard Javascript test frameworks (Mocha) and is able to integrate with all the usual actions.
# Packaging your extension
Packaging is as easy as running `vsce package` from the root of the extension.
* The first time you run this, you'll see errors if you didn't edit your Readme and other key files
* Update Readme.md so it's not a default value
* Similarly delete Changelog contents or update as needed
* Delete the **vsc-extension-quickstart.md` file
Now if you re-run, you'll get a .vsix file
## Installing your extension for testing
* In Azure Data Studio, hit `Ctrl+Shift+P` and choose **Extensions: Install from VSIX...**
* Pick your file and click OK
* It'll install and be available - no reload necessary!
## Publishing your extension
Follow our [Extension Authoring](https://github.com/Microsoft/azuredatastudio/wiki/Extension-Authoring) guide which has details on publishing to the extension gallery. If you have any issues reach out to us on Twitter [@AzureDataStudio](https://twitter.com/azuredatastudio)
| github_jupyter |
# Convolutional Autoencoder
Sticking with the MNIST dataset, let's improve our autoencoder's performance using convolutional layers. Again, loading modules and the data.
```
%matplotlib inline
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', validation_size=0)
img = mnist.train.images[2]
plt.imshow(img.reshape((28, 28)), cmap='Greys_r')
```
## Network Architecture
The encoder part of the network will be a typical convolutional pyramid. Each convolutional layer will be followed by a max-pooling layer to reduce the dimensions of the layers. The decoder though might be something new to you. The decoder needs to convert from a narrow representation to a wide reconstructed image. For example, the representation could be a 4x4x8 max-pool layer. This is the output of the encoder, but also the input to the decoder. We want to get a 28x28x1 image out from the decoder so we need to work our way back up from the narrow decoder input layer. A schematic of the network is shown below.
<img src='assets/convolutional_autoencoder.png' width=500px>
Here our final encoder layer has size 4x4x8 = 128. The original images have size 28x28 = 784, so the encoded vector is roughly 16% the size of the original image. These are just suggested sizes for each of the layers. Feel free to change the depths and sizes, but remember our goal here is to find a small representation of the input data.
### What's going on with the decoder
Okay, so the decoder has these "Upsample" layers that you might not have seen before. First off, I'll discuss a bit what these layers *aren't*. Usually, you'll see **transposed convolution** layers used to increase the width and height of the layers. They work almost exactly the same as convolutional layers, but in reverse. A stride in the input layer results in a larger stride in the transposed convolution layer. For example, if you have a 3x3 kernel, a 3x3 patch in the input layer will be reduced to one unit in a convolutional layer. Comparatively, one unit in the input layer will be expanded to a 3x3 path in a transposed convolution layer. The TensorFlow API provides us with an easy way to create the layers, [`tf.nn.conv2d_transpose`](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d_transpose).
However, transposed convolution layers can lead to artifacts in the final images, such as checkerboard patterns. This is due to overlap in the kernels which can be avoided by setting the stride and kernel size equal. In [this Distill article](http://distill.pub/2016/deconv-checkerboard/) from Augustus Odena, *et al*, the authors show that these checkerboard artifacts can be avoided by resizing the layers using nearest neighbor or bilinear interpolation (upsampling) followed by a convolutional layer. In TensorFlow, this is easily done with [`tf.image.resize_images`](https://www.tensorflow.org/versions/r1.1/api_docs/python/tf/image/resize_images), followed by a convolution. Be sure to read the Distill article to get a better understanding of deconvolutional layers and why we're using upsampling.
> **Exercise:** Build the network shown above. Remember that a convolutional layer with strides of 1 and 'same' padding won't reduce the height and width. That is, if the input is 28x28 and the convolution layer has stride = 1 and 'same' padding, the convolutional layer will also be 28x28. The max-pool layers are used the reduce the width and height. A stride of 2 will reduce the size by a factor of 2. Odena *et al* claim that nearest neighbor interpolation works best for the upsampling, so make sure to include that as a parameter in `tf.image.resize_images` or use [`tf.image.resize_nearest_neighbor`]( `https://www.tensorflow.org/api_docs/python/tf/image/resize_nearest_neighbor). For convolutional layers, use [`tf.layers.conv2d`](https://www.tensorflow.org/api_docs/python/tf/layers/conv2d). For example, you would write `conv1 = tf.layers.conv2d(inputs, 32, (5,5), padding='same', activation=tf.nn.relu)` for a layer with a depth of 32, a 5x5 kernel, stride of (1,1), padding is 'same', and a ReLU activation. Similarly, for the max-pool layers, use [`tf.layers.max_pooling2d`](https://www.tensorflow.org/api_docs/python/tf/layers/max_pooling2d).
```
inputs_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='inputs')
targets_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='targets')
### Encoder
conv1 = tf.layers.conv2d(inputs_, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x16
maxpool1 = tf.layers.max_pooling2d(conv1, (2,2), (2,2), padding='same')
# Now 14x14x16
conv2 = tf.layers.conv2d(maxpool1, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x8
maxpool2 = tf.layers.max_pooling2d(conv2, (2,2), (2,2), padding='same')
# Now 7x7x8
conv3 = tf.layers.conv2d(maxpool2, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x8
encoded = tf.layers.max_pooling2d(conv3, (2,2), (2,2), padding='same')
# Now 4x4x8
### Decoder
upsample1 = tf.image.resize_nearest_neighbor(encoded, (7,7))
# Now 7x7x8
conv4 = tf.layers.conv2d(upsample1, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x8
upsample2 = tf.image.resize_nearest_neighbor(conv4, (14,14))
# Now 14x14x8
conv5 = tf.layers.conv2d(upsample2, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x8
upsample3 = tf.image.resize_nearest_neighbor(conv5, (28,28))
# Now 28x28x8
conv6 = tf.layers.conv2d(upsample3, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x16
logits = tf.layers.conv2d(conv6, 1, (3,3), padding='same', activation=None)
#Now 28x28x1
decoded = tf.nn.sigmoid(logits, name='decoded')
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=targets_, logits=logits)
cost = tf.reduce_mean(loss)
opt = tf.train.AdamOptimizer(0.001).minimize(cost)
```
## Training
As before, here wi'll train the network. Instead of flattening the images though, we can pass them in as 28x28x1 arrays.
```
sess = tf.Session()
epochs = 1
batch_size = 200
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
imgs = batch[0].reshape((-1, 28, 28, 1))
batch_cost, _ = sess.run([cost, opt], feed_dict={inputs_: imgs,
targets_: imgs})
print("Epoch: {}/{}...".format(e+1, epochs),
"Training loss: {:.4f}".format(batch_cost))
fig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
in_imgs = mnist.test.images[:10]
reconstructed = sess.run(decoded, feed_dict={inputs_: in_imgs.reshape((10, 28, 28, 1))})
for images, row in zip([in_imgs, reconstructed], axes):
for img, ax in zip(images, row):
ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
fig.tight_layout(pad=0.1)
sess.close()
```
## Denoising
As I've mentioned before, autoencoders like the ones you've built so far aren't too useful in practive. However, they can be used to denoise images quite successfully just by training the network on noisy images. We can create the noisy images ourselves by adding Gaussian noise to the training images, then clipping the values to be between 0 and 1. We'll use noisy images as input and the original, clean images as targets. Here's an example of the noisy images I generated and the denoised images.

Since this is a harder problem for the network, we'll want to use deeper convolutional layers here, more feature maps. I suggest something like 32-32-16 for the depths of the convolutional layers in the encoder, and the same depths going backward through the decoder. Otherwise the architecture is the same as before.
> **Exercise:** Build the network for the denoising autoencoder. It's the same as before, but with deeper layers. I suggest 32-32-16 for the depths, but you can play with these numbers, or add more layers.
```
inputs_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='inputs')
targets_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='targets')
### Encoder
conv1 = tf.layers.conv2d(inputs_, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x32
maxpool1 = tf.layers.max_pooling2d(conv1, (2,2), (2,2), padding='same')
# Now 14x14x32
conv2 = tf.layers.conv2d(maxpool1, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x32
maxpool2 = tf.layers.max_pooling2d(conv2, (2,2), (2,2), padding='same')
# Now 7x7x32
conv3 = tf.layers.conv2d(maxpool2, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x16
encoded = tf.layers.max_pooling2d(conv3, (2,2), (2,2), padding='same')
# Now 4x4x16
### Decoder
upsample1 = tf.image.resize_nearest_neighbor(encoded, (7,7))
# Now 7x7x16
conv4 = tf.layers.conv2d(upsample1, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x16
upsample2 = tf.image.resize_nearest_neighbor(conv4, (14,14))
# Now 14x14x16
conv5 = tf.layers.conv2d(upsample2, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x32
upsample3 = tf.image.resize_nearest_neighbor(conv5, (28,28))
# Now 28x28x32
conv6 = tf.layers.conv2d(upsample3, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x32
logits = tf.layers.conv2d(conv6, 1, (3,3), padding='same', activation=None)
#Now 28x28x1
decoded = tf.nn.sigmoid(logits, name='decoded')
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=targets_, logits=logits)
cost = tf.reduce_mean(loss)
opt = tf.train.AdamOptimizer(0.001).minimize(cost)
sess = tf.Session()
epochs = 100
batch_size = 200
# Set's how much noise we're adding to the MNIST images
noise_factor = 0.5
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
# Get images from the batch
imgs = batch[0].reshape((-1, 28, 28, 1))
# Add random noise to the input images
noisy_imgs = imgs + noise_factor * np.random.randn(*imgs.shape)
# Clip the images to be between 0 and 1
noisy_imgs = np.clip(noisy_imgs, 0., 1.)
# Noisy images as inputs, original images as targets
batch_cost, _ = sess.run([cost, opt], feed_dict={inputs_: noisy_imgs,
targets_: imgs})
print("Epoch: {}/{}...".format(e+1, epochs),
"Training loss: {:.4f}".format(batch_cost))
```
## Checking out the performance
Here I'm adding noise to the test images and passing them through the autoencoder. It does a suprising great job of removing the noise, even though it's sometimes difficult to tell what the original number is.
```
fig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
in_imgs = mnist.test.images[:10]
noisy_imgs = in_imgs + noise_factor * np.random.randn(*in_imgs.shape)
noisy_imgs = np.clip(noisy_imgs, 0., 1.)
reconstructed = sess.run(decoded, feed_dict={inputs_: noisy_imgs.reshape((10, 28, 28, 1))})
for images, row in zip([noisy_imgs, reconstructed], axes):
for img, ax in zip(images, row):
ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
fig.tight_layout(pad=0.1)
```
| github_jupyter |
Practice geospatial aggregations in geopandas before writing them to .py files
```
%load_ext autoreload
%autoreload 2
import sys
sys.path.append('../utils')
import wd_management
wd_management.set_wd_root()
import geopandas as gp
import pandas as pd
import requests
res = requests.get('https://services5.arcgis.com/GfwWNkhOj9bNBqoJ/arcgis/rest/services/NYC_Public_Use_Microdata_Areas_PUMAs_2010/FeatureServer/0/query?where=1=1&outFields=*&outSR=4326&f=pgeojson')
res_json = res.json()
NYC_PUMAs = gp.GeoDataFrame.from_features(res_json['features'])
NYC_PUMAs.set_crs('EPSG:4326',inplace=True)
NYC_PUMAs.set_index('PUMA', inplace=True)
NYC_PUMAs.head(5)
NYC_PUMAs.plot()
```
Ok looks good. Load in historic districts. [This stackoverflow post](https://gis.stackexchange.com/questions/327197/typeerror-input-geometry-column-must-contain-valid-geometry-objects) was helpful
```
from shapely import wkt
hd= gp.read_file('.library/lpc_historic_district_areas.csv')
hd['the_geom'] = hd['the_geom'].apply(wkt.loads)
hd.set_geometry(col='the_geom', inplace=True, crs='EPSG:4326')
hd= hd.explode(column='the_geom')
hd.set_geometry('the_geom',inplace=True)
hd = hd.to_crs('EPSG:2263')
hd = hd.reset_index()
hd.plot()
```
Ok great next do some geospatial analysis. Start only with PUMA 3807 as it has a lot of historic area
```
def fraction_area_historic(PUMA, hd):
try:
gdf = gp.GeoDataFrame(geometry = [PUMA.geometry], crs = 'EPSG:4326')
gdf = gdf.to_crs('EPSG:2263')
overlay = gp.overlay(hd, gdf, 'intersection')
if overlay.empty:
return 0, 0
else:
fraction = overlay.area.sum()/gdf.geometry.area.sum()
return fraction, overlay.area.sum()/(5280**2)
except Exception as e:
print(f'broke on {PUMA}')
print(e)
NYC_PUMAs[['fraction_area_historic', 'total_area_historic']] = NYC_PUMAs.apply(fraction_area_historic, axis=1, args=(hd,), result_type='expand')
NYC_PUMAs.sort_values('fraction_area_historic', ascending=False)
```
Superimpose PUMA 3801's historic districts on it to see if 38% looks right
```
def visualize_overlay(PUMA):
test_PUMA = NYC_PUMAs.loc[[PUMA]].to_crs('EPSG:2263')
base = test_PUMA.plot(color='green', edgecolor='black')
overlay = gp.overlay(hd, test_PUMA, 'intersection')
overlay.plot(ax=base, color='red');
visualize_overlay('3810')
```
Ok great that looks like about a third to me
From eyeballing map, more than 20% of PUMA 3806 on UWS looks to be historic
```
visualize_overlay('3806')
```
Ah ok the PUMA geography from includes central park. Worth flagging
### Question from Renae:
Renae points out that description of historic districts says "including items that may have been denied designation or overturned."
Look at dataset to see if columns point to this clearly
```
hd.head(5)
hd.groupby('status_of_').size()
hd.groupby('current_').size()
hd.groupby('last_actio').size()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/prateekjoshi565/Fine-Tuning-BERT/blob/master/Fine_Tuning_BERT_for_Spam_Classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Install Transformers Library
```
!pip install transformers
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import transformers
from transformers import AutoModel, BertTokenizerFast
# specify GPU
device = torch.device("cuda")
```
# Load Dataset
```
df = pd.read_csv("spamdata_v2.csv")
df.head()
df.shape
# check class distribution
df['label'].value_counts(normalize = True)
```
# Split train dataset into train, validation and test sets
```
train_text, temp_text, train_labels, temp_labels = train_test_split(df['text'], df['label'],
random_state=2018,
test_size=0.3,
stratify=df['label'])
# we will use temp_text and temp_labels to create validation and test set
val_text, test_text, val_labels, test_labels = train_test_split(temp_text, temp_labels,
random_state=2018,
test_size=0.5,
stratify=temp_labels)
```
# Import BERT Model and BERT Tokenizer
```
# import BERT-base pretrained model
bert = AutoModel.from_pretrained('bert-base-uncased')
# Load the BERT tokenizer
tokenizer = BertTokenizerFast.from_pretrained('bert-base-uncased')
# sample data
text = ["this is a bert model tutorial", "we will fine-tune a bert model"]
# encode text
sent_id = tokenizer.batch_encode_plus(text, padding=True, return_token_type_ids=False)
# output
print(sent_id)
```
# Tokenization
```
# get length of all the messages in the train set
seq_len = [len(i.split()) for i in train_text]
pd.Series(seq_len).hist(bins = 30)
max_seq_len = 25
# tokenize and encode sequences in the training set
tokens_train = tokenizer.batch_encode_plus(
train_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
# tokenize and encode sequences in the validation set
tokens_val = tokenizer.batch_encode_plus(
val_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
# tokenize and encode sequences in the test set
tokens_test = tokenizer.batch_encode_plus(
test_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
```
# Convert Integer Sequences to Tensors
```
# for train set
train_seq = torch.tensor(tokens_train['input_ids'])
train_mask = torch.tensor(tokens_train['attention_mask'])
train_y = torch.tensor(train_labels.tolist())
# for validation set
val_seq = torch.tensor(tokens_val['input_ids'])
val_mask = torch.tensor(tokens_val['attention_mask'])
val_y = torch.tensor(val_labels.tolist())
# for test set
test_seq = torch.tensor(tokens_test['input_ids'])
test_mask = torch.tensor(tokens_test['attention_mask'])
test_y = torch.tensor(test_labels.tolist())
```
# Create DataLoaders
```
from torch.utils.data import TensorDataset, DataLoader, RandomSampler, SequentialSampler
#define a batch size
batch_size = 32
# wrap tensors
train_data = TensorDataset(train_seq, train_mask, train_y)
# sampler for sampling the data during training
train_sampler = RandomSampler(train_data)
# dataLoader for train set
train_dataloader = DataLoader(train_data, sampler=train_sampler, batch_size=batch_size)
# wrap tensors
val_data = TensorDataset(val_seq, val_mask, val_y)
# sampler for sampling the data during training
val_sampler = SequentialSampler(val_data)
# dataLoader for validation set
val_dataloader = DataLoader(val_data, sampler = val_sampler, batch_size=batch_size)
```
# Freeze BERT Parameters
```
# freeze all the parameters
for param in bert.parameters():
param.requires_grad = False
```
# Define Model Architecture
```
class BERT_Arch(nn.Module):
def __init__(self, bert):
super(BERT_Arch, self).__init__()
self.bert = bert
# dropout layer
self.dropout = nn.Dropout(0.1)
# relu activation function
self.relu = nn.ReLU()
# dense layer 1
self.fc1 = nn.Linear(768,512)
# dense layer 2 (Output layer)
self.fc2 = nn.Linear(512,2)
#softmax activation function
self.softmax = nn.LogSoftmax(dim=1)
#define the forward pass
def forward(self, sent_id, mask):
#pass the inputs to the model
_, cls_hs = self.bert(sent_id, attention_mask=mask)
x = self.fc1(cls_hs)
x = self.relu(x)
x = self.dropout(x)
# output layer
x = self.fc2(x)
# apply softmax activation
x = self.softmax(x)
return x
# pass the pre-trained BERT to our define architecture
model = BERT_Arch(bert)
# push the model to GPU
model = model.to(device)
# optimizer from hugging face transformers
from transformers import AdamW
# define the optimizer
optimizer = AdamW(model.parameters(), lr = 1e-3)
```
# Find Class Weights
```
from sklearn.utils.class_weight import compute_class_weight
#compute the class weights
class_wts = compute_class_weight('balanced', np.unique(train_labels), train_labels)
print(class_wts)
# convert class weights to tensor
weights= torch.tensor(class_wts,dtype=torch.float)
weights = weights.to(device)
# loss function
cross_entropy = nn.NLLLoss(weight=weights)
# number of training epochs
epochs = 10
```
# Fine-Tune BERT
```
# function to train the model
def train():
model.train()
total_loss, total_accuracy = 0, 0
# empty list to save model predictions
total_preds=[]
# iterate over batches
for step,batch in enumerate(train_dataloader):
# progress update after every 50 batches.
if step % 50 == 0 and not step == 0:
print(' Batch {:>5,} of {:>5,}.'.format(step, len(train_dataloader)))
# push the batch to gpu
batch = [r.to(device) for r in batch]
sent_id, mask, labels = batch
# clear previously calculated gradients
model.zero_grad()
# get model predictions for the current batch
preds = model(sent_id, mask)
# compute the loss between actual and predicted values
loss = cross_entropy(preds, labels)
# add on to the total loss
total_loss = total_loss + loss.item()
# backward pass to calculate the gradients
loss.backward()
# clip the the gradients to 1.0. It helps in preventing the exploding gradient problem
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
# update parameters
optimizer.step()
# model predictions are stored on GPU. So, push it to CPU
preds=preds.detach().cpu().numpy()
# append the model predictions
total_preds.append(preds)
# compute the training loss of the epoch
avg_loss = total_loss / len(train_dataloader)
# predictions are in the form of (no. of batches, size of batch, no. of classes).
# reshape the predictions in form of (number of samples, no. of classes)
total_preds = np.concatenate(total_preds, axis=0)
#returns the loss and predictions
return avg_loss, total_preds
# function for evaluating the model
def evaluate():
print("\nEvaluating...")
# deactivate dropout layers
model.eval()
total_loss, total_accuracy = 0, 0
# empty list to save the model predictions
total_preds = []
# iterate over batches
for step,batch in enumerate(val_dataloader):
# Progress update every 50 batches.
if step % 50 == 0 and not step == 0:
# Calculate elapsed time in minutes.
elapsed = format_time(time.time() - t0)
# Report progress.
print(' Batch {:>5,} of {:>5,}.'.format(step, len(val_dataloader)))
# push the batch to gpu
batch = [t.to(device) for t in batch]
sent_id, mask, labels = batch
# deactivate autograd
with torch.no_grad():
# model predictions
preds = model(sent_id, mask)
# compute the validation loss between actual and predicted values
loss = cross_entropy(preds,labels)
total_loss = total_loss + loss.item()
preds = preds.detach().cpu().numpy()
total_preds.append(preds)
# compute the validation loss of the epoch
avg_loss = total_loss / len(val_dataloader)
# reshape the predictions in form of (number of samples, no. of classes)
total_preds = np.concatenate(total_preds, axis=0)
return avg_loss, total_preds
```
# Start Model Training
```
# set initial loss to infinite
best_valid_loss = float('inf')
# empty lists to store training and validation loss of each epoch
train_losses=[]
valid_losses=[]
#for each epoch
for epoch in range(epochs):
print('\n Epoch {:} / {:}'.format(epoch + 1, epochs))
#train model
train_loss, _ = train()
#evaluate model
valid_loss, _ = evaluate()
#save the best model
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'saved_weights.pt')
# append training and validation loss
train_losses.append(train_loss)
valid_losses.append(valid_loss)
print(f'\nTraining Loss: {train_loss:.3f}')
print(f'Validation Loss: {valid_loss:.3f}')
```
# Load Saved Model
```
#load weights of best model
path = 'saved_weights.pt'
model.load_state_dict(torch.load(path))
```
# Get Predictions for Test Data
```
# get predictions for test data
with torch.no_grad():
preds = model(test_seq.to(device), test_mask.to(device))
preds = preds.detach().cpu().numpy()
# model's performance
preds = np.argmax(preds, axis = 1)
print(classification_report(test_y, preds))
# confusion matrix
pd.crosstab(test_y, preds)
```
| github_jupyter |
# WeatherPy
----
#### Note
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
import random
import json
import scipy.stats as st
from scipy.stats import linregress
# Import API key
from api_keys import weather_api_key
from api_keys import g_key
# Incorporated citipy to determine city based on latitude and longitude
from citipy import citipy
# Output File (CSV)
output_data_file = "output_data/cities.csv"
# Range of latitudes and longitudes
lat_range = (-90, 90)
lng_range = (-180, 180)
```
## Generate Cities List
```
# List for holding lat_lngs and cities
lat_lngs = []
cities = []
# Create a set of random lat and lng combinations
lats = np.random.uniform(lat_range[0], lat_range[1], size=1500)
lngs = np.random.uniform(lng_range[0], lng_range[1], size=1500)
lat_lngs = zip(lats, lngs)
# Identify nearest city for each lat, lng combination
for lat_lng in lat_lngs:
city = citipy.nearest_city(lat_lng[0], lat_lng[1]).city_name
# If the city is unique, then add it to a our cities list
if city not in cities:
cities.append(city)
# Print the city count to confirm sufficient count
len(cities)
city_names_ls = []
cloudiness_ls = []
country_ls = []
date_ls = []
humidity_ls = []
lat_ls = []
lng_ls = []
max_temp_ls = []
wind_speed_ls = []
index_counter = 0
set_counter = 1
```
### Perform API Calls
* Perform a weather check on each city using a series of successive API calls.
* Include a print log of each city as it'sbeing processed (with the city number and city name).
```
print("Beginning Data Retrieval")
print("-------------------------------")
base_url = "http://api.openweathermap.org/data/2.5/weather?"
units = "imperial"
url = f"{base_url}appid={weather_api_key}&units={units}&q="
for index, city in enumerate(cities, start = 1):
try:
response = requests.get(url + city).json()
city_names_ls.append(response["name"])
cloudiness_ls.append(response["clouds"]["all"])
country_ls.append(response["sys"]["country"])
date_ls.append(response["dt"])
humidity_ls.append(response["main"]["humidity"])
lat_ls.append(response["coord"]["lat"])
lng_ls.append(response["coord"]["lon"])
max_temp_ls.append(response["main"]["temp_max"])
wind_speed_ls.append(response["wind"]["speed"])
if index_counter > 49:
index_counter = 0
set_counter = set_counter + 1
else:
index_counter = index_counter + 1
print(f"Processing Record {index_counter} of Set {set_counter} : {city}")
except(KeyError, IndexError):
print("City not found. Skipping...")
print("-------------------------------")
print("Data Retrieval Complete")
print("-------------------------------")
```
### Convert Raw Data to DataFrame
* Export the city data into a .csv.
* Display the DataFrame
```
weather_df = pd.DataFrame({
"City" : city_names_ls,
"Cloudiness" : cloudiness_ls,
"Country" : country_ls,
"Date" : date_ls,
"Humidity" : humidity_ls,
"Lat" : lat_ls,
"Lng" : lng_ls,
"Max Temp" : max_temp_ls,
"Wind Speed" : wind_speed_ls
})
weather_df.count()
weather_df
weather_df.to_csv('../output_data/cities.csv')
```
## Inspect the data and remove the cities where the humidity > 100%.
----
Skip this step if there are no cities that have humidity > 100%.
```
# Get the indices of cities that have humidity over 100%.
# Make a new DataFrame equal to the city data to drop all humidity outliers by index.
# Passing "inplace=False" will make a copy of the city_data DataFrame, which we call "clean_city_data".
# Extract relevant fields from the data frame
# Export the City_Data into a csv
```
## Plotting the Data
* Use proper labeling of the plots using plot titles (including date of analysis) and axes labels.
* Save the plotted figures as .pngs.
## Latitude vs. Temperature Plot
```
plt.scatter(weather_df["Lat"], weather_df["Max Temp"], facecolor = "darkblue", edgecolor = "darkgrey")
plt.title("City Latitude vs. Max Temperature (07/13/20)")
plt.ylabel("Max Temperature (F)")
plt.xlabel("Latitude")
plt.grid(True)
plt.savefig("../Images/City Latitude vs Max Temperature.png")
plt.show()
print("This plot shows that as cities get further away from equator that they are cooler")
```
## Latitude vs. Humidity Plot
```
plt.scatter(weather_df["Lat"], weather_df["Humidity"], facecolor = "darkblue", edgecolor = "darkgrey")
plt.title("City Latitude vs. Humidity (07/13/20)")
plt.ylabel("Humidity (%)")
plt.xlabel("Latitude")
plt.grid(True)
plt.savefig("../Images/City Latitude vs Humidity.png")
plt.show()
print("This plot shows that humidity is well spread throughout cities despite location")
```
## Latitude vs. Cloudiness Plot
```
plt.scatter(weather_df["Lat"], weather_df["Cloudiness"], facecolor = "darkblue", edgecolor = "darkgrey")
plt.title("City Latitude vs. Cloudiness (07/13/20)")
plt.ylabel("Cloudiness (%)")
plt.xlabel("Latitude")
plt.grid(True)
plt.savefig("../Images/City Latitude vs Cloudiness.png")
plt.show()
print("This plot shows that cloudiness is well spread throughout cities despite location")
```
## Latitude vs. Wind Speed Plot
```
plt.scatter(weather_df["Lat"], weather_df["Wind Speed"], facecolor = "darkblue", edgecolor = "darkgrey")
plt.title("City Latitude vs. Windspeed (07/13/20)")
plt.ylabel("Windspeed (mph)")
plt.xlabel("Latitude")
plt.grid(True)
plt.savefig("../Images/City Latitude vs Windspeed.png")
plt.show()
print("This plot shows that windspeed is well spread throughout cities despite location")
```
## Linear Regression
```
# OPTIONAL: Create a function to create Linear Regression plots
nor_hemi = weather_df.loc[weather_df["Lat"] >= 0]
sou_hemi = weather_df.loc[weather_df["Lat"] < 0]
def linear_agression(x,y):
print(f"The r-squared is : {round(st.pearsonr(x, y)[0],2)}")
(slope, intercept, rvalue, pvalue, stderr) = linregress(x, y)
regress_values = x * slope + intercept
line_eq = "y = " + str(round(slope,2)) + "x + " + str(round(intercept,2))
plt.scatter(x, y)
plt.plot(x,regress_values,"r-")
return line_eq
def annotate(line_eq, a, b):
plt.annotate(line_eq,(a,b),fontsize=15,color="red")
```
#### Northern Hemisphere - Max Temp vs. Latitude Linear Regression
```
equation = linear_agression(nor_hemi["Lat"], nor_hemi["Max Temp"])
annotate(equation, 10, 40)
plt.ylabel("Max Temp (F)")
plt.xlabel("Latitude")
plt.savefig("../Images/NorHemi Max Temp vs. Latitude Linear Regression.png")
print("This linear regression shows that cities gets hotter as get closer to equator in northern hemisphere")
```
#### Southern Hemisphere - Max Temp vs. Latitude Linear Regression
```
equation = linear_agression(sou_hemi["Lat"], sou_hemi["Max Temp"])
annotate(equation, -50, 80)
plt.ylabel("Max Temperature (F)")
plt.xlabel("Latitude")
plt.savefig("../Images/SouHemi Max Temp vs. Latitude Linear Regression.png")
print("This linear regression shows that cities gets colder as get away to equator in southern hemisphere")
```
#### Northern Hemisphere - Humidity (%) vs. Latitude Linear Regression
```
equation = linear_agression(nor_hemi["Lat"], nor_hemi["Humidity"])
annotate(equation, 1, 5)
plt.ylabel("Humidity")
plt.xlabel("Latitude")
plt.savefig("../Images/NorHemi Humidity vs. Latitude Linear Regression.png")
print("This linear regression shows that cities' humidity doesn't change much as get closer to equator in northern hemisphere")
```
#### Southern Hemisphere - Humidity (%) vs. Latitude Linear Regression
```
equation = linear_agression(sou_hemi["Lat"], sou_hemi["Humidity"])
annotate(equation, -50, 20)
plt.ylabel("Humidity")
plt.xlabel("Latitude")
plt.savefig("../Images/SouHemi Humidity vs. Latitude Linear Regression.png")
print("This linear regression shows that cities' humidity doesn't change much as get closer to equator in southern hemisphere")
```
#### Northern Hemisphere - Cloudiness (%) vs. Latitude Linear Regression
```
equation = linear_agression(nor_hemi["Lat"], nor_hemi["Cloudiness"])
annotate(equation, 0, 0)
plt.ylabel("Cloudiness")
plt.xlabel("Latitude")
plt.savefig("../Images/NorHemi Cloudiness vs. Latitude Linear Regression.png")
print("This linear regression shows that cities' cloudiness doesn't change much as get closer to equator in northern hemisphere")
```
#### Southern Hemisphere - Cloudiness (%) vs. Latitude Linear Regression
```
equation = linear_agression(sou_hemi["Lat"], sou_hemi["Cloudiness"])
annotate(equation, -50, 50)
plt.ylabel("Cloudiness")
plt.xlabel("Latitude")
plt.savefig("../Images/SouHemi Cloudiness vs. Latitude Linear Regression.png")
print("This linear regression shows that cities' cloudiness doesn't change much as get closer to equator in southern hemisphere")
```
#### Northern Hemisphere - Wind Speed (mph) vs. Latitude Linear Regression
```
equation = linear_agression(nor_hemi["Lat"], nor_hemi["Wind Speed"])
annotate(equation, 40, 25)
plt.ylabel("Wind Speed")
plt.xlabel("Latitude")
plt.savefig("../Images/NorHemi Wind Speed vs. Latitude Linear Regression.png")
print("This linear regression shows that cities' windiness doesn't change much as get closer to equator in northern hemisphere")
```
#### Southern Hemisphere - Wind Speed (mph) vs. Latitude Linear Regression
```
equation = linear_agression(sou_hemi["Lat"], sou_hemi["Wind Speed"])
annotate(equation, -50, 25)
plt.ylabel("Wind Speed")
plt.xlabel("Latitude")
plt.savefig("../Images/SouHemi Wind Speed vs. Latitude Linear Regression.png")
print("This linear regression shows that cities' windiness doesn't change much as get closer to equator in northern hemisphere")
#Three Observable Trends
#1- Out of the cities analyzed, tends to be hotter by the equatator
#2- This time of year there tends to be more wind in cities away from equator in southern hemisphere
#3- Humidty, cloudiness, and wind speeds did not any obvious trends in the nothern hemisphere.
```
| github_jupyter |
<a href="https://colab.research.google.com/github/jorge23amury/daa_2021_1/blob/master/4_diciembre1358.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
"""
Array2D
"""
class Array2D:
def __init__(self,rows, cols, value):
self.__cols = cols
self.__rows = rows
self.__array=[[value for x in range(self.__cols)] for y in range(self.__rows)]
def to_string(self):
[print("---",end="") for x in range(self.__cols)]
print("")
for ren in self.__array:
print(ren)
[print("---",end="") for x in range(self.__cols)]
print("")
def get_num_rows(self):
return self.__rows
def get_num_cols(self):
return self.__cols
def get_item(self,row,col):
return self.__array[row][col]
def set_item( self , row , col , valor ):
self.__array[row][col]=valor
def clearing(self, valor=0):
for ren in range(self.__rows):
for col in range(self.__cols):
self.__array[ren][col]=valor
class Stack:
def __init__(self):
self.__data = []
self.__size = 0
def pop(self):
return self.__data.pop()
def get_size(self):
return self.__size
def peak(self):
if len(self.__data) > 0:
return self.__data[-1]
else:
return None
def push(self,value):
self.__data.append(value)
self.__size += 1
def to_string(self):
print("-"*6)
for dato in self.__data[::-1]:
print(f"| {dato} |")
print("/" * 6)
print("")
class Laberinto_ADT:
def __init__(self, archivo):
self.__laberinto = Array2D(0, 0, 0)
self.__camino = Stack()
self.__rens = 0
self.__cols = 0
self.__entrada = (0, 0)
entrada = open(archivo, 'rt')
datos = entrada.readlines()
#print(datos)
self.__rens = int(datos.pop(0).strip())
self.__cols = int(datos.pop(0).strip())
self.__entrada = list(datos[0].strip().split(','))
self.__entrada[0] = int(self.__entrada[0])
self.__entrada[1] = int(self.__entrada[1])
self.__camino.push((self.__entrada[1],[0]))
datos.pop(0) #eleminamos la tupla
print(self.__rens, self.__cols, self.__entrada)
print(datos)
self.__laberinto = Array2D(self.__rens, self.__cols, '1')
for renglon in range(self.__rens):
info_ren = datos[renglon].strip().split(',')
for columna in range(self.__cols):
self.__laberinto.set_item(renglon, columna, info_ren[columna])
self.__laberinto.to_string()
def resolver(self):
actual = self.__camino.peek()
def imprime_camino(self):
self.__camino.to_string()
def mostrar(self):
self.__laberinto.to_string()
if self.__laberinto.get_item( actual[0], actual[1] - 1 ) == '0' and self.__laberinto.get_item( actual[0], actual[1] - 1 ) != 'X' and self.__previa ! = actual[0], actual[1] - 1:
self.__previa = actual
self.__camino.push(actual[0], actual[1]-1)
elif self.__laberinto.get_item(actual[0]-1 , actual[1]) == '0' and self.__
elif l ==2 :
pass
elif l== 2:
pass
else:
self.__laberinto.set_item(actual[0])
def otros():
pass
#main
laberinto = Laberinto_ADT("entrada.txt")
laberinto.mostrar()
laberinto.imprime_camino()
```
| github_jupyter |
# Run hacked AlphaFold2 on the designed bound states
### Imports
```
%load_ext lab_black
# Python standard library
from glob import glob
import os
import socket
import sys
# 3rd party library imports
import dask
import matplotlib.pyplot as plt
import pandas as pd
import pyrosetta
import numpy as np
import scipy
import seaborn as sns
from tqdm.auto import tqdm # jupyter compatible progress bar
tqdm.pandas() # link tqdm to pandas
# Notebook magic
# save plots in the notebook
%matplotlib inline
# reloads modules automatically before executing cells
%load_ext autoreload
%autoreload 2
print(f"running in directory: {os.getcwd()}") # where are we?
print(f"running on node: {socket.gethostname()}") # what node are we on?
```
### Set working directory to the root of the crispy_shifty repo
TODO set to projects dir
```
os.chdir("/home/pleung/projects/crispy_shifty")
# os.chdir("/projects/crispy_shifty")
```
### Run AF2 on the designed bound states
TODO
```
from crispy_shifty.utils.io import gen_array_tasks
simulation_name = "03_fold_bound_states"
design_list_file = os.path.join(
os.getcwd(),
"projects/crispy_shifties/02_mpnn_bound_states/test_mpnn_states.pair", # TODO
)
output_path = os.path.join(os.getcwd(), f"projects/crispy_shifties/{simulation_name}")
options = " ".join(
[
"out:level 200",
]
)
extra_kwargs = {"models": "1"}
gen_array_tasks(
distribute_func="crispy_shifty.protocols.folding.fold_bound_state",
design_list_file=design_list_file,
output_path=output_path,
queue="gpu", # TODO
cores=2,
memory="16G", # TODO
gres="--gres=gpu:rtx2080:1", # TODO
# TODO perlmutter_mode=True,
nstruct=1,
nstruct_per_task=1,
options=options,
extra_kwargs=extra_kwargs,
simulation_name=simulation_name,
)
# !sbatch -a 1-$(cat /mnt/home/pleung/projects/crispy_shifty/projects/crispy_shifties/02_mpnn_bound_states/tasks.cmds | wc -l) /mnt/home/pleung/projects/crispy_shifty/projects/crispy_shifties/02_mpnn_bound_states/run.sh
```
### Collect scorefiles of designed bound states and concatenate
TODO change to projects dir
```
sys.path.insert(0, "~/projects/crispy_shifty") # TODO
from crispy_shifty.utils.io import collect_score_file
simulation_name = "03_fold_bound_states"
output_path = os.path.join(os.getcwd(), f"projects/crispy_shifties/{simulation_name}")
if not os.path.exists(os.path.join(output_path, "scores.json")):
collect_score_file(output_path, "scores")
```
### Load resulting concatenated scorefile
TODO change to projects dir
```
sys.path.insert(0, "~/projects/crispy_shifty") # TODO
from crispy_shifty.utils.io import parse_scorefile_linear
output_path = os.path.join(os.getcwd(), f"projects/crispy_shifties/{simulation_name}")
scores_df = parse_scorefile_linear(os.path.join(output_path, "scores.json"))
scores_df = scores_df.convert_dtypes()
```
### Setup for plotting
```
sns.set(
context="talk",
font_scale=1, # make the font larger; default is pretty small
style="ticks", # make the background white with black lines
palette="colorblind", # a color palette that is colorblind friendly!
)
```
### Data exploration
Gonna remove the Rosetta sfxn scoreterms for now
```
from crispy_shifty.protocols.design import beta_nov16_terms
scores_df = scores_df[
[term for term in scores_df.columns if term not in beta_nov16_terms]
]
print(len(scores_df))
j = 0
for i, r in scores_df.iterrows():
if (r["designed_by"]) == "rosetta":
j += 1
print(j)
```
### Save a list of outputs
```
# simulation_name = "03_fold_bound_states"
# output_path = os.path.join(os.getcwd(), f"projects/crispy_shifties/{simulation_name}")
# with open(os.path.join(output_path, "folded_states.list"), "w") as f:
# for path in tqdm(scores_df.index):
# print(path, file=f)
```
### Prototyping blocks
test `fold_bound_state`
```
%%time
from operator import gt, lt
import pyrosetta
filter_dict = {
"mean_plddt": (gt, 85.0),
"rmsd_to_reference": (lt, 2.2),
"mean_pae_interaction": (lt, 10.0),
}
rank_on = "mean_plddt"
prefix = "mpnn_seq"
pyrosetta.init()
sys.path.insert(0, "~/projects/crispy_shifty/") # TODO projects
from crispy_shifty.protocols.folding import fold_bound_state
t = fold_bound_state(
None,
**{
'fasta_path': '/mnt/home/pleung/projects/crispy_shifty/projects/crispy_shifties/02_mpnn_bound_states/fastas/0000/02_mpnn_bound_states_25a76fae39514121922e2b477b5b9813.fa',
"filter_dict": filter_dict,
"models": [1], # TODO
'pdb_path': '/mnt/home/pleung/projects/crispy_shifty/projects/crispy_shifties/02_mpnn_bound_states/decoys/0000/02_mpnn_bound_states_25a76fae39514121922e2b477b5b9813.pdb.bz2',
'prefix': prefix,
'rank_on': rank_on,
# 'fasta_path': 'bar.fa',
# "models": [1, 2], # TODO
# 'pdb_path': 'foo.pdb.bz2',
}
)
for i, tppose in enumerate(t):
tppose.pose.dump_pdb(f"{i}.pdb")
tppose.pose.scores
```
test `generate_decoys_from_pose`
```
from operator import gt, lt
from crispy_shifty.protocols.folding import generate_decoys_from_pose
filter_dict = {
"mean_plddt": (gt, 85.0),
"rmsd_to_reference": (lt, 2.2),
"mean_pae_interaction": (lt, 10.0),
}
rank_on = "mean_plddt"
prefix = "mpnn_seq"
tpose = tppose.pose.clone()
genr = generate_decoys_from_pose(
tpose, prefix=prefix, rank_on=rank_on, filter_dict=filter_dict
)
for d in genr:
print(d.sequence())
```
| github_jupyter |
<a href="https://colab.research.google.com/github/parshwa1999/Map-Segmentation/blob/master/ResNet_RoadTest.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Segmentation of Road from Satellite imagery
## Importing Libraries
```
import warnings
warnings.filterwarnings('ignore')
import os
import cv2
#from google.colab.patches import cv2_imshow
import numpy as np
import tensorflow as tf
import pandas as pd
from keras.models import Model, load_model
from skimage.morphology import label
import pickle
from keras import backend as K
from matplotlib import pyplot as plt
from tqdm import tqdm_notebook
import random
from skimage.io import imread, imshow, imread_collection, concatenate_images
from matplotlib import pyplot as plt
import h5py
seed = 56
from google.colab import drive
drive.mount('/content/gdrive/')
base_path = "gdrive/My\ Drive/MapSegClean/"
%cd gdrive/My\ Drive/MapSegClean/
```
## Defining Custom Loss functions and accuracy Metric.
```
#Source: https://towardsdatascience.com/metrics-to-evaluate-your-semantic-segmentation-model-6bcb99639aa2
from keras import backend as K
def iou_coef(y_true, y_pred, smooth=1):
intersection = K.sum(K.abs(y_true * y_pred), axis=[1,2,3])
union = K.sum(y_true,[1,2,3])+K.sum(y_pred,[1,2,3])-intersection
iou = K.mean((intersection + smooth) / (union + smooth), axis=0)
return iou
def dice_coef(y_true, y_pred, smooth = 1):
y_true_f = K.flatten(y_true)
y_pred_f = K.flatten(y_pred)
intersection = K.sum(y_true_f * y_pred_f)
return (2. * intersection + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth)
def soft_dice_loss(y_true, y_pred):
return 1-dice_coef(y_true, y_pred)
```
## Defining Our Model
```
pip install -U segmentation-models
from keras.models import Model, load_model
import tensorflow as tf
from keras.layers import Input
from keras.layers.core import Dropout, Lambda
from keras.layers.convolutional import Conv2D, Conv2DTranspose
from keras.layers.pooling import MaxPooling2D
from keras.layers.merge import concatenate
from keras import optimizers
from keras.layers import BatchNormalization
import keras
from segmentation_models import Unet
from segmentation_models import get_preprocessing
from segmentation_models.losses import bce_jaccard_loss
from segmentation_models.metrics import iou_score
model = Unet('resnet101', input_shape=(256, 256, 3), encoder_weights=None)
#model = Unet(input_shape=(256, 256, 3), weights=None, activation='elu')
model.summary()
# fit model
```
### HYPER_PARAMETERS
```
LEARNING_RATE = 0.0001
```
### Initializing Callbacks
```
#from tensorboardcolab import TensorBoardColab, TensorBoardColabCallback
from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau
from datetime import datetime
model_path = "./Models/Resnet_road_weights.h5"
checkpointer = ModelCheckpoint(model_path,
monitor="val_loss",
mode="min",
save_best_only = True,
verbose=1)
earlystopper = EarlyStopping(monitor = 'val_loss',
min_delta = 0,
patience = 5,
verbose = 1,
restore_best_weights = True)
lr_reducer = ReduceLROnPlateau(monitor='val_loss',
factor=0.1,
patience=4,
verbose=1,
epsilon=1e-4)
```
### Compiling the model
```
opt = keras.optimizers.adam(LEARNING_RATE)
model.compile(
optimizer=opt,
loss=soft_dice_loss,
metrics=[iou_coef])
```
## Testing our Model
### On Test Images
```
model.load_weights("Models/Resnet_road_weights.h5")
import cv2
import glob
import numpy as np
import h5py
#test_images = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/I/")])
#test_masks = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/M/")])
test_masks = []
test_images = []
files = glob.glob ("TestI/*.png")
for myFile in files:
print(myFile)
image = cv2.imread (myFile)
test_images.append (image)
myFile = 'TestM' + myFile[5:len(myFile)]
image = cv2.cvtColor(cv2.imread (myFile), cv2.COLOR_BGR2GRAY)
test_masks.append (image)
#files = glob.glob ("TestM/*.png")
#for myFile in files:
# print(myFile)
#test_images = cv2.imread("/home/bisag/Desktop/Road-Segmentation/I/1.png")
#test_masks = cv2.imread("/home/bisag/Desktop/Road-Segmentation/M/1.png")
test_images = np.array(test_images)
test_masks = np.array(test_masks)
test_masks = np.expand_dims(test_masks, -1)
print("Unique elements in the train mask:", np.unique(test_masks))
print(test_images.shape)
print(test_masks.shape)
test_images = test_images.astype(np.float16)/255
test_masks = test_masks.astype(np.float16)/255
import sys
def sizeof_fmt(num, suffix='B'):
''' by Fred Cirera, https://stackoverflow.com/a/1094933/1870254, modified'''
for unit in ['','Ki','Mi','Gi','Ti','Pi','Ei','Zi']:
if abs(num) < 1024.0:
return "%3.1f %s%s" % (num, unit, suffix)
num /= 1024.0
return "%.1f %s%s" % (num, 'Yi', suffix)
for name, size in sorted(((name, sys.getsizeof(value)) for name, value in locals().items()),
key= lambda x: -x[1])[:10]:
print("{:>30}: {:>8}".format(name, sizeof_fmt(size)))
test_masks_tmp = []
for i in test_masks:
image = cv2.cvtColor(i, cv2.COLOR_BGR2GRAY)
test_masks_tmp.append (image)
test_images = np.array(test_images)
test_masks = np.array(test_masks_tmp)
test_masks = np.expand_dims(test_masks, -1)
#print(np.unique(test_masks))
print(test_images.shape)
print(test_masks.shape)
del test_masks_tmp
model.evaluate(test_images, test_masks)
predictions = model.predict(test_images, verbose=1)
thresh_val = 0.1
predicton_threshold = (predictions > thresh_val).astype(np.uint8)
plt.figure()
#plt.subplot(2, 1, 1)
plt.imshow(np.squeeze(predictions[19][:,:,0]))
plt.show()
import matplotlib
for i in range(len(predictions)):
#print("Results/" + str(i) + "Image.png")
matplotlib.image.imsave( "Results/" + str(i) + "Image.png" , np.squeeze(test_images[i][:,:,0]))
matplotlib.image.imsave( "Results/" + str(i) + "GroundTruth.png" , np.squeeze(test_masks[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#matplotlib.image.imsave('/home/bisag/Desktop/Road-Segmentation/Results/000.png', np.squeeze(predicton_threshold[0][:,:,0]))
matplotlib.image.imsave("Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
matplotlib.image.imsave( "Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#imshow(np.squeeze(predictions[0][:,:,0]))
#import scipy.misc
#scipy.misc.imsave('/home/bisag/Desktop/Road-Segmentation/Results/00.png', np.squeeze(predictions[0][:,:,0]))
model.load_weights("/home/parshwa/Desktop/Road-Segmentation/Models/weights.h5")
```
### Just Test
```
"""Test"""
import cv2
import glob
import numpy as np
import h5py
#test_images = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/I/")])
#test_masks = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/M/")])
test_images = []
files = glob.glob ("/home/parshwa/Desktop/Road-Segmentation/Test/*.png")
for myFile in files:
print(myFile)
image = cv2.imread (myFile)
test_images.append (image)
#test_images = cv2.imread("/home/bisag/Desktop/Road-Segmentation/I/1.png")
#test_masks = cv2.imread("/home/bisag/Desktop/Road-Segmentation/M/1.png")
test_images = np.array(test_images)
print(test_images.shape)
predictions = model.predict(test_images, verbose=1)
thresh_val = 0.1
predicton_threshold = (predictions > thresh_val).astype(np.uint8)
import matplotlib
for i in range(len(predictions)):
cv2.imwrite( "/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Image.png" , np.squeeze(test_images[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#matplotlib.image.imsave('/home/bisag/Desktop/Road-Segmentation/Results/000.png', np.squeeze(predicton_threshold[0][:,:,0]))
matplotlib.image.imsave("/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
matplotlib.image.imsave( "/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#imshow(np.squeeze(predictions[0][:,:,0]))
imshow(np.squeeze(predictions[0][:,:,0]))
#import scipy.misc
#scipy.misc.imsave('/home/bisag/Desktop/Road-Segmentation/Results/00.png', np.squeeze(predictions[0][:,:,0]))
"""Visualise"""
def layer_to_visualize(layer):
inputs = [K.learning_phase()] + model.inputs
_convout1_f = K.function(inputs, [layer.output])
def convout1_f(X):
# The [0] is to disable the training phase flag
return _convout1_f([0] + [X])
convolutions = convout1_f(img_to_visualize)
convolutions = np.squeeze(convolutions)
print ('Shape of conv:', convolutions.shape)
n = convolutions.shape[0]
n = int(np.ceil(np.sqrt(n)))
# Visualization of each filter of the layer
fig = plt.figure(figsize=(12,8))
for i in range(len(convolutions)):
ax = fig.add_subplot(n,n,i+1)
ax.imshow(convolutions[i], cmap='gray')
```
| github_jupyter |
```
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
from torchvision.utils import make_grid
import numpy as np
import pandas as pd
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
%matplotlib inline
import time
transform = transforms.ToTensor()
train_data = datasets.MNIST(root='../Data', train=True, download=True, transform=transform)
test_data = datasets.MNIST(root='../Data', train=False, download=True, transform=transform)
train_data
test_data
train_loader = DataLoader(train_data, batch_size=10, shuffle=True)
test_loader = DataLoader(test_data, batch_size=10, shuffle=False)
conv1 = nn.Conv2d(1, 6, 3, 1)
conv2 = nn.Conv2d(6, 16, 3, 1)
for i, (X_train, y_train) in enumerate(train_data):
break
x = X_train.view(1, 1, 28, 28)
x = F.relu(conv1(x))
x.shape
x = F.max_pool2d(x, 2, 2)
x.shape
x = F.relu(conv2(x))
x.shape
x = F.max_pool2d(x, 2, 2)
x.shape
x.view(-1, 16 * 5 * 5).shape
class ConvolutionalNetwork(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 6, 3, 1)
self.conv2 = nn.Conv2d(6, 16, 3, 1)
self.fc1 = nn.Linear(5 * 5 * 16, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, X):
X = F.relu(self.conv1(X))
X = F.max_pool2d(X, 2, 2)
X = F.relu(self.conv2(X))
X = F.max_pool2d(X, 2, 2)
X = X.view(-1, 16 * 5 * 5)
X = F.relu(self.fc1(X))
X = F.relu(self.fc2(X))
X = F.log_softmax(self.fc3(X), dim=1)
return X
torch.manual_seed(42)
model = ConvolutionalNetwork()
model
for param in model.parameters():
print(param.numel())
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
start_time = time.time()
epochs = 5
train_losses = []
test_losses = []
train_correct = []
test_correct = []
for i in range(epochs):
trn_corr = 0
tst_corr = 0
for b, (X_train, y_train) in enumerate(train_loader):
b += 1
y_pred = model(X_train)
loss = criterion(y_pred, y_train)
predicted = torch.max(y_pred.data, 1)[1]
batch_corr = (predicted == y_train).sum()
trn_corr += batch_corr
optimizer.zero_grad()
loss.backward()
optimizer.step()
if b % 600 == 0:
print(f"Epoch: {i} BATCH: {b} LOSS: {loss.item()}")
train_losses.append(loss)
train_correct.append(trn_corr)
with torch.no_grad():
for b, (X_test, y_test) in enumerate(test_loader):
y_val = model(X_test)
predicted = torch.max(y_val.data, 1)[1]
tst_corr += (predicted == y_test).sum()
loss = criterion(y_val, y_test)
test_losses.append(loss)
test_correct.append(tst_corr)
current_time = time.time()
total = current_time - start_time
print(f"Training took {total / 60} minutes")
with torch.no_grad():
plt.plot(train_losses, label='train loss')
plt.plot(test_losses, label='validation loss')
plt.title('LOSS AT EPOCH')
plt.legend()
plt.plot([t / 600 for t in train_correct], label='training accuracy')
plt.plot([t / 100 for t in test_correct], label='validation accuracy')
plt.title('Accuracy at the end of each epoch')
plt.legend()
test_load_all = DataLoader(test_data, batch_size=10000, shuffle=False)
with torch.no_grad():
correct = 0
for X_test, y_test in test_load_all:
y_val = model(X_test)
predicted = torch.max(y_val, 1)[1]
correct += (predicted == y_test).sum()
correct.item() * 100 / len(test_data)
np.set_printoptions(formatter=dict(int=lambda x: f'{x:4}'))
print(np.arange(10).reshape(1, 10))
print()
print(confusion_matrix(predicted.view(-1), y_test.view(-1)))
plt.imshow(test_data[333][0].reshape(28, 28))
model.eval()
with torch.no_grad():
new_prediction = model(test_data[333][0].view(1, 1, 28, 28))
new_prediction
new_prediction.argmax()
```
| github_jupyter |
## Homework 4
Today we'll start by reproducing the DQN and then try improving it with the tricks we learned on the lecture:
* Target networks
* Double q-learning
* Prioritized experience replay
* Dueling DQN
* Bootstrap DQN
```
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# If you are running on a server, launch xvfb to record game videos
# Please make sure you have xvfb installed
import os
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
!bash ../xvfb start
os.environ['DISPLAY'] = ':1'
```
# Processing game image (2 pts)
Raw Atari images are large, 210x160x3 by default. However, we don't need that level of detail in order to learn them.
We can thus save a lot of time by preprocessing game image, including
* Resizing to a smaller shape
* Converting to grayscale
* Cropping irrelevant image parts
```
from gym.core import ObservationWrapper
from gym.spaces import Box
from scipy.misc import imresize
class PreprocessAtari(ObservationWrapper):
def __init__(self, env):
"""A gym wrapper that crops, scales image into the desired shapes and optionally grayscales it."""
ObservationWrapper.__init__(self, env)
self.img_size = (64, 64)
self.observation_space = Box(0.0, 1.0, self.img_size)
def observation(self, img):
"""what happens to each observation"""
# Here's what you need to do:
# * crop image, remove irrelevant parts
# * resize image to self.img_size
# (use imresize imported above or any library you want,
# e.g. opencv, skimage, PIL, keras)
# * cast image to grayscale
# * convert image pixels to (0,1) range, float32 type
<Your code here>
return <YOUR CODE>
import gym
def make_env():
env = gym.make("KungFuMasterDeterministic-v0") # create raw env
return PreprocessAtari(env) # apply your wrapper
# spawn game instance for tests
env = make_env()
observation_shape = env.observation_space.shape
n_actions = env.action_space.n
obs = env.reset()
# test observation
assert obs.shape == observation_shape
assert obs.dtype == 'float32'
assert len(np.unique(obs)) > 2, "your image must not be binary"
assert 0 <= np.min(obs) and np.max(
obs) <= 1, "convert image pixels to (0,1) range"
print "Formal tests seem fine. Here's an example of what you'll get."
plt.title("what your network gonna see")
plt.imshow(obs, interpolation='none', cmap='gray')
plt.figure(figsize=[12, 12])
env.reset()
for i in range(16):
for _ in range(10):
new_obs = env.step(env.action_space.sample())[0]
plt.subplot(4, 4, i+1)
plt.imshow(new_obs, interpolation='none', cmap='gray')
# dispose of the game instance
del env
```
# Building a DQN (2 pts)
Here we define a simple agent that maps game images into Qvalues using simple convolutional neural network.
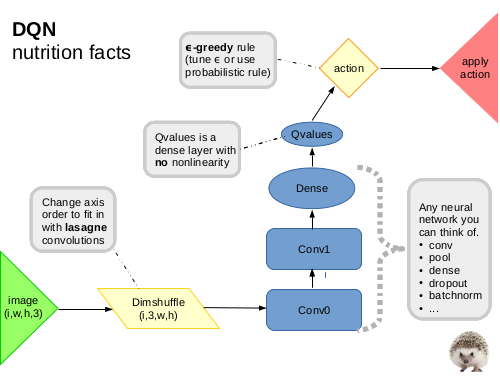
```
# setup theano/lasagne. Prefer GPU. Fallback to CPU (will print warning)
%env THEANO_FLAGS = floatX = float32
import theano
import lasagne
from lasagne.layers import *
from theano import tensor as T
# observation
observation_layer = InputLayer(
(None,)+observation_shape) # game image, [batch,64,64]
# 4-tick window over images
from agentnet.memory import WindowAugmentation
# window size [batch,4,64,64]
prev_wnd = InputLayer((None, 4)+observation_shape)
new_wnd = WindowAugmentation( < current observation layer> , prev_wnd)
# if you changed img size, remove assert
assert new_wnd.output_shape == (None, 4, 64, 64)
from lasagne.nonlinearities import elu, tanh, softmax, rectify
<network body, growing from new_wnd. several conv layers or something similar would do>
dense = <final dense layer with 256 neurons>
# qvalues layer
qvalues_layer = <a dense layer that predicts q-values>
assert qvalues_layer.nonlinearity is not rectify
# sample actions proportionally to policy_layer
from agentnet.resolver import EpsilonGreedyResolver
action_layer = EpsilonGreedyResolver(qvalues_layer)
```
### Define agent
Here you will need to declare how your agent works
* `observation_layers` and `action_layers` are the input and output of agent in MDP.
* `policy_estimators` must contain whatever you need for training
* In our case, that's `qvalues_layer`, but you'll need to add more when implementing target network.
* agent_states contains our frame buffer.
* The code `{new_wnd:prev_wnd}` reads as "`new_wnd becomes prev_wnd next turn`"
```
from agentnet.agent import Agent
# agent
agent = Agent(observation_layers=<YOUR CODE>,
policy_estimators=<YOUR CODE>,
action_layers=<YOUR CODE>,
agent_states={new_wnd: prev_wnd},)
```
# Create and manage a pool of Atari sessions to play with
* To make training more stable, we shall have an entire batch of game sessions each happening independent of others
* Why several parallel agents help training: http://arxiv.org/pdf/1602.01783v1.pdf
* Alternative approach: store more sessions: https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf
```
from agentnet.experiments.openai_gym.pool import EnvPool
pool = EnvPool(agent, make_env, n_games=16) # 16 parallel game sessions
%%time
# interact for 7 ticks
_, action_log, reward_log, _, _, _ = pool.interact(5)
print('actions:')
print(action_log[0])
print("rewards")
print(reward_log[0])
# load first sessions (this function calls interact and remembers sessions)
SEQ_LENGTH = 10 # sub-session length
pool.update(SEQ_LENGTH)
```
# Q-learning
We train our agent based on sessions it has played in `pool.update(SEQ_LENGTH)`
To do so, we first obtain sequences of observations, rewards, actions, q-values, etc.
Actions and rewards have shape `[n_games,seq_length]`, q-values are `[n_games,seq_length,n_actions]`
```
# get agent's Qvalues obtained via experience replay
replay = pool.experience_replay
actions, rewards, is_alive = replay.actions[0], replay.rewards, replay.is_alive
_, _, _, _, qvalues = agent.get_sessions(
replay,
session_length=SEQ_LENGTH,
experience_replay=True,
)
assert actions.ndim == rewards.ndim == is_alive.ndim == 2, "actions, rewards and is_alive must have shape [batch,time]"
assert qvalues.ndim == 3, "q-values must have shape [batch,time,n_actions]"
# compute V(s) as Qvalues of best actions.
# For homework assignment, you will need to use target net
# or special double q-learning objective here
state_values_target = <YOUR CODE: compute V(s) 2d tensor by taking T.argmax of qvalues over correct axis>
assert state_values_target.eval().shape = qvalues.eval().shape[:2]
from agentnet.learning.generic import get_n_step_value_reference
# get reference Q-values via Q-learning algorithm
reference_qvalues = get_n_step_value_reference(
state_values=state_values_target,
rewards=rewards/100.,
is_alive=is_alive,
n_steps=10,
gamma_or_gammas=0.99,
)
# consider it constant
from theano.gradient import disconnected_grad
reference_qvalues = disconnected_grad(reference_qvalues)
# get predicted Q-values for committed actions by both current and target networks
from agentnet.learning.generic import get_values_for_actions
action_qvalues = get_values_for_actions(qvalues, actions)
# loss for Qlearning =
# (Q(s,a) - (r+ gamma*r' + gamma^2*r'' + ... +gamma^10*Q(s_{t+10},a_max)))^2
elwise_mse_loss = <mean squared error between action qvalues and reference qvalues>
# mean over all batches and time ticks
loss = (elwise_mse_loss*is_alive).mean()
# Since it's a single lasagne network, one can get it's weights, output, etc
weights = <YOUR CODE: get all trainable params>
weights
# Compute weight updates
updates = <your favorite optimizer>
# compile train function
train_step = theano.function([], loss, updates=updates)
```
# Demo run
as usual...
```
action_layer.epsilon.set_value(0.05)
untrained_reward = np.mean(pool.evaluate(save_path="./records",
record_video=True))
# show video
from IPython.display import HTML
import os
video_names = list(
filter(lambda s: s.endswith(".mp4"), os.listdir("./records/")))
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format("./records/" + video_names[-1])) # this may or may not be _last_ video. Try other indices
```
# Training loop
```
# starting epoch
epoch_counter = 1
# full game rewards
rewards = {}
loss, reward_per_tick, reward = 0, 0, 0
from tqdm import trange
from IPython.display import clear_output
for i in trange(150000):
# update agent's epsilon (in e-greedy policy)
current_epsilon = 0.05 + 0.45*np.exp(-epoch_counter/20000.)
action_layer.epsilon.set_value(np.float32(current_epsilon))
# play
pool.update(SEQ_LENGTH)
# train
loss = 0.95*loss + 0.05*train_step()
if epoch_counter % 10 == 0:
# average reward per game tick in current experience replay pool
reward_per_tick = 0.95*reward_per_tick + 0.05 * \
pool.experience_replay.rewards.get_value().mean()
print("iter=%i\tepsilon=%.3f\tloss=%.3f\treward/tick=%.3f" % (epoch_counter,
current_epsilon,
loss,
reward_per_tick))
# record current learning progress and show learning curves
if epoch_counter % 100 == 0:
action_layer.epsilon.set_value(0.05)
reward = 0.95*reward + 0.05*np.mean(pool.evaluate(record_video=False))
action_layer.epsilon.set_value(np.float32(current_epsilon))
rewards[epoch_counter] = reward
clear_output(True)
plt.plot(*zip(*sorted(rewards.items(), key=lambda (t, r): t)))
plt.show()
epoch_counter += 1
# Time to drink some coffee!
```
# Evaluating results
* Here we plot learning curves and sample testimonials
```
import pandas as pd
plt.plot(*zip(*sorted(rewards.items(), key=lambda k: k[0])))
from agentnet.utils.persistence import save, load
save(action_layer, "pacman.pcl")
action_layer.epsilon.set_value(0.05)
rw = pool.evaluate(n_games=20, save_path="./records", record_video=False)
print("mean session score=%f.5" % np.mean(rw))
# show video
from IPython.display import HTML
import os
video_names = list(
filter(lambda s: s.endswith(".mp4"), os.listdir("./records/")))
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format("./videos/" + video_names[-1])) # this may or may not be _last_ video. Try other indices
```
## Assignment part I (5 pts)
We'll start by implementing target network to stabilize training.
There are two ways to do so:
__1)__ Manually write lasagne network, or clone it via [one of those methods](https://github.com/Lasagne/Lasagne/issues/720).
You will need to implement loading weights from original network to target network.
We recommend thoroughly debugging your code on simple tests before applying it in Atari dqn.
__2)__ Use pre-build functionality from [here](http://agentnet.readthedocs.io/en/master/modules/target_network.html)
```
from agentnet.target_network import TargetNetwork
target_net = TargetNetwork(qvalues_layer)
old_qvalues = target_net.output_layers
#agent's policy_estimators must now become (qvalues,old_qvalues)
_,_,_,_,(qvalues,old_qvalues) = agent.get_sessions(...) #replaying experience
target_net.load_weights()#loads weights, so target network is now exactly same as main network
target_net.load_weights(0.01)# w_target = 0.99*w_target + 0.01*w_new
```
## Bonus I (2+ pts)
Implement and train double q-learning.
This task contains of
* Implementing __double q-learning__ or __dueling q-learning__ or both (see tips below)
* Training a network till convergence
* Full points will be awwarded if your network gets average score of >=10 (see "evaluating results")
* Higher score = more points as usual
* If you're running out of time, it's okay to submit a solution that hasn't converged yet and updating it when it converges. _Lateness penalty will not increase for second submission_, so submitting first one in time gets you no penalty.
#### Tips:
* Implementing __double q-learning__ shouldn't be a problem if you've already have target networks in place.
* As one option, use `get_values_for_actions(<some q-values tensor3>,<some indices>)`.
* You will probably need `T.argmax` to select best actions
* Here's an original [article](https://arxiv.org/abs/1509.06461)
* __Dueling__ architecture is also quite straightforward if you have standard DQN.
* You will need to change network architecture, namely the q-values layer
* It must now contain two heads: V(s) and A(s,a), both dense layers
* You should then add them up via elemwise sum layer or a [custom](http://lasagne.readthedocs.io/en/latest/user/custom_layers.html) layer.
* Here's an [article](https://arxiv.org/pdf/1511.06581.pdf)
Here's a template for your convenience:
```
from lasagne.layers import *
class DuelingQvaluesLayer(MergeLayer):
def get_output_for(self, inputs, **tags):
V, A = inputs
return <YOUR CODE: add them up :)>
def get_output_shape_for(self, input_shapes, **tags):
V_shape, A_shape=input_shapes
assert len(
V_shape) == 2 and V_shape[-1] == 1, "V layer (first param) shape must be [batch,tick,1]"
return A_shape # shape of q-values is same as predicted advantages
# mock-up tests
import theano.tensor as T
v_tensor = -T.arange(10).reshape((10, 1))
V = InputLayer((None, 1), v_tensor)
a_tensor = T.arange(30).reshape((10, 3))
A = InputLayer((None, 1), a_tensor)
Q = DuelingQvaluesLayer([V, A])
import numpy as np
assert np.allclose(get_output(Q).eval(), (v_tensor+a_tensor).eval())
print("looks good")
```
## Bonus II (5+ pts): Prioritized experience replay
In this section, you're invited to implement prioritized experience replay
* You will probably need to provide a custom data structure
* Once pool.update is called, collect the pool.experience_replay.observations, actions, rewards and is_alive and store them in your data structure
* You can now sample such transitions in proportion to the error (see [article](https://arxiv.org/abs/1511.05952)) for training.
It's probably more convenient to explicitly declare inputs for "sample observations", "sample actions" and so on to plug them into q-learning.
Prioritized (and even normal) experience replay should greatly reduce amount of game sessions you need to play in order to achieve good performance.
While it's effect on runtime is limited for atari, more complicated envs (further in the course) will certainly benefit for it.
Prioritized experience replay only supports off-policy algorithms, so pls enforce `n_steps=1` in your q-learning reference computation (default is 10).
| github_jupyter |
```
# installing keras
!pip install keras
# installing opencv
!pip install opencv-python
# installing opencv full package
!pip install opencv-contrib-python
import cv2
from keras.models import load_model
import numpy as np
face_detect = cv2.CascadeClassifier('haarcascade_frontalface_default.xml')
def face_detection(img,size=0.5):
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # converting image into grayscale image
face_roi = face_detect.detectMultiScale(img_gray, 1.3,1) # ROI (region of interest of detected face)
class_labels = ['Angry','Happy','Neutral','Fear']
if face_roi is (): # checking if face_roi is empty that is if no face detected
return img
for(x,y,w,h) in face_roi: # iterating through faces and draw rectangle over each face
x = x - 5
w = w + 10
y = y + 7
h = h + 2
cv2.rectangle(img, (x,y),(x+w,y+h),(125,125,10), 1) # (x,y)- top left point ; (x+w,y+h)-bottom right point ; (125,125,10)-colour of rectangle ; 1- thickness
img_gray_crop = img_gray[y:y+h,x:x+w] # croping gray scale image
img_color_crop = img[y:y+h,x:x+w] # croping color image
model=load_model('model.h5')
final_image = cv2.resize(img_color_crop, (48,48)) # size of colured image is resized to 48,48
final_image = np.expand_dims(final_image, axis = 0) # array is expanded by inserting axis at position 0
final_image = final_image/255.0 # feature scaling of final image
prediction = model.predict(final_image) # predicting emotion of captured image from the trained model
label=class_labels[prediction.argmax()] # finding the label of class which has maximaum probalility
cv2.putText(frame,label, (50,60), cv2.FONT_HERSHEY_SCRIPT_COMPLEX,2, (120,10,200),3)
# putText is used to draw a detected emotion on image
# (50,60)-top left coordinate FONT_HERSHEY_SCRIPT_COMPLEX-font type
# 2-fontscale (120,10,200)-font colour 3-font thickness
img_color_crop = cv2.flip(img_color_crop, 1) # fliping the image
return img
cap = cv2.VideoCapture(0) # capturing the video that is live webcam
while True:
ret, frame = cap.read()
cv2.imshow('LIVE', face_detection(frame)) # captured frame will be sent to face_detection function for emotion detection
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
```
| github_jupyter |
```
# (c) amantay from https://github.com/AmantayAbdurakhmanov/misc/blob/master/Geabox-Yearn.ipynb
import json
import os
from dotenv import load_dotenv
from web3 import Web3
from multicall import Call, Multicall
load_dotenv() # add this line
RPC_Endpoint = os.getenv('RPC_NODE')
GearboxAddressProvider = Web3.toChecksumAddress('0xcF64698AFF7E5f27A11dff868AF228653ba53be0') #gearbox address provider
yVaultUSDC = Web3.toChecksumAddress('0xa354F35829Ae975e850e23e9615b11Da1B3dC4DE') #Yearn Vault Address
ABI = """[{"name":"getAccountFactory",
"inputs":[],
"outputs":[{"internalType":"address","name":"","type":"address"}],
"stateMutability":"view","type":"function"},
{"name":"countCreditAccounts",
"inputs":[],
"outputs":[{"internalType":"uint256","name":"","type":"uint256"}],
"stateMutability":"view","type":"function"},
{"name":"decimals",
"inputs":[],
"outputs":[{"name":"","type":"uint256"}],
"stateMutability":"view","type":"function"
}
]
"""
def chunks(lst, n):
"""Yield successive n-sized chunks from lst."""
for i in range(0, len(lst), n):
yield lst[i:i + n]
w3_eth = Web3(Web3.HTTPProvider(RPC_Endpoint, request_kwargs={'timeout': 20}))
print ('Ethereum connected:', w3_eth.isConnected())
AccountFactory = w3_eth.eth.contract(address=GearboxAddressProvider, abi=ABI).functions.getAccountFactory().call()
print('AccountFactory:', AccountFactory)
countCreditAccounts = w3_eth.eth.contract(address=AccountFactory, abi=ABI).functions.countCreditAccounts().call()
print('countCreditAccounts:', countCreditAccounts)
yVaultUSDC_decimals = w3_eth.eth.contract(address=yVaultUSDC, abi=ABI).functions.decimals().call()
print('yVaultUSDC_decimals:', yVaultUSDC_decimals)
idList = list(range(countCreditAccounts))
multi_idCA = {}
for ids in list(chunks(idList, 400)): #chunk size for multicall = 400
#d_ca = get_data_multicall(df.loc[id_range], 'creditAccounts', df_abi, AccountFactory)
multi_result = Multicall([
Call(AccountFactory, ['creditAccounts(uint256)(address)', x], [[x, Web3.toChecksumAddress]]) for x in ids
]
,_w3 = w3_eth)
multi_result = multi_result()
multi_idCA.update(multi_result)
multi_idBalance = {}
for ids in list(chunks(list(multi_idCA), 400)): #chunk size for multicall = 400
multi_result = Multicall([
Call(yVaultUSDC, ['balanceOf(address)(uint256)', multi_idCA[x]], [[x, None]]) for x in ids
]
,_w3 = w3_eth)
multi_result = multi_result()
multi_idBalance.update(multi_result)
multi_CA = {multi_idCA[x]:multi_idBalance[x] for x in multi_idCA}
#only with existing balance
{key:value for key, value in multi_CA.items() if value > 0}
#decimal values
{key:value*10**(-yVaultUSDC_decimals) for key, value in multi_CA.items() if value > 0}
```
| github_jupyter |
```
#!/usr/bin/env python
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.tri as tri
from mpl_toolkits.axes_grid1.anchored_artists import AnchoredSizeBar
from matplotlib import ticker, cm
import numpy as np
from numpy import ma
import csv
degree_sign= u'\N{DEGREE SIGN}'
CSV_FILE_PATH = '../../../Data/ISER2021/Sabattus-catabot-20201006.csv'
#CSV_FILE_PATH2 = '../../../Data/ISER2021/Sunapee-20200715-path-2.csv'
#CSV_FILE_PATH3 = '../../../Data/ISER2021/Sunapee-20200715-path-3.csv'
with open(CSV_FILE_PATH, 'r') as csv_file:
reader = csv.reader(csv_file)
path1_list = np.array(list(reader))
"""
with open(CSV_FILE_PATH2, 'r') as csv_file:
reader = csv.reader(csv_file)
path2_list = np.array(list(reader))
with open(CSV_FILE_PATH3, 'r') as csv_file:
reader = csv.reader(csv_file)
path3_list = np.array(list(reader))
"""
#=============================== 07/15 ===============================
# one independent
# temp
#z = path1_list[0:1833,23]
#z = z.astype('float32')
# DO
z = path1_list[0:1833,30]
z = z.astype('float32')
# gps x,y
x = path1_list[0:1833,2]
x = x.astype('float32')
y = path1_list[0:1833,1]
y = y.astype('float32')
"""
# PATH 1
# temp
z1 = path1_list[0:2126,23]
z1 = z1.astype('float32')
# gps x,y
x1 = path1_list[0:2126,2]
x1 = x1.astype('float32')
y1 = path1_list[0:2126,1]
y1 = y1.astype('float32')
## PATH 2
# temp
z2 = path2_list[0:998,23]
z2 = z2.astype('float32')
# gps x,y
x2 = path2_list[0:998,2]
x2 = x2.astype('float32')
y2 = path2_list[0:998,1]
y2 = y2.astype('float32')
## PATH 3
# temp
z3 = path3_list[0:597,23]
z3 = z3.astype('float32')
# gps x,y
x3 = path3_list[0:597,2]
x3 = x3.astype('float32')
y3 = path3_list[0:597,1]
y3 = y3.astype('float32')
x = np.concatenate([x1, x2, x3])
y = np.concatenate([y1, y2, y3])
z = np.concatenate([z1, z2, z3])
"""
#=====================================================================
f, ax = plt.subplots()
#ax.set_title('Catabot 10/06 Lake Sabattus: Temperature (' + degree_sign + 'C)')
ax.set_title('Catabot 10/06 Lake Sabattus: DO (%sat)')
vmax=96.4
vmin=82.4
levels = np.linspace(vmin,vmax, 100)
cs = ax.tricontourf(x,y,z, 10, norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03), levels=levels,vmax=vmax,vmin=vmin)
#cs = ax.tricontourf(x,y,z, 20, vmin=24.35, vmax=26.94)
#cs = ax.tricontourf(x,y,z, 20)
cb_ticklabel = np.linspace(82.4, 96.4, 10)
#cb = f.colorbar(cs, ticks=cb_ticklabel, orientation='horizontal', format='%.1f')
ax.set_xlabel('Longitude')
plt.xlim([-70.1070, -70.1040])
ax.set_xticks(np.arange(-70.1070, -70.1039, 0.001))
f.canvas.draw()
ax.set_xticklabels(['-70.1070', '-70.1060', '-70.1050', '-70.1040'])
ax.set_ylabel('Latitude')
plt.ylim([44.1230, 44.1255])
ax.set_yticks(np.arange(44.1230, 44.1256, 0.0005))
f.canvas.draw()
ax.set_yticklabels(['44.1230', '44.1235', '44.1240', '44.1245', '44.1250', '44.1255'])
# path 1,2,3
ax.plot(x,y,marker='o', color='k', markersize=0.1)
#ax.plot(x2,y2,marker='o', color='b', markersize=0.1)
#ax.plot(x3,y3,marker='o', color='r', markersize=0.1)
ax.set_aspect('equal')
plt.grid(True)
# boathouse
ax.plot(np.array([-70.1060711]), np.array([44.1251027]), color='k', marker=(5,1), markersize=16)
ax.plot(np.array([-70.1060711]), np.array([44.1251027]), color='#FF4500', marker=(5,1), markersize=8)
"""
# summer buoy
ax.plot(np.array([-72.033128]), np.array([43.4096079]), color='k', marker='o', markersize=13)
ax.plot(np.array([-72.033128]), np.array([43.4096079]), color='yellow', marker='o', markersize=8)
# boathouse
ax.plot(np.array([-72.0369625]), np.array([43.4100466]), color='k', marker=(5,1), markersize=16)
ax.plot(np.array([-72.0369625]), np.array([43.4100466]), color='#FF4500', marker=(5,1), markersize=8)
# winter buoy
ax.plot(np.array([-72.0365116]), np.array([43.410345]), color='k', marker='o', markersize=13)
ax.plot(np.array([-72.0365116]), np.array([43.410345]), color='m', marker='o', markersize=8)
"""
bar = AnchoredSizeBar(ax.transData, 0.00046, '40 m', 'upper right', pad=0.6, frameon=False)
ax.add_artist(bar)
plt.show()
#f.savefig('1006-Sabattus-DO.pdf', bbox_inches ='tight')
min(x)
max(x)
min(y)
max(y)
```
| github_jupyter |
__mlmachine - GroupbyImputer, KFoldEncoder, and Skew Correction__
<br><br>
Welcome to Example Notebook 2. If you're new to mlmachine, check out [Example Notebook 1](https://github.com/petersontylerd/mlmachine/blob/master/notebooks/mlmachine_part_1.ipynb).
<br><br>
Check out the [GitHub repository](https://github.com/petersontylerd/mlmachine).
<br><br>
1. [Missing Values - Assessment & GroupbyImputer](#Missing-Values-Assessment-&-GroupbyImputer)
1. [Assessment](#Assessment)
1. [GroupbyImputer](#GroupbyImputer)
1. [Imputation](#Imputation)
1. [KFold Encoding - Exotic Encoding Without the Leakage](#KFold-Encoding-Exotic-Encoding-Without-the-Leakage)
1. [KFoldEncoder](#KFoldEncoder)
1. [Box, Cox, Yeo & Johnson - Skew Correctors](#Box,-Cox,-Yeo-&-Johnson-Skew-Correctors)
1. [Assessment](#Assessment-1)
1. [Skew correction](#Skew-correction)
---
# Missing Values - Assessment & GroupbyImputer
---
<br><br>
Let's start by instantiating a couple `Machine()` objects, one for our training data and a second for our validation data:
<br><br>
<a id = 'Missing-Values-Assessment-&-GroupbyImputer'></a>
```
# import libraries
import numpy as np
import pandas as pd
# import mlmachine tools
import mlmachine as mlm
from mlmachine.data import titanic
# use titanic() function to create DataFrames for training and validation datasets
df_train, df_valid = titanic()
# ordinal encoding hierarchy
ordinal_encodings = {"Pclass": [1, 2, 3]}
# instantiate a Machine object for the training data
mlmachine_titanic_train = mlm.Machine(
data=df_train,
target="Survived",
remove_features=["PassengerId","Ticket","Name"],
identify_as_continuous=["Age","Fare"],
identify_as_count=["Parch","SibSp"],
identify_as_nominal=["Embarked"],
identify_as_ordinal=["Pclass"],
ordinal_encodings=ordinal_encodings,
is_classification=True,
)
# instantiate a Machine object for the validation data
mlmachine_titanic_valid = mlm.Machine(
data=df_valid,
remove_features=["PassengerId","Ticket","Name"],
identify_as_continuous=["Age","Fare"],
identify_as_count=["Parch","SibSp"],
identify_as_nominal=["Embarked"],
identify_as_ordinal=["Pclass"],
ordinal_encodings=ordinal_encodings,
is_classification=True,
)
```
---
## Assessment
---
<br><br>
Each `Machine()` object contains a method for summarizing missingness in tabular form and in graphical form:
<br><br>
<a id = 'Assessment'></a>
```
# generate missingness summary for training data
mlmachine_titanic_train.eda_missing_summary(display_df=True)
```
---
<br><br>
By default, this method acts on the `data` attribute associated with `mlmachine_train`. Let's do the same for the validation dataset:
<br><br>
```
# generate missingness summary for validation data
mlmachine_titanic_valid.eda_missing_summary(display_df=True)
```
---
<br><br>
Next, we need to determine if there are features with missing values in the training data, but not the validation data, and vice versa. This informs how we should set up our transformation pipeline. For example, if a feature has missing values in the validation dataset, but not the training dataset, we will still want to `fit_transform()` this feature on the training data to learn imputation values to apply on the nulls in the validation dataset.
<br><br>
We could eyeball the tables and visuals above to compare the state of missingness in the two datasets, but this can be tedious, particularly with large datasets. Instead, we will leverage a method within our `Machine()` object. We simply pass the validation dataset to `mlmachine_titanic_train`'s method `missing_col_compare`, which returns a bidirectional missingness summary.
<br><br>
```
# generate missingness comparison summary
mlmachine_titanic_train.missing_column_compare(
validation_data=mlmachine_titanic_valid.data,
)
```
---
<br><br>
The key observation here is that "Fare" is fully populated in the training data, but not the validation data. We need to make sure our pipeline learns how to impute these missing values based on the training data, despite the fact that the training data is not missing any values in this feature.
<br><br>
---
## GroupbyImputer
---
<br><br>
mlmachine includes a transformer called `GroupbyImputer()`, which makes it easy to perform the same basic imputation techniques provided by Scikit-learn's `SimpleImputer()`, but with the added ability to group by another feature in the dataset. Let's see an example:
<br><br>
<a id = 'GroupbyImputer'></a>
```
# import mlmachine tools
from mlmachine.features.preprocessing import GroupbyImputer
# instantiate GroupbyImputer to fill "Age" mean, grouped by "SibSp"
impute = GroupbyImputer(null_column="Age", groupby_column="SibSp", strategy="mean")
impute.fit_transform(mlmachine_titanic_train.data[["Age","SibSp"]])
display(impute.train_value)
```
---
<br><br>
In the code snippet above, we mean impute "Age", grouped by "SibSp". We pass "Age" to the `null_column` parameter to indicate which column contains the nulls, and pass "SibSp" to the `groupby_column` parameter. The strategy parameter receives the same instructions as Scikit-learn's `SimpleImputer()` - "mean", "median" and "most_frequent".
<br><br>
To inspect the learned values, we can display the object's `train_value` attribute, which is a `DataFrame` containing the category/value pairs
<br><br>
`GroupbyImputer` uses these pairs to impute the missing values in "Age". If, in the unlikely circumstance, a level in `groupby_column` has only null values in `null_column`, then the missing values associated with that level will be imputed with the mean, median or mode of the entire feature.
<br><br>
---
## Imputation
---
<br><br>
Now we're going to use `GroupbyImputer()` within `PandasFeatureUnion()` to impute nulls in both the training and validation datasets.
<br><br>
<a id = 'Imputation'></a>
```
# import libraries
from sklearn.impute import SimpleImputer
from sklearn.pipeline import make_pipeline
# import mlmachine tools
from mlmachine.features.preprocessing import (
DataFrameSelector,
PandasTransformer,
PandasFeatureUnion,
)
# create imputation PandasFeatureUnion pipeline
impute_pipe = PandasFeatureUnion([
("age", make_pipeline(
DataFrameSelector(include_columns=["Age","SibSp"]),
GroupbyImputer(null_column="Age", groupby_column="SibSp", strategy="mean")
)),
("fare", make_pipeline(
DataFrameSelector(include_columns=["Fare","Pclass"]),
GroupbyImputer(null_column="Fare", groupby_column="Pclass", strategy="mean")
)),
("embarked", make_pipeline(
DataFrameSelector(include_columns=["Embarked"]),
PandasTransformer(SimpleImputer(strategy="most_frequent"))
)),
("cabin", make_pipeline(
DataFrameSelector(include_columns=["Cabin"]),
PandasTransformer(SimpleImputer(strategy="constant", fill_value="X"))
)),
("diff", make_pipeline(
DataFrameSelector(exclude_columns=["Age","Fare","Embarked","Cabin"])
)),
])
# fit and transform training data, transform validation data
mlmachine_titanic_train.data = impute_pipe.fit_transform(mlmachine_titanic_train.data)
mlmachine_titanic_valid.data = impute_pipe.transform(mlmachine_titanic_valid.data)
mlmachine_titanic_train.data[:20]
```
---
<br><br>
`GroupbyImputer()` makes two appearances in this `PandasFeatureUnion()` operation. On line 4, we groupby the feature "SibSp" to impute the mean "Age" value, and on line 8 we groupby the feature "Pclass" to impute the mean "Fare" value.
<br><br>
Imputations for "Embarked" and "Cabin" are completed in straightforward fashion - "Embarked" is simply imputed with the mode, and "Cabin" is imputed with the constant value of "X".
<br><br>
Lastly, we `fit_transform()` the `PandasFeatureUnion()` on `mlmachine_titanic_train.data` and finish filling our nulls by calling `transform()` on `mlmachine_titanic_valid.data`.
<br><br>
---
# KFold Encoding - Exotic Encoding Without the Leakage
---
<br><br>
Target value-based encoding techniques such as mean encoding, CatBoost Encoding, and Weight of Evidence encoding are often discussed in the context of Kaggle competitions. The primary advantage of these techniques is that they use the target variable to inform the encoded feature's values. However, this comes with the risk of leaking target information into the encoded values.
<br><br>
KFold cross-validation assists in avoiding this problem. The key is to apply the encoded values to the out-of-fold observations only. This visualization illustrates the general pattern:
<br><br>
<br><br>

<br><br>
- Separate a validation subset from the training dataset.
- Learn the encoded values from the training data and the associated target values.
- Apply the learned values to the validation observations only.
- Repeat the process on the K-1 remaining folds.
<a id = 'KFold-Encoding-Exotic-Encoding-Without-the-Leakage'></a>
---
## KFoldEncoder
---
<br><br>
mlmachine has a class called `KFoldEncoder` that facilitates KFold encoding with an encoder of choice. Let's use a small subset of our features to see how this works.
<br><br>
We want to target encode two features: "Pclass" and "Age". Since "Age" is a continuous feature, we first need to map the values to bins, which is effectively an ordinal categorical column. We handle all of this in the simple `PandasFeatureUnion` below:
<br><br>
<a id = 'KFoldEncoder'></a>
```
# import libraries
from sklearn.preprocessing import KBinsDiscretizer
# create simple encoding PandasFeatureUnion pipeline
encode_pipe = PandasFeatureUnion([
("bin", make_pipeline(
DataFrameSelector(include_columns=["Age"]),
PandasTransformer(KBinsDiscretizer(encode="ordinal"))
)),
("select", make_pipeline(
DataFrameSelector(include_columns=["Age","Pclass"])
)),
])
# fit and transform training data, transform validation data
mlmachine_titanic_train.data = encode_pipe.fit_transform(mlmachine_titanic_train.data)
mlmachine_titanic_valid.data = encode_pipe.fit_transform(mlmachine_titanic_valid.data)
# update mlm_dtypes
mlmachine_titanic_train.update_dtypes()
mlmachine_titanic_valid.update_dtypes()
```
---
<br><br>
This operation returns a binned version of "Age", as well as the original "Age" and "Pclass" features.
<br><br>
```
mlmachine_titanic_train.data[:10]
```
---
<br><br>
Next, we target encode both "Pclass" and "Age_binned_5" using mean encoding, CatBoost encoding and Weight of Evidence encoding as provided by the package category_encoders.
<br><br>
```
# import libraries
from sklearn.model_selection import KFold
from category_encoders import WOEEncoder, TargetEncoder, CatBoostEncoder
# import mlmachine tools
from mlmachine.features.preprocessing import KFoldEncoder
# create KFold encoding PandasFeatureUnion pipeline
target_encode_pipe = PandasFeatureUnion([
("target", make_pipeline(
DataFrameSelector(include_mlm_dtypes=["category"], exclude_columns=["Cabin"]),
KFoldEncoder(
target=mlmachine_titanic_train.target,
cv=KFold(n_splits=5, shuffle=True, random_state=0),
encoder=TargetEncoder,
),
)),
("woe", make_pipeline(
DataFrameSelector(include_mlm_dtypes=["category"]),
KFoldEncoder(
target=mlmachine_titanic_train.target,
cv=KFold(n_splits=5, shuffle=False),
encoder=WOEEncoder,
),
)),
("catboost", make_pipeline(
DataFrameSelector(include_mlm_dtypes=["category"]),
KFoldEncoder(
target=mlmachine_titanic_train.target,
cv=KFold(n_splits=5, shuffle=False),
encoder=CatBoostEncoder,
),
)),
("diff", make_pipeline(
DataFrameSelector(exclude_mlm_dtypes=["category"]),
)),
])
# fit and transform training data, transform validation data
mlmachine_titanic_train.data = target_encode_pipe.fit_transform(mlmachine_titanic_train.data)
mlmachine_titanic_valid.data = target_encode_pipe.transform(mlmachine_titanic_valid.data)
# update mlm_dtypes
mlmachine_titanic_train.update_dtypes()
mlmachine_titanic_valid.update_dtypes()
mlmachine_titanic_train.data[:10]
```
---
<br><br>
Let's review the key `KFoldEncoder()` parameters:
- `target`: the target attribute of our mlmachine_titanic_train object
- `cv`: a cross-validation object
- `encoder`: a target encoder class
<br><br>
`KFoldEncoder()` learns the encoded values on the training data, and applies the values to the out-of-fold observations.
<br><br>
On the validation data, the process is simpler: we calculate the average out-of-fold encodings applied to the training data and apply these values to all validation observations.
<br><br>
---
# Box, Cox, Yeo & Johnson - Skew Correctors
---
<a id = 'Box,-Cox,-Yeo-&-Johnson-Skew-Correctors'></a>
---
## Assessment
---
<br><br>
Just as we have a quick method for evaluating missingness, we have a quick method for evaluating skew.
<br><br>
<a id = 'Assessment-1'></a>
```
# generate skewness summary
mlmachine_titanic_train.skew_summary()
```
---
<br><br>
The `skew_summary()` method returns a `DataFrame` that summarizes the skew for each feature, along with a "Percent zero" column, which informs us of the percentage of values in the feature that are zero.
<br><br>
---
## Skew correction
---
<br><br>
mlmachine contains a class called `DualTransformer()`, which, by default, applies both Yeo-Johnson and Box-Cox transformations to the specified features with the intent of correcting skew. The Box-Cox transformation automatically seeks the lambda value which maximizes the log-likelihood function.
<br><br>
Since Box-Cox transformation requires all values in a feature to be greater than zero, `DualTransformer()` applies one of two simple feature adjustments when this rule is violated:
<br><br>
- If the minimum value in a feature is zero, each value in that feature is increased by a value of 1 prior to transformation.
- If the minimum value is less than zero, then each feature value is increased by the absolute value of the minimum value in the feature plus 1 prior to transformation.
<br><br>
Let's use `DualTransformer()` to see if we can minimize the skew in the original "Age" feature:
<br><br>
<a id = 'Skew-correction'></a>
```
# import mlmachine tools
from mlmachine.features.preprocessing import DualTransformer
# create skew correction PandasFeatureUnion pipeline
skew_pipe = PandasFeatureUnion([
("skew", make_pipeline(
DataFrameSelector(include_columns=["Age"]),
DualTransformer(),
)),
])
# fit and transform training data, transform validation data
mlmachine_titanic_train.data = skew_pipe.fit_transform(mlmachine_titanic_train.data)
mlmachine_titanic_valid.data = skew_pipe.transform(mlmachine_titanic_valid.data)
# update mlm_dtypes
mlmachine_titanic_train.update_dtypes()
mlmachine_titanic_valid.update_dtypes()
mlmachine_titanic_train.data[:10]
```
---
<br><br>
`DualTransformer()` adds the features "Age_BoxCox" and "Age_YeoJohnson". Let's execute `skew_summary()` again to see if `DualTransformer()` addressed the skew in our original feature:
<br><br>
"Age_BoxCox" and "Age_YeoJohnson" have a skew of 0.0286 and 0.0483, respectively.
<br><br>
```
# generate skewness summary
mlmachine_titanic_train.skew_summary()
```
---
<br><br>
Star the [GitHub repository](https://github.com/petersontylerd/mlmachine), and stay tuned for additional notebooks.
<br><br>
| github_jupyter |
```
# default_exp analysis
```
# Tools to analyze the results of Gate simulations
```
#hide
from nbdev.showdoc import *
```
## Dependencies
```
#export
import pandas as pd
import uproot as rt
import awkward as ak
from scipy.stats import moyal
import matplotlib.pyplot as plt
import numpy as np
import math
from scipy import stats
from scipy.stats import rv_continuous
# import pylandau
from matplotlib.pyplot import hist2d
import matplotlib.colors as mcolors
import glob
#export
def find_max_nonzero(array_hist):
"""returns an upper boundary of the continuos non-zero bins
input a histogram array output from plt.hist
"""
previous = -1
preprevious = -1
p_b = -1
pp_b = -1
for v, b in zip(array_hist[0],array_hist[1]):
if preprevious != 0 and previous == 0 and v == 0:
return math.ceil(p_b)
pp_b = p_b
p_b = b
preprevious = previous
previous = v
show_doc(find_max_nonzero)
#export
def find_range(param):
"""removes a tail in the upper range of the histogram"""
array_hist = plt.hist(param, bins=100)
upper_limit = find_max_nonzero(array_hist)
ret = -1
for _ in range(10):
print(f'upper limit: {upper_limit}')
ret = upper_limit
array_hist = plt.hist(param[param < upper_limit], bins=100)
upper_limit = find_max_nonzero(array_hist)
if ret == upper_limit:
break
return ret
show_doc(find_range)
#export
def get_edep_data(df, sensor=-1):
"""returns an array of energies deposited in each event (keV)"""
# sum all energy deposited in each event and convert the result to keV
if sensor == -1:
edep = df.groupby(['eventID'])['edep'].sum()*1000
else:
edep = (df[df['volumeID'] == sensor].groupby(['eventID']))['edep'].sum()*1000
return edep
show_doc(get_edep_data)
#export
def get_df_subentry2(root_file_name):
"""returns a dataframe that contains only subentry 2 data
This subentry seems to contain all the relevant information"""
df = pd.DataFrame()
with rt.open(f'{root_file_name}:Hits') as tree:
df = ak.to_pandas(tree.arrays())
return df.xs(2, level='subentry')
show_doc(get_df_subentry2)
#export
def get_phasespace_df(timestamp, layer):
root_file = f"../results/tracker_{timestamp}_{layer}.root:PhaseSpace"
df = pd.DataFrame()
with rt.open(root_file) as tree:
df = ak.to_pandas(tree.arrays())
return df
root_file = "../results/dose_2021May10_181812_1-Dose.root"
file = rt.open(root_file)
file.keys()
#export
def get_Ekin(df, particle='proton'):
return df[df['ParticleName'] == particle]['Ekine']
#export
def extract_dose(timestamp):
'''return numpy array of the dose for all phantom layers
'''
# get all the Dose files for a give timestamp
files = glob.glob(f'../results/dose_{timestamp}_*-Dose.txt')
# sort them by the layer number
files.sort(key=lambda x: int(x.split('_')[-1].rstrip('-Dose.txt')))
dose = []
for file in files:
d = []
with open(file) as f:
for line in f:
# ignore the lines starting with #
if not line.startswith('#'):
d.append(float(line))
# The beam is in the negative 'y' direction
# so is the numbering of layers
# while the data in the files is in positive direction
# so it needs to be reversed
dose += reversed(d)
return np.array(dose)
```
```
get_Ekin(ph0).hist(bins=50)
get_Ekin(ph19).hist(bins=50)
print(round(stats.tstd(get_Ekin(ph0), (175, 200)), 2), 'MeV')
print(round(stats.tstd(get_Ekin(ph19), (55, 90)), 2), 'MeV')
from matplotlib import colors
x0 = ph19[(ph19["ParticleName"]=='proton') & (ph19['CreatorProcess'] == 0) & (ph19['NuclearProcess'] == 0)]['X']
z0 = ph19[(ph19["ParticleName"]=='proton') & (ph19['CreatorProcess'] == 0) & (ph19['NuclearProcess'] == 0)]['Z']
x1 = ph19[(ph19["ParticleName"]=='proton')]['X']
z1 = ph19[(ph19["ParticleName"]=='proton')]['Z']
fig, (ax_all, ax_prim) = plt.subplots(1,2, figsize = (14, 5))
__ =ax_all.hist2d(x1, z1, bins=50, range=[[-50, 50],[-50,50]], norm=colors.LogNorm())
ax_all.set_title("lateral position of all protons in the last phantom layer")
ax_all.set_xlabel('X (mm)')
ax_all.set_ylabel('Z (mm)')
__ = ax_prim.hist2d(x0, z0, bins=50, range=[[-50, 50],[-50,50]], norm=colors.LogNorm())
ax_prim.set_xlabel('X (mm)')
ax_prim.set_ylabel('Z (mm)')
_ =ax_prim.set_title("lateral position of primary protons that only experienced Coulomb scattering")
```
Lateral positions of protons in the last phantom layer. On the left are all protons, on the right are only the primary protons that did not experience nuclear scattering.
```
x0 = ph19[(ph19["ParticleName"]=='proton') & (ph19['CreatorProcess'] == 0) & (ph19['NuclearProcess'] == 0)]['X']
ekin0 = ph19[(ph19["ParticleName"]=='proton') & (ph19['CreatorProcess'] == 0) & (ph19['NuclearProcess'] == 0)]['Ekine']
x1 = ph19[(ph19["ParticleName"]=='proton')]['X']
ekin1 = ph19[(ph19["ParticleName"]=='proton')]['Ekine']
fig, (ax_all, ax_prim) = plt.subplots(1,2, figsize = (14, 5), sharey=True)
__ =ax_all.hist2d(x1, ekin1, bins=50, norm=colors.LogNorm(), range=[[-70, 70],[0, 90]])
ax_all.set_ylabel('E_kin (MeV)')
ax_all.set_xlabel('X (mm)')
__ = ax_prim.hist2d(x0, ekin0, bins=50, norm=colors.LogNorm(), range=[[-70, 70],[0, 90]])
ax_prim.set_xlabel('X (mm)')
```
Kinetic energy deposited by particle versus the position of the hit (left) all protons (right) protons from the primary beam that did not experience nuclear scattering
```
ph = pd.merge(ph0, ph5, on="EventID", suffixes=("", "_5"))
ph = pd.merge(ph, ph10, on="EventID", suffixes=("", "_10"))
ph = pd.merge(ph, ph15, on="EventID", suffixes=("", "_15"))
ph = pd.merge(ph, ph19, on="EventID", suffixes=("", "_19"))
def select(ph):
result = (ph[f"CreatorProcess"] == 0) & (ph[f"ParticleName"] == "proton")
for x in [ "_5", "_10", "_15", "_19"]:
result = result & (ph[f"CreatorProcess{x}"] == 0) & (ph[f"ParticleName{x}"] == "proton")
return result
ph100 = ph[(ph["EventID"]<100) & select(ph)]
x = np.array(ph100[ph100["EventID"] == 1][["X", "X_5", "X_10", "X_15", "X_19"]]).flatten()
y = np.array(ph100[ph100["EventID"] == 1][["Y", "Y_5", "Y_10", "Y_15", "Y_19"]]).flatten()
y = np.array(y).flatten()
x = np.array(x).flatten()
plt.plot(y,x, 'o')
ph100["EventID"].head()
from mpl_toolkits.mplot3d import Axes3D
```
## Example showing energy deposition with 3 sensors
```
df2 = get_df_subentry2('results/TrackerHits.root')
edep = get_edep_data(df2, sensor=0)
_ = plt.hist(edep, bins=100, range=(0,1000))
_ = plt.hist(get_edep_data(df2, sensor=1), bins=100, range=(0,1000))
_ = plt.hist(get_edep_data(df2, sensor=2), bins=100, range=(0,1000))
null_columns = [col for col in df2.columns if df2[col].max() == 0 and df2[col].min() == 0]
df2.drop(columns=null_columns, inplace=True)
single_value_columns = [col for col in df2.columns if df2[col].max() == df2[col].min()]
df2.drop(columns=single_value_columns, inplace=True)
df2.head()
_ = plt.hist2d(df2['posX']-df2['sourcePosX'], df2['posY'], bins=(100, 80), norm=mcolors.LogNorm())
df2_sensor0 = df2[df2.volumeID == 0]
_= plt.hist((df2_sensor0[(df2_sensor0['processName']=='Transportation') & (df2_sensor0['posY']==-47.25)]).edep,log=True, density=True, bins = 100)
_= plt.hist((df2_sensor0[(df2_sensor0['processName']=='Transportation') & (df2_sensor0['posY']==-47.75)]).edep,log=True, density=True,bins = 100)
_= hist2d(df2.volumeID, df2.posY, bins=(12,100), norm=mcolors.LogNorm())
_ = hist2d(df2.trackLength, df2.volumeID, bins=(100, 12), norm=mcolors.LogNorm())
import pylandau
class landau_gen(rv_continuous):
r"""A Landau continuous random variable.
%(before_notes)s
Notes
-----
The probability density function for `Landau` is:
for a real number :math:`x`.
%(after_notes)s
This distribution has utility in high-energy physics and radiation
detection. It describes the energy loss of a charged relativistic
particle due to ionization of the medium .
"""
def _pdf(self, x):
return pylandau.landau_pdf(np.float64(x))
landau = landau_gen(name="landau")
#hide
from nbdev.export import notebook2script; notebook2script()
loc,scale = moyal.fit(edep)
print(loc, scale)
fig1, ax1 = plt.subplots(figsize=(7, 3))
x = np.linspace(0, 100, 200)
ax1.plot(x, moyal.pdf(x, loc, scale), label = 'Moyal MLE fit')
_ = ax1.hist(edep[edep < 100], bins = 100, histtype='step', density= True, label = 'sim data')
ax1.plot(x, landau.pdf(x, 23.973851592546183, 2.921658875656049), label='Landau MLE fit')
ax1.plot(x, landau.pdf(x, 24.13, 2.629), label='Meine Landau mit deine fit Parametern')
#ax1.scatter(GeV8_data.energy, GeV8_data.counts/4400, label = 'data', marker='o', c = 'green', alpha = 0.5)
plt.xlabel('keV')
ax1.legend()
loc,scale = moyal.fit(edep[edep < 50])
print(loc, scale)
m = np.mean(edep)
em = stats.sem(edep)
tm = stats.tmean(edep, limits=(edep.min(),np.mean(edep) + 1 * np.std(edep) + 2))
etm = stats.tsem(edep, limits=(edep.min(),np.mean(edep) + 1 * np.std(edep) + 2))
print(f'Mean: {m}, Error on mean: {em}, SNR: {m/em}')
print(f'Trimmed mean {tm}, Error on trimmed mean: {etm}, SNR: {tm/etm}')
#print(stats.mode(np.round(edep, 0)))
## edep.to_csv('simdata.csv', sep =',', mode='w')
```
| github_jupyter |
# 序列到序列学习(seq2seq)
在`seq2seq`中,
特定的“<eos>”表示序列结束词元。
一旦输出序列生成此词元,模型就会停止预测。
在循环神经网络解码器的初始化时间步,有两个特定的设计决定:
首先,特定的“<bos>”表示序列开始词元,它是解码器的输入序列的第一个词元。
其次,使用循环神经网络编码器最终的隐状态来初始化解码器的隐状态。
这种设计将输入序列的编码信息送入到解码器中来生成输出序列的。
在其他一些设计中 :cite:`Cho.Van-Merrienboer.Gulcehre.ea.2014`,
编码器最终的隐状态在每一个时间步都作为解码器的输入序列的一部分。
类似于 :`language_model`中语言模型的训练,
可以允许标签成为原始的输出序列,
从源序列词元“<bos>”、“Ils”、“regardent”、“.”
到新序列词元
“Ils”、“regardent”、“.”、“<eos>”来移动预测的位置。
下面,我们动手构建 :`seq2seq`的设计,
并将基于 :`machine_translation`中
介绍的“英-法”数据集来训练这个机器翻译模型。
```
import collections
import math
import tensorflow as tf
from d2l import tensorflow as d2l
```
## 编码器
从技术上讲,编码器将长度可变的输入序列转换成
形状固定的上下文变量$\mathbf{c}$,
并且将输入序列的信息在该上下文变量中进行编码。
如 :numref:`fig_seq2seq`所示,可以使用循环神经网络来设计编码器。
考虑由一个序列组成的样本(批量大小是$1$)。
假设输入序列是$x_1, \ldots, x_T$,
其中$x_t$是输入文本序列中的第$t$个词元。
在时间步$t$,循环神经网络将词元$x_t$的输入特征向量
$\mathbf{x}_t$和$\mathbf{h} _{t-1}$(即上一时间步的隐状态)
转换为$\mathbf{h}_t$(即当前步的隐状态)。
使用一个函数$f$来描述循环神经网络的循环层所做的变换:
$$\mathbf{h}_t = f(\mathbf{x}_t, \mathbf{h}_{t-1}). $$
总之,编码器通过选定的函数$q$,
将所有时间步的隐状态转换为上下文变量:
$$\mathbf{c} = q(\mathbf{h}_1, \ldots, \mathbf{h}_T).$$
比如,当选择$q(\mathbf{h}_1, \ldots, \mathbf{h}_T) = \mathbf{h}_T$时
(就像 :numref:`fig_seq2seq`中一样),
上下文变量仅仅是输入序列在最后时间步的隐状态$\mathbf{h}_T$。
到目前为止,我们使用的是一个单向循环神经网络来设计编码器,
其中隐状态只依赖于输入子序列,
这个子序列是由输入序列的开始位置到隐状态所在的时间步的位置
(包括隐状态所在的时间步)组成。
我们也可以使用双向循环神经网络构造编码器,
其中隐状态依赖于两个输入子序列,
两个子序列是由隐状态所在的时间步的位置之前的序列和之后的序列
(包括隐状态所在的时间步),
因此隐状态对整个序列的信息都进行了编码。
现在,让我们[**实现循环神经网络编码器**]。
注意,我们使用了*嵌入层*(embedding layer)
来获得输入序列中每个词元的特征向量。
嵌入层的权重是一个矩阵,
其行数等于输入词表的大小(`vocab_size`),
其列数等于特征向量的维度(`embed_size`)。
对于任意输入词元的索引$i$,
嵌入层获取权重矩阵的第$i$行(从$0$开始)以返回其特征向量。
另外,本文选择了一个多层门控循环单元来实现编码器。
```
class Encoder(tf.keras.layers.Layer):
"""编码器-解码器架构的基本编码器接口"""
def __init__(self, **kwargs):
super(Encoder, self).__init__(**kwargs)
def call(self, X, *args, **kwargs):
raise NotImplementedError
#@save
class Seq2SeqEncoder(d2l.Encoder):
"""用于序列到序列学习的循环神经网络编码器"""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers, dropout=0, **kwargs):
super().__init__(*kwargs)
# 嵌入层
self.embedding = tf.keras.layers.Embedding(vocab_size, embed_size)
self.rnn = tf.keras.layers.RNN(tf.keras.layers.StackedRNNCells(
[tf.keras.layers.GRUCell(num_hiddens, dropout=dropout)
for _ in range(num_layers)]), return_sequences=True,
return_state=True)
def call(self, X, *args, **kwargs):
# 输入'X'的形状:(`batch_size`, `num_steps`)
# 输出'X'的形状:(`batch_size`, `num_steps`, `embed_size`)
X = self.embedding(X)
output = self.rnn(X, **kwargs)
state = output[1:]
return output[0], state
```
循环层返回变量的说明可以参考 :numref:`sec_rnn-concise`。
下面,我们实例化[**上述编码器的实现**]:
我们使用一个两层门控循环单元编码器,其隐藏单元数为$16$。
给定一小批量的输入序列`X`(批量大小为$4$,时间步为$7$)。
在完成所有时间步后,
最后一层的隐状态的输出是一个张量(`output`由编码器的循环层返回),
其形状为(时间步数,批量大小,隐藏单元数)。
```
encoder = Seq2SeqEncoder(vocab_size=10, embed_size=8, num_hiddens=16, num_layers=2)
X = tf.zeros((4, 7))
output, state = encoder(X, training=False)
output.shape
```
由于这里使用的是门控循环单元,
所以在最后一个时间步的多层隐状态的形状是
(隐藏层的数量,批量大小,隐藏单元的数量)。
如果使用长短期记忆网络,`state`中还将包含记忆单元信息。
```
len(state), [element.shape for element in state]
```
## [**解码器**]
:label:`sec_seq2seq_decoder`
正如上文提到的,编码器输出的上下文变量$\mathbf{c}$
对整个输入序列$x_1, \ldots, x_T$进行编码。
来自训练数据集的输出序列$y_1, y_2, \ldots, y_{T'}$,
对于每个时间步$t'$(与输入序列或编码器的时间步$t$不同),
解码器输出$y_{t'}$的概率取决于先前的输出子序列
$y_1, \ldots, y_{t'-1}$和上下文变量$\mathbf{c}$,
即$P(y_{t'} \mid y_1, \ldots, y_{t'-1}, \mathbf{c})$。
为了在序列上模型化这种条件概率,
我们可以使用另一个循环神经网络作为解码器。
在输出序列上的任意时间步$t^\prime$,
循环神经网络将来自上一时间步的输出$y_{t^\prime-1}$
和上下文变量$\mathbf{c}$作为其输入,
然后在当前时间步将它们和上一隐状态
$\mathbf{s}_{t^\prime-1}$转换为
隐状态$\mathbf{s}_{t^\prime}$。
因此,可以使用函数$g$来表示解码器的隐藏层的变换:
$$\mathbf{s}_{t^\prime} = g(y_{t^\prime-1}, \mathbf{c}, \mathbf{s}_{t^\prime-1}).$$
:eqlabel:`eq_seq2seq_s_t`
在获得解码器的隐状态之后,
我们可以使用输出层和softmax操作
来计算在时间步$t^\prime$时输出$y_{t^\prime}$的条件概率分布
$P(y_{t^\prime} \mid y_1, \ldots, y_{t^\prime-1}, \mathbf{c})$。
根据 :numref:`fig_seq2seq`,当实现解码器时,
我们直接使用编码器最后一个时间步的隐状态来初始化解码器的隐状态。
这就要求使用循环神经网络实现的编码器和解码器具有相同数量的层和隐藏单元。
为了进一步包含经过编码的输入序列的信息,
上下文变量在所有的时间步与解码器的输入进行拼接(concatenate)。
为了预测输出词元的概率分布,
在循环神经网络解码器的最后一层使用全连接层来变换隐状态。
### 解码器输入: hidden state ‘c’, 当前词向量 ‘x’, 输出:目标语言词向量 ‘output’
### 解码器要得到解码是的hidden state需要c和x, 所以解码器的RNNcell的输入是embed_size + num_hiddens 维
### 解码器最后要根据hidden state得到目标语言,所以最后要加一个nn.Linear(num_hiddens, vocab_size)
```
class Decoder(tf.keras.layers.Layer):
"""编码器-解码器架构的基本解码器接口"""
def __init__(self, **kwargs):
super(Decoder, self).__init__(**kwargs)
def init_state(self, enc_outputs, *args):
raise NotImplementedError
def call(self, X, state, **kwargs):
raise NotImplementedError
class Seq2SeqDecoder(d2l.Decoder):
"""用于序列到序列学习的循环神经网络解码器"""
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super().__init__(**kwargs)
self.embedding = tf.keras.layers.Embedding(vocab_size, embed_size)
self.rnn = tf.keras.layers.RNN(tf.keras.layers.StackedRNNCells(
[tf.keras.layers.GRUCell(num_hiddens, dropout=dropout)
for _ in range(num_layers)]), return_sequences=True,
return_state=True)
self.dense = tf.keras.layers.Dense(vocab_size)
def init_state(self, enc_outputs, *args):
return enc_outputs[1]
def call(self, X, state, **kwargs):
# 输出'X'的形状:(`batch_size`, `num_steps`, `embed_size`)
X = self.embedding(X)
# 广播`context`,使其具有与`X`相同的`num_steps`
context = tf.repeat(tf.expand_dims(state[-1], axis=1), repeats=X.shape[1], axis=1)
X_and_context = tf.concat((X, context), axis=2)
rnn_output = self.rnn(X_and_context, state, **kwargs)
output = self.dense(rnn_output[0])
# `output`的形状: (`batch_size`, `num_steps`, `vocab_size`)
# `state`是一个包含`num_layers`个元素的列表,每个元素的形状: (`batch_size`, `num_hiddens`)
return output, rnn_output[1:]
```
下面,我们用与前面提到的编码器中相同的超参数来[**实例化解码器**]。
如我们所见,解码器的输出形状变为(批量大小,时间步数,词表大小),
其中张量的最后一个维度存储预测的词元分布。
```
decoder = Seq2SeqDecoder(vocab_size=10, embed_size=8, num_hiddens=16, num_layers=2)
state = decoder.init_state(encoder(X))
output, state = decoder(X, state, training=False)
output.shape, len(state), state[0].shape
```
## 损失函数
在每个时间步,解码器预测了输出词元的概率分布。
类似于语言模型,可以使用softmax来获得分布,
并通过计算交叉熵损失函数来进行优化。
回想一下 :`machine_translation`中,
特定的填充词元被添加到序列的末尾,
因此不同长度的序列可以以相同形状的小批量加载。
但是,我们应该将填充词元的预测排除在损失函数的计算之外。
为此,我们可以使用下面的`sequence_mask`函数
[**通过零值化屏蔽不相关的项**],
以便后面任何不相关预测的计算都是与零的乘积,结果都等于零。
例如,如果两个序列的有效长度(不包括填充词元)分别为$1$和$2$,
则第一个序列的第一项和第二个序列的前两项之后的剩余项将被清除为零。
```
#@save
def sequence_mask(X, valid_len, value=0):
"""在序列中屏蔽不相关的项"""
maxlen = X.shape[1]
mask = tf.range(start=0, limit=maxlen, dtype=tf.float32)[
None, :] < tf.cast(valid_len[:, None], dtype=tf.float32)
if len(X.shape) == 3:
return tf.where(tf.expand_dims(mask, axis=-1), X, value)
else:
return tf.where(mask, X, value)
X = tf.constant([[1, 2, 3], [4, 5, 6]])
sequence_mask(X, tf.constant([1, 2]))
```
(**我们还可以使用此函数屏蔽最后几个轴上的所有项。**)如果愿意,也可以使用指定的非零值来替换这些项。
```
X = tf.ones((2,3,4))
sequence_mask(X, tf.constant([1, 2]), value=-1)
```
现在,我们可以[**通过扩展softmax交叉熵损失函数来遮蔽不相关的预测**]。
最初,所有预测词元的掩码都设置为1。
一旦给定了有效长度,与填充词元对应的掩码将被设置为0。
最后,将所有词元的损失乘以掩码,以过滤掉损失中填充词元产生的不相关预测。
```
#@save
class MaskedSoftmaxCELoss(tf.keras.losses.Loss):
"""带遮蔽的softmax交叉熵损失函数"""
def __init__(self, valid_len):
super().__init__(reduction='none')
self.valid_len = valid_len
# `pred` 的形状:(`batch_size`, `num_steps`, `vocab_size`)
# `label` 的形状:(`batch_size`, `num_steps`)
# `valid_len` 的形状:(`batch_size`,)
def call(self, label, pred):
weights = tf.ones_like(label, dtype=tf.float32)
weights = sequence_mask(weights, self.valid_len)
label_one_hot = tf.one_hot(label, depth=pred.shape[-1])
unweighted_loss = tf.keras.losses.CategoricalCrossentropy(
from_logits=True, reduction='none')(label_one_hot, pred)
weighted_loss = tf.reduce_mean((unweighted_loss*weights), axis=1)
return weighted_loss
```
我们可以创建三个相同的序列来进行[**代码健全性检查**],
然后分别指定这些序列的有效长度为$4$、$2$和$0$。
结果就是,第一个序列的损失应为第二个序列的两倍,而第三个序列的损失应为零。
```
loss = MaskedSoftmaxCELoss(tf.constant([4, 2, 0]))
loss(tf.ones((3,4), dtype = tf.int32), tf.ones((3, 4, 10))).numpy()
```
## [**训练**]
:label:`sec_seq2seq_training`
在下面的循环训练过程中,如 :numref:`fig_seq2seq`所示,
特定的序列开始词元(“<bos>”)和
原始的输出序列(不包括序列结束词元“<eos>”)
拼接在一起作为解码器的输入。
这被称为*强制教学*(teacher forcing),
因为原始的输出序列(词元的标签)被送入解码器。
或者,将来自上一个时间步的*预测*得到的词元作为解码器的当前输入。
```
#@save
def train_seq2seq(net, data_iter, lr, num_epochs, tgt_vocab, device):
"""训练序列到序列模型"""
optimizer = tf.keras.optimizers.Adam(learning_rate=lr)
animator = d2l.Animator(xlabel="epoch", ylabel="loss",
xlim=[10, num_epochs])
for epoch in range(num_epochs):
timer = d2l.Timer()
metric = d2l.Accumulator(2) # 训练损失总和,词元数量
for batch in data_iter:
X, X_valid_len, Y, Y_valid_len = [x for x in batch]
bos = tf.reshape(tf.constant([tgt_vocab['<bos>']] * Y.shape[0]),
shape=(-1, 1))
dec_input = tf.concat([bos, Y[:, :-1]], 1) # 强制教学
with tf.GradientTape() as tape:
Y_hat, _ = net(X, dec_input, X_valid_len, training=True)
l = MaskedSoftmaxCELoss(Y_valid_len)(Y, Y_hat)
gradients = tape.gradient(l, net.trainable_variables)
gradients = d2l.grad_clipping(gradients, 1)
optimizer.apply_gradients(zip(gradients, net.trainable_variables))
num_tokens = tf.reduce_sum(Y_valid_len).numpy()
metric.add(tf.reduce_sum(l), num_tokens)
if (epoch + 1) % 10 == 0:
animator.add(epoch + 1, (metric[0] / metric[1],))
print(f'loss {metric[0] / metric[1]:.3f}, {metric[1] / timer.stop():.1f} '
f'tokens/sec on {str(device)}')
```
现在,在机器翻译数据集上,我们可以
[**创建和训练一个循环神经网络“编码器-解码器”模型**]用于序列到序列的学习。
```
class EncoderDecoder(tf.keras.Model):
"""编码器-解码器架构的基类"""
def __init__(self, encoder, decoder, **kwargs):
super(EncoderDecoder, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
def call(self, enc_X, dec_X, *args, **kwargs):
enc_outputs = self.encoder(enc_X, *args, **kwargs)
dec_state = self.decoder.init_state(enc_outputs, *args)
return self.decoder(dec_X, dec_state, **kwargs)
embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 300, d2l.try_gpu()
train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = Seq2SeqEncoder(len(src_vocab), embed_size, num_hiddens, num_layers,
dropout)
decoder = Seq2SeqDecoder(len(tgt_vocab), embed_size, num_hiddens, num_layers,
dropout)
net = EncoderDecoder(encoder, decoder)
train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)
```
## [**预测**]
为了采用一个接着一个词元的方式预测输出序列,
每个解码器当前时间步的输入都将来自于前一时间步的预测词元。
与训练类似,序列开始词元(“<bos>”)
在初始时间步被输入到解码器中。
该预测过程如 :`seq2seq_predict`所示,
当输出序列的预测遇到序列结束词元(“<eos>”)时,预测就结束了。
我们将在 :`beam-search`中介绍不同的序列生成策略。
```
#@save
def predict_seq2seq(net, src_sentence, src_vocab, tgt_vocab, num_steps,
save_attention_weights=False):
"""序列到序列模型的预测"""
src_tokens = src_vocab[src_sentence.lower().split(' ')] + [
src_vocab['<eos>']]
enc_valid_len = tf.constant([len(src_tokens)])
src_tokens = d2l.truncate_pad(src_tokens, num_steps, src_vocab['<pad>'])
# 添加批量轴
enc_X = tf.expand_dims(src_tokens, axis=0)
enc_outputs = net.encoder(enc_X, enc_valid_len, training=False)
dec_state = net.decoder.init_state(enc_outputs, enc_valid_len)
# 添加批量轴
dec_X = tf.expand_dims(tf.constant([tgt_vocab['<bos>']]), axis=0)
output_seq, attention_weight_seq = [], []
for _ in range(num_steps):
Y, dec_state = net.decoder(dec_X, dec_state, training=False)
# 我们使用具有预测最高可能性的词元,作为解码器在下一时间步的输入
dec_X = tf.argmax(Y, axis=2)
pred = tf.squeeze(dec_X, axis=0)
# 保存注意力权重
if save_attention_weights:
attention_weight_seq.append(net.decoder.attention_weights)
# 一旦序列结束词元被预测,输出序列的生成就完成了
if pred == tgt_vocab['<eos>']:
break
output_seq.append(pred.numpy())
return ' '.join(tgt_vocab.to_tokens(tf.reshape(output_seq,
shape = -1).numpy().tolist())), attention_weight_seq
```
## 预测序列的评估
我们可以通过与真实的标签序列进行比较来评估预测序列。
虽然 :cite:`Papineni.Roukos.Ward.ea.2002`
提出的BLEU(bilingual evaluation understudy)
最先是用于评估机器翻译的结果,
但现在它已经被广泛用于测量许多应用的输出序列的质量。
原则上说,对于预测序列中的任意$n$元语法(n-grams),
BLEU的评估都是这个$n$元语法是否出现在标签序列中。
我们将BLEU定义为:
$$ \exp\left(\min\left(0, 1 - \frac{\mathrm{len}_{\text{label}}}{\mathrm{len}_{\text{pred}}}\right)\right) \prod_{n=1}^k p_n^{1/2^n},$$
:eqlabel:`eq_bleu`
其中$\mathrm{len}_{\text{label}}$表示标签序列中的词元数和
$\mathrm{len}_{\text{pred}}$表示预测序列中的词元数,
$k$是用于匹配的最长的$n$元语法。
另外,用$p_n$表示$n$元语法的精确度,它是两个数量的比值:
第一个是预测序列与标签序列中匹配的$n$元语法的数量,
第二个是预测序列中$n$元语法的数量的比率。
具体地说,给定标签序列$A$、$B$、$C$、$D$、$E$、$F$
和预测序列$A$、$B$、$B$、$C$、$D$,
我们有$p_1 = 4/5$、$p_2 = 3/4$、$p_3 = 1/3$和$p_4 = 0$。
根据 :eqref:`eq_bleu`中BLEU的定义,
当预测序列与标签序列完全相同时,BLEU为$1$。
此外,由于$n$元语法越长则匹配难度越大,
所以BLEU为更长的$n$元语法的精确度分配更大的权重。
具体来说,当$p_n$固定时,$p_n^{1/2^n}$
会随着$n$的增长而增加(原始论文使用$p_n^{1/n}$)。
而且,由于预测的序列越短获得的$p_n$值越高,
所以 :eqref:`eq_bleu`中乘法项之前的系数用于惩罚较短的预测序列。
例如,当$k=2$时,给定标签序列$A$、$B$、$C$、$D$、$E$、$F$
和预测序列$A$、$B$,尽管$p_1 = p_2 = 1$,
惩罚因子$\exp(1-6/2) \approx 0.14$会降低BLEU。
[**BLEU的代码实现**]如下。
```
def bleu(pred_seq, label_seq, k): #@save
"""计算BLEU"""
pred_tokens, label_tokens = pred_seq.split(' '), label_seq.split(' ')
len_pred, len_label = len(pred_tokens), len(label_tokens)
score = math.exp(min(0, 1 - len_label / len_pred))
for n in range(1, k + 1):
num_matches, label_subs = 0, collections.defaultdict(int)
for i in range(len_label - n + 1):
label_subs[''.join(label_tokens[i: i + n])] += 1
for i in range(len_pred - n + 1):
if label_subs[''.join(pred_tokens[i: i + n])] > 0:
num_matches += 1
label_subs[''.join(pred_tokens[i: i + n])] -= 1
score *= math.pow(num_matches / (len_pred - n + 1), math.pow(0.5, n))
return score
```
最后,利用训练好的循环神经网络“编码器-解码器”模型,
[**将几个英语句子翻译成法语**],并计算BLEU的最终结果。
```
engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
translation, attention_weight_seq = predict_seq2seq(
net, eng, src_vocab, tgt_vocab, num_steps)
print(f'{eng} => {translation}, bleu {bleu(translation, fra, k=2):.3f}')
```
| github_jupyter |
# Now You Code 2: Character Frequency
Write a program to input some text (a word or a sentence). The program should create a histogram of each character in the text and it's frequency. For example the text `apple` has a frequency `a:1, p:2, l:1, e:1`
Some advice:
- build a dictionary of each character where the character is the key and the value is the number of occurences of that character.
- omit spaces, in the input text, and they cannot be represented as dictionary keys
- convert the input text to lower case, so that `A` and `a` are counted as the same character.
After you count the characters:
- sort the dictionary keys alphabetically,
- print out the character distribution
Example Run:
```
Enter some text: Michael is a Man from Mississppi.
. : 1
a : 3
c : 1
e : 1
f : 1
h : 1
i : 5
l : 1
m : 4
n : 1
o : 1
p : 2
r : 1
s : 5
```
## Step 1: Problem Analysis
Inputs: string
Outputs: frequency of each character (besides space)
Algorithm (Steps in Program):
- create empty dictionary
- input the string
- make string lowercase and remove spaces
- for each character in the text, set its dictionary value to 0
- for each character in the text, increase its dictionary value by one
- sort the dictionary keys alphabetically
- for each key, print the key and its corresponding value
```
## Step 2: Write code here
fr = {}
text = input("Enter text: ")
text = text.lower().replace(' ','')
for char in text:
fr[char] = 0
for char in text:
fr[char] = fr[char] + 1
for key in sorted(fr.keys()):
print(key, ':', fr[key])
```
## Step 3: Questions
1. Explain how you handled the situation where the dictionary key does not exist? (For instance the first time you encounter a character?)
I made a first loop that goes through all the characters and sets their values to 0 to make sure all the dictionary keys exist when I increase them by 1.
2. What happens when you just press `ENTER` as opposed to entering some actual text? What can be done about this to provide better feedback.
The program finishes without displaying anything. I could improve on this by printing that the string is empty if the dictionary is empty by the end of the program.
3. This program is similar to the popular word cloud generators [http://www.wordclouds.com/] you can find on the Web. Describe how this program could be modified to count words instead of characters.
I could split the string up into a list of words and then have the program go through the list of words instead of going through each character in the string.
## Reminder of Evaluation Criteria
1. What the problem attempted (analysis, code, and answered questions) ?
2. What the problem analysis thought out? (does the program match the plan?)
3. Does the code execute without syntax error?
4. Does the code solve the intended problem?
5. Is the code well written? (easy to understand, modular, and self-documenting, handles errors)
| github_jupyter |
## Deep face recognition with Keras, Dlib and OpenCV
Face recognition identifies persons on face images or video frames. In a nutshell, a face recognition system extracts features from an input face image and compares them to the features of labeled faces in a database. Comparison is based on a feature similarity metric and the label of the most similar database entry is used to label the input image. If the similarity value is below a certain threshold the input image is labeled as *unknown*. Comparing two face images to determine if they show the same person is known as face verification.
This notebook uses a deep convolutional neural network (CNN) to extract features from input images. It follows the approach described in [[1]](https://arxiv.org/abs/1503.03832) with modifications inspired by the [OpenFace](http://cmusatyalab.github.io/openface/) project. [Keras](https://keras.io/) is used for implementing the CNN, [Dlib](http://dlib.net/) and [OpenCV](https://opencv.org/) for aligning faces on input images. Face recognition performance is evaluated on a small subset of the [LFW](http://vis-www.cs.umass.edu/lfw/) dataset which you can replace with your own custom dataset e.g. with images of your family and friends if you want to further experiment with this notebook. After an overview of the CNN architecure and how the model can be trained, it is demonstrated how to:
- Detect, transform, and crop faces on input images. This ensures that faces are aligned before feeding them into the CNN. This preprocessing step is very important for the performance of the neural network.
- Use the CNN to extract 128-dimensional representations, or *embeddings*, of faces from the aligned input images. In embedding space, Euclidean distance directly corresponds to a measure of face similarity.
- Compare input embedding vectors to labeled embedding vectors in a database. Here, a support vector machine (SVM) and a KNN classifier, trained on labeled embedding vectors, play the role of a database. Face recognition in this context means using these classifiers to predict the labels i.e. identities of new inputs.
### Environment setup
For running this notebook, create and activate a new [virtual environment](https://docs.python.org/3/tutorial/venv.html) and install the packages listed in [requirements.txt](requirements.txt) with `pip install -r requirements.txt`. Furthermore, you'll need a local copy of Dlib's face landmarks data file for running face alignment:
```
import bz2
import os
from urllib.request import urlopen
def download_landmarks(dst_file):
url = 'http://dlib.net/files/shape_predictor_68_face_landmarks.dat.bz2'
decompressor = bz2.BZ2Decompressor()
with urlopen(url) as src, open(dst_file, 'wb') as dst:
data = src.read(1024)
while len(data) > 0:
dst.write(decompressor.decompress(data))
data = src.read(1024)
dst_dir = 'models'
dst_file = os.path.join(dst_dir, 'landmarks.dat')
if not os.path.exists(dst_file):
os.makedirs(dst_dir)
download_landmarks(dst_file)
```
### CNN architecture and training
The CNN architecture used here is a variant of the inception architecture [[2]](https://arxiv.org/abs/1409.4842). More precisely, it is a variant of the NN4 architecture described in [[1]](https://arxiv.org/abs/1503.03832) and identified as [nn4.small2](https://cmusatyalab.github.io/openface/models-and-accuracies/#model-definitions) model in the OpenFace project. This notebook uses a Keras implementation of that model whose definition was taken from the [Keras-OpenFace](https://github.com/iwantooxxoox/Keras-OpenFace) project. The architecture details aren't too important here, it's only useful to know that there is a fully connected layer with 128 hidden units followed by an L2 normalization layer on top of the convolutional base. These two top layers are referred to as the *embedding layer* from which the 128-dimensional embedding vectors can be obtained. The complete model is defined in [model.py](model.py) and a graphical overview is given in [model.png](model.png). A Keras version of the nn4.small2 model can be created with `create_model()`.
```
from model import create_model
nn4_small2 = create_model()
```
Model training aims to learn an embedding $f(x)$ of image $x$ such that the squared L2 distance between all faces of the same identity is small and the distance between a pair of faces from different identities is large. This can be achieved with a *triplet loss* $L$ that is minimized when the distance between an anchor image $x^a_i$ and a positive image $x^p_i$ (same identity) in embedding space is smaller than the distance between that anchor image and a negative image $x^n_i$ (different identity) by at least a margin $\alpha$.
$$L = \sum^{m}_{i=1} \large[ \small {\mid \mid f(x_{i}^{a}) - f(x_{i}^{p})) \mid \mid_2^2} - {\mid \mid f(x_{i}^{a}) - f(x_{i}^{n})) \mid \mid_2^2} + \alpha \large ] \small_+$$
$[z]_+$ means $max(z,0)$ and $m$ is the number of triplets in the training set. The triplet loss in Keras is best implemented with a custom layer as the loss function doesn't follow the usual `loss(input, target)` pattern. This layer calls `self.add_loss` to install the triplet loss:
```
from keras import backend as K
from keras.models import Model
from keras.layers import Input, Layer
# Input for anchor, positive and negative images
in_a = Input(shape=(96, 96, 3))
in_p = Input(shape=(96, 96, 3))
in_n = Input(shape=(96, 96, 3))
# Output for anchor, positive and negative embedding vectors
# The nn4_small model instance is shared (Siamese network)
emb_a = nn4_small2(in_a)
emb_p = nn4_small2(in_p)
emb_n = nn4_small2(in_n)
class TripletLossLayer(Layer):
def __init__(self, alpha, **kwargs):
self.alpha = alpha
super(TripletLossLayer, self).__init__(**kwargs)
def triplet_loss(self, inputs):
a, p, n = inputs
p_dist = K.sum(K.square(a-p), axis=-1)
n_dist = K.sum(K.square(a-n), axis=-1)
return K.sum(K.maximum(p_dist - n_dist + self.alpha, 0), axis=0)
def call(self, inputs):
loss = self.triplet_loss(inputs)
self.add_loss(loss)
return loss
# Layer that computes the triplet loss from anchor, positive and negative embedding vectors
triplet_loss_layer = TripletLossLayer(alpha=0.2, name='triplet_loss_layer')([emb_a, emb_p, emb_n])
# Model that can be trained with anchor, positive negative images
nn4_small2_train = Model([in_a, in_p, in_n], triplet_loss_layer)
```
During training, it is important to select triplets whose positive pairs $(x^a_i, x^p_i)$ and negative pairs $(x^a_i, x^n_i)$ are hard to discriminate i.e. their distance difference in embedding space should be less than margin $\alpha$, otherwise, the network is unable to learn a useful embedding. Therefore, each training iteration should select a new batch of triplets based on the embeddings learned in the previous iteration. Assuming that a generator returned from a `triplet_generator()` call can generate triplets under these constraints, the network can be trained with:
```
from data import triplet_generator
# triplet_generator() creates a generator that continuously returns
# ([a_batch, p_batch, n_batch], None) tuples where a_batch, p_batch
# and n_batch are batches of anchor, positive and negative RGB images
# each having a shape of (batch_size, 96, 96, 3).
generator = triplet_generator()
nn4_small2_train.compile(loss=None, optimizer='adam')
nn4_small2_train.fit_generator(generator, epochs=10, steps_per_epoch=100)
# Please note that the current implementation of the generator only generates
# random image data. The main goal of this code snippet is to demonstrate
# the general setup for model training. In the following, we will anyway
# use a pre-trained model so we don't need a generator here that operates
# on real training data. I'll maybe provide a fully functional generator
# later.
```
The above code snippet should merely demonstrate how to setup model training. But instead of actually training a model from scratch we will now use a pre-trained model as training from scratch is very expensive and requires huge datasets to achieve good generalization performance. For example, [[1]](https://arxiv.org/abs/1503.03832) uses a dataset of 200M images consisting of about 8M identities.
The OpenFace project provides [pre-trained models](https://cmusatyalab.github.io/openface/models-and-accuracies/#pre-trained-models) that were trained with the public face recognition datasets [FaceScrub](http://vintage.winklerbros.net/facescrub.html) and [CASIA-WebFace](http://arxiv.org/abs/1411.7923). The Keras-OpenFace project converted the weights of the pre-trained nn4.small2.v1 model to [CSV files](https://github.com/iwantooxxoox/Keras-OpenFace/tree/master/weights) which were then [converted here](face-recognition-convert.ipynb) to a binary format that can be loaded by Keras with `load_weights`:
```
nn4_small2_pretrained = create_model()
nn4_small2_pretrained.load_weights('weights/nn4.small2.v1.h5')
```
### Custom dataset
To demonstrate face recognition on a custom dataset, a small subset of the [LFW](http://vis-www.cs.umass.edu/lfw/) dataset is used. It consists of 100 face images of [10 identities](images). The metadata for each image (file and identity name) are loaded into memory for later processing.
```
import numpy as np
import os.path
class IdentityMetadata():
def __init__(self, base, name, file):
# dataset base directory
self.base = base
# identity name
self.name = name
# image file name
self.file = file
def __repr__(self):
return self.image_path()
def image_path(self):
return os.path.join(self.base, self.name, self.file)
def load_metadata(path):
metadata = []
for i in os.listdir(path):
for f in os.listdir(os.path.join(path, i)):
#checking file extention. Allowing only '.jpg' and '.jpeg' files.
ext = os.path.splitext(f)[1]
if ext == '.jpg' or ext == '.jpeg':
metadata.append(IdentityMetadata(path, i, f))
return np.array(metadata)
metadata = load_metadata('images')
```
### Face alignment
The nn4.small2.v1 model was trained with aligned face images, therefore, the face images from the custom dataset must be aligned too. Here, we use [Dlib](http://dlib.net/) for face detection and [OpenCV](https://opencv.org/) for image transformation and cropping to produce aligned 96x96 RGB face images. By using the [AlignDlib](align.py) utility from the OpenFace project this is straightforward:
```
import cv2
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from align import AlignDlib
%matplotlib inline
def load_image(path):
img = cv2.imread(path, 1)
# OpenCV loads images with color channels
# in BGR order. So we need to reverse them
return img[...,::-1]
# Initialize the OpenFace face alignment utility
alignment = AlignDlib('models/landmarks.dat')
# Load an image of Jacques Chirac
jc_orig = load_image(metadata[2].image_path())
# Detect face and return bounding box
bb = alignment.getLargestFaceBoundingBox(jc_orig)
# Transform image using specified face landmark indices and crop image to 96x96
jc_aligned = alignment.align(96, jc_orig, bb, landmarkIndices=AlignDlib.OUTER_EYES_AND_NOSE)
# Show original image
plt.subplot(131)
plt.imshow(jc_orig)
# Show original image with bounding box
plt.subplot(132)
plt.imshow(jc_orig)
plt.gca().add_patch(patches.Rectangle((bb.left(), bb.top()), bb.width(), bb.height(), fill=False, color='red'))
# Show aligned image
plt.subplot(133)
plt.imshow(jc_aligned);
```
As described in the OpenFace [pre-trained models](https://cmusatyalab.github.io/openface/models-and-accuracies/#pre-trained-models) section, landmark indices `OUTER_EYES_AND_NOSE` are required for model nn4.small2.v1. Let's implement face detection, transformation and cropping as `align_image` function for later reuse.
```
def align_image(img):
return alignment.align(96, img, alignment.getLargestFaceBoundingBox(img),
landmarkIndices=AlignDlib.OUTER_EYES_AND_NOSE)
```
### Embedding vectors
Embedding vectors can now be calculated by feeding the aligned and scaled images into the pre-trained network.
```
embedded = np.zeros((metadata.shape[0], 128))
for i, m in enumerate(metadata):
img = load_image(m.image_path())
img = align_image(img)
# scale RGB values to interval [0,1]
img = (img / 255.).astype(np.float32)
# obtain embedding vector for image
embedded[i] = nn4_small2_pretrained.predict(np.expand_dims(img, axis=0))[0]
```
Let's verify on a single triplet example that the squared L2 distance between its anchor-positive pair is smaller than the distance between its anchor-negative pair.
```
def distance(emb1, emb2):
return np.sum(np.square(emb1 - emb2))
def show_pair(idx1, idx2):
plt.figure(figsize=(8,3))
plt.suptitle(f'Distance = {distance(embedded[idx1], embedded[idx2]):.2f}')
plt.subplot(121)
plt.imshow(load_image(metadata[idx1].image_path()))
plt.subplot(122)
plt.imshow(load_image(metadata[idx2].image_path()));
show_pair(2, 3)
show_pair(2, 12)
```
As expected, the distance between the two images of Jacques Chirac is smaller than the distance between an image of Jacques Chirac and an image of Gerhard Schröder (0.30 < 1.12). But we still do not know what distance threshold $\tau$ is the best boundary for making a decision between *same identity* and *different identity*.
### Distance threshold
To find the optimal value for $\tau$, the face verification performance must be evaluated on a range of distance threshold values. At a given threshold, all possible embedding vector pairs are classified as either *same identity* or *different identity* and compared to the ground truth. Since we're dealing with skewed classes (much more negative pairs than positive pairs), we use the [F1 score](https://en.wikipedia.org/wiki/F1_score) as evaluation metric instead of [accuracy](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.accuracy_score.html).
```
from sklearn.metrics import f1_score, accuracy_score
distances = [] # squared L2 distance between pairs
identical = [] # 1 if same identity, 0 otherwise
num = len(metadata)
for i in range(num - 1):
for j in range(1, num):
distances.append(distance(embedded[i], embedded[j]))
identical.append(1 if metadata[i].name == metadata[j].name else 0)
distances = np.array(distances)
identical = np.array(identical)
thresholds = np.arange(0.3, 1.0, 0.01)
f1_scores = [f1_score(identical, distances < t) for t in thresholds]
acc_scores = [accuracy_score(identical, distances < t) for t in thresholds]
opt_idx = np.argmax(f1_scores)
# Threshold at maximal F1 score
opt_tau = thresholds[opt_idx]
# Accuracy at maximal F1 score
opt_acc = accuracy_score(identical, distances < opt_tau)
# Plot F1 score and accuracy as function of distance threshold
plt.plot(thresholds, f1_scores, label='F1 score');
plt.plot(thresholds, acc_scores, label='Accuracy');
plt.axvline(x=opt_tau, linestyle='--', lw=1, c='lightgrey', label='Threshold')
plt.title(f'Accuracy at threshold {opt_tau:.2f} = {opt_acc:.3f}');
plt.xlabel('Distance threshold')
plt.legend();
```
The face verification accuracy at $\tau$ = 0.56 is 95.7%. This is not bad given a baseline of 89% for a classifier that always predicts *different identity* (there are 980 pos. pairs and 8821 neg. pairs) but since nn4.small2.v1 is a relatively small model it is still less than what can be achieved by state-of-the-art models (> 99%).
The following two histograms show the distance distributions of positive and negative pairs and the location of the decision boundary. There is a clear separation of these distributions which explains the discriminative performance of the network. One can also spot some strong outliers in the positive pairs class but these are not further analyzed here.
```
dist_pos = distances[identical == 1]
dist_neg = distances[identical == 0]
plt.figure(figsize=(12,4))
plt.subplot(121)
plt.hist(dist_pos)
plt.axvline(x=opt_tau, linestyle='--', lw=1, c='lightgrey', label='Threshold')
plt.title('Distances (pos. pairs)')
plt.legend();
plt.subplot(122)
plt.hist(dist_neg)
plt.axvline(x=opt_tau, linestyle='--', lw=1, c='lightgrey', label='Threshold')
plt.title('Distances (neg. pairs)')
plt.legend();
```
### Face recognition
Given an estimate of the distance threshold $\tau$, face recognition is now as simple as calculating the distances between an input embedding vector and all embedding vectors in a database. The input is assigned the label (i.e. identity) of the database entry with the smallest distance if it is less than $\tau$ or label *unknown* otherwise. This procedure can also scale to large databases as it can be easily parallelized. It also supports one-shot learning, as adding only a single entry of a new identity might be sufficient to recognize new examples of that identity.
A more robust approach is to label the input using the top $k$ scoring entries in the database which is essentially [KNN classification](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm) with a Euclidean distance metric. Alternatively, a linear [support vector machine](https://en.wikipedia.org/wiki/Support_vector_machine) (SVM) can be trained with the database entries and used to classify i.e. identify new inputs. For training these classifiers we use 50% of the dataset, for evaluation the other 50%.
```
from sklearn.preprocessing import LabelEncoder
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import LinearSVC
targets = np.array([m.name for m in metadata])
encoder = LabelEncoder()
encoder.fit(targets)
# Numerical encoding of identities
y = encoder.transform(targets)
train_idx = np.arange(metadata.shape[0]) % 2 != 0
test_idx = np.arange(metadata.shape[0]) % 2 == 0
# 50 train examples of 10 identities (5 examples each)
X_train = embedded[train_idx]
# 50 test examples of 10 identities (5 examples each)
X_test = embedded[test_idx]
y_train = y[train_idx]
y_test = y[test_idx]
knn = KNeighborsClassifier(n_neighbors=1, metric='euclidean')
svc = LinearSVC()
knn.fit(X_train, y_train)
svc.fit(X_train, y_train)
acc_knn = accuracy_score(y_test, knn.predict(X_test))
acc_svc = accuracy_score(y_test, svc.predict(X_test))
print(f'KNN accuracy = {acc_knn}, SVM accuracy = {acc_svc}')
```
The KNN classifier achieves an accuracy of 96% on the test set, the SVM classifier 98%. Let's use the SVM classifier to illustrate face recognition on a single example.
```
import warnings
# Suppress LabelEncoder warning
warnings.filterwarnings('ignore')
example_idx = 29
example_image = load_image(metadata[test_idx][example_idx].image_path())
example_prediction = svc.predict([embedded[test_idx][example_idx]])
example_identity = encoder.inverse_transform(example_prediction)[0]
plt.imshow(example_image)
plt.title(f'Recognized as {example_identity}');
```
Seems reasonable :-) Classification results should actually be checked whether (a subset of) the database entries of the predicted identity have a distance less than $\tau$, otherwise one should assign an *unknown* label. This step is skipped here but can be easily added.
### Dataset visualization
To embed the dataset into 2D space for displaying identity clusters, [t-distributed Stochastic Neighbor Embedding](https://en.wikipedia.org/wiki/T-distributed_stochastic_neighbor_embedding) (t-SNE) is applied to the 128-dimensional embedding vectors. Except from a few outliers, identity clusters are well separated.
```
from sklearn.manifold import TSNE
X_embedded = TSNE(n_components=2).fit_transform(embedded)
for i, t in enumerate(set(targets)):
idx = targets == t
plt.scatter(X_embedded[idx, 0], X_embedded[idx, 1], label=t)
plt.legend(bbox_to_anchor=(1, 1));
```
### References
- [1] [FaceNet: A Unified Embedding for Face Recognition and Clustering](https://arxiv.org/abs/1503.03832)
- [2] [Going Deeper with Convolutions](https://arxiv.org/abs/1409.4842)
| github_jupyter |
```
dtypes = {
'MachineIdentifier': 'category',
'ProductName': 'category',
'EngineVersion': 'category',
'AppVersion': 'category',
'AvSigVersion': 'category',
'IsBeta': 'int8',
'RtpStateBitfield': 'float16',
'IsSxsPassiveMode': 'int8',
'DefaultBrowsersIdentifier': 'float16',
'AVProductStatesIdentifier': 'float32',
'AVProductsInstalled': 'float16',
'AVProductsEnabled': 'float16',
'HasTpm': 'int8',
'CountryIdentifier': 'int16',
'CityIdentifier': 'float32',
'OrganizationIdentifier': 'float16',
'GeoNameIdentifier': 'float16',
'LocaleEnglishNameIdentifier': 'int8',
'Platform': 'category',
'Processor': 'category',
'OsVer': 'category',
'OsBuild': 'int16',
'OsSuite': 'int16',
'OsPlatformSubRelease': 'category',
'OsBuildLab': 'category',
'SkuEdition': 'category',
'IsProtected': 'float16',
'AutoSampleOptIn': 'int8',
'PuaMode': 'category',
'SMode': 'float16',
'IeVerIdentifier': 'float16',
'SmartScreen': 'category',
'Firewall': 'float16',
'UacLuaenable': 'float32',
'Census_MDC2FormFactor': 'category',
'Census_DeviceFamily': 'category',
'Census_OEMNameIdentifier': 'float16',
'Census_OEMModelIdentifier': 'float32',
'Census_ProcessorCoreCount': 'float16',
'Census_ProcessorManufacturerIdentifier': 'float16',
'Census_ProcessorModelIdentifier': 'float16',
'Census_ProcessorClass': 'category',
'Census_PrimaryDiskTotalCapacity': 'float32',
'Census_PrimaryDiskTypeName': 'category',
'Census_SystemVolumeTotalCapacity': 'float32',
'Census_HasOpticalDiskDrive': 'int8',
'Census_TotalPhysicalRAM': 'float32',
'Census_ChassisTypeName': 'category',
'Census_InternalPrimaryDiagonalDisplaySizeInInches': 'float16',
'Census_InternalPrimaryDisplayResolutionHorizontal': 'float16',
'Census_InternalPrimaryDisplayResolutionVertical': 'float16',
'Census_PowerPlatformRoleName': 'category',
'Census_InternalBatteryType': 'category',
'Census_InternalBatteryNumberOfCharges': 'float32',
'Census_OSVersion': 'category',
'Census_OSArchitecture': 'category',
'Census_OSBranch': 'category',
'Census_OSBuildNumber': 'int16',
'Census_OSBuildRevision': 'int32',
'Census_OSEdition': 'category',
'Census_OSSkuName': 'category',
'Census_OSInstallTypeName': 'category',
'Census_OSInstallLanguageIdentifier': 'float16',
'Census_OSUILocaleIdentifier': 'int16',
'Census_OSWUAutoUpdateOptionsName': 'category',
'Census_IsPortableOperatingSystem': 'int8',
'Census_GenuineStateName': 'category',
'Census_ActivationChannel': 'category',
'Census_IsFlightingInternal': 'float16',
'Census_IsFlightsDisabled': 'float16',
'Census_FlightRing': 'category',
'Census_ThresholdOptIn': 'float16',
'Census_FirmwareManufacturerIdentifier': 'float16',
'Census_FirmwareVersionIdentifier': 'float32',
'Census_IsSecureBootEnabled': 'int8',
'Census_IsWIMBootEnabled': 'float16',
'Census_IsVirtualDevice': 'float16',
'Census_IsTouchEnabled': 'int8',
'Census_IsPenCapable': 'int8',
'Census_IsAlwaysOnAlwaysConnectedCapable': 'float16',
'Wdft_IsGamer': 'float16',
'Wdft_RegionIdentifier': 'float16',
'HasDetections': 'int8'
}
import numpy as np
import pandas as pd
import lightgbm as lgb
import xgboost as xgb
import time, datetime
from sklearn import *
train = pd.read_csv('../input/train.csv', iterator=True, chunksize=1_500_000, dtype=dtypes)
test = pd.read_csv('../input/test.csv', iterator=True, chunksize=1_000_000, dtype=dtypes)
gf_defaults = {'col': [], 'ocol':[], 'dcol' : ['EngineVersion', 'AppVersion', 'AvSigVersion', 'OsBuildLab', 'Census_OSVersion']}
one_hot = {}
def get_features(df, gf_train=False):
global one_hot
global gf_defaults
for c in gf_defaults['dcol']:
for i in range(5):
df[c + str(i)] = df[c].map(lambda x: str(x).split('.')[i] if len(str(x).split('.'))>i else -1)
col = [c for c in df.columns if c not in ['MachineIdentifier', 'HasDetections']]
if gf_train:
for c in col:
if df[c].dtype == 'O' or df[c].dtype.name == 'category':
gf_defaults['ocol'].append(c)
else:
gf_defaults['col'].append(c)
one_hot = {c: list(df[c].value_counts().index) for c in gf_defaults['ocol']}
#train and test
for c in one_hot:
if len(one_hot[c])>1 and len(one_hot[c]) < 20:
for val in one_hot[c]:
df[c+'_oh_' + str(val)] = (df[c].values == val).astype(np.int)
if gf_train:
gf_defaults['col'].append(c+'_oh_' + str(val))
return df[gf_defaults['col']+['MachineIdentifier', 'HasDetections']]
col = gf_defaults['col']
model = []
params = {'objective':'binary', "boosting": "gbdt", 'learning_rate': 0.02, 'max_depth': -1,
"feature_fraction": 0.8, "bagging_freq": 1, "bagging_fraction": 0.8 , "bagging_seed": 11,
"metric": 'auc', "lambda_l1": 0.1, 'num_leaves': 60, 'min_data_in_leaf': 60, "verbosity": -1, "random_state": 3}
online_start = True
for df in train:
if online_start:
df = get_features(df, True)
x1, x2, y1, y2 = model_selection.train_test_split(df[col], df['HasDetections'], test_size=0.2, random_state=25)
model = lgb.train(params, lgb.Dataset(x1, y1), 2500, lgb.Dataset(x2, y2), verbose_eval=100, early_stopping_rounds=200)
model.save_model('lgb.model')
else:
df = get_features(df)
x1, x2, y1, y2 = model_selection.train_test_split(df[col], df['HasDetections'], test_size=0.2, random_state=25)
model = lgb.train(params, lgb.Dataset(x1, y1), 2500, lgb.Dataset(x2, y2), verbose_eval=100, early_stopping_rounds=200, init_model='lgb.model')
model.save_model('lgb.model')
online_start = False
print('training...')
predictions = []
for df in test:
df['HasDetections'] = 0.0
df = get_features(df)
df['HasDetections'] = model.predict(df[col], num_iteration=model.best_iteration + 50)
predictions.append(df[['MachineIdentifier', 'HasDetections']].values)
print('testing...')
sub = np.concatenate(predictions)
sub = pd.DataFrame(sub, columns = ['MachineIdentifier', 'HasDetections'])
sub.to_csv('submission.csv', index=False)
```
| github_jupyter |
```
import pytorch_lightning as pl
import torch.nn as nn
import torch.nn.functional as F
from torch import optim
from torch.utils.data import DataLoader, random_split
from torch.utils.data.distributed import DistributedSampler
import numpy as np
import pandas as pd
import torch as torch
from pathlib import Path
import pickle
import warnings
import numpy as np
import pandas as pd
from pandas.core.common import SettingWithCopyWarning
import pytorch_lightning as pl
from pytorch_lightning.callbacks import EarlyStopping, LearningRateMonitor
from pytorch_lightning.loggers import TensorBoardLogger
import torch
from pytorch_forecasting import GroupNormalizer, TemporalFusionTransformer, TimeSeriesDataSet
from pytorch_forecasting.data.examples import get_stallion_data
from pytorch_forecasting.metrics import MAE, RMSE, SMAPE, PoissonLoss, QuantileLoss
from pytorch_forecasting.models.temporal_fusion_transformer.tuning import optimize_hyperparameters
from pytorch_forecasting.utils import profile
from torch.utils.data import Dataset, DataLoader, IterableDataset
warnings.simplefilter("error", category=SettingWithCopyWarning)
class MQCNNEncoder(nn.Module):
def __init__(self, time_step, static_features, timevarying_features, num_static_features, num_timevarying_features):
super().__init__()
self.time_step = time_step
self.static_features = static_features
self.timevarying_features = timevarying_features
self.num_static_features = num_static_features
self.num_timevarying_features = num_timevarying_features
self.static = StaticLayer(in_channels = self.num_static_features,
time_step = self.time_step,
static_features = self.static_features)
self.conv = ConvLayer(in_channels = self.num_timevarying_features,
timevarying_features = self.timevarying_features,
time_step = self.time_step)
def forward(self, x):
x_s = self.static(x)
x_t = self.conv(x)
return torch.cat((x_s, x_t), axis = 2)
class MQCNNDecoder(nn.Module):
"""Decoder implementation for MQCNN
Parameters
----------
config
Configurations
ltsp : list of tuple of int
List of lead-time / span tuples to make predictions for
expander : HybridBlock
Overrides default future data expander if not None
hf1 : HybridBlock
Overrides default global future layer if not None
hf2 : HybridBlock
Overrides default local future layer if not None
ht1 : HybridBlock
Overrides horizon-specific layer if not None
ht2 : HybridBlock
Overrides horizon-agnostic layer if not None
h : HybridBlock
Overrides local MLP if not None
span_1 : HybridBlock
Overrides span 1 layer if not None
span_N : HybridBlock
Overrides span N layer if not None
Inputs:
- **xf** : Future data of shape
(batch_size, Trnn + lead_future - 1, num_future_ts_features)
- **encoded** : Encoded input tensor of shape
(batch_size, Trnn, n) for some n
Outputs:
- **pred_1** : Span 1 predictions of shape
(batch_size, Trnn, Tpred * num_quantiles)
- **pred_N** : Span N predictions of shape
(batch_size, Trnn, span_N_count * num_quantiles)
In both outputs, the last dimensions has the predictions grouped
together by quantile. For example, the quantiles are P10 and P90
then the span 1 predictions will be:
Tpred_0_p50, Tpred_1_p50, ..., Tpred_N_p50, Tpred_0_p90,
Tpred_1_p90, ... Tpred_N_90
"""
def __init__(self, time_step, lead_future, ltsp, future_information, num_future_features,
global_hidden_units, horizon_specific_hidden_units, horizon_agnostic_hidden_units,
local_mlp_hidden_units, local_mlp_output_units,
num_quantiles=2, expander=None, hf1=None, hf2=None,
ht1=None, ht2=None, h=None, span_1=None, span_N=None,
**kwargs):
super(MQCNNDecoder, self).__init__(**kwargs)
self.future_features_count = num_future_features
self.future_information = future_information
self.time_step = time_step
self.lead_future = lead_future
self.ltsp = ltsp
self.num_quantiles = num_quantiles
self.global_hidden_units = global_hidden_units
self.horizon_specific_hidden_units = horizon_specific_hidden_units
self.horizon_agnostic_hidden_units = horizon_agnostic_hidden_units
self.local_mlp_hidden_units = local_mlp_hidden_units
self.local_mlp_output_units = local_mlp_output_units
# We assume that Tpred == span1_count.
# Tpred = forecast_end_index
# self.Tpred = max(map(lambda x: x[0] + x[1], self.ltsp))
self.Tpred = 6
# span1_count = len(list(filter(lambda x: x[1] == 1, self.ltsp)))
span1_count = 1
#print(self.Tpred, span1_count)
#assert span1_count == self.Tpred, f"Number of span 1 horizons: {span1_count}\
#does not match Tpred: {self.Tpred}"
# self.spanN_count = len(list(filter(lambda x: x[1] != 1, self.ltsp)))
self.spanN_count = 1
# Setting default components:
if expander is None:
expander = ExpandLayer(self.time_step, self.lead_future, self.future_information)
if hf1 is None:
hf1 = GlobalFutureLayer(self.time_step, self.lead_future, self.future_features_count, out_channels=self.global_hidden_units)
if ht1 is None:
ht1 = HorizonSpecific(self.Tpred, self.time_step, num = self.horizon_specific_hidden_units)
if ht2 is None:
ht2 = HorizonAgnostic(self.horizon_agnostic_hidden_units, self.lead_future)
if h is None:
h = LocalMlp(self.local_mlp_hidden_units, self.local_mlp_output_units)
if span_1 is None:
span_1 = Span1(self.time_step, self.lead_future, self.num_quantiles)
if span_N is None:
span_N = SpanN(self.time_step, self.lead_future, self.num_quantiles, self.spanN_count)
self.expander = expander
self.hf1 = hf1
self.hf2 = hf2
self.ht1 = ht1
self.ht2 = ht2
self.h = h
self.span_1 = span_1
self.span_N = span_N
def forward(self, x, encoded):
xf = x['future_information']
expanded = self.expander(xf)
hf1 = self.hf1(expanded)
hf2 = F.relu(expanded)
ht = torch.cat((encoded, hf1), dim=-1)
ht1 = self.ht1(ht)
ht2 = self.ht2(ht)
h = torch.cat((ht1, ht2, hf2), dim=-1)
h = self.h(h)
return self.span_1(h)#, self.span_N(h)
# submodule
class StaticLayer(nn.Module):
def __init__(self, in_channels, time_step, static_features, out_channels = 30, dropout = 0.4):
super().__init__()
self.time_step = time_step
#self.static_features = static_features
self.dropout = nn.Dropout(dropout)
self.in_channels = in_channels
self.out_channels = out_channels
self.static = nn.Linear(self.in_channels, self.out_channels)
def forward(self, x):
x = x['static_features'][:,:1,:]
x = self.dropout(x)
x = self.static(x)
return x.repeat(1, self.time_step, 1)
class ConvLayer(nn.Module):
def __init__(self, time_step, timevarying_features, in_channels, out_channels = 30, kernel_size = 2):
super().__init__()
self.in_channels = in_channels
self.out_channels = out_channels
self.kernel_size = kernel_size
self.timevarying_features = timevarying_features
self.time_step = time_step
self.c1 = nn.Conv1d(self.in_channels, self.out_channels, self.kernel_size, dilation = 1)
self.c2 = nn.Conv1d(self.out_channels, self.out_channels, self.kernel_size, dilation = 2)
self.c3 = nn.Conv1d(self.out_channels, self.out_channels, self.kernel_size, dilation = 4)
self.c4 = nn.Conv1d(self.out_channels, self.out_channels, self.kernel_size, dilation = 8)
self.c5 = nn.Conv1d(self.out_channels, self.out_channels, self.kernel_size, dilation = 16)
#self.c6 = nn.Conv1d(self.out_channels, self.out_channels, self.kernel_size, dilation = 32)
def forward(self, x):
x_t = x['timevarying_features'][:, :self.time_step, :]
x_t = x_t.permute(0, 2, 1)
x_t = F.pad(x_t, (1,0), "constant", 0)
x_t = self.c1(x_t)
x_t = F.pad(x_t, (2,0), "constant", 0)
x_t = self.c2(x_t)
x_t = F.pad(x_t, (4,0), "constant", 0)
x_t = self.c3(x_t)
x_t = F.pad(x_t, (8,0), "constant", 0)
x_t = self.c4(x_t)
x_t = F.pad(x_t, (16,0), "constant", 0)
x_t = self.c5(x_t)
return x_t.permute(0, 2, 1)
class ExpandLayer(nn.Module):
"""Expands the dimension referred to as `expand_axis` into two
dimensions by applying a sliding window. For example, a tensor of
shape (1, 4, 2) as follows:
[[[0. 1.]
[2. 3.]
[4. 5.]
[6. 7.]]]
where `expand_axis` = 1 and `time_step` = 3 (number of windows) and
`lead_future` = 2 (window length) will become:
[[[[0. 1.]
[2. 3.]]
[[2. 3.]
[4. 5.]]
[[4. 5.]
[6. 7.]]]]
Used for expanding future information tensors
Parameters
----------
time_step : int
Length of the time sequence (number of windows)
lead_future : int
Number of future time points (window length)
expand_axis : int
Axis to expand"""
def __init__(self, time_step, lead_future, future_information, **kwargs):
super(ExpandLayer, self).__init__(**kwargs)
self.time_step = time_step
self.future_information = future_information
self.lead_future = lead_future
def forward(self, x):
# First create a matrix of indices, which we will use to slice
# `input` along `expand_axis`. For example, for time_step=3 and
# lead_future=2,
# idx = [[0. 1.]
# [1. 2.]
# [2. 3.]]
# We achieve this by doing a broadcast add of
# [[0.] [1.] [2.]] and [[0. 1.]]
idx = torch.add(torch.arange(self.time_step).unsqueeze(axis = 1),
torch.arange(self.lead_future).unsqueeze(axis = 0))
# Now we slice `input`, taking elements from `input` that correspond to
# the indices in `idx` along the `expand_axis` dimension
return x[:, idx, :]
class GlobalFutureLayer(nn.Module):
def __init__(self, time_step, lead_future, future_features_count, out_channels = 30):
super().__init__()
self.time_step = time_step
self.lead_future = lead_future
self.future_features_count = future_features_count
self.out_channels = out_channels
self.l1 = nn.Linear(self.lead_future * self.future_features_count, out_channels)
def forward(self, x):
x = x.contiguous().view(-1, self.time_step, self.lead_future * self.future_features_count)
return self.l1(x)
class HorizonSpecific(nn.Module):
def __init__(self, Tpred, time_step, num = 20):
super().__init__()
self.Tpred = Tpred
self.time_step = time_step
self.num = num
def forward(self, x):
x = nn.Linear(x.size(-1), self.Tpred * self.num)(x)
x = F.relu(x)
return x.view(-1, self.time_step, self.Tpred, 20)
class HorizonAgnostic(nn.Module):
def __init__(self, out_channels, lead_future):
super().__init__()
self.out_channels = out_channels
self.lead_future = lead_future
def forward(self, x):
x = nn.Linear(x.size(-1), self.out_channels)(x)
x = F.relu(x)
x = x.unsqueeze(axis = 2)
x = x.repeat(1,1, self.lead_future, 1)
return x
class LocalMlp(nn.Module):
def __init__(self, hidden, output):
super().__init__()
self.hidden = hidden
self.output = output
def forward(self, x):
x = nn.Linear(x.size(-1), self.hidden)(x)
x = F.relu(x)
x = nn.Linear(self.hidden, self.output)(x)
x = F.relu(x)
return x
class Span1(nn.Module):
def __init__(self, time_step, lead_future, num_quantiles):
super().__init__()
self.time_step = time_step
self.lead_future = lead_future
self.num_quantiles = num_quantiles
def forward(self, x):
x = nn.Linear(x.size(-1), self.num_quantiles)(x)
x = F.relu(x.contiguous().view(-1, x.size(-2), x.size(-1)))
x = x.view(-1, self.time_step, self.lead_future, self.num_quantiles)
x = x.view(-1, self.time_step, self.lead_future*self.num_quantiles)
return x
class SpanN(nn.Module):
def __init__(self, time_step, lead_future, num_quantiles, spanN_count):
super().__init__()
self.time_step = time_step
self.lead_future = lead_future
self.num_quantiles = num_quantiles
self.spanN_count = spanN_count
def forward(self, x):
x = x.permute(0, 1, 3, 2)
x = x.contiguous().view(-1, self.time_step, x.size(-2) * x.size(-1))
x = nn.Linear(x.size(-1), self.spanN_count * self.num_quantiles)(x)
return x
class MQCNNModel(pl.LightningModule):
def __init__(self, static_features, timevarying_features, future_information, time_step, ltsp, lead_future,
global_hidden_units, horizon_specific_hidden_units,
horizon_agnostic_hidden_units, local_mlp_hidden_units, local_mlp_output_units):
super(MQCNNModel, self).__init__()
#self.input_tensor = input_tensor
self.time_step = time_step
self.static_features = static_features
self.num_static_features = len(static_features)
self.timevarying_features = timevarying_features
self.num_timevarying_features = len(timevarying_features)
self.future_information = future_information
self.num_future_features = len(future_information)
self.ltsp = ltsp
self.lead_future = lead_future
self.global_hidden_units = global_hidden_units
self.horizon_specific_hidden_units = horizon_specific_hidden_units
self.horizon_agnostic_hidden_units = horizon_agnostic_hidden_units
self.local_mlp_hidden_units = local_mlp_hidden_units
self.local_mlp_output_units = local_mlp_output_units
self.encoder = MQCNNEncoder(self.time_step, self.static_features, self.timevarying_features,
self.num_static_features, self.num_timevarying_features)
self.decoder = MQCNNDecoder(self.time_step, self.lead_future, self.ltsp, self.future_information,
self.num_future_features, self.global_hidden_units, self.horizon_specific_hidden_units,
self.horizon_agnostic_hidden_units, self.local_mlp_hidden_units,
self.local_mlp_output_units)
def forward(self, x):
encoding = self.encoder(x)
output = self.decoder(x, encoding)
return output
def configure_optimizers(self):
optimizer = optim.SGD(self.parameters(), lr = 1e-2)
return optimizer
def training_step(self, batch, batch_idx):
x, y = batch, batch['targets']
quantiles = torch.tensor([0.5, 0.9]).view(2, 1)
outputs = self(x)
loss = self.loss(outputs, y, quantiles)
print(f'loss: {loss}')
pbar = {'train_loss': loss[0] + loss[1]}
train_loss = loss[0] + loss[1]
return {"loss": train_loss, "progress_bar": pbar}
def loss(self, outputs, targets, quantiles):
l = outputs - targets.repeat_interleave(2, dim=2)
p50 = torch.mul(torch.where(l > torch.zeros(l.shape), l, torch.zeros_like(l)), 1 - quantiles[0]) + \
torch.mul(torch.where(l < torch.zeros(l.shape), -l, torch.zeros_like(l)), quantiles[0])
p90 = torch.mul(torch.where(l > torch.zeros(l.shape), l, torch.zeros_like(l)), 1 - quantiles[1]) + \
torch.mul(torch.where(l < torch.zeros(l.shape), -l, torch.zeros_like(l)), quantiles[1])
p50 = p50.mean()
p90 = p90.mean()
print(f' p50: {p50}, p90: {p90}')
return p50, p90
class InstockMask(nn.Module):
def __init__(self, time_step, ltsp, min_instock_ratio = 0.5, eps_instock_dph = 1e-3,
eps_total_dph = 1e-3, **kwargs):
super(InstockMask, self).__init__(**kwargs)
if not eps_total_dph > 0:
raise ValueError(f"epsilon_total_dph of {eps_total_dph} is invalid! \
This parameter must be > 0 to avoid division by 0.")
self.min_instock_ratio = min_instock_ratio
self.eps_instock_dph = eps_instock_dph
self.eps_total_dph = eps_total_dph
def forward(self, demand, total_dph, instock_dph):
if total_dph is not None and instock_dph is not None:
total_dph = total_dph + self.eps_total_dph
instock_dph = instock_dph + self.eps_instock_dph
instock_rate = torch.round(instock_dph/total_dph)
demand = torch.where(instock_rate >= self.min_instock_ratio, demand,
-torch.ones_like(demand))
return demand
class _BaseInstockMask(nn.Module):
def __init__(self, time_step, ltsp, min_instock_ratio = 0.5, eps_total_dph = 1e-3,
eps_instock_dph = 1e-3, **kwargs):
super(_BaseInstockMask, self).__init__(**kwargs)
if not eps_total_dph > 0:
raise ValueError(f"epsilon_total_dph of {eps_total_dph} is invalid! \
This parameter must be > 0 to avoid division by 0.")
self.instock_mask = InstockMask(time_step, ltsp, min_instock_ratio=min_instock_ratio,
eps_instock_dph = eps_instock_dph,
eps_total_dph = eps_total_dph)
def forward(self):
raise NotImplementedError
class HorizonMask(_BaseInstockMask):
def __init__(self, time_step, ltsp, min_instock_ratio = 0.5, eps_instock_dph=1e-3,
eps_total_dph=1e-3, **kwargs):
super(HorizonMask, self).__init__(time_step, ltsp,
min_instock_ratio = min_instock_ratio,
eps_instock_dph=eps_instock_dph,
eps_total_dph=eps_total_dph, **kwargs)
self.mask_idx = _compute_horizon_mask(time_step, ltsp)
def forward(self, demand, total_dph, instock_dph):
demand_instock = self.instock_mask(demand, total_dph, instock_dph).float()
mask = mask_idx.repeat(demand_instock.shape[0], 1, 1)
print(f'demand shape: {demand_instock.shape}, mask shape: {mask_idx.shape}')
masked_demand = torch.where(mask, demand_instock,
-torch.ones_like(demand_instock))
return masked_demand
def _compute_horizon_mask(time_step, ltsp):
horizon = np.array(list(map(lambda _ltsp: _ltsp[0] + _ltsp[1], ltsp))).\
reshape((1, len(ltsp)))
forecast_date_range = np.arange(time_step).reshape((time_step, 1))
relative_distance = forecast_date_range + horizon
mask = relative_distance < time_step
return torch.tensor(mask)
class DemandExpander(nn.Module):
def __init__(self, time_step, ltsp, normalize = True,
mask_func = HorizonMask, min_instock_ratio=0.5,
eps_instock_dph = 1e-3, eps_total_dph = 1e-3, **kwargs):
super(DemandExpander, self).__init__(**kwargs)
if not eps_total_dph > 0:
raise ValueError("eps_total_dph can't be 0")
Tpred = max(map(lambda x: x[0] + x[1], ltsp))
pos_sp1 = [i for i, x in enumerate(ltsp) if x[1] == 1]
pos_spN = [i for i, x in enumerate(ltsp) if x[1] != 1]
self.pos_sp1 = pos_sp1
self.pos_spN = pos_spN
self.ltsp_kernel = _ltsp_kernel(Tpred, ltsp, normalize)
self.ltsp_idx = _ltsp_idx(time_step, Tpred)
self.demand_mask = mask_func(time_step, ltsp, min_instock_ratio=min_instock_ratio,
eps_instock_dph=eps_instock_dph,
eps_total_dph = eps_total_dph)
def forward(self, demand):
ltsp_demand = _apply_ltsp_kernel(demand, self.ltsp_idx, self.ltsp_kernel)
#ltsp_idph = _apply_ltsp_kernel(instock_dph, self.ltsp_idx, self.ltsp_kernel)
#ltsp_dph = _apply_ltsp_kernel(total_dph, self.ltsp_idx, self.ltsp_kernel)
#masked_demand = self.demand_mask(ltsp_demand, ltsp_dph, ltsp_idph)
masked_demand_sp1 = ltsp_demand[:, :, self.pos_sp1]
masked_demand_spN = ltsp_demand[:, :, self.pos_spN]
return masked_demand_sp1#, masked_demand_spN
def _ltsp_idx(time_step, Tpred):
idx = np.arange(time_step).reshape(-1, 1) + np.arange(Tpred)
return torch.tensor(idx)
def _ltsp_kernel(Tpred, ltsp, normalize = True):
ltsp_count = len(ltsp)
kernel = np.zeros((Tpred, ltsp_count), dtype = 'float32')
for i in range(len(ltsp)):
lead_time = ltsp[i][0]
span = ltsp[i][1]
if normalize:
kernel[lead_time:lead_time + span, i] = 1.0/span
else:
kernel[lead_time:lead_time + span, i] = 1.0
return torch.tensor(kernel)
def _apply_ltsp_kernel(s, ltsp_idx, ltsp_kernel):
s_ltsp = s[:, ltsp_idx].float()
return s_ltsp @ ltsp_kernel
class Dataset(Dataset):
def __init__(self, data, static_features, timevarying_features, future_information,
target, train_time_step, predict_time_step, num_quantiles, ltsp, mask_func):
self.data = data
self.train_time_step = train_time_step
self.predict_time_step = predict_time_step
self.num_quantiles = num_quantiles
self.ltsp = ltsp
self.mask_func = mask_func
self.static_features = torch.tensor(self.data.\
loc[self.data['time_idx'] < self.train_time_step][static_features].\
to_numpy(np.float64).reshape(-1, self.train_time_step, len(static_features))).float()
self.timevarying_features = torch.tensor(self.data.\
loc[self.data['time_idx'] < self.train_time_step][timevarying_features].\
to_numpy(np.float64).reshape(-1, self.train_time_step, len(timevarying_features))).float()
self.future_information = torch.tensor(self.data[future_information].\
to_numpy(np.float64).reshape(-1, (self.train_time_step + self.predict_time_step), len(future_information))).float()
self.targets = torch.tensor(self.data[target].\
to_numpy(np.float64).reshape(-1, (self.train_time_step + self.predict_time_step))).float()
self.expander = DemandExpander(self.train_time_step,
self.ltsp,
mask_func = self.mask_func)
self.targets = self.expander(self.targets)
def __len__(self):
return self.timevarying_features.shape[1]
def __getitem__(self, idx):
static_features = self.static_features[idx, :, :]
timevarying_features = self.timevarying_features[idx, :, :]
future_information = self.future_information[idx, :, :]
targets = self.targets[idx, :, :]
return dict(static_features = static_features, timevarying_features = timevarying_features,
future_information = future_information, targets = targets)
data = get_stallion_data()
# add time index
data["time_idx"] = data["date"].dt.year * 12 + data["date"].dt.month
data["time_idx"] -= data["time_idx"].min()
# add additional features
# show sample data
data.sample(10, random_state=521)
data['month'] = data['date'].dt.month
data_sorted = data.sort_values(['agency', 'sku', 'date'])
data_sorted = pd.get_dummies(data_sorted, columns=['month'])
static_cols=['avg_population_2017']
timevarying_cols=['volume', 'industry_volume', 'soda_volume', 'price_regular']
future_cols=['month_1', 'month_2','month_3', 'month_4', 'month_5', 'month_6', 'month_7', 'month_8',
'month_9', 'month_10', 'month_11', 'month_12', 'price_regular']
ltsp = [(i, 1) for i in range(6)]
len(ltsp)
training = Dataset(data_sorted,
static_features = static_cols,
timevarying_features = timevarying_cols,
future_information = future_cols,
target=['volume'],
train_time_step=54,
predict_time_step=6,
num_quantiles = 2,
ltsp = ltsp,
mask_func = HorizonMask)
MQCNN = MQCNNModel(static_cols, timevarying_cols, future_cols,
54, ltsp, 6, 50, 20, 100, 50, 10)
trainer = pl.Trainer(max_epochs = 10)
train_loader = DataLoader(training, 32)
trainer.fit(MQCNN, train_loader)
```
| github_jupyter |
```
import numpy as np
import nibabel as nb
import matplotlib.pyplot as plt
# helper function to plot 3D NIfTI
def plot_slice (fname):
# Load image
img = nb.load (fname)
data = img.get_data ()
# cut in the middle of brain
cut = int (data.shape[-1]/2) + 10
# plot data
plt.imshow (np.rot90 (data[...,cut]), cmap = 'gray')
plt.gca().set_axis_off()
# skull strip
# smooth original img
# mask smoothed img
# Example 1 : shell command line execution
# ----------------------------------------
%%bash
ANAT_NAME=sub-2019A_T1w
ANAT="/home/jiyang/Work/sub-2019A/anat/${ANAT_NAME}"
bet ${ANAT} /home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_brain -m -f 0.5
fslmaths ${ANAT} -s 2 /home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_smooth
fslmaths /home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_smooth \
-mas /home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_brain_mask \
/home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_smooth_mask
# plot
f = plt.figure (figsize=(12,4))
for i, img in enumerate(['T1w', 'T1w_smooth', 'T1w_brain_mask', 'T1w_smooth_mask']):
f.add_subplot (1, 4, i + 1)
if i == 0:
plot_slice ('/home/jiyang/Work/sub-2019A/anat/sub-2019A_%s.nii.gz' % img)
else:
plot_slice ('/home/jiyang/Work/sub-2019A/derivatives/sub-2019A_%s.nii.gz' % img)
plt.title(img)
# Example 2 : interface execution
import matplotlib.pyplot as plt
from nipype.interfaces import fsl
skullstrip = fsl.BET (in_file = "/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz",
out_file = "/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain.nii.gz",
mask = True)
skullstrip.run()
smooth = fsl.IsotropicSmooth (in_file = "/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz",
out_file = "/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth.nii.gz",
fwhm = 4)
smooth.run()
mask = fsl.ApplyMask (in_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth.nii.gz',
out_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth_brain.nii.gz',
mask_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain_mask.nii.gz')
mask.run()
# visualise
f = plt.figure (figsize = (12,4))
for i, img in enumerate (['T1w', 'T1w_smooth',
'T1w_brain_mask', 'T1w_smooth_brain']):
f.add_subplot (1, 4, i + 1)
if i == 0:
plot_slice ('/Users/jiyang/Desktop/test/anat/sub-3625A_%s.nii.gz' % img)
else:
plot_slice ('/Users/jiyang/Desktop/test/derivatives/sub-3625A_%s.nii.gz' % img)
plt.title (img)
# Example 2 can be simplified
skullstrip = fsl.BET (in_file = "/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz",
out_file = "/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain.nii.gz",
mask = True)
bet_result = skullstrip.run()
smooth = fsl.IsotropicSmooth (in_file = skullstrip.inputs.in_file,
out_file = "/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth.nii.gz",
fwhm = 4)
smooth_result = smooth.run()
# # There is a bug here bet_result.outputs.mask_file point to cwd
# mask = fsl.ApplyMask (in_file = smooth_result.outputs.out_file,
# mask_file = bet_result.outputs.mask_file,
# out_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth_brain.nii.gz')
# mask_result = mask.run()
mask = fsl.ApplyMask (in_file = smooth_result.outputs.out_file,
mask_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain_mask.nii.gz',
out_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth_brain.nii.gz')
mask_result = mask.run()
# visualise
f = plt.figure (figsize = (12, 4))
for i, img in enumerate ([skullstrip.inputs.in_file, smooth_result.outputs.out_file,
'/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain_mask.nii.gz',
mask_result.outputs.out_file]):
f.add_subplot (1, 4, i + 1)
plot_slice (img)
plt.title (img.split('/')[-1].split('.')[0].split('A_')[-1])
skullstrip.inputs.in_file
smooth_result.outputs.out_file
bet_result.outputs.mask_file
bet_result.outputs # bug with bet_result.outputs.mask_file
# Example 3 : Workflow execution
from nipype import Node, Workflow
from nipype.interfaces import fsl
from os.path import abspath # passing absolute path is clearer
in_file = abspath ('/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz')
# workflow will take care of out_file
# only need to specify the very original in_file
# bet_out_file = abspath ('/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain.nii.gz')
# smooth_out_file = abspath ('/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth.nii.gz')
skullstrip = Node (fsl.BET (in_file = in_file,
mask = True),
name = 'skullstrip')
smooth = Node (fsl.IsotropicSmooth (in_file = in_file,
fwhm = 4),
name = 'smooth')
mask = Node (fsl.ApplyMask (), name = 'mask')
# Initiate a workflow
wf = Workflow (name = 'smoothflow', base_dir = '/Users/jiyang/Desktop/test/derivatives')
# Two ways to connect nodes
#
# Way 1
# connect (source_node, "source_node_output", dest_node, "dest_node_input")
#
# Way 2
# connect ([(source_node, dest_node, [("source_node_output1", "dest_node_input1"),
# ("source_node_output2", "dest_node_input2")
# ]
# )])
#
#
# Way 1 can establish one connection at a time. Way 2 can establish multiple connections btw two nodes at once.
#
# In either case, four pieces of info are needed :
# - source node object
# - output field from source node
# - dest node object
# - input field from dest node
# Way 1
wf.connect (skullstrip, "mask_file", mask, "mask_file")
# Way 2
wf.connect ([(smooth, mask, [("out_file", "in_file")])])
# display workflow
wf.write_graph ('workflow_graph.dot')
from IPython.display import Image
Image (filename = '/Users/jiyang/Desktop/test/derivatives/smoothflow/workflow_graph.png')
wf.write_graph (graph2use = 'flat')
from IPython.display import Image
Image (filename = "/Users/jiyang/Desktop/test/derivatives/smoothflow/graph_detailed.png")
# execute
wf.base_dir = '/Users/jiyang/Desktop/test/derivatives'
wf.run()
# Note that specifying base_dir is very important (and is why we needed to use absolute paths above),
# because otherwise all outputs would be saved somewhere in temporary files.
# Unlike interfaces which by default split out results to local direcotries, Workflow engine execute
# things off in its own directory hierarchy.
f = plt.figure (figsize = (12, 4))
for i, img in enumerate (['/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz',
'/Users/jiyang/Desktop/test/derivatives/smoothflow/smooth/sub-3625A_T1w_smooth.nii.gz',
'/Users/jiyang/Desktop/test/derivatives/smoothflow/skullstrip/sub-3625A_T1w_brain_mask.nii.gz',
'/Users/jiyang/Desktop/test/derivatives/smoothflow/mask/sub-3625A_T1w_smooth_masked.nii.gz']):
f.add_subplot (1, 4, i + 1)
plot_slice (img)
!tree /Users/jiyang/Desktop/test/derivatives/smoothflow -I '*js|*json|*html|*pklz|_report'
# running workflow will return a graph object
#
# workflow does not have inputs/outputs, you can access them through Node
#
# A workflow inside a workflow
# ------------------------------------------------------------------------
#
# calling create_susan_smooth will return a workflow object
from nipype.workflows.fmri.fsl import create_susan_smooth
susan = create_susan_smooth (separate_masks = False)
```
| github_jupyter |
# Mapping water extent and rainfall using WOfS and CHIRPS
* **Products used:**
[wofs_ls](https://explorer.digitalearth.africa/products/wofs_ls),
[rainfall_chirps_monthly](https://explorer.digitalearth.africa/products/rainfall_chirps_monthly)
## Background
The United Nations have prescribed 17 "Sustainable Development Goals" (SDGs). This notebook attempts to monitor SDG Indicator 6.6.1 - change in the extent of water-related ecosystems. Indicator 6.6.1 has 4 sub-indicators:
i. The spatial extent of water-related ecosystems
ii. The quantity of water contained within these ecosystems
iii. The quality of water within these ecosystems
iv. The health or state of these ecosystems
This notebook primarily focuses on the first sub-indicator - spatial extents.
## Description
The notebook loads WOfS feature layers to map the spatial extent of water bodies. It also loads and plots monthly total rainfall from CHIRPS. The last section will compare the water extent between two periods to allow visulazing where change is occuring.
***
## Load packages
Import Python packages that are used for the analysis.
```
%matplotlib inline
import datacube
import matplotlib.pyplot as plt
from deafrica_tools.dask import create_local_dask_cluster
from deafrica_tools.datahandling import wofs_fuser
from long_term_water_extent import (
load_vector_file,
get_resampled_labels,
resample_water_observations,
resample_rainfall_observations,
calculate_change_in_extent,
compare_extent_and_rainfall,
)
```
## Set up a Dask cluster
Dask can be used to better manage memory use and conduct the analysis in parallel.
```
create_local_dask_cluster()
```
## Connect to Data Cube
```
dc = datacube.Datacube(app="long_term_water_extent")
```
## Analysis parameters
The following cell sets the parameters, which define the area of interest and the length of time to conduct the analysis over.
* Upload a vector file for your water extent and your catchment to the `data` folder.
* Set the time range you want to use.
* Set the resampling strategy. Possible options include:
* `"1Y"` - Annual resampling, use this option for longer term monitoring
* `"QS-DEC"` - Quarterly resampling from December
* `"3M"` - Three-monthly resampling
* `"1M"` - Monthly resampling
For more details on resampling timeframes, see the [xarray](https://xarray.pydata.org/en/v0.8.2/generated/xarray.Dataset.resample.html#r29) and [pandas](https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html#dateoffset-objects) documentation.
```
water_extent_vector_file = "data/lake_baringo_extent.geojson"
water_catchment_vector_file = "data/lake_baringo_catchment.geojson"
time_range = ("2018-07", "2021")
resample_strategy = "Q-DEC"
dask_chunks = dict(x=1000, y=1000)
```
## Get waterbody and catchment geometries
The next cell will extract the waterbody and catchment geometries from the supplied vector files, which will be used to load Water Observations from Space and the CHIRPS rainfall products.
```
extent, extent_geometry = load_vector_file(water_extent_vector_file)
catchment, catchment_geometry = load_vector_file(water_catchment_vector_file)
```
## Load Water Observation from Space for Waterbody
The first step is to load the Water Observations from Space product using the extent geometry.
```
extent_query = {
"time": time_range,
"resolution": (-30, 30),
"output_crs": "EPSG:6933",
"geopolygon": extent_geometry,
"group_by": "solar_day",
"dask_chunks":dask_chunks
}
wofs_ds = dc.load(product="wofs_ls", fuse_func=wofs_fuser, **extent_query)
```
### Identify water in each resampling period
The second step is to resample the observations to get a consistent measure of the waterbody, and then calculate the classified as water for each period.
```
resampled_water_ds, resampled_water_area_ds = resample_water_observations(
wofs_ds, resample_strategy
)
date_range_labels = get_resampled_labels(wofs_ds, resample_strategy)
```
### Plot the change in water area over time
```
fig, ax = plt.subplots(figsize=(15, 5))
ax.plot(
date_range_labels,
resampled_water_area_ds.values,
color="red",
marker="^",
markersize=4,
linewidth=1,
)
plt.xticks(date_range_labels, rotation=65)
plt.title(f"Observed Area of Water from {time_range[0]} to {time_range[1]}")
plt.ylabel("Waterbody area (km$^2$)")
plt.tight_layout()
```
## Load CHIRPS monthly rainfall
```
catchment_query = {
"time": time_range,
"resolution": (-5000, 5000),
"output_crs": "EPSG:6933",
"geopolygon": catchment_geometry,
"group_by": "solar_day",
"dask_chunks":dask_chunks
}
rainfall_ds = dc.load(product="rainfall_chirps_monthly", **catchment_query)
```
### Resample to estimate rainfall for each time period
This is done by taking calculating the average rainfall over the extent of the catchment, then summing these averages over the resampling period to estimate the total rainfall for the catchment.
```
catchment_rainfall_resampled_ds = resample_rainfall_observations(
rainfall_ds, resample_strategy, catchment
)
```
## Compare waterbody area to catchment rainfall
This step plots the summed average rainfall for the catchment area over each period as a histogram, overlaid with the waterbody area calculated previously.
```
figure = compare_extent_and_rainfall(
resampled_water_area_ds, catchment_rainfall_resampled_ds, "mm", date_range_labels
)
```
### Save the figure
```
figure.savefig("waterarea_and_rainfall.png", bbox_inches="tight")
```
## Compare water extent for two different periods
For the next step, enter a baseline date, and an analysis date to construct a plot showing where water appeared, as well as disappeared, by comparing the two dates.
```
baseline_time = "2018-07-01"
analysis_time = "2021-10-01"
figure = calculate_change_in_extent(baseline_time, analysis_time, resampled_water_ds)
```
### Save figure
```
figure.savefig("waterarea_change.png", bbox_inches="tight")
```
---
## Additional information
**License:** The code in this notebook is licensed under the [Apache License, Version 2.0](https://www.apache.org/licenses/LICENSE-2.0).
Digital Earth Africa data is licensed under the [Creative Commons by Attribution 4.0](https://creativecommons.org/licenses/by/4.0/) license.
**Contact:** If you need assistance, please post a question on the [Open Data Cube Slack channel](http://slack.opendatacube.org/) or on the [GIS Stack Exchange](https://gis.stackexchange.com/questions/ask?tags=open-data-cube) using the `open-data-cube` tag (you can view previously asked questions [here](https://gis.stackexchange.com/questions/tagged/open-data-cube)).
If you would like to report an issue with this notebook, you can file one on [Github](https://github.com/digitalearthafrica/deafrica-sandbox-notebooks).
**Compatible datacube version:**
```
print(datacube.__version__)
```
**Last Tested:**
```
from datetime import datetime
datetime.today().strftime('%Y-%m-%d')
```
| github_jupyter |
# Overview
1. Project Instructions & Prerequisites
2. Learning Objectives
3. Data Preparation
4. Create Categorical Features with TF Feature Columns
5. Create Continuous/Numerical Features with TF Feature Columns
6. Build Deep Learning Regression Model with Sequential API and TF Probability Layers
7. Evaluating Potential Model Biases with Aequitas Toolkit
# 1. Project Instructions & Prerequisites
## Project Instructions
**Context**: EHR data is becoming a key source of real-world evidence (RWE) for the pharmaceutical industry and regulators to [make decisions on clinical trials](https://www.fda.gov/news-events/speeches-fda-officials/breaking-down-barriers-between-clinical-trials-and-clinical-care-incorporating-real-world-evidence). You are a data scientist for an exciting unicorn healthcare startup that has created a groundbreaking diabetes drug that is ready for clinical trial testing. It is a very unique and sensitive drug that requires administering the drug over at least 5-7 days of time in the hospital with frequent monitoring/testing and patient medication adherence training with a mobile application. You have been provided a patient dataset from a client partner and are tasked with building a predictive model that can identify which type of patients the company should focus their efforts testing this drug on. Target patients are people that are likely to be in the hospital for this duration of time and will not incur significant additional costs for administering this drug to the patient and monitoring.
In order to achieve your goal you must build a regression model that can predict the estimated hospitalization time for a patient and use this to select/filter patients for your study.
**Expected Hospitalization Time Regression Model:** Utilizing a synthetic dataset(denormalized at the line level augmentation) built off of the UCI Diabetes readmission dataset, students will build a regression model that predicts the expected days of hospitalization time and then convert this to a binary prediction of whether to include or exclude that patient from the clinical trial.
This project will demonstrate the importance of building the right data representation at the encounter level, with appropriate filtering and preprocessing/feature engineering of key medical code sets. This project will also require students to analyze and interpret their model for biases across key demographic groups.
Please see the project rubric online for more details on the areas your project will be evaluated.
### Dataset
Due to healthcare PHI regulations (HIPAA, HITECH), there are limited number of publicly available datasets and some datasets require training and approval. So, for the purpose of this exercise, we are using a dataset from UC Irvine(https://archive.ics.uci.edu/ml/datasets/Diabetes+130-US+hospitals+for+years+1999-2008) that has been modified for this course. Please note that it is limited in its representation of some key features such as diagnosis codes which are usually an unordered list in 835s/837s (the HL7 standard interchange formats used for claims and remits).
**Data Schema**
The dataset reference information can be https://github.com/udacity/nd320-c1-emr-data-starter/blob/master/project/data_schema_references/
. There are two CSVs that provide more details on the fields and some of the mapped values.
## Project Submission
When submitting this project, make sure to run all the cells before saving the notebook. Save the notebook file as "student_project_submission.ipynb" and save another copy as an HTML file by clicking "File" -> "Download as.."->"html". Include the "utils.py" and "student_utils.py" files in your submission. The student_utils.py should be where you put most of your code that you write and the summary and text explanations should be written inline in the notebook. Once you download these files, compress them into one zip file for submission.
## Prerequisites
- Intermediate level knowledge of Python
- Basic knowledge of probability and statistics
- Basic knowledge of machine learning concepts
- Installation of Tensorflow 2.0 and other dependencies(conda environment.yml or virtualenv requirements.txt file provided)
## Environment Setup
For step by step instructions on creating your environment, please go to https://github.com/udacity/nd320-c1-emr-data-starter/blob/master/project/README.md.
# 2. Learning Objectives
By the end of the project, you will be able to
- Use the Tensorflow Dataset API to scalably extract, transform, and load datasets and build datasets aggregated at the line, encounter, and patient data levels(longitudinal)
- Analyze EHR datasets to check for common issues (data leakage, statistical properties, missing values, high cardinality) by performing exploratory data analysis.
- Create categorical features from Key Industry Code Sets (ICD, CPT, NDC) and reduce dimensionality for high cardinality features by using embeddings
- Create derived features(bucketing, cross-features, embeddings) utilizing Tensorflow feature columns on both continuous and categorical input features
- SWBAT use the Tensorflow Probability library to train a model that provides uncertainty range predictions that allow for risk adjustment/prioritization and triaging of predictions
- Analyze and determine biases for a model for key demographic groups by evaluating performance metrics across groups by using the Aequitas framework
# 3. Data Preparation
```
# from __future__ import absolute_import, division, print_function, unicode_literals
import os
import numpy as np
import seaborn as sns
import tensorflow as tf
from tensorflow.keras import layers
import tensorflow_probability as tfp
import matplotlib.pyplot as plt
import pandas as pd
import aequitas as ae
from sklearn.metrics import roc_auc_score, accuracy_score, f1_score, classification_report, precision_score, recall_score
# Put all of the helper functions in utils
from utils import build_vocab_files, show_group_stats_viz, aggregate_dataset, preprocess_df, df_to_dataset, posterior_mean_field, prior_trainable
from functools import partial
pd.set_option('display.max_columns', 500)
# this allows you to make changes and save in student_utils.py and the file is reloaded every time you run a code block
%load_ext autoreload
%autoreload
#OPEN ISSUE ON MAC OSX for TF model training
import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'
```
## Dataset Loading and Schema Review
Load the dataset and view a sample of the dataset along with reviewing the schema reference files to gain a deeper understanding of the dataset. The dataset is located at the following path https://github.com/udacity/nd320-c1-emr-data-starter/blob/master/project/starter_code/data/final_project_dataset.csv. Also, review the information found in the data schema https://github.com/udacity/nd320-c1-emr-data-starter/blob/master/project/data_schema_references/
```
dataset_path = "./data/final_project_dataset.csv"
df = pd.read_csv(dataset_path)
# Line Test
try:
assert len(df) > df['encounter_id'].nunique()
print("Dataset could be at the line level")
except:
print("Dataset is not at the line level")
```
## Determine Level of Dataset (Line or Encounter)
**Question 1**: Based off of analysis of the data, what level is this dataset? Is it at the line or encounter level? Are there any key fields besides the encounter_id and patient_nbr fields that we should use to aggregate on? Knowing this information will help inform us what level of aggregation is necessary for future steps and is a step that is often overlooked.
**Student Response** : The dataset is at line level and needs to be converted to encounter level. The dataset should be aggregated on encounter_id, patient_nbr and principal_diagnosis_code.
## Analyze Dataset
**Question 2**: Utilizing the library of your choice (recommend Pandas and Seaborn or matplotlib though), perform exploratory data analysis on the dataset. In particular be sure to address the following questions:
- a. Field(s) with high amount of missing/zero values
- b. Based off the frequency histogram for each numerical field, which numerical field(s) has/have a Gaussian(normal) distribution shape?
- c. Which field(s) have high cardinality and why (HINT: ndc_code is one feature)
- d. Please describe the demographic distributions in the dataset for the age and gender fields.
**OPTIONAL**: Use the Tensorflow Data Validation and Analysis library to complete.
- The Tensorflow Data Validation and Analysis library(https://www.tensorflow.org/tfx/data_validation/get_started) is a useful tool for analyzing and summarizing dataset statistics. It is especially useful because it can scale to large datasets that do not fit into memory.
- Note that there are some bugs that are still being resolved with Chrome v80 and we have moved away from using this for the project.
**Student Response**:
1. Fields with high amount of missing/null values are:
*weight, payer_code, medical_speciality, number_outpatients, number_inpatients, number_emergency, num_procedures, ndc_codes.*
1. Numerical values having Gaussian Distribution are: *num_lab_procedures, number_medication.*
1. Fields having high cardinality are: *encounter_id, patient_nbr, other_diagnosis_codes.* It is because there there are 71,518 patients and more than 1 Lac encounters in the dataset and each encounter have various diagnoisis codes. This can also be reviewed by looking the Tensorflow Data Validation statistics.
1. Demographic distributions is shown below.
```
def check_null_df(df):
return pd.DataFrame({
'percent_null' : df.isna().sum() / len(df) * 100,
'percent_zero' : df.isin([0]).sum() / len(df) * 100,
'percent_missing' : df.isin(['?', '?|?', 'Unknown/Invalid']).sum() / len(df) * 100,
})
check_null_df(df)
plt.figure(figsize=(8, 5))
sns.countplot(x = 'age', data = df)
plt.figure(figsize=(8, 5))
sns.countplot(x = 'gender', data = df)
plt.figure(figsize=(8, 5))
sns.countplot(x = 'age', hue = 'gender', data = df)
plt.figure(figsize=(8, 5))
sns.distplot(df['num_lab_procedures'])
plt.figure(figsize=(8, 5))
sns.distplot(df['num_medications'])
######NOTE: The visualization will only display in Chrome browser. ########
# First install below libraries and then restart the kernel to visualize.
# !pip install tensorflow-data-validation
# !pip install apache-beam[interactive]
import tensorflow_data_validation as tfdv
full_data_stats = tfdv.generate_statistics_from_dataframe(dataframe=df)
tfdv.visualize_statistics(full_data_stats)
schema = tfdv.infer_schema(statistics=full_data_stats)
tfdv.display_schema(schema=schema)
categorical_columns_list = ['A1Cresult', 'age', 'change', 'gender', 'max_glu_serum', 'medical_specialty', 'payer_code', 'race',
'readmitted', 'weight']
def count_unique_values(df):
cat_df = df
return pd.DataFrame({
'columns' : cat_df.columns,
'cardinality' : cat_df.nunique()
}).reset_index(drop = True).sort_values(by = 'cardinality', ascending = False)
count_unique_values(df)
```
## Reduce Dimensionality of the NDC Code Feature
**Question 3**: NDC codes are a common format to represent the wide variety of drugs that are prescribed for patient care in the United States. The challenge is that there are many codes that map to the same or similar drug. You are provided with the ndc drug lookup file https://github.com/udacity/nd320-c1-emr-data-starter/blob/master/project/data_schema_references/ndc_lookup_table.csv derived from the National Drug Codes List site(https://ndclist.com/). Please use this file to come up with a way to reduce the dimensionality of this field and create a new field in the dataset called "generic_drug_name" in the output dataframe.
```
#NDC code lookup file
ndc_code_path = "./medication_lookup_tables/final_ndc_lookup_table"
ndc_code_df = pd.read_csv(ndc_code_path)
from student_utils import reduce_dimension_ndc
def reduce_dimension_ndc(df, ndc_code_df):
'''
df: pandas dataframe, input dataset
ndc_df: pandas dataframe, drug code dataset used for mapping in generic names
return:
df: pandas dataframe, output dataframe with joined generic drug name
'''
mapping = dict(ndc_code_df[['NDC_Code', 'Non-proprietary Name']].values)
mapping['nan'] = np.nan
df['generic_drug_name'] = df['ndc_code'].astype(str).apply(lambda x : mapping[x])
return df
reduce_dim_df = reduce_dimension_ndc(df, ndc_code_df)
reduce_dim_df.head()
# Number of unique values should be less for the new output field
assert df['ndc_code'].nunique() > reduce_dim_df['generic_drug_name'].nunique()
print('Number of ndc_code: ', df['ndc_code'].nunique())
print('Number of drug name: ', reduce_dim_df['generic_drug_name'].nunique())
```
## Select First Encounter for each Patient
**Question 4**: In order to simplify the aggregation of data for the model, we will only select the first encounter for each patient in the dataset. This is to reduce the risk of data leakage of future patient encounters and to reduce complexity of the data transformation and modeling steps. We will assume that sorting in numerical order on the encounter_id provides the time horizon for determining which encounters come before and after another.
```
def select_first_encounter(df):
'''
df: pandas dataframe, dataframe with all encounters
return:
- first_encounter_df: pandas dataframe, dataframe with only the first encounter for a given patient
'''
df.sort_values(by = 'encounter_id')
first_encounters = df.groupby('patient_nbr')['encounter_id'].first().values
first_encounter_df = df[df['encounter_id'].isin(first_encounters)]
# first_encounter_df = first_encounter_df.groupby('encounter_id').first().reset_index()
return first_encounter_df
first_encounter_df = select_first_encounter(reduce_dim_df)
first_encounter_df.head()
# unique patients in transformed dataset
unique_patients = first_encounter_df['patient_nbr'].nunique()
print("Number of unique patients:{}".format(unique_patients))
# unique encounters in transformed dataset
unique_encounters = first_encounter_df['encounter_id'].nunique()
print("Number of unique encounters:{}".format(unique_encounters))
original_unique_patient_number = reduce_dim_df['patient_nbr'].nunique()
# number of unique patients should be equal to the number of unique encounters and patients in the final dataset
assert original_unique_patient_number == unique_patients
assert original_unique_patient_number == unique_encounters
print("Tests passed!!")
```
## Aggregate Dataset to Right Level for Modeling
In order to provide a broad scope of the steps and to prevent students from getting stuck with data transformations, we have selected the aggregation columns and provided a function to build the dataset at the appropriate level. The 'aggregate_dataset" function that you can find in the 'utils.py' file can take the preceding dataframe with the 'generic_drug_name' field and transform the data appropriately for the project.
To make it simpler for students, we are creating dummy columns for each unique generic drug name and adding those are input features to the model. There are other options for data representation but this is out of scope for the time constraints of the course.
```
exclusion_list = [ 'generic_drug_name', 'ndc_code']
grouping_field_list = [c for c in first_encounter_df.columns if c not in exclusion_list]
agg_drug_df, ndc_col_list = aggregate_dataset(first_encounter_df, grouping_field_list, 'generic_drug_name')
assert len(agg_drug_df) == agg_drug_df['patient_nbr'].nunique() == agg_drug_df['encounter_id'].nunique()
ndc_col_list
```
## Prepare Fields and Cast Dataset
### Feature Selection
**Question 5**: After you have aggregated the dataset to the right level, we can do feature selection (we will include the ndc_col_list, dummy column features too). In the block below, please select the categorical and numerical features that you will use for the model, so that we can create a dataset subset.
For the payer_code and weight fields, please provide whether you think we should include/exclude the field in our model and give a justification/rationale for this based off of the statistics of the data. Feel free to use visualizations or summary statistics to support your choice.
**Student response**: We should exclude both payer_code and weight in our model because of large missing values.
```
plt.figure(figsize=(8, 5))
sns.countplot(x = 'payer_code', data = agg_drug_df)
plt.figure(figsize=(8, 5))
sns.countplot(x = 'number_emergency', data = agg_drug_df)
count_unique_values(agg_drug_df[grouping_field_list])
'''
Please update the list to include the features you think are appropriate for the model
and the field that we will be using to train the model. There are three required demographic features for the model
and I have inserted a list with them already in the categorical list.
These will be required for later steps when analyzing data splits and model biases.
'''
required_demo_col_list = ['race', 'gender', 'age']
student_categorical_col_list = [ 'change', 'primary_diagnosis_code'
] + required_demo_col_list + ndc_col_list
student_numerical_col_list = [ 'number_inpatient', 'number_emergency', 'num_lab_procedures', 'number_diagnoses','num_medications','num_procedures']
PREDICTOR_FIELD = 'time_in_hospital'
def select_model_features(df, categorical_col_list, numerical_col_list, PREDICTOR_FIELD, grouping_key='patient_nbr'):
selected_col_list = [grouping_key] + [PREDICTOR_FIELD] + categorical_col_list + numerical_col_list
return agg_drug_df[selected_col_list]
selected_features_df = select_model_features(agg_drug_df, student_categorical_col_list, student_numerical_col_list,
PREDICTOR_FIELD)
```
### Preprocess Dataset - Casting and Imputing
We will cast and impute the dataset before splitting so that we do not have to repeat these steps across the splits in the next step. For imputing, there can be deeper analysis into which features to impute and how to impute but for the sake of time, we are taking a general strategy of imputing zero for only numerical features.
OPTIONAL: What are some potential issues with this approach? Can you recommend a better way and also implement it?
```
processed_df = preprocess_df(selected_features_df, student_categorical_col_list,
student_numerical_col_list, PREDICTOR_FIELD, categorical_impute_value='nan', numerical_impute_value=0)
```
## Split Dataset into Train, Validation, and Test Partitions
**Question 6**: In order to prepare the data for being trained and evaluated by a deep learning model, we will split the dataset into three partitions, with the validation partition used for optimizing the model hyperparameters during training. One of the key parts is that we need to be sure that the data does not accidently leak across partitions.
Please complete the function below to split the input dataset into three partitions(train, validation, test) with the following requirements.
- Approximately 60%/20%/20% train/validation/test split
- Randomly sample different patients into each data partition
- **IMPORTANT** Make sure that a patient's data is not in more than one partition, so that we can avoid possible data leakage.
- Make sure that the total number of unique patients across the splits is equal to the total number of unique patients in the original dataset
- Total number of rows in original dataset = sum of rows across all three dataset partitions
```
def patient_dataset_splitter(df, patient_key='patient_nbr'):
'''
df: pandas dataframe, input dataset that will be split
patient_key: string, column that is the patient id
return:
- train: pandas dataframe,
- validation: pandas dataframe,
- test: pandas dataframe,
'''
df[student_numerical_col_list] = df[student_numerical_col_list].astype(float)
train_val_df = df.sample(frac = 0.8, random_state=3)
train_df = train_val_df.sample(frac = 0.8, random_state=3)
val_df = train_val_df.drop(train_df.index)
test_df = df.drop(train_val_df.index)
return train_df.reset_index(drop = True), val_df.reset_index(drop = True), test_df.reset_index(drop = True)
#from student_utils import patient_dataset_splitter
d_train, d_val, d_test = patient_dataset_splitter(processed_df, 'patient_nbr')
assert len(d_train) + len(d_val) + len(d_test) == len(processed_df)
print("Test passed for number of total rows equal!")
assert (d_train['patient_nbr'].nunique() + d_val['patient_nbr'].nunique() + d_test['patient_nbr'].nunique()) == agg_drug_df['patient_nbr'].nunique()
print("Test passed for number of unique patients being equal!")
```
## Demographic Representation Analysis of Split
After the split, we should check to see the distribution of key features/groups and make sure that there is representative samples across the partitions. The show_group_stats_viz function in the utils.py file can be used to group and visualize different groups and dataframe partitions.
### Label Distribution Across Partitions
Below you can see the distributution of the label across your splits. Are the histogram distribution shapes similar across partitions?
```
show_group_stats_viz(processed_df, PREDICTOR_FIELD)
show_group_stats_viz(d_train, PREDICTOR_FIELD)
show_group_stats_viz(d_test, PREDICTOR_FIELD)
```
## Demographic Group Analysis
We should check that our partitions/splits of the dataset are similar in terms of their demographic profiles. Below you can see how we might visualize and analyze the full dataset vs. the partitions.
```
# Full dataset before splitting
patient_demo_features = ['race', 'gender', 'age', 'patient_nbr']
patient_group_analysis_df = processed_df[patient_demo_features].groupby('patient_nbr').head(1).reset_index(drop=True)
show_group_stats_viz(patient_group_analysis_df, 'gender')
# Training partition
show_group_stats_viz(d_train, 'gender')
# Test partition
show_group_stats_viz(d_test, 'gender')
```
## Convert Dataset Splits to TF Dataset
We have provided you the function to convert the Pandas dataframe to TF tensors using the TF Dataset API.
Please note that this is not a scalable method and for larger datasets, the 'make_csv_dataset' method is recommended -https://www.tensorflow.org/api_docs/python/tf/data/experimental/make_csv_dataset.
```
# Convert dataset from Pandas dataframes to TF dataset
batch_size = 128
diabetes_train_ds = df_to_dataset(d_train, PREDICTOR_FIELD, batch_size=batch_size)
diabetes_val_ds = df_to_dataset(d_val, PREDICTOR_FIELD, batch_size=batch_size)
diabetes_test_ds = df_to_dataset(d_test, PREDICTOR_FIELD, batch_size=batch_size)
# We use this sample of the dataset to show transformations later
diabetes_batch = next(iter(diabetes_train_ds))[0]
def demo(feature_column, example_batch):
feature_layer = tf.keras.layers.DenseFeatures(feature_column)
print(feature_layer(example_batch))
```
# 4. Create Categorical Features with TF Feature Columns
## Build Vocabulary for Categorical Features
Before we can create the TF categorical features, we must first create the vocab files with the unique values for a given field that are from the **training** dataset. Below we have provided a function that you can use that only requires providing the pandas train dataset partition and the list of the categorical columns in a list format. The output variable 'vocab_file_list' will be a list of the file paths that can be used in the next step for creating the categorical features.
```
vocab_file_list = build_vocab_files(d_train, student_categorical_col_list)
assert len(vocab_file_list) == len(student_categorical_col_list)
```
## Create Categorical Features with Tensorflow Feature Column API
**Question 7**: Using the vocab file list from above that was derived fromt the features you selected earlier, please create categorical features with the Tensorflow Feature Column API, https://www.tensorflow.org/api_docs/python/tf/feature_column. Below is a function to help guide you.
```
def create_tf_categorical_feature_cols(categorical_col_list,
vocab_dir='./diabetes_vocab/'):
'''
categorical_col_list: list, categorical field list that will be transformed with TF feature column
vocab_dir: string, the path where the vocabulary text files are located
return:
output_tf_list: list of TF feature columns
'''
output_tf_list = []
for c in categorical_col_list:
vocab_file_path = os.path.join(vocab_dir, c + "_vocab.txt")
'''
Which TF function allows you to read from a text file and create a categorical feature
You can use a pattern like this below...
tf_categorical_feature_column = tf.feature_column.......
'''
diagnosis_vocab = tf.feature_column.categorical_column_with_vocabulary_file(c, vocab_file_path, num_oov_buckets = 1)
tf_categorical_feature_column = tf.feature_column.indicator_column(diagnosis_vocab)
output_tf_list.append(tf_categorical_feature_column)
return output_tf_list
tf_cat_col_list = create_tf_categorical_feature_cols(student_categorical_col_list)
test_cat_var1 = tf_cat_col_list[0]
print("Example categorical field:\n{}".format(test_cat_var1))
demo(test_cat_var1, diabetes_batch)
```
# 5. Create Numerical Features with TF Feature Columns
**Question 8**: Using the TF Feature Column API(https://www.tensorflow.org/api_docs/python/tf/feature_column/), please create normalized Tensorflow numeric features for the model. Try to use the z-score normalizer function below to help as well as the 'calculate_stats_from_train_data' function.
```
from student_utils import create_tf_numeric_feature
def create_tf_numeric_feature(col, MEAN, STD, default_value=0):
'''
col: string, input numerical column name
MEAN: the mean for the column in the training data
STD: the standard deviation for the column in the training data
default_value: the value that will be used for imputing the field
return:
tf_numeric_feature: tf feature column representation of the input field
'''
normalizer_fn = lambda col, m, s : (col - m) / s
normalizer = partial(normalizer_fn, m = MEAN, s = STD)
tf_numeric_feature = tf.feature_column.numeric_column(col, normalizer_fn = normalizer, dtype = tf.float64,
default_value = default_value)
return tf_numeric_feature
```
For simplicity the create_tf_numerical_feature_cols function below uses the same normalizer function across all features(z-score normalization) but if you have time feel free to analyze and adapt the normalizer based off the statistical distributions. You may find this as a good resource in determining which transformation fits best for the data https://developers.google.com/machine-learning/data-prep/transform/normalization.
```
def calculate_stats_from_train_data(df, col):
mean = df[col].describe()['mean']
std = df[col].describe()['std']
return mean, std
def create_tf_numerical_feature_cols(numerical_col_list, train_df):
tf_numeric_col_list = []
for c in numerical_col_list:
mean, std = calculate_stats_from_train_data(train_df, c)
tf_numeric_feature = create_tf_numeric_feature(c, mean, std)
tf_numeric_col_list.append(tf_numeric_feature)
return tf_numeric_col_list
tf_cont_col_list = create_tf_numerical_feature_cols(student_numerical_col_list, d_train)
test_cont_var1 = tf_cont_col_list[0]
print("Example continuous field:\n{}\n".format(test_cont_var1))
demo(test_cont_var1, diabetes_batch)
```
# 6. Build Deep Learning Regression Model with Sequential API and TF Probability Layers
## Use DenseFeatures to combine features for model
Now that we have prepared categorical and numerical features using Tensorflow's Feature Column API, we can combine them into a dense vector representation for the model. Below we will create this new input layer, which we will call 'claim_feature_layer'.
```
claim_feature_columns = tf_cat_col_list + tf_cont_col_list
claim_feature_layer = tf.keras.layers.DenseFeatures(claim_feature_columns)
```
## Build Sequential API Model from DenseFeatures and TF Probability Layers
Below we have provided some boilerplate code for building a model that connects the Sequential API, DenseFeatures, and Tensorflow Probability layers into a deep learning model. There are many opportunities to further optimize and explore different architectures through benchmarking and testing approaches in various research papers, loss and evaluation metrics, learning curves, hyperparameter tuning, TF probability layers, etc. Feel free to modify and explore as you wish.
**OPTIONAL**: Come up with a more optimal neural network architecture and hyperparameters. Share the process in discovering the architecture and hyperparameters.
```
def build_sequential_model(feature_layer):
model = tf.keras.Sequential([
feature_layer,
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(64, activation='relu'),
tfp.layers.DenseVariational(1+1, posterior_mean_field, prior_trainable),
tfp.layers.DistributionLambda(
lambda t:tfp.distributions.Normal(loc=t[..., :1],
scale=1e-3 + tf.math.softplus(0.01 * t[...,1:])
)
),
])
return model
def build_diabetes_model(train_ds, val_ds, feature_layer, epochs=5, loss_metric='mse'):
model = build_sequential_model(feature_layer)
model.compile(optimizer='rmsprop', loss=loss_metric, metrics=[loss_metric])
early_stop = tf.keras.callbacks.EarlyStopping(monitor=loss_metric, patience=3)
model_checkpoint = tf.keras.callbacks.ModelCheckpoint('saved_models/bestmodel.h5', monitor='val_loss', verbose=0, save_best_only=True, mode='auto')
history = model.fit(train_ds, validation_data=val_ds,
callbacks=[early_stop],
epochs=epochs)
return model, history
diabetes_model, history = build_diabetes_model(diabetes_train_ds, diabetes_val_ds, claim_feature_layer, epochs=20)
```
## Show Model Uncertainty Range with TF Probability
**Question 9**: Now that we have trained a model with TF Probability layers, we can extract the mean and standard deviation for each prediction. Please fill in the answer for the m and s variables below. The code for getting the predictions is provided for you below.
```
feature_list = student_categorical_col_list + student_numerical_col_list
diabetes_x_tst = dict(d_test[feature_list])
diabetes_yhat = diabetes_model(diabetes_x_tst)
preds = diabetes_model.predict(diabetes_test_ds)
def get_mean_std_from_preds(diabetes_yhat):
'''
diabetes_yhat: TF Probability prediction object
'''
m = diabetes_yhat.mean()
s = diabetes_yhat.stddev()
return m, s
m, s = get_mean_std_from_preds(diabetes_yhat)
```
## Show Prediction Output
```
prob_outputs = {
"pred": preds.flatten(),
"actual_value": d_test['time_in_hospital'].values,
"pred_mean": m.numpy().flatten(),
"pred_std": s.numpy().flatten()
}
prob_output_df = pd.DataFrame(prob_outputs)
prob_output_df.head()
```
## Convert Regression Output to Classification Output for Patient Selection
**Question 10**: Given the output predictions, convert it to a binary label for whether the patient meets the time criteria or does not (HINT: use the mean prediction numpy array). The expected output is a numpy array with a 1 or 0 based off if the prediction meets or doesnt meet the criteria.
```
def get_student_binary_prediction(df, col):
'''
df: pandas dataframe prediction output dataframe
col: str, probability mean prediction field
return:
student_binary_prediction: pandas dataframe converting input to flattened numpy array and binary labels
'''
student_binary_prediction = df[col].apply(lambda x : 1 if x >= 5 else 0)
return student_binary_prediction
student_binary_prediction = get_student_binary_prediction(prob_output_df, 'pred_mean')
```
### Add Binary Prediction to Test Dataframe
Using the student_binary_prediction output that is a numpy array with binary labels, we can use this to add to a dataframe to better visualize and also to prepare the data for the Aequitas toolkit. The Aequitas toolkit requires that the predictions be mapped to a binary label for the predictions (called 'score' field) and the actual value (called 'label_value').
```
def add_pred_to_test(test_df, pred_np, demo_col_list):
for c in demo_col_list:
test_df[c] = test_df[c].astype(str)
test_df['score'] = pred_np
test_df['label_value'] = test_df['time_in_hospital'].apply(lambda x: 1 if x >=5 else 0)
return test_df
pred_test_df = add_pred_to_test(d_test, student_binary_prediction, ['race', 'gender'])
pred_test_df[['patient_nbr', 'gender', 'race', 'time_in_hospital', 'score', 'label_value']].head()
```
## Model Evaluation Metrics
**Question 11**: Now it is time to use the newly created binary labels in the 'pred_test_df' dataframe to evaluate the model with some common classification metrics. Please create a report summary of the performance of the model and be sure to give the ROC AUC, F1 score(weighted), class precision and recall scores.
For the report please be sure to include the following three parts:
- With a non-technical audience in mind, explain the precision-recall tradeoff in regard to how you have optimized your model.
- What are some areas of improvement for future iterations?
### Precision-Recall Tradeoff
* Tradeoff means increasing one parameter leads to decreasing of the other.
* Precision is the fraction of correct positives among the total predicted positives.
* Recall is the fraction of correct positives among the total positives in the dataset.
* precision-recall tradeoff occur due to increasing one of the parameter(precision or recall) while keeping the model same.
### Improvements
* Recall seems to be quite low, so we can further try to improve the score.
```
# AUC, F1, precision and recall
# Summary
print(classification_report(pred_test_df['label_value'], pred_test_df['score']))
f1_score(pred_test_df['label_value'], pred_test_df['score'], average='weighted')
accuracy_score(pred_test_df['label_value'], pred_test_df['score'])
roc_auc_score(pred_test_df['label_value'], pred_test_df['score'])
precision_score(pred_test_df['label_value'], pred_test_df['score'])
recall_score(pred_test_df['label_value'], pred_test_df['score'])
```
# 7. Evaluating Potential Model Biases with Aequitas Toolkit
## Prepare Data For Aequitas Bias Toolkit
Using the gender and race fields, we will prepare the data for the Aequitas Toolkit.
```
# Aequitas
from aequitas.preprocessing import preprocess_input_df
from aequitas.group import Group
from aequitas.plotting import Plot
from aequitas.bias import Bias
from aequitas.fairness import Fairness
ae_subset_df = pred_test_df[['race', 'gender', 'score', 'label_value']]
ae_df, _ = preprocess_input_df(ae_subset_df)
g = Group()
xtab, _ = g.get_crosstabs(ae_df)
absolute_metrics = g.list_absolute_metrics(xtab)
clean_xtab = xtab.fillna(-1)
aqp = Plot()
b = Bias()
```
## Reference Group Selection
Below we have chosen the reference group for our analysis but feel free to select another one.
```
# test reference group with Caucasian Male
bdf = b.get_disparity_predefined_groups(clean_xtab,
original_df=ae_df,
ref_groups_dict={'race':'Caucasian', 'gender':'Male'
},
alpha=0.05,
check_significance=False)
f = Fairness()
fdf = f.get_group_value_fairness(bdf)
```
## Race and Gender Bias Analysis for Patient Selection
**Question 12**: For the gender and race fields, please plot two metrics that are important for patient selection below and state whether there is a significant bias in your model across any of the groups along with justification for your statement.
```
# Plot two metrics
# Is there significant bias in your model for either race or gender?
aqp.plot_group_metric(clean_xtab, 'fpr', min_group_size=0.05)
aqp.plot_group_metric(clean_xtab, 'tpr', min_group_size=0.05)
aqp.plot_group_metric(clean_xtab, 'fnr', min_group_size=0.05)
aqp.plot_group_metric(clean_xtab, 'tnr', min_group_size=0.05)
```
#### There isn't any significant bias in the model for either race or gender.
## Fairness Analysis Example - Relative to a Reference Group
**Question 13**: Earlier we defined our reference group and then calculated disparity metrics relative to this grouping. Please provide a visualization of the fairness evaluation for this reference group and analyze whether there is disparity.
```
# Reference group fairness plot
aqp.plot_fairness_disparity(bdf, group_metric='fnr', attribute_name='race', significance_alpha=0.05, min_group_size=0.05)
aqp.plot_fairness_disparity(fdf, group_metric='fnr', attribute_name='gender', significance_alpha=0.05, min_group_size=0.05)
aqp.plot_fairness_disparity(fdf, group_metric='fpr', attribute_name='race', significance_alpha=0.05, min_group_size=0.05)
```
#### There isn't any disparity in the model for either race or gender.
```
aqp.plot_fairness_group(fdf, group_metric='fpr', title=True, min_group_size=0.05)
aqp.plot_fairness_group(fdf, group_metric='fnr', title=True)
```
#### Nearly all races and gender seem to have the same probability of falsely non-identifying them. The model is unbiased towards race or gender.
| github_jupyter |
<font size ='3'>*First, let's read in the data and necessary libraries*<font/>
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from mypy import print_side_by_side
from mypy import display_side_by_side
#https://stackoverflow.com/a/44923103/8067752
%matplotlib inline
pd.options.mode.chained_assignment = None
b_cal = pd.read_csv('boston_calendar.csv')
s_cal = pd.read_csv('seatle_calendar.csv')
b_list = pd.read_csv('boston_listings.csv')
s_list = pd.read_csv('seatle_listings.csv')
b_rev = pd.read_csv('boston_reviews.csv')
s_rev = pd.read_csv('seatle_reviews.csv')
```
_______________________________________________________________________________________________________________________
## Task 1: Business Understanding <font size="2"> *(With some Data Preperation)*</font>
<font size="3"> *My work flow will be as follows, I will explore the data with some cleaning to get enough insights to formulate questions, then, within every question I will follow the rest of the steps of the CRISP-DM framework.*</font>
### Step 1: Basic Exploration with some cleaning
<font size ='3'>*To be familiarized with the Data and to gather insights to formulate questions*<font/>
> **Boston & Seatle Calendar**
```
display_side_by_side(b_cal.head(), s_cal.head(), titles = ['b_cal', 's_cal'])
```
<font size ='3'>*Check the sizes of cols and rows & check Nulls*<font/>
```
print_side_by_side('Boston Cal:', 'Seatle Cal:', b=0)
print_side_by_side('Shape:',b_cal.shape,"Shape:", s_cal.shape)
print_side_by_side("Cols with nulls: ", b_cal.isnull().sum()[b_cal.isnull().sum()>0].index[0],"Cols with nulls: ", s_cal.isnull().sum()[s_cal.isnull().sum()>0].index[0])
print_side_by_side("Null prop of price column: ", round(b_cal.price.isnull().sum()/b_cal.shape[0], 2),"Null prop of price column: ", round(s_cal.price.isnull().sum()/s_cal.shape[0], 2))
print_side_by_side("Proportion of False(unit unavailable):", round(b_cal.available[b_cal.available =='f' ].count()/b_cal.shape[0],2),"Proportion of False(unit unavailable):", round(s_cal.available[s_cal.available =='f' ].count()/s_cal.shape[0],2))
print_side_by_side("Nulls when units are available: ", b_cal[b_cal['available']== 't']['price'].isnull().sum(),"Nulls when units are available: ", s_cal[s_cal['available']== 't']['price'].isnull().sum() )
print('\n')
```
<font size ='3'>*Let's do some cleaning, first, let's transfer `date` column to datetime to ease manipulation and analysis. I will also create a dataframe with seperate date items from the Date column, to check the time interval along which the data was collected. In addition to that, let's transform `price` and `available` into numerical values*<font/>
```
def create_dateparts(df, date_col):
"""
INPUT
df -pandas dataframe
date_col -list of columns to break down into columns of years,months and days.
OUTPUT
df - a dataframe with columns of choice transformed in to columns of date parts(years,months and days)
"""
df['date'] = pd.to_datetime(df.date)
b_date_df = pd.DataFrame()
b_date_df['year'] = df['date'].dt.year
b_date_df['month'] = df['date'].dt.month
b_date_df['day'] =df['date'].dt.strftime("%A")
#b_date_df['dow'] =df['date'].dt.day
df = df.join(b_date_df)
return df
#######################
def get_period_df(df):
"""
INPUT
df -pandas dataframe
OUTPUT
df - a dataframe grouped to show the span of all the entries
"""
period =pd.DataFrame(df.groupby(['year','month'], sort = True)['day'].value_counts())
period = period.rename(columns={'day':'count'}, level=0)
period = period.reset_index().sort_values(by=['year', 'month', 'day']).reset_index(drop = True)
return period
#############################
def to_float(df, float_cols):
"""
INPUT
df -pandas dataframe
float_cols -list of columns to transform to float
OUTPUT
df - a dataframe with columns of choice transformed to float
"""
for col in float_cols:
df[col] = df[col].str.replace('$', "", regex = False)
df[col] = df[col].str.replace('%', "", regex = False)
df[col] = df[col].str.replace(',', "", regex = False)
for col in float_cols:
df[col] = df[col].astype(float)
return df
#############################
def bool_nums(df, bool_cols):
"""
INPUT
df -pandas dataframe
bool_cols -list of columns with true or false strings
OUTPUT
df - a dataframe with columns of choice transforemed into binary values
"""
for col in bool_cols:
df[col] = df[col].apply(lambda x: 1 if x == 't' else 0 )
df = df.reset_index(drop= True)
return df
```
<font size = '3'>*Let's take a look at the resulted DataFrames after executing the previous fuc=nctions. I flipped the Boston calendar to have it start in ascending order like Seatle.*<font/>
```
b_cal_1 = to_float(b_cal, ['price'])
s_cal_1 = to_float(s_cal, ['price'])
b_cal_1 = create_dateparts(b_cal_1, 'date')
s_cal_1 = create_dateparts(s_cal_1, 'date')
b_cal_1 = bool_nums(b_cal_1, ['available'])
s_cal_1 = bool_nums(s_cal_1, ['available'])
b_cal_1 = b_cal_1.iloc[::-1].reset_index(drop=True)
display_side_by_side(b_cal_1.head(3),s_cal_1.head(3), titles = ['b_cal_1', 's_cal_1'])
```
<font size = '3'>*Let's take a look at the resulted time intervals for Both Boston and Seatle calendar tables*<font/>
```
b_period =get_period_df(b_cal_1)
s_period =get_period_df(s_cal_1)
display_side_by_side(b_period.head(1), b_period.tail(1), titles = ['Boston Period'])
display_side_by_side(s_period.head(1), s_period.tail(1), titles = ['Seatle Period'])
print("Number of unique Listing IDs in Boston Calendar: ", len(b_cal_1.listing_id.unique()))
print("Number of unique Listing IDs in Seatle Calendar: ", len(s_cal_1.listing_id.unique()))
print('\n')
#b_period.iloc[0], s_period.iloc[0], b =0)
```
<font size ='3'>*Seems like they both span a year, through which all the listings are tracked in terms of availability. When we group by year and month; the count is equivalent to the numbers of the unique ids because all the ids are spanning the same interval. Let's check any anomalies*<font/>
```
def check_anomalies(df, col):
list_ids_not_year_long = []
for i in sorted(list(df[col].unique())):
if df[df[col]== i].shape[0] != 365:
list_ids_not_year_long.append(i)
print("Entry Ids that don't span 1 year: " , list_ids_not_year_long)
#Boston
check_anomalies(b_cal_1, 'listing_id')
#Seatle
check_anomalies(s_cal_1, 'listing_id')
## check this entry in Boston Calendar
print("Span of the entries for this listing, should be 365: ", b_cal_1[b_cal_1['listing_id']== 12898806].shape[0])
## 2 years, seems like a duplicate as 730 = 365 * 2
one_or_two = pd.DataFrame(b_cal_1[b_cal_1['listing_id']==12898806].groupby(['year', 'month', 'day'])['day'].count()).day.unique()[0]
print("Should be 1: ", one_or_two)
## It indeed is :)
b_cal_1 = b_cal_1.drop_duplicates()
print("Size of anomaly listing, Should be = 365: ", b_cal_1.drop_duplicates()[b_cal_1.drop_duplicates().listing_id==12898806]['listing_id'].size)
print("After removing duplicates, Span of the entries for this listing, should be 365: ", b_cal_1[b_cal_1['listing_id']== 12898806].shape[0])
print("After removing duplicates, shape is: ", b_cal_1.shape)
# b_cal_1.to_csv('b_cal_1.csv')
# s_cal_1.to_csv('s_cal_1.csv')
```
_______________________________________________________________________________________________________________________
### Comments:
[Boston & Seatle Calendar]
- The datasets have information about listing dates, availability and price tracked over a year for ever listing id
- There are no data entry errors, all nulls are due to the structuring of the Data (the listings that weren't available has no price)
- I added 4 cols that contain dateparts that will aid further analysis and modeling
- The Boston calendar Dataset ranges through `365`days from `6th of September'16` to `5th of September'17`, No nulls with `1308525` rows and `8` cols
- The Seatle calendar Dataset ranges through `365`days from `4th of January'16` to `2nd of January'17`, No nulls with `1393570` rows and `8` cols
- Number of unique Listing IDs in Boston Calendar: `3585`
- Number of unique Listing IDs in Seatle Calendar: `3818`
- It seems that the table is not documenting any rentals it just shows if the unit is available at a certain time and the price then.
_______________________________________________________________________________________________________________________
## Step 1: Continue -
> **Boston & Seatle Listings**
```
b_list.head(1)
#s_list.head(10)
```
<font size ='3'>*Check the sizes of cols & rows & check Nulls*<font/>
```
print_side_by_side("Boston listings size :", b_list.shape, "Seatle listings size :", s_list.shape)
print_side_by_side("Number of Non-null cols in Boston listings: ", np.sum(b_list.isnull().sum()==0) ,"Number of Non-null cols in Seatle listings: ", np.sum(s_list.isnull().sum()==0))
set_difference = set(b_list.columns) - set(s_list.columns)
print("Columns in Boston but not in Seatle: ", set_difference)
print('\n')
```
<font size ='3'>*Let's go through the columns of this table as they are a lot, decide on which would be useful, which would be ignored and which would be transformed based on intuition.* <font/>
> **to_parts:**<br><font size = '2'>(Divide into ranges)<font/><br>
>* *maximum_nights*
><br>
>
> **to_count:** <br><font size = '2'>(Provide a count)<font/><br>
> * *amenities* <br>
> * *host_verifications*
><br>
>
>**to_dummy:** <br><font size = '2'>(Convert into dummy variables)<font/><br>
>* *amenities*
><br>
>
>**to_len_text:** <br><font size = '2'>(provide length of text)<font/><br>
>* *name*
>* *host_about*
>* *summary*
>* *description*
>* *neighborhood_overview*
>* *transit*
><br>
>
>**to_days:** <br><font size = '2'>(calculate the difference between both columns to have a meaningful value of host_since in days)<font/><br>
>* *host_since*
>* *last_review*
><br>
>
>**to_float:**<br><font size = '2'>(Transform to float)<font/><br>
>* *cleaning_fee* <br>
>* *host_response_rate* <br>
>* *host_acceptance_rate* <br>
>* *host_response_rate* <br>
>* *host_acceptance_rate* <br>
>* *extra_people* <br>
>* *price* <br>
><br>
>
> **to_binary:** <br><font size = '2'>(Transform to binary)<font/><br>
>* *host_has_profile_pic*
>* *host_identity_verified*
>* *host_is_superhost*
>* *is_location_exact*
>* *instant_bookable*
>* *require_guest_profile_picture*
>* *require_guest_phone_verification*
><br>
>
>**to_drop:**<br><font size = '2'>(Columns to be dropped)<font/>
<br><br>
>**reason: little use:** <br>
>* *listing_url, scrape_id, last_scraped, experiences_offered, thumbnail_url,xl_picture_url, medium_url,*
>* *host_id, host_url, host_thumbnail_url, host_picture_url, host_total_listings_count, neighbourhood,*
>* *neighbourhood_group_cleansed, state, country_code, country, latitude, longitude,*
>* *has_availability, calendar_last_scraped, host_name, picture_url, space, first_review, *
><br><br>
>
>**reason: Nulls, text, only in Boston:** <br>
>* *access , interaction, house_rules*
><br><br>
>
>**reason> Nulls, 0 variability or extreme variability:** <br>
>* *square_feet* ------------- *90% Null boston 97% Null seatle* <br>
>* *weekly_price*-------------*75% Null boston 47% Null seatle* <br>
>* *monthly_price*------------*75% Null boston 60% Null seatle* <br>
>* *security_deposit*---------*65% Null boston 51% Null seatle* <br>
>* *notes*---------------------*55% Null boston 42% Null seatle* <br>
>* *jurisdiction_names*---------*100% Null in both* <br>
>* *license*--------------------*100% Null in both*
>* *required_license*-----------*100% Null in both* <br>
>* *street*---------------------*High variability* <br>
<font size = '3' >*Let's write anymore functions needed to carry on these suggested changes*<font/>
```
drop_cols = ['listing_url', 'scrape_id', 'last_scraped', 'experiences_offered', 'thumbnail_url','xl_picture_url',
'medium_url', 'host_id', 'host_url', 'host_thumbnail_url', 'host_picture_url', 'host_total_listings_count',
'neighbourhood', 'neighbourhood_group_cleansed','state', 'country_code', 'country', 'latitude', 'longitude',
'has_availability', 'calendar_last_scraped', 'host_name','square_feet',
'weekly_price', 'monthly_price', 'security_deposit', 'notes', 'jurisdiction_names', 'license', 'requires_license',
'street', 'picture_url', 'space','first_review', 'house_rules', 'access', 'interaction']
float_cols = ['cleaning_fee', 'host_response_rate','host_acceptance_rate','host_response_rate',
'host_acceptance_rate','extra_people','price']
len_text_cols = ['name', 'host_about', 'summary', 'description','neighborhood_overview', 'transit']
count_cols = ['amenities', 'host_verifications']
d_col = [ 'amenities']
part_col = ['maximum_nights']
bool_cols = ['host_has_profile_pic', 'host_identity_verified', 'host_is_superhost', 'is_location_exact',
'instant_bookable', 'require_guest_profile_picture' , 'require_guest_phone_verification' ]
day_cols = [ 'host_since', 'last_review']
###########################################################################################################################
def to_drop(df, drop_cols):
"""
INPUT
df -pandas dataframe
drop_cols -list of columns to drop
OUTPUT
df - a dataframe with columns of choice dropped
"""
for col in drop_cols:
if col in list(df.columns):
df = df.drop(col, axis = 1)
else:
continue
return df
#################################
def to_len_text(df, len_text_cols):
"""
INPUT
df -pandas dataframe
len_text_cols- list of columns to return the length of text of their values
OUTPUT
df - a dataframe with columns of choice transformed to len(values) instead of long text
"""
df_new = df.copy()
len_text = []
new_len_text_cols = []
for col in len_text_cols:
new_len_text_cols.append("len_"+col)
for i in df_new[col]:
#print(col,i)
try:
len_text.append(len(i))
except:
len_text.append(i)
#print('\n'*10)
df_new = df_new.drop(col, axis = 1)
len_text_col = pd.Series(len_text)
len_text_col = len_text_col.reset_index(drop = True)
#print(len_text_col)
df_new['len_'+col]= len_text_col
len_text = []
df_new[new_len_text_cols] = df_new[new_len_text_cols].fillna(0)
return df_new, new_len_text_cols
#########################
def to_parts(df, part_col):
"""
INPUT
df -pandas dataframe
part_col -list of columns to divide into "week or less" and "more than a week" depending on values
OUTPUT
df - a dataframe with columns of choice transformed to ranges of "week or less" and "more than a week"
"""
def to_apply(val):
if val <= 7:
val = '1 Week or less'
elif (val >7) and (val<=14):
val = '1 week to 2 weeks'
elif (val >14) and (val<=30):
val = '2 weeks to 1 month'
elif (val >30) and (val>=60):
val = '1 month to 2 months'
elif (val >60) and (val>=90):
val = '2 month to 3 months'
elif (val >90) and (val>=180):
val = '3 month to 6 months'
else:
val = 'More than 6 months'
return val
for part in part_col:
df[part]= df[part].apply(to_apply)
return df
############################
def to_count(df, count_cols):
"""
INPUT
df -pandas dataframe
count_cols -list of columns to count the string items within each value
OUTPUT
df - a dataframe with columns of choice transformed to a count of values
"""
def to_apply(val):
if "{" in val:
val = val.replace('}', "").replace('{', "").replace("'","" ).replace('"',"" ).replace("''", "").strip().split(',')
elif "[" in val:
val = val.replace('[',"" ).replace(']',"" ).replace("'","" ).strip().split(",")
return len(val)
for col in count_cols:
df['count_'+col]= df[col].apply(to_apply)
return df
########################
def to_items(df, d_col):
"""
INPUT
df -pandas dataframe
d_col -list of columns to divide the values to clean list of items
OUTPUT
df - a dataframe with columns of choice cleaned and returns the values as lists
"""
def to_apply(val):
if "{" in val:
val = val.replace('}', "").replace('{', "").replace("'","" ).replace('"',"" ).replace("''", "").lower().split(',')
elif "[" in val:
val = val.replace('[',"" ).replace(']',"" ).replace("'","" ).lower().split(",")
return val
def to_apply1(val):
new_val = []
if val == 'None':
new_val.append(val)
for i in list(val):
if (i != "") and ('translation' not in i.lower()):
new_val.append(i.strip())
return new_val
def to_apply2(val):
if 'None' in val:
return ['none']
elif len((val)) == 0:
return ['none']
else:
return list(val)
for col in d_col:
df[col]= df[col].apply(to_apply)
df[col]= df[col].apply(to_apply1)
df[col]= df[col].apply(to_apply2)
return df
def items_counter(df, d_col):
"""
INPUT
df -pandas dataframe
count_col -list of columns to with lists as values to count
OUTPUT
all_strings - a dictionary with the count of every value every list within every series
"""
all_strings= {}
def to_apply(val):
for i in val:
if i in list(all_strings.keys()):
all_strings[i]+=1
else:
all_strings[i]=1
df[d_col].apply(to_apply)
return all_strings
###################################
def to_days(df, day_cols, na_date):
"""
INPUT
df -pandas dataframe
day_cols -list of columns to divide the values to clean list of items
OUTPUT
df - a dataframe with columns of choice cleaned and returns the values as lists
"""
#Since Boston lisitngs span from September'16 to september'17, we can impute using the month of march'16
#Since Seatle lisitngs span from January'16 to January'17, we can impute using the month of june'16
df = df.copy()
df[[day_cols[0], day_cols[1]]]=df[[day_cols[0], day_cols[1]]].apply(pd.to_datetime)
df = df.dropna(subset= [day_cols[0]], how ='any', axis = 0)
df[day_cols[1]] = df[day_cols[1]].fillna(pd.to_datetime(na_date))
df[day_cols[0]]= (df[day_cols[1]] - df[day_cols[0]]).apply(lambda x: round(x.value/(864*1e11)),2)
df= df.drop(day_cols[1], axis =1 )
df = df.reset_index(drop= True)
return df
###########################################################################################################################
def applier(df1,df2,drop = True, float_=True, len_text= True, count= True, items = True,
parts = True , count_items = True, bool_num = True, days = True):
"""
INPUT
df1,df2 - 2 pandas dataframes
drop,float_,len_text, count, parts, date_time - Boolean values that corresponds to previosuly defined functions
OUTPUT
df - a clean dataframe that has undergone previously defined functions according to the boolean prameters passed
"""
while drop:
df1 = to_drop(df1, drop_cols)
df2 =to_drop(df2, drop_cols)
break
while float_:
df1 =to_float(df1, float_cols)
df2 =to_float(df2, float_cols)
break
while len_text:
df1, nltc = to_len_text(df1, len_text_cols)
df2, nltc = to_len_text(df2, len_text_cols)
break
while parts:
df1 = to_parts(df1, part_col)
df2 = to_parts(df2, part_col)
break
while count:
df1 = to_count(df1, count_cols)
df2 = to_count(df2, count_cols)
df1 = df1.drop('host_verifications', axis =1 )
df2 = df2.drop('host_verifications', axis =1 )
break
while items:
df1 = to_items(df1, d_col)
df2 = to_items(df2, d_col)
break
while count_items:
b_amens_count = pd.Series(items_counter(df1,'amenities')).reset_index().rename(columns = {'index':'amenities', 0:'count'}).sort_values(by='count', ascending =False).reset_index(drop =True)
s_amens_count = pd.Series(items_counter(df2, 'amenities')).reset_index().rename(columns = {'index':'amenities', 0:'count'}).sort_values(by='count', ascending =False).reset_index(drop =True)
a_counts = [b_amens_count,s_amens_count]
break
while bool_num:
df1 = bool_nums(df1, bool_cols)
df2 = bool_nums(df2, bool_cols)
break
while days:
df1 = to_days(df1, day_cols, '2016-04-1')
df2 = to_days(df2, day_cols, '2016-06-1')
break
if count_items:
return df1, df2 ,a_counts
else:
return df1,df2
b_list_1, s_list_1, a_counts = applier(b_list, s_list)
```
<font size = '3' >*Amenities seems like a good indicator of price as a response variable so let's have it dummified*<font/>
<br>
<font size = '2.75' >**This function takes forever(6 mins),so, it's commented out and I use the resulted dataframes that were written to CSV files**<font/>
```
# %%time
# def to_dummy(df1,df2, col1, cols_ref1,cols_ref2):
# def construct(df,col, cols_ref):
# count = 0
# for val2 in df[col]:
# lister = []
# for val1 in cols_ref[col]:
# if val1 in val2:
# lister.append(1)
# else:
# lister.append(0)
# cols_ref = cols_ref.join(pd.Series(lister, name = count))
# count+=1
# cols_ref = cols_ref.drop('count', axis = 1).transpose()
# cols_ref.columns = list(cols_ref.iloc[0,:])
# return cols_ref
# b_amens_1 =construct(df1, col1,cols_ref1)
# s_amens_1 =construct(df2, col1,cols_ref2)
# b_amens_1 = b_amens_1.drop('none', axis = 1) #.drop(0,axis=0).reset_index(drop= True)
# b_amens_1 = b_amens_1.iloc[1:,:]
# b_amens_1.columns = ["{}_{}".format(col1,col) for col in b_amens_1.columns]
# s_amens_1 = s_amens_1.iloc[1:,:]
# s_amens_1 = s_amens_1.drop('none', axis = 1)
# s_amens_1.columns = ["{}_{}".format(col1,col) for col in s_amens_1.columns]
# b_dummies = b_amens_1.reset_index(drop =True)
# s_dummies = s_amens_1.reset_index(drop =True)
# df1 = df1.join(b_dummies)
# df2 = df2.join(s_dummies)
# df1 = df1.drop([col1], axis = 1)
# df2 = df2.drop([col1], axis = 1)
# return b_dummies, s_dummies, df1, df2
# b_d, s_d,b_list_d, s_list_d = to_dummy(b_list_1, s_list_1, 'amenities',
# b_a_counts, s_a_counts)
# b_list_d.to_csv('b_list_d.csv')
# s_list_d.to_csv('s_list_d.csv')
b_list_d = pd.read_csv('b_list_d.csv', index_col = 0)
s_list_d = pd.read_csv('s_list_d.csv', index_col = 0)
```
<font size = '3' >*Check the nulls again*<font/><br>
```
df1= (b_list_d.isnull().sum()[b_list_d.isnull().sum()>0]/b_list_d.shape[0]*100).reset_index().rename(columns ={'index':'col_name',0:'nulls_proportion'})
df2 = (s_list_d.isnull().sum()[s_list_d.isnull().sum()>0]/s_list_d.shape[0]*100).reset_index().rename(columns ={'index':'col_name',0:'nulls_proportion'})
display_side_by_side(df1,df2, titles =['b_list_d_Nulls','s_list_d_Nulls' ])
```
_______________________________________________________________________________________________________________________
### Comments:
[Boston & Seatle Listings]
- Boston listings size : `3585`, `95`/ Seatle listings size : `3818`, `92`
- Number of Non-null cols in Boston listings: `51`, around half
- Number of Non-null cols in Seatle listings: `47`, around half<br>
- I wrote a series of functions that commenced some basic cleaning to ease analysis, with the option to switch off any of them depending on the future requirements of the analyses, some of what was done:
>- Columns with relatively high number nulls or that have little to no forseeable use were removed
>- Took the charachter length of the values in some of the cols with long text entries and many unique values, possibly the length of some fields maybe correlated somewhat with price.
>- Columns with dates are transformed into Datetime, numerical values that were in text to floats
>- Columns `amenities`and `host_verifications`were taken as counts, `amenities` was then dummified, for its seeming importance.
>- `maximum_nights`column seems to lack some integrity so I divided it into time periods
> Columns with t and f strings were converted into binary data.
>- Difference between `host_since`and `last_review` was computed in days to `host_since`<br>
>- All columns with only 't' or 'f' values were transformed in to binary values.
- **After the basic cleaning and the dummification of `amenities`:** <br>
~Boston listings size : `3585`, `98`/ Seatle listings size : `3818`, `98`. <br>
~There are still nulls to deal with in case of modeling, but that depends on the requirements of each question.
_______________________________________________________________________________________________________________________
### Step 1: Continue -
> **Boston & Seatle Reviews**
```
#b_rev.head(3)
s_rev.head(3)
```
<font size = '3' >*Check the sizes of cols & rows & check Nulls*<font/>
```
print_side_by_side("Boston reviews size:", b_rev.shape,"Seatle reviews size:", s_rev.shape)
print_side_by_side("No. of unique listing ids:", b_rev.listing_id.unique().size,"No. of unique listing ids:", s_rev.listing_id.unique().size)
print_side_by_side("Number of Non-null cols in Boston Reviews:", np.sum(b_rev.isnull().sum()==0),
"Number of Non-null cols in Seatle Reviews:", np.sum(s_rev.isnull().sum()==0))
print_side_by_side("Null cols % in Boston:", (b_rev.isnull().sum()[b_rev.isnull().sum()>0]/b_rev.shape[0]*100).to_string(),
"Null cols % in Seatle:", (s_rev.isnull().sum()[s_rev.isnull().sum()>0]/s_rev.shape[0]*100).to_string())
print_side_by_side("Null cols no. in Boston:",(b_rev.isnull().sum()[b_rev.isnull().sum()>0]).to_string(),
"Null cols no. in Seatle:", (s_rev.isnull().sum()[s_rev.isnull().sum()>0]).to_string())
print('\n')
```
<font size = '3' >**To extract analytical insights from the reviews entries, they ought to be transformed from text to numerical scores, to do so I will follow some steps:**<font/>
<font size = '3' >*1) Find all the words -excluding any non alphanumeric charachters - in each Dataset*<font/><br>
<font size = '2' >**As the function takes 4 mins to execute, I commented it out and passed the resulted word lists as dfs to CSV files that were added to the project instead of running it in the notebook again.**<font/>
```
#%%time
# def get_words(df, col):
# """
# INPUT
# df -pandas dataframe
# col -column of which the values are text
#
# OUTPUT
# df - a dataframe with a single colum of all the words
# """
# all_strings = []
# for val in df[col]:
# try:
# val_strings = [''.join(filter(str.isalnum, i.lower())) for i in val.split() if len(i)>3]
# except:
# continue
# for word in val_strings:
# if word not in all_strings:
# all_strings.append(word)
# val_strings = []
# return pd.Series(all_strings).to_frame().reset_index(drop = True).rename(columns = {0:'words'})
# boston_words = get_words(b_rev, 'comments')
# seatle_words = get_words(s_rev, 'comments')
# boston_words.to_csv('boston_words.csv')
# seatle_words.to_csv('seatle_words.csv')
boston_words = pd.read_csv('drafts/boston_words.csv', index_col= 0)
seatle_words = pd.read_csv('drafts/seatle_words.csv', index_col= 0)
print("Boston words no.: ", boston_words.shape[0])
print("Seatle words no.: ", seatle_words.shape[0])
display_side_by_side(boston_words.head(5), seatle_words.head(5), titles = [ 'Boston', 'Seatle'])
```
<font size = '3' >*2) Read in positive and negative english word lists that are used for sentiment analysis*<font/>
### Citation:
* Using this resource https://www.cs.uic.edu/~liub/FBS/sentiment-analysis.html#lexicon I downloaded a list of words with positive and negative connotations used for sentiment analysis
* *Based on the book*:
> Sentiment Analysis and Opinion Mining (Introduction and Survey), Morgan & Claypool, May 2012.
```
positive_words = pd.read_csv('drafts/positive-words.txt', sep = '\t',encoding="ISO-8859-1")
negative_words = pd.read_csv('drafts/negative-words.txt', sep = '\t',encoding="ISO-8859-1")
positive_words = positive_words.iloc[29:,:].reset_index(drop = True).rename(columns = {';;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;':'words'})
negative_words = negative_words.iloc[31:,:].reset_index(drop = True).rename(columns = {';;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;':'words'})
b_pos = np.intersect1d(np.array(boston_words['words'].astype(str)), np.array(positive_words['words']),assume_unique=True)
b_neg = np.intersect1d(np.array(boston_words['words'].astype(str)), np.array(negative_words['words']),assume_unique=True)
s_pos = np.intersect1d(np.array(seatle_words['words'].astype(str)), np.array(positive_words['words']),assume_unique=True)
s_neg = np.intersect1d(np.array(seatle_words['words'].astype(str)), np.array(negative_words['words']),assume_unique=True)
print_side_by_side('Positive words count: ', positive_words.shape[0]
,'Negative words count: ', negative_words.shape[0])
print_side_by_side("No. of positive words in Boston Reviews: ", len(b_pos)
,"No. of negative words in Boston Reviews: ", len(b_neg))
print_side_by_side("No. of positive words in Seatle Reviews: ", len(s_pos)
,"No. of negative words in Seatle Reviews: ", len(s_neg))
print('\n')
```
<font size = '3' >*3) Let's translate the reviews from other languages to English*<font/>
<br>
<font size='3'>*Let's start with dropping the nulls, check the language of the reviews using `langdetect`, prepare the non english `comments` to be translated*<font/>
```
##Dependency googletrans-4.0.0rc1
##langdetect
# b_rev = b_rev.dropna(subset=['comments'], how = 'any', axis = 0)
# s_rev = s_rev.dropna(subset=['comments'], how = 'any', axis = 0)
# %%time
# b_rev_t = b_rev.copy()
# s_rev_t = s_rev.copy()
# from langdetect import detect
# def lang_check(val):
# try:
# return detect(val)
# except:
# return val
# b_rev_t['review_lang']=b_rev['comments'].apply(lang_check)
# s_rev_t['review_lang']=s_rev['comments'].apply(lang_check)
# b_rev_t.to_csv('b_rev_t.csv')
# s_rev_t.to_csv('s_rev_t.csv')
# b_rev_t = pd.read_csv('b_rev_t.csv', index_col = 0)
#s_rev_t = pd.read_csv('s_rev_t.csv', index_col = 0)
# print('Proportion of non English reviews in Boston: ' ,b_rev_t[b_rev_t['review_lang']!= 'en'].shape[0]/b_rev_t.shape[0])
# print('Proportion of non English reviews in Seattle: ',s_rev_t[s_rev_t['review_lang']!= 'en'].shape[0]/s_rev_t.shape[0])
print(f"""Proportion of non English reviews in Boston: 0.05436662660138958
Proportion of non English reviews in Seattle: 0.012424703233487757""")
# b_to_trans =b_rev_t[b_rev_t['review_lang']!= 'en']
# s_to_trans =s_rev_t[s_rev_t['review_lang']!= 'en']
# b_to_trans['comments'] = b_to_trans['comments'].map(lambda val : str([re.sub(r"[^a-zA-Z0-9]+", '. ', k) for k in val.split("\n")]).replace('['," ").replace(']',"").replace("'",""))
# s_to_trans['comments'] = s_to_trans['comments'].map(lambda val : str([re.sub(r"[^a-zA-Z0-9]+", '. ', k) for k in val.split("\n")]).replace('['," ").replace(']',"").replace("'",""))
```
<font size='3'>*Since googletrans library is extremely unstable, I break down the non-English reviews in Boston into 4 dataframes*<font/>
```
# def trans_slicer(df,df1 = 0,df2 = 0,df3 = 0, df4 = 0):
# dfs=[]
# for i in [df1,df2,df3,df4]:
# i = df[0:1000]
# df = df.drop(index = i.index.values,axis = 0).reset_index(drop= True)
# dfs.append(i.reset_index(drop =True))
# # df = df.drop(index = range(0,df.shape[0],1),axis = 0).reset_index(drop= True)
# return dfs
# df1, df2, df3, df4 = trans_slicer(b_to_trans)
# %%time
# import re
# import time
# import googletrans
# import httpx
# from googletrans import Translator
# timeout = httpx.Timeout(10) # 5 seconds timeout
# translator = Translator(timeout=timeout)
# def text_trans(val):
# vals = translator.translate(val, dest='en').text
# time.sleep(10)
# return vals
# ############################################################
# df1['t_comments'] = df2['comments'].apply(text_trans)
# df1.to_csv('df2.csv')
# df2['t_comments'] = df2['comments'].apply(text_trans)
# df2.to_csv('df2.csv')
# df3['t_comments'] = df3['comments'].apply(text_trans)
# df3.to_csv('df3.csv')
# df4['t_comments'] = df4['comments'].apply(text_trans)
# df4.to_csv('df4.csv')
# #4###########################################################
# s_to_trans['t_comments'] = s_to_trans['comments'].apply(text_trans)
# s_to_trans.to_csv('s_translate.csv')
# dfs = df1.append(df2)
# dfs = dfs.append(df3)
# dfs = dfs.append(df4)
# dfs.index = b_to_trans.index
# b_to_trans = dfs
# b_to_trans['comments'] = b_to_trans['t_comments']
# b_to_trans = b_to_trans.drop(columns =['t_comments'],axis = 1)
#b_rev_t = b_rev_t.drop(index =b_to_trans.index,axis = 0)
#b_rev_t = b_rev_t.append(b_to_trans)
#b_rev_t = b_rev_t.sort_index(axis = 0).reset_index(drop= True)
# b_rev_t['comments'] = b_rev_t['comments'].apply(lambda x: x.replace('.',' '))
# b_rev_t.to_csv('b_rev_translated.csv')
# s_to_trans['comments'] = s_to_trans['t_comments']
# s_to_trans = s_to_trans.drop(columns =['t_comments'],axis = 1)
# s_rev_t = s_rev_t.drop(index =s_to_trans.index,axis = 0)
# s_rev_t = s_rev_t.append(s_to_trans)
# s_rev_t = s_rev_t.sort_index(axis = 0).reset_index(drop= True)
# s_rev_t['comments'] = s_rev_t['comments'].apply(lambda x: x.replace('.',' '))
# s_rev_t.to_csv('s_rev_translated.csv')
```
<font size='3'>*Since googletrans takes around 3 hours to translate 1000 entries, that took some time, here are the resulted DataFrames*<font/>
```
b_rev_trans = pd.read_csv('b_rev_translated.csv', index_col =0)
s_rev_trans = pd.read_csv('s_rev_translated.csv', index_col =0)
```
<font size = '3' >*4) Add a scores column using the previous resource as a reference to evaulate the score of each review*<font/><br>
```
# %%time
# def create_scores(df,col, df_pos_array, df_neg_array):
# """
# INPUT
# df -pandas dataframe
# col -column with text reviews to be transformed in to positive and negative scores
# pos_array- array with reference positive words for the passed df
# neg_array- array with reference negative words for the passed df
# OUTPUT
# df - a dataframe with a score column containing positive and negative scores"
# """
# def get_score(val):
# val_strings = [''.join(filter(str.isalnum, i.lower())) for i in str(val).split() if len(i)>3]
# pos_score = len(np.intersect1d(np.array(val_strings).astype(object), df_pos_array, assume_unique =True))
# neg_score = len(np.intersect1d(np.array(val_strings).astype(object), df_neg_array, assume_unique =True))
# return pos_score - neg_score +1
# df['score']= df[col].apply(get_score)
# return df
# b_rev_score = create_scores(b_rev_trans, 'comments', b_pos, b_neg)
# s_rev_score = create_scores(s_rev_trans, 'comments', s_pos, s_neg)
# b_rev_score.to_csv('b_rev_score.csv')
# s_rev_score.to_csv('s_rev_score.csv')
```
<font size = '3' >*As this function takes a while as well, let's write the results into to csv files and read the frames again and then show some samples.*<font/>
```
b_rev_score = pd.read_csv('b_rev_score.csv', index_col = 0)
s_rev_score = pd.read_csv('s_rev_score.csv', index_col = 0)
sub_b_rev = b_rev_score.iloc[:,[5,6,7]]
sub_s_rev = s_rev_score.iloc[:,[5,6,7]]
display_side_by_side(sub_b_rev.head(3), sub_s_rev.head(3), titles= ['Boston Reviews', 'Seatle_reviews'])
```
_______________________________________________________________________________________________________________________
### Comments:
[Boston & Seatle Reviews]
- Boston reviews size : (68275, 6)
- Seatle reviews size : (84849, 6)
- Nulls are only in `comments`columns in both Datasets:
- Null percentage in Boston Reviews: 0.08%
- Null percentage in Seatle Reviews: 0.02%
- I added a score column to both tables to reflect positive or negative reviews numerically with the aid of an external resource.
_______________________________________________________________________________________________________________________
### Step 2: Formulating Questions
<font size = '3' >*After going through the data I think those questions would be of interest:*<font/>
### *Q: How can you compare the reviews in both cities ?*
### *Q: What aspects of a listing influences the price in both cities?*
### *Q: How can we predict the price?*
### *Q: How do prices vary through the year in both cities ? when is the season and off season in both cities?*
_______________________________________________________________________________________________________________________
### *Q: How can you compare the reviews in both cities ?*
<font size = '3' >*Let's attempt to statistically describe the reviews in both cities*<font/>
```
print_side_by_side(' Boston: ', ' Seattle: ', b = 0)
print_side_by_side(' Maximum score : ', b_rev_score.iloc[b_rev_score.score.idxmax()].score,
' Maximum Score : ', s_rev_score.iloc[s_rev_score.score.idxmax()].score)
print_side_by_side(' Minimum Score : ', b_rev_score.iloc[b_rev_score.score.idxmin()].score,
' Minimum Score : ', s_rev_score.iloc[s_rev_score.score.idxmin()].score)
print_side_by_side(' Most common score: ', b_rev_score['score'].mode().to_string(),
' Most common score: ', s_rev_score['score'].mode().to_string())
print_side_by_side(' Mean score: ', round(b_rev_score['score'].mean(),2)
,' Mean score: ', round(s_rev_score['score'].mean(),2))
print_side_by_side(' Median score: ',round( b_rev_score['score'].median(),2),
' Median score: ', s_rev_score['score'].median())
print_side_by_side(' Standard deviation: ', round(b_rev_score['score'].std(),2)
,' Standard deviation: ', round(s_rev_score['score'].std(),2))
# print_side_by_side(' Z score of -2: ', round(b_rev_score['score'].mean()-2*round(b_rev_score['score'].std(),2),1)
# ,' Z score of -2: ', round(s_rev_score['score'].mean()-2*round(s_rev_score['score'].std(),2)),1)
# print('Score: ', b_rev_score.iloc[b_rev_score.score.idxmax()].score)
# b_rev_score.iloc[b_rev_score.score.idxmax()].comments
plt.figure(figsize = (14,8))
plt.subplot(2,1,1)
plt.title('Boston Reviews', fontsize = 18)
sns.kdeplot(b_rev_score.score, bw_adjust=2)
plt.axvline(x= b_rev_score['score'].mean(), color = 'orange', alpha = 0.6)
plt.axvline(x= b_rev_score['score'].median(), color = 'gray', alpha = 0.6)
plt.xlim(-15,30)
plt.xlabel('', fontsize = 14)
plt.ylabel('Count', fontsize = 14)
plt.legend(['Scores','mean', 'median'])
order = np.arange(-15,31,3)
plt.xticks(order,order, fontsize = 12)
plt.subplot(2,1,2)
plt.title('Seattle Reviews', fontsize = 18)
sns.kdeplot(s_rev_score.score, bw_adjust=2)
plt.axvline(x= s_rev_score['score'].mean(), color = 'orange', alpha = 0.6)
plt.axvline(x= s_rev_score['score'].median(), color = 'gray', alpha = 0.6)
plt.xlim(-15,30)
plt.xlabel('Scores', fontsize = 18)
plt.ylabel('Count', fontsize = 14)
plt.legend(['Scores','mean','median'])
plt.xticks(order,order, fontsize = 12)
plt.tight_layout();
```
>* <font size = '3'>**The scores clearly follow a normal distribution in both cities, with close standard deviations**</font>
>* <font size = '3'>**The mean score of Seattle (6.55) is a bit higher than Boston (5.84)**</font>
>* <font size = '3'>**The median score in both cities is a bit less than the mean which indicates a slight right skew**</font>
<font size = '3' >*Let'stake a look on the boxplots to have more robust insights*<font/>
```
plt.figure(figsize = (15,6))
plt.subplot(2,1,1)
plt.title('Boston Reviews', fontsize = 18)
sns.boxplot(data = b_rev_score, x = b_rev_score.score)
plt.axvline(x= b_rev_score['score'].mean(), color = 'orange', alpha = 0.6)
# plt.axvline(x= b_rev_score['score'].mean()+2*round(b_rev_score['score'].std(),2), color = 'red', alpha = 0.6)
# plt.axvline(x= b_rev_score['score'].mean()-2*round(b_rev_score['score'].std(),2), color = 'red', alpha = 0.6)
plt.xlim(-3,15)
plt.ylabel('Count', fontsize = 16)
order = np.arange(-3,15,1)
plt.xticks(order,order, fontsize = 13)
plt.xlabel('')
plt.subplot(2,1,2)
plt.title('Seattle Reviews', fontsize = 18)
sns.boxplot(data = s_rev_score, x = s_rev_score.score)
plt.axvline(x= s_rev_score['score'].mean(), color = 'orange', alpha = 0.6)
# plt.axvline(x= s_rev_score['score'].mean()+2*round(s_rev_score['score'].std(),2), color = 'red', alpha = 0.6)
# plt.axvline(x= s_rev_score['score'].mean()-2*round(s_rev_score['score'].std(),2), color = 'red', alpha = 0.6)
plt.xlim(-3,15)
plt.xlabel('Scores', fontsize = 18)
plt.ylabel('Count', fontsize = 16)
plt.xticks(order,order, fontsize = 13)
plt.tight_layout();
```
>* <font size = '3'>**50% of The scores in both cities lies between 4 and 8**</font>
>* <font size = '3'>**The IQR of the scores in both cities lies between -2 to 14**</font>
<font size = '3' >*Finally, what's the proportion of negative scores in both cities*<font/>
```
b_rev_score['grade']= b_rev_score['score'].apply(lambda x: 1 if x >0 else 0)
s_rev_score['grade']= s_rev_score['score'].apply(lambda x: 1 if x >0 else 0)
print_side_by_side('Boston: ', 'Seattle: ', b=0)
print_side_by_side('Negative reviews proportion: ',
round(b_rev_score['grade'][b_rev_score.grade == 0].count()/b_rev_score.shape[0],3),
'Negative reviews proportion: ',
round(s_rev_score['grade'][s_rev_score.grade == 0].count()/s_rev_score.shape[0],3))
```
><font size = '3'>**Further exploration:**</font>
<br>
>* <font size = '3'>**Use an NLP model be used to better classify the sentiment in the reviews**</font>
>* <font size = '3'>**Explore how to predict reviews using aspects of a listing**</font>
>* <font size = '3'>**Explore the relatioship between average price per meter in each city's estates/ temperature trends and reviews**</font>
_______________________________________________________________________________________________________________________
| github_jupyter |
# Appendix
Hao Lu 04/04/2020
In this notebook, we simulated EEG data with the method described in the paper by Bharadwaj and Shinn-Cunningham (2014) and analyzed the data with the toolbox proposed in the same paper.
The function was modifed so the values of thee variables within the function can be extracted and studied.
Reference:
Bharadwaj, H. M., & Shinn-Cunningham, B. G. (2014). Rapid acquisition of auditory subcortical steady state responses using multichannel recordings. Clinical Neurophysiology, 125(9), 1878-1888.
```
# import packages
import numpy as np
import matplotlib.pyplot as plt
import pickle
import random
from scipy import linalg
from anlffr import spectral,dpss
sfreq = 10000
random.seed(2020)
phase_list = [random.uniform(-np.pi,np.pi) for i in range(32)]
```
The phase of the signal from 32 channels were randomly sampled from a uniform distribution
```
plt.plot(phase_list)
plt.xlabel('Number of Channel')
plt.ylabel('Phase of signal')
```
The signal is defined as 100 Hz SSSR
```
signal = np.zeros((32,200,int(sfreq*0.2)))
xt = np.linspace(0,0.2,sfreq*0.2)
for iChannel in range(32):
for iTrial in range(200):
signal[iChannel,iTrial,:] = np.sin(xt*100*2*np.pi+phase_list[iChannel])
# plot first two channels to show the phase differences
plt.plot(xt,signal[0:2,0,:].transpose())
```
The signal to noise ratio (SNR) in the simulated data was set as -40 dB for all channels
```
std = 10**(40/20)*np.sqrt((signal**2).mean())
noise = np.random.normal(0,std,signal.shape)
```
The simulated data was analyzed through the code from the function anlffr.spectral.mtcplv
```
params = dict(Fs = sfreq, tapers = [1,1], fpass = [80, 120], itc = 0, pad = 1)
x=signal + noise
#codes from the dpss tool of anlffr to make sure the multitaper part is consistent
if(len(x.shape) == 3):
timedim = 2
trialdim = 1
ntrials = x.shape[trialdim]
nchans = x.shape[0]
nfft, f, fInd = spectral._get_freq_vector(x, params, timedim)
ntaps = params['tapers'][1]
TW = params['tapers'][0]
w, conc = dpss.dpss_windows(x.shape[timedim], TW, ntaps)
# the original version of mtcplv
plv = np.zeros((ntaps, len(fInd)))
for k, tap in enumerate(w):
xw = np.fft.rfft(tap * x, n=nfft, axis=timedim)
if params['itc']:
C = (xw.mean(axis=trialdim) /
(abs(xw).mean(axis=trialdim))).squeeze()
else:
C = (xw / abs(xw)).mean(axis=trialdim).squeeze()
for fi in np.arange(0, C.shape[1]):
Csd = np.outer(C[:, fi], C[:, fi].conj())
vals = linalg.eigh(Csd, eigvals_only=True)
plv[k, fi] = vals[-1] / nchans
# Average over tapers and squeeze to pretty shapes
plv = (plv.mean(axis=0)).squeeze()
plv = plv[fInd]
```
The mtcplv did capture the 100 Hz component
```
plt.plot(f,plv)
plt.xlabel('frequency')
plt.ylabel('output of mtcPLV')
```
However, the output of mtcplv perfectly overlaps with the average of squared single-channel PLV stored in matrix C
```
plt.plot(f,abs(C**2).mean(0)[fInd], label='average of square', alpha=0.5)
plt.plot(f,plv,label = 'mtcplv', alpha = 0.5)
plt.plot(f,abs(C**2).mean(0)[fInd] - plv, label='difference')
plt.legend()
plt.xlabel('frequency')
plt.ylabel('PLV')
```
We then check the eigen value decomposition around the 100 Hz peak and there is only one non-zero eigen value as expected
```
fi = np.argmax(plv)+np.argwhere(fInd==True).min()
Csd = np.outer(C[:, fi], C[:, fi].conj())
vals = linalg.eigh(Csd, eigvals_only=True)
plt.bar(np.arange(32),vals[::-1])
plt.xlabel('Principle Components')
plt.ylabel('Eigen Values')
```
| github_jupyter |
# Statistics
## Introduction
In this chapter, you'll learn about how to do statistics with code. We already saw some statistics in the chapter on probability and random processes: here we'll focus on computing basic statistics and using statistical tests. We'll make use of the excellent [*pingouin*](https://pingouin-stats.org/index.html) statistics package and its documentation for many of the examples and methods in this chapter {cite}`vallat2018pingouin`. This chapter also draws on Open Intro Statistics {cite}`diez2012openintro`.
### Notation and basic definitions
Greek letters, like $\beta$, are the truth and represent parameters. Modified Greek letters are an estimate of the truth, for example $\hat{\beta}$. Sometimes Greek letters will stand in for vectors of parameters. Most of the time, upper case Latin characters such as $X$ will represent random variables (which could have more than one dimension). Lower case letters from the Latin alphabet denote realised data, for instance $x$ (which again could be multi-dimensional). Modified Latin alphabet letters denote computations performed on data, for instance $\bar{x} = \frac{1}{n} \displaystyle\sum_{i} x_i$ where $n$ is number of samples. Parameters are given following a vertical bar, for example if $f(x|\mu, \sigma)$ is a probability density function, the vertical line indicates that its parameters are $\mu$ and $\sigma$. The set of distributions with densities $f_\theta(x)$, $\theta \in \Theta$ is called a parametric family, eg there is a family of different distributions that are parametrised by $\theta$.
A **statistic** $T(x)$ is a function of the data $x=(x_1, \dots, x_n)$.
An **estimator** of a parameter $\theta$ is a function $T=T(x)$ which is used to estimate $\theta$ based on observations of data. $T$ is an unbiased estimator if $\mathbb{E}(T) = \theta$.
If $X$ has PDF $f(x|\theta)$ then, given the observed value $x$ of $X$, the **likelihood** of $\theta$ is defined by $\text{lik}(\theta) = f(x | \theta)$. For independent and identically distributed observed values, then $\text{lik}(\theta) = f(x_1, \dots, x_n| \theta) = \Pi_{i=1}^n f(x_i | \theta)$. The $\hat{\theta}$ such that this function attains its maximum value is the **maximum likelihood estimator (MLE)** of $\theta$.
Given an MLE $\hat{\theta}$ of $\theta$, $\hat{\theta}$ is said to be **consistent** if $\mathbb{P}(\hat{\theta} - \theta > \epsilon) \rightarrow 0$ as $n\rightarrow \infty$.
An estimator *W* is **efficient** relative to another estimator $V$ if $\text{Var}(W) < \text{Var}(V)$.
Let $\alpha$ be the 'significance level' of a test statistic $T$.
Let $\gamma(X)$ and $\delta(X)$ be two statistics satisfying $\gamma(X) < \delta(X)$ for all $X$. If on observing $X = x$, the inference can be made that $\gamma(x) \leq \theta \leq \delta(x)$. Then $[\delta(x), \gamma(x)]$ is an **interval estimate** and $[\delta(X), \gamma(X)]$ is an **interval estimator**. The random interval (random because the *endpoints* are random variables) $[\delta(X), \gamma(X)]$ is called a $100\cdot\alpha \%$ **confidence interval** for $\theta$. Of course, there is a true $\theta$, so either it is in this interval or it is not. But if the confidence interval was constructed many times over using samples, $\theta$ would be contained within it $100\cdot\alpha \%$ of the times.
A **hypothesis test** is a conjecture about the distribution of one or more random variables, and a test of a hypothesis is a procedure for deciding whether or not to reject that conjecture. The **null hypothesis**, $H_0$, is only ever conservatively rejected and represents the default positiion. The **alternative hypothesis**, $H_1$, is the conclusion contrary to this.
A type I error occurs when $H_0$ is rejected when it is true, ie when a *true* null hypothesis is rejected. Mistakenly failing to reject a false null hypothesis is called a type II error.
In the most simple situations, the upper bound on the probability of a type I error is called the size or **significance level** of the *test*. The **p-value** of a random variable $X$ is the smallest value of the significance level (denoted $\alpha$) for which $H_0$ would be rejected on the basis of seeing $x$. The p-value is sometimes called the significance level of $X$. The probability that a test will reject the null is called the power of the test. The probability of a type II error is equal to 1 minus the power of the test.
Recall that there are two types of statistics out there: parametrised, eg by $\theta$, and non-parametrised. The latter are often distribution free (ie don't involve a PDF) or don't require parameters to be specified.
### Imports
First we need to import the packages we'll be using
```
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pandas as pd
import pingouin as pg
import statsmodels.formula.api as smf
from numpy.random import Generator, PCG64
# Set seed for random numbers
seed_for_prng = 78557
prng = Generator(PCG64(seed_for_prng))
```
## Basic statistics
Let's start with computing the simplest statistics you can think of using some synthetic data. Many of the functions have lots of extra options that we won't explore here (like weights or normalisation); remember that you can see these using the `help()` method.
We'll generate a vector with 100 entries:
```
data = np.array(range(100))
data
from myst_nb import glue
import sympy
import warnings
warnings.filterwarnings("ignore")
dict_fns = {'mean': np.mean(data),
'std': np.std(data),
'mode': stats.mode([0, 1, 2, 3, 3, 3, 5])[0][0],
'median': np.median(data)}
for name, eval_fn in dict_fns.items():
glue(name, f'{eval_fn:.1f}')
# Set max rows displayed for readability
pd.set_option('display.max_rows', 6)
# Plot settings
plt.style.use('plot_style.txt')
```
Okay, let's see how some basic statistics are computed. The mean is `np.mean(data)=` {glue:}`mean`, the standard deviation is `np.std(data)=` {glue:}`std`, and the median is given by `np.median(data)= `{glue:}`median`. The mode is given by `stats.mode([0, 1, 2, 3, 3, 3, 5])[0]=` {glue:}`mode` (access the counts using `stats.mode(...)[1]`).
Less famous quantiles than the median are given by, for example for $q=0.25$,
```
np.quantile(data, 0.25)
```
As with **pandas**, **numpy** and **scipy** work on scalars, vectors, matrices, and tensors: you just need to specify the axis that you'd like to apply a function to:
```
data = np.fromfunction(lambda i, j: i + j, (3, 6), dtype=int)
data
np.mean(data, axis=0)
```
Remember that, for discrete data points, the $k$th (unnormalised) moment is
$$
\hat{m}_k = \frac{1}{n}\displaystyle\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^k
$$
To compute this use scipy's `stats.moment(a, moment=1)`. For instance for the kurtosis ($k=4$), it's
```
stats.moment(data, moment=4, axis=1)
```
Covariances are found using `np.cov`.
```
np.cov(np.array([[0, 1, 2], [2, 1, 0]]))
```
Note that, as expected, the $C_{01}$ term is -1 as the vectors are anti-correlated.
## Parametric tests
Reminder: parametric tests assume that data are effectively drawn a probability distribution that can be described with fixed parameters.
### One-sample t-test
The one-sample t-test tells us whether a given parameter for the mean, i.e. a suspected $\mu$, is likely to be consistent with the sample mean. The null hypothesis is that $\mu = \bar{x}$. Let's see an example using the default `tail='two-sided'` option. Imagine we have data on the number of hours people spend working each day and we want to test the (alternative) hypothesis that $\bar{x}$ is not $\mu=$8 hours:
```
x = [8.5, 5.4, 6.8, 9.6, 4.2, 7.2, 8.8, 8.1]
pg.ttest(x, 8).round(2)
```
(The returned object is a **pandas** dataframe.) We only have 8 data points, and so that is a great big confidence interval! It's worth remembering what a t-statistic and t-test really are. In this case, the statistic that is constructed to test whether the sample mean is different from a known parameter $\mu$ is
$$
T = \frac{\sqrt{n}(\bar{x}-\mu)}{\hat{\sigma}} \thicksim t_{n-1}
$$
where $t_{n-1}$ is the student's t-distribution and $n-1$ is the number of degrees of freedom. The $100\cdot(1-\alpha)\%$ test interval in this case is given by
$$
1 - \alpha = \mathbb{P}\left(-t_{n-1, \alpha/2} \leq \frac{\sqrt{n}(\bar{x} - \mu)}{\hat{\sigma}} \leq t_{n-1,\alpha/2}\right)
$$
where we define $t_{n-1, \alpha/2}$ such that $\mathbb{P}(T > t_{n-1, \alpha/2}) = \alpha/2$. For $\alpha=0.05$, implying confidence intervals of 95%, this looks like:
```
import scipy.stats as st
def plot_t_stat(x, mu):
T = np.linspace(-7, 7, 500)
pdf_vals = st.t.pdf(T, len(x)-1)
sigma_hat = np.sqrt(np.sum( (x-np.mean(x))**2)/(len(x)-1))
actual_T_stat = (np.sqrt(len(x))*(np.mean(x) - mu))/sigma_hat
alpha = 0.05
T_alpha_over_2 = st.t.ppf(1.0-alpha/2, len(x)-1)
interval_T = T[((T>-T_alpha_over_2) & (T<T_alpha_over_2))]
interval_y = pdf_vals[((T>-T_alpha_over_2) & (T<T_alpha_over_2))]
fig, ax = plt.subplots()
ax.plot(T, pdf_vals, label=f'Student t: dof={len(x)-1}', zorder=2)
ax.fill_between(interval_T, 0, interval_y, alpha=0.2, label=r'95% interval', zorder=1)
ax.plot(actual_T_stat, st.t.pdf(actual_T_stat, len(x)-1), 'bo', ms=15, label=r'$\sqrt{n}(\bar{x} - \mu)/\hat{\sigma}}$',
color='orchid', zorder=4)
ax.vlines(actual_T_stat, 0, st.t.pdf(actual_T_stat, len(x)-1), color='orchid', zorder=3)
ax.set_xlabel('Value of statistic T')
ax.set_ylabel('PDF')
ax.set_xlim(-7, 7)
ax.set_ylim(0., 0.4)
ax.legend(frameon=False)
plt.show()
mu = 8
plot_t_stat(x, mu)
```
In this case, we would reject the alternative hypothesis. You can see why from the plot; the test statistic we have constructed lies within the interval where we cannot reject the null hypothesis. $\bar{x}-\mu$ is close enough to zero to give us cause for concern. (You can also see from the plot why this is a two-tailed test: we don't care if $\bar{x}$ is greater or less than $\mu$, just that it's different--and so the test statistic could appear in either tail of the distribution for us to accept $H_1$.)
We accept the null here, but about if there were many more data points? Let's try adding some generated data (pretend it is from making extra observations).
```
# 'Observe' extra data
extra_data = prng.uniform(5.5, 8.5, size=(30))
# Add it in to existing vector
x_prime = np.concatenate((np.array(x), extra_data), axis=None)
# Run t-test
pg.ttest(x_prime, 8).round(2)
```
Okay, what happened? Our extra observations have seen the confidence interval shrink considerably, and the p-value is effectively 0. There's a large negative t-statistic too. Unsurprisingly, as we chose a uniform distribution that only just included 8 but was centered on $(8-4.5)/2$ *and* we had more points, the test now rejects the null hypothesis that $\mu=8$ . Because the alternative hypothesis is just $\mu\neq8$, and these tests are conservative, we haven't got an estimate of what the mean actually is; we just know that our test rejects that it's $8$.
We can see this in a new version of the chart that uses the extra data:
```
plot_t_stat(x_prime, mu)
```
Now our test statistic is safely outside the interval.
#### Connection to linear regression
Note that testing if $\mu\neq0$ is equivalent to having the alternative hypothesis that a single, non-zero scalar value is a good expected value for $x$, i.e. that $\mathbb{E}(x) \neq 0$. Which may sound familiar if you've run **linear regression** and, indeed, this t-test has an equivalent linear model! It's just regressing $X$ on a constant--a single, non-zero scalar value. In general, t-tests appear in linear regression to test whether any coefficient $\beta \neq 0$.
We can see this connection by running a hypothesis test of whether the sample mean is not zero. Note the confidence interval, t-statistic, and p-value.
```
pg.ttest(x, 0).round(3)
```
And, as an alternative, regressing x on a constant, again noting the interval, t-stat, and p-value:
```
import statsmodels.formula.api as smf
df = pd.DataFrame(x, columns=['x'])
res = smf.ols(formula='x ~ 1', data=df).fit()
# Show only the info relevant to the intercept (there are no other coefficients)
print(res.summary().tables[1])
```
Many tests have an equivalent linear model.
#### Other information provided by **Pingouin** tests
We've covered the degrees of freedom, the T statistic, the p-value, and the confidence interval. So what's all that other gunk in our t-test? Cohen's d is a measure of whether the difference being measured in our test is large or not (this is important; you can have statistically significant differences that are so small as to be inconsequential). Cohen suggested that $d = 0.2$ be considered a 'small' effect size, 0.5 represents a 'medium' effect size and 0.8 a 'large' effect size. BF10 represents the Bayes factor, the ratio (given the data) of the likelihood of the alternative hypothesis relative to the null hypothesis. Values greater than unity therefore favour the alternative hypothesis. Finally, power is the achieved power of the test, which is $1 - \mathbb{P}(\text{type II error})$. A common default to have in mind is a power greater than 0.8.
### Two-sample t-test
The two-sample t-test is used to determine if two population means are equal (with the null being that they *are* equal). Let's look at an example with synthetic data of equal length, which means we can use the *paired* version of this. We'll imagine we are looking at an intervention with a pre- and post- dataset.
```
pre = [5.5, 2.4, 6.8, 9.6, 4.2, 5.9]
post = [6.4, 3.4, 6.4, 11., 4.8, 6.2]
pg.ttest(pre, post, paired=True, tail='two-sided').round(2)
```
In this case, we cannot reject the null hypothesis that the means are the same pre- and post-intervention.
### Pearson correlation
The Pearson correlation coefficient measures the linear relationship between two datasets. Strictly speaking, it requires that each dataset be normally distributed.
```
mean, cov = [4, 6], [(1, .5), (.5, 1)]
x, y = prng.multivariate_normal(mean, cov, 30).T
# Compute Pearson correlation
pg.corr(x, y).round(3)
```
### Welch's t-test
In the case where you have two samples with unequal variances (or, really, unequal sample sizes too), Welch's t-test is appropriate. With `correction='true'`, it assumes that variances are not equal.
```
x = prng.normal(loc=7, size=20)
y = prng.normal(loc=6.5, size=15)
pg.ttest(x, y, correction='true')
```
### One-way ANOVA
Analysis of variance (ANOVA) is a technique for testing hypotheses about means, for example testing the equality of the means of $k>2$ groups. The model would be
$$
X_{ij} = \mu_i + \epsilon_{ij} \quad j=1, \dots, n_i \quad i=1, \dots, k.
$$
so that the $i$th group has $n_i$ observations. The null hypothesis of one-way ANOVA is that $H_0: \mu_1 = \mu_2 = \dots = \mu_k$, with the alternative hypothesis that this is *not* true.
```
df = pg.read_dataset('mixed_anova')
df.head()
# Run the ANOVA
pg.anova(data=df, dv='Scores', between='Group', detailed=True)
```
### Multiple pairwise t-tests
There's a problem with running multiple t-tests: if you run enough of them, something is bound to come up as significant! As such, some *post-hoc* adjustments exist that correct for the fact that multiple tests are occurring simultaneously. In the example below, multiple pairwise comparisons are made between the scores by time group. There is a corrected p-value, `p-corr`, computed using the Benjamini/Hochberg FDR correction.
```
pg.pairwise_ttests(data=df, dv='Scores', within='Time', subject='Subject',
parametric=True, padjust='fdr_bh', effsize='hedges').round(3)
```
### One-way ANCOVA
Analysis of covariance (ANCOVA) is a general linear model which blends ANOVA and regression. ANCOVA evaluates whether the means of a dependent variable (dv) are equal across levels of a categorical independent variable (between) often called a treatment, while statistically controlling for the effects of other continuous variables that are not of primary interest, known as covariates or nuisance variables (covar).
```
df = pg.read_dataset('ancova')
df.head()
pg.ancova(data=df, dv='Scores', covar='Income', between='Method')
```
### Power calculations
Often, it's quite useful to know what sample size is needed to avoid certain types of testing errors. **Pingouin** offers ways to compute effect sizes and test powers to help with these questions.
As an example, let's assume we have a new drug (`x`) and an old drug (`y`) that are both intended to reduce blood pressure. The standard deviation of the reduction in blood pressure of those receiving the old drug is 12 units. The null hypothesis is that the new drug is no more effective than the new drug. But it will only be worth switching production to the new drug if it reduces blood pressure by more than 3 units versus the old drug. In this case, the effect size of interest is 3 units.
Let's assume for a moment that the true difference is 3 units and we want to perform a test with $\alpha=0.05$. The problem is that, for small differences in the effect, the distribution of effects under the null and the distribution of effects under the alternative have a great deal of overlap. So the chances of making a Type II error - accepting the null hypothesis when it is actually false - is quite high. Let's say we'd ideally have at most a 20% chance of making a Type II error: what sample size do we need?
We can compute this, but we need an extra piece of information first: a normalised version of the effect size called Cohen's $d$. We need to transform the difference in means to compute this. For independent samples, $d$ is:
$$ d = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{(n_{1} - 1)\sigma_{1}^{2} + (n_{2} - 1)\sigma_{2}^{2}}{n_1 + n_2 - 2}}}$$
(If you have real data samples, you can compute this using `pg.compute_effsize`.)
For this case, $d$ is $-3/12 = -1/4$ if we assume the standard deviations are the same across the old (`y`) and new (`x`) drugs. So we will plug that $d$ in and look at a range of possible sample sizes along with a standard value for $alpha$ of 0.05. In the below `tail=less` tests the alternative that `x` has a smaller mean than `y`.
```
cohen_d = -0.25 # Fixed effect size
sample_size_array = np.arange(1, 500, 50) # Incrementing sample size
# Compute the achieved power
pwr = pg.power_ttest(d=cohen_d, n=sample_size_array, alpha=0.05,
contrast='two-samples', tail='less')
fig, ax = plt.subplots()
ax.plot(sample_size_array, pwr, 'ko-.')
ax.axhline(0.8, color='r', ls=':')
ax.set_xlabel('Sample size')
ax.set_ylabel('Power (1 - type II error)')
ax.set_title('Achieved power of a T-test')
plt.show()
```
From this, we can see we need a sample size of at least 200 in order to have a power of 0.8.
The `pg.power_ttest` function takes any three of the four of `d`, `n`, `power`, and `alpha` (ie leave one of these out), and then returns what the missing parameter should be. We passed in `d`, `n`, and `alpha`, and so the `power` was returned.
## Non-parametric tests
Reminder: non-parametrics tests do not make any assumptions about the distribution from which data are drawn or that it can be described by fixed parameters.
### Wilcoxon Signed-rank Test
This tests the null hypothesis that two related paired samples come from the same distribution. It is the non-parametric equivalent of the t-test.
```
x = [20, 22, 19, 20, 22, 18, 24, 20, 19, 24, 26, 13]
y = [38, 37, 33, 29, 14, 12, 20, 22, 17, 25, 26, 16]
pg.wilcoxon(x, y, tail='two-sided').round(2)
```
### Mann-Whitney U Test (aka Wilcoxon rank-sum test)
The Mann–Whitney U test is a non-parametric test of the null hypothesis that it is equally likely that a randomly selected value from one sample will be less than or greater than a randomly selected value from a second sample. It is the non-parametric version of the two-sample T-test.
Like many non-parametric **pingouin** tests, it can take values of tail that are 'two-sided', 'one-sided', 'greater', or 'less'. Below, we ask if a randomly selected value from `x` is greater than one from `y`, with the null that it is not.
```
x = prng.uniform(low=0, high=1, size=20)
y = prng.uniform(low=0.2, high=1.2, size=20)
pg.mwu(x, y, tail='greater')
```
### Spearman Correlation
The Spearman correlation coefficient is the Pearson correlation coefficient between the rank variables, and does not assume normality of data.
```
mean, cov = [4, 6], [(1, .5), (.5, 1)]
x, y = prng.multivariate_normal(mean, cov, 30).T
pg.corr(x, y, method="spearman").round(2)
```
### Kruskal-Wallace
The Kruskal-Wallis H-test tests the null hypothesis that the population median of all of the groups are equal. It is a non-parametric version of ANOVA. The test works on 2 or more independent samples, which may have different sizes.
```
df = pg.read_dataset('anova')
df.head()
pg.kruskal(data=df, dv='Pain threshold', between='Hair color')
```
### The Chi-Squared Test
The chi-squared test is used to determine whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories. This test can be used to evaluate the quality of a categorical variable in a classification problem or to check the similarity between two categorical variables.
There are two conditions for a chi-squared test:
- Independence: Each case that contributes a count to the table must be independent of all the other cases in the table.
- Sample size or distribution: Each particular case (ie cell count) must have at least 5 expected cases.
Let's see an example from the **pingouin** docs: whether gender is a good predictor of heart disease. First, let's load the data and look at the gender split in total:
```
chi_data = pg.read_dataset('chi2_independence')
chi_data['sex'].value_counts(ascending=True)
```
If gender is *not* a predictor, we would expect a roughly similar split between those who have heart disease and those who do not. Let's look at the observerd versus the expected split once we categorise by gender and 'target' (heart disease or not).
```
expected, observed, stats = pg.chi2_independence(chi_data, x='sex', y='target')
observed - expected
```
So we have fewer in the 0, 0 and 1, 1 buckets than expected but more in the 0, 1 and 1, 0 buckets. Let's now see how the test interprets this:
```
stats.round(3)
```
From these, it is clear we can reject the null and therefore it seems like gender is a good predictor of heart disease.
### Shapiro-Wilk Test for Normality
Note that the null here is that the distribution *is* normal, so normality is only rejected when the p-value is sufficiently small.
```
x = prng.normal(size=20)
pg.normality(x)
```
The test can also be run on multiple variables in a dataframe:
```
df = pg.read_dataset('ancova')
pg.normality(df[['Scores', 'Income', 'BMI']], method='normaltest').round(3)
```
| github_jupyter |
```
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import savefig
import cv2
np.set_printoptions(threshold=np.inf)
num_images = 3670
dataset = []
for i in range(1, num_images+1):
img = cv2.imread("color_images/color_" +str(i) +".jpg" )
dataset.append(np.array(img))
dataset_source = np.asarray(dataset)
print(dataset_source.shape)
dataset_tar = []
for i in range(1, num_images+1):
img = cv2.imread("gray_images/gray_" +str(i) +".jpg", 0)
dataset_tar.append(np.array(img))
dataset_target = np.asarray(dataset_tar)
print(dataset_target.shape)
dataset_target = dataset_target[:, :, :, np.newaxis]
def autoencoder(inputs): # Undercomplete Autoencoder
# Encoder
net = tf.layers.conv2d(inputs, 128, 2, activation = tf.nn.relu)
print(net.shape)
net = tf.layers.max_pooling2d(net, 2, 2, padding = 'same')
print(net.shape)
# Decoder
net = tf.image.resize_nearest_neighbor(net, tf.constant([129, 129]))
net = tf.layers.conv2d(net, 1, 2, activation = None, name = 'outputOfAuto')
print(net.shape)
return net
ae_inputs = tf.placeholder(tf.float32, (None, 128, 128, 3), name = 'inputToAuto')
ae_target = tf.placeholder(tf.float32, (None, 128, 128, 1))
ae_outputs = autoencoder(ae_inputs)
lr = 0.001
loss = tf.reduce_mean(tf.square(ae_outputs - ae_target))
train_op = tf.train.AdamOptimizer(learning_rate = lr).minimize(loss)
# Intialize the network
init = tf.global_variables_initializer()
```
#### If you don't want to train the network skip the cell righ below and dowload the pre-trained model. After downloading the pre-trained model run the cell below to the immediate below cell.
```
batch_size = 32
epoch_num = 50
saving_path = 'K:/autoencoder_color_to_gray/SavedModel/AutoencoderColorToGray.ckpt'
saver_ = tf.train.Saver(max_to_keep = 3)
batch_img = dataset_source[0:batch_size]
batch_out = dataset_target[0:batch_size]
num_batches = num_images//batch_size
sess = tf.Session()
sess.run(init)
for ep in range(epoch_num):
batch_size = 0
for batch_n in range(num_batches): # batches loop
_, c = sess.run([train_op, loss], feed_dict = {ae_inputs: batch_img, ae_target: batch_out})
print("Epoch: {} - cost = {:.5f}" .format((ep+1), c))
batch_img = dataset_source[batch_size: batch_size+32]
batch_out = dataset_target[batch_size: batch_size+32]
batch_size += 32
saver_.save(sess, saving_path, global_step = ep)
recon_img = sess.run([ae_outputs], feed_dict = {ae_inputs: batch_img})
sess.close()
saver = tf.train.Saver()
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
saver.restore(sess, 'K:/autoencoder_color_to_gray/SavedModel/AutoencoderColorToGray.ckpt-49')
import glob as gl
filenames = gl.glob('flower_images/*.png')
test_data = []
for file in filenames[0:100]:
test_data.append(np.array(cv2.imread(file)))
test_dataset = np.asarray(test_data)
print(test_dataset.shape)
# Running the test data on the autoencoder
batch_imgs = test_dataset
gray_imgs = sess.run(ae_outputs, feed_dict = {ae_inputs: batch_imgs})
print(gray_imgs.shape)
for i in range(gray_imgs.shape[0]):
cv2.imwrite('gen_gray_images/gen_gray_' +str(i) +'.jpeg', gray_imgs[i])
```
| github_jupyter |
# CarND Object Detection Lab
Let's get started!
```
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from PIL import ImageDraw
from PIL import ImageColor
import time
from scipy.stats import norm
%matplotlib inline
plt.style.use('ggplot')
```
## MobileNets
[*MobileNets*](https://arxiv.org/abs/1704.04861), as the name suggests, are neural networks constructed for the purpose of running very efficiently (high FPS, low memory footprint) on mobile and embedded devices. *MobileNets* achieve this with 3 techniques:
1. Perform a depthwise convolution followed by a 1x1 convolution rather than a standard convolution. The 1x1 convolution is called a pointwise convolution if it's following a depthwise convolution. The combination of a depthwise convolution followed by a pointwise convolution is sometimes called a separable depthwise convolution.
2. Use a "width multiplier" - reduces the size of the input/output channels, set to a value between 0 and 1.
3. Use a "resolution multiplier" - reduces the size of the original input, set to a value between 0 and 1.
These 3 techniques reduce the size of cummulative parameters and therefore the computation required. Of course, generally models with more paramters achieve a higher accuracy. *MobileNets* are no silver bullet, while they perform very well larger models will outperform them. ** *MobileNets* are designed for mobile devices, NOT cloud GPUs**. The reason we're using them in this lab is automotive hardware is closer to mobile or embedded devices than beefy cloud GPUs.
### Convolutions
#### Vanilla Convolution
Before we get into the *MobileNet* convolution block let's take a step back and recall the computational cost of a vanilla convolution. There are $N$ kernels of size $D_k * D_k$. Each of these kernels goes over the entire input which is a $D_f * D_f * M$ sized feature map or tensor (if that makes more sense). The computational cost is:
$$
D_g * D_g * M * N * D_k * D_k
$$
Let $D_g * D_g$ be the size of the output feature map. Then a standard convolution takes in a $D_f * D_f * M$ input feature map and returns a $D_g * D_g * N$ feature map as output.
(*Note*: In the MobileNets paper, you may notice the above equation for computational cost uses $D_f$ instead of $D_g$. In the paper, they assume the output and input are the same spatial dimensions due to stride of 1 and padding, so doing so does not make a difference, but this would want $D_g$ for different dimensions of input and output.)

#### Depthwise Convolution
A depthwise convolution acts on each input channel separately with a different kernel. $M$ input channels implies there are $M$ $D_k * D_k$ kernels. Also notice this results in $N$ being set to 1. If this doesn't make sense, think about the shape a kernel would have to be to act upon an individual channel.
Computation cost:
$$
D_g * D_g * M * D_k * D_k
$$

#### Pointwise Convolution
A pointwise convolution performs a 1x1 convolution, it's the same as a vanilla convolution except the kernel size is $1 * 1$.
Computation cost:
$$
D_k * D_k * D_g * D_g * M * N =
1 * 1 * D_g * D_g * M * N =
D_g * D_g * M * N
$$

Thus the total computation cost is for separable depthwise convolution:
$$
D_g * D_g * M * D_k * D_k + D_g * D_g * M * N
$$
which results in $\frac{1}{N} + \frac{1}{D_k^2}$ reduction in computation:
$$
\frac {D_g * D_g * M * D_k * D_k + D_g * D_g * M * N} {D_g * D_g * M * N * D_k * D_k} =
\frac {D_k^2 + N} {D_k^2*N} =
\frac {1}{N} + \frac{1}{D_k^2}
$$
*MobileNets* use a 3x3 kernel, so assuming a large enough $N$, separable depthwise convnets are ~9x more computationally efficient than vanilla convolutions!
### Width Multiplier
The 2nd technique for reducing the computational cost is the "width multiplier" which is a hyperparameter inhabiting the range [0, 1] denoted here as $\alpha$. $\alpha$ reduces the number of input and output channels proportionally:
$$
D_f * D_f * \alpha M * D_k * D_k + D_f * D_f * \alpha M * \alpha N
$$
### Resolution Multiplier
The 3rd technique for reducing the computational cost is the "resolution multiplier" which is a hyperparameter inhabiting the range [0, 1] denoted here as $\rho$. $\rho$ reduces the size of the input feature map:
$$
\rho D_f * \rho D_f * M * D_k * D_k + \rho D_f * \rho D_f * M * N
$$
Combining the width and resolution multipliers results in a computational cost of:
$$
\rho D_f * \rho D_f * a M * D_k * D_k + \rho D_f * \rho D_f * a M * a N
$$
Training *MobileNets* with different values of $\alpha$ and $\rho$ will result in different speed vs. accuracy tradeoffs. The folks at Google have run these experiments, the result are shown in the graphic below:

MACs (M) represents the number of multiplication-add operations in the millions.
### Exercise 1 - Implement Separable Depthwise Convolution
In this exercise you'll implement a separable depthwise convolution block and compare the number of parameters to a standard convolution block. For this exercise we'll assume the width and resolution multipliers are set to 1.
Docs:
* [depthwise convolution](https://www.tensorflow.org/api_docs/python/tf/nn/depthwise_conv2d)
```
def vanilla_conv_block(x, kernel_size, output_channels):
"""
Vanilla Conv -> Batch Norm -> ReLU
"""
x = tf.layers.conv2d(
x, output_channels, kernel_size, (2, 2), padding='SAME')
x = tf.layers.batch_normalization(x)
return tf.nn.relu(x)
# TODO: implement MobileNet conv block
def mobilenet_conv_block(x, kernel_size, output_channels):
"""
Depthwise Conv -> Batch Norm -> ReLU -> Pointwise Conv -> Batch Norm -> ReLU
"""
pass
```
**[Sample solution](./exercise-solutions/e1.py)**
Let's compare the number of parameters in each block.
```
# constants but you can change them so I guess they're not so constant :)
INPUT_CHANNELS = 32
OUTPUT_CHANNELS = 512
KERNEL_SIZE = 3
IMG_HEIGHT = 256
IMG_WIDTH = 256
with tf.Session(graph=tf.Graph()) as sess:
# input
x = tf.constant(np.random.randn(1, IMG_HEIGHT, IMG_WIDTH, INPUT_CHANNELS), dtype=tf.float32)
with tf.variable_scope('vanilla'):
vanilla_conv = vanilla_conv_block(x, KERNEL_SIZE, OUTPUT_CHANNELS)
with tf.variable_scope('mobile'):
mobilenet_conv = mobilenet_conv_block(x, KERNEL_SIZE, OUTPUT_CHANNELS)
vanilla_params = [
(v.name, np.prod(v.get_shape().as_list()))
for v in tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, 'vanilla')
]
mobile_params = [
(v.name, np.prod(v.get_shape().as_list()))
for v in tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, 'mobile')
]
print("VANILLA CONV BLOCK")
total_vanilla_params = sum([p[1] for p in vanilla_params])
for p in vanilla_params:
print("Variable {0}: number of params = {1}".format(p[0], p[1]))
print("Total number of params =", total_vanilla_params)
print()
print("MOBILENET CONV BLOCK")
total_mobile_params = sum([p[1] for p in mobile_params])
for p in mobile_params:
print("Variable {0}: number of params = {1}".format(p[0], p[1]))
print("Total number of params =", total_mobile_params)
print()
print("{0:.3f}x parameter reduction".format(total_vanilla_params /
total_mobile_params))
```
Your solution should show the majority of the parameters in *MobileNet* block stem from the pointwise convolution.
## *MobileNet* SSD
In this section you'll use a pretrained *MobileNet* [SSD](https://arxiv.org/abs/1512.02325) model to perform object detection. You can download the *MobileNet* SSD and other models from the [TensorFlow detection model zoo](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/detection_model_zoo.md) (*note*: we'll provide links to specific models further below). [Paper](https://arxiv.org/abs/1611.10012) describing comparing several object detection models.
Alright, let's get into SSD!
### Single Shot Detection (SSD)
Many previous works in object detection involve more than one training phase. For example, the [Faster-RCNN](https://arxiv.org/abs/1506.01497) architecture first trains a Region Proposal Network (RPN) which decides which regions of the image are worth drawing a box around. RPN is then merged with a pretrained model for classification (classifies the regions). The image below is an RPN:

The SSD architecture is a single convolutional network which learns to predict bounding box locations and classify the locations in one pass. Put differently, SSD can be trained end to end while Faster-RCNN cannot. The SSD architecture consists of a base network followed by several convolutional layers:

**NOTE:** In this lab the base network is a MobileNet (instead of VGG16.)
#### Detecting Boxes
SSD operates on feature maps to predict bounding box locations. Recall a feature map is of size $D_f * D_f * M$. For each feature map location $k$ bounding boxes are predicted. Each bounding box carries with it the following information:
* 4 corner bounding box **offset** locations $(cx, cy, w, h)$
* $C$ class probabilities $(c_1, c_2, ..., c_p)$
SSD **does not** predict the shape of the box, rather just where the box is. The $k$ bounding boxes each have a predetermined shape. This is illustrated in the figure below:

The shapes are set prior to actual training. For example, In figure (c) in the above picture there are 4 boxes, meaning $k$ = 4.
### Exercise 2 - SSD Feature Maps
It would be a good exercise to read the SSD paper prior to a answering the following questions.
***Q: Why does SSD use several differently sized feature maps to predict detections?***
A: Your answer here
**[Sample answer](./exercise-solutions/e2.md)**
The current approach leaves us with thousands of bounding box candidates, clearly the vast majority of them are nonsensical.
### Exercise 3 - Filtering Bounding Boxes
***Q: What are some ways which we can filter nonsensical bounding boxes?***
A: Your answer here
**[Sample answer](./exercise-solutions/e3.md)**
#### Loss
With the final set of matched boxes we can compute the loss:
$$
L = \frac {1} {N} * ( L_{class} + L_{box})
$$
where $N$ is the total number of matched boxes, $L_{class}$ is a softmax loss for classification, and $L_{box}$ is a L1 smooth loss representing the error of the matched boxes with the ground truth boxes. L1 smooth loss is a modification of L1 loss which is more robust to outliers. In the event $N$ is 0 the loss is set 0.
### SSD Summary
* Starts from a base model pretrained on ImageNet.
* The base model is extended by several convolutional layers.
* Each feature map is used to predict bounding boxes. Diversity in feature map size allows object detection at different resolutions.
* Boxes are filtered by IoU metrics and hard negative mining.
* Loss is a combination of classification (softmax) and dectection (smooth L1)
* Model can be trained end to end.
## Object Detection Inference
In this part of the lab you'll detect objects using pretrained object detection models. You can download the latest pretrained models from the [model zoo](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/detection_model_zoo.md), although do note that you may need a newer version of TensorFlow (such as v1.8) in order to use the newest models.
We are providing the download links for the below noted files to ensure compatibility between the included environment file and the models.
[SSD_Mobilenet 11.6.17 version](http://download.tensorflow.org/models/object_detection/ssd_mobilenet_v1_coco_11_06_2017.tar.gz)
[RFCN_ResNet101 11.6.17 version](http://download.tensorflow.org/models/object_detection/rfcn_resnet101_coco_11_06_2017.tar.gz)
[Faster_RCNN_Inception_ResNet 11.6.17 version](http://download.tensorflow.org/models/object_detection/faster_rcnn_inception_resnet_v2_atrous_coco_11_06_2017.tar.gz)
Make sure to extract these files prior to continuing!
```
# Frozen inference graph files. NOTE: change the path to where you saved the models.
SSD_GRAPH_FILE = 'ssd_mobilenet_v1_coco_11_06_2017/frozen_inference_graph.pb'
RFCN_GRAPH_FILE = 'rfcn_resnet101_coco_11_06_2017/frozen_inference_graph.pb'
FASTER_RCNN_GRAPH_FILE = 'faster_rcnn_inception_resnet_v2_atrous_coco_11_06_2017/frozen_inference_graph.pb'
```
Below are utility functions. The main purpose of these is to draw the bounding boxes back onto the original image.
```
# Colors (one for each class)
cmap = ImageColor.colormap
print("Number of colors =", len(cmap))
COLOR_LIST = sorted([c for c in cmap.keys()])
#
# Utility funcs
#
def filter_boxes(min_score, boxes, scores, classes):
"""Return boxes with a confidence >= `min_score`"""
n = len(classes)
idxs = []
for i in range(n):
if scores[i] >= min_score:
idxs.append(i)
filtered_boxes = boxes[idxs, ...]
filtered_scores = scores[idxs, ...]
filtered_classes = classes[idxs, ...]
return filtered_boxes, filtered_scores, filtered_classes
def to_image_coords(boxes, height, width):
"""
The original box coordinate output is normalized, i.e [0, 1].
This converts it back to the original coordinate based on the image
size.
"""
box_coords = np.zeros_like(boxes)
box_coords[:, 0] = boxes[:, 0] * height
box_coords[:, 1] = boxes[:, 1] * width
box_coords[:, 2] = boxes[:, 2] * height
box_coords[:, 3] = boxes[:, 3] * width
return box_coords
def draw_boxes(image, boxes, classes, thickness=4):
"""Draw bounding boxes on the image"""
draw = ImageDraw.Draw(image)
for i in range(len(boxes)):
bot, left, top, right = boxes[i, ...]
class_id = int(classes[i])
color = COLOR_LIST[class_id]
draw.line([(left, top), (left, bot), (right, bot), (right, top), (left, top)], width=thickness, fill=color)
def load_graph(graph_file):
"""Loads a frozen inference graph"""
graph = tf.Graph()
with graph.as_default():
od_graph_def = tf.GraphDef()
with tf.gfile.GFile(graph_file, 'rb') as fid:
serialized_graph = fid.read()
od_graph_def.ParseFromString(serialized_graph)
tf.import_graph_def(od_graph_def, name='')
return graph
```
Below we load the graph and extract the relevant tensors using [`get_tensor_by_name`](https://www.tensorflow.org/api_docs/python/tf/Graph#get_tensor_by_name). These tensors reflect the input and outputs of the graph, or least the ones we care about for detecting objects.
```
detection_graph = load_graph(SSD_GRAPH_FILE)
# detection_graph = load_graph(RFCN_GRAPH_FILE)
# detection_graph = load_graph(FASTER_RCNN_GRAPH_FILE)
# The input placeholder for the image.
# `get_tensor_by_name` returns the Tensor with the associated name in the Graph.
image_tensor = detection_graph.get_tensor_by_name('image_tensor:0')
# Each box represents a part of the image where a particular object was detected.
detection_boxes = detection_graph.get_tensor_by_name('detection_boxes:0')
# Each score represent how level of confidence for each of the objects.
# Score is shown on the result image, together with the class label.
detection_scores = detection_graph.get_tensor_by_name('detection_scores:0')
# The classification of the object (integer id).
detection_classes = detection_graph.get_tensor_by_name('detection_classes:0')
```
Run detection and classification on a sample image.
```
# Load a sample image.
image = Image.open('./assets/sample1.jpg')
image_np = np.expand_dims(np.asarray(image, dtype=np.uint8), 0)
with tf.Session(graph=detection_graph) as sess:
# Actual detection.
(boxes, scores, classes) = sess.run([detection_boxes, detection_scores, detection_classes],
feed_dict={image_tensor: image_np})
# Remove unnecessary dimensions
boxes = np.squeeze(boxes)
scores = np.squeeze(scores)
classes = np.squeeze(classes)
confidence_cutoff = 0.8
# Filter boxes with a confidence score less than `confidence_cutoff`
boxes, scores, classes = filter_boxes(confidence_cutoff, boxes, scores, classes)
# The current box coordinates are normalized to a range between 0 and 1.
# This converts the coordinates actual location on the image.
width, height = image.size
box_coords = to_image_coords(boxes, height, width)
# Each class with be represented by a differently colored box
draw_boxes(image, box_coords, classes)
plt.figure(figsize=(12, 8))
plt.imshow(image)
```
## Timing Detection
The model zoo comes with a variety of models, each its benefits and costs. Below you'll time some of these models. The general tradeoff being sacrificing model accuracy for seconds per frame (SPF).
```
def time_detection(sess, img_height, img_width, runs=10):
image_tensor = sess.graph.get_tensor_by_name('image_tensor:0')
detection_boxes = sess.graph.get_tensor_by_name('detection_boxes:0')
detection_scores = sess.graph.get_tensor_by_name('detection_scores:0')
detection_classes = sess.graph.get_tensor_by_name('detection_classes:0')
# warmup
gen_image = np.uint8(np.random.randn(1, img_height, img_width, 3))
sess.run([detection_boxes, detection_scores, detection_classes], feed_dict={image_tensor: gen_image})
times = np.zeros(runs)
for i in range(runs):
t0 = time.time()
sess.run([detection_boxes, detection_scores, detection_classes], feed_dict={image_tensor: image_np})
t1 = time.time()
times[i] = (t1 - t0) * 1000
return times
with tf.Session(graph=detection_graph) as sess:
times = time_detection(sess, 600, 1000, runs=10)
# Create a figure instance
fig = plt.figure(1, figsize=(9, 6))
# Create an axes instance
ax = fig.add_subplot(111)
plt.title("Object Detection Timings")
plt.ylabel("Time (ms)")
# Create the boxplot
plt.style.use('fivethirtyeight')
bp = ax.boxplot(times)
```
### Exercise 4 - Model Tradeoffs
Download a few models from the [model zoo](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/detection_model_zoo.md) and compare the timings.
## Detection on a Video
Finally run your pipeline on [this short video](https://s3-us-west-1.amazonaws.com/udacity-selfdrivingcar/advanced_deep_learning/driving.mp4).
```
# Import everything needed to edit/save/watch video clips
from moviepy.editor import VideoFileClip
from IPython.display import HTML
HTML("""
<video width="960" height="600" controls>
<source src="{0}" type="video/mp4">
</video>
""".format('driving.mp4'))
```
### Exercise 5 - Object Detection on a Video
Run an object detection pipeline on the above clip.
```
clip = VideoFileClip('driving.mp4')
# TODO: Complete this function.
# The input is an NumPy array.
# The output should also be a NumPy array.
def pipeline(img):
pass
```
**[Sample solution](./exercise-solutions/e5.py)**
```
with tf.Session(graph=detection_graph) as sess:
image_tensor = sess.graph.get_tensor_by_name('image_tensor:0')
detection_boxes = sess.graph.get_tensor_by_name('detection_boxes:0')
detection_scores = sess.graph.get_tensor_by_name('detection_scores:0')
detection_classes = sess.graph.get_tensor_by_name('detection_classes:0')
new_clip = clip.fl_image(pipeline)
# write to file
new_clip.write_videofile('result.mp4')
HTML("""
<video width="960" height="600" controls>
<source src="{0}" type="video/mp4">
</video>
""".format('result.mp4'))
```
## Further Exploration
Some ideas to take things further:
* Finetune the model on a new dataset more relevant to autonomous vehicles. Instead of loading the frozen inference graph you'll load the checkpoint.
* Optimize the model and get the FPS as low as possible.
* Build your own detector. There are several base model pretrained on ImageNet you can choose from. [Keras](https://keras.io/applications/) is probably the quickest way to get setup in this regard.
| github_jupyter |
```
import sys
import json
sys.path.insert(0, "../")
print(sys.path)
import pymongo
#31470/5/1
import sys
import json
import cobrakbase
import cobrakbase.core.model
import cobra
import logging
#from cobra.core import Gene, Metabolite, Model, Reaction
#from pyeda import *
#from pyeda.inter import *
#from pyeda.boolalg import expr
import pandas as pd
fbamodel = None
data = None
with open('community_model.json', 'r') as fh:
data = json.loads(fh.read())
fbamodel = cobrakbase.core.KBaseFBAModel(data)
for r in data['modelreactions']:
if 'rxn0020_c0' in r['id']:
print(r)
for r in fbamodel.get_reactions():
r = fbamodel.get_reaction(r['id'])
o = b.convert_modelreaction(r)
if 'rxn0020_c0' in o.id:
print(o, r.id)
kbase_api = cobrakbase.KBaseAPI("64XQ7SABQILQWSEW3CQKZXJA63DXZBGH")
#ref = kbase_api.get_object_info_from_ref(fbamodel.data['genome_ref'])
modelseed = cobrakbase.modelseed.from_local('../../../../ModelSEEDDatabase')
for seed_id in modelseed.reactions:
seed_rxn = modelseed.get_seed_reaction(seed_id)
ec_numbers = set()
if 'Enzyme Class' in seed_rxn.ec_numbers:
for ec in seed_rxn.ec_numbers['Enzyme Class']:
if ec.startswith('EC-'):
ec_numbers.add(ec[3:])
else:
ec_numbers.add(ec)
def annotate_model_reactions_with_modelseed(model, modelseed):
for r in model.reactions:
seed_id = None
if 'seed.reaction' in r.annotation:
annotation = {}
seed_id = r.annotation['seed.reaction']
seed_rxn = modelseed.get_seed_reaction(seed_id)
if not seed_rxn == None:
1
else:
print('!', r.id)
print(seed_id)
break
return r
r= annotate_model_reactions_with_modelseed(model, modelseed)
r
r.annotation
b = cobrakbase.core.converters.KBaseFBAModelToCobraBuilder(fbamodel)
if 'genome_ref' in fbamodel.data:
logging.info(f"Annotating model with genome information: {fbamodel.data['genome_ref']}")
#ref = kbase_api.get_object_info_from_ref(fbamodel.data['genome_ref'])
#genome_data = kbase_api.get_object(ref.id, ref.ws)
#genome = self.dfu.get_objects(
# {'object_refs': [ret['data']['genome_ref']]})['data'][0]['data']
# #adding Genome to the Builder
# builder.with_genome(KBaseGenome(genome))
model = b.build()
print(cobrakbase.annotate_model_with_modelseed(model, modelseed))
model.summary()
model = cobra.io.read_sbml_model('../../../../data/sbml/saccharomyces.xml')
cobra.io.write_sbml_model
solution = model.optimize()
solution
o_data = kbase_dev.get_object('GCF_000005845.2.beta.fba', 'filipeliu:narrative_1556512034170')
fba = cobrakbase.core.KBaseFBA(o_data)
fba.data.keys('FBAReactionVariables')
with open('../../../../data/www/mpa19/flux.txt', 'w+') as f:
for o in fba.data['FBAReactionVariables']:
v = o['value']
rxn_id = o['modelreaction_ref'].split('/')[-1]
#print(rxn_id, v)
f.write("{},{}\n".format(rxn_id, v))
#model = cobra.io.read_sbml_model('/Users/fliu/Downloads/iML1515.kb.SBML/iML1515.kb.xml')
kbase = cobrakbase.KBaseAPI("YAFOCRSMRNDXZ7KMW7GCK5AC3SBNTEFD")
kbase_dev = cobrakbase.KBaseAPI("YAFOCRSMRNDXZ7KMW7GCK5AC3SBNTEFD", dev=True)
#12998
kbase.ws_client.ver.get_workspace_info({'id' : 23938})
kbase.ws_client.get_workspace_info({'id' : 12998})
ref_info = kbase.get_object_info_from_ref('12998/1/2')
print(ref_info.id, ref_info.workspace_id, ref_info.workspace_uid, ref_info.uid, ref_info)
a = kbase_dev.ws_client.get_workspace_info({'workspace' : 'NewKBaseModelTemplates'})
kbase_dev.list_objects('NewKBaseModelTemplates')
kmodel = kbase_dev.get_object('Escherichia_coli_K-12_MG1655_output', 'filipeliu:narrative_1564175222344')
kmodel.keys()
kmodel['genome_ref']
kmodel['template_ref'] = '50/1/2'
genome_ref = '31470/4/1'
for mr in kmodel['modelreactions']:
#print(mr)
for mrp in mr['modelReactionProteins']:
#print(modelReactionProtein)
for mrps in mrp['modelReactionProteinSubunits']:
for i in range(len(mrps['feature_refs'])):
a, b = mrps['feature_refs'][i].split('features')
#print(a, b)
mrps['feature_refs'][i] = kmodel['genome_ref'] + '/features' + b
#mrps['feature_refs'][i] = kmodel['genome_ref'] + f_block
#print(i, mrps['feature_refs'][i], f_block)
kbase_dev.save_object('Escherichia_coli_K-12_MG1655_output', 'filipeliu:narrative_1564175222344', 'KBaseFBA.FBAModel', kmodel)
kmodel['genome_ref']
kbase_dev.ws_client.get_object_info3({'objects' : [{'ref' : '31470/5/2'}]})
%run ../../../scripts/bios_utils.py
with open('aww.json', 'w') as f:
f.write(json.dumps(kmodel, indent=4, sort_keys=True))
kbase_dev.list_objects('filipeliu:narrative_1564175222344')
os = kbase.list_objects('filipeliu:narrative_1564417971147')
kmodel = kbase.get_object('test', 'filipeliu:narrative_1564417971147')
kmodel['gapfillings']
os[4] #31470/3/1
o_data['gapfillings']
ref = kbase.get_object_info_from_ref('262/34/1')
ref.id
for o in os:
if not o[2].startswith('KBaseNarrative.Narrative') and not o[2].startswith('KBaseGenomes.Genome'):
print(o)
o_data = kbase.get_object(o[1], 'zahmeeth:narrative_1561761748173')
if 'genome_ref' in o_data:
o_data['genome_ref'] = '31470/2/1'
if 'gapfillings' in o_data:
for gapfilling in o_data['gapfillings']:
print(o[1], gapfilling['gapfill_id'])
if 'media_ref' in gapfilling:
gapfilling['media_ref'] = '31470/3/1'
#kbase_dev.save_object(o[1], 'filipeliu:narrative_1564175222344', o[2].split('-')[0], o_data)
kmodel = kbase.get_object('iML1515.kb', 'zahmeeth:narrative_1561761748173')
ref = kbase.get_object_info_from_ref(kmodel['genome_ref'])
kgenome = kbase.get_object(ref.id, ref.workspace_id)
genome = cobrakbase.core.KBaseGenome(kgenome)
builder = cobrakbase.core.converters.KBaseFBAModelToCobraBuilder(cobrakbase.core.model.KBaseFBAModel(kmodel))
builder = builder.with_genome(genome)
model = builder.build()
gene = model.genes[5]
gene.annotation
cobrakbase.COBRA_DEFAULT_LB = -1000
cobrakbase.COBRA_DEFAULT_UB = 1000
kmodel = kbase.get_object('iAF1260.fix2.kb', 'filipeliu:narrative_1504192868437')
exprvar
os = kbase.list_objects('jplfaria:narrative_1524466549180')
genomes = set()
for o in os:
if o[1].endswith('RAST'):
genomes.add(o[1])
print(len(genomes))
os = kbase.list_objects('filipeliu:narrative_1549385719110')
genomes2 = set()
for o in os:
if o[1].endswith('RAST.mdl.gfrelease.Carbon-D-Glucose'):
id = o[1].split('.mdl.')[0]
genomes2.add(id)
print(len(genomes2))
#genomes2
genomes3 = set()
for o in os:
if o[1].endswith('RAST.mdl.gfrelease.Carbon-D-Glucose.fba'):
id = o[1].split('.mdl.')[0]
genomes3.add(id)
print(len(genomes3))
kmedia = kbase.get_object('Carbon-D-Glucose', 'filipeliu:narrative_1549385719110')
media_const = cobrakbase.convert_media(kmedia)
genome_id = 'GCF_000005845.2.RAST'
def eval_fba(genome_id):
kmodel = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose', 'filipeliu:narrative_1549385719110')
#genome = kbase.get_object('GCF_000005845.2.RAST', 'jplfaria:narrative_1524466549180')
enforce_direaction_bounds(kmodel)
kmodel_fba = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose.fba', 'filipeliu:narrative_1549385719110')
fbamodel = cobrakbase.core.model.KBaseFBAModel(kmodel)
kbase_fba = kmodel_fba['objectiveValue']
model = cobrakbase.convert_kmodel(kmodel, media_const)
solution = model.optimize()
cobra_fba = solution.objective_value
print(kbase_fba, cobra_fba, cobra_fba - cobra_fba)
return kbase_fba, cobra_fba, cobra_fba - cobra_fba
kmodel = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose', 'filipeliu:narrative_1549385719110')
#genome = kbase.get_object('GCF_000005845.2.RAST', 'jplfaria:narrative_1524466549180')
enforce_direaction_bounds(kmodel)
kmodel_fba = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose.fba', 'filipeliu:narrative_1549385719110')
fbamodel = cobrakbase.core.model.KBaseFBAModel(kmodel)
cpd_ref_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Compound_Aliases.txt'
rxn_ref_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Reaction_Aliases.txt'
rxn_ec_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Reaction_ECs.txt'
cpd_stru_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Structures/ModelSEED_Structures.txt'
cpd_df = pd.read_csv(cpd_ref_file, sep='\t')
rxn_df = pd.read_csv(rxn_ref_file, sep='\t')
rxn_ec_df = pd.read_csv(rxn_ec_file, sep='\t')
stru_df = pd.read_csv(cpd_stru_file, sep='\t')
structures = cobrakbase.read_modelseed_compound_structures(stru_df)
rxn_aliases = cobrakbase.read_modelseed_reaction_aliases2(rxn_df)
cpd_aliases = cobrakbase.read_modelseed_compound_aliases2(cpd_df)
gene_aliases = cobrakbase.read_genome_aliases(genome)
def annotate_model(model, cpd_aliases, rxn_aliases, gene_aliases, structures):
for m in model.metabolites:
seed_id = None
if 'seed.compound' in m.annotation:
seed_id = m.annotation['seed.compound']
if seed_id in structures:
m.annotation.update(structures[seed_id])
if seed_id in cpd_aliases:
m.annotation.update(cpd_aliases[seed_id])
for r in model.reactions:
seed_id = None
if 'seed.reaction' in r.annotation:
seed_id = r.annotation['seed.reaction']
if seed_id in rxn_aliases:
r.annotation.update(rxn_aliases[seed_id])
for g in model.genes:
if g.id in gene_aliases:
g.annotation.update(gene_aliases[g.id])
for r in model.reactions:
if cobrakbase.is_translocation(r):
if cobrakbase.is_transport(r):
r.annotation['sbo'] = 'SBO:0000655'
else:
r.annotation['sbo'] = 'SBO:0000185'
kbase_sinks = ['rxn13783_c0', 'rxn13784_c0', 'rxn13782_c0']
for r in model.reactions:
#r.annotation['ec-code'] = '1.1.1.1'
#r.annotation['metanetx.reaction'] = 'MNXR103371'
if r.id in kbase_sinks:
r.annotation['sbo'] = 'SBO:0000632'
if r.id.startswith('DM_'):
r.annotation['sbo'] = 'SBO:0000628'
#
cpd_ref_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Compound_Aliases.txt'
rxn_ref_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Reaction_Aliases.txt'
rxn_ec_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Reaction_ECs.txt'
cpd_stru_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Structures/ModelSEED_Structures.txt'
cpd_df = pd.read_csv(cpd_ref_file, sep='\t')
rxn_df = pd.read_csv(rxn_ref_file, sep='\t')
rxn_ec_df = pd.read_csv(rxn_ec_file, sep='\t')
stru_df = pd.read_csv(cpd_stru_file, sep='\t')
structures = cobrakbase.read_modelseed_compound_structures(stru_df)
rxn_aliases = cobrakbase.read_modelseed_reaction_aliases2(rxn_df)
cpd_aliases = cobrakbase.read_modelseed_compound_aliases2(cpd_df)
exclude = genomes - genomes2
i = 0
for genome_id in genomes:
if not genome_id in exclude:
kmodel = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose', 'filipeliu:narrative_1549385719110')
genome = kbase.get_object(genome_id, 'jplfaria:narrative_1524466549180')
enforce_direaction_bounds(kmodel)
#kmodel_fba = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose.fba', 'filipeliu:narrative_1549385719110')
fbamodel = cobrakbase.core.model.KBaseFBAModel(kmodel)
gene_aliases = cobrakbase.read_genome_aliases(genome)
model = cobrakbase.convert_kmodel(kmodel, media_const)
annotate_model(model, cpd_aliases, rxn_aliases, gene_aliases, structures)
for r in model.reactions:
ub = r.upper_bound
lb = r.lower_bound
if ub == 1000000:
ub = 1000
if lb == -1000000:
lb = -1000
r.upper_bound = ub
r.lower_bound = lb
cobra.io.write_sbml_model(model, '../../data/memote_models/' + genome_id.split('.RAST')[0] + '.xml')
print(i, genome_id)
i += 1
data = {
'genome_id' : [],
'cobra' : []
}
for genome_id in genomes:
if not genome_id in exclude:
print(genome_id)
model = cobra.io.read_sbml_model('../../data/memote_models/' + genome_id.split('.RAST')[0] + '.xml')
solution = model.optimize()
cobra_fba = solution.objective_value
data['genome_id'].append(genome_id)
data['cobra'].append(cobra_fba)
df = pd.DataFrame(data)
df = df.set_index('genome_id')
df.to_csv('../../data/export_fba.tsv', sep='\t')
data = {
'genome_id' : [],
'kbase' : [],
'cobra' : [],
'error' : [],
}
exclude = genomes - genomes3
for genome_id in genomes:
break
if not genome_id in exclude:
kbase_fba, cobra_fba, e = eval_fba(genome_id)
data['genome_id'].append(genome_id)
data['kbase'].append(kbase_fba)
data['cobra'].append(cobra_fba)
data['error'].append(e)
df = pd.DataFrame(data)
df = df.set_index('genome_id')
#df.to_csv('../../data/cobrakbase_fba.tsv', sep='\t')
print()
kmodel_fba.keys()
def enforce_direaction_bounds(kmodel):
for r in kmodel['modelreactions']:
direction = r['direction']
if direction == '>':
r['maxrevflux'] = 0
r['maxforflux'] = 1000
elif direction == '=':
r['maxrevflux'] = 1000
r['maxforflux'] = 1000
elif direction == '<':
r['maxrevflux'] = 1000
r['maxforflux'] = 0
for r in kmodel_fba['FBAReactionVariables']:
break
r_id = r['modelreaction_ref'].split('/')[-1]
frxn = fbamodel.get_reaction(r_id)
#print(frxn.data)
rxn = model.reactions.get_by_id(r_id)
cobra_bound = (rxn.lower_bound, rxn.upper_bound)
lb_ub = (r['lowerBound'], r['upperBound'])
min_max = (r['min'], r['max'])
direction = frxn.data['direction']
if direction == '>':
rxn.lower_bound = 0
rxn.upper_bound = 1000
elif direction == '=':
rxn.lower_bound = -1000
rxn.upper_bound = 1000
elif direction == '<':
rxn.lower_bound = -1000
rxn.upper_bound = 0
print(frxn.data['direction'], cobra_bound, lb_ub, min_max, rxn.flux, r['value'], rxn)
break
solution = model.optimize()
print(solution.objective_value)
b0002 = exprvar('b0002')
f1 = b0002 & z
f1
expr.expr("(b0078 & b0077) | (b3670 & (b3671 | k))").to_dnf().cover
f10 = Or(And(Not(a), b), And(c, Not(d)))
f10
a, b, c, d, k, z, w = map(exprvar, "abcdkzw")
f0 = a & (b | c) | k & (z | w)
dnf = f0.to_dnf()
dnf
def get_protein_sets(dnf):
print('get_protein_sets', dnf)
protein_sets = []
for k in dnf.iter_dfs():
print(type(k))
if type(k) == expr.AndOp:
protein_set = set()
for gene in k.iter_dfs():
if type(gene) == expr.Variable:
protein_set.add(gene)
#print(k, gene)
protein_sets.append(protein_set)
elif type(k) == expr.Variable:
1
#protein_sets.append(set([k]))
elif type(k) == expr.OrOp:
for k_childs in k.iter_dfs():
1
#print(k_childs)
#protein_sets.append(set([k]))
return protein_sets
def get_protein_sets2(dnf):
protein_sets = []
for k in dnf.iter_dfs():
if type(k) == expr.Variable:
protein_set = set()
for gene in k.iter_dfs():
if type(gene) == expr.Variable:
protein_set.add(gene)
#print(k, gene)
protein_sets.append(protein_set)
return protein_sets
protein_sets = get_protein_sets(dnf)
print(dnf, protein_sets)
f100 = expr.expr("(b0078 | b0077) | (b3670 & b3671)").to_dnf()
protein_sets = get_protein_sets(f100)
print(f100, protein_sets)
ast = f100.to_ast()
def get_protein_sets(ast, protein_sets):
print('get_protein_sets', ast)
#protein_sets = []
t = ast[0]
if t == 'or':
for child in ast:
if type(child) == tuple:
get_protein_sets(child, protein_sets)
elif t == 'and':
get_protein_set = set()
for child in ast:
if type(child) == tuple:
get_protein_set.add(child[1])
protein_sets.append(get_protein_set)
elif t == 'lit':
protein_sets.append(set([ast[1]]))
else:
print('invalid type', t)
return protein_sets
f100.NAME
print(f100, get_protein_sets(ast, []))
def get_protein_sets(e, protein_sets):
for var in e.xs:
if var.depth == 0:
for a in var.cover:
#print(type(a.))
print(a)
protein_sets.append(set([a]))
else:
for a in var.xs:
print(a)
print(var, var.depth)
return protein_sets
print(f100, get_protein_sets(f100, []))
for var in ast:
print(var)
dnf.cover
f0.to_cnf()
model = cobrakbase.convert_kmodel(kmodel)
"(b0078 and b0077) or (b3670 and b3671)".replace('and', '&').replace('or', '|')
a = ['b0241', 'b0002']
print(a)
a.sort()
print(a)
mapping = pd.read_csv('/Volumes/My Passport/var/argonne/annotation/manual/iAF1260_rxn_pred.tsv', sep='\t')
to_seed = {}
for _, row in mapping.iterrows():
if not pd.isna(row['ModelSeedReaction']):
to_seed[row['iAF1260'][2:]] = row['ModelSeedReaction']
prot_to_rxn = {}
for r in model_bigg.reactions:
gpr = r.gene_name_reaction_rule
gpr = gpr.replace('and', '&').replace('or', '|')
if len(gpr) > 0:
gpr_expression = expr.expr(gpr)
gpr_expression = gpr_expression.to_dnf()
psets = gpr_expression.cover
for pset in psets:
prot = []
for p in pset:
#print(type(p), str(p))
prot.append(str(p))
prot.sort()
prot = ';'.join(prot)
if not prot in prot_to_rxn:
prot_to_rxn[prot] = set()
prot_to_rxn[prot].add(r.id)
#print(gpr_expression, psets)
data = []
for gene in prot_to_rxn:
#print(gene)
rxn_ids = []
for rxn_id in prot_to_rxn[gene]:
seed_id = to_seed[rxn_id]
rxn_ids.append(seed_id)
data.append([gene, ';'.join(rxn_ids)])
df = pd.DataFrame(data, columns=['genes', 'reactions'])
df.to_csv('iAF1260.csv')
model_bigg = cobra.io.read_sbml_model('iAF1260.xml')
media = None
with open('glucose_media.json', 'r') as f:
data = json.loads(f.read())
media = cobrakbase.convert_media(data)
model = None
with open('test_model.json', 'r') as f:
data = json.loads(f.read())
model = cobrakbase.convert_kmodel(data, media)
model.summary()
for m in model.metabolites:
print(m.id)
print(m.annotation)
break
"cpd11".startswith('cpd')
#https://raw.githubusercontent.com/ModelSEED/ModelSEEDDatabase/dev/Biochemistry/Aliases/Compounds_Aliases.tsv
import pandas as pd
from urllib.request import urlopen
data = urlopen('https://raw.githubusercontent.com/ModelSEED/ModelSEEDDatabase/dev/Biochemistry/Aliases/Compounds_Aliases.tsv')
df = pd.read_csv(data, sep='\t')
data = urlopen('https://raw.githubusercontent.com/ModelSEED/ModelSEEDDatabase/dev/Biochemistry/Aliases/Reactions_Aliases.tsv')
rxn_df = pd.read_csv(data, sep='\t')
data = urlopen('https://raw.githubusercontent.com/ModelSEED/ModelSEEDDatabase/dev/Biochemistry/Structures/ModelSEED_Structures.txt')
stru_df = pd.read_csv(data, sep='\t')
def read_modelseed_compound_aliases(df):
aliases = {}
for a, row in df.iterrows():
if row[3] == 'BiGG':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['bigg.metabolite'] = row[2]
if row[3] == 'MetaCyc':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['biocyc'] = row[2]
if row[3] == 'KEGG' and row[2][0] == 'C':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['kegg.compound'] = row[2]
return aliases
def read_modelseed_reaction_aliases(df):
aliases = {}
for a, row in df.iterrows():
if row[3] == 'BiGG':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['bigg.reaction'] = row[2]
if row[3] == 'MetaCyc':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['biocyc'] = row[2]
if row[3] == 'KEGG' and row[2][0] == 'R':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['kegg.reaction'] = row[2]
return aliases
def read_modelseed_compound_structures(df):
structures = {}
for _, row in df.iterrows():
#print(row[0], row[1], row[3])
if row[1] == 'InChIKey':
if not row[0] in structures:
structures[row[0]] = {}
structures[row[0]]['inchikey'] = row[3]
return structures
structures = read_modelseed_compound_structures(stru_df)
structures['cpd00001']
rxn_aliases = read_modelseed_reaction_aliases(rxn_df)
print(len(rxn_aliases))
print(aliases['cpd00001'])
print(rxn_aliases['rxn00001'])
#jplfaria:narrative_1492808527866
#jplfaria:narrative_1524466549180
kbase = cobrakbase.KBaseAPI('SHO64Q2X7HKU4PP4BV7XQMY3WYIK2QRJ')
#31045/4997/1
kbase.get_object_info_from_ref('31045/4997/1')
wsos = kbase.list_objects('jplfaria:narrative_1492808527866')
#KBaseGenomes.Genome
#KBaseFBA.FBAModel
models = set()
for o in wsos:
if 'KBaseFBA.FBAModel' in o[2]:
models.add(o[1])
kmodel = kbase.get_object('GCF_000005845.2.RAST.mdl', 'jplfaria:narrative_1492808527866')
for m_id in models:
kmodel = kbase.get_object(m_id, 'jplfaria:narrative_1492808527866')
save_model_mongo(kmodel)
mclient = pymongo.MongoClient('mongodb://localhost:27017/')
database = mclient['Models']
kbasemodels = database['TemplateV1']
a = set()
a.add(1)
a.update([2, 3])
a
def save_model_mongo(kmodel):
model_id = kmodel['id']
genome_info = kbase.get_object_info_from_ref(kmodel['genome_ref'])
genome = genome_info['infos'][0][1]
rxn_to_genes = {}
for modelreactions in kmodel['modelreactions']:
rxn_id = modelreactions['reaction_ref'].split('/')[-1].split('_')[0]
genes = []
for modelReactionProteins in modelreactions['modelReactionProteins']:
for modelReactionProteinSubunits in modelReactionProteins['modelReactionProteinSubunits']:
for feature_refs in modelReactionProteinSubunits['feature_refs']:
gene = feature_refs.split('/')[-1]
genes.append(gene)
if len(genes) > 0:
if not rxn_id in rxn_to_genes:
rxn_to_genes[rxn_id] = set()
rxn_to_genes[rxn_id].update(genes)
#break
for k in rxn_to_genes:
rxn_to_genes[k] = list(rxn_to_genes[k])
data = {'genome' : genome, 'ws' : 'jplfaria:narrative_1492808527866', 'rxn_to_genes' : rxn_to_genes}
kbasemodels.update_one({'_id' : model_id}, {'$set' : data}, upsert=True)
%%HTML
<b>Why not R-r0317 in master_fungal_template_fix mapped</b><br>
<i>H2O[c0] + LACT[c0] <=> D-glucose[c0] + Galactose[c0]</i><br>
<i>rxn00816 Lactose galactohydrolase 1 H2O [0] + 1 LACT [0] 1 D-Glucose [0] + 1 Galactose [0]</i><br>
<b>Answer: 1 compound is not integrated:</b> D-glucose[c0] > '~/modelcompounds/id/M-dglc-c_c0'<br>
<br>
<b>ATP Synthases! MERGE</b>
Asppeni1_model = cobrakbase.API.get_object(id="Asppeni1_model", ws="janakakbase:narrative_1540435363582")
for r in Asppeni1_model['modelreactions']:
if '/' in r['id']:
id = r['id']
if id[:2] == 'R-':
id = id[2:]
id = id.replace('/','-')
print(r['id'], '->', id)
r['id'] = id
def save_object(wsc, o, id, ws, t):
wsc.save_objects(
{'workspace': ws,
'objects' : [{'data' : o, 'name' : id, 'type' : t}]
})
save_object(cobrakbase.API.wsClient, Asppeni1_model, "Asppeni1_model_fix", "janakakbase:narrative_1540435363582", "KBaseFBA.FBAModel")
template = cobrakbase.API.get_object(id="Fungi", ws="NewKBaseModelTemplates")
master_fungal_template_fix = cobrakbase.API.get_object(id="master_fungal_template_fix", ws="jplfaria:narrative_1510597445008")
#rxn08617 GLCtex
#rxn08606
lookup = ["rxn08617", "rxn08606", "rxn05226"]
for r in template['reactions']:
#print(r['id'], r['name'])
if r['id'] in lookup:
print(r)
#print(r)
#break
print(template.keys())
for r in template['reactions']:
atp = False
adp = False
h = False
pi = False
h2o = False
for c in r['templateReactionReagents']:
if 'cpd00002' in c['templatecompcompound_ref']:
atp = True
if 'cpd00008' in c['templatecompcompound_ref']:
adp = True
if 'cpd00009' in c['templatecompcompound_ref']:
pi = True
if 'cpd00067' in c['templatecompcompound_ref']:
h = True
if 'cpd00001' in c['templatecompcompound_ref']:
h2o = True
if atp and adp and h and pi and h2o and 'rxf' and len(r['templateReactionReagents']) == 5:
print(r)
for r in template['reactions']:
#print(r['id'])
1
for r in master_fungal_template_fix['modelreactions']:
for c in r['modelReactionReagents']:
if not 'modelcompounds/id/cpd' in c['modelcompound_ref']:
1 #print(c)
#if 'R-r0317' in r['id']:
# print(r)
fmodel = cobrakbase.API.get_object(id="Asppeni1_model_fix_GP_GMM", ws="janakakbase:narrative_1540435363582")
template.keys()
for r in template['modelreactions']:
#print(r['id'])
if 'R-r0317' in r['id']:
print(r)
gmedia = cobrakbase.API.get_object(id="Carbon-D-Glucose", ws="janakakbase:narrative_1540435363582")
media = cobrakbase.convert_media(gmedia)
#cobrakbase.
model = cobrakbase.convert_kmodel(fmodel, media=media)
for r in model.sinks:
print("SK", r)
for r in model.demands:
print("DM", r)
for r in model.exchanges:
#print("EX", r, r.lower_bound)
1
for r in model.reactions:
#print(r)
1
def demand(cpd, value, model):
dm = Reaction(id="DM_" + cpd, name="Demand for " + cpd, lower_bound=value, upper_bound=1000)
dm.add_metabolites({model.metabolites.get_by_id(cpd) : -1})
print(cpd, value, dm)
model.add_reaction(dm)
1
bio = model.reactions.get_by_id('bio1_biomass')
print(bio)
for a in bio.metabolites:
#print(a.id, a.name, bio.metabolites[a])
#demand(a.id, -1, model)
1
for a in bio.metabolites:
model.reactions.get_by_id("DM_" + a.id).lower_bound = -1
model.reactions.get_by_id('DM_cpd00030_c0').lower_bound = 0.0 #Mn2+
model.reactions.get_by_id('DM_cpd00205_c0').lower_bound = 0.0 #K+
model.reactions.get_by_id('DM_cpd00149_c0').lower_bound = 0.0 #Co2+
model.reactions.get_by_id('DM_cpd00063_c0').lower_bound = 0.0 #Ca2+
model.reactions.get_by_id('DM_cpd11416_c0').lower_bound = 0.0 #Biomass
model.reactions.get_by_id('DM_cpd00107_c0').lower_bound = -0.1 #L-Leucine
model.reactions.get_by_id('DM_cpd00069_c0').lower_bound = 0.0 #L-Tyrosine
model.reactions.get_by_id('DM_cpd12370_c0').lower_bound = 0.0 #apo-ACP
model.reactions.get_by_id('DM_cpd00003_c0').lower_bound = 0.0 #NAD
model.reactions.get_by_id('DM_cpd00006_c0').lower_bound = 0.0 #NADP
model.summary()
for a in bio.metabolites:
coef = bio.get_coefficient(a)
z = "+"
if coef < 0:
z = "-"
flux = model.reactions.get_by_id("DM_" + a.id).flux
if not flux == 0.0:
print(a, z, a.name, flux)
1
#print(model.reactions.DM_cpd00053_c0.flux)
#model.metabolites.get_by_id("cpd00205_c0").summary()
def get_flux_distribution(fba):
fdist = {}
for a in fba['FBAReactionVariables']:
flux = a['value']
#if '~/fbamodel/modelreactions/id/pi_m0' == a['modelreaction_ref']:
# a['modelreaction_ref'] = '~/fbamodel/modelreactions/id/tr-succ/pi_m0'
id = cobrakbase.get_id_from_ref(a['modelreaction_ref'], stok='/')
#print(a['modelreaction_ref'], id, flux)
fdist[id] = flux
biomass = "bio1_biomass"
if not fba['objectiveValue'] == 0:
flux = fba['objectiveValue']
fdist[biomass] = flux
return fdist
def get_net_convertion(model, fdist):
net = {}
for rxnId in fdist:
flux = fdist[rxnId]
rselect = rxnId
#print(rselect)
if "R-" in rselect:
rselect = rselect[2:]
#print(rselect)
id = rxnId
#id = cobrakbase.get_id_from_ref(rxnId)
#print(id)
if "R-" in id:
id = id[2:]
#print(id)
#print(id, a['value'])
if not flux == 0:
r = model.reactions.get_by_id(id)
#print(r, flux)
#print(dir(r))
for k in r.reactants:
if not k in net:
net[k] = 0
net[k] += r.get_coefficient(k) * flux
for k in r.products:
if not k in net:
net[k] = 0
net[k] += r.get_coefficient(k) * flux
return net
cobrakbase.login("TUEVGXRO3JJUJCEPAHBSGW67ZM7UURGC", dev=False)
fba = cobrakbase.API.get_object("Asppeni1_model_fix_GP_GMM.gf.1", "janakakbase:narrative_1540435363582")
print(fba['objectiveValue'])
fdist = get_flux_distribution(fba)
#model.reactions.get_by_id("r0516_m0")
print(model.reactions.get_by_id("tr-succ-pi_m0"))
net = get_net_convertion(model, fdist)
#cpd11416
e = 1e-3
for cpd in net:
flux = net[cpd]
if flux > e or flux < -e:
if False or "_c0" in cpd.id:
print(cpd, flux)
cobra_model = cobrakbase.read_model_with_media("GCF_000005845.2", "Carbon-D-Glucose", "filipeliu:narrative_1504192868437")
#jsonMedia = cobrakbase.API.get_object("Carbon-D-Glucose", "filipeliu:narrative_1504192868437")
#jsonModel = cobrakbase.API.get_object("GCF_000005845.2", "filipeliu:narrative_1504192868437")
#for r in jsonModel['modelreactions']:
# if "rxn00159_c0" in r['id']:
# print(r)
cobra_model.reactions.get_by_id("rxn00159_c0")
#cobra_model.medium
#met = cobra_model.metabolites.get_by_id("cpd00011_e0")
#object_stoichiometry = {met : -1}
#reaction = Reaction(id="EX_cpd00011_e0", name="Exchange for " + met.name, lower_bound=-8, upper_bound=1000)
#cobra_model.add_reaction(reaction)
#with open('iMR1_799.json', 'w') as outfile:
# json.dump(model, outfile)
#cobra_model.summary()
for r in model.reactions:
if False or "EX_" in r.id and r.lower_bound == 0:
#print(r)
#if r.lower_bound == 0:
#r.lower_bound = -1
#print(r, ":", r.lower_bound, r.upper_bound)
1
#cobra_model.reactions.get_by_id("EX_cpd00011_e0").lower_bound = 7.99
#cobra_model.objective = "bio1_biomass"
#cobra_model.summary()
#cobra_model.metabolites.cpd00011_c0.summary()
CONSUMING REACTIONS -- CO2_c0 (cpd0001...)
------------------------------------------
% FLUX RXN ID REACTION
--- ------ ---------- --------------------------------------------------
87% 7.99 rxn0546... cpd00011_e0 <=> cpd00011_c0
15% 1.39 rxn0534... cpd11466_c0 + cpd11492_c0 <=> cpd00011_c0 + cpd...
3% 0.255 rxn0292... 2 cpd00001_c0 + 2 cpd00067_c0 + cpd02103_c0 <=>...
2% 0.206 rxn0920... 2 cpd00067_c0 + cpd15555_c0 <=> cpd00011_c0 + c...
2% 0.175 rxn0293... cpd00067_c0 + cpd02893_c0 <=> cpd00011_c0 + cpd...
CONSUMING REACTIONS -- CO2_c0 (cpd0001...)
------------------------------------------
% FLUX RXN ID REACTION
--- ------ ---------- --------------------------------------------------
32% 1.9 rxn0534... cpd11466_c0 + cpd11492_c0 <=> cpd00011_c0 + cpd...
28% 1.67 rxn0916... cpd00001_c0 + cpd00020_c0 + cpd15560_c0 <=> cpd...
20% 1.21 rxn0015... cpd00003_c0 + cpd00130_c0 <=> cpd00004_c0 + cpd...
6% 0.347 rxn0292... 2 cpd00001_c0 + 2 cpd00067_c0 + cpd02103_c0 <=>...
5% 0.321 rxn0637... cpd00033_c0 + cpd00067_c0 + cpd12005_c0 <=> cpd...
5% 0.281 rxn0920... 2 cpd00067_c0 + cpd15555_c0 <=> cpd00011_c0 + c...
4% 0.239 rxn0293... cpd00067_c0 + cpd02893_c0 <=> cpd00011_c0 + cpd...
#jsonModel = cobrakbase.API.get_object("GCF_000005845.2", "filipeliu:narrative_1504192868437")
#jsonMedia = cobrakbase.API.get_object("Carbon-D-Glucose", "filipeliu:narrative_1504192868437")
def fix_flux_bounds(m):
for r in m['modelreactions']:
lb = -1 * r['maxrevflux']
ub = r['maxforflux']
di = r['direction']
cdi = "="
if lb == 0 and ub > 0:
cdi = ">"
elif ub == 0 and lb < 0:
cdi = '<'
if not cdi == di:
if di == '>':
r['maxrevflux'] = 0
elif di == '<':
r['maxforflux'] = 0
else:
1
print(r['id'], di, cdi, lb, ub)
fix_flux_bounds(jsonModel)
cobra_model = cobrakbase.convert_kmodel(jsonModel, media=cobrakbase.convert_media(jsonMedia))
from memote.suite.cli.reports import report
import memote.suite.api as api
from memote.suite.reporting import ReportConfiguration
#a, results = api.test_model(cobra_model, results=True)
config = ReportConfiguration.load()
html = api.snapshot_report(results, config)
with open("report.html", "w") as text_file:
print(html, file=text_file)
```
| github_jupyter |
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix, f1_score
from sklearn.metrics import make_scorer, f1_score, accuracy_score, recall_score, precision_score, classification_report, precision_recall_fscore_support
import itertools
# file used to write preserve the results of the classfier
# confusion matrix and precision recall fscore matrix
def plot_confusion_matrix(cm,
target_names,
title='Confusion matrix',
cmap=None,
normalize=True):
"""
given a sklearn confusion matrix (cm), make a nice plot
Arguments
---------
cm: confusion matrix from sklearn.metrics.confusion_matrix
target_names: given classification classes such as [0, 1, 2]
the class names, for example: ['high', 'medium', 'low']
title: the text to display at the top of the matrix
cmap: the gradient of the values displayed from matplotlib.pyplot.cm
see http://matplotlib.org/examples/color/colormaps_reference.html
plt.get_cmap('jet') or plt.cm.Blues
normalize: If False, plot the raw numbers
If True, plot the proportions
Usage
-----
plot_confusion_matrix(cm = cm, # confusion matrix created by
# sklearn.metrics.confusion_matrix
normalize = True, # show proportions
target_names = y_labels_vals, # list of names of the classes
title = best_estimator_name) # title of graph
Citiation
---------
http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html
"""
accuracy = np.trace(cm) / float(np.sum(cm))
misclass = 1 - accuracy
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
if cmap is None:
cmap = plt.get_cmap('Blues')
plt.figure(figsize=(8, 6))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
if target_names is not None:
tick_marks = np.arange(len(target_names))
plt.xticks(tick_marks, target_names, rotation=45)
plt.yticks(tick_marks, target_names)
thresh = cm.max() / 1.5 if normalize else cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
if normalize:
plt.text(j, i, "{:0.4f}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
else:
plt.text(j, i, "{:,}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label\naccuracy={:0.4f}; misclass={:0.4f}'.format(accuracy, misclass))
plt.tight_layout()
return plt
##saving the classification report
def pandas_classification_report(y_true, y_pred):
metrics_summary = precision_recall_fscore_support(
y_true=y_true,
y_pred=y_pred)
cm = confusion_matrix(y_true, y_pred)
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
avg = list(precision_recall_fscore_support(
y_true=y_true,
y_pred=y_pred,
average='macro'))
avg.append(accuracy_score(y_true, y_pred, normalize=True))
metrics_sum_index = ['precision', 'recall', 'f1-score', 'support','accuracy']
list_all=list(metrics_summary)
list_all.append(cm.diagonal())
class_report_df = pd.DataFrame(
list_all,
index=metrics_sum_index)
support = class_report_df.loc['support']
total = support.sum()
avg[-2] = total
class_report_df['avg / total'] = avg
return class_report_df.T
from commen_preprocess import *
from sklearn.metrics import accuracy_score
import joblib
from sklearn.model_selection import StratifiedKFold as skf
###all classifier
from catboost import CatBoostClassifier
from xgboost.sklearn import XGBClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn import tree
from sklearn import neighbors
from sklearn import ensemble
from sklearn import neural_network
from sklearn import linear_model
import lightgbm as lgbm
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
from lightgbm import LGBMClassifier
from nltk.classify.scikitlearn import SklearnClassifier
eng_train_dataset = pd.read_csv('../Data/hindi_dataset/hindi_dataset.tsv', sep='\t')
eng_train_dataset.head()
l=eng_train_dataset['task_1'].value_counts()
print("the total dataset size:",len(eng_train_dataset),'\n',l)
import numpy as np
from tqdm import tqdm
import pickle
####loading laser embeddings for english dataset
def load_laser_embeddings():
dim = 1024
engX_commen = np.fromfile("../Data/hindi_dataset/embeddings_hin_task1_commen.raw", dtype=np.float32, count=-1)
engX_lib = np.fromfile("../Data/hindi_dataset/embeddings_hin_task1_lib.raw", dtype=np.float32, count=-1)
engX_commen.resize(engX_commen.shape[0] // dim, dim)
engX_lib.resize(engX_lib.shape[0] // dim, dim)
return engX_commen,engX_lib
def load_bert_embeddings():
file = open('../Data/hindi_dataset/no_preprocess_bert_embed_task1.pkl', 'rb')
embeds = pickle.load(file)
return np.array(embeds)
def merge_feature(*args):
feat_all=[]
print(args[0].shape)
for i in tqdm(range(args[0].shape[0])):
feat=[]
for arg in args:
feat+=list(arg[i])
feat_all.append(feat)
return feat_all
convert_label={
'HOF':1,
'NOT':0
}
convert_reverse_label={
1:'HOF',
0:'NOT'
}
labels=eng_train_dataset['task_1'].values
engX_commen,engX_lib=load_laser_embeddings()
bert_embeds =load_bert_embeddings()
feat_all=merge_feature(engX_commen,engX_lib,bert_embeds)
#feat_all=merge_feature(engX_lib)
# feat_all=[]
# for i in range(len(labels)):
# feat=list(engX_commen[i])+list(engX_lib[i])
# feat_all.append(feat)
len(feat_all[0])
from sklearn.utils.multiclass import type_of_target
Classifier_Train_X=np.array(feat_all)
labels_int=[]
for i in range(len(labels)):
labels_int.append(convert_label[labels[i]])
Classifier_Train_Y=np.array(labels_int,dtype='float64')
print(type_of_target(Classifier_Train_Y))
Classifier_Train_Y
def train_model_no_ext(Classifier_Train_X,Classifier_Train_Y,model_type,save_model=False):
kf = skf(n_splits=10,shuffle=True)
y_total_preds=[]
y_total=[]
count=0
img_name = 'cm.png'
report_name = 'report.csv'
scale=list(Classifier_Train_Y).count(0)/list(Classifier_Train_Y).count(1)
print(scale)
if(save_model==True):
Classifier=get_model(scale,m_type=model_type)
Classifier.fit(Classifier_Train_X,Classifier_Train_Y)
filename = model_type+'_hin_task_1.joblib.pkl'
joblib.dump(Classifier, filename, compress=9)
# filename1 = model_name+'select_features_eng_task1.joblib.pkl'
# joblib.dump(model_featureSelection, filename1, compress=9)
else:
for train_index, test_index in kf.split(Classifier_Train_X,Classifier_Train_Y):
X_train, X_test = Classifier_Train_X[train_index], Classifier_Train_X[test_index]
y_train, y_test = Classifier_Train_Y[train_index], Classifier_Train_Y[test_index]
classifier=get_model(scale,m_type=model_type)
print(type(y_train))
classifier.fit(X_train,y_train)
y_preds = classifier.predict(X_test)
for ele in y_test:
y_total.append(ele)
for ele in y_preds:
y_total_preds.append(ele)
y_pred_train = classifier.predict(X_train)
print(y_pred_train)
print(y_train)
count=count+1
print('accuracy_train:',accuracy_score(y_train, y_pred_train),'accuracy_test:',accuracy_score(y_test, y_preds))
print('TRAINING:')
print(classification_report( y_train, y_pred_train ))
print("TESTING:")
print(classification_report( y_test, y_preds ))
report = classification_report( y_total, y_total_preds )
cm=confusion_matrix(y_total, y_total_preds)
plt=plot_confusion_matrix(cm,normalize= True,target_names = ['NOT','HOF'],title = "Confusion Matrix")
plt.savefig('hin_task1'+model_type+'_'+img_name)
print(classifier)
print(report)
print(accuracy_score(y_total, y_total_preds))
df_result=pandas_classification_report(y_total,y_total_preds)
df_result.to_csv('hin_task1'+model_type+'_'+report_name, sep=',')
def get_model(scale,m_type=None):
if not m_type:
print("ERROR: Please specify a model type!")
return None
if m_type == 'decision_tree_classifier':
logreg = tree.DecisionTreeClassifier(max_features=1000,max_depth=3,class_weight='balanced')
elif m_type == 'gaussian':
logreg = GaussianNB()
elif m_type == 'logistic_regression':
logreg = LogisticRegression(n_jobs=10, random_state=42,class_weight='balanced',solver='liblinear')
elif m_type == 'MLPClassifier':
# logreg = neural_network.MLPClassifier((500))
logreg = neural_network.MLPClassifier((100),random_state=42,early_stopping=True)
elif m_type == 'KNeighborsClassifier':
# logreg = neighbors.KNeighborsClassifier(n_neighbors = 10)
logreg = neighbors.KNeighborsClassifier()
elif m_type == 'ExtraTreeClassifier':
logreg = tree.ExtraTreeClassifier()
elif m_type == 'ExtraTreeClassifier_2':
logreg = ensemble.ExtraTreesClassifier()
elif m_type == 'RandomForestClassifier':
logreg = ensemble.RandomForestClassifier(n_estimators=100, class_weight='balanced', n_jobs=12, max_depth=7)
elif m_type == 'SVC':
#logreg = LinearSVC(dual=False,max_iter=200)
logreg = SVC(kernel='linear',random_state=1526)
elif m_type == 'Catboost':
logreg = CatBoostClassifier(iterations=100,learning_rate=0.2,l2_leaf_reg=500,depth=10,use_best_model=False, random_state=42,scale_pos_weight=SCALE_POS_WEIGHT)
# logreg = CatBoostClassifier(scale_pos_weight=0.8, random_seed=42,);
elif m_type == 'XGB_classifier':
# logreg=XGBClassifier(silent=False,eta=0.1,objective='binary:logistic',max_depth=5,min_child_weight=0,gamma=0.2,subsample=0.8, colsample_bytree = 0.8,scale_pos_weight=1,n_estimators=500,reg_lambda=3,nthread=12)
logreg=XGBClassifier(silent=False,objective='binary:logistic',scale_pos_weight=SCALE_POS_WEIGHT,reg_lambda=3,nthread=12, random_state=42)
elif m_type == 'light_gbm':
logreg = LGBMClassifier(objective='binary',max_depth=3,learning_rate=0.2,num_leaves=20,scale_pos_weight=scale,boosting_type='gbdt',
metric='binary_logloss',random_state=5,reg_lambda=20,silent=False)
else:
print("give correct model")
print(logreg)
return logreg
models_name=['decision_tree_classifier','gaussian','logistic_regression','MLPClassifier','RandomForestClassifier',
'SVC','light_gbm']
for model in models_name:
train_model_no_ext(Classifier_Train_X,Classifier_Train_Y,model)
train_model_no_ext(Classifier_Train_X,Classifier_Train_Y,models_name[-1],save_model=True)
train_model_no_ext(Classifier_Train_X,Classifier_Train_Y,'SVC')
```
| github_jupyter |
```
# importing
import tensorflow as tf
import matplotlib.pyplot as plt
import os
# loading images
path_dir = "/content/drive/MyDrive/Dataset/malariya_cell_data_set/cell_images/"
loaded = 0
path = path_dir+"Uninfected/"
uninfected_list = os.listdir(path)
path = path_dir + "Parasitized"
infected_list = os.listdir(path)
img = plt.imread(path_dir+"Uninfected/"+uninfected_list[0])
plt.imshow(img)
img = plt.imread(path_dir+"Parasitized/"+infected_list[0])
plt.imshow(img)
# Kearas implementation
print("uninfected count: ",len(os.listdir(path_dir+"/Uninfected")))
print("Parasitized count: ",len(os.listdir(path_dir+"/Parasitized")))
dataGen = tf.keras.preprocessing.image.ImageDataGenerator(rescale=1/255.0,validation_split=0.2)
dataset_train = dataGen.flow_from_directory(path_dir,target_size=(128,128),batch_size=32,class_mode="binary",shuffle=True,seed=10,subset="training")
dataset_test = dataGen.flow_from_directory(path_dir,target_size=(128,128),batch_size=32,class_mode="binary",shuffle=True,seed=10,subset="validation")
# printintg the loaded classes
dataset_train
# designing the model
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(32,(3,3),padding="same",input_shape=(128,128,3),activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.MaxPool2D(pool_size=(2,2),strides=2,padding="same"))
model.add(tf.keras.layers.Conv2D(64,(3,3),strides=(1,1),padding="same",input_shape=(128,128,3),activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.MaxPool2D(strides=2,padding="same"))
model.add(tf.keras.layers.Conv2D(128,(3,3),strides=(1,1),padding="same",input_shape=(128,128,3),activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.MaxPool2D(strides=2,padding="same"))
model.add(tf.keras.layers.Conv2D(256,3,strides=(1,1),padding="same",input_shape=(128,128,3),activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.MaxPool2D(strides=2,padding="same"))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(128,activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.Dropout(0.2))
model.add(tf.keras.layers.Dense(64,activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.Dropout(0.2))
model.add(tf.keras.layers.Dense(1,activation='sigmoid'))
# compiling the model
model.compile(optimizer="adam",loss="binary_crossentropy",metrics=["accuracy"])
# model summary
model.summary()
# defining early stoping
early_stop = tf.keras.callbacks.EarlyStopping(monitor="val_loss",patience=2,verbose=1)
model_history = model.fit(dataset_train,epochs=20,callbacks=early_stop,validation_data=dataset_test)
plt.plot(model_history.history["accuracy"])
plt.plot(model_history.history["val_accuracy"])
plt.title("Model Accuracy")
plt.xlabel('epochs')
plt.ylabel('acuracy')
plt.show()
model.save("./malariya_classification_acc94.h5")
```
| github_jupyter |
# Using Neural Network Formulations in OMLT
In this notebook we show how OMLT can be used to build different optimization formulations of neural networks within Pyomo. It specifically demonstrates the following examples:<br>
1.) A neural network with smooth sigmoid activation functions represented using full-space and reduced-space formulations <br>
2.) A neural network with non-smooth ReLU activation functions represented using complementarity and mixed integer formulations <br>
3.) A neural network with mixed ReLU and sigmoid activation functions represented using complementarity (for ReLU) and full-space (for sigmoid) formulations <br>
<br>
After building the OMLT formulations, we minimize each representation of the function and compare the results.
## Library Setup
This notebook assumes you have a working Tensorflow environment in addition to necessary Python packages described here. We use Keras to train neural networks of interest for our example which requires the Python Tensorflow package. The neural networks are then formulated in Pyomo using OMLT which therefore requires working Pyomo and OMLT installations.
The required Python libraries used this notebook are as follows: <br>
- `pandas`: used for data import and management <br>
- `matplotlib`: used for plotting the results in this example
- `tensorflow`: the machine learning language we use to train our neural network
- `pyomo`: the algebraic modeling language for Python, it is used to define the optimization model passed to the solver
- `omlt`: The package this notebook demonstates. OMLT can formulate machine learning models (such as neural networks) within Pyomo
```
#Start by importing the following libraries
#data manipulation and plotting
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc('font', size=24)
plt.rc('axes', titlesize=24)
#tensorflow objects
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Dense, Input
from tensorflow.keras.optimizers import Adam
#pyomo for optimization
import pyomo.environ as pyo
#omlt for interfacing our neural network with pyomo
from omlt import OmltBlock
from omlt.neuralnet import NetworkDefinition, NeuralNetworkFormulation, ReducedSpaceNeuralNetworkFormulation
from omlt.neuralnet.activations import ComplementarityReLUActivation
from omlt.io import keras_reader
import omlt
```
## Import the Data
We begin by training neural networks that learn from data given the following imported dataframe. In practice, this data could represent the output of a simulation, real sensor measurements, or some other external data source. The data contains a single input `x` and a single output `y` and contains 10,000 total samples
```
df = pd.read_csv("../data/sin_quadratic.csv",index_col=[0]);
```
The data we use for training is plotted below (on the left figure). We also scale the training data to a mean of zero with unit standard deviation. The scaled inputs and outputs are added to the dataframe and plotted next to the original data values (on the right).
```
#retrieve input 'x' and output 'y' from the dataframe
x = df["x"]
y = df["y"]
#calculate mean and standard deviation, add scaled 'x' and scaled 'y' to the dataframe
mean_data = df.mean(axis=0)
std_data = df.std(axis=0)
df["x_scaled"] = (df['x'] - mean_data['x']) / std_data['x']
df["y_scaled"] = (df['y'] - mean_data['y']) / std_data['y']
#create plots for unscaled and scaled data
f, (ax1, ax2) = plt.subplots(1, 2,figsize = (16,8))
ax1.plot(x, y)
ax1.set_xlabel("x")
ax1.set_ylabel("y");
ax1.set_title("Training Data")
ax2.plot(df["x_scaled"], df["y_scaled"])
ax2.set_xlabel("x_scaled")
ax2.set_ylabel("y_scaled");
ax2.set_title("Scaled Training Data")
plt.tight_layout()
```
## Train the Neural Networks
After importing the dataset we use Tensorflow (with Keras) to train three neural network models. Each neural network contains 2 layers with 100 nodes per layer with a single output layer. <br>
1.) The first network (`nn1`) uses sigmoid activation functions for both layers.<br>
2.) The second network (`nn2`) uses ReLU activations<br>
3.) The last network (`nn3`) mixes ReLU and sigmoid activation functions. The first layer is sigmoid, the second layer is ReLU. <br>
We use the ADAM optimizer and train the first two neural networks for 50 epochs. We train `nn3` for 150 epochs since we observe difficulty obtaining a good fit with the mixed network.
```
#sigmoid neural network
nn1 = Sequential(name='sin_wave_sigmoid')
nn1.add(Input(1))
nn1.add(Dense(100, activation='sigmoid'))
nn1.add(Dense(100, activation='sigmoid'))
nn1.add(Dense(1))
nn1.compile(optimizer=Adam(), loss='mse')
#relu neural network
nn2 = Sequential(name='sin_wave_relu')
nn2.add(Input(1))
nn2.add(Dense(100, activation='relu'))
nn2.add(Dense(100, activation='relu'))
nn2.add(Dense(1))
nn2.compile(optimizer=Adam(), loss='mse')
#mixed neural network
nn3 = Sequential(name='sin_wave_mixed')
nn3.add(Input(1))
nn3.add(Dense(100, activation='sigmoid'))
nn3.add(Dense(100, activation='relu'))
nn3.add(Dense(1))
nn3.compile(optimizer=Adam(), loss='mse')
#train all three neural networks
history1 = nn1.fit(x=df['x_scaled'], y=df['y_scaled'],verbose=1, epochs=50)
history2 = nn2.fit(x=df['x_scaled'], y=df['y_scaled'],verbose=1, epochs=50)
history3 = nn3.fit(x=df['x_scaled'], y=df['y_scaled'],verbose=1, epochs=150)
```
## Check the predictions
Before we formulate our trained neural networks in OMLT, we check to see that they adequately represent the data. While we would normally use some accuracy measure, we suffice with a visual plot of the fits.
```
#note: we calculate the unscaled output for each neural network to check the predictions
#nn1
y_predict_scaled_sigmoid = nn1.predict(x=df['x_scaled'])
y_predict_sigmoid = y_predict_scaled_sigmoid*(std_data['y']) + mean_data['y']
#nn2
y_predict_scaled_relu = nn2.predict(x=df['x_scaled'])
y_predict_relu = y_predict_scaled_relu*(std_data['y']) + mean_data['y']
#nn3
y_predict_scaled_mixed = nn3.predict(x=df['x_scaled'])
y_predict_mixed = y_predict_scaled_mixed*(std_data['y']) + mean_data['y']
#create a single plot with the original data and each neural network's predictions
fig,ax = plt.subplots(1,figsize = (8,8))
ax.plot(x,y,linewidth = 3.0,label = "data", alpha = 0.5)
ax.plot(x,y_predict_relu,linewidth = 3.0,linestyle="dotted",label = "relu")
ax.plot(x,y_predict_sigmoid,linewidth = 3.0,linestyle="dotted",label = "sigmoid")
ax.plot(x,y_predict_mixed,linewidth = 3.0,linestyle="dotted",label = "mixed")
plt.xlabel("x")
plt.ylabel("y")
plt.legend();
```
## Formulating Neural Networks with OMLT
We now show how OMLT can formulate neural networks within Pyomo. We specifically show how to specify and build different neural network optimization formulations and how to connect them with a broader Pyomo model. In these examples we use Pyomo solvers to find the input that minimizes each neural network output.
<br><br>
OMLT can formulate what we call full-space and reduced-space neural network representations using the `NeuralNetworkFormulation` object (for full-space) and `ReducedSpaceNeuralNetworkFormulation` object (for reduced-space). The reduced-space representation can be represented more compactly than the full-space within an optimization setting (i.e. it produces less variables and constraints), but we will see that full-space representation is necessary to represent non-smooth activation formulations (e.g. ReLU with binary variables).
### Reduced Space (supports smooth activations) <br>
The reduced-space representation (`ReducedSpaceNeuralNetworkFormulation`) provided by OMLT hides intermediate neural network variables and activation functions from the underlying optimizer and represents the neural network using one constraint as following:
$\hat{y} = N(x)$
Here, $\hat{y}$ is a vector of outputs from the neural network, $x$ is a vector of inputs, and $N(\cdot)$ represents the encoded neural network function that internally uses weights, biases, and activation functions to map $x \rightarrow \hat{y}$. From an implementation standpoint, OMLT builds the reduced-space formulation by encoding the sequential layer logic and activation functions as Pyomo `Expression` objects that depend only on the input variables.
### Full Space (supports smooth and non-smooth activations) <br>
The full space formulation (`NeuralNetworkFormulation`) creates intermediate variables associated with the neural network nodes and activation functions and exposes them to the optimizer. This is represented by the following set of equations where $x$ and $\hat{y}$ are again the neural network input and output vectors, and we introduce $\hat{z}_{\ell}$ and $z_{\ell}$ to represent pre-activation and post-activation vectors for each each layer $\ell$. We further use the notation $\hat z_{\ell,i}$ to denote node $i$ in layer $\ell$ where $N_\ell$ is the number of nodes in layer $\ell$ and $N_L$ is the number of layers in the neural network. As such, the first equation maps the input to the first layer values $z_0$, the second equation represents the pre-activation values obtained from the weights, biases, and outputs of the previous layer, the third equation applies the activation function, and the last equation maps the final layer to the output. Note that the reduced-space formulation effectively captures these equations using a single constraint.
$\begin{align*}
& x = z_0 &\\
& \hat z_{\ell,i} = \sum_{j{=}1}^{N_{\ell-1}} w_{ij} z_j + b_i & \forall i \in \{1,...,N_\ell \}, \quad \ell \in \{1,...N_L\} \\
& z_{\ell,i} = \sigma(\hat z_{\ell}) & \forall i \in \{1,...,N_\ell \}, \quad \ell \in \{1,...N_L\} \\
& \hat{y} = z_{N_L} &
\end{align*}
$
### Full Space ReLU with Binary Variables
The full space formulation supports non-smooth ReLU activation functions (i.e. the function $z_i = max(0,\hat{z}_i)$) by using binary indicator variables. When using `NeuralNetworkFormulation` with a neural network that contains ReLU activations, OMLT will formulate the below set of variables and constraints for each node in a ReLU layer. Here, $q_{\ell,i}$ is a binary indicator variable that determines whether the output from node $i$ on layer $\ell$ is $0$ or whether it is $\hat{z}_{\ell,i}$. $M_{\ell,i}^U$ and $M_{\ell,i}^L$ are 'BigM' constants used to enforce the ReLU logic. Values for 'BigM' are often taken to be arbitrarily large numbers, but OMLT will automatically determine values by propagating the bounds on the input variables.
$
\begin{align*}
& z_{\ell,i} \ge \hat{z}_{\ell,i} & \forall i \in \{1,...,N_\ell \}, \quad \ell \in \{1,...N_L\}\\
& z_{\ell,i} \ge 0 & \forall i \in \{1,...,N_\ell \}, \quad \ell \in \{1,...N_L\}\\
& z_{\ell,i} \le M_{\ell,i}^L q_{\ell,i} & \forall i \in \{1,...,N_\ell \}, \quad \ell \in \{1,...N_L\} \\
& z_{\ell,i} \le \hat{z}_{\ell,i} - M_{\ell,i}^U(1-q_{\ell,i}) & \forall i \in \{1,...,N_\ell \}, \quad \ell \in \{1,...N_L\}
\end{align*}
$
### Full Space ReLU with Complementarity Constraints
ReLU activation functions can also be represented using the following complementarity condition:
$
\begin{align*}
0 \le (z_{\ell,i} - \hat{z}_{\ell,i}) \perp z_{\ell,i} \ge 0 & \quad \forall i \in \{1,...,N_\ell \}, \quad \ell \in \{1,...N_L\}
\end{align*}
$
This condition means that both of the expressions must be satisfied, where exactly one expression must be satisfied with equality. Hence, we must have that $z_{\ell,i} \ge \hat{z}_{\ell,i}$ and $z_{\ell,i} \ge 0$ with either $z_{\ell,i} = \hat{z}_{\ell,i}$, or $z_{\ell,i} = 0$.
OMLT uses a `ComplementarityReLUActivation` object to specify that ReLU activation functions should be formulated using complementarity conditions. Within the formulation code, it uses `pyomo.mpec` to transform this complementarity condition into nonlinear constraints which facilitates using smooth optimization solvers (such as Ipopt) to optimize over ReLU activation functions.
## Solving Optimization Problems with Neural Networks using OMLT
We now show how to use the above neural network formulations in OMLT for our trained neural networks: `nn1`, `nn2`, and `nn3`. For each formulation we solve the simple optimization problem below using Pyomo where we find the input $x$ that minimizes the output $\hat y$ of the neural network.
$
\begin{align*}
& \min_x \ \hat{y}\\
& s.t. \hat{y} = N(x)
\end{align*}
$
For each neural network we trained, we instantiate a Pyomo `ConcreteModel` and create variables that represent the neural network input $x$ and output $\hat y$. We also create an objective function that seeks to minimize the output $\hat y$.
Each example uses the same general workflow:
- Use the `keras_reader` to import the neural network into a OMLT `NetworkDefinition` object.
- Create a Pyomo model with variables `x` and `y` where we intend to minimize `y`.
- Create an `OmltBlock`.
- Create a formulation object. Note that we use `ReducedSpaceNeuralNetworkFormulation` for the reudced-space and `NeuralNetworkFormulation` for full-space and ReLU.
- Build the formulation object on the `OmltBlock`.
- Add constraints connecting `x` to the neural network input and `y` to the neural network output.
- Solve with an optimization solver (this example uses ipopt).
- Query the solution.
We also print model size and solution time following each cell where we optimize the Pyomo model.
### Setup scaling and input bounds
We assume that our Pyomo model operates in the unscaled space with respect to our neural network inputs and outputs. We additionally assume input bounds to our neural networks are given by the limits of our training data.
To handle this, OMLT can be given scaling information (in the form of an OMLT scaling object) and input bounds (in the form of a dictionary where indices correspond to neural network indices and values are 2-length tuples of lower and upper bounds). This maintains the space of the optimization problem and scaling is handled by OMLT underneath. The scaling object and input bounds are passed to keras reader method `load_keras_sequential` when importing the associated neural networks.
```
#create an omlt scaling object
scaler = omlt.scaling.OffsetScaling(offset_inputs=[mean_data['x']],
factor_inputs=[std_data['x']],
offset_outputs=[mean_data['y']],
factor_outputs=[std_data['y']])
#create the input bounds. note that the key `0` corresponds to input `0` and that we also scale the input bounds
input_bounds={0:((min(df['x']) - mean_data['x'])/std_data['x'],
(max(df['x']) - mean_data['x'])/std_data['x'])};
print(scaler)
print("Scaled input bounds: ",input_bounds)
```
## Neural Network 1: Sigmoid Activations with Full-Space and Reduced-Space Formulations
The first neural network contains sigmoid activation functions which we formulate with full-space and reduced-space representations and solve with Ipopt.
### Reduced Space Model
We begin with the reduced-space formulation and build the Pyomo model according to the above workflow. Note that the reduced-space model only contains 6 variables (`x` and `y` created on the Pyomo model, and the `OmltBlock` scaled and unscaled input and output which get created internally). The full-space formulation (shown next) will contain many more.
```
#create a network definition
net_sigmoid = keras_reader.load_keras_sequential(nn1,scaler,input_bounds)
#create a pyomo model with variables x and y
model1_reduced = pyo.ConcreteModel()
model1_reduced.x = pyo.Var(initialize = 0)
model1_reduced.y = pyo.Var(initialize = 0)
model1_reduced.obj = pyo.Objective(expr=(model1_reduced.y))
#create an OmltBlock
model1_reduced.nn = OmltBlock()
#use the reduced-space formulation
formulation1_reduced = ReducedSpaceNeuralNetworkFormulation(net_sigmoid)
model1_reduced.nn.build_formulation(formulation1_reduced)
#connect pyomo variables to the neural network
@model1_reduced.Constraint()
def connect_inputs(mdl):
return mdl.x == mdl.nn.inputs[0]
@model1_reduced.Constraint()
def connect_outputs(mdl):
return mdl.y == mdl.nn.outputs[0]
#solve the model and query the solution
status_1_reduced = pyo.SolverFactory('ipopt').solve(model1_reduced, tee=True)
solution_1_reduced = (pyo.value(model1_reduced.x),pyo.value(model1_reduced.y))
#print out model size and solution values
print("Reduced Space Solution:")
print("# of variables: ",model1_reduced.nvariables())
print("# of constraints: ",model1_reduced.nconstraints())
print("x = ", solution_1_reduced[0])
print("y = ", solution_1_reduced[1])
print("Solve Time: ", status_1_reduced['Solver'][0]['Time'])
```
### Full Space Model
For the full-space representation we use `NeuralNetworkFormulation` instead of `ReducedSpaceNeuralNetworkFormulation`. The key difference is that this formulation creates additional variables and constraints to represent each node and activation function in the neural network.
Note that when we print this model there are over 400 variables and constraints each owing to the number of neural network nodes. The solution consequently takes longer with more iterations (this effect is more pronounced for larger models). The full-space also finds a different local minima, but this was by no means guaranteed to happen.
```
net_sigmoid = keras_reader.load_keras_sequential(nn1,scaler,input_bounds)
model1_full = pyo.ConcreteModel()
model1_full.x = pyo.Var(initialize = 0)
model1_full.y = pyo.Var(initialize = 0)
model1_full.obj = pyo.Objective(expr=(model1_full.y))
model1_full.nn = OmltBlock()
formulation2_full = NeuralNetworkFormulation(net_sigmoid)
model1_full.nn.build_formulation(formulation2_full)
@model1_full.Constraint()
def connect_inputs(mdl):
return mdl.x == mdl.nn.inputs[0]
@model1_full.Constraint()
def connect_outputs(mdl):
return mdl.y == mdl.nn.outputs[0]
status_1_full = pyo.SolverFactory('ipopt').solve(model1_full, tee=True)
solution_1_full = (pyo.value(model1_full.x),pyo.value(model1_full.y))
#print out model size and solution values
print("Full Space Solution:")
print("# of variables: ",model1_full.nvariables())
print("# of constraints: ",model1_full.nconstraints())
print("x = ", solution_1_full[0])
print("y = ", solution_1_full[1])
print("Solve Time: ", status_1_full['Solver'][0]['Time'])
```
## Neural Network 2: ReLU Neural Network using Complementarity Constraints and Binary Variables
The second neural network contains ReLU activation functions which we represent using complementarity constraints and binary variables.
### ReLU Complementarity Constraints
To represent ReLU using complementarity constraints we use the `ComplementarityReLUActivation` object which we pass as a keyword argument to a `NeuralNetworkFormulation`. This overrides the default ReLU behavior which uses binary variables (shown in the next model). Importantly, the complementarity formulation allows us to solve the model using a continuous solver (in this case using Ipopt).
```
net_relu = keras_reader.load_keras_sequential(nn2,scaler,input_bounds)
model2_comp = pyo.ConcreteModel()
model2_comp.x = pyo.Var(initialize = 0)
model2_comp.y = pyo.Var(initialize = 0)
model2_comp.obj = pyo.Objective(expr=(model2_comp.y))
model2_comp.nn = OmltBlock()
formulation2_comp = NeuralNetworkFormulation(net_relu,activation_constraints={
"relu": ComplementarityReLUActivation()})
model2_comp.nn.build_formulation(formulation2_comp)
@model2_comp.Constraint()
def connect_inputs(mdl):
return mdl.x == mdl.nn.inputs[0]
@model2_comp.Constraint()
def connect_outputs(mdl):
return mdl.y == mdl.nn.outputs[0]
status_2_comp = pyo.SolverFactory('ipopt').solve(model2_comp, tee=True)
solution_2_comp = (pyo.value(model2_comp.x),pyo.value(model2_comp.y))
#print out model size and solution values
print("ReLU Complementarity Solution:")
print("# of variables: ",model2_comp.nvariables())
print("# of constraints: ",model2_comp.nconstraints())
print("x = ", solution_2_comp[0])
print("y = ", solution_2_comp[1])
print("Solve Time: ", status_2_comp['Solver'][0]['Time'])
```
### ReLU with Binary Variables and BigM Constraints
For the binary variable formulation of ReLU we use the default activation function settings. These are applied automatically if a `NetworkDefinition` contains ReLU activation functions.
Note that we solve the optimization problem with Cbc which can handle binary decisions. While the solution takes considerably longer than the continuous complementarity formulation, it is guaranteed to find the global minimum.
```
net_relu = keras_reader.load_keras_sequential(nn2,scaler,input_bounds)
model2_bigm = pyo.ConcreteModel()
model2_bigm.x = pyo.Var(initialize = 0)
model2_bigm.y = pyo.Var(initialize = 0)
model2_bigm.obj = pyo.Objective(expr=(model2_bigm.y))
model2_bigm.nn = OmltBlock()
formulation2_bigm = NeuralNetworkFormulation(net_relu)
model2_bigm.nn.build_formulation(formulation2_bigm)
@model2_bigm.Constraint()
def connect_inputs(mdl):
return mdl.x == mdl.nn.inputs[0]
@model2_bigm.Constraint()
def connect_outputs(mdl):
return mdl.y == mdl.nn.outputs[0]
status_2_bigm = pyo.SolverFactory('cbc').solve(model2_bigm, tee=True)
solution_2_bigm = (pyo.value(model2_bigm.x),pyo.value(model2_bigm.y))
#print out model size and solution values
print("ReLU BigM Solution:")
print("# of variables: ",model2_bigm.nvariables())
print("# of constraints: ",model2_bigm.nconstraints())
print("x = ", solution_2_bigm[0])
print("y = ", solution_2_bigm[1])
print("Solve Time: ", status_2_bigm['Solver'][0]['Time'])
```
## Neural Network 3: Mixed ReLU and Sigmoid Activation Functions
The last neural network contains both ReLU and sigmoid activation functions. These networks can be represented by using the complementarity formulation of relu and mixing it with the full-space formulation for the sigmoid functions.
```
net_mixed = keras_reader.load_keras_sequential(nn3,scaler,input_bounds)
model3_mixed = pyo.ConcreteModel()
model3_mixed.x = pyo.Var(initialize = 0)
model3_mixed.y = pyo.Var(initialize = 0)
model3_mixed.obj = pyo.Objective(expr=(model3_mixed.y))
model3_mixed.nn = OmltBlock()
formulation3_mixed = NeuralNetworkFormulation(net_mixed,activation_constraints={
"relu": ComplementarityReLUActivation()})
model3_mixed.nn.build_formulation(formulation3_mixed)
@model3_mixed.Constraint()
def connect_inputs(mdl):
return mdl.x == mdl.nn.inputs[0]
@model3_mixed.Constraint()
def connect_outputs(mdl):
return mdl.y == mdl.nn.outputs[0]
status_3_mixed = pyo.SolverFactory('ipopt').solve(model3_mixed, tee=True)
solution_3_mixed = (pyo.value(model3_mixed.x),pyo.value(model3_mixed.y))
#print out model size and solution values
print("Mixed NN Solution:")
print("# of variables: ",model3_mixed.nvariables())
print("# of constraints: ",model3_mixed.nconstraints())
print("x = ", solution_3_mixed[0])
print("y = ", solution_3_mixed[1])
print("Solve Time: ", status_3_mixed['Solver'][0]['Time'])
```
### Final Plots and Discussion
We lastly plot the results of each optimization problem. Some of the main take-aways from this notebook are as follows:
- A broad set of dense neural network architectures can be represented in Pyomo using OMLT. This notebook used the Keras reader to import sequential Keras models but OMLT also supports using ONNX models (see `import_network.ipynb`). OMLT additionally supports Convolutional Neural Networks (see `mnist_example_cnn.ipynb`).
- The reduced-space formulation provides a computationally tractable means to represent neural networks that contain smooth activation functions and can be used with continuous optimizers to obtain local solutions.
- The full-space formulation permits representing ReLU activation functions using either complementarity or 'BigM' approaches with binary variables (as well as partition-based approaches not shown in this notebook).
- The full-space formulation further allows one to optimize over neural networks that contain mixed activation functions by formulating ReLU logic as complementarity conditions.
- Using binary variables to represent ReLU can attain global solutions (if the rest of the problem is convex), whereas the complementarity formulation provides local solutions but tends to be more scalable.
```
#create a plot with 3 subplots
fig,axs = plt.subplots(1,3,figsize = (24,8))
#nn1 - sigmoid
axs[0].plot(x,y_predict_sigmoid,linewidth = 3.0,linestyle="dotted",color = "orange")
axs[0].set_title("sigmoid")
axs[0].scatter([solution_1_reduced[0]],[solution_1_reduced[1]],color = "black",s = 300, label="reduced space")
axs[0].scatter([solution_1_full[0]],[solution_1_full[1]],color = "blue",s = 300, label="full space")
axs[0].legend()
#nn2 - relu
axs[1].plot(x,y_predict_relu,linewidth = 3.0,linestyle="dotted",color = "green")
axs[1].set_title("relu")
axs[1].scatter([solution_2_comp[0]],[solution_2_comp[1]],color = "black",s = 300, label="complementarity")
axs[1].scatter([solution_2_bigm[0]],[solution_2_bigm[1]],color = "blue",s = 300, label="bigm")
axs[1].legend()
#nn3 - mixed
axs[2].plot(x,y_predict_mixed,linewidth = 3.0,linestyle="dotted", color = "red")
axs[2].set_title("mixed")
axs[2].scatter([solution_3_mixed[0]],[solution_3_mixed[1]],color = "black",s = 300);
```
| github_jupyter |
# transmissibility-based TPA: FRF based
In this example a numerical example is used to demonstrate a FRF based TPA example.
```
import pyFBS
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.colors import LogNorm
%matplotlib inline
```
## Example datasets
Load the required predefined datasets:
```
pyFBS.download_lab_testbench()
xlsx_pos = r"./lab_testbench/Measurements/TPA_synt.xlsx"
stl_A = r"./lab_testbench/STL/A.stl"
stl_B = r"./lab_testbench/STL/B.stl"
stl_AB = r"./lab_testbench/STL/AB.stl"
df_acc_AB = pd.read_excel(xlsx_pos, sheet_name='Sensors_AB')
df_chn_AB = pd.read_excel(xlsx_pos, sheet_name='Channels_AB')
df_imp_AB = pd.read_excel(xlsx_pos, sheet_name='Impacts_AB')
df_vp = pd.read_excel(xlsx_pos, sheet_name='VP_Channels')
df_vpref = pd.read_excel(xlsx_pos, sheet_name='VP_RefChannels')
```
## Numerical model
Load the corresponding .full and .ress file from the example datasets:
```
full_file_AB = r"./lab_testbench/FEM/AB.full"
ress_file_AB = r"./lab_testbench/FEM/AB.rst"
```
Create an MK model for each component:
```
MK_AB = pyFBS.MK_model(ress_file_AB, full_file_AB, no_modes=100, recalculate=False)
```
The locations and directions of responses and excitations often do not match exactly with the numerical model, so we need to find the nodes closest to these points. Only the locations are updated, the directions remain the same.
```
df_chn_AB_up = MK_AB.update_locations_df(df_chn_AB)
df_imp_AB_up = MK_AB.update_locations_df(df_imp_AB)
```
## 3D view
Open 3D viewer in the background. With the 3D viewer the subplot capabilities of PyVista can be used.
```
view3D = pyFBS.view3D(show_origin=False, show_axes=False, title="TPA")
```
Add the STL file of structure AB to the plot and show the corresponding accelerometer, channels and impacts.
```
view3D.plot.add_text("AB", position='upper_left', font_size=10, color="k", font="times", name="AB_structure")
view3D.add_stl(stl_AB, name="AB_structure", color="#8FB1CC", opacity=.1)
view3D.plot.add_mesh(MK_AB.mesh, scalars=np.zeros(MK_AB.mesh.points.shape[0]), show_scalar_bar=False, name="mesh_AB", cmap="coolwarm", show_edges=True)
view3D.show_chn(df_chn_AB_up, color="green", overwrite=True)
view3D.show_imp(df_imp_AB_up, color="red", overwrite=True);
view3D.show_acc(df_acc_AB, overwrite=True)
view3D.show_vp(df_vp, color="blue", overwrite=True)
view3D.label_imp(df_imp_AB_up)
view3D.label_acc(df_acc_AB)
```
## FRF sythetization
Perform the FRF sythetization for each component based on the updated locations:
```
MK_AB.FRF_synth(df_chn_AB_up, df_imp_AB_up, f_start=0, modal_damping=0.003, frf_type="accelerance")
```
First, structural admittance $\boldsymbol{\text{Y}}_{31}^{\text{AB}}$ is obtained.
```
imp_loc = 10
Y31_AB = MK_AB.FRF[:, 9:12, imp_loc:imp_loc+1]
Y31_AB.shape
```
Then, structural admittance $\boldsymbol{\text{Y}}_{41}^{\text{AB}}$ is obtained.
```
Y41_AB = MK_AB.FRF[:, :9, imp_loc:imp_loc+1]
Y41_AB.shape
```
## Aplication of the FRF based TPA
Calculation of transmissibility matrix $\boldsymbol{\text{T}}_{34, f_1}^{\text{AB}}$:
```
T34 = Y31_AB @ np.linalg.pinv(Y41_AB)
T34.shape
```
Define operational displacements $\boldsymbol{\text{u}}_4$:
```
u4 = MK_AB.FRF[:, :9, imp_loc:imp_loc+1]
u4.shape
```
Calcualting response $\boldsymbol{\text{u}}_3^{\text{TPA}}$.
```
u3 = T34 @ u4
u3.shape
```
On board validation: comparison of predicted $\boldsymbol{\text{u}}_{3}^{\text{TPA}}$ and operational $\boldsymbol{\text{u}}_{3}^{\text{MK}}$:
```
plt.figure(figsize=(10, 5))
u3_MK = MK_AB.FRF[:, 9:12, imp_loc:imp_loc+1]
sel = 0
plt.subplot(211)
plt.semilogy(np.abs(u3_MK[:,sel,0]), label='MK');
plt.semilogy(np.abs(u3[:,sel,0]), '--', label='TPA');
plt.ylim(10**-8, 10**4);
plt.xlim(0, 2000)
plt.legend(loc=0);
plt.subplot(413)
plt.plot(np.angle(u3_MK[:,sel,0]));
plt.plot(np.angle(u3[:,sel,0]), '--');
plt.xlim(0, 2000);
```
| github_jupyter |
```
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
import pandas as pd
import numpy as np
import sklearn.metrics
pd.reset_option('all')
# 84575189_0_6365692015941409487 -> no matches at all
data = pd.read_csv('/Users/summ7t/dev/novartis/table-linker/SemTab2019/embedding_evaluation_files/14067031_0_559833072073397908.csv')
data
data = data.fillna('')
data
```
### Which is better text embedding or graph embedding?
```
# define this question
data[(data['kg_id'] == data['GT_kg_id']) & (data['kg_id'] != '')]
```
### By cell linking task. Count/compute
- Number of tasks
- Number and fraction of tasks with known ground truth
- Number and fraction of tasks with ground truth in the candidate set
- Number and fraction of singleton candidate sets
- Number and fraction of singleton candidate sets containing ground truth
- Top-1 accuracy, Top-5 accuracy and NDCG using retrieval_score, text-embedding-score and graph-embedding-score. In our case with binary relevance I think NDCG is the same as DCG.
- Average Top-1, Top-5 and NDCG metrics
```
row_idx, col_idx = 2, 0
relevant_df = data[(data['column'] == col_idx) & (data['row'] == row_idx) & (data['kg_id'] != '')]
num_tasks = len(relevant_df)
num_tasks
num_tasks_known_gt = len(relevant_df[relevant_df['GT_kg_id'] != ''])
num_tasks_known_gt
is_gt_in_candidate = len(relevant_df[relevant_df['GT_kg_id'] == relevant_df['kg_id']])
is_gt_in_candidate
is_candidate_set_singleton = len(relevant_df) == 1
is_candidate_set_singleton
is_top_one_accurate = False
top_one_row = relevant_df.iloc[0]
if top_one_row['kg_id'] == top_one_row['GT_kg_id']:
is_top_one_accurate = True
is_top_one_accurate
is_top_five_accurate = False
top_five_rows = relevant_df.iloc[0:5]
for i, row in top_five_rows.iterrows():
if row['kg_id'] == row['GT_kg_id']:
is_top_five_accurate = True
is_top_five_accurate
is_top_ten_accurate = False
top_ten_rows = relevant_df.iloc[0:10]
for i, row in top_ten_rows.iterrows():
if row['kg_id'] == row['GT_kg_id']:
is_top_ten_accurate = True
is_top_ten_accurate
# parse eval file
def parse_eval_file_stats(file_name=None, eval_data=None):
if file_name is not None and eval_data is None:
eval_data = pd.read_csv(file_name)
eval_data = eval_data.fillna('')
parsed_eval_data = {}
for ei, erow in eval_data.iterrows():
if 'table_id' not in erow:
table_id = file_name.split('/')[-1].split('.csv')[0]
else:
table_id = erow['table_id']
row_idx, col_idx = erow['row'], erow['column']
if (table_id, row_idx, col_idx) in parsed_eval_data:
continue
relevant_df = eval_data[(eval_data['column'] == col_idx) & (eval_data['row'] == row_idx) & (eval_data['kg_id'] != '')]
if len(relevant_df) == 0:
parsed_eval_data[(row_idx, col_idx)] = {
'table_id': table_id,
'GT_kg_id': erow['GT_kg_id'],
'row': row_idx,
'column': col_idx,
'num_candidate': 0,
'num_candidate_known_gt': 0,
'is_gt_in_candidate': False,
'is_candidate_set_singleton': False,
'is_top_one_accurate': False,
'is_top_five_accurate': False
}
continue
row_col_stats = {}
row_col_stats['table_id'] = table_id
row_col_stats['GT_kg_id'] = erow['GT_kg_id']
row_col_stats['row'] = erow['row']
row_col_stats['column'] = erow['column']
row_col_stats['num_candidate'] = len(relevant_df)
row_col_stats['num_candidate_known_gt'] = len(relevant_df[relevant_df['GT_kg_id'] != ''])
row_col_stats['is_gt_in_candidate'] = len(relevant_df[relevant_df['GT_kg_id'] == relevant_df['kg_id']]) > 0
row_col_stats['is_candidate_set_singleton'] = len(relevant_df) == 1
is_top_one_accurate = False
top_one_row = relevant_df.iloc[0]
if top_one_row['kg_id'] == top_one_row['GT_kg_id']:
is_top_one_accurate = True
row_col_stats['is_top_one_accurate'] = is_top_one_accurate
is_top_five_accurate = False
top_five_rows = relevant_df.iloc[0:5]
for i, row in top_five_rows.iterrows():
if row['kg_id'] == row['GT_kg_id']:
is_top_five_accurate = True
row_col_stats['is_top_five_accurate'] = is_top_five_accurate
parsed_eval_data[(table_id, row_idx, col_idx)] = row_col_stats
return parsed_eval_data
e_data = parse_eval_file_stats(file_name='/Users/summ7t/dev/novartis/table-linker/SemTab2019/embedding_evaluation_files/84575189_0_6365692015941409487.csv')
len(e_data), e_data[("84575189_0_6365692015941409487", 0, 2)]
e_data = parse_eval_file_stats(eval_data=all_data)
len(e_data), e_data[("84575189_0_6365692015941409487", 0, 2)]
import json
with open('./eval_all.json', 'w') as f:
json.dump(list(e_data.values()), f, indent=4)
import json
with open('./eval_14067031_0_559833072073397908.json', 'w') as f:
json.dump(list(e_data.values()), f, indent=4)
len([k for k in e_data if e_data[k]['is_gt_in_candidate']])
import os
eval_file_names = []
for (dirpath, dirnames, filenames) in os.walk('/Users/summ7t/dev/novartis/table-linker/SemTab2019/embedding_evaluation_files/'):
for fn in filenames:
if "csv" not in fn:
continue
abs_fn = dirpath + fn
assert os.path.isfile(abs_fn)
if os.path.getsize(abs_fn) == 0:
continue
eval_file_names.append(abs_fn)
len(eval_file_names)
eval_file_names
# merge all eval files in one df
def merge_df(file_names: list):
df_list = []
for fn in file_names:
fid = fn.split('/')[-1].split('.csv')[0]
df = pd.read_csv(fn)
df['table_id'] = fid
# df = df.fillna('')
df_list.append(df)
return pd.concat(df_list)
all_data = merge_df(eval_file_names)
all_data
all_data[all_data['table_id'] == '14067031_0_559833072073397908']
# filter out empty task: NaN in candidate
no_nan_all_data = all_data[pd.notna(all_data['kg_id'])]
no_nan_all_data
all_data[pd.isna(all_data['kg_id'])]
# parse eval file
from pandas.core.common import SettingWithCopyError
import numpy as np
import sklearn.metrics
pd.options.mode.chained_assignment = 'raise'
def parse_eval_files_stats(eval_data):
res = {}
candidate_eval_data = eval_data.groupby(['table_id', 'row', 'column'])['table_id'].count().reset_index(name="count")
res['num_tasks'] = len(eval_data.groupby(['table_id', 'row', 'column']))
res['num_tasks_with_gt'] = len(eval_data[pd.notna(eval_data['GT_kg_id'])].groupby(['table_id', 'row', 'column']))
res['num_tasks_with_gt_in_candidate'] = len(eval_data[eval_data['evaluation_label'] == 1].groupby(['table_id', 'row', 'column']))
res['num_tasks_with_singleton_candidate'] = len(candidate_eval_data[candidate_eval_data['count'] == 1].groupby(['table_id', 'row', 'column']))
singleton_eval_data = candidate_eval_data[candidate_eval_data['count'] == 1]
num_tasks_with_singleton_candidate_with_gt = 0
for i, row in singleton_eval_data.iterrows():
table_id, row_idx, col_idx = row['table_id'], row['row'], row['column']
c_e_data = eval_data[(eval_data['table_id'] == table_id) & (eval_data['row'] == row_idx) & (eval_data['column'] == col_idx)]
assert len(c_e_data) == 1
if c_e_data.iloc[0]['evaluation_label'] == 1:
num_tasks_with_singleton_candidate_with_gt += 1
res['num_tasks_with_singleton_candidate_with_gt'] = num_tasks_with_singleton_candidate_with_gt
num_tasks_with_retrieval_top_one_accurate = []
num_tasks_with_retrieval_top_five_accurate = []
num_tasks_with_text_top_one_accurate = []
num_tasks_with_text_top_five_accurate = []
num_tasks_with_graph_top_one_accurate = []
num_tasks_with_graph_top_five_accurate = []
ndcg_score_r_list = []
ndcg_score_t_list = []
ndcg_score_g_list = []
has_gt_list = []
has_gt_in_candidate = []
# candidate_eval_data = candidate_eval_data[:1]
for i, row in candidate_eval_data.iterrows():
table_id, row_idx, col_idx = row['table_id'], row['row'], row['column']
# print(f"working on {table_id}: {row_idx}, {col_idx}")
c_e_data = eval_data[(eval_data['table_id'] == table_id) & (eval_data['row'] == row_idx) & (eval_data['column'] == col_idx)]
assert len(c_e_data) > 0
if np.nan not in set(c_e_data['GT_kg_id']):
has_gt_list.append(1)
else:
has_gt_list.append(0)
if 1 in set(c_e_data['evaluation_label']):
has_gt_in_candidate.append(1)
else:
has_gt_in_candidate.append(0)
# handle retrieval score
s_data = c_e_data.sort_values(by=['retrieval_score'], ascending=False)
if s_data.iloc[0]['evaluation_label'] == 1:
num_tasks_with_retrieval_top_one_accurate.append(1)
else:
num_tasks_with_retrieval_top_one_accurate.append(0)
if 1 in set(s_data.iloc[0:5]['evaluation_label']):
num_tasks_with_retrieval_top_five_accurate.append(1)
else:
num_tasks_with_retrieval_top_five_accurate.append(0)
# handle text-embedding-score
s_data = c_e_data.sort_values(by=['text-embedding-score'], ascending=False)
if s_data.iloc[0]['evaluation_label'] == 1:
num_tasks_with_text_top_one_accurate.append(1)
else:
num_tasks_with_text_top_one_accurate.append(0)
if 1 in set(s_data.iloc[0:5]['evaluation_label']):
num_tasks_with_text_top_five_accurate.append(1)
else:
num_tasks_with_text_top_five_accurate.append(0)
# handle graph-embedding-score
s_data = c_e_data.sort_values(by=['graph-embedding-score'], ascending=False)
if s_data.iloc[0]['evaluation_label'] == 1:
num_tasks_with_graph_top_one_accurate.append(1)
else:
num_tasks_with_graph_top_one_accurate.append(0)
if 1 in set(s_data.iloc[0:5]['evaluation_label']):
num_tasks_with_graph_top_five_accurate.append(1)
else:
num_tasks_with_graph_top_five_accurate.append(0)
cf_e_data = c_e_data.copy()
cf_e_data['evaluation_label'] = cf_e_data['evaluation_label'].replace(-1, 0)
cf_e_data['text-embedding-score'] = cf_e_data['text-embedding-score'].replace(np.nan, 0)
cf_e_data['graph-embedding-score'] = cf_e_data['graph-embedding-score'].replace(np.nan, 0)
try:
ndcg_score_r_list.append(
sklearn.metrics.ndcg_score(
np.array([list(cf_e_data['evaluation_label'])]),
np.array([list(cf_e_data['retrieval_score'])])
)
)
except:
if len(cf_e_data['evaluation_label']) == 1 and cf_e_data['evaluation_label'].iloc[0] == 1:
ndcg_score_r_list.append(1.0)
elif len(cf_e_data['evaluation_label']) == 1 and cf_e_data['evaluation_label'].iloc[0] != 1:
ndcg_score_r_list.append(0.0)
else:
print("why am i here")
try:
ndcg_score_t_list.append(
sklearn.metrics.ndcg_score(
np.array([list(cf_e_data['evaluation_label'])]),
np.array([list(cf_e_data['text-embedding-score'])])
)
)
except:
if len(cf_e_data['evaluation_label']) == 1 and cf_e_data['evaluation_label'].iloc[0] == 1:
ndcg_score_t_list.append(1.0)
elif len(cf_e_data['evaluation_label']) == 1 and cf_e_data['evaluation_label'].iloc[0] != 1:
ndcg_score_t_list.append(0.0)
else:
print("text", cf_e_data['evaluation_label'], cf_e_data['text-embedding-score'] )
print("why am i here")
try:
ndcg_score_g_list.append(
sklearn.metrics.ndcg_score(
np.array([list(cf_e_data['evaluation_label'])]),
np.array([list(cf_e_data['graph-embedding-score'])])
)
)
except:
if len(cf_e_data['evaluation_label']) == 1 and cf_e_data['evaluation_label'].iloc[0] == 1:
ndcg_score_g_list.append(1.0)
elif len(cf_e_data['evaluation_label']) == 1 and cf_e_data['evaluation_label'].iloc[0] != 1:
ndcg_score_g_list.append(0.0)
else:
print("graph", cf_e_data['evaluation_label'], cf_e_data['graph-embedding-score'])
print("why am i here")
candidate_eval_data['r_ndcg'] = ndcg_score_r_list
candidate_eval_data['t_ndcg'] = ndcg_score_t_list
candidate_eval_data['g_ndcg'] = ndcg_score_g_list
candidate_eval_data['retrieval_top_one_accurate'] = num_tasks_with_retrieval_top_one_accurate
candidate_eval_data['retrieval_top_five_accurate'] = num_tasks_with_retrieval_top_five_accurate
candidate_eval_data['text_top_one_accurate'] = num_tasks_with_text_top_one_accurate
candidate_eval_data['text_top_five_accurate'] = num_tasks_with_text_top_five_accurate
candidate_eval_data['graph_top_one_accurate'] = num_tasks_with_graph_top_one_accurate
candidate_eval_data['graph_top_five_accurate'] = num_tasks_with_graph_top_five_accurate
candidate_eval_data['has_gt'] = has_gt_list
candidate_eval_data['has_gt_in_candidate'] = has_gt_in_candidate
res['num_tasks_with_retrieval_top_one_accurate'] = sum(num_tasks_with_retrieval_top_one_accurate)
res['num_tasks_with_retrieval_top_five_accurate'] = sum(num_tasks_with_retrieval_top_five_accurate)
res['num_tasks_with_text_top_one_accurate'] = sum(num_tasks_with_text_top_one_accurate)
res['num_tasks_with_text_top_five_accurate'] = sum(num_tasks_with_text_top_five_accurate)
res['num_tasks_with_graph_top_one_accurate'] = sum(num_tasks_with_graph_top_one_accurate)
res['num_tasks_with_graph_top_five_accurate'] = sum(num_tasks_with_graph_top_five_accurate)
return res, candidate_eval_data
# no_nan_all_data[no_nan_all_data['table_id'] == "84575189_0_6365692015941409487"]
res, candidate_eval_data = parse_eval_files_stats(no_nan_all_data[no_nan_all_data['table_id'] == "84575189_0_6365692015941409487"])
res
res, candidate_eval_data = parse_eval_files_stats(no_nan_all_data)
print(res)
display(candidate_eval_data)
candidate_eval_data['has_gt'].sum(), candidate_eval_data['has_gt_in_candidate'].sum()
candidate_eval_data.to_csv('./candidate_eval_no_empty.csv', index=False)
# Conclusion of exact-match on all tasks with ground truth (no filtering)
print(f"number of tasks: {res['num_tasks']}")
print(f"number of tasks with ground truth: {res['num_tasks_with_gt']}")
print(f"number of tasks with ground truth in candidate set: {res['num_tasks_with_gt_in_candidate']}, which is {res['num_tasks_with_gt_in_candidate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks has singleton candidate set: {res['num_tasks_with_singleton_candidate']}, which is {res['num_tasks_with_singleton_candidate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks has singleton candidate set which is ground truth: {res['num_tasks_with_singleton_candidate_with_gt']}, which is {res['num_tasks_with_singleton_candidate_with_gt']/res['num_tasks_with_gt'] * 100}%")
print()
print(f"number of tasks with top-1 accuracy in terms of retrieval score: {res['num_tasks_with_retrieval_top_one_accurate']}, which is {res['num_tasks_with_retrieval_top_one_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-5 accuracy in terms of retrieval score: {res['num_tasks_with_retrieval_top_five_accurate']}, which is {res['num_tasks_with_retrieval_top_five_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-1 accuracy in terms of text embedding score: {res['num_tasks_with_text_top_one_accurate']}, which is {res['num_tasks_with_text_top_one_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-5 accuracy in terms of text embedding score: {res['num_tasks_with_text_top_five_accurate']}, which is {res['num_tasks_with_text_top_five_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-1 accuracy in terms of graph embedding score: {res['num_tasks_with_graph_top_one_accurate']}, which is {res['num_tasks_with_graph_top_one_accurate']/res['num_tasks_with_gt'] * 100}%")
print(f"number of tasks with top-5 accuracy in terms of graph embedding score: {res['num_tasks_with_graph_top_five_accurate']}, which is {res['num_tasks_with_graph_top_five_accurate']/res['num_tasks_with_gt'] * 100}%")
print()
candidate_eval_data_with_gt = candidate_eval_data[candidate_eval_data['has_gt'] == 1]
print(f"average ndcg score ranked by retrieval score: {candidate_eval_data_with_gt['r_ndcg'].mean()}")
print(f"average ndcg score ranked by text-embedding-score: {candidate_eval_data_with_gt['t_ndcg'].mean()}")
print(f"average ndcg score ranked by graph-embedding-score: {candidate_eval_data_with_gt['g_ndcg'].mean()}")
# Conclusion of exact-match on filtered tasks: candidate set is non singleton and has ground truth
f_candidate_eval_data = candidate_eval_data[(candidate_eval_data['has_gt'] == 1) & (candidate_eval_data['count'] > 1)]
f_candidate_eval_data
num_tasks = len(f_candidate_eval_data)
df_has_gt_in_candidate = f_candidate_eval_data[f_candidate_eval_data['has_gt_in_candidate'] == 1]
df_singleton_candidate = f_candidate_eval_data[f_candidate_eval_data['count'] == 1]
df_singleton_candidate_has_gt = f_candidate_eval_data[(f_candidate_eval_data['count'] == 1) & (f_candidate_eval_data['has_gt_in_candidate'] == 1)]
df_retrieval_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['retrieval_top_one_accurate'] == 1]
df_retrieval_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['retrieval_top_five_accurate'] == 1]
df_text_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['text_top_one_accurate'] == 1]
df_text_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['text_top_five_accurate'] == 1]
df_graph_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['graph_top_one_accurate'] == 1]
df_graph_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['graph_top_five_accurate'] == 1]
print(f"number of tasks with ground truth: {num_tasks}")
print(f"number of tasks with ground truth in candidate set: {len(df_has_gt_in_candidate)}, which is {len(df_has_gt_in_candidate)/num_tasks * 100}%")
print(f"number of tasks has singleton candidate set: {len(df_singleton_candidate)}, which is {len(df_singleton_candidate)/num_tasks * 100}%")
print(f"number of tasks has singleton candidate set which is ground truth: {len(df_singleton_candidate_has_gt)}, which is {len(df_singleton_candidate_has_gt)/num_tasks * 100}%")
print()
print(f"number of tasks with top-1 accuracy in terms of retrieval score: {len(df_retrieval_top_one_accurate)}, which is {len(df_retrieval_top_one_accurate)/num_tasks * 100}%")
print(f"number of tasks with top-5 accuracy in terms of retrieval score: {len(df_retrieval_top_five_accurate)}, which is {len(df_retrieval_top_five_accurate)/num_tasks * 100}%")
print(f"number of tasks with top-1 accuracy in terms of text embedding score: {len(df_text_top_one_accurate)}, which is {len(df_text_top_one_accurate)/num_tasks * 100}%")
print(f"number of tasks with top-5 accuracy in terms of text embedding score: {len(df_text_top_five_accurate)}, which is {len(df_text_top_five_accurate)/num_tasks * 100}%")
print(f"number of tasks with top-1 accuracy in terms of graph embedding score: {len(df_graph_top_one_accurate)}, which is {len(df_graph_top_one_accurate)/num_tasks * 100}%")
print(f"number of tasks with top-5 accuracy in terms of graph embedding score: {len(df_graph_top_five_accurate)}, which is {len(df_graph_top_five_accurate)/num_tasks * 100}%")
print()
print(f"average ndcg score ranked by retrieval score: {df_has_gt_in_candidate['r_ndcg'].mean()}")
print(f"average ndcg score ranked by text-embedding-score: {df_has_gt_in_candidate['t_ndcg'].mean()}")
print(f"average ndcg score ranked by graph-embedding-score: {df_has_gt_in_candidate['g_ndcg'].mean()}")
test_data = all_data[(all_data['table_id'] == "14067031_0_559833072073397908") & (all_data['row'] == 3) & (all_data['column'] == 0)]
test_data
sklearn.metrics.ndcg_score(np.array([list(all_data[:5]['evaluation_label'])]), np.array([list(all_data[:5]['retrieval_score'])]))
# Some ground truth is empty??? why???
all_data[all_data['GT_kg_id'] == '']
```
### Graphs
```
import matplotlib.pyplot as plt
import sys
candidate_eval_data = pd.read_csv('./candidate_eval_no_empty.csv', index_col=False)
candidate_eval_data
# Line plot of top-1, top-5 and NDCG versus size of candidate set
x_candidate_set_size = list(pd.unique(candidate_eval_data['count']))
x_candidate_set_size.sort()
y_r_top_one = []
y_r_top_five = []
y_t_top_one = []
y_t_top_five = []
y_g_top_one = []
y_g_top_five = []
y_avg_r_ndcg = []
y_avg_t_ndcg = []
y_avg_g_ndcg = []
for c in x_candidate_set_size:
dff = candidate_eval_data[candidate_eval_data['count'] == c]
y_r_top_one.append(len(dff[dff['retrieval_top_one_accurate'] == 1])/len(dff) * 100)
y_r_top_five.append(len(dff[dff['retrieval_top_five_accurate'] == 1])/len(dff) * 100)
y_t_top_one.append(len(dff[dff['text_top_one_accurate'] == 1])/len(dff) * 100)
y_t_top_five.append(len(dff[dff['text_top_five_accurate'] == 1])/len(dff) * 100)
y_g_top_one.append(len(dff[dff['graph_top_one_accurate'] == 1])/len(dff) * 100)
y_g_top_five.append(len(dff[dff['graph_top_five_accurate'] == 1])/len(dff) * 100)
y_avg_r_ndcg.append(dff['r_ndcg'].mean())
y_avg_t_ndcg.append(dff['t_ndcg'].mean())
y_avg_g_ndcg.append(dff['g_ndcg'].mean())
len(y_r_top_one), len(y_g_top_one), len(y_t_top_one), len(y_avg_r_ndcg)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.set_ylabel('percent')
ax.set_xlabel('candidate set size')
ax.plot(x_candidate_set_size, y_r_top_one, 'ro', label='retrieval_top_one_accurate')
ax.plot(x_candidate_set_size, y_r_top_five, 'bo', label='retrieval_top_five_accurate')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
fig, ax = plt.subplots()
ax.set_ylabel('percent')
ax.set_xlabel('candidate set size')
ax.plot(x_candidate_set_size, y_t_top_one, 'ro', label='text_top_one_accurate')
ax.plot(x_candidate_set_size, y_t_top_five, 'bo', label='text_top_five_accurate')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
fig, ax = plt.subplots()
ax.set_ylabel('percent')
ax.set_xlabel('candidate set size')
ax.plot(x_candidate_set_size, y_g_top_one, 'ro', label='graph_top_one_accurate')
ax.plot(x_candidate_set_size, y_g_top_five, 'bo', label='graph_top_five_accurate')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
fig, ax = plt.subplots()
ax.set_ylabel('average ndcg')
ax.set_xlabel('candidate set size')
ax.plot(x_candidate_set_size, y_avg_r_ndcg, 'ro', label='average ndcg score ranked by retrieval score')
ax.plot(x_candidate_set_size, y_avg_t_ndcg, 'bo', label='average ndcg score ranked by text-embedding-score')
ax.plot(x_candidate_set_size, y_avg_g_ndcg, 'go', label='average ndcg score ranked by graph-embedding-score')
fig.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
```
### 02/16 stats on each eval file
```
import pandas as pd
candidate_eval_data = pd.read_csv('./candidate_eval.csv', index_col=False)
candidate_eval_data
# candidate_eval_data = candidate_eval_data.drop(['Unnamed: 0'], axis=1)
# candidate_eval_data
import os
eval_file_names = []
eval_file_ids = []
for (dirpath, dirnames, filenames) in os.walk('/Users/summ7t/dev/novartis/table-linker/SemTab2019/embedding_evaluation_files/'):
for fn in filenames:
if "csv" not in fn:
continue
abs_fn = dirpath + fn
assert os.path.isfile(abs_fn)
if os.path.getsize(abs_fn) == 0:
continue
eval_file_names.append(abs_fn)
eval_file_ids.append(fn.split('.csv')[0])
len(eval_file_names), len(eval_file_ids)
eval_file_ids
f_candidate_eval_data = candidate_eval_data[candidate_eval_data['table_id'] == '52299421_0_4473286348258170200']
f_candidate_eval_data
def compute_eval_file_stats(f_candidate_eval_data):
res = {}
num_tasks = len(f_candidate_eval_data)
df_has_gt = f_candidate_eval_data[f_candidate_eval_data['has_gt'] == 1]
df_has_gt_in_candidate = f_candidate_eval_data[f_candidate_eval_data['has_gt_in_candidate'] == 1]
df_singleton_candidate = f_candidate_eval_data[f_candidate_eval_data['count'] == 1]
df_singleton_candidate_has_gt = f_candidate_eval_data[(f_candidate_eval_data['count'] == 1) & (f_candidate_eval_data['has_gt_in_candidate'] == 1)]
df_retrieval_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['retrieval_top_one_accurate'] == 1]
df_retrieval_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['retrieval_top_five_accurate'] == 1]
df_text_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['text_top_one_accurate'] == 1]
df_text_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['text_top_five_accurate'] == 1]
df_graph_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['graph_top_one_accurate'] == 1]
df_graph_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['graph_top_five_accurate'] == 1]
res['table_id'] = f_candidate_eval_data['table_id'].iloc[0]
res['num_tasks'] = num_tasks
res['num_tasks_with_gt'] = len(df_has_gt)
res['num_tasks_with_gt_in_candidate'] = len(df_has_gt_in_candidate) / len(df_has_gt) * 100
res['num_tasks_with_singleton_candidate'] = len(df_singleton_candidate) / len(df_has_gt) * 100
res['num_tasks_with_singleton_candidate_with_gt'] = len(df_singleton_candidate_has_gt) / len(df_has_gt) * 100
res['num_tasks_with_retrieval_top_one_accurate'] = len(df_retrieval_top_one_accurate) / len(df_has_gt) * 100
res['num_tasks_with_retrieval_top_five_accurate'] = len(df_retrieval_top_five_accurate) / len(df_has_gt) * 100
res['num_tasks_with_text_top_one_accurate'] = len(df_text_top_one_accurate) / len(df_has_gt) * 100
res['num_tasks_with_text_top_five_accurate'] = len(df_text_top_five_accurate) / len(df_has_gt) * 100
res['num_tasks_with_graph_top_one_accurate'] = len(df_graph_top_one_accurate) / len(df_has_gt) * 100
res['num_tasks_with_graph_top_five_accurate'] = len(df_graph_top_five_accurate) / len(df_has_gt) * 100
res['average_ndcg_retrieval'] = df_has_gt['r_ndcg'].mean()
res['average_ndcg_text'] = df_has_gt['t_ndcg'].mean()
res['average_ndcg_graph'] = df_has_gt['g_ndcg'].mean()
return res
def compute_eval_file_stats_count(f_candidate_eval_data):
res = {}
num_tasks = len(f_candidate_eval_data)
df_has_gt = f_candidate_eval_data[f_candidate_eval_data['has_gt'] == 1]
df_has_gt_in_candidate = f_candidate_eval_data[f_candidate_eval_data['has_gt_in_candidate'] == 1]
df_singleton_candidate = f_candidate_eval_data[f_candidate_eval_data['count'] == 1]
df_singleton_candidate_has_gt = f_candidate_eval_data[(f_candidate_eval_data['count'] == 1) & (f_candidate_eval_data['has_gt_in_candidate'] == 1)]
df_retrieval_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['retrieval_top_one_accurate'] == 1]
df_retrieval_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['retrieval_top_five_accurate'] == 1]
df_text_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['text_top_one_accurate'] == 1]
df_text_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['text_top_five_accurate'] == 1]
df_graph_top_one_accurate = f_candidate_eval_data[f_candidate_eval_data['graph_top_one_accurate'] == 1]
df_graph_top_five_accurate = f_candidate_eval_data[f_candidate_eval_data['graph_top_five_accurate'] == 1]
res['table_id'] = f_candidate_eval_data['table_id'].iloc[0]
res['num_tasks'] = num_tasks
res['num_tasks_with_gt'] = len(df_has_gt)
res['num_tasks_with_gt_in_candidate'] = len(df_has_gt_in_candidate)
res['num_tasks_with_singleton_candidate'] = len(df_singleton_candidate)
res['num_tasks_with_singleton_candidate_with_gt'] = len(df_singleton_candidate_has_gt)
res['num_tasks_with_retrieval_top_one_accurate'] = len(df_retrieval_top_one_accurate) / len(df_has_gt) * 100
res['num_tasks_with_retrieval_top_five_accurate'] = len(df_retrieval_top_five_accurate) / len(df_has_gt) * 100
res['num_tasks_with_text_top_one_accurate'] = len(df_text_top_one_accurate) / len(df_has_gt) * 100
res['num_tasks_with_text_top_five_accurate'] = len(df_text_top_five_accurate) / len(df_has_gt) * 100
res['num_tasks_with_graph_top_one_accurate'] = len(df_graph_top_one_accurate) / len(df_has_gt) * 100
res['num_tasks_with_graph_top_five_accurate'] = len(df_graph_top_five_accurate) / len(df_has_gt) * 100
res['average_ndcg_retrieval'] = df_has_gt['r_ndcg'].mean()
res['average_ndcg_text'] = df_has_gt['t_ndcg'].mean()
res['average_ndcg_graph'] = df_has_gt['g_ndcg'].mean()
return res
res = compute_eval_file_stats(f_candidate_eval_data)
print(f"table id is {res['table_id']}")
print(f"number of tasks: {res['num_tasks']}")
print(f"number of tasks with ground truth: {res['num_tasks_with_gt']}")
print(f"number of tasks with ground truth in candidate set: {res['num_tasks_with_gt_in_candidate']}")
print(f"number of tasks has singleton candidate set: {res['num_tasks_with_singleton_candidate']}")
print(f"number of tasks has singleton candidate set which is ground truth: {res['num_tasks_with_singleton_candidate_with_gt']}")
print()
print(f"number of tasks with top-1 accuracy in terms of retrieval score: {res['num_tasks_with_retrieval_top_one_accurate']}")
print(f"number of tasks with top-5 accuracy in terms of retrieval score: {res['num_tasks_with_retrieval_top_five_accurate']}")
print(f"number of tasks with top-1 accuracy in terms of text embedding score: {res['num_tasks_with_text_top_one_accurate']}")
print(f"number of tasks with top-5 accuracy in terms of text embedding score: {res['num_tasks_with_text_top_five_accurate']}")
print(f"number of tasks with top-1 accuracy in terms of graph embedding score: {res['num_tasks_with_graph_top_one_accurate']}")
print(f"number of tasks with top-5 accuracy in terms of graph embedding score: {res['num_tasks_with_graph_top_five_accurate']}")
print()
print(f"average ndcg score ranked by retrieval score: {res['average_ndcg_retrieval']}")
print(f"average ndcg score ranked by text-embedding-score: {res['average_ndcg_text']}")
print(f"average ndcg score ranked by graph-embedding-score: {res['average_ndcg_graph']}")
all_tables = {}
for tid in eval_file_ids:
f_candidate_eval_data = candidate_eval_data[candidate_eval_data['table_id'] == tid]
all_tables[tid] = compute_eval_file_stats(f_candidate_eval_data)
all_tables
all_tables = {}
for tid in eval_file_ids:
f_candidate_eval_data = candidate_eval_data[candidate_eval_data['table_id'] == tid]
all_tables[tid] = compute_eval_file_stats_count(f_candidate_eval_data)
all_tables
eval_file_ids
# visualize ten dev eval file stats
# Recompute all tables if needed
x_eval_fid = [
'movies',
'players I',
'video games',
'magazines',
'companies',
'country I',
'players II',
'pope',
'country II'
]
x_eval_fidx = range(len(x_eval_fid))
y_num_tasks_with_gt_in_candidate = []
y_num_tasks_with_singleton_candidate = []
y_num_tasks_with_singleton_candidate_with_gt = []
y_num_tasks_with_retrieval_top_one_accurate = []
y_num_tasks_with_retrieval_top_five_accurate = []
y_num_tasks_with_text_top_one_accurate = []
y_num_tasks_with_text_top_five_accurate = []
y_num_tasks_with_graph_top_one_accurate = []
y_num_tasks_with_graph_top_five_accurate = []
y_average_ndcg_retrieval = []
y_average_ndcg_text = []
y_average_ndcg_graph = []
for idx in range(len(x_eval_fid)):
table_id = eval_file_ids[idx]
y_num_tasks_with_gt_in_candidate.append(all_tables[table_id]['num_tasks_with_gt_in_candidate'])
y_num_tasks_with_singleton_candidate.append(all_tables[table_id]['num_tasks_with_singleton_candidate'])
y_num_tasks_with_singleton_candidate_with_gt.append(all_tables[table_id]['num_tasks_with_singleton_candidate_with_gt'])
y_num_tasks_with_retrieval_top_one_accurate.append(all_tables[table_id]['num_tasks_with_retrieval_top_one_accurate'])
y_num_tasks_with_retrieval_top_five_accurate.append(all_tables[table_id]['num_tasks_with_retrieval_top_five_accurate'])
y_num_tasks_with_text_top_one_accurate.append(all_tables[table_id]['num_tasks_with_text_top_one_accurate'])
y_num_tasks_with_text_top_five_accurate.append(all_tables[table_id]['num_tasks_with_text_top_five_accurate'])
y_num_tasks_with_graph_top_one_accurate.append(all_tables[table_id]['num_tasks_with_graph_top_one_accurate'])
y_num_tasks_with_graph_top_five_accurate.append(all_tables[table_id]['num_tasks_with_graph_top_five_accurate'])
y_average_ndcg_retrieval.append(all_tables[table_id]['average_ndcg_retrieval'])
y_average_ndcg_text.append(all_tables[table_id]['average_ndcg_text'])
y_average_ndcg_graph.append(all_tables[table_id]['average_ndcg_graph'])
y_num_tasks_with_text_top_five_accurate
import statistics
def compute_list_stats(l):
return min(l), max(l), statistics.median(l), statistics.mean(l), statistics.stdev(l)
print('% tasks_with_gt_in_candidate : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_gt_in_candidate)))
print('% tasks_with_singleton_candidate : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_singleton_candidate)))
print('% tasks_with_singleton_candidate_with_gt : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_singleton_candidate_with_gt)))
print('% tasks_with_retrieval_top_one_accurate : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_retrieval_top_one_accurate)))
print('% tasks_with_retrieval_top_five_accurate : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_retrieval_top_five_accurate)))
print('% tasks_with_text_top_one_accurate : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_text_top_one_accurate)))
print('% tasks_with_text_top_five_accurate : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_text_top_five_accurate)))
print('% tasks_with_graph_top_one_accurate : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_graph_top_one_accurate)))
print('% tasks_with_graph_top_five_accurate : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_average_ndcg_retrieval)))
print('average_ndcg_retrieval : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_num_tasks_with_graph_top_five_accurate)))
print('average_ndcg_text : \n min is {},\n max is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_average_ndcg_text)))
print('average_ndcg_graph : \n min is {}, \nmax is {},\n median is {},\n mean is {},\n std is {}'.format(*compute_list_stats(y_average_ndcg_graph)))
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 10))
ax.set_ylabel('average ndcg')
ax.set_xlabel('table content')
ax.plot(x_eval_fid, y_average_ndcg_retrieval, 'rx', label='average ndcg score ranked by retrieval score')
ax.plot(x_eval_fid, y_average_ndcg_text, 'bx', label='average ndcg score ranked by text embedding score')
ax.plot(x_eval_fid, y_average_ndcg_graph, 'gx', label='average ndcg score ranked by graph embedding score')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
fig, ax = plt.subplots(figsize=(10, 10))
ax.set_ylabel('percent')
ax.set_xlabel('table content')
ax.plot(x_eval_fid, y_num_tasks_with_retrieval_top_one_accurate, 'rx', label='ranked by retrieval score top-1 accuracy')
ax.plot(x_eval_fid, y_num_tasks_with_text_top_one_accurate, 'bx', label='ranked by text embedding score top-1 accuracy')
ax.plot(x_eval_fid, y_num_tasks_with_graph_top_one_accurate, 'gx', label='ranked by graph embedding score top-1 accuracy')
ax.plot(x_eval_fid, y_num_tasks_with_retrieval_top_five_accurate, 'ro', label='ranked by retrieval score top-5 accuracy')
ax.plot(x_eval_fid, y_num_tasks_with_text_top_five_accurate, 'bo', label='ranked by text embedding score top-5 accuracy')
ax.plot(x_eval_fid, y_num_tasks_with_graph_top_five_accurate, 'go', label='ranked by graph embedding score top-5 accuracy')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
# fig, ax = plt.subplots(figsize=(10, 10))
# ax.set_ylabel('percent')
# ax.set_xlabel('table_id idx')
# ax.plot(x_eval_fid, y_num_tasks_with_retrieval_top_five_accurate, 'rx', label='ranked by retrieval score top-5 accuracy')
# ax.plot(x_eval_fid, y_num_tasks_with_text_top_five_accurate, 'bx', label='ranked by text embedding score top-5 accuracy')
# ax.plot(x_eval_fid, y_num_tasks_with_graph_top_five_accurate, 'gx', label='ranked by graph embedding score top-5 accuracy')
# ax.legend(bbox_to_anchor=(1,1), loc="upper left")
# fig.show()
fig, ax = plt.subplots(figsize=(10, 10))
ax.set_ylabel('percent')
ax.set_xlabel('table content')
ax.plot(x_eval_fid, y_num_tasks_with_singleton_candidate, 'rx', label='percent of tasks with singleton candidate set')
ax.plot(x_eval_fid, y_num_tasks_with_singleton_candidate_with_gt, 'bx', label='percent of tasks with ground truth in singleton candidate set')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
```
### 02/17 More plots
```
candidate_eval_data[candidate_eval_data['count'] == 1]
[all_tables[tid]['num_tasks_with_singleton_candidate'] for tid in all_tables]
# x_axis percetage of singleton
x_pos = [all_tables[tid]['num_tasks_with_singleton_candidate'] for tid in all_tables]
x_posgt = [all_tables[tid]['num_tasks_with_singleton_candidate_with_gt'] for tid in all_tables]
len(x_pos), len(x_posgt)
fig, ax = plt.subplots()
ax.set_ylabel('average ndcg')
# ax.set_xlabel('percentage of singleton candidate set')
ax.set_xlabel('number of singleton candidate set')
ax.plot(x_pos, y_average_ndcg_retrieval, 'rx', label='average ndcg score ranked by retrieval score')
ax.plot(x_pos, y_average_ndcg_text, 'bx', label='average ndcg score ranked by text embedding score')
ax.plot(x_pos, y_average_ndcg_graph, 'gx', label='average ndcg score ranked by graph embedding score')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
fig, ax = plt.subplots()
ax.set_ylabel('percent')
# ax.set_xlabel('percentage of singleton candidate set')
ax.set_xlabel('number of singleton candidate set')
ax.plot(x_pos, y_num_tasks_with_retrieval_top_one_accurate, 'rx', label='ranked by retrieval score top-1 accuracy')
ax.plot(x_pos, y_num_tasks_with_text_top_one_accurate, 'bx', label='ranked by text embedding score top-1 accuracy')
ax.plot(x_pos, y_num_tasks_with_graph_top_one_accurate, 'gx', label='ranked by graph embedding score top-1 accuracy')
ax.plot(x_pos, y_num_tasks_with_retrieval_top_five_accurate, 'ro', label='ranked by retrieval score top-5 accuracy')
ax.plot(x_pos, y_num_tasks_with_text_top_five_accurate, 'bo', label='ranked by text embedding score top-5 accuracy')
ax.plot(x_pos, y_num_tasks_with_graph_top_five_accurate, 'go', label='ranked by graph embedding score top-5 accuracy')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
fig, ax = plt.subplots()
ax.set_ylabel('percent')
# ax.set_xlabel('percentage of singleton candidate set with ground truth')
ax.set_xlabel('number of singleton candidate set with ground truth')
ax.plot(x_posgt, y_num_tasks_with_retrieval_top_one_accurate, 'rx', label='ranked by retrieval score top-1 accuracy')
ax.plot(x_posgt, y_num_tasks_with_text_top_one_accurate, 'bx', label='ranked by text embedding score top-1 accuracy')
ax.plot(x_posgt, y_num_tasks_with_graph_top_one_accurate, 'gx', label='ranked by graph embedding score top-1 accuracy')
ax.plot(x_posgt, y_num_tasks_with_retrieval_top_five_accurate, 'ro', label='ranked by retrieval score top-5 accuracy')
ax.plot(x_posgt, y_num_tasks_with_text_top_five_accurate, 'bo', label='ranked by text embedding score top-5 accuracy')
ax.plot(x_posgt, y_num_tasks_with_graph_top_five_accurate, 'go', label='ranked by graph embedding score top-5 accuracy')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
fig, ax = plt.subplots()
ax.set_ylabel('average ndcg')
ax.set_xlabel('number of singleton candidate set with ground truth')
# ax.set_xlabel('percentage of singleton candidate set with ground truth')
ax.plot(x_posgt, y_average_ndcg_retrieval, 'rx', label='average ndcg score ranked by retrieval score')
ax.plot(x_posgt, y_average_ndcg_text, 'bx', label='average ndcg score ranked by text embedding score')
ax.plot(x_posgt, y_average_ndcg_graph, 'gx', label='average ndcg score ranked by graph embedding score')
ax.legend(bbox_to_anchor=(1,1), loc="upper left")
fig.show()
```
### 02/19 More experiments: wrong singleton
```
import pandas as pd
candidate_eval_data = pd.read_csv('./candidate_eval_no_empty.csv', index_col=False)
candidate_eval_data
# Sub all singleton candidate set to see how "good" the algorithm can be
subbed_candidate_eval_data = candidate_eval_data.copy()
for i, row in subbed_candidate_eval_data.iterrows():
if row['count'] == 1:
subbed_candidate_eval_data.loc[i, 'retrieval_top_one_accurate'] = 1
subbed_candidate_eval_data.loc[i, 'retrieval_top_five_accurate'] = 1
subbed_candidate_eval_data.loc[i, 'text_top_one_accurate'] = 1
subbed_candidate_eval_data.loc[i, 'text_top_five_accurate'] = 1
subbed_candidate_eval_data.loc[i, 'graph_top_one_accurate'] = 1
subbed_candidate_eval_data.loc[i, 'graph_top_five_accurate'] = 1
subbed_candidate_eval_data.loc[i, 'has_gt'] = 1
subbed_candidate_eval_data.loc[i, 'has_gt_in_candidate'] = 1
subbed_candidate_eval_data.loc[i, 'r_ndcg'] = 1
subbed_candidate_eval_data.loc[i, 't_ndcg'] = 1
subbed_candidate_eval_data.loc[i, 'g_ndcg'] = 1
subbed_candidate_eval_data
dropped_candidate_eval_data = candidate_eval_data.copy()[(candidate_eval_data['count'] != 1) | (candidate_eval_data['has_gt_in_candidate'] == 1)]
dropped_candidate_eval_data
candidate_eval_data[candidate_eval_data['count'] == 1]
subbed_candidate_eval_data[subbed_candidate_eval_data['count'] == 1]
dropped_candidate_eval_data[dropped_candidate_eval_data['count'] == 1]
# compute the same metrics
import os
eval_file_names = []
eval_file_ids = []
for (dirpath, dirnames, filenames) in os.walk('/Users/summ7t/dev/novartis/table-linker/SemTab2019/embedding_evaluation_files/'):
for fn in filenames:
if "csv" not in fn:
continue
abs_fn = dirpath + fn
assert os.path.isfile(abs_fn)
if os.path.getsize(abs_fn) == 0:
continue
eval_file_names.append(abs_fn)
eval_file_ids.append(fn.split('.csv')[0])
len(eval_file_names), len(eval_file_ids)
subbed_all_tables = {}
for tid in eval_file_ids:
f_candidate_eval_data = subbed_candidate_eval_data[subbed_candidate_eval_data['table_id'] == tid]
subbed_all_tables[tid] = compute_eval_file_stats(f_candidate_eval_data)
subbed_all_tables
dropped_all_tables = {}
for tid in eval_file_ids:
f_candidate_eval_data = dropped_candidate_eval_data[dropped_candidate_eval_data['table_id'] == tid]
dropped_all_tables[tid] = compute_eval_file_stats(f_candidate_eval_data)
dropped_all_tables
# visualize ten dev eval file stats
# Same process as before
x_eval_fid = [
'movies',
'players I',
'video games',
'magazines',
'companies',
'country I',
'players II',
'pope',
'country II'
]
x_eval_fidx = range(len(x_eval_fid))
r_y_num_tasks_with_gt_in_candidate = []
r_y_num_tasks_with_singleton_candidate = []
r_y_num_tasks_with_singleton_candidate_with_gt = []
r_y_num_tasks_with_retrieval_top_one_accurate = []
r_y_num_tasks_with_retrieval_top_five_accurate = []
r_y_num_tasks_with_text_top_one_accurate = []
r_y_num_tasks_with_text_top_five_accurate = []
r_y_num_tasks_with_graph_top_one_accurate = []
r_y_num_tasks_with_graph_top_five_accurate = []
r_y_average_ndcg_retrieval = []
r_y_average_ndcg_text = []
r_y_average_ndcg_graph = []
for idx in range(len(x_eval_fid)):
table_id = eval_file_ids[idx]
r_y_num_tasks_with_gt_in_candidate.append(subbed_all_tables[table_id]['num_tasks_with_gt_in_candidate'])
r_y_num_tasks_with_singleton_candidate.append(subbed_all_tables[table_id]['num_tasks_with_singleton_candidate'])
r_y_num_tasks_with_singleton_candidate_with_gt.append(subbed_all_tables[table_id]['num_tasks_with_singleton_candidate_with_gt'])
r_y_num_tasks_with_retrieval_top_one_accurate.append(subbed_all_tables[table_id]['num_tasks_with_retrieval_top_one_accurate'])
r_y_num_tasks_with_retrieval_top_five_accurate.append(subbed_all_tables[table_id]['num_tasks_with_retrieval_top_five_accurate'])
r_y_num_tasks_with_text_top_one_accurate.append(subbed_all_tables[table_id]['num_tasks_with_text_top_one_accurate'])
r_y_num_tasks_with_text_top_five_accurate.append(subbed_all_tables[table_id]['num_tasks_with_text_top_five_accurate'])
r_y_num_tasks_with_graph_top_one_accurate.append(subbed_all_tables[table_id]['num_tasks_with_graph_top_one_accurate'])
r_y_num_tasks_with_graph_top_five_accurate.append(subbed_all_tables[table_id]['num_tasks_with_graph_top_five_accurate'])
r_y_average_ndcg_retrieval.append(subbed_all_tables[table_id]['average_ndcg_retrieval'])
r_y_average_ndcg_text.append(subbed_all_tables[table_id]['average_ndcg_text'])
r_y_average_ndcg_graph.append(subbed_all_tables[table_id]['average_ndcg_graph'])
r_y_average_ndcg_retrieval, y_average_ndcg_retrieval
x_eval_fid = [
'movies',
'players I',
'video games',
'magazines',
'companies',
'country I',
'players II',
'pope',
'country II'
]
x_eval_fidx = range(len(x_eval_fid))
d_y_num_tasks_with_gt_in_candidate = []
d_y_num_tasks_with_singleton_candidate = []
d_y_num_tasks_with_singleton_candidate_with_gt = []
d_y_num_tasks_with_retrieval_top_one_accurate = []
d_y_num_tasks_with_retrieval_top_five_accurate = []
d_y_num_tasks_with_text_top_one_accurate = []
d_y_num_tasks_with_text_top_five_accurate = []
d_y_num_tasks_with_graph_top_one_accurate = []
d_y_num_tasks_with_graph_top_five_accurate = []
d_y_average_ndcg_retrieval = []
d_y_average_ndcg_text = []
d_y_average_ndcg_graph = []
for idx in range(len(x_eval_fid)):
table_id = eval_file_ids[idx]
d_y_num_tasks_with_gt_in_candidate.append(dropped_all_tables[table_id]['num_tasks_with_gt_in_candidate'])
d_y_num_tasks_with_singleton_candidate.append(dropped_all_tables[table_id]['num_tasks_with_singleton_candidate'])
d_y_num_tasks_with_singleton_candidate_with_gt.append(dropped_all_tables[table_id]['num_tasks_with_singleton_candidate_with_gt'])
d_y_num_tasks_with_retrieval_top_one_accurate.append(dropped_all_tables[table_id]['num_tasks_with_retrieval_top_one_accurate'])
d_y_num_tasks_with_retrieval_top_five_accurate.append(dropped_all_tables[table_id]['num_tasks_with_retrieval_top_five_accurate'])
d_y_num_tasks_with_text_top_one_accurate.append(dropped_all_tables[table_id]['num_tasks_with_text_top_one_accurate'])
d_y_num_tasks_with_text_top_five_accurate.append(dropped_all_tables[table_id]['num_tasks_with_text_top_five_accurate'])
d_y_num_tasks_with_graph_top_one_accurate.append(dropped_all_tables[table_id]['num_tasks_with_graph_top_one_accurate'])
d_y_num_tasks_with_graph_top_five_accurate.append(dropped_all_tables[table_id]['num_tasks_with_graph_top_five_accurate'])
d_y_average_ndcg_retrieval.append(dropped_all_tables[table_id]['average_ndcg_retrieval'])
d_y_average_ndcg_text.append(dropped_all_tables[table_id]['average_ndcg_text'])
d_y_average_ndcg_graph.append(dropped_all_tables[table_id]['average_ndcg_graph'])
d_y_average_ndcg_retrieval, y_average_ndcg_retrieval
# import matplotlib.pyplot as plt
# fig, ax = plt.subplots(figsize=(10, 10))
# ax.set_ylabel('average ndcg')
# ax.set_xlabel('table content')
# ax.plot(x_eval_fid, r_y_average_ndcg_retrieval, 'ro', label='R: average ndcg score ranked by retrieval score')
# ax.plot(x_eval_fid, r_y_average_ndcg_text, 'bo', label='R: average ndcg score ranked by text embedding score')
# ax.plot(x_eval_fid, r_y_average_ndcg_graph, 'go', label='R: average ndcg score ranked by graph embedding score')
# ax.plot(x_eval_fid, y_average_ndcg_retrieval, 'rx', label='average ndcg score ranked by retrieval score')
# ax.plot(x_eval_fid, y_average_ndcg_text, 'bx', label='average ndcg score ranked by text embedding score')
# ax.plot(x_eval_fid, y_average_ndcg_graph, 'gx', label='average ndcg score ranked by graph embedding score')
# ax.legend(bbox_to_anchor=(1,1), loc="upper left")
# fig.show()
# fig, ax = plt.subplots(figsize=(10, 10))
# ax.set_ylabel('R: percent')
# ax.set_xlabel('table content')
# ax.plot(x_eval_fid, r_y_num_tasks_with_retrieval_top_one_accurate, 'rx', label='ranked by retrieval score top-1 accuracy')
# ax.plot(x_eval_fid, r_y_num_tasks_with_text_top_one_accurate, 'bx', label='ranked by text embedding score top-1 accuracy')
# ax.plot(x_eval_fid, r_y_num_tasks_with_graph_top_one_accurate, 'gx', label='ranked by graph embedding score top-1 accuracy')
# ax.plot(x_eval_fid, r_y_num_tasks_with_retrieval_top_five_accurate, 'ro', label='ranked by retrieval score top-5 accuracy')
# ax.plot(x_eval_fid, r_y_num_tasks_with_text_top_five_accurate, 'bo', label='ranked by text embedding score top-5 accuracy')
# ax.plot(x_eval_fid, r_y_num_tasks_with_graph_top_five_accurate, 'go', label='ranked by graph embedding score top-5 accuracy')
# ax.legend(bbox_to_anchor=(1,1), loc="upper left")
# fig.show()
# p_min, p_max, p_median, p_mean, p_std = compute_list_stats(y_num_tasks_with_text_top_five_accurate)
# r_min, r_max, r_median, r_mean, r_std = compute_list_stats(r_y_num_tasks_with_text_top_five_accurate)
# r_min - p_min, r_max - p_max, r_median - p_median, r_mean - p_mean, r_std - p_std
# Plot dropped wrong singleton
# import matplotlib.pyplot as plt
# fig, ax = plt.subplots(figsize=(10, 10))
# ax.set_ylabel('average ndcg')
# ax.set_xlabel('table content')
# ax.plot(x_eval_fid, d_y_average_ndcg_retrieval, 'ro', label='D: average ndcg score ranked by retrieval score')
# ax.plot(x_eval_fid, d_y_average_ndcg_text, 'bo', label='D: average ndcg score ranked by text embedding score')
# ax.plot(x_eval_fid, d_y_average_ndcg_graph, 'go', label='D: average ndcg score ranked by graph embedding score')
# ax.plot(x_eval_fid, r_y_average_ndcg_retrieval, 'r+', label='R: average ndcg score ranked by retrieval score')
# ax.plot(x_eval_fid, r_y_average_ndcg_text, 'b+', label='R: average ndcg score ranked by text embedding score')
# ax.plot(x_eval_fid, r_y_average_ndcg_graph, 'g+', label='R: average ndcg score ranked by graph embedding score')
# ax.plot(x_eval_fid, y_average_ndcg_retrieval, 'rx', label='average ndcg score ranked by retrieval score')
# ax.plot(x_eval_fid, y_average_ndcg_text, 'bx', label='average ndcg score ranked by text embedding score')
# ax.plot(x_eval_fid, y_average_ndcg_graph, 'gx', label='average ndcg score ranked by graph embedding score')
# ax.legend(bbox_to_anchor=(1,1), loc="upper left")
# fig.show()
# fig, ax = plt.subplots(figsize=(10, 10))
# ax.set_ylabel('D: percent')
# ax.set_xlabel('table content')
# ax.plot(x_eval_fid, d_y_num_tasks_with_retrieval_top_one_accurate, 'rx', label='ranked by retrieval score top-1 accuracy')
# ax.plot(x_eval_fid, d_y_num_tasks_with_text_top_one_accurate, 'bx', label='ranked by text embedding score top-1 accuracy')
# ax.plot(x_eval_fid, d_y_num_tasks_with_graph_top_one_accurate, 'gx', label='ranked by graph embedding score top-1 accuracy')
# ax.plot(x_eval_fid, d_y_num_tasks_with_retrieval_top_five_accurate, 'ro', label='ranked by retrieval score top-5 accuracy')
# ax.plot(x_eval_fid, d_y_num_tasks_with_text_top_five_accurate, 'bo', label='ranked by text embedding score top-5 accuracy')
# ax.plot(x_eval_fid, d_y_num_tasks_with_graph_top_five_accurate, 'go', label='ranked by graph embedding score top-5 accuracy')
# ax.legend(bbox_to_anchor=(1,1), loc="upper left")
# fig.show()
dropped_all_tables
# construct differene table
diff_ndcg_df = pd.DataFrame(columns=['table_content', 'r_ndcg', 'R: r_ndcg', 'D: r_ndcg', 't_ndcg', 'R: t_ndcg', 'D: t_ndcg', 'g_ndcg', 'R: g_ndcg', 'D: g_ndcg'])
for idx in range(len(x_eval_fid)):
table_id = eval_file_ids[idx]
diff_ndcg_df.loc[table_id] = [
x_eval_fid[idx],
y_average_ndcg_retrieval[idx],
r_y_average_ndcg_retrieval[idx],
d_y_average_ndcg_retrieval[idx],
y_average_ndcg_text[idx],
r_y_average_ndcg_text[idx],
d_y_average_ndcg_text[idx],
y_average_ndcg_graph[idx],
r_y_average_ndcg_graph[idx],
d_y_average_ndcg_graph[idx]
]
diff_ndcg_df
diff_accuracy_df = pd.DataFrame(columns=[
'table_content', 'top1-retr', 'R: top1-retr', 'D: top1-retr',
'top1-text', 'R: top1-text', 'D: top1-text',
'top1-graph', 'R: top1-graph', 'D: top1-graph'
])
for idx in range(len(x_eval_fid)):
table_id = eval_file_ids[idx]
diff_accuracy_df.loc[table_id] = [
x_eval_fid[idx],
y_num_tasks_with_retrieval_top_one_accurate[idx],
r_y_num_tasks_with_retrieval_top_one_accurate[idx],
d_y_num_tasks_with_retrieval_top_one_accurate[idx],
y_num_tasks_with_text_top_one_accurate[idx],
r_y_num_tasks_with_text_top_one_accurate[idx],
d_y_num_tasks_with_text_top_one_accurate[idx],
y_num_tasks_with_graph_top_one_accurate[idx],
r_y_num_tasks_with_graph_top_one_accurate[idx],
d_y_num_tasks_with_graph_top_one_accurate[idx]
]
diff_accuracy_df
diff_accuracy_f_df = pd.DataFrame(columns=[
'table_content',
'top5-retr', 'R: top5-retr', 'D: top5-retr',
'top5-text', 'R: top5-text', 'D: top5-text',
'top5-graph', 'R: top5-graph', 'D: top5-graph'
])
for idx in range(len(x_eval_fid)):
table_id = eval_file_ids[idx]
diff_accuracy_f_df.loc[table_id] = [
x_eval_fid[idx],
y_num_tasks_with_retrieval_top_five_accurate[idx],
r_y_num_tasks_with_retrieval_top_five_accurate[idx],
d_y_num_tasks_with_retrieval_top_five_accurate[idx],
y_num_tasks_with_text_top_five_accurate[idx],
r_y_num_tasks_with_text_top_five_accurate[idx],
d_y_num_tasks_with_text_top_five_accurate[idx],
y_num_tasks_with_graph_top_five_accurate[idx],
r_y_num_tasks_with_graph_top_five_accurate[idx],
d_y_num_tasks_with_graph_top_five_accurate[idx]
]
diff_accuracy_f_df
# distribution of wrong singleton
wrong_singleton_df = candidate_eval_data[(candidate_eval_data['count'] == 1) & (candidate_eval_data['has_gt_in_candidate'] != 1)]
wrong_singleton_df
# get candidate from eval file + get label from ground truth file
wrong_files = list(pd.unique(wrong_singleton_df['table_id']))
wrong_tasks_df = pd.DataFrame(columns=['table_id', 'row', 'column', 'GT_kg_label', 'GT_kg_id', 'candidates'])
for fid in wrong_files:
f_data = pd.read_csv(f'/Users/summ7t/dev/novartis/table-linker/SemTab2019/embedding_evaluation_files/{fid}.csv')
f_wrong_tasks = wrong_singleton_df[wrong_singleton_df['table_id'] == fid]
for i, row in f_wrong_tasks.iterrows():
candidates_df = f_data[(f_data['row'] == row['row']) & (f_data['column'] == row['column'])]
candidates_df = candidates_df.fillna("")
# print(row)
# display(candidates_df)
assert row['count'] == len(candidates_df)
c_list = list(pd.unique(candidates_df['kg_id']))
GT_kg_id = candidates_df['GT_kg_id'].iloc[0]
GT_kg_label = candidates_df['GT_kg_label'].iloc[0]
# print(row['row'], row['column'], GT_kg_label, GT_kg_id)
# print(c_list)
wrong_tasks_df = wrong_tasks_df.append({
'table_id': fid,
'row': row['row'],
'column': row['column'],
'GT_kg_label': GT_kg_label,
'GT_kg_id': GT_kg_id,
'candidates': " ".join(c_list)
}, ignore_index=True)
wrong_tasks_df
pd.unique(wrong_tasks_df['candidates'])
wrong_tasks_df[wrong_tasks_df['candidates'] > '']
data[242:245]
```
| github_jupyter |
# Homework 5: Problems
## Due Wednesday 28 October, before class
### PHYS 440/540, Fall 2020
https://github.com/gtrichards/PHYS_440_540/
## Problems 1&2
Complete Chapters 1 and 2 in the *unsupervised learning* course in Data Camp. The last video (and the two following code examples) in Chapter 2 are off topic, but we'll discuss those next week, so this will be a good intro. The rest is highly relevant to this week's material. These are worth 1000 and 900 points, respectively. I'll be grading on the number of points earned instead of completion (as I have been), so try to avoid using the hints unless you really need them.
## Problem 3
Fill in the blanks below. This exercise will take you though an example of everything that we did this week. Please copy the relevant import statements (below) to the cells where they are used (so that they can be run out of order).
If a question is calling for a word-based answer, I'm not looking for more than ~1 sentence.
---
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.metrics.cluster import homogeneity_score
from sklearn.datasets import make_blobs
from sklearn.neighbors import KernelDensity
from astroML.density_estimation import KNeighborsDensity
from sklearn.model_selection import GridSearchCV
from sklearn.mixture import GaussianMixture
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN
```
Setup up the data set. We will do both density estimation and clustering on it.
```
from sklearn.datasets import make_blobs
#Make two blobs with 3 features and 1000 samples
N=1000
X,y = make_blobs(n_samples=N, centers=5, n_features=2, random_state=25)
plt.figure(figsize=(10,10))
plt.scatter(X[:, 0], X[:, 1], s=100, c=y)
```
Start with kernel density estimation, including a grid search to find the best bandwidth
```
bwrange = np.linspace(____,____,____) # Test 30 bandwidths from 0.1 to 1.0 ####
K = ____ # 5-fold cross validation ####
grid = GridSearchCV(KernelDensity(), {'bandwidth': ____}, cv=K) ####
grid.fit(X) #Fit the histogram data that we started the lecture with.
h_opt = ____.best_params_['bandwidth'] ####
print(h_opt)
kde = KernelDensity(kernel='gaussian', bandwidth=h_opt)
kde.fit(X) #fit the model to the data
u = v = np.linspace(-15,15,100)
Xgrid = np.vstack(map(np.ravel, np.meshgrid(u, v))).T
dens = np.exp(kde.score_samples(Xgrid)) #evaluate the model on the grid
plt.scatter(____[:,0],____[:,1], c=dens, cmap="Purples", edgecolor="None") ####
plt.colorbar()
```
---
Now try a nearest neighbors approach to estimating the density.
#### What value of $k$ do you need to make the plot look similar to the one above?
```
# Compute density with Bayesian nearest neighbors
k=____ ####
nbrs = KNeighborsDensity('bayesian',n_neighbors=____) ####
nbrs.____(X) ####
dens_nbrs = nbrs.eval(Xgrid) / N
plt.scatter(Xgrid[:,0],Xgrid[:,1], c=dens_nbrs, cmap="Purples", edgecolor="None")
plt.colorbar()
```
---
Now do a Gaussian mixture model. Do a grid search for between 1 and 10 components.
```
#Kludge to fix the bug with draw_ellipse in astroML v1.0
from matplotlib.patches import Ellipse
def draw_ellipse(mu, C, scales=[1, 2, 3], ax=None, **kwargs):
if ax is None:
ax = plt.gca()
# find principal components and rotation angle of ellipse
sigma_x2 = C[0, 0]
sigma_y2 = C[1, 1]
sigma_xy = C[0, 1]
alpha = 0.5 * np.arctan2(2 * sigma_xy,
(sigma_x2 - sigma_y2))
tmp1 = 0.5 * (sigma_x2 + sigma_y2)
tmp2 = np.sqrt(0.25 * (sigma_x2 - sigma_y2) ** 2 + sigma_xy ** 2)
sigma1 = np.sqrt(tmp1 + tmp2)
sigma2 = np.sqrt(tmp1 - tmp2)
for scale in scales:
ax.add_patch(Ellipse((mu[0], mu[1]),
2 * scale * sigma1, 2 * scale * sigma2,
alpha * 180. / np.pi,
**kwargs))
ncomps = np.arange(____,____,____) # Test 10 bandwidths from 1 to 10 ####
K = 5 # 5-fold cross validation
grid = ____(GaussianMixture(), {'n_components': ncomps}, cv=____) ####
grid.fit(X) #Fit the histogram data that we started the lecture with.
ncomp_opt = grid.____['n_components'] ####
print(ncomp_opt)
gmm = ____(n_components=ncomp_opt) ####
gmm.fit(X)
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111)
ax.scatter(X[:,0],X[:,1])
ax.scatter(gmm.means_[:,0], gmm.means_[:,1], marker='s', c='red', s=80)
for mu, C, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
draw_ellipse(mu, 1*C, scales=[2], ax=ax, fc='none', ec='k') #2 sigma ellipses for each component
```
#### Do you get the same answer (the same number of components) each time you run it?
---
Now try Kmeans. Here we will scale the data.
```
kmeans = KMeans(n_clusters=5)
scaler = StandardScaler()
X_scaled = ____.____(X) ####
kmeans.fit(X_scaled)
centers=kmeans.____ #location of the clusters ####
labels=kmeans.predict(____) #labels for each of the points ####
centers_unscaled = scaler.____(centers) ####
fig,ax = plt.subplots(1,2,figsize=(16, 8))
ax[0].scatter(X[:,0],X[:,1],c=labels)
ax[0].scatter(centers_unscaled[:,0], centers_unscaled[:,1], marker='s', c='red', s=80)
ax[0].set_title("Predictions")
ax[1].scatter(X[:, 0], X[:, 1], c=y)
ax[1].set_title("Truth")
```
Let's evaluate how well we did in two other ways: a matrix and a score.
```
df = pd.DataFrame({'predictions': labels, 'truth': y})
ct = pd.crosstab(df['predictions'], df['truth'])
print(ct)
from sklearn.metrics.cluster import homogeneity_score
score = homogeneity_score(df['truth'], df['predictions'])
print(score)
```
#### What is the score for 3 clusters?
---
Finally, let's use DBSCAN. Note that outliers are flagged as `labels_=-1`, so there is one more class that you might think.
Full credit if you can get a score of 0.6 or above. Extra credit (0.1 of 5 points) for a score of 0.85 or above.
```
def plot_dbscan(dbscan, X, size, show_xlabels=True, show_ylabels=True):
core_mask = np.zeros_like(dbscan.labels_, dtype=bool)
core_mask[dbscan.core_sample_indices_] = True
anomalies_mask = dbscan.labels_ == -1
non_core_mask = ~(core_mask | anomalies_mask)
cores = dbscan.components_
anomalies = X[anomalies_mask]
non_cores = X[non_core_mask]
plt.scatter(cores[:, 0], cores[:, 1],
c=dbscan.labels_[core_mask], marker='o', s=size, cmap="Paired")
plt.scatter(cores[:, 0], cores[:, 1], marker='*', s=20, c=dbscan.labels_[core_mask])
plt.scatter(anomalies[:, 0], anomalies[:, 1],
c="r", marker="x", s=100)
plt.scatter(non_cores[:, 0], non_cores[:, 1], c=dbscan.labels_[non_core_mask], marker=".")
if show_xlabels:
plt.xlabel("$x_1$", fontsize=14)
else:
plt.tick_params(labelbottom=False)
if show_ylabels:
plt.ylabel("$x_2$", fontsize=14, rotation=0)
else:
plt.tick_params(labelleft=False)
plt.title("eps={:.2f}, min_samples={}".format(dbscan.eps, dbscan.min_samples), fontsize=14)
dbscan = DBSCAN(eps=0.15, min_samples=7)
dbscan.fit(X_scaled)
plt.figure(figsize=(10, 10))
plot_dbscan(dbscan, X_scaled, size=100)
n_clusters=np.unique(dbscan.labels_)
print(len(n_clusters)) #Number of clusters found (+1)
df2 = pd.DataFrame({'predictions': dbscan.labels_, 'truth': y})
ct2 = pd.crosstab(df2['predictions'], df2['truth'])
print(ct2)
from sklearn.metrics.cluster import homogeneity_score
score2 = homogeneity_score(df2['truth'], df2['predictions'])
print(score2)
```
#### Why do you think DBSCAN is having a hard time? Think about what the Gaussian Mixture Model result showed.
| github_jupyter |
### Dataset Source:
About this file
Boston House Price dataset
### columns:
* CRIM per capita crime rate by town
* ZN proportion of residential land zoned for lots over 25,000 sq.ft.
* INDUS proportion of non-retail business acres per town
* CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
* NOX nitric oxides concentration (parts per 10 million)
* RM average number of rooms per dwelling
* AGE proportion of owner-occupied units built prior to 1940
* DIS weighted distances to five Boston employment centres
* RAD index of accessibility to radial highways
* TAX full-value property-tax rate per 10,000
* PTRATIO pupil-teacher ratio by town
* B where Bk is the proportion of blacks by town
* LSTAT percentage lower status of the population
* MEDV Median value of owner-occupied homes in 1000$
### Load Modules
```
import numpy as np # linear algebra python library
import pandas as pd # data structure for tabular data.
import matplotlib.pyplot as plt # visualization library
%matplotlib inline
```
<br>
Loading data
```
filename = "housing.csv"
boston_data = pd.read_csv(filename, delim_whitespace=True, header=None)
header = ["CRIM","ZN","INDUS","CHAS","NOX","RM",
"AGE","DIS","RAD","TAX","PTRATIO","B","LSTAT","MEDV"]
boston_data.columns = header
# display the first 10 rows of dataframe.
boston_data.head(10)
```
<br>
Inspecting variable types
```
boston_data.dtypes
```
<p class="alert alert-warning">In many datasets, integer variables are cast as float. So, after inspecting
the data type of the variable, even if you get float as output, go ahead
and check the unique values to make sure that those variables are discrete
and not continuous.</p>
### Inspecting all variables
<br>
inspecting distinct values of `RAD`(index of accessibility to radial highways).
```
boston_data['RAD'].unique()
```
<br>
inspecting distinct values of `CHAS` Charles River dummy variable (= 1 if tract bounds river; 0 otherwise).
```
boston_data['CHAS'].unique()
```
<br>
#### inspecting the first 20 distinct values of all continous variables as following:
* CRIM per capita crime rate by town
* ZN proportion of residential land zoned for lots over 25,000 sq.ft.
* INDUS proportion of non-retail business acres per town
* NOX nitric oxides concentration (parts per 10 million)
* RM average number of rooms per dwelling
* AGE proportion of owner-occupied units built prior to 1940
* DIS weighted distances to five Boston employment centres
* TAX full-value property-tax rate per 10,000
* PTRATIO pupil-teacher ratio by town
* B where Bk is the proportion of blacks by town
* LSTAT percentage lower status of the population
* MEDV Median value of owner-occupied homes in 1000$
<br>
CRIM per capita crime rate by town.
```
boston_data['CRIM'].unique()[0:20]
```
<br>
ZN proportion of residential land zoned for lots over 25,000 sq.ft.
```
boston_data['ZN'].unique()[0:20]
```
<br>
INDUS proportion of non-retail business acres per town
```
boston_data['INDUS'].unique()[0:20]
```
<br>
NOX nitric oxides concentration (parts per 10 million)
```
boston_data['NOX'].unique()[0:20]
```
<br>
RM average number of rooms per dwelling
```
boston_data['RM'].unique()[0:20]
```
<br>
AGE proportion of owner-occupied units built prior to 1940
```
boston_data['AGE'].unique()[0:20]
```
<br>
DIS weighted distances to five Boston employment centres
```
boston_data['DIS'].unique()[0:20]
```
<br>
TAX full-value property-tax rate per 10,000
```
boston_data['TAX'].unique()[0:20]
```
<br>
PTRATIO pupil-teacher ratio by town
```
boston_data['PTRATIO'].unique()
```
<br>
B where Bk is the proportion of blacks by town
```
boston_data['B'].unique()[0:20]
```
<br>
LSTAT percentage lower status of the population
```
boston_data['LSTAT'].unique()[0:20]
```
<br>
MEDV Median value of owner-occupied homes in 1000$
```
boston_data['MEDV'].unique()[0:20]
```
<p class="alert alert-info" role="alert">after we checked the dat type of each variable. we have 2 discrete numerical variable and 10 floating or continuous variales.</p>
#### To understand wheather a variable is contious or discrete. we can also make a histogram for each:
* CRIM per capita crime rate by town
* ZN proportion of residential land zoned for lots over 25,000 sq.ft.
* INDUS proportion of non-retail business acres per town
* CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
* NOX nitric oxides concentration (parts per 10 million)
* RM average number of rooms per dwelling
* AGE proportion of owner-occupied units built prior to 1940
* DIS weighted distances to five Boston employment centres
* RAD index of accessibility to radial highways
* TAX full-value property-tax rate per 10,000
* PTRATIO pupil-teacher ratio by town
* B where Bk is the proportion of blacks by town
* LSTAT percentage lower status of the population
* MEDV Median value of owner-occupied homes in 1000$
<br>
making histogram for crime rate by town `CRIM` vatiable by dividing the variable range into intervals.
```
n_data = len(boston_data['CRIM'])
bins = int(np.sqrt(n_data))
boston_data['CRIM'].hist(bins=bins)
```
<br>
making histogram for proportion of residential land zoned for lots over 25,000 sq.ft `ZN`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['ZN'])
bins = int(np.sqrt(n_data))
boston_data['ZN'].hist(bins=bins)
```
<br>
making histogram for proportion of non-retail business acres per town `INDUS`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['INDUS'])
bins = int(np.sqrt(n_data))
boston_data['INDUS'].hist(bins=bins)
```
<br>
making histogram for nitric oxides concentration (parts per 10 million) `NOX`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['NOX'])
bins = int(np.sqrt(n_data))
boston_data['NOX'].hist(bins=bins)
```
<br>
making histogram for average number of rooms per dwelling `RM`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['RM'])
bins = int(np.sqrt(n_data))
boston_data['RM'].hist(bins=bins)
```
<br>
making histogram for proportion of owner-occupied units built prior to 1940 `AGE`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['AGE'])
bins = int(np.sqrt(n_data))
boston_data['AGE'].hist(bins=bins)
```
<br>
making histogram for weighted distances to five Boston employment centres `DIS`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['DIS'])
bins = int(np.sqrt(n_data))
boston_data['DIS'].hist(bins=bins)
```
<br>
making histogram for full-value property-tax rate per 10,000 `TAX`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['TAX'])
bins = int(np.sqrt(n_data))
boston_data['TAX'].hist(bins=bins)
```
<br>
making histogram for pupil-teacher ratio by town `PTRATIO`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['PTRATIO'])
bins = int(np.sqrt(n_data))
boston_data['PTRATIO'].hist(bins=bins)
```
<br>
making histogram where Bk is the proportion of blacks by town `B`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['B'])
bins = int(np.sqrt(n_data))
boston_data['B'].hist(bins=bins)
```
<br>
making histogram for percentage lower status of the population `LSTAT `, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['LSTAT'])
bins = int(np.sqrt(n_data))
boston_data['LSTAT'].hist(bins=bins)
```
<br>
making histogram for Median value of owner-occupied homes in 1000$ ` MEDV`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['MEDV'])
bins = int(np.sqrt(n_data))
boston_data['MEDV'].hist(bins=bins)
```
<br>
<br>
making histogram for index of accessibility to radial highways`RAD`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['RAD'])
bins = int(np.sqrt(n_data))
boston_data['RAD'].hist(bins=bins)
```
<br>
<p class="alert alert-success">by taking a look to histogram of features we noticing that the continuous variables values range is not discrete.</p>
making histogram for Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) ` CHAS`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['CHAS'])
bins = int(np.sqrt(n_data))
boston_data['CHAS'].hist(bins=bins)
```
<p class="alert alert-info">
we noticing here the values of this variable is discrete.
</p>
#### Quantifying Missing Data
calculating the missing values in the dataset.
```
boston_data.isnull().sum()
```
<p class="alert alert-info">There is no Missing Values</p>
<br>
#### Determining the cardinality in cateogrical varaibles
<br>
find unique values in each categorical variable
```
boston_data.nunique()
```
<p class="alert alert-info">The <b>nunique()</b> method ignores missing values by default. If we want to
consider missing values as an additional category, we should set the
dropna argument to <i>False</i>: <b>data.nunique(dropna=False).</b><p>
<br>
let's print out the unique category in Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) ` CHAS`
```
boston_data['CHAS'].unique()
```
<p class="alert alert-info">pandas <b>nunique()</b> can be used in the entire dataframe. pandas
<b>unique()</b>, on the other hand, works only on a pandas Series. Thus, we
need to specify the column name that we want to return the unique values
for.</p>
<br>
```
boston_data[['CHAS','RAD']].nunique().plot.bar(figsize=(12,6))
plt.xlabel("Variables")
plt.ylabel("Number Of Unique Values")
plt.title("Cardinality")
plt.show()
```
| github_jupyter |
# 第5章 計算機を作る
## 5.1.2 スタックマシン
```
def calc(expression: str):
# 空白で分割して字句にする
tokens = expression.split()
stack = []
for token in tokens:
if token.isdigit():
# 数値はスタックに push する
stack.append(int(token))
continue
# 数値でないなら,演算子として処理する
x = stack.pop()
y = stack.pop()
if token == '+':
stack.append(x+y)
elif token == '*':
stack.append(x*y)
return stack.pop()
calc('1 2 + 2 3 + *')
# !pip install pegtree
import pegtree as pg
from pegtree.colab import peg, pegtree, example
```
構文木を表示するためには、graphviz があらかじめインストールされている必要がある。
```
%%peg
Expr = Prod ("+" Prod)*
Prod = Value ("*" Value)*
Value = { [0-9]+ #Int } _
example Expr 1+2+3
%%peg
Expr = { Prod ("+" Prod)* #Add }
Prod = { Value ("*" Value)* #Mul }
Value = { [0-9]+ #Int } _
example Expr 1+2+3
%%peg
Expr = Prod {^ "+" Prod #Add }*
Prod = Value {^ "*" Value #Mul }*
Value = { [0-9]+ #Int } _
example Expr 1+2+3
%%peg
Expr = Prod {^ "+" Prod #Add }*
Prod = Value {^ "*" Value #Mul }*
Value = "(" Expr ")" / Int
Int = { [0-9]+ #Int} _
example Expr 1+(2+3)
```
## PegTree によるパーザ生成
```
%%peg calc.pegtree
Start = Expr EOF // 未消費文字を構文エラーに
Expr = Prod ({^ "+" Prod #Add } / {^ "-" Prod #Sub } )*
Prod = Value ({^ "*" Value #Mul } / {^ "/" Value #Div } )*
Value = { [0-9]+ #Int} _ / "(" Expr ")"
example Expr 1+2*3
example Expr (1+2)*3
example Expr 1*2+3
```
## PegTree 文法のロード
```
peg = pg.grammar('calc.pegtree')
GRAMMAR = '''
Start = Expr EOF
Expr = Prod ({^ "+" Prod #Add } / {^ "-" Prod #Sub } )*
Prod = Value ({^ "*" Value #Mul } / {^ "/" Value #Div } )*
Value = { [0-9]+ #Int} _ / "(" Expr ")"
'''
peg = pg.grammar(GRAMMAR)
peg['Expr']
```
## 5.3.2 パーザの生成
```
parser = pg.generate(peg)
tree = parser('1+2')
print(repr(tree))
tree = parser('3@14')
print(repr(tree))
```
## 構文木とVisitor パターン
```
peg = pg.grammar('calc.pegtree')
parser = pg.generate(peg)
tree = parser('1+2*3')
tree.getTag()
len(tree)
left = tree[0]
left.getTag()
left = tree[0]
str(left)
def calc(tree):
tag = tree.getTag()
if tag == 'Add':
t0 = tree[0]
t1 = tree[1]
return calc(t0) + calc(t1)
if tag == 'Mul':
t0 = tree[0]
t1 = tree[1]
return calc(t0) * calc(t1)
if tag == 'Int':
token = tree.getToken()
return int(token)
print(f'TODO: {tag}') # 未実装のタグの報告
return 0
tree = parser('1+2*3')
print(calc(tree))
```
## Visitor パターン
```
class Visitor(object):
def visit(self, tree):
tag = tree.getTag()
name = f'accept{tag}'
if hasattr(self, name): # accept メソッドがあるか調べる
# メソッド名からメソッドを得る
acceptMethod = getattr(self, name)
return acceptMethod(tree)
print(f'TODO: accept{tag} method')
return None
class Calc(Visitor): # Visitor の継承
def __init__(self, parser):
self.parser = parser
def eval(self, source):
tree = self.parser(source)
return self.visit(tree)
def acceptInt(self, tree):
token = tree.getToken()
return int(token)
def acceptAdd(self, tree):
t0 = tree.get(0)
t1 = tree.get(1)
v0 = self.visit(t0)
v1 = self.visit(t1)
return v0 + v1
def acceptMul(self, tree):
t0 = tree.get(0)
t1 = tree.get(1)
v0 = self.visit(t0)
v1 = self.visit(t1)
return v0 * v1
def accepterr(self, tree):
print(repr(tree))
raise SyntaxError()
calc = Calc(parser)
print(calc.eval("1+2*3"))
print(calc.eval("(1+2)*3"))
print(calc.eval("1*2+3"))
calc.eval('1@2')
```
| github_jupyter |
# Week 3 - Ungraded Lab: Data Labeling
Welcome to the ungraded lab for week 3 of Machine Learning Engineering for Production. In this lab, you will see how the data labeling process affects the performance of a classification model. Labeling data is usually a very labor intensive and costly task but it is of great importance.
As you saw in the lectures there are many ways to label data, this is dependant on the strategy used. Recall the example with the iguanas, all of the following are valid labeling alternatives but they clearly follow different criteria.
<table><tr><td><img src='assets/iguanas1.png'></td><td><img src='assets/iguanas2.png'></td><td><img src='assets/iguanas3.png'></td></tr></table>
**You can think of every labeling strategy as a result of different labelers following different labeling rules**. If your data is labeled by people using different criteria this will have a negative impact on your learning algorithm. It is desired to have consistent labeling across your dataset.
This lab will touch on the effect of labeling strategies from a slighlty different angle. You will explore how different strategies affect the performance of a machine learning model by simulating the process of having different labelers label the data. This, by defining a set of rules and performing automatic labeling based on those rules.
**The main objective of this ungraded lab is to compare performance across labeling options to understand the role that good labeling plays on the performance of Machine Learning models**, these options are:
1. Randomly generated labels (performance lower bound)
2. Automatic generated labels based on three different label strategies
3. True labels (performance upper bound)
Although the example with the iguanas is a computer vision task, the same concepts regarding labeling can be applied to other types of data. In this lab you will be working with text data, concretely you will be using a dataset containing comments from the 2015 top 5 most popular Youtube videos. Each comment has been labeled as `spam` or `not_spam` depending on its contents.
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
## Loading the dataset
The dataset consists of 5 CSV files, one for each video. Pandas `DataFrame` are very powerful to handle data in CSV format. The following helper function will load the data using pandas:
```
def load_labeled_spam_dataset():
"""Load labeled spam dataset."""
# Path where csv files are located
base_path = "./data/"
# List of csv files with full path
csv_files = [os.path.join(base_path, csv) for csv in os.listdir(base_path)]
# List of dataframes for each file
dfs = [pd.read_csv(filename) for filename in csv_files]
# Concatenate dataframes into a single one
df = pd.concat(dfs)
# Rename columns
df = df.rename(columns={"CONTENT": "text", "CLASS": "label"})
# Set a seed for the order of rows
df = df.sample(frac=1, random_state=824)
return df.reset_index()
# Save the dataframe into the df_labeled variable
df_labeled = load_labeled_spam_dataset()
```
To have a feeling of how the data is organized, let's inspect the top 5 rows of the data:
```
# Take a look at the first 5 rows
df_labeled.head()
```
## Further inspection and preprocessing
### Checking for data imbalance
It is fairly common to assume that the data you are working on is balanced. This means that the dataset contains a similar proportion of examples for all classes. Before moving forward let's actually test this assumption:
```
# Print actual value count
print(f"Value counts for each class:\n\n{df_labeled.label.value_counts()}\n")
# Display pie chart to visually check the proportion
df_labeled.label.value_counts().plot.pie(y='label', title='Proportion of each class')
plt.show()
```
There is roughly the same number of data points for each class so class imbalance is not an issue for this particular dataset.
### Cleaning the dataset
If you scroll back to the cell where you inspected the data, you will realize that the dataframe includes information that is not relevant for the task at hand. At the moment, you are only interested in the comments and the corresponding labels (the video that each comment belongs to will be used later). Let's drop the remaining columns.
```
# Drop unused columns
df_labeled = df_labeled.drop(['index', 'COMMENT_ID', 'AUTHOR', 'DATE'], axis=1)
# Look at the cleaned dataset
df_labeled.head()
```
Now the dataset only includes the information you are going to use moving forward.
### Splitting the dataset
Before jumping to the data labeling section let's split the data into training and test sets so you can use the latter to measure the performance of models that were trained using data labeled through different methods. As a safety measure when doing this split, remember to use stratification so the proportion of classes is maintained within each split.
```
from sklearn.model_selection import train_test_split
# Save the text into the X variable
X = df_labeled.drop("label", axis=1)
# Save the true labels into the y variable
y = df_labeled["label"]
# Use 1/5 of the data for testing later
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)
# Print number of comments for each set
print(f"There are {X_train.shape[0]} comments for training.")
print(f"There are {X_test.shape[0]} comments for testing")
```
Let's do a visual to check that the stratification actually worked:
```
plt.subplot(1, 3, 1)
y_train.value_counts().plot.pie(y='label', title='Proportion of each class for train set', figsize=(10, 6))
plt.subplot(1, 3, 3)
y_test.value_counts().plot.pie(y='label', title='Proportion of each class for test set', figsize=(10, 6))
plt.tight_layout()
plt.show()
```
Both, the training and test sets a balanced proportion of examples per class. So, the code successfully implemented stratification.
Let's get going!
## Data Labeling
### Establishing performance lower and upper bounds for reference
To properly compare different labeling strategies you need to establish a baseline for model accuracy, in this case you will establish both a lower and an upper bound to compare against.
### Calculate accuracy of a labeling strategy
[CountVectorizer](https://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html#sklearn.feature_extraction.text.CountVectorizer) is a handy tool included in the sklearn ecosystem to encode text based data.
For more information on how to work with text data using sklearn check out this [resource](https://scikit-learn.org/stable/tutorial/text_analytics/working_with_text_data.html).
```
from sklearn.feature_extraction.text import CountVectorizer
# Allow unigrams and bigrams
vectorizer = CountVectorizer(ngram_range=(1, 5))
```
Now that the text encoding is defined, you need to select a model to make predictions. For simplicity you will use a [Multinomial Naive Bayes](https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.MultinomialNB.html) classifier. This model is well suited for text classification and is fairly quick to train.
Let's define a function which will handle the model fitting and print out the accuracy on the test data:
```
from sklearn.metrics import accuracy_score
from sklearn.naive_bayes import MultinomialNB
def calculate_accuracy(X_tr, y_tr, X_te=X_test, y_te=y_test,
clf=MultinomialNB(), vectorizer=vectorizer):
# Encode train text
X_train_vect = vectorizer.fit_transform(X_tr.text.tolist())
# Fit model
clf.fit(X=X_train_vect, y=y_tr)
# Vectorize test text
X_test_vect = vectorizer.transform(X_te.text.tolist())
# Make predictions for the test set
preds = clf.predict(X_test_vect)
# Return accuracy score
return accuracy_score(preds, y_te)
```
Now let's create a dictionary to store the accuracy of each labeling method:
```
# Empty dictionary
accs = dict()
```
### Random Labeling
Generating random labels is a natural way to establish a lower bound. You will expect that any successful alternative labeling model to outperform randomly generated labels.
Now let's calculate the accuracy for the random labeling method
```
# Calculate random labels
rnd_labels = np.random.randint(0, 2, X_train.shape[0])
# Feed them alongside X_train to calculate_accuracy function
rnd_acc = calculate_accuracy(X_train, rnd_labels)
rnd_acc
```
You will see a different accuracy everytime you run the previous cell. This is due to the fact that the labeling is done randomly. Remember, this is a binary classification problem and both classes are balanced, so you can expect to see accuracies that revolve around 50%.
To further gain intuition let's look at the average accuracy over 10 runs:
```
# Empty list to save accuracies
rnd_accs = []
for _ in range(10):
# Add every accuracy to the list
rnd_accs.append(calculate_accuracy(X_train, np.random.randint(0, 2, X_train.shape[0])))
# Save result in accs dictionary
accs['random-labels'] = sum(rnd_accs)/len(rnd_accs)
# Print result
print(f"The random labelling method achieved and accuracy of {accs['random-labels']*100:.2f}%")
```
Random labelling is completely disregarding the information from the solution space you are working on, and is just guessing the correct label. You can't probably do worse than this (or maybe you can). For this reason, this method serves as reference for comparing other labeling methods
### Labeling with true values
Now let's look at the other end of the spectrum, this is using the correct labels for your data points. Let's retrain the Multinomial Naive Bayes classifier with the actual labels
```
# Calculate accuracy when using the true labels
true_acc = calculate_accuracy(X_train, y_train)
# Save the result
accs['true-labels'] = true_acc
print(f"The true labelling method achieved and accuracy of {accs['true-labels']*100:.2f}%")
```
Training with the true labels produced a noticeable boost in accuracy. This is expected as the classifier is now able to properly identify patterns in the training data which were lacking with randomly generated labels.
Achieving higher accuracy is possible by either fine-tunning the model or even selecting a different one. For the time being you will keep the model as it is and use this accuracy as what we should strive for with the automatic labeling algorithms you will see next.
## Automatic labeling - Trying out different labeling strategies
Let's suppose that for some reason you don't have access to the true labels associated with each data point in this dataset. It is a natural idea to think that there are patterns in the data that will provide clues of which are the correct labels. This is of course very dependant on the kind of data you are working with and to even hypothesize which patterns exist requires great domain knowledge.
The dataset used in this lab was used for this reason. It is reasonable for many people to come up with rules that might help identify a spam comment from a non-spam one for a Youtube video. In the following section you will be performing automatic labeling using such rules. **You can think of each iteration of this process as a labeler with different criteria for labeling** and your job is to hire the most promising one.
Notice the word **rules**. In order to perform automatic labeling you will define some rules such as "if the comment contains the word 'free' classify it as spam".
First things first. Let's define how we are going to encode the labeling:
- `SPAM` is represented by 1
- `NOT_SPAM` by 0
- `NO_LABEL` as -1
You might be wondering about the `NO_LABEL` keyword. Depending on the rules you come up with, these might not be applicable to some data points. For such cases it is better to refuse from giving a label rather than guessing, which you already saw yields poor results.
### First iteration - Define some rules
For this first iteration you will create three rules based on the intuition of common patterns that appear on spam comments. The rules are simple, classify as SPAM if any of the following patterns is present within the comment or NO_LABEL otherwise:
- `free` - spam comments usually lure users by promoting free stuff
- `subs` - spam comments tend to ask users to subscribe to some website or channel
- `http` - spam comments include links very frequently
```
def labeling_rules_1(x):
# Convert text to lowercase
x = x.lower()
# Define list of rules
rules = [
"free" in x,
"subs" in x,
"http" in x
]
# If the comment falls under any of the rules classify as SPAM
if any(rules):
return 1
# Otherwise, NO_LABEL
return -1
# Apply the rules the comments in the train set
labels = [labeling_rules_1(label) for label in X_train.text]
# Convert to a numpy array
labels = np.asarray(labels)
# Take a look at the automatic labels
labels
```
For lots of points the automatic labeling algorithm decided to not settle for a label, this is expected given the nature of the rules that were defined. These points should be deleted since they don't provide information about the classification process and tend to hurt performance.
```
# Create the automatic labeled version of X_train by removing points with NO_LABEL label
X_train_al = X_train[labels != -1]
# Remove predictions with NO_LABEL label
labels_al = labels[labels != -1]
print(f"Predictions with concrete label have shape: {labels_al.shape}")
print(f"Proportion of data points kept: {labels_al.shape[0]/labels.shape[0]*100:.2f}%")
```
Notice that only 379 data points remained out of the original 1564. The rules defined didn't provide enough context for the labeling algorithm to settle on a label, so around 75% of the data has been trimmed.
Let's test the accuracy of the model when using these automatic generated labels:
```
# Compute accuracy when using these labels
iter_1_acc = calculate_accuracy(X_train_al, labels_al)
# Display accuracy
print(f"First iteration of automatic labeling has an accuracy of {iter_1_acc*100:.2f}%")
# Save the result
accs['first-iteration'] = iter_1_acc
```
Let's compare this accuracy to the baselines by plotting:
```
def plot_accuracies(accs=accs):
colors = list("rgbcmy")
items_num = len(accs)
cont = 1
for x, y in accs.items():
if x in ['true-labels', 'random-labels', 'true-labels-best-clf']:
plt.hlines(y, 0, (items_num-2)*2, colors=colors.pop())
else:
plt.scatter(cont, y, s=100)
cont+=2
plt.legend(accs.keys(), loc="center left",bbox_to_anchor=(1, 0.5))
plt.show()
plot_accuracies()
```
This first iteration had an accuracy very close to the random labeling, we should strive to do better than this.
Before moving forward let's define the `label_given_rules` function that performs all of the steps you just saw, these are:
- Apply the rules to a dataframe of comments
- Cast the resulting labels to a numpy array
- Delete all data points with NO_LABEL as label
- Calculate the accuracy of the model using the automatic labels
- Save the accuracy for plotting
- Print some useful metrics of the process
```
def label_given_rules(df, rules_function, name,
accs_dict=accs, verbose=True):
# Apply labeling rules to the comments
labels = [rules_function(label) for label in df.text]
# Convert to a numpy array
labels = np.asarray(labels)
# Save initial number of data points
initial_size = labels.shape[0]
# Trim points with NO_LABEL label
X_train_al = df[labels != -1]
labels = labels[labels != -1]
# Save number of data points after trimming
final_size = labels.shape[0]
# Compute accuracy
acc = calculate_accuracy(X_train_al, labels)
# Print useful information
if verbose:
print(f"Proportion of data points kept: {final_size/initial_size*100:.2f}%\n")
print(f"{name} labeling has an accuracy of {acc*100:.2f}%\n")
# Save accuracy to accuracies dictionary
accs_dict[name] = acc
return X_train_al, labels, acc
```
Going forward we should come up with rules that have a better coverage of the training data, thus making pattern discovery an easier task. Also notice how the rules were only able to label as either SPAM or NO_LABEL, we should also create some rules that help the identification of NOT_SPAM comments.
### Second iteration - Coming up with better rules
If you inspect the comments in the dataset you might be able to distinguish certain patterns at a glimpse. For example, not spam comments often make references to either the number of views since these were the most watched videos of 2015 or the song in the video and its contents . As for spam comments other common patterns are to promote gifts or ask to follow some channel or website.
Let's create some new rules that include these patterns:
```
def labeling_rules_2(x):
# Convert text to lowercase
x = x.lower()
# Define list of rules to classify as NOT_SPAM
not_spam_rules = [
"view" in x,
"song" in x
]
# Define list of rules to classify as SPAM
spam_rules = [
"free" in x,
"subs" in x,
"gift" in x,
"follow" in x,
"http" in x
]
# Classify depending on the rules
if any(not_spam_rules):
return 0
if any(spam_rules):
return 1
return -1
```
This new set of rules looks more promising as it includes more patterns to classify as SPAM as well as some patterns to classify as NOT_SPAM. This should result in more data points with a label different to NO_LABEL.
Let's check if this is the case.
```
label_given_rules(X_train, labeling_rules_2, "second-iteration")
plot_accuracies()
```
This time 44% of the original dataset was given a decisive label and there were data points for both labels, this helped the model reach a higher accuracy when compared to the first iteration. Now the accuracy is considerably higher than the random labeling but it is still very far away from the upper bound.
Let's see if we can make it even better!
### Third Iteration - Even more rules
The rules we have defined so far are doing a fair job. Let's add two additional rules, one for classifying SPAM comments and the other for the opposite task.
At a glimpse it looks like NOT_SPAM comments are usually shorter. This may be due to them not including hyperlinks but also in general they tend to be more concrete such as "I love this song!".
Let's take a look at the average number of characters for SPAM comments vs NOT_SPAM oned:
```
from statistics import mean
print(f"NOT_SPAM comments have an average of {mean([len(t) for t in df_labeled[df_labeled.label==0].text]):.2f} characters.")
print(f"SPAM comments have an average of {mean([len(t) for t in df_labeled[df_labeled.label==1].text]):.2f} characters.")
```
It sure looks like there is a big difference in the number of characters for both types of comments.
To decide on a threshold to classify as NOT_SPAM let's plot a histogram of the number of characters for NOT_SPAM comments:
```
plt.hist([len(t) for t in df_labeled[df_labeled.label==0].text], range=(0,100))
plt.show()
```
The majority of NOT_SPAM comments have 30 or less characters so we'll use that as a threshold.
Another prevalent pattern in spam comments is to ask users to "check out" a channel, website or link.
Let's add these two new rules:
```
def labeling_rules_3(x):
# Convert text to lowercase
x = x.lower()
# Define list of rules to classify as NOT_SPAM
not_spam_rules = [
"view" in x,
"song" in x,
len(x) < 30
]
# Define list of rules to classify as SPAM
spam_rules = [
"free" in x,
"subs" in x,
"gift" in x,
"follow" in x,
"http" in x,
"check out" in x
]
# Classify depending on the rules
if any(not_spam_rules):
return 0
if any(spam_rules):
return 1
return -1
label_given_rules(X_train, labeling_rules_3, "third-iteration")
plot_accuracies()
```
These new rules do a pretty good job at both, covering the dataset and having a good model accuracy. To be more concrete this labeling strategy reached an accuracy of ~86%! We are getting closer and closer to the upper bound defined by using the true labels.
We could keep going on adding more rules to improve accuracy and we do encourage you to try it out yourself!
### Come up with your own rules
The following cells contain some code to help you inspect the dataset for patterns and to test out these patterns. The ones used before are commented out in case you want start from scratch or re-use them.
```
# Configure pandas to print out all rows to check the complete dataset
pd.set_option('display.max_rows', None)
# Check NOT_SPAM comments
df_labeled[df_labeled.label==0]
# Check SPAM comments
df_labeled[df_labeled.label==1]
def your_labeling_rules(x):
# Convert text to lowercase
x = x.lower()
# Define your rules for classifying as NOT_SPAM
not_spam_rules = [
# "view" in x,
# "song" in x,
# len(x) < 30
]
# Define your rules for classifying as SPAM
spam_rules = [
# "free" in x,
# "subs" in x,
# "gift" in x,
# "follow" in x,
# "http" in x,
# "check out" in x
]
# Classify depending on your rules
if any(not_spam_rules):
return 0
if any(spam_rules):
return 1
return -1
try:
label_given_rules(X_train, your_labeling_rules, "your-iteration")
plot_accuracies()
except ValueError:
print("You have not defined any rules.")
```
**Congratulations on finishing this ungraded lab!**
By now you should have a better understanding of having good labelled data. In general, **the better your labels are, the better your models will be**. Also it is important to realize that the process of correctly labeling data is a very complex one. **Remember, you can think of each one of the iterations of the automatic labeling process to be a different labeler with different criteria for labeling**. If you assume you are hiring labelers you will want to hire the latter for sure!
Another important point to keep in mind is that establishing baselines to compare against is really important as they provide perspective on how well your data and models are performing.
**Keep it up!**
| github_jupyter |
# A Whirlwind Tour of Python
*Jake VanderPlas, Summer 2016*
These are the Jupyter Notebooks behind my O'Reilly report,
[*A Whirlwind Tour of Python*](http://www.oreilly.com/programming/free/a-whirlwind-tour-of-python.csp).
The full notebook listing is available [on Github](https://github.com/jakevdp/WhirlwindTourOfPython).
*A Whirlwind Tour of Python* is a fast-paced introduction to essential
components of the Python language for researchers and developers who are
already familiar with programming in another language.
The material is particularly aimed at those who wish to use Python for data
science and/or scientific programming, and in this capacity serves as an
introduction to my upcoming book, *The Python Data Science Handbook*.
These notebooks are adapted from lectures and workshops I've given on these
topics at University of Washington and at various conferences, meetings, and
workshops around the world.
## Index
1. [Introduction](00-Introduction.ipynb)
2. [How to Run Python Code](01-How-to-Run-Python-Code.ipynb)
3. [Basic Python Syntax](02-Basic-Python-Syntax.ipynb)
4. [Python Semantics: Variables](03-Semantics-Variables.ipynb)
5. [Python Semantics: Operators](04-Semantics-Operators.ipynb)
6. [Built-In Scalar Types](05-Built-in-Scalar-Types.ipynb)
7. [Built-In Data Structures](06-Built-in-Data-Structures.ipynb)
8. [Control Flow Statements](07-Control-Flow-Statements.ipynb)
9. [Defining Functions](08-Defining-Functions.ipynb)
10. [Errors and Exceptions](09-Errors-and-Exceptions.ipynb)
11. [Iterators](10-Iterators.ipynb)
12. [List Comprehensions](11-List-Comprehensions.ipynb)
13. [Generators and Generator Expressions](12-Generators.ipynb)
14. [Modules and Packages](13-Modules-and-Packages.ipynb)
15. [Strings and Regular Expressions](14-Strings-and-Regular-Expressions.ipynb)
16. [Preview of Data Science Tools](15-Preview-of-Data-Science-Tools.ipynb)
17. [Resources for Further Learning](16-Further-Resources.ipynb)
18. [Appendix: Code To Reproduce Figures](17-Figures.ipynb)
## License
This material is released under the "No Rights Reserved" [CC0](LICENSE)
license, and thus you are free to re-use, modify, build-on, and enhance
this material for any purpose.
That said, I request (but do not require) that if you use or adapt this material,
you include a proper attribution and/or citation; for example
> *A Whirlwind Tour of Python* by Jake VanderPlas (O’Reilly). Copyright 2016 O’Reilly Media, Inc., 978-1-491-96465-1
Read more about CC0 [here](https://creativecommons.org/share-your-work/public-domain/cc0/).
| github_jupyter |
```
epochs = 5
```
# Example - Simple Vertically Partitioned Split Neural Network
- <b>Alice</b>
- Has model Segment 1
- Has the handwritten Images
- <b>Bob</b>
- Has model Segment 2
- Has the image Labels
Based on [SplitNN - Tutorial 3](https://github.com/OpenMined/PySyft/blob/master/examples/tutorials/advanced/split_neural_network/Tutorial%203%20-%20Folded%20Split%20Neural%20Network.ipynb) from Adam J Hall - Twitter: [@AJH4LL](https://twitter.com/AJH4LL) · GitHub: [@H4LL](https://github.com/H4LL)
Authors:
- Pavlos Papadopoulos · GitHub: [@pavlos-p](https://github.com/pavlos-p)
- Tom Titcombe · GitHub: [@TTitcombe](https://github.com/TTitcombe)
- Robert Sandmann · GitHub: [@rsandmann](https://github.com/rsandmann)
```
class SplitNN:
def __init__(self, models, optimizers):
self.models = models
self.optimizers = optimizers
self.data = []
self.remote_tensors = []
def forward(self, x):
data = []
remote_tensors = []
data.append(self.models[0](x))
if data[-1].location == self.models[1].location:
remote_tensors.append(data[-1].detach().requires_grad_())
else:
remote_tensors.append(
data[-1].detach().move(self.models[1].location).requires_grad_()
)
i = 1
while i < (len(models) - 1):
data.append(self.models[i](remote_tensors[-1]))
if data[-1].location == self.models[i + 1].location:
remote_tensors.append(data[-1].detach().requires_grad_())
else:
remote_tensors.append(
data[-1].detach().move(self.models[i + 1].location).requires_grad_()
)
i += 1
data.append(self.models[i](remote_tensors[-1]))
self.data = data
self.remote_tensors = remote_tensors
return data[-1]
def backward(self):
for i in range(len(models) - 2, -1, -1):
if self.remote_tensors[i].location == self.data[i].location:
grads = self.remote_tensors[i].grad.copy()
else:
grads = self.remote_tensors[i].grad.copy().move(self.data[i].location)
self.data[i].backward(grads)
def zero_grads(self):
for opt in self.optimizers:
opt.zero_grad()
def step(self):
for opt in self.optimizers:
opt.step()
import sys
sys.path.append('../')
import torch
from torchvision import datasets, transforms
from torch import nn, optim
from torchvision.datasets import MNIST
from torchvision.transforms import ToTensor
import syft as sy
from src.dataloader import VerticalDataLoader
from src.psi.util import Client, Server
from src.utils import add_ids
hook = sy.TorchHook(torch)
# Create dataset
data = add_ids(MNIST)(".", download=True, transform=ToTensor()) # add_ids adds unique IDs to data points
# Batch data
dataloader = VerticalDataLoader(data, batch_size=128) # partition_dataset uses by default "remove_data=True, keep_order=False"
```
## Check if the datasets are unordered
In MNIST, we have 2 datasets (the images and the labels).
```
# We need matplotlib library to plot the dataset
import matplotlib.pyplot as plt
# Plot the first 10 entries of the labels and the dataset
figure = plt.figure()
num_of_entries = 10
for index in range(1, num_of_entries + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(dataloader.dataloader1.dataset.data[index].numpy().squeeze(), cmap='gray_r')
print(dataloader.dataloader2.dataset[index][0], end=" ")
```
## Implement PSI and order the datasets accordingly
```
# Compute private set intersection
client_items = dataloader.dataloader1.dataset.get_ids()
server_items = dataloader.dataloader2.dataset.get_ids()
client = Client(client_items)
server = Server(server_items)
setup, response = server.process_request(client.request, len(client_items))
intersection = client.compute_intersection(setup, response)
# Order data
dataloader.drop_non_intersecting(intersection)
dataloader.sort_by_ids()
```
## Check again if the datasets are ordered
```
# We need matplotlib library to plot the dataset
import matplotlib.pyplot as plt
# Plot the first 10 entries of the labels and the dataset
figure = plt.figure()
num_of_entries = 10
for index in range(1, num_of_entries + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(dataloader.dataloader1.dataset.data[index].numpy().squeeze(), cmap='gray_r')
print(dataloader.dataloader2.dataset[index][0], end=" ")
torch.manual_seed(0)
# Define our model segments
input_size = 784
hidden_sizes = [128, 640]
output_size = 10
models = [
nn.Sequential(
nn.Linear(input_size, hidden_sizes[0]),
nn.ReLU(),
nn.Linear(hidden_sizes[0], hidden_sizes[1]),
nn.ReLU(),
),
nn.Sequential(nn.Linear(hidden_sizes[1], output_size), nn.LogSoftmax(dim=1)),
]
# Create optimisers for each segment and link to them
optimizers = [
optim.SGD(model.parameters(), lr=0.03,)
for model in models
]
# create some workers
alice = sy.VirtualWorker(hook, id="alice")
bob = sy.VirtualWorker(hook, id="bob")
# Send Model Segments to model locations
model_locations = [alice, bob]
for model, location in zip(models, model_locations):
model.send(location)
#Instantiate a SpliNN class with our distributed segments and their respective optimizers
splitNN = SplitNN(models, optimizers)
def train(x, target, splitNN):
#1) Zero our grads
splitNN.zero_grads()
#2) Make a prediction
pred = splitNN.forward(x)
#3) Figure out how much we missed by
criterion = nn.NLLLoss()
loss = criterion(pred, target)
#4) Backprop the loss on the end layer
loss.backward()
#5) Feed Gradients backward through the nework
splitNN.backward()
#6) Change the weights
splitNN.step()
return loss, pred
for i in range(epochs):
running_loss = 0
correct_preds = 0
total_preds = 0
for (data, ids1), (labels, ids2) in dataloader:
# Train a model
data = data.send(models[0].location)
data = data.view(data.shape[0], -1)
labels = labels.send(models[-1].location)
# Call model
loss, preds = train(data, labels, splitNN)
# Collect statistics
running_loss += loss.get()
correct_preds += preds.max(1)[1].eq(labels).sum().get().item()
total_preds += preds.get().size(0)
print(f"Epoch {i} - Training loss: {running_loss/len(dataloader):.3f} - Accuracy: {100*correct_preds/total_preds:.3f}")
print("Labels pointing to: ", labels)
print("Images pointing to: ", data)
```
| github_jupyter |
## 1-3. 複数量子ビットの記述
ここまでは1量子ビットの状態とその操作(演算)の記述について学んできた。この章の締めくくりとして、$n$個の量子ビットがある場合の状態の記述について学んでいこう。テンソル積がたくさん出てきてややこしいが、コードをいじりながら身につけていってほしい。
$n$個の**古典**ビットの状態は$n$個の$0,1$の数字によって表現され、そのパターンの総数は$2^n$個ある。
量子力学では、これらすべてのパターンの重ね合わせ状態が許されているので、$n$個の**量子**ビットの状態$|\psi \rangle$はどのビット列がどのような重みで重ね合わせになっているかという$2^n$個の複素確率振幅で記述される:
$$
\begin{eqnarray}
|\psi \rangle &= &
c_{00...0} |00...0\rangle +
c_{00...1} |00...1\rangle + \cdots +
c_{11...1} |11...1\rangle =
\left(
\begin{array}{c}
c_{00...0}
\\
c_{00...1}
\\
\vdots
\\
c_{11...1}
\end{array}
\right).
\end{eqnarray}
$$
ただし、
複素確率振幅は規格化
$\sum _{i_1,..., i_n} |c_{i_1...i_n}|^2=1$
されているものとする。
そして、この$n$量子ビットの量子状態を測定するとビット列$i_1 ... i_n$が確率
$$
\begin{eqnarray}
p_{i_1 ... i_n} &=&|c_{i_1 ... i_n}|^2
\label{eq02}
\end{eqnarray}
$$
でランダムに得られ、測定後の状態は$|i_1 \dotsc i_n\rangle$となる。
**このように**$n$**量子ビットの状態は、**$n$**に対して指数的に大きい**$2^n$**次元の複素ベクトルで記述する必要があり、ここに古典ビットと量子ビットの違いが顕著に現れる**。
そして、$n$量子ビット系に対する操作は$2^n \times 2^n$次元のユニタリ行列として表される。
言ってしまえば、量子コンピュータとは、量子ビット数に対して指数的なサイズの複素ベクトルを、物理法則に従ってユニタリ変換するコンピュータのことなのである。
※ここで、複数量子ビットの順番と表記の関係について注意しておく。状態をケットで記述する際に、「1番目」の量子ビット、「2番目」の量子ビット、……の状態に対応する0と1を左から順番に並べて表記した。例えば$|011\rangle$と書けば、1番目の量子ビットが0、2番目の量子ビットが1、3番目の量子ビットが1である状態を表す。一方、例えば011を2進数の表記と見た場合、上位ビットが左、下位ビットが右となることに注意しよう。すなわち、一番左の0は最上位ビットであって$2^2$の位に対応し、真ん中の1は$2^1$の位、一番右の1は最下位ビットであって$2^0=1$の位に対応する。つまり、「$i$番目」の量子ビットは、$n$桁の2進数表記の$n-i+1$桁目に対応している。このことは、SymPyなどのパッケージで複数量子ビットを扱う際に気を付ける必要がある(下記「SymPyを用いた演算子のテンソル積」も参照)。
(詳細は Nielsen-Chuang の `1.2.1 Multiple qbits` を参照)
### 例:2量子ビットの場合
2量子ビットの場合は、 00, 01, 10, 11 の4通りの状態の重ね合わせをとりうるので、その状態は一般的に
$$
c_{00} |00\rangle + c_{01} |01\rangle + c_{10}|10\rangle + c_{11} |11\rangle =
\left(
\begin{array}{c}
c_{00}
\\
c_{01}
\\
c_{10}
\\
c_{11}
\end{array}
\right)
$$
とかける。
一方、2量子ビットに対する演算は$4 \times 4$行列で書け、各列と各行はそれぞれ $\langle00|,\langle01|,\langle10|, \langle11|, |00\rangle,|01\rangle,|10\rangle, |01\rangle$ に対応する。
このような2量子ビットに作用する演算としてもっとも重要なのが**制御NOT演算(CNOT演算)**であり、
行列表示では
$$
\begin{eqnarray}
\Lambda(X) =
\left(
\begin{array}{cccc}
1 & 0 & 0& 0
\\
0 & 1 & 0& 0
\\
0 & 0 & 0 & 1
\\
0 & 0 & 1& 0
\end{array}
\right)
\end{eqnarray}
$$
となる。
CNOT演算が2つの量子ビットにどのように作用するか見てみよう。まず、1つ目の量子ビットが$|0\rangle$の場合、$c_{10} = c_{11} = 0$なので、
$$
\Lambda(X)
\left(
\begin{array}{c}
c_{00}\\
c_{01}\\
0\\
0
\end{array}
\right) =
\left(
\begin{array}{c}
c_{00}\\
c_{01}\\
0\\
0
\end{array}
\right)
$$
となり、状態は変化しない。一方、1つ目の量子ビットが$|1\rangle$の場合、$c_{00} = c_{01} = 0$なので、
$$
\Lambda(X)
\left(
\begin{array}{c}
0\\
0\\
c_{10}\\
c_{11}
\end{array}
\right) =
\left(
\begin{array}{c}
0\\
0\\
c_{11}\\
c_{10}
\end{array}
\right)
$$
となり、$|10\rangle$と$|11\rangle$の確率振幅が入れ替わる。すなわち、2つ目の量子ビットが反転している。
つまり、CNOT演算は1つ目の量子ビットをそのままに保ちつつ、
- 1つ目の量子ビットが$|0\rangle$の場合は、2つ目の量子ビットにも何もしない(恒等演算$I$が作用)
- 1つ目の量子ビットが$|1\rangle$の場合は、2つ目の量子ビットを反転させる($X$が作用)
という効果を持つ。
そこで、1つ目の量子ビットを**制御量子ビット**、2つ目の量子ビットを**ターゲット量子ビット**と呼ぶ。
このCNOT演算の作用は、$\oplus$を mod 2の足し算、つまり古典計算における排他的論理和(XOR)とすると、
$$
\begin{eqnarray}
\Lambda(X) |ij \rangle = |i \;\; (i\oplus j)\rangle \:\:\: (i,j=0,1)
\end{eqnarray}
$$
とも書ける。よって、CNOT演算は古典計算でのXORを可逆にしたものとみなせる
(ユニタリー行列は定義$U^\dagger U = U U^\dagger = I$より可逆であることに注意)。
例えば、1つ目の量子ビットを$|0\rangle$と$|1\rangle$の
重ね合わせ状態にし、2つ目の量子ビットを$|0\rangle$として
$$
\begin{eqnarray}
\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle )\otimes |0\rangle =
\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1
\\
0
\\
1
\\
0
\end{array}
\right)
\end{eqnarray}
$$
にCNOTを作用させると、
$$
\begin{eqnarray}
\frac{1}{\sqrt{2}}( |00\rangle + |11\rangle ) =
\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1
\\
0
\\
0
\\
1
\end{array}
\right)
\end{eqnarray}
$$
が得られ、2つ目の量子ビットがそのままである状態$|00\rangle$と反転された状態$|11\rangle$の重ね合わせになる。(記号$\otimes$については次節参照)
さらに、CNOT ゲートを組み合わせることで重要な2量子ビットゲートである**SWAP ゲート**を作ることができる。
$$\Lambda(X)_{i,j}$$
を$i$番目の量子ビットを制御、$j$番目の量子ビットをターゲットとするCNOT ゲートとして、
$$
\begin{align}
\mathrm{SWAP} &= \Lambda(X)_{1,2} \Lambda(X)_{2,1} \Lambda(X)_{1,2}\\
&=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}
\right)
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}
\right)
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}
\right)\\
&=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
\end{align}
$$
のように書ける。これは1 番目の量子ビットと2 番目の量子ビットが交換するゲートであることが分かる。
このことは、上記のmod 2の足し算$\oplus$を使った表記で簡単に確かめることができる。3つのCNOTゲート$\Lambda(X)_{1,2} \Lambda(X)_{2,1} \Lambda(X)_{1,2}$の$|ij\rangle$への作用を1ステップずつ書くと、$i \oplus (i \oplus j) = (i \oplus i) \oplus j = 0 \oplus j = j$であることを使って、
$$
\begin{align}
|ij\rangle &\longrightarrow
|i \;\; (i\oplus j)\rangle\\
&\longrightarrow
|(i\oplus (i\oplus j)) \;\; (i\oplus j)\rangle =
|j \;\; (i\oplus j)\rangle\\
&\longrightarrow
|j \;\; (j\oplus (i\oplus j))\rangle =
|ji\rangle
\end{align}
$$
となり、2つの量子ビットが交換されていることが分かる。
(詳細は Nielsen-Chuang の `1.3.2 Multiple qbit gates` を参照)
### テンソル積の計算
手計算や解析計算で威力を発揮するのは、**テンソル積**($\otimes$)である。
これは、複数の量子ビットがある場合に、それをどのようにして、上で見た大きな一つのベクトルへと変換するのか?という計算のルールを与えてくれる。
量子力学の世界では、2つの量子系があってそれぞれの状態が$|\psi \rangle$と$|\phi \rangle$のとき、
$$
|\psi \rangle \otimes |\phi\rangle
$$
とテンソル積 $\otimes$ を用いて書く。このような複数の量子系からなる系のことを**複合系**と呼ぶ。例えば2量子ビット系は複合系である。
基本的にはテンソル積は、**多項式と同じような計算ルール**で計算してよい。
例えば、
$$
(\alpha |0\rangle + \beta |1\rangle )\otimes (\gamma |0\rangle + \delta |1\rangle )
= \alpha \gamma |0\rangle |0\rangle + \alpha \delta |0\rangle |1\rangle + \beta \gamma |1 \rangle | 0\rangle + \beta \delta |1\rangle |1\rangle
$$
のように計算する。列ベクトル表示すると、$|00\rangle$, $|01\rangle$, $|10\rangle$, $|11\rangle$に対応する4次元ベクトル、
$$
\left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right)
\otimes
\left(
\begin{array}{c}
\gamma
\\
\delta
\end{array}
\right) =
\left(
\begin{array}{c}
\alpha \gamma
\\
\alpha \delta
\\
\beta \gamma
\\
\beta \delta
\end{array}
\right)
$$
を得る計算になっている。
### SymPyを用いたテンソル積の計算
```
from IPython.display import Image, display_png
from sympy import *
from sympy.physics.quantum import *
from sympy.physics.quantum.qubit import Qubit,QubitBra
from sympy.physics.quantum.gate import X,Y,Z,H,S,T,CNOT,SWAP, CPHASE
init_printing() # ベクトルや行列を綺麗に表示するため
# Google Colaboratory上でのみ実行してください
from IPython.display import HTML
def setup_mathjax():
display(HTML('''
<script>
if (!window.MathJax && window.google && window.google.colab) {
window.MathJax = {
'tex2jax': {
'inlineMath': [['$', '$'], ['\\(', '\\)']],
'displayMath': [['$$', '$$'], ['\\[', '\\]']],
'processEscapes': true,
'processEnvironments': true,
'skipTags': ['script', 'noscript', 'style', 'textarea', 'code'],
'displayAlign': 'center',
},
'HTML-CSS': {
'styles': {'.MathJax_Display': {'margin': 0}},
'linebreaks': {'automatic': true},
// Disable to prevent OTF font loading, which aren't part of our
// distribution.
'imageFont': null,
},
'messageStyle': 'none'
};
var script = document.createElement("script");
script.src = "https://colab.research.google.com/static/mathjax/MathJax.js?config=TeX-AMS_HTML-full,Safe";
document.head.appendChild(script);
}
</script>
'''))
get_ipython().events.register('pre_run_cell', setup_mathjax)
a,b,c,d = symbols('alpha,beta,gamma,delta')
psi = a*Qubit('0')+b*Qubit('1')
phi = c*Qubit('0')+d*Qubit('1')
TensorProduct(psi, phi) #テンソル積
represent(TensorProduct(psi, phi))
```
さらに$|\psi\rangle$とのテンソル積をとると8次元のベクトルになる:
```
represent(TensorProduct(psi,TensorProduct(psi, phi)))
```
### 演算子のテンソル積
演算子についても何番目の量子ビットに作用するのか、というのをテンソル積をもちいて表現することができる。たとえば、1つめの量子ビットには$A$という演算子、2つめの量子ビットには$B$という演算子を作用させるという場合には、
$$ A \otimes B$$
としてテンソル積演算子が与えられる。
$A$と$B$をそれぞれ、2×2の行列とすると、$A\otimes B$は4×4の行列として
$$
\left(
\begin{array}{cc}
a_{11} & a_{12}
\\
a_{21} & a_{22}
\end{array}
\right)
\otimes
\left(
\begin{array}{cc}
b_{11} & b_{12}
\\
b_{21} & b_{22}
\end{array}
\right) =
\left(
\begin{array}{cccc}
a_{11} b_{11} & a_{11} b_{12} & a_{12} b_{11} & a_{12} b_{12}
\\
a_{11} b_{21} & a_{11} b_{22} & a_{12} b_{21} & a_{12} b_{22}
\\
a_{21} b_{11} & a_{21} b_{12} & a_{22} b_{11} & a_{22} b_{12}
\\
a_{21} b_{21} & a_{21} b_{22} & a_{22} b_{21} & a_{22} b_{22}
\end{array}
\right)
$$
のように計算される。
テンソル積状態
$$|\psi \rangle \otimes | \phi \rangle $$
に対する作用は、
$$ (A|\psi \rangle ) \otimes (B |\phi \rangle )$$
となり、それぞれの部分系$|\psi \rangle$と$|\phi\rangle$に$A$と$B$が作用する。
足し算に対しては、多項式のように展開してそれぞれの項を作用させればよい。
$$
(A+C)\otimes (B+D) |\psi \rangle \otimes | \phi \rangle =
(A \otimes B +A \otimes D + C \otimes B + C \otimes D) |\psi \rangle \otimes | \phi \rangle\\ =
(A|\psi \rangle) \otimes (B| \phi \rangle)
+(A|\psi \rangle) \otimes (D| \phi \rangle)
+(C|\psi \rangle) \otimes (B| \phi \rangle)
+(C|\psi \rangle) \otimes (D| \phi \rangle)
$$
テンソル積やテンソル積演算子は左右横並びで書いているが、本当は
$$
\left(
\begin{array}{c}
A
\\
\otimes
\\
B
\end{array}
\right)
\begin{array}{c}
|\psi \rangle
\\
\otimes
\\
|\phi\rangle
\end{array}
$$
のように縦に並べた方がその作用の仕方がわかりやすいのかもしれない。
例えば、CNOT演算を用いて作られるエンタングル状態は、
$$
\left(
\begin{array}{c}
|0\rangle \langle 0|
\\
\otimes
\\
I
\end{array}
+
\begin{array}{c}
|1\rangle \langle 1|
\\
\otimes
\\
X
\end{array}
\right)
\left(
\begin{array}{c}
\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
\\
\otimes
\\
|0\rangle
\end{array}
\right) =
\frac{1}{\sqrt{2}}\left(
\begin{array}{c}
|0 \rangle
\\
\otimes
\\
|0\rangle
\end{array}
+
\begin{array}{c}
|1 \rangle
\\
\otimes
\\
|1\rangle
\end{array}
\right)
$$
のようになる。
### SymPyを用いた演算子のテンソル積
SymPyで演算子を使用する時は、何桁目の量子ビットに作用する演算子かを常に指定する。「何**番目**」ではなく2進数表記の「何**桁目**」であることに注意しよう。$n$量子ビットのうちの左から$i$番目の量子ビットを指定する場合、SymPyのコードでは`n-i`を指定する(0を基点とするインデックス)。
`H(0)` は、1量子ビット空間で表示すると
```
represent(H(0),nqubits=1)
```
2量子ビット空間では$H \otimes I$に対応しており、その表示は
```
represent(H(1),nqubits=2)
```
CNOT演算は、
```
represent(CNOT(1,0),nqubits=2)
```
パウリ演算子のテンソル積$X\otimes Y \otimes Z$も、
```
represent(X(2)*Y(1)*Z(0),nqubits=3)
```
このようにして、上記のテンソル積のルールを実際にたしかめてみることができる。
### 複数の量子ビットの一部分だけを測定した場合
複数の量子ビットを全て測定した場合の測定結果の確率については既に説明した。複数の量子ビットのうち、一部だけを測定することもできる。その場合、測定結果の確率は、測定結果に対応する(部分系の)基底で射影したベクトルの長さの2乗になり、測定後の状態は射影されたベクトルを規格化したものになる。
具体的に見ていこう。以下の$n$量子ビットの状態を考える。
\begin{align}
|\psi\rangle &=
c_{00...0} |00...0\rangle +
c_{00...1} |00...1\rangle + \cdots +
c_{11...1} |11...1\rangle\\
&= \sum_{i_1 \dotsc i_n} c_{i_1 \dotsc i_n} |i_1 \dotsc i_n\rangle =
\sum_{i_1 \dotsc i_n} c_{i_1 \dotsc i_n} |i_1\rangle \otimes \cdots \otimes |i_n\rangle
\end{align}
1番目の量子ビットを測定するとしよう。1つ目の量子ビットの状態空間の正規直交基底$|0\rangle$, $|1\rangle$に対する射影演算子はそれぞれ$|0\rangle\langle0|$, $|1\rangle\langle1|$と書ける。1番目の量子ビットを$|0\rangle$に射影し、他の量子ビットには何もしない演算子
$$
|0\rangle\langle0| \otimes I \otimes \cdots \otimes I
$$
を使って、測定値0が得られる確率は
$$
\bigl\Vert \bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) |\psi\rangle \bigr\Vert^2 =
\langle \psi | \bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) | \psi \rangle
$$
である。ここで
$$
\bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) | \psi \rangle =
\sum_{i_2 \dotsc i_n} c_{0 i_2 \dotsc i_n} |0\rangle \otimes |i_2\rangle \otimes \cdots \otimes |i_n\rangle
$$
なので、求める確率は
$$
p_0 = \sum_{i_2 \dotsc i_n} |c_{0 i_2 \dotsc i_n}|^2
$$
となり、測定後の状態は
$$
\frac{1}{\sqrt{p_0}}\sum_{i_2 \dotsc i_n} c_{0 i_2 \dotsc i_n} |0\rangle \otimes |i_2\rangle \otimes \cdots \otimes |i_n\rangle
$$
となる。0と1を入れ替えれば、測定値1が得られる確率と測定後の状態が得られる。
ここで求めた$p_0$, $p_1$の表式は、測定値$i_1, \dotsc, i_n$が得られる同時確率分布$p_{i_1, \dotsc, i_n}$から計算される$i_1$の周辺確率分布と一致することに注意しよう。実際、
$$
\sum_{i_2, \dotsc, i_n} p_{i_1, \dotsc, i_n} = \sum_{i_2, \dotsc, i_n} |c_{i_1, \dotsc, i_n}|^2 = p_{i_1}
$$
である。
測定される量子ビットを増やし、最初の$k$個の量子ビットを測定する場合も同様に計算できる。測定結果$i_1, \dotsc, i_k$を得る確率は
$$
p_{i_1, \dotsc, i_k} = \sum_{i_{k+1}, \dotsc, i_n} |c_{i_1, \dotsc, i_n}|^2
$$
であり、測定後の状態は
$$
\frac{1}{\sqrt{p_{i_1, \dotsc, i_k}}}\sum_{i_{k+1} \dotsc i_n} c_{i_1 \dotsc i_n} |i_1 \rangle \otimes \cdots \otimes |i_n\rangle
$$
となる。(和をとるのは$i_{k+1},\cdots,i_n$だけであることに注意)
SymPyを使ってさらに具体的な例を見てみよう。H演算とCNOT演算を組み合わせて作られる次の状態を考える。
$$
|\psi\rangle = \Lambda(X) (H \otimes H) |0\rangle \otimes |0\rangle = \frac{|00\rangle + |10\rangle + |01\rangle + |11\rangle}{2}
$$
```
psi = qapply(CNOT(1, 0)*H(1)*H(0)*Qubit('00'))
psi
```
この状態の1つ目の量子ビットを測定して0になる確率は
$$
p_0 = \langle \psi | \bigl( |0\rangle\langle0| \otimes I \bigr) | \psi \rangle =
\left(\frac{\langle 00 | + \langle 10 | + \langle 01 | + \langle 11 |}{2}\right)
\left(\frac{| 00 \rangle + | 01 \rangle}{2}\right) =
\frac{1}{2}
$$
で、測定後の状態は
$$
\frac{1}{\sqrt{p_0}} \bigl( |0\rangle\langle0| \otimes I \bigr) | \psi \rangle =
\frac{| 00 \rangle + | 01 \rangle}{\sqrt{2}}
$$
である。
この結果をSymPyでも計算してみよう。SymPyには測定用の関数が数種類用意されていて、一部の量子ビットを測定した場合の確率と測定後の状態を計算するには、`measure_partial`を用いればよい。測定する状態と、測定を行う量子ビットのインデックスを引数として渡すと、測定後の状態と測定の確率の組がリストとして出力される。1つめの量子ビットが0だった場合の量子状態と確率は`[0]`要素を参照すればよい。
```
from sympy.physics.quantum.qubit import measure_all, measure_partial
measured_state_and_probability = measure_partial(psi, (1,))
measured_state_and_probability[0]
```
上で手計算した結果と合っていることが分かる。測定結果が1だった場合も同様に計算できる。
```
measured_state_and_probability[1]
```
---
## コラム:ユニバーサルゲートセットとは
古典計算機では、NANDゲート(論理積ANDの出力を反転したもの)さえあれば、これをいくつか組み合わせることで、任意の論理演算が実行できることが知られている。
それでは、量子計算における対応物、すなわち任意の量子計算を実行するために最低限必要な量子ゲートは何であろうか?
実は、本節で学んだ
$$\{H, T, {\rm CNOT} \}$$
の3種類のゲートがその役割を果たしている、いわゆる**ユニバーサルゲートセット**であることが知られている。
これらをうまく組み合わせることで、任意の量子計算を実行できる、すなわち「**万能量子計算**」が可能である。
### 【より詳しく知りたい人のための注】
以下では$\{H, T, {\rm CNOT} \}$の3種のゲートの組が如何にしてユニバーサルゲートセットを構成するかを、順を追って説明する。
流れとしては、一般の$n$量子ビットユニタリ演算からスタートし、これをより細かい部品にブレイクダウンしていくことで、最終的に上記3種のゲートに行き着くことを見る。
#### ◆ $n$量子ビットユニタリ演算の分解
まず、任意の$n$量子ビットユニタリ演算は、以下の手順を経て、いくつかの**1量子ビットユニタリ演算**と**CNOTゲート**に分解できる。
1. 任意の$n$量子ビットユニタリ演算は、いくつかの**2準位ユニタリ演算**の積に分解できる。ここで2準位ユニタリ演算とは、例として3量子ビットの場合、$2^3=8$次元空間のうち2つの基底(e.g., $\{|000\rangle, |111\rangle \}$)の張る2次元部分空間にのみ作用するユニタリ演算である
2. 任意の2準位ユニタリ演算は、**制御**$U$**ゲート**(CNOTゲートのNOT部分を任意の1量子ビットユニタリ演算$U$に置き換えたもの)と**Toffoliゲート**(CNOTゲートの制御量子ビットが2つになったもの)から構成できる
3. 制御$U$ゲートとToffoliゲートは、どちらも**1量子ビットユニタリ演算**と**CNOTゲート**から構成できる
#### ◆ 1量子ビットユニタリ演算の構成
さらに、任意の1量子ビットユニタリ演算は、$\{H, T\}$の2つで構成できる。
1. 任意の1量子ビットユニタリ演算は、オイラーの回転角の法則から、回転ゲート$\{R_X(\theta), R_Z(\theta)\}$で(厳密に)実現可能である
2. 実は、ブロッホ球上の任意の回転は、$\{H, T\}$のみを用いることで実現可能である(注1)。これはある軸に関する$\pi$の無理数倍の回転が$\{H, T\}$のみから実現できること(**Solovay-Kitaevアルゴリズム**)に起因する
(注1) ブロッホ球上の連続的な回転を、離散的な演算である$\{H, T\}$で実現できるか疑問に思われる読者もいるかもしれない。実際、厳密な意味で1量子ビットユニタリ演算を離散的なゲート操作で実現しようとすると、無限個のゲートが必要となる。しかし実際には厳密なユニタリ演算を実現する必要はなく、必要な計算精度$\epsilon$で任意のユニタリ演算を近似できれば十分である。ここでは、多項式個の$\{H, T\}$を用いることで、任意の1量子ビットユニタリ演算を**十分良い精度で近似的に構成できる**ことが、**Solovay-Kitaevの定理** [3] により保証されている。
<br>
以上の議論により、3種のゲート$\{H, T, {\rm CNOT} \}$があれば、任意の$n$量子ビットユニタリ演算が実現できることがわかる。
ユニバーサルゲートセットや万能量子計算について、より詳しくは以下を参照されたい:
[1] Nielsen-Chuang の `4.5 Universal quantum gates`
[2] 藤井 啓祐 「量子コンピュータの基礎と物理との接点」(第62回物性若手夏の学校 講義)DOI: 10.14989/229039 http://mercury.yukawa.kyoto-u.ac.jp/~bussei.kenkyu/archives/1274.html
[3] レビューとして、C. M. Dawson, M. A. Nielsen, “The Solovay-Kitaev algorithm“, https://arxiv.org/abs/quant-ph/0505030
| github_jupyter |
# Evaluation of a Pipeline and its Components
[](https://colab.research.google.com/github/deepset-ai/haystack/blob/master/tutorials/Tutorial5_Evaluation.ipynb)
To be able to make a statement about the quality of results a question-answering pipeline or any other pipeline in haystack produces, it is important to evaluate it. Furthermore, evaluation allows determining which components of the pipeline can be improved.
The results of the evaluation can be saved as CSV files, which contain all the information to calculate additional metrics later on or inspect individual predictions.
### Prepare environment
#### Colab: Enable the GPU runtime
Make sure you enable the GPU runtime to experience decent speed in this tutorial.
**Runtime -> Change Runtime type -> Hardware accelerator -> GPU**
<img src="https://raw.githubusercontent.com/deepset-ai/haystack/master/docs/_src/img/colab_gpu_runtime.jpg">
```
# Make sure you have a GPU running
!nvidia-smi
# Install the latest release of Haystack in your own environment
#! pip install farm-haystack
# Install the latest master of Haystack
!pip install --upgrade pip
!pip install git+https://github.com/deepset-ai/haystack.git#egg=farm-haystack[colab]
```
## Start an Elasticsearch server
You can start Elasticsearch on your local machine instance using Docker. If Docker is not readily available in your environment (eg., in Colab notebooks), then you can manually download and execute Elasticsearch from source.
```
# If Docker is available: Start Elasticsearch as docker container
# from haystack.utils import launch_es
# launch_es()
# Alternative in Colab / No Docker environments: Start Elasticsearch from source
! wget https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-7.9.2-linux-x86_64.tar.gz -q
! tar -xzf elasticsearch-7.9.2-linux-x86_64.tar.gz
! chown -R daemon:daemon elasticsearch-7.9.2
import os
from subprocess import Popen, PIPE, STDOUT
es_server = Popen(
["elasticsearch-7.9.2/bin/elasticsearch"], stdout=PIPE, stderr=STDOUT, preexec_fn=lambda: os.setuid(1) # as daemon
)
# wait until ES has started
! sleep 30
```
## Fetch, Store And Preprocess the Evaluation Dataset
```
from haystack.utils import fetch_archive_from_http
# Download evaluation data, which is a subset of Natural Questions development set containing 50 documents with one question per document and multiple annotated answers
doc_dir = "data/tutorial5"
s3_url = "https://s3.eu-central-1.amazonaws.com/deepset.ai-farm-qa/datasets/nq_dev_subset_v2.json.zip"
fetch_archive_from_http(url=s3_url, output_dir=doc_dir)
# make sure these indices do not collide with existing ones, the indices will be wiped clean before data is inserted
doc_index = "tutorial5_docs"
label_index = "tutorial5_labels"
# Connect to Elasticsearch
from haystack.document_stores import ElasticsearchDocumentStore
# Connect to Elasticsearch
document_store = ElasticsearchDocumentStore(
host="localhost",
username="",
password="",
index=doc_index,
label_index=label_index,
embedding_field="emb",
embedding_dim=768,
excluded_meta_data=["emb"],
)
from haystack.nodes import PreProcessor
# Add evaluation data to Elasticsearch Document Store
# We first delete the custom tutorial indices to not have duplicate elements
# and also split our documents into shorter passages using the PreProcessor
preprocessor = PreProcessor(
split_length=200,
split_overlap=0,
split_respect_sentence_boundary=False,
clean_empty_lines=False,
clean_whitespace=False,
)
document_store.delete_documents(index=doc_index)
document_store.delete_documents(index=label_index)
# The add_eval_data() method converts the given dataset in json format into Haystack document and label objects. Those objects are then indexed in their respective document and label index in the document store. The method can be used with any dataset in SQuAD format.
document_store.add_eval_data(
filename="data/tutorial5/nq_dev_subset_v2.json",
doc_index=doc_index,
label_index=label_index,
preprocessor=preprocessor,
)
```
## Initialize the Two Components of an ExtractiveQAPipeline: Retriever and Reader
```
# Initialize Retriever
from haystack.nodes import ElasticsearchRetriever
retriever = ElasticsearchRetriever(document_store=document_store)
# Alternative: Evaluate dense retrievers (EmbeddingRetriever or DensePassageRetriever)
# The EmbeddingRetriever uses a single transformer based encoder model for query and document.
# In contrast, DensePassageRetriever uses two separate encoders for both.
# Please make sure the "embedding_dim" parameter in the DocumentStore above matches the output dimension of your models!
# Please also take care that the PreProcessor splits your files into chunks that can be completely converted with
# the max_seq_len limitations of Transformers
# The SentenceTransformer model "sentence-transformers/multi-qa-mpnet-base-dot-v1" generally works well with the EmbeddingRetriever on any kind of English text.
# For more information and suggestions on different models check out the documentation at: https://www.sbert.net/docs/pretrained_models.html
# from haystack.retriever import EmbeddingRetriever, DensePassageRetriever
# retriever = EmbeddingRetriever(document_store=document_store, model_format="sentence_transformers",
# embedding_model="sentence-transformers/multi-qa-mpnet-base-dot-v1")
# retriever = DensePassageRetriever(document_store=document_store,
# query_embedding_model="facebook/dpr-question_encoder-single-nq-base",
# passage_embedding_model="facebook/dpr-ctx_encoder-single-nq-base",
# use_gpu=True,
# max_seq_len_passage=256,
# embed_title=True)
# document_store.update_embeddings(retriever, index=doc_index)
# Initialize Reader
from haystack.nodes import FARMReader
reader = FARMReader("deepset/roberta-base-squad2", top_k=4, return_no_answer=True)
# Define a pipeline consisting of the initialized retriever and reader
from haystack.pipelines import ExtractiveQAPipeline
pipeline = ExtractiveQAPipeline(reader=reader, retriever=retriever)
# The evaluation also works with any other pipeline.
# For example you could use a DocumentSearchPipeline as an alternative:
# from haystack.pipelines import DocumentSearchPipeline
# pipeline = DocumentSearchPipeline(retriever=retriever)
```
## Evaluation of an ExtractiveQAPipeline
Here we evaluate retriever and reader in open domain fashion on the full corpus of documents i.e. a document is considered
correctly retrieved if it contains the gold answer string within it. The reader is evaluated based purely on the
predicted answer string, regardless of which document this came from and the position of the extracted span.
The generation of predictions is seperated from the calculation of metrics. This allows you to run the computation-heavy model predictions only once and then iterate flexibly on the metrics or reports you want to generate.
```
from haystack.schema import EvaluationResult, MultiLabel
# We can load evaluation labels from the document store
# We are also opting to filter out no_answer samples
eval_labels = document_store.get_all_labels_aggregated(drop_negative_labels=True, drop_no_answers=False)
eval_labels = [label for label in eval_labels if not label.no_answer] # filter out no_answer cases
## Alternative: Define queries and labels directly
# eval_labels = [
# MultiLabel(
# labels=[
# Label(
# query="who is written in the book of life",
# answer=Answer(
# answer="every person who is destined for Heaven or the World to Come",
# offsets_in_context=[Span(374, 434)]
# ),
# document=Document(
# id='1b090aec7dbd1af6739c4c80f8995877-0',
# content_type="text",
# content='Book of Life - wikipedia Book of Life Jump to: navigation, search This article is
# about the book mentioned in Christian and Jewish religious teachings...'
# ),
# is_correct_answer=True,
# is_correct_document=True,
# origin="gold-label"
# )
# ]
# )
# ]
# Similar to pipeline.run() we can execute pipeline.eval()
eval_result = pipeline.eval(labels=eval_labels, params={"Retriever": {"top_k": 5}})
# The EvaluationResult contains a pandas dataframe for each pipeline node.
# That's why there are two dataframes in the EvaluationResult of an ExtractiveQAPipeline.
retriever_result = eval_result["Retriever"]
retriever_result.head()
reader_result = eval_result["Reader"]
reader_result.head()
# We can filter for all documents retrieved for a given query
query = "who is written in the book of life"
retriever_book_of_life = retriever_result[retriever_result["query"] == query]
# We can also filter for all answers predicted for a given query
reader_book_of_life = reader_result[reader_result["query"] == query]
# Save the evaluation result so that we can reload it later and calculate evaluation metrics without running the pipeline again.
eval_result.save("../")
```
## Calculating Evaluation Metrics
Load an EvaluationResult to quickly calculate standard evaluation metrics for all predictions,
such as F1-score of each individual prediction of the Reader node or recall of the retriever.
To learn more about the metrics, see [Evaluation Metrics](https://haystack.deepset.ai/guides/evaluation#metrics-retrieval)
```
saved_eval_result = EvaluationResult.load("../")
metrics = saved_eval_result.calculate_metrics()
print(f'Retriever - Recall (single relevant document): {metrics["Retriever"]["recall_single_hit"]}')
print(f'Retriever - Recall (multiple relevant documents): {metrics["Retriever"]["recall_multi_hit"]}')
print(f'Retriever - Mean Reciprocal Rank: {metrics["Retriever"]["mrr"]}')
print(f'Retriever - Precision: {metrics["Retriever"]["precision"]}')
print(f'Retriever - Mean Average Precision: {metrics["Retriever"]["map"]}')
print(f'Reader - F1-Score: {metrics["Reader"]["f1"]}')
print(f'Reader - Exact Match: {metrics["Reader"]["exact_match"]}')
```
## Generating an Evaluation Report
A summary of the evaluation results can be printed to get a quick overview. It includes some aggregated metrics and also shows a few wrongly predicted examples.
```
pipeline.print_eval_report(saved_eval_result)
```
## Advanced Evaluation Metrics
As an advanced evaluation metric, semantic answer similarity (SAS) can be calculated. This metric takes into account whether the meaning of a predicted answer is similar to the annotated gold answer rather than just doing string comparison.
To this end SAS relies on pre-trained models. For English, we recommend "cross-encoder/stsb-roberta-large", whereas for German we recommend "deepset/gbert-large-sts". A good multilingual model is "sentence-transformers/paraphrase-multilingual-mpnet-base-v2".
More info on this metric can be found in our [paper](https://arxiv.org/abs/2108.06130) or in our [blog post](https://www.deepset.ai/blog/semantic-answer-similarity-to-evaluate-qa).
```
advanced_eval_result = pipeline.eval(
labels=eval_labels, params={"Retriever": {"top_k": 1}}, sas_model_name_or_path="cross-encoder/stsb-roberta-large"
)
metrics = advanced_eval_result.calculate_metrics()
print(metrics["Reader"]["sas"])
```
## Isolated Evaluation Mode
The isolated node evaluation uses labels as input to the Reader node instead of the output of the preceeding Retriever node.
Thereby, we can additionally calculate the upper bounds of the evaluation metrics of the Reader. Note that even with isolated evaluation enabled, integrated evaluation will still be running.
```
eval_result_with_upper_bounds = pipeline.eval(
labels=eval_labels, params={"Retriever": {"top_k": 5}, "Reader": {"top_k": 5}}, add_isolated_node_eval=True
)
pipeline.print_eval_report(eval_result_with_upper_bounds)
```
## Evaluation of Individual Components: Retriever
Sometimes you might want to evaluate individual components, for example, if you don't have a pipeline but only a retriever or a reader with a model that you trained yourself.
Here we evaluate only the retriever, based on whether the gold_label document is retrieved.
```
## Evaluate Retriever on its own
# Note that no_answer samples are omitted when evaluation is performed with this method
retriever_eval_results = retriever.eval(top_k=5, label_index=label_index, doc_index=doc_index)
# Retriever Recall is the proportion of questions for which the correct document containing the answer is
# among the correct documents
print("Retriever Recall:", retriever_eval_results["recall"])
# Retriever Mean Avg Precision rewards retrievers that give relevant documents a higher rank
print("Retriever Mean Avg Precision:", retriever_eval_results["map"])
```
Just as a sanity check, we can compare the recall from `retriever.eval()` with the multi hit recall from `pipeline.eval(add_isolated_node_eval=True)`.
These two recall metrics are only comparable since we chose to filter out no_answer samples when generating eval_labels.
```
metrics = eval_result_with_upper_bounds.calculate_metrics()
print(metrics["Retriever"]["recall_multi_hit"])
```
## Evaluation of Individual Components: Reader
Here we evaluate only the reader in a closed domain fashion i.e. the reader is given one query
and its corresponding relevant document and metrics are calculated on whether the right position in this text is selected by
the model as the answer span (i.e. SQuAD style)
```
# Evaluate Reader on its own
reader_eval_results = reader.eval(document_store=document_store, label_index=label_index, doc_index=doc_index)
# Evaluation of Reader can also be done directly on a SQuAD-formatted file without passing the data to Elasticsearch
# reader_eval_results = reader.eval_on_file("../data/nq", "nq_dev_subset_v2.json", device=device)
# Reader Top-N-Accuracy is the proportion of predicted answers that match with their corresponding correct answer
print("Reader Top-N-Accuracy:", reader_eval_results["top_n_accuracy"])
# Reader Exact Match is the proportion of questions where the predicted answer is exactly the same as the correct answer
print("Reader Exact Match:", reader_eval_results["EM"])
# Reader F1-Score is the average overlap between the predicted answers and the correct answers
print("Reader F1-Score:", reader_eval_results["f1"])
```
## About us
This [Haystack](https://github.com/deepset-ai/haystack/) notebook was made with love by [deepset](https://deepset.ai/) in Berlin, Germany
We bring NLP to the industry via open source!
Our focus: Industry specific language models & large scale QA systems.
Some of our other work:
- [German BERT](https://deepset.ai/german-bert)
- [GermanQuAD and GermanDPR](https://deepset.ai/germanquad)
- [FARM](https://github.com/deepset-ai/FARM)
Get in touch:
[Twitter](https://twitter.com/deepset_ai) | [LinkedIn](https://www.linkedin.com/company/deepset-ai/) | [Slack](https://haystack.deepset.ai/community/join) | [GitHub Discussions](https://github.com/deepset-ai/haystack/discussions) | [Website](https://deepset.ai)
By the way: [we're hiring!](https://www.deepset.ai/jobs)
| github_jupyter |
```
%matplotlib inline
from __future__ import print_function, unicode_literals
import sys, os
import seaborn as sns
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
from pygaarst import raster
sys.path.append('../firedetection/')
import landsat8fire as lfire
sns.set(rc={'image.cmap': 'gist_heat'})
sns.set(rc={'image.cmap': 'bone'})
sns.set_context("poster")
myfontsize = 20
font = {'family' : 'Calibri',
'weight': 'bold',
'size' : myfontsize}
matplotlib.rc('font', **font)
matplotlib.axes.rcParams['axes.labelsize']=myfontsize-4
matplotlib.axes.rcParams['axes.titlesize']=myfontsize
cmap1 = matplotlib.colors.ListedColormap(sns.xkcd_palette(['white', 'red']))
cmap2 = matplotlib.colors.ListedColormap(sns.xkcd_palette(['white', 'neon green']))
cmap3 = matplotlib.colors.ListedColormap(sns.xkcd_palette(['white', 'orange']))
landsatpath = '/Volumes/SCIENCE_mobile_Mac/Fire/DATA_BY_PROJECT/2015VIIRSMODIS/Landsat/L8 OLI_TIRS Sockeye'
lsscene = 'LC80700172015166LGN00'
landsat = raster.Landsatscene(os.path.join(landsatpath, lsscene))
landsat.infix = '_clip'
rho7 = landsat.band7.reflectance
rho6 = landsat.band6.reflectance
rho5 = landsat.band5.reflectance
rho4 = landsat.band4.reflectance
rho3 = landsat.band3.reflectance
rho2 = landsat.band2.reflectance
rho1 = landsat.band1.reflectance
R75 = rho7/rho5
R76 = rho7/rho6
xmax = landsat.band7.ncol
ymax = landsat.band7.nrow
```
"Unambiguous fire pixels" test 1 (daytime, normal conditions).
```
firecond1 = np.logical_and(R75 > 2.5, rho7 > .5)
firecond1 = np.logical_and(firecond1, rho7 - rho5 > .3)
firecond1_masked = np.ma.masked_where(
~firecond1, np.ones((ymax, xmax)))
```
"Unambiguous fire pixels" test 2 (daytime, sensor anomalies)
```
firecond2 = np.logical_and(rho6 > .8, rho1 < .2)
firecond2 = np.logical_and(firecond2,
np.logical_or(rho5 > .4, rho7 < .1)
)
firecond2_masked = np.ma.masked_where(
~firecond2, np.ones((ymax, xmax)))
```
"Relaxed conditions"
```
firecond3 = np.logical_and(R75 > 1.8, rho7 - rho5 > .17)
firecond3_masked = np.ma.masked_where(
~firecond3, np.ones((ymax, xmax)))
```
"Extra tests" for relaxed conditions:
1. R76 > 1.6
2. R75 at least 3 sigma and 0.8 larger than avg of a 61x61 window of valid pixels
3. rho7 at least 3 sigma and 0.08 larger than avg of a 61x61 window of valid pixels
Valid pixels are:
1. Not "unambiguous fire pixel"
2. rho7 > 0
3. Not water as per water test 1: rho4 > rho5 AND rho5 > rho6 AND rho6 > rho7 AND rho1 - rho7 < 0.2
4. Not water as per test 2: rho3 > rho2 OR ( rho1 > rho2 AND rho2 > rho3 AND rho3 > rho4 )
So let's get started on the validation tests...
```
newfirecandidates = np.logical_and(~firecond1, ~firecond2)
newfirecandidates = np.logical_and(newfirecandidates, firecond3)
newfirecandidates = np.logical_and(newfirecandidates, R76 > 0)
sum(sum(newfirecandidates))
```
We'll need a +-30 pixel window around a coordinate pair to carry out the averaging for the contextual tests
```
iidxmax, jidxmax = landsat.band1.data.shape
def get_window(ii, jj, N, iidxmax, jidxmax):
"""Return 2D Boolean array that is True where a window of size N
around a given point is masked out """
imin = max(0, ii-N)
imax = min(iidxmax, ii+N)
jmin = max(0, jj-N)
jmax = min(jidxmax, jj+N)
mask1 = np.zeros((iidxmax, jidxmax))
mask1[imin:imax+1, jmin:jmax+1] = 1
return mask1 == 1
plt.imshow(get_window(100, 30, 30, iidxmax, jidxmax) , cmap=cmap3, vmin=0, vmax=1)
```
We can then get the union of those windows over all detected fire pixel candidates.
```
windows = [get_window(ii, jj, 30, iidxmax, jidxmax) for ii, jj in np.argwhere(newfirecandidates)]
window = np.any(windows, axis=0)
plt.imshow(window , cmap=cmap3, vmin=0, vmax=1)
```
We also need a water mask...
```
def get_l8watermask_frombands(
rho1, rho2, rho3,
rho4, rho5, rho6, rho7):
"""
Takes L8 bands, returns 2D Boolean numpy array of same shape
"""
turbidwater = get_l8turbidwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
deepwater = get_l8deepwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
return np.logical_or(turbidwater, deepwater)
def get_l8commonwater(rho1, rho4, rho5, rho6, rho7):
"""Returns Boolean numpy array common to turbid and deep water schemes"""
water1cond = np.logical_and(rho4 > rho5, rho5 > rho6)
water1cond = np.logical_and(water1cond, rho6 > rho7)
water1cond = np.logical_and(water1cond, rho1 - rho7 < 0.2)
return water1cond
def get_l8turbidwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7):
"""Returns Boolean numpy array that marks shallow, turbid water"""
watercond2 = get_l8commonwater(rho1, rho4, rho5, rho6, rho7)
watercond2 = np.logical_and(watercond2, rho3 > rho2)
return watercond2
def get_l8deepwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7):
"""Returns Boolean numpy array that marks deep, clear water"""
watercond3 = get_l8commonwater(rho1, rho4, rho5, rho6, rho7)
watercondextra = np.logical_and(rho1 > rho2, rho2 > rho3)
watercondextra = np.logical_and(watercondextra, rho3 > rho4)
return np.logical_and(watercond3, watercondextra)
water = get_l8watermask_frombands(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
plt.imshow(~water , cmap=cmap3, vmin=0, vmax=1)
```
Let's try out the two components, out of interest... apparently, only the "deep water" test catches the water bodies here.
```
turbidwater = get_l8turbidwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
deepwater = get_l8deepwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
plt.imshow(~turbidwater , cmap=cmap3, vmin=0, vmax=1)
plt.show()
plt.imshow(~deepwater , cmap=cmap3, vmin=0, vmax=1)
def get_valid_pixels(otherfirecond, rho1, rho2, rho3,
rho4, rho5, rho6, rho7, mask=None):
"""returns masked array of 1 for valid, 0 for not"""
if not np.any(mask):
mask = np.zeros(otherfirecond.shape)
rho = {}
for rho in [rho1, rho2, rho3, rho4, rho5, rho6, rho7]:
rho = np.ma.masked_array(rho, mask=mask)
watercond = get_l8watermask_frombands(
rho1, rho2, rho3,
rho4, rho5, rho6, rho7)
greater0cond = rho7 > 0
finalcond = np.logical_and(greater0cond, ~watercond)
finalcond = np.logical_and(finalcond, ~otherfirecond)
return np.ma.masked_array(finalcond, mask=mask)
otherfirecond = np.logical_or(firecond1, firecond2)
validpix = get_valid_pixels(otherfirecond, rho1, rho2, rho3,
rho4, rho5, rho6, rho7, mask=~window)
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(validpix), cmap=cmap3, vmin=0, vmax=1)
iidxmax, jidxmax = landsat.band1.data.shape
output = np.zeros((iidxmax, jidxmax))
for ii, jj in np.argwhere(firecond3):
window = get_window(ii, jj, 30, iidxmax, jidxmax)
newmask = np.logical_or(~window, ~validpix.data)
rho7_win = np.ma.masked_array(rho7, mask=newmask)
R75_win = np.ma.masked_array(rho7/rho5, mask=newmask)
rho7_bar = np.mean(rho7_win.flatten())
rho7_std = np.std(rho7_win.flatten())
R75_bar = np.mean(R75_win.flatten())
R75_std = np.std(R75_win.flatten())
rho7_test = rho7_win[ii, jj] - rho7_bar > max(3*rho7_std, 0.08)
R75_test = R75_win[ii, jj]- R75_bar > max(3*R75_std, 0.8)
if rho7_test and R75_test:
output[ii, jj] = 1
lowfirecond = output == 1
sum(sum(lowfirecond))
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(lowfirecond), cmap=cmap1, vmin=0, vmax=1)
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(firecond1), cmap=cmap3, vmin=0, vmax=1)
allfirecond = np.logical_or(firecond1, firecond2)
allfirecond = np.logical_or(allfirecond, lowfirecond)
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(allfirecond), cmap=cmap1, vmin=0, vmax=1)
```
So this works! Now we can do the same using the module that incorporates the above code:
```
testfire, highfire, anomfire, lowfire = lfire.get_l8fire(landsat)
sum(sum(lowfire))
sum(sum(testfire))
firecond1_masked = np.ma.masked_where(
~testfire, np.ones((ymax, xmax)))
firecondlow_masked = np.ma.masked_where(
~lowfire, np.ones((ymax, xmax)))
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(firecond1_masked), cmap=cmap1, vmin=0, vmax=1)
ax1.pcolormesh(np.flipud(firecondlow_masked), cmap=cmap3, vmin=0, vmax=1)
```
| github_jupyter |
# Finding fraud patterns with FP-growth
# Data Collection and Investigation
```
import pandas as pd
# Input data files are available in the "../input/" directory
df = pd.read_csv('D:/Python Project/Credit Card Fraud Detection/benchmark dataset/Test FP-Growth.csv')
# printing the first 5 columns for data visualization
df.head()
```
## Execute FP-growth algorithm
## Spark
```
# import environment path to pyspark
import os
import sys
spark_path = r"D:\apache-spark" # spark installed folder
os.environ['SPARK_HOME'] = spark_path
sys.path.insert(0, spark_path + "/bin")
sys.path.insert(0, spark_path + "/python/pyspark/")
sys.path.insert(0, spark_path + "/python/lib/pyspark.zip")
sys.path.insert(0, spark_path + "/python/lib/py4j-0.10.7-src.zip")
# Export csv to txt file
df.to_csv('processed_itemsets.txt', index=None, sep=' ', mode='w+')
import csv
# creating necessary variable
new_itemsets_list = []
skip_first_iteration = 1
# find the duplicate item and add a counter at behind
with open("processed_itemsets.txt", 'r') as fp:
itemsets_list = csv.reader(fp, delimiter =' ', skipinitialspace=True)
for itemsets in itemsets_list:
unique_itemsets = []
counter = 2
for item in itemsets:
if itemsets.count(item) > 1:
if skip_first_iteration == 1:
unique_itemsets.append(item)
skip_first_iteration = skip_first_iteration + 1
continue
duplicate_item = item + "__(" + str(counter) + ")"
unique_itemsets.append(duplicate_item)
counter = counter + 1
else:
unique_itemsets.append(item)
print(itemsets)
new_itemsets_list.append(unique_itemsets)
# write the new itemsets into file
with open('processed_itemsets.txt', 'w+') as f:
for items in new_itemsets_list:
for item in items:
f.write("{} ".format(item))
f.write("\n")
from pyspark import SparkContext
from pyspark.mllib.fpm import FPGrowth
# initialize spark
sc = SparkContext.getOrCreate()
data = sc.textFile('processed_itemsets.txt').cache()
transactions = data.map(lambda line: line.strip().split(' '))
```
__minSupport__: The minimum support for an itemset to be identified as frequent. <br>
For example, if an item appears 3 out of 5 transactions, it has a support of 3/5=0.6.
__minConfidence__: Minimum confidence for generating Association Rule. Confidence is an indication of how often an association rule has been found to be true. For example, if in the transactions itemset X appears 4 times, X and Y co-occur only 2 times, the confidence for the rule X => Y is then 2/4 = 0.5.
__numPartitions__: The number of partitions used to distribute the work. By default the param is not set, and number of partitions of the input dataset is used
```
model = FPGrowth.train(transactions, minSupport=0.6, numPartitions=10)
result = model.freqItemsets().collect()
print("Frequent Itemsets : Item Support")
print("====================================")
for index, frequent_itemset in enumerate(result):
print(str(frequent_itemset.items) + ' : ' + str(frequent_itemset.freq))
rules = sorted(model._java_model.generateAssociationRules(0.8).collect(), key=lambda x: x.confidence(), reverse=True)
print("Antecedent => Consequent : Min Confidence")
print("========================================")
for rule in rules[:200]:
print(rule)
# stop spark session
sc.stop()
```
| github_jupyter |
```
import pandas as pd
import sqlite3
import datetime
def main():
data_list = [("ml-latest-small/", "small_output/", "small"), ("ml-20m/", "20M_output/","20M")]
for item in data_list:
start_time = datetime.datetime.now()
process_data(item[0], item[1])
end_time = datetime.datetime.now()
diff = end_time - start_time
print("Pre-processing time for ", item[2], " dataset ----> ", diff)
def process_data(input_path, output_path):
# --------------------------------------------------------
# read data to make a revised movies table and genre table
# --------------------------------------------------------
movies = input_path + "movies.csv"
movies_data = pd.read_csv(movies)
# print((movies_data.head(10)))
data = {'movieId':[],
'title': [],
'genreID': []
}
genre_dict = {}
gen_id = 1
# genre_dict = dict([v,k] for k,v in genre_dict.items())
# print(genre_dict)
for item in movies_data.iterrows():
mID = item[1][0]
ttle = item[1][1]
genre_list = item[1][2]
for gen in genre_list.split('|'):
if gen not in genre_dict:
genre_dict[gen] = gen_id
gen_id += 1
data['movieId'].append(mID)
data['title'].append(ttle)
data['genreID'].append(genre_dict[gen])
# print(genre_dict)
# print(data)
movies_df = pd.DataFrame(data)
# print(df.head(20))
print("There are ", len(movies_df), "rows in the revised movies table")
# --------------------------------------------------------
# create revised_movies.csv
# --------------------------------------------------------
revised_movies = output_path + "revised_movies.csv"
movies_df.to_csv(revised_movies, index=False)
# --------------------------------------------------------
# get genre information
# --------------------------------------------------------
temp = {'genreID':[], 'genre':[]}
for k,v in genre_dict.items():
temp['genreID'].append(v)
temp['genre'].append(k)
# print(temp)
genre_df = pd.DataFrame(temp)
# print(genre_df.head(20))
print("There are : ", len(genre_df), "rows in the genre table")
# --------------------------------------------------------
# create genres.csv
# --------------------------------------------------------
genres = output_path + "genres.csv"
genre_df.to_csv(genres, index=False)
# --------------------------------------------------------
# timestamps in tags needs to be changed.
# --------------------------------------------------------
tags = input_path + "tags.csv"
tags_data = pd.read_csv(tags)
new_ts_list = []
for item in tags_data['timestamp']:
start_time = datetime.datetime(year=1970, month=1, day=1, hour=00, minute=00, second=00)
t_delta=datetime.timedelta(seconds=item)
dtime = start_time + t_delta
new_ts_list.append(dtime)
tags_data['tags_timestamp'] = new_ts_list
del tags_data['timestamp']
# print(tags_data.head(10))
# # --------------------------------------------------------
# # create revised_tags.csv
# # --------------------------------------------------------
revised_tags = output_path + "revised_tags.csv"
tags_data.to_csv(revised_tags, index=False)
print("There are ", len(tags_data), "rows in the tags table")
# --------------------------------------------------------
# timestamps in ratings needs to be changed.
# --------------------------------------------------------
ratings = input_path + "ratings.csv"
ratings_data = pd.read_csv(ratings)
new_ts_list = []
for item in ratings_data['timestamp']:
start_time = datetime.datetime(year=1970, month=1, day=1, hour=00, minute=00, second=00)
t_delta=datetime.timedelta(seconds=item)
dtime = start_time + t_delta
new_ts_list.append(dtime)
ratings_data['ratings_timestamp'] = new_ts_list
del ratings_data['timestamp']
# print(ratings_data.head(10))
# --------------------------------------------------------
# create revised_ratings.csv
# --------------------------------------------------------
revised_ratings = output_path + "revised_ratings.csv"
ratings_data.to_csv(revised_ratings, index=False)
print("There are ", len(ratings_data), "rows in the ratings table")
# ---------------------------------------------------------------------------------
# links.csv remains the same.
# ---------------------------------------------------------------------------------
# --------------------------------------------------------
# How many rows are there in the links table
# --------------------------------------------------------
links = input_path + "links.csv"
links_data = pd.read_csv(links)
print("There are ", len(links_data), "rows in the links table")
main()
```
| github_jupyter |
```
%cd ..
%ls
import pandas as pd
import datetime
import numpy as np
# xls to csv
xls = pd.read_excel(u'107年 竹苗空品區/107年新竹站_20190315.xls', index_col=0)
xls.to_csv('107年 竹苗空品區/107年新竹站_20190315.csv', encoding='big5')
train = pd.read_csv('107年 竹苗空品區/107年新竹站_20190315.csv', encoding='big5', index_col = False)
train.iloc[26].ffill()
def str_2(x):
x = str(x).rjust(2, '0')
return x
def get_next(col, i): # 下一個時間
col = int(col) + 1
if col > 23:
col = 0
i += 18
while(pd.isnull(train[str_2(col)][i]) \
or '*' in train[str_2(col)][i][-1] \
or '#' in train[str_2(col)][i][-1] \
or 'x' in train[str_2(col)][i][-1] \
or 'A' in train[str_2(col)][i][-1]):
col += 1
if col > 23:
col = 0
i += 18
return float(train[str_2(col)][i])
def get_last(col, i): # 上一個時間
col = int(col) - 1
if col < 0:
col = 23
i -= 18
while(pd.isnull(train[str_2(col)][i]) \
or '*' in train[str_2(col)][i][-1] \
or '#' in train[str_2(col)][i][-1] \
or 'x' in train[str_2(col)][i][-1] \
or 'A' in train[str_2(col)][i][-1]):
col -= 1
if col < 0:
col = 23
i -= 18
return float(train[str_2(col)][i])
# 表示儀器檢核為無效值,* 表示程式檢核為無效值,x 表示人工檢核為無效值,NR 表示無降雨,空白 表示缺值。
#,A 係指因儀器疑似故障警報所產生的無效值。
feat = train.columns
print(feat)
for col in feat:
for i in range(len(train)):
token = str(train[col][i])[-1]
if train[col][i] == "NR":
# c. NR表示無降雨,以0取代
print(f' NR 表示無降雨 col: {col} index:{i}')
train[col][i] = '0'
elif pd.isnull(train[col][i]):
print(f' 空白 表示缺值 col: {col} index:{i}')
elif token =='*':
print(f' * 表示程式檢核為無效值 col: {col} index:{i}')
elif token =='#':
print(f' # 表示儀器檢核為無效值 col: {col} index:{i}')
elif token == 'A':
print(f' A 係指因儀器疑似故障警報所產生的無效值 col: {col} index:{i}')
elif token == 'x':
if col != '測項':
print(f' x 表示人工檢核為無效值 col: {col} index:{i}')
# 表示儀器檢核為無效值,* 表示程式檢核為無效值,x 表示人工檢核為無效值,NR 表示無降雨,空白 表示缺值
#,A 係指因儀器疑似故障警報所產生的無效值。
feat = train.columns
print(feat)
for col in feat:
for i in range(len(train)):
token = str(train[col][i])[-1]
if train[col][i] == "NR":
train[col][i] = '0'
elif pd.isnull(train[col][i]):
train[col][i] = str((get_last(col, i) + get_next(col, i)) / 2)
elif token =='*':
train[col][i] = str((get_last(col, i) + get_next(col, i)) / 2)
elif token =='A':
train[col][i] = str((get_last(col, i) + get_next(col, i)) / 2)
elif token =='#':
train[col][i] = str((get_last(col, i) + get_next(col, i)) / 2)
elif token == 'x':
if col != '測項':
train[col][i] = str((get_last(col, i) + get_next(col, i)) / 2)
month_slice = train['日期'].apply(lambda x: int(x[5:7]))
# Truth value of a Series is ambiguous. Use a.empty, a.bool(), a.item(), a.any() or a.all()
df_train = train[(month_slice < 12) & (month_slice > 9)].reset_index(drop=True)
df_test = train[ month_slice == 12].reset_index(drop=True)
# kill 日期測站測項
df_train.drop(columns=['日期', '測站', '測項'], axis=1, inplace=True)
df_test.drop(columns=['日期', '測站', '測項'], axis=1, inplace=True)
df_train = np.array(df_train).reshape(18, -1)
df_test = np.array(df_test).reshape(18, -1)
df_test.shape
# test_item = list(train['測項'][0:18])
# time_list = list(np.arange('2018-10-01', '2018-12-01', dtype='datetime64[h]'))
# df_train = pd.DataFrame(data=df_train, index=test_item, columns=time_list)
x_train_list=[]
y_train_list=[]
for i in range(0, df_train.shape[1]-6):
x_train_list.append(df_train[:, i:i+6])
for i in range(0, df_test.shape[1]-6):
y_train_list.append(df_test[:, i:i+6])
len(x_train_list)
len(y_train_list)
x_train_list_np = np.array(x_train_list).reshape(1458, -1)
y_train_list_np = np.array(y_train_list).reshape(738, -1)
from sklearn.linear_model import LinearRegression
x_train = x_train_list_np
y_train = df_train[9][6:]
lr = LinearRegression()
lr.fit(x_train, y_train)
x_test = y_train_list_np
pred = lr.predict(x_test)
x_test.shape
from sklearn import metrics
pred.shape
df_test[9][6:].shape
metrics.mean_squared_error(pred, df_test[9][6:])
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
c = np.concatenate((a,b), axis=1)
c
```
| github_jupyter |
```
### MODULE 1
### Basic Modeling in scikit-learn
```
```
### Seen vs. unseen data
# The model is fit using X_train and y_train
model.fit(X_train, y_train)
# Create vectors of predictions
train_predictions = model.predict(X_train)
test_predictions = model.predict(X_test)
# Train/Test Errors
train_error = mae(y_true=y_train, y_pred=train_predictions)
test_error = mae(y_true=y_test, y_pred=test_predictions)
# Print the accuracy for seen and unseen data
print("Model error on seen data: {0:.2f}.".format(train_error))
print("Model error on unseen data: {0:.2f}.".format(test_error))
# Set parameters and fit a model
# Set the number of trees
rfr.n_estimators = 1000
# Add a maximum depth
rfr.max_depth = 6
# Set the random state
rfr.random_state = 11
# Fit the model
rfr.fit(X_train, y_train)
## Feature importances
# Fit the model using X and y
rfr.fit(X_train, y_train)
# Print how important each column is to the model
for i, item in enumerate(rfr.feature_importances_):
# Use i and item to print out the feature importance of each column
print("{0:s}: {1:.2f}".format(X_train.columns[i], item))
### lassification predictions
# Fit the rfc model.
rfc.fit(X_train, y_train)
# Create arrays of predictions
classification_predictions = rfc.predict(X_test)
probability_predictions = rfc.predict_proba(X_test)
# Print out count of binary predictions
print(pd.Series(classification_predictions).value_counts())
# Print the first value from probability_predictions
print('The first predicted probabilities are: {}'.format(probability_predictions[0]))
## Reusing model parameters
rfc = RandomForestClassifier(n_estimators=50, max_depth=6, random_state=1111)
# Print the classification model
print(rfc)
# Print the classification model's random state parameter
print('The random state is: {}'.format(rfc.random_state))
# Print all parameters
print('Printing the parameters dictionary: {}'.format(rfc.get_params()))
## Random forest classifier
from sklearn.ensemble import RandomForestClassifier
# Create a random forest classifier
rfc = RandomForestClassifier(n_estimators=50, max_depth=6, random_state=1111)
# Fit rfc using X_train and y_train
rfc.fit(X_train, y_train)
# Create predictions on X_test
predictions = rfc.predict(X_test)
print(predictions[0:5])
# Print model accuracy using score() and the testing data
print(rfc.score(X_test, y_test))
## MODULE 2
## Validation Basics
```
```
## Create one holdout set
# Create dummy variables using pandas
X = pd.get_dummies(tic_tac_toe.iloc[:,0:9])
y = tic_tac_toe.iloc[:, 9]
# Create training and testing datasets. Use 10% for the test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.1, random_state=1111)
## Create two holdout sets
# Create temporary training and final testing datasets
X_temp, X_test, y_temp, y_test =\
train_test_split(X, y, test_size=.2, random_state=1111)
# Create the final training and validation datasets
X_train, X_val, y_train, y_val = train_test_split(X_temp, y_temp, test_size=.25, random_state=1111)
### Mean absolute error
from sklearn.metrics import mean_absolute_error
# Manually calculate the MAE
n = len(predictions)
mae_one = sum(abs(y_test - predictions)) / n
print('With a manual calculation, the error is {}'.format(mae_one))
# Use scikit-learn to calculate the MAE
mae_two = mean_absolute_error(y_test, predictions)
print('Using scikit-lean, the error is {}'.format(mae_two))
# <script.py> output:
# With a manual calculation, the error is 5.9
# Using scikit-lean, the error is 5.9
### Mean squared error
from sklearn.metrics import mean_squared_error
n = len(predictions)
# Finish the manual calculation of the MSE
mse_one = sum(abs(y_test - predictions)**2) / n
print('With a manual calculation, the error is {}'.format(mse_one))
# Use the scikit-learn function to calculate MSE
mse_two = mean_squared_error(y_test, predictions)
print('Using scikit-lean, the error is {}'.format(mse_two))
### Performance on data subsets
# Find the East conference teams
east_teams = labels == "E"
# Create arrays for the true and predicted values
true_east = y_test[east_teams]
preds_east = predictions[east_teams]
# Print the accuracy metrics
print('The MAE for East teams is {}'.format(
mae(true_east, preds_east)))
# Print the West accuracy
print('The MAE for West conference is {}'.format(west_error))
### Confusion matrices
# Calculate and print the accuracy
accuracy = (324 + 491) / (953)
print("The overall accuracy is {0: 0.2f}".format(accuracy))
# Calculate and print the precision
precision = (491) / (491 + 15)
print("The precision is {0: 0.2f}".format(precision))
# Calculate and print the recall
recall = (491) / (491 + 123)
print("The recall is {0: 0.2f}".format(recall))
### Confusion matrices, again
from sklearn.metrics import confusion_matrix
# Create predictions
test_predictions = rfc.predict(X_test)
# Create and print the confusion matrix
cm = confusion_matrix(y_test, test_predictions)
print(cm)
# Print the true positives (actual 1s that were predicted 1s)
print("The number of true positives is: {}".format(cm[1, 1]))
## <script.py> output:
## [[177 123]
## [ 92 471]]
## The number of true positives is: 471
## Row 1, column 1 represents the number of actual 1s that were predicted 1s (the true positives).
## Always make sure you understand the orientation of the confusion matrix before you start using it!
### Precision vs. recall
from sklearn.metrics import precision_score
test_predictions = rfc.predict(X_test)
# Create precision or recall score based on the metric you imported
score = precision_score(y_test, test_predictions)
# Print the final result
print("The precision value is {0:.2f}".format(score))
### Error due to under/over-fitting
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=2)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.88
## The testing error is 9.15
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=11)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.57
## The testing error is 10.05
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=4)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.60
## The testing error is 8.79
### Am I underfitting?
from sklearn.metrics import accuracy_score
test_scores, train_scores = [], []
for i in [1, 2, 3, 4, 5, 10, 20, 50]:
rfc = RandomForestClassifier(n_estimators=i, random_state=1111)
rfc.fit(X_train, y_train)
# Create predictions for the X_train and X_test datasets.
train_predictions = rfc.predict(X_train)
test_predictions = rfc.predict(X_test)
# Append the accuracy score for the test and train predictions.
train_scores.append(round(accuracy_score(y_train, train_predictions), 2))
test_scores.append(round(accuracy_score(y_test, test_predictions), 2))
# Print the train and test scores.
print("The training scores were: {}".format(train_scores))
print("The testing scores were: {}".format(test_scores))
### MODULE 3
### Cross Validation
```
```
### Two samples
# Create two different samples of 200 observations
sample1 = tic_tac_toe.sample(200, random_state=1111)
sample2 = tic_tac_toe.sample(200, random_state=1171)
# Print the number of common observations
print(len([index for index in sample1.index if index in sample2.index]))
# Print the number of observations in the Class column for both samples
print(sample1['Class'].value_counts())
print(sample2['Class'].value_counts())
### scikit-learn's KFold()
from sklearn.model_selection import KFold
# Use KFold
kf = KFold(n_splits=5, shuffle=True, random_state=1111)
# Create splits
splits = kf.split(X)
# Print the number of indices
for train_index, val_index in splits:
print("Number of training indices: %s" % len(train_index))
print("Number of validation indices: %s" % len(val_index))
### Using KFold indices
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
rfc = RandomForestRegressor(n_estimators=25, random_state=1111)
# Access the training and validation indices of splits
for train_index, val_index in splits:
# Setup the training and validation data
X_train, y_train = X[train_index], y[train_index]
X_val, y_val = X[val_index], y[val_index]
# Fit the random forest model
rfc.fit(X_train, y_train)
# Make predictions, and print the accuracy
predictions = rfc.predict(X_val)
print("Split accuracy: " + str(mean_squared_error(y_val, predictions)))
### scikit-learn's methods
# Instruction 1: Load the cross-validation method
from sklearn.model_selection import cross_val_score
# Instruction 2: Load the random forest regression model
from sklearn.ensemble import RandomForestClassifier
# Instruction 3: Load the mean squared error method
# Instruction 4: Load the function for creating a scorer
from sklearn.metrics import mean_squared_error, make_scorer
## It is easy to see how all of the methods can get mixed up, but
## it is important to know the names of the methods you need.
## You can always review the scikit-learn documentation should you need any help
### Implement cross_val_score()
rfc = RandomForestRegressor(n_estimators=25, random_state=1111)
mse = make_scorer(mean_squared_error)
# Set up cross_val_score
cv = cross_val_score(estimator=rfc,
X=X_train,
y=y_train,
cv=10,
scoring=mse)
# Print the mean error
print(cv.mean())
### Leave-one-out-cross-validation
from sklearn.metrics import mean_absolute_error, make_scorer
# Create scorer
mae_scorer = make_scorer(mean_absolute_error)
rfr = RandomForestRegressor(n_estimators=15, random_state=1111)
# Implement LOOCV
scores = cross_val_score(estimator=rfr, X=X, y=y, cv=85, scoring=mae_scorer)
# Print the mean and standard deviation
print("The mean of the errors is: %s." % np.mean(scores))
print("The standard deviation of the errors is: %s." % np.std(scores))
### MODULE 4
### Selecting the best model with Hyperparameter tuning.
```
```
### Creating Hyperparameters
# Review the parameters of rfr
print(rfr.get_params())
# Maximum Depth
max_depth = [4, 8, 12]
# Minimum samples for a split
min_samples_split = [2, 5, 10]
# Max features
max_features = [4, 6, 8, 10]
### Running a model using ranges
from sklearn.ensemble import RandomForestRegressor
# Fill in rfr using your variables
rfr = RandomForestRegressor(
n_estimators=100,
max_depth=random.choice(max_depth),
min_samples_split=random.choice(min_samples_split),
max_features=random.choice(max_features))
# Print out the parameters
print(rfr.get_params())
### Preparing for RandomizedSearch
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import make_scorer, mean_squared_error
# Finish the dictionary by adding the max_depth parameter
param_dist = {"max_depth": [2, 4, 6, 8],
"max_features": [2, 4, 6, 8, 10],
"min_samples_split": [2, 4, 8, 16]}
# Create a random forest regression model
rfr = RandomForestRegressor(n_estimators=10, random_state=1111)
# Create a scorer to use (use the mean squared error)
scorer = make_scorer(mean_squared_error)
# Import the method for random search
from sklearn.model_selection import RandomizedSearchCV
# Build a random search using param_dist, rfr, and scorer
random_search =\
RandomizedSearchCV(
estimator=rfr,
param_distributions=param_dist,
n_iter=10,
cv=5,
scoring=scorer)
### Selecting the best precision model
from sklearn.metrics import precision_score, make_scorer
# Create a precision scorer
precision = make_scorer(precision_score)
# Finalize the random search
rs = RandomizedSearchCV(
estimator=rfc, param_distributions=param_dist,
scoring = precision,
cv=5, n_iter=10, random_state=1111)
rs.fit(X, y)
# print the mean test scores:
print('The accuracy for each run was: {}.'.format(rs.cv_results_['mean_test_score']))
# print the best model score:
print('The best accuracy for a single model was: {}'.format(rs.best_score_))
```
| github_jupyter |
# Goals
### Learn how to change train validation splits
# Table of Contents
## [0. Install](#0)
## [1. Load experiment with defaut transforms](#1)
## [2. Reset Transforms andapply new transforms](#2)
<a id='0'></a>
# Install Monk
- git clone https://github.com/Tessellate-Imaging/monk_v1.git
- cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
- (Select the requirements file as per OS and CUDA version)
```
!git clone https://github.com/Tessellate-Imaging/monk_v1.git
# Select the requirements file as per OS and CUDA version
!cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
```
## Dataset - Broad Leaved Dock Image Classification
- https://www.kaggle.com/gavinarmstrong/open-sprayer-images
```
! wget --load-cookies /tmp/cookies.txt "https://docs.google.com/uc?export=download&confirm=$(wget --save-cookies /tmp/cookies.txt --keep-session-cookies --no-check-certificate 'https://docs.google.com/uc?export=download&id=1uL-VV4nV_u0kry3gLH1TATUTu8hWJ0_d' -O- | sed -rn 's/.*confirm=([0-9A-Za-z_]+).*/\1\n/p')&id=1uL-VV4nV_u0kry3gLH1TATUTu8hWJ0_d" -O open_sprayer_images.zip && rm -rf /tmp/cookies.txt
! unzip -qq open_sprayer_images.zip
```
# Imports
```
# Monk
import os
import sys
sys.path.append("monk_v1/monk/");
#Using mxnet-gluon backend
from gluon_prototype import prototype
```
<a id='1'></a>
# Load experiment with default transforms
```
gtf = prototype(verbose=1);
gtf.Prototype("project", "understand_transforms");
gtf.Default(dataset_path="open_sprayer_images/train",
model_name="resnet18_v1",
freeze_base_network=True,
num_epochs=5);
#Read the summary generated once you run this cell.
```
## Default Transforms are
Train Transforms
{'RandomHorizontalFlip': {'p': 0.8}},
{'Normalize': {'mean': [0.485, 0.456, 0.406], 'std': [0.229, 0.224, 0.225]}}]
Val Transforms
{'RandomHorizontalFlip': {'p': 0.8}},
{'Normalize': {'mean': [0.485, 0.456, 0.406], 'std': [0.229, 0.224, 0.225]}}
In that order
<a id='2'></a>
# Reset transforms
```
# Reset train and validation transforms
gtf.reset_transforms();
# Reset test transforms
gtf.reset_transforms(test=True);
```
## Apply new transforms
```
gtf.List_Transforms();
# Transform applied to only train and val
gtf.apply_center_crop(224,
train=True,
val=True,
test=False)
# Transform applied to all train, val and test
gtf.apply_normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225],
train=True,
val=True,
test=True
)
# Very important to reload post update
gtf.Reload();
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
import sklearn
from sklearn.ensemble import RandomForestClassifier
import catboost as cat
from catboost import CatBoostClassifier
from sklearn import preprocessing
import sklearn.model_selection as ms
from sklearn.model_selection import GridSearchCV, KFold, StratifiedKFold
from sklearn.metrics import log_loss, confusion_matrix, accuracy_score
import xgboost as xgb
import lightgbm as lgb
def fill_missing_values(data):
'''
Function to input missing values based on the column object type
'''
cols = list(data.columns)
for col in cols:
if data[col].dtype == 'int64' or data[col].dtype == 'float64':
data[col] = data[col].fillna(data[col].mean())
#elif data[col].dtype == 'O' or data[col].dtype == 'object':
# data[col] = data[col].fillna(data[col].mode()[0])
else:
data[col] = data[col].fillna(data[col].mode()[0])
return data
def one_hot_encoding(traindata, *args):
for ii in args:
traindata = pd.get_dummies(traindata, prefix=[ii], columns=[ii])
return traindata
def drop_columns(traindata, *args):
#labels = np.array(traindata[target])
columns = []
for _ in args:
columns.append(_)
traindata = traindata.drop(columns, axis=1)
#traindata = traindata.drop(target, axis=1)
#testdata = testdata.drop(columns, axis=1)
return traindata
def process(traindata):
cols = list(traindata.columns)
for _ in cols:
traindata[_] = np.where(traindata[_] == np.inf, -999, traindata[_])
traindata[_] = np.where(traindata[_] == np.nan, -999, traindata[_])
traindata[_] = np.where(traindata[_] == -np.inf, -999, traindata[_])
return traindata
def show_evaluation(pred, true):
print(f'Default score: {score(true.values, pred)}')
print(f'Accuracy is: {accuracy_score(true, pred)}')
print(f'F1 is: {f1_score(pred, true.values, average="weighted")}')
def freq_encode(data, cols):
for i in cols:
encoding = data.groupby(i).size()
encoding = encoding/len(data)
data[i + '_enc'] = data[i].map(encoding)
return data
def mean_target(data, cols):
kf = KFold(5)
a = pd.DataFrame()
for tr_ind, val_ind in kf.split(data):
X_tr, X_val= data.iloc[tr_ind].copy(), data.iloc[val_ind].copy()
for col in cols:
means = X_val[col].map(X_tr.groupby(col).FORCE_2020_LITHOFACIES_LITHOLOGY.mean())
X_val[col + '_mean_target'] = means + 0.0001
a = pd.concat((a, X_val))
#prior = FORCE_2020_LITHOFACIES_LITHOLOGY.mean()
#a.fillna(prior, inplace=True)
return a
def make_submission(prediction, filename):
path = './'
test = pd.read_csv('./Test.csv', sep=';')
#test_prediction = model.predict(testdata)
#test_prediction
category_to_lithology = {y:x for x,y in lithology_numbers.items()}
test_prediction_for_submission = np.vectorize(category_to_lithology.get)(prediction)
np.savetxt(path+filename+'.csv', test_prediction_for_submission, header='lithology', fmt='%i')
A = np.load('penalty_matrix.npy')
def score(y_true, y_pred):
S = 0.0
y_true = y_true.astype(int)
y_pred = y_pred.astype(int)
for i in range(0, y_true.shape[0]):
S -= A[y_true[i], y_pred[i]]
return S/y_true.shape[0]
def evaluate(model, prediction, true_label):
feat_imp = pd.Series(model.feature_importances_).sort_values(ascending=False)
plt.figure(figsize=(12,8))
feat_imp.plot(kind='bar', title=f'Feature Importances {len(model.feature_importances_)}')
plt.ylabel('Feature Importance Score')
#importing files
train = pd.read_csv('Train.csv', sep=';')
test = pd.read_csv('Test.csv', sep=';')
ntrain = train.shape[0]
ntest = test.shape[0]
target = train.FORCE_2020_LITHOFACIES_LITHOLOGY.copy()
df = pd.concat((train, test)).reset_index(drop=True)
plt.scatter(train.X_LOC, train.Y_LOC)
plt.scatter(test.X_LOC, test.Y_LOC)
test.describe()
train.describe()
train.WELL.value_counts()
test.WELL.value_counts()
#importing files
train = pd.read_csv('Train.csv', sep=';')
test = pd.read_csv('Test.csv', sep=';')
ntrain = train.shape[0]
ntest = test.shape[0]
target = train.FORCE_2020_LITHOFACIES_LITHOLOGY.copy()
df = pd.concat((train, test)).reset_index(drop=True)
lithology = train['FORCE_2020_LITHOFACIES_LITHOLOGY']
lithology_numbers = {30000: 0,
65030: 1,
65000: 2,
80000: 3,
74000: 4,
70000: 5,
70032: 6,
88000: 7,
86000: 8,
99000: 9,
90000: 10,
93000: 11}
lithology = lithology.map(lithology_numbers)
np.array(lithology)
test.describe()
train.describe()
(train.isna().sum()/train.shape[0]) * 100
(df.isna().sum()/df.shape[0]) * 100
(df.WELL.value_counts()/df.WELL.shape[0]) * 100
print(df.shape)
cols = ['FORCE_2020_LITHOFACIES_CONFIDENCE', 'SGR',
'DTS', 'DCAL', 'MUDWEIGHT', 'RMIC', 'ROPA', 'RXO']
df = drop_columns(df, *cols)
print(df.shape)
train.FORMATION.value_counts()
train.WELL.value_counts()
one_hot_cols = ['GROUP']
df = one_hot_encoding(df, *one_hot_cols)
print(df.shape)
df = freq_encode(df, ['FORMATION','WELL'])
df = df.copy()
print(df.shape)
#df.isna().sum()
df = mean_target(df, ['FORMATION', 'WELL'])
df.shape
df = df.drop(['FORMATION', 'WELL'], axis=1)
df.shape
df = df.fillna(-999)
data = df.copy()
train2 = data[:ntrain].copy()
target = train2.FORCE_2020_LITHOFACIES_LITHOLOGY.copy()
train2.drop(['FORCE_2020_LITHOFACIES_LITHOLOGY'], axis=1, inplace=True)
test2 = data[ntrain:].copy()
test2.drop(['FORCE_2020_LITHOFACIES_LITHOLOGY'], axis=1, inplace=True)
test2 = test2.reset_index(drop=True)
train2.shape, train.shape, test.shape, test2.shape
traindata = train2
testdata = test2
#using StandardScaler function to scale the numeric features
scaler = preprocessing.StandardScaler().fit(traindata)
traindata = pd.DataFrame(scaler.transform(traindata))
traindata.head()
testdata = pd.DataFrame(scaler.transform(testdata))
testdata.head()
class Model():
def __init__(self, train, test, label):
self.train = train
self.test = test
self.label = label
def __call__(self, plot = True):
return self.fit(plot)
def fit(self, plot):
#SPLIT ONE
self.x_train, self.x_test, self.y_train, self.y_test = ms.train_test_split(self.train,
pd.DataFrame(np.array(self.label)),
test_size=0.25,
random_state=42)
#SPLIT TWO
self.x_test1, self.x_test2, self.y_test1, self.y_test2 = ms.train_test_split(self.x_test,
self.y_test,
test_size=0.5,
random_state=42)
lgbm = CatBoostClassifier(n_estimators=15, max_depth=6,
random_state=42, learning_rate=0.033,
use_best_model=True, task_type='CPU',
eval_metric='MultiClass')
def show_evaluation(pred, true):
print(f'Default score: {score(true.values, pred)}')
print(f'Accuracy is: {accuracy_score(true, pred)}')
print(f'F1 is: {f1_score(pred, true.values, average="weighted")}')
split = 3
kf = StratifiedKFold(n_splits=split, shuffle=False)
#TEST DATA
pred_test = np.zeros((len(self.x_test1), 12))
pred_val = np.zeros((len(self.x_test2), 12))
pred_val = np.zeros((len(self.test), 12))
for (train_index, test_index) in kf.split(pd.DataFrame(self.x_train), pd.DataFrame(self.y_train)):
X_train,X_test = pd.DataFrame(self.x_train).iloc[train_index], pd.DataFrame(self.x_train).iloc[test_index]
y_train,y_test = pd.DataFrame(self.y_train).iloc[train_index],pd.DataFrame(self.y_train).iloc[test_index]
lgbm.fit(X_train, y_train, early_stopping_rounds=2, eval_set=[(X_test,y_test)])
#scores.append(metric(lgbm.predict_proba(X_test),y_test))
pred_test+=lgbm.predict_proba(self.x_test1)
pred_val+=lgbm.predict_proba(self.x_test2)
open_test_pred+=lgbm.predict_proba(self.test)
pred_test_avg = pred_test/split
pred_val_avg = pred_test/split
print('----------------TEST EVALUATION------------------')
show_evaluation(pred_test_avg, self.y_test1)
print('----------------HOLD OUT EVALUATION------------------')
show_evaluation(pred_val_avg, self.y_test2)
if plot: self.plot_feat_imp(model)
return open_test_pred, lgbm
def plot_feat_imp(self, model):
feat_imp = pd.Series(model.get_fscore()).sort_values(ascending=False)
plt.figure(figsize=(12,8))
feat_imp.plot(kind='bar', title='Feature Importances')
plt.ylabel('Feature Importance Score')
func_= Model(traindata, testdata, lithology)
val_p2, test_p2, model2 = func_()
pd.DataFrame(lithology)
i, j = Model(df, test, lithology)
params = {'n_estimators': 3000,
'max_depth': 6,
'learning_rate': 0.033,
'verbose': 2}
a = Model(train, test, 'FORCE_2020_LITHOFACIES_LITHOLOGY', 0.3, params)
```
| github_jupyter |
# Dataproc - Submit Hadoop Job
## Intended Use
A Kubeflow Pipeline component to submit a Apache Hadoop MapReduce job on Apache Hadoop YARN in Google Cloud Dataproc service.
## Run-Time Parameters:
Name | Description
:--- | :----------
project_id | Required. The ID of the Google Cloud Platform project that the cluster belongs to.
region | Required. The Cloud Dataproc region in which to handle the request.
cluster_name | Required. The cluster to run the job.
main_jar_file_uri | The HCFS URI of the jar file containing the main class. Examples: `gs://foo-bucket/analytics-binaries/extract-useful-metrics-mr.jar` `hdfs:/tmp/test-samples/custom-wordcount.jar` `file:///home/usr/lib/hadoop-mapreduce/hadoop-mapreduce-examples.jar`
main_class | The name of the driver's main class. The jar file that contains the class must be in the default CLASSPATH or specified in jarFileUris.
args | Optional. The arguments to pass to the driver. Do not include arguments, such as -libjars or -Dfoo=bar, that can be set as job properties, since a collision may occur that causes an incorrect job submission.
hadoop_job | Optional. The full payload of a [HadoopJob](https://cloud.google.com/dataproc/docs/reference/rest/v1/HadoopJob).
job | Optional. The full payload of a [Dataproc job](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs).
wait_interval | Optional. The wait seconds between polling the operation. Defaults to 30s.
## Output:
Name | Description
:--- | :----------
job_id | The ID of the created job.
## Sample
Note: the sample code below works in both IPython notebook or python code directly.
### Setup a Dataproc cluster
Follow the [guide](https://cloud.google.com/dataproc/docs/guides/create-cluster) to create a new Dataproc cluster or reuse an existing one.
### Prepare Hadoop job
Upload your Hadoop jar file to a Google Cloud Storage (GCS) bucket. In the sample, we will use a jar file that is pre-installed in the main cluster, so there is no need to provide the `main_jar_file_uri`. We only set `main_class` to be `org.apache.hadoop.examples.WordCount`.
Here is the [source code of example](https://github.com/apache/hadoop/blob/trunk/hadoop-mapreduce-project/hadoop-mapreduce-examples/src/main/java/org/apache/hadoop/examples/WordCount.java).
To package a self-contained Hadoop MapReduct application from source code, follow the [instructions](https://hadoop.apache.org/docs/current/hadoop-mapreduce-client/hadoop-mapreduce-client-core/MapReduceTutorial.html).
### Set sample parameters
```
PROJECT_ID = '<Please put your project ID here>'
CLUSTER_NAME = '<Please put your existing cluster name here>'
OUTPUT_GCS_PATH = '<Please put your output GCS path here>'
REGION = 'us-central1'
MAIN_CLASS = 'org.apache.hadoop.examples.WordCount'
INTPUT_GCS_PATH = 'gs://ml-pipeline-playground/shakespeare1.txt'
EXPERIMENT_NAME = 'Dataproc - Submit Hadoop Job'
COMPONENT_SPEC_URI = 'https://raw.githubusercontent.com/kubeflow/pipelines/7622e57666c17088c94282ccbe26d6a52768c226/components/gcp/dataproc/submit_hadoop_job/component.yaml'
```
### Insepct Input Data
The input file is a simple text file:
```
!gsutil cat $INTPUT_GCS_PATH
```
### Clean up existing output files (Optional)
This is needed because the sample code requires the output folder to be a clean folder.
To continue to run the sample, make sure that the service account of the notebook server has access to the `OUTPUT_GCS_PATH`.
**CAUTION**: This will remove all blob files under `OUTPUT_GCS_PATH`.
```
!gsutil rm $OUTPUT_GCS_PATH/**
```
### Install KFP SDK
Install the SDK (Uncomment the code if the SDK is not installed before)
```
# KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.12/kfp.tar.gz'
# !pip3 install $KFP_PACKAGE --upgrade
```
### Load component definitions
```
import kfp.components as comp
dataproc_submit_hadoop_job_op = comp.load_component_from_url(COMPONENT_SPEC_URI)
display(dataproc_submit_hadoop_job_op)
```
### Here is an illustrative pipeline that uses the component
```
import kfp.dsl as dsl
import kfp.gcp as gcp
import json
@dsl.pipeline(
name='Dataproc submit Hadoop job pipeline',
description='Dataproc submit Hadoop job pipeline'
)
def dataproc_submit_hadoop_job_pipeline(
project_id = PROJECT_ID,
region = REGION,
cluster_name = CLUSTER_NAME,
main_jar_file_uri = '',
main_class = MAIN_CLASS,
args = json.dumps([
INTPUT_GCS_PATH,
OUTPUT_GCS_PATH
]),
hadoop_job='',
job='{}',
wait_interval='30'
):
dataproc_submit_hadoop_job_op(project_id, region, cluster_name, main_jar_file_uri, main_class,
args, hadoop_job, job, wait_interval).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
### Compile the pipeline
```
pipeline_func = dataproc_submit_hadoop_job_pipeline
pipeline_filename = pipeline_func.__name__ + '.pipeline.tar.gz'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
```
### Submit the pipeline for execution
```
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
```
### Inspect the outputs
The sample in the notebook will count the words in the input text and output them in sharded files. Here is the command to inspect them:
```
!gsutil cat $OUTPUT_GCS_PATH/*
```
| github_jupyter |
# Random Variables
:label:`sec_random_variables`
In :numref:`sec_prob` we saw the basics of how to work with discrete random variables, which in our case refer to those random variables which take either a finite set of possible values, or the integers. In this section, we develop the theory of *continuous random variables*, which are random variables which can take on any real value.
## Continuous Random Variables
Continuous random variables are a significantly more subtle topic than discrete random variables. A fair analogy to make is that the technical jump is comparable to the jump between adding lists of numbers and integrating functions. As such, we will need to take some time to develop the theory.
### From Discrete to Continuous
To understand the additional technical challenges encountered when working with continuous random variables, let us perform a thought experiment. Suppose that we are throwing a dart at the dart board, and we want to know the probability that it hits exactly $2 \text{cm}$ from the center of the board.
To start with, we imagine measuring a single digit of accuracy, that is to say with bins for $0 \text{cm}$, $1 \text{cm}$, $2 \text{cm}$, and so on. We throw say $100$ darts at the dart board, and if $20$ of them fall into the bin for $2\text{cm}$ we conclude that $20\%$ of the darts we throw hit the board $2 \text{cm}$ away from the center.
However, when we look closer, this does not match our question! We wanted exact equality, whereas these bins hold all that fell between say $1.5\text{cm}$ and $2.5\text{cm}$.
Undeterred, we continue further. We measure even more precisely, say $1.9\text{cm}$, $2.0\text{cm}$, $2.1\text{cm}$, and now see that perhaps $3$ of the $100$ darts hit the board in the $2.0\text{cm}$ bucket. Thus we conclude the probability is $3\%$.
However, this does not solve anything! We have just pushed the issue down one digit further. Let us abstract a bit. Imagine we know the probability that the first $k$ digits match with $2.00000\ldots$ and we want to know the probability it matches for the first $k+1$ digits. It is fairly reasonable to assume that the ${k+1}^{\mathrm{th}}$ digit is essentially a random choice from the set $\{0, 1, 2, \ldots, 9\}$. At least, we cannot conceive of a physically meaningful process which would force the number of micrometers away form the center to prefer to end in a $7$ vs a $3$.
What this means is that in essence each additional digit of accuracy we require should decrease probability of matching by a factor of $10$. Or put another way, we would expect that
$$
P(\text{distance is}\; 2.00\ldots, \;\text{to}\; k \;\text{digits} ) \approx p\cdot10^{-k}.
$$
The value $p$ essentially encodes what happens with the first few digits, and the $10^{-k}$ handles the rest.
Notice that if we know the position accurate to $k=4$ digits after the decimal. that means we know the value falls within the interval say $[(1.99995,2.00005]$ which is an interval of length $2.00005-1.99995 = 10^{-4}$. Thus, if we call the length of this interval $\epsilon$, we can say
$$
P(\text{distance is in an}\; \epsilon\text{-sized interval around}\; 2 ) \approx \epsilon \cdot p.
$$
Let us take this one final step further. We have been thinking about the point $2$ the entire time, but never thinking about other points. Nothing is different there fundamentally, but it is the case that the value $p$ will likely be different. We would at least hope that a dart thrower was more likely to hit a point near the center, like $2\text{cm}$ rather than $20\text{cm}$. Thus, the value $p$ is not fixed, but rather should depend on the point $x$. This tells us that we should expect
$$P(\text{distance is in an}\; \epsilon \text{-sized interval around}\; x ) \approx \epsilon \cdot p(x).$$
:eqlabel:`eq_pdf_deriv`
Indeed, :eqref:`eq_pdf_deriv` precisely defines the *probability density function*. It is a function $p(x)$ which encodes the relative probability of hitting near one point vs. another. Let us visualize what such a function might look like.
```
%matplotlib inline
from d2l import mxnet as d2l
from IPython import display
from mxnet import np, npx
npx.set_np()
# Plot the probability density function for some random variable
x = np.arange(-5, 5, 0.01)
p = 0.2*np.exp(-(x - 3)**2 / 2)/np.sqrt(2 * np.pi) + \
0.8*np.exp(-(x + 1)**2 / 2)/np.sqrt(2 * np.pi)
d2l.plot(x, p, 'x', 'Density')
```
The locations where the function value is large indicates regions where we are more likely to find the random value. The low portions are areas where we are unlikely to find the random value.
### Probability Density Functions
Let us now investigate this further. We have already seen what a probability density function is intuitively for a random variable $X$, namely the density function is a function $p(x)$ so that
$$P(X \; \text{is in an}\; \epsilon \text{-sized interval around}\; x ) \approx \epsilon \cdot p(x).$$
:eqlabel:`eq_pdf_def`
But what does this imply for the properties of $p(x)$?
First, probabilities are never negative, thus we should expect that $p(x) \ge 0$ as well.
Second, let us imagine that we slice up the $\mathbb{R}$ into an infinite number of slices which are $\epsilon$ wide, say with slices $(\epsilon\cdot i, \epsilon \cdot (i+1)]$. For each of these, we know from :eqref:`eq_pdf_def` the probability is approximately
$$
P(X \; \text{is in an}\; \epsilon\text{-sized interval around}\; x ) \approx \epsilon \cdot p(\epsilon \cdot i),
$$
so summed over all of them it should be
$$
P(X\in\mathbb{R}) \approx \sum_i \epsilon \cdot p(\epsilon\cdot i).
$$
This is nothing more than the approximation of an integral discussed in :numref:`sec_integral_calculus`, thus we can say that
$$
P(X\in\mathbb{R}) = \int_{-\infty}^{\infty} p(x) \; dx.
$$
We know that $P(X\in\mathbb{R}) = 1$, since the random variable must take on *some* number, we can conclude that for any density
$$
\int_{-\infty}^{\infty} p(x) \; dx = 1.
$$
Indeed, digging into this further shows that for any $a$, and $b$, we see that
$$
P(X\in(a, b]) = \int _ {a}^{b} p(x) \; dx.
$$
We may approximate this in code by using the same discrete approximation methods as before. In this case we can approximate the probability of falling in the blue region.
```
# Approximate probability using numerical integration
epsilon = 0.01
x = np.arange(-5, 5, 0.01)
p = 0.2*np.exp(-(x - 3)**2 / 2) / np.sqrt(2 * np.pi) + \
0.8*np.exp(-(x + 1)**2 / 2) / np.sqrt(2 * np.pi)
d2l.set_figsize()
d2l.plt.plot(x, p, color='black')
d2l.plt.fill_between(x.tolist()[300:800], p.tolist()[300:800])
d2l.plt.show()
f'approximate Probability: {np.sum(epsilon*p[300:800])}'
```
It turns out that these two properties describe exactly the space of possible probability density functions (or *p.d.f.*'s for the commonly encountered abbreviation). They are non-negative functions $p(x) \ge 0$ such that
$$\int_{-\infty}^{\infty} p(x) \; dx = 1.$$
:eqlabel:`eq_pdf_int_one`
We interpret this function by using integration to obtain the probability our random variable is in a specific interval:
$$P(X\in(a, b]) = \int _ {a}^{b} p(x) \; dx.$$
:eqlabel:`eq_pdf_int_int`
In :numref:`sec_distributions` we will see a number of common distributions, but let us continue working in the abstract.
### Cumulative Distribution Functions
In the previous section, we saw the notion of the p.d.f. In practice, this is a commonly encountered method to discuss continuous random variables, but it has one significant pitfall: that the values of the p.d.f. are not themselves probabilities, but rather a function that we must integrate to yield probabilities. There is nothing wrong with a density being larger than $10$, as long as it is not larger than $10$ for more than an interval of length $1/10$. This can be counter-intuitive, so people often also think in terms of the *cumulative distribution function*, or c.d.f., which *is* a probability.
In particular, by using :eqref:`eq_pdf_int_int`, we define the c.d.f. for a random variable $X$ with density $p(x)$ by
$$
F(x) = \int _ {-\infty}^{x} p(x) \; dx = P(X \le x).
$$
Let us observe a few properties.
* $F(x) \rightarrow 0$ as $x\rightarrow -\infty$.
* $F(x) \rightarrow 1$ as $x\rightarrow \infty$.
* $F(x)$ is non-decreasing ($y > x \implies F(y) \ge F(x)$).
* $F(x)$ is continuous (has no jumps) if $X$ is a continuous random variable.
With the fourth bullet point, note that this would not be true if $X$ were discrete, say taking the values $0$ and $1$ both with probability $1/2$. In that case
$$
F(x) = \begin{cases}
0 & x < 0, \\
\frac{1}{2} & x < 1, \\
1 & x \ge 1.
\end{cases}
$$
In this example, we see one of the benefits of working with the c.d.f., the ability to deal with continuous or discrete random variables in the same framework, or indeed mixtures of the two (flip a coin: if heads return the roll of a die, if tails return the distance of a dart throw from the center of a dart board).
### Means
Suppose that we are dealing with a random variables $X$. The distribution itself can be hard to interpret. It is often useful to be able to summarize the behavior of a random variable concisely. Numbers that help us capture the behavior of a random variable are called *summary statistics*. The most commonly encountered ones are the *mean*, the *variance*, and the *standard deviation*.
The *mean* encodes the average value of a random variable. If we have a discrete random variable $X$, which takes the values $x_i$ with probabilities $p_i$, then the mean is given by the weighted average: sum the values times the probability that the random variable takes on that value:
$$\mu_X = E[X] = \sum_i x_i p_i.$$
:eqlabel:`eq_exp_def`
The way we should interpret the mean (albeit with caution) is that it tells us essentially where the random variable tends to be located.
As a minimalistic example that we will examine throughout this section, let us take $X$ to be the random variable which takes the value $a-2$ with probability $p$, $a+2$ with probability $p$ and $a$ with probability $1-2p$. We can compute using :eqref:`eq_exp_def` that, for any possible choice of $a$ and $p$, the mean is
$$
\mu_X = E[X] = \sum_i x_i p_i = (a-2)p + a(1-2p) + (a+2)p = a.
$$
Thus we see that the mean is $a$. This matches the intuition since $a$ is the location around which we centered our random variable.
Because they are helpful, let us summarize a few properties.
* For any random variable $X$ and numbers $a$ and $b$, we have that $\mu_{aX+b} = a\mu_X + b$.
* If we have two random variables $X$ and $Y$, we have $\mu_{X+Y} = \mu_X+\mu_Y$.
Means are useful for understanding the average behavior of a random variable, however the mean is not sufficient to even have a full intuitive understanding. Making a profit of $\$10 \pm \$1$ per sale is very different from making $\$10 \pm \$15$ per sale despite having the same average value. The second one has a much larger degree of fluctuation, and thus represents a much larger risk. Thus, to understand the behavior of a random variable, we will need at minimum one more measure: some measure of how widely a random variable fluctuates.
### Variances
This leads us to consider the *variance* of a random variable. This is a quantitative measure of how far a random variable deviates from the mean. Consider the expression $X - \mu_X$. This is the deviation of the random variable from its mean. This value can be positive or negative, so we need to do something to make it positive so that we are measuring the magnitude of the deviation.
A reasonable thing to try is to look at $\left|X-\mu_X\right|$, and indeed this leads to a useful quantity called the *mean absolute deviation*, however due to connections with other areas of mathematics and statistics, people often use a different solution.
In particular, they look at $(X-\mu_X)^2.$ If we look at the typical size of this quantity by taking the mean, we arrive at the variance
$$\sigma_X^2 = \mathrm{Var}(X) = E\left[(X-\mu_X)^2\right] = E[X^2] - \mu_X^2.$$
:eqlabel:`eq_var_def`
The last equality in :eqref:`eq_var_def` holds by expanding out the definition in the middle, and applying the properties of expectation.
Let us look at our example where $X$ is the random variable which takes the value $a-2$ with probability $p$, $a+2$ with probability $p$ and $a$ with probability $1-2p$. In this case $\mu_X = a$, so all we need to compute is $E\left[X^2\right]$. This can readily be done:
$$
E\left[X^2\right] = (a-2)^2p + a^2(1-2p) + (a+2)^2p = a^2 + 8p.
$$
Thus, we see that by :eqref:`eq_var_def` our variance is
$$
\sigma_X^2 = \mathrm{Var}(X) = E[X^2] - \mu_X^2 = a^2 + 8p - a^2 = 8p.
$$
This result again makes sense. The largest $p$ can be is $1/2$ which corresponds to picking $a-2$ or $a+2$ with a coin flip. The variance of this being $4$ corresponds to the fact that both $a-2$ and $a+2$ are $2$ units away from the mean, and $2^2 = 4$. On the other end of the spectrum, if $p=0$, this random variable always takes the value $0$ and so it has no variance at all.
We will list a few properties of variance below:
* For any random variable $X$, $\mathrm{Var}(X) \ge 0$, with $\mathrm{Var}(X) = 0$ if and only if $X$ is a constant.
* For any random variable $X$ and numbers $a$ and $b$, we have that $\mathrm{Var}(aX+b) = a^2\mathrm{Var}(X)$.
* If we have two *independent* random variables $X$ and $Y$, we have $\mathrm{Var}(X+Y) = \mathrm{Var}(X) + \mathrm{Var}(Y)$.
When interpreting these values, there can be a bit of a hiccup. In particular, let us try imagining what happens if we keep track of units through this computation. Suppose that we are working with the star rating assigned to a product on the web page. Then $a$, $a-2$, and $a+2$ are all measured in units of stars. Similarly, the mean $\mu_X$ is then also measured in stars (being a weighted average). However, if we get to the variance, we immediately encounter an issue, which is we want to look at $(X-\mu_X)^2$, which is in units of *squared stars*. This means that the variance itself is not comparable to the original measurements. To make it interpretable, we will need to return to our original units.
### Standard Deviations
This summary statistics can always be deduced from the variance by taking the square root! Thus we define the *standard deviation* to be
$$
\sigma_X = \sqrt{\mathrm{Var}(X)}.
$$
In our example, this means we now have the standard deviation is $\sigma_X = 2\sqrt{2p}$. If we are dealing with units of stars for our review example, $\sigma_X$ is again in units of stars.
The properties we had for the variance can be restated for the standard deviation.
* For any random variable $X$, $\sigma_{X} \ge 0$.
* For any random variable $X$ and numbers $a$ and $b$, we have that $\sigma_{aX+b} = |a|\sigma_{X}$
* If we have two *independent* random variables $X$ and $Y$, we have $\sigma_{X+Y} = \sqrt{\sigma_{X}^2 + \sigma_{Y}^2}$.
It is natural at this moment to ask, "If the standard deviation is in the units of our original random variable, does it represent something we can draw with regards to that random variable?" The answer is a resounding yes! Indeed much like the mean told we the typical location of our random variable, the standard deviation gives the typical range of variation of that random variable. We can make this rigorous with what is known as Chebyshev's inequality:
$$P\left(X \not\in [\mu_X - \alpha\sigma_X, \mu_X + \alpha\sigma_X]\right) \le \frac{1}{\alpha^2}.$$
:eqlabel:`eq_chebyshev`
Or to state it verbally in the case of $\alpha=10$, $99\%$ of the samples from any random variable fall within $10$ standard deviations of the mean. This gives an immediate interpretation to our standard summary statistics.
To see how this statement is rather subtle, let us take a look at our running example again where $X$ is the random variable which takes the value $a-2$ with probability $p$, $a+2$ with probability $p$ and $a$ with probability $1-2p$. We saw that the mean was $a$ and the standard deviation was $2\sqrt{2p}$. This means, if we take Chebyshev's inequality :eqref:`eq_chebyshev` with $\alpha = 2$, we see that the expression is
$$
P\left(X \not\in [a - 4\sqrt{2p}, a + 4\sqrt{2p}]\right) \le \frac{1}{4}.
$$
This means that $75\%$ of the time, this random variable will fall within this interval for any value of $p$. Now, notice that as $p \rightarrow 0$, this interval also converges to the single point $a$. But we know that our random variable takes the values $a-2, a$, and $a+2$ only so eventually we can be certain $a-2$ and $a+2$ will fall outside the interval! The question is, at what $p$ does that happen. So we want to solve: for what $p$ does $a+4\sqrt{2p} = a+2$, which is solved when $p=1/8$, which is *exactly* the first $p$ where it could possibly happen without violating our claim that no more than $1/4$ of samples from the distribution would fall outside the interval ($1/8$ to the left, and $1/8$ to the right).
Let us visualize this. We will show the probability of getting the three values as three vertical bars with height proportional to the probability. The interval will be drawn as a horizontal line in the middle. The first plot shows what happens for $p > 1/8$ where the interval safely contains all points.
```
# Define a helper to plot these figures
def plot_chebyshev(a, p):
d2l.set_figsize()
d2l.plt.stem([a-2, a, a+2], [p, 1-2*p, p], use_line_collection=True)
d2l.plt.xlim([-4, 4])
d2l.plt.xlabel('x')
d2l.plt.ylabel('p.m.f.')
d2l.plt.hlines(0.5, a - 4 * np.sqrt(2 * p),
a + 4 * np.sqrt(2 * p), 'black', lw=4)
d2l.plt.vlines(a - 4 * np.sqrt(2 * p), 0.53, 0.47, 'black', lw=1)
d2l.plt.vlines(a + 4 * np.sqrt(2 * p), 0.53, 0.47, 'black', lw=1)
d2l.plt.title(f'p = {p:.3f}')
d2l.plt.show()
# Plot interval when p > 1/8
plot_chebyshev(0.0, 0.2)
```
The second shows that at $p = 1/8$, the interval exactly touches the two points. This shows that the inequality is *sharp*, since no smaller interval could be taken while keeping the inequality true.
```
# Plot interval when p = 1/8
plot_chebyshev(0.0, 0.125)
```
The third shows that for $p < 1/8$ the interval only contains the center. This does not invalidate the inequality since we only needed to ensure that no more than $1/4$ of the probability falls outside the interval, which means that once $p < 1/8$, the two points at $a-2$ and $a+2$ can be discarded.
```
# Plot interval when p < 1/8
plot_chebyshev(0.0, 0.05)
```
### Means and Variances in the Continuum
This has all been in terms of discrete random variables, but the case of continuous random variables is similar. To intuitively understand how this works, imagine that we split the real number line into intervals of length $\epsilon$ given by $(\epsilon i, \epsilon (i+1)]$. Once we do this, our continuous random variable has been made discrete and we can use :eqref:`eq_exp_def` say that
$$
\begin{aligned}
\mu_X & \approx \sum_{i} (\epsilon i)P(X \in (\epsilon i, \epsilon (i+1)]) \\
& \approx \sum_{i} (\epsilon i)p_X(\epsilon i)\epsilon, \\
\end{aligned}
$$
where $p_X$ is the density of $X$. This is an approximation to the integral of $xp_X(x)$, so we can conclude that
$$
\mu_X = \int_{-\infty}^\infty xp_X(x) \; dx.
$$
Similarly, using :eqref:`eq_var_def` the variance can be written as
$$
\sigma^2_X = E[X^2] - \mu_X^2 = \int_{-\infty}^\infty x^2p_X(x) \; dx - \left(\int_{-\infty}^\infty xp_X(x) \; dx\right)^2.
$$
Everything stated above about the mean, the variance, and the standard deviation still applies in this case. For instance, if we consider the random variable with density
$$
p(x) = \begin{cases}
1 & x \in [0,1], \\
0 & \text{otherwise}.
\end{cases}
$$
we can compute
$$
\mu_X = \int_{-\infty}^\infty xp(x) \; dx = \int_0^1 x \; dx = \frac{1}{2}.
$$
and
$$
\sigma_X^2 = \int_{-\infty}^\infty x^2p(x) \; dx - \left(\frac{1}{2}\right)^2 = \frac{1}{3} - \frac{1}{4} = \frac{1}{12}.
$$
As a warning, let us examine one more example, known as the *Cauchy distribution*. This is the distribution with p.d.f. given by
$$
p(x) = \frac{1}{1+x^2}.
$$
```
# Plot the Cauchy distribution p.d.f.
x = np.arange(-5, 5, 0.01)
p = 1 / (1 + x**2)
d2l.plot(x, p, 'x', 'p.d.f.')
```
This function looks innocent, and indeed consulting a table of integrals will show it has area one under it, and thus it defines a continuous random variable.
To see what goes astray, let us try to compute the variance of this. This would involve using :eqref:`eq_var_def` computing
$$
\int_{-\infty}^\infty \frac{x^2}{1+x^2}\; dx.
$$
The function on the inside looks like this:
```
# Plot the integrand needed to compute the variance
x = np.arange(-20, 20, 0.01)
p = x**2 / (1 + x**2)
d2l.plot(x, p, 'x', 'integrand')
```
This function clearly has infinite area under it since it is essentially the constant one with a small dip near zero, and indeed we could show that
$$
\int_{-\infty}^\infty \frac{x^2}{1+x^2}\; dx = \infty.
$$
This means it does not have a well-defined finite variance.
However, looking deeper shows an even more disturbing result. Let us try to compute the mean using :eqref:`eq_exp_def`. Using the change of variables formula, we see
$$
\mu_X = \int_{-\infty}^{\infty} \frac{x}{1+x^2} \; dx = \frac{1}{2}\int_1^\infty \frac{1}{u} \; du.
$$
The integral inside is the definition of the logarithm, so this is in essence $\log(\infty) = \infty$, so there is no well-defined average value either!
Machine learning scientists define their models so that we most often do not need to deal with these issues, and will in the vast majority of cases deal with random variables with well-defined means and variances. However, every so often random variables with *heavy tails* (that is those random variables where the probabilities of getting large values are large enough to make things like the mean or variance undefined) are helpful in modeling physical systems, thus it is worth knowing that they exist.
### Joint Density Functions
The above work all assumes we are working with a single real valued random variable. But what if we are dealing with two or more potentially highly correlated random variables? This circumstance is the norm in machine learning: imagine random variables like $R_{i, j}$ which encode the red value of the pixel at the $(i, j)$ coordinate in an image, or $P_t$ which is a random variable given by a stock price at time $t$. Nearby pixels tend to have similar color, and nearby times tend to have similar prices. We cannot treat them as separate random variables, and expect to create a successful model (we will see in :numref:`sec_naive_bayes` a model that under-performs due to such an assumption). We need to develop the mathematical language to handle these correlated continuous random variables.
Thankfully, with the multiple integrals in :numref:`sec_integral_calculus` we can develop such a language. Suppose that we have, for simplicity, two random variables $X, Y$ which can be correlated. Then, similar to the case of a single variable, we can ask the question:
$$
P(X \;\text{is in an}\; \epsilon \text{-sized interval around}\; x \; \text{and} \;Y \;\text{is in an}\; \epsilon \text{-sized interval around}\; y ).
$$
Similar reasoning to the single variable case shows that this should be approximately
$$
P(X \;\text{is in an}\; \epsilon \text{-sized interval around}\; x \; \text{and} \;Y \;\text{is in an}\; \epsilon \text{-sized interval around}\; y ) \approx \epsilon^{2}p(x, y),
$$
for some function $p(x, y)$. This is referred to as the joint density of $X$ and $Y$. Similar properties are true for this as we saw in the single variable case. Namely:
* $p(x, y) \ge 0$;
* $\int _ {\mathbb{R}^2} p(x, y) \;dx \;dy = 1$;
* $P((X, Y) \in \mathcal{D}) = \int _ {\mathcal{D}} p(x, y) \;dx \;dy$.
In this way, we can deal with multiple, potentially correlated random variables. If we wish to work with more than two random variables, we can extend the multivariate density to as many coordinates as desired by considering $p(\mathbf{x}) = p(x_1, \ldots, x_n)$. The same properties of being non-negative, and having total integral of one still hold.
### Marginal Distributions
When dealing with multiple variables, we oftentimes want to be able to ignore the relationships and ask, "how is this one variable distributed?" Such a distribution is called a *marginal distribution*.
To be concrete, let us suppose that we have two random variables $X, Y$ with joint density given by $p _ {X, Y}(x, y)$. We will be using the subscript to indicate what random variables the density is for. The question of finding the marginal distribution is taking this function, and using it to find $p _ X(x)$.
As with most things, it is best to return to the intuitive picture to figure out what should be true. Recall that the density is the function $p _ X$ so that
$$
P(X \in [x, x+\epsilon]) \approx \epsilon \cdot p _ X(x).
$$
There is no mention of $Y$, but if all we are given is $p _{X, Y}$, we need to include $Y$ somehow. We can first observe that this is the same as
$$
P(X \in [x, x+\epsilon] \text{, and } Y \in \mathbb{R}) \approx \epsilon \cdot p _ X(x).
$$
Our density does not directly tell us about what happens in this case, we need to split into small intervals in $y$ as well, so we can write this as
$$
\begin{aligned}
\epsilon \cdot p _ X(x) & \approx \sum _ {i} P(X \in [x, x+\epsilon] \text{, and } Y \in [\epsilon \cdot i, \epsilon \cdot (i+1)]) \\
& \approx \sum _ {i} \epsilon^{2} p _ {X, Y}(x, \epsilon\cdot i).
\end{aligned}
$$

:label:`fig_marginal`
This tells us to add up the value of the density along a series of squares in a line as is shown in :numref:`fig_marginal`. Indeed, after canceling one factor of epsilon from both sides, and recognizing the sum on the right is the integral over $y$, we can conclude that
$$
\begin{aligned}
p _ X(x) & \approx \sum _ {i} \epsilon p _ {X, Y}(x, \epsilon\cdot i) \\
& \approx \int_{-\infty}^\infty p_{X, Y}(x, y) \; dy.
\end{aligned}
$$
Thus we see
$$
p _ X(x) = \int_{-\infty}^\infty p_{X, Y}(x, y) \; dy.
$$
This tells us that to get a marginal distribution, we integrate over the variables we do not care about. This process is often referred to as *integrating out* or *marginalized out* the unneeded variables.
### Covariance
When dealing with multiple random variables, there is one additional summary statistic which is helpful to know: the *covariance*. This measures the degree that two random variable fluctuate together.
Suppose that we have two random variables $X$ and $Y$, to begin with, let us suppose they are discrete, taking on values $(x_i, y_j)$ with probability $p_{ij}$. In this case, the covariance is defined as
$$\sigma_{XY} = \mathrm{Cov}(X, Y) = \sum_{i, j} (x_i - \mu_X) (y_j-\mu_Y) p_{ij}. = E[XY] - E[X]E[Y].$$
:eqlabel:`eq_cov_def`
To think about this intuitively: consider the following pair of random variables. Suppose that $X$ takes the values $1$ and $3$, and $Y$ takes the values $-1$ and $3$. Suppose that we have the following probabilities
$$
\begin{aligned}
P(X = 1 \; \text{and} \; Y = -1) & = \frac{p}{2}, \\
P(X = 1 \; \text{and} \; Y = 3) & = \frac{1-p}{2}, \\
P(X = 3 \; \text{and} \; Y = -1) & = \frac{1-p}{2}, \\
P(X = 3 \; \text{and} \; Y = 3) & = \frac{p}{2},
\end{aligned}
$$
where $p$ is a parameter in $[0,1]$ we get to pick. Notice that if $p=1$ then they are both always their minimum or maximum values simultaneously, and if $p=0$ they are guaranteed to take their flipped values simultaneously (one is large when the other is small and vice versa). If $p=1/2$, then the four possibilities are all equally likely, and neither should be related. Let us compute the covariance. First, note $\mu_X = 2$ and $\mu_Y = 1$, so we may compute using :eqref:`eq_cov_def`:
$$
\begin{aligned}
\mathrm{Cov}(X, Y) & = \sum_{i, j} (x_i - \mu_X) (y_j-\mu_Y) p_{ij} \\
& = (1-2)(-1-1)\frac{p}{2} + (1-2)(3-1)\frac{1-p}{2} + (3-2)(-1-1)\frac{1-p}{2} + (3-2)(3-1)\frac{p}{2} \\
& = 4p-2.
\end{aligned}
$$
When $p=1$ (the case where they are both maximally positive or negative at the same time) has a covariance of $2$. When $p=0$ (the case where they are flipped) the covariance is $-2$. Finally, when $p=1/2$ (the case where they are unrelated), the covariance is $0$. Thus we see that the covariance measures how these two random variables are related.
A quick note on the covariance is that it only measures these linear relationships. More complex relationships like $X = Y^2$ where $Y$ is randomly chosen from $\{-2, -1, 0, 1, 2\}$ with equal probability can be missed. Indeed a quick computation shows that these random variables have covariance zero, despite one being a deterministic function of the other.
For continuous random variables, much the same story holds. At this point, we are pretty comfortable with doing the transition between discrete and continuous, so we will provide the continuous analogue of :eqref:`eq_cov_def` without any derivation.
$$
\sigma_{XY} = \int_{\mathbb{R}^2} (x-\mu_X)(y-\mu_Y)p(x, y) \;dx \;dy.
$$
For visualization, let us take a look at a collection of random variables with tunable covariance.
```
# Plot a few random variables adjustable covariance
covs = [-0.9, 0.0, 1.2]
d2l.plt.figure(figsize=(12, 3))
for i in range(3):
X = np.random.normal(0, 1, 500)
Y = covs[i]*X + np.random.normal(0, 1, (500))
d2l.plt.subplot(1, 4, i+1)
d2l.plt.scatter(X.asnumpy(), Y.asnumpy())
d2l.plt.xlabel('X')
d2l.plt.ylabel('Y')
d2l.plt.title(f'cov = {covs[i]}')
d2l.plt.show()
```
Let us see some properties of covariances:
* For any random variable $X$, $\mathrm{Cov}(X, X) = \mathrm{Var}(X)$.
* For any random variables $X, Y$ and numbers $a$ and $b$, $\mathrm{Cov}(aX+b, Y) = \mathrm{Cov}(X, aY+b) = a\mathrm{Cov}(X, Y)$.
* If $X$ and $Y$ are independent then $\mathrm{Cov}(X, Y) = 0$.
In addition, we can use the covariance to expand a relationship we saw before. Recall that is $X$ and $Y$ are two independent random variables then
$$
\mathrm{Var}(X+Y) = \mathrm{Var}(X) + \mathrm{Var}(Y).
$$
With knowledge of covariances, we can expand this relationship. Indeed, some algebra can show that in general,
$$
\mathrm{Var}(X+Y) = \mathrm{Var}(X) + \mathrm{Var}(Y) + 2\mathrm{Cov}(X, Y).
$$
This allows us to generalize the variance summation rule for correlated random variables.
### Correlation
As we did in the case of means and variances, let us now consider units. If $X$ is measured in one unit (say inches), and $Y$ is measured in another (say dollars), the covariance is measured in the product of these two units $\text{inches} \times \text{dollars}$. These units can be hard to interpret. What we will often want in this case is a unit-less measurement of relatedness. Indeed, often we do not care about exact quantitative correlation, but rather ask if the correlation is in the same direction, and how strong the relationship is.
To see what makes sense, let us perform a thought experiment. Suppose that we convert our random variables in inches and dollars to be in inches and cents. In this case the random variable $Y$ is multiplied by $100$. If we work through the definition, this means that $\mathrm{Cov}(X, Y)$ will be multiplied by $100$. Thus we see that in this case a change of units change the covariance by a factor of $100$. Thus, to find our unit-invariant measure of correlation, we will need to divide by something else that also gets scaled by $100$. Indeed we have a clear candidate, the standard deviation! Indeed if we define the *correlation coefficient* to be
$$\rho(X, Y) = \frac{\mathrm{Cov}(X, Y)}{\sigma_{X}\sigma_{Y}},$$
:eqlabel:`eq_cor_def`
we see that this is a unit-less value. A little mathematics can show that this number is between $-1$ and $1$ with $1$ meaning maximally positively correlated, whereas $-1$ means maximally negatively correlated.
Returning to our explicit discrete example above, we can see that $\sigma_X = 1$ and $\sigma_Y = 2$, so we can compute the correlation between the two random variables using :eqref:`eq_cor_def` to see that
$$
\rho(X, Y) = \frac{4p-2}{1\cdot 2} = 2p-1.
$$
This now ranges between $-1$ and $1$ with the expected behavior of $1$ meaning most correlated, and $-1$ meaning minimally correlated.
As another example, consider $X$ as any random variable, and $Y=aX+b$ as any linear deterministic function of $X$. Then, one can compute that
$$\sigma_{Y} = \sigma_{aX+b} = |a|\sigma_{X},$$
$$\mathrm{Cov}(X, Y) = \mathrm{Cov}(X, aX+b) = a\mathrm{Cov}(X, X) = a\mathrm{Var}(X),$$
and thus by :eqref:`eq_cor_def` that
$$
\rho(X, Y) = \frac{a\mathrm{Var}(X)}{|a|\sigma_{X}^2} = \frac{a}{|a|} = \mathrm{sign}(a).
$$
Thus we see that the correlation is $+1$ for any $a > 0$, and $-1$ for any $a < 0$ illustrating that correlation measures the degree and directionality the two random variables are related, not the scale that the variation takes.
Let us again plot a collection of random variables with tunable correlation.
```
# Plot a few random variables adjustable correlations
cors = [-0.9, 0.0, 1.0]
d2l.plt.figure(figsize=(12, 3))
for i in range(3):
X = np.random.normal(0, 1, 500)
Y = cors[i] * X + np.sqrt(1 - cors[i]**2) * np.random.normal(0, 1, 500)
d2l.plt.subplot(1, 4, i + 1)
d2l.plt.scatter(X.asnumpy(), Y.asnumpy())
d2l.plt.xlabel('X')
d2l.plt.ylabel('Y')
d2l.plt.title(f'cor = {cors[i]}')
d2l.plt.show()
```
Let us list a few properties of the correlation below.
* For any random variable $X$, $\rho(X, X) = 1$.
* For any random variables $X, Y$ and numbers $a$ and $b$, $\rho(aX+b, Y) = \rho(X, aY+b) = \rho(X, Y)$.
* If $X$ and $Y$ are independent with non-zero variance then $\rho(X, Y) = 0$.
As a final note, you may feel like some of these formulae are familiar. Indeed, if we expand everything out assuming that $\mu_X = \mu_Y = 0$, we see that this is
$$
\rho(X, Y) = \frac{\sum_{i, j} x_iy_ip_{ij}}{\sqrt{\sum_{i, j}x_i^2 p_{ij}}\sqrt{\sum_{i, j}y_j^2 p_{ij}}}.
$$
This looks like a sum of a product of terms divided by the square root of sums of terms. This is exactly the formula for the cosine of the angle between two vectors $\mathbf{v}, \mathbf{w}$ with the different coordinates weighted by $p_{ij}$:
$$
\cos(\theta) = \frac{\mathbf{v}\cdot \mathbf{w}}{\|\mathbf{v}\|\|\mathbf{w}\|} = \frac{\sum_{i} v_iw_i}{\sqrt{\sum_{i}v_i^2}\sqrt{\sum_{i}w_i^2}}.
$$
Indeed if we think of norms as being related to standard deviations, and correlations as being cosines of angles, much of the intuition we have from geometry can be applied to thinking about random variables.
## Summary
* Continuous random variables are random variables that can take on a continuum of values. They have some technical difficulties that make them more challenging to work with compared to discrete random variables.
* The probability density function allows us to work with continuous random variables by giving a function where the area under the curve on some interval gives the probability of finding a sample point in that interval.
* The cumulative distribution function is the probability of observing the random variable to be less than a given threshold. It can provide a useful alternate viewpoint which unifies discrete and continuous variables.
* The mean is the average value of a random variable.
* The variance is the expected square of the difference between the random variable and its mean.
* The standard deviation is the square root of the variance. It can be thought of as measuring the range of values the random variable may take.
* Chebyshev's inequality allows us to make this intuition rigorous by giving an explicit interval that contains the random variable most of the time.
* Joint densities allow us to work with correlated random variables. We may marginalize joint densities by integrating over unwanted random variables to get the distribution of the desired random variable.
* The covariance and correlation coefficient provide a way to measure any linear relationship between two correlated random variables.
## Exercises
1. Suppose that we have the random variable with density given by $p(x) = \frac{1}{x^2}$ for $x \ge 1$ and $p(x) = 0$ otherwise. What is $P(X > 2)$?
2. The Laplace distribution is a random variable whose density is given by $p(x = \frac{1}{2}e^{-|x|}$. What is the mean and the standard deviation of this function? As a hint, $\int_0^\infty xe^{-x} \; dx = 1$ and $\int_0^\infty x^2e^{-x} \; dx = 2$.
3. I walk up to you on the street and say "I have a random variable with mean $1$, standard deviation $2$, and I observed $25\%$ of my samples taking a value larger than $9$." Do you believe me? Why or why not?
4. Suppose that you have two random variables $X, Y$, with joint density given by $p_{XY}(x, y) = 4xy$ for $x, y \in [0,1]$ and $p_{XY}(x, y) = 0$ otherwise. What is the covariance of $X$ and $Y$?
[Discussions](https://discuss.d2l.ai/t/415)
| github_jupyter |
# Capstone Project - Madiun Cafe Location
## Introduction / business problem
i am looking to open a cafe in Madiun City, **the question is**, where is the best location for open new cafe? **The background of the problem** it is not worth setting up a cafe in the close promixity of existing ones. because the location of the new cafe has a significant impact on the expected returns.
## Data
**A description of the data**: the data used to solve this problem is geolocation data collected from [FourSquare](https://foursquare.com/). Data is a single tabel, containing location of the existing cafe. **Explanation** of the location data are column `(lat, lng)`, where `lat` stands for latitude and `lng` for longitude. **Example** of the data:
| Name | Shortname | Latitude | Londitude |
| ------------------------ | ------------ | --------- | ---------- |
| Markas Kopi | Coffee Shop | -7.648215 | 111.530610 |
| Cafe Latté | Coffee Shop | -7.635934 | 111.519315 |
| Coffee Toffee | Coffee Shop | -7.622158 | 111.536357 |
**Data will be used**: by knowing the locations of already existing cafes, i will be using Kernel Density Estimation to determine the area of influence of the existing cafes, and recommend a new location which is not in the area of influence from existing cafe.
## Prep
```
!conda install -c conda-forge folium=0.5.0 --yes
import pandas as pd
import folium
import requests
# The code was removed by Watson Studio for sharing.
request_parameters = {
"client_id": CLIENT_ID,
"client_secret": CLIENT_SECRET,
"v": VERSION,
"section": "coffee",
"near": "Madiun",
"radius": 1000,
"limit": 50}
data = requests.get("https://api.foursquare.com/v2/venues/explore", params=request_parameters)
d = data.json()["response"]
d.keys()
d["headerLocationGranularity"], d["headerLocation"], d["headerFullLocation"]
d["suggestedBounds"], d["totalResults"]
d["geocode"]
d["groups"][0].keys()
d["groups"][0]["type"], d["groups"][0]["name"]
items = d["groups"][0]["items"]
print("items: %i" % len(items))
items[0]
items[1]
df_raw = []
for item in items:
venue = item["venue"]
categories, uid, name, location = venue["categories"], venue["id"], venue["name"], venue["location"]
assert len(categories) == 1
shortname = categories[0]["shortName"]
if not "address" in location:
address = ''
else:
address = location["address"]
if not "postalCode" in location:
postalcode = ''
else:
postalcode = location["postalCode"]
lat = location["lat"]
lng = location["lng"]
datarow = (uid, name, shortname, address, postalcode, lat, lng)
df_raw.append(datarow)
df = pd.DataFrame(df_raw, columns=["uid", "name", "shortname", "address", "postalcode", "lat", "lng"])
print("total %i cafes" % len(df))
df.head()
madiun_center = d["geocode"]["center"]
madiun_center
```
## Applying Heatmap to Map
Some density based estimator is a good to be used to determine where to start a new coffee business. Using HeatMap plugin in Folium, to visualize all the existing Cafes to same map:
```
from folium import plugins
# create map of Helsinki using latitude and longitude values
map_madiun = folium.Map(location=[madiun_center["lat"], madiun_center["lng"]], zoom_start=14)
folium.LatLngPopup().add_to(map_madiun)
def add_markers(df):
for (j, row) in df.iterrows():
label = folium.Popup(row["name"], parse_html=True)
folium.CircleMarker(
[row["lat"], row["lng"]],
radius=10,
popup=label,
color='blue',
fill=True,
fill_color='#3186cc',
fill_opacity=0.7,
parse_html=False).add_to(map_madiun)
add_markers(df)
hm_data = df[["lat", "lng"]].as_matrix().tolist()
map_madiun.add_child(plugins.HeatMap(hm_data))
map_madiun
```
## Result
After further analysis, the best location for a new cafe is on Tulus Bakti Street, because it is not in close proximity with other cafe, and located near school and on densest population region in madiun. [BPS DATA](https://madiunkota.bps.go.id/statictable/2015/06/08/141/jumlah-penduduk-menurut-kecamatan-dan-agama-yang-dianut-di-kota-madiun-2013-.html)
```
lat = -7.6393
lng = 111.5285
school_1_lat = -7.6403
school_1_lng = 111.5316
map_best = folium.Map(location=[lat, lng], zoom_start=17)
add_markers(df)
folium.CircleMarker(
[school_1_lat, school_1_lng],
radius=15,
popup="School",
color='Yellow',
fill=True,
fill_color='#3186cc',
fill_opacity=0.7,
parse_html=False).add_to(map_best)
folium.CircleMarker(
[lat, lng],
radius=15,
popup="Best Location!",
color='red',
fill=True,
fill_color='#3186cc',
fill_opacity=0.7,
parse_html=False).add_to(map_best)
map_best
```
| github_jupyter |
<div>
<img src="https://drive.google.com/uc?export=view&id=1vK33e_EqaHgBHcbRV_m38hx6IkG0blK_" width="350"/>
</div>
#**Artificial Intelligence - MSc**
This notebook is designed specially for the module
ET5003 - MACHINE LEARNING APPLICATIONS
Instructor: Enrique Naredo
###ET5003_BayesianNN
© All rights reserved to the author, do not share outside this module.
## Introduction
A [Bayesian network](https://en.wikipedia.org/wiki/Bayesian_network) (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG).
* Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor.
* For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms.
* Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
**Acknowledgement**
This notebook is refurbished taking source code from Alessio Benavoli's webpage and from the libraries numpy, GPy, pylab, and pymc3.
## Libraries
```
# Suppressing Warnings:
import warnings
warnings.filterwarnings("ignore")
# https://pypi.org/project/GPy/
!pip install gpy
import GPy as GPy
import numpy as np
import pylab as pb
import pymc3 as pm
%matplotlib inline
```
## Data generation
Generate data from a nonlinear function and use a Gaussian Process to sample it.
```
# seed the legacy random number generator
# to replicate experiments
seed = None
#seed = 7
np.random.seed(seed)
# Gaussian Processes
# https://gpy.readthedocs.io/en/deploy/GPy.kern.html
# Radial Basis Functions
# https://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html
# kernel is a function that specifies the degree of similarity
# between variables given their relative positions in parameter space
kernel = GPy.kern.RBF(input_dim=1,lengthscale=0.15,variance=0.2)
print(kernel)
# number of samples
num_samples_train = 250
num_samples_test = 200
# intervals to sample
a, b, c = 0.2, 0.6, 0.8
# points evenly spaced over [0,1]
interval_1 = np.random.rand(int(num_samples_train/2))*b - c
interval_2 = np.random.rand(int(num_samples_train/2))*b + c
X_new_train = np.sort(np.hstack([interval_1,interval_2]))
X_new_test = np.linspace(-1,1,num_samples_test)
X_new_all = np.hstack([X_new_train,X_new_test]).reshape(-1,1)
# vector of the means
μ_new = np.zeros((len(X_new_all)))
# covariance matrix
C_new = kernel.K(X_new_all,X_new_all)
# noise factor
noise_new = 0.1
# generate samples path with mean μ and covariance C
TF_new = np.random.multivariate_normal(μ_new,C_new,1)[0,:]
y_new_train = TF_new[0:len(X_new_train)] + np.random.randn(len(X_new_train))*noise_new
y_new_test = TF_new[len(X_new_train):] + np.random.randn(len(X_new_test))*noise_new
TF_new = TF_new[len(X_new_train):]
```
In this example, first generate a nonlinear functions and then generate noisy training data from that function.
The constrains are:
* Training samples $x$ belong to either interval $[-0.8,-0.2]$ or $[0.2,0.8]$.
* There is not data training samples from the interval $[-0.2,0.2]$.
* The goal is to evaluate the extrapolation error outside in the interval $[-0.2,0.2]$.
```
# plot
pb.figure()
pb.plot(X_new_test,TF_new,c='b',label='True Function',zorder=100)
# training data
pb.scatter(X_new_train,y_new_train,c='g',label='Train Samples',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.legend()
pb.savefig("New_data.pdf")
```
## Bayesian NN
We address the previous nonlinear regression problem by using a Bayesian NN.
**The model is basically very similar to polynomial regression**. We first define the nonlinear function (NN)
and the place a prior over the unknown parameters. We then compute the posterior.
```
# https://theano-pymc.readthedocs.io/en/latest/
import theano
# add a column of ones to include an intercept in the model
x1 = np.vstack([np.ones(len(X_new_train)), X_new_train]).T
floatX = theano.config.floatX
l = 15
# Initialize random weights between each layer
# we do that to help the numerical algorithm that computes the posterior
init_1 = np.random.randn(x1.shape[1], l).astype(floatX)
init_out = np.random.randn(l).astype(floatX)
# pymc3 model as neural_network
with pm.Model() as neural_network:
# we convert the data in theano type so we can do dot products with the correct type.
ann_input = pm.Data('ann_input', x1)
ann_output = pm.Data('ann_output', y_new_train)
# Priors
# Weights from input to hidden layer
weights_in_1 = pm.Normal('w_1', 0, sigma=10,
shape=(x1.shape[1], l), testval=init_1)
# Weights from hidden layer to output
weights_2_out = pm.Normal('w_0', 0, sigma=10,
shape=(l,),testval=init_out)
# Build neural-network using tanh activation function
# Inner layer
act_1 = pm.math.tanh(pm.math.dot(ann_input,weights_in_1))
# Linear layer, like in Linear regression
act_out = pm.Deterministic('act_out',pm.math.dot(act_1, weights_2_out))
# standard deviation of noise
sigma = pm.HalfCauchy('sigma',5)
# Normal likelihood
out = pm.Normal('out',
act_out,
sigma=sigma,
observed=ann_output)
# this can be slow because there are many parameters
# some parameters
par1 = 100 # start with 100, then use 1000+
par2 = 1000 # start with 1000, then use 10000+
# neural network
with neural_network:
posterior = pm.sample(par1,tune=par2,chains=1)
```
Specifically, PyMC3 supports the following Variational Inference (VI) methods:
* Automatic Differentiation Variational Inference (ADVI): 'advi'
* ADVI full rank: 'fullrank_advi'
* Stein Variational Gradient Descent (SVGD): 'svgd'
* Amortized Stein Variational Gradient Descent (ASVGD): 'asvgd'
* Normalizing Flow with default scale-loc flow (NFVI): 'nfvi'
```
# we can do instead an approximated inference
param3 = 1000 # start with 1000, then use 50000+
VI = 'advi' # 'advi', 'fullrank_advi', 'svgd', 'asvgd', 'nfvi'
OP = pm.adam # pm.adam, pm.sgd, pm.adagrad, pm.adagrad_window, pm.adadelta
LR = 0.01
with neural_network:
approx = pm.fit(param3, method=VI, obj_optimizer=pm.adam(learning_rate=LR))
# plot
pb.plot(approx.hist, label='Variational Inference: '+ VI.upper(), alpha=.3)
pb.legend(loc='upper right')
# Evidence Lower Bound (ELBO)
# https://en.wikipedia.org/wiki/Evidence_lower_bound
pb.ylabel('ELBO')
pb.xlabel('iteration');
# draw samples from variational posterior
D = 500
posterior = approx.sample(draws=D)
```
Now, we compute the prediction for each sample.
* Note that we use `np.tanh` instead of `pm.math.tanh`
for speed reason.
* `pm.math.tanh` is slower outside a Pymc3 model because it converts all data in theano format.
* It is convenient to do GPU-based training, but it is slow when we only need to compute predictions.
```
# add a column of ones to include an intercept in the model
x2 = np.vstack([np.ones(len(X_new_test)), X_new_test]).T
y_pred = []
for i in range(posterior['w_1'].shape[0]):
#inner layer
t1 = np.tanh(np.dot(posterior['w_1'][i,:,:].T,x2.T))
#outer layer
y_pred.append(np.dot(posterior['w_0'][i,:],t1))
# predictions
y_pred = np.array(y_pred)
```
We first plot the mean of `y_pred`, this is very similar to the prediction that Keras returns
```
# plot
pb.plot(X_new_test,TF_new,label='true')
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean')
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.legend()
pb.ylim([-1,1])
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.savefig("BayesNN_mean.pdf")
```
Now, we plot the uncertainty, by plotting N nonlinear regression lines from the posterior
```
# plot
pb.plot(X_new_test,TF_new,label='true',Zorder=100)
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean',Zorder=100)
N = 500
# nonlinear regression lines
for i in range(N):
pb.plot(X_new_test,y_pred[i,:],c='gray',alpha=0.05)
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.ylim([-1,1.5])
pb.legend()
pb.savefig("BayesNN_samples.pdf")
# plot
pb.plot(X_new_test,TF_new,label='true',Zorder=100)
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean',Zorder=100)
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.ylim([-1,1.5])
pb.legend()
pb.savefig("BayesNN_mean.pdf")
```
| github_jupyter |
# 函数
- 函数可以用来定义可重复代码,组织和简化
- 一般来说一个函数在实际开发中为一个小功能
- 一个类为一个大功能
- 同样函数的长度不要超过一屏
Python中的所有函数实际上都是有返回值(return None),
如果你没有设置return,那么Python将不显示None.
如果你设置return,那么将返回出return这个值.
```
def HJN():
print('Hello')
return 1000
b=HJN()
print(b)
HJN
def panduan(number):
if number % 2 == 0:
print('O')
else:
print('J')
panduan(number=1)
panduan(2)
```
## 定义一个函数
def function_name(list of parameters):
do something

- 以前使用的random 或者range 或者print.. 其实都是函数或者类
函数的参数如果有默认值的情况,当你调用该函数的时候:
可以不给予参数值,那么就会走该参数的默认值
否则的话,就走你给予的参数值.
```
import random
def hahah():
n = random.randint(0,5)
while 1:
N = eval(input('>>'))
if n == N:
print('smart')
break
elif n < N:
print('太小了')
elif n > N:
print('太大了')
```
## 调用一个函数
- functionName()
- "()" 就代表调用
```
def H():
print('hahaha')
def B():
H()
B()
def A(f):
f()
A(B)
```

## 带返回值和不带返回值的函数
- return 返回的内容
- return 返回多个值
- 一般情况下,在多个函数协同完成一个功能的时候,那么将会有返回值

- 当然也可以自定义返回None
## EP:

```
def main():
print(min(min(5,6),(51,6)))
def min(n1,n2):
a = n1
if n2 < a:
a = n2
main()
```
## 类型和关键字参数
- 普通参数
- 多个参数
- 默认值参数
- 不定长参数
## 普通参数
## 多个参数
## 默认值参数
## 强制命名
```
def U(str_):
xiaoxie = 0
for i in str_:
ASCII = ord(i)
if 97<=ASCII<=122:
xiaoxie +=1
elif xxxx:
daxie += 1
elif xxxx:
shuzi += 1
return xiaoxie,daxie,shuzi
U('HJi12')
```
## 不定长参数
- \*args
> - 不定长,来多少装多少,不装也是可以的
- 返回的数据类型是元组
- args 名字是可以修改的,只是我们约定俗成的是args
- \**kwargs
> - 返回的字典
- 输入的一定要是表达式(键值对)
- name,\*args,name2,\**kwargs 使用参数名
```
def TT(a,b)
def TT(*args,**kwargs):
print(kwargs)
print(args)
TT(1,2,3,4,6,a=100,b=1000)
{'key':'value'}
TT(1,2,4,5,7,8,9,)
def B(name1,nam3):
pass
B(name1=100,2)
def sum_(*args,A='sum'):
res = 0
count = 0
for i in args:
res +=i
count += 1
if A == "sum":
return res
elif A == "mean":
mean = res / count
return res,mean
else:
print(A,'还未开放')
sum_(-1,0,1,4,A='var')
'aHbK134'.__iter__
b = 'asdkjfh'
for i in b :
print(i)
2,5
2 + 22 + 222 + 2222 + 22222
```
## 变量的作用域
- 局部变量 local
- 全局变量 global
- globals 函数返回一个全局变量的字典,包括所有导入的变量
- locals() 函数会以字典类型返回当前位置的全部局部变量。
```
a = 1000
b = 10
def Y():
global a,b
a += 100
print(a)
Y()
def YY(a1):
a1 += 100
print(a1)
YY(a)
print(a)
```
## 注意:
- global :在进行赋值操作的时候需要声明
- 官方解释:This is because when you make an assignment to a variable in a scope, that variable becomes local to that scope and shadows any similarly named variable in the outer scope.
- 
# Homework
- 1

```
def getPentagonalNumber(n):
count = 0
for n in range(100):
y=int(n*(3*n-1)/2)
print(y,end=' ')
count += 1
if count %10 == 0:
print()
getPentagonalNumber(100)
```
- 2

```
def sumDigits(n):
bai=n//100
shi=n//10%10
ge=n%10
y=bai+shi+ge
print('%d(%d+%d+%d)'%(y,bai,shi,ge))
sumDigits(234)
```
- 3

```
def displaySortedNumber():
num1,num2,num3=map(float,input('Enter three number:').split(','))
a=[num1,num2,num3]
a.sort()
print(a)
displaySortedNumber()
```
- 4

```
def futureInvestmentValue(principal,rate,years):
for i in range(years):
principal = principal * (1+rate)
print("{}年内总额{}: ".format(i+1,principal))
principal = eval(input("输入存款金额: "))
rate = eval(input("输入利率: "))
years = eval(input("输入年份:" ))
futureInvestmentValue(principal,rate,years)
```
- 5

```
def printChars():
count=0
for i in range(49,91):
print(chr(i),end=' ')
count=count+1
if count%10==0:
print()
printChars()
```
- 6

```
def numberofDaysInAYear():
for year in range(2010,2021):
if (year%4==0 and year%100!=0) or (year%400==0):
print('%d年366天'%year)
else:
print('%d年365天'%year)
numberofDaysInAYear()
```
- 7

```
import numpy as np
import math
def xsj(x1,y1,x2,y2):
p1=np.array([x1,y1])
p2=np.array([x2,y2])
p3=p2-p1
p4=math.hypot(p3[0],p3[1])
print(p4)
x1,y1,x2,y2=map(int,input().split(','))
xsj(x1,y1,x2,y2)
```
- 8

- 9


```
import time
localtime = time.asctime(time.localtime(time.time()))
print("本地时间为 :", localtime)
2019 - 1970
```
- 10

```
import random
num1=random.randrange(1,7)
num2=random.randrange(1,7)
sum_=num1+num2
if sum_==2 or sum_==3 or sum_==12:
print('You rolled %d+%d=%d'%(num1,num2,sum_))
print('you lose')
elif sum_==7 or sum_==11:
print('You rolled %d+%d=%d'%(num1,num2,sum_))
print('you win')
else:
print('You rolled %d+%d=%d'%(num1,num2,sum_))
print('point is %d'%sum_)
num1=random.randrange(1,7)
num2=random.randrange(1,7)
sum_1=num1+num2
if sum_1==sum_:
print('You rolled %d+%d=%d'%(num1,num2,sum_1))
print('you win')
else:
print('You rolled %d+%d=%d'%(num1,num2,sum_1))
print('you lose')
```
- 11
### 去网上寻找如何用Python代码发送邮件
| github_jupyter |
```
import tensorflow as tf
import os
import pickle
import numpy as np
CIFAR_DIR = "./../../cifar-10-batches-py"
print(os.listdir(CIFAR_DIR))
def load_data(filename):
"""read data from data file."""
with open(filename, 'rb') as f:
data = pickle.load(f, encoding='bytes')
return data[b'data'], data[b'labels']
# tensorflow.Dataset.
class CifarData:
def __init__(self, filenames, need_shuffle):
all_data = []
all_labels = []
for filename in filenames:
data, labels = load_data(filename)
all_data.append(data)
all_labels.append(labels)
self._data = np.vstack(all_data)
self._data = self._data / 127.5 - 1
self._labels = np.hstack(all_labels)
print(self._data.shape)
print(self._labels.shape)
self._num_examples = self._data.shape[0]
self._need_shuffle = need_shuffle
self._indicator = 0
if self._need_shuffle:
self._shuffle_data()
def _shuffle_data(self):
# [0,1,2,3,4,5] -> [5,3,2,4,0,1]
p = np.random.permutation(self._num_examples)
self._data = self._data[p]
self._labels = self._labels[p]
def next_batch(self, batch_size):
"""return batch_size examples as a batch."""
end_indicator = self._indicator + batch_size
if end_indicator > self._num_examples:
if self._need_shuffle:
self._shuffle_data()
self._indicator = 0
end_indicator = batch_size
else:
raise Exception("have no more examples")
if end_indicator > self._num_examples:
raise Exception("batch size is larger than all examples")
batch_data = self._data[self._indicator: end_indicator]
batch_labels = self._labels[self._indicator: end_indicator]
self._indicator = end_indicator
return batch_data, batch_labels
train_filenames = [os.path.join(CIFAR_DIR, 'data_batch_%d' % i) for i in range(1, 6)]
test_filenames = [os.path.join(CIFAR_DIR, 'test_batch')]
train_data = CifarData(train_filenames, True)
test_data = CifarData(test_filenames, False)
x = tf.placeholder(tf.float32, [None, 3072])
# [None], eg: [0,5,6,3]
y = tf.placeholder(tf.int64, [None])
hidden1 = tf.layers.dense(x, 100, activation=tf.nn.relu)
hidden2 = tf.layers.dense(hidden1, 100, activation=tf.nn.relu)
hidden3 = tf.layers.dense(hidden2, 50, activation=tf.nn.relu)
y_ = tf.layers.dense(hidden3, 10)
loss = tf.losses.sparse_softmax_cross_entropy(labels=y, logits=y_)
# y_ -> sofmax
# y -> one_hot
# loss = ylogy_
# indices
predict = tf.argmax(y_, 1)
# [1,0,1,1,1,0,0,0]
correct_prediction = tf.equal(predict, y)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float64))
with tf.name_scope('train_op'):
train_op = tf.train.AdamOptimizer(1e-3).minimize(loss)
init = tf.global_variables_initializer()
batch_size = 20
train_steps = 100000
test_steps = 100
# train: 100k: 51.%
with tf.Session() as sess:
sess.run(init)
for i in range(train_steps):
batch_data, batch_labels = train_data.next_batch(batch_size)
loss_val, acc_val, _ = sess.run(
[loss, accuracy, train_op],
feed_dict={
x: batch_data,
y: batch_labels})
if (i+1) % 500 == 0:
print('[Train] Step: %d, loss: %4.5f, acc: %4.5f'
% (i+1, loss_val, acc_val))
if (i+1) % 5000 == 0:
test_data = CifarData(test_filenames, False)
all_test_acc_val = []
for j in range(test_steps):
test_batch_data, test_batch_labels \
= test_data.next_batch(batch_size)
test_acc_val = sess.run(
[accuracy],
feed_dict = {
x: test_batch_data,
y: test_batch_labels
})
all_test_acc_val.append(test_acc_val)
test_acc = np.mean(all_test_acc_val)
print('[Test ] Step: %d, acc: %4.5f'
% (i+1, test_acc))
```
| github_jupyter |
```
import pandas as pd
import numpy as np
X_raw = pd.read_csv("/Users/joejohns/data_bootcamp/GitHub/final_project_nhl_prediction/Data/Shaped_Data/data_bet_stats_mp.csv")
##note it is against, for .. then sometimes *by itself* stat% = for/(for+against); stat%_against would be 1-stat%
##basic features to add:
##pp %
##pk stats,
##pk%
##sh%
##sv%
##goal_diff = gf -ga
##goal% = gf/(gf+ga)
##total points (prolly adjust for stupid OT, SO shit)
##pts %
##league rank (based on pts%)
feat_drop = [
'startRinkSide'
'HoA', #this is mp ###many of these are repeated from mp_data
'HoA_bet',
'VH',
'home_or_away',
'team',
'name',
'Team',
'Unnamed: 0',
'playerTeam',
'position',
'blocked', ## Same as bSAAgainst
'pim', ## same as penaltyminFor
'goals', ##goalsFor
'shots',
'giveaways',
'hits',
]
#################################first round
feat_goals = [
'goalsAgainst',
'goalsFor',]
##do ga - gf and maybe gf/(gf+ga) ... can I get rid of OT and SO ? Not so easy ... would need to use situation stuff.
##
feat_SOG = [
'shotsOnGoalAgainst',
'shotsOnGoalFor',
]
##sh%, sv%
feat_saves = [
'savedShotsOnGoalAgainst',
'savedShotsOnGoalFor',
#pair with shots for sv%, sh%
]
##pp, pk, penalties
feat_pen_pp_pk = [
'penalityMinutesAgainst', #Penalties
'penalityMinutesFor',
# 'penaltiesAgainst',
# 'penaltiesFor', not sure so useful compared to minutes
'powerPlayGoals',
'powerPlayOpportunities', #Powerplay
]
##! Need to create pk stat and pp%, pk%
##xgoals
feat_xgoals =[
'xGoalsAgainst', #(measure of quality of chances for and against)
'xGoalsFor',
'xGoalsPercentage', #derived from above two
]
##possession
feat_SA = [
'unblockedShotAttemptsAgainst',
'unblockedShotAttemptsFor',
'shotAttemptsAgainst',
'shotAttemptsFor',
'corsiPercentage', ##derived from 4 above
'fenwickPercentage',
]
##a way to get possession
feat_FO = [
'faceOffsWonAgainst',
'faceOffsWonFor',
'faceOffWinPercentage',] #has missing nan ... re-do it using last 2.
##measures of possession loss/gain
feat_give_aways = [
'giveawaysAgainst',
'giveawaysFor',
]
feat_dzone_give_aways = [
'dZoneGiveawaysAgainst',
'dZoneGiveawaysFor',]
##should cause more give aways and recoveries
feat_hits = [
'hitsAgainst',
'hitsFor',
]
#measures defensive stat ... also ability to get shots thru
feat_blocked = [
'blockedShotAttemptsAgainst',
'blockedShotAttemptsFor',]
##measures shooting skill to hit the net or ability to make guys shoot wide if you are in lane (kind of like block)
feat_missed = [
'missedShotsAgainst',
'missedShotsFor',]
##measures how many rebounds you give up (degense)... and how many you generate (offense)
##g/rb
##sht/rb
##hml sht/rb
## xg/rb
feat_rebounds = [
'reboundGoalsAgainst', #could put with goals ... prolly want g/rb; pair with high rebounds for
'reboundGoalsFor',
'reboundsAgainst',
'reboundsFor',
]
##ability to maintain pressure ...
feat_pressure = [
'playContinuedInZoneAgainst', #after a shot is next shot in zone (no events outside+ same players on ice)
'playContinuedInZoneFor',
'playContinuedOutsideZoneAgainst',
'playContinuedOutsideZoneFor',
]
feat_pressure_stoppage = [
'freezeAgainst', # "freeze after shot attempt For/Against"
'freezeFor',
'playStoppedAgainst',
'playStoppedFor', #non-freeze reason
]
################################second round
feat_goals_hml_danger = [
'highDangerGoalsAgainst',
'highDangerGoalsFor',
'mediumDangerGoalsAgainst',
'mediumDangerGoalsFor',
'lowDangerGoalsAgainst',
'lowDangerGoalsFor',
]
feat_saves_fen = [
'savedUnblockedShotAttemptsAgainst', ##mised shots plus saved SOG
'savedUnblockedShotAttemptsFor', #pair with unblocked shots for Fsv%
]
feat_xgoals_adj = [
'scoreVenueAdjustedxGoalsAgainst', ##probably select one of these 3 versions?
'scoreVenueAdjustedxGoalsFor',
'flurryAdjustedxGoalsAgainst',
'flurryAdjustedxGoalsFor',
'flurryScoreVenueAdjustedxGoalsAgainst',
'flurryScoreVenueAdjustedxGoalsFor',
]
feat_xgoals_hml_danger = [
'highDangerxGoalsAgainst',
'highDangerxGoalsFor',
'mediumDangerxGoalsAgainst',
'mediumDangerxGoalsFor',
'lowDangerxGoalsAgainst',
'lowDangerxGoalsFor',
]
feat_xgoals_rebounds = [
'xGoalsFromActualReboundsOfShotsAgainst',
'xGoalsFromActualReboundsOfShotsFor',
'xGoalsFromxReboundsOfShotsAgainst',
'xGoalsFromxReboundsOfShotsFor',
'totalShotCreditAgainst', ##xgoals + xgoalsfromxreb -reboundxgoals ?
'totalShotCreditFor',
]
feat_SA_adj = [
'scoreAdjustedShotsAttemptsAgainst',
'scoreAdjustedShotsAttemptsFor',
'scoreAdjustedUnblockedShotAttemptsAgainst',
'scoreAdjustedUnblockedShotAttemptsFor',
]
feat_SOG_hml_danger = [
'highDangerShotsAgainst',
'highDangerShotsFor',
'mediumDangerShotsAgainst',
'mediumDangerShotsFor',
'lowDangerShotsAgainst',
'lowDangerShotsFor',
]
feat_xrebounds = [
'reboundxGoalsAgainst',
'reboundxGoalsFor',
'xReboundsAgainst',
'xReboundsFor']
feat_xpressure = [
'xPlayStoppedAgainst',
'xPlayStoppedFor',
'xPlayContinuedInZoneAgainst', ##maybe do PCIZA and PCIZA - xPCIZA (measures lucky/unlucky)
'xPlayContinuedInZoneFor',
'xPlayStoppedAgainst',
'xPlayStoppedFor',
]
#I_F means individual for player; from player stats dictionary ... team level version there should be no difference if
#cacluated from shot level data; but I guess he just averaged them ... I think the xgoalsonsshots is calculated from shot level data ... so these
##avges only sometimes match
#I_F_xGoalsFromxReboundsOfShots,"Expected Goals from Expected Rebounds of player's shots. Even if a shot does not actually generate a rebound, if it's a shot that is likely to generate a rebound the player is credited with xGoalsFromxRebounds"
#I_F_xGoalsFromActualReboundsOfShots,Expected Goals from actual rebounds shots of player's shots.
#I_F_reboundxGoals,Expected Goal on rebound shots
X_raw.head()
```
Goals for Total number of goals scored so far this season
Goals against
Total number of goals conceded so far thisseason
Goals Differential Goals for – Goals against
Power Play Success Rate Ratio – scoring a goal when 5 on 4
Power Kill Success Rate Ratio – not conceding a goal when 4 on 5
Shot % Goal scored/shots taken
Save % Goals conceded/shots saved
Winning Streak Number of consecutive games won
Conference Standing Latest ranking on conference table
Fenwick Close % Possession ratio
PDO Luck parameter
5/5 Goal For/Against Ratio – 5 on 5 Goals For/Against
```
feat_Pisch = [ 'faceOffWinPercentage',
```
| github_jupyter |
# Linear Regression
We will implement a linear regression model by using the Keras library.
```
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
```
## Data set: Weight and height
Active Drive and read the csv file with the weight and height data
```
df = pd.read_csv('/content/drive/My Drive/Colab Notebooks/DeepLearning-Intro-part2/weight-height.csv')
df.head()
df.plot(kind='scatter',
x='Height',
y='Weight',
title='Weight and Height in adults')
```
## Model building
```
# Import the type of model: Sequential, because we will add elements to this model in a sequence
from keras.models import Sequential
# To build a linear model we will need only dense layers
from keras.layers import Dense
# Import the optimizers, they change the weights and biases looking for the minimum cost
from keras.optimizers import Adam, SGD
```
### Define the model
```
# define the model to be sequential
model = Sequential()
```
```
Dense(units, activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None, **kwargs)
```
Just your regular densely-connected NN layer.
Dense implements the operation: $output = activation(dot(input, kernel) + bias)$ where activation is the element-wise activation function passed as the activation argument, kernel is a weights matrix created by the layer, and bias is a bias vector created by the layer (only applicable if use_bias is True).
```
# we add to the model a dense layer
# the first parammeter is the number of units that is how many outputs this layer will have
# Since this is a linear regression we will require a model with one output and one input
model.add(Dense(1, input_shape=(1,))) #this code implements a model x*w+b
model.summary()
```
We have a single layer called 'dense_1' the Output Shape is 1 number and it has 2 parameters.
The reason that the Output Shape is (None, 1) is because the model can accept multiple points at once, instead of passing a single value we can ask for many values of x in one single call.
When we compile the model, Keras will construct the model based on the backend software that we define (here we are using TensorFlow model).
```
model.compile(optimizer, loss=None, metrics=None, loss_weights=None, sample_weight_mode=None, weighted_metrics=None, target_tensors=None, **kwargs)
```
```
# we will compile using the cost function (loss) 'mean_squared_error'
model.compile(Adam(lr=0.8), 'mean_squared_error')
```
### Fit the model
```
X = df[['Height']].values #input data
y_true = df['Weight'].values #output data
```
Fit the model by using the input data, X, and the output data, y_true. In each iteration the loss is decreasing by looking for the W and B values. In this example it will search 40 times (40 epochs).
```
model.fit(X, y_true, epochs=40)
y_pred = model.predict(X)
df.plot(kind='scatter',
x='Height',
y='Weight',
title='Weight and Height in adults')
plt.plot(X, y_pred, color='red')
```
Extract the values of W (slope) and B (bias).
```
W, B = model.get_weights()
W
B
```
## Performance of the model
```
from sklearn.metrics import r2_score
print("The R2 score is {:0.3f}".format(r2_score(y_true, y_pred)))
```
### Train/test split
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y_true,
test_size=0.2)
len(X_train)
len(X_test)
#reset the parameters of the model
W[0, 0] = 0.0
B[0] = 0.0
model.set_weights((W, B))
#retrain the model in the selected sample
model.fit(X_train, y_train, epochs=50, verbose=0) #verbose=0 doesn't show each iteration
y_train_pred = model.predict(X_train).ravel()
y_test_pred = model.predict(X_test).ravel()
from sklearn.metrics import mean_squared_error as mse
print("The Mean Squared Error on the Train set is:\t{:0.1f}".format(mse(y_train, y_train_pred)))
print("The Mean Squared Error on the Test set is:\t{:0.1f}".format(mse(y_test, y_test_pred)))
print("The R2 score on the Train set is:\t{:0.3f}".format(r2_score(y_train, y_train_pred)))
print("The R2 score on the Test set is:\t{:0.3f}".format(r2_score(y_test, y_test_pred)))
```
The score for the training set is close to the one in the test set, therefore this model is good in generalization.
| github_jupyter |
```
print(__doc__)
from time import time
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn import metrics
from sklearn.cluster import KMeans
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.preprocessing import scale
np.random.seed(42)
digits = load_digits()
data = scale(digits.data)
n_samples, n_features = data.shape
n_digits = len(np.unique(digits.target))
labels = digits.target
sample_size = 300
print(digits.data.shape)
print(digits.data[0].shape)
#plt.imshow(digits.data[0].reshape([8,8]), cmap='gray')
print(data.shape)
print(data[0].shape)
plt.imshow(data[8].reshape([8,8]), cmap='gray')
print(labels[8])
```
# # A demo of K-Means clustering on the handwritten digits data
In this example we compare the various initialization strategies for
K-means in terms of runtime and quality of the results.
As the ground truth is known here, we also apply different cluster
quality metrics to judge the goodness of fit of the cluster labels to the
ground truth.
Cluster quality metrics evaluated (see `clustering_evaluation` for
definitions and discussions of the metrics):
| Shorthand | Full name |
|------------|----------------------------:|
| homo | homogeneity score |
| compl | completeness score |
| v-meas | V measure |
| ARI | adjusted Rand index |
| AMI | adjusted mutual information |
| silhouette | silhouette coefficient |
```
def bench_k_means(estimator, name, data):
t0 = time()
estimator.fit(data)
print('%-9s\t%.2fs\t%i\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f\t%.3f'
% (name, (time() - t0), estimator.inertia_,
metrics.homogeneity_score(labels, estimator.labels_),
metrics.completeness_score(labels, estimator.labels_),
metrics.v_measure_score(labels, estimator.labels_),
metrics.adjusted_rand_score(labels, estimator.labels_),
metrics.adjusted_mutual_info_score(labels, estimator.labels_,
average_method='arithmetic'),
metrics.silhouette_score(data, estimator.labels_,
metric='euclidean',
sample_size=sample_size)))
print("n_digits: %d, \t n_samples %d, \t n_features %d"
% (n_digits, n_samples, n_features))
print(82 * '_')
print('init\t\ttime\tinertia\thomo\tcompl\tv-meas\tARI\tAMI\tsilhouette')
bench_k_means(KMeans(init='k-means++', n_clusters=n_digits, n_init=10),
name="k-means++", data=data)
bench_k_means(KMeans(init='random', n_clusters=n_digits, n_init=10),
name="random", data=data)
# in this case the seeding of the centers is deterministic, hence we run the
# kmeans algorithm only once with n_init=1
pca = PCA(n_components=n_digits).fit(data)
bench_k_means(KMeans(init=pca.components_, n_clusters=n_digits, n_init=1),
name="PCA-based", data=data)
print(82 * '_')
# Visualize the results on PCA-reduced data
reduced_data = PCA(n_components=2).fit_transform(data)
kmeans = KMeans(init='k-means++', n_clusters=n_digits, n_init=10)
kmeans.fit(reduced_data)
# Step size of the mesh. Decrease to increase the quality of the VQ.
h = .02 # point in the mesh [x_min, x_max]x[y_min, y_max].
# Plot the decision boundary. For that, we will assign a color to each
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Obtain labels for each point in mesh. Use last trained model.
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1)
plt.clf()
plt.imshow(Z, interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
cmap=plt.cm.Paired,
aspect='auto', origin='lower')
plt.plot(reduced_data[:, 0], reduced_data[:, 1], 'k.', markersize=2)
# Plot the centroids as a white X
centroids = kmeans.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1],
marker='x', s=169, linewidths=3,
color='w', zorder=10)
plt.title('K-means clustering on the digits dataset (PCA-reduced data)\n'
'Centroids are marked with white cross')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()
from sklearn.metrics import normalized_mutual_info_score
normalized_mutual_info_score(kmeans.labels_, labels)
```
| github_jupyter |
# Training vs validation loss
[](https://colab.research.google.com/github/parrt/fundamentals-of-deep-learning/blob/main/notebooks/3.train-test-diabetes.ipynb)
By [Terence Parr](https://explained.ai).
This notebook explores how to use a validation set to estimate how well a model generalizes from its training data to unknown test vectors. We will see that deep learning models often have so many parameters that we can drive training loss to zero, but unfortunately the validation loss usually grows as the model overfits. We will also compare how deep learning performs compared to a random forest model as a baseline. Instead of the cars data set, we will use the [diabetes data set](https://scikit-learn.org/stable/datasets/toy_dataset.html#diabetes-dataset) loaded via sklearn.
## Support code
```
import os
import sys
import torch
import copy
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
from sklearn.metrics import r2_score
from sklearn.ensemble import RandomForestRegressor
import matplotlib.pyplot as plt
from matplotlib import colors
! pip install -q -U colour
import colour
%config InlineBackend.figure_format = 'retina'
import tsensor
def plot_history(history, ax=None, maxy=None, file=None):
if ax is None:
fig, ax = plt.subplots(1,1, figsize=(3.5,3))
ax.set_ylabel("Loss")
ax.set_xlabel("Epochs")
loss = history[:,0]
val_loss = history[:,1]
if maxy:
ax.set_ylim(0,maxy)
else:
ax.set_ylim(0,torch.max(val_loss))
ax.spines['top'].set_visible(False) # turns off the top "spine" completely
ax.spines['right'].set_visible(False)
ax.spines['left'].set_linewidth(.5)
ax.spines['bottom'].set_linewidth(.5)
ax.plot(loss, label='train_loss')
ax.plot(val_loss, label='val_loss')
ax.legend(loc='upper right')
plt.tight_layout()
if file:
# plt.savefig(f"/Users/{os.environ['USER']}/Desktop/{file}.pdf")
plt.savefig(f"{os.environ['HOME']}/{file}.pdf")
```
## Load diabetes data set
From [sklearn diabetes data set](https://scikit-learn.org/stable/datasets/toy_dataset.html#diabetes-dataset):
"<i>Ten baseline variables, age, sex, body mass index, average blood pressure, and six blood serum measurements were obtained for each of n = 442 diabetes patients, as well as the response of interest, a quantitative measure of disease progression one year after baseline.</i>"
So, the goal is to predict disease progression based upon all of these features.
```
d = load_diabetes()
len(d.data)
df = pd.DataFrame(d.data, columns=d.feature_names)
df['disease'] = d.target # "quantitative measure of disease progression one year after baseline"
df.head(3)
```
## Split data into train, validation sets
Any sufficiently powerful model is able to effectively drive down the training loss (error). What we really care about, though, is how well the model generalizes. That means we have to look at the validation or test error, computed from records the model was not trained on. (We'll use "test" as shorthand for "validation" often, but technically they are not the same.) For non-time-sensitive data sets, we can simply randomize and hold out 20% of our data as our validation set:
```
np.random.seed(1) # set a random seed for consistency across runs
n = len(df)
X = df.drop('disease',axis=1).values
y = df['disease'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20) # hold out 20%
len(X), len(X_train), len(X_test)
```
Let's also make sure to normalize the data to make training easier:
```
m = np.mean(X_train,axis=0)
std = np.std(X_train,axis=0)
X_train = (X_train-m)/std
X_test = (X_test-m)/std # use training data only when prepping test sets
```
## Baseline with random forest
When building machine learning models, it's always important to ask how good your model is. One of the best ways is to choose a baseline model, such as a random forest or a linear regression model, and compare your new model to make sure it can beat the old model. Random forests are easy to use, understand, and train so they are a good baseline. Training the model is as simple as calling `fit()` (`min_samples_leaf=20` gives a bit more generality):
```
rf = RandomForestRegressor(n_estimators=100, n_jobs=-1, min_samples_leaf=20)
rf.fit(X_train, y_train.reshape(-1))
```
To evaluate our models, let's compute the mean squared error (MSE) for both training and validation sets:
```
y_pred = rf.predict(X_train)
mse = np.mean((y_pred - y_train.reshape(-1))**2)
y_pred_test = rf.predict(X_test)
mse_test = np.mean((y_pred_test - y_test.reshape(-1))**2)
print(f"Training MSE {mse:.2f} validation MSE {mse_test:.2f}")
```
Let's check $R^2$ as well.
```
rf.score(X_train, y_train), rf.score(X_test, y_test)
```
#### Exercise
Why is the validation error much larger than the training error?
<details>
<summary>Solution</summary>
Because the model was trained on the training set, one would expect it to generally perform better on it than any other data set. The more the validation error diverges from the training error, the less general you should assume your model is.
</details>
## Train neural network model
Ok, so now we have a baseline and an understanding of how well a decent model performs on this data set. Let's see if we can beat that baseline with a neural network. First we will see how easy it is to drive the training error down and then show how the validation error is not usually very good in that case. We will finish by considering ways to get better validation errors, which means more general models.
### Most basic network training
A basic training loop for a neural network model simply measures and tracks the training loss or error/metric. (In this case, our loss and metric are the same.) The following function embodies such a training loop:
```
def train0(model, X_train, y_train,
learning_rate = .5, nepochs=2000):
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
for epoch in range(nepochs+1):
y_pred = model(X_train)
loss = torch.mean((y_pred - y_train)**2)
if epoch % (nepochs//10) == 0:
print(f"Epoch {epoch:4d} MSE train loss {loss:12.3f}")
optimizer.zero_grad()
loss.backward() # autograd computes w1.grad, b1.grad, ...
optimizer.step()
```
To use this method, we have to convert the training and validation data sets to pytorch tensors from numpy (they are already normalized):
```
X_train = torch.tensor(X_train).float()
X_test = torch.tensor(X_test).float()
y_train = torch.tensor(y_train).float().reshape(-1,1) # column vector
y_test = torch.tensor(y_test).float().reshape(-1,1)
```
Let's create a model with one hidden layer and an output layer, glued together with a ReLU nonlinearity. The network looks something like the following except of course we have many more input features and neurons than shown here:
<img src="images/diabetes-relu.png" width="300">
There is an implied input layer which is really just the input vector of features. The output layer takes the output of the hidden layer and generates a single output, our $\hat{y}$:
```
ncols = X.shape[1]
n_neurons = 150
model = nn.Sequential(
nn.Linear(ncols, n_neurons), # hidden layer
nn.ReLU(), # nonlinearity
nn.Linear(n_neurons, 1) # output layer
)
train0(model, X_train, y_train, learning_rate=.08, nepochs=5000)
```
Run this a few times and you'll see that we can drive the training error very close to zero with 150 neurons and many iterations (epochs). Compare this to the RF training MSE which is orders of magnitude bigger (partly due to the `min_samples_leaf` hyperparameter).
#### Exercise
Why does the training loss sometimes pop up and then go back down? Why is it not monotonically decreasing?
<details>
<summary>Solution</summary>
The only source of randomness is the initialization of the model parameters, but that does not explain the lack of monotonicity. In this situation, it is likely that the learning rate is too high and therefore, as we approach the minimum of the lost function, our steps are too big. We are jumping back and forth across the location of the minimum in parameter space.
</details>
#### Exercise
Change the learning rate from 0.08 to 0.001 and rerun the example. What happens to the training loss? Is it better or worse than the baseline random forest and the model trained with learning rate 0.08?
<details>
<summary>Solution</summary>
The training loss continues to decrease but much lower than before and stops long before reaching a loss near zero. On the other hand, it is better than the training error from the baseline random forest.
</details>
## Reducing the learning rate to zero in on the minimum
In one of the above exercises we discussed that the learning rate was probably too high in the vicinity of the lost function minimum. There are ways to throttle the learning rate down as we approach the minimum, but we are using a fixed learning rate here. In order to get a smooth, monotonic reduction in loss function let's start with a smaller learning rate, but that means increasing the number of epochs:
```
ncols = X.shape[1]
n_neurons = 150
model = nn.Sequential(
nn.Linear(ncols, n_neurons), # hidden layer
nn.ReLU(), # nonlinearity
nn.Linear(n_neurons, 1) # output layer
)
train0(model, X_train, y_train, learning_rate=.017, nepochs=15000)
```
Notice now that we can reliably drive that training error down to zero without bouncing around, although it takes longer with the smaller learning rate.
#### Exercise
Play around with the learning rate and nepochs to see how fast you can reliably get MSE down to 0.
### Tracking validation loss
A low training error doesn't really tell us that much, other than the model is able to capture the relationship between the features and the target variable. What we really want is a general model, which means evaluating the model's performance on a validation set. We have both sets, so let's now track the training and validation error in the loop. We will see that our model performs much worse on the records in the validation set (on which the model was not trained).
```
def train1(model, X_train, X_test, y_train, y_test,
learning_rate = .5, nepochs=2000):
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
history = [] # track training and validation loss
for epoch in range(nepochs+1):
y_pred = model(X_train)
loss = torch.mean((y_pred - y_train)**2)
y_pred_test = model(X_test)
loss_test = torch.mean((y_pred_test - y_test)**2)
history.append((loss, loss_test))
if epoch % (nepochs//10) == 0:
print(f"Epoch {epoch:4d} MSE train loss {loss:12.3f} test loss {loss_test:12.3f}")
optimizer.zero_grad()
loss.backward() # autograd computes w1.grad, b1.grad, ...
optimizer.step()
return torch.tensor(history)
```
Let's create the exact same model that we had before but plot train/validation errors against the number of epochs:
```
ncols = X.shape[1]
n_neurons = 150
model = nn.Sequential(
nn.Linear(ncols, n_neurons),
nn.ReLU(),
nn.Linear(n_neurons, 1)
)
history = train1(model, X_train, X_test, y_train, y_test,
learning_rate=.02, nepochs=8000)
plot_history(torch.clamp(history, 0, 12000), file="train-test")
```
Wow. The validation error is much much worse than the training error, which is almost 0. That tells us that the model is severely overfit to the training data and is not general at all. Well, the validation error actually makes a lot of progress initially but then after a few thousand epochs immediately starts to grow (we'll use this fact later). Unless we do something fancier, the best solution can be obtained by selecting the model parameters that gives us the lowest validation loss.
### Track best loss and choose best model
We saw in the previous section that the most general model appears fairly soon in the training cycle. So, despite being able to drive the training error to zero if we keep going long enough, the most general model actually is known very early in the training process. This is not always the case, but it certainly is here for this data. Let's exploit this by tracking the best model, the one with the lowest validation error. There is [some indication](https://moultano.wordpress.com/2020/10/18/why-deep-learning-works-even-though-it-shouldnt/) that a good approach is to (sometimes crank up the power of the model and then) just stop early, or at least pick the model with the lowest validation error. The following function embodies that by making a copy of our neural net model when it finds an improved version.
```
def train2(model, X_train, X_test, y_train, y_test,
learning_rate = .5, nepochs=2000, weight_decay=0):
optimizer = torch.optim.Adam(model.parameters(),
lr=learning_rate, weight_decay=weight_decay)
history = [] # track training and validation loss
best_loss = 1e10
best_model = None
for epoch in range(nepochs+1):
y_pred = model(X_train)
loss = torch.mean((y_pred - y_train)**2)
y_pred_test = model(X_test)
loss_test = torch.mean((y_pred_test - y_test)**2)
history.append((loss, loss_test))
if loss_test < best_loss:
best_loss = loss_test
best_model = copy.deepcopy(model)
best_epoch = epoch
if epoch % (nepochs//10) == 0:
print(f"Epoch {epoch:4d} MSE train loss {loss:12.3f} test loss {loss_test:12.3f}")
optimizer.zero_grad()
loss.backward() # autograd computes w1.grad, b1.grad, ...
optimizer.step()
print(f"BEST MSE test loss {best_loss:.3f} at epoch {best_epoch}")
return torch.tensor(history), best_model
```
Let's use the exact same model and learning rate with no weight decay and see what happens.
```
ncols = X.shape[1]
n_neurons = 150
model = nn.Sequential(
nn.Linear(ncols, n_neurons),
nn.ReLU(),
nn.Linear(n_neurons, 1)
)
history, best_model = train2(model, X_train, X_test, y_train, y_test,
learning_rate=.02, nepochs=1000,
weight_decay=0)
# verify we got the best model out
y_pred = best_model(X_test)
loss_test = torch.mean((y_pred - y_test)**2)
plot_history(torch.clamp(history, 0, 12000))
```
Let's also look at $R^2$:
```
y_pred = best_model(X_train).detach().numpy()
y_pred_test = best_model(X_test).detach().numpy()
r2_score(y_train, y_pred), r2_score(y_test, y_pred_test)
```
The best MSE bounces around a loss value of 3000 from run to run, a bit above it or a bit below, depending on the run. And this decent result occurs without having to understand or use weight decay (more on this next). Compare the validation R^2 to that of the RF; the network does much better!
### Weight decay to reduce overfitting
Other than stopping early, one of the most common ways to reduce model overfitting is to use weight decay, otherwise known as L2 (Ridge) regression, to constrain the model parameters. Without constraints, model parameters can get very large, which typically leads to a lack of generality. Using the `Adam` optimizer, we turn on weight decay with parameter `weight_decay`, but otherwise the training loop is the same:
```
def train3(model, X_train, X_test, y_train, y_test,
learning_rate = .5, nepochs=2000, weight_decay=0, trace=True):
optimizer = torch.optim.Adam(model.parameters(),
lr=learning_rate, weight_decay=weight_decay)
history = [] # track training and validation loss
for epoch in range(nepochs+1):
y_pred = model(X_train)
loss = torch.mean((y_pred - y_train)**2)
y_pred_test = model(X_test)
loss_test = torch.mean((y_pred_test - y_test)**2)
history.append((loss, loss_test))
if trace and epoch % (nepochs//10) == 0:
print(f"Epoch {epoch:4d} MSE train loss {loss:12.3f} test loss {loss_test:12.3f}")
optimizer.zero_grad()
loss.backward() # autograd computes w1.grad, b1.grad, ...
optimizer.step()
return torch.tensor(history)
```
How do we know what the right value of the weight decay is? Typically we try a variety of weight decay values and then see which one gives us the best validation error, so let's do that using a grid of images. The following loop uses the same network and learning rate for each run but varies the weight decay:
```
ncols = X.shape[1]
n_neurons = 150
fig, axes = plt.subplots(1, 4, figsize=(12.5,2.5))
for wd,ax in zip([0,.3,.6,1.5],axes):
model = nn.Sequential(
nn.Linear(ncols, n_neurons),
nn.ReLU(),
nn.Linear(n_neurons, 1)
)
history = train3(model, X_train, X_test, y_train, y_test,
learning_rate=.05, nepochs=1000, weight_decay=wd,
trace=False)
mse_valid = history[-1][1]
ax.set_title(f"wd={wd:.1f}, valid MSE {mse_valid:.0f}")
plot_history(torch.clamp(history, 0, 10000), ax=ax, maxy=10_000)
plt.tight_layout()
plt.show()
```
From this experiment, we can conclude that a weight decay of 1.5 gives the best final mean squared error. But, the experiment is reporting the final MSE all the way on the right side of the graph.
The minimum MSE in the above experiment (of four side-by-side graphs), however, appears before the right edge and the validation error simply gets worse after that. That tells us that we should not pick the parameters simply as the parameters where the training leaves off. We should pick the model parameters that give the minimum loss, as we did before.
#### Exercise
Set the weight decay to something huge like 100. What do you observe about the training and validation curves?
<details>
<summary>Solution</summary>
The two curves are flat, and about the same level. The minimum validation error is about 6000 so much worse than with more reasonable weight decay. We have seriously biased the model because we cannot even drive the training error downwards. The bias comes from the extreme constraint we've placed on the model parameters.
<pre>
model = nn.Sequential(
nn.Linear(ncols, n_neurons),
nn.ReLU(),
nn.Linear(n_neurons, 1)
)
history = train2(model, X_train, X_test, y_train, y_test,
learning_rate=.05, nepochs=1000, weight_decay=100,
trace=False)
mse_valid = history[-1][1]
ax.set_title(f"wd={wd:.1f}, valid MSE {mse_valid:.0f}")
plot_history(torch.clamp(history, 0, 10000), ax=ax, maxy=10_000)
</pre>
</details>
| github_jupyter |
# Simple Attack
In this notebook, we will examine perhaps the simplest possible attack on an individual's private data and what the OpenDP library can do to mitigate it.
## Loading the data
The vetting process is currently underway for the code in the OpenDP Library.
Any constructors that have not been vetted may still be accessed if you opt-in to "contrib".
```
import numpy as np
from opendp.mod import enable_features
enable_features('contrib')
```
We begin with loading up the data.
```
import os
data_path = os.path.join('.', 'data', 'PUMS_california_demographics_1000', 'data.csv')
with open(data_path) as input_file:
data = input_file.read()
col_names = ["age", "sex", "educ", "race", "income", "married"]
print(col_names)
print('\n'.join(data.split('\n')[:6]))
```
The following code parses the data into a vector of incomes.
More details on preprocessing can be found [here](https://github.com/opendp/opendp/blob/main/python/example/basic_data_analysis.ipynb).
```
from opendp.trans import make_split_dataframe, make_select_column, make_cast, make_impute_constant
income_preprocessor = (
# Convert data into a dataframe where columns are of type Vec<str>
make_split_dataframe(separator=",", col_names=col_names) >>
# Selects a column of df, Vec<str>
make_select_column(key="income", TOA=str)
)
# make a transformation that casts from a vector of strings to a vector of floats
cast_str_float = (
# Cast Vec<str> to Vec<Option<floats>>
make_cast(TIA=str, TOA=float) >>
# Replace any elements that failed to parse with 0., emitting a Vec<float>
make_impute_constant(0.)
)
# replace the previous preprocessor: extend it with the caster
income_preprocessor = income_preprocessor >> cast_str_float
incomes = income_preprocessor(data)
print(incomes[:7])
```
## A simple attack
Say there's an attacker who's target is the income of the first person in our data (i.e. the first income in the csv). In our case, its simply `0` (but any number is fine, i.e. 5000).
```
person_of_interest = incomes[0]
print('person of interest:\n\n{0}'.format(person_of_interest))
```
Now consider the case an attacker that doesn't know the POI income, but do know the following: (1) the average income without the POI income, and (2) the number of persons in the database.
As we show next, if he would also get the average income (including the POI's one), by simple manipulation he can easily back out the individual's income.
```
# attacker information: everyone's else mean, and their count.
known_mean = np.mean(incomes[1:])
known_obs = len(incomes) - 1
# assume the attackers know legitimately get the overall mean (and hence can infer the total count)
overall_mean = np.mean(incomes)
n_obs = len(incomes)
# back out POI's income
poi_income = overall_mean * n_obs - known_obs * known_mean
print('poi_income: {0}'.format(poi_income))
```
The attacker now knows with certainty that the POI has an income of $0.
## Using OpenDP
Let's see what happens if the attacker were made to interact with the data through OpenDP and was given a privacy budget of $\epsilon = 1$.
We will assume that the attacker is reasonably familiar with differential privacy and believes that they should use tighter data bounds than they would anticipate being in the data in order to get a less noisy estimate.
They will need to update their `known_mean` accordingly.
```
from opendp.trans import make_clamp, make_sized_bounded_mean, make_bounded_resize
from opendp.meas import make_base_laplace
enable_features("floating-point")
max_influence = 1
count_release = 100
income_bounds = (0.0, 100_000.0)
clamp_and_resize_data = (
make_clamp(bounds=income_bounds) >>
make_bounded_resize(size=count_release, bounds=income_bounds, constant=10_000.0)
)
known_mean = np.mean(clamp_and_resize_data(incomes)[1:])
mean_measurement = (
clamp_and_resize_data >>
make_sized_bounded_mean(size=count_release, bounds=income_bounds) >>
make_base_laplace(scale=1.0)
)
dp_mean = mean_measurement(incomes)
print("DP mean:", dp_mean)
print("Known mean:", known_mean)
```
We will be using `n_sims` to simulate the process a number of times to get a sense for various possible outcomes for the attacker.
In practice, they would see the result of only one simulation.
```
# initialize vector to store estimated overall means
n_sims = 10_000
n_queries = 1
poi_income_ests = []
estimated_means = []
# get estimates of overall means
for i in range(n_sims):
query_means = [mean_measurement(incomes) for j in range(n_queries)]
# get estimates of POI income
estimated_means.append(np.mean(query_means))
poi_income_ests.append(estimated_means[i] * count_release - (count_release - 1) * known_mean)
# get mean of estimates
print('Known Mean Income (after truncation): {0}'.format(known_mean))
print('Observed Mean Income: {0}'.format(np.mean(estimated_means)))
print('Estimated POI Income: {0}'.format(np.mean(poi_income_ests)))
print('True POI Income: {0}'.format(person_of_interest))
```
We see empirically that, in expectation, the attacker can get a reasonably good estimate of POI's income. However, they will rarely (if ever) get it exactly and would have no way of knowing if they did.
In our case, indeed the mean estimated POI income approaches the true income, as the number of simulations `n_sims` increases.
Below is a plot showing the empirical distribution of estimates of POI income. Notice about its concentration around `0`, and the Laplacian curve of the graph.
```
import warnings
import seaborn as sns
# hide warning created by outstanding scipy.stats issue
warnings.simplefilter(action='ignore', category=FutureWarning)
# distribution of POI income
ax = sns.distplot(poi_income_ests, kde = False, hist_kws = dict(edgecolor = 'black', linewidth = 1))
ax.set(xlabel = 'Estimated POI income')
```
| github_jupyter |
```
import tensorflow as tf
import h5py
import shutil
import numpy as np
from torch.utils.data import DataLoader
import keras
from tqdm.notebook import tqdm
from keras.models import Sequential
from keras.layers import Dense, Flatten, Conv3D, Dropout, MaxPooling3D,MaxPooling2D
from keras.utils import to_categorical
from tensorflow.keras.callbacks import ModelCheckpoint
from keras.utils.vis_utils import plot_model
from sklearn.model_selection import train_test_split
from keras.layers import Conv2D,Dropout
from keras.layers import Activation,Average
from keras.layers import GlobalAveragePooling2D,BatchNormalization
from keras.optimizers import Adam
import time
import collections
from keras.losses import categorical_crossentropy
```
ConvPool_CNN Model
```
def ConvPool_CNN_C():
model = Sequential()
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(MaxPooling2D(pool_size=(3,3),strides=2))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(MaxPooling2D(pool_size=(3,3),strides=2))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(1,1),activation='relu'))
model.add(Conv2D(5,(1,1)))
model.add(GlobalAveragePooling2D())
model.add(Flatten())
model.add(Dense(5, activation='softmax'))
model.build(input_shape)
model.compile(loss=categorical_crossentropy,optimizer=keras.optimizers.Adam(0.001),metrics=['accuracy'])
return model
```
ALL_CNN_MODEL
```
def all_cnn_c(X,y,learningRate=0.001,lossFunction='categorical_crossentropy'):
model = Sequential()
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(1,1),activation='relu'))
model.add(GlobalAveragePooling2D())
model.add(Dense(5, activation='softmax'))
model.build(input_shape)
model.compile(loss=categorical_crossentropy,optimizer=Adam(0.001),metrics=['accuracy'])
return model
```
NIN_CNN_MODEL
```
def nin_cnn_c():
model = Sequential()
model.add(Conv2D(32,kernel_size=(5,5),activation='relu',padding='valid'))
model.add(Conv2D(32,kernel_size=(5,5),activation='relu'))
model.add(Conv2D(32,kernel_size=(5,5),activation='relu'))
model.add(MaxPooling2D(pool_size=(3,3),strides=2))
model.add(Dropout(0.5))
model.add(Conv2D(64,(3,3),activation='relu',padding='same'))
model.add(Conv2D(64,(1,1),activation='relu',padding='same'))
model.add(Conv2D(64,(1,1),activation='relu',padding='same'))
model.add(MaxPooling2D(pool_size=(3,3),strides=2))
model.add(Dropout(0.5))
model.add(Conv2D(128,(3,3),activation='relu',padding='same'))
model.add(Conv2D(32,(1,1),activation='relu'))
model.add(Conv2D(5,(1,1)))
model.add(GlobalAveragePooling2D())
model.add(Flatten())
model.add(Dense(5, activation='softmax'))
model.build(input_shape)
model.compile(loss=categorical_crossentropy,optimizer=Adam(0.001),metrics=['accuracy'])
return model
```
| github_jupyter |
© 2018 Suzy Beeler and Vahe Galstyan. This work is licensed under a [Creative Commons Attribution License CC-BY 4.0](https://creativecommons.org/licenses/by/4.0/). All code contained herein is licensed under an [MIT license](https://opensource.org/licenses/MIT)
This exercise was generated from a Jupyter notebook. You can download the notebook [here](diffusion_via_coin_flips.ipynb).
___
# Objective
In this tutorial, we will computationally simulate the process of diffusion with "coin flips," where at each time step, the particle can either move to the left or the right, each with probability $0.5$. From here, we can see how the distance a diffusing particle travels scale with time.
# Modeling 1-D diffusion with coin flips
Diffusion can be understood as random motion in space caused by thermal fluctuations in the environment. In the cytoplasm of the cell different molecules undergo a 3-dimensional diffusive motion. On the other hand, diffusion on the cell membrane is chiefly 2-dimensional. Here we will consider a 1-dimensional diffusion motion to make the treatment simpler, but the ideas can be extended into higher dimensions.
```
# Import modules
import numpy as np
import matplotlib.pyplot as plt
# Show figures in the notebook
%matplotlib inline
# For pretty plots
import seaborn as sns
rc={'lines.linewidth': 2, 'axes.labelsize': 14, 'axes.titlesize': 14, \
'xtick.labelsize' : 14, 'ytick.labelsize' : 14}
sns.set(rc=rc)
```
To simulate the flipping of a coin, we will make use of `numpy`'s `random.uniform()` function that produces a random number between $0$ and $1$. Let's see it in action by printing a few random numbers:
```
for i in range(10):
print(np.random.uniform())
```
We can now use these randomly generated numbers to simulate the process of a diffusing particle moving in one dimension, where any value below $0.5$ corresponds to step to the left and any value above $0.5$ corresponds to a step to the right. Below, we keep track of the position of a particle for $1000$ steps, where each position is $+1$ or $-1$ from the previous position, as determined by the result of a coin flip.
```
# Number of steps
n_steps = 1000
# Array to store walker positions
positions = np.zeros(n_steps)
# simulate the particle moving and store the new position
for i in range(1, n_steps):
# generate random number
rand = np.random.uniform()
# step in the positive direction
if rand > 0.5:
positions[i] = positions[i-1] + 1
# step in the negative direction
else:
positions[i] = positions[i-1] - 1
# Show the trajectory
plt.plot(positions)
plt.xlabel('steps')
plt.ylabel('position');
```
As we can see, the position of the particle moves about the origin in an undirected fashion as a result of the randomness of the steps taken. However, it's hard to conclude anything from this single trace. Only by simulating many of these trajectories can we begin to conclude some of the scaling properties of diffusing particles.
# Average behavior of diffusing particles
Now let's generate multiple random trajectories and see their collective behavior. To do that, we will create a 2-dimensional `numpy` array where each row will be a different trajectory. 2D arrays can be sliced such that `[i,:]` refers to all the values in the `i`th row, and `[:,j]` refers to all the values in `j`th column.
```
# Number of trajectories
n_traj = 1000
# 2d array for storing the trajectories
positions_2D = np.zeros([n_traj, n_steps])
# first iterate through the trajectories
for i in range(n_traj):
# then iterate through the steps
for j in range(1, n_steps):
# generate random number
rand = np.random.uniform()
# step in the positive direction
if rand > 0.5:
positions_2D[i, j] = positions_2D[i, j-1] + 1
# step in the negative direction
else:
positions_2D[i, j] = positions_2D[i, j-1] - 1
```
Now let's plot the results, once again by looping.
```
# iterate through each trajectory and plot
for i in range(n_traj):
plt.plot(positions_2D[i,:])
# label
plt.xlabel('steps')
plt.ylabel('position');
```
The overall tendency is that the average displacement from the origin increases with the number of time steps. Because each trajectory is assigned a solid color and all trajectories are overlaid on top of each other, it's hard to see the distribution of the walker position at a given number of times steps. To get a better intuition about the distribution of the walker's position at different steps, we will assign the same color to each trajectory and add transparency to each of them so that the more densely populated regions have a darker color.
```
# iterate through each trajectory and plot
for i in range(n_traj):
# lower alpha corresponds to lighter lines
plt.plot(positions_2D[i,:], alpha=0.01, color='k')
# label
plt.xlabel('steps')
plt.ylabel('position');
```
As we can see, over the course of diffusion the distribution of the walker's position becomes wider but remains centered around the origin, indicative of the unbiased nature of the random walk. To see how the walkers are distributed at this last time point, let's make a histogram of the walker's final positions.
```
# Make a histogram of final positions
_ = plt.hist(positions_2D[:,-1], bins=20)
plt.xlabel('final position')
plt.ylabel('frequency');
```
As expected, the distribution is centered around the origin and has a Gaussian-like shape. The more trajectories we sample, the "more Gaussian" the distribution will become. However, we may notice that the distribution appears to change depending on the number of bins we choose. This is known as *bin bias* and doesn't reflect anything about our data itself, just how we choose to represent it. An alternative (and arguably better) way to present the data is as a *empirical cumulative distribution function* (or ECDF), where we don't specify a number of bins, but instead plot each data point. For our cumulative frequency distribution, the $x$-axis corresponds to the final position of a particle and the $y$-axis corresponds to the proportion of particles that ended at this position or a more negative position.
```
# sort the final positions
sorted_positons = np.sort(positions_2D[:,-1])
# make the corresponding y_values (i.e. percentiles)
y_values = np.linspace(start=0, stop=1, num=len(sorted_positons))
# plot the cumulative histogram
plt.plot(sorted_positons, y_values, '.')
plt.xlabel("final position")
plt.ylabel("cumulative frequency");
```
This way of visualizing the data makes it easier to tell that distribution of walkers is in fact symmetric around 0. That is, 50% of the walkers ended on a negative position, while 50% of the walkers ended on a positive position.
| github_jupyter |
# 1. Python and notebook basics
In this first chapter, we will cover the very essentials of Python and notebooks such as creating a variable, importing packages, using functions, seeing how variables behave in the notebook etc. We will see more details on some of these topics, but this very short introduction will then allow us to quickly dive into more applied and image processing specific topics without having to go through a full Python introduction.
## Variables
Like we would do in mathematics when we define variables in equations such as $x=3$, we can do the same in all programming languages. Python has one of the simplest syntax for this, i.e. exactly as we would do it naturally. Let's define a variable in the next cell:
```
a = 3
```
As long as we **don't execute the cell** using Shift+Enter or the play button in the menu, the above cell is **purely text**. We can close our Jupyter session and then re-start it and this line of text will still be there. However other parts of the notebook are not "aware" that this variable has been defined and so we can't re-use anywhere else. For example if we type ```a``` again and execute the cell, we get an error:
```
a
```
So we actually need to **execute** the cell so that Python reads that line and executes the command. Here it's a very simple command that just says that the value of the variable ```a``` is three. So let's go back to the cell that defined ```a``` and now execute it (click in the cell and hit Shift+Enter). Now this variable is **stored in the computing memory** of the computer and we can re-use it anywhere in the notebook (but only in **this** notebook)!
We can again just type ```a```
```
a
```
We see that now we get an *output* with the value three. Most variables display an output when they are not involved in an operation. For example the line ```a=3``` didn't have an output.
Now we can define other variables in a new cell. Note that we can put as **many lines** of commands as we want in a single cell. Each command just need to be on a new line.
```
b = 5
c = 2
```
As variables are defined for the entire notebook we can combine information that comes from multiple cells. Here we do some basic mathematics:
```
a + b
```
Here we only see the output. We can't re-use that ouput for further calculations as we didn't define a new variable to contain it. Here we do it:
```
d = a + b
d
```
```d``` is now a new variable. It is purely numerical and not a mathematical formula as the above cell could make you believe. For example if we change the value of ```a```:
```
a = 100
```
and check the value of ```d```:
```
d
```
it has not change. We would have to rerun the operation and assign it again to ```d``` for it to update:
```
d = a + b
d
```
We will see many other types of variables during the course. Some are just other types of data, for example we can define a **text** variable by using quotes ```' '``` around a given text:
```
my_text = 'This is my text'
my_text
```
Others can contain multiple elements like lists:
```
my_list = [3, 8, 5, 9]
my_list
```
but more on these data structures later...
## Functions
We have seen that we could define variables and do some basic operations with them. If we want to go beyond simple arithmetic we need more **complex functions** that can operate on variables. Imagine for example that we need a function $f(x, a, b) = a * x + b$. For this we can use and **define functions**. Here's how we can define the previous function:
```
def my_fun(x, a, b):
out = a * x + b
return out
```
We see a series of Python rules to define a function:
- we use the word **```def```** to signal that we are creating a function
- we pick a **function name**, here ```my_fun```
- we open the **parenthesis** and put all our **variables ```x```, ```a```, ```b```** in there, just like when we do mathematics
- we do some operation inside the function. **Inside** the function is signal with the **indentation**: everything that belong inside the function (there could be many more lines) is shifted by a *single tab* or *three space* to the right
- we use the word **```return```** to tell what is the output of the function, here the variable ```out```
We can now use this function as if we were doing mathematics: we pick a a value for the three parameters e.g. $f(3, 2, 5)$
```
my_fun(3, 2, 5)
```
Note that **some functions are defined by default** in Python. For example if I define a variable which is a string:
```
my_text = 'This is my text'
```
I can count the number of characters in this text using the ```len()``` function which comes from base Python:
```
len(my_text)
```
The ```len``` function has not been manually defined within a ```def``` statement, it simply exist by default in the Python language.
## Variables as objects
In the Python world, variables are not "just" variables, they are actually more complex objects. So for example our variable ```my_text``` does indeed contain the text ```This is my text``` but it contains also additional features. The way to access those features is to use the dot notation ```my_text.some_feature```. There are two types of featues:
- functions, called here methods, that do some computation or modify the variable itself
- properties, that contain information about the variable
For example the object ```my_text``` has a function attached to it that allows us to put all letters to lower case:
```
my_text
my_text.lower()
```
If we define a complex number:
```
a = 3 + 5j
```
then we can access the property ```real``` that gives us only the real part of the number:
```
a.real
```
Note that when we use a method (function) we need to use the parenthesis, just like for regular functions, while for properties we don't.
## Packages
In the examples above, we either defined a function ourselves or used one generally accessible in base Python but there is a third solution: **external packages**. These packages are collections of functions used in a specific domain that are made available to everyone via specialized online repositories. For example we will be using in this course a package called [scikit-image](https://scikit-image.org/) that implements a large number of functions for image processing. For example if we want to filter an image stored in a variable ```im_in``` with a median filter, we can then just use the ```median()``` function of scikit-image and apply it to an image ```im_out = median(im_in)```. The question is now: how do we access these functions?
### Importing functions
The answer is that we have to **import** the functions we want to use in a *given notebook* from a package to be able to use them. First the package needs to be **installed**. One of the most popular place where to find such packages is the PyPi repository. We can install packages from there using the following command either in a **terminal or directly in the notebook**. For example for [scikit-image](https://pypi.org/project/scikit-image/):
```
pip install scikit-image
```
Once installed we can **import** the packakge in a notebook in the following way (note that the name of the package is scikit-image, but in code we use an abbreviated name ```skimage```):
```
import skimage
```
The import is valid for the **entire notebook**, we don't need that line in each cell.
Now that we have imported the package we can access all function that we define in it using a *dot notation* ```skimage.myfun```. Most packages are organized into submodules and in that case to access functions of a submodule we use ```skimage.my_submodule.myfun```.
To come back to the previous example: the ```median``` filtering function is in the ```filters``` submodule that we could now use as:
```python
im_out = skimage.filters.median(im_in)
```
We cannot execute this command as the variables ```im_in``` and ```im_out``` are not yet defined.
Note that there are multiple ways to import packages. For example we could give another name to the package, using the ```as``` statement:
```
import skimage as sk
```
Nowe if we want to use the ```median``` function in the filters sumodule we would write:
```python
im_out = sk.filters.median(im_in)
```
We can also import only a certain submodule using:
```
from skimage import filters
```
Now we have to write:
```python
im_out = filters.median(im_in)
```
Finally, we can import a **single** function like this:
```
from skimage.filters import median
```
and now we have to write:
```python
im_out = median(im_in)
```
## Structures
As mentioned above we cannot execute those various lines like ```im_out = median(im_in)``` because the image variable ```im_in``` is not yet defined. This variable should be an image, i.e. it cannot be a single number like in ```a=3``` but an entire grid of values, each value being one pixel. We therefore need a specific variable type that can contain such a structure.
We have already seen that we can define different types of variables. Single numbers:
```
a = 3
```
Text:
```
b = 'my text'
```
or even lists of numbers:
```
c = [6,2,8,9]
```
This last type of variable is called a ```list``` in Python and is one of the **structures** that is available in Python. If we think of an image that has multiple lines and columns of pixels, we could now imagine that we can represent it as a list of lists, each single list being e.g. one row pf pixels. For example a 3 x 3 image could be:
```
my_image = [[4,8,7], [6,4,3], [5,3,7]]
my_image
```
While in principle we could use a ```list``` for this, computations on such objects would be very slow. For example if we wanted to do background correction and subtract a given value from our image, effectively we would have to go through each element of our list (each pixel) one by one and sequentially remove the background from each pixel. If the background is 3 we would have therefore to compute:
- 4-3
- 8-3
- 7-3
- 6-3
etc. Since operations are done sequentially this would be very slow as we couldn't exploit the fact that most computers have multiple processors. Also it would be tedious to write such an operation.
To fix this, most scientific areas that use lists of numbers of some kind (time-series, images, measurements etc.) resort to an **external package** called ```Numpy``` which offers a **computationally efficient list** called an **array**.
To make this clearer we now import an image in our notebook to see such a structure. We will use a **function** from the scikit-image package to do this import. That function called ```imread``` is located in the submodule called ```io```. Remember that we can then access this function with ```skimage.io.imread()```. Just like we previously defined a function $f(x, a, b)$ that took inputs $x, a, b$, this ```imread()``` function also needs an input. Here it is just the **location of the image**, and that location can either be the **path** to the file on our computer or a **url** of an online place where the image is stored. Here we use an image that can be found at https://github.com/guiwitz/PyImageCourse_beginner/raw/master/images/19838_1252_F8_1.tif. As you can see it is a tif file. This address that we are using as an input should be formatted as text:
```
my_address = 'https://github.com/guiwitz/PyImageCourse_beginner/raw/master/images/19838_1252_F8_1.tif'
```
Now we can call our function:
```
skimage.io.imread(my_address)
```
We see here an output which is what is returned by our function. It is as expected a list of numbers, and not all numbers are shown because the list is too long. We see that we also have ```[]``` to specify rows, columns etc. The main difference compared to our list of lists that we defined previously is the ```array``` indication at the very beginning of the list of numbers. This ```array``` indication tells us that we are dealing with a ```Numpy``` array, this alternative type of list of lists that will allow us to do efficient computations.
## Plotting
We will see a few ways to represent data during the course. Here we just want to have a quick look at the image we just imported. For plotting we will use yet another **external library** called Matplotlib. That library is extensively used in the Python world and offers extensive choices of plots. We will mainly use one **function** from the library to display images: ```imshow```. Again, to access that function, we first need to import the package. Here we need a specific submodule:
```
import matplotlib.pyplot as plt
```
Now we can use the ```plt.imshow()``` function. There are many options for plot, but we can use that function already by just passing an ```array``` as an input. First we need to assign the imported array to a variable:
```
import skimage.io
image = skimage.io.imread(my_address)
plt.imshow(image);
```
We see that we are dealing with a multi-channel image and can already distinguish cell nuclei (blue) and cytoplasm (red).
| github_jupyter |
<a href="http://cocl.us/pytorch_link_top">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/Pytochtop.png" width="750" alt="IBM Product " />
</a>
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/cc-logo-square.png" width="200" alt="cognitiveclass.ai logo" />
<h1>Multiple Linear Regression</h1>
<h2>Objective</h2><ul><li> How to make the prediction for multiple inputs.</li><li> How to use linear class to build more complex models.</li><li> How to build a custom module.</li></ul>
<h2>Table of Contents</h2>
<p>In this lab, you will review how to make a prediction in several different ways by using PyTorch.</p>
<ul>
<li><a href="#Prediction">Prediction</a></li>
<li><a href="#Linear">Class Linear</a></li>
<li><a href="#Cust">Build Custom Modules</a></li>
</ul>
<p>Estimated Time Needed: <strong>15 min</strong></p>
<hr>
<h2>Preparation</h2>
Import the libraries and set the random seed.
```
# Import the libraries and set the random seed
from torch import nn
import torch
torch.manual_seed(1)
```
<!--Empty Space for separating topics-->
<h2 id="Prediction">Prediction</h2>
Set weight and bias.
```
# Set the weight and bias
w = torch.tensor([[2.0], [3.0]], requires_grad=True)
b = torch.tensor([[1.0]], requires_grad=True)
```
Define the parameters. <code>torch.mm</code> uses matrix multiplication instead of scaler multiplication.
```
# Define Prediction Function
def forward(x):
yhat = torch.mm(x, w) + b
return yhat
```
The function <code>forward</code> implements the following equation:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter2/2.6.1_matrix_eq.png" width="600" alt="Matrix Linear Regression"/>
If we input a <i>1x2</i> tensor, because we have a <i>2x1</i> tensor as <code>w</code>, we will get a <i>1x1</i> tensor:
```
# Calculate yhat
x = torch.tensor([[1.0, 2.0]])
yhat = forward(x)
print("The result: ", yhat)
```
<img src = "https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter2/2.6.1example.png" width = "300" alt="Linear Regression Matrix Sample One" />
# Each row of the following tensor represents a sample:
```
# Sample tensor X
X = torch.tensor([[1.0, 1.0], [1.0, 2.0], [1.0, 3.0]])
# Make the prediction of X
yhat = forward(X)
print("The result: ", yhat)
```
<!--Empty Space for separating topics-->
<h2 id="Linear">Class Linear</h2>
We can use the linear class to make a prediction. You'll also use the linear class to build more complex models.
Let us create a model.
```
# Make a linear regression model using build-in function
model = nn.Linear(2, 1)
```
Make a prediction with the first sample:
```
# Make a prediction of x
yhat = model(x)
print("The result: ", yhat)
```
Predict with multiple samples <code>X</code>:
```
# Make a prediction of X
yhat = model(X)
print("The result: ", yhat)
```
The function performs matrix multiplication as shown in this image:
<img src = "https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter2/2.6.1multi_sample_example.png" width = "600" alt="Linear Regression Matrix Sample One" />
<!--Empty Space for separating topics-->
<h2 id="Cust">Build Custom Modules </h2>
Now, you'll build a custom module. You can make more complex models by using this method later.
```
# Create linear_regression Class
class linear_regression(nn.Module):
# Constructor
def __init__(self, input_size, output_size):
super(linear_regression, self).__init__()
self.linear = nn.Linear(input_size, output_size)
# Prediction function
def forward(self, x):
yhat = self.linear(x)
return yhat
```
Build a linear regression object. The input feature size is two.
```
model = linear_regression(2, 1)
```
This will input the following equation:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter2/2.6.1_matrix_eq.png" width="600" alt="Matrix Linear Regression" />
You can see the randomly initialized parameters by using the <code>parameters()</code> method:
```
# Print model parameters
print("The parameters: ", list(model.parameters()))
```
You can also see the parameters by using the <code>state_dict()</code> method:
```
# Print model parameters
print("The parameters: ", model.state_dict())
```
Now we input a 1x2 tensor, and we will get a 1x1 tensor.
```
# Make a prediction of x
yhat = model(x)
print("The result: ", yhat)
```
The shape of the output is shown in the following image:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter2/2.6.1_matrix_eq.png" width="600" alt="Matrix Linear Regression" />
Make a prediction for multiple samples:
```
# Make a prediction of X
yhat = model(X)
print("The result: ", yhat)
```
The shape is shown in the following image:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter2/2.6.1Multi_sample.png" width="600" alt="Multiple Samples Linear Regression" />
<!--Empty Space for separating topics-->
<h3>Practice</h3>
Build a model or object of type <code>linear_regression</code>. Using the <code>linear_regression</code> object will predict the following tensor:
```
# Practice: Build a model to predict the follow tensor.
X = torch.tensor([[11.0, 12.0, 13, 14], [11, 12, 13, 14]])
```
Double-click <b>here</b> for the solution.
<!-- Your answer is below:
model = linear_regression(4, 1)
yhat = model(X)
print("The result: ", yhat)
-->
<!--Empty Space for separating topics-->
<a href="http://cocl.us/pytorch_link_bottom">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/notebook_bottom%20.png" width="750" alt="PyTorch Bottom" />
</a>
<h2>About the Authors:</h2>
<a href="https://www.linkedin.com/in/joseph-s-50398b136/">Joseph Santarcangelo</a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
Other contributors: <a href="https://www.linkedin.com/in/michelleccarey/">Michelle Carey</a>, <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
## Change Log
| Date (YYYY-MM-DD) | Version | Changed By | Change Description |
| ----------------- | ------- | ---------- | ----------------------------------------------------------- |
| 2020-09-23 | 2.0 | Shubham | Migrated Lab to Markdown and added to course repo in GitLab |
<hr>
Copyright © 2018 <a href="cognitiveclass.ai?utm_source=bducopyrightlink&utm_medium=dswb&utm_campaign=bdu">cognitiveclass.ai</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.
| github_jupyter |
# Classifying Fashion-MNIST
Now it's your turn to build and train a neural network. You'll be using the [Fashion-MNIST dataset](https://github.com/zalandoresearch/fashion-mnist), a drop-in replacement for the MNIST dataset. MNIST is actually quite trivial with neural networks where you can easily achieve better than 97% accuracy. Fashion-MNIST is a set of 28x28 greyscale images of clothes. It's more complex than MNIST, so it's a better representation of the actual performance of your network, and a better representation of datasets you'll use in the real world.
<img src='assets/fashion-mnist-sprite.png' width=500px>
In this notebook, you'll build your own neural network. For the most part, you could just copy and paste the code from Part 3, but you wouldn't be learning. It's important for you to write the code yourself and get it to work. Feel free to consult the previous notebooks though as you work through this.
First off, let's load the dataset through torchvision.
```
import torch
from torchvision import datasets, transforms
import helper
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
trainset.classes
trainset
```
Here we can see one of the images.
```
image, label = next(iter(trainloader))
print(image.shape, label.shape)
helper.imshow(image[0,:]);
```
## Building the network
Here you should define your network. As with MNIST, each image is 28x28 which is a total of 784 pixels, and there are 10 classes. You should include at least one hidden layer. We suggest you use ReLU activations for the layers and to return the logits or log-softmax from the forward pass. It's up to you how many layers you add and the size of those layers.
```
# TODO: Define your network architecture here
from torch import nn
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128,32),
nn.ReLU(),
nn.Linear(32,10))
model.parameters
```
# Train the network
Now you should create your network and train it. First you'll want to define [the criterion](http://pytorch.org/docs/master/nn.html#loss-functions) ( something like `nn.CrossEntropyLoss`) and [the optimizer](http://pytorch.org/docs/master/optim.html) (typically `optim.SGD` or `optim.Adam`).
Then write the training code. Remember the training pass is a fairly straightforward process:
* Make a forward pass through the network to get the logits
* Use the logits to calculate the loss
* Perform a backward pass through the network with `loss.backward()` to calculate the gradients
* Take a step with the optimizer to update the weights
By adjusting the hyperparameters (hidden units, learning rate, etc), you should be able to get the training loss below 0.4.
```
# TODO: Create the network, define the criterion and optimizer
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(params=model.parameters(), lr=0.01)
len(trainloader), 60000/64
# TODO: Train the network here
epochs = 10
for e in range(epochs):
running_loss = 0
for image,label in iter(trainloader):
optimizer.zero_grad()
output = model(image.view(image.shape[0],-1))
loss = criterion(output, label)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
print(f"Epoch {e} - loss {running_loss/len(trainloader)}")
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import helper
# Test out your network!
dataiter = iter(testloader)
images, labels = dataiter.next()
img = images[2]
# Convert 2D image to 1D vector
img = img.resize_(1, 784)
# TODO: Calculate the class probabilities (softmax) for img
with torch.no_grad():
ps = model(img)
# Plot the image and probabilities
helper.view_classify(img.resize_(1, 28, 28), ps, version='Fashion')
```
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.