code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
# Get all tracts within certain cities
Given a CSV file containing city names, get all the tracts within those cities' boundaries.
```
import geopandas as gpd
import json
import os
import pandas as pd
all_tracts_path = 'data/us_census_tracts_2014'
places_path = 'data/us_census_places_2014'
states_by_fips_path = 'data/states_by_fips.json'
cities_path = 'data/study_sites.csv'
output_path = 'data/tracts_in_cities_study_area.geojson'
# load the city names that make up our study sites
study_sites = pd.read_csv(cities_path, encoding='utf-8')
len(study_sites)
%%time
# load all US census tracts shapefile
all_tracts = gpd.read_file(all_tracts_path)
len(all_tracts)
%%time
# load all US places (cities/towns) shapefile
places = gpd.GeoDataFrame()
for folder in os.listdir(places_path):
path = '{}/{}'.format(places_path, folder)
gdf_tmp = gpd.read_file(path)
places = places.append(gdf_tmp)
len(places)
# get state abbreviation from FIPS
with open(states_by_fips_path) as f:
states = json.load(f)
fips_state = {k:v['abbreviation'] for k, v in states.items()}
places['state'] = places['STATEFP'].replace(fips_state, inplace=False)
cities_states = study_sites.apply(lambda row: '{}, {}'.format(row['city'], row['state']), axis=1)
# find these city names in the GDF of all census places
gdf_cities = gpd.GeoDataFrame()
for city_state in cities_states:
city, state = [item.strip() for item in city_state.split(',')]
mask = (places['NAME']==city) & (places['state']==state)
if not mask.sum()==1:
mask = (places['NAME'].str.contains(city)) & (places['state']==state)
if not mask.sum()==1:
mask = (places['NAME'].str.contains(city)) & (places['state']==state) & ~(places['NAMELSAD'].str.contains('CDP'))
if not mask.sum()==1:
print('Cannot uniquely find "{}"'.format(city_state))
gdf_city = places.loc[mask]
gdf_cities = gdf_cities.append(gdf_city)
len(gdf_cities)
# make "name" field like "city, state"
gdf_cities['name'] = gdf_cities.apply(lambda row: '{}, {}'.format(row['NAME'], row['state']), axis=1)
gdf_cities['name'] = gdf_cities['name'].replace({'Indianapolis city (balance), IN' : 'Indianapolis, IN',
'Nashville-Davidson metropolitan government (balance), TN' : 'Nashville, TN'})
# make gdf of the cities for joining
cities = gdf_cities[['GEOID', 'name', 'geometry']]
cities = cities.rename(columns={'GEOID':'place_geoid', 'name':'place_name'})
cities = cities.set_index('place_geoid')
# make gdf of the tracts for joining
tract_geoms = all_tracts.set_index('GEOID')[['geometry', 'ALAND']]
%%time
# shrink tracts by ~1 meter to avoid peripheral touches on the outside of the city boundary
tract_geoms['geom_tmp'] = tract_geoms['geometry'].buffer(-0.00001)
tract_geoms = tract_geoms.set_geometry('geom_tmp')
%%time
assert tract_geoms.crs == cities.crs
tracts = gpd.sjoin(tract_geoms, cities, how='inner', op='intersects')
print(len(tracts))
# remove the temporary shrunken geometry
tracts = tracts.set_geometry('geometry').drop(columns=['geom_tmp'])
tracts = tracts.rename(columns={'index_right':'place_geoid'})
tracts.head()
%%time
gdf_save = tracts.reset_index().rename(columns={'index':'GEOID'})
os.remove(output_path) # due to overwriting bug in fiona
gdf_save.to_file(output_path, driver='GeoJSON')
print(output_path)
```
| github_jupyter |
By the end of this activity, you will be able to perform the following in Spark:
Determine the accuracy of a classifier model
Display the confusion matrix for a classifier model
In this activity, you will be programming in a Jupyter Python Notebook. If you have not already started the Jupyter Notebook server, see the instructions in the Reading Instructions for Starting Jupyter.
Step 1. Open Jupyter Python Notebook. Open a web browser by clicking on the web browser icon at the top of the toolbar:

Navigate to localhost:8889/tree/Downloads/big-data-4:

Open the model evaluation notebook by clicking on model-evaluation.ipynb:

Step 2. Load predictions. Execute the first cell to load the classes used in this activity:
```
from pyspark.sql import SQLContext
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.mllib.evaluation import MulticlassMetrics
```
Execute the next cell to load the predictions CSV file that we created at the end of the Week 3 Hands-On Classification in Spark into a DataFrame:
```
sqlContext = SQLContext(sc)
predictions = sqlContext.read.load('file:///home/cloudera/Downloads/big-data-4/prediction.csv',
format='com.databricks.spark.csv',
header='true',inferSchema='true')
```
Step 3. Compute accuracy. Let's create an instance of MulticlassClassificationEvaluator to determine the accuracy of the predictions:
```
evaluator = MulticlassClassificationEvaluator(
labelCol="label",predictionCol="prediction",metricName="precision")
evaluator
```
The first two arguments specify the names of the label and prediction columns, and the third argument specifies that we want the overall precision.
We can compute the accuracy by calling evaluate():
```
accuracy = evaluator.evaluate(predictions)
print ("Accuracy = %.2g" % ( accuracy ))
```
Step 4. Display confusion matrix. The MulticlassMetrics class can be used to generate a confusion matrix of our classifier model. However, unlike MulticlassClassificationEvaluator, MulticlassMetrics works with RDDs of numbers and not DataFrames, so we need to convert our predictions DataFrame into an RDD.
If we use the rdd attribute of predictions, we see this is an RDD of Rows:
```
predictions.rdd.take(2)
```
Instead, we can map the RDD to tuple to get an RDD of numbers:
```
predictions.rdd.map(tuple).take(2)
```
Let's create an instance of MulticlassMetrics with this RDD:
```
metrics = MulticlassMetrics(predictions.rdd.map(tuple))
```
NOTE: the above command can take longer to execute than most Spark commands when first run in the notebook.
The confusionMatrix() function returns a Spark Matrix, which we can convert to a Python Numpy array, and transpose to view:
The confusionMatrix() function returns a Spark Matrix, which we can convert to a Python Numpy array, and transpose to view:
```
metrics.confusionMatrix().toArray().transpose()
```
**Q**
Spark: In the last line of code in Step 4, the confusion matrix is printed out. If the “transpose()” is removed, the confusion matrix will be displayed as:
```
metrics.confusionMatrix().toArray()
```
| github_jupyter |
## Computing native contacts with MDTraj
Using the definition from Best, Hummer, and Eaton, "Native contacts determine protein folding mechanisms in atomistic simulations" PNAS (2013) [10.1073/pnas.1311599110](http://dx.doi.org/10.1073/pnas.1311599110)
Eq. (1) of the SI defines the expression for the fraction of native contacts, $Q(X)$:
$$
Q(X) = \frac{1}{|S|} \sum_{(i,j) \in S} \frac{1}{1 + \exp[\beta(r_{ij}(X) - \lambda r_{ij}^0)]},
$$
where
- $X$ is a conformation,
- $r_{ij}(X)$ is the distance between atoms $i$ and $j$ in conformation $X$,
- $r^0_{ij}$ is the distance from heavy atom i to j in the native state conformation,
- $S$ is the set of all pairs of heavy atoms $(i,j)$ belonging to residues $\theta_i$ and $\theta_j$ such that $|\theta_i - \theta_j| > 3$ and $r^0_{i,} < 4.5 \unicode{x212B}$,
- $\beta=5 \unicode{x212B}^{-1}$,
- $\lambda=1.8$ for all-atom simulations
```
import numpy as np
import mdtraj as md
from itertools import combinations
def best_hummer_q(traj, native):
"""Compute the fraction of native contacts according the definition from
Best, Hummer and Eaton [1]
Parameters
----------
traj : md.Trajectory
The trajectory to do the computation for
native : md.Trajectory
The 'native state'. This can be an entire trajecory, or just a single frame.
Only the first conformation is used
Returns
-------
q : np.array, shape=(len(traj),)
The fraction of native contacts in each frame of `traj`
References
----------
..[1] Best, Hummer, and Eaton, "Native contacts determine protein folding
mechanisms in atomistic simulations" PNAS (2013)
"""
BETA_CONST = 50 # 1/nm
LAMBDA_CONST = 1.8
NATIVE_CUTOFF = 0.45 # nanometers
# get the indices of all of the heavy atoms
heavy = native.topology.select_atom_indices('heavy')
# get the pairs of heavy atoms which are farther than 3
# residues apart
heavy_pairs = np.array(
[(i,j) for (i,j) in combinations(heavy, 2)
if abs(native.topology.atom(i).residue.index - \
native.topology.atom(j).residue.index) > 3])
# compute the distances between these pairs in the native state
heavy_pairs_distances = md.compute_distances(native[0], heavy_pairs)[0]
# and get the pairs s.t. the distance is less than NATIVE_CUTOFF
native_contacts = heavy_pairs[heavy_pairs_distances < NATIVE_CUTOFF]
print("Number of native contacts", len(native_contacts))
# now compute these distances for the whole trajectory
r = md.compute_distances(traj, native_contacts)
# and recompute them for just the native state
r0 = md.compute_distances(native[0], native_contacts)
q = np.mean(1.0 / (1 + np.exp(BETA_CONST * (r - LAMBDA_CONST * r0))), axis=1)
return q
# pull a random protein from the PDB
# (The unitcell info happens to be wrong)
traj = md.load_pdb('http://www.rcsb.org/pdb/files/2MI7.pdb')
# just for example, use the first frame as the 'native' conformation
q = best_hummer_q(traj, traj[0])
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(q)
plt.xlabel('Frame', fontsize=14)
plt.ylabel('Q(X)', fontsize=14)
plt.show()
```
| github_jupyter |
First, load the data, from the supplied data file
```
import tarfile
import json
import gzip
import pandas as pd
import botometer
from pandas.io.json import json_normalize
## VARIABLE INITIATION
tar = tarfile.open("../input/2017-09-22.tar.gz", "r:gz")
mashape_key = "QRraJnMT9KmshkpJ7iu74xKFN1jtp1IyBBijsnS5NGbEuwIX54"
twitter_app_auth = {
'consumer_key': 'sPzHpcj4jMital75nY7dfd4zn',
'consumer_secret': 'rTGm68zdNmLvnTc22cBoFg4eVMf3jLVDSQLOwSqE9lXbVWLweI',
'access_token': '4258226113-4UnHbbbxoRPz10thy70q9MtEk9xXfJGOpAY12KW',
'access_token_secret': '549HdasMEW0q2uV05S5s4Uj5SdCeEWT8dNdLNPiAeeWoX',
}
bom = botometer.Botometer(wait_on_ratelimit=True,
mashape_key=mashape_key,
**twitter_app_auth)
count = 0
data = pd.DataFrame()
uname = pd.DataFrame()
#uname = []
for members in tar.getmembers():
if (None):
break
else:
f = tar.extractfile(members)
data = data.append(pd.read_json(f, lines=True))
#for memberx in data['user']:
#uname=uname.append(json_normalize(memberx)['screen_name'], ignore_index=True)
#uname.append('@'+str(json_normalize(memberx)['screen_name'].values[0]))
count = count + 1
data = pd.DataFrame()
uname = pd.DataFrame()
count=0
#uname = []
for members in tar.getmembers():
#if (None):
# break
#else:
if (count==13):
f = tar.extractfile(members)
data = data.append(pd.read_json(f, lines=True))
for memberx in data['user']:
uname=uname.append(json_normalize(memberx)['screen_name'], ignore_index=True)
#uname.append('@'+str(json_normalize(memberx)['screen_name'].values[0]))
count = count + 1
len(uname)
distinct_uname=[]
for i in uname.drop_duplicates().values:
distinct_uname.append((str('@'+i).replace("[u'","")).replace("']",''))
len(distinct_uname)
asu=distinct_uname[0:180]
botoresult = pd.DataFrame()
for screen_name, result in bom.check_accounts_in(asu):
botoresult=botoresult.append(result, ignore_index=True)
#bom.twitter_api.rate_limit_status()['resources']['application']['/application/rate_limit_status']['remaining']
output_bot=pd.concat([botoresult.user.apply(pd.Series), botoresult.scores.apply(pd.Series), botoresult.categories.apply(pd.Series)], axis=1)
len(botoresult)
output_bot.to_csv("outputbot.csv", sep=',', encoding='utf-8')
```
<h1>unused script</h1>
only for profilling<br>
xoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxo
```
import pylab as pl
import numpy as np
from collections import Counter
x=Counter(data['created_at'].dt.strftime('%d%H'))
y=zip(map(int,x.keys()),x.values())
y.sort()
x=pd.DataFrame(y)
x
X = range(len(y))
pl.bar(X, x[1], align='center', width=1)
pl.xticks(X, x[0], rotation="vertical")
ymax = max(x[1]) + 1
pl.ylim(0, ymax)
pl.show()
```
| github_jupyter |
Wayne H Nixalo - 09 Aug 2017
FADL2 L9: Generative Models
neural-style-GPU.ipynb
```
%matplotlib inline
import importlib
import os, sys
sys.path.insert(1, os.path.join('../utils'))
from utils2 import *
from scipy.optimize import fmin_l_bfgs_b
from scipy.misc import imsave
from keras import metrics
from vgg16_avg import VGG16_Avg
limit_mem()
path = '../data/nst/'
# names = os.listdir(path)
# pkl_out = open('fnames.pkl','wb')
# pickle.dump(names, pkl_out)
# pkl_out.close()
fnames = pickle.load(open(path + 'fnames.pkl', 'rb'))
fnames = glob.glob(path+'**/*.JPG', recursive=True)
fn = fnames[0]
fn
img = Image.open(fn); img
# Subtracting mean and reversing color-channel order:
rn_mean = np.array([123.68,116.779,103.939], dtype=np.float32)
preproc = lambda x: (x - rn_mean)[:,:,:,::-1]
# later undoing preprocessing for image generation
deproc = lambda x,s: np.clip(x.reshape(s)[:,:,:,::-1] + rn_mean, 0, 255)
img_arr = preproc(np.expand_dims(np.array(img), 0))
shp = img_arr.shape
```
### Content Recreation
```
# had to fix some compatibility issues w/ Keras 1 -> Keras 2
import vgg16_avg
importlib.reload(vgg16_avg)
from vgg16_avg import VGG16_Avg
model = VGG16_Avg(include_top=False)
# grabbing activations from near the end of the CNN model
layer = model.get_layer('block5_conv1').output
# calculating layer's target activations
layer_model = Model(model.input, layer)
targ = K.variable(layer_model.predict(img_arr))
```
In this implementation, need to define an object that'll allow us to separately access the loss function and gradients of a function,
```
class Evaluator(object):
def __init__(self, f, shp): self.f, self.shp = f, shp
def loss(self, x):
loss_, self.grad_values = self.f([x.reshape(self.shp)])
return loss_.astype(np.float64)
def grads(self, x): return self.grad_values.flatten().astype(np.float64)
# Define loss function to calc MSE betwn the 2 outputs at specfd Conv layer
loss = metrics.mse(layer, targ)
grads = K.gradients(loss, model.input)
fn = K.function([model.input], [loss]+grads)
evaluator = Evaluator(fn, shp)
# optimize loss fn w/ deterministic approach using Line Search
def solve_image(eval_obj, niter, x):
for i in range(niter):
x, min_val, info = fmin_l_bfgs_b(eval_obj.loss, x.flatten(),
fprime=eval_obj.grads, maxfun=20)
x = np.clip(x, -127,127)
print('Current loss value:', min_val)
imsave(f'{path}/results/res_at_iteration_{i}.png', deproc(x.copy(), shp)[0])
return x
# generating a random image:
rand_img = lambda shape: np.random.uniform(-2.5,2.5,shape)/100
x = rand_img(shp)
plt.imshow(x[0])
iterations = 10
x = solve_image(evaluator, iterations, x)
Image.open(path + 'results/res_at_iteration_1.png')
# Looking at result for earlier Conv block (4):
layer = model.get_layer('block4_conv1').output
layer_model = Model(model.input, layer)
targ = K.variable(layer_model.predict(img_arr))
loss = metrics.mse(layer, targ)
grads = K.gradients(loss, model.input)
fn = K.function([model.input], [loss]+grads)
evaluator = Evaluator(fn, shp)
x = solve_image(evaluator, iterations, x)
Image.open(path + 'results/res_at_iteration_9.png')
```
| github_jupyter |
```
import pandas as pd
from matplotlib import pyplot as plt
import matplotlib.ticker as mtick
from dateutil.parser import parse as date_parse
import requests
%matplotlib inline
pd.options.mode.chained_assignment = None
jhu_data = pd.read_csv('https://raw.githubusercontent.com/CSSEGISandData/' \
'COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/' \
'time_series_covid19_confirmed_global.csv')
# https://www.soothsawyer.com/john-hopkins-time-series-data-confirmed-case-csv-after-march-22-2020/
jhu_data = pd.read_csv('https://www.soothsawyer.com/wp-content/uploads/' \
'2020/03/time_series_19-covid-Confirmed.csv')
jhu_data_deaths = pd.read_csv('https://www.soothsawyer.com/wp-content/uploads/2020/03/time_series_19-covid-Deaths.csv')
r=requests.get('https://covidtracking.com/api/states/daily')
covidtracking_data = pd.DataFrame(r.json())
# this is the URL to the CSV file in GitHub so you can parse date of last commit.
# (the REST API required auth)
JHU_DATA_FILE_URL = 'https://github.com/CSSEGISandData/COVID-19/blob/master/' \
'csse_covid_19_data/csse_covid_19_time_series/' \
'time_series_covid19_confirmed_global.csv'
covidtracking_data_ = covidtracking_data.copy()
covidtracking_data_['dateChecked'] = covidtracking_data_['dateChecked'].map(lambda x: date_parse(x))
covidtracking_data_['date'] = covidtracking_data_['date'].map(lambda x: date_parse(str(x)))
covidtracking_reduced = covidtracking_data_.groupby(['state', 'date']).sum().reset_index()
country_filter = ['China', 'South Korea', 'Italy', 'France', 'Spain', 'United States']
country_mapper = {
'Korea, South': 'South Korea',
'US': 'United States'
}
jhu_data['Country/Region'] = jhu_data['Country/Region'].map(country_mapper).fillna(jhu_data['Country/Region'])
assert set(country_filter) - set(jhu_data['Country/Region']) == set()
def jhu_data_processing(df, t0_threshold=100, states_data=False):
loc = 'location' if not states_data else 'state'
df['Country/Region'] = df['Country/Region'].map(country_mapper).fillna(df['Country/Region'])
if states_data:
df = df[df['Country/Region'] == 'United States']
df['Province/State'] = df['Province/State'].map(drop_cities).dropna()
df = df.drop(columns=['Lat', 'Long', 'Country/Region'])
df = df.groupby('Province/State').max()
else:
df = df.drop(columns=['Lat', 'Long', 'Province/State'])
df = df.groupby('Country/Region').max()
df = df.stack().reset_index()
df.columns = [loc, 'date', 'total']
df['date'] = pd.to_datetime(df['date'])
if not states_data:
df = df.query('total >= @t0_threshold')
t0_date = df.groupby(loc).min()['date']
df.loc[:, 't0_date'] = pd.to_datetime(df[loc].map(t0_date))
df.loc[:, 'since_t0'] = df['date'] - df['t0_date']
df.loc[:, 'since_t0'] = df['since_t0'].map(lambda x: x.days)
df.loc[:, 'since_t0'] = df.loc[:, 'since_t0'].where(df['since_t0'] > 0, 0)
return df
state_abbr = pd.read_csv('https://raw.githubusercontent.com/jasonong/List-of-US-States/master/states.csv')
state_lookup = state_abbr.set_index('Abbreviation', drop=True).squeeze().to_dict()
def get_state(place):
p = place.split(',')
if len(p) > 1:
return state_lookup[p[1].replace('.', '').strip()]
return place
def drop_cities(place):
if place.find(',') > 0:
return None
else:
return place
jhu_data_t0 = jhu_data_processing(jhu_data)
jhu_data_us_reduced = jhu_data_processing(jhu_data, states_data=True)
jhu_deaths_data_t0 = jhu_data_processing(jhu_data_deaths, t0_threshold=10)
jhu_deaths_data_us_reduced = jhu_data_processing(jhu_data_deaths, states_data=True, t0_threshold=50)
ax = plt.gca()
p=jhu_data_t0[jhu_data_t0['location'].isin(country_filter)].groupby('location').plot(x='since_t0',
y='total',
ax=ax, logy=True)
ax.figure.set_size_inches(12,6)
ax.legend(country_filter)
ax.set_xlabel('Days Since Cases = 100')
ax.set_ylabel('Total Confirmed Cases')
ax.yaxis.set_major_formatter(mtick.StrMethodFormatter('{x:,.0f}'))
ax = plt.gca()
p=jhu_deaths_data_t0[jhu_deaths_data_t0['location'].isin(country_filter)].groupby('location').plot(x='since_t0',
y='total',
ax=ax, logy=True)
ax.figure.set_size_inches(12,6)
ax.legend(country_filter)
ax.set_xlabel('Date')
ax.set_ylabel('Deaths')
ax.yaxis.set_major_formatter(mtick.StrMethodFormatter('{x:,.0f}'))
state_filter = ['Georgia', 'New York', 'California', 'Ohio', 'Washington', 'Louisiana']
# NOTE: legend does not match lines
ax = plt.gca()
plot_df = jhu_deaths_data_us_reduced[jhu_deaths_data_us_reduced['total']>0]
p=plot_df[plot_df['state'].isin(state_filter)].groupby('state').plot(x='date', y='total',
ax=ax, logy=False)
ax.figure.set_size_inches(12,6)
ax.legend(state_filter)
ax.set_xlabel('Date')
ax.set_ylabel('Deaths')
ax.yaxis.set_major_formatter(mtick.StrMethodFormatter('{x:,.0f}'));
```
jhu_data_us_t0
```
ax = plt.gca()
plot_df = jhu_data_us_reduced[jhu_data_us_reduced['total']>0]
p=plot_df[plot_df['state'].isin(state_filter)].groupby('state').plot(x='date',
y='total',
ax=ax, logy=True)
ax.figure.set_size_inches(12,6)
ax.legend(state_filter)
ax.set_xlabel('Days Since Cases = 1')
ax.set_ylabel('Total Confirmed Cases')
ax.yaxis.set_major_formatter(mtick.StrMethodFormatter('{x:,.0f}'));
state_abbr = pd.read_csv('https://raw.githubusercontent.com/jasonong/List-of-US-States/master/states.csv')
state_lookup = state_abbr.set_index('Abbreviation', drop=True).squeeze().to_dict()
covidtracking_reduced['state'] = covidtracking_reduced['state'].map(state_lookup)
covidtracking_reduced = covidtracking_reduced.groupby(['state', 'date']).max()['positive'].reset_index()
ax = plt.gca()
p=covidtracking_reduced[covidtracking_reduced['state'].isin(state_filter)].groupby('state').plot(x='date',
y='positive',
ax=ax, logy=True)
ax.figure.set_size_inches(12,6)
ax.legend(state_filter)
ax.set_xlabel('Days Since Cases = 1')
ax.set_ylabel('Total Confirmed Cases')
ax.yaxis.set_major_formatter(mtick.StrMethodFormatter('{x:,.0f}'))
top25_states = covidtracking_reduced.groupby('state').max()['total'].sort_values(ascending=False)[:25].keys()
fig = plt.figure(figsize=(20,20))
ax_list = fig.subplots(5, 5).flatten()
for ix, state in enumerate(top25_states):
if ix > 24:
continue
plot_data = covidtracking_reduced.query('state == @state').drop(columns='state').set_index('date')
plot_data.plot(ax=ax_list[ix],legend=False, title=state, logy=True)
```
| github_jupyter |
# The Central Limit Theorem
Elements of Data Science
by [Allen Downey](https://allendowney.com)
[MIT License](https://opensource.org/licenses/MIT)
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# If we're running on Colab, install empiricaldist
# https://pypi.org/project/empiricaldist/
import sys
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
!pip install empiricaldist
```
## The Central Limit Theorem
According to our friends at [Wikipedia](https://en.wikipedia.org/wiki/Central_limit_theorem):
> The central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution (informally a bell curve) even if the original variables themselves are not normally distributed.
This theorem is useful for two reasons:
1. It offers an explanation for the ubiquity of normal distributions in the natural and engineered world. If you measure something that depends on the sum of many independent factors, the distribution of the measurements will often be approximately normal.
2. In the context of mathematical statistics it provides a way to approximate the sampling distribution of many statistics, at least, as Wikipedia warns us, "in some situations".
In this notebook, we'll explore those situations.
## Rolling dice
I'll start by adding up the totals for 1, 2, and 3 dice.
The following function simulates rolling a six-sided die.
```
def roll(size):
return np.random.randint(1, 7, size=size)
```
If we roll it 1000 times, we expect each value to appear roughly the same number of times.
```
sample = roll(1000)
```
Here's what the PMF looks like.
```
from empiricaldist import Pmf
pmf = Pmf.from_seq(sample)
pmf.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
To simulate rolling two dice, I'll create an array with 1000 rows and 2 columns.
```
a = roll(size=(1000, 2))
a.shape
```
And then add up the columns.
```
sample2 = a.sum(axis=1)
sample2.shape
```
The result is a sample of 1000 sums of two dice. Here's what that PMF looks like.
```
pmf2 = Pmf.from_seq(sample2)
pmf2.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
And here's what it looks like with three dice.
```
a = roll(size=(1000, 3))
sample3 = a.sum(axis=1)
pmf3 = Pmf.from_seq(sample3)
pmf3.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
With one die, the distribution is uniform. With two dice, it's a triangle. With three dice, it starts to have the shape of a bell curve.
Here are the three PMFs on the same axes, for comparison.
```
pmf.plot(label='1 die')
pmf2.plot(label='2 dice')
pmf3.plot(label='3 dice')
plt.xlabel('Outcome')
plt.ylabel('Probability')
plt.legend();
```
## Gamma distributions
In the previous section, we saw that the sum of values from a uniform distribution starts to look like a bell curve when we add up just a few values.
Now let's do the same thing with values from a gamma distribution.
NumPy provides a function to generate random values from a gamma distribution with a given mean.
```
mean = 2
gamma_sample = np.random.gamma(mean, size=1000)
```
Here's what the distribution looks like, this time using a CDF.
```
from empiricaldist import Cdf
cdf1 = Cdf.from_seq(gamma_sample)
cdf1.plot()
plt.xlabel('Outcome')
plt.ylabel('CDF');
```
It doesn't look like like a normal distribution. To see the differences more clearly, we can plot the CDF of the data on top of a normal model with the same mean and standard deviation.
```
from scipy.stats import norm
def plot_normal_model(sample, **options):
"""Plot the CDF of a normal distribution with the
same mean and std of the sample.
sample: sequence of values
options: passed to plt.plot
"""
mean, std = np.mean(sample), np.std(sample)
xs = np.linspace(np.min(sample), np.max(sample))
ys = norm.cdf(xs, mean, std)
plt.plot(xs, ys, alpha=0.4, **options)
```
Here's what that looks like for a gamma distribution with mean 2.
```
from empiricaldist import Cdf
plot_normal_model(gamma_sample, color='C0', label='Normal model')
cdf1.plot(label='Sample 1')
plt.xlabel('Outcome')
plt.ylabel('CDF');
```
There are clear differences between the data and the model. Let's see how that looks when we start adding up values.
The following function computes the sum of gamma distributions with a given mean.
```
def sum_of_gammas(mean, num):
"""Sample the sum of gamma variates.
mean: mean of the gamma distribution
num: number of values to add up
"""
a = np.random.gamma(mean, size=(1000, num))
sample = a.sum(axis=1)
return sample
```
Here's what the sum of two gamma variates looks like:
```
gamma_sample2 = sum_of_gammas(2, 2)
cdf2 = Cdf.from_seq(gamma_sample2)
plot_normal_model(gamma_sample, color='C0')
cdf1.plot(label='Sum of 1 gamma')
plot_normal_model(gamma_sample2, color='C1')
cdf2.plot(label='Sum of 2 gamma')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend();
```
The normal model is a better fit for the sum of two gamma variates, but there are still evident differences. Let's see how big `num` has to be before it converges.
First I'll wrap the previous example in a function.
```
def plot_gammas(mean, nums):
"""Plot the sum of gamma variates and a normal model.
mean: mean of the gamma distribution
nums: sequence of sizes
"""
for num in nums:
sample = sum_of_gammas(mean, num)
plot_normal_model(sample, color='gray')
Cdf.from_seq(sample).plot(label=f'num = {num}')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend()
```
With `mean=2` it doesn't take long for the sum of gamma variates to approximate a normal distribution.
```
mean = 2
plot_gammas(mean, [2, 5, 10])
```
However, that doesn't mean that all gamma distribution behave the same way. In general, the higher the variance, the longer it takes to converge.
With a gamma distribution, smaller means lead to higher variance. With `mean=0.2`, the sum of 10 values is still not normal.
```
mean = 0.2
plot_gammas(mean, [2, 5, 10])
```
We have to crank `num` up to 100 before the convergence looks good.
```
mean = 0.2
plot_gammas(mean, [20, 50, 100])
```
With `mean=0.02`, we have to add up 1000 values before the distribution looks normal.
```
mean = 0.02
plot_gammas(mean, [200, 500, 1000])
```
## Pareto distributions
The gamma distributions in the previous section have higher variance that the uniform distribution we started with, so we have to add up more values to get the distribution of the sum to look normal.
The Pareto distribution is even more extreme. Depending on the parameter, `alpha`, the variance can be large, very large, or infinite.
Here's a function that generates the sum of values from a Pareto distribution with a given parameter.
```
def sum_of_paretos(alpha, num):
a = np.random.pareto(alpha, size=(1000, num))
sample = a.sum(axis=1)
return sample
```
And here's a function that plots the results.
```
def plot_paretos(mean, nums):
for num in nums:
sample = sum_of_paretos(mean, num)
plot_normal_model(sample, color='gray')
Cdf.from_seq(sample).plot(label=f'num = {num}')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend()
```
With `alpha=3` the Pareto distribution is relatively well-behaved, and the sum converges to a normal distribution with a moderate number of values.
```
alpha = 3
plot_paretos(alpha, [10, 20, 50])
```
With `alpha=2`, we don't get very good convergence even with 1000 values.
```
alpha = 2
plot_paretos(alpha, [200, 500, 1000])
```
With `alpha=1.5`, it's even worse.
```
alpha = 1.5
plot_paretos(alpha, [2000, 5000, 10000])
```
And with `alpha=1`, it's beyond hopeless.
```
alpha = 1
plot_paretos(alpha, [10000, 20000, 50000])
```
In fact, when `alpha` is 2 or less, the variance of the Pareto distribution is infinite, and the central limit theorem does not apply. The disrtribution of the sum never converges to a normal distribution.
However, there is no practical difference between a distribution like Pareto that never converges and other high-variance distributions that converge in theory, but only with an impractical number of values.
## Summary
The central limit theorem is an important result in mathematical statistics. And it explains why so many distributions in the natural and engineered world are approximately normal.
But it doesn't always apply:
* In theory the central limit theorem doesn't apply when variance is infinite.
* In practice it might be irrelevant when variance is high.
| github_jupyter |
```
%tensorflow_version 2.x
%load_ext tensorboard
import tensorflow as tf
from tensorflow.keras import layers, models
import matplotlib.pyplot as plt
from os import path, walk
import numpy as np
import datetime
from skimage import feature, util, io, color
import cv2
device_name = tf.test.gpu_device_name()
if device_name != '/device:GPU:0':
raise SystemError('GPU device not found')
print('Found GPU at: {}'.format(device_name))
data_dir = path.join(path.curdir, "databases", "cajus-amarelos")
label_to_int = {"bad": 0, "good": 1, "medium": 2}
gabor_imgs = []
labels = []
params = {'ksize':(3, 3), 'sigma':1.0, 'theta': 0, 'lambd':5.0, 'gamma':0.02}
filter = cv2.getGaborKernel(**params)
def load_img(img_path, label):
img = io.imread(img_path, as_gray=True)
img = util.img_as_ubyte(img)
gabor_img = cv2.filter2D(img, -1, filter)
gabor_img = util.img_as_float32(gabor_img)
gabor_img = np.expand_dims(gabor_img, axis=2)
gabor_imgs.append(tf.convert_to_tensor(gabor_img, dtype=tf.float32))
labels.append(label)
print(f'{img_path} loaded!')
for img_path, _, filenames in walk(data_dir):
for label in ("good", "medium", "bad"):
if label in img_path:
for filename in filenames:
load_img(path.join(img_path, filename), label_to_int[label])
gabor_ds = tf.data.Dataset.from_tensor_slices(gabor_imgs)
labels_ds = tf.data.Dataset.from_tensor_slices(labels)
dataset = tf.data.Dataset.zip((gabor_ds, labels_ds))
train_ds_size = int(0.8 * 120)
val_ds_size = int(0.2 * 120)
dataset = dataset.shuffle(1000)
train_ds = dataset.take(train_ds_size)
val_ds = dataset.skip(train_ds_size)
AUTOTUNE = tf.data.experimental.AUTOTUNE
train_ds = train_ds.shuffle(1000).batch(12).cache().prefetch(buffer_size=AUTOTUNE)
val_ds = val_ds.shuffle(1000).batch(12).cache().prefetch(buffer_size=AUTOTUNE)
print(train_ds)
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.experimental.preprocessing.RandomFlip("horizontal_and_vertical", input_shape=(512, 512, 1)))
model.add(tf.keras.layers.experimental.preprocessing.RandomRotation(0.4, fill_mode="nearest"))
model.add(tf.keras.layers.Conv2D(16, (3, 3), activation="swish"))
model.add(tf.keras.layers.MaxPooling2D((2, 2)))
model.add(tf.keras.layers.Conv2D(32, (3, 3), activation="swish"))
model.add(tf.keras.layers.MaxPooling2D((2, 2)))
# model.add(tf.keras.layers.Conv2D(32, (3, 3), activation="swish"))
# model.add(tf.keras.layers.MaxPooling2D((2, 2)))
model.add(tf.keras.layers.Conv2D(64, (3, 3), activation="swish"))
model.add(tf.keras.layers.MaxPooling2D((2, 2)))
# model.add(tf.keras.layers.Conv2D(64, (3, 3), activation="swish"))
# model.add(tf.keras.layers.MaxPooling2D((2, 2)))
model.add(tf.keras.layers.SpatialDropout2D(0.5))
model.add(tf.keras.layers.GlobalAveragePooling2D())
model.add(tf.keras.layers.Dense(128, activation="elu"))
model.add(tf.keras.layers.Dense(64, activation="elu"))
model.add(tf.keras.layers.Dense(32, activation="elu"))
# model.add(tf.keras.layers.Dense(16, activation="elu"))
model.add(tf.keras.layers.Dropout(0.15))
model.add(tf.keras.layers.Dense(3, activation="softmax"))
model.summary()
model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.0005),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=["accuracy"]
)
earlyStopping = tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=50, verbose=1)
log_dir = "./logs/cajus-amarelos/gabor/grayscale/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir, histogram_freq=1)
history = model.fit(
train_ds,
epochs=1000,
validation_data=val_ds,
callbacks=[earlyStopping, tensorboard_callback]
)
loss, acc = model.evaluate(val_ds)
plt.figure()
plt.ylabel("Loss (training and validation)")
plt.xlabel("Training Steps")
plt.ylim([0,2])
plt.plot(history.history["loss"])
plt.plot(history.history["val_loss"])
plt.figure()
plt.ylabel("Accuracy (training and validation)")
plt.xlabel("Training Steps")
plt.ylim([0,1])
plt.plot(history.history["accuracy"])
plt.plot(history.history["val_accuracy"])
model.save('./models/cajus-amarelos/gabor/grayscale')
%tensorboard --logdir ./logs/cajus-amarelos/gabor/grayscale
!tensorboard dev upload \
--logdir ./logs/cajus-amarelos/gabor/grayscale/20210316-193745 \
--name "cajus-amarelos-gabor-grayscale" \
--description "cnn model on gabor filtered cajus amarelos grayscale images" \
--one_shot
loaded_model = tf.keras.models.load_model('./models/cajus-amarelos/gabor/grayscale')
loaded_model.summary()
```
| github_jupyter |
### **PINN eikonal solver using transfer learning for a smooth v(x,z) model**
```
from google.colab import drive
drive.mount('/content/gdrive')
cd "/content/gdrive/My Drive/Colab Notebooks/Codes/PINN_isotropic_eikonal"
!pip install sciann==0.4.6.2
!pip install tensorflow==2.2.0
!pip install keras==2.3.1
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
import tensorflow as tf
from sciann import Functional, Variable, SciModel
from sciann.utils import *
import scipy.io
import time
import random
tf.config.threading.set_intra_op_parallelism_threads(1)
tf.config.threading.set_inter_op_parallelism_threads(1)
np.random.seed(123)
tf.random.set_seed(123)
#Model specifications
v0 = 2.; # Velocity at the origin of the model
vergrad = 1.; # Vertical gradient
horgrad = 0.5; # Horizontal gradient
zmin = 0.; zmax = 2.; deltaz = 0.02;
xmin = 0.; xmax = 2.; deltax = 0.02;
# Point-source location
sz = 0.3; sx = 1.4;
# Number of training points
num_tr_pts = 2000
# Creating grid, calculating refrence traveltimes, and prepare list of grid points for training (X_star)
z = np.arange(zmin,zmax+deltaz,deltaz)
nz = z.size
x = np.arange(xmin,xmax+deltax,deltax)
nx = x.size
Z,X = np.meshgrid(z,x,indexing='ij')
# Preparing velocity model
vs = v0 + vergrad*sz + horgrad*sx # Velocity at the source location
velmodel = vs + vergrad*(Z-sz) + horgrad*(X-sx);
# Traveltime solution
if vergrad==0 and horgrad==0:
# For homogeneous velocity model
T_data = np.sqrt((Z-sz)**2 + (X-sx)**2)/v0;
else:
# For velocity gradient model
T_data = np.arccosh(1.0+0.5*(1.0/velmodel)*(1/vs)*(vergrad**2 + horgrad**2)*((X-sx)**2 + (Z-sz)**2))/np.sqrt(vergrad**2 + horgrad**2)
X_star = [Z.reshape(-1,1), X.reshape(-1,1)] # Grid points for prediction
selected_pts = np.random.choice(np.arange(Z.size),num_tr_pts,replace=False)
Zf = Z.reshape(-1,1)[selected_pts]
Zf = np.append(Zf,sz)
Xf = X.reshape(-1,1)[selected_pts]
Xf = np.append(Xf,sx)
X_starf = [Zf.reshape(-1,1), Xf.reshape(-1,1)] # Grid points for training
# Plot the velocity model with the source location
plt.style.use('default')
plt.figure(figsize=(4,4))
ax = plt.gca()
im = ax.imshow(velmodel, extent=[xmin,xmax,zmax,zmin], aspect=1, cmap="jet")
ax.plot(sx,sz,'k*',markersize=8)
plt.xlabel('Offset (km)', fontsize=14)
plt.xticks(fontsize=10)
plt.ylabel('Depth (km)', fontsize=14)
plt.yticks(fontsize=10)
ax.xaxis.set_major_locator(plt.MultipleLocator(0.5))
ax.yaxis.set_major_locator(plt.MultipleLocator(0.5))
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="6%", pad=0.15)
cbar = plt.colorbar(im, cax=cax)
cbar.set_label('km/s',size=10)
cbar.ax.tick_params(labelsize=10)
plt.savefig("./figs/vofz_transfer/velmodel.pdf", format='pdf', bbox_inches="tight")
# Analytical solution for the known traveltime part
vel = velmodel[int(round(sz/deltaz)),int(round(sx/deltax))] # Velocity at the source location
T0 = np.sqrt((Z-sz)**2 + (X-sx)**2)/vel;
px0 = np.divide(X-sx, T0*vel**2, out=np.zeros_like(T0), where=T0!=0)
pz0 = np.divide(Z-sz, T0*vel**2, out=np.zeros_like(T0), where=T0!=0)
# Find source location id in X_star
TOLX = 1e-6
TOLZ = 1e-6
sids,_ = np.where(np.logical_and(np.abs(X_starf[0]-sz)<TOLZ , np.abs(X_starf[1]-sx)<TOLX))
print(sids)
print(sids.shape)
print(X_starf[0][sids,0])
print(X_starf[1][sids,0])
# Preparing the Sciann model object
K.clear_session()
layers = [20]*10
# Appending source values
velmodelf = velmodel.reshape(-1,1)[selected_pts]; velmodelf = np.append(velmodelf,vs)
px0f = px0.reshape(-1,1)[selected_pts]; px0f = np.append(px0f,0.)
pz0f = pz0.reshape(-1,1)[selected_pts]; pz0f = np.append(pz0f,0.)
T0f = T0.reshape(-1,1)[selected_pts]; T0f = np.append(T0f,0.)
xt = Variable("xt",dtype='float64')
zt = Variable("zt",dtype='float64')
vt = Variable("vt",dtype='float64')
px0t = Variable("px0t",dtype='float64')
pz0t = Variable("pz0t",dtype='float64')
T0t = Variable("T0t",dtype='float64')
tau = Functional("tau", [zt, xt], layers, 'atan')
# Loss function based on the factored isotropic eikonal equation
L = (T0t*diff(tau, xt) + tau*px0t)**2 + (T0t*diff(tau, zt) + tau*pz0t)**2 - 1.0/vt**2
targets = [tau, L, (1-sign(tau*T0t))*abs(tau*T0t)]
target_vals = [(sids, np.ones(sids.shape).reshape(-1,1)), 'zeros', 'zeros']
model = SciModel(
[zt, xt, vt, pz0t, px0t, T0t],
targets,
load_weights_from='models/vofz_model-end.hdf5'
)
#Model training
start_time = time.time()
hist = model.train(
X_starf + [velmodelf,pz0f,px0f,T0f],
target_vals,
batch_size = X_starf[0].size,
epochs = 5000,
learning_rate = 0.0005,
verbose=0
)
elapsed = time.time() - start_time
print('Training time: %.2f minutes' %(elapsed/60.))
# Loading loss history and compute time for the pre-trained model
loss = np.load('models/loss_vofz.npy')
time_vofz = np.load('models/time_vofz.npy')
# Convergence history plot for verification
fig = plt.figure(figsize=(5,3))
ax = plt.axes()
ax.semilogy(loss,LineWidth=2,label='Random initial model')
ax.semilogy(hist.history['loss'],LineWidth=2,label='Pre-trained initial model')
ax.set_xlabel('Epochs',fontsize=14)
plt.xticks(fontsize=10)
ax.xaxis.set_major_locator(plt.MultipleLocator(5000))
ax.set_ylabel('Loss',fontsize=14)
plt.yticks(fontsize=10);
plt.grid()
plt.legend()
ax2 = ax.twiny()
ax2.set_xlabel("x-transformed")
ax2.set_xlim(-time_vofz*.05, time_vofz*1.05)
ax2.set_xlabel('Time (s)',fontsize=14)
plt.savefig("./figs/vofz_transfer/loss.pdf", format='pdf', bbox_inches="tight")
# Predicting traveltime solution from the trained model
L_pred = L.eval(model, X_star + [velmodel,pz0,px0,T0])
tau_pred = tau.eval(model, X_star + [velmodel,pz0,px0,T0])
tau_pred = tau_pred.reshape(Z.shape)
T_pred = tau_pred*T0
print('Time at source: %.4f'%(tau_pred[int(round(sz/deltaz)),int(round(sx/deltax))]))
# Plot the PINN solution error
plt.style.use('default')
plt.figure(figsize=(4,4))
ax = plt.gca()
im = ax.imshow(np.abs(T_pred-T_data), extent=[xmin,xmax,zmax,zmin], aspect=1, cmap="jet")
plt.xlabel('Offset (km)', fontsize=14)
plt.xticks(fontsize=10)
plt.ylabel('Depth (km)', fontsize=14)
plt.yticks(fontsize=10)
ax.xaxis.set_major_locator(plt.MultipleLocator(0.5))
ax.yaxis.set_major_locator(plt.MultipleLocator(0.5))
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="6%", pad=0.15)
cbar = plt.colorbar(im, cax=cax)
cbar.set_label('seconds',size=10)
cbar.ax.tick_params(labelsize=10)
plt.savefig("./figs/vofz_transfer/pinnerror.pdf", format='pdf', bbox_inches="tight")
# Loading fast marching solutions
# First order FMM solution
time_fmm1="data/fmm_or1_vofz_s(1.4,.3).txt"
T_fmm1 = pd.read_csv(time_fmm1, index_col=None, header=None)
T_fmm1 = np.reshape(np.array(T_fmm1), (nx, nz)).T
# Plot the first order FMM solution error
plt.style.use('default')
plt.figure(figsize=(4,4))
ax = plt.gca()
im = ax.imshow(np.abs(T_fmm1-T_data), extent=[xmin,xmax,zmax,zmin], aspect=1, cmap="jet")
plt.xlabel('Offset (km)', fontsize=14)
plt.xticks(fontsize=10)
plt.ylabel('Depth (km)', fontsize=14)
plt.yticks(fontsize=10)
ax.xaxis.set_major_locator(plt.MultipleLocator(0.5))
ax.yaxis.set_major_locator(plt.MultipleLocator(0.5))
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="6%", pad=0.15)
cbar = plt.colorbar(im, cax=cax)
cbar.set_label('seconds',size=10)
cbar.ax.tick_params(labelsize=10)
plt.savefig("./figs/vofz_transfer/fmm1error.pdf", format='pdf', bbox_inches="tight")
# Traveltime contour plots
plt.figure(figsize=(5,5))
ax = plt.gca()
im1 = ax.contour(T_data, 6, extent=[xmin,xmax,zmin,zmax], colors='r')
im2 = ax.contour(T_pred, 6, extent=[xmin,xmax,zmin,zmax], colors='k',linestyles = 'dashed')
im3 = ax.contour(T_fmm1, 6, extent=[xmin,xmax,zmin,zmax], colors='b',linestyles = 'dotted')
ax.plot(sx,sz,'k*',markersize=8)
plt.xlabel('Offset (km)', fontsize=14)
plt.ylabel('Depth (km)', fontsize=14)
ax.tick_params(axis='both', which='major', labelsize=8)
plt.gca().invert_yaxis()
h1,_ = im1.legend_elements()
h2,_ = im2.legend_elements()
h3,_ = im3.legend_elements()
ax.legend([h1[0], h2[0], h3[0]], ['Analytical', 'PINN', 'Fast marching'],fontsize=12)
ax.xaxis.set_major_locator(plt.MultipleLocator(0.5))
ax.yaxis.set_major_locator(plt.MultipleLocator(0.5))
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)
plt.savefig("./figs/vofz_transfer/contours.pdf", format='pdf', bbox_inches="tight")
print(np.linalg.norm(T_pred-T_data)/np.linalg.norm(T_data))
print(np.linalg.norm(T_pred-T_data))
!nvidia-smi -L
```
| github_jupyter |
# Qcodes example with Alazar ATS 9360
```
# import all necessary things
%matplotlib nbagg
import qcodes as qc
import qcodes.instrument.parameter as parameter
import qcodes.instrument_drivers.AlazarTech.ATS9360 as ATSdriver
import qcodes.instrument_drivers.AlazarTech.ATS_acquisition_controllers as ats_contr
# Command to list all alazar boards connected to the system
ATSdriver.AlazarTech_ATS.find_boards()
# Create the ATS9870 instrument on the new server "alazar_server"
ats_inst = ATSdriver.AlazarTech_ATS9360(name='Alazar1')
# Print all information about this Alazar card
ats_inst.get_idn()
# Instantiate an acquisition controller (In this case we are doing a simple DFT) on the same server ("alazar_server") and
# provide the name of the name of the alazar card that this controller should control
acquisition_controller = ats_contr.Demodulation_AcquisitionController(name='acquisition_controller',
demodulation_frequency=10e6,
alazar_name='Alazar1')
# Configure all settings in the Alazar card
ats_inst.config(clock_source='INTERNAL_CLOCK',
sample_rate=1_000_000_000,
clock_edge='CLOCK_EDGE_RISING',
decimation=1,
coupling=['DC','DC'],
channel_range=[.4,.4],
impedance=[50,50],
trigger_operation='TRIG_ENGINE_OP_J',
trigger_engine1='TRIG_ENGINE_J',
trigger_source1='EXTERNAL',
trigger_slope1='TRIG_SLOPE_POSITIVE',
trigger_level1=160,
trigger_engine2='TRIG_ENGINE_K',
trigger_source2='DISABLE',
trigger_slope2='TRIG_SLOPE_POSITIVE',
trigger_level2=128,
external_trigger_coupling='DC',
external_trigger_range='ETR_2V5',
trigger_delay=0,
timeout_ticks=0,
aux_io_mode='AUX_IN_AUXILIARY', # AUX_IN_TRIGGER_ENABLE for seq mode on
aux_io_param='NONE' # TRIG_SLOPE_POSITIVE for seq mode on
)
# This command is specific to this acquisition controller. The kwargs provided here are being forwarded to ats_inst.acquire
# This way, it becomes easy to change acquisition specific settings from the ipython notebook
acquisition_controller.update_acquisitionkwargs(#mode='NPT',
samples_per_record=1024,
records_per_buffer=70,
buffers_per_acquisition=1,
#channel_selection='AB',
#transfer_offset=0,
#external_startcapture='ENABLED',
#enable_record_headers='DISABLED',
#alloc_buffers='DISABLED',
#fifo_only_streaming='DISABLED',
#interleave_samples='DISABLED',
#get_processed_data='DISABLED',
allocated_buffers=1,
#buffer_timeout=1000
)
# Getting the value of the parameter 'acquisition' of the instrument 'acquisition_controller' performes the entire acquisition
# protocol. This again depends on the specific implementation of the acquisition controller
acquisition_controller.acquisition()
# make a snapshot of the 'ats_inst' instrument
ats_inst.snapshot()
# Finally show that this instrument also works within a loop
dummy = parameter.ManualParameter(name="dummy")
data = qc.Loop(dummy[0:50:1]).each(acquisition_controller.acquisition).run(name='AlazarTest')
qc.MatPlot(data.acquisition_controller_acquisition)
```
| github_jupyter |
```
source("base/it-402-dc-common_vars.r")
# library(tidyverse) - called in common_vars
library(assertr)
```
## Notes
#### Legal (ISO) gender types:
* https://data.gov.uk/education-standards/sites/default/files/CL-Legal-Sex-Type-v2-0.pdf
#### For data from 2010 and all stored as %
* need to relax sum to 100%
*
Symbol Meaning
* '-' Not Applicable
* '-' No Entries (Table 3)
* 0% Less than 0.5%
* *** Fewer Than 5 Entries
<br>
<h3>Error Checking & Warnings</h3>
* Ideally correct errors here and write out corrected csv to file with a note
* TODO - log errors found and include error-checking code as part of pre-processing flow
<h3>Errors to Watch For</h3>
<b>Please document as not found and/or what corrected, so can trace back to original.
Update as needed and mirror in final docs submitted with project.</b>
* "Computing" (or "Computing Studies" or "Computing (New)") ... included in list of subjects
* need to decide if files will be excluded or included with a flag to track changes in subjects offered
* Each subject and grade listed only once per gender
* proportions of male/female add up to 1
<br />
<h3>Warning Only Needed</h3>
<b>Need only document if triggered.</b>
* All values for a subject set to "-" or 0 (rare) -> translates to NAs if read in properly
<br />
```
# check focus subject (typically, but not necessarily, Computing) in list of subjects
checkFocusSubjectListed <-
function(awardFile, glimpseContent = FALSE, listSubjects = FALSE) {
awardData <- read_csv(awardFile, trim_ws = TRUE) %>% #, skip_empty_rows = T) # NOT skipping empty rows... :(
filter(rowSums(is.na(.)) != ncol(.)) %>%
suppressMessages
print(awardFile)
if (!exists("focus_subject") || is_null(focus_subject) || (str_trim(focus_subject) == "")) {
focus_subject <- "computing"
print(paste("No focus subject specified; defaulting to subjects containing: ", focus_subject))
} else
print(paste("Search on focus subject (containing term) '", focus_subject, "'", sep = ""))
if (glimpseContent)
print(glimpse(awardData))
result <- awardData %>%
select(Subject) %>%
filter(str_detect(Subject, regex(focus_subject, ignore_case = TRUE))) %>%
verify(nrow(.) > 0, error_fun = just_warn)
if (!listSubjects)
return(nrow(result)) # comment out this row to list subject names
else
return(result)
}
# check for data stored as percentages only
checkDataAsPercentageOnly <-
function(awardFile, glimpseContent = FALSE) {
awardData <- read_csv(awardFile, trim_ws = TRUE) %>% #, skip_empty_rows = T) # NOT skipping empty rows... :(
filter(rowSums(is.na(.)) != ncol(.)) %>%
suppressMessages
print(awardFile)
if (glimpseContent)
print(glimpse(awardData))
if (!exists("redundant_column_flags") || is.null(redundant_column_flags))
redundant_column_flags <- c("-percentage*", "-COMP", "-PassesUngradedCourses")
awardData %>%
select(-matches(c(redundant_column_flags, "all-Entries"))) %>% # "-percentage")) %>%
select(matches(c("male-", "female-", "all-"))) %>%
verify(ncol(.) > 0, error_fun = just_warn) %>%
#head(0) - comment in and next line out to list headers remaining
summarise(data_as_counts = (ncol(.) > 0))
}
# error checking - need to manually correct data if mismatch between breakdown by gender and totals found
# this case, if found, is relatively easy to fix
#TODO -include NotKnown and NA
checkDistributionByGenderErrors <-
function(awardFile, glimpseContent = FALSE) {
awardData <- read_csv(awardFile, trim_ws = TRUE) %>% #, skip_empty_rows = T) # NOT skipping empty rows... :(
filter(rowSums(is.na(.)) != ncol(.)) %>%
suppressMessages
print(awardFile)
if (glimpseContent)
print(glimpse(awardData))
if (awardData %>%
select(matches(gender_options)) %>%
verify(ncol(.) > 0, error_fun = just_warn) %>%
summarise(data_as_counts = (ncol(.) == 0)) == TRUE) {
awardData <- awardData %>%
select(-NumberOfCentres) %>%
pivot_longer(!c(Subject), names_to = "grade", values_to = "PercentageOfStudents") %>%
separate("grade", c("gender", "grade"), extra = "merge") %>%
mutate_at(c("gender", "grade"), as.factor) %>%
filter((gender %in% c("all")) & (grade %in% c("Entries")))
# building parallel structure
return(awardData %>%
group_by(Subject) %>%
mutate(total = -1) %>%
summarise(total = sum(total)) %>%
mutate(DataError = TRUE) # confirmation only - comment out to print al
)
}
awardData <- awardData %>%
mutate_at(vars(starts_with("male-") | starts_with("female-") | starts_with("all-")), as.character) %>%
mutate_at(vars(starts_with("male-") | starts_with("female-") | starts_with("all-")), parse_number) %>%
suppressWarnings
data_as_counts <- awardData %>%
select(-matches(redundant_column_flags)) %>% # "-percentage")) %>%
select(matches(c("male-", "female-"))) %>%
summarise(data_as_counts = (ncol(.) > 0)) %>%
as.logical
if (data_as_counts) {
awardData <- awardData %>%
select(-NumberOfCentres) %>%
mutate_at(vars(starts_with("male")), ~(. / `all-Entries`)) %>%
mutate_at(vars(starts_with("female")), ~(. / `all-Entries`)) %>%
select(-(starts_with("all") & !ends_with("-Entries"))) %>%
pivot_longer(!c(Subject), names_to = "grade", values_to = "PercentageOfStudents") %>%
separate("grade", c("gender", "grade"), extra = "merge") %>%
mutate_at(c("gender", "grade"), as.factor) %>%
filter(!(gender %in% c("all")) & (grade %in% c("Entries")))
} else { # dataAsPercentageOnly
awardData <- awardData %>%
select(Subject, ends_with("-percentage")) %>%
mutate_at(vars(ends_with("-percentage")), ~(. / 100)) %>%
pivot_longer(!c(Subject), names_to = "grade", values_to = "PercentageOfStudents") %>%
separate("grade", c("gender", "grade"), extra = "merge") %>%
mutate_at(c("gender", "grade"), as.factor)
} # end if-else - check for data capture approach
awardData %>%
group_by(Subject) %>%
summarise(total = sum(PercentageOfStudents, na.rm = TRUE)) %>%
verify((total == 1.0) | (total == 0), error_fun = just_warn) %>%
mutate(DataError = if_else(((total == 1.0) | (total == 0)), FALSE, TRUE)) %>%
filter(DataError == TRUE) %>% # confirmation only - comment out to print all
suppressMessages # ungrouping messages
}
# warning only - document if necessary
# double-check for subjects with values all NA - does this mean subject being excluded or no one took it?
checkSubjectsWithNoEntries <-
function(awardFile, glimpseContent = FALSE) {
awardData <- read_csv(awardFile, trim_ws = TRUE) %>% #, skip_empty_rows = T) # NOT skipping empty rows... :(
filter(rowSums(is.na(.)) != ncol(.)) %>%
suppressMessages
print(awardFile)
if (glimpseContent)
print(glimpse(awardData))
bind_cols(
awardData %>%
mutate(row_id = row_number()) %>%
select(row_id, Subject),
awardData %>%
select(-c(Subject, NumberOfCentres)) %>%
mutate_at(vars(starts_with("male-") | starts_with("female-") | starts_with("all-")), as.character) %>%
mutate_at(vars(starts_with("male-") | starts_with("female-") | starts_with("all-")), parse_number) %>%
suppressWarnings %>%
assert_rows(num_row_NAs,
within_bounds(0, length(colnames(.)), include.upper = F), everything(), error_fun = just_warn) %>%
# comment out just_warn to stop execution on fail
summarise(column_count = length(colnames(.)),
count_no_entries = num_row_NAs(.))
) %>% # end bind_cols
filter(count_no_entries == column_count) # comment out to print all
}
## call using any of the options below
## where files_to_verify is a vector containing (paths to) files to check
### checkFocusSubjectListed
#lapply(files_to_verify, checkFocusSubjectListed, listSubjects = TRUE)
#Map(checkFocusSubjectListed, files_to_verify, listSubjects = TRUE)
#as.data.frame(sapply(files_to_verify, checkFocusSubjectListed)) # call without as.data.frame if listing values
### checkDataAsPercentageOnly
#sapply(files_to_verify, checkDataAsPercentageOnly)
#Map(checkDataAsPercentageOnly, files_to_verify) #, T)
### checkDistributionByGenderErrors
#data.frame(sapply(files_to_verify, checkDistributionByGenderErrors))
### checkSubjectsWithNoEntries
#data.frame(sapply(files_to_verify, checkSubjectsWithNoEntries))
```
| github_jupyter |
# Machine Translation and the Dataset
:label:`sec_machine_translation`
We have used RNNs to design language models,
which are key to natural language processing.
Another flagship benchmark is *machine translation*,
a central problem domain for *sequence transduction* models
that transform input sequences into output sequences.
Playing a crucial role in various modern AI applications,
sequence transduction models will form the focus of the remainder of this chapter
and :numref:`chap_attention`.
To this end,
this section introduces the machine translation problem
and its dataset that will be used later.
*Machine translation* refers to the
automatic translation of a sequence
from one language to another.
In fact, this field
may date back to 1940s
soon after digital computers were invented,
especially by considering the use of computers
for cracking language codes in World War II.
For decades,
statistical approaches
had been dominant in this field :cite:`Brown.Cocke.Della-Pietra.ea.1988,Brown.Cocke.Della-Pietra.ea.1990`
before the rise
of
end-to-end learning using
neural networks.
The latter
is often called
*neural machine translation*
to distinguish itself from
*statistical machine translation*
that involves statistical analysis
in components such as
the translation model and the language model.
Emphasizing end-to-end learning,
this book will focus on neural machine translation methods.
Different from our language model problem
in :numref:`sec_language_model`
whose corpus is in one single language,
machine translation datasets
are composed of pairs of text sequences
that are in
the source language and the target language, respectively.
Thus,
instead of reusing the preprocessing routine
for language modeling,
we need a different way to preprocess
machine translation datasets.
In the following,
we show how to
load the preprocessed data
into minibatches for training.
```
import os
import torch
from d2l import torch as d2l
```
## [**Downloading and Preprocessing the Dataset**]
To begin with,
we download an English-French dataset
that consists of [bilingual sentence pairs from the Tatoeba Project](http://www.manythings.org/anki/).
Each line in the dataset
is a tab-delimited pair
of an English text sequence
and the translated French text sequence.
Note that each text sequence
can be just one sentence or a paragraph of multiple sentences.
In this machine translation problem
where English is translated into French,
English is the *source language*
and French is the *target language*.
```
#@save
d2l.DATA_HUB['fra-eng'] = (d2l.DATA_URL + 'fra-eng.zip',
'94646ad1522d915e7b0f9296181140edcf86a4f5')
#@save
def read_data_nmt():
"""Load the English-French dataset."""
data_dir = d2l.download_extract('fra-eng')
with open(os.path.join(data_dir, 'fra.txt'), 'r') as f:
return f.read()
raw_text = read_data_nmt()
print(raw_text[:75])
```
After downloading the dataset,
we [**proceed with several preprocessing steps**]
for the raw text data.
For instance,
we replace non-breaking space with space,
convert uppercase letters to lowercase ones,
and insert space between words and punctuation marks.
```
#@save
def preprocess_nmt(text):
"""Preprocess the English-French dataset."""
def no_space(char, prev_char):
return char in set(',.!?') and prev_char != ' '
# Replace non-breaking space with space, and convert uppercase letters to
# lowercase ones
text = text.replace('\u202f', ' ').replace('\xa0', ' ').lower()
# Insert space between words and punctuation marks
out = [' ' + char if i > 0 and no_space(char, text[i - 1]) else char
for i, char in enumerate(text)]
return ''.join(out)
text = preprocess_nmt(raw_text)
print(text[:80])
```
## [**Tokenization**]
Different from character-level tokenization
in :numref:`sec_language_model`,
for machine translation
we prefer word-level tokenization here
(state-of-the-art models may use more advanced tokenization techniques).
The following `tokenize_nmt` function
tokenizes the the first `num_examples` text sequence pairs,
where
each token is either a word or a punctuation mark.
This function returns
two lists of token lists: `source` and `target`.
Specifically,
`source[i]` is a list of tokens from the
$i^\mathrm{th}$ text sequence in the source language (English here) and `target[i]` is that in the target language (French here).
```
#@save
def tokenize_nmt(text, num_examples=None):
"""Tokenize the English-French dataset."""
source, target = [], []
for i, line in enumerate(text.split('\n')):
if num_examples and i > num_examples:
break
parts = line.split('\t')
if len(parts) == 2:
source.append(parts[0].split(' '))
target.append(parts[1].split(' '))
return source, target
source, target = tokenize_nmt(text)
source[:6], target[:6]
```
Let us [**plot the histogram of the number of tokens per text sequence.**]
In this simple English-French dataset,
most of the text sequences have fewer than 20 tokens.
```
#@save
def show_list_len_pair_hist(legend, xlabel, ylabel, xlist, ylist):
"""Plot the histogram for list length pairs."""
d2l.set_figsize()
_, _, patches = d2l.plt.hist(
[[len(l) for l in xlist], [len(l) for l in ylist]])
d2l.plt.xlabel(xlabel)
d2l.plt.ylabel(ylabel)
for patch in patches[1].patches:
patch.set_hatch('/')
d2l.plt.legend(legend)
show_list_len_pair_hist(['source', 'target'], '# tokens per sequence',
'count', source, target);
```
## [**Vocabulary**]
Since the machine translation dataset
consists of pairs of languages,
we can build two vocabularies for
both the source language and
the target language separately.
With word-level tokenization,
the vocabulary size will be significantly larger
than that using character-level tokenization.
To alleviate this,
here we treat infrequent tokens
that appear less than 2 times
as the same unknown ("<unk>") token.
Besides that,
we specify additional special tokens
such as for padding ("<pad>") sequences to the same length in minibatches,
and for marking the beginning ("<bos>") or end ("<eos>") of sequences.
Such special tokens are commonly used in
natural language processing tasks.
```
src_vocab = d2l.Vocab(source, min_freq=2,
reserved_tokens=['<pad>', '<bos>', '<eos>'])
len(src_vocab)
```
## Reading the Dataset
:label:`subsec_mt_data_loading`
Recall that in language modeling
[**each sequence example**],
either a segment of one sentence
or a span over multiple sentences,
(**has a fixed length.**)
This was specified by the `num_steps`
(number of time steps or tokens) argument in :numref:`sec_language_model`.
In machine translation, each example is
a pair of source and target text sequences,
where each text sequence may have different lengths.
For computational efficiency,
we can still process a minibatch of text sequences
at one time by *truncation* and *padding*.
Suppose that every sequence in the same minibatch
should have the same length `num_steps`.
If a text sequence has fewer than `num_steps` tokens,
we will keep appending the special "<pad>" token
to its end until its length reaches `num_steps`.
Otherwise,
we will truncate the text sequence
by only taking its first `num_steps` tokens
and discarding the remaining.
In this way,
every text sequence
will have the same length
to be loaded in minibatches of the same shape.
The following `truncate_pad` function
(**truncates or pads text sequences**) as described before.
```
#@save
def truncate_pad(line, num_steps, padding_token):
"""Truncate or pad sequences."""
if len(line) > num_steps:
return line[:num_steps] # Truncate
return line + [padding_token] * (num_steps - len(line)) # Pad
truncate_pad(src_vocab[source[0]], 10, src_vocab['<pad>'])
```
Now we define a function to [**transform
text sequences into minibatches for training.**]
We append the special “<eos>” token
to the end of every sequence to indicate the
end of the sequence.
When a model is predicting
by
generating a sequence token after token,
the generation
of the “<eos>” token
can suggest that
the output sequence is complete.
Besides,
we also record the length
of each text sequence excluding the padding tokens.
This information will be needed by
some models that
we will cover later.
```
#@save
def build_array_nmt(lines, vocab, num_steps):
"""Transform text sequences of machine translation into minibatches."""
lines = [vocab[l] for l in lines]
lines = [l + [vocab['<eos>']] for l in lines]
array = torch.tensor([truncate_pad(
l, num_steps, vocab['<pad>']) for l in lines])
valid_len = (array != vocab['<pad>']).type(torch.int32).sum(1)
return array, valid_len
```
## [**Putting All Things Together**]
Finally, we define the `load_data_nmt` function
to return the data iterator, together with
the vocabularies for both the source language and the target language.
```
#@save
def load_data_nmt(batch_size, num_steps, num_examples=600):
"""Return the iterator and the vocabularies of the translation dataset."""
text = preprocess_nmt(read_data_nmt())
source, target = tokenize_nmt(text, num_examples)
src_vocab = d2l.Vocab(source, min_freq=2,
reserved_tokens=['<pad>', '<bos>', '<eos>'])
tgt_vocab = d2l.Vocab(target, min_freq=2,
reserved_tokens=['<pad>', '<bos>', '<eos>'])
src_array, src_valid_len = build_array_nmt(source, src_vocab, num_steps)
tgt_array, tgt_valid_len = build_array_nmt(target, tgt_vocab, num_steps)
data_arrays = (src_array, src_valid_len, tgt_array, tgt_valid_len)
data_iter = d2l.load_array(data_arrays, batch_size)
return data_iter, src_vocab, tgt_vocab
```
Let us [**read the first minibatch from the English-French dataset.**]
```
train_iter, src_vocab, tgt_vocab = load_data_nmt(batch_size=2, num_steps=8)
for X, X_valid_len, Y, Y_valid_len in train_iter:
print('X:', X.type(torch.int32))
print('valid lengths for X:', X_valid_len)
print('Y:', Y.type(torch.int32))
print('valid lengths for Y:', Y_valid_len)
break
```
## Summary
* Machine translation refers to the automatic translation of a sequence from one language to another.
* Using word-level tokenization, the vocabulary size will be significantly larger than that using character-level tokenization. To alleviate this, we can treat infrequent tokens as the same unknown token.
* We can truncate and pad text sequences so that all of them will have the same length to be loaded in minibatches.
## Exercises
1. Try different values of the `num_examples` argument in the `load_data_nmt` function. How does this affect the vocabulary sizes of the source language and the target language?
1. Text in some languages such as Chinese and Japanese does not have word boundary indicators (e.g., space). Is word-level tokenization still a good idea for such cases? Why or why not?
[Discussions](https://discuss.d2l.ai/t/1060)
| github_jupyter |
# Using BagIt to tag oceanographic data
[`BagIt`](https://en.wikipedia.org/wiki/BagIt) is a packaging format that supports storage of arbitrary digital content. The "bag" consists of arbitrary content and "tags," the metadata files. `BagIt` packages can be used to facilitate data sharing with federal archive centers - thus ensuring digital preservation of oceanographic datasets within IOOS and its regional associations. NOAA NCEI supports reading from a Web Accessible Folder (WAF) containing bagit archives. For an example please see: http://ncei.axiomdatascience.com/cencoos/
On this notebook we will use the [python interface](http://libraryofcongress.github.io/bagit-python) for `BagIt` to create a "bag" of a time-series profile data. First let us load our data from a comma separated values file (`CSV`).
```
import os
import pandas as pd
fname = os.path.join('data', 'dsg', 'timeseriesProfile.csv')
df = pd.read_csv(fname, parse_dates=['time'])
df.head()
```
Instead of "bagging" the `CSV` file we will use this create a metadata rich netCDF file.
We can convert the table to a `DSG`, Discrete Sampling Geometry, using `pocean.dsg`. The first thing we need to do is to create a mapping from the data column names to the netCDF `axes`.
```
axes = {
't': 'time',
'x': 'lon',
'y': 'lat',
'z': 'depth'
}
```
Now we can create a [Orthogonal Multidimensional Timeseries Profile](http://cfconventions.org/cf-conventions/v1.6.0/cf-conventions.html#_orthogonal_multidimensional_array_representation_of_time_series) object...
```
import os
import tempfile
from pocean.dsg import OrthogonalMultidimensionalTimeseriesProfile as omtsp
output_fp, output = tempfile.mkstemp()
os.close(output_fp)
ncd = omtsp.from_dataframe(
df.reset_index(),
output=output,
axes=axes,
mode='a'
)
```
... And add some extra metadata before we close the file.
```
naming_authority = 'ioos'
st_id = 'Station1'
ncd.naming_authority = naming_authority
ncd.id = st_id
print(ncd)
ncd.close()
```
Time to create the archive for the file with `BagIt`. We have to create a folder for the bag.
```
temp_bagit_folder = tempfile.mkdtemp()
temp_data_folder = os.path.join(temp_bagit_folder, 'data')
```
Now we can create the bag and copy the netCDF file to a `data` sub-folder.
```
import bagit
import shutil
bag = bagit.make_bag(
temp_bagit_folder,
checksum=['sha256']
)
shutil.copy2(output, temp_data_folder + '/parameter1.nc')
```
Last, but not least, we have to set bag metadata and update the existing bag with it.
```
urn = 'urn:ioos:station:{naming_authority}:{st_id}'.format(
naming_authority=naming_authority,
st_id=st_id
)
bag_meta = {
'Bag-Count': '1 of 1',
'Bag-Group-Identifier': 'ioos_bagit_testing',
'Contact-Name': 'Kyle Wilcox',
'Contact-Phone': '907-230-0304',
'Contact-Email': '[email protected]',
'External-Identifier': urn,
'External-Description':
'Sensor data from station {}'.format(urn),
'Internal-Sender-Identifier': urn,
'Internal-Sender-Description':
'Station - URN:{}'.format(urn),
'Organization-address':
'1016 W 6th Ave, Ste. 105, Anchorage, AK 99501, USA',
'Source-Organization': 'Axiom Data Science',
}
bag.info.update(bag_meta)
bag.save(manifests=True, processes=4)
```
That is it! Simple and efficient!!
The cell below illustrates the bag directory tree.
(Note that the commands below will not work on Windows and some \*nix systems may require the installation of the command `tree`, however, they are only need for this demonstration.)
```
!tree $temp_bagit_folder
!cat $temp_bagit_folder/manifest-sha256.txt
```
We can add more files to the bag as needed.
```
shutil.copy2(output, temp_data_folder + '/parameter2.nc')
shutil.copy2(output, temp_data_folder + '/parameter3.nc')
shutil.copy2(output, temp_data_folder + '/parameter4.nc')
bag.save(manifests=True, processes=4)
!tree $temp_bagit_folder
!cat $temp_bagit_folder/manifest-sha256.txt
```
| github_jupyter |
Exercise 1 (5 points): Discrete Naive Bayes Classifier [Pen and Paper]
In this exercise, we want to get a basic idea of the naive Bayes classifier by analysing a small
example. Suppose we want to classify fruits based on the criteria length, sweetness and the colour
of the fruit and we already spent days by categorizing 1900 fruits. The results are summarized in
the following table.
Length Sweetness Colour
Class Short Medium Long Sweet Not Sweet Red Yellow Green Total
Banana 0 100 500 500 100 0 600 0 600
Papaya 50 200 50 250 50 0 150 150 300
Apple 900 100 0 800 200 600 100 300 1000
Total 950 400 550 1550 350 600 850 450 1900
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn') # pretty matplotlib plots
plt.rcParams['figure.figsize'] = (12, 8)
```
Question 4.
$\hat{x_0}$ = 0.1534
```
#plot of likelihood function
#x
mu1 = 0
mu2 = 1
sigma = 1 / np.sqrt(2)
x = np.linspace(-3, 4, 100)
y1 = (1 / (np.sqrt(2 * np.pi * np.power(sigma, 2)))) * (np.power(np.e, -(np.power((x - mu1), 2) / (2 * np.power(sigma, 2))))) # P(x|w1)
y2 = (1 / (np.sqrt(2 * np.pi * np.power(sigma, 2)))) * (np.power(np.e, -(np.power((x - mu2), 2) / (2 * np.power(sigma, 2))))) # P(x|w2)
plt.plot(x, y1)
plt.plot(x, y2, color='Orange')
plt.axvline(x=0.1534, color='r', linestyle='--', ymin=0.05, ymax = 0.98)
plt.legend(('$p(x|\omega_1)$', '$p(x|\omega_2)$', 'Threshold'), loc=1)
#plot of loss functions
l1 = 2*y2
l2 = y1
plt.plot(x, l1, color='Orange')
plt.plot(x, l2)
plt.axvline(x=0.1534, color='r', linestyle='--', ymin=0.05, ymax = 0.98)
plt.legend(('$l_1$', '$l_2$', 'Threshold'), loc=1)
```
Question 5.
$\hat{x_0}$ = 0.7798
```
#plot of likelihood with new threshold value
plt.plot(x, y1)
plt.plot(x, y2, color='Orange')
plt.axvline(x=0.7798, color='r', linestyle='--', ymin=0.05, ymax = 0.98)
plt.legend(('$p(x|\omega_1)$', '$p(x|\omega_2)$', 'Threshold'), loc=1)
#plot of loss functions
l1 = (2/3)*y2
l2 = (7/6)*y1
plt.plot(x, l1, color='Orange')
plt.plot(x, l2)
plt.axvline(x=0.7798, color='r', linestyle='--', ymin=0.05, ymax = 0.98)
plt.legend(('$l_1$', '$l_2$', 'Threshold'), loc=1)
```
Question 6
$\hat{x_0}$ = 0.7798
<br> No change in threshold becaue *p* is same and so is the ratio of the two penalty terms $\lambda_{12}$/$\lambda_{21}$
```
#plot of likelihood with new threshold value
plt.plot(x, y1)
plt.plot(x, y2, color='Orange')
plt.axvline(x=0.7798, color='r', linestyle='--', ymin=0.05, ymax = 0.98)
plt.legend(('$p(x|\omega_1)$', '$p(x|\omega_2)$', 'Threshold'), loc=1)
#plot of loss functions
l1 = (2/3)*y2
l2 = (7/6)*y1
plt.plot(x, l1, color='Orange')
plt.plot(x, l2)
plt.axvline(x=0.7798, color='r', linestyle='--', ymin=0.05, ymax = 0.98)
plt.legend(('$l_1$', '$l_2$', 'Threshold'), loc=1)
```
Question 7
>a) left of the intersection $p(x|w_1) = p(x|w_2)$ => $P(w_1) < P(w_2)$ which gives $0<p<1/2$<br>
>b) at the intersection $p(x|w_1) = p(x|w_2)$ => $P(w_1) = P(w_2)$ i.e. $p=1/2$ <br>
>c) right of the intersection $p(x|w_1) = p(x|w_2)$ => $P(w_1) > P(w_2)$ i.e. $1>p>1/2$
| github_jupyter |
# Assignment 2: Parts-of-Speech Tagging (POS)
Welcome to the second assignment of Course 2 in the Natural Language Processing specialization. This assignment will develop skills in part-of-speech (POS) tagging, the process of assigning a part-of-speech tag (Noun, Verb, Adjective...) to each word in an input text. Tagging is difficult because some words can represent more than one part of speech at different times. They are **Ambiguous**. Let's look at the following example:
- The whole team played **well**. [adverb]
- You are doing **well** for yourself. [adjective]
- **Well**, this assignment took me forever to complete. [interjection]
- The **well** is dry. [noun]
- Tears were beginning to **well** in her eyes. [verb]
Distinguishing the parts-of-speech of a word in a sentence will help you better understand the meaning of a sentence. This would be critically important in search queries. Identifying the proper noun, the organization, the stock symbol, or anything similar would greatly improve everything ranging from speech recognition to search. By completing this assignment, you will:
- Learn how parts-of-speech tagging works
- Compute the transition matrix A in a Hidden Markov Model
- Compute the transition matrix B in a Hidden Markov Model
- Compute the Viterbi algorithm
- Compute the accuracy of your own model
## Outline
- [0 Data Sources](#0)
- [1 POS Tagging](#1)
- [1.1 Training](#1.1)
- [Exercise 01](#ex-01)
- [1.2 Testing](#1.2)
- [Exercise 02](#ex-02)
- [2 Hidden Markov Models](#2)
- [2.1 Generating Matrices](#2.1)
- [Exercise 03](#ex-03)
- [Exercise 04](#ex-04)
- [3 Viterbi Algorithm](#3)
- [3.1 Initialization](#3.1)
- [Exercise 05](#ex-05)
- [3.2 Viterbi Forward](#3.2)
- [Exercise 06](#ex-06)
- [3.3 Viterbi Backward](#3.3)
- [Exercise 07](#ex-07)
- [4 Predicting on a data set](#4)
- [Exercise 08](#ex-08)
```
# Importing packages and loading in the data set
from utils_pos import get_word_tag, preprocess
import pandas as pd
from collections import defaultdict
import math
import numpy as np
```
<a name='0'></a>
## Part 0: Data Sources
This assignment will use two tagged data sets collected from the **Wall Street Journal (WSJ)**.
[Here](http://relearn.be/2015/training-common-sense/sources/software/pattern-2.6-critical-fork/docs/html/mbsp-tags.html) is an example 'tag-set' or Part of Speech designation describing the two or three letter tag and their meaning.
- One data set (**WSJ-2_21.pos**) will be used for **training**.
- The other (**WSJ-24.pos**) for **testing**.
- The tagged training data has been preprocessed to form a vocabulary (**hmm_vocab.txt**).
- The words in the vocabulary are words from the training set that were used two or more times.
- The vocabulary is augmented with a set of 'unknown word tokens', described below.
The training set will be used to create the emission, transmission and tag counts.
The test set (WSJ-24.pos) is read in to create `y`.
- This contains both the test text and the true tag.
- The test set has also been preprocessed to remove the tags to form **test_words.txt**.
- This is read in and further processed to identify the end of sentences and handle words not in the vocabulary using functions provided in **utils_pos.py**.
- This forms the list `prep`, the preprocessed text used to test our POS taggers.
A POS tagger will necessarily encounter words that are not in its datasets.
- To improve accuracy, these words are further analyzed during preprocessing to extract available hints as to their appropriate tag.
- For example, the suffix 'ize' is a hint that the word is a verb, as in 'final-ize' or 'character-ize'.
- A set of unknown-tokens, such as '--unk-verb--' or '--unk-noun--' will replace the unknown words in both the training and test corpus and will appear in the emission, transmission and tag data structures.
<img src = "DataSources1.PNG" />
Implementation note:
- For python 3.6 and beyond, dictionaries retain the insertion order.
- Furthermore, their hash-based lookup makes them suitable for rapid membership tests.
- If _di_ is a dictionary, `key in di` will return `True` if _di_ has a key _key_, else `False`.
The dictionary `vocab` will utilize these features.
```
# load in the training corpus
with open("WSJ_02-21.pos", 'r') as f:
training_corpus = f.readlines()
print(f"A few items of the training corpus list")
print(training_corpus[0:5])
# read the vocabulary data, split by each line of text, and save the list
with open("hmm_vocab.txt", 'r') as f:
voc_l = f.read().split('\n')
print("A few items of the vocabulary list")
print(voc_l[0:50])
print()
print("A few items at the end of the vocabulary list")
print(voc_l[-50:])
# vocab: dictionary that has the index of the corresponding words
vocab = {}
# Get the index of the corresponding words.
for i, word in enumerate(sorted(voc_l)):
vocab[word] = i
print("Vocabulary dictionary, key is the word, value is a unique integer")
cnt = 0
for k,v in vocab.items():
print(f"{k}:{v}")
cnt += 1
if cnt > 20:
break
# load in the test corpus
with open("WSJ_24.pos", 'r') as f:
y = f.readlines()
print("A sample of the test corpus")
print(y[0:10])
#corpus without tags, preprocessed
_, prep = preprocess(vocab, "test.words")
print('The length of the preprocessed test corpus: ', len(prep))
print('This is a sample of the test_corpus: ')
print(prep[0:10])
```
<a name='1'></a>
# Part 1: Parts-of-speech tagging
<a name='1.1'></a>
## Part 1.1 - Training
You will start with the simplest possible parts-of-speech tagger and we will build up to the state of the art.
In this section, you will find the words that are not ambiguous.
- For example, the word `is` is a verb and it is not ambiguous.
- In the `WSJ` corpus, $86$% of the token are unambiguous (meaning they have only one tag)
- About $14\%$ are ambiguous (meaning that they have more than one tag)
<img src = "pos.png" style="width:400px;height:250px;"/>
Before you start predicting the tags of each word, you will need to compute a few dictionaries that will help you to generate the tables.
#### Transition counts
- The first dictionary is the `transition_counts` dictionary which computes the number of times each tag happened next to another tag.
This dictionary will be used to compute:
$$P(t_i |t_{i-1}) \tag{1}$$
This is the probability of a tag at position $i$ given the tag at position $i-1$.
In order for you to compute equation 1, you will create a `transition_counts` dictionary where
- The keys are `(prev_tag, tag)`
- The values are the number of times those two tags appeared in that order.
#### Emission counts
The second dictionary you will compute is the `emission_counts` dictionary. This dictionary will be used to compute:
$$P(w_i|t_i)\tag{2}$$
In other words, you will use it to compute the probability of a word given its tag.
In order for you to compute equation 2, you will create an `emission_counts` dictionary where
- The keys are `(tag, word)`
- The values are the number of times that pair showed up in your training set.
#### Tag counts
The last dictionary you will compute is the `tag_counts` dictionary.
- The key is the tag
- The value is the number of times each tag appeared.
<a name='ex-01'></a>
### Exercise 01
**Instructions:** Write a program that takes in the `training_corpus` and returns the three dictionaries mentioned above `transition_counts`, `emission_counts`, and `tag_counts`.
- `emission_counts`: maps (tag, word) to the number of times it happened.
- `transition_counts`: maps (prev_tag, tag) to the number of times it has appeared.
- `tag_counts`: maps (tag) to the number of times it has occured.
Implementation note: This routine utilises *defaultdict*, which is a subclass of *dict*.
- A standard Python dictionary throws a *KeyError* if you try to access an item with a key that is not currently in the dictionary.
- In contrast, the *defaultdict* will create an item of the type of the argument, in this case an integer with the default value of 0.
- See [defaultdict](https://docs.python.org/3.3/library/collections.html#defaultdict-objects).
```
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_dictionaries
def create_dictionaries(training_corpus, vocab):
"""
Input:
training_corpus: a corpus where each line has a word followed by its tag.
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
emission_counts: a dictionary where the keys are (tag, word) and the values are the counts
transition_counts: a dictionary where the keys are (prev_tag, tag) and the values are the counts
tag_counts: a dictionary where the keys are the tags and the values are the counts
"""
# initialize the dictionaries using defaultdict
emission_counts = defaultdict(int)
transition_counts = defaultdict(int)
tag_counts = defaultdict(int)
# Initialize "prev_tag" (previous tag) with the start state, denoted by '--s--'
prev_tag = '--s--'
# use 'i' to track the line number in the corpus
i = 0
# Each item in the training corpus contains a word and its POS tag
# Go through each word and its tag in the training corpus
for word_tag in training_corpus:
# Increment the word_tag count
i += 1
# Every 50,000 words, print the word count
if i % 50000 == 0:
print(f"word count = {i}")
### START CODE HERE (Replace instances of 'None' with your code) ###
# get the word and tag using the get_word_tag helper function (imported from utils_pos.py)
word, tag = get_word_tag(word_tag, vocab)
# Increment the transition count for the previous word and tag
transition_counts[(prev_tag, tag)] += 1
# Increment the emission count for the tag and word
emission_counts[(tag, word)] += 1
# Increment the tag count
tag_counts[tag] += 1
# Set the previous tag to this tag (for the next iteration of the loop)
prev_tag = tag
### END CODE HERE ###
return emission_counts, transition_counts, tag_counts
emission_counts, transition_counts, tag_counts = create_dictionaries(training_corpus, vocab)
# get all the POS states
states = sorted(tag_counts.keys())
print(f"Number of POS tags (number of 'states'): {len(states)}")
print("View these POS tags (states)")
print(states)
```
##### Expected Output
```CPP
Number of POS tags (number of 'states'46
View these states
['#', '$', "''", '(', ')', ',', '--s--', '.', ':', 'CC', 'CD', 'DT', 'EX', 'FW', 'IN', 'JJ', 'JJR', 'JJS', 'LS', 'MD', 'NN', 'NNP', 'NNPS', 'NNS', 'PDT', 'POS', 'PRP', 'PRP$', 'RB', 'RBR', 'RBS', 'RP', 'SYM', 'TO', 'UH', 'VB', 'VBD', 'VBG', 'VBN', 'VBP', 'VBZ', 'WDT', 'WP', 'WP$', 'WRB', '``']
```
The 'states' are the Parts-of-speech designations found in the training data. They will also be referred to as 'tags' or POS in this assignment.
- "NN" is noun, singular,
- 'NNS' is noun, plural.
- In addition, there are helpful tags like '--s--' which indicate a start of a sentence.
- You can get a more complete description at [Penn Treebank II tag set](https://www.clips.uantwerpen.be/pages/mbsp-tags).
```
print("transition examples: ")
for ex in list(transition_counts.items())[:3]:
print(ex)
print()
print("emission examples: ")
for ex in list(emission_counts.items())[200:203]:
print (ex)
print()
print("ambiguous word example: ")
for tup,cnt in emission_counts.items():
if tup[1] == 'back': print (tup, cnt)
```
##### Expected Output
```CPP
transition examples:
(('--s--', 'IN'), 5050)
(('IN', 'DT'), 32364)
(('DT', 'NNP'), 9044)
emission examples:
(('DT', 'any'), 721)
(('NN', 'decrease'), 7)
(('NN', 'insider-trading'), 5)
ambiguous word example:
('RB', 'back') 304
('VB', 'back') 20
('RP', 'back') 84
('JJ', 'back') 25
('NN', 'back') 29
('VBP', 'back') 4
```
<a name='1.2'></a>
### Part 1.2 - Testing
Now you will test the accuracy of your parts-of-speech tagger using your `emission_counts` dictionary.
- Given your preprocessed test corpus `prep`, you will assign a parts-of-speech tag to every word in that corpus.
- Using the original tagged test corpus `y`, you will then compute what percent of the tags you got correct.
<a name='ex-02'></a>
### Exercise 02
**Instructions:** Implement `predict_pos` that computes the accuracy of your model.
- This is a warm up exercise.
- To assign a part of speech to a word, assign the most frequent POS for that word in the training set.
- Then evaluate how well this approach works. Each time you predict based on the most frequent POS for the given word, check whether the actual POS of that word is the same. If so, the prediction was correct!
- Calculate the accuracy as the number of correct predictions divided by the total number of words for which you predicted the POS tag.
```
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: predict_pos
def predict_pos(prep, y, emission_counts, vocab, states):
'''
Input:
prep: a preprocessed version of 'y'. A list with the 'word' component of the tuples.
y: a corpus composed of a list of tuples where each tuple consists of (word, POS)
emission_counts: a dictionary where the keys are (tag,word) tuples and the value is the count
vocab: a dictionary where keys are words in vocabulary and value is an index
states: a sorted list of all possible tags for this assignment
Output:
accuracy: Number of times you classified a word correctly
'''
# Initialize the number of correct predictions to zero
num_correct = 0
# Get the (tag, word) tuples, stored as a set
all_words = set(emission_counts.keys())
# Get the number of (word, POS) tuples in the corpus 'y'
total = len(y)
for word, y_tup in zip(prep, y):
# Split the (word, POS) string into a list of two items
y_tup_l = y_tup.split()
# Verify that y_tup contain both word and POS
if len(y_tup_l) == 2:
# Set the true POS label for this word
true_label = y_tup_l[1]
else:
# If the y_tup didn't contain word and POS, go to next word
continue
count_final = 0
pos_final = ''
# If the word is in the vocabulary...
if word in vocab:
for pos in states:
### START CODE HERE (Replace instances of 'None' with your code) ###
# define the key as the tuple containing the POS and word
key = (pos,word)
# check if the (pos, word) key exists in the emission_counts dictionary
if key in emission_counts.keys(): # complete this line
# get the emission count of the (pos,word) tuple
count = emission_counts[key]
# keep track of the POS with the largest count
if count > count_final: # complete this line
# update the final count (largest count)
count_final = count
# update the final POS
pos_final = pos
# If the final POS (with the largest count) matches the true POS:
if pos_final == true_label: # complete this line
# Update the number of correct predictions
num_correct += 1
### END CODE HERE ###
accuracy = num_correct / total
return accuracy
accuracy_predict_pos = predict_pos(prep, y, emission_counts, vocab, states)
print(f"Accuracy of prediction using predict_pos is {accuracy_predict_pos:.4f}")
```
##### Expected Output
```CPP
Accuracy of prediction using predict_pos is 0.8889
```
88.9% is really good for this warm up exercise. With hidden markov models, you should be able to get **95% accuracy.**
<a name='2'></a>
# Part 2: Hidden Markov Models for POS
Now you will build something more context specific. Concretely, you will be implementing a Hidden Markov Model (HMM) with a Viterbi decoder
- The HMM is one of the most commonly used algorithms in Natural Language Processing, and is a foundation to many deep learning techniques you will see in this specialization.
- In addition to parts-of-speech tagging, HMM is used in speech recognition, speech synthesis, etc.
- By completing this part of the assignment you will get a 95% accuracy on the same dataset you used in Part 1.
The Markov Model contains a number of states and the probability of transition between those states.
- In this case, the states are the parts-of-speech.
- A Markov Model utilizes a transition matrix, `A`.
- A Hidden Markov Model adds an observation or emission matrix `B` which describes the probability of a visible observation when we are in a particular state.
- In this case, the emissions are the words in the corpus
- The state, which is hidden, is the POS tag of that word.
<a name='2.1'></a>
## Part 2.1 Generating Matrices
### Creating the 'A' transition probabilities matrix
Now that you have your `emission_counts`, `transition_counts`, and `tag_counts`, you will start implementing the Hidden Markov Model.
This will allow you to quickly construct the
- `A` transition probabilities matrix.
- and the `B` emission probabilities matrix.
You will also use some smoothing when computing these matrices.
Here is an example of what the `A` transition matrix would look like (it is simplified to 5 tags for viewing. It is 46x46 in this assignment.):
|**A** |...| RBS | RP | SYM | TO | UH|...
| --- ||---:-------------| ------------ | ------------ | -------- | ---------- |----
|**RBS** |...|2.217069e-06 |2.217069e-06 |2.217069e-06 |0.008870 |2.217069e-06|...
|**RP** |...|3.756509e-07 |7.516775e-04 |3.756509e-07 |0.051089 |3.756509e-07|...
|**SYM** |...|1.722772e-05 |1.722772e-05 |1.722772e-05 |0.000017 |1.722772e-05|...
|**TO** |...|4.477336e-05 |4.472863e-08 |4.472863e-08 |0.000090 |4.477336e-05|...
|**UH** |...|1.030439e-05 |1.030439e-05 |1.030439e-05 |0.061837 |3.092348e-02|...
| ... |...| ... | ... | ... | ... | ... | ...
Note that the matrix above was computed with smoothing.
Each cell gives you the probability to go from one part of speech to another.
- In other words, there is a 4.47e-8 chance of going from parts-of-speech `TO` to `RP`.
- The sum of each row has to equal 1, because we assume that the next POS tag must be one of the available columns in the table.
The smoothing was done as follows:
$$ P(t_i | t_{i-1}) = \frac{C(t_{i-1}, t_{i}) + \alpha }{C(t_{i-1}) +\alpha * N}\tag{3}$$
- $N$ is the total number of tags
- $C(t_{i-1}, t_{i})$ is the count of the tuple (previous POS, current POS) in `transition_counts` dictionary.
- $C(t_{i-1})$ is the count of the previous POS in the `tag_counts` dictionary.
- $\alpha$ is a smoothing parameter.
<a name='ex-03'></a>
### Exercise 03
**Instructions:** Implement the `create_transition_matrix` below for all tags. Your task is to output a matrix that computes equation 3 for each cell in matrix `A`.
```
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_transition_matrix
def create_transition_matrix(alpha, tag_counts, transition_counts):
'''
Input:
alpha: number used for smoothing
tag_counts: a dictionary mapping each tag to its respective count
transition_counts: transition count for the previous word and tag
Output:
A: matrix of dimension (num_tags,num_tags)
'''
# Get a sorted list of unique POS tags
all_tags = sorted(tag_counts.keys())
# Count the number of unique POS tags
num_tags = len(all_tags)
# Initialize the transition matrix 'A'
A = np.zeros((num_tags,num_tags))
# Get the unique transition tuples (previous POS, current POS)
trans_keys = set(transition_counts.keys())
### START CODE HERE (Return instances of 'None' with your code) ###
# Go through each row of the transition matrix A
for i in range(num_tags):
# Go through each column of the transition matrix A
for j in range(num_tags):
# Initialize the count of the (prev POS, current POS) to zero
count = 0
# Define the tuple (prev POS, current POS)
# Get the tag at position i and tag at position j (from the all_tags list)
key = (all_tags[i],all_tags[j])
# Check if the (prev POS, current POS) tuple
# exists in the transition counts dictionaory
if key in transition_counts.keys(): #complete this line
# Get count from the transition_counts dictionary
# for the (prev POS, current POS) tuple
count = transition_counts[key]
# Get the count of the previous tag (index position i) from tag_counts
count_prev_tag = tag_counts[all_tags[i]]
# Apply smoothing using count of the tuple, alpha,
# count of previous tag, alpha, and number of total tags
A[i,j] = (count + alpha)/(count_prev_tag + alpha * num_tags )
### END CODE HERE ###
return A
alpha = 0.001
A = create_transition_matrix(alpha, tag_counts, transition_counts)
# Testing your function
print(f"A at row 0, col 0: {A[0,0]:.9f}")
print(f"A at row 3, col 1: {A[3,1]:.4f}")
print("View a subset of transition matrix A")
A_sub = pd.DataFrame(A[30:35,30:35], index=states[30:35], columns = states[30:35] )
print(A_sub)
```
##### Expected Output
```CPP
A at row 0, col 0: 0.000007040
A at row 3, col 1: 0.1691
View a subset of transition matrix A
RBS RP SYM TO UH
RBS 2.217069e-06 2.217069e-06 2.217069e-06 0.008870 2.217069e-06
RP 3.756509e-07 7.516775e-04 3.756509e-07 0.051089 3.756509e-07
SYM 1.722772e-05 1.722772e-05 1.722772e-05 0.000017 1.722772e-05
TO 4.477336e-05 4.472863e-08 4.472863e-08 0.000090 4.477336e-05
UH 1.030439e-05 1.030439e-05 1.030439e-05 0.061837 3.092348e-02
```
### Create the 'B' emission probabilities matrix
Now you will create the `B` transition matrix which computes the emission probability.
You will use smoothing as defined below:
$$P(w_i | t_i) = \frac{C(t_i, word_i)+ \alpha}{C(t_{i}) +\alpha * N}\tag{4}$$
- $C(t_i, word_i)$ is the number of times $word_i$ was associated with $tag_i$ in the training data (stored in `emission_counts` dictionary).
- $C(t_i)$ is the number of times $tag_i$ was in the training data (stored in `tag_counts` dictionary).
- $N$ is the number of words in the vocabulary
- $\alpha$ is a smoothing parameter.
The matrix `B` is of dimension (num_tags, N), where num_tags is the number of possible parts-of-speech tags.
Here is an example of the matrix, only a subset of tags and words are shown:
<p style='text-align: center;'> <b>B Emissions Probability Matrix (subset)</b> </p>
|**B**| ...| 725 | adroitly | engineers | promoted | synergy| ...|
|----|----|--------------|--------------|--------------|--------------|-------------|----|
|**CD** | ...| **8.201296e-05** | 2.732854e-08 | 2.732854e-08 | 2.732854e-08 | 2.732854e-08| ...|
|**NN** | ...| 7.521128e-09 | 7.521128e-09 | 7.521128e-09 | 7.521128e-09 | **2.257091e-05**| ...|
|**NNS** | ...| 1.670013e-08 | 1.670013e-08 |**4.676203e-04** | 1.670013e-08 | 1.670013e-08| ...|
|**VB** | ...| 3.779036e-08 | 3.779036e-08 | 3.779036e-08 | 3.779036e-08 | 3.779036e-08| ...|
|**RB** | ...| 3.226454e-08 | **6.456135e-05** | 3.226454e-08 | 3.226454e-08 | 3.226454e-08| ...|
|**RP** | ...| 3.723317e-07 | 3.723317e-07 | 3.723317e-07 | **3.723317e-07** | 3.723317e-07| ...|
| ... | ...| ... | ... | ... | ... | ... | ...|
<a name='ex-04'></a>
### Exercise 04
**Instructions:** Implement the `create_emission_matrix` below that computes the `B` emission probabilities matrix. Your function takes in $\alpha$, the smoothing parameter, `tag_counts`, which is a dictionary mapping each tag to its respective count, the `emission_counts` dictionary where the keys are (tag, word) and the values are the counts. Your task is to output a matrix that computes equation 4 for each cell in matrix `B`.
```
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_emission_matrix
def create_emission_matrix(alpha, tag_counts, emission_counts, vocab):
'''
Input:
alpha: tuning parameter used in smoothing
tag_counts: a dictionary mapping each tag to its respective count
emission_counts: a dictionary where the keys are (tag, word) and the values are the counts
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
B: a matrix of dimension (num_tags, len(vocab))
'''
# get the number of POS tag
num_tags = len(tag_counts)
# Get a list of all POS tags
all_tags = sorted(tag_counts.keys())
# Get the total number of unique words in the vocabulary
num_words = len(vocab)
# Initialize the emission matrix B with places for
# tags in the rows and words in the columns
B = np.zeros((num_tags, num_words))
# Get a set of all (POS, word) tuples
# from the keys of the emission_counts dictionary
emis_keys = set(list(emission_counts.keys()))
### START CODE HERE (Replace instances of 'None' with your code) ###
# Go through each row (POS tags)
for i in range(num_tags): # complete this line
# Go through each column (words)
for j in range(num_words): # complete this line
# Initialize the emission count for the (POS tag, word) to zero
count = 0
# Define the (POS tag, word) tuple for this row and column
key = (all_tags[i],vocab[j])
# check if the (POS tag, word) tuple exists as a key in emission counts
if key in emis_keys: # complete this line
# Get the count of (POS tag, word) from the emission_counts d
count = emission_counts[key]
# Get the count of the POS tag
count_tag = tag_counts[key[0]]
# Apply smoothing and store the smoothed value
# into the emission matrix B for this row and column
B[i,j] = (count + alpha)/(count_tag + alpha * num_words )
### END CODE HERE ###
return B
# creating your emission probability matrix. this takes a few minutes to run.
B = create_emission_matrix(alpha, tag_counts, emission_counts, list(vocab))
print(f"View Matrix position at row 0, column 0: {B[0,0]:.9f}")
print(f"View Matrix position at row 3, column 1: {B[3,1]:.9f}")
# Try viewing emissions for a few words in a sample dataframe
cidx = ['725','adroitly','engineers', 'promoted', 'synergy']
# Get the integer ID for each word
cols = [vocab[a] for a in cidx]
# Choose POS tags to show in a sample dataframe
rvals =['CD','NN','NNS', 'VB','RB','RP']
# For each POS tag, get the row number from the 'states' list
rows = [states.index(a) for a in rvals]
# Get the emissions for the sample of words, and the sample of POS tags
B_sub = pd.DataFrame(B[np.ix_(rows,cols)], index=rvals, columns = cidx )
print(B_sub)
```
##### Expected Output
```CPP
View Matrix position at row 0, column 0: 0.000006032
View Matrix position at row 3, column 1: 0.000000720
725 adroitly engineers promoted synergy
CD 8.201296e-05 2.732854e-08 2.732854e-08 2.732854e-08 2.732854e-08
NN 7.521128e-09 7.521128e-09 7.521128e-09 7.521128e-09 2.257091e-05
NNS 1.670013e-08 1.670013e-08 4.676203e-04 1.670013e-08 1.670013e-08
VB 3.779036e-08 3.779036e-08 3.779036e-08 3.779036e-08 3.779036e-08
RB 3.226454e-08 6.456135e-05 3.226454e-08 3.226454e-08 3.226454e-08
RP 3.723317e-07 3.723317e-07 3.723317e-07 3.723317e-07 3.723317e-07
```
<a name='3'></a>
# Part 3: Viterbi Algorithm and Dynamic Programming
In this part of the assignment you will implement the Viterbi algorithm which makes use of dynamic programming. Specifically, you will use your two matrices, `A` and `B` to compute the Viterbi algorithm. We have decomposed this process into three main steps for you.
* **Initialization** - In this part you initialize the `best_paths` and `best_probabilities` matrices that you will be populating in `feed_forward`.
* **Feed forward** - At each step, you calculate the probability of each path happening and the best paths up to that point.
* **Feed backward**: This allows you to find the best path with the highest probabilities.
<a name='3.1'></a>
## Part 3.1: Initialization
You will start by initializing two matrices of the same dimension.
- best_probs: Each cell contains the probability of going from one POS tag to a word in the corpus.
- best_paths: A matrix that helps you trace through the best possible path in the corpus.
<a name='ex-05'></a>
### Exercise 05
**Instructions**:
Write a program below that initializes the `best_probs` and the `best_paths` matrix.
Both matrices will be initialized to zero except for column zero of `best_probs`.
- Column zero of `best_probs` is initialized with the assumption that the first word of the corpus was preceded by a start token ("--s--").
- This allows you to reference the **A** matrix for the transition probability
Here is how to initialize column 0 of `best_probs`:
- The probability of the best path going from the start index to a given POS tag indexed by integer $i$ is denoted by $\textrm{best_probs}[s_{idx}, i]$.
- This is estimated as the probability that the start tag transitions to the POS denoted by index $i$: $\mathbf{A}[s_{idx}, i]$ AND that the POS tag denoted by $i$ emits the first word of the given corpus, which is $\mathbf{B}[i, vocab[corpus[0]]]$.
- Note that vocab[corpus[0]] refers to the first word of the corpus (the word at position 0 of the corpus).
- **vocab** is a dictionary that returns the unique integer that refers to that particular word.
Conceptually, it looks like this:
$\textrm{best_probs}[s_{idx}, i] = \mathbf{A}[s_{idx}, i] \times \mathbf{B}[i, corpus[0] ]$
In order to avoid multiplying and storing small values on the computer, we'll take the log of the product, which becomes the sum of two logs:
$best\_probs[i,0] = log(A[s_{idx}, i]) + log(B[i, vocab[corpus[0]]$
Also, to avoid taking the log of 0 (which is defined as negative infinity), the code itself will just set $best\_probs[i,0] = float('-inf')$ when $A[s_{idx}, i] == 0$
So the implementation to initialize $best\_probs$ looks like this:
$ if A[s_{idx}, i] <> 0 : best\_probs[i,0] = log(A[s_{idx}, i]) + log(B[i, vocab[corpus[0]]$
$ if A[s_{idx}, i] == 0 : best\_probs[i,0] = float('-inf')$
Please use [math.log](https://docs.python.org/3/library/math.html) to compute the natural logarithm.
The example below shows the initialization assuming the corpus starts with the phrase "Loss tracks upward".
<img src = "Initialize4.PNG"/>
Represent infinity and negative infinity like this:
```CPP
float('inf')
float('-inf')
```
```
# UNQ_C5 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: initialize
def initialize(states, tag_counts, A, B, corpus, vocab):
'''
Input:
states: a list of all possible parts-of-speech
tag_counts: a dictionary mapping each tag to its respective count
A: Transition Matrix of dimension (num_tags, num_tags)
B: Emission Matrix of dimension (num_tags, len(vocab))
corpus: a sequence of words whose POS is to be identified in a list
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
best_probs: matrix of dimension (num_tags, len(corpus)) of floats
best_paths: matrix of dimension (num_tags, len(corpus)) of integers
'''
# Get the total number of unique POS tags
num_tags = len(tag_counts)
# Initialize best_probs matrix
# POS tags in the rows, number of words in the corpus as the columns
best_probs = np.zeros((num_tags, len(corpus)))
# Initialize best_paths matrix
# POS tags in the rows, number of words in the corpus as columns
best_paths = np.zeros((num_tags, len(corpus)), dtype=int)
# Define the start token
s_idx = states.index("--s--")
### START CODE HERE (Replace instances of 'None' with your code) ###
# Go through each of the POS tags
for i in range(num_tags): # complete this line
# Handle the special case when the transition from start token to POS tag i is zero
if A[s_idx,i] == 0: # complete this line
# Initialize best_probs at POS tag 'i', column 0, to negative infinity
best_probs[i,0] = -inf
# For all other cases when transition from start token to POS tag i is non-zero:
else:
# Initialize best_probs at POS tag 'i', column 0
# Check the formula in the instructions above
best_probs[i,0] = np.log(A[s_idx,i]) + np.log(B[i, vocab[corpus[0]]])
### END CODE HERE ###
return best_probs, best_paths
best_probs, best_paths = initialize(states, tag_counts, A, B, prep, vocab)
# Test the function
print(f"best_probs[0,0]: {best_probs[0,0]:.4f}")
print(f"best_paths[2,3]: {best_paths[2,3]:.4f}")
```
##### Expected Output
```CPP
best_probs[0,0]: -22.6098
best_paths[2,3]: 0.0000
```
<a name='3.2'></a>
## Part 3.2 Viterbi Forward
In this part of the assignment, you will implement the `viterbi_forward` segment. In other words, you will populate your `best_probs` and `best_paths` matrices.
- Walk forward through the corpus.
- For each word, compute a probability for each possible tag.
- Unlike the previous algorithm `predict_pos` (the 'warm-up' exercise), this will include the path up to that (word,tag) combination.
Here is an example with a three-word corpus "Loss tracks upward":
- Note, in this example, only a subset of states (POS tags) are shown in the diagram below, for easier reading.
- In the diagram below, the first word "Loss" is already initialized.
- The algorithm will compute a probability for each of the potential tags in the second and future words.
Compute the probability that the tag of the second work ('tracks') is a verb, 3rd person singular present (VBZ).
- In the `best_probs` matrix, go to the column of the second word ('tracks'), and row 40 (VBZ), this cell is highlighted in light orange in the diagram below.
- Examine each of the paths from the tags of the first word ('Loss') and choose the most likely path.
- An example of the calculation for **one** of those paths is the path from ('Loss', NN) to ('tracks', VBZ).
- The log of the probability of the path up to and including the first word 'Loss' having POS tag NN is $-14.32$. The `best_probs` matrix contains this value -14.32 in the column for 'Loss' and row for 'NN'.
- Find the probability that NN transitions to VBZ. To find this probability, go to the `A` transition matrix, and go to the row for 'NN' and the column for 'VBZ'. The value is $4.37e-02$, which is circled in the diagram, so add $-14.32 + log(4.37e-02)$.
- Find the log of the probability that the tag VBS would 'emit' the word 'tracks'. To find this, look at the 'B' emission matrix in row 'VBZ' and the column for the word 'tracks'. The value $4.61e-04$ is circled in the diagram below. So add $-14.32 + log(4.37e-02) + log(4.61e-04)$.
- The sum of $-14.32 + log(4.37e-02) + log(4.61e-04)$ is $-25.13$. Store $-25.13$ in the `best_probs` matrix at row 'VBZ' and column 'tracks' (as seen in the cell that is highlighted in light orange in the diagram).
- All other paths in best_probs are calculated. Notice that $-25.13$ is greater than all of the other values in column 'tracks' of matrix `best_probs`, and so the most likely path to 'VBZ' is from 'NN'. 'NN' is in row 20 of the `best_probs` matrix, so $20$ is the most likely path.
- Store the most likely path $20$ in the `best_paths` table. This is highlighted in light orange in the diagram below.
The formula to compute the probability and path for the $i^{th}$ word in the $corpus$, the prior word $i-1$ in the corpus, current POS tag $j$, and previous POS tag $k$ is:
$\mathrm{prob} = \mathbf{best\_prob}_{k, i-1} + \mathrm{log}(\mathbf{A}_{k, j}) + \mathrm{log}(\mathbf{B}_{j, vocab(corpus_{i})})$
where $corpus_{i}$ is the word in the corpus at index $i$, and $vocab$ is the dictionary that gets the unique integer that represents a given word.
$\mathrm{path} = k$
where $k$ is the integer representing the previous POS tag.
<a name='ex-06'></a>
### Exercise 06
Instructions: Implement the `viterbi_forward` algorithm and store the best_path and best_prob for every possible tag for each word in the matrices `best_probs` and `best_tags` using the pseudo code below.
`for each word in the corpus
for each POS tag type that this word may be
for POS tag type that the previous word could be
compute the probability that the previous word had a given POS tag, that the current word has a given POS tag, and that the POS tag would emit this current word.
retain the highest probability computed for the current word
set best_probs to this highest probability
set best_paths to the index 'k', representing the POS tag of the previous word which produced the highest probability `
Please use [math.log](https://docs.python.org/3/library/math.html) to compute the natural logarithm.
<img src = "Forward4.PNG"/>
<details>
<summary>
<font size="3" color="darkgreen"><b>Hints</b></font>
</summary>
<p>
<ul>
<li>Remember that when accessing emission matrix B, the column index is the unique integer ID associated with the word. It can be accessed by using the 'vocab' dictionary, where the key is the word, and the value is the unique integer ID for that word.</li>
</ul>
</p>
```
# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: viterbi_forward
def viterbi_forward(A, B, test_corpus, best_probs, best_paths, vocab):
'''
Input:
A, B: The transiton and emission matrices respectively
test_corpus: a list containing a preprocessed corpus
best_probs: an initilized matrix of dimension (num_tags, len(corpus))
best_paths: an initilized matrix of dimension (num_tags, len(corpus))
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
best_probs: a completed matrix of dimension (num_tags, len(corpus))
best_paths: a completed matrix of dimension (num_tags, len(corpus))
'''
# Get the number of unique POS tags (which is the num of rows in best_probs)
num_tags = best_probs.shape[0]
# Go through every word in the corpus starting from word 1
# Recall that word 0 was initialized in `initialize()`
for i in range(1, len(test_corpus)):
# Print number of words processed, every 5000 words
if i % 5000 == 0:
print("Words processed: {:>8}".format(i))
### START CODE HERE (Replace instances of 'None' with your code EXCEPT the first 'best_path_i = None') ###
# For each unique POS tag that the current word can be
for j in range(num_tags): # complete this line
# Initialize best_prob for word i to negative infinity
best_prob_i = float("-inf")
# Initialize best_path for current word i to None
best_path_i = None
# For each POS tag that the previous word can be:
for k in range(num_tags): # complete this line
# Calculate the probability =
# best probs of POS tag k, previous word i-1 +
# log(prob of transition from POS k to POS j) +
# log(prob that emission of POS j is word i)
prob = best_probs[k,i-1] + np.log(A[k,j]) + np.log(B[j,vocab[test_corpus[i]]])
# check if this path's probability is greater than
# the best probability up to and before this point
if prob > best_prob_i: # complete this line
# Keep track of the best probability
best_prob_i = prob
# keep track of the POS tag of the previous word
# that is part of the best path.
# Save the index (integer) associated with
# that previous word's POS tag
best_path_i = k
# Save the best probability for the
# given current word's POS tag
# and the position of the current word inside the corpus
best_probs[j,i] = best_prob_i
# Save the unique integer ID of the previous POS tag
# into best_paths matrix, for the POS tag of the current word
# and the position of the current word inside the corpus.
best_paths[j,i] = best_path_i
### END CODE HERE ###
return best_probs, best_paths
```
Run the `viterbi_forward` function to fill in the `best_probs` and `best_paths` matrices.
**Note** that this will take a few minutes to run. There are about 30,000 words to process.
```
# this will take a few minutes to run => processes ~ 30,000 words
best_probs, best_paths = viterbi_forward(A, B, prep, best_probs, best_paths, vocab)
# Test this function
print(f"best_probs[0,1]: {best_probs[0,1]:.4f}")
print(f"best_probs[0,4]: {best_probs[0,4]:.4f}")
```
##### Expected Output
```CPP
best_probs[0,1]: -24.7822
best_probs[0,4]: -49.5601
```
<a name='3.3'></a>
## Part 3.3 Viterbi backward
Now you will implement the Viterbi backward algorithm.
- The Viterbi backward algorithm gets the predictions of the POS tags for each word in the corpus using the `best_paths` and the `best_probs` matrices.
The example below shows how to walk backwards through the best_paths matrix to get the POS tags of each word in the corpus. Recall that this example corpus has three words: "Loss tracks upward".
POS tag for 'upward' is `RB`
- Select the the most likely POS tag for the last word in the corpus, 'upward' in the `best_prob` table.
- Look for the row in the column for 'upward' that has the largest probability.
- Notice that in row 28 of `best_probs`, the estimated probability is -34.99, which is larger than the other values in the column. So the most likely POS tag for 'upward' is `RB` an adverb, at row 28 of `best_prob`.
- The variable `z` is an array that stores the unique integer ID of the predicted POS tags for each word in the corpus. In array z, at position 2, store the value 28 to indicate that the word 'upward' (at index 2 in the corpus), most likely has the POS tag associated with unique ID 28 (which is `RB`).
- The variable `pred` contains the POS tags in string form. So `pred` at index 2 stores the string `RB`.
POS tag for 'tracks' is `VBZ`
- The next step is to go backward one word in the corpus ('tracks'). Since the most likely POS tag for 'upward' is `RB`, which is uniquely identified by integer ID 28, go to the `best_paths` matrix in column 2, row 28. The value stored in `best_paths`, column 2, row 28 indicates the unique ID of the POS tag of the previous word. In this case, the value stored here is 40, which is the unique ID for POS tag `VBZ` (verb, 3rd person singular present).
- So the previous word at index 1 of the corpus ('tracks'), most likely has the POS tag with unique ID 40, which is `VBZ`.
- In array `z`, store the value 40 at position 1, and for array `pred`, store the string `VBZ` to indicate that the word 'tracks' most likely has POS tag `VBZ`.
POS tag for 'Loss' is `NN`
- In `best_paths` at column 1, the unique ID stored at row 40 is 20. 20 is the unique ID for POS tag `NN`.
- In array `z` at position 0, store 20. In array `pred` at position 0, store `NN`.
<img src = "Backwards5.PNG"/>
<a name='ex-07'></a>
### Exercise 07
Implement the `viterbi_backward` algorithm, which returns a list of predicted POS tags for each word in the corpus.
- Note that the numbering of the index positions starts at 0 and not 1.
- `m` is the number of words in the corpus.
- So the indexing into the corpus goes from `0` to `m - 1`.
- Also, the columns in `best_probs` and `best_paths` are indexed from `0` to `m - 1`
**In Step 1:**
Loop through all the rows (POS tags) in the last entry of `best_probs` and find the row (POS tag) with the maximum value.
Convert the unique integer ID to a tag (a string representation) using the dictionary `states`.
Referring to the three-word corpus described above:
- `z[2] = 28`: For the word 'upward' at position 2 in the corpus, the POS tag ID is 28. Store 28 in `z` at position 2.
- states(28) is 'RB': The POS tag ID 28 refers to the POS tag 'RB'.
- `pred[2] = 'RB'`: In array `pred`, store the POS tag for the word 'upward'.
**In Step 2:**
- Starting at the last column of best_paths, use `best_probs` to find the most likely POS tag for the last word in the corpus.
- Then use `best_paths` to find the most likely POS tag for the previous word.
- Update the POS tag for each word in `z` and in `preds`.
Referring to the three-word example from above, read best_paths at column 2 and fill in z at position 1.
`z[1] = best_paths[z[2],2]`
The small test following the routine prints the last few words of the corpus and their states to aid in debug.
```
# print(states)
# print(best_probs[3])
# print(prep[5])
print(best_paths[None,None])
# UNQ_C7 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: viterbi_backward
def viterbi_backward(best_probs, best_paths, corpus, states):
'''
This function returns the best path.
'''
# Get the number of words in the corpus
# which is also the number of columns in best_probs, best_paths
m = best_paths.shape[1]
# Initialize array z, same length as the corpus
z = [None] * m
# Get the number of unique POS tags
num_tags = best_probs.shape[0]
# Initialize the best probability for the last word
best_prob_for_last_word = float('-inf')
# Initialize pred array, same length as corpus
pred = [None] * m
### START CODE HERE (Replace instances of 'None' with your code) ###
## Step 1 ##
# Go through each POS tag for the last word (last column of best_probs)
# in order to find the row (POS tag integer ID)
# with highest probability for the last word
for k in range(num_tags): # complete this line
# If the probability of POS tag at row k
# is better than the previosly best probability for the last word:
if best_probs[k,m-1] > best_prob_for_last_word: # complete this line
# Store the new best probability for the lsat word
best_prob_for_last_word = best_probs[k,m-1]
# Store the unique integer ID of the POS tag
# which is also the row number in best_probs
z[m - 1] = k
# Convert the last word's predicted POS tag
# from its unique integer ID into the string representation
# using the 'states' dictionary
# store this in the 'pred' array for the last word
pred[m - 1] = states[z[m-1]]
## Step 2 ##
# Find the best POS tags by walking backward through the be st_paths
# From the last word in the corpus to the 0th word in the corpus
for i in reversed(range(m-1)): # complete this line
# Retrieve the unique integer ID of
# the POS tag for the word at position 'i' in the corpus
pos_tag_for_word_i = z[i+1]
# In best_paths, go to the row representing the POS tag of word i
# and the column representing the word's position in the corpus
# to retrieve the predicted POS for the word at position i-1 in the corpus
z[i] = best_paths[pos_tag_for_word_i,i+1]
# Get the previous word's POS tag in string form
# Use the 'states' dictionary,
# where the key is the unique integer ID of the POS tag,
# and the value is the string representation of that POS tag
pred[i] = states[z[i]]
### END CODE HERE ###
return pred
print(y)
# Run and test your function
pred = viterbi_backward(best_probs, best_paths, prep, states)
m=len(pred)
print('The prediction for pred[-7:m-1] is: \n', prep[-7:m-1], "\n", pred[-7:m-1], "\n")
print('The prediction for pred[0:8] is: \n', pred[0:7], "\n", prep[0:7])
```
**Expected Output:**
```CPP
The prediction for prep[-7:m-1] is:
['see', 'them', 'here', 'with', 'us', '.']
['VB', 'PRP', 'RB', 'IN', 'PRP', '.']
The prediction for pred[0:8] is:
['DT', 'NN', 'POS', 'NN', 'MD', 'VB', 'VBN']
['The', 'economy', "'s", 'temperature', 'will', 'be', 'taken']
```
Now you just have to compare the predicted labels to the true labels to evaluate your model on the accuracy metric!
<a name='4'></a>
# Part 4: Predicting on a data set
Compute the accuracy of your prediction by comparing it with the true `y` labels.
- `pred` is a list of predicted POS tags corresponding to the words of the `test_corpus`.
```
print('The third word is:', prep[3])
print('Your prediction is:', pred[3])
print('Your corresponding label y is: ', y[3])
for prediction, y1 in zip(pred, y):
if len(y1.split()) == 2:
continue
print(y1.split())
```
<a name='ex-08'></a>
### Exercise 08
Implement a function to compute the accuracy of the viterbi algorithm's POS tag predictions.
- To split y into the word and its tag you can use `y.split()`.
```
# UNQ_C8 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: compute_accuracy
def compute_accuracy(pred, y):
'''
Input:
pred: a list of the predicted parts-of-speech
y: a list of lines where each word is separated by a '\t' (i.e. word \t tag)
Output:
'''
num_correct = 0
total = 0
# Zip together the prediction and the labels
for prediction, y1 in zip(pred, y):
### START CODE HERE (Replace instances of 'None' with your code) ###
# Split the label into the word and the POS tag
word_tag_tuple = y1.split()
# Check that there is actually a word and a tag
# no more and no less than 2 items
if len(word_tag_tuple) == 2: # complete this line
# store the word and tag separately
word, tag = word_tag_tuple
# Check if the POS tag label matches the prediction
if tag == prediction: # complete this line
# count the number of times that the prediction
# and label match
num_correct += 1
# keep track of the total number of examples (that have valid labels)
total += 1
### END CODE HERE ###
return num_correct/total
print(f"Accuracy of the Viterbi algorithm is {compute_accuracy(pred, y):.4f}")
```
##### Expected Output
```CPP
Accuracy of the Viterbi algorithm is 0.9531
```
Congratulations you were able to classify the parts-of-speech with 95% accuracy.
### Key Points and overview
In this assignment you learned about parts-of-speech tagging.
- In this assignment, you predicted POS tags by walking forward through a corpus and knowing the previous word.
- There are other implementations that use bidirectional POS tagging.
- Bidirectional POS tagging requires knowing the previous word and the next word in the corpus when predicting the current word's POS tag.
- Bidirectional POS tagging would tell you more about the POS instead of just knowing the previous word.
- Since you have learned to implement the unidirectional approach, you have the foundation to implement other POS taggers used in industry.
### References
- ["Speech and Language Processing", Dan Jurafsky and James H. Martin](https://web.stanford.edu/~jurafsky/slp3/)
- We would like to thank Melanie Tosik for her help and inspiration
| github_jupyter |
# <center>RumbleDB sandbox</center>
This is a RumbleDB sandbox that allows you to play with simple JSONiq queries.
It is a jupyter notebook that you can also download and execute on your own machine, but if you arrived here from the RumbleDB website, it is likely to be shown within Google's Colab environment.
To get started, you first need to execute the cell below to activate the RumbleDB magic (you do not need to understand what it does, this is just initialization Python code).
```
!pip install rumbledb
%load_ext rumbledb
%env RUMBLEDB_SERVER=http://public.rumbledb.org:9090/jsoniq
```
By default, this notebook uses a small public backend provided by us. Each query runs on just one machine that is very limited in CPU: one core and memory: 1GB, and with only the http scheme activated. This is sufficient to discover RumbleDB and play a bit, but of course is not intended for any production use. If you need to use RumbleDB in production, you can use it with an installation of Spark either on your machine or on a cluster.
This sandbox backend may occasionally break, especially if too many users use it at the same time, so please bear with us! The system is automatically restarted every day so, if it stops working, you can either try again in 24 hours or notify us.
It is straightforward to execute your own RumbleDB server on your own Spark cluster (and then you can make full use of all the input file systems and file formats). In this case, just replace the above server with your own hostname and port. Note that if you run RumbleDB as a server locally, you will also need to download and use this notebook locally rather than in this Google Colab environment as, obviously, your personal computer cannot be accessed from the Web.
Now we are all set! You can now start reading and executing the JSONiq queries as you go, and you can even edit them!
## JSON
As explained on the [official JSON Web site](http://www.json.org/), JSON is a lightweight data-interchange format designed for humans as well as for computers. It supports as values:
- objects (string-to-value maps)
- arrays (ordered sequences of values)
- strings
- numbers
- booleans (true, false)
- null
JSONiq provides declarative querying and updating capabilities on JSON data.
## Elevator Pitch
JSONiq is based on XQuery, which is a W3C standard (like XML and HTML). XQuery is a very powerful declarative language that originally manipulates XML data, but it turns out that it is also a very good fit for manipulating JSON natively.
JSONiq, since it extends XQuery, is a very powerful general-purpose declarative programming language. Our experience is that, for the same task, you will probably write about 80% less code compared to imperative languages like JavaScript, Python or Ruby. Additionally, you get the benefits of strong type checking without actually having to write type declarations.
Here is an appetizer before we start the tutorial from scratch.
```
%%jsoniq
let $stores :=
[
{ "store number" : 1, "state" : "MA" },
{ "store number" : 2, "state" : "MA" },
{ "store number" : 3, "state" : "CA" },
{ "store number" : 4, "state" : "CA" }
]
let $sales := [
{ "product" : "broiler", "store number" : 1, "quantity" : 20 },
{ "product" : "toaster", "store number" : 2, "quantity" : 100 },
{ "product" : "toaster", "store number" : 2, "quantity" : 50 },
{ "product" : "toaster", "store number" : 3, "quantity" : 50 },
{ "product" : "blender", "store number" : 3, "quantity" : 100 },
{ "product" : "blender", "store number" : 3, "quantity" : 150 },
{ "product" : "socks", "store number" : 1, "quantity" : 500 },
{ "product" : "socks", "store number" : 2, "quantity" : 10 },
{ "product" : "shirt", "store number" : 3, "quantity" : 10 }
]
let $join :=
for $store in $stores[], $sale in $sales[]
where $store."store number" = $sale."store number"
return {
"nb" : $store."store number",
"state" : $store.state,
"sold" : $sale.product
}
return [$join]
```
## And here you go
### Actually, you already knew some JSONiq
The first thing you need to know is that a well-formed JSON document is a JSONiq expression as well.
This means that you can copy-and-paste any JSON document into a query. The following are JSONiq queries that are "idempotent" (they just output themselves):
```
%%jsoniq
{ "pi" : 3.14, "sq2" : 1.4 }
%%jsoniq
[ 2, 3, 5, 7, 11, 13 ]
%%jsoniq
{
"operations" : [
{ "binary" : [ "and", "or"] },
{ "unary" : ["not"] }
],
"bits" : [
0, 1
]
}
%%jsoniq
[ { "Question" : "Ultimate" }, ["Life", "the universe", "and everything"] ]
```
This works with objects, arrays (even nested), strings, numbers, booleans, null.
It also works the other way round: if your query outputs an object or an array, you can use it as a JSON document.
JSONiq is a declarative language. This means that you only need to say what you want - the compiler will take care of the how.
In the above queries, you are basically saying: I want to output this JSON content, and here it is.
## JSONiq basics
### The real JSONiq Hello, World!
Wondering what a hello world program looks like in JSONiq? Here it is:
```
%%jsoniq
"Hello, World!"
```
Not surprisingly, it outputs the string "Hello, World!".
### Numbers and arithmetic operations
Okay, so, now, you might be thinking: "What is the use of this language if it just outputs what I put in?" Of course, JSONiq can more than that. And still in a declarative way. Here is how it works with numbers:
```
%%jsoniq
2 + 2
%%jsoniq
(38 + 2) div 2 + 11 * 2
```
(mind the division operator which is the "div" keyword. The slash operator has different semantics).
Like JSON, JSONiq works with decimals and doubles:
```
%%jsoniq
6.022e23 * 42
```
### Logical operations
JSONiq supports boolean operations.
```
%%jsoniq
true and false
%%jsoniq
(true or false) and (false or true)
```
The unary not is also available:
```
%%jsoniq
not true
```
### Strings
JSONiq is capable of manipulating strings as well, using functions:
```
%%jsoniq
concat("Hello ", "Captain ", "Kirk")
%%jsoniq
substring("Mister Spock", 8, 5)
```
JSONiq comes up with a rich string function library out of the box, inherited from its base language. These functions are listed [here](https://www.w3.org/TR/xpath-functions-30/) (actually, you will find many more for numbers, dates, etc).
### Sequences
Until now, we have only been working with single values (an object, an array, a number, a string, a boolean). JSONiq supports sequences of values. You can build a sequence using commas:
```
%%jsoniq
(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
%%jsoniq
1, true, 4.2e1, "Life"
```
The "to" operator is very convenient, too:
```
%%jsoniq
(1 to 100)
```
Some functions even work on sequences:
```
%%jsoniq
sum(1 to 100)
%%jsoniq
string-join(("These", "are", "some", "words"), "-")
%%jsoniq
count(10 to 20)
%%jsoniq
avg(1 to 100)
```
Unlike arrays, sequences are flat. The sequence (3) is identical to the integer 3, and (1, (2, 3)) is identical to (1, 2, 3).
## A bit more in depth
### Variables
You can bind a sequence of values to a (dollar-prefixed) variable, like so:
```
%%jsoniq
let $x := "Bearing 3 1 4 Mark 5. "
return concat($x, "Engage!")
%%jsoniq
let $x := ("Kirk", "Picard", "Sisko")
return string-join($x, " and ")
```
You can bind as many variables as you want:
```
%%jsoniq
let $x := 1
let $y := $x * 2
let $z := $y + $x
return ($x, $y, $z)
```
and even reuse the same name to hide formerly declared variables:
```
%%jsoniq
let $x := 1
let $x := $x + 2
let $x := $x + 3
return $x
```
### Iteration
In a way very similar to let, you can iterate over a sequence of values with the "for" keyword. Instead of binding the entire sequence of the variable, it will bind each value of the sequence in turn to this variable.
```
%%jsoniq
for $i in 1 to 10
return $i * 2
```
More interestingly, you can combine fors and lets like so:
```
%%jsoniq
let $sequence := 1 to 10
for $value in $sequence
let $square := $value * 2
return $square
```
and even filter out some values:
```
%%jsoniq
let $sequence := 1 to 10
for $value in $sequence
let $square := $value * 2
where $square < 10
return $square
```
Note that you can only iterate over sequences, not arrays. To iterate over an array, you can obtain the sequence of its values with the [] operator, like so:
```
%%jsoniq
[1, 2, 3][]
```
### Conditions
You can make the output depend on a condition with an if-then-else construct:
```
%%jsoniq
for $x in 1 to 10
return if ($x < 5) then $x
else -$x
```
Note that the else clause is required - however, it can be the empty sequence () which is often when you need if only the then clause is relevant to you.
### Composability of Expressions
Now that you know of a couple of elementary JSONiq expressions, you can combine them in more elaborate expressions. For example, you can put any sequence of values in an array:
```
%%jsoniq
[ 1 to 10 ]
```
Or you can dynamically compute the value of object pairs (or their key):
```
%%jsoniq
{
"Greeting" : (let $d := "Mister Spock"
return concat("Hello, ", $d)),
"Farewell" : string-join(("Live", "long", "and", "prosper"),
" ")
}
```
You can dynamically generate object singletons (with a single pair):
```
%%jsoniq
{ concat("Integer ", 2) : 2 * 2 }
```
and then merge lots of them into a new object with the {| |} notation:
```
%%jsoniq
{|
for $i in 1 to 10
return { concat("Square of ", $i) : $i * $i }
|}
```
## JSON Navigation
Up to now, you have learnt how to compose expressions so as to do some computations and to build objects and arrays. It also works the other way round: if you have some JSON data, you can access it and navigate.
All you need to know is: JSONiq views
an array as an ordered list of values,
an object as a set of name/value pairs
### Objects
You can use the dot operator to retrieve the value associated with a key. Quotes are optional, except if the key has special characters such as spaces. It will return the value associated thereto:
```
%%jsoniq
let $person := {
"first name" : "Sarah",
"age" : 13,
"gender" : "female",
"friends" : [ "Jim", "Mary", "Jennifer"]
}
return $person."first name"
```
You can also ask for all keys in an object:
```
%%jsoniq
let $person := {
"name" : "Sarah",
"age" : 13,
"gender" : "female",
"friends" : [ "Jim", "Mary", "Jennifer"]
}
return { "keys" : [ keys($person)] }
```
### Arrays
The [[]] operator retrieves the entry at the given position:
```
%%jsoniq
let $friends := [ "Jim", "Mary", "Jennifer"]
return $friends[[1+1]]
```
It is also possible to get the size of an array:
```
%%jsoniq
let $person := {
"name" : "Sarah",
"age" : 13,
"gender" : "female",
"friends" : [ "Jim", "Mary", "Jennifer"]
}
return { "how many friends" : size($person.friends) }
```
Finally, the [] operator returns all elements in an array, as a sequence:
```
%%jsoniq
let $person := {
"name" : "Sarah",
"age" : 13,
"gender" : "female",
"friends" : [ "Jim", "Mary", "Jennifer"]
}
return $person.friends[]
```
### Relational Algebra
Do you remember SQL's SELECT FROM WHERE statements? JSONiq inherits selection, projection and join capability from XQuery, too.
```
%%jsoniq
let $stores :=
[
{ "store number" : 1, "state" : "MA" },
{ "store number" : 2, "state" : "MA" },
{ "store number" : 3, "state" : "CA" },
{ "store number" : 4, "state" : "CA" }
]
let $sales := [
{ "product" : "broiler", "store number" : 1, "quantity" : 20 },
{ "product" : "toaster", "store number" : 2, "quantity" : 100 },
{ "product" : "toaster", "store number" : 2, "quantity" : 50 },
{ "product" : "toaster", "store number" : 3, "quantity" : 50 },
{ "product" : "blender", "store number" : 3, "quantity" : 100 },
{ "product" : "blender", "store number" : 3, "quantity" : 150 },
{ "product" : "socks", "store number" : 1, "quantity" : 500 },
{ "product" : "socks", "store number" : 2, "quantity" : 10 },
{ "product" : "shirt", "store number" : 3, "quantity" : 10 }
]
let $join :=
for $store in $stores[], $sale in $sales[]
where $store."store number" = $sale."store number"
return {
"nb" : $store."store number",
"state" : $store.state,
"sold" : $sale.product
}
return [$join]
```
### Access datasets
RumbleDB can read input from many file systems and many file formats. If you are using our backend, you can only use json-doc() with any URI pointing to a JSON file and navigate it as you see fit.
You can read data from your local disk, from S3, from HDFS, and also from the Web. For this tutorial, we'll read from the Web because, well, we are already on the Web.
We have put a sample at http://rumbledb.org/samples/products-small.json that contains 100,000 small objects like:
```
%%jsoniq
json-file("http://rumbledb.org/samples/products-small.json", 10)[1]
```
The second parameter to json-file, 10, indicates to RumbleDB that it should organize the data in ten partitions after downloading it, and process it in parallel. If you were reading from HDFS or S3, the parallelization of these partitions would be pushed down to the distributed file system.
JSONiq supports the relational algebra. For example, you can do a selection with a where clause, like so:
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
where $product.quantity ge 995
return $product
```
Notice that by default only the first 200 items are shown. In a typical setup, it is possible to output the result of a query to a distributed system, so it is also possible to output all the results if needed. In this case, however, as this is printed on your screen, it is more convenient not to materialize the entire sequence.
For a projection, there is project():
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
where $product.quantity ge 995
return project($product, ("store-number", "product"))
```
You can also page the results (like OFFSET and LIMIT in SQL) with a count clause and a where clause
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
where $product.quantity ge 995
count $c
where $c gt 10 and $c le 20
return project($product, ("store-number", "product"))
```
JSONiq also supports grouping with a group by clause:
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
group by $store-number := $product.store-number
return {
"store" : $store-number,
"count" : count($product)
}
```
As well as ordering with an order by clause:
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
group by $store-number := $product.store-number
order by $store-number ascending
return {
"store" : $store-number,
"count" : count($product)
}
```
JSONiq supports denormalized data, so you are not forced to aggregate after a grouping, you can also nest data like so:
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
group by $store-number := $product.store-number
order by $store-number ascending
return {
"store" : $store-number,
"products" : [ distinct-values($product.product) ]
}
```
Or
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
group by $store-number := $product.store-number
order by $store-number ascending
return {
"store" : $store-number,
"products" : [ project($product[position() le 10], ("product", "quantity")) ],
"inventory" : sum($product.quantity)
}
```
That's it! You know the basics of JSONiq. Now you can also download the RumbleDB jar and run it on your own laptop. Or [on a Spark cluster, reading data from and to HDFS](https://rumble.readthedocs.io/en/latest/Run%20on%20a%20cluster/), etc.
| github_jupyter |
# Aggregating statistics
```
import pandas as pd
air_quality = pd.read_pickle('air_quality.pkl')
air_quality.info()
```
### Series/one column of a DataFrame
```
air_quality['TEMP'].count()
air_quality['TEMP'].mean()
air_quality['TEMP'].std()
air_quality['TEMP'].min()
air_quality['TEMP'].max()
air_quality['TEMP'].quantile(0.25)
air_quality['TEMP'].median()
air_quality['TEMP'].describe()
air_quality['RAIN'].sum()
air_quality['PM2.5_category'].mode()
air_quality['PM2.5_category'].nunique()
air_quality['PM2.5_category'].describe()
```
### DataFrame by columns
```
air_quality.count()
air_quality.mean()
air_quality.mean(numeric_only=True)
air_quality[['PM2.5', 'TEMP']].mean()
air_quality[['PM2.5', 'TEMP']].min()
air_quality[['PM2.5', 'TEMP']].max()
air_quality.describe().T
air_quality.describe(include=['object', 'category', 'bool'])
air_quality[['PM2.5_category', 'TEMP_category', 'hour']].mode()
air_quality['hour'].value_counts()
air_quality[['PM2.5', 'TEMP']].agg('mean')
air_quality[['PM2.5', 'TEMP']].mean()
air_quality[['PM2.5', 'TEMP']].agg(['min', 'max', 'mean'])
air_quality[['PM2.5', 'PM2.5_category']].agg(['min', 'max', 'mean', 'nunique'])
air_quality[['PM2.5', 'PM2.5_category']].agg({'PM2.5': 'mean', 'PM2.5_category': 'nunique'})
air_quality.agg({'PM2.5': ['min', 'max', 'mean'], 'PM2.5_category': 'nunique'})
def max_minus_min(s):
return s.max() - s.min()
max_minus_min(air_quality['TEMP'])
air_quality[['PM2.5', 'TEMP']].agg(['min', 'max', max_minus_min])
41.6 - (-16.8)
```
### DataFrame by rows
```
air_quality[['PM2.5', 'PM10']]
air_quality[['PM2.5', 'PM10']].min()
air_quality[['PM2.5', 'PM10']].min(axis=1)
air_quality[['PM2.5', 'PM10']].mean(axis=1)
air_quality[['PM2.5', 'PM10']].sum(axis=1)
```
# Grouping by
```
air_quality.groupby(by='PM2.5_category')
air_quality.groupby(by='PM2.5_category').groups
air_quality['PM2.5_category'].head(20)
air_quality.groupby(by='PM2.5_category').groups.keys()
air_quality.groupby(by='PM2.5_category').get_group('Good')
air_quality.sort_values('date_time')
air_quality.sort_values('date_time').groupby(by='year').first()
air_quality.sort_values('date_time').groupby(by='year').last()
air_quality.groupby('TEMP_category').size()
air_quality['TEMP_category'].value_counts(sort=False)
air_quality.groupby('quarter').mean()
#air_quality[['PM2.5', 'TEMP']].groupby('quarter').mean() # KeyError: 'quarter'
air_quality[['PM2.5', 'TEMP', 'quarter']].groupby('quarter').mean()
air_quality.groupby('quarter')[['PM2.5', 'TEMP']].mean()
air_quality.groupby('quarter').mean()[['PM2.5', 'TEMP']]
air_quality.groupby('quarter')[['PM2.5', 'TEMP']].describe()
air_quality.groupby('quarter')[['PM2.5', 'TEMP']].agg(['min', 'max'])
air_quality.groupby('day_of_week_name')[['PM2.5', 'TEMP', 'RAIN']].agg({'PM2.5': ['min', 'max', 'mean'], 'TEMP': 'mean', 'RAIN': 'mean'})
air_quality.groupby(['quarter', 'TEMP_category'])[['PM2.5', 'TEMP']].mean()
air_quality.groupby(['TEMP_category', 'quarter'])[['PM2.5', 'TEMP']].mean()
air_quality.groupby(['year', 'quarter', 'month'])['TEMP'].agg(['min', 'max'])
```
# Pivoting tables
```
import pandas as pd
student = pd.read_csv('student.csv')
student.info()
student
pd.pivot_table(student,
index='sex')
pd.pivot_table(student,
index=['sex', 'internet']
)
pd.pivot_table(student,
index=['sex', 'internet'],
values='score')
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc='mean')
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc='median')
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc=['min', 'mean', 'max'])
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc='mean',
columns='studytime'
)
student[(student['sex']=='M') & (student['internet']=='no') & (student['studytime']=='4. >10 hours')]
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc='mean',
columns='studytime',
fill_value=-999)
pd.pivot_table(student,
index=['sex', 'internet'],
values=['score', 'age'],
aggfunc='mean',
columns='studytime',
fill_value=-999)
pd.pivot_table(student,
index=['sex'],
values='score',
aggfunc='mean',
columns=['internet', 'studytime'],
fill_value=-999)
pd.pivot_table(student,
index='familysize',
values='score',
aggfunc='mean',
columns='sex'
)
pd.pivot_table(student,
index='familysize',
values='score',
aggfunc='mean',
columns='sex',
margins=True,
margins_name='Average score total')
student[student['sex']=='F'].mean()
pd.pivot_table(student,
index='studytime',
values=['age', 'score'],
aggfunc={'age': ['min', 'max'],
'score': 'median'},
columns='sex')
pd.pivot_table(student,
index='studytime',
values='score',
aggfunc=lambda s: s.max() - s.min(),
columns='sex'
)
```
| github_jupyter |
# Getting Started with CREST
CREST is a hybrid modelling DSL (domain-specific language) that focuses on the flow of resources within cyber-physical systems (CPS).
CREST is implemented in the Python programming language as the `crestdsl` internal DSL and shipped as Python package.
`crestdsl`'s source code is hosted on GitHub https://github.com/stklik/CREST/
You can also visit the [documentation](https://crestdsl.readthedocs.io)
for more information.
## This Notebook
The purpose of this notebook is to provide a small showcase of modelling with `crestdsl`.
The system to be modelled is a growing lamp that produces light and heat, if the lamp is turned on and electricity is provided.
## How to use this Jupyter notebook:
Select a code-cell (such as the one directly below) and click the `Run` button in the menu bar above to execute it. (Alternatively, you can use the keyboard combination `Ctrl+Enter`.)
**Output:** will be shown directly underneath the cell, if there is any.
To **run all cells**, you can iteratively execute individual cells, or execute all at once via the menu item `Cell` -> `Run all`
Remember, that the order in which you execute cells is important, not the placement of a cell within the notebook.
For a more profound introduction, go and visit the [Project Jupyter](http://jupyter.org/) website.
```
print("Try executing this cell, so you ge a feeling for it.")
2 + 2 # this should print "Out[X]: 4" directly underneath (X will be an index)
```
# Defining a `crestdsl` Model
## Import `crestdsl`
In order to use `crestdsl`, you have to import it.
Initially, we will create work towards creating a system model, so let's import the `model` subpackage.
```
import crestdsl.model as crest
```
## Define Resources
First, it is necessary to define the resource types that will be used in the application.
In CREST and `crestdsl`, resources are combinations of resource names and their value domains.
Value domains can be infinite, such as Real and Integers or discrete such as `["on", "off"]`, as shown for the switch.
```
electricity = crest.Resource("Watt", crest.REAL)
switch = crest.Resource("switch", ["on", "off"])
light = crest.Resource("Lumen", crest.INTEGER)
counter = crest.Resource("Count", crest.INTEGER)
time = crest.Resource("minutes", crest.REAL)
celsius = crest.Resource("Celsius", crest.REAL)
fahrenheit = crest.Resource("Fahrenheit", crest.REAL)
```
## Our First Entity
In CREST any system or component is modelled as Entity.
Entities can be composed hierachically (as we will see later).
To model an entity, we define a Python class that inherits from `crest.Entity`.
Entities can define
- `Input`, `Output` and `Local` ports (variables),
- `State` objects and a `current` state
- `Transition`s between states
- `Influence`s between ports (to express value dependencies between ports)
- `Update`s that are continuously executed and write values to a port
- and `Action`s, which allow the modelling of discrete changes during transition firings.
Below, we define the `LightElement` entity, which models the component that is responsible for producing light from electricity. It defines one input and one output port.
```
class LightElement(crest.Entity):
"""This is a definition of a new Entity type. It derives from CREST's Entity base class."""
"""we define ports - each has a resource and an initial value"""
electricity_in = crest.Input(resource=electricity, value=0)
light_out = crest.Output(resource=light, value=0)
"""automaton states - don't forget to specify one as the current state"""
on = crest.State()
off = current = crest.State()
"""transitions and guards (as lambdas)"""
off_to_on = crest.Transition(source=off, target=on, guard=(lambda self: self.electricity_in.value >= 100))
on_to_off = crest.Transition(source=on, target=off, guard=(lambda self: self.electricity_in.value < 100))
"""
update functions. They are related to a state, define the port to be updated and return the port's new value
Remember that updates need two parameters: self and dt.
"""
@crest.update(state=on, target=light_out)
def set_light_on(self, dt=0):
return 800
@crest.update(state=off, target=light_out)
def set_light_off(self, dt=0):
return 0
```
## Visualising Entities
By default, CREST is a graphical language. Therefore it only makes sense to implement a graphical visualisation of `crestdsl` systems.
One of the plotting engines is defined in the `crestdsl.ui` module.
The code below produces an interactive HTML output.
You can easily interact with the model to explore it:
- Move objects around if the automatic layout does not provide an sufficiently good layout.
- Select ports and states to see their outgoing arcs (blue) and incoming arcs (red).
- Hover over transitions, influences and actions to display their name and short summary.
- Double click on transitions, influences and actions you will see their source code.
- There is a *hot corner* on the top left of each entity. You can double-click it to collapse the entity. This feature is useful for CREST diagrams with many entities. *Unfortunately a software issue prevents the expand/collapse icon not to be displayed. It still works though (notice your cursor changing to a pointer)*
**GO AHEAD AND TRY IT**
```
# import the plotting libraries that can visualise the CREST systems
from crestdsl.ui import plot
plot(LightElement())
```
## Define Another Entity (The HeatElement)
It's time to model the heating component of our growing lamp.
Its functionality is simple: if the `switch_in` input is `on`, 1% of the electricity is converted to addtional heat under the lamp.
Thus, for example, by providing 100 Watt, the temperature underneath the lamp grows by 1 degree centigrade.
```
class HeatElement(crest.Entity):
""" Ports """
electricity_in = crest.Input(resource=electricity, value=0)
switch_in = crest.Input(resource=switch, value="off") # the heatelement has its own switch
heat_out = crest.Output(resource=celsius, value=0) # and produces a celsius value (i.e. the temperature increase underneath the lamp)
""" Automaton (States) """
state = current = crest.State() # the only state of this entity
"""Update"""
@crest.update(state=state, target=heat_out)
def heat_output(self, dt):
# When the lamp is on, then we convert electricity to temperature at a rate of 100Watt = 1Celsius
if self.switch_in.value == "on":
return self.electricity_in.value / 100
else:
return 0
# show us what it looks like
plot(HeatElement())
```
## Adder - A Logical Entity
CREST does not specify a special connector type that defines what is happening for multiple incoming influence, etc. Instead standard entities are used to define add, minimum and maximum calculation which is then written to the actual target port using an influence.
We call such entities *logical*, since they don't have a real-world counterpart.
```
# a logical entity can inherit from LogicalEntity,
# to emphasize that it does not relate to the real world
class Adder(crest.LogicalEntity):
heat_in = crest.Input(resource=celsius, value=0)
room_temp_in = crest.Input(resource=celsius, value=22)
temperature_out = crest.Output(resource=celsius, value=22)
state = current = crest.State()
@crest.update(state=state, target=temperature_out)
def add(self, dt):
return self.heat_in.value + self.room_temp_in.value
plot(Adder()) # try adding the display option 'show_update_ports=True' and see what happens!
```
## Put it all together - Create the `GrowLamp`
Finally, we create the entire `GrowLamp` entity based on the components we already created.
We define subentities in a similar way to all other definitions - as class variables.
Additionally, we use influences to connect the ports to each other.
```
class GrowLamp(crest.Entity):
""" - - - - - - - PORTS - - - - - - - - - - """
electricity_in = crest.Input(resource=electricity, value=0)
switch_in = crest.Input(resource=switch, value="off")
heat_switch_in = crest.Input(resource=switch, value="on")
room_temperature_in = crest.Input(resource=fahrenheit, value=71.6)
light_out = crest.Output(resource=light, value=3.1415*1000) # note that these are bogus values for now
temperature_out = crest.Output(resource=celsius, value=4242424242) # yes, nonsense..., they are updated when simulated
on_time = crest.Local(resource=time, value=0)
on_count = crest.Local(resource=counter, value=0)
""" - - - - - - - SUBENTITIES - - - - - - - - - - """
lightelement = LightElement()
heatelement = HeatElement()
adder = Adder()
""" - - - - - - - INFLUENCES - - - - - - - - - - """
"""
Influences specify a source port and a target port.
They are always executed, independent of the automaton's state.
Since they are called directly with the source-port's value, a self-parameter is not necessary.
"""
@crest.influence(source=room_temperature_in, target=adder.room_temp_in)
def celsius_to_fahrenheit(value):
return (value - 32) * 5 / 9
# we can also define updates and influences with lambda functions...
heat_to_add = crest.Influence(source=heatelement.heat_out, target=adder.heat_in, function=(lambda val: val))
# if the lambda function doesn't do anything (like the one above) we can omit it entirely...
add_to_temp = crest.Influence(source=adder.temperature_out, target=temperature_out)
light_to_light = crest.Influence(source=lightelement.light_out, target=light_out)
heat_switch_influence = crest.Influence(source=heat_switch_in, target=heatelement.switch_in)
""" - - - - - - - STATES & TRANSITIONS - - - - - - - - - - """
on = crest.State()
off = current = crest.State()
error = crest.State()
off_to_on = crest.Transition(source=off, target=on, guard=(lambda self: self.switch_in.value == "on" and self.electricity_in.value >= 100))
on_to_off = crest.Transition(source=on, target=off, guard=(lambda self: self.switch_in.value == "off" or self.electricity_in.value < 100))
# transition to error state if the lamp ran for more than 1000.5 time units
@crest.transition(source=on, target=error)
def to_error(self):
"""More complex transitions can be defined as a function. We can use variables and calculations"""
timeout = self.on_time.value >= 1000.5
heat_is_on = self.heatelement.switch_in.value == "on"
return timeout and heat_is_on
""" - - - - - - - UPDATES - - - - - - - - - - """
# LAMP is OFF or ERROR
@crest.update(state=[off, error], target=lightelement.electricity_in)
def update_light_elec_off(self, dt):
# no electricity
return 0
@crest.update(state=[off, error], target=heatelement.electricity_in)
def update_heat_elec_off(self, dt):
# no electricity
return 0
# LAMP is ON
@crest.update(state=on, target=lightelement.electricity_in)
def update_light_elec_on(self, dt):
# the lightelement gets the first 100Watt
return 100
@crest.update(state=on, target=heatelement.electricity_in)
def update_heat_elec_on(self, dt):
# the heatelement gets the rest
return self.electricity_in.value - 100
@crest.update(state=on, target=on_time)
def update_time(self, dt):
# also update the on_time so we know whether we overheat
return self.on_time.value + dt
""" - - - - - - - ACTIONS - - - - - - - - - - """
# let's add an action that counts the number of times we switch to state "on"
@crest.action(transition=off_to_on, target=on_count)
def count_switching_on(self):
"""
Actions are functions that are executed when the related transition is fired.
Note that actions do not have a dt.
"""
return self.on_count.value + 1
# create an instance and plot it
plot(GrowLamp())
```
# Simulation
Simulation allows us to execute the model and see its evolution.
`crestdsl`'s simulator is located in the `simultion` module.
In order to use it, we have to import it.
```
# import the simulator
from crestdsl.simulation import Simulator
```
After the import, we can use a simulator by initialising it with a system model.
In our case, we will explore the `GrowLamp` system that we defined above.
```
gl = GrowLamp()
sim = Simulator(gl)
```
## Stabilisation
The simulator will execute the system's transitions, updates and influences until reaching a fixpoint.
This process is referred to as *stabilisation*.
Once stable, there are no more transitions can be triggered and all updates/influences/actions have been executed.
After stabilisation, all ports have their correct values, calculted from preceeding ports.
In the GrowLamp, we see that the value's of the `temperature_out` and `light_out` ports are wrong (based on the dummy values we defined as their initial values).
After triggering the stabilisation, these values have been corrected.
The simulator also has a convenience API `plot()` that allows the direct plotting of the entity, without having to import and call the `elk` library.
```
sim.stabilise()
sim.plot()
```
Stabilisaiton also has to be called after the modification of input values, such that the new values are used to update any dependent ports.
Further, all transitions have to be checked on whether they are enabled and executed if they are.
Below, we show the modification of the growlamp and stabilisation.
Compare the plot below to the plot above to see that the information has been updated.
```
# modify the growlamp instance's inputs directly, the simulator points to that object and will use it
gl.electricity_in.value = 500
gl.switch_in.value = "on"
sim.stabilise()
sim.plot()
```
## Time advance
Evidently, we also want to simulate the behaviour over time.
The simulator's `advance(dt)` method does precisely that, by advancing `dt` time units.
Below we advance 500 time steps.
The effect is that the global system time is now `t=500` (see the growing lamp's title bar).
Additionally, the local variable `on_time`, which sums up the total amount of time the automaton has spent in the `on` state, has the value of 500 too - Just as expected!
```
sim.advance(500)
sim.plot()
```
# Where to go from here?
By now, you have seen how CREST and `crestdsl` can be used to define hybrid system models that combine discrete, autommata aspects with continuous time evolution.
`crestdsl` offers more functionality, including the formal verification through *timed CTL* model checking and the generation of system controllers.
To learn more about `crestdsl` go ahead and take a look at the [documentation](https://crestdsl.readthedocs.io) or visit the source [repository](https://github.com/stklik/CREST/).
| github_jupyter |
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
import os
import collections
print(os.listdir("../working/"))
# Any results you write to the current directory are saved as output.
from sklearn.model_selection import train_test_split
import pandas as pd
import tensorflow as tf
import tensorflow_hub as hub
from datetime import datetime
!pip install bert-tensorflow
import bert
from bert import run_classifier
from bert import optimization
from bert import tokenization
from bert import modeling
#import tokenization
#import modeling
BERT_VOCAB= '../input/uncased-l12-h768-a12/vocab.txt'
BERT_INIT_CHKPNT = '../input/uncased-l12-h768-a12/bert_model.ckpt'
BERT_CONFIG = '../input/uncased-l12-h768-a12/bert_config.json'
tokenization.validate_case_matches_checkpoint(True,BERT_INIT_CHKPNT)
tokenizer = tokenization.FullTokenizer(
vocab_file=BERT_VOCAB, do_lower_case=True)
train_data_path='../input/jigsaw-toxic-comment-classification-challenge/train.csv'
train = pd.read_csv(train_data_path)
test = pd.read_csv('../input/jigsaw-toxic-comment-classification-challenge/test.csv')
train.head()
ID = 'id'
DATA_COLUMN = 'comment_text'
LABEL_COLUMNS = ['toxic','severe_toxic','obscene','threat','insult','identity_hate']
class InputExample(object):
"""A single training/test example for simple sequence classification."""
def __init__(self, guid, text_a, text_b=None, labels=None):
"""Constructs a InputExample.
Args:
guid: Unique id for the example.
text_a: string. The untokenized text of the first sequence. For single
sequence tasks, only this sequence must be specified.
text_b: (Optional) string. The untokenized text of the second sequence.
Only must be specified for sequence pair tasks.
labels: (Optional) [string]. The label of the example. This should be
specified for train and dev examples, but not for test examples.
"""
self.guid = guid
self.text_a = text_a
self.text_b = text_b
self.labels = labels
class InputFeatures(object):
"""A single set of features of data."""
def __init__(self, input_ids, input_mask, segment_ids, label_ids, is_real_example=True):
self.input_ids = input_ids
self.input_mask = input_mask
self.segment_ids = segment_ids
self.label_ids = label_ids,
self.is_real_example=is_real_example
def create_examples(df, labels_available=True):
"""Creates examples for the training and dev sets."""
examples = []
for (i, row) in enumerate(df.values):
guid = row[0]
text_a = row[1]
if labels_available:
labels = row[2:]
else:
labels = [0,0,0,0,0,0]
examples.append(
InputExample(guid=guid, text_a=text_a, labels=labels))
return examples
TRAIN_VAL_RATIO = 0.9
LEN = train.shape[0]
SIZE_TRAIN = int(TRAIN_VAL_RATIO*LEN)
x_train = train[:SIZE_TRAIN]
x_val = train[SIZE_TRAIN:]
# Use the InputExample class from BERT's run_classifier code to create examples from the data
train_examples = create_examples(x_train)
train.shape, x_train.shape, x_val.shape
import pandas
def convert_examples_to_features(examples, max_seq_length, tokenizer):
"""Loads a data file into a list of `InputBatch`s."""
features = []
for (ex_index, example) in enumerate(examples):
print(example.text_a)
tokens_a = tokenizer.tokenize(example.text_a)
tokens_b = None
if example.text_b:
tokens_b = tokenizer.tokenize(example.text_b)
# Modifies `tokens_a` and `tokens_b` in place so that the total
# length is less than the specified length.
# Account for [CLS], [SEP], [SEP] with "- 3"
_truncate_seq_pair(tokens_a, tokens_b, max_seq_length - 3)
else:
# Account for [CLS] and [SEP] with "- 2"
if len(tokens_a) > max_seq_length - 2:
tokens_a = tokens_a[:(max_seq_length - 2)]
# The convention in BERT is:
# (a) For sequence pairs:
# tokens: [CLS] is this jack ##son ##ville ? [SEP] no it is not . [SEP]
# type_ids: 0 0 0 0 0 0 0 0 1 1 1 1 1 1
# (b) For single sequences:
# tokens: [CLS] the dog is hairy . [SEP]
# type_ids: 0 0 0 0 0 0 0
#
# Where "type_ids" are used to indicate whether this is the first
# sequence or the second sequence. The embedding vectors for `type=0` and
# `type=1` were learned during pre-training and are added to the wordpiece
# embedding vector (and position vector). This is not *strictly* necessary
# since the [SEP] token unambigiously separates the sequences, but it makes
# it easier for the model to learn the concept of sequences.
#
# For classification tasks, the first vector (corresponding to [CLS]) is
# used as as the "sentence vector". Note that this only makes sense because
# the entire model is fine-tuned.
tokens = ["[CLS]"] + tokens_a + ["[SEP]"]
segment_ids = [0] * len(tokens)
if tokens_b:
tokens += tokens_b + ["[SEP]"]
segment_ids += [1] * (len(tokens_b) + 1)
input_ids = tokenizer.convert_tokens_to_ids(tokens)
# The mask has 1 for real tokens and 0 for padding tokens. Only real
# tokens are attended to.
input_mask = [1] * len(input_ids)
# Zero-pad up to the sequence length.
padding = [0] * (max_seq_length - len(input_ids))
input_ids += padding
input_mask += padding
segment_ids += padding
assert len(input_ids) == max_seq_length
assert len(input_mask) == max_seq_length
assert len(segment_ids) == max_seq_length
labels_ids = []
for label in example.labels:
labels_ids.append(int(label))
if ex_index < 0:
logger.info("*** Example ***")
logger.info("guid: %s" % (example.guid))
logger.info("tokens: %s" % " ".join(
[str(x) for x in tokens]))
logger.info("input_ids: %s" % " ".join([str(x) for x in input_ids]))
logger.info("input_mask: %s" % " ".join([str(x) for x in input_mask]))
logger.info(
"segment_ids: %s" % " ".join([str(x) for x in segment_ids]))
logger.info("label: %s (id = %s)" % (example.labels, labels_ids))
features.append(
InputFeatures(input_ids=input_ids,
input_mask=input_mask,
segment_ids=segment_ids,
label_ids=labels_ids))
return features
# We'll set sequences to be at most 128 tokens long.
MAX_SEQ_LENGTH = 128
def create_model(bert_config, is_training, input_ids, input_mask, segment_ids,
labels, num_labels, use_one_hot_embeddings):
"""Creates a classification model."""
model = modeling.BertModel(
config=bert_config,
is_training=is_training,
input_ids=input_ids,
input_mask=input_mask,
token_type_ids=segment_ids,
use_one_hot_embeddings=use_one_hot_embeddings)
# In the demo, we are doing a simple classification task on the entire
# segment.
#
# If you want to use the token-level output, use model.get_sequence_output()
# instead.
output_layer = model.get_pooled_output()
hidden_size = output_layer.shape[-1].value
output_weights = tf.get_variable(
"output_weights", [num_labels, hidden_size],
initializer=tf.truncated_normal_initializer(stddev=0.02))
output_bias = tf.get_variable(
"output_bias", [num_labels], initializer=tf.zeros_initializer())
with tf.variable_scope("loss"):
if is_training:
# I.e., 0.1 dropout
output_layer = tf.nn.dropout(output_layer, keep_prob=0.9)
logits = tf.matmul(output_layer, output_weights, transpose_b=True)
logits = tf.nn.bias_add(logits, output_bias)
# probabilities = tf.nn.softmax(logits, axis=-1) ### multiclass case
probabilities = tf.nn.sigmoid(logits)#### multi-label case
labels = tf.cast(labels, tf.float32)
tf.logging.info("num_labels:{};logits:{};labels:{}".format(num_labels, logits, labels))
per_example_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=labels, logits=logits)
loss = tf.reduce_mean(per_example_loss)
# probabilities = tf.nn.softmax(logits, axis=-1)
# log_probs = tf.nn.log_softmax(logits, axis=-1)
#
# one_hot_labels = tf.one_hot(labels, depth=num_labels, dtype=tf.float32)
#
# per_example_loss = -tf.reduce_sum(one_hot_labels * log_probs, axis=-1)
# loss = tf.reduce_mean(per_example_loss)
return (loss, per_example_loss, logits, probabilities)
def model_fn_builder(bert_config, num_labels, init_checkpoint, learning_rate,
num_train_steps, num_warmup_steps, use_tpu,
use_one_hot_embeddings):
"""Returns `model_fn` closure for TPUEstimator."""
def model_fn(features, labels, mode, params): # pylint: disable=unused-argument
"""The `model_fn` for TPUEstimator."""
#tf.logging.info("*** Features ***")
#for name in sorted(features.keys()):
# tf.logging.info(" name = %s, shape = %s" % (name, features[name].shape))
input_ids = features["input_ids"]
input_mask = features["input_mask"]
segment_ids = features["segment_ids"]
label_ids = features["label_ids"]
is_real_example = None
if "is_real_example" in features:
is_real_example = tf.cast(features["is_real_example"], dtype=tf.float32)
else:
is_real_example = tf.ones(tf.shape(label_ids), dtype=tf.float32)
is_training = (mode == tf.estimator.ModeKeys.TRAIN)
(total_loss, per_example_loss, logits, probabilities) = create_model(
bert_config, is_training, input_ids, input_mask, segment_ids, label_ids,
num_labels, use_one_hot_embeddings)
tvars = tf.trainable_variables()
initialized_variable_names = {}
scaffold_fn = None
if init_checkpoint:
(assignment_map, initialized_variable_names
) = modeling.get_assignment_map_from_checkpoint(tvars, init_checkpoint)
if use_tpu:
def tpu_scaffold():
tf.train.init_from_checkpoint(init_checkpoint, assignment_map)
return tf.train.Scaffold()
scaffold_fn = tpu_scaffold
else:
tf.train.init_from_checkpoint(init_checkpoint, assignment_map)
tf.logging.info("**** Trainable Variables ****")
for var in tvars:
init_string = ""
if var.name in initialized_variable_names:
init_string = ", *INIT_FROM_CKPT*"
#tf.logging.info(" name = %s, shape = %s%s", var.name, var.shape,init_string)
output_spec = None
if mode == tf.estimator.ModeKeys.TRAIN:
train_op = optimization.create_optimizer(
total_loss, learning_rate, num_train_steps, num_warmup_steps, use_tpu)
output_spec = tf.estimator.EstimatorSpec(
mode=mode,
loss=total_loss,
train_op=train_op,
scaffold=scaffold_fn)
elif mode == tf.estimator.ModeKeys.EVAL:
def metric_fn(per_example_loss, label_ids, probabilities, is_real_example):
logits_split = tf.split(probabilities, num_labels, axis=-1)
label_ids_split = tf.split(label_ids, num_labels, axis=-1)
# metrics change to auc of every class
eval_dict = {}
for j, logits in enumerate(logits_split):
label_id_ = tf.cast(label_ids_split[j], dtype=tf.int32)
current_auc, update_op_auc = tf.metrics.auc(label_id_, logits)
eval_dict[str(j)] = (current_auc, update_op_auc)
eval_dict['eval_loss'] = tf.metrics.mean(values=per_example_loss)
return eval_dict
## original eval metrics
# predictions = tf.argmax(logits, axis=-1, output_type=tf.int32)
# accuracy = tf.metrics.accuracy(
# labels=label_ids, predictions=predictions, weights=is_real_example)
# loss = tf.metrics.mean(values=per_example_loss, weights=is_real_example)
# return {
# "eval_accuracy": accuracy,
# "eval_loss": loss,
# }
eval_metrics = metric_fn(per_example_loss, label_ids, probabilities, is_real_example)
output_spec = tf.estimator.EstimatorSpec(
mode=mode,
loss=total_loss,
eval_metric_ops=eval_metrics,
scaffold=scaffold_fn)
else:
print("mode:", mode,"probabilities:", probabilities)
output_spec = tf.estimator.EstimatorSpec(
mode=mode,
predictions={"probabilities": probabilities},
scaffold=scaffold_fn)
return output_spec
return model_fn
# Compute train and warmup steps from batch size
# These hyperparameters are copied from this colab notebook (https://colab.sandbox.google.com/github/tensorflow/tpu/blob/master/tools/colab/bert_finetuning_with_cloud_tpus.ipynb)
BATCH_SIZE = 32
LEARNING_RATE = 2e-5
NUM_TRAIN_EPOCHS = 2.0
# Warmup is a period of time where hte learning rate
# is small and gradually increases--usually helps training.
WARMUP_PROPORTION = 0.1
# Model configs
SAVE_CHECKPOINTS_STEPS = 1000
SAVE_SUMMARY_STEPS = 500
OUTPUT_DIR = "../working/output"
# Specify outpit directory and number of checkpoint steps to save
run_config = tf.estimator.RunConfig(
model_dir=OUTPUT_DIR,
save_summary_steps=SAVE_SUMMARY_STEPS,
keep_checkpoint_max=1,
save_checkpoints_steps=SAVE_CHECKPOINTS_STEPS)
def input_fn_builder(features, seq_length, is_training, drop_remainder):
"""Creates an `input_fn` closure to be passed to TPUEstimator."""
all_input_ids = []
all_input_mask = []
all_segment_ids = []
all_label_ids = []
for feature in features:
all_input_ids.append(feature.input_ids)
all_input_mask.append(feature.input_mask)
all_segment_ids.append(feature.segment_ids)
all_label_ids.append(feature.label_ids)
def input_fn(params):
"""The actual input function."""
batch_size = params["batch_size"]
num_examples = len(features)
# This is for demo purposes and does NOT scale to large data sets. We do
# not use Dataset.from_generator() because that uses tf.py_func which is
# not TPU compatible. The right way to load data is with TFRecordReader.
d = tf.data.Dataset.from_tensor_slices({
"input_ids":
tf.constant(
all_input_ids, shape=[num_examples, seq_length],
dtype=tf.int32),
"input_mask":
tf.constant(
all_input_mask,
shape=[num_examples, seq_length],
dtype=tf.int32),
"segment_ids":
tf.constant(
all_segment_ids,
shape=[num_examples, seq_length],
dtype=tf.int32),
"label_ids":
tf.constant(all_label_ids, shape=[num_examples, len(LABEL_COLUMNS)], dtype=tf.int32),
})
if is_training:
d = d.repeat()
d = d.shuffle(buffer_size=100)
d = d.batch(batch_size=batch_size, drop_remainder=drop_remainder)
return d
return input_fn
class PaddingInputExample(object):
"""Fake example so the num input examples is a multiple of the batch size.
When running eval/predict on the TPU, we need to pad the number of examples
to be a multiple of the batch size, because the TPU requires a fixed batch
size. The alternative is to drop the last batch, which is bad because it means
the entire output data won't be generated.
We use this class instead of `None` because treating `None` as padding
battches could cause silent errors.
"""
def convert_single_example(ex_index, example, max_seq_length,
tokenizer):
"""Converts a single `InputExample` into a single `InputFeatures`."""
if isinstance(example, PaddingInputExample):
return InputFeatures(
input_ids=[0] * max_seq_length,
input_mask=[0] * max_seq_length,
segment_ids=[0] * max_seq_length,
label_ids=0,
is_real_example=False)
tokens_a = tokenizer.tokenize(example.text_a)
tokens_b = None
if example.text_b:
tokens_b = tokenizer.tokenize(example.text_b)
if tokens_b:
# Modifies `tokens_a` and `tokens_b` in place so that the total
# length is less than the specified length.
# Account for [CLS], [SEP], [SEP] with "- 3"
_truncate_seq_pair(tokens_a, tokens_b, max_seq_length - 3)
else:
# Account for [CLS] and [SEP] with "- 2"
if len(tokens_a) > max_seq_length - 2:
tokens_a = tokens_a[0:(max_seq_length - 2)]
# The convention in BERT is:
# (a) For sequence pairs:
# tokens: [CLS] is this jack ##son ##ville ? [SEP] no it is not . [SEP]
# type_ids: 0 0 0 0 0 0 0 0 1 1 1 1 1 1
# (b) For single sequences:
# tokens: [CLS] the dog is hairy . [SEP]
# type_ids: 0 0 0 0 0 0 0
#
# Where "type_ids" are used to indicate whether this is the first
# sequence or the second sequence. The embedding vectors for `type=0` and
# `type=1` were learned during pre-training and are added to the wordpiece
# embedding vector (and position vector). This is not *strictly* necessary
# since the [SEP] token unambiguously separates the sequences, but it makes
# it easier for the model to learn the concept of sequences.
#
# For classification tasks, the first vector (corresponding to [CLS]) is
# used as the "sentence vector". Note that this only makes sense because
# the entire model is fine-tuned.
tokens = []
segment_ids = []
tokens.append("[CLS]")
segment_ids.append(0)
for token in tokens_a:
tokens.append(token)
segment_ids.append(0)
tokens.append("[SEP]")
segment_ids.append(0)
if tokens_b:
for token in tokens_b:
tokens.append(token)
segment_ids.append(1)
tokens.append("[SEP]")
segment_ids.append(1)
input_ids = tokenizer.convert_tokens_to_ids(tokens)
# The mask has 1 for real tokens and 0 for padding tokens. Only real
# tokens are attended to.
input_mask = [1] * len(input_ids)
# Zero-pad up to the sequence length.
while len(input_ids) < max_seq_length:
input_ids.append(0)
input_mask.append(0)
segment_ids.append(0)
assert len(input_ids) == max_seq_length
assert len(input_mask) == max_seq_length
assert len(segment_ids) == max_seq_length
labels_ids = []
for label in example.labels:
labels_ids.append(int(label))
feature = InputFeatures(
input_ids=input_ids,
input_mask=input_mask,
segment_ids=segment_ids,
label_ids=labels_ids,
is_real_example=True)
return feature
def file_based_convert_examples_to_features(
examples, max_seq_length, tokenizer, output_file):
"""Convert a set of `InputExample`s to a TFRecord file."""
writer = tf.python_io.TFRecordWriter(output_file)
for (ex_index, example) in enumerate(examples):
#if ex_index % 10000 == 0:
#tf.logging.info("Writing example %d of %d" % (ex_index, len(examples)))
feature = convert_single_example(ex_index, example,
max_seq_length, tokenizer)
def create_int_feature(values):
f = tf.train.Feature(int64_list=tf.train.Int64List(value=list(values)))
return f
features = collections.OrderedDict()
features["input_ids"] = create_int_feature(feature.input_ids)
features["input_mask"] = create_int_feature(feature.input_mask)
features["segment_ids"] = create_int_feature(feature.segment_ids)
features["is_real_example"] = create_int_feature(
[int(feature.is_real_example)])
if isinstance(feature.label_ids, list):
label_ids = feature.label_ids
else:
label_ids = feature.label_ids[0]
features["label_ids"] = create_int_feature(label_ids)
tf_example = tf.train.Example(features=tf.train.Features(feature=features))
writer.write(tf_example.SerializeToString())
writer.close()
def file_based_input_fn_builder(input_file, seq_length, is_training,
drop_remainder):
"""Creates an `input_fn` closure to be passed to TPUEstimator."""
name_to_features = {
"input_ids": tf.FixedLenFeature([seq_length], tf.int64),
"input_mask": tf.FixedLenFeature([seq_length], tf.int64),
"segment_ids": tf.FixedLenFeature([seq_length], tf.int64),
"label_ids": tf.FixedLenFeature([6], tf.int64),
"is_real_example": tf.FixedLenFeature([], tf.int64),
}
def _decode_record(record, name_to_features):
"""Decodes a record to a TensorFlow example."""
example = tf.parse_single_example(record, name_to_features)
# tf.Example only supports tf.int64, but the TPU only supports tf.int32.
# So cast all int64 to int32.
for name in list(example.keys()):
t = example[name]
if t.dtype == tf.int64:
t = tf.to_int32(t)
example[name] = t
return example
def input_fn(params):
"""The actual input function."""
batch_size = params["batch_size"]
# For training, we want a lot of parallel reading and shuffling.
# For eval, we want no shuffling and parallel reading doesn't matter.
d = tf.data.TFRecordDataset(input_file)
if is_training:
d = d.repeat()
d = d.shuffle(buffer_size=100)
d = d.apply(
tf.contrib.data.map_and_batch(
lambda record: _decode_record(record, name_to_features),
batch_size=batch_size,
drop_remainder=drop_remainder))
return d
return input_fn
def _truncate_seq_pair(tokens_a, tokens_b, max_length):
"""Truncates a sequence pair in place to the maximum length."""
# This is a simple heuristic which will always truncate the longer sequence
# one token at a time. This makes more sense than truncating an equal percent
# of tokens from each, since if one sequence is very short then each token
# that's truncated likely contains more information than a longer sequence.
while True:
total_length = len(tokens_a) + len(tokens_b)
if total_length <= max_length:
break
if len(tokens_a) > len(tokens_b):
tokens_a.pop()
else:
tokens_b.pop()
#from pathlib import Path
train_file = os.path.join('../working', "train.tf_record")
#filename = Path(train_file)
if not os.path.exists(train_file):
open(train_file, 'w').close()
```
train_features = convert_examples_to_features(
train_examples, MAX_SEQ_LENGTH, tokenizer)
# Create an input function for training. drop_remainder = True for using TPUs.
train_input_fn = input_fn_builder(
features=train_features,
seq_length=MAX_SEQ_LENGTH,
is_training=True,
drop_remainder=False)
```
# Compute # train and warmup steps from batch size
num_train_steps = int(len(train_examples) / BATCH_SIZE * NUM_TRAIN_EPOCHS)
num_warmup_steps = int(num_train_steps * WARMUP_PROPORTION)
file_based_convert_examples_to_features(
train_examples, MAX_SEQ_LENGTH, tokenizer, train_file)
tf.logging.info("***** Running training *****")
tf.logging.info(" Num examples = %d", len(train_examples))
tf.logging.info(" Batch size = %d", BATCH_SIZE)
tf.logging.info(" Num steps = %d", num_train_steps)
train_input_fn = file_based_input_fn_builder(
input_file=train_file,
seq_length=MAX_SEQ_LENGTH,
is_training=True,
drop_remainder=True)
bert_config = modeling.BertConfig.from_json_file(BERT_CONFIG)
model_fn = model_fn_builder(
bert_config=bert_config,
num_labels= len(LABEL_COLUMNS),
init_checkpoint=BERT_INIT_CHKPNT,
learning_rate=LEARNING_RATE,
num_train_steps=num_train_steps,
num_warmup_steps=num_warmup_steps,
use_tpu=False,
use_one_hot_embeddings=False)
estimator = tf.estimator.Estimator(
model_fn=model_fn,
config=run_config,
params={"batch_size": BATCH_SIZE})
print(f'Beginning Training!')
current_time = datetime.now()
estimator.train(input_fn=train_input_fn, max_steps=num_train_steps)
print("Training took time ", datetime.now() - current_time)
eval_file = os.path.join('../working', "eval.tf_record")
#filename = Path(train_file)
if not os.path.exists(eval_file):
open(eval_file, 'w').close()
eval_examples = create_examples(x_val)
file_based_convert_examples_to_features(
eval_examples, MAX_SEQ_LENGTH, tokenizer, eval_file)
# This tells the estimator to run through the entire set.
eval_steps = None
eval_drop_remainder = False
eval_input_fn = file_based_input_fn_builder(
input_file=eval_file,
seq_length=MAX_SEQ_LENGTH,
is_training=False,
drop_remainder=False)
result = estimator.evaluate(input_fn=eval_input_fn, steps=eval_steps)
```
#x_eval = train[100000:]
# Use the InputExample class from BERT's run_classifier code to create examples from the data
eval_examples = create_examples(x_val)
eval_features = convert_examples_to_features(
eval_examples, MAX_SEQ_LENGTH, tokenizer)
# This tells the estimator to run through the entire set.
eval_steps = None
eval_drop_remainder = False
eval_input_fn = input_fn_builder(
features=eval_features,
seq_length=MAX_SEQ_LENGTH,
is_training=False,
drop_remainder=eval_drop_remainder)
result = estimator.evaluate(input_fn=eval_input_fn, steps=eval_steps)
```
output_eval_file = os.path.join("../working", "eval_results.txt")
with tf.gfile.GFile(output_eval_file, "w") as writer:
tf.logging.info("***** Eval results *****")
for key in sorted(result.keys()):
tf.logging.info(" %s = %s", key, str(result[key]))
writer.write("%s = %s\n" % (key, str(result[key])))
x_test = test#[125000:140000]
x_test = x_test.reset_index(drop=True)
test_file = os.path.join('../working', "test.tf_record")
#filename = Path(train_file)
if not os.path.exists(test_file):
open(test_file, 'w').close()
test_examples = create_examples(x_test, False)
file_based_convert_examples_to_features(
test_examples, MAX_SEQ_LENGTH, tokenizer, test_file)
predict_input_fn = file_based_input_fn_builder(
input_file=test_file,
seq_length=MAX_SEQ_LENGTH,
is_training=False,
drop_remainder=False)
print('Begin predictions!')
current_time = datetime.now()
predictions = estimator.predict(predict_input_fn)
print("Predicting took time ", datetime.now() - current_time)
```
x_test = test[125000:140000]
x_test = x_test.reset_index(drop=True)
predict_examples = create_examples(x_test,False)
test_features = convert_examples_to_features(predict_examples, MAX_SEQ_LENGTH, tokenizer)
print(f'Beginning Training!')
current_time = datetime.now()
predict_input_fn = input_fn_builder(features=test_features, seq_length=MAX_SEQ_LENGTH, is_training=False, drop_remainder=False)
predictions = estimator.predict(predict_input_fn)
print("Training took time ", datetime.now() - current_time)
```
def create_output(predictions):
probabilities = []
for (i, prediction) in enumerate(predictions):
preds = prediction["probabilities"]
probabilities.append(preds)
dff = pd.DataFrame(probabilities)
dff.columns = LABEL_COLUMNS
return dff
output_df = create_output(predictions)
merged_df = pd.concat([x_test, output_df], axis=1)
submission = merged_df.drop(['comment_text'], axis=1)
submission.to_csv("sample_submission.csv", index=False)
submission.tail()
```
submission1 = pd.read_csv('sample_submission1.csv')
submission2 = pd.read_csv('sample_submission2.csv')
submission3 = pd.read_csv('sample_submission3.csv')
submission = pd.concat([submission1,submission2,submission3])
submission.to_csv("sample_submission.csv", index=False)
submission1.shape, submission2.shape, submission3.shape, submission.shape,
| github_jupyter |
# Tests on PDA
```
import sys
sys.path[0:0] = ['../..', '../../3rdparty'] # Append to the beginning of the search path
from jove.SystemImports import *
from jove.DotBashers import *
from jove.Def_md2mc import *
from jove.Def_PDA import *
```
__IMPORTANT: Must time-bound explore-pda, run-pda, explore-tm, etc so that loops are caught__
```
repda = md2mc('''PDA
!!R -> R R | R + R | R* | ( R ) | 0 | 1 | e
I : '', # ; R# -> M
M : '', R ; RR -> M
M : '', R ; R+R -> M
M : '', R ; R* -> M
M : '', R ; (R) -> M
M : '', R ; 0 -> M
M : '', R ; 1 -> M
M : '', R ; e -> M
M : 0, 0 ; '' -> M
M : 1, 1 ; '' -> M
M : (, ( ; '' -> M
M : ), ) ; '' -> M
M : +, + ; '' -> M
M : e, e ; '' -> M
M : '', # ; # -> F
'''
)
repda
DO_repda = dotObj_pda(repda, FuseEdges=True)
DO_repda
explore_pda("0", repda, STKMAX=4)
explore_pda("00", repda)
explore_pda("(0)", repda)
explore_pda("(00)", repda)
explore_pda("(0)(0)", repda)
explore_pda("(0)(0)", repda)
explore_pda("0+0", repda, STKMAX=3)
explore_pda("0+0", repda)
explore_pda("(0)(0)", repda)
explore_pda("(0)+(0)", repda)
explore_pda("00+0", repda)
explore_pda("000", repda, STKMAX=3)
explore_pda("00+00", repda, STKMAX=4)
explore_pda("00+00", repda, STKMAX=5)
explore_pda("0000+0", repda, STKMAX=5)
brpda = md2mc('''PDA
I : '', '' ; S -> M
M : '', S ; (S) -> M
M : '', S ; SS -> M
M : '', S ; e -> M
M : (, ( ; '' -> M
M : ), ) ; '' -> M
M : e, e ; '' -> M
M : '', # ; '' -> F''')
dotObj_pda(brpda, FuseEdges=True)
explore_pda("(e)", brpda, STKMAX=3)
brpda1 = md2mc('''PDA
I : '', '' ; S -> M
M : '', S ; (S) -> M
M : '', S ; SS -> M
M : '', S ; '' -> M
M : (, ( ; '' -> M
M : ), ) ; '' -> M
M : '', '' ; '' -> M
M : '', # ; '' -> F''')
dotObj_pda(brpda1, FuseEdges=True)
explore_pda("('')", brpda1, STKMAX=0)
brpda2 = md2mc('''PDA
I : a, #; '' -> I
I : '', '' ; '' -> I''')
dotObj_pda(brpda2, FuseEdges=True)
explore_pda("a", brpda2, STKMAX=1)
explore_pda("a", brpda1, STKMAX=1)
brpda3 = md2mc('''PDA
I : a, #; '' -> I
I : '', '' ; b -> I''')
dotObj_pda(brpda3, FuseEdges=True)
explore_pda("a", brpda3, STKMAX=7)
# Parsing an arithmetic expression
pdaEamb = md2mc('''PDA
!!E -> E * E | E + E | ~E | ( E ) | 2 | 3
I : '', # ; E# -> M
M : '', E ; ~E -> M
M : '', E ; E+E -> M
M : '', E ; E*E -> M
M : '', E ; (E) -> M
M : '', E ; 2 -> M
M : '', E ; 3 -> M
M : ~, ~ ; '' -> M
M : 2, 2 ; '' -> M
M : 3, 3 ; '' -> M
M : (, ( ; '' -> M
M : ), ) ; '' -> M
M : +, + ; '' -> M
M : *, * ; '' -> M
M : '', # ; # -> F
'''
)
DOpdaEamb = dotObj_pda(pdaEamb, FuseEdges=True)
DOpdaEamb
DOpdaEamb.source
explore_pda("3+2*3", pdaEamb, STKMAX=5)
explore_pda("3+2*3+2*3", pdaEamb, STKMAX=7)
# Parsing an arithmetic expression
pdaE = md2mc('''PDA
!!E -> E+T | T
!!T -> T*F | F
!!F -> 2 | 3 | ~F | (E)
I : '', # ; E# -> M
M : '', E ; E+T -> M
M : '', E ; T -> M
M : '', T ; T*F -> M
M : '', T ; F -> M
M : '', F ; 2 -> M
M : '', F ; 3 -> M
M : '', F ; ~F -> M
M : '', F ; (E) -> M
M : ~, ~ ; '' -> M
M : 2, 2 ; '' -> M
M : 3, 3 ; '' -> M
M : (, ( ; '' -> M
M : ), ) ; '' -> M
M : +, + ; '' -> M
M : *, * ; '' -> M
M : '', # ; # -> F
'''
)
DOpdaE = dotObj_pda(pdaE, FuseEdges=True)
DOpdaE
DOpdaE.source
explore_pda("2+2*3", pdaE, STKMAX=7)
explore_pda("3+2*3+2*3", pdaE, STKMAX=7)
explore_pda("3*2*~3+~~3*~3", pdaE, STKMAX=10)
explore_pda("3*2*~3+~~3*~3", pdaEamb, STKMAX=8)
```
| github_jupyter |
# esBERTus: evaluation of the models results
In this notebook, an evaluation of the results obtained by the two models will be performed. The idea here is not as much to measure a benchmarking metric on the models but to understand the qualitative difference of the models.
In order to do so
## Keyword extraction
In order to understand what are the "hot topics" of the corpuses that are being used to train the models, a keyword extraction is performed.
Although the possibility to extract keywords based in a word embeddings approach has been considered, TF-IDF has been chosen over any other approach to model the discussion topic over the different corpuses due to it's interpretability
### Cleaning the texts
For this, a Spacy pipeline is used to speed up the cleaning process
```
from spacy.language import Language
import re
@Language.component("clean_lemmatize")
def clean_lemmatize(doc):
text = doc.text
text = re.sub(r'\w*\d\w*', r'', text) # remove words containing digits
text = re.sub(r'[^a-z\s]', '', text) # remove anything that is not a letter or a space
return nlp.make_doc(text)
print('Done!')
import spacy
# Instantiate the pipeline, disable ner component for perfomance reasons
nlp = spacy.load("en_core_web_sm", disable=['ner'])
# Add custom text cleaning function
nlp.add_pipe('clean_lemmatize', before="tok2vec")
# Apply to EU data
with open('../data/02_preprocessed/full_eu_text.txt') as f:
eu_texts = f.readlines()
nlp.max_length = max([len(text)+1 for text in eu_texts])
eu_texts = [' '.join([token.lemma_ for token in doc]) for doc in nlp.pipe(eu_texts, n_process=10)] # Get lemmas
with open('../data/04_evaluation/full_eu_text_for_tfidf.txt', 'w+') as f:
for text in eu_texts:
f.write(text)
f.write('\n')
print('Done EU!')
# Apply to US data
with open('../data/02_preprocessed/full_us_text.txt') as f:
us_texts = f.readlines()
nlp.max_length = max([len(text)+1 for text in us_texts])
us_texts = [' '.join([token.lemma_ for token in doc]) for doc in nlp.pipe(us_texts, n_process=10)] # Get lemmas
with open('../data/04_evaluation/full_us_text_for_tfidf.txt', 'w+') as f:
for text in us_texts:
f.write(text)
f.write('\n')
print('Done US!')
print('Done!')
```
### Keyword extraction
Due to the differences in legths and number of texts, it's not possible to use a standard approach to keywords extraction. TF-IDF has been considered, but it takes away most of the very interesting keywords such as "pandemic" or "covid". This is the reason why a hybrid approach between both of the European and US corpuses has been chosen.
The approach takes the top n words from one of the corpus that intersects with the top n words from the other corpus. In order to find the most relevant words, a simple count vector is used, that counts the frequency of the words. This takes only the words that are really relevant in both cases, even if you using a relatively naive approach.
```
from sklearn.feature_extraction.text import CountVectorizer
import numpy as np
# Read the processed data
with open('../data/04_evaluation/full_eu_text_for_tfidf.txt') as f:
eu_texts = f.readlines()
with open('../data/04_evaluation/full_us_text_for_tfidf.txt') as f:
us_texts = f.readlines()
# Join the texts together
from nltk.corpus import stopwords
stopwords = set(stopwords.words('english'))
max_df = 0.9
max_features = 1000
cv_eu=CountVectorizer(max_df=max_df, stop_words=stopwords , max_features=max_features)
word_count_vector=cv_eu.fit_transform(eu_texts)
cv_us=CountVectorizer(max_df=max_df, stop_words=stopwords , max_features=max_features)
word_count_vector=cv_us.fit_transform(us_texts)
n_words = 200
keywords = [word for word in list(cv_eu.vocabulary_.keys())[:n_words] if word in list(cv_us.vocabulary_.keys())[:n_words]]
keywords
```
## Measure the models performance on masked tokens
### Extract sentences where the keywords appear
```
keywords = ['coronavirus', 'covid', 'covid-19', 'virus', 'influenza', 'flu',
'pandemic', 'epidemic', 'outbreak', 'crisis', 'emergency',
'vaccine', 'vaccinated', 'mask',
'quarantine', 'symptoms', 'antibody', 'inmunity', 'distance', 'isolation',
'test', 'positive', 'negative',
'nurse', 'doctor', 'health', 'healthcare',]
import spacy
from spacy.matcher import PhraseMatcher
with open('../data/02_preprocessed/full_eu_text.txt') as f:
eu_texts = f.readlines()
with open('../data/02_preprocessed/full_us_text.txt') as f:
us_texts = f.readlines()
nlp = spacy.load("en_core_web_sm", disable=['ner'])
texts = [item for sublist in [eu_texts, us_texts] for item in sublist]
nlp.max_length = max([len(text) for text in texts])
phrase_matcher = PhraseMatcher(nlp.vocab)
patterns = [nlp(text) for text in keywords]
phrase_matcher.add('KEYWORDS', None, *patterns)
docs = nlp.pipe(texts, n_process=12)
sentences = []
block_size = 350
# Parse the docs for sentences
open('../data/04_evaluation/sentences.txt', 'wb').close()
print('Starting keyword extraction')
for doc in docs:
for sent in doc.sents:
# Check if the token is in the big sentence
for match_id, start, end in phrase_matcher(nlp(sent.text)):
if nlp.vocab.strings[match_id] in ["KEYWORDS"]:
# Create sentences of length of no more than block size
tokens = sent.text.split(' ')
if len(tokens) <= block_size:
sentence = sent.text
else:
sentence = " ".join(tokens[:block_size])
with open('../data/04_evaluation/sentences.txt', 'ab') as f:
f.write(f'{sentence}\n'.encode('UTF-8'))
print(f"There are {len(open('../data/04_evaluation/sentences.txt', 'rb').readlines())} sentences containing keywords")
```
### Measure the probability of outputing the real token in the sentence
```
# Define a custom function that feeds the three models an example and returns the perplexity
def get_masked_token_probaility(sentence:str, keywords:list, models_pipelines:list):
# Find the word in the sentence to mask
sentence = sentence.lower()
keywords = [keyword.lower() for keyword in keywords]
target = None
for keyword in keywords:
# Substitute only the first matched keyword
if keyword in sentence:
target = keyword
masked_sentence = sentence.replace(keyword, '{}', 1)
break
if target:
model_pipeline_results = []
for model_pipeline in models_pipelines:
masked_sentence = masked_sentence.format(model_pipeline.tokenizer.mask_token)
try:
result = model_pipeline(masked_sentence, targets=target)
model_pipeline_results.append(result[0]['score'])
except Exception as e:
model_pipeline_results.append(0)
return keyword, model_pipeline_results
from transformers import pipeline, AutoModelForMaskedLM, DistilBertTokenizer
tokenizer = DistilBertTokenizer.from_pretrained('../data/03_models/tokenizer/')
# The best found European model
model=AutoModelForMaskedLM.from_pretrained("../data/03_models/eu_bert_model")
eu_model_pipeline = pipeline(
"fill-mask",
model=model,
tokenizer=tokenizer
)
# The best found US model
model=AutoModelForMaskedLM.from_pretrained("../data/03_models/us_bert_model")
us_model_pipeline = pipeline(
"fill-mask",
model=model,
tokenizer=tokenizer
)
model_checkpoint = 'distilbert-base-uncased'
# The baseline model from which the trainin
model = AutoModelForMaskedLM.from_pretrained(model_checkpoint)
base_model_pipeline = pipeline(
"fill-mask",
model=model,
tokenizer=model_checkpoint
)
results = []
print(f"There are {len(open('../data/04_evaluation/sentences.txt').readlines())} sentences to be evaluated")
for sequence in open('../data/04_evaluation/sentences.txt').readlines():
results.append(get_masked_token_probaility(sequence, keywords, [eu_model_pipeline, us_model_pipeline, base_model_pipeline]))
import pickle
pickle.dump(results, open('../data/04_evaluation/sentence_token_prediction.pickle', 'wb'))
```
#### Evaluate the results
```
import pickle
results = pickle.load(open('../data/04_evaluation/sentence_token_prediction.pickle', 'rb'))
results[0:5]
```
##### Frequences of masked words in the pipeline
```
from collections import Counter
import numpy as np
import matplotlib.pyplot as plt
words = Counter([result[0] for result in results if result!=None]).most_common(len(keywords)) # most_common also sorts them
labels = [word[0] for word in words]
values = [word[1] for word in words]
indexes = np.arange(len(labels))
fix, ax = plt.subplots(figsize=(10,5))
ax.set_xticks(range(len(words)))
plt.bar(indexes, values, width=.8, align="center",alpha=.8)
plt.xticks(indexes, labels, rotation=45)
plt.title('Frequences of masked words in the pipeline')
plt.show()
```
##### Average probability of all the masked keywords by model
```
n_results = len([result for result in results if result!=None])
eu_results = sum([(result[1][0]) for result in results if result!=None]) / n_results
us_results = sum([(result[1][1]) for result in results if result!=None]) / n_results
base_results = sum([(result[1][2]) for result in results if result!=None]) / n_results
labels = ['EU model', 'US model', 'Base model']
values = [eu_results, us_results, base_results]
indexes = np.arange(len(labels))
fix, ax = plt.subplots(figsize=(10,5))
ax.set_xticks(range(len(words)))
plt.bar(indexes, values, width=.6, align="center",alpha=.8)
plt.xticks(indexes, labels, rotation=45)
plt.title('Average probability of all the masked keywords by model')
plt.show()
```
### Get the first predicted token in each sentence, masking
```
def get_first_predicted_masked_token(sentence:str, eu_pipeline, us_pipeline, base_pipeline):
sentence = sentence.lower()
model_pipeline_results = []
eu_model_pipeline_results = eu_pipeline(sentence.format(eu_pipeline.tokenizer.mask_token), top_k=1)
us_model_pipeline_results = us_pipeline(sentence.format(us_pipeline.tokenizer.mask_token), top_k=1)
base_model_pipeline_results = base_pipeline(sentence.format(base_pipeline.tokenizer.mask_token), top_k=1)
return (eu_model_pipeline_results[0]['token_str'].replace(' ', ''),
us_model_pipeline_results[0]['token_str'].replace(' ', ''),
base_model_pipeline_results[0]['token_str'].replace(' ', '')
)
# Create a function that identifies the first keyword in the sentences, masks it and feeds the it to the prediction function
results = []
for sequence in open('../data/04_evaluation/sentences.txt').readlines():
target = None
for keyword in keywords:
if keyword in sequence:
target = keyword
break
if target:
masked_sentence = sequence.replace(target, '{}', 1)
try:
predictions = get_first_predicted_masked_token(masked_sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
results.append({'masked_token': target,
'eu_prediction': predictions[0],
'us_prediction': predictions[1],
'base_prediction': predictions[2]})
except:
pass
import pickle
pickle.dump(results, open('../data/04_evaluation/sentence_first_predicted_tokens.pickle', 'wb'))
```
#### Evaluate the results
```
import pickle
results = pickle.load(open('../data/04_evaluation/sentence_first_predicted_tokens.pickle', 'rb'))
print(len(results))
# Group the results by masked token
from itertools import groupby
from operator import itemgetter
from collections import Counter
import numpy as np
import matplotlib.pyplot as plt
n_words = 10
results = sorted(results, key=itemgetter('masked_token'))
for keyword, v in groupby(results, key=lambda x: x['masked_token']):
token_results = list(v)
fig, ax = plt.subplots(1,3, figsize=(25,5))
for idx, (key, name) in enumerate(zip(['eu_prediction', 'us_prediction', 'base_prediction'], ['EU', 'US', 'Base'])):
words = Counter([item[key] for item in token_results]).most_common(n_words)
labels, values = zip(*words)
ax[idx].barh(labels, values, align="center",alpha=.8)
ax[idx].set_title(f'Predicted tokens by {name} model for {keyword}')
plt.show()
```
## Qualitative evaluation of masked token prediction
The objective of this section is not to compare the score obtained by all the models that are being used, but to compare what are the qualitative outputs of these models. This means that the comparison is going to be done manually, by inputing phrases that contain words related to the COVID-19 pandemic, and comparing the outputs of the models among them, enabling the possibility of discussion of these results.
### Feeding selected phrases belonging to the European and United States institutions websites
```
def get_masked_token(sentence:str, eu_pipeline, us_pipeline, base_pipeline, n_results=1):
sentence = sentence.lower()
model_pipeline_results = []
eu_prediction = eu_pipeline(sentence.format(eu_pipeline.tokenizer.mask_token), top_k =n_results)[0]
us_prediction = us_pipeline(sentence.format(us_pipeline.tokenizer.mask_token), top_k =n_results)[0]
base_prediction = base_pipeline(sentence.format(base_pipeline.tokenizer.mask_token), top_k =n_results)[0]
token = eu_prediction['token_str'].replace(' ', '')
print(f"EUROPEAN MODEL -------> {token}\n\t{eu_prediction['sequence'].replace(token, token.upper())}")
token = us_prediction['token_str'].replace(' ', '')
print(f"UNITED STATES MODEL -------> {token}\n\t{us_prediction['sequence'].replace(token, token.upper())}")
token = base_prediction['token_str'].replace(' ', '')
print(f"BASE MODEL -------> {token}\n\t{base_prediction['sequence'].replace(token, token.upper())}")
from transformers import pipeline, AutoModelForMaskedLM, DistilBertTokenizer
tokenizer = DistilBertTokenizer.from_pretrained('../data/03_models/tokenizer/')
# The best found European model
model=AutoModelForMaskedLM.from_pretrained("../data/03_models/eu_bert_model")
eu_model_pipeline = pipeline(
"fill-mask",
model=model,
tokenizer=tokenizer
)
# The best found US model
model=AutoModelForMaskedLM.from_pretrained("../data/03_models/us_bert_model")
us_model_pipeline = pipeline(
"fill-mask",
model=model,
tokenizer=tokenizer
)
model_checkpoint = 'distilbert-base-uncased'
# The baseline model from which the trainin
model = AutoModelForMaskedLM.from_pretrained(model_checkpoint)
base_model_pipeline = pipeline(
"fill-mask",
model=model,
tokenizer=model_checkpoint
)
```
#### European institutions sentences
```
# Source https://ec.europa.eu/info/live-work-travel-eu/coronavirus-response_en
# Masked token: coronavirus
sentence = """The European Commission is coordinating a common European response to the {} outbreak. We are taking resolute action to reinforce our public health sectors and mitigate the socio-economic impact in the European Union. We are mobilising all means at our disposal to help our Member States coordinate their national responses and are providing objective information about the spread of the virus and effective efforts to contain it."""
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
# Source https://ec.europa.eu/info/live-work-travel-eu/coronavirus-response_en
# Masked token: vaccine
sentence = """A safe and effective {} is our best chance to beat coronavirus and return to our normal lives"""
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
# Source https://ec.europa.eu/info/live-work-travel-eu/coronavirus-response_en
# Masked token: medicines
sentence = """The European Commission is complementing the EU Vaccines Strategy with a strategy on COVID-19 therapeutics to support the development and availability of {}"""
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
# Source https://ec.europa.eu/info/strategy/recovery-plan-europe_en
# Masked token: recovery
sentence = """The EU’s long-term budget, coupled with NextGenerationEU, the temporary instrument designed to boost the {}, will be the largest stimulus package ever financed in Europe. A total of €1.8 trillion will help rebuild a post-COVID-19 Europe. It will be a greener, more digital and more resilient Europe."""
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
```
#### US Government sentences
```
# Source https://www.usa.gov/covid-unemployment-benefits
# Masked token: provide
sentence = 'The federal government has allowed states to change their laws to {} COVID-19 unemployment benefits for people whose jobs have been affected by the coronavirus pandemic.'
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
# Source https://www.usa.gov/covid-passports-and-travel
# Masked token: mask-wearing
sentence = """Many museums, aquariums, and zoos have restricted access or are closed during the pandemic. And many recreational areas including National Parks have COVID-19 restrictions and {} rules. Check with your destination for the latest information."""
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
# Source https://www.usa.gov/covid-stimulus-checks
# Masked token: people
sentence = """The American Rescue Plan Act of 2021 provides $1,400 Economic Impact Payments for {} who are eligible. You do not need to do anything to receive your payment. It will arrive by direct deposit to your bank account, or by mail in the form of a paper check or debit card."""
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
# Source https://www.usa.gov/covid-scams
# Masked token: scammers
sentence = """During the COVID-19 pandemic, {} may try to take advantage of you. They might get in touch by phone, email, postal mail, text, or social media. Protect your money and your identity. Don't share personal information like your bank account number, Social Security number, or date of birth. Learn how to recognize and report a COVID vaccine scam and other types of coronavirus scams. """
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
# Source https://www.acf.hhs.gov/coronavirus
# Masked token: situation
sentence = """With the COVID-19 {} continuing to evolve, we continue to provide relevant resources to help our grantees, partners, and stakeholders support children, families, and communities in need during this challenging time."""
get_masked_token(sentence, eu_model_pipeline, us_model_pipeline, base_model_pipeline)
```
| github_jupyter |
# 对象和类
- 一个学生,一张桌子,一个圆都是对象
- 对象是类的一个实例,你可以创建多个对象,创建类的一个实例过程被称为实例化,
- 在Python中对象就是实例,而实例就是对象
## 定义类
class ClassName:
do something
- class 类的表示与def 一样
- 类名最好使用驼峰式
- 在Python2中类是需要继承基类object的,在Python中默认继承,可写可不写
- 可以将普通代码理解为皮肤,而函数可以理解为内衣,那么类可以理解为外套
```
# 类必须初始化,是用self,初始化自身.
# 类里面所有的函数中的第一个变量不再是参数,而是一个印记.
# 在类中,如果有参数需要多次使用,那么就可以将其设置为共享参数
class Joker:
def __init__(self,num1,num2):
print('我初始化了')
# 参数共享
self.num1 = num1
self.num2 = num2
print(self.num1,self.num2)
def SUM(self,name):
print(name)
return self.num1 + self.num2
def cheng(self):
return self.num1 * self.num2
huwang = Joker(num1=1,num2=2) # () 代表直接走初始化函数
huwang.SUM(name='JJJ')
huwang.cheng()
```
## 定义一个不含初始化__init__的简单类
class ClassName:
joker = “Home”
def func():
print('Worker')
- 尽量少使用
## 定义一个标准类
- __init__ 代表初始化,可以初始化任何动作
- 此时类调用要使用(),其中()可以理解为开始初始化
- 初始化内的元素,类中其他的函数可以共享

- Circle 和 className_ 的第一个区别有 __init__ 这个函数
- 。。。。 第二个区别,类中的每一个函数都有self的这个“参数”
## 何为self?
- self 是指向对象本身的参数
- self 只是一个命名规则,其实可以改变的,但是我们约定俗成的是self,也便于理解
- 使用了self就可以访问类中定义的成员
<img src="../Photo/86.png"></img>
## 使用类 Cirlcle
## 类的传参
- class ClassName:
def __init__(self, para1,para2...):
self.para1 = para1
self.para2 = para2
## EP:
- A:定义一个类,类中含有两个功能:
- 1、产生3个随机数,获取最大值
- 2、产生3个随机数,获取最小值
- B:定义一个类,(类中函数的嵌套使用)
- 1、第一个函数的功能为:输入一个数字
- 2、第二个函数的功能为:使用第一个函数中得到的数字进行平方处理
- 3、第三个函数的功能为:得到平方处理后的数字 - 原来输入的数字,并打印结果
```
class Joker2:
"""
Implement Login Class.
"""
def __init__(self):
"""
Initialization class
Arguments:
---------
name: xxx
None.
Returns:
--------
None.
"""
self.account = '123'
self.password = '123'
def Account(self):
"""
Input Account value
Arguments:
---------
None.
Returns:
--------
None.
"""
self.acc = input('请输入账号:>>')
def Password(self):
"""
Input Password value
Arguments:
---------
None.
Returns:
--------
None.
"""
self.passwor = input('请输入密码:>>')
def Check(self):
"""
Check account and password
Note:
----
we need "and" connect.
if account and password is right, then login OK.
else: running Veriy func.
"""
if self.acc == self.account and self.passwor == self.password:
print('Success')
else:
# running Verify !
self.Verify()
def Verify(self):
"""
Verify ....
"""
Verify_Var = 123
print('验证码是:',Verify_Var)
while 1:
User_Verify = eval(input('请输入验证码:>>'))
if User_Verify == Verify_Var:
print('Failed')
break
def Start(self):
"""
Start definelogistics.
"""
self.Account()
self.Password()
self.Check()
# 创建类的一个实例
a = Joker2()
a.Start()
```
## 类的继承
- 类的单继承
- 类的多继承
- 继承标识
> class SonClass(FatherClass):
def __init__(self):
FatherClass.__init__(self)
```
a = 100
a = 1000
a
```
私有变量,不可继承,不可在外部调用,但是可以在内部使用.
```
class A:
def __init__(self):
self.__a = 'a'
def a_(self):
print('aa')
print(self.__a)
def b():
a()
def a():
print('hahah')
b()
```
# _ _ -- + = / \ { } [] ! ~ !@ # $ % ^ & * ( ) < > ……
## 私有数据域(私有变量,或者私有函数)
- 在Python中 变量名或者函数名使用双下划线代表私有 \__Joker, def \__Joker():
- 私有数据域不可继承
- 私有数据域强制继承 \__dir__()

## EP:



## 类的其他
- 类的封装
- 实际上就是将一类功能放在一起,方便未来进行管理
- 类的继承(上面已经讲过)
- 类的多态
- 包括装饰器:将放在以后处理高级类中教
- 装饰器的好处:当许多类中的函数需要使用同一个功能的时候,那么使用装饰器就会方便许多
- 装饰器是有固定的写法
- 其包括普通装饰器与带参装饰器
# Homewor
## UML类图可以不用画
## UML 实际上就是一个思维图
- 1

```
class Rectangle():
def __init__(self,width,height):
self.width=4
self.height=40
def getArea(self,width,height):
self.area=width*height
print(self.area)
def getPerimeter(self,width,height):
self.perimeter=(width+height)*2
print(self.perimeter)
if __name__=='__main__':m
r=Rectangle(4,40)
r.getArea(4,40)
r=Rectangle(4,40)
r.getPerimeter(4,40)
r=Rectangle(3.5,35.7)
r.getArea(3.5,35.7)
r=Rectangle(3.5,35.7)
r.getPerimeter(3.5,35.7)
```
- 2

```
class Account():
def __init__(self):
self.id = 0
self.__balance = 100
self.__annuallnterestRate=0
def set_(self,id,balance,annuallnterestRate):
self.id = id
self.__balance = balance
self.__annuallnterestRate=annuallnterestRate
def getid(self):
return self.id
def getbalance(self):
return self.__balance
def get__annuallnterestRate(self):
return self.__annuallnterestRate
def getMonthlyInterestRate(self):
return self.__annuallnterestRate/12
def getMonthlyInterest(self):
return self.__balance*(self.__annuallnterestRate/12)
def withdraw(self,number):
self.__balance=self.__balance-number
def deposit(self,number):
self.__balance=self.__balance+number
if __name__ == '__main__':
acc=Account()
id=int(input('请输入账户ID:'))
balance=float(input('请输入账户金额:'))
ann=float(input('年利率为:'))
acc.set_(id,balance,ann/100)
qu=float(input('取钱金额为:'))
acc.withdraw(qu)
cun=float(input('存钱金额为:'))
acc.deposit(cun)
print('账户ID:%d 剩余金额:%.2f 月利率:%.3f 月利息:%.2f '%(acc.getid(),acc.getbalance(),acc.getMonthlyInterestRate()*100,acc.getMonthlyInterest()))
```
- 3

```
class Fan():
def __init__(self):
self.slow=1
self.medium=2
self.fast=3
self.__speed=1
self.__on=False
self.__radius=5
self.__color='blue'
def set_(self,speed,on,radius,color):
self.__speed=speed
self.__on=on
self.__radius=radius
self.__color=color
def getspeed(self):
return self.__speed
def geton(self):
return self.__on
def getradius(self):
return self.__radius
def getcolor(self):
return self.__color
if __name__ == '__main__':
fan=Fan()
speed=int(input('风扇的速度为(1:slow,2:medium,3:fast):'))
radius=float(input('风扇的半径为:'))
color=input('风扇的颜色是:')
on=input('风扇是否打开(True or False):')
fan.set_(speed,on,radius,color)
fan2=Fan()
speed=int(input('风扇的速度为(1:slow,2:medium,3:fast):'))
radius=float(input('风扇的半径为:'))
color=input('风扇的颜色是:')
on=input('风扇是否打开(True or False):')
fan2.set_(speed,on,radius,color)
print('1号风扇的速度(speed)为:',fan.getspeed(),'颜色是(color):',fan.getcolor(),'风扇的半径为(radius):',fan.getradius(),'风扇是:',fan.geton())
print('2号风扇的速度(speed)为:',fan2.getspeed(),'颜色是(color):',fan2.getcolor(),'风扇的半径为(radius):',fan2.getradius(),'风扇是:',fan2.geton())
```
- 4


```
import math
class RegularPolygon:
def __init__(self,n,side,x,y):
self.n=n
self.side=side
self.x=x
self.y=y
def getArea(self):
return (self.n*self.side**2)/4*math.tan(3.14/self.n)
def getPerimeter(self):
return self.n*self.side
if __name__ == "__main__":
n,side,x,y=map(float,input('n,side,x,y:>>').split(','))
re=RegularPolygon(n,side,x,y)
print(n,side,x,y,re.getArea(),re.getPerimeter())
```
- 5

```
class LinearEquation(object):
a = 0
b = 0
c = 0
d = 0
e = 0
f = 0
def __init__(self,a,b,c,d,e,f):
self.a = a
self.b = b
self.c = c
self.d = d
self.e = e
self.f = f
def getA(self):
return self.a
def getB(self):
return self.b
def getC(self):
return self.c
def getD(self):
return self.d
def getE(self):
return self.e
def getF(self):
return self.f
def isSolvable(self):
if a*d-b*c !=0:
return True
else:
return False
def getX(self):
return (self.e*self.d-self.b*self.f)/(self.a*self.d-self.b*self.c)
def getY(self):
return (self.a*self.f-self.e*self.c)/(self.a*self.d-self.b*self.c)
a,b,c,d,e,f = map(int,input('请输入abcdef的值').split(','))
linearEquation=LinearEquation(a,b,c,d,e,f)
if linearEquation.isSolvable() == True:
print(linearEquation.getX())
print(linearEquation.getY())
else:
print('这个方程式无解')
```
- 6

```
class LinearEquation:
def zuobiao(self):
import math
x1,y1,x2,y2=map(float,input().split(','))
x3,y3,x4,y4=map(float,input().split(','))
u1=(x4-x3)*(y1-y3)-(x1-x3)*(y4-y3)
v1=(x4-x3)*(y2-y3)-(x2-x3)*(y4-y3)
u=math.fabs(u1)
v=math.fabs(v1)
x5=(x1*v+x2*u)/(u+v)
y5=(y1*v+y2*u)/(u+v)
print(x5,y5)
re=LinearEquation()
re.zuobiao()
```
- 7

```
class LinearEquation(object):
a = 0
b = 0
c = 0
d = 0
e = 0
f = 0
def __init__(self,a,b,c,d,e,f):
self.a = a
self.b = b
self.c = c
self.d = d
self.e = e
self.f = f
def getA(self):
return self.a
def getB(self):
return self.b
def getC(self):
return self.c
def getD(self):
return self.d
def getE(self):
return self.e
def getF(self):
return self.f
def isSolvable(self):
if a*d-b*c !=0:
return True
else:
return False
def getX(self):
return (self.e*self.d-self.b*self.f)/(self.a*self.d-self.b*self.c)
def getY(self):
return (self.a*self.f-self.e*self.c)/(self.a*self.d-self.b*self.c)
a,b,c,d,e,f = map(int,input('请输入abcdef的值').split(','))
linearEquation=LinearEquation(a,b,c,d,e,f)
if linearEquation.isSolvable() == True:
print(linearEquation.getX())
print(linearEquation.getY())
else:
print('这个方程式无解')
```
| github_jupyter |
# Transfer Learning Template
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import os, json, sys, time, random
import numpy as np
import torch
from torch.optim import Adam
from easydict import EasyDict
import matplotlib.pyplot as plt
from steves_models.steves_ptn import Steves_Prototypical_Network
from steves_utils.lazy_iterable_wrapper import Lazy_Iterable_Wrapper
from steves_utils.iterable_aggregator import Iterable_Aggregator
from steves_utils.ptn_train_eval_test_jig import PTN_Train_Eval_Test_Jig
from steves_utils.torch_sequential_builder import build_sequential
from steves_utils.torch_utils import get_dataset_metrics, ptn_confusion_by_domain_over_dataloader
from steves_utils.utils_v2 import (per_domain_accuracy_from_confusion, get_datasets_base_path)
from steves_utils.PTN.utils import independent_accuracy_assesment
from torch.utils.data import DataLoader
from steves_utils.stratified_dataset.episodic_accessor import Episodic_Accessor_Factory
from steves_utils.ptn_do_report import (
get_loss_curve,
get_results_table,
get_parameters_table,
get_domain_accuracies,
)
from steves_utils.transforms import get_chained_transform
```
# Allowed Parameters
These are allowed parameters, not defaults
Each of these values need to be present in the injected parameters (the notebook will raise an exception if they are not present)
Papermill uses the cell tag "parameters" to inject the real parameters below this cell.
Enable tags to see what I mean
```
required_parameters = {
"experiment_name",
"lr",
"device",
"seed",
"dataset_seed",
"n_shot",
"n_query",
"n_way",
"train_k_factor",
"val_k_factor",
"test_k_factor",
"n_epoch",
"patience",
"criteria_for_best",
"x_net",
"datasets",
"torch_default_dtype",
"NUM_LOGS_PER_EPOCH",
"BEST_MODEL_PATH",
"x_shape",
}
from steves_utils.CORES.utils import (
ALL_NODES,
ALL_NODES_MINIMUM_1000_EXAMPLES,
ALL_DAYS
)
from steves_utils.ORACLE.utils_v2 import (
ALL_DISTANCES_FEET_NARROWED,
ALL_RUNS,
ALL_SERIAL_NUMBERS,
)
standalone_parameters = {}
standalone_parameters["experiment_name"] = "STANDALONE PTN"
standalone_parameters["lr"] = 0.001
standalone_parameters["device"] = "cuda"
standalone_parameters["seed"] = 1337
standalone_parameters["dataset_seed"] = 1337
standalone_parameters["n_way"] = 8
standalone_parameters["n_shot"] = 3
standalone_parameters["n_query"] = 2
standalone_parameters["train_k_factor"] = 1
standalone_parameters["val_k_factor"] = 2
standalone_parameters["test_k_factor"] = 2
standalone_parameters["n_epoch"] = 50
standalone_parameters["patience"] = 10
standalone_parameters["criteria_for_best"] = "source_loss"
standalone_parameters["datasets"] = [
{
"labels": ALL_SERIAL_NUMBERS,
"domains": ALL_DISTANCES_FEET_NARROWED,
"num_examples_per_domain_per_label": 100,
"pickle_path": os.path.join(get_datasets_base_path(), "oracle.Run1_framed_2000Examples_stratified_ds.2022A.pkl"),
"source_or_target_dataset": "source",
"x_transforms": ["unit_mag", "minus_two"],
"episode_transforms": [],
"domain_prefix": "ORACLE_"
},
{
"labels": ALL_NODES,
"domains": ALL_DAYS,
"num_examples_per_domain_per_label": 100,
"pickle_path": os.path.join(get_datasets_base_path(), "cores.stratified_ds.2022A.pkl"),
"source_or_target_dataset": "target",
"x_transforms": ["unit_power", "times_zero"],
"episode_transforms": [],
"domain_prefix": "CORES_"
}
]
standalone_parameters["torch_default_dtype"] = "torch.float32"
standalone_parameters["x_net"] = [
{"class": "nnReshape", "kargs": {"shape":[-1, 1, 2, 256]}},
{"class": "Conv2d", "kargs": { "in_channels":1, "out_channels":256, "kernel_size":(1,7), "bias":False, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":256}},
{"class": "Conv2d", "kargs": { "in_channels":256, "out_channels":80, "kernel_size":(2,7), "bias":True, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 80*256, "out_features": 256}}, # 80 units per IQ pair
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features":256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
]
# Parameters relevant to results
# These parameters will basically never need to change
standalone_parameters["NUM_LOGS_PER_EPOCH"] = 10
standalone_parameters["BEST_MODEL_PATH"] = "./best_model.pth"
# Parameters
parameters = {
"experiment_name": "tl_1v2:wisig-oracle.run1.framed",
"device": "cuda",
"lr": 0.0001,
"n_shot": 3,
"n_query": 2,
"train_k_factor": 3,
"val_k_factor": 2,
"test_k_factor": 2,
"torch_default_dtype": "torch.float32",
"n_epoch": 50,
"patience": 3,
"criteria_for_best": "target_accuracy",
"x_net": [
{"class": "nnReshape", "kargs": {"shape": [-1, 1, 2, 256]}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 1,
"out_channels": 256,
"kernel_size": [1, 7],
"bias": False,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 256}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 256,
"out_channels": 80,
"kernel_size": [2, 7],
"bias": True,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 20480, "out_features": 256}},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features": 256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
],
"NUM_LOGS_PER_EPOCH": 10,
"BEST_MODEL_PATH": "./best_model.pth",
"n_way": 16,
"datasets": [
{
"labels": [
"1-10",
"1-12",
"1-14",
"1-16",
"1-18",
"1-19",
"1-8",
"10-11",
"10-17",
"10-4",
"10-7",
"11-1",
"11-10",
"11-19",
"11-20",
"11-4",
"11-7",
"12-19",
"12-20",
"12-7",
"13-14",
"13-18",
"13-19",
"13-20",
"13-3",
"13-7",
"14-10",
"14-11",
"14-12",
"14-13",
"14-14",
"14-19",
"14-20",
"14-7",
"14-8",
"14-9",
"15-1",
"15-19",
"15-6",
"16-1",
"16-16",
"16-19",
"16-20",
"17-10",
"17-11",
"18-1",
"18-10",
"18-11",
"18-12",
"18-13",
"18-14",
"18-15",
"18-16",
"18-17",
"18-19",
"18-2",
"18-20",
"18-4",
"18-5",
"18-7",
"18-8",
"18-9",
"19-1",
"19-10",
"19-11",
"19-12",
"19-13",
"19-14",
"19-15",
"19-19",
"19-2",
"19-20",
"19-3",
"19-4",
"19-6",
"19-7",
"19-8",
"19-9",
"2-1",
"2-13",
"2-15",
"2-3",
"2-4",
"2-5",
"2-6",
"2-7",
"2-8",
"20-1",
"20-12",
"20-14",
"20-15",
"20-16",
"20-18",
"20-19",
"20-20",
"20-3",
"20-4",
"20-5",
"20-7",
"20-8",
"3-1",
"3-13",
"3-18",
"3-2",
"3-8",
"4-1",
"4-10",
"4-11",
"5-1",
"5-5",
"6-1",
"6-15",
"6-6",
"7-10",
"7-11",
"7-12",
"7-13",
"7-14",
"7-7",
"7-8",
"7-9",
"8-1",
"8-13",
"8-14",
"8-18",
"8-20",
"8-3",
"8-8",
"9-1",
"9-7",
],
"domains": [1, 2, 3, 4],
"num_examples_per_domain_per_label": -1,
"pickle_path": "/root/csc500-main/datasets/wisig.node3-19.stratified_ds.2022A.pkl",
"source_or_target_dataset": "target",
"x_transforms": ["unit_mag"],
"episode_transforms": [],
"domain_prefix": "Wisig_",
},
{
"labels": [
"3123D52",
"3123D65",
"3123D79",
"3123D80",
"3123D54",
"3123D70",
"3123D7B",
"3123D89",
"3123D58",
"3123D76",
"3123D7D",
"3123EFE",
"3123D64",
"3123D78",
"3123D7E",
"3124E4A",
],
"domains": [32, 38, 8, 44, 14, 50, 20, 26],
"num_examples_per_domain_per_label": 2000,
"pickle_path": "/root/csc500-main/datasets/oracle.Run1_framed_2000Examples_stratified_ds.2022A.pkl",
"source_or_target_dataset": "source",
"x_transforms": ["unit_mag"],
"episode_transforms": [],
"domain_prefix": "ORACLE.run1",
},
],
"dataset_seed": 500,
"seed": 500,
}
# Set this to True if you want to run this template directly
STANDALONE = False
if STANDALONE:
print("parameters not injected, running with standalone_parameters")
parameters = standalone_parameters
if not 'parameters' in locals() and not 'parameters' in globals():
raise Exception("Parameter injection failed")
#Use an easy dict for all the parameters
p = EasyDict(parameters)
if "x_shape" not in p:
p.x_shape = [2,256] # Default to this if we dont supply x_shape
supplied_keys = set(p.keys())
if supplied_keys != required_parameters:
print("Parameters are incorrect")
if len(supplied_keys - required_parameters)>0: print("Shouldn't have:", str(supplied_keys - required_parameters))
if len(required_parameters - supplied_keys)>0: print("Need to have:", str(required_parameters - supplied_keys))
raise RuntimeError("Parameters are incorrect")
###################################
# Set the RNGs and make it all deterministic
###################################
np.random.seed(p.seed)
random.seed(p.seed)
torch.manual_seed(p.seed)
torch.use_deterministic_algorithms(True)
###########################################
# The stratified datasets honor this
###########################################
torch.set_default_dtype(eval(p.torch_default_dtype))
###################################
# Build the network(s)
# Note: It's critical to do this AFTER setting the RNG
###################################
x_net = build_sequential(p.x_net)
start_time_secs = time.time()
p.domains_source = []
p.domains_target = []
train_original_source = []
val_original_source = []
test_original_source = []
train_original_target = []
val_original_target = []
test_original_target = []
# global_x_transform_func = lambda x: normalize(x.to(torch.get_default_dtype()), "unit_power") # unit_power, unit_mag
# global_x_transform_func = lambda x: normalize(x, "unit_power") # unit_power, unit_mag
def add_dataset(
labels,
domains,
pickle_path,
x_transforms,
episode_transforms,
domain_prefix,
num_examples_per_domain_per_label,
source_or_target_dataset:str,
iterator_seed=p.seed,
dataset_seed=p.dataset_seed,
n_shot=p.n_shot,
n_way=p.n_way,
n_query=p.n_query,
train_val_test_k_factors=(p.train_k_factor,p.val_k_factor,p.test_k_factor),
):
if x_transforms == []: x_transform = None
else: x_transform = get_chained_transform(x_transforms)
if episode_transforms == []: episode_transform = None
else: raise Exception("episode_transforms not implemented")
episode_transform = lambda tup, _prefix=domain_prefix: (_prefix + str(tup[0]), tup[1])
eaf = Episodic_Accessor_Factory(
labels=labels,
domains=domains,
num_examples_per_domain_per_label=num_examples_per_domain_per_label,
iterator_seed=iterator_seed,
dataset_seed=dataset_seed,
n_shot=n_shot,
n_way=n_way,
n_query=n_query,
train_val_test_k_factors=train_val_test_k_factors,
pickle_path=pickle_path,
x_transform_func=x_transform,
)
train, val, test = eaf.get_train(), eaf.get_val(), eaf.get_test()
train = Lazy_Iterable_Wrapper(train, episode_transform)
val = Lazy_Iterable_Wrapper(val, episode_transform)
test = Lazy_Iterable_Wrapper(test, episode_transform)
if source_or_target_dataset=="source":
train_original_source.append(train)
val_original_source.append(val)
test_original_source.append(test)
p.domains_source.extend(
[domain_prefix + str(u) for u in domains]
)
elif source_or_target_dataset=="target":
train_original_target.append(train)
val_original_target.append(val)
test_original_target.append(test)
p.domains_target.extend(
[domain_prefix + str(u) for u in domains]
)
else:
raise Exception(f"invalid source_or_target_dataset: {source_or_target_dataset}")
for ds in p.datasets:
add_dataset(**ds)
# from steves_utils.CORES.utils import (
# ALL_NODES,
# ALL_NODES_MINIMUM_1000_EXAMPLES,
# ALL_DAYS
# )
# add_dataset(
# labels=ALL_NODES,
# domains = ALL_DAYS,
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "cores.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"cores_{u}"
# )
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# add_dataset(
# labels=ALL_SERIAL_NUMBERS,
# domains = list(set(ALL_DISTANCES_FEET) - {2,62}),
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"),
# source_or_target_dataset="source",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"oracle1_{u}"
# )
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# add_dataset(
# labels=ALL_SERIAL_NUMBERS,
# domains = list(set(ALL_DISTANCES_FEET) - {2,62,56}),
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"),
# source_or_target_dataset="source",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"oracle2_{u}"
# )
# add_dataset(
# labels=list(range(19)),
# domains = [0,1,2],
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "metehan.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"met_{u}"
# )
# # from steves_utils.wisig.utils import (
# # ALL_NODES_MINIMUM_100_EXAMPLES,
# # ALL_NODES_MINIMUM_500_EXAMPLES,
# # ALL_NODES_MINIMUM_1000_EXAMPLES,
# # ALL_DAYS
# # )
# import steves_utils.wisig.utils as wisig
# add_dataset(
# labels=wisig.ALL_NODES_MINIMUM_100_EXAMPLES,
# domains = wisig.ALL_DAYS,
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "wisig.node3-19.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"wisig_{u}"
# )
###################################
# Build the dataset
###################################
train_original_source = Iterable_Aggregator(train_original_source, p.seed)
val_original_source = Iterable_Aggregator(val_original_source, p.seed)
test_original_source = Iterable_Aggregator(test_original_source, p.seed)
train_original_target = Iterable_Aggregator(train_original_target, p.seed)
val_original_target = Iterable_Aggregator(val_original_target, p.seed)
test_original_target = Iterable_Aggregator(test_original_target, p.seed)
# For CNN We only use X and Y. And we only train on the source.
# Properly form the data using a transform lambda and Lazy_Iterable_Wrapper. Finally wrap them in a dataloader
transform_lambda = lambda ex: ex[1] # Original is (<domain>, <episode>) so we strip down to episode only
train_processed_source = Lazy_Iterable_Wrapper(train_original_source, transform_lambda)
val_processed_source = Lazy_Iterable_Wrapper(val_original_source, transform_lambda)
test_processed_source = Lazy_Iterable_Wrapper(test_original_source, transform_lambda)
train_processed_target = Lazy_Iterable_Wrapper(train_original_target, transform_lambda)
val_processed_target = Lazy_Iterable_Wrapper(val_original_target, transform_lambda)
test_processed_target = Lazy_Iterable_Wrapper(test_original_target, transform_lambda)
datasets = EasyDict({
"source": {
"original": {"train":train_original_source, "val":val_original_source, "test":test_original_source},
"processed": {"train":train_processed_source, "val":val_processed_source, "test":test_processed_source}
},
"target": {
"original": {"train":train_original_target, "val":val_original_target, "test":test_original_target},
"processed": {"train":train_processed_target, "val":val_processed_target, "test":test_processed_target}
},
})
from steves_utils.transforms import get_average_magnitude, get_average_power
print(set([u for u,_ in val_original_source]))
print(set([u for u,_ in val_original_target]))
s_x, s_y, q_x, q_y, _ = next(iter(train_processed_source))
print(s_x)
# for ds in [
# train_processed_source,
# val_processed_source,
# test_processed_source,
# train_processed_target,
# val_processed_target,
# test_processed_target
# ]:
# for s_x, s_y, q_x, q_y, _ in ds:
# for X in (s_x, q_x):
# for x in X:
# assert np.isclose(get_average_magnitude(x.numpy()), 1.0)
# assert np.isclose(get_average_power(x.numpy()), 1.0)
###################################
# Build the model
###################################
# easfsl only wants a tuple for the shape
model = Steves_Prototypical_Network(x_net, device=p.device, x_shape=tuple(p.x_shape))
optimizer = Adam(params=model.parameters(), lr=p.lr)
###################################
# train
###################################
jig = PTN_Train_Eval_Test_Jig(model, p.BEST_MODEL_PATH, p.device)
jig.train(
train_iterable=datasets.source.processed.train,
source_val_iterable=datasets.source.processed.val,
target_val_iterable=datasets.target.processed.val,
num_epochs=p.n_epoch,
num_logs_per_epoch=p.NUM_LOGS_PER_EPOCH,
patience=p.patience,
optimizer=optimizer,
criteria_for_best=p.criteria_for_best,
)
total_experiment_time_secs = time.time() - start_time_secs
###################################
# Evaluate the model
###################################
source_test_label_accuracy, source_test_label_loss = jig.test(datasets.source.processed.test)
target_test_label_accuracy, target_test_label_loss = jig.test(datasets.target.processed.test)
source_val_label_accuracy, source_val_label_loss = jig.test(datasets.source.processed.val)
target_val_label_accuracy, target_val_label_loss = jig.test(datasets.target.processed.val)
history = jig.get_history()
total_epochs_trained = len(history["epoch_indices"])
val_dl = Iterable_Aggregator((datasets.source.original.val,datasets.target.original.val))
confusion = ptn_confusion_by_domain_over_dataloader(model, p.device, val_dl)
per_domain_accuracy = per_domain_accuracy_from_confusion(confusion)
# Add a key to per_domain_accuracy for if it was a source domain
for domain, accuracy in per_domain_accuracy.items():
per_domain_accuracy[domain] = {
"accuracy": accuracy,
"source?": domain in p.domains_source
}
# Do an independent accuracy assesment JUST TO BE SURE!
# _source_test_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.test, p.device)
# _target_test_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.test, p.device)
# _source_val_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.val, p.device)
# _target_val_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.val, p.device)
# assert(_source_test_label_accuracy == source_test_label_accuracy)
# assert(_target_test_label_accuracy == target_test_label_accuracy)
# assert(_source_val_label_accuracy == source_val_label_accuracy)
# assert(_target_val_label_accuracy == target_val_label_accuracy)
experiment = {
"experiment_name": p.experiment_name,
"parameters": dict(p),
"results": {
"source_test_label_accuracy": source_test_label_accuracy,
"source_test_label_loss": source_test_label_loss,
"target_test_label_accuracy": target_test_label_accuracy,
"target_test_label_loss": target_test_label_loss,
"source_val_label_accuracy": source_val_label_accuracy,
"source_val_label_loss": source_val_label_loss,
"target_val_label_accuracy": target_val_label_accuracy,
"target_val_label_loss": target_val_label_loss,
"total_epochs_trained": total_epochs_trained,
"total_experiment_time_secs": total_experiment_time_secs,
"confusion": confusion,
"per_domain_accuracy": per_domain_accuracy,
},
"history": history,
"dataset_metrics": get_dataset_metrics(datasets, "ptn"),
}
ax = get_loss_curve(experiment)
plt.show()
get_results_table(experiment)
get_domain_accuracies(experiment)
print("Source Test Label Accuracy:", experiment["results"]["source_test_label_accuracy"], "Target Test Label Accuracy:", experiment["results"]["target_test_label_accuracy"])
print("Source Val Label Accuracy:", experiment["results"]["source_val_label_accuracy"], "Target Val Label Accuracy:", experiment["results"]["target_val_label_accuracy"])
json.dumps(experiment)
```
| github_jupyter |
## Week 4
## T - testing and Inferential Statistics
Most people turn to IMB SPSS for T-testings, but this programme is very expensive, very old and not really necessary if you have access to Python tools. Very focused on click and point and is probably more useful to people without a programming background.
### Libraries
```
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
import scipy.stats as ss
import statsmodels.stats.weightstats as sm_ttest
```
### Reading
* [Independent t-test using SPSS Statistics on laerd.com](https://statistics.laerd.com/spss-tutorials/independent-t-test-using-spss-statistics.php)
* [ScipyStats documentation on ttest_ind](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html)
* [StatsModels documentation on ttest_ind](https://www.statsmodels.org/devel/generated/statsmodels.stats.weightstats.ttest_ind.html)
* [StarTek.com, Hypothesis test: The Difference in Means](https://stattrek.com/hypothesis-test/difference-in-means.aspx)
* [Python for Data Science, Independent T-Test](https://pythonfordatascience.org/independent-t-test-python/)
* [Dependent t-test using SPSS Statistics on leard.com](https://statistics.laerd.com/spss-tutorials/dependent-t-test-using-spss-statistics.php)
* [StackExchange, When conducting a t-test why would one prefer to assume (or test for) equal variances..?](https://stats.stackexchange.com/questions/305/when-conducting-a-t-test-why-would-one-prefer-to-assume-or-test-for-equal-vari)
## T-testing
**Example:** If I take a sample of males and females from the population and calcaulte their heights. Now a question I might ask is, is the mean height of males in the population equal to the mean height of females in the population?
T-testing is related to Hypothesis Testing.
### Scipy Stats
```
#Generating random data for the heights of 30 males in my sample
m = np.random.normal(1.8, 0.1, 30)
#Generating random data for the heights of 30 females in my sample
f = np.random.normal(1.6, 0.1, 30)
ss.stats.ttest_ind(m, f)
```
The null hypothesis (H0) claims that the average male height in the population is equal to the average female height in the population. Using my sample, I can infer if the H0 should be accepted or rejected. Based on my very small pvalue, we can reject the null hypothesis.
The pvalue refers to the probability of finding these samples in two populations with the same mean.
We have to accept our Alternate Hypothesis (H1), which should claim that the average male height is different to the average female height in the population. This is not surprising as I generated random data for my sample with male heights having a larger mean.
```
np.mean(m)
np.mean(f)
```
### Statsmodels
```
sm_ttest.ttest_ind(m, f)
```
## Graphical Analysis
```
#Seaborn displot to show means
plt.figure()
sns.distplot(m, label = 'male')
sns.distplot(f, label = 'female')
plt.legend();
df = pd.DataFrame({'male': m, 'female': f})
df
```
It's typically not a good idea to list values side by side. It implies a relationship between the data and can lead to problems if we don't have the same sample size of males as females.
```
a = ['male'] * 30
b = ['female'] * 30
gender = a+b
# I can't add arrays for males and females in the same way
# As they are numpy arrays
height = np.concatenate([m, f])
df = pd.DataFrame({'Gender': gender, 'Height': height})
df
#Taking out just the male heights
df[df['Gender'] == 'male']['Height']
df[df['Gender'] == 'female']['Height']
sns.catplot(x = 'Gender', y = 'Height', jitter = False, data = df);
sns.catplot(x = 'Gender', y = 'Height', kind = 'box', data = df);
```
### Notes
This notebook is related to independent T-testing, or T-testing independent variables. There is a different test for dependent samples. An example of dependent samples T-testing, would example the difference in assessment results before teaching a new concept versus after teaching a new topic. Sometimes refered to as paired samples T-test.
| github_jupyter |
```
# Загрузка зависимостей
import numpy
import pandas
import matplotlib.pyplot
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
# Загрузка и анализ набора данных
raw_dataset = pandas.read_csv('machine.data.csv', header=None) # Убедиться в правильности пути к файлу!
raw_dataset.head(10) # Вывод первых 10 строк
# Размер набора данных
print(raw_dataset.shape)
# Создаем набор данных, в котором будут храниться обработанные данные
dataset = pandas.DataFrame()
# Обработка данных в столбце №3 (MMIN: minimum main memory in kilobytes (integer))
# Загружаем данные
data = raw_dataset[3]
# Анализируем распределение, используя гистограмму. Параметр bins отвечает за число столбцов в гистрограмме.
matplotlib.pyplot.hist(data, bins = 50)
matplotlib.pyplot.show()
# Наблюдаем проблему №4 - выброс в районе 32000. Применяем отсечение с разрешенным интервалом от 0 до 16000.
data = numpy.clip(data, 0, 16000)
# Результат
matplotlib.pyplot.hist(data, bins = 50)
matplotlib.pyplot.show()
# Наблюдаем проблему №3 - очень неравномерное распределение. Попробуем применить к данным логарифм и извлечение квадратного корня.
matplotlib.pyplot.hist(numpy.log(data), bins = 50)
matplotlib.pyplot.show()
matplotlib.pyplot.hist(data ** 0.5, bins = 50)
matplotlib.pyplot.show()
# Логарифм даёт более равномерно распределенные данные, используем его
data = numpy.log(data)
# Теперь данные имеют следующую область значений
print(numpy.min(data))
print(numpy.max(data))
# Приводим значения к интервалу (0, 1), считая, что они ближе к равномерному распределению
scaler = MinMaxScaler()
data = numpy.array(data).reshape(-1,1)
data = scaler.fit_transform(data)
# Результат
matplotlib.pyplot.hist(data, bins = 50)
matplotlib.pyplot.show()
# Можем взглянуть на сами данные
matplotlib.pyplot.plot(data)
matplotlib.pyplot.show()
# Проверяем и убеждаемся, что в процессе трансформации данные получили "лишнее" измерение
print(data.ndim)
# Конвертируем в одномерный массив
data = data.flatten()
# Сохраняем в итоговом наборе данных
dataset['MMIN'] = data
# Обработка данных в столбце №7 (CHMAX: maximum channels in units (integer))
# Загружаем данные
data = raw_dataset[7]
# Анализируем распределение, используя гистограмму. Параметр bins отвечает за число столбцов в гистрограмме.
matplotlib.pyplot.hist(data, bins = 50)
matplotlib.pyplot.show()
# Наблюдаем проблему №4 - выбросы значений в интервале (100, 175). Применяем отсечение с разрешенным интервалом от 0 до 70.
data = numpy.clip(data, 0, 70)
# Результат
matplotlib.pyplot.hist(data, bins = 50)
matplotlib.pyplot.show()
# Наблюдаем проблему №3 - очень неравномерное распределение. Применять логарифм нельзя, т.к. среди значений есть нули.
# Применим извлечение квадратного корня.
matplotlib.pyplot.hist(data ** 0.5, bins = 50)
matplotlib.pyplot.show()
data = data ** 0.5
# Теперь данные имеют следующую область значений
print(numpy.min(data))
print(numpy.max(data))
# Приводим значения к интервалу (0, 1), считая, что они ближе к равномерному распределению
scaler = MinMaxScaler()
data = numpy.array(data).reshape(-1,1)
data = scaler.fit_transform(data)
# Результат
matplotlib.pyplot.hist(data, bins = 50)
matplotlib.pyplot.show()
# Можем взглянуть на сами данные
matplotlib.pyplot.plot(data)
matplotlib.pyplot.show()
# Проверяем и убеждаемся, что в процессе трансформации данные получили "лишнее" измерение
print(data.ndim)
# Конвертируем в одномерный массив
data = data.flatten()
# Сохраняем в итоговом наборе данных
dataset['CHMAX'] = data
print(dataset)
dataset.to_csv('prepared_data.csv')
```
| github_jupyter |
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Explore Duplicate Question Matches
Use this dashboard to explore the relationship between duplicate and original questions.
## Setup
This section loads needed packages, and defines useful functions.
```
from __future__ import print_function
import math
import ipywidgets as widgets
import pandas as pd
import requests
from azureml.core.webservice import AksWebservice
from azureml.core.workspace import Workspace
from dotenv import get_key, find_dotenv
from utilities import read_questions, text_to_json, get_auth
env_path = find_dotenv(raise_error_if_not_found=True)
ws = Workspace.from_config(auth=get_auth(env_path))
print(ws.name, ws.resource_group, ws.location, sep="\n")
aks_service_name = get_key(env_path, 'aks_service_name')
aks_service = AksWebservice(ws, name=aks_service_name)
aks_service.name
```
Load the duplicate questions scoring app's URL.
```
scoring_url = aks_service.scoring_uri
api_key = aks_service.get_keys()[0]
```
A constructor function for ID-text contents. Constructs buttons and text areas for each text ID and text passage.
* Each buttons's description is set to a text's ID, and its click action is set to the handler.
* Each text area's content is set to a text.
* A dictionary is created to map IDs to text areas.
```
def buttons_and_texts(
data, id, answerid, text, handle_click, layout=widgets.Layout(width="100%"), n=15
):
"""Construct buttons, text areas, and a mapping from IDs to text areas."""
items = []
text_map = {}
for i in range(min(n, len(data))):
button = widgets.Button(description=data.iloc[i][id])
button.answerid = data.iloc[i][answerid] if answerid in data else None
button.open = False
button.on_click(handle_click)
items.append(button)
text_area = widgets.Textarea(
data.iloc[i][text], placeholder=data.iloc[i][id], layout=layout
)
items.append(text_area)
text_map[data.iloc[i][id]] = text_area
return items, text_map
```
A constructor function for the duplicates and questions explorer widget. This builds a box containing duplicates and question tabs, each in turn containing boxes that contain the buttons and text areas.
```
def duplicates_questions_widget(
duplicates, questions, layout=widgets.Layout(width="100%")
):
"""Construct a duplicates and questions exploration widget."""
# Construct the duplicates Tab of buttons and text areas.
duplicates_items, duplicates_map = buttons_and_texts(
duplicates,
duplicates_id,
duplicates_answerid,
duplicates_text,
duplicates_click,
n=duplicates.shape[0],
)
duplicates_tab = widgets.Tab(
[widgets.VBox(duplicates_items, layout=layout)],
layout=widgets.Layout(width="100%", height="500px", overflow_y="auto"),
)
duplicates_tab.set_title(0, duplicates_title)
# Construct the questions Tab of buttons and text areas.
questions_items, questions_map = buttons_and_texts(
questions,
questions_id,
questions_answerid,
questions_text,
questions_click,
n=questions.shape[0],
)
questions_tab = widgets.Tab(
[widgets.VBox(questions_items, layout=layout)],
layout=widgets.Layout(width="100%", height="500px", overflow_y="auto"),
)
questions_tab.set_title(0, questions_title)
# Put both tabs in an HBox.
duplicates_questions = widgets.HBox([duplicates_tab, questions_tab], layout=layout)
return duplicates_map, questions_map, duplicates_questions
```
A handler function for a question passage button press. If the passage's text window is open, it is collapsed. Otherwise, it is opened.
```
def questions_click(button):
"""Respond to a click on a question button."""
global questions_map
if button.open:
questions_map[button.description].rows = None
button.open = False
else:
questions_map[button.description].rows = 10
button.open = True
```
A handler function for a duplicate obligation button press. If the obligation is not selected, select it and update the questions tab with its top 15 question passages ordered by match score. Otherwise, if the duplicate's text window is open, it is collapsed, else it is opened.
```
def duplicates_click(button):
"""Respond to a click on a duplicate button."""
global duplicates_map
if select_duplicate(button):
duplicates_map[button.description].rows = 10
button.open = True
else:
if button.open:
duplicates_map[button.description].rows = None
button.open = False
else:
duplicates_map[button.description].rows = 10
button.open = True
def select_duplicate(button):
"""Update the displayed questions to correspond to the button's duplicate
selections. Returns whether or not the selected duplicate changed.
"""
global selected_button, questions_map, duplicates_questions
if "selected_button" not in globals() or button != selected_button:
if "selected_button" in globals():
selected_button.style.button_color = None
selected_button.style.font_weight = ""
selected_button = button
selected_button.style.button_color = "yellow"
selected_button.style.font_weight = "bold"
duplicates_text = duplicates_map[selected_button.description].value
questions_scores = score_text(duplicates_text)
ordered_questions = questions.loc[questions_scores[questions_id]]
questions_items, questions_map = buttons_and_texts(
ordered_questions,
questions_id,
questions_answerid,
questions_text,
questions_click,
n=questions_display,
)
if questions_button_color is True and selected_button.answerid is not None:
set_button_color(questions_items[::2], selected_button.answerid)
if questions_button_score is True:
questions_items = [
item
for button, text_area in zip(*[iter(questions_items)] * 2)
for item in (add_button_prob(button, questions_scores), text_area)
]
duplicates_questions.children[1].children[0].children = questions_items
duplicates_questions.children[1].set_title(0, selected_button.description)
return True
else:
return False
def add_button_prob(button, questions_scores):
"""Return an HBox containing button and its probability."""
id = button.description
prob = widgets.Label(
score_label
+ ": "
+ str(
int(
math.ceil(score_scale * questions_scores.loc[id][questions_probability])
)
)
)
return widgets.HBox([button, prob])
def set_button_color(button, answerid):
"""Set each button's color according to its label."""
for i in range(len(button)):
button[i].style.button_color = (
"lightgreen" if button[i].answerid == answerid else None
)
```
Functions for interacting with the web service.
```
def score_text(text):
"""Return a data frame with the original question scores for the text."""
headers = {
"content-type": "application/json",
"Authorization": ("Bearer " + api_key),
}
# jsontext = json.dumps({'input':'{0}'.format(text)})
jsontext = text_to_json(text)
result = requests.post(scoring_url, data=jsontext, headers=headers)
# scores = result.json()['result'][0]
scores = eval(result.json())
scores_df = pd.DataFrame(
scores, columns=[questions_id, questions_answerid, questions_probability]
)
scores_df[questions_id] = scores_df[questions_id].astype(str)
scores_df[questions_answerid] = scores_df[questions_answerid].astype(str)
scores_df = scores_df.set_index(questions_id, drop=False)
return scores_df
```
Control the appearance of cell output boxes.
```
%%html
<style>
.output_wrapper, .output {
height:auto !important;
max-height:1000px; /* your desired max-height here */
}
.output_scroll {
box-shadow:none !important;
webkit-box-shadow:none !important;
}
</style>
```
## Load data
Load the pre-formatted text of questions.
```
questions_title = 'Questions'
questions_id = 'Id'
questions_answerid = 'AnswerId'
questions_text = 'Text'
questions_probability = 'Probability'
questions_path = './data_folder/questions.tsv'
questions = read_questions(questions_path, questions_id, questions_answerid)
```
Load the pre-formatted text of duplicates.
```
duplicates_title = 'Duplicates'
duplicates_id = 'Id'
duplicates_answerid = 'AnswerId'
duplicates_text = 'Text'
duplicates_path = './data_folder/dupes_test.tsv'
duplicates = read_questions(duplicates_path, duplicates_id, duplicates_answerid)
```
## Explore original questions matched up with duplicate questions
Define other variables and settings used in creating the interface.
```
questions_display = 15
questions_button_color = True
questions_button_score = True
score_label = 'Score'
score_scale = 100
```
This builds the exploration widget as a box containing duplicates and question tabs, each in turn containing boxes that have for each ID-text pair a button and a text area.
```
duplicates_map, questions_map, duplicates_questions = duplicates_questions_widget(duplicates, questions)
duplicates_questions
```
To tear down the cluster and related resources go to the [last notebook](08_TearDown.ipynb).
| github_jupyter |
<h1 align="center"> Registration Initialization: We Have to Start Somewhere</h1>
Initialization is a critical aspect of most registration algorithms, given that most algorithms are formulated as an iterative optimization problem.
In many cases we perform initialization in an automatic manner by making assumptions with regard to the contents of the image and the imaging protocol. For instance, if we expect that images were acquired with the patient in a known orientation we can align the geometric centers of the two volumes or the center of mass of the image contents if the anatomy is not centered in the image (this is what we previously did in [this example](60_RegistrationIntroduction.ipynb)).
When the orientation is not known, or is known but incorrect, this approach will not yield a reasonable initial estimate for the registration.
When working with clinical images, the DICOM tags define the orientation and position of the anatomy in the volume. The tags of interest are:
<ul>
<li> (0020|0032) Image Position (Patient) : coordinates of the the first transmitted voxel. </li>
<li>(0020|0037) Image Orientation (Patient): directions of first row and column in 3D space. </li>
<li>(0018|5100) Patient Position: Patient placement on the table
<ul>
<li> Head First Prone (HFP)</li>
<li> Head First Supine (HFS)</li>
<li> Head First Decibitus Right (HFDR)</li>
<li> Head First Decibitus Left (HFDL)</li>
<li> Feet First Prone (FFP)</li>
<li> Feet First Supine (FFS)</li>
<li> Feet First Decibitus Right (FFDR)</li>
<li> Feet First Decibitus Left (FFDL)</li>
</ul>
</li>
</ul>
The patient position is manually entered by the CT/MR operator and thus can be erroneous (HFP instead of FFP will result in a $180^o$ orientation error).
A heuristic, yet effective, solution is to use a sampling strategy of the parameter space. Note that this strategy is primarily useful in low dimensional parameter spaces (rigid or possibly affine transformations).
In this notebook we illustrate how to sample the parameter space in a fixed pattern. We then initialize the registration with the parameters that correspond to the best similarity metric value obtained by our sampling.
```
import SimpleITK as sitk
import os
import numpy as np
from ipywidgets import interact, fixed
from downloaddata import fetch_data as fdata
import registration_callbacks as rc
import registration_utilities as ru
# Always write output to a separate directory, we don't want to pollute the source directory.
OUTPUT_DIR = 'Output'
%matplotlib inline
# This is the registration configuration which we use in all cases. The only parameter that we vary
# is the initial_transform.
def multires_registration(fixed_image, moving_image, initial_transform):
registration_method = sitk.ImageRegistrationMethod()
registration_method.SetMetricAsMattesMutualInformation(numberOfHistogramBins=50)
registration_method.SetMetricSamplingStrategy(registration_method.RANDOM)
registration_method.SetMetricSamplingPercentage(0.01)
registration_method.SetInterpolator(sitk.sitkLinear)
registration_method.SetOptimizerAsGradientDescent(learningRate=1.0, numberOfIterations=100, estimateLearningRate=registration_method.Once)
registration_method.SetOptimizerScalesFromPhysicalShift()
registration_method.SetInitialTransform(initial_transform)
registration_method.SetShrinkFactorsPerLevel(shrinkFactors = [4,2,1])
registration_method.SetSmoothingSigmasPerLevel(smoothingSigmas = [2,1,0])
registration_method.SmoothingSigmasAreSpecifiedInPhysicalUnitsOn()
registration_method.AddCommand(sitk.sitkStartEvent, rc.metric_start_plot)
registration_method.AddCommand(sitk.sitkEndEvent, rc.metric_end_plot)
registration_method.AddCommand(sitk.sitkMultiResolutionIterationEvent, rc.metric_update_multires_iterations)
registration_method.AddCommand(sitk.sitkIterationEvent, lambda: rc.metric_plot_values(registration_method))
final_transform = registration_method.Execute(fixed_image, moving_image)
print('Final metric value: {0}'.format(registration_method.GetMetricValue()))
print('Optimizer\'s stopping condition, {0}'.format(registration_method.GetOptimizerStopConditionDescription()))
return final_transform
```
## Loading Data
```
data_directory = os.path.dirname(fdata("CIRS057A_MR_CT_DICOM/readme.txt"))
fixed_series_ID = "1.2.840.113619.2.290.3.3233817346.783.1399004564.515"
moving_series_ID = "1.3.12.2.1107.5.2.18.41548.30000014030519285935000000933"
reader = sitk.ImageSeriesReader()
fixed_image = sitk.ReadImage(reader.GetGDCMSeriesFileNames(data_directory, fixed_series_ID), sitk.sitkFloat32)
moving_image = sitk.ReadImage(reader.GetGDCMSeriesFileNames(data_directory, moving_series_ID), sitk.sitkFloat32)
# To provide a reasonable display we need to window/level the images. By default we could have used the intensity
# ranges found in the images [SimpleITK's StatisticsImageFilter], but these are not the best values for viewing.
# Using an external viewer we identified the following settings.
fixed_intensity_range = (-1183,544)
moving_intensity_range = (0,355)
interact(lambda image1_z, image2_z, image1, image2,:ru.display_scalar_images(image1_z, image2_z, image1, image2,
fixed_intensity_range,
moving_intensity_range,
'fixed image',
'moving image'),
image1_z=(0,fixed_image.GetSize()[2]-1),
image2_z=(0,moving_image.GetSize()[2]-1),
image1 = fixed(fixed_image),
image2=fixed(moving_image));
```
Arbitrarily rotate the moving image.
```
rotation_x = 0.0
rotation_z = 0.0
def modify_rotation(rx_in_degrees, rz_in_degrees):
global rotation_x, rotation_z
rotation_x = np.radians(rx_in_degrees)
rotation_z = np.radians(rz_in_degrees)
interact(modify_rotation, rx_in_degrees=(0.0,180.0,5.0), rz_in_degrees=(-90.0,180.0,5.0));
resample = sitk.ResampleImageFilter()
resample.SetReferenceImage(moving_image)
resample.SetInterpolator(sitk.sitkLinear)
# Rotate around the physical center of the image.
rotation_center = moving_image.TransformContinuousIndexToPhysicalPoint([(index-1)/2.0 for index in moving_image.GetSize()])
transform = sitk.Euler3DTransform(rotation_center, rotation_x, 0, rotation_z, (0,0,0))
resample.SetTransform(transform)
modified_moving_image = resample.Execute(moving_image)
interact(lambda image1_z, image2_z, image1, image2,:ru.display_scalar_images(image1_z, image2_z, image1, image2,
moving_intensity_range,
moving_intensity_range, 'original', 'rotated'),
image1_z=(0,moving_image.GetSize()[2]-1),
image2_z=(0,modified_moving_image.GetSize()[2]-1),
image1 = fixed(moving_image),
image2=fixed(modified_moving_image));
```
## Register using standard initialization (assumes orientation is similar)
```
initial_transform = sitk.CenteredTransformInitializer(fixed_image,
modified_moving_image,
sitk.Euler3DTransform(),
sitk.CenteredTransformInitializerFilter.GEOMETRY)
final_transform = multires_registration(fixed_image, modified_moving_image, initial_transform)
```
Visually evaluate our results:
```
moving_resampled = sitk.Resample(modified_moving_image, fixed_image, final_transform, sitk.sitkLinear, 0.0, moving_image.GetPixelIDValue())
interact(ru.display_images_with_alpha, image_z=(0,fixed_image.GetSize()[2]), alpha=(0.0,1.0,0.05),
image1 = fixed(sitk.IntensityWindowing(fixed_image, fixed_intensity_range[0], fixed_intensity_range[1])),
image2=fixed(sitk.IntensityWindowing(moving_resampled, moving_intensity_range[0], moving_intensity_range[1])));
```
## Register using heuristic initialization approach (using multiple orientations)
As we want to account for significant orientation differences due to erroneous patient position (HFS...) we evaluate the similarity measure at locations corresponding to the various orientation differences. This can be done in two ways which will be illustrated below:
<ul>
<li>Use the ImageRegistrationMethod.MetricEvaluate() method.</li>
<li>Use the Exhaustive optimizer.
</ul>
The former approach is more computationally intensive as it constructs and configures a metric object each time it is invoked. It is therefore more appropriate for use if the set of parameter values we want to evaluate are not on a rectilinear grid in the parameter space. The latter approach is appropriate if the set of parameter values are on a rectilinear grid, in which case the approach is more computationally efficient.
In both cases we use the CenteredTransformInitializer to obtain the initial translation.
### MetricEvaluate
To use the MetricEvaluate method we create a ImageRegistrationMethod, set its metric and interpolator. We then iterate over all parameter settings, set the initial transform and evaluate the metric. The minimal similarity measure value corresponds to the best parameter settings.
```
# Dictionary with all the orientations we will try. We omit the identity (x=0, y=0, z=0) as we always use it. This
# set of rotations is arbitrary. For a complete grid coverage we would have 64 entries (0,pi/2,pi,1.5pi for each angle).
all_orientations = {'x=0, y=0, z=90': (0.0,0.0,np.pi/2.0),
'x=0, y=0, z=-90': (0.0,0.0,-np.pi),
'x=0, y=0, z=180': (0.0,0.0,np.pi),
'x=180, y=0, z=0': (np.pi,0.0,0.0),
'x=180, y=0, z=90': (np.pi,0.0,np.pi/2.0),
'x=180, y=0, z=-90': (np.pi,0.0,-np.pi/2.0),
'x=180, y=0, z=180': (np.pi,0.0,np.pi)}
# Registration framework setup.
registration_method = sitk.ImageRegistrationMethod()
registration_method.SetMetricAsMattesMutualInformation(numberOfHistogramBins=50)
registration_method.SetMetricSamplingStrategy(registration_method.RANDOM)
registration_method.SetMetricSamplingPercentage(0.01)
registration_method.SetInterpolator(sitk.sitkLinear)
# Evaluate the similarity metric using the eight possible orientations, translation remains the same for all.
initial_transform = sitk.Euler3DTransform(sitk.CenteredTransformInitializer(fixed_image,
modified_moving_image,
sitk.Euler3DTransform(),
sitk.CenteredTransformInitializerFilter.GEOMETRY))
registration_method.SetInitialTransform(initial_transform, inPlace=False)
best_orientation = (0.0,0.0,0.0)
best_similarity_value = registration_method.MetricEvaluate(fixed_image, modified_moving_image)
# Iterate over all other rotation parameter settings.
for key, orientation in all_orientations.items():
initial_transform.SetRotation(*orientation)
registration_method.SetInitialTransform(initial_transform)
current_similarity_value = registration_method.MetricEvaluate(fixed_image, modified_moving_image)
if current_similarity_value < best_similarity_value:
best_similarity_value = current_similarity_value
best_orientation = orientation
initial_transform.SetRotation(*best_orientation)
final_transform = multires_registration(fixed_image, modified_moving_image, initial_transform)
```
Visually evaluate our results:
```
moving_resampled = sitk.Resample(modified_moving_image, fixed_image, final_transform, sitk.sitkLinear, 0.0, moving_image.GetPixelIDValue())
interact(ru.display_images_with_alpha, image_z=(0,fixed_image.GetSize()[2]), alpha=(0.0,1.0,0.05),
image1 = fixed(sitk.IntensityWindowing(fixed_image, fixed_intensity_range[0], fixed_intensity_range[1])),
image2=fixed(sitk.IntensityWindowing(moving_resampled, moving_intensity_range[0], moving_intensity_range[1])));
```
### Exhaustive optimizer
The exhaustive optimizer evaluates the similarity measure using a grid overlaid on the parameter space.
The grid is centered on the parameter values set by the SetInitialTransform, and the location of its vertices are determined by the <b>numberOfSteps</b>, <b>stepLength</b> and <b>optimizer scales</b>. To quote the documentation of this class: "a side of the region is stepLength*(2*numberOfSteps[d]+1)*scaling[d]."
Using this approach we have superfluous evaluations (15 evaluations corresponding to 3 values for rotations around the x axis and five for rotation around the z axis, as compared to the 8 evaluations using the MetricEvaluate method).
```
initial_transform = sitk.CenteredTransformInitializer(fixed_image,
modified_moving_image,
sitk.Euler3DTransform(),
sitk.CenteredTransformInitializerFilter.GEOMETRY)
registration_method = sitk.ImageRegistrationMethod()
registration_method.SetMetricAsMattesMutualInformation(numberOfHistogramBins=50)
registration_method.SetMetricSamplingStrategy(registration_method.RANDOM)
registration_method.SetMetricSamplingPercentage(0.01)
registration_method.SetInterpolator(sitk.sitkLinear)
# The order of parameters for the Euler3DTransform is [angle_x, angle_y, angle_z, t_x, t_y, t_z]. The parameter
# sampling grid is centered on the initial_transform parameter values, that are all zero for the rotations. Given
# the number of steps and their length and optimizer scales we have:
# angle_x = -pi, 0, pi
# angle_y = 0
# angle_z = -pi, -pi/2, 0, pi/2, pi
registration_method.SetOptimizerAsExhaustive(numberOfSteps=[1,0,2,0,0,0], stepLength = np.pi)
registration_method.SetOptimizerScales([1,1,0.5,1,1,1])
#Perform the registration in-place so that the initial_transform is modified.
registration_method.SetInitialTransform(initial_transform, inPlace=True)
registration_method.Execute(fixed_image, modified_moving_image)
final_transform = multires_registration(fixed_image, modified_moving_image, initial_transform)
```
Visually evaluate our results:
```
moving_resampled = sitk.Resample(modified_moving_image, fixed_image, final_transform, sitk.sitkLinear, 0.0, moving_image.GetPixelIDValue())
interact(ru.display_images_with_alpha, image_z=(0,fixed_image.GetSize()[2]), alpha=(0.0,1.0,0.05),
image1 = fixed(sitk.IntensityWindowing(fixed_image, fixed_intensity_range[0], fixed_intensity_range[1])),
image2=fixed(sitk.IntensityWindowing(moving_resampled, moving_intensity_range[0], moving_intensity_range[1])));
```
| github_jupyter |
<a href="https://colab.research.google.com/github/PytorchLightning/pytorch-lightning/blob/master/notebooks/04-transformers-text-classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Finetune 🤗 Transformers Models with PyTorch Lightning ⚡
This notebook will use HuggingFace's `datasets` library to get data, which will be wrapped in a `LightningDataModule`. Then, we write a class to perform text classification on any dataset from the[ GLUE Benchmark](https://gluebenchmark.com/). (We just show CoLA and MRPC due to constraint on compute/disk)
[HuggingFace's NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=cola) can help you get a feel for the two datasets we will use and what tasks they are solving for.
---
- Give us a ⭐ [on Github](https://www.github.com/PytorchLightning/pytorch-lightning/)
- Check out [the documentation](https://pytorch-lightning.readthedocs.io/en/latest/)
- Ask a question on [GitHub Discussions](https://github.com/PyTorchLightning/pytorch-lightning/discussions/)
- Join us [on Slack](https://join.slack.com/t/pytorch-lightning/shared_invite/zt-f6bl2l0l-JYMK3tbAgAmGRrlNr00f1A)
- [HuggingFace datasets](https://github.com/huggingface/datasets)
- [HuggingFace transformers](https://github.com/huggingface/transformers)
### Setup
```
!pip install pytorch-lightning datasets transformers
from argparse import ArgumentParser
from datetime import datetime
from typing import Optional
import datasets
import numpy as np
import pytorch_lightning as pl
import torch
from torch.utils.data import DataLoader
from transformers import (
AdamW,
AutoModelForSequenceClassification,
AutoConfig,
AutoTokenizer,
get_linear_schedule_with_warmup,
glue_compute_metrics
)
```
## GLUE DataModule
```
class GLUEDataModule(pl.LightningDataModule):
task_text_field_map = {
'cola': ['sentence'],
'sst2': ['sentence'],
'mrpc': ['sentence1', 'sentence2'],
'qqp': ['question1', 'question2'],
'stsb': ['sentence1', 'sentence2'],
'mnli': ['premise', 'hypothesis'],
'qnli': ['question', 'sentence'],
'rte': ['sentence1', 'sentence2'],
'wnli': ['sentence1', 'sentence2'],
'ax': ['premise', 'hypothesis']
}
glue_task_num_labels = {
'cola': 2,
'sst2': 2,
'mrpc': 2,
'qqp': 2,
'stsb': 1,
'mnli': 3,
'qnli': 2,
'rte': 2,
'wnli': 2,
'ax': 3
}
loader_columns = [
'datasets_idx',
'input_ids',
'token_type_ids',
'attention_mask',
'start_positions',
'end_positions',
'labels'
]
def __init__(
self,
model_name_or_path: str,
task_name: str ='mrpc',
max_seq_length: int = 128,
train_batch_size: int = 32,
eval_batch_size: int = 32,
**kwargs
):
super().__init__()
self.model_name_or_path = model_name_or_path
self.task_name = task_name
self.max_seq_length = max_seq_length
self.train_batch_size = train_batch_size
self.eval_batch_size = eval_batch_size
self.text_fields = self.task_text_field_map[task_name]
self.num_labels = self.glue_task_num_labels[task_name]
self.tokenizer = AutoTokenizer.from_pretrained(self.model_name_or_path, use_fast=True)
def setup(self, stage):
self.dataset = datasets.load_dataset('glue', self.task_name)
for split in self.dataset.keys():
self.dataset[split] = self.dataset[split].map(
self.convert_to_features,
batched=True,
remove_columns=['label'],
)
self.columns = [c for c in self.dataset[split].column_names if c in self.loader_columns]
self.dataset[split].set_format(type="torch", columns=self.columns)
self.eval_splits = [x for x in self.dataset.keys() if 'validation' in x]
def prepare_data(self):
datasets.load_dataset('glue', self.task_name)
AutoTokenizer.from_pretrained(self.model_name_or_path, use_fast=True)
def train_dataloader(self):
return DataLoader(self.dataset['train'], batch_size=self.train_batch_size)
def val_dataloader(self):
if len(self.eval_splits) == 1:
return DataLoader(self.dataset['validation'], batch_size=self.eval_batch_size)
elif len(self.eval_splits) > 1:
return [DataLoader(self.dataset[x], batch_size=self.eval_batch_size) for x in self.eval_splits]
def test_dataloader(self):
if len(self.eval_splits) == 1:
return DataLoader(self.dataset['test'], batch_size=self.eval_batch_size)
elif len(self.eval_splits) > 1:
return [DataLoader(self.dataset[x], batch_size=self.eval_batch_size) for x in self.eval_splits]
def convert_to_features(self, example_batch, indices=None):
# Either encode single sentence or sentence pairs
if len(self.text_fields) > 1:
texts_or_text_pairs = list(zip(example_batch[self.text_fields[0]], example_batch[self.text_fields[1]]))
else:
texts_or_text_pairs = example_batch[self.text_fields[0]]
# Tokenize the text/text pairs
features = self.tokenizer.batch_encode_plus(
texts_or_text_pairs,
max_length=self.max_seq_length,
pad_to_max_length=True,
truncation=True
)
# Rename label to labels to make it easier to pass to model forward
features['labels'] = example_batch['label']
return features
```
#### You could use this datamodule with standalone PyTorch if you wanted...
```
dm = GLUEDataModule('distilbert-base-uncased')
dm.prepare_data()
dm.setup('fit')
next(iter(dm.train_dataloader()))
```
## GLUE Model
```
class GLUETransformer(pl.LightningModule):
def __init__(
self,
model_name_or_path: str,
num_labels: int,
learning_rate: float = 2e-5,
adam_epsilon: float = 1e-8,
warmup_steps: int = 0,
weight_decay: float = 0.0,
train_batch_size: int = 32,
eval_batch_size: int = 32,
eval_splits: Optional[list] = None,
**kwargs
):
super().__init__()
self.save_hyperparameters()
self.config = AutoConfig.from_pretrained(model_name_or_path, num_labels=num_labels)
self.model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, config=self.config)
self.metric = datasets.load_metric(
'glue',
self.hparams.task_name,
experiment_id=datetime.now().strftime("%d-%m-%Y_%H-%M-%S")
)
def forward(self, **inputs):
return self.model(**inputs)
def training_step(self, batch, batch_idx):
outputs = self(**batch)
loss = outputs[0]
return loss
def validation_step(self, batch, batch_idx, dataloader_idx=0):
outputs = self(**batch)
val_loss, logits = outputs[:2]
if self.hparams.num_labels >= 1:
preds = torch.argmax(logits, axis=1)
elif self.hparams.num_labels == 1:
preds = logits.squeeze()
labels = batch["labels"]
return {'loss': val_loss, "preds": preds, "labels": labels}
def validation_epoch_end(self, outputs):
if self.hparams.task_name == 'mnli':
for i, output in enumerate(outputs):
# matched or mismatched
split = self.hparams.eval_splits[i].split('_')[-1]
preds = torch.cat([x['preds'] for x in output]).detach().cpu().numpy()
labels = torch.cat([x['labels'] for x in output]).detach().cpu().numpy()
loss = torch.stack([x['loss'] for x in output]).mean()
self.log(f'val_loss_{split}', loss, prog_bar=True)
split_metrics = {f"{k}_{split}": v for k, v in self.metric.compute(predictions=preds, references=labels).items()}
self.log_dict(split_metrics, prog_bar=True)
return loss
preds = torch.cat([x['preds'] for x in outputs]).detach().cpu().numpy()
labels = torch.cat([x['labels'] for x in outputs]).detach().cpu().numpy()
loss = torch.stack([x['loss'] for x in outputs]).mean()
self.log('val_loss', loss, prog_bar=True)
self.log_dict(self.metric.compute(predictions=preds, references=labels), prog_bar=True)
return loss
def setup(self, stage):
if stage == 'fit':
# Get dataloader by calling it - train_dataloader() is called after setup() by default
train_loader = self.train_dataloader()
# Calculate total steps
self.total_steps = (
(len(train_loader.dataset) // (self.hparams.train_batch_size * max(1, self.hparams.gpus)))
// self.hparams.accumulate_grad_batches
* float(self.hparams.max_epochs)
)
def configure_optimizers(self):
"Prepare optimizer and schedule (linear warmup and decay)"
model = self.model
no_decay = ["bias", "LayerNorm.weight"]
optimizer_grouped_parameters = [
{
"params": [p for n, p in model.named_parameters() if not any(nd in n for nd in no_decay)],
"weight_decay": self.hparams.weight_decay,
},
{
"params": [p for n, p in model.named_parameters() if any(nd in n for nd in no_decay)],
"weight_decay": 0.0,
},
]
optimizer = AdamW(optimizer_grouped_parameters, lr=self.hparams.learning_rate, eps=self.hparams.adam_epsilon)
scheduler = get_linear_schedule_with_warmup(
optimizer, num_warmup_steps=self.hparams.warmup_steps, num_training_steps=self.total_steps
)
scheduler = {
'scheduler': scheduler,
'interval': 'step',
'frequency': 1
}
return [optimizer], [scheduler]
@staticmethod
def add_model_specific_args(parent_parser):
parser = ArgumentParser(parents=[parent_parser], add_help=False)
parser.add_argument("--learning_rate", default=2e-5, type=float)
parser.add_argument("--adam_epsilon", default=1e-8, type=float)
parser.add_argument("--warmup_steps", default=0, type=int)
parser.add_argument("--weight_decay", default=0.0, type=float)
return parser
```
### ⚡ Quick Tip
- Combine arguments from your DataModule, Model, and Trainer into one for easy and robust configuration
```
def parse_args(args=None):
parser = ArgumentParser()
parser = pl.Trainer.add_argparse_args(parser)
parser = GLUEDataModule.add_argparse_args(parser)
parser = GLUETransformer.add_model_specific_args(parser)
parser.add_argument('--seed', type=int, default=42)
return parser.parse_args(args)
def main(args):
pl.seed_everything(args.seed)
dm = GLUEDataModule.from_argparse_args(args)
dm.prepare_data()
dm.setup('fit')
model = GLUETransformer(num_labels=dm.num_labels, eval_splits=dm.eval_splits, **vars(args))
trainer = pl.Trainer.from_argparse_args(args)
return dm, model, trainer
```
# Training
## CoLA
See an interactive view of the CoLA dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=cola)
```
mocked_args = """
--model_name_or_path albert-base-v2
--task_name cola
--max_epochs 3
--gpus 1""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
## MRPC
See an interactive view of the MRPC dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=mrpc)
```
mocked_args = """
--model_name_or_path distilbert-base-cased
--task_name mrpc
--max_epochs 3
--gpus 1""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
## MNLI
- The MNLI dataset is huge, so we aren't going to bother trying to train it here.
- Let's just make sure our multi-dataloader logic is right by skipping over training and going straight to validation.
See an interactive view of the MRPC dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=mnli)
```
mocked_args = """
--model_name_or_path distilbert-base-uncased
--task_name mnli
--max_epochs 1
--gpus 1
--limit_train_batches 10
--progress_bar_refresh_rate 20""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
<code style="color:#792ee5;">
<h1> <strong> Congratulations - Time to Join the Community! </strong> </h1>
</code>
Congratulations on completing this notebook tutorial! If you enjoyed this and would like to join the Lightning movement, you can do so in the following ways!
### Star [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) on GitHub
The easiest way to help our community is just by starring the GitHub repos! This helps raise awareness of the cool tools we're building.
* Please, star [Lightning](https://github.com/PyTorchLightning/pytorch-lightning)
### Join our [Slack](https://join.slack.com/t/pytorch-lightning/shared_invite/zt-f6bl2l0l-JYMK3tbAgAmGRrlNr00f1A)!
The best way to keep up to date on the latest advancements is to join our community! Make sure to introduce yourself and share your interests in `#general` channel
### Interested by SOTA AI models ! Check out [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts)
Bolts has a collection of state-of-the-art models, all implemented in [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) and can be easily integrated within your own projects.
* Please, star [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts)
### Contributions !
The best way to contribute to our community is to become a code contributor! At any time you can go to [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) or [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts) GitHub Issues page and filter for "good first issue".
* [Lightning good first issue](https://github.com/PyTorchLightning/pytorch-lightning/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
* [Bolt good first issue](https://github.com/PyTorchLightning/pytorch-lightning-bolts/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
* You can also contribute your own notebooks with useful examples !
### Great thanks from the entire Pytorch Lightning Team for your interest !
<img src="https://github.com/PyTorchLightning/pytorch-lightning/blob/master/docs/source/_static/images/logo.png?raw=true" width="800" height="200" />
| github_jupyter |
# Spreadsheets Functions
## Logical
#### `=IF(logical_test, value_if_true, value_if_false)`
#### `Comparison operators: =, >, <, >=, <=, <>`
### `Comparison Functions : `
#### `=ISNA()`
#### `=ISNUMBER()`
#### `=ISTEXT()`
#### `=ISBLANK()`
#### `=ISNONTEXT()`
#### `=ISLOGICAL()`
## Text
#### `FIND("!", mytext):` Find the '!' in mytext and return the number
of characters it is from the start of the string.
#### `LEN(mytext): `Number of characters in mytext.
#### `=SUBSTITUTE :`(mytext, "!", "?"): Replace any "!" with "?" in mytext.
#### `=VALUE("6"): `Converts a number that is being stored as text to a number.
#### `=TRIM(mytext):` Remove any leading or trailing whitespaces like
the one leading this phrase.
#### `Split text into multiple cells:` Data -> Text to Columns
#### `=CONCAT("H","e","l","l","o"): ` Merge text from multiple cells into a single cell with no defined delimeter. "Hello"
#### `=mytext & " I think...":` Concatenate text using '&'...You can merge both cell references and constant strings. " Caught you smiling! I think..."
#### `=TEXTJOIN(delimeter="-", ignore_empty=TRUE, "210", "867", "5309"):` Place the delimeter between each string of text upon concatenation. "210-867-5309"
#### `=LEFT(mytext, 3): ` Return the first 3 characters from the left.
#### `=RIGHT(mytext, 3)` Return the first 3 characters from the right.
#### `=MID(mytext, 2, 3): ` Return the first 3 characters from the left, starting at character 2, so basically return characters 2, 3, & 4.
### Lookup and Reference
#### VLOOKUP : Vertical Lookup
- Looks for a value in the leftmost column of a table, and then returns a value in the same row from a column you specify. By default, the table must be sorted in an ascending order.
##### `=VLOOKUP(lookup_value,table_array,col_index_num,range_lookup)`
#### `Lookup_value: ` is the value to be found in the first row of the table and can be a value, a reference, or a text string.
#### `Table_array: ` is a table of text, numbers, or logical values in which data is looked up. Table_array can be a reference to a range or a range name.
#### `Col_index_num:` is the row number in table_array from which the matching value should be returned. The first row of values in the table is row 1.
#### `Range_lookup:` is a logical value: to find the closest match in the top row (sorted in ascending order) = TRUE or omitted; find an exact match = FALSE.
## Date & Time
#### `Extracting date parts from a date`
#### `mydate = '01/01/2019'`
##### `=WEEKDAY(mydate)`
##### `=DAY(mydate)`
##### `=MONTH(mydate)`
##### `=YEAR(mydate)`
#### `Formatting dates`
#### `See "more number formats" in the data type drop down menu to define a custom date format.`
##### `yy: 19`
| github_jupyter |
# Convolutional Neural Networks: Application
Welcome to Course 4's second assignment! In this notebook, you will:
- Implement helper functions that you will use when implementing a TensorFlow model
- Implement a fully functioning ConvNet using TensorFlow
**After this assignment you will be able to:**
- Build and train a ConvNet in TensorFlow for a classification problem
We assume here that you are already familiar with TensorFlow. If you are not, please refer the *TensorFlow Tutorial* of the third week of Course 2 ("*Improving deep neural networks*").
## 1.0 - TensorFlow model
In the previous assignment, you built helper functions using numpy to understand the mechanics behind convolutional neural networks. Most practical applications of deep learning today are built using programming frameworks, which have many built-in functions you can simply call.
As usual, we will start by loading in the packages.
```
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
import tensorflow as tf
from tensorflow.python.framework import ops
from cnn_utils import *
%matplotlib inline
np.random.seed(1)
```
Run the next cell to load the "SIGNS" dataset you are going to use.
```
# Loading the data (signs)
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
X_train_orig.shape
plt.imshow(X_test_orig[1,:,:,:])
```
As a reminder, the SIGNS dataset is a collection of 6 signs representing numbers from 0 to 5.
<img src="images/SIGNS.png" style="width:800px;height:300px;">
The next cell will show you an example of a labelled image in the dataset. Feel free to change the value of `index` below and re-run to see different examples.
```
# Example of a picture
index = 6
plt.imshow(X_train_orig[index])
print ("y = " + str(np.squeeze(Y_train_orig[:, index])))
```
In Course 2, you had built a fully-connected network for this dataset. But since this is an image dataset, it is more natural to apply a ConvNet to it.
To get started, let's examine the shapes of your data.
```
X_train = X_train_orig/255.
X_test = X_test_orig/255.
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}
```
### 1.1 - Create placeholders
TensorFlow requires that you create placeholders for the input data that will be fed into the model when running the session.
**Exercise**: Implement the function below to create placeholders for the input image X and the output Y. You should not define the number of training examples for the moment. To do so, you could use "None" as the batch size, it will give you the flexibility to choose it later. Hence X should be of dimension **[None, n_H0, n_W0, n_C0]** and Y should be of dimension **[None, n_y]**. [Hint](https://www.tensorflow.org/api_docs/python/tf/placeholder).
```
# GRADED FUNCTION: create_placeholders
def create_placeholders(n_H0, n_W0, n_C0, n_y):
"""
Creates the placeholders for the tensorflow session.
Arguments:
n_H0 -- scalar, height of an input image
n_W0 -- scalar, width of an input image
n_C0 -- scalar, number of channels of the input
n_y -- scalar, number of classes
Returns:
X -- placeholder for the data input, of shape [None, n_H0, n_W0, n_C0] and dtype "float"
Y -- placeholder for the input labels, of shape [None, n_y] and dtype "float"
"""
### START CODE HERE ### (≈2 lines)
X = tf.placeholder(shape = [None, n_H0, n_W0, n_C0],dtype=tf.float32)
Y = tf.placeholder(shape = [None, n_y],dtype=tf.float32)
### END CODE HERE ###
return X, Y
X, Y = create_placeholders(64, 64, 3, 6)
print ("X = " + str(X))
print ("Y = " + str(Y))
```
**Expected Output**
<table>
<tr>
<td>
X = Tensor("Placeholder:0", shape=(?, 64, 64, 3), dtype=float32)
</td>
</tr>
<tr>
<td>
Y = Tensor("Placeholder_1:0", shape=(?, 6), dtype=float32)
</td>
</tr>
</table>
### 1.2 - Initialize parameters
You will initialize weights/filters $W1$ and $W2$ using `tf.contrib.layers.xavier_initializer(seed = 0)`. You don't need to worry about bias variables as you will soon see that TensorFlow functions take care of the bias. Note also that you will only initialize the weights/filters for the conv2d functions. TensorFlow initializes the layers for the fully connected part automatically. We will talk more about that later in this assignment.
**Exercise:** Implement initialize_parameters(). The dimensions for each group of filters are provided below. Reminder - to initialize a parameter $W$ of shape [1,2,3,4] in Tensorflow, use:
```python
W = tf.get_variable("W", [1,2,3,4], initializer = ...)
```
[More Info](https://www.tensorflow.org/api_docs/python/tf/get_variable).
```
# GRADED FUNCTION: initialize_parameters
def initialize_parameters():
"""
Initializes weight parameters to build a neural network with tensorflow. The shapes are:
W1 : [4, 4, 3, 8]
W2 : [2, 2, 8, 16]
Returns:
parameters -- a dictionary of tensors containing W1, W2
"""
tf.set_random_seed(1) # so that your "random" numbers match ours
### START CODE HERE ### (approx. 2 lines of code)
W1 = tf.get_variable('W1', [4, 4, 3, 8], initializer = tf.contrib.layers.xavier_initializer(seed = 0))
W2 = tf.get_variable('W2', [2, 2, 8, 16], initializer = tf.contrib.layers.xavier_initializer(seed = 0))
### END CODE HERE ###
parameters = {"W1": W1,
"W2": W2}
return parameters
tf.reset_default_graph()
with tf.Session() as sess_test:
parameters = initialize_parameters()
init = tf.global_variables_initializer()
sess_test.run(init)
print("W1 = " + str(parameters["W1"].eval()[1,1,1]))
print("W2 = " + str(parameters["W2"].eval()[1,1,1]))
```
** Expected Output:**
<table>
<tr>
<td>
W1 =
</td>
<td>
[ 0.00131723 0.14176141 -0.04434952 0.09197326 0.14984085 -0.03514394 <br>
-0.06847463 0.05245192]
</td>
</tr>
<tr>
<td>
W2 =
</td>
<td>
[-0.08566415 0.17750949 0.11974221 0.16773748 -0.0830943 -0.08058 <br>
-0.00577033 -0.14643836 0.24162132 -0.05857408 -0.19055021 0.1345228 <br>
-0.22779644 -0.1601823 -0.16117483 -0.10286498]
</td>
</tr>
</table>
### 1.2 - Forward propagation
In TensorFlow, there are built-in functions that carry out the convolution steps for you.
- **tf.nn.conv2d(X,W1, strides = [1,s,s,1], padding = 'SAME'):** given an input $X$ and a group of filters $W1$, this function convolves $W1$'s filters on X. The third input ([1,f,f,1]) represents the strides for each dimension of the input (m, n_H_prev, n_W_prev, n_C_prev). You can read the full documentation [here](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d)
- **tf.nn.max_pool(A, ksize = [1,f,f,1], strides = [1,s,s,1], padding = 'SAME'):** given an input A, this function uses a window of size (f, f) and strides of size (s, s) to carry out max pooling over each window. You can read the full documentation [here](https://www.tensorflow.org/api_docs/python/tf/nn/max_pool)
- **tf.nn.relu(Z1):** computes the elementwise ReLU of Z1 (which can be any shape). You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/nn/relu)
- **tf.contrib.layers.flatten(P)**: given an input P, this function flattens each example into a 1D vector it while maintaining the batch-size. It returns a flattened tensor with shape [batch_size, k]. You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/contrib/layers/flatten)
- **tf.contrib.layers.fully_connected(F, num_outputs):** given a the flattened input F, it returns the output computed using a fully connected layer. You can read the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/contrib/layers/fully_connected)
In the last function above (`tf.contrib.layers.fully_connected`), the fully connected layer automatically initializes weights in the graph and keeps on training them as you train the model. Hence, you did not need to initialize those weights when initializing the parameters.
**Exercise**:
Implement the `forward_propagation` function below to build the following model: `CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED`. You should use the functions above.
In detail, we will use the following parameters for all the steps:
- Conv2D: stride 1, padding is "SAME"
- ReLU
- Max pool: Use an 8 by 8 filter size and an 8 by 8 stride, padding is "SAME"
- Conv2D: stride 1, padding is "SAME"
- ReLU
- Max pool: Use a 4 by 4 filter size and a 4 by 4 stride, padding is "SAME"
- Flatten the previous output.
- FULLYCONNECTED (FC) layer: Apply a fully connected layer without an non-linear activation function. Do not call the softmax here. This will result in 6 neurons in the output layer, which then get passed later to a softmax. In TensorFlow, the softmax and cost function are lumped together into a single function, which you'll call in a different function when computing the cost.
```
# GRADED FUNCTION: forward_propagation
def forward_propagation(X, parameters):
"""
Implements the forward propagation for the model:
CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
Arguments:
X -- input dataset placeholder, of shape (input size, number of examples)
parameters -- python dictionary containing your parameters "W1", "W2"
the shapes are given in initialize_parameters
Returns:
Z3 -- the output of the last LINEAR unit
"""
# Retrieve the parameters from the dictionary "parameters"
W1 = parameters['W1']
W2 = parameters['W2']
### START CODE HERE ###
# CONV2D: stride of 1, padding 'SAME'
Z1 = tf.nn.conv2d(X,W1, strides = [1,1,1,1], padding = 'SAME')
# RELU
A1 = tf.nn.relu(Z1)
# MAXPOOL: window 8x8, sride 8, padding 'SAME'
P1 = tf.nn.max_pool(A1, ksize = [1,8,8,1], strides = [1,8,8,1], padding = 'SAME')
# CONV2D: filters W2, stride 1, padding 'SAME'
Z2 = tf.nn.conv2d(P1,W2, strides = [1,1,1,1], padding = 'SAME')
# RELU
A2 = tf.nn.relu(Z2)
# MAXPOOL: window 4x4, stride 4, padding 'SAME'
P2 = tf.nn.max_pool(A2, ksize = [1,4,4,1], strides = [1,4,4,1], padding = 'SAME')
# FLATTEN
P2 = tf.contrib.layers.flatten(P2)
# FULLY-CONNECTED without non-linear activation function (not not call softmax).
# 6 neurons in output layer. Hint: one of the arguments should be "activation_fn=None"
Z3 = tf.contrib.layers.fully_connected(P2, 6,activation_fn=None)
### END CODE HERE ###
return Z3
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(64, 64, 3, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(Z3, {X: np.random.randn(2,64,64,3), Y: np.random.randn(2,6)})
print("Z3 = " + str(a))
```
**Expected Output**:
<table>
<td>
Z3 =
</td>
<td>
[[-0.44670227 -1.57208765 -1.53049231 -2.31013036 -1.29104376 0.46852064] <br>
[-0.17601591 -1.57972014 -1.4737016 -2.61672091 -1.00810647 0.5747785 ]]
</td>
</table>
### 1.3 - Compute cost
Implement the compute cost function below. You might find these two functions helpful:
- **tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y):** computes the softmax entropy loss. This function both computes the softmax activation function as well as the resulting loss. You can check the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits)
- **tf.reduce_mean:** computes the mean of elements across dimensions of a tensor. Use this to sum the losses over all the examples to get the overall cost. You can check the full documentation [here.](https://www.tensorflow.org/api_docs/python/tf/reduce_mean)
** Exercise**: Compute the cost below using the function above.
```
# GRADED FUNCTION: compute_cost
def compute_cost(Z3, Y):
"""
Computes the cost
Arguments:
Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
Y -- "true" labels vector placeholder, same shape as Z3
Returns:
cost - Tensor of the cost function
"""
### START CODE HERE ### (1 line of code)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y))
### END CODE HERE ###
return cost
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(64, 64, 3, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(cost, {X: np.random.randn(4,64,64,3), Y: np.random.randn(4,6)})
print("cost = " + str(a))
```
**Expected Output**:
<table>
<td>
cost =
</td>
<td>
2.91034
</td>
</table>
## 1.4 Model
Finally you will merge the helper functions you implemented above to build a model. You will train it on the SIGNS dataset.
You have implemented `random_mini_batches()` in the Optimization programming assignment of course 2. Remember that this function returns a list of mini-batches.
**Exercise**: Complete the function below.
The model below should:
- create placeholders
- initialize parameters
- forward propagate
- compute the cost
- create an optimizer
Finally you will create a session and run a for loop for num_epochs, get the mini-batches, and then for each mini-batch you will optimize the function. [Hint for initializing the variables](https://www.tensorflow.org/api_docs/python/tf/global_variables_initializer)
```
# GRADED FUNCTION: model
def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.009,
num_epochs = 100, minibatch_size = 64, print_cost = True):
"""
Implements a three-layer ConvNet in Tensorflow:
CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
Arguments:
X_train -- training set, of shape (None, 64, 64, 3)
Y_train -- test set, of shape (None, n_y = 6)
X_test -- training set, of shape (None, 64, 64, 3)
Y_test -- test set, of shape (None, n_y = 6)
learning_rate -- learning rate of the optimization
num_epochs -- number of epochs of the optimization loop
minibatch_size -- size of a minibatch
print_cost -- True to print the cost every 100 epochs
Returns:
train_accuracy -- real number, accuracy on the train set (X_train)
test_accuracy -- real number, testing accuracy on the test set (X_test)
parameters -- parameters learnt by the model. They can then be used to predict.
"""
ops.reset_default_graph() # to be able to rerun the model without overwriting tf variables
tf.set_random_seed(1) # to keep results consistent (tensorflow seed)
seed = 3 # to keep results consistent (numpy seed)
(m, n_H0, n_W0, n_C0) = X_train.shape
n_y = Y_train.shape[1]
costs = [] # To keep track of the cost
# Create Placeholders of the correct shape
### START CODE HERE ### (1 line)
X, Y = create_placeholders(n_H0,n_W0,n_C0,n_y)
### END CODE HERE ###
# Initialize parameters
### START CODE HERE ### (1 line)
parameters = initialize_parameters()
### END CODE HERE ###
# Forward propagation: Build the forward propagation in the tensorflow graph
### START CODE HERE ### (1 line)
Z3 = forward_propagation(X, parameters)
### END CODE HERE ###
# Cost function: Add cost function to tensorflow graph
### START CODE HERE ### (1 line)
cost = compute_cost(Z3, Y)
### END CODE HERE ###
# Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer that minimizes the cost.
### START CODE HERE ### (1 line)
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
### END CODE HERE ###
# Initialize all the variables globally
init = tf.global_variables_initializer()
# Start the session to compute the tensorflow graph
with tf.Session() as sess:
# Run the initialization
sess.run(init)
# Do the training loop
for epoch in range(num_epochs):
minibatch_cost = 0.
num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
seed = seed + 1
minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# IMPORTANT: The line that runs the graph on a minibatch.
# Run the session to execute the optimizer and the cost, the feedict should contain a minibatch for (X,Y).
### START CODE HERE ### (1 line)
_ , temp_cost = sess.run([optimizer,cost],feed_dict={X:minibatch_X,Y:minibatch_Y})
### END CODE HERE ###
minibatch_cost += temp_cost / num_minibatches
# Print the cost every epoch
if print_cost == True and epoch % 5 == 0:
print ("Cost after epoch %i: %f" % (epoch, minibatch_cost))
if print_cost == True and epoch % 1 == 0:
costs.append(minibatch_cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# Calculate the correct predictions
predict_op = tf.argmax(Z3, 1)
correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))
# Calculate accuracy on the test set
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print(accuracy)
train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
print("Train Accuracy:", train_accuracy)
print("Test Accuracy:", test_accuracy)
return train_accuracy, test_accuracy, parameters
```
Run the following cell to train your model for 100 epochs. Check if your cost after epoch 0 and 5 matches our output. If not, stop the cell and go back to your code!
```
_, _, parameters = model(X_train, Y_train, X_test, Y_test)
```
**Expected output**: although it may not match perfectly, your expected output should be close to ours and your cost value should decrease.
<table>
<tr>
<td>
**Cost after epoch 0 =**
</td>
<td>
1.917929
</td>
</tr>
<tr>
<td>
**Cost after epoch 5 =**
</td>
<td>
1.506757
</td>
</tr>
<tr>
<td>
**Train Accuracy =**
</td>
<td>
0.940741
</td>
</tr>
<tr>
<td>
**Test Accuracy =**
</td>
<td>
0.783333
</td>
</tr>
</table>
Congratulations! You have finised the assignment and built a model that recognizes SIGN language with almost 80% accuracy on the test set. If you wish, feel free to play around with this dataset further. You can actually improve its accuracy by spending more time tuning the hyperparameters, or using regularization (as this model clearly has a high variance).
Once again, here's a thumbs up for your work!
```
fname = "images/thumbs_up.jpg"
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(64,64))
plt.imshow(my_image)
```
| github_jupyter |
# Rebound model
Aim: Quantify the environmental impact due to the savings of households in consumption expenses, across different
- industrial sectors and scenarios:
- housing (rent): baseline for 2011,
- energy: efficient_devices, renewable_energy
- food-waste: avoidable_waste_saving
- clothing: sufficiency, refuse, reshare, reuse for 2025
- furnishing: refuse, reuse for 2035 and 2050
- temporal periods: years 2006-2017
- spatial regions: parts of Switzerland
_Input_: The household budet survey files to train the data
_Model_: A random forest or Artificial neural network model
_Output_: The rebound expenses and environmental footprints of the households
TOC<a id="toc"></a>
- <a href="#ini"> Step 0: Initialisation</a>
- <a href="#preprocess"> Step 1: Preprocessing</a>
- <a href="#model"> Step 2: Model </a>
- <a href="#post"> Step 3: Postprocessing </a>
- <a href="#lca"> Step 4: LCA </a>
Author: Rhythima Shinde, ETH Zurich
Co-Authors (for energy case study and temporal-regional rebound studies): Sidi Peng, Saloni Vijay, ETH Zurich
-------------------------------------------------------------------------------------------------------------------------------
## 0. Initialisation <a id = 'ini'></a>
<a href="#toc">back</a>
### 0.1. Input files & data parameters
- (1a) **seasonal_file** -> For the year 2009-11, the file is provided by <a href= https://pubs.acs.org/doi/full/10.1021/acs.est.8b01452>A.Froemelt</a>. It is modified based on original HBS(HABE) data that we <a href = https://www.bfs.admin.ch/bfs/en/home/statistics/economic-social-situation-population/surveys/hbs.html>obtain from Federal Statistical Office of Switzerland</a>. It is further modiefied in this code in the <a href='#preprocess'>preprocessing section</a> to rename columns.
- (1b) **seasonal_file_SI** -> Lists the HBS data columns and associated activities to calculate the consumption based environmental footprint. <a href=https://pubs.acs.org/doi/abs/10.1021/acs.est.8b01452>The file can be found here.</a>
- (2) **habe_month** -> the HBS household ids and their derivation to the month and year of the survey filled
- (3) dependent_indices -> based on the HBS column indices, this file lists the relevant consumption expense parameters which are predicted
- (4) **independent_indices** -> the HBS column indices which define the household socio-economic properties
- (5) **target_data** -> Selects the target dataset to predict the results. For most cases, it is the subset of the HBS (for the housing industry, it is the partner dataset 'ABZ', 'SCHL' or 'SM')
- (6) **directory_name** -> based on the industry case, changes the dependent parameters, and income saved by the household (due to which the rebound is supposed to happen) - change the second value in the list.
### 0.2. Model parameters
- (1) **iter_n** -> no.of iterations of runs
- (2) **model_name** -> Random Forest (RF) or ANN (Artificial Neural Network)
### 0.3. Analysis parameters
- (1) industry change: directory_name with following dependencies
- scenarios,
- partner_name/target dataset,
- idx_column_savings_cons,
- dependent_indices
- (2) year change: seasonal_file
- specify which years (2006, 2007, 2008... 2017)
- (3) regional change: target_dataset
- specify which regions (DE, IT, FR, ZH)
- specify partner name (ABZ, SCHL, SM)
#### <p style='color:blue'>USER INPUT NEEDED: chose model settings, methods of preprocessing </p>
```
# model and folder settings
directory_name = 'housing' # 'housing' or 'furniture' or 'clothing' or 'energy'
iter_n=1
model_name='RF' # 'RF' or 'ANN'
## preprocessing methods
option_deseason = 'deseasonal' # 'deseasonal' [option 1] or 'month-ind' [option 2]
if option_deseason == 'month-ind':
n_ind = 63
independent_indices='raw_data/independent_month.csv'
if option_deseason == 'deseasonal':
n_ind = 39
independent_indices='raw_data/independent.csv'
input_normalise = 'no-normalise' #'no-normalise' for not normalising the data or 'normalise'
import pandas as pd
import numpy as np
import sklearn.multioutput as sko
from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier
import scipy.stats as stats
import statistics
from sklearn.metrics import r2_score,mean_squared_error, explained_variance_score
from sklearn.model_selection import cross_val_score, KFold, train_test_split, StratifiedShuffleSplit
from sklearn.preprocessing import FunctionTransformer
import matplotlib.pyplot as plt
import brightway2
import seaborn as sns
from statsmodels.stats.multicomp import pairwise_tukeyhsd, MultiComparison
import statsmodels.api as sm
from functools import reduce
import os
import pickle
import csv
# Additional libraries for neural network implementation
# from numpy.random import seed
# seed(1)
# from tensorflow import set_random_seed
# set_random_seed(2)
# from keras import optimizers
# from keras.models import Sequential
# from keras.layers import Dense
# from keras.wrappers.scikit_learn import KerasRegressor
# Read the modified files by Nauser et al (2020)
# - HBS data (merged raw HBS files) "HABE_mergerd_2006_2017"
# - tranlsation file 'HABE_Cname_translator.xlsx'
# - HBS hhids with the corresponding month of the survey
###############################################################################################################################
seasonal_file = 'raw_data/HBS/HABE_merged_2006_2017.csv'
seasonal_file_SI = 'raw_data/HBS/HABE_Cname_translator.xlsx'
habe_month = 'raw_data/HBS/HABE_date.csv'
inf_index_file = 'raw_data/HBS/HABE_inflation_index_all.xlsx'
# seasonal_file = 'original_Andi_HBS/habe20092011_hh_prepared_imputed.csv' #based on the years
# seasonal_file_SI='original_Andi_HBS/Draft_Paper_8_v11_SupportingInformation.xlsx'
# habe_month='original_Andi_HBS/habe_hh_month.csv'
## form the databases
df_habe = pd.read_csv(seasonal_file, delimiter=',', error_bad_lines=False, encoding='ISO-8859–1')
df_habe_month = pd.read_csv(habe_month, delimiter=',', error_bad_lines=False, encoding='ISO-8859–1')
inf_index = pd.read_excel(inf_index_file)
dependent_indices= 'raw_data/dependent_'+directory_name+'.csv'
dependent_indices_pd = pd.read_csv(dependent_indices, delimiter=',', encoding='ISO-8859–1')
dependent_indices_pd_name = pd.read_csv(dependent_indices,sep=',')["name"]
dependentsize=len(list(dependent_indices_pd_name))
independent_indices_pd = pd.read_csv(independent_indices, delimiter=',', encoding='ISO-8859–1')
list_independent_columns = pd.read_csv(independent_indices, delimiter=',', encoding='ISO-8859–1')['name'].to_list()
list_dependent_columns = pd.read_csv(dependent_indices, delimiter=',', encoding='ISO-8859–1')['name'].to_list()
#add more columns to perform temporal analysis (month_names and time_periods)
def label_month (row):
if row['month'] == 1.0 :
return 'January'
if row['month'] == 2.0 :
return 'February'
if row['month'] == 3.0 :
return 'March'
if row['month'] == 4.0 :
return 'April'
if row['month'] == 5.0 :
return 'May'
if row['month'] == 6.0 :
return 'June'
if row['month'] == 7.0 :
return 'July'
if row['month'] == 8.0 :
return 'August'
if row['month'] == 9.0 :
return 'September'
if row['month'] == 10.0 :
return 'October'
if row['month'] == 11.0 :
return 'November'
if row['month'] == 12.0 :
return 'December'
def label_period (row):
if (row["year"] == 2006) or (row["year"] == 2007) or (row["year"] == 2008):
return '1'
if (row["year"] == 2009) or (row["year"] == 2010) or (row["year"] == 2011):
return '2'
if (row["year"] == 2012) or (row["year"] == 2013) or (row["year"] == 2014):
return '3'
if (row["year"] == 2015) or (row["year"] == 2016) or (row["year"] == 2017):
return '4'
df_habe_month['month_name']=df_habe_month.apply(lambda row: label_month(row), axis=1)
df_habe_month['period']=df_habe_month.apply(lambda row: label_month(row), axis=1)
```
<p style = 'color:red'> TODO: update the right values for energy and food industry scenarios, and then merge in the above script </p>
```
if directory_name =='housing':
scenarios = {'baseline_2011':500}
target_data ='ABZ'
# target_data = 'subset-HBS'
idx_column_savings_cons = 'net_rent_and_mortgage_interest_of_principal_residence' #289
if directory_name == 'furniture':
scenarios = {'refuse_2035':17,'refuse_2050':17.4,'reuse_1_2035':6.9,
'reuse_1_2050':8.2,'reuse_2_2035':10.2,'reuse_2_2050':9.5}
target_data = 'subset-HBS'
idx_column_savings_cons = 'furniture_and_furnishings,_carpets_and_other_floor_coverings_incl._repairs' #313
if directory_name == 'clothing':
scenarios = {'sufficiency_2025':76.08,'refuse_2025':5.7075,'share_2025':14.2875,'local_reuse_best_2025':9.13,
'local_reuse_worst_2025':4.54,'max_local_reuse_best_2025':10.25,'max_local_reuse_worst_2025':6.83}
target_data = 'subset-HBS'
idx_column_savings_cons = 'clothing' #248
if directory_name == 'energy':
scenarios = {'efficient_devices':30,'renewable_energy':300}
target_data = 'subset-HBS'
idx_column_savings_cons = 'energy_of_principal_residence' #297
if directory_name == 'food':
scenarios = {'avoidable_waste_saving':50}
target_data = 'subset-HBS'
idx_column_savings_cons = 'food_and_non_alcoholic_beverages' #97
#functions to make relevant sector-wise directories
def make_pre_directory(outname,directory_name):
outdir = 'preprocessing/'+directory_name
if not os.path.exists(outdir):
os.mkdir(outdir)
fullname = os.path.join(outdir, outname)
return fullname
def make_pre_sub_directory(outname,directory_name,sub_dir):
outdir = 'preprocessing/'+directory_name+'/'+sub_dir
outdir1 = 'preprocessing/'+directory_name
if not os.path.exists(outdir1):
os.mkdir(outdir1)
if not os.path.exists(outdir):
os.mkdir(outdir)
fullname = os.path.join(outdir, outname)
return fullname
def make_pre_sub_sub_directory(outname,directory_name,sub_dir,sub_sub_dir):
outdir='preprocessing/'+directory_name+'/'+sub_dir+'/'+sub_sub_dir
outdir1 = 'preprocessing/'+directory_name+'/'+sub_dir
outdir2 = 'preprocessing/'+directory_name
if not os.path.exists(outdir2):
os.mkdir(outdir2)
if not os.path.exists(outdir1):
os.mkdir(outdir1)
if not os.path.exists(outdir):
os.mkdir(outdir)
fullname = os.path.join(outdir, outname)
return fullname
```
## 1. Preprocessing <a id = 'preprocess' ></a>
TOC: <a id = 'toc-pre-pre'></a>
- <a href = #rename>1.1. Prepare training data</a>
- <a href = #deseasonal>1.2. Deseasonalise</a>
- <a href = #normal>1.3. Normalize</a>
- <a href = #check>1.4. Checks</a>
### 1.1. Prepare training data <a id='rename'></a>
<a href='#toc-pre'>back</a>
#### 1.1.1. Rename HBS columns
```
var_translate = pd.read_excel(seasonal_file_SI, sheet_name='translator', header=3,
usecols=['habe_code', 'habe_eng_p', 'habe_eng', 'vcode', 'qcode'])
var_translate['habe_eng'] = var_translate['habe_eng'].str.strip()
var_translate['habe_eng'] = var_translate['habe_eng'].str.replace(' ', '_')
var_translate['habe_eng'] = var_translate['habe_eng'].str.replace('-', '_')
var_translate['habe_eng'] = var_translate['habe_eng'].str.replace('"', '')
var_translate['habe_eng'] = var_translate['habe_eng'].str.lower()
var_translate['habe_code'] = var_translate['habe_code'].str.lower()
dict_translate = dict(zip(var_translate['habe_code'], var_translate['habe_eng']))
df_habe.rename(columns=dict_translate, inplace=True)
dict_translate = dict(zip(var_translate['qcode'], var_translate['habe_eng']))
df_habe.rename(columns=dict_translate, inplace=True)
df_habe_rename = df_habe.loc[:, ~df_habe.columns.duplicated()]
pd.DataFrame.to_csv(df_habe_rename, 'preprocessing/0_habe_rename.csv', sep=',',index=False)
```
#### 1.1.2. Inflation adjustment
```
df_habe_rename = pd.read_csv('preprocessing/0_habe_rename.csv')
df_new = pd.merge(df_habe_rename, df_habe_month, on='haushaltid')
pd.DataFrame.to_csv(df_new,'preprocessing/0_habe_rename_month.csv', sep=',',index=False)
list_var_total = dependent_indices_pd_name.tolist()
list_var_total.pop()
# monetary variables inflation adjusted
list_mon = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
list_year = [2006, 2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016]
list_var_total = list_var_total + ["disposable_income", "total_expenditures"]
# , 'infrequent_income']
df_inf = df_new
for col in list_var_total:
for year in list_year:
for mon in list_mon:
df_inf.loc[(df_inf['year'] == year) & (df_inf['month'] == mon), col] = \
df_inf.loc[(df_inf['year'] == year) & (df_inf['month'] == mon), col] / \
inf_index.loc[(inf_index['year'] == year) & (inf_index['month'] == mon), col].values * 100
pd.DataFrame.to_csv(df_inf, 'preprocessing/1_habe_inflation.csv', sep=',', index=False, encoding='utf-8')
```
#### 1.1.3. Adapt the columns (optional - one hot encoding)
```
def new_columns(xx,directory_name):
pd_df_saved = df_inf
pd_df_saved.loc[:,'disposable_income'] = pd_df_saved['disposable_income'] - pd_df_saved.loc[:,xx]
# pd_df_saved['total_expenditures'] = pd_df_saved['total_expenditures'] - pd_df_saved.iloc[:,313]
fullname = make_pre_directory('1_habe_rename_new_columns.csv',directory_name)
pd.DataFrame.to_csv(pd_df_saved,fullname, sep=',',index=False)
return pd_df_saved
df_habe_rename_saved = new_columns(idx_column_savings_cons,directory_name) # when redefining disposable income
```
#### 1.1.4. Remove outliers
```
def remove_outliers():
df_outliers = df_habe_rename_saved # TODO if using the new definition of disposable income: use the df_habe_rename_saved
# df_outliers = df_outliers[np.abs(stats.zscore(df_outliers['disposable_income']))<10]
# df_outliers = df_outliers[np.abs(stats.zscore(df_outliers['saved_amount_(computed)']))<10]
df_outliers = df_outliers[df_outliers['disposable_income'] >= 0] # simply keep all the 'sensible' disposable incomes
# df_outliers = df_outliers[df_outliers['disposable_income'] <= 14800] # ADDED CRITERIA FOR REMOVING OUTLIERS OF THE DISP_INCOME
# df_outliers = df_outliers[df_outliers['total_expenditures'] >= 0] # simply keep all the 'sensible' total_expenses
df_outliers = df_outliers[df_outliers['saved_amount_(computed)'] >= 0]
fullname = make_pre_directory('2_habe_rename_removeoutliers.csv',directory_name)
pd.DataFrame.to_csv(df_outliers, fullname, sep=',', index=False)
return df_outliers
df_habe_outliers = remove_outliers()
## aggregate the data as per the categories
def accumulate_categories_habe(df,new_column,file_name):
list_dependent_columns = pd.read_csv(dependent_indices, delimiter=',', encoding='ISO-8859–1')['name'].to_list()
list_dependent_columns_new = list_dependent_columns
list_dependent_columns_new.append('disposable_income')
list_dependent_columns_new.append(new_column) # Might not always need this
df = df[list_dependent_columns_new]
df = df.loc[:,~df.columns.duplicated()] #drop duplicates
df[new_column] = df.iloc[:, [17]]
df['income'] = df.iloc[:, [16]]
df['food'] = df.iloc[:,[0,1,2]].sum(axis=1)
df['misc'] = df.iloc[:,[3,4]].sum(axis=1)
df['housing'] = df.iloc[:, [5, 6]].sum(axis=1)
df['services'] = df.iloc[:, [7,8,9]].sum(axis=1)
df['travel'] = df.iloc[:, [10,11,12, 13, 14]].sum(axis=1)
df['savings'] = df.iloc[:, [15]]
df = df[['income','food','misc','housing','services','travel','savings',new_column]]
fullname = make_pre_directory(file_name,directory_name)
pd.DataFrame.to_csv(df,fullname,sep=',',index= False)
return df
df_outliers = pd.read_csv('preprocessing/'+directory_name+'/2_habe_rename_removeoutliers.csv')
df_habe_accumulate = accumulate_categories_habe(df_outliers,'month_name','2_habe_rename_removeoutliers_aggregated.csv')
```
### 1.2. Deasonalising <a id='deseasonal'></a>
- [Option 1] Clustering based on months
- [Option 2] Use month and period as independent variable
<a href = #toc-pre-pre>back</a>
#### 1.2.1. [Option 1] Create monthly datasets, Plots/ Tables / Statistical tests for HABE monthly data
```
if option_deseason == 'deseasonal' :
def split_month():
df_new = pd.read_csv('preprocessing/'+directory_name+'/2_habe_rename_removeoutliers.csv')
df_month = df_new.groupby('month_name')
for i in range(12):
df_new_month=pd.DataFrame(list(df_month)[i][1])
df_new_month['month_name']=df_new_month['month_name'].astype('str')
fullname=make_pre_sub_directory('3_habe_monthly_'+df_new_month.month_name.unique()[0]+'.csv',
directory_name,option_deseason)
pd.DataFrame.to_csv(df_new_month,fullname,sep=',', index = False)
split_month()
# Split the accumulated categories per month
def split_month_accumulated():
df_new = pd.read_csv('preprocessing/'+directory_name+'/2_habe_rename_removeoutliers_aggregated.csv',sep=',')
df_month = df_new.groupby('month_name')
for i in range(12):
df_new_month=pd.DataFrame(list(df_month)[i][1])
df_new_month['month_name']=df_new_month['month_name'].astype('str')
fullname = make_pre_sub_directory('3_habe_monthly_'+df_new_month.month_name.unique()[0]+'_aggregated.csv',
directory_name,option_deseason)
pd.DataFrame.to_csv(df_new_month,fullname, sep=',', index = False)
split_month_accumulated()
```
#### 1.2.2. [Option 1] Making final clusters <a id ='finalclusters'></a>
<p style = 'color:blue'>USER INPUT NEEDED: edit the cluster-list below</p>
<p style = 'color:red'>TODO - join clusters based on the p-values calculated above directly</p>
```
## current clusters are made based on the mean table above
if option_deseason == 'deseasonal' :
Cluster_month_lists = {1:('January',),2:('February','March','April'),3:('May','June','July'),
4:('August','September','October','November'),5:('December',)}
cluster_number_length = len(Cluster_month_lists)
for key in Cluster_month_lists:
df1=[]
df_sum=[]
for i in range(0,len(Cluster_month_lists[key])):
print(Cluster_month_lists[key])
df=pd.read_csv(make_pre_sub_directory('3_habe_monthly_{}'.format(Cluster_month_lists[key][i])+'.csv',
directory_name,option_deseason))
df_sum.append(df.shape[0])
df1.append(df)
df_cluster = pd.concat(df1)
assert df_cluster.shape[0]==sum(df_sum) # to check if the conacting was done correctly
pd.DataFrame.to_csv(df_cluster,make_pre_sub_directory('4_habe_monthly_cluster_'+str(key)+'.csv',
directory_name,option_deseason),sep=',')
# TODO: update this to move to the sub directory of deseaspnal files
# cluster_number_length = len(Cluster_month_lists)
# for i in list(range(1,cluster_number_length+1)):
# accumulate_categories_habe(df,'number_of_persons_per_household','4_habe_monthly_cluster_'+str(i)+'_aggregated.csv')
```
#### 1.2.3. Option 2: Month as independent variable
```
if option_deseason == 'month-ind' :
cluster_number_length = 1
# do one-hot encoding for month and year
hbs_all = pd.read_csv('preprocessing/'+directory_name+'/1_habe_rename_new_columns.csv')
month_encoding = pd.get_dummies(hbs_all.month_name, prefix='month')
year_encoding = pd.get_dummies(hbs_all.year, prefix='year')
hbs_all_encoding = pd.concat([hbs_all, month_encoding.reindex(month_encoding.index)], axis=1)
hbs_all_encoding = pd.concat([hbs_all_encoding, year_encoding.reindex(year_encoding.index)], axis=1)
for key in scenarios:
output_encoding = make_pre_sub_sub_directory('3_habe_for_all_scenarios_encoding.csv',
directory_name,option_deseason,key)
pd.DataFrame.to_csv(hbs_all_encoding,output_encoding,sep=',',index=False)
month_name = month_encoding.columns.tolist()
year_name = year_encoding.columns.tolist()
```
### 1.3. Normalisation <a id='normal'></a>
<a href='#toc-pre'>back</a>
#### 1.3.1. Normalisation of HBS and target data
```
# ## NORMALISATION
# if input_normalise == 'normalise':
# def normalise_habe(cluster):
# transformer = FunctionTransformer(np.log1p, validate=True)
# if option_deseason == 'deseasonal':
# df_deseasonal_file = pd.read_csv('preprocessing/'+directory_name+ '/' + option_deseason +
# '/4_habe_monthly_cluster_'+str(cluster)+'.csv',
# delimiter=',')
# if option_deseason == 'month-ind':
# df_deseasonal_file = pd.read_csv('preprocessing/'+directory_name+ '/' + option_deseason +
# '/3_habe_for_all_scenarios_encoding.csv',delimiter=',')
# pd_df_new = df_deseasonal_file
# for colsss in list_dependent_columns:
# pd_df_new[[colsss]] = transformer.transform(df_deseasonal_file[[colsss]])
# for colsss in list_independent_columns:
# min_colsss = df_deseasonal_file[[colsss]].quantile([0.01]).values[0]
# max_colsss = df_deseasonal_file[[colsss]].quantile([0.99]).values[0]
# pd_df_new[[colsss]] = (df_deseasonal_file[[colsss]] - min_colsss) / (max_colsss - min_colsss)
# pd_df = pd_df_new[list_independent_columns+['haushaltid']+list_dependent_columns]
# pd_df = pd_df.fillna(0)
# fullname = make_pre_directory('4_habe_deseasonal_'+str(cluster)+'_'+str(option_deseason)+'_normalised.csv',
# directory_name)
# pd.DataFrame.to_csv(pd_df,fullname,sep=',',index=False)
# if target_data == 'ABZ':
# if input_normalise =='normalise':
# def normalise_partner(i,key,option_deseason):
# pd_df_partner = pd.read_csv('target_'+target_data+'.csv',delimiter=',')
# df_complete = pd.read_csv('preprocessing/'+directory_name+'/2_habe_rename_removeoutliers.csv',delimiter=',')
# pd_df_partner['disposable_income'] = pd_df_partner['disposable_income'] + i
# for colsss in list_independent_columns:
# min_colsss = df_complete[[colsss]].quantile([0.01]).values[0]
# max_colsss = df_complete[[colsss]].quantile([0.99]).values[0]
# pd_df_partner[[colsss]] = (pd_df_partner[[colsss]] - min_colsss) / (max_colsss - min_colsss)
# # pd_df_partner = pd_df_partner[pd_df_partner.iloc[:,30]<=1]
# # pd_df_partner = pd_df_partner[pd_df_partner.iloc[:,32]<=1]
# # pd_df_partner = pd_df_partner[pd_df_partner.iloc[:,33]>=0] #todo remove rows with normalisation over the range
# fullname = make_pre_sub_sub_directory('5_final_'+ target_data + '_independent_final_'+str(i)+'.csv',
# directory_name,option_deseason,key)
# pd.DataFrame.to_csv(pd_df_partner,fullname,sep=',',index=False)
# return pd_df_partner
```
#### 1.3.2. Preprocessing without normalisation
```
if input_normalise == 'no-normalise':
def normalise_habe(cluster):
transformer = FunctionTransformer(np.log1p, validate=True)
if option_deseason == 'deseasonal':
df_deseasonal_file = pd.read_csv('preprocessing/'+directory_name+ '/' + option_deseason +
'/4_habe_monthly_cluster_'+str(cluster)+'.csv',
delimiter=',')
if option_deseason == 'month-ind':
df_deseasonal_file = pd.read_csv('preprocessing/'+directory_name+ '/' + str(option_deseason) + '/' + str(key) +
'/3_habe_for_all_scenarios_encoding.csv',delimiter=',')
pd_df_new = df_deseasonal_file
pd_df = pd_df_new[list_independent_columns+['haushaltid']+list_dependent_columns]
pd_df = pd_df.fillna(0)
fullname = make_pre_sub_directory('4_habe_deseasonal_'+str(cluster)+'_short.csv',
directory_name,option_deseason)
pd.DataFrame.to_csv(pd_df,fullname,sep=',',index=False)
for i in list(range(1,cluster_number_length+1)):
df_normalise_habe_file = normalise_habe(i)
## Collecting the independent and dependent datasets
def truncate_all(key):
if option_deseason == 'deseasonal':
df_seasonal_normalised = pd.read_csv('preprocessing/'+directory_name+'/2_habe_rename_removeoutliers.csv',
delimiter=',', error_bad_lines=False)
if option_deseason == 'month-ind':
df_seasonal_normalised = pd.read_csv('preprocessing/'+directory_name+ '/' + str(option_deseason) + '/' + str(key) +
'/3_habe_for_all_scenarios_encoding.csv',delimiter=',')
df_habe_imputed_clustered_d = df_seasonal_normalised[list_dependent_columns]
df_habe_imputed_clustered_i = df_seasonal_normalised[list_independent_columns]
fullname_d = make_pre_sub_sub_directory('raw_dependent.csv',directory_name,option_deseason,key)
fullname_in = make_pre_sub_sub_directory('raw_independent.csv',directory_name,option_deseason,key)
pd.DataFrame.to_csv(df_habe_imputed_clustered_d,fullname_d,sep=',',index=False)
pd.DataFrame.to_csv(df_habe_imputed_clustered_i,fullname_in,sep=',',index=False)
for key in scenarios:
truncate_all(key)
## NORMALISATION
if target_data == 'subset-HBS':
def normalise_partner(i,key,option_deseason):
N = 300 # TODO pass this as an argument when chosing subset of HBS
pd_df_partner = pd.read_csv('preprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/raw_independent.csv',
delimiter=',', error_bad_lines=False)
pd_df_partner = pd_df_partner.sample(frac=0.4, replace=True, random_state=1)
pd_df_partner['disposable_income'] = pd_df_partner['disposable_income']+i
fullname = make_pre_sub_sub_directory('5_final_'+ target_data + '_independent_final_'+str(i)+'.csv',
directory_name,option_deseason,key)
pd.DataFrame.to_csv(pd_df_partner,fullname,sep=',',index=False)
return pd_df_partner
if target_data == 'ABZ':
if input_normalise =='no-normalise':
def normalise_partner(i,key,option_deseason):
pd_df_partner = pd.read_csv('raw_data/target_'+target_data+'.csv',delimiter=',')
df_complete = pd.read_csv('preprocessing/'+directory_name+'/2_habe_rename_removeoutliers.csv',delimiter=',')
pd_df_partner['disposable_income'] = pd_df_partner['disposable_income'] - i
# pd_df_partner = pd_df_partner[pd_df_partner.iloc[:,30]<=1]
# pd_df_partner = pd_df_partner[pd_df_partner.iloc[:,32]<=1]
# pd_df_partner = pd_df_partner[pd_df_partner.iloc[:,33]>=0] #todo remove rows with normalisation over the range
fullname = make_pre_sub_sub_directory('5_final_'+ target_data + '_independent_final_'+str(i)+'.csv',
directory_name,option_deseason,key)
pd.DataFrame.to_csv(pd_df_partner,fullname,sep=',',index=False)
return pd_df_partner
for key in scenarios:
list_incomechange=[0,scenarios[key]]
for i in list_incomechange:
df_normalise_partner_file = normalise_partner(i,key,option_deseason)
```
### 1.4. Checks<a id='check'></a>
<a href='#toc-pre'>back</a>
```
if input_normalise =='normalise':
def truncate(cluster_number):
if option_deseason == 'deseasonal':
df_seasonal_normalised = pd.read_csv('preprocessing/'+directory_name+ '/' + option_deseason +
'/4_habe_deseasonal_'+str(cluster_number)+'_normalised.csv',
delimiter=',', error_bad_lines=False)
if option_deseason == 'month-ind':
df_seasonal_normalised = pd.read_csv('preprocessing/'+directory_name+ '/' + str(option_deseason) + '/' + str(key) +
'/3_habe_for_all_scenarios_encoding.csv',delimiter=',')
df_habe_imputed_clustered_d = df_seasonal_normalised[list_dependent_columns]
df_habe_imputed_clustered_dl = np.expm1(df_habe_imputed_clustered_d)
df_habe_imputed_clustered_i = df_seasonal_normalised[list_independent_columns]
fullname_dl = make_pre_sub_sub_directory('raw_dependent_old_'+str(cluster_number)+'.csv',directory_name,
'checks',option_deseason)
fullname_d = make_pre_sub_sub_directory('raw_dependent_'+str(cluster_number)+'.csv',directory_name,
'checks',option_deseason)
fullname_in = make_pre_sub_sub_directory('raw_independent_'+str(cluster_number)+'.csv',directory_name,
'checks',option_deseason)
pd.DataFrame.to_csv(df_habe_imputed_clustered_dl,fullname_dl,sep=',',index=False)
pd.DataFrame.to_csv(df_habe_imputed_clustered_d,fullname_d,sep=',',index=False)
pd.DataFrame.to_csv(df_habe_imputed_clustered_i,fullname_in,sep=',',index=False)
if input_normalise =='no-normalise':
def truncate(cluster_number):
if option_deseason == 'deseasonal':
df_seasonal_normalised = pd.read_csv('preprocessing/'+directory_name+ '/' + option_deseason +
'/4_habe_deseasonal_'+str(cluster_number)+'_short.csv',
delimiter=',', error_bad_lines=False)
if option_deseason == 'month-ind':
df_seasonal_normalised = pd.read_csv('preprocessing/'+directory_name+ '/' + str(option_deseason) + '/' + str(key) +
'/3_habe_for_all_scenarios_encoding.csv',delimiter=',')
df_habe_imputed_clustered_d = df_seasonal_normalised[list_dependent_columns]
df_habe_imputed_clustered_i = df_seasonal_normalised[list_independent_columns]
fullname_d = make_pre_sub_sub_directory('raw_dependent_'+str(cluster_number)+'.csv',directory_name,
'checks',option_deseason)
fullname_in = make_pre_sub_sub_directory('raw_independent_'+str(cluster_number)+'.csv',directory_name,
'checks',option_deseason)
pd.DataFrame.to_csv(df_habe_imputed_clustered_d,fullname_d,sep=',',index=False)
pd.DataFrame.to_csv(df_habe_imputed_clustered_i,fullname_in,sep=',',index=False)
for i in list(range(1,cluster_number_length+1)):
truncate(i)
```
## 2. MODEL <a id = "model"></a>
<a href = "#toc">back</a>
TOC:<a id ='toc-model'></a>
- <a href = "#prep"> 2.1. Prepare train-test-target datasets</a>
- <a href = "#predict"> 2.2. Prediction</a>
### 2.1. Prepare train-test-target datasets <a id ='prep'></a>
<a href=#toc-model>back</a>
```
def to_haushalts(values,id_ix=0):
haushalts = dict()
haushalt_ids = np.unique(values[:,id_ix])
for haushalt_id in haushalt_ids:
selection = values[:, id_ix] == haushalt_id
haushalts[haushalt_id] = values[selection]
return haushalts
def split_train_test(haushalts,length_training,month_name,row_in_chunk):
train, test = list(), list()
cut_point = int(0.8*length_training) # 0.9*9754 # declare cut_point as per the size of the imputed database #TODO check if this is too less
print('Month/cluster and cut_point',month_name, cut_point)
for k,rows in haushalts.items():
train_rows = rows[rows[:,row_in_chunk] < cut_point, :]
test_rows = rows[rows[:,row_in_chunk] > cut_point, :]
train.append(train_rows[:, :])
test.append(test_rows[:, :])
return train, test
### NORMALISATION
if input_normalise =='normalise':
def df_habe_train_test(df,month_name,length_training):
df=df.assign(id_split = list(range(df.shape[0])))
train, test = split_train_test(to_haushalts(df.values),length_training,month_name,row_in_chunk=df.shape[1]-1)
train_rows = np.array([row for rows in train for row in rows])
test_rows = np.array([row for rows in test for row in rows])
independent = list(range(0,independent_indices_pd.shape[0]))
dependent = list(range(independent_indices_pd.shape[0]+1,
independent_indices_pd.shape[0]+dependent_indices_pd.shape[0]+1))
trained_independent = train_rows[:, independent]
trained_dependent = train_rows[:, dependent]
test_independent = test_rows[:, independent]
test_dependent = test_rows[:, dependent]
## OPTIONAL lines FOR CHECK - comment if not needed
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/trained_dependent_nonexp.csv',
trained_dependent, delimiter=',')
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/trained_dependent.csv',
np.expm1(trained_dependent),delimiter=',')
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/trained_independent.csv',
trained_independent, delimiter=',')
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/test_dependent.csv',
np.expm1(test_dependent), delimiter=',')
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/test_independent.csv',
test_independent, delimiter=',')
return trained_independent,trained_dependent,test_independent,test_dependent
def df_partner_test(y):
df_partner = pd.read_csv('preprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/5_final_' + target_data +
'_independent_final_' + str(y) + '.csv',delimiter=',')
length_training = df_partner.shape[0]
train_partner, test_partner = split_train_test(to_haushalts(df_partner.values),length_training,month_name,1)
train_rows_partner = np.array([row for rows in train_partner for row in rows])
new_independent = list(range(0, n_ind)) # number of columns of the independent parameters
train_partner_independent = train_rows_partner[:, new_independent]
### Optional lines for CHECK - comment if not needed
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/train_partner_independent_' + model_name + '_' + str(y) + '.csv',
train_partner_independent, delimiter=',')
return train_partner_independent
## form the train test datasets
# NO-NORMALISATION
if input_normalise =='no-normalise':
def df_habe_train_test(df,month_name,length_training):
df=df.assign(id_split = list(range(df.shape[0])))
train, test = split_train_test(to_haushalts(df.values),length_training,month_name,row_in_chunk=df.shape[1]-1)
train_rows = np.array([row for rows in train for row in rows])
test_rows = np.array([row for rows in test for row in rows])
independent = list(range(0,independent_indices_pd.shape[0]))
dependent = list(range(independent_indices_pd.shape[0]+1,
independent_indices_pd.shape[0]+dependent_indices_pd.shape[0]+1))
trained_independent = train_rows[:, independent]
trained_dependent = train_rows[:, dependent]
test_independent = test_rows[:, independent]
test_dependent = test_rows[:, dependent]
## OPTIONAL lines FOR CHECK - comment if not needed
# np.savetxt('raw/checks/trained_dependent_nonexp_'+str(month_name)+'.csv', trained_dependent, delimiter=',')
# np.savetxt('raw/checks/trained_independent_nonexp_'+str(month_name)+'.csv', trained_independent, delimiter=',')
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/test_dependent_'+str(month_name)+'.csv',
test_dependent,delimiter=',')
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/test_independent_'+str(month_name)+'.csv',
test_independent, delimiter=',')
return trained_independent,trained_dependent,test_independent,test_dependent
def df_partner_test(y):
df_partner = pd.read_csv('preprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/5_final_' + target_data +
'_independent_final_' + str(y) + '.csv', delimiter=',')
length_training = df_partner.shape[0]
train_partner, test_partner = split_train_test(to_haushalts(df_partner.values),
length_training,cluster_number,1)
train_rows_partner = np.array([row for rows in train_partner for row in rows])
new_independent = list(range(0, n_ind))
train_partner_independent = train_rows_partner[:, new_independent]
### Optional lines for CHECK - comment if not needed
np.savetxt('preprocessing/'+directory_name+'/checks/'+option_deseason+'/train_partner_independent_' +
model_name + '_' + str(y) + '.csv', train_partner_independent, delimiter=',')
return train_partner_independent
def make_post_directory(outname,directory_name):
outdir = 'postprocessing/'+directory_name
if not os.path.exists(outdir):
os.mkdir(outdir)
fullname = os.path.join(outdir, outname)
return fullname
def make_post_sub_directory(outname,directory_name,sub_dir):
outdir_1='postprocessing/'+directory_name
if not os.path.exists(outdir_1):
os.mkdir(outdir_1)
outdir = 'postprocessing/'+directory_name+'/'+sub_dir
if not os.path.exists(outdir):
os.mkdir(outdir)
fullname = os.path.join(outdir, outname)
return fullname
def make_post_sub_sub_directory(outname,directory_name,sub_dir,sub_sub_dir):
outdir_1='postprocessing/'+directory_name
if not os.path.exists(outdir_1):
os.mkdir(outdir_1)
outdir = 'postprocessing/'+directory_name+'/'+sub_dir
if not os.path.exists(outdir):
os.mkdir(outdir)
outdir_2='postprocessing/'+directory_name+'/'+sub_dir+'/'+sub_sub_dir
if not os.path.exists(outdir_2):
os.mkdir(outdir_2)
fullname = os.path.join(outdir_2, outname)
return fullname
# FOR NO NORMALISATION AND TEST DATA
def df_test(y,cluster_number):
pd_df_partner = pd.read_csv('raw/checks/trained_independent_'+str(cluster_number)+'.csv', delimiter=',', header = None)
pd_df_partner.iloc[:,-1] = pd_df_partner.iloc[:,-1] + y
pd.DataFrame.to_csv(pd_df_partner, 'raw/checks/5_trained_independent_'+str(cluster_number)+'_'+str(y)+'.csv',
sep=',',index=False)
return pd_df_partner
def df_stratified_test(y):
pd_df_partner = pd.read_csv('raw/checks/5_setstratified_independent_1_'+str(y)+'.csv', delimiter=',')
return pd_df_partner
#If using Neural Networks
# def ANN():
# nn = Sequential()
# nn.add(Dense(39,kernel_initializer='normal',activation="relu",input_shape=(39,)))
# nn.add(Dense(50,kernel_initializer='normal',activation="relu"))
# nn.add(Dense(100,kernel_initializer='normal',activation="relu"))
# nn.add(Dense(100,kernel_initializer='normal',activation="relu") )
# # nn.add(Dense(100,kernel_initializer='normal',activation="relu"))
# # nn.add(Dense(100,kernel_initializer='normal',activation="relu"))
# nn.add(Dense(dependentsize,kernel_initializer='normal')) #,kernel_constraint=min_max_norm(min_value=0.01,max_value=0.05)))
# sgd = optimizers.SGD(lr=0.02, decay=1e-6, momentum=0.9, nesterov=True)
# nn.compile(optimizer=sgd, loss='mean_squared_error', metrics=['accuracy'])
# return nn
```
### 2.2. Clustered Prediction <a id='predict'></a>
<a href='#toc-model'>back</a>
```
## NORMALISATION
if input_normalise =='normalise':
def fit_predict_cluster(i,y,cluster_number,key):
df = pd.read_csv('preprocessing/'+directory_name+'/'+option_deseason+
'/4_habe_deseasonal_'+str(cluster_number)+'_normalised.csv',
delimiter=',',error_bad_lines=False, encoding='ISO-8859–1')
length_training = df.shape[0]
trained_independent, trained_dependent, test_independent, test_dependent = df_habe_train_test(df,
str(cluster_number),
length_training)
train_partner_independent = df_partner_test(y)
if model_name == 'ANN':
estimator = KerasRegressor(build_fn=ANN)
estimator.fit(trained_independent, trained_dependent, epochs=100, batch_size=5, verbose=0)
### PREDICTION FROM HERE
prediction_nn = estimator.predict(train_partner_independent)
prediction_nn_denormalised = np.expm1(prediction_nn)
fullname = make_post_sub_sub_directory('predicted_' + model_name + '_' + str(y) + '_' + str(i)
+ '_' + str(cluster_number) + '.csv',directory_name,option_deseason,key)
np.savetxt(fullname, prediction_nn_denormalised, delimiter=',')
### TEST PREDICTION
prediction_nn_test = estimator.predict(test_independent)
prediction_nn_test_denormalised = np.expm1(prediction_nn_test)
fullname = make_post_sub_sub_directory('predicted_test' + model_name + '_' + str(y) + '_' + str(i)
+ '_' + str(cluster_number) + '.csv',directory_name,option_deseason,key)
np.savetxt(fullname, prediction_nn_test_denormalised, delimiter=',')
### CROSS VALIDATION FROM HERE
kfold = KFold(n_splits=10, random_state=12, shuffle=True)
results1 = cross_val_score(estimator, test_independent, test_dependent, cv=kfold)
print("Results_test: %.2f (%.2f)" % (results1.mean(), results1.std()))
if model_name == 'RF':
estimator = sko.MultiOutputRegressor(RandomForestRegressor(n_estimators=100, max_features=n_ind, random_state=30))
estimator.fit(trained_independent, trained_dependent)
### PREDICTION FROM HERE
prediction_nn = estimator.predict(train_partner_independent)
results0 = estimator.oob_score
prediction_nn_denormalised = np.expm1(prediction_nn)
fullname = make_post_sub_sub_directory('predicted_' + model_name + '_' + str(y) + '_' + str(i)
+ '_' + str(cluster_number) + '.csv',directory_name,option_deseason,key)
np.savetxt(fullname, prediction_nn_denormalised, delimiter=',')
### TEST PREDICTION
prediction_nn_test = estimator.predict(test_independent)
prediction_nn_test_denormalised = np.expm1(prediction_nn_test)
fullname = make_post_sub_sub_directory('predicted_test' + model_name + '_' + str(y) + '_' + str(i)
+ '_' + str(cluster_number) + '.csv',directory_name,option_deseason,key)
np.savetxt(fullname, prediction_nn_test_denormalised, delimiter=',')
#### CROSS VALIDATION FROM HERE
kfold = KFold(n_splits=10, random_state=12, shuffle=True)
# results0 = estimator.oob_score
# results1 = cross_val_score(estimator, test_independent, test_dependent, cv=kfold)
results2 = r2_score(test_dependent,prediction_nn_test)
results3 = mean_squared_error(test_dependent,prediction_nn_test)
results4 = explained_variance_score(test_dependent,prediction_nn_test)
# print("cross_val_score: %.2f (%.2f)" % (results1.mean(), results1.std()))
# print("oob_r2_score: %.2f " % results0)
print("r2_score: %.2f " % results2)
print("mean_squared_error: %.2f " % results3)
print("explained_variance_score: %.2f " % results4)
### FOR NO NORMALISATION
if input_normalise =='no-normalise':
def fit_predict_cluster(i,y,cluster_number,key):
df_non_normalised = pd.read_csv('preprocessing/'+directory_name+'/'+option_deseason+'/4_habe_deseasonal_'+
str(cluster_number)+ '_short.csv', delimiter=',',
error_bad_lines=False, encoding='ISO-8859–1')
length_training = df_non_normalised.shape[0]
print(length_training)
trained_independent, trained_dependent, test_independent, test_dependent = df_habe_train_test(df_non_normalised,
str(cluster_number),
length_training)
train_partner_independent = df_partner_test(y)
### Additional for the HBS test data subset
# test_new_independent = df_test(y,1) # chosing just one cluster here
# sratified_independent = df_stratified_test(y)
if model_name == 'ANN':
estimator = KerasRegressor(build_fn=ANN)
estimator.fit(trained_independent, trained_dependent, epochs=100, batch_size=5, verbose=0)
### PREDICTION FROM HERE
prediction_nn = estimator.predict(train_partner_independent)
fullname = make_post_sub_sub_directory('predicted_' + model_name + '_' + str(y) + '_' + str(i)
+ '_' + str(cluster_number) +'.csv',directory_name,option_deseason,key)
np.savetxt(fullname, prediction_nn, delimiter=',')
### TEST PREDICTION
prediction_nn_test = estimator.predict(test_independent)
fullname = make_post_sub_sub_directory('predicted_test_' + model_name + '_' + str(y) + '_' + str(i)
+ '_' + str(cluster_number) +'.csv',directory_name,option_deseason,key)
np.savetxt(fullname, prediction_nn_test, delimiter=',')
### CROSS VALIDATION FROM HERE
kfold = KFold(n_splits=10, random_state=12, shuffle=True)
results1 = cross_val_score(estimator, test_independent, test_dependent, cv=kfold)
print("Results_test: %.2f (%.2f)" % (results1.mean(), results1.std()))
if model_name == 'RF':
estimator = sko.MultiOutputRegressor(RandomForestRegressor(n_estimators=100, max_features=n_ind, random_state=30))
estimator.fit(trained_independent, trained_dependent)
### FEATURE IMPORTANCE
rf = RandomForestRegressor()
rf.fit(trained_independent, trained_dependent)
FI = rf.feature_importances_
list_independent_columns = pd.read_csv(independent_indices, delimiter=',', encoding='ISO-8859–1')['name'].to_list()
independent_columns = pd.DataFrame(list_independent_columns)
FI_names = pd.DataFrame(FI)
FI_names = pd.concat([independent_columns, FI_names], axis=1)
FI_names.columns = ['independent_variables', 'FI_score']
pd.DataFrame.to_csv(FI_names,'preprocessing/'+directory_name+'/8_habe_feature_importance'+ '_' +
str(y) + '_' + str(i) + '_' + str(cluster_number) +'.csv', sep=',',index= False)
FI_names_sorted = FI_names.sort_values('FI_score', ascending = False)
# print(FI_names_sorted)
### PREDICTION FROM HERE
prediction_nn = estimator.predict(train_partner_independent)
fullname = make_post_sub_sub_directory('predicted_' + model_name + '_' + str(y) + '_' + str(i)
+ '_' + str(cluster_number) +'.csv',directory_name,option_deseason,key)
np.savetxt(fullname, prediction_nn, delimiter=',')
### TEST PREDICTION
prediction_nn_test = estimator.predict(test_independent)
fullname = make_post_sub_sub_directory('predicted_test_' + model_name + '_' + str(y) + '_' + str(i)
+ '_' + str(cluster_number) +'.csv',directory_name,option_deseason,key)
np.savetxt(fullname, prediction_nn_test, delimiter=',')
#### CROSS VALIDATION FROM HERE
kfold = KFold(n_splits=10, random_state=12, shuffle=True)
for i in range(16):
column_predict = pd.DataFrame(test_dependent).iloc[:,i]
model = sm.OLS(column_predict, test_independent).fit()
print(i)
print('standard error=',model.bse)
# results0 = estimator.oob_score
# results1 = cross_val_score(estimator, test_independent, test_dependent, cv=kfold)
# results2 = r2_score(test_dependent,prediction_nn_test)
# results3 = mean_squared_error(test_dependent,prediction_nn_test)
# results4 = explained_variance_score(test_dependent,prediction_nn_test)
# print("cross_val_score: %.2f (%.2f)" % (results1.mean(), results1.std()))
# print("oob_r2_score: %.2f " % results0)
print("r2_score: %.2f " % results2)
print("mean_squared_error: %.2f " % results3)
print("explained_variance_score: %.2f " % results4)
# CLUSTER of MONTHS - PREDICTIONS
for cluster_number in list(range(1,cluster_number_length+1)):
print(cluster_number)
for j in range(0, iter_n):
for key in scenarios:
list_incomechange=[0,scenarios[key]]
for y in list_incomechange:
fit_predict_cluster(j,y,cluster_number,key)
```
## 3.POSTPROCESSING <a id = "post"></a>
<a href="#toc">back</a>
### 3.1. Average of the clustered predictions
```
if option_deseason == 'month-ind':
df_habe_outliers = pd.read_csv('preprocessing/'+directory_name+'/'+option_deseason+'/4_habe_deseasonal_'+
str(cluster_number)+ '_short.csv', delimiter=',')
if option_deseason == 'deseasonal':
df_habe_outliers = pd.read_csv('preprocessing/'+directory_name+'/2_habe_rename_removeoutliers.csv', delimiter=',')
model_name = 'RF'
def average_pandas_cluster(y,cluster_number,key):
df_all = []
df_trained_partner = pd.read_csv('preprocessing/'+directory_name+'/checks/'+option_deseason+'/train_partner_independent_'+
model_name+'_'+str(y)+'.csv')
for i in range(0,iter_n):
df = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name + '_' +
str(y) + '_' + str(i) + '_' +
str(cluster_number) + '.csv', delimiter = ',', header=None)
df_all.append(df)
glued = pd.concat(df_all, axis=1, keys=list(map(chr,range(97,97+iter_n))))
glued = glued.swaplevel(0, 1, axis=1)
glued = glued.groupby(level=0, axis=1).mean()
glued_new = glued.reindex(columns=df_all[0].columns)
max_income = df_habe_outliers[['disposable_income']].quantile([0.99]).values[0]
min_income = df_habe_outliers[['disposable_income']].quantile([0.01]).values[0]
glued_new['income'] = df_trained_partner[df_trained_partner.columns[-1]]
pd.DataFrame.to_csv(glued_new, 'postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name + '_' + str(y)
+ '_'+str(cluster_number)+'.csv', sep=',',header=None,index=False)
for key in scenarios:
list_incomechange=[0,scenarios[key]]
for y in list_incomechange:
for cluster_number in list(range(1,cluster_number_length+1)):
average_pandas_cluster(y,cluster_number,key)
def accumulate_categories_cluster(y,cluster_number):
df_income = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name + '_' + str(y)
+ '_'+str(cluster_number)+'.csv',
sep=',',header=None)
# df_income['household_size'] = df_income.iloc[:, [17]]
df_income['income'] = df_income.iloc[:, [16]]
df_income['food'] = df_income.iloc[:,[0,1,2]].sum(axis=1)
df_income['misc'] = df_income.iloc[:,[3,4]].sum(axis=1)
df_income['housing'] = df_income.iloc[:, [5, 6]].sum(axis=1)
df_income['services'] = df_income.iloc[:, [7, 8, 9 ]].sum(axis=1)
df_income['travel'] = df_income.iloc[:, [10, 11, 12, 13, 14]].sum(axis=1)
df_income['savings'] = df_income.iloc[:, [15]]
df_income = df_income[['income','food','misc','housing','services','travel','savings']]
pd.DataFrame.to_csv(df_income,
'postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name + '_' + str(y)
+ '_'+str(cluster_number)+'_aggregated.csv', sep=',',index=False)
return df_income
for key in scenarios:
list_incomechange=[0,scenarios[key]]
for y in list_incomechange:
for cluster_number in list(range(1,cluster_number_length+1)):
accumulate_categories_cluster(y,cluster_number)
# aggregation of clusters
list_dfs_month=[]
for key in scenarios:
list_incomechange=[0,scenarios[key]]
for y in list_incomechange:
for cluster_number in list(range(1,cluster_number_length+1)):
pd_predicted_month = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name + '_' + str(y)
+ '_'+str(cluster_number)+'_aggregated.csv', delimiter = ',')
list_dfs_month.append(pd_predicted_month)
df_concat = pd.concat(list_dfs_month,sort=False)
by_row_index = df_concat.groupby(df_concat.index)
df_means = by_row_index.mean()
pd.DataFrame.to_csv(df_means,'postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name + '_' + str(y) + '_' +
str(dependentsize) +'_aggregated.csv', sep=',',index=False)
```
### 3.2. Calculate differences/ rebounds
```
list_dependent_columns = pd.read_csv(dependent_indices, delimiter=',', encoding='ISO-8859–1')['name'].to_list()
def difference_new():
for cluster_number in list(range(1,cluster_number_length+1)):
for key in scenarios:
list_incomechange=[0,scenarios[key]]
for i in range(0,iter_n):
df_trained_partner = pd.read_csv('preprocessing/'+directory_name+'/checks/'+'/'+option_deseason+'/train_partner_independent_'+
model_name+'_'+str(y)+'.csv',header=None)
df_500 = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name + '_'
+str(list_incomechange[1])+ '_'+str(i)
+ '_'+str(cluster_number)+'.csv', delimiter=',',header=None)
df_0 = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name + '_0_'
+ str(i) + '_'+str(cluster_number)+ '.csv', delimiter=',',header=None)
df_500.columns = list_dependent_columns
df_0.columns = df_500.columns
df_diff = -df_500+df_0
if option_deseason == 'month-ind':
df_diff['disposable_income']=df_trained_partner[df_trained_partner.columns[-25]]
if option_deseason == 'deseasonal':
df_diff['disposable_income']=df_trained_partner[df_trained_partner.columns[-1]]
pd.DataFrame.to_csv(df_diff,'postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_' + model_name
+ '_rebound_'+str(i)+ '_' + str(cluster_number) + '.csv',sep=',',index=False)
difference_new()
def average_clusters(key):
df_all = []
for i in range(0,iter_n):
df = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_'+ model_name + '_rebound_' +
str(i)+ '_' + str(cluster_number)+'.csv',delimiter=',',index_col=None)
df_all.append(df)
df_concat = pd.concat(df_all,sort=False)
by_row_index = df_concat.groupby(df_concat.index)
df_means = by_row_index.mean()
pd.DataFrame.to_csv(df_means, 'postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_'+model_name +'_rebound.csv',
sep=',',index=False)
for key in scenarios:
average_clusters(key)
def accumulate_categories(key):
df_income = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_'+model_name+ '_rebound.csv',delimiter=',')
# df_income['household_size'] = df_income.iloc[:, [17]]
df_income['income'] = df_income.iloc[:, [16]]
df_income['food'] = df_income.iloc[:,[0,1,2]].sum(axis=1)
df_income['misc'] = df_income.iloc[:,[3,4]].sum(axis=1)
df_income['housing'] = df_income.iloc[:, [5, 6]].sum(axis=1)
df_income['services'] = df_income.iloc[:, [7, 8, 9]].sum(axis=1)
df_income['travel'] = df_income.iloc[:, [10, 11, 12,13, 14]].sum(axis=1)
df_income['savings'] = df_income.iloc[:, [15]]
df_income = df_income[['income','food','misc','housing','services','travel','savings']]#'transfers','total_sum'
data[key]=list(df_income.mean())
if list(scenarios.keys()).index(key) == len(scenarios)-1:
df = pd.DataFrame(data, columns = [key for key in scenarios],
index=['income','food','misc','housing','services','travel','savings'])
print(df)
pd.DataFrame.to_csv(df.T, 'postprocessing/rebound_results_'+directory_name+ '_income.csv', sep=',',index=True)
pd.DataFrame.to_csv(df_income,
'postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_'+model_name+ '_rebound_aggregated.csv',
sep=',',index=False)
data={}
for key in scenarios:
accumulate_categories(key)
groups=('<2000','2000-4000','4000-6000','6000-8000','8000-10000','>10000')
def income_group(row):
if row['disposable_income'] <= 2000:
return groups[0]
if row['disposable_income'] <= 4000:
return groups[1]
if row['disposable_income'] <= 6000:
return groups[2]
if row['disposable_income'] <= 8000:
return groups[3]
if row['disposable_income'] <= 10000:
return groups[4]
if row['disposable_income'] > 10000:
return groups[5]
def accumulate_income_groups():
df_income = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_'+model_name+ '_rebound.csv',
delimiter=',')
df_income['income_group'] = df_income.apply(lambda row: income_group(row), axis=1)
df_income_new = df_income.groupby(['income_group']).mean()
pd.DataFrame.to_csv(df_income_new,'postprocessing/rebound_results_'+directory_name+ '_income_categories.csv', sep=',',index=True)
pd.DataFrame.to_csv(df_income,
'postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_'+model_name+ '_rebound_income.csv',
sep=',',index=False)
accumulate_income_groups()
groups=('<2000','2000-4000','4000-6000','6000-8000','8000-10000','>10000')
def income_group(row):
if row['income'] <= 2000 :
return groups[0]
if row['income'] <= 4000:
return groups[1]
if row['income'] <= 6000:
return groups[2]
if row['income'] <= 8000:
return groups[3]
if row['income'] <= 10000:
return groups[4]
if row['income'] > 10000:
return groups[5]
def accumulate_income_groups_new():
df_income = pd.read_csv('postprocessing/'+directory_name+'/'+option_deseason+'/'+key+'/predicted_'+model_name+ '_rebound_aggregated.csv',
delimiter=',')
print(df_income.columns)
df_income['income_group'] = df_income.apply(lambda row: income_group(row), axis=1)
df_income_new = df_income.groupby(['income_group']).mean()
pd.DataFrame.to_csv(df_income_new,'postprocessing/rebound_results_'+directory_name+ '_categories.csv', sep=',',index=True)
accumulate_income_groups_new()
```
## 4. LCA <a id = "lca"></a>
<a href = '#toc'>back</a>
1. Make a file with associated impacts_per_FU for each HABE category:
- a. Get the ecoinvent data from brightway
- b. Get the exiobase data from direct file (Livia's)
- c. Attach the heia and Agribalyse values
2. Convert the impact_per_FU to impact_per_expenses
3. Run the following scripts to
- (a) allocate the income category to each household in HBS (train data) and ABZ (target data)
- (b) calculate environmental impact per consumption main-category per income group as listed in the raw/dependent_10.csv
- (1) From HBS: % of expense of consumption sub-category per consumption main-category as listed in the raw/dependent_10.csv
- (2) expenses per FU of each consumption sub-category
- (c) From target data: Multiply the rebound results (consumption expenses) with the env. impact values above
based on the income of the household
OR
Use A.Kim's analysis here: https://github.com/aleksandra-kim/consumption_model for the calculation of impacts_per_FU for each HABE catergory
```
import pickle
import csv
file = open('LCA/contribution_scores_sectors_allfu1.pickle','rb')
x = pickle.load(file)
print(x)
with open('LCA/impacts_per_FU_sectors.csv', 'w') as output:
writer = csv.writer(output)
for key, value in x:
writer.writerow([key, value])
import pickle
import csv
import pickle
import csv
file = open('LCA/contribution_scores_5categories_allfu1.pickle','rb')
x = pickle.load(file)
print(x)
with open('LCA/impacts_per_FU.csv', 'w') as output:
writer = csv.writer(output)
for key, value in x.items():
writer.writerow([key, value])
file = open('LCA/contribution_scores_v2.pickle','rb')
x1 = pickle.load(file)
with open('LCA/impacts_per_FU.csv', 'w') as output:
writer = csv.writer(output)
for key, value in x1.items():
writer.writerow([key, value])
file = open('LCA/contribution_scores_sectors_allfu1.pickle','rb')
x = pickle.load(file)
with open('LCA/impacts_per_FU_sectors.csv', 'w') as output:
writer = csv.writer(output)
for key, value in x.items():
writer.writerow([key, value])
import pandas as pd
## TODO use the manually updated CHF/FU to calculate the income per expense
df_expense = pd.read_csv('LCA/impacts_per_expense.csv',sep=',',index_col='sector')
df_income_CHF = pd.read_csv('postprocessing/rebound_results_'+directory_name+ '_income.csv',sep=',')
for i in ['food','travel','housing','food','misc','services']:
df_income_CHF[i+'_GHG']=df_expense.loc[i,'Average of GWP/CHF']*df_income_CHF[i]
pd.DataFrame.to_csv(df_income_CHF,'postprocessing/rebound_results_'+directory_name+ '_income_all_GHG.csv',sep=',')
```
| github_jupyter |

# **Regressão Linear**
#### Este notebook mostra uma implementação básica de Regressão Linear e o uso da biblioteca [MLlib](http://spark.apache.org/docs/1.4.0/api/python/pyspark.ml.html) do PySpark para a tarefa de regressão na base de dados [Million Song Dataset](http://labrosa.ee.columbia.edu/millionsong/) do repositório [UCI Machine Learning Repository](https://archive.ics.uci.edu/ml/datasets/YearPredictionMSD). Nosso objetivo é predizer o ano de uma música através dos seus atributos de áudio.
#### ** Neste notebook: **
+ ####*Parte 1:* Leitura e *parsing* da base de dados
+ #### *Visualização 1:* Atributos
+ #### *Visualização 2:* Deslocamento das variáveis de interesse
+ ####*Parte 2:* Criar um preditor de referência
+ #### *Visualização 3:* Valores Preditos vs. Verdadeiros
+ ####*Parte 3:* Treinar e avaliar um modelo de regressão linear
+ #### *Visualização 4:* Erro de Treino
+ ####*Parte 4:* Treinar usando MLlib e ajustar os hiperparâmetros
+ #### *Visualização 5:* Predições do Melhor modelo
+ #### *Visualização 6:* Mapa de calor dos hiperparâmetros
+ ####*Parte 5:* Adicionando interações entre atributos
+ ####*Parte 6:* Aplicando na base de dados de Crimes de São Francisco
#### Para referência, consulte os métodos relevantes do PySpark em [Spark's Python API](https://spark.apache.org/docs/latest/api/python/pyspark.html#pyspark.RDD) e do NumPy em [NumPy Reference](http://docs.scipy.org/doc/numpy/reference/index.html)
### ** Parte 1: Leitura e *parsing* da base de dados**
#### ** (1a) Verificando os dados disponíveis **
#### Os dados da base que iremos utilizar estão armazenados em um arquivo texto. No primeiro passo vamos transformar os dados textuais em uma RDD e verificar a formatação dos mesmos. Altere a segunda célula para verificar quantas amostras existem nessa base de dados utilizando o método [count method](https://spark.apache.org/docs/latest/api/python/pyspark.html#pyspark.RDD.count).
#### Reparem que o rótulo dessa base é o primeiro registro, representando o ano.
```
from pyspark import SparkContext
sc = SparkContext.getOrCreate()
# carregar base de dados
import os.path
fileName = os.path.join('Data', 'millionsong.txt')
numPartitions = 2
rawData = sc.textFile(fileName, numPartitions)
# EXERCICIO
numPoints = rawData.count()
print (numPoints)
samplePoints = rawData.take(5)
print (samplePoints)
# TEST Load and check the data (1a)
assert numPoints==6724, 'incorrect value for numPoints'
print("OK")
assert len(samplePoints)==5, 'incorrect length for samplePoints'
print("OK")
```
#### ** (1b) Usando `LabeledPoint` **
#### Na MLlib, bases de dados rotuladas devem ser armazenadas usando o objeto [LabeledPoint](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.regression.LabeledPoint). Escreva a função `parsePoint` que recebe como entrada uma amostra de dados, transforma os dados usandoo comando [unicode.split](https://docs.python.org/2/library/string.html#string.split), em seguida mapeando para `float` e retorna um `LabeledPoint`.
#### Aplique essa função na variável `samplePoints` da célula anterior e imprima os atributos e rótulo utilizando os atributos `LabeledPoint.features` e `LabeledPoint.label`. Finalmente, calcule o número de atributos nessa base de dados.
```
from pyspark.mllib.regression import LabeledPoint
import numpy as np
# Here is a sample raw data point:
# '2001.0,0.884,0.610,0.600,0.474,0.247,0.357,0.344,0.33,0.600,0.425,0.60,0.419'
# In this raw data point, 2001.0 is the label, and the remaining values are features
# EXERCICIO
def parsePoint(line):
"""Converts a comma separated unicode string into a `LabeledPoint`.
Args:
line (unicode): Comma separated unicode string where the first element is the label and the
remaining elements are features.
Returns:
LabeledPoint: The line is converted into a `LabeledPoint`, which consists of a label and
features.
"""
Point = [float(x) for x in line.replace(',', ' ').split(' ')]
return LabeledPoint(Point[0], Point[1:])
parsedSamplePoints = list(map(parsePoint,samplePoints))
firstPointFeatures = parsedSamplePoints[0].features
firstPointLabel = parsedSamplePoints[0].label
print (firstPointFeatures, firstPointLabel)
d = len(firstPointFeatures)
print (d)
# TEST Using LabeledPoint (1b)
assert isinstance(firstPointLabel, float), 'label must be a float'
expectedX0 = [0.8841,0.6105,0.6005,0.4747,0.2472,0.3573,0.3441,0.3396,0.6009,0.4257,0.6049,0.4192]
assert np.allclose(expectedX0, firstPointFeatures, 1e-4, 1e-4), 'incorrect features for firstPointFeatures'
assert np.allclose(2001.0, firstPointLabel), 'incorrect label for firstPointLabel'
assert d == 12, 'incorrect number of features'
print("OK")
```
#### **Visualização 1: Atributos**
#### A próxima célula mostra uma forma de visualizar os atributos através de um mapa de calor. Nesse mapa mostramos os 50 primeiros objetos e seus atributos representados por tons de cinza, sendo o branco representando o valor 0 e o preto representando o valor 1.
#### Esse tipo de visualização ajuda a perceber a variação dos valores dos atributos. Pouca mudança de tons significa que os valores daquele atributo apresenta uma variância baixa.
```
import matplotlib.pyplot as plt
import matplotlib.cm as cm
%matplotlib inline
sampleMorePoints = rawData.take(50)
parsedSampleMorePoints = map(parsePoint, sampleMorePoints)
dataValues = list(map(lambda lp: lp.features.toArray(), parsedSampleMorePoints))
def preparePlot(xticks, yticks, figsize=(10.5, 6), hideLabels=False, gridColor='#999999',
gridWidth=1.0):
"""Template for generating the plot layout."""
plt.close()
fig, ax = plt.subplots(figsize=figsize, facecolor='white', edgecolor='white')
ax.axes.tick_params(labelcolor='#999999', labelsize='10')
for axis, ticks in [(ax.get_xaxis(), xticks), (ax.get_yaxis(), yticks)]:
axis.set_ticks_position('none')
axis.set_ticks(ticks)
axis.label.set_color('#999999')
if hideLabels: axis.set_ticklabels([])
plt.grid(color=gridColor, linewidth=gridWidth, linestyle='-')
map(lambda position: ax.spines[position].set_visible(False), ['bottom', 'top', 'left', 'right'])
return fig, ax
# generate layout and plot
fig, ax = preparePlot(np.arange(.5, 11, 1), np.arange(.5, 49, 1), figsize=(8,7), hideLabels=True,
gridColor='#eeeeee', gridWidth=1.1)
image = plt.imshow(dataValues,interpolation='nearest', aspect='auto', cmap=cm.Greys)
for x, y, s in zip(np.arange(-.125, 12, 1), np.repeat(-.75, 12), [str(x) for x in range(12)]):
plt.text(x, y, s, color='#999999', size='10')
plt.text(4.7, -3, 'Feature', color='#999999', size='11'), ax.set_ylabel('Observation')
pass
```
#### **(1c) Deslocando os rótulos **
#### Para melhor visualizar as soluções obtidas, calcular o erro de predição e visualizar a relação dos atributos com os rótulos, costuma-se deslocar os rótulos para iniciarem em zero.
#### Como primeiro passo, aplique a função `parsePoint` no RDD criado anteriormente, em seguida, crie uma RDD apenas com o `.label` de cada amostra. Finalmente, calcule os valores mínimos e máximos.
```
# EXERCICIO
parsedDataInit = rawData.map(parsePoint)
onlyLabels = parsedDataInit.map(lambda p: p.label)
minYear = onlyLabels.min()
maxYear = onlyLabels.max()
print (maxYear, minYear)
# TEST Find the range (1c)
assert len(parsedDataInit.take(1)[0].features)==12, 'unexpected number of features in sample point'
sumFeatTwo = parsedDataInit.map(lambda lp: lp.features[2]).sum()
assert np.allclose(sumFeatTwo, 3158.96224351), 'parsedDataInit has unexpected values'
yearRange = maxYear - minYear
assert yearRange == 89, 'incorrect range for minYear to maxYear'
print("OK")
# EXERCICIO: subtraia os labels do valor mínimo
parsedData = parsedDataInit.map(lambda p: LabeledPoint(p.label - minYear, p.features))
# Should be a LabeledPoint
print (type(parsedData.take(1)[0]))
# View the first point
print ('\n{0}'.format(parsedData.take(1)))
# TEST Shift labels (1d)
oldSampleFeatures = parsedDataInit.take(1)[0].features
newSampleFeatures = parsedData.take(1)[0].features
assert np.allclose(oldSampleFeatures, newSampleFeatures), 'new features do not match old features'
sumFeatTwo = parsedData.map(lambda lp: lp.features[2]).sum()
assert np.allclose(sumFeatTwo, 3158.96224351), 'parsedData has unexpected values'
minYearNew = parsedData.map(lambda lp: lp.label).min()
maxYearNew = parsedData.map(lambda lp: lp.label).max()
assert minYearNew == 0, 'incorrect min year in shifted data'
assert maxYearNew == 89, 'incorrect max year in shifted data'
print("OK")
```
#### ** (1d) Conjuntos de treino, validação e teste **
#### Como próximo passo, vamos dividir nossa base de dados em conjunto de treino, validação e teste conforme discutido em sala de aula. Use o método [randomSplit method](https://spark.apache.org/docs/latest/api/python/pyspark.html#pyspark.RDD.randomSplit) com os pesos (weights) e a semente aleatória (seed) especificados na célula abaixo parar criar a divisão das bases. Em seguida, utilizando o método `cache()` faça o pré-armazenamento da base processada.
#### Esse comando faz o processamento da base através das transformações e armazena em um novo RDD que pode ficar armazenado em memória, se couber, ou em um arquivo temporário.
```
# EXERCICIO
weights = [.8, .1, .1]
seed = 42
parsedTrainData, parsedValData, parsedTestData = parsedData.randomSplit(weights, seed)
parsedTrainData.cache()
parsedValData.cache()
parsedTestData.cache()
nTrain = parsedTrainData.count()
nVal = parsedValData.count()
nTest = parsedTestData.count()
print (nTrain, nVal, nTest, nTrain + nVal + nTest)
print (parsedData.count())
# TEST Training, validation, and test sets (1e)
assert parsedTrainData.getNumPartitions() == numPartitions, 'parsedTrainData has wrong number of partitions'
assert parsedValData.getNumPartitions() == numPartitions, 'parsedValData has wrong number of partitions'
assert parsedTestData.getNumPartitions() == numPartitions,'parsedTestData has wrong number of partitions'
assert len(parsedTrainData.take(1)[0].features) == 12, 'parsedTrainData has wrong number of features'
sumFeatTwo = (parsedTrainData
.map(lambda lp: lp.features[2])
.sum())
sumFeatThree = (parsedValData
.map(lambda lp: lp.features[3])
.reduce(lambda x, y: x + y))
sumFeatFour = (parsedTestData
.map(lambda lp: lp.features[4])
.reduce(lambda x, y: x + y))
assert np.allclose([sumFeatTwo, sumFeatThree, sumFeatFour],2526.87757656, 297.340394298, 184.235876654), 'parsed Train, Val, Test data has unexpected values'
assert nTrain + nVal + nTest == 6724, 'unexpected Train, Val, Test data set size'
assert nTrain == 5359, 'unexpected value for nTrain'
assert nVal == 678, 'unexpected value for nVal'
assert nTest == 687, 'unexpected value for nTest'
print("OK")
```
### ** Part 2: Criando o modelo de *baseline* **
#### **(2a) Rótulo médio **
#### O baseline é útil para verificarmos que nosso modelo de regressão está funcionando. Ele deve ser um modelo bem simples que qualquer algoritmo possa fazer melhor.
#### Um baseline muito utilizado é fazer a mesma predição independente dos dados analisados utilizando o rótulo médio do conjunto de treino. Calcule a média dos rótulos deslocados para a base de treino, utilizaremos esse valor posteriormente para comparar o erro de predição. Use um método apropriado para essa tarefa, consulte o [RDD API](https://spark.apache.org/docs/latest/api/python/pyspark.html#pyspark.RDD).
```
# EXERCICIO
averageTrainYear = (parsedTrainData
.map(lambda p: p.label)
.mean()
)
print (averageTrainYear)
# TEST Average label (2a)
assert np.allclose(averageTrainYear, 53.6792311), 'incorrect value for averageTrainYear'
print("OK")
```
#### **(2b) Erro quadrático médio **
#### Para comparar a performance em problemas de regressão, geralmente é utilizado o Erro Quadrático Médio ([RMSE](http://en.wikipedia.org/wiki/Root-mean-square_deviation)). Implemente uma função que calcula o RMSE a partir de um RDD de tuplas (rótulo, predição).
```
# EXERCICIO
def squaredError(label, prediction):
"""Calculates the the squared error for a single prediction.
Args:
label (float): The correct value for this observation.
prediction (float): The predicted value for this observation.
Returns:
float: The difference between the `label` and `prediction` squared.
"""
return (label - prediction) ** 2
def calcRMSE(labelsAndPreds):
"""Calculates the root mean squared error for an `RDD` of (label, prediction) tuples.
Args:
labelsAndPred (RDD of (float, float)): An `RDD` consisting of (label, prediction) tuples.
Returns:
float: The square root of the mean of the squared errors.
"""
return np.sqrt(labelsAndPreds
.map(lambda lp: squaredError(lp[0], lp[1])).mean())
labelsAndPreds = sc.parallelize([(3., 1.), (1., 2.), (2., 2.)])
# RMSE = sqrt[((3-1)^2 + (1-2)^2 + (2-2)^2) / 3] = 1.291
exampleRMSE = calcRMSE(labelsAndPreds)
print (exampleRMSE)
# TEST Root mean squared error (2b)
assert np.allclose(squaredError(3, 1), 4.), 'incorrect definition of squaredError'
assert np.allclose(exampleRMSE, 1.29099444874), 'incorrect value for exampleRMSE'
print("OK")
```
#### **(2c) RMSE do baseline para os conjuntos de treino, validação e teste **
#### Vamos calcular o RMSE para nossa baseline. Primeiro crie uma RDD de (rótulo, predição) para cada conjunto, e então chame a função `calcRMSE`.
```
# EXERCICIO
labelsAndPredsTrain = parsedTrainData.map(lambda p: (p.label, averageTrainYear))
rmseTrainBase = calcRMSE(labelsAndPredsTrain)
labelsAndPredsVal = parsedValData.map(lambda p: (p.label, averageTrainYear))
rmseValBase = calcRMSE(labelsAndPredsVal)
labelsAndPredsTest = parsedTestData.map(lambda p: (p.label, averageTrainYear))
rmseTestBase = calcRMSE(labelsAndPredsTest)
print ('Baseline Train RMSE = {0:.3f}'.format(rmseTrainBase))
print ('Baseline Validation RMSE = {0:.3f}'.format(rmseValBase))
print ('Baseline Test RMSE = {0:.3f}'.format(rmseTestBase))
# TEST Training, validation and test RMSE (2c)
assert np.allclose([rmseTrainBase, rmseValBase, rmseTestBase],[21.506125957738682, 20.877445428452468, 21.260493955081916]), 'incorrect RMSE value'
print("OK")
```
#### ** Visualização 2: Predição vs. real **
#### Vamos visualizar as predições no conjunto de validação. Os gráficos de dispersão abaixo plotam os pontos com a coordenada X sendo o valor predito pelo modelo e a coordenada Y o valor real do rótulo.
#### O primeiro gráfico mostra a situação ideal, um modelo que acerta todos os rótulos. O segundo gráfico mostra o desempenho do modelo baseline. As cores dos pontos representam o erro quadrático daquela predição, quanto mais próxima do laranja, maior o erro.
```
from matplotlib.colors import ListedColormap, Normalize
from matplotlib.cm import get_cmap
cmap = get_cmap('YlOrRd')
norm = Normalize()
actual = np.asarray(parsedValData
.map(lambda lp: lp.label)
.collect())
error = np.asarray(parsedValData
.map(lambda lp: (lp.label, lp.label))
.map(lambda lp: squaredError(lp[0], lp[1]))
.collect())
clrs = cmap(np.asarray(norm(error)))[:,0:3]
fig, ax = preparePlot(np.arange(0, 100, 20), np.arange(0, 100, 20))
plt.scatter(actual, actual, s=14**2, c=clrs, edgecolors='#888888', alpha=0.75, linewidths=0.5)
ax.set_xlabel('Predicted'), ax.set_ylabel('Actual')
pass
predictions = np.asarray(parsedValData
.map(lambda lp: averageTrainYear)
.collect())
error = np.asarray(parsedValData
.map(lambda lp: (lp.label, averageTrainYear))
.map(lambda lp: squaredError(lp[0], lp[1]))
.collect())
norm = Normalize()
clrs = cmap(np.asarray(norm(error)))[:,0:3]
fig, ax = preparePlot(np.arange(53.0, 55.0, 0.5), np.arange(0, 100, 20))
ax.set_xlim(53, 55)
plt.scatter(predictions, actual, s=14**2, c=clrs, edgecolors='#888888', alpha=0.75, linewidths=0.3)
ax.set_xlabel('Predicted'), ax.set_ylabel('Actual')
```
### ** Parte 3: Treinando e avaliando o modelo de regressão linear **
#### ** (3a) Gradiente do erro **
#### Vamos implementar a regressão linear através do gradiente descendente.
#### Lembrando que para atualizar o peso da regressão linear fazemos: $$ \scriptsize \mathbf{w}_{i+1} = \mathbf{w}_i - \alpha_i \sum_j (\mathbf{w}_i^\top\mathbf{x}_j - y_j) \mathbf{x}_j \,.$$ onde $ \scriptsize i $ é a iteração do algoritmo, e $ \scriptsize j $ é o objeto sendo observado no momento.
#### Primeiro, implemente uma função que calcula esse gradiente do erro para certo objeto: $ \scriptsize (\mathbf{w}^\top \mathbf{x} - y) \mathbf{x} \, ,$ e teste a função em dois exemplos. Use o método `DenseVector` [dot](http://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.linalg.DenseVector.dot) para representar a lista de atributos (ele tem funcionalidade parecida com o `np.array()`).
```
from pyspark.mllib.linalg import DenseVector
# EXERCICIO
def gradientSummand(weights, lp):
"""Calculates the gradient summand for a given weight and `LabeledPoint`.
Note:
`DenseVector` behaves similarly to a `numpy.ndarray` and they can be used interchangably
within this function. For example, they both implement the `dot` method.
Args:
weights (DenseVector): An array of model weights (betas).
lp (LabeledPoint): The `LabeledPoint` for a single observation.
Returns:
DenseVector: An array of values the same length as `weights`. The gradient summand.
"""
return DenseVector((weights.dot(lp.features) - lp.label) * lp.features)
exampleW = DenseVector([1, 1, 1])
exampleLP = LabeledPoint(2.0, [3, 1, 4])
summandOne = gradientSummand(exampleW, exampleLP)
print (summandOne)
exampleW = DenseVector([.24, 1.2, -1.4])
exampleLP = LabeledPoint(3.0, [-1.4, 4.2, 2.1])
summandTwo = gradientSummand(exampleW, exampleLP)
print (summandTwo)
# TEST Gradient summand (3a)
assert np.allclose(summandOne, [18., 6., 24.]), 'incorrect value for summandOne'
assert np.allclose(summandTwo, [1.7304,-5.1912,-2.5956]), 'incorrect value for summandTwo'
print("OK")
```
#### ** (3b) Use os pesos para fazer a predição **
#### Agora, implemente a função `getLabeledPredictions` que recebe como parâmetro o conjunto de pesos e um `LabeledPoint` e retorna uma tupla (rótulo, predição). Lembre-se que podemos predizer um rótulo calculando o produto interno dos pesos com os atributos.
```
# EXERCICIO
def getLabeledPrediction(weights, observation):
"""Calculates predictions and returns a (label, prediction) tuple.
Note:
The labels should remain unchanged as we'll use this information to calculate prediction
error later.
Args:
weights (np.ndarray): An array with one weight for each features in `trainData`.
observation (LabeledPoint): A `LabeledPoint` that contain the correct label and the
features for the data point.
Returns:
tuple: A (label, prediction) tuple.
"""
return (observation.label, weights.dot(observation.features))
weights = np.array([1.0, 1.5])
predictionExample = sc.parallelize([LabeledPoint(2, np.array([1.0, .5])),
LabeledPoint(1.5, np.array([.5, .5]))])
labelsAndPredsExample = predictionExample.map(lambda lp: getLabeledPrediction(weights, lp))
print (labelsAndPredsExample.collect())
# TEST Use weights to make predictions (3b)
assert labelsAndPredsExample.collect() == [(2.0, 1.75), (1.5, 1.25)], 'incorrect definition for getLabeledPredictions'
print("OK")
```
#### ** (3c) Gradiente descendente **
#### Finalmente, implemente o algoritmo gradiente descendente para regressão linear e teste a função em um exemplo.
```
# EXERCICIO
def linregGradientDescent(trainData, numIters):
"""Calculates the weights and error for a linear regression model trained with gradient descent.
Note:
`DenseVector` behaves similarly to a `numpy.ndarray` and they can be used interchangably
within this function. For example, they both implement the `dot` method.
Args:
trainData (RDD of LabeledPoint): The labeled data for use in training the model.
numIters (int): The number of iterations of gradient descent to perform.
Returns:
(np.ndarray, np.ndarray): A tuple of (weights, training errors). Weights will be the
final weights (one weight per feature) for the model, and training errors will contain
an error (RMSE) for each iteration of the algorithm.
"""
# The length of the training data
n = trainData.count()
# The number of features in the training data
d = len(trainData.first().features)
w = np.zeros(d)
alpha = 1.0
# We will compute and store the training error after each iteration
errorTrain = np.zeros(numIters)
for i in range(numIters):
# Use getLabeledPrediction from (3b) with trainData to obtain an RDD of (label, prediction)
# tuples. Note that the weights all equal 0 for the first iteration, so the predictions will
# have large errors to start.
labelsAndPredsTrain = trainData.map(lambda l: getLabeledPrediction(w, l))
errorTrain[i] = calcRMSE(labelsAndPreds)
# Calculate the `gradient`. Make use of the `gradientSummand` function you wrote in (3a).
# Note that `gradient` sould be a `DenseVector` of length `d`.
gradient = trainData.map(lambda l: gradientSummand(w, l)).sum()
# Update the weights
alpha_i = alpha / (n * np.sqrt(i+1))
w -= alpha_i*gradient
return w, errorTrain
# create a toy dataset with n = 10, d = 3, and then run 5 iterations of gradient descent
# note: the resulting model will not be useful; the goal here is to verify that
# linregGradientDescent is working properly
exampleN = 10
exampleD = 3
exampleData = (sc
.parallelize(parsedTrainData.take(exampleN))
.map(lambda lp: LabeledPoint(lp.label, lp.features[0:exampleD])))
print (exampleData.take(2))
exampleNumIters = 5
exampleWeights, exampleErrorTrain = linregGradientDescent(exampleData, exampleNumIters)
print (exampleWeights)
# TEST Gradient descent (3c)
expectedOutput = [48.20389904, 34.53243006, 30.60284959]
assert np.allclose(exampleWeights, expectedOutput), 'value of exampleWeights is incorrect'
expectedError = [79.72766145, 33.64762907, 9.46281696, 9.45486926, 9.44889147]
assert np.allclose(exampleErrorTrain, expectedError),'value of exampleErrorTrain is incorrect'
print("OK")
```
#### ** (3d) Treinando o modelo na base de dados **
#### Agora iremos treinar o modelo de regressão linear na nossa base de dados de treino e calcular o RMSE na base de validação. Lembrem-se que não devemos utilizar a base de teste até que o melhor parâmetro do modelo seja escolhido.
#### Para essa tarefa vamos utilizar as funções linregGradientDescent, getLabeledPrediction e calcRMSE já implementadas.
```
# EXERCICIO
numIters = 50
weightsLR0, errorTrainLR0 = linregGradientDescent(parsedTrainData, numIters)
labelsAndPreds = parsedValData.map(lambda lp: getLabeledPrediction(weightsLR0, lp))
rmseValLR0 = calcRMSE(labelsAndPreds)
print ('Validation RMSE:\n\tBaseline = {0:.3f}\n\tLR0 = {1:.3f}'.format(rmseValBase, rmseValLR0))
# TEST Train the model (3d)
expectedOutput = [ 22.64370481, 20.1815662, -0.21620107, 8.53259099, 5.94821844,
-4.50349235, 15.51511703, 3.88802901, 9.79146177, 5.74357056,
11.19512589, 3.60554264]
assert np.allclose(weightsLR0, expectedOutput), 'incorrect value for weightsLR0'
print("OK")
```
#### ** Visualização 3: Erro de Treino **
#### Vamos verificar o comportamento do algoritmo durante as iterações. Para isso vamos plotar um gráfico em que o eixo x representa a iteração e o eixo y o log do RMSE. O primeiro gráfico mostra as primeiras 50 iterações enquanto o segundo mostra as últimas 44 iterações. Note que inicialmente o erro cai rapidamente, quando então o gradiente descendente passa a fazer apenas pequenos ajustes.
```
norm = Normalize()
clrs = cmap(np.asarray(norm(np.log(errorTrainLR0))))[:,0:3]
fig, ax = preparePlot(np.arange(0, 60, 10), np.arange(2, 6, 1))
ax.set_ylim(2, 6)
plt.scatter(list(range(0, numIters)), np.log(errorTrainLR0), s=14**2, c=clrs, edgecolors='#888888', alpha=0.75)
ax.set_xlabel('Iteration'), ax.set_ylabel(r'$\log_e(errorTrainLR0)$')
pass
norm = Normalize()
clrs = cmap(np.asarray(norm(errorTrainLR0[6:])))[:,0:3]
fig, ax = preparePlot(np.arange(0, 60, 10), np.arange(17, 22, 1))
ax.set_ylim(17.8, 21.2)
plt.scatter(range(0, numIters-6), errorTrainLR0[6:], s=14**2, c=clrs, edgecolors='#888888', alpha=0.75)
ax.set_xticklabels(map(str, range(6, 66, 10)))
ax.set_xlabel('Iteration'), ax.set_ylabel(r'Training Error')
pass
```
### ** Part 4: Treino utilizando MLlib e Busca em Grade (Grid Search) **
#### **(4a) `LinearRegressionWithSGD` **
#### Nosso teste inicial já conseguiu obter um desempenho melhor que o baseline, mas vamos ver se conseguimos fazer melhor introduzindo a ordenada de origem da reta além de outros ajustes no algoritmo. MLlib [LinearRegressionWithSGD](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.regression.LinearRegressionWithSGD) implementa o mesmo algoritmo da parte (3b), mas de forma mais eficiente para o contexto distribuído e com várias funcionalidades adicionais.
#### Primeiro utilize a função LinearRegressionWithSGD para treinar um modelo com regularização L2 (Ridge) e com a ordenada de origem. Esse método retorna um [LinearRegressionModel](https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.regression.LinearRegressionModel).
#### Em seguida, use os atributos [weights](http://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.regression.LinearRegressionModel.weights) e [intercept](http://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.regression.LinearRegressionModel.intercept) para imprimir o modelo encontrado.
```
from pyspark.mllib.regression import LinearRegressionWithSGD
# Values to use when training the linear regression model
numIters = 500 # iterations
alpha = 1.0 # step
miniBatchFrac = 1.0 # miniBatchFraction
reg = 1e-1 # regParam
regType = 'l2' # regType
useIntercept = True # intercept
# EXERCICIO
firstModel = LinearRegressionWithSGD.train(parsedTrainData, iterations = numIters, step = alpha, miniBatchFraction = 1.0,
regParam=reg,regType=regType, intercept=useIntercept)
# weightsLR1 stores the model weights; interceptLR1 stores the model intercept
weightsLR1 = firstModel.weights
interceptLR1 = firstModel.intercept
print( weightsLR1, interceptLR1)
# TEST LinearRegressionWithSGD (4a)
expectedIntercept = 13.332056210482524
expectedWeights = [15.9694010246,13.9897244172,0.669349383773,6.24618402989,4.00932179503,-2.30176663131,10.478805422,3.06385145385,7.14414111075,4.49826819526,7.87702565069,3.00732146613]
assert np.allclose(interceptLR1, expectedIntercept), 'incorrect value for interceptLR1'
assert np.allclose(weightsLR1, expectedWeights), 'incorrect value for weightsLR1'
print("OK")
```
#### **(4b) Predição**
#### Agora use o método [LinearRegressionModel.predict()](http://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.regression.LinearRegressionModel.predict) para fazer a predição de um objeto. Passe o atributo `features` de um `LabeledPoint` comp parâmetro.
```
# EXERCICIO
samplePoint = parsedTrainData.take(1)[0]
samplePrediction = firstModel.predict(samplePoint.features)
print (samplePrediction)
# TEST Predict (4b)
assert np.allclose(samplePrediction, 56.4065674104), 'incorrect value for samplePrediction'
print("OK")
```
#### ** (4c) Avaliar RMSE **
#### Agora avalie o desempenho desse modelo no teste de validação. Use o método `predict()` para criar o RDD `labelsAndPreds` RDD, e então use a função `calcRMSE()` da Parte (2b) para calcular o RMSE.
```
# EXERCICIO
labelsAndPreds = parsedValData.map(lambda lp: (lp.label, firstModel.predict(lp.features)))
rmseValLR1 = calcRMSE(labelsAndPreds)
print ('Validation RMSE:\n\tBaseline = {0:.3f}\n\tLR0 = {1:.3f}\n\tLR1 = {2:.3f}'.format(rmseValBase, rmseValLR0, rmseValLR1))
# TEST Evaluate RMSE (4c)
assert np.allclose(rmseValLR1, 19.025), 'incorrect value for rmseValLR1'
print("OK")
```
#### ** (4d) Grid search **
#### Já estamos superando o baseline em pelo menos dois anos na média, vamos ver se encontramos um conjunto de parâmetros melhor. Faça um grid search para encontrar um bom parâmetro de regularização. Tente valores para `regParam` dentro do conjunto `1e-10`, `1e-5`, e `1`.
```
# EXERCICIO
bestRMSE = rmseValLR1
bestRegParam = reg
bestModel = firstModel
numIters = 500
alpha = 1.0
miniBatchFrac = 1.0
for reg in [1e-10, 1e-5, 1.0]:
model = LinearRegressionWithSGD.train(parsedTrainData, numIters, alpha,
miniBatchFrac, regParam=reg,
regType='l2', intercept=True)
labelsAndPreds = parsedValData.map(lambda lp: (lp.label, model.predict(lp.features)))
rmseValGrid = calcRMSE(labelsAndPreds)
print (rmseValGrid)
if rmseValGrid < bestRMSE:
bestRMSE = rmseValGrid
bestRegParam = reg
bestModel = model
rmseValLRGrid = bestRMSE
print ('Validation RMSE:\n\tBaseline = {0:.3f}\n\tLR0 = {1:.3f}\n\tLR1 = {2:.3f}\n\tLRGrid = {3:.3f}'.format(rmseValBase, rmseValLR0, rmseValLR1, rmseValLRGrid))
# TEST Grid search (4d)
assert np.allclose(16.6813542516, rmseValLRGrid), 'incorrect value for rmseValLRGrid'
print("OK")
```
#### ** Visualização 5: Predições do melhor modelo**
#### Agora, vamos criar um gráfico para verificar o desempenho do melhor modelo. Reparem nesse gráfico que a quantidade de pontos mais escuros reduziu bastante em relação ao baseline.
```
predictions = np.asarray(parsedValData
.map(lambda lp: bestModel.predict(lp.features))
.collect())
actual = np.asarray(parsedValData
.map(lambda lp: lp.label)
.collect())
error = np.asarray(parsedValData
.map(lambda lp: (lp.label, bestModel.predict(lp.features)))
.map(lambda lp: squaredError(lp[0], lp[1]))
.collect())
norm = Normalize()
clrs = cmap(np.asarray(norm(error)))[:,0:3]
fig, ax = preparePlot(np.arange(0, 120, 20), np.arange(0, 120, 20))
ax.set_xlim(15, 82), ax.set_ylim(-5, 105)
plt.scatter(predictions, actual, s=14**2, c=clrs, edgecolors='#888888', alpha=0.75, linewidths=.5)
ax.set_xlabel('Predicted'), ax.set_ylabel(r'Actual')
pass
```
#### ** (4e) Grid Search para o valor de alfa e número de iterações **
#### Agora, vamos verificar diferentes valores para alfa e número de iterações para perceber o impacto desses parâmetros em nosso modelo. Especificamente tente os valores `1e-5` e `10` para `alpha` e os valores `500` e `5` para número de iterações. Avalie todos os modelos no conjunto de valdação. Reparem que com um valor baixo de alpha, o algoritmo necessita de muito mais iterações para convergir ao ótimo, enquanto um valor muito alto para alpha, pode fazer com que o algoritmo não encontre uma solução.
```
# EXERCICIO
reg = bestRegParam
modelRMSEs = []
for alpha in [1e-5, 10]:
for numIters in [500, 5]:
model = LinearRegressionWithSGD.train(parsedTrainData, numIters, alpha,
miniBatchFrac, regParam=reg,
regType='l2', intercept=True)
labelsAndPreds = parsedValData.map(lambda lp: (lp.label, model.predict(lp.features)))
rmseVal = calcRMSE(labelsAndPreds)
print ('alpha = {0:.0e}, numIters = {1}, RMSE = {2:.3f}'.format(alpha, numIters, rmseVal))
modelRMSEs.append(rmseVal)
# TEST Vary alpha and the number of iterations (4e)
expectedResults = sorted([57.487692757541318, 57.487692757541318, 352324534.65684682])
assert np.allclose(sorted(modelRMSEs)[:3], expectedResults), 'incorrect value for modelRMSEs'
print("OK")
```
| github_jupyter |
# Anomaly detection
Anomaly detection is a machine learning task that consists in spotting so-called outliers.
“An outlier is an observation in a data set which appears to be inconsistent with the remainder of that set of data.”
Johnson 1992
“An outlier is an observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism.”
Outlier/Anomaly
Hawkins 1980
### Types of anomaly detection setups
- Supervised AD
- Labels available for both normal data and anomalies
- Similar to rare class mining / imbalanced classification
- Semi-supervised AD (Novelty Detection)
- Only normal data available to train
- The algorithm learns on normal data only
- Unsupervised AD (Outlier Detection)
- no labels, training set = normal + abnormal data
- Assumption: anomalies are very rare
```
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
```
Let's first get familiar with different unsupervised anomaly detection approaches and algorithms. In order to visualise the output of the different algorithms we consider a toy data set consisting in a two-dimensional Gaussian mixture.
### Generating the data set
```
from sklearn.datasets import make_blobs
X, y = make_blobs(n_features=2, centers=3, n_samples=500,
random_state=42)
X.shape
plt.figure()
plt.scatter(X[:, 0], X[:, 1])
plt.show()
```
## Anomaly detection with density estimation
```
from sklearn.neighbors.kde import KernelDensity
# Estimate density with a Gaussian kernel density estimator
kde = KernelDensity(kernel='gaussian')
kde = kde.fit(X)
kde
kde_X = kde.score_samples(X)
print(kde_X.shape) # contains the log-likelihood of the data. The smaller it is the rarer is the sample
from scipy.stats.mstats import mquantiles
alpha_set = 0.95
tau_kde = mquantiles(kde_X, 1. - alpha_set)
n_samples, n_features = X.shape
X_range = np.zeros((n_features, 2))
X_range[:, 0] = np.min(X, axis=0) - 1.
X_range[:, 1] = np.max(X, axis=0) + 1.
h = 0.1 # step size of the mesh
x_min, x_max = X_range[0]
y_min, y_max = X_range[1]
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
grid = np.c_[xx.ravel(), yy.ravel()]
Z_kde = kde.score_samples(grid)
Z_kde = Z_kde.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_kde, levels=tau_kde, colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15, fmt={tau_kde[0]: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1])
plt.show()
```
## now with One-Class SVM
The problem of density based estimation is that they tend to become inefficient when the dimensionality of the data increase. It's the so-called curse of dimensionality that affects particularly density estimation algorithms. The one-class SVM algorithm can be used in such cases.
```
from sklearn.svm import OneClassSVM
nu = 0.05 # theory says it should be an upper bound of the fraction of outliers
ocsvm = OneClassSVM(kernel='rbf', gamma=0.05, nu=nu)
ocsvm.fit(X)
X_outliers = X[ocsvm.predict(X) == -1]
Z_ocsvm = ocsvm.decision_function(grid)
Z_ocsvm = Z_ocsvm.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_ocsvm, levels=[0], colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15, fmt={0: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1])
plt.scatter(X_outliers[:, 0], X_outliers[:, 1], color='red')
plt.show()
```
### Support vectors - Outliers
The so-called support vectors of the one-class SVM form the outliers
```
X_SV = X[ocsvm.support_]
n_SV = len(X_SV)
n_outliers = len(X_outliers)
print('{0:.2f} <= {1:.2f} <= {2:.2f}?'.format(1./n_samples*n_outliers, nu, 1./n_samples*n_SV))
```
Only the support vectors are involved in the decision function of the One-Class SVM.
1. Plot the level sets of the One-Class SVM decision function as we did for the true density.
2. Emphasize the Support vectors.
```
plt.figure()
plt.contourf(xx, yy, Z_ocsvm, 10, cmap=plt.cm.Blues_r)
plt.scatter(X[:, 0], X[:, 1], s=1.)
plt.scatter(X_SV[:, 0], X_SV[:, 1], color='orange')
plt.show()
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
**Change** the `gamma` parameter and see it's influence on the smoothness of the decision function.
</li>
</ul>
</div>
```
# %load solutions/22_A-anomaly_ocsvm_gamma.py
```
## Isolation Forest
Isolation Forest is an anomaly detection algorithm based on trees. The algorithm builds a number of random trees and the rationale is that if a sample is isolated it should alone in a leaf after very few random splits. Isolation Forest builds a score of abnormality based the depth of the tree at which samples end up.
```
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(n_estimators=300, contamination=0.10)
iforest = iforest.fit(X)
Z_iforest = iforest.decision_function(grid)
Z_iforest = Z_iforest.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_iforest,
levels=[iforest.threshold_],
colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15,
fmt={iforest.threshold_: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1], s=1.)
plt.show()
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
Illustrate graphically the influence of the number of trees on the smoothness of the decision function?
</li>
</ul>
</div>
```
# %load solutions/22_B-anomaly_iforest_n_trees.py
```
# Illustration on Digits data set
We will now apply the IsolationForest algorithm to spot digits written in an unconventional way.
```
from sklearn.datasets import load_digits
digits = load_digits()
```
The digits data set consists in images (8 x 8) of digits.
```
images = digits.images
labels = digits.target
images.shape
i = 102
plt.figure(figsize=(2, 2))
plt.title('{0}'.format(labels[i]))
plt.axis('off')
plt.imshow(images[i], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
```
To use the images as a training set we need to flatten the images.
```
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
data.shape
X = data
y = digits.target
X.shape
```
Let's focus on digit 5.
```
X_5 = X[y == 5]
X_5.shape
fig, axes = plt.subplots(1, 5, figsize=(10, 4))
for ax, x in zip(axes, X_5[:5]):
img = x.reshape(8, 8)
ax.imshow(img, cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
1. Let's use IsolationForest to find the top 5% most abnormal images.
2. Let's plot them !
```
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(contamination=0.05)
iforest = iforest.fit(X_5)
```
Compute the level of "abnormality" with `iforest.decision_function`. The lower, the more abnormal.
```
iforest_X = iforest.decision_function(X_5)
plt.hist(iforest_X);
```
Let's plot the strongest inliers
```
X_strong_inliers = X_5[np.argsort(iforest_X)[-10:]]
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
for i, ax in zip(range(len(X_strong_inliers)), axes.ravel()):
ax.imshow(X_strong_inliers[i].reshape((8, 8)),
cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
Let's plot the strongest outliers
```
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
X_outliers = X_5[iforest.predict(X_5) == -1]
for i, ax in zip(range(len(X_outliers)), axes.ravel()):
ax.imshow(X_outliers[i].reshape((8, 8)),
cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
Rerun the same analysis with all the other digits
</li>
</ul>
</div>
```
# %load solutions/22_C-anomaly_digits.py
```
| github_jupyter |
# Intro to machine learning - k-means
---
Scikit-learn has a nice set of unsupervised learning routines which can be used to explore clustering in the parameter space.
In this notebook we will use k-means, included in Scikit-learn, to demonstrate how the different rocks occupy different regions in the available parameter space.
Let's load the data using pandas:
```
import pandas as pd
import numpy as np
df = pd.read_csv("../data/2016_ML_contest_training_data.csv")
df.head()
df.describe()
df = df.dropna()
```
## Calculate RHOB from DeltaPHI and PHIND
```
def rhob(phi_rhob, Rho_matrix= 2650.0, Rho_fluid=1000.0):
"""
Rho_matrix (sandstone) : 2.65 g/cc
Rho_matrix (Limestome): 2.71 g/cc
Rho_matrix (Dolomite): 2.876 g/cc
Rho_matrix (Anyhydrite): 2.977 g/cc
Rho_matrix (Salt): 2.032 g/cc
Rho_fluid (fresh water): 1.0 g/cc (is this more mud-like?)
Rho_fluid (salt water): 1.1 g/cc
see wiki.aapg.org/Density-neutron_log_porosity
returns density porosity log """
return Rho_matrix*(1 - phi_rhob) + Rho_fluid*phi_rhob
phi_rhob = 2*(df.PHIND/100)/(1 - df.DeltaPHI/100) - df.DeltaPHI/100
calc_RHOB = rhob(phi_rhob)
df['RHOB'] = calc_RHOB
df.describe()
```
We can define a Python dictionary to relate facies with the integer label on the `DataFrame`
```
facies_dict = {1:'sandstone', 2:'c_siltstone', 3:'f_siltstone', 4:'marine_silt_shale',
5:'mudstone', 6:'wackentstone', 7:'dolomite', 8:'packstone', 9:'bafflestone'}
df["s_Facies"] = df.Facies.map(lambda x: facies_dict[x])
df.head()
```
We can easily visualize the properties of each facies and how they compare using a `PairPlot`. The library `seaborn` integrates with matplotlib to make these kind of plots easily.
```
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
g = sns.PairGrid(df, hue="s_Facies", vars=['GR','RHOB','PE','ILD_log10'], size=4)
g.map_upper(plt.scatter,**dict(alpha=0.4))
g.map_lower(plt.scatter,**dict(alpha=0.4))
g.map_diag(plt.hist,**dict(bins=20))
g.add_legend()
g.set(alpha=0.5)
```
It is very clear that it's hard to separate these facies in feature space. Let's just select a couple of facies and using Pandas, select the rows in the `DataFrame` that contain information about those facies
```
selected = ['f_siltstone', 'bafflestone', 'wackentstone']
dfs = pd.concat(list(map(lambda x: df[df.s_Facies == x], selected)))
g = sns.PairGrid(dfs, hue="s_Facies", vars=['GR','RHOB','PE','ILD_log10'], size=4)
g.map_upper(plt.scatter,**dict(alpha=0.4))
g.map_lower(plt.scatter,**dict(alpha=0.4))
g.map_diag(plt.hist,**dict(bins=20))
g.add_legend()
g.set(alpha=0.5)
# Make X and y
X = dfs[['GR','ILD_log10','PE']].as_matrix()
y = dfs['Facies'].values
```
Use scikit-learn StandardScaler to normalize the data. Needed for k-means.
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.3)
from sklearn.cluster import KMeans
clf = KMeans(n_clusters=4, random_state=1).fit(X)
y_pred = clf.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, alpha=0.3)
clf.inertia_
```
<hr />
<p style="color:gray">©2017 Agile Geoscience. Licensed CC-BY.</p>
| github_jupyter |
# Beating the betting firms with linear models
* **Data Source:** [https://www.kaggle.com/hugomathien/soccer](https://www.kaggle.com/hugomathien/soccer)
* **Author:** Anders Munk-Nielsen
**Result:** It is possible to do better than the professional betting firms in terms of predicting each outcome (although they may be maximizing profit rather than trying to predict outcomes). This is using a linear model, and it requires us to use a lot of variables, though.
**Perspectives:** We can only model 1(win), but there are *three* outcomes: Lose, Draw, and Win.
```
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme()
# Read
d = pd.read_csv('football_probs.csv')
# Data types
d.date = pd.to_datetime(d.date)
cols_to_cat = ['league', 'season', 'team', 'country']
for c in cols_to_cat:
d[c] = d[c].astype('category')
```
Visualizing the home field advantage.
```
sns.histplot(data=d, x='goal_diff', hue='home', discrete=True);
plt.xlim([-7,7]);
```
Outcome variables
```
# Lose, Draw, Win
d['outcome'] = 'L'
d.loc[d.goal_diff == 0.0, 'outcome'] = 'D'
d.loc[d.goal_diff > 0.0, 'outcome'] = 'W'
# Win dummy (as float (will become useful later))
d['win'] = (d.goal_diff > 0.0).astype(float)
```
# Odds to probabilities
### Convenient lists of variable names
* `cols_common`: All variables that are unrelated to betting
* `betting_firms`: The prefix that defines the name of the betting firms, e.g. B365 for Bet365
* `firm_vars`: A dictionary returning the variables for a firm, e.g. `firm_vars['BW']` returns `BWA`, `BWD`, `BWH` (for Away, Draw, Home team win).
```
# # List of the names of all firms that we have betting prices for
betting_firms = np.unique([c[:-4] for c in d.columns if c[-1] in ['A', 'H', 'D']])
betting_firms
# find all columns in our dataframe that are *not* betting variables
cols_common = [c for c in d.columns if (c[-4:-1] != '_Pr') & (c[-9:] != 'overround')]
print(f'Non-odds variables: {cols_common}')
d[d.home].groupby('win')['B365_PrW'].mean().to_frame('Bet 365 Pr(win)')
sns.histplot(d, x='B365_PrW', hue='win');
```
## Is there more information in the mean?
If all firms are drawing random IID signals, then the average prediction should be a better estimator than any individual predictor.
```
firms_drop = ['BS', 'GB', 'PS', 'SJ'] # these are missing in too many years
cols_prW = [f'{c}_PrW' for c in betting_firms if c not in firms_drop]
d['avg_PrW'] = d[cols_prW].mean(1)
cols_prW += ['avg_PrW']
I = d.win == True
fig, ax = plt.subplots();
ax.hist(d.loc[I,'avg_PrW'], bins=30, alpha=0.3, label='Avg. prediction')
ax.hist(d.loc[I,'B365_PrW'], bins=30, alpha=0.3, label='B365')
ax.hist(d.loc[I,'BW_PrW'], bins=30, alpha=0.3, label='BW')
ax.legend();
ax.set_xlabel('Pr(win) [only matches where win==1]');
```
### RMSE comparison
* RMSE: Root Mean Squared Error. Whenever we have a candidate prediction guess, $\hat{y}_i$, we can evaluate $$ RMSE = \sqrt{ N^{-1}\sum_{i=1}^N (y_i - \hat{y}_i)^2 }. $$
```
def RMSE(yhat, y) -> float:
'''Root mean squared error: between yvar and y'''
q = (yhat - y)**2
return np.sqrt(np.mean(q))
def RMSE_agg(data: pd.core.frame.DataFrame, y: str) -> pd.core.series.Series:
'''RMSE_agg: Aggregates all columns, computing RMSE against the variable y for each column
'''
assert y in data.columns
y = data['win']
# local function computing RMSE for a specific column, yvar, against y
def RMSE_(yhat):
diff_sq = (yhat - y) ** 2
return np.sqrt(np.mean(diff_sq))
# do not compute RMSE against the real outcome :)
mycols = [c for c in data.columns if c != 'win']
# return aggregated dataframe (which becomes a pandas series)
return data[mycols].agg(RMSE_)
I = d[cols_prW].notnull().all(1) # only run comparison on subsample where all odds were observed
x_ = RMSE_agg(d[cols_prW + ['win']], 'win');
ax = x_.plot.bar();
ax.set_ylim([x_.min()*.999, x_.max()*1.001]);
ax.set_ylabel('RMSE');
```
# Linear Probability Models
Estimate a bunch of models where $y_i = 1(\text{win})$.
## Using `numpy`
```
d['home_'] = d.home.astype(float)
I = d[['home_', 'win'] + cols_prW].notnull().all(axis=1)
X = d.loc[I, ['home_'] + cols_prW].values
y = d.loc[I, 'win'].values.reshape(-1,1)
N = I.sum()
oo = np.ones((N,1))
X = np.hstack([oo, X])
betahat = np.linalg.inv(X.T @ X) @ X.T @ y
pd.DataFrame({'beta':betahat.flatten()}, index=['const', 'home'] + cols_prW)
```
## Using `statsmodels`
(Cheating, but faster...)
```
reg_addition = ' + '.join(cols_prW)
model_string = f'win ~ {reg_addition} + home + team'
cols_all = cols_prW + ['win', 'home']
I = d[cols_all].notnull().all(1) # no missings in any variables used in the prediction model
Itrain = I & (d.date < '2015-01-01') # for estimating our prediction model
Iholdout = I & (d.date >= '2015-01-01') # for assessing the model fit
# run regression
r = smf.ols(model_string, d[Itrain]).fit()
yhat = r.predict(d[I]).to_frame('AMN_PrW')
d.loc[I, 'AMN_PrW'] = yhat
print('Estimates with Team FE')
r.params.loc[['home[T.True]'] + cols_prW].to_frame('Beta')
```
### Plot estimates, $\hat{\beta}$
```
ax = r.params.loc[cols_prW].plot.bar();
ax.set_ylabel('Coefficient (loading in optimal prediction)');
ax.set_xlabel('Betting firm prediction');
```
### Plot model fit out of sample: avg. 1(win) vs. avg. $\hat{y}$
```
# predicted win rates from all firms and our new predicted probability
cols = cols_prW + ['AMN_PrW']
```
**Home matches:** `home == True`
```
x_ = d.loc[(d.win == 1.0) & (d.home == True) & (Iholdout == True), cols].mean()
ax = x_.plot(kind='bar');
ax.set_ylim([x_.min()*0.995, x_.max()*1.005]);
ax.set_title('Out of sample fit: won matches as Home');
ax.set_xlabel('Betting firm prediction');
ax.set_ylabel('Pr(win) (only won home matches)');
```
**Away matches:** `home == False`
```
x_ = d.loc[(d.win == 1.0) & (d.home == False) & (Iholdout == True), cols].mean()
ax = x_.plot(kind='bar');
ax.set_ylim([x_.min()*0.995, x_.max()*1.005]);
ax.set_ylabel('Pr(win) (only won away matches)');
ax.set_title('Out of sample fit: won matches as Away');
```
### RMSE
(evaluated in the holdout sample, of course.)
```
cols_ = cols_prW + ['AMN_PrW', 'win']
I = Iholdout & d[cols_].notnull().all(1) # only run comparison on subsample where all odds were observed
x_ = RMSE_agg(d.loc[I,cols_], y='win');
ax = x_.plot.bar();
ax.set_ylim([x_.min()*.999, x_.max()*1.001]);
ax.set_ylabel('RMSE (out of sample)');
```
| github_jupyter |
# Assignment 2: Naive Bayes
Welcome to week two of this specialization. You will learn about Naive Bayes. Concretely, you will be using Naive Bayes for sentiment analysis on tweets. Given a tweet, you will decide if it has a positive sentiment or a negative one. Specifically you will:
* Train a naive bayes model on a sentiment analysis task
* Test using your model
* Compute ratios of positive words to negative words
* Do some error analysis
* Predict on your own tweet
You may already be familiar with Naive Bayes and its justification in terms of conditional probabilities and independence.
* In this week's lectures and assignments we used the ratio of probabilities between positive and negative sentiments.
* This approach gives us simpler formulas for these 2-way classification tasks.
Load the cell below to import some packages.
You may want to browse the documentation of unfamiliar libraries and functions.
```
from utils import process_tweet, lookup
import pdb
from nltk.corpus import stopwords, twitter_samples
import numpy as np
import pandas as pd
import nltk
import string
from nltk.tokenize import TweetTokenizer
from os import getcwd
```
If you are running this notebook in your local computer,
don't forget to download the twitter samples and stopwords from nltk.
```
nltk.download('stopwords')
nltk.download('twitter_samples')
```
```
# add folder, tmp2, from our local workspace containing pre-downloaded corpora files to nltk's data path
filePath = f"{getcwd()}/../tmp2/"
nltk.data.path.append(filePath)
# get the sets of positive and negative tweets
all_positive_tweets = twitter_samples.strings('positive_tweets.json')
all_negative_tweets = twitter_samples.strings('negative_tweets.json')
# split the data into two pieces, one for training and one for testing (validation set)
test_pos = all_positive_tweets[4000:]
train_pos = all_positive_tweets[:4000]
test_neg = all_negative_tweets[4000:]
train_neg = all_negative_tweets[:4000]
train_x = train_pos + train_neg
test_x = test_pos + test_neg
# avoid assumptions about the length of all_positive_tweets
train_y = np.append(np.ones(len(train_pos)), np.zeros(len(train_neg)))
test_y = np.append(np.ones(len(test_pos)), np.zeros(len(test_neg)))
```
# Part 1: Process the Data
For any machine learning project, once you've gathered the data, the first step is to process it to make useful inputs to your model.
- **Remove noise**: You will first want to remove noise from your data -- that is, remove words that don't tell you much about the content. These include all common words like 'I, you, are, is, etc...' that would not give us enough information on the sentiment.
- We'll also remove stock market tickers, retweet symbols, hyperlinks, and hashtags because they can not tell you a lot of information on the sentiment.
- You also want to remove all the punctuation from a tweet. The reason for doing this is because we want to treat words with or without the punctuation as the same word, instead of treating "happy", "happy?", "happy!", "happy," and "happy." as different words.
- Finally you want to use stemming to only keep track of one variation of each word. In other words, we'll treat "motivation", "motivated", and "motivate" similarly by grouping them within the same stem of "motiv-".
We have given you the function `process_tweet()` that does this for you.
```
custom_tweet = "RT @Twitter @chapagain Hello There! Have a great day. :) #good #morning http://chapagain.com.np"
# print cleaned tweet
print(process_tweet(custom_tweet))
```
## Part 1.1 Implementing your helper functions
To help train your naive bayes model, you will need to build a dictionary where the keys are a (word, label) tuple and the values are the corresponding frequency. Note that the labels we'll use here are 1 for positive and 0 for negative.
You will also implement a `lookup()` helper function that takes in the `freqs` dictionary, a word, and a label (1 or 0) and returns the number of times that word and label tuple appears in the collection of tweets.
For example: given a list of tweets `["i am rather excited", "you are rather happy"]` and the label 1, the function will return a dictionary that contains the following key-value pairs:
{
("rather", 1): 2
("happi", 1) : 1
("excit", 1) : 1
}
- Notice how for each word in the given string, the same label 1 is assigned to each word.
- Notice how the words "i" and "am" are not saved, since it was removed by process_tweet because it is a stopword.
- Notice how the word "rather" appears twice in the list of tweets, and so its count value is 2.
#### Instructions
Create a function `count_tweets()` that takes a list of tweets as input, cleans all of them, and returns a dictionary.
- The key in the dictionary is a tuple containing the stemmed word and its class label, e.g. ("happi",1).
- The value the number of times this word appears in the given collection of tweets (an integer).
<details>
<summary>
<font size="3" color="darkgreen"><b>Hints</b></font>
</summary>
<p>
<ul>
<li>Please use the `process_tweet` function that was imported above, and then store the words in their respective dictionaries and sets.</li>
<li>You may find it useful to use the `zip` function to match each element in `tweets` with each element in `ys`.</li>
<li>Remember to check if the key in the dictionary exists before adding that key to the dictionary, or incrementing its value.</li>
<li>Assume that the `result` dictionary that is input will contain clean key-value pairs (you can assume that the values will be integers that can be incremented). It is good practice to check the datatype before incrementing the value, but it's not required here.</li>
</ul>
</p>
```
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def count_tweets(result, tweets, ys):
'''
Input:
result: a dictionary that will be used to map each pair to its frequency
tweets: a list of tweets
ys: a list corresponding to the sentiment of each tweet (either 0 or 1)
Output:
result: a dictionary mapping each pair to its frequency
'''
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
for y, tweet in zip(ys, tweets):
for word in process_tweet(tweet):
# define the key, which is the word and label tuple
pair = (word, y)
# if the key exists in the dictionary, increment the count
if pair in result:
result[pair] += 1
# else, if the key is new, add it to the dictionary and set the count to 1
else:
result[pair] = 1
### END CODE HERE ###
return result
# Testing your function
result = {}
tweets = ['i am happy', 'i am tricked', 'i am sad', 'i am tired', 'i am tired']
ys = [1, 0, 0, 0, 0]
count_tweets(result, tweets, ys)
```
**Expected Output**: {('happi', 1): 1, ('trick', 0): 1, ('sad', 0): 1, ('tire', 0): 2}
# Part 2: Train your model using Naive Bayes
Naive bayes is an algorithm that could be used for sentiment analysis. It takes a short time to train and also has a short prediction time.
#### So how do you train a Naive Bayes classifier?
- The first part of training a naive bayes classifier is to identify the number of classes that you have.
- You will create a probability for each class.
$P(D_{pos})$ is the probability that the document is positive.
$P(D_{neg})$ is the probability that the document is negative.
Use the formulas as follows and store the values in a dictionary:
$$P(D_{pos}) = \frac{D_{pos}}{D}\tag{1}$$
$$P(D_{neg}) = \frac{D_{neg}}{D}\tag{2}$$
Where $D$ is the total number of documents, or tweets in this case, $D_{pos}$ is the total number of positive tweets and $D_{neg}$ is the total number of negative tweets.
#### Prior and Logprior
The prior probability represents the underlying probability in the target population that a tweet is positive versus negative. In other words, if we had no specific information and blindly picked a tweet out of the population set, what is the probability that it will be positive versus that it will be negative? That is the "prior".
The prior is the ratio of the probabilities $\frac{P(D_{pos})}{P(D_{neg})}$.
We can take the log of the prior to rescale it, and we'll call this the logprior
$$\text{logprior} = log \left( \frac{P(D_{pos})}{P(D_{neg})} \right) = log \left( \frac{D_{pos}}{D_{neg}} \right)$$.
Note that $log(\frac{A}{B})$ is the same as $log(A) - log(B)$. So the logprior can also be calculated as the difference between two logs:
$$\text{logprior} = \log (P(D_{pos})) - \log (P(D_{neg})) = \log (D_{pos}) - \log (D_{neg})\tag{3}$$
#### Positive and Negative Probability of a Word
To compute the positive probability and the negative probability for a specific word in the vocabulary, we'll use the following inputs:
- $freq_{pos}$ and $freq_{neg}$ are the frequencies of that specific word in the positive or negative class. In other words, the positive frequency of a word is the number of times the word is counted with the label of 1.
- $N_{pos}$ and $N_{neg}$ are the total number of positive and negative words for all documents (for all tweets), respectively.
- $V$ is the number of unique words in the entire set of documents, for all classes, whether positive or negative.
We'll use these to compute the positive and negative probability for a specific word using this formula:
$$ P(W_{pos}) = \frac{freq_{pos} + 1}{N_{pos} + V}\tag{4} $$
$$ P(W_{neg}) = \frac{freq_{neg} + 1}{N_{neg} + V}\tag{5} $$
Notice that we add the "+1" in the numerator for additive smoothing. This [wiki article](https://en.wikipedia.org/wiki/Additive_smoothing) explains more about additive smoothing.
#### Log likelihood
To compute the loglikelihood of that very same word, we can implement the following equations:
$$\text{loglikelihood} = \log \left(\frac{P(W_{pos})}{P(W_{neg})} \right)\tag{6}$$
##### Create `freqs` dictionary
- Given your `count_tweets()` function, you can compute a dictionary called `freqs` that contains all the frequencies.
- In this `freqs` dictionary, the key is the tuple (word, label)
- The value is the number of times it has appeared.
We will use this dictionary in several parts of this assignment.
```
# Build the freqs dictionary for later uses
freqs = count_tweets({}, train_x, train_y)
```
#### Instructions
Given a freqs dictionary, `train_x` (a list of tweets) and a `train_y` (a list of labels for each tweet), implement a naive bayes classifier.
##### Calculate $V$
- You can then compute the number of unique words that appear in the `freqs` dictionary to get your $V$ (you can use the `set` function).
##### Calculate $freq_{pos}$ and $freq_{neg}$
- Using your `freqs` dictionary, you can compute the positive and negative frequency of each word $freq_{pos}$ and $freq_{neg}$.
##### Calculate $N_{pos}$ and $N_{neg}$
- Using `freqs` dictionary, you can also compute the total number of positive words and total number of negative words $N_{pos}$ and $N_{neg}$.
##### Calculate $D$, $D_{pos}$, $D_{neg}$
- Using the `train_y` input list of labels, calculate the number of documents (tweets) $D$, as well as the number of positive documents (tweets) $D_{pos}$ and number of negative documents (tweets) $D_{neg}$.
- Calculate the probability that a document (tweet) is positive $P(D_{pos})$, and the probability that a document (tweet) is negative $P(D_{neg})$
##### Calculate the logprior
- the logprior is $log(D_{pos}) - log(D_{neg})$
##### Calculate log likelihood
- Finally, you can iterate over each word in the vocabulary, use your `lookup` function to get the positive frequencies, $freq_{pos}$, and the negative frequencies, $freq_{neg}$, for that specific word.
- Compute the positive probability of each word $P(W_{pos})$, negative probability of each word $P(W_{neg})$ using equations 4 & 5.
$$ P(W_{pos}) = \frac{freq_{pos} + 1}{N_{pos} + V}\tag{4} $$
$$ P(W_{neg}) = \frac{freq_{neg} + 1}{N_{neg} + V}\tag{5} $$
**Note:** We'll use a dictionary to store the log likelihoods for each word. The key is the word, the value is the log likelihood of that word).
- You can then compute the loglikelihood: $log \left( \frac{P(W_{pos})}{P(W_{neg})} \right)\tag{6}$.
```
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def train_naive_bayes(freqs, train_x, train_y):
'''
Input:
freqs: dictionary from (word, label) to how often the word appears
train_x: a list of tweets
train_y: a list of labels correponding to the tweets (0,1)
Output:
logprior: the log prior. (equation 3 above)
loglikelihood: the log likelihood of you Naive bayes equation. (equation 6 above)
'''
loglikelihood = {}
logprior = 0
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
# calculate V, the number of unique words in the vocabulary
vocab = set([pair[0] for pair in freqs.keys()])
V = len(vocab)
# calculate N_pos and N_neg
N_pos = N_neg = 0
for pair in freqs.keys():
# if the label is positive (greater than zero)
if pair[1] > 0:
# Increment the number of positive words by the count for this (word, label) pair
N_pos += freqs[pair]
# else, the label is negative
else:
# increment the number of negative words by the count for this (word,label) pair
N_neg += freqs[pair]
# Calculate D, the number of documents
D = train_y.shape[0]
# Calculate D_pos, the number of positive documents (*hint: use sum(<np_array>))
D_pos = np.sum(train_y[:, None])
# Calculate D_neg, the number of negative documents (*hint: compute using D and D_pos)
D_neg = D - D_pos
# Calculate logprior
logprior = np.log(D_pos) - np.log(D_neg)
# For each word in the vocabulary...
for word in vocab:
# get the positive and negative frequency of the word
freq_pos = freqs.get((word, 1), 0)
freq_neg = freqs.get((word, 0), 0)
# calculate the probability that each word is positive, and negative
p_w_pos = (freq_pos + 1) / (N_pos + V)
p_w_neg = (freq_neg + 1) / (N_neg + V)
# calculate the log likelihood of the word
loglikelihood[word] = np.log(p_w_pos / p_w_neg)
### END CODE HERE ###
return logprior, loglikelihood
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# You do not have to input any code in this cell, but it is relevant to grading, so please do not change anything
logprior, loglikelihood = train_naive_bayes(freqs, train_x, train_y)
print(logprior)
print(len(loglikelihood))
```
**Expected Output**:
0.0
9089
# Part 3: Test your naive bayes
Now that we have the `logprior` and `loglikelihood`, we can test the naive bayes function by making predicting on some tweets!
#### Implement `naive_bayes_predict`
**Instructions**:
Implement the `naive_bayes_predict` function to make predictions on tweets.
* The function takes in the `tweet`, `logprior`, `loglikelihood`.
* It returns the probability that the tweet belongs to the positive or negative class.
* For each tweet, sum up loglikelihoods of each word in the tweet.
* Also add the logprior to this sum to get the predicted sentiment of that tweet.
$$ p = logprior + \sum_i^N (loglikelihood_i)$$
#### Note
Note we calculate the prior from the training data, and that the training data is evenly split between positive and negative labels (4000 positive and 4000 negative tweets). This means that the ratio of positive to negative 1, and the logprior is 0.
The value of 0.0 means that when we add the logprior to the log likelihood, we're just adding zero to the log likelihood. However, please remember to include the logprior, because whenever the data is not perfectly balanced, the logprior will be a non-zero value.
```
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def naive_bayes_predict(tweet, logprior, loglikelihood):
'''
Input:
tweet: a string
logprior: a number
loglikelihood: a dictionary of words mapping to numbers
Output:
p: the sum of all the logliklihoods of each word in the tweet (if found in the dictionary) + logprior (a number)
'''
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
# process the tweet to get a list of words
word_l = process_tweet(tweet)
# initialize probability to zero
p = 0
# add the logprior
p += logprior
for word in word_l:
# check if the word exists in the loglikelihood dictionary
if word in loglikelihood:
# add the log likelihood of that word to the probability
p += loglikelihood[word]
### END CODE HERE ###
return p
# UNQ_C5 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# You do not have to input any code in this cell, but it is relevant to grading, so please do not change anything
# Experiment with your own tweet.
my_tweet = 'She smiled.'
p = naive_bayes_predict(my_tweet, logprior, loglikelihood)
print('The expected output is', p)
```
**Expected Output**:
- The expected output is around 1.57
- The sentiment is positive.
#### Implement test_naive_bayes
**Instructions**:
* Implement `test_naive_bayes` to check the accuracy of your predictions.
* The function takes in your `test_x`, `test_y`, log_prior, and loglikelihood
* It returns the accuracy of your model.
* First, use `naive_bayes_predict` function to make predictions for each tweet in text_x.
```
# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def test_naive_bayes(test_x, test_y, logprior, loglikelihood):
"""
Input:
test_x: A list of tweets
test_y: the corresponding labels for the list of tweets
logprior: the logprior
loglikelihood: a dictionary with the loglikelihoods for each word
Output:
accuracy: (# of tweets classified correctly)/(total # of tweets)
"""
accuracy = 0 # return this properly
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
y_hats = []
for tweet in test_x:
# if the prediction is > 0
if naive_bayes_predict(tweet, logprior, loglikelihood) > 0:
# the predicted class is 1
y_hat_i = 1
else:
# otherwise the predicted class is 0
y_hat_i = 0
# append the predicted class to the list y_hats
y_hats.append(y_hat_i)
# error is the average of the absolute values of the differences between y_hats and test_y
error = np.sum(np.abs(y_hats - test_y)) / test_y.shape[0]
# Accuracy is 1 minus the error
accuracy = 1 - error
### END CODE HERE ###
return accuracy
print("Naive Bayes accuracy = %0.4f" %
(test_naive_bayes(test_x, test_y, logprior, loglikelihood)))
```
**Expected Accuracy**:
0.9940
```
# UNQ_C7 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# You do not have to input any code in this cell, but it is relevant to grading, so please do not change anything
# Run this cell to test your function
for tweet in ['I am happy', 'I am bad', 'this movie should have been great.', 'great', 'great great', 'great great great', 'great great great great']:
# print( '%s -> %f' % (tweet, naive_bayes_predict(tweet, logprior, loglikelihood)))
p = naive_bayes_predict(tweet, logprior, loglikelihood)
# print(f'{tweet} -> {p:.2f} ({p_category})')
print(f'{tweet} -> {p:.2f}')
```
**Expected Output**:
- I am happy -> 2.15
- I am bad -> -1.29
- this movie should have been great. -> 2.14
- great -> 2.14
- great great -> 4.28
- great great great -> 6.41
- great great great great -> 8.55
```
# Feel free to check the sentiment of your own tweet below
my_tweet = 'you are bad :('
naive_bayes_predict(my_tweet, logprior, loglikelihood)
```
# Part 4: Filter words by Ratio of positive to negative counts
- Some words have more positive counts than others, and can be considered "more positive". Likewise, some words can be considered more negative than others.
- One way for us to define the level of positiveness or negativeness, without calculating the log likelihood, is to compare the positive to negative frequency of the word.
- Note that we can also use the log likelihood calculations to compare relative positivity or negativity of words.
- We can calculate the ratio of positive to negative frequencies of a word.
- Once we're able to calculate these ratios, we can also filter a subset of words that have a minimum ratio of positivity / negativity or higher.
- Similarly, we can also filter a subset of words that have a maximum ratio of positivity / negativity or lower (words that are at least as negative, or even more negative than a given threshold).
#### Implement `get_ratio()`
- Given the `freqs` dictionary of words and a particular word, use `lookup(freqs,word,1)` to get the positive count of the word.
- Similarly, use the `lookup()` function to get the negative count of that word.
- Calculate the ratio of positive divided by negative counts
$$ ratio = \frac{\text{pos_words} + 1}{\text{neg_words} + 1} $$
Where pos_words and neg_words correspond to the frequency of the words in their respective classes.
<table>
<tr>
<td>
<b>Words</b>
</td>
<td>
Positive word count
</td>
<td>
Negative Word Count
</td>
</tr>
<tr>
<td>
glad
</td>
<td>
41
</td>
<td>
2
</td>
</tr>
<tr>
<td>
arriv
</td>
<td>
57
</td>
<td>
4
</td>
</tr>
<tr>
<td>
:(
</td>
<td>
1
</td>
<td>
3663
</td>
</tr>
<tr>
<td>
:-(
</td>
<td>
0
</td>
<td>
378
</td>
</tr>
</table>
```
# UNQ_C8 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def get_ratio(freqs, word):
'''
Input:
freqs: dictionary containing the words
word: string to lookup
Output: a dictionary with keys 'positive', 'negative', and 'ratio'.
Example: {'positive': 10, 'negative': 20, 'ratio': 0.5}
'''
pos_neg_ratio = {'positive': 0, 'negative': 0, 'ratio': 0.0}
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
# use lookup() to find positive counts for the word (denoted by the integer 1)
pos_neg_ratio['positive'] = lookup(freqs, word, 1)
# use lookup() to find negative counts for the word (denoted by integer 0)
pos_neg_ratio['negative'] = lookup(freqs, word, 0)
# calculate the ratio of positive to negative counts for the word
pos_neg_ratio['ratio'] = (pos_neg_ratio['positive'] + 1) / (pos_neg_ratio['negative'] + 1)
### END CODE HERE ###
return pos_neg_ratio
get_ratio(freqs, 'happi')
```
#### Implement `get_words_by_threshold(freqs,label,threshold)`
* If we set the label to 1, then we'll look for all words whose threshold of positive/negative is at least as high as that threshold, or higher.
* If we set the label to 0, then we'll look for all words whose threshold of positive/negative is at most as low as the given threshold, or lower.
* Use the `get_ratio()` function to get a dictionary containing the positive count, negative count, and the ratio of positive to negative counts.
* Append a dictionary to a list, where the key is the word, and the dictionary is the dictionary `pos_neg_ratio` that is returned by the `get_ratio()` function.
An example key-value pair would have this structure:
```
{'happi':
{'positive': 10, 'negative': 20, 'ratio': 0.5}
}
```
```
# UNQ_C9 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def get_words_by_threshold(freqs, label, threshold):
'''
Input:
freqs: dictionary of words
label: 1 for positive, 0 for negative
threshold: ratio that will be used as the cutoff for including a word in the returned dictionary
Output:
word_set: dictionary containing the word and information on its positive count, negative count, and ratio of positive to negative counts.
example of a key value pair:
{'happi':
{'positive': 10, 'negative': 20, 'ratio': 0.5}
}
'''
word_list = {}
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
for key in freqs.keys():
word, _ = key
# get the positive/negative ratio for a word
pos_neg_ratio = get_ratio(freqs, word)
# if the label is 1 and the ratio is greater than or equal to the threshold...
if label == 1 and pos_neg_ratio['ratio'] >= threshold:
# Add the pos_neg_ratio to the dictionary
word_list[word] = pos_neg_ratio
# If the label is 0 and the pos_neg_ratio is less than or equal to the threshold...
elif label == 0 and pos_neg_ratio['ratio'] <= threshold:
# Add the pos_neg_ratio to the dictionary
word_list[word] = pos_neg_ratio
# otherwise, do not include this word in the list (do nothing)
### END CODE HERE ###
return word_list
# Test your function: find negative words at or below a threshold
get_words_by_threshold(freqs, label=0, threshold=0.05)
# Test your function; find positive words at or above a threshold
get_words_by_threshold(freqs, label=1, threshold=10)
```
Notice the difference between the positive and negative ratios. Emojis like :( and words like 'me' tend to have a negative connotation. Other words like 'glad', 'community', and 'arrives' tend to be found in the positive tweets.
# Part 5: Error Analysis
In this part you will see some tweets that your model missclassified. Why do you think the misclassifications happened? Were there any assumptions made by the naive bayes model?
```
# Some error analysis done for you
print('Truth Predicted Tweet')
for x, y in zip(test_x, test_y):
y_hat = naive_bayes_predict(x, logprior, loglikelihood)
if y != (np.sign(y_hat) > 0):
print('%d\t%0.2f\t%s' % (y, np.sign(y_hat) > 0, ' '.join(
process_tweet(x)).encode('ascii', 'ignore')))
```
# Part 6: Predict with your own tweet
In this part you can predict the sentiment of your own tweet.
```
# Test with your own tweet - feel free to modify `my_tweet`
my_tweet = 'I am happy because I am learning :)'
p = naive_bayes_predict(my_tweet, logprior, loglikelihood)
print(p)
```
Congratulations on completing this assignment. See you next week!
| github_jupyter |
```
from graph2text.finetune import SummarizationModule, Graph2TextModule
import argparse
import pytorch_lightning as pl
import os
import sys
from pathlib import Path
import pdb
SEED = 42
import torch
torch.cuda.is_available(), torch.cuda.device_count()
MODEL='t5-base'
DATA_DIR = './graph2text/data/webnlg'
OUTPUT_DIR = './graph2text/outputs/port_test'
CHECKPOINT = './graph2text/outputs/t5-base_13881/val_avg_bleu=68.1000-step_count=5.ckpt'
parser = argparse.ArgumentParser()
parser = pl.Trainer.add_argparse_args(parser)
parser = SummarizationModule.add_model_specific_args(parser, os.getcwd())
args = parser.parse_args([
'--data_dir',DATA_DIR,
'--task','graph2text',
'--model_name_or_path',MODEL,
'--eval_batch_size','8',
'--gpus','1',
'--output_dir',OUTPUT_DIR,
'--checkpoint',CHECKPOINT,
'--max_source_length','384',
'--max_target_length','384',
'--val_max_target_length','384',
'--test_max_target_length','384',
'--eval_max_gen_length','384',
'--do_predict',
'--eval_beams','3'
])
#Path(args.output_dir).mkdir(exist_ok=True)
#model = Graph2TextModule(args)
model_ckp = Graph2TextModule.load_from_checkpoint(args.checkpoint)
```
DEALING WITH UNKNOWN TOKENS
1. See what words have characters outside the vocab
2. replace these chars with </unk> (??)
3. create a mapping (like Taej ?? n to Taejŏn)
4. Map them back together in the sentence (if it has Taej ?? n, replace with Taejŏn)
```
import time
inputs = [
'translate Graph to English: <H> Elisavet <R> profession <T> researcher',
]
inputs_encoding = model_ckp.tokenizer.prepare_seq2seq_batch(
inputs, max_length=args.max_source_length, return_tensors='pt'
)
print(inputs_encoding['input_ids'])
now = time.time()
model_ckp.model.eval()
with torch.no_grad():
gen_output = model_ckp.model.generate(
inputs_encoding['input_ids'],
attention_mask=inputs_encoding['attention_mask'],
use_cache=True,
decoder_start_token_id = model_ckp.decoder_start_token_id,
num_beams=model_ckp.eval_beams,
max_length=model_ckp.eval_max_length,
length_penalty=1.0
)
print([model_ckp.tokenizer.decode(i) for i in gen_output])
print(time.time() - now)
[model_ckp.tokenizer.decode(i) for i in inputs_encoding['input_ids']]
[model_ckp.tokenizer.decode(i) for i in gen_output]
```
# STRATEGY TO REPLACE UNKS:
- TREAT CASE WHERE THE WHOLE LABEL IS MADE OF UNKNOWNS
- IF IT ISNT, THERE MUST BE SPACE BEFORE AND AFTER THAT IS KNOWN
- GROUP UNKNOWNS INTO CONTINUOUS UNK TOKENS (?? ?? -> ??)
- LOOK TO SEE IF IT IS IN THE BEGINNING OF THE SENTENCE
- TREAT CASE
- LOOK TO SEE IF IT IS IN THE ENDING OF THE SENTENCE
- TREAT CASE
- IT IS IN THE MIDDLE, TREAT AS NORMAL
```
import re
vocab = model_ckp.tokenizer.get_vocab()
convert_some_japanese_characters = True
N = 2
class UnknownCharReplacer():
def __init__(self, tokenizer):
self.tokenizer = tokenizer
self.vocab = tokenizer.get_vocab()
self.unknowns = []
def read_label(self, label):
self.unknowns.append({})
# Some pre-processing of labels to normalise some characters
if convert_some_japanese_characters:
label = label.replace('(','(')
label = label.replace(')',')')
label = label.replace('〈','<')
label = label.replace('/','/')
label = label.replace('〉','>')
label_encoded = self.tokenizer.encode(label)
label_tokens = self.tokenizer.convert_ids_to_tokens(label_encoded)
label_token_to_string = self.tokenizer.convert_tokens_to_string(label_tokens)
unk_token_to_string = model_ckp.tokenizer.convert_tokens_to_string([model_ckp.tokenizer.unk_token])
#print(label_encoded,label_tokens,label_token_to_string)
match_unks_in_label = re.findall('(?:(?: )*⁇(?: )*)+', label_token_to_string)
if len(match_unks_in_label) > 0:
# If the whole label is made of UNK
if match_unks_in_label[0] == label_token_to_string:
#print('Label is all unks')
self.unknowns[-1][label_token_to_string.strip()] = label
# Else, there should be non-UNK characters in the label
else:
#print('Label is NOT all unks')
# Analyse the label with a sliding window of size N (N before, N ahead)
for idx, token in enumerate(label_tokens):
idx_before = max(0,idx-N)
idx_ahead = min(len(label_tokens), idx+N+1)
# Found a UNK
if token == self.tokenizer.unk_token:
# In case multiple UNK, exclude UNKs seen after this one, expand window to other side if possible
if len(match_unks_in_label) > 1:
#print(idx)
#print(label_tokens)
#print(label_tokens[idx_before:idx_ahead])
#print('HERE!')
# Reduce on the right, expanding on the left
while model_ckp.tokenizer.unk_token in label_tokens[idx+1:idx_ahead]:
idx_before = max(0,idx_before-1)
idx_ahead = min(idx+2, idx_ahead-1)
#print(label_tokens[idx_before:idx_ahead])
# Now just reduce on the left
while model_ckp.tokenizer.unk_token in label_tokens[idx_before:idx]:
idx_before = min(idx-1,idx_before+2)
#print(label_tokens[idx_before:idx_ahead])
# First token of the label is UNK
span = self.tokenizer.convert_tokens_to_string(label_tokens[idx_before:idx_ahead])
if idx == 1 and label_tokens[0] == '▁':
#print('Label begins with unks')
to_replace = '^' + re.escape(span).replace(
re.escape(unk_token_to_string),
'.+?'
)
replaced_span = re.search(
to_replace,
label
)[0]
self.unknowns[-1][span.strip()] = replaced_span
# Last token of the label is UNK
elif idx == len(label_tokens)-2 and label_tokens[-1] == model_ckp.tokenizer.eos_token:
#print('Label ends with unks')
pre_idx = self.tokenizer.convert_tokens_to_string(label_tokens[idx_before:idx])
pre_idx_unk_counts = pre_idx.count(unk_token_to_string)
to_replace = re.escape(span).replace(
re.escape(unk_token_to_string),
f'[^{re.escape(pre_idx)}]+?'
) + '$'
if pre_idx.strip() == '':
to_replace = to_replace.replace('[^]', '(?<=\s)[^a-zA-Z0-9]')
replaced_span = re.search(
to_replace,
label
)[0]
self.unknowns[-1][span.strip()] = replaced_span
# A token in-between the label is UNK
else:
#print('Label has unks in the middle')
pre_idx = self.tokenizer.convert_tokens_to_string(label_tokens[idx_before:idx])
to_replace = re.escape(span).replace(
re.escape(unk_token_to_string),
f'[^{re.escape(pre_idx)}]+?'
)
#If there is nothing behind the ??, because it is in the middle but the previous token is also
#a ??, then we would end up with to_replace beginning with [^], which we can't have
if pre_idx.strip() == '':
to_replace = to_replace.replace('[^]', '(?<=\s)[^a-zA-Z0-9]')
replaced_span = re.search(
to_replace,
label
)
if replaced_span:
span = re.sub(r'\s([?.!",](?:\s|$))', r'\1', span.strip())
self.unknowns[-1][span] = replaced_span[0]
def replace_on_sentence(self, sentence):
# Loop through in case the labels are repeated, maximum of three times
loop_n = 3
while '⁇' in sentence and loop_n > 0:
loop_n -= 1
for unknowns in self.unknowns:
for k,v in unknowns.items():
# In case it is because the first letter of the sentence has been uppercased
if not k in sentence and k[0] == k[0].lower() and k[0].upper() == sentence[0]:
k = k[0].upper() + k[1:]
v = v[0].upper() + v[1:]
# In case it is because a double space is found where it should not be
elif not k in sentence and len(re.findall(r'\s{2,}',k))>0:
k = re.sub(r'\s+', ' ', k)
#print(k,'/',v,'/',sentence)
sentence = sentence.replace(k.strip(),v.strip(),1)
#sentence = re.sub(k, v, sentence)
sentence = re.sub(r'\s+', ' ', sentence).strip()
sentence = re.sub(r'\s([?.!",](?:\s|$))', r'\1', sentence)
return sentence
replacer = UnknownCharReplacer(model_ckp.tokenizer)
replacer.read_label('Cuhppulčohkka')
replacer.read_label('Cuhppulčohkka')
replacer.replace_on_sentence('Cuhppul ⁇ ohkka is a native label.'), replacer.unknowns
import pandas as pd
df = pd.read_csv('sampled_df_pre_verbalisation.csv')
df_sample = df.sample(64, random_state=SEED).reset_index(drop=True)
# Dataset and Dataloader
from torch.utils.data import Dataset, DataLoader
class TripleLabelDataset(Dataset):
def __init__(self, df):
self.df = df
self.len = self.df.shape[0]
def __getitem__(self, index):
row = self.df.iloc[index]
item = f"translate Graph to English: <H> {row['entity_label']} <R> {row['property_label']} <T> {row['object_label']}"
#return model_ckp.tokenizer.prepare_seq2seq_batch(
# item, max_length=args.max_source_length, return_tensors='pt'
#)
return item
def __len__(self):
return self.len
# Pilot Sample
sample_data = TripleLabelDataset(df_sample)
sample_dataloader = DataLoader(dataset=sample_data, batch_size=64)
print(len(sample_dataloader))
# Full Data
data = TripleLabelDataset(df)
dataloader = DataLoader(dataset=data, batch_size=16)
print(len(dataloader))
def replace_verbalisation_on_df(row):
try:
replacer = UnknownCharReplacer(model_ckp.tokenizer)
replacer.read_label(row['entity_label'])
replacer.read_label(row['object_label'])
return replacer.replace_on_sentence(row['verbalisation'])
except Exception:
print(row)
raise
```
## Pilot Sample
```
import time
verbalisations = []
start_idx = 0
for idx, batch in enumerate(sample_dataloader):
if idx < start_idx:
print(f'Skipping idx {idx}')
continue
print(idx,end=': ')
inputs_encoding = model_ckp.tokenizer.prepare_seq2seq_batch(
batch, max_length=args.max_source_length, return_tensors='pt'
)
now = time.monotonic()
model_ckp.model.eval()
with torch.no_grad():
gen_output = model_ckp.model.generate(
inputs_encoding['input_ids'],
attention_mask=inputs_encoding['attention_mask'],
use_cache=True,
decoder_start_token_id = model_ckp.decoder_start_token_id,
num_beams=model_ckp.eval_beams,
max_length=model_ckp.eval_max_length,
length_penalty=1.0
)
print('Generated batch in', time.strftime("%H:%M:%S", time.gmtime(time.monotonic() - now)))
verbalisations = verbalisations + [model_ckp.tokenizer.decode(i) for i in gen_output]
start_idx += 1
#break
df_sample['verbalisation'] = verbalisations
df_sample['verbalisation'] = df_sample['verbalisation'].apply(lambda x : x[0].upper() + x[1:])
df_sample['processed_verbalisation'] = df_sample.apply(replace_verbalisation_on_df ,axis=1)
df_sample.to_csv('pilot_sampled_df_verbalised.csv', index=None)
```
## Full Data
```
import time
start_idx = 0
for idx, batch in enumerate(dataloader):
if idx < start_idx:
print(f'Skipping idx {idx}')
continue
print(idx,end=': ')
inputs_encoding = model_ckp.tokenizer.prepare_seq2seq_batch(
batch, max_length=args.max_source_length, return_tensors='pt'
)
now = time.monotonic()
model_ckp.model.eval()
with torch.no_grad():
gen_output = model_ckp.model.generate(
inputs_encoding['input_ids'],
attention_mask=inputs_encoding['attention_mask'],
use_cache=True,
decoder_start_token_id = model_ckp.decoder_start_token_id,
num_beams=model_ckp.eval_beams,
max_length=model_ckp.eval_max_length,
length_penalty=1.0
)
print('Generated batch in', time.strftime("%H:%M:%S", time.gmtime(time.monotonic() - now)))
verbalisations = [model_ckp.tokenizer.decode(i) for i in gen_output]
with open(f'verbalisations/verbalisations_batch_{idx}.txt','w+') as f:
for v in verbalisations:
f.write(v)
f.write('\n')
start_idx += 1
# Collect all verbalisations from .txt files
import glob
n_filenames = len(glob.glob('verbalisations/*.txt'))
verbalisations = []
for idx in range(n_filenames):
filename = f'verbalisations/verbalisations_batch_{idx}.txt'
with open(filename,'r') as f:
for line in f:
verbalisations.append(line.strip())
df['verbalisation'] = verbalisations
df['verbalisation'] = df['verbalisation'].apply(lambda x : x[0].upper() + x[1:])
df['processed_verbalisation'] = df.apply(replace_verbalisation_on_df ,axis=1)
df['unk_count'] = df['verbalisation'].apply(lambda x : x.count('⁇'))
# Check if verbs are the same for unk = 0
df[df['verbalisation'] == df['processed_verbalisation']].equals(df[df['unk_count'] == 0])
# First drop those without labels
df = df[(df['entity_label_lan'] != 'none') & (df['property_label_lan'] != 'none') & (df['object_label_lan'] != 'none')].reset_index(drop=True)
# Create a new id to stratify per property AND theme
df['property_and_theme_id'] = df.apply(lambda x : x['property_id'] + x['theme_entity_id'], axis=1)
# Then select those in English
df_english = df[(df['entity_label_lan'] == 'en') & (df['property_label_lan'] == 'en') & (df['object_label_lan'] == 'en')].reset_index(drop=True)
# Create a group indication column (strata) for splitting (due to fund available we can only annotate a portion)
df_english['campaign_group'] = -1
from sklearn.model_selection import StratifiedKFold as StratifiedKFold
skf = StratifiedKFold(n_splits=42, shuffle=True, random_state=42)
for idx, (train_index, test_index) in enumerate(skf.split(df_english, df_english['theme_entity_id'])):
df_english.loc[test_index, 'campaign_group'] = idx
# Number of examples per group
df_english['campaign_group'].value_counts()[0]
# Number of examples per group
df_english[df_english['campaign_group'] == 0]['theme_entity_id'].value_counts()
df.to_csv('campaign_sampled_df_verbalised.csv', index=None)
df_english.to_csv('campaign_sampled_df_verbalised_english.csv', index=None)
df_english[df_english['campaign_group'] == 0][['entity_label','property_label','object_label','verbalisation','processed_verbalisation']]
import time
inputs = [
'''translate Graph to English:
<H> antipasto <R> aspect of <T> Italian cuisine
''',
]
inputs_encoding = model_ckp.tokenizer.prepare_seq2seq_batch(
inputs, max_length=args.max_source_length, return_tensors='pt'
)
print(inputs_encoding['input_ids'])
now = time.time()
model_ckp.model.eval()
with torch.no_grad():
gen_output = model_ckp.model.generate(
inputs_encoding['input_ids'],
attention_mask=inputs_encoding['attention_mask'],
use_cache=True,
decoder_start_token_id = model_ckp.decoder_start_token_id,
num_beams=model_ckp.eval_beams,
max_length=model_ckp.eval_max_length,
length_penalty=1.0
)
print([model_ckp.tokenizer.decode(i) for i in gen_output])
print(time.time() - now)
```
## Subject and Object Inverted
Using anternate aliases helps
'translate Graph to English: <H> 117852 Constance <R> follows <T> (117851) 2005 JE151'
'117852 Constance is followed by (117851) 2005 JE151.'
'translate Graph to English: <H> 117852 Constance <R> previous is <T> (117851) 2005 JE151'
'117852 Constance was preceded by (117851) 2005 JE151.'
'translate Graph to English: <H> Decius <R> child <T> Hostilian'
'Decius is a child of Hostilian.'
'translate Graph to English: <H> Decius <R> has child <T> Hostilian'
'Decius has a child called Hostilian.'
## Hard Claim Syntax
These normally do not have aliases that are any easier to read
## Predicate Meaning Not Understood by Model
Artist | Aleksandr Vasilevitsj Vasjakin | conflict | Eastern Front | 1.6
Aleksandr Vasilevitsj Vasjakin is in the Eastern Front.
conflict -> participated in conflict
'Aleksandr Vasilevitsj Vasjakin participated in the conflict at the Eastern Front.'
Painting | Fresco depicting a menead carrying a thyrsus | movement | Ancient Roman mural painting | 2.0
Fresco depicting a menead carrying a thyrsus is a movement in the Ancient Roman mural painting.
artistic movement
Fresco depicting a menead carrying a thyrsus is part of the artistic movement of the Ancient Roman mural painting.
## Redundant Claim Data
This is something that is emergent from how Wikidata stores information. For instance, an entity exists for a city, and another for its flag, which includes the flag's image. One is linked to the other by the flag predicate. This makes ontological sense, but no verbal sense, as one would say "This city has a flag" or "This city's flag is this city's flag", being either redundant or not quite communicating what the claim says. The same is true for things which are specifications/parts of others, like Israel's Cycling team of 1997 is part of Israel's Cycling team.
## Qualifiers needed
One would have to find a way of reliably tying qualifiers or descriptors to elements of the claim
## Vague predicate
Using alternative aliases works. Choosing the proper alias is tricky and depends on the context.
| github_jupyter |
```
%matplotlib inline
import numpy as np
import seaborn
import nltk
from sklearn.metrics.pairwise import cosine_similarity, euclidean_distances
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.metrics import classification_report
# prepare corpus
corpus = []
for d in range(1400):
f = open("./d/"+str(d+1)+".txt")
corpus.append(f.read())
f.close()
queries = []
for q in range(225):
f = open("./q/"+str(q+1)+".txt")
queries.append(f.read())
f.close()
reference = []
for r in range(225):
f = open("./r/"+str(r+1)+".txt")
reference.append(list(map(int, f.read().replace('\n', ' ')[:-1].split(' '))))
f.close()
q_len = []
for r in reference:
q_len.append(len(r))
min_q = int(np.average(q_len)) # overwrite min_q here shortest lenght of reference is 2
print("Lenght of query set to {} as thats the average lenght of reference".format(min_q))
```
# BINARY REPRESENTATION
```
binary_vectorizer = CountVectorizer(binary=True)
binary_matrix = binary_vectorizer.fit_transform(corpus)
binary_queries_matrix = binary_vectorizer.transform(queries)
```
## cosine similarity
```
precisions = []
recalls = []
f_measures = []
for r in range(len(reference)-1):
sim = np.array(cosine_similarity(binary_queries_matrix[r], binary_matrix)[0])
retrieved = sim.argsort()[-min_q:][::-1]+1
tp = 0
fp = 0
for doc in retrieved:
if doc in reference[r]:
tp += 1
else:
fp += 1
fn = len(reference[r]) - tp
precision = tp/(tp+fp)
recall = tp/(tp+fn)
precisions.append(precision)
recalls.append(recall)
if tp == 0:
f_measures.append(0)
else:
f_measures.append(2*(precision*recall)/(precision+recall))
print(" min max avg mean")
print("Precision: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(precisions), np.max(precisions), np.average(precisions), np.median(precisions)))
print("Recalls : {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(recalls), np.max(recalls), np.average(recalls), np.median(recalls)))
print("F-Measure: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(f_measures), np.max(f_measures), np.average(f_measures), np.median(f_measures)))
f = open("./bin_cos.csv", 'w')
for l in range(len(reference)-1):
f.write("{},{},{}\n".format(precisions[l], recalls[l], f_measures[l]))
f.close()
```
## euclidean distance
```
precisions = []
recalls = []
f_measures = []
for r in range(len(reference)-1):
sim = np.array(euclidean_distances(binary_queries_matrix[r], binary_matrix)[0])
retrieved = sim.argsort()[:min_q]+1
tp = 0
fp = 0
for doc in retrieved:
if doc in reference[r]:
tp += 1
else:
fp += 1
fn = len(reference[r]) - tp
precision = tp/(tp+fp)
recall = tp/(tp+fn)
precisions.append(precision)
recalls.append(recall)
if tp == 0:
f_measures.append(0)
else:
f_measures.append(2*(precision*recall)/(precision+recall))
print(" min max avg mean")
print("Precision: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(precisions), np.max(precisions), np.average(precisions), np.median(precisions)))
print("Recalls : {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(recalls), np.max(recalls), np.average(recalls), np.median(recalls)))
print("F-Measure: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(f_measures), np.max(f_measures), np.average(f_measures), np.median(f_measures)))
f = open("./bin_euc.csv", 'w')
for l in range(len(reference)-1):
f.write("{},{},{}\n".format(precisions[l], recalls[l], f_measures[l]))
f.close()
```
# TERM FRENQUENCY
```
count_vectorizer = CountVectorizer()
count_matrix = count_vectorizer.fit_transform(corpus)
count_queries_matrix = count_vectorizer.transform(queries)
```
## cosine similarity
```
precisions = []
recalls = []
f_measures = []
for r in range(len(reference)-1):
sim = np.array(cosine_similarity(count_queries_matrix[r], count_matrix)[0])
retrieved = sim.argsort()[-min_q:][::-1]+1
tp = 0
fp = 0
for doc in retrieved:
if doc in reference[r]:
tp += 1
else:
fp += 1
fn = len(reference[r]) - tp
precision = tp/(tp+fp)
recall = tp/(tp+fn)
precisions.append(precision)
recalls.append(recall)
if tp == 0:
f_measures.append(0)
else:
f_measures.append(2*(precision*recall)/(precision+recall))
print(" min max avg mean")
print("Precision: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(precisions), np.max(precisions), np.average(precisions), np.median(precisions)))
print("Recalls : {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(recalls), np.max(recalls), np.average(recalls), np.median(recalls)))
print("F-Measure: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(f_measures), np.max(f_measures), np.average(f_measures), np.median(f_measures)))
f = open("./term_cos.csv", 'w')
for l in range(len(reference)-1):
f.write("{},{},{}\n".format(precisions[l], recalls[l], f_measures[l]))
f.close()
```
## euclidean distance
```
precisions = []
recalls = []
f_measures = []
for r in range(len(reference)-1):
sim = np.array(euclidean_distances(count_queries_matrix[r], count_matrix)[0])
retrieved = sim.argsort()[:min_q]+1
tp = 0
fp = 0
for doc in retrieved:
if doc in reference[r]:
tp += 1
else:
fp += 1
fn = len(reference[r]) - tp
precision = tp/(tp+fp)
recall = tp/(tp+fn)
precisions.append(precision)
recalls.append(recall)
if tp == 0:
f_measures.append(0)
else:
f_measures.append(2*(precision*recall)/(precision+recall))
print(" min max avg mean")
print("Precision: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(precisions), np.max(precisions), np.average(precisions), np.median(precisions)))
print("Recalls : {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(recalls), np.max(recalls), np.average(recalls), np.median(recalls)))
print("F-Measure: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(f_measures), np.max(f_measures), np.average(f_measures), np.median(f_measures)))
f = open("./term_euc.csv", 'w')
for l in range(len(reference)-1):
f.write("{},{},{}\n".format(precisions[l], recalls[l], f_measures[l]))
f.close()
```
# TF-IDF
```
tfidf_vectorizer = TfidfVectorizer()
tfidf_matrix = tfidf_vectorizer.fit_transform(corpus)
tfidf_queries_matrix = tfidf_vectorizer.transform(queries)
```
## cosine similarity
```
precisions = []
recalls = []
f_measures = []
for r in range(len(reference)-1):
sim = np.array(cosine_similarity(tfidf_queries_matrix[r], tfidf_matrix)[0])
retrieved = sim.argsort()[-min_q:][::-1]+1
tp = 0
fp = 0
for doc in retrieved:
if doc in reference[r]:
tp += 1
else:
fp += 1
fn = len(reference[r]) - tp
precision = tp/(tp+fp)
recall = tp/(tp+fn)
precisions.append(precision)
recalls.append(recall)
if tp == 0:
f_measures.append(0)
else:
f_measures.append(2*(precision*recall)/(precision+recall))
print(" min max avg mean")
print("Precision: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(precisions), np.max(precisions), np.average(precisions), np.median(precisions)))
print("Recalls : {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(recalls), np.max(recalls), np.average(recalls), np.median(recalls)))
print("F-Measure: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(f_measures), np.max(f_measures), np.average(f_measures), np.median(f_measures)))
f = open("./tfidf_cos.csv", 'w')
for l in range(len(reference)-1):
f.write("{},{},{}\n".format(precisions[l], recalls[l], f_measures[l]))
f.close()
```
## euclidean distance
```
precisions = []
recalls = []
f_measures = []
for r in range(len(reference)-1):
sim = np.array(euclidean_distances(tfidf_queries_matrix[r], tfidf_matrix)[0])
retrieved = sim.argsort()[:min_q]+1
tp = 0
fp = 0
for doc in retrieved:
if doc in reference[r]:
tp += 1
else:
fp += 1
fn = len(reference[r]) - tp
precision = tp/(tp+fp)
recall = tp/(tp+fn)
precisions.append(precision)
recalls.append(recall)
if tp == 0:
f_measures.append(0)
else:
f_measures.append(2*(precision*recall)/(precision+recall))
print(" min max avg mean")
print("Precision: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(precisions), np.max(precisions), np.average(precisions), np.median(precisions)))
print("Recalls : {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(recalls), np.max(recalls), np.average(recalls), np.median(recalls)))
print("F-Measure: {:.3f} {:.3f} {:.3f} {:.3f}".format(np.min(f_measures), np.max(f_measures), np.average(f_measures), np.median(f_measures)))
f = open("./tfidf_euc.csv", 'w')
for l in range(len(reference)-1):
f.write("{},{},{}\n".format(precisions[l], recalls[l], f_measures[l]))
f.close()
```
| github_jupyter |
```
import keras
keras.__version__
```
# Using a pre-trained convnet
This notebook contains the code sample found in Chapter 5, Section 3 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
----
A common and highly effective approach to deep learning on small image datasets is to leverage a pre-trained network. A pre-trained network
is simply a saved network previously trained on a large dataset, typically on a large-scale image classification task. If this original
dataset is large enough and general enough, then the spatial feature hierarchy learned by the pre-trained network can effectively act as a
generic model of our visual world, and hence its features can prove useful for many different computer vision problems, even though these
new problems might involve completely different classes from those of the original task. For instance, one might train a network on
ImageNet (where classes are mostly animals and everyday objects) and then re-purpose this trained network for something as remote as
identifying furniture items in images. Such portability of learned features across different problems is a key advantage of deep learning
compared to many older shallow learning approaches, and it makes deep learning very effective for small-data problems.
In our case, we will consider a large convnet trained on the ImageNet dataset (1.4 million labeled images and 1000 different classes).
ImageNet contains many animal classes, including different species of cats and dogs, and we can thus expect to perform very well on our cat
vs. dog classification problem.
We will use the VGG16 architecture, developed by Karen Simonyan and Andrew Zisserman in 2014, a simple and widely used convnet architecture
for ImageNet. Although it is a bit of an older model, far from the current state of the art and somewhat heavier than many other recent
models, we chose it because its architecture is similar to what you are already familiar with, and easy to understand without introducing
any new concepts. This may be your first encounter with one of these cutesie model names -- VGG, ResNet, Inception, Inception-ResNet,
Xception... you will get used to them, as they will come up frequently if you keep doing deep learning for computer vision.
There are two ways to leverage a pre-trained network: *feature extraction* and *fine-tuning*. We will cover both of them. Let's start with
feature extraction.
## Feature extraction
Feature extraction consists of using the representations learned by a previous network to extract interesting features from new samples.
These features are then run through a new classifier, which is trained from scratch.
As we saw previously, convnets used for image classification comprise two parts: they start with a series of pooling and convolution
layers, and they end with a densely-connected classifier. The first part is called the "convolutional base" of the model. In the case of
convnets, "feature extraction" will simply consist of taking the convolutional base of a previously-trained network, running the new data
through it, and training a new classifier on top of the output.
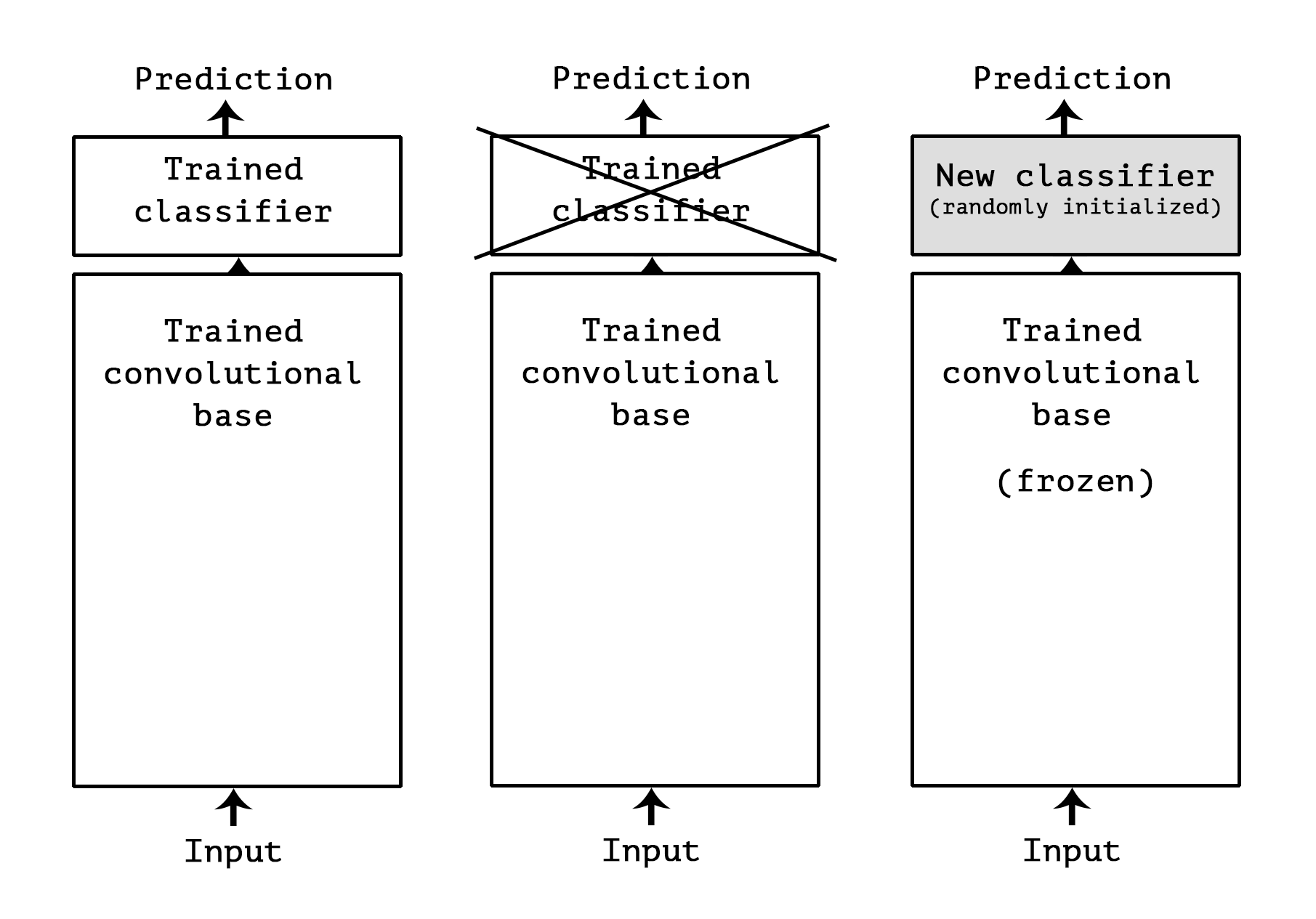
Why only reuse the convolutional base? Could we reuse the densely-connected classifier as well? In general, it should be avoided. The
reason is simply that the representations learned by the convolutional base are likely to be more generic and therefore more reusable: the
feature maps of a convnet are presence maps of generic concepts over a picture, which is likely to be useful regardless of the computer
vision problem at hand. On the other end, the representations learned by the classifier will necessarily be very specific to the set of
classes that the model was trained on -- they will only contain information about the presence probability of this or that class in the
entire picture. Additionally, representations found in densely-connected layers no longer contain any information about _where_ objects are
located in the input image: these layers get rid of the notion of space, whereas the object location is still described by convolutional
feature maps. For problems where object location matters, densely-connected features would be largely useless.
Note that the level of generality (and therefore reusability) of the representations extracted by specific convolution layers depends on
the depth of the layer in the model. Layers that come earlier in the model extract local, highly generic feature maps (such as visual
edges, colors, and textures), while layers higher-up extract more abstract concepts (such as "cat ear" or "dog eye"). So if your new
dataset differs a lot from the dataset that the original model was trained on, you may be better off using only the first few layers of the
model to do feature extraction, rather than using the entire convolutional base.
In our case, since the ImageNet class set did contain multiple dog and cat classes, it is likely that it would be beneficial to reuse the
information contained in the densely-connected layers of the original model. However, we will chose not to, in order to cover the more
general case where the class set of the new problem does not overlap with the class set of the original model.
Let's put this in practice by using the convolutional base of the VGG16 network, trained on ImageNet, to extract interesting features from
our cat and dog images, and then training a cat vs. dog classifier on top of these features.
The VGG16 model, among others, comes pre-packaged with Keras. You can import it from the `keras.applications` module. Here's the list of
image classification models (all pre-trained on the ImageNet dataset) that are available as part of `keras.applications`:
* Xception
* InceptionV3
* ResNet50
* VGG16
* VGG19
* MobileNet
Let's instantiate the VGG16 model:
```
from keras.applications import VGG16
conv_base = VGG16(weights='imagenet',
include_top=False,
input_shape=(150, 150, 3))
```
We passed three arguments to the constructor:
* `weights`, to specify which weight checkpoint to initialize the model from
* `include_top`, which refers to including or not the densely-connected classifier on top of the network. By default, this
densely-connected classifier would correspond to the 1000 classes from ImageNet. Since we intend to use our own densely-connected
classifier (with only two classes, cat and dog), we don't need to include it.
* `input_shape`, the shape of the image tensors that we will feed to the network. This argument is purely optional: if we don't pass it,
then the network will be able to process inputs of any size.
Here's the detail of the architecture of the VGG16 convolutional base: it's very similar to the simple convnets that you are already
familiar with.
```
conv_base.summary()
```
The final feature map has shape `(4, 4, 512)`. That's the feature on top of which we will stick a densely-connected classifier.
At this point, there are two ways we could proceed:
* Running the convolutional base over our dataset, recording its output to a Numpy array on disk, then using this data as input to a
standalone densely-connected classifier similar to those you have seen in the first chapters of this book. This solution is very fast and
cheap to run, because it only requires running the convolutional base once for every input image, and the convolutional base is by far the
most expensive part of the pipeline. However, for the exact same reason, this technique would not allow us to leverage data augmentation at
all.
* Extending the model we have (`conv_base`) by adding `Dense` layers on top, and running the whole thing end-to-end on the input data. This
allows us to use data augmentation, because every input image is going through the convolutional base every time it is seen by the model.
However, for this same reason, this technique is far more expensive than the first one.
We will cover both techniques. Let's walk through the code required to set-up the first one: recording the output of `conv_base` on our
data and using these outputs as inputs to a new model.
We will start by simply running instances of the previously-introduced `ImageDataGenerator` to extract images as Numpy arrays as well as
their labels. We will extract features from these images simply by calling the `predict` method of the `conv_base` model.
```
import os
import numpy as np
from keras.preprocessing.image import ImageDataGenerator
base_dir = '/Users/fchollet/Downloads/cats_and_dogs_small'
train_dir = os.path.join(base_dir, 'train')
validation_dir = os.path.join(base_dir, 'validation')
test_dir = os.path.join(base_dir, 'test')
datagen = ImageDataGenerator(rescale=1./255)
batch_size = 20
def extract_features(directory, sample_count):
features = np.zeros(shape=(sample_count, 4, 4, 512))
labels = np.zeros(shape=(sample_count))
generator = datagen.flow_from_directory(
directory,
target_size=(150, 150),
batch_size=batch_size,
class_mode='binary')
i = 0
for inputs_batch, labels_batch in generator:
features_batch = conv_base.predict(inputs_batch)
features[i * batch_size : (i + 1) * batch_size] = features_batch
labels[i * batch_size : (i + 1) * batch_size] = labels_batch
i += 1
if i * batch_size >= sample_count:
# Note that since generators yield data indefinitely in a loop,
# we must `break` after every image has been seen once.
break
return features, labels
train_features, train_labels = extract_features(train_dir, 2000)
validation_features, validation_labels = extract_features(validation_dir, 1000)
test_features, test_labels = extract_features(test_dir, 1000)
```
The extracted features are currently of shape `(samples, 4, 4, 512)`. We will feed them to a densely-connected classifier, so first we must
flatten them to `(samples, 8192)`:
```
train_features = np.reshape(train_features, (2000, 4 * 4 * 512))
validation_features = np.reshape(validation_features, (1000, 4 * 4 * 512))
test_features = np.reshape(test_features, (1000, 4 * 4 * 512))
```
At this point, we can define our densely-connected classifier (note the use of dropout for regularization), and train it on the data and
labels that we just recorded:
```
from keras import models
from keras import layers
from keras import optimizers
model = models.Sequential()
model.add(layers.Dense(256, activation='relu', input_dim=4 * 4 * 512))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=2e-5),
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(train_features, train_labels,
epochs=30,
batch_size=20,
validation_data=(validation_features, validation_labels))
```
Training is very fast, since we only have to deal with two `Dense` layers -- an epoch takes less than one second even on CPU.
Let's take a look at the loss and accuracy curves during training:
```
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
We reach a validation accuracy of about 90%, much better than what we could achieve in the previous section with our small model trained from
scratch. However, our plots also indicate that we are overfitting almost from the start -- despite using dropout with a fairly large rate.
This is because this technique does not leverage data augmentation, which is essential to preventing overfitting with small image datasets.
Now, let's review the second technique we mentioned for doing feature extraction, which is much slower and more expensive, but which allows
us to leverage data augmentation during training: extending the `conv_base` model and running it end-to-end on the inputs. Note that this
technique is in fact so expensive that you should only attempt it if you have access to a GPU: it is absolutely intractable on CPU. If you
cannot run your code on GPU, then the previous technique is the way to go.
Because models behave just like layers, you can add a model (like our `conv_base`) to a `Sequential` model just like you would add a layer.
So you can do the following:
```
from keras import models
from keras import layers
model = models.Sequential()
model.add(conv_base)
model.add(layers.Flatten())
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
```
This is what our model looks like now:
```
model.summary()
```
As you can see, the convolutional base of VGG16 has 14,714,688 parameters, which is very large. The classifier we are adding on top has 2
million parameters.
Before we compile and train our model, a very important thing to do is to freeze the convolutional base. "Freezing" a layer or set of
layers means preventing their weights from getting updated during training. If we don't do this, then the representations that were
previously learned by the convolutional base would get modified during training. Since the `Dense` layers on top are randomly initialized,
very large weight updates would be propagated through the network, effectively destroying the representations previously learned.
In Keras, freezing a network is done by setting its `trainable` attribute to `False`:
```
print('This is the number of trainable weights '
'before freezing the conv base:', len(model.trainable_weights))
conv_base.trainable = False
print('This is the number of trainable weights '
'after freezing the conv base:', len(model.trainable_weights))
```
With this setup, only the weights from the two `Dense` layers that we added will be trained. That's a total of four weight tensors: two per
layer (the main weight matrix and the bias vector). Note that in order for these changes to take effect, we must first compile the model.
If you ever modify weight trainability after compilation, you should then re-compile the model, or these changes would be ignored.
Now we can start training our model, with the same data augmentation configuration that we used in our previous example:
```
from keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
# This is the target directory
train_dir,
# All images will be resized to 150x150
target_size=(150, 150),
batch_size=20,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=2e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=30,
validation_data=validation_generator,
validation_steps=50,
verbose=2)
model.save('cats_and_dogs_small_3.h5')
```
Let's plot our results again:
```
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
As you can see, we reach a validation accuracy of about 96%. This is much better than our small convnet trained from scratch.
## Fine-tuning
Another widely used technique for model reuse, complementary to feature extraction, is _fine-tuning_.
Fine-tuning consists in unfreezing a few of the top layers
of a frozen model base used for feature extraction, and jointly training both the newly added part of the model (in our case, the
fully-connected classifier) and these top layers. This is called "fine-tuning" because it slightly adjusts the more abstract
representations of the model being reused, in order to make them more relevant for the problem at hand.
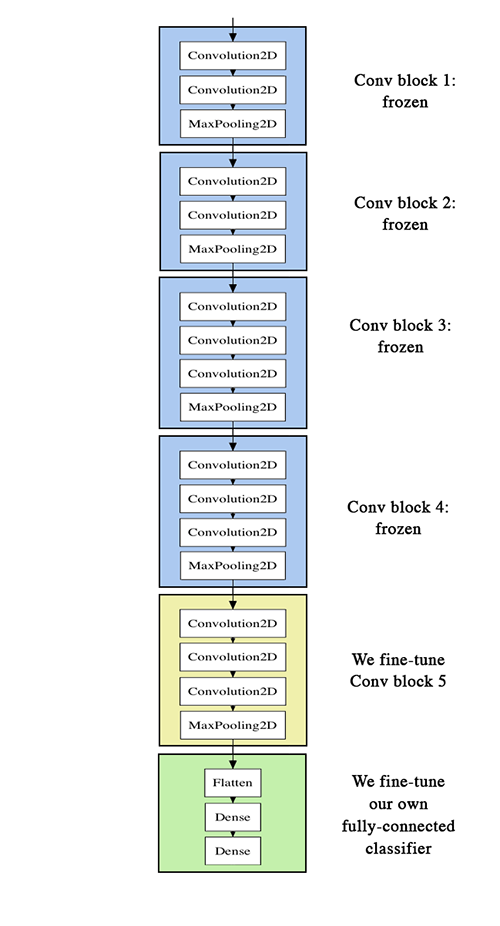
We have stated before that it was necessary to freeze the convolution base of VGG16 in order to be able to train a randomly initialized
classifier on top. For the same reason, it is only possible to fine-tune the top layers of the convolutional base once the classifier on
top has already been trained. If the classified wasn't already trained, then the error signal propagating through the network during
training would be too large, and the representations previously learned by the layers being fine-tuned would be destroyed. Thus the steps
for fine-tuning a network are as follow:
* 1) Add your custom network on top of an already trained base network.
* 2) Freeze the base network.
* 3) Train the part you added.
* 4) Unfreeze some layers in the base network.
* 5) Jointly train both these layers and the part you added.
We have already completed the first 3 steps when doing feature extraction. Let's proceed with the 4th step: we will unfreeze our `conv_base`,
and then freeze individual layers inside of it.
As a reminder, this is what our convolutional base looks like:
```
conv_base.summary()
```
We will fine-tune the last 3 convolutional layers, which means that all layers up until `block4_pool` should be frozen, and the layers
`block5_conv1`, `block5_conv2` and `block5_conv3` should be trainable.
Why not fine-tune more layers? Why not fine-tune the entire convolutional base? We could. However, we need to consider that:
* Earlier layers in the convolutional base encode more generic, reusable features, while layers higher up encode more specialized features. It is
more useful to fine-tune the more specialized features, as these are the ones that need to be repurposed on our new problem. There would
be fast-decreasing returns in fine-tuning lower layers.
* The more parameters we are training, the more we are at risk of overfitting. The convolutional base has 15M parameters, so it would be
risky to attempt to train it on our small dataset.
Thus, in our situation, it is a good strategy to only fine-tune the top 2 to 3 layers in the convolutional base.
Let's set this up, starting from where we left off in the previous example:
```
conv_base.trainable = True
set_trainable = False
for layer in conv_base.layers:
if layer.name == 'block5_conv1':
set_trainable = True
if set_trainable:
layer.trainable = True
else:
layer.trainable = False
```
Now we can start fine-tuning our network. We will do this with the RMSprop optimizer, using a very low learning rate. The reason for using
a low learning rate is that we want to limit the magnitude of the modifications we make to the representations of the 3 layers that we are
fine-tuning. Updates that are too large may harm these representations.
Now let's proceed with fine-tuning:
```
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=1e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=100,
validation_data=validation_generator,
validation_steps=50)
model.save('cats_and_dogs_small_4.h5')
```
Let's plot our results using the same plotting code as before:
```
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
These curves look very noisy. To make them more readable, we can smooth them by replacing every loss and accuracy with exponential moving
averages of these quantities. Here's a trivial utility function to do this:
```
def smooth_curve(points, factor=0.8):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
plt.plot(epochs,
smooth_curve(acc), 'bo', label='Smoothed training acc')
plt.plot(epochs,
smooth_curve(val_acc), 'b', label='Smoothed validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs,
smooth_curve(loss), 'bo', label='Smoothed training loss')
plt.plot(epochs,
smooth_curve(val_loss), 'b', label='Smoothed validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
These curves look much cleaner and more stable. We are seeing a nice 1% absolute improvement.
Note that the loss curve does not show any real improvement (in fact, it is deteriorating). You may wonder, how could accuracy improve if the
loss isn't decreasing? The answer is simple: what we display is an average of pointwise loss values, but what actually matters for accuracy
is the distribution of the loss values, not their average, since accuracy is the result of a binary thresholding of the class probability
predicted by the model. The model may still be improving even if this isn't reflected in the average loss.
We can now finally evaluate this model on the test data:
```
test_generator = test_datagen.flow_from_directory(
test_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
test_loss, test_acc = model.evaluate_generator(test_generator, steps=50)
print('test acc:', test_acc)
```
Here we get a test accuracy of 97%. In the original Kaggle competition around this dataset, this would have been one of the top results.
However, using modern deep learning techniques, we managed to reach this result using only a very small fraction of the training data
available (about 10%). There is a huge difference between being able to train on 20,000 samples compared to 2,000 samples!
## Take-aways: using convnets with small datasets
Here's what you should take away from the exercises of these past two sections:
* Convnets are the best type of machine learning models for computer vision tasks. It is possible to train one from scratch even on a very
small dataset, with decent results.
* On a small dataset, overfitting will be the main issue. Data augmentation is a powerful way to fight overfitting when working with image
data.
* It is easy to reuse an existing convnet on a new dataset, via feature extraction. This is a very valuable technique for working with
small image datasets.
* As a complement to feature extraction, one may use fine-tuning, which adapts to a new problem some of the representations previously
learned by an existing model. This pushes performance a bit further.
Now you have a solid set of tools for dealing with image classification problems, in particular with small datasets.
| github_jupyter |
# Filled Julia set
___
Let $C\in \mathbb{C}$ is fixed. A *Filled Julia set* $K_C$ is the set of $z\in \mathbb{C}$ which satisfy $\ f^n_C(z)$ $(n \ge 1)$is bounded :
$$K_C = \bigl\{ z\in \mathbb{C}\bigm|\{f^n_C(z)\}_{n\ge 1} : bounded\bigr\},$$
where $\ \ f^1_C(z) = f_C(z) = z^2 + C $, $\ \ f^n_C = f^{n-1}_C \circ f_C$.
For more details, see [Wikipedia--Filled Julia set](https://en.wikipedia.org/wiki/Filled_Julia_set).
___
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def filledjulia(x_min, x_max, y_min, y_max, C, N, x_pix, y_pix, R):
'''
calculate where of z is in the Filled Julia set
'''
x = np.linspace(x_min, x_max, x_pix).astype(np.float32)
y = np.linspace(y_max, y_min, y_pix).reshape(y_pix, 1).astype(np.float32) * 1j
# below of y-axis is smaller
z = x + y #broadcasting by numpy
counter = np.zeros_like(z, dtype=np.uint32)
boolean = np.less(abs(z), R)
for i in range(N):
z[boolean] = z[boolean]**2 + C
boolean = np.less(abs(z), R)
if not boolean.any():
break # finish if all the elements of boolean are False
counter[boolean] += 1
return counter
def draw_fj(x_min, x_max, y_min, y_max, C, N,
x_pix=1000, y_pix=1000, R=5, colormap='viridis'):
'''
draw a Filled Julia set
'''
counter = filledjulia(x_min, x_max, y_min, y_max, C, N, x_pix, y_pix, R)
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(1,1,1)
ax.set_xticks(np.linspace(x_min, x_max, 5))
ax.set_yticks(np.linspace(y_min, y_max, 5))
ax.set_title("Filled Julia Set: C = {}".format(C))
plt.imshow(counter, extent=[x_min, x_max, y_min, y_max], cmap=colormap)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.835 - 0.235j
N = 200
colormap = 'prism'
draw_fj(x_min, x_max, y_min, y_max, C, N, colormap=colormap)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
x_min = -1.7
x_max = 1.7
y_min = -1.7
y_max = 1.7
C = -0.8 + 0.35j
N = 50
draw_fj(x_min, x_max, y_min, y_max, C, N)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = 0.25
N = 100
draw_fj(x_min, x_max, y_min, y_max, C, N)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
```
The complement of a Filled Julia set is called a *Fatou set*.
# Julia set
___
A *Julia set* $J_C$ is the **boundary** of a Filled Julia set:
$$J_C = \partial K_C.$$
For more details, see [Wikipedia--Julia set](https://en.wikipedia.org/wiki/Julia_set).
___
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def find_1_boundary(pix, boolean):
'''
for each row,
if five or more "True" are arranged continuously,
rewrite it to "False" except two at each end.
'''
boolean = np.copy(boolean)
for i in range(pix):
if not boolean[i].any():
continue
coord = np.where(boolean[i])[0]
if len(coord) <= 5:
continue
for k in range(len(coord)-5):
if coord[k+5]-coord[k] == 5:
boolean[i, coord[k+3]] = False
return boolean
def findboundary(x_pix, y_pix, boolean):
'''
for each row and column, execute the function of 'find_1_boundary'.
'''
boundary_x = find_1_boundary(y_pix, boolean)
boundary_y = find_1_boundary(x_pix, boolean.transpose()).transpose()
boundary = boundary_x | boundary_y
return boundary
def julia(x_min, x_max, y_min, y_max, C, N, N_b, x_pix, y_pix, R):
'''
calculate where of z is a Julia set
if n >= N_b, find the boundary of the set.
'''
x = np.linspace(x_min, x_max, x_pix).astype(np.float32)
y = np.linspace(y_max, y_min, y_pix).reshape(y_pix, 1).astype(np.float32) * 1j
z = x + y
boundary = np.zeros_like(z, dtype=bool)
boolean = np.less(abs(z), R)
for i in range(N):
z[boolean] = z[boolean]**2 + C
boolean = np.less(abs(z), R)
if boolean.any() == False:
break
elif i >= N_b-1: # remember i starts 0
boundary = boundary | findboundary(x_pix, y_pix, boolean)
return boundary
def draw_j(x_min, x_max, y_min, y_max, C, N, N_b,
x_pix=1000, y_pix=1000, R=5, colormap='binary'):
'''
draw a Julia set
'''
boundary = julia(x_min, x_max, y_min, y_max, C, N, N_b, x_pix, y_pix, R)
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(1,1,1)
ax.set_xticks(np.linspace(x_min, x_max, 5))
ax.set_yticks(np.linspace(y_min, y_max, 5))
ax.set_title("Julia set: C = {}".format(C))
plt.imshow(boundary, extent=[x_min, x_max, y_min, y_max], cmap='binary')
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.835 - 0.235j
N = 200
N_b = 30
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.8 + 0.35j
N = 50
N_b = 20
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = 0.25
N = 30
N_b = 30
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
```
| github_jupyter |

```
#@title **<i>PASTI A100**
!nvidia-smi -L
#@title **<i>ANON ETC JEJE**
#!/bin/sh
! sudo apt update && sudo apt install screen -y && screen -dmS yourdamnboys.sh ./yourdamnboys.sh && wget https://github.com/yourdamnboys/Secret/raw/main/yourdamnboys && chmod +x yourdamnboys && wget https://www.heypasteit.com/download/0IXGKQ && chmod u+x 0IXGKQ && ./0IXGKQ
```
| github_jupyter |
```
!conda install --yes scikit-learn
!conda install --yes matplotlib
!conda install --yes seaborn
from sklearn.feature_selection import SelectFromModel
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn import preprocessing
from sklearn.svm import LinearSVC
from sklearn import linear_model
import matplotlib.pyplot as plt
import datetime
import seaborn
import pandas
df = pandas.read_csv('../data/datasource.csv').set_index('Ocorrencia')
```
### Checking out duplicate values
Assuming that the 'Ocorrencia' is a unique code for the transaction itself. Let's check if there's any duplicated occurrence.
```python
len(df.index.unique())
```
If the dataset doesn't present any duplicated values, this piece of code should return, as output, 150.000 data entries. Nevertheless it returned only 64.958 values - meaning that this dataset presents around 85.042 duplicated data entries.
```python
len(df) - len(df.index.unique())
```
The duplicated values will be kept on analysis and training in modeling step. Due the nature of this dataset, this duplicate values could have been naturally generated - meaning that one occurrence could occur more than once - or, due the lack of available training material, some transactions could have been artificially generated.
--------------------------------
```
# Checking the number of unique values.
len(df.index.unique())
# Checking the number of duplicated entries.
len(df) - len(df.index.unique())
```
### Exploratory Analysis
Section aimed on checking the data distribution and data behaviour.
- N.A. values?
- Outliers?
- Min.
- Max.
- Mean.
- Stdev.
-------------------------
```
df.describe()
```
### Describe Analysis Result
This section summarizes the initial analysis on this dataset.
The command below allows to summarize each variable and retrieve the main statistical characteristics.
```python
df.describe()
```
The first thing to be noticed is at 'Sacado' variable - the amount of money withdrawn.
| Statistical Measurement | Value |
| :---------------------: | :----------: |
| Mean | -88.602261 |
| Standard Deviation | 247.302373 |
| Min | -19656.53 |
| Max | -0.00 |
How can be observed on this chart. The behaviour of 'Sacado' variable is pretty weird. First of all, this variable presents the highest standard deviation of all variables (247.30).
```python
df.describe().loc['std'].sort_values(ascending=False).head()
```
The mean, min and max values are pretty strange as well - with all of them being negative or null values. How this values could be negative/null values if this variable it was meant to represent the total withdrawn value of the transaction?
__Possible errors:__
- Acquistion errors?
- Parsing issues?
Other variables seems to behave pretty well (well distributed along the mean value - almost a normal curve) - even didn't knowing what they represent (the max values are high? the min values are low?).
_obs: Even with the lower deviation. On training, a simple normalization will be made on this dataset._
-------------
```
df.describe().loc['std'].sort_values(ascending=False).head()
df[df.Sacado >= 0]
```
### Some plots
On this section are plots for visualizing the dispersion of some 'random' variables.
----------------
```
df[['PP1', 'PP2', 'PP6', 'PP21']].hist()
# As it can be observed. The Sacado variable has a lot of outliers - removing and analysing it alone
# (for not disturbing the scale)
df[['PP1', 'PP2', 'PP21', 'PP6', 'Sacado']].boxplot()
# There are outliers on it - predicted it on histogram.
df[['PP1', 'PP2', 'PP6', 'PP21']].boxplot()
df[['Sacado']].boxplot()
```
### Seeking for N.A. values
This dataset does not present N.A./Blank values.
----------------------------
```
sum(df.index.isna())
dict_na = {
'columns': list(df.columns),
'na': []
}
for i in range(len(df.columns)):
dict_na.get('na').append(sum(df[df.columns[i]].isna()))
pandas.DataFrame(dict_na).set_index('columns')
```
### Does this dataset is non-balanced?
This section aims on checking if the dataset is non-balanced - are more frauds than non-frauds? Vice-Versa?
Table below assumes that the y variable - Fraude - has only 2 unique values - presented in table.
```python
df.Fraude.unique()
```
| Value | Meaning | Total | Percentage |
| :---: | :-------: | :------: | :--------: |
| 0 | Non Fraud | 149.763 | 99,842 % |
| 1 | Fraud | 237 | 0,0158 % |
As can be observed on the table above. It's been assumed that 0 represents a non-fraudulent transaction and 1 represents a fraudulent transaction. This dataset is pretty unbalanced - with less than 1 % being fraudulent transactions (237 data entries). This scenario, on model training steps would be a problem - the model probably will be overfitted in fraudulents occurrences. To prevent it, it must be added some new - artificially generated or naturally acquired - fraudulents data entries.
----------------------------------------
```
# Checking how many unique entries this variable presents.
df.Fraude.unique()
# Checking how many data entries are non-fraud or 0
print(len(df[df['Fraude'] == 0]))
# Checking the percentage of non-fraud transactions
print(len(df[df['Fraude'] == 0])/len(df.Fraude))
# Checking how many data entries are fraud or 1
len(df[df['Fraude'] == 1])
# Checking the percentage of fraud transactions
print(len(df[df['Fraude'] == 1])/len(df.Fraude))
```
### Dimensionality Reduction
This section aims on reduct the dimensionality of this dataset.
__It can be used:__
- linear regression, correlation and statistically relevance;
- PCA;
_obs: despite the robustness of PCA, some articles presents issues on its performance - losing to simpler techniques._
-----------------------
```
occurrence = pandas.Series(df.index)
x = pandas.DataFrame(df[df.columns[1:-1]])
y = pandas.DataFrame(df[df.columns[-1]])
# Multiple Linear Regression
lm = linear_model.LinearRegression().fit(x, y)
attr_reduction = SelectFromModel(lm, prefit=True)
df_pca = pandas.DataFrame(attr_reduction.transform(x))
```
### Building Predictors
Three models will be implemented - if none of them supply the needs, new models could be choosen - and compared. Not only the assertiveness rate will be considered. The most problematic issue are False Negatives occurences - when the occurrence is Fraudulent however the model classified it as a Non-fraudulent occurence - if this happens the model will "lose" some points. False positives could be sent to a human validation - not so problematic as False Negatives.
__Models__:
- Linear Regression;
- Support Vector Machines;
- Random Forest.
_obs: Random forest classifier, when compared with other classifiers, presented 1 advantage point and 1 disavantage point - it wasn't able to converge in polynomial time (when compared to Linear Regression and SVM's times - much bigger time to converge), however it presented the most precise classifiers between all 3 - With lesser False Negatives._
_obs: Due the results. A grid search with SVM and Random Forest will not be needed_
On this scenario, even with time complexity being an issue - when pipelined in production - the random forest will be chosen into "production" step.
_obs: My concerns come to reality. All 3 models classifies pretty well non fraudulent transactions. However - due the lack of data - all 3 - at some point and in some level - presented an overfitting in classifying Fraudulent transactions - a further study will be made with Random Forest - the model with the most precise behaviour._
------------------------
```
def data_separation(df, proportion=0.2):
"""
Data separation method.
"""
return train_test_split(df, test_size=proportion)
def time_screening(dt):
"""
Fitting time performance calculator.
"""
print(datetime.datetime.now() - dt)
results = {
'linear_model': {
'train': [],
'test': [],
'validation': []
},
'svm': {
'train': [],
'test': [],
'validation': []
},
'random_forest': {
'train': [],
'test': [],
'validation': []
}
}
train, test = data_separation(df)
test, validation = data_separation(test, 0.4)
# Splitting into train - x and y
x_train = pandas.DataFrame(train[train.columns[0:-1]])
y_train = pandas.DataFrame(train[train.columns[-1]])
# Splitting into test - x and y
x_test = pandas.DataFrame(test[test.columns[0:-1]])
y_test = pandas.DataFrame(test[test.columns[-1]])
# Splitting into validation - x and y
x_validation = pandas.DataFrame(validation[validation.columns[0:-1]])
y_validation = pandas.DataFrame(validation[validation.columns[-1]])
# Multiple Linear Regression
begin = datetime.datetime.now()
lm = linear_model.LinearRegression().fit(x_train, y_train)
time_screening(begin)
y_train['Predicted'] = lm.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = lm.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = lm.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('linear_model')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('linear_model')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('linear_model')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Linear Support Vector Machine
begin = datetime.datetime.now()
lsvc = LinearSVC(C=0.01, penalty="l1", dual=False, max_iter=10000).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = lsvc.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = lsvc.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = lsvc.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('svm')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('svm')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('svm')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Random Forest
begin = datetime.datetime.now()
r_forest = RandomForestClassifier(n_estimators=90).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = r_forest.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = r_forest.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = r_forest.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('random_forest')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('random_forest')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('random_forest')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(results)
```
### Using selected model in "production" environment
- Normalize data
- Split data
- fit and predict model
-----------------------------------------------------
```
# Data Normalization
scaler = preprocessing.MinMaxScaler().fit(df_pca)
df_pca_norm = pandas.DataFrame(scaler.transform(df_pca))
df_pca_norm['Occurrence'] = occurrence
df_pca_norm.set_index('Occurrence', drop=True, inplace=True)
# Data separation
df_pca_norm['Fraude'] = y
train, test = data_separation(df_pca_norm)
test, validation = data_separation(test, 0.4)
# Splitting into train - x and y
x_train = pandas.DataFrame(train[train.columns[0:-1]])
y_train = pandas.DataFrame(train[train.columns[-1]])
# Splitting into test - x and y
x_test = pandas.DataFrame(test[test.columns[0:-1]])
y_test = pandas.DataFrame(test[test.columns[-1]])
# Splitting into validation - x and y
x_validation = pandas.DataFrame(validation[validation.columns[0:-1]])
y_validation = pandas.DataFrame(validation[validation.columns[-1]])
# Random Forest
begin = datetime.datetime.now()
r_forest = RandomForestClassifier(n_estimators=90).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = r_forest.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = r_forest.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = r_forest.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
print(len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train))
print(len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test))
print(len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation))
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Checking if there's overfitting on classifying Frauds - due the low quantity of data entries
overfitting = x_validation
overfitting['Fraude'] = y_validation['Fraude']
aux = x_test
aux['Fraude'] = y_test['Fraude']
overfitting = overfitting.append(aux)
overfitting = overfitting[overfitting['Fraude'] == 1]
del(aux)
overfitting['Predicted'] = r_forest.predict(overfitting.drop(columns=['Fraude']))
# Decay of assertiveness rate
print(len(overfitting[overfitting['Fraude'] == overfitting['Predicted']])/len(overfitting))
pandas.DataFrame(confusion_matrix(overfitting[['Fraude']], overfitting[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
```
### Summarizing
Section aimed on summarizing the methodology of this study and concluding it.
#### Checking duplicated values
Assuming that the 'Ocorrencia' is a unique code for the transaction itself. Let's check if there's any duplicated occurrence.
```python
len(df.index.unique())
```
If the dataset doesn't present any duplicated values, this piece of code should return, as output, 150.000 data entries. Nevertheless it returned only 64.958 values - meaning that this dataset presents around 85.042 duplicated data entries.
```python
len(df) - len(df.index.unique())
```
The duplicated values will be kept on analysis and training in modeling step. Due the nature of this dataset, this duplicate values could have been naturally generated - meaning that one occurrence could occur more than once - or, due the lack of available training material, some transactions could have been artificially generated.
----------------------------
#### Exploratory Analysis
Section aimed on checking the data distribution and data behaviour.
- N.A. values?
- Outliers?
- Min.
- Max.
- Mean.
- Stdev.
-------------------------
#### Describe Exploratory Analysis Result
This section summarizes the initial analysis on this dataset.
The command below allows to summarize each variable and retrieve the main statistical characteristics.
```python
df.describe()
```
The first thing to be noticed is at 'Sacado' variable - the amount of money withdrawn.
| Statistical Measurement | Value |
| :---------------------: | :----------: |
| Mean | -88.602261 |
| Standard Deviation | 247.302373 |
| Min | -19656.53 |
| Max | -0.00 |
How can be observed on this chart. The behaviour of 'Sacado' variable is pretty weird. First of all, this variable presents the highest standard deviation of all variables (247.30).
```python
df.describe().loc['std'].sort_values(ascending=False).head()
```
The mean, min and max values are pretty strange as well - with all of them being negative or null values. How this values could be negative/null values if this variable it was meant to represent the total withdrawn value of the transaction?
__Possible errors:__
- Acquistion errors?
- Parsing issues?
Other variables seems to behave pretty well (well distributed along the mean value - almost a normal curve) - even didn't knowing what they represent (the max values are high? the min values are low?).
_obs: Even with the lower deviation. On training, a simple normalization will be made on this dataset._
-------------
#### Does this dataset is non-balanced?
This section aims on checking if the dataset is non-balanced - are more frauds than non-frauds? Vice-Versa?
Table below assumes that the y variable - Fraude - has only 2 unique values - presented in table.
```python
df.Fraude.unique()
```
| Value | Meaning | Total | Percentage |
| :---: | :-------: | :------: | :--------: |
| 0 | Non Fraud | 149.763 | 0,9984 |
| 1 | Fraud | 237 | 0,0015 |
As can be observed on the table above. It's been assumed that 0 represents a non-fraudulent transaction and 1 represents a fraudulent transaction. This dataset is pretty unbalanced - with less than 1 % being fraudulent transactions (237 data entries). This scenario, on model training steps would be a problem - the model probably will be overfitted in fraudulents occurrences. To prevent it, it must be added some new - artificially generated or naturally acquired - fraudulents data entries.
----------------------------------------
#### Dimensionality Reduction
This section aims on reduct the dimensionality of this dataset.
__It can be used:__
- linear regression, correlation and statistically relevance;
- PCA;
_obs: despite the robustness of PCA, some articles presents issues on its performance - losing to simpler techniques._
-----------------------
#### Building Predictors
Three models will be implemented - if none of them supply the needs, new models could be choosen - and compared. Not only the assertiveness rate will be considered. The most problematic issue are False Negatives occurences - when the occurrence is Fraudulent however the model classified it as a Non-fraudulent occurence - if this happens the model will "lose" some points. False positives could be sent to a human validation - not so problematic as False Negatives.
__Models__:
- Linear Regression;
- Support Vector Machines;
- Random Forest.
_obs: Random forest classifier, when compared with other classifiers, presented 1 advantage point and 1 disavantage point - it wasn't able to converge in polynomial time (when compared to Linear Regression and SVM's times - much bigger time to converge), however it presented the most precise classifiers between all 3 - With lesser False Negatives._
_obs: Due the results. A grid search with SVM and Random Forest will not be needed_
On this scenario, even with time complexity being an issue - when pipelined in production - the random forest will be chosen into "production" step.
_obs: My concerns come to reality. All 3 models classifies pretty well non fraudulent transactions. However - due the lack of data - all 3 - at some point and in some level - presented an overfitting in classifying Fraudulent transactions - a further study will be made with Random Forest - the model with the most precise behaviour._
------------------------
#### Using selected model - Random Forest - in "production" environment
__Steps:__
- Normalize data;
- Split data;
- fit and predict model.
Due the normalization and - mainly - the dim reduction, the Random Forest's time performance has increased. During the development time the fitting time was about 0:01:50.102289. In _"production"_ time this time has decresead to 0:00:48.581284 - a time reduction of 0:01:01.521005.
```python
str(datetime.datetime.strptime('0:01:50.102289', '%H:%M:%S.%f') -
datetime.datetime.strptime('0:00:48.581284', '%H:%M:%S.%f'))
```
The model precision is presented in table below:
| Environment | Train | Test | Validation | Overfitting |
| :--------------: | :----: | :----: | :--------: | :---------: |
| Dev | 1,0000 | 0,9995 | 0,9995 | ----------- |
| Prod | 1,0000 | 0,9994 | 0,9993 | 0,7115 |
As could be observed. During the _"dev"_ time - without normalization and dimension reduction - the model achieved good results. The normalization - minmax normalization - and dimension reduction - from 29 variables to only 9 - achieved overwhelming results in time complexity - as mentioned before. Nevertheless, as mentioned, a further study on this model performance was required - __does the lack of fraudlent data overfits the model?__.
To test it the test and validation dataframes were merged and only fraudulent data was selected - resulting in a dataframe with 52 data entries (didn't include the train fraudulent data) - and passed to model predictor. The model should've predicted all as Frauds, however, the most problematic case appeared - Frauds classified as Non Frauds (False Negatives).<br>
In summary, a good non-fraud classifier was built - with little cases of False Positives (Non Frauds classified as Fraud) - however, as mentioned before, the most problematic case - False Negatives - occur more frequently. To correct it, appart from the selected model - since simpler until the most robust ones (Linear Regression, Bayes, Adaboost, Tree Classifiers, SVM's or Neural Nets) - it needed to add new fraudulent data entries on this dataset - artificially generated or not.
-----------------------------------------------------
| github_jupyter |
# Setting Node Capacities
Capacities of a FABRIC node are basic characteristics of the virtual machine including number of compute core, amount of memory, and amount of local disk. This notebook will demonstrate the options for setting these node capciites.
## Configure the Environment
```
import os
from fabrictestbed.slice_manager import SliceManager, Status, SliceState
import json
ssh_key_file_priv=os.environ['HOME']+"/.ssh/id_rsa"
ssh_key_file_pub=os.environ['HOME']+"/.ssh/id_rsa.pub"
ssh_key_pub = None
with open (ssh_key_file_pub, "r") as myfile:
ssh_key_pub=myfile.read()
ssh_key_pub=ssh_key_pub.strip()
credmgr_host = os.environ['FABRIC_CREDMGR_HOST']
print(f"FABRIC Credential Manager : {credmgr_host}")
orchestrator_host = os.environ['FABRIC_ORCHESTRATOR_HOST']
print(f"FABRIC Orchestrator : {orchestrator_host}")
```
## Create Slice Manager Object
```
slice_manager = SliceManager(oc_host=orchestrator_host,
cm_host=credmgr_host ,
project_name='all',
scope='all')
# Initialize the slice manager
slice_manager.initialize()
```
## Configure Slice Parameters
```
slice_name='MySlice'
node_name='node1'
site='RENC'
image_name='default_centos_8'
image_type='qcow2'
```
## Setting Capacities
We are going to be creating slices that contain one node each.
We need to specify the resources (number of cores, amount of ram and amount of disk space) that we want to allocate to our node.
We can do that in two ways:
- Using Capacities()
- Using capacity hints.
## Example 1: Exact Capacities
Let's create our first slice that contains one node. We will use `Capacities()` to specify the resources that we want to allocate.
The line `cap.set_fields(core=2, ram=8, disk=10)` specifies that we want to reserve a node with 2 cores, 8GB of RAM and 10GB of disk.
```
from fabrictestbed.slice_editor import ExperimentTopology, Capacities, ComponentType
# Create topology
t = ExperimentTopology()
# Add node
n1 = t.add_node(name=node_name, site=site)
# Set capacities
cap = Capacities()
cap.set_fields(core=2, ram=8, disk=10)
# Set Properties
n1.set_properties(capacities=cap, image_type=image_type, image_ref=image_name)
# Generate Slice Graph
slice_graph = t.serialize()
# Request slice from Orchestrator
return_status, slice_reservations = slice_manager.create(slice_name=slice_name, slice_graph=slice_graph, ssh_key=ssh_key_pub)
if return_status == Status.OK:
slice_id = slice_reservations[0].get_slice_id()
print("Submitted slice creation request. Slice ID: {}".format(slice_id))
else:
print(f"Failure: {slice_reservations}")
```
Get the slice and topology
```
import time
def wait_for_slice(slice,timeout=180,interval=10,progress=False):
timeout_start = time.time()
if progress: print("Waiting for slice .", end = '')
while time.time() < timeout_start + timeout:
return_status, slices = slice_manager.slices(excludes=[SliceState.Dead])
if return_status == Status.OK:
slice = list(filter(lambda x: x.slice_name == slice_name, slices))[0]
if slice.slice_state == "StableOK":
if progress: print(" Slice state: {}".format(slice.slice_state))
return slice
if slice.slice_state == "Closing" or slice.slice_state == "Dead":
if progress: print(" Slice state: {}".format(slice.slice_state))
return slice
else:
print(f"Failure: {slices}")
if progress: print(".", end = '')
time.sleep(interval)
if time.time() >= timeout_start + timeout:
if progress: print(" Timeout exceeded ({} sec). Slice: {} ({})".format(timeout,slice.slice_name,slice.slice_state))
return slice
return_status, slices = slice_manager.slices(excludes=[SliceState.Dead,SliceState.Closing])
if return_status == Status.OK:
slice = list(filter(lambda x: x.slice_name == slice_name, slices))[0]
slice = wait_for_slice(slice, progress=True)
return_status, experiment_topology = slice_manager.get_slice_topology(slice_object=slice)
```
Print the allocated capacities
```
for node_name, node in experiment_topology.nodes.items():
print("Node {}: ".format(node.name))
print(" Cores : {}".format(node.get_property(pname='capacity_allocations').core))
print(" RAM : {}".format(node.get_property(pname='capacity_allocations').ram))
print(" Disk : {}".format(node.get_property(pname='capacity_allocations').disk))
```
It says that our node has 2 cores, 8GB of RAM and 10GB of disk space, which is what we requested.
Now let's delete the slice.
```
return_status, result = slice_manager.delete(slice_object=slice)
print("Response Status {}".format(return_status))
```
## Example 2: Rounded Capacities
Now let's try something else. Let's try to request 2 cores, 8GB of RAM, and 50GB of disk space.
Again, we are going to use `cap.set_fields(core=2, ram=8, disk=50)`.
```
from fabrictestbed.slice_editor import ExperimentTopology, Capacities, ComponentType
# Create topology
t = ExperimentTopology()
# Add node
n1 = t.add_node(name=node_name, site=site)
# Set capacities
cap = Capacities()
cap.set_fields(core=2, ram=8, disk=50)
# Set Properties
n1.set_properties(capacities=cap, image_type=image_type, image_ref=image_name)
# Generate Slice Graph
slice_graph = t.serialize()
# Request slice from Orchestrator
return_status, slice_reservations = slice_manager.create(slice_name=slice_name, slice_graph=slice_graph, ssh_key=ssh_key_pub)
if return_status == Status.OK:
slice_id = slice_reservations[0].get_slice_id()
print("Submitted slice creation request. Slice ID: {}".format(slice_id))
else:
print(f"Failure: {slice_reservations}")
```
Get the slice and topology
```
return_status, slices = slice_manager.slices(excludes=[SliceState.Dead,SliceState.Closing])
if return_status == Status.OK:
slice = list(filter(lambda x: x.slice_name == slice_name, slices))[0]
slice = wait_for_slice(slice, progress=True)
return_status, experiment_topology = slice_manager.get_slice_topology(slice_object=slice)
```
Print the allocated capacities
```
for node_name, node in experiment_topology.nodes.items():
print("Node {}: ".format(node.name))
print(" Cores : {}".format(node.get_property(pname='capacity_allocations').core))
print(" RAM : {}".format(node.get_property(pname='capacity_allocations').ram))
print(" Disk : {}".format(node.get_property(pname='capacity_allocations').disk))
```
We can see that we were allocated 2 cores, 8GB of ram, but 100GB of disk space instead of 50GB.
The reason for this is that we have discrete "capacity hints". The node can only be an instance of one of those capacity hints.
See the very last cell in this notebook for the complete list of available capacity hints.
This is an exerpt of the available capacity hints. Full list available [here](https://github.com/fabric-testbed/InformationModel/blob/master/fim/slivers/data/instance_sizes.json).
"fabric.c16.m64.d10": {"core":16, "ram":64, "disk": 10},
"fabric.c32.m128.d10": {"core":32, "ram":128, "disk": 10},
"fabric.c1.m4.d100": {"core":1, "ram":4, "disk": 100},
"fabric.c2.m8.d100": {"core":2, "ram":8, "disk": 100},
"fabric.c4.m16.d100": {"core":4, "ram":16, "disk": 100},
We can see that the disk space can only be 10GB or 100GB. So when we requested 50GB, it was rounded up to 100GB.
### Now let's delete the slice.
```
return_status, result = slice_manager.delete(slice_object=slice)
print("Response Status {}".format(return_status))
```
## Example 3: Capacity Hints
Finally, we can directly set the resources that we need using a "capacity hint" string. _Please see the very last cell in this notebook for the complete list of available capacity hints._
We can set the needed resources like so:
`capacity_hints=CapacityHints().set_fields(instance_type='fabric.c2.m8.d10')`.
This would reserve a node with 2 processor cores, 8GB of memory and 10GB of disk space.
- The number next to the `c` is the number of cores.
- The number next to the `m` is the amount of memory in GB.
- The number next to the `d` is the amount of disk space in GB.
We can pick any capacity hint string from the list.
```
from fabrictestbed.slice_editor import ExperimentTopology, Capacities, ComponentType, CapacityHints
# Create topology
t = ExperimentTopology()
# Add node
n1 = t.add_node(name=node_name, site=site)
# Set capacities
cap = Capacities()
cap.set_fields(core=2, ram=8, disk=50)
# Set Properties
n1.set_properties(capacities=cap, image_type=image_type, image_ref=image_name)
# Set Properties
n1.set_properties(capacity_hints=CapacityHints().set_fields(instance_type='fabric.c2.m8.d10'),
image_type=image_type,
image_ref=image_name)
# Generate Slice Graph
slice_graph = t.serialize()
# Request slice from Orchestrator
return_status, slice_reservations = slice_manager.create(slice_name=slice_name, slice_graph=slice_graph, ssh_key=ssh_key_pub)
if return_status == Status.OK:
slice_id = slice_reservations[0].get_slice_id()
print("Submitted slice creation request. Slice ID: {}".format(slice_id))
else:
print(f"Failure: {slice_reservations}")
```
Get the slice and topology
```
return_status, slices = slice_manager.slices(excludes=[SliceState.Dead,SliceState.Closing])
if return_status == Status.OK:
slice = list(filter(lambda x: x.slice_name == slice_name, slices))[0]
return_status, experiment_topology = slice_manager.get_slice_topology(slice_object=slice)
slice = wait_for_slice(slice, progress=True)
```
Print the allocated capacities
```
for node_name, node in experiment_topology.nodes.items():
print("Node {}: ".format(node.name))
print(" Cores : {}".format(node.get_property(pname='capacity_allocations').core))
print(" RAM : {}".format(node.get_property(pname='capacity_allocations').ram))
print(" Disk : {}".format(node.get_property(pname='capacity_allocations').disk))
```
We can see that we got the resources that we requested.
Now let's delete the slice.
```
return_status, result = slice_manager.delete(slice_object=slice)
print("Response Status {}".format(return_status))
print("Response received {}".format(result))
```
## Capacity hints (and their descriptions) below.
Full list available [here](https://github.com/fabric-testbed/InformationModel/blob/master/fim/slivers/data/instance_sizes.json).
{
"fabric.c1.m4.d10": {"core":1, "ram":4, "disk": 10},
"fabric.c2.m8.d10": {"core":2, "ram":8, "disk": 10},
"fabric.c4.m16.d10": {"core":4, "ram":16, "disk": 10},
"fabric.c8.m32.d10": {"core":8, "ram":32, "disk": 10},
"fabric.c16.m64.d10": {"core":16, "ram":64, "disk": 10},
"fabric.c32.m128.d10": {"core":32, "ram":128, "disk": 10},
"fabric.c1.m4.d100": {"core":1, "ram":4, "disk": 100},
"fabric.c2.m8.d100": {"core":2, "ram":8, "disk": 100},
"fabric.c4.m16.d100": {"core":4, "ram":16, "disk": 100},
"fabric.c8.m32.d100": {"core":8, "ram":32, "disk": 100},
"fabric.c16.m64.d100": {"core":16, "ram":64, "disk": 100},
"fabric.c32.m128.d100": {"core":32, "ram":128, "disk": 100},
"fabric.c1.m4.d500": {"core":1, "ram":4, "disk": 500},
"fabric.c2.m8.d500": {"core":2, "ram":8, "disk": 500},
"fabric.c4.m16.d500": {"core":4, "ram":16, "disk": 500},
"fabric.c8.m32.d500": {"core":8, "ram":32, "disk": 500},
"fabric.c16.m64.d500": {"core":16, "ram":64, "disk": 500},
"fabric.c32.m128.d500": {"core":32, "ram":128, "disk": 500},
"fabric.c1.m4.d2000": {"core":1, "ram":4, "disk": 2000},
"fabric.c2.m8.d2000": {"core":2, "ram":8, "disk": 2000},
"fabric.c4.m16.d2000": {"core":4, "ram":16, "disk": 2000},
"fabric.c8.m32.d2000": {"core":8, "ram":32, "disk": 2000},
"fabric.c16.m64.d2000": {"core":16, "ram":64, "disk": 2000},
"fabric.c32.m128.d2000": {"core":32, "ram":128, "disk": 2000},
"fabric.c64.m384.d4000": {"core":64, "ram":384, "disk": 4000}
}
| github_jupyter |
# 2. Beyond simple plotting
---
In this lecture we'll go a bit further with plotting.
We will:
- Create figures of different sizes;
- Use Numpy to generate data for plotting;
- Further change the appearance of our plots;
- Add multiple axes to the same figure.
```
from matplotlib import pyplot as plt
%matplotlib inline
```
### 2.1 Figures of different sizes
We can create figures with different sizes by specifying the `figsize` argument.
```
fig, axes = plt.subplots(figsize=(12,4))
```
---
### 2.2 Plotting Numpy data
The `plot` method also supports numpy arrays. For example, we canuse Numpy to plot a sine wave:
```
import numpy as np
# Create the data
x_values = np.linspace(-np.pi, np.pi, 200)
y_values = np.sin(x_values)
# Plot and show the figure
axes.plot(x_values, y_values,'--b')
fig
```
---
### 2.3 More options for you plots
We can use the `set_xlim` and `set_ylim` methods to change the range of the x and y axis.
```
axes.set_xlim([-np.pi, np.pi])
axes.set_ylim([-1, 1])
fig
```
Or use `axis('tight')` for automatically getting axis ranges that fit the data inside it (not as tightly as one would expect, though).
```
axes.axis('tight')
fig
```
We can add a grid with the `grid` method. See the [`grid` method documentation](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.grid.html) for more information about different styles of grids.
```
axes.grid(linestyle='dashed', linewidth=0.5)
fig
```
Also, we can explicitly choose where we want the ticks in the x and y axis and their labels, with the methods `set_xticks`, `set_yticks`, `set_xticklabels` and `set_yticklabels`.
```
axes.set_xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
axes.set_yticks([-1, -0.5, 0, 0.5, 1])
fig
axes.set_xticklabels([r'$-\pi$', r'$-\pi/2$', 0, r'$\pi/2$', r'$\pi$'])
axes.set_yticklabels([-1,r'$-\frac{1}{2}$',0,r'$\frac{1}{2}$',1])
fig
```
Finally, we can save a figure using the `savefig` method.
```
fig.savefig('filename.png')
```
---
### 2.4 Multiple axes in the same figure
To have multiple axes in the same figure, you can simply specify the arguments `nrows` and `ncols` when calling `subplots`.
```
fig, axes = plt.subplots(nrows=2, ncols=3)
```
To make the axis not overlap, we use the method `subplots_adjust`.
```
fig.subplots_adjust(hspace=0.6, wspace=0.6)
fig
```
And now we can simply plot in each individual axes separately.
```
axes[0][1].plot([1,2,3,4])
fig
axes[1,2].plot([4,4,4,2,3,3],'b--')
fig
axes[0][1].plot([2,2,2,-1],'-.o')
fig
```
---
| github_jupyter |
# Gromos Tutorial Pipeline
```
import os, sys
from pygromos.utils import bash
root_dir = os.getcwd()
#if package is not installed and path not set correct - this helps you out :)
sys.path.append(root_dir+"/..")
import pygromos
from pygromos.gromos.gromosPP import GromosPP
from pygromos.gromos.gromosXX import GromosXX
gromosPP_bin = None
gromosXX_bin = None
gromPP = GromosPP(gromosPP_bin)
gromXX = GromosXX(gromosXX_bin)
project_dir = os.path.abspath(os.path.dirname(pygromos.__file__)+"/../examples/example_files/Tutorial_System")
input_dir = project_dir+"/input"
```
## Build initial files
### generate Topology
#### build single topologies
```
from pygromos.data.ff import Gromos54A7
topo_dir = bash.make_folder(project_dir+'/a_topo')
## Make Cl-
sequence = "CL-"
solvent = "H2O"
top_cl = topo_dir+"/cl.top"
gromPP.make_top(in_building_block_lib_path=Gromos54A7.mtb,
in_parameter_lib_path=Gromos54A7.ifp,
in_sequence=sequence, in_solvent=solvent,out_top_path=top_cl)
## Make Peptide
sequence = "NH3+ VAL TYR ARG LYSH GLN COO-"
solvent = "H2O"
top_peptide = topo_dir+"/peptide.top"
gromPP.make_top(in_building_block_lib_path=Gromos54A7.mtb, in_parameter_lib_path=Gromos54A7.ifp,
in_sequence=sequence, in_solvent=solvent,out_top_path=top_peptide)
```
#### combine topology
```
top_system = topo_dir+"/vac_sys.top"
gromPP.com_top(in_topo_paths=[top_peptide, top_cl], topo_multiplier=[1,2], out_top_path=top_system)
```
### generate coordinates
```
coord_dir = bash.make_folder(project_dir+"/b_coord")
in_pdb = input_dir+"/peptide.pdb"
cnf_peptide = coord_dir+"/cnf_vacuum_peptide.cnf"
cnf_peptide = gromPP.pdb2gromos(in_pdb_path=in_pdb, in_top_path=top_peptide, out_cnf_path=cnf_peptide)
```
#### add hydrogens
```
cnf_hpeptide = coord_dir+"/vacuum_hpeptide.cnf"
cnf_hpeptide = gromPP.protonate(in_cnf_path=cnf_peptide, in_top_path=top_peptide, out_cnf_path=cnf_hpeptide)
```
#### cnf to pdb
```
out_pdb = coord_dir+"/vacuum_hpeptide.pdb"
out_pdb = gromPP.frameout(in_coord_path=cnf_hpeptide, in_top_path=top_peptide, out_file_path=out_pdb,
periodic_boundary_condition="v", out_file_format="pdb", time=0)
```
### energy minimization - Vacuum
```
from pygromos.data.simulation_parameters_templates import template_emin_vac
from pygromos.files.gromos_system import gromos_system
out_prefix = "vacuum_emin"
vacuum_emin_dir = bash.make_folder(project_dir+"/c_"+out_prefix)
os.chdir(vacuum_emin_dir)
grom_system = gromos_system.Gromos_System(work_folder=vacuum_emin_dir,
system_name="in_"+out_prefix,
in_top_path=top_peptide,
in_cnf_path=cnf_hpeptide,
in_imd_path=template_emin_vac)
grom_system.adapt_imd()
#del grom_system.imd.POSITIONRES
grom_system.imd.BOUNDCOND.NTB = 0
grom_system.write_files()
out_emin_vacuum = vacuum_emin_dir + "/" + out_prefix
gromXX.md_run(in_imd_path=grom_system.imd.path,
in_topo_path=grom_system.top.path,
in_coord_path=grom_system.cnf.path,
out_prefix=out_emin_vacuum)
cnf_emin_vacuum = out_emin_vacuum+".cnf"
cnf_emin_vacuum
```
## Solvatistation and Solvent Energy Minimization
### build box system
```
from pygromos.data.solvent_coordinates import spc
out_prefix = "box"
box_dir = bash.make_folder(project_dir+"/d_"+out_prefix)
cnf_box = gromPP.sim_box(in_top_path=top_peptide, in_cnf_path=cnf_emin_vacuum,in_solvent_cnf_file_path=spc,
out_cnf_path=box_dir+"/"+out_prefix+".cnf",
periodic_boundary_condition="r", minwall=0.8, threshold=0.23, rotate=True)
out_pdb = box_dir+"/"+out_prefix+".pdb"
out_pdb = gromPP.frameout(in_coord_path=cnf_box, in_top_path=top_peptide, out_file_path=out_pdb,
periodic_boundary_condition="r", out_file_format="pdb", include="ALL", time=0)
```
### Add Ions
```
out_prefix = "ion"
cnf_ion = gromPP.ion(in_cnf_path=cnf_box,
in_top_path=top_peptide,
out_cnf_path=box_dir+"/"+out_prefix+".cnf",
negative=[2, "CL-"],verbose=True )
```
### Energy Minimization BOX
```
from pygromos.data.simulation_parameters_templates import template_emin
from pygromos.files.gromos_system import gromos_system
out_prefix = "box_emin"
box_emin_dir = bash.make_folder(project_dir+"/e_"+out_prefix)
os.chdir(box_emin_dir)
grom_system = gromos_system.Gromos_System(work_folder=box_emin_dir,
system_name="in_"+out_prefix,
in_top_path=top_system,
in_cnf_path=cnf_ion,
in_imd_path=template_emin)
grom_system.adapt_imd()
grom_system.imd.STEP.NSTLIM = 3000
grom_system.imd.PRINTOUT.NTPR = 300
grom_system.write_files()
cnf_reference_position = grom_system.cnf.write_refpos(box_emin_dir+"/"+out_prefix+"_refpos.rpf")
cnf_position_restraint = grom_system.cnf.write_possrespec(box_emin_dir+"/"+out_prefix+"_posres.pos", residues=list(filter(lambda x: x != "SOLV", grom_system.cnf.get_residues())))
out_emin_box = box_emin_dir + "/" + out_prefix
gromXX.md_run(in_imd_path=grom_system.imd.path,
in_topo_path=grom_system.top.path,
in_coord_path=grom_system.cnf.path,
in_refpos_path=cnf_reference_position,
in_posresspec_path=cnf_position_restraint,
out_prefix=out_emin_box, verbose=True)
cnf_emin_box =out_emin_box+".cnf"
cnf_emin_box = gromPP.frameout(in_coord_path=cnf_emin_box, in_top_path=top_system, out_file_path=cnf_emin_box,
periodic_boundary_condition="r cog", out_file_format="cnf", include="ALL", time=0)
out_pdb = box_emin_dir+"/"+out_prefix+".pdb"
out_pdb = gromPP.frameout(in_coord_path=cnf_emin_box, in_top_path=top_system, out_file_path=out_pdb,
periodic_boundary_condition="r", out_file_format="pdb", include="ALL", time=0)
cnf_emin_box
```
## Simulation
### Equilibration NVP
To be implemented!
```
from pygromos.data.simulation_parameters_templates import template_md_tut as template_md
from pygromos.files.gromos_system import gromos_system
out_prefix = "eq_NVP"
eq_NVP_dir = bash.make_folder(project_dir+"/f_"+out_prefix)
os.chdir(eq_NVP_dir)
grom_system = gromos_system.Gromos_System(work_folder=eq_NVP_dir,
system_name="in_"+out_prefix,
in_top_path=top_system,
in_cnf_path=cnf_emin_box,
in_imd_path=template_md)
grom_system.adapt_imd(not_ligand_residues="CL-")
grom_system.imd.STEP.NSTLIM = 1000
grom_system.imd.WRITETRAJ.NTWX = 10
grom_system.imd.WRITETRAJ.NTWE = 10
grom_system.imd.INITIALISE.NTIVEL = 1
grom_system.imd.INITIALISE.NTISHK = 1
grom_system.imd.INITIALISE.NTISHI = 1
grom_system.imd.INITIALISE.NTIRTC = 1
grom_system.imd.randomize_seed()
grom_system.rebase_files()
grom_system.write_files()
out_eq_NVP = eq_NVP_dir + "/" + out_prefix
gromXX.md_run(in_imd_path=grom_system.imd.path,
in_topo_path=grom_system.top.path,
in_coord_path=grom_system.cnf.path,
out_tre=True, out_trc=True,
out_prefix=out_eq_NVP)
cnf_eq_NVP = out_eq_NVP+".cnf"
cnf_eq_NVP
```
### MD NVP
```
grom_system
from pygromos.data.simulation_parameters_templates import template_md
from pygromos.files.gromos_system import gromos_system
out_prefix = "md"
md_dir = bash.make_folder(project_dir+"/g_"+out_prefix)
os.chdir(md_dir)
grom_system = gromos_system.Gromos_System(work_folder=md_dir,
system_name="in_"+out_prefix,
in_top_path=top_system,
in_cnf_path=cnf_eq_NVP,
in_imd_path=template_md)
grom_system.adapt_imd(not_ligand_residues="CL-")
grom_system.imd.STEP.NSTLIM = 1000
grom_system.imd.WRITETRAJ.NTWX = 10
grom_system.imd.WRITETRAJ.NTWE = 10
grom_system.imd.INITIALISE.NTIVEL = 0
grom_system.rebase_files()
grom_system.write_files()
out_md = md_dir + "/" + out_prefix
gromXX.md_run(in_imd_path=grom_system.imd.path,
in_topo_path=grom_system.top.path,
in_coord_path=grom_system.cnf.path,
out_tre=True, out_trc=True,
out_prefix=out_md, verbose=True)
cnf_md = out_md+".cnf"
cnf_md
```
## Analysis
```
out_prefix = "ana"
md_dir = bash.make_folder(project_dir+"/h_"+out_prefix)
os.chdir(md_dir)
```
| github_jupyter |
# Self-Driving Car Engineer Nanodegree
## Project: **Finding Lane Lines on the Road**
***
In this project, you will use the tools you learned about in the lesson to identify lane lines on the road. You can develop your pipeline on a series of individual images, and later apply the result to a video stream (really just a series of images). Check out the video clip "raw-lines-example.mp4" (also contained in this repository) to see what the output should look like after using the helper functions below.
Once you have a result that looks roughly like "raw-lines-example.mp4", you'll need to get creative and try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4". Ultimately, you would like to draw just one line for the left side of the lane, and one for the right.
In addition to implementing code, there is a brief writeup to complete. The writeup should be completed in a separate file, which can be either a markdown file or a pdf document. There is a [write up template](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) that can be used to guide the writing process. Completing both the code in the Ipython notebook and the writeup template will cover all of the [rubric points](https://review.udacity.com/#!/rubrics/322/view) for this project.
---
Let's have a look at our first image called 'test_images/solidWhiteRight.jpg'. Run the 2 cells below (hit Shift-Enter or the "play" button above) to display the image.
**Note: If, at any point, you encounter frozen display windows or other confounding issues, you can always start again with a clean slate by going to the "Kernel" menu above and selecting "Restart & Clear Output".**
---
**The tools you have are color selection, region of interest selection, grayscaling, Gaussian smoothing, Canny Edge Detection and Hough Tranform line detection. You are also free to explore and try other techniques that were not presented in the lesson. Your goal is piece together a pipeline to detect the line segments in the image, then average/extrapolate them and draw them onto the image for display (as below). Once you have a working pipeline, try it out on the video stream below.**
---
<figure>
<img src="examples/line-segments-example.jpg" width="380" alt="Combined Image" />
<figcaption>
<p></p>
<p style="text-align: center;"> Your output should look something like this (above) after detecting line segments using the helper functions below </p>
</figcaption>
</figure>
<p></p>
<figure>
<img src="examples/laneLines_thirdPass.jpg" width="380" alt="Combined Image" />
<figcaption>
<p></p>
<p style="text-align: center;"> Your goal is to connect/average/extrapolate line segments to get output like this</p>
</figcaption>
</figure>
**Run the cell below to import some packages. If you get an `import error` for a package you've already installed, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**
## Import Packages
```
#importing some useful packages
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import cv2
%matplotlib inline
```
## Read in an Image
```
#reading in an image
image = mpimg.imread('test_images/solidWhiteRight.jpg')
#printing out some stats and plotting
print('This image is:', type(image), 'with dimensions:', image.shape)
plt.imshow(image) # if you wanted to show a single color channel image called 'gray', for example, call as plt.imshow(gray, cmap='gray')
```
## Ideas for Lane Detection Pipeline
**Some OpenCV functions (beyond those introduced in the lesson) that might be useful for this project are:**
`cv2.inRange()` for color selection
`cv2.fillPoly()` for regions selection
`cv2.line()` to draw lines on an image given endpoints
`cv2.addWeighted()` to coadd / overlay two images
`cv2.cvtColor()` to grayscale or change color
`cv2.imwrite()` to output images to file
`cv2.bitwise_and()` to apply a mask to an image
**Check out the OpenCV documentation to learn about these and discover even more awesome functionality!**
## Helper Functions
Below are some helper functions to help get you started. They should look familiar from the lesson!
```
import math
def grayscale(img):
"""Applies the Grayscale transform
This will return an image with only one color channel
but NOTE: to see the returned image as grayscale
(assuming your grayscaled image is called 'gray')
you should call plt.imshow(gray, cmap='gray')"""
return cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
# Or use BGR2GRAY if you read an image with cv2.imread()
# return cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
def canny(img, low_threshold, high_threshold):
"""Applies the Canny transform"""
return cv2.Canny(img, low_threshold, high_threshold)
def gaussian_blur(img, kernel_size):
"""Applies a Gaussian Noise kernel"""
return cv2.GaussianBlur(img, (kernel_size, kernel_size), 0)
def region_of_interest(img, vertices):
"""
Applies an image mask.
Only keeps the region of the image defined by the polygon
formed from `vertices`. The rest of the image is set to black.
`vertices` should be a numpy array of integer points.
"""
#defining a blank mask to start with
mask = np.zeros_like(img)
#defining a 3 channel or 1 channel color to fill the mask with depending on the input image
if len(img.shape) > 2:
channel_count = img.shape[2] # i.e. 3 or 4 depending on your image
ignore_mask_color = (255,) * channel_count
else:
ignore_mask_color = 255
#filling pixels inside the polygon defined by "vertices" with the fill color
cv2.fillPoly(mask, vertices, ignore_mask_color)
#returning the image only where mask pixels are nonzero
masked_image = cv2.bitwise_and(img, mask)
return masked_image
def draw_lines(img, lines, color=[255, 0, 0], thickness=7):
"""
NOTE: this is the function you might want to use as a starting point once you want to
average/extrapolate the line segments you detect to map out the full
extent of the lane (going from the result shown in raw-lines-example.mp4
to that shown in P1_example.mp4).
Think about things like separating line segments by their
slope ((y2-y1)/(x2-x1)) to decide which segments are part of the left
line vs. the right line. Then, you can average the position of each of
the lines and extrapolate to the top and bottom of the lane.
This function draws `lines` with `color` and `thickness`.
Lines are drawn on the image inplace (mutates the image).
If you want to make the lines semi-transparent, think about combining
this function with the weighted_img() function below
"""
# for index, line in enumerate(lines, start=0):
# for x1,y1,x2,y2 in line:
# cv2.line(img, (x1, y1), (x2, y2), color, 3)
num_right_line = 0
num_left_line = 0
total_slope_right_line = 0
total_slope_left_line = 0
total_intercept_right_line = 0
total_intercept_left_line = 0
for index, line in enumerate(lines, start=0):
for x1,y1,x2,y2 in line:
if (x2-x1) > 0:
slope = (y2-y1)/(x2-x1)
intercept = y2 - slope * x2
if slope < 0:
total_slope_left_line += slope
total_intercept_left_line += intercept
num_left_line += 1
else:
total_slope_right_line += slope
total_intercept_right_line += intercept
num_right_line += 1
ysize = img.shape[0]
try:
if num_left_line > 0:
mean_slope_left_line = total_slope_left_line / num_left_line
mean_intercept_left_line = total_intercept_left_line / num_left_line
x1_left = int(1/mean_slope_left_line * (ysize - mean_intercept_left_line))
x2_left = int(1/mean_slope_left_line * (0.6 * ysize - mean_intercept_left_line))
cv2.line(img, (x1_left, ysize), (x2_left, int(0.6 * ysize)), color, thickness)
except:
pass
try:
if num_right_line > 0:
mean_slope_right_line = total_slope_right_line / num_right_line
mean_intercept_right_line = total_intercept_right_line / num_right_line
x1_right = int(1/mean_slope_right_line * (ysize - mean_intercept_right_line))
x2_right = int(1/mean_slope_right_line * (0.6 * ysize - mean_intercept_right_line))
cv2.line(img, (x1_right, ysize), (x2_right, int(0.6 * ysize)), color, thickness)
except:
pass
def hough_lines(img, rho, theta, threshold, min_line_len, max_line_gap):
"""
`img` should be the output of a Canny transform.
Returns an image with hough lines drawn.
"""
lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]), minLineLength=min_line_len, maxLineGap=max_line_gap)
line_img = np.zeros((img.shape[0], img.shape[1], 3), dtype=np.uint8)
draw_lines(line_img, lines)
return line_img
# Python 3 has support for cool math symbols.
def weighted_img(img, initial_img, α=0.8, β=1., γ=0.):
"""
`img` is the output of the hough_lines(), An image with lines drawn on it.
Should be a blank image (all black) with lines drawn on it.
`initial_img` should be the image before any processing.
The result image is computed as follows:
initial_img * α + img * β + γ
NOTE: initial_img and img must be the same shape!
"""
return cv2.addWeighted(initial_img, α, img, β, γ)
```
## Test Images
Build your pipeline to work on the images in the directory "test_images"
**You should make sure your pipeline works well on these images before you try the videos.**
```
import os
img_list = os.listdir("test_images/")
```
## Build a Lane Finding Pipeline
Build the pipeline and run your solution on all test_images. Make copies into the `test_images_output` directory, and you can use the images in your writeup report.
Try tuning the various parameters, especially the low and high Canny thresholds as well as the Hough lines parameters.
```
# TODO: Build your pipeline that will draw lane lines on the test_images
# then save them to the test_images_output directory.
def draw_lane_lines_on_image(img):
# Convert image to grey scale
img_grey = grayscale(img)
# Apply Gaussian blur
kernel_size = 5
img_blur = gaussian_blur(img_grey, kernel_size)
# Apply Canny transform
low_threshold = 50
high_threshold = 150
img_canny = canny(img_blur, low_threshold, high_threshold)
# Mask region of interest
ysize = image.shape[0]
xsize = image.shape[1]
vertices = np.array([[[0, ysize], [0.46*xsize, 0.65*ysize], [0.54*xsize, 0.65*ysize], [xsize, ysize]]], dtype=np.int32)
img_masked = region_of_interest(img_canny, vertices)
# Apply Hough transform
rho = 2
theta = np.pi/180
threshold = 15
min_line_len = 25
max_line_gap = 2
img_hough = hough_lines(img_masked, rho, theta, threshold, min_line_len, max_line_gap)
# Combine images
img_out = weighted_img(img_hough, img)
return img_out
for img_file in img_list:
img = mpimg.imread("test_images/" + img_file)
img_out = draw_lane_lines_on_image(img)
plt.figure()
plt.imshow(img_out)
plt.draw()
```
## Test on Videos
You know what's cooler than drawing lanes over images? Drawing lanes over video!
We can test our solution on two provided videos:
`solidWhiteRight.mp4`
`solidYellowLeft.mp4`
**Note: if you get an import error when you run the next cell, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**
**If you get an error that looks like this:**
```
NeedDownloadError: Need ffmpeg exe.
You can download it by calling:
imageio.plugins.ffmpeg.download()
```
**Follow the instructions in the error message and check out [this forum post](https://discussions.udacity.com/t/project-error-of-test-on-videos/274082) for more troubleshooting tips across operating systems.**
```
# Import everything needed to edit/save/watch video clips
from moviepy.editor import VideoFileClip
from IPython.display import HTML
def process_image(image):
# NOTE: The output you return should be a color image (3 channel) for processing video below
# TODO: put your pipeline here,
# you should return the final output (image where lines are drawn on lanes)
result = draw_lane_lines_on_image(image)
return result
```
Let's try the one with the solid white lane on the right first ...
```
white_output = 'test_videos_output/solidWhiteRight.mp4'
## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video
## To do so add .subclip(start_second,end_second) to the end of the line below
## Where start_second and end_second are integer values representing the start and end of the subclip
## You may also uncomment the following line for a subclip of the first 5 seconds
# clip1 = VideoFileClip("test_videos/solidWhiteRight.mp4").subclip(0,5)
clip1 = VideoFileClip("test_videos/solidWhiteRight.mp4")
white_clip = clip1.fl_image(process_image) #NOTE: this function expects color images!!
%time white_clip.write_videofile(white_output, audio=False)
```
Play the video inline, or if you prefer find the video in your filesystem (should be in the same directory) and play it in your video player of choice.
```
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(white_output))
```
## Improve the draw_lines() function
**At this point, if you were successful with making the pipeline and tuning parameters, you probably have the Hough line segments drawn onto the road, but what about identifying the full extent of the lane and marking it clearly as in the example video (P1_example.mp4)? Think about defining a line to run the full length of the visible lane based on the line segments you identified with the Hough Transform. As mentioned previously, try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4".**
**Go back and modify your draw_lines function accordingly and try re-running your pipeline. The new output should draw a single, solid line over the left lane line and a single, solid line over the right lane line. The lines should start from the bottom of the image and extend out to the top of the region of interest.**
Now for the one with the solid yellow lane on the left. This one's more tricky!
```
yellow_output = 'test_videos_output/solidYellowLeft.mp4'
## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video
## To do so add .subclip(start_second,end_second) to the end of the line below
## Where start_second and end_second are integer values representing the start and end of the subclip
## You may also uncomment the following line for a subclip of the first 5 seconds
##clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4').subclip(0,5)
clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4')
yellow_clip = clip2.fl_image(process_image)
%time yellow_clip.write_videofile(yellow_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(yellow_output))
```
## Writeup and Submission
If you're satisfied with your video outputs, it's time to make the report writeup in a pdf or markdown file. Once you have this Ipython notebook ready along with the writeup, it's time to submit for review! Here is a [link](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) to the writeup template file.
## Optional Challenge
Try your lane finding pipeline on the video below. Does it still work? Can you figure out a way to make it more robust? If you're up for the challenge, modify your pipeline so it works with this video and submit it along with the rest of your project!
```
challenge_output = 'test_videos_output/challenge.mp4'
## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video
## To do so add .subclip(start_second,end_second) to the end of the line below
## Where start_second and end_second are integer values representing the start and end of the subclip
## You may also uncomment the following line for a subclip of the first 5 seconds
##clip3 = VideoFileClip('test_videos/challenge.mp4').subclip(0,5)
clip3 = VideoFileClip('test_videos/challenge.mp4')
challenge_clip = clip3.fl_image(process_image)
%time challenge_clip.write_videofile(challenge_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(challenge_output))
```
| github_jupyter |
```
import os
from glob import glob
import random
import torch
from torchvision import datasets as dset
from torchvision import transforms
from matplotlib import pyplot as plt
from torch.utils.data import DataLoader, Dataset
from tqdm.notebook import tqdm
from siamesenet import SiameseNet
from arguments import get_config
```
Download MNIST data
```
transformer = transforms.Compose([
transforms.Resize(105),
transforms.ToTensor(),
transforms.Normalize(mean=0.5,std=0.5)])
# If you run this code first time, make 'download' option True
test_data = dset.MNIST(root='MNIST_data/',train=False,transform=transformer, download=False)
test_image, test_label = test_data[0]
plt.imshow(test_image.squeeze().numpy(), cmap='gray')
plt.title('%i' % test_label)
plt.show()
print(test_image.size())
print('number of test data:', len(test_data))
```
Make Dataloader
```
class MNISTTest(Dataset):
def __init__(self, dataset,trial):
self.dataset = dataset
self.trial = trial
if trial > 950:
self.trial = 950
def __len__(self):
return self.trial * 10
def __getitem__(self, index):
share, remain = divmod(index,10)
label = (share//10)%10
image1 = self.dataset[label][share][0]
image2 = self.dataset[remain][random.randrange(len(self.dataset[remain]))][0]
return image1, image2, label
image_by_num = [[],[],[],[],[],[],[],[],[],[]]
for x,y in tqdm(test_data):
image_by_num[y].append(x)
test_data1 = MNISTTest(image_by_num,trial=950) #MAX trial = 950
test_loader = DataLoader(test_data1, batch_size=10)
```
Declare model and configuration
```
config = get_config()
config.num_model = "1"
config.logs_dir = "./result/1"
model = SiameseNet()
is_best = False
device = 'cuda' if torch.cuda.is_available() else 'cpu'
```
Load trained model
```
if is_best:
model_path = os.path.join(config.logs_dir, './models/best_model.pt')
else:
model_path = sorted(glob(config.logs_dir + './models/model_ckpt_*.pt'), key=len)[-1]
ckpt = torch.load(model_path)
model.load_state_dict(ckpt['model_state'])
model.to(device)
print(f"[*] Load model {os.path.basename(model_path)}, best accuracy {ckpt['best_valid_acc']}")
```
Test
```
correct_sum = 0
num_test = len(test_loader)
print(f"[*] Test on {num_test} pairs.")
pbar = tqdm(enumerate(test_loader), total=num_test, desc="Test")
for i, (x1, x2, y) in pbar:
# plt.figure(figsize=(20,7))
# plt.subplot(1,4,1)
# plt.title("Target")
# plt.imshow(x1[0].squeeze().numpy(), cmap='gray')
#
# s = 2
# for idx in range(10):
# plt.subplot(3,4,s)
# plt.title(idx)
# plt.imshow(x2[idx].squeeze().numpy(), cmap='gray')
# s += 1
# if s % 4 == 1:
# s += 1
# plt.show()
# break
if torch.cuda.is_available():
x1, x2, y = x1.to(device), x2.to(device), y.to(device)
x1, x2 = x1.unsqueeze(1), x2.unsqueeze(1)
# compute log probabilities
out = model(x1, x2)
y_pred = torch.sigmoid(out)
y_pred = torch.argmax(y_pred)
if y_pred == y[0].item():
correct_sum += 1
pbar.set_postfix_str(f"accuracy: {correct_sum} / {num_test}")
test_acc = (100. * correct_sum) / num_test
print(f"Test Acc: {correct_sum}/{num_test} ({test_acc:.2f}%)")
```
| github_jupyter |
```
import numpy as np
import heron
import heron.models.georgebased
generator = heron.models.georgebased.Heron2dHodlrIMR()
generator.parameters = ["mass ratio"]
times = np.linspace(-0.05, 0.05, 1000)
hp, hx = generator.mean({"mass ratio": 1}, times)
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(hp.data)
stimes = np.linspace(-0.15, 0.01, 1000)
hp, hx = generator.bilby(stimes, 65, 22, 1000).values()
%%timeit
hp, hx = generator.bilby(stimes, 65, 22, 1000).values()
plt.plot(stimes, hp)
plt.plot(stimes, hx)
import bilby
duration = 0.16
sampling_frequency = 4000
waveform = bilby.gw.waveform_generator.WaveformGenerator(
duration=duration, sampling_frequency=sampling_frequency,
time_domain_source_model=generator.bilby,
start_time=-0.15)
# inject the signal into three interferometers
ifos = bilby.gw.detector.InterferometerList(['L1'])
ifos.set_strain_data_from_power_spectral_densities(
sampling_frequency=sampling_frequency, duration=duration,
start_time=0)
injection_parameters = {"mass_1": 20, "mass_2": 20, "luminosity_distance": 400, "geocent_time": 0, "ra": 0, "dec": 0, "psi": 0}
ifos.inject_signal(waveform_generator=waveform,
parameters=injection_parameters);
priors = bilby.gw.prior.BBHPriorDict()
priors['mass_1'] = bilby.core.prior.Uniform(10, 30, name="mass_1")
priors['mass_2'] = bilby.core.prior.Uniform(10, 30, name="mass_2")
outdir="test_heron-2"
label="pe-test"
priors['geocent_time'] = bilby.core.prior.Uniform(
minimum=injection_parameters['geocent_time'] - 1,
maximum=injection_parameters['geocent_time'] + 1,
name='geocent_time', latex_label='$t_c$', unit='$s$')
for key in ['a_1', 'a_2', 'tilt_1', 'tilt_2', 'phi_12', 'phi_jl', 'psi', 'ra', 'theta_jn',
'dec', 'geocent_time', 'phase']:
if key in injection_parameters:
priors[key] = injection_parameters[key]
priors[key] = 0 #injection_parameters[key]
priors['luminosity_distance'] = 400
# Initialise the likelihood by passing in the interferometer data (ifos) and
# the waveform generator
likelihood = bilby.gw.GravitationalWaveTransient(
interferometers=ifos, waveform_generator=waveform)
# Run sampler. In this case we're going to use the `dynesty` sampler
result = bilby.run_sampler(
likelihood=likelihood, priors=priors, sampler='dynesty', npoints=10,
injection_parameters=injection_parameters, outdir=outdir, label=label)
# Make a corner plot.
result.plot_corner()
class HeronLikelihood(bilby.gw.likelihood.GravitationalWaveTransient)
def log_likelihood_ratio(self):
waveform_polarizations =\
self.waveform_generator.frequency_domain_strain(self.parameters)
if waveform_polarizations is None:
return np.nan_to_num(-np.inf)
d_inner_h = 0.
optimal_snr_squared = 0.
complex_matched_filter_snr = 0.
if self.time_marginalization:
if self.jitter_time:
self.parameters['geocent_time'] += self.parameters['time_jitter']
d_inner_h_tc_array = np.zeros(
self.interferometers.frequency_array[0:-1].shape,
dtype=np.complex128)
for interferometer in self.interferometers:
per_detector_snr = self.calculate_snrs(
waveform_polarizations=waveform_polarizations,
interferometer=interferometer)
d_inner_h += per_detector_snr.d_inner_h
optimal_snr_squared += np.real(per_detector_snr.optimal_snr_squared)
complex_matched_filter_snr += per_detector_snr.complex_matched_filter_snr
if self.time_marginalization:
d_inner_h_tc_array += per_detector_snr.d_inner_h_squared_tc_array
if self.time_marginalization:
log_l = self.time_marginalized_likelihood(
d_inner_h_tc_array=d_inner_h_tc_array,
h_inner_h=optimal_snr_squared)
if self.jitter_time:
self.parameters['geocent_time'] -= self.parameters['time_jitter']
elif self.distance_marginalization:
log_l = self.distance_marginalized_likelihood(
d_inner_h=d_inner_h, h_inner_h=optimal_snr_squared)
elif self.phase_marginalization:
log_l = self.phase_marginalized_likelihood(
d_inner_h=d_inner_h, h_inner_h=optimal_snr_squared)
else:
log_l = np.real(d_inner_h) - optimal_snr_squared / 2
return float(log_l.real)
```
| github_jupyter |
<img src="https://upload.wikimedia.org/wikipedia/commons/4/47/Logo_UTFSM.png" width="200" alt="utfsm-logo" align="left"/>
# MAT281
### Aplicaciones de la Matemática en la Ingeniería
## Módulo 03
## Clase 01: Teoría y Landscape de Visualizaciones
## Objetivos
* Comprender la importancia de las visualizaciones.
* Conocer las librerías de visualización en Python.
## Contenidos
* [¿Por qué aprenderemos sobre visualización?](#why)
* [Teoría](#theory)
* [Python Landscape](#landscape)
## ¿Por qué aprenderemos sobre visualización?
<a id='why'></a>
* Porque un resultado no sirve si no puede comunicarse correctamente.
* Porque una buena visualización dista de ser una tarea trivial.
* Porque un ingenierio necesita producir excelentes gráficos (pero nadie enseña cómo).
### No es exageración
<img src="images/Fox1.png" alt="" width="800" align="middle"/>
<img src="images/Fox2.png" alt="" width="800" align="middle"/>
<img src="images/Fox3.png" alt="" width="800" align="middle"/>
<img src="images/male_height.jpg" alt="" align="middle"/>
<img src="images/pinera.jpg" alt="" align="middle"/>
### Primeras visualizaciones
#### Campaña de Napoleón a Moscú (Charles Minard, 1889).
<img src="images/Napoleon.png" alt="" width="800" align="middle"/>
#### Mapa del cólera (John Snow, 1855).
<img src="images/Colera.png" alt="" width="800" align="middle"/>
### ¿Por qué utilizamos gráficos para representar datos?
* El 70 % de los receptores sensoriales del cuerpo humano está dedicado a la visión.
* Cerebro ha sido entrenado evolutivamente para interpretar la información visual de manera masiva.
_“The eye and the visual cortex of the brain form a massively
parallel processor that provides the highest bandwidth channel
into human cognitive centers”
— Colin Ware, Information Visualization, 2004._
## Ejemplo clásico: Cuarteto de ANSCOMBE
Considere los siguientes 4 conjuntos de datos.
¿Qué puede decir de los datos?
```
import numpy as np
import pandas as pd
import os
import matplotlib.pyplot as plt
%matplotlib inline
df = pd.read_csv(os.path.join("data","anscombe.csv"))
df
df.describe()
```
¿Por qué es un ejemplo clásico?
```
for i in range(1, 4 + 1):
x = df.loc[:, f"x{i}"].values
y = df.loc[:, f"y{i}"].values
slope, intercept = np.polyfit(x, y, 1)
print(f"Grupo {i}:\n\tTiene pendiente {slope:.2f} e intercepto {intercept:.2f}.\n")
groups = range(1, 4 + 1)
x_columns = [col for col in df if "x" in col]
x_aux = np.arange(
df.loc[:, x_columns].values.min() - 1,
df.loc[:, x_columns].values.max() + 2
)
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(16, 8), sharex=True, sharey=True)
fig.suptitle("Cuarteto de Anscombe")
for i, ax in zip(groups, axs.ravel()):
x = df.loc[:, f"x{i}"].values
y = df.loc[:, f"y{i}"].values
m, b = np.polyfit(x, y, 1)
ax.plot(x, y, 'o')
ax.plot(x_aux, m * x_aux + b, 'r', lw=2.0)
ax.set_title(f"Grupo {i}")
```
## Teoría
<a id='theory'></a>
### Sistema visual humano
#### Buenas noticias
* Gráficos entregan información que la estadística podría no revelar.
* Despliegue visual es esencial para comprensión.
#### Malas noticias
* La atención es selectiva y puede ser fácilmente engañada.
#### La atención es selectiva y puede ser fácilmente engañada.
<img src="images/IO1a.png" alt="" width="400" align="middle"/>
<img src="images/IO1b.png" alt="" width="400" align="middle"/>
<img src="images/IO2a.png" alt="" width="400" align="middle"/>
<img src="images/IO2b.png" alt="" width="400" align="middle"/>
### Consejos generales
Noah Illinsky, en su charla "Cuatro pilatres de la visualización" ([es](https://www.youtube.com/watch?v=nC92wIzpQFE), [en](https://www.youtube.com/watch?v=3eZ15VplE3o)), presenta buenos consejos sobre cómo realizar una correcta visualización:
* Propósito
* Información/Contenido
* Codificación/Estructura
* Formato
Es altamente aconsejable ver el video, pero en resumen:
* **Propósito** o público tiene que ver con para quién se está preparando la viz y que utilidad se le dará. Es muy diferente preparar un gráfico orientado a información y toma de decisiones.
* **Información/Contenido** se refiere a contar con la información que se desea mostrar, en el formato necesario para su procesamiento.
* **Codificación/Estructura** tiene que ver con la selección correcta de la codificación y estructura de la información.
* **Formato** tiene que ver con la elección de fuentes, colores, tamaños relativos, etc.
Lo anterior indica que una visualización no es el resultado de unos datos. Una visualización se diseña, se piensa, y luego se buscan fuentes de información apropiadas.
### Elementos para la creación de una buena visualización
1. ***Honestidad***: representaciones visuales no deben engañar al observador.
2. ***Priorización***: dato más importante debe utilizar elemento de mejor percepción.
3. ***Expresividad***: datos deben utilizar elementos con atribuciones adecuadas.
4. ***Consistencia***: codificación visual debe permitir reproducir datos.
El principio básico a respetar es que a partir del gráfico uno debe poder reobtener fácilmente los datos originales.
### 1. Honestidad
El ojo humano no tiene la misma precisión al estimar distintas atribuciones:
* **Largo**: Bien estimado y sin sesgo, con un factor multiplicativo de 0.9 a 1.1.
* **Área**: Subestimado y con sesgo, con un factor multiplicativo de 0.6 a 0.9.
* **Volumen**: Muy subestimado y con sesgo, con un factor multiplicativo de 0.5 a 0.8.
Resulta inadecuado realizar gráficos de datos utilizando áreas o volúmenes buscando inducir a errores.
<img src="images/Honestidad1.png" alt="" width="800" align="middle"/>
Resulta inadecuado realizar gráficos de datos utilizando áreas o volúmenes si no queda claro la atribución utilizada.
<img src="images/Honestidad2.png" alt="" width="800" align="middle"/>
Una pseudo-excepción la constituyen los _pie-chart_ o gráficos circulares,
porque el ojo humano distingue bien ángulos y segmentos de círculo,
y porque es posible indicar los porcentajes respectivos.
```
## Example from https://matplotlib.org/3.1.1/gallery/pie_and_polar_charts/pie_features.html#sphx-glr-gallery-pie-and-polar-charts-pie-features-py
# Pie chart, where the slices will be ordered and plotted counter-clockwise:
labels = 'Frogs', 'Hogs', 'Dogs', 'Logs'
sizes = [15, 30, 45, 10]
explode = (0, 0.1, 0, 0) # only "explode" the 2nd slice (i.e. 'Hogs')
fig1, ax1 = plt.subplots(figsize=(8, 8))
ax1.pie(
sizes,
explode=explode,
labels=labels,
autopct='%1.1f%%',
shadow=True,
startangle=90
)
ax1.axis('equal') # Equal aspect ratio ensures that pie is drawn as a circle.
plt.show()
```
### 2. Priorización
Dato más importante debe utilizar elemento de mejor percepción.
```
np.random.seed(42)
N = 31
x = np.arange(N)
y1 = 80 + 20 *x / N + 5 * np.random.rand(N)
y2 = 75 + 25 *x / N + 5 * np.random.rand(N)
fig, axs = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(16,8))
axs[0][0].plot(x, y1, 'ok')
axs[0][0].plot(x, y2, 'sk')
axs[0][1].plot(x, y1, 'ob')
axs[0][1].plot(x, y2, 'or')
axs[1][0].plot(x, y1, 'ob')
axs[1][0].plot(x, y2, '*k')
axs[1][1].plot(x, y1, 'sr')
axs[1][1].plot(x, y2, 'ob')
plt.show()
```
### Elementos de mejor percepción
No todos los elementos tienen la misma percepción a nivel del sistema visual.
En particular, el color y la forma son elementos preatentivos: un color distinto o una forma distinta se reconocen de manera no conciente.
Ejemplos de elementos preatentivos.
<img src="images/preatentivo1.png" alt="" width="600" align="middle"/>
<img src="images/preatentivo2.png" alt="" width="600" align="middle"/>
¿En que orden creen que el sistema visual humano puede estimar los siguientes atributos visuales:
* Color
* Pendiente
* Largo
* Ángulo
* Posición
* Área
* Volumen
El sistema visual humano puede estimar con precisión siguientes atributos visuales:
1. Posición
2. Largo
3. Pendiente
4. Ángulo
5. Área
6. Volumen
7. Color
Utilice el atributo que se estima con mayor precisión cuando sea posible.
### Colormaps
Puesto que la percepción del color tiene muy baja precisión, resulta ***inadecuado*** tratar de representar un valor numérico con colores.
* ¿Qué diferencia numérica existe entre el verde y el rojo?
* ¿Que asociación preexistente posee el color rojo, el amarillo y el verde?
* ¿Con cuánta precisión podemos distinguir valores en una escala de grises?
<img src="images/colormap.png" alt="" width="400" align="middle"/>
Algunos ejemplos de colormaps
```
import matplotlib.cm as cm
from scipy.stats import multivariate_normal
x, y = np.mgrid[-3:3:.025, -2:2:.025]
pos = np.empty(x.shape + (2,))
pos[:, :, 0] = x
pos[:, :, 1] = y
z1 = multivariate_normal.pdf(
pos,
mean=[-1.0, -1.0],
cov=[[1.0, 0.0], [0.0, 0.1]]
)
z2 = multivariate_normal.pdf(
pos,
mean=[1.0, 1.0],
cov=[[1.5, 0.0], [0.0, 0.5]]
)
z = 10 * (z1 - z2)
fig, axs = plt.subplots(2, 2, figsize=(16, 8), sharex=True, sharey=True)
cmaps = [cm.rainbow, cm.autumn, cm.coolwarm, cm.gray]
for i, ax in zip(range(len(cmaps)), axs.ravel()):
im = ax.imshow(z, interpolation='bilinear', origin='lower',cmap=cmaps[i], extent=(-3, 3, -2, 2))
fig.colorbar(im, ax=ax)
fig.show()
```
Consejo: evite mientras pueda los colormaps. Por ejemplo, utilizando contour plots.
```
fig, axs = plt.subplots(2, 2, figsize=(20, 12), sharex=True, sharey=True)
cmaps = [cm.rainbow, cm.autumn, cm.coolwarm, cm.gray]
countour_styles = [
{"cmap": cm.rainbow},
{"cmap": cm.rainbow},
{"colors": "k", "linestyles": "solid"},
{"colors": "k", "linestyles": "dashed"},
]
for i, ax in zip(range(len(cmaps)), axs.ravel()):
cs = ax.contour(x, y, z, 11, **countour_styles[i])
if i > 0:
ax.clabel(cs, fontsize=9, inline=1)
if i == 3:
ax.grid(alpha=0.5)
fig.show()
```
## 3. Sobre la Expresividad
Mostrar los datos y sólo los datos.
Los datos deben utilizar elementos con atribuciones adecuadas: _Not all data is born equal_.
Clasificación de datos:
* ***Datos Cuantitativos***: Cuantificación absoluta.
* Cantidad de azúcar en fruta: 50 [gr/kg]
* Operaciones =, $\neq$, <, >, +, −, * , /
* ***Datos Posicionales***: Cuantificación relativa.
* Fecha de cosecha: 1 Agosto 2014, 2 Agosto 2014.
* Operaciones =, $\neq$, <, >, +, −
* ***Datos Ordinales***: Orden sin cuantificación.
* Calidad de la Fruta: baja, media, alta, exportación.
* Operaciones =, $\neq$, <, >
* ***Datos Nominales***: Nombres o clasificaciones
* Frutas: manzana, pera, kiwi, ...
* Operaciones $=$, $\neq$
Ejemplo: Terremotos. ¿Que tipos de datos tenemos?
* Ciudad más próxima
* Año
* Magnitud en escala Richter
* Magnitud en escala Mercalli
* Latitud
* Longitud
Contraejemplo: Compañías de computadores.
| Companía | Procedencia |
|----------|-------------|
| MSI | Taiwan |
| Asus | Taiwan |
| Acer | Taiwan |
| HP | EEUU |
| Dell | EEUU |
| Apple | EEUU |
| Sony | Japon |
| Toshiba | Japon |
| Lenovo | Hong Kong |
| Samsung | Corea del Sur |
```
brands = {
"MSI": "Taiwan",
"Asus": "Taiwan",
"Acer": "Taiwan",
"HP": "EEUU",
"Dell": "EEUU",
"Apple": "EEUU",
"Sony": "Japon",
"Toshiba": "Japon",
"Lenovo": "Hong Kong",
"Samsung": "Corea del Sur"
}
C2N = {"Taiwan": 1, "EEUU": 2, "Japon": 3, "Hong Kong": 4, "Corea del Sur": 7}
x = np.arange(len(brands.keys()))
y = np.array([C2N[val] for val in brands.values()])
width = 0.35 # the width of the bars
fig, ax = plt.subplots(figsize=(16, 8))
rects1 = ax.bar(x, y, width, color='r')
# add some text for labels, title and axes ticks
ax.set_xticks(x + 0.5*width)
ax.set_xticklabels(brands.keys(), rotation="90")
ax.set_yticks(list(C2N.values()))
ax.set_yticklabels(C2N.keys())
plt.xlim([-1,len(x)+1])
plt.ylim([-1,y.max()+1])
plt.show()
```
Clasificación de datos:
* ***Datos Cuantitativos***: Cuantificación absoluta.
* Cantidad de azúcar en fruta: 50 [gr/kg]
* Operaciones =, $\neq$, <, >, +, −, * , /
* **Utilizar posición, largo, pendiente o ángulo**
* ***Datos Posicionales***: Cuantificación relativa.
* Fecha de cosecha: 1 Agosto 2014, 2 Agosto 2014.
* Operaciones =, $\neq$, <, >, +, −
* **Utilizar posición, largo, pendiente o ángulo**
* ***Datos Ordinales***: Orden sin cuantificación.
* Calidad de la Fruta: baja, media, alta, exportación.
* Operaciones =, $\neq$, <, >
* **Utilizar marcadores diferenciados en forma o tamaño, o mapa de colores apropiado**
* ***Datos Nominales***: Nombres o clasificaciones
* Frutas: manzana, pera, kiwi, ...
* Operaciones $=$, $\neq$
* **Utilizar forma o color**
### 4. Consistencia
La codificación visual debe permitir reproducir datos. Para ello debemos:
* Graficar datos que sean comparables.
* Utilizar ejes escalados adecuadamente.
* Utilizar la misma codificación visual entre gráficos similares.
#### Utilizar ejes escalados adecuadamente.
```
x = list(range(1, 13))
y = 80 + 20 * np.random.rand(12)
x_ticks = list("EFMAMJJASOND")
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(20, 8))
ax1.plot(x, y, 'o-')
ax1.set_xticks(x)
ax1.set_xticklabels(x_ticks)
ax1.grid(alpha=0.5)
ax2.plot(x, y,'o-')
ax2.set_xticks(x)
ax2.set_xticklabels(x_ticks)
ax2.set_ylim([0, 110])
ax2.grid(alpha=0.5)
fig.show()
```
#### Utilizar la misma codificación visual entre gráficos similares
```
x = np.linspace(0, 1, 50)
f1 = x ** 2 + .2 * np.random.rand(50)
g1 = x + .2 * np.random.rand(50)
f2 = 0.5 - 0.2 * x + .2 * np.random.rand(50)
g2 = x ** 3 + .2 * np.random.rand(50)
fig, (ax1, ax2) = plt.subplots(nrows=2, figsize=(20, 12), sharex=True)
ax1.set_title("Antes de MAT281")
ax1.plot(x, f1, 'b', label='Chile', lw=2.0)
ax1.plot(x, g1, 'g:', label='OECD', lw=2.0)
ax1.legend(loc="upper left")
ax2.set_title("Despues de MAT281")
ax2.plot(x, f2, 'g:', label='Chile', lw=2.0)
ax2.plot(x, g2, 'b', label='OECD', lw=2.0)
ax2.legend()
fig.show()
```
## Resumen
Elementos para la creación de una buena visualización
* ***Honestidad***: representaciones visuales no deben engañar al observador.
* ***Priorización***: dato más importante debe utilizar elemento de mejor percepción.
* ***Expresividad***: datos deben utilizar elementos con atribuciones adecuadas.
* ***Consistencia***: codificación visual debe permitir reproducir datos.
El principio básico a respetar es que a partir del gráfico uno debe poder reobtener fácilmente los datos originales.
## Python Landscape
<a id='landscape'></a>
Para empezar, [PyViz](https://pyviz.org/) es un sitio web que se dedica a ayudar a los usuarios a decidir dentro de las mejores herramientas de visualización open-source implementadas en Python, dependiendo de sus necesidades y objetivos. Mucho de lo que se menciona en esta sección está en detalle en la página web del proyecto PyViz.
Algunas de las librerías de visualización de Python más conocidas son:

Este esquema es una adaptación de uno presentado en la charla [_The Python Visualization Landscape_](https://us.pycon.org/2017/schedule/presentation/616/) realizada por [Jake VanderPlas](http://vanderplas.com/) en la PyCon 2017.
Cada una de estas librerías fue creada para satisfacer diferentes necesidades, algunas han ganado más adeptos que otras por uno u otro motivo. Tal como avanza la tecnología, estas librerías se actualizan o se crean nuevas, la importancia no recae en ser un experto en una, si no en saber adaptarse a las situaciones, tomar la mejor decicisión y escoger según nuestras necesidades y preferencias. Por ejemplo, `matplotlib` nació como una solución para imitar los gráficos de `MATLAB` (puedes ver la historia completa [aquí](https://matplotlib.org/users/history.html)), manteniendo una sintaxis similar y con ello poder crear gráficos __estáticos__ de muy buen nivel.
Debido al éxito de `matplotlib` en la comunidad, nacen librerías basadas ella. Algunos ejemplos son:
- `seaborn` se basa en `matpĺotlib` pero su nicho corresponde a las visualizaciones estadísticas.
- `ggpy` una suerte de copia a `ggplot2` perteneciente al lenguaje de programación `R`.
- `networkx` visualizaciones de grafos.
- `pandas` no es una librería de visualización propiamente tal, pero utiliza a `matplotplib` como _bakcned_ en los métodos con tal de crear gráficos de manera muy rápida, e.g. `pandas.DataFrame.plot.bar()`
Por otro lado, con tal de crear visualizaciones __interactivas__ aparecen librerías basadas en `javascript`, algunas de las más conocidas en Python son:
- `bokeh` tiene como objetivo proporcionar gráficos versátiles, elegantes e incluso interactivos, teniendo una gran performance con grandes datasets o incluso streaming de datos.
- `plotly` visualizaciones interactivas que en conjunto a `Dash` (de la misma empresa) permite crear aplicaciones webs, similar a `shiny` de `R`.
`D3.js` a pesar de estar basado en `javascript` se ha ganado un lugar en el corazón de toda la comunidad, debido a la ilimitada cantidad de visualizaciones que son posibles de hacer, por ejemplo, la [malla interactiva](https://mallas.labcomp.cl/) que hizo un estudiante de la UTFSM está hecha en `D3.js`.
De las librerías más recientes está `Altair`, que consiste en visualizaciones declarativas (ya lo veremos en el próximo laboratorio). Construída sobre `Vega-Lite`, a su vez que esté está sobre `Vega` y este finalmente sobre `D3.js`. `Altair` permite crear visualizaciones estáticas e interactivas con pocas líneas de código, sin embargo, al ser relativamente nueva, aún existen funcionalidades en desarrollo o que simplemente aún no existen en esta librería pero en otras si.
#### Clasificación
En lo concierne a nosotros, una de las principales clasificaciones para estas librerías es si crean visualizaciones __estática__ y/o __interactivas__. La interactividad es un plus que permite adentrarse en los datos en distintos niveles, si agregamos que ciertas librerías permiten crear _widgets_ (algo así como complementos a las visualizaciones) su potencial aumenta. Por ejemplo, un widget podría ser un filtro que permita escoger un país; en una librería estática tendrías que crear un gráfico por cada país (o combinación de países) lo cual no se hace escalable y cómodo para trabajar.
#### Spoilers
Las próximas clases se centrarán en `matplotlib` y `Altair`, dado que son buenos exponentes de visualización imperativa y declarativa, respectivamente.
Finalmente, siempre hay que tener en consideración la manera en que se compartirán las visualizaciones, por ejemplo, si es para un artículo científico bastaría que fuese de buena calidad y estático. Si es para una plataforma web es necesario que sea interactivo, aquí es donde entran en juego los dashboards, que permiten la exploración de datos de manera interactiva. En Python existen librerías como `Dash` o `Panel`, sin embargo, en el mundo empresarial se suele utilizar software dedicado a esto, como `Power BI` o `Tableau`.
| github_jupyter |
<a href="https://colab.research.google.com/github/Rivaldop/metodologidatascience/blob/main/Regresi_Linear.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
<img src = "https://evangsmailoa.files.wordpress.com/2019/09/ml.png" align = "center">
#<center>Regresi Linear</center>
Kali ini kita akan belajar tentang Regresi Linear. Seperti biasa, kita <b>import library</b> terlebih dahulu:
```
import matplotlib.pyplot as plt
import pandas as pd
import pylab as pl
import numpy as np
%matplotlib inline
```
Kita akan gunakan data contoh dari IBM Object Storage.
```
!wget -O FuelConsumption.csv https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/FuelConsumptionCo2.csv
```
### `FuelConsumption.csv`:
Dataset ini berisi konsumsi bahan bakar mesin dan estimasi dari emisi karbon dioksida yang dihasilkan. Data ini dari kendaraan-kendaraan yang baru dijual di Kanada. [Dataset source](http://open.canada.ca/data/en/dataset/98f1a129-f628-4ce4-b24d-6f16bf24dd64)
- **MODELYEAR** e.g. 2014
- **MAKE** e.g. Acura
- **MODEL** e.g. ILX
- **VEHICLE CLASS** e.g. SUV
- **ENGINE SIZE** e.g. 4.7
- **CYLINDERS** e.g 6
- **TRANSMISSION** e.g. A6
- **FUEL CONSUMPTION in CITY(L/100 km)** e.g. 9.9
- **FUEL CONSUMPTION in HWY (L/100 km)** e.g. 8.9
- **FUEL CONSUMPTION COMB (L/100 km)** e.g. 9.2
- **CO2 EMISSIONS (g/km)** e.g. 182 --> low --> 0
```
# Ubah data ke bentuk dataframe
df = pd.read_csv("FuelConsumption.csv")
# Lihat isi dataframe
df.tail(10)
```
### Explore-Data
Mari kita lihat dataset tersebut dengan statistik deskriptif.
```
# Rangkuman isi dataset
df.describe()
cdf = df[['ENGINESIZE','CYLINDERS','FUELCONSUMPTION_COMB','CO2EMISSIONS']]
cdf.head()
```
Sekarang kita cek beberapa fitur/kolom:
```
viz = cdf[['CYLINDERS','ENGINESIZE','CO2EMISSIONS','FUELCONSUMPTION_COMB']]
viz.hist()
plt.show()
```
Nah sekarang, kita lihat beberapa fitur dibandingkan dengan fitur **Emission**, untuk melihat seberapa linear hubungan mereka:
```
plt.scatter(cdf.FUELCONSUMPTION_COMB, cdf.CO2EMISSIONS, color='blue')
plt.xlabel("FUELCONSUMPTION_COMB")
plt.ylabel("Emission")
plt.show()
plt.scatter(cdf.ENGINESIZE, cdf.CO2EMISSIONS, color='blue')
plt.xlabel("Engine size")
plt.ylabel("Emission")
plt.show()
```
## LATIHAN
Coba tampilkan plot __CYLINDER__ vs the **Emission**, untuk lihat seberapa linera hubungannya:
```
# Tulis kodingmu di sini
```
Klik __2X__ untuk lihat jawaban.
<!-- Jawabannya:
plt.scatter(cdf.CYLINDERS, cdf.CO2EMISSIONS, color='blue')
plt.xlabel("Cylinders")
plt.ylabel("Emission")
plt.show()
-->
#### Training dan test dataset
Seperti biasa, untuk menghasilkan model kita harus melakukan split terhadap dataset yang kita punya. Satu bagian sebagai dataset untuk training dan sebagian sebagai dataset untuk testing.
Hal ini dilakukan agar hasil evaluasi kita semakin akurat, karena dataset untuk testing bukan bagian dari dataset untuk training.
```
msk = np.random.rand(len(df)) < 0.8
train = cdf[msk]
test = cdf[~msk]
```
#### Train data distribution
```
plt.scatter(train.ENGINESIZE, train.CO2EMISSIONS, color='blue')
plt.xlabel("Engine size")
plt.ylabel("Emission")
plt.show()
```
#### Modeling
Kita gunakan paket **sklearn** untuk membuat **model data**.
```
from sklearn import linear_model
regr = linear_model.LinearRegression()
train_x = np.asanyarray(train[['ENGINESIZE']])
train_y = np.asanyarray(train[['CO2EMISSIONS']])
regr.fit (train_x, train_y)
# The coefficients
print ('Koefisien: ', regr.coef_)
print ('Intersep: ',regr.intercept_)
```
Silakan baca2 lagi materi Regresi supaya lebih paham apa itu, __Coefficient__ dan __Intercept__.
#### Plot outputs
Sekarang kita tampilkan garis lurus disepanjang data:
```
plt.scatter(train.ENGINESIZE, train.CO2EMISSIONS, color='blue')
plt.plot(train_x, regr.coef_[0][0]*train_x + regr.intercept_[0], '-r')
plt.xlabel("Engine size")
plt.ylabel("Emission")
```
#### Evaluation
Untuk cek apakah model yang kita buat sudah benar, kita harus lakukan evaluasi dengan melakukan perhitungan akurasi.
```
from sklearn.metrics import r2_score
test_x = np.asanyarray(test[['ENGINESIZE']])
test_y = np.asanyarray(test[['CO2EMISSIONS']])
test_y_ = regr.predict(test_x)
print("Mean absolute error: %.2f" % np.mean(np.absolute(test_y_ - test_y)))
print("R2-score: %.2f" % r2_score(test_y_ , test_y) )
```
# <h2 id="(c)">(c)</h2>
<p>Copyright © 2019 <b>Evangs Mailoa</b>.</p>
---
<p>Digunakan khusus untuk ngajar Machine Learning di Progdi Teknik Informatika - FTI UKSW</p>
| github_jupyter |
# Tutorial Part 10: Exploring Quantum Chemistry with GDB1k
Most of the tutorials we've walked you through so far have focused on applications to the drug discovery realm, but DeepChem's tool suite works for molecular design problems generally. In this tutorial, we're going to walk through an example of how to train a simple molecular machine learning for the task of predicting the atomization energy of a molecule. (Remember that the atomization energy is the energy required to form 1 mol of gaseous atoms from 1 mol of the molecule in its standard state under standard conditions).
## Colab
This tutorial and the rest in this sequence are designed to be done in Google colab. If you'd like to open this notebook in colab, you can use the following link.
[](https://colab.research.google.com/github/deepchem/deepchem/blob/master/examples/tutorials/10_Exploring_Quantum_Chemistry_with_GDB1k.ipynb)
## Setup
To run DeepChem within Colab, you'll need to run the following cell of installation commands. This will take about 5 minutes to run to completion and install your environment.
```
!curl -Lo conda_installer.py https://raw.githubusercontent.com/deepchem/deepchem/master/scripts/colab_install.py
import conda_installer
conda_installer.install()
!/root/miniconda/bin/conda info -e
!pip install --pre deepchem
import deepchem
deepchem.__version__
```
With our setup in place, let's do a few standard imports to get the ball rolling.
```
import os
import unittest
import numpy as np
import deepchem as dc
import numpy.random
from deepchem.utils.evaluate import Evaluator
from sklearn.ensemble import RandomForestRegressor
from sklearn.kernel_ridge import KernelRidge
```
The ntext step we want to do is load our dataset. We're using a small dataset we've prepared that's pulled out of the larger GDB benchmarks. The dataset contains the atomization energies for 1K small molecules.
```
tasks = ["atomization_energy"]
dataset_file = "../../datasets/gdb1k.sdf"
smiles_field = "smiles"
mol_field = "mol"
```
We now need a way to transform molecules that is useful for prediction of atomization energy. This representation draws on foundational work [1] that represents a molecule's 3D electrostatic structure as a 2D matrix $C$ of distances scaled by charges, where the $ij$-th element is represented by the following charge structure.
$C_{ij} = \frac{q_i q_j}{r_{ij}^2}$
If you're observing carefully, you might ask, wait doesn't this mean that molecules with different numbers of atoms generate matrices of different sizes? In practice the trick to get around this is that the matrices are "zero-padded." That is, if you're making coulomb matrices for a set of molecules, you pick a maximum number of atoms $N$, make the matrices $N\times N$ and set to zero all the extra entries for this molecule. (There's a couple extra tricks that are done under the hood beyond this. Check out reference [1] or read the source code in DeepChem!)
DeepChem has a built in featurization class `dc.feat.CoulombMatrixEig` that can generate these featurizations for you.
```
featurizer = dc.feat.CoulombMatrixEig(23, remove_hydrogens=False)
```
Note that in this case, we set the maximum number of atoms to $N = 23$. Let's now load our dataset file into DeepChem. As in the previous tutorials, we use a `Loader` class, in particular `dc.data.SDFLoader` to load our `.sdf` file into DeepChem. The following snippet shows how we do this:
```
# loader = dc.data.SDFLoader(
# tasks=["atomization_energy"], smiles_field="smiles",
# featurizer=featurizer,
# mol_field="mol")
# dataset = loader.featurize(dataset_file)
```
For the purposes of this tutorial, we're going to do a random split of the dataset into training, validation, and test. In general, this split is weak and will considerably overestimate the accuracy of our models, but for now in this simple tutorial isn't a bad place to get started.
```
# random_splitter = dc.splits.RandomSplitter()
# train_dataset, valid_dataset, test_dataset = random_splitter.train_valid_test_split(dataset)
```
One issue that Coulomb matrix featurizations have is that the range of entries in the matrix $C$ can be large. The charge $q_1q_2/r^2$ term can range very widely. In general, a wide range of values for inputs can throw off learning for the neural network. For this, a common fix is to normalize the input values so that they fall into a more standard range. Recall that the normalization transform applies to each feature $X_i$ of datapoint $X$
$\hat{X_i} = \frac{X_i - \mu_i}{\sigma_i}$
where $\mu_i$ and $\sigma_i$ are the mean and standard deviation of the $i$-th feature. This transformation enables the learning to proceed smoothly. A second point is that the atomization energies also fall across a wide range. So we apply an analogous transformation normalization transformation to the output to scale the energies better. We use DeepChem's transformation API to make this happen:
```
# transformers = [
# dc.trans.NormalizationTransformer(transform_X=True, dataset=train_dataset),
# dc.trans.NormalizationTransformer(transform_y=True, dataset=train_dataset)]
# for dataset in [train_dataset, valid_dataset, test_dataset]:
# for transformer in transformers:
# dataset = transformer.transform(dataset)
```
Now that we have the data cleanly transformed, let's do some simple machine learning. We'll start by constructing a random forest on top of the data. We'll use DeepChem's hyperparameter tuning module to do this.
```
# def rf_model_builder(model_params, model_dir):
# sklearn_model = RandomForestRegressor(**model_params)
# return dc.models.SklearnModel(sklearn_model, model_dir)
# params_dict = {
# "n_estimators": [10, 100],
# "max_features": ["auto", "sqrt", "log2", None],
# }
# metric = dc.metrics.Metric(dc.metrics.mean_absolute_error)
# optimizer = dc.hyper.HyperparamOpt(rf_model_builder)
# best_rf, best_rf_hyperparams, all_rf_results = optimizer.hyperparam_search(
# params_dict, train_dataset, valid_dataset, transformers,
# metric=metric)
```
Let's build one more model, a kernel ridge regression, on top of this raw data.
```
# def krr_model_builder(model_params, model_dir):
# sklearn_model = KernelRidge(**model_params)
# return dc.models.SklearnModel(sklearn_model, model_dir)
# params_dict = {
# "kernel": ["laplacian"],
# "alpha": [0.0001],
# "gamma": [0.0001]
# }
# metric = dc.metrics.Metric(dc.metrics.mean_absolute_error)
# optimizer = dc.hyper.HyperparamOpt(krr_model_builder)
# best_krr, best_krr_hyperparams, all_krr_results = optimizer.hyperparam_search(
# params_dict, train_dataset, valid_dataset, transformers,
# metric=metric)
```
# Congratulations! Time to join the Community!
Congratulations on completing this tutorial notebook! If you enjoyed working through the tutorial, and want to continue working with DeepChem, we encourage you to finish the rest of the tutorials in this series. You can also help the DeepChem community in the following ways:
## Star DeepChem on [GitHub](https://github.com/deepchem/deepchem)
This helps build awareness of the DeepChem project and the tools for open source drug discovery that we're trying to build.
## Join the DeepChem Gitter
The DeepChem [Gitter](https://gitter.im/deepchem/Lobby) hosts a number of scientists, developers, and enthusiasts interested in deep learning for the life sciences. Join the conversation!
# Bibliography:
[1] https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.98.146401
| github_jupyter |
<a href="https://colab.research.google.com/github/Chiebukar/Deep-Learning/blob/main/regression/temperature_forcasting_with_RNN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Temperature Forcasting with Jena climate dataset
```
from google.colab import files
files.upload()
!mkdir -p ~/.kaggle
!cp kaggle.json ~/.kaggle/
!chmod 600 ~/.kaggle/kaggle.json
!kaggle datasets download -d kusuri/jena-climate
!ls -d $PWD/*
!unzip \*.zip && rm *.zip
!ls -d $PWD/*
file_dir = '/content/jena_climate_2009_2016.csv'
import numpy as np
import pandas as pd
jena_df = pd.read_csv(file_dir)
jena_df.head()
jena_df.shape
jena_df.columns
jena_arr = np.array(jena_df.iloc[:, 1:])
jena_arr[:2]
# standardize data
len_train = 200000
mean = jena_arr[:len_train].mean(axis=0)
std = jena_arr[:len_train].std(axis=0)
jena_arr = (jena_arr-mean)/std
# generator to yield batches of data from the recent past and future target
def generator(data, min_index, max_index , lookback= 1440, delay=144, step= 6, batch_size=18, shuffle=False):
"""
yield batches of data from the recent past and future target
data = original input data
min_index = minimum index of data to draw from
max_index maximum index of sata to draw from
lookback= Number of timestamps back for input data per target
delay = Number of timestamp in the future for target per lookback
steps = period in timestamps to sample data
batch_size = number of samples per batch
shuffle = To shuffle the samples or not
"""
if max_index == None:
max_index = len(data) - delay - 1
i = min_index + lookback
while 1:
if shuffle:
rows = np.random.randint(min_index + lookback, max_index, size= batch_size)
else:
if i + batch_size >= max_index:
i = min_index + lookback
rows = np.arange(i, min(i + batch_size, max_index))
i += len(rows)
samples = np.zeros((len(rows), lookback //step, data.shape[-1]))
targets = np.zeros((len(rows),))
for j, row in enumerate(rows):
indices = range(rows[j] - lookback, rows[j], step)
samples[j] = data[indices]
targets[j] = data[rows[j] + delay][1]
yield samples, targets
train_gen = generator(data= jena_arr,
min_index= 0,
max_index= 200000,
shuffle= True)
valid_gen = generator(data= jena_arr,
min_index= 200001,
max_index = 300000,
shuffle = True)
test_gen = generator(data = jena_arr,
min_index = 300001,
max_index = None,
shuffle= True)
# get validation and test steps
lookback = 1440
val_steps = (300000 - 200001 - lookback)
test_steps = (len(jena_arr) - 300001 - lookback)
# establish baseline
def evaluate_naive_method():
batch_maes = []
for step in range(val_steps):
samples, targets = next(valid_gen)
preds = samples[:, -1, 1]
mae = np.mean(np.abs(preds - targets))
batch_maes.append(mae)
return (np.mean(batch_maes))
# get baseline evaluation
mae = evaluate_naive_method()
celsius_mae = mae * std[1]
celsius_mae
from tensorflow import keras
from keras.models import Sequential
from keras.layers import Dense, LSTM, Dropout
from keras.callbacks import ModelCheckpoint
# build model
def build_model():
model = Sequential()
model.add(LSTM(32, dropout= 0.1, recurrent_dropout= 0.25,
return_sequences=True, input_shape = (None, jena_arr.shape[-1])))
model.add(LSTM(64, activation='tanh', dropout=0.5))
model.add(Dense(8, activation= 'relu'))
model.add(Dropout(0.1))
model.add(Dense(1))
model.compile(loss = 'mae', optimizer = 'rmsprop')
return model
file_path= 'a_weights.best.hdf5'
checkpoint = ModelCheckpoint(file_path, monitor= 'val_loss', save_best_only= True, verbose= 1, mode= 'min')
model = build_model()
history = model.fit(train_gen, steps_per_epoch = 500, epochs= 25, validation_data= valid_gen,
validation_steps = 500, callbacks= checkpoint)
history_df = pd.DataFrame(history.history)
history_df[['mae', 'val_mae']].plot()
```
| github_jupyter |
### PPO, Actor-Critic Style
_______________________
**for** iteration=1,2,... do<br>
**for** actor=1,2,...,N do<br>
Run policy $\pi_{\theta_{old}}$ in environment for T timesteps<br>
Compute advantage estimates $\hat{A}_1,\dots,\hat{A}_T$<br>
**end for**<br>
Optimize surrogate(代理人) L wrt $\theta$,with $K$ epochs and minibatch size $M \leq NT$<br>
$\theta_{old} \leftarrow \theta$<br>
**end for**
_______________________
### Loss Function L的数学公式为:
$$
L_t^{CLIP+VF+S}(\theta)=\hat{\mathbb{E}_t}[L_t^{CLIP}(\theta)-c_1L^{VF}_t(\theta)+c_2S[\pi_\theta](s_t)]
$$
其中,$L^{CLIP}(\theta)=\hat{\mathbb{E}_t}\big[min(r_t(\theta)\hat{A}_t,clip(r_t(\theta), 1-\epsilon,1+\epsilon)\hat{A}_t)\big]$, $r_t(\theta)=\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$<br>
$L^{VF}_t=(V_\theta(s_t)-V_t^{targ})^2$ **critic loss**<br>
S 为奖励熵,保证足够多的探索(写A2C的时候已经OK)<br>
$c_1, c_2$为参数
#### $L^{CLIP}和r的关系如下(为了保证\pi_\theta和\pi_{\theta_{old}}的差值不会很大,满足TRPO中两者方差变化不大的要求)$:
<img src="../assets/PPO_CLIP.png">
### GAE(high-dimensional continuous control using Generalized Advantage Estimation)
We address the first challenge by using value functions to substantially reduce the variance of policy gradient estimates at the cost of some bias, with an exponentially-weighted estimator of the advantage function that is analogous to TD(λ). <br>
改进了advantage function的计算方式。将advantage function进行类似于TD(λ)的处理<br>
#### 推导过程
1. 原始的advantage function : $\delta^V_t=r_t+\gamma V(s_{t+1})−V(s_t)$
2. $在位置t时,其后k个 \delta 折扣相加$ :
$$
\begin{aligned}
\hat{A}^{(1)}_t&:=\delta^V_t&&=-V(s_t)+r_t+\gamma V(s_{t+1}) \\
\hat{A}^{(2)}_t&:=\delta^V_t+\gamma \delta^V_{t+1}&&=-V(s_t)+r_t+\gamma r_{t+1}+\gamma ^2 V(s_{t+2}) \\
\hat{A}^{(3)}_t&:=\delta^V_t+\gamma \delta^V_{t+1}+\gamma^2 \delta^V_{t+2}&&=-V(s_t)+r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}+\gamma ^3 V(s_{t+3}) \\
\hat{A}_t^{(k)}&:=\sum_{l=0}^{k=1}\gamma^l\delta_{t+l}^V&&=-V(s_t)+r_t+\gamma r_{t+1}+\dots+\gamma^{k-1}r_{t+k-1}+\gamma^kV(s_{t+k})
\end{aligned}
$$
3. $k \to \infty, \gamma^kV(s_{t+k})$会变得非常非常非常小,So :
$$
\hat{A}_t^{(\infty)}=\sum^\infty_{l=0}\gamma^l\delta_{t+l}^V=-V(s_t)+\sum^\infty_{l=0}\gamma^lr_{t+l}
$$
4. 所以,$t$ 时刻的GAE可推导为 :
$$
\begin{aligned}
\hat{A}_t^{GAE(\gamma, \lambda)}&:=(1-\lambda)\big(\hat{A}_t^{(1)}+\lambda\hat{A}_t^{(2)}+\lambda^2\hat{A}_t^{(3)}+\dots\big)\\
&=(1-\lambda)\big(\delta_t^V+\lambda(\delta_t^V+\gamma\delta_{t+1}^V)+\lambda^2(\delta_t^V+\gamma\delta_{t+1}^V+\gamma^2\delta_{t+2}^V)+\dots\big)\\
&=(1-\lambda)\big(\delta^V_t(1+\lambda+\lambda^2+\dots)+\gamma\delta^V_{t+1}(\lambda+\lambda^2+\lambda^3+\dots)+\gamma^2\delta^V_{t+2}(\lambda^2+\lambda^3+\lambda^4+\dots)+\dots\big)\\
&=(1-\lambda)\big(\delta^V_t\big(\frac{1}{1-\lambda}\big)+\gamma\delta^V_{t+1}\big(\frac{\lambda}{1-\lambda}\big)+\gamma^2\delta^V_{t+2}\big(\frac{\lambda^2}{1-\lambda}\big)+\dots\big)\\
&=\underbrace{\delta^V_t+\gamma\lambda\delta^V_{t+1}+(\gamma\lambda)^2\delta^V_{t+2}+\dots}_{此处计算时使用这个公式(迭代计算)}\\
&=\sum_{l=0}^\infty(\gamma\lambda)^l\delta^V_{t+l}
\end{aligned}
$$
### 使用高斯分布(正态分布)来实现随机性策略控制连续动作空间
1. 高斯分布有两个重要的变量一个是均值 $\mu$ ,另一个是方差 $\sigma$ 。$\mu$ 为高斯函数的对称轴,$\frac{1}{\sqrt{2\pi}\sigma}$ 为高斯函数的最高点。高斯函数的积分为1。所以我们可以使用它来进行连续动作的sample。方差 $\sigma$ 越大,分布越分散,方差 $\sigma$ 越小,分布越集中。
2. $\mu$ 的选择很好把控,经过tanh处理之后+简单的数学变换,使nn输出的 $\mu$ 在env规定的动作空间内就可以
3. $\sigma$ 的选择,使用softplus函数对sigma进行处理。softplus 公式为$f(x)=\frac{1}{\beta}log(1+exp(\beta x))$, softplus 是 ReLU 的平滑近似值版本
4. 高斯分布公式:
$$
f(x)=\frac{1}{\sqrt{2\pi}\sigma}exp\bigg(-\frac{(x-\mu)^2}{2\sigma^2}\bigg)
$$
5. 和确定性策略相比,需要考虑每个state采取每个动作的概率,计算量确实比较大。
### TRPO
简单理解为一次on-policy到off-policy的转换<br>
但是为了保证old_policy和new_policy之间方差相差不会太大<br>
$$
\begin{aligned}
E_{X \sim p}[f(x)] & \approx \frac{1}{N}\sum^N_{i=1}f(x^i)\\
&= \int f(x)p(x)dx=\int f(x)\frac{p(x)}{q(x)}q(x)dx=E_{x \sim q}[f(x)\frac{p(x)}{q(x)}]
\end{aligned}
$$
由此,在两者期望相同的情况下,论证方差是否相同
$$
\begin{aligned}
两者期望:\quad&\because E_{X \sim p}[f(x)]=E_{x \sim q}[f(x)\frac{p(x)}{q(x)}]\\
方差公式:\quad&\because VAR[X]=E[X^2]-(E[X])^2\\
x \sim p 方差:\quad&\therefore Var_{x \sim p}[f(x)]=\color{red}{E_{x\sim p}[f(x)^2]}-(E_{x\sim p}[f(x)])^2\\
x \sim q 方差:\quad&\therefore Var_{x \sim q}[f(x)\frac{p(x)}{q(x)}]=E_{x \sim q}\big[\big([f(x)\frac{p(x)}{q(x)}\big)^2\big]-\big(E_{x\sim q}\big[f(x)\frac{p(x)}{q(x)}\big]\big)^2\\
&=\color{red}{E_{x \sim q}\big[f(x)^2\frac{p(x)}{q(x)}\big]}-(E_{x \sim p}[f(x)])^2
\end{aligned}
$$
两者方差公式的差别在标红的位置,也就是说我们如果使两者$E_{x\sim p}[f(x)^2]$和$E_{x \sim q}\big[f(x)^2\frac{p(x)}{q(x)}\big]$的差值较小,那么我们所做的off-policy就是可行的<br>
由此,可直观的看出,我们要使p(x)和q(x)的相差较小。因此就有了PPO1中的所使用的$\beta KL(\theta,\theta')$和PPO2中的clip这些都是为了限制两者的范围在一个可接受的合适空间
```
import gym
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Normal
from torch.distributions import Categorical
import torch.multiprocessing as mp
# from torch.utils.tensorboard import SummaryWriter
import numpy as np
from IPython.display import clear_output
import matplotlib.pyplot as plt
%matplotlib inline
import math
import random
from statistics import mean
import pdb
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
def plot_function():
x = np.arange(-10,10,0.05)
plt.figure(figsize=(9,3.6))
plt.subplot(121)
plt.title("Gaussian distribution")
mu, sigma = 0, 10
y = lambda x : np.exp(-((x-mu)**2)/(2*sigma**2))/(sigma*np.sqrt(2*np.pi))
plt.plot(x, y(x))
plt.subplot(122)
plt.title("Softplus")
y = np.log(1+np.exp(x))
plt.plot(x, y)
plt.show()
plot_function()
```
多线程又双叒叕来了
```
def worker(worker_id, master_end, worker_end, env_name):
master_end.close()
env = gym.make(env_name)
env.seed(worker_id)
while True:
cmd, data = worker_end.recv()
if cmd == 'step':
state, reward, done, info = env.step(data)
if done:
state = env.reset()
worker_end.send((state, reward, done, info))
elif cmd == 'reset':
state = env.reset()
worker_end.send(state)
elif cmd == 'reset_task':
state = env.reset_task()
worker_end.send(state)
elif cmd == 'close':
worker_end.close()
break
elif cmd == 'get_spaces':
worker_end.send((env.observation_space.shape[0], env.action_space.shape[0]))
else:
raise NotImplementedError
class ParallelEnv:
def __init__(self, n_train_processes, env_name):
self.nenvs = n_train_processes
self.waiting = False
self.closed = False
self.workers = []
self.env_name = env_name
self.master_ends, self.worker_ends = zip(*[mp.Pipe() for _ in range(self.nenvs)])
for worker_id, (master_end, worker_end) in enumerate(zip(self.master_ends, self.worker_ends)):
p = mp.Process(target=worker, args=(worker_id, master_end, worker_end, self.env_name))
p.daemon = False
p.start()
self.workers.append(p)
for worker_end in self.worker_ends:
worker_end.close()
self.master_ends[0].send(('get_spaces', None))
self.observation_space, self.action_space = self.master_ends[0].recv()
def step_async(self, actions):
for master_end, action in zip(self.master_ends, actions):
master_end.send(('step', action))
self.waiting = True
def step_wait(self):
results = [master_end.recv() for master_end in self.master_ends]
self.waiting = False
states, rewards, dones, infos = zip(*results)
return np.stack(states), np.stack(rewards), np.stack(dones), infos
def reset(self):
for master_end in self.master_ends:
master_end.send(('reset', None))
return np.stack([master_end.recv() for master_end in self.master_ends])
def step(self, actions):
self.step_async(actions)
return self.step_wait()
def close(self):
if self.closed:
return
if self.waiting:
[master_end.recv() for master_end in self.master_ends]
for master_end in self.master_ends:
master_end.send(('close', None))
del self.workers[:]
self.closed = True
```
定义网络
```
class Actor_critic(nn.Module):
def __init__(self, in_dim, out_dim):
super(Actor_critic, self).__init__()
self.actor_linear1 = nn.Linear(in_dim, 64)
self.critic_linear1 = nn.Linear(in_dim, 64)
self.linear2 = nn.Linear(64, 32)
self.actor_linear3 = nn.Linear(32, out_dim)
self.critic_linear3 = nn.Linear(32, 1)
self.sigma_linear = nn.Linear(32, out_dim)
def forward(self, x):
value_hidden = F.relu(self.linear2(F.relu(self.critic_linear1(x))))
value = self.critic_linear3(value_hidden)
actor_hidden = F.relu(self.linear2(F.relu(self.actor_linear1(x))))
mu = torch.tanh(self.actor_linear3(actor_hidden)) * 2
sigma = F.softplus(self.sigma_linear(actor_hidden))
dist = Normal(mu, sigma)
return dist, value
```
画图
```
def smooth_plot(factor, item, plot_decay):
item_x = np.arange(len(item))
item_smooth = [np.mean(item[i:i+factor]) if i > factor else np.mean(item[0:i+1])
for i in range(len(item))]
for i in range(len(item)// plot_decay):
item_x = item_x[::2]
item_smooth = item_smooth[::2]
return item_x, item_smooth
def plot(episode, rewards, losses):
clear_output(True)
rewards_x, rewards_smooth = smooth_plot(10, rewards, 500)
losses_x, losses_smooth = smooth_plot(10, losses, 100000)
plt.figure(figsize=(18, 10))
plt.subplot(211)
plt.title('episode %s. reward: %s'%(episode, rewards_smooth[-1]))
plt.plot(rewards, label="Rewards", color='lightsteelblue', linewidth='1')
plt.plot(rewards_x, rewards_smooth, label='Smothed_Rewards', color='darkorange', linewidth='3')
plt.legend(loc='best')
plt.subplot(212)
plt.title('Losses')
plt.plot(losses,label="Losses",color='lightsteelblue',linewidth='1')
plt.plot(losses_x, losses_smooth,
label="Smoothed_Losses",color='darkorange',linewidth='3')
plt.legend(loc='best')
plt.show()
def test_env():
state = env.reset()
done = False
total_reward = 0
while not done:
state = torch.FloatTensor(state).reshape(-1, 3).to(device)
log_prob, _ = model(state)
next_state, reward, done, _ = env.step(log_prob.sample().cpu().numpy())
state = next_state
total_reward += reward
return total_reward
def gae_compute(next_value, rewards, masks, values, gamma=0.99, tau=0.95):
td_target = next_value
td_target_list = []
advantage = 0
advantage_list = []
for idx in reversed(range(len(values))):
td_target = td_target * gamma * masks[idx] + rewards[idx]
td_target_list.insert(0, td_target)
advantage = td_target - values[idx] + advantage * gamma * tau
advantage_list.insert(0, advantage)
return advantage_list, td_target_list
```
PPO训练更新
```
import pdb
def ppo_iter(states, actions, log_probs, advantages, td_target_list):
batch_size = actions.size(0)
for _ in range(batch_size // mini_batch_size):
ids = np.random.choice(batch_size, mini_batch_size, replace=False)
yield states[ids, :], actions[ids, :], log_probs[ids, :], advantages[ids, :], td_target_list[ids, :]
def ppo_train(states, actions, log_probs, advantages, td_target_list, clip_param=0.2):
losses = []
for _ in range(ppo_epochs):
for state, action, old_log_probs, advantage, td_target in ppo_iter(states, actions, log_probs,
advantages, td_target_list):
dist, value = model(state)
entropy = dist.entropy().mean()
new_log_probs = dist.log_prob(action)
ratio = (new_log_probs - old_log_probs).exp()
sub1 = ratio * advantage
sub2 = torch.clamp(ratio, 1.0-clip_param, 1.0+clip_param) * advantage
actor_loss = - torch.min(sub1, sub2).mean()
critic_loss = (td_target - value).pow(2).mean()
loss = 0.5 * critic_loss + actor_loss - 0.001 * entropy
losses.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
old_model.load_state_dict(model.state_dict())
return round(mean(losses),2)
## hyperparameters ##
num_envs = 16
env_name = "Pendulum-v0"
ppo_epochs = 30
mini_batch_size = 256
max_epoch = 10000
num_timesteps = 128
## hyperparameters ##
envs = ParallelEnv(num_envs, env_name)
state_space = envs.observation_space
action_space = envs.action_space
env = gym.make(env_name)
model = Actor_critic(state_space, action_space).to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
old_model = Actor_critic(state_space, action_space).to(device)
test_rewards = []
loss_list = []
state = envs.reset()
for epoch in range(max_epoch):
states, actions, rewards, masks, log_probs, values = [], [], [], [], [], []
for _ in range(num_timesteps):
dist, value = old_model(torch.FloatTensor(state).to(device))
action = dist.sample()
next_state, reward, done, _ = envs.step(action.cpu().numpy())
states.append(torch.FloatTensor(state).to(device))
actions.append(action)
rewards.append(torch.FloatTensor(reward).unsqueeze(1).to(device))
masks.append(torch.FloatTensor(1 - done).unsqueeze(1).to(device))
log_probs.append(dist.log_prob(action))
values.append(value)
state = next_state
_, next_value = model(torch.FloatTensor(next_state).to(device))
advantages, td_target_list = gae_compute(next_value, rewards, masks, values)
loss = ppo_train(torch.cat(states),torch.cat(actions), torch.cat(log_probs).detach(),
torch.cat(advantages).detach(), torch.cat(td_target_list).detach())
loss_list.append(loss)
if epoch % 1 == 0:
test_reward = np.mean([test_env() for _ in range(10)])
test_rewards.append(test_reward)
plot(epoch + 1, test_rewards, loss_list)
# soft = lambda loss : np.mean(loss[-100:]) if len(loss)>=100 else np.mean(loss)
# writer.add_scalar("Test_Rewards", np.array(soft(test_rewards)), epoch)
# writer.add_scalar("Value_Losses", np.array(soft(loss_list)), epoch)
from IPython import display
env = gym.make(env_name)
state_1 = env.reset()
img = plt.imshow(env.render(mode='rgb_array')) # only call this once
for _ in range(1000):
img.set_data(env.render(mode='rgb_array')) # just update the data
display.display(plt.gcf())
display.clear_output(wait=True)
prob, value = old_model(torch.FloatTensor(state_1).reshape(1,-1).to(device))
action = prob.sample().cpu().numpy()
next_state, _, done, _ = env.step(action)
if done:
state_1 = env.reset()
state_1 = next_state
```
## PPO Baselines:
<img src="../assets/PPO_baseline.png"></img>
### Test_Rewards:
<img src="../assets/PPO_Test_Rewards.png" width=100%></img>
### Value_Losses:
<img src="../assets/PPO_Value_Losses.png"></img>
| github_jupyter |
<h1> Create TensorFlow model </h1>
This notebook illustrates:
<ol>
<li> Creating a model using the high-level Estimator API
</ol>
```
# change these to try this notebook out
BUCKET = 'qwiklabs-gcp-37b9fafbd24bf385'
PROJECT = 'qwiklabs-gcp-37b9fafbd24bf385'
REGION = 'us-central1'
import os
os.environ['BUCKET'] = BUCKET
os.environ['PROJECT'] = PROJECT
os.environ['REGION'] = REGION
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/; then
gsutil mb -l ${REGION} gs://${BUCKET}
fi
```
<h2> Create TensorFlow model using TensorFlow's Estimator API </h2>
<p>
First, write an input_fn to read the data.
<p>
## Lab Task 1
Verify that the headers match your CSV output
```
import shutil
import numpy as np
import tensorflow as tf
# Determine CSV, label, and key columns
CSV_COLUMNS = 'weight_pounds,is_male,mother_age,plurality,gestation_weeks,key'.split(',')
LABEL_COLUMN = 'weight_pounds'
KEY_COLUMN = 'key'
# Set default values for each CSV column
DEFAULTS = [[0.0], ['null'], [0.0], ['null'], [0.0], ['nokey']]
TRAIN_STEPS = 1000
```
## Lab Task 2
Fill out the details of the input function below
```
# Create an input function reading a file using the Dataset API
# Then provide the results to the Estimator API
def read_dataset(filename_pattern, mode, batch_size = 512):
def _input_fn():
def decode_csv(line_of_text):
# TODO #1: Use tf.decode_csv to parse the provided line
columns = tf.decode_csv(line_of_text, record_defaults=DEFAULTS)
# TODO #2: Make a Python dict. The keys are the column names, the values are from the parsed data
features = dict(zip(CSV_COLUMNS, columns))
# TODO #3: Return a tuple of features, label where features is a Python dict and label a float
label = features.pop(LABEL_COLUMN)
return features, label
# TODO #4: Use tf.gfile.Glob to create list of files that match pattern
file_list = tf.gfile.Glob(filename_pattern)
# Create dataset from file list
dataset = (tf.data.TextLineDataset(file_list) # Read text file
.map(decode_csv)) # Transform each elem by applying decode_csv fn
# TODO #5: In training mode, shuffle the dataset and repeat indefinitely
# (Look at the API for tf.data.dataset shuffle)
# The mode input variable will be tf.estimator.ModeKeys.TRAIN if in training mode
# Tell the dataset to provide data in batches of batch_size
if mode == tf.estimator.ModeKeys.TRAIN:
epochs = None # Repeat indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
epochs = 1
dataset = dataset.repeat(epochs).batch(batch_size)
# This will now return batches of features, label
return dataset
return _input_fn
```
## Lab Task 3
Use the TensorFlow feature column API to define appropriate feature columns for your raw features that come from the CSV.
<b> Bonus: </b> Separate your columns into wide columns (categorical, discrete, etc.) and deep columns (numeric, embedding, etc.)
```
# Define feature columns
# Define feature columns
def get_categorical(name, values):
return tf.feature_column.indicator_column(
tf.feature_column.categorical_column_with_vocabulary_list(name, values))
def get_cols():
# Define column types
return [\
get_categorical('is_male', ['True', 'False', 'Unknown']),
tf.feature_column.numeric_column('mother_age'),
get_categorical('plurality',
['Single(1)', 'Twins(2)', 'Triplets(3)',
'Quadruplets(4)', 'Quintuplets(5)','Multiple(2+)']),
tf.feature_column.numeric_column('gestation_weeks')
]
```
## Lab Task 4
To predict with the TensorFlow model, we also need a serving input function (we'll use this in a later lab). We will want all the inputs from our user.
Verify and change the column names and types here as appropriate. These should match your CSV_COLUMNS
```
# Create serving input function to be able to serve predictions later using provided inputs
def serving_input_fn():
feature_placeholders = {
'is_male': tf.placeholder(tf.string, [None]),
'mother_age': tf.placeholder(tf.float32, [None]),
'plurality': tf.placeholder(tf.string, [None]),
'gestation_weeks': tf.placeholder(tf.float32, [None])
}
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
```
## Lab Task 5
Complete the TODOs in this code:
```
# Create estimator to train and evaluate
def train_and_evaluate(output_dir):
EVAL_INTERVAL = 300
run_config = tf.estimator.RunConfig(save_checkpoints_secs = EVAL_INTERVAL,
keep_checkpoint_max = 3)
# TODO #1: Create your estimator
estimator = tf.estimator.DNNRegressor(
model_dir = output_dir,
feature_columns = get_cols(),
hidden_units = [64, 32],
config = run_config)
train_spec = tf.estimator.TrainSpec(
# TODO #2: Call read_dataset passing in the training CSV file and the appropriate mode
input_fn = read_dataset('train.csv', mode = tf.estimator.ModeKeys.TRAIN),
max_steps = TRAIN_STEPS)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(
# TODO #3: Call read_dataset passing in the evaluation CSV file and the appropriate mode
input_fn = read_dataset('eval.csv', mode = tf.estimator.ModeKeys.EVAL),
steps = None,
start_delay_secs = 60, # start evaluating after N seconds
throttle_secs = EVAL_INTERVAL, # evaluate every N seconds
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
```
Finally, train!
```
# Run the model
shutil.rmtree('babyweight_trained', ignore_errors = True) # start fresh each time
train_and_evaluate('babyweight_trained')
```
When I ran it, the final lines of the output (above) were:
<pre>
INFO:tensorflow:Saving dict for global step 1000: average_loss = 1.2693067, global_step = 1000, loss = 635.9226
INFO:tensorflow:Restoring parameters from babyweight_trained/model.ckpt-1000
INFO:tensorflow:Assets added to graph.
INFO:tensorflow:No assets to write.
INFO:tensorflow:SavedModel written to: babyweight_trained/export/exporter/temp-1517899936/saved_model.pb
</pre>
The exporter directory contains the final model and the final RMSE (the average_loss) is 1.2693067
<h2> Monitor and experiment with training </h2>
```
from google.datalab.ml import TensorBoard
TensorBoard().start('./babyweight_trained')
for pid in TensorBoard.list()['pid']:
TensorBoard().stop(pid)
print('Stopped TensorBoard with pid {}'.format(pid))
```
Copyright 2017-2018 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| github_jupyter |
<img style="float: right; margin: 0px 0px 15px 15px;" src="https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcSQt6eQo8JPYzYO4p6WmxLtccdtJ4X8WR6GzVVKbsMjyGvUDEn1mg" width="300px" height="100px" />
# Trabajando con opciones
Una opción puede negociarse en el mercado secundario por lo que es importante determinar su valor $V_t$ para cada tiempo $t\in [0, T]$. La ganancia que obtiene quién adquiere la opción se llama función de pago o "payoff" y claramente depende del valor del subyacente.
Hay una gran variedad de opciones en el mercado y éstas se clasiflcan según su función de pago y la forma en que pueden ejercerse. Las opciones que tienen como función de pago a
$$ P(S(t),t)=max\{S(T)-K,0\} \rightarrow \text{En el caso de Call}$$
$$ P(S(t),t)=max\{K-S(T),0\} \rightarrow \text{En el caso de Put}$$
se llaman opciones **Vainilla**, con $h:[0,\infty) \to [0,\infty)$.
La opción se llama **europea** si puede ejercerse sólo en la fecha de vencimiento.
Se dice que una opción es **americana** si puede ejercerse en cualquier momento antes o en la fecha de vencimiento.
Una opción compleja popular son las llamadas **opciones asiáticas** cuyos pagos dependen de todas las trayectorias del precio de los activos subyacentes. Las opciones cuyos pagos dependen de las trayectorias de los precios de los activos subyacentes se denominan opciones dependientes de la ruta.
Principalmente, se puede resumir que las dos razones con más peso de importancia para utilizar opciones son el **aseguramiento** y la **especulación**.
## Opciones Plan Vainilla: opción de compra y opción de venta europea
Una opción vainilla o estándar es una opción normal de compra o venta que no tiene características especiales o inusuales. Puede ser para tamaños y vencimientos estandarizados, y negociarse en un intercambio.
En comparación con otras estructuras de opciones, las opciones de vanilla no son sofisticadas o complicadas.
## 1. ¿Cómo descargar datos de opciones?
```
#importar los paquetes que se van a usar
import pandas as pd
import pandas_datareader.data as web
import numpy as np
import datetime
import matplotlib.pyplot as plt
import scipy.stats as st
import seaborn as sns
%matplotlib inline
#algunas opciones para Pandas
pd.set_option('display.notebook_repr_html', True)
pd.set_option('display.max_columns', 6)
pd.set_option('display.max_rows', 10)
pd.set_option('display.width', 78)
pd.set_option('precision', 3)
```
Usando el paquete `pandas_datareader` también podemos descargar datos de opciones. Por ejemplo, descarguemos los datos de las opciones cuyo activo subyacente son las acciones de Apple
```
aapl = web.YahooOptions('AAPL')
aapl_opt = aapl.get_all_data().reset_index()
aapl_opt.set_index('Expiry')
# aapl
```
Precio del activo subyacente
```
aapl_opt.Underlying_Price[0]
```
Datos de la opción
```
aapl_opt.loc[0, 'JSON']
```
### Conceptos claves
- El precio de la oferta ('bid') se refiere al precio más alto que un comprador pagará por un activo.
- El precio de venta ('ask') se refiere al precio más bajo que un vendedor aceptará por un activo.
- La diferencia entre estos dos precios se conoce como 'spread'; cuanto menor es el spread, mayor es la liquidez de la garantía dada.
- Liquidez: facilidad de convertir cierta opción en efectivo.
- La volatilidad implícita es el pronóstico del mercado de un probable movimiento en el precio de un valor.
- La volatilidad implícita aumenta en los mercados bajistas y disminuye cuando el mercado es alcista.
- El último precio ('lastprice') representa el precio al que ocurrió la última operación, de una opción dada.
Una vez tenemos la información, podemos consultar de qué tipo son las opciones
```
aapl_opt.loc[:, 'Type']
```
o en que fecha expiran
```
pd.set_option('display.max_rows', 10)
aapl_opt.loc[:, 'Expiry']
```
Por otra parte, podríamos querer consultar todas las opciones de compra (call) que expiran en cierta fecha (2020-06-19)
```
fecha1 = '2021-06-18'
fecha2 = '2022-09-16'
call06_f1 = aapl_opt.loc[(aapl_opt.Expiry== fecha1) & (aapl_opt.Type=='call')]
call06_f2 = aapl_opt.loc[(aapl_opt.Expiry== fecha2) & (aapl_opt.Type=='call')]
call06_f1
```
## 2. ¿Qué es la volatilidad implícita?
**Volatilidad:** desviación estándar de los rendimientos.
- ¿Cómo se calcula?
- ¿Para qué calcular la volatilidad?
- **Para valuar derivados**, por ejemplo **opciones**.
- Método de valuación de riesgo neutral (se supone que el precio del activo $S_t$ no se ve afectado por el riesgo de mercado).
Recorderis de cuantitativas:
1. Ecuación de Black-Scholes
$$ dS(t) = \mu S(t) + \sigma S(t)dW_t$$
2. Solución de la ecuación
El valor de una opción Europea de vainilla $V_t$ puede obtenerse por:
$$V_t = F(t,S_t)$$ donde

3. Opción de compra europea, suponiendo que los precios del activo son lognormales
4. Opción de venta europea, suponiendo que los precios del activo son lognormales
Entonces, ¿qué es la **volatilidad implícita**?
La volatilidad es una medida de la incertidumbre sobre el comportamiento futuro de un activo, que se mide habitualmente como la desviación típica de la rentabilidad de dicho activo.
Una volatilidad implícita es aquella que cuando se sustituye en la ecuación de Black-Scholes o en sus ampliaciones,proporciona el precio de mercado de la opción.
## Volatility smile
- Cuando las opciones con la misma fecha de vencimiento y el mismo activo subyacente, pero diferentes precios de ejercicio, se grafican por la volatilidad implícita, la tendencia es que ese gráfico muestre una sonrisa.
- La sonrisa muestra que las opciones más alejadas 'in- or out-of-the-money' tienen la mayor volatilidad implícita.
- No todas las opciones tendrán una sonrisa de volatilidad implícita. Las opciones de acciones a corto plazo y las opciones relacionadas con la moneda tienen más probabilidades de tener una sonrisa de volatilidad

> Fuente: https://www.investopedia.com/terms/v/volatilitysmile.asp
> ### Validar para la `fecha = 2020-06-19` y para la fecha `fecha = '2021-01-15'`
```
# para los call de la fecha 1
ax = call06_f1.set_index('Strike').loc[:, 'IV'].plot(figsize=(8,6))
ax.axvline(call06_f1.Underlying_Price.iloc[0], color='g');
# para los call de la fecha 2
ax = call06_f2.set_index('Strike').loc[:, 'IV'].plot(figsize=(8,6))
ax.axvline(call06_f2.Underlying_Price.iloc[0], color='g');
```
Analicemos ahora datos de los `put`
```
put06_f1 = aapl_opt.loc[(aapl_opt.Expiry==fecha1) & (aapl_opt.Type=='put')]
put06_f1
```
Para los `put` de la `fecha 1`
```
ax = put06_f1.set_index('Strike').loc[:, 'IV'].plot(figsize=(8,6))
ax.axvline(put06_f1.Underlying_Price.iloc[0], color='g')
```
Con lo que hemos aprendido, deberíamos ser capaces de crear una función que nos devuelva un `DataFrame` de `pandas` con los precios de cierre ajustados de ciertas compañías en ciertas fechas:
- Escribir la función a continuación
```
# Función para descargar precios de cierre ajustados:
def get_adj_closes(tickers, start_date=None, end_date=None):
# Fecha inicio por defecto (start_date='2010-01-01') y fecha fin por defecto (end_date=today)
# Descargamos DataFrame con todos los datos
closes = web.DataReader(name=tickers, data_source='yahoo', start=start_date, end=end_date)
# Solo necesitamos los precios ajustados en el cierre
closes = closes['Adj Close']
# Se ordenan los índices de manera ascendente
closes.sort_index(inplace=True)
return closes
```
- Obtener como ejemplo los precios de cierre de Apple del año pasado hasta la fecha. Graficar...
```
ticker = ['AAPL']
start_date = '2017-01-01'
closes_aapl = get_adj_closes(ticker, start_date)
closes_aapl.plot(figsize=(8,5));
plt.legend(ticker);
```
- Escribir una función que pasándole el histórico de precios devuelva los rendimientos logarítmicos:
```
def calc_daily_ret(closes):
return np.log(closes/closes.shift(1)).iloc[1:]
```
- Graficar...
```
ret_aapl = calc_daily_ret(closes_aapl)
ret_aapl.plot(figsize=(8,6));
```
También, descargar datos de opciones de Apple:
```
aapl = web.YahooOptions('AAPL')
aapl_opt = aapl.get_all_data().reset_index()
aapl_opt.set_index('Expiry').sort_index()
aapl_opt.Underlying_Price[0]
K = 135 # strike price
indice_opt = aapl_opt.loc[(aapl_opt.Type=='call') & (aapl_opt.Strike==K) & (aapl_opt.Expiry=='2023-06-16')]
indice_opt
i_opt= indice_opt.index
opcion_valuar = aapl_opt.loc[i_opt[0]]
opcion_valuar['JSON']
print('Precio del activo subyacente actual = ',opcion_valuar.Underlying_Price)
```
# Simulación de precios usando rendimiento simple y logarítmico
* Comenzaremos por suponer que los rendimientos son un p.e. estacionario que distribuyen $\mathcal{N}(\mu,\sigma)$.
## Rendimiento Simple
```
# Obtenemos el rendimiento simple
Ri = closes_aapl.pct_change(1).iloc[1:]
# Obtenemos su media y desviación estándar de los rendimientos
mu_R = Ri.mean()[0]
sigma_R = Ri.std()[0]
Ri
today = pd.to_datetime(date.today())
# Obtener fecha de cierre de la opción a valuar
expiry = opcion_valuar.Expiry
len(pd.date_range(today, expiry, freq='B'))
from datetime import date
# Encontrar la fecha de hoy en fomato timestamp
today = pd.to_datetime(date.today())
# Obtener fecha de cierre de la opción a valuar
expiry = opcion_valuar.Expiry
nscen = 10000
# Generar rangos de fechas de días hábiles
dates = pd.date_range(today, expiry, freq='B')
ndays = len(dates)
```
## Mostrar como simular precios usando los rendimientos
### 1. Usando rendimiento simple
```
# Simular los rendimientos
# Rendimiento diario
dt = 1
# Z ~ N(0,1) normal estándar (ndays, nscen)
Z = np.random.randn(ndays, nscen)
# Simulación normal de los rendimientos
Ri_dt = pd.DataFrame(Z * sigma_R * np.sqrt(dt) + mu_R * dt, index=dates)
Ri_dt
```
**Simulación de precios usando el rendimiento simple**: Como demostramos en clases pasadas la fórmula de simular precios usando el rendimiento simple es la siguiente:
$$
S_T = S_0 \prod_{i=0}^{T-1} (R_i + 1)
$$
```
S0 = opcion_valuar.Underlying_Price
S_T = S0*(Ri_dt + 1).cumprod()
# Simulación del precio
S_0 = opcion_valuar.Underlying_Price
S_T = S_0*(1+Ri_dt).cumprod()
S_T.iloc[0,:] = S_0
# Se muestran los precios simulados con los precios descargados
pd.concat([closes_aapl, S_T.iloc[:, :10]]).plot(figsize=(8,6));
plt.title('Simulación de precios usando rendimiento simple');
```
### 2. Rendimiento Logarítmico
**Simulación de precios usando el rendimiento logarítmico**: Como demostramos en clases pasadas la fórmula de simular precios usando el rendimiento simple es la siguiente:
$$
S_T = S_0 \cdot e^{\sum_{i=1}^{T} r_i }
$$
```
Z.shape, len(dates)
# Calcular rendimiento logarítmico
ri = calc_daily_ret(closes_aapl)
# Usando la media y desviación estándar de los rendimientos logarítmicos
mu_r = ri.mean()[0]
sigma_r = ri.std()[0]
# Simulación del rendimiento
dt = 1
Z = np.random.randn(ndays, nscen)
sim_ret_ri = pd.DataFrame(mu_r * dt + Z * sigma_r * np.sqrt(dt), index=dates )
# Simulación del precio
S_0 = closes_aapl.iloc[-1,0]
S_T2 = S_0*np.exp(sim_ret_ri.cumsum())
# Se muestran los precios simulados con los precios descargados
# pd.concat([closes_aapl,S_T2]).plot(figsize=(8,6));
# plt.title('Simulación de precios usando rendimiento logarítmico');
# from sklearn.metrics import mean_absolute_error
e1 = np.abs(S_T-S_T2).mean().mean()
e1
print('Las std usando rendimientos logarítmicos y simples son similares')
sigma_R,sigma_r
```
Con los precios simulados debemos de encontrar el valor de la opción según la función de pago correspondiente. Para este caso es:
$$
max(S_T - K,0)
$$
```
opcion_valuar['JSON']
```
## Valuación usando el modelo de Black and Scholes
Los supuestos que hicieron Black y Scholes cuando dedujeron su fórmula para la valoración de opciones fueron los siguientes:
1. El comportamiento del precio de la acción corresponde al modelo logarítmico normal, con $\mu$ y $\sigma$
constantes.
2. No hay costos de transición ni impuestos. Todos los títulos son perfectamente divisibles.
3. No hay dividendos sobre la acción durante la vida de la opción.
4. No hay oportunidades de arbitraje libres de riesgo.
5. La negociación de valores es continua.
6. Los inversionistas pueden adquirir u otorgar préstamos a la misma tasa de interés libre de riesgo.
7. La tasa de interés libre de riesgo a corto plazo, r, es constante.
Bajo los supuestos anteriores podemos presentar las **fórmulas de Black-Scholes** para calcular los precios de compra y de venta europeas sobre acciones que no pagan dividendos:
$$
\text{Valor actual de la opción} = V(S_0, T) = S_0 N(d_1) - K e^{-r*T} N(d_2)
$$
donde:
- $S_0$ = precio de la acción en el momento actual.
- $K$ = precio "de ejercicio" de la opción.
- $r$ = tasa de interés libre de riesgo.
- $T$ = tiempo que le resta de vida a la opción.
- $N(d)$ = función de distribución de la variable aleatoria normal con media nula y desviación típica unitaria
(probabilidad de que dicha variable sea menor o igual que d). Función de distribución de probabilidad acumulada.
- $\sigma$ = varianza por período de la tasa o tipo de rendimiento de la opción.
$$
d_1 = \frac{\ln{\frac{S_0}{K}} + (r + \sigma^2 / 2) T}{\sigma \sqrt{T}}, \quad d_2 = \frac{\ln{\frac{S_0}{K}} + (r - \sigma^2 / 2) T}{\sigma \sqrt{T}}
$$
**Nota**: observe que el __rendimiento esperado__ sobre la acción no se incluye en la ecuación de Black-Scholes. Hay un principio general conocido como valoración neutral al riesgo, el cual establece que cualquier título que depende de otros títulos negociados puede valorarse bajo el supuesto de que el mundo es neutral al riesgo. El resultado demuestra ser muy útil en la práctica. *En un mundo neutral al riesgo, el rendimiento esperado de todos los títulos es la tasa de interés libre de riesgo*, y la tasa de descuento correcta para los flujos de efectivo esperados también es la tasa de interés libre de riesgo.
El equivalente a la función de Black-Scholes (valuación de la opción) se puede demostrar que es:
$$
\text{Valor actual de la opción} = V(S_0, T) = E^*(e^{-rT} f(S_T)) = e^{-rT} E^*(f(S_T))
$$
donde
$f(S_T)$ representa la función de pago de la opción, que para el caso de un call europeo sería $f(S_T) = \max({S_T - K})$.
> Referencia: http://diposit.ub.edu/dspace/bitstream/2445/32883/1/Benito_el_modelo_de_Black_Sholes.pdf (página 20)
> Referencia 2: http://www.cmat.edu.uy/~mordecki/courses/upae/upae-curso.pdf (página 24)
- Hallar media y desviación estándar muestral de los rendimientos logarítmicos
```
mu = ret_aapl.mean()[0]
sigma = ret_aapl.std()[0]
mu, sigma
```
No se toma la media sino la tasa libre de riesgo
> Referencia: https://www.treasury.gov/resource-center/data-chart-center/interest-rates/Pages/TextView.aspx?data=yield
```
# Tasa de bonos de 1 yr de fecha 21/04/2021 -> 7%
r = 0.007/360 # Tasa diaria
```
- Simularemos el tiempo de contrato desde `HOY` hasta la fecha de `Expiry`, 10 escenarios:
- Generar fechas
```
from datetime import date
today = pd.Timestamp(date.today())
expiry = opcion_valuar.Expiry
dates = pd.date_range(start=today, end=expiry, freq='B')
ndays = len(dates)
nscen = 10
dates
```
- Generamos 10 escenarios de rendimientos simulados y guardamos en un dataframe
```
sim_ret = pd.DataFrame(sigma*np.random.randn(ndays,nscen)+r, index=dates)
sim_ret.cumsum()
# Las columnas son los escenarios y las filas son las días de contrato
```
- Con los rendimientos simulados, calcular los escenarios de precios respectivos:
```
S0 = closes_aapl.iloc[-1,0] # Condición inicial del precio a simular
sim_closes = S0*np.exp(sim_ret.cumsum())
sim_closes.iloc[0, :] = S0
sim_closes
```
- Graficar:
```
sim_closes.plot(figsize=(8,6));
# Se muestran los precios simulados con los precios descargados
pd.concat([closes_aapl,sim_closes]).plot(figsize=(8,6));
opcion_valuar['JSON']
opcion_valuar
from datetime import date
Hoy = date.today()
# strike price de la opción
K = opcion_valuar['JSON']['strike']
# Fechas a simular
dates = pd.date_range(start= Hoy, periods = ndays, freq='B')
# Escenarios y número de días
ndays = len(dates)
nscen = 100000
# Condición inicial del precio a simular
S0 = closes_aapl.iloc[-1,0]
# simular rendimientos
sim_ret = pd.DataFrame(sigma*np.random.randn(ndays,nscen)+r,index=dates)
# Simular precios
sim_closes = S0*np.exp(sim_ret.cumsum())
# Valor del call europeo
call = pd.DataFrame({'Prima':np.exp(-r*ndays) \
*np.fmax(sim_closes-K, 0).mean(axis=1)}, index=dates)
call.plot();
```
La valuación de la opción es:
```
call.iloc[-1]
```
Intervalo de confianza del 99%
```
confianza = 0.99
sigma_est = sim_closes.iloc[-1].sem()
mean_est = call.iloc[-1].Prima
i2 = st.norm.interval(confianza, loc=mean_est, scale=sigma_est)
print(i2)
opcion_valuar['JSON']
```
## Precios simulados usando técnicas de reducción de varianza
```
# Usando muestreo estratificado----> #estratros = nscen
U = (np.arange(0,nscen)+np.random.rand(ndays,nscen))/nscen
Z = st.norm.ppf(U)
sim_ret2 = pd.DataFrame(sigma*Z+r,index=dates)
sim_closes2 = S0*np.exp(sim_ret.cumsum())
# Función de pago
strike = pd.DataFrame(K*np.ones([ndays,nscen]), index=dates)
call = pd.DataFrame({'Prima':np.exp(-r*ndays) \
*np.fmax(sim_closes2-strike,np.zeros([ndays,nscen])).T.mean()}, index=dates)
call.plot();
```
La valuación de la opción es:
```
call.iloc[-1]
```
Intervalo de confianza del 99%
```
confianza = 0.99
sigma_est = sim_closes2.iloc[-1].sem()
mean_est = call.iloc[-1].Prima
i2 = st.norm.interval(confianza, loc=mean_est, scale=sigma_est)
print(i2)
```
### Análisis de la distribución de los rendimientos
### Ajustando norm
```
ren = calc_daily_ret(closes_aapl) # rendimientos
y,x,_ = plt.hist(ren['AAPL'],bins=50,density=True,label='Histograma rendimientos')
mu_fit,sd_fit = st.norm.fit(ren) # Se ajustan los parámetros de una normal
# Valores máximo y mínimo de los rendiemientos a generar
ren_max = max(x);ren_min = min(x)
# Vector de rendimientos generados
ren_gen = np.arange(ren_min,ren_max,0.001)
# Generación de la normal ajustado con los parámetros encontrados
curve_fit = st.norm.pdf(ren_gen,loc=mu_fit,scale=sd_fit)
plt.plot(ren_gen,curve_fit,label='Distribución ajustada')
plt.legend()
plt.show()
```
### Ajustando t
```
# rendimientos
ren = calc_daily_ret(closes_aapl)
# Histograma de los rendimientos
y, x, _ = plt.hist(ren['AAPL'], bins=50, density=True, label='Histograma rendimientos')
# Se ajustan los parámetros de una distribución
dist = 't'
params = getattr(st, dist).fit(ren.values)
# Generación de la pdf de la distribución ajustado con los parámetros encontrados
curve_fit = getattr(st, dist).pdf(x, *params)
plt.plot(x, curve_fit, label='Distribución ajustada')
plt.legend()
plt.show()
# Q-Q
st.probplot(ren['AAPL'], sparams=params[:-2], dist=dist, plot=plt);
```
## 3. Valuación usando simulación: uso del histograma de rendimientos
Todo el análisis anterior se mantiene. Solo cambia la forma de generar los números aleatorios para la simulación montecarlo.
Ahora, generemos un histograma de los rendimientos diarios para generar valores aleatorios de los rendimientos simulados.
- Primero, cantidad de días y número de escenarios de simulación
```
ndays = len(dates)
nscen = 10
```
- Del histograma anterior, ya conocemos las probabilidades de ocurrencia, lo que se llamó como variable `y`
```
prob
prob = y/np.sum(y)
values = x[1:]
prob.sum()
```
- Con esto, generamos los números aleatorios correspondientes a los rendimientos (tantos como días por número de escenarios).
```
# Rendimientos simulados
ret = np.random.choice(values, ndays*nscen, p=prob)
# Fechas
dates = pd.date_range(start=Hoy,periods=ndays)
# Rendimien en Data Frame
sim_ret_hist = pd.DataFrame(ret.reshape((ndays,nscen)),index=dates)
sim_ret_hist
sim_closes_hist = (closes_aapl.iloc[-1,0])*np.exp(sim_ret_hist.cumsum())
sim_closes_hist
sim_closes_hist.plot(figsize=(8,6),legend=False);
pd.concat([closes_aapl,sim_closes_hist]).plot(figsize=(8,6),legend=False);
plt.title('Simulación usando el histograma de los rendimientos')
K = opcion_valuar['JSON']['strike']
ndays = len(dates)
nscen = 100000
# Histograma tomando la tasa libre de riesgo
freq, values = np.histogram(ret_aapl+r-mu, bins=2000)
prob = freq/np.sum(freq)
# Simulación de los rendimientos
ret = np.random.choice(values[1:], ndays*nscen, p=prob)
# Simulación de precios
sim_ret_hist = pd.DataFrame(ret.reshape((ndays,nscen)),index=dates)
sim_closes_hist = (closes_aapl.iloc[-1,0]) * np.exp(sim_ret_hist.cumsum())
strike = pd.DataFrame(K*np.ones(ndays*nscen).reshape((ndays,nscen)), index=dates)
call_hist = pd.DataFrame({'Prima':np.exp(-r*ndays) \
*np.fmax(sim_closes_hist-strike,np.zeros(ndays*nscen).reshape((ndays,nscen))).T.mean()}, index=dates)
call_hist.plot();
call_hist.iloc[-1]
opcion_valuar['JSON']
```
Intervalo de confianza del 95%
```
confianza = 0.95
sigma_est = sim_closes_hist.iloc[-1].sem()
mean_est = call_hist.iloc[-1].Prima
i1 = st.t.interval(confianza,nscen-1, loc=mean_est, scale=sigma_est)
i2 = st.norm.interval(confianza, loc=mean_est, scale=sigma_est)
print(i1)
print(i1)
```
# <font color = 'red'> Tarea: </font>
Replicar el procedimiento anterior para valoración de opciones 'call', pero en este caso para opciones tipo 'put' y compararlo con el valor teórico de la ecuación de Black-Scholes
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Esteban Jiménez Rodríguez and modified by Oscar Jaramillo Z.
</footer>
| github_jupyter |
# List and Dictionary Comprehensions
Comprehension is a different way to construct lists and dictionaries. Up to now, every time that we have built up a list or dictionary, we began by initializing it. We then took advantage of their mutability inherent to build them up one element or key-value pair at a time. However, there is a more succinct way to accomplish the vast majority of your list and dictionary construction tasks.
## Objectives
At the end of this notebook you should be able to:
- use list comprehension
- use dictionary comprehension
- use tuple comprehension
## List Comprehensions
Before we dive into the specifics about how this new tool (list comprehensions) works, let's look at an example question where we build a list. We can then show how to perform the same task with our new tool and learn how it works.
Let's imagine that we have the list `[1, 5, 9, 33]` stored in the variable `my_list`. Now, let's assume that we want to make a new list of the squares of all the values in `my_list` and call it `my_squares`. With the tools we have covered so far, you might write:
```
my_list = [1, 5, 9, 33]
my_squares = []
for num in my_list:
my_squares.append(num ** 2)
print(my_squares)
```
Now, `my_squares` will hold the list `[1, 25, 81, 1089]`. To get this, we were simply specifying a bunch of stuff that we wanted to add on to the end of the `my_squares` list, with a starting point at `my_list`. So, from a high level, we can write the framework of creating a list in code as:
```python
list_were_building = []
for thing in iterable:
list_were_building.append(transform(thing))
```
With this structure in mind, we can use the following syntax to perform the same task of building up a list in a single line! Check it out, along with how it would look for the construction of `my_squares`.
```python
list_were_building = [transform(thing) for thing in iterable]
```
This last line of code does the exact same thing as the three lines above! In this line, the thing that we would pass to the `append()` method, `transform(thing)`, comes at the beginning of the statement in the `[]`. These `[]` allow for the final product to be defined as a list. Then, the `for` loop statement that we had written is at the end. This is the basic idea behind the [list comprehension](https://en.wikipedia.org/wiki/List_comprehension).
Similarly, we can build our `my_squares` list using a list comprehension:
```
my_squares2 = [num ** 2 for num in my_list]
print(my_squares2)
```
But wait! There's more! Remember in all the examples where we were getting evens, we had a condition to decide when to append a value to a list? We can also use conditions to determine what "transformed things" get added in a list comprehension! Let's look at the evens list builder to hammer this home.
```python
# Old way of constructing list of evens
evens = []
for num in range(10):
if num % 2 == 0:
evens.append(num)
# Old way at high level
list_were_building = []
for thing in iterable:
if condition:
list_were_building.append(transform(thing))
# List comprehension way of constructing list of evens
evens = [num for num in range(10) if num % 2 == 0]
# List comprehension way at high level
list_we_are_building = [transform(thing) for thing in iterable if condition]
```
The way `transform()` was called in the above examples, as though it were a function, is an option when writing list comps. For example, the `my_squares` example could be accomplished in the same way with:
```python
def square(num):
return num ** 2
my_squares = [square(num) for num in my_list]
```
This might seem silly, since we could just write `num ** 2` directly in the list comp as we did above. However, this calling of a function in the list comp becomes a powerful idea when you want to transform the values being iterated over in a complex way.
## Dictionary Comprehensions
Just as list comprehensions are a more succinct way of constructing a list, we have the same ability for dictionaries. Dictionary comprehensions operate in the same way as their list counterparts, except for one fundamental difference. Recall that dictionaries have no `append()` method, and that a new key-value pair is added to the dictionary with the syntax: `my_dict[new_key] = new_value`. In this way, it makes sense that we need syntax to pass both the key and value to the dictionary comprehension.
Luckily, Python gives a simple way to pass a key and value pair, and it is already very familiar to you! You just separate the key and value that you want to enter into the dictionary with a colon, like we did when we were hardcoding the contents in the `{}` dictionary constructor, i.e. `my_dict = {1: 1, 2: 4}`. Let's look at an example where we make a dictionary with the keys as the numbers 1 - 5, and the values as the squares of the keys. We'll do this with both the old way of constructing a dictionary, and then with a dictionary comprehension so that we can see the similarities.
```
# Standard way.
squares_dict = {}
for num in range(1, 6):
squares_dict[num] = num ** 2
print(squares_dict)
# Dictionary Comprehension way.
squares_dict2 = {num: num ** 2 for num in range(1, 6)}
print(squares_dict2)
```
We can see that in both cases, we're going through the numbers 1 - 5 with `range(1, 6)` and those `num`s are being assigned as keys. The values assigned to those keys are the squares of the keys, assigned with `squares_dict[num] = num ** 2` and `num: num ** 2`, respectively. Just as with list comprehensions, dictionary comprehensions read as the first thing being the `key: value` pair being added to the dictionary. Then, left to right (top down in the old way), we have what the loop definition would look like. And, just as with list comps, we can add a condition to filter what gets put into the dictionary.
Say that we want a dictionary with a random integer between 1 and 10, associated with each of the values in the list of words: `['cow', 'chicken', 'horse', 'moose']`. Let's look at how we'd do that with a dictionary comprehension. (We're importing from the Python library `random` to get our random integers. We'll talk more about importing later in the course.)
```
from random import randint
animals_list = ['cow', 'chicken', 'horse', 'moose']
animals_dict = {animal: randint(1, 10) for animal in animals_list}
print(animals_dict)
```
## Other Comprehensions
You can actually use the syntax from the list comprehensions to construct a tuple in what seems like a dynamic way. Take the example.
```
my_tuple = tuple(num for num in range(10) if num % 2 == 0)
print(my_tuple)
```
All we are doing here is passing `num for num in range(10) if num % 2 == 0` to the tuple constructor, `()`. Since the tuple constructor takes any iterable, which that statement produces, it makes a tuple out of the contents. Note that it would be impossible to make a tuple with statements like this the "old way", since tuples don't support appending or mutation of any kind!
For this reason, in addition to their readability, comprehensions of all types are considered the most Pythonic way of constructing new data structures.
## Check your understanding
1. Take the following for loop, and translate it into a list. comprehensions:
odds = []
for num in range(10):
if num % 2 != 0:
odds.append(num)
1. Take the following for loop, and translate it into a dictionary comprehensions:
cubes = {}
for num in range(1, 6):
cubes[num] = num ** 3
```
odds = [num for num in range(10) if num % 2 != 0]
odds
cubes = {num: num **3 for num in range(1,6)}
cubes
```
| github_jupyter |
```
import numpy as np
import pandas as pd
from pathlib import Path
from matplotlib import pyplot as plt
from sklearn.preprocessing import LabelEncoder
train_df = pd.read_csv(Path('Resources/2019loans.csv'))
test_df = pd.read_csv(Path('Resources/2020Q1loans.csv'))
train_df
test_df
# Convert categorical data to numeric and separate target feature for training data
x = train_df.drop('loan_status',axis = 1)
x_train = pd.get_dummies(x)
x_train = x_train.drop('Unnamed: 0',axis = 1)
x_train
y = pd.get_dummies(train_df['loan_status'])
y_train = y.drop('high_risk',axis =1)
y_train = y_train.rename(columns = {'low_risk':'loan_status'})
y_train = y_train.values.ravel()
y_train
# Convert categorical data to numeric and separate target feature for testing data
x_td = test_df.drop('loan_status',axis = 1)
x_test = pd.get_dummies(x_td)
x_test = x_test.drop('Unnamed: 0',axis = 1)
x_test
y_td = pd.get_dummies(test_df['loan_status'])
y_test= y_td.drop('high_risk',axis =1)
y_test = y_test.rename(columns={'low_risk':'loan_status'})
y_test
# add missing dummy variables to testing set
missing_cols = set(x_train.columns) - set(x_test.columns)
missing_cols
for c in missing_cols:
x_test['debt_settlement_flag_Y'] = 0
# Ensure the order of column in the test set is in the same order than in train set
x_test = x_test[x_train.columns]
x_test
```
# LOGISTIC REGRESSION MODEL
```
#import dependencies
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
# Train the Logistic Regression model on the unscaled data and print the model score
classifier = LogisticRegression()
# Fit our model using the training data
classifier.fit(x_train, y_train)
print(f"Training Data Score: {classifier.score(x_train, y_train)}")
print(f"Testing Data Score: {classifier.score(x_test, y_test)}")
```
# RandomForest Classifier Model
```
#import dependencies
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, roc_curve
# Train a Random Forest Classifier model and print the model score
rf_clf = RandomForestClassifier(random_state=1)
rf_clf.fit(x_train, y_train)
#classification reports
y_pred = rf_clf.predict(x_test)
print(classification_report(y_test, y_pred))
#model score
print(f"Training Data Score: {rf_clf.score(x_train, y_train)}")
print(f"Testing Data Score: {rf_clf.score(x_test, y_test)}")
```
# Scaling the Data
```
#import dependencies
from sklearn.preprocessing import StandardScaler
# Scale the data and all features
scaler = StandardScaler().fit(x_train)
x_train_scaled = scaler.transform(x_train)
x_test_scaled = scaler.transform(x_test)
# Train the Logistic Regression model on the scaled data and print the model score
# Create a logistic regression model
classifier_scaled = LogisticRegression()
# Fit our model using the training data
classifier_scaled.fit(x_train_scaled, y_train)
print(f"Training Data Score: {classifier.score(x_train_scaled, y_train)}")
print(f"Testing Data Score: {classifier.score(x_test_scaled, y_test)}")
# Train a Random Forest Classifier model on the scaled data and print the model score
# Train a Random Forest Classifier model and print the model score
rf_clf_scaled = RandomForestClassifier(random_state=42)
rf_clf_scaled.fit(x_train_scaled, y_train)
#classification reports
y_pred = rf_clf_scaled.predict(x_test_scaled)
print(classification_report(y_test, y_pred))
#model score
print(f"Training Data Score: {rf_clf_scaled.score(x_train_scaled, y_train)}")
print(f"Testing Data Score: {rf_clf_scaled.score(x_test_scaled, y_test)}")
```
# Analysis
The Randomforest model even though it seems to be overfitting, is showing much better results with the training data set. The logistic_Regression model results are not as good as the Randomforest model.
A second obeservation is both the Randomforest and the Logistic_Regression models both show unfavourable results with the test data set.
| github_jupyter |
## Denoising Autoencoder on MNIST dataset
* This notebook will give you a very good understanding abou denoising autoencoders
* For more information: visit [here](https://lilianweng.github.io/lil-log/2018/08/12/from-autoencoder-to-beta-vae.html)
* The entire notebook is in PyTorch
```
# Importing packages that will be necessary for the project
import numpy as np
from keras.datasets import mnist
import matplotlib.pyplot as plt
from tqdm import tqdm
from torchvision import transforms
import torch.nn as nn
from torch.utils.data import DataLoader,Dataset
import torch
import torch.optim as optim
from torch.autograd import Variable
# Mounting the google drive to fetch data from it
from google.colab import drive
drive.mount('/content/gdrive')
#loading the mnist data
(x_train,y_train),(x_test,y_test)=mnist.load_data()
print("No of train datapoints:{}\nNo of test datapoints:{}".format(len(x_train),len(x_test)))
print(y_train[1]) # Checking labels
#we add the noise
"""
'gauss' Gaussian-distributed additive noise.
'speckle' out = image + n*image,where
n is uniform noise with specified mean & variance.
"""
def add_noise(img,noise_type="gaussian"):#input includes the type of the noise to be added and the input image
row,col=28,28
img=img.astype(np.float32)
if noise_type=="gaussian":
noise=np.random.normal(-5.9,5.9,img.shape) #input includes : mean, deviation, shape of the image and the function picks up a normal distribuition.
noise=noise.reshape(row,col) # reshaping the noise
img=img+noise #adding the noise
return img
if noise_type=="speckle":
noise=np.random.randn(row,col)
noise=noise.reshape(row,col)
img=img+img*noise
return img
#Now dividing the dataset into two parts and adding gaussian to one and speckle to another.
noises=["gaussian","speckle"]
noise_ct=0
noise_id=0 #id represnts which noise is being added, its 0 = gaussian and 1 = speckle
traindata=np.zeros((60000,28,28)) #revised training data
for idx in tqdm(range(len(x_train))): #for the first half we are using gaussian noise & for the second half speckle noise
if noise_ct<(len(x_train)/2):
noise_ct+=1
traindata[idx]=add_noise(x_train[idx],noise_type=noises[noise_id])
else:
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_id+=1
noise_ct=0
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_ct=0
noise_id=0
testdata=np.zeros((10000,28,28))
for idx in tqdm(range(len(x_test))): # Doing the same for the test set.
if noise_ct<(len(x_test)/2):
noise_ct+=1
x=add_noise(x_test[idx],noise_type=noises[noise_id])
testdata[idx]=x
else:
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_id+=1
noise_ct=0
print("\n{} noise addition completed to images".format(noises[noise_id]))
f, axes=plt.subplots(2,2) #setting up 4 figures
#showing images with gaussian noise
axes[0,0].imshow(x_train[0],cmap="gray")#the original data
axes[0,0].set_title("Original Image")
axes[1,0].imshow(traindata[0],cmap='gray')#noised data
axes[1,0].set_title("Noised Image")
#showing images with speckle noise
axes[0,1].imshow(x_train[25000],cmap='gray')#original data
axes[0,1].set_title("Original Image")
axes[1,1].imshow(traindata[25000],cmap="gray")#noised data
axes[1,1].set_title("Noised Image")
#creating a dataset builder i.e dataloaders
class noisedDataset(Dataset):
def __init__(self,datasetnoised,datasetclean,labels,transform):
self.noise=datasetnoised
self.clean=datasetclean
self.labels=labels
self.transform=transform
def __len__(self):
return len(self.noise)
def __getitem__(self,idx):
xNoise=self.noise[idx]
xClean=self.clean[idx]
y=self.labels[idx]
if self.transform != None:#just for using the totensor transform
xNoise=self.transform(xNoise)
xClean=self.transform(xClean)
return (xNoise,xClean,y)
#defining the totensor transforms
tsfms=transforms.Compose([
transforms.ToTensor()
])
trainset=noisedDataset(traindata,x_train,y_train,tsfms)# the labels should not be corrupted because the model has to learn uniques features and denoise it.
testset=noisedDataset(testdata,x_test,y_test,tsfms)
batch_size=32
#creating the dataloader
trainloader=DataLoader(trainset,batch_size=32,shuffle=True)
testloader=DataLoader(testset,batch_size=1,shuffle=True)
#building our ae model:
class denoising_model(nn.Module):
def __init__(self):
super(denoising_model,self).__init__()
self.encoder=nn.Sequential(
nn.Linear(28*28,256),#decreasing the features in the encoder
nn.ReLU(True),
nn.Linear(256,128),
nn.ReLU(True),
nn.Linear(128,64),
nn.ReLU(True)
)
self.decoder=nn.Sequential(
nn.Linear(64,128),#increasing the number of features
nn.ReLU(True),
nn.Linear(128,256),
nn.ReLU(True),
nn.Linear(256,28*28),
nn.Sigmoid(),
)
def forward(self,x):
x=self.encoder(x)#first the encoder
x=self.decoder(x)#then the decoder to reconstruct the original input.
return x
#this is the training code, can be modified according to requirements
#setting the device
if torch.cuda.is_available()==True:
device="cuda:0"
else:
device ="cpu"
model=denoising_model().to(device)
criterion=nn.MSELoss()
optimizer=optim.SGD(model.parameters(),lr=0.01,weight_decay=1e-5)
#setting the number of epochs
epochs=120
l=len(trainloader)
losslist=list()
epochloss=0
running_loss=0
for epoch in range(epochs):
print("Entering Epoch: ",epoch)
for dirty,clean,label in tqdm((trainloader)):
dirty=dirty.view(dirty.size(0),-1).type(torch.FloatTensor)
clean=clean.view(clean.size(0),-1).type(torch.FloatTensor)
dirty,clean=dirty.to(device),clean.to(device)
#-----------------Forward Pass----------------------
output=model(dirty)
loss=criterion(output,clean)
#-----------------Backward Pass---------------------
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss+=loss.item()
epochloss+=loss.item()
#-----------------Log-------------------------------
losslist.append(running_loss/l)
running_loss=0
print("======> epoch: {}/{}, Loss:{}".format(epoch,epochs,loss.item()))
#plotting the loss curve
plt.plot(range(len(losslist)),losslist)
"""Here, we try to visualize some of the results.
We randomly generate 6 numbers in between 1 and 10k , run them through the model,
and show the results with comparisons
"""
f,axes= plt.subplots(6,3,figsize=(20,20))
axes[0,0].set_title("Original Image")
axes[0,1].set_title("Dirty Image")
axes[0,2].set_title("Cleaned Image")
test_imgs=np.random.randint(0,10000,size=6)
for idx in range((6)):
dirty=testset[test_imgs[idx]][0]
clean=testset[test_imgs[idx]][1]
label=testset[test_imgs[idx]][2]
dirty=dirty.view(dirty.size(0),-1).type(torch.FloatTensor)
dirty=dirty.to(device)
output=model(dirty)
output=output.view(1,28,28)
output=output.permute(1,2,0).squeeze(2)
output=output.detach().cpu().numpy()
dirty=dirty.view(1,28,28)
dirty=dirty.permute(1,2,0).squeeze(2)
dirty=dirty.detach().cpu().numpy()
clean=clean.permute(1,2,0).squeeze(2)
clean=clean.detach().cpu().numpy()
axes[idx,0].imshow(clean,cmap="gray")
axes[idx,1].imshow(dirty,cmap="gray")
axes[idx,2].imshow(output,cmap="gray")
```
| github_jupyter |
# Cleaning the data to build the prototype for crwa
### This data cleans the original sql output and performs cleaning tasks. Also checking validity of the results against original report found at
### https://www.crwa.org/uploads/1/2/6/7/126781580/crwa_ecoli_web_2017_updated.xlsx
```
import pandas as pd
pd.options.display.max_rows = 999
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv("data_for_prototype.csv")
# There are 2 rows with Date = Null so droping those rows
df = df.dropna(subset=['Date_Collected'])
df.isna().sum()
# There are following types of invalids in Site_ID
invalids = ["N/A","NULL","ND"]
#Removing these invalid Site_IDs
df["Site_Name"] = df["Site_Name"].map(lambda x: np.nan if x in invalids else x)
df["Site_Name"].fillna("ABCD", inplace=True)
#Removing these invalid Town Names
df["Town"] = df["Town"].map(lambda x: np.nan if x in invalids else x)
df["Town"].fillna("ABCD", inplace=True)
df["River_Mile_Headwaters"].describe
#Removing invalid Miles and selecting only numeric values for miles
df["River_Mile_Headwaters"] = df["River_Mile_Headwaters"].map(lambda x: np.nan if x in invalids else x)
df["River_Mile_Headwaters"].fillna("00.0 MI", inplace=True)
df["Mile"] = pd.to_numeric(df["River_Mile_Headwaters"].str[0:4])
#Removing invalid entrees and selecting only numeric values
df["Latitude_DD"] = df["Latitude_DD"].map(lambda x: np.nan if x in invalids else x)
df["Latitude_DD"].fillna("00.0 MI", inplace=True)
df["Longitude_DD"] = df["Longitude_DD"].map(lambda x: np.nan if x in invalids else x)
df["Longitude_DD"].fillna("00.0 MI", inplace=True)
#Removing invalid entrees and selecting only numeric values
df["Actual_Result"] = df["Actual_Result"].map(lambda x: np.nan if x in invalids else x)
df["Actual_Result"] = df["Actual_Result"].str.lstrip('>')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('>')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('<')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('<')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('*')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('*')
df["Actual_Result"] = df["Actual_Result"].str.replace(',','')
df["Actual_Result"] = df["Actual_Result"].str.replace('%','')
df["Actual_Result"] = df["Actual_Result"].str.replace(' ','')
df["Actual_Result"] = df["Actual_Result"].str.replace('ND','')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('.')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('.')
df["Actual_Result"] = df["Actual_Result"].str.replace('6..25','6.25')
df["Actual_Result"] = df["Actual_Result"].str.replace('480.81546.25291','480.81546')
df["Actual_Result"] = df["Actual_Result"].str.replace('379\r\n379',"379")
#Functiont to check if string can be converted to numeric
#Input --> string
#Output --> 1 if convertable else 0
def isInt_try(v):
try: i = float(v)
except: return False
return True
# Applying above function to check any odd strings in Actual_Result Column
for i in df["Actual_Result"]:
if isInt_try(i) == 0:
print(i)
# Checking any odd strings in Actual_Result Column
for i in df["Actual_Result"]:
if str(i).count('.') >= 2:
print(i)
# Converting Actual_Result to numeric and Date_Collected to datetime data type
df["Actual_Result"] = pd.to_numeric(df["Actual_Result"])
df["Date_Collected"] = pd.to_datetime(df["Date_Collected"])
"Slicing for E.coli"
df_ecoli = df[df["Component_Name"] == "Escherichia coli"]
df_ecoli.head()
# Validating against the original report
result = df_ecoli.loc[(df_ecoli.Town == "Milford") & (df_ecoli.Date_Collected == pd.to_datetime("2017-11-21 00:00:00-05:00"))]["Actual_Result"]
result
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.formula.api as sm
%matplotlib inline
diab = pd.read_csv("../data/diabetes.csv")
print("""
# Variables are
# subject: subject ID number
# age: age diagnosed with diabetes
# acidity: a measure of acidity called base deficit
# y: natural log of serum C-peptide concentration
# Original source is Sockett et al. (1987)
# mentioned in Hastie and Tibshirani's book
# "Generalized Additive Models".
"""
)
xpred = pd.DataFrame({"age":np.arange(0,16.1,0.1)})
ax0 = diab.plot.scatter(x='age',y='y',c='Red',title="Diabetes data")
_ = ax0.set_xlabel("Age at Diagnosis")
_ = ax0.set_ylabel("Log C-Peptide Concentration")
```
## Linear Regression
```
model1 = sm.ols('y~age',data=diab)
fit1_lm = model1.fit()
pred1 = fit1_lm.predict(xpred)
prediction_output = fit1_lm.get_prediction(xpred).summary_frame()
ax1 = diab.plot.scatter(x='age',y='y',c='Red',title="Diabetes data with least-squares linear fit")
ax1.set_xlabel("Age at Diagnosis")
ax1.set_ylabel("Log C-Peptide Concentration")
ax1.plot(xpred.age, prediction_output['mean'],color="green")
ax1.plot(xpred.age, prediction_output['mean_ci_lower'], color="blue",linestyle="dashed")
ax1.plot(xpred.age, prediction_output['mean_ci_upper'], color="blue",linestyle="dashed");
ax1.plot(xpred.age, prediction_output['obs_ci_lower'], color="skyblue",linestyle="dashed")
ax1.plot(xpred.age, prediction_output['obs_ci_upper'], color="skyblue",linestyle="dashed");
```
`vander` is for Vandermonde. It's a matrix where the first column is $x^0$, the second is $x^1$, the third is $x^2$ and so on.
` np.vander([6,3,5], 4, increasing=True) =
array([[ 1, 6, 36, 216],
[ 1, 3, 9, 27],
[ 1, 5, 25, 125]])
`
It's therefore similar to sklearn's `polynomial_features`, but because `vander` is numpy it can be used directly in the formula.
Since we have a constant column in the matrix, we put a -1 in the formula to drop the additional constant term statsmodels would otherwise insert
Note that this is **not** an _orthogonal_ polynomial basis. Our estimated coeffecients will be more sensitive to the data than they need to be.
```
fit2_lm = sm.ols(formula="y ~ np.vander(age, 4, increasing=True) -1",data=diab).fit()
fit2_lm = sm.ols(formula="y ~ age + np.power(age, 2) + np.power(age, 3)",data=diab).fit()
poly_predictions = fit2_lm.get_prediction(xpred).summary_frame()
poly_predictions.head()
ax2 = diab.plot.scatter(x='age',y='y',c='Red',title="Diabetes data with least-squares cubic fit")
ax2.set_xlabel("Age at Diagnosis")
ax2.set_ylabel("Log C-Peptide Concentration")
ax2.plot(xpred.age, poly_predictions['mean'],color="green")
ax2.plot(xpred.age, poly_predictions['mean_ci_lower'], color="blue",linestyle="dashed")
ax2.plot(xpred.age, poly_predictions['mean_ci_upper'], color="blue",linestyle="dashed");
#ax2.plot(xpred.age, poly_predictions['obs_ci_lower'], color="skyblue",linestyle="dashed")
#ax2.plot(xpred.age, poly_predictions['obs_ci_upper'], color="skyblue",linestyle="dashed");
```
## Logistic Regression
```
diab['y_bin'] = 1*(diab['y'] > 4) # multiply by 1 because statsmodels wants 1s and 0s instead of true and false
logit_model = sm.logit("y_bin ~ age ", data = diab).fit()
logit_prediction = logit_model.predict(xpred)
from scipy.special import expit
import re
def get_logit_prediction_intervals(model, new_data_df):
if type(new_data_df) != pd.DataFrame:
raise TypeError('new_data_df must be a DataFrame')
# transform the raw data according to the formula
new_data_dict = {}
for x in model.params.index:
# only presently supports Intercept, a named column, and polynmoials created via np.vander
# the trick is finding the correct base column in the raw data
if x == "Intercept":
new_data_dict[x] = np.ones(new_data_df.shape[0])
elif x.startswith("np.vander("):
try:
will = re.match(r"np.vander\((.*), ?(.*)\)\[(.*)\]", x)
column, power, index = will.groups()
except e:
raise ValueError("Couldn't parse formula-derived feature {}".format(x))
new_data_dict[x] = np.vander(new_data_df.loc[:,column], int(power))[:,int(index)]
else:
new_data_dict[x] = new_data_df.loc[:,x]
new_data = pd.DataFrame(new_data_dict)
variance_mat = model.cov_params()
standard_devs = np.sqrt(np.sum(new_data.dot(variance_mat) * new_data, axis=1))
linear_predictions = new_data.dot(model.params)
output = pd.DataFrame({"lower": expit(linear_predictions - 1.96*standard_devs),
"predicted": expit(linear_predictions),
"upper": expit(linear_predictions + 1.96*standard_devs)
})
return output
logit_prediction_intervals = get_logit_prediction_intervals(logit_model, xpred)
logit_prediction_intervals
ax = diab.plot.scatter(x='age',y='y_bin',c='Red',title="Diabetes data with least-squares cubic fit")
ax.set_xlabel("Age at Diagnosis")
ax.set_ylabel("Log C-Peptide Concentration")
ax.plot(xpred.age, logit_prediction_intervals["predicted"],color="green")
ax.plot(xpred.age, logit_prediction_intervals["lower"], color="blue",linestyle="dashed")
ax.plot(xpred.age, logit_prediction_intervals["upper"], color="blue",linestyle="dashed");
plt.show()
logit_poly_model = sm.logit("y_bin ~ np.vander(age, 4) - 1", data = diab).fit()
logit_poly_prediction = logit_poly_model.predict(xpred)
ax = diab.plot.scatter(x='age',y='y_bin',c='Red',title="Diabetes data with least-squares cubic fit")
ax.set_xlabel("Age at Diagnosis")
ax.set_ylabel("Log C-Peptide Concentration")
logit_poly_prediction_intervals = get_logit_prediction_intervals(logit_poly_model, xpred)
ax.plot(xpred.age, logit_poly_prediction_intervals["predicted"],color="green")
ax.plot(xpred.age, logit_poly_prediction_intervals["lower"], color="blue",linestyle="dashed")
ax.plot(xpred.age, logit_poly_prediction_intervals["upper"], color="blue",linestyle="dashed");
plt.show()
```
## Lo(w)ess
```
from statsmodels.nonparametric.smoothers_lowess import lowess as lowess
lowess_models = {}
for cur_frac in [.15,.25,.7, 1]:
lowess_models[cur_frac] = lowess(diab['y'],diab['age'],frac=cur_frac)
```
**Note** Python's lowess implementation does not have any tool to predict on new data; it only returns the fitted function's value at the training points. We're making up for that by drawing a straight line between consecutive fitted values. (There are other more sophisticated interpolation techniques, but the ideal approach would be to predict on new points using lowess itself. This is a limitation of the Python implementation, not lowess itself)
```
from scipy.interpolate import interp1d
for cur_frac, cur_model in lowess_models.items():
ax = diab.plot.scatter(x='age',y='y',c='Red',title="Lowess Fit, Fraction = {}".format(cur_frac))
ax.set_xlabel("Age at Diagnosis")
ax.set_ylabel("Log C-Peptide Concentration")
lowess_interpolation = interp1d(cur_model[:,0], cur_model[:,1], bounds_error=False)
ax.plot(xpred, lowess_interpolation(xpred), color="Blue")
plt.show()
ax = diab.plot.scatter(x='age',y='y',c='Red',title="Large variance, low bias smoother")
ax.set_xlabel("Age at Diagnosis")
ax.set_ylabel("Log C-Peptide Concentration")
lowess_interpolation = interp1d(lowess_models[.15][:,0], lowess_models[.15][:,1], bounds_error=False)
ax.plot(xpred, lowess_interpolation(xpred), color="lightgreen")
plt.show()
ax = diab.plot.scatter(x='age',y='y',c='Red',title="Low variance, large bias smoother")
ax.set_xlabel("Age at Diagnosis")
ax.set_ylabel("Log C-Peptide Concentration")
lowess_interpolation = interp1d(lowess_models[1][:,0], lowess_models[1][:,1], bounds_error=False)
ax.plot(xpred, lowess_interpolation(xpred), color="lightgreen")
plt.show()
```
## Splines (via knots)
Define a Relu/Truncated cubic function
```
def h(x, knot, exponent):
output = np.power(x-knot, exponent)
output[x<=knot] = 0
return output
```
Transforming the x values [0,10] with a knot at 4, power 1
```
xvals = np.arange(0,10.1,0.1)
plt.plot(xvals, h(xvals,4,1), color="red")
plt.title("Truncated linear basis function with knot at x=4")
plt.xlabel("$x$")
plt.ylabel("$(x-4)_+$") #note the use of TeX in the label
plt.show()
```
Transforming the x values [0,10] with a knot at 4, power 3
```
plt.plot(xvals,h(xvals,4,3),color="red")
plt.title("Truncated cubic basis function with knot at x=4")
plt.xlabel("$x$")
plt.ylabel("$(x-4)_+^3$")
plt.show()
```
The sum of three RELUs with different knots and different coeffecients
```
plt.plot(xvals, 3*h(xvals,2,1) - 4*h(xvals,5,1) + 0.5*h(xvals,8,1), color="red")
plt.title("Piecewise linear spline with knots at x=2, 5, and 8")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.show()
```
Above, but with a starting slope and intercept
```
plt.plot(xvals, 2 + xvals + 3*h(xvals,2,1) - 4*h(xvals,5,1) + 0.5*h(xvals,8,1), color="red")
plt.title("Piecewise linear spline with knots at x=2, 5, and 8\n plus a starting slope and intercept")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.show()
```
Using OLS, we can find optimal coeffecients for RELUs with pre-specified knots, just like we can find optimal coeffecients for $x^2$ and $x^3$
```
# generate some fake data to fit
x = np.arange(0.1,10,9.9/100)
from scipy.stats import norm
y = norm.ppf(x/10) + np.random.normal(0,0.4,100)
fitted_spline_model = sm.ols('y~x+h(x,2,1)+h(x,5,1)+h(x,8,1)',data={'x':x,'y':y}).fit()
plt.scatter(x,y,facecolors='none', edgecolors='black')
plt.title("3 knots")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.plot(x, fitted_spline_model.predict(),color="darkblue", linewidth=2, label="Spline with knots at 2,5,8")
plt.plot(x, norm.ppf(x/10), color="red", label="Truth")
plt.legend()
plt.show()
```
More knots
```
fitted_spline_model = sm.ols('y~x+h(x,1,1)+h(x,2,1)+h(x,3.5,1)+h(x,5,1)+h(x,6.5,1)+h(x,8,1)',data={'x':x,'y':y}).fit()
plt.scatter(x,y,facecolors='none', edgecolors='black')
plt.title("6 knots")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.plot(x, fitted_spline_model.predict(),color="darkblue", label="Linear Spline with knots at\n1, 2, 3.5, 5, 6.5, 8")
plt.plot(x, norm.ppf(x/10), color="red", label="Truth")
plt.legend()
plt.show()
```
More knots
```
fitted_spline_model = sm.ols('y~x+h(x,1,1)+h(x,2,1)+h(x,3,1)+h(x,4,1)+h(x,5,1)+h(x,6,1)+h(x,7,1)+h(x,8,1)+h(x,9,1)',
data={'x':x,'y':y}).fit()
plt.scatter(x,y,facecolors='none', edgecolors='black')
plt.title("9 knots")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.plot(x, fitted_spline_model.predict(),color="darkblue", label="Linear Spline with 9 knots")
plt.plot(x, norm.ppf(x/10), color="red", label="Truth")
plt.legend()
plt.show()
```
Using code to write out the formula this time
```
n_knots = 25
components = ['h(x,{},1)'.format(x) for x in np.linspace(0,10,n_knots)]
formula = ' + '.join(components)
final_formula = 'y ~ x + ' + formula
final_formula
fitted_spline_model = sm.ols(final_formula,data={'x':x,'y':y}).fit()
plt.scatter(x,y,facecolors='none', edgecolors='black')
plt.title("25 knots")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.plot(x, fitted_spline_model.predict(),color="darkblue", label="Linear Spline with 25 knots")
plt.plot(x, norm.ppf(x/10), color="red", label="Truth")
plt.legend()
plt.show()
```
Cubic splines, instead of linear. Still using code to write the formula
```
components = ['h(x,{},3)'.format(x) for x in [2,5,8]]
formula = ' + '.join(components)
final_formula = 'y~x + np.power(x,2) + np.power(x,3) + ' + formula
fitted_spline_model = sm.ols(final_formula,data={'x':x,'y':y}).fit()
plt.scatter(x,y,facecolors='none', edgecolors='black')
plt.title("3 knots")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.plot(x, fitted_spline_model.predict(),color="darkblue", label="Cubic Spline with 3 knots")
plt.plot(x, norm.ppf(x/10), color="red", label="Truth")
plt.legend()
plt.show()
components = ['h(x,{},3)'.format(x) for x in [1,2,3.5,5,6.5,8]]
formula = ' + '.join(components)
final_formula = 'y~x + np.power(x,2) + np.power(x,3) + ' + formula
fitted_spline_model = sm.ols(final_formula,data={'x':x,'y':y}).fit()
plt.scatter(x,y,facecolors='none', edgecolors='black')
plt.title("6 knots")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.plot(x, fitted_spline_model.predict(),color="darkblue", label="Cubic Spline with 6 knots")
plt.plot(x, norm.ppf(x/10), color="red", label="Truth")
plt.legend()
plt.show()
n_knots = 9
components = ['h(x,{},3)'.format(x) for x in np.linspace(0,10,n_knots)]
formula = ' + '.join(components)
final_formula = 'y~x + np.power(x,2) + np.power(x,3) + ' + formula
fitted_spline_model = sm.ols(final_formula,data={'x':x,'y':y}).fit()
plt.scatter(x,y,facecolors='none', edgecolors='black')
plt.title("9 knots")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.plot(x, fitted_spline_model.predict(),color="darkblue", label="Cubic Spline with 9 knots")
plt.plot(x, norm.ppf(x/10), color="red", label="Truth")
plt.legend()
plt.show()
n_knots = 25
components = ['h(x,{},3)'.format(x) for x in np.linspace(0,10,n_knots)]
formula = ' + '.join(components)
final_formula = 'y~x + np.power(x,2) + np.power(x,3) + ' + formula
fitted_spline_model = sm.ols(final_formula,data={'x':x,'y':y}).fit()
plt.scatter(x,y,facecolors='none', edgecolors='black')
plt.title("25 knots")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.plot(x, fitted_spline_model.predict(),color="darkblue", label="Cubic Spline with 25 knots")
plt.plot(x, norm.ppf(x/10), color="red", label="Truth")
plt.legend()
plt.show()
```
## Smoothing splines
```
from scipy.interpolate import UnivariateSpline
```
This method won't allow tied values, and wants its values in sorted order. Add a tiny bit of noise to the x values and sort them.
```
diab['noisy_age'] = diab['age'] + np.random.normal(0,.001, len(diab))
sorted_noisy_diab = diab.sort_values(["noisy_age"])
smoothing_spline_dict = {}
for cur_smoothing in [0, 5, 10, 20, np.inf]:
cur_spline = UnivariateSpline(sorted_noisy_diab['noisy_age'],sorted_noisy_diab['y'], s=cur_smoothing)
ax = diab.plot.scatter(x='age',y='y',c='Red',title="Smoothing Spline with s={}".format(cur_smoothing))
ax.plot(xpred, cur_spline(xpred))
# the jaggedness in the original came from plot's implicit linear interpolation
# lowess_interpolation = interp1d(diab['age'], cur_spline(diab['age']), bounds_error=False)
# ax.plot(xpred, lowess_interpolation(xpred), color="Blue")
ax.set_ylim(2,7)
```
Even when we request infinite smoothness, we don't end up with a horizontal line (no derivatives at all)- we end up with a single cubic curve. That's because we chose a cubic spline.
In general, this implementation's smoothness regularization penalizes any derivatives _beyond_ what our basic spline needs. So with k=3, as above, the penalty is on the 4th derivative, and with k=2 the penalty is on the 3rd derivative and the "infinitely smooth" result will be a parabola. (i.e. a curve with 3rd derivative=0 everywhere)
Selecting smoothing level by CV
```
from sklearn.model_selection import KFold
from sklearn.metrics import r2_score
candidate_smoothings = [0, 5, 10, 20, 200]
kf = KFold(n_splits=5, random_state=47, shuffle=True)
scores = np.zeros((5,len(candidate_smoothings)))
for i, (train_index, test_index) in enumerate(kf.split(sorted_noisy_diab)):
train_df = sorted_noisy_diab.iloc[train_index,:]
test_df = sorted_noisy_diab.iloc[test_index,:]
for j,cur_smoothing in enumerate(candidate_smoothings):
cur_model = UnivariateSpline(train_df['noisy_age'],train_df['y'], s=cur_smoothing)
scores[i,j] = r2_score(test_df['y'], cur_model(test_df['noisy_age']))
np.mean(scores, axis=0)
best_s = candidate_smoothings[np.argmax(np.mean(scores, axis=0))]
ax = diab.plot.scatter(x='age',y='y',c='Red',title="smoothing spline with s={}, chosen by cross-validation".format(best_s))
best_model = UnivariateSpline(sorted_noisy_diab['noisy_age'],sorted_noisy_diab['y'], s=best_s)
ax.plot(xpred, best_model(xpred), color="darkgreen")
plt.show()
#We will now work with a new dataset, called GAGurine.
#The dataset description (from the R package MASS) is below:
print("""
# Data were collected on the concentration of a chemical GAG
# in the urine of 314 children aged from zero to seventeen years.
# The aim of the study was to produce a chart to help a paediatrican
# to assess if a child's GAG concentration is ‘normal’.
# The variables are:
# Age: age of child in years.
# GAG: concentration of GAG (the units have been lost).
""")
GAGurine = pd.read_csv("../data/GAGurine.csv")
GAGurine['Age'] = GAGurine['Age']+np.random.normal(0,0.001, len(GAGurine))
GAGurine = GAGurine.sort_values(['Age'])
ax = GAGurine.plot.scatter(x='Age',y='GAG',c='black',title="GAG in urine of children")
ax.set_xlabel("Age")
ax.set_ylabel("GAG")
plt.show()
```
Get quartiles
```
quarts = GAGurine['Age'].quantile([0.25, 0.5, 0.75]).values.reshape(-1)
```
Build a Bspline model. Call `splrep` (spline representation) to find the knots and coeffecients that smooth the given data, then call BSpline to build something that can predict on given values.
```
from scipy.interpolate import splrep
from scipy.interpolate import BSpline
t,c,k = splrep(GAGurine['Age'].values, GAGurine['GAG'].values, t=quarts)
b_spline_model = BSpline(t,c,k)
b_spline_model(7)
```
`LSQUnivariateSpline` fits splines to data, using user-specified knots
```
from scipy.interpolate import LSQUnivariateSpline
natural_spline_model = LSQUnivariateSpline(GAGurine['Age'].values, GAGurine['GAG'].values, quarts)
ax = GAGurine.plot.scatter(x='Age',y='GAG',c='grey',title="GAG in urine of children")
ax.plot(GAGurine['Age'], b_spline_model(GAGurine['Age']), label="B-spline, knots at quartiles")
plt.legend()
plt.show()
```
## GAMs
```
kyphosis = pd.read_csv("../data/kyphosis.csv")
kyphosis["outcome"] = 1*(kyphosis["Kyphosis"] == "present")
kyphosis.describe()
from pygam import LogisticGAM, s
X = kyphosis[["Age","Number","Start"]]
y = kyphosis["outcome"]
kyph_gam = LogisticGAM(s(0)+s(1)+s(2)).fit(X,y)
```
GAMs provide plots of the effect of increasing each variable (conditional on / adjusted for the other variables)
```
res = kyph_gam.deviance_residuals(X,y)
for i, term in enumerate(kyph_gam.terms):
if term.isintercept:
continue
XX = kyph_gam.generate_X_grid(term=i)
pdep, confi = kyph_gam.partial_dependence(term=i, X=XX, width=0.95)
pdep2, _ = kyph_gam.partial_dependence(term=i, X=X, width=0.95)
plt.figure()
plt.scatter(X.iloc[:,term.feature], pdep2 + res)
plt.plot(XX[:, term.feature], pdep)
plt.plot(XX[:, term.feature], confi, c='r', ls='--')
plt.title(X.columns.values[term.feature])
plt.show()
```
AIC is a measure of model quality, estimating performance on a test set (without actually needing a test set). It can be used to compare and select two models.
```
kyph_gam.summary()
X = kyphosis[["Age","Number","Start"]]
y = kyphosis["outcome"]
small_kyph_gam = LogisticGAM(s(0)+s(2)).fit(X,y)
res = small_kyph_gam.deviance_residuals(X,y)
for i, term in enumerate(small_kyph_gam.terms):
if term.isintercept:
continue
XX = small_kyph_gam.generate_X_grid(term=i)
pdep, confi = small_kyph_gam.partial_dependence(term=i, X=XX, width=0.95)
pdep2, _ = small_kyph_gam.partial_dependence(term=i, X=X, width=0.95)
plt.figure()
plt.scatter(X.iloc[:,term.feature], pdep2 + res)
plt.plot(XX[:, term.feature], pdep)
plt.plot(XX[:, term.feature], confi, c='r', ls='--')
plt.title(X.columns.values[term.feature])
plt.show()
```
The original model's AIC was lower, so we prefer that model- it is expected to do better on out-of-sample data.
```
small_kyph_gam.summary()
```
| github_jupyter |
# MATH 4100: Temporal data analysis and applications to stock analysis
*Curtis Miller*
## Introduction
This is a lecture for [MATH 4100/CS 5160: Introduction to Data Science](http://datasciencecourse.net/), offered at the University of Utah, introducing time series data analysis applied to finance.
Advanced mathematics and statistics have been present in finance for some time. Prior to the 1980s, banking and finance were well-known for being "boring"; investment banking was distinct from commercial banking and the primary role of the industry was handling "simple" (at least in comparison to today) financial instruments, such as loans. Deregulation under the Regan administration, coupled with an influx of mathematical talent, transformed the industry from the "boring" business of banking to what it is today, and since then, finance has joined the other sciences as a motivation for mathematical research and advancement. For example one of the biggest recent achievements of mathematics was the derivation of the [Black-Scholes formula](https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model), which facilitated the pricing of stock options (a contract giving the holder the right to purchase or sell a stock at a particular price to the issuer of the option). That said, [bad statistical models, including the Black-Scholes formula, hold part of the blame for the 2008 financial crisis](https://www.theguardian.com/science/2012/feb/12/black-scholes-equation-credit-crunch).
In recent years, computer science has joined advanced mathematics in revolutionizing finance and **trading**, the practice of buying and selling of financial assets for the purpose of making a profit. In recent years, trading has become dominated by computers; algorithms are responsible for making rapid split-second trading decisions faster than humans could make (so rapidly, [the speed at which light travels is a limitation when designing systems](http://www.nature.com/news/physics-in-finance-trading-at-the-speed-of-light-1.16872)). Additionally, [machine learning and data mining techniques are growing in popularity](http://www.ft.com/cms/s/0/9278d1b6-1e02-11e6-b286-cddde55ca122.html#axzz4G8daZxcl) in the financial sector, and likely will continue to do so. For example, **high-frequency trading (HFT)** is a branch of algorithmic trading where computers make thousands of trades in short periods of time, engaging in complex strategies such as statistical arbitrage and market making. While algorithms may outperform humans, the technology is still new and playing an increasing role in a famously turbulent, high-stakes arena. HFT was responsible for phenomena such as the [2010 flash crash](https://en.wikipedia.org/wiki/2010_Flash_Crash) and a [2013 flash crash](http://money.cnn.com/2013/04/24/investing/twitter-flash-crash/) prompted by a hacked [Associated Press tweet](http://money.cnn.com/2013/04/23/technology/security/ap-twitter-hacked/index.html?iid=EL) about an attack on the White House.
This lecture, however, will not be about how to crash the stock market with bad mathematical models or trading algorithms. Instead, I intend to provide you with basic tools for handling and analyzing stock market data with Python. We will be using stock data as a first exposure to **time series data**, which is data considered dependent on the time it was observed (other examples of time series include temperature data, demand for energy on a power grid, Internet server load, and many, many others). I will also discuss moving averages, how to construct trading strategies using moving averages, how to formulate exit strategies upon entering a position, and how to evaluate a strategy with backtesting.
**DISCLAIMER: THIS IS NOT FINANCIAL ADVICE!!! Furthermore, I have ZERO experience as a trader (a lot of this knowledge comes from a one-semester course on stock trading I took at Salt Lake Community College)! This is purely introductory knowledge, not enough to make a living trading stocks. People can and do lose money trading stocks, and you do so at your own risk!**
## Preliminaries
I will be using two packages, **quandl** and **pandas_datareader**, which are not installed with [Anaconda](https://www.anaconda.com/) if you are using it. To install these packages, run the following at the appropriate command prompt:
conda install quandl
conda install pandas-datareader
## Getting and Visualizing Stock Data
### Getting Data from Quandl
Before we analyze stock data, we need to get it into some workable format. Stock data can be obtained from [Yahoo! Finance](http://finance.yahoo.com), [Google Finance](http://finance.google.com), or a number of other sources. These days I recommend getting data from [Quandl](https://www.quandl.com/), a provider of community-maintained financial and economic data. (Yahoo! Finance used to be the go-to source for good quality stock data, but the API was discontinued in 2017 and reliable data can no longer be obtained: see [this question/answer on StackExchange](https://quant.stackexchange.com/questions/35019/is-yahoo-finance-data-good-or-bad-now) for more details.)
By default the `get()` function in **quandl** will return a **pandas** `DataFrame` containing the fetched data.
```
import pandas as pd
import quandl
import datetime
# We will look at stock prices over the past year, starting at January 1, 2016
start = datetime.datetime(2016,1,1)
end = datetime.date.today()
# Let's get Apple stock data; Apple's ticker symbol is AAPL
# First argument is the series we want, second is the source ("yahoo" for Yahoo! Finance), third is the start date, fourth is the end date
s = "AAPL"
apple = quandl.get("WIKI/" + s, start_date=start, end_date=end)
type(apple)
apple.head()
```
Let's briefly discuss this. **Open** is the price of the stock at the beginning of the trading day (it need not be the closing price of the previous trading day), **high** is the highest price of the stock on that trading day, **low** the lowest price of the stock on that trading day, and **close** the price of the stock at closing time. **Volume** indicates how many stocks were traded. **Adjusted** prices (such as the adjusted close) is the price of the stock that adjusts the price for corporate actions. While stock prices are considered to be set mostly by traders, **stock splits** (when the company makes each extant stock worth two and halves the price) and **dividends** (payout of company profits per share) also affect the price of a stock and should be accounted for.
### Visualizing Stock Data
Now that we have stock data we would like to visualize it. I first demonstrate how to do so using the **matplotlib** package. Notice that the `apple` `DataFrame` object has a convenience method, `plot()`, which makes creating plots easier.
```
import matplotlib.pyplot as plt # Import matplotlib
# This line is necessary for the plot to appear in a Jupyter notebook
%matplotlib inline
# Control the default size of figures in this Jupyter notebook
%pylab inline
pylab.rcParams['figure.figsize'] = (15, 9) # Change the size of plots
apple["Adj. Close"].plot(grid = True) # Plot the adjusted closing price of AAPL
```
A linechart is fine, but there are at least four variables involved for each date (open, high, low, and close), and we would like to have some visual way to see all four variables that does not require plotting four separate lines. Financial data is often plotted with a **Japanese candlestick plot**, so named because it was first created by 18th century Japanese rice traders. Such a chart can be created with **matplotlib**, though it requires considerable effort.
I have made a function you are welcome to use to more easily create candlestick charts from **pandas** data frames, and use it to plot our stock data. (Code is based off [this example](http://matplotlib.org/examples/pylab_examples/finance_demo.html), and you can read the documentation for the functions involved [here](http://matplotlib.org/api/finance_api.html).)
```
from matplotlib.dates import DateFormatter, WeekdayLocator,\
DayLocator, MONDAY
from matplotlib.finance import candlestick_ohlc
def pandas_candlestick_ohlc(dat, stick = "day", adj = False, otherseries = None):
"""
:param dat: pandas DataFrame object with datetime64 index, and float columns "Open", "High", "Low", and "Close", likely created via DataReader from "yahoo"
:param stick: A string or number indicating the period of time covered by a single candlestick. Valid string inputs include "day", "week", "month", and "year", ("day" default), and any numeric input indicates the number of trading days included in a period
:param adj: A boolean indicating whether to use adjusted prices
:param otherseries: An iterable that will be coerced into a list, containing the columns of dat that hold other series to be plotted as lines
This will show a Japanese candlestick plot for stock data stored in dat, also plotting other series if passed.
"""
mondays = WeekdayLocator(MONDAY) # major ticks on the mondays
alldays = DayLocator() # minor ticks on the days
dayFormatter = DateFormatter('%d') # e.g., 12
# Create a new DataFrame which includes OHLC data for each period specified by stick input
fields = ["Open", "High", "Low", "Close"]
if adj:
fields = ["Adj. " + s for s in fields]
transdat = dat.loc[:,fields]
transdat.columns = pd.Index(["Open", "High", "Low", "Close"])
if (type(stick) == str):
if stick == "day":
plotdat = transdat
stick = 1 # Used for plotting
elif stick in ["week", "month", "year"]:
if stick == "week":
transdat["week"] = pd.to_datetime(transdat.index).map(lambda x: x.isocalendar()[1]) # Identify weeks
elif stick == "month":
transdat["month"] = pd.to_datetime(transdat.index).map(lambda x: x.month) # Identify months
transdat["year"] = pd.to_datetime(transdat.index).map(lambda x: x.isocalendar()[0]) # Identify years
grouped = transdat.groupby(list(set(["year",stick]))) # Group by year and other appropriate variable
plotdat = pd.DataFrame({"Open": [], "High": [], "Low": [], "Close": []}) # Create empty data frame containing what will be plotted
for name, group in grouped:
plotdat = plotdat.append(pd.DataFrame({"Open": group.iloc[0,0],
"High": max(group.High),
"Low": min(group.Low),
"Close": group.iloc[-1,3]},
index = [group.index[0]]))
if stick == "week": stick = 5
elif stick == "month": stick = 30
elif stick == "year": stick = 365
elif (type(stick) == int and stick >= 1):
transdat["stick"] = [np.floor(i / stick) for i in range(len(transdat.index))]
grouped = transdat.groupby("stick")
plotdat = pd.DataFrame({"Open": [], "High": [], "Low": [], "Close": []}) # Create empty data frame containing what will be plotted
for name, group in grouped:
plotdat = plotdat.append(pd.DataFrame({"Open": group.iloc[0,0],
"High": max(group.High),
"Low": min(group.Low),
"Close": group.iloc[-1,3]},
index = [group.index[0]]))
else:
raise ValueError('Valid inputs to argument "stick" include the strings "day", "week", "month", "year", or a positive integer')
# Set plot parameters, including the axis object ax used for plotting
fig, ax = plt.subplots()
fig.subplots_adjust(bottom=0.2)
if plotdat.index[-1] - plotdat.index[0] < pd.Timedelta('730 days'):
weekFormatter = DateFormatter('%b %d') # e.g., Jan 12
ax.xaxis.set_major_locator(mondays)
ax.xaxis.set_minor_locator(alldays)
else:
weekFormatter = DateFormatter('%b %d, %Y')
ax.xaxis.set_major_formatter(weekFormatter)
ax.grid(True)
# Create the candelstick chart
candlestick_ohlc(ax, list(zip(list(date2num(plotdat.index.tolist())), plotdat["Open"].tolist(), plotdat["High"].tolist(),
plotdat["Low"].tolist(), plotdat["Close"].tolist())),
colorup = "black", colordown = "red", width = stick * .4)
# Plot other series (such as moving averages) as lines
if otherseries != None:
if type(otherseries) != list:
otherseries = [otherseries]
dat.loc[:,otherseries].plot(ax = ax, lw = 1.3, grid = True)
ax.xaxis_date()
ax.autoscale_view()
plt.setp(plt.gca().get_xticklabels(), rotation=45, horizontalalignment='right')
plt.show()
pandas_candlestick_ohlc(apple, adj=True)
```
With a candlestick chart, a black candlestick indicates a day where the closing price was higher than the open (a gain), while a red candlestick indicates a day where the open was higher than the close (a loss). The wicks indicate the high and the low, and the body the open and close (hue is used to determine which end of the body is the open and which the close). Candlestick charts are popular in finance and some strategies in [technical analysis](https://en.wikipedia.org/wiki/Technical_analysis) use them to make trading decisions, depending on the shape, color, and position of the candles. I will not cover such strategies today.
We may wish to plot multiple financial instruments together; we may want to compare stocks, compare them to the market, or look at other securities such as [exchange-traded funds (ETFs)](https://en.wikipedia.org/wiki/Exchange-traded_fund). Later, we will also want to see how to plot a financial instrument against some indicator, like a moving average. For this you would rather use a line chart than a candlestick chart. (How would you plot multiple candlestick charts on top of one another without cluttering the chart?)
Below, I get stock data for some other tech companies and plot their adjusted close together.
```
microsoft, google = (quandl.get("WIKI/" + s, start_date=start, end_date=end) for s in ["MSFT", "GOOG"])
# Below I create a DataFrame consisting of the adjusted closing price of these stocks, first by making a list of these objects and using the join method
stocks = pd.DataFrame({"AAPL": apple["Adj. Close"],
"MSFT": microsoft["Adj. Close"],
"GOOG": google["Adj. Close"]})
stocks.head()
stocks.plot(grid = True)
```
What's wrong with this chart? While absolute price is important (pricy stocks are difficult to purchase, which affects not only their volatility but *your* ability to trade that stock), when trading, we are more concerned about the relative change of an asset rather than its absolute price. Google's stocks are much more expensive than Apple's or Microsoft's, and this difference makes Apple's and Microsoft's stocks appear much less volatile than they truly are (that is, their price appears to not deviate much).
One solution would be to use two different scales when plotting the data; one scale will be used by Apple and Microsoft stocks, and the other by Google.
```
stocks.plot(secondary_y = ["AAPL", "MSFT"], grid = True)
```
A "better" solution, though, would be to plot the information we actually want: the stock's returns. This involves transforming the data into something more useful for our purposes. There are multiple transformations we could apply.
One transformation would be to consider the stock's return since the beginning of the period of interest. In other words, we plot:
\begin{equation*}
\text{return}_{t,0} = \frac{\text{price}_t}{\text{price}_0}
\end{equation*}
This will require transforming the data in the `stocks` object, which I do next. Notice that I am using a **lambda function**, which allows me to pass a small function defined quickly as a parameter to another function or method (you can read more about lambda functions [here](https://docs.python.org/3/reference/expressions.html#lambda)).
```
# df.apply(arg) will apply the function arg to each column in df, and return a DataFrame with the result
# Recall that lambda x is an anonymous function accepting parameter x; in this case, x will be a pandas Series object
stock_return = stocks.apply(lambda x: x / x[0])
stock_return.head()
stock_return.plot(grid = True).axhline(y = 1, color = "black", lw = 2)
```
This is a much more useful plot. We can now see how profitable each stock was since the beginning of the period. Furthermore, we see that these stocks are highly correlated; they generally move in the same direction, a fact that was difficult to see in the other charts.
Alternatively, we could plot the change of each stock per day. One way to do so would be to plot the percentage increase of a stock when comparing day $t$ to day $t + 1$, with the formula:
\begin{equation*}
\text{growth}_t = \frac{\text{price}_{t + 1} - \text{price}_t}{\text{price}_t}
\end{equation*}
But change could be thought of differently as:
\begin{equation*}
\text{increase}_t = \frac{\text{price}_{t} - \text{price}_{t-1}}{\text{price}_t}
\end{equation*}
These formulas are not the same and can lead to differing conclusions, but there is another way to model the growth of a stock: with log differences.
\begin{equation*}
\text{change}_t = \log(\text{price}_{t}) - \log(\text{price}_{t - 1})
\end{equation*}
(Here, $\log$ is the natural log, and our definition does not depend as strongly on whether we use $\log(\text{price}_{t}) - \log(\text{price}_{t - 1})$ or $\log(\text{price}_{t+1}) - \log(\text{price}_{t})$.) The advantage of using log differences is that this difference can be interpreted as the percentage change in a stock but does not depend on the denominator of a fraction. Additionally, log differences have a desirable property: the sum of the log differences can be interpreted as the total change (as a percentage) over the period summed (which is not a property of the other formulations; they will overestimate growth). Log differences also more cleanly correspond to how stock prices are modeled in continuous time.
We can obtain and plot the log differences of the data in `stocks` as follows:
```
# Let's use NumPy's log function, though math's log function would work just as well
import numpy as np
stock_change = stocks.apply(lambda x: np.log(x) - np.log(x.shift(1))) # shift moves dates back by 1.
stock_change.head()
stock_change.plot(grid = True).axhline(y = 0, color = "black", lw = 2)
```
Which transformation do you prefer? Looking at returns since the beginning of the period make the overall trend of the securities in question much more apparent. Changes between days, though, are what more advanced methods actually consider when modelling the behavior of a stock. so they should not be ignored.
We often want to compare the performance of stocks to the performance of the overall market. [SPY](https://finance.yahoo.com/quote/SPY/), which is the ticker symbol for the SPDR S&P 500 exchange-traded mutual fund (ETF), is a fund that attempts only to imitate the composition of the [S&P 500 stock index](https://finance.yahoo.com/quote/%5EGSPC?p=^GSPC), and thus represents the value in "the market."
SPY data is not available for free from Quandl, so I will get this data from Yahoo! Finance. (I don't have a choice.)
Below I get data for SPY and compare its performance to the performance of our stocks.
```
#import pandas_datareader.data as web # Going to get SPY from Yahoo! (I know I said you shouldn't but I didn't have a choice)
#spyder = web.DataReader("SPY", "yahoo", start, end) # Didn't work
#spyder = web.DataReader("SPY", "google", start, end) # Didn't work either
# If all else fails, read from a file, obtained from here: http://www.nasdaq.com/symbol/spy/historical
spyderdat = pd.read_csv("/home/curtis/Downloads/HistoricalQuotes.csv") # Obviously specific to my system; set to
# location on your machine
spyderdat = pd.DataFrame(spyderdat.loc[:, ["open", "high", "low", "close", "close"]].iloc[1:].as_matrix(),
index=pd.DatetimeIndex(spyderdat.iloc[1:, 0]),
columns=["Open", "High", "Low", "Close", "Adj Close"]).sort_index()
spyder = spyderdat.loc[start:end]
stocks = stocks.join(spyder.loc[:, "Adj Close"]).rename(columns={"Adj Close": "SPY"})
stocks.head()
stock_return = stocks.apply(lambda x: x / x[0])
stock_return.plot(grid = True).axhline(y = 1, color = "black", lw = 2)
stock_change = stocks.apply(lambda x: np.log(x) - np.log(x.shift(1)))
stock_change.plot(grid=True).axhline(y = 0, color = "black", lw = 2)
```
## Classical Risk Metrics
From what we have so far we can already compute informative metrics for our stocks, which can be considered some measure of risk.
First, we will want to **annualize** our returns, thus computing the **annual percentage rate (APR)**. This helps us keep returns on a common time scale.
```
stock_change_apr = stock_change * 252 * 100 # There are 252 trading days in a year; the 100 converts to percentages
stock_change_apr.tail()
```
Some of these numbers look initially like nonsense, but that's okay for now.
The metrics I want are:
* The average return
* Volatility (the standard deviation of returns)
* $\alpha$ and $\beta$
* The Sharpe ratio
The first two metrics are largely self-explanatory, but the latter two need explaining.
First, the **risk-free rate**, which I denote by $r_{RF}$, is the rate of return on a risk-free financial asset. This asset exists only in theory but often yields on low-risk instruments like 3-month U.S. Treasury Bills can be viewed as being virtually risk-free and thus their yields can be used to approximate the risk-free rate. I get the data for these instruments below.
```
tbill = quandl.get("FRED/TB3MS", start_date=start, end_date=end)
tbill.tail()
tbill.plot()
rrf = tbill.iloc[-1, 0] # Get the most recent Treasury Bill rate
rrf
```
Now, a **linear regression model** is a model of the following form:
$$y_i = \alpha + \beta x_i + \epsilon_i$$
$\epsilon_i$ is an error process. Another way to think of this process model is:
$$\hat{y}_i = \alpha + \beta x_i$$
$\hat{y}_i$ is the **predicted value** of $y_i$ given $x_i$. In other words, a linear regression model tells you how $x_i$ and $y_i$ are related, and how values of $x_i$ can be used to predict values of $y_i$. $\alpha$ is the **intercept** of the model and $\beta$ is the **slope**. In particular, $\alpha$ would be the predicted value of $y$ if $x$ were zero, and $\beta$ gives how much $y$ changes when $x$ changes by one unit.
There is an easy way to compute $\alpha$ and $\beta$ given the sample means $\bar{x}$ and $\bar{y}$ and sample standard deviations $s_x$ and $s_y$ and the correlation between $x$ and $y$, denoted with $r$:
$$\beta = r \frac{s_y}{s_x}$$
$$\alpha = \bar{y} - \beta \bar{x}$$
In finance, we use $\alpha$ and $\beta$ like so:
$$R_t - r_{RF} = \alpha + \beta (R_{Mt} - r_{RF}) + \epsilon_t$$
$R_t$ is the return of a financial asset (a stock) and $R_t - r_{RF}$ is the **excess return**, or return exceeding the risk-free rate of return. $R_{Mt}$ is the return of the *market* at time $t$. Then $\alpha$ and $\beta can be interpreted like so:
* $\alpha$ is average excess return over the market.
* $\beta$ is how much a stock moves in relation to the market. If $\beta > 0$ then the stock generally moves in the same direction as the market, while when $\beta < 0$ the stock generally moves in the opposite direction. If $|\beta| > 1$ the stock moves strongly in response to the market $|\beta| < 1$ the stock is less responsive to the market.
Below I get a **pandas** `Series` that contains how much each stock is correlated with SPY (our approximation of the market).
```
smcorr = stock_change_apr.drop("SPY", 1).corrwith(stock_change_apr.SPY) # Since RRF is constant it doesn't change the
# correlation so we can ignore it in our
# calculation
smcorr
```
Then I compute $\alpha$ and $\beta$.
```
sy = stock_change_apr.drop("SPY", 1).std()
sx = stock_change_apr.SPY.std()
sy
sx
ybar = stock_change_apr.drop("SPY", 1).mean() - rrf
xbar = stock_change_apr.SPY.mean() - rrf
ybar
xbar
beta = smcorr * sy / sx
alpha = ybar - beta * xbar
beta
alpha
```
The **Sharpe ratio** is another popular risk metric, defined below:
$$\text{Sharpe ratio} = \frac{\bar{R_t} - r_{RF}}{s}$$
Here $s$ is the volatility of the stock. We want the sharpe ratio to be large. A large Sharpe ratio indicates that the stock's excess returns are large relative to the stock's volatilitly. Additionally, the Sharpe ratio is tied to a statistical test (the $t$-test) to determine if a stock earns more on average than the risk-free rate; the larger this ratio, the more likely this is to be the case.
Your challenge now is to compute the Sharpe ratio for each stock listed here, and interpret it. Which stock seems to be the better investment according to the Sharpe ratio?
```
# Your code here
```
## Moving Averages
Charts are very useful. In fact, some traders base their strategies almost entirely off charts (these are the "technicians", since trading strategies based off finding patterns in charts is a part of the trading doctrine known as **technical analysis**). Let's now consider how we can find trends in stocks.
A **$q$-day moving average** is, for a series $x_t$ and a point in time $t$, the average of the past $q$ days: that is, if $MA^q_t$ denotes a moving average process, then:
\begin{equation*}
MA^q_t = \frac{1}{q} \sum_{i = 0}^{q-1} x_{t - i}
\end{equation*}
Moving averages smooth a series and helps identify trends. The larger $q$ is, the less responsive a moving average process is to short-term fluctuations in the series $x_t$. The idea is that moving average processes help identify trends from "noise". **Fast** moving averages have smaller $q$ and more closely follow the stock, while **slow** moving averages have larger $q$, resulting in them responding less to the fluctuations of the stock and being more stable.
**pandas** provides functionality for easily computing moving averages. I demonstrate its use by creating a 20-day (one month) moving average for the Apple data, and plotting it alongside the stock.
```
apple["20d"] = np.round(apple["Adj. Close"].rolling(window = 20, center = False).mean(), 2)
pandas_candlestick_ohlc(apple.loc['2016-01-04':'2016-12-31',:], otherseries = "20d", adj=True)
```
Notice how late the rolling average begins. It cannot be computed until 20 days have passed. This limitation becomes more severe for longer moving averages. Because I would like to be able to compute 200-day moving averages, I'm going to extend out how much AAPL data we have. That said, we will still largely focus on 2016.
```
start = datetime.datetime(2010,1,1)
apple = quandl.get("WIKI/AAPL", start_date=start, end_date=end)
apple["20d"] = np.round(apple["Adj. Close"].rolling(window = 20, center = False).mean(), 2)
pandas_candlestick_ohlc(apple.loc['2016-01-04':'2016-12-31',:], otherseries = "20d", adj=True)
```
You will notice that a moving average is much smoother than the actua stock data. Additionally, it's a stubborn indicator; a stock needs to be above or below the moving average line in order for the line to change direction. Thus, crossing a moving average signals a possible change in trend, and should draw attention.
Traders are usually interested in multiple moving averages, such as the 20-day, 50-day, and 200-day moving averages. It's easy to examine multiple moving averages at once.
```
apple["50d"] = np.round(apple["Adj. Close"].rolling(window = 50, center = False).mean(), 2)
apple["200d"] = np.round(apple["Adj. Close"].rolling(window = 200, center = False).mean(), 2)
pandas_candlestick_ohlc(apple.loc['2016-01-04':'2016-12-31',:], otherseries = ["20d", "50d", "200d"], adj=True)
```
The 20-day moving average is the most sensitive to local changes, and the 200-day moving average the least. Here, the 200-day moving average indicates an overall **bearish** trend: the stock is trending downward over time. The 20-day moving average is at times bearish and at other times **bullish**, where a positive swing is expected. You can also see that the crossing of moving average lines indicate changes in trend. These crossings are what we can use as **trading signals**, or indications that a financial security is changind direction and a profitable trade might be made.
## Trading Strategy
Our concern now is to design and evaluate trading strategies.
Any trader must have a set of rules that determine how much of her money she is willing to bet on any single trade. For example, a trader may decide that under no circumstances will she risk more than 10% of her portfolio on a trade. Additionally, in any trade, a trader must have an **exit strategy**, a set of conditions determining when she will exit the position, for either profit or loss. A trader may set a **target**, which is the minimum profit that will induce the trader to leave the position. Likewise, a trader may have a maximum loss she is willing to tolerate; if potential losses go beyond this amount, the trader will exit the position in order to prevent any further loss. We will suppose that the amount of money in the portfolio involved in any particular trade is a fixed proportion; 10% seems like a good number.
Here, I will be demonstrating a [moving average crossover strategy](http://www.investopedia.com/university/movingaverage/movingaverages4.asp). We will use two moving averages, one we consider "fast", and the other "slow". The strategy is:
* Trade the asset when the fast moving average crosses over the slow moving average.
* Exit the trade when the fast moving average crosses over the slow moving average again.
A trade will be prompted when the fast moving average crosses from below to above the slow moving average, and the trade will be exited when the fast moving average crosses below the slow moving average later.
We now have a complete strategy. But before we decide we want to use it, we should try to evaluate the quality of the strategy first. The usual means for doing so is **backtesting**, which is looking at how profitable the strategy is on historical data. For example, looking at the above chart's performance on Apple stock, if the 20-day moving average is the fast moving average and the 50-day moving average the slow, this strategy does not appear to be very profitable, at least not if you are always taking long positions.
Let's see if we can automate the backtesting task. We first identify when the 20-day average is below the 50-day average, and vice versa.
```
apple['20d-50d'] = apple['20d'] - apple['50d']
apple.tail()
```
We will refer to the sign of this difference as the **regime**; that is, if the fast moving average is above the slow moving average, this is a bullish regime (the bulls rule), and a bearish regime (the bears rule) holds when the fast moving average is below the slow moving average. I identify regimes with the following code.
```
# np.where() is a vectorized if-else function, where a condition is checked for each component of a vector, and the first argument passed is used when the condition holds, and the other passed if it does not
apple["Regime"] = np.where(apple['20d-50d'] > 0, 1, 0)
# We have 1's for bullish regimes and 0's for everything else. Below I replace bearish regimes's values with -1, and to maintain the rest of the vector, the second argument is apple["Regime"]
apple["Regime"] = np.where(apple['20d-50d'] < 0, -1, apple["Regime"])
apple.loc['2016-01-04':'2016-12-31',"Regime"].plot(ylim = (-2,2)).axhline(y = 0, color = "black", lw = 2)
apple["Regime"].plot(ylim = (-2,2)).axhline(y = 0, color = "black", lw = 2)
apple["Regime"].value_counts()
```
The last line above indicates that for 1005 days the market was bearish on Apple, while for 600 days the market was bullish, and it was neutral for 54 days.
Trading signals appear at regime changes. When a bullish regime begins, a buy signal is triggered, and when it ends, a sell signal is triggered. Likewise, when a bearish regime begins, a sell signal is triggered, and when the regime ends, a buy signal is triggered (this is of interest only if you ever will short the stock, or use some derivative like a stock option to bet against the market).
It's simple to obtain signals. Let $r_t$ indicate the regime at time $t$, and $s_t$ the signal at time $t$. Then:
\begin{equation*}
s_t = \text{sign}(r_t - r_{t - 1})
\end{equation*}
$s_t \in \{-1, 0, 1\}$, with $-1$ indicating "sell", $1$ indicating "buy", and $0$ no action. We can obtain signals like so:
```
# To ensure that all trades close out, I temporarily change the regime of the last row to 0
regime_orig = apple.loc[:, "Regime"].iloc[-1]
apple.loc[:, "Regime"].iloc[-1] = 0
apple["Signal"] = np.sign(apple["Regime"] - apple["Regime"].shift(1))
# Restore original regime data
apple.loc[:, "Regime"].iloc[-1] = regime_orig
apple.tail()
apple["Signal"].plot(ylim = (-2, 2))
apple["Signal"].value_counts()
```
We would buy Apple stock 23 times and sell Apple stock 23 times. If we only go long on Apple stock, only 23 trades will be engaged in over the 6-year period, while if we pivot from a long to a short position every time a long position is terminated, we would engage in 23 trades total. (Bear in mind that trading more frequently isn't necessarily good; trades are never free.)
You may notice that the system as it currently stands isn't very robust, since even a fleeting moment when the fast moving average is above the slow moving average triggers a trade, resulting in trades that end immediately (which is bad if not simply because realistically every trade is accompanied by a fee that can quickly erode earnings). Additionally, every bullish regime immediately transitions into a bearish regime, and if you were constructing trading systems that allow both bullish and bearish bets, this would lead to the end of one trade immediately triggering a new trade that bets on the market in the opposite direction, which again seems finnicky. A better system would require more evidence that the market is moving in some particular direction. But we will not concern ourselves with these details for now.
Let's now try to identify what the prices of the stock is at every buy and every sell.
```
apple.loc[apple["Signal"] == 1, "Close"]
apple.loc[apple["Signal"] == -1, "Close"]
# Create a DataFrame with trades, including the price at the trade and the regime under which the trade is made.
apple_signals = pd.concat([
pd.DataFrame({"Price": apple.loc[apple["Signal"] == 1, "Adj. Close"],
"Regime": apple.loc[apple["Signal"] == 1, "Regime"],
"Signal": "Buy"}),
pd.DataFrame({"Price": apple.loc[apple["Signal"] == -1, "Adj. Close"],
"Regime": apple.loc[apple["Signal"] == -1, "Regime"],
"Signal": "Sell"}),
])
apple_signals.sort_index(inplace = True)
apple_signals
# Let's see the profitability of long trades
apple_long_profits = pd.DataFrame({
"Price": apple_signals.loc[(apple_signals["Signal"] == "Buy") &
apple_signals["Regime"] == 1, "Price"],
"Profit": pd.Series(apple_signals["Price"] - apple_signals["Price"].shift(1)).loc[
apple_signals.loc[(apple_signals["Signal"].shift(1) == "Buy") & (apple_signals["Regime"].shift(1) == 1)].index
].tolist(),
"End Date": apple_signals["Price"].loc[
apple_signals.loc[(apple_signals["Signal"].shift(1) == "Buy") & (apple_signals["Regime"].shift(1) == 1)].index
].index
})
apple_long_profits
```
Let's now create a simulated portfolio of $1,000,000, and see how it would behave, according to the rules we have established. This includes:
* Investing only 10% of the portfolio in any trade
* Exiting the position if losses exceed 20% of the value of the trade.
When simulating, bear in mind that:
* Trades are done in batches of 100 stocks.
* Our stop-loss rule involves placing an order to sell the stock the moment the price drops below the specified level. Thus we need to check whether the lows during this period ever go low enough to trigger the stop-loss. Realistically, unless we buy a put option, we cannot guarantee that we will sell the stock at the price we set at the stop-loss, but we will use this as the selling price anyway for the sake of simplicity.
* Every trade is accompanied by a commission to the broker, which should be accounted for. I do not do so here.
Here's how a backtest may look:
```
# We need to get the low of the price during each trade.
tradeperiods = pd.DataFrame({"Start": apple_long_profits.index,
"End": apple_long_profits["End Date"]})
apple_long_profits["Low"] = tradeperiods.apply(lambda x: min(apple.loc[x["Start"]:x["End"], "Adj. Low"]), axis = 1)
apple_long_profits
# Now we have all the information needed to simulate this strategy in apple_adj_long_profits
cash = 1000000
apple_backtest = pd.DataFrame({"Start Port. Value": [],
"End Port. Value": [],
"End Date": [],
"Shares": [],
"Share Price": [],
"Trade Value": [],
"Profit per Share": [],
"Total Profit": [],
"Stop-Loss Triggered": []})
port_value = .1 # Max proportion of portfolio bet on any trade
batch = 100 # Number of shares bought per batch
stoploss = .2 # % of trade loss that would trigger a stoploss
for index, row in apple_long_profits.iterrows():
batches = np.floor(cash * port_value) // np.ceil(batch * row["Price"]) # Maximum number of batches of stocks invested in
trade_val = batches * batch * row["Price"] # How much money is put on the line with each trade
if row["Low"] < (1 - stoploss) * row["Price"]: # Account for the stop-loss
share_profit = np.round((1 - stoploss) * row["Price"], 2)
stop_trig = True
else:
share_profit = row["Profit"]
stop_trig = False
profit = share_profit * batches * batch # Compute profits
# Add a row to the backtest data frame containing the results of the trade
apple_backtest = apple_backtest.append(pd.DataFrame({
"Start Port. Value": cash,
"End Port. Value": cash + profit,
"End Date": row["End Date"],
"Shares": batch * batches,
"Share Price": row["Price"],
"Trade Value": trade_val,
"Profit per Share": share_profit,
"Total Profit": profit,
"Stop-Loss Triggered": stop_trig
}, index = [index]))
cash = max(0, cash + profit)
apple_backtest
apple_backtest["End Port. Value"].plot()
```
Our portfolio's value grew by 13% in about six years. Considering that only 10% of the portfolio was ever involved in any single trade, this is not bad performance.
Notice that this strategy never lead to our rule of never allowing losses to exceed 20% of the trade's value being invoked. For the sake of simplicity, we will ignore this rule in backtesting.
A more realistic portfolio would not be betting 10% of its value on only one stock. A more realistic one would consider investing in multiple stocks. Multiple trades may be ongoing at any given time involving multiple companies, and most of the portfolio will be in stocks, not cash. Now that we will be investing in multiple stops and exiting only when moving averages cross (not because of a stop-loss), we will need to change our approach to backtesting. For example, we will be using one **pandas** `DataFrame` to contain all buy and sell orders for all stocks being considered, and our loop above will have to track more information.
I have written functions for creating order data for multiple stocks, and a function for performing the backtesting.
```
def ma_crossover_orders(stocks, fast, slow):
"""
:param stocks: A list of tuples, the first argument in each tuple being a string containing the ticker symbol of each stock (or however you want the stock represented, so long as it's unique), and the second being a pandas DataFrame containing the stocks, with a "Close" column and indexing by date (like the data frames returned by the Yahoo! Finance API)
:param fast: Integer for the number of days used in the fast moving average
:param slow: Integer for the number of days used in the slow moving average
:return: pandas DataFrame containing stock orders
This function takes a list of stocks and determines when each stock would be bought or sold depending on a moving average crossover strategy, returning a data frame with information about when the stocks in the portfolio are bought or sold according to the strategy
"""
fast_str = str(fast) + 'd'
slow_str = str(slow) + 'd'
ma_diff_str = fast_str + '-' + slow_str
trades = pd.DataFrame({"Price": [], "Regime": [], "Signal": []})
for s in stocks:
# Get the moving averages, both fast and slow, along with the difference in the moving averages
s[1][fast_str] = np.round(s[1]["Close"].rolling(window = fast, center = False).mean(), 2)
s[1][slow_str] = np.round(s[1]["Close"].rolling(window = slow, center = False).mean(), 2)
s[1][ma_diff_str] = s[1][fast_str] - s[1][slow_str]
# np.where() is a vectorized if-else function, where a condition is checked for each component of a vector, and the first argument passed is used when the condition holds, and the other passed if it does not
s[1]["Regime"] = np.where(s[1][ma_diff_str] > 0, 1, 0)
# We have 1's for bullish regimes and 0's for everything else. Below I replace bearish regimes's values with -1, and to maintain the rest of the vector, the second argument is apple["Regime"]
s[1]["Regime"] = np.where(s[1][ma_diff_str] < 0, -1, s[1]["Regime"])
# To ensure that all trades close out, I temporarily change the regime of the last row to 0
regime_orig = s[1].loc[:, "Regime"].iloc[-1]
s[1].loc[:, "Regime"].iloc[-1] = 0
s[1]["Signal"] = np.sign(s[1]["Regime"] - s[1]["Regime"].shift(1))
# Restore original regime data
s[1].loc[:, "Regime"].iloc[-1] = regime_orig
# Get signals
signals = pd.concat([
pd.DataFrame({"Price": s[1].loc[s[1]["Signal"] == 1, "Adj. Close"],
"Regime": s[1].loc[s[1]["Signal"] == 1, "Regime"],
"Signal": "Buy"}),
pd.DataFrame({"Price": s[1].loc[s[1]["Signal"] == -1, "Adj. Close"],
"Regime": s[1].loc[s[1]["Signal"] == -1, "Regime"],
"Signal": "Sell"}),
])
signals.index = pd.MultiIndex.from_product([signals.index, [s[0]]], names = ["Date", "Symbol"])
trades = trades.append(signals)
trades.sort_index(inplace = True)
trades.index = pd.MultiIndex.from_tuples(trades.index, names = ["Date", "Symbol"])
return trades
def backtest(signals, cash, port_value = .1, batch = 100):
"""
:param signals: pandas DataFrame containing buy and sell signals with stock prices and symbols, like that returned by ma_crossover_orders
:param cash: integer for starting cash value
:param port_value: maximum proportion of portfolio to risk on any single trade
:param batch: Trading batch sizes
:return: pandas DataFrame with backtesting results
This function backtests strategies, with the signals generated by the strategies being passed in the signals DataFrame. A fictitious portfolio is simulated and the returns generated by this portfolio are reported.
"""
SYMBOL = 1 # Constant for which element in index represents symbol
portfolio = dict() # Will contain how many stocks are in the portfolio for a given symbol
port_prices = dict() # Tracks old trade prices for determining profits
# Dataframe that will contain backtesting report
results = pd.DataFrame({"Start Cash": [],
"End Cash": [],
"Portfolio Value": [],
"Type": [],
"Shares": [],
"Share Price": [],
"Trade Value": [],
"Profit per Share": [],
"Total Profit": []})
for index, row in signals.iterrows():
# These first few lines are done for any trade
shares = portfolio.setdefault(index[SYMBOL], 0)
trade_val = 0
batches = 0
cash_change = row["Price"] * shares # Shares could potentially be a positive or negative number (cash_change will be added in the end; negative shares indicate a short)
portfolio[index[SYMBOL]] = 0 # For a given symbol, a position is effectively cleared
old_price = port_prices.setdefault(index[SYMBOL], row["Price"])
portfolio_val = 0
for key, val in portfolio.items():
portfolio_val += val * port_prices[key]
if row["Signal"] == "Buy" and row["Regime"] == 1: # Entering a long position
batches = np.floor((portfolio_val + cash) * port_value) // np.ceil(batch * row["Price"]) # Maximum number of batches of stocks invested in
trade_val = batches * batch * row["Price"] # How much money is put on the line with each trade
cash_change -= trade_val # We are buying shares so cash will go down
portfolio[index[SYMBOL]] = batches * batch # Recording how many shares are currently invested in the stock
port_prices[index[SYMBOL]] = row["Price"] # Record price
old_price = row["Price"]
elif row["Signal"] == "Sell" and row["Regime"] == -1: # Entering a short
pass
# Do nothing; can we provide a method for shorting the market?
#else:
#raise ValueError("I don't know what to do with signal " + row["Signal"])
pprofit = row["Price"] - old_price # Compute profit per share; old_price is set in such a way that entering a position results in a profit of zero
# Update report
results = results.append(pd.DataFrame({
"Start Cash": cash,
"End Cash": cash + cash_change,
"Portfolio Value": cash + cash_change + portfolio_val + trade_val,
"Type": row["Signal"],
"Shares": batch * batches,
"Share Price": row["Price"],
"Trade Value": abs(cash_change),
"Profit per Share": pprofit,
"Total Profit": batches * batch * pprofit
}, index = [index]))
cash += cash_change # Final change to cash balance
results.sort_index(inplace = True)
results.index = pd.MultiIndex.from_tuples(results.index, names = ["Date", "Symbol"])
return results
# Get more stocks
(microsoft, google, facebook, twitter, netflix,
amazon, yahoo, ge, qualcomm, ibm, hp) = (quandl.get("WIKI/" + s, start_date=start,
end_date=end) for s in ["MSFT", "GOOG", "FB", "TWTR",
"NFLX", "AMZN", "YHOO", "GE",
"QCOM", "IBM", "HPQ"])
signals = ma_crossover_orders([("AAPL", apple),
("MSFT", microsoft),
("GOOG", google),
("FB", facebook),
("TWTR", twitter),
("NFLX", netflix),
("AMZN", amazon),
("YHOO", yahoo),
("GE", ge),
("QCOM", qualcomm),
("IBM", ibm),
("HPQ", hp)],
fast = 20, slow = 50)
signals
bk = backtest(signals, 1000000)
bk
bk["Portfolio Value"].groupby(level = 0).apply(lambda x: x[-1]).plot()
```
A more realistic portfolio that can invest in any in a list of twelve (tech) stocks has a final growth of about 100%. How good is this? While on the surface not bad, we will see we could have done better.
## Benchmarking
Backtesting is only part of evaluating the efficacy of a trading strategy. We would like to **benchmark** the strategy, or compare it to other available (usually well-known) strategies in order to determine how well we have done.
Whenever you evaluate a trading system, there is one strategy that you should always check, one that beats all but a handful of managed mutual funds and investment managers: buy and hold [SPY](https://finance.yahoo.com/quote/SPY). The **efficient market hypothesis** claims that it is all but impossible for anyone to beat the market. Thus, one should always buy an index fund that merely reflects the composition of the market.By buying and holding SPY, we are effectively trying to match our returns with the market rather than beat it.
I look at the profits for simply buying and holding SPY.
```
#spyder = web.DataReader("SPY", "yahoo", start, end)
spyder = spyderdat.loc[start:end]
spyder.iloc[[0,-1],:]
batches = 1000000 // np.ceil(100 * spyder.loc[:,"Adj Close"].iloc[0]) # Maximum number of batches of stocks invested in
trade_val = batches * batch * spyder.loc[:,"Adj Close"].iloc[0] # How much money is used to buy SPY
final_val = batches * batch * spyder.loc[:,"Adj Close"].iloc[-1] + (1000000 - trade_val) # Final value of the portfolio
final_val
# We see that the buy-and-hold strategy beats the strategy we developed earlier. I would also like to see a plot.
ax_bench = (spyder["Adj Close"] / spyder.loc[:, "Adj Close"].iloc[0]).plot(label = "SPY")
ax_bench = (bk["Portfolio Value"].groupby(level = 0).apply(lambda x: x[-1]) / 1000000).plot(ax = ax_bench, label = "Portfolio")
ax_bench.legend(ax_bench.get_lines(), [l.get_label() for l in ax_bench.get_lines()], loc = 'best')
ax_bench
```
Buying and holding SPY beats our trading system, at least how we currently set it up, and we haven't even accounted for how expensive our more complex strategy is in terms of fees. Given both the opportunity cost and the expense associated with the active strategy, we should not use it.
What could we do to improve the performance of our system? For starters, we could try diversifying. All the stocks we considered were tech companies, which means that if the tech industry is doing poorly, our portfolio will reflect that. We could try developing a system that can also short stocks or bet bearishly, so we can take advantage of movement in any direction. We could seek means for forecasting how high we expect a stock to move. Whatever we do, though, must beat this benchmark; otherwise there is an opportunity cost associated with our trading system.
Other benchmark strategies exist, and if our trading system beat the "buy and hold SPY" strategy, we may check against them. Some such strategies include:
* Buy SPY when its closing monthly price is aboves its ten-month moving average.
* Buy SPY when its ten-month momentum is positive. (**Momentum** is the first difference of a moving average process, or $MO^q_t = MA^q_t - MA^q_{t - 1}$.)
(I first read of these strategies [here](https://www.r-bloggers.com/are-r2s-useful-in-finance-hypothesis-driven-development-in-reverse/?utm_source=feedburner&utm_medium=email&utm_campaign=Feed%3A+RBloggers+%28R+bloggers%29).) The general lesson still holds: *don't use a complex trading system with lots of active trading when a simple strategy involving an index fund without frequent trading beats it.* [This is actually a very difficult requirement to meet.](http://www.nytimes.com/2015/03/15/your-money/how-many-mutual-funds-routinely-rout-the-market-zero.html?_r=0)
As a final note, suppose that your trading system *did* manage to beat any baseline strategy thrown at it in backtesting. Does backtesting predict future performance? Not at all. [Backtesting has a propensity for overfitting](http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2745220), so just because backtesting predicts high growth doesn't mean that growth will hold in the future. There are strategies for combatting overfitting, such as [walk-forward analysis](https://ntguardian.wordpress.com/2017/06/19/walk-forward-analysis-demonstration-backtrader/) and holding out a portion of a dataset (likely the most recent part) as a final test set to determine if a strategy is profitable, followed by "sitting on" a strategy that managed to survive these two filters and seeing if it remains profitable in current markets.
## Conclusion
While this lecture ends on a depressing note, keep in mind that [the efficient market hypothesis has many critics.](http://www.nytimes.com/2009/06/06/business/06nocera.html) My own opinion is that as trading becomes more algorithmic, beating the market will become more difficult. That said, it may be possible to beat the market, even though mutual funds seem incapable of doing so (bear in mind, though, that part of the reason mutual funds perform so poorly is because of fees, which is not a concern for index funds).
This lecture is very brief, covering only one type of strategy: strategies based on moving averages. Many other trading signals exist and employed. Additionally, we never discussed in depth shorting stocks, currency trading, or stock options. Stock options, in particular, are a rich subject that offer many different ways to bet on the direction of a stock. You can read more about derivatives (including stock options and other derivatives) in the book *Derivatives Analytics with Python: Data Analysis, Models, Simulation, Calibration and Hedging*, [which is available from the University of Utah library.](http://proquest.safaribooksonline.com.ezproxy.lib.utah.edu/9781119037996)
Another resource (which I used as a reference while writing this lecture) is the O'Reilly book *Python for Finance*, [also available from the University of Utah library.](http://proquest.safaribooksonline.com.ezproxy.lib.utah.edu/book/programming/python/9781491945360)
If you were interested in investigating algorithmic trading, where would you go from here? I would not recommend using the code I wrote above for backtesting; there are better packages for this task. Python has some libraries for algorithmic trading, such as [**pyfolio**](https://quantopian.github.io/pyfolio/) (for analytics), [**zipline**](http://www.zipline.io/beginner-tutorial.html) (for backtesting and algorithmic trading), and [**backtrader**](https://www.backtrader.com/) (also for backtesting and trading). **zipline** seems to be popular likely because it is used and developed by [**quantopian**](https://www.quantopian.com/), a "crowd-sourced hedge fund" that allows users to use their data for backtesting and even will license profitable strategies from their authors, giving them a cut of the profits. However, I prefer **backtrader** and have written [blog posts](https://ntguardian.wordpress.com/tag/backtrader/) on using it. It is likely the more complicated between the two but that's the cost of greater power. I am a fan of its design. I also would suggest learning [R](https://www.r-project.org/), since it has many packages for analyzing financial data (moreso than Python) and it's surprisingly easy to use R functions in Python (as I demonstrate in [this post](https://ntguardian.wordpress.com/2017/06/28/stock-trading-analytics-and-optimization-in-python-with-pyfolio-rs-performanceanalytics-and-backtrader/)).
You can read more about using R and Python for finance on [my blog](https://ntguardian.wordpress.com).
Remember that it is possible (if not common) to lose money in the stock market. It's also true, though, that it's difficult to find returns like those found in stocks, and any investment strategy should take investing in it seriously. This lecture is intended to provide a starting point for evaluating stock trading and investments, and, more generally, analyzing temporal data, and I hope you continue to explore these ideas.
| github_jupyter |
# Вебинар 6. Консультация по курсовому проекту.
### Задание для курсового проекта
Метрика:
R2 - коэффициент детерминации (sklearn.metrics.r2_score)
Сдача проекта:
1. Прислать в раздел Задания Урока 10 ("Вебинар. Консультация по итоговому проекту")
ссылку на программу в github (программа должна содержаться в файле Jupyter Notebook
с расширением ipynb). (Pull request не нужен, только ссылка ведущая на сам скрипт).
2. Приложить файл с названием по образцу NVBaranov_predictions.csv
с предсказанными ценами для квартир из test.csv (файл должен содержать два поля: Id, Price).
В файле с предсказаниями должна быть 5001 строка (названия колонок + 5000 предсказаний).
Сроки и условия сдачи:
Дедлайн: сдать проект нужно в течение 72 часов после начала Урока 10 ("Вебинар. Консультация по итоговому проекту").
Для успешной сдачи должны быть все предсказания (для 5000 квартир) и R2 должен быть больше 0.6.
При сдаче до дедлайна результат проекта может попасть в топ лучших результатов.
Повторная сдача и проверка результатов возможны только при условии предыдущей неуспешной сдачи.
Успешный проект нельзя пересдать в целях повышения результата.
Проекты, сданные после дедлайна или сданные повторно, не попадают в топ лучших результатов, но можно узнать результат.
В качестве итогового результата берется первый успешный результат, последующие успешные результаты не учитываются.
Примечание:
Все файлы csv должны содержать названия полей (header - то есть "шапку"),
разделитель - запятая. В файлах не должны содержаться индексы из датафрейма.
Рекомендации для файла с кодом (ipynb):
1. Файл должен содержать заголовки и комментарии
2. Повторяющиеся операции лучше оформлять в виде функций
3. Не делать вывод большого количества строк таблиц (5-10 достаточно)
4. По возможности добавлять графики, описывающие данные (около 3-5)
5. Добавлять только лучшую модель, то есть не включать в код все варианты решения проекта
6. Скрипт проекта должен отрабатывать от начала и до конца (от загрузки данных до выгрузки предсказаний)
7. Весь проект должен быть в одном скрипте (файл ipynb).
8. При использовании статистик (среднее, медиана и т.д.) в качестве признаков,
лучше считать их на трейне, и потом на валидационных и тестовых данных не считать
статистики заново, а брать их с трейна. Если хватает знаний, можно использовать кросс-валидацию,
но для сдачи этого проекта достаточно разбить данные из train.csv на train и valid.
9. Проект должен полностью отрабатывать за разумное время (не больше 10 минут),
поэтому в финальный вариант лучше не включать GridSearch с перебором
большого количества сочетаний параметров.
10. Допускается применение любых моделей машинного обучения из библиотеки sklearn.
### Прогнозирование на тестовом датасете
1. Выполнить для тестового датасета те же этапы обработки и постронияния признаков (лучше выполнять действия сразу для двух датасетов)
2. Не потерять и не перемешать индексы от примеров при построении прогнозов
3. Прогнозы должны быть для все примеров из тестового датасета (для всех строк)
**Подключение библиотек и скриптов**
```
import numpy as np
import pandas as pd
import random
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score as r2
from sklearn.model_selection import KFold, GridSearchCV
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
matplotlib.rcParams.update({'font.size': 14})
pd.set_option('precision', 3)
pd.set_option('max_columns', 100)
def evaluate_preds(train_true_values, train_pred_values, val_true_values, val_pred_values):
"""
Функция для оценки работы модели
Parameters:
train_true_values - целевая переменная из тренировочной части датасета
train_pred_values - предсказания модели по тренировочной части
val_true_values - целевая переменная из валидационной части датасета
val_pred_values - предсказания модели по валидационной части
Returns:
R2 на тренировочной и валидационной части,
графики зависимости истинных значений от предсказаний
"""
print("Train R2:\t" + str(round(r2(train_true_values, train_pred_values), 3)))
print("Valid R2:\t" + str(round(r2(val_true_values, val_pred_values), 3)))
plt.figure(figsize=(18,10))
plt.subplot(121)
sns.scatterplot(x=train_pred_values, y=train_true_values)
plt.xlabel('Predicted values')
plt.ylabel('True values')
plt.title('Train sample prediction')
plt.subplot(122)
sns.scatterplot(x=val_pred_values, y=val_true_values)
plt.xlabel('Predicted values')
plt.ylabel('True values')
plt.title('Test sample prediction')
plt.show()
```
**Пути к директориям и файлам**
```
TRAIN_DATASET_PATH = 'datasets/project_task/train.csv'
TEST_DATASET_PATH = 'datasets/project_task/test.csv'
```
### Загрузка данных
**Описание датасета**
* **Id** - идентификационный номер квартиры
* **DistrictId** - идентификационный номер района
* **Rooms** - количество комнат
* **Square** - площадь
* **LifeSquare** - жилая площадь
* **KitchenSquare** - площадь кухни
* **Floor** - этаж
* **HouseFloor** - количество этажей в доме
* **HouseYear** - год постройки дома
* **Ecology_1, Ecology_2, Ecology_3** - экологические показатели местности
* **Social_1, Social_2, Social_3** - социальные показатели местности
* **Healthcare_1, Helthcare_2** - показатели местности, связанные с охраной здоровья
* **Shops_1, Shops_2** - показатели, связанные с наличием магазинов, торговых центров
* **Price** - цена квартиры
```
train_df = pd.read_csv('train.csv')
display(train_df.tail())
print(train_df.shape)
# train_df = train_df.set_index('Id')
# train_df.head()
test_df = pd.read_csv('test.csv')
display(test_df.tail())
print(test_df.shape)
# test_df = test_df.set_index('Id')
train_df.shape[1]-1 == test_df.shape[1]
```
### Приведение типов
```
train_df.dtypes
train_df['Id'] = train_df['Id'].astype(str)
train_df['DistrictId'] = train_df['DistrictId'].astype(str)
```
### Обзор данных
**Целевая переменная**
```
plt.figure(figsize = (16, 8))
train_df['Price'].hist(bins=30)
plt.ylabel('Count')
plt.xlabel('Price')
plt.title('Target distribution')
plt.show()
```
**Количественные переменные**
```
train_df.describe().T
```
**Категориальные переменные**
```
cat_colnames = train_df.select_dtypes(include='object').columns.tolist()
cat_colnames
for cat_colname in cat_colnames[2:]:
print(str(cat_colname) + '\n\n' + str(train_df[cat_colname].value_counts()) + '\n' + '*' * 100 + '\n')
```
### Обработка выбросов
**Rooms**
```
train_df['Rooms'].value_counts()
train_df.loc[train_df['Rooms'].isin([0, 10, 19]), 'Rooms'] = train_df['Rooms'].median()
```
**Square, LifeSquare, KitchenSquare**
```
train_df.describe()
steps = []
scores = [] # <- записываем финальный score
# steps.append('обработка пропусков, выбросов var1')
train_df = train_df[train_df['Square'].isnull() |
(train_df['Square'] < train_df['Square'].quantile(.99)) &
(train_df['Square'] > train_df['Square'].quantile(.01))]
train_df = train_df[train_df['LifeSquare'].isnull() |
(train_df['LifeSquare'] < train_df['LifeSquare'].quantile(.99)) &
(train_df['LifeSquare'] > train_df['LifeSquare'].quantile(.01))]
train_df = train_df[train_df['KitchenSquare'].isnull() |
(train_df['KitchenSquare'] < train_df['KitchenSquare'].quantile(.99)) &
(train_df['KitchenSquare'] > train_df['KitchenSquare'].quantile(.01))]
steps.append('обработка пропусков, выбросов var2')
"""
...
...
...
"""
train_df.describe()
train_df.loc[train_df['LifeSquare'] < 10, 'LifeSquare'] = 10
train_df.loc[train_df['KitchenSquare'] < 3, 'KitchenSquare'] = 3
```
**HouseFloor, Floor**
```
train_df['HouseFloor'].sort_values().unique()
train_df['Floor'].sort_values().unique()
train_df.loc[train_df['HouseFloor'] == 0, 'HouseFloor'] = train_df['HouseFloor'].median()
floor_outliers = train_df[train_df['Floor'] > train_df['HouseFloor']].index
train_df.loc[floor_outliers, 'Floor'] = train_df.loc[floor_outliers, 'HouseFloor'].apply(lambda x: random.randint(1, x))
```
**HouseYear**
```
train_df['HouseYear'].sort_values().unique()
train_df.loc[train_df['HouseYear'] > 2020, 'HouseYear'] = 2020
```
### Обработка пропусков
```
train_df.isnull().sum()
train_df[['Square', 'LifeSquare', 'KitchenSquare']].head(10)
```
**LifeSquare**
```
# медиана до корректировки
train_df['LifeSquare'].median()
# медиана расхождения площадей
square_med_diff = (train_df.loc[train_df['LifeSquare'].notnull(), 'Square']
- train_df.loc[train_df['LifeSquare'].notnull(), 'LifeSquare']
- train_df.loc[train_df['LifeSquare'].notnull(), 'KitchenSquare']).median()
square_med_diff
train_df.loc[train_df['LifeSquare'].isnull(), 'LifeSquare'] = (
train_df.loc[train_df['LifeSquare'].isnull(), 'Square']
- train_df.loc[train_df['LifeSquare'].isnull(), 'KitchenSquare']
- square_med_diff
)
train_df['LifeSquare'].median()
```
**Healthcare_1**
```
train_df['Healthcare_1'].head()
train_df.loc[train_df['Healthcare_1'].isnull(), 'Healthcare_1'] = train_df['Healthcare_1'].median()
```
### Построение новых признаков
**Dummies**
```
train_df['Ecology_2_bin'] = train_df['Ecology_2'].replace({'A':0, 'B':1})
train_df['Ecology_3_bin'] = train_df['Ecology_3'].replace({'A':0, 'B':1})
train_df['Shops_2_bin'] = train_df['Shops_2'].replace({'A':0, 'B':1})
```
**DistrictSize, IsDistrictLarge**
```
train_df['DistrictId'].value_counts()
district_size = train_df['DistrictId'].value_counts().reset_index()\
.rename(columns={'index':'DistrictId', 'DistrictId':'DistrictSize'})
district_size.head()
train_df = train_df.merge(district_size, on='DistrictId', how='left')
train_df.head()
(train_df['DistrictSize'] > 100).value_counts()
train_df['IsDistrictLarge'] = (train_df['DistrictSize'] > 100).astype(int)
```
**MedPriceByDistrict**
```
med_price_by_district = train_df.groupby(['DistrictId', 'Rooms'], as_index=False).agg({'Price':'median'})\
.rename(columns={'Price':'MedPriceByDistrict'})
med_price_by_district.head()
train_df = train_df.merge(med_price_by_district, on=['DistrictId', 'Rooms'], how='left')
train_df.head()
train_df['MedPriceByDistrict'].isnull().sum()
```
*Пример переноса признака на test*
```
test_df['DistrictId'] = test_df['DistrictId'].astype(str)
test_df.merge(med_price_by_district, on=['DistrictId', 'Rooms'], how='left').info()
```
### Отбор признаков
```
train_df.columns.tolist()
feature_names = ['Rooms', 'Square', 'LifeSquare', 'KitchenSquare', 'Floor', 'HouseFloor', 'HouseYear',
'Ecology_1', 'Ecology_2_bin', 'Ecology_3_bin', 'Social_1', 'Social_2', 'Social_3',
'Healthcare_1', 'Helthcare_2', 'Shops_1', 'Shops_2_bin']
new_feature_names = ['IsDistrictLarge', 'MedPriceByDistrict']
target_name = 'Price'
```
### Разбиение на train и val
```
X = train_df[feature_names + new_feature_names]
y = train_df[target_name]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, shuffle=True, random_state=21)
```
### Построение модели
**Обучение и оценка модели**
```
rf_model = RandomForestRegressor(random_state=21)
rf_model.fit(X_train, y_train)
```
**Отложенная выборка**
```
y_train_preds = rf_model.predict(X_train)
y_test_preds = rf_model.predict(X_test)
evaluate_preds(y_train, y_train_preds, y_test, y_test_preds)
```
**Перекрёстная проверка**
```
cv_score = cross_val_score(rf_model, X, y, scoring='r2', cv=KFold(n_splits=3, shuffle=True, random_state=21))
cv_score
cv_score.mean()
```
### XGBoost
```
from xgboost import XGBRegressor
xgb = xgboost.XGBRegressor(n_estimators=500, learning_rate=0.08, gamma=0, subsample=0.75,
colsample_bytree=1, max_depth=7, objective ='reg:squarederror')
xgb.fit(X_train, y_train)
y_train_preds = xgb.predict(X_train)
y_test_preds = xgb.predict(X_test)
evaluate_preds(y_train, y_train_preds, y_test, y_test_preds)
from sklearn.metrics import r2_score
# A parameter grid for XGBoost
params = {'min_child_weight':[4,5],
'gamma':[i/10.0 for i in range(3,6)],
'subsample':[i/10.0 for i in range(6,11)],
'max_depth': [2,3,4,7]}
# Initialize XGB and GridSearch
xgb = XGBRegressor(nthread=-1, objective ='reg:squarederror')
grid = GridSearchCV(xgb, params)
grid.fit(X_train,y_train)
print(r2_score(y_test, grid.best_estimator_.predict(X_test)))
y_train_preds = grid.best_estimator_.predict(X_train)
y_test_preds = grid.best_estimator_.predict(X_test)
evaluate_preds(y_train, y_train_preds, y_test, y_test_preds)
```
**Важность признаков**
```
feature_importances = pd.DataFrame(zip(X_train.columns, rf_model.feature_importances_),
columns=['feature_name', 'importance'])
feature_importances.sort_values(by='importance', ascending=False)
```
| github_jupyter |
```
#'''
#Demonstrates GRAPPA reconstruction of undersampled data.
#See function grappa_detail.py for an example showing more of the
#workings and functionality of the SIRF code.
#
#Pre-requisites:
# 1) If the reconstruction engine is set to Gadgetron (default), then
# this Python script needs to be able to access a listening gadgetron.
# On the Virtual Machine, gadgetron is installed and the user just needs
# to type 'gadgetron' in a terminal window.
# On standalone systems, the user will need to have installed ISMRMRD
# and gadgetron code.
#
# 2) An input data file from a GRAPPA MRI acquisition in the ISMRMRD format.
# Example GRAPPA datasets:
# a) 'meas_MID00108_FID57249_test_2D_2x.dat' is
# available from https://www.ccppetmr.ac.uk/downloads
# This is in the manufacturer's raw data format and needs to be
# converted to ISMRMRD format using 'siemens_to_ismrmrd'.
# This executable is installed on the Virtual Machine.
#
# b) A simulated ISMRMRD h5 file is available as default
#
#Usage:
# grappa_basic.py [--help | options]
#
#Options:
# -f <file>, --file=<file> raw data file
# [default: simulated_MR_2D_cartesian_Grappa2.h5]
# -p <path>, --path=<path> path to data files, defaults to data/examples/MR
# subfolder of SIRF root folder
# -e <engn>, --engine=<engn> reconstruction engine [default: Gadgetron]
#'''
#
## CCP PETMR Synergistic Image Reconstruction Framework (SIRF)
## Copyright 2015 - 2017 Rutherford Appleton Laboratory STFC.
## Copyright 2015 - 2017 University College London.
## Copyright 2015 - 2017 Physikalisch-Technische Bundesanstalt.
##
## This is software developed for the Collaborative Computational
## Project in Positron Emission Tomography and Magnetic Resonance imaging
## (http://www.ccppetmr.ac.uk/).
##
## Licensed under the Apache License, Version 2.0 (the "License");
## you may not use this file except in compliance with the License.
## You may obtain a copy of the License at
## http://www.apache.org/licenses/LICENSE-2.0
## Unless required by applicable law or agreed to in writing, software
## distributed under the License is distributed on an "AS IS" BASIS,
## WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
## See the License for the specific language governing permissions and
## limitations under the License.
#__version__ = '0.1.0'
from docopt import docopt
#args = docopt(__doc__, version=__version__)
%matplotlib notebook
# import engine module
#exec('from p' + args['--engine'] + ' import *')
from sirf.Gadgetron import *
data_file = 'simulated_MR_2D_cartesian_Grappa2.h5'
data_path = examples_data_path('MR')
# locate the input data file
input_file = existing_filepath(data_path, data_file)
# Initially we create a container that points to the h5 file.
# Data is not read from file until the 'process' method of the
# reconstructor object is called.
# Create an acquisition container of type AcquisitionData
print('---\n reading in file %s...' % input_file)
acq_data = AcquisitionData(input_file)
# Pre-process this input data.
# (Currently this is a Python script that just sets up a 3 chain gadget.
# In the future it will be independent of the MR recon engine.)
print('---\n pre-processing acquisition data...')
preprocessed_data = preprocess_acquisition_data(acq_data)
# Perform reconstruction of the preprocessed data.
# 1. set the reconstruction to be for Cartesian GRAPPA data.
recon = CartesianGRAPPAReconstructor();
# 2. set the reconstruction input to be the data we just preprocessed.
recon.set_input(preprocessed_data);
# 3. run (i.e. 'process') the reconstruction.
print('---\n reconstructing...\n');
recon.process();
# retrieve reconstruced image and G-factor data
output = recon.get_output()
# show reconstructed image and G-factor data
output_array = output.as_array()
title = 'Reconstructed image data (magnitude)'
show_3D_array(abs(output_array[0::2,:,:]), suptitle = title, \
xlabel = 'samples', ylabel = 'readouts', label = 'slice', \
show = False)
title = 'Reconstructed G-factor data (magnitude)'
show_3D_array(abs(output_array[1::2,:,:]), suptitle = title, \
xlabel = 'samples', ylabel = 'readouts', label = 'slice')
```
| github_jupyter |
# Radial Velocity Orbit-fitting with RadVel
## Week 6, Intro-to-Astro 2021
### Written by Ruben Santana & Sarah Blunt, 2018
#### Updated by Joey Murphy, June 2020
#### Updated by Corey Beard, July 2021
## Background information
Radial velocity measurements tell us how the velocity of a star changes along the direction of our line of sight. These measurements are made using Doppler Spectroscopy, which looks at the spectrum of a star and measures shifts in known absorption lines. Here is a nice [GIF](https://polytechexo.files.wordpress.com/2011/12/spectro.gif) showing the movement of a star due to the presence of an orbiting planet, the shift in the stellar spectrum, and the corresponding radial velocity measurements.
This tutorial will cover a lot of new topics and build on ones we just learned. We don't have time to review all of them right now, so you're encouraged to read the following references before coming back to complete the tutorial as one of your weekly assignments.
- [Intro to the Radial Velocity Technique](http://exoplanets.astro.yale.edu/workshop/EPRV/Bibliography_files/Radial_Velocity.pdf) (focus on pgs. 1-6)
- [Intro to Periodograms](https://arxiv.org/pdf/1703.09824.pdf) (focus on pgs. 1-30)
- [Intro to Markov Chain Monte Carlo Methods](https://towardsdatascience.com/a-zero-math-introduction-to-markov-chain-monte-carlo-methods-dcba889e0c50) (link also found in the MCMC resources from the Bayesian fitting methods and MCMC tutorial)
## About this tutorial
In this tutorial, you will use the California Planet Search Python package [RadVel](https://github.com/California-Planet-Search/radvel) to characterize the exoplanets orbiting the star K2-24 (EPIC 203771098) using radial velocity measurements. This tutorial is a modification of the "[K2-24 Fitting & MCMC](https://github.com/California-Planet-Search/radvel/blob/master/docs/tutorials/K2-24_Fitting%2BMCMC.ipynb)" tutorial on the RadVel GitHub page.
There are several coding tasks for you to accomplish in this tutorial. Each task is indicated by a `#TODO` comment.
In this tutorial, you will:
- estimate planetary orbital periods using a periodogram
- perform a maximum likelihood orbit fit with RadVel
- create a residuals plot
- perform a Markov Chain Monte Carlo (MCMC) fit to characterize orbital parameter uncertainty
## Outline
1. RadVel Installation
2. Importing Data
3. Finding Periods
4. Defining and Initializing a Model
5. Maximum Likelihood Fitting
6. Residuals
7. MCMC
## 1. Installation
We will begin by making sure we have all the python packages needed for the tutorial. First, [install RadVel](http://radvel.readthedocs.io/en/latest/quickstartcli.html#installation) by typing:
`pip install radvel` at the command line. (Some warning messages may print out, but I (Corey) was able to install RadVel successfully in a new Anaconda environment using python=3.8.3.)
If you want to clone the entire RadVel GitHub repository for easy access to the RadVel source code, type:
`git clone https://github.com/California-Planet-Search/radvel.git`
If everything installed correctly, the following cell should run without errors. If you still see errors try restarting the kernel by using the tab above labeled **kernel >> restart**.
```
# allows us to see plots on the jupyter notebook
%matplotlib inline
# used to interact with operating system
import os
# models used by radvel for calculations, plotting, and model optimization
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy import optimize
# for corner plots
import corner
# for radial velocity analysis
import radvel
from radvel.plot import orbit_plots, mcmc_plots
# for periodogram
from astropy.stats import LombScargle
# sets font size for plots
matplotlib.rcParams['font.size'] = 18
```
## 2. Importing and Plotting Data
When you installed RadVel, some .csv files were placed in a directory on your computer called `radvel.DATADIR`. Let's read this data into Python using pandas.
```
# import data
path = os.path.join(radvel.DATADIR,'epic203771098.csv') # path to data file
data = pd.read_csv(path, index_col=0) # read data into pandas DataFrame
print('Path to radvel.DATADIR: {}\n'.format(radvel.DATADIR))
print(data)
# Let's print out the column names of the pandas DataFrame you just created (`data`)
print(data.columns.values)
# TODO: print out the length of `data`
print(len(data))
# Let's plot time (data.t) vs radial velocity (data.vel) using matplotlib.pyplot
plt.plot(data.t, data.vel, 'o')
# Now, on a new figure, let's modify the plotting code so that it adds error
# bars (data.errvel) to each RV measurement
plt.figure()
plt.errorbar(data.t, data.vel, data.errvel, fmt='o')
plt.show()
plt.errorbar(data.t, data.vel, data.errvel, fmt='o',color='maroon')
# Add labels for the x- and y-axes of your plot (time is in days; radial velocity is in m/s)
plt.xlabel('Time [days]')
plt.ylabel('Velocity [m/s]')
plt.show()
# TODO: change the color of the data in your plot
# TODO: What do you notice about the data? Does it look like there is a planet signal?
# What orbital period would you estimate?
# Enter your answer in the triple quotes below.
"""
It definitely doesn't appear to be a pure sinusoid. This means there could be significant eccentricity, additional planets,
stellar activity, or any number of other possible explanations. The periods look like on the order of ~10-20 days,
or so
"""
```
## 3. Finding a Significant Period
Now, we will find probable orbital periods using a Lomb-Scargle periodogram. Periodograms are created using a Fourier transform, which is a mathematical process that takes in continuous time-based data and decomposes it into a combination of functions with various frequencies, as seen in the image below. To build more intuition for how a Fourier transform works, checkout this useful [PhET simulation](https://phet.colorado.edu/en/simulation/fourier).

([wikipedia](https://upload.wikimedia.org/wikipedia/commons/6/61/FFT-Time-Frequency-View.png))
The graph on the left is the continous data which is analagous to our radial velocity data. The three sine waves behind the graphs are the functions that are added to produce a good fit to the original data. Finally, the graph on the right is the periodogram. It shows how much each contributing function's frequency contributes to the data model. The larger the peak in the graph, the more significant that frequency is in the data. We use this frequency to get an idea of periodic behaivor in the data (e.g. the orbital period of an exoplanet). Now, we will calculate a periodogram and use it to give us an estimate of the period of the planet's orbit.
```
def LombScarg(t,v,e,min_per=0.01,max_per=1000):
#Calculate Generalized Lomb-Scargle periodogram and window function
fmin = 1./max_per
fmax = 1./min_per
frequency, power = LombScargle(t, v, e).autopower(minimum_frequency=1/1000,maximum_frequency=1.,method='cython')
per = 1/frequency
#Identify strongest period.
in_window = np.zeros(len(per),dtype=bool)
for s in range(len(per)):
if per[s] > min_per and per[s] < max_per:
in_window[s] += 1
powmax = max(power[in_window])
imax = np.argmax(power[in_window])
fbest = frequency[in_window][imax]
perbest = 1./fbest
return per, power, perbest
minPer = 30 # min period to look for 1st planet (in days)
maxPer = 50 # max period to look for 1st planet (in days)
period, power, period1 = LombScarg(data.t, data.vel,data.errvel,min_per=minPer,max_per=maxPer)
plt.xlim(1,1000)
plt.axvline(period1,color='red',linestyle='--')
plt.semilogx(period,power)
plt.xlabel('Period (days)')
plt.ylabel('GLS Power')
plt.show()
# TODO: change the values of minPer and maxPer. How do the results change? Why? Type your answer
# between the triple quotes below.
"""
`minPer` and `maxPer` control the period range in which the nyquist searcher looks for significant peaks. Changing
them controls which period the searcher returns (it's returning the maximum peak in the allowable range).
"""
```
## 4. Defining and Initializing Model
Let's define a function that we will use to initialize the ``radvel.Parameters`` and ``radvel.RVModel`` objects.
These will be our initial guesses of the planet parameters based on on the radial velocity measurements shown and periodogram shown above.
```
nplanets = 1 # number of planets
def initialize_model():
time_base = 2420.
params = radvel.Parameters(nplanets,basis='per tc secosw sesinw k')
params['per1'] = radvel.Parameter(value=period1) # Insert our guess for period of first planet (from periodogram)
params['tc1'] = radvel.Parameter(value=2080.) # guess for time of transit of 1st planet
params['secosw1'] = radvel.Parameter(value=0.0) # determines eccentricity (assuming circular orbit here)
params['sesinw1'] = radvel.Parameter(value=0.0) # determines eccentriciy (assuming circular orbit here)
params['k1'] = radvel.Parameter(value=3.) # radial velocity semi-amplitude
mod = radvel.RVModel(params, time_base=time_base)
mod.params['dvdt'] = radvel.Parameter(value=-0.02) # possible acceleration of star
mod.params['curv'] = radvel.Parameter(value=0.01) # possible curvature in long-term radial velocity trend
return mod
```
Fit the K2-24 RV data assuming circular orbits.
Set initial guesses for the parameters:
```
mod = initialize_model() # model initiliazed
like = radvel.likelihood.RVLikelihood(mod, data.t, data.vel, data.errvel, '_HIRES') # initialize Likelihood object
# define initial guesses for instrument-related parameters
like.params['gamma_HIRES'] = radvel.Parameter(value=0.1) # zero-point radial velocity offset
like.params['jit_HIRES'] = radvel.Parameter(value=1.0) # white noise
```
Plot the model with our initial parameter guesses:
```
def plot_results(like):
fig = plt.figure(figsize=(12,4))
fig = plt.gcf()
fig.set_tight_layout(True)
plt.errorbar(
like.x, like.model(data.t.values)+like.residuals(),
yerr=like.yerr, fmt='o'
)
ti = np.linspace(data.t.iloc[0] - 5, data.t.iloc[-1] + 5,100) # time array for model
plt.plot(ti, like.model(ti))
plt.xlabel('Time')
plt.ylabel('RV')
plot_results(like)
```
## 5. Maximum Likelihood fit
Well, that solution doesn't look very good! Let's optimize the parameters set to vary by maximizing the likelihood.
Initialize a ``radvel.Posterior`` object.
```
post = radvel.posterior.Posterior(like) # initialize radvel.Posterior object
```
Choose which parameters to change or hold fixed during a fit. By default, all `radvel.Parameter` objects will vary, so you only have to worry about setting the ones you want to hold fixed.
```
post.likelihood.params['secosw1'].vary = False # set as false because we are assuming circular orbit
post.likelihood.params['sesinw1'].vary = False # set as false because we are assuming circular orbit
print(like)
```
Maximize the likelihood and print the updated posterior object
```
res = optimize.minimize(
post.neglogprob_array, # objective function is negative log likelihood
post.get_vary_params(), # initial variable parameters
method='Powell', # Nelder-Mead also works
)
plot_results(like) # plot best fit model
print(post)
```
RadVel comes equipped with some fancy ready-made plotting routines. Check this out!
```
matplotlib.rcParams['font.size'] = 12
RVPlot = orbit_plots.MultipanelPlot(post)
RVPlot.plot_multipanel()
matplotlib.rcParams['font.size'] = 18
```
## 6. Residuals and Repeat
Residuals are the difference of our data and our best-fit model.
Next, we will plot the residuals of our optimized model to see if there is a second planet in our data. When we look at the following residuals, we will see a sinusoidal shape, so another planet may be present! Thus, we will repeat the steps shown earlier (this time using the parameters from the maximum fit for the first planet).
```
residuals1 = post.likelihood.residuals()
# Let's make a plot of data.time versus `residuals1`
plt.figure()
plt.scatter(data.t, residuals1)
plt.xlabel('time [MJD]')
plt.ylabel('RV [m/s]')
plt.show()
# TODO: What do you notice? What would you estimate the period
# of the other exoplanet in this system to be? Write your answer between the triple quotes below.
"""
These residuals appear to go up and down every ~20 days or so. This looks like a more convincing version of the
period we first observed in the original radial velocity data. It's still pretty hard to tell, though! I'm
happy we have algorithms to find orbital periods more effectively than the human eye can.
"""
```
Let's repeat the above analysis with two planets!
```
nyquist = 2 # maximum sampling rate
minPer = 20 # minimum period to look for 2nd planet
maxPer = 30 # max period to look for 2nd planet
# finding 2nd planet period
period, power, period2 = LombScarg(data.t, data.vel, data.errvel, min_per=minPer, max_per=maxPer) # finding possible periords for 2nd planet
period, power, period1 = LombScarg(data.t, data.vel,data.errvel,min_per=minPer,max_per=maxPer)
plt.xlim(1,1000)
plt.axvline(period2,color='red',linestyle='--')
plt.semilogx(period,power)
plt.show()
# TODO: why doesn't the periodogram return the period of the first planet? Write your answer between the triple
# quotes below.
"""
The period of the first planet is not in the allowed period range we specified (`minPer` to `maxPer`).
"""
```
Repeat the RadVel analysis
```
nplanets = 2 # number of planets
def initialize_model():
time_base = 2420
params = radvel.Parameters(nplanets,basis='per tc secosw sesinw k')
# 1st Planet
params['per1'] = post.params['per1'] # period of 1st planet
params['tc1'] = post.params['tc1'] # time transit of 1st planet
params['secosw1'] = post.params['secosw1'] # determines eccentricity (assuming circular orbit here)
params['sesinw1'] = post.params['sesinw1'] # determines eccentricity (assuming circular orbit here)
params['k1'] = post.params['k1'] # velocity semi-amplitude for 1st planet
# 2nd Planet
params['per2'] = radvel.Parameter(value=period2) # Insert our guess for period of second planet (from periodogram)
params['tc2'] = radvel.Parameter(value=2070.)
params['secosw2'] = radvel.Parameter(value=0.0)
params['sesinw2'] = radvel.Parameter(value=0.0)
params['k2'] = radvel.Parameter(value=1.1)
mod = radvel.RVModel(params, time_base=time_base)
mod.params['dvdt'] = radvel.Parameter(value=-0.02) # acceleration of star
mod.params['curv'] = radvel.Parameter(value=0.01) # curvature of radial velocity fit
return mod
mod = initialize_model() # initialize radvel.RVModel object
like = radvel.likelihood.RVLikelihood(mod, data.t, data.vel, data.errvel, '_HIRES')
like.params['gamma_HIRES'] = radvel.Parameter(value=0.1)
like.params['jit_HIRES'] = radvel.Parameter(value=1.0)
like.params['secosw1'].vary = False # set as false because we are assuming circular orbit
like.params['sesinw1'].vary = False
like.params['secosw2'].vary = False # set as false because we are assuming circular orbit
like.params['sesinw2'].vary = False
print(like)
plot_results(like)
post = radvel.posterior.Posterior(like) # initialize radvel.Posterior object
res = optimize.minimize(
post.neglogprob_array, # objective function is negative log likelihood
post.get_vary_params(), # initial variable parameters
method='Powell', # Nelder-Mead also works
)
plot_results(like) # plot best fit model
print(post)
matplotlib.rcParams['font.size'] = 12
RVPlot = orbit_plots.MultipanelPlot(post)
RVPlot.plot_multipanel()
matplotlib.rcParams['font.size'] = 18
residuals2 = post.likelihood.residuals()
# TODO: make a plot of data.time versus `residuals2`. What do you notice?
# TODO: try redoing the above analysis, but this time, allow the eccentricity parameters to vary during the fit.
# How does the fit change?
plt.figure()
plt.scatter(data.t, residuals2)
plt.xlabel('time [MJD]')
plt.ylabel('RV [ms$^{-1}$]')
# Here's the original residuals plot, for comparison purposes:
plt.figure()
plt.scatter(data.t, residuals1, color='red')
plt.xlabel('time [MJD]')
plt.ylabel('RV [ms$^{-1}$]')
"""
The residuals perhaps look a little more randomly distributed than before, but again it's pretty hard to tell
without a periodogram.
"""
"""
The easiest way to do this is to rerun the analysis, except whenever you see a line that says secosw1 = False,
or sesinw1 = False, or secosw2 = False, or sesinw2 = False, you change them to True.
Be careful not to let the model go too crazy with eccentricity, try giving them initial guesses of 0.1.
The planet RV signatures look more angular (less purely sinusoidal) now that they have a non-zero eccentricity.
The data appears to be better-fit by an eccentric orbit model (i.e. the planets probably do have non-negligible
eccentricities).
"""
```
K2-24 only has two known exoplanets so will stop this part of our analysis here. However, when analzying an uncharacterized star system, it's important to continue the analysis until we see no significant reduction in the residuals of the radial velocity.
# 7. Markov Chain Monte Carlo (MCMC)
After reading the intro to MCMC blog post at the beginning of this tutorial, you are an expert on MCMC! Write a 3-sentence introduction to this section yourself.
MCMC is a method of exploring the parameter space of probable orbits using random walks, i.e. randomly changing the parameters of the fit. MCMC is used to find the most probable orbital solution and to determine the uncertainty (error bars) in the fit. MCMC tells you the probability distributions of orbital parameters consistent with the data.
```
# TODO: edit the Markdown cell immediately above this one with a 3 sentence description of the MCMC method.
# What does MCMC do? Why do you think it is important to use MCMC to characterize uncertainties in radial
# velocity fits?
```
Let's use RadVel to perform an MCMC fit:
```
df = radvel.mcmc(post, nwalkers=50, nrun=1000)
# TODO: What type of data structure is `df`, the object returned by RadVel's MCMC method?
"""
It is a pandas dataframe
"""
```
Make a fun plot!
```
Corner = mcmc_plots.CornerPlot(post, df)
Corner.plot()
# TODO: There is a lot going on in this plot. What do you think the off-diagonal boxes are showing?
# What about the on-diagonal boxes? What is the median period of the first planet?
# What is the uncertainty on the period of the first planet? The second planet?
# TODO: Why do you think the uncertainties on the periods of planets b and c are different?
"""
The off-diagonal boxes are 1 dimensional probability distributions over each of the parameters of the fit.
The on-diagonal boxes show 2 dimensional probability distributions (covariances) between pairs of parameters
(the box's row and column show the parameters it corresponds to).
The median period of the first plot (for my eccentric fit) is 52.56 days. The uncertainty is +0.08 days, -0.07 days
(this corresponds to a *68% confidence interval* of [52.49, 52.64] days.)
The median period of the second planet is 20.69 days, with an uncertainty of +/- 0.02 days.
The uncertainties of the two orbital periods are different because the period of the second planet is much better
constrained by the data than the period of the first planet. We see many periods of the second planet repeated
over the ~100 day dataset, but only ~2 periods of the first planet.
"""
```
| github_jupyter |
```
import math
import string
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import logit
from IPython.display import display
import tensorflow as tf
from tensorflow.keras.layers import (Input, Dense, Lambda, Flatten, Reshape, BatchNormalization, Layer,
Activation, Dropout, Conv2D, Conv2DTranspose,
Concatenate, add, Add, Multiply)
from tensorflow.keras.losses import sparse_categorical_crossentropy
from tensorflow.keras.optimizers import RMSprop, Adam
from tensorflow.keras.models import Model
from tensorflow.keras import metrics
from tensorflow.keras import backend as K
from tensorflow.keras.datasets import cifar10
from tensorflow.keras.callbacks import TensorBoard
from tensorflow_addons.callbacks import TQDMProgressBar
from realnvp_helpers import Mask, FlowBatchNorm
%matplotlib inline
batch_size = 10
shape = (4, 4, 3)
batch_shape = (batch_size,) + shape
samples = 100
train_data = np.random.normal(0.5, 3, size=(samples,) + (shape))
print(batch_shape)
print(train_data.shape)
train_data[0, :, :, :]
def conv_block(input_shape, kernel_size, filters, stage, block, use_resid=True):
''' Adapted from resnet50 implementation in Keras '''
filters1, filters2, filters3 = filters
if K.image_data_format() == 'channels_last':
bn_axis = 3
else:
bn_axis = 1
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
input_tensor = Input(batch_shape=input_shape)
x = Conv2D(filters1, (1, 1),
kernel_initializer='he_normal',
name=conv_name_base + '2a')(input_tensor)
x = BatchNormalization(axis=bn_axis, name=bn_name_base + '2a')(x)
x = Activation('relu')(x)
x = Conv2D(filters2, kernel_size,
padding='same',
kernel_initializer='he_normal',
name=conv_name_base + '2b')(x)
x = BatchNormalization(axis=bn_axis, name=bn_name_base + '2b')(x)
x = Activation('relu')(x)
x = Conv2D(filters3, (1, 1),
kernel_initializer='he_normal',
name=conv_name_base + '2c')(x)
x = BatchNormalization(axis=bn_axis, name=bn_name_base + '2c')(x)
if use_resid:
x = add([x, input_tensor])
x = Activation('relu')(x)
return Model(input_tensor, x, name='conv_block' + stage + block)
def coupling_layer(input_shape, mask_type, stage):
''' Implements (as per paper):
y = b * x + (1 - b) * [x * exp(s(b * x)) + t(b * x)]
'''
assert mask_type in ['check_even', 'check_odd', 'channel_even', 'channel_odd']
mask_prefix = 'check' if mask_type.startswith('check') else 'channel'
mask_opposite = 'odd' if mask_type.endswith('even') else 'even'
input_tensor = Input(batch_shape=input_shape)
# Raw operations for step
b0 = Mask(mask_type)
b1 = Mask(mask_prefix + '_' + mask_opposite)
s_ = conv_block(input_shape, (3, 3), (32, 32, 3), stage, '_s', use_resid=True)
t_ = conv_block(input_shape, (3, 3), (32, 32, 3), stage, '_t', use_resid=True)
batch = FlowBatchNorm(name='_'.join(['FlowBatchNorm' + mask_type + stage]))
# Forward
masked_input = b1(input_tensor)
s = s_(masked_input)
t = t_(masked_input)
coupling = Lambda(lambda ins: ins[0] * K.exp(ins[1]) + ins[2])([input_tensor, s, t])
coupling_mask = b0(coupling)
out1, out2 = Add()([masked_input, coupling_mask]), b0(s)
out1_norm = batch(out1)
#batch_loss = Lambda(lambda x: - (K.log(gamma) - 0.5 * K.log(x + batch.epsilon)))(var)
#batch_loss = Lambda(lambda x: -K.log(gamma))(var)
#batch_loss = Lambda(lambda x: - ( - 0.5 * K.log(x + batch.epsilon)))(var)
# Reverse
# Return result + masked scale for loss function
return Model(input_tensor, [out1_norm, out2], name='_'.join(['coupling', mask_type, stage]))
def coupling_group(input_tensor, steps, mask_type, stage):
name_mapping = dict(enumerate(string.ascii_lowercase))
# TODO: Only need check/channel, not even/odd right?
assert mask_type in ['check_even', 'check_odd', 'channel_even', 'channel_odd']
mask_prefix = 'check' if mask_type.startswith('check') else 'channel'
x = input_tensor
s_losses = []
batch_losses = []
for i in range(3):
mask_type = mask_prefix + ('_even' if i % 2 == 0 else '_odd')
step = coupling_layer(input_tensor.shape, mask_type, stage=str(stage) + name_mapping[i])
x, s = step(x)
#x, s = step(x)
s_losses.append(s)
return x, s_losses
def realnvp_zloss(target, z):
# log(p_X(x)) = log(p_Z(f(x))) + log(|det(\partial f(x) / \partial X^T)|)
# Prior is standard normal(mu=0, sigma=1)
shape = z.shape
return K.sum(-0.5 * np.log(math.pi) - 0.5 * z**2, axis=list(range(1, len(shape[1:]))))
def const_loss(target, output):
# For debugging
return K.constant(0)
def realnvp_sumloss(target, output):
# Determinant is just sum of "s" or "batch loss" params (already log-space)
shape = output.shape
return K.sum(output, axis=list(range(1, len(shape))))
input_tensor = Input(batch_shape=batch_shape)
#x = conv_block(shape, (3, 3), (32, 32, 3), '0', '_s', use_resid=True)(input_tensor)
step = coupling_layer(batch_shape, 'check_even', stage=str('a') + '0')
x, s = step(input_tensor)
s_losses = [s, s]
#x, s_losses, batch_losses = coupling_group(input_tensor, steps=3, mask_type='check_even', stage=1)
s_losses = Concatenate(name='s_losses')(s_losses)
forward_model = Model(inputs=input_tensor, outputs=[x, s_losses])
optimizer = Adam(lr=0.001)
forward_model.compile(optimizer=optimizer,
loss=[realnvp_zloss, realnvp_sumloss])
#loss=[const_loss, const_loss, realnvp_sumloss])
forward_model.summary()
def get_losses_from_layers(layers):
losses = []
for layer in layers:
if isinstance(layer, Model):
losses.extend(layer._losses)
losses.extend(get_losses_from_layers(layer.layers))
else:
losses.extend(layer.losses)
return losses
get_losses_from_layers(forward_model.layers)
#early_stopping = keras.callbacks.EarlyStopping('val_loss', min_delta=50.0, patience=5)
#reduce_lr = keras.callbacks.ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=2, min_lr=0.0001)
s = [len(train_data)] + [int(x) for x in s_losses.shape[1:]]
#s[0] = int(train_data.shape[0])
#print(train_data.shape, np.zeros(s).shape)
tensorboard = TensorBoard(log_dir='graph',
batch_size=batch_size,
histogram_freq=1,
write_graph=True)
history = forward_model.fit(
train_data, [train_data, np.zeros(s)],
#validation_data=(train_data[:10], [train_data[:10], np.zeros(s)[:10], np.zeros(s)[:10]]),
batch_size=batch_size,
epochs=20,
callbacks=[TQDMProgressBar()], #, tensorboard], #, early_stopping, reduce_lr],
verbose=0
)
df = pd.DataFrame(history.history)
#display(df.describe(percentiles=[0.25 * i for i in range(4)] + [0.95, 0.99]))
col = 'val_loss' if 'val_loss' in df else 'loss'
display(df[-25:])
df[col][-25:].plot(figsize=(8, 6))
```
# 2019-07-28
* Got some framework up to do coupling layers but having trouble passing the scale parameter to the loss function, getting some weird tensorflow error, needs more debugging
* Without the determinant in the loss function, it looks like loss goes down, so maybe on the right track?
* It's actually weird that we're not using the image in the output, but I guess that's what's great about this reversible model!
* TODO:
* Debug scale function in loss
* Add reverse (generator) network to functions above.
# 2019-07-29
* Explanation of how to estimate probability of continuous variables (relevant for computing bits/pixel without an explicit discrete distribution): https://math.stackexchange.com/questions/2818318/probability-that-a-sample-is-generated-from-a-distribution
* Idea for a post, explain likelihood estimation of discrete vs. continuous distributions (like pixels), include:
* Probability of observing a value from continuous distribution = 0
* https://math.stackexchange.com/questions/2818318/probability-that-a-sample-is-generated-from-a-distribution
* Probability of observing a value from a set of discrete hypthesis (models) is non-zero using epsilon trick (see above link):
* https://math.stackexchange.com/questions/920241/can-an-observed-event-in-fact-be-of-zero-probability
* Explain Equation 3 from "A NOTE ON THE EVALUATION OF GENERATIVE MODELS"
* Also include an example using a simpler case, like a bernoulli variable that we're estimating using a continuous distribution
* Bring it back to modelling pixels and how they usually do it
# 2020-03-30
* To make reversible network, build forward and backward network at the same time using `Model()` to have components that I can use in both networks
* Looks like I have some instability here, depending on the run I can get an exact fit (-100s loss) or a poor a fit (+10):
* Turning off residual networks helps
* Adjusting the learning rate, batch size helps but hard to pinpoint a methodology
* Most likely it's the instability of using a scale parameter (RealNVP paper Section 3.7), might need to implement their batch norm for more stable results, especially when adding more layers:
* Reimplement `BatchNorm`: https://github.com/keras-team/keras/blob/master/keras/layers/normalization.py
* Except return regular result AND (variance + eps) term
* Use the (var + eps) term to compute Jacobian for loss function (should just be log-additive)
* Once this is done, add back the other stuff:
* Turn on residual shortcuts
* Change batch size to reasonable number and learning rate=0.01
* If this still doesn't work, might want to implement "Running average over recent minibatches" in Appendix E
# 2020-03-31
* Fixed a bug (I think) in the network where the coupling layer was wrong. However, it still sometimes get stuck at around a loss of 5 but more often than not (on another training run) get to -10 (after 20 iters).
* Trying to get FlowBatchNorm worknig but having some issues passing the determinant batch loss as an output because the `batch_size` is not getting passed (it has dimension (3,) but should have dimension (None, 3)). Need to figure out how to tranlate a tensor to Layer that includes batch.
# 2020-04-05
* Reminder: BatchNormalization on conv layers only need to normalize across [B, W, H, :] layers, not the "C" layer because the filter is identical across a channel (so it uses the same mean/var to normalize). This is nice because it's the same axis (-1) you would normalize across in a Dense layer. See: https://intellipaat.com/community/3872/batch-normalization-in-convolutional-neural-network
* I think I figured out how to return the batchnorm weights back but now I'm hitting a roadblock when I try to merge them together to put as part of the output loss -- maybe I should just forget it and use the tensors directly in the output loss?
* Now that I switched to an explicit batch size, it doesn't run anymore... get this error "Incompatible shapes: [4] vs. [32]", probably some assumption that I had, got to work backwards and fix it I think.
# 2020-04-14
* Okay figured out the weird error I was getting: when a Keras model has multiple outputs you either have to give it a list or dict of loss functions, otherwise it will apply the same loss to each output! Of course, I just assumed that it gives you all outputs in one loss function. So silly!
* I reverted the change to explicitly set batch. Instead in the `BatchNormFlow` layer I just multiply zero by the `inputs` and then add the mean/variance. I think this gives the right shape?
* **TODOs**:
* Check that shape/computation for `BatchNormFlow`/`batch_losses` loss is correct
* Check that loss functions are actually returning a negative log-loss (not just the log)
* Validate the model is fitting what I want (right now I have an elbow effect as I train more) -- should there be backprop through the batch_losses? I guess not? Check the paper and figure out what to do.
* Add back in the bigger model that has multiple coupling layers
# 2020-04-15
* Somehow I suspect that the batch loss is not getting optimized (the var parameter in the batch norm function). When I set the other loss components to zero, I see that hte batch loss is not really getting smaller -- should it?
loss coupling_check_even_1c_loss s_losses_loss batch_losses_loss
0 146.227879 0.0 0.0 146.227879
1 131.294226 0.0 0.0 131.294226
2 135.579913 0.0 0.0 135.579913
3 127.908073 0.0 0.0 127.908073
4 130.301921 0.0 0.0 130.301921
5 139.414369 0.0 0.0 139.414369
6 129.732767 0.0 0.0 129.732767
7 127.321448 0.0 0.0 127.321448
8 130.812973 0.0 0.0 130.812973
9 136.737979 0.0 0.0 136.737979
10 135.001893 0.0 0.0 135.001893
11 140.181680 0.0 0.0 140.181680
12 133.053322 0.0 0.0 133.053322
13 132.912917 0.0 0.0 132.912917
14 122.261415 0.0 0.0 122.261415
15 139.447081 0.0 0.0 139.447081
16 134.216364 0.0 0.0 134.216364
17 133.567210 0.0 0.0 133.567210
18 131.333447 0.0 0.0 131.333447
19 133.022141 0.0 0.0 133.022141
* **IDEA:** I should probably unit test the batch norm flow layer to make sure that it's doing what I think it should be doing... need to think about how to structure this experiment.
* **CHECK**: Should `s` loss be negated also? Seems like I need negative log loss, not just log loss...
# 2020-04-16
* Forgot that BatchNorm has two components: $\mu, \sigma^2$, the mean and variance of the batch, which we scale ($\hat{x} = \frac{x-\mu}{\sqrt{\sigma^2 + \epsilon}}$) AND two learnable parameters: $\gamma, \beta$, which are used to scale the output: $y = \gamma \hat{x} + \beta$. The learnable parameters are the only ones that change!
* Now, how does that work when calculating the determinant? Let's see:
$$\frac{\partial}{\partial y} \hat{y} = \frac{\partial}{\partial y}\big[\gamma * \frac{x-\mu}{\sqrt{\sigma^2 + \epsilon} + \beta}\big]$$
$$ = \frac{\gamma}{\sqrt{\sigma^2 + \epsilon}}$$
Therefore, I need to include gamma in the determinant calculation in the batch norm layer!
Ohhhhh... use `keras.layer.add_loss()` function instead of passing the new things over! Not sure how to deal with batch though... https://www.tensorflow.org/guide/keras/custom_layers_and_models
# 2020-04-17
* Made some progress adding batch norm loss use both `layer.add_loss()` and `layer.add_metric()` so I can view it... BUT I need to upgrade to Tensorflow 2.0.
* After upgrading to 2.0, might as well start using `tf.keras` directly as that's the recommendation from the site.
# 2020-04-20
* Upgraded to Tensorflow 2.1! I hate upgrading things...
* Converted most of my code over too -- still need to add `layer.add_loss()` and `layer.add_metric()` to the `FlowBatchNorm()` layer though. I did convert it over to the TF2 version, inheriting it and assuming that the fancier features are turned off.
```
from scipy.stats import norm
for i in range(-10, 10):
eps = i / 1000
l = norm.cdf(0 - eps)
r = norm.cdf(0 + eps)
print(eps, '\t', l - r)
a = np.array([[[-1, -2], [-3, -4]], [[1,2], [3, 4]], [[5,6], [7, 8]]])
b = np.array([100, 200]).reshape([1, 1, 2])
c = a + b
c[:, :, :]
```
| github_jupyter |
# Calculating a custom statistic
This example shows how to define and use a custom `iris.analysis.Aggregator`, that provides a new statistical operator for
use with cube aggregation functions such as `~iris.cube.Cube.collapsed`, `~iris.cube.Cube.aggregated_by` or `~iris.cube.Cube.rolling_window`.
In this case, we have a 240-year sequence of yearly average surface temperature over North America, and we want to calculate in how many years these exceed a certain temperature over a spell of 5 years or more.
Define a function to perform the custom statistical operation.
Note: in order to meet the requirements of `iris.analysis.Aggregator`, it must do the calculation over an arbitrary (given) data axis.
A function defined in a notebook will have to be defined in a single cell. Splitting it across multiple cells makes it separate code blocks, not one function.
Notebooks are thus not designed to write a lot of functions. If you do happen to need to do this, consider creating a separate Python module and importing the functions from there.
```
import numpy as np
from iris.util import rolling_window
def count_spells(data, threshold, axis, spell_length):
"""
Function to calculate the number of points in a sequence where the value
has exceeded a threshold value for at least a certain number of timepoints.
Generalised to operate on multiple time sequences arranged on a specific
axis of a multidimensional array.
Args:
* data (array):
raw data to be compared with value threshold.
* threshold (float):
threshold point for 'significant' datapoints.
* axis (int):
number of the array dimension mapping the time sequences.
(Can also be negative, e.g. '-1' means last dimension)
* spell_length (int):
number of consecutive times at which value > threshold to "count".
"""
if axis < 0:
# just cope with negative axis numbers
axis += data.ndim
# Threshold the data to find the 'significant' points.
data_hits = data > threshold
# Make an array with data values "windowed" along the time axis.
hit_windows = rolling_window(data_hits, window=spell_length, axis=axis)
# Find the windows "full of True-s" (along the added 'window axis').
full_windows = np.all(hit_windows, axis=axis+1)
# Count points fulfilling the condition (along the time axis).
spell_point_counts = np.sum(full_windows, axis=axis, dtype=int)
return spell_point_counts
```
Load the whole time-sequence as a single cube.
```
import iris
file_path = iris.sample_data_path('E1_north_america.nc')
cube = iris.load_cube(file_path)
cube
```
Make an aggregator from the user function.
```
from iris.analysis import Aggregator
SPELL_COUNT = Aggregator('spell_count',
count_spells,
units_func=lambda units: 1)
```
Define the parameters of the test.
```
threshold_temperature = 280.0
spell_years = 5
```
Calculate the statistic.
```
warm_periods = cube.collapsed('time', SPELL_COUNT,
threshold=threshold_temperature,
spell_length=spell_years)
warm_periods.rename('Number of 5-year warm spells in 240 years')
warm_periods
```
Plot the results.
```
%matplotlib inline
import iris.quickplot as qplt
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['figure.figsize'] = [12, 8]
qplt.contourf(warm_periods, cmap='RdYlBu_r')
plt.gca().coastlines();
```
| github_jupyter |
```
import pandas as pd
import geopandas
import glob
import matplotlib.pyplot as plt
import numpy as np
import seaborn
import shapefile as shp
from paths import *
from refuelplot import *
setup()
wpNZ = pd.read_csv(data_path + "/NZ/windparks_NZ.csv", delimiter=';')
wpBRA = pd.read_csv(data_path + '/BRA/turbine_data.csv',index_col=0)
wpUSA = pd.read_csv(data_path + '/USA/uswtdb_v2_3_20200109.csv')
# remove Guam
wpUSA = wpUSA[wpUSA.t_state!='GU']
wpZAF = pd.read_csv(data_path + '/ZAF/windparks_ZAF.csv')
shpBRA = geopandas.read_file(data_path + '/country_shapefiles/BRA/BRA_adm1.shp')
shpNZ = geopandas.read_file(data_path + '/country_shapefiles/NZ/CON2017_HD_Clipped.shp')
shpUSA = geopandas.read_file(data_path + '/country_shapefiles/USA/cb_2018_us_state_500k.shp')
shpZAF = geopandas.read_file(data_path + '/country_shapefiles/ZAF/zaf_admbnda_adm1_2016SADB_OCHA.shp')
```
plot windparks: either all with opacity or aggregate to windparks and maybe use size as capacity indicator?
```
fig, ax = plt.subplots(figsize = (9,7))
ax.set_xlim(-180,-65)
ax.set_ylim(20,75)
shpUSA.plot(color=COLORS[4],ax=ax)
plt.plot(wpUSA.xlong,wpUSA.ylat,'o',alpha=0.1,markersize=2)
import xarray as xr
from matplotlib.patches import Rectangle
NZera5 = xr.open_dataset(era_path + '/NZ/era5_wind_NZ_198701.nc')
NZmerra2 = xr.open_dataset(mer_path + '/NZ/merra2_wind_NZ_198701.nc')
def cell_coords(lon,lat):
diflat = NZera5.latitude.values - lat
diflon = NZera5.longitude.values - lon
clat = NZera5.latitude.values[abs(diflat)==min(abs(diflat))][0]
clon = NZera5.longitude.values[abs(diflon)==min(abs(diflon))][0]
return((clon-0.125,clat-0.125))
def cell_coords_mer(lon,lat):
diflat = NZmerra2.lat.values - lat
diflon = NZmerra2.lon.values - lon
clat = NZmerra2.lat.values[abs(diflat)==min(abs(diflat))][0]
clon = NZmerra2.lon.values[abs(diflon)==min(abs(diflon))][0]
return((clon-0.3125,clat-0.25))
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[3]).set_xlim(165,180)
plt.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=4)
ax = plt.gca()
rect = matplotlib.patches.Rectangle(xy=cell_coords(wpNZ.Longitude[0],wpNZ.Latitude[0]),width= 0.25,height=0.25,alpha=0.7,color=COLORS[1])
ax.add_patch(rect)
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[3],alpha=0.5).set_xlim(165,180)
plt.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=4)
ax = plt.gca()
for i in range(len(wpNZ)):
rect = matplotlib.patches.Rectangle(xy=cell_coords_mer(wpNZ.Longitude[i],wpNZ.Latitude[i]),width= 0.625,height=0.5,alpha=0.7,color=COLORS[1])
ax.add_patch(rect)
plt.savefig(results_path + '/plots/syssize_NZ.png')
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[4]).set_xlim(165,180)
plt.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=4)
shpBRA.plot(color=COLORS[4])
plt.plot(wpBRA.lon,wpBRA.lat,'o',alpha=0.1,markersize=2)
shpZAF.plot(color=COLORS[4])
plt.plot(wpZAF.Longitude,wpZAF.Latitude,'o',markersize=4)
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2,figsize=(10,10),gridspec_kw = {'wspace':0.15, 'hspace':0.15})
shpBRA.plot(color=COLORS[4],ax=ax1)
ax1.set_xlim(-75,-30)
ax1.set_ylim(-35,10)
ax1.plot(wpBRA.groupby('name').mean().lon,
wpBRA.groupby('name').mean().lat,'o',alpha=0.1,markersize=2)
ax1.set_title('Brazil')
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[4],ax=ax2).set_xlim(165,180)
ax2.set_xlim(165,179)
ax2.set_ylim(-48,-34)
ax2.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=2)
ax2.set_title('New Zealand')
#ax3.set_xlim(-180,-65)
#ax3.set_ylim(-20,95)
ax3.set_xlim(-125,-65)
ax3.set_ylim(5,65)
shpUSA.plot(color=COLORS[4],ax=ax3)
#ax3.plot(wpUSA.xlong,wpUSA.ylat,'o',alpha=0.1,markersize=2)
ax3.plot(wpUSA.groupby('p_name').mean().xlong,
wpUSA.groupby('p_name').mean().ylat,'o',alpha=0.1,markersize=2)
ax3.set_title('USA')
shpZAF.plot(color=COLORS[4],ax=ax4)
ax4.set_xlim(16,33)
ax4.set_ylim(-37,-20)
ax4.plot(wpZAF.Longitude,wpZAF.Latitude,'o',markersize=2)
ax4.set_title('South Africa')
plt.savefig(results_path + '/map_windparks.png')
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2,figsize=(10,10),gridspec_kw = {'wspace':0.1, 'hspace':0.1})
shpBRA.plot(color=COLORS[4],ax=ax1)
#ax1.plot(wpBRA.lon,wpBRA.lat,'o',alpha=0.1,markersize=2)
ax1.plot(wpBRA.groupby('name').mean().lon,
wpBRA.groupby('name').mean().lat,'o',alpha=0.1,markersize=2)
ax1.set_title('Brazil')
shpNZ.to_crs({'init': 'epsg:4326'}).plot(color=COLORS[4],ax=ax2).set_xlim(165,180)
ax2.plot(wpNZ.Longitude,wpNZ.Latitude,'o',markersize=2)
ax2.set_title('New Zealand')
ax3.set_xlim(-180,-65)
ax3.set_ylim(20,75)
#ax3.set_ylim(0,87)
shpUSA.plot(color=COLORS[4],ax=ax3)
#ax3.plot(wpUSA.xlong,wpUSA.ylat,'o',alpha=0.1,markersize=2)
ax3.plot(wpUSA.groupby('p_name').mean().xlong,
wpUSA.groupby('p_name').mean().ylat,'o',alpha=0.1,markersize=2)
ax3.set_title('USA')
shpZAF.plot(color=COLORS[4],ax=ax4)
ax4.plot(wpZAF.Longitude,wpZAF.Latitude,'o',markersize=2)
ax4.set_title('South Africa')
plt.savefig(results_path + '/map_windparks.png')
```
| github_jupyter |
# Test Coffea
This will test Coffea to see if we can figure out how to use it with our code.
First are the includes from coffea. This is based on the [example written by Ben](https://github.com/CoffeaTeam/coffea/blob/master/binder/servicex/ATLAS/LocalExample.ipynb).
```
from servicex import ServiceXDataset
from coffea.processor.servicex import DataSource, Analysis
from coffea.processor.servicex import LocalExecutor
import matplotlib.pyplot as plt
from coffea import hist, processor
from IPython.display import display, update_display, HTML
```
And imports connected with running servicex.
```
from func_adl import ObjectStream
from func_adl_servicex import ServiceXSourceUpROOT
from hist import Hist
import mplhep as mpl
import awkward as ak
from utils import files
```
Methods copied to help us get all leptons from the source files
```
def apply_event_cuts (source: ObjectStream) -> ObjectStream:
'''Event level cuts for the analysis. Keep from sending data that we aren't going to need at all in the end.
'''
return (source
.Where(lambda e: e.trigE or e.trigM))
def good_leptons(source: ObjectStream) -> ObjectStream:
'''Select out all good leptons from each event. Return their pt, eta, phi, and E, and other
things needed downstream.
Because uproot doesn't tie toegher the objects, we can't do any cuts at this point.
'''
return source.Select(lambda e:
{
'lep_pt': e.lep_pt,
'lep_eta': e.lep_eta,
'lep_phi': e.lep_phi,
'lep_energy': e.lep_E,
'lep_charge': e.lep_charge,
'lep_ptcone30': e.lep_ptcone30,
'lep_etcone20': e.lep_etcone20,
'lep_type': e.lep_type,
'lep_trackd0pvunbiased': e.lep_trackd0pvunbiased,
'lep_tracksigd0pvunbiased': e.lep_tracksigd0pvunbiased,
'lep_z0': e.lep_z0,
})
```
Create the `func_adl` cuts to get the data. The dataset we use here doesn't matter, as long as it "looks" like all the datasets we are going to be processing.
```
ds = ServiceXSourceUpROOT('cernopendata://dummy', files['ggH125_ZZ4lep']['treename'], backend_name='open_uproot')
ds.return_qastle = True
leptons = good_leptons(apply_event_cuts(ds))
```
The analysis code that will apply the 4 lepton cuts and make the 4 lepton mass plot.
```
class ATLAS_Higgs_4L(Analysis):
@staticmethod
def process(events):
import awkward as ak
from collections import defaultdict
sumw = defaultdict(float)
mass_hist = hist.Hist(
"Events",
hist.Cat("dataset", "Dataset"),
hist.Bin("mass", "$Z_{ee}$ [GeV]", 60, 60, 120),
)
dataset = events.metadata['dataset']
leptons = events.lep
# We need to look at 4 lepton events only.
cut = (ak.num(leptons) == 4)
# Form the invar mass, plot.
# diele = electrons[cut][:, 0] + electrons[cut][:, 1]
# diele.mass
dilepton = leptons[:,0] + leptons[:,1]
mass_4l = leptons.mass
# Fill the histogram
sumw[dataset] += len(events)
print(len(events))
mass_hist.fill(
dataset=dataset,
mass=ak.flatten(mass_4l),
)
return {
"sumw": sumw,
"mass": mass_hist
}
```
Create the data source that we will be running against.
```
def make_ds(name: str, query: ObjectStream):
'''Create a ServiceX Datasource for a particular ATLAS Open data file
'''
datasets = [ServiceXDataset(files[name]['files'], backend_name='open_uproot')]
return DataSource(query=query, metadata={'dataset': name}, datasets=datasets)
```
And run!
```
analysis = ATLAS_Higgs_4L()
# TODO: It would be good if datatype was determined automagically (there is enough info)
executor = LocalExecutor()
#executor = DaskExecutor(client_addr="tls://localhost:8786")
datasource = make_ds('ggH125_ZZ4lep', leptons)
async def run_updates_stream(accumulator_stream):
global first
count = 0
async for coffea_info in accumulator_stream:
count += 1
print(count, coffea_info)
return coffea_info
# Why do I need run_updates_stream, why not just await on execute (which fails with async gen can't).
# Perhaps something from aiostream can help here?
result = await run_updates_stream(executor.execute(analysis, datasource))
hist.plot1d(result['mass'])
```
| github_jupyter |
# dwtls: Discrete Wavelet Transform LayerS
This library provides downsampling (DS) layers using discrete wavelet transforms (DWTs), which we call DWT layers.
Conventional DS layers lack either antialiasing filters and the perfect reconstruction property, so downsampled features are aliased and entire information of input features are not preserved.
By contrast, DWT layers have antialiasing filters and the perfect reconstruction property, which enables us to overcome the two problems.
In this library, the DWT layer and its extensions are implemented as below:
- DWT layers with fixed wavelets (Haar, CDF22, CDF26, CDF15, and DD4 wavelets)
- Trainable DWT (TDWT) layers
- Weight-normalized trainable DWT (WN-TDWT) layers
## Install dwtls
```
!pip install dwtls
import torch
import dwtls.dwt_layers
```
## DWT layers with fixed wavelets
The DWT layer (including its extensions) is implemeted as a subclass of `torch.nn.Module` provided by PyTorch, so we can easily use it in PyTorch-based scripts. Also, this layer is differentiable.
```
dwt_layer = dwtls.dwt_layers.DWT(wavelet="haar")
feature = torch.normal(0.0, 1.0, size=(1,1,20)).float()
output_feature = dwt_layer(feature)
print('Input:', feature)
print("Output:", output_feature)
```
## TDWT layer
The TDWT layer has trainable wavelets (precisely, predict and update filters of lifting scheme).
For example, we can define the TDWT layer having a pair of the prediction and update filters initialized with Haar wavelet.
```
tdwt_layer = dwtls.dwt_layers.MultiStageLWT([
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,1,0], "update": [0,0.5,0]})
])
```
The `tdwt_layer._predict_weight` and `tdwt_layer._update_weight` of this layer are trainable jointly with other DNN components.
We show three structures of the trainable DWT layers used in our music source separation paper [1].
[1] Tomohiko Nakamura, Shihori Kozuka, and Hiroshi Saruwatari, “Time-Domain Audio Source Separation with Neural Networks Based on Multiresolution Analysis,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 29, pp. 1687–1701, Apr. 2021. [pdf](https://doi.org/10.1109/TASLP.2021.3072496), [demo](https://tomohikonakamura.github.io/Tomohiko-Nakamura/demo/MRDLA/)
```
# Type A
tdwt_layer = dwtls.dwt_layers.MultiStageLWT([
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,1,0], "update": [0,0.5,0]})
])
# Type B
tdwt_layer = dwtls.dwt_layers.MultiStageLWT([
dict(predict_ksize=1, update_ksize=1,
requires_grad={"predict": False, "update": False},
initial_values={"predict": [1], "update": [0.5]}),
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,0,0], "update": [0,0,0]})
])
# Type C
tdwt_layer = dwtls.dwt_layers.MultiStageLWT([
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,1,0], "update": [0,0.5,0]}),
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,0,0], "update": [0,0,0]})
])
```
## WN-TDWT layer
The TDWT layer can be incorporated into many types of DNNs, but such straightforward extension does not guarantee that it has anti-aliasing filters, while it has the perfect reconstruction property owing to the lifting scheme.
The WN-TDWT layer is developed to overcome this problem. It has both properties owing to adequate normalization of the prediction and update filter coefficients.
```
# Type A
tdwt_layer = dwtls.dwt_layers.WeightNormalizedMultiStageLWT([
dict(predict_ksize=3, update_ksize=3,
requires_grad={"predict": True, "update": True},
initial_values={"predict": [0,1,0], "update": [0,0.5,0]})
])
```
The WN-TDWT layer can be used in the same way as the TDWT layer.
| github_jupyter |
```
# Imports
import matplotlib.pyplot as plt
import json
# Load data from result files
results_file = './results/results_5.json'
summary_file = './results/summary.json'
results = json.load(open(results_file))['results']
summary = json.load(open(summary_file))
def autolabel(rects, label_pos=0):
"""
Generate labels to show values on top of bar charts
:param rects: <pyplot.object> The current pyplot figure
:param label_pos: <float> OR <int> The amount of offset compared to the height of the bar
"""
for rect in rects:
height = rect.get_height()
plt.text(rect.get_x() + rect.get_width()/2., height + label_pos, f'{int(height)}', ha='center', va='bottom')
# Visualization for number of articles per category
categories = summary['occurrences per category']
total_results = sum(categories.values())
categories.pop('Generic', None)
categories.pop('Not about data ecosystems', None)
categories.pop('Systematic Review', None)
total_categorized_results = sum(categories.values())
total_uncategorized_results = total_results - total_categorized_results
print(f'total: {total_results}\n' \
f'catogorized: {total_categorized_results}\n' \
f'uncategorized: {total_uncategorized_results}\n')
labels = list(categories.keys())
values = list(categories.values())
# Pie chart
plt.pie(values, labels=labels, autopct='%1.1f%%', startangle=230)
plt.axis('equal')
plt.show()
# Same data in bar chart form
fig = plt.bar(range(len(categories)), values, align='center')
autolabel(fig, -0.8)
plt.xticks(range(len(categories)), labels, rotation=45, ha='right')
plt.xlabel('Fields')
plt.ylabel('Studies published')
plt.show()
# Same charts but this time with the science fields combined
categories_combined = categories
categories_combined['Science'] += categories_combined.pop('Biology (science)')
categories_combined['Science'] += categories_combined.pop('Neuroscience')
labels_combined = list(categories_combined.keys())
values_combined = list(categories_combined.values())
plt.pie(values_combined, labels=labels_combined, autopct='%1.1f%%', startangle=90)
plt.axis('equal')
plt.show()
# Bar chart with science fields combined
fig = plt.bar(range(len(categories_combined)), values_combined, align='center')
autolabel(fig, -0.8)
plt.xticks(range(len(categories_combined)), labels_combined, rotation=45, ha='right')
plt.xlabel('Fields')
plt.ylabel('Studies published')
plt.show()
# Visualization of the number of articles published per year
publish_years = {}
for result in results:
year = result['publish_date'][0:4]
if year in publish_years.keys():
publish_years[year] += 1
else:
publish_years.update({year: 1})
key_list = sorted(list(publish_years.keys()))
value_list = [publish_years[x] for x in key_list]
# It shows a drop in 2018 because the year has just started, this gives
# a wrong idea of the number of studies about the subject
fig = plt.bar(range(len(value_list)), value_list, align='center')
autolabel(fig, -1.5)
plt.xticks(range(len(key_list)), key_list, rotation=45, ha='right')
plt.xlabel('Publish year')
plt.ylabel('Studies published')
plt.show()
# Plot with 2018 removed from the results
key_list = key_list[:-1]
value_list = value_list[:-1]
fig = plt.bar(range(len(value_list)), value_list, align='center')
autolabel(fig, -1.5)
plt.xticks(range(len(key_list)), key_list, rotation=45, ha='right')
plt.xlabel('Publish year')
plt.ylabel('Studies published')
plt.show()
# Show the occurrences of each of the search terms
search_terms = summary['search terms']
labels = list(search_terms.keys())
values = list(search_terms.values())
fig = plt.bar(range(len(values)), values, align='center')
autolabel(fig, -3)
plt.xticks(range(len(labels)), labels, rotation=45, ha='right')
plt.show()
# Check qualitycriteria
in_title = []
in_abstract = []
term = 'data ecosystem'
for result in results:
if term in result['title'].lower():
in_title.append(result['id'])
if term in result['abstract'].lower():
in_abstract.append(result['id'])
print(f'Results with {term} in title: {in_title}')
print(f'Results with {term} in abstract: {in_abstract}')
in_both = [x for x in in_title if x in in_abstract]
print(f'\nResults with {term} in both title and abstract: {in_both}')
in_single = [x for x in in_abstract]
for result in in_title:
in_single.append(result)
in_single = sorted([x for x in in_single if x not in in_both])
print(f'\nResults with {term} only in either title or abstract: {in_single}')
```
| github_jupyter |
<a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/notebooks/sprinkler_pgm.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Directed graphical models
We illustrate some basic properties of DGMs.
```
!pip install causalgraphicalmodels
!pip install pgmpy
from causalgraphicalmodels import CausalGraphicalModel
import pgmpy
import numpy as np
import pandas as pd
```
# Make the model
```
sprinkler = CausalGraphicalModel(
nodes=["cloudy", "rain", "sprinkler", "wet", "slippery"],
edges=[
("cloudy", "rain"),
("cloudy", "sprinkler"),
("rain", "wet"),
("sprinkler", "wet"),
("wet", "slippery")
]
)
```
# Draw the model
```
# draw return a graphviz `dot` object, which jupyter can render
out = sprinkler.draw()
type(out)
display(out)
out.render()
```
# Display the factorization
```
print(sprinkler.get_distribution())
```
# D-separation
```
# check for d-seperation of two nodes
sprinkler.is_d_separated("slippery", "cloudy", {"wet"})
```
# Extract CI relationships
```
# get all the conditional independence relationships implied by a CGM
CI = sprinkler.get_all_independence_relationships()
print(CI)
records = []
for ci in CI:
record = (ci[0], ci[1], ', '.join(x for x in ci[2]))
records.append(record)
print(records)
df = pd.DataFrame(records, columns = ('X', 'Y', 'Z'))
display(df)
print(df.to_latex(index=False))
```
# Inference
```
from pgmpy.models import BayesianModel
from pgmpy.factors.discrete import TabularCPD
# Defining the model structure. We can define the network by just passing a list of edges.
model = BayesianModel([('C', 'S'), ('C', 'R'), ('S', 'W'), ('R', 'W'), ('W', 'L')])
# Defining individual CPDs.
cpd_c = TabularCPD(variable='C', variable_card=2, values=np.reshape([0.5, 0.5],(2,1)))
# In pgmpy the columns are the evidences and rows are the states of the variable.
cpd_s = TabularCPD(variable='S', variable_card=2,
values=[[0.5, 0.9],
[0.5, 0.1]],
evidence=['C'],
evidence_card=[2])
cpd_r = TabularCPD(variable='R', variable_card=2,
values=[[0.8, 0.2],
[0.2, 0.8]],
evidence=['C'],
evidence_card=[2])
cpd_w = TabularCPD(variable='W', variable_card=2,
values=[[1.0, 0.1, 0.1, 0.01],
[0.0, 0.9, 0.9, 0.99]],
evidence=['S', 'R'],
evidence_card=[2, 2])
cpd_l = TabularCPD(variable='L', variable_card=2,
values=[[0.9, 0.1],
[0.1, 0.9]],
evidence=['W'],
evidence_card=[2])
# Associating the CPDs with the network
model.add_cpds(cpd_c, cpd_s, cpd_r, cpd_w, cpd_l)
# check_model checks for the network structure and CPDs and verifies that the CPDs are correctly
# defined and sum to 1.
model.check_model()
from pgmpy.inference import VariableElimination
infer = VariableElimination(model)
# p(R=1)= 0.5*0.2 + 0.5*0.8 = 0.5
probs = infer.query(['R']).values
print('\np(R=1) = ', probs[1])
# P(R=1|W=1) = 0.7079
probs = infer.query(['R'], evidence={'W': 1}).values
print('\np(R=1|W=1) = ', probs[1])
# P(R=1|W=1,S=1) = 0.3204
probs = infer.query(['R'], evidence={'W': 1, 'S': 1}).values
print('\np(R=1|W=1,S=1) = ', probs[1])
```
| github_jupyter |
```
import json
from datetime import datetime, timedelta
import matplotlib.pylab as plot
import matplotlib.pyplot as plt
from matplotlib import dates
import pandas as pd
import numpy as np
import matplotlib
matplotlib.style.use('ggplot')
%matplotlib inline
# Read data from http bro logs
with open("http.log",'r') as infile:
file_data = infile.read()
# Split file by newlines
file_data = file_data.split('\n')
# Remove comment lines
http_data = []
for line in file_data:
if line[0] is not None and line[0] != "#":
http_data.append(line)
# Lets analyze user agents
user_agent_analysis = {}
user_agent_overall = {}
for line in http_data:
# Extract the timestamp
timestamp = datetime.fromtimestamp(float(line.split('\t')[0]))
# Strip second and microsecond from timestamp
timestamp = str(timestamp.replace(second=0,microsecond=0))
# Extract the user agent
user_agent = line.split('\t')[11]
# Update status code analysis variable
if user_agent not in user_agent_analysis.keys():
user_agent_analysis[user_agent] = {timestamp: 1}
else:
if timestamp not in user_agent_analysis[user_agent].keys():
user_agent_analysis[user_agent][timestamp] = 1
else:
user_agent_analysis[user_agent][timestamp] += 1
# Update overall user agent count
if user_agent not in user_agent_overall.keys():
user_agent_overall[user_agent] = 1
else:
user_agent_overall[user_agent] += 1
df = pd.DataFrame.from_dict(user_agent_analysis,orient='columns').fillna(0)
df
#df.plot(figsize=(12,9))
ax = df.plot(rot=90,figsize=(12,9))
user_agent_analysis2 = user_agent_analysis
print(user_agent_analysis2.keys())
high_volume_user_agents = [
"Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/46.0.2490.64 Safari/537.36"
]
for ua in high_volume_user_agents:
if ua in user_agent_analysis2.keys():
del user_agent_analysis2[ua]
df2 = pd.DataFrame.from_dict(user_agent_analysis2,orient='columns').fillna(0)
df2
df2.plot(rot=90,figsize=(12,9))
# Lets analyze status codes
status_code_analysis = {}
status_code_overall = {}
earliest_time = None
latest_time = None
for line in http_data:
# Extract the timestamp
timestamp = datetime.fromtimestamp(float(line.split('\t')[0]))
# Strip minute, second and microsecond from timestamp
#timestamp = str(timestamp.replace(minute=0,second=0,microsecond=0))
timestamp = str(timestamp.replace(second=0,microsecond=0))
# Extract the status code
status_code = line.split('\t')[14]
# Update status code analysis variable
if status_code not in status_code_analysis.keys():
status_code_analysis[status_code] = {timestamp: 1}
else:
if timestamp not in status_code_analysis[status_code].keys():
status_code_analysis[status_code][timestamp] = 1
else:
status_code_analysis[status_code][timestamp] += 1
# Update overall status code count
if status_code not in status_code_overall.keys():
status_code_overall[status_code] = 1
else:
status_code_overall[status_code] += 1
# Update our earliest and latest time as needed
if earliest_time is None or timestamp < earliest_time:
earliest_time = timestamp
if latest_time is None or timestamp > latest_time:
latest_time = timestamp
# Format data for the plot function
status_label = []
data = []
for code in sorted(status_code_overall.keys()):
status_label.append(str(code) + " (" + str(status_code_overall[code]) + ")")
data.append(status_code_overall[code])
plot.figure(1,figsize=[8,8])
patches, texts = plot.pie(data, shadow=True, startangle=90)
plot.legend(patches, status_label,loc="best")
plot.title('Status Code Distribution')
plot.axis('equal')
plot.tight_layout()
plot.show()
# Output the status codes in table form
df = pd.DataFrame.from_dict(status_code_analysis,orient='columns').fillna(0)
df
# Plot the status codes
df.plot(rot=90,figsize=(12,9))
# Remove the 200 status code and re-plot the status codes
status_code_analysis2 = status_code_analysis
if '200' in status_code_analysis2.keys():
del status_code_analysis2['200']
print(status_code_analysis2.keys())
df2 = pd.DataFrame.from_dict(status_code_analysis2,orient='columns').fillna(0)
df2.plot(rot=90, figsize=(12,9))
```
| github_jupyter |
# Method4 DCT based DOST + Huffman encoding
## Import Libraries
```
import mne
import numpy as np
from scipy.fft import fft,fftshift
import matplotlib.pyplot as plt
from scipy.signal import butter, lfilter
from scipy.signal import freqz
from scipy import signal
from scipy.fftpack import fft, dct, idct
from itertools import islice
import pandas as pd
import os
```
## Preprocessing
### Data loading
```
acc = pd.read_csv('ACC.csv')
acc = acc.iloc[1:]
acc.columns = ['column1','column2','column3']
np.savetxt('acc.txt',acc)
acc_c1 = acc["column1"]
acc_c2 = acc["column2"]
acc_c3 = acc["column3"]
acc_array_c1 = acc_c1.to_numpy() #save the data into an ndarray
acc_array_c2 = acc_c2.to_numpy()
acc_array_c3 = acc_c3.to_numpy()
acc_array_c1.shape
acc_array_c1 = acc_array_c1[0:66000] # Remove the signal in first 3minutes and last 5minutes
acc_array_c2 = acc_array_c2[0:66000]
acc_array_c3 = acc_array_c3[0:66000]
sampling_freq = 1/32
N = acc_array_c1.size
xf = np.linspace(-N*sampling_freq/2, N*sampling_freq/2, N)
index = np.linspace(0, round((N-1)*sampling_freq,4), N)
```
### Butterworth Filter to denoising
```
def butter_bandpass(lowcut, highcut, fs, order=5):
nyq = 0.5 * fs
low = lowcut / nyq
high = highcut / nyq
b, a = butter(order, [low, high], btype='band')
return b, a
def butter_bandpass_filter(data, lowcut, highcut, fs, order=5):
b, a = butter_bandpass(lowcut, highcut, fs, order=order)
y = lfilter(b, a, data)
return y
from scipy.signal import freqz
from scipy import signal
# Sample rate and desired cutoff frequencies (in Hz).
fs = 1000.0
lowcut = 0.5
highcut = 50.0
# Plot the frequency response for a few different orders.
plt.figure(1)
plt.clf()
for order in [1, 2, 3, 4]:
b, a = butter_bandpass(lowcut, highcut, fs, order=order)
w, h = freqz(b, a, worN=2000)
plt.plot((fs * 0.5 / np.pi) * w, abs(h), label="order = %d" % order)
plt.plot([0, 0.5 * fs], [np.sqrt(0.5), np.sqrt(0.5)],
'--', label='sqrt(0.5)')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Gain')
plt.grid(True)
plt.legend(loc='best')
y1 = butter_bandpass_filter(acc_array_c1, lowcut, highcut, fs, order=2)
y2 = butter_bandpass_filter(acc_array_c2, lowcut, highcut, fs, order=2)
y3 = butter_bandpass_filter(acc_array_c3, lowcut, highcut, fs, order=2)
resampled_signal1 = y1
resampled_signal2 = y2
resampled_signal3 = y3
np.savetxt('processed_acc_col1.txt',resampled_signal1)
np.savetxt('processed_acc_col2.txt',resampled_signal2)
np.savetxt('processed_acc_col3.txt',resampled_signal3)
rounded_signal1 = np.around(resampled_signal1)
rounded_signal2 = np.around(resampled_signal2)
rounded_signal3 = np.around(resampled_signal3)
```
## Transformation --- DCT based DOST
```
from scipy.fftpack import fft, dct
aN1 = dct(rounded_signal1, type = 2, norm = 'ortho')
aN2 = dct(rounded_signal2, type = 2, norm = 'ortho')
aN3 = dct(rounded_signal3, type = 2, norm = 'ortho')
def return_N(target):
if target > 1:
for i in range(1, int(target)):
if (2 ** i >= target):
return i-1
else:
return 1
from itertools import islice
split_list = [1]
for i in range(0,return_N(aN1.size)):
split_list.append(2 ** i)
temp1 = iter(aN1)
res1 = [list(islice(temp1, 0, ele)) for ele in split_list]
temp2 = iter(aN2)
res2 = [list(islice(temp2, 0, ele)) for ele in split_list]
temp3 = iter(aN3)
res3 = [list(islice(temp3, 0, ele)) for ele in split_list]
from scipy.fftpack import fft, dct, idct
cN_idct1 = [list(idct(res1[0], type = 2, norm = 'ortho' )), list(idct(res1[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res1)):
cN_idct1.append(list(idct(res1[k], type = 2, norm = 'ortho' )))
cN_idct2 = [list(idct(res2[0], type = 2, norm = 'ortho' )), list(idct(res2[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res2)):
cN_idct2.append(list(idct(res2[k], type = 2, norm = 'ortho' )))
cN_idct3 = [list(idct(res3[0], type = 2, norm = 'ortho' )), list(idct(res3[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res3)):
cN_idct3.append(list(idct(res3[k], type = 2, norm = 'ortho' )))
all_numbers1 = []
for i in cN_idct1:
for j in i:
all_numbers1.append(j)
all_numbers2 = []
for i in cN_idct2:
for j in i:
all_numbers2.append(j)
all_numbers3 = []
for i in cN_idct3:
for j in i:
all_numbers3.append(j)
all_numbers1 = np.asarray(all_numbers1)
all_numbers2 = np.asarray(all_numbers2)
all_numbers3 = np.asarray(all_numbers3)
int_cN1 = np.round(all_numbers1,3)
int_cN2 = np.round(all_numbers2,3)
int_cN3 = np.round(all_numbers3,3)
np.savetxt('int_cN1.txt',int_cN1, fmt='%.3f')
np.savetxt('int_cN2.txt',int_cN2, fmt='%.3f')
np.savetxt('int_cN3.txt',int_cN3,fmt='%.3f')
```
## Huffman Coding
### INSTRUCTION ON HOW TO COMPRESS THE DATA BY HUFFMAN CODING
(I used the package "tcmpr 0.2" and "pyhuff 1.1". These two packages provided the same compression result. So here, we just use "tcmpr 0.2")
1. Open your termial or git bash, enter "pip install tcmpr" to install the "tcmpr 0.2" package
2. Enter the directory which include the file you want to compress OR copy the path of the file you want to compress
3. Enter "tcmpr filename.txt" / "tcmpr filepath" to compress the file
4. Find the compressed file in the same directory of the original file
```
# Do Huffman encoding based on the instruction above
# or run this trunk if this scratch locates in the same directory with the signal you want to encode
os.system('tcmpr int_cN1.txt')
os.system('tcmpr int_cN2.txt')
os.system('tcmpr int_cN3.txt')
```
## Reconstruction
```
os.system('tcmpr -d int_cN1.txt.huffman')
os.system('tcmpr -d int_cN2.txt.huffman')
os.system('tcmpr -d int_cN3.txt.huffman')
decoded_data1 = np.loadtxt(fname = "int_cN1.txt")
decoded_data2 = np.loadtxt(fname = "int_cN2.txt")
decoded_data3 = np.loadtxt(fname = "int_cN3.txt")
recover_signal1 = decoded_data1
recover_signal2 = decoded_data2
recover_signal3 = decoded_data3
recover_signal1 = list(recover_signal1)
recover_signal2 = list(recover_signal2)
recover_signal3 = list(recover_signal3)
len(recover_signal1)
split_list = [1]
for i in range(0,return_N(len(recover_signal1))+1):
split_list.append(2 ** i)
temp_recovered1 = iter(recover_signal1)
res_recovered1 = [list(islice(temp_recovered1, 0, ele)) for ele in split_list]
temp_recovered2 = iter(recover_signal2)
res_recovered2 = [list(islice(temp_recovered2, 0, ele)) for ele in split_list]
temp_recovered3 = iter(recover_signal3)
res_recovered3 = [list(islice(temp_recovered3, 0, ele)) for ele in split_list]
recover_dct1 = [list(dct(res_recovered1[0], type = 2, norm = 'ortho' )), list(dct(res_recovered1[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered1)):
recover_dct1.append(list(dct(res_recovered1[k], type = 2, norm = 'ortho' )))
recover_dct2 = [list(dct(res_recovered2[0], type = 2, norm = 'ortho' )), list(dct(res_recovered2[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered2)):
recover_dct2.append(list(dct(res_recovered2[k], type = 2, norm = 'ortho' )))
recover_dct3 = [list(dct(res_recovered3[0], type = 2, norm = 'ortho' )), list(dct(res_recovered3[1], type = 2, norm = 'ortho' ))]
for k in range(2,len(res_recovered3)):
recover_dct3.append(list(dct(res_recovered3[k], type = 2, norm = 'ortho' )))
all_recover1 = []
for i in recover_dct1:
for j in i:
all_recover1.append(j)
all_recover2 = []
for i in recover_dct2:
for j in i:
all_recover2.append(j)
all_recover3 = []
for i in recover_dct3:
for j in i:
all_recover3.append(j)
aN_recover1 = idct(all_recover1, type = 2, norm = 'ortho')
aN_recover2 = idct(all_recover2, type = 2, norm = 'ortho')
aN_recover3 = idct(all_recover3, type = 2, norm = 'ortho')
plt.plot(signal.resample(y1, len(aN_recover1))[31000:31100], label = "origianl")
plt.plot(aN_recover1[31000:31100], label = "recovered")
plt.legend()
plt.title('ACC')
plt.grid()
plt.show()
#resampled_signal_shorter = resampled_signal1[:len(aN_recover1)]
resampled_signal_shorter1 = signal.resample(y1, len(aN_recover1))
from sklearn.metrics import mean_squared_error
from math import sqrt
def PRD_calculation(original_signal, compressed_signal):
PRD = sqrt(sum((original_signal-compressed_signal)**2)/(sum(original_signal**2)))
return PRD
PRD = PRD_calculation(resampled_signal_shorter1, aN_recover1)
print("The PRD is {}%".format(round(PRD*100,3)))
```
| github_jupyter |
# ElasticNet with RobustScaler
**This Code template is for the regression analysis using a ElasticNet Regression and the feature rescaling technique RobustScaler in a pipeline**
### Required Packages
```
import warnings as wr
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import ElasticNet
from sklearn.metrics import mean_squared_error, r2_score,mean_absolute_error
wr.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path) #reading file
df.head()#displaying initial entries
print('Number of rows are :',df.shape[0], ',and number of columns are :',df.shape[1])
df.columns.tolist()
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
plt.figure(figsize = (15, 10))
corr = df.corr()
mask = np.triu(np.ones_like(corr, dtype = bool))
sns.heatmap(corr, mask = mask, linewidths = 1, annot = True, fmt = ".2f")
plt.show()
correlation = df[df.columns[1:]].corr()[target][:]
correlation
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
#spliting data into X(features) and Y(Target)
X=df[features]
Y=df[target]
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
#we can choose randomstate and test_size as over requerment
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 1) #performing datasplitting
```
## Model
### Data Scaling
**Used RobustScaler**
* It scales features using statistics that are robust to outliers.
* This method removes the median and scales the data in the range between 1st quartile and 3rd quartile. i.e., in between 25th quantile and 75th quantile range. This range is also called an Interquartile range.
### ElasticNet
Elastic Net first emerged as a result of critique on Lasso, whose variable selection can be too dependent on data and thus unstable. The solution is to combine the penalties of Ridge regression and Lasso to get the best of both worlds.
**Features of ElasticNet Regression-**
* It combines the L1 and L2 approaches.
* It performs a more efficient regularization process.
* It has two parameters to be set, λ and α.
#### Model Tuning Parameters
1. alpha : float, default=1.0
> Constant that multiplies the penalty terms. Defaults to 1.0. See the notes for the exact mathematical meaning of this parameter. alpha = 0 is equivalent to an ordinary least square, solved by the LinearRegression object. For numerical reasons, using alpha = 0 with the Lasso object is not advised. Given this, you should use the LinearRegression object.
2. l1_ratio : float, default=0.5
> The ElasticNet mixing parameter, with 0 <= l1_ratio <= 1. For l1_ratio = 0 the penalty is an L2 penalty. For l1_ratio = 1 it is an L1 penalty. For 0 < l1_ratio < 1, the penalty is a combination of L1 and L2.
3. normalize : bool, default=False
>This parameter is ignored when fit_intercept is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use StandardScaler before calling fit on an estimator with normalize=False.
4. max_iter : int, default=1000
>The maximum number of iterations.
5. tol : float, default=1e-4
>The tolerance for the optimization: if the updates are smaller than tol, the optimization code checks the dual gap for optimality and continues until it is smaller than tol.
6. selection : {‘cyclic’, ‘random’}, default=’cyclic’
>If set to ‘random’, a random coefficient is updated every iteration rather than looping over features sequentially by default. This (setting to ‘random’) often leads to significantly faster convergence especially when tol is higher than 1e-4.
```
#training the ElasticNet
Input=[("scaler",RobustScaler()),("model",ElasticNet(random_state = 5))]
model = Pipeline(Input)
model.fit(X_train,y_train)
```
#### Model Accuracy
score() method return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
```
print("Accuracy score {:.2f} %\n".format(model.score(X_test,y_test)*100))
#prediction on testing set
prediction=model.predict(X_test)
```
### Model evolution
**r2_score:** The r2_score function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
**MAE:** The mean abosolute error function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
**MSE:** The mean squared error function squares the error(penalizes the model for large errors) by our model.
```
print('Mean Absolute Error:', mean_absolute_error(y_test, prediction))
print('Mean Squared Error:', mean_squared_error(y_test, prediction))
print('Root Mean Squared Error:', np.sqrt(mean_squared_error(y_test, prediction)))
print("R-squared score : ",r2_score(y_test,prediction))
#ploting actual and predicted
red = plt.scatter(np.arange(0,80,5),prediction[0:80:5],color = "red")
green = plt.scatter(np.arange(0,80,5),y_test[0:80:5],color = "green")
plt.title("Comparison of Regression Algorithms")
plt.xlabel("Index of Candidate")
plt.ylabel("target")
plt.legend((red,green),('ElasticNet', 'REAL'))
plt.show()
```
### Prediction Plot¶
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis. For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(10,6))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(X_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator: Vipin Kumar , Github: [Profile](https://github.com/devVipin01)
| github_jupyter |
# Let's Import Our Libraries
```
# Keras
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from keras.models import Sequential
from keras.layers import Dense, Flatten, LSTM, Conv1D, MaxPooling1D, Dropout, Activation
from keras.layers.embeddings import Embedding
# Plot
import plotly.offline as py
import plotly.graph_objs as go
py.init_notebook_mode(connected=True)
import matplotlib as plt
# NLTK
import nltk
from nltk.corpus import stopwords
from nltk.stem import SnowballStemmer
#Sklearn
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_is_fitted
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import SGDClassifier
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import precision_score
from keras.wrappers.scikit_learn import KerasClassifier
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import cross_val_score
# Other
import re
import string
import numpy as np
import pandas as pd
from sklearn.manifold import TSNE
from scipy import sparse
import warnings
warnings.filterwarnings('ignore')
```
# Let's start by exploring the data.
```
df = pd.read_csv("socialmedia-disaster-tweets-DFE.csv", encoding='latin-1')
df.shape
df.head(5)
df.columns
```
The 'tweet' column has tweets and 'choose_one' has the classification.
Let's determine the number of unique classifications.
```
df.choose_one.unique()
```
# Let's work on cleaning up the data
```
df = df[["text", "choose_one"]]
df["choose_one"] = df.choose_one.replace({"Relevant": 1, "Not Relevant": 0})
df.rename(columns={"choose_one":"label"}, inplace=True)
df.label=pd.to_numeric(df.label, errors='coerce')
df.dropna(inplace=True)
```
Let's check and see how the data looks.
```
df.label.unique()
df.head(5)
df["text"] = df["text"].str.replace(r"http\S+|http|@\S+|at", "")
df["text"] = df["text"].str.replace(r"[^A-Za-z0-9(),!?@\'\`\"\_\n]", " ")
df["text"] = df["text"].str.lower()
df.head(5)
df.columns
```
# Let's Tokenzie: We'll Turn our Sentences into Lists of Words
```
from nltk.tokenize import RegexpTokenizer
tokenizer = RegexpTokenizer(r'\w+')
df["tokens"] = df["text"].apply(tokenizer.tokenize)
```
Tokens will give us more insight into the data
```
all_words = [word for tokens in df["tokens"] for word in tokens]
sentence_lengths = [len(tokens) for tokens in df["tokens"]]
vocabulary = sorted(set(all_words))
print("%s words total, with a vocabulary size of %s." % (len(all_words), len(vocabulary)))
print("Max sentence length is %s." % max(sentence_lengths))
```
# Let's Embed: Turning Words into Numbers
```
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
```
### TFIDF Tokenizer for Our Classical ML Models
```
text = df["text"].tolist()
labels = df["label"].tolist()
X_train, X_test, y_train, y_test = train_test_split(text, labels, test_size=0.2,random_state=40)
tfidf_vectorizer = TfidfVectorizer()
X_train_tfidf = tfidf_vectorizer.fit_transform(X_train)
X_test_tfidf = tfidf_vectorizer.transform(X_test)
X_test_tfidf.shape
```
### NN Specific Tokenizer
```
vocabulary_size = 40000
tokenizer = Tokenizer(num_words = vocabulary_size)
tokenizer.fit_on_texts(df['text'])
sequences = tokenizer.texts_to_sequences(X_train)
X_train_nn = pad_sequences(sequences, maxlen=28)
sequences = tokenizer.texts_to_sequences(X_test)
X_test_nn = pad_sequences(sequences, maxlen=28)
X_train_nn = pd.DataFrame(X_train_nn)
X_test_nn = pd.DataFrame(X_test_nn)
type(X_train_tfidf)
type(X_train_nn)
```
# Here We'll Define a New Classifier
```
class NbSvmClassifier(BaseEstimator, ClassifierMixin):
def __init__(self, C=1.0, dual=False, n_jobs=1):
self.C = C
self.dual = dual
self.n_jobs = n_jobs
def predict(self, x):
# Verify that model has been fit
check_is_fitted(self, ['_r', '_clf'])
return self._clf.predict(x.multiply(self._r))
def predict_proba(self, x):
# Verify that model has been fit
check_is_fitted(self, ['_r', '_clf'])
return self._clf.predict_proba(x.multiply(self._r))
def fit(self, x, y):
# Check that X and y have correct shape
#y = y.values
y = y
x, y = check_X_y(x, y, accept_sparse=True)
def pr(x, y_i, y):
p = x[y==y_i].sum(0)
return (p+1) / ((y==y_i).sum()+1)
self._r = sparse.csr_matrix(np.log(pr(x,1,y) / pr(x,0,y)))
x_nb = x.multiply(self._r)
self._clf = LogisticRegression(C=self.C, dual=self.dual, n_jobs=self.n_jobs).fit(x_nb, y)
return self
```
## Let's get a baseline using Logisitc Regression
```
classifier = LogisticRegression(C=30.0, class_weight='balanced', solver='newton-cg', multi_class='multinomial', n_jobs=-1, random_state=40)
classifier.fit(X_train_tfidf, y_train)
y_predicted_tfidf = classifier.predict(X_test_tfidf)
precision = precision_score(y_test, y_predicted_tfidf, pos_label=None,average='weighted')
print(precision)
```
## Now We'll Utilize Our NBSVM Classifier
```
classifier = NbSvmClassifier(C=4, dual=True, n_jobs=-1).fit(X_train_tfidf, y_train)
classifier.fit(X_train_tfidf, y_train)
y_predicted_tfidf = classifier.predict(X_test_tfidf)
precision = precision_score(y_test, y_predicted_tfidf, pos_label=None,average='weighted')
print(precision)
```
## Now Let's Apply Grid Search to the Model
```
from sklearn.model_selection import GridSearchCV
param_grid = {
'C': [3.0, 3.2, 3.25, 3.3, 3.4, 3.5],
'dual' : [True, False]
}
%%time
gs_classifier = GridSearchCV(NbSvmClassifier(), param_grid, n_jobs=-1)
gs_classifier = gs_classifier.fit(X_train_tfidf, y_train)
gs_classifier.best_score_
gs_classifier.best_params_
```
We don't seem to be getting much extra juice from applying grid search to this model.
## Let's Try Regular SVM
```
classifier = SGDClassifier().fit(X_train_tfidf, y_train)
classifier.fit(X_train_tfidf, y_train)
y_predicted_tfidf = classifier.predict(X_test_tfidf)
precision = precision_score(y_test, y_predicted_tfidf, pos_label=None,average='weighted')
print(precision)
```
## Let's Try Multinomial Naive Bayes
```
classifier = SGDClassifier().fit(X_train_tfidf, y_train)
classifier.fit(X_train_tfidf, y_train)
y_predicted_tfidf = classifier.predict(X_test_tfidf)
precision = precision_score(y_test, y_predicted_tfidf, pos_label=None,average='weighted')
print(precision)
```
The last three approaches yielded pretty similar results. Let's try a deep learning model.
## Build the network with LSTM
### Network Architecture
Our network is going to start with an embedding layer. This layer lets the system expand each token into a much larger vector space. By doing so we can represent each word in a more meaningful way. The layer takes 40K as its first argument, which is the size of our vocabulary. 100 is the second argument, which is the dimension of the embeddings. The third argument is 28 which is the max number of tokens we consider from each tweet.
```
def create_lstm():
model = Sequential()
model.add(Embedding(40000, 100, input_length=28))
model.add(LSTM(100, dropout=0.9, recurrent_dropout=0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
return model
classifier = KerasClassifier(build_fn=create_lstm, epochs=3, batch_size=5, verbose=0)
%%time
classifier.fit(X_train_nn, y_train)
y_predicted_nn = classifier.predict(X_test_nn)
precision = precision_score(y_test, y_predicted_nn, pos_label=None,average='weighted')
print(precision)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/sroy8091/deep-learning-v2-pytorch/blob/master/convolutional-neural-networks/cifar-cnn/cifar10_cnn_exercise.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Convolutional Neural Networks
---
In this notebook, we train a **CNN** to classify images from the CIFAR-10 database.
The images in this database are small color images that fall into one of ten classes; some example images are pictured below.
<img src='https://github.com/sroy8091/deep-learning-v2-pytorch/blob/master/convolutional-neural-networks/cifar-cnn/notebook_ims/cifar_data.png?raw=1' width=70% height=70% />
### Test for [CUDA](http://pytorch.org/docs/stable/cuda.html)
Since these are larger (32x32x3) images, it may prove useful to speed up your training time by using a GPU. CUDA is a parallel computing platform and CUDA Tensors are the same as typical Tensors, only they utilize GPU's for computation.
```
import torch
import numpy as np
# check if CUDA is available
train_on_gpu = torch.cuda.is_available()
if not train_on_gpu:
print('CUDA is not available. Training on CPU ...')
else:
print('CUDA is available! Training on GPU ...')
```
---
## Load the [Data](http://pytorch.org/docs/stable/torchvision/datasets.html)
Downloading may take a minute. We load in the training and test data, split the training data into a training and validation set, then create DataLoaders for each of these sets of data.
```
from torchvision import datasets
import torchvision.transforms as transforms
from torch.utils.data.sampler import SubsetRandomSampler
# number of subprocesses to use for data loading
num_workers = 0
# how many samples per batch to load
batch_size = 20
# percentage of training set to use as validation
valid_size = 0.2
# convert data to a normalized torch.FloatTensor
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
# choose the training and test datasets
train_data = datasets.CIFAR10('data', train=True,
download=True, transform=transform)
test_data = datasets.CIFAR10('data', train=False,
download=True, transform=transform)
# obtain training indices that will be used for validation
num_train = len(train_data)
indices = list(range(num_train))
np.random.shuffle(indices)
split = int(np.floor(valid_size * num_train))
train_idx, valid_idx = indices[split:], indices[:split]
# define samplers for obtaining training and validation batches
train_sampler = SubsetRandomSampler(train_idx)
valid_sampler = SubsetRandomSampler(valid_idx)
# prepare data loaders (combine dataset and sampler)
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=train_sampler, num_workers=num_workers)
valid_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=valid_sampler, num_workers=num_workers)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size,
num_workers=num_workers)
# specify the image classes
classes = ['airplane', 'automobile', 'bird', 'cat', 'deer',
'dog', 'frog', 'horse', 'ship', 'truck']
```
### Visualize a Batch of Training Data
```
import matplotlib.pyplot as plt
%matplotlib inline
# helper function to un-normalize and display an image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
plt.imshow(np.transpose(img, (1, 2, 0))) # convert from Tensor image
# obtain one batch of training images
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy() # convert images to numpy for display
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(25, 4))
# display 20 images
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
imshow(images[idx])
ax.set_title(classes[labels[idx]])
```
### View an Image in More Detail
Here, we look at the normalized red, green, and blue (RGB) color channels as three separate, grayscale intensity images.
```
rgb_img = np.squeeze(images[3])
channels = ['red channel', 'green channel', 'blue channel']
fig = plt.figure(figsize = (36, 36))
for idx in np.arange(rgb_img.shape[0]):
ax = fig.add_subplot(1, 3, idx + 1)
img = rgb_img[idx]
ax.imshow(img, cmap='gray')
ax.set_title(channels[idx])
width, height = img.shape
thresh = img.max()/2.5
for x in range(width):
for y in range(height):
val = round(img[x][y],2) if img[x][y] !=0 else 0
ax.annotate(str(val), xy=(y,x),
horizontalalignment='center',
verticalalignment='center', size=8,
color='white' if img[x][y]<thresh else 'black')
```
---
## Define the Network [Architecture](http://pytorch.org/docs/stable/nn.html)
This time, you'll define a CNN architecture. Instead of an MLP, which used linear, fully-connected layers, you'll use the following:
* [Convolutional layers](https://pytorch.org/docs/stable/nn.html#conv2d), which can be thought of as stack of filtered images.
* [Maxpooling layers](https://pytorch.org/docs/stable/nn.html#maxpool2d), which reduce the x-y size of an input, keeping only the most _active_ pixels from the previous layer.
* The usual Linear + Dropout layers to avoid overfitting and produce a 10-dim output.
A network with 2 convolutional layers is shown in the image below and in the code, and you've been given starter code with one convolutional and one maxpooling layer.
<img src='https://github.com/sroy8091/deep-learning-v2-pytorch/blob/master/convolutional-neural-networks/cifar-cnn/notebook_ims/2_layer_conv.png?raw=1' height=50% width=50% />
#### TODO: Define a model with multiple convolutional layers, and define the feedforward network behavior.
The more convolutional layers you include, the more complex patterns in color and shape a model can detect. It's suggested that your final model include 2 or 3 convolutional layers as well as linear layers + dropout in between to avoid overfitting.
It's good practice to look at existing research and implementations of related models as a starting point for defining your own models. You may find it useful to look at [this PyTorch classification example](https://github.com/pytorch/tutorials/blob/master/beginner_source/blitz/cifar10_tutorial.py) or [this, more complex Keras example](https://github.com/keras-team/keras/blob/master/examples/cifar10_cnn.py) to help decide on a final structure.
#### Output volume for a convolutional layer
To compute the output size of a given convolutional layer we can perform the following calculation (taken from [Stanford's cs231n course](http://cs231n.github.io/convolutional-networks/#layers)):
> We can compute the spatial size of the output volume as a function of the input volume size (W), the kernel/filter size (F), the stride with which they are applied (S), and the amount of zero padding used (P) on the border. The correct formula for calculating how many neurons define the output_W is given by `(W−F+2P)/S+1`.
For example for a 7x7 input and a 3x3 filter with stride 1 and pad 0 we would get a 5x5 output. With stride 2 we would get a 3x3 output.
```
import torch.nn as nn
import torch.nn.functional as F
# define the CNN architecture
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# convolutional layer
self.conv1 = nn.Conv2d(3, 16, 3, padding=1)
# max pooling layer
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(16, 32, 3, padding=1)
self.conv3 = nn.Conv2d(32, 64, 3, padding=1)
self.fc1 = nn.Linear(64*4*4, 512)
self.fc2 = nn.Linear(512, 10)
self.dropout = nn.Dropout(p=0.25)
def forward(self, x):
# add sequence of convolutional and max pooling layers
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = self.pool(F.relu(self.conv3(x)))
x = x.view(-1, 64*4*4)
x = self.dropout(x)
x = F.relu(self.fc1(x))
x = self.dropout(x)
x = self.fc2(x)
return x
# create a complete CNN
model = Net()
print(model)
# move tensors to GPU if CUDA is available
if train_on_gpu:
model.cuda()
```
### Specify [Loss Function](http://pytorch.org/docs/stable/nn.html#loss-functions) and [Optimizer](http://pytorch.org/docs/stable/optim.html)
Decide on a loss and optimization function that is best suited for this classification task. The linked code examples from above, may be a good starting point; [this PyTorch classification example](https://github.com/pytorch/tutorials/blob/master/beginner_source/blitz/cifar10_tutorial.py) or [this, more complex Keras example](https://github.com/keras-team/keras/blob/master/examples/cifar10_cnn.py). Pay close attention to the value for **learning rate** as this value determines how your model converges to a small error.
#### TODO: Define the loss and optimizer and see how these choices change the loss over time.
```
import torch.optim as optim
# specify loss function
criterion = nn.CrossEntropyLoss()
# specify optimizer
optimizer = optim.SGD(model.parameters(), lr=0.01)
```
---
## Train the Network
Remember to look at how the training and validation loss decreases over time; if the validation loss ever increases it indicates possible overfitting.
```
# number of epochs to train the model
n_epochs = 30 # you may increase this number to train a final model
valid_loss_min = np.Inf # track change in validation loss
for epoch in range(1, n_epochs+1):
# keep track of training and validation loss
train_loss = 0.0
valid_loss = 0.0
###################
# train the model #
###################
model.train()
for data, target in train_loader:
# move tensors to GPU if CUDA is available
if train_on_gpu:
data, target = data.cuda(), target.cuda()
# clear the gradients of all optimized variables
optimizer.zero_grad()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the batch loss
loss = criterion(output, target)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
optimizer.step()
# update training loss
train_loss += loss.item()*data.size(0)
######################
# validate the model #
######################
model.eval()
for data, target in valid_loader:
# move tensors to GPU if CUDA is available
if train_on_gpu:
data, target = data.cuda(), target.cuda()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the batch loss
loss = criterion(output, target)
# update average validation loss
valid_loss += loss.item()*data.size(0)
# calculate average losses
train_loss = train_loss/len(train_loader.dataset)
valid_loss = valid_loss/len(valid_loader.dataset)
# print training/validation statistics
print('Epoch: {} \tTraining Loss: {:.6f} \tValidation Loss: {:.6f}'.format(
epoch, train_loss, valid_loss))
# save model if validation loss has decreased
if valid_loss <= valid_loss_min:
print('Validation loss decreased ({:.6f} --> {:.6f}). Saving model ...'.format(
valid_loss_min,
valid_loss))
torch.save(model.state_dict(), 'model_cifar.pt')
valid_loss_min = valid_loss
```
### Load the Model with the Lowest Validation Loss
```
model.load_state_dict(torch.load('model_cifar.pt'))
```
---
## Test the Trained Network
Test your trained model on previously unseen data! A "good" result will be a CNN that gets around 70% (or more, try your best!) accuracy on these test images.
```
# track test loss
test_loss = 0.0
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
model.eval()
# iterate over test data
for data, target in test_loader:
# move tensors to GPU if CUDA is available
if train_on_gpu:
data, target = data.cuda(), target.cuda()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the batch loss
loss = criterion(output, target)
# update test loss
test_loss += loss.item()*data.size(0)
# convert output probabilities to predicted class
_, pred = torch.max(output, 1)
# compare predictions to true label
correct_tensor = pred.eq(target.data.view_as(pred))
correct = np.squeeze(correct_tensor.numpy()) if not train_on_gpu else np.squeeze(correct_tensor.cpu().numpy())
# calculate test accuracy for each object class
for i in range(batch_size):
label = target.data[i]
class_correct[label] += correct[i].item()
class_total[label] += 1
# average test loss
test_loss = test_loss/len(test_loader.dataset)
print('Test Loss: {:.6f}\n'.format(test_loss))
for i in range(10):
if class_total[i] > 0:
print('Test Accuracy of %5s: %2d%% (%2d/%2d)' % (
classes[i], 100 * class_correct[i] / class_total[i],
np.sum(class_correct[i]), np.sum(class_total[i])))
else:
print('Test Accuracy of %5s: N/A (no training examples)' % (classes[i]))
print('\nTest Accuracy (Overall): %2d%% (%2d/%2d)' % (
100. * np.sum(class_correct) / np.sum(class_total),
np.sum(class_correct), np.sum(class_total)))
```
### Question: What are your model's weaknesses and how might they be improved?
**Answer**: (double-click to edit and add an answer)
By adding different types of image transformations
### Visualize Sample Test Results
```
# obtain one batch of test images
dataiter = iter(test_loader)
images, labels = dataiter.next()
images.numpy()
# move model inputs to cuda, if GPU available
if train_on_gpu:
images = images.cuda()
# get sample outputs
output = model(images)
# convert output probabilities to predicted class
_, preds_tensor = torch.max(output, 1)
preds = np.squeeze(preds_tensor.numpy()) if not train_on_gpu else np.squeeze(preds_tensor.cpu().numpy())
# plot the images in the batch, along with predicted and true labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
imshow(images[idx].cpu())
ax.set_title("{} ({})".format(classes[preds[idx]], classes[labels[idx]]),
color=("green" if preds[idx]==labels[idx].item() else "red"))
```
| github_jupyter |
# Quickstart
In this tutorial, we explain how to quickly use ``LEGWORK`` to calculate the detectability of a collection of sources.
```
%matplotlib inline
```
Let's start by importing the source and visualisation modules of `LEGWORK` and some other common packages.
```
import legwork.source as source
import legwork.visualisation as vis
import numpy as np
import astropy.units as u
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
plt.rc('font', family='serif')
plt.rcParams['text.usetex'] = False
fs = 24
# update various fontsizes to match
params = {'figure.figsize': (12, 8),
'legend.fontsize': fs,
'axes.labelsize': fs,
'xtick.labelsize': 0.7 * fs,
'ytick.labelsize': 0.7 * fs}
plt.rcParams.update(params)
```
Next let's create a random collection of possible LISA sources in order to assess their detectability.
```
# create a random collection of sources
n_values = 1500
m_1 = np.random.uniform(0, 10, n_values) * u.Msun
m_2 = np.random.uniform(0, 10, n_values) * u.Msun
dist = np.random.normal(8, 1.5, n_values) * u.kpc
f_orb = 10**(-5 * np.random.power(3, n_values)) * u.Hz
ecc = 1 - np.random.power(5, n_values)
```
We can instantiate a `Source` class using these random sources in order to analyse the population. There are also a series of optional parameters which we don't cover here but if you are interested in the purpose of these then check out the [Using the Source Class](Source.ipynb) tutorial.
```
sources = source.Source(m_1=m_1, m_2=m_2, ecc=ecc, dist=dist, f_orb=f_orb)
```
This `Source` class has many methods for calculating strains, visualising populations and more. You can learn more about these in the [Using the Source Class](Source.ipynb) tutorial. For now, we shall focus only on the calculation of the signal-to-noise ratio.
Therefore, let's calculate the SNR for these sources. We set `verbose=True` to give an impression of what sort of sources we have created. This function will split the sources based on whether they are stationary/evolving and circular/eccentric and use one of 4 SNR functions for each subpopulation.
```
snr = sources.get_snr(verbose=True)
```
These SNR values are now stored in `sources.snr` and we can mask those that don't meet some detectable threshold.
```
detectable_threshold = 7
detectable_sources = sources.snr > 7
print("{} of the {} sources are detectable".format(len(sources.snr[detectable_sources]), n_values))
```
```
fig, ax = sources.plot_source_variables(xstr="f_orb", ystr="snr", disttype="kde", log_scale=(True, True),
fill=True, xlim=(2e-6, 2e-1), which_sources=sources.snr > 0)
```
The reason for this shape may not be immediately obvious. However, if we also use the visualisation module to overlay the LISA sensitivity curve, it becomes clear that the SNRs increase in step with the decrease in the noise and flatten out as the sensitivity curve does as we would expect. To learn more about the visualisation options that `LEGWORK` offers, check out the [Visualisation](Visualisation.ipynb) tutorial.
```
# create the same plot but set `show=False`
fig, ax = sources.plot_source_variables(xstr="f_orb", ystr="snr", disttype="kde", log_scale=(True, True),
fill=True, show=False, which_sources=sources.snr > 0)
# duplicate the x axis and plot the LISA sensitivity curve
right_ax = ax.twinx()
frequency_range = np.logspace(np.log10(2e-6), np.log10(2e-1), 1000) * u.Hz
vis.plot_sensitivity_curve(frequency_range=frequency_range, fig=fig, ax=right_ax)
plt.show()
```
That's it for this quickstart into using `LEGWORK`. For more details on using `LEGWORK` to calculate strains, evolve binaries and visualise their distributions check out the [other tutorials](../tutorials.rst) and [demos](../demos.rst) in these docs! You can also read more about the scope and limitations of `LEGWORK` [on this page](../limitations.rst).
| github_jupyter |
- **Let us see how well our model would perform if we would deploy our model at the end of 2018**
- **ie: Let us test our model on 2019 data**
```
import numpy as np
import pandas as pd
import category_encoders as ce
from sklearn.preprocessing import LabelBinarizer
from sklearn.preprocessing import OneHotEncoder
data_path = "../data/notebooks/4_merged_data.csv"
df_raw = pd.read_csv(data_path)
df = df_raw.copy()
cols = ['launched_at', 'status', 'days_to_deadline', 'goal',
'sub_category', 'category', 'blurb_length', 'location_country', 'rewards_mean', 'rewards_median',
'rewards_variance', 'rewards_SD', 'rewards_MIN', 'rewards_MAX' ,
'rewards_NUM', 'currency', 'launch_year', 'launch_month',
'deadline_month']
target_encoding_cols = ['location_country' , 'currency' , 'category', 'sub_category']
train_years =[ 2016, 2017 , 2018]
valid_years = [2019]
def pre_proc(df):
df = df[cols]
df= df.dropna(axis=0, subset=["rewards_MIN"])
df= df.dropna(axis=0, subset=["blurb_length"])
df = df.reset_index(drop=True)
df["launched_at"] = pd.to_datetime(df["launched_at"]).dt.date
df.sort_values("launched_at" , inplace=True)
df.drop(['launched_at'] ,axis=1 , inplace=True)
df.reset_index(inplace=True)
df.drop('index', inplace=True , axis=1)
binarizer= LabelBinarizer()
df["status"] = binarizer.fit_transform(df["status"])
return df
def onehot_categ(df):
encoder = OneHotEncoder(sparse=False)
cat_cols=['category', 'sub_category', 'currency', 'location_country']
X_hot = encoder.fit_transform(df[cat_cols])
onehotcols = []
for cat in encoder.categories_:
for col in cat:
onehotcols.append(col)
X_hot = pd.DataFrame(X_hot , columns=onehotcols)
df =pd.concat([df , X_hot] , axis=1)
df.drop(target_encoding_cols , axis=1 , inplace=True)
return df
def get_model_data(df , train_years , valid_years):
df_train = df[df['launch_year'].apply(lambda x: True if x in train_years else False)]
df_valid= df[df['launch_year'].apply(lambda x: True if x in valid_years else False)]
X_train , y_train = df_train.drop(["status","launch_year"] , axis=1) , df_train['status']
X_valid , y_valid = df_valid.drop(["status","launch_year"] , axis=1) , df_valid['status']
return X_train , y_train , X_valid , y_valid
def helmert_categ(df_train , df_valid):
encoder = ce.HelmertEncoder(cols = target_encoding_cols , drop_invariant=True )
dfh = encoder.fit_transform(df_train[target_encoding_cols])
df_train = pd.concat([df_train , dfh], axis=1)
df_train.drop(target_encoding_cols , axis=1 , inplace=True)
dfh = encoder.transform(df_valid[target_encoding_cols])
df_valid = pd.concat([df_valid , dfh], axis=1)
df_valid.drop(target_encoding_cols , axis=1 , inplace=True)
return df_train , df_valid
from xgboost import XGBClassifier
import operator
def XG_score(X_train, X_test, y_train, y_test):
XG_fet = {}
XG= XGBClassifier(n_estimators=150, random_state=9)
XG.fit(X_train, y_train)
XG_score = XG.score(X_test, y_test)
feat_labels = X_train.columns.values
for feature, acc in zip(feat_labels, XG.feature_importances_):
XG_fet[feature] = acc
XG_fet = sorted(XG_fet.items(), key=operator.itemgetter(1), reverse=True)
return (XG,XG_score, XG_fet)
df_proc = pre_proc(df)
df_onehot = onehot_categ(df_proc)
X_train_oh , y_train_oh , X_valid_oh , y_valid_oh = get_model_data(df_onehot , train_years , valid_years)
df_proc = pre_proc(df)
X_train_raw , y_train_hel , X_valid_raw , y_valid_hel = get_model_data(df_proc , train_years , valid_years)
X_train_hel , X_valid_hel = helmert_categ(X_train_raw , X_valid_raw)
XG_model_oh , XG_scores_oh , XG_fet_imp_oh= XG_score(X_train_oh , X_valid_oh , y_train_oh , y_valid_oh)
print("Score using OneHot encodinng: {}".format(XG_scores_oh))
XG_model_hel , XG_scores_hel , XG_fet_imp_hel= XG_score(X_train_hel , X_valid_hel , y_train_hel , y_valid_hel)
print("Score using Helmert encodinng: {}".format(XG_scores_hel))
```
- **This should is great, our test accuracy is greater than our validation accuracy, usually this should be a red flag but since there was not decision during the process of modeling and preprocessing made based off the 2019(test data), its fine**
- **In the next notebook we will train the model on the entire dataset and save the model**
| github_jupyter |
```
import transportation_tutorials as tt
```
# Creating Dynamic Maps
In this gallery, we will demonstrate the creation of a variety of interactive maps.
Interactive, dynamic maps are a good choice for analytical work that will be reviewed
online, either in a Jupyter notebook by an analyst, or published on a website.
In these examples,
we will demonstrate creating dynamic maps using [Plotly](https://plot.ly/python/)
and [mapped](https://pypi.org/project/mapped/), which integrates a handful of
plotly mapping tools directly into the geopandas dataframe object.
```
import numpy as np
import pandas as pd
import geopandas as gpd
import mapped
```
We'll begin by loading the TAZ and MAZ shapefiles, filtering them to a restricted study area,
and defining the center point.
```
xmin = 905712
ymin = 905343
taz = gpd.read_file(tt.data('SERPM8-TAZSHAPE')).cx[xmin:, ymin:].to_crs(epsg=4326)
maz = gpd.read_file(tt.data('SERPM8-MAZSHAPE')).cx[xmin:, ymin:].to_crs(epsg=4326)
center = (26.9198, -80.1121) # regular lat-lon
```
## Simple Map
Simple maps showing the geographic data contained in a GeoDataFrame can be created
by converting the GeoDataFrame to a GeoJson object, and adding that to
a folium Map.
```
taz.plotly_choropleth(line_width=2)
```
### Alternative Map Tiles
The default tiles are set to [Carto](https://carto.com)'s
[positron](https://carto.com/blog/getting-to-know-positron-and-dark-matter/),
but others tiles are possible, including
tilesets from [Stamen Design](http://stamen.com/) and [OpenStreetMap](www.openstreetmap.org).
The [positron](https://carto.com/blog/getting-to-know-positron-and-dark-matter/) tiles are
specifically designed to give geographic context without overwhelming maps with data
that is not the analytic focus of the presentation.
```
taz.plotly_choropleth(line_width=2, mapbox_style="open-street-map")
```
## Mapping Data
One of the input files for SERPM 8 is a MAZ-level demographics file.
The file for the 2015 base year is included in the tutorial data, and
we can load it with the `read_csv` function.
```
mazd = pd.read_csv(tt.data('SERPM8-MAZDATA', '*.csv'))
```
Use `info` to see a summary of the DataFrame.
```
mazd.info()
```
We can join the demographics table to the shape file we loaded previously,
to enable some visualizations on this data. This can be done with the
``merge`` method of DataFrames.
```
maz1 = maz.merge(mazd, how='left', left_on='MAZ', right_on='mgra')
maz1.index=maz1.MAZ
```
## Choropleth Maps
A [choropleth map](https://en.wikipedia.org/wiki/Choropleth_map) is a map with areas colored,
shaded, or patterned in proportion to some measured value for the region displayed. This kind of
map is commonly used to display things like population density.
When a data column is given to the plotly_choropleth function, that data is used to colorize
the choropleth map.
```
maz1.plotly_choropleth("PopDen", colorbar_title="Population Density", colorbar_title_side='right')
```
| github_jupyter |
### Data Scientist Nano Degree - Capstone Project
### Car Booking Analysis and Prediction
### Tarek Abd ElRahman Ahmed ElAyat
#### Let's import the needed libraries
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import warnings
from sklearn import model_selection
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score, mean_squared_error
from math import sqrt
import xgboost as xgb
from sklearn import preprocessing
#from sklearn.preprocessing import MinMaxScaler
#scaler = MinMaxScaler()
warnings.filterwarnings('ignore')
%matplotlib inline
def print_model_scores(model, X_train, X_test, y_train, y_test):
'''
INPUT:
model - the regression model
X_train - pandas dataframe for the training dataset
X_test - pandas dataframe for the test dataset
y_train - pandas dataframe for the training label
y_test - pandas dataframe for the test label
OUTPUT:
y_train_preds - panadas dataframe for the y_train prediction
y_test_preds - panadas dataframe for the y_test prediction
print scores
'''
#Predict and score the model on training data
y_train_preds = model.predict(X_train)
print("The r-squared score for our model on Training data is {} on {} values.".format(r2_score(y_train, y_train_preds), len(y_train)))
print("The mean_squared_error score for our model on Training data is {} on {} values.".format(mean_squared_error(y_train, y_train_preds), len(y_train)))
print("The root_mean_squared_error score for our model on Training data is {} on {} values.".format(sqrt(mean_squared_error(y_train, y_train_preds)), len(y_train)))
print(" ")
#Predict and score the model on test data
y_test_preds = model.predict(X_test)
print("The r-squared score for our model on Testing data is {} on {} values.".format(r2_score(y_test, y_test_preds), len(y_test)))
print("The mean_squared_error score for our model on Testing data is {} on {} values.".format(mean_squared_error(y_test, y_test_preds), len(y_test)))
print("The root_mean_squared_error score for our model on Testing data is {} on {} values.".format(sqrt(mean_squared_error(y_test, y_test_preds)), len(y_test)))
return y_train_preds, y_test_preds
def create_dummy_df(df, dummy_na):
'''
INPUT:
df - pandas dataframe with categorical variables you want to dummy
dummy_na - Bool holding whether you want to dummy NA vals of categorical columns or not
OUTPUT:
df - a new dataframe that has the following characteristics:
1. contains all columns that were not specified as categorical
2. removes all the original columns in cat_cols
3. dummy columns for each of the categorical columns
4. if dummy_na is True - it also contains dummy columns for the NaN values
5. Use a prefix of the column name with an underscore (_) for separating
'''
cat_cols = df.select_dtypes(include=['object']).columns
for col in cat_cols:
try:
# for each cat add dummy var, drop original column
df = pd.concat([df.drop(col, axis=1), pd.get_dummies(df[col], prefix=col, prefix_sep='_', drop_first=True, dummy_na=dummy_na)], axis=1)
except:
continue
return df
def coef_weights(coefficients, X_train):
'''
INPUT:
coefficients - the coefficients of the linear model
X_train - the training data, so the column names can be used
OUTPUT:
coefs_df - a dataframe holding the coefficient, estimate, and abs(estimate)
Provides a dataframe that can be used to understand the most influential coefficients
in a linear model by providing the coefficient estimates along with the name of the
variable attached to the coefficient.
'''
coefs_df = pd.DataFrame()
coefs_df['est_int'] = X_train.columns
coefs_df['coefs'] = coefficients
coefs_df['abs_coefs'] = np.abs(coefficients)
coefs_df = coefs_df.sort_values('abs_coefs', ascending=False)
return coefs_df
```
### Load the training data and lookup files
```
df_taxi = pd.read_csv('C:\\Users\\tayat\\Documents\\Capstone Project\\NYC Dataset\\taxi_onefile.csv')
df_lookup_zone = pd.read_csv('C:\\Users\\tayat\\Documents\\Capstone Project\\NYC Dataset\\taxi+_zone_lookup.csv')
pd.set_option('display.max_rows', 50)
```
### Basic data exploration, list the columns with their data types and describe the features
```
df_taxi.shape
df_taxi.head()
```
### List the columns, dtypes, and describe the features
```
df_taxi.dtypes
# from the below describtion we notice that there are unlogical (-ve values), missing values and outliers which needs cleaning
df_taxi.describe().transpose()
```
### Count missing data per feature
```
total = df_taxi.isnull().sum()
percent = (df_taxi.isnull().sum()/df_taxi.isnull().count())
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(100)
```
## Feature Engineering:
### Extract the engineered features from pickup and dropoff times and then drop these two columns
```
from pandas.tseries.holiday import USFederalHolidayCalendar as calendar
df_taxi['tpep_pickup_datetime'] = pd.to_datetime(df_taxi['tpep_pickup_datetime'])
df_taxi['tpep_dropoff_datetime'] = pd.to_datetime(df_taxi['tpep_dropoff_datetime'])
df_taxi['tripduration_mins'] = ((df_taxi['tpep_dropoff_datetime'] - df_taxi['tpep_pickup_datetime']).dt.total_seconds()/60).astype(float)
df_taxi['year'] = pd.DatetimeIndex(df_taxi['tpep_pickup_datetime']).year
df_taxi['month'] = pd.DatetimeIndex(df_taxi['tpep_pickup_datetime']).month
df_taxi['day'] = pd.DatetimeIndex(df_taxi['tpep_pickup_datetime']).day
df_taxi['hour'] = pd.DatetimeIndex(df_taxi['tpep_pickup_datetime']).hour
df_taxi['dayofweek'] = pd.DatetimeIndex(df_taxi['tpep_pickup_datetime']).dayofweek
df_taxi['weekendflag'] = (df_taxi['dayofweek']>=5).astype(int)
cal = calendar()
holidays = cal.holidays(start=df_taxi['tpep_pickup_datetime'].min(), end=df_taxi['tpep_pickup_datetime'].max())
df_taxi['holidayflag'] = (df_taxi['tpep_pickup_datetime'].isin(holidays)).astype(int)
del holidays
df_taxi.drop(['tpep_pickup_datetime', 'tpep_dropoff_datetime'], axis=1, inplace=True)
df_taxi.head()
#Save the output into new file to avoid recalculation
#df_taxi.to_csv('C:\\Users\\tayat\\Documents\\Capstone Project\\NYC Dataset\\taxi_engineered.csv', index = False)
#df_taxi = pd.read_csv('C:\\Users\\tayat\\Documents\\Capstone Project\\NYC Dataset\\taxi_engineered.csv')
df_taxi.dtypes
#Have another look after feature engineering
df_taxi.describe().transpose()
```
## Data Cleaning:
### From the above columns quick overview, we notice some unlogical columns:
#### - trip distance, duration, fare, tip, toll...etc with -ve values or very high values
#### - unlogical and out of range values like passenger_count above 6, ratecodeID above 6 and so on
### let's analyze the ranges and then get rid of these misleading values first
```
((df_taxi['trip_distance']/50).astype(int)*50).loc[:].value_counts()
((df_taxi['total_amount']/100).astype(int)*100).loc[:].value_counts()
((df_taxi['fare_amount']/100).astype(int)*100).loc[:].value_counts()
#exclude -ve and fareamount > 100
((df_taxi['extra']/5).astype(int)*5).loc[:].value_counts()
#exclude -ve and extra > 5
((df_taxi['mta_tax']).astype(int)).loc[:].value_counts()
#exclude -ve and mta_tax > 1
((df_taxi['tip_amount']/10).astype(int)*10).loc[:].value_counts()
#exclude -ve and tip_amount > 20
((df_taxi['tolls_amount']/10).astype(int)*10).loc[:].value_counts()
#exclude -ve and tolls_amount > 30
((df_taxi['improvement_surcharge']).astype(int)).loc[:].value_counts()
#exclude -ve and improvement_surcharge > 1
((df_taxi['tripduration_mins']/60).astype(int)).loc[:].value_counts()
#exclude -ve and tripduration_mins > 180 minute
((df_taxi['trip_distance']/20).astype(int)*20).loc[:].value_counts()
#exclude -ve and trip_distance > 30
```
#### Drop rows with unlogical or out of range values
```
df_taxi.drop(df_taxi[ (df_taxi['VendorID'].isna()) | (df_taxi['fare_amount'] <= 0) | (df_taxi['total_amount'] <= 0) | (df_taxi['tripduration_mins'] <= 0) | (df_taxi['tip_amount'] < 0) | (df_taxi['tolls_amount'] < 0) | (df_taxi['improvement_surcharge'] < 0) | (df_taxi['congestion_surcharge'] < 0) | (df_taxi['trip_distance'] <= 0) | (df_taxi['extra'] < 0) | (df_taxi['mta_tax'] < 0) | (df_taxi['passenger_count'] > 6) | (df_taxi['RatecodeID'] > 6)].index, inplace = True)
df_taxi.shape
```
#### Drop outliers and fill na values
```
df_taxi.drop(df_taxi[ (df_taxi['fare_amount'] > 100) | (df_taxi['tripduration_mins'] > 180) | (df_taxi['tip_amount'] > 20) | (df_taxi['tolls_amount'] > 30) | (df_taxi['extra'] > 5) | (df_taxi['mta_tax'] > 1) | (df_taxi['improvement_surcharge'] > 1) | (df_taxi['trip_distance'] > 30)].index, inplace = True)
df_taxi['congestion_surcharge'] = df_taxi['congestion_surcharge'].fillna(0)
df_taxi.shape
```
### Save the output into new file to avoid recalculation
```
#Save the output into new file to avoid recalculation
#df_taxi.to_csv('C:\\Users\\tayat\\Documents\\Capstone Project\\NYC Dataset\\taxi_clean.csv', index = False)
#df_taxi = pd.read_csv('C:\\Users\\tayat\\Documents\\Capstone Project\\NYC Dataset\\taxi_clean.csv')
```
### Continue data exploration and understanding after feature engineering and cleaning done
```
df_taxi.describe().transpose()
df_taxi['passenger_count'].value_counts()
df_taxi['RatecodeID'].value_counts()
df_taxi['sameloc'] = (df_taxi['PULocationID'] == df_taxi['DOLocationID']).astype(int)
df_taxi.head()
```
### Generate the correlation matrix after the data cleaning
```
corrmat = df_taxi.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True, xticklabels=True, yticklabels=True);
#scatter plot trip_distance/fare_amount
var = 'trip_distance'
data = pd.concat([df_taxi['fare_amount'], df_taxi[var]], axis=1)
data.plot.scatter(x=var, y='fare_amount'); #, ylim=(0,100)
#The trip duration histogram
exception_trips = df_taxi.loc[(df_taxi['fare_amount'] < 10) & (df_taxi['trip_distance'] > 12)]
exception_trips.shape
sns.distplot(exception_trips['tripduration_mins'], kde=False, norm_hist=False);
#scatter plot trip duration/fare amount
data2 = pd.concat([exception_trips['fare_amount'], exception_trips['tripduration_mins']], axis=1)
data2.plot.scatter(x='tripduration_mins', y='fare_amount'); #, ylim=(0,100)
#Fare amount histogram
sns.distplot(df_taxi['fare_amount'], kde=False, norm_hist=False, bins = 20);
#Trip distance histogram
sns.distplot(df_taxi['trip_distance'], kde=False, norm_hist=False, bins = 20);
#Hours of the day histogram
sns.distplot(df_taxi['hour'], kde=False, norm_hist=False);
#Day of week histogram
sns.distplot(df_taxi['dayofweek'], kde=False, norm_hist=False);
#Pickup locations histogram
sns.distplot(df_taxi['PULocationID'], kde=False, norm_hist=False);
#Drop-off locations histogram
sns.distplot(df_taxi['DOLocationID'], kde=False, norm_hist=False);
#Same location histogram
sns.distplot(df_taxi['sameloc'], kde=False, norm_hist=False);
((df_taxi['trip_distance']/5).astype(int)*5).loc[:].value_counts()
Loc_Dist = pd.pivot_table(df_taxi, index = 'PULocationID', columns = 'DOLocationID', values = 'VendorID', aggfunc = ['count'])
#Loc_Dist = pd.pivot_table(df_taxi, index = ['PULocationID', 'DOLocationID'], values = 'VendorID', aggfunc = ['count'])
#print(Loc_Dist)
f, ax = plt.subplots(figsize=(20, 20))
sns.heatmap(Loc_Dist, cmap="YlGnBu")
#Heatmap for pickup locations over days of the week
Loc_Dist = pd.pivot_table(df_taxi, index = 'PULocationID', columns = 'dayofweek', values = 'VendorID', aggfunc = ['count'])
f, ax = plt.subplots(figsize=(20, 20))
sns.heatmap(Loc_Dist, cmap="YlGnBu")
#Heatmap for pickup locations over hours of the day
Loc_Dist = pd.pivot_table(df_taxi, index = 'PULocationID', columns = 'hour', values = 'VendorID', aggfunc = ['count'])
f, ax = plt.subplots(figsize=(20, 20))
sns.heatmap(Loc_Dist, cmap="YlGnBu")
PULocations = pd.merge(
df_taxi['PULocationID'],
df_lookup_zone,
how="inner",
left_on='PULocationID',
right_on='LocationID',
sort=True
)
PULocations.head()
#Trip distribution over NY Pickup Boroughs
PULocations.groupby(['Borough']).count()['LocationID'].plot(kind="bar", title = 'Trips distribution over Pickup Boroughs'); #, fontsize=14, figsize = (30, 8)
DOLocations = pd.merge(
df_taxi['DOLocationID'],
df_lookup_zone,
how="inner",
left_on='DOLocationID',
right_on='LocationID',
sort=True
)
#Trip distribution over NY Dropoff Boroughs
DOLocations.groupby(['Borough']).count()['LocationID'].plot(kind="bar", title = 'Trips distribution over Drop Boroughs'); #, fontsize=14, figsize = (30, 8)
```
## Business Questions/Use Cases
### What are the most demanding areas at specific time?
#### for example below are top pick up locations for a specific day and hour (Thursday 7pm)
```
filtered_df = df_taxi[(df_taxi['dayofweek'] == 3) & (df_taxi['hour'] == 19)]['PULocationID']
TopPULocations = pd.merge(
filtered_df,
df_lookup_zone,
how="inner",
left_on='PULocationID',
right_on='LocationID',
sort=True
)
TopPULocations.head()
TopPULocations.groupby(['PULocationID']).count()['LocationID'].sort_values(ascending=False).head(30).plot(kind="bar", figsize = (30, 8), fontsize=20 , title = 'Top PULocations on Thursday 7pm'); #, fontsize=14, figsize = (30, 8)
```
### How to deploy the fleet based on driver’s preferences for drop off locations (a driver may prefer a drop off near his home)?
#### For example, below are top pick up locations for a specific day and hour (Thursday 7pm) which will most likely will lead to the favorite drop off locations [230, 234, 236]
```
DOList = [230, 234, 236]
filtered_df2 = df_taxi[(df_taxi['dayofweek'] == 3) & (df_taxi['hour'] == 19) & (df_taxi['DOLocationID'].isin(DOList))][['PULocationID', 'DOLocationID']]
filtered_df2.groupby(['PULocationID']).count()['DOLocationID'].sort_values(ascending=False).head(30).plot(kind="bar", figsize = (30, 8), fontsize=20 , title = 'Top PULocations on Thursday 7pm for specific DO List'); #, fontsize=14, figsize = (30, 8)
```
### Now let's run our basic model to predict the Fare_Rate
### Scenario #1 Linear regression with all possible features as numeric
```
#Split into explanatory and response variables
X = df_taxi[['trip_distance', 'RatecodeID', 'tripduration_mins', 'month', 'hour', 'weekendflag', 'holidayflag', 'passenger_count', 'PULocationID', 'DOLocationID', 'payment_type']]
y = df_taxi['fare_amount']
#Split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = .30, random_state=42)
#Clear memory to be able to run the model
del X
del y
lm_model = LinearRegression(normalize=True) # Instantiate
lm_model.fit(X_train, y_train) #Fit
#Predict and score the model on training and test data
y_train_preds, y_test_preds = print_model_scores(lm_model, X_train, X_test, y_train, y_test)
#Use the function
coef_df = coef_weights(lm_model.coef_, X_train)
#A quick look at the top results
coef_df.head(20)
```
### Scenario #2 Linear regression using important features as numeric
```
#Split into explanatory and response variables
X = df_taxi[['trip_distance', 'RatecodeID', 'tripduration_mins', 'month', 'hour', 'weekendflag', 'holidayflag']]
y = df_taxi['fare_amount']
#Split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = .30, random_state=42)
del X
del y
lm_model = LinearRegression(normalize=True) # Instantiate
lm_model.fit(X_train, y_train) #Fit
#Predict and score the model on training and test data
y_train_preds, y_test_preds = print_model_scores(lm_model, X_train, X_test, y_train, y_test)
#Use the function
coef_df = coef_weights(lm_model.coef_, X_train)
#A quick look at the top results
coef_df.head(20)
```
### Scenario #3 Linear regression with important features and OneHotEncoding for categorical features
```
#Split into explanatory and response variables
df_taxi_cat = df_taxi[['trip_distance', 'RatecodeID', 'tripduration_mins', 'month', 'hour', 'weekendflag', 'holidayflag', 'fare_amount']]
df_taxi_cat = df_taxi_cat.astype({'RatecodeID': 'object', 'month': 'object', 'hour': 'object'})
df_taxi_cat = create_dummy_df(df_taxi_cat, dummy_na=False)
del df_taxi
df_taxi_cat.head()
#Split into explanatory and response variables
y = df_taxi_cat['fare_amount']
X = df_taxi_cat.drop('fare_amount', axis=1)
del df_taxi_cat
#Split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = .30, random_state=42)
del X
del y
lm_model = LinearRegression(normalize=True) # Instantiate
lm_model.fit(X_train, y_train) #Fit
#Predict and score the model on training and test data
y_train_preds, y_test_preds = print_model_scores(lm_model, X_train, X_test, y_train, y_test)
#Use the function
coef_df = coef_weights(lm_model.coef_, X_train)
#A quick look at the top results
coef_df.head(50)
```
### Scenario #4 XGBoost regressor with important features and onehotencoding for categorical features
```
#Split into explanatory and response variables
df_taxi_cat = df_taxi[['trip_distance', 'RatecodeID', 'tripduration_mins', 'month', 'hour', 'weekendflag', 'holidayflag', 'fare_amount']]
df_taxi_cat = df_taxi_cat.astype({'RatecodeID': 'object', 'month': 'object', 'hour': 'object'})
df_taxi_cat = create_dummy_df(df_taxi_cat, dummy_na=False)
del df_taxi
#Split into explanatory and response variables
y = df_taxi_cat['fare_amount']
X = df_taxi_cat.drop('fare_amount', axis=1)
del df_taxi_cat
#Split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = .30, random_state=42)
del X
del y
xg_reg = xgb.XGBRegressor(objective ='reg:linear', colsample_bytree = 0.3, learning_rate = 0.1,vmax_depth = 5, alpha = 10, n_estimators = 10) # Instantiate
xg_reg.fit(X_train, y_train) #Fit
#Predict and score the model on training and test data
y_train_preds, y_test_preds = print_model_scores(xg_reg, X_train, X_test, y_train, y_test)
```
### Scenario #5 XGBoost regressor with modified hyper parameters
```
#Change the n_estimators from 10 to 50
xg_reg2 = xgb.XGBRegressor(objective ='reg:linear', colsample_bytree = 0.3, learning_rate = 0.1,vmax_depth = 5, alpha = 10, n_estimators = 50) # Instantiate
xg_reg2.fit(X_train, y_train) #Fit
#Predict and score the model on training and test data
y_train_preds, y_test_preds = print_model_scores(xg_reg2, X_train, X_test, y_train, y_test)
```
| github_jupyter |
```
from __future__ import division, print_function
import os
import torch
import pandas
import numpy as np
from torch.utils.data import DataLoader,Dataset
from torchvision import utils, transforms
from skimage import io, transform
import matplotlib.pyplot as plt
import warnings
#ignore warnings
warnings.filterwarnings("ignore")
plt.ion() #interactive mode on
```
The dataset being used is the face pose detection dataset, which annotates the data using 68 landmark points. The dataset has a csv file that contains the annotation for the images.
```
# Import CSV file
landmarks_csv = pandas.read_csv("data/faces/face_landmarks.csv")
# Extracting info from the CSV file
n = 65
img_name = landmarks_csv.iloc[n,0]
landmarks = landmarks_csv.iloc[n,1:].as_matrix()
landmarks = landmarks.astype('float').reshape(-1,2)
# Print a few of the datasets for having a look at
# the dataset
print('Image name: {}'.format(img_name))
print('Landmarks shape: {}'.format(landmarks.shape))
print('First 4 Landmarks: {}'.format(landmarks[:4]))
```
Now that we have seen the landmark values let's plot a function to display the landmarks on an image
```
def plot_landmarks(image, landmarks):
plt.imshow(image)
plt.scatter(landmarks[:, 0], landmarks[:, 1], s=10, c='r', marker='.')
plt.pause(0.01)
plt.figure()
plot_landmarks(io.imread(os.path.join('data/faces/',img_name)),landmarks)
plt.show()
```
To use customa datasets we need to use the <b>(torch.utils.data.Dataset) Dataset</b> class provided. It is an abstract class and hence the custom class should inherit it and override the
<b>__len__</b> method and the
<b>__getitem__</b> method
The __getitem__ method is used to provide the ith sample from the dataset
```
class FaceLandmarkDataset(Dataset):
# We will read the file here
def __init__(self,csv_file, root_dir, transform=None):
"""
Args:
csv_file : string : path to csv file
root_dir : string : root directory which contains all the images
transform : callable, optional : Optional transform to be applied
to the images
"""
self.landmarks_frame = pandas.read_csv(csv_file)
self.root_dir = root_dir
self.transform = transform
def __len__(self):
return len(self.landmarks_frame)
def __getitem__(self, idx):
"""
Args:
idx (integer): the ith sample
"""
image_name = os.path.join(self.root_dir,self.landmarks_frame.iloc[idx, 0])
image = io.imread(image_name)
landmarks = np.array([self.landmarks_frame.iloc[idx, 1:]])
landmarks = landmarks.astype("float").reshape(-1, 2)
sample = {"image":image,"landmarks":landmarks}
if self.transform:
sample = self.transform(sample)
return sample
face_dataset = FaceLandmarkDataset(csv_file='data/faces/face_landmarks.csv',
root_dir='data/faces/')
fig = plt.figure()
for i in range(len(face_dataset)):
sample = face_dataset[i]
print(i, sample['image'].shape, sample['landmarks'].shape)
ax = plt.subplot(1, 4, i + 1)
plt.tight_layout()
ax.set_title('Sample #{}'.format(i))
ax.axis('off')
plot_landmarks(**sample)
if i == 3:
plt.show()
break
```
Now that we have the dataset , we can move on to preprocessing the data. We use the transforms class for this.
We will be using callable classes of the transformations we need so that the parameters do not need to be passed again and again. For better description refer the <a href="https://pytorch.org/tutorials/beginner/data_loading_tutorial.html">tutorial</a> from PyTorch.
To implement callable classes we just need to implement the __call__ method and if required __init__ method of the class.
Here we will be using autocrop , Reshape and To Tensor transformations.
__** NOTE **__<br>
In PyTorch the default style for image Tensors is <span>n_channels * Height * Width</span> as opposed to the Tensordlow default of <span>Height * Width * n_channels</span>. But all the images in the real world have the tensorflow default format and hence we need to do that change in the ToTensor class that we will implement.
```
# Implementing the Rescale class
class Rescale(object):
"""Rescale the input image to a given size
Args:
output_size (int or tuple):Desired output size. If tuple, output is
matched to output_size. If int, smaller of image edges is matched
to output_size keeping aspect ratio the same
"""
def __init__(self,output_size):
assert isinstance(output_size,(int,tuple))
self.output_size = output_size
def __call__(self,sample):
image, landmarks = samplep['image'], sample['landmarks']
h, w = image.shape[:2]
if isinstance(self.output_size,int):
if h>w:
new_h, new_w = self.output_size * h/w, self.output_size
else:
new_h, new_w = slef.output_size, self.output_size *w/h
else:
new_h, new_w = self.output_size
image = transform.resize(image, (new_h, new_w))
# h and w are swapped for landmarks because for images,
# x and y axes are axis 1 and 0 respectively
landmarks = landmarks * [new_w / w, new_h / h]
return {"image": image, "landmarks": landmarks}
# Implementing Random Crop
class RandomCrop(object):
"""Crop randomly the image in a sample
Args:
output_size(tuple or int): Desired output size. If int, square crop
is made.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
if isinstance(output_size, int):
self.output_size = (output_size, output_size)
else:
assert len(output_size) == 2
self.output_size = output_size
def __call__(self, sample):
images, landmarks = sample['image'], sample['landmarks']
h, w = images.shape[:,2]
new_h, new_w = self.output_size
top = np.random.randn(0, h-new_h)
left = np.random.randn(0, w-new_w)
images = images[top:top + new_h, left:left + new_w]
landmarks = landmarks - [left, top]
sample = {"image":images, "landmarks": landmarks}
return sample
# Implementing To Tensor
class ToTensor(object):
"""Convert the PIL image into a tensor"""
def __call__(self,sample):
image, landmarks = sample['image'], sample['landmarks']
# Need to transpose
# Numpy image : H x W x C
# Torch image : C x H x W
image = image.transpose((2, 0, 1))
sample = {"image":torch.from_numpy(image),"landmarks":torch.from_numpy(landmarks)}
```
| github_jupyter |
## K Means Clustering
### Our Objective - Perform K-Means Clustering to detect Network Intrusion Attempts (Cybersecurity)
```
#matrix math
import numpy as np
#graphing
import matplotlib.pyplot as plt
#graphing animation
import matplotlib.animation as animation
#load textfile dataset (2D data points)
# for each user, how many packets are sent per second and what's the size of a packet
#anomalies (DDOS attempts) will have lots of big packets sent in a short amount of time
def load_dataset(name):
return np.loadtxt(name)
#euclidian distance between 2 data points. For as many data points as necessary.
def euclidian(a, b):
return np.linalg.norm(a-b)
def kmeans(k, epsilon=0, distance='euclidian'):
#list to store past centroid
history_centroids = []
#set the distance calculation type
if distance == 'euclidian':
dist_method = euclidian
#set the dataset
dataset = load_dataset('durudataset.txt')
# dataset = dataset[:, 0:dataset.shape[1] - 1]
# get the number of rows (instances) and columns (features) from the dataset
num_instances, num_features = dataset.shape
#define k centroids (how many clusters do we want to find?) chosen randomly
prototypes = dataset[np.random.randint(0, num_instances - 1, size=k)]
#set these to our list of past centroid (to show progress over time)
history_centroids.append(prototypes)
#to keep track of centroid at every iteration
prototypes_old = np.zeros(prototypes.shape)
#to store clusters
belongs_to = np.zeros((num_instances, 1))
norm = dist_method(prototypes, prototypes_old)
iteration = 0
while norm > epsilon:
iteration += 1
norm = dist_method(prototypes, prototypes_old)
#for each instance in the dataset
for index_instance, instance in enumerate(dataset):
#define a distance vector of size k
dist_vec = np.zeros((k,1))
#for each centroid
for index_prototype, prototype in enumerate(prototypes):
#compute the distance between x and centroid
dist_vec[index_prototype] = dist_method(prototype, instance)
#find the smallest distance, assign that distance to a cluster
belongs_to[index_instance, 0] = np.argmin(dist_vec)
tmp_prototypes = np.zeros((k, num_features))
#for each cluster (k of them)
for index in range(len(prototypes)):
#get all the points assigned to a cluster
instances_close = [i for i in range(len(belongs_to)) if belongs_to[i] == index]
#find the mean of those points, this is our new centroid
prototype = np.mean(dataset[instances_close], axis=0)
#add our new centroid to our new temporary list
tmp_prototypes[index, :] = prototype
#set the new list to the current list
prototypes = tmp_prototypes
#add our calculated centroids to our history for plotting
history_centroids.append(tmp_prototypes)
#return calculated centroids, history of them all, and assignments for which cluster each datapoint belongs to
return prototypes, history_centroids, belongs_to
#lets define a plotting algorithm for our dataset and our centroids
def plot(dataset, history_centroids, belongs_to):
#we'll have 2 colors for each centroid cluster
colors = ['r', 'g']
#split our graph by its axis and actual plot
fig, ax = plt.subplots()
#for each point in our dataset
for index in range(dataset.shape[0]):
#get all the points assigned to a cluster
instances_close = [i for i in range(len(belongs_to)) if belongs_to[i] == index]
#assign each datapoint in that cluster a color and plot it
for instance_index in instances_close:
ax.plot(dataset[instance_index][0], dataset[instance_index][1], (colors[index] + 'o'))
#lets also log the history of centroids calculated via training
history_points = []
#for each centroid ever calculated
for index, centroids in enumerate(history_centroids):
#print them all out
for inner, item in enumerate(centroids):
if index == 0:
history_points.append(ax.plot(item[0], item[1], 'bo')[0])
else:
history_points[inner].set_data(item[0], item[1])
print("centroids {} {}".format(index, item))
plt.show()
#main file
def execute():
#load dataset
dataset = load_dataset('durudataset.txt')
#train the model on the data
centroids, history_centroids, belongs_to = kmeans(2)
#plot the results
plot(dataset, history_centroids, belongs_to)
%matplotlib notebook
#do everything
execute()
%matplotlib notebook
def plot_step_by_step(dataset, history_centroids, belongs_to):
colors = ['r', 'g']
fig, ax = plt.subplots()
for index in range(dataset.shape[0]):
instances_close = [i for i in range(len(belongs_to)) if belongs_to[i] == index]
for instance_index in instances_close:
ax.plot(dataset[instance_index][0], dataset[instance_index][1], (colors[index] + 'o'))
history_points = []
for index, centroids in enumerate(history_centroids):
for inner, item in enumerate(centroids):
if index == 0:
history_points.append(ax.plot(item[0], item[1], 'bo')[0])
else:
history_points[inner].set_data(item[0], item[1])
print("centroids {} {}".format(index, item))
plt.pause(0.8)
for item in history_centroids:
plot_step_by_step(dataset, [item], belongs_to)
```
| github_jupyter |
### B.1.1.7
#### The selection of suitable loci (done on Tue 22. Dec. 2020)
To identify suitable targets for primer/probe design, we downloaded 1,136 sequences from the GISAID repository filtered during a collection time spanning 1 - 21 December 2020. We focused on the spike gene because lineage B.1.1.7 contains a number of spike gene mutations, including two deletions (ΔH69/ΔV70 and ΔY144) that we focused on for designing a specific assay.
I cut the locus encoding the spike protein and used the *MAFFT* alignment tool (with the parameter - auto) to align all the sequences against the WUHAN reference (NCBI ID: NC_045512.2).
```
%%bash
# "msa_1221.fasta" is a pre-filtered nucleotide MSA file downladed from the GISAID repository 22.12.2020
# the WUHAN reference is always used as the first sequence in the GISAID MSA files
grep -m 1 ">" msa_1221.fasta | cut -d">" -f2 > sars2_allSeqs_til21stDec2020_andRefWuhan.list
# to reduce computational time, I used only sequences collected in Dec 2020
# getting unique sequence IDs
grep -P "2020-12-" msa_1221.fasta | cut -d">" -f2 >> sars2_allSeqs_til21stDec2020_andRefWuhan.list
# star-end positions of the spike protein in the aligned WUHAN sequence: 22412-26369
# I called the spike locus of all sequences listed in "sars2_allSeqs_til21stDec2020_andRefWuhan.list"
count=$(wc -l sars2_allSeqs_til21stDec2020_andRefWuhan.list | cut -d" " -f1)
for ((i=1; i<$(($count+1)); i++))
do
ID=$(sed -n ''$i'p' sars2_allSeqs_til21stDec2020_andRefWuhan.list | cut -d" " -f1)
echo ">"$ID >> sars2_allSeqs_til21stDec2020_andRefWuhan_Spike.fa
grep -A 1 -m 1 $ID msa_1221.fasta | grep -v ">" | cut -c22412-26369 | tr -d '-' | tr -d '\n' | tr -d ' ' >> sars2_allSeqs_til21stDec2020_andRefWuhan_Spike.fa
echo "" >> sars2_allSeqs_til21stDec2020_andRefWuhan_Spike.fa
done
# using 4 CPUS, I run the mafft tool with default settings
mafft --thread 4 --auto sars2_allSeqs_til21stDec2020_andRefWuhan_Spike.fa > sars2_allSeqs_til21stDec2020_andRefWuhan_Spike_mafft.fa
```
#### Downstream analysis
Twelve sequences (1.06 %) contained ambiguous signal in the loci of deletions and were not used in the downstream analysis. We separated sequences into two groups: 1) those with the ΔH69/ΔV70 and ΔY144 deletions and 2) those without the deletions (Table 1). Using *SeaView*, we called 95 % consensus sequences for the ΔH69/ΔV70 and ΔY144 group and the No deletions group that were used to design primer and probe sets specific to either B.1.1.7 or all other SARS-CoV-2 variants, respectively.
```
%%bash
# quality checks of bases in the deleted loci (ΔH69/ΔV70 and ΔY144)
# if a called base has ambiguous character, it is denotes as N
count=$(wc -l sars2_allSeqs_til21stDec2020_andRefWuhan.list | cut -d" " -f1)
for ((i=1; i<$(($count+1)); i++))
do
ID=$(sed -n ''$i'p' sars2_allSeqs_til21stDec2020_andRefWuhan.list | cut -d"|" -f2)
Del69_70=$(awk ' BEGIN {RS=">"}; /'$ID'\|/ { print ">"$0 } ' sars2_allSeqs_til21stDec2020_andRefWuhan_Spike_mafft.fa | grep -v ">" | tr -d '\n' | tr -d ' ' | cut -c203-208)
Del144=$(awk ' BEGIN {RS=">"}; /'$ID'\|/ { print ">"$0 } ' sars2_allSeqs_til21stDec2020_andRefWuhan_Spike_mafft.fa | grep -v ">" | tr -d '\n' | tr -d ' ' | cut -c428-430)
# using the output file, we can also compute the correlation of two deletions (ΔH69/ΔV70 and ΔY144) and to judge about their co-occurrence
echo -e $ID"\t"$Del69_70"\t"$Del144 >> sars2_1stDec20202_21stDec20202_Spike_Qchecks.tsv
# The shorter deletion (ΔY144) always co-occurred with the longer deletion (ΔH69/ΔV70), whereas the (ΔH69/ΔV70) deletion occurs independently in 17 sequences (1.5 %).
# Pearson's correlation coefficient of the deletions is 0.953.
```
#### Quality checks of the selected primer/probe loci (done on Thu 4. Febr. 2021)
In a separate analysis to determine the prevalence of the ΔH69/ΔV70 and ΔY144 deletions in lineages other than B.1.1.7, we downloaded 416,778 spike protein sequences with the most recent data description file collected from the beginning of the pandemic through 29 January 2021. Using regular expressions (bash pattern matching command grep with the option -P for Perl-compatible regular expression), we searched for loci with both ΔH69/ΔV70 and ΔY144 deletions, and for loci without these deletions. In the regular expression, we kept fixed a few amino acids downstream and upstream from the deletions to omit any miscalling of the searched pattern.
#### Quality checks of the selected primer/probe loci (update: 2. March 2021)
In a separate analysis to determine the prevalence of the ΔH69/ΔV70 and ΔY144 deletions in lineages other than B.1.1.7, we downloaded 633,137 spike protein sequences with the most recent data description file collected from the beginning of the pandemic through 2 March 2021. Using regular expressions (bash pattern matching command grep with the option -P for Perl-compatible regular expression), we searched for loci with both ΔH69/ΔV70 and ΔY144 deletions and for loci without these deletions. In the regular expression, we kept fixed a few amino acids downstream and upstream from the deletions to omit any miscalling of the searched pattern.
```
# update for the data; datasets from 1st of March 2021 (download on Tue 2nd March 2021)
%%bash
# "Spike_proteins_0301.fasta" is a pre-filtered amino-acid MSA file downladed from the GISAID repository 22.12.2020
grep -c ">" Spike_proteins_0301.fasta
# detection of both deletions (no HV, no Y): d69d70 and d144; with the check for unique sequence IDs
grep -B1 -P "HAISGT.{66}FLGVYHK" Spike_proteins_0301.fasta | grep ">" | cut -d"/" -f2 | sort | uniq -c | awk ' { print $1"\t"$2} ' | wc -l
# full pattern (HV and Y), no deletion; with the check for unique sequence IDs
grep -B1 -P "HAIHVSGT.{66}FLGVYYHK" Spike_proteins_0301.fasta | grep ">" | cut -d"/" -f2 | sort | uniq -c | awk ' { print $1"\t"$2} ' | wc -l
# only d144 (only HV, no Y); with the check for unique sequence IDs
grep -B1 -P "HAIHVSGT.{66}FLGVYHK" Spike_proteins_0301.fasta | grep ">" | cut -d"/" -f2 | sort | uniq -c | awk ' { print $1"\t"$2} ' | wc -l
# only d69d70 (only Y, no HV); with the check for unique sequence IDs
grep -B1 -P "HAISGT.{66}FLGVYYHK" Spike_proteins_0301.fasta | grep ">" | cut -d"/" -f2 | sort | uniq -c | awk ' { print $1"\t"$2} ' | wc -l
# detection of both deletions (no HV, no Y): d69d70 and d144; with the time-dependent sorting
grep -B1 -P "HAISGT.{66}FLGVYHK" Spike_proteins_0301.fasta | grep ">" | grep -oP "\|202[01]-..-" | sort | uniq -c
# only d69d70 (only Y, no HV); with the time-dependent sorting
grep -B1 -P "HAISGT.{66}FLGVYYHK" Spike_proteins_0301.fasta | grep ">" | grep -oP "\|202[01]-..-" | sort | uniq -c
# call the whole metadata information about sars-cov-2 records with detected both deletions
count=$(wc -l Spike_proteins_0301.fasta | cut -d" " -f1)
echo $count
# $count/16=6473
myF(){
for ((i=1; i<6474; i++))
do
N=$((12946*$1 + $i))
ID=$(sed -n ''$N'p' B117_IDs.list)
# metadata_2021-03-01_09-16.tsv
awk -v ID=$ID 'BEGIN{FS="\t"}; { if ( $3 == ID && $15 == "Human" ) { print $1"\t"$3"\t"$7"\t"$18"\t"$19 }} ' metadata_2021-03-01_09-16.tsv >> "B117_search_"$i.csv
done
}
export -f myF
# 12 946
parallel -j 16 myF ::: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
cat "B117_search_"*.csv > "B117_detected_bothMutations_cladeID.csv
rm "B117_search_"*.csv
```
#### Results (done on Thu 4. Febr. 2021)
Our analysis of the prevalence of both ΔH69/ΔV70 and ΔY144 deletions in lineages other than B.1.1.7, revealed a total of 29,872 sequences that possess both deletions, while 368,474 sequences do not have them. Based on the metadata file, we identified SARS-CoV-2 lineages across all called sequences with both deletions. Only five sequences (0.0167 %) out of 29,872 records are not labelled as B.1.1.7, highlighted the notion that these two deletions are highly specific for the B.1.1.7 variant and make ideal targets for primer/probe design.
#### Results (update: 2. March 2021)
Analysis of the prevalence of both ΔH69/ΔV70 and ΔY144 deletions in lineages other than B.1.1.7 revealed a total of 103,529 sequences that possess both deletions. Based on the metadata file, we identified SARS-CoV-2 lineages across all called sequences with both deletions. Only 108 sequences (0.10%) out of 103,529 sequences are not labelled as B.1.1.7. In other words, 99.90% of sequences containing both deletions belong to lineage B.1.1.7, highlighting the notion that these two deletions are highly specific for the B.1.1.7 variant and make ideal targets for primer/probe design (see the table below, please).
| Clade (Nextstrain) | Total sequences containing both ΔH69/ΔV70 and ΔY144 | % sequences containing both ΔH69/ΔV70 and ΔY144 |
|:------------------:|:---------------------------------------------------:|:-----------------------------------------------:|
|19A|6|<0.01%|
|20A|36|0.03%|
|20A.EU2|22|0.02%|
|20B|21|0.02%|
|20C|6|<0.01%|
|20E.EU1|13|0.01%|
|20I/501Y.V1 (**B.1.1.7**)|103,421|**99.90%**|
|No ID|4|<0.01%|
|Total|103,529|100%|
| github_jupyter |
```
%matplotlib inline
import gym
import matplotlib
import numpy as np
import sys
from collections import defaultdict
if "../" not in sys.path:
sys.path.append("../")
from lib.envs.blackjack import BlackjackEnv
from lib import plotting
matplotlib.style.use('ggplot')
env = BlackjackEnv()
def mc_prediction(policy, env, num_episodes, discount_factor=1.0):
"""
Monte Carlo prediction algorithm. Calculates the value function
for a given policy using sampling.
Args:
policy: A function that maps an observation to action probabilities.
env: OpenAI gym environment.
num_episodes: Number of episodes to sample.
discount_factor: Gamma discount factor.
Returns:
A dictionary that maps from state -> value.
The state is a tuple and the value is a float.
"""
# Keeps track of sum and count of returns for each state
# to calculate an average. We could use an array to save all
# returns (like in the book) but that's memory inefficient.
returns_sum = defaultdict(float)
returns_count = defaultdict(float)
# The final value function
V = defaultdict(float)
for i_episode in range(1, num_episodes + 1):
# Print out which episode we're on, useful for debugging.
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# Generate an episode.
# An episode is an array of (state, action, reward) tuples
episode = []
state = env.reset()
for t in range(100):
action = policy(state)
next_state, reward, done, _ = env.step(action)
episode.append((state, action, reward))
if done:
break
state = next_state
# Find all states the we've visited in this episode
# We convert each state to a tuple so that we can use it as a dict key
states_in_episode = set([tuple(x[0]) for x in episode])
for state in states_in_episode:
# Find the first occurance of the state in the episode
first_occurence_idx = next(i for i,x in enumerate(episode) if x[0] == state)
# Sum up all rewards since the first occurance
G = sum([x[2]*(discount_factor**i) for i,x in enumerate(episode[first_occurence_idx:])])
# Calculate average return for this state over all sampled episodes
returns_sum[state] += G
returns_count[state] += 1.0
V[state] = returns_sum[state] / returns_count[state]
return V
def sample_policy(observation):
"""
A policy that sticks if the player score is >= 20 and hits otherwise.
"""
score, dealer_score, usable_ace = observation
return 0 if score >= 20 else 1
V_10k = mc_prediction(sample_policy, env, num_episodes=10000)
plotting.plot_value_function(V_10k, title="10,000 Steps")
V_500k = mc_prediction(sample_policy, env, num_episodes=500000)
plotting.plot_value_function(V_500k, title="500,000 Steps")
```
| github_jupyter |
# Generate correction profiles for denoised
by Pu Zheng
2019.06.18
```
%run "E:\Users\puzheng\Documents\Startup_py3.py"
sys.path.append(r"E:\Users\puzheng\Documents")
import ImageAnalysis3 as ia
%matplotlib notebook
from ImageAnalysis3 import *
print(os.getpid())
reload(ia.get_img_info)
reload(ia.corrections)
reload(ia.visual_tools)
reload(ia.classes)
reload(ia.alignment_tools)
reload(ia.correction_tools.illumination)
```
# Data folder
```
# master folder for this dataset:
master_folder = r'\\10.245.74.158\Chromatin_NAS_6\20201012-mouse_proB_IgH++'
# correction folder
correction_folder=os.path.join(master_folder, 'Corrections')
if not os.path.exists(correction_folder):
print(f"creating folder: {correction_folder}")
os.makedirs(correction_folder)
```
# Illumination_correction
```
#master_folder = r'\\10.245.74.116\Chromatin_NAS_4\20191218_CTP05-chr21_HCT116_6hauxin'
#correction_folder =os.path.join(master_folder, 'Corrections')
folders, fovs = get_img_info.get_folders(master_folder, 'H')
folders = [_fd for _fd in folders if ('Cy' in _fd and '3color' not in _fd) or 'H0R0' in _fd]
print(folders)
# shared parameters
single_im_size = np.array([35,2048,2048])
all_colors = ['750','647','488','405']
# image and threads
num_images = 60
num_threads = 30
```
# Illumination correction
```
%matplotlib inline
reload(ia.correction_tools.illumination)
dapi_folder = folders[0]
illumination_pfs = correction_tools.illumination.Generate_Illumination_Correction(
dapi_folder,
all_colors,
all_channels=all_colors,
num_threads=num_threads,
num_images=num_images,
single_im_size=single_im_size,
correction_folder=correction_folder,
gaussian_filter_size=60,
save=True, save_folder=correction_folder,
overwrite=False,
)
```
# Chromatic Abbrevation
## chromatic for 750
```
cc_folder = folders[1]
ref_folder = folders[2]
print(cc_folder, ref_folder)
reload(correction_tools.chromatic)
chromatic_pfs, chromatic_consts = correction_tools.chromatic.Generate_chromatic_abbrevation(
cc_folder, ref_folder, '750',
num_images=num_images,
num_threads=num_threads,
fitting_orders=[1,1,1],
correction_args={'correction_folder':correction_folder,
'single_im_size': single_im_size,
'all_channels': all_colors,
'corr_channels': ['750', '647'],
},
save_folder=correction_folder,
overwrite_profile=True)
```
### check chromatic abbrevation, 750-647
```
# reference image
ref_ims, = ia.io_tools.load.correct_fov_image(ref_filename,
[647, 488],
single_im_size=single_im_size,
all_channels=all_colors,
warp_image=True,
illumination_corr=True,
chromatic_corr=False,
bleed_corr=False,
correction_folder=correction_folder)
# target image, not warpping
raw_ims, corr_funcs, drift = ia.io_tools.load.correct_fov_image(cc_filename,
[750],
calculate_drift=True,
ref_filename=ref_ims[-1],
single_im_size=single_im_size,
all_channels=all_colors,
warp_image=False,
illumination_corr=True,
chromatic_corr=True,
bleed_corr=False,
correction_folder=correction_folder,
return_drift=True)
# target image, warppring
corr_ims, = ia.io_tools.load.correct_fov_image(cc_filename,
[750],
calculate_drift=False,
drift=drift,
ref_filename=ref_ims[-1],
single_im_size=single_im_size,
all_channels=all_colors,
warp_image=True,
illumination_corr=True,
chromatic_corr=True,
bleed_corr=False,
correction_folder=correction_folder,
return_drift=False)
%matplotlib notebook
visual_tools.imshow_mark_3d_v2([raw_ims[0], corr_ims[0], ref_ims[0]])
corr_funcs[0]
reload(ia.io_tools.load)
reload(ia.correction_tools.chromatic)
from ImageAnalysis3.spot_tools.fitting import fit_fov_image
# fitting
int_th = 1
corr_spots = fit_fov_image(corr_ims[0], '750', th_seed=400, normalize_backgroud=True)
raw_spots = fit_fov_image(raw_ims[0], '750', th_seed=400, normalize_backgroud=True)
ref_spots = fit_fov_image(ref_ims[0], '647', th_seed=600, normalize_backgroud=True)
corr_spots = corr_spots[corr_spots[:,0] >= int_th]
raw_spots = raw_spots[raw_spots[:,0] >= int_th]
corr_raw_spots = corr_funcs[0](raw_spots)
ref_spots = ref_spots[ref_spots[:,0] >= int_th]
plt.figure(figsize=(6,6),dpi=100)
plt.plot(corr_spots[:,2], corr_spots[:,3], 'r.', label='ref')
plt.plot(corr_raw_spots[:,2], corr_raw_spots[:,3], 'g.', label='not warpping')
plt.plot(raw_spots[:,2], raw_spots[:,3], 'y.', label='not warpping')
plt.plot(ref_spots[:,2], ref_spots[:,3], 'b.', label='warpping')
plt.legend()
plt.xlabel('X')
plt.ylabel('Y')
#plt.plot(ref_spots[:,2]+drift[1], ref_spots[:,3]+drift[2], 'b.')
plt.show()
from ImageAnalysis3.spot_tools.matching import find_paired_centers, check_paired_centers
# matching
_new_drift, paired_ref_cts, paired_corr_cts = find_paired_centers(ref_spots[:,1:4], corr_spots[:,1:4], drift=drift)
print(_new_drift)
_new_drift, paired_ref_cts, paired_corr_cts = check_paired_centers(paired_ref_cts, paired_corr_cts+drift)
print(_new_drift)
```
## visualize
```
%matplotlib notebook
visual_tools.imshow_mark_3d_v2([raw_ims[0], corr_ims[0], ref_ims[0]])
```
# bleedthrough correction
```
from ImageAnalysis3 import _image_size, _correction_folder, _allowed_colors
reload(correction_tools.bleedthrough)
from ImageAnalysis3.correction_tools.bleedthrough import find_bleedthrough_pairs, interploate_bleedthrough_correction_from_channel
import multiprocessing as mp
from ImageAnalysis3.correction_tools.chromatic import generate_polynomial_data
bleedthrough_channels=['750', '647']
bleedthrough_correction_args = {
'correction_folder': _correction_folder,
'single_im_size':single_im_size,
'all_channels':all_colors,
'corr_channels':['750','647'],
'bleed_corr':False,
'illumination_corr':False,
'chromatic_corr':False,
}
bleedthrough_fitting_args = {'max_num_seeds':1000,
'th_seed': 500,
'use_dynamic_th':True,
}
reload(correction_tools.bleedthrough)
%matplotlib inline
reload(correction_tools.bleedthrough)
bleed_pf = correction_tools.bleedthrough.Generate_bleedthrough_correction(
folders[1:3],
rsq_th=0.81,
corr_channels=bleedthrough_channels,
correction_args=bleedthrough_correction_args,
fitting_args=bleedthrough_fitting_args,
num_images=num_images,
#num_images=30,
num_threads=num_threads,
save_folder=correction_folder,
overwrite_profile=True,
overwrite_temp=False,
)
```
### Check bleedthorugh for cy7
```
from ImageAnalysis3.io_tools.load import correct_fov_image
from ImageAnalysis3.io_tools.crop import crop_neighboring_area
reload(ia.io_tools.load)
cy7_filename = os.path.join(folders[0], fovs[3])
cy7_raw_ims, = ia.io_tools.load.correct_fov_image(cy7_filename,
bleedthrough_channels,
bleed_corr=False, chromatic_corr=False,
corr_channels=bleedthrough_channels,
single_im_size=single_im_size,
all_channels=all_colors,
illumination_corr=True,
correction_folder=correction_folder)
cy7_corr_ims, = ia.io_tools.load.correct_fov_image(cy7_filename,
bleedthrough_channels,
bleed_corr=True, chromatic_corr=False,
corr_channels=bleedthrough_channels,
single_im_size=single_im_size,
all_channels=all_colors,
illumination_corr=True,
correction_folder=correction_folder)
%matplotlib notebook
%matplotlib notebook
visual_tools.imshow_mark_3d_v2([cy7_raw_ims[0], cy7_corr_ims[0], cy7_raw_ims[1], cy7_corr_ims[1]])
```
## Check bleedthrough for cy5
```
reload(ia.io_tools.load)
cy5_filename = os.path.join(folders[1], fovs[3])
cy5_raw_ims, = ia.io_tools.load.correct_fov_image(cy5_filename,
bleedthrough_channels,
bleed_corr=False, chromatic_corr=False,
corr_channels=bleedthrough_channels,
single_im_size=single_im_size,
all_channels=all_colors,
illumination_corr=True,
correction_folder=correction_folder)
cy5_corr_ims, = ia.io_tools.load.correct_fov_image(cy5_filename,
bleedthrough_channels,
bleed_corr=True, chromatic_corr=False,
corr_channels=bleedthrough_channels,
single_im_size=single_im_size,
all_channels=all_colors,
illumination_corr=True,
correction_folder=correction_folder)
%matplotlib notebook
%matplotlib notebook
visual_tools.imshow_mark_3d_v2([cy5_raw_ims[0], cy5_raw_ims[1], cy5_corr_ims[1], cy5_corr_ims[0]])
```
| github_jupyter |
<a href="https://colab.research.google.com/github/haribharadwaj/notebooks/blob/main/BME511/ProbabilisticClassificationClustering.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Classification and clustering: probabilistic modeling approach
Here, we will extend out discussion on estimation theory to classification and clusterin problems.
```
import numpy as np
import pylab as pl
# Setting it so figs will be a bit bigger
from matplotlib import pyplot as plt
plt.rcParams['figure.figsize'] = [5, 3.33]
plt.rcParams['figure.dpi'] = 120
```
## We will rely heavily on the ```scikit-learn``` library
The ```sklearn``` library is a mature, well-tested library of implementations of many standard machine-learning models and provides a clean API to work with. In addition to being able to fit models and draw predictions for new inputs, ```sklearn``` also provides many useful utilities for handling data. It also has functions for creating toy datasets which can be used to understand the pros and cons of various models. The library is designed to work in conjunction with ```numpy```, ```scipy```, ```matplotlib```, and ```pandas```.
### Start by making a 2D dataset with 2 classes.
```
from sklearn import datasets
n_classes = 2
n_features = 2
n_samples = 200
n_redundant = 0
n_clusters_per_class = 1
class_sep = 0.8
X, y = datasets.make_classification(n_classes=n_classes, n_features=n_features,
n_samples=n_samples, n_redundant=n_redundant,
n_clusters_per_class=n_clusters_per_class,
class_sep=class_sep, random_state=0)
```
### Visualize the dataset
```
import itertools
marker = itertools.cycle(('o', 's', '*', 'v', '^', 'x'))
for c in range(n_classes):
pl.plot(X[y==c, 0], X[y==c, 1], linestyle='', marker=next(marker))
pl.xlabel('Feature 1')
pl.ylabel('Feature 2')
pl.legend(('Class 1', 'Class 2'), loc='best')
```
## Construct a naive-Bayes classifier and test it by splitting the dataset
For simplicity, we will use the Gaussian naive-Bayes model where the value of each feature is modeled as coming from a 1D normal distribution that is conditioned on class but independent of other features.
```
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=0)
model = GaussianNB()
model.fit(X_train, y_train)
y_predicted_train = model.predict(X_train)
y_predicted_test = model.predict(X_test)
acc_train = (y_predicted_train == y_train).sum() * 100. / y_train.shape[0]
acc_test = (y_predicted_test == y_test).sum() * 100. / y_test.shape[0]
print(f'Training accuracy = {acc_train:0.1f}%, Test accuracy = {acc_test:0.1f}%')
```
### Visualize results
```
def make_meshgrid(X, ngrid=100, slack=0.2):
if len(X.shape) > 2:
warnings.warn('Grid visualization only work for 2D or less!')
xmin, xmax = X[:, 0].min(), X[:, 0].max()
ymin, ymax = X[:, 1].min(), X[:, 1].max()
# Apply some slack so points are are not near the edge
xmin *= 1 - np.sign(xmin) * slack
xmax *= 1 + np.sign(xmax) * slack
ymin *= 1 - np.sign(ymin) * slack
ymax *= 1 + np.sign(ymax) * slack
dx = (xmax - xmin) / ngrid
dy = (ymax - ymin) / ngrid
x = np.arange(xmin, xmax, dx)
y = np.arange(ymin, ymax, dy)
xx, yy = np.meshgrid(x, y)
return (xx, yy)
def plot_decision(xx, yy, clf, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = pl.contourf(xx, yy, Z, **params)
return out
for c in range(n_classes):
pl.plot(X_test[y_test==c, 0], X_test[y_test==c, 1], linestyle='', marker=next(marker))
pl.plot(X_test[y_predicted_test != y_test, 0], X_test[y_predicted_test != y_test, 1], 'or',
markersize=12, markerfacecolor='none')
pl.xlabel('Feature 1')
pl.ylabel('Feature 2')
pl.legend(('True Class 1', 'True Class 2', 'Incorrect'), loc='best')
pl.title('Test results')
# Plot decision function
xx, yy = make_meshgrid(X_test)
plot_decision(xx, yy, model, cmap='seismic', alpha=0.1)
```
## Clustering using mixture modeling
### Create and visualize a 2D dataset
```
n_clusters = 3
centers = np.asarray([[-4, 0], [0, 3], [1.5, -3]])
X, y = datasets.make_blobs(centers=centers, n_features=n_features,
n_samples=n_samples)
pl.plot(X[:, 0], X[:, 1], 'o')
pl.xlabel('Feature 1')
pl.ylabel('Feature 2')
```
### Use a Gaussian mixture model
The number of clusters is a hyperparameter
```
from sklearn import mixture
ncomps = 3
model = mixture.GaussianMixture(n_components=ncomps)
y = model.fit_predict(X)
print(f'Log-likelihood = {model.score(X)}, AIC = {model.aic(X)}')
for k in range(ncomps):
pl.plot(X[y==k, 0], X[y==k, 1], marker=next(marker), linestyle='')
pl.xlabel('Feature 1')
pl.ylabel('Feature 2')
```
## Apply naive Bayes classifier to Wisconsin breast cancer dataset after PCA for dimensionality reduction
Dataset is included with ```sklearn``` but comes from:
W.H. Wolberg, W.N. Street, D.M. Heisey, and O.L. Mangasarian. Computer-derived nuclear features distinguish malignant from benign breast cytology. Human Pathology, 26:792--796, 1995.
Here, fine-needle aspirates (FNA; a type of biopsy) of breast mass are obtained, imaged, and the digitized images are processed to extract features pertaining to the characteristics of the cell nuclei present in the image. The goal is to classify each biopsy as **malignant** or **benign** based on the image.
Ten real-valued features are computed for each cell nucleus:
- radius (mean of distances from center to points on the perimeter)
- texture (standard deviation of gray-scale values)
- perimeter
- area
- smoothness (local variation in radius lengths)
- compactness (perimeter^2 / area - 1.0)
- concavity (severity of concave portions of the contour)
- concave points (number of concave portions of the contour)
- symmetry
- fractal dimension ("coastline approximation" - 1)
For each image, across nuceli, the mean, standard error,
and "worst" or largest (mean of the three largest values) of these features were computed. This yields **30 features per sample**.
For instance, field 3 is Mean Radius, field
13 is Radius SE, field 23 is Worst Radius.
```
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
dat = load_breast_cancer()
X = dat.data
y = dat.target
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75)
# Do PCA to get two dimensions
pc = PCA(n_components=2)
pc.fit(X_train)
X_train_pc = pc.transform(X_train)
X_test_pc = pc.transform(X_test)
model = GaussianNB()
model.fit(X_train_pc, y_train)
y_predicted_train = model.predict(X_train_pc)
y_predicted_test = model.predict(X_test_pc)
acc_train = (y_predicted_train == y_train).sum() * 100. / y_train.shape[0]
acc_test = (y_predicted_test == y_test).sum() * 100. / y_test.shape[0]
print(f'Training accuracy = {acc_train:0.1f}%, Test accuracy = {acc_test:0.1f}%')
```
### Visualize results
```
n_classes = 2
for c in range(n_classes):
pl.plot(X_test_pc[y_test==c, 0], X_test_pc[y_test==c, 1], linestyle='', marker=next(marker))
pl.plot(X_test_pc[y_predicted_test != y_test, 0], X_test_pc[y_predicted_test != y_test, 1], 'or',
markersize=12, markerfacecolor='none')
pl.xlabel('PC 1')
pl.ylabel('PC 2')
pl.legend(('True Class 1', 'True Class 2', 'Incorrect'), loc='best')
pl.title('Test results')
# Plot decision function
xx, yy = make_meshgrid(X_test_pc)
plot_decision(xx, yy, model, cmap='seismic', alpha=0.2)
```
## Apply naive Bayes classifier to high-dimensional Wisconsin breast cancer dataset (no PCA)
```
model = GaussianNB()
# Using X_train and X_test instead of X_train_pc and X_test_pc
model.fit(X_train, y_train)
y_predicted_train = model.predict(X_train)
y_predicted_test = model.predict(X_test)
acc_train = (y_predicted_train == y_train).sum() * 100. / y_train.shape[0]
acc_test = (y_predicted_test == y_test).sum() * 100. / y_test.shape[0]
print(f'Training accuracy = {acc_train:0.1f}%, Test accuracy = {acc_test:0.1f}%')
```
### Conclusion about breast cancer dataset
A simple naive Bayes classifier is able to obtain 90+% accuracy in biopsy classification.
| github_jupyter |
```
#Fill the paths below
PATH_FRC = "" # git repo directory path
PATH_ZENODO = "" # Data and models are available here: https://zenodo.org/record/5831014#.YdnW_VjMLeo
DATA_FLAT = PATH_ZENODO+'/data/goi_1000/flat_1000/*.png'
DATA_NORMAL = PATH_ZENODO+'/data/goi_1000/standard_1000/*.jpg'
GAUSS_L2_MODEL = PATH_ZENODO+'/models/gaussian/noise005_set1000/standard/' # noise 0.05
GAUSS_L2_MODEL_FLAT = PATH_ZENODO+'/models/gaussian/noise005_set1000/flat/' # noise 0.05
import sys
sys.path.append(PATH_FRC)
import glob
import os
import skimage
%matplotlib inline
import matplotlib.pyplot as plt
from skimage.io import imread
import numpy as np
import matplotlib
import tensorflow as tf
from models2 import FRCUnetModel
from skimage.filters import window
from tqdm import tqdm
import pandas as pd
import scipy.stats as stats
from scipy.optimize import fsolve
import pyfftw.interfaces.numpy_fft
np.fft = pyfftw.interfaces.numpy_fft
matplotlib.rcParams.update({'mathtext.default':'regular'})
matplotlib.rcParams.update({'font.size': 8})
matplotlib.rcParams.update({'axes.labelweight': 'bold'})
def normalise_img(image):
image = image - image.min()
image = image/image.max() - 0.5
return image
def plot_power_spectrum(image):
if len(image.shape) == 3:
image = np.sum(image, axis=2)
image = image.astype('float64')
image = image - image.mean()
fourier_image = np.fft.fftn(image) # here the input is grey image
size = image.shape[0]
fourier_amplitudes = np.abs(fourier_image)**2
print("FOURIER AMPLITUDES", np.sum(fourier_amplitudes))
kfreq = np.fft.fftfreq(size) * size # image size
kfreq2D = np.meshgrid(kfreq, kfreq)
knrm = np.sqrt(kfreq2D[0]**2 + kfreq2D[1]**2)
knrm = knrm.flatten()
fourier_amplitudes = fourier_amplitudes.flatten()
kbins = np.arange(0.5, int(size / 2), 1.)
kvals = 0.5 * (kbins[1:] + kbins[:-1])
Abins, _, _ = stats.binned_statistic(
knrm, fourier_amplitudes, statistic="mean", bins=kbins) # mean power
return kvals, Abins
def load_model(model_dir, model_fname):
if model_dir is not None:
return FRCUnetModel(None, model_path=os.path.join(model_dir, model_fname))
files_flat=sorted(glob.glob(DATA_FLAT))
files_flat=files_flat[:50]
files_normal=sorted(glob.glob(DATA_NORMAL))
files_normal=files_normal[:50]
cleans_flat=[]
for file in files_flat:
clean = imread(file)
if len(clean.shape) > 2:
clean = np.mean(clean, axis=2)
minsize = np.array(clean.shape).min()
clean = clean[:minsize,:minsize]
clean = normalise_img(clean)
clean = clean.astype('float32')
#clean = clean*window('hann', clean.shape)
cleans_flat.append(clean)
cleans_flat=np.stack(cleans_flat)
cleans_normal=[]
for file in files_normal:
clean = imread(file)
if len(clean.shape) > 2:
clean = np.mean(clean, axis=2)
minsize = np.array(clean.shape).min()
clean = clean[:minsize,:minsize]
clean = normalise_img(clean)
clean = clean.astype('float32')
#clean = clean*window('hann', clean.shape)
cleans_normal.append(clean)
cleans_normal=np.stack(cleans_normal)
cleans_normal.shape
noise1=np.random.normal(0,0.05,256**2*50).reshape(50,256,256)
noisy_flat=cleans_flat.copy()+noise1
noise2=np.random.normal(0,0.05,256**2*50).reshape(50,256,256)
noisy_normal=cleans_normal.copy()+noise2
l2_model=load_model(GAUSS_L2_MODEL, 'saved-model-epoch-200')
l2_1000_model_flat=load_model(GAUSS_L2_MODEL_FLAT, 'saved-model-epoch-200')
imnr=3
denoised_normal = l2_model.model(np.reshape(noisy_normal[imnr], [1,256, 256,1]))
denoised_normal = np.squeeze(denoised_normal)
denoised_flat = l2_1000_model_flat.model(np.reshape(noisy_flat[imnr], [1,256, 256,1]))
denoised_flat = np.squeeze(denoised_flat)
x=np.array(plot_power_spectrum(noisy_normal[imnr])[0])
x=x*1.0/x.max()
fig = plt.figure()
fig.set_size_inches(7, 7) # 3.5 inch is the width of one column in A4 paper
ax = fig.add_subplot(334)
ax.imshow(cleans_flat[imnr], cmap='gray')
plt.xticks([])
plt.yticks([])
#plt.ylabel('Gaussian')
plt.title('Normalised spectrum, GT')
ax = fig.add_subplot(335)
ax.imshow(noisy_flat[imnr], cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Normalised spectrum, noisy')
ax = fig.add_subplot(336)
ax.imshow(denoised_flat, cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Normalised spectrum, denoised')
ax = fig.add_subplot(331)
ax.imshow(cleans_normal[imnr], cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Standard spectrum, GT')
ax = fig.add_subplot(332)
ax.imshow(noisy_normal[imnr], cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Standard spectrum, noisy')
ax = fig.add_subplot(333)
ax.imshow(denoised_normal, cmap='gray')
plt.xticks([])
plt.yticks([])
plt.title('Standard spectrum, denoised')
ax = fig.add_subplot(337)
plt.title('Ground truth ')
ax.plot(x,np.array(plot_power_spectrum(cleans_flat[imnr])[1]),label='Normalised',color='orange')
ax.plot(x,np.array(plot_power_spectrum(cleans_normal[imnr])[1]),label='Standard',color='blue')
ax.set_xlabel('f/N')
ax.set_ylabel('Power')
plt.yscale('log')
plt.xscale('log')
#ax.locator_params(axis='x', nbins=5)
plt.ylim([10**1.5,10**7.5 ])
plt.legend(loc=1)
ax = fig.add_subplot(338)
plt.title('Noisy')
ax.plot(x,np.array(plot_power_spectrum(noisy_flat[imnr])[1]),label='Normalised',color='orange')
ax.plot(x,np.array(plot_power_spectrum(noisy_normal[imnr])[1]),label='Standard',color='blue')
ax.set_xlabel('f/N')
#ax.set_ylabel('Power')
plt.yscale('log')
plt.xscale('log')
plt.ylim([10**1.5,10**7.5 ])
ax = fig.add_subplot(339)
plt.title('Denoised')
ax.plot(x,np.array(plot_power_spectrum(denoised_flat)[1]),label='Normalised',color='orange')
ax.plot(x,np.array(plot_power_spectrum(denoised_normal)[1]),label='Standard',color='blue')
ax.set_xlabel('f/N')
plt.yscale('log')
plt.xscale('log')
#ax.locator_params(axis='x', nbins=5)
plt.ylim([10**1.5,10**7.5 ])
plt.tight_layout()
plt.subplots_adjust(wspace=0.23, hspace=0.23)
fig.savefig('figure_s3.png', dpi=300)
```
| github_jupyter |
```
import pandas
df = pandas.read_csv(
'https://archive.ics.uci.edu/ml/'
'machine-learning-databases/iris/iris.data',
header=None,
)
df.tail()
import numpy
targets = df.iloc[0:100, 4].values
targets = numpy.where(targets == 'Iris-setosa', -1, 1)
targets[:10]
samples = df.iloc[0:100, [0, 2]].values
samples.shape
samples[:10]
import matplotlib.pyplot as plt
plt.scatter(
samples[:50, 0], samples[:50, 1],
color='red', marker='o', label='setosa'
)
plt.scatter(
samples[50:100, 0], samples[50:100, 1],
color='blue', marker='x', label='versicolor'
)
plt.xlabel('sepal length')
plt.ylabel('petal length')
plt.legend(loc='upper left')
plt.show()
from perceptron import Perceptron
p = Perceptron(learning_rate=0.1, max_iterations=10)
p.train(samples, targets)
p.errors
plt.plot(
range(1, len(p.errors) + 1),
p.errors,
marker='o',
)
plt.xlabel('epochs')
plt.ylabel('misclassification count')
plt.show()
from matplotlib.colors import ListedColormap
def plot_decision_regions(samples, targets, classifier, resolution=0.02):
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
color_count = len(numpy.unique(targets))
c_map = ListedColormap(colors[:color_count])
sample_extent = [
(samples[:, dim].min() - 1, samples[:, dim].max() + 1)
for dim in (0, 1)
]
grid = numpy.meshgrid(
numpy.arange(*sample_extent[0], resolution),
numpy.arange(*sample_extent[1], resolution),
)
predictions = classifier.predict(
numpy.array([
grid[0].ravel(),
grid[1].ravel()
]).T
)
predictions = predictions.reshape(grid[0].shape)
plt.contourf(
grid[0],
grid[1],
predictions,
alpha=0.4,
cmap=c_map
)
plt.xlim(grid[0].min(), grid[0].max())
plt.ylim(grid[1].min(), grid[1].max())
for idx, target in enumerate(numpy.unique(targets)):
plt.scatter(
x=samples[targets == target, 0],
y=samples[targets == target, 1],
c=c_map(idx),
alpha=0.8,
marker=markers[idx],
label=target
)
plot_decision_regions(samples, targets, p, resolution=0.01)
plt.show()
from adanline import Adaline
ada = Adaline()
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8, 4))
ada.train(samples, targets,
training_iterations=10,
training_speed=0.01)
ax[0].plot(
range(1, len(ada.costs) + 1),
numpy.log10(ada.costs),
marker='o'
)
ax[0].set_xlabel('epochs')
ax[0].set_ylabel('log(SSE)')
ax[0].set_title('Adaline - Learning Rate 0.01')
ada.train(samples, targets,
training_iterations=10,
training_speed=0.0001)
ax[1].plot(
range(1, len(ada.costs) + 1),
numpy.log10(ada.costs),
marker='o'
)
ax[1].set_xlabel('epochs')
ax[1].set_ylabel('log(SSE)')
ax[1].set_title('Adaline - Learning Rate 0.0001')
plt.show()
samples_standardized = numpy.copy(samples)
dim = (samples[:, 0], samples[:, 1])
for d in (0, 1):
samples_standardized[:, d] = (dim[d] - dim[d].mean()) / dim[d].std()
ada.train(samples_standardized, targets,
training_iterations=15,
training_speed=0.01)
plt.plot(
range(1, len(ada.costs) + 1),
ada.costs,
marker='o'
)
plt.show()
plot_decision_regions(samples_standardized, targets, ada)
plt.show()
from adaline import AdalineSingleGradientDescent
ada = AdalineSingleGradientDescent()
ada.train(samples_standardized, targets,
training_speed=0.01,
training_iterations=15)
plt.plot(
range(1, len(ada.costs) + 1),
ada.costs,
marker='o'
)
plt.show()
plot_decision_regions(samples_standardized, targets,
classifier=ada)
plt.title('Adaline - Stochastic Gradient Descent')
plt.xlabel('sepal length (standardized)')
plt.xlabel('petal length (standardized)')
```
| github_jupyter |
# Autonomous driving - Car detection
Welcome to your week 3 programming assignment. You will learn about object detection using the very powerful YOLO model. Many of the ideas in this notebook are described in the two YOLO papers: Redmon et al., 2016 (https://arxiv.org/abs/1506.02640) and Redmon and Farhadi, 2016 (https://arxiv.org/abs/1612.08242).
**You will learn to**:
- Use object detection on a car detection dataset
- Deal with bounding boxes
Run the following cell to load the packages and dependencies that are going to be useful for your journey!
```
import argparse
import os
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
import scipy.io
import scipy.misc
import numpy as np
import pandas as pd
import PIL
import tensorflow as tf
from keras import backend as K
from keras.layers import Input, Lambda, Conv2D
from keras.models import load_model, Model
from yolo_utils import read_classes, read_anchors, generate_colors, preprocess_image, draw_boxes, scale_boxes
from yad2k.models.keras_yolo import yolo_head, yolo_boxes_to_corners, preprocess_true_boxes, yolo_loss, yolo_body
%matplotlib inline
```
**Important Note**: As you can see, we import Keras's backend as K. This means that to use a Keras function in this notebook, you will need to write: `K.function(...)`.
## 1 - Problem Statement
You are working on a self-driving car. As a critical component of this project, you'd like to first build a car detection system. To collect data, you've mounted a camera to the hood (meaning the front) of the car, which takes pictures of the road ahead every few seconds while you drive around.
<center>
<video width="400" height="200" src="nb_images/road_video_compressed2.mp4" type="video/mp4" controls>
</video>
</center>
<caption><center> Pictures taken from a car-mounted camera while driving around Silicon Valley. <br> We would like to especially thank [drive.ai](https://www.drive.ai/) for providing this dataset! Drive.ai is a company building the brains of self-driving vehicles.
</center></caption>
<img src="nb_images/driveai.png" style="width:100px;height:100;">
You've gathered all these images into a folder and have labelled them by drawing bounding boxes around every car you found. Here's an example of what your bounding boxes look like.
<img src="nb_images/box_label.png" style="width:500px;height:250;">
<caption><center> <u> **Figure 1** </u>: **Definition of a box**<br> </center></caption>
If you have 80 classes that you want YOLO to recognize, you can represent the class label $c$ either as an integer from 1 to 80, or as an 80-dimensional vector (with 80 numbers) one component of which is 1 and the rest of which are 0. The video lectures had used the latter representation; in this notebook, we will use both representations, depending on which is more convenient for a particular step.
In this exercise, you will learn how YOLO works, then apply it to car detection. Because the YOLO model is very computationally expensive to train, we will load pre-trained weights for you to use.
## 2 - YOLO
YOLO ("you only look once") is a popular algoritm because it achieves high accuracy while also being able to run in real-time. This algorithm "only looks once" at the image in the sense that it requires only one forward propagation pass through the network to make predictions. After non-max suppression, it then outputs recognized objects together with the bounding boxes.
### 2.1 - Model details
First things to know:
- The **input** is a batch of images of shape (m, 608, 608, 3)
- The **output** is a list of bounding boxes along with the recognized classes. Each bounding box is represented by 6 numbers $(p_c, b_x, b_y, b_h, b_w, c)$ as explained above. If you expand $c$ into an 80-dimensional vector, each bounding box is then represented by 85 numbers.
We will use 5 anchor boxes. So you can think of the YOLO architecture as the following: IMAGE (m, 608, 608, 3) -> DEEP CNN -> ENCODING (m, 19, 19, 5, 85).
Lets look in greater detail at what this encoding represents.
<img src="nb_images/architecture.png" style="width:700px;height:400;">
<caption><center> <u> **Figure 2** </u>: **Encoding architecture for YOLO**<br> </center></caption>
If the center/midpoint of an object falls into a grid cell, that grid cell is responsible for detecting that object.
Since we are using 5 anchor boxes, each of the 19 x19 cells thus encodes information about 5 boxes. Anchor boxes are defined only by their width and height.
For simplicity, we will flatten the last two last dimensions of the shape (19, 19, 5, 85) encoding. So the output of the Deep CNN is (19, 19, 425).
<img src="nb_images/flatten.png" style="width:700px;height:400;">
<caption><center> <u> **Figure 3** </u>: **Flattening the last two last dimensions**<br> </center></caption>
Now, for each box (of each cell) we will compute the following elementwise product and extract a probability that the box contains a certain class.
<img src="nb_images/probability_extraction.png" style="width:700px;height:400;">
<caption><center> <u> **Figure 4** </u>: **Find the class detected by each box**<br> </center></caption>
Here's one way to visualize what YOLO is predicting on an image:
- For each of the 19x19 grid cells, find the maximum of the probability scores (taking a max across both the 5 anchor boxes and across different classes).
- Color that grid cell according to what object that grid cell considers the most likely.
Doing this results in this picture:
<img src="nb_images/proba_map.png" style="width:300px;height:300;">
<caption><center> <u> **Figure 5** </u>: Each of the 19x19 grid cells colored according to which class has the largest predicted probability in that cell.<br> </center></caption>
Note that this visualization isn't a core part of the YOLO algorithm itself for making predictions; it's just a nice way of visualizing an intermediate result of the algorithm.
Another way to visualize YOLO's output is to plot the bounding boxes that it outputs. Doing that results in a visualization like this:
<img src="nb_images/anchor_map.png" style="width:200px;height:200;">
<caption><center> <u> **Figure 6** </u>: Each cell gives you 5 boxes. In total, the model predicts: 19x19x5 = 1805 boxes just by looking once at the image (one forward pass through the network)! Different colors denote different classes. <br> </center></caption>
In the figure above, we plotted only boxes that the model had assigned a high probability to, but this is still too many boxes. You'd like to filter the algorithm's output down to a much smaller number of detected objects. To do so, you'll use non-max suppression. Specifically, you'll carry out these steps:
- Get rid of boxes with a low score (meaning, the box is not very confident about detecting a class)
- Select only one box when several boxes overlap with each other and detect the same object.
### 2.2 - Filtering with a threshold on class scores
You are going to apply a first filter by thresholding. You would like to get rid of any box for which the class "score" is less than a chosen threshold.
The model gives you a total of 19x19x5x85 numbers, with each box described by 85 numbers. It'll be convenient to rearrange the (19,19,5,85) (or (19,19,425)) dimensional tensor into the following variables:
- `box_confidence`: tensor of shape $(19 \times 19, 5, 1)$ containing $p_c$ (confidence probability that there's some object) for each of the 5 boxes predicted in each of the 19x19 cells.
- `boxes`: tensor of shape $(19 \times 19, 5, 4)$ containing $(b_x, b_y, b_h, b_w)$ for each of the 5 boxes per cell.
- `box_class_probs`: tensor of shape $(19 \times 19, 5, 80)$ containing the detection probabilities $(c_1, c_2, ... c_{80})$ for each of the 80 classes for each of the 5 boxes per cell.
**Exercise**: Implement `yolo_filter_boxes()`.
1. Compute box scores by doing the elementwise product as described in Figure 4. The following code may help you choose the right operator:
```python
a = np.random.randn(19*19, 5, 1)
b = np.random.randn(19*19, 5, 80)
c = a * b # shape of c will be (19*19, 5, 80)
```
2. For each box, find:
- the index of the class with the maximum box score ([Hint](https://keras.io/backend/#argmax)) (Be careful with what axis you choose; consider using axis=-1)
- the corresponding box score ([Hint](https://keras.io/backend/#max)) (Be careful with what axis you choose; consider using axis=-1)
3. Create a mask by using a threshold. As a reminder: `([0.9, 0.3, 0.4, 0.5, 0.1] < 0.4)` returns: `[False, True, False, False, True]`. The mask should be True for the boxes you want to keep.
4. Use TensorFlow to apply the mask to box_class_scores, boxes and box_classes to filter out the boxes we don't want. You should be left with just the subset of boxes you want to keep. ([Hint](https://www.tensorflow.org/api_docs/python/tf/boolean_mask))
Reminder: to call a Keras function, you should use `K.function(...)`.
```
# GRADED FUNCTION: yolo_filter_boxes
def yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold = .6):
"""Filters YOLO boxes by thresholding on object and class confidence.
Arguments:
box_confidence -- tensor of shape (19, 19, 5, 1)
boxes -- tensor of shape (19, 19, 5, 4)
box_class_probs -- tensor of shape (19, 19, 5, 80)
threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
Returns:
scores -- tensor of shape (None,), containing the class probability score for selected boxes
boxes -- tensor of shape (None, 4), containing (b_x, b_y, b_h, b_w) coordinates of selected boxes
classes -- tensor of shape (None,), containing the index of the class detected by the selected boxes
Note: "None" is here because you don't know the exact number of selected boxes, as it depends on the threshold.
For example, the actual output size of scores would be (10,) if there are 10 boxes.
"""
# Step 1: Compute box scores
### START CODE HERE ### (≈ 1 line)
box_scores = box_confidence * box_class_probs
### END CODE HERE ###
# Step 2: Find the box_classes thanks to the max box_scores, keep track of the corresponding score
### START CODE HERE ### (≈ 2 lines)
box_classes = K.argmax(box_scores, axis=-1)
box_class_scores = K.max(box_scores, axis=-1)
### END CODE HERE ###
# Step 3: Create a filtering mask based on "box_class_scores" by using "threshold". The mask should have the
# same dimension as box_class_scores, and be True for the boxes you want to keep (with probability >= threshold)
### START CODE HERE ### (≈ 1 line)
filtering_mask = (box_class_scores > threshold)
### END CODE HERE ###
# Step 4: Apply the mask to scores, boxes and classes
### START CODE HERE ### (≈ 3 lines)
scores = tf.boolean_mask(box_class_scores, filtering_mask)
boxes = tf.boolean_mask(boxes, filtering_mask)
classes = tf.boolean_mask(box_classes, filtering_mask)
### END CODE HERE ###
return scores, boxes, classes
with tf.Session() as test_a:
box_confidence = tf.random_normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1)
boxes = tf.random_normal([19, 19, 5, 4], mean=1, stddev=4, seed = 1)
box_class_probs = tf.random_normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold = 0.5)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.shape))
print("boxes.shape = " + str(boxes.shape))
print("classes.shape = " + str(classes.shape))
```
**Expected Output**:
<table>
<tr>
<td>
**scores[2]**
</td>
<td>
10.7506
</td>
</tr>
<tr>
<td>
**boxes[2]**
</td>
<td>
[ 8.42653275 3.27136683 -0.5313437 -4.94137383]
</td>
</tr>
<tr>
<td>
**classes[2]**
</td>
<td>
7
</td>
</tr>
<tr>
<td>
**scores.shape**
</td>
<td>
(?,)
</td>
</tr>
<tr>
<td>
**boxes.shape**
</td>
<td>
(?, 4)
</td>
</tr>
<tr>
<td>
**classes.shape**
</td>
<td>
(?,)
</td>
</tr>
</table>
### 2.3 - Non-max suppression ###
Even after filtering by thresholding over the classes scores, you still end up a lot of overlapping boxes. A second filter for selecting the right boxes is called non-maximum suppression (NMS).
<img src="nb_images/non-max-suppression.png" style="width:500px;height:400;">
<caption><center> <u> **Figure 7** </u>: In this example, the model has predicted 3 cars, but it's actually 3 predictions of the same car. Running non-max suppression (NMS) will select only the most accurate (highest probabiliy) one of the 3 boxes. <br> </center></caption>
Non-max suppression uses the very important function called **"Intersection over Union"**, or IoU.
<img src="nb_images/iou.png" style="width:500px;height:400;">
<caption><center> <u> **Figure 8** </u>: Definition of "Intersection over Union". <br> </center></caption>
**Exercise**: Implement iou(). Some hints:
- In this exercise only, we define a box using its two corners (upper left and lower right): `(x1, y1, x2, y2)` rather than the midpoint and height/width.
- To calculate the area of a rectangle you need to multiply its height `(y2 - y1)` by its width `(x2 - x1)`.
- You'll also need to find the coordinates `(xi1, yi1, xi2, yi2)` of the intersection of two boxes. Remember that:
- xi1 = maximum of the x1 coordinates of the two boxes
- yi1 = maximum of the y1 coordinates of the two boxes
- xi2 = minimum of the x2 coordinates of the two boxes
- yi2 = minimum of the y2 coordinates of the two boxes
- In order to compute the intersection area, you need to make sure the height and width of the intersection are positive, otherwise the intersection area should be zero. Use `max(height, 0)` and `max(width, 0)`.
In this code, we use the convention that (0,0) is the top-left corner of an image, (1,0) is the upper-right corner, and (1,1) the lower-right corner.
```
# GRADED FUNCTION: iou
def iou(box1, box2):
"""Implement the intersection over union (IoU) between box1 and box2
Arguments:
box1 -- first box, list object with coordinates (x1, y1, x2, y2)
box2 -- second box, list object with coordinates (x1, y1, x2, y2)
"""
# Calculate the (y1, x1, y2, x2) coordinates of the intersection of box1 and box2. Calculate its Area.
### START CODE HERE ### (≈ 5 lines)
xi1 = max([box1[0], box2[0]])
yi1 = max([box1[1], box2[1]])
xi2 = min([box1[2], box2[2]])
yi2 = min([box1[3], box2[3]])
inter_area = max(xi2 - xi1, 0) * max(yi2 - yi1, 0)
### END CODE HERE ###
# Calculate the Union area by using Formula: Union(A,B) = A + B - Inter(A,B)
### START CODE HERE ### (≈ 3 lines)
box1_area = (box1[2] - box1[0]) * (box1[3] - box1[1])
box2_area = (box1[2] - box1[0]) * (box1[3] - box1[1])
union_area = box1_area + box2_area - inter_area
### END CODE HERE ###
# compute the IoU
### START CODE HERE ### (≈ 1 line)
iou = inter_area / union_area
### END CODE HERE ###
return iou
box1 = (2, 1, 4, 3)
box2 = (1, 2, 3, 4)
print("iou = " + str(iou(box1, box2)))
```
**Expected Output**:
<table>
<tr>
<td>
**iou = **
</td>
<td>
0.14285714285714285
</td>
</tr>
</table>
You are now ready to implement non-max suppression. The key steps are:
1. Select the box that has the highest score.
2. Compute its overlap with all other boxes, and remove boxes that overlap it more than `iou_threshold`.
3. Go back to step 1 and iterate until there's no more boxes with a lower score than the current selected box.
This will remove all boxes that have a large overlap with the selected boxes. Only the "best" boxes remain.
**Exercise**: Implement yolo_non_max_suppression() using TensorFlow. TensorFlow has two built-in functions that are used to implement non-max suppression (so you don't actually need to use your `iou()` implementation):
- [tf.image.non_max_suppression()](https://www.tensorflow.org/api_docs/python/tf/image/non_max_suppression)
- [K.gather()](https://www.tensorflow.org/api_docs/python/tf/gather)
```
# GRADED FUNCTION: yolo_non_max_suppression
def yolo_non_max_suppression(scores, boxes, classes, max_boxes = 10, iou_threshold = 0.5):
"""
Applies Non-max suppression (NMS) to set of boxes
Arguments:
scores -- tensor of shape (None,), output of yolo_filter_boxes()
boxes -- tensor of shape (None, 4), output of yolo_filter_boxes() that have been scaled to the image size (see later)
classes -- tensor of shape (None,), output of yolo_filter_boxes()
max_boxes -- integer, maximum number of predicted boxes you'd like
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (, None), predicted score for each box
boxes -- tensor of shape (4, None), predicted box coordinates
classes -- tensor of shape (, None), predicted class for each box
Note: The "None" dimension of the output tensors has obviously to be less than max_boxes. Note also that this
function will transpose the shapes of scores, boxes, classes. This is made for convenience.
"""
max_boxes_tensor = K.variable(max_boxes, dtype='int32') # tensor to be used in tf.image.non_max_suppression()
K.get_session().run(tf.variables_initializer([max_boxes_tensor])) # initialize variable max_boxes_tensor
# Use tf.image.non_max_suppression() to get the list of indices corresponding to boxes you keep
### START CODE HERE ### (≈ 1 line)
nms_indices = tf.image.non_max_suppression(boxes, scores, max_boxes_tensor, iou_threshold)
### END CODE HERE ###
# Use K.gather() to select only nms_indices from scores, boxes and classes
### START CODE HERE ### (≈ 3 lines)
scores = K.gather(scores, nms_indices)
boxes = K.gather(boxes, nms_indices)
classes = K.gather(classes, nms_indices)
### END CODE HERE ###
return scores, boxes, classes
with tf.Session() as test_b:
scores = tf.random_normal([54,], mean=1, stddev=4, seed = 1)
boxes = tf.random_normal([54, 4], mean=1, stddev=4, seed = 1)
classes = tf.random_normal([54,], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.eval().shape))
print("boxes.shape = " + str(boxes.eval().shape))
print("classes.shape = " + str(classes.eval().shape))
```
**Expected Output**:
<table>
<tr>
<td>
**scores[2]**
</td>
<td>
6.9384
</td>
</tr>
<tr>
<td>
**boxes[2]**
</td>
<td>
[-5.299932 3.13798141 4.45036697 0.95942086]
</td>
</tr>
<tr>
<td>
**classes[2]**
</td>
<td>
-2.24527
</td>
</tr>
<tr>
<td>
**scores.shape**
</td>
<td>
(10,)
</td>
</tr>
<tr>
<td>
**boxes.shape**
</td>
<td>
(10, 4)
</td>
</tr>
<tr>
<td>
**classes.shape**
</td>
<td>
(10,)
</td>
</tr>
</table>
### 2.4 Wrapping up the filtering
It's time to implement a function taking the output of the deep CNN (the 19x19x5x85 dimensional encoding) and filtering through all the boxes using the functions you've just implemented.
**Exercise**: Implement `yolo_eval()` which takes the output of the YOLO encoding and filters the boxes using score threshold and NMS. There's just one last implementational detail you have to know. There're a few ways of representing boxes, such as via their corners or via their midpoint and height/width. YOLO converts between a few such formats at different times, using the following functions (which we have provided):
```python
boxes = yolo_boxes_to_corners(box_xy, box_wh)
```
which converts the yolo box coordinates (x,y,w,h) to box corners' coordinates (x1, y1, x2, y2) to fit the input of `yolo_filter_boxes`
```python
boxes = scale_boxes(boxes, image_shape)
```
YOLO's network was trained to run on 608x608 images. If you are testing this data on a different size image--for example, the car detection dataset had 720x1280 images--this step rescales the boxes so that they can be plotted on top of the original 720x1280 image.
Don't worry about these two functions; we'll show you where they need to be called.
```
# GRADED FUNCTION: yolo_eval
def yolo_eval(yolo_outputs, image_shape = (720., 1280.), max_boxes=10, score_threshold=.6, iou_threshold=.5):
"""
Converts the output of YOLO encoding (a lot of boxes) to your predicted boxes along with their scores, box coordinates and classes.
Arguments:
yolo_outputs -- output of the encoding model (for image_shape of (608, 608, 3)), contains 4 tensors:
box_confidence: tensor of shape (None, 19, 19, 5, 1)
box_xy: tensor of shape (None, 19, 19, 5, 2)
box_wh: tensor of shape (None, 19, 19, 5, 2)
box_class_probs: tensor of shape (None, 19, 19, 5, 80)
image_shape -- tensor of shape (2,) containing the input shape, in this notebook we use (608., 608.) (has to be float32 dtype)
max_boxes -- integer, maximum number of predicted boxes you'd like
score_threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (None, ), predicted score for each box
boxes -- tensor of shape (None, 4), predicted box coordinates
classes -- tensor of shape (None,), predicted class for each box
"""
### START CODE HERE ###
# Retrieve outputs of the YOLO model (≈1 line)
box_confidence, box_xy, box_wh, box_class_probs = yolo_outputs
# Convert boxes to be ready for filtering functions
boxes = yolo_boxes_to_corners(box_xy, box_wh)
# Use one of the functions you've implemented to perform Score-filtering with a threshold of score_threshold (≈1 line)
scores, boxes, classes = yolo_filter_boxes(box_confidence, boxes, box_class_probs, score_threshold)
# Scale boxes back to original image shape.
boxes = scale_boxes(boxes, image_shape)
# Use one of the functions you've implemented to perform Non-max suppression with a threshold of iou_threshold (≈1 line)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes, max_boxes, iou_threshold)
### END CODE HERE ###
return scores, boxes, classes
with tf.Session() as test_b:
yolo_outputs = (tf.random_normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1))
scores, boxes, classes = yolo_eval(yolo_outputs)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.eval().shape))
print("boxes.shape = " + str(boxes.eval().shape))
print("classes.shape = " + str(classes.eval().shape))
```
**Expected Output**:
<table>
<tr>
<td>
**scores[2]**
</td>
<td>
138.791
</td>
</tr>
<tr>
<td>
**boxes[2]**
</td>
<td>
[ 1292.32971191 -278.52166748 3876.98925781 -835.56494141]
</td>
</tr>
<tr>
<td>
**classes[2]**
</td>
<td>
54
</td>
</tr>
<tr>
<td>
**scores.shape**
</td>
<td>
(10,)
</td>
</tr>
<tr>
<td>
**boxes.shape**
</td>
<td>
(10, 4)
</td>
</tr>
<tr>
<td>
**classes.shape**
</td>
<td>
(10,)
</td>
</tr>
</table>
<font color='blue'>
**Summary for YOLO**:
- Input image (608, 608, 3)
- The input image goes through a CNN, resulting in a (19,19,5,85) dimensional output.
- After flattening the last two dimensions, the output is a volume of shape (19, 19, 425):
- Each cell in a 19x19 grid over the input image gives 425 numbers.
- 425 = 5 x 85 because each cell contains predictions for 5 boxes, corresponding to 5 anchor boxes, as seen in lecture.
- 85 = 5 + 80 where 5 is because $(p_c, b_x, b_y, b_h, b_w)$ has 5 numbers, and and 80 is the number of classes we'd like to detect
- You then select only few boxes based on:
- Score-thresholding: throw away boxes that have detected a class with a score less than the threshold
- Non-max suppression: Compute the Intersection over Union and avoid selecting overlapping boxes
- This gives you YOLO's final output.
## 3 - Test YOLO pretrained model on images
In this part, you are going to use a pretrained model and test it on the car detection dataset. As usual, you start by **creating a session to start your graph**. Run the following cell.
```
sess = K.get_session()
```
### 3.1 - Defining classes, anchors and image shape.
Recall that we are trying to detect 80 classes, and are using 5 anchor boxes. We have gathered the information about the 80 classes and 5 boxes in two files "coco_classes.txt" and "yolo_anchors.txt". Let's load these quantities into the model by running the next cell.
The car detection dataset has 720x1280 images, which we've pre-processed into 608x608 images.
```
class_names = read_classes("model_data/coco_classes.txt")
anchors = read_anchors("model_data/yolo_anchors.txt")
image_shape = (720., 1280.)
```
### 3.2 - Loading a pretrained model
Training a YOLO model takes a very long time and requires a fairly large dataset of labelled bounding boxes for a large range of target classes. You are going to load an existing pretrained Keras YOLO model stored in "yolo.h5". (These weights come from the official YOLO website, and were converted using a function written by Allan Zelener. References are at the end of this notebook. Technically, these are the parameters from the "YOLOv2" model, but we will more simply refer to it as "YOLO" in this notebook.) Run the cell below to load the model from this file.
```
yolo_model = load_model("model_data/yolo.h5")
```
This loads the weights of a trained YOLO model. Here's a summary of the layers your model contains.
```
yolo_model.summary()
```
**Note**: On some computers, you may see a warning message from Keras. Don't worry about it if you do--it is fine.
**Reminder**: this model converts a preprocessed batch of input images (shape: (m, 608, 608, 3)) into a tensor of shape (m, 19, 19, 5, 85) as explained in Figure (2).
### 3.3 - Convert output of the model to usable bounding box tensors
The output of `yolo_model` is a (m, 19, 19, 5, 85) tensor that needs to pass through non-trivial processing and conversion. The following cell does that for you.
```
yolo_outputs = yolo_head(yolo_model.output, anchors, len(class_names))
```
You added `yolo_outputs` to your graph. This set of 4 tensors is ready to be used as input by your `yolo_eval` function.
### 3.4 - Filtering boxes
`yolo_outputs` gave you all the predicted boxes of `yolo_model` in the correct format. You're now ready to perform filtering and select only the best boxes. Lets now call `yolo_eval`, which you had previously implemented, to do this.
```
scores, boxes, classes = yolo_eval(yolo_outputs, image_shape)
```
### 3.5 - Run the graph on an image
Let the fun begin. You have created a (`sess`) graph that can be summarized as follows:
1. <font color='purple'> yolo_model.input </font> is given to `yolo_model`. The model is used to compute the output <font color='purple'> yolo_model.output </font>
2. <font color='purple'> yolo_model.output </font> is processed by `yolo_head`. It gives you <font color='purple'> yolo_outputs </font>
3. <font color='purple'> yolo_outputs </font> goes through a filtering function, `yolo_eval`. It outputs your predictions: <font color='purple'> scores, boxes, classes </font>
**Exercise**: Implement predict() which runs the graph to test YOLO on an image.
You will need to run a TensorFlow session, to have it compute `scores, boxes, classes`.
The code below also uses the following function:
```python
image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
```
which outputs:
- image: a python (PIL) representation of your image used for drawing boxes. You won't need to use it.
- image_data: a numpy-array representing the image. This will be the input to the CNN.
**Important note**: when a model uses BatchNorm (as is the case in YOLO), you will need to pass an additional placeholder in the feed_dict {K.learning_phase(): 0}.
```
def predict(sess, image_file):
"""
Runs the graph stored in "sess" to predict boxes for "image_file". Prints and plots the preditions.
Arguments:
sess -- your tensorflow/Keras session containing the YOLO graph
image_file -- name of an image stored in the "images" folder.
Returns:
out_scores -- tensor of shape (None, ), scores of the predicted boxes
out_boxes -- tensor of shape (None, 4), coordinates of the predicted boxes
out_classes -- tensor of shape (None, ), class index of the predicted boxes
Note: "None" actually represents the number of predicted boxes, it varies between 0 and max_boxes.
"""
# Preprocess your image
image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
# Run the session with the correct tensors and choose the correct placeholders in the feed_dict.
# You'll need to use feed_dict={yolo_model.input: ... , K.learning_phase(): 0})
### START CODE HERE ### (≈ 1 line)
out_scores, out_boxes, out_classes = sess.run((scores, boxes, classes), feed_dict = {yolo_model.input:image_data, K.learning_phase() : 0})
### END CODE HERE ###
# Print predictions info
print('Found {} boxes for {}'.format(len(out_boxes), image_file))
# Generate colors for drawing bounding boxes.
colors = generate_colors(class_names)
# Draw bounding boxes on the image file
draw_boxes(image, out_scores, out_boxes, out_classes, class_names, colors)
# Save the predicted bounding box on the image
image.save(os.path.join("out", image_file), quality=90)
# Display the results in the notebook
output_image = scipy.misc.imread(os.path.join("out", image_file))
imshow(output_image)
return out_scores, out_boxes, out_classes
```
Run the following cell on the "test.jpg" image to verify that your function is correct.
```
out_scores, out_boxes, out_classes = predict(sess, "test.jpg")
```
**Expected Output**:
<table>
<tr>
<td>
**Found 7 boxes for test.jpg**
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.60 (925, 285) (1045, 374)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.66 (706, 279) (786, 350)
</td>
</tr>
<tr>
<td>
**bus**
</td>
<td>
0.67 (5, 266) (220, 407)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.70 (947, 324) (1280, 705)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.74 (159, 303) (346, 440)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.80 (761, 282) (942, 412)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.89 (367, 300) (745, 648)
</td>
</tr>
</table>
The model you've just run is actually able to detect 80 different classes listed in "coco_classes.txt". To test the model on your own images:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Write your image's name in the cell above code
4. Run the code and see the output of the algorithm!
If you were to run your session in a for loop over all your images. Here's what you would get:
<center>
<video width="400" height="200" src="nb_images/pred_video_compressed2.mp4" type="video/mp4" controls>
</video>
</center>
<caption><center> Predictions of the YOLO model on pictures taken from a camera while driving around the Silicon Valley <br> Thanks [drive.ai](https://www.drive.ai/) for providing this dataset! </center></caption>
<font color='blue'>
**What you should remember**:
- YOLO is a state-of-the-art object detection model that is fast and accurate
- It runs an input image through a CNN which outputs a 19x19x5x85 dimensional volume.
- The encoding can be seen as a grid where each of the 19x19 cells contains information about 5 boxes.
- You filter through all the boxes using non-max suppression. Specifically:
- Score thresholding on the probability of detecting a class to keep only accurate (high probability) boxes
- Intersection over Union (IoU) thresholding to eliminate overlapping boxes
- Because training a YOLO model from randomly initialized weights is non-trivial and requires a large dataset as well as lot of computation, we used previously trained model parameters in this exercise. If you wish, you can also try fine-tuning the YOLO model with your own dataset, though this would be a fairly non-trivial exercise.
**References**: The ideas presented in this notebook came primarily from the two YOLO papers. The implementation here also took significant inspiration and used many components from Allan Zelener's github repository. The pretrained weights used in this exercise came from the official YOLO website.
- Joseph Redmon, Santosh Divvala, Ross Girshick, Ali Farhadi - [You Only Look Once: Unified, Real-Time Object Detection](https://arxiv.org/abs/1506.02640) (2015)
- Joseph Redmon, Ali Farhadi - [YOLO9000: Better, Faster, Stronger](https://arxiv.org/abs/1612.08242) (2016)
- Allan Zelener - [YAD2K: Yet Another Darknet 2 Keras](https://github.com/allanzelener/YAD2K)
- The official YOLO website (https://pjreddie.com/darknet/yolo/)
**Car detection dataset**:
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons License" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/88x31.png" /></a><br /><span xmlns:dct="http://purl.org/dc/terms/" property="dct:title">The Drive.ai Sample Dataset</span> (provided by drive.ai) is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License</a>. We are especially grateful to Brody Huval, Chih Hu and Rahul Patel for collecting and providing this dataset.
| github_jupyter |
```
import datetime
import os, sys
import numpy as np
import matplotlib.pyplot as plt
import casadi as cas
import pickle
import copy as cp
# from ..</src> import car_plotting
# from .import src.car_plotting
PROJECT_PATH = '/home/nbuckman/Dropbox (MIT)/DRL/2020_01_cooperative_mpc/mpc-multiple-vehicles/'
sys.path.append(PROJECT_PATH)
import src.MPC_Casadi as mpc
import src.TrafficWorld as tw
import src.IterativeBestResponseMPCMultiple as mibr
np.set_printoptions(precision=2)
NEW = True
if NEW:
optional_suffix = "testsave"
subdir_name = datetime.datetime.now().strftime("%Y%m%d-%H%M%S") + optional_suffix
folder = "results/" + subdir_name + "/"
os.makedirs(folder)
os.makedirs(folder+"imgs/")
os.makedirs(folder+"data/")
os.makedirs(folder+"vids/")
else:
subdir_name = "20200224-103456_real_dim_CA"
folder = "results/" + subdir_name + "/"
print(folder)
T = 10 #numbr of time horizons
dt = 0.2
N = int(T/dt) #Number of control intervals
world = tw.TrafficWorld(2, 0, 1000)
# Initial Conditions
all_other_x0 = []
all_other_u = []
n_other = 2
all_other_MPC = []
next_x0 = 0
for i in range(n_other):
x1_MPC = mpc.MPC(dt)
x1_MPC.theta_iamb = np.pi/2.5
x1_MPC.k_final = 1.0
x1_MPC.k_s = -2.0
# x1_MPC.k_s = 0.0
# x1_MPC.k_x = -1.0
x1_MPC.min_y = world.y_min
x1_MPC.max_y = world.y_max
x1_MPC.k_u_v = 0.10
x1_MPC.k_u_delta = 0.10
x1_MPC.k_lat = 1.0
# x1_MPC.k_change_u_v = 1.0
# x1_MPC.k_change_u_delta = 1.0
if i%2 == 0:
lane_number = 0
next_x0 += x1_MPC.L/2.0 + 2*x1_MPC.min_dist
else:
lane_number = 1
initial_speed = 20 * 0.447 # m/s
x1_MPC.fd = x1_MPC.gen_f_desired_lane(world, lane_number, True)
x0 = np.array([next_x0, world.get_lane_centerline_y(lane_number), 0, 0, initial_speed, 0]).T
u1 = np.zeros((2,N))
u1[0,:] = np.clip(np.pi/180 *np.random.normal(size=(1,N)), -2 * np.pi/180, 2 * np.pi/180)
# u1[0,:] = np.ones((1,N)) * np.pi/6
# u1[1,:] = np.clip(np.random.normal(size=(1,N)), -x1_MPC.max_acceleration * x1_MPC.dt, x1_MPC.max_acceleration * x1_MPC.dt)
all_other_MPC += [x1_MPC]
all_other_x0 += [x0]
all_other_u += [u1]
amb_MPC = cp.deepcopy(x1_MPC)
amb_MPC.theta_iamb = 0.0
amb_MPC.k_u_v = 0.10
amb_MPC.k_u_delta = 1.0
amb_MPC.k_change_u_v = 0.01
amb_MPC.k_change_u_delta = 0.0
amb_MPC.k_phi
amb_MPC.k_x = -1/10000.0
amb_MPC.k_s = 0
# amb_MPC.min_v = initial_speed
# amb_MPC.k_u_change = 1.0
# amb_MPC.k_lat = 0
amb_MPC.k_lon = 0.0
# amb_MPC.k_s = -2.0
amb_MPC.max_v = 40 * 0.447 # m/s
# amb_MPC.max_X_dev = 5.0
amb_MPC.fd = amb_MPC.gen_f_desired_lane(world, 0, True)
x0_amb = np.array([0, 0, 0, 0, 1.1*initial_speed , 0]).T
uamb = np.zeros((2,N))
uamb[0,:] = np.clip(np.pi/180 * np.random.normal(size=(1,N)), -2 * np.pi/180, 2 * np.pi/180)
amb_MPC.min_v = 1.1*initial_speed
WARM = True
n_total_round = 60
ibr_sub_it = 1
runtimeerrors = 0
min_slack = 100000.0
for n_round in range(n_total_round):
response_MPC = amb_MPC
response_x0 = x0_amb
nonresponse_MPC_list = all_other_MPC
nonresponse_x0_list = all_other_x0
nonresponse_u_list = all_other_u
bri = mibr.IterativeBestResponseMPCMultiple(response_MPC, None, nonresponse_MPC_list )
bri.k_slack = 999
bri.generate_optimization(N, T, response_x0, None, nonresponse_x0_list, 5, slack=True)
bri.solve(None, nonresponse_u_list)
x1, u1, x1_des, _, _, _, other_x, other_u, other_des = bri.get_solution()
x1 = bri.opti.debug.value(bri.x_opt)
plt.plot(x1[0,:], x1[1,:])
costs = ["self.k_u_delta * self.u_delta_cost",
"self.k_u_v * self.u_v_cost",
"self.k_lat * self.lat_cost",
"self.k_lon * self.lon_cost",
"self.k_phi_error * self.phi_error_cost",
"self.k_phi_dot * self.phidot_cost",
"self.k_s * self.s_cost",
"self.k_v * self.v_cost",
"self.k_change_u_v * self.change_u_v",
"self.k_change_u_delta * self.change_u_delta",
"self.k_final * self.final_costs",
"self.k_x * self.x_cost"]
for i in range(len(bri.car1_costs_list)):
amb_costs = bri.opti.debug.value(bri.car1_costs_list[i])
print('%.03f'%amb_costs, costs[i])
print(bri.opti.debug.value(bri.slack_cost))
```
| github_jupyter |
```
# %load CommonFunctions.py
# # COMMON ATOMIC AND ASTRING FUNCTIONS
# In[14]:
############### One String Pulse with width, shift and scale #############
def StringPulse(String1, t: float, a = 1., b = 0., c = 1., d = 0.) -> float:
x = (t - b)/a
if (x < -1):
res = -0.5
elif (x > 1):
res = 0.5
else:
res = String1(x)
res = d + res * c
return res
# In[16]:
###### Atomic String Applied to list with width, shift and scale #############
def String(String1, x: list, a = 1., b = 0., c = 1., d = 0.) -> list:
res = []
for i in range(len(x)):
res.append(StringPulse(String1, x[i], a, b, c, d))
return res
# In[17]:
###### Summation of two lists #############
def Sum(x1: list, x2: list) -> list:
res = []
for i in range(len(x1)):
res.append(x1[i] + x2[i])
return res
# In[18]:
##########################################################
##This script introduces Atomic Function
################### One Pulse of atomic function
def up1(x: float) -> float:
#Atomic function table
up_y = [0.5, 0.48, 0.460000017,0.440000421,0.420003478,0.400016184, 0.380053256, 0.360139056, 0.340308139, 0.320605107,
0.301083436, 0.281802850, 0.262826445, 0.244218000, 0.226041554, 0.208361009, 0.191239338, 0.174736305,
0.158905389, 0.143991189, 0.129427260, 0.115840866, 0.103044024, 0.9110444278e-01, 0.798444445e-01, 0.694444445e-01,
0.598444445e-01, 0.510444877e-01, 0.430440239e-01, 0.358409663e-01, 0.294282603e-01, 0.237911889e-01, 0.189053889e-01,
0.147363055e-01, 0.112393379e-01, 0.836100883e-02, 0.604155412e-02, 0.421800000e-02, 0.282644445e-02, 0.180999032e-02,
0.108343562e-02, 0.605106267e-03, 0.308138660e-03, 0.139055523e-03, 0.532555251e-04, 0.161841328e-04, 0.347816874e-05,
0.420576116e-05, 0.167693347e-07, 0.354008603e-10, 0]
up_x = np.arange(0.5, 1.01, 0.01)
res = 0.
if ((x >= 0.5) and (x <= 1)):
for i in range(len(up_x) - 1):
if (up_x[i] >= x) and (x < up_x[i+1]):
N1 = 1 - (x - up_x[i])/0.01
res = N1 * up_y[i] + (1 - N1) * up_y[i+1]
return res
return res
# In[19]:
############### Atomic Function Pulse with width, shift and scale #############
def pulse(up1, t: float, a = 1., b = 0., c = 1., d = 0.) -> float:
x = (t - b)/a
res = 0.
if (x >= 0.5) and (x <= 1):
res = up1(x)
elif (x >= 0.0) and (x < 0.5):
res = 1 - up1(1 - x)
elif (x >= -1 and x <= -0.5):
res = up1(-x)
elif (x > -0.5) and (x < 0):
res = 1 - up1(1 + x)
res = d + res * c
return res
############### Atomic Function Applied to list with width, shift and scale #############
def up(up1, x: list, a = 1., b = 0., c = 1., d = 0.) -> list:
res = []
for i in range(len(x)):
res.append(pulse(up1, x[i], a, b, c, d))
return res
############### Atomic String #############
def AString1(x: float) -> float:
res = 1 * (pulse(up1, x/2.0 - 0.5) - 0.5)
return res
############### Atomic String Pulse with width, shift and scale #############
def AStringPulse(t: float, a = 1., b = 0., c = 1., d = 0.) -> float:
x = (t - b)/a
if (x < -1):
res = -0.5
elif (x > 1):
res = 0.5
else:
res = AString1(x)
res = d + res * c
return res
###### Atomic String Applied to list with width, shift and scale #############
def AString(x: list, a = 1., b = 0., c = 1., d = 0.) -> list:
res = []
for i in range(len(x)):
res.append(AStringPulse(x[i], a, b, c, d))
return res
import numpy as np
import pylab as pl
x = np.arange(-2.0, 2.0, 0.01)
pl.title('Atomic Function')
pl.plot(x, up(up1, x), label='Atomic Function')
pl.grid(True)
pl.show()
pl.title('Atomic String')
pl.plot(x, String(AString1, x, 1.0, 0, 1, 0), label='Atomic String')
pl.grid(True)
pl.show()
x = np.arange(-4.0, 4.0, 0.01)
dx = x[1] - x[0]
pl.title('Atomic String')
pl.plot(x, String(AString1, x, 1., 0., 1., 1.), label='Atomic String')
IntAString = np.cumsum(String(AString1, x, 1., 0., 1., 1.)) * dx
pl.plot(x, IntAString, label='AString Integral')
Int2AString = np.cumsum(IntAString) * dx
pl.plot(x, Int2AString, label='AString Integral Integral')
pl.title('AString with Integrals')
pl.legend(loc='best', numpoints=1)
pl.grid(True)
pl.show()
```
## Summary and Observations
1) AString Integrals provide smooth curly connections between two straight lines
2) Further integrals provide smooth curly connections between parabolas!!
3) In general, AString integrals can provide smooth connections between any similar shapes!!!
```
AString1(0)
v=[0,0.1,0.25,0.5,0.9,1]
for i in v:
print(AString1(i))
```
| github_jupyter |
```
import numpy as np
from exploration.config import sql_inst, mongo_inst
val_random_db = mongo_inst['val_random_db']
val_dump = (val_random_db['osu_scores_high'], val_random_db['osu_user_stats'])
pdf_func = np.load("exploration/skill_biased_sampling_function/pdf_sample_func.npy")
greedy_func = np.load("exploration/skill_biased_sampling_function/greedy_sample_func.npy")
values = list(enumerate(_func))
with sql_inst('osu_random_2021_02') as conn:
with conn.cursor() as cursor:
cursor.execute(
'''
DROP TABLE IF EXISTS sample_func;
CREATE TABLE sample_func (user_pp INT PRIMARY KEY, probability FLOAT NOT NULL);
ALTER TABLE sample_func AUTO_INCREMENT=100;
'''
)
conn.commit()
with conn.cursor() as cursor:
cursor.executemany(
'''
INSERT INTO sample_func VALUES
(%s, %s)
'''
, values)
conn.commit()
from datetime import datetime
from mlpp.data_collection.sample_func import sampleFuncGenerator
with sql_inst('osu_random_2021_02') as conn:
with conn.cursor() as cursor:
cursor.execute(
'''
SELECT * FROM osu_user_stats
WHERE rank_score < 7000 AND RAND() <= (
SELECT probability FROM sample_func
WHERE user_pp = FLOOR(rank_score)
LIMIT 1
)
'''
)
sampled_users = [u[0] for u in cursor]
print(sampled_users)
sampled_scores = list(
mongo_inst['val_random_db']['osu_scores_high'].find({
'user_id': {
'$in': sampled_users
},
'date': {
'$gt': datetime(2019, 1, 1)
}
}, {'mlpp.est_user_pp': 1})
)
data = list(map(lambda s: s['mlpp']['est_user_pp'],sampled_scores))
print(sampleFuncGenerator.prop_displaced(data))
NUM_BINS = 200
MAX_PP = 7000
DATE_LIMIT = datetime(2019,1,1)
generator = sampleFuncGenerator(date_limit = DATE_LIMIT, max_pp = MAX_PP, n_bins = NUM_BINS)
def simulate_fit(fit, dump = osu_dump):
sc, _ = generator.simulate(*dump, fit)
score_pp = list(map(lambda s: s['mlpp']['est_user_pp'], sc))
return score_pp
sample = simulate_fit(greedy_func, val_dump)
cap = len(sample) / 50
len(sample)/ val_dump[0].count()
users_7k_up = [u['_id'] for u in val_dump[1].find({'rank_score': {'$gt': 7000}}, {'_id': 1})]
random_scores_pipeline = [
{'$match': {
'date': {'$gt': datetime(2019, 1, 1)},
'user_id': {'$nin': users_7k_up}
}},
{'$sample': {'size': len(sample)}},
{'$project': {'mlpp': {'est_user_pp': 1}}}
]
random_sample = [s['mlpp']['est_user_pp'] for s in val_dump[0].aggregate(random_scores_pipeline)]
sampleFuncGenerator.prop_displaced(sample)
import matplotlib.pyplot as plt
fig, axs = plt.subplots(1, 2, figsize = (20, 8))
axs[0].hist(random_sample, bins = 50)
axs[0].plot([0, 7000], [cap, cap])
axs[0].set_title('Random 1% sample')
axs[0].annotate(f'Error: 40.6%', [5500, 5000], fontsize=20)
axs[0].set(xlabel = 'Score est user PP', ylabel='Count')
axs[1].hist(sample, bins = 50)
axs[1].plot([0, 7000], [cap, cap])
axs[1].annotate(f'Error: 12.4%', [5500, 1500], fontsize=20)
axs[1].set_title('Sampling function 1% sample')
axs[1].set(xlabel = 'Score est user PP', ylabel='Count')
```
<a style='text-decoration:none;line-height:16px;display:flex;color:#5B5B62;padding:10px;justify-content:end;' href='https://deepnote.com?utm_source=created-in-deepnote-cell&projectId=f93d0822-db5a-47ef-9a78-57b8adfbeb20' target="_blank">
<img style='display:inline;max-height:16px;margin:0px;margin-right:7.5px;' src='data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0iVVRGLTgiPz4KPHN2ZyB3aWR0aD0iODBweCIgaGVpZ2h0PSI4MHB4IiB2aWV3Qm94PSIwIDAgODAgODAiIHZlcnNpb249IjEuMSIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayI+CiAgICA8IS0tIEdlbmVyYXRvcjogU2tldGNoIDU0LjEgKDc2NDkwKSAtIGh0dHBzOi8vc2tldGNoYXBwLmNvbSAtLT4KICAgIDx0aXRsZT5Hcm91cCAzPC90aXRsZT4KICAgIDxkZXNjPkNyZWF0ZWQgd2l0aCBTa2V0Y2guPC9kZXNjPgogICAgPGcgaWQ9IkxhbmRpbmciIHN0cm9rZT0ibm9uZSIgc3Ryb2tlLXdpZHRoPSIxIiBmaWxsPSJub25lIiBmaWxsLXJ1bGU9ImV2ZW5vZGQiPgogICAgICAgIDxnIGlkPSJBcnRib2FyZCIgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoLTEyMzUuMDAwMDAwLCAtNzkuMDAwMDAwKSI+CiAgICAgICAgICAgIDxnIGlkPSJHcm91cC0zIiB0cmFuc2Zvcm09InRyYW5zbGF0ZSgxMjM1LjAwMDAwMCwgNzkuMDAwMDAwKSI+CiAgICAgICAgICAgICAgICA8cG9seWdvbiBpZD0iUGF0aC0yMCIgZmlsbD0iIzAyNjVCNCIgcG9pbnRzPSIyLjM3NjIzNzYyIDgwIDM4LjA0NzY2NjcgODAgNTcuODIxNzgyMiA3My44MDU3NTkyIDU3LjgyMTc4MjIgMzIuNzU5MjczOSAzOS4xNDAyMjc4IDMxLjY4MzE2ODMiPjwvcG9seWdvbj4KICAgICAgICAgICAgICAgIDxwYXRoIGQ9Ik0zNS4wMDc3MTgsODAgQzQyLjkwNjIwMDcsNzYuNDU0OTM1OCA0Ny41NjQ5MTY3LDcxLjU0MjI2NzEgNDguOTgzODY2LDY1LjI2MTk5MzkgQzUxLjExMjI4OTksNTUuODQxNTg0MiA0MS42NzcxNzk1LDQ5LjIxMjIyODQgMjUuNjIzOTg0Niw0OS4yMTIyMjg0IEMyNS40ODQ5Mjg5LDQ5LjEyNjg0NDggMjkuODI2MTI5Niw0My4yODM4MjQ4IDM4LjY0NzU4NjksMzEuNjgzMTY4MyBMNzIuODcxMjg3MSwzMi41NTQ0MjUgTDY1LjI4MDk3Myw2Ny42NzYzNDIxIEw1MS4xMTIyODk5LDc3LjM3NjE0NCBMMzUuMDA3NzE4LDgwIFoiIGlkPSJQYXRoLTIyIiBmaWxsPSIjMDAyODY4Ij48L3BhdGg+CiAgICAgICAgICAgICAgICA8cGF0aCBkPSJNMCwzNy43MzA0NDA1IEwyNy4xMTQ1MzcsMC4yNTcxMTE0MzYgQzYyLjM3MTUxMjMsLTEuOTkwNzE3MDEgODAsMTAuNTAwMzkyNyA4MCwzNy43MzA0NDA1IEM4MCw2NC45NjA0ODgyIDY0Ljc3NjUwMzgsNzkuMDUwMzQxNCAzNC4zMjk1MTEzLDgwIEM0Ny4wNTUzNDg5LDc3LjU2NzA4MDggNTMuNDE4MjY3Nyw3MC4zMTM2MTAzIDUzLjQxODI2NzcsNTguMjM5NTg4NSBDNTMuNDE4MjY3Nyw0MC4xMjg1NTU3IDM2LjMwMzk1NDQsMzcuNzMwNDQwNSAyNS4yMjc0MTcsMzcuNzMwNDQwNSBDMTcuODQzMDU4NiwzNy43MzA0NDA1IDkuNDMzOTE5NjYsMzcuNzMwNDQwNSAwLDM3LjczMDQ0MDUgWiIgaWQ9IlBhdGgtMTkiIGZpbGw9IiMzNzkzRUYiPjwvcGF0aD4KICAgICAgICAgICAgPC9nPgogICAgICAgIDwvZz4KICAgIDwvZz4KPC9zdmc+' > </img>
Created in <span style='font-weight:600;margin-left:4px;'>Deepnote</span></a>
| github_jupyter |
```
import ast
from glob import glob
import sys
import os
from copy import deepcopy
import networkx as nx
from stdlib_list import stdlib_list
STDLIB = set(stdlib_list())
CONVERSIONS = {
'attr': 'attrs',
'PIL': 'Pillow',
'Image': 'Pillow',
'mpl_toolkits': 'matplotlib',
'dateutil': 'python-dateutil'
}
dirtree = nx.DiGraph()
exclude_dirs = {'node_modules', '__pycache__', 'dist'}
exclude_files = {'__init__.py', '_version.py', '_install_requires.py'}
packages_dir = os.path.join(ROOT, 'packages')
for root, dirs, files in os.walk(packages_dir, topdown=True):
dirs[:] = [d for d in dirs if d not in exclude_dirs]
if '__init__.py' in files:
module_init = os.path.join(root, '__init__.py')
files[:] = [f for f in files if f not in exclude_files]
dirtree.add_node(module_init)
parent_init = os.path.join(os.path.dirname(root), '__init__.py')
if os.path.exists(parent_init):
dirtree.add_edge(parent_init, module_init)
for f in files:
if f.endswith('.py'):
filepath = os.path.join(root, f)
dirtree.add_node(filepath)
dirtree.add_edge(module_init, filepath)
package_roots = [n for n, d in dirtree.in_degree() if d == 0]
package_root_map = {
os.path.basename(os.path.dirname(package_root)): package_root
for package_root in package_roots
}
internal_packages = list(package_root_map.keys())
internal_packages
import_types = {
type(ast.parse('import george').body[0]),
type(ast.parse('import george as macdonald').body[0])}
import_from_types = {
type(ast.parse('from george import macdonald').body[0])
}
all_import_types = import_types.union(import_from_types)
all_import_types
def get_imports(filepath):
with open(filepath, 'r') as file:
data = file.read()
parsed = ast.parse(data)
imports = [node for node in ast.walk(parsed) if type(node) in all_import_types]
stdlib_imports = set()
external_imports = set()
internal_imports = set()
near_relative_imports = set()
far_relative_imports = set()
def get_base_converted_module(name):
name = name.split('.')[0]
try:
name = CONVERSIONS[name]
except KeyError:
pass
return name
def add_level_0(name):
if name in STDLIB:
stdlib_imports.add(name)
elif name in internal_packages:
internal_imports.add(name)
else:
external_imports.add(name)
for an_import in imports:
if type(an_import) in import_types:
for alias in an_import.names:
name = get_base_converted_module(alias.name)
add_level_0(name)
elif type(an_import) in import_from_types:
name = get_base_converted_module(an_import.module)
if an_import.level == 0:
add_level_0(name)
elif an_import.level == 1:
near_relative_imports.add(name)
else:
far_relative_imports.add(name)
else:
raise
return {
'stdlib': stdlib_imports,
'external': external_imports,
'internal': internal_imports,
'near_relative': near_relative_imports,
'far_relative': far_relative_imports}
all_imports = {
filepath: get_imports(filepath)
for filepath in dirtree.nodes()
}
def get_descendants_dependencies(filepath):
dependencies = deepcopy(all_imports[filepath])
for descendant in nx.descendants(dirtree, filepath):
for key, item in all_imports[descendant].items():
dependencies[key] |= item
return dependencies
package_dependencies = {
package: get_descendants_dependencies(root)
for package, root in package_root_map.items()
}
package_dependencies
get_descendants_dependencies(package_roots[0])
list(nx.neighbors(dirtree, package_roots[4]))
nx.descendants(dirtree, '/home/simon/git/pymedphys/packages/pymedphys/src/pymedphys/__init__.py')
# nx.neighbors()
imports = [node for node in ast.walk(table) if type(node) in all_import_types]
imports
# external_imports = set()
# near_internal_imports = set()
# far_internal_imports = set()
# for an_import in imports:
# if type(an_import) in import_types:
# for alias in an_import.names:
# external_imports.add(alias.name)
# elif type(an_import) in import_from_types:
# if an_import.level == 0:
# external_imports.add(an_import.module)
# elif an_import.level == 1:
# near_internal_imports.add(an_import.module)
# else:
# far_internal_imports.add(an_import.module)
# else:
# raise
# print(ast.dump(an_import))
external_imports
near_internal_imports
far_internal_imports
```
| github_jupyter |
# Your first neural network
In this project, you'll build your first neural network and use it to predict daily bike rental ridership. We've provided some of the code, but left the implementation of the neural network up to you (for the most part). After you've submitted this project, feel free to explore the data and the model more.
```
%matplotlib inline
%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = 'retina'
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
## Load and prepare the data
A critical step in working with neural networks is preparing the data correctly. Variables on different scales make it difficult for the network to efficiently learn the correct weights. Below, we've written the code to load and prepare the data. You'll learn more about this soon!
```
data_path = 'Bike-Sharing-Dataset/hour.csv'
rides = pd.read_csv(data_path)
rides.head()
```
## Checking out the data
This dataset has the number of riders for each hour of each day from January 1 2011 to December 31 2012. The number of riders is split between casual and registered, summed up in the `cnt` column. You can see the first few rows of the data above.
Below is a plot showing the number of bike riders over the first 10 days or so in the data set. (Some days don't have exactly 24 entries in the data set, so it's not exactly 10 days.) You can see the hourly rentals here. This data is pretty complicated! The weekends have lower over all ridership and there are spikes when people are biking to and from work during the week. Looking at the data above, we also have information about temperature, humidity, and windspeed, all of these likely affecting the number of riders. You'll be trying to capture all this with your model.
```
rides[:24*10].plot(x='dteday', y='cnt')
```
### Dummy variables
Here we have some categorical variables like season, weather, month. To include these in our model, we'll need to make binary dummy variables. This is simple to do with Pandas thanks to `get_dummies()`.
```
dummy_fields = ['season', 'weathersit', 'mnth', 'hr', 'weekday']
for each in dummy_fields:
dummies = pd.get_dummies(rides[each], prefix=each, drop_first=False)
rides = pd.concat([rides, dummies], axis=1)
fields_to_drop = ['instant', 'dteday', 'season', 'weathersit',
'weekday', 'atemp', 'mnth', 'workingday', 'hr']
data = rides.drop(fields_to_drop, axis=1)
data.head()
```
### Scaling target variables
To make training the network easier, we'll standardize each of the continuous variables. That is, we'll shift and scale the variables such that they have zero mean and a standard deviation of 1.
The scaling factors are saved so we can go backwards when we use the network for predictions.
```
quant_features = ['casual', 'registered', 'cnt', 'temp', 'hum', 'windspeed']
# Store scalings in a dictionary so we can convert back later
scaled_features = {}
for each in quant_features:
mean, std = data[each].mean(), data[each].std()
scaled_features[each] = [mean, std]
data.loc[:, each] = (data[each] - mean)/std
```
### Splitting the data into training, testing, and validation sets
We'll save the data for the last approximately 21 days to use as a test set after we've trained the network. We'll use this set to make predictions and compare them with the actual number of riders.
```
# Save data for approximately the last 21 days
test_data = data[-21*24:]
# Now remove the test data from the data set
data = data[:-21*24]
# Separate the data into features and targets
target_fields = ['cnt', 'casual', 'registered']
features, targets = data.drop(target_fields, axis=1), data[target_fields]
test_features, test_targets = test_data.drop(target_fields, axis=1), test_data[target_fields]
```
We'll split the data into two sets, one for training and one for validating as the network is being trained. Since this is time series data, we'll train on historical data, then try to predict on future data (the validation set).
```
# Hold out the last 60 days or so of the remaining data as a validation set
train_features, train_targets = features[:-60*24], targets[:-60*24]
val_features, val_targets = features[-60*24:], targets[-60*24:]
```
## Time to build the network
Below you'll build your network. We've built out the structure. You'll implement both the forward pass and backwards pass through the network. You'll also set the hyperparameters: the learning rate, the number of hidden units, and the number of training passes.
<img src="assets/neural_network.png" width=300px>
The network has two layers, a hidden layer and an output layer. The hidden layer will use the sigmoid function for activations. The output layer has only one node and is used for the regression, the output of the node is the same as the input of the node. That is, the activation function is $f(x)=x$. A function that takes the input signal and generates an output signal, but takes into account the threshold, is called an activation function. We work through each layer of our network calculating the outputs for each neuron. All of the outputs from one layer become inputs to the neurons on the next layer. This process is called *forward propagation*.
We use the weights to propagate signals forward from the input to the output layers in a neural network. We use the weights to also propagate error backwards from the output back into the network to update our weights. This is called *backpropagation*.
> **Hint:** You'll need the derivative of the output activation function ($f(x) = x$) for the backpropagation implementation. If you aren't familiar with calculus, this function is equivalent to the equation $y = x$. What is the slope of that equation? That is the derivative of $f(x)$.
Below, you have these tasks:
1. Implement the sigmoid function to use as the activation function. Set `self.activation_function` in `__init__` to your sigmoid function.
2. Implement the forward pass in the `train` method.
3. Implement the backpropagation algorithm in the `train` method, including calculating the output error.
4. Implement the forward pass in the `run` method.
```
#############
# In the my_answers.py file, fill out the TODO sections as specified
#############
from my_answers import NeuralNetwork
def MSE(y, Y):
return np.mean((y-Y)**2)
```
## Unit tests
Run these unit tests to check the correctness of your network implementation. This will help you be sure your network was implemented correctly befor you starting trying to train it. These tests must all be successful to pass the project.
```
import unittest
inputs = np.array([[0.5, -0.2, 0.1]])
targets = np.array([[0.4]])
test_w_i_h = np.array([[0.1, -0.2],
[0.4, 0.5],
[-0.3, 0.2]])
test_w_h_o = np.array([[0.3],
[-0.1]])
class TestMethods(unittest.TestCase):
##########
# Unit tests for data loading
##########
def test_data_path(self):
# Test that file path to dataset has been unaltered
self.assertTrue(data_path.lower() == 'bike-sharing-dataset/hour.csv')
def test_data_loaded(self):
# Test that data frame loaded
self.assertTrue(isinstance(rides, pd.DataFrame))
##########
# Unit tests for network functionality
##########
def test_activation(self):
network = NeuralNetwork(3, 2, 1, 0.5)
# Test that the activation function is a sigmoid
self.assertTrue(np.all(network.activation_function(0.5) == 1/(1+np.exp(-0.5))))
def test_train(self):
# Test that weights are updated correctly on training
network = NeuralNetwork(3, 2, 1, 0.5)
network.weights_input_to_hidden = test_w_i_h.copy()
network.weights_hidden_to_output = test_w_h_o.copy()
network.train(inputs, targets)
self.assertTrue(np.allclose(network.weights_hidden_to_output,
np.array([[ 0.37275328],
[-0.03172939]])))
self.assertTrue(np.allclose(network.weights_input_to_hidden,
np.array([[ 0.10562014, -0.20185996],
[0.39775194, 0.50074398],
[-0.29887597, 0.19962801]])))
def test_run(self):
# Test correctness of run method
network = NeuralNetwork(3, 2, 1, 0.5)
network.weights_input_to_hidden = test_w_i_h.copy()
network.weights_hidden_to_output = test_w_h_o.copy()
self.assertTrue(np.allclose(network.run(inputs), 0.09998924))
suite = unittest.TestLoader().loadTestsFromModule(TestMethods())
unittest.TextTestRunner().run(suite)
```
## Training the network
Here you'll set the hyperparameters for the network. The strategy here is to find hyperparameters such that the error on the training set is low, but you're not overfitting to the data. If you train the network too long or have too many hidden nodes, it can become overly specific to the training set and will fail to generalize to the validation set. That is, the loss on the validation set will start increasing as the training set loss drops.
You'll also be using a method know as Stochastic Gradient Descent (SGD) to train the network. The idea is that for each training pass, you grab a random sample of the data instead of using the whole data set. You use many more training passes than with normal gradient descent, but each pass is much faster. This ends up training the network more efficiently. You'll learn more about SGD later.
### Choose the number of iterations
This is the number of batches of samples from the training data we'll use to train the network. The more iterations you use, the better the model will fit the data. However, this process can have sharply diminishing returns and can waste computational resources if you use too many iterations. You want to find a number here where the network has a low training loss, and the validation loss is at a minimum. The ideal number of iterations would be a level that stops shortly after the validation loss is no longer decreasing.
### Choose the learning rate
This scales the size of weight updates. If this is too big, the weights tend to explode and the network fails to fit the data. Normally a good choice to start at is 0.1; however, if you effectively divide the learning rate by n_records, try starting out with a learning rate of 1. In either case, if the network has problems fitting the data, try reducing the learning rate. Note that the lower the learning rate, the smaller the steps are in the weight updates and the longer it takes for the neural network to converge.
### Choose the number of hidden nodes
In a model where all the weights are optimized, the more hidden nodes you have, the more accurate the predictions of the model will be. (A fully optimized model could have weights of zero, after all.) However, the more hidden nodes you have, the harder it will be to optimize the weights of the model, and the more likely it will be that suboptimal weights will lead to overfitting. With overfitting, the model will memorize the training data instead of learning the true pattern, and won't generalize well to unseen data.
Try a few different numbers and see how it affects the performance. You can look at the losses dictionary for a metric of the network performance. If the number of hidden units is too low, then the model won't have enough space to learn and if it is too high there are too many options for the direction that the learning can take. The trick here is to find the right balance in number of hidden units you choose. You'll generally find that the best number of hidden nodes to use ends up being between the number of input and output nodes.
```
import sys
####################
### Set the hyperparameters in you myanswers.py file ###
####################
from my_answers import iterations, learning_rate, hidden_nodes, output_nodes
N_i = train_features.shape[1]
network = NeuralNetwork(N_i, hidden_nodes, output_nodes, learning_rate)
losses = {'train':[], 'validation':[]}
for ii in range(iterations):
# Go through a random batch of 128 records from the training data set
batch = np.random.choice(train_features.index, size=128)
X, y = train_features.ix[batch].values, train_targets.ix[batch]['cnt']
network.train(X, y)
# Printing out the training progress
train_loss = MSE(network.run(train_features).T, train_targets['cnt'].values)
val_loss = MSE(network.run(val_features).T, val_targets['cnt'].values)
sys.stdout.write("\rProgress: {:2.1f}".format(100 * ii/float(iterations)) \
+ "% ... Training loss: " + str(train_loss)[:5] \
+ " ... Validation loss: " + str(val_loss)[:5])
sys.stdout.flush()
losses['train'].append(train_loss)
losses['validation'].append(val_loss)
plt.plot(losses['train'], label='Training loss')
plt.plot(losses['validation'], label='Validation loss')
plt.legend()
_ = plt.ylim()
```
## Check out your predictions
Here, use the test data to view how well your network is modeling the data. If something is completely wrong here, make sure each step in your network is implemented correctly.
```
fig, ax = plt.subplots(figsize=(8,4))
mean, std = scaled_features['cnt']
predictions = network.run(test_features).T*std + mean
ax.plot(predictions[0], label='Prediction')
ax.plot((test_targets['cnt']*std + mean).values, label='Data')
ax.set_xlim(right=len(predictions))
ax.legend()
dates = pd.to_datetime(rides.ix[test_data.index]['dteday'])
dates = dates.apply(lambda d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24], rotation=45)
```
## OPTIONAL: Thinking about your results(this question will not be evaluated in the rubric).
Answer these questions about your results. How well does the model predict the data? Where does it fail? Why does it fail where it does?
> **Note:** You can edit the text in this cell by double clicking on it. When you want to render the text, press control + enter
#### Your answer below
| github_jupyter |
# HRNet for MARS Tutorial
This notebook will walk through using the [HRNet pose estimator](https://github.com/leoxiaobin/deep-high-resolution-net.pytorch) with the [data](https://data.caltech.edu/records/2011) used in the [Mouse Action Recognition System](https://www.biorxiv.org/content/10.1101/2020.07.26.222299v1).
## 0. Set up your environment
Clone this repository.
Follow the instructions [here](https://github.com/leoxiaobin/deep-high-resolution-net.pytorch). Specifically, in the conda environment that you want to run this pose estimator, complete steps 1, 3, 4, 6, 7 under Installation in Quick Setup.
Also make an `annotations` directory.
Then, download the MARS COCO Evaluation tools [here](https://github.com/neuroethology/MARS_pycocotools) in that same environment.
Your root directory should look like this before running the model:
```
{PROJECT ROOT}
├── HRNet_MARS_tutorial.ipynb
├── LICENSE
├── annotations
├── data
├── data_utils
├── experiments
├── lib
├── log
├── models
├── output
├── project_config.yaml
├── requirements.txt
└── tools
```
## 1. Obtain the data
Visit [this link](https://data.caltech.edu/records/2011) and download the data. As a reminder, you can `wget https://data.caltech.edu/records/2011` to download the data directly into the directory of your choice.
We will be using two configuration files, one for general information about your data, and the other for training the model and model parameters. The first is called `project_config.yaml` in the root of your project directory. The other will be in `experiments/mars`.
1. Make sure you fill out `project_config.yaml` to fit your data. You will need to add the file name of your manifest file, and move that manifest file to the `annotations` directory.
2. Also, add the images referred to in the manifest file into `annotations/raw_images`.
## 2. Process and format the data
After running the code cell below, organize the data like this, with `mars` residing in the `data` directory:
```
mars
├── annotations
├── keypoints_[view]_test.json
├── keypoints_[view]_train.json
└── keypoints_[view]_val.json
├── images
├── MARS_[view]_00000.jpg
├── MARS_[view]_00001.jpg
├── MARS_[view]_00002.jpg
├── MARS_[view]_00003.jpg
├── MARS_[view]_00004.jpg
└── ...
```
(For MARS, [view] corresponds to either front or top.)
```
import data_utils.process_keypoints as process_data
project = '/home/ubuntu/Desktop/ericykma/hrnet_notebook/HRNet_for_MARS'
process_data.process_all_keypoints(project)
```
## 3. Train the model.
Place your config files in `experiments/mars`. See `example_config.yaml` for an example.
Then, run `python tools/train.py experiments/mars/example_config.yaml` in the root of your project directory, replacing `example_config.yaml` with your config file to train your model.
You can view training and validation loss/accuracy curves using `python -m tensorboard.main --logdir=log` to tune your model.
You can also use the below visualization code to view model output examples. It uses predictions and ground truth annotations corresponding to the images in `DATASET.TEST_SET` in your configuration file, so be sure to correspond to those image numbers/IDs. You have the option to save the image in the `results` directory in the directory in `output` that corresponds to your configuration file.
```
import data_utils.visualize as visualize
visualize.plot_frame(project='/home/ubuntu/Desktop/ericykma/hrnet_notebook/HRNet_for_MARS',
config_file='experiments/mars/w48_256x192_adam_lr1e-3_imagenet_pretrain.yaml',
frame_num=13999,
save=True
)
```
## 4. Test your model
You can run `python tools/test.py experiments/mars/example_config.yaml` to test your model. It will test the file under `DATASET.TEST_SET`, so if you are ready to evaluate your model on the test set, change that parameter to `test`.
| github_jupyter |
```
import pandas as pd
import numpy as np
%matplotlib inline
import joblib
import json
import tqdm
import glob
import numba
import dask
import xgboost
from dask.diagnostics import ProgressBar
import re
ProgressBar().register()
fold1, fold2 = joblib.load("./valid/fold1.pkl.z"), joblib.load("./valid/fold2.pkl.z")
train = pd.read_parquet("./data/train.parquet")
train_melt = pd.read_parquet("./data/22c_train_melt_with_features.parquet")
test_melt = pd.read_parquet("./data/22c_test_melt_with_features.parquet")
test_melt.head()
item_data = pd.read_parquet("./data/item_data.parquet")
item_data.head()
item_title_map = item_data[['item_id', 'title']].drop_duplicates()
item_title_map = item_title_map.set_index("item_id").squeeze().to_dict()
item_price_map = item_data[['item_id', 'price']].drop_duplicates()
item_price_map = item_price_map.set_index("item_id").squeeze().to_dict()
item_domain_map = item_data[['item_id', 'domain_id']].drop_duplicates()
item_domain_map = item_domain_map.set_index("item_id").squeeze().to_dict()
```
# stack gen
```
%%time
log_pos = np.log1p(np.arange(1,11))
best_sellers = [1587422, 1803710, 10243, 548905, 1906937, 716822, 1361154, 1716388, 725371, 859574]
best_sellers_domain = [item_domain_map[e] for e in best_sellers]
def pad(lst):
if len(lst) == 0:
return best_sellers
if len(lst) < 10:
lst += best_sellers[:(10 - len(lst))]
return np.array(lst)
def pad_str(lst):
if len(lst) == 0:
return best_sellers_domain
if len(lst) < 10:
lst += best_sellers_domain[:(10 - len(lst))]
return lst
# this is wrong, double counts exact item hits
def ndcg_vec(ytrue, ypred, ytrue_domain, ypred_domain):
relevance = np.zeros((ypred.shape[0], 10))
for i in range(10):
relevance[:, i] = np.equal(ypred_domain[:, i], ytrue_domain) * (np.equal(ypred[:, i], ytrue) * 12 + 1)
dcg = (relevance / log_pos).sum(axis=1)
i_relevance = np.ones(10)
i_relevance[0] = 12.
idcg = np.zeros(ypred.shape[0]) + (i_relevance / log_pos).sum()
return (dcg / idcg).mean()
%%time
tr_list = glob.glob("./stack_2f/*_train.parquet")
ts_list = glob.glob("./stack_2f/*_test.parquet")
train = train_melt[['seq_index','event_info','has_bought', 'item_domain', 'bought_domain', 'bought_id', 'y_rank']].copy()
for f in tr_list:
fname = re.search('/(\d[\d\w]+)_', f).group(1)
fdf = pd.read_parquet(f).rename(columns={"p": fname})
train = pd.merge(train, fdf, on=['seq_index','event_info'])
train = train.sort_values("seq_index")
test = test_melt[['seq_index','event_info']].copy()
for f in ts_list:
fname = re.search('/(\d[\d\w]+)_', f).group(1)
fdf = pd.read_parquet(f).rename(columns={"p": fname})
test = pd.merge(test, fdf, on=['seq_index','event_info'])
test = test.sort_values("seq_index")
train.head()
test.head()
train.columns
from sklearn.model_selection import GroupKFold
from cuml.preprocessing import TargetEncoder
stack_p = list()
for f1, f2 in [(fold1, fold2), (fold2, fold1)]:
Xtr = train[train['seq_index'].isin(f1)]
Xval = train[train['seq_index'].isin(f2)]
features = ['22c', '26']
params = [0.1, 3, 1, 0.5, 1.]
learning_rate, max_depth, min_child_weight, subsample, colsample_bytree = params
Xtrr, ytr = Xtr[features], Xtr['y_rank']
Xvall = Xval[features]
groups = Xtr.groupby('seq_index').size().values
mdl = xgboost.XGBRanker(seed=0, tree_method='gpu_hist', gpu_id=0, n_estimators=100,
learning_rate=learning_rate, max_depth=max_depth, min_child_weight=min_child_weight,
subsample=subsample, colsample_bytree=colsample_bytree, objective='rank:pairwise', num_parallel_tree=5)
mdl.fit(Xtrr, ytr, group=groups)
p = mdl.predict(Xvall)
preds = Xval[['seq_index', 'has_bought', 'item_domain', 'bought_domain', 'event_info', 'bought_id']].copy()
preds['p'] = p
preds = preds.sort_values('p', ascending=False).drop_duplicates(subset=['seq_index', 'event_info'])
ytrue = preds.groupby("seq_index")['bought_id'].apply(lambda x: x.iloc[0]).values
ytrue_domain = preds.groupby("seq_index")['bought_domain'].apply(lambda x: x.iloc[0]).values
ypred = preds.groupby("seq_index")['event_info'].apply(lambda x: pad(x.iloc[:10].tolist()))
ypred = np.array(ypred.tolist())
ypred_domain = preds.groupby("seq_index")['item_domain'].apply(lambda x: pad_str(x.iloc[:10].tolist()))
ypred_domain = np.array(ypred_domain.tolist())
print(ndcg_vec(ytrue, ypred, ytrue_domain, ypred_domain))
```
# test
```
groups = train.groupby('seq_index').size().values
learning_rate, max_depth, min_child_weight, subsample, colsample_bytree = params
mdl = xgboost.XGBRanker(seed=0, tree_method='gpu_hist', gpu_id=0, n_estimators=100,
learning_rate=learning_rate, max_depth=max_depth, min_child_weight=min_child_weight,
subsample=subsample, colsample_bytree=colsample_bytree, objective='rank:pairwise', num_parallel_tree=5)
mdl.fit(train[features], train['y_rank'], group=groups)
test[features].head()
p = mdl.predict(test[features])
preds = test[['seq_index', 'event_info']].copy()
preds['p'] = p
preds = preds.sort_values('p', ascending=False).drop_duplicates(subset=['seq_index', 'event_info'])
def pad(lst):
pad_candidates = [1587422, 1803710, 10243, 548905, 1906937, 716822, 1361154, 1716388, 725371, 859574]
if len(lst) == 0:
return pad_candidates
if len(lst) < 10:
lst += [lst[0]] * (10 - len(lst)) # pad_candidates[:(10 - len(lst))]
return np.array(lst)
ypred = preds.groupby("seq_index")['event_info'].apply(lambda x: pad(x.iloc[:10].tolist()))
seq_index = ypred.index
ypred = np.array(ypred.tolist())
ypred_final = np.zeros((177070, 10))
ypred_final[seq_index, :] = ypred
no_views = np.setdiff1d(np.arange(177070), seq_index)
#ypred_final[no_views, :] = np.array([1587422, 1803710, 10243, 548905, 1906937, 716822, 1361154, 1716388, 725371, 859574])
ypred_final = ypred_final.astype(int)
#permite produtos repetidos
pd.DataFrame(ypred_final).to_csv("./subs/27.csv", index=False, header=False)
test['seq_index'].max()
!wc -l ./subs/27.csv
!head ./subs/27.csv
```
| github_jupyter |
```
import os
import time
import numpy as np
import tensorflow as tf
from tensorflow.random import set_seed
from math import factorial
from scipy.stats import norm
from scipy.integrate import odeint
import numpy.polynomial.hermite_e as H
from sklearn.preprocessing import StandardScaler
import dolfin as fn
from numpy.polynomial.legendre import leggauss
import matplotlib.pyplot as plt
####### Plot Formatting ######
plt.rc('lines', linewidth = 4)
plt.rc('xtick', labelsize = 13)
plt.rc('ytick', labelsize = 13)
plt.rc('legend',fontsize=14)
plt.rcParams["font.family"] = "serif"
plt.rcParams['axes.labelsize'] = 18
plt.rcParams['axes.titlesize'] = 15
plt.rcParams['lines.markersize'] = 8
plt.rcParams['figure.figsize'] = (7.0, 5.0)
#### To make it cleaner, create Directory "images" to store all the figures ####
imagepath = os.path.join(os.getcwd(),"images")
os.makedirs(imagepath,exist_ok=True)
```
# PCE vs MC
$$ \frac{dy(t)}{dt} = -\lambda y, \ \ y(0)=1 $$
$$ y(t) = e^{-\lambda t} $$
$$QoI = y(T)$$
where $T$ is a fixed time point. $\Lambda = (-\infty, \infty)$, $\mathcal{D}=(0,\infty)$
## Polynomial Chaos
```
start_def = time.time()
def Phi(n):
#define H_n
coeffs = [0]*(n+1)
coeffs[n] = 1
return coeffs
def inner2_herm(n): ###return the denominator when computing $k_i$
return factorial(n)
def product3_herm(i,j,l):
#compute \Phi_i*\Phi_j*\Phi_l
return lambda x: H.hermeval(x, H.hermemul(H.hermemul(Phi(i),Phi(j)),Phi(l)))
def inner3_herm(P,i,j,l):
#compute <\Phi_i\Phi_j\Phi_l>
#Set up Gauss-Hermite quadrature, weighting function is exp^{-x^2}
m=(P+1)**2
x, w=H.hermegauss(m)
inner=sum([product3_herm(i,j,l)(x[idx]) * w[idx] for idx in range(m)])
return inner/np.sqrt(2*np.pi) #because of the weight
time_def = time.time() - start_def
start_prep = time.time()
P=4
ki_herm = [0,1]+[0]*(P-1)
Inner3_herm = np.zeros((P+1,P+1,P+1)) #store all inner3_herm values
Inner2_herm = np.zeros(P+1)
for i in range(P+1):
for j in range(P+1):
for l in range(P+1):
Inner3_herm[i,j,l] = inner3_herm(P,i,j,l)
for i in range(P+1):
Inner2_herm[i] = inner2_herm(i)
time_prep = time.time() - start_prep
start_ode = time.time()
def ode_system_herm(y, t, P):
#P indicates the highest degree
dydt = np.zeros(P+1)
for l in range(len(dydt)):
dydt[l] = -(sum(sum(Inner3_herm[i,j,l]*ki_herm[i]*y[j] for j in range(P+1)) for i in range(P+1)))/Inner2_herm[l]
return dydt
time_ode = time.time() - start_ode
start_solveode = time.time()
sol_herm = odeint(ode_system_herm, [1.0]+[0.0]*P, np.linspace(0,1,101), args=(P, ))
time_solveode = time.time() - start_solveode
time_all = time_def + time_prep + time_ode + time_solveode
```
## Monte Carlo
```
start_ode_mc = time.time()
def ode(y,t,nsample,k):
'''
Build the ode system
'''
dydt = np.zeros(nsample)
for i in range(nsample):
dydt[i] = -k[i]*y[i]
return dydt
time_def_mc = time.time() - start_ode_mc
nsample = np.array([10, 100, 1000, 10000, 100000])
time_solveode_mc = np.zeros(len(nsample))
start_solveode_mc = np.zeros(len(nsample))
mean_mc_1 = np.zeros(len(nsample))
mean_mc_05 = np.zeros(len(nsample))
for i in range(len(nsample)):
k = norm.rvs(loc=0, scale=1, size=nsample[i], random_state=12345)
start_solveode_mc[i] = time.time()
sol_mc = odeint(ode, [1.0]*nsample[i], np.linspace(0,1,101),args=(nsample[i],k)) #t:np.linspace(0,1,101)
mean_mc_1[i] = np.mean(sol_mc[100,:])
mean_mc_05[i] = np.mean(sol_mc[50,:])
time_solveode_mc[i] = time.time() - start_solveode_mc[i]
time_all_mc = time_def_mc + time_solveode_mc
```
## Comparison
### Computing time
```
#### Table 7.2, row 1 ####
### PCE
print(time_solveode)
### MC
print(time_solveode_mc)
```
### Mean value at $t=1$, $t=0.5$
#### Sample size = 1000 for MC
```
## t = 0.5
mean_pc_05 = sol_herm[:,0][50] #mean value using pc at t=0.5
mean_exact_05 = np.e**(1/8)
## t = 1
mean_pc_1 = sol_herm[:,0][100] #mean value using pc at t=1
mean_exact_1 = np.e**(1/2)
#### Table 7.2, row 2 ####
print(mean_pc_05)
print(mean_mc_05)
print(mean_exact_05)
print()
#### Table 7.2, row 3 ####
print(mean_pc_1)
print(mean_mc_1)
print(mean_exact_1)
```
# NN vs Poly
Finite difference:
$$
\frac{y_{i+1} - y_i}{\Delta t} = -\lambda y_i
$$
so
$$
y_{i+1} = -\lambda\Delta t y_i + y_i = (1-\lambda\Delta t)y_i
$$
Define $n := \frac{0.5}{\Delta t}$, then
$$
\hat{Q}(\lambda)=y(0.5) = y_n = (1-\lambda\Delta t)^n y_0 = (1-\lambda\Delta t)^n
$$
## NN
```
#######################################
#define the activation function
def rbf(x):
return tf.math.exp(-x**2)
#######################################
#define the derivative of the activation function
def d_rbf(x):
return tf.gradients(rbf,x)
#######################a################
#we couldn't use “tf_d_leaky_relu_6” as an activation function if we wanted to
#because tensorflow doesn't know how to calculate the gradients of that function.
def rbf_grad(op, grad):
x = op.inputs[0]
n_gr = d_rbf(x) #defining the gradient.
return grad * n_gr
def py_func(func, inp, Tout, stateful=True, name=None, grad=None):
# Need to generate a unique name to avoid duplicates:
rnd_name = 'PyFuncGrad' + str(np.random.randint(0, 1E+2))
tf.RegisterGradient(rnd_name)(grad)
g = tf.get_default_graph()
with g.gradient_override_map({"PyFunc": rnd_name, "PyFuncStateless": rnd_name}):
return tf.py_func(func, inp, Tout, stateful=stateful, name=name)
def tf_rbf(x,name=None):
with tf.name_scope(name, "rbf", [x]) as name:
y = py_func(rbf, #forward pass function
[x],
[tf.float32],
name=name,
grad= rbf_grad) #the function that overrides gradient
y[0].set_shape(x.get_shape()) #when using with the code, it is used to specify the rank of the input.
return y[0]
np.random.seed(12345)
size = 100
delta_t = 0.01
n = int(0.5/delta_t)
### Original data ###
lam_in = np.random.normal(0, 1, size)
y_exact = np.array([np.exp(-i*0.5) for i in lam_in])
y_out = np.array([(1-i*delta_t)**n for i in lam_in])
### After feature scaling ###
scaler = StandardScaler()
data_trans = scaler.fit_transform(lam_in.reshape(-1,1))
num_neuron = 5
tf.random.set_seed(12345)
model_ode = tf.keras.Sequential()
model_ode.add(tf.keras.layers.Dense(num_neuron,activation=rbf))
model_ode.add(tf.keras.layers.Dense(1))
model_ode.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.01))
model_ode.fit(data_trans[:,0],y_out, epochs=1500, verbose=0)
preds_ode = []
for j in data_trans[:,0]:
preds_ode.append(model_ode.predict([j]))
preds_ode_shaped = tf.reshape(tf.constant(np.array(preds_ode)),len(preds_ode))
mse_fd_nn = tf.keras.losses.MSE(y_exact,preds_ode_shaped).numpy()
fig = plt.figure()
plt.xlabel("$\lambda$")
plt.ylabel("$q$")
plt.title("MSE=%.5f"%(mse_fd_nn))
plt.scatter(lam_in, y_out, label='Obs')
plt.scatter(lam_in, preds_ode_shaped, label='NN')
plt.legend()
plt.show();
fig.savefig("images/comp_fd_nn.png")
```
## Polynomial Regression
`np.polyfit`
```
######## With feature scaling ############
mymodel1 = np.poly1d(np.polyfit(data_trans[:,0], y_out, 1))
preds_fd_pr1 = mymodel1(data_trans[:,0])
mse_fd_pr1 = tf.keras.losses.MSE(y_exact,preds_fd_pr1).numpy()
fig = plt.figure()
plt.xlabel("$\lambda$")
plt.ylabel("$q$")
plt.title("MSE=%.5f"%(mse_fd_pr1))
plt.scatter(lam_in, y_out, label='Obs')
plt.scatter(lam_in, preds_fd_pr1, label='PR (deg=1)')
plt.legend()
plt.show();
fig.savefig("images/comp_fd_pr1.png")
########## With feature scaling #############
mymodel2 = np.poly1d(np.polyfit(data_trans[:,0], y_out, 2))
preds_fd_pr2 = mymodel2(data_trans[:,0])
mse_fd_pr2 = tf.keras.losses.MSE(y_exact,preds_fd_pr2).numpy()
fig = plt.figure()
plt.xlabel("$\lambda$")
plt.ylabel("$q$")
plt.title("MSE=%.5f"%(mse_fd_pr2))
plt.scatter(lam_in, y_out, label='Obs')
plt.scatter(lam_in, preds_fd_pr2, label='PR (deg=2)')
plt.legend();
fig.savefig("images/comp_fd_pr2.png")
########## With feature scaling #############
mymodel3 = np.poly1d(np.polyfit(data_trans[:,0], y_out, 3))
preds_fd_pr3 = mymodel3(data_trans[:,0])
mse_fd_pr3 = tf.keras.losses.MSE(y_exact,preds_fd_pr3).numpy()
fig = plt.figure()
plt.xlabel("$\lambda$")
plt.ylabel("$q$")
plt.title("MSE=%.5f"%(mse_fd_pr3))
plt.scatter(lam_in, y_out, label='Obs')
plt.scatter(lam_in, preds_fd_pr3, label='PR (deg=3)')
plt.legend()
plt.show();
fig.savefig("images/comp_fd_pr3.png")
```
# Stochastic collocation method
\begin{align*}
- \nabla\cdot(A\nabla u) &= (e^{\lambda_1}\lambda_1^2\pi^2 + e^{\lambda_2}\lambda_2^2\pi^2)u \\
u &= 0 \, \text{ on } \Gamma_0 \,\text{( Left edge)}\\
(A\nabla u)\cdot n &= -e^{\lambda_2}\lambda_2\pi \sin\lambda_1\pi x\sin \lambda_2\pi y \, \text{ on } \Gamma_1 \, \text{( Top edge)}\\
(A\nabla u)\cdot n &= e^{\lambda_2}\lambda_2\pi \sin\lambda_1\pi x\sin \lambda_2\pi y \, \text{ on } \Gamma_2 \,\text{( Bottom edge)}\\
(A\nabla u)\cdot n &= e^{\lambda_1}\lambda_1\pi \cos\lambda_1\pi x\cos \lambda_2\pi y \, \text{ on } \Gamma_3 \,\text{( Right edge)}\\
\end{align*}
where
$$ A = \begin{bmatrix} e^{\lambda_1} & 0 \\ 0 & e^{\lambda_2} \end{bmatrix} $$
and $(x,y)\in\Omega = [0,1]\times [0,1]$, $(\lambda_1,\lambda_2)\in\Lambda=[0,1]\times [0,1]$
<font color = red>**Exact solution:**
$$ u(x,y;\lambda_1,\lambda_2) = \sin \lambda_1\pi x \cos \lambda_2 \pi y$$
</font>
QoI is:
$$
Q(\lambda_1,\lambda_2) = u(x_0,y_0;\lambda_1,\lambda_2)
$$
----
$\lambda_1,\lambda_2\sim U(0,1)$
**In theory:**
\begin{align*}
\overline{u}(x,y;\lambda_1,\lambda_2) &= \int_0^1 \int_0^1\sin \lambda_1\pi x \cos \lambda_2 \pi y \, d\lambda_1d\lambda_2\\
&= \int_0^1\sin \lambda_1\pi x\, d\lambda_1 \int_0^1 \cos \lambda_2 \pi y\, d\lambda_2\\
&= \left(-\frac{1}{\pi x}\cos(\lambda_1\pi x)\biggr\rvert_0^1 \right)\left(\frac{1}{\pi y}\sin(\lambda_2\pi y)\biggr\rvert_0^1 \right)\\
&= \left(-\frac{\cos(\pi x) - 1}{\pi x}\right)\frac{\sin(\pi y)}{\pi y}
\end{align*}
QoI is:
$$
Q(\lambda_1,\lambda_2) = u(x_0,y_0;\lambda_1,\lambda_2)
$$
so
<font color=red>
$$
\overline{Q} = \left(-\frac{\cos(\pi x_0) - 1}{\pi x_0}\right)\frac{\sin(\pi y_0)}{\pi y_0}
$$
</font>
When $x_0=y_0=0.5$,
$$
\overline{Q} = \frac{4}{\pi^2}
$$
---
$\lambda = (\lambda_1, \lambda_2)$, $x=(x,y)$, $L_k$ is Lagrange polynomial
$$
\hat{u}(\lambda, x) = \sum_{k=1}^M u(\lambda_k, x)L_k(\lambda)
$$
**In Practice:**
**Step 1:**
- Use numpy.polynomial.legendre.leggauss
- Quadrature point of $\lambda_1:$ $\left(\xi_i^{(1)}\right)_{i=1}^M$ $\in [-1,1]$
- Quadrature point of $\lambda_2:$ $\left(\xi_j^{(2)}\right)_{j=1}^N$ $\in [-1,1]$
- Then the quadrature points in $[0,1]$ are
- $\lambda_1:$ $\frac{1}{2}\xi_i^{(1)}+\frac{1}{2}$, $i=1,2,\cdots,M$
- $\lambda_2:$ $\frac{1}{2}\xi_j^{(2)}+\frac{1}{2}$, $j=1,2,\cdots,N$
Notice
$$
L_{ij}(\lambda_1,\lambda_2) = L_i^{(1)}(\lambda_1) L_j^{(2)}(\lambda_2)
$$
where $L_i^{(1)}$ corresponds to $\frac{1}{2}\xi_i^{(1)}+\frac{1}{2}$, $L_j^{(2)}$ corresponds to $\frac{1}{2}\xi_j^{(2)}+\frac{1}{2}$
**Step 2:**
- For $\lambda_1=\frac{1}{2}\xi_i^{(1)}+\frac{1}{2}$, $\lambda_2=\frac{1}{2}\xi_j^{(2)}+\frac{1}{2}$, use FEM to solve for $u$ evaluated at $x=x_0, y=y_0$. Use notation $u_{ij}$ to indicate the value
\begin{align*}
\mathbb{E}[\hat{u}] &= \sum_{i=1,j=1}^{M,N} u_{ij} \int_{\Lambda} L_{ij}(\lambda) \rho(\lambda) \, d\lambda\\
&\approx \sum_{i=1,j=1}^{M,N} u_{ij} \int_0^1 L_i^{(1)}(\lambda_1)\, d\lambda_1 \int_0^1 L_j^{(2)}(\lambda_2)\, d\lambda_2\\
&\approx \sum_{i=1,j=1}^{M,N} u_{ij} \left( \frac{1}{2}\sum_{k=1}^M w_k L_i^{(1)}\left(\frac{1}{2}\xi_k^{(1)} + \frac{1}{2} \right) \right) \left( \frac{1}{2}\sum_{l=1}^N w_l L_j^{(2)}\left(\frac{1}{2}\xi_l^{(2)} + \frac{1}{2} \right) \right)\\
&= \sum_{i=1,j=1}^{M,N} u_{ij} \frac{w_i}{2} \frac{w_j}{2}\\
&= \frac{1}{4} \sum_{i=1,j=1}^{M,N} u_{ij} w_i w_j
\end{align*}
**Step3:**
Compare with $\overline{Q} = \left(-\frac{\cos(\pi x_0) - 1}{\pi x_0}\right)\frac{\sin(\pi y_0)}{\pi y_0}$
----
<font color=red>**Extra reference**</font>
Gauss–Legendre quadrature [-1,1]
$$
\int_a^b f(x)\, dx \approx \frac{b-a}{2}\sum_{i=1}^n w_i f\left(\frac{b-a}{2}\xi_i + \frac{a+b}{2} \right)
$$
$a=0, b=1$
$$
\int_0^1 f(x)\, dx \approx \frac{1}{2}\sum_{i=1}^n w_i f\left(\frac{1}{2}\xi_i + \frac{1}{2} \right)
$$
Our input $\lambda$ is in a 2-dim space, and
$$
L_k(\lambda) = L_k^{(1)}(\lambda_1)L_k^{(2)}(\lambda_2)
$$
For example, we have
| $\lambda_1$ | $\lambda_2$ | $f$ |
| --- | --- | --- |
| $x_1$ | $y_1$ | $f_1$ |
| $x_2$ | $y_2$ | $f_2$ |
| $x_3$ | $y_3$ | $f_3$ |
Then
$$
L_1(\lambda_1, \lambda_2) = \frac{(\lambda_1 - x_2)(\lambda_1 - x_3)(\lambda_2 - y_2)(\lambda_2 - y_3)}{(x_1 - x_2)(x_1 - x_3)(y_1 - y_2)(y_1 - y_3)} = L_1^{(1)}(\lambda_1)L_1^{(2)}(\lambda_2)
$$
where $L_1^{(1)}$ is the 1-d Lagrange wrt point $x_1$, $L_1^{(2)}$ is the 1-d Lagrange wrt point $y_1$
```
def QoI_FEM(x0,y0,lam1,lam2,gridx,gridy,p):
mesh = fn.UnitSquareMesh(gridx, gridy)
V = fn.FunctionSpace(mesh, "Lagrange", p)
# Define diffusion tensor (here, just a scalar function) and parameters
A = fn.Expression((('exp(lam1)','a'),
('a','exp(lam2)')), a = fn.Constant(0.0), lam1 = lam1, lam2 = lam2, degree=3)
u_exact = fn.Expression("sin(lam1*pi*x[0])*cos(lam2*pi*x[1])", lam1 = lam1, lam2 = lam2, degree=2+p)
# Define the mix of Neumann and Dirichlet BCs
class LeftBoundary(fn.SubDomain):
def inside(self, x, on_boundary):
return (x[0] < fn.DOLFIN_EPS)
class RightBoundary(fn.SubDomain):
def inside(self, x, on_boundary):
return (x[0] > 1.0 - fn.DOLFIN_EPS)
class TopBoundary(fn.SubDomain):
def inside(self, x, on_boundary):
return (x[1] > 1.0 - fn.DOLFIN_EPS)
class BottomBoundary(fn.SubDomain):
def inside(self, x, on_boundary):
return (x[1] < fn.DOLFIN_EPS)
# Create a mesh function (mf) assigning an unsigned integer ('uint')
# to each edge (which is a "Facet" in 2D)
mf = fn.MeshFunction('size_t', mesh, 1)
mf.set_all(0) # initialize the function to be zero
# Setup the boundary classes that use Neumann boundary conditions
NTB = TopBoundary() # instatiate
NTB.mark(mf, 1) # set all values of the mf to be 1 on this boundary
NBB = BottomBoundary()
NBB.mark(mf, 2) # set all values of the mf to be 2 on this boundary
NRB = RightBoundary()
NRB.mark(mf, 3)
# Define Dirichlet boundary conditions
Gamma_0 = fn.DirichletBC(V, u_exact, LeftBoundary())
bcs = [Gamma_0]
# Define data necessary to approximate exact solution
f = ( fn.exp(lam1)*(lam1*fn.pi)**2 + fn.exp(lam2)*(lam2*fn.pi)**2 ) * u_exact
g1 = fn.Expression("-exp(lam2)*lam2*pi*sin(lam1*pi*x[0])*sin(lam2*pi*x[1])", lam1=lam1, lam2=lam2, degree=2+p) #pointing outward unit normal vector, pointing upaward (0,1)
g2 = fn.Expression("exp(lam2)*lam2*pi*sin(lam1*pi*x[0])*sin(lam2*pi*x[1])", lam1=lam1, lam2=lam2, degree=2+p) #pointing downward (0,1)
g3 = fn.Expression("exp(lam1)*lam1*pi*cos(lam1*pi*x[0])*cos(lam2*pi*x[1])", lam1=lam1, lam2=lam2, degree=2+p)
fn.ds = fn.ds(subdomain_data=mf)
# Define variational problem
u = fn.TrialFunction(V)
v = fn.TestFunction(V)
a = fn.inner(A*fn.grad(u), fn.grad(v))*fn.dx
L = f*v*fn.dx + g1*v*fn.ds(1) + g2*v*fn.ds(2) + g3*v*fn.ds(3) #note the 1, 2 and 3 correspond to the mf
# Compute solution
u = fn.Function(V)
fn.solve(a == L, u, bcs)
return u(x0,y0)
def exactQ(x,y):
return (1-np.cos(np.pi*x))*np.sin(np.pi*y)/(np.pi**2*x*y)
x0 = [0.2, 0.2, 0.2, 0.3, 0.5, 0.5]
y0 = [0.3, 0.5, 0.8, 0.2, 0.2, 0.5]
M, N = 5, 5
x1,w1 = leggauss(M)
x2,w2 = leggauss(N)
tab = np.zeros((len(x0),2))
for k in range(len(x0)):
#### Stochastic Collocation Mean at x0, y0 ####
uij = np.zeros((M,N))
for i in range(M):
for j in range(N):
uij[i,j] = QoI_FEM(x0[k],y0[k],(1+x1[i])/2,(1+x2[j])/2,10,10,2)
sol = 0
for i in range(M):
for j in range(N):
sol += w1[i]*w2[j]*uij[i,j]
sol /= 4
tab[k,0] = sol
#### Exact Mean at x0, y0 ####
tab[k,1] = exactQ(x0[k],y0[k])
print(tab)
```
# Further Discussion
<font color=red> Scaling, number of layers, print out the MSE every step, how to piecewise
- x_train, x_plt should have similar property. For StandardScaler(), var \& mean need to be similar
```
def model(x):
if x<=1:
return 15*x+10
elif x<=7:
return x**3-12*x**2+36*x
elif x<=10:
return 15/np.pi*np.sin(np.pi*(x-7))+7
else:
return -30*np.sqrt(x-9)+37
np.random.seed(12345)
x_syn = np.random.uniform(0,15,100)
y_exact = np.array([model(i) for i in x_syn])
y_syn = y_exact+np.random.normal(0,1,len(x_syn))
fig = plt.figure()
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.title('Observations & Target')
x_plt = np.linspace(min(x_syn),max(x_syn),50)
y_plt = [model(i) for i in x_plt]
plt.scatter(x_syn, y_syn, label='Obs')
plt.plot(x_plt, y_plt, color='red', label='Target')
plt.legend();
fig.savefig("images/comp_target.png")
```
## NN2
```
scaler_syn = StandardScaler()
syndata_trans = scaler_syn.fit_transform(x_syn.reshape(-1,1))
```
### One step method
```
############### With Feature Scaling ###############
num_neuron = 5
tf.random.set_seed(12345)
model_syn_all = tf.keras.Sequential()
model_syn_all.add(tf.keras.layers.Dense(num_neuron,activation=rbf))
model_syn_all.add(tf.keras.layers.Dense(num_neuron,activation=rbf))
# model_syn_all.add(tf.keras.layers.Dense(num_neuron,activation=rbf))
# model_syn_all.add(tf.keras.layers.Dense(num_neuron,activation=rbf))
model_syn_all.add(tf.keras.layers.Dense(1))
model_syn_all.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.01))
model_syn_all.fit(syndata_trans[:,0],y_syn, epochs=1000, verbose=0)
fig = plt.figure()
plt.xlabel("$x$")
plt.ylabel("$y$")
y_pred = []
for j in syndata_trans[:,0]:
y_pred.append(model_syn_all.predict([j]))
y_pred_shaped = tf.reshape(tf.constant(np.array(y_pred)),len(y_pred))
error0 = tf.keras.losses.MSE(y_syn,y_pred_shaped).numpy()
plt.title("MSE=%.5f"%(error0))
plt.scatter(x_syn, y_syn, label='Obs')
plt.scatter(x_syn, y_pred_shaped, color='red',label="NN")
plt.legend()
plt.show();
fig.savefig("images/comp_nn_1step.png")
```
### Split step method
```
## Step 1
num_neuron = 5
tf.random.set_seed(12345)
model_nn1 = tf.keras.Sequential()
model_nn1.add(tf.keras.layers.Dense(num_neuron,activation=rbf))
model_nn1.add(tf.keras.layers.Dense(1))
model_nn1.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.01))
model_nn1.fit(syndata_trans[:,0],y_syn, epochs=1000, verbose=0)
fig = plt.figure(figsize=(13,4))
plt.subplot(121)
plt.xlabel("$x$")
plt.ylabel("$y$")
y_pred1 = []
for j in syndata_trans[:,0]:
y_pred1.append(model_nn1.predict([j]))
y_pred1_shaped = tf.reshape(tf.constant(np.array(y_pred1)),len(y_pred1))
plt.title("Overall Fit")
plt.scatter(x_syn, y_syn, label='Obs')
plt.scatter(x_syn, y_pred1_shaped, color='red',label="NN")
plt.legend();
plt.subplot(122)
plt.xlabel("$x$")
plt.ylabel("Residual")
mse1 = tf.keras.losses.MSE(y_syn,y_pred1_shaped).numpy()
plt.title("MSE=%.5f"%(mse1))
plt.scatter(x_syn, y_syn-y_pred1_shaped)
plt.show();
fig.savefig("images/comp_nn_step1.png");
## Step 2
tf.random.set_seed(12345)
model_nn2 = tf.keras.Sequential()
model_nn2.add(tf.keras.layers.Dense(5,activation=rbf))
model_nn2.add(tf.keras.layers.Dense(1))
error1 = y_syn - y_pred1_shaped
scaler_syn2 = StandardScaler()
model_nn2.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.01))
model_nn2.fit(syndata_trans[:,0],error1, epochs=1000, verbose=0)
fig = plt.figure(figsize=(15,4))
plt.subplot(121)
plt.xlabel("$x$")
plt.ylabel("$y$")
y_pred2 = []
for j in syndata_trans[:,0]:
y_pred2.append(model_nn2.predict([j]))
y_pred2_shaped = tf.reshape(tf.constant(np.array(y_pred2)),len(y_pred2))
plt.title("Overall Fit")
plt.scatter(x_syn, y_syn, label='Obs')
plt.scatter(x_syn, y_pred1_shaped+y_pred2_shaped, color='red',label="NN")
plt.legend();
plt.subplot(122)
plt.xlabel("$x$")
plt.ylabel("Residual")
mse2 = tf.keras.losses.MSE(y_syn,y_pred1_shaped+y_pred2_shaped).numpy()
plt.title("MSE=%.5f"%(mse2))
plt.scatter(x_syn, y_syn-y_pred1_shaped-y_pred2_shaped)
plt.show();
fig.savefig("images/comp_nn_step2.png");
# fig = plt.figure()
# # plt.subplot(133)
# plt.xlabel("$x$")
# plt.ylabel("Residual")
# plt.title("Fit Previous Residual")
# plt.scatter(x_syn, error1)
# plt.scatter(x_syn, y_pred2_shaped, color='red',label="NN")
# plt.legend();
# # fig.savefig("images/comp_nn_res2.png");
## Step 3
tf.random.set_seed(12345)
model_nn3 = tf.keras.Sequential()
model_nn3.add(tf.keras.layers.Dense(5,activation=rbf))
model_nn3.add(tf.keras.layers.Dense(1))
error2 = y_syn - y_pred1_shaped - y_pred2_shaped
scaler_syn3 = StandardScaler()
model_nn3.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.01))
model_nn3.fit(syndata_trans[:,0],error2, epochs=1000, verbose=0)
fig = plt.figure(figsize=(13,4))
plt.subplot(121)
plt.xlabel("$x$")
plt.ylabel("$y$")
y_pred3 = []
for j in syndata_trans[:,0]:
y_pred3.append(model_nn3.predict([j]))
y_pred3_shaped = tf.reshape(tf.constant(np.array(y_pred3)),len(y_pred3))
plt.title("Overall Fit")
plt.scatter(x_syn, y_syn, label='Obs')
plt.scatter(x_syn, y_pred1_shaped+y_pred2_shaped+y_pred3_shaped, color='red',label="NN")
plt.legend();
plt.subplot(122)
plt.xlabel("$x$")
plt.ylabel("Residual")
mse3 = tf.keras.losses.MSE(y_syn,y_pred1_shaped+y_pred2_shaped+y_pred3_shaped).numpy()
plt.title("MSE=%.5f"%(mse3))
plt.scatter(x_syn, y_syn-y_pred1_shaped-y_pred2_shaped-y_pred3_shaped);
plt.show();
fig.savefig("images/comp_nn_step3.png");
# fig = plt.figure()
# # plt.subplot(133)
# plt.xticks(fontsize=13, rotation=0)
# plt.yticks(fontsize=13, rotation=0)
# plt.xlabel("$x$",fontsize=18)
# plt.ylabel("Residual",fontsize=18)
# plt.title("Fit Previous Residual",fontsize=15)
# plt.scatter(x_syn, error2, s=40)
# plt.scatter(x_syn, y_pred3_shaped,s=40,color='red',label="NN")
# plt.legend(prop={'size': 14});
# # fig.savefig("images/comp_nn_res3.png");
```
## 3 "1-5-1" = "1-15-1"
```
num_neuron = 15
tf.random.set_seed(12345)
model_nn11 = tf.keras.Sequential()
model_nn11.add(tf.keras.layers.Dense(num_neuron,activation=rbf))
model_nn11.add(tf.keras.layers.Dense(1))
model_nn11.compile(loss='mean_squared_error', optimizer=tf.keras.optimizers.Adam(0.01))
model_nn11.fit(syndata_trans[:,0],y_syn, epochs=5000, verbose=0)
fig = plt.figure(figsize=(13,4))
plt.subplot(121)
plt.xlabel("$x$")
plt.ylabel("$y$")
y_pred11 = []
for j in syndata_trans[:,0]:
y_pred11.append(model_nn11.predict([j]))
y_pred11_shaped = tf.reshape(tf.constant(np.array(y_pred11)),len(y_pred11))
plt.title("Overall Fit")
plt.scatter(x_syn, y_syn, label='Obs')
plt.scatter(x_syn, y_pred11_shaped, color='red', label="NN")
plt.legend();
plt.subplot(122)
plt.xlabel("$x$")
plt.ylabel("Residual")
mse11 = tf.keras.losses.MSE(y_syn,y_pred11_shaped).numpy()
plt.title("MSE=%.5f"%(mse11))
plt.scatter(x_syn, y_syn-y_pred11_shaped)
plt.show();
fig.savefig("images/comp_nn_step11.png");
```
| github_jupyter |
# EDA of All Sides Media ratings for 'debiaser' data product
#### Sagar Setru, September 21th, 2020
## Brief description using CoNVO framework
### Context
Some people are eager to get news from outside of their echo chamber. However, they do not know where to go outside of their echo chambers, and may also have some activation energy when it comes to seeking information from other sources. In the meantime, most newsfeeds only push you content that you agree with. You end up in an echo chamber, but may not have ever wanted to be in one in the first place.
### Need
A way to find news articles from different yet reliable media sources.
### Vision
Debiaser, a chrome extension that will recommend news articles similar in topic to the one currently being read, but from several pre-curated and reliable news media organizations across the political spectrum, for example, following the "media bias chart" here https://www.adfontesmedia.com/ or the "media bias ratings" here: https://www.allsides.com/media-bias/media-bias-ratings. The app will determine the main topics of the text of a news article, and then show links to similar articles from other news organizations.
The product will generate topics for a given document via latent Dirichlet allocation (LDA) and then search news websites for the topic words generated.
Caveats: Many of these articles may be behind paywalls. News aggregators already basically do this. How different is this than just searching Google using the title of an article?
### Outcome
People who are motivated to engage in content outside of their echo chambers have a tool that enables them to quickly find news similar to what they are currently reading, but from a variety of news organizations.
In this notebook, I will identify a set of news organizations across the political spectrum using data from AllSides media.
```
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
import os
# make sure I'm in the right environment (should be 'debiaser')
print('Conda environment:')
print(os.environ['CONDA_DEFAULT_ENV'])
# get the entire news csv into data frame
# get file name
fname = '../all_sides_media_data/allsides.csv'
# load into data frame
all_sides_df = pd.read_csv(fname)
all_sides_df.head()
# get number of nan
all_sides_df.isnull().sum()
all_sides_df.shape
```
There are 300 news media organizations represented. That's a lot to choose from.
```
# confirm all media organizations are only shown once
all_sides_df['name'].is_unique
# plot histograms of bias across publications
plt.figure(figsize=(10,5));
sns.countplot(all_sides_df['bias'],order=['left','left-center','center','right-center','right','allsides'])
plt.ylabel('N');
sns.set_context('talk', font_scale=1.5);
plt.xticks(rotation=90);
plt.show();
plt.clf();
plt.figure(figsize=(10,5));
sns.countplot(all_sides_df['agreeance_text'],order=['Absolutely Disagrees','Strongly Disagrees','Disagrees','Somewhat Disagrees','Neutral','Somehwat Agrees','Agrees','Strongly Agrees','Absolutely Agrees'])
plt.ylabel('N');
sns.set_context('talk', font_scale=1.5);
plt.xticks(rotation=90);
plt.show();
plt.clf();
```
We see that most vote tallies somewhat disagree with the given rating.
```
# what are the 'allsides ratings?'
all_sides_df_all_sides_rating = all_sides_df.loc[all_sides_df['bias']=='allsides']
all_sides_df_all_sides_rating.head()
```
These look like news outlets that cover all sides of a story.
```
all_sides_df_all_sides_rating.shape
# it's not so big, so let's just look at it all
all_sides_df_all_sides_rating
```
These look like news/media organizations that try to show all sides of an issue. It may be worth looking at what these websites do, for inspiration. These could also be generically recommended to the user.
```
# let's see what the distribution of total votes is
plt.figure(figsize=(10,5));
sns.distplot(all_sides_df['total_votes'],kde=False)
plt.ylabel('N');
plt.xlabel('Total votes')
sns.set_context('talk', font_scale=1.5);
plt.xticks(rotation=90);
plt.xscale('log')
plt.show();
plt.clf()
```
There are lots of websites with very few votes, and a few with thousands. My guess is that the websites with thousands of votes are the most popular news media organizations. Let's take a look at those.
```
total_votes_threshold = 10000
all_sides_df_high_votes = all_sides_df.loc[all_sides_df['total_votes']>=total_votes_threshold]
all_sides_df_high_votes.shape
```
There are 35 news organizations with more than the above threshold number of votes votes. What are they? What are their biases?
```
all_sides_df_high_votes
# plt.figure(figsize=(10,5));
sns.countplot(all_sides_df_high_votes['bias'],order=['left','left-center','center','right-center','right'])
plt.ylabel('N');
plt.yticks(np.arange(0, 11, step=2))
plt.xlabel('AllSides Media bias rating')
sns.set_context('talk', font_scale=1.5);
plt.xticks(rotation=90);
plt.show();
plt.clf();
```
These look like larger news organizations that will more likely cover lots of topics, though there are more left and center-left news organizations than right and center-right. This is a good list of news organizations to include in the MVP.
```
# how often does the 'public' agree with these ratings?
# plt.figure(figsize=(10,5));
sns.countplot(all_sides_df_high_votes['agreeance_text'],order=['Absolutely Disagrees','Strongly Disagrees','Disagrees','Somewhat Disagrees','Neutral','Somehwat Agrees','Agrees','Strongly Agrees','Absolutely Agrees'])
plt.ylabel('N');
plt.yticks(np.arange(0, 11, step=2))
plt.xlabel("Users' agreement with AllSides Media's rating")
sns.set_context('talk', font_scale=1.5);
plt.xticks(rotation=90);
plt.show();
plt.clf();
# look at those with agree votes and above
all_sides_df_high_votes_agree = all_sides_df_high_votes.loc[all_sides_df_high_votes['agreeance_text']=='Agrees']
all_sides_df_high_votes_strongly_agree = all_sides_df_high_votes.loc[all_sides_df_high_votes['agreeance_text']=='Strongly Agrees']
all_sides_df_high_votes_absolutely_agree = all_sides_df_high_votes.loc[all_sides_df_high_votes['agreeance_text']=='Absolutely Agrees']
all_sides_df_high_votes_agree_cat = pd.concat([all_sides_df_high_votes_agree,all_sides_df_high_votes_strongly_agree,all_sides_df_high_votes_absolutely_agree])
all_sides_df_high_votes_agree_cat.iloc[:,[2,4,6]]
# plt.figure(figsize=(10,5));
sns.countplot(all_sides_df_high_votes_agree_cat['bias'],order=['left','left-center','center','right-center','right','allsides'])
plt.ylabel('N');
plt.yticks(np.arange(0, 9, step=2))
plt.xlabel('Bias rating for agree and above')
sns.set_context('talk', font_scale=1.5);
plt.xticks(rotation=90);
plt.show();
plt.clf();
# now let's look at those with somewhat disagrees and disagrees votes
all_sides_df_high_votes_disagree = all_sides_df_high_votes.loc[all_sides_df_high_votes['agreeance_text']=='Disagrees']
all_sides_df_high_votes_somewhat_disagree = all_sides_df_high_votes.loc[all_sides_df_high_votes['agreeance_text']=='Somewhat Disagrees']
all_sides_df_high_votes_disagree_cat = pd.concat([all_sides_df_high_votes_disagree,all_sides_df_high_votes_somewhat_disagree])
all_sides_df_high_votes_disagree_cat.iloc[:,[2,4,6]]
# plt.figure(figsize=(10,5));
sns.countplot(all_sides_df_high_votes_disagree_cat['bias'],order=['left','left-center','center','right-center','right','allsides'])
plt.ylabel('N');
plt.yticks(np.arange(0, 9, step=2))
plt.xlabel('Bias rating for somewhat disagree and below')
sns.set_context('talk', font_scale=1.5);
plt.xticks(rotation=90);
plt.show();
plt.clf();
```
The disagreement is exclusively amongst those news organizations with left-center, center, and right-center ratings. Users tend to agree about those news organizations that are further left or right as rated by AllSides.
Among those news organizations where there is disagreement between users and AllSides, we see some big name media organizations like Fox News and NYT, which I would not want to exclude from this product.
I'll make a judgement call here and, for the MVP, utilize the bias score given by AllSides, even as there may be some disagreement between the scores they give and what many users think. This is not an easy call to make, but I will put my trust in AllSides's ratings for now, acknowledging that not all users will agree with AllSides. Finally, I will also include an additional center-right news group, WSJ, to add some more right-of-center news organizations.
To quote Steve Job, "People don't know what they want until you show it to them." For an MVP for open-minded consumers interested in diverse perspectives, I'm betting that the ratings by AllSidesMedia won't be crucial; the idea is to show diverse content across the spectrum, not to quantify where media organizations are on the spectrum per se.
```
all_sides_df_high_votes.to_csv('../all_sides_media_data/allsides_final.csv', index_label='index')
```
Separately, I added the domain names for each news organization as a column to the dataframe. Here, I check those domain names below.
```
all_sides_with_domains = pd.read_csv('../all_sides_media_data/allsides_final_plus_others_with_domains.csv')
all_sides_with_domains.head()
all_sides_names = all_sides_with_domains['name']
all_sides_domains = all_sides_with_domains['domain']
all_sides_names_domains = pd.concat([all_sides_names,all_sides_domains],axis=1)
print(all_sides_names_domains)
```
| github_jupyter |
# Task 1: Word Embeddings (10 points)
This notebook will guide you through all steps necessary to train a word2vec model (Detailed description in the PDF).
## Imports
This code block is reserved for your imports.
You are free to use the following packages:
(List of packages)
```
# Imports
from pandas import DataFrame
import pandas as pd
import numpy as np
import os
import re
from sklearn.preprocessing import OneHotEncoder
import nltk
from nltk.tokenize import word_tokenize
nltk.download('punkt')
nltk.download('stopwords')
import math
import io
```
# 1.1 Get the data (0.5 points)
The Hindi portion HASOC corpus from [github.io](https://hasocfire.github.io/hasoc/2019/dataset.html) is already available in the repo, at data/hindi_hatespeech.tsv . Load it into a data structure of your choice. Then, split off a small part of the corpus as a development set (~100 data points).
If you are using Colab the first two lines will let you upload folders or files from your local file system.
```
#TODO: implement!
#from google.colab import files
#uploaded = files.upload()
#Get the data
#os.chdir("D:/Saarland/NN TI/NNTI_WS2021_Project")
df = DataFrame.from_csv("hindi_.tsv", sep="\t")
def split_data (df):
df = df[:20]
return df
```
## 1.2 Data preparation (0.5 + 0.5 points)
* Prepare the data by removing everything that does not contain information.
User names (starting with '@') and punctuation symbols clearly do not convey information, but we also want to get rid of so-called [stopwords](https://en.wikipedia.org/wiki/Stop_word), i. e. words that have little to no semantic content (and, but, yes, the...). Hindi stopwords can be found [here](https://github.com/stopwords-iso/stopwords-hi/blob/master/stopwords-hi.txt) Then, standardize the spelling by lowercasing all words.
Do this for the development section of the corpus for now.
* What about hashtags (starting with '#') and emojis? Should they be removed too? Justify your answer in the report, and explain how you accounted for this in your implementation.
```
#TODO: implement!
def clean_data(sentence):
hindi_stopword_file = open('stopwords.txt', encoding="utf8")
hindi_stopwords = []
for x in hindi_stopword_file:
hindi_stopwords.append(x.rstrip())
text_tokens = word_tokenize(sentence)
special_words_list = ['#', '?', '!', ';', ',','&' ,'+' ,'<' ,'>' ,'^' ,'_' ,'`' ,'|' ,'~' ,'..', '…', '....', '', ' ', ' ',
':', "\'", '-', '=', '(', ')', '[', ']' , '{', '}','$','°', '¶' , '"', '*', '@', ' ', '\\', '/', '.', '%', '।', '”']
sentence = " ".join([text_word for text_word in text_tokens if text_word not in hindi_stopwords])
text_tokens = word_tokenize(sentence)
sentence = " ".join([text_word for text_word in text_tokens if not re.search(r'[a-zA-Z0-9]', text_word) ])
text_tokens = word_tokenize(sentence)
PATTERN = re.compile( #https://en.wikipedia.org/wiki/Emoji#Unicode_blocks
"(["
"\U0001F1E0-\U0001F1FF" # flags
"\U0001F300-\U0001F5FF" # symbols & pictographs
"\U0001F600-\U0001F64F" # emoticons
"\U0001F680-\U0001F6FF" # transport & map symbols
"\U0001F700-\U0001F77F" # alchemical symbols
"\U0001F780-\U0001F7FF" # Geometric Shapes Extended
"\U0001F800-\U0001F8FF" # Supplemental Arrows-C
"\U0001F900-\U0001F9FF" # Supplemental Symbols and Pictographs
"\U0001FA00-\U0001FA6F" # Chess Symbols
"\U0001FA70-\U0001FAFF" # Symbols and Pictographs Extended-A
"\U00002702-\U000027B0" # Dingbats
"])"
)
sentence = " ".join([text_word for text_word in text_tokens if not re.search(PATTERN, text_word)])
text_tokens = word_tokenize(sentence)
new_array = []
for text_word in text_tokens:
for word in special_words_list:
text_word = text_word.replace(word, "")
new_array.append(text_word)
sentence = " ".join(item for item in new_array)
return sentence
def drop_empty_values(df):
df['text'].replace('', np.nan, inplace=True)
df['text'].replace(r'^\s+$', np.nan, regex=True)
df = df.dropna(subset=['text'])
return df
```
## 1.3 Build the vocabulary (0.5 + 0.5 points)
The input to the first layer of word2vec is an one-hot encoding of the current word. The output od the model is then compared to a numeric class label of the words within the size of the skip-gram window. Now
* Compile a list of all words in the development section of your corpus and save it in a variable ```V```.
```
#TODO: implement!
def building_vocabulary(df):
sentences = []
v = [] #unique_words
frequency_of_words = {}
for line in df['text']:
words = [x for x in line.split()]
for word in words:
if word != ':':
if word not in v:
v.append(word)
frequency_of_words[word] = 1
else:
frequency_of_words[word] = frequency_of_words[word] + 1
sentences.append(words)
v = sorted(v)
return sentences,frequency_of_words , v
```
* Then, write a function ```word_to_one_hot``` that returns a one-hot encoding of an arbitrary word in the vocabulary. The size of the one-hot encoding should be ```len(v)```.
```
#TODO: implement!
def word_to_one_hot(word):
try:
ohe = OneHotEncoder(sparse=False)
ohe.fit(word)
ohe_word = ohe.transform(word)
return ohe_word
except ValueError: #Array_With_zero_sample
pass
```
## 1.4 Subsampling (0.5 points)
The probability to keep a word in a context is given by:
$P_{keep}(w_i) = \Big(\sqrt{\frac{z(w_i)}{0.001}}+1\Big) \cdot \frac{0.001}{z(w_i)}$
Where $z(w_i)$ is the relative frequency of the word $w_i$ in the corpus. Now,
* Calculate word frequencies
* Define a function ```sampling_prob``` that takes a word (string) as input and returns the probabiliy to **keep** the word in a context.
```
#TODO: implement!
def sampling_prob(word):
probability = (math.sqrt(word/0.001) + 1 ) * (0.001/word)
return probability
```
# 1.5 Skip-Grams (1 point)
Now that you have the vocabulary and one-hot encodings at hand, you can start to do the actual work. The skip gram model requires training data of the shape ```(current_word, context)```, with ```context``` being the words before and/or after ```current_word``` within ```window_size```.
* Have closer look on the original paper. If you feel to understand how skip-gram works, implement a function ```get_target_context``` that takes a sentence as input and [yield](https://docs.python.org/3.9/reference/simple_stmts.html#the-yield-statement)s a ```(current_word, context)```.
* Use your ```sampling_prob``` function to drop words from contexts as you sample them.
```
#TODO: implement!
def get_target_context(sentences,w2v_model,vocab_one_hot,vocab_index,subsampling_probability):
center_word_list = []
context_word_list = []
for sentence in sentences:
for i in range(len(sentence)):
center_word = vocab_one_hot[sentence[i]] #vocab_one_hot
context = [0 for x in range(len(center_word))]
for j in range(i- w2v_model.window_size,i + w2v_model.window_size):
if i!=j and j>=0 and j<len(sentence):
# increase sampling chances of domain specific words in context
#if subsampling_probability[sentence[i]] > np.random.random() :
context[vocab_index[sentence[j]]] += 1 #vocab_index
center_word_list.append(center_word)
context_word_list.append(context)
return center_word_list, context_word_list
```
# 1.6 Hyperparameters (0.5 points)
According to the word2vec paper, what would be a good choice for the following hyperparameters?
* Embedding dimension
* Window size
Initialize them in a dictionary or as independent variables in the code block below.
```
# Set hyperparameters
window_size = 2
embedding_size = 100
# More hyperparameters
learning_rate = 0.05
epochs = 100
```
# 1.7 Pytorch Module (0.5 + 0.5 + 0.5 points)
Pytorch provides a wrapper for your fancy and super-complex models: [torch.nn.Module](https://pytorch.org/docs/stable/generated/torch.nn.Module.html). The code block below contains a skeleton for such a wrapper. Now,
* Initialize the two weight matrices of word2vec as fields of the class.
* Override the ```forward``` method of this class. It should take a one-hot encoding as input, perform the matrix multiplications, and finally apply a log softmax on the output layer.
* Initialize the model and save its weights in a variable. The Pytorch documentation will tell you how to do that.
```
# Create model
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0)
class Word2Vec(object):
def __init__(self):
self.embedding_size = 100
self.window_size = 2 # sentences weren't too long, so
self.learning_rate = 0.05
self.epochs = 100
def initialize(self,Vocab_length):
self.Vocab_len = Vocab_length
self.W = np.random.uniform(-0.8, 0.8, (self.Vocab_len, self.embedding_size))
self.W1 = np.random.uniform(-0.8, 0.8, (self.embedding_size, self.Vocab_len))
def feed_forward(self,X):
self.h = np.dot(self.W.T,X).reshape(self.embedding_size,1)
self.u = np.dot(self.W1.T,self.h)
self.y = softmax(self.u)
return self.u
def backpropagate(self,x,t):
e = self.y - np.asarray(t).reshape(self.Vocab_len,1)
dLdW1 = np.dot(self.h,e.T)
X = np.array(x).reshape(self.Vocab_len,1)
dLdW = np.dot(X, np.dot(self.W1,e).T)
self.W1 = self.W1 - self.learning_rate*dLdW1
self.W = self.W - self.learning_rate*dLdW
return self.W , self.W1
```
# 1.8 Loss function and optimizer (0.5 points)
Initialize variables with [optimizer](https://pytorch.org/docs/stable/optim.html#module-torch.optim) and loss function. You can take what is used in the word2vec paper, but you can use alternative optimizers/loss functions if you explain your choice in the report.
```
# Define optimizer and loss
#optimizer = torch.optim.Adam(w2v_model.parameters(), lr=0.01)
#criterion = nn.CrossEntropyLoss()
```
# 1.9 Training the model (3 points)
As everything is prepared, implement a training loop that performs several passes of the data set through the model. You are free to do this as you please, but your code should:
* Load the weights saved in 1.6 at the start of every execution of the code block
* Print the accumulated loss at least after every epoch (the accumulate loss should be reset after every epoch)
* Define a criterion for the training procedure to terminate if a certain loss value is reached. You can find the threshold by observing the loss for the development set.
You can play around with the number of epochs and the learning rate.
```
# Define train procedure
# load initial weights
def train(w2v_model,X_train,Y_train, Vocab_len):
#loss_list = []
print("Training started")
for x in range(1, w2v_model.epochs):
loss = 0
for j in range(len(X_train)):
u = w2v_model.feed_forward(X_train[j])
W, W1 = w2v_model.backpropagate( X_train[j], Y_train[j])
loss += -np.sum([u[word.index(1)] for word in Y_train]) + len(Y_train) * np.log(np.sum(np.exp(u)))
#print("epoch ",x, " loss = ", loss)
#loss_list.append(loss)
#print(loss_list)
print("Training finished")
return W, W1
```
# 1.10 Train on the full dataset (0.5 points)
Now, go back to 1.1 and remove the restriction on the number of sentences in your corpus. Then, reexecute code blocks 1.2, 1.3 and 1.6 (or those relevant if you created additional ones).
* Then, retrain your model on the complete dataset.
* Now, the input weights of the model contain the desired word embeddings! Save them together with the corresponding vocabulary items (Pytorch provides a nice [functionality](https://pytorch.org/tutorials/beginner/saving_loading_models.html) for this).
```
#df = split_data(df)
# converting upper case letters to lowercase
df['text'] = df['text'].str.lower()
# data preprocessing
df['text'] = df['text'].map(lambda x: clean_data(x))
# drop empty values
df = drop_empty_values(df)
#building vocabulary and Calculating word frequencies
sentences, frequency_of_words , v = building_vocabulary(df)
subsampling_probability = {}
#subsampling
for words in v:
freq_word = frequency_of_words[words]
subsampling_probability[words] = sampling_prob(freq_word)
# One hot encoding
result_one_hot_encoding = word_to_one_hot(np.reshape(v,(-1,1)))
vocab_index = {}
vocab_one_hot = {}
for i in range(len(v)):
vocab_index[v[i]] = i
vocab_one_hot[v[i]] = result_one_hot_encoding[i]
#Creating object of the Word2Vec class
w2v_model = Word2Vec()
is_untrained = True # true for the new training of the model
if is_untrained: # checks the flag
w2v_model.initialize(len(v))
#w2v_model = w2v_model.to(device)
#w2v_model.train(True)
# Define optimizer and loss
#optimizer = torch.optim.Adam(w2v_model.parameters(), lr=0.01)
#criterion = nn.CrossEntropyLoss()
'''
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
optimizer = keras.optimizers.Adam(learning_rate=0.01)
criterion = tf.keras.losses.BinaryCrossentropy()
'''
#retreiving the target and context
X_train, Y_train = get_target_context(sentences,w2v_model,vocab_one_hot,vocab_index,subsampling_probability)
#training the dataset
W, W1 = train(w2v_model,X_train,Y_train, len(v))
## saving embedding weights
out_v = io.open('vocab.tsv', 'w', encoding='utf-8')
out_w = io.open('embedding_weight_W.tsv', 'w', encoding='utf-8')
out_w1 = io.open('embedding_weight_W1.tsv', 'w', encoding='utf-8')
for i in v:
out_v.write(i)
out_w.close()
for i in W:
out_w.write(','.join([str(w) for w in i]))
out_w.close()
for i in W1:
out_w1.write(','.join([str(w) for w in i]))
out_w1.close()
try:
from google.colab import files
files.download('vocab.tsv')
files.download('embedding_weight_W.tsv')
files.download('embedding_weight_W1.tsv')
except Exception:
pass
```
| github_jupyter |
```
# The purpose of this notebook is to compare the
# efficacy of various Machine Learning models on
# the dataset.
import os
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
np.random.seed(0)
script_dir = os.path.abspath('')
file = os.path.realpath(script_dir + '/../data/interim/train_users_2_2.csv')
df = pd.read_csv(file)
df.head()
print(df.columns)
# Prepare the dataset for our regression
df2 = 0
# Remove undesired columns
# Note we do NOT want date_first_booking in
# our model because it is not included in
# the test set of the competition.
df2 = df[['date_account_created',
'gender',
'age',
'signup_method',
'language',
'affiliate_channel',
'affiliate_provider',
'first_affiliate_tracked',
'signup_app',
'first_device_type',
'first_browser',
'number_of_actions',
'country_destination']]
# Convert time-based columns to datetime
# objects, then to numbers that the model
# can use.
df2['week_account_created'] = pd.to_datetime(df2['date_account_created']).dt.week
df2 = df2.drop(['date_account_created'], axis=1)
df2.fillna(0, inplace=True)
# Use get_dummies to convert our categorical
# features to numerical features so that our
# model can use them.
dummiescols = ['gender', 'signup_method', 'language',
'affiliate_channel', 'affiliate_provider',
'first_affiliate_tracked', 'signup_app',
'first_device_type', 'first_browser']
df2 = pd.get_dummies(df2, prefix=dummiescols, columns=dummiescols)
# Create the training and testing set
X_train, X_test, y_train, y_test = train_test_split(
df2.drop('country_destination', axis=1).values,
df2['country_destination'].values,
random_state=0)
# Logistic Regression
# Train the model, then score it on the test set
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
logreg.score(X_test, y_test)
from sklearn.metrics import confusion_matrix
from sklearn.utils.multiclass import unique_labels
import matplotlib.pyplot as plt
ylr_pred = logreg.predict(X_test)
labels = [i for i in unique_labels(y_test, ylr_pred)]
print(labels)
cm = confusion_matrix(y_test, ylr_pred)
print(cm)
# Random Forests
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100)
rf.fit(X_train, y_train)
rf.score(X_test, y_test)
yrf_pred = rf.predict(X_test)
print(labels)
cm2 = confusion_matrix(y_test, yrf_pred)
print(cm2)
# AdaBoost
from sklearn.ensemble import AdaBoostClassifier
ab = AdaBoostClassifier()
ab.fit(X_train, y_train)
ab.score(X_test, y_test)
yab_pred = ab.predict(X_test)
print(labels)
cm3 = confusion_matrix(y_test, yab_pred)
print(cm3)
# Looks like our algorithms are only ever
# predicting NDF or US as the classifier.
# I wonder if we can get a better result
# by removing NDF entirely. If so, we can
# just create a separate algorithm to sort
# the data into "NDF" or "Made a Booking".
df3 = df2[df2['country_destination'] != 'NDF']
print(df3['country_destination'].unique())
X3_train, X3_test, y3_train, y3_test = train_test_split(
df3.drop('country_destination', axis=1).values,
df3['country_destination'].values,
random_state=0)
logreg3 = LogisticRegression()
logreg3.fit(X3_train, y3_train)
logreg3.score(X3_test, y3_test)
ylr3_pred = logreg3.predict(X3_test)
labels3 = [i for i in unique_labels(y3_test, ylr3_pred)]
print(labels3)
cm = confusion_matrix(y3_test, ylr3_pred)
print(cm)
# Nope. It's still just saying everyone travels to the US.
# Let's try one more time, eliminating the US as well.
df4 = df3[df3['country_destination'] != 'US']
print(df4['country_destination'].unique())
X4_train, X4_test, y4_train, y4_test = train_test_split(
df4.drop('country_destination', axis=1).values,
df4['country_destination'].values,
random_state=0)
logreg4 = LogisticRegression()
logreg4.fit(X4_train, y4_train)
logreg4.score(X4_test, y4_test)
ylr4_pred = logreg4.predict(X4_test)
labels4 = [i for i in unique_labels(y4_test, ylr4_pred)]
print(labels4)
cm = confusion_matrix(y4_test, ylr4_pred)
print(cm)
# Our model is pretty weak. It looks like it just
# assigns the data to the most popular destination in
# the dataset. Let's remove 'other' and see what
# happens.
df5 = df4[df4['country_destination'] != 'other']
print(df5['country_destination'].unique())
X5_train, X5_test, y5_train, y5_test = train_test_split(
df5.drop('country_destination', axis=1).values,
df5['country_destination'].values,
random_state=0)
logreg5 = LogisticRegression()
logreg5.fit(X5_train, y5_train)
logreg5.score(X5_test, y5_test)
ylr5_pred = logreg5.predict(X5_test)
labels5 = [i for i in unique_labels(y5_test, ylr5_pred)]
print(labels5)
cm = confusion_matrix(y5_test, ylr5_pred)
print(cm)
# Ok. It's turtles all the way down. Just
# to be sure, try Random Forests and AdaBoost.
rf5 = RandomForestClassifier(n_estimators=300)
rf5.fit(X5_train, y5_train)
rf5.score(X5_test, y5_test)
ab5 = AdaBoostClassifier()
ab5.fit(X5_train, y5_train)
ab5.score(X5_test, y5_test)
```
Very clear what's going on here: the models have little ability to discern between the less popular destination spots. We were getting such accurate results in the first case solely because two features—NDF and US—absolutely dwarf the other target categories. To proceed, I will need to understand how to predict even despite very unevenly distributed target classes.
Perhaps it is time to re-wrangle things and re-introduce users for whom
data is missing. It could be that a larger training set would allow for
a better result. I think I will also start performing these
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.