code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
### Import Library and Dataset
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime
pd.set_option('display.max_columns', None)
data_train = pd.read_excel('Data_Train.xlsx')
data_test = pd.read_excel('Data_Test.xlsx')
```
### Combining the Dataset
```
price_train = data_train.Price
# Concatenate training and test sets
data = pd.concat([data_train.drop(['Price'], axis=1), data_test])
data.columns
```
### Exploratory Data Analysis
```
data.head()
data.info()
data.describe()
data = data.drop_duplicates()
data.isnull().sum()
data = data.drop(data.loc[data['Route'].isnull()].index)
```
## Feature Engineering
```
data['Airline'].unique()
import seaborn as sns
sns.countplot(x='Airline', data=data)
plt.xticks(rotation=90)
data['Airline'] = np.where(data['Airline']=='Vistara Premium economy', 'Vistara', data['Airline'])
data['Airline'] = np.where(data['Airline']=='Jet Airways Business', 'Jet Airways', data['Airline'])
data['Airline'] = np.where(data['Airline']=='Multiple carriers Premium economy', 'Multiple carriers', data['Airline'])
sns.countplot(x='Airline', data=data)
plt.xticks(rotation=90)
data['Destination'].unique()
data['Destination'] = np.where(data['Destination']=='Delhi','New Delhi', data['Destination'])
data['Date_of_Journey']
data['Date_of_Journey'] = pd.to_datetime(data['Date_of_Journey'])
data['Date_of_Journey']
data['day_of_week'] = data['Date_of_Journey'].dt.day_name()
data['day_of_week']
sns.countplot(x='day_of_week', data=data)
plt.xticks(rotation=90)
data['Journey_Month'] = pd.to_datetime(data.Date_of_Journey, format='%d/%m/%Y').dt.month_name()
sns.countplot(x='Journey_Month', data=data)
plt.xticks(rotation=90)
data['Departure_t'] = pd.to_datetime(data.Dep_Time, format='%H:%M')
a = data.assign(dept_session=pd.cut(data.Departure_t.dt.hour,[0,6,12,18,24],labels=['Night','Morning','Afternoon','Evening']))
data['Departure_S'] = a['dept_session']
sns.countplot(x='dept_session', data=a)
plt.xticks(rotation=90)
data['Departure_S'].fillna("Night", inplace = True)
duration = list(data['Duration'])
for i in range(len(duration)) :
if len(duration[i].split()) != 2:
if 'h' in duration[i] :
duration[i] = duration[i].strip() + ' 0m'
elif 'm' in duration[i] :
duration[i] = '0h {}'.format(duration[i].strip())
dur_hours = []
dur_minutes = []
for i in range(len(duration)) :
dur_hours.append(int(duration[i].split()[0][:-1]))
dur_minutes.append(int(duration[i].split()[1][:-1]))
data['Duration_hours'] = dur_hours
data['Duration_minutes'] =dur_minutes
data.loc[:,'Duration_hours'] *= 60
data['Duration_Total_mins']= data['Duration_hours']+data['Duration_minutes']
# Get names of indexes for which column Age has value 30
indexNames = data[data.Duration_Total_mins < 60].index
# Delete these row indexes from dataFrame
data.drop(indexNames , inplace=True)
data.drop(labels = ['Arrival_Time','Dep_Time','Date_of_Journey','Duration','Departure_t','Duration_hours','Duration_minutes'], axis=1, inplace = True)
cat_vars = ['Airline', 'Source', 'Destination', 'Route', 'Total_Stops',
'Additional_Info', 'day_of_week', 'Journey_Month', 'Departure_S' ]
for var in cat_vars:
catList = 'var'+'_'+var
catList = pd.get_dummies(data[var], prefix=var)
data1 = data.join(catList)
data = data1
data_vars = data.columns.values.tolist()
to_keep = [i for i in data_vars if i not in cat_vars]
data_final=data[to_keep]
data
```
| github_jupyter |
```
# Import dependencies
import pandas as pd
import pathlib
# Identifying CSV file path
csv_path = pathlib.Path('../../Resources/Raw/COVID-19_Case_Surveillance_Public_Use_Data_with_Geography.csv')
# Reading and previewing CSV file
data_df = pd.read_csv(csv_path, low_memory=False)
data_df.head()
# Filtering for only California cases
ca_data_df = data_df.loc[data_df['res_state'] == 'CA']
ca_data_df.head()
# Dropping unused columns
ca_data_df = ca_data_df.drop(columns=[
'state_fips_code',
'case_positive_specimen_interval',
'case_onset_interval', 'process',
'exposure_yn', 'symptom_status',
'hosp_yn',
'icu_yn',
'underlying_conditions_yn'])
ca_data_df.head()
# Extracting year and month from 'case_month'
ca_data_df['year'] = ca_data_df['case_month'].str[:4].astype(int)
ca_data_df['month'] = ca_data_df['case_month'].str[-2:].astype(int)
ca_data_df.head()
# ----------------------- Data Cleanup -----------------------
# County: dropping rows with N/A
ca_data_df = pd.DataFrame(ca_data_df[ca_data_df['res_county'].notna()])
# Age Group: removing rows with 'Missing'
ca_data_df['age_group'] = ca_data_df['age_group'].str.replace('Missing','Unknown')
ca_data_df['age_group'] = ca_data_df['age_group'].str.replace('NA','Unknown')
value = {'age_group': 'Unknown'}
ca_data_df = ca_data_df.fillna(value=value)
# Sex: If 'Missing' then 'Unknown'
ca_data_df['sex'] = ca_data_df['sex'].str.replace('NA','Unknown')
value = {'sex': 'Unknown'}
ca_data_df = ca_data_df.fillna(value=value)
# Current Status: removing Probable Cases
ca_data_df = ca_data_df.drop(ca_data_df[ca_data_df.current_status == 'Probable Case'].index)
# Death Y/N: removing 'Missing' or 'Unknown'
ca_data_df = ca_data_df.drop(ca_data_df[ca_data_df.death_yn == 'Missing'].index)
ca_data_df = ca_data_df.drop(ca_data_df[ca_data_df.death_yn == 'NA'].index)
ca_data_df = ca_data_df.drop(ca_data_df[ca_data_df.death_yn == 'Unknown'].index)
# Create new column for 'race/ethnicity' and set initially to the value of 'race'
ca_data_df['race/ethnicity'] = ca_data_df['race']
# If 'race' equals "Unknown" then set 'race/ethnicity' to the value of 'ethnicity'
ca_data_df.loc[ca_data_df["race"] == "Unknown", "race/ethnicity"] = ca_data_df["ethnicity"]
ca_data_df.loc[ca_data_df['race'] == 'Unknown'].head()
# If 'race' equals "Missing" then set 'race/ethnicity' to the value of 'ethnicity'
ca_data_df.loc[ca_data_df["race"] == "Missing", "race/ethnicity"] = ca_data_df["ethnicity"]
ca_data_df.loc[ca_data_df["race"] == "Missing"].head()
# If 'race/ethnicity' equals "Missing" then set 'race/ethnicity' to "Unknown"
ca_data_df.loc[ca_data_df["race/ethnicity"] == "Missing"] = "Unknown"
ca_data_df['race/ethnicity'].value_counts()
# If 'race' equals "White" and ethnicity equals "Hispanic/Latino" then set 'race/ethnicity' to "Hispanic/Latino"
ca_data_df.loc[((ca_data_df['race'] == 'White') & (ca_data_df['ethnicity'] == 'Hispanic/Latino')), 'race/ethnicity'] = 'Hispanic/Latino'
ca_data_df.loc[((ca_data_df['race'] == 'White') & (ca_data_df['ethnicity'] == 'Hispanic/Latino'))].head()
# Replace blanks in 'race/ethnicity' with "Unknown"
ca_data_df['race/ethnicity'] = ca_data_df['race/ethnicity'].fillna('Unknown')
# Reviewing 'race/ethnicity' column
ca_data_df['race/ethnicity'].value_counts()
# Reorganizing columns
ca_data_df = ca_data_df[['year','month','case_month','res_county','res_state','county_fips_code','age_group','sex','race/ethnicity','current_status','death_yn']]
ca_data_df.head()
# Export to CSV for review
ca_data_df.to_csv('../../Resources/Clean/ca_data_df.csv', index=False)
```
| github_jupyter |
```
# Load dependencies
import numpy as np
import pandas as pd
from uncertainties import ufloat
from uncertainties import unumpy
```
# Biomass C content estimation
Biomass is presented in the paper on a dry-weight basis. As part of the biomass calculation, we converted biomass in carbon-weight basis to dry-weight basis by multiplying by a conversion factor.
## Conversion factor calculation
The conversion factor was calculated based on C content estimates of the different plant compartments (leaves, stems and roots) of different biomes, from [Tang et al.](https://doi.org/10.1073/pnas.1700295114) (units: (mg/g)).
```
# Upload C content data from Tang et al., units [mg/g]
c_content = pd.read_excel("C_content_Tang.xlsx")
c_content
# Save parameters to unumpy arrays
cleaf = unumpy.uarray(list(c_content['leaf']), list(c_content['leaf std']))
cstem = unumpy.uarray(list(c_content['stem'].fillna(0)), list(c_content['stem std'].fillna(0)))
croot = unumpy.uarray(list(c_content['root']), list(c_content['root std']))
```
For each biome, we calculate the weighted average C content according to the mass fraction of each plant compartment. Information on plants compartmental mass composition was obtained from [Poorter et al.](https://nph.onlinelibrary.wiley.com/doi/full/10.1111/j.1469-8137.2011.03952.x).
```
# Upload compartmental mass composition, from Poorter et al., classified according to Tang et al. biomes
compart_comp = pd.read_excel("compartment_comp_Poorter.xlsx")
compart_comp
# Save parameters to unumpy arrays
fleaf = unumpy.uarray(list(compart_comp['leaf']), list(compart_comp['leaf std']))
fstem = unumpy.uarray(list(compart_comp['stem'].fillna(0)), list(compart_comp['stem std'].fillna(0)))
froot = unumpy.uarray(list(compart_comp['root']), list(compart_comp['root std']))
# Calculate the weighted average for each biome
cbiome = (cleaf*fleaf)+(cstem*fstem)+(croot*froot)
```
Next, we calculate the plants conversion factor, according to the mass fraction of each biome, which was calculated by the corresponding mass of each of the biome categories, derived from [Erb et al.](https://doi.org/10.1038/nature25138).
```
# Upload biomes biomass, from Erb et al., classified according to Tang et al. biomes
mbiome = pd.read_excel('biome_mass_Erb.xlsx')
mbiome
# Save to unumpy array
mbiomes = unumpy.uarray(list(mbiome['biomass [Gt C]']), list(mbiome['biomass std']))
# Calculate the overall conversion factor
cplants_factor = 1000/np.sum((cbiome* (mbiomes/np.sum(mbiomes))))
```
In the overall carbon-weight to dry-weight conversion factor, we also accounted the C content of non-plant biomass, which was based on estimates from [Heldal et al.](https://aem.asm.org/content/50/5/1251.short) and [von Stockar](https://www.sciencedirect.com/science/article/pii/S0005272899000651). We used the current estimate of non-plant biomass fraction - about 10% of the total biomass, according to [Bar-On et al.](https://doi.org/10.1073/pnas.1711842115) and [updates](https://doi.org/10.1038/s41561-018-0221-6).
```
# Upload non plant C content data, units [g/g]
cnon_plant = pd.read_excel('C_content_non_plant.xlsx')
cnon_plant
# Calculate conversion factors
cnon_plant_factor = ufloat(np.average(cnon_plant['C content']) ,np.std(cnon_plant['C content'], ddof = 1))
cfactor = (cplants_factor*0.9) +(0.1*(1/cnon_plant_factor))
cfactor
print 'Our best estimate of the C content conversion factor is: ' + "%.2f" % (cfactor.n) + ', with uncertainty (±1 standard deviation): ' + "%.2f" % (cfactor.s)
```
| github_jupyter |
```
!pip install -q efficientnet
import math, re, os, random
import tensorflow as tf, tensorflow.keras.backend as K
import numpy as np
import pandas as pd
import efficientnet.tfkeras as efn
from matplotlib import pyplot as plt
from kaggle_datasets import KaggleDatasets
from sklearn.metrics import f1_score, precision_score, recall_score, confusion_matrix
from sklearn.model_selection import KFold
print("Tensorflow version " + tf.__version__)
AUTO = tf.data.experimental.AUTOTUNE
```
# TPU or GPU detection
```
# Detect hardware, return appropriate distribution strategy
try:
tpu = tf.distribute.cluster_resolver.TPUClusterResolver() # TPU detection. No parameters necessary if TPU_NAME environment variable is set. On Kaggle this is always the case.
print('Running on TPU ', tpu.master())
except ValueError:
tpu = None
if tpu:
tf.config.experimental_connect_to_cluster(tpu)
tf.tpu.experimental.initialize_tpu_system(tpu)
strategy = tf.distribute.experimental.TPUStrategy(tpu)
else:
strategy = tf.distribute.get_strategy() # default distribution strategy in Tensorflow. Works on CPU and single GPU.
print("REPLICAS: ", strategy.num_replicas_in_sync)
```
# Competition data access
TPUs read data directly from Google Cloud Storage (GCS). This Kaggle utility will copy the dataset to a GCS bucket co-located with the TPU. If you have multiple datasets attached to the notebook, you can pass the name of a specific dataset to the get_gcs_path function. The name of the dataset is the name of the directory it is mounted in. Use `!ls /kaggle/input/` to list attached datasets.
```
GCS_DS_PATH = KaggleDatasets().get_gcs_path() # you can list the bucket with "!gsutil ls $GCS_DS_PATH"
```
# Configuration
```
IMAGE_SIZE = [512, 512] # at this size, a GPU will run out of memory. Use the TPU
BATCH_SIZE = 16 * strategy.num_replicas_in_sync
SEED = 42
FOLDS = 3
GCS_PATH_SELECT = { # available image sizes
192: GCS_DS_PATH + '/tfrecords-jpeg-192x192',
224: GCS_DS_PATH + '/tfrecords-jpeg-224x224',
331: GCS_DS_PATH + '/tfrecords-jpeg-331x331',
512: GCS_DS_PATH + '/tfrecords-jpeg-512x512'
}
GCS_PATH = GCS_PATH_SELECT[IMAGE_SIZE[0]]
TRAINING_FILENAMES = tf.io.gfile.glob(GCS_PATH + '/train/*.tfrec') + tf.io.gfile.glob(GCS_PATH + '/val/*.tfrec')
TEST_FILENAMES = tf.io.gfile.glob(GCS_PATH + '/test/*.tfrec') # predictions on this dataset should be submitted for the competition
CLASSES = ['pink primrose', 'hard-leaved pocket orchid', 'canterbury bells', 'sweet pea', 'wild geranium', 'tiger lily', 'moon orchid', 'bird of paradise', 'monkshood', 'globe thistle', # 00 - 09
'snapdragon', "colt's foot", 'king protea', 'spear thistle', 'yellow iris', 'globe-flower', 'purple coneflower', 'peruvian lily', 'balloon flower', 'giant white arum lily', # 10 - 19
'fire lily', 'pincushion flower', 'fritillary', 'red ginger', 'grape hyacinth', 'corn poppy', 'prince of wales feathers', 'stemless gentian', 'artichoke', 'sweet william', # 20 - 29
'carnation', 'garden phlox', 'love in the mist', 'cosmos', 'alpine sea holly', 'ruby-lipped cattleya', 'cape flower', 'great masterwort', 'siam tulip', 'lenten rose', # 30 - 39
'barberton daisy', 'daffodil', 'sword lily', 'poinsettia', 'bolero deep blue', 'wallflower', 'marigold', 'buttercup', 'daisy', 'common dandelion', # 40 - 49
'petunia', 'wild pansy', 'primula', 'sunflower', 'lilac hibiscus', 'bishop of llandaff', 'gaura', 'geranium', 'orange dahlia', 'pink-yellow dahlia', # 50 - 59
'cautleya spicata', 'japanese anemone', 'black-eyed susan', 'silverbush', 'californian poppy', 'osteospermum', 'spring crocus', 'iris', 'windflower', 'tree poppy', # 60 - 69
'gazania', 'azalea', 'water lily', 'rose', 'thorn apple', 'morning glory', 'passion flower', 'lotus', 'toad lily', 'anthurium', # 70 - 79
'frangipani', 'clematis', 'hibiscus', 'columbine', 'desert-rose', 'tree mallow', 'magnolia', 'cyclamen ', 'watercress', 'canna lily', # 80 - 89
'hippeastrum ', 'bee balm', 'pink quill', 'foxglove', 'bougainvillea', 'camellia', 'mallow', 'mexican petunia', 'bromelia', 'blanket flower', # 90 - 99
'trumpet creeper', 'blackberry lily', 'common tulip', 'wild rose'] # 100 - 102
```
## Visualization utilities
data -> pixels, nothing of much interest for the machine learning practitioner in this section.
```
# numpy and matplotlib defaults
np.set_printoptions(threshold=15, linewidth=80)
def batch_to_numpy_images_and_labels(data):
images, labels = data
numpy_images = images.numpy()
numpy_labels = labels.numpy()
if numpy_labels.dtype == object: # binary string in this case, these are image ID strings
numpy_labels = [None for _ in enumerate(numpy_images)]
# If no labels, only image IDs, return None for labels (this is the case for test data)
return numpy_images, numpy_labels
def title_from_label_and_target(label, correct_label):
if correct_label is None:
return CLASSES[label], True
correct = (label == correct_label)
return "{} [{}{}{}]".format(CLASSES[label], 'OK' if correct else 'NO', u"\u2192" if not correct else '',
CLASSES[correct_label] if not correct else ''), correct
def display_one_flower(image, title, subplot, red=False, titlesize=16):
plt.subplot(*subplot)
plt.axis('off')
plt.imshow(image)
if len(title) > 0:
plt.title(title, fontsize=int(titlesize) if not red else int(titlesize/1.2), color='red' if red else 'black', fontdict={'verticalalignment':'center'}, pad=int(titlesize/1.5))
return (subplot[0], subplot[1], subplot[2]+1)
def display_batch_of_images(databatch, predictions=None):
"""This will work with:
display_batch_of_images(images)
display_batch_of_images(images, predictions)
display_batch_of_images((images, labels))
display_batch_of_images((images, labels), predictions)
"""
# data
images, labels = batch_to_numpy_images_and_labels(databatch)
if labels is None:
labels = [None for _ in enumerate(images)]
# auto-squaring: this will drop data that does not fit into square or square-ish rectangle
rows = int(math.sqrt(len(images)))
cols = len(images)//rows
# size and spacing
FIGSIZE = 13.0
SPACING = 0.1
subplot=(rows,cols,1)
if rows < cols:
plt.figure(figsize=(FIGSIZE,FIGSIZE/cols*rows))
else:
plt.figure(figsize=(FIGSIZE/rows*cols,FIGSIZE))
# display
for i, (image, label) in enumerate(zip(images[:rows*cols], labels[:rows*cols])):
title = '' if label is None else CLASSES[label]
correct = True
if predictions is not None:
title, correct = title_from_label_and_target(predictions[i], label)
dynamic_titlesize = FIGSIZE*SPACING/max(rows,cols)*40+3 # magic formula tested to work from 1x1 to 10x10 images
subplot = display_one_flower(image, title, subplot, not correct, titlesize=dynamic_titlesize)
#layout
plt.tight_layout()
if label is None and predictions is None:
plt.subplots_adjust(wspace=0, hspace=0)
else:
plt.subplots_adjust(wspace=SPACING, hspace=SPACING)
plt.show()
def display_confusion_matrix(cmat, score, precision, recall):
plt.figure(figsize=(15,15))
ax = plt.gca()
ax.matshow(cmat, cmap='Reds')
ax.set_xticks(range(len(CLASSES)))
ax.set_xticklabels(CLASSES, fontdict={'fontsize': 7})
plt.setp(ax.get_xticklabels(), rotation=45, ha="left", rotation_mode="anchor")
ax.set_yticks(range(len(CLASSES)))
ax.set_yticklabels(CLASSES, fontdict={'fontsize': 7})
plt.setp(ax.get_yticklabels(), rotation=45, ha="right", rotation_mode="anchor")
titlestring = ""
if score is not None:
titlestring += 'f1 = {:.3f} '.format(score)
if precision is not None:
titlestring += '\nprecision = {:.3f} '.format(precision)
if recall is not None:
titlestring += '\nrecall = {:.3f} '.format(recall)
if len(titlestring) > 0:
ax.text(101, 1, titlestring, fontdict={'fontsize': 18, 'horizontalalignment':'right', 'verticalalignment':'top', 'color':'#804040'})
plt.show()
def display_training_curves(training, validation, title, subplot):
if subplot%10==1: # set up the subplots on the first call
plt.subplots(figsize=(10,10), facecolor='#F0F0F0')
plt.tight_layout()
ax = plt.subplot(subplot)
ax.set_facecolor('#F8F8F8')
ax.plot(training)
ax.plot(validation)
ax.set_title('model '+ title)
ax.set_ylabel(title)
#ax.set_ylim(0.28,1.05)
ax.set_xlabel('epoch')
ax.legend(['train', 'valid.'])
```
# Datasets
```
def decode_image(image_data):
image = tf.image.decode_jpeg(image_data, channels=3)
image = tf.cast(image, tf.float32) / 255.0 # convert image to floats in [0, 1] range
image = tf.reshape(image, [*IMAGE_SIZE, 3]) # explicit size needed for TPU
return image
def read_labeled_tfrecord(example):
LABELED_TFREC_FORMAT = {
"image": tf.io.FixedLenFeature([], tf.string), # tf.string means bytestring
"class": tf.io.FixedLenFeature([], tf.int64), # shape [] means single element
}
example = tf.io.parse_single_example(example, LABELED_TFREC_FORMAT)
image = decode_image(example['image'])
label = tf.cast(example['class'], tf.int32)
return image, label # returns a dataset of (image, label) pairs
def read_unlabeled_tfrecord(example):
UNLABELED_TFREC_FORMAT = {
"image": tf.io.FixedLenFeature([], tf.string), # tf.string means bytestring
"id": tf.io.FixedLenFeature([], tf.string), # shape [] means single element
# class is missing, this competitions's challenge is to predict flower classes for the test dataset
}
example = tf.io.parse_single_example(example, UNLABELED_TFREC_FORMAT)
image = decode_image(example['image'])
idnum = example['id']
return image, idnum # returns a dataset of image(s)
def load_dataset(filenames, labeled=True, ordered=False):
# Read from TFRecords. For optimal performance, reading from multiple files at once and
# disregarding data order. Order does not matter since we will be shuffling the data anyway.
ignore_order = tf.data.Options()
if not ordered:
ignore_order.experimental_deterministic = False # disable order, increase speed
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=AUTO) # automatically interleaves reads from multiple files
dataset = dataset.with_options(ignore_order) # uses data as soon as it streams in, rather than in its original order
dataset = dataset.map(read_labeled_tfrecord if labeled else read_unlabeled_tfrecord, num_parallel_calls=AUTO)
# returns a dataset of (image, label) pairs if labeled=True or (image, id) pairs if labeled=False
return dataset
def data_augment(image, label):
# data augmentation. Thanks to the dataset.prefetch(AUTO) statement in the next function (below),
# this happens essentially for free on TPU. Data pipeline code is executed on the "CPU" part
# of the TPU while the TPU itself is computing gradients.
image = tf.image.random_flip_left_right(image)
return image, label
def get_training_dataset(dataset, do_aug=True):
dataset = dataset.map(data_augment, num_parallel_calls=AUTO)
if do_aug: dataset = dataset.map(transform, num_parallel_calls=AUTO)
dataset = dataset.repeat() # the training dataset must repeat for several epochs
dataset = dataset.shuffle(2048)
dataset = dataset.batch(BATCH_SIZE)
dataset = dataset.prefetch(AUTO) # prefetch next batch while training (autotune prefetch buffer size)
return dataset
def get_validation_dataset(dataset):
dataset = dataset.batch(BATCH_SIZE)
dataset = dataset.cache()
dataset = dataset.prefetch(AUTO) # prefetch next batch while training (autotune prefetch buffer size)
return dataset
def get_test_dataset(ordered=False):
dataset = load_dataset(TEST_FILENAMES, labeled=False, ordered=ordered)
dataset = dataset.batch(BATCH_SIZE)
dataset = dataset.prefetch(AUTO) # prefetch next batch while training (autotune prefetch buffer size)
return dataset
def count_data_items(filenames):
# the number of data items is written in the name of the .tfrec files, i.e. flowers00-230.tfrec = 230 data items
n = [int(re.compile(r"-([0-9]*)\.").search(filename).group(1)) for filename in filenames]
return np.sum(n)
NUM_TRAINING_IMAGES = int( count_data_items(TRAINING_FILENAMES) * (FOLDS-1.)/FOLDS )
NUM_VALIDATION_IMAGES = int( count_data_items(TRAINING_FILENAMES) * (1./FOLDS) )
NUM_TEST_IMAGES = count_data_items(TEST_FILENAMES)
STEPS_PER_EPOCH = NUM_TRAINING_IMAGES // BATCH_SIZE
print('Dataset: {} training images, {} validation images, {} unlabeled test images'.format(NUM_TRAINING_IMAGES, NUM_VALIDATION_IMAGES, NUM_TEST_IMAGES))
```
# Enhanced Data Augmentation
```
def get_mat(rotation, shear, height_zoom, width_zoom, height_shift, width_shift):
# returns 3x3 transformmatrix which transforms indicies
# CONVERT DEGREES TO RADIANS
rotation = math.pi * rotation / 180.
shear = math.pi * shear / 180.
# ROTATION MATRIX
c1 = tf.math.cos(rotation)
s1 = tf.math.sin(rotation)
one = tf.constant([1],dtype='float32')
zero = tf.constant([0],dtype='float32')
rotation_matrix = tf.reshape( tf.concat([c1,s1,zero, -s1,c1,zero, zero,zero,one],axis=0),[3,3] )
# SHEAR MATRIX
c2 = tf.math.cos(shear)
s2 = tf.math.sin(shear)
shear_matrix = tf.reshape( tf.concat([one,s2,zero, zero,c2,zero, zero,zero,one],axis=0),[3,3] )
# ZOOM MATRIX
zoom_matrix = tf.reshape( tf.concat([one/height_zoom,zero,zero, zero,one/width_zoom,zero, zero,zero,one],axis=0),[3,3] )
# SHIFT MATRIX
shift_matrix = tf.reshape( tf.concat([one,zero,height_shift, zero,one,width_shift, zero,zero,one],axis=0),[3,3] )
return K.dot(K.dot(rotation_matrix, shear_matrix), K.dot(zoom_matrix, shift_matrix))
def transform(image,label):
# input image - is one image of size [dim,dim,3] not a batch of [b,dim,dim,3]
# output - image randomly rotated, sheared, zoomed, and shifted
DIM = IMAGE_SIZE[0]
XDIM = DIM%2 #fix for size 331
rot = 15. * tf.random.normal([1],dtype='float32')
shr = 5. * tf.random.normal([1],dtype='float32')
h_zoom = 1.0 + tf.random.normal([1],dtype='float32')/10.
w_zoom = 1.0 + tf.random.normal([1],dtype='float32')/10.
h_shift = 16. * tf.random.normal([1],dtype='float32')
w_shift = 16. * tf.random.normal([1],dtype='float32')
# GET TRANSFORMATION MATRIX
m = get_mat(rot,shr,h_zoom,w_zoom,h_shift,w_shift)
# LIST DESTINATION PIXEL INDICES
x = tf.repeat( tf.range(DIM//2,-DIM//2,-1), DIM )
y = tf.tile( tf.range(-DIM//2,DIM//2),[DIM] )
z = tf.ones([DIM*DIM],dtype='int32')
idx = tf.stack( [x,y,z] )
# ROTATE DESTINATION PIXELS ONTO ORIGIN PIXELS
idx2 = K.dot(m,tf.cast(idx,dtype='float32'))
idx2 = K.cast(idx2,dtype='int32')
idx2 = K.clip(idx2,-DIM//2+XDIM+1,DIM//2)
# FIND ORIGIN PIXEL VALUES
idx3 = tf.stack( [DIM//2-idx2[0,], DIM//2-1+idx2[1,]] )
d = tf.gather_nd(image,tf.transpose(idx3))
return tf.reshape(d,[DIM,DIM,3]),label
```
# Model Selector
```
#selecting which models will be trained and used in inference. Options: Ensamble, Model No.
MODEL_SELECT = 'Model1'
EPOCHS = 15
```
# Model 1
DenseNet201
```
def get_model1():
with strategy.scope():
dn201 = tf.keras.applications.DenseNet201(weights='imagenet', include_top=False, input_shape=[*IMAGE_SIZE, 3])
dn201.trainable = True # Full Training
model1 = tf.keras.Sequential([
dn201,
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(len(CLASSES), activation='softmax')
])
model1.compile(
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001, beta_1=0.9, beta_2=0.999, amsgrad=False),
loss = 'sparse_categorical_crossentropy',
metrics=['sparse_categorical_accuracy']
)
return model1
```
# Model 2
Efficient Net B7
```
def get_model2():
with strategy.scope():
enb7 = efn.EfficientNetB7(weights='noisy-student', include_top=False, input_shape=[*IMAGE_SIZE, 3])
enb7.trainable = True # Full Training
model2 = tf.keras.Sequential([
enb7,
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(len(CLASSES), activation='softmax')
])
model2.compile(
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001, beta_1=0.9, beta_2=0.999, amsgrad=False),
loss = 'sparse_categorical_crossentropy',
metrics=['sparse_categorical_accuracy']
)
return model2
```
# Callbacks
```
LR_START = 0.0001
LR_MAX = 0.00005 * strategy.num_replicas_in_sync
LR_MIN = 0.00001
LR_RAMPUP_EPOCHS = 3
LR_SUSTAIN_EPOCHS = 0
LR_EXP_DECAY = .8
def lrfn(epoch):
if epoch < LR_RAMPUP_EPOCHS:
lr = np.random.random_sample() * LR_START # Using random learning rate for initial epochs.
elif epoch < LR_RAMPUP_EPOCHS + LR_SUSTAIN_EPOCHS:
lr = LR_MAX
else:
lr = (LR_MAX - LR_MIN) * LR_EXP_DECAY**(epoch - LR_RAMPUP_EPOCHS - LR_SUSTAIN_EPOCHS) + LR_MIN # Rapid decay of learning rate to improve convergence.
return lr
lr_callback = tf.keras.callbacks.LearningRateScheduler(lrfn, verbose=True)
es_callback = tf.keras.callbacks.EarlyStopping(min_delta=0, patience=5, verbose=1, mode='auto', restore_best_weights=True)
```
# Custom Training Fuction
```
def train_cross_validate(folds = 5):
histories = []
models = []
kfold = KFold(folds, shuffle = True, random_state = SEED)
for f, (trn_ind, val_ind) in enumerate(kfold.split(TRAINING_FILENAMES)):
print(); print('#'*25)
print('### FOLD',f+1)
print('#'*25)
train_dataset = load_dataset(list(pd.DataFrame({'TRAINING_FILENAMES': TRAINING_FILENAMES}).loc[trn_ind]['TRAINING_FILENAMES']), labeled = True)
val_dataset = load_dataset(list(pd.DataFrame({'TRAINING_FILENAMES': TRAINING_FILENAMES}).loc[val_ind]['TRAINING_FILENAMES']), labeled = True, ordered = True)
if MODEL_SELECT is 'Ensamble' or MODEL_SELECT is 'Model1':
model1 = get_model1()
history1 = model1.fit(
get_training_dataset(train_dataset),
steps_per_epoch = STEPS_PER_EPOCH,
epochs = EPOCHS,
callbacks = [lr_callback, es_callback],
validation_data = get_validation_dataset(val_dataset),
verbose=2
)
models.append(model1)
histories.append(history1)
if MODEL_SELECT is 'Ensamble' or MODEL_SELECT is 'Model2':
model2 = get_model2()
history2 = model2.fit(
get_training_dataset(train_dataset),
steps_per_epoch = STEPS_PER_EPOCH,
epochs = EPOCHS,
callbacks = [lr_callback, es_callback],
validation_data = get_validation_dataset(val_dataset),
verbose=2
)
models.append(model2)
histories.append(history2)
return histories, models
def train_and_predict(folds = 5):
test_ds = get_test_dataset(ordered=True) # since we are splitting the dataset and iterating separately on images and ids, order matters.
test_images_ds = test_ds.map(lambda image, idnum: image)
print('Start training %i folds'%folds)
histories, models = train_cross_validate(folds = folds)
print('Computing predictions...')
# get the mean probability of the folds models
probabilities = np.average([models[i].predict(test_images_ds) for i in range(len(models))], axis = 0)
predictions = np.argmax(probabilities, axis=-1)
print('Generating submission.csv file...')
test_ids_ds = test_ds.map(lambda image, idnum: idnum).unbatch()
test_ids = next(iter(test_ids_ds.batch(NUM_TEST_IMAGES))).numpy().astype('U') # all in one batch
np.savetxt('submission.csv', np.rec.fromarrays([test_ids, predictions]), fmt=['%s', '%d'], delimiter=',', header='id,label', comments='')
return histories, models
```
# Training
```
histories, models = train_and_predict(folds = FOLDS)
for h in range(len(histories)):
display_training_curves(histories[h].history['loss'], histories[h].history['val_loss'], 'loss', 211)
display_training_curves(histories[h].history['sparse_categorical_accuracy'], histories[h].history['val_sparse_categorical_accuracy'], 'accuracy', 212)
```
# Confusion matrix
```
all_labels = []; all_prob = []; all_pred = []
kfold = KFold(FOLDS, shuffle = True, random_state = SEED)
for j, (trn_ind, val_ind) in enumerate( kfold.split(TRAINING_FILENAMES) ):
print('Inferring fold',j+1,'validation images...')
VAL_FILES = list(pd.DataFrame({'TRAINING_FILENAMES': TRAINING_FILENAMES}).loc[val_ind]['TRAINING_FILENAMES'])
NUM_VALIDATION_IMAGES = count_data_items(VAL_FILES)
cmdataset = get_validation_dataset(load_dataset(VAL_FILES, labeled = True, ordered = True))
images_ds = cmdataset.map(lambda image, label: image)
labels_ds = cmdataset.map(lambda image, label: label).unbatch()
all_labels.append( next(iter(labels_ds.batch(NUM_VALIDATION_IMAGES))).numpy() ) # get everything as one batch
prob = models[j].predict(images_ds)
all_prob.append( prob )
all_pred.append( np.argmax(prob, axis=-1) )
cm_correct_labels = np.concatenate(all_labels)
cm_probabilities = np.concatenate(all_prob)
cm_predictions = np.concatenate(all_pred)
print("Correct labels: ", cm_correct_labels.shape, cm_correct_labels)
print("Predicted labels: ", cm_predictions.shape, cm_predictions)
cmat = confusion_matrix(cm_correct_labels, cm_predictions, labels=range(len(CLASSES)))
score = f1_score(cm_correct_labels, cm_predictions, labels=range(len(CLASSES)), average='macro')
precision = precision_score(cm_correct_labels, cm_predictions, labels=range(len(CLASSES)), average='macro')
recall = recall_score(cm_correct_labels, cm_predictions, labels=range(len(CLASSES)), average='macro')
display_confusion_matrix(cmat, score, precision, recall)
print('f1 score: {:.3f}, precision: {:.3f}, recall: {:.3f}'.format(score, precision, recall))
```
| github_jupyter |
## A Simple Pair Trading Strategy
**_Please go through the "building strategies" notebook before looking at this notebook._**
Let's build a aimple pair trading strategy to show how you can trade multiple symbols in a strategy. We will trade 2 stocks, Coca-Cola (KO) and Pepsi (PEP)
1. We will buy KO and sell PEP when the price ratio KO / PEP is more than 1 standard deviation lower than its 5 day simple moving average.
2. We will buy PEP and sell KO when the price ratio KO / PEP is more than 1 standard deviation higher than its 5 day simple moving average.
3. We will exit when the price ratio is less than +/- 0.5 standard deviations away from its simple moving average
4. We will size the trades in 1 and 2 by allocating 10% of our capital to each trade.
First lets load some price data in fifteen minute bars.
```
import math
import datetime
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats
import os
from types import SimpleNamespace
import pyqstrat as pq
pq.set_defaults() # Set some display defaults to make dataframes and plots easier to look at
try:
ko_file = os.path.dirname(os.path.realpath(__file__)) + './support/coke_15_min_prices.csv.gz'
pep_file = os.path.dirname(os.path.realpath(__file__)) + './support/pepsi_15_min_prices.csv.gz' # If we are running from unit tests
except:
ko_file_path = '../notebooks/support/coke_15_min_prices.csv.gz'
pep_file_path = '../notebooks/support/pepsi_15_min_prices.csv.gz'
ko_prices = pd.read_csv(ko_file_path)
pep_prices = pd.read_csv(pep_file_path)
ko_prices['timestamp'] = pd.to_datetime(ko_prices.date)
pep_prices['timestamp'] = pd.to_datetime(pep_prices.date)
timestamps = ko_prices.timestamp.values
ko_contract_group = pq.ContractGroup.create('KO')
pep_contract_group = pq.ContractGroup.create('PEP')
```
Lets compute the ratio of the two prices and add it to the market data. Since the two price series have the exact same timestamps, we can simply divide the two close price series
```
ratio = ko_prices.c / pep_prices.c
```
Next, lets create an indicator for the zscore, and plot it.
```
def zscore_indicator(symbol, timestamps, indicators, strategy_context): # simple moving average
ratio = indicators.ratio
r = pd.Series(ratio).rolling(window = 130)
mean = r.mean()
std = r.std(ddof = 0)
zscore = (ratio - mean) / std
zscore = np.nan_to_num(zscore)
return zscore
ko_zscore = zscore_indicator(None, None, SimpleNamespace(ratio = ratio), None)
ratio_subplot = pq.Subplot([pq.TimeSeries('ratio', timestamps, ratio)], ylabel = 'Ratio')
zscore_subplot = pq.Subplot([pq.TimeSeries('zscore', timestamps, ko_zscore)], ylabel = 'ZScore')
plot = pq.Plot([ratio_subplot, zscore_subplot], title = 'KO')
plot.draw();
```
Now lets create the signal that will tell us to get in when the zscore is +/-1 and get out when its less than +/- 0.5. We use a signal value of 2 to figure out when to go long, and -2 to figure out when to go short. A value of 1 means get out of a long position, and -1 means get out of a short position. We also plot the signal to check it.
```
def pair_strategy_signal(contract_group, timestamps, indicators, parent_signals, strategy_context):
zscore = indicators.zscore
signal = np.where(zscore > 1, 2, 0)
signal = np.where(zscore < -1, -2, signal)
signal = np.where((zscore > 0.5) & (zscore < 1), 1, signal)
signal = np.where((zscore < -0.5) & (zscore > -1), -1, signal)
if contract_group.name == 'PEP': signal = -1. * signal
return signal
signal = pair_strategy_signal(ko_contract_group, timestamps, SimpleNamespace(zscore = ko_zscore), None, None)
signal_subplot = pq.Subplot([pq.TimeSeries('signal', timestamps, signal)], ylabel = 'Signal')
plot = pq.Plot([signal_subplot], title = 'KO', show_date_gaps = False)
plot.draw();
```
Finally we create the trading rule and market simulator functions
```
def pair_trading_rule(contract_group, i, timestamps, indicators, signal, account, strategy_context):
timestamp = timestamps[i]
curr_pos = account.position(contract_group, timestamp)
signal_value = signal[i]
risk_percent = 0.1
orders = []
symbol = contract_group.name
contract = contract_group.get_contract(symbol)
if contract is None:
contract = pq.Contract.create(symbol, contract_group = contract_group)
# if we don't already have a position, check if we should enter a trade
if math.isclose(curr_pos, 0):
if signal_value == 2 or signal_value == -2:
curr_equity = account.equity(timestamp)
order_qty = np.round(curr_equity * risk_percent / indicators.c[i] * np.sign(signal_value))
trigger_price = indicators.c[i]
reason_code = pq.ReasonCode.ENTER_LONG if order_qty > 0 else pq.ReasonCode.ENTER_SHORT
orders.append(pq.MarketOrder(contract, timestamp, order_qty, reason_code = reason_code))
else: # We have a current position, so check if we should exit
if (curr_pos > 0 and signal_value == -1) or (curr_pos < 0 and signal_value == 1):
order_qty = -curr_pos
reason_code = pq.ReasonCode.EXIT_LONG if order_qty < 0 else pq.ReasonCode.EXIT_SHORT
orders.append(pq.MarketOrder(contract, timestamp, order_qty, reason_code = reason_code))
return orders
def market_simulator(orders, i, timestamps, indicators, signals, strategy_context):
trades = []
timestamp = timestamps[i]
for order in orders:
trade_price = np.nan
contract_group = order.contract.contract_group
ind = indicators[contract_group]
o, h, l, c = ind.o[i], ind.h[i], ind.l[i], ind.c[i]
if isinstance(order, pq.MarketOrder):
trade_price = 0.5 * (o + h) if order.qty > 0 else 0.5 * (o + l)
else:
raise Exception(f'unexpected order type: {order}')
if np.isnan(trade_price): continue
trade = pq.Trade(order.contract, order, timestamp, order.qty, trade_price, commission = 0, fee = 0)
order.status = 'filled'
trades.append(trade)
return trades
```
Lets run the strategy, plot the results and look at the returns
```
def get_price(contract, timestamps, i, strategy_context):
if contract.symbol == 'KO':
return strategy_context.ko_price[i]
elif contract.symbol == 'PEP':
return strategy_context.pep_price[i]
raise Exception(f'Unknown symbol: {symbol}')
strategy_context = SimpleNamespace(ko_price = ko_prices.c.values, pep_price = pep_prices.c.values)
strategy = pq.Strategy(timestamps, [ko_contract_group, pep_contract_group], get_price, trade_lag = 1, strategy_context = strategy_context)
for tup in [(ko_contract_group, ko_prices), (pep_contract_group, pep_prices)]:
for column in ['o', 'h', 'l', 'c']:
strategy.add_indicator(column, tup[1][column].values, contract_groups = [tup[0]])
strategy.add_indicator('ratio', ratio)
strategy.add_indicator('zscore', zscore_indicator, depends_on = ['ratio'])
strategy.add_signal('pair_strategy_signal', pair_strategy_signal, depends_on_indicators = ['zscore'])
# ask pqstrat to call our trading rule when the signal has one of the values [-2, -1, 1, 2]
strategy.add_rule('pair_trading_rule', pair_trading_rule,
signal_name = 'pair_strategy_signal', sig_true_values = [-2, -1, 1, 2])
strategy.add_market_sim(market_simulator)
portfolio = pq.Portfolio()
portfolio.add_strategy('pair_strategy', strategy)
portfolio.run()
strategy.plot(primary_indicators = ['c'], secondary_indicators = ['zscore'])
strategy.evaluate_returns();
```
| github_jupyter |
# Introduction
<div class="alert alert-info">
**Code not tidied, but should work OK**
</div>
<img src="../Udacity_DL_Nanodegree/031%20RNN%20Super%20Basics/SimpleRNN01.png" align="left"/>
# Neural Network
```
import numpy as np
import matplotlib.pyplot as plt
import pdb
```
**Sigmoid**
```
def sigmoid(x):
return 1/(1+np.exp(-x))
def sigmoid_der(x):
return sigmoid(x) * (1 - sigmoid(x))
```
**Hyperbolic Tangent**
```
def tanh(x):
return np.tanh(x)
def tanh_der(x):
return 1.0 - np.tanh(x)**2
```
**Mean Squared Error**
```
def mse(x, y, Wxh, Whh, Who):
y_hat = forward(x, Wxh, Whh, Who)
return 0.5 * np.mean((y-y_hat)**2)
```
**Forward Pass**
```
def forward(x, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
x_t0 = x[:,0,:]
x_t1 = x[:,1,:]
x_t2 = x[:,2,:]
x_t3 = x[:,3,:]
s_init = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
z_t0 = s_init @ Whh + x_t0 @ Wxh
s_t0 = tanh(z_t0)
z_t1 = s_t0 @ Whh + x_t1 @ Wxh
s_t1 = tanh(z_t1)
z_t2 = s_t1 @ Whh + x_t2 @ Wxh
s_t2 = tanh(z_t2)
z_t3 = s_t2 @ Whh + x_t3 @ Wxh
s_t3 = tanh(z_t3)
z_out = s_t3 @ Who
y_hat = sigmoid( z_out )
return y_hat
def forward(x, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
x_t = {}
s_t = {}
z_t = {}
s_t[-1] = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
T = x.shape[1]
for t in range(T):
x_t[t] = x[:,t,:]
z_t[t] = s_t[t-1] @ Whh + x_t[t] @ Wxh
s_t[t] = tanh(z_t[t])
z_out = s_t[t] @ Who
y_hat = sigmoid( z_out )
return y_hat
```
**Backpropagation**
```
def backward(x, y, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
assert y.ndim==2 and y.shape[1:]==(1,)
assert len(x) == len(y)
# Forward
x_t0 = x[:,0,:]
x_t1 = x[:,1,:]
x_t2 = x[:,2,:]
x_t3 = x[:,3,:]
s_init = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
z_t0 = s_init @ Whh + x_t0 @ Wxh
s_t0 = tanh(z_t0)
z_t1 = s_t0 @ Whh + x_t1 @ Wxh
s_t1 = tanh(z_t1)
z_t2 = s_t1 @ Whh + x_t2 @ Wxh
s_t2 = tanh(z_t2)
z_t3 = s_t2 @ Whh + x_t3 @ Wxh
s_t3 = tanh(z_t3)
z_out = s_t3 @ Who
y_hat = sigmoid( z_out )
# Backward
dWxh = np.zeros_like(Wxh)
dWhh = np.zeros_like(Whh)
dWho = np.zeros_like(Who)
err = -(y-y_hat)/len(x) * sigmoid_der( z_out )
dWho = s_t3.T @ err
ro_t3 = err @ Who.T * tanh_der(z_t3)
dWxh += x_t3.T @ ro_t3
dWhh += s_t2.T @ ro_t3
ro_t2 = ro_t3 @ Whh.T * tanh_der(z_t2)
dWxh += x_t2.T @ ro_t2
dWhh += s_t1.T @ ro_t2
ro_t1 = ro_t2 @ Whh.T * tanh_der(z_t1)
dWxh += x_t1.T @ ro_t1
dWhh += s_t0.T @ ro_t1
ro_t0 = ro_t1 @ Whh.T * tanh_der(z_t0)
dWxh += x_t0.T @ ro_t0
dWhh += s_init.T @ ro_t0
return y_hat, dWxh, dWhh, dWho
def backward(x, y, Wxh, Whh, Who):
assert x.ndim==3 and x.shape[1:]==(4, 3)
assert y.ndim==2 and y.shape[1:]==(1,)
assert len(x) == len(y)
# Init
x_t = {}
s_t = {}
z_t = {}
s_t[-1] = np.zeros([len(x), len(Whh)]) # [n_batch, n_hid]
T = x.shape[1]
# Forward
for t in range(T): # t = [0, 1, 2, 3]
x_t[t] = x[:,t,:] # pick time-step input x_[t].shape = (n_batch, n_in)
z_t[t] = s_t[t-1] @ Whh + x_t[t] @ Wxh
s_t[t] = tanh(z_t[t])
z_out = s_t[t] @ Who
y_hat = sigmoid( z_out )
# Backward
dWxh = np.zeros_like(Wxh)
dWhh = np.zeros_like(Whh)
dWho = np.zeros_like(Who)
ro = -(y-y_hat)/len(x) * sigmoid_der( z_out ) # Backprop through loss funt.
dWho = s_t[t].T @ ro #
ro = ro @ Who.T * tanh_der(z_t[t]) # Backprop into hidden state
for t in reversed(range(T)): # t = [3, 2, 1, 0]
dWxh += x_t[t].T @ ro
dWhh += s_t[t-1].T @ ro
if t != 0: # don't backprop into t=-1
ro = ro @ Whh.T * tanh_der(z_t[t-1]) # Backprop into previous time step
return y_hat, dWxh, dWhh, dWho
```
**Train Loop**
```
def train_rnn(x, y, nb_epochs, learning_rate, Wxh, Whh, Who):
losses = []
for e in range(nb_epochs):
y_hat, dWxh, dWhh, dWho = backward(x, y, Wxh, Whh, Who)
Wxh += -learning_rate * dWxh
Whh += -learning_rate * dWhh
Who += -learning_rate * dWho
# Log and print
loss_train = mse(x, y, Wxh, Whh, Who)
losses.append(loss_train)
if e % (nb_epochs / 10) == 0:
print('loss ', loss_train.round(4))
return losses
```
# Example: Count Letter 'a'
**Create Dataset**
```
# Encoding: 'a'=[0,0,1] 'b'=[0,1,0] 'c'=[1,0,0]
# < ----- 4x time steps ----- >
x_train = np.array([
[ [0, 1, 0], [0, 1, 0], [1, 0, 0], [0, 1, 0] ], # 'bbcb'
[ [1, 0, 0], [0, 1, 0], [1, 0, 0], [0, 1, 0] ], # 'cbcb' ^
[ [0, 1, 0], [1, 0, 0], [0, 1, 0], [1, 0, 0] ], # 'bcbc' ^
[ [1, 0, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0] ], # 'cbbc' ^
[ [1, 0, 0], [1, 0, 0], [0, 1, 0], [1, 0, 0] ], # 'ccbc' ^
[ [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0] ], # 'bacb' | 9x batch size
[ [1, 0, 0], [1, 0, 0], [0, 1, 0], [0, 0, 1] ], # 'ccba' v
[ [0, 0, 1], [1, 0, 0], [0, 1, 0], [1, 0, 0] ], # 'acbc' ^
[ [1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0] ], # 'cbac' ^
[ [0, 1, 0], [0, 0, 1], [0, 0, 1], [0, 1, 0] ], # 'baab'
[ [0, 0, 1], [0, 0, 1], [0, 1, 0], [1, 0, 0] ], # 'aabc'
[ [0, 0, 1], [1, 0, 0], [0, 0, 1], [0, 0, 1] ], # 'acaa'
])
y_train = np.array([ [0], # <-> no timesteps
[0], #
[0], #
[0], #
[0], #
[1], # ^
[1], # | 9x batch size
[1], # ^
[1], # | 9x batch size
[0], # v
[0], #
[1] ]) #
x_test = np.array([
[ [0,1,0], [1,0,0], [1,0,0], [0,1,0] ], # 'bccb' -> 0
[ [1,0,0], [1,0,0], [0,1,0], [1,0,0] ], # 'ccbb' -> 0
[ [0,1,0], [1,0,0], [0,0,1], [1,0,0] ], # 'bcac' -> 1
[ [0,1,0], [0,0,1], [1,0,0], [0,1,0] ], # 'bacb' -> 1
])
y_test = np.array([ [0], # <-> no timesteps
[0], #
[1], #
[1], ])
test_gradient()
```
#### Train
```
np.random.seed(0)
W_xh = 0.1 * np.random.randn(3, 2) # Wxh.shape: [n_in, n_hid]
W_hh = 0.1 * np.random.randn(2, 2) # Whh.shape: [n_hid, n_hid]
W_ho = 0.1 * np.random.randn(2, 1) # Who.shape: [n_hid, n_out]
losses = train_rnn(x_train, y_train, 3000, 0.1, W_xh, W_hh, W_ho)
y_hat = forward(x_train, W_xh, W_hh, W_ho).round(0)
y_hat
y_hat == y_train
y_hat = forward(x_test, W_xh, W_hh, W_ho).round(0)
y_hat
y_hat == y_test
plt.plot(losses)
```
# Gradient Check
```
def numerical_gradient(x, y, Wxh, Whh, Who):
dWxh = np.zeros_like(Wxh)
dWhh = np.zeros_like(Whh)
dWho = np.zeros_like(Who)
eps = 1e-4
for r in range(len(Wxh)):
for c in range(Wxh.shape[1]):
Wxh_pls = Wxh.copy()
Wxh_min = Wxh.copy()
Wxh_pls[r, c] += eps
Wxh_min[r, c] -= eps
l_pls = mse(x, y, Wxh_pls, Whh, Who)
l_min = mse(x, y, Wxh_min, Whh, Who)
dWxh[r, c] = (l_pls - l_min) / (2*eps)
for r in range(len(Whh)):
for c in range(Whh.shape[1]):
Whh_pls = Whh.copy()
Whh_min = Whh.copy()
Whh_pls[r, c] += eps
Whh_min[r, c] -= eps
l_pls = mse(x, y, Wxh, Whh_pls, Who)
l_min = mse(x, y, Wxh, Whh_min, Who)
dWhh[r, c] = (l_pls - l_min) / (2*eps)
for r in range(len(Who)):
for c in range(Who.shape[1]):
Who_pls = Who.copy()
Who_min = Who.copy()
Who_pls[r, c] += eps
Who_min[r, c] -= eps
l_pls = mse(x, y, Wxh, Whh, Who_pls)
l_min = mse(x, y, Wxh, Whh, Who_min)
dWho[r, c] = (l_pls - l_min) / (2*eps)
return dWxh, dWhh, dWho
def test_gradients():
for i in range(100):
W_xh = 0.1 * np.random.randn(3, 2) # Wxh.shape: [n_in, n_hid]
W_hh = 0.1 * np.random.randn(2, 2) # Whh.shape: [n_hid, n_hid]
W_ho = 0.1 * np.random.randn(2, 1) # Who.shape: [n_hid, n_out]
xx = np.random.randn(100, 4, 3)
yy = np.random.randint(0, 2, size=[100, 1])
_, dW_xh, dW_hh, dW_ho = backward(xx, yy, W_xh, W_hh, W_ho)
ngW_xh, ngW_hh, ngW_ho = numerical_gradient(xx, yy, W_xh, W_hh, W_ho)
assert np.allclose(dW_xh, ngW_xh)
assert np.allclose(dW_hh, ngW_hh)
assert np.allclose(dW_ho, ngW_ho)
test_gradients()
```
| github_jupyter |
<a id="title_ID"></a>
# JWST Pipeline Validation Notebook: calwebb_detector1, dark_current unit tests
<span style="color:red"> **Instruments Affected**</span>: NIRCam, NIRISS, NIRSpec, MIRI, FGS
### Table of Contents
<div style="text-align: left">
<br> [Introduction](#intro)
<br> [JWST Unit Tests](#unit)
<br> [Defining Terms](#terms)
<br> [Test Description](#description)
<br> [Data Description](#data_descr)
<br> [Imports](#imports)
<br> [Convenience Functions](#functions)
<br> [Perform Tests](#testing)
<br> [About This Notebook](#about)
<br>
</div>
<a id="intro"></a>
# Introduction
This is the validation notebook that displays the unit tests for the Dark Current step in calwebb_detector1. This notebook runs and displays the unit tests that are performed as a part of the normal software continuous integration process. For more information on the pipeline visit the links below.
* Pipeline description: https://jwst-pipeline.readthedocs.io/en/latest/jwst/dark_current/index.html
* Pipeline code: https://github.com/spacetelescope/jwst/tree/master/jwst/
[Top of Page](#title_ID)
<a id="unit"></a>
# JWST Unit Tests
JWST unit tests are located in the "tests" folder for each pipeline step within the [GitHub repository](https://github.com/spacetelescope/jwst/tree/master/jwst/), e.g., ```jwst/dark_current/tests```.
* Unit test README: https://github.com/spacetelescope/jwst#unit-tests
[Top of Page](#title_ID)
<a id="terms"></a>
# Defining Terms
These are terms or acronymns used in this notebook that may not be known a general audience.
* JWST: James Webb Space Telescope
* NIRCam: Near-Infrared Camera
[Top of Page](#title_ID)
<a id="description"></a>
# Test Description
Unit testing is a software testing method by which individual units of source code are tested to determine whether they are working sufficiently well. Unit tests do not require a separate data file; the test creates the necessary test data and parameters as a part of the test code.
[Top of Page](#title_ID)
<a id="data_descr"></a>
# Data Description
Data used for unit tests is created on the fly within the test itself, and is typically an array in the expected format of JWST data with added metadata needed to run through the pipeline.
[Top of Page](#title_ID)
<a id="imports"></a>
# Imports
* tempfile for creating temporary output products
* pytest for unit test functions
* jwst for the JWST Pipeline
* IPython.display for display pytest reports
[Top of Page](#title_ID)
```
import tempfile
import pytest
import jwst
from IPython.display import IFrame
```
<a id="functions"></a>
# Convenience Functions
Here we define any convenience functions to help with running the unit tests.
[Top of Page](#title_ID)
```
def display_report(fname):
'''Convenience function to display pytest report.'''
return IFrame(src=fname, width=700, height=600)
```
<a id="testing"></a>
# Perform Tests
Below we run the unit tests for the Dark Current step.
[Top of Page](#title_ID)
```
with tempfile.TemporaryDirectory() as tmpdir:
!pytest jwst/dark_current -v --ignore=jwst/associations --ignore=jwst/datamodels --ignore=jwst/stpipe --ignore=jwst/regtest --html=tmpdir/unit_report.html --self-contained-html
report = display_report('tmpdir/unit_report.html')
report
```
<a id="about"></a>
## About This Notebook
**Author:** Alicia Canipe, Staff Scientist, NIRCam
<br>**Updated On:** 01/07/2021
[Top of Page](#title_ID)
<img style="float: right;" src="./stsci_pri_combo_mark_horizonal_white_bkgd.png" alt="stsci_pri_combo_mark_horizonal_white_bkgd" width="200px"/>
| github_jupyter |
## Dự án 01: Xây dựng Raspberry PI thành máy tính cho Data Scientist (PIDS)
## Bài 01. Cài đặt TensorFlow và các thư viện cần thiết
##### Người soạn: Dương Trần Hà Phương
##### Website: [Mechasolution Việt Nam](https://mechasolution.vn)
##### Email: [email protected]
---
## 1. Mở đầu
Nếu bạn muốn chạy một Neural network model hoặc một thuật toán dự đoán nào đó trên một hệ thống nhúng thì Raspberry PI là một lựa chọn hoàn hảo cho bạn.
Chỉ cần lựa chọn phiên bản Raspberry phù hợp với dự án của bạn. Sau đó, cài đặt hệ điều hành mới nhất và xong. Bạn đã sẵn sàng để khám phá thế giới Raspberry kì diệu rồi đó.
## 2. Yêu cầu cần thiết
**Hệ điều hành: Raspbian**
* Tải xuống phiên bản mới nhất của hệ điều hành Raspbian tại [ĐÂY](https://downloads.raspberrypi.org/raspbian_latest)
* Sử dụng [Etcher](https://etcher.io/) để copy Raspbian lên thẻ nhớ (MicroSD)
* Tham khảo cách cài đặt và chạy Raspbian tại bài viết [**Thiết lập Raspberry PI**](https://mechasolution.vn/Blog/bai-1-thiet-lap-raspberry-pi)
**Python**
* Ở đây chúng ta sẽ dùng Python làm ngôn ngữ chính để lập trình vì nhiều lý do như: hiện thực thuật toán nhanh, đơn giản, hệ thống thư viện hỗ trợ đa dạng.
* Phiên bản Raspbian mới nhất ([2018–04–18-raspbian-stretch](https://downloads.raspberrypi.org/raspbian_latest)) đã được cài đặt 2 phiên bản Python là Python 3.5.2 và 2.7.13. Ở đây tôi sử dụng phiên bản Python 3.5.x để demo.
## 3. Cài đặt Numpy
Numpy là thư viện toán học cho ngôn ngữ lập trình Python. Numpy hỗ trợ mảng, ma trận có kích thước và số chiều lớn cùng các toán tử đa dạng để tính toán trên mảng, ma trận. Cơ sở của Machine Learning dự trên phần lớn là toán học nên Numpy là một thư viện nền tảng không thể thiếu. Số lượng Commits và Contributors trên Github cũng cực kì ấn tượng: Commits: 15980, Contributors: 522.
Chúng ta cài đặt Numpy với dòng lệnh sau:
> `sudo apt-get install python3-numpy`
## 4. Cài đặt Scipy
Scipy là thư viện dành cho các nhà khoa học và kĩ sư. SciPy bao gồm các modules: linear algebra, optimization, integration, and statistics. Đây cũng là một thư viện nền tảng không thể thiếu cho các dự án Machine Learning. Scipy cũng có số lượng Commits và Contributors trên Github rất lớn: **Commits: 17213, Contributors: 489**
Chúng ta cài đặt Scipy và các thư viện liên quan với các dòng lệnh sau:
> `sudo apt-get install libblas-dev`
> `sudo apt-get install liblapack-dev`
> `sudo apt-get install python3-dev # Có thể đã được cài đặt sẵn`
> `sudo apt-get install libatlas-base-dev # Tuỳ chọn`
> `sudo apt-get install gfortran`
> `sudo apt-get install python3-setuptools # Có thể đã được cài đặt sẵn`
> `sudo apt-get install python3-scipy`
## 5. Cài đặt Scikit-learn
Scikit-learn (Sklearn) là các gói bổ sung của SciPy Stack được thiết kế cho các chức năng cụ thể như xử lý hình ảnh và Machine learning được dễ dàng hơn, nhanh hơn và tiện dụng hơn. Lượt Commits và Contributors trên Github lần lượt là: **Commits: 21793, Contributors: 842**.
> `sudo pip3 install scikit-learn`
> `sudo pip3 install pillow`
> `sudo apt-get install python3-h5py`
## 6. Cài đặt Matplotlib
Matplotlib là một thư viện hỗ trợ trực quan hoá dữ liệu một cách đơn giản nhưng không kém phần mạnh mẽ. Với một chút nỗ lực, bạn có thể trực quan hoá bất kỳ dữ liệu nào: Line plots; Scatter plots; Bar charts and Histograms; Pie charts; Stem plots; Contour plots; Quiver plots; Spectrograms. Số lượng Commits và Contributors trên Github là: **Commits: 21754, Contributors: 588**.
> `sudo apt-get install python3-matplotlib`
## 7. Upgrade pip
Chúng ta hãy cập nhật pip trước khi tiến hành cài đặt thư viện tiếp theo - Jupyter notebook.
> `sudo pip3 install --upgrade pip`
> `reboot`
## 8. Cài đặt Jupyter Notebook
[Jupyter Notebook](http://jupyter.org/) là một ứng dụng web mã nguồn mở cho phép bạn tạo hoặc chia sẻ những văn bản chứa:
* live code
* mô phỏng
* văn bản diễn giải
Sau đó, bạn chạy các lệnh dưới đây trên Terminal:
> `sudo pip3 install jupyter`
Khi cài đặt xong, chạy dòng lệnh dưới đây để khởi động Jupyter Notebook
> `jupyter notebook`
Kết quả, bạn sẽ thấy trình duyệt web được mở lên cùng với giao diện Jupyter Notebook như sau:

Xem bài viết [Sử dụng Jupyter Notebook cho Python](https://mechasolution.vn/Blog/bai-3-su-dung-jupyter-notebook-cho-python) để xem thêm về cách sử dụng Jupyter Notebook
## 9. Cài đặt TensorFlow
[**TensorFlow**](https://www.tensorflow.org/) là một hệ thống chuyên dùng để tính toán trên đồ thị (graph-based computation). Một ví dụ điển hình là sử dụng trong máy học (machine learning).
Ở đây, tôi sử dụng **Python Wheel Package (*.WHL)** được cung cấp bởi [lhelontra](https://github.com/lhelontra) tại [tensorflow-on-arm](https://github.com/lhelontra/tensorflow-on-arm)
### * Với Raspberry PI 2 / 3
###### ♦ Với Python version 3.5.x
> `wget https://github.com/lhelontra/tensorflow-on-arm/releases/download/v1.8.0/tensorflow-1.8.0-cp35-none-linux_armv7l.whl`
> `sudo pip3 install tensorflow-1.8.0-cp35-none-linux_armv7l.whl`
> `sudo pip3 uninstall mock`
> `sudo pip3 install mock`
###### ♦ Với Python version 2.7.x
> `wget https://github.com/lhelontra/tensorflow-on-arm/releases/download/v1.8.0/tensorflow-1.8.0-cp27-none-linux_armv7l.wh`
> `sudo pip3 install tensorflow-1.8.0-cp35-none-linux_armv7l.whl`
> `sudo pip3 uninstall mock`
> `sudo pip3 install mock`
### * Với Raspberry PI One / Zero
###### ♦ Với Python version 3.5.x
> `wget https://github.com/lhelontra/tensorflow-on-arm/releases/download/v1.8.0/tensorflow-1.8.0-cp35-none-linux_armv6l.whl`
> `sudo pip3 install tensorflow-1.8.0-cp35-none-linux_armv6l.whl`
> `sudo pip3 uninstall mock`
> `sudo pip3 install mock`
###### ♦ Với Python version 2.7.x
> `wget https://github.com/lhelontra/tensorflow-on-arm/releases/download/v1.8.0/tensorflow-1.8.0-cp27-none-linux_armv6l.whl`
> `sudo pip3 install tensorflow-1.8.0-cp27-none-linux_armv6l.whl`
> `sudo pip3 uninstall mock`
> `sudo pip3 install mock`
Sau khi cài đặt xong, bạn có thể kiểm tra xem mình có cài đặt thành công không bằng cách import TensorFlow và in ra phiên bản hiện tại (như hình):

### Tham khảo:
* https://medium.com/@abhizcc/installing-latest-tensor-flow-and-keras-on-raspberry-pi-aac7dbf95f2
* https://medium.com/activewizards-machine-learning-company/top-15-python-libraries-for-data-science-in-in-2017-ab61b4f9b4a7
* http://www.instructables.com/id/Installing-Keras-on-Raspberry-Pi-3/
---
Nếu có thắc mắc hoặc góp ý, các bạn hãy comment bên dưới để bài viết có thể được hoàn thiện hơn.
Xin cảm ơn,
Hà Phương - Mechasolution Việt Nam.
| github_jupyter |
# Transform points from pitch to texture and vice-versa
### Matrix P - Projection
The P matrix is a 3x4 matrix that given a 3D point in the world reference frame, it is projected into the 2D image in **texture coordinate** reference frame, i.e:
\begin{align}
\mathbf{pt_{world}} = (x, y, z, 1) \\
\mathbf{pt_{pitch}} = (a, b, c) = \mathbf{P_{texture}} * \mathbf{pt_{world}} \\
\mathbf{pt_{texture}} = (i, j) = (a/c, b/c)
\end{align}
**Texture coordinate range** is [0.0, 1.0]
<img src="pitch.png" style="width: 400px;">
### Matrix H - Homography
The H matrix is a 3x3 Matrix that transforms points from one plane to another. In our case from pitch to texture and from texture to pitch which is the inverse of the first (pitch to texture homography). **Pitch is the world plane where z=0.** Hence, get matrix **H*pith2texture*** is as simple as discard 3th matrix P column:
<img src="homo.png" style="width: 500px;">
### How to convert from pitch (world) to texture coordinate system
\begin{align}
\mathbf{pt_{texture}} = \mathbf{H_{pitch2texture}} * \mathbf{pt_{pitch}}
\end{align}
### How to convert from texture to pitch (world) coordinate system
\begin{align}
\mathbf{pt_{pitch}} = \mathbf{H_{texture2pitch}} * \mathbf{pt_{texture}}
\end{align}
Where,
\begin{align}
\mathbf{H_{texture2pitch}} = \mathbf{H_{pitch2texture}^{-1}}
\end{align}
### How to convert from texture to video image coordinate system
\begin{equation*}
\mathbf{P_{image}} = \begin{vmatrix}
Width & 0 & 0 \\ 0 & Height & 0 \\ 0 & 0 & 1
\end{vmatrix} * \mathbf{P_{texture}}
\end{equation*}
Where **`Width`** and **`Height`** refer to the video frame size.
```
# import what we need
import numpy as np
import math
def rodrigues(r):
'''
Rodrigues formula
:param r: 1x3 array of rotations about x, y, and z
:return: the 3x3 rotation matrix
'''
def S(n):
Sn = np.array([
[0.0, -n[2], n[1]],
[n[2], 0.0, -n[0]],
[-n[1], n[0], 0]])
return Sn
theta = np.linalg.norm(r)
if theta > 1e-30:
n = r/theta
Sn = S(n)
R = np.eye(3) + np.sin(theta) * Sn + (1.0 - np.cos(theta)) * np.dot(Sn, Sn)
else:
Sr = S(r)
theta2 = theta ** 2.0
R = np.eye(3) + (1.0 - theta2 / 6.0)*Sr + (0.5 - theta2 / 24.0) * np.dot(Sr, Sr)
return np.mat(R)
def world_to_texture(pw, P):
"""
Projects a world point to texture projection plane
:param pw: world point (x, y, z)
:param P: projection matrix P
:return: texture point (i, j)
"""
pw_h = np.append(pw, 1.0)
pp = P.dot(pw_h)
return np.array([pp[0]/pp[2], pp[1]/pp[2]])
def homography_pitch_to_texture(P):
"""
Returns the homografy to transform points from the pitch (world Z=0) to texture image
:param matrixP: Full matrix P
:return: homography_pitch_to_texture matrix
"""
# delete the 3th column, the z component
return np.delete(P, 2, axis=1)
def pitch_to_texture(pitch, P):
"""
Project a point from pitch plane to texture plane
:param pitch: pitch point (x, y)
:param P: projection matrix P
:return: texture point (i, j)
"""
pitch_h = np.append(pitch, 1.0)
H = homography_pitch_to_texture(P)
transformed = H.dot(pitch_h)
#print(projected)
return np.array([transformed[0]/transformed[2], transformed[1]/transformed[2]])
def texture_to_pitch(texture, P):
"""
Project a point from texture plane to pitch plane
:param texture: texture point (i, j)
:param P: projection matrix P
:return: pitch point (x, y)
"""
texture_h = np.append(texture, 1.0)
H = homography_pitch_to_texture(P)
Hinv = np.linalg.inv(H)
transformed = Hinv.dot(texture_h)
return np.array([transformed[0]/transformed[2], transformed[1]/transformed[2]])
def texture_to_image(texture, width, height):
"""
Converts a texture coordinate to image coordinate system
"""
return np.array([int(float(width)*texture[0]), int(float(height)*texture[1])])
def image_to_texture(image, width, height):
"""
Converts a image coordinate to texture coordinate system
"""
return np.array([float(image[0])/float(width), float(image[1])/float(height)])
```
# Projection matrix P from an individual camera
The funciton `camera_full_projection_matrix` is only valid for individual cameras.
## How to get camera parameters: *aspect_ratio, zoom, skew, pan, tilt, roll, Tx, Ty, Tz*
You can find camera parameters **`aspect_ratio, zoom, skew, pan, tilt, roll, Tx, Ty, Tz`** in `C:\AutomaticTV\data\cameras\{id}.xml`. In XML `<modelcalibration>` tag, for instance:
```
<modelsCalibration>
<modelCalibration computed="true" sportFieldName="Football11">
<Zoom>1.2124214</Zoom>
<AspectRatio>1.7777778</AspectRatio>
<Skew>0</Skew>
<Pan>-28.826538</Pan>
<Tilt>110.37401</Tilt>
<Roll>-10.530287</Roll>
<Tx>34.07756</Tx>
<Ty>-3.4855517</Ty>
<Tz>74.498503</Tz>
</modelCalibration>
</modelsCalibration>
```
```
def camera_full_projection_matrix(aspect_ratio, zoom, skew, pan, tilt, roll, Tx, Ty, Tz):
"""
Creates projection matrix P from camera model parameters
:param aspect_ratio: camera aspect ratio = image width / image height
:param zoom: camera focal
:param skew:
:param pan:
:param tilt:
:param roll:
:param Tx:
:param Ty:
:param Tz:
:return: the projection Matrix P
"""
K = np.array([[zoom, skew, 0.5], [0.0, zoom * aspect_ratio, 0.5], [0.0, 0.0, 1.0]])
# Rotation matrix
Rpan = rodrigues(np.array([0.0, 0.0, pan*math.pi/180.0]))
Rtilt = rodrigues(np.array([tilt*math.pi/180.0, 0.0, 0.0]))
Rroll = rodrigues(np.array([0.0, 0.0, roll*math.pi/180.0]))
Mrot = Rroll * Rtilt * Rpan
# Translation vector
t = np.array([Tx, Ty, Tz])
KR = K * Mrot
Kt = np.dot(K, t)
# Projection Martix P
P = np.zeros((3, 4))
P[:, 0] = KR[:, 0].T
P[:, 1] = KR[:, 1].T
P[:, 2] = KR[:, 2].T
P[:, 3] = Kt
return P
```
### Individual camera matrix P Testing
```
# test
# test matrixP_from_camera_model
camera_model = {
"aspect_ratio": 5.333333333,
"zoom": 0.45361389,
"skew": 0.0,
"pan": -2.0953152,
"tilt": 108.76381,
"roll": 0.0,
"Tx": 0.48063888,
"Ty": -0.30635475,
"Tz": 87.349004}
P = camera_full_projection_matrix(**camera_model)
P_expected = np.array([[0.436, 0.4897, -0.1608, 43.893],
[0.01114, -0.3046, -2.4515, 42.933],
[-0.03462, 0.9462, -0.3217, 87.349]])
assert(np.allclose(P, P_expected, rtol=1e-3))
# ML
camera_model = {
"aspect_ratio": 1.7777778,
"zoom": 1.2124214,
"skew": 0.0,
"pan": -28.826538,
"tilt": 110.37401,
"roll": -10.530287,
"Tx": 34.07756,
"Ty": -3.4855517,
"Tz": 74.498503}
P = camera_full_projection_matrix(**camera_model)
print(P)
P_expected = np.array([[0.8555, 0.9178, -0.3818, 78.566],
[-0.2154, -0.4256, -2.1606, 29.736],
[-0.452, 0.8213, -0.3481, 74.499]])
assert(np.allclose(P, P_expected, rtol=1e-3))
print()
# project world point
x = -10.0
y = 3.0
world = np.array([x, y, 0.0])
print("world: {}".format(world))
texture = world_to_texture(world, P)
print("texture: {}".format(texture))
"""
if (texture > 1.0).any() or (texture < 0.0).any():
print("point is out the texture limits")
else:
print("point is in the texture limits")
"""
print()
# transform point from pitch to texture plane
pitch = np.array([x, y])
print("pitch: {}".format(pitch))
texture = pitch_to_texture(pitch, P)
print("texture: {}".format(texture))
print()
# transform point from texture to pitch
print("texture: {}".format(texture))
pitch = texture_to_pitch(texture, P)
print("pitch: {}".format(pitch))
```
## Matrix P for Panorama
## How to get Panorama camera parameters: *src_width, src_height, zoom, skew, pan, tilt, roll, Tx, Ty, Tz*
You can find camera parameters **`zoom, skew, pan, tilt, roll, Tx, Ty, Tz`** in `C:\AutomaticTV\data\virtual_cameras\{id}.xml`. In XML `<CameraModel name="PANORAMA">` tag, for instance:
```
<CameraModel name="PANORAMA">
<Width>5760</Width>
<Height>1080</Height>
<Zoom>0.45361389</Zoom>
<AspectRatio>5.3333333</AspectRatio>
<Skew>0</Skew>
<Pan>-2.0953152</Pan>
<Tilt>108.76381</Tilt>
<Roll>10</Roll>
<Tx>0.48063888</Tx>
<Ty>-0.30635475</Ty>
<Tz>87.349004</Tz>
</CameraModel>
```
* **src_width** is `5760`
* **src_height** is `1080`
**NOTE: Do not use this `AspectRatio`.**
## How to get Panorama camera *offset_x* and *offset_y*
You can find **`offset_x`** and **`offset_y`** in `C:\AutomaticTV\data\virtual_cameras\{id}.xml` file tag `<PanoramaOffsetX>` and `<PanoramaOffsetY>`
```
<PanoramaOffsetX>0</PanoramaOffsetX>
<PanoramaOffsetY>0</PanoramaOffsetY>
```
## How to get Panorama camera *src_width* and *src_height*
It can be found in `C:\AutomaticTV\data\productions\{id}.xml`. In XML `<panorama><realization>` tag, for instance:`
```
<width>3840</width>
<height>1080</height>
```
## How to get Panorama camera *aspect_ratio, state_x, state_y, state_zoom*
It can be found in `C:\AutomaticTV\data\productions\{id}.xml`. In XML `<panorama><realization><operators><operator name="panorama"><currentState>` tag, for instance:
```
<currentState>
<elem>0.500000</elem>
<elem>0.500000</elem>
<elem>1.000000</elem>
<elem>0.453614</elem>
<elem>3.555556</elem>
<elem>0.000000</elem>
<elem>-2.095315</elem>
<elem>108.763810</elem>
<elem>0.000000</elem>
<elem>0.480639</elem>
<elem>-0.306355</elem>
<elem>87.349004</elem>
</currentState>
```
where:
* ***aspect_ratio*** is the 4th elem `3.555556`
* ***state_x*** is the 1st elem `0.500000`
* ***state_y*** is the 2nd elem `0.500000`
* ***state_zoom*** is the 3rd elem `1.000000`
```
def camera_full_projection_matrix_with_crop(aspect_ratio, zoom, skew, pan, tilt, roll, Tx, Ty, Tz, crop_tx, crop_ty, crop_zoom):
"""
Creates projection matrix P from camera model parameters
:param aspect_ratio: camera aspect ratio = dst_width / dst_height
:param zoom: camera focal
:param skew:
:param pan:
:param tilt:
:param roll:
:param Tx:
:param Ty:
:param Tz:
:param crop_tx:
:param crop_ty:
:param crop_zoom:
:return: the projection Matrix P
"""
K = np.array([[crop_zoom * zoom, crop_zoom * skew, 0.5 + crop_tx],
[0.0, crop_zoom * zoom * aspect_ratio, 0.5 + crop_ty],
[0.0, 0.0, 1.0]])
# Rotation matrix
Rpan = rodrigues(np.array([0.0, 0.0, pan*math.pi/180.0]))
Rtilt = rodrigues(np.array([tilt*math.pi/180.0, 0.0, 0.0]))
Rroll = rodrigues(np.array([0.0, 0.0, roll*math.pi/180.0]))
Mrot = Rroll * Rtilt * Rpan
# Translation vector
t = np.array([Tx, Ty, Tz])
KR = K * Mrot
Kt = np.dot(K, t)
# Projection Martix P
P = np.zeros((3, 4))
P[:, 0] = KR[:, 0].T
P[:, 1] = KR[:, 1].T
P[:, 2] = KR[:, 2].T
P[:, 3] = Kt
return P
def get_crop_params(src_width, src_height, offset_x, offset_y, dst_width, dst_height, state_x, state_y, state_zoom):
"""
Computes crop parameters taking in account source and destination dimensions
: return crop_tx:
: return crop_ty:
: return crop_zoom:
"""
width_ratio_inv = float(src_width) / float(dst_width)
height_ratio_inv = float(src_height) / float(dst_height)
crop_tx = (0.5 - state_x + offset_y) * (state_zoom * width_ratio_inv)
crop_ty = (0.5 - state_x + offset_y) * (state_zoom * height_ratio_inv)
crop_zoom = state_zoom * max(width_ratio_inv, height_ratio_inv)
return crop_tx, crop_ty, crop_zoom
```
### Panorama matrix P Testing
```
camera_model = {
"aspect_ratio": 3.5555555820465088,
"zoom": 0.45361389,
"skew": 0.0,
"pan": -2.0953152,
"tilt": 108.76381,
"roll": 10.0,
"Tx": 0.48063888,
"Ty": -0.30635475,
"Tz": 87.349004}
crop_params = {
"src_width": 5760,
"src_height": 1080,
"offset_x": 0.0,
"offset_y": 0.0,
"dst_width": 3840,
"dst_height": 1080,
"state_x": 0.5,
"state_y": 0.5,
"state_zoom": 1.0}
# compute crop from params
crop_tx, crop_ty, crop_zoom = get_crop_params(**crop_params)
print("crop: {}, {}, {}".format(crop_tx, crop_ty, crop_zoom))
# compute matrix P
P = camera_full_projection_matrix_with_crop(**camera_model, crop_tx=crop_tx, crop_ty=crop_ty, crop_zoom=crop_zoom)
print(P)
P_expected = np.array([[0.6509, 0.53559, -0.04896, 44.0015],
[0.4305, -0.2774, -2.4167, 42.933],
[-0.034618, 0.946219, -0.321667, 87.3490]])
assert(np.allclose(P, P_expected, rtol=1e-3))
```
## How to transform points from an image A to an image B
<img src="imageA2imageB.png">
### How to get frames from video
```
ffmpeg -i "CleanFeed.mp4" "frames/out-%03d.jpg"
```
| github_jupyter |
# House Price Prediction With TensorFlow
[![open_in_colab][colab_badge]][colab_notebook_link]
[![open_in_binder][binder_badge]][binder_notebook_link]
[colab_badge]: https://colab.research.google.com/assets/colab-badge.svg
[colab_notebook_link]: https://colab.research.google.com/github/UnfoldedInc/examples/blob/master/notebooks/09%20-%20Tensorflow_prediction.ipynb
[binder_badge]: https://mybinder.org/badge_logo.svg
[binder_notebook_link]: https://mybinder.org/v2/gh/UnfoldedInc/examples/master?urlpath=lab/tree/notebooks/09%20-%20Tensorflow_prediction.ipynb
This example demonstrates how the Unfolded Map SDK allows for more engaging exploratory data visualization, helping to simplify the process of building a machine learning model for predicting median house prices in California.
## Dependencies
This notebook uses the following dependencies:
- pandas
- numpy
- scikit-learn
- scipy
- seaborn
- matplotlib
- tensorflow
If running this notebook in Binder, these dependencies should already be installed. If running in Colab, the next cell will install these dependencies. In another environment, you'll need to make sure these dependencies are available by running the following `pip` command in a shell.
```bash
pip install pandas numpy scikit-learn scipy seaborn matplotlib tensorflow
```
This notebook was originally tested with the following package versions, but likely works with a broad range of versions:
- pandas==1.3.2
- numpy==1.19.5
- scikit-learn==0.24.2
- scipy==1.7.1
- seaborn==0.11.2
- matplotlib==3.4.3
- tensorflow==2.6.0
```
# If in Colab, install this notebook's required dependencies
import sys
if "google.colab" in sys.modules:
!pip install 'unfolded.map_sdk>=0.6.3' pandas numpy scikit-learn scipy seaborn matplotlib tensorflow
```
## Imports
If you're running this notebook on Binder, you may see a notification like the following when running the next cell.
```
Could not load dynamic library 'libcudart.so.11.0'; dlerror: libcudart.so.11.0: cannot open shared object file: No such file or directory
Ignore above cudart dlerror if you do not have a GPU set up on your machine.
```
This is expected behavior because the machines on which Binder is running are not equipped with GPUs. The notebook will still function fine, it will just run slightly slower than on a machine with a GPU available.
```
from uuid import uuid4
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from unfolded.map_sdk import UnfoldedMap
```
## Data Loading
For this example we'll use data from Kaggle's [California Housing Prices](https://www.kaggle.com/camnugent/california-housing-prices) dataset under the CC0 license. This dataset contains information about the housing in each census area in California, as of the 1990 census.
```
dataset_url = "https://raw.githubusercontent.com/UnfoldedInc/examples/master/notebooks/data/housing.csv"
housing = pd.read_csv(dataset_url)
housing.head()
```
## Feature Engineering
First, let's take a look at the input data and try to visualize different aspects of them in a map.
### Population Clustering
In the next cell we'll create a map that clusters rows of the dataset according to population. Note that since the clustering happens within Unfolded Studio, the clusters are re-computed as you zoom in, allowing you to explore your data at various resolutions.
```
population_in_CA = UnfoldedMap()
population_in_CA
# Create a persistent dataset ID that we can reference in both add_dataset and add_layer
dataset_id = uuid4()
population_in_CA.add_dataset(
{"uuid": dataset_id, "label": "Population_in_CA", "data": housing},
auto_create_layers=False,
)
population_in_CA.add_layer(
{
"id": "population_CA",
"type": "cluster",
"config": {
"label": "population in CA",
"data_id": dataset_id,
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "population", "type": "real"},
},
}
)
population_in_CA.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 5}
)
```
### Distances from housing areas to largest cities
Next, we want to explore where the housing areas in our dataset are located in comparison to the largest cities in California. For example purposes, we'll take the five largest cities in California and compare our input data against these locations.
```
# Longitude-latitude pairs for large cities
cities = {
"Los Angeles": (-118.244, 34.052),
"San Diego": (-117.165, 32.716),
"San Jose": (-121.895, 37.339),
"San Francisco": (-122.419, 37.775),
"Fresno": (-119.772, 36.748),
}
```
Next we need to find the closest city for each row in our data sample. First we'll define a couple functions to help compute the distance between cities and the city closest to a specific point. Then we'll apply these functions on our data.
```
def distance(lng1, lat1, lng2, lat2):
"""Vectorized Haversine formula
Computes distances between two sets of points.
From: https://stackoverflow.com/a/51722117
"""
# approximate radius of earth in km
R = 6371.009
lat1 = lat1*np.pi/180.0
lng1 = np.deg2rad(lng1)
lat2 = np.deg2rad(lat2)
lng2 = np.deg2rad(lng2)
d = np.sin((lat2 - lat1)/2)**2 + np.cos(lat1)*np.cos(lat2) * np.sin((lng2 - lng1)/2)**2
return 2 * R * np.arcsin(np.sqrt(d))
def closest_city(lng_array, lat_array, cities):
"""Find the closest_city for each row in lng_array and lat_array input
"""
distances = []
# Compute distance from each row of arrays to each of our city inputs
for city_name, coord in cities.items():
distances.append(distance(lng_array, lat_array, *coord))
# Convert this list of numpy arrays into a 2D numpy array
distances = np.array(distances)
# Find the shortest distance value for each row
shortest_distances = np.amin(distances, axis=0)
# Find the _index_ of the shortest distance for each row. Then use this value to
# lookup the longitude-latitude pair of the closest city
city_index = np.argmin(distances, axis=0)
# Create a 2D numpy array of location coordinates
# Then use the indexes from above to perform a lookup against the order of cities as
# input. (Note: this relies on the fact that in Python 3.6+ dictionaries are
# ordered)
input_coords = np.array(list(cities.values()))
closest_city_coords = input_coords[city_index]
# Return a 2D array with three columns:
# - Distance to closest city
# - Longitude of closest city
# - Latitude of closest city
return np.hstack((shortest_distances[:, np.newaxis], closest_city_coords))
```
Then use the `closest_city` function on our data to create three new columns:
```
housing[['closest_city_dist', 'closest_city_lng', 'closest_city_lat']] = closest_city(
housing['longitude'], housing['latitude'], cities
)
```
The map created in the next cell uses the new columns we computed above in relation to the largest cities in California:
```
distance_to_big_cities = UnfoldedMap()
distance_to_big_cities
dist_data_id = uuid4()
distance_to_big_cities.add_dataset(
{
"uuid": dist_data_id,
"label": "Distance to closest big city",
"data": housing,
},
auto_create_layers=False,
)
distance_to_big_cities.add_layer(
{
"id": "closest_distance",
"type": "arc",
"config": {
"data_id": dist_data_id,
"label": "distance to closest big city",
"columns": {
"lng0": "longitude",
"lat0": "latitude",
"lng1": "closest_city_lng",
"lat1": "closest_city_lat",
},
"visConfig": {"opacity": 0.8, "thickness": 0.3},
"is_visible": True,
},
}
)
distance_to_big_cities.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 4.5}
)
```
## Data Preprocessing
In this next section, we want to prepare our dataset to be used for training a TensorFlow model. First, we'll drop rows with null values, since they're quite rare in the dataset.
```
pct_null_rows = housing.isnull().any(axis=1).sum() / len(housing) * 100
print(f'{pct_null_rows:.1f}% of rows have null values')
housing = housing.dropna()
```
In the model we're training, we want to predict the median house value of an area. Thus we split the columns from our dataset `housing` into a dataset `y` with the column `median_house_value` and a dataset `X` with all other columns.
```
predicted_column = ['median_house_value']
other_columns = housing.columns.difference(predicted_column)
X = housing.loc[:, other_columns]
y = housing.loc[:, predicted_column]
```
Most of the columns in `X` are numeric, but one is not. `ocean_proximity` is of type `object`, which here is a string.
```
X.dtypes
```
Looking closer, we see that `ocean_proximity` is a categorical string with only five values.
```
X['ocean_proximity'].value_counts()
```
In order to use this column in our numeric model, we call [`pandas.get_dummies`](https://pandas.pydata.org/docs/reference/api/pandas.get_dummies.html) to create five new boolean columns. Each of these columns contains a `1` if the value of `ocean_proximity` is equal to the value that's now the column name.
```
X = pd.get_dummies(
data=X, columns=["ocean_proximity"], prefix=["ocean_proximity"], drop_first=True
)
```
## Data Splitting
In line with standard machine learning practice, we split our dataset into training, validation and test sets. We first take out 20% of our full dataset to use for testing the model after training. Then of the remaining 80%, we take out 75% to use for training the model and 25% to use for validation.
```
# dividing training data into test, validation and train
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, test_size=0.25, random_state=1
)
# We save a copy of our test data to use after model prediction
start_values = X_test.copy(deep=True)
```
## Feature Scaling
We use standard scaling with mean and standard deviation from our training dataset to avoid data leakage.
```
# feature standardization
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_val = scaler.transform(X_val)
X_test = scaler.transform(X_test)
```
## Price Prediction Model
Next we specify the parameters for the TensorFlow model:
```
# We use a Sequential model from Keras
# https://keras.io/api/models/sequential/
model = Sequential()
# Each column from X is an input feature into our model.
number_of_features = len(X.columns)
# input Layer
model.add(Dense(number_of_features, activation="relu", input_dim=number_of_features))
# hidden Layer
model.add(Dense(512, activation="relu"))
model.add(Dense(512, activation="relu"))
model.add(Dense(256, activation="relu"))
model.add(Dense(128, activation="relu"))
model.add(Dense(64, activation="relu"))
model.add(Dense(32, activation="relu"))
# output Layer
model.add(Dense(1, activation="linear"))
model.compile(loss="mse", optimizer="adam", metrics=["mse", "mae"])
model.summary()
```
### Training
Next we begin model training. Model training can take a long time; the higher the number of epochs, the better the model will be fit, but the longer training will take. Here we default to only 10 epochs because the focus of this notebook is integration with Unfolded Studio, not the machine learning itself.
```
EPOCHS = 10
# Or uncomment the following line if you're happy to wait longer for a better model fit.
# EPOCHS = 70
history = model.fit(
X_train,
y_train.to_numpy(),
batch_size=10,
epochs=EPOCHS,
verbose=1,
validation_data=(X_val, y_val),
)
```
### Evaluation
Next we want to find out how well the model was trained:
```
# summarize history for loss
loss_train = history.history["loss"]
loss_val = history.history["val_loss"]
epochs = range(1, EPOCHS + 1)
plt.figure(figsize=(10, 8))
plt.plot(epochs, loss_train, "g", label="Training loss")
plt.plot(epochs, loss_val, "b", label="Validation loss")
plt.title("Training and Validation loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()
```
In the above chart we can see that the training loss and validation loss are quite close to each other.
Now we can use our trained model to predict home prices on the _test_ data, which was not used in the training process.
```
y_pred = model.predict(X_test)
```
We can see that loss function value on the test data is similar to the loss value on the training data
```
model.evaluate(X_test, y_test)
```
### Prediction
Let's now visualize our housing price predictions using Unfolded Studio. Here we create a dataframe with predicted values obtained from the model.
```
predict_data = start_values.loc[:, ['longitude', 'latitude']]
predict_data["price"] = y_pred
```
### Visualization
The map we create in the next cell depicts the prices we've predicted for houses in each census area in California.
```
housing_predict_prices = UnfoldedMap()
housing_predict_prices
price_data_id = uuid4()
housing_predict_prices.add_dataset(
{
"uuid": price_data_id,
"label": "Predict housing prices in CA",
"data": predict_data,
},
auto_create_layers=False,
)
housing_predict_prices.add_layer(
{
"id": "housing_prices",
"type": "hexagon",
"config": {
"label": "housing prices",
"data_id": price_data_id,
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "price", "type": "real"},
"vis_config": {
"colorRange": {
"colors": [
"#E6F598",
"#ABDDA4",
"#66C2A5",
"#3288BD",
"#5E4FA2",
"#9E0142",
"#D53E4F",
"#F46D43",
"#FDAE61",
"#FEE08B",
]
}
},
},
}
)
housing_predict_prices.set_view_state(
{"longitude": -119.417931, "latitude": 36.6, "zoom": 6}
)
```
## Clustering Model
We'll now cluster the predicted data by price levels using the KMeans algorithm.
```
k = 5
km = KMeans(n_clusters=k, init="k-means++")
X = predict_data.loc[:, ["latitude", "longitude", "price"]]
# Run clustering and add to prediction dataset dataset
predict_data["cluster"] = km.fit_predict(X)
```
### Visualization
Let's show the price clusters in a chart
```
fig, ax = plt.subplots()
sns.scatterplot(
x="latitude",
y="longitude",
data=predict_data,
palette=sns.color_palette("bright", k),
hue="cluster",
size_order=[1, 0],
ax=ax,
).set_title(f"Clustering (k={k})")
```
The next map shows the same clusters in a geographic context. Here we can see that house prices are highest for areas close to the largest cities.
```
unfolded_map_prices = UnfoldedMap()
unfolded_map_prices
prices_dataset_id = uuid4()
unfolded_map_prices.add_dataset(
{"uuid": prices_dataset_id, "label": "Prices", "data": predict_data},
auto_create_layers=False,
)
unfolded_map_prices.add_layer(
{
"id": "prices_CA",
"type": "point",
"config": {
"data_id": prices_dataset_id,
"label": "clustering of prices",
"columns": {"lat": "latitude", "lng": "longitude"},
"is_visible": True,
"color_scale": "quantize",
"color_field": {"name": "cluster", "type": "real"},
"vis_config": {
"colorRange": {
"colors": ["#7FFFD4", "#8A2BE2", "#00008B", "#FF8C00", "#FF1493"]
}
},
},
}
)
unfolded_map_prices.set_view_state(
{"longitude": -119.417931, "latitude": 36.778259, "zoom": 4}
)
```
| github_jupyter |
Lambda School Data Science
*Unit 2, Sprint 2, Module 3*
---
<p style="padding: 10px; border: 2px solid red;">
<b>Before you start:</b> Today is the day you should submit the dataset for your Unit 2 Build Week project. You can review the guidelines and make your submission in the Build Week course for your cohort on Canvas.</p>
```
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge/main/data/'
!pip install category_encoders==2.*
!pip install pandas-profiling==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
```
# Module Project: Hyperparameter Tuning
This sprint, the module projects will focus on creating and improving a model for the Tanazania Water Pump dataset. Your goal is to create a model to predict whether a water pump is functional, non-functional, or needs repair.
Dataset source: [DrivenData.org](https://www.drivendata.org/competitions/7/pump-it-up-data-mining-the-water-table/).
## Directions
The tasks for this project are as follows:
- **Task 1:** Use `wrangle` function to import training and test data.
- **Task 2:** Split training data into feature matrix `X` and target vector `y`.
- **Task 3:** Establish the baseline accuracy score for your dataset.
- **Task 4:** Build `clf_dt`.
- **Task 5:** Build `clf_rf`.
- **Task 6:** Evaluate classifiers using k-fold cross-validation.
- **Task 7:** Tune hyperparameters for best performing classifier.
- **Task 8:** Print out best score and params for model.
- **Task 9:** Create `submission.csv` and upload to Kaggle.
You should limit yourself to the following libraries for this project:
- `category_encoders`
- `matplotlib`
- `pandas`
- `pandas-profiling`
- `sklearn`
# I. Wrangle Data
```
def wrangle(fm_path, tv_path=None):
if tv_path:
df = pd.merge(pd.read_csv(fm_path,
na_values=[0, -2.000000e-08]),
pd.read_csv(tv_path)).set_index('id')
else:
df = pd.read_csv(fm_path,
na_values=[0, -2.000000e-08],
index_col='id')
# Drop constant columns
df.drop(columns=['recorded_by'], inplace=True)
# Drop HCCCs
cutoff = 100
drop_cols = [col for col in df.select_dtypes('object').columns
if df[col].nunique() > cutoff]
df.drop(columns=drop_cols, inplace=True)
# Drop duplicate columns
dupe_cols = [col for col in df.head(15).T.duplicated().index
if df.head(15).T.duplicated()[col]]
df.drop(columns=dupe_cols, inplace=True)
return df
```
**Task 1:** Using the above `wrangle` function to read `train_features.csv` and `train_labels.csv` into the DataFrame `df`, and `test_features.csv` into the DataFrame `X_test`.
```
df = ...
X_test = ...
```
# II. Split Data
**Task 2:** Split your DataFrame `df` into a feature matrix `X` and the target vector `y`. You want to predict `'status_group'`.
**Note:** You won't need to do a train-test split because you'll use cross-validation instead.
```
X = ...
y = ...
```
# III. Establish Baseline
**Task 3:** Since this is a **classification** problem, you should establish a baseline accuracy score. Figure out what is the majority class in `y_train` and what percentage of your training observations it represents.
```
baseline_acc = ...
print('Baseline Accuracy Score:', baseline_acc)
```
# IV. Build Models
**Task 4:** Build a `Pipeline` named `clf_dt`. Your `Pipeline` should include:
- an `OrdinalEncoder` transformer for categorical features.
- a `SimpleImputer` transformer fot missing values.
- a `DecisionTreeClassifier` Predictor.
**Note:** Do not train `clf_dt`. You'll do that in a subsequent task.
```
clf_dt = ...
```
**Task 5:** Build a `Pipeline` named `clf_rf`. Your `Pipeline` should include:
- an `OrdinalEncoder` transformer for categorical features.
- a `SimpleImputer` transformer fot missing values.
- a `RandomForestClassifier` predictor.
**Note:** Do not train `clf_rf`. You'll do that in a subsequent task.
```
clf_rf = ...
```
# V. Check Metrics
**Task 6:** Evaluate the performance of both of your classifiers using k-fold cross-validation.
```
cv_scores_dt = ...
cv_scores_rf = ...
print('CV scores DecisionTreeClassifier')
print(cv_scores_dt)
print('Mean CV accuracy score:', cv_scores_dt.mean())
print('STD CV accuracy score:', cv_scores_dt.std())
print('CV score RandomForestClassifier')
print(cv_scores_rf)
print('Mean CV accuracy score:', cv_scores_rf.mean())
print('STD CV accuracy score:', cv_scores_rf.std())
```
# VI. Tune Model
**Task 7:** Choose the best performing of your two models and tune its hyperparameters using a `RandomizedSearchCV` named `model`. Make sure that you include cross-validation and that `n_iter` is set to at least `25`.
**Note:** If you're not sure which hyperparameters to tune, check the notes from today's guided project and the `sklearn` documentation.
```
model = ...
```
**Task 8:** Print out the best score and best params for `model`.
```
best_score = ...
best_params = ...
print('Best score for `model`:', best_score)
print('Best params for `model`:', best_params)
```
# Communicate Results
**Task 9:** Create a DataFrame `submission` whose index is the same as `X_test` and that has one column `'status_group'` with your predictions. Next, save this DataFrame as a CSV file and upload your submissions to our competition site.
**Note:** Check the `sample_submission.csv` file on the competition website to make sure your submissions follows the same formatting.
```
submission = ...
```
| github_jupyter |
# Semantic Image Clustering
**Author:** [Khalid Salama](https://www.linkedin.com/in/khalid-salama-24403144/)<br>
**Date created:** 2021/02/28<br>
**Last modified:** 2021/02/28<br>
**Description:** Semantic Clustering by Adopting Nearest neighbors (SCAN) algorithm.
## Introduction
This example demonstrates how to apply the [Semantic Clustering by Adopting Nearest neighbors
(SCAN)](https://arxiv.org/abs/2005.12320) algorithm (Van Gansbeke et al., 2020) on the
[CIFAR-10](https://www.cs.toronto.edu/~kriz/cifar.html) dataset. The algorithm consists of
two phases:
1. Self-supervised visual representation learning of images, in which we use the
[simCLR](https://arxiv.org/abs/2002.05709) technique.
2. Clustering of the learned visual representation vectors to maximize the agreement
between the cluster assignments of neighboring vectors.
The example requires [TensorFlow Addons](https://www.tensorflow.org/addons),
which you can install using the following command:
```python
pip install tensorflow-addons
```
## Setup
```
from collections import defaultdict
import random
import numpy as np
import tensorflow as tf
import tensorflow_addons as tfa
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
from tqdm import tqdm
```
## Prepare the data
```
num_classes = 10
input_shape = (32, 32, 3)
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
x_data = np.concatenate([x_train, x_test])
y_data = np.concatenate([y_train, y_test])
print("x_data shape:", x_data.shape, "- y_data shape:", y_data.shape)
classes = [
"airplane",
"automobile",
"bird",
"cat",
"deer",
"dog",
"frog",
"horse",
"ship",
"truck",
]
```
## Define hyperparameters
```
target_size = 32 # Resize the input images.
representation_dim = 512 # The dimensions of the features vector.
projection_units = 128 # The projection head of the representation learner.
num_clusters = 20 # Number of clusters.
k_neighbours = 5 # Number of neighbours to consider during cluster learning.
tune_encoder_during_clustering = False # Freeze the encoder in the cluster learning.
```
## Implement data preprocessing
The data preprocessing step resizes the input images to the desired `target_size` and applies
feature-wise normalization. Note that, when using `keras.applications.ResNet50V2` as the
visual encoder, resizing the images into 255 x 255 inputs would lead to more accurate results
but require a longer time to train.
```
data_preprocessing = keras.Sequential(
[
layers.experimental.preprocessing.Resizing(target_size, target_size),
layers.experimental.preprocessing.Normalization(),
]
)
# Compute the mean and the variance from the data for normalization.
data_preprocessing.layers[-1].adapt(x_data)
```
## Data augmentation
Unlike simCLR, which randomly picks a single data augmentation function to apply to an input
image, we apply a set of data augmentation functions randomly to the input image.
(You can experiment with other image augmentation techniques by following the [data augmentation tutorial](https://www.tensorflow.org/tutorials/images/data_augmentation).)
```
data_augmentation = keras.Sequential(
[
layers.experimental.preprocessing.RandomTranslation(
height_factor=(-0.2, 0.2), width_factor=(-0.2, 0.2), fill_mode="nearest"
),
layers.experimental.preprocessing.RandomFlip(mode="horizontal"),
layers.experimental.preprocessing.RandomRotation(
factor=0.15, fill_mode="nearest"
),
layers.experimental.preprocessing.RandomZoom(
height_factor=(-0.3, 0.1), width_factor=(-0.3, 0.1), fill_mode="nearest"
)
]
)
```
Display a random image
```
image_idx = np.random.choice(range(x_data.shape[0]))
image = x_data[image_idx]
image_class = classes[y_data[image_idx][0]]
plt.figure(figsize=(3, 3))
plt.imshow(x_data[image_idx].astype("uint8"))
plt.title(image_class)
_ = plt.axis("off")
```
Display a sample of augmented versions of the image
```
plt.figure(figsize=(10, 10))
for i in range(9):
augmented_images = data_augmentation(np.array([image]))
ax = plt.subplot(3, 3, i + 1)
plt.imshow(augmented_images[0].numpy().astype("uint8"))
plt.axis("off")
```
## Self-supervised representation learning
### Implement the vision encoder
```
def create_encoder(representation_dim):
encoder = keras.Sequential(
[
keras.applications.ResNet50V2(
include_top=False, weights=None, pooling="avg"
),
layers.Dense(representation_dim),
]
)
return encoder
```
### Implement the unsupervised contrastive loss
```
class RepresentationLearner(keras.Model):
def __init__(
self,
encoder,
projection_units,
num_augmentations,
temperature=1.0,
dropout_rate=0.1,
l2_normalize=False,
**kwargs
):
super(RepresentationLearner, self).__init__(**kwargs)
self.encoder = encoder
# Create projection head.
self.projector = keras.Sequential(
[
layers.Dropout(dropout_rate),
layers.Dense(units=projection_units, use_bias=False),
layers.BatchNormalization(),
layers.ReLU(),
]
)
self.num_augmentations = num_augmentations
self.temperature = temperature
self.l2_normalize = l2_normalize
self.loss_tracker = keras.metrics.Mean(name="loss")
@property
def metrics(self):
return [self.loss_tracker]
def compute_contrastive_loss(self, feature_vectors, batch_size):
num_augmentations = tf.shape(feature_vectors)[0] // batch_size
if self.l2_normalize:
feature_vectors = tf.math.l2_normalize(feature_vectors, -1)
# The logits shape is [num_augmentations * batch_size, num_augmentations * batch_size].
logits = (
tf.linalg.matmul(feature_vectors, feature_vectors, transpose_b=True)
/ self.temperature
)
# Apply log-max trick for numerical stability.
logits_max = tf.math.reduce_max(logits, axis=1)
logits = logits - logits_max
# The shape of targets is [num_augmentations * batch_size, num_augmentations * batch_size].
# targets is a matrix consits of num_augmentations submatrices of shape [batch_size * batch_size].
# Each [batch_size * batch_size] submatrix is an identity matrix (diagonal entries are ones).
targets = tf.tile(tf.eye(batch_size), [num_augmentations, num_augmentations])
# Compute cross entropy loss
return keras.losses.categorical_crossentropy(
y_true=targets, y_pred=logits, from_logits=True
)
def call(self, inputs):
# Preprocess the input images.
preprocessed = data_preprocessing(inputs)
# Create augmented versions of the images.
augmented = []
for _ in range(self.num_augmentations):
augmented.append(data_augmentation(preprocessed))
augmented = layers.Concatenate(axis=0)(augmented)
# Generate embedding representations of the images.
features = self.encoder(augmented)
# Apply projection head.
return self.projector(features)
def train_step(self, inputs):
batch_size = tf.shape(inputs)[0]
# Run the forward pass and compute the contrastive loss
with tf.GradientTape() as tape:
feature_vectors = self(inputs, training=True)
loss = self.compute_contrastive_loss(feature_vectors, batch_size)
# Compute gradients
trainable_vars = self.trainable_variables
gradients = tape.gradient(loss, trainable_vars)
# Update weights
self.optimizer.apply_gradients(zip(gradients, trainable_vars))
# Update loss tracker metric
self.loss_tracker.update_state(loss)
# Return a dict mapping metric names to current value
return {m.name: m.result() for m in self.metrics}
def test_step(self, inputs):
batch_size = tf.shape(inputs)[0]
feature_vectors = self(inputs, training=False)
loss = self.compute_contrastive_loss(feature_vectors, batch_size)
self.loss_tracker.update_state(loss)
return {"loss": self.loss_tracker.result()}
```
### Train the model
```
# Create vision encoder.
encoder = create_encoder(representation_dim)
# Create representation learner.
representation_learner = RepresentationLearner(
encoder, projection_units, num_augmentations=2, temperature=0.1
)
# Create a a Cosine decay learning rate scheduler.
lr_scheduler = keras.experimental.CosineDecay(
initial_learning_rate=0.001, decay_steps=500, alpha=0.1
)
# Compile the model.
representation_learner.compile(
optimizer=tfa.optimizers.AdamW(learning_rate=lr_scheduler, weight_decay=0.0001),
)
# Fit the model.
history = representation_learner.fit(
x=x_data,
batch_size=512,
epochs=50, # for better results, increase the number of epochs to 500.
)
```
Plot training loss
```
plt.plot(history.history["loss"])
plt.ylabel("loss")
plt.xlabel("epoch")
plt.show()
```
## Compute the nearest neighbors
### Generate the embeddings for the images
```
batch_size = 500
# Get the feature vector representations of the images.
feature_vectors = encoder.predict(x_data, batch_size=batch_size, verbose=1)
# Normalize the feature vectores.
feature_vectors = tf.math.l2_normalize(feature_vectors, -1)
```
### Find the *k* nearest neighbours for each embedding
```
neighbours = []
num_batches = feature_vectors.shape[0] // batch_size
for batch_idx in tqdm(range(num_batches)):
start_idx = batch_idx * batch_size
end_idx = start_idx + batch_size
current_batch = feature_vectors[start_idx:end_idx]
# Compute the dot similarity.
similarities = tf.linalg.matmul(current_batch, feature_vectors, transpose_b=True)
# Get the indices of most similar vectors.
_, indices = tf.math.top_k(similarities, k=k_neighbours + 1, sorted=True)
# Add the indices to the neighbours.
neighbours.append(indices[..., 1:])
neighbours = np.reshape(np.array(neighbours), (-1, k_neighbours))
```
Let's display some neighbors on each row
```
nrows = 4
ncols = k_neighbours + 1
plt.figure(figsize=(12, 12))
position = 1
for _ in range(nrows):
anchor_idx = np.random.choice(range(x_data.shape[0]))
neighbour_indicies = neighbours[anchor_idx]
indices = [anchor_idx] + neighbour_indicies.tolist()
for j in range(ncols):
plt.subplot(nrows, ncols, position)
plt.imshow(x_data[indices[j]].astype("uint8"))
plt.title(classes[y_data[indices[j]][0]])
plt.axis("off")
position += 1
```
You notice that images on each row are visually similar, and belong to similar classes.
## Semantic clustering with nearest neighbours
### Implement clustering consistency loss
This loss tries to make sure that neighbours have the same clustering assignments.
```
class ClustersConsistencyLoss(keras.losses.Loss):
def __init__(self):
super(ClustersConsistencyLoss, self).__init__()
def __call__(self, target, similarity, sample_weight=None):
# Set targets to be ones.
target = tf.ones_like(similarity)
# Compute cross entropy loss.
loss = keras.losses.binary_crossentropy(
y_true=target, y_pred=similarity, from_logits=True
)
return tf.math.reduce_mean(loss)
```
### Implement the clusters entropy loss
This loss tries to make sure that cluster distribution is roughly uniformed, to avoid
assigning most of the instances to one cluster.
```
class ClustersEntropyLoss(keras.losses.Loss):
def __init__(self, entropy_loss_weight=1.0):
super(ClustersEntropyLoss, self).__init__()
self.entropy_loss_weight = entropy_loss_weight
def __call__(self, target, cluster_probabilities, sample_weight=None):
# Ideal entropy = log(num_clusters).
num_clusters = tf.cast(tf.shape(cluster_probabilities)[-1], tf.dtypes.float32)
target = tf.math.log(num_clusters)
# Compute the overall clusters distribution.
cluster_probabilities = tf.math.reduce_mean(cluster_probabilities, axis=0)
# Replacing zero probabilities - if any - with a very small value.
cluster_probabilities = tf.clip_by_value(
cluster_probabilities, clip_value_min=1e-8, clip_value_max=1.0
)
# Compute the entropy over the clusters.
entropy = -tf.math.reduce_sum(
cluster_probabilities * tf.math.log(cluster_probabilities)
)
# Compute the difference between the target and the actual.
loss = target - entropy
return loss
```
### Implement clustering model
This model takes a raw image as an input, generated its feature vector using the trained
encoder, and produces a probability distribution of the clusters given the feature vector
as the cluster assignments.
```
def create_clustering_model(encoder, num_clusters, name=None):
inputs = keras.Input(shape=input_shape)
# Preprocess the input images.
preprocessed = data_preprocessing(inputs)
# Apply data augmentation to the images.
augmented = data_augmentation(preprocessed)
# Generate embedding representations of the images.
features = encoder(augmented)
# Assign the images to clusters.
outputs = layers.Dense(units=num_clusters, activation="softmax")(features)
# Create the model.
model = keras.Model(inputs=inputs, outputs=outputs, name=name)
return model
```
### Implement clustering learner
This model receives the input `anchor` image and its `neighbours`, produces the clusters
assignments for them using the `clustering_model`, and produces two outputs:
1. `similarity`: the similarity between the cluster assignments of the `anchor` image and
its `neighbours`. This output is fed to the `ClustersConsistencyLoss`.
2. `anchor_clustering`: cluster assignments of the `anchor` images. This is fed to the `ClustersEntropyLoss`.
```
def create_clustering_learner(clustering_model):
anchor = keras.Input(shape=input_shape, name="anchors")
neighbours = keras.Input(
shape=tuple([k_neighbours]) + input_shape, name="neighbours"
)
# Changes neighbours shape to [batch_size * k_neighbours, width, height, channels]
neighbours_reshaped = tf.reshape(neighbours, shape=tuple([-1]) + input_shape)
# anchor_clustering shape: [batch_size, num_clusters]
anchor_clustering = clustering_model(anchor)
# neighbours_clustering shape: [batch_size * k_neighbours, num_clusters]
neighbours_clustering = clustering_model(neighbours_reshaped)
# Convert neighbours_clustering shape to [batch_size, k_neighbours, num_clusters]
neighbours_clustering = tf.reshape(
neighbours_clustering,
shape=(-1, k_neighbours, tf.shape(neighbours_clustering)[-1]),
)
# similarity shape: [batch_size, 1, k_neighbours]
similarity = tf.linalg.einsum(
"bij,bkj->bik", tf.expand_dims(anchor_clustering, axis=1), neighbours_clustering
)
# similarity shape: [batch_size, k_neighbours]
similarity = layers.Lambda(lambda x: tf.squeeze(x, axis=1), name="similarity")(
similarity
)
# Create the model.
model = keras.Model(
inputs=[anchor, neighbours],
outputs=[similarity, anchor_clustering],
name="clustering_learner",
)
return model
```
### Train model
```
# If tune_encoder_during_clustering is set to False,
# then freeze the encoder weights.
for layer in encoder.layers:
layer.trainable = tune_encoder_during_clustering
# Create the clustering model and learner.
clustering_model = create_clustering_model(encoder, num_clusters, name="clustering")
clustering_learner = create_clustering_learner(clustering_model)
# Instantiate the model losses.
losses = [ClustersConsistencyLoss(), ClustersEntropyLoss(entropy_loss_weight=5)]
# Create the model inputs and labels.
inputs = {"anchors": x_data, "neighbours": tf.gather(x_data, neighbours)}
labels = tf.ones(shape=(x_data.shape[0]))
# Compile the model.
clustering_learner.compile(
optimizer=tfa.optimizers.AdamW(learning_rate=0.0005, weight_decay=0.0001),
loss=losses,
)
# Begin training the model.
clustering_learner.fit(x=inputs, y=labels, batch_size=512, epochs=50)
```
Plot training loss
```
plt.plot(history.history["loss"])
plt.ylabel("loss")
plt.xlabel("epoch")
plt.show()
```
## Cluster analysis
### Assign images to clusters
```
# Get the cluster probability distribution of the input images.
clustering_probs = clustering_model.predict(x_data, batch_size=batch_size, verbose=1)
# Get the cluster of the highest probability.
cluster_assignments = tf.math.argmax(clustering_probs, axis=-1).numpy()
# Store the clustering confidence.
# Images with the highest clustering confidence are considered the 'prototypes'
# of the clusters.
cluster_confidence = tf.math.reduce_max(clustering_probs, axis=-1).numpy()
```
Let's compute the cluster sizes
```
clusters = defaultdict(list)
for idx, c in enumerate(cluster_assignments):
clusters[c].append((idx, cluster_confidence[idx]))
for c in range(num_clusters):
print("cluster", c, ":", len(clusters[c]))
```
Notice that the clusters have roughly balanced sizes.
### Visualize cluster images
Display the *prototypes*—instances with the highest clustering confidence—of each cluster:
```
num_images = 8
plt.figure(figsize=(15, 15))
position = 1
for c in range(num_clusters):
cluster_instances = sorted(clusters[c], key=lambda kv: kv[1], reverse=True)
for j in range(num_images):
image_idx = cluster_instances[j][0]
plt.subplot(num_clusters, num_images, position)
plt.imshow(x_data[image_idx].astype("uint8"))
plt.title(classes[y_data[image_idx][0]])
plt.axis("off")
position += 1
```
### Compute clustering accuracy
First, we assign a label for each cluster based on the majority label of its images.
Then, we compute the accuracy of each cluster by dividing the number of image with the
majority label by the size of the cluster.
```
cluster_label_counts = dict()
for c in range(num_clusters):
cluster_label_counts[c] = [0] * num_classes
instances = clusters[c]
for i, _ in instances:
cluster_label_counts[c][y_data[i][0]] += 1
cluster_label_idx = np.argmax(cluster_label_counts[c])
correct_count = np.max(cluster_label_counts[c])
cluster_size = len(clusters[c])
accuracy = (
np.round((correct_count / cluster_size) * 100, 2) if cluster_size > 0 else 0
)
cluster_label = classes[cluster_label_idx]
print("cluster", c, "label is:", cluster_label, " - accuracy:", accuracy, "%")
```
## Conclusion
To improve the accuracy results, you can: 1) increase the number
of epochs in the representation learning and the clustering phases; 2)
allow the encoder weights to be tuned during the clustering phase; and 3) perform a final
fine-tuning step through self-labeling, as described in the [original SCAN paper](https://arxiv.org/abs/2005.12320).
Note that unsupervised image clustering techniques are not expected to outperform the accuracy
of supervised image classification techniques, rather showing that they can learn the semantics
of the images and group them into clusters that are similar to their original classes.
| github_jupyter |
```
import json
import numpy as np
from sklearn.model_selection import train_test_split
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import random
import librosa
import math
# path to json
data_path = "C:\\Users\\Saad\\Desktop\\Project\\MGC\\Data\\data.json"
def load_data(data_path):
with open(data_path, "r") as f:
data = json.load(f)
# convert lists to numpy arrays
X = np.array(data["mfcc"])
y = np.array(data["labels"])
print("No Problems, go ahead!")
return X, y
# load data
X, y = load_data(data_path)
X.shape
```
## ANN
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = keras.Sequential([
keras.layers.Flatten(input_shape=(X.shape[1], X.shape[2])),
keras.layers.Dense(512, activation='relu'),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dense(64, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.summary()
history = model.fit(X_train, y_train, validation_data=(X_test, y_test), batch_size=32, epochs=50)
def plot_history(history):
fig, axs = plt.subplots(2)
axs[0].plot(history.history["accuracy"], label="train accuracy")
axs[0].plot(history.history["val_accuracy"], label="test accuracy")
axs[0].set_ylabel("Accuracy")
axs[0].legend(loc="lower right")
axs[0].set_title("Accuracy eval")
axs[1].plot(history.history["loss"], label="train error")
axs[1].plot(history.history["val_loss"], label="test error")
axs[1].set_ylabel("Error")
axs[1].set_xlabel("Epoch")
axs[1].legend(loc="upper right")
axs[1].set_title("Error eval")
plt.show()
plot_history(history)
model_regularized = keras.Sequential([
keras.layers.Flatten(input_shape=(X.shape[1], X.shape[2])),
keras.layers.Dense(512, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(256, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(64, activation='relu', kernel_regularizer=keras.regularizers.l2(0.001)),
keras.layers.Dropout(0.3),
keras.layers.Dense(10, activation='softmax')
])
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model_regularized.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model_regularized.fit(X_train, y_train, validation_data=(X_test, y_test), batch_size=32, epochs=100)
plot_history(history)
```
## CNN
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
X_train, X_validation, y_train, y_validation = train_test_split(X_train, y_train, test_size=0.2)
X_train = X_train[..., np.newaxis]
X_validation = X_validation[..., np.newaxis]
X_test = X_test[..., np.newaxis]
X_train.shape
input_shape = (X_train.shape[1], X_train.shape[2], 1)
model_cnn = keras.Sequential()
model_cnn.add(keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=input_shape))
model_cnn.add(keras.layers.MaxPooling2D((3, 3), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Conv2D(32, (3, 3), activation='relu'))
model_cnn.add(keras.layers.MaxPooling2D((3, 3), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Conv2D(32, (2, 2), activation='relu'))
model_cnn.add(keras.layers.MaxPooling2D((2, 2), strides=(2, 2), padding='same'))
model_cnn.add(keras.layers.BatchNormalization())
model_cnn.add(keras.layers.Flatten())
model_cnn.add(keras.layers.Dense(64, activation='relu'))
model_cnn.add(keras.layers.Dropout(0.3))
model_cnn.add(keras.layers.Dense(10, activation='softmax'))
optimiser = keras.optimizers.Adam(learning_rate=0.0001)
model_cnn.compile(optimizer=optimiser,
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model_cnn.summary()
history = model_cnn.fit(X_train, y_train, validation_data=(X_validation, y_validation), batch_size=32, epochs=50)
plot_history(history)
test_loss, test_acc = model_cnn.evaluate(X_test, y_test, verbose=1)
print('\nTest accuracy:', test_acc)
model_cnn.save("Genre_Classifier.h5")
for n in range(10):
i = random.randint(0,len(X_test))
# pick a sample to predict from the test set
X_to_predict = X_test[i]
y_to_predict = y_test[i]
print("\nReal Genre :", y_to_predict)
X_to_predict = X_to_predict[np.newaxis, ...]
prediction = model_cnn.predict(X_to_predict)
# get index with max value
predicted_index = np.argmax(prediction, axis=1)
print("Predicted Genre:", int(predicted_index))
```
| github_jupyter |
# Notebook 3 - Advanced Data Structures
So far, we have seen numbers, strings, and lists. In this notebook, we will learn three more data structures, which allow us to organize data. The data structures are `tuple`, `set`, and `dict` (dictionary).
## Tuples
A tuple is like a list, but is immutable, meaning that it cannot be modified.
```
tup = (1,'a',[1,2])
tup
print(tup[1])
print(tup[2][0])
tup[1] = 3
# We can turn a list into a tuple, and visa versa
print(list(tup))
print(tuple(list(tup)))
# We can have a tuple with a single item
single_tup = (1,)
print(single_tup)
```
## Sets
We consider the `set` data structure. The `set` is thought of similarly to how it is defined in mathematics: it is unordered, and has no duplicates. Let's contrast with the data structures we have seen thus far.
* A `list` is an ordered, mutable collection of items
* A `tuple` is an ordered, immutable collection of items
* A `str` is an ordered, immutable collection of characters
* A `set` is an unordered, mutable collection of distinct items
```
some_numbers = [0,2,1,1,2]
my_set = set(some_numbers) # create a set out of the numbers
print(my_set)
```
We observed that, by turning a list into a set, we automatically removed the duplicates. This idea will work on any collection.
```
my_string = 'aabbccda'
my_set = set(my_string)
print(my_set)
'a' in my_set
'a' in my_set and 'e' not in my_set
```
Suppose we wanted to remove `'a'` from `my_set`, but don't know the syntax for it.
Fortunately, there is built-in help features.
* Typing `my_set.<tab>` lists different member functions of `my_set`.
* The function `help(my_set)` also lists different functions, along with explanations.
```
my_set.
help(my_set)
```
## Dictionaries
These are *very* useful!
Given $n$ values, a list `l` store $n$ values, which can be accessed by `l[i]` for each $i = 0,\ldots,n-1$.
A *dictionary* is a data structure that allows us to access values by general types of keys. This is useful in designing efficient algorithms and writing simple code.
```
# Create a dictionary of produce and their prices
product_prices = {}
# Add produce and prices to the dictionary
product_prices['apple'] = 2
product_prices['banana'] = 2
product_prices['carrot'] = 3
# View the dictionary
print(product_prices)
```
Dictionaries behave in ways similar to a list.
```
# Print the price of a banana
print(product_prices['banana'])
# Check if 'banana' is a key in the dictionary.
print('banana' in product_prices)
# Check if `donut` is a key in the dictonary.
print('donut' in product_prices)
```
Dictionaries allow us to access their keys and values directly.
```
# View the keys of the dictionary
produce = product_prices.keys()
print(produce)
# The keys are a list
type(produce)
# Using list comprehensions, we can find all produce that
# have 6 characters in their name.
print([name for name in product_prices if len(name) == 6])
# Python knows that we want to iterate through the keys of product_prices.
# Equivalently, we can use the following syntax.
print([name for name in produce if len(name) == 6])
# We can find all produce that have a price of 2 dollars.
print([name for name in product_prices if product_prices[name] == 2])
# Similarly, we can access the values of the dictionary
print(product_prices.values())
```
Dictionaries don't have to be indexed by strings. It can be indexed by numbers.
```
my_dict = {1: 5, 'abc': '123'}
print(my_dict)
```
Dictionaries can be created in several ways. We have seen two so far.
* Creating an empty dictionary with `{}`, then adding (key,value) pairs, one at a time.
* Creating an dictionary at once as `{key1:val1, key2:val2, ...}`
There are more ways to create dictionaries, that are convenient in different situations. We will see one more way.
* Dictionary comprehension
* Combining lists
```
# Create a dictionary, with a key of i^2 and a value of i for each i in 0,...,1000
squared_numbers = {i**2: i for i in range(10)}
print(81 in squared_numbers)
print(squared_numbers[81])
names = ['alice','bob','cindy']
sports = [['Archery', 'Badmitton'], ['Archery', 'Curling'], ['Badmitton', 'Diving']]
# Create a dictionary mapping names to sports
print({names[i]:sports[i] for i in range(len(names))})
# Alternative approach
print(dict(zip(names,sports)))
```
## Exercise
### Part 1
Obtain the list of common English words from the 'english_words.txt' file.
### Part 2
Create a dictionary called `length_to_words` that maps an integer `i` to the list of common English words that have that have `i` letters.
Example: If the words were `['and','if','the']`, then the dictionary would be `{2: ['if'], 3: ['and','the']}`.
Question: Why is a dictionary the correct choice for this data structure?
### Part 3
Create a dictionary named `length_to_num_words` that maps each length in `length_to_words` to the number of words with that length.
Example: If the words were `['and','if','the']`, then the dictionary would be `{2: 1, 3: 2}`.
| github_jupyter |
### Mount Google Drive (Works only on Google Colab)
```
from google.colab import drive
drive.mount('/content/gdrive')
```
# Import Packages
```
import os
import numpy as np
import pandas as pd
from zipfile import ZipFile
from PIL import Image
from tqdm.autonotebook import tqdm
from IPython.display import display
from IPython.display import Image as Dimage
```
# Define Paths
Define paths of all the required directories
```
# Root path of the dataset
ROOT_DATA_DIR = '/content/gdrive/My Drive/modest_museum_dataset.zip'
```
# Data Visualization
Let's visualize some of the foreground and background images
```
def make_grid(images_list, height=140, margin=8, aspect_ratio=False):
"""Combine Images to form a grid.
Args:
images (list): List of PIL images to display in grid.
height (int): Height to which the image will be resized.
margin (int): Amount of padding between the images in grid.
aspect_ratio (bool, optional): Create grid while maintaining
the aspect ratio of the images. (default: False)
Returns:
Image grid.
"""
# Create grid template
widths = []
if aspect_ratio:
for image in images_list:
# Find width according to aspect ratio
h_percent = height / image.size[1]
widths.append(int(image.size[0] * h_percent))
else:
widths = [height] * len(images_list)
start = 0
background = Image.new(
'RGBA', (sum(widths) + (len(images_list) - 1) * margin, height)
)
# Add images to grid
for idx, image in enumerate(images_list):
image = image.resize((widths[idx], height))
offset = (start, 0)
start += (widths[idx] + margin)
background.paste(image, offset)
return background
```
# Data Statistics
Let's calculate mean, standard deviation and total number of images for each type of image category.
## Mean
Mean is calculated using the formula
<center>
<img src="https://www.gstatic.com/education/formulas/images_long_sheet/en/mean.svg" height="50">
</center>
where, `sum of the terms` represents a pixel value and `number of terms` represents the total number of pixels across all the images.
## Standard Deviation
Standard Deviation is calculated using the formula
<center>
<img src="https://www.gstatic.com/education/formulas/images_long_sheet/en/population_standard_deviation.svg" height="50">
</center>
where, `x` represents a pixel value, `u` represents the mean calculated above and `N` represents the total number of pixels across all the images.
```
def statistics(filename, channel_num, filetype):
"""Calculates data statistics
Args:
path (str): Path of the directory for which statistics is to be calculated
Returns:
Mean, standard deviation, number of images
"""
counter = 0
mean = []
std = []
images = [] # store PIL instance of the image
pixel_num = 0 # store all pixel number in the dataset
channel_sum = np.zeros(channel_num) # store channel-wise sum
channel_sum_squared = np.zeros(channel_num) # store squared channel-wise sum
with ZipFile(filename) as archive:
img_list = [
x for x in archive.infolist()
if x.filename.split('/')[1] == filetype and x.filename.split('/')[2].endswith('.jpeg')
]
for entry in tqdm(img_list):
with archive.open(entry) as file:
img = Image.open(file)
if len(images) < 5:
images.append(img)
im = np.array(img)
im = im / 255.0
pixel_num += (im.size / channel_num)
channel_sum += np.sum(im, axis=(0, 1))
channel_sum_squared += np.sum(np.square(im), axis=(0, 1))
counter += 1
bgr_mean = channel_sum / pixel_num
bgr_std = np.sqrt(channel_sum_squared / pixel_num - np.square(bgr_mean))
# change the format from bgr to rgb
mean = [round(x, 5) for x in list(bgr_mean)[::-1]]
std = [round(x, 5) for x in list(bgr_std)[::-1]]
return mean, std, counter, im.shape, images
```
# Statistics for Background images
```
# Background
print('Calculating statistics for Backgrounds...')
bg_mean, bg_std, bg_counter, bg_dim, bg_images = statistics(ROOT_DATA_DIR, 3, 'bg')
# Display
print('Background Images:')
make_grid(bg_images, margin=30)
print('Data Statistics for Background images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_mean, bg_std, bg_counter, bg_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground images
```
# Background-Foreground
print('Calculating statistics for Background-Foreground Images...')
bg_fg_mean, bg_fg_std, bg_fg_counter, bg_fg_dim, bg_fg_image = statistics(ROOT_DATA_DIR, 3, 'bg_fg')
# Display
print('Background-Foreground Images:')
make_grid(bg_fg_image, margin=30)
print('Data Statistics for Background-Foreground images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_fg_mean, bg_fg_std, bg_fg_counter, bg_fg_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground Masks
```
#Foreground-Background Masks
print('Calculating statistics for Foreground-Background Masks...')
bg_fg_mask_mean, bg_fg_mask_std, bg_fg_mask_counter, bg_fg_mask_dim, bg_fg_mask_images = statistics(ROOT_DATA_DIR, 1, 'bg_fg_mask')
# Display
print('Background-Foreground Masks:')
make_grid(bg_fg_mask_images, margin=30, aspect_ratio=True)
print('Data Statistics for Background-Foreground Masks images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [bg_fg_mask_mean, bg_fg_mask_std, bg_fg_mask_counter, bg_fg_mask_dim]
}
data = pd.DataFrame(stats)
data
```
# Statistics for Background-Foreground Depth Maps
```
#Foreground-Background Depth Map
print('Calculating statistics for Foreground-Background Depth Map...')
depth_mean, depth_std, depth_counter, depth_dim, depth_images = statistics(ROOT_DATA_DIR, 1, 'bg_fg_depth_map')
# Display
print('Background-Foreground Depth Maps:')
make_grid(depth_images, margin=30)
print('Data Statistics for Background-Foreground Depth Map images')
stats = {
'Statistics': ['Mean', 'Standard deviation', 'Number of images', 'Dimension'],
'Data': [depth_mean, depth_std, depth_counter, depth_dim]
}
data = pd.DataFrame(stats)
data
```
| github_jupyter |
<a id='pd'></a>
<div id="qe-notebook-header" align="right" style="text-align:right;">
<a href="https://quantecon.org/" title="quantecon.org">
<img style="width:250px;display:inline;" width="250px" src="https://assets.quantecon.org/img/qe-menubar-logo.svg" alt="QuantEcon">
</a>
</div>
# Pandas
<a id='index-1'></a>
## Contents
- [Pandas](#Pandas)
- [Overview](#Overview)
- [Series](#Series)
- [DataFrames](#DataFrames)
- [On-Line Data Sources](#On-Line-Data-Sources)
- [Exercises](#Exercises)
- [Solutions](#Solutions)
In addition to what’s in Anaconda, this lecture will need the following libraries:
```
!pip install --upgrade pandas-datareader
```
## Overview
[Pandas](http://pandas.pydata.org/) is a package of fast, efficient data analysis tools for Python.
Its popularity has surged in recent years, coincident with the rise
of fields such as data science and machine learning.
Here’s a popularity comparison over time against STATA, SAS, and [dplyr](https://dplyr.tidyverse.org/) courtesy of Stack Overflow Trends
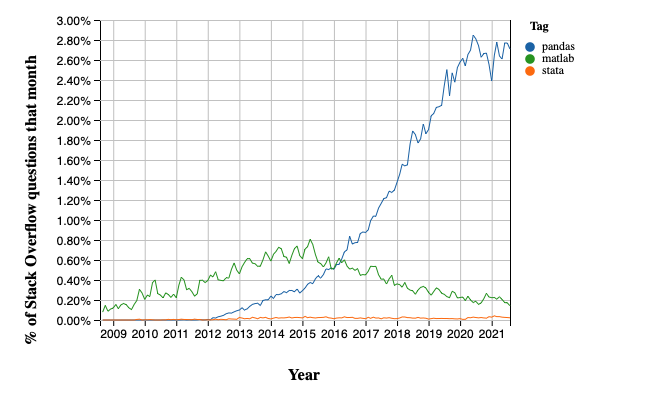
Just as [NumPy](http://www.numpy.org/) provides the basic array data type plus core array operations, pandas
1. defines fundamental structures for working with data and
1. endows them with methods that facilitate operations such as
- reading in data
- adjusting indices
- working with dates and time series
- sorting, grouping, re-ordering and general data munging <sup><a href=#mung id=mung-link>[1]</a></sup>
- dealing with missing values, etc., etc.
More sophisticated statistical functionality is left to other packages, such
as [statsmodels](http://www.statsmodels.org/) and [scikit-learn](http://scikit-learn.org/), which are built on top of pandas.
This lecture will provide a basic introduction to pandas.
Throughout the lecture, we will assume that the following imports have taken
place
```
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = [10,8] # Set default figure size
import requests
```
## Series
<a id='index-2'></a>
Two important data types defined by pandas are `Series` and `DataFrame`.
You can think of a `Series` as a “column” of data, such as a collection of observations on a single variable.
A `DataFrame` is an object for storing related columns of data.
Let’s start with Series
```
s = pd.Series(np.random.randn(4), name='daily returns')
s
```
Here you can imagine the indices `0, 1, 2, 3` as indexing four listed
companies, and the values being daily returns on their shares.
Pandas `Series` are built on top of NumPy arrays and support many similar
operations
```
s * 100
np.abs(s)
```
But `Series` provide more than NumPy arrays.
Not only do they have some additional (statistically oriented) methods
```
s.describe()
```
But their indices are more flexible
```
s.index = ['AMZN', 'AAPL', 'MSFT', 'GOOG']
s
```
Viewed in this way, `Series` are like fast, efficient Python dictionaries
(with the restriction that the items in the dictionary all have the same
type—in this case, floats).
In fact, you can use much of the same syntax as Python dictionaries
```
s['AMZN']
s['AMZN'] = 0
s
'AAPL' in s
```
## DataFrames
<a id='index-3'></a>
While a `Series` is a single column of data, a `DataFrame` is several columns, one for each variable.
In essence, a `DataFrame` in pandas is analogous to a (highly optimized) Excel spreadsheet.
Thus, it is a powerful tool for representing and analyzing data that are naturally organized into rows and columns, often with descriptive indexes for individual rows and individual columns.
Here’s the content of `test_pwt.csv`
```text
"country","country isocode","year","POP","XRAT","tcgdp","cc","cg"
"Argentina","ARG","2000","37335.653","0.9995","295072.21869","75.716805379","5.5788042896"
"Australia","AUS","2000","19053.186","1.72483","541804.6521","67.759025993","6.7200975332"
"India","IND","2000","1006300.297","44.9416","1728144.3748","64.575551328","14.072205773"
"Israel","ISR","2000","6114.57","4.07733","129253.89423","64.436450847","10.266688415"
"Malawi","MWI","2000","11801.505","59.543808333","5026.2217836","74.707624181","11.658954494"
"South Africa","ZAF","2000","45064.098","6.93983","227242.36949","72.718710427","5.7265463933"
"United States","USA","2000","282171.957","1","9898700","72.347054303","6.0324539789"
"Uruguay","URY","2000","3219.793","12.099591667","25255.961693","78.978740282","5.108067988"
```
Supposing you have this data saved as `test_pwt.csv` in the present working directory (type `%pwd` in Jupyter to see what this is), it can be read in as follows:
```
df = pd.read_csv('https://raw.githubusercontent.com/QuantEcon/lecture-python-programming/master/source/_static/lecture_specific/pandas/data/test_pwt.csv')
type(df)
df
```
We can select particular rows using standard Python array slicing notation
```
df[2:5]
```
To select columns, we can pass a list containing the names of the desired columns represented as strings
```
df[['country', 'tcgdp']]
```
To select both rows and columns using integers, the `iloc` attribute should be used with the format `.iloc[rows, columns]`
```
df.iloc[2:5, 0:4]
```
To select rows and columns using a mixture of integers and labels, the `loc` attribute can be used in a similar way
```
df.loc[df.index[2:5], ['country', 'tcgdp']]
```
Let’s imagine that we’re only interested in population (`POP`) and total GDP (`tcgdp`).
One way to strip the data frame `df` down to only these variables is to overwrite the dataframe using the selection method described above
```
df = df[['country', 'POP', 'tcgdp']]
df
```
Here the index `0, 1,..., 7` is redundant because we can use the country names as an index.
To do this, we set the index to be the `country` variable in the dataframe
```
df = df.set_index('country')
df
```
Let’s give the columns slightly better names
```
df.columns = 'population', 'total GDP'
df
```
Population is in thousands, let’s revert to single units
```
df['population'] = df['population'] * 1e3
df
```
Next, we’re going to add a column showing real GDP per capita, multiplying by 1,000,000 as we go because total GDP is in millions
```
df['GDP percap'] = df['total GDP'] * 1e6 / df['population']
df
```
One of the nice things about pandas `DataFrame` and `Series` objects is that they have methods for plotting and visualization that work through Matplotlib.
For example, we can easily generate a bar plot of GDP per capita
```
ax = df['GDP percap'].plot(kind='bar')
ax.set_xlabel('country', fontsize=12)
ax.set_ylabel('GDP per capita', fontsize=12)
plt.show()
```
At the moment the data frame is ordered alphabetically on the countries—let’s change it to GDP per capita
```
df = df.sort_values(by='GDP percap', ascending=False)
df
```
Plotting as before now yields
```
ax = df['GDP percap'].plot(kind='bar')
ax.set_xlabel('country', fontsize=12)
ax.set_ylabel('GDP per capita', fontsize=12)
plt.show()
```
## On-Line Data Sources
<a id='index-4'></a>
Python makes it straightforward to query online databases programmatically.
An important database for economists is [FRED](https://research.stlouisfed.org/fred2/) — a vast collection of time series data maintained by the St. Louis Fed.
For example, suppose that we are interested in the [unemployment rate](https://research.stlouisfed.org/fred2/series/UNRATE).
Via FRED, the entire series for the US civilian unemployment rate can be downloaded directly by entering
this URL into your browser (note that this requires an internet connection)
```text
https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv
```
(Equivalently, click here: [https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv](https://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv))
This request returns a CSV file, which will be handled by your default application for this class of files.
Alternatively, we can access the CSV file from within a Python program.
This can be done with a variety of methods.
We start with a relatively low-level method and then return to pandas.
### Accessing Data with requests
<a id='index-6'></a>
One option is to use [requests](https://requests.readthedocs.io/en/master/), a standard Python library for requesting data over the Internet.
To begin, try the following code on your computer
```
r = requests.get('http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv')
```
If there’s no error message, then the call has succeeded.
If you do get an error, then there are two likely causes
1. You are not connected to the Internet — hopefully, this isn’t the case.
1. Your machine is accessing the Internet through a proxy server, and Python isn’t aware of this.
In the second case, you can either
- switch to another machine
- solve your proxy problem by reading [the documentation](https://requests.readthedocs.io/en/master/)
Assuming that all is working, you can now proceed to use the `source` object returned by the call `requests.get('http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv')`
```
url = 'http://research.stlouisfed.org/fred2/series/UNRATE/downloaddata/UNRATE.csv'
source = requests.get(url).content.decode().split("\n")
source[0]
source[1]
source[2]
```
We could now write some additional code to parse this text and store it as an array.
But this is unnecessary — pandas’ `read_csv` function can handle the task for us.
We use `parse_dates=True` so that pandas recognizes our dates column, allowing for simple date filtering
```
data = pd.read_csv(url, index_col=0, parse_dates=True)
```
The data has been read into a pandas DataFrame called `data` that we can now manipulate in the usual way
```
type(data)
data.head() # A useful method to get a quick look at a data frame
pd.set_option('precision', 1)
data.describe() # Your output might differ slightly
```
We can also plot the unemployment rate from 2006 to 2012 as follows
```
ax = data['2006':'2012'].plot(title='US Unemployment Rate', legend=False)
ax.set_xlabel('year', fontsize=12)
ax.set_ylabel('%', fontsize=12)
plt.show()
```
Note that pandas offers many other file type alternatives.
Pandas has [a wide variety](https://pandas.pydata.org/pandas-docs/stable/user_guide/io.html) of top-level methods that we can use to read, excel, json, parquet or plug straight into a database server.
### Using pandas_datareader to Access Data
<a id='index-8'></a>
The maker of pandas has also authored a library called pandas_datareader that gives programmatic access to many data sources straight from the Jupyter notebook.
While some sources require an access key, many of the most important (e.g., FRED, [OECD](https://data.oecd.org/), [EUROSTAT](https://ec.europa.eu/eurostat/data/database) and the World Bank) are free to use.
For now let’s work through one example of downloading and plotting data — this
time from the World Bank.
The World Bank [collects and organizes data](http://data.worldbank.org/indicator) on a huge range of indicators.
For example, [here’s](http://data.worldbank.org/indicator/GC.DOD.TOTL.GD.ZS/countries) some data on government debt as a ratio to GDP.
The next code example fetches the data for you and plots time series for the US and Australia
```
from pandas_datareader import wb
govt_debt = wb.download(indicator='GC.DOD.TOTL.GD.ZS', country=['US', 'AU'], start=2005, end=2016).stack().unstack(0)
ind = govt_debt.index.droplevel(-1)
govt_debt.index = ind
ax = govt_debt.plot(lw=2)
ax.set_xlabel('year', fontsize=12)
plt.title("Government Debt to GDP (%)")
plt.show()
```
The [documentation](https://pandas-datareader.readthedocs.io/en/latest/index.html) provides more details on how to access various data sources.
## Exercises
<a id='pd-ex1'></a>
### Exercise 1
With these imports:
```
import datetime as dt
from pandas_datareader import data
```
Write a program to calculate the percentage price change over 2019 for the following shares:
```
ticker_list = {'INTC': 'Intel',
'MSFT': 'Microsoft',
'IBM': 'IBM',
'BHP': 'BHP',
'TM': 'Toyota',
'AAPL': 'Apple',
'AMZN': 'Amazon',
'BA': 'Boeing',
'QCOM': 'Qualcomm',
'KO': 'Coca-Cola',
'GOOG': 'Google',
'SNE': 'Sony',
'PTR': 'PetroChina'}
```
Here’s the first part of the program
```
def read_data(ticker_list,
start=dt.datetime(2019, 1, 2),
end=dt.datetime(2019, 12, 31)):
"""
This function reads in closing price data from Yahoo
for each tick in the ticker_list.
"""
ticker = pd.DataFrame()
for tick in ticker_list:
prices = data.DataReader(tick, 'yahoo', start, end)
closing_prices = prices['Close']
ticker[tick] = closing_prices
return ticker
ticker = read_data(ticker_list)
```
Complete the program to plot the result as a bar graph like this one:
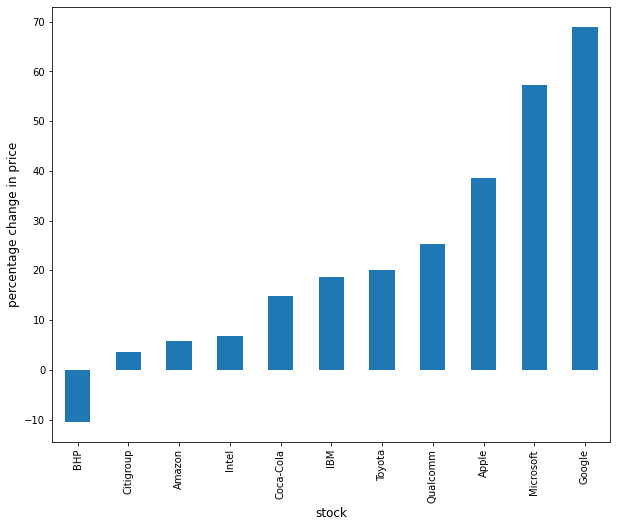
<a id='pd-ex2'></a>
### Exercise 2
Using the method `read_data` introduced in [Exercise 1](#pd-ex1), write a program to obtain year-on-year percentage change for the following indices:
```
indices_list = {'^GSPC': 'S&P 500',
'^IXIC': 'NASDAQ',
'^DJI': 'Dow Jones',
'^N225': 'Nikkei'}
```
Complete the program to show summary statistics and plot the result as a time series graph like this one:
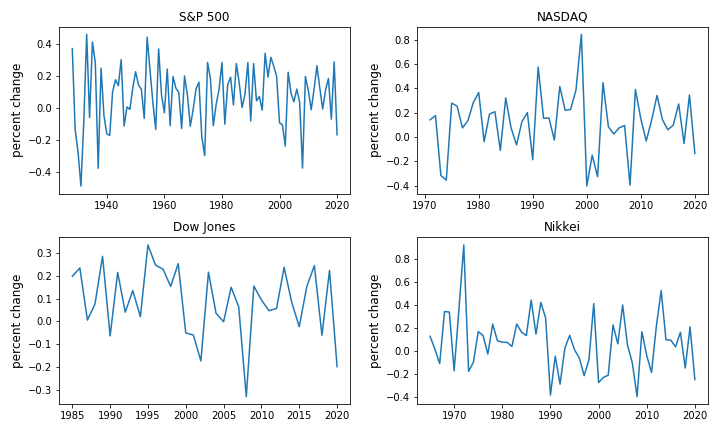
## Solutions
### Exercise 1
There are a few ways to approach this problem using Pandas to calculate
the percentage change.
First, you can extract the data and perform the calculation such as:
```
p1 = ticker.iloc[0] #Get the first set of prices as a Series
p2 = ticker.iloc[-1] #Get the last set of prices as a Series
price_change = (p2 - p1) / p1 * 100
price_change
```
Alternatively you can use an inbuilt method `pct_change` and configure it to
perform the correct calculation using `periods` argument.
```
change = ticker.pct_change(periods=len(ticker)-1, axis='rows')*100
price_change = change.iloc[-1]
price_change
```
Then to plot the chart
```
price_change.sort_values(inplace=True)
price_change = price_change.rename(index=ticker_list)
fig, ax = plt.subplots(figsize=(10,8))
ax.set_xlabel('stock', fontsize=12)
ax.set_ylabel('percentage change in price', fontsize=12)
price_change.plot(kind='bar', ax=ax)
plt.show()
```
### Exercise 2
Following the work you did in [Exercise 1](#pd-ex1), you can query the data using `read_data` by updating the start and end dates accordingly.
```
indices_data = read_data(
indices_list,
start=dt.datetime(1928, 1, 2),
end=dt.datetime(2020, 12, 31)
)
```
Then, extract the first and last set of prices per year as DataFrames and calculate the yearly returns such as:
```
yearly_returns = pd.DataFrame()
for index, name in indices_list.items():
p1 = indices_data.groupby(indices_data.index.year)[index].first() # Get the first set of returns as a DataFrame
p2 = indices_data.groupby(indices_data.index.year)[index].last() # Get the last set of returns as a DataFrame
returns = (p2 - p1) / p1
yearly_returns[name] = returns
yearly_returns
```
Next, you can obtain summary statistics by using the method `describe`.
```
yearly_returns.describe()
```
Then, to plot the chart
```
fig, axes = plt.subplots(2, 2, figsize=(10, 8))
for iter_, ax in enumerate(axes.flatten()): # Flatten 2-D array to 1-D array
index_name = yearly_returns.columns[iter_] # Get index name per iteration
ax.plot(yearly_returns[index_name]) # Plot pct change of yearly returns per index
ax.set_ylabel("percent change", fontsize = 12)
ax.set_title(index_name)
plt.tight_layout()
```
<p><a id=mung href=#mung-link><strong>[1]</strong></a> Wikipedia defines munging as cleaning data from one raw form into a structured, purged one.
| github_jupyter |
```
import numpy
import scipy
import scipy.sparse
import sklearn.metrics.pairwise
from sklearn import datasets
from sklearn.metrics.pairwise import pairwise_distances
#%%
descriptions = []
with open('descriptions.txt', encoding = "utf8") as f:
for line in f:
text = line.lower() ## Lowercase all characters
text = text.replace("[comma]"," ") ## Replace [commas] with empty space
for ch in text:
if ch < "0" or (ch < "a" and ch > "9") or ch > "z": ## The cleaning operation happens here, remove all special characters
text = text.replace(ch," ")
text = ' '.join(text.split()) ## Remove double spacing from sentences
descriptions.append(text)
dataSet = numpy.array(descriptions)
f.close()
#%%
vect = sklearn.feature_extraction.text.CountVectorizer()
##alternative vect = sklearn.feature_extraction.text.TfidfVectorizer
count = vect.fit_transform(descriptions)
cossim = sklearn.metrics.pairwise.cosine_similarity(count)
euclid = pairwise_distances(count, metric='euclidean')
manhat = pairwise_distances(count, metric='manhattan')
print(euclid[1][3])
print(euclid[1][2])
print(euclid[2][3])
print(euclid[21][344])
#from nltk.corpus import stopwords
#stop = stopwords.words('english')
from nltk.stem import PorterStemmer
st = PorterStemmer()
## Stemming removes -ly, -ing, -ly, etc.
import numpy
descriptions = []
with open('descriptions.txt', encoding = "utf8") as f:
for line in f:
text = line.lower() ## Lowercase all characters
text = text.replace("[comma]"," ") ## Replace [commas] with empty space
for ch in text:
if ch < "0" or (ch < "a" and ch > "9") or ch > "z": ## The cleaning operation happens here, remove all special characters
text = text.replace(ch," ")
text = ' '.join(text.split()) ## Remove double spacing from sentences
descriptions.append(text)
dataSet = numpy.array(descriptions)
f.close()
numpy.save("descriptions_cleaned_array.npy",dataSet)#numpy.
dataSet = numpy.load("descriptions_cleaned_array.npy")
#dataSet = numpy.load("coco_val.npy")
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer()
TfIdf_dataSet = vectorizer.fit_transform(dataSet)
print("What our Tf-Idf looks like: ")
print()
print(TfIdf_dataSet[1:2])
vectorVocab = vectorizer._validate_vocabulary()
## COSINE
cosineSimilarity = sklearn.metrics.pairwise.cosine_similarity(TfIdf_dataSet)
cosineSimilaritySorted = numpy.argsort(cosineSimilarity, axis=1)
top5Similar = cosineSimilaritySorted[:,0:5]
print(top5Similar)
from nltk.tokenize import sent_tokenize, word_tokenize
print(sent_tokenize(descriptions[2]))
print(word_tokenize(descriptions[2]))
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize
stop_words = set(stopwords.words("english"))
# removes standard words such as "have" "just" "until" "it" "did"...
words = word_tokenize(descriptions[123])
filtered = []
for w in words:
if w not in stop_words:
filtered.append(w)
print(filtered)
## Stemming
from nltk.stem import PorterStemmer
from nltk.tokenize import word_tokenize
ps = PorterStemmer()
for w in descriptions:
print(ps.stem(w))
## Speech tagging
from nltk.tokenize import PunktSentenceTokenizer
train_text = descriptions[2]
sample_text = descriptions[22]
custom_tokenizer = PunktSentenceTokenizer(train_text)
tokenized = custom_tokenizer.tokenize(sample_text)
def tagging():
for x in tokenized:
words = nltk.word_tokenize(x)
tagged = nltk.pos_tag(words)
print(tagged)
tagging()
##Lemmatizing
from nltk.stem import WordNetLemmatizer
lemmatizer = WordNetLemmatizer()
print(lemmatizer.lemmatize("better", pos = "a"))
## WordNet = find synonyms (better accuracy)
from nltk.corpus import wordnet
syns = wordnet.synsets("program")
print(syns)
print(descriptions[1])
print(len(descriptions))
a = 'Panama'
b = 'Pamela'
def hamming(a,b):
distance = 0
for index in range(len(a)):
# print(a[index], b[index]) # prints each nth letter next to each other
if a[index] != b[index]:
distance +=1
#print(distance)
return distance
hamming(a,b)
## Haming only for strings of the same length
def minkowski_distance(self,x,y,p_value):
""" return minkowski distance between two lists """
return self.nth_root(sum(pow(abs(a-b),p_value) for a,b in zip(x, y)),
p_value)
#!/usr/bin/env python
from math import*
from decimal import Decimal
def nth_root(value, n_root):
root_value = 1/float(n_root)
return round (Decimal(value) ** Decimal(root_value),3)
def minkowski_distance(x,y,p_value):
return nth_root(sum(pow(abs(a-b),p_value) for a,b in zip(x, y)),p_value)
#print minkowski_distance([0,3,4,5],[7,6,3,-1],3)
```
Also other distance metrics are present, such as chebyshev, minkowski, mahalanobis, haversine, hamming, canberra, braycurtis and many more.
```
minkowski_distance(x=[7,6,3,-1], y=[0,3,4,5], p_value=3)
```
| github_jupyter |
# Anna KaRNNa
In this notebook, I'll build a character-wise RNN trained on Anna Karenina, one of my all-time favorite books. It'll be able to generate new text based on the text from the book.
This network is based off of Andrej Karpathy's [post on RNNs](http://karpathy.github.io/2015/05/21/rnn-effectiveness/) and [implementation in Torch](https://github.com/karpathy/char-rnn). Also, some information [here at r2rt](http://r2rt.com/recurrent-neural-networks-in-tensorflow-ii.html) and from [Sherjil Ozair](https://github.com/sherjilozair/char-rnn-tensorflow) on GitHub. Below is the general architecture of the character-wise RNN.
<img src="assets/charseq.jpeg" width="500">
```
import time
from collections import namedtuple
import numpy as np
import tensorflow as tf
```
First we'll load the text file and convert it into integers for our network to use. Here I'm creating a couple dictionaries to convert the characters to and from integers. Encoding the characters as integers makes it easier to use as input in the network.
```
with open('anna.txt', 'r') as f:
text=f.read()
vocab = sorted(set(text))
vocab_to_int = {c: i for i, c in enumerate(vocab)}
int_to_vocab = dict(enumerate(vocab))
encoded = np.array([vocab_to_int[c] for c in text], dtype=np.int32)
```
Let's check out the first 100 characters, make sure everything is peachy. According to the [American Book Review](http://americanbookreview.org/100bestlines.asp), this is the 6th best first line of a book ever.
```
text[:100]
```
And we can see the characters encoded as integers.
```
encoded[:100]
```
Since the network is working with individual characters, it's similar to a classification problem in which we are trying to predict the next character from the previous text. Here's how many 'classes' our network has to pick from.
```
len(vocab)
```
## Making training mini-batches
Here is where we'll make our mini-batches for training. Remember that we want our batches to be multiple sequences of some desired number of sequence steps. Considering a simple example, our batches would look like this:
<img src="assets/[email protected]" width=500px>
<br>
We start with our text encoded as integers in one long array in `encoded`. Let's create a function that will give us an iterator for our batches. I like using [generator functions](https://jeffknupp.com/blog/2013/04/07/improve-your-python-yield-and-generators-explained/) to do this. Then we can pass `encoded` into this function and get our batch generator.
The first thing we need to do is discard some of the text so we only have completely full batches. Each batch contains $N \times M$ characters, where $N$ is the batch size (the number of sequences) and $M$ is the number of steps. Then, to get the total number of batches, $K$, we can make from the array `arr`, you divide the length of `arr` by the number of characters per batch. Once you know the number of batches, you can get the total number of characters to keep from `arr`, $N * M * K$.
After that, we need to split `arr` into $N$ sequences. You can do this using `arr.reshape(size)` where `size` is a tuple containing the dimensions sizes of the reshaped array. We know we want $N$ sequences (`batch_size` below), let's make that the size of the first dimension. For the second dimension, you can use `-1` as a placeholder in the size, it'll fill up the array with the appropriate data for you. After this, you should have an array that is $N \times (M * K)$.
Now that we have this array, we can iterate through it to get our batches. The idea is each batch is a $N \times M$ window on the $N \times (M * K)$ array. For each subsequent batch, the window moves over by `n_steps`. We also want to create both the input and target arrays. Remember that the targets are the inputs shifted over one character.
The way I like to do this window is use `range` to take steps of size `n_steps` from $0$ to `arr.shape[1]`, the total number of steps in each sequence. That way, the integers you get from `range` always point to the start of a batch, and each window is `n_steps` wide.
```
def get_batches(arr, batch_size, n_steps):
'''Create a generator that returns batches of size
batch_size x n_steps from arr.
Arguments
---------
arr: Array you want to make batches from
batch_size: Batch size, the number of sequences per batch
n_steps: Number of sequence steps per batch
'''
# Get the number of characters per batch and number of batches we can make
chars_per_batch = batch_size * n_steps
n_batches = len(arr)//chars_per_batch
# Keep only enough characters to make full batches
arr = arr[:n_batches * chars_per_batch]
# Reshape into batch_size rows
arr = arr.reshape((batch_size, -1))
for n in range(0, arr.shape[1], n_steps):
# The features
x = arr[:, n:n+n_steps]
# The targets, shifted by one
y_temp = arr[:, n+1:n+n_steps+1]
# For the very last batch, y will be one character short at the end of
# the sequences which breaks things. To get around this, I'll make an
# array of the appropriate size first, of all zeros, then add the targets.
# This will introduce a small artifact in the last batch, but it won't matter.
y = np.zeros(x.shape, dtype=x.dtype)
y[:,:y_temp.shape[1]] = y_temp
yield x, y
```
Now I'll make my data sets and we can check out what's going on here. Here I'm going to use a batch size of 10 and 50 sequence steps.
```
batches = get_batches(encoded, 10, 50)
x, y = next(batches)
print('x\n', x[:10, :10])
print('\ny\n', y[:10, :10])
```
If you implemented `get_batches` correctly, the above output should look something like
```
x
[[55 63 69 22 6 76 45 5 16 35]
[ 5 69 1 5 12 52 6 5 56 52]
[48 29 12 61 35 35 8 64 76 78]
[12 5 24 39 45 29 12 56 5 63]
[ 5 29 6 5 29 78 28 5 78 29]
[ 5 13 6 5 36 69 78 35 52 12]
[63 76 12 5 18 52 1 76 5 58]
[34 5 73 39 6 5 12 52 36 5]
[ 6 5 29 78 12 79 6 61 5 59]
[ 5 78 69 29 24 5 6 52 5 63]]
y
[[63 69 22 6 76 45 5 16 35 35]
[69 1 5 12 52 6 5 56 52 29]
[29 12 61 35 35 8 64 76 78 28]
[ 5 24 39 45 29 12 56 5 63 29]
[29 6 5 29 78 28 5 78 29 45]
[13 6 5 36 69 78 35 52 12 43]
[76 12 5 18 52 1 76 5 58 52]
[ 5 73 39 6 5 12 52 36 5 78]
[ 5 29 78 12 79 6 61 5 59 63]
[78 69 29 24 5 6 52 5 63 76]]
```
although the exact numbers will be different. Check to make sure the data is shifted over one step for `y`.
## Building the model
Below is where you'll build the network. We'll break it up into parts so it's easier to reason about each bit. Then we can connect them up into the whole network.
<img src="assets/charRNN.png" width=500px>
### Inputs
First off we'll create our input placeholders. As usual we need placeholders for the training data and the targets. We'll also create a placeholder for dropout layers called `keep_prob`.
```
def build_inputs(batch_size, num_steps):
''' Define placeholders for inputs, targets, and dropout
Arguments
---------
batch_size: Batch size, number of sequences per batch
num_steps: Number of sequence steps in a batch
'''
# Declare placeholders we'll feed into the graph
inputs = tf.placeholder(tf.int32, [batch_size, num_steps], name='inputs')
targets = tf.placeholder(tf.int32, [batch_size, num_steps], name='targets')
# Keep probability placeholder for drop out layers
keep_prob = tf.placeholder(tf.float32, name='keep_prob')
return inputs, targets, keep_prob
```
### LSTM Cell
Here we will create the LSTM cell we'll use in the hidden layer. We'll use this cell as a building block for the RNN. So we aren't actually defining the RNN here, just the type of cell we'll use in the hidden layer.
We first create a basic LSTM cell with
```python
lstm = tf.contrib.rnn.BasicLSTMCell(num_units)
```
where `num_units` is the number of units in the hidden layers in the cell. Then we can add dropout by wrapping it with
```python
tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
```
You pass in a cell and it will automatically add dropout to the inputs or outputs. Finally, we can stack up the LSTM cells into layers with [`tf.contrib.rnn.MultiRNNCell`](https://www.tensorflow.org/versions/r1.0/api_docs/python/tf/contrib/rnn/MultiRNNCell). With this, you pass in a list of cells and it will send the output of one cell into the next cell. Previously with TensorFlow 1.0, you could do this
```python
tf.contrib.rnn.MultiRNNCell([cell]*num_layers)
```
This might look a little weird if you know Python well because this will create a list of the same `cell` object. However, TensorFlow 1.0 will create different weight matrices for all `cell` objects. But, starting with TensorFlow 1.1 you actually need to create new cell objects in the list. To get it to work in TensorFlow 1.1, it should look like
```python
def build_cell(num_units, keep_prob):
lstm = tf.contrib.rnn.BasicLSTMCell(num_units)
drop = tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
return drop
tf.contrib.rnn.MultiRNNCell([build_cell(num_units, keep_prob) for _ in range(num_layers)])
```
Even though this is actually multiple LSTM cells stacked on each other, you can treat the multiple layers as one cell.
We also need to create an initial cell state of all zeros. This can be done like so
```python
initial_state = cell.zero_state(batch_size, tf.float32)
```
Below, we implement the `build_lstm` function to create these LSTM cells and the initial state.
```
def build_lstm(lstm_size, num_layers, batch_size, keep_prob):
''' Build LSTM cell.
Arguments
---------
keep_prob: Scalar tensor (tf.placeholder) for the dropout keep probability
lstm_size: Size of the hidden layers in the LSTM cells
num_layers: Number of LSTM layers
batch_size: Batch size
'''
### Build the LSTM Cell
def build_cell(lstm_size, keep_prob):
# Use a basic LSTM cell
lstm = tf.contrib.rnn.BasicLSTMCell(lstm_size)
# Add dropout to the cell
drop = tf.contrib.rnn.DropoutWrapper(lstm, output_keep_prob=keep_prob)
return drop
# Stack up multiple LSTM layers, for deep learning
cell = tf.contrib.rnn.MultiRNNCell([build_cell(lstm_size, keep_prob) for _ in range(num_layers)])
initial_state = cell.zero_state(batch_size, tf.float32)
return cell, initial_state
```
### RNN Output
Here we'll create the output layer. We need to connect the output of the RNN cells to a full connected layer with a softmax output. The softmax output gives us a probability distribution we can use to predict the next character.
If our input has batch size $N$, number of steps $M$, and the hidden layer has $L$ hidden units, then the output is a 3D tensor with size $N \times M \times L$. The output of each LSTM cell has size $L$, we have $M$ of them, one for each sequence step, and we have $N$ sequences. So the total size is $N \times M \times L$.
We are using the same fully connected layer, the same weights, for each of the outputs. Then, to make things easier, we should reshape the outputs into a 2D tensor with shape $(M * N) \times L$. That is, one row for each sequence and step, where the values of each row are the output from the LSTM cells.
One we have the outputs reshaped, we can do the matrix multiplication with the weights. We need to wrap the weight and bias variables in a variable scope with `tf.variable_scope(scope_name)` because there are weights being created in the LSTM cells. TensorFlow will throw an error if the weights created here have the same names as the weights created in the LSTM cells, which they will be default. To avoid this, we wrap the variables in a variable scope so we can give them unique names.
```
def build_output(lstm_output, in_size, out_size):
''' Build a softmax layer, return the softmax output and logits.
Arguments
---------
x: Input tensor
in_size: Size of the input tensor, for example, size of the LSTM cells
out_size: Size of this softmax layer
'''
# Reshape output so it's a bunch of rows, one row for each step for each sequence.
# That is, the shape should be batch_size*num_steps rows by lstm_size columns
seq_output = tf.concat(lstm_output, axis=1)
x = tf.reshape(seq_output, [-1, in_size])
# Connect the RNN outputs to a softmax layer
with tf.variable_scope('softmax'):
softmax_w = tf.Variable(tf.truncated_normal((in_size, out_size), stddev=0.1))
softmax_b = tf.Variable(tf.zeros(out_size))
# Since output is a bunch of rows of RNN cell outputs, logits will be a bunch
# of rows of logit outputs, one for each step and sequence
logits = tf.matmul(x, softmax_w) + softmax_b
# Use softmax to get the probabilities for predicted characters
out = tf.nn.softmax(logits, name='predictions')
return out, logits
```
### Training loss
Next up is the training loss. We get the logits and targets and calculate the softmax cross-entropy loss. First we need to one-hot encode the targets, we're getting them as encoded characters. Then, reshape the one-hot targets so it's a 2D tensor with size $(M*N) \times C$ where $C$ is the number of classes/characters we have. Remember that we reshaped the LSTM outputs and ran them through a fully connected layer with $C$ units. So our logits will also have size $(M*N) \times C$.
Then we run the logits and targets through `tf.nn.softmax_cross_entropy_with_logits` and find the mean to get the loss.
```
def build_loss(logits, targets, lstm_size, num_classes):
''' Calculate the loss from the logits and the targets.
Arguments
---------
logits: Logits from final fully connected layer
targets: Targets for supervised learning
lstm_size: Number of LSTM hidden units
num_classes: Number of classes in targets
'''
# One-hot encode targets and reshape to match logits, one row per batch_size per step
y_one_hot = tf.one_hot(targets, num_classes)
y_reshaped = tf.reshape(y_one_hot, logits.get_shape())
# Softmax cross entropy loss
loss = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=y_reshaped)
loss = tf.reduce_mean(loss)
return loss
```
### Optimizer
Here we build the optimizer. Normal RNNs have have issues gradients exploding and disappearing. LSTMs fix the disappearance problem, but the gradients can still grow without bound. To fix this, we can clip the gradients above some threshold. That is, if a gradient is larger than that threshold, we set it to the threshold. This will ensure the gradients never grow overly large. Then we use an AdamOptimizer for the learning step.
```
def build_optimizer(loss, learning_rate, grad_clip):
''' Build optmizer for training, using gradient clipping.
Arguments:
loss: Network loss
learning_rate: Learning rate for optimizer
'''
# Optimizer for training, using gradient clipping to control exploding gradients
tvars = tf.trainable_variables()
grads, _ = tf.clip_by_global_norm(tf.gradients(loss, tvars), grad_clip)
train_op = tf.train.AdamOptimizer(learning_rate)
optimizer = train_op.apply_gradients(zip(grads, tvars))
return optimizer
```
### Build the network
Now we can put all the pieces together and build a class for the network. To actually run data through the LSTM cells, we will use [`tf.nn.dynamic_rnn`](https://www.tensorflow.org/versions/r1.0/api_docs/python/tf/nn/dynamic_rnn). This function will pass the hidden and cell states across LSTM cells appropriately for us. It returns the outputs for each LSTM cell at each step for each sequence in the mini-batch. It also gives us the final LSTM state. We want to save this state as `final_state` so we can pass it to the first LSTM cell in the the next mini-batch run. For `tf.nn.dynamic_rnn`, we pass in the cell and initial state we get from `build_lstm`, as well as our input sequences. Also, we need to one-hot encode the inputs before going into the RNN.
```
class CharRNN:
def __init__(self, num_classes, batch_size=64, num_steps=50,
lstm_size=128, num_layers=2, learning_rate=0.001,
grad_clip=5, sampling=False):
# When we're using this network for sampling later, we'll be passing in
# one character at a time, so providing an option for that
if sampling == True:
batch_size, num_steps = 1, 1
else:
batch_size, num_steps = batch_size, num_steps
tf.reset_default_graph()
# Build the input placeholder tensors
self.inputs, self.targets, self.keep_prob = build_inputs(batch_size, num_steps)
# Build the LSTM cell
cell, self.initial_state = build_lstm(lstm_size, num_layers, batch_size, self.keep_prob)
### Run the data through the RNN layers
# First, one-hot encode the input tokens
x_one_hot = tf.one_hot(self.inputs, num_classes)
# Run each sequence step through the RNN and collect the outputs
outputs, state = tf.nn.dynamic_rnn(cell, x_one_hot, initial_state=self.initial_state)
self.final_state = state
# Get softmax predictions and logits
self.prediction, self.logits = build_output(outputs, lstm_size, num_classes)
# Loss and optimizer (with gradient clipping)
self.loss = build_loss(self.logits, self.targets, lstm_size, num_classes)
self.optimizer = build_optimizer(self.loss, learning_rate, grad_clip)
```
## Hyperparameters
Here I'm defining the hyperparameters for the network.
* `batch_size` - Number of sequences running through the network in one pass.
* `num_steps` - Number of characters in the sequence the network is trained on. Larger is better typically, the network will learn more long range dependencies. But it takes longer to train. 100 is typically a good number here.
* `lstm_size` - The number of units in the hidden layers.
* `num_layers` - Number of hidden LSTM layers to use
* `learning_rate` - Learning rate for training
* `keep_prob` - The dropout keep probability when training. If you're network is overfitting, try decreasing this.
Here's some good advice from Andrej Karpathy on training the network. I'm going to copy it in here for your benefit, but also link to [where it originally came from](https://github.com/karpathy/char-rnn#tips-and-tricks).
> ## Tips and Tricks
>### Monitoring Validation Loss vs. Training Loss
>If you're somewhat new to Machine Learning or Neural Networks it can take a bit of expertise to get good models. The most important quantity to keep track of is the difference between your training loss (printed during training) and the validation loss (printed once in a while when the RNN is run on the validation data (by default every 1000 iterations)). In particular:
> - If your training loss is much lower than validation loss then this means the network might be **overfitting**. Solutions to this are to decrease your network size, or to increase dropout. For example you could try dropout of 0.5 and so on.
> - If your training/validation loss are about equal then your model is **underfitting**. Increase the size of your model (either number of layers or the raw number of neurons per layer)
> ### Approximate number of parameters
> The two most important parameters that control the model are `lstm_size` and `num_layers`. I would advise that you always use `num_layers` of either 2/3. The `lstm_size` can be adjusted based on how much data you have. The two important quantities to keep track of here are:
> - The number of parameters in your model. This is printed when you start training.
> - The size of your dataset. 1MB file is approximately 1 million characters.
>These two should be about the same order of magnitude. It's a little tricky to tell. Here are some examples:
> - I have a 100MB dataset and I'm using the default parameter settings (which currently print 150K parameters). My data size is significantly larger (100 mil >> 0.15 mil), so I expect to heavily underfit. I am thinking I can comfortably afford to make `lstm_size` larger.
> - I have a 10MB dataset and running a 10 million parameter model. I'm slightly nervous and I'm carefully monitoring my validation loss. If it's larger than my training loss then I may want to try to increase dropout a bit and see if that helps the validation loss.
> ### Best models strategy
>The winning strategy to obtaining very good models (if you have the compute time) is to always err on making the network larger (as large as you're willing to wait for it to compute) and then try different dropout values (between 0,1). Whatever model has the best validation performance (the loss, written in the checkpoint filename, low is good) is the one you should use in the end.
>It is very common in deep learning to run many different models with many different hyperparameter settings, and in the end take whatever checkpoint gave the best validation performance.
>By the way, the size of your training and validation splits are also parameters. Make sure you have a decent amount of data in your validation set or otherwise the validation performance will be noisy and not very informative.
```
batch_size = 100 # Sequences per batch
num_steps = 100 # Number of sequence steps per batch
lstm_size = 512 # Size of hidden layers in LSTMs
num_layers = 2 # Number of LSTM layers
learning_rate = 0.001 # Learning rate
keep_prob = 0.5 # Dropout keep probability
```
## Time for training
This is typical training code, passing inputs and targets into the network, then running the optimizer. Here we also get back the final LSTM state for the mini-batch. Then, we pass that state back into the network so the next batch can continue the state from the previous batch. And every so often (set by `save_every_n`) I save a checkpoint.
Here I'm saving checkpoints with the format
`i{iteration number}_l{# hidden layer units}.ckpt`
```
epochs = 20
# Print losses every N interations
print_every_n = 50
# Save every N iterations
save_every_n = 200
model = CharRNN(len(vocab), batch_size=batch_size, num_steps=num_steps,
lstm_size=lstm_size, num_layers=num_layers,
learning_rate=learning_rate)
saver = tf.train.Saver(max_to_keep=100)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
# Use the line below to load a checkpoint and resume training
#saver.restore(sess, 'checkpoints/______.ckpt')
counter = 0
for e in range(epochs):
# Train network
new_state = sess.run(model.initial_state)
loss = 0
for x, y in get_batches(encoded, batch_size, num_steps):
counter += 1
start = time.time()
feed = {model.inputs: x,
model.targets: y,
model.keep_prob: keep_prob,
model.initial_state: new_state}
batch_loss, new_state, _ = sess.run([model.loss,
model.final_state,
model.optimizer],
feed_dict=feed)
if (counter % print_every_n == 0):
end = time.time()
print('Epoch: {}/{}... '.format(e+1, epochs),
'Training Step: {}... '.format(counter),
'Training loss: {:.4f}... '.format(batch_loss),
'{:.4f} sec/batch'.format((end-start)))
if (counter % save_every_n == 0):
saver.save(sess, "checkpoints/i{}_l{}.ckpt".format(counter, lstm_size))
saver.save(sess, "checkpoints/i{}_l{}.ckpt".format(counter, lstm_size))
```
#### Saved checkpoints
Read up on saving and loading checkpoints here: https://www.tensorflow.org/programmers_guide/variables
```
tf.train.get_checkpoint_state('checkpoints')
```
## Sampling
Now that the network is trained, we'll can use it to generate new text. The idea is that we pass in a character, then the network will predict the next character. We can use the new one, to predict the next one. And we keep doing this to generate all new text. I also included some functionality to prime the network with some text by passing in a string and building up a state from that.
The network gives us predictions for each character. To reduce noise and make things a little less random, I'm going to only choose a new character from the top N most likely characters.
```
def pick_top_n(preds, vocab_size, top_n=5):
p = np.squeeze(preds)
p[np.argsort(p)[:-top_n]] = 0
p = p / np.sum(p)
c = np.random.choice(vocab_size, 1, p=p)[0]
return c
def sample(checkpoint, n_samples, lstm_size, vocab_size, prime="The "):
samples = [c for c in prime]
model = CharRNN(len(vocab), lstm_size=lstm_size, sampling=True)
saver = tf.train.Saver()
with tf.Session() as sess:
saver.restore(sess, checkpoint)
new_state = sess.run(model.initial_state)
for c in prime:
x = np.zeros((1, 1))
x[0,0] = vocab_to_int[c]
feed = {model.inputs: x,
model.keep_prob: 1.,
model.initial_state: new_state}
preds, new_state = sess.run([model.prediction, model.final_state],
feed_dict=feed)
c = pick_top_n(preds, len(vocab))
samples.append(int_to_vocab[c])
for i in range(n_samples):
x[0,0] = c
feed = {model.inputs: x,
model.keep_prob: 1.,
model.initial_state: new_state}
preds, new_state = sess.run([model.prediction, model.final_state],
feed_dict=feed)
c = pick_top_n(preds, len(vocab))
samples.append(int_to_vocab[c])
return ''.join(samples)
```
Here, pass in the path to a checkpoint and sample from the network.
```
tf.train.latest_checkpoint('checkpoints')
checkpoint = tf.train.latest_checkpoint('checkpoints')
samp = sample(checkpoint, 2000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i200_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i600_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
checkpoint = 'checkpoints/i1200_l512.ckpt'
samp = sample(checkpoint, 1000, lstm_size, len(vocab), prime="Far")
print(samp)
```
| github_jupyter |
```
print('Kazuma Shachou')
nome_do_filme = "Bakamon"
print(nome_do_filme)
nome_do_filme
import pandas as pd
filmes = pd.read_csv("https://raw.githubusercontent.com/alura-cursos/introducao-a-data-science/master/aula0/ml-latest-small/movies.csv")
filmes.columns = ["filmeid", "titulo", "generos"]
filmes.head()
# Lendo a documwentação de um método atributo
?filmes.head
#Lendo a documentação do tipo(docstring)
?filmes
avaliacoes = pd.read_csv("https://raw.githubusercontent.com/alura-cursos/introducao-a-data-science/master/aula0/ml-latest-small/ratings.csv")
avaliacoes.head()
avaliacoes.shape
len(avaliacoes)
avaliacoes.columns = ["usuárioid", "filmeid", "nota", "momento"]
avaliacoes.head()
avaliacoes.query("filmeid==1")
avaliacoes.describe()
avaliacoes["nota"]
avaliacoes.query("filmeid == 1").describe()
avaliacoes.query("filmeid == 1").mean()
avaliacoes.query("filmeid == 1")["nota"].mean()
notas_media_por_filme = avaliacoes.groupby("filmeid")["nota"].mean()
notas_media_por_filme.head()
#risco de filmes nao estarem em quantidade exata
#filme["nota media"] = notas_media_por_filme
#filmes.head()
```
##desafio 1:
Encontre os 18 filmes que não tiveram avaliação
```
filmes_com_media = filmes.join(notas_media_por_filme, on = "filmeid")
filmes_com_media.head()
```
##desafio 2
mudar o nome da coluna nota para media apos o join
```
filmes_com_media.sort_values("nota", ascending=False).head(15)
```
##desafio 3
coloque o numero de avaliações por filme
```
import matplotlib.pyplot as plt
avaliacoes.query("filmeid == 1")["nota"].plot(kind = 'hist',
title= "avaliações do filme toy story")
#plt.title("Avaliações do filme toy story")
plt.show()
avaliacoes.query("filmeid == 1")["nota"].plot(kind = 'hist')
avaliacoes.query("filmeid == 2")["nota"].plot(kind = 'hist')
avaliacoes.query("filmeid == 102084")["nota"].plot(kind = 'hist')
```
##desafio4
arredondar o valor da coluna de nota media em 2 casas
##desafio5
descobrir os generos de filmes(quais são eles, unicos) (esse daqui o bicho pega)
##desafio6
contar o numero de aparições de cada genero.
##desafio7
plotar o gráfico de aparições por genero, pode ser um gráfico de tipo igual a
barra
```
```
# Aula 2
```
filmes["generos"].str.get_dummies('|').sum() #srt é string, para cortar a parte que você quer, get dummies cria variaveis que true é 1 e 0 falso, por ultimo o | é para separação, por ultimo "sum" é somar generos
filmes["generos"].str.get_dummies('|').sum().sort_values(ascending=False) #ordenar por ordem decrescente generos
filmes.index #dataframe do filme, tem o indice que vai do 0 até 9742
filmes
filmes.values
filmes['generos'].str.get_dummies('|').sum().sort_values(ascending=False).index
filmes['generos'].str.get_dummies('|').sum().sort_values(ascending=False).values #valores
filmes['generos'].str.get_dummies('|').sum().sort_index() #ordenar pelo indice, ordem alfabetica
filmes['generos'].str.get_dummies('|').sum().sort_values(ascending=False).plot()
#naofaz sentido nenhum porque esta se referindo diferentamente ao genero, nao ao genero mais visto
filmes['generos'].str.get_dummies('|').sum().sort_values(ascending=False).plot(
kind='pie',
title = 'gráfico de generos',
figsize =(8,8))
plt.show()
filmes['generos'].str.get_dummies('|').sum().sort_values(ascending=False).plot(
kind='bar',
title = 'gráfico de generos',
figsize =(8,8))
plt.show()
import seaborn as sns
sns.set_style("whitegrid")
filmes_por_genero = filmes['generos'].str.get_dummies('|').sum().sort_index().sort_values(ascending = False)
plt.figure(figsize = (16,8))
plt.xticks(rotation=45)
sns.barplot(x = filmes_por_genero.index,
y = filmes_por_genero.values,
palette=sns.color_palette("BuGn_r",n_colors =len(filmes_por_genero) + 10 ))
plt.show()
pop = 1000
sal = 1000000
salario999 = 1
media = (sal * 1 + salario999 * 999)/1000
media
notas_media_por_filme.describe()
filmes_com_media.sort_values('nota', ascending=False)[2450:2500] #selecionando para ver os filmes entre o numero 2450 e 2500
notas_do_filme_2 = avaliacoes.query("filmeid==1")["nota"]
print(notas_do_filme_2.mean())
avaliacoes.query("filmeid==1")["nota"].plot(kind='hist')
notas_do_filme_2.describe()
avaliacoes.groupby("filmeid").mean()
filmes
filmes_com_media.sort_values("nota", ascending= False)[2450:2500]
def plot_filme(n) :
notas_do_filme = avaliacoes.query(f"filmeid=={n}")["nota"]
notas_do_filme.plot(kind='hist')
return notas_do_filme.describe()
plot_filme(919)
plot_filme(46578)
def plot_filme(n) :
notas_do_filme = avaliacoes.query(f"filmeid=={n}")["nota"]
notas_do_filme.plot(kind='hist')
plt.show()
notas_do_filme.plot.box()
plt.show
return notas_do_filme.describe()
plot_filme(919)
sns.boxplot(data = avaliacoes.query('filmeid in [1,2,919,46578]'), x = "filmeid", y= "nota")
```
```
```
| github_jupyter |
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# You can write up to 5GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
print(os.listdir("../input/dogs-vs-cats-redux-kernels-edition/"))
import numpy as np
import tensorflow as tf
import pandas as pd
import seaborn as sns
from sklearn.model_selection import train_test_split
from tensorflow import keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Activation, Dense, Flatten, BatchNormalization, Conv2D, MaxPool2D
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.metrics import categorical_crossentropy
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from sklearn.metrics import confusion_matrix
import itertools
import os
import shutil
import random
import glob
import matplotlib.pyplot as plt
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
%matplotlib inline
!unzip -q ../input/dogs-vs-cats-redux-kernels-edition/train.zip
!unzip -q ../input/dogs-vs-cats-redux-kernels-edition/test.zip
filenames = os.listdir("/kaggle/working/test")
for filename in filenames:
test_df = pd.DataFrame({
'filename': filenames
})
test_df.index = test_df.index + 1
test_df.head()
print(os.listdir("/kaggle/working"))
filenames = os.listdir("/kaggle/working/train")
categories = []
for filename in filenames:
category = filename.split('.')[0]
if category == 'dog':
categories.append(1)
else:
categories.append(0)
df = pd.DataFrame({
'filename': filenames,
'category': categories
})
df.head()
sns.countplot(df['category'])
df['category'] = df['category'].astype(str)
train_df, validate_df = train_test_split(df, test_size=0.1)
train_df = train_df.reset_index()
validate_df = validate_df.reset_index()
total_train = train_df.shape[0]
total_validate = validate_df.shape[0]
print(total_train)
print(total_validate)
train_batches = ImageDataGenerator(
rotation_range=15,
rescale=1./255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest',
width_shift_range=0.1,
height_shift_range=0.1) \
.flow_from_dataframe(
train_df,
"/kaggle/working/train",
x_col='filename',
y_col='category',
class_mode='binary',
target_size=(224, 224),
batch_size=124)
valid_batches = ImageDataGenerator(rescale=1./255) \
.flow_from_dataframe(
validate_df,
"/kaggle/working/train",
x_col='filename',
y_col='category',
class_mode='binary',
target_size=(224, 224),
batch_size=124)
test_batches = ImageDataGenerator(rescale=1./255) \
.flow_from_dataframe(
test_df,
"/kaggle/working/test",
x_col='filename',
y_col=None,
class_mode=None,
batch_size=124,
target_size=(224, 224),
shuffle=False
)
assert train_batches.n == 22500
assert valid_batches.n == 2500
imgs, labels = next(train_batches)
# This function will plot images in the form of a grid with 1 row and 10 columns where images are placed in each column.
def plotImages(images_arr):
fig, axes = plt.subplots(1, 10, figsize=(20,20))
axes = axes.flatten()
for img, ax in zip( images_arr, axes):
ax.imshow(img)
ax.axis('off')
plt.tight_layout()
plt.show()
plotImages(imgs)
print(labels[0:10])
model= tf.keras.models.Sequential(
[tf.keras.layers.Conv2D(filters = 64, kernel_size = (3,3), activation = 'relu', input_shape = (224,224,3)),
tf.keras.layers.Conv2D(filters = 64, kernel_size = (3,3), activation = 'relu'),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Dropout(.25),
tf.keras.layers.Conv2D(filters = 64, kernel_size = (3,3), activation = 'relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')]
)
model.summary()
model.compile(optimizer=Adam(learning_rate=0.0001),
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x=train_batches,
steps_per_epoch=len(train_batches),
validation_data=valid_batches,
validation_steps=len(valid_batches),
epochs=2,
verbose=2
)
```
Since accuracy is not that great, we will use a pre-trained model with transfer learning.
```
train_batches1 = ImageDataGenerator(preprocessing_function=tf.keras.applications.vgg16.preprocess_input) \
.flow_from_dataframe(
train_df,
"/kaggle/working/train",
x_col='filename',
y_col='category',
class_mode='binary',
target_size=(224, 224),
batch_size=124)
valid_batches1 = ImageDataGenerator(preprocessing_function=tf.keras.applications.vgg16.preprocess_input) \
.flow_from_dataframe(
validate_df,
"/kaggle/working/train",
x_col='filename',
y_col='category',
class_mode='binary',
target_size=(224, 224),
batch_size=124)
test_batches1 = ImageDataGenerator(preprocessing_function=tf.keras.applications.vgg16.preprocess_input) \
.flow_from_dataframe(
test_df,
"/kaggle/working/test",
x_col='filename',
y_col=None,
class_mode=None,
batch_size=124,
target_size=(224, 224),
shuffle=False
)
imgs, labels = next(train_batches1)
plotImages(imgs)
print(labels[0:10])
vgg16_model = tf.keras.applications.vgg16.VGG16()
vgg16_model.summary()
```
Removing the Last Layer
```
model = Sequential()
for layer in vgg16_model.layers[:-1]:
model.add(layer)
model.summary()
for layer in model.layers:
layer.trainable = False
model.add(Dense(units=1, activation='sigmoid'))
model.summary()
model.compile(optimizer=Adam(learning_rate=0.0001),
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x=train_batches1,
steps_per_epoch=len(train_batches1),
validation_data=valid_batches1,
validation_steps=len(valid_batches1),
epochs=3,
verbose=2)
```
Predict
```
results = model.predict(test_batches)
test_df['category'] = np.where(results > 0.5, 1,0)
```
Submission
```
submission_df = test_df.copy()
submission_df['id'] = submission_df['filename'].str.split('.').str[0]
submission_df['label'] = submission_df['category']
submission_df.drop(['filename', 'category'], axis=1, inplace=True)
submission_df.to_csv('submission.csv', index=False)
```
| github_jupyter |
# Import Dependencies
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
# scaling and dataset split
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
# OLS, Ridge
from sklearn.linear_model import LinearRegression, Ridge
# model evaluation
from sklearn.metrics import r2_score, mean_squared_error
```
# Read the CSV and Perform Basic Data Cleaning
```
data_to_load = "new_folder/googleplaystore.csv"
df_apps = pd.read_csv(data_to_load)
categories = list(df_apps["Category"].unique())
#Remove Category 1.9
categories.remove('1.9')
a = df_apps.loc[df_apps["Category"] == "1.9"]
df_apps = df_apps.drop(int(a.index.values),axis=0)
#df_apps = df_apps[df_apps['Category']!= "1.9"]
df_apps = df_apps.drop(df_apps[df_apps['Rating'].isnull()].index, axis=0)
df_apps["Type"] = (df_apps["Type"] == "Paid").astype(int)
#Extract App, Installs, & Content Rating from df_apps
popApps = df_apps.copy()
popApps = popApps.drop_duplicates()
#Remove characters preventing values from being floats and integers
popApps["Installs"] = popApps["Installs"].str.replace("+","")
popApps["Installs"] = popApps["Installs"].str.replace(",","")
popApps["Installs"] = popApps["Installs"].astype("int64")
popApps["Price"] = popApps["Price"].str.replace("$","")
popApps["Price"] = popApps["Price"].astype("float64")
popApps["Size"] = popApps["Size"].str.replace("Varies with device","0")
popApps["Size"] = (popApps["Size"].replace(r'[kM]+$', '', regex=True).astype(float) *\
popApps["Size"].str.extract(r'[\d\.]+([kM]+)', expand=False).fillna(1).replace(['k','M'], [10**3, 10**6]).astype(int))
popApps["Reviews"] = popApps["Reviews"].astype("int64")
popApps.reset_index(inplace=True)
popApps.drop(["index"],axis=1,inplace=True)
popAppsCopy = popApps.drop(["App","Last Updated","Current Ver","Android Ver","Type"],axis=1)
X = popAppsCopy.drop("Installs", axis = 1)
y = popAppsCopy["Installs"]
y = y.replace({1:'1000+',5: '1000+', 10: '1000+',50:'1000+',100:'1000+',500:'1000+',
1000: '1000+',5000:'10000+',10000: '10000+', 50000:'100000+',100000:'100000+',
500000:'1000000+', 1000000:'1000000+',5000000:'10000000+',10000000:'10000000+',
50000000:'100000000+',100000000:'100000000+', 500000000:'1000000000+',
1000000000:'1000000000+' })
print(X.shape, y.shape)
import seaborn as sns
corr = X.apply(lambda x: x.factorize()[0]).corr()
plt.figure(figsize=(12,7))
sns.heatmap(corr, xticklabels=corr.columns, yticklabels=corr.columns,annot=True)
plt.savefig('Correlation_matrix.png')
data = popAppsCopy
data = data.drop("Genres",axis =1)
data_binary_encoded = pd.get_dummies(data, columns=["Category"])
data_binary_encoded_1 = pd.get_dummies(data_binary_encoded, columns=["Content Rating"])
data_binary_encoded_1.head()
X = data_binary_encoded_1.drop("Installs", axis = 1)
y = data_binary_encoded_1["Installs"]
y = y.replace({1:'1000+',5: '1000+', 10: '1000+',50:'1000+',100:'1000+',500:'1000+',
1000: '1000+',5000:'10000+',10000: '10000+', 50000:'100000+',100000:'100000+',
500000:'1000000+', 1000000:'1000000+',5000000:'10000000+',10000000:'10000000+',
50000000:'100000000+',100000000:'100000000+', 500000000:'1000000000+',
1000000000:'1000000000+' })
print(X.shape, y.shape)
#X = X.drop(["Content Rating_Adults only 18+","Content Rating_Unrated"], axis = 1)
feature_names = X.columns
feature_names
```
# Split the data into training and testing
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
from sklearn.preprocessing import LabelEncoder, MinMaxScaler
X_scaler = MinMaxScaler().fit(X_train)
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
```
# SVC Model
```
# Support vector machine linear classifier
from sklearn.svm import SVC
model = SVC(kernel='linear')
model.fit(X_train_scaled, y_train)
print('Test Acc: %.3f' % model.score(X_test_scaled, y_test))
print(f"Training Data Score: {model.score(X_train_scaled, y_train)}")
print(f"Testing Data Score: {model.score(X_test_scaled, y_test)}")
import seaborn as sns
corr = X.apply(lambda x: x.factorize()[0]).corr()
plt.figure(figsize=(12,7))
sns.heatmap(corr, xticklabels=corr.columns, yticklabels=corr.columns,annot=True)
plt.savefig('large_cor.png')
plt.show()
```
# Random Forest Model
```
from sklearn import tree
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X_train, y_train)
print('Test_score:', clf.score(X_test, y_test))
print('Train_score:', clf.score(X_train, y_train))
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X_train_scaled, y_train)
print('Test_score:', clf.score(X_test_scaled, y_test))
print('Train_score:', clf.score(X_train_scaled, y_train))
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=200)
rf = rf.fit(X_train_scaled, y_train)
print('Test_score:', rf.score(X_test_scaled, y_test))
print('Train_score:',rf.score(X_train_scaled, y_train))
y_pred = rf.predict(X_test_scaled)
import seaborn as sns
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
labels = np.unique(y_test)
cm = confusion_matrix(y_test, y_pred, labels=labels)
df_cm = pd.DataFrame(cm, index=labels, columns=labels)
plt.figure(figsize = (10,7))
sns.set(font_scale=1.4)#for label size
sns.heatmap(df_cm, annot=True,annot_kws={"size": 16})# font size
print('Accuracy' , accuracy_score(y_test, y_pred))
plt.savefig("correlation_rf.png")
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=200)
rf = rf.fit(X_train_scaled, y_train)
rf.score(X_test_scaled, y_test)
```
# Hyperparameter Tuning
```
# Create the GridSearch estimator along with a parameter object containing the values to adjust
from sklearn.model_selection import GridSearchCV
param_grid = {'n_estimators':[100,200,300,400,500,600,700,800,900,1000],
'max_depth':[1,5,10,15,20]}
grid = GridSearchCV(rf,param_grid,verbose=3)
grid.fit(X_train,y_train)
# List the best parameters for this dataset
print(grid.best_params_)
# List the best score
print(grid.best_score_)
# Create the GridSearchCV model
predictions = grid.predict(X_test)
predictions_train = grid.predict(X_train)
# Train the model with GridSearch
from sklearn.metrics import classification_report
print(classification_report(y_test, predictions))
imp_features = sorted(zip(rf.feature_importances_, feature_names), reverse=True)
imp_features
y_v = [lis[0] for lis in imp_features]
x = [lis[1] for lis in imp_features]
plt.figure(figsize=(12,7))
plt.bar(y_v,x, align='center', alpha=0.5)
plt.savefig('Knee_effect.png')
```
# Remove least imp features
```
X_red = popAppsCopy.drop(["Genres","Category","Installs","Content Rating","Genres"], axis = 1)
y_red = popApps["Installs"]
y = y_red.replace({1:'1000+',5: '1000+', 10: '1000+',50:'1000+',100:'1000+',500:'1000+',
1000: '1000+',5000:'10000+',10000: '10000+', 50000:'100000+',100000:'100000+',
500000:'1000000+', 1000000:'1000000+',5000000:'10000000+',10000000:'10000000+',
50000000:'100000000+',100000000:'100000000+', 500000000:'1000000000+',
1000000000:'1000000000+' })
print(X_red.shape, y_red.shape)
X_red.head()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_red, y_red, random_state=42)
from sklearn import tree
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X_train, y_train)
clf.score(X_test, y_test)
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=200)
rf = rf.fit(X_train, y_train)
rf.score(X_test, y_test)
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=200)
rf = rf.fit(X_train_scaled, y_train)
rf.score(X_test_scaled, y_test)
# Create the GridSearch estimator along with a parameter object containing the values to adjust
from sklearn.model_selection import GridSearchCV
param_grid = {'n_estimators':[100,200,300,400,500,600,700,800,900,1000],
'max_depth':[5,10,15,20]}
grid = GridSearchCV(rf,param_grid,verbose=3)
grid.fit(X_train,y_train)
# List the best score
print(grid.best_score_)
grid.score(X_train,y_train)
```
# PCA
```
X.head()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
from sklearn.decomposition import PCA
pca = PCA()
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
explained_variance = pca.explained_variance_ratio_
explained_variance
from sklearn.decomposition import PCA
pca = PCA(n_components=39)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(max_depth=2, random_state=0)
classifier.fit(X_train, y_train)
# Predicting the Test set results
y_pred = classifier.predict(X_test)
import seaborn as sns
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
labels = np.unique(y_test)
cm = confusion_matrix(y_test, y_pred, labels=labels)
df_cm = pd.DataFrame(cm, index=labels, columns=labels)
plt.figure(figsize = (10,7))
sns.set(font_scale=1.4)#for label size
sns.heatmap(df_cm, annot=True,annot_kws={"size": 16})# font size
print('Accuracy' , accuracy_score(y_test, y_pred))
```
# Remove the least 2 values from knee effect
```
X_knee = X.drop(["Content Rating_Adults only 18+","Content Rating_Unrated"], axis = 1)
y_knee = y
print(X_knee.shape, y_knee.shape)
from sklearn.model_selection import train_test_split
X_train_k, X_test_k, y_train_k, y_test_k = train_test_split(X_knee, y_knee, random_state=42)
from sklearn.preprocessing import LabelEncoder, MinMaxScaler
X_scaler_k = MinMaxScaler().fit(X_train_k)
X_train_scaled_k = X_scaler_k.transform(X_train_k)
X_test_scaled_k = X_scaler_k.transform(X_test_k)
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=200)
rf = rf.fit(X_train_scaled_k, y_train_k)
rf.score(X_test_scaled_k, y_test_k)
rf.score(X_train_scaled_k, y_train_k)
```
| github_jupyter |
# Regression on Decison Trees and Random Forest
```
#importing important libraries
#libraries for reading dataset
import numpy as np
import pandas as pd
#libraries for data visualisation
import matplotlib.pyplot as plt
import seaborn as sns
#libraries for model building and understanding
import sklearn
from sklearn.model_selection import train_test_split
#importing label encoder
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
#importing libraries for decision tree regression
from IPython.display import Image
from six import StringIO
import graphviz, pydotplus
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor, export_graphviz
from sklearn import metrics
from sklearn.metrics import r2_score,mean_squared_log_error
#importing libraries for boosting
from sklearn.ensemble import GradientBoostingRegressor
from xgboost import XGBRegressor
#libraries for hyper parameter tuning
from sklearn.model_selection import KFold
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import RandomizedSearchCV
#library to deal with warning
import warnings
warnings.filterwarnings('ignore')
#to display all the columns in the dataset
pd.set_option('display.max_columns', 500)
```
## Reading Data
```
cp = pd.read_csv('carprice.csv')
```
### Understanding the data
```
cp.head()
cp.shape
cp.info()
cp.describe()
#symboling is a categorical data so we convert to the specified type
cp['symboling'] = cp['symboling'].apply(str)
```
#### There are 11 categorical data and remaining are the numerical data
```
#as per the bussiness requirements we only need name of the carcompany and not the carmodel
#so we drop carmodel and only keep carCompany
cp['CarName'] = cp['CarName'].str.lower()
cp['carCompany'] = cp['CarName'].str.split(' ').str[0]
cp = cp.drop('CarName',axis = 1)
cp.head()
```
## Data visualization and understanding using EDA
### Price is a dependent variable
#### Visualising numerical data
```
#Finding correlation
cor = cp.corr()
cor
# visulaising correlation using heatmap
plt.subplots(figsize=(20, 20))
plt.title('Correlation between each data variable')
sns.heatmap(cor, xticklabels=cor.columns.values,
yticklabels=cor.columns.values,annot= True,linecolor="black",linewidths=2, cmap="viridis")
plt.show()
```
`citympg` and `highwaympg` have negative correlation with price
`carlength`,`carwidth`,`curbweight`,`enginesize` and `horsepower` have positve correlation with price
```
#scatter plot for numerical data with yaxis fixed as price
plt.figure(figsize=[18,12])
plt.subplot(3,3,1)
plt.scatter(cp.wheelbase, cp.price)
plt.title('wheelbase vs price')
plt.subplot(3,3,2)
plt.scatter(cp.peakrpm, cp.price)
plt.title('peakrpm vs price')
plt.subplot(3,3,3)
plt.scatter(cp.carheight, cp.price)
plt.title('carheight vs price')
plt.subplot(3,3,4)
plt.scatter(cp.compressionratio, cp.price)
plt.title('compressionratio vs price')
plt.subplot(3,3,5)
plt.scatter(cp.stroke, cp.price)
plt.title('Stroke vs price')
plt.subplot(3,3,6)
plt.scatter(cp.boreratio, cp.price)
plt.title('boreratio vs price')
plt.subplot(3,3,7)
plt.scatter(cp.enginesize, cp.price)
plt.title('enginesize vs price')
plt.subplot(3,3,8)
plt.scatter(cp.horsepower, cp.price)
plt.title('horsepower vs price')
plt.subplot(3,3,9)
plt.scatter(cp.curbweight, cp.price)
plt.title('curbweight vs price')
plt.show()
plt.figure(figsize=[15,8])
plt.subplot(2,2,1)
plt.scatter(cp.carlength, cp.price)
plt.title('carlength vs price')
plt.subplot(2,2,2)
plt.scatter(cp.carwidth, cp.price)
plt.title('carwidth vs price')
plt.subplot(2,2,3)
plt.scatter(cp.citympg, cp.price)
plt.title('citympg vs price')
plt.subplot(2,2,4)
plt.scatter(cp.highwaympg, cp.price)
plt.title('highwaympg vs price')
plt.show()
print(np.corrcoef(cp['carlength'], cp['carwidth'])[0, 1])
print(np.corrcoef(cp['citympg'], cp['highwaympg'])[0, 1])
```
#### Visualising categorical data
```
plt.figure(figsize=(20, 15))
plt.subplot(3,3,1)
sns.countplot(cp.fueltype)
plt.subplot(3,3,2)
sns.countplot(cp.aspiration)
plt.subplot(3,3,3)
sns.countplot(cp.doornumber)
plt.subplot(3,3,4)
sns.countplot(cp.drivewheel)
plt.subplot(3,3,5)
sns.countplot(cp.carbody)
plt.subplot(3,3,6)
sns.countplot(cp.enginelocation)
plt.subplot(3,3,7)
sns.countplot(cp.enginetype)
plt.subplot(3,3,8)
sns.countplot(cp.cylindernumber)
plt.subplot(3,3,9)
sns.countplot(cp.symboling)
plt.show()
```
`ohc` is the most preferred enginetype
most cars have `four cylinders`
`sedan` and `hatchback` are most common carbody
most cars prefer `gas` fueltype
```
plt.figure(figsize=(30,25))
plt.subplot(2,1,1)
sns.countplot(cp.fuelsystem)
plt.subplot(2,1,2)
sns.countplot(cp.carCompany)
plt.show()
```
`mpfi` and `2bbl` are most common fuelsystem
`Toyota` is most favoured carcompany
##### we can observe that numerous carcompanies are misspelled
```
# replcaing incorrect carcompanies with correct ones so we replace them with correct spellings
cp['carCompany'] = cp['carCompany'].str.replace('vok','volk')
cp['carCompany'] = cp['carCompany'].str.replace('ou','o')
cp['carCompany'] = cp['carCompany'].str.replace('cshce','sche')
cp['carCompany'] = cp['carCompany'].str.replace('vw','volkswagen')
cp['carCompany'] = cp['carCompany'].str.replace('xd','zd')
# visualising categorical data vs price
plt.figure(figsize = (25,15))
plt.subplot(3,3,1)
sns.boxplot(x = 'fueltype',y='price', data = cp)
plt.subplot(3,3,2)
sns.boxplot(x = 'symboling',y='price', data = cp)
plt.subplot(3,3,3)
sns.boxplot(x = 'aspiration',y='price', data = cp)
plt.subplot(3,3,4)
sns.boxplot(x = 'doornumber',y='price', data = cp)
plt.subplot(3,3,5)
sns.boxplot(x = 'carbody',y='price', data = cp)
plt.subplot(3,3,6)
sns.boxplot(x = 'drivewheel',y='price', data = cp)
plt.subplot(3,3,7)
sns.boxplot(x = 'enginelocation',y='price', data = cp)
plt.subplot(3,3,8)
sns.boxplot(x = 'enginetype',y='price', data = cp)
plt.subplot(3,3,9)
sns.boxplot(x = 'cylindernumber',y='price', data = cp)
plt.show()
```
`ohcv` are most expensive of the enginetype
`doornumber` don't have much impact on the price
`hardtop` and `covertible` are most expensive among the carbody
cars that are `rwd` have higher price
```
plt.figure(figsize=(30,25))
plt.subplot(2,1,1)
sns.boxplot(x = 'fuelsystem',y='price', data = cp)
plt.subplot(2,1,2)
sns.boxplot(x = 'carCompany',y='price', data = cp)
plt.show()
```
`buick`, `jaguar`, `porsche` and `bmw` are most expensive carCompany
`mpfi` and `idi` having the highest price range.
### Encoding categorical data
```
#defining fucntion for binary encoding of features with only 2 types of data
def number_map(x):
return x.map({'gas':1,'diesel':0,'std':0,'turbo':1,'two':0,'four':1,'front':0,'rear':1})
cp[['aspiration']] =cp[['aspiration']].apply(number_map)
cp[['doornumber']] =cp[['doornumber']].apply(number_map)
cp[['fueltype']] =cp[['fueltype']].apply(number_map)
cp[['enginelocation']] =cp[['enginelocation']].apply(number_map)
#applying label encoder on categorical variables
cp['carCompany'] = le.fit_transform(cp['carCompany'])
cp['symboling'] = le.fit_transform(cp['symboling'])
cp['carbody'] = le.fit_transform(cp['carbody'])
cp['drivewheel'] = le.fit_transform(cp['drivewheel'])
cp['enginetype'] = le.fit_transform(cp['enginetype'])
cp['cylindernumber'] = le.fit_transform(cp['cylindernumber'])
cp['fuelsystem'] = le.fit_transform(cp['fuelsystem'])
#and dropping columns that are not required for the analysis
cp = cp.drop(['car_ID'],axis = 1)
# converting price to thousands i.e 12.1K
cp['price']=cp['price'].apply(lambda val: round(val/1000,3))
pd.options.display.float_format = '{:,.2f}'.format
cp.info()
cp.head(100)
X=cp.drop(["price"],axis=1)
y=cp["price"]
```
### Splitting data into test and train datasets
```
#splitting the data into test and train for evaluation
# taking the test data as 30% and train data as 70%
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
```
## Gradient Boosting
```
# fitting the model on train data
model = GradientBoostingRegressor()
gbr = model.fit(X_train,y_train)
# predicting on test data
y_pred = gbr.predict(X_test)
# checking the goodness of the model
metrics.r2_score(y_test, y_pred)
```
### Hyper parameter tuning
```
# hyper parameter tuning for GBR
GBR = GradientBoostingRegressor()
param_dist = {"learning_rate": np.linspace(0.05, 0.15,5),"subsample": [0.3, 0.6, 0.9]}
rand = RandomizedSearchCV(GBR, param_dist, cv=5,n_iter=10, random_state=100)
rand.fit(X_train,y_train)
print(rand.best_params_)
GBR = GradientBoostingRegressor(learning_rate= 0.15, subsample= 0.6)
GBR.fit(X_train,y_train)
# predicting on test data
y_pred = GBR.predict(X_test)
np.sqrt(mean_squared_log_error(y_test, y_pred))
# checking the goodness of the model
metrics.r2_score(y_test, y_pred)
# plotting feature importance
importance = GBR.feature_importances_
fig = plt.figure(figsize=(10, 10))
x = X_test.columns.values
plt.barh(x, 100*importance)
plt.title('Feature Importance', loc='left')
plt.xlabel('Percentage')
plt.grid()
plt.show()
```
## XGboost
```
# fitting XGB on training data
XGB = XGBRegressor()
XGB = XGB.fit(X_train,y_train)
# predicting on test data
Y_pred = XGB.predict(X_test)
np.sqrt(mean_squared_log_error(y_test,Y_pred))
# checking the goodness of the model
metrics.r2_score(y_test, Y_pred)
importance = XGB.feature_importances_
# plotting feature importance
fig = plt.figure(figsize=(10, 10))
x = X_train.columns.values
plt.barh(x, 100*importance)
plt.title('Feature Importance', loc='left')
plt.xlabel('Percentage')
plt.grid()
plt.show()
```
### Hyperparameter tuning
```
# hyper parameter tuning for XGB
XGB = XGBRegressor()
param_grid = {"learning_rate": np.linspace(0.05, 0.15,5),
"subsample": [0.3, 0.6, 0.9]}
rand = RandomizedSearchCV(XGB, param_grid, cv=5,n_iter=10, random_state=100)
rand.fit(X_train,y_train)
print(rand.best_params_)
xgb = XGBRegressor(learning_rate= 0.15, subsample= 0.6)
xgb.fit(X_train,y_train)
Y_pred = xgb.predict(X_test)
np.sqrt(mean_squared_log_error(y_test,Y_pred))
# checking the goodness of the model
metrics.r2_score(y_test, Y_pred)
importance = xgb.feature_importances_
# plotting feature importance
fig = plt.figure(figsize=(10, 10))
x = X_test.columns.values
plt.barh(x, 100*importance)
plt.title('Feature Importance', loc='left')
plt.xlabel('Percentage')
plt.grid()
plt.show()
```
| github_jupyter |
# In this note book the following steps are taken:
1. Remove highly correlated attributes
2. Find the best hyper parameters for estimator
3. Find the most important features by tunned random forest
4. Find f1 score of the tunned full model
5. Find best hyper parameter of model with selected features
6. Find f1 score of the tuned seleccted model
7. Compare the two f1 scores
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.feature_selection import RFECV,RFE
from sklearn.model_selection import train_test_split, GridSearchCV, KFold,RandomizedSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn import metrics
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score,f1_score
import numpy as np
from sklearn.metrics import make_scorer
f1_score = make_scorer(f1_score)
#import data
Data=pd.read_csv("Halifax-Transfomed-Data-BS-NoBreak - Copy.csv")
X = Data.iloc[:,:-1]
y = Data.iloc[:,-1]
#split test and training set.
np.random.seed(60)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2,
random_state = 1000)
#Define estimator and model
classifiers = {}
classifiers.update({"Random Forest": RandomForestClassifier(random_state=1000)})
#Define range of hyperparameters for estimator
np.random.seed(60)
parameters = {}
parameters.update({"Random Forest": { "classifier__n_estimators": [100,105,110,115,120,125,130,135,140,145,150,155,160,170,180,190,200],
# "classifier__n_estimators": [2,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150,160,170,180,190,200],
#"classifier__class_weight": [None, "balanced"],
"classifier__max_features": ["auto", "sqrt", "log2"],
"classifier__max_depth" : [4,6,8,10,11,12,13,14,15,16,17,18,19,20,22],
#"classifier__max_depth" : [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20],
"classifier__criterion" :["gini", "entropy"]
}})
# Make correlation matrix
corr_matrix = X_train.corr(method = "spearman").abs()
# Draw the heatmap
sns.set(font_scale = 1.0)
f, ax = plt.subplots(figsize=(11, 9))
sns.heatmap(corr_matrix, cmap= "YlGnBu", square=True, ax = ax)
f.tight_layout()
plt.savefig("correlation_matrix.png", dpi = 1080)
# Select upper triangle of matrix
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k = 1).astype(np.bool))
# Find index of feature columns with correlation greater than 0.8
to_drop = [column for column in upper.columns if any(upper[column] > 0.8)]
# Drop features
X_train = X_train.drop(to_drop, axis = 1)
X_test = X_test.drop(to_drop, axis = 1)
X_train
FEATURE_IMPORTANCE = {"Random Forest"}
selected_classifier = "Random Forest"
classifier = classifiers[selected_classifier]
scaler = StandardScaler()
steps = [("scaler", scaler), ("classifier", classifier)]
pipeline = Pipeline(steps = steps)
#Define parameters that we want to use in gridsearch cv
param_grid = parameters[selected_classifier]
# Initialize GridSearch object for estimator
gscv = RandomizedSearchCV(pipeline, param_grid, cv = 3, n_jobs= -1, verbose = 1, scoring = f1_score, n_iter=30)
# Fit gscv (Tunes estimator)
print(f"Now tuning {selected_classifier}. Go grab a beer or something.")
gscv.fit(X_train, np.ravel(y_train))
#Getting the best hyperparameters
best_params = gscv.best_params_
best_params
#Getting the best score of model
best_score = gscv.best_score_
best_score
#Check overfitting of the estimator
from sklearn.model_selection import cross_val_score
mod = RandomForestClassifier(#class_weight= None,
criterion= 'gini',
max_depth= 16,
max_features= 'auto',
n_estimators= 155 ,random_state=10000)
scores_test = cross_val_score(mod, X_test, y_test, scoring='f1', cv=5)
scores_test
tuned_params = {item[12:]: best_params[item] for item in best_params}
classifier.set_params(**tuned_params)
#Find f1 score of the model with all features (Model is tuned for all features)
results={}
model=classifier.set_params(criterion= 'gini',
max_depth= 16,
max_features= 'auto',
n_estimators= 155 ,random_state=10000)
model.fit(X_train,y_train)
y_pred = model.predict(X_test)
F1 = metrics.f1_score(y_test, y_pred)
results = {"classifier": model,
"Best Parameters": best_params,
"Training f1": best_score*100,
"Test f1": F1*100}
results
# Select Features using RFECV
class PipelineRFE(Pipeline):
# Source: https://ramhiser.com/post/2018-03-25-feature-selection-with-scikit-learn-pipeline/
def fit(self, X, y=None, **fit_params):
super(PipelineRFE, self).fit(X, y, **fit_params)
self.feature_importances_ = self.steps[-1][-1].feature_importances_
return self
steps = [("scaler", scaler), ("classifier", classifier)]
pipe = PipelineRFE(steps = steps)
np.random.seed(60)
# Initialize RFECV object
feature_selector = RFECV(pipe, cv = 5, step = 1, verbose = 1)
# Fit RFECV
feature_selector.fit(X_train, np.ravel(y_train))
# Get selected features
feature_names = X_train.columns
selected_features = feature_names[feature_selector.support_].tolist()
performance_curve = {"Number of Features": list(range(1, len(feature_names) + 1)),
"F1": feature_selector.grid_scores_}
performance_curve = pd.DataFrame(performance_curve)
# Performance vs Number of Features
# Set graph style
sns.set(font_scale = 1.75)
sns.set_style({"axes.facecolor": "1.0", "axes.edgecolor": "0.85", "grid.color": "0.85",
"grid.linestyle": "-", 'axes.labelcolor': '0.4', "xtick.color": "0.4",
'ytick.color': '0.4'})
colors = sns.color_palette("RdYlGn", 20)
line_color = colors[3]
marker_colors = colors[-1]
# Plot
f, ax = plt.subplots(figsize=(13, 6.5))
sns.lineplot(x = "Number of Features", y = "F1", data = performance_curve,
color = line_color, lw = 4, ax = ax)
sns.regplot(x = performance_curve["Number of Features"], y = performance_curve["F1"],
color = marker_colors, fit_reg = False, scatter_kws = {"s": 200}, ax = ax)
# Axes limits
plt.xlim(0.5, len(feature_names)+0.5)
plt.ylim(0.60, 1)
# Generate a bolded horizontal line at y = 0
ax.axhline(y = 0.625, color = 'black', linewidth = 1.3, alpha = .7)
# Turn frame off
ax.set_frame_on(False)
# Tight layout
plt.tight_layout()
#Define new training and test set based based on selected features by RFECV
X_train_rfecv = X_train[selected_features]
X_test_rfecv= X_test[selected_features]
np.random.seed(60)
classifier.fit(X_train_rfecv, np.ravel(y_train))
#Finding important features
np.random.seed(60)
feature_importance = pd.DataFrame(selected_features, columns = ["Feature Label"])
feature_importance["Feature Importance"] = classifier.feature_importances_
feature_importance = feature_importance.sort_values(by="Feature Importance", ascending=False)
feature_importance
# Initialize GridSearch object for model with selected features
np.random.seed(60)
gscv = RandomizedSearchCV(pipeline, param_grid, cv = 3, n_jobs= -1, verbose = 1, scoring = f1_score, n_iter=30)
#Tuning random forest classifier with selected features
np.random.seed(60)
gscv.fit(X_train_rfecv,y_train)
#Getting the best parameters of model with selected features
best_params = gscv.best_params_
best_params
#Getting the score of model with selected features
best_score = gscv.best_score_
best_score
#Check overfitting of the tuned model with selected features
from sklearn.model_selection import cross_val_score
mod = RandomForestClassifier(#class_weight= None,
criterion= 'entropy',
max_depth= 16,
max_features= 'auto',
n_estimators= 100 ,random_state=10000)
scores_test = cross_val_score(mod, X_test_rfecv, y_test, scoring='f1', cv=5)
scores_test
results={}
model=classifier.set_params(criterion= 'entropy',
max_depth= 16,
max_features= 'auto',
n_estimators= 100 ,random_state=10000)
scores_test = cross_val_score(mod, X_test_rfecv, y_test, scoring='f1', cv=5)
model.fit(X_train_rfecv,y_train)
y_pred = model.predict(X_test_rfecv)
F1 = metrics.f1_score(y_test, y_pred)
results = {"classifier": model,
"Best Parameters": best_params,
"Training f1": best_score*100,
"Test f1": F1*100}
results
```
| github_jupyter |
# Anailís ghramadaí trí [deplacy](https://koichiyasuoka.github.io/deplacy/)
## le [Stanza](https://stanfordnlp.github.io/stanza)
```
!pip install deplacy stanza
import stanza
stanza.download("ga")
nlp=stanza.Pipeline("ga")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [UDPipe 2](http://ufal.mff.cuni.cz/udpipe/2)
```
!pip install deplacy
def nlp(t):
import urllib.request,urllib.parse,json
with urllib.request.urlopen("https://lindat.mff.cuni.cz/services/udpipe/api/process?model=ga&tokenizer&tagger&parser&data="+urllib.parse.quote(t)) as r:
return json.loads(r.read())["result"]
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [COMBO-pytorch](https://gitlab.clarin-pl.eu/syntactic-tools/combo)
```
!pip install --index-url https://pypi.clarin-pl.eu/simple deplacy combo
import combo.predict
nlp=combo.predict.COMBO.from_pretrained("irish-ud27")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [Trankit](https://github.com/nlp-uoregon/trankit)
```
!pip install deplacy trankit transformers
import trankit
nlp=trankit.Pipeline("irish")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spacy-udpipe](https://github.com/TakeLab/spacy-udpipe)
```
!pip install deplacy spacy-udpipe
import spacy_udpipe
spacy_udpipe.download("ga")
nlp=spacy_udpipe.load("ga")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spaCy-COMBO](https://github.com/KoichiYasuoka/spaCy-COMBO)
```
!pip install deplacy spacy_combo
import spacy_combo
nlp=spacy_combo.load("ga_idt")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [spaCy-jPTDP](https://github.com/KoichiYasuoka/spaCy-jPTDP)
```
!pip install deplacy spacy_jptdp
import spacy_jptdp
nlp=spacy_jptdp.load("ga_idt")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
## le [Camphr-Udify](https://camphr.readthedocs.io/en/latest/notes/udify.html)
```
!pip install deplacy camphr en-udify@https://github.com/PKSHATechnology-Research/camphr_models/releases/download/0.7.0/en_udify-0.7.tar.gz
import pkg_resources,imp
imp.reload(pkg_resources)
import spacy
nlp=spacy.load("en_udify")
doc=nlp("Táimid faoi dhraíocht ag ceol na farraige.")
import deplacy
deplacy.render(doc)
deplacy.serve(doc,port=None)
# import graphviz
# graphviz.Source(deplacy.dot(doc))
```
| github_jupyter |
<a href="https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_python.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# MMClassification Python API tutorial on Colab
In this tutorial, we will introduce the following content:
* How to install MMCls
* Inference a model with Python API
* Fine-tune a model with Python API
## Install MMClassification
Before using MMClassification, we need to prepare the environment with the following steps:
1. Install Python, CUDA, C/C++ compiler and git
2. Install PyTorch (CUDA version)
3. Install mmcv
4. Clone mmcls source code from GitHub and install it
Because this tutorial is on Google Colab, and the basic environment has been completed, we can skip the first two steps.
### Check environment
```
%cd /content
!pwd
# Check nvcc version
!nvcc -V
# Check GCC version
!gcc --version
# Check PyTorch installation
import torch, torchvision
print(torch.__version__)
print(torch.cuda.is_available())
```
### Install MMCV
MMCV is the basic package of all OpenMMLab packages. We have pre-built wheels on Linux, so we can download and install them directly.
Please pay attention to PyTorch and CUDA versions to match the wheel.
In the above steps, we have checked the version of PyTorch and CUDA, and they are 1.9.0 and 11.1 respectively, so we need to choose the corresponding wheel.
In addition, we can also install the full version of mmcv (mmcv-full). It includes full features and various CUDA ops out of the box, but needs a longer time to build.
```
# Install mmcv
!pip install mmcv -f https://download.openmmlab.com/mmcv/dist/cu111/torch1.9.0/index.html
# !pip install mmcv-full -f https://download.openmmlab.com/mmcv/dist/cu110/torch1.9.0/index.html
```
### Clone and install MMClassification
Next, we clone the latest mmcls repository from GitHub and install it.
```
# Clone mmcls repository
!git clone https://github.com/open-mmlab/mmclassification.git
%cd mmclassification/
# Install MMClassification from source
!pip install -e .
# Check MMClassification installation
import mmcls
print(mmcls.__version__)
```
## Inference a model with Python API
MMClassification provides many pre-trained models, and you can check them by the link of [model zoo](https://mmclassification.readthedocs.io/en/latest/model_zoo.html). Almost all models can reproduce the results in original papers or reach higher metrics. And we can use these models directly.
To use the pre-trained model, we need to do the following steps:
- Prepare the model
- Prepare the config file
- Prepare the checkpoint file
- Build the model
- Inference with the model
```
# Get the demo image
!wget https://www.dropbox.com/s/k5fsqi6qha09l1v/banana.png?dl=0 -O demo/banana.png
from PIL import Image
Image.open('demo/banana.png')
```
### Prepare the config file and checkpoint file
We configure a model with a config file and save weights with a checkpoint file.
On GitHub, you can find all these pre-trained models in the config folder of MMClassification. For example, you can find the config files and checkpoints of Mobilenet V2 in [this link](https://github.com/open-mmlab/mmclassification/tree/master/configs/mobilenet_v2).
We have integrated many config files for various models in the MMClassification repository. As for the checkpoint, we can download it in advance, or just pass an URL to API, and MMClassification will download it before load weights.
```
# Confirm the config file exists
!ls configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py
# Specify the path of the config file and checkpoint file.
config_file = 'configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py'
checkpoint_file = 'https://download.openmmlab.com/mmclassification/v0/mobilenet_v2/mobilenet_v2_batch256_imagenet_20200708-3b2dc3af.pth'
```
### Inference the model
MMClassification provides high-level Python API to inference models.
At first, we build the MobilenetV2 model and load the checkpoint.
```
import mmcv
from mmcls.apis import inference_model, init_model, show_result_pyplot
# Specify the device, if you cannot use GPU, you can also use CPU
# by specifying `device='cpu'`.
device = 'cuda:0'
# device = 'cpu'
# Build the model according to the config file and load the checkpoint.
model = init_model(config_file, checkpoint_file, device=device)
# The model's inheritance relationship
model.__class__.__mro__
# The inference result in a single image
img = 'demo/banana.png'
img_array = mmcv.imread(img)
result = inference_model(model, img_array)
result
%matplotlib inline
# Visualize the inference result
show_result_pyplot(model, img, result)
```
## Fine-tune a model with Python API
Fine-tuning is to re-train a model which has been trained on another dataset (like ImageNet) to fit our target dataset. Compared with training from scratch, fine-tuning is much faster can avoid over-fitting problems during training on a small dataset.
The basic steps of fine-tuning are as below:
1. Prepare the target dataset and meet MMClassification's requirements.
2. Modify the training config.
3. Start training and validation.
More details are in [the docs](https://mmclassification.readthedocs.io/en/latest/tutorials/finetune.html).
### Prepare the target dataset
Here we download the cats & dogs dataset directly. You can find more introduction about the dataset in the [tools tutorial](https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_tools.ipynb).
```
# Download the cats & dogs dataset
!wget https://www.dropbox.com/s/wml49yrtdo53mie/cats_dogs_dataset_reorg.zip?dl=0 -O cats_dogs_dataset.zip
!mkdir -p data
!unzip -qo cats_dogs_dataset.zip -d ./data/
```
### Read the config file and modify the config
In the [tools tutorial](https://colab.research.google.com/github/open-mmlab/mmclassification/blob/master/docs/tutorials/MMClassification_tools.ipynb), we have introduced all parts of the config file, and here we can modify the loaded config by Python code.
```
# Load the base config file
from mmcv import Config
cfg = Config.fromfile('configs/mobilenet_v2/mobilenet-v2_8xb32_in1k.py')
# Modify the number of classes in the head.
cfg.model.head.num_classes = 2
cfg.model.head.topk = (1, )
# Load the pre-trained model's checkpoint.
cfg.model.backbone.init_cfg = dict(type='Pretrained', checkpoint=checkpoint_file, prefix='backbone')
# Specify sample size and number of workers.
cfg.data.samples_per_gpu = 32
cfg.data.workers_per_gpu = 2
# Specify the path and meta files of training dataset
cfg.data.train.data_prefix = 'data/cats_dogs_dataset/training_set/training_set'
cfg.data.train.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the path and meta files of validation dataset
cfg.data.val.data_prefix = 'data/cats_dogs_dataset/val_set/val_set'
cfg.data.val.ann_file = 'data/cats_dogs_dataset/val.txt'
cfg.data.val.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the path and meta files of test dataset
cfg.data.test.data_prefix = 'data/cats_dogs_dataset/test_set/test_set'
cfg.data.test.ann_file = 'data/cats_dogs_dataset/test.txt'
cfg.data.test.classes = 'data/cats_dogs_dataset/classes.txt'
# Specify the normalization parameters in data pipeline
normalize_cfg = dict(type='Normalize', mean=[124.508, 116.050, 106.438], std=[58.577, 57.310, 57.437], to_rgb=True)
cfg.data.train.pipeline[3] = normalize_cfg
cfg.data.val.pipeline[3] = normalize_cfg
cfg.data.test.pipeline[3] = normalize_cfg
# Modify the evaluation metric
cfg.evaluation['metric_options']={'topk': (1, )}
# Specify the optimizer
cfg.optimizer = dict(type='SGD', lr=0.005, momentum=0.9, weight_decay=0.0001)
cfg.optimizer_config = dict(grad_clip=None)
# Specify the learning rate scheduler
cfg.lr_config = dict(policy='step', step=1, gamma=0.1)
cfg.runner = dict(type='EpochBasedRunner', max_epochs=2)
# Specify the work directory
cfg.work_dir = './work_dirs/cats_dogs_dataset'
# Output logs for every 10 iterations
cfg.log_config.interval = 10
# Set the random seed and enable the deterministic option of cuDNN
# to keep the results' reproducible.
from mmcls.apis import set_random_seed
cfg.seed = 0
set_random_seed(0, deterministic=True)
cfg.gpu_ids = range(1)
```
### Fine-tune the model
Use the API `train_model` to fine-tune our model on the cats & dogs dataset.
```
import time
import mmcv
import os.path as osp
from mmcls.datasets import build_dataset
from mmcls.models import build_classifier
from mmcls.apis import train_model
# Create the work directory
mmcv.mkdir_or_exist(osp.abspath(cfg.work_dir))
# Build the classifier
model = build_classifier(cfg.model)
model.init_weights()
# Build the dataset
datasets = [build_dataset(cfg.data.train)]
# Add `CLASSES` attributes to help visualization
model.CLASSES = datasets[0].CLASSES
# Start fine-tuning
train_model(
model,
datasets,
cfg,
distributed=False,
validate=True,
timestamp=time.strftime('%Y%m%d_%H%M%S', time.localtime()),
meta=dict())
%matplotlib inline
# Validate the fine-tuned model
img = mmcv.imread('data/cats_dogs_dataset/training_set/training_set/cats/cat.1.jpg')
model.cfg = cfg
result = inference_model(model, img)
show_result_pyplot(model, img, result)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/EnzoGolfetti/imersaoalura_dados_3/blob/main/aula05_imersao_alura_dados.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Análise de Drugs Discovery - Imersão Dados Alura
Desafio 1: Investigar por que a classe tratamento é tão desbalanceada
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
url_dados = 'https://github.com/alura-cursos/imersaodados3/blob/main/dados/dados_experimentos.zip?raw=true'
dados = pd.read_csv(url_dados, compression = 'zip') #compression = 'zip' serve par aarquivos que estejam comprimidos, isso é bom para arquivos muito grandes
dados
```
Cada linha é um experimento de cultura de células que foi submetida a alguma droga com determinada dosagem e por determinada quantidade de tempo.
```
dados.info() #para ver as primeiras infos dos dados, número de index (linhas)
#colunas
# e tipo dos dados, no caso são 872 de float64, 1 de int64 e 4 object (string)
dados.isnull().sum() #o .isnull .summ serve para somar por coluna os valores nulos, da um parecer inicial sobre quais colunas tem nulos e dar uma ideia
#do que vamos precisar fazer
dados['tratamento']
dados['tratamento'].value_counts()
```
Os tratamentos tem expressiva quantidade de experimentos 'com_droga' e apenas 1866 de 23814 sendo 'com_controle'.
Com controle significa, aqueles que não recebem os tratamentos para testar como os com experimento reagiram a droga, para saber que foi a droga que mudou a resposta, temos que ter o grupo controle que esteja no mesmo ambiente, exceto a presença da droga para ver a resposta.
```
#próxima variável a ser analisada = tempo
dados['tempo']
dados['tempo'].value_counts()
```
Podemos ver que o tempo está disposto em unidades de 'hora', respectivamente:
24, 48, 72.
48 horas foi a maioria do tempo observado nos experimentos, e 24 horas a que menos foi (segundo a bióloga da imersão, devido a que, muitas vezes, 24 horas não é o suficiente para as células desenvolverem respostas à droga aplicada.
```
dados['dose'].value_counts()
```
Observamos que tem apenas dois tipos doses (D1, D2), D1 tendo a maioria dos registros - 12147
```
dados['droga'].value_counts()
```
Nas drogas, podemos ver que a droga 'cacb2b860' foi a mais usada (1866 vezes)
E a droga '87d714366' foi a segunda mais usada com 718 vezes.
O nome das drogas, é "confuso", pois foram anonimizados para evitar vieses nas análises.
O total de drogas investigados foi de 3289 (registrado em 'length')
```
dados['g-0'].value_counts()
```
Os 'g' são abreviação de genes, portanto, existem observações das respostas de vários deles, que estão dispostos nas colunas, e os valores que vemos é a expressão dos genes frente à droga, dose e tempo de exposição.
Os valores provavelmente estão normalizados para permitir o entendimento e a comparação deles
```
#contando quantos valores maiores que 0, temos em 'g-0'
dados[dados['g-0'] > 0].count()
#máscara para os dados g-0 maiores que '0'
dados_g0_maior_zero = dados[dados['g-0'] > 0]
dados_g0_maior_zero.head()
```
###Desafio 2: Plotar as últimas 5 linhas do Dataframe
```
#plotando últimas 5 linhas
dados.iloc[23809:,:]
```
###Desafio 3: Registrar a proporção da classe tratamento
```
#usando método matemático
(dados['tratamento'].value_counts() * 100) / 23814
#usando função value_counts do Pandas
dados['tratamento'].value_counts(normalize=True) #o normalize nos dá os porcent deles
```
É interessante termos um comparativo com dados da própria tabela, porém de outras colunas, nesse caso, vamos comparar com a distribuição das doses
```
dados['dose'].value_counts(normalize=True)
#plotando gráfico de pizza para mostrar as proporções dos valores em tratamento
fig, ax = plt.subplots(figsize=(20,6))
labels = ['com_droga', 'com_controle']
ax.pie(dados['tratamento'].value_counts(normalize=True), labels=labels, autopct='%1.1f%%')
ax.set_title('Distribuição dos tipos de tratamentos')
```
###Observando graficamente os valores de tempo
```
barplot_time = dados['tempo'].value_counts().plot.bar()
barplot_time.set_title('Distribuição dos experimentos por tempo')
barplot_time.set_xlabel('Tempo observado')
barplot_time.set_ylabel('Nº de experimentos')
fig, ax = plt.subplots(figsize=(15,6))
ax.bar(dados['tempo'].unique(), height=dados['tempo'].value_counts(ascending=True), width=20, color='red')
ax.set_xticks(dados['tempo'].unique())
ax.set_title('Distribuição dos experimentos por tempo')
ax.set_xlabel('Tempo observado')
ax.set_ylabel('Nº de experimentos')
barplot_dose = dados['dose'].value_counts().plot.bar()
barplot_dose.set_title('Distribuição dos experimentos por dose')
barplot_dose.set_xlabel('Dose administrada')
barplot_dose.set_ylabel('Nº de experimentos')
```
###Desafio 4: Quantos tipos de drogas foram investigados?
```
dados['droga'].nunique()
```
###Desafio 5: Procurar a documentação do query (no pandas) e resolver o desafio de criar a máscara de valores g-0 maiores que zero
```
dados.query('g0 > 0')
dados.query('dose == "D1"') #fazendo mais um uso do Query
```
###Desafio 6: Renomear as colunas tirando o hífen
```
dados.columns = dados.columns.str.replace("-","")
dados.head()
```
###Desafio 7: Fazer um resumo das descobertas
Preferi deixar as anotações ao longo das células, se você leu até aqui, provavelmente viu minhas notas!
##Observando a distribuição dos genes g0 e g1
```
#histograma da distribuição dos resultados de g0
ax = sns.displot(data=dados, x='g0', kde=True)
print(dados['g0'].min())
print(dados['g0'].max())
print(dados['g0'].mean())
print(dados['g0'].median())
print(dados['g0'].var())
print(dados['g0'].skew())
sns.displot(data=dados, x='g1', kde=True)
print(dados['g1'].min())
print(dados['g1'].max())
print(dados['g1'].mean())
print(dados['g1'].median())
print(dados['g1'].var())
print(dados['g1'].skew())
```
###Aula 02
```
#forma interessante de substituir nome de coluna
#através de um mapa
mapa = {'droga':'composto'}
dados.rename(columns=mapa, inplace=True)
```
Criando um countplot com os primeiros 5 compostos mais usados
```
comp = dados['composto'].value_counts().index[:5]
#coletando as infos dos 5 compostos com o query
d_comp = dados.query('composto in @comp') #o @ serve para declarar que a váriavel foi definida pelo python e não pelo dados
```
###Desafio 9: Melhorar a visualização e estética dos gráficos
```
#usando o Seaborn
fig, ax = plt.subplots(figsize=(15,6))
sns.set() #rodar pelo menos uma vez o .set() tras as novas configurações automáticas de estilização do Seaborn
ax = sns.countplot(data=d_comp, x='composto')
ax.set_title('5 compostos mais usados', )
ax.set_xlabel('Composto')
ax.set_ylabel('vezes usado')
plt.show() #colocar ele mesmo com o matplotlib inline some com o text que vem em cima do gráfico
#loc nos genes 'g'
dados.loc[:,'g0':'g771'].describe()
```
Histograma das médias dos genes 'g'
```
#com o .T fazemos a transposição do DataFrame
describe_g = dados.loc[:,'g0':'g771'].describe().T
#plotando o histograma das médias
hist_g = sns.histplot(describe_g, x='mean', kde=True)
plt.show()
#histograma dos desvios-padrão
hist_g = sns.histplot(describe_g, x='std', kde=True)
plt.show()
```
Observando as variáveis 'c'
```
describe_c = dados.loc[:,'c0':'c99'].describe().T
#histograma das médias
sns.histplot(data=describe_c, x='mean', kde=True)
plt.show()
```
No Dataframe, cada 'c' respresenta linhagens de células, o pressuposto de ter vários tipos de células é para garantir a famosa independência estatística, e não gerar o viés de que o o medicamento agiu em determinado tipo, ou que foi o tipo que gerou o resultado da célula, e também garantir saber possíveis colaterais.
Os valores registrados em c são as viabilidades, ou seja, "o quanto as células sobreviveram" à exposição daqueles compostos
###Plotando Boxplots
```
sns.boxplot(data=dados, x='g0')
#boxplot da resposta de g0 por dose administrada
plt.figure(figsize=(10,6))
sns.boxplot(data=dados, x='g0', y='dose', )
#boxplot da resposta de g0 por tratamento
sns.boxplot(data=dados, x='g0', y='tratamento')
```
Plotando um boxplot mais bonito e mais completo
```
fig, ax = plt.subplots(figsize=(10,9))
sns.set_style('darkgrid')
sns.set_context('talk')
ax = sns.boxplot(data=dados, x='tratamento', y='g0', hue='dose', palette='Paired')
ax.set_xlabel('Tipo de tratamento', fontdict={'fontsize':20})
ax.set_ylabel('gene g0')
ax.set_title('Quartis e mediana por tratamento e dose', fontdict={'fontsize':20, 'verticalalignment':'center'})
plt.show()
```
##Dia 3
Função nova: ".crosstab" que cria uma frequency table
Para filtrar mais de um dado, nas colunas ou linhas (e criar um MultiIndex) devemos inserir os **colchetes antes**(procedimento padrão no Pandas).
Podemos normalizar os valores de várias formas (ver documetação) com o **'normalize='**.
Para adicionar um valor específico que desejamos ver os dados correspondentes a ele, usar **'value='** e podemos inclusive, colocar uma função (média, mediana, std, etc.) com o **'aggfunc='**.
```
pd.crosstab(dados['dose'], [dados['tratamento'], dados['tempo']])
#outra forma de fazer
pd.crosstab([dados['dose'], dados['tempo']], dados['tratamento'])
#plotando as proporções
pd.crosstab([dados['dose'], dados['tempo']], dados['tratamento'], normalize=True) * 100
#plotando as proporções pelo index (nesse caso será em relação as linhas)
pd.crosstab([dados['dose'], dados['tempo']], dados['tratamento'], normalize='index')
pd.crosstab([dados['dose'], dados['tempo']], dados['tratamento'], values=dados['g0'], aggfunc='mean')
```
###Desafio 08: Fazer uma tabela parecida com a crosstab mas utilizando o Groupby
Nota pessoal: Eu gosto muito de Groupby, ela é muito poderosa
```
groupby = dados.groupby(by=['dose', 'tratamento','tempo']).count()
groupby.iloc[:13,2:3]
groupby.iloc[:13,2:3].T
```
###Desafio 9: Normalizar o crosstab pela coluna
```
pd.crosstab([dados['dose'],dados['tempo']], dados['tratamento'], normalize='columns')
```
###Desafio 10: Quais outros agregadores existem?
Média
```
pd.crosstab([dados['dose'], dados['tempo']], dados['tratamento'], values=dados['g0'], aggfunc='mean')
```
Mediana
```
pd.crosstab([dados['dose'], dados['tempo']], dados['tratamento'], values=dados['g0'], aggfunc='median')
```
Standard Deviation a.k.a Desvio-padrão
```
pd.crosstab([dados['dose'], dados['tempo']], dados['tratamento'], values=dados['g0'], aggfunc='std')
```
Variância
```
pd.crosstab([dados['dose'], dados['tempo']], dados['tratamento'], values=dados['g0'], aggfunc='var')
```
###Desafio 11: Explorar o Melt
Esse método pode ser aplicado tanto em pd (pandas) quanto diretamente no Dataframe
```
pd.melt(dados, id_vars=['dose','tratamento', 'tempo'], value_vars=['g0'])
dados.melt(id_vars=['dose','tratamento','tempo'], value_vars=['g0'])
dados.melt(id_vars=['dose','tratamento','tempo'], value_vars=['g0'])[:5]
#podemos aplicar o index como sempre para dar uma filtrada
dados.melt(id_vars=['dose','tratamento','tempo'], value_vars=['g0'], value_name='respostas do gene 0').mean()
#observando a média do gene 0 pela dose, tratamento e tempo
```
###Explorando as correlações e variações de g0 e g1
```
#usando a dispersão
sns.scatterplot(data=dados, x='g0', y='g1')
sns.scatterplot(data=dados, x='g0', y='g3', )
#o jointplot mostra a distruibuição junto com a dispersão
sns.jointplot(data=dados, x='g0', y='g3', kind='reg')
#outra forma de ver a linha de distribuição é com o lmplot
sns.lmplot(data=dados, x='g0', y='g3', line_kws={'color':'red'})
sns.lmplot(data=dados, x='g0', y='g3', line_kws={'color':'red'}, hue='dose', col='tratamento', row='tempo')
```
Observando as correlações
O Próprio Pandas pode nos mostrar as correlações
```
#.corr()
dados.loc[:,'g0':'g771'].corr()
```
No geral, utilizamos um gráfico 'heatmap' para ver as correlações.
Aqui, usaremos um ctrl+c ctrl+v da matriz diagonal de correlação
```
corr = dados.loc[:,'g0':'g50'].corr()
# Generate a mask for the upper triangle
mask = np.triu(np.ones_like(corr, dtype=bool))
# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(30, 15))
# Generate a custom diverging colormap
cmap = sns.diverging_palette(230, 20, as_cmap=True)
# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr, mask=mask, cmap=cmap, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5})
```
VELHO LEMBRETE: **Correlação não é causalidade!**
Correlações de C
```
corr_c = dados.loc[:,'c0':'c50'].corr()
# Generate a mask for the upper triangle
mask = np.triu(np.ones_like(corr_c, dtype=bool))
# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(30, 15))
# Generate a custom diverging colormap
cmap = sns.diverging_palette(230, 20, as_cmap=True)
# Draw the heatmap with the mask and correct aspect ratio
sns.heatmap(corr_c, mask=mask, cmap=cmap, center=0,
square=True, linewidths=.5, cbar_kws={"shrink": .5})
```
###Desafio 12: Explorar a correlação entre expressões gênicas g e os tipos célulares c
```
```
##Dia 4
###Hoje vamos observar os resultados dos testes experimentais
```
dados_resultados = pd.read_csv('https://github.com/alura-cursos/imersaodados3/blob/main/dados/dados_resultados.csv?raw=true')
dados_resultados.head()
```
De forma superficial, essa base contém os mecanismos de ação, se 1, foi ativado pelo experimento, se 0 é que não foi ativado pelo experimento
```
dados_resultados.info()
```
###Três formas de fazer a contagem dos mecanismos de ação
Com o Iloc
```
contagem_moa = dados_resultados.iloc[:,1:].sum().sort_values(ascending=False)
contagem_moa
```
COm o select_dtypes
```
contagem_moa = dados_resultados.select_dtypes('int64').sum().sort_values(ascending=False)
contagem_moa
```
Com o drop
```
contagem_moa = dados_resultados.drop('id', axis=1).sum().sort_values(ascending=False)
contagem_moa
dados_resultados['n_moa'] = dados_resultados.drop('id', axis=1).sum(axis=1)
dados_resultados['moa_ativado'] = dados_resultados['n_moa'] != 0
dados_resultados.head()
dados_final = pd.merge(dados, dados_resultados[['id', 'n_moa', 'moa_ativado']], on='id')
dados_final.head(2)
```
###Desafio 01: Encontrar o top10 das ações do MoA (inibidor, agonista, etc.)
```
copy_dados = dados_resultados
copy_dados
#contando quantos tem inhibitor
len(copy_dados.columns[copy_dados.columns.str.contains('inhibitor')])
#Contando quantos tem agonist
len(copy_dados.columns[copy_dados.columns.str.contains('agonist')])
#vendo os que não contém nem inhibitor nem agonist
copy_dados.columns[(copy_dados.columns.str.contains('agonist') == False) & (copy_dados.columns.str.contains('inhibitor')==False)]
```
###Desafio 2: Criar uma coluna True False (0,1) para a coluna tratamento
```
dados_final['eh_controle'] = dados_final['tratamento'] == 'com_controle'
dados_final['eh_controle'].value_counts()
```
###Desafio 3: Criar colunas para 24, 48 e 72 de True e False
```
dados_final['tempo'].dtype
dados_final['24h'] = dados_final['tempo'] == 24
dados_final.head(2)
dados_final['48h'] = dados_final['tempo'] == 48
dados_final['72h'] = dados_final['tempo'] == 72
```
###Desafio 4: Criar coluna para dose
```
dados_final['d1'] = dados_final['dose'] == 'D1'
dados_final['d2'] = dados_final['dose'] == 'D2'
```
###Desafio 4: Análise mais profunda para quando há tempo e dose
```
dados_final['composto'].value_counts()
#não esquecer: para teste boleano não aplicar o filtro (nome do dataset no início), para fazer slice ai sim se coloca o filtro, como no caso abaixo
analise_comp = dados_final[(dados_final['composto'] == 'cacb2b860') | (dados_final['composto'] == '5628cb3ee')]
analise_comp
sns.catplot(data=analise_comp, x='composto', y='g0', hue='tratamento', col='dose', row='tempo', kind='box')
```
Observando a partir da coluna eh_controle True False que criamos
```
sns.catplot(data=analise_comp, x='composto', y='g0', hue='eh_controle', col='dose', row='tempo', kind='box')
```
Passando ordem explícita para o hue de como ordenar
```
sns.catplot(data=analise_comp, x='composto', y='g0', hue='tratamento', col='dose', row='tempo', kind='box', hue_order=['com_droga','com_controle'])
```
##Dia 5
No último dia da imersão, estamos implementando alguns modelos de machine learning para auxiliar no Drug Discovery
```
dados_final.head()
```
No train test split, podemos passar algumas variáveis, para que tenhamos um modelo de comparação para os outros modelos que vamos testar (a benchmark), são eles: random_state, que vai travar em determinada acurácia o modelo e stratify que vai garantir que a acurácia seja igual à realidade.
```
from sklearn.model_selection import train_test_split #biblioteca para separar as bases de dados para treinar e testar a capacidade do modelo
x = dados_final.select_dtypes('float64')
y = dados_final['moa_ativado']
x_treino, x_teste, y_treino, y_teste = train_test_split(x,y, test_size=0.2, stratify=y, random_state=350)
from sklearn.linear_model import LogisticRegression #modelo de regressão logística
from sklearn.model_selection import train_test_split
modelo_rlogistica = LogisticRegression(max_iter=1000)
modelo_rlogistica.fit(x_treino, y_treino)
modelo_rlogistica.score(x_teste, y_teste)
```
Um método interessante para comparar a capacidade do modelo é o uso de modelo Dummy (bobo e simples) para ver se nosso modelo realmente está fazendo uma previsão melhor que "chutando".
Obs: na página do Sklearn sobre o Dummy há um alerta de não usá-lo para problemas reais.
```
from sklearn.dummy import DummyClassifier
from sklearn.metrics import accuracy_score
dummy_model = DummyClassifier('most_frequent')
dummy_model.fit(x_treino, y_treino)
previsao_dummy = dummy_model.predict(x_teste)
accuracy_score(y_teste, previsao_dummy)
```
Com o benchmark feito, agora podemos construir nossa tentativa de um novo modelo com melhor capacidade de previsão, o proposto foi: árvore de decisão (Decision Tree)
```
from sklearn.tree import DecisionTreeClassifier
x = dados_final.select_dtypes('float64')
y = dados_final['moa_ativado']
x_treino, x_teste, y_treino, y_teste = train_test_split(x,y, test_size=0.2, stratify=y, random_state=350)
tree = DecisionTreeClassifier(max_depth=3)
tree.fit(x_treino, y_treino)
tree.score(x_teste, y_teste)
```
O max_depth é a profundidade dos níveis de decisão da árvore, nesse caso, ela está com 3, isso PODE SER um dos problemas da baixa acurácia.
Vamos testar para uma profundidade maior e ver o que acontece.
```
tree = DecisionTreeClassifier(max_depth=10)
tree.fit(x_treino, y_treino)
tree.score(x_teste, y_teste)
teste=[]
treino=[]
for i in range(1,15):
modelo_arvore = DecisionTreeClassifier(max_depth = i)
modelo_arvore.fit(x_treino, y_treino)
teste.append(modelo_arvore.score(x_teste, y_teste))
treino.append(modelo_arvore.score(x_treino, y_treino))
teste
treino
sns.lineplot(x=range(1,15), y=treino, label='treino')
sns.lineplot(x=range(1,15), y=teste, label='teste')
```
Podemos ver que ao contrário do esperado, o algoritmo passou a performar melhor no treino e pior no teste, esse é um processo conhecido como 'overfitting', ou uma especialização do algoritmo na base de treino e que portanto, perde a capacidade de generalização.
Já que aprofundar não é uma forma sempre perfeita de aplicar, podemos fazer com que o dataset seja varrido por várias árvores de decisão, esse é o algoritmo chamado de Random Forest.
Como funciona?
Ele divide o dataset em várias amostras e aplica as árvores de decisão nelas
```
from sklearn.ensemble import RandomForestClassifier
#aplicação é semelhante ao Decision Tree
x = dados_final.drop(columns=['id', 'moa_ativado', 'n_moa', 'tratamento','tempo','dose','composto']) #podemos ver que o Random Forest consegue arcar com tipos diversos de dados
y = dados_final['moa_ativado']
x_treino, x_teste, y_treino, y_teste = train_test_split(x,y, test_size=0.2, stratify=y, random_state=350)
```
Testei minha Random Forest para vários parâmetros e cheguei a esses resultados:
```
random_forest = RandomForestClassifier(n_estimators=1000)
random_forest.fit(x_treino, y_treino)
random_forest.score(x_teste, y_teste)
random_forest = RandomForestClassifier(n_estimators=1000, max_depth=8)
random_forest.fit(x_treino, y_treino)
random_forest.score(x_teste, y_teste)
random_forest = RandomForestClassifier()
random_forest.fit(x_treino, y_treino)
random_forest.score(x_teste, y_teste)
lista_treino = []
lista_teste = []
for i in range(200,238):
random_forest = RandomForestClassifier(n_estimators=i)
random_forest.fit(x_treino, y_treino)
lista_treino.append(random_forest.score(x_treino, y_treino))
lista_teste.append(random_forest.score(x_teste, y_teste))
lista_treino
lista_teste
```
| github_jupyter |
<div class="alert alert-block alert-info">
<b><h1>ENGR 1330 Computational Thinking with Data Science </h1></b>
</div>
Copyright © 2021 Theodore G. Cleveland and Farhang Forghanparast
Last GitHub Commit Date:
# 14: Visual display of data
This lesson is a prelude to the `matplotlib` external module package, used to construct
line charts, scatter plots, bar charts, box plot, and histograms. `matplotlib` is used herein to generate some different plots; with additional detail in a subseqent lesson.
- plot types
- plot uses
- plot conventions
---
## Objectives
- List common plot types and their uses
- Identify the parts of a line (or scatter) plot
1. Define the ordinate, abscissa
2. Define independent and dependent variables
- Define how to plot experimental data (observations) and theoretical data (model)
1. Marker conventions
2. Line conventions
3. Legends
---
### About `matplotlib`
Quoting from: https://matplotlib.org/tutorials/introductory/pyplot.html#sphx-glr-tutorials-introductory-pyplot-py
`matplotlib.pyplot` is a collection of functions that make matplotlib work like MATLAB. Each pyplot function makes some change to a figure: e.g., creates a figure, creates a plotting area in a figure, plots some lines in a plotting area, decorates the plot with labels, etc.
In `matplotlib.pyplot` various states are preserved across function calls, so that it keeps track of things like the current figure and plotting area, and the plotting functions are directed to the current axes (please note that "axes" here and in most places in the documentation refers to the axes part of a figure and not the strict mathematical term for more than one axis).
**Computational thinking (CT)** concepts involved are:
- `Decomposition` : Break a problem down into smaller pieces; separating plotting from other parts of analysis simplifies maintenace of scripts
- `Abstraction` : Pulling out specific differences to make one solution work for multiple problems; wrappers around generic plot calls enhances reuse
- `Algorithms` : A list of steps that you can follow to finish a task; Often the last step and most important to make professional graphics to justify the expense (of paying you to do engineering) to the client.
---
## Graphics Conventions for Plots
```{note}
This section needs to have graphics replaced with author generated examples in future editions
```
### Terminology: Ordinate, Abscissa, Dependent and Independent Variables
A few terms are used in describing plots:
- Abscissa – the horizontal axis on a plot (the left-right axis)
- Ordinate – the vertical axis on a plot (the up-down axis)
A few terms in describing data models
- Independent Variable (Explainatory, Predictor, Feature, ...) – a variable that can be controlled/manipulated in an experiment or theoretical analysis
- Dependent Variable (Response, Prediction, ...) – the variable that measured/observed as a function of the independent variable
Plotting convention in most cases assigns explainatory variables to the horizontal axis (e.g. Independent variable is plotted on the Abscissa) and the response variable(s) to the vertical axis (e.g. Dependent Variable is plotted on the Ordinate)
---

---
#### Conventions for Proper Plots
- Include a title OR a caption with a brief description of the plot
- Label both axes clearly
- Include the variable name, the variable, and the unit in each label
---

---
- If possible, select increments for both the x and y axes that provide for easy interpolation
---

---
- Include gridlines
- Show experimental measurements as symbols
- Show model (theoretical) relationships as lines
---

---
- Use portrait orientation when making your plot
- Make the plot large enough to be easily read
- If more than one experimental dataset is plotted
- Use different shapes for each dataset
- Use different colors for each dataset
- Include a legend defining the datasets
---


---

---
### Line Charts using `matplotlib`
A line chart or line plot or line graph or curve chart is a type of chart which displays information as a series of data points called 'markers' connected by straight line segments.
It is a basic type of chart common in many fields. It is similar to a scatter plot (below) except that the measurement points are **ordered** (typically by their x-axis value) and joined with straight line segments.
A line chart is often used to visualize a trend in data over intervals of time – a time series – thus the line is often drawn chronologically.
The x-axis spacing is sometimes tricky, hence line charts can unintentionally decieve - so be careful that it is the appropriate chart for your application.
#### Example
Consider the experimental data below
|Elapsed Time (s)|Speed (m/s)|
|---:|---:|
|0 |0|
|1.0 |3|
|2.0 |7|
|3.0 |12|
|4.0 |20|
|5.0 |30|
|6.0 | 45.6|
Show the relationship between time and speed. Is the relationship indicating acceleration? How much?
```
# import the package
from matplotlib import pyplot as plt
# Create two lists; time and speed.
time = [0,1.0,2.0,3.0,4.0,5.0,6.0]
speed = [0,3,7,12,20,30,45.6]
# Create a line chart of speed on y axis and time on x axis
mydata = plt.figure(figsize = (10,5)) # build a square drawing canvass from figure class
plt.plot(time, speed, c='red', marker='v',linewidth=1) # basic line plot
plt.show()
time = [0,1.0,4.0,5.0,6.0,2.0,3.0]
speed = [0,3,20,30,45.6,7,12]
# Create a line chart of speed on y axis and time on x axis
mydata = plt.figure(figsize = (10,5)) # build a square drawing canvass from figure class
plt.plot(time, speed, c='green', marker='o',linewidth=1) # basic line plot
plt.show()
# Estimate acceleration (naive)
dvdt = (max(speed) - min(speed))/(max(time)-min(time))
plottitle = 'Average acceleration %.1f' % (dvdt) + r' ($\frac{m}{s^2}$)'
seriesnames = ['Data','Model']
modely = [min(speed),max(speed)]
modelx = [min(time),max(time)]
mydata = plt.figure(figsize = (10,5)) # build a square drawing canvass from figure class
plt.plot(time, speed, c='red', marker='v',linewidth=1) # basic line plot
plt.plot(modelx, modely, c='blue',linewidth=1) # basic line plot
plt.xlabel('Time (sec)')
plt.ylabel('Speed '+r'($\frac{m}{s}$)')
plt.legend(seriesnames)
plt.title(plottitle)
plt.show()
```
---
### Line Charts in Pandas
The next few examples use graphics in pandas. The example below uses a database table from [census_18.csv](http://54.243.252.9/engr-1330-webroot/1-Lessons/Lesson12/census_18.csv)
```
import pandas as pd
df = pd.read_csv('census_18.csv')
df.head()
df.plot.line(x="AGE", y="2010", label="Born in 2014", c="blue")
ax = df.plot.line(x="AGE", y="2010", label="Born in 2014", c="blue")
df.plot.line(x="AGE", y="2014", label="Born in 2015", c="red", ax=ax)
import matplotlib.pyplot as plt
age = df['AGE']
born2010 = df['2010']
born2014 = df['2014']
plt.plot(age, born2010, c='blue')
plt.show()
plt.plot(age, born2010, c='blue', label='Born in 2010')
plt.plot(age, born2014, c='red', label='Born in 2014')
plt.legend()
plt.show()
```
## References
1. Grus, Joel (2015-04-14). Data Science from Scratch: First Principles with Python
(Kindle Locations 1190-1191). O'Reilly Media. Kindle Edition.
2. Call Expressions in "Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science" https://www.inferentialthinking.com/chapters/03/3/Calls.html
3. Functions and Tables in "Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science" https://www.inferentialthinking.com/chapters/08/Functions_and_Tables.html
4. Visualization in "Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science" https://www.inferentialthinking.com/chapters/07/Visualization.html
5. Documentation; The Python Standard Library; 9. Numeric and Mathematical Modules https://docs.python.org/2/library/math.html
6. https://matplotlib.org/gallery/lines_bars_and_markers/horizontal_barchart_distribution.html?highlight=horizontal%20bar%20chart
7. https://www.geeksforgeeks.org/bar-plot-in-matplotlib/
## Addendum (Scripts that are Interactive)
:::{note}
The addendum is intended for in-class demonstration
:::
```
# python script to illustrate plotting
# CODE BELOW IS ADAPTED FROM:
# Grus, Joel (2015-04-14). Data Science from Scratch: First Principles with Python
# (Kindle Locations 1190-1191). O'Reilly Media. Kindle Edition.
#
from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
years = [1950, 1960, 1970, 1980, 1990, 2000, 2010] # define one list for years
gdp = [300.2, 543.3, 1075.9, 2862.5, 5979.6, 10289.7, 14958.3] # and another one for Gross Domestic Product (GDP)
plt.plot( years, gdp, color ='green', marker ='o', linestyle ='solid') # create a line chart, years on x-axis, gdp on y-axis
# what if "^", "P", "*" for marker?
# what if "red" for color?
# what if "dashdot", '--' for linestyle?
plt.title("Nominal GDP")# add a title
plt.ylabel("Billions of $")# add a label to the x and y-axes
plt.xlabel("Year")
plt.show() # display the plot
```
Now lets put the plotting script into a function so we can make line charts of any two numeric lists
```
def plotAline(list1,list2,strx,stry,strtitle): # plot list1 on x, list2 on y, xlabel, ylabel, title
from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
plt.plot( list1, list2, color ='green', marker ='o', linestyle ='solid') # create a line chart, years on x-axis, gdp on y-axis
plt.title(strtitle)# add a title
plt.ylabel(stry)# add a label to the x and y-axes
plt.xlabel(strx)
plt.show() # display the plot
return #null return
# wrapper
years = [1950, 1960, 1970, 1980, 1990, 2000, 2010] # define two lists years and gdp
gdp = [300.2, 543.3, 1075.9, 2862.5, 5979.6, 10289.7, 14958.3]
print(type(years[0]))
print(type(gdp[0]))
plotAline(years,gdp,"Year","Billions of $","Nominal GDP")
```
## Example
Use the plotting script and create a function that draws a straight line between two points.
```
def Line():
from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
x1 = input('Please enter x value for point 1')
y1 = input('Please enter y value for point 1')
x2 = input('Please enter x value for point 2')
y2 = input('Please enter y value for point 2')
xlist = [x1,x2]
ylist = [y1,y2]
plt.plot( xlist, ylist, color ='orange', marker ='*', linestyle ='solid')
#plt.title(strtitle)# add a title
plt.ylabel("Y-axis")# add a label to the x and y-axes
plt.xlabel("X-axis")
plt.show() # display the plot
return #null return
```
---
## Laboratory 14
**Examine** (click) Laboratory 15 as a webpage at [Laboratory 14.html](http://54.243.252.9/engr-1330-webroot/8-Labs/Lab14/Lab14.html)
**Download** (right-click, save target as ...) Laboratory 15 as a jupyterlab notebook from [Laboratory 14.ipynb](http://54.243.252.9/engr-1330-webroot/8-Labs/Lab14/Lab14.ipynb)
<hr><hr>
## Exercise Set 14
**Examine** (click) Exercise Set 15 as a webpage at [Exercise 14.html](http://54.243.252.9/engr-1330-webroot/8-Labs/Lab14/Lab14-TH.html)
**Download** (right-click, save target as ...) Exercise Set 15 as a jupyterlab notebook at [Exercise Set 14.ipynb](http://54.243.252.9/engr-1330-webroot/8-Labs/Lab14/Lab14-TH.ipynb)
| github_jupyter |
```
from os import listdir
from numpy import array
from keras.preprocessing.text import Tokenizer, one_hot
from keras.preprocessing.sequence import pad_sequences
from keras.models import Model, Sequential, model_from_json
from keras.utils import to_categorical
from keras.layers.core import Dense, Dropout, Flatten
from keras.optimizers import RMSprop
from keras.layers.convolutional import Conv2D
from keras.callbacks import ModelCheckpoint
from keras.layers import Embedding, TimeDistributed, RepeatVector, LSTM, concatenate , Input, Reshape, Dense
from keras.preprocessing.image import array_to_img, img_to_array, load_img
import numpy as np
dir_name = 'resources/eval_light/'
# Read a file and return a string
def load_doc(filename):
file = open(filename, 'r')
text = file.read()
file.close()
return text
def load_data(data_dir):
text = []
images = []
# Load all the files and order them
all_filenames = listdir(data_dir)
all_filenames.sort()
for filename in (all_filenames):
if filename[-3:] == "npz":
# Load the images already prepared in arrays
image = np.load(data_dir+filename)
images.append(image['features'])
else:
# Load the boostrap tokens and rap them in a start and end tag
syntax = '<START> ' + load_doc(data_dir+filename) + ' <END>'
# Seperate all the words with a single space
syntax = ' '.join(syntax.split())
# Add a space after each comma
syntax = syntax.replace(',', ' ,')
text.append(syntax)
images = np.array(images, dtype=float)
return images, text
train_features, texts = load_data(dir_name)
# Initialize the function to create the vocabulary
tokenizer = Tokenizer(filters='', split=" ", lower=False)
# Create the vocabulary
tokenizer.fit_on_texts([load_doc('resources/bootstrap.vocab')])
# Add one spot for the empty word in the vocabulary
vocab_size = len(tokenizer.word_index) + 1
# Map the input sentences into the vocabulary indexes
train_sequences = tokenizer.texts_to_sequences(texts)
# The longest set of boostrap tokens
max_sequence = max(len(s) for s in train_sequences)
# Specify how many tokens to have in each input sentence
max_length = 48
def preprocess_data(sequences, features):
X, y, image_data = list(), list(), list()
for img_no, seq in enumerate(sequences):
for i in range(1, len(seq)):
# Add the sentence until the current count(i) and add the current count to the output
in_seq, out_seq = seq[:i], seq[i]
# Pad all the input token sentences to max_sequence
in_seq = pad_sequences([in_seq], maxlen=max_sequence)[0]
# Turn the output into one-hot encoding
out_seq = to_categorical([out_seq], num_classes=vocab_size)[0]
# Add the corresponding image to the boostrap token file
image_data.append(features[img_no])
# Cap the input sentence to 48 tokens and add it
X.append(in_seq[-48:])
y.append(out_seq)
return np.array(X), np.array(y), np.array(image_data)
X, y, image_data = preprocess_data(train_sequences, train_features)
#Create the encoder
image_model = Sequential()
image_model.add(Conv2D(16, (3, 3), padding='valid', activation='relu', input_shape=(256, 256, 3,)))
image_model.add(Conv2D(16, (3,3), activation='relu', padding='same', strides=2))
image_model.add(Conv2D(32, (3,3), activation='relu', padding='same'))
image_model.add(Conv2D(32, (3,3), activation='relu', padding='same', strides=2))
image_model.add(Conv2D(64, (3,3), activation='relu', padding='same'))
image_model.add(Conv2D(64, (3,3), activation='relu', padding='same', strides=2))
image_model.add(Conv2D(128, (3,3), activation='relu', padding='same'))
image_model.add(Flatten())
image_model.add(Dense(1024, activation='relu'))
image_model.add(Dropout(0.3))
image_model.add(Dense(1024, activation='relu'))
image_model.add(Dropout(0.3))
image_model.add(RepeatVector(max_length))
visual_input = Input(shape=(256, 256, 3,))
encoded_image = image_model(visual_input)
language_input = Input(shape=(max_length,))
language_model = Embedding(vocab_size, 50, input_length=max_length, mask_zero=True)(language_input)
language_model = LSTM(128, return_sequences=True)(language_model)
language_model = LSTM(128, return_sequences=True)(language_model)
#Create the decoder
decoder = concatenate([encoded_image, language_model])
decoder = LSTM(512, return_sequences=True)(decoder)
decoder = LSTM(512, return_sequences=False)(decoder)
decoder = Dense(vocab_size, activation='softmax')(decoder)
# Compile the model
model = Model(inputs=[visual_input, language_input], outputs=decoder)
optimizer = RMSprop(lr=0.0001, clipvalue=1.0)
model.compile(loss='categorical_crossentropy', optimizer=optimizer)
#Save the model for every 2nd epoch
filepath="org-weights-epoch-{epoch:04d}--val_loss-{val_loss:.4f}--loss-{loss:.4f}.hdf5"
checkpoint = ModelCheckpoint(filepath, monitor='val_loss', verbose=1, save_weights_only=True, period=2)
callbacks_list = [checkpoint]
# Train the model
model.fit([image_data, X], y, batch_size=1, shuffle=False, validation_split=0.1, callbacks=callbacks_list, verbose=1, epochs=50)
```
| github_jupyter |
```
```
# **Deep Convolutional Generative Adversarial Network (DC-GAN):**
DC-GAN is a foundational adversarial framework developed in 2015.
It had a major contribution in streamlining the process of designing adversarial frameworks and visualizing intermediate representations, thus, making GANs more accessible to both researchers and practitioners. This was achieved by enhancing the concept of adversarial training (introduced by [Ian Goodfellow](https://arxiv.org/abs/1406.2661) one year prior) with then-state-of-the-art advances in deep learning such as strided and fractional-strided convolutions, batch normalization and LeakyReLU activations.
In this programming exercise, you are tasking with creating a miniature [Deep Convolutional Generative Adversarial Network](https://arxiv.org/pdf/1511.06434.pdf) (DC-GAN) framework for the generation of MNIST digits. The goal is to bridge the gap between the theoretical concept and the practical implementation of GANs.

The desired DC-GAN network should consist of two principal components: the generator $G$ and the discriminator $D$. The generator should receive as input a 100-dimensional random noise vector $z$ and outputs a synthetically generated MNIST digit $G(z)$ of pixel size $28 \times 28 \times 1$. As the adversarial training continues over time, the output digits should increasingly resemble handwritten digits as shown below.

The discriminator network receives both the synthetically generated digits as well as ground-truth MNIST digits $x$ as inputs. $D$ is trained as a binary classifier. In other words, it is trained to assign the correct label (real vs fake) to both sets of input images. On the other hand side, $G$ is motivated to fool the discriminator into making a false decision by implicitly improving the quality of the output synthetic image. This adversarial training procedure, where both networks are trained with opposing goals, is represented by the following min-max optimization task:
>$\underset{G}{\min} \underset{D}{\max} \mathcal{L}_{\textrm{adv}} =\underset{G}{\min} \underset{D}{\max} \; \mathbb{E}_{x} \left[\textrm{log} D(x) \right] + \mathbb{E}_{z} \left[\textrm{log} \left( 1 - D\left(G(z)\right) \right) \right]$
# Implementation
### Import Import TensorFlow and other libraries
```
from __future__ import absolute_import, division, print_function, unicode_literals
!pip install tensorflow-gpu==2.0.0-alpha0
import tensorflow as tf
tf.__version__
# To generate GIFs for illustration
!pip install imageio
import glob
import imageio
import matplotlib.pyplot as plt
import numpy as np
import os
import PIL
from tensorflow.keras import layers
import time
from IPython import display
```
### Load and prepare the dataset
You will use the MNIST dataset to train the generator and the discriminator. The generator will generate handwritten digits resembling the MNIST data.
You can also repeat the exercise for other avaliable variations of the MNIST dataset such as: EMNIST, Fashio-MNIST or KMNIST. For more details, please refer to [tensorflow_datasets](https://www.tensorflow.org/datasets/datasets).
```
(train_images, train_labels), (_, _) = tf.keras.datasets.mnist.load_data()
train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')
train_images = (train_images - 127.5) / 127.5 # Normalize the images to [-1, 1]
BUFFER_SIZE = 60000
BATCH_SIZE = 256
# Batch and shuffle the data
train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
```
## Create the models
Both the generator and discriminator are defined using the [Keras Sequential API](https://www.tensorflow.org/guide/keras#sequential_model).
### The Generator
The generator uses `tf.keras.layers.Conv2DTranspose` (fractional-strided convolutional) layers to produce an image from an input noise vector. Start with a fully connected layer that takes this vector as input, then upsample several times until you reach the desired image size of $28\times 28 \times 1$. Utilize the `tf.keras.layers.LeakyReLU` activation and batch normalization for each intermediate layer, except the output layer which should use tanh.
```
def make_generator_model():
model = tf.keras.Sequential()
model.add(layers.Dense(7*7*256, use_bias=False, input_shape=(100,)))
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
model.add(layers.Reshape((7, 7, 256)))
assert model.output_shape == (None, 7, 7, 256) # Note: None is the batch size
# Layer 2: Hint use layers.Conv2DTranspose with 5x5 kernels and appropriate stride
model.add(layers.Conv2DTranspose(128, (5, 5), strides=(1, 1), padding='same', use_bias=False))
assert model.output_shape == (None, 7, 7, 128)
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
# Layer 3
model.add(layers.Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', use_bias=False))
assert model.output_shape == (None, 14, 14, 64)
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU())
#Layer4
model.add(layers.Conv2DTranspose(1, (5, 5), strides=(2, 2), padding='same', use_bias=False, activation='tanh'))
assert model.output_shape == (None, 28, 28, 1)
return model
```
Use the (as yet untrained) generator to create an image.
```
generator = make_generator_model()
noise = tf.random.normal([1, 100])
generated_image = generator(noise, training=False)
plt.imshow(generated_image[0, :, :, 0], cmap='gray')
```
### The Discriminator
The discriminator is a CNN-based image classifier.
```
def make_discriminator_model():
model = tf.keras.Sequential()
model.add(layers.Conv2D(64, (5, 5), strides=(2, 2), padding='same',
input_shape=[28, 28, 1]))
model.add(layers.LeakyReLU())
model.add(layers.Dropout(0.3))
model.add(layers.Conv2D(128, (5, 5), strides=(2, 2), padding='same'))
model.add(layers.LeakyReLU())
model.add(layers.Dropout(0.3))
model.add(layers.Flatten())
model.add(layers.Dense(1))
return model
```
Use the (as yet untrained) discriminator to classify the generated images as real or fake. The model will be trained to output positive values for real images, and negative values for fake images.
```
discriminator = make_discriminator_model()
decision = discriminator(generated_image)
print (decision)
```
## Define the loss and optimizers
Define loss functions and optimizers for both models.
```
# This method returns a helper function to compute the binary cross entropy loss
cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True)
```
### Discriminator loss
Define the discriminator loss function. [Hint](https://www.tensorflow.org/api_docs/python/tf/keras/losses/BinaryCrossentropy): compare the discriminator's predictions on real images to an array of 1s.
```
def discriminator_loss(real_output, fake_output):
real_loss = cross_entropy(tf.ones_like(real_output), real_output)
fake_loss = cross_entropy(tf.zeros_like(fake_output), fake_output)
total_loss = real_loss + fake_loss
return total_loss
```
### Generator loss
The generator's loss quantifies how well it was able to trick the discriminator. Intuitively, if the generator is performing well, the discriminator will classify the fake images as real (or 1). Again, use the same principle used to define the real_loss to define the generator_loss.
```
def generator_loss(fake_output):
generator_loss = cross_entropy(tf.ones_like(fake_output), fake_output)
return generator_loss
```
The discriminator and the generator optimizers are different since both networks are trained separately. Hint: use Adam optimizers. Experiment with the learning rates.
```
generator_optimizer = tf.keras.optimizers.Adam(1e-4)
discriminator_optimizer = tf.keras.optimizers.Adam(1e-4)
```
### Save checkpoints
This notebook also demonstrates how to save and restore models, which can be helpful in case a long running training task is interrupted (especially for larger datasets).
```
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
```
## Define the training loop
```
EPOCHS = 100
noise_dim = 100
num_examples_to_generate = 16 # For visualization
# We will reuse this noise_vector overtime (so it's easier)
# to visualize progress in the animated GIF)
noise_vector = tf.random.normal([num_examples_to_generate, noise_dim])
```
The training loop should begin with generator receiving a random vector as input. That vector will be used to produce an image. The discriminator should then be used to classify real images (drawn from the training set) and fakes images (produced by the generator). The loss will be calculated for each of these models, and the gradients used to update the generator and discriminator
```
# Notice the use of `tf.function`
# This annotation causes the function to be "compiled".
@tf.function
def train_step(images):
noise = tf.random.normal([BATCH_SIZE, noise_dim])
with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
# Generator output
generated_images = generator(noise, training=True)
# Discriminator output
real_output = discriminator(images, training=True)
fake_output = discriminator(generated_images, training=True)
# Loss functions
gen_loss = generator_loss(fake_output)
disc_loss = discriminator_loss(real_output, fake_output)
# Gradients
gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables)
gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)
# Update both networks
generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))
discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))
def train(dataset, epochs):
for epoch in range(epochs):
start = time.time()
for image_batch in dataset:
train_step(image_batch)
# Produce images for the GIF as we go
display.clear_output(wait=True)
generate_and_save_images(generator,
epoch + 1,
noise_vector)
# Save the model every 15 epochs
if (epoch + 1) % 15 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print ('Time for epoch {} is {} sec'.format(epoch + 1, time.time()-start))
# Generate after the final epoch
display.clear_output(wait=True)
generate_and_save_images(generator,
epochs,
noise_vector)
```
**Generate and save images**
```
def generate_and_save_images(model, epoch, test_input):
# Notice `training` is set to False.
# This is so all layers run in inference mode (batchnorm).
predictions = model(test_input, training=False)
fig = plt.figure(figsize=(4,4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i+1)
plt.imshow(predictions[i, :, :, 0] * 127.5 + 127.5, cmap='gray')
plt.axis('off')
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
```
## Train the model
Call the `train()` method defined above to train the generator and discriminator simultaneously. Note, training GANs can be tricky. It's important that the generator and discriminator do not overpower each other (e.g., that they train at a similar rate).
At the beginning of the training, the generated images look like random noise. As training progresses, the generated digits will look increasingly real. After about 50 epochs, they resemble MNIST digits. This may take about one minute / epoch with the default settings on Colab.
```
%%time
train(train_dataset, EPOCHS)
```
Restore the latest checkpoint.
```
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
```
## Create a GIF
```
# Display a single image using the epoch number
def display_image(epoch_no):
return PIL.Image.open('image_at_epoch_{:04d}.png'.format(epoch_no))
display_image(EPOCHS)
```
Use imageio to create an animated gif using the images saved during training.
```
anim_file = 'dcgan.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
last = -1
for i,filename in enumerate(filenames):
frame = 8*(i**0.25)
if round(frame) > round(last):
last = frame
else:
continue
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)
import IPython
if IPython.version_info > (6,2,0,''):
display.Image(filename=anim_file)
```
If you're working in Colab you can download the animation with the code below:
```
try:
from google.colab import files
except ImportError:
pass
else:
files.download(anim_file)
```
## Next Steps
How does the generated digits compare with the original MNIST? Optimize the network design and training hyperparameters further for better results.
Repeat the above steps for other similar datasets such as Fashion-MNIST or expand the capacities of the network appropriately to suit larger datasets such as the Large-scale Celeb Faces Attributes (CelebA) dataset.
| github_jupyter |
## Code Equivalence
```
import ast
import astpretty
import showast
import sys
import re
sys.path.insert(0, '../preprocess/')
sys.path.insert(0, '../../coarse2fine.git/src')
from sketch_generation import Sketch
from tree import SketchRepresentation
import table
SKP_WORD = '<sk>'
RIG_WORD = '<]>'
LFT_WORD = '<[>'
def is_code_eq(tokens1, tokens2, not_layout=False):
if isinstance(tokens1, SketchRepresentation):
tokens1 = str(tokens1)
else:
tokens1 = ' '.join(tokens1)
if isinstance(tokens2, SketchRepresentation):
tokens2 = str(tokens2)
else:
tokens2 = ' '.join(tokens2)
tokens1 = ['\"' if it in (RIG_WORD, LFT_WORD) else it for it in tokens1.split(' ')]
tokens2 = ['\"' if it in (RIG_WORD, LFT_WORD) else it for it in tokens2.split(' ')]
if len(tokens1) != len(tokens2):
return False
return all(map(lambda tk1, tk2: tk1 == tk2, tokens1, tokens2))
# AST => Node Type [AST]
class Node:
def __init__(self, val, *kids):
self.val = val
self.kids = kids
def __str__(self):
return Node.to_string(self, indent=2, c=' ')
def __repr__(self):
return str(self)
@staticmethod
def val_to_string(val):
if len(val) == 1:
n, f = val[0]
if n == 'body':
f = f[0]
s = "%s: %s\n" % (n, f.__class__.__name__)
else:
s = ', '.join(['%s: %s' % (n, f.__class__.__name__) for n, f in val]) + "\n"
return s
@staticmethod
def to_string(node, indent=2, c=' '):
if node.val == []:
return ''
s = Node.val_to_string(node.val)
for k in node.kids:
_s = Node.to_string(k, indent*2)
if _s != '':
s += (c * indent) + _s
return s
class Nil(Node):
def __init__(self):
self.val = None
self.kids = []
def __str__(self):
return "x"
def __repr__(self):
return str(self)
class Leaf(Node):
def __init__(self, val):
self.val = val
self.kids = []
def __str__(self):
return '%d' % self.val
def __repr__(self):
return str(self)
# TODO
def cons_tree(t):
val = list(ast.iter_fields(t))
kids = list(ast.iter_child_nodes(t))
return Node(val, *[cons_tree(k) for k in kids])
def zip_tree_pred(pred, t1, t2):
zs = [pred(t1.val, t2.val)]
for k1, k2 in zip(t1.kids, t2.kids):
zs.append(zip_tree_pred(pred, k1, k2))
return all(zs)
code1 = '[x for x in range(10)]'
code2 = '[i for i in [1,2,3]]'
tree1 = ast.parse(code1)
tree2 = ast.parse(code2)
t1 = cons_tree(tree1)
t2 = cons_tree(tree2)
def cmp_func(x, y):
s1 = Node.val_to_string(x)
s2 = Node.val_to_string(y)
return s1 == s2
zip_tree_pred(cmp_func, t1, t2)
%%showast
x = self.func(1, 'test', var)
%%showast
raise RuntimeError('[%s]' % self.get_err_msg(timestamp[:2]))
# tree = Node(Assign, [Attribute(Name(self), var), Name(x)])
# astpretty.pprint(tree1.body[0], indent=' ' * 4)
astpretty.pprint(tree2.body[0], indent=' ' * 4)
```
## Eval framework
```
## TODO
```
| github_jupyter |
# Import Scikit Learn, Pandas and Numpy
```
import sklearn
import numpy as np
import pandas as pd
```
# 1. Read the Dataset using Pandas
```
data = pd.read_csv("data/amazon_baby.csv")
data
```
# 2. Exploratory Data Analysis
```
data.head()
data.info()
```
### The first observation is that we have cells with null review and they have rating. Those rows which contain those cells should be dropped from the data as they will confuse the model by acting like noise.
```
data.describe()
import matplotlib.pyplot as plt
import seaborn as sns
fig = sns.countplot(x='rating', data=data)
```
### The second observation is that we have imbalanced classes in our Data. At this project we will just use different metrics to measure model performance besides accuracy like recall, $F_{1}$ score and ROC.
# 3. Data Preprocessing
### Drop null rows using DataFrame.dropna()
```
data.dropna(inplace=True)
data.reset_index(drop=True, inplace=True)
data.info()
```
### Ignore the three stars ratings.
Because they are neutral, and dropp those rows with neutral reviews.
This step is done before building the word count vector to save memory space and computational power by not getting the word count vector for those neutral reviews.
```
data = data[data['rating'] != 3]
data.reset_index(drop=True, inplace=True)
data.info()
```
### Build word count vectors
```
import pandas as pd
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
def dictionarize(row):
cv = CountVectorizer(
analyzer = "word",
token_pattern = '[a-zA-Z0-9$&+:;=?@#|<>.^*()%!]+'
)
text = [row.loc['review']]
cv_fit=cv.fit_transform(text)
word_list = cv.get_feature_names()
count_list = cv_fit.toarray().sum(axis=0)
dictionary = dict(zip(word_list,count_list))
row['word_count'] = dictionary
return row
data = data.apply(dictionarize, axis=1)
data.head()
data = data.assign(sentiment = (data['rating'] >= 4).astype(int))
data.head()
fig = sns.countplot(x='sentiment', data=data)
```
# 4. Train-Test Split
```
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(data, test_size=0.2, random_state=42)
```
# 5. Logistic Regression Pipeline
```
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import TfidfVectorizer, TfidfTransformer
sentiment_pipeline = Pipeline(
[
('Count_Vectorizer', CountVectorizer()),
('TF-IDF', TfidfTransformer()),
('Logistic_Regression', LogisticRegression(solver='lbfgs', max_iter=1000, class_weight='dict'))
],
verbose=True
)
from sklearn import set_config
set_config(display='diagram')
sentiment_pipeline
```
# 6. Pipeline Training
```
sentiment_pipeline.fit(train_set['review'], train_set['sentiment'])
```
### Plot Learning Curves
```
from sklearn.model_selection import learning_curve
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
"""
Generate a simple plot of the test and traning learning curve.
Parameters
----------
estimator : object type that implements the "fit" and "predict" methods
An object of that type which is cloned for each validation.
title : string
Title for the chart.
X : array-like, shape (n_samples, n_features)
Training vector, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape (n_samples) or (n_samples, n_features), optional
Target relative to X for classification or regression;
None for unsupervised learning.
ylim : tuple, shape (ymin, ymax), optional
Defines minimum and maximum yvalues plotted.
cv : integer, cross-validation generator, optional
If an integer is passed, it is the number of folds (defaults to 3).
Specific cross-validation objects can be passed, see
sklearn.cross_validation module for the list of possible objects
n_jobs : integer, optional
Number of jobs to run in parallel (default 1).
"""
estimator.verbose = False
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="best")
estimator.verbose = True
return plt
```
# 7. Metrics
```
from sklearn.metrics import classification_report
y_pred = sentiment_pipeline.predict(test_set['review'])
print('Classification report:\n\n{}'.format(
classification_report(test_set['sentiment'], y_pred))
)
plot_learning_curve(sentiment_pipeline\
, 'Pipeline Learning Curves', train_set['review'], train_set['sentiment'])
from sklearn.metrics import plot_precision_recall_curve, plot_roc_curve
from sklearn.metrics import average_precision_score
average_precision = average_precision_score(test_set['sentiment'], y_pred)
disp = plot_precision_recall_curve(sentiment_pipeline, test_set['review'], test_set['sentiment'])
disp.ax_.set_title('Two-class Precision-Recall curve')
disp = plot_roc_curve(sentiment_pipeline, test_set['review'], test_set['sentiment'])
disp.ax_.set_title('Two-class ROC curve')
from sklearn.metrics import accuracy_score
y_pred_selected_words = sentiment_pipeline.predict(test_set['review'])
y_true_selected_words = test_set['sentiment']
accuracy_score(y_true_selected_words, y_pred_selected_words)
print('The accuracy of the sentiment_pipeline is',accuracy_score(y_true_selected_words, y_pred_selected_words))
```
# Assignment
## 1. Use .apply() to build a new feature with the counts for each of the selected_words.
```
selected_words = ['awesome', 'great', 'fantastic', 'amazing',\
'love', 'horrible', 'bad', 'terrible', 'awful', 'wow', 'hate']
def dictionary_count(row):
count_list = []
for word in selected_words:
count_list.append(row['word_count'].get(word, 0))
dictionary = dict(zip(selected_words, count_list))
row['selected_words'] = dictionary
return row
data = data.apply(dictionary_count, axis=1)
data.head()
from collections import Counter
counts = sum(map(Counter, data['selected_words']), Counter())
results = pd.DataFrame.from_dict(counts, orient='index', columns=['Sums'])\
.sort_values(by=['Sums'], ascending=False)
results
```
## 2. Create a new sentiment analysis model using only the selected_words as features
```
from sklearn.preprocessing import StandardScaler
from sklearn.feature_extraction import DictVectorizer
from sklearn.preprocessing import Normalizer
selected_words_pipeline = Pipeline(
[
('Dictionary_Vectorizer', DictVectorizer(sparse=False, sort=False)),
('Scaler', StandardScaler()),
('Logistic_Regression', LogisticRegression(solver='lbfgs', max_iter=1000, class_weight='dict'))
],
verbose=True
)
from sklearn import set_config
set_config(display='diagram')
selected_words_pipeline
```
### Train-Test split
```
train_set, test_set = train_test_split(data, test_size=0.2, random_state=15)
```
### Training the selected_words_pipeline
```
selected_words_pipeline.fit(train_set['selected_words'], train_set['sentiment'])
```
### selected_words_pipeline Metrics
```
from sklearn.metrics import classification_report
y_pred = selected_words_pipeline.predict(test_set['selected_words'])
print('Classification report:\n\n{}'.format(
classification_report(test_set['sentiment'], y_pred))
)
disp = plot_learning_curve(selected_words_pipeline, 'selected_words_pipeline Learning Curves', \
train_set['selected_words'], train_set['sentiment'])
average_precision = average_precision_score(test_set['sentiment'], y_pred)
disp = plot_precision_recall_curve(selected_words_pipeline, test_set['selected_words'], test_set['sentiment'])
disp.ax_.set_title('Two-class Precision-Recall curve')
disp = plot_roc_curve(selected_words_pipeline, test_set['selected_words'], test_set['sentiment'])
disp.ax_.set_title('Two-class POC curve')
weights = dict(zip(selected_words, selected_words_pipeline['Logistic_Regression'].coef_[0]))
sorted_weights = pd.DataFrame.from_dict(weights, orient='index', columns=['Weights'])\
.sort_values(by=['Weights'], ascending=False)
sorted_weights
```
## 3. Comparing the accuracy of different sentiment analysis models: Using .predict()
In this task the accuracy of the sentiment_pipeline, selected_words_pipeline and majority_class. The first one has been calculated above.
```
from sklearn.metrics import accuracy_score
y_pred_selected_words = selected_words_pipeline.predict(test_set['selected_words'])
y_true_selected_words = test_set['sentiment']
accuracy_score(y_true_selected_words, y_pred_selected_words)
print('The accuracy of the selected_words_pipeline is',
accuracy_score(y_true_selected_words, y_pred_selected_words))
majority_class = float(test_set[test_set['sentiment'] == 1].shape[0] / test_set.shape[0])
majority_class
```
## 4. Interpreting the difference in performance between the models
```
diaper_champ_reviews = data.loc[data['name']=='Baby Trend Diaper Champ',\
['review', 'selected_words', 'sentiment']]
diaper_champ_reviews
diaper_champ_reviews['predicted_sentiment'] = \
sentiment_pipeline.predict_proba(diaper_champ_reviews['review'])[:, 1].tolist()
diaper_champ_reviews
diaper_champ_reviews = diaper_champ_reviews.sort_values(by=['predicted_sentiment'], ascending=False)
diaper_champ_reviews.head()
diaper_champ_reviews['predicted_selected_word'] = \
selected_words_pipeline\
.predict_proba(diaper_champ_reviews['selected_words'])[:, 1].tolist()
diaper_champ_reviews.iloc[1]
diaper_champ_reviews.iloc[1]['review']
diaper_champ_reviews.iloc[1]['selected_words']
```
| github_jupyter |
```
%autosave 0
```
# MCPC rehearsal problem Oct 25 2017 at UCSY
## Problem E: Stacking Plates
### Input format
- 1st Line: 1 integer, Number of Test Case, each Test Case has following data
+ 1 Line: 1 integer, **n**(Number of Stacks)
+ **n** Lines: first integer: **h** (Number of Plates), and **h** integers (Plate size)
### Output format
Case: (test case number): Number of Operations
### Sample Input
```
3
2
3 1 2 4
2 3 5
3
4 1 1 1 1
4 1 1 1 1
4 1 1 1 1
2
15 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
15 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
```
### Sample Output
```
Case 1:5
Case 2:2
Case 3:5
```
### Explanation of sample I/O
- 3 test cases
+ Stack of (1,2,4) and (3,5)
+ Stack of 3 (1,1,1,1)
+ Stack of 2 (1,1,1,1,1,2,2,2,2,2,3,3,3,3,3)
- 1st case:
Split between 2 and 4, 3 and 5, Move 4 on 5, 3 on 4, (1,2) on 3 ==> Total 5 operations
- 2nd case:
Move 1st stack (1,1,1,1,1) on 2nd stack, move (1st+2nd stack) on 3rd stack ==> Total 2 operations
- 3rd case:
Split between 1 and 2 of 1st stack, between 2 and 3 of 2nd stack, move (2,2,2,2,2,3,3,3,3,3) of 1st stack on (3,3,3,3,3) of 2nd, move (1,1,1,1,1,2,2,2,2,2) of 2nd stack on it, move (1,1,1,1,1) on top ==> Total 5 operations
### Specific vs Abstract, Find a General Rule from Detail
When solving problems and puzzles that you can not find how to solve, thinking specificlly then abstractly is important. Finding general rules from specific examples give you a path to the answer.
- Think about simple cases
- Find general pattern (idea, rule) from there
- Proove the rule (if possible)
- Extend the rule to more complex cases
### How to calculate number of operation(movement)
If there are N stacks and each contains just 1 piece (Split is not necessary), (N-1) operations are reuired. (N-1) is a minimum number of oprations.
For each Split operation, Join operation is required to create single stack. Total number of operation increases by 2 for each Split operations (S). The order of Split and Join does not affect total number of movement. (Split-Split-Join-Join) = (Split-Join-Split-Join) \begin{equation} Nmber Of Movement = 2S + (N-1) \end{equation}
Same size of pieces in original stacks (Case 2 and Case 3) can be considered to be same as single piece. Case 2: 3 stack of (1), Case 3: 2 stack of (1,2,3)
### Optimized movement
Reverse-Thinking is sometimes very effective. Create Final Stack and check the boundary. If the combination of the boundary exists in original stacks, it can be used (not necessary to split). **Stack ID needs to be checked, as for detail see later**.
$S = (Maximum Number Of Split) - (Number Of Reused Boundary)$
- Case 1: [1,2,3,4,5] is final form. Boundary of [1,2] exist in Original Stack-1, $S=(2+1)-1=2, Movement=2*2+(2-1)=5$
- Case 2: Convert original stacks to [1], $Movement=2*0+(3-1)=2$
- Case 3: Convert original stacks to [1,2,3], Final form is [1,1,2,2,3,3]. Boundary of [1,2] and [2,3] exists. $S=(2+2)-2=2$
### Sample I/O gives hint
Sample Input/Output often gives great hint to solve problems. Same number in original stack cause problem in above idea, but same number can be considered to be 1 digit, so convert input data to eliminate duplicate number.
### Stack ID checking
- Assign stack ID
- Merge every plates and sort by radius (size of plate)
- Manage the list of candidate for boundary reuse (top and bottom)
- Boundary assignment can be done greedy, if there is only 1 combination between top of stack and next, use it
```
#!/usr/bin/python3
# -*- coding: utf-8 -*-
'''
2017 MCPC at UCSY
Problem-E: Stacking Plates
'''
import sys
class TestCase():
pass
class Plates():
# Groupt of same radius plates in merged stack
# id_list: list of stack ID
def __init__(self, radius, id_list):
self.radius = radius
self.id_list = id_list
self.top = None
self.bottom = None
def match_prev(self, prev_bottom):
self.top = list()
for stack_id in self.id_list:
if stack_id in prev_bottom:
self.top.append(stack_id)
self.bottom = self.id_list.copy()
if len(self.top) == 1 and len(self.bottom) != 1:
self.bottom.remove(self.top[0])
return
def __repr__(self):
return ('Plates {}: {}, top: {} bottom: {}'.format(self.radius, self.id_list, self.top, self.bottom))
def parse_tc(tc):
'''
Input: Test Case
Update:
Return: None
'''
tc.n = int(tc.stdin.readline())
tc.stacks = list()
for i in range(tc.n):
stack = tc.stdin.readline().split()[1:] # 2d List, 1st=len
tc.stacks.append(stack)
return
def reform_stack(org):
'''
Input: tc.stacks
Output: cosolidated stacks (no prefix, no duplicate)
'''
stacks = list()
stack_id = 0
for stack in org:
prev_radius = None
new_stack = list()
for radius in stack:
if radius != prev_radius:
new_stack.append((radius, stack_id))
prev_radius = radius
stacks.append(new_stack)
stack_id += 1
return stacks
def merge(stacks):
'''
stacks: 2D List of tuple(radius, id)
Return: 1D sorted List
'''
merged_stack = list()
for stack in stacks:
merged_stack.extend(stack)
merged_stack.sort()
return merged_stack
def stack2plates(merged_stack):
'''
merged_stack: List of Tuple(radius, id)
return: List of Plates
'''
plates_list = list()
id_list = list()
prev_size = None
for plate in merged_stack:
radius, plate_id = plate
if radius != prev_size:
if id_list:
plates_list.append(Plates(prev_size, id_list))
id_list = [plate_id]
else:
id_list.append(plate_id)
prev_size = radius
if id_list:
plates_list.append(Plates(radius, id_list))
return plates_list
def max_reuse(plates_list):
reuse = 0
prev_bottom = list()
for plates in plates_list:
plates.match_prev(prev_bottom)
if plates.top: reuse += 1
prev_bottom = plates.bottom
#print(plates, file=sys.stderr)
return reuse
def solve(tc):
'''
Input: Test Case
Return: Numper of movement
'''
parse_tc(tc)
stacks = reform_stack(tc.stacks)
#print(stacks)
num_merge = len(stacks) - 1 ## Join Stacks
for stack in stacks:
num_merge += (len(stack) - 1) * 2 ## Split and Join
merged_stack = merge(stacks)
plates_list = stack2plates(merged_stack) # list of Plates
#return (num_merge - check_bound(merged_stack, stack_bound) * 2)
return (num_merge - max_reuse(plates_list) * 2)
### Main routine
infile = open('reh_e.in', 'r')
tc = TestCase()
tc.stdin = infile
tc.t = int(tc.stdin.readline())
for i in range(tc.t):
print('Case {}:{}'.format(i+1, solve(tc)))
```
| github_jupyter |
```
%matplotlib inline
import matplotlib.pyplot as plt
from functools import reduce
import seaborn as sns; sns.set(rc={'figure.figsize':(15,15)})
import numpy as np
import pandas as pd
from sqlalchemy import create_engine
from sklearn.preprocessing import MinMaxScaler
engine = create_engine('postgresql://postgres:[email protected]:5555/mimic')
common_index = ['hadm_id', 'icustay_id', 'ts']
def get_mortality_label():
label = pd.read_sql("""
select icustay_id, hadm_id, date_trunc('day', outtime) as ts, hospital_expire_flag, thirtyday_expire_flag
from sepsis3
where excluded=0
""", engine)
label.set_index(common_index, inplace=True)
return label
def get_demo():
demo = pd.read_sql("""
select icustay_id, hadm_id, date_trunc('day', intime) as ts
, age, is_male, race_white, race_black, race_hispanic, race_other
from sepsis3
where excluded=0
""", engine)
demo.set_index(common_index, inplace=True)
return demo
def get_admit():
admit = pd.read_sql("""
select icustay_id, hadm_id, date_trunc('day', intime) as ts, icu_los, hosp_los
from sepsis3
where excluded=0
""", engine)
admit.set_index(common_index, inplace=True)
return admit
def get_comorbidity():
com = pd.read_sql('''
select s.icustay_id, date_trunc('day', admittime) as ts, c.*
from comorbidity c
inner join (select icustay_id, hadm_id from sepsis3 where excluded=0) s
on c.hadm_id=s.hadm_id
''', engine)
del com['subject_id']
del com['admittime']
com.set_index(common_index, inplace=True)
return com
def get_gcs():
gcs = pd.read_sql('''
select v.*
from gcsdaily v
inner join (select hadm_id from sepsis3 where excluded=0) s
on v.hadm_id=s.hadm_id
where charttime_by_day is not null
''', engine)
del gcs['subject_id']
gcs.rename(columns = {'charttime_by_day': 'ts'}, inplace=True)
gcs.set_index(common_index, inplace=True)
return gcs
def get_vitalsign():
vital = pd.read_sql('''
select v.*
from vitalsdaily v
inner join (select hadm_id from sepsis3 where excluded=0) s
on v.hadm_id=s.hadm_id
''', engine)
del vital['subject_id']
vital.rename(columns = {'charttime_by_day': 'ts'}, inplace=True)
vital.set_index(common_index, inplace=True)
return vital
def get_drug():
# (48761, 1770) --> (48761, 8)
list_of_abx = ['adoxa','ala-tet','alodox','amikacin','amikin','amoxicillin',
'amoxicillin%claulanate','clavulanate','ampicillin','augmentin',
'avelox','avidoxy','azactam','azithromycin','aztreonam','axetil',
'bactocill','bactrim','bethkis','biaxin','bicillin l-a','cayston',
'cefazolin','cedax','cefoxitin','ceftazidime','cefaclor','cefadroxil',
'cefdinir','cefditoren','cefepime','cefotetan','cefotaxime','cefpodoxime',
'cefprozil','ceftibuten','ceftin','cefuroxime ','cefuroxime','cephalexin',
'chloramphenicol','cipro','ciprofloxacin','claforan','clarithromycin',
'cleocin','clindamycin','cubicin','dicloxacillin','doryx','doxycycline',
'duricef','dynacin','ery-tab','eryped','eryc','erythrocin','erythromycin',
'factive','flagyl','fortaz','furadantin','garamycin','gentamicin',
'kanamycin','keflex','ketek','levaquin','levofloxacin','lincocin',
'macrobid','macrodantin','maxipime','mefoxin','metronidazole',
'minocin','minocycline','monodox','monurol','morgidox','moxatag',
'moxifloxacin','myrac','nafcillin sodium','nicazel doxy 30','nitrofurantoin',
'noroxin','ocudox','ofloxacin','omnicef','oracea','oraxyl','oxacillin',
'pc pen vk','pce dispertab','panixine','pediazole','penicillin',
'periostat','pfizerpen','piperacillin','tazobactam','primsol','proquin',
'raniclor','rifadin','rifampin','rocephin','smz-tmp','septra','septra ds',
'septra','solodyn','spectracef','streptomycin sulfate','sulfadiazine',
'sulfamethoxazole','trimethoprim','sulfatrim','sulfisoxazole','suprax',
'synercid','tazicef','tetracycline','timentin','tobi','tobramycin','trimethoprim',
'unasyn','vancocin','vancomycin','vantin','vibativ','vibra-tabs','vibramycin',
'zinacef','zithromax','zmax','zosyn','zyvox']
drug = pd.read_sql("""
select p.icustay_id, p.hadm_id
, startdate as ts
, 'prescription' as category
, drug
, sum((EXTRACT(EPOCH FROM enddate - startdate))/ 60 / 60 / 24) as duration
from prescriptions p
inner join (select hadm_id, icustay_id from sepsis3 where excluded=0) s
on p.hadm_id=s.hadm_id and p.icustay_id=s.icustay_id
group by p.icustay_id, p.hadm_id, ts, drug
""", engine)
drug.duration = drug.duration.replace(0, 1) # avoid null of instant prescription
drug = drug[drug.drug.str.contains('|'.join(list_of_abx), case=False)]
pivot_drug = pd.pivot_table(drug,
index=common_index,
columns=['drug'],
values='duration',
fill_value=0)
return pivot_drug
def get_lab():
lab = pd.read_sql("""
select s.icustay_id, c.hadm_id, date_trunc('day', c.charttime) as ts
, d.label
, valuenum
from labevents c
inner join (select hadm_id, icustay_id from sepsis3 where excluded=0) s
on c.hadm_id=s.hadm_id
join d_labitems d using (itemid)
where itemid in (
50912 -- 크레아티닌(creatinine)
,50905, 50906 -- LDL-콜레스테롤(LDL-cholesterol)
,50852 -- 당화혈색소(HbA1c/Hemoglobin A1c)
,50809, 50931 -- 공복혈당(fasting plasma glucose)
,50889 -- C-반응성 단백질(C-reactive protein)
,50811, 51222 -- 헤모글로빈(hemoglobin)
,50907 -- 총콜레스테롤(total cholesterol)
,50945 -- 호모시스테인(Homocysteine)
,51006 -- 혈액 요소 질소(blood urea nitrogen)
,51000 -- 중성지방(triglyceride)
,51105 -- 요산(uric acid)
,50904 -- HDL-콜레스테롤(HDL-cholesterol)
,51265 -- 혈소판(platelet)
,51288 -- 적혈구침강속도(Erythrocyte sedimentation rate)
,51214 -- 피브리노겐(fibrinogen)
,51301 -- 백혈구(white blood cell)
,50963 -- B형 나트륨 이뇨펩타이드(B-type Natriuretic Peptide)
,51002, 51003 -- 트로포닌(Troponin)
,50908 -- 크레아티닌키나제-MB(Creatine Kinase - Muscle Brain)
,50862 -- 알부민(albumin)
,50821 -- 동맥 산소분압(arterial pO2)
,50818 -- 이산화탄소분압(pCO2)
,50820 -- 동맥혈의 산도(arterial PH)
,50910 -- 크레아틴키나제(CK)
,51237 -- 혈액응고검사(PT (INR)/aPTT)
,50885 -- 빌리루빈(bilirubin)
,51144 -- 대상핵세포(band cells)
,50863 -- 알칼리 인산염(alkaline phosphatase)
)
""", engine)
pivot_lab = pd.pivot_table(lab,
index=common_index,
columns=['label'],
values='valuenum',
# aggfunc=['min', 'max', np.mean]
fill_value=0)
return pivot_lab
def get_vaso():
vaso = pd.read_sql("""
select c.icustay_id, s.hadm_id, date_trunc('day', c.starttime) as ts
, duration_hours as vaso_duration_hours
from vasopressordurations c
inner join (select hadm_id, icustay_id from sepsis3 where excluded=0) s
on c.icustay_id=s.icustay_id
""", engine)
vaso.set_index(common_index, inplace=True)
return vaso
def get_sepsis():
s = pd.read_sql("""
select icustay_id, hadm_id, date_trunc('day', intime) as ts
, sofa, qsofa
from sepsis3
where excluded=0
""", engine)
s.set_index(common_index, inplace=True)
return s
def fig_corr_heatmap(labels, df, feature_df):
cols = [labels[0]] + feature_df.columns.tolist()
df_grp = df[cols].groupby(level=0).agg('mean')
corr = df_grp.corr()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
cols[0] = labels[1]
df_grp = df[cols].groupby(level=0).agg('mean')
corr_30d = df_grp.corr()
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(15, 5))
sns.heatmap(corr, ax=ax1, mask=mask, vmin=0, vmax=1)
sns.heatmap(corr_30d, ax=ax2, mask=mask, vmin=0, vmax=1)
ax1.set_title('In-hospital Death')
ax2.set_title('30-day Death')
```
- 패혈증 진단받은 환자수, 입원수
```
pd.read_sql(
"""
select count(distinct hadm_id), count(distinct icustay_id) from sepsis3 where excluded=0
""", engine)
```
- ICU, 입원 기간의 최소, 최대
```
pd.read_sql(
"""
select min(icu_los), max(icu_los), min(hosp_los), max(hosp_los) from sepsis3 where excluded=0
""", engine)
```
## 라벨
- 사망: 원내 사망, 30일 이내 사망
```
label = get_mortality_label()
label.head()
```
## 변수 : 인구통계, 입원, 진단
```
demo = get_demo()
demo.head()
admit = get_admit()
admit.head()
com = get_comorbidity()
com.head()
```
## 변수 : 바이탈사인, 투약, 검사, 승압제
```
gcs = get_gcs()
gcs.head()
vital = get_vitalsign()
vital.head()
drug = get_drug()
drug.head()
lab = get_lab()
lab.head()
vaso = get_vaso()
vaso.head()
sepsis = get_sepsis()
sepsis.head()
data_frames = [
label,
demo,
admit,
com,
gcs,
vital,
drug,
lab,
vaso,
sepsis
]
df_merged = reduce(lambda left,right: pd.merge(left, right, how='outer', left_index=True, right_index=True),
data_frames)
df_merged.head()
```
- hdf 포맷으로 저장
```
filename_sepsis = "mimiciii_sepsis_mortality.h5"
df_merged.to_hdf(filename_sepsis, key='all')
```
# 탐색
```
df = pd.read_hdf(filename_sepsis, key='all')
df.head()
```
# Correlation
## mortality and features
```
labels = ['hospital_expire_flag', 'thirtyday_expire_flag']
for f in data_frames[1:]:
fig_corr_heatmap(labels, df, f)
```
# Feature, Label
```
y = df[labels].groupby(level=0).agg('max').fillna(0).values
X = df.drop(columns=labels).groupby(level=0).agg(['mean','max', 'min']).fillna(0)
X.shape, y.shape
y.sum(axis=0) / y.shape[0]
```
# In-hospital Death - Train and Validation
```
from sklearn.ensemble import GradientBoostingClassifier, RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_auc_score, confusion_matrix, f1_score, accuracy_score
import numpy as np
random_state = 2
X_train, X_test, y_train, y_test = train_test_split(X, y[:, 0], test_size=0.3, random_state=random_state)
clf = LogisticRegression(penalty='l1',
solver='liblinear',
# tol=1e-6,
# max_iter=int(1e6),
# warm_start=True,
random_state=random_state)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
params = {'n_estimators': 1000, 'max_leaf_nodes': None, 'max_depth': None, 'random_state': random_state,
'min_samples_split': 4,
'learning_rate': 0.1}
clf = GradientBoostingClassifier(**params)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
clf = RandomForestClassifier(n_estimators=1000, random_state=random_state)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
```
# 30day Death - Train and Validation
```
X_train, X_test, y_train, y_test = train_test_split(X, y[:, 1], test_size=0.3, random_state=random_state)
clf = LogisticRegression(penalty='l1',
solver='liblinear',
# tol=1e-6,
# max_iter=int(1e6),
# warm_start=True,
random_state=random_state)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
clf = GradientBoostingClassifier(**params)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
clf = RandomForestClassifier(n_estimators=1000, random_state=random_state)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('auroc :', roc_auc_score(y_test, y_pred))
print('accuracy:', accuracy_score(y_test, y_pred))
```
| github_jupyter |
[View in Colaboratory](https://colab.research.google.com/github/tjh48/DCGAN/blob/master/dcgan.ipynb)
First we'll import all the tools we need and set some initial parameters
```
import numpy as np
from sklearn.utils import shuffle
import matplotlib.pyplot as plt
import os
from keras.models import *
from keras.layers import *
from keras.optimizers import *
from keras.callbacks import EarlyStopping
from keras.datasets import mnist
from keras.utils import np_utils
from keras.initializers import RandomNormal
import keras.backend as K
import time
# Just in case we're re-running, clear the Keras session data.
K.clear_session()
# Shall we use BatchNormalization layers?
useBN = False
# Shall we use bias?
useBias = True
# Logging directory and label
LOG_DIR = './log'
logSub = "mnistDCGAN"
```
This is an optional code block for creating an ngrok tunnel to a tensorboard instance. Useful for running on cloud services
```
if not os.path.isfile('./ngrok'):
!wget https://bin.equinox.io/c/4VmDzA7iaHb/ngrok-stable-linux-amd64.zip
!unzip ngrok-stable-linux-amd64.zip
get_ipython().system_raw(
'tensorboard --logdir ' + LOG_DIR + ' --host 0.0.0.0 --port 6006 &'
)
get_ipython().system_raw('./ngrok http 6006 &')
! curl -s http://localhost:4040/api/tunnels | python3 -c \
"import sys, json; print(json.load(sys.stdin)['tunnels'][0]['public_url'])"
```
This code block imports manual logging functionality and defines a couple of extra functions required for GANs in Keras, since we need to use train_on_batch rather than fit. train_on_batch does not log automatically to tensorboard, hence we'll perform the logging manually.
```
if os.path.isfile('tensorboard_logging.py'): os.remove('tensorboard_logging.py')
!wget https://gist.githubusercontent.com/tjh48/bf56684801d641544e49a5e66bf15fba/raw/9c6e04cca49288ab0920d9a3aeb3283da13d1a39/tensorboard_logging.py
import tensorboard_logging as tbl
subdir = LOG_DIR + "/" + logSub + '_' + str(int(np.round(time.time())))
logger = tbl.Logger(subdir)
```
Next we'll download the MNIST data set, in lieu of anything more interesting to work with.
We'll also define a function for plotting MNIST-type images so that we can see the output of the generator.
```
from keras.datasets import mnist
(x_train, _), (x_test, _) = mnist.load_data()
# just for fun, you can drop in the fashion_mnist dataset here instead of standard mnist
#from keras.datasets import fashion_mnist
#(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
x_train = x_train.astype('float32') / 127.5 - 1
x_test = x_test.astype('float32') / 127.5 - 1
x_train = x_train[:, :, :, np.newaxis]
def plotImages(images, n = 25):
plt.figure(figsize=(32, 32))
for i in range(n):
ax = plt.subplot(2, n, i + 1)
x = images[i]
if x.shape[2] == 1: x = x.reshape(x.shape[0:2])
plt.imshow((x + 1) / 2)
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
plotImages(x_train)
def genfun(inputLayer, initialFeatures = 256, outputDim = 32, outputFeatures = 3, minimumDim = 5):
# Here we find the number of times the output dimension is divisible by 2
# while still keeping the initial dimension of the data above some threshold.
# Letting the threshold go too low results in model collapse; ad hoc experimentation suggests that
# an initial dimension >= 5 is ok.
for loop in range(int(np.log2(outputDim)) + 1):
if(outputDim % np.power(2, loop) != 0 or outputDim / np.power(2, loop) < minimumDim):
break
# Given the number of times the output dimension is divisible by 2,
# we can determine the initial dimension of the dense layer from a random vector.
initialDim = outputDim // np.power(2, loop - 1)
if initialDim == outputDim:
raise ValueError("The outputDim is not divisible by 2 - there's no clean way to upsample.")
x = Dense(initialDim*initialDim*initialFeatures, kernel_initializer='glorot_normal', use_bias = useBias)(inputLayer)
x = LeakyReLU(0.2)(x)
if useBN: x = BatchNormalization()(x)
x = Reshape((initialDim, initialDim, initialFeatures))(x)
# Now we can repeatedly upsample doubling the dimension each time
# and convolute, halving the number of features
# until we arrive at (half the) right output dimension
for ii in range(loop - 1):
x = UpSampling2D(size=(2, 2), data_format='channels_last')(x)
if ii < loop - 2:
x = Conv2D(initialFeatures // np.power(2, ii + 1), kernel_size = 5, padding ='same', use_bias = useBias, strides = 1)(x)
x = LeakyReLU(0.2)(x)
if useBN: x = BatchNormalization()(x)
# now reduce the features to one (for MNIST) - for colour images we may need three or more channels in output
x = Conv2D(outputFeatures, kernel_size = 5, padding ='same', use_bias = useBias, strides = 1)(x)
x = Activation('tanh')(x)
return x
```
Here's a function to define the generator layer. We want to upsample from a random vector to an image, with a convolutional layer at each upsampling. Each upsampling with a 2x2 shape doubles the size of the image, so we can start with with a low-dimensional image with a large number of features and upsample until we get to the right size.
Starting with a too-low dimensional image gives model failure, particularly if you don't use batch normalisation. Ad hoc experimentation suggests that an initial dimension > 5 is required to avoid this scenario.
And here's a function to define a discriminator layer. In the original DCGAN paper, this is envisaged as an almost direct mirror image of the generator. It need not be - we could have fewer layers (to make the discriminator less efficient) as long as we end with a dense layer mapping to a single output.
```
def disfun(inputImage, initialFeatures= 64, numLayers = 2):
x = inputImage
for ii in range(numLayers):
x = Conv2D(initialFeatures * np.power(2, ii), kernel_size = 5, padding='same', strides=(2,2), use_bias = useBias)(x)
x = LeakyReLU(0.2)(x)
if useBN: x = BatchNormalization()(x)
x = Flatten()(x)
x = Dense(1, activation = 'sigmoid', use_bias = useBias)(x)
return x
```
Now comes the conceptually tricky bit. The best way I've found to think about this is found on ctmakro's github page:

This map of the model makes it clear what we're trying to do in each training pass. We generate a random input 'z' which we feed into the generator along with the weights 'Wg' (the generator's weights, which we want to train). That produces a set of generated images, which we feed into a copy of the discriminator.
The generator's performance ('G_loss') is measured on its ability to get the discriminator to regard the generated images as true positives - what the discriminator says about the input images is irrelevant to the generator's loss. Then we update (green arrow) the generator's weights based on the generator's loss.
The discriminator's performance ('D_loss') is measured on its ability to separate the generated images (the output of 'D(copy1)'') from the true images (the output of 'D(copy2)'). We update (blue arrow) the discriminator's weights based on the discriminator's loss.
In native Keras, we don't have a way to update one set of weights 'Wg' based on the 'G_loss' and another set of weights 'Wd' based on the 'D_loss' and so we have to split this update process.
In each training step, we first produce a set of generated images to feed into the discriminator (along with the true images) and train the discriminator's loss. Then we freeze the discriminator's weights (make it untrainable) and train the generator by feeding the generated images into the discriminator, with the generator being scored on how strongly the discriminator predicts that the generated images are true.
[ctmakro's github - Fast DCGAN in Keras](https://ctmakro.github.io/site/on_learning/fast_gan_in_keras.html) has a method for rewriting the necessary update steps in tensorflow, making it possible to update both sets of weights in one step, making for a faster update process. For the moment, we'll stick with the longer method as this tends to be the one that gets implemented (but often not explained)
Here we can build the models. We need a discriminator model that can be trained on true/fake images, a generator model that will be used to create fake images, and a combined model that will link the generator to the discriminator to produce the loss on the generator.
Since the loss on the generator is measured by assuming the fake images are real, we need to freeze (set untrainable) the discriminator model so as not to disrupt the training of the discriminator by feeding it false information.
I'm wrapping the whole thing up in a function so that we can easily generate fresh models for use with a tweaked training regime.
```
optimizer = Adam(0.0002, 0.5)
def dcganModels():
inputRandom = Input(shape=(100,))
generator = Model(inputRandom, genfun(inputRandom, initialFeatures = 128, outputDim = x_train.shape[2], outputFeatures = x_train.shape[3]))
generator.compile(loss = 'binary_crossentropy', optimizer = optimizer)
inputImage = Input(shape=x_train.shape[1:4]) # adapt this if using `channels_first` image data format
discriminator = Model(inputImage, disfun(inputImage))
discriminator.compile(loss = 'binary_crossentropy', optimizer = optimizer)
discriminator.trainable = False
gan = Model(inputRandom, discriminator(generator(inputRandom)))
gan.compile(loss = 'binary_crossentropy', optimizer = optimizer)
discriminator.trainable = True
return(gan, discriminator, generator)
```
Next we'll create a function that creates the data for each training batch.
One trick for improving performance of GANs is to add random noise to both the true and fake images as they go into the discriminator. This weakens the discriminator by creating more overlap between (the distribution of) true and fake images (http://www.inference.vc/instance-noise-a-trick-for-stabilising-gan-training/). As the generator improves, we require less noise to confuse the discriminator, and so we can weaken the amount of noise being added over time. This seems to offer considerably faster training, and more convincing output.
```
def makeBatch(x_train, batchSize = 128, noisyEpochs = 0.0):
noise_factor = 0
if noisyEpochs > 0:
noise_factor = np.clip(1 - i/noisyEpochs, 0, 1)
trueImages = x_train[np.random.randint(0, x_train.shape[0], batchSize),]
trueImages = trueImages + np.random.normal(loc=0.0, scale=noise_factor, size=trueImages.shape)
trueImages = np.clip(trueImages, -1, 1)
randomInput = np.random.normal(0, 1, (batchSize,100))
generatedImages = generator.predict(randomInput)
generatedImages = generatedImages + np.random.normal(loc=0.0, scale=noise_factor, size=generatedImages.shape)
generatedImages = np.clip(generatedImages, -1, 1)
return randomInput, trueImages, generatedImages
```
Now we can train the models. We first generate the fake images, then train the discriminator on these and an equal sized random batch of the true images. Then we train the generator.
Every fifty epochs, we'll take a look at a sample of the current output and log the various metrics of interest.
```
nbEpoch = 10000
dLoss = []
gLoss = []
from IPython.display import clear_output, Image
gan, discriminator, generator = dcganModels()
batchSize = 128
for epoch in range(nbEpoch):
randomInput, trueImages, generatedImages = makeBatch(x_train)
discriminatorLoss = 0.5 * (discriminator.train_on_batch(generatedImages, np.zeros(generatedImages.shape[0])) + discriminator.train_on_batch(trueImages, np.ones(trueImages.shape[0])))
dcganLabels = np.ones(generatedImages.shape[0]).astype(int)
discriminator.trainable = False
dcganLoss = gan.train_on_batch(randomInput, dcganLabels)
discriminator.trainable = True
dLoss.append(discriminatorLoss)
gLoss.append(dcganLoss)
if (epoch % 50 == 0) or (epoch == 0):
print('after epoch: ', epoch)
print ('dcgan Loss: ', dcganLoss, '\t discriminator loss', discriminatorLoss)
clear_output(wait=True)
fig, ax1 = plt.subplots(1,1)
fig.set_size_inches(16, 8)
ax1.plot(range(len(dLoss)), dLoss, label="loss generator")
ax1.plot(range(len(gLoss)), gLoss, label="loss disc-true")
plt.show()
plotImages(generatedImages)
tbl.logModel(logger, epoch, generator, "generator")
tbl.logModel(logger, epoch, discriminator, "discriminator")
logger.log_scalar('generator_loss', gLoss[epoch], epoch)
logger.log_scalar('discriminator_loss', dLoss[epoch], epoch)
```
| github_jupyter |
## Preprocessing
```
# Import our dependencies
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import pandas as pd
import tensorflow as tf
# Import and read the charity_data.csv.
import pandas as pd
application_df = pd.read_csv("Resources/charity_data.csv")
application_df.head()
# Drop the non-beneficial ID columns, 'EIN' and 'NAME'.
application_df = application_df.drop(columns=['EIN','NAME'],axis=1)
application_df
# Determine the number of unique values in each column.
application_df.nunique()
# Look at APPLICATION_TYPE value counts for binning
app_type = application_df['APPLICATION_TYPE'].value_counts()
app_type
# Choose a cutoff value and create a list of application types to be replaced
# use the variable name `application_types_to_replace
application_types_to_replace = list(app_type[app_type<200].index)
# Replace in dataframe
for app in application_types_to_replace:
application_df['APPLICATION_TYPE'] = application_df['APPLICATION_TYPE'].replace(app,"Other")
# Check to make sure binning was successful
application_df['APPLICATION_TYPE'].value_counts()
# Look at CLASSIFICATION value counts for binning
app_class = application_df['CLASSIFICATION'].value_counts()
app_class
# You may find it helpful to look at CLASSIFICATION value counts >1
for i in app_class:
if i > 1:
print(i)
# Choose a cutoff value and create a list of classifications to be replaced
# use the variable name `classifications_to_replace`
classifications_to_replace = list(app_class[app_class<800].index)
# Replace in dataframe
for cls in classifications_to_replace:
application_df['CLASSIFICATION'] = application_df['CLASSIFICATION'].replace(cls,"Other")
# Check to make sure binning was successful
application_df['CLASSIFICATION'].value_counts()
# Convert categorical data to numeric with `pd.get_dummies`
application_df = pd.get_dummies(application_df, dtype=float)
application_df
# Split our preprocessed data into our features and target arrays
y = application_df.IS_SUCCESSFUL.values
X = application_df.drop('IS_SUCCESSFUL', axis=1).values
# Split the preprocessed data into a training and
# testing dataset
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state= 42)
# Create a StandardScaler instances
scaler = StandardScaler()
# Fit the StandardScaler
X_scaler = scaler.fit(X_train)
# Scale the data
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
```
## Compile, Train and Evaluate the Model
```
# # Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
# number_input_features = len( X_train_scaled[0])
# hidden_nodes_layer1=88
# hidden_nodes_layer2=44
# attempt 2
number_input_features = len( X_train_scaled[0])
hidden_nodes_layer1=10
hidden_nodes_layer2=20
# # attempt 3
# number_input_features = len( X_train_scaled[0])
# hidden_nodes_layer1=15
# hidden_nodes_layer2=40
nn = tf.keras.models.Sequential()
# First hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer1, input_dim=number_input_features, activation='relu'))
# Second hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer2, activation='relu'))
# Output layer
nn.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))
# Check the structure of the model
nn.summary()
# Compile the model
nn.compile(loss = 'binary_crossentropy', optimizer = 'adam', metrics=['accuracy', tf.keras.metrics.Recall()])
# Train the model
fit_model = nn.fit(X_train_scaled,y_train,validation_split=0.15, epochs=100)
# Evaluate the model using the test data
model_loss, model_accuracy, model_recall = nn.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
# Export our model to HDF5 file
from google.colab import files
nn.save('AlphabetSoupCharity_Optimization.h5')
files.download('AlphabetSoupCharity_Optimization.h5')
```
| github_jupyter |
# Puts ALL WISE Astrometry reference catalogues into GAIA reference frame
<img src=https://avatars1.githubusercontent.com/u/7880370?s=200&v=4>
The WISE catalogues were produced by ../dmu16_allwise/make_wise_samples_for_stacking.csh
In the catalogue, we keep:
- The position;
- The chi^2
This astrometric correction is adapted from master list code (dmu1_ml_XMM-LSS/1.8_SERVS.ipynb) written by Yannick Rohlly and Raphael Shirley
```
field="XMM-LSS"
from herschelhelp_internal import git_version
print("This notebook was run with herschelhelp_internal version: \n{}".format(git_version()))
%matplotlib inline
#%config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
plt.rc('figure', figsize=(10, 6))
from collections import OrderedDict
import os
from astropy import units as u
from astropy.coordinates import SkyCoord
from astropy.table import Column, Table
import numpy as np
from herschelhelp_internal.flagging import gaia_flag_column
from herschelhelp_internal.masterlist import nb_astcor_diag_plot, remove_duplicates
from herschelhelp_internal.utils import astrometric_correction, flux_to_mag
OUT_DIR = os.environ.get('TMP_DIR', "../dmu16_allwise/data/")
try:
os.makedirs(OUT_DIR)
except FileExistsError:
pass
RA_COL = "servs_ra"
DEC_COL = "servs_dec"
## I - Reading in WISE astrometric catalogue
wise = Table.read(f"../dmu16_allwise/data/Allwise_PSF_stack_{field}.fits")
wise_coords=SkyCoord(wise['ra'], wise['dec'])
epoch = 2009
wise[:10].show_in_notebook()
```
## III - Astrometry correction
We match the astrometry to the Gaia one. We limit the Gaia catalogue to sources with a g band flux between the 30th and the 70th percentile. Some quick tests show that this give the lower dispersion in the results.
```
#gaia = Table.read("./dmu17_XMM-LSS/data/GAIA_XMM-LSS.fits")
print(f"../../dmu0/dmu0_GAIA/data/GAIA_{field}.fits")
gaia = Table.read(f"../../dmu0/dmu0_GAIA/data/GAIA_{field}.fits")
gaia_coords = SkyCoord(gaia['ra'], gaia['dec'])
nb_astcor_diag_plot(wise_coords.ra, wise_coords.dec,
gaia_coords.ra, gaia_coords.dec, near_ra0=True)
delta_ra, delta_dec = astrometric_correction(
wise_coords,
gaia_coords, near_ra0=True
)
print("RA correction: {}".format(delta_ra))
print("Dec correction: {}".format(delta_dec))
print( wise["ra"])
print(delta_ra.to(u.deg))
#wise["ra"] += delta_ra.to(u.deg)
wise["ra"] = wise["ra"]+ delta_ra.to(u.deg)
wise["dec"] = wise["dec"]+ delta_dec.to(u.deg)
nb_astcor_diag_plot(wise["ra"], wise["dec"],
gaia_coords.ra, gaia_coords.dec, near_ra0=True)
```
## V - Saving to disk
```
wise.write(f"../dmu16_allwise/data/Allwise_PSF_stack_GAIA_{field}.fits", overwrite=True)
```
| github_jupyter |
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# Any results you write to the current directory are saved as output.
```
This is the post about **Introduction to Data Scinece**, I am going to write about* handling tabular/dataframe* data in python3.
### Importing Data
```
import pandas as pd
df = pd.read_csv('/kaggle/input/california-housing-prices/housing.csv')
display(df.head())
```
During data analysis, we need to use our data to perform some calculations and generate some new data or output from it. Pandas makes it very easy to apply user-defined operations, in Python terminology, on individual data items, rows, and columns of a dataframe.
Pandas has an **apply** function which applies the provided function to the data. One of the reasons for the success of pandas is how fast the apply function performs.
In the Dataset, the field **median_income** has values which are written in tens of thousands of dollars. During analysis, we might want to convert this to Dollars. Let’s see how we can do that with the apply function.
```
def convert(n):
return n * 10000
converted = df['median_income'].apply(convert)
display(converted.head())
# update value
df['median_income'] = converted
display(df.head())
```
### Converting numerical values to categories
----
During analysis, sometimes we want to classify our data into separate classes based on some criteria. For instance, we might want to separate these housing blocks into three distinct categories based on the median income of the households i.e.
* High-incomes
* Moderate-incomes
* Low-incomes
```
def category(n):
value = n / 10000
if value > 10:
return 'high-income'
elif value > 2 and value < 10:
return 'moderate-income'
else:
return 'low-income'
categories = df['median_income'].apply(category)
df['income-category'] = categories
display(df.head())
print(df['income-category'].value_counts())
```
| github_jupyter |
```
from pykat import finesse
from pykat.commands import *
import numpy as np
import matplotlib.pyplot as plt
import scipy
from IPython import display
pykat.init_pykat_plotting(dpi=200)
base1 = """
l L0 10 0 n0 #input laser
tem L0 0 0 1 0 #tem modes
tem L0 1 0 1 0
tem L0 2 0 1 0
tem L0 3 0 1 0
tem L0 4 0 1 0
tem L0 5 0 1 0
tem L0 6 0 1 0
tem L0 7 0 1 0
s s1 1 n0 n5
m itmx0 0 1 0 n5 n6 #ITM surface 1
s itmx_l 0.035 1.44963 n6 n7 #thickness of mirror
m2 itmx 0.99 50u 0 n7 n8 #ITM surface 2
s s2 9.1 n8 n9 #cavity length
m2 etmx 0.998 50u 0 n9 n10 #ETM surface 2
s etmx_l 0.035 1.44963 n10 n11 #thickness of mirror
m etmx0 0 1 0 n11 n12 #ETM surface 1
attr etmx Rcx 34 #roc of mirror
attr etmx Rcy 34
xaxis etmx Rcx lin 20 40 6000
func g = 1-(9.1/$x1)
put etmx Rcy $x1
ad order0 0 0 0 n12 #ad detectors
ad order1 1 0 0 n12
ad order2 2 0 0 n12
ad order3 3 0 0 n12
ad order4 4 0 0 n12
ad order5 5 0 0 n12
ad order6 6 0 0 n12
ad order7 7 0 0 n12
cav FP itmx n8 etmx n9
cp FP x finesse
maxtem 7
phase 2
#noplot Rc2
"""
basekat = finesse.kat()
basekat.verbose = 1
basekat.parse(base1)
out = basekat.run()
out.info()
#out.plot(['FP_x_w'])
y=[]
x= out['g']
colors = ['b','g','r','c','m','y','k','teal','violet','pink','olive']
#plt.figure(figsize=(8,4))
#append all output detectors in an array
for i in range(0,7,1):
y.append(out['order'+str(i+1)]/out['order0'])
#plot all outputs
for k in range(0,7,1):
plt.semilogy(x,y[k],antialiased=False,label='order'+str(k),c=colors[k])
#label and other stuff
plt.grid(linewidth=1)
plt.legend(["order1","order2","order3","order4","order5","order6","order7","order8","order9","order10"],loc='center left', bbox_to_anchor=(1, 0.5))
plt.xlabel("g (1-L/R) \n Finesse = "+str(out['FP_x_finesse'][1]))
plt.ylabel("HG modes intensity(rel to fund. mode)",verticalalignment='center')
plt.axvline(x = 0.708, color = 'r', linestyle = 'dashed')
plt.axvline(x = 0.73, color = 'b', linestyle = 'dashed')
display.Image("C:/Users/Parivesh/Desktop/9.1m.jpg",width = 500, height = 300)
base2 = """
l L0 10 0 n0 #input laser
s s1 1 n0 n1 #laser cav
bs bs1 0.5 0.5 0 0 n1 n2 n3 n4 #beam splitter
s sx 1 n2 n5 #BS to ITMx cav
m itmx0 0 1 0 n5 n6 #ITM surface 1
s itmx_l 0.035 1.44963 n6 n7 #thickness of mirror
m2 itmx 0.99 50u 0 n7 n8 #ITM surface 2
s s2 9.1 n8 n9 #arm length
m2 etmx 0.998 50u 0 n9 n10 #ETM surface 2
s etmx_l 0.035 1.44963 n10 n11 #thickness of mirror
m etmx0 0 1 0 n11 dump #ETM surface 1
s sy 1 n3 n13 #BS to ITMy cav
m itmy0 0 1 0 n13 n14
s itmy_l 0.035 1.44963 n14 n15
m2 itmy 0.99 50u 0 n15 n16
s s3 9.1 n16 n17
m2 etmy 0.998 50u 0 n17 n18
s etmy_l 0.035 1.44963 n18 n19
m etmy0 0 1 0 n19 n20
attr etmy Rc 34 #roc of mirror
attr etmx Rc 34
xaxis etmy phi lin -220 220 7000
#maxtem 7
#phase 2
pd pd_out n4
#ad order0 0 0 0 n20 #ad detectors
#ad order1 1 0 0 n20
#ad order2 2 0 0 n20
"""
basekat1 = finesse.kat()
basekat1.verbose = 1
basekat1.parse(base2)
out = basekat1.run()
out.info()
out.plot(['pd_out'])
#out.plot(['order0','order1','order2'])
print("Contrast Ratio : ",(np.max(out['pd_out'])-np.min(out['pd_out']))/(np.max(out['pd_out'])+np.min(out['pd_out'])))
```
| github_jupyter |
-> Associated lecture videos:
in Neural Networks/Lesson 4 - Deep Learning with PyTorch: video 4, video 5, video 6, video 7
# Introduction to Deep Learning with PyTorch
In this notebook, you'll get introduced to [PyTorch](http://pytorch.org/), a framework for building and training neural networks. PyTorch in a lot of ways behaves like the arrays you love from Numpy. These Numpy arrays, after all, are just tensors. PyTorch takes these tensors and makes it simple to move them to GPUs for the faster processing needed when training neural networks. It also provides a module that automatically calculates gradients (for backpropagation!) and another module specifically for building neural networks. All together, PyTorch ends up being more coherent with Python and the Numpy/Scipy stack compared to TensorFlow and other frameworks.
## Neural Networks
Deep Learning is based on artificial neural networks which have been around in some form since the late 1950s. The networks are built from individual parts approximating neurons, typically called units or simply "neurons." Each unit has some number of weighted inputs. These weighted inputs are summed together (a linear combination) then passed through an activation function to get the unit's output.
<img src="assets/simple_neuron.png" width=400px>
Mathematically this looks like:
$$
\begin{align}
y &= f(w_1 x_1 + w_2 x_2 + b) \\
y &= f\left(\sum_i w_i x_i +b \right)
\end{align}
$$
With vectors this is the dot/inner product of two vectors:
$$
h = \begin{bmatrix}
x_1 \, x_2 \cdots x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_1 \\
w_2 \\
\vdots \\
w_n
\end{bmatrix}
$$
## Tensors
It turns out neural network computations are just a bunch of linear algebra operations on *tensors*, a generalization of vectors and matrices. A vector is a 1-dimensional tensor, a matrix is a 2-dimensional tensor, an array with three indices is a 3-dimensional tensor (RGB color images for example). The fundamental data structure for neural networks are tensors and PyTorch (as well as pretty much every other deep learning framework) is built around tensors.
<img src="assets/tensor_examples.svg" width=600px>
With the basics covered, it's time to explore how we can use PyTorch to build a simple neural network.
```
# First, import PyTorch
import torch
def activation(x):
""" Sigmoid activation function
Arguments
---------
x: torch.Tensor
"""
return 1/(1+torch.exp(-x))
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 5 random normal variables (input features: x1, x2, x3, x4, x5 for each dataset example)
features = torch.randn((1, 5)) # creates a 2D tensor ('features') of random normal variables, of size (1, 5)
# True weights for our data, random normal variables again
weights = torch.randn_like(features) # creates a tensor ('weights') with same shape as the 'features' 2D tensor
# and a true bias term
bias = torch.randn((1, 1)) # a single random normal variable
```
Above I generated data we can use to get the output of our simple network. This is all just random for now, going forward we'll start using normal data. Going through each relevant line:
`features = torch.randn((1, 5))` creates a tensor with shape `(1, 5)`, one row and five columns, that contains values randomly distributed according to the normal distribution with a mean of zero and standard deviation of one.
`weights = torch.randn_like(features)` creates another tensor with the same shape as `features`, again containing values from a normal distribution.
Finally, `bias = torch.randn((1, 1))` creates a single value from a normal distribution.
PyTorch tensors can be added, multiplied, subtracted, etc, just like Numpy arrays. In general, you'll use PyTorch tensors pretty much the same way you'd use Numpy arrays. They come with some nice **benefits though such as GPU acceleration** which we'll get to later. For now, use the generated data to calculate the output of this simple single layer network.
> **Exercise**: Calculate the output of the network with input features `features`, weights `weights`, and bias `bias`. Similar to Numpy, PyTorch has a [`torch.sum()`](https://pytorch.org/docs/stable/torch.html#torch.sum) function, as well as a `.sum()` method on tensors, for taking sums. Use the function `activation` defined above as the activation function.
```
## Calculate the output of this network using the weights and bias tensors
h = torch.sum(features * weights) + bias
output_y = activation(h)
# or using (features * weights).sum() instead of torch.sum()
### Recall
# features * weights -> this multiplies each element (5 in total) of 'features' with each element in 'weights'
## This is called an 'element-wise' operation, here the operation being the multiplication
output_y
```
You can do the multiplication and sum in the same operation using a matrix multiplication, instead of writing `torch.sum(features * weights)`. In general, you'll want to use matrix multiplications since they are more efficient and accelerated using modern libraries and high-performance computing on GPUs.
Here, we want to do a matrix multiplication of the features and the weights. For this we can use [`torch.mm()`](https://pytorch.org/docs/stable/torch.html#torch.mm) or [`torch.matmul()`](https://pytorch.org/docs/stable/torch.html#torch.matmul) which is somewhat more complicated and supports broadcasting. If we try to do it with `features` and `weights` as they are, we'll get an error
```python
>> torch.mm(features, weights)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-13-15d592eb5279> in <module>()
----> 1 torch.mm(features, weights)
RuntimeError: size mismatch, m1: [1 x 5], m2: [1 x 5] at /Users/soumith/minicondabuild3/conda-bld/pytorch_1524590658547/work/aten/src/TH/generic/THTensorMath.c:2033
```
As you're building neural networks in any framework, you'll see this often. Really often. What's happening here is our tensors aren't the correct shapes to perform a matrix multiplication. **Remember that for matrix multiplications, the number of columns in the first tensor must equal to the number of rows in the second column**. Both `features` and `weights` have the same shape, `(1, 5)`. This means we need to change the shape of `weights` to get the matrix multiplication to work.
**Note:** To see the shape of a tensor called `tensor`, use `tensor.shape`. If you're building neural networks, you'll be using this method often.
There are a few options here: [`weights.reshape()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.reshape), [`weights.resize_()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.resize_), and [`weights.view()`](https://pytorch.org/docs/stable/tensors.html#torch.Tensor.view).
* `weights.reshape(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)` sometimes, and sometimes a clone, as in it copies the data to another part of memory.
* `weights.resize_(a, b)` returns the same tensor with a different shape. However, if the new shape results in fewer elements than the original tensor, some elements will be removed from the tensor (but not from memory). If the new shape results in more elements than the original tensor, new elements will be uninitialized in memory. Here I should note that the underscore at the end of the method denotes that this method is performed **in-place**. Here is a great forum thread to [read more about in-place operations](https://discuss.pytorch.org/t/what-is-in-place-operation/16244) in PyTorch.
**BEST OPTION:**
* `weights.view(a, b)` will return a new tensor with the same data as `weights` with size `(a, b)`.
I usually use `.view()`, but any of the three methods will work for this. So, now we can reshape `weights` to have five rows and one column with something like `weights.view(5, 1)`.
> **Exercise**: Calculate the output of our little network using matrix multiplication.
```
## Calculate the output of this network using matrix multiplication
h = torch.mm(features, weights.view(5,1)) + bias
output_y = activation(h)
output_y
```
### Stack them up! -> Multilayer neural networks
That's how you can calculate the output for a single neuron. The real power of this algorithm happens when you start stacking these individual units into layers and stacks of layers, into a network of neurons. The output of one layer of neurons becomes the input for the next layer. With multiple input units and output units, we now need to express the weights as a matrix.
<img src='assets/multilayer_diagram_weights.png' width=450px>
The first layer shown on the bottom here are the inputs, understandably called the **input layer**. The middle layer is called the **hidden layer**, and the final layer (on top) is the **output layer**. We can express this network mathematically with matrices again and use matrix multiplication to get linear combinations for each unit in one operation. For example, the hidden layer ($h_1$ and $h_2$ here) can be calculated
$$
\vec{h} = [h_1 \, h_2] =
\begin{bmatrix}
x_1 \, x_2 \cdots \, x_n
\end{bmatrix}
\cdot
\begin{bmatrix}
w_{11} & w_{12} \\
w_{21} &w_{22} \\
\vdots &\vdots \\
w_{n1} &w_{n2}
\end{bmatrix}
$$
The output for this small network is found by treating the hidden layer as inputs for the output unit. The network output is expressed simply
$$
y = f_2 \! \left(\, f_1 \! \left(\vec{x} \, \mathbf{W_1}\right) \mathbf{W_2} \right)
$$
```
### Generate some data
torch.manual_seed(7) # Set the random seed so things are predictable
# Features are 3 random normal variables: x1, x2 and x3
features = torch.randn((1, 3))
# Define the size of each layer in our network
n_input = features.shape[1] # Number of input units, must match number of input features
n_hidden = 2 # Number of hidden units
n_output = 1 # Number of output units
# Weights for inputs to hidden layer
W1 = torch.randn(n_input, n_hidden)
# Weights for hidden layer to output layer
W2 = torch.randn(n_hidden, n_output)
# and bias terms for hidden and output layers
B1 = torch.randn((1, n_hidden))
B2 = torch.randn((1, n_output))
```
> **Exercise:** Calculate the output for this multi-layer network using the weights `W1` & `W2`, and the biases, `B1` & `B2`.
```
## Your solution here
H = activation(torch.mm(features, W1) + B1) # 2D tensor (shape: 1,2) containing h1 and h2
output_y = activation(torch.mm(H, W2) + B2) # 1D tensor (shape: 1,1) containg the single ouput
output_y
```
If you did this correctly, you should see the output `tensor([[ 0.3171]])`.
The number of hidden units is a parameter of the network, often called a **hyperparameter** to differentiate it from the weights and biases parameters. As you'll see later when we discuss training a neural network, the more hidden units a network has, and the more layers, the better able it is to learn from data and make accurate predictions.
## Numpy to Torch and back
Special bonus section! PyTorch has a great feature for converting between Numpy arrays and Torch tensors. To create a tensor from a Numpy array, use `torch.from_numpy()`. To convert a tensor to a Numpy array, use the `.numpy()` method.
```
import numpy as np
a = np.random.rand(4,3)
a # a nd numpy array
b = torch.from_numpy(a)
b # a 2D tensor
b.numpy()
```
The memory is shared between the Numpy array and Torch tensor, so if you change the values in-place of one object, the other will change as well.
```
# Multiply PyTorch Tensor by 2, in place (symbol: _)
b.mul_(2) # in place multiplication by 2
# Numpy array matches new values from Tensor b
a
```
| github_jupyter |
# Chapter 7 - Iterations
-------------------------------
Computers do not get bored. If you want the computer to repeat a certain task hundreds of thousands of times, it does not protest. Humans hate too much repetition. Therefore, repetitious tasks should be performed by computers. All programming languages support repetitions. The general class of programming constructs that allow the definition of repetitions are called "iterations". A term which is even more common for such tasks is "loops".
This chapter explains all you need to know about loops in Python. Students who are completely new to programming often find loops the first really hard topic in programming that they encounter. If that is the case for you, then make sure you take your time for this chapter, and work on it until you understand it completely. Loops are such a basic concept in programming that you need to understand them in all their details. Each and every chapter after this one needs loops.
---
## `while` loop
Suppose you have to ask the user for five numbers, then add them up, and show the total. With the material from the previous chapter, you would program that as follows:
```
from pcinput import getInteger
num1 = getInteger( "Number 1: " )
num2 = getInteger( "Number 2: " )
num3 = getInteger( "Number 3: " )
num4 = getInteger( "Number 4: " )
num5 = getInteger( "Number 5: " )
print( "Total is", num1 + num2 + num3 + num4 + num5 )
```
But what if I want you to ask the user for 500 numbers? Are you going to create a block of code of more than 500 lines long? Surely there must be an easier way to do this?
Of course there is. You can use a loop to do this.
The first loop I am going to present to you is the `while` loop. A `while` statement is quite similar to an `if` statement. The syntax is:
while <boolean expression>:
<statements>
Just like an `if` statement, the `while` statement tests a boolean expression, and if the expression evaluates to `True`, it executes the code block below it. However, contrary to the `if` statement, once the code block has finished, the code "loops" back to the boolean expression to test it again. If it still evaluates to `True`, the code block below it gets executed once more. And after it has finished, it loops back again, and again, and again...
Note: if the boolean expression immediately evaluates to `False`, then the code block below the `while` is skipped completely, just like with an `if` statement.
### `while` loop, first example
Let's take a simple example: printing the numbers 1 to 5. With a `while` loop, that can be done as follows:
```
num = 1
while num <= 5:
print( num )
num += 1
print( "Done" )
```
This code is represented by the flow chart below.
<img src="img/Chart4en.png" alt="Simple while-loop" style="width:300px;"><br>
<div align="center">Figure 7.1: Simple while-loop.</div>
It is crucial that you understand this code, so let's discuss it step by step.
The first line initializes a variable `num`. This is the variable that the code will print, so it is initialized to `1`, as `1` is the first value that must be printed.
Then the `while` loop starts. The boolean expression says `num <= 5`. Since `num` is `1`, and `1` is actually smaller than (or equal to) `5`, the boolean expression evaluates to `True`. Therefore, the code block below the `while` gets executed.
The first line of the code block below the `while` prints the value of `num`, which is `1`. The second line adds `1` to the value of `num`, which makes `num` hold the value `2`. Then the code loops back to the boolean expression (i.e., the last line of the code, the printing of "Done", is not executed as it is not part of the loop and the loop has not finished yet).
Since `num` is `2`, the boolean expression still evaluates to `True`. The code block gets executed once more. `2` is displayed, `num` gets the value `3`, and the code loops back to the boolean expression.
Since `num` is `3`, the boolean expression still evaluates to `True`. The code block gets executed once more. `3` is displayed, `num` gets the value `4`, and the code loops back to the boolean expression.
Since `num` is `4`, the boolean expression still evaluates to `True`. The code block gets executed once more. `4` is displayed, `num` gets the value `5`, and the code loops back to the boolean expression.
Since `num` is `5`, the boolean expression still evaluates to `True` (because `5 <= 5`). The code block gets executed once more. `5` is displayed, `num` gets the value `6`, and the code loops back to the boolean expression.
Since `num` is `6`, the boolean expression now evaluates to `False` (because `6` is bigger than `5`). Therefore, the code block gets skipped, and the code continues with the first line below the code block, which is the last line of the code. The word `Done` is printed, and the code ends.
**Exercise**: Change the code above so that it prints the numbers 1, 3, 5, 7, and 9.
### `while` loop, second example
If you understand the first example, you probably also understand how to ask the user for five numbers and print the total. This is implemented as follows:
```
from pcinput import getInteger
total = 0
count = 0
while count < 5:
total += getInteger( "Please give a number: " )
count += 1
print( "Total is", total )
```
Study this code closely. There are two variables used. `total` is used to add up the five numbers that the user enters. It is started at zero, as at the start of the code the user has not yet entered any numbers, so the total is still zero. `count` is used to count how often the code has gone through the loop. Since the loop must be done five times, `count` is started at `0` and the boolean expression for the loop continues until `count` is `5` (or higher). Thus, in the loop `count` gets increased by `1` at the end of every cycle through the loop.
You may wonder why `count` is started at `0` and the boolean expression checks if `count < 5`. Why not start `count` at `1` and check if `count <= 5`? The reason is convention: programmers are used to start indices at `0`, and if they count, they count "up to but not including". When you continue with programming, you will find that most code sticks to this convention. Most standard programming constructs that use indices or count things apply this convention too. My advice is therefore that you get used to it, as it makes code easier to read.
Note: The variable `count` is what programmers call a "throw-away variable". Its only purpose is to count how often the loop has been cycled through, and it has no real meaning before the loop, in the loop, or after the loop has ended. Programmers often choose a single-character variable name for such a variable, usually `i` or `j`. In this example I chose the name `count` because it is illustrative of what the variable does for the code, but a single-character name for this variable would have been acceptable.
**Exercise**: Change the code block above so that it not only prints the total, but also the average of the five numbers.
**Exercise**: The first code block of this chapter also asks the user for five numbers, and prints the total. However, that code block uses "Enter number *x*: " as a prompt, whereby *x* is a digit. Can you change the code block above so that it also uses such a changing prompt to ask for each number? Hint: you can construct a string that represents the prompt by adding a couple of strings together; remember that you can use the `str()` function to turn a number into a string.
### Putting the `while` loop under user control
Suppose that, in the second example, you do not want the user to be restricted to entering exactly five numbers. You want the user to enter as many numbers as he wants, including none. This means that you cannot predict how many iterations through the `while` loop are needed. Instead, it is the user who controls when the loop ends. You therefore have to give the user the means to indicate that the loop should end.
The code block below shows how to use a `while` loop to allow the user to enter numbers as long as he wants, until he enters a zero. Once a zero is entered, the total is printed, and the program ends.
```
from pcinput import getInteger
num = -1
total = 0
while num != 0:
num = getInteger( "Enter a number: " )
total += num
print( "Total is", total )
```
This code works, but there are (at least) two ugly things about it. First, `num` is initialized to `-1`. The `-1` is meaningless, I just needed an initialization that would ensure that the `while` loop would be entered at least once. Second, when the user enters zero, `total` still gets increased by `num`. Since `num` is zero at that point, it does not matter for the total, but if I wanted the user to end the program by typing something else (for instance, a negative number), then `total` would now hold the wrong value.
Because of these ugly elements, some programmers prefer to write this code as follows:
```
from pcinput import getInteger
num = getInteger( "Enter a number: " )
total = 0
while num != 0:
total += num
num = getInteger( "Enter a number: " )
print( "Total is", total )
```
This solves the ugly parts from the previous code, but introduces something new that is ugly, namely the repetition of the `getInteger()` function. How this can be solved follows at the end of this chapter. For now, make sure that you understand how `while` loops work.
### Endless loops
The code below is supposed to start at number 1, and add up numbers, until it encounters a number that, when squared, is dividable by 1000. The code contains an error, though. See if you can spot it (without running the code!).
```
number = 1
total = 0
while (number * number) % 1000 != 0:
total += number
print( "Total is", total )
```
The heading of this subsection gave away the answer, of course: this code contains a loop that never terminates. If you run it, it looks like the program "hangs", i.e., sits there and does nothing. It is not doing nothing, it is actually highly active, but it is in a neverending addition. `number` starts at `1`, and is never increased in the loop, so the boolean expression will always be `True`. This is called an "endless loop", and it is the single one great danger in using `while` loops.
If you did run this code, you can go the the "Kernel" menu and choose "Interrupt". If you ran the code without modifications, you will have to do that.
If you did not spot that this is an example of an endless loop, you might have seen what happened if I had written code that prints something in the loop. Unfortunately, browsers tend not to handle notebooks that print a lot of stuff well, and you would probably need a reboot of your computer, or at least the shutdown of the browser via a task manager, to resolve the problem. That's not very nice, so I did not do that.
Since every programmer writes endless loops by accident now and again, it is good practice when you program a loop to immediately add a statement to a loop that makes a change that is tested in the boolean expression, so that you do not forget about it.
Should you still write an endless loop and have troubles interrupting the kernel, if you are on the notebook server the instructor can shut down your kernel for you.
**Exercise**: Fix the code above so that it no longer is an endless loop.
### `while` loop practice exercises
You should now practice a bit with simple `while` loops.
**Exercise**: In the code block below, write a countdown function. It starts with a given number (in this case 10, but you should be able to change it), and counts down to zero, printing each number it encounters (10, 9, 8, ...). It does not print `0`, instead it prints "Blast off!".
```
# Countdown.
count = 10
```
**Exercise**: The factorial of a positive integer is that integer, multiplied by all positive integers that are lower (excluding zero). You write the factorial as the number with an exclamation mark after it. E.g., the factorial of 5 is `5! = 5 * 4 * 3 * 2 * 1 = 120`. Write some code that calculates the factorial of a number. The number is given here as `num`. You can try out different values for `num`, but do not make them too high, as factorials grow exponentially. Hint: to do this with a `while` loop, you need at least one more variable.
```
# Factorial.
num = 5
```
---
## `for` loop
An alternative way of implementing loops is by using a `for` loop. `for` loops tends to be easier and safer to use than `while` loops, but cannot be applied to all iteration problems. `while` loops are more general. In other words, everything that a `for` loop can do, a `while` loop can do too, but not the other way around.
The syntax of a `for` loop is as follows:
for <variable> in <collection>:
<statements>
A `for` loop gets presented with a collection of items, and it will process these items, in order, one by one. Every cycle through the loop will put one item in the variable given next to the `for`, and can then be used in the code block under the `for`. The variable does *not* need to exist before the `for` loop is encountered. If it does, it gets overwritten. It is a real variable, by the way, in the sense that it still exists after the loop has finished. It will contain the last value that it got assigned during the processing of the loop.
At this point you might wonder what a "collection" is. There are many different kinds of collections in Python, and in this section I will introduce a few. In later chapters collections will be discussed in more detail.
### `for` loop with strings
The only collection introduced until now is the string. A string is a collection of characters, e.g., the string "banana" is a collection of the characters "b", "a", "n", "a", "n", and "a", in that specific order. The following code loops through each of these letters:
```
for letter in "banana":
print( letter )
print( "Done" )
```
While this code is fairly trivial, let's go through it step by step.
When the `for` loop is encountered, Python takes the collection (i.e., the string "banana") and turns it into an "iterable". What that is exactly I will get to in a later chapter, but for now assume that it is a list of all the letters in the string, in the order that they appear in the string. Python then takes the first of those letters, and puts it in the variable `letter`. It then executes the code block below the `for`.
The code block contains only one statement, which is the printing of `letter`. So the program prints "b", and then loops back to the `for`.
Python then takes the next letter, which is an "a", and it executes the code block with `letter` being an "a".
It then repeats this process for each of the remaining letters.
Once all the letters have been used, the `for` loop ends, and Python executes the last line of the code, which is the printing of the word "Done".
To be absolutely clear: In a `for` loop you do *not* have to write code that explicitly increases some kind of variable that then grabs the next letter, or something like that. The `for` statement handles that automatically: every time it is looped back to, it takes the next item from the collection.
### `for` loop using a variable as collection
In the code above, the literal string "banana" was used as the collection, but it could also be a variable that contains a string. For instance, the following code runs similar to the previous code:
```
fruit = "banana"
for letter in fruit:
print( letter )
print( "Done" )
```
You might wonder if this isn't dangerous. What happens if the programmer changes the contents of the variable `fruit` *in* the loop's code block? Let's try that out:
```
fruit = "banana"
for letter in fruit:
print( letter )
if letter == "n":
fruit = "orange"
print( "Done" )
```
As you can see when you run this code, changing the contents of the variable `fruit` in the loop has *no effect* on the loop's processing. The sequence of characters that the loop processes is only constituted once, when the `for` loop is first entered. This is a great feature of `for` loops, because it means they are *guaranteed* to end. No `for` loops are endless! (Unfortunately, I will have to revise this statement in a much later chapter, but it requires knowledge of pretty advanced Python to create an endless `for` loop -- for now, and in general practice, you may assume that `for` loops are guaranteed to end.)
Note that there is a conditional statement in the loop above. There is nothing that stops you from putting conditions in the code block for a loop. There is also nothing against putting loops in the code block for a condition, or even putting loops inside loops (more on that last option follows later in this chapter). Most students probably are not surprised to hear that, but for the few who are completely new to programming: as long as you stick to the syntactic requirements, you can use conditional statements and loops wherever you can write Python statements.
### `for` loop using a range of numbers
Python offers a `range()` function that generates a collection of sequential numbers, which is often used for `for` loops. The simplest call to `range()` has one parameter, which is a number. It will generate all integers, starting at zero, up to but not including the parameter.
```
for x in range( 10 ):
print( x )
```
`range()` can get multiple parameters. If you give two parameters, then the first will be the starting number (default is zero), while the second will be the "up to but not including" number. If you give three parameters, the third will be a step size (default is `1`). You can choose a negative step size if you want to count down. With a negative step size, make sure that the starting number is higher than the number that you want to count up to (or down to, in this case).
```
for x in range( 1, 11, 2 ):
print( x )
```
**Exercise:** Change the three parameters above to observe their effect, until you fully understand the `range()` function.
**Exercise:** Use the `for` loop and `range()` function to print multiples of 3, starting at 21, counting down to 3, in just two lines of code.
```
# Counting down by threes.
```
### `for` loop with manual collections
If you want to use a `for` loop to cycle through items in a collection that you create manually, you can do so by listing all your items between parentheses. This defines a "tuple" for the items of your collection. Tuples will be discussed later.
```
for x in ( 10, 100, 1000, 10000 ):
print( x )
```
Or:
```
for x in ( "apple", "pear", "orange", "banana", "mango", "cherry" ):
print( x )
```
Your collection can even consist of mixed types.
### Practice with `for` loops
To get strong grips on how to use `for` loops, do the following exercises.
**Exercise**: You already created code with a `while` loop that asked the user for five numbers, and displayed their total. Create code for this task, but now use a `for` loop.
```
# Total of five numbers.
```
**Exercise**: Create a countdown function that starts at a certain count, and counts down to zero. Instead of zero, print "Blast off!". Use a `for` loop.
```
# Count down with for loop.
```
**Exercise**: I am not going to ask you to build a `for` loop that asks the user to enter numbers until the user enters zero. Why not? Hint: How often do you think that the user will enter a number that is not zero?
---
## Loop control statements
There are three extra statements that help you control the flow in a loop. They are `else`, `break`, and `continue`.
### `else`
Just like with an `if` statement, you can add an `else` statement to the end of a `while` or `for` loop. The code block for the `else` is executed whenever the loop ends, i.e., when the boolean expression for the `while` loop evaluates to `False`, or when the last item of the collection of the `for` loop is processed.
Here is an example of using the `else` clause for a `while` loop:
```
i = 0
while i < 5:
print( i )
i += 1
else:
print( "The loop ends, i is now", i )
print( "Done" )
```
This code is represented by the flow chart below.
<img src="img/Chart5en.png" alt="Example of an else-branch in a loop" style="width:300px;"><br>
<div align="center">Figure 7.2: Example of an else-branch in a loop.</div>
And here is an example of using `else` for a `for` loop:
```
for fruit in ( "apple", "orange", "strawberry" ):
print( fruit )
else:
print( "The loop ends, fruit is now", fruit )
print( "Done" )
```
### `break`
The `break` statement allows you to prematurely break out of a loop. I.e., when Python encounters the `break` statement, it will no longer process the remainder of the code block for the loop, and will not loop back to the boolean expression. It will simply continue with the first statement after the loop's code block.
To see why this is useful, here follows an interesting exercise. I am looking for a number that starts with a 1, and when you transfer that 1 to the end of the number, the result is a number that is three times as high. For example, if I check the number 1867, I move the 1 from the start to the end, which gives 8671. If 8671 would be three times 1867, that is the answer I seek. It is not, so 1867 is not correct. The code to solve this is actually fairly short, and gives the lowest number for which the comparison holds:
```
i = 1
while i <= 1000000:
num1 = int( "1" + str( i ) )
num2 = int( str( i ) + "1" )
if num2 == 3 * num1:
print( num2, "is three times", num1 )
break
i += 1
else:
print( "No answer found" )
```
This code is represented by the flow chart below.
<img src="img/Chart6en.png" alt="Example of a break in a loop" style="width:400px;"><br>
<div align="center">Figure 7.3: Example of a break in a loop.</div>
In this example we see the `break` statement used to good effect. Since I have no idea which number I am looking for, I am just going to check a whole bunch of numbers. I let a counter `i` run up to `1000000`. Of course, I don't know if I find the answer before `i` has reached `1000000`, but I should set a limit somewhere, because I don't know if a number with the requested property exists at all, and I do not want to create an endless loop. I might find the answer at any point, and when I do, I `break` out of the loop, because further testing of numbers no longer serves a purpose.
The point here is that the setting of the maximum value of `i` to `1000000` is not because I know that I have to generate one million numbers. I have no idea how many times I have to cycle through the loop. I just know that if I encounter the requested number at some point, I am done and can skip the remainder of the cycles. That is exactly what the purpose of the `break` is.
With some juggling I could make sure that the boolean expression for the loop actually does the comparison for me. It would be something like `while (i < 1000000) and (num1 != 3 * num2):`. This becomes a bit convoluted, and I would also have to give `num1` and `num2` starting values before the loop starts. Still, it is always possible to avoid using a `break`, but applying the `break` might make code more readable and flow better, as it does in this case.
The `break` statement also works for `for` loops.
The `break` statement cannot be used outside a loop. It is only defined for loops. (Take note of this. I very often see students putting `break` statements in conditions that are not inside a loop, and then look mystified when Python reports a runtime error.)
Note that when a `break` statement is encountered, and the loop also has an `else` clause, the code block for the `else` will *not* be executed. I use this to good effect in the code above, by ensuring that the text that indicates that no answer is found, only will be printed if the loop ends by checking all the numbers without finding an answer.
The following code checks a list of grades for a student. As long as all grades are 5.5 or higher, the student passes. When one or more grades are lower than 5.5, the student fails. The grades are in a collection that is given to a `for` loop.
```
for grade in ( 8, 7.5, 9, 6, 6, 6, 5.5, 7, 5, 8, 7, 7.5 ):
if grade < 5.5:
print( "The student fails!" )
break
else:
print( "The student passes!" )
```
**Exercise**: Remove the 5 from the list of grades and notice that the student now passes. Study this code carefully until you understand it.
### `continue`
When the `continue` statement is encountered in the code block of a loop, the current cycle ends immediately and the code loops back to the start of the loop. For a `while` loop, that means that the boolean expression is evaluated again. For a `for` loop, that means that the next item is taken from the collection and processed.
The following code prints all numbers between 1 and 100 that cannot be divided by 2 or 3, and do not end in a 7 or 9.
```
num = 0
while num < 100:
num += 1
if num%2 == 0:
continue
if num%3 == 0:
continue
if num%10 == 7:
continue
if num%10 == 9:
continue
print( num )
```
This code is represented by the flow chart below.
<img src="img/Chart7.png" alt="Example of a continue in a loop" style="width:300px;"><br>
<div align="center">Figure 7.4: Example of a continue in a loop.</div>
I don't know why you would want this list, but the use of `continue` statements to implement it helps. Alternatively, you could have created one big boolean expression for an `if` statement, but that would become unreadable quickly. Still, just like `break` statements, `continue` statements can always be avoided if you really want to, but they do help keeping code understandable.
Note that `continue` statements, just like `break` statements, can only be used inside loops.
Be very, very careful when using a `continue` in a `while` loop. Most `while` loops use a number that restricts the number of cycles through the loop. Usually such a number is increased at the bottom of the code block for the loop. A `continue` statement would loop back to the boolean expression immediately, without increasing the number, and thus such a `continue` could easily cause an endless loop. I.e.:
i = 0
while i < 10:
if i == 5:
continue
i += 1
causes an endless loop!
**Exercise**: Write a program that processes a collection of numbers using a `for` loop. The program should end immediately, printing only the word "Done", when a zero is encountered (use a `break` for this). Negative numbers should be ignored (use a `continue` for this; I know you can also easily do this with a condition, but I want you to practice with `continue`). If no zero is encountered, the program should display the sum of all numbers (do this in an `else` clause). Always display "Done" at the end of the program.
```
for num in ( 12, 4, 3, 33, -2, -5, 7, 0, 22, 4 ):
# Write your code here
```
With the numbers provided, the program should display only "Done". If you remove the zero, it should display 85 (and "Done").
-------
## Nested loops
You can put a loop inside another loop.
That is a simple statement, but it is one of the hardest concepts for students to wrap their minds around.
Let's first look at an example of a double-nested loop, i.e., a loop which contains one other loop. Usually programmers talk about an "outer loop" and an "inner loop". The inner loop is part of the code block for the outer loop.
```
for i in range( 3 ):
print( "Entering the outer loop for i =", i )
for j in range( 3 ):
print( " Entering the inner loop for j =", j )
print( " (i,j) = ({},{})".format( i, j ) )
print( " Leaving the inner loop for j =", j )
print( "Leaving the outer loop for i =", i )
```
Study this code and its output until you fully understand it!
The code first gives `i` the value `0`, and then lets `j` take on the values `0`, `1`, and `2`. It then gives `i` the value `1`, and then lets `j` take on the values `0`, `1`, and `2`. Finally, it gives `i` the value `2`, and then lets `j` take on the values `0`, `1`, and `2`. So this code runs through all possible pairs of `(i,j)` with `i` and `j` being `0`, `1`, or `2`.
Notice how variables for the outer loop are also accessible by the inner loop. `i` exists in both the outer and the inner loop.
Suppose that you want to print all pairs `(i,j)` where `i` and `j` can take on the values `0` to `3`, but `j` must be higher than `i`. Code that does that is:
```
for i in range( 4 ):
for j in range( i+1, 4 ):
print( "({},{})".format( i, j ) )
```
See how I cleverly use `i` to set the range for `j`?
**Exercise**: Write code that prints all pairs `(i,j)` where `i` and `j` can take on the values `0` to `3`, but they cannot be equal.
```
# Pairs of (i,j) where i != j.
```
You can, of course, also nest `while` loops, or mix nesting `for` loops with `while` loops.
You should be aware that when you use a `break` or `continue` in an inner loop, it will only `break` out of the inner loop or `continue` with the inner loop, respectively. There is no command that you can give in an inner loop that breaks out of both the inner and outer loop immediately.
Once you understand double-nested loops, it should come as no surpise that you can also triple-nest loops, quadruple-nest loops, or go even deeper. However, in practice I have seldom seen a nesting deeper than triple-nested.
```
for i in range( 3 ):
for j in range( 3 ):
for k in range( 3 ):
print( "({},{},{})".format( i, j, k ) )
```
---
## The loop-and-a-half
Suppose you want to ask the user for two numbers in a loop. For every two numbers that the user enters, you want to show their multiplication. You allow the user to stop the program when he enters zero for any of the numbers. For some reason, if the numbers are dividers of each other, that is an error and the program also stops, but with an error message. Finally, you will not process numbers higher than 1000 or smaller than zero, but that is not an error; you just want to allow the user to enter new numbers. How do you program that? Here is a first attempt:
```
from pcinput import getInteger
x = 3
y = 7
while (x != 0) and (y != 0) and (x%y != 0) and (y%x != 0):
x = getInteger( "Enter number 1: " )
y = getInteger( "Enter number 2: " )
if (x > 1000) or (y > 1000) or (x < 0) or (y < 0):
print( "Numbers should both be between 0 and 1000" )
continue
print( "Multiplication of", x, "and", y, "gives", x * y )
if x == 0 or y == 0:
print( "Goodbye!" )
else:
print( "Error: the numbers cannot be dividers of each other" )
```
**Exercise**: Study this code and make a list of everything that you feel is bad about it. Once you have done that, continue reading and compare your notes to the list below. If you noted things that are bad about it that are not on the list below, inform the instructor of the course.
There are many things bad about this code. Here is a list:
- To ensure that the loop is run at least once, `x` and `y` must be initialized. Why did I choose 3 and 7 for that? That was arbitrary, but I had to pick two numbers that are not dividers of each other. Otherwise the loop would not have been entered. On the whole, having to give variables some arbitrary starting values just to make sure that they exist is not nice, as their initial values are meaningless. You want to avoid that.
- When you enter something that should end the loop (e.g., zero for `x`), the multiplication will still be executed before the loop really has ended. That was not supposed to happen.
- If you enter 0 for `x`, the code will still ask for a value for `y`, even if it does not need it anymore.
- The boolean expression next to the `while` is rather complex. In this code it is still readable, but you can imagine what happens when you have many more requirements.
- The error message for the dividers is not next to the actual test where you decide to leave the loop (i.e., the boolean expression next to the `while`).
The solution to some of these issues that certain programmers prefer, is to initialize `x` and `y` with values that you read from the input. This solves the arbitrary initialization, and also gets around the problem that you print the result of the multiplication even when the loop was already supposed to end. If you do this, however, in the loop you have to move the asking for input to the end of the loop, and if you ever have a `continue` in the loop, you also have to copy it there. The code becomes something like this:
```
from pcinput import getInteger
x = getInteger( "Enter number 1: " )
y = getInteger( "Enter number 2: " )
while (x != 0) and (y != 0) and (x%y != 0) and (y%x != 0):
if (x > 1000) or (y > 1000) or (x < 0) or (y < 0):
print( "Numbers should both be between 0 and 1000" )
x = getInteger( "Enter number 1: " )
y = getInteger( "Enter number 2: " )
continue
print( "Multiplication of", x, "and", y, "gives", x * y )
x = getInteger( "Enter number 1: " )
y = getInteger( "Enter number 2: " )
if x == 0 or y == 0:
print( "Goodbye!" )
else:
print( "Error: the numbers cannot be dividers of each other" )
```
So this code removes two of the issues, but it adds a new one, which makes the code a lot worse. The list of issues now is:
- The statements that ask for input for each of the variables occur no less than three times in the code.
- If you enter 0 for `x`, the code will still ask for a value for `y`.
- The boolean expression next to the `while` is rather complex.
- The error message for the dividers is not next to the actual test where you decide to leave the loop.
The trick to get around these issues is to control the loop solely through `continue`s and `break`s (and perhaps the occasional `exit` when errors occur, though later in the course you will learn to use the much "cleaner" `return` for that). I.e., you do the loop "always", but decide to leave the loop or redo the loop when certain events occur which you notice *in* the loop. Doing the loop "always" you can effectuate with the statement `while True` (as this simply means: the test that decides whether or not you have to do the loop again, always results in `True`).
```
from pcinput import getInteger
from sys import exit
while True:
x = getInteger( "Enter number 1: " )
if x == 0:
break
y = getInteger( "Enter number 2: " )
if y == 0:
break
if (x < 0 or x > 1000) or (y < 0 or y > 1000):
print( "The numbers should be between 0 and 1000" )
continue
if x%y == 0 or y%x == 0:
print( "Error: the numbers cannot be dividers of each other" )
exit()
print( "Multiplication of", x, "and", y, "gives", x * y )
print( "Goodbye!" )
```
This code gets around almost all the problems. It asks for the input for `x` and `y` only once. There is no arbitrary initialization for `x` and `y`. The loop stops as soon as you enter zero for one of the numbers. It prints error messages at the moment that the errors are noted. There is no complex boolean expression needed with lots of `and`s and `or`s.
The only issue that is still remaining is that when the user enters a value outside the range 0 to 1000 for `x`, he still gets to enter `y` before the program says that he has to enter the numbers again. That is best solved by writing your own functions, which follows in the next chapter. (If you really want to solve it now, you can do that with a nested loop, but I wouldn't bother.)
The code is slightly longer than the first version, but length is no issue, and the code is a lot more readable.
A loop like this one, that uses `while True`, is sometimes called a "loop-and-a-half". It is a common approach to writing loops for which you cannot predict when they will end.
**Exercise**: The user must enter a positive integer. You use the `getInteger()` function from `pcinput` for that. This function also allows entering negative numbers. If the user enters a negative number, you want to print a message and ask him again, until he entered a positive number. Once a positive number is entered, you print that number and the program ends. Such a problem is typically solved using a loop-and-a-half, as you cannot predict how often the user will enter a negative number before he gets wise. Write such a loop-and-a-half in the code block below (you will need exactly one `break`, and you need at most one `continue`). Print the final number that the user entered *after* you have exited the loop. The reason to do it afterwards is that the loop is just there to control the entering of the input, not the processing of the resulting variable.
```
# Input entering.
```
I have noted in the past that many students find the use of `while True` confusing. They see it often in example code, but do not really grasp what the point of it is. And then they start inserting `while True` in their code whenever they do not know exactly what they need to do. If you have troubles understanding the loop-and-a-half, study this section again, until you do.
---
## Being smart about loops
To complete this chapter, I want to discuss a few strategies on loop design.
### When to use a loop
If you roll five 6-sided dice, how big is the chance that you roll five sixes? The answer is `1/(6**5)`, but suppose that you did not know that, and wanted to use a simulation to estimate the chance. You can imitate the rolling of a die using `randint()`, and so you can imitate the rolling of five dice this way. You can check whether they all show a 6. You can do that a large number of times, and then divide the number of times that you rolled five sixes by the number of times that you rolled five dice, to get an estimate. When I put this problem to students (in a slightly more complicated form, so that the answer cannot easily be calculated), I often get code that looks like this:
```
from random import randint
TESTS = 10000
success = 0
for i in range( TESTS ):
die1 = randint( 1, 6 )
die2 = randint( 1, 6 )
die3 = randint( 1, 6 )
die4 = randint( 1, 6 )
die5 = randint( 1, 6 )
if die1 == 6 and die2 == 6 and die3 == 6 and die4 == 6 and die5 == 6:
success += 1
print( "Chance at five sixes is", success / TESTS )
```
(You would need a bigger number of tests to get a more accurate estimate, but I did not want this code to run too long.)
When I see code like this, I ask: "What if I had asked you to roll one hundred dice? Would you really repeat that die rolling line 100 times?" Whenever you see lines of code repeated with just a slight change between them (or when you are copying/pasting within a block of code), you should start thinking about loops. You can roll five dice by stating:
```
from random import randint
for i in range( 5 ):
die = randint( 1, 6 )
```
"But", you might argue: "I need the value of all the five dice to see if they are all sixes! Every time you cycle through the loop, you lose the value of the previous roll!"
True enough, but the line that checks all the dice by using five boolean expressions concatenated with `and`s is particularly ugly too. Can't you streamline this? Is there no way that you can draw some conclusion upon the rolling of one die?
By thinking a bit about it, you might come to the following conclusion: as soon as you roll a die that is not a six, you already have failed on your try, and you can skip to the next try. There are many ways to effectuate this, but here is a brief one using a `break` and an `else`:
```
from random import randint
TESTS = 10000
success = 0
for i in range( TESTS ):
for j in range( 5 ):
if randint( 1, 6 ) != 6:
break
else:
success += 1
print( "Chance at five sixes is", success / TESTS )
```
You might think this is difficult to come up with, but there are other ways too. You can, for instance, add up the values of the rolls and test if the total is 30 after the inner loop. Or you can keep track of how many dice were rolled to a value of 6 and check if that is 5 after the inner loop. Or you can set a boolean variable to `True` before the inner loop, then set it to `False` as soon as you roll something that is not 6 in the inner loop, and then test the variable after the inner loop.
The point is that the arbitrary long repetition of pieces of code can probably be replaced by a loop.
### Processing data items one by one
Usually, when a loop is applied, you are working through a long series of data items. Each cycle through the loop will process one of those data items. You then often need to remember something about the data items that you have processed so far, for which you need extra variables. You have to be smart in thinking about such variables.
Take the following example: I will provide you with ten numbers, and I need you to create a program that tells me which is the largest, which is the smallest, and how many are dividable by 3. You might say: "It is easy to determine the largest and the smallest; I just use the `max()` and `min()` functions. Dividable by 3 is a bit tricky, I have to think about that." But `max()` and `min()` require you to keep all the numbers in memory. That's fine for 10 numbers, but what about one hundred? Or a million?
Since you will have to process all the numbers, you have to think about a loop, and in particular, a loop wherein you have only one of the numbers available each cycle through the loop (but you will see them all before the loop ends). You must now think about variables that you can use to remember something each cycle through the loop, that allows you to determine, at the end, which number was the largest, which the smallest, and how many are dividable by 3. Which variables do you need?
The answer, which comes easy to anyone who has been doing some programming, is that you need to remember, each cycle through the loop, which is the largest number *until now*, which is the smallest number *until now*, and how many numbers are dividable by 3 *until now*. That means that every cycle through the loop you compare the new number with the variables in which you retain the largest and smallest, and replace them with the new number if that is appropriate. You also check if the new number is dividable by three, and if so, increase the variable that you use to keep track of that.
You will have to find good initial values for the three variables. The dividable-by-3 variable can start at zero, but the largest and smallest need an appropriate value. The best solution in this case is to fill them with the first number, as that number is both the largest and the smallest at that point.
I give this problem as an exercise below. Use the algorithm described here to solve it.
### Start with the smallest unit and build outward
Suppose that I give you the following assignment: Of all the books on all the shelves in the library, count the number of words and report the average number of words for the books. If you ask a human to perform this task, he or she will probably think: "I go to the library, get the first book from the first shelf, count the words, write that number down, then take the second book and do the same thing, etcetera. When I finished the first shelf, I go to the second shelf and treat that one in the same way, until I have done all the books on all the shelves in the library. Then I add up the counts and divide by the number of books." For humans this approach works, but when you need to tell a computer how to do this, the task seems hard.
To solve this problem, I should start with the smallest unit that I need to work with. In this case, the smallest unit is a "book". It is not "word", because I don't need to do anything with a "word"; what I need to do is count the words in a book. In pseudocode, that would be something like:
wordcount = 0
for word in book:
wordcount += 1
When I code something like this, I can already test it. Once I am satisfied that I can count the words in a book, I can move up to the next smallest unit, which is the shelf. How do I process all the books on a shelf? In pseudocode, it is something like:
for book on shelf:
process_book()
But what does `process_book()` do? It counts the words. I already wrote pseudocode for that, which I simply need to insert in place of the statement `process_book()`. This then becomes:
for book on shelf:
wordcount = 0
for word in book:
wordcount += 1
When I test this, I run into a problem. I find that I am counting the words per book, but I am not doing anything with those word counts. I just overwrite them. To get the average, I first need a count of all the words in all the books. This means I have to initialize `wordcount` only once.
wordcount = 0
for book on shelf:
for word in book:
wordcount += 1
To calculate the average, I need to also count the books. Again, I only need to initialize the `bookcount` once, at the start, and I have to increase the `bookcount` every time I have processed one book. At the end, I can then print the average.
wordcount = 0
bookcount = 0
for book on shelf:
for word in book:
wordcount += 1
bookcount += 1
print( wordcount / bookcount )
Finally, I can go up to the highest level: the library as a whole. I know how to process one shelf, now I need to process all the shelves. I should, of course, remember that the initialization of `wordcount` and `bookcount` only should be done once, and the printing of the average too. With that in mind, it is easy to extend the pseudocode to encompass the library as a whole:
wordcount = 0
bookcount = 0
for shelf in library:
for book on shelf:
for word in book:
wordcount += 1
bookcount += 1
print( wordcount / bookcount )
As you can see, I built a triple-nested loop, working from the inner loop outward. To learn how to deal with nested loops, this is usually the best approach.
---
## On designing algorithms
At this point in the course, you will often run into exercises and coding problems for which you are unsure how to solve them. I gave an example of such a problem above (finding of ten numbers the largest, the smallest, and the number dividable by 3), and the solution I came to. Such a solution approach is called an "algorithm". But how do you design such algorithms?
I often see students typing code without really knowing what they are doing. They are trying to solve a problem but do not know how, so they start typing. You may realize that this is not a good approach to creating solutions (even though experimenting a bit might help).
What you have to do in such a situation is sit back, leave the keyboard alone, and think "How would I solve this problem as a human?" Try to write down what you would do if you would do it by hand. It does not matter if what you would do is a very boring task that you would never *want* to do by hand -- you have a computer to do the boring things for you.
Once you have figured out what you would do, then try to think about how you would translate that to code. Because basically, that is what you need to tell the computer: the steps that you as a human would take to get to a solution. If you really cannot think of any way that you as a human would use to solve a problem, then you sure as hell won't be able to tell the computer how to do it for you.
---
## What you learned
In this chapter, you learned about:
- What loops are
- `while` loops
- `for` loops
- Endless loops
- Loop control via `else`, `break`, and `continue`
- Nested loops
- The loop-and-a-half
- Being smart about loops
-------
## Exercises
Since loops are incredibly important and students often have problems with them, I provide a considerable number of exercises here. I recommend that you do them all. You will learn a lot.
### Exercise 7.1
Write a program that lets the user enter a number. Then the program displays the multiplication table for that number from 1 to 10. E.g., when the user enters `12`, the first line printed is "`1 * 12 = 12`" and the last line printed is "`10 * 12 = 120`".
```
# Multiplication table.
```
### Exercise 7.2
If you did the previous exercise with a `while` loop, then do it again with a `for` loop. If you did it with a `for` loop, then do it again with a `while` loop. If you did not use a loop at all, you should be ashamed of yourself.
```
# Multiplication table (again).
```
### Exercise 7.3
Write a program that asks the user for ten numbers, and then prints the largest, the smallest, and how many are dividable by 3. Use the algorithm described earlier in this chapter.
```
# Largest, smallest, dividable by 3.
```
### Exercise 7.4
"99 bottles of beer" is a traditional song in the United States and Canada. It is popular to sing on long trips, as it has a very repetitive format which is easy to memorize, and can take a long time to sing. The song's simple lyrics are as follows: "99 bottles of beer on the wall, 99 bottles of beer. Take one down, pass it around, 98 bottles of beer on the wall." The same verse is repeated, each time with one fewer bottle. The song is completed when the singer or singers reach zero. Write a program that generates all the verses of the song (though you might start a bit lower, for instance with 10 bottles). Make sure that your loop is not endless, and that you use the proper inflection for the word "bottle".
```
# Bottles of beer.
```
### Exercise 7.5
The Fibonacci sequence is a sequence of numbers that starts with 1, followed by 1 again. Every next number is the sum of the two previous numbers. I.e., the sequence starts with 1, 1, 2, 3, 5, 8, 13, 21,... Write a program that calculates and prints the Fibonacci sequence until the numbers get higher than 1000.
```
# Fibonacci.
```
### Exercise 7.6
Write a program that asks the user for two words. Then print all the characters that the words have in common. You can consider capitals different from lower case letters, but each character that you report, should be reported only once (e.g., the strings "bee" and "peer" only have one character in common, namely the letter "e"). Hint: Gather the characters in a third string, and when you find a character that the two words have in common, check if it is already in the third string before reporting it.
```
# Common characters.
```
### Exercise 7.7
Write a program that approximates the value of `pi` by using random numbers, as follows. Consider a square measuring 1 by 1. If you throw a dart into that square in a random location, the probability that it will have a distance of 1 or less to the lower left corner is `pi/4`. To see why that is, remember that the area of a circle with a radius of 1 is `pi`, so the area of a quarter circle is `pi/4`. Thus, if a dart lands in a random point in the square, the chance that it lands in the quarter circle with its centre at the lower left corner is `pi/4`. Therefore, if you throw `N` darts into the square, and `M` of those land inside a distance of 1 to the lower left corner, then `4M/N` approximates `pi` if `N` is very large.
The program holds a constant that determines how many darts it will simulate. It prints an approximation of `pi` derived by simulating the throwing of that number of darts. Remember that the distance of a point `(x,y)` to the lower-left corner is calculated as `sqrt( x*x + y*y )`. Use the `random()` function from the `random` module.
<img src="img/pi4.png" alt="quarter circle" style="width:100px;">
```
# Approximation of pi.
```
### Exercise 7.8
Write a program that takes a random integer between 1 and 1000 (you can use the `randint()` function for that). The program then asks the user to guess the number. After every guess, the program will say either "Lower" if the number it took is lower, "Higher" if the number it took is higher, and "You guessed it!" if the number it took is equal to the number that the user entered. It will end with displaying how many guesses the user needed. It might be wise, for testing purposes, to also display the number that the program randomly picks, until you are sure that the program works correctly.
```
# Number guessing.
```
### Exercise 7.9
Write a program that is the opposite of the previous one: now *you* take a number in mind, and the computer will try to guess it. You respond to the computer's guesses by entering a letter: "L" for lower, "H" for higher, and "C" for correct (you can use the `getLetter()` function from `pcinput` for that). Once the computer has guessed your number, it displays how many guesses it needed. Make sure that you let the computer recognize when there is no answer (maybe because you made a mistake or because you tried to fool the computer).
```
# Opposite number guessing.
```
### Exercise 7.10
A prime number is a positive integer that is dividable by exactly two different numbers, namely 1 and itself. The lowest (and only even) prime number is 2. The first 10 prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. Write a program that asks the user for a number and then displays whether or not it is prime. Hint: In a loop where you test the possible dividers of the number, you can conclude that the number is not prime as soon as you encounter a number other than 1 or itself that divides it. However, you can *only* conclude that it actually *is* prime after you have tested all possible dividers.
```
# Prime number tester.
```
### Exercise 7.11
Write a program that prints a multiplication table for digits 1 to a certain number `num` (you may assume for the output that num is one digit). A multiplication table for the numbers 1 to `num = 3` looks as follows:
`. | 1 2 3`<br>
`------------`<br>
`1 | 1 2 3`<br>
`2 | 2 4 6`<br>
`3 | 3 6 9`
So the labels on the rows are multiplied by the labels on the columns, and the result is shown in the cell that is on that row/column combination.
```
# Multiplication table.
num = 9
```
### Exercise 7.12
Write a program that displays all integers between 1 and 100 that can be written as the sum of two squares. Produce output in the form of `z = x**2 + y**2`, e.g., `58 = 3**2 + 7**2`. If a number occurs on the list with multiple *different* ways of writing it as the sum of two squares, that is acceptable.
```
# Sum of two squares.
```
### Exercise 7.13
You roll five six-sided dice, one by one. How big is the probability that the value of each die is greater than or equal to the value of the previous die that you rolled? For example, the sequence "1, 1, 4, 4, 6" is a success, but "1, 1, 4, 3, 6" is not. Determine the probability of success using a simulation of a large number of trials.
```
# Increasing die values.
```
### Exercise 7.14
A, B, C, and D are all different digits. The number DCBA is equal to 4 times the number ABCD. What are the digits? Note: to make ABCD and DCBA conventional numbers, neither A nor D can be zero. Use a quadruple-nested loop.
```
# Solve 4*ABCD == DCBA.
```
### Exercise 7.15
According to an old puzzle, five pirates and their monkey are stranded on an island. During the day they gather coconuts, which they put in a big pile. When night falls, they go asleep.
In the middle of the night, the first pirate wakes up, and, not trusting his buddies, he divides the pile into five equal parts, takes what he believes to be his share and hides it. Since he had one coconut left after the division, he gives it to the monkey. Then he goes back to sleep.
An hour later, the next pirate wakes up. He behaves in the same way as the first pirate: he divides the pile into five equal shares, with one coconut left over which he gives to the monkey, hides what he believes to be his share, and goes to sleep again.
The same happens to the other pirates: they wake up one by one, divide the pile, give one coconut to the monkey, hide their share, and go back to sleep.
In the morning they all wake up. They divide what remains of the coconuts equally among them. Since that leaves one coconut, they give it to the monkey.
The question is: what is the smallest number of coconuts that they can have started with?
Write a Python program that solves this puzzle. If you can solve it for any number of pirates, all the better.
```
# The monkey and the coconuts.
```
### Exercise 7.16
Consider the triangle shown below. This triangle houses a colony of Triangle Crawlers, and one big Eater of Triangle Crawlers. The Eater is located in point D. All Triangle Crawlers are born in point A. A Triangle Crawler which ends up in point D gets eaten.
Every day, each Triangle Crawler moves over one of the lines to a randomly-determined neighboring point, but not to the point where he was the day before. This movement takes one day. For instance, a Triangle Crawler that was just born in A, on the first day of his life will move to B, C, or D. If he moves to B, the next day he will move to C or D (but not back to A). If on his first day he moves to C instead, the next day he will move to B or D (but not back to A). If he moves to D, he gets eaten.
There is a one-third probability that Triangle Crawler on the first day of his life immediately goes to D, and therefore only lives one day. In principle, a Triangle Crawler may reach any age, however high, by moving in circles from A to B to C and back to A again (or counterclockwise, from A to C to B and back to A again). However, since every day he makes a random choice between the two possible follow-up directions, every day after the first there is a one-half probability that he ends up in point D, and dies.
Write a program that calculates an approximation of the average age that a Triangle Crawler reaches. Do this by simulating the lives of 100,000 Triangle Crawlers, counting the days that they live, and dividing the total by 100,000. The output of your program should be a single floating point number, rounded to two decimals.
Hint 1: You can follow two different approaches: either you simulate the behavior of one single Triangle Crawler and repeat that 100,000 times, or you start with a population of 100,000 triangle crawlers in point A, and divide these over variables that keep track of how many Triangles are in each point, each day, including the point that they came from (assigning a remaining odd Triangle Crawler to a randomly determined neighboring point). The first method is short and simple but slow, the second is long and complex but fast. You may use either method.
Hint 2: Do not use 100,000 Triangle Crawlers in your first attempts. Start with 1000 (or even only 1), and only try it out with 100,000 once your program is more or less finished. Testing is much quicker with fewer Triangle Crawlers. 1000 Triangle Crawlers should be done in under a second, so if your program takes longer, you probably have created an endless loop.
Hint 3: I won't be too specific, but the final answer is somewhere between 1 and 5 days. If you get something outside that range, it is definitely wrong. You may try to determine the exact answer mathematically before starting on the exercise, which is doable though quite hard.
<img src="img/Triangle.png" alt="Triangle" style="width:200px;">
```
# Triangle crawlers.
```
---
## Python 2
In Python 3, the `range()` function is an iterator. This entails that it needs very little memory space: it only retains the last number generated, the step size, and the limit that it should reach. In Python 2 `range()` is implemented differently: it produces all the numbers of the range in memory at once. This means that a statement like `range(1000000000)` in Python 2 requires so much memory that it may very well crash the program. In Python 3, such issues do not exist. In Python 2 it is therefore recommended not to use `range()` for more than 10,000 numbers or so, while in Python 3 no restrictions exist.
---
End of Chapter 7. Version 1.3.
| github_jupyter |
# 2D Advection-Diffusion equation
in this notebook we provide a simple example of the DeepMoD algorithm and apply it on the 2D advection-diffusion equation.
```
# General imports
import numpy as np
import torch
import matplotlib.pylab as plt
# DeepMoD functions
from deepymod import DeepMoD
from deepymod.model.func_approx import NN, Siren
from deepymod.model.library import Library2D_third
from deepymod.model.constraint import LeastSquares
from deepymod.model.sparse_estimators import Threshold,PDEFIND
from deepymod.training import train
from deepymod.training.sparsity_scheduler import TrainTestPeriodic
from scipy.io import loadmat
# Settings for reproducibility
np.random.seed(42)
torch.manual_seed(0)
%load_ext autoreload
%autoreload 2
```
## Prepare the data
Next, we prepare the dataset.
```
data = np.load('data_paper.npy')
down_data= np.take(np.take(np.take(data,np.arange(0,data.shape[0],6),axis=0),np.arange(0,data.shape[1],6),axis=1),np.arange(0,data.shape[2],1),axis=2)
down_data.shape
steps = down_data.shape[2]
width = down_data.shape[0]
width_2 = down_data.shape[1]
x_arr = np.arange(0,width)
y_arr = np.arange(0,width_2)
t_arr = np.arange(0,steps)
x_grid, y_grid, t_grid = np.meshgrid(x_arr, y_arr, t_arr, indexing='ij')
X = np.transpose((t_grid.flatten(), x_grid.flatten(), y_grid.flatten()))
fig = plt.figure(figsize=(15,5))
plt.subplot(1,3, 1)
plt.imshow(down_data[:,:,1], aspect=0.5)
plt.subplot(1,3, 2)
plt.imshow(down_data[:,:,9], aspect=0.5)
plt.subplot(1,3, 3)
plt.imshow(down_data[:,:,19], aspect=0.5)
```
We flatten it to give it the right dimensions for feeding it to the network:
```
X = np.transpose((t_grid.flatten()/np.max(t_grid), x_grid.flatten()/np.max(y_grid), y_grid.flatten()/np.max(y_grid)))
y = np.float32(down_data.reshape((down_data.size, 1)))
y = y/np.max(y)
len(y)
number_of_samples = 10000
idx = np.random.permutation(y.shape[0])
X_train = torch.tensor(X[idx, :][:number_of_samples], dtype=torch.float32, requires_grad=True)
y_train = torch.tensor(y[idx, :][:number_of_samples], dtype=torch.float32)
```
## Configuration of DeepMoD
Configuration of the function approximator: Here the first argument is the number of input and the last argument the number of output layers.
```
network = NN(3, [30, 30, 30, 30], 1)
```
Configuration of the library function: We select athe library with a 2D spatial input. Note that that the max differential order has been pre-determined here out of convinience. So, for poly_order 1 the library contains the following 12 terms:
* [$1, u_x, u_y, u_{xx}, u_{yy}, u_{xy}, u, u u_x, u u_y, u u_{xx}, u u_{yy}, u u_{xy}$]
```
library = Library2D_third(poly_order=0)
```
Configuration of the sparsity estimator and sparsity scheduler used. In this case we use the most basic threshold-based Lasso estimator and a scheduler that asseses the validation loss after a given patience. If that value is smaller than 1e-5, the algorithm is converged.
```
estimator = Threshold(0.025)
sparsity_scheduler = TrainTestPeriodic(periodicity=50, patience=200, delta=1e-5)
```
Configuration of the sparsity estimator
```
constraint = LeastSquares()
# Configuration of the sparsity scheduler
```
Now we instantiate the model and select the optimizer
```
model = DeepMoD(network, library, estimator, constraint)
# Defining optimizer
optimizer = torch.optim.Adam(model.parameters(), betas=(0.99, 0.999), amsgrad=True, lr=1e-3)
```
## Run DeepMoD
We can now run DeepMoD using all the options we have set and the training data:
* The directory where the tensorboard file is written (log_dir)
* The ratio of train/test set used (split)
* The maximum number of iterations performed (max_iterations)
* The absolute change in L1 norm considered converged (delta)
* The amount of epochs over which the absolute change in L1 norm is calculated (patience)
```
train(model, X_train, y_train, optimizer,sparsity_scheduler, log_dir='runs/space_new/', split=0.8, max_iterations=100000, delta=1e-5, patience=200)
```
Sparsity masks provide the active and non-active terms in the PDE:
```
sol = model(torch.tensor(X, dtype=torch.float32))[0].reshape((width,width_2,steps)).detach().numpy()
ux = model(torch.tensor(X, dtype=torch.float32))[2][0][:,1].reshape((width,width_2,steps)).detach().numpy()
uy = model(torch.tensor(X, dtype=torch.float32))[2][0][:,2].reshape((width,width_2,steps)).detach().numpy()
uxx = model(torch.tensor(X, dtype=torch.float32))[2][0][:,3].reshape((width,width_2,steps)).detach().numpy()
uyy = model(torch.tensor(X, dtype=torch.float32))[2][0][:,4].reshape((width,width_2,steps)).detach().numpy()
import pysindy as ps
fd_spline = ps.SINDyDerivative(kind='spline', s=1e-2)
fd_spectral = ps.SINDyDerivative(kind='spectral')
fd_sg = ps.SINDyDerivative(kind='savitzky_golay', left=0.5, right=0.5, order=3)
y = down_data[5,:,1]
x = y_arr
plt.plot(x,y, 'bo--')
plt.plot(x,sol[5,:,1]*np.max(down_data),'b', label='t = 1',linewidth=3)
y = down_data[5,:,5]
x = y_arr
plt.plot(x,y, 'go--')
plt.plot(x,sol[5,:,5]*np.max(down_data),'g', label='t = 5',linewidth=3)
y = down_data[5,:,10]
x = y_arr
plt.plot(x,y, 'ro--')
plt.plot(x,sol[5,:,10]*np.max(down_data),'r', label='t = 10',linewidth=3)
plt.legend()
y = down_data[5,:,1]
x = y_arr
plt.plot(x,fd_sg(y,x), 'bo--')
plt.plot(x,uy[5,:,1]*np.max(down_data)/np.max(y_grid),'b', label='x = 1',linewidth=3)
y = down_data[5,:,5]
x = y_arr
plt.plot(x,fd_sg(y,x), 'go--')
plt.plot(x,uy[5,:,5]*np.max(down_data)/np.max(y_grid),'g', label='x = 5',linewidth=3)
y = down_data[5,:,10]
x = y_arr
plt.plot(x,fd_sg(y,x), 'ro--')
plt.plot(x,uy[5,:,10]*np.max(down_data)/np.max(y_grid),'r', label='x = 10',linewidth=3)
plt.legend()
y = down_data[5,:,1]
x = y_arr
plt.plot(x,fd_sg(fd_sg(y,x)), 'bo--')
plt.plot(x,uyy[5,:,1]*np.max(down_data)/(np.max(y_grid)*np.max(y_grid)),'b',linewidth=3)
y = down_data[5,:,5]
x = y_arr
plt.plot(x,fd_sg(fd_sg(y,x)), 'go--')
plt.plot(x,uyy[5,:,5]*np.max(down_data)/(np.max(y_grid)*np.max(y_grid)),'g',linewidth=3)
y = down_data[5,:,10]
x = y_arr
plt.plot(x,fd_sg(fd_sg(y,x)), 'ro--')
plt.plot(x,uyy[5,:,10]*np.max(down_data)/(np.max(y_grid)*np.max(y_grid)),'r',linewidth=3)
fig = plt.figure(figsize=(15,5))
plt.subplot(1,3, 1)
plt.imshow(sol[:,:,1], aspect=0.5)
plt.subplot(1,3, 2)
plt.imshow(sol[:,:,5], aspect=0.5)
plt.subplot(1,3, 3)
plt.imshow(sol[:,:,10], aspect=0.5)
#plt.savefig('reconstruction.pdf')
fig = plt.figure(figsize=(15,5))
plt.subplot(1,3, 1)
plt.imshow(down_data[:,:,1], aspect=0.5)
plt.subplot(1,3, 2)
plt.imshow(down_data[:,:,19], aspect=0.5)
plt.subplot(1,3, 3)
plt.imshow(down_data[:,:,39], aspect=0.5)
plt.savefig('original_20_20_40.pdf')
np.max(down_data)
plt.plot(x,sol[5,:,10]*np.max(down_data))
noise_level = 0.025
y_noisy = y + noise_level * np.std(y) * np.random.randn(y.size)
plt.plot(x,uy[25,:,10])
plt.plot(x,ux[25,:,10])
fig = plt.figure(figsize=(15,5))
plt.subplot(1,3, 1)
plt.plot(fd_spline(y.reshape(-1,1),x), label='Ground truth',linewidth=3)
plt.plot(fd_spline(y_noisy.reshape(-1,1),x), label='Spline',linewidth=3)
plt.legend()
plt.subplot(1,3, 2)
plt.plot(fd_spline(y.reshape(-1,1),x), label='Ground truth',linewidth=3)
plt.plot(fd_sg(y_noisy.reshape(-1,1),x), label='Savitzky Golay',linewidth=3)
plt.legend()
plt.subplot(1,3, 3)
plt.plot(fd_spline(y.reshape(-1,1),x), label='Ground truth',linewidth=3)
plt.plot(uy[25,:,10],linewidth=3, label='DeepMoD')
plt.legend()
plt.show()
plt.plot(ux[10,:,5])
ax = plt.subplot(1,1,1)
ax.plot(fd(y.reshape(-1,1),x), label='Ground truth')
ax.plot(fd_sline(y_noisy.reshape(-1,1),x), label='Spline')
ax.plot(fd_sg(y_noisy.reshape(-1,1),x), label='Savitzky Golay')
ax.legend()
plt.plot(model(torch.tensor(X, dtype=torch.float32))[2][0].detach().numpy())
sol = model(torch.tensor(X, dtype=torch.float32))[0]
plt.imshow(sol[:,:,4].detach().numpy())
plt.plot(sol[10,:,6].detach().numpy())
plt.plot(down_data[10,:,6]/np.max(down_data))
x = np.arange(0,len(y))
import pysindy as ps
diffs = [
('PySINDy Finite Difference', ps.FiniteDifference()),
('Smoothed Finite Difference', ps.SmoothedFiniteDifference()),
('Savitzky Golay', ps.SINDyDerivative(kind='savitzky_golay', left=0.5, right=0.5, order=3)),
('Spline', ps.SINDyDerivative(kind='spline', s=1e-2)),
('Trend Filtered', ps.SINDyDerivative(kind='trend_filtered', order=0, alpha=1e-2)),
('Spectral', ps.SINDyDerivative(kind='spectral')),
]
fd = ps.SINDyDerivative(kind='spline', s=1e-2)
y = down_data[:,10,9]/np.max(down_data)
x = np.arange(0,len(y))
t = np.linspace(0,1,5)
X = np.vstack((np.sin(t),np.cos(t))).T
plt.plot(y)
plt.plot(fd(y.reshape(-1,1),x))
y.shape
plt.plot(fd._differentiate(y.reshape(-1,1),x))
plt.plot(ux[:,10,6])
plt.plot(sol[:,10,6].detach().numpy())
plt.plot(down_data[:,10,6]/np.max(down_data))
model.sparsity_masks
```
estimatior_coeffs gives the magnitude of the active terms:
```
print(model.estimator_coeffs())
plt.contourf(ux[:,:,10])
plt.plot(ux[25,:,2])
ax = plt.subplot(1,1,1)
ax.plot(fd(y.reshape(-1,1),x), label='Ground truth')
ax.plot(fd_sline(y_noisy.reshape(-1,1),x), label='Spline')
ax.plot(fd_sg(y_noisy.reshape(-1,1),x), label='Savitzky Golay')
ax.legend()
import pysindy as ps
fd_spline = ps.SINDyDerivative(kind='spline', s=1e-2)
fd_spectral = ps.SINDyDerivative(kind='spectral')
fd_sg = ps.SINDyDerivative(kind='savitzky_golay', left=0.5, right=0.5, order=3)
y = u_v[25,:,2]
x = y_v[25,:,2]
plt.scatter(x,y)
y.shape
noise_level = 0.025
y_noisy = y + noise_level * np.std(y) * np.random.randn(y.size)
ax = plt.subplot(1,1,1)
ax.plot(x,y_noisy, label="line 1")
ax.plot(x,y, label="line 2")
ax.legend()
ax = plt.subplot(1,1,1)
ax.plot(fd(y.reshape(-1,1),x), label='Ground truth')
ax.plot(fd_sline(y_noisy.reshape(-1,1),x), label='Spline')
ax.plot(fd_sg(y_noisy.reshape(-1,1),x), label='Savitzky Golay')
ax.legend()
```
| github_jupyter |
# Web crawling exercise
```
from selenium import webdriver
```
## Quiz 1
- 아래 URL의 NBA 데이터를 크롤링하여 판다스 데이터 프레임으로 나타내세요.
- http://stats.nba.com/teams/traditional/?sort=GP&dir=-1
### 1.1 webdriver를 실행하고 사이트에 접속하기
```
driver = webdriver.Chrome()
url = "http://stats.nba.com/teams/traditional/?sort=GP&dir=-1"
driver.get(url)
```
링크로 들어가면 GP로 정렬되어 있는 상태임

### 1.2 표 데이터 받아오기
#### (1) column 이름을 받아와서 pandas dataframe 만들기
```
columns = driver.find_elements_by_css_selector("div.nba-stat-table__overflow > table > thead > tr > th")[:28]
len(columns)
ls_column = []
for column in columns:
ls_column.append(column.text)
ls_column
df = pd.DataFrame(columns = ls_column)
df
```
#### (2) 각 row의 팀별 데이터를 받아와서 dataframe에 넣기
```
team_stat = driver.find_elements_by_css_selector("div.nba-stat-table__overflow > table > tbody > tr")
len(team_stat)
for stat in team_stat:
stats = stat.find_elements_by_css_selector("td")
stat = {}
for i in range(len(stats)):
stat[ls_column[i]] = stats[i].text
df.loc[len(df)] = stat
df
driver.quit()
```
## Quiz 2
- Selenium을 이용하여 네이버 IT/과학 기사의 10 페이지 까지의 최신 제목 리스트를 크롤링하세요.
- http://news.naver.com/main/main.nhn?mode=LSD&mid=shm&sid1=105
### 2.1 webdriver를 실행하고 사이트에 접속하기
```
driver = webdriver.Chrome()
def make_url(page=1):
return "http://news.naver.com/main/main.nhn?mode=LSD&mid=shm&sid1=105#&date=%2000:00:00&page="\
+ str(page)
url = make_url()
driver.get(url)
```
### 2.2 기사 제목 리스트 가져오기
#### (1) 1페이지에 대해 기사 제목 가져오기
##### 1페이지의 기사 리스트 가져오기
- 한 페이지에 20개의 기사가 있음
```
articles = driver.find_elements_by_css_selector("#section_body > ul > li")
len(articles)
```
##### 1페이지 안의 기사 제목 가져오기
```
dict_list = []
for article in articles:
dict_list.append({
"title": article.find_element_by_css_selector("dt:nth-child(2)").text
})
df = pd.DataFrame(dict_list)
df.tail()
```
#### (2) 1-10페이지에서 기사 제목 가져오기
- 2페이지와 7페이지에서 에러가 발생해서 try & except 처리함
```
dict_list = []
for i in range(1, 11):
driver.get(make_url(i))
articles = driver.find_elements_by_css_selector("#section_body > ul > li")
print(len(articles))
try:
for article in articles:
dict_list.append({"title": article.find_element_by_css_selector("dl > dt:nth-child(2)").text})
except:
print(str(i)+"페이지 에러 발생")
df = pd.DataFrame(dict_list)
df.tail()
```
총 168개의 기사 제목이 크롤링됨
```
driver.quit()
```
#### 참고자료
- 패스트캠퍼스, ⟪데이터사이언스스쿨 8기⟫ 수업자료
| github_jupyter |
### Functions
```
# syntax
# Declaring a function
def function_name():
codes
codes
# Calling a function
function_name()
def generate_full_name ():
first_name = 'Ayush'
last_name = 'Jindal'
space = ' '
full_name = first_name + space + last_name
print(full_name)
generate_full_name () # calling a function
def add_two_numbers ():
num_one = 2
num_two = 3
total = num_one + num_two
print(total)
add_two_numbers()
```
### Function Returning a Value - Part 1
```
def generate_full_name ():
first_name = 'Ayush'
last_name = 'Jindal'
space = ' '
full_name = first_name + space + last_name
return full_name
print(generate_full_name () )
def add_two_numbers ():
num_one = 2
num_two = 3
total = num_one + num_two
return total
print(add_two_numbers())
```
### Function with Parameters
- Single Parameter: If our function takes a parameter we should call our function with an argument
```
def greetings(name):
message = name + ', Welcome to my Youtube Channel'
return message
print(greetings('Ayush'))
def add_ten(num):
ten = 10
return num + 10
print(add_ten(10))
def sq(x):
return x*x
print(sq(9))
def area(r):
PI = 3.14
area=PI*r**2
return area
print(area(1))
def sum_of_numbers(n):
total = 0
for i in range(n+1):
total+=i
print(total)
sum_of_numbers(10) # 55
sum_of_numbers(100) # 5050
```
- Two Parameter: A function may or may not have a parameter or parameters. A function may have two or more parameters. If our function takes parameters we should call it with arguments. Let's check a function with two parameters:
```
def generate_full_name (first_name, last_name):
space = ' '
full_name = first_name + space + last_name
return full_name
print('Full Name: ', generate_full_name('Ayush','Jindal'))
```
### Passing Arguments with Key and Value
If we pass the arguments with key and value, the order of the arguments does not matter.
```
def add_two_numbers (num1, num2):
total = num1 + num2
print(total)
add_two_numbers(num2 = 3, num1 = 2)
```
### Function Returning a Value - Part 2
- Returning a string:
```
def print_name(firstname):
return firstname
print_name('Asabeneh')
```
- Returning a number:
```
def add_two_numbers (num1, num2):
total = num1 + num2
return total
print(add_two_numbers(2, 3))
```
- Returning a boolean:
```
def is_even (n):
if n % 2 == 0:
print('even')
return True # return stops further execution of the function, similar to break
return False
print(is_even(10))
print(is_even(7))
```
- Returning a list:
```
def find_even_numbers(n):
evens = []
for i in range(n+1):
if i % 2 == 0:
evens.append(i)
return evens
print(find_even_numbers(10))
```
### Arbitrary Number of Arguments
If we do not know the number of arguments we pass to our function, we can create a function which can take arbitrary number of arguments by adding * before the parameter name.
```
def sum_all_nums(*nums):
total = 0
for num in nums:
total += num # same as total = total + num
return total
print(sum_all_nums(2, 3, 5))
```
### Default and Arbitrary Number of Parameters in Functions
```
def generate_groups (team,*args):
print(team)
for i in args:
print(i)
generate_groups('Team-1','Asabeneh','Brook','David','Eyob')
```
### Function as a Parameter of Another Function
```
def square_number (n):
return n * n
def do_something(f, x):
return f(x)
print(do_something(square_number, 3))
```
| github_jupyter |
# Custom Building Recurrent Neural Network
**Notation**:
- Superscript $[l]$ denotes an object associated with the $l^{th}$ layer.
- Superscript $(i)$ denotes an object associated with the $i^{th}$ example.
- Superscript $\langle t \rangle$ denotes an object at the $t^{th}$ time-step.
- **Sub**script $i$ denotes the $i^{th}$ entry of a vector.
Example:
- $a^{(2)[3]<4>}_5$ denotes the activation of the 2nd training example (2), 3rd layer [3], 4th time step <4>, and 5th entry in the vector.
Let's first import all the packages.
```
import numpy as np
from rnn_utils import *
```
## Forward propagation for the basic Recurrent Neural Network
## RNN cell
```
# GRADED FUNCTION: rnn_cell_forward
def rnn_cell_forward(xt, a_prev, parameters):
# Retrieve parameters from "parameters"
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# compute next activation state using the formula given above
a_next = a_next = np.tanh(np.dot(Wax, xt) + np.dot(Waa, a_prev) + ba)
# compute output of the current cell using the formula given above
yt_pred = softmax(np.dot(Wya, a_next) + by)
# store values you need for backward propagation in cache
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, yt_pred_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)
print("a_next[4] = \n", a_next_tmp[4])
print("a_next.shape = \n", a_next_tmp.shape)
print("yt_pred[1] =\n", yt_pred_tmp[1])
print("yt_pred.shape = \n", yt_pred_tmp.shape)
```
## 1.2 - RNN forward pass
```
# GRADED FUNCTION: rnn_forward
def rnn_forward(x, a0, parameters):
# Initialize "caches" which will contain the list of all caches
caches = []
# Retrieve dimensions from shapes of x and parameters["Wya"]
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
# initialize "a" and "y_pred" with zeros (≈2 lines)
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
# Initialize a_next (≈1 line)
a_next = a0
# loop over all time-steps of the input 'x' (1 line)
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache (≈1 line)
a_next, yt_pred, cache = rnn_cell_forward(x[:,:,t], a_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y_pred[:,:,t] = yt_pred
# Append "cache" to "caches" (≈1 line)
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
np.random.seed(1)
x_tmp = np.random.randn(3,10,4)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_pred_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp)
print("a[4][1] = \n", a_tmp[4][1])
print("a.shape = \n", a_tmp.shape)
print("y_pred[1][3] =\n", y_pred_tmp[1][3])
print("y_pred.shape = \n", y_pred_tmp.shape)
print("caches[1][1][3] =\n", caches_tmp[1][1][3])
print("len(caches) = \n", len(caches_tmp))
```
## Long Short-Term Memory (LSTM) network
### Overview of gates and states
#### - Forget gate $\mathbf{\Gamma}_{f}$
* Let's assume we are reading words in a piece of text, and plan to use an LSTM to keep track of grammatical structures, such as whether the subject is singular ("puppy") or plural ("puppies").
* If the subject changes its state (from a singular word to a plural word), the memory of the previous state becomes outdated, so we "forget" that outdated state.
* The "forget gate" is a tensor containing values that are between 0 and 1.
* If a unit in the forget gate has a value close to 0, the LSTM will "forget" the stored state in the corresponding unit of the previous cell state.
* If a unit in the forget gate has a value close to 1, the LSTM will mostly remember the corresponding value in the stored state.
##### Equation
$$\mathbf{\Gamma}_f^{\langle t \rangle} = \sigma(\mathbf{W}_f[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_f)\tag{1} $$
##### Explanation of the equation:
* $\mathbf{W_{f}}$ contains weights that govern the forget gate's behavior.
* The previous time step's hidden state $[a^{\langle t-1 \rangle}$ and current time step's input $x^{\langle t \rangle}]$ are concatenated together and multiplied by $\mathbf{W_{f}}$.
* A sigmoid function is used to make each of the gate tensor's values $\mathbf{\Gamma}_f^{\langle t \rangle}$ range from 0 to 1.
* The forget gate $\mathbf{\Gamma}_f^{\langle t \rangle}$ has the same dimensions as the previous cell state $c^{\langle t-1 \rangle}$.
* This means that the two can be multiplied together, element-wise.
* Multiplying the tensors $\mathbf{\Gamma}_f^{\langle t \rangle} * \mathbf{c}^{\langle t-1 \rangle}$ is like applying a mask over the previous cell state.
* If a single value in $\mathbf{\Gamma}_f^{\langle t \rangle}$ is 0 or close to 0, then the product is close to 0.
* This keeps the information stored in the corresponding unit in $\mathbf{c}^{\langle t-1 \rangle}$ from being remembered for the next time step.
* Similarly, if one value is close to 1, the product is close to the original value in the previous cell state.
* The LSTM will keep the information from the corresponding unit of $\mathbf{c}^{\langle t-1 \rangle}$, to be used in the next time step.
##### Variable names in the code
The variable names in the code are similar to the equations, with slight differences.
* `Wf`: forget gate weight $\mathbf{W}_{f}$
* `Wb`: forget gate bias $\mathbf{W}_{b}$
* `ft`: forget gate $\Gamma_f^{\langle t \rangle}$
#### Candidate value $\tilde{\mathbf{c}}^{\langle t \rangle}$
* The candidate value is a tensor containing information from the current time step that **may** be stored in the current cell state $\mathbf{c}^{\langle t \rangle}$.
* Which parts of the candidate value get passed on depends on the update gate.
* The candidate value is a tensor containing values that range from -1 to 1.
* The tilde "~" is used to differentiate the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ from the cell state $\mathbf{c}^{\langle t \rangle}$.
##### Equation
$$\mathbf{\tilde{c}}^{\langle t \rangle} = \tanh\left( \mathbf{W}_{c} [\mathbf{a}^{\langle t - 1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{c} \right) \tag{3}$$
##### Explanation of the equation
* The 'tanh' function produces values between -1 and +1.
##### Variable names in the code
* `cct`: candidate value $\mathbf{\tilde{c}}^{\langle t \rangle}$
#### - Update gate $\mathbf{\Gamma}_{i}$
* We use the update gate to decide what aspects of the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ to add to the cell state $c^{\langle t \rangle}$.
* The update gate decides what parts of a "candidate" tensor $\tilde{\mathbf{c}}^{\langle t \rangle}$ are passed onto the cell state $\mathbf{c}^{\langle t \rangle}$.
* The update gate is a tensor containing values between 0 and 1.
* When a unit in the update gate is close to 1, it allows the value of the candidate $\tilde{\mathbf{c}}^{\langle t \rangle}$ to be passed onto the hidden state $\mathbf{c}^{\langle t \rangle}$
* When a unit in the update gate is close to 0, it prevents the corresponding value in the candidate from being passed onto the hidden state.
* Notice that we use the subscript "i" and not "u", to follow the convention used in the literature.
##### Equation
$$\mathbf{\Gamma}_i^{\langle t \rangle} = \sigma(\mathbf{W}_i[a^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_i)\tag{2} $$
##### Explanation of the equation
* Similar to the forget gate, here $\mathbf{\Gamma}_i^{\langle t \rangle}$, the sigmoid produces values between 0 and 1.
* The update gate is multiplied element-wise with the candidate, and this product ($\mathbf{\Gamma}_{i}^{\langle t \rangle} * \tilde{c}^{\langle t \rangle}$) is used in determining the cell state $\mathbf{c}^{\langle t \rangle}$.
##### Variable names in code (Please note that they're different than the equations)
In the code, we'll use the variable names found in the academic literature. These variables don't use "u" to denote "update".
* `Wi` is the update gate weight $\mathbf{W}_i$ (not "Wu")
* `bi` is the update gate bias $\mathbf{b}_i$ (not "bu")
* `it` is the forget gate $\mathbf{\Gamma}_i^{\langle t \rangle}$ (not "ut")
#### - Cell state $\mathbf{c}^{\langle t \rangle}$
* The cell state is the "memory" that gets passed onto future time steps.
* The new cell state $\mathbf{c}^{\langle t \rangle}$ is a combination of the previous cell state and the candidate value.
##### Equation
$$ \mathbf{c}^{\langle t \rangle} = \mathbf{\Gamma}_f^{\langle t \rangle}* \mathbf{c}^{\langle t-1 \rangle} + \mathbf{\Gamma}_{i}^{\langle t \rangle} *\mathbf{\tilde{c}}^{\langle t \rangle} \tag{4} $$
##### Explanation of equation
* The previous cell state $\mathbf{c}^{\langle t-1 \rangle}$ is adjusted (weighted) by the forget gate $\mathbf{\Gamma}_{f}^{\langle t \rangle}$
* and the candidate value $\tilde{\mathbf{c}}^{\langle t \rangle}$, adjusted (weighted) by the update gate $\mathbf{\Gamma}_{i}^{\langle t \rangle}$
##### Variable names and shapes in the code
* `c`: cell state, including all time steps, $\mathbf{c}$ shape $(n_{a}, m, T)$
* `c_next`: new (next) cell state, $\mathbf{c}^{\langle t \rangle}$ shape $(n_{a}, m)$
* `c_prev`: previous cell state, $\mathbf{c}^{\langle t-1 \rangle}$, shape $(n_{a}, m)$
#### - Output gate $\mathbf{\Gamma}_{o}$
* The output gate decides what gets sent as the prediction (output) of the time step.
* The output gate is like the other gates. It contains values that range from 0 to 1.
##### Equation
$$ \mathbf{\Gamma}_o^{\langle t \rangle}= \sigma(\mathbf{W}_o[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{o})\tag{5}$$
##### Explanation of the equation
* The output gate is determined by the previous hidden state $\mathbf{a}^{\langle t-1 \rangle}$ and the current input $\mathbf{x}^{\langle t \rangle}$
* The sigmoid makes the gate range from 0 to 1.
##### Variable names in the code
* `Wo`: output gate weight, $\mathbf{W_o}$
* `bo`: output gate bias, $\mathbf{b_o}$
* `ot`: output gate, $\mathbf{\Gamma}_{o}^{\langle t \rangle}$
### LSTM cell
```
# GRADED FUNCTION: lstm_cell_forward
def lstm_cell_forward(xt, a_prev, c_prev, parameters):
# Retrieve parameters from "parameters"
Wf = parameters["Wf"] # forget gate weight
bf = parameters["bf"]
Wi = parameters["Wi"] # update gate weight (notice the variable name)
bi = parameters["bi"] # (notice the variable name)
Wc = parameters["Wc"] # candidate value weight
bc = parameters["bc"]
Wo = parameters["Wo"] # output gate weight
bo = parameters["bo"]
Wy = parameters["Wy"] # prediction weight
by = parameters["by"]
# Retrieve dimensions from shapes of xt and Wy
n_x, m = xt.shape
n_y, n_a = Wy.shape
# Concatenate a_prev and xt (≈1 line)
concat = np.zeros((n_a + n_x, m))
concat[: n_a, :] = a_prev
concat[n_a :, :] = xt
# Compute values for ft (forget gate), it (update gate),
# cct (candidate value), c_next (cell state),
# ot (output gate), a_next (hidden state) (≈6 lines)
ft = sigmoid(np.dot(Wf, concat) + bf)
it = sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_next = ft * c_prev + it * cct
ot = sigmoid(np.dot(Wo, concat) + bo)
a_next = ot * np.tanh(c_next)
# Compute prediction of the LSTM cell (≈1 line)
yt_pred = softmax(np.dot(Wy, a_next) + by)
# store values needed for backward propagation in cache
cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)
return a_next, c_next, yt_pred, cache
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
c_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)
print("a_next[4] = \n", a_next_tmp[4])
print("a_next.shape = ", c_next_tmp.shape)
print("c_next[2] = \n", c_next_tmp[2])
print("c_next.shape = ", c_next_tmp.shape)
print("yt[1] =", yt_tmp[1])
print("yt.shape = ", yt_tmp.shape)
print("cache[1][3] =\n", cache_tmp[1][3])
print("len(cache) = ", len(cache_tmp))
```
### Forward pass for LSTM
```
# GRADED FUNCTION: lstm_forward
def lstm_forward(x, a0, parameters):
# Initialize "caches", which will track the list of all the caches
caches = []
# Retrieve dimensions from shapes of x and Wy (≈2 lines)
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wy"].shape
# initialize "a", "c" and "y" with zeros (≈3 lines)
a = np.zeros((n_a, m, T_x))
c = np.zeros((n_a, m, T_x))
y = np.zeros((n_y, m, T_x))
# Initialize a_next and c_next (≈2 lines)
a_next = a0
c_next = np.zeros(a_next.shape)
# loop over all time-steps
for t in range(T_x):
# Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line)
a_next, c_next, yt, cache = lstm_cell_forward(x[:, :, t], a_next, c_next, parameters)
# Save the value of the new "next" hidden state in a (≈1 line)
a[:,:,t] = a_next
# Save the value of the prediction in y (≈1 line)
y[:,:,t] = yt
# Save the value of the next cell state (≈1 line)
c[:,:,t] = c_next
# Append the cache into caches (≈1 line)
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y, c, caches
np.random.seed(1)
x_tmp = np.random.randn(3,10,7)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi']= np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)
print("a[4][3][6] = ", a_tmp[4][3][6])
print("a.shape = ", a_tmp.shape)
print("y[1][4][3] =", y_tmp[1][4][3])
print("y.shape = ", y_tmp.shape)
print("caches[1][1][1] =\n", caches_tmp[1][1][1])
print("c[1][2][1]", c_tmp[1][2][1])
print("len(caches) = ", len(caches_tmp))
```
**Expected Output**:
```Python
a[4][3][6] = 0.172117767533
a.shape = (5, 10, 7)
y[1][4][3] = 0.95087346185
y.shape = (2, 10, 7)
caches[1][1][1] =
[ 0.82797464 0.23009474 0.76201118 -0.22232814 -0.20075807 0.18656139
0.41005165]
c[1][2][1] -0.855544916718
len(caches) = 2
```
## Backpropagation in recurrent neural networks
This section is optional and ungraded. It is more difficult and has fewer details regarding its implementation. This section only implements key elements of the full path.
### Basic RNN backward pass
##### Equations
To compute the rnn_cell_backward you can utilize the following equations. It is a good exercise to derive them by hand. Here, $*$ denotes element-wise multiplication while the absence of a symbol indicates matrix multiplication.
$a^{\langle t \rangle} = \tanh(W_{ax} x^{\langle t \rangle} + W_{aa} a^{\langle t-1 \rangle} + b_{a})\tag{-}$
$\displaystyle \frac{\partial \tanh(x)} {\partial x} = 1 - \tanh^2(x) \tag{-}$
$\displaystyle {dW_{ax}} = da_{next} * ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) ) x^{\langle t \rangle T}\tag{1}$
$\displaystyle dW_{aa} = da_{next} * (( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) ) a^{\langle t-1 \rangle T}\tag{2}$
$\displaystyle db_a = da_{next} * \sum_{batch}( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{3}$
$\displaystyle dx^{\langle t \rangle} = da_{next} * { W_{ax}}^T ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{4}$
$\displaystyle da_{prev} = da_{next} * { W_{aa}}^T ( 1-\tanh^2(W_{ax}x^{\langle t \rangle}+W_{aa} a^{\langle t-1 \rangle} + b_{a}) )\tag{5}$
#### Implementing rnn_cell_backward
```
def rnn_cell_backward(da_next, cache):
# Retrieve values from cache
(a_next, a_prev, xt, parameters) = cache
# Retrieve values from parameters
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# compute the gradient of the loss with respect to z (optional) (≈1 line)
dtanh = (1 - a_next ** 2) * da_next
# compute the gradient of the loss with respect to Wax (≈2 lines)
dxt = np.dot(Wax.T, dtanh)
dWax = np.dot(dtanh, xt.T)
# compute the gradient with respect to Waa (≈2 lines)
da_prev = np.dot(Waa.T, dtanh)
dWaa = np.dot(dtanh, a_prev.T)
# compute the gradient with respect to b (≈1 line)
dba = np.sum(dtanh, axis = 1,keepdims=1)
# Store the gradients in a python dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}
return gradients
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wax'] = np.random.randn(5,3)
parameters_tmp['Waa'] = np.random.randn(5,5)
parameters_tmp['Wya'] = np.random.randn(2,5)
parameters_tmp['ba'] = np.random.randn(5,1)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, yt_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp)
da_next_tmp = np.random.randn(5,10)
gradients_tmp = rnn_cell_backward(da_next_tmp, cache_tmp)
print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients_tmp["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients_tmp["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients_tmp["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients_tmp["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients_tmp["dba"][4])
print("gradients[\"dba\"].shape =", gradients_tmp["dba"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dxt"][1][2]** =
</td>
<td>
-1.3872130506
</td>
</tr>
<tr>
<td>
**gradients["dxt"].shape** =
</td>
<td>
(3, 10)
</td>
</tr>
<tr>
<td>
**gradients["da_prev"][2][3]** =
</td>
<td>
-0.152399493774
</td>
</tr>
<tr>
<td>
**gradients["da_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWax"][3][1]** =
</td>
<td>
0.410772824935
</td>
</tr>
<tr>
<td>
**gradients["dWax"].shape** =
</td>
<td>
(5, 3)
</td>
</tr>
<tr>
<td>
**gradients["dWaa"][1][2]** =
</td>
<td>
1.15034506685
</td>
</tr>
<tr>
<td>
**gradients["dWaa"].shape** =
</td>
<td>
(5, 5)
</td>
</tr>
<tr>
<td>
**gradients["dba"][4]** =
</td>
<td>
[ 0.20023491]
</td>
</tr>
<tr>
<td>
**gradients["dba"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
#### Backward pass through the RNN
```
def rnn_backward(da, caches):
# Retrieve values from the first cache (t=1) of caches (≈2 lines)
(caches, x) = caches
(a1, a0, x1, parameters) = caches[0]
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈6 lines)
dx = np.zeros((n_x, m, T_x))
dWax = np.zeros((n_a, n_x))
dWaa = np.zeros((n_a, n_a))
dba = np.zeros((n_a, 1))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
# Loop through all the time steps
for t in reversed(range(T_x)):
# Compute gradients at time step t. Choose wisely the "da_next" and the "cache" to use in the backward propagation step. (≈1 line)
gradients = rnn_cell_backward(da[:,:,t] + da_prevt, caches[t])
# Retrieve derivatives from gradients (≈ 1 line)
dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"]
# Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines)
dx[:, :, t] = dxt
dWax += dWaxt
dWaa += dWaat
dba += dbat
# Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line)
da0 = da_prevt
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba}
return gradients
np.random.seed(1)
x = np.random.randn(3,10,4)
a0 = np.random.randn(5,10)
Wax = np.random.randn(5,3)
Waa = np.random.randn(5,5)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)
print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dx"][1][2]** =
</td>
<td>
[-2.07101689 -0.59255627 0.02466855 0.01483317]
</td>
</tr>
<tr>
<td>
**gradients["dx"].shape** =
</td>
<td>
(3, 10, 4)
</td>
</tr>
<tr>
<td>
**gradients["da0"][2][3]** =
</td>
<td>
-0.314942375127
</td>
</tr>
<tr>
<td>
**gradients["da0"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWax"][3][1]** =
</td>
<td>
11.2641044965
</td>
</tr>
<tr>
<td>
**gradients["dWax"].shape** =
</td>
<td>
(5, 3)
</td>
</tr>
<tr>
<td>
**gradients["dWaa"][1][2]** =
</td>
<td>
2.30333312658
</td>
</tr>
<tr>
<td>
**gradients["dWaa"].shape** =
</td>
<td>
(5, 5)
</td>
</tr>
<tr>
<td>
**gradients["dba"][4]** =
</td>
<td>
[-0.74747722]
</td>
</tr>
<tr>
<td>
**gradients["dba"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
## LSTM backward pass
### One Step backward
### Gate derivatives
Note the location of the gate derivatives ($\gamma$..) between the dense layer and the activation function (see graphic above). This is convenient for computing parameter derivatives in the next step.
$d\gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*\left(1-\Gamma_o^{\langle t \rangle}\right)\tag{7}$
$dp\widetilde{c}^{\langle t \rangle} = \left(dc_{next}*\Gamma_u^{\langle t \rangle}+ \Gamma_o^{\langle t \rangle}* (1-\tanh^2(c_{next})) * \Gamma_u^{\langle t \rangle} * da_{next} \right) * \left(1-\left(\widetilde c^{\langle t \rangle}\right)^2\right) \tag{8}$
$d\gamma_u^{\langle t \rangle} = \left(dc_{next}*\widetilde{c}^{\langle t \rangle} + \Gamma_o^{\langle t \rangle}* (1-\tanh^2(c_{next})) * \widetilde{c}^{\langle t \rangle} * da_{next}\right)*\Gamma_u^{\langle t \rangle}*\left(1-\Gamma_u^{\langle t \rangle}\right)\tag{9}$
$d\gamma_f^{\langle t \rangle} = \left(dc_{next}* c_{prev} + \Gamma_o^{\langle t \rangle} * (1-\tanh^2(c_{next})) * c_{prev} * da_{next}\right)*\Gamma_f^{\langle t \rangle}*\left(1-\Gamma_f^{\langle t \rangle}\right)\tag{10}$
### Parameter derivatives
$ dW_f = d\gamma_f^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{11} $
$ dW_u = d\gamma_u^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{12} $
$ dW_c = dp\widetilde c^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{13} $
$ dW_o = d\gamma_o^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{14}$
To calculate $db_f, db_u, db_c, db_o$ you just need to sum across the horizontal (axis= 1) axis on $d\gamma_f^{\langle t \rangle}, d\gamma_u^{\langle t \rangle}, dp\widetilde c^{\langle t \rangle}, d\gamma_o^{\langle t \rangle}$ respectively. Note that you should have the `keepdims = True` option.
$\displaystyle db_f = \sum_{batch}d\gamma_f^{\langle t \rangle}\tag{15}$
$\displaystyle db_u = \sum_{batch}d\gamma_u^{\langle t \rangle}\tag{16}$
$\displaystyle db_c = \sum_{batch}d\gamma_c^{\langle t \rangle}\tag{17}$
$\displaystyle db_o = \sum_{batch}d\gamma_o^{\langle t \rangle}\tag{18}$
Finally, you will compute the derivative with respect to the previous hidden state, previous memory state, and input.
$ da_{prev} = W_f^T d\gamma_f^{\langle t \rangle} + W_u^T d\gamma_u^{\langle t \rangle}+ W_c^T dp\widetilde c^{\langle t \rangle} + W_o^T d\gamma_o^{\langle t \rangle} \tag{19}$
Here, to account for concatenation, the weights for equations 19 are the first n_a, (i.e. $W_f = W_f[:,:n_a]$ etc...)
$ dc_{prev} = dc_{next}*\Gamma_f^{\langle t \rangle} + \Gamma_o^{\langle t \rangle} * (1- \tanh^2(c_{next}))*\Gamma_f^{\langle t \rangle}*da_{next} \tag{20}$
$ dx^{\langle t \rangle} = W_f^T d\gamma_f^{\langle t \rangle} + W_u^T d\gamma_u^{\langle t \rangle}+ W_c^T dp\widetilde c^{\langle t \rangle} + W_o^T d\gamma_o^{\langle t \rangle}\tag{21} $
where the weights for equation 21 are from n_a to the end, (i.e. $W_f = W_f[:,n_a:]$ etc...)
**Exercise:** Implement `lstm_cell_backward` by implementing equations $7-21$ below.
Note: In the code:
$d\gamma_o^{\langle t \rangle}$ is represented by `dot`,
$dp\widetilde{c}^{\langle t \rangle}$ is represented by `dcct`,
$d\gamma_u^{\langle t \rangle}$ is represented by `dit`,
$d\gamma_f^{\langle t \rangle}$ is represented by `dft`
```
def lstm_cell_backward(da_next, dc_next, cache):
# Retrieve information from "cache"
(a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
# Retrieve dimensions from xt's and a_next's shape (≈2 lines)
n_x, m = xt.shape
n_a, m = a_next.shape
# Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
dot = da_next * np.tanh(c_next) * ot * (1 - ot)
dcct = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * it * (1 - cct ** 2)
dit = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * cct * (1 - it) * it
dft = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * c_prev * ft * (1 - ft)
# Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
dWf = np.dot(dft, np.hstack([a_prev.T, xt.T]))
dWi = np.dot(dit, np.hstack([a_prev.T, xt.T]))
dWc = np.dot(dcct, np.hstack([a_prev.T, xt.T]))
dWo = np.dot(dot, np.hstack([a_prev.T, xt.T]))
dbf = np.sum(dft, axis=1, keepdims=True)
dbi = np.sum(dit, axis=1, keepdims=True)
dbc = np.sum(dcct, axis=1, keepdims=True)
dbo = np.sum(dot, axis=1, keepdims=True)
# Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
da_prev = np.dot(Wf[:, :n_a].T, dft) + np.dot(Wc[:, :n_a].T, dcct) + np.dot(Wi[:, :n_a].T, dit) + np.dot(Wo[:, :n_a].T, dot)
dc_prev = (da_next * ot * (1 - np.tanh(c_next) ** 2) + dc_next) * ft
dxt = np.dot(Wf[:, n_a:].T, dft) + np.dot(Wc[:, n_a:].T, dcct) + np.dot(Wi[:, n_a:].T, dit) + np.dot(Wo[:, n_a:].T, dot)
# Save gradients in dictionary
gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
xt_tmp = np.random.randn(3,10)
a_prev_tmp = np.random.randn(5,10)
c_prev_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.random.randn(2,5)
parameters_tmp['by'] = np.random.randn(2,1)
a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp)
da_next_tmp = np.random.randn(5,10)
dc_next_tmp = np.random.randn(5,10)
gradients_tmp = lstm_cell_backward(da_next_tmp, dc_next_tmp, cache_tmp)
print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients_tmp["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients_tmp["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dxt"][1][2]** =
</td>
<td>
3.23055911511
</td>
</tr>
<tr>
<td>
**gradients["dxt"].shape** =
</td>
<td>
(3, 10)
</td>
</tr>
<tr>
<td>
**gradients["da_prev"][2][3]** =
</td>
<td>
-0.0639621419711
</td>
</tr>
<tr>
<td>
**gradients["da_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dc_prev"][2][3]** =
</td>
<td>
0.797522038797
</td>
</tr>
<tr>
<td>
**gradients["dc_prev"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWf"][3][1]** =
</td>
<td>
-0.147954838164
</td>
</tr>
<tr>
<td>
**gradients["dWf"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWi"][1][2]** =
</td>
<td>
1.05749805523
</td>
</tr>
<tr>
<td>
**gradients["dWi"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWc"][3][1]** =
</td>
<td>
2.30456216369
</td>
</tr>
<tr>
<td>
**gradients["dWc"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWo"][1][2]** =
</td>
<td>
0.331311595289
</td>
</tr>
<tr>
<td>
**gradients["dWo"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dbf"][4]** =
</td>
<td>
[ 0.18864637]
</td>
</tr>
<tr>
<td>
**gradients["dbf"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbi"][4]** =
</td>
<td>
[-0.40142491]
</td>
</tr>
<tr>
<td>
**gradients["dbi"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbc"][4]** =
</td>
<td>
[ 0.25587763]
</td>
</tr>
<tr>
<td>
**gradients["dbc"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbo"][4]** =
</td>
<td>
[ 0.13893342]
</td>
</tr>
<tr>
<td>
**gradients["dbo"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
### LSTM BACKWARD
```
def lstm_backward(da, caches):
# Retrieve values from the first cache (t=1) of caches.
(caches, x) = caches
(a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]
# Retrieve dimensions from da's and x1's shapes (≈2 lines)
n_a, m, T_x = da.shape
n_x, m = x1.shape
# initialize the gradients with the right sizes (≈12 lines)
dx = np.zeros((n_x, m, T_x))
da0 = np.zeros((n_a, m))
da_prevt = np.zeros((n_a, m))
dc_prevt = np.zeros((n_a, m))
dWf = np.zeros((n_a, n_a + n_x))
dWi = np.zeros((n_a, n_a + n_x))
dWc = np.zeros((n_a, n_a + n_x))
dWo = np.zeros((n_a, n_a + n_x))
dbf = np.zeros((n_a, 1))
dbi = np.zeros((n_a, 1))
dbc = np.zeros((n_a, 1))
dbo = np.zeros((n_a, 1))
# loop back over the whole sequence
for t in reversed(range(T_x)):
# Compute all gradients using lstm_cell_backward
gradients = lstm_cell_backward(da[:,:,t] + da_prevt, dc_prevt, caches[t])
# Store or add the gradient to the parameters' previous step's gradient
dx[:,:,t] = gradients["dxt"]
dWf += gradients["dWf"]
dWi += gradients["dWi"]
dWc += gradients["dWc"]
dWo += gradients["dWo"]
dbf += gradients["dbf"]
dbi += gradients["dbi"]
dbc += gradients["dbc"]
dbo += gradients["dbo"]
# Set the first activation's gradient to the backpropagated gradient da_prev.
da0 = gradients["da_prev"]
# Store the gradients in a python dictionary
gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
"dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}
return gradients
np.random.seed(1)
x_tmp = np.random.randn(3,10,7)
a0_tmp = np.random.randn(5,10)
parameters_tmp = {}
parameters_tmp['Wf'] = np.random.randn(5, 5+3)
parameters_tmp['bf'] = np.random.randn(5,1)
parameters_tmp['Wi'] = np.random.randn(5, 5+3)
parameters_tmp['bi'] = np.random.randn(5,1)
parameters_tmp['Wo'] = np.random.randn(5, 5+3)
parameters_tmp['bo'] = np.random.randn(5,1)
parameters_tmp['Wc'] = np.random.randn(5, 5+3)
parameters_tmp['bc'] = np.random.randn(5,1)
parameters_tmp['Wy'] = np.zeros((2,5)) # unused, but needed for lstm_forward
parameters_tmp['by'] = np.zeros((2,1)) # unused, but needed for lstm_forward
a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp)
da_tmp = np.random.randn(5, 10, 4)
gradients_tmp = lstm_backward(da_tmp, caches_tmp)
print("gradients[\"dx\"][1][2] =", gradients_tmp["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients_tmp["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients_tmp["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients_tmp["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
```
**Expected Output**:
<table>
<tr>
<td>
**gradients["dx"][1][2]** =
</td>
<td>
[0.00218254 0.28205375 -0.48292508 -0.43281115]
</td>
</tr>
<tr>
<td>
**gradients["dx"].shape** =
</td>
<td>
(3, 10, 4)
</td>
</tr>
<tr>
<td>
**gradients["da0"][2][3]** =
</td>
<td>
0.312770310257
</td>
</tr>
<tr>
<td>
**gradients["da0"].shape** =
</td>
<td>
(5, 10)
</td>
</tr>
<tr>
<td>
**gradients["dWf"][3][1]** =
</td>
<td>
-0.0809802310938
</td>
</tr>
<tr>
<td>
**gradients["dWf"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWi"][1][2]** =
</td>
<td>
0.40512433093
</td>
</tr>
<tr>
<td>
**gradients["dWi"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWc"][3][1]** =
</td>
<td>
-0.0793746735512
</td>
</tr>
<tr>
<td>
**gradients["dWc"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dWo"][1][2]** =
</td>
<td>
0.038948775763
</td>
</tr>
<tr>
<td>
**gradients["dWo"].shape** =
</td>
<td>
(5, 8)
</td>
</tr>
<tr>
<td>
**gradients["dbf"][4]** =
</td>
<td>
[-0.15745657]
</td>
</tr>
<tr>
<td>
**gradients["dbf"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbi"][4]** =
</td>
<td>
[-0.50848333]
</td>
</tr>
<tr>
<td>
**gradients["dbi"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbc"][4]** =
</td>
<td>
[-0.42510818]
</td>
</tr>
<tr>
<td>
**gradients["dbc"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
<tr>
<td>
**gradients["dbo"][4]** =
</td>
<td>
[ -0.17958196]
</td>
</tr>
<tr>
<td>
**gradients["dbo"].shape** =
</td>
<td>
(5, 1)
</td>
</tr>
</table>
| github_jupyter |
# Data description:
I'm going to solve the International Airline Passengers prediction problem. This is a problem where given a year and a month, the task is to predict the number of international airline passengers in units of 1,000. The data ranges from January 1949 to December 1960 or 12 years, with 144 observations.
# Workflow:
- Load the Time Series (TS) by Pandas Library
- Prepare the data, i.e. convert the problem to a supervised ML problem
- Build and evaluate the RNN model:
- Fit the best RNN model
- Evaluate model by in-sample prediction: Calculate RMSE
- Forecast the future trend: Out-of-sample prediction
Note: For data exploration of this TS, please refer to the notebook of my alternative solution with "Seasonal ARIMA model"
```
import keras
import sklearn
import tensorflow as tf
import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import metrics
from sklearn import preprocessing
import random as rn
import math
%matplotlib inline
from keras import backend as K
session_conf = tf.ConfigProto(intra_op_parallelism_threads=5, inter_op_parallelism_threads=5)
sess = tf.Session(graph=tf.get_default_graph(), config=session_conf)
K.set_session(sess)
import warnings
warnings.filterwarnings("ignore")
# Load data using Series.from_csv
from pandas import Series
#TS = Series.from_csv('C:/Users/rhash/Documents/Datasets/Time Series analysis/daily-minimum-temperatures.csv', header=0)
# Load data using pandas.read_csv
# in case, specify your own date parsing function and use the date_parser argument
from pandas import read_csv
TS = read_csv('C:/Users/rhash/Documents/Datasets/Time Series analysis/AirPassengers.csv', header=0, parse_dates=[0], index_col=0, squeeze=True)
print(TS.head())
#TS=pd.to_numeric(TS, errors='coerce')
TS.dropna(inplace=True)
data=pd.DataFrame(TS.values)
# prepare the data (i.e. convert problem to a supervised ML problem)
def prepare_data(data, lags=1):
"""
Create lagged data from an input time series
"""
X, y = [], []
for row in range(len(data) - lags - 1):
a = data[row:(row + lags), 0]
X.append(a)
y.append(data[row + lags, 0])
return np.array(X), np.array(y)
# normalize the dataset
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(data)
# split into train and test sets
train = dataset[0:120, :]
test = dataset[120:, :]
# LSTM RNN model: _________________________________________________________________
from keras.models import Sequential, Model
from keras.layers import Dense, LSTM, Dropout, average, Input, merge, concatenate
from keras.layers.merge import concatenate
from keras.regularizers import l2, l1
from keras.callbacks import EarlyStopping, ModelCheckpoint
from sklearn.utils.class_weight import compute_sample_weight
from keras.layers.normalization import BatchNormalization
# reshape into X=t and Y=t+1
lags = 3
X_train, y_train = prepare_data(train, lags)
X_test, y_test = prepare_data(test, lags)
# reshape input to be [samples, time steps, features]
X_train = np.reshape(X_train, (X_train.shape[0], lags, 1))
X_test = np.reshape(X_test, (X_test.shape[0], lags, 1))
# create and fit the LSTM network
mdl = Sequential()
#mdl.add(Dense(3, input_shape=(1, lags), activation='relu'))
mdl.add(LSTM(4, activation='relu'))
#mdl.add(Dropout(0.1))
mdl.add(Dense(1))
mdl.compile(loss='mean_squared_error', optimizer='adam')
monitor=EarlyStopping(monitor='loss', min_delta=0.001, patience=100, verbose=1, mode='auto')
history=mdl.fit(X_train, y_train, epochs=1000, batch_size=1, validation_data=(X_test, y_test), callbacks=[monitor], verbose=0)
# To measure RMSE and evaluate the RNN model:
from sklearn.metrics import mean_squared_error
# make predictions
train_predict = mdl.predict(X_train)
test_predict = mdl.predict(X_test)
# invert transformation
train_predict = scaler.inverse_transform(pd.DataFrame(train_predict))
y_train = scaler.inverse_transform(pd.DataFrame(y_train))
test_predict = scaler.inverse_transform(pd.DataFrame(test_predict))
y_test = scaler.inverse_transform(pd.DataFrame(y_test))
# calculate root mean squared error
train_score = math.sqrt(mean_squared_error(y_train, train_predict[:,0]))
print('Train Score: {:.2f} RMSE'.format(train_score))
test_score = math.sqrt(mean_squared_error(y_test, test_predict[:,0]))
print('Test Score: {:.2f} RMSE'.format(test_score))
# list all data in history
#print(history.history.keys())
# summarize history for loss
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
mdl.save('passenger_model.h5')
# shift train predictions for plotting
train_predict_plot =np.full(data.shape, np.nan)
train_predict_plot[lags:len(train_predict)+lags, :] = train_predict
# shift test predictions for plotting
test_predict_plot =np.full(data.shape, np.nan)
test_predict_plot[len(train_predict) + (lags * 2)+1:len(data)-1, :] = test_predict
# plot observation and predictions
plt.figure(figsize=(8,6))
plt.plot(data, label='Observed', color='#006699');
plt.plot(train_predict_plot, label='Prediction for Train Set', color='#006699', alpha=0.5);
plt.plot(test_predict_plot, label='Prediction for Test Set', color='#ff0066');
plt.legend(loc='upper left')
plt.title('LSTM Recurrent Neural Net')
plt.show()
mse = mean_squared_error(y_test, test_predict[:,0])
plt.title('Prediction quality: {:.2f} MSE ({:.2f} RMSE)'.format(mse, math.sqrt(mse)))
plt.plot(y_test.reshape(-1, 1), label='Observed', color='#006699')
plt.plot(test_predict.reshape(-1, 1), label='Prediction', color='#ff0066')
plt.legend(loc='upper left');
plt.show()
```
| github_jupyter |
<font color ='0c6142' size=6)> Chemistry </font> <font color ='708090' size=3)> for Technology Students at GGC </font>
<font color ='708090' size=3)> Measurement Uncertainty, Accuracy, and Precision </font>
[Textbook: Chapter 1, section 5](https://openstax.org/books/chemistry-2e/pages/1-5-measurement-uncertainty-accuracy-and-precision)
### Measurement Uncertainty
Most measurements are very much _not_ like that. You can easily imagine getting 4.34 gallons of gasoline at the gas station, right? Or 2.47 pounds of catfish at the deli?
Python has a way to deal with these numbers. And they're called __floats__. It turns out the difference between these numbers is not going to be a big deal in most applications, but it's a fundamental concept, and sometimes it matters. Computers store integers and floats differently and use them differently, and when we are doing really big calculations, it could mean the difference between _can_ and _can't_.
Try `print(type(3.14159))`.
What would you say if your friend told you he measured the diameter of a hair with a yardstick? Nonsense, right? Or the length of a cellphone with a car's odometer?
In order to do that, he would have to take a cellphone and put it on the ground - hopefully his own. Then he would have to drive over the phone, checking his odometer as the center of the wheel passed over the first edge, and then again as it passed over the far edge.
What's the problem with those examples? Besides the fact dude just ruined his cellphone, in both cases, the measurements exceed the limits of the apparatus. Yardsticks aren't made to measure lengths smaller than the markings on the stick, let alone lengths much, much smaller.
This is where _significant figures_ comes in. The number of sig figs gives us a measure of how precise our measurement is.
Python has a way of formatting strings, so when your calcuation makes an output, and you send it to a file, you can show how precisely your measurement was taken.
`d = 1.00 # inches`
`pi = 3.1415926`
`c = pi*d`
`print ("The circumference of the circle is {:.2f}".format(c))`
Try it.
```
d = 1.00 # inches
pi = 3.1415926
c = pi*d
print ("The circumference of the circle is {:.2f} inches.".format(c))
```
## Exercises
1. In the last example above, the circumference of a circle is given to 2 decimal places - or 3 significant figures. Suppose we had a way of measuring the diameter to a much higher precision. Namely, suppose we knew it was 1.0000 inches. Copy the code and alter it so that this is reflected in the output string.
2. Set two variables, `exact_nums` and `uncertain_nums`. Go to your textbook and draft good definitions of those.
***
[Table of Contents](../../../chem4tech.ipynb)
[Chapter 1, section 6](../sections/chem4tech01_06.ipynb)
| github_jupyter |
```
import sys
sys.path.insert(1, '/home/maria/Documents/EnsemblePursuit')
from EnsemblePursuit.EnsemblePursuit import EnsemblePursuit
import numpy as np
from scipy.stats import zscore
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter, gaussian_filter1d
data_path='/home/maria/Documents/data_for_suite2p/TX39/'
dt=1
spks= np.load(data_path+'spks.npy')
print('Shape of the data matrix, neurons by timepoints:',spks.shape)
iframe = np.load(data_path+'iframe.npy') # iframe[n] is the microscope frame for the image frame n
ivalid = iframe+dt<spks.shape[-1] # remove timepoints outside the valid time range
iframe = iframe[ivalid]
S = spks[:, iframe+dt]
print(S.shape)
#Uncomment to compute U and V
ep=EnsemblePursuit(n_components=200,lam=0.01,n_kmeans=200)
model=ep.fit(S.T[:10000,:])
V=model.components_
U=model.weights
np.save('U.npy',U)
#13
print(U.shape)
print(np.nonzero(U[:,13])[0])
print(S.shape)
print(S[np.nonzero(U[:,13])[0],:].shape)
stat = np.load(('/home/maria/Documents/data_for_suite2p/TX39/'+'stat.npy'), allow_pickle=True) # these are the per-neuron stats returned by suite2p
# these are the neurons' 2D coordinates
ypos = np.array([stat[n]['med'][0] for n in range(len(stat))])
# (notice the python list comprehension [X(n) for n in range(N)])
xpos = np.array([stat[n]['med'][1] for n in range(len(stat))])
comp=U[:,13]
comp= comp/np.max(np.abs(comp))
lam = np.abs(comp)
plt.scatter(xpos, -ypos, s = 50 * lam, c = comp, cmap='bwr', alpha = .5)
```
# Inject activity patterns without plasticity
```
np.random.seed(7)
input_patterns=S[np.nonzero(U[:,13])[0],:]
input_patterns=zscore(input_patterns,axis=1)
v_lst=[]
w=np.random.normal(loc=0,size=(656,))
v_lst=[np.dot(w,input_patterns[:,0])]
for j in range(1,30560):
v_lst.append(np.dot(w,input_patterns[:,j]))
plt.plot(zscore(v_lst[:100]))
plt.show()
plt.plot(input_patterns[1,:100])
v_lst=np.array(zscore(v_lst))
print(v_lst.shape)
def train_test_split(NT):
nsegs = 20
nt=NT
nlen = nt/nsegs
ninds = np.linspace(0,nt-nlen,nsegs).astype(int)
itest = (ninds[:,np.newaxis] + np.arange(0,nlen*0.25,1,int)).flatten()
itrain = np.ones(nt, np.bool)
itrain[itest] = 0
return itrain, itest
mov=np.load(data_path+'mov.npy')
mov = mov[:, :, ivalid]
ly, lx, nstim = mov.shape
#print(nstim)
NT = v_lst.shape[0]
NN=1
mov=mov[:,:,:NT]
print(NT)
itrain,itest=train_test_split(NT)
X = np.reshape(mov, [-1, NT]) # reshape to Npixels by Ntimepoints
X = X-0.5 # subtract the background
X = np.abs(X) # does not matter if a pixel is black (0) or white (1)
X = zscore(X, axis=1)/NT**.5 # z-score each pixel separately
npix = X.shape[0]
lam = 0.1
ncomps = Sp.shape[0]
B0 = np.linalg.solve((X[:,itrain] @ X[:,itrain].T + lam * np.eye(npix)), (X[:,itrain] @ v_lst[itrain].T)) # get the receptive fields for each neuron
B0 = np.reshape(B0, (ly, lx, 1))
B0 = gaussian_filter(B0, [.5, .5, 0]) # smooth each receptive field a littleb
rf = B0[:,:,0]
rfmax = np.max(B0)
# rfmax = np.max(np.abs(rf))
plt.imshow(rf, aspect='auto', cmap = 'bwr', vmin = -rfmax, vmax = rfmax)
```
# Inject patterns with plasticity
```
#Using Euler's method to calculate the weight increments
h=0.001
input_patterns=S[np.nonzero(U[:,13])[0],:]
input_patterns=zscore(input_patterns,axis=1)
print(input_patterns.shape)
v_lst=[]
w_lst=[]
w=np.random.normal(loc=0,size=(656,))
v_lst=[np.dot(w,input_patterns[:,1])]
for j in range(0,1000):
v_lst.append(np.dot(w,input_patterns[:,j]))
w=w+h*v_lst[-1]*input_patterns[:,j]
w=np.clip(w,a_min=-100,a_max=100)
w_lst.append(w)
w_arr=np.array(w_lst).T
print(w_arr.shape)
plt.plot(w_arr[0,:])
for j in range(0,10):
plt.plot(w_arr[j,:])
v_lst=np.array(zscore(v_lst))
mov=np.load(data_path+'mov.npy')
mov = mov[:, :, ivalid]
ly, lx, nstim = mov.shape
#print(nstim)
NT = v_lst.shape[0]
NN=1
mov=mov[:,:,:NT]
print(NT)
itrain,itest=train_test_split(NT)
X = np.reshape(mov, [-1, NT]) # reshape to Npixels by Ntimepoints
X = X-0.5 # subtract the background
X = np.abs(X) # does not matter if a pixel is black (0) or white (1)
X = zscore(X, axis=1)/NT**.5 # z-score each pixel separately
npix = X.shape[0]
lam = 0.1
ncomps = Sp.shape[0]
B0 = np.linalg.solve((X[:,itrain] @ X[:,itrain].T + lam * np.eye(npix)), (X[:,itrain] @ v_lst[itrain].T)) # get the receptive fields for each neuron
B0 = np.reshape(B0, (ly, lx, 1))
B0 = gaussian_filter(B0, [.5, .5, 0]) # smooth each receptive field a littleb
rf = B0[:,:,0]
rfmax = np.max(B0)
# rfmax = np.max(np.abs(rf))
plt.imshow(rf, aspect='auto', cmap = 'bwr', vmin = -rfmax, vmax = rfmax)
```
| github_jupyter |
# Comparing soundings from NCEP Reanalysis and various models
We are going to plot the global, annual mean sounding (vertical temperature profile) from observations.
Read in the necessary NCEP reanalysis data from the online server.
The catalog is here: <https://psl.noaa.gov/psd/thredds/catalog/Datasets/ncep.reanalysis.derived/catalog.html>
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
ncep_url = "https://psl.noaa.gov/thredds/dodsC/Datasets/ncep.reanalysis.derived/"
ncep_air = xr.open_dataset( ncep_url + "pressure/air.mon.1981-2010.ltm.nc", decode_times=False)
level = ncep_air.level
lat = ncep_air.lat
```
Take global averages and time averages.
```
Tzon = ncep_air.air.mean(dim=('lon','time'))
weight = np.cos(np.deg2rad(lat)) / np.cos(np.deg2rad(lat)).mean(dim='lat')
Tglobal = (Tzon * weight).mean(dim='lat')
```
Here is code to make a nicely labeled sounding plot.
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000))
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Global, annual mean sounding from NCEP Reanalysis', fontsize = 24)
ax2 = ax.twinx()
ax2.plot( Tglobal + 273.15, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Now compute the Radiative Equilibrium solution for the grey-gas column model
```
import climlab
from climlab import constants as const
col = climlab.GreyRadiationModel()
print(col)
col.subprocess['LW'].diagnostics
col.integrate_years(1)
print("Surface temperature is " + str(col.Ts) + " K.")
print("Net energy in to the column is " + str(col.ASR - col.OLR) + " W / m2.")
```
### Plot the radiative equilibrium temperature on the same plot with NCEP reanalysis
```
pcol = col.lev
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=20 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue) and radiative equilibrium in grey gas model (red)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Now use convective adjustment to compute a Radiative-Convective Equilibrium temperature profile
```
dalr_col = climlab.RadiativeConvectiveModel(adj_lapse_rate='DALR')
print(dalr_col)
dalr_col.integrate_years(2.)
print("After " + str(dalr_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(dalr_col.Ts) + " K.")
print("Net energy in to the column is " + str(dalr_col.ASR - dalr_col.OLR) + " W / m2.")
dalr_col.param
```
Now plot this "Radiative-Convective Equilibrium" on the same graph:
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red) and dry RCE (black)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
The convective adjustment gets rid of the unphysical temperature difference between the surface and the overlying air.
But now the surface is colder! Convection acts to move heat upward, away from the surface.
Also, we note that the observed lapse rate (blue) is always shallower than $\Gamma_d$ (temperatures decrease more slowly with height).
## "Moist" Convective Adjustment
To approximately account for the effects of latent heat release in rising air parcels, we can just adjust to a lapse rate that is a little shallow than $\Gamma_d$.
We will choose 6 K / km, which gets close to the observed mean lapse rate.
We will also re-tune the longwave absorptivity of the column to get a realistic surface temperature of 288 K:
```
rce_col = climlab.RadiativeConvectiveModel(adj_lapse_rate=6, abs_coeff=1.7E-4)
print(rce_col)
rce_col.integrate_years(2.)
print("After " + str(rce_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(rce_col.Ts) + " K.")
print("Net energy in to the column is " + str(rce_col.ASR - rce_col.OLR) + " W / m2.")
```
Now add this new temperature profile to the graph:
```
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + 273.15, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.plot( rce_col.Tatm, np.log( pcol / const.ps ), 'm-' )
ax.plot( rce_col.Ts, 0, 'mo', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red), dry RCE (black), and moist RCE (magenta)', fontsize = 18)
ax2 = ax.twinx()
ax2.plot( Tglobal + const.tempCtoK, -8*np.log(level/1000) );
ax2.set_ylabel('Approx. height above surface (km)', fontsize=16 );
ax.grid()
```
## Adding stratospheric ozone
Our model has no equivalent of the stratosphere, where temperature increases with height. That's because our model has been completely transparent to shortwave radiation up until now.
We can load some climatogical ozone data:
```
# Put in some ozone
import xarray as xr
ozonepath = "http://thredds.atmos.albany.edu:8080/thredds/dodsC/CLIMLAB/ozone/apeozone_cam3_5_54.nc"
ozone = xr.open_dataset(ozonepath)
ozone
```
Take the global average of the ozone climatology, and plot it as a function of pressure (or height)
```
# Taking annual, zonal, and global averages of the ozone data
O3_zon = ozone.OZONE.mean(dim=("time","lon"))
weight_ozone = np.cos(np.deg2rad(ozone.lat)) / np.cos(np.deg2rad(ozone.lat)).mean(dim='lat')
O3_global = (O3_zon * weight_ozone).mean(dim='lat')
O3_global.shape
ax = plt.figure(figsize=(10,8)).add_subplot(111)
ax.plot( O3_global * 1.E6, np.log(O3_global.lev/const.ps) )
ax.invert_yaxis()
ax.set_xlabel('Ozone (ppm)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
yticks = np.array([1000., 500., 250., 100., 50., 20., 10., 5.])
ax.set_yticks( np.log(yticks/1000.) )
ax.set_yticklabels( yticks )
ax.set_title('Global, annual mean ozone concentration', fontsize = 24);
```
This shows that most of the ozone is indeed in the stratosphere, and peaks near the top of the stratosphere.
Now create a new column model object **on the same pressure levels as the ozone data**. We are also going set an adjusted lapse rate of 6 K / km, and tune the longwave absorption
```
oz_col = climlab.RadiativeConvectiveModel(lev = ozone.lev,
abs_coeff=1.82E-4,
adj_lapse_rate=6,
albedo=0.315)
```
Now we will do something new: let the column absorb some shortwave radiation. We will assume that the shortwave absorptivity is proportional to the ozone concentration we plotted above. We need to weight the absorptivity by the pressure (mass) of each layer.
```
ozonefactor = 75
dp = oz_col.Tatm.domain.axes['lev'].delta
sw_abs = O3_global * dp * ozonefactor
oz_col.subprocess.SW.absorptivity = sw_abs
oz_col.compute()
oz_col.compute()
print(oz_col.SW_absorbed_atm)
```
Now run it out to Radiative-Convective Equilibrium, and plot
```
oz_col.integrate_years(2.)
print("After " + str(oz_col.time['days_elapsed']) + " days of integration:")
print("Surface temperature is " + str(oz_col.Ts) + " K.")
print("Net energy in to the column is " + str(oz_col.ASR - oz_col.OLR) + " W / m2.")
pozcol = oz_col.lev
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/1000), 'b-', col.Tatm, np.log( pcol/const.ps ), 'r-' )
ax.plot( col.Ts, 0, 'ro', markersize=16 )
ax.plot( dalr_col.Tatm, np.log( pcol / const.ps ), 'k-' )
ax.plot( dalr_col.Ts, 0, 'ko', markersize=16 )
ax.plot( rce_col.Tatm, np.log( pcol / const.ps ), 'm-' )
ax.plot( rce_col.Ts, 0, 'mo', markersize=16 )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/1000) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RE (red), dry RCE (black), moist RCE (magenta), RCE with ozone (cyan)', fontsize = 18)
ax.grid()
```
And we finally have something that looks looks like the tropopause, with temperature increasing above at about the correct rate. Though the tropopause temperature is off by 15 degrees or so.
## Greenhouse warming in the RCE model with ozone
```
oz_col2 = climlab.process_like( oz_col )
oz_col2.subprocess['LW'].absorptivity *= 1.2
oz_col2.integrate_years(2.)
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/const.ps), 'b-' )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.plot( oz_col2.Tatm, np.log( pozcol / const.ps ), 'c--' )
ax.plot( oz_col2.Ts, 0, 'co', markersize=16 )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/const.ps) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RCE with ozone (cyan)', fontsize = 18)
ax.grid()
```
And we find that the troposphere warms, while the stratosphere cools!
### Vertical structure of greenhouse warming in CESM model
```
datapath = "http://thredds.atmos.albany.edu:8080/thredds/dodsC/CESMA/"
atmstr = ".cam.h0.clim.nc"
cesm_ctrl = xr.open_dataset(datapath + 'som_1850_f19/clim/som_1850_f19' + atmstr)
cesm_2xCO2 = xr.open_dataset(datapath + 'som_1850_2xCO2/clim/som_1850_2xCO2' + atmstr)
cesm_ctrl.T
T_cesm_ctrl_zon = cesm_ctrl.T.mean(dim=('time', 'lon'))
T_cesm_2xCO2_zon = cesm_2xCO2.T.mean(dim=('time', 'lon'))
weight = np.cos(np.deg2rad(cesm_ctrl.lat)) / np.cos(np.deg2rad(cesm_ctrl.lat)).mean(dim='lat')
T_cesm_ctrl_glob = (T_cesm_ctrl_zon*weight).mean(dim='lat')
T_cesm_2xCO2_glob = (T_cesm_2xCO2_zon*weight).mean(dim='lat')
fig = plt.figure( figsize=(10,8) )
ax = fig.add_subplot(111)
ax.plot( Tglobal + const.tempCtoK, np.log(level/const.ps), 'b-' )
ax.plot( oz_col.Tatm, np.log( pozcol / const.ps ), 'c-' )
ax.plot( oz_col.Ts, 0, 'co', markersize=16 )
ax.plot( oz_col2.Tatm, np.log( pozcol / const.ps ), 'c--' )
ax.plot( oz_col2.Ts, 0, 'co', markersize=16 )
ax.plot( T_cesm_ctrl_glob, np.log( cesm_ctrl.lev/const.ps ), 'r-' )
ax.plot( T_cesm_2xCO2_glob, np.log( cesm_ctrl.lev/const.ps ), 'r--' )
ax.invert_yaxis()
ax.set_xlabel('Temperature (K)', fontsize=16)
ax.set_ylabel('Pressure (hPa)', fontsize=16 )
ax.set_yticks( np.log(level/const.ps) )
ax.set_yticklabels( level.values )
ax.set_title('Temperature profiles: observed (blue), RCE with ozone (cyan), CESM (red)', fontsize = 18)
ax.grid()
```
And we find that CESM has the same tendency for increased CO2: warmer troposphere, colder stratosphere.
| github_jupyter |
<a href="https://colab.research.google.com/github/boopathiviky/Eulers-Project/blob/repo/euler's.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#1.multiples of 3 and 5
```
sum1=0
x=int(input())
for i in range(1,x):
if(i%3==0 or i%5==0):
sum1=sum1+i
print(sum1)
```
#2.even fib numbers
```
a=0
b=1
c=0
sum2=0
for i in range(0,10):
c=a+b
a=b
b=c
print(c)
if(c%2==0):
sum2=sum2+c
print('sum',sum2)
```
#3.prime fact of
```
def isprime(n):
pr=1
for i in range(2,int(n/2)):
if(n%i==0):
pr=0
break
if(pr==1):
print(n)
x=int(input())
for i in range(2,x):
if(x%i==0):
isprime(i)
```
#4.Largest palindrome product
```
li=[]
def ispalindrome(c):
if(str(c) == str(c)[::-1]):
li.append(c)
#print(list)
li.sort()
for i in range(100,1000):
for k in range(i,1000):
a=i*k
ispalindrome(a)
print("Largest palindrome is:", li[-1])
```
#5.Smallest multiple
```
n=1
while (n>=1):
n=n+1
c=1
for i in range(1,11):
if (n%i==0):
c=c+1
if (c>10):
print(n)
break
```
#6.Sum square difference
```
sq1=0
sq=0
# i insiate start,stop 10 1,9 1,11
for i in range(1,100+1):
sq=i**2
sq1=sq1+sq
sqr=0
for j in range(1,100+1):
sqr=sqr+j
s1=sqr**2
final=s1-sq1
print(sq1)
print(s1)
print(final)
# sq1=0
# for i in range(1,10+1):
# sq=i**2
# sq1=sq1+sq
# print(sq)
# print('\t',sq1)
```
#7.10001st prime
```
def isprime(n):
pr=1
for i in range(2,int(n/2)):
if(n%i==0):
pr=0
break
if(pr==1):
return 1
c=0
for i in range(3,1000000):
if (isprime(i)==1):
c=c+1
if (c>=10001):
print (i)
break
```
#8.Largest product in a series
```
n='731671765313306249192251196744265747423553491949349698352031277450632623957831801698480186947885184385861560789112949495459501737958331952853208805511\
125406987471585238630507156932909632952274430435576689664895044524452316173185640309871112172238311362229893423380308135336276614282806444486645238749\
303589072962904915604407723907138105158593079608667017242712188399879790879227492190169972088809377665727333001053367881220235421809751254540594752243\
525849077116705560136048395864467063244157221553975369781797784617406495514929086256932197846862248283972241375657056057490261407972968652414535100474\
821663704844031998900088952434506585412275886668811642717147992444292823086346567481391912316282458617866458359124566529476545682848912883142\
60769004224219022671055626321111109370544217506941658960408\
0719840385096245544436298123098787992724428490918884580156166097919133875499200524063689912560717606\
0588611646710940507754100225698315520005593572972571636269561882670428252483600823257530420752963450'
lst=[]
h=1
lst=str(n)
p=13
for i in range(0,1000):
temp=lst[i:i+p]
sum1=1
for j in range(len(temp)):
v=int(temp[j])
sum1=sum1*v
if h<sum1 :
h=sum1
print(h)
```
#9.Special Pythagorean triplet
```
for i in range(500):
for j in range(500):
for k in range(500):
if i+j+k == 1000:
if i<j<k:
if i**2+j**2==k**2:
print (i,j,k)
```
#10.Summation of primes
```
num1=[]
pr=0
for num in range(0,11):
if num>=1:
for i in range(2,num):
if(num%i==0):
pr=0
break
else:
pr=1
if(pr==1):
num1.append(num)
print(sum(num1))
```
#11.Largest product in a grid
```
import numpy as np
lst1=[]
lst2=[]
lst3=[]
lst4=[]
dt=np.genfromtxt('data.txt', delimiter=' ')
rows, cols=dt.shape
print(dt[0])
su=1
for i in range(0,rows):
for j in range(0,cols):
# forward
if(j+4<=cols):
su=dt[i,j]*dt[i,j+1]*dt[i,j+2]*dt[i,j+3]
lst1.append(su)
su=1
#downward
if(i+4<=rows):
su=dt[i,j]*dt[i+1,j]*dt[i+2,j]*dt[i+3,j]
lst2.append(su)
su=1
# diagonal l-r
if(i+4<=rows and j+4<=cols):
su=dt[i,j]*dt[i+1,j+1]*dt[i+2,j+2]*dt[i+3,j+3]
lst3.append(su)
su=1
# diagonal r-l
if(j>2 and i<cols-3):
su=dt[i,j]*dt[i+1,j-1]*dt[i+2,j-2]*dt[i+3,j-3]
lst4.append(su)
su=1
print(max(lst1),max(lst2),max(lst3),max(lst4))
```
| github_jupyter |
# `numpy`
မင်္ဂလာပါ၊ welcome to the week 07 of Data Science Using Python.
We will go into details of `numpy` this week (as well as do some linear algebra stuffs).
## `numpy` အကြောင်း သိပြီးသမျှ
* `numpy` ဟာ array library ဖြစ်တယ်၊
* efficient ဖြစ်တယ်၊
* vector နဲ့ matrix တွေကို လွယ်လွယ်ကူကူ ကိုင်တွယ်နိုင်တယ်၊
* tensor တွေကို ရောပဲ ???
```
# tensor ဆိုတာ 2 ထက်များတဲ့ dimension ရှိတဲ့ array ကြီးတွေကို သင်္ချာဆန်ဆန် ခေါ်တာပါပဲ။
import numpy as np
tensor_3d = np.array(
[
[
[1, 2],
[3, 4]
],
[
[10, 20],
[30, 40]
],
]
)
print (tensor_3d.ndim, tensor_3d.shape, tensor_3d.size)
```
* **array indexing** `numpy` array တွေကို index လုပ်ဖို့ square bracket '[]' ထဲမှာ comma ',' ခံပြီး ရေးရတယ်။ dimension အရေအတွက် ရှိတဲ့အတိုင်း အကုန်ရေးရတယ်။ ချန်ထားရင် ကျန်တဲ့ dimensional တွေအတွက် အကုန်လို့ ယူဆတယ်။
* **slicing/dicing** `numpy` array တွေရဲ့ view တခုကို dimension အတွက် index ဂဏန်း နေရာမှာ start:end:step syntax သုံးပြီး slice လုပ်နိုင်တယ်။
```
from utils import my_data, np_data
print (my_data)
print ('---')
print (np_data)
# so, how to get the id, length, width view and height view ?
```
## `numpy` array creation
`numpy` မှာ array ဖန်တီးဖို့ short-cut function တွေရှိတယ်။
```
import numpy as np
a = np.zeros((2,2)) # Create an array of all zeros
print(a) # Prints "[[ 0. 0.]
# [ 0. 0.]]"
b = np.ones((1,2)) # Create an array of all ones
print(b) # Prints "[[ 1. 1.]]"
c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
e = np.random.random((2,2)) # Create an array filled with random values
print(e) # Might print "[[ 0.91940167 0.08143941]
# [ 0.68744134 0.87236687]]"
r = np.arange(35)
print (r)
```
အသုံးများတာကတော့ ...
* `arange`
* `zeros`
* `ones`
* `full`
* `eye` နဲ့
* `random.random` တို့ ဖြစ်တယ်။
အပြည့်အစုံကို [Numpy official documentation](https://numpy.org/doc/stable/reference/routines.array-creation.html) မှာ ကြည့်နိုင်တယ်။
## `numpy` array manipulation
အသုံးအများဆုံး array manipulation ကတော့ ...
* `copy`
* `reshape`
* `vstack`
* `hstack` နဲ့
* `block` တို့ပဲ ဖြစ်တယ်။
```
v1 = np_data[::2]
v2 = np_data[1::2,0]
print (v1.shape, v2.shape)
print (v1)
print (v2)
v2 =v2.reshape(-1,1) # here, -1 means "ကိုယ့်ဟာကိုယ် ကြည့်ဖြည့်လိုက်"
print (v2.shape)
np.hstack((v1, v2))
A = np.zeros((3,3)) # သတိထားစရာက tuple တွေကို parameter pass တာပဲ
print (A)
print ("---")
B = np.eye(2, 2)
print (B)
print ("---")
A_sub = A[1:3, 1:3]
A_sub += B
print (A)
A = np.zeros((3,3))
print (A)
print ("---")
B = np.eye(2, 2)
print (B)
print ("---")
A_sub = A[1:3, 1:3].copy() # this copy make sure A_sub is a copy (not a view)
A_sub += B
print (A)
A = np.ones(2, 2) # this will give you an error. check it out
B = np.zeros((2, 2))
C = np.block([[A, B, B], [B, A, B]])
print (C)
D = np.hstack((A, B))
E = np.vstack((A, B))
print (D)
print (E)
```
နောက်ထပ် အသုံးများတဲ့ property တခုကတော့ `T` ပဲ။ transpose လုပ်တာ။
```
print (D.T)
print (E.T)
```
## vector/matrix calculations
`dot` function ဟာ matrix/vector တွေကို လွယ်ကူစွာ မြှောက်နိုင်စေတယ်။
```
x = np.array(
[
[1,2],
[3,4]
])
y = np.array(
[
[5,6],
[7,8]
])
v = np.array([9,10])
w = np.array([11, 12])
# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))
# Matrix / vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(x, v))
# Matrix / matrix product; both produce the rank 2 array
# [[19 22]
# [43 50]]
print(x.dot(y))
print(np.dot(x, y))
```
## Special Array indexing
`numpy` မှာ array တခုရဲ့ dimension တခုစီအတွက် list တခုနှုန်းနဲ့ (အဲဒီ list ထဲမှာ ကိုယ်လိုချင်တဲ့ element အရေအတွက်အတိုင်း ပါရ) index လုပ်တဲ့ special indexing method လဲ ရှိတယ်။
```
r = np.arange(35).reshape(5, 7)
print (r)
index_x0 = [3, 4, 4]
index_x1 = [6, 2, 3]
print (r[index_x0, index_x1])
```
### `numpy` special boolean ability and boolean indexing
```
r_index = r % 2 == 0
print (r_index)
```
အဲဒီလို boolean array (size တူရမယ်) ကို အသုံးပြုပြီး မူလ array ကနေ data retrieval လုပ်နိုင်တယ်။
```
r_selected = r[r_index]
print (r_selected)
```
| github_jupyter |
# Building your Deep Neural Network: Step by Step
Welcome to your week 4 assignment (part 1 of 2)! Previously you trained a 2-layer Neural Network with a single hidden layer. This week, you will build a deep neural network with as many layers as you want!
- In this notebook, you'll implement all the functions required to build a deep neural network.
- For the next assignment, you'll use these functions to build a deep neural network for image classification.
**By the end of this assignment, you'll be able to:**
- Use non-linear units like ReLU to improve your model
- Build a deeper neural network (with more than 1 hidden layer)
- Implement an easy-to-use neural network class
**Notation**:
- Superscript $[l]$ denotes a quantity associated with the $l^{th}$ layer.
- Example: $a^{[L]}$ is the $L^{th}$ layer activation. $W^{[L]}$ and $b^{[L]}$ are the $L^{th}$ layer parameters.
- Superscript $(i)$ denotes a quantity associated with the $i^{th}$ example.
- Example: $x^{(i)}$ is the $i^{th}$ training example.
- Lowerscript $i$ denotes the $i^{th}$ entry of a vector.
- Example: $a^{[l]}_i$ denotes the $i^{th}$ entry of the $l^{th}$ layer's activations).
Let's get started!
## Table of Contents
- [1 - Packages](#1)
- [2 - Outline](#2)
- [3 - Initialization](#3)
- [3.1 - 2-layer Neural Network](#3-1)
- [Exercise 1 - initialize_parameters](#ex-1)
- [3.2 - L-layer Neural Network](#3-2)
- [Exercise 2 - initialize_parameters_deep](#ex-2)
- [4 - Forward Propagation Module](#4)
- [4.1 - Linear Forward](#4-1)
- [Exercise 3 - linear_forward](#ex-3)
- [4.2 - Linear-Activation Forward](#4-2)
- [Exercise 4 - linear_activation_forward](#ex-4)
- [4.3 - L-Layer Model](#4-3)
- [Exercise 5 - L_model_forward](#ex-5)
- [5 - Cost Function](#5)
- [Exercise 6 - compute_cost](#ex-6)
- [6 - Backward Propagation Module](#6)
- [6.1 - Linear Backward](#6-1)
- [Exercise 7 - linear_backward](#ex-7)
- [6.2 - Linear-Activation Backward](#6-2)
- [Exercise 8 - linear_activation_backward](#ex-8)
- [6.3 - L-Model Backward](#6-3)
- [Exercise 9 - L_model_backward](#ex-9)
- [6.4 - Update Parameters](#6-4)
- [Exercise 10 - update_parameters](#ex-10)
<a name='1'></a>
## 1 - Packages
First, import all the packages you'll need during this assignment.
- [numpy](www.numpy.org) is the main package for scientific computing with Python.
- [matplotlib](http://matplotlib.org) is a library to plot graphs in Python.
- dnn_utils provides some necessary functions for this notebook.
- testCases provides some test cases to assess the correctness of your functions
- np.random.seed(1) is used to keep all the random function calls consistent. It helps grade your work. Please don't change the seed!
```
import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases import *
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
from public_tests import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2
np.random.seed(1)
```
<a name='2'></a>
## 2 - Outline
To build your neural network, you'll be implementing several "helper functions." These helper functions will be used in the next assignment to build a two-layer neural network and an L-layer neural network.
Each small helper function will have detailed instructions to walk you through the necessary steps. Here's an outline of the steps in this assignment:
- Initialize the parameters for a two-layer network and for an $L$-layer neural network
- Implement the forward propagation module (shown in purple in the figure below)
- Complete the LINEAR part of a layer's forward propagation step (resulting in $Z^{[l]}$).
- The ACTIVATION function is provided for you (relu/sigmoid)
- Combine the previous two steps into a new [LINEAR->ACTIVATION] forward function.
- Stack the [LINEAR->RELU] forward function L-1 time (for layers 1 through L-1) and add a [LINEAR->SIGMOID] at the end (for the final layer $L$). This gives you a new L_model_forward function.
- Compute the loss
- Implement the backward propagation module (denoted in red in the figure below)
- Complete the LINEAR part of a layer's backward propagation step
- The gradient of the ACTIVATE function is provided for you(relu_backward/sigmoid_backward)
- Combine the previous two steps into a new [LINEAR->ACTIVATION] backward function
- Stack [LINEAR->RELU] backward L-1 times and add [LINEAR->SIGMOID] backward in a new L_model_backward function
- Finally, update the parameters
<img src="images/final outline.png" style="width:800px;height:500px;">
<caption><center><b>Figure 1</b></center></caption><br>
**Note**:
For every forward function, there is a corresponding backward function. This is why at every step of your forward module you will be storing some values in a cache. These cached values are useful for computing gradients.
In the backpropagation module, you can then use the cache to calculate the gradients. Don't worry, this assignment will show you exactly how to carry out each of these steps!
<a name='3'></a>
## 3 - Initialization
You will write two helper functions to initialize the parameters for your model. The first function will be used to initialize parameters for a two layer model. The second one generalizes this initialization process to $L$ layers.
<a name='3-1'></a>
### 3.1 - 2-layer Neural Network
<a name='ex-1'></a>
### Exercise 1 - initialize_parameters
Create and initialize the parameters of the 2-layer neural network.
**Instructions**:
- The model's structure is: *LINEAR -> RELU -> LINEAR -> SIGMOID*.
- Use this random initialization for the weight matrices: `np.random.randn(shape)*0.01` with the correct shape
- Use zero initialization for the biases: `np.zeros(shape)`
```
# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
parameters -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(1)
#(≈ 4 lines of code)
# W1 = ...
# b1 = ...
# W2 = ...
# b2 = ...
# YOUR CODE STARTS HERE
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros([n_h,1])
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros([n_y,1])
# YOUR CODE ENDS HERE
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
parameters = initialize_parameters(3,2,1)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
initialize_parameters_test(initialize_parameters)
```
***Expected output***
```
W1 = [[ 0.01624345 -0.00611756 -0.00528172]
[-0.01072969 0.00865408 -0.02301539]]
b1 = [[0.]
[0.]]
W2 = [[ 0.01744812 -0.00761207]]
b2 = [[0.]]
```
<a name='3-2'></a>
### 3.2 - L-layer Neural Network
The initialization for a deeper L-layer neural network is more complicated because there are many more weight matrices and bias vectors. When completing the `initialize_parameters_deep` function, you should make sure that your dimensions match between each layer. Recall that $n^{[l]}$ is the number of units in layer $l$. For example, if the size of your input $X$ is $(12288, 209)$ (with $m=209$ examples) then:
<table style="width:100%">
<tr>
<td> </td>
<td> <b>Shape of W</b> </td>
<td> <b>Shape of b</b> </td>
<td> <b>Activation</b> </td>
<td> <b>Shape of Activation</b> </td>
<tr>
<tr>
<td> <b>Layer 1</b> </td>
<td> $(n^{[1]},12288)$ </td>
<td> $(n^{[1]},1)$ </td>
<td> $Z^{[1]} = W^{[1]} X + b^{[1]} $ </td>
<td> $(n^{[1]},209)$ </td>
<tr>
<tr>
<td> <b>Layer 2</b> </td>
<td> $(n^{[2]}, n^{[1]})$ </td>
<td> $(n^{[2]},1)$ </td>
<td>$Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]}$ </td>
<td> $(n^{[2]}, 209)$ </td>
<tr>
<tr>
<td> $\vdots$ </td>
<td> $\vdots$ </td>
<td> $\vdots$ </td>
<td> $\vdots$</td>
<td> $\vdots$ </td>
<tr>
<tr>
<td> <b>Layer L-1</b> </td>
<td> $(n^{[L-1]}, n^{[L-2]})$ </td>
<td> $(n^{[L-1]}, 1)$ </td>
<td>$Z^{[L-1]} = W^{[L-1]} A^{[L-2]} + b^{[L-1]}$ </td>
<td> $(n^{[L-1]}, 209)$ </td>
<tr>
<tr>
<td> <b>Layer L</b> </td>
<td> $(n^{[L]}, n^{[L-1]})$ </td>
<td> $(n^{[L]}, 1)$ </td>
<td> $Z^{[L]} = W^{[L]} A^{[L-1]} + b^{[L]}$</td>
<td> $(n^{[L]}, 209)$ </td>
<tr>
</table>
Remember that when you compute $W X + b$ in python, it carries out broadcasting. For example, if:
$$ W = \begin{bmatrix}
w_{00} & w_{01} & w_{02} \\
w_{10} & w_{11} & w_{12} \\
w_{20} & w_{21} & w_{22}
\end{bmatrix}\;\;\; X = \begin{bmatrix}
x_{00} & x_{01} & x_{02} \\
x_{10} & x_{11} & x_{12} \\
x_{20} & x_{21} & x_{22}
\end{bmatrix} \;\;\; b =\begin{bmatrix}
b_0 \\
b_1 \\
b_2
\end{bmatrix}\tag{2}$$
Then $WX + b$ will be:
$$ WX + b = \begin{bmatrix}
(w_{00}x_{00} + w_{01}x_{10} + w_{02}x_{20}) + b_0 & (w_{00}x_{01} + w_{01}x_{11} + w_{02}x_{21}) + b_0 & \cdots \\
(w_{10}x_{00} + w_{11}x_{10} + w_{12}x_{20}) + b_1 & (w_{10}x_{01} + w_{11}x_{11} + w_{12}x_{21}) + b_1 & \cdots \\
(w_{20}x_{00} + w_{21}x_{10} + w_{22}x_{20}) + b_2 & (w_{20}x_{01} + w_{21}x_{11} + w_{22}x_{21}) + b_2 & \cdots
\end{bmatrix}\tag{3} $$
<a name='ex-2'></a>
### Exercise 2 - initialize_parameters_deep
Implement initialization for an L-layer Neural Network.
**Instructions**:
- The model's structure is *[LINEAR -> RELU] $ \times$ (L-1) -> LINEAR -> SIGMOID*. I.e., it has $L-1$ layers using a ReLU activation function followed by an output layer with a sigmoid activation function.
- Use random initialization for the weight matrices. Use `np.random.randn(shape) * 0.01`.
- Use zeros initialization for the biases. Use `np.zeros(shape)`.
- You'll store $n^{[l]}$, the number of units in different layers, in a variable `layer_dims`. For example, the `layer_dims` for last week's Planar Data classification model would have been [2,4,1]: There were two inputs, one hidden layer with 4 hidden units, and an output layer with 1 output unit. This means `W1`'s shape was (4,2), `b1` was (4,1), `W2` was (1,4) and `b2` was (1,1). Now you will generalize this to $L$ layers!
- Here is the implementation for $L=1$ (one layer neural network). It should inspire you to implement the general case (L-layer neural network).
```python
if L == 1:
parameters["W" + str(L)] = np.random.randn(layer_dims[1], layer_dims[0]) * 0.01
parameters["b" + str(L)] = np.zeros((layer_dims[1], 1))
```
```
# GRADED FUNCTION: initialize_parameters_deep
def initialize_parameters_deep(layer_dims):
"""
Arguments:
layer_dims -- python array (list) containing the dimensions of each layer in our network
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
bl -- bias vector of shape (layer_dims[l], 1)
"""
np.random.seed(3)
parameters = {}
l = len(layer_dims) # number of layers in the network
for l in range(1, l):
#(≈ 2 lines of code)
# parameters['W' + str(l)] = ...
# parameters['b' + str(l)] = ...
# YOUR CODE STARTS HERE
parameters["W" + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])* 0.01
parameters["b" + str(l)] = np.zeros((layer_dims[l], 1))
# YOUR CODE ENDS HERE
assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters
parameters = initialize_parameters_deep([5,4,3])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
initialize_parameters_deep_test(initialize_parameters_deep)
```
***Expected output***
```
W1 = [[ 0.01788628 0.0043651 0.00096497 -0.01863493 -0.00277388]
[-0.00354759 -0.00082741 -0.00627001 -0.00043818 -0.00477218]
[-0.01313865 0.00884622 0.00881318 0.01709573 0.00050034]
[-0.00404677 -0.0054536 -0.01546477 0.00982367 -0.01101068]]
b1 = [[0.]
[0.]
[0.]
[0.]]
W2 = [[-0.01185047 -0.0020565 0.01486148 0.00236716]
[-0.01023785 -0.00712993 0.00625245 -0.00160513]
[-0.00768836 -0.00230031 0.00745056 0.01976111]]
b2 = [[0.]
[0.]
[0.]]
```
<a name='4'></a>
## 4 - Forward Propagation Module
<a name='4-1'></a>
### 4.1 - Linear Forward
Now that you have initialized your parameters, you can do the forward propagation module. Start by implementing some basic functions that you can use again later when implementing the model. Now, you'll complete three functions in this order:
- LINEAR
- LINEAR -> ACTIVATION where ACTIVATION will be either ReLU or Sigmoid.
- [LINEAR -> RELU] $\times$ (L-1) -> LINEAR -> SIGMOID (whole model)
The linear forward module (vectorized over all the examples) computes the following equations:
$$Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}\tag{4}$$
where $A^{[0]} = X$.
<a name='ex-3'></a>
### Exercise 3 - linear_forward
Build the linear part of forward propagation.
**Reminder**:
The mathematical representation of this unit is $Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}$. You may also find `np.dot()` useful. If your dimensions don't match, printing `W.shape` may help.
```
# GRADED FUNCTION: linear_forward
def linear_forward(A, W, b):
"""
Implement the linear part of a layer's forward propagation.
Arguments:
A -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
Returns:
Z -- the input of the activation function, also called pre-activation parameter
cache -- a python tuple containing "A", "W" and "b" ; stored for computing the backward pass efficiently
"""
#(≈ 1 line of code)
# Z = ...
# YOUR CODE STARTS HERE
Z = np.dot(W,A)+ b
# YOUR CODE ENDS HERE
cache = (A, W, b)
return Z, cache
t_A, t_W, t_b = linear_forward_test_case()
t_Z, t_linear_cache = linear_forward(t_A, t_W, t_b)
print("Z = " + str(t_Z))
linear_forward_test(linear_forward)
```
***Expected output***
```
Z = [[ 3.26295337 -1.23429987]]
```
<a name='4-2'></a>
### 4.2 - Linear-Activation Forward
In this notebook, you will use two activation functions:
- **Sigmoid**: $\sigma(Z) = \sigma(W A + b) = \frac{1}{ 1 + e^{-(W A + b)}}$. You've been provided with the `sigmoid` function which returns **two** items: the activation value "`a`" and a "`cache`" that contains "`Z`" (it's what we will feed in to the corresponding backward function). To use it you could just call:
``` python
A, activation_cache = sigmoid(Z)
```
- **ReLU**: The mathematical formula for ReLu is $A = RELU(Z) = max(0, Z)$. You've been provided with the `relu` function. This function returns **two** items: the activation value "`A`" and a "`cache`" that contains "`Z`" (it's what you'll feed in to the corresponding backward function). To use it you could just call:
``` python
A, activation_cache = relu(Z)
```
For added convenience, you're going to group two functions (Linear and Activation) into one function (LINEAR->ACTIVATION). Hence, you'll implement a function that does the LINEAR forward step, followed by an ACTIVATION forward step.
<a name='ex-4'></a>
### Exercise 4 - linear_activation_forward
Implement the forward propagation of the *LINEAR->ACTIVATION* layer. Mathematical relation is: $A^{[l]} = g(Z^{[l]}) = g(W^{[l]}A^{[l-1]} +b^{[l]})$ where the activation "g" can be sigmoid() or relu(). Use `linear_forward()` and the correct activation function.
```
# GRADED FUNCTION: linear_activation_forward
def linear_activation_forward(A_prev, W, b, activation):
"""
Implement the forward propagation for the LINEAR->ACTIVATION layer
Arguments:
A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
A -- the output of the activation function, also called the post-activation value
cache -- a python tuple containing "linear_cache" and "activation_cache";
stored for computing the backward pass efficiently
"""
if activation == "sigmoid":
#(≈ 2 lines of code)
# Z, linear_cache = ...
# A, activation_cache = ...
# YOUR CODE STARTS HERE
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
# YOUR CODE ENDS HERE
elif activation == "relu":
#(≈ 2 lines of code)
# Z, linear_cache = ...
# A, activation_cache = ...
# YOUR CODE STARTS HERE
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = relu(Z)
# YOUR CODE ENDS HERE
cache = (linear_cache, activation_cache)
return A, cache
t_A_prev, t_W, t_b = linear_activation_forward_test_case()
t_A, t_linear_activation_cache = linear_activation_forward(t_A_prev, t_W, t_b, activation = "sigmoid")
print("With sigmoid: A = " + str(t_A))
t_A, t_linear_activation_cache = linear_activation_forward(t_A_prev, t_W, t_b, activation = "relu")
print("With ReLU: A = " + str(t_A))
linear_activation_forward_test(linear_activation_forward)
```
***Expected output***
```
With sigmoid: A = [[0.96890023 0.11013289]]
With ReLU: A = [[3.43896131 0. ]]
```
**Note**: In deep learning, the "[LINEAR->ACTIVATION]" computation is counted as a single layer in the neural network, not two layers.
<a name='4-3'></a>
### 4.3 - L-Layer Model
For even *more* convenience when implementing the $L$-layer Neural Net, you will need a function that replicates the previous one (`linear_activation_forward` with RELU) $L-1$ times, then follows that with one `linear_activation_forward` with SIGMOID.
<img src="images/model_architecture_kiank.png" style="width:600px;height:300px;">
<caption><center> <b>Figure 2</b> : *[LINEAR -> RELU] $\times$ (L-1) -> LINEAR -> SIGMOID* model</center></caption><br>
<a name='ex-5'></a>
### Exercise 5 - L_model_forward
Implement the forward propagation of the above model.
**Instructions**: In the code below, the variable `AL` will denote $A^{[L]} = \sigma(Z^{[L]}) = \sigma(W^{[L]} A^{[L-1]} + b^{[L]})$. (This is sometimes also called `Yhat`, i.e., this is $\hat{Y}$.)
**Hints**:
- Use the functions you've previously written
- Use a for loop to replicate [LINEAR->RELU] (L-1) times
- Don't forget to keep track of the caches in the "caches" list. To add a new value `c` to a `list`, you can use `list.append(c)`.
```
# GRADED FUNCTION: L_model_forward
def L_model_forward(X, parameters):
"""
Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
Arguments:
X -- data, numpy array of shape (input size, number of examples)
parameters -- output of initialize_parameters_deep()
Returns:
AL -- activation value from the output (last) layer
caches -- list of caches containing:
every cache of linear_activation_forward() (there are L of them, indexed from 0 to L-1)
"""
caches = []
A = X
L = len(parameters) // 2 # number of layers in the neural network
# Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
# The for loop starts at 1 because layer 0 is the input
for l in range(1, L):
A_prev = A
#(≈ 2 lines of code)
# A, cache = ...
# caches ...
# YOUR CODE STARTS HERE
A, cache = linear_activation_forward(A, parameters['W' + str(l)], parameters['b' + str(l)], "relu")
caches.append(cache)
# YOUR CODE ENDS HERE
# Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
#(≈ 2 lines of code)
# AL, cache = ...
# caches ...
# YOUR CODE STARTS HERE
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
caches.append(cache)
# YOUR CODE ENDS HERE
return AL, caches
t_X, t_parameters = L_model_forward_test_case_2hidden()
t_AL, t_caches = L_model_forward(t_X, t_parameters)
print("AL = " + str(t_AL))
L_model_forward_test(L_model_forward)
```
***Expected output***
```
AL = [[0.03921668 0.70498921 0.19734387 0.04728177]]
```
**Awesome!** You've implemented a full forward propagation that takes the input X and outputs a row vector $A^{[L]}$ containing your predictions. It also records all intermediate values in "caches". Using $A^{[L]}$, you can compute the cost of your predictions.
<a name='5'></a>
## 5 - Cost Function
Now you can implement forward and backward propagation! You need to compute the cost, in order to check whether your model is actually learning.
<a name='ex-6'></a>
### Exercise 6 - compute_cost
Compute the cross-entropy cost $J$, using the following formula: $$-\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right)) \tag{7}$$
```
# GRADED FUNCTION: compute_cost
def compute_cost(AL, Y):
"""
Implement the cost function defined by equation (7).
Arguments:
AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)
Returns:
cost -- cross-entropy cost
"""
m = Y.shape[1]
# Compute loss from aL and y.
# (≈ 1 lines of code)
# cost = ...
# YOUR CODE STARTS HERE
cost = (-1/m)*(np.dot(Y,np.log(AL).T)+np.dot(1-Y,np.log(1-AL).T))
# YOUR CODE ENDS HERE
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
return cost
t_Y, t_AL = compute_cost_test_case()
t_cost = compute_cost(t_AL, t_Y)
print("Cost: " + str(t_cost))
compute_cost_test(compute_cost)
```
**Expected Output**:
<table>
<tr>
<td><b>cost</b> </td>
<td> 0.2797765635793422</td>
</tr>
</table>
<a name='6'></a>
## 6 - Backward Propagation Module
Just as you did for the forward propagation, you'll implement helper functions for backpropagation. Remember that backpropagation is used to calculate the gradient of the loss function with respect to the parameters.
**Reminder**:
<img src="images/backprop_kiank.png" style="width:650px;height:250px;">
<caption><center><font color='purple'><b>Figure 3</b>: Forward and Backward propagation for LINEAR->RELU->LINEAR->SIGMOID <br> <i>The purple blocks represent the forward propagation, and the red blocks represent the backward propagation.</font></center></caption>
<!--
For those of you who are experts in calculus (which you don't need to be to do this assignment!), the chain rule of calculus can be used to derive the derivative of the loss $\mathcal{L}$ with respect to $z^{[1]}$ in a 2-layer network as follows:
$$\frac{d \mathcal{L}(a^{[2]},y)}{{dz^{[1]}}} = \frac{d\mathcal{L}(a^{[2]},y)}{{da^{[2]}}}\frac{{da^{[2]}}}{{dz^{[2]}}}\frac{{dz^{[2]}}}{{da^{[1]}}}\frac{{da^{[1]}}}{{dz^{[1]}}} \tag{8} $$
In order to calculate the gradient $dW^{[1]} = \frac{\partial L}{\partial W^{[1]}}$, use the previous chain rule and you do $dW^{[1]} = dz^{[1]} \times \frac{\partial z^{[1]} }{\partial W^{[1]}}$. During backpropagation, at each step you multiply your current gradient by the gradient corresponding to the specific layer to get the gradient you wanted.
Equivalently, in order to calculate the gradient $db^{[1]} = \frac{\partial L}{\partial b^{[1]}}$, you use the previous chain rule and you do $db^{[1]} = dz^{[1]} \times \frac{\partial z^{[1]} }{\partial b^{[1]}}$.
This is why we talk about **backpropagation**.
!-->
Now, similarly to forward propagation, you're going to build the backward propagation in three steps:
1. LINEAR backward
2. LINEAR -> ACTIVATION backward where ACTIVATION computes the derivative of either the ReLU or sigmoid activation
3. [LINEAR -> RELU] $\times$ (L-1) -> LINEAR -> SIGMOID backward (whole model)
For the next exercise, you will need to remember that:
- `b` is a matrix(np.ndarray) with 1 column and n rows, i.e: b = [[1.0], [2.0]] (remember that `b` is a constant)
- np.sum performs a sum over the elements of a ndarray
- axis=1 or axis=0 specify if the sum is carried out by rows or by columns respectively
- keepdims specifies if the original dimensions of the matrix must be kept.
- Look at the following example to clarify:
```
A = np.array([[1, 2], [3, 4]])
print('axis=1 and keepdims=True')
print(np.sum(A, axis=1, keepdims=True))
print('axis=1 and keepdims=False')
print(np.sum(A, axis=1, keepdims=False))
print('axis=0 and keepdims=True')
print(np.sum(A, axis=0, keepdims=True))
print('axis=0 and keepdims=False')
print(np.sum(A, axis=0, keepdims=False))
```
<a name='6-1'></a>
### 6.1 - Linear Backward
For layer $l$, the linear part is: $Z^{[l]} = W^{[l]} A^{[l-1]} + b^{[l]}$ (followed by an activation).
Suppose you have already calculated the derivative $dZ^{[l]} = \frac{\partial \mathcal{L} }{\partial Z^{[l]}}$. You want to get $(dW^{[l]}, db^{[l]}, dA^{[l-1]})$.
<img src="images/linearback_kiank.png" style="width:250px;height:300px;">
<caption><center><font color='purple'><b>Figure 4</b></font></center></caption>
The three outputs $(dW^{[l]}, db^{[l]}, dA^{[l-1]})$ are computed using the input $dZ^{[l]}$.
Here are the formulas you need:
$$ dW^{[l]} = \frac{\partial \mathcal{J} }{\partial W^{[l]}} = \frac{1}{m} dZ^{[l]} A^{[l-1] T} \tag{8}$$
$$ db^{[l]} = \frac{\partial \mathcal{J} }{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}\tag{9}$$
$$ dA^{[l-1]} = \frac{\partial \mathcal{L} }{\partial A^{[l-1]}} = W^{[l] T} dZ^{[l]} \tag{10}$$
$A^{[l-1] T}$ is the transpose of $A^{[l-1]}$.
<a name='ex-7'></a>
### Exercise 7 - linear_backward
Use the 3 formulas above to implement `linear_backward()`.
**Hint**:
- In numpy you can get the transpose of an ndarray `A` using `A.T` or `A.transpose()`
```
# GRADED FUNCTION: linear_backward
def linear_backward(dZ, cache):
"""
Implement the linear portion of backward propagation for a single layer (layer l)
Arguments:
dZ -- Gradient of the cost with respect to the linear output (of current layer l)
cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
A_prev, W, b = cache
m = A_prev.shape[1]
### START CODE HERE ### (≈ 3 lines of code)
# dW = ...
# db = ... sum by the rows of dZ with keepdims=True
# dA_prev = ...
# YOUR CODE STARTS HERE
dW = (1/m)*(np.dot(dZ,A_prev.T))
db = (1/m)*(np.sum(dZ,axis=1,keepdims=True))
dA_prev = np.dot(W.T,dZ)
# YOUR CODE ENDS HERE
return dA_prev, dW, db
t_dZ, t_linear_cache = linear_backward_test_case()
t_dA_prev, t_dW, t_db = linear_backward(t_dZ, t_linear_cache)
print("dA_prev: " + str(t_dA_prev))
print("dW: " + str(t_dW))
print("db: " + str(t_db))
linear_backward_test(linear_backward)
```
**Expected Output**:
```
dA_prev: [[-1.15171336 0.06718465 -0.3204696 2.09812712]
[ 0.60345879 -3.72508701 5.81700741 -3.84326836]
[-0.4319552 -1.30987417 1.72354705 0.05070578]
[-0.38981415 0.60811244 -1.25938424 1.47191593]
[-2.52214926 2.67882552 -0.67947465 1.48119548]]
dW: [[ 0.07313866 -0.0976715 -0.87585828 0.73763362 0.00785716]
[ 0.85508818 0.37530413 -0.59912655 0.71278189 -0.58931808]
[ 0.97913304 -0.24376494 -0.08839671 0.55151192 -0.10290907]]
db: [[-0.14713786]
[-0.11313155]
[-0.13209101]]
```
<a name='6-2'></a>
### 6.2 - Linear-Activation Backward
Next, you will create a function that merges the two helper functions: **`linear_backward`** and the backward step for the activation **`linear_activation_backward`**.
To help you implement `linear_activation_backward`, two backward functions have been provided:
- **`sigmoid_backward`**: Implements the backward propagation for SIGMOID unit. You can call it as follows:
```python
dZ = sigmoid_backward(dA, activation_cache)
```
- **`relu_backward`**: Implements the backward propagation for RELU unit. You can call it as follows:
```python
dZ = relu_backward(dA, activation_cache)
```
If $g(.)$ is the activation function,
`sigmoid_backward` and `relu_backward` compute $$dZ^{[l]} = dA^{[l]} * g'(Z^{[l]}). \tag{11}$$
<a name='ex-8'></a>
### Exercise 8 - linear_activation_backward
Implement the backpropagation for the *LINEAR->ACTIVATION* layer.
```
# GRADED FUNCTION: linear_activation_backward
def linear_activation_backward(dA, cache, activation):
"""
Implement the backward propagation for the LINEAR->ACTIVATION layer.
Arguments:
dA -- post-activation gradient for current layer l
cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
linear_cache, activation_cache = cache
if activation == "relu":
#(≈ 2 lines of code)
# dZ = ...
# dA_prev, dW, db = ...
# YOUR CODE STARTS HERE
dZ = relu_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
# YOUR CODE ENDS HERE
elif activation == "sigmoid":
#(≈ 2 lines of code)
# dZ = ...
# dA_prev, dW, db = ...
# YOUR CODE STARTS HERE
dZ = sigmoid_backward(dA, activation_cache)
dA_prev, dW, db = linear_backward(dZ, linear_cache)
# YOUR CODE ENDS HERE
return dA_prev, dW, db
t_dAL, t_linear_activation_cache = linear_activation_backward_test_case()
t_dA_prev, t_dW, t_db = linear_activation_backward(t_dAL, t_linear_activation_cache, activation = "sigmoid")
print("With sigmoid: dA_prev = " + str(t_dA_prev))
print("With sigmoid: dW = " + str(t_dW))
print("With sigmoid: db = " + str(t_db))
t_dA_prev, t_dW, t_db = linear_activation_backward(t_dAL, t_linear_activation_cache, activation = "relu")
print("With relu: dA_prev = " + str(t_dA_prev))
print("With relu: dW = " + str(t_dW))
print("With relu: db = " + str(t_db))
linear_activation_backward_test(linear_activation_backward)
```
**Expected output:**
```
With sigmoid: dA_prev = [[ 0.11017994 0.01105339]
[ 0.09466817 0.00949723]
[-0.05743092 -0.00576154]]
With sigmoid: dW = [[ 0.10266786 0.09778551 -0.01968084]]
With sigmoid: db = [[-0.05729622]]
With relu: dA_prev = [[ 0.44090989 0. ]
[ 0.37883606 0. ]
[-0.2298228 0. ]]
With relu: dW = [[ 0.44513824 0.37371418 -0.10478989]]
With relu: db = [[-0.20837892]]
```
<a name='6-3'></a>
### 6.3 - L-Model Backward
Now you will implement the backward function for the whole network!
Recall that when you implemented the `L_model_forward` function, at each iteration, you stored a cache which contains (X,W,b, and z). In the back propagation module, you'll use those variables to compute the gradients. Therefore, in the `L_model_backward` function, you'll iterate through all the hidden layers backward, starting from layer $L$. On each step, you will use the cached values for layer $l$ to backpropagate through layer $l$. Figure 5 below shows the backward pass.
<img src="images/mn_backward.png" style="width:450px;height:300px;">
<caption><center><font color='purple'><b>Figure 5</b>: Backward pass</font></center></caption>
**Initializing backpropagation**:
To backpropagate through this network, you know that the output is:
$A^{[L]} = \sigma(Z^{[L]})$. Your code thus needs to compute `dAL` $= \frac{\partial \mathcal{L}}{\partial A^{[L]}}$.
To do so, use this formula (derived using calculus which, again, you don't need in-depth knowledge of!):
```python
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL)) # derivative of cost with respect to AL
```
You can then use this post-activation gradient `dAL` to keep going backward. As seen in Figure 5, you can now feed in `dAL` into the LINEAR->SIGMOID backward function you implemented (which will use the cached values stored by the L_model_forward function).
After that, you will have to use a `for` loop to iterate through all the other layers using the LINEAR->RELU backward function. You should store each dA, dW, and db in the grads dictionary. To do so, use this formula :
$$grads["dW" + str(l)] = dW^{[l]}\tag{15} $$
For example, for $l=3$ this would store $dW^{[l]}$ in `grads["dW3"]`.
<a name='ex-9'></a>
### Exercise 9 - L_model_backward
Implement backpropagation for the *[LINEAR->RELU] $\times$ (L-1) -> LINEAR -> SIGMOID* model.
```
# GRADED FUNCTION: L_model_backward
def L_model_backward(AL, Y, caches):
"""
Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
Arguments:
AL -- probability vector, output of the forward propagation (L_model_forward())
Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
caches -- list of caches containing:
every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2)
the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1])
Returns:
grads -- A dictionary with the gradients
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
#(1 line of code)
# dAL = ...
# YOUR CODE STARTS HERE
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
# YOUR CODE ENDS HERE
# Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "dAL, current_cache". Outputs: "grads["dAL-1"], grads["dWL"], grads["dbL"]
#(approx. 5 lines)
# current_cache = ...
# dA_prev_temp, dW_temp, db_temp = ...
# grads["dA" + str(L-1)] = ...
# grads["dW" + str(L)] = ...
# grads["db" + str(L)] = ...
# YOUR CODE STARTS HERE
current_cache = caches[1]
grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache,'sigmoid')
# YOUR CODE ENDS HERE
# Loop from l=L-2 to l=0
for l in reversed(range(L-1)):
# lth layer: (RELU -> LINEAR) gradients.
# Inputs: "grads["dA" + str(l + 1)], current_cache". Outputs: "grads["dA" + str(l)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)]
#(approx. 5 lines)
# current_cache = ...
# dA_prev_temp, dW_temp, db_temp = ...
# grads["dA" + str(l)] = ...
# grads["dW" + str(l + 1)] = ...
# grads["db" + str(l + 1)] = ...
# YOUR CODE STARTS HERE
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 1)], current_cache, 'relu')
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
# YOUR CODE ENDS HERE
return grads
t_AL, t_Y_assess, t_caches = L_model_backward_test_case()
grads = L_model_backward(t_AL, t_Y_assess, t_caches)
print("dA0 = " + str(grads['dA0']))
print("dA1 = " + str(grads['dA1']))
print("dW1 = " + str(grads['dW1']))
print("dW2 = " + str(grads['dW2']))
print("db1 = " + str(grads['db1']))
print("db2 = " + str(grads['db2']))
L_model_backward_test(L_model_backward)
```
**Expected output:**
```
dA0 = [[ 0. 0.52257901]
[ 0. -0.3269206 ]
[ 0. -0.32070404]
[ 0. -0.74079187]]
dA1 = [[ 0.12913162 -0.44014127]
[-0.14175655 0.48317296]
[ 0.01663708 -0.05670698]]
dW1 = [[0.41010002 0.07807203 0.13798444 0.10502167]
[0. 0. 0. 0. ]
[0.05283652 0.01005865 0.01777766 0.0135308 ]]
dW2 = [[-0.39202432 -0.13325855 -0.04601089]]
db1 = [[-0.22007063]
[ 0. ]
[-0.02835349]]
db2 = [[0.15187861]]
```
<a name='6-4'></a>
### 6.4 - Update Parameters
In this section, you'll update the parameters of the model, using gradient descent:
$$ W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]} \tag{16}$$
$$ b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]} \tag{17}$$
where $\alpha$ is the learning rate.
After computing the updated parameters, store them in the parameters dictionary.
<a name='ex-10'></a>
### Exercise 10 - update_parameters
Implement `update_parameters()` to update your parameters using gradient descent.
**Instructions**:
Update parameters using gradient descent on every $W^{[l]}$ and $b^{[l]}$ for $l = 1, 2, ..., L$.
```
# GRADED FUNCTION: update_parameters
def update_parameters(params, grads, learning_rate):
"""
Update parameters using gradient descent
Arguments:
params -- python dictionary containing your parameters
grads -- python dictionary containing your gradients, output of L_model_backward
Returns:
parameters -- python dictionary containing your updated parameters
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
parameters = params.copy()
L = len(parameters) // 2 # number of layers in the neural network
# Update rule for each parameter. Use a for loop.
#(≈ 2 lines of code)
for l in range(L):
# parameters["W" + str(l+1)] = ...
# parameters["b" + str(l+1)] = ...
# YOUR CODE STARTS HERE
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
# YOUR CODE ENDS HERE
return parameters
t_parameters, grads = update_parameters_test_case()
t_parameters = update_parameters(t_parameters, grads, 0.1)
print ("W1 = "+ str(t_parameters["W1"]))
print ("b1 = "+ str(t_parameters["b1"]))
print ("W2 = "+ str(t_parameters["W2"]))
print ("b2 = "+ str(t_parameters["b2"]))
update_parameters_test(update_parameters)
```
**Expected output:**
```
W1 = [[-0.59562069 -0.09991781 -2.14584584 1.82662008]
[-1.76569676 -0.80627147 0.51115557 -1.18258802]
[-1.0535704 -0.86128581 0.68284052 2.20374577]]
b1 = [[-0.04659241]
[-1.28888275]
[ 0.53405496]]
W2 = [[-0.55569196 0.0354055 1.32964895]]
b2 = [[-0.84610769]]
```
### Congratulations!
You've just implemented all the functions required for building a deep neural network, including:
- Using non-linear units improve your model
- Building a deeper neural network (with more than 1 hidden layer)
- Implementing an easy-to-use neural network class
This was indeed a long assignment, but the next part of the assignment is easier. ;)
In the next assignment, you'll be putting all these together to build two models:
- A two-layer neural network
- An L-layer neural network
You will in fact use these models to classify cat vs non-cat images! (Meow!) Great work and see you next time.
| github_jupyter |
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
from sklearn.feature_extraction import DictVectorizer
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# You can write up to 20GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
```
**Load training data**
```
train_df = pd.read_csv("/kaggle/input/house-prices-advanced-regression-techniques/train.csv")
```
**Remove categorical features, handle missing data, cast improper types**
```
train_df['MSSubClass'] = train_df['MSSubClass'].apply(str)
train_df['MoSold'] = train_df['MoSold'].astype(str)
train_df['YrSold'] = train_df['YrSold'].astype(str)
cat_features = train_df.select_dtypes(include = 'object').columns
train_df.drop(cat_features, axis=1, inplace=True)
for c in train_df.columns:
train_df[c].fillna(train_df[c].median(), inplace=True)
```
**Split the data into X(test/train) and Y(test/train) datasets**
```
y = train_df['SalePrice']
x = train_df.loc[:, train_df.columns != 'SalePrice']
X_dict = x.to_dict(orient='records')
dv_X = DictVectorizer(sparse=False)
X_encoded = dv_X.fit_transform(X_dict)
X_Train, X_Test, Y_Train, Y_Test = train_test_split(X_encoded, y.to_numpy(), test_size=0.33, random_state=42)
```
**Train a Linear Regression Model**
```
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(X_Train, Y_Train)
```
**Predict from the testing set**
```
# Make predictions using the testing set
preds = regr.predict(X_Test)
```
**Score the model**
```
regr.score(X_Test, Y_Test)
```
| github_jupyter |
```
import pandas as pd
import datetime
from finquant.portfolio import build_portfolio
from finquant.moving_average import compute_ma, ema
from finquant.moving_average import plot_bollinger_band
from finquant.efficient_frontier import EfficientFrontier
### DOES OUR OPTIMIZATION ACTUALLY WORK?
# COMPARING AN OPTIMIZED PORTFOLIO WITH OTHER 2: THE FIRST WITH THE SAME AMOUNT OF ALL CURRENCIES AND ONE WITH ETH ONLY
# TIME-FRAME: WINTER 2021 IN WHICH ALL CURRENCIES WERE WERE GOING UP
# NO STABLECOINS
L = ['ETH', 'BTC', 'USDT', 'USDC','ENJ', 'MANA']
names = ['ETH-USD', 'BTC-USD', 'ENJ-USD', 'MANA-USD']
start_date = '2021-01-01'
end_date = '2021-03-01' #datetime.date.today()
pf = build_portfolio(names=names, data_api="yfinance", start_date=start_date,end_date=end_date)
pf.data=pf.data.fillna('nan')
for i in range(pf.data.shape[0]):
for k in range(pf.data.shape[1]):
if pf.data.iloc[i,k]=='nan':
pf.data.iloc[i,k]=pf.data.iloc[i-1,k]
pf.data.head()
pf.properties()
ef=EfficientFrontier(pf.comp_mean_returns(freq=30), pf.comp_cov(), risk_free_rate=0.0232)
max_sr=ef.maximum_sharpe_ratio().reset_index().rename({"index":"Crypto"},axis=1)
data = {i : {'Name':max_sr.iloc[i,0], "Allocation":max_sr.iloc[i,1]}for i in range(max_sr.shape[0])}
alloc=[max_sr.iloc[i,1] for i in range(max_sr.shape[0])]
data
pf_allocation = pd.DataFrame.from_dict(data, orient="index")
names=pf_allocation["Name"].values.tolist()
pf_opt = build_portfolio(names=names,pf_allocation=pf_allocation, start_date=start_date ,end_date=end_date,data_api="yfinance")
pf_opt.properties()
# OUR OPTIMIZATION EXPECTS A RETURN OF 578%
start_date = '2021-03-01'
end_date = '2021-04-01'
pf_real = build_portfolio(names=names, data_api="yfinance", start_date=start_date,end_date=end_date)
pf_real.data=pf_real.data.fillna('nan')
for i in range(pf_real.data.shape[0]):
for k in range(pf_real.data.shape[1]):
if pf_real.data.iloc[i,k]=='nan':
pf_real.data.iloc[i,k]=pf_real.data.iloc[i-1,k]
ds=pf_real.data
ds
returns = {i : {'Name':ds.columns[i], "Returns":(ds.iloc[-1,i]-ds.iloc[0,i])/ds.iloc[0,i]}for i in range(ds.shape[1])}
r=[(ds.iloc[-1,i]-ds.iloc[0,i])/ds.iloc[0,i] for i in range(ds.shape[1])]
returns,r
DATA = pd.DataFrame(names, columns=['Crypto'])
DATA["p_1"]=alloc
DATA["p_2"]=0.2
DATA["p_3"]=0
DATA.iloc[0,3]=1
DATA["Returns"]=r
DATA
p_1_returns = 0
p_2_returns = 0
p_3_returns = 0
for i in range(DATA.shape[0]):
p_1_returns+=DATA.iloc[i,1]*DATA.iloc[i,4]
p_2_returns+=DATA.iloc[i,2]*DATA.iloc[i,4]
p_3_returns+=DATA.iloc[i,3]*DATA.iloc[i,4]
p_1_returns,p_2_returns,p_3_returns
# AS WE CAN SEE, OUR PORTFOLIO PERFORMED MUCH BETTER, WITH 240% ACTUAL RETURN RATE
# TIME_FRAME: SUMMER 2021, WHEN CRYPTOS WERE GOING DOWN
# WITH STABLECOINS
L = ['ETH', 'BTC', 'USDT', 'USDC','ENJ', 'MANA']
names = ['ETH-USD', 'BTC-USD', 'ENJ-USD', 'MANA-USD', 'USDC-USD','USDT-USD']
start_date = '2021-06-01'
end_date = '2021-09-01' #datetime.date.today()
pf = build_portfolio(names=names, data_api="yfinance", start_date=start_date,end_date=end_date)
pf.data=pf.data.fillna('nan')
for i in range(pf.data.shape[0]):
for k in range(pf.data.shape[1]):
if pf.data.iloc[i,k]=='nan':
pf.data.iloc[i,k]=pf.data.iloc[i-1,k]
pf.data.head()
ef=EfficientFrontier(pf.comp_mean_returns(freq=30), pf.comp_cov(), risk_free_rate=0.0232)
max_sr=ef.maximum_sharpe_ratio().reset_index().rename({"index":"Crypto"},axis=1)
data = {i : {'Name':max_sr.iloc[i,0], "Allocation":max_sr.iloc[i,1]}for i in range(max_sr.shape[0])}
alloc=[max_sr.iloc[i,1] for i in range(max_sr.shape[0])]
pf_allocation = pd.DataFrame.from_dict(data, orient="index")
names=pf_allocation["Name"].values.tolist()
pf_opt = build_portfolio(names=names,pf_allocation=pf_allocation, start_date=start_date ,end_date=end_date,data_api="yfinance")
pf_opt.properties()
# OUR OPTIMIZATION EXPECTS A RETURN OF 6.5%
start_date = '2021-09-01'
end_date = '2021-10-01'
pf_real = build_portfolio(names=names, data_api="yfinance", start_date=start_date,end_date=end_date)
pf_real.data=pf_real.data.fillna('nan')
for i in range(pf_real.data.shape[0]):
for k in range(pf_real.data.shape[1]):
if pf_real.data.iloc[i,k]=='nan':
pf_real.data.iloc[i,k]=pf_real.data.iloc[i-1,k]
ds=pf_real.data
ds.head()
returns = {i : {'Name':ds.columns[i], "Returns":(ds.iloc[-1,i]-ds.iloc[0,i])/ds.iloc[0,i]}for i in range(ds.shape[1])}
r=[(ds.iloc[-1,i]-ds.iloc[0,i])/ds.iloc[0,i] for i in range(ds.shape[1])]
DATA = pd.DataFrame(names, columns=['Crypto'])
DATA["p_1"]=alloc
DATA["p_2"]=0.2
DATA["p_3"]=0
DATA.iloc[0,3]=1
DATA["Returns"]=r
DATA
p_1_returns = 0
p_2_returns = 0
p_3_returns = 0
for i in range(DATA.shape[0]):
p_1_returns+=DATA.iloc[i,1]*DATA.iloc[i,4]
p_2_returns+=DATA.iloc[i,2]*DATA.iloc[i,4]
p_3_returns+=DATA.iloc[i,3]*DATA.iloc[i,4]
p_1_returns,p_2_returns,p_3_returns
# ACTUAL RETURN RATE IS -0.8%, WAY LOWER THAN THE OTHER PORTFOLIOS
```
| github_jupyter |
# Isolation Forest (IF) outlier detector deployment
Wrap a scikit-learn Isolation Forest python model for use as a prediction microservice in seldon-core and deploy on seldon-core running on minikube or a Kubernetes cluster using GCP.
## Dependencies
- [helm](https://github.com/helm/helm)
- [minikube](https://github.com/kubernetes/minikube)
- [s2i](https://github.com/openshift/source-to-image) >= 1.1.13
python packages:
- scikit-learn: pip install scikit-learn --> 0.20.1
## Task
The outlier detector needs to detect computer network intrusions using TCP dump data for a local-area network (LAN) simulating a typical U.S. Air Force LAN. A connection is a sequence of TCP packets starting and ending at some well defined times, between which data flows to and from a source IP address to a target IP address under some well defined protocol. Each connection is labeled as either normal, or as an attack.
There are 4 types of attacks in the dataset:
- DOS: denial-of-service, e.g. syn flood;
- R2L: unauthorized access from a remote machine, e.g. guessing password;
- U2R: unauthorized access to local superuser (root) privileges;
- probing: surveillance and other probing, e.g., port scanning.
The dataset contains about 5 million connection records.
There are 3 types of features:
- basic features of individual connections, e.g. duration of connection
- content features within a connection, e.g. number of failed log in attempts
- traffic features within a 2 second window, e.g. number of connections to the same host as the current connection
The outlier detector is only using 40 out of 41 features.
## Train locally
Train on small dataset where you roughly know the fraction of outliers, defined by the "contamination" parameter.
```
# define columns to keep
cols=['duration','protocol_type','flag','src_bytes','dst_bytes','land',
'wrong_fragment','urgent','hot','num_failed_logins','logged_in',
'num_compromised','root_shell','su_attempted','num_root','num_file_creations',
'num_shells','num_access_files','num_outbound_cmds','is_host_login',
'is_guest_login','count','srv_count','serror_rate','srv_serror_rate',
'rerror_rate','srv_rerror_rate','same_srv_rate','diff_srv_rate',
'srv_diff_host_rate','dst_host_count','dst_host_srv_count','dst_host_same_srv_rate',
'dst_host_diff_srv_rate','dst_host_same_src_port_rate','dst_host_srv_diff_host_rate',
'dst_host_serror_rate','dst_host_srv_serror_rate','dst_host_rerror_rate',
'dst_host_srv_rerror_rate','target']
cols_str = str(cols)
!python train.py \
--dataset 'kddcup99' \
--samples 50000 \
--keep_cols "$cols_str" \
--contamination .1 \
--n_estimators 100 \
--max_samples .8 \
--max_features 1. \
--save_path './models/'
```
## Test using Kubernetes cluster on GCP or Minikube
Run the outlier detector as a model or a transformer. If you want to run the anomaly detector as a transformer, change the SERVICE_TYPE variable from MODEL to TRANSFORMER [here](./.s2i/environment), set MODEL = False and change ```OutlierIsolationForest.py``` to:
```python
from CoreIsolationForest import CoreIsolationForest
class OutlierIsolationForest(CoreIsolationForest):
""" Outlier detection using Isolation Forests.
Parameters
----------
threshold (float) : anomaly score threshold; scores below threshold are outliers
"""
def __init__(self,threshold=0.,load_path='./models/'):
super().__init__(threshold=threshold, load_path=load_path)
```
```
MODEL = True
```
Pick Kubernetes cluster on GCP or Minikube.
```
MINIKUBE = True
if MINIKUBE:
!minikube start --memory 4096
else:
!gcloud container clusters get-credentials standard-cluster-1 --zone europe-west1-b --project seldon-demos
```
Create a cluster-wide cluster-admin role assigned to a service account named “default” in the namespace “kube-system”.
```
!kubectl create clusterrolebinding kube-system-cluster-admin --clusterrole=cluster-admin \
--serviceaccount=kube-system:default
!kubectl create namespace seldon
```
Add current context details to the configuration file in the seldon namespace.
```
!kubectl config set-context $(kubectl config current-context) --namespace=seldon
```
Create tiller service account and give it a cluster-wide cluster-admin role.
```
!kubectl -n kube-system create sa tiller
!kubectl create clusterrolebinding tiller --clusterrole cluster-admin --serviceaccount=kube-system:tiller
!helm init --service-account tiller
```
Check deployment rollout status and deploy seldon/spartakus helm charts.
```
!kubectl rollout status deploy/tiller-deploy -n kube-system
!helm install ../../../helm-charts/seldon-core-operator --name seldon-core --set usage_metrics.enabled=true --namespace seldon-system
```
Check deployment rollout status for seldon core.
```
!kubectl rollout status deploy/seldon-controller-manager -n seldon-system
```
Install Ambassador API gateway
```
!helm install stable/ambassador --name ambassador --set crds.keep=false
!kubectl rollout status deployment.apps/ambassador
```
If Minikube used: create docker image for outlier detector inside Minikube using s2i. Besides the transformer image and the demo specific model image, the general model image for the Isolation Forest outlier detector is also available from Docker Hub as ***seldonio/outlier-if-model:0.1***.
```
if MINIKUBE & MODEL:
!eval $(minikube docker-env) && \
s2i build . seldonio/seldon-core-s2i-python3:0.4 seldonio/outlier-if-model-demo:0.1
elif MINIKUBE:
!eval $(minikube docker-env) && \
s2i build . seldonio/seldon-core-s2i-python3:0.4 seldonio/outlier-if-transformer:0.1
```
Install outlier detector helm charts either as a model or transformer and set *threshold* hyperparameter value.
```
if MODEL:
!helm install ../../../helm-charts/seldon-od-model \
--name outlier-detector \
--namespace=seldon \
--set model.type=isolationforest \
--set model.isolationforest.image.name=seldonio/outlier-if-model-demo:0.1 \
--set model.isolationforest.threshold=0 \
--set oauth.key=oauth-key \
--set oauth.secret=oauth-secret \
--set replicas=1
else:
!helm install ../../../helm-charts/seldon-od-transformer \
--name outlier-detector \
--namespace=seldon \
--set outlierDetection.enabled=true \
--set outlierDetection.name=outlier-if \
--set outlierDetection.type=isolationforest \
--set outlierDetection.isolationforest.image.name=seldonio/outlier-if-transformer:0.1 \
--set outlierDetection.isolationforest.threshold=0 \
--set oauth.key=oauth-key \
--set oauth.secret=oauth-secret \
--set model.image.name=seldonio/mock_classifier:1.0
```
## Port forward Ambassador
Run command in terminal:
```
kubectl port-forward $(kubectl get pods -n seldon -l app.kubernetes.io/name=ambassador -o jsonpath='{.items[0].metadata.name}') -n seldon 8003:8080
```
## Import rest requests, load data and test requests
```
from utils import get_payload, rest_request_ambassador, send_feedback_rest, get_kdd_data, generate_batch
data = get_kdd_data(keep_cols=cols,percent10=True) # load dataset
print(data.shape)
```
Generate a random batch from the data
```
import numpy as np
samples = 1
fraction_outlier = 0.
X, labels = generate_batch(data,samples,fraction_outlier)
print(X.shape)
print(labels.shape)
```
Test the rest requests with the generated data. It is important that the order of requests is respected. First we make predictions, then we get the "true" labels back using the feedback request. If we do not respect the order and eg keep making predictions without getting the feedback for each prediction, there will be a mismatch between the predicted and "true" labels. This will result in errors in the produced metrics.
```
request = get_payload(X)
response = rest_request_ambassador("outlier-detector","seldon",request,endpoint="localhost:8003")
```
If the outlier detector is used as a transformer, the output of the anomaly detection is added as part of the metadata. If it is used as a model, we send model feedback to retrieve custom performance metrics.
```
if MODEL:
send_feedback_rest("outlier-detector","seldon",request,response,0,labels,endpoint="localhost:8003")
```
## Analytics
Install the helm charts for prometheus and the grafana dashboard
```
!helm install ../../../helm-charts/seldon-core-analytics --name seldon-core-analytics \
--set grafana_prom_admin_password=password \
--set persistence.enabled=false \
--namespace seldon
```
## Port forward Grafana dashboard
Run command in terminal:
```
kubectl port-forward $(kubectl get pods -n seldon -l app=grafana-prom-server -o jsonpath='{.items[0].metadata.name}') -n seldon 3000:3000
```
You can then view an analytics dashboard inside the cluster at http://localhost:3000/dashboard/db/prediction-analytics?refresh=5s&orgId=1. Your IP address may be different. get it via minikube ip. Login with:
Username : admin
password : password (as set when starting seldon-core-analytics above)
Import the outlier-detector-if dashboard from ../../../helm-charts/seldon-core-analytics/files/grafana/configs.
## Run simulation
- Sample random network intrusion data with a certain outlier probability.
- Get payload for the observation.
- Make a prediction.
- Send the "true" label with the feedback if the detector is run as a model.
It is important that the prediction-feedback order is maintained. Otherwise there will be a mismatch between the predicted and "true" labels.
View the progress on the grafana "Outlier Detection" dashboard. Most metrics need the outlier detector to be run as a model since they need model feedback.
```
import time
n_requests = 100
samples = 1
for i in range(n_requests):
fraction_outlier = .1
X, labels = generate_batch(data,samples,fraction_outlier)
request = get_payload(X)
response = rest_request_ambassador("outlier-detector","seldon",request,endpoint="localhost:8003")
if MODEL:
send_feedback_rest("outlier-detector","seldon",request,response,0,labels,endpoint="localhost:8003")
time.sleep(1)
if MINIKUBE:
!minikube delete
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import os
import spacy
import en_core_web_sm
from spacy.lang.en import English
from spacy.lang.en.stop_words import STOP_WORDS
import string
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.feature_extraction import DictVectorizer
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer,HashingVectorizer
from sklearn.base import TransformerMixin
from sklearn.pipeline import Pipeline
!pip install vaderSentiment
import vaderSentiment
from vaderSentiment.vaderSentiment import SentimentIntensityAnalyzer
!pip install -U -q PyDrive
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
from google.colab import drive
drive.mount('/content/gdrive')
# preprocessing the data file
# read the data
df1 = pd.read_csv("/content/gdrive/My Drive/Colab Notebooks/drugsComTrain_raw.csv")
df2 = pd.read_csv("/content/gdrive/My Drive/Colab Notebooks/drugsComTest_raw.csv")
# combine two file
df = pd.concat([df1, df2])
df
# rename the cols
df.columns = ['ID','drug name','condition','review','rating','date','useful count']
df2 = df[df['useful count'] > 10]
df_condition = df2.groupby(['condition'])['drug name'].nunique().sort_values(ascending=False)
df_condition = pd.DataFrame(df_condition).reset_index()
df_condition.tail(20)
df_condition_1 = df_condition[df_condition['drug name'] == 1].reset_index()
all_list = set(df.index)
# deleting them
condition_list = []
for i,j in enumerate(df['condition']):
for c in list(df_condition_1['condition']):
if j == c:
condition_list.append(i)
new_idx = all_list.difference(set(condition_list))
df = df.iloc[list(new_idx)].reset_index()
del df['index']
df.shape
# removing the conditions with <span> in it.
all_list = set(df.index)
span_list = []
for i,j in enumerate(df['condition']):
if "</span>" in str(j):
span_list.append(i)
new_idx = all_list.difference(set(span_list))
df = df.iloc[list(new_idx)].reset_index()
del df['index']
import re
from bs4 import BeautifulSoup
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
from nltk.stem.snowball import SnowballStemmer
from nltk.stem.porter import PorterStemmer
# removing some stopwords from the list of stopwords as they are important for drug recommendation
stops = set(stopwords.words('english'))
not_stop = ["aren't","couldn't","didn't","doesn't","don't","hadn't","hasn't","haven't","isn't","mightn't",
"mustn't","needn't","no","nor","not","shan't","shouldn't","wasn't","weren't","wouldn't"]
for i in not_stop:
stops.remove(i)
stemmer = SnowballStemmer('english')
def review_to_words(raw_review):
# 1. Delete HTML
review_text = BeautifulSoup(raw_review, 'html.parser').get_text()
# 2. Make a space
letters_only = re.sub('[^a-zA-Z]', ' ', review_text)
# 3. lower letters
words = letters_only.lower().split()
# 5. Stopwords
meaningful_words = [w for w in words if not w in stops]
# 6. Stemming
stemming_words = [stemmer.stem(w) for w in meaningful_words]
# 7. space join words
return( ' '.join(stemming_words))
# create a list of stopwords
nlp = spacy.load('en_core_web_sm')
stop_words = spacy.lang.en.stop_words.STOP_WORDS
parser = English()
punctuations = string.punctuation
# Creating our tokenizer function
def spacy_tokenizer(sentence):
# Creating our token object, which is used to create documents with linguistic annotations.
mytokens = parser(sentence)
# Lemmatizing each token and converting each token into lowercase
mytokens = [ word.lemma_.lower().strip() if word.lemma_ != "-PRON-" else word.lower_ for word in mytokens ]
# Removing stop words
mytokens = [ word for word in mytokens if word not in stop_words and word not in punctuations ]
# return preprocessed list of tokens
return mytokens
%time df['review_clean'] = df['review'].apply(review_to_words)
df.head()
bow_vector = CountVectorizer(tokenizer = spacy_tokenizer, ngram_range=(1,2))
# tf-idf vector
tfidf_vector = TfidfVectorizer(tokenizer = spacy_tokenizer)
# part 1---vader sentiment analyzer for c_review
analyzer = SentimentIntensityAnalyzer()
# create new col vaderReviewScore based on C-review
df['vaderReviewScore'] = df['review_clean'].apply(lambda x: analyzer.polarity_scores(x)['compound'])
# define the positive, neutral and negative
positive_num = len(df[df['vaderReviewScore'] >=0.05])
neutral_num = len(df[(df['vaderReviewScore'] >-0.05) & (df['vaderReviewScore']<0.05)])
negative_num = len(df[df['vaderReviewScore']<=-0.05])
# create new col vaderSentiment based on vaderReviewScore
df['vaderSentiment'] = df['vaderReviewScore'].map(lambda x:int(2) if x>=0.05 else int(1) if x<=-0.05 else int(0) )
df['vaderSentiment'].value_counts() # 2-pos: 99519; 1-neg: 104434; 0-neu: 11110
# label pos/neg/neu based on vaderSentiment result
df.loc[df['vaderReviewScore'] >=0.05,"vaderSentimentLabel"] ="positive"
df.loc[(df['vaderReviewScore'] >-0.05) & (df['vaderReviewScore']<0.05),"vaderSentimentLabel"]= "neutral"
df.loc[df['vaderReviewScore']<=-0.05,"vaderSentimentLabel"] = "negative"
df['vaderReviewScore'].max()
df['vaderReviewScore'].min()
criteria = [df['vaderReviewScore'].between(-0.997, -0.799), df['vaderReviewScore'].between(-0.798, -0.601), df['vaderReviewScore'].between(-0.600, 0.403), df['vaderReviewScore'].between(-0.402, -0.205), df['vaderReviewScore'].between(-0.204, -0.007), df['vaderReviewScore'].between(-0.006,0.191), df['vaderReviewScore'].between(0.192, 0.389), df['vaderReviewScore'].between(0.390, 0.587), df['vaderReviewScore'].between(0.588, 0.785), df['vaderReviewScore'].between(0.786, 1)]
values = [1, 2, 3,4,5,6,7,8,9,10]
df['normalVaderScore'] = np.select(criteria, values, 0)
df
df['meanNormalizedScore'] = (df['rating'] + df['normalVaderScore'])/2
df.head()
grouped = df.groupby(['condition','drug name', 'ID']).agg({'meanNormalizedScore' : ['mean']})
grouped.to_csv('Medicare_Normalized_results')
grouped1 = grouped.reset_index()
grouped1.head(100)
grouped1.set_index('ID')
user_ratings = grouped1.pivot_table(index = ['condition'], columns = ['ID'], values = 'meanNormalizedScore')
user_ratings1 = grouped1.pivot_table(index = ['condition'], columns = ['ID'], values = 'meanNormalizedScore')
user_ratings.head(20)
user_ratings.to_csv('Itemtoitem_recom.csv')
user_ratings.iloc[0,:].sum(axis=0)
#Let's predict the rating for the first drug for the 1st condition.
#Therefore, we need to find the similarity between the them
import math as np
def takesec(num):
return num[1]
cosine_vector = []
num = 0
l1 = 0
l2 = 0
for i in range(1,user_ratings.shape[0]):
num = 0
l1 = 0
l2 = 0
for j in range(user_ratings.shape[1]):
if not np.isnan(user_ratings.iloc[i,j]) and not np.isnan(user_ratings.iloc[0,j]):
num = num + (user_ratings.iloc[i,j] * user_ratings.iloc[0,j])
if not np.isnan(user_ratings.iloc[i,j]):
l1 = l1 + (user_ratings.iloc[i,j] * user_ratings.iloc[i,j])
if not np.isnan(user_ratings.iloc[0,j]):
l2 = l2 + (user_ratings.iloc[0,j] * user_ratings.iloc[0,j])
eventual_prod = np.sqrt(l1) * np.sqrt(l2)
if eventual_prod != 0 :
eventual_div = num/eventual_prod
cosine_vector.append([i,eventual_div])
cosine_vector.sort(key=takesec, reverse=True)
cosine_vector[:100000]
user_ratings1.iloc[4,1]
import csv
# opening the csv file in 'w+' mode
file = open('cosine_vec.csv', 'w+', newline ='')
# writing the data into the file
with file:
write = csv.writer(file)
write.writerows(cosine_vector)
#Let's consider the top 50 similar rated drugs and predict the output.
predict_drug = int(input ("Enter a drug ID within range 0 to 1000000 : "))
count = 0
num1 = 0
den1 = 0
for i in cosine_vector:
if user_ratings1.iloc[i[0],predict_drug] > 0:
count = count + 1
num1 = num1 + i[1] * user_ratings1.iloc[i[0],predict_drug]
#print(num1)
den1 = den1 + i[1]
#print(den1)
#print("{}..{}".format(i[0],i[1]))
if count == 50:
print ("Reached 50 :)")
break
print("Expected Rating for 1st Drug for condition: {} is :{}".format(predict_drug,num1/den1))
for i in range(user_ratings1.shape[1]):
if user_ratings1.iloc[0,i] > 0:
print("Id = {} , Rating = {}".format(i,user_ratings1.iloc[0,i]))
```
| github_jupyter |
# Implementing logistic regression from scratch
The goal of this notebook is to implement your own logistic regression classifier. We will:
* Extract features from Amazon product reviews.
* Convert an SFrame into a NumPy array.
* Implement the link function for logistic regression.
* Write a function to compute the derivative of the log likelihood function with respect to a single coefficient.
* Implement gradient ascent.
* Given a set of coefficients, predict sentiments.
* Compute classification accuracy for the logistic regression model.
Let's get started!
## Fire up Turi Create
Make sure you have the latest version of Turi Create.
```
import turicreate
## utils for this notebooks moved into its own package
import sys
sys.path.append("../common")
from utils import time_it, assert_all, get_numpy_data, load_important_words
```
## Load review dataset
For this assignment, we will use a subset of the Amazon product review dataset. The subset was chosen to contain similar numbers of positive and negative reviews, as the original dataset consisted primarily of positive reviews.
```
products = turicreate.SFrame('../data/amazon_baby_subset.sframe/')
```
One column of this dataset is 'sentiment', corresponding to the class label with +1 indicating a review with positive sentiment and -1 indicating one with negative sentiment.
```
products['sentiment'][1:20]
```
Let us quickly explore more of this dataset. The 'name' column indicates the name of the product. Here we list the first 10 products in the dataset. We then count the number of positive and negative reviews.
```
products.head(10)['name']
print('# of positive reviews =', len(products[products['sentiment'] == 1]))
print('# of negative reviews =', len(products[products['sentiment'] == -1]))
```
**Note:** For this assignment, we eliminated class imbalance by choosing
a subset of the data with a similar number of positive and negative reviews.
## Apply text cleaning on the review data
In this section, we will perform some simple feature cleaning using **SFrames**. The last assignment used all words in building bag-of-words features, but here we limit ourselves to 193 words (for simplicity). We compiled a list of 193 most frequent words into a JSON file.
Now, we will load these words from this JSON file:
```
important_words = load_important_words()
important_words[0:10], len(important_words)
```
Now, we will perform 2 simple data transformations:
1. Remove punctuation using [Python's built-in](https://docs.python.org/2/library/string.html) string functionality.
2. Compute word counts (only for **important_words**)
We start with *Step 1* which can be done as follows:
```
import string
def remove_punctuation(text):
translator = text.maketrans('', '', string.punctuation)
return text.translate(translator)
products['review_clean'] = products['review'].apply(remove_punctuation)
```
Now we proceed with *Step 2*. For each word in **important_words**, we compute a count for the number of times the word occurs in the review. We will store this count in a separate column (one for each word). The result of this feature processing is a single column for each word in **important_words** which keeps a count of the number of times the respective word occurs in the review text.
**Note:** There are several ways of doing this. In this assignment, we use the built-in *count* function for Python lists. Each review string is first split into individual words and the number of occurances of a given word is counted.
```
for word in important_words:
products[word] = products['review_clean'].apply(lambda s: s.split().count(word))
products.column_names()[0:10], len(products.column_names())
```
The SFrame **products** now contains one column for each of the 193 **important_words**. As an example, the column **perfect** contains a count of the number of times the word **perfect** occurs in each of the reviews.
```
products['perfect'][0:10], len(products['perfect'])
```
Now, write some code to compute the number of product reviews that contain the word **perfect**.
**Hint**:
* First create a column called `contains_perfect` which is set to 1 if the count of the word **perfect** (stored in column **perfect**) is >= 1.
* Sum the number of 1s in the column `contains_perfect`.
```
products['contains_perfect'] = products['perfect'].apply(lambda c: 1 if c >= 1 else 0)
sum(products['contains_perfect'])
sum(products['great'].apply(lambda c: 1 if c >= 1 else 0)), sum(products['quality'].apply(lambda c: 1 if c >= 1 else 0))
```
**Quiz Question**. How many reviews contain the word **perfect**?
- cf. above cell.
## Convert SFrame to NumPy array
As you have seen previously, NumPy is a powerful library for doing matrix manipulation. Let us convert our data to matrices and then implement our algorithms with matrices.
First, make sure you can perform the following import. If it doesn't work, you need to go back to the terminal and run
`pip install numpy`.
```
import numpy as np
```
We now provide you with a function that extracts columns from an SFrame and converts them into a NumPy array. Two arrays are returned: one representing features and another representing class labels. Note that the feature matrix includes an additional column 'intercept' to take account of the intercept term.
Let us convert the data into NumPy arrays.
```
# Warning: This may take a few minutes...
feature_matrix, sentiment = get_numpy_data(products, important_words, 'sentiment')
```
**Are you running this notebook on an Amazon EC2 t2.micro instance?** (If you are using your own machine, please skip this section)
It has been reported that t2.micro instances do not provide sufficient power to complete the conversion in acceptable amount of time. For interest of time, please refrain from running `get_numpy_data` function. Instead, download the [binary file](https://s3.amazonaws.com/static.dato.com/files/coursera/course-3/numpy-arrays/module-3-assignment-numpy-arrays.npz) containing the four NumPy arrays you'll need for the assignment. To load the arrays, run the following commands:
```
arrays = np.load('module-3-assignment-numpy-arrays.npz')
feature_matrix, sentiment = arrays['feature_matrix'], arrays['sentiment']
```
**Quiz Question:** How many features are there in the **feature_matrix**?
```
feature_matrix.shape, feature_matrix.shape[1] ## == number of features / number of important word + 1 (interept)
```
**Quiz Question:** Assuming that the intercept is present, how does the number of features in **feature_matrix** relate to the number of features in the logistic regression model? <br />
Let x = [number of features in feature_matrix] and y = [number of features in logistic regression model].
- [ ] y = x - 1
- [x] y = x
- [ ] y = x + 1
- [ ] None of the above
Now, let us see what the **sentiment** column looks like:
```
sentiment
```
## Estimating conditional probability with link function
Recall from lecture that the link function is given by:
$$
P(y_i = +1 | \mathbf{x}_i,\mathbf{w}) = \frac{1}{1 + \exp(-\mathbf{w}^T h(\mathbf{x}_i))},
$$
where the feature vector $h(\mathbf{x}_i)$ represents the word counts of **important_words** in the review $\mathbf{x}_i$. Complete the following function that implements the link function:
```
'''
produces probablistic estimate for P(y_i = +1 | x_i, w).
estimate ranges between 0 and 1.
'''
def predict_probability(feature_matrix, coefficients):
score = np.dot(feature_matrix, coefficients) ## Take dot product of feature_matrix and coefficients
return 1. / (1. + np.exp(-score)) # Compute P(y_i = +1 | x_i, w) using the link function
```
**Aside**. How the link function works with matrix algebra
Since the word counts are stored as columns in **feature_matrix**, each $i$-th row of the matrix corresponds to the feature vector $h(\mathbf{x}_i)$:
$$
[\text{feature_matrix}] =
\left[
\begin{array}{c}
h(\mathbf{x}_1)^T \\
h(\mathbf{x}_2)^T \\
\vdots \\
h(\mathbf{x}_N)^T
\end{array}
\right] =
\left[
\begin{array}{cccc}
h_0(\mathbf{x}_1) & h_1(\mathbf{x}_1) & \cdots & h_D(\mathbf{x}_1) \\
h_0(\mathbf{x}_2) & h_1(\mathbf{x}_2) & \cdots & h_D(\mathbf{x}_2) \\
\vdots & \vdots & \ddots & \vdots \\
h_0(\mathbf{x}_N) & h_1(\mathbf{x}_N) & \cdots & h_D(\mathbf{x}_N)
\end{array}
\right]
$$
By the rules of matrix multiplication, the score vector containing elements $\mathbf{w}^T h(\mathbf{x}_i)$ is obtained by multiplying **feature_matrix** and the coefficient vector $\mathbf{w}$.
$$
[\text{score}] =
[\text{feature_matrix}]\mathbf{w} =
\left[
\begin{array}{c}
h(\mathbf{x}_1)^T \\
h(\mathbf{x}_2)^T \\
\vdots \\
h(\mathbf{x}_N)^T
\end{array}
\right]
\mathbf{w}
= \left[
\begin{array}{c}
h(\mathbf{x}_1)^T\mathbf{w} \\
h(\mathbf{x}_2)^T\mathbf{w} \\
\vdots \\
h(\mathbf{x}_N)^T\mathbf{w}
\end{array}
\right]
= \left[
\begin{array}{c}
\mathbf{w}^T h(\mathbf{x}_1) \\
\mathbf{w}^T h(\mathbf{x}_2) \\
\vdots \\
\mathbf{w}^T h(\mathbf{x}_N)
\end{array}
\right]
$$
**Checkpoint**
Just to make sure we are on the right track, we have provided a few examples. If our `predict_probability` function is implemented correctly, then the following should pass:
```
dummy_feature_matrix = np.array([[1., 2., 3.], [1., -1., -1]])
dummy_coefficients = np.array([1., 3., -1.])
correct_scores = np.array([1.*1. + 2.*3. + 3.*(-1.), 1.*1. + (-1.)*3. + (-1.)*(-1.)])
correct_preds = np.array([1. / (1 + np.exp(-correct_scores[0])), 1. / (1 + np.exp(-correct_scores[1]))])
eps = 1e-7
assert_all(lambda t: abs(t[0] - t[1]) <= eps, zip(predict_probability(dummy_feature_matrix, dummy_coefficients), correct_preds))
```
## Compute derivative of log likelihood with respect to a single coefficient
Recall from lecture:
$$
\frac{\partial\ell}{\partial w_j} = \sum_{i=1}^N h_j(\mathbf{x}_i)\left(\mathbf{1}[y_i = +1] - P(y_i = +1 | \mathbf{x}_i, \mathbf{w})\right)
$$
We will now write a function that computes the derivative of log likelihood with respect to a single coefficient $w_j$. The function accepts two arguments:
* `errors` vector containing $\mathbf{1}[y_i = +1] - P(y_i = +1 | \mathbf{x}_i, \mathbf{w})$ for all $i$.
* `feature` vector containing $h_j(\mathbf{x}_i)$ for all $i$.
Complete the following code block:
```
def feature_derivative(errors, features):
return np.dot(errors, features) # Compute the dot product...
```
In the main lecture, our focus was on the likelihood. In the advanced optional video, however, we introduced a transformation of this likelihood---called the log likelihood---that simplifies the derivation of the gradient and is more numerically stable. Due to its numerical stability, we will use the log likelihood instead of the likelihood to assess the algorithm.
The log likelihood is computed using the following formula (see the advanced optional video if you are curious about the derivation of this equation):
$$\ell\ell(\mathbf{w}) = \sum_{i=1}^N \Big( (\mathbf{1}[y_i = +1] - 1)\mathbf{w}^T h(\mathbf{x}_i) - \ln\left(1 + \exp(-\mathbf{w}^T h(\mathbf{x}_i))\right) \Big) $$
We provide a function to compute the log likelihood for the entire dataset.
```
def compute_log_likelihood(feature_matrix, sentiment, coefficients):
indic = (sentiment == +1)
scores = np.dot(feature_matrix, coefficients)
logexp = np.log(1. + np.exp(-scores))
# Simple check to prevent overflow
mask = np.isinf(logexp)
logexp[mask] = -scores[mask]
return np.sum((indic - 1) * scores - logexp)
```
**Checkpoint**
Just to make sure we are on the same page, run the following code block and check that the outputs match.
```
dummy_feature_matrix = np.array([[1.,2.,3.], [1.,-1.,-1]])
dummy_coefficients = np.array([1., 3., -1.])
dummy_sentiment = np.array([-1, 1])
correct_indicators = np.array( [-1 == +1, 1 == +1])
correct_scores = np.array( [1.*1. + 2.*3. + 3.*(-1.), 1.*1. + (-1.)*3. + (-1.)*(-1.)])
correct_first_term = np.array( [(correct_indicators[0]-1)*correct_scores[0], (correct_indicators[1]-1)*correct_scores[1]])
correct_second_term = np.array( [np.log(1. + np.exp(-correct_scores[0])), np.log(1. + np.exp(-correct_scores[1]))])
correct_ll = sum([correct_first_term[0] - correct_second_term[0], correct_first_term[1] - correct_second_term[1]])
assert abs(compute_log_likelihood(dummy_feature_matrix, dummy_sentiment, dummy_coefficients) - correct_ll) <= eps
```
## Taking gradient steps
Now we are ready to implement our own logistic regression. All we have to do is to write a gradient ascent function that takes gradient steps towards the optimum.
Complete the following function to solve the logistic regression model using gradient ascent:
```
from math import sqrt
def logistic_regression(feature_matrix, sentiment, initial_coefficients, step_size, max_iter):
coeffs = np.array(initial_coefficients) # make sure it's a numpy array
for itr in range(max_iter):
# Predict P(y_i = +1|x_i,w) using your predict_probability() function
preds = predict_probability(feature_matrix, coeffs)
indic = (sentiment == +1) ## Compute indicator value for (y_i = +1)
errors = indic - preds ## Compute the errors as indicator - predictions
for jx in range(len(coeffs)): # loop over each coefficient
# Recall that feature_matrix[:, jx] is the feature column associated with coeffs[j].
# Compute the derivative for coeffs[jx]. Save it in a variable called derivative
derivative = feature_derivative(errors, feature_matrix[:, jx])
# add the step size times the derivative to the current coefficient
coeffs[jx] += step_size * derivative
# Checking whether log likelihood is increasing
if itr <= 15 or (itr <= 100 and itr % 10 == 0) or (itr <= 1000 and itr % 100 == 0) \
or (itr <= 10000 and itr % 1000 == 0) or itr % 10000 == 0:
lp = compute_log_likelihood(feature_matrix, sentiment, coeffs)
print('iteration %*d: log likelihood of observed labels = %.8f' % \
(int(np.ceil(np.log10(max_iter))), itr, lp))
return coeffs
```
Now, let us run the logistic regression solver.
```
coefficients = logistic_regression(feature_matrix, sentiment, initial_coefficients=np.zeros(194),
step_size=1e-7, max_iter=301)
```
**Quiz Question:** As each iteration of gradient ascent passes, does the log likelihood increase or decrease?
- increase
## Predicting sentiments
Recall from lecture that class predictions for a data point $\mathbf{x}$ can be computed from the coefficients $\mathbf{w}$ using the following formula:
$$
\hat{y}_i =
\left\{
\begin{array}{ll}
+1 & \mathbf{x}_i^T\mathbf{w} > 0 \\
-1 & \mathbf{x}_i^T\mathbf{w} \leq 0 \\
\end{array}
\right.
$$
Now, we will write some code to compute class predictions. We will do this in two steps:
* **Step 1**: First compute the **scores** using **feature_matrix** and **coefficients** using a dot product.
* **Step 2**: Using the formula above, compute the class predictions from the scores.
Step 1 can be implemented as follows:
```
# Compute the scores as a dot product between feature_matrix and coefficients.
scores = np.dot(feature_matrix, coefficients)
len(scores), scores
```
Now, complete the following code block for **Step 2** to compute the class predictions using the **scores** obtained above:
```
preds = np.where(scores > 0., 1, -1)
len(scores), scores
```
**Quiz Question:** How many reviews were predicted to have positive sentiment?
```
n_pos = np.where(scores > 0., 1, 0).sum()
n_neg = np.where(scores > 0., 0, 1).sum()
assert n_pos + n_neg == len(scores)
n_pos
n_pos, n_neg = len(preds[preds == 1]), len(preds[preds == -1])
assert n_pos + n_neg == len(scores)
n_pos
```
## Measuring accuracy
We will now measure the classification accuracy of the model. Recall from the lecture that the classification accuracy can be computed as follows:
$$
\mbox{accuracy} = \frac{\mbox{# correctly classified data points}}{\mbox{# total data points}}
$$
Complete the following code block to compute the accuracy of the model.
```
np.where(sentiment - preds != 0, 1, 0).sum()
n = len(products)
num_mistakes = np.where(sentiment - preds != 0, 1, 0).sum()
accuracy = (n - num_mistakes) / n
print("-----------------------------------------------------")
print(f'# Reviews correctly classified = {n - num_mistakes}')
print(f'# Reviews incorrectly classified = {num_mistakes}')
print(f'# Reviews total = {n}')
print("-----------------------------------------------------")
print(f'Accuracy = {accuracy:.2f}')
```
**Quiz Question**: What is the accuracy of the model on predictions made above? (round to 2 digits of accuracy)
## Which words contribute most to positive & negative sentiments?
Recall that in Module 2 assignment, we were able to compute the "**most positive words**". These are words that correspond most strongly with positive reviews. In order to do this, we will first do the following:
* Treat each coefficient as a tuple, i.e. (**word**, **coefficient_value**).
* Sort all the (**word**, **coefficient_value**) tuples by **coefficient_value** in descending order.
```
def top_n(words=important_words, coeffs=list(coefficients[1:]), key='positive'):
return sorted(
[(word, coeff) for word, coeff in zip(words, coeffs)],
key=lambda x: x[1],
reverse=True if key == 'positive' else False
)
```
Now, **word_coefficient_tuples** contains a sorted list of (**word**, **coefficient_value**) tuples. The first 10 elements in this list correspond to the words that are most positive.
### Ten "most positive" words
Now, we compute the 10 words that have the most positive coefficient values. These words are associated with positive sentiment.
```
list(map(lambda t: t[0], top_n()[0:10]))
```
**Quiz Question:** Which word is **NOT** present in the top 10 "most positive" words?
- [ ] love
- [ ] easy
- [ ] great
- [ ] perfect
- [x] cheap
### Ten "most negative" words
Next, we repeat this exercise on the 10 most negative words. That is, we compute the 10 words that have the most negative coefficient values. These words are associated with negative sentiment.
```
list(map(lambda t: t[0], top_n(key='negative')[0:10]))
```
**Quiz Question:** Which word is **NOT** present in the top 10 "most negative" words?
- [x] need
- [ ] work
- [ ] disappointed
- [ ] even
- [ ] return
| github_jupyter |
## Demo: MultiContainer feeder example
The basic steps to set up an OpenCLSim simulation are:
* Import libraries
* Initialise simpy environment
* Define object classes
* Create objects
* Create sites
* Create vessels
* Create activities
* Register processes and run simpy
----
#### 0. Import libraries
```
import datetime, time
import simpy
import numpy as np
import pandas as pd
import shapely.geometry
import openclsim.core as core
import openclsim.model as model
import openclsim.plot as plot
```
#### 1. Initialise simpy environment
```
NR_BARGES = 3
TOTAL_AMOUNT = 100
BARGE_CAPACITY=10
# setup environment
simulation_start = 0
my_env = simpy.Environment(initial_time=simulation_start)
registry = {}
```
#### 2. Define object classes
```
# create a Site object based on desired mixin classes
Site = type(
"Site",
(
core.Identifiable,
core.Log,
core.Locatable,
core.HasMultiContainer,
core.HasResource,
),
{},
)
# create a TransportProcessingResource object based on desired mixin classes
TransportProcessingResource = type(
"TransportProcessingResource",
(
core.Identifiable,
core.Log,
core.MultiContainerDependentMovable,
core.Processor,
core.HasResource,
),
{"key": "MultiStoreHopper"},
)
```
#### 3. Create objects
##### 3.1. Create site object(s)
```
location_from_site = shapely.geometry.Point(4.18055556, 52.18664444)
data_from_site = {"env": my_env,
"name": "from_site",
"geometry": location_from_site,
"store_capacity": 4,
"nr_resources": 1,
"initials": [
{
"id": "Cargo type 1",
"level": TOTAL_AMOUNT,
"capacity": TOTAL_AMOUNT
},
],
}
from_site = Site(**data_from_site)
location_to_site = shapely.geometry.Point(4.25222222, 52.11428333)
data_to_site = {"env": my_env,
"name": "to_site",
"geometry": location_to_site,
"store_capacity": 4,
"nr_resources": 1,
"initials": [
{
"id": "Cargo type 1",
"level": 0,
"capacity": TOTAL_AMOUNT
},
],
}
to_site = Site(**data_to_site)
```
##### 3.2. Create vessel object(s)
```
vessels = {}
for i in range(NR_BARGES):
vessels[f"vessel{i}"] = TransportProcessingResource(
env=my_env,
name=f"vessel{i}",
geometry=location_from_site,
store_capacity=4,
nr_resources=1,
compute_v=lambda x: 10,
initials=[
{
"id": "Cargo type 1",
"level": 0,
"capacity": BARGE_CAPACITY
},
],
)
# prepare input data for installer01
data_installer01 = {"env": my_env,
"name": "installer01",
"geometry": location_to_site,
"store_capacity": 4,
"nr_resources": 1,
"compute_v": lambda x: 10,
"initials": [
{
"id": "Cargo type 1",
"level": 0,
"capacity": NR_BARGES, # Bug we need a watchtower for this
},
],
}
# instantiate vessel_02
installer01 = TransportProcessingResource(**data_installer01)
```
##### 3.3 Create activity/activities
```
processes = []
for i in range(NR_BARGES):
vessel = vessels[f"vessel{i}"]
requested_resources={}
processes.append(
model.WhileActivity(
env=my_env,
name=f"while {vessel.name}",
registry=registry,
sub_processes=[
model.SequentialActivity(
env=my_env,
name=f"sequence {vessel.name}",
registry=registry,
sub_processes=[
model.MoveActivity(
env=my_env,
name=f"sailing empty {vessel.name}",
registry=registry,
mover=vessel,
destination=from_site,
duration=10,
),
model.ShiftAmountActivity(
env=my_env,
name=f"load cargo type 1 {vessel.name}",
registry=registry,
processor=vessel,
origin=from_site,
destination=vessel,
amount=BARGE_CAPACITY,
duration=10,
id_="Cargo type 1",
requested_resources=requested_resources,
),
model.MoveActivity(
env=my_env,
name=f"sailing filled {vessel.name}",
registry=registry,
mover=vessel,
destination=to_site,
duration=10,
),
model.WhileActivity(
env=my_env,
name=f"unload cycle {vessel.name}",
registry=registry,
condition_event={
"type": "container",
"concept": vessel,
"state": "empty",
"id_":"Cargo type 1"
},
sub_processes=[
model.ShiftAmountActivity(
env=my_env,
name=f"unload cargo type 1 {vessel.name}",
registry=registry,
processor=installer01,
origin=vessel,
destination=installer01,
amount=1,
duration=10,
id_="Cargo type 1",
requested_resources=requested_resources,
start_event={
"type": "container",
"concept": installer01,
"state": "lt",
"level":1,
"id_":"Cargo type 1"
}
),
]
)
],
)
],
condition_event={
"type": "container",
"concept": from_site,
"state": "empty",
"id_":"Cargo type 1_reservations"
},
)
)
install_process = model.WhileActivity(
env=my_env,
name=f"While installer",
registry=registry,
condition_event={
"type": "container",
"concept": to_site,
"state": "full",
"id_":"Cargo type 1"
},
sub_processes=[
model.ShiftAmountActivity(
env=my_env,
name=f"Install Cargo type 1",
registry=registry,
processor=installer01,
origin=installer01,
destination=to_site,
amount=1,
duration=2,
id_="Cargo type 1",
start_event={
"type": "container",
"concept": installer01,
"state": "ge",
"level":1,
"id_":"Cargo type 1"
}
)
],
)
```
#### 4. Register processes and run simpy
```
model.register_processes([install_process, *processes])
my_env.run()
def extend_id_map(activity, id_map):
if hasattr(activity, "sub_processes"):
for sub_process in activity.sub_processes:
id_map = extend_id_map(sub_process, id_map)
return {**id_map, activity.id: activity }
activity_map = {}
for activity in [*processes, install_process]:
activity_map = extend_id_map(activity, activity_map)
id_map = {key:val.name for (key,val) in activity_map.items()}
```
#### 5. Inspect results
##### 5.1 Inspect logs
```
plot.get_log_dataframe(installer01, list(activity_map.values())).head()
```
##### 5.2 Visualise gantt charts
```
acts = []
for proc in processes:
acts.extend(proc.sub_processes[0].sub_processes)
plot.get_gantt_chart([*install_process.sub_processes, *acts])
plot.get_gantt_chart(
[installer01],
id_map=id_map
)
```
##### 5.3 Visualise step charts
```
fig = plot.get_step_chart([installer01])
fig = plot.get_step_chart([from_site, *vessels.values(), installer01, to_site])
```
| github_jupyter |
```
from IPython.display import Latex
# Latex(r"""\begin{eqnarray} \large
# Z_{n+1} = Z_{n}^(-e^(Z_{n}^p)^(e^(Z_{n}^p)^(-e^(Z_{n}^p)^(e^(Z_{n}^p)^(-e^(Z_{n}^p))))))
# \end{eqnarray}""")
```
# Parameterized machine learning algo:
## tanh(Z) = (a exp(Z) - b exp(-Z)) / (c exp(Z) + d exp(-Z))
### with parameters a,b,c,d s.t. ad - bc = 1
Sequential iteration of difference equation:
Z =
```
import warnings
warnings.filterwarnings('ignore')
import os
import sys
import numpy as np
import time
from IPython.display import display
sys.path.insert(1, '../src');
import z_plane as zp
import graphic_utility as gu;
import itergataters as ig
import numcolorpy as ncp
def rnd_lambda(s=1):
""" random parameters s.t. a*d - b*c = 1 """
b = np.random.random()
c = np.random.random()
ad = b*c + 1
a = np.random.random()
d = ad / a
lamb0 = {'a': a, 'b': b, 'c': c, 'd': d}
lamb0 = np.array([a, b, c, d]) * s
return lamb0
def tanh_lmbd(Z, p, Z0=None, ET=None):
""" Z = starfish_ish(Z, p)
Args:
Z: a real or complex number
p: a real of complex number
Returns:
Z: the result (complex)
"""
Zp = np.exp(Z)
Zm = np.exp(-Z)
return (p[0] * Zp - p[1] * Zm) / (p[2] * Zp + p[3] * Zm)
def plane_gradient(X):
""" DX, DY = plane_gradient(X)
Args:
X: matrix
Returns:
DX: gradient in X direction
DY: gradient in Y direction
"""
n_rows = X.shape[0]
n_cols = X.shape[1]
DX = np.zeros(X.shape)
DY = np.zeros(X.shape)
for r in range(0, n_rows):
xr = X[r, :]
for c in range(0, n_cols - 1):
DX[r,c] = xr[c+1] - xr[c]
for c in range(0, n_cols):
xc = X[:, c]
for r in range(0, n_rows -1):
DY[r, c] = xc[r+1] - xc[r]
return DX, DY
def grad_Im(X):
"""
Args:
X: matrix
Returns:
Gradient_Image: positive matrix representation of the X-Y gradient of X
"""
DX, DY = plane_gradient(X)
return gu.graphic_norm(DX + DY * 1j)
def grad_pct(X):
""" percentage of X s.t gradient > 0 """
I = grad_Im(X)
return (I > 0).sum() / (X.shape[0] * X.shape[1])
def get_half_n_half(X):
""" box counting, fractal dimension submatrix shortcut """
x_rows = X.shape[0]
x_cols = X.shape[1]
x_numel = x_rows * x_cols
y_rows = np.int(np.ceil(x_rows / 2))
y_cols = np.int(np.ceil(x_cols / 2))
y_numel = y_rows * y_cols
Y = np.zeros([y_rows, y_cols])
for r in range(0, y_rows):
for c in range(0, y_cols):
Y[r,c] = X[2*r, 2*c]
return Y, y_numel, x_numel
def get_fractal_dim(X):
""" estimate fractal dimension by box counting """
Y, y_numel, x_numel = get_half_n_half(X)
X_pct = grad_pct(X) + 1
Y_pct = grad_pct(Y) + 1
return X_pct / Y_pct
X = np.random.random([5,5])
X[X < 0.5] = 0
Y, y_numel, x_numel = get_half_n_half(X)
X_pct = grad_pct(X)
Y_pct = grad_pct(Y)
print(X_pct, Y_pct)
print('y_numel', y_numel, '\nx_numel', x_numel)
print(X_pct / Y_pct)
# print(Y)
# print(X)
print(get_fractal_dim(X))
# -- machine with 8 cores --
P0 = [ 1.68458678, 1.72346312, 0.53931956, 2.92623535]
P1 = [ 1.99808082, 0.68298986, 0.80686446, 2.27772581]
P2 = [ 1.97243201, 1.32849475, 0.24972699, 2.19615225]
P3 = [ 1.36537498, 1.02648965, 0.60966423, 3.38794403]
p_scale = 2
P = rnd_lambda(p_scale)
# P = np.array(P3)
N = 200
par_set = {'n_rows': N, 'n_cols': N}
par_set['center_point'] = 0.0 + 0.0j
par_set['theta'] = np.pi / 2
par_set['zoom'] = 1/2
par_set['it_max'] = 16
par_set['max_d'] = 12 / par_set['zoom']
par_set['dir_path'] = os.getcwd()
list_tuple = [(tanh_lmbd, (P))]
t0 = time.time()
ET, Z, Z0 = ig.get_primitives(list_tuple, par_set)
tt = time.time() - t0
print(P, '\n', tt, '\t total time')
Zd, Zr, ETn = ncp.etg_norm(Z0, Z, ET)
print('Fractal Dimensionn = ', get_fractal_dim(ETn) - 1)
ZrN = ncp.range_norm(Zr, lo=0.25, hi=1.0)
display(ncp.gray_mat(ZrN))
ZrN = ncp.range_norm(gu.grad_Im(ETn), lo=0.25, hi=1.0)
R = ncp.gray_mat(ZrN)
display(R)
# -- machine with 4 cores --
p_scale = 2
# P = rnd_lambda(p_scale)
P = np.array([1.97243201, 1.32849475, 0.24972699, 2.19615225])
N = 800
par_set = {'n_rows': N, 'n_cols': N}
par_set['center_point'] = 0.0 + 0.0j
par_set['theta'] = np.pi / 2
par_set['zoom'] = 1/2
par_set['it_max'] = 16
par_set['max_d'] = 12 / par_set['zoom']
par_set['dir_path'] = os.getcwd()
list_tuple = [(tanh_lmbd, (P))]
t0 = time.time()
ET, Z, Z0 = ig.get_primitives(list_tuple, par_set)
tt = time.time() - t0
print(P, '\n', tt, '\t total time')
t0 = time.time()
Zd, Zr, ETn = ncp.etg_norm(Z0, Z, ET)
print('converstion time =\t', time.time() - t0)
t0 = time.time()
# ZrN = ncp.range_norm(Zr, lo=0.25, hi=1.0)
# R = ncp.gray_mat(ZrN)
ZrN = ncp.range_norm(gu.grad_Im(ETn), lo=0.25, hi=1.0)
R = ncp.gray_mat(ZrN)
print('coloring time =\t',time.time() - t0)
display(R)
# def grad_pct(X):
# """ percentage of X s.t gradient > 0 """
# I = gu.grad_Im(X)
# nz = (I == 0).sum()
# if nz > 0:
# grad_pct = (I > 0).sum() / nz
# else:
# grad_pct = 1
# return grad_pct
I = gu.grad_Im(ETn)
nz = (I == 0).sum()
nb = (I > 0).sum()
print(nz, nb, ETn.shape[0] * ETn.shape[1], nz + nb)
P0 = [ 1.68458678, 1.72346312, 0.53931956, 2.92623535]
P1 = [ 1.99808082, 0.68298986, 0.80686446, 2.27772581]
P2 = [ 1.97243201, 1.32849475, 0.24972699, 2.19615225]
P3 = [ 1.36537498, 1.02648965, 0.60966423, 3.38794403]
H = ncp.range_norm(1 - Zd, lo=0.5, hi=1.0)
S = ncp.range_norm(1 - ETn, lo=0.0, hi=0.15)
V = ncp.range_norm(Zr, lo=0.2, hi=1.0)
t0 = time.time()
Ihsv = ncp.rgb_2_hsv_mat(H, S, V)
print('coloring time:\t',time.time() - t0)
display(Ihsv)
H = ncp.range_norm(Zd, lo=0.05, hi=0.55)
S = ncp.range_norm(1 - ETn, lo=0.0, hi=0.35)
V = ncp.range_norm(Zr, lo=0.0, hi=0.7)
t0 = time.time()
Ihsv = ncp.rgb_2_hsv_mat(H, S, V)
print('coloring time:\t',time.time() - t0)
display(Ihsv)
# smaller for analysis
par_set = {'n_rows': 200, 'n_cols': 200}
par_set['center_point'] = 0.0 + 0.0j
par_set['theta'] = 0.0
par_set['zoom'] = 5/8
par_set['it_max'] = 16
par_set['max_d'] = 10 / par_set['zoom']
par_set['dir_path'] = os.getcwd()
# list_tuple = [(starfish_ish, (-0.040431211565+0.388620268274j))]
list_tuple = [(tanh_lmbd, (P))]
t0 = time.time()
ET_sm, Z_sm, Z0_zm = ig.get_primitives(list_tuple, par_set)
tt = time.time() - t0
print(tt, '\t total time')
# view smaller - individual escape time starting points
for t in range(1,7):
print('ET =\t',t)
I = np.ones(ET_sm.shape)
I[ET_sm == t] = 0
display(ncp.mat_to_gray(I))
I = np.ones(ET_sm.shape)
I[ET_sm > 7] = 0
display(ncp.mat_to_gray(I))
# view smaller - individual escape time frequency
for k in range(0,int(ET_sm.max())):
print(k, (ET_sm == k).sum())
print('\nHow many never escaped:\n>',(ET_sm > k).sum())
# get the list of unescaped starting points and look for orbit points
Z_overs = Z0_zm[ET_sm == ET_sm.max()]
v1 = Z_overs[0]
d = '%0.2f'%(np.abs(v1))
theta = '%0.1f'%(180*np.arctan2(np.imag(v1), np.real(v1))/np.pi)
print('One Unescaped Vector:\n\tV = ', d, theta, 'degrees\n')
print('%9d'%Z_overs.size, 'total unescaped points\n')
print('%9s'%('points'), 'near V', ' (plane units)')
for denom0 in range(1,12):
neighbor_distance = np.abs(v1) * 1/denom0
v1_list = Z_overs[np.abs(Z_overs-v1) < neighbor_distance]
print('%9d'%len(v1_list), 'within V/%2d (%0.3f)'%(denom0, neighbor_distance))
```
| github_jupyter |
# Hashtags
```
from nltk.tokenize import TweetTokenizer
import os
import pandas as pd
import re
import sys
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation
from IPython.display import clear_output
def squeal(text=None):
clear_output(wait=True)
if not text is None: print(text)
DATADIR = "../data/text/"
ID_STR = "id_str"
TEXT = "text"
TOPICQUERY = "corona|covid|huisarts|mondkapje|rivm|blijfthuis|flattenthecurve|houvol"
PANDEMICQUERY = "|".join([TOPICQUERY, r'virus|besmet|ziekenhui|\bic\b|intensive.care|^zorg|vaccin|[^ad]arts|uitbraak|uitbrak|pandemie|ggd|'+
r'mondkapje|quarantaine|\bwho\b|avondklok|variant|verple|sympto|e.golf|mutant|^omt$|umc|hcq|'+
r'hydroxychloroquine|virolo|zkh|oversterfte|patiënt|patient|intensivist|🦠|ivermectin'])
DISTANCEQUERY = "1[.,]5[ -]*m|afstand.*hou|hou.*afstand|anderhalve[ -]*meter"
LOCKDOWNQUERY = "lock.down|lockdown"
VACCINQUERY = "vaccin|ingeënt|ingeent|inent|prik|spuit|bijwerking|-->|💉|pfizer|moderna|astrazeneca|astra|zeneca|novavax|biontech"
TESTQUERY = r'\btest|getest|sneltest|pcr'
QUERY = "|".join([PANDEMICQUERY, TESTQUERY, VACCINQUERY, LOCKDOWNQUERY, DISTANCEQUERY])
BASEQUERY = "corona|covid"
HAPPY_QUERY = r'\b(geluk|gelukkig|gelukkige|blij|happy)\b'
LONELY_QUERY = r'eenza|alleen.*voel|voel.*alleen|lonely|loneli'
IK_QUERY = r'\b(ik|mij|mijn|me|mn|m\'n|zelf|mezelf|mijzelf|i)\b'
def get_tweets(file_pattern, query, query2="", spy=False):
tweets = []
file_names = sorted(os.listdir(DATADIR))
for file_name in file_names:
if re.search('^' + file_pattern, file_name):
if spy:
squeal(file_name)
df = pd.read_csv(DATADIR+file_name,index_col=ID_STR)
if query2 == "":
df_query = df[df[TEXT].str.contains(query, flags=re.IGNORECASE)]
else:
df_query = df[df[TEXT].str.contains(query, flags=re.IGNORECASE) & df[TEXT].str.contains(query2, flags=re.IGNORECASE)]
tweets.extend(list(df_query[TEXT]))
return(tweets)
def get_hashtags(tweet):
hashtags = []
for token in TweetTokenizer().tokenize(tweet):
if re.search(r'#', token):
hashtags.append(token)
return(hashtags)
def process_month(month, query=BASEQUERY, query2=""):
tweets = [re.sub(r'\\n', ' ', tweet) for tweet in get_tweets(month, query, query2=query2, spy=False)]
hashtags = {}
for tweet in tweets:
if re.search(r'#', tweet):
for hashtag in get_hashtags(tweet):
if hashtag in hashtags:
hashtags[hashtag] += 1
else:
hashtags[hashtag] = 1
print(month, " ".join([hashtag for hashtag in sorted(hashtags.keys(), key=lambda hashtag:hashtags[hashtag], reverse=True)][:200]))
pd.DataFrame([{"202105": "measures", "202106": "pandemic", "202107": "measures",
"202108": "pandemic", "202109": "entry pass", "202110": "entry pass"},
{"202105": "pandemic", "202106": "measures", "202107": "pandemic",
"202108": "measures", "202109": "measures", "202110": "measures"},
{"202105": "vaccination", "202106": "vaccination", "202107": "vaccination",
"202108": "vaccination obligation", "202109": "vaccination obligation", "202110": "pandemic"},
{"202105": "entry pass", "202106": "FVD", "202107": "vaccination obligation",
"202108": "vaccination", "202109": "pandemic", "202110": "vaccination obligation"},
{"202105": "Netherlands", "202106": "Netherlands", "202107": "FVD",
"202108": "Netherlands", "202109": "press conference", "202110": "press conference"},
{"202105": "testing", "202106": "facemasks", "202107": "Netherlands",
"202108": "lockdown", "202109": "FVD", "202110": "unvaccinated"},
{"202105": "FVD", "202106": "entry pass", "202107": "lockdown",
"202108": "press conference", "202109": "Hugo de Jonge", "202110": "3 October protest"},
{"202105": "ivermectine", "202106": "app", "202107": "press conference",
"202108": "entry pass", "202109": "hospitality business", "202110": "Netherlands"},
{"202105": "long covid", "202106": "variants", "202107": "long covid",
"202108": "FVD", "202109": "Mark Rutte", "202110": "Hugo de Jonge"},
{"202105": "lockdown", "202106": "lab leak", "202107": "Hugo de Jonge",
"202108": "long covid", "202109": "Mona Keizer", "202110": "FVD"},
])
for month in "202105 202106 202107 202108 202109 202110".split():
process_month(month)
for month in "202105".split():
tweets = [re.sub(r'\\n', ' ', tweet) for tweet in get_tweets(month, LONELY_QUERY, query2=IK_QUERY, spy=False)]
hashtags = {}
for tweet in tweets:
if re.search(r'#', tweet):
for hashtag in get_hashtags(tweet):
if hashtag in hashtags:
hashtags[hashtag] += 1
else:
hashtags[hashtag] = 1
print(month, " ".join([hashtag for hashtag in sorted(hashtags.keys(), key=lambda hashtag:hashtags[hashtag], reverse=True)][:200]))
for month in "202002 202003 202004 202005 202006 202007 202008 202009 202010 202011 202012 201201".split():
tweets = [re.sub(r'\\n', ' ', tweet) for tweet in get_tweets(month, BASEQUERY, spy=False)]
hashtags = {}
for tweet in tweets:
if re.search(r'#', tweet):
for hashtag in get_hashtags(tweet):
if hashtag in hashtags:
hashtags[hashtag] += 1
else:
hashtags[hashtag] = 1
print(month, " ".join([hashtag for hashtag in sorted(hashtags.keys(), key=lambda hashtag:hashtags[hashtag], reverse=True)][:200]))
for month in "202101 202102 202103 202104".split():
tweets = [re.sub(r'\\n', ' ', tweet) for tweet in get_tweets(month, BASEQUERY, spy=False)]
hashtags = {}
for tweet in tweets:
if re.search(r'#', tweet):
for hashtag in get_hashtags(tweet):
if hashtag in hashtags:
hashtags[hashtag] += 1
else:
hashtags[hashtag] = 1
print(month, " ".join([hashtag for hashtag in sorted(hashtags.keys(), key=lambda hashtag:hashtags[hashtag], reverse=True)][:200]))
```
| github_jupyter |
```
from IPython.core.display import HTML
HTML("<style>.container { width:95% !important; }</style>")
```
# Lecture 11, Solution methods for multiobjective optimization
## Reminder:
### Mathematical formulation of multiobjective optimization problems
Multiobjective optimization problems are often formulated as
$$
\begin{align} \
\min \quad &\{f_1(x),\ldots,f_k(x)\}\\
\text{s.t.} \quad & g_j(x) \geq 0\text{ for all }j=1,\ldots,J\\
& h_q(x) = 0\text{ for all }q=1,\ldots,Q\\
&a_i\leq x_i\leq b_i\text{ for all } i=1,\ldots,n\\
&x\in \mathbb R^n,
\end{align}
$$
where $$f_1,\ldots,f_k:\{x\in\mathbb R^n: g_j(x) \geq 0 \text{ for all }j=1,\ldots,J \text{ and } h_q(x) = 0\text{ for all }q=1,\ldots,Q\}\mapsto\mathbb R$$ are the objective functions.
## Pareto optimality
A feasible solution $x_1$ is Pareto optimal to the multiobjective optimization problem, if there does not exist a feasible solution $x_2$, $x_1\neq x_2$, such that
$$
\left\{
\begin{align}
&f_i(x_2)\leq f_i(x_1)\text{ for all }i\in \{1,\ldots,k\}\\
&f_j(x_2)<f_j(x_1)\text{ for some }j\in \{1,\ldots,k\}.\\
\end{align}
\right.
$$
### Basic concepts
* There is no single optimal solution, instead we have a set of solutions called pareto optimal set.
* All the objectives don’t have the same optimal solution → optimality needs to be modified
### PARETO OPTIMALITY (PO)
* A solution is pareto optimal if none of the objectives can be improved without impairing at least one of the others
It means:
$$
\text{“Take from Sami to pay Anna”}
$$
* Optimal solutions are located at the boundary to the down & left (for minimization problems)*

* There are to spaces connected to the problem: the space $\mathbb R^n$ is called the decision space and $\mathbb R^k$ is called the objective space.
1. **Decision space**: includes the **Pareto optimal solution set**
2. **Objective space**: consists of the image of Pareto optimal solutions (**Pareto frontier**)

## Some more concepts:
In addition to Pareto optimality, two more concepts are important, which are called the ideal and the nadir vector.
* **Ideal objective vector $𝒛^∗$:** best values for each objective (when optimized independently)
* **Nadir objective vector $𝒛^𝑛𝑎𝑑$:** worst values for each objective in PO set

Mathematically the ideal vector $z^{ideal}$ can be defined as having
$$
z^{ideal}_i = \begin{align} \
\min \quad &f_i(x)\\
\text{s.t.} \quad &x\text{ is feasible}
\end{align}
$$
for all $i=1,\ldots,k$ (i.e., by **solving single-objective optimization problems, one for each objective**).
The nadir vector $z^{nadir}$ on the other hand has
$$
z^{nadir}_i =
\begin{align}
\max \quad &f_i(x)\\
\text{s.t.} \quad &x\text{ is Pareto optimal},
\end{align}
$$
for all $i=1,\ldots,k$ (**not as straightforward as calculating the ideal points for more than two objectives**).
## Optimization problem formulation
* By optimizing only one criterion, the rest are not considered
* Objective vs. constraint
* Summation of the objectives
* adding apples and oranges
* Converting the objectives (e.g. as costs)
* not easy, includes uncertainteis
* Multiobjective formulation reveals interdependences between the objectives
## Example
Consider multiobjective optimization problem
$$
\min \{f_1(x,y)=x^2+y,\quad f_2(x,y)=1-x\}\\
\text{s.t. }x\in[0,1], y\geq0.
$$
#### Pareto optimal solutions
Now, the set of Pareto optimal solutions is
$$
\{(x,0):x\in[0,1]\}.
$$
How to show this?
Let's show that $(x',0)$ is Pareto optimal for all $x'\in[0,1]$. *The idea of the proof: assume that $(x',0)$ is not Pareto optimal and then deduce a contradiction.*
Let's assume $(x,y)$ with $x\in[0,1]$ and $y\geq0$ such that
$$
\left\{
\begin{align}
f_1(x,y)=x^2+y\leq x'^2=f_1(x',0),\textbf{ and}\\
f_2(x,y)=1-x\leq 1-x'=f_2(x',0).
\end{align}
\right.
$$
and
$$
\left\{
\begin{align}
f_1(x,y)=x^2+y< x'^2 =f_1(x',0)\textbf{ or}\\
f_2(x,y)=1-x< 1-x'=f_2(x',0).
\end{align}
\right.
$$
Second inequality in the first system of inequalities gives $x\geq x'$. This yields from the first inequality in that same system of inequalities
$$
y\leq x'^2-x^2\leq 0.
$$
Thus, $y=0$. This means that $x=x'$ using again the first inequality.
This means that the solution cannot satisfy the second system of strict inequalities. We have a contradiction and, therefore, $(x',0)$ has to be Pareto optimal.
Now, we show that any other feasible solution can not be Pareto optimal. Let's assume a solution $(x,y)$, where $x\in[0,1]$ and $y>0$ and show that this is not Pareto optimal:
By choosing solution $(x,0)$, we have
$$
\left\{
\begin{align}
f_1(x,0)=x^2<x^2+y=f_1(x,y) ,\text{ and}\\
f_2(x,0)=1-x\leq 1-x=f_2(x,y).
\end{align}
\right.
$$
Thus, the solution $(x,y)$ cannot be Pareto optimal.
#### Ideal
Now
$$
\begin{align}
\min x^2+y\\
\text{s.t. }x\in[0,1],\ y\geq0
\end{align}
= 0
$$
and
$$
\begin{align}
\min 1-x\\
\text{s.t. }x\in[0,1],\ y\geq0
\end{align}
= 0.
$$
Thus, the ideal is
$$
z^{ideal} = (0,0)^T
$$
#### Nadir
Now,
$$
\begin{align}
\max x^2+y\\
\text{s.t. }x\in[0,1],\ y=0
\end{align}
= 1
$$
and
$$
\begin{align}
\max 1-x\\
\text{s.t. }x\in[0,1],\ y=0
\end{align}
= 1.
$$
Thus,
$$
z^{nadir}=(1,1)^T.
$$
# What means solving a multiobjective optimization problem?
* **Find all Pareto optimal solutions**
* As we learned in the previous lecture, there can be infinitely many Pareto optimal solutions for problems having real valued variables $\rightarrow$ extremely difficult and possible only in some simple special cases
* **Find a set of solutions that approximate the set of all Pareto optimal solutions**
* How to evaluate the goodness of the approximation? (closeness, spread, ...)
* The number of solutions required for a good approximation grows exponentially with the number of objectives!
* Works well with two objectives and, in some cases, for three objectives
* **Find a solution/solutions that best satisfies the preferences of a decision maker**
* Usually in practical problems one solution has to be finally selected for further analysis
* Sometimes, more than one (but not that many) are needed $\rightarrow$ e.g. choose best design for different types of cars to be manufactured (small and economic sedan, spacious vagon, efficient sports model, etc.)
* does not depend on the number of objectives
If you want to know more about the topic of this lecture, I urge you to read Professor Miettinen's book Nonlinear Multiobjective Optimization

## Scalarization
* One way to consider a multiobjective optimization problem is to convert it to a single objective subproblem whose solution is Pareto optimal for the original problem
* The subproblem is called a *scalarization* and it can be solved by using a suitable single objective optimization method
* By changing the values of the parameters in the scalarization, different (Pareto optimal) solutions can be computed
## Classification of methods
Methods for multiobjective optimization are often characterized by the involvement of the decision maker in the process.
The types of methods are
* **no preference methods**, where the decision maker does not play a role,
* **a priori methods**, where the decision maker gives his/her preference information at first and then the optimization method finds the best match to that preference information,
* **a posteriori methods**, where the optimization methods try to characterize all/find a good representation of the Pareto optimal solutions and the decision maker chooses the most preferred one of those,
* **interactive methods**, where the optimization method and the decision maker alternate in iterative search for the most preferred solution.
## Multiple Criteria Decision Making (MCDM)
* The related research field is called multiple criteria decision making
* More information in the website of the <a href="http://www.mcdmsociety.org/">International Society on MCDM</a>
## Our example problem for this lecture
We study a hypothetical decision problem of buying a car, when you can choose to have a car with power between (denoted by $p$) 50 and 200 kW and average consumption (denoted by $c$) per 100 km between 3 and 10 l. However, in addition to the average consumption and power, you need to decide the volume of the cylinders (v), which may be between 1000 $cm^3$ and 4000 $cm^3$. Finally, the price of the car follows now a function
$$
\left(\sqrt{\frac{p-50}{50}}\\
+\left(\frac{p-50}{50}\right)^2+0.3(10-c)\\ +10^{-5}\left(v-\left(1000+3000\frac{p-50}{150}\right)\right)^2\right)10000\\+5000
$$
in euros. This problem can be formulated as a multiobjective optimization problem
$$
\begin{align}
\min \quad & \{c,-p,P\},\\
\text{s.t. }\quad
&50\leq p\leq 200\\
&3\leq c\leq 10\\
&1000\leq v\leq 4000,\\
\text{where }\quad&P = \left(\sqrt{\frac{p-50}{50}}+\left(\frac{p-50}{50}\right)^2+0.3(10-c)\right.\\
& \left.+ 10^{-5}\left(v-\left(1000+3000\frac{p-50}{150}\right)\right)^2\right)10000+5000
\end{align}
$$
```
#Let us define a Python function which returns the value of this
import math
def car_problem(c,p,v):
# import pdb; pdb.set_trace()
return [#Objective function values
c,-p,
(math.sqrt((p-50.)/50.)+((p-50.)/50.)**2+
0.3*(10.-c)+0.00001*(v-(1000.+3000.*(p-50.)/150.))**2)*10000.
+5000.]
print("Car with 3 l/100km consumption, 50kW and 1000cm^3 engine would cost "
+str(car_problem(3,50,1000)[2])+"€")
print("Car with 3 l/100km consumption, 100kW and 2000cm^3 engine would cost "
+str(car_problem(3,100,2000)[2])+"€")
print("Car with 3 l/100km consumption, 100kW and 1000cm^3 engine would cost "
+str(car_problem(3,100,1000)[2])+"€")
```
## Normalization of the objectives
**In many of the methods, the normalization of the objectives is necessary.**
We can normalize the objectives using the nadir and ideal and setting the normalized objective as
$$ \tilde f_i = \frac{f_i-z_i^{ideal}}{z_i^{nadir}-z_i^{ideal}}$$
## Calculating the ideal
**Finding the ideal for problems is usually easy, if you can optimize the objective functions separately.**
For the car problem, ideal can be computed easily using the script:
```
#Calculating the ideal
from scipy.optimize import minimize
import ad
def calc_ideal(f):
ideal = [0]*3 #Because three objectives
solutions = [] #list for storing the actual solutions, which give the ideal
bounds = ((3,10),(50,200),(1000,4000)) #Bounds of the problem
starting_point = [3,50,1000]
for i in range(3):
res=minimize(
#Minimize each objective at the time
lambda x: f(x[0],x[1],x[2])[i], starting_point, method='SLSQP'
#Jacobian using automatic differentiation (note: SLSQP can estimate gradiants itself with some extra function evaluations)
#,jac=ad.gh(lambda x: f(x[0],x[1],x[2])[i])[0]
#bounds given above
,bounds = bounds
,options = {'disp':True, 'ftol': 1e-20, 'maxiter': 1000})
solutions.append(f(res.x[0],res.x[1],res.x[2]))
ideal[i]=res.fun
return ideal,solutions
ideal, solutions= calc_ideal(car_problem)
print ("ideal is "+str(ideal))
```
## Pay-off table method
**Finding the nadir value is however, usually much harder.**
Usually, the nadir value is estimated using the so-called pay-off table method.
The pay-off table method does not guarantee to find the exact nadir for problems with more than two objectives. <!--(One of your exercises this week will be to show this.)-->
The method is, however, a generally accepted way of approximating the nadir vector.
In the pay-off table method:
1. the objective values for attaining the individual minima are added in table
2. the nadir is estimated by each objectives maxima in the table.
3. the ideal values are located in the diagonal of the pay-off table

### $x^{(*,i)} =$ optimal solution for $f_i$
### The nadir for the car selection problem
The table now becomes by using the *solutions* that we returned while calculating the ideal
```
for solution in solutions:
print(solution)
```
Thus, the esimation of the nadir vector is
$$(10,-50,1033320.5080756888)$$
This is actually the real Nadir vector for this problem.
### Normalized car problem
```
#Let us define a Python function which returns the value of this
import math
def car_problem_normalized(c,p,v):
z_ideal = [3.0, -200.0, 5000]
z_nadir = [10,-50,1033320.5080756888]
z = car_problem(c,p,v)
return [(zi-zideali)/(znadiri-zideali) for
(zi,zideali,znadiri) in zip(z,z_ideal,z_nadir)]
```
<a href="https://docs.python.org/3.3/library/functions.html#zip">the zip function</a> in Python
```
print("Normalized value of the car problem at (3,50,1000) is "
+str(car_problem_normalized(3,50,1000)))
print("Normalized value of the car problem at (3,125,2500) is "
+str(car_problem_normalized(3,125,2500)))
print("Normalized value of the car problem at (10,100,1000) is "
+str(car_problem_normalized(10,100,1000)))
```
**So, value 1 now indicates the worst value on the Pareto frontier and value 0 indicates the best values**
Let's set the ideal and nadir for later reference:
```
z_ideal = [3.0, -200.0, 5000]
z_nadir = [10.,-50,1033320.5080756888]
```
**From now on, we will deal with the normalized problem, although, we write just $f$.** The aim of this is to simplify presentation.
| github_jupyter |
```
import pandas as pd
import os, sys
from sklearn.gaussian_process import GaussianProcessRegressor
import shapefile
from functools import partial
import pyproj
from shapely.geometry import shape, Point, mapping
from shapely.ops import transform
processeddir = "../data/processed/"
rawdir = "../data/raw/"
df = pd.read_csv(os.path.join(processeddir,"nyctaxiclean.csv"), dtype={"store_and_fwd_flag": "object"})
df["pickup_float"] = pd.to_datetime(df["pickup_datetime"]).apply(lambda x: x.timestamp())
df["pickup_datetime"] = pd.to_datetime(df["pickup_datetime"])
df["dropoff_datetime"] = pd.to_datetime(df["dropoff_datetime"])
df["pickup_datetime"] = pd.to_datetime(df["pickup_datetime"])
df["dropoff_datetime"] = pd.to_datetime(df["dropoff_datetime"])
df["trip_time_in_secs"].describe()
df["pickup_hour"] = df["pickup_datetime"].apply(lambda x: x.hour)
df["pickup_dayofweek"] = df["pickup_datetime"].apply(lambda x: x.weekday())
df["pickup_dayofmonth"] = df["pickup_datetime"].apply(lambda x: x.day)
from statsmodels.nonparametric.kernel_density import KDEMultivariate
from sklearn.model_selection import KFold
# 4 POC neighbourhoods
chosen_neighbourhoods = ["Upper East Side South", "Midtown Center", "Flatiron", "JFK Airport"]
filtered_df = df[df["pickup_neighbourhood"].isin(chosen_neighbourhoods)]
# as this dataset is not aggregated we can use random 4-fold CV
kf = KFold(n_splits=4, shuffle=True)
kde_models = []
x_models = []
likelihood = []
filtered_df = filtered_df[["pickup_hour", "pickup_dayofweek", "trip_time_in_secs"]]
x_df = filtered_df[["pickup_hour", "pickup_dayofweek"]]
for train_index, test_index in list(kf.split(filtered_df))[:2]:
train_df = filtered_df.iloc[train_index]
test_df = filtered_df.iloc[test_index][:100]
kde_models.append(KDEMultivariate(train_df, var_type='ooc'))
x_models.append(KDEMultivariate(x_df, var_type='oo'))
likelihood.append(np.exp(kde_models[-1].pdf(test_df))/np.exp(x_models[-1].pdf(test_df[["pickup_hour", "pickup_dayofweek"]])))
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
plt.plot(likelihood[0])
plt.title("Likelihood for trip time KDE")
plt.ylabel("Likelihood")
plt.xlabel("Test index")
#likelihood is sufficiently high for held out test set - 99-100%
#now assess some predictions
import numpy as np
triptime = np.linspace(0,960,25) #test up to 3rd percentile; no point assesing the long tail as
#we're looking for short trips here
x_data = [[4, x] for x in range(24)]
yx_data = np.asarray([[x+[y] for x in x_data] for y in triptime])
x_data = np.asarray(x_data)
kde_time = kde_models[-1]
x_model = x_models[-1]
probs = []
for i in range(len(yx_data)):
probs.append(np.exp(kde_time.cdf(yx_data[i])))
plt.plot(probs[18])
```
| github_jupyter |
# Graph
> in progress
- toc: true
- badges: true
- comments: true
- categories: [self-taught]
- image: images/bone.jpeg
- hide: true
https://towardsdatascience.com/using-graph-convolutional-neural-networks-on-structured-documents-for-information-extraction-c1088dcd2b8f
CNNs effectively capture patterns in data in Euclidean space
data is represented in the form of a Graph and lack a grid-like regularity.
As Graphs can be irregular, they may have a variable size of un-ordered nodes and each node may have a different number of neighbors, resulting in mathematical operations such as convolutions difficult to apply to the Graph domain.
Some examples of such non-Euclidean data include:
- Protein-Protein Interaction Data where interactions between molecules are modeled as graphs
- Citation Networks where scientific papers are nodes and citations are uni- or bi-directional edges
- Social Networks where people on the network are nodes and their relationships are edges
This article particularly discusses the use of Graph Convolutional Neural Networks (GCNs) on structured documents such as Invoices and Bills to automate the extraction of meaningful information by learning positional relationships between text entities.
What is a Graph?
**How to convert Structured Documents to Graphs?**
Such recurring structural information along with text attributes can help a Graph Neural Network learn neighborhood representations and perform node classification as a result
Geometric Algorithm: Connecting objects based on visibility
**Convolution on Document Graphs for Information Extraction**
# References
https://towardsdatascience.com/overview-of-deep-learning-on-graph-embeddings-4305c10ad4a4
Graph embedding
https://towardsdatascience.com/graph-convolutional-networks-for-geometric-deep-learning-1faf17dee008m
Graph Conv
https://arxiv.org/pdf/1611.08097.pdf
https://arxiv.org/pdf/1901.00596.pdf
https://towardsdatascience.com/graph-theory-and-deep-learning-know-hows-6556b0e9891b
**Everything you need to know about Graph Theory for Deep Learning**
Graph Theory — crash course
1. What is a graph?
A graph, in the context of graph theory, is a structured datatype that has nodes (entities that hold information) and edges (connections between nodes that can also hold information). A graph is a way of structuring data, but can be a datapoint itself. Graphs are a type of Non-Euclidean data, which means they exist in 3D, unlike other datatypes like images, text, and audio.
- Graphs can have labels on their edges and/or nodes
- Labels can also be considered weights, but that’s up to the graph’s designer.
- Labels don’t have to be numerical, they can be textual.
- Labels don’t have to be unique;
- Graphs can have features (a.k.a attributes).
Take care not to mix up features and labels.
> Note: a node is a person, a node’s label is a person’s name, and the node’s features are the person’s characteristics.
- Graphs can be directed or undirected
- A node in the graph can even have an edge that points/connects to itself. This is known as a self-loop.
Graphs can be either:
- Heterogeneous — composed of different types of nodes
- Homogeneous — composed of the same type of nodes
and are either:
- Static — nodes and edges do not change, nothing is added or taken away
- Dynamic — nodes and edges change, added, deleted, moved, etc.
graphs can be vaguely described as either
- Dense — composed of many nodes and edges
- Sparse — composed of fewer nodes and edges
Graphs can be made to look neater by turning them into their planar form, which basically means rearranging nodes such that edges don’t intersect
2. Graph Analysis
3. E-graphs — graphs on computers
https://medium.com/@flawnsontong1/what-is-geometric-deep-learning-b2adb662d91d
**What is Geometric Deep Learning?**
The vast majority of deep learning is performed on Euclidean data. This includes datatypes in the 1-dimensional and 2-dimensional domain.
Images, text, audio, and many others are all euclidean data.
`Non-euclidean data` can represent more complex items and concepts with more accuracy than 1D or 2D representation:
When we represent things in a non-euclidean way, we are giving it an inductive bias.
An inductive bias allows a learning algorithm to prioritize one solution (or interpretation) over another, independent of the observed data. Inductive biases can express assumptions about either the data-generating process or the space of solutions.
In the majority of current research pursuits and literature, the inductive bias that is used is relational.
Building on this intuition, `Geometric Deep Learning (GDL)` is the niche field under the umbrella of deep learning that aims to build neural networks that can learn from non-euclidean data.
The prime example of a non-euclidean datatype is a graph. `Graphs` are a type of data structure that consists of `nodes` (entities) that are connected with `edges` (relationships). This abstract data structure can be used to model almost anything.
We want to be able to learn from graphs because:
`
Graphs allow us to represent individual features, while also providing information regarding relationships and structure.
`
`Graph theory` is the study of graphs and what we can learn from them. There are various types of graphs, each with a set of rules, properties, and possible actions.
Examples of Geometric Deep Learning
- Molecular Modeling and learning:
One of the bottlenecks in computational chemistry, biology, and physics is the representation concepts, entities, and interactions. Our current methods of representing these concepts computationally can be considered “lossy”, since we lose a lot of valuable information. By treating atoms as nodes, and bonds as edges, we can save structural information that can be used downstream in prediction or classification.
- 3D Modeling and Learning
5 types of bias
https://twitter.com/math_rachel/status/1113203073051033600
https://arxiv.org/pdf/1806.01261.pdf
https://stackoverflow.com/questions/35655267/what-is-inductive-bias-in-machine-learning
| github_jupyter |
# All those moments will be los(s)t in time, like tears in rain.
> I am completely operational, and all my circuits are functioning perfectly.
- toc: true
- badges: true
- comments: true
- categories: [jupyter]
- image: images/posts/2020-12-10-Tears-In-Rain/Tears-In-Rain.jpg
```
#hide
!pip install -Uqq fastbook
import fastbook
fastbook.setup_book()
#hide
from fastai.vision.all import *
from fastbook import *
matplotlib.rc('image', cmap='Greys')
```
# Under the Hood: Training a Digit Classifier
This one is the big one. Now we have made it past the introduction of the course it is time to get under the hood and start implementing some of the functionality for ourselves. I am going to be taking quite thorough notes as I want to make sure I understand everything before I move onto Chapter 5.
So far all the heavy lifting has been done for us, the fastai library is a nice high level API written on top of PyTorch and abstracted in such a way that the "magic" / "obfuscation" is a little hard to determine what is actually happening. So in this chapter we will be making a hand written digit classifier, a simple classifier that can determine whether or not a 28px * 28px image of a hand written digit is either a **3** or a **7**. We will try to figure out a good baseline from which we can assess our model and then proceed to write out each element of the model in simple python, before seeing it all wrapped up in the nice and tidy fastai API.
## Pixels: The Foundations of Computer Vision
Here we are going to take a look at what we are actually dealing with when it comes to our hand written digits. Thankfully there is a great training set put together by Yann LeCun called the [MNIST](https://en.wikipedia.org/wiki/MNIST_database) or Modified National Institute of Standards and Technology database. It contains thousands of individual hand written digits that have been collated as 28px * 28px grayscale images. This is the data we will be using to build our classifier.
The team at fastai have made it simple to download and unzip the data we are going to use for this lesson. Instead of having to manually go to the [fastai datasets](https://course.fast.ai/datasets) documentation page, download the tar file, unzip it in a location accessible to your notebooks they have a handy [utility](https://github.com/fastai/fastai/blob/715c027b0ad8586feda09e29fb2b483dfe30c910/fastai/data/external.py) that will do all of that in single line of code:
```
path = untar_data(URLs.MNIST_SAMPLE)
#hide
Path.BASE_PATH = path
```
The have also added the UNIX [ls()](https://en.wikipedia.org/wiki/Ls) function to Python [path](https://docs.python.org/3/library/pathlib.html) to give a handy way to see what is in our directory. Here you can see we have our training and validation directory along with a label.csv file.
```
path.ls()
```
Inside each of the training and validation directories we have a folder which contains all of our **3's** and **7's** respectively
```
(path/'train').ls()
```
Now we can create a list of the file paths and store them in variables
```
threes = (path/'train'/'3').ls().sorted()
sevens = (path/'train'/'7').ls().sorted()
threes
```
Let's take a look at what we are working with. By indexing into the above **threes** list we can retrive the first path in the list. Using [PIL](https://pillow.readthedocs.io/en/stable/) the Python Imaging Library, we can display the data at that path.
```
im3_path = threes[1]
im3 = Image.open(im3_path)
im3
```
At this point it may not be entirely intuative what image information is. It is just an array of values for 0 to 255 for an 8-bit grayscale image like we have above. By casting into a Numpy array and taking a slice we can se what that might look like.
```
array(im3)[4:10,4:10]
```
As we have seen earlier in the course the PyTorch tensors have very similar functionality to Numpy arrays, but have the added benefit of being pushed to the GPU, this is a optimization and can be used in replacement of standard Numpy arrays. As a huge fan of Numpy my natural propensity is to use them all the time. But I think I need to reconsider . . .
```
tensor(im3)[4:10,4:10]
```
By loading the tensor into a Pandas Dataframe we are able to see what the pixel values look like by using the .background_gradients method
```
im3_t = tensor(im3)
df = pd.DataFrame(im3_t[4:15,4:22])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')
```

## First Try: Pixel Similarity
Before we start building our model we should consider if there are feasible alternatives to our problem. Working with Deep Learning is like weilding a very large hammer and every problem can appear to us as a nail. But for small self contained problem that do not require scale, simple alternatives are preferable. Here we are exploring an alternative to determine a baseline. What results can we achieve with a naive approach, is this sufficient to solve our problem and can they be improved by the use of a deep learning model. This is an important step, making sure that you are making headway on your problem is more important than having a shiny new model.
### Problem Statement
Can we create a simple baseline application that can classify an unseen 28px * 28px image of a **3** or a **7**. Theoretically, this is a simpler task than differentiating between a **3** and an **8** for example because both have similar curves at the top of the number and the bottom which might be difficult to disambiguate. If we try making a `mean` image from all the data in the **threes** folder and another for the **sevens** and compare the `pixel similarity` of an unseen image with this `mean` image we might be able to classify it with some manner of accuracy
### Process
Let's create two more arrays that store a tensor of each image in our **threes** and **sevens** folders.
```
seven_tensors = [tensor(Image.open(o)) for o in sevens]
three_tensors = [tensor(Image.open(o)) for o in threes]
len(three_tensors),len(seven_tensors)
```
In a similar way to the method above to cast our image to an array or tensor, we can use the fastai `show_image` method to take a tensor and display it as an image, this will be useful for debugging
```
show_image(three_tensors[1]);
```
Our next operation is to normalize the values of the images between 0 and 1, first we stack the images on top of one another using `torch.stack`, convert the integer values in the tensor stack to a float to ensure that values aren't rounded after our division operation, and then we divide the image by 255.
By looking at the shape of the torch tensor stack we can see that we have 6131 image tensors that have 28 rows and 28 columns
```
stacked_sevens = torch.stack(seven_tensors).float()/255
stacked_threes = torch.stack(three_tensors).float()/255
stacked_threes.shape
```
The length of the tensor.shape is the same as the tensor rank or number of dimensions, we can see that below by using the `ndim` method. This is a fast way of checking that your tensors have the correct rank before moving forward building your model or baseline
```
len(stacked_threes.shape)
stacked_threes.ndim
```
Now that we have all of our image tensors stack on top of one another and normalized, we can use the `mean` method to find the average. By passing in the argument 0, we are telling the operation to take the `mean` across the first axis. In this example this is the `mean` of the 6131 images.
```
mean3 = stacked_threes.mean(0)
show_image(mean3);
mean7 = stacked_sevens.mean(0)
show_image(mean7);
```
Now that we have our `mean` images, we can compare one of the images against them to see what the `pixel similarity` is and determine if the image is either a **3** or a **7**
```
a_3 = stacked_threes[1]
show_image(a_3);
```
### L1 and L2 norm
- Take the mean of the absolute value of differences (absolute value is the function that replaces negative values with positive values). This is called the mean absolute difference or L1 norm
- Take the mean of the square of differences (which makes everything positive) and then take the square root (which undoes the squaring). This is called the root mean squared error (RMSE) or L2 norm.
To determine the `pixel similarity` of our test image and our mean image we are going to use the `mean absolte difference` or the `L1 Norm` and the `root mean squared error` or the `L2 Norm`.
If we were simply going to subtract one for the other we could end up with negative values, which once averaged would negate positive values and give us inconcluse information. By comparing the test image againt the mean of the **3's** and the mean of the **7's** we can see that error is lower when comparing to the mean of the **3's** giving us a classification that this image is of a **3**
```
dist_3_abs = (a_3 - mean3).abs().mean()
dist_3_sqr = ((a_3 - mean3)**2).mean().sqrt()
dist_3_abs,dist_3_sqr
dist_7_abs = (a_3 - mean7).abs().mean()
dist_7_sqr = ((a_3 - mean7)**2).mean().sqrt()
dist_7_abs,dist_7_sqr
```
Here we can see by using the `l1_loss` and the `mse_loss` methods we are getting the same answers our implementations above
```
F.l1_loss(a_3.float(),mean7), F.mse_loss(a_3,mean7).sqrt()
```
## Computing Metrics Using Broadcasting
At this point we could simply use a loop and iterate through each of the images in the validation set, calculate the `L1` loss for each image and determine whether or not our baseline application determines the number to be a **3** or a **7**, check the prediction against and determine an accuracy. This would take a very long time and wouldn't make use of the GPU accelleration needed for Deep Learning.
Here we are going to look at the secret sauce that makes Python (an interpreted language) powerful enough to be used in Deep Learning applications. What is that secret sauce you ask? `Broadcasting`
So lets start by stacking the images from our validation directories in the same way we did with our training images. We will normalize them and check the shape of the tensor stack
```
valid_3_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'3').ls()])
valid_3_tens = valid_3_tens.float()/255
valid_7_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'7').ls()])
valid_7_tens = valid_7_tens.float()/255
valid_3_tens.shape,valid_7_tens.shape
```
Here we are going to write our `L1 Norm` in the form of a function, here taking the mean across the rows and columns of the absolute difference of the tow images.
```
def mnist_distance(a,b): return (a-b).abs().mean((-1,-2))
mnist_distance(a_3, mean3)
```
But by using `Broadcasting`, we can instead use our entire tensor stack and compare it against the `mean` image of the **3** all at once. What is happening under the hood is that PyTorch is making a "virtual" copy of the mean image tensor for every image tensor in the validation stack so it can determine the `pixel similarity` for all of them at once. What it returns is a tensor of all of the results.
```
valid_3_dist = mnist_distance(valid_3_tens, mean3)
valid_3_dist, valid_3_dist.shape
```
Now lets create a simple definition to determine if the prediction is a **3** if the result is `False` then we assume that the image is classified as a **7**
If the `mnist_distance` measured againt the `mean` **3** is lower than the `mean` **7** then the function will return `True`
```
def is_3(x): return mnist_distance(x,mean3) < mnist_distance(x,mean7)
```
Here by passing in our test image we can see that it returns `True`, but by casting it to a float we can get a value instead
```
is_3(a_3), is_3(a_3).float()
```
Taking advantage of `Broadcasting` we can pass the entire tensor stack to the function and we get back an array of predictions
```
is_3(valid_3_tens)
```
Lets check the accuracy of our classification application. We are expecting every image tensor in the `valid_3_tens` tensor to return true and all the image tensors in the `valid_7_tens` tensor to return false. We can convert them to a floating point value and take the `mean` to determine the accuracy
```
accuracy_3s = is_3(valid_3_tens).float() .mean()
accuracy_7s = (1 - is_3(valid_7_tens).float()).mean()
accuracy_3s,accuracy_7s,(accuracy_3s+accuracy_7s)/2
```
Wow! It looks like our naive `pixel similarity` application gives us a **95%** accuracy on this task!
We have only used PyTorch for its power tensor operations in this task and proven that with a simple baseline we can determine a highly accurate classifier. Let's see if making a Deep Learning model we can improve the accuracy even further!
## Stochastic Gradient Descent (SGD)
Up until this point we have a classifier but it really does follow the description by Arthur Samuel
**Suppose we arrange for some automatic means of testing the effectiveness of any current weight assignment in terms of actual performance and provide a mechanism for altering the weight assignment so as to maximize the performance. We need not go into the details of such a procedure to see that it could be made entirely automatic and to see that a machine so programmed would "learn" from its experience.**
To turn our function into a machine learning classifier we will need:
- Initialize the weights.
- For each image, use these weights to predict whether it appears to be a 3 or a 7.
- Based on these predictions, calculate how good the model is (its loss).
- Calculate the gradient, which measures for each weight, how changing that weight would change the loss
- Step (that is, change) all the weights based on that calculation.
- Go back to the step 2, and repeat the process.
- Iterate until you decide to stop the training process (for instance, because the model is good enough or you don't want to wait any longer).
```
gv('''
init->predict->loss->gradient->step->stop
step->predict[label=repeat]
''')
```

To understand `SGD` a little better lets start with a simpler example using this quadratic function:
```
def f(x): return x**2
```
Let's plot what that function looks like:
```
plot_function(f, 'x', 'x**2')
```
The sequence of steps we described earlier starts by picking some random value for a parameter, and calculating the value of the loss:
```
plot_function(f, 'x', 'x**2')
plt.scatter(-1.5, f(-1.5), color='red');
```
Now we look to see what would happen if we increased or decreased our parameter by a little bit—the adjustment. This is simply the slope at a particular point:

We can change our weight by a little in the direction of the slope, calculate our loss and adjustment again, and repeat this a few times. Eventually, we will get to the lowest point on our curve:

This basic idea goes all the way back to Isaac Newton, who pointed out that we can optimize arbitrary functions in this way
### Calculating Gradients
*This is a lot of text from this portion of the book, its **really** important and I getting it right is paramount*
"The one magic step is the bit where we calculate the gradients. As we mentioned, we use calculus as a performance optimization; it allows us to more quickly calculate whether our loss will go up or down when we adjust our parameters up or down. In other words, the gradients will tell us how much we have to change each weight to make our model better."
Thankfully PyTorch is a very powerful auto-differential library. It utilises the [Chain Rule](https://medium.com/machine-learning-and-math/deep-learning-and-chain-rule-of-calculus-80896a1e91f9) to [calculate the derivative](https://pytorch.org/docs/stable/notes/autograd.html) of our functions.
First, let's pick a tensor value which we want gradients at:
```
xt = tensor(3.).requires_grad_()
```
Notice the special method requires_grad_? That's the magical incantation we use to tell PyTorch that we want to calculate gradients with respect to that variable at that value. It is essentially tagging the variable, so PyTorch will remember to keep track of how to compute gradients of the other, direct calculations on it that you will ask for.
This API might throw you off if you're coming from math or physics. In those contexts the "gradient" of a function is just another function (i.e., its derivative), so you might expect gradient-related APIs to give you a new function. **But in deep learning, "gradients" usually means the value of a function's derivative at a particular argument value**. The PyTorch API also puts the focus on the argument, not the function you're actually computing the gradients of. It may feel backwards at first, but it's just a different perspective.
Now we calculate our function with that value. Notice how PyTorch prints not just the value calculated, but also a note that it has a gradient function it'll be using to calculate our gradients when needed:
```
yt = f(xt)
yt
```
Calculating the derivative value of our function at this input tensor is simple, we just call the `backward` method.
```
yt.backward()
```
The "backward" here refers to backpropagation, which is the name given to the process of calculating the derivative of each layer.
We can now view the gradients by checking the grad attribute of our tensor:
```
xt.grad
```
If you remember your high school calculus rules, the derivative of x***2 is 2*x, and we have x=3, so the gradients should be 2*3=6, which is what PyTorch calculated for us!
Now we'll repeat the preceding steps, but with a vector argument for our function:
```
xt = tensor([3.,4.,10.]).requires_grad_()
xt
```
And we'll add sum to our function so it can take a vector (i.e., a rank-1 tensor), and return a scalar (i.e., a rank-0 tensor):
```
def f(x): return (x**2).sum()
yt = f(xt)
yt
```
Our gradients are 2*xt, as we'd expect!
```
yt.backward()
xt.grad
```
The gradients only tell us the slope of our function, they don't actually tell us exactly how far to adjust the parameters. But it gives us some idea of how far; if the slope is very large, then that may suggest that we have more adjustments to do, whereas if the slope is very small, that may suggest that we are close to the optimal value.
### Stepping With a Learning Rate
Because our gradient only shows the slope, or the direction, in which we need to change our parameters. We will need to figure out how much we move in this direction. This is where we introduce the learning rate. The learning rate is often a number between 0.001 and 0.1, although it could be anything.
Once you've picked a learning rate, you can adjust your parameters using this simple function:
```
w -= gradient(w) * lr
```
If you pick a learning rate that's too low, it can mean having to do a lot of steps

But picking a learning rate that's too high is even worse—it can actually result in the loss getting worse

If the learning rate is too high, it may also "bounce" around, rather than actually diverging

### An End-to-End SGD Example
Let's work through a practical example from end-to-end. First we will make a float tensor that represents our time variable. Each index is a time in seconds
```
time = torch.arange(0,20).float(); time
```
Here we create a quadratic function, a function of the form a*(time***2)+(b*time)+c, and add some noiose to simulate realworld measurments
```
speed = torch.randn(20)*3 + 0.75*(time-9.5)**2 + 1
plt.scatter(time,speed);
```
We want to distinguish clearly between the function's input (the time when we are measuring the coaster's speed) and its parameters (the values that define which quadratic we're trying). So, let's collect the parameters in one argument and thus separate the input, t, and the parameters, params, in the function's signature:
```
def f(t, params):
a,b,c = params
return a*(t**2) + (b*t) + c
```
We need to determine which loss function we would like to use. For continuous data, it's common to use mean squared error:
```
def mse(preds, targets): return ((preds-targets)**2).mean().sqrt()
```
#### Step 1: Initialize the parameters
First thing we want to do is create a tensor for our parameters and to tell PyTorch that this tensor `requires_grad_()`.
```
params = torch.randn(3).requires_grad_()
#hide
orig_params = params.clone()
```
#### Step 2: Calculate the predictions
Lets pass our time tensor and our params into our function
```
preds = f(time, params)
```
Here we are creating a small matplotlib function to show a comparison between our predictions and our observations
```
def show_preds(preds, ax=None):
if ax is None: ax=plt.subplots()[1]
ax.scatter(time, speed)
ax.scatter(time, to_np(preds), color='red')
ax.set_ylim(-300,100)
show_preds(preds)
```
#### Step 3: Calculate the loss
Now we can use our `L2` or `RMSE` function to determine our loss
```
loss = mse(preds, speed)
loss
```
#### Step 4: Calculate the gradients
By performing `Back Propogation` with our `backward()` method on the loss, we can calculate the slope of our gradient and which direction the we need to move in to improve our loss
```
loss.backward()
params.grad
```
Here we use a small learning rate and multiply that to our parameter's gradient to make sure we move towards the optimal solution over each iteration
```
params.grad * 1e-5
params
```
#### Step 5: Step the weights.
```
lr = 1e-5
params.data -= lr * params.grad.data
params.grad = None
```
**Understanding this bit depends on remembering recent history. To calculate the gradients we call backward on the loss. But this loss was itself calculated by mse, which in turn took preds as an input, which was calculated using f taking as an input params, which was the object on which we originally called required_grads_—which is the original call that now allows us to call backward on loss. This chain of function calls represents the mathematical composition of functions, which enables PyTorch to use calculus's chain rule under the hood to calculate these gradients.**
```
preds = f(time,params)
mse(preds, speed)
show_preds(preds)
```
Here we simply wrap our previous steps into a function
- Make a prediction
- Calculate the loss
- Perform back propogation on the loss, see above for details
- Apply the learning rate
- Zero our gradients
- Return our predictions
```
def apply_step(params, prn=True):
preds = f(time, params)
loss = mse(preds, speed)
loss.backward()
params.data -= lr * params.grad.data
params.grad = None
if prn: print(loss.item())
return preds
```
#### Step 6: Repeat the process
Now we simply call our `apply_step` function a number of times, as we can see our loss improves each iteration
```
for i in range(10): apply_step(params)
#hide
params = orig_params.detach().requires_grad_()
_,axs = plt.subplots(1,4,figsize=(12,3))
for ax in axs: show_preds(apply_step(params, False), ax)
plt.tight_layout()
```
#### Step 7: stop
Either we can stop after a certain accuracy or simply after a number of iterations
### Summarizing Gradient Descent
```
gv('''
init->predict->loss->gradient->step->stop
step->predict[label=repeat]
''')
```

- Initialize the weights.
- For each image, use these weights to predict whether it appears to be a 3 or a 7.
- Based on these predictions, calculate how good the model is (its loss).
- Calculate the gradient, which measures for each weight, how changing that weight would change the loss
- Step (that is, change) all the weights based on that calculation.
- Go back to the step 2, and repeat the process.
- Iterate until you decide to stop the training process (for instance, because the model is good enough or you don't want to wait any longer).
To summarize, at the beginning, the weights of our model can be random (training from scratch) or come from a pretrained model (transfer learning). In the first case, the output we will get from our inputs won't have anything to do with what we want, and even in the second case, it's very likely the pretrained model won't be very good at the specific task we are targeting. So the model will need to learn better weights.
We begin by comparing the outputs the model gives us with our targets (we have labeled data, so we know what result the model should give) using a loss function, which returns a number that we want to make as low as possible by improving our weights. To do this, we take a few data items (such as images) from the training set and feed them to our model. We compare the corresponding targets using our loss function, and the score we get tells us how wrong our predictions were. We then change the weights a little bit to make it slightly better.
To find how to change the weights to make the loss a bit better, we use calculus to calculate the gradients. (Actually, we let PyTorch do it for us!) Let's consider an analogy. Imagine you are lost in the mountains with your car parked at the lowest point. To find your way back to it, you might wander in a random direction, but that probably wouldn't help much. Since you know your vehicle is at the lowest point, you would be better off going downhill. By always taking a step in the direction of the steepest downward slope, you should eventually arrive at your destination. We use the magnitude of the gradient (i.e., the steepness of the slope) to tell us how big a step to take; specifically, we multiply the gradient by a number we choose called the learning rate to decide on the step size. We then iterate until we have reached the lowest point, which will be our parking lot, then we can stop.
## The MNIST Loss Function
Now we have seen how the mothod works on a simple function, we can now put this into practice on our MNIST **3's** and **7's** problem. As we have our dependent variable x:
Remember:
- **Dependent Variable** == input variables
- **Independent Varibale** == output variables
Our dependent variable in this is example are the images themselves. Here we concatinate the stacked image tensors of the **3's** and the **7's**. Having the image as Matrix is irrelevant we can use the Pytorch `view` method to reshape every tensor to rank 1,
```
train_x = torch.cat([stacked_threes, stacked_sevens]).view(-1, 28*28)
```
We also need a label for each of the images, here we can simply create a tensor by combining an array of 1's of length of the number of **3's** and an array of 0's the length of the number of **7's**. We use the PyTorch function `unsqueeze` to transpose the tensor from a vector with 123396 elements into a tensor with 12396 rows and a single column
```
train_y = tensor([1]*len(threes) + [0]*len(sevens)).unsqueeze(1)
train_x.shape,train_y.shape
```
Now we need to create a dataset, a dataset needs to be able to be indexable, and at that index we expect a tuple (data, label). Here we are using the python `zip` function to take the `train_x` and `train_y` varibles and combine them into a tuple at each index as described
```
dset = list(zip(train_x,train_y))
x,y = dset[0]
x.shape,y
```
We need to do the same operations above for our validation set as well
- Concatinate the images and reshape
- Create labels and unsqueeze
- Zip data and label into dataset
```
valid_x = torch.cat([valid_3_tens, valid_7_tens]).view(-1, 28*28)
valid_y = tensor([1]*len(valid_3_tens) + [0]*len(valid_7_tens)).unsqueeze(1)
valid_dset = list(zip(valid_x,valid_y))
```
Here is a simple function that will initialize our parameters with random values. PyTorch `randn` returns a tensor the shape and size of its argument with normalized values between 0 and 1. We can use a variance argument here to scale the random values if necessary, but not in this example. We want to be able to calculate the gradient of this tensor, so we use the `requires_grad` method
```
def init_params(size, std=1.0): return (torch.randn(size)*std).requires_grad_()
```
We create and initialize our weights and bias variables
```
weights = init_params((28*28,1))
bias = init_params(1)
```
In neural networks, the w in the equation y=w*x+b is called the weights, and the b is called the bias. Together, the weights and bias make up the parameters.
We can now calculate a prediction for one image:
```
(train_x[0]*weights.T).sum() + bias
```
While we could use a Python for loop to calculate the prediction for each image, that would be very slow. Because Python loops don't run on the GPU, and because Python is a slow language for loops in general, we need to represent as much of the computation in a model as possible using higher-level functions.
In this case, there's an extremely convenient mathematical operation that calculates w*x for every row of a matrix—it's called matrix multiplication.

In Python, matrix multiplication is represented with the @ operator. Let's try it:
```
def linear1(xb): return xb@weights + bias
preds = linear1(train_x)
preds
```
Lets check how good our random initialization is. Here is make a determination that if a prediction is over 0 it's a **3** else its a **7** and we compare it against our labels
```
corrects = (preds>0.0).float() == train_y
corrects
```
As you can see, and could have predicted, a random initilization is correct roughly 50% of the time.
```
corrects.float().mean().item()
```
So lets change one of our parameters a little bit and see if that changes our result
```
weights[0] *= 1.0001
preds = linear1(train_x)
((preds>0.0).float() == train_y).float().mean().item()
```
As we can see above changing one parameter a little has absolutely no affect on the results of our network. What does this mean practically?
By changing this pixel by some small amount is not sufficient in itself to change the prediction of an image from a **3** to a **7**
Becaue there is no change we cannot calculate a gradient and we cannot make a step to improve our predictions. This is because of the thresholding in our determining our correctness.
**In mathematical terms, accuracy is a function that is constant almost everywhere (except at the threshold, 0.5), so its derivative is nil almost everywhere (and infinity at the threshold). This then gives gradients that are 0 or infinite, which are useless for updating the model.**
So how do we fix this?
```
trgts = tensor([1,0,1])
prds = tensor([0.9, 0.4, 0.2])
```
Here's a first try at a loss function that measures the distance between predictions and targets:
```
def mnist_loss(predictions, targets):
return torch.where(targets==1, 1-predictions, predictions).mean()
```
**Read the Docs: It's important to learn about PyTorch functions like this, because looping over tensors in Python performs at Python speed, not C/CUDA speed! Try running help(torch.where) now to read the docs for this function, or, better still, look it up on the PyTorch documentation site.**
```
torch.where(trgts==1, 1-prds, prds)
```
You can see that this function returns a lower number when predictions are more accurate, when accurate predictions are more confident (higher absolute values), and when inaccurate predictions are less confident. In PyTorch, we always assume that a lower value of a loss function is better. Since we need a scalar for the final loss, mnist_loss takes the mean of the previous tensor:
```
mnist_loss(prds,trgts)
```
For instance, if we change our prediction for the one "false" target from 0.2 to 0.8 the loss will go down, indicating that this is a better prediction:
```
mnist_loss(tensor([0.9, 0.4, 0.8]),trgts)
```
One problem with mnist_loss as currently defined is that it assumes that predictions are always between 0 and 1. We need to ensure, then, that this is actually the case! As it happens, there is a function that does exactly that—let's take a look.
### Sigmoid
The sigmoid function always outputs a number between 0 and 1. It's defined as follows:
```
def sigmoid(x): return 1/(1+torch.exp(-x))
plot_function(torch.sigmoid, title='Sigmoid', min=-4, max=4)
```
As you can see, it takes any input value, positive or negative, and smooshes it onto an output value between 0 and 1. It's also a smooth curve that only goes up, which makes it easier for SGD to find meaningful gradients.
Let's update mnist_loss to first apply sigmoid to the inputs:
```
def mnist_loss(predictions, targets):
predictions = predictions.sigmoid()
return torch.where(targets==1, 1-predictions, predictions).mean()
```
### SGD and Mini-Batches
In the context of SGD, "Minibatch" means that the gradient is calculated across the entire batch before updating weights. If you are not using a "minibatch", every training example in a "batch" updates the learning algorithm's parameters independently.
```
coll = range(15)
dl = DataLoader(coll, batch_size=5, shuffle=True)
list(dl)
ds = L(enumerate(string.ascii_lowercase))
ds
dl = DataLoader(ds, batch_size=6, shuffle=True)
list(dl)
```
## Putting It All Together
First, let's re-initialize our parameters:
```
weights = init_params((28*28,1))
bias = init_params(1)
```
A DataLoader can be created from a Dataset and we can set our bacth size here:
```
dl = DataLoader(dset, batch_size=256)
xb,yb = first(dl)
xb.shape,yb.shape
```
We'll do the same for the validation set:
```
valid_dl = DataLoader(valid_dset, batch_size=256)
```
Let's create a mini-batch of size 4 for testing:
```
batch = train_x[:4]
batch.shape
preds = linear1(batch)
preds
loss = mnist_loss(preds, train_y[:4])
loss
```
Now we can calculate the gradients:
```
loss.backward()
weights.grad.shape,weights.grad.mean(),bias.grad
```
Let's put this into a function:
```
def calc_grad(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
```
But look what happens if we call it twice:
```
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad
```
The gradients have changed! The reason for this is that loss.backward actually adds the gradients of loss to any gradients that are currently stored. So, we have to set the current gradients to 0 first:
```
weights.grad.zero_()
bias.grad.zero_();
```
**Inplace Operations: Methods in PyTorch whose names end in an underscore modify their objects in place. For instance, bias.zero_() sets all elements of the tensor bias to 0.**
Our only remaining step is to update the weights and biases based on the gradient and learning rate. When we do so, we have to tell PyTorch not to take the gradient of this step too—otherwise things will get very confusing when we try to compute the derivative at the next batch!
**If we assign to the data attribute of a tensor then PyTorch will not take the gradient of that step. Here's our basic training loop for an epoch:**
```
def train_epoch(model, lr, params):
for xb,yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_()
```
We also want to check how we're doing, by looking at the accuracy of the validation set. To decide if an output represents a 3 or a 7, we can just check whether it's greater than 0. So our accuracy for each item can be calculated (using broadcasting, so no loops!) with:
```
(preds>0.0).float() == train_y[:4]
```
That gives us this function to calculate our validation accuracy:
```
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds>0.5) == yb
return correct.float().mean()
batch_accuracy(linear1(batch), train_y[:4])
```
and then put the batches together:
```
def validate_epoch(model):
accs = [batch_accuracy(model(xb), yb) for xb,yb in valid_dl]
return round(torch.stack(accs).mean().item(), 4)
validate_epoch(linear1)
```
That's our starting point. Let's train for one epoch, and see if the accuracy improves:
```
lr = 1.
params = weights,bias
train_epoch(linear1, lr, params)
validate_epoch(linear1)
```
Then do a few more:
```
for i in range(20):
train_epoch(linear1, lr, params)
print(validate_epoch(linear1), end=' ')
```
Looking good! We're already about at the same accuracy as our "pixel similarity" approach, and we've created a general-purpose foundation we can build on. Our next step will be to create an object that will handle the SGD step for us. In PyTorch, it's called an optimizer.
### Creating an Optimizer
PyTorch's `nn.Linear` does the same thing as our init_params and linear together. It contains both the weights and biases in a single class. Here's how we replicate our model from the previous section:
```
linear_model = nn.Linear(28*28,1)
```
Every PyTorch module knows what parameters it has that can be trained; they are available through the parameters method:
```
w,b = linear_model.parameters()
w.shape,b.shape
```
Now, let's create an optimizer:
```
class BasicOptim:
def __init__(self,params,lr): self.params,self.lr = list(params),lr
def step(self, *args, **kwargs):
for p in self.params: p.data -= p.grad.data * self.lr
def zero_grad(self, *args, **kwargs):
for p in self.params: p.grad = None
```
We can create our optimizer by passing in the model's parameters:
```
opt = BasicOptim(linear_model.parameters(), lr)
def train_epoch(model):
for xb,yb in dl:
calc_grad(xb, yb, model)
opt.step()
opt.zero_grad()
validate_epoch(linear_model)
def train_model(model, epochs):
for i in range(epochs):
train_epoch(model)
print(validate_epoch(model), end=' ')
train_model(linear_model, 20)
```
fastai provides the SGD class which, by default, does the same thing as our BasicOptim:
```
linear_model = nn.Linear(28*28,1)
opt = SGD(linear_model.parameters(), lr)
train_model(linear_model, 20)
```
fastai also provides Learner.fit, which we can use instead of train_model. To create a Learner we first need to create a DataLoaders, by passing in our training and validation DataLoaders:
```
dls = DataLoaders(dl, valid_dl)
```
To create a Learner without using an application (such as cnn_learner) we need to pass in all the elements that we've created in this chapter: the DataLoaders, the model, the optimization function (which will be passed the parameters), the loss function, and optionally any metrics to print:
```
learn = Learner(dls, nn.Linear(28*28,1), opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)
learn.fit(10, lr=lr)
```
## Adding a Nonlinearity
So far we have a general procedure for optimizing the parameters of a function, and we have tried it out on a very boring function: a simple linear classifier. A linear classifier is very constrained in terms of what it can do. To make it a bit more complex (and able to handle more tasks), we need to add something nonlinear between two linear classifiers—this is what gives us a neural network.
Here is the entire definition of a basic neural network:
```
def simple_net(xb):
res = xb@w1 + b1
res = res.max(tensor(0.0))
res = res@w2 + b2
return res
```
That's it! All we have in simple_net is two linear classifiers with a max function between them.
Here, w1 and w2 are weight tensors, and b1 and b2 are bias tensors; that is, parameters that are initially randomly initialized, just like we did in the previous section:
```
w1 = init_params((28*28,30))
b1 = init_params(30)
w2 = init_params((30,1))
b2 = init_params(1)
```
The key point about this is that w1 has 30 output activations (which means that w2 must have 30 input activations, so they match). That means that the first layer can construct 30 different features, each representing some different mix of pixels. You can change that 30 to anything you like, to make the model more or less complex.
That little function res.max(tensor(0.0)) is called a rectified linear unit, also known as ReLU. We think we can all agree that rectified linear unit sounds pretty fancy and complicated... But actually, there's nothing more to it than res.max(tensor(0.0))—in other words, replace every negative number with a zero. This tiny function is also available in PyTorch as F.relu:
```
plot_function(F.relu)
```
**Mathematically, we say the composition of two linear functions is another linear function. So, we can stack as many linear classifiers as we want on top of each other, and without nonlinear functions between them, it will just be the same as one linear classifier.**
```
simple_net = nn.Sequential(
nn.Linear(28*28,30),
nn.ReLU(),
nn.Linear(30,1)
)
```
nn.Sequential creates a module that will call each of the listed layers or functions in turn.
nn.ReLU is a PyTorch module that does exactly the same thing as the F.relu function. Most functions that can appear in a model also have identical forms that are modules. Generally, it's just a case of replacing F with nn and changing the capitalization. When using nn.Sequential, PyTorch requires us to use the module version. Since modules are classes, we have to instantiate them, which is why you see nn.ReLU() in this example.
Because nn.Sequential is a module, we can get its parameters, which will return a list of all the parameters of all the modules it contains. Let's try it out! As this is a deeper model, we'll use a lower learning rate and a few more epochs.
```
learn = Learner(dls, simple_net, opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)
learn.fit(40, 0.1)
plt.plot(L(learn.recorder.values).itemgot(2));
```
And we can view the final accuracy:
```
learn.recorder.values[-1][2]
```
At this point we have something that is rather magical:
A function that can solve any problem to any level of accuracy (the neural network) given the correct set of parameters
A way to find the best set of parameters for any function (stochastic gradient descent)
### Going Deeper
Here what happens when we train an 18-layer model . . .
```
dls = ImageDataLoaders.from_folder(path)
learn = cnn_learner(dls, resnet18, pretrained=False,
loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(1, 0.1)
```
Almost 100% accuracy!
## Jargon Recap
- **ReLU :** Function that returns 0 for negative numbers and doesn't change positive numbers.
- **Mini-batch :** A small group of inputs and labels gathered together in two arrays. A gradient descent step is updated on this batch (rather than a whole epoch).
- **Forward pass :** Applying the model to some input and computing the predictions.
- **Loss :** A value that represents how well (or badly) our model is doing.
- **Gradient :** The derivative of the loss with respect to some parameter of the model.
- **Backward pass :** Computing the gradients of the loss with respect to all model parameters.
- **Gradient descent :** Taking a step in the directions opposite to the gradients to make the model parameters a little bit better.
- **Learning rate :** The size of the step we take when applying SGD to update the parameters of the model.
## Questionnaire
**How is a grayscale image represented on a computer? How about a color image?**
Images are represented by arrays with pixel values representing the content of the image. For greyscale images, a 2-dimensional array is used with the pixels representing the greyscale values, with a range of 256 integers. A value of 0 would represent white, and a value of 255 represents black, and different shades of greyscale in between. For color images, three color channels (red, green, blue) are typicall used, with a separate 256-range 2D array used for each channel. A pixel value of 0 again represents white, with 255 representing solid red, green, or blue. The three 2-D arrays form a final 3-D array (rank 3 tensor) representing the color image.
**How are the files and folders in the `MNIST_SAMPLE` dataset structured? Why?**
There are two subfolders, train and valid, the former contains the data for model training, the latter contains the data for validating model performance after each training step. Evaluating the model on the validation set serves two purposes: a) to report a human-interpretable metric such as accuracy (in contrast to the often abstract loss functions used for training), b) to facilitate the detection of overfitting by evaluating the model on a dataset it hasn’t been trained on (in short, an overfitting model performs increasingly well on the training set but decreasingly so on the validation set). Of course, every practicioner could generate their own train/validation-split of the data. Public datasets are usually pre-split to simplifiy comparing results between implementations/publications.
Each subfolder has two subsubfolders 3 and 7 which contain the .jpg files for the respective class of images. This is a common way of organizing datasets comprised of pictures. For the full MNIST dataset there are 10 subsubfolders, one for the images for each digit.
**Explain how the "pixel similarity" approach to classifying digits works.**
In the “pixel similarity” approach, we generate an archetype for each class we want to identify. In our case, we want to distinguish images of 3’s from images of 7’s. We define the archetypical 3 as the pixel-wise mean value of all 3’s in the training set. Analoguously for the 7’s. You can visualize the two archetypes and see that they are in fact blurred versions of the numbers they represent.
In order to tell if a previously unseen image is a 3 or a 7, we calculate its distance to the two archetypes (here: mean pixel-wise absolute difference). We say the new image is a 3 if its distance to the archetypical 3 is lower than two the archetypical 7.
**What is a list comprehension? Create one now that selects odd numbers from a list and doubles them.**
Lists (arrays in other programming languages) are often generated using a for-loop. A list comprehension is a Pythonic way of condensing the creation of a list using a for-loop into a single expression. List comprehensions will also often include if clauses for filtering.
```
lst_in = range(10)
lst_out = [2*el for el in lst_in if el%2==1]
# is equivalent to:
lst_out = []
for el in lst_in:
if el%2==1:
lst_out.append(2*el)
```
**What is a "rank-3 tensor"?**
The rank of a tensor is the number of dimensions it has. An easy way to identify the rank is the number of indices you would need to reference a number within a tensor. A scalar can be represented as a tensor of rank 0 (no index), a vector can be represented as a tensor of rank 1 (one index, e.g., v[i]), a matrix can be represented as a tensor of rank 2 (two indices, e.g., a[i,j]), and a tensor of rank 3 is a cuboid or a “stack of matrices” (three indices, e.g., b[i,j,k]). In particular, the rank of a tensor is independent of its shape or dimensionality, e.g., a tensor of shape 2x2x2 and a tensor of shape 3x5x7 both have rank 3.
Note that the term “rank” has different meanings in the context of tensors and matrices (where it refers to the number of linearly independent column vectors).
**What is the difference between tensor rank and shape? How do you get the rank from the shape?**
Rank is the number of axes or dimensions in a tensor; shape is the size of each axis of a tensor.
**How do you get the rank from the shape?**
The length of a tensor’s shape is its rank.
So if we have the images of the 3 folder from the MINST_SAMPLE dataset in a tensor called stacked_threes and we find its shape like this.
```
stacked_threes.shape
```
torch.Size([6131, 28, 28])
We just need to find its length to know its rank. This is done as follows.
```
len(stacked_threes.shape)
```
3
You can also get a tensor’s rank directly with ndim .
```
stacked_threes.ndim
```
3
**What are RMSE and L1 norm?**
Root mean square error (RMSE), also called the L2 norm, and mean absolute difference (MAE), also called the L1 norm, are two commonly used methods of measuring “distance”. Simple differences do not work because some difference are positive and others are negative, canceling each other out. Therefore, a function that focuses on the magnitudes of the differences is needed to properly measure distances. The simplest would be to add the absolute values of the differences, which is what MAE is. RMSE takes the mean of the square (makes everything positive) and then takes the square root (undoes squaring).
**How can you apply a calculation on thousands of numbers at once, many thousands of times faster than a Python loop?**
As loops are very slow in Python, it is best to represent the operations as array operations rather than looping through individual elements. If this can be done, then using NumPy or PyTorch will be thousands of times faster, as they use underlying C code which is much faster than pure Python. Even better, PyTorch allows you to run operations on GPU, which will have significant speedup if there are parallel operations that can be done.
**Create a 3×3 tensor or array containing the numbers from 1 to 9. Double it. Select the bottom-right four numbers.**
```
a = torch.Tensor(list(range(1,10))).view(3,3); print(a)
```
tensor([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])
```
b = 2*a;
print(b)
```
tensor([[ 2., 4., 6.],
[ 8., 10., 12.],
[14., 16., 18.]])
```
b[1:,1:]
```
tensor([[10., 12.],
[16., 18.]])
**What is broadcasting?**
Scientific/numerical Python packages like NumPy and PyTorch will often implement broadcasting that often makes code easier to write. In the case of PyTorch, tensors with smaller rank are expanded to have the same size as the larger rank tensor. In this way, operations can be performed between tensors with different rank.
**Are metrics generally calculated using the training set, or the validation set? Why?**
Metrics are generally calculated on a validation set. As the validation set is unseen data for the model, evaluating the metrics on the validation set is better in order to determine if there is any overfitting and how well the model might generalize if given similar data.
**What is SGD?**
SGD, or stochastic gradient descent, is an optimization algorithm. Specifically, SGD is an algorithm that will update the parameters of a model in order to minimize a given loss function that was evaluated on the predictions and target. The key idea behind SGD (and many optimization algorithms, for that matter) is that the gradient of the loss function provides an indication of how that loss function changes in the parameter space, which we can use to determine how best to update the parameters in order to minimize the loss function. This is what SGD does.
**Why does SGD use mini-batches?**
We need to calculate our loss function (and our gradient) on one or more data points. We cannot calculate on the whole datasets due to compute limitations and time constraints. If we iterated through each data point, however, the gradient will be unstable and imprecise, and is not suitable for training. As a compromise, we calculate the average loss for a small subset of the dataset at a time. This subset is called a mini-batch. Using mini-batches are also more computationally efficient than single items on a GPU.
**What are the seven steps in SGD for machine learning?**
- Initialize the weights.
- For each image, use these weights to predict whether it appears to be a 3 or a 7.
- Based on these predictions, calculate how good the model is (its loss).
- Calculate the gradient, which measures for each weight, how changing that weight would change the loss
- Step (that is, change) all the weights based on that calculation.
- Go back to the step 2, and repeat the process.
- Iterate until you decide to stop the training process (for instance, because the model is good enough or you don't want to wait any longer).
**How do we initialize the weights in a model?**
Random weights work pretty well.
**What is "loss"?**
The loss function will return a value based on the given predictions and targets, where lower values correspond to better model predictions.
**Why can't we always use a high learning rate?**
The loss may “bounce” around (oscillate) or even diverge, as the optimizer is taking steps that are too large, and updating the parameters faster than it should be.
**What is a "gradient"?**
The gradients tell us how much we have to change each weight to make our model better. It is essentially a measure of how the loss function changes with changes of the weights of the model (the derivative).
**Do you need to know how to calculate gradients yourself?**
Manual calculation of the gradients are not required, as deep learning libraries will automatically calculate the gradients for you. This feature is known as automatic differentiation. In PyTorch, if requires_grad=True, the gradients can be returned by calling the backward method: a.backward()
**Why can't we use accuracy as a loss function?**
A loss function needs to change as the weights are being adjusted. Accuracy only changes if the predictions of the model change. So if there are slight changes to the model that, say, improves confidence in a prediction, but does not change the prediction, the accuracy will still not change. Therefore, the gradients will be zero everywhere except when the actual predictions change. The model therefore cannot learn from the gradients equal to zero, and the model’s weights will not update and will not train. A good loss function gives a slightly better loss when the model gives slightly better predictions. Slightly better predictions mean if the model is more confident about the correct prediction. For example, predicting 0.9 vs 0.7 for probability that a MNIST image is a 3 would be slightly better prediction. The loss function needs to reflect that.
**Draw the sigmoid function. What is special about its shape?**

Sigmoid function is a smooth curve that squishes all values into values between 0 and 1. Most loss functions assume that the model is outputting some form of a probability or confidence level between 0 and 1 so we use a sigmoid function at the end of the model in order to do this.
**What is the difference between a loss function and a metric?**
The key difference is that metrics drive human understanding and losses drive automated learning. In order for loss to be useful for training, it needs to have a meaningful derivative. Many metrics, like accuracy are not like that. Metrics instead are the numbers that humans care about, that reflect the performance of the model.
**What is the function to calculate new weights using a learning rate?**
The optimizer step function
**What does the `DataLoader` class do?**
The DataLoader class can take any Python collection and turn it into an iterator over many batches.
**Write pseudocode showing the basic steps taken in each epoch for SGD.**
```
for x,y in dl:
pred = model(x)
loss = loss_func(pred, y)
loss.backward()
parameters -= parameters.grad * lr
```
**Create a function that, if passed two arguments `[1,2,3,4]` and `'abcd'`, returns `[(1, 'a'), (2, 'b'), (3, 'c'), (4, 'd')]`. What is special about that output data structure?**
```
def func(a,b): return list(zip(a,b))
```
This data structure is useful for machine learning models when you need lists of tuples where each tuple would contain input data and a label.
**What does `view` do in PyTorch?**
It changes the shape of a Tensor without changing its contents.
**What are the "bias" parameters in a neural network? Why do we need them?**
Without the bias parameters, if the input is zero, the output will always be zero. Therefore, using bias parameters adds additional flexibility to the model.
**What does the `@` operator do in Python?**
This is the matrix multiplication operator.
**What does the `backward` method do?**
This method returns the current gradients.
**Why do we have to zero the gradients?**
PyTorch will add the gradients of a variable to any previously stored gradients. If the training loop function is called multiple times, without zeroing the gradients, the gradient of current loss would be added to the previously stored gradient value.
**What information do we have to pass to `Learner`?**
We need to pass in the DataLoaders, the model, the optimization function, the loss function, and optionally any metrics to print.
**Show Python or pseudocode for the basic steps of a training loop.**
```
def train_epoch(model, lr, params):
for xb,yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_()
for i in range(20):
train_epoch(model, lr, params)
```
**What is "ReLU"? Draw a plot of it for values from `-2` to `+2`.**
ReLU just means “replace any negative numbers with zero”. It is a commonly used activation function.

**What is an "activation function"?**
The activation function is another function that is part of the neural network, which has the purpose of providing non-linearity to the model. The idea is that without an activation function, we just have multiple linear functions of the form y=mx+b. However, a series of linear layers is equivalent to a single linear layer, so our model can only fit a line to the data. By introducing a non-linearity in between the linear layers, this is no longer true. Each layer is somewhat decoupled from the rest of the layers, and the model can now fit much more complex functions. In fact, it can be mathematically proven that such a model can solve any computable problem to an arbitrarily high accuracy, if the model is large enough with the correct weights. This is known as the universal approximation theorem.
**What's the difference between `F.relu` and `nn.ReLU`?**
F.relu is a Python function for the relu activation function. On the other hand, nn.ReLU is a PyTorch module. This means that it is a Python class that can be called as a function in the same way as F.relu.
**The universal approximation theorem shows that any function can be approximated as closely as needed using just one nonlinearity. So why do we normally use more?**
There are practical performance benefits to using more than one nonlinearity. We can use a deeper model with less number of parameters, better performance, faster training, and less compute/memory requirements.
### Further Research
1. Create your own implementation of `Learner` from scratch, based on the training loop shown in this chapter.
1. Complete all the steps in this chapter using the full MNIST datasets (that is, for all digits, not just 3s and 7s). This is a significant project and will take you quite a bit of time to complete! You'll need to do some of your own research to figure out how to overcome some obstacles you'll meet on the way.
| github_jupyter |
# 08 - Common problems & bad data situations
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons Licence" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/88x31.png" title='This work is licensed under a Creative Commons Attribution 4.0 International License.' align="right"/></a>
In this notebook, we will revise common problems that might come up when dealing with real-world data.
Maintainers: [@thempel](https://github.com/thempel), [@cwehmeyer](https://github.com/cwehmeyer), [@marscher](https://github.com/marscher), [@psolsson](https://github.com/psolsson)
**Remember**:
- to run the currently highlighted cell, hold <kbd>⇧ Shift</kbd> and press <kbd>⏎ Enter</kbd>;
- to get help for a specific function, place the cursor within the function's brackets, hold <kbd>⇧ Shift</kbd>, and press <kbd>⇥ Tab</kbd>;
- you can find the full documentation at [PyEMMA.org](http://www.pyemma.org).
---
Most problems in Markov modeling of MD data arise from bad sampling combined with a poor discretization.
For estimating a Markov model, it is required to have a connected data set,
i.e., we must have observed each process we want to describe in both directions.
PyEMMA checks if this requirement is fulfilled but, however, in certain situations this might be less obvious.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import mdshare
import pyemma
```
## Case 1: preprocessed, two-dimensional data (toy model)
### well-sampled double-well potential
Let's again have a look at the double-well potential.
Since we are only interested in the problematic situations here,
we will simplify our data a bit and work with a 1D projection.
```
file = mdshare.fetch('hmm-doublewell-2d-100k.npz', working_directory='data')
with np.load(file) as fh:
data = [fh['trajectory'][:, 1]]
```
Since this particular example is simple enough, we can define a plotting function that combines histograms with trajectory data:
```
def plot_1D_histogram_trajectories(data, cluster=None, max_traj_length=200, ax=None):
if ax is None:
fig, ax = plt.subplots()
for n, _traj in enumerate(data):
ax.hist(_traj, bins=30, alpha=.33, density=True, color='C{}'.format(n));
ylims = ax.get_ylim()
xlims = ax.get_xlim()
for n, _traj in enumerate(data):
ax.plot(
_traj[:min(len(_traj), max_traj_length)],
np.linspace(*ylims, min(len(_traj), max_traj_length)),
alpha=0.6, color='C{}'.format(n), label='traj {}'.format(n))
if cluster is not None:
ax.plot(
cluster.clustercenters[cluster.dtrajs[n][:min(len(_traj), max_traj_length)], 0],
np.linspace(*ylims, min(len(_traj), max_traj_length)),
'.-', alpha=.6, label='dtraj {}'.format(n), linewidth=.3)
ax.annotate(
'', xy=(0.8500001 * xlims[1], 0.7 * ylims[1]), xytext=(0.85 * xlims[1], 0.3 * ylims[1]),
arrowprops=dict(fc='C0', ec='None', alpha=0.6, width=2))
ax.text(0.86 * xlims[1], 0.5 * ylims[1], '$x(time)$', ha='left', va='center', rotation=90)
ax.set_xlabel('TICA coordinate')
ax.set_ylabel('histogram counts & trajectory time')
ax.legend(loc=2)
```
As a reference, we visualize the histogram of this well-sampled trajectory along with the first $200$ steps (left panel) and the MSM implied timescales (right panel):
```
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
cluster = pyemma.coordinates.cluster_regspace(data, dmin=0.05)
plot_1D_histogram_trajectories(data, cluster=cluster, ax=axes[0])
lags = [i + 1 for i in range(10)]
its = pyemma.msm.its(cluster.dtrajs, lags=lags)
pyemma.plots.plot_implied_timescales(its, marker='o', ax=axes[1], nits=4)
fig.tight_layout()
```
We see a nice, reversibly connected trajectory.
That means we have sampled transitions between the basins in both directions that are correctly resolved by the discretization.
As we see from the almost perfect overlay of discrete and continuous trajectory, nearly no discretization error is made.
### irreversibly connected double-well trajectories
In MD simulations, we often face the problem that a process is sampled only in one direction.
For example, consider protein-protein binding.
The unbinding might take on the order of seconds to minutes and is thus difficult to sample.
We will have a look what happens with the MSM in this case.
Our example are two trajectories sampled from a double-well potential, each started in a different basin.
They will be color coded.
```
file = mdshare.fetch('doublewell_oneway.npy', working_directory='data')
data = [trj for trj in np.load(file)]
plot_1D_histogram_trajectories(data, max_traj_length=data[0].shape[0])
```
We note that the orange trajectory does not leave its potential well while the blue trajectory does overcome the barrier exactly once.
⚠️ Even though we have sampled one direction of the process,
we do not sample the way out of one of the potential wells, thus effectively finding a sink state in our data.
Let's have a look at the MSM.
Since in higher dimensions, we often face the problem of poor discretization,
we will simulate this situation by using too few cluster centers.
```
cluster_fine = pyemma.coordinates.cluster_regspace(data, dmin=0.1)
cluster_poor = pyemma.coordinates.cluster_regspace(data, dmin=0.7)
print(cluster_fine.n_clusters, cluster_poor.n_clusters)
fig, axes = plt.subplots(2, 2, figsize=(10, 8), sharey='col')
for cluster, ax in zip([cluster_poor, cluster_fine], axes):
plot_1D_histogram_trajectories(data, cluster=cluster, max_traj_length=data[0].shape[0], ax=ax[0])
its = pyemma.msm.its(cluster.dtrajs, lags=[1, 10, 100, 200, 300, 500, 800, 1000])
pyemma.plots.plot_implied_timescales(its, marker='o', ax=ax[1], nits=4)
axes[0, 0].set_title('poor discretization')
axes[1, 0].set_title('fine discretization')
fig.tight_layout()
```
#### What do we see?
1) We observe implied timescales that even look converged in the fine discretization case.
2) With poor clustering, the process cannot be resolved any more, i.e., the ITS does not convergence before the lag time exceeds the implied time scale.
The obvious question is, what is the process that can be observed in the fine discretization case?
PyEMMA checks for disconnectivity and thus should not find the process between the two wells.
We follow this question by taking a look at the first eigenvector, which corresponds to that process.
```
msm = pyemma.msm.estimate_markov_model(cluster_fine.dtrajs, 200)
fig, ax = plt.subplots()
ax.plot(
cluster_fine.clustercenters[msm.active_set, 0],
msm.eigenvectors_right()[:, 1],
'o:',
label='first eigvec')
tx = ax.twinx()
tx.hist(np.concatenate(data), bins=30, alpha=0.33)
tx.set_yticklabels([])
tx.set_yticks([])
fig.legend()
fig.tight_layout()
```
We observe a process which is entirely taking place in the left potential well.
How come?
PyEMMA estimates MSMs only on the largest connected set because they are only defined on connected sets.
In this particular example, the largest connected set is the microstates in the left potential well.
That means that we find a transition between the right and the left side of this well.
This is not wrong, it might just be non-informative or even irrelevant.
The set of microstates which is used for the MSM estimation is stored in the MSM object `msm` and can be retrieved via `.active_set`.
```
print('Active set: {}'.format(msm.active_set))
print('Active state fraction: {:.2}'.format(msm.active_state_fraction))
```
In this example we clearly see that some states are missing.
### disconnected double-well trajectories with cross-overs
This example covers the worst-case scenario.
We have two trajectories that live in two separated wells and never transition to the other one.
Due to a very bad clustering, we believe that the data is connected.
This can happen if we cluster a large dataset in very high dimensions where it is especially difficult to debug.
```
file = mdshare.fetch('doublewell_disconnected.npy', working_directory='data')
data = [trj for trj in np.load(file)]
plot_1D_histogram_trajectories(data, max_traj_length=data[0].shape[0])
```
We, again, compare a reasonable to a deliberately poor discretization:
```
cluster_fine = pyemma.coordinates.cluster_regspace(data, dmin=0.1)
cluster_poor = pyemma.coordinates.cluster_regspace(data, dmin=0.7)
print(cluster_fine.n_clusters, cluster_poor.n_clusters)
fig, axes = plt.subplots(2, 2, figsize=(10, 8), sharey='col')
for cluster, ax in zip([cluster_poor, cluster_fine], axes):
plot_1D_histogram_trajectories(data, cluster=cluster, max_traj_length=data[0].shape[0], ax=ax[0])
its = pyemma.msm.its(cluster.dtrajs, lags=[1, 10, 100, 200, 300, 500, 800, 1000])
pyemma.plots.plot_implied_timescales(its, marker='o', ax=ax[1], nits=4)
axes[0, 0].set_title('poor discretization')
axes[1, 0].set_title('fine discretization')
fig.tight_layout()
```
#### What do we see?
1) With the fine discretization, we observe some timescales that are converged. These are most probably processes within one of the wells, similar to the ones we saw before.
2) The poor discretization induces a large error and describes artificial short visits to the other basin.
3) The timescales in the poor discretization are much higher but not converged.
The reason for the high timescales in 3) are in fact the artificial cross-over events created by the poor discretization.
This process was not actually sampled and is an artifact of bad clustering.
Let's look at it in more detail and see what happens if we estimate an MSM and even compute metastable states with PCCA++.
```
msm = pyemma.msm.estimate_markov_model(cluster_poor.dtrajs, 200)
nstates = 2
msm.pcca(nstates)
index_order = np.argsort(cluster_poor.clustercenters[:, 0])
fig, axes = plt.subplots(1, 3, figsize=(12, 3))
axes[0].plot(
cluster_poor.clustercenters[index_order, 0],
msm.eigenvectors_right()[index_order, 1],
'o:',
label='1st eigvec')
axes[0].set_title('first eigenvector')
for n, metastable_distribution in enumerate(msm.metastable_distributions):
axes[1].step(
cluster_poor.clustercenters[index_order, 0],
metastable_distribution[index_order],
':',
label='md state {}'.format(n + 1),
where='mid')
axes[1].set_title('metastable distributions (md)')
axes[2].step(
cluster_poor.clustercenters[index_order, 0],
msm.pi[index_order],
'k--',
label='$\pi$',
where='mid')
axes[2].set_title('stationary distribution $\pi$')
for ax in axes:
tx = ax.twinx()
tx.hist(np.concatenate(data), bins=30, alpha=0.33)
tx.set_yticklabels([])
tx.set_yticks([])
fig.legend(loc=7)
fig.tight_layout()
```
We observe that the first eigenvector represents a process that does not exist, i.e., is an artifact.
Nevertheless, the PCCA++ algorithm can separate metastable states in a way we would expect.
It finds the two disconnected states. However, the stationary distribution yields arbitrary results.
#### How to detect disconnectivity?
Generally, hidden Markov models (HMMs) are much more reliable because they come with an additional layer of hidden states.
Cross-over events are thus unlikely to be counted as "real" transitions.
Thus, it is a good idea to estimate an HMM.
What happens if we try to estimate a two state HMM on the same, poorly discretized data?
⚠️ It is important to note that the HMM estimation is initialized from the PCCA++ metastable states that we already analyzed.
```
hmm = pyemma.msm.estimate_hidden_markov_model(cluster_poor.dtrajs, nstates, msm.lag)
```
We are getting an error message which already explains what is going wrong, i.e.,
that the (macro-) states are not connected and thus no unique stationary distribution can be estimated.
This is equivalent to having two eigenvalues of magnitude 1 or an implied timescale of infinity which is what we observe in the implied timescales plot.
```
its = pyemma.msm.timescales_hmsm(cluster_poor.dtrajs, nstates, lags=[1, 3, 4, 10, 100])
pyemma.plots.plot_implied_timescales(its, marker='o', ylog=True);
```
As we see, the requested timescales above $4$ steps could not be computed because the underlying HMM is disconnected,
i.e., the corresponding timescales are infinity.
The implied timescales that could be computed are most likely the same process that we observed from the fine clustering before, i.e., jumps within one basin.
In general, it is a non-trivial problem to show that processes were not sampled reversibly.
In our experience, HMMs are a good choice here, even though situations can occur where they might not detect the problem as easily as in this example.
<a id="poorly_sampled_dw"></a>
### poorly sampled double-well trajectories
Let's now assume that everything worked out fine but our sampling is somewhat poor.
This is a realistic scenario when dealing with large systems that were well-sampled but still contain only few events of interest.
We expect that our trajectories are just long enough to sample a certain process but are too short to capture them with a large lag time.
To rule out discretization issues and to make the example clear, we use the full data set for discretization.
```
file = mdshare.fetch('hmm-doublewell-2d-100k.npz', working_directory='data')
with np.load(file) as fh:
data = [fh['trajectory'][:, 1]]
cluster = pyemma.coordinates.cluster_regspace(data, dmin=0.05)
```
We want to simulate a process that happens on a timescale that is on the order of magnitude of the trajectory length.
To do so, we choose `n_trajs` chunks from the full data set that contain `traj_length` steps by splitting the original trajectory:
```
traj_length = 10
n_trajs = 50
data_short_trajs = list(data[0].reshape((data[0].shape[0] // traj_length, traj_length)))[:n_trajs]
dtrajs_short = list(cluster.dtrajs[0].reshape((data[0].shape[0] // traj_length, traj_length)))[:n_trajs]
```
Now, let's plot the trajectories (left panel) and estimate implied timescales (right panel) as above.
Since we know the true ITS of this process, we visualize it as a dotted line.
```
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
for n, _traj in enumerate(data_short_trajs):
axes[0].plot(_traj, np.linspace(0, 1, _traj.shape[0]) + n)
lags = [i + 1 for i in range(9)]
its = pyemma.msm.its(dtrajs_short, lags=lags)
pyemma.plots.plot_implied_timescales(its, marker='o', ax=axes[1], nits=1)
its_reference = pyemma.msm.its(cluster.dtrajs, lags=lags)
pyemma.plots.plot_implied_timescales(its_reference, linestyle=':', ax=axes[1], nits=1)
fig.tight_layout()
```
We note that the slowest process is clearly contained in the data chunks and is reversibly sampled (left panel, short trajectory pieces color coded and stacked).
Due to very short trajectories, we find that this process can only be captured at a very short MSM lag time (right panel).
Above that interval, the slowest timescale diverges.
Luckily, here we know that it is already converged at $\tau = 1$, so we estimate an MSM:
```
msm_short_trajectories = pyemma.msm.estimate_markov_model(dtrajs_short, 1)
```
Let's now have a look at the CK-test:
```
pyemma.plots.plot_cktest(msm_short_trajectories.cktest(2), marker='.');
```
As already discussed, we cannot expect new estimates above a certain lag time to agree with the model prediction due to too short trajectories.
Indeed, we find that new estimates and model predictions diverge at very high lag times.
This does not necessarily mean that the model at $\tau=1$ is wrong and in this particular case,
we can even explain the divergence and find that it fits to the implied timescales divergence.
This example mirrors another incarnation of the sampling problem: Working with large systems,
we often have comparably short trajectories with few rare events.
Thus, implied timescales convergence can often be achieved only in a certain interval and CK-tests will not converge up to arbitrary multiples of the lag time.
It is the responsibility of the modeler to interpret these results and to ensure that a valid model can be obtained from the data.
Please note that this is only a special case of a failed CK test.
More general information about CK tests and what it means if it fails are explained in
[Notebook 03 ➜ 📓](03-msm-estimation-and-validation.ipynb).
## Case 2: low-dimensional molecular dynamics data (alanine dipeptide)
In this example, we will show how an ill-conducted TICA analysis can yield results that look metastable in the 2D histogram,
but in fact are not describing the slow dynamics.
Please note that this was deliberately broken with a nonsensical TICA-lagtime of almost trajectory length, which is 250 ns.
We start off with adding all atom coordinates.
That is a non-optimal choice because it artificially blows up the dimensionality,
but might still be a reasonable choice depending on the problem.
A well-conducted TICA projection can extract the slow coordinates, as we will see at the end of this example.
```
pdb = mdshare.fetch('alanine-dipeptide-nowater.pdb', working_directory='data')
files = mdshare.fetch('alanine-dipeptide-*-250ns-nowater.xtc', working_directory='data')
feat = pyemma.coordinates.featurizer(pdb)
feat.add_all()
data = pyemma.coordinates.load(files, features=feat)
```
TICA analysis is conducted with an extremely high lag time of almost $249.9$ ns. We map down to two dimensions.
```
tica = pyemma.coordinates.tica(data, lag=data[0].shape[0] - 100, dim=2)
tica_output = tica.get_output()
pyemma.plots.plot_free_energy(*np.concatenate(tica_output).T, legacy=False);
```
In the free energy plot, we recognize two defined basins that are nicely separated by the first TICA component. We thus continue with a discretization of this space and estimate MSM implied timescales.
```
cluster = pyemma.coordinates.cluster_kmeans(tica_output, k=200, max_iter=30, stride=100)
its = pyemma.msm.its(cluster.dtrajs, lags=[1, 5, 10, 20, 30, 50])
pyemma.plots.plot_implied_timescales(its, marker='o', units='ps', nits=3);
```
Indeed, we observe a converged implied timescale.
In this example we already know that it is way lower than expected,
but in the general case we are unaware of the real dynamics of the system.
Thus, we estimate an MSM at lag time $20 $ ps.
Coarse graining and validation will be done with $2$ metastable states since we found $2$ basins in the free energy landscape and have one slow process in the ITS plot.
```
msm = pyemma.msm.estimate_markov_model(cluster.dtrajs, 20)
nstates = 2
msm.pcca(nstates);
stride = 10
metastable_trajs_strided = [msm.metastable_assignments[dtrj[::stride]] for dtrj in cluster.dtrajs]
tica_output_strided = [i[::stride] for i in tica_output]
_, _, misc = pyemma.plots.plot_state_map(*np.concatenate(tica_output_strided).T,
np.concatenate(metastable_trajs_strided));
misc['cbar'].set_ticklabels(range(1, nstates + 1)) # set state numbers 1 ... nstates
```
As we see, the PCCA++ algorithm is perfectly able to separate the two basins.
Let's go on with a Chapman-Kolmogorow validation.
```
pyemma.plots.plot_cktest(msm.cktest(nstates), units='ps');
```
Congratulations, we have estimated a well-validated MSM.
The only question remaining is: What does it actually describe?
For this, we usually extract representative structures as described in [Notebook 00 ➜ 📓](00-pentapeptide-showcase.ipynb).
We will not do this here but look at the metastable trajectories instead.
#### What could be wrong about it?
Let's have a look at the trajectories as assigned to PCCA++ metastable states.
We have already computed them before but not looked at their time dependence.
```
fig, ax = plt.subplots(1, 1, figsize=(15, 6), sharey=True, sharex=True)
ax_yticks_labels = []
for n, pcca_traj in enumerate(metastable_trajs_strided):
ax.plot(range(len(pcca_traj)), msm.n_metastable * n + pcca_traj, color='k', linewidth=0.3)
ax.scatter(range(len(pcca_traj)), msm.n_metastable * n + pcca_traj, c=pcca_traj, s=0.1)
ax_yticks_labels.append(((msm.n_metastable * (2 * n + 1) - 1) / 2, n + 1))
ax.set_yticks([l[0] for l in ax_yticks_labels])
ax.set_yticklabels([str(l[1]) for l in ax_yticks_labels])
ax.set_ylabel('Trajectory #')
ax.set_xlabel('time / {} ps'.format(stride))
fig.tight_layout()
```
#### What do we see?
The above figure shows the metastable states visited by the trajectory over time.
Each metastable state is color-coded, the trajectory is shown by the black line.
This is clearly not a metastable trajectory as we would have expected.
What did we do wrong?
Let's have a look at the TICA trajectories, not only the histogram!
```
fig, axes = plt.subplots(2, 3, figsize=(12, 6), sharex=True, sharey='row')
for n, trj in enumerate(tica_output):
for dim, traj1d in enumerate(trj.T):
axes[dim, n].plot(traj1d[::stride], linewidth=.5)
for ax in axes[1]:
ax.set_xlabel('time / {} ps'.format(stride))
for dim, ax in enumerate(axes[:, 0]):
ax.set_ylabel('IC {}'.format(dim + 1))
for n, ax in enumerate(axes[0]):
ax.set_title('Trajectory # {}'.format(n + 1))
fig.tight_layout()
```
This is essentially noise, so it is not surprising that the metastable trajectories do not show significant metastability.
The MSM nevertheless found a process in the above TICA components which, however,
does not seem to describe any of the slow dynamics.
Thus, the model is not wrong, it is just not informative.
As we see in this example, it can be instructive to keep the trajectories in mind and not to rely on the histograms alone.
⚠️ Histograms are no proof of metastability,
they can only give us a hint towards defined states in a multi-dimensional state space which can be metastable.
#### How to fix it?
In this particular example, we already know the issue:
the TICA lag time was deliberately chosen way too high.
That's easy to fix.
Let's now have a look at how the metastable trajectories should look for a decent model such as the one estimated in [Notebook 05 ➜ 📓](05-pcca-tpt.ipynb).
We will take the same input data,
do a TICA transform with a realistic lag time of $10$ ps,
and coarse grain into $2$ metastable states in order to compare with the example above.
```
tica = pyemma.coordinates.tica(data, lag=10, dim=2)
tica_output = tica.get_output()
cluster = pyemma.coordinates.cluster_kmeans(tica_output, k=200, max_iter=30, stride=100)
pyemma.plots.plot_free_energy(*np.concatenate(tica_output).T, legacy=False);
```
As wee see, TICA yields a very nice state separation.
We will see that these states are in fact metastable.
```
msm = pyemma.msm.estimate_markov_model(cluster.dtrajs, lag=20)
msm.pcca(nstates);
metastable_trajs_strided = [msm.metastable_assignments[dtrj[::stride]] for dtrj in cluster.dtrajs]
stride = 10
tica_output_strided = [i[::stride] for i in tica_output]
_, _, misc = pyemma.plots.plot_state_map(*np.concatenate(tica_output_strided).T,
np.concatenate(metastable_trajs_strided));
misc['cbar'].set_ticklabels(range(1, nstates + 1)) # set state numbers 1 ... nstates
```
We note that PCCA++ separates the two basins of the free energy plot.
Let's have a look at the metastable trajectories:
```
fig, ax = plt.subplots(1, 1, figsize=(12, 6), sharey=True, sharex=True)
ax_yticks_labels = []
for n, pcca_traj in enumerate(metastable_trajs_strided):
ax.plot(range(len(pcca_traj)), msm.n_metastable * n + pcca_traj, color='k', linewidth=0.3)
ax.scatter(range(len(pcca_traj)), msm.n_metastable * n + pcca_traj, c=pcca_traj, s=0.1)
ax_yticks_labels.append(((msm.n_metastable * (2 * n + 1) - 1) / 2, n + 1))
ax.set_yticks([l[0] for l in ax_yticks_labels])
ax.set_yticklabels([str(l[1]) for l in ax_yticks_labels])
ax.set_ylabel('Trajectory #')
ax.set_xlabel('time / {} ps'.format(stride))
fig.tight_layout()
```
These trajectories show the expected behavior of a metastable trajectory,
i.e., it does not quickly jump back and forth between the states.
## Wrapping up
In this notebook, we have learned about some problems that can arise when estimating MSMs with "real world" data at simple examples.
In detail, we have seen
- irreversibly connected dynamics and what it means for MSM estimation,
- fully disconnected trajectories and how to identify them,
- connected but poorly sampled trajectories and how convergence looks in this case,
- ill-conducted TICA analysis and what it yields.
The most important lesson from this tutorial is that histograms, which are usually calculated in a projected space, are not a sufficient means of identifying metastability or connectedness.
It is crucial to remember that the underlying trajectories play the role of ground truth for the model.
Ultimately, histograms only help us to understand this ground truth but cannot provide a complete picture.
| github_jupyter |
## Define the Convolutional Neural Network
After you've looked at the data you're working with and, in this case, know the shapes of the images and of the keypoints, you are ready to define a convolutional neural network that can *learn* from this data.
In this notebook and in `models.py`, you will:
1. Define a CNN with images as input and keypoints as output
2. Construct the transformed FaceKeypointsDataset, just as before
3. Train the CNN on the training data, tracking loss
4. See how the trained model performs on test data
5. If necessary, modify the CNN structure and model hyperparameters, so that it performs *well* **\***
**\*** What does *well* mean?
"Well" means that the model's loss decreases during training **and**, when applied to test image data, the model produces keypoints that closely match the true keypoints of each face. And you'll see examples of this later in the notebook.
---
## CNN Architecture
Recall that CNN's are defined by a few types of layers:
* Convolutional layers
* Maxpooling layers
* Fully-connected layers
You are required to use the above layers and encouraged to add multiple convolutional layers and things like dropout layers that may prevent overfitting. You are also encouraged to look at literature on keypoint detection, such as [this paper](https://arxiv.org/pdf/1710.00977.pdf), to help you determine the structure of your network.
### TODO: Define your model in the provided file `models.py` file
This file is mostly empty but contains the expected name and some TODO's for creating your model.
---
## PyTorch Neural Nets
To define a neural network in PyTorch, you define the layers of a model in the function `__init__` and define the feedforward behavior of a network that employs those initialized layers in the function `forward`, which takes in an input image tensor, `x`. The structure of this Net class is shown below and left for you to fill in.
Note: During training, PyTorch will be able to perform backpropagation by keeping track of the network's feedforward behavior and using autograd to calculate the update to the weights in the network.
#### Define the Layers in ` __init__`
As a reminder, a conv/pool layer may be defined like this (in `__init__`):
```
# 1 input image channel (for grayscale images), 32 output channels/feature maps, 3x3 square convolution kernel
self.conv1 = nn.Conv2d(1, 32, 3)
# maxpool that uses a square window of kernel_size=2, stride=2
self.pool = nn.MaxPool2d(2, 2)
```
#### Refer to Layers in `forward`
Then referred to in the `forward` function like this, in which the conv1 layer has a ReLu activation applied to it before maxpooling is applied:
```
x = self.pool(F.relu(self.conv1(x)))
```
Best practice is to place any layers whose weights will change during the training process in `__init__` and refer to them in the `forward` function; any layers or functions that always behave in the same way, such as a pre-defined activation function, should appear *only* in the `forward` function.
#### Why models.py
You are tasked with defining the network in the `models.py` file so that any models you define can be saved and loaded by name in different notebooks in this project directory. For example, by defining a CNN class called `Net` in `models.py`, you can then create that same architecture in this and other notebooks by simply importing the class and instantiating a model:
```
from models import Net
net = Net()
```
```
# import the usual resources
import matplotlib.pyplot as plt
import numpy as np
# watch for any changes in model.py, if itchanges, re-load it automatically
%load_ext autoreload
%autoreload 2
## TODO: Define the Net in models.py
import torch
import torch.nn as nn
import torch.nn.functional as F
## TODO: Once you've define the network, you can instantiate it
# one example conv layer has been provided for you
from models import Net
net = Net()
print(net)
```
## Transform the dataset
To prepare for training, create a transformed dataset of images and keypoints.
### TODO: Define a data transform
In PyTorch, a convolutional neural network expects a torch image of a consistent size as input. For efficient training, and so your model's loss does not blow up during training, it is also suggested that you normalize the input images and keypoints. The necessary transforms have been defined in `data_load.py` and you **do not** need to modify these; take a look at this file (you'll see the same transforms that were defined and applied in Notebook 1).
To define the data transform below, use a [composition](http://pytorch.org/tutorials/beginner/data_loading_tutorial.html#compose-transforms) of:
1. Rescaling and/or cropping the data, such that you are left with a square image (the suggested size is 224x224px)
2. Normalizing the images and keypoints; turning each RGB image into a grayscale image with a color range of [0, 1] and transforming the given keypoints into a range of [-1, 1]
3. Turning these images and keypoints into Tensors
These transformations have been defined in `data_load.py`, but it's up to you to call them and create a `data_transform` below. **This transform will be applied to the training data and, later, the test data**. It will change how you go about displaying these images and keypoints, but these steps are essential for efficient training.
As a note, should you want to perform data augmentation (which is optional in this project), and randomly rotate or shift these images, a square image size will be useful; rotating a 224x224 image by 90 degrees will result in the same shape of output.
```
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms, utils
# the dataset we created in Notebook 1 is copied in the helper file `data_load.py`
from data_load import FacialKeypointsDataset
# the transforms we defined in Notebook 1 are in the helper file `data_load.py`
from data_load import Rescale, RandomCrop, Normalize, ToTensor
## TODO: define the data_transform using transforms.Compose([all tx's, . , .])
# order matters! i.e. rescaling should come before a smaller crop
data_transform = transforms.Compose([Rescale(256), RandomCrop(224),Normalize(), ToTensor()])
#data_transform = transforms.Compose([Rescale((224,224)),Normalize(), ToTensor()])
# testing that you've defined a transform
assert(data_transform is not None), 'Define a data_transform'
# create the transformed dataset
transformed_dataset = FacialKeypointsDataset(csv_file='data/training_frames_keypoints.csv',
root_dir='data/training/',
transform=data_transform)
print('Number of images: ', len(transformed_dataset))
# iterate through the transformed dataset and print some stats about the first few samples
for i in range(4):
sample = transformed_dataset[i]
print(i, sample['image'].size(), sample['keypoints'].size())
```
## Batching and loading data
Next, having defined the transformed dataset, we can use PyTorch's DataLoader class to load the training data in batches of whatever size as well as to shuffle the data for training the model. You can read more about the parameters of the DataLoader, in [this documentation](http://pytorch.org/docs/master/data.html).
#### Batch size
Decide on a good batch size for training your model. Try both small and large batch sizes and note how the loss decreases as the model trains.
**Note for Windows users**: Please change the `num_workers` to 0 or you may face some issues with your DataLoader failing.
```
# load training data in batches
batch_size = 128
train_loader = DataLoader(transformed_dataset,
batch_size=batch_size,
shuffle=True,
num_workers=4)
```
## Before training
Take a look at how this model performs before it trains. You should see that the keypoints it predicts start off in one spot and don't match the keypoints on a face at all! It's interesting to visualize this behavior so that you can compare it to the model after training and see how the model has improved.
#### Load in the test dataset
The test dataset is one that this model has *not* seen before, meaning it has not trained with these images. We'll load in this test data and before and after training, see how your model performs on this set!
To visualize this test data, we have to go through some un-transformation steps to turn our images into python images from tensors and to turn our keypoints back into a recognizable range.
```
# load in the test data, using the dataset class
# AND apply the data_transform you defined above
# create the test dataset
test_dataset = FacialKeypointsDataset(csv_file='data/test_frames_keypoints.csv',
root_dir='data/test/',
transform=data_transform)
# load test data in batches
batch_size = 128
test_loader = DataLoader(test_dataset,
batch_size=batch_size,
shuffle=True,
num_workers=4)
```
## Apply the model on a test sample
To test the model on a test sample of data, you have to follow these steps:
1. Extract the image and ground truth keypoints from a sample
2. Make sure the image is a FloatTensor, which the model expects.
3. Forward pass the image through the net to get the predicted, output keypoints.
This function test how the network performs on the first batch of test data. It returns the images, the transformed images, the predicted keypoints (produced by the model), and the ground truth keypoints.
```
# test the model on a batch of test images
def net_sample_output():
# iterate through the test dataset
for i, sample in enumerate(test_loader):
# get sample data: images and ground truth keypoints
images = sample['image']
key_pts = sample['keypoints']
# convert images to FloatTensors
images = images.type(torch.FloatTensor)
# forward pass to get net output
output_pts = net(images)
# reshape to batch_size x 68 x 2 pts
output_pts = output_pts.view(output_pts.size()[0], 68, -1)
# break after first image is tested
if i == 0:
return images, output_pts, key_pts
```
#### Debugging tips
If you get a size or dimension error here, make sure that your network outputs the expected number of keypoints! Or if you get a Tensor type error, look into changing the above code that casts the data into float types: `images = images.type(torch.FloatTensor)`.
```
# call the above function
# returns: test images, test predicted keypoints, test ground truth keypoints
test_images, test_outputs, gt_pts = net_sample_output()
# print out the dimensions of the data to see if they make sense
print(test_images.data.size())
print(test_outputs.data.size())
print(gt_pts.size())
```
## Visualize the predicted keypoints
Once we've had the model produce some predicted output keypoints, we can visualize these points in a way that's similar to how we've displayed this data before, only this time, we have to "un-transform" the image/keypoint data to display it.
Note that I've defined a *new* function, `show_all_keypoints` that displays a grayscale image, its predicted keypoints and its ground truth keypoints (if provided).
```
def show_all_keypoints(image, predicted_key_pts, gt_pts=None):
"""Show image with predicted keypoints"""
# image is grayscale
plt.imshow(image, cmap='gray')
plt.scatter(predicted_key_pts[:, 0], predicted_key_pts[:, 1], s=20, marker='.', c='m')
# plot ground truth points as green pts
if gt_pts is not None:
plt.scatter(gt_pts[:, 0], gt_pts[:, 1], s=20, marker='.', c='g')
```
#### Un-transformation
Next, you'll see a helper function. `visualize_output` that takes in a batch of images, predicted keypoints, and ground truth keypoints and displays a set of those images and their true/predicted keypoints.
This function's main role is to take batches of image and keypoint data (the input and output of your CNN), and transform them into numpy images and un-normalized keypoints (x, y) for normal display. The un-transformation process turns keypoints and images into numpy arrays from Tensors *and* it undoes the keypoint normalization done in the Normalize() transform; it's assumed that you applied these transformations when you loaded your test data.
```
# visualize the output
# by default this shows a batch of 10 images
def visualize_output(test_images, test_outputs, gt_pts=None, batch_size=10):
for i in range(batch_size):
plt.figure(figsize=(20,10))
ax = plt.subplot(1, batch_size, i+1)
# un-transform the image data
image = test_images[i].data # get the image from it's wrapper
image = image.numpy() # convert to numpy array from a Tensor
image = np.transpose(image, (1, 2, 0)) # transpose to go from torch to numpy image
# un-transform the predicted key_pts data
predicted_key_pts = test_outputs[i].data
predicted_key_pts = predicted_key_pts.numpy()
# undo normalization of keypoints
predicted_key_pts = predicted_key_pts*50.0+100
# plot ground truth points for comparison, if they exist
ground_truth_pts = None
if gt_pts is not None:
ground_truth_pts = gt_pts[i]
ground_truth_pts = ground_truth_pts*50.0+100
# call show_all_keypoints
show_all_keypoints(np.squeeze(image), predicted_key_pts, ground_truth_pts)
plt.axis('off')
plt.show()
# call it
#visualize_output(test_images, test_outputs, gt_pts)
```
## Training
#### Loss function
Training a network to predict keypoints is different than training a network to predict a class; instead of outputting a distribution of classes and using cross entropy loss, you may want to choose a loss function that is suited for regression, which directly compares a predicted value and target value. Read about the various kinds of loss functions (like MSE or L1/SmoothL1 loss) in [this documentation](http://pytorch.org/docs/master/_modules/torch/nn/modules/loss.html).
### TODO: Define the loss and optimization
Next, you'll define how the model will train by deciding on the loss function and optimizer.
---
```
## TODO: Define the loss and optimization
import torch.optim as optim
#criterion = nn.MSELoss()
criterion = nn.SmoothL1Loss()
optimizer = optim.Adam(net.parameters(), lr=1e-3, betas=(0.9, 0.999))
#optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
```
## Training and Initial Observation
Now, you'll train on your batched training data from `train_loader` for a number of epochs.
To quickly observe how your model is training and decide on whether or not you should modify it's structure or hyperparameters, you're encouraged to start off with just one or two epochs at first. As you train, note how your the model's loss behaves over time: does it decrease quickly at first and then slow down? Does it take a while to decrease in the first place? What happens if you change the batch size of your training data or modify your loss function? etc.
Use these initial observations to make changes to your model and decide on the best architecture before you train for many epochs and create a final model.
```
from livelossplot import PlotLosses
def train_net(n_epochs):
# prepare the net for training
net.train()
liveloss = PlotLosses()
for epoch in range(n_epochs): # loop over the dataset multiple times
epoch_loss = 0.0
epoch_correct = 0
epoch_loss_val = 0.0
epoch_correct_val = 0
running_loss = 0.0
# train on batches of data, assumes you already have train_loader
for batch_i, data in enumerate(train_loader):
# get the input images and their corresponding labels
images = data['image']
key_pts = data['keypoints']
# flatten pts
key_pts = key_pts.view(key_pts.size(0), -1)
# convert variables to floats for regression loss
key_pts = key_pts.type(torch.FloatTensor)
images = images.type(torch.FloatTensor)
# forward pass to get outputs
output_pts = net(images)
# calculate the loss between predicted and target keypoints
loss = criterion(output_pts, key_pts)
# zero the parameter (weight) gradients
optimizer.zero_grad()
# backward pass to calculate the weight gradients
loss.backward()
# update the weights
optimizer.step()
epoch_loss += loss.data[0]
epoch_correct += (output_pts.max(1)[1] == key_pts).sum().data[0]
# print loss statistics
# to convert loss into a scalar and add it to the running_loss, use .item()
running_loss += loss.item()
if batch_i % 10 == 9: # print every 10 batches
print('Epoch: {}, Batch: {}, Avg. Loss: {}'.format(epoch + 1, batch_i+1, running_loss/1000))
running_loss = 0.0
avg_loss = epoch_loss / len(train_loader.dataset)
avg_accuracy = epoch_correct / len(train_loader.dataset)
liveloss.update({
'log loss': avg_loss,
'val_log loss': avg_loss_val,
'accuracy': avg_accuracy,
'val_accuracy': avg_accuracy_val})
liveloss.draw()
print('Finished Training')
def train_net (n_epochs):
# prepare the net for training
net.train()
for epoch in range(n_epochs): # loop over the dataset multiple times
running_loss = 0.0
# train on batches of data, assumes you already have train_loader
for batch_i, data in enumerate(train_loader):
# get the input images and their corresponding labels
images = data['image']
key_pts = data['keypoints']
# flatten pts
key_pts = key_pts.view(key_pts.size(0), -1)
# convert variables to floats for regression loss
key_pts = key_pts.type(torch.FloatTensor)
images = images.type(torch.FloatTensor)
# forward pass to get outputs
output_pts = net(images)
# calculate the loss between predicted and target keypoints
loss = criterion(output_pts, key_pts)
# zero the parameter (weight) gradients
optimizer.zero_grad()
# backward pass to calculate the weight gradients
loss.backward()
# update the weights
optimizer.step()
# print loss statistics
# to convert loss into a scalar and add it to the running_loss, use .item()
running_loss += loss.item()
if batch_i % 10 == 9: # print every 10 batches
print('Epoch: {}, Batch: {}, Avg. Loss: {}'.format(epoch + 1, batch_i+1, running_loss/1000))
running_loss = 0.0
model_dir = 'saved_models/'
model_name = 'model_3200_1600_smoothL1.pt'
# after training, save your model parameters in the dir 'saved_models'
#torch.save(net.state_dict(), model_dir+model_name)
print('Finished Training')
net.load_state_dict(torch.load('saved_models/model_3200_1600_smoothL1.pt'))
# train your network
n_epochs = 5 # start small, and increase when you've decided on your model structure and hyperparams
train_net(n_epochs)
```
## Test data
See how your model performs on previously unseen, test data. We've already loaded and transformed this data, similar to the training data. Next, run your trained model on these images to see what kind of keypoints are produced. You should be able to see if your model is fitting each new face it sees, if the points are distributed randomly, or if the points have actually overfitted the training data and do not generalize.
```
# get a sample of test data again
test_images, test_outputs, gt_pts = net_sample_output()
torch.cuda.get_device_name(0)
print(test_images.data.size())
print(test_outputs.data.size())
print(gt_pts.size())
visualize_output(test_images, test_outputs, gt_pts)
## TODO: visualize your test output
# you can use the same function as before, by un-commenting the line below:
visualize_output(test_images, test_outputs, gt_pts)
```
Once you've found a good model (or two), save your model so you can load it and use it later!
```
## TODO: change the name to something uniqe for each new model
model_dir = 'saved_models/'
model_name = 'model_3200_1600_smoothL1.pt'
# after training, save your model parameters in the dir 'saved_models'
torch.save(net.state_dict(), model_dir+model_name)
```
After you've trained a well-performing model, answer the following questions so that we have some insight into your training and architecture selection process. Answering all questions is required to pass this project.
### Question 1: What optimization and loss functions did you choose and why?
**Answer**: write your answer here (double click to edit this cell)
I use the ADAM optimization and MSE loss functions. I choose it because the network's output error should be as close as the desire value ( not classification). Therefore the ADAM and MSE works well.
### Question 2: What kind of network architecture did you start with and how did it change as you tried different architectures? Did you decide to add more convolutional layers or any layers to avoid overfitting the data?
**Answer**: write your answer here
Firstly, i try to apply LeNet architecture because it simple and fast. However, the result looks not good. Therefore, i change to the NaimishNet. This CNN apply many dropout layers to avoid overfitting the data.
### Question 3: How did you decide on the number of epochs and batch_size to train your model?
**Answer**: write your answer here
• Epoch: 30. The bigger the epoch, the better model is. Because there mare many dropout() layer, the network does not overfit the data with 30 epoch.
• Batch size: 10 . The bigger the batch size, the faster model is.
## Feature Visualization
Sometimes, neural networks are thought of as a black box, given some input, they learn to produce some output. CNN's are actually learning to recognize a variety of spatial patterns and you can visualize what each convolutional layer has been trained to recognize by looking at the weights that make up each convolutional kernel and applying those one at a time to a sample image. This technique is called feature visualization and it's useful for understanding the inner workings of a CNN.
In the cell below, you can see how to extract a single filter (by index) from your first convolutional layer. The filter should appear as a grayscale grid.
```
# Get the weights in the first conv layer, "conv1"
# if necessary, change this to reflect the name of your first conv layer
weights1 = net.conv1.weight.data
w = weights1.numpy()
filter_index = 0
print(w[filter_index][0])
print(w[filter_index][0].shape)
# display the filter weights
plt.imshow(w[filter_index][0], cmap='gray')
```
## Feature maps
Each CNN has at least one convolutional layer that is composed of stacked filters (also known as convolutional kernels). As a CNN trains, it learns what weights to include in it's convolutional kernels and when these kernels are applied to some input image, they produce a set of **feature maps**. So, feature maps are just sets of filtered images; they are the images produced by applying a convolutional kernel to an input image. These maps show us the features that the different layers of the neural network learn to extract. For example, you might imagine a convolutional kernel that detects the vertical edges of a face or another one that detects the corners of eyes. You can see what kind of features each of these kernels detects by applying them to an image. One such example is shown below; from the way it brings out the lines in an the image, you might characterize this as an edge detection filter.
<img src='images/feature_map_ex.png' width=50% height=50%/>
Next, choose a test image and filter it with one of the convolutional kernels in your trained CNN; look at the filtered output to get an idea what that particular kernel detects.
### TODO: Filter an image to see the effect of a convolutional kernel
---
```
##TODO: load in and display any image from the transformed test dataset
## TODO: Using cv's filter2D function,
## apply a specific set of filter weights (like the one displayed above) to the test image
fig = plt.figure(figsize=(120, 4))
for idx in np.arange(4):
ax = fig.add_subplot(2, 128/2, idx+1, xticks=[], yticks=[])
image = test_dataset[idx]['image'].numpy()
ax.imshow(np.squeeze(image), cmap='gray')
import cv2
num = 3
img = np.squeeze(test_dataset[num]['image'].numpy())
plt.imshow(img, cmap='gray')
weights = net.conv1.weight.data
w = weights.numpy()
fig=plt.figure(figsize=(30, 10))
columns = 5*2
rows = 2
for i in range(0, columns*rows):
fig.add_subplot(rows, columns, i+1)
if ((i%2)==0):
plt.imshow(w[int(i/2)][0], cmap='gray')
else:
c = cv2.filter2D(img, -1, w[int((i-1)/2)][0])
plt.imshow(c, cmap='gray')
plt.show()
```
### Question 4: Choose one filter from your trained CNN and apply it to a test image; what purpose do you think it plays? What kind of feature do you think it detects?
**Answer**: (does it detect vertical lines or does it blur out noise, etc.) write your answer here
---
## Moving on!
Now that you've defined and trained your model (and saved the best model), you are ready to move on to the last notebook, which combines a face detector with your saved model to create a facial keypoint detection system that can predict the keypoints on *any* face in an image!
| github_jupyter |
```
import tensorflow as tf
import tensorflow as tf
from tensorflow.python.keras.applications.vgg19 import VGG19
model=VGG19(
include_top=False,
weights='imagenet'
)
model.trainable=False
model.summary()
from tensorflow.python.keras.preprocessing.image import load_img, img_to_array
from tensorflow.python.keras.applications.vgg19 import preprocess_input
from tensorflow.python.keras.models import Model
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def load_and_process_image(image_path):
img=load_img(image_path)
img=img_to_array(img)
img=preprocess_input(img)
img=np.expand_dims(img,axis=0)
return img
def deprocess(x):
x[:,:,0]+=103.939
x[:,:,1]+=116.779
x[:,:,2]+=123.68
x=x[:,:,::-1]
x=np.clip(x,0,255).astype('uint8')
return x
def display_image(image):
if len(image.shape)==4:
img=np.squeeze(image,axis=0)
img=deprocess(img)
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img)
return
display_image(load_and_process_image('style.jpg'))
style_layers = [
'block1_conv1',
'block3_conv1',
'block5_conv1'
]
content_layer = 'block5_conv2'
# intermediate models
content_model = Model(
inputs = model.input,
outputs = model.get_layer(content_layer).output
)
style_models = [Model(inputs = model.input,
outputs = model.get_layer(layer).output) for layer in style_layers]
# Content Cost
def content_cost(content, generated):
a_C = content_model(content)
a_G = content_model(generated)
cost = tf.reduce_mean(tf.square(a_C - a_G))
return cost
def gram_matrix(A):
channels = int(A.shape[-1])
a = tf.reshape(A, [-1, channels])
n = tf.shape(a)[0]
gram = tf.matmul(a, a, transpose_a = True)
return gram / tf.cast(n, tf.float32)
lam = 1. / len(style_models)
def style_cost(style, generated):
J_style = 0
for style_model in style_models:
a_S = style_model(style)
a_G = style_model(generated)
GS = gram_matrix(a_S)
GG = gram_matrix(a_G)
current_cost = tf.reduce_mean(tf.square(GS - GG))
J_style += current_cost * lam
return J_style
import time
generated_images = []
def training_loop(content_path, style_path, iterations = 20, a = 10., b = 20.):
# initialise
content = load_and_process_image(content_path)
style = load_and_process_image(style_path)
generated = tf.Variable(content, dtype = tf.float32)
opt = tf.optimizers.Adam(learning_rate = 7.)
best_cost = 1e12+0.1
best_image = None
start_time = time.time()
for i in range(iterations):
with tf.GradientTape() as tape:
J_content = content_cost(content, generated)
J_style = style_cost(style, generated)
J_total = a * J_content + b * J_style
grads = tape.gradient(J_total, generated)
opt.apply_gradients([(grads, generated)])
if J_total < best_cost:
best_cost = J_total
best_image = generated.numpy()
if i % int(iterations/10) == 0:
time_taken = time.time() - start_time
print('Cost at {}: {}. Time elapsed: {}'.format(i, J_total, time_taken))
generated_images.append(generated.numpy())
return best_image
final = training_loop('content.jpg','style.jpg')
plt.figure(figsize = (12, 12))
for i in range(10):
plt.subplot(5, 2, i + 1)
display_image(generated_images[i])
plt.show()
```
| github_jupyter |
```
from sklearn import datasets
wine = datasets.load_wine()
print(wine.DESCR)
print('Features: ', wine.feature_names)
print('Labels: ', wine.target_names)
#wine=wine.sample(frac=1)
data = wine.data
target = wine.target
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=.3, random_state=109)
print('Xtrain : ',X_train.shape)
print('Xtest : ',X_test.shape)
print('Ytrain : ',y_train.shape)
print('Ytest : ',y_test.shape)
print('Xtrain : ',X_train[:5])
print('Xtest : ',X_test[:5])
print('Ytrain : ',y_train[:5])
print('Ytest : ',y_test[:5])
from sklearn.naive_bayes import GaussianNB
nb = GaussianNB()
nb.fit(X_train, y_train)
y_pred = nb.predict(X_test)
from sklearn import metrics
scores = metrics.accuracy_score(y_test, y_pred)
print('Accuracy: ','{:2.2%}'.format(scores))
cm = metrics.confusion_matrix(y_test, y_pred)
print(cm)
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))
import numpy as np
print(np.sum(np.diag(cm)/np.sum(cm)))
import itertools
import matplotlib.pyplot as plt
%matplotlib inline
def plot_confusion_matrix(cm,
target_names,
title='Confusion matrix',
cmap=None,
normalize=True):
"""
given a sklearn confusion matrix (cm), make a nice plot
Arguments
---------
cm: confusion matrix from sklearn.metrics.confusion_matrix
target_names: given classification classes such as [0, 1, 2]
the class names, for example: ['high', 'medium', 'low']
title: the text to display at the top of the matrix
cmap: the gradient of the values displayed from matplotlib.pyplot.cm
see http://matplotlib.org/examples/color/colormaps_reference.html
plt.get_cmap('jet') or plt.cm.Blues
normalize: If False, plot the raw numbers
If True, plot the proportions
Usage
-----
plot_confusion_matrix(cm = cm, # confusion matrix created by
# sklearn.metrics.confusion_matrix
normalize = True, # show proportions
target_names = y_labels_vals, # list of names of the classes
title = best_estimator_name) # title of graph
Citiation
---------
https://www.kaggle.com/grfiv4/plot-a-confusion-matrix
"""
accuracy = np.trace(cm) / float(np.sum(cm))
misclass = 1 - accuracy
if cmap is None:
cmap = plt.get_cmap('Blues')
plt.figure(figsize=(8, 6))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
if target_names is not None:
tick_marks = np.arange(len(target_names))
plt.xticks(tick_marks, target_names, rotation=45)
plt.yticks(tick_marks, target_names)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
thresh = cm.max() / 1.5 if normalize else cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
if normalize:
plt.text(j, i, "{:0.4f}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
else:
plt.text(j, i, "{:,}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label\naccuracy={:0.4f}; misclass={:0.4f}'.format(accuracy, misclass))
plt.show()
plot_confusion_matrix(cm,wine.target_names)
```
| github_jupyter |
```
%reload_ext watermark
%matplotlib inline
from os.path import exists
from metapool.metapool import *
from metapool import (validate_plate_metadata, assign_emp_index, make_sample_sheet, KLSampleSheet, parse_prep, validate_and_scrub_sample_sheet, generate_qiita_prep_file)
%watermark -i -v -iv -m -h -p metapool,sample_sheet,openpyxl -u
```
# Knight Lab Amplicon Sample Sheet and Mapping (preparation) File Generator
### What is it?
This Jupyter Notebook allows you to automatically generate sample sheets for amplicon sequencing.
### Here's how it should work.
You'll start out with a **basic plate map** (platemap.tsv) , which just links each sample to it's approprite row and column.
You can use this google sheet template to generate your plate map:
https://docs.google.com/spreadsheets/d/1xPjB6iR3brGeG4bm2un4ISSsTDxFw5yME09bKqz0XNk/edit?usp=sharing
Next you'll automatically assign EMP barcodes in order to produce a **sample sheet** (samplesheet.csv) that can be used in combination with the rest of the sequence processing pipeline.
**Please designate what kind of amplicon sequencing you want to perform:**
```
seq_type = '16S'
#options are ['16S', '18S', 'ITS']
```
## Step 1: read in plate map
**Enter the correct path to the plate map file**. This will serve as the plate map for relating all subsequent information.
```
plate_map_fp = './test_data/amplicon/compressed-map.tsv'
if not exists(plate_map_fp):
print("Error: %s is not a path to a valid file" % plate_map_fp)
```
**Read in the plate map**. It should look something like this:
```
Sample Row Col Blank
GLY_01_012 A 1 False
GLY_14_034 B 1 False
GLY_11_007 C 1 False
GLY_28_018 D 1 False
GLY_25_003 E 1 False
GLY_06_106 F 1 False
GLY_07_011 G 1 False
GLY_18_043 H 1 False
GLY_28_004 I 1 False
```
**Make sure there a no duplicate IDs.** If each sample doesn't have a different name, an error will be thrown and you won't be able to generate a sample sheet.
```
plate_df = read_plate_map_csv(open(plate_map_fp,'r'))
plate_df.head()
```
# Assign barcodes according to primer plate
This portion of the notebook will assign a barcode to each sample according to the primer plate number.
As inputs, it requires:
1. A plate map dataframe (from previous step)
2. Preparation metadata for the plates, importantly we need the Primer Plate # so we know what **EMP barcodes** to assign to each plate.
The workflow then:
1. Joins the preparation metadata with the plate metadata.
2. Assigns indices per sample
## Enter and validate the plating metadata
- In general you will want to update all the fields, but the most important ones are the `Primer Plate #` and the `Plate Position`. `Primer Plate #` determines which EMP barcodes will be used for this plate. `Plate Position` determines the physical location of the plate.
- If you are plating less than four plates, then remove the metadata for that plate by deleting the text between the curly braces.
- For missing fields, write NA between the single quotes for example `'NA'`.
- To enter a plate copy and paste the contents from the plates below.
```
_metadata = [
{
# top left plate
'Plate Position': '1',
'Primer Plate #': '1',
'Sample Plate': 'THDMI_UK_Plate_2',
'Project_Name': 'THDMI UK',
'Plating': 'SF',
'Extraction Kit Lot': '166032128',
'Extraction Robot': 'Carmen_HOWE_KF3',
'TM1000 8 Tool': '109379Z',
'Primer Date': '2021-08-17', # yyyy-mm-dd
'MasterMix Lot': '978215',
'Water Lot': 'RNBJ0628',
'Processing Robot': 'Echo550',
'Original Name': ''
},
{
# top right plate
'Plate Position': '2',
'Primer Plate #': '2',
'Sample Plate': 'THDMI_UK_Plate_3',
'Project_Name': 'THDMI UK',
'Plating':'AS',
'Extraction Kit Lot': '166032128',
'Extraction Robot': 'Carmen_HOWE_KF4',
'TM1000 8 Tool': '109379Z',
'Primer Date': '2021-08-17', # yyyy-mm-dd
'MasterMix Lot': '978215',
'Water Lot': 'RNBJ0628',
'Processing Robot': 'Echo550',
'Original Name': ''
},
{
# bottom left plate
'Plate Position': '3',
'Primer Plate #': '3',
'Sample Plate': 'THDMI_UK_Plate_4',
'Project_Name': 'THDMI UK',
'Plating':'MB_SF',
'Extraction Kit Lot': '166032128',
'Extraction Robot': 'Carmen_HOWE_KF3',
'TM1000 8 Tool': '109379Z',
'Primer Date': '2021-08-17', # yyyy-mm-dd
'MasterMix Lot': '978215',
'Water Lot': 'RNBJ0628',
'Processing Robot': 'Echo550',
'Original Name': ''
},
{
# bottom right plate
'Plate Position': '4',
'Primer Plate #': '4',
'Sample Plate': 'THDMI_US_Plate_6',
'Project_Name': 'THDMI US',
'Plating':'AS',
'Extraction Kit Lot': '166032128',
'Extraction Robot': 'Carmen_HOWE_KF4',
'TM1000 8 Tool': '109379Z',
'Primer Date': '2021-08-17', # yyyy-mm-dd
'MasterMix Lot': '978215',
'Water Lot': 'RNBJ0628',
'Processing Robot': 'Echo550',
'Original Name': ''
},
]
plate_metadata = validate_plate_metadata(_metadata)
plate_metadata
```
The `Plate Position` and `Primer Plate #` allow us to figure out which wells are associated with each of the EMP barcodes.
```
if plate_metadata is not None:
plate_df = assign_emp_index(plate_df, plate_metadata, seq_type).reset_index()
plate_df.head()
else:
print('Error: Please fix the errors in the previous cell')
```
As you can see in the table above, the resulting table is now associated with the corresponding EMP barcodes (`Golay Barcode`, `Forward Primer Linker`, etc), and the plating metadata (`Primer Plate #`, `Primer Date`, `Water Lot`, etc).
```
plate_df.head()
```
# Combine plates (optional)
If you would like to combine existing plates with these samples, enter the path to their corresponding sample sheets and mapping (preparation) files below. Otherwise you can skip to the next section.
- sample sheet and mapping (preparation)
```
files = [
# uncomment the line below and point to the correct filepaths to combine with previous plates
# ['test_output/amplicon/2021_08_17_THDMI-4-6_samplesheet.csv', 'test_output/amplicon/2021-08-01-515f806r_prep.tsv'],
]
sheets, preps = [], []
for sheet, prep in files:
sheets.append(KLSampleSheet(sheet))
preps.append(parse_prep(prep))
if len(files):
print('%d pair of files loaded' % len(files))
```
# Make Sample Sheet
This workflow takes the pooled sample information and writes an Illumina sample sheet that can be given directly to the sequencing center or processing pipeline. Note that as of writing `bcl2fastq` does not support error-correction in Golay barcodes so the sample sheet is used to generate a mapping (preparation) file but not to demultiplex sequences. Demultiplexing takes place in [Qiita](https://qiita.ucsd.edu).
As inputs, this notebook requires:
1. A plate map DataFrame (from previous step)
The workflow:
1. formats sample names as bcl2fastq-compatible
2. formats sample data
3. sets values for sample sheet fields and formats sample sheet.
4. writes the sample sheet to a file
## Step 1: Format sample names to be bcl2fastq-compatible
bcl2fastq requires *only* alphanumeric, hyphens, and underscore characters. We'll replace all non-those characters
with underscores and add the bcl2fastq-compatible names to the DataFrame.
```
plate_df['sample sheet Sample_ID'] = plate_df['Sample'].map(bcl_scrub_name)
plate_df.head()
```
## Format the sample sheet data
This step formats the data columns appropriately for the sample sheet, using the values we've calculated previously.
The newly-created `bcl2fastq`-compatible names will be in the `Sample ID` and `Sample Name` columns. The original sample names will be in the Description column.
Modify lanes to indicate which lanes this pool will be sequenced on.
The `Project Name` and `Project Plate` columns will be placed in the `Sample_Project` and `Sample_Name` columns, respectively.
sequencer is important for making sure the i5 index is in the correct orientation for demultiplexing. `HiSeq4000`, `HiSeq3000`, `NextSeq`, and `MiniSeq` all require reverse-complemented i5 index sequences. If you enter one of these exact strings in for sequencer, it will revcomp the i5 sequence for you.
`HiSeq2500`, `MiSeq`, and `NovaSeq` will not revcomp the i5 sequence.
```
sequencer = 'HiSeq4000'
lanes = [1]
metadata = {
'Bioinformatics': [
{
'Sample_Project': 'THDMI_10317',
'QiitaID': '10317',
'BarcodesAreRC': 'False',
'ForwardAdapter': '',
'ReverseAdapter': '',
'HumanFiltering': 'True',
'library_construction_protocol': 'Illumina EMP protocol 515fbc, 806r amplification of 16S rRNA V4',
'experiment_design_description': 'Equipment',
},
],
'Contact': [
{
'Sample_Project': 'THDMI_10317',
# non-admin contacts who want to know when the sequences
# are available in Qiita
'Email': '[email protected],[email protected]'
},
],
'Chemistry': 'Amplicon',
'Assay': 'TruSeq HT',
}
sheet = make_sample_sheet(metadata, plate_df, sequencer, lanes)
sheet.Settings['Adapter'] = 'AGATCGGAAGAGCACACGTCTGAACTCCAGTCA'
sheet.Settings['AdapterRead2'] = 'AGATCGGAAGAGCGTCGTGTAGGGAAAGAGTGT'
```
Check for any possible errors in the sample sheet
```
sheet = validate_and_scrub_sample_sheet(sheet)
```
Add the other sample sheets
```
if len(sheets):
sheet.merge(sheets)
```
## Step 3: Write the sample sheet to file
```
# write sample sheet as .csv
sample_sheet_fp = './test_output/amplicon/2021_08_17_THDMI-4-6_samplesheet16S.csv'
if exists(sample_sheet_fp):
print("Warning! This file exists already.")
with open(sample_sheet_fp,'w') as f:
sheet.write(f)
!head -n 30 {sample_sheet_fp}
!echo ...
!tail -n 15 {sample_sheet_fp}
```
# Create a mapping (preparation) file for Qiita
```
output_filename = 'test_output/amplicon/2021-08-01-515f806r_prep.tsv'
qiita_df = generate_qiita_prep_file(plate_df, seq_type)
qiita_df.head()
qiita_df.set_index('sample_name', verify_integrity=True).to_csv(output_filename, sep='\t')
```
Add the previous sample sheets
```
if len(preps):
prep = prep.append(preps, ignore_index=True)
!head -n 5 {output_filename}
```
| github_jupyter |
<p align="center">
<h1 align="center">Machine Learning and Statistics Tasks 2020</h1>
<h1 align="center"> Task 1: Python function sqrt2</h1>
<h2 align="center"> Author: Ezekiel Onaloye</h2>
<h2 align="center"> Created: November 2020 </h2>
</p>

### Task 1
Write a Python function called sqrt2 that calculates and prints to the screen the square root of 2 to 100 decimal places.
### Introduction
A square root of a number is a value that gives the original number when multiplied by itself. For example, 2 x 2 = 4, so a square root of 4 is 2. -2 x -2 is 4 too, so -2 is also a square root of 4.
A square root is like asking ourselves, "what value can we multiply by itself to get this outcome?". That multiplication by itself, is also called squaring. So, in other words, 3 squared is 9, and so the square root of 9 is 3.
### Simple Python function sqrt2
<h4 align="left"> Algorithm </h4>
1. Take the input from the user
2. Create a function that takes one argument
3. Then, if the number is negative, return nothing
4. As a square root of a number is simply the number raised to the power 0.5, raise the given number to the power of 0.5
5. This will give us the square root of the number; return it
6. Print out the result to the user
```
# Python function called sqrt2
# Adapted from https://www.educative.io/edpresso/how-to-take-the-square-root-of-a-number-in-python
# Function takes input,calculates and prints to the screen the square root of 2 to 100 decimal places
n = int(input("Please input the base value: "))
def sqrt(n):
if n < 0:
return
else:
return n**0.5
print("The square root of", n, "is", format(sqrt(n),'.100f'))
```
### Python function sqrt2
<h4 align="left"> Algorithm </h4>
1. Let n be the given number
2. create function sqrt2(takes a parameter)
3. Given number stored as variable x
4. y equate given number + 1 divided by 2
5. while y is less than x
6. then x = y
7. y store the value of x+n divided by itself and overall by 2
8. return y as the square root
```
# Python function called sqrt2
# Adapted from
# Function takes input,calculates and prints to the screen the square root of 2 to 100 decimal places
# user asked to enter a number
print("")
n = int(input("Please enter any number to find square root: "))
# function declared
def sqrt2(n):
# number entered stored as x, x is a variable carrying entered number
x = n
# y store x + 1 divided by 2 based on
y = (x + 1) / 2
while y < x:
x = y
y = (x + n / x) / 2
return y;
print("Square root of", n, "the given number is %.100f" % sqrt2(n))
```
### References
[1] https://www.educative.io/edpresso/how-to-take-the-square-root-of-a-number-in-python
[2] https://www.codegrepper.com/code-examples/python/python+print+upto+two+decimal+places
[3] https://kodify.net/python/math/square-root/
[4] https://www.educba.com/square-root-in-python/
| github_jupyter |
```
%load_ext autoreload
%autoreload 2
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from tqdm.autonotebook import tqdm
from joblib import Parallel, delayed
import umap
import pandas as pd
from avgn.utils.paths import DATA_DIR, most_recent_subdirectory, ensure_dir
DATASET_ID = 'swamp_sparrow'
from avgn.utils.hparams import HParams
from avgn.dataset import DataSet
from avgn.signalprocessing.create_spectrogram_dataset import prepare_wav, create_label_df, get_row_audio
```
### create dataset
```
hparams = HParams(
num_mel_bins = 32,
mel_lower_edge_hertz=100,
mel_upper_edge_hertz=22000,
butter_lowcut = 100,
butter_highcut = 22000,
ref_level_db = 25,
min_level_db = -50,
mask_spec = True,
win_length_ms = 5,
hop_length_ms = .5,
mask_spec_kwargs = {"spec_thresh": 0.9, "offset": 1e-10}
)
# create a dataset object
dataset = DataSet(DATASET_ID, hparams = hparams)
dataset.sample_json
```
#### Create dataset based upon JSON
```
from joblib import Parallel, delayed
n_jobs = -1; verbosity = 10
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
syllable_dfs = parallel(
delayed(create_label_df)(
dataset.data_files[key].data,
hparams=dataset.hparams,
labels_to_retain=["syllable", "pos_in_syllable"],
unit="elements",
key = key,
)
for key in tqdm(dataset.data_files.keys())
)
syllable_df = pd.concat(syllable_dfs)
len(syllable_df)
syllable_df[:3]
syllable_df
```
### get audio for dataset
```
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
syllable_dfs = parallel(
delayed(get_row_audio)(
syllable_df[syllable_df.key == key],
dataset.data_files[key].data['wav_loc'],
dataset.hparams
)
for key in tqdm(syllable_df.key.unique())
)
syllable_df = pd.concat(syllable_dfs)
len(syllable_df)
syllable_df[:3]
syllable_df.indvi.values[:100]
sylls = syllable_df.audio.values
nrows = 5
ncols = 10
zoom = 2
fig, axs = plt.subplots(ncols=ncols, nrows = nrows,figsize = (ncols*zoom, nrows+zoom/1.5))
for i, syll in tqdm(enumerate(sylls), total = nrows*ncols):
ax = axs.flatten()[i]
ax.plot(syll)
if i == nrows*ncols -1:
break
```
### Create spectrograms
```
from avgn.visualization.spectrogram import draw_spec_set
from avgn.signalprocessing.create_spectrogram_dataset import make_spec, mask_spec, log_resize_spec, pad_spectrogram
syllables_wav = syllable_df.audio.values
syllables_rate = syllable_df.rate.values
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
# create spectrograms
syllables_spec = parallel(
delayed(make_spec)(
syllable,
rate,
hparams=dataset.hparams,
mel_matrix=dataset.mel_matrix,
use_mel=True,
use_tensorflow=False,
)
for syllable, rate in tqdm(
zip(syllables_wav, syllables_rate),
total=len(syllables_rate),
desc="getting syllable spectrograms",
leave=False,
)
)
```
### Rescale spectrogram
- using log rescaling
```
log_scaling_factor = 4
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
syllables_spec = parallel(
delayed(log_resize_spec)(spec, scaling_factor=log_scaling_factor)
for spec in tqdm(syllables_spec, desc="scaling spectrograms", leave=False)
)
draw_spec_set(syllables_spec, zoom=1, maxrows=10, colsize=25)
```
### Pad spectrograms
```
syll_lens = [np.shape(i)[1] for i in syllables_spec]
pad_length = np.max(syll_lens)
plt.hist(syll_lens)
with Parallel(n_jobs=n_jobs, verbose=verbosity) as parallel:
syllables_spec = parallel(
delayed(pad_spectrogram)(spec, pad_length)
for spec in tqdm(
syllables_spec, desc="padding spectrograms", leave=False
)
)
draw_spec_set(syllables_spec, zoom=1, maxrows=10, colsize=25)
```
### save dataset
```
np.shape(syllables_spec)
syllable_df[:3]
syllable_df['spectrogram'] = syllables_spec
save_loc = DATA_DIR / 'syllable_dfs' / DATASET_ID / 'swampsparrow.pickle'
ensure_dir(save_loc)
syllable_df.to_pickle(save_loc)
```
| github_jupyter |
<img src="../../images/banners/python-basics.png" width="600"/>
# <img src="../../images/logos/python.png" width="23"/> Conda Environments
## <img src="../../images/logos/toc.png" width="20"/> Table of Contents
* [Understanding Conda Environments](#understanding_conda_environments)
* [Understanding Basic Package Management With Conda](#understanding_basic_package_management_with_conda)
* [Searching and Installing Packages](#searching_and_installing_packages)
* [Updating and Removing Packages](#updating_and_removing_packages)
* [Cheat Sheet](#cheat_sheet)
* [<img src="../../images/logos/web.png" width="20"/> Read More](#<img_src="../../images/logos/web.png"_width="20"/>_read_more)
---
<a class="anchor" id="understanding_conda_environments"></a>
## Understanding Conda Environments
When you start developing a project from scratch, it’s recommended that you use the latest versions of the libraries you need. However, when working with someone else’s project, such as when running an example from [Kaggle](https://www.kaggle.com/) or [Github](https://github.com/), you may need to install specific versions of packages or even another version of Python due to compatibility issues.
This problem may also occur when you try to run an application you’ve developed long ago, which uses a particular library version that does not work with your application anymore due to updates.
Virtual environments are a solution to this kind of problem. By using them, it is possible to create multiple environments, each one with different versions of packages. A typical Python set up includes [Virtualenv](https://virtualenv.pypa.io/en/stable/#), a tool to create isolated Python virtual environments, widely used in the Python community.
Conda includes its own environment manager and presents some advantages over Virtualenv, especially concerning numerical applications, such as the ability to manage non-Python dependencies and the ability to manage different versions of Python, which is not possible with Virtualenv. Besides that, Conda environments are entirely compatible with default [Python packages](https://realpython.com/python-modules-packages/) that may be installed using pip.
Miniconda installation provides Conda and a root environment with a version of Python and some basic packages installed. Besides this root environment, it is possible to set up additional environments including different versions of Python and packages.
<a class="anchor" id="conda_environments:"></a>
Using the Anaconda prompt, it is possible to check the available Conda environments by running `conda env list`:
```bash
$ (base) ~ % conda env list
# conda environments:
#
base * /home/ali/anaconda3
```
<a class="anchor" id="package_plan_##"></a>
This base environment is the root environment, created by the Miniconda installer. It is possible to create another environment, named `otherenv`, by running `conda create --name otherenv`:
```bash
$ (base) ~ % conda create --name otherenv
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\otherenv
Proceed ([y]/n)? y
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
# $ conda activate otherenv
#
# To deactivate an active environment, use
#
# $ conda deactivate
```
As notified after the environment creation process is finished, it is possible to activate the otherenv environment by running `conda activate otherenv`. You’ll notice the environment has changed by the indication between parentheses in the beginning of the prompt:
```bash
$ (base) ~ % conda activate otherenv
$ (otherenv) ~ %
```
You can open the Python interpreter within this environment by running `python`:
```bash
$ (otherenv) ~ % python
Python 3.7.0 (default, Jun 28 2018, 08:04:48) [MSC v.1912 64 bit (AMD64)] :: Anaconda, Inc. on win32
Type "help", "copyright", "credits" or "license" for more information.
>>>
```
The environment includes Python 3.7.0, the same version included in the root base environment. To exit the Python interpreter, just run `quit()`:
```bash
>>> quit()
(otherenv) ~ %
```
To deactivate the otherenv environment and go back to the root base environment, you should run `deactivate`:
```bash
(otherenv) ~ % conda deactivate
(base) ~ %
```
<a class="anchor" id="package_plan_##"></a>
As mentioned earlier, Conda allows you to easily create environments with different versions of Python, which is not straightforward with Virtualenv. To include a different Python version within an environment, you have to specify it by using `python=<version>` when running conda create. For example, to create an environment named `py2` with `Python 2.7`, you have to run `conda create --name py2 python=2.7`:
```bash
(base) ~ % create --name py2 python=2.7
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\py2
added / updated specs:
- python=2.7
The following NEW packages will be INSTALLED:
certifi: 2018.8.24-py27_1
pip: 10.0.1-py27_0
python: 2.7.15-he216670_0
setuptools: 40.2.0-py27_0
vc: 9-h7299396_1
vs2008_runtime: 9.00.30729.1-hfaea7d5_1
wheel: 0.31.1-py27_0
wincertstore: 0.2-py27hf04cefb_0
Proceed ([y]/n)? y
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
# $ conda activate py2
#
# To deactivate an active environment, use
#
# $ conda deactivate
(base) /mnt/c/Users/username%
```
As shown by the output of `conda create`, this time some new packages were installed, since the new environment uses Python 2. You can check the new environment indeed uses Python 2 by activating it and running the Python interpreter:
```
(base) ~ % conda activate py2
```
<a class="anchor" id="conda_environments:"></a>
Now, if you run `conda env list`, you should see the two environments that were created, besides the root base environment:
```bash
(py2) ~ % conda env list
# conda environments:
#
base C:\Users\IEUser\Miniconda3
otherenv C:\Users\IEUser\Miniconda3\envs\otherenv
py2 * C:\Users\IEUser\Miniconda3\envs\py2
(py2) ~ %
```
<a class="anchor" id="package_plan_##"></a>
In the list, the asterisk indicates the activated environment. It is possible to remove an environment by running `conda remove --name <environment name> --all`. Since it is not possible to remove an activated environment, you should first deactivate the `py2` environment, to remove it:
```bash
(py2) ~ % conda deactivate
(base) ~ % conda remove --name py2 --all
Remove all packages in environment C:\Users\IEUser\Miniconda3\envs\py2:
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\py2
The following packages will be REMOVED:
certifi: 2018.8.24-py27_1
pip: 10.0.1-py27_0
python: 2.7.15-he216670_0
setuptools: 40.2.0-py27_0
vc: 9-h7299396_1
vs2008_runtime: 9.00.30729.1-hfaea7d5_1
wheel: 0.31.1-py27_0
wincertstore: 0.2-py27hf04cefb_0
Proceed ([y]/n)? y
(base) /mnt/c/Users/username%
```
Now that you’ve covered the basics of managing environments with Conda, let’s see how to manage packages within the environments.
<a class="anchor" id="understanding_basic_package_management_with_conda"></a>
## Understanding Basic Package Management With Conda
Within each environment, packages of software can be installed using the Conda package manager. The root base environment created by the Miniconda installer includes some packages by default that are not part of Python standard library.
<a class="anchor" id="packages_in_environment_at_c:\users\ieuser\miniconda3:"></a>
The default installation includes the minimum packages necessary to use Conda. To check the list of installed packages in an environment, you just have to make sure it is activated and run `conda list`. In the root environment, the following packages are installed by default:
```bash
(base) ~ % conda list
# packages in environment at C:\Users\IEUser\Miniconda3:
#
# Name Version Build Channel
asn1crypto 0.24.0 py37_0
ca-certificates 2018.03.07 0
certifi 2018.8.24 py37_1
cffi 1.11.5 py37h74b6da3_1
chardet 3.0.4 py37_1
conda 4.5.11 py37_0
conda-env 2.6.0 1
console_shortcut 0.1.1 3
cryptography 2.3.1 py37h74b6da3_0
idna 2.7 py37_0
menuinst 1.4.14 py37hfa6e2cd_0
openssl 1.0.2p hfa6e2cd_0
pip 10.0.1 py37_0
pycosat 0.6.3 py37hfa6e2cd_0
pycparser 2.18 py37_1
pyopenssl 18.0.0 py37_0
pysocks 1.6.8 py37_0
python 3.7.0 hea74fb7_0
pywin32 223 py37hfa6e2cd_1
requests 2.19.1 py37_0
ruamel_yaml 0.15.46 py37hfa6e2cd_0
setuptools 40.2.0 py37_0
six 1.11.0 py37_1
urllib3 1.23 py37_0
vc 14 h0510ff6_3
vs2015_runtime 14.0.25123 3
wheel 0.31.1 py37_0
win_inet_pton 1.0.1 py37_1
wincertstore 0.2 py37_0
yaml 0.1.7 hc54c509_2
```
To manage the packages, you should also use Conda. Next, let’s see how to search, install, update, and remove packages using Conda.
<a class="anchor" id="searching_and_installing_packages"></a>
### Searching and Installing Packages
Packages are installed from repositories called **channels** by Conda, and some default channels are configured by the installer. To search for a specific package, you can run `conda search <package name>`. For example, this is how you search for the `keras` package (a machine learning library):
```bash
(base) ~ % conda search keras
Loading channels: done
# Name Version Build Channel
keras 2.0.8 py35h15001cb_0 pkgs/main
keras 2.0.8 py36h65e7a35_0 pkgs/main
keras 2.1.2 py35_0 pkgs/main
keras 2.1.2 py36_0 pkgs/main
keras 2.1.3 py35_0 pkgs/main
keras 2.1.3 py36_0 pkgs/main
... (more)
```
According to the previous output, there are different versions of the package and different builds for each version, such as for Python 3.5 and 3.6.
<a class="anchor" id="name_version_build_channel"></a>
The previous search shows only exact matches for packages named `keras`. To perform a broader search, including all packages containing `keras` in their names, you should use the wildcard `*`. For example, when you run conda search `*keras*`, you get the following:
```bash
(base) ~ % conda search "*keras*"
Loading channels: done
# Name Version Build Channel
keras 2.0.8 py35h15001cb_0 pkgs/main
keras 2.0.8 py36h65e7a35_0 pkgs/main
keras 2.1.2 py35_0 pkgs/main
keras 2.1.2 py36_0 pkgs/main
keras 2.1.3 py35_0 pkgs/main
keras 2.1.3 py36_0 pkgs/main
... (more)
keras-applications 1.0.2 py35_0 pkgs/main
keras-applications 1.0.2 py36_0 pkgs/main
keras-applications 1.0.4 py35_0 pkgs/main
... (more)
keras-base 2.2.0 py35_0 pkgs/main
keras-base 2.2.0 py36_0 pkgs/main
... (more)
```
As the previous output shows, there are some other keras related packages in the default channels.
<a class="anchor" id="package_plan_##"></a>
To install a package, you should run `conda install <package name>`. By default, the newest version of the package will be installed in the active environment. So, let’s install the package `keras` in the environment `otherenv` that you’ve already created:
```bash
(base) ~ % conda activate otherenv
(otherenv) ~ % conda install keras
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\otherenv
added / updated specs:
- keras
The following NEW packages will be INSTALLED:
_tflow_1100_select: 0.0.3-mkl
absl-py: 0.4.1-py36_0
astor: 0.7.1-py36_0
blas: 1.0-mkl
certifi: 2018.8.24-py36_1
gast: 0.2.0-py36_0
grpcio: 1.12.1-py36h1a1b453_0
h5py: 2.8.0-py36h3bdd7fb_2
hdf5: 1.10.2-hac2f561_1
icc_rt: 2017.0.4-h97af966_0
intel-openmp: 2018.0.3-0
keras: 2.2.2-0
keras-applications: 1.0.4-py36_1
keras-base: 2.2.2-py36_0
keras-preprocessing: 1.0.2-py36_1
libmklml: 2018.0.3-1
libprotobuf: 3.6.0-h1a1b453_0
markdown: 2.6.11-py36_0
mkl: 2019.0-117
mkl_fft: 1.0.4-py36h1e22a9b_1
mkl_random: 1.0.1-py36h77b88f5_1
numpy: 1.15.1-py36ha559c80_0
numpy-base: 1.15.1-py36h8128ebf_0
pip: 10.0.1-py36_0
protobuf: 3.6.0-py36he025d50_0
python: 3.6.6-hea74fb7_0
pyyaml: 3.13-py36hfa6e2cd_0
scipy: 1.1.0-py36h4f6bf74_1
setuptools: 40.2.0-py36_0
six: 1.11.0-py36_1
tensorboard: 1.10.0-py36he025d50_0
tensorflow: 1.10.0-mkl_py36hb361250_0
tensorflow-base: 1.10.0-mkl_py36h81393da_0
termcolor: 1.1.0-py36_1
vc: 14-h0510ff6_3
vs2013_runtime: 12.0.21005-1
vs2015_runtime: 14.0.25123-3
werkzeug: 0.14.1-py36_0
wheel: 0.31.1-py36_0
wincertstore: 0.2-py36h7fe50ca_0
yaml: 0.1.7-hc54c509_2
zlib: 1.2.11-h8395fce_2
Proceed ([y]/n)?
```
Conda manages the necessary dependencies for a package when it is installed. Since the package keras has a lot of dependencies, when you install it, Conda manages to install this big list of packages.
> **Note:** The paragraph below may not happen when you run it as newer versions of `keras` may be available that use python 3.7.
It’s worth noticing that, since the keras package’s newest build uses Python 3.6 and the otherenv environment was created using Python 3.7, the package python version 3.6.6 was included as a dependency. After confirming the installation, you can check that the Python version for the otherenv environment is downgraded to the 3.6.6 version.
Sometimes, you don’t want packages to be downgraded, and it would be better to just create a new environment with the necessary version of Python. To check the list of new packages, updates, and downgrades necessary for a package without installing it, you should use the parameter `--dry-run`. For example, to check the packages that will be changed by the installation of the package keras, you should run the following:
```
(base) ~ % conda install keras --dry-run
```
<a class="anchor" id="package_plan_##"></a>
However, if necessary, it is possible to change the default Python of a Conda environment by installing a specific version of the package python. To demonstrate that, let’s create a new environment called envpython:
```bash
(otherenv) ~ % conda create --name envpython
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\envpython
Proceed ([y]/n)? y
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
# $ conda activate envpython
#
# To deactivate an active environment, use
#
# $ conda deactivate
```
As you saw before, since the root base environment uses Python 3.7, envpython is created including this same version of Python:
```bash
(base) ~ % conda activate envpython
(envpython) ~ % python
Python 3.7.0 (default, Jun 28 2018, 08:04:48) [MSC v.1912 64 bit (AMD64)] :: Anaconda, Inc. on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> quit()
```
<a class="anchor" id="package_plan_##"></a>
To install a specific version of a package, you can run `conda install <package name>=<version>`. For example, this is how you install Python 3.6 in the envpython environment:
```bash
(envpython) ~ % conda install python=3.6
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3\envs\envpython
added / updated specs:
- python=3.6
The following NEW packages will be INSTALLED:
certifi: 2018.8.24-py36_1
pip: 10.0.1-py36_0
python: 3.6.6-hea74fb7_0
setuptools: 40.2.0-py36_0
vc: 14-h0510ff6_3
vs2015_runtime: 14.0.25123-3
wheel: 0.31.1-py36_0
wincertstore: 0.2-py36h7fe50ca_0
Proceed ([y]/n)?
```
<a class="anchor" id="package_plan_##"></a>
In case you need to install more than one package in an environment, it is possible to run conda install only once, passing the names of the packages. To illustrate that, let’s install `numpy`, `scipy`, and `matplotlib`, basic packages for numerical computation:
```bash
(envpython) ~ % conda install numpy scipy matplotlib
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3
added / updated specs:
- matplotlib
- numpy
- scipy
The following packages will be downloaded:
package | build
---------------------------|-----------------
libpng-1.6.34 | h79bbb47_0 1.3 MB
mkl_random-1.0.1 | py37h77b88f5_1 267 KB
intel-openmp-2019.0 | 117 1.7 MB
qt-5.9.6 | vc14h62aca36_0 92.5 MB
matplotlib-2.2.3 | py37hd159220_0 6.5 MB
tornado-5.1 | py37hfa6e2cd_0 668 KB
pyqt-5.9.2 | py37ha878b3d_0 4.6 MB
pytz-2018.5 | py37_0 232 KB
scipy-1.1.0 | py37h4f6bf74_1 13.5 MB
jpeg-9b | hb83a4c4_2 313 KB
python-dateutil-2.7.3 | py37_0 260 KB
numpy-base-1.15.1 | py37h8128ebf_0 3.9 MB
numpy-1.15.1 | py37ha559c80_0 37 KB
mkl_fft-1.0.4 | py37h1e22a9b_1 120 KB
kiwisolver-1.0.1 | py37h6538335_0 61 KB
pyparsing-2.2.0 | py37_1 96 KB
cycler-0.10.0 | py37_0 13 KB
freetype-2.9.1 | ha9979f8_1 470 KB
icu-58.2 | ha66f8fd_1 21.9 MB
sqlite-3.24.0 | h7602738_0 899 KB
sip-4.19.12 | py37h6538335_0 283 KB
------------------------------------------------------------
Total: 149.5 MB
The following NEW packages will be INSTALLED:
blas: 1.0-mkl
cycler: 0.10.0-py37_0
freetype: 2.9.1-ha9979f8_1
icc_rt: 2017.0.4-h97af966_0
icu: 58.2-ha66f8fd_1
intel-openmp: 2019.0-117
jpeg: 9b-hb83a4c4_2
kiwisolver: 1.0.1-py37h6538335_0
libpng: 1.6.34-h79bbb47_0
matplotlib: 2.2.3-py37hd159220_0
mkl: 2019.0-117
mkl_fft: 1.0.4-py37h1e22a9b_1
mkl_random: 1.0.1-py37h77b88f5_1
numpy: 1.15.1-py37ha559c80_0
numpy-base: 1.15.1-py37h8128ebf_0
pyparsing: 2.2.0-py37_1
pyqt: 5.9.2-py37ha878b3d_0
python-dateutil: 2.7.3-py37_0
pytz: 2018.5-py37_0
qt: 5.9.6-vc14h62aca36_0
scipy: 1.1.0-py37h4f6bf74_1
sip: 4.19.12-py37h6538335_0
sqlite: 3.24.0-h7602738_0
tornado: 5.1-py37hfa6e2cd_0
zlib: 1.2.11-h8395fce_2
Proceed ([y]/n)?
```
Now that you’ve covered how to search and install packages, let’s see how to update and remove them using Conda.
<a class="anchor" id="updating_and_removing_packages"></a>
### Updating and Removing Packages
Sometimes, when new packages are released, you need to update them. To do so, you may run `conda update <package name>`. In case you wish to update all the packages within one environment, you should activate the environment and run `conda update --all`.
<a class="anchor" id="package_plan_##"></a>
To remove a package, you can run `conda remove <package name>`. For example, this is how you remove numpy from the root base environment:
```bash
(envpython) ~ % conda remove numpy
Solving environment: done
## Package Plan ##
environment location: C:\Users\IEUser\Miniconda3
removed specs:
- numpy
The following packages will be REMOVED:
matplotlib: 2.2.3-py37hd159220_0
mkl_fft: 1.0.4-py37h1e22a9b_1
mkl_random: 1.0.1-py37h77b88f5_1
numpy: 1.15.1-py37ha559c80_0
scipy: 1.1.0-py37h4f6bf74_1
Proceed ([y]/n)?
```
> **Note:** It’s worth noting that when you remove a package, all packages that depend on it are also removed.
<a class="anchor" id="cheat_sheet"></a>
## Cheat Sheet
[Click here to get access to a Conda cheat sheet](https://static.realpython.com/conda-cheatsheet.pdf) with handy usage examples for managing your Python environment and packages.
<a class="anchor" id="read_more"></a>
## <img src="../../images/logos/web.png" width="20"/> Read More
Also, if you’d like a deeper understanding of Anaconda and Conda, check out the following links:
- [Why you need Python environments and how to manage them with Conda](https://medium.freecodecamp.org/why-you-need-python-environments-and-how-to-manage-them-with-conda-85f155f4353c)
- [Conda: Myths and Misconceptions](http://jakevdp.github.io/blog/2016/08/25/conda-myths-and-misconceptions/)
| github_jupyter |
# Configuraciones para el Grupo de Estudio
<img src="./img/f_mail.png" style="width: 700px;"/>
## Contenidos
- ¿Por qué jupyter notebooks?
- Bash
- ¿Que es un *kernel*?
- Instalación
- Deberes
## Python y proyecto Jupyter
<img src="./img/py.jpg" style="width: 500px;"/>
<img src="./img/jp.png" style="width: 100px;"/>
- Necesitamos llevar un registro del avance de cada integrante.
- Lenguaje de programación interpretado de alto nivel.
- Jupyter notebooks: son fáciles de usar
- `Necesitamos que todos tengan una versión de Python con jupyter lab`
## ¿Cómo funciona Jupyter?
- Es un derivado del proyecto `iPython`, que ofrece una interfaz interactiva para programadores.
- Tiene formato `.ipynb`
- Es posible usar otros lenguajes de programación diferentes a Python.
- Permite al usuario configurar cómo se visualiza su código mediante `Markdown`.
- Ahora una demostración
<img src="./img/jupex.png" style="width: 500px;"/>
```
import matplotlib.pyplot as plt
import numpy as np
import math
# constantes
pi = math.pi; h = 6.626e-34; kB = 1.380e-23; c = 3.0e+8;
Temps = [9940.00, 8500.00, 7500.00, 6627.00, 5810.93, 4231.15, 3000.00, 2973.15, 288.15]
labels = ['Sirius', 'White star', 'Yellow-white star', 'Polaris', 'Sol', 'HfC', 'Bombilla', 'TaN', 'Atmósfera ']
colors = ['r','g','#FF9633','c','m','#eeefff','y','b','k']
# arreglo de frecuencias
freq = np.arange(0.25e14,3e15,0.25e14)
# funcion spectral energy density (SED)
def SED(f, T):
energyDensity = ( 8*pi*h*(np.power(f, 3.0))/(c**3) ) / (np.exp((h/kB)*f/T) - 1)
return energyDensity
# Calculo de SED para temperaturas
for i in range(len(Temps)):
r = SED(freq,Temps[i])
plt.plot(freq*1e-12,r,color=colors[i],label=labels[i])
plt.legend(); plt.xlabel('frequency ( THz )'); plt.ylabel('SED_frequency ( J $m^{-3}$ $Hz^{-1}$ )')
plt.xlim(0.25e2,2.5e3); plt.show()
```
### Permite escribir expresiones matemáticas complejas
Es posible escribir código en $\LaTeX$ si es necesario
\begin{align}
\frac{\partial u(\lambda, T)}{\partial \lambda} &= \frac{\partial}{\partial \lambda} \left( \frac{C_{1}}{\lambda^{5}}\left(\frac{1}{e^{C_{2}/T\lambda} -1}\right) \right) \\
0 &= \left(\frac{-5}{e^{C_{2}/T\lambda} -1}\frac{1}{\lambda^{6}}\right) + \left( \frac{C_{2}e^{C_{2}/T\lambda}}{T\lambda^{7}} \right)\left(\frac{1}{e^{C_{2}/T\lambda} -1}\right)^{2} \\
0 &= \frac{-\lambda T5}{C_{2}} + \frac{e^{C_{2}/T\lambda}}{e^{C_{2}/T\lambda} -1} \\
0 &= -5 + \left(\frac{C_{2}}{\lambda T}\right) \left(\frac{e^{C_{2}/T\lambda}}{e^{C_{2}/T\lambda} -1}\right)
\end{align}
## ¿Cómo es que usa un lenguaje diferente a Python?
- Un kernel es una especie de `motor computacional` que ejecuta el código dentro de un archivo `.ipynb`.
- Los kernels hay para varios lengajes de programación, como R, Bash, C++, julia.
<img src="./img/ker.png" style="width: 250px;"/>
## ¿Por qué Bash?
- Bash es un lenguaje de scripting que se comunica con la shell e históricamente ha ayudado a científicos a llevarse mejor con la bioinformática.
## ¿Dónde encontramos las instrucciones para instalar Python?
- Es posible hacerlo de varias maneras: `Anaconda` y el `intérprete oficial` desde https://www.python.org/downloads/
- Usaremos el intérprete de `Anaconda`: es más fácil la instalación si no te acostumbras a usar la línea de comandos.
- Si ustedes ya están familiarizados con Python y no desean instalar el intérprete de `Anaconda` pueden usar `pip` desde https://pypi.org/project/bash_kernel/
<img src="./img/qrgit.png" style="width: 250px;"/>
## Deberes
- Creamos una carpeta en `google Drive` donde harán subirán los archivos `.ipynb` y una conversión a HTML, u otro tipo de archivo dependiendo de la sesión.
- Vamos a tener un quiz cada semana, que les enviaremos por el servidor de Discord del grupo de estudio.
- El deber para la siguiente semana:
1. Instalar Ubuntu si aún no lo poseen usando cualquiera de las alternativas presentadas.
2. Instalar Anaconda, jupyter lab y el kernel de bash.
Se deben enviar un documento word o pdf con capturas de pantalla que compruebe esto.
Si tienen algún problema, usen por favor los foros de `Discord` y nos ayudamos entre todos.
<img src="./img/deberes.png" style="width: 500px;"/>
| github_jupyter |
# Generación de observaciones aleatorias a partir de una distribución de probabilidad
La primera etapa de la simulación es la **generación de números aleatorios**. Los números aleatorios sirven como el bloque de construcción de la simulación. La segunda etapa de la simulación es la **generación de variables aleatorias basadas en números aleatorios**. Esto incluye generar variables aleatorias <font color ='red'> discretas y continuas de distribuciones conocidas </font>. En esta clase, estudiaremos técnicas para generar variables aleatorias.
Intentaremos dar respuesta a el siguiente interrogante:
>Dada una secuencia de números aleatorios, ¿cómo se puede generar una secuencia de observaciones aleatorias a partir de una distribución de probabilidad dada? Varios enfoques diferentes están disponibles, dependiendo de la naturaleza de la distribución
Considerando la generación de números alestorios estudiados previamente, asumiremos que tenemos disponble una secuencia $U_1,U_2,\cdots$ variables aleatorias independientes, para las cuales se satisface que:
$$
P(U_i\leq u) = \begin{cases}0,& u<0\\ u,&0\leq u \leq 1\\ 1,& u>1 \end{cases}
$$
es decir, cada variable se distribuye uniformemente entre 0 y 1.
**Recordar:** En clases pasadas, observamos como transformar un número p-seudoaletorio distribuido uniformemte entre 0 y 1, en una distribución normalmente distribuida con media $(\mu,\sigma^2)\longrightarrow$ <font color='red'> [Médoto de Box Muller](http://www.lmpt.univ-tours.fr/~nicolis/Licence_NEW/08-09/boxmuller.pdf) </font> como un caso particular.
En esta sesión, se presentarán dos de los técnicas más ampliamente utilizados para generar variables aletorias, a partir de una distribución de probabilidad.
## 1. Método de la transformada inversa
Este método puede ser usado en ocasiones para generar una observación aleatoria. Tomando $X$ como la variable aletoria involucrada, denotaremos la función de distribución de probabilidad acumulada por
$$F(x)=P(X\leq x),\quad \forall x$$
<font color ='blue'> Dibujar graficamente esta situación en el tablero</font>
El método de la transformada inversa establece
$$X = F^{-1}(U),\quad U \sim \text{Uniforme[0,1]}$$
donde $F^{-1}$ es la transformada inversa de $F$.
Recordar que $F^{-1}$ está bien definida si $F$ es estrictamente creciente, de otro modo necesitamos una regla para solucionar los casos donde esta situación no se satisface. Por ejemplo, podríamos tomar
$$F^{-1}(u)=\inf\{x:F(x)\geq u\}$$
Si hay muchos valores de $x$ para los cuales $F(x)=u$, esta regla escoje el valor mas pequeño. Observar esta situación en el siguiente ejemplo:

Observe que en el intervalo $(a,b]$ si $X$ tiene distribución $F$, entonces
$$P(a<X\leq b)=F(b)-F(a)=0\longrightarrow \text{secciones planas}$$
Por lo tanto si $F$ tienen una densidad continua, entonces $F$ es estrictamente creciente y su inversa está bien definida.
Ahora observemos cuando se tienen las siguientes funciones:

Observemos que sucede en $x_0$
$$\lim_{x \to x_0^-} F(x)\equiv F(x^-)<F(x^+)\equiv \lim_{x\to x_0^+}F(x)$$
Bajo esta distribución el resultado $x_0$ tiene probabilidad $F(x^+)-F(x^-)$. Por otro lado todos los valores de $u$ entre $[u_2,u_1]$ serán mapeados a $x_0$.
Los siguientes ejemplos mostrarán una implementación directa de este método.
### Ejemplo 1: Distribución exponencial
La distribución exponencial con media $\theta$ tiene distribución
$$F(x)=1-e^{-x/\theta}, \quad x\geq 0$$
> Distrubución exponencial python: https://en.wikipedia.org/wiki/Exponential_distribution
>### <font color= blue> Mostrar en el tablero la demostración
```
# Importamos las librerías principales
import numpy as np
import matplotlib.pyplot as plt
# Creamos la función que crea muestras distribuidas exponencialmente
def D_exponential(theta,N):
return -np.log(np.random.random(N))*theta
theta = 4 # Media
N = 10**6 # Número de muestras
# creamos muestras exponenciales con la función que esta en numpy
x = np.random.exponential(theta,N)
# creamos muestras exponenciales con la función creada
x2 = D_exponential(theta,N)
# Graficamos el historial para x
plt.hist(x,100,density=True)
plt.xlabel('valores aleatorios')
plt.ylabel('probabilidad')
plt.title('histograma función de numpy')
print(np.mean(x))
plt.show()
plt.hist(x2,100,density=True)
plt.xlabel('valores aleatorios')
plt.ylabel('probabilidad')
plt.title('histograma función creada')
print(np.mean(x2))
plt.show()
```
### Ejemplo 2
Se sabe que la distribución Erlang resulta de la suma de $k$ variables distribuidas exponencialmente cada una con media $\theta$, y por lo tanto esta variable resultante tiene distribución Erlang de tamaño $k$ y media $theta$.
> Enlace distribución Erlang: https://en.wikipedia.org/wiki/Erlang_distribution
```
N = 10**4
# Variables exponenciales
x1 = np.random.exponential(4,N)
x2 = np.random.exponential(4,N)
x3 = np.random.exponential(4,N)
x4 = np.random.exponential(4,N)
x5 = np.random.exponential(4,N)
# Variables erlang
e0 = x1
e1 = (x1+x2)
e2 = (x3+x4+x5)
e3 = (x1+x2+x3+x4)
e4 = x1+x2+x3+x4+x5
plt.hist(e0,100,density=True,label='1 exponencial')
plt.hist(e1,100,density=True,label='suma de 2 exp')
plt.hist(e2,100,density=True,label='suma de 3 exp')
plt.hist(e3,100,density=True,label='suma de 4 exp')
plt.hist(e4,100,density=True,label='suma de 5 exp')
plt.legend()
plt.show()
# Función para crear variables aleatorias Erlang
def D_erlang(theta:'media distrubucion',k,N):
f = np.random.rand(N,k) # Matriz de variables aleatorias de dim N*k mejora la velocidad del algoritmo
y =list(map(lambda i:-(theta)*np.log(np.prod(f[i,:])),range(N)))
return y
# Prueba de la función creada
N = 10**4
ks = [1,2,3,4,5]
theta = 4
y = list(map(lambda k:D_erlang(theta,k,N),ks))
[plt.hist(y[i],bins=100,density=True,label='suma de %i exp'%(i+1)) for i in range(len(y))]
plt.legend()
plt.show()
```
### Función de densidad variables Erlang
$$p(x)=x^{k-1}\frac{e^{-x/\theta}}{\theta^k\Gamma(k)}\equiv x^{k-1}\frac{e^{-x/\theta}}{\theta^k(k-1)!}$$
```
#Librería que tiene la función gamma y factorial
# Para mostrar la equivalencia entre el factorial y la función gamma
import scipy.special as sps
from math import factorial as fac
k = 4
theta = 4
x = np.arange(0,60,0.01)
plt.show()
y= x**(k-1)*(np.exp(-x/theta) /(sps.gamma(k)*theta**k))
y2 = x**(k-1)*(np.exp(-x/theta) /(fac(k-1)*theta**k))
plt.plot(x,y,'r')
plt.plot(x,y2,'b--')
# plt.show()
# Creo variables aleatorias erlang y obtengo su histograma en la misma gráfica anterior
N = 10**4
r1 = D_erlang(theta,k,N)
plt.hist(r1,bins=50,density=True)
plt.show()
```
Para mejorar la eficiencia, creemos una función que grafique la misma gráfica anterior pero este caso que le podamos variar los parámetros `k` y $\theta$ de la distribución
```
# Función que grafica subplots para cada señal de distribución Erlang
def histograma_erlang(signal:'señal que desea graficar',
k:'Parámetro de la función Erlang'):
plt.figure(figsize=(8,3))
count, x, _ = plt.hist(signal,100,density=True,label='k=%d'%k)
y = x**(k-1)*(np.exp(-x/theta) /(sps.gamma(k)*theta**k))
plt.plot(x, y, linewidth=2,color='k')
plt.ylabel('Probabilidad')
plt.xlabel('Muestras')
plt.legend()
plt.show()
```
Con la función anterior, graficar la función de distribución de una Erlang con parámetros $\theta = 4$ y `Ks = [1,8,3,6] `
```
theta = 4 # media
N = 10**5 # Número de muestras
Ks = [1,8,3,6] # Diferentes valores de k para la distribución Erlang
# Obtengo
Y = list(map(lambda k:D_erlang(theta,k,N),Ks))
list(map(histograma_erlang,Y,Ks));
```
### Ejemplo 4
Distribución de Rayleigh
$$F(x)=1-e^{-2x(x-b)},\quad x\geq b $$
> Fuente: https://en.wikipedia.org/wiki/Rayleigh_distribution
```
# Función del ejemplo 4
def D_rayleigh(b,N):
return (b/2)+np.sqrt(b**2-2*np.log(np.random.rand(N)))/2
np.random.rayleigh?
# Función de Raylegh que contiene numpy
def D_rayleigh2(sigma,N):
return np.sqrt(-2*sigma**2*np.log(np.random.rand(N)))
b = 0.5; N =10**6;sigma = 2
r = D_rayleigh(b,N) # Función del ejemplo
r2 = np.random.rayleigh(sigma,N) # Función que contiene python
r3 = D_rayleigh2(sigma,N) # Función creada de acuerdo a la función de python
plt.figure(1,figsize=(10,8))
plt.subplot(311)
plt.hist(r3,100,density=True)
plt.xlabel('valores aleatorios')
plt.ylabel('probabilidad')
plt.title('histograma función D_rayleigh2')
plt.subplot(312)
plt.hist(r2,100,density=True)
plt.xlabel('valores aleatorios')
plt.ylabel('probabilidad')
plt.title('histograma función numpy')
plt.subplot(313)
plt.hist(r,100,density=True)
plt.xlabel('valores aleatorios')
plt.ylabel('probabilidad')
plt.title('histograma función D_rayleigh')
plt.subplots_adjust(top=0.92, bottom=0.08, left=0.10, right=0.95,
hspace=.5,wspace=0)
plt.show()
```
## Distribuciones discretas
Para una variable dicreta, evaluar $F^{-1}$ se reduce a buscar en una tabla. Considere por ejemplo una variable aleatoria discreta, cuyos posibles valores son $c_1<c_2<\cdots<c_n$. Tome $p_i$ la probabilidad alcanzada por $c_i$, $i=1,\cdots,n$ y tome $q_0=0$, en donde $q_i$ representa las **probabilidades acumuladas asociadas con $c_i$** y está definido como:
$$q_i=\sum_{j=1}^{i}p_j,\quad i=1,\cdots,n \longrightarrow q_i=F(c_i)$$
Entonces, para tomar muestras de esta distribución se deben de realizar los siguientes pasos:
1. Generar un número uniforme $U$ entre (0,1).
2. Encontrar $k\in\{1,\cdots,n\}$ tal que $q_{k-1}<U\leq q_k$
3. Tomar $X=c_k$.
### Ejemplo numérico
```
# Librería para crear tablas
import pandas as pd
val = [1,2,3,4,5]
p_ocur = [.1,.2,.4,.2,.1]
p_acum = np.cumsum(p_ocur)
df = pd.DataFrame(index=val,columns=['Probabilidades','Probabilidad acumulada'], dtype='float')
df.index.name = "Valores (índices)"
df.loc[val,'Probabilidades'] = p_ocur
df.loc[val,'Probabilidad acumulada'] = p_acum
df
u = .5
print(sum(1 for i in p_acum if i<u) + 1)
def Gen_distr_discreta(U:'vector de números aleatorios',
p_acum: 'P.Acumulada de la distribución a generar'):
'''Tener en cuenta que este arreglo cuenta números empezando del 0'''
v = np.array(list(map(lambda j:sum(1 for i in p_acum if i<U[j]),range(len(U)))))
return v
```
# Lo que no se debe de hacer, cuando queremos graficar el histograma de una distribución discreta
```
N = 10**4
u =np.random.rand(N)
v = Gen_distr_discreta(u,p_acum)+1
plt.hist(v,bins = 6)
plt.show()
N = 10**4
u =np.random.rand(N)
v = Gen_distr_discreta(u,p_acum)+1 #+1 porque los índices comienzan en 1
# print(u,v)
# Método 1 (Correcto)
hist,bins = np.histogram(v,bins=len(val))
# print(hist,bins)
plt.bar(val,hist)
plt.title('METODO CORRECTO')
plt.xlabel('valores (índices)')
plt.ylabel('frecuencias')
plt.show()
# Método 2 (incorrecto)
y,x,_ = plt.hist(v,bins=len(val))
plt.title('METODO INCORRECTO')
plt.xlabel('valores (índices)')
plt.ylabel('frecuencias')
plt.legend(['incorrecto'])
plt.show()
def plot_histogram_discrete(distribucion:'distribución a graficar histograma',
label:'label del legend'):
# len(set(distribucion)) cuenta la cantidad de elementos distintos de la variable 'distribucion'
plt.figure(figsize=[8,4])
y,x = np.histogram(distribucion,bins = len(set(distribucion)))
plt.bar(list(set(distribucion)),y,label=label)
plt.legend()
plt.show()
```
>### <font color ='red'> **Tarea 4**
> 1. Generación variable aleatoria continua
>El tiempo en el cual un movimiento browniano se mantiene sobre su punto máximo en el intervalo [0,1] tiene una distribución
>$$F(x)=\frac{2}{\pi}\sin^{-1}(\sqrt x),\quad 0\leq x\leq 1$$ </font>
> 2. Generación variable aleatoria Discreta
> La distribución binomial modela el número de éxitos de n ensayos independientes donde hay una probabilidad p de éxito en cada ensayo.
> Generar una variable aletoria binomial con parámetros $n=10$ y $p=0.7$. Recordar que $$X\sim binomial(n,p) \longrightarrow p_i=P(X=i)=\frac{n!}{i!(n-i)!}p^i(1-p)^{n-i},\quad i=0,1,\cdots,n$$
> Por propiedades de la operación factorial la anterior $p_i$ se puede escribir como:
> $$p_{i+1}=\frac{n-i}{i+1}\frac{p}{1-p} p_i $$
> **Nota:** Por notación recuerde que para el caso continuo $f(x)$ es la distribución de probabilidad (PDF), mientras $F(x)$ corresponde a la distribución de probabilidad acumulada (CDF). Para el caso discreto, $P(X=i)$ corresponde a su distribución de probabilidad (PMF) y $ F_{X}(x)=\operatorname {P} (X\leq x)=\sum _{x_{i}\leq x}\operatorname {P} (X=x_{i})=\sum _{x_{i}\leq x}p(x_{i})$, corresponde a su distribución de probabilidad acumulada (CDF).
Genere muestres aleatorias que distribuyan según la función dada usando el método de la transformada inversa y grafique el histograma de 100 muestras generadas con el método y compárela con el función $f(x)$ dada, esto con el fín de validar que el procedimiento fue realizado de manera correcta
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Oscar David Jaramillo Z.
</footer>
| github_jupyter |
# MHKiT Quality Control Module
The following example runs a simple quality control analysis on wave elevation data using the [MHKiT QC module](https://mhkit-software.github.io/MHKiT/mhkit-python/api.qc.html). The data file used in this example is stored in the [\\\\MHKiT\\\\examples\\\\data](https://github.com/MHKiT-Software/MHKiT-Python/tree/master/examples/data) directory.
Start by importing the necessary Python packages and MHKiT modules.
```
import pandas as pd
from mhkit import qc, utils
```
## Load Data
The wave elevation data used in this example includes several issues, including timestamps that are out of order, corrupt data with values of -999, data outside the expected range, and stagnant data.
The data is loaded into a pandas DataFrame using the pandas method `read_csv`. The first 5 rows of data are shown below, along with a plot.
```
# Load data from the csv file into a DataFrame
data = pd.read_csv('data/qc/wave_elevation_data.csv', index_col='Time')
# Plot the data
data.plot(figsize=(15,5), ylim=(-60,60))
# Print the first 5 rows of data
print(data.head())
```
The data is indexed by time in seconds. To use the quality control functions, the data must be indexed by datetime. The index can be converted to datetime using the following utility function.
```
# Convert the index to datetime
data.index = utils.index_to_datetime(data.index, origin='2019-05-20')
# Print the first 5 rows of data
print(data.head())
```
## Quality control tests
The following quality control tests are used to identify timestamp issues, corrupt data, data outside the expected range, and stagnant data.
Each quality control tests results in the following information:
* Cleaned data, which is a DataFrame that has *NaN* in place of data that did not pass the quality control test
* Boolean mask, which is a DataFrame with True/False that indicates if each data point passed the quality control test
* Summary of the quality control test results, the summary includes the variable name (which is blank for timestamp issues), the start and end time of the test failure, and an error flag for each test failure
### Check timestamp
Quality control analysis generally starts by checking the timestamp index of the data.
The following test checks to see if 1) the data contains duplicate timestamps, 2) timestamps are not monotonically increasing, and 3) timestamps occur at irregular intervals (an interval of 0.002s is expected for this data).
If duplicate timestamps are found, the resulting DataFrames (cleaned data and mask) keep the first occurrence. If timestamps are not monotonic, the timestamps in the resulting DataFrames are reordered.
```
# Define expected frequency of the data, in seconds
frequency = 0.002
# Run the timestamp quality control test
results = qc.check_timestamp(data, frequency)
```
The cleaned data, boolean mask, and test results summary are shown below. The summary is transposed (using .T) so that it is easier to read.
```
# Plot cleaned data
results['cleaned_data'].plot(figsize=(15,5), ylim=(-60,60))
# Print the first 5 rows of the cleaned data
print(results['cleaned_data'].head())
# Print the first 5 rows of the mask
print(results['mask'].head())
# Print the test results summary
# The summary is transposed (using .T) so that it is easier to read.
print(results['test_results'].T)
```
### Check for corrupt data
In the following quality control tests, the cleaned data from the previous test is used as input to the subsequent test. For each quality control test, a plot of the cleaned data is shown along with the test results summary.
Note, that if you want to run a series of quality control tests before extracting the cumulative cleaned data, boolean mask, and summary, we recommend using Pecos directly with the object-oriented approach, see https://pecos.readthedocs.io/ for more details.
The quality control test below checks for corrupt data, indicated by a value of -999.
```
# Define corrupt values
corrupt_values = [-999]
# Run the corrupt data quality control test
results = qc.check_corrupt(results['cleaned_data'], corrupt_values)
# Plot cleaned data
results['cleaned_data'].plot(figsize=(15,5), ylim=(-60,60))
# Print test results summary
print(results['test_results'].T)
```
### Check for data outside the expected range
The next quality control test checks for data that is greater than 50 or less than -50. Note that expected range tests can also be used to compare measured values to a model, or analyze the expected relationships between data columns.
```
# Define expected lower and upper bound ([lower bound, upper bound])
expected_bounds = [-50, 50]
# Run expected range quality control test
results = qc.check_range(results['cleaned_data'], expected_bounds)
# Plot cleaned data
results['cleaned_data'].plot(figsize=(15,5), ylim=(-60,60))
# Print test results summary
print(results['test_results'].T)
```
### Check for stagnant data
The final quality control test checks for stagnant data by looking for data that changes by less than 0.001 within a 0.02 second moving window.
```
# Define expected lower bound (no upper bound is specified in this example)
expected_bound = [0.001, None]
# Define the moving window, in seconds
window = 0.02
# Run the delta quality control test
results = qc.check_delta(results['cleaned_data'], expected_bound, window)
# Plot cleaned data
results['cleaned_data'].plot(figsize=(15,5), ylim=(-60,60))
# Print test results summary
print(results['test_results'].T)
```
## Cleaned Data
The cleaned data can be used directly in MHKiT analysis, or the missing values can be replaced using various methods before analysis is run.
Data replacement strategies are generally defined on a case by case basis. Pandas includes methods to interpolate, replace, and fill missing values.
```
# Extract final cleaned data for MHKiT analysis
cleaned_data = results['cleaned_data']
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import scipy as sp
from scipy.stats import mode
from sklearn import linear_model
import matplotlib
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn import preprocessing
import sklearn as sk
import sklearn.discriminant_analysis as da
import sklearn.neighbors as knn
from IPython.display import Markdown, display
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import Imputer
from sklearn.linear_model import LinearRegression
from sklearn import cross_validation, ensemble, preprocessing, metrics
from sklearn.externals import joblib
%matplotlib inline
df = pd.read_csv('listings_new_york_2018.csv')
```
## 全部的columns名稱
```
df.columns.values
```
## 把全部的分數相關的平均起來成新的column
```
col = df.loc[: , "review_scores_accuracy":"review_scores_value"]
df['review_scores_mean'] = col.mean(axis=1)
```
## 留下來的attributes
```
cols_to_keep = [
'latitude',
'longitude',
'property_type',
'room_type',
'accommodates',
'bathrooms',
'bedrooms',
'beds',
'price','review_scores_mean'
]
df = df[cols_to_keep]
```
## 清理price的符號 只剩下數字和小數點
```
df['price'] = df['price'].replace('[^(0-9).]','', regex=True).replace('[(]','-', regex=True).astype(float)
display(df.head())
```
## 要預測的欄位 price換成log price
```
df['log_price'] = np.log(df['price'].values)
```
## drop price
```
data = df.drop('price', axis=1)
list(data.columns.values)
data.head()
```
## Missing Values
找出各欄位有多少NAN
```
#Replace blanks with NaNs
data = data.replace('_', np.nan)
data = data.replace(' ', np.nan)
data = data.replace([np.inf, -np.inf], np.nan)
col_analysis = []
for column in data.columns:
numNulls = len(data[column][data[column].isnull()])
totalLength = len(data[column])
dict1 = {'Name':column,'DataType':data[column].dtype, 'NumberOfNulls':numNulls, 'PercentageNulls':numNulls*100.0/totalLength}
col_analysis.append(dict1)
col_anal_df = pd.DataFrame(col_analysis)[['Name', 'DataType','NumberOfNulls','PercentageNulls']].sort_values(by='PercentageNulls', ascending=False)
useful_cols = col_anal_df[col_anal_df.PercentageNulls < 50.0]
print('List of Predictors and their respective percentages of missing values')
display(useful_cols.head(28))
for cols in data.columns.values:
if (np.any(useful_cols.Name.values == cols) == False):
data.drop(cols, axis=1, inplace=True)
data.head(5)
```
## Impute Missing Values
把空白的填補成整個欄位的平均值
```
#Use Mean for Real values Columns
real_value_cols = useful_cols[useful_cols.DataType == 'float64']
imp = Imputer(missing_values='NaN', strategy='mean', axis=0)
data[real_value_cols.Name.values] = imp.fit_transform(data[real_value_cols.Name.values])
#Use Highest frequency for categorical columns
categorical_value_cols = useful_cols[useful_cols.DataType == 'object'].Name.values
data[categorical_value_cols] = data[categorical_value_cols].apply(lambda x:x.fillna(x.value_counts().index[0]))
data.head()
data.dtypes
data = data.dropna()
```
## log_price的直方圖 (可以看出試常態分佈)
```
data.log_price.hist()
```
## Convert Categorical Variables to dummy integer values here
- We convert the categorical variables to numeric here such that we can run models that work only with numbers
## One-Hot Encoding
把nomial的欄位換成數字
```
data_ohe = data.copy(deep= True)
#Encode categorical variables
def encode_categorical(array):
return preprocessing.LabelEncoder().fit_transform(array)
categorical_value_cols = useful_cols[useful_cols.DataType == 'object'].Name.values
#print(categorical_value_cols)
#Convert Categories to numbers here
data_ohe[categorical_value_cols] = data_ohe[categorical_value_cols].apply(encode_categorical)
#data_ohe['property_type'] = data_ohe['property_type'].apply(encode_categorical)
# Apply one hot endcoing
# Leads to inferior performance and hence we disable for now
#data_ohe = pd.get_dummies(data_ohe.ix[:,:-1], columns=categorical_value_cols)
print ('Final Dataset ready for modelling after filling in missing values, and encoding categorical variables')
data_ohe.head()
```
## Separate response from predictors
```
x = data_ohe.values[:, :-1]
y = data_ohe.values[:, -1]
#response = df_filtered[['log_price']]
#predictors = df_filtered.drop(['log_price'], axis=1)
```
## Split into train/test
```
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4, random_state=42)
```
## Simple Regression Model
```
#OLS regression
clf = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
clf.fit(x_train, y_train)
predicted = clf.predict(x_test)
score = sk.metrics.r2_score(y_test, predicted)
print('sklearn: R2 score for Linear Regression is: {}'.format(score))
from sklearn import cross_validation, ensemble, preprocessing, metrics
# 建立 random forest 模型
forest = ensemble.RandomForestClassifier(n_estimators = 100)
y_train = np.array(y_train, dtype=int)
forest_fit = forest.fit(x_train, y_train)
# 預測
test_y_predicted = forest.predict(x_test)
y_test = np.array(y_test, dtype=int)
# 績效
score = sk.metrics.r2_score(y_test, test_y_predicted)
print('sklearn: R2 score for Random Forest is: {}'.format(score))
```
## 把model打包
```
joblib.dump(clf, 'predicted.pkl')
estimator = joblib.load('predicted.pkl')
estimator
```
| github_jupyter |
```
import random
import copy
import os
import time
import numpy as np
import matplotlib.pyplot as plt
import warnings
# warnings.filterwarnings("ignore")
%matplotlib inline
class Dataset:
def __init__(self,X,y,proportion=0.8,shuffle=True, mini_batch=0):
"""
Dataset class provide tools to manage dataset
:param X: ndarray, features, highly recommand ndarray
:param y: ndarray, labels
:param proportion: number between 0 and 1, the proportion of train dataset and test dataset
:param shuffle: boolean,
:param mini_batch mini batch size, 0 by default, in this case no mini batch size dataset will be generated
"""
self.X = X
self.y = y
self.trainset = None
self.testset = None
self.validationset = None
self.proportion = proportion
self.shuffle = shuffle
self.mini_batch = mini_batch
self.allset = np.concatenate((X,y),axis=1)
self.minisets = []
if self.shuffle:
# automatic distribution
self.distribute()
# @classmethod
# def imageset(cls, path, proportion = 0.8, shuffle = None):
# pass
def distribute(self):
"""
This function will automatically distribute train and test dataset
call this function to reshuffle all the dataset and also generate new train and test set
"""
n = np.shape(self.X)[0]
samples = np.concatenate((self.X,self.y),axis=1)
random.shuffle(samples)
# sample train and test dataset
self.trainset = samples[0:round(n * self.proportion),:]
self.testset = samples[round(n * self.proportion) + 1:, :]
def getX(self):
return self.X
def gety(self):
return self.y
def getminibatch(self):
return self.mini_batch
def gettrainset(self):
"""
:return: return train dataset with respect of proportion
"""
return Dataset(self.trainset[:, 0:self.X.shape[1]], self.trainset[:, self.X.shape[1]:], mini_batch=self.mini_batch)
def gettestset(self):
"""
:return: test dataset with respect of proportion
"""
return Dataset(self.testset[:, 0:self.X.shape[1]], self.testset[:, self.X.shape[1]:], mini_batch=self.mini_batch)
def getminiset(self):
"""
get mini sets with mini batch size
:return: Dataset array
"""
spilit_list = np.arange(self.mini_batch, self.allset.shape[0], self.mini_batch)
minisets = np.split(self.allset, spilit_list)
for i in range(len(minisets)):
self.minisets.append(Dataset(minisets[i][:, 0:self.X.shape[1]], minisets[i][:, self.X.shape[1]:],shuffle =False, mini_batch=self.mini_batch))
return self.minisets
class NN:
import numpy as np
def __init__(self,dataset):
"""
This class contains Activation function util class, Layer class for construct networks, it contains several extend classes like LinearLayer, Conv2D etc.
Examples:
layer_list = [NN.Layer('Linear',3,10,'sigmoid',BN=True), NN.Layer('Linear',10,100,'sigmoid',BN=True),
NN.Layer('Linear',100,10,'sigmoid',BN=True),NN.Layer('Linear',10,3,'none') ]
dataset = Dataset(X, y, mini_batch= 64)
nn = NN(dataset)
layer_list is a list has 4 layers all are Layer class. Note that here we don't use LinearLayer,
to use LinearLayer, replace NN.Layer('Linear',3,10,'sigmoid',BN=True) as NN.LinearLayer(,3,10,'sigmoid',BN=True) or
NN.LinearLayer(3,10,'sigmoid'), NN.BN()
:param dataset: Dataset class
"""
# self.input = input
self.dataset = dataset
self.layer_list = []
def addlayers(self,layers):
self.layer_list = layers
def getlayers(self):
return self.layer_list
# activation functions
class ActivationFunc:
"""
ActivationFunc is an util class with different types of activation function.
it can
"""
@staticmethod
def sigmoid(x):
"""
Sigmoid function
"""
return 1.0 / (1.0 + np.exp(-x))
@staticmethod
def ReLU(x):
"""
:param x: ndarray,
:return:
"""
return np.maximum(0, x)
@staticmethod
def LeakyReLU(x):
return np.where(x > 0, x, x * 0.01)
@staticmethod
def tanh(x):
return np.tanh(x)
@staticmethod
def none(x):
return x
# Layer class
class Layer:
def __init__(self, type, input_dim, output_dim, activation, BN = False):
"""
Define a layer contains activation function or other normalization.
:param type: Layer type, choose 'Linear', 'Conv' etc
:param input_dim: input dim or previous layer's output
:param output_dim: output dim of this layer
:param activation: activation function, it now support "sigmoid", "ReLU", "LeakyReLU", "tanh" and "none" for no activation function
:param BN, batch normalization , Default False
Examples:
A linear layer with input dim = 3 and output dim = 10, following batch normalization and a sigmoid activation function
NN.Layer('Linear',3,10,'sigmoid',BN=True)
"""
self.type = type
self.input_dim = input_dim
self.output_dim = output_dim
self.activation = activation
self.BN = BN
def getinputdim(self):
return self.input_dim
def getoutputdim(self):
return self.output_dim
def gettype(self):
return self.type
def getact(self, x):
func_name = "NN.ActivationFunc."+self.activation
func = eval(func_name)
return func(x)
def getactname(self):
return self.activation
def getBN(self):
return self.BN
class LinearLayer(Layer):
"""
Define a linear layer
As same as Layer except no need to clarify type
"""
def __init__(self, input_dim, output_dim):
self.type = "Linear"
self.input_dim = input_dim
self.output_dim = output_dim
class Conv2DLayer(Layer):
"""
Define a 2D convolutional layer_
"""
def __init__(self, input_size, kernel_size, stride, padding):
"""
initialize 2D conv layer
:param input_size: Union[tuple, ndarray] layer's input size
:param kernel_size: Union[tuple, ndarray] layer's kernel size
:param stride: Int
:param padding: Int
"""
self.type = "Conv2D"
self.input_size = input_size
self.kernel_size = kernel_size
self.stride = stride
self.padding = padding
def getimagesize(self):
return self.image_size
def getkernelsize(self):
return self.kernel_size
def getstride(self):
return self.stride
def getpadding(self):
return self.padding
class BN(Layer):
def __init__(self):
"""
Define a batch normalization layer
"""
self.type = "BN"
self.activation ="none"
class Optimizer:
def __init__(self,nn ,optimizer,loss_function, batch_size=8,epoch=20000,lr=0.0001,decay_rate=0):
"""
:param nn: input an NN class
:param optimizer: optimizer as "GD", "SGD" etc
:param batch_size: batch size for mini batch optimization
:param epoch: epoch number
:param lr: learning rate
:param decay_rate: float, learning rate decay rate by default is 0
"""
self.nn = nn
self.optimizer = optimizer
self.loss_function = loss_function
self.batch_size = batch_size
self.epoch = epoch
self.lr = lr
self.weight_list = None
self.gradient_list = None
self.loss_list = None
self.passer_list = None
self.decay_rate = decay_rate
def getgradientlist(self):
return self.gradient_list
def getlosslist(self):
return self.loss_list
def getweightlist(self):
return self.weight_list
class LossFunc:
class Logarithmic:
def __init__(self, y_true=None, y_pred=None, eps=1e-16):
self.y_true = y_true
self.y_pred = y_pred
self.eps = eps
"""
Loss function we would like to optimize (minimize)
We are using Logarithmic Loss
http://scikit-learn.org/stable/modules/model_evaluation.html#log-loss
"""
def loss(self):
self.y_pred = np.maximum(self.y_pred, self.eps)
self.y_pred = np.minimum(self.y_pred, (1 - self.eps))
return -(np.sum(self.y_true * np.log(self.y_pred)) + np.sum((1 - self.y_true) * np.log(1 - self.y_pred))) / len(self.y_true)
class Quadratic:
def __init__(self, y_true=None, y_pred=None, norm = 0):
self.y_true = y_true
self.y_pred = y_pred
self.norm = norm
def loss(self):
return 1 / self.y_true.shape[0] * 0.5 * np.sum((self.y_pred - self.y_true) ** 2)
def diff(self):
return 2 * (self.y_pred - self.y_true)
class MSE:
def __init__(self, y_true=None, y_pred=None, x=None):
self.y_true = y_true
self.y_pred = y_pred
self.x = x
def loss(self):
return 1 / np.shape(self.y_true)[0] * np.sum((self.y_pred - self.y_true) ** 2)
def diff(self):
return 2 / np.shape(self.y_true)[0] * np.sum(self.x @ (self.y_pred - self.y_true))
class Node:
def __init__(self, data: np.ndarray, type : str):
"""
Node class, is the node of binary tree which has two child node: left and right.
It can also be presented as weight. Every passer during the back propagation is saved as
a node class contains data, type, back and cache for calculation
:param data: ndarray, value given during forward propagation
:param type: str, the type of node, it can be "weight", "data" or calculation like "@", "+" etc
:param back: ndarray, value updated during back propagation
:param cache: array_like stock forward propagation's detail and middle value for the convenient of back propagation
"""
self.left = None
self.right = None
self.data = data
self.type = type
self.back = None
self.cache = None
self.momentum = None
def getleft(self):
return self.left
def getright(self):
return self.right
def gettype(self):
return self.type
def getdata(self):
return self.data
def getback(self):
return self.back
def getmomentum(self):
return self.momentum
class WeightIni:
"""
Provide weight initial functions. util class
"""
@staticmethod
def init_linear_weight(input_dim, output_dim):
return np.random.uniform(-1, 1, (input_dim, output_dim))
@staticmethod
def init_BN_weight(dim):
return np.ones((1, dim)), np.ones((1, dim), dtype="float32")
@staticmethod
def init_conv2D_kernel(shape):
"""
:param shape: Union[tuple, int, float] shape of kernel
:return:
"""
return np.random.random(shape)
@staticmethod
def initial_weight_list(layer_list):
"""
@Staticmethod. Given layer list and return respected initiall weight list
:param layer_list: list, layer list
:return: list, list of weight in Node class
"""
weight_list = []
# initial weights in weight list by their type
layer_num = len(layer_list)
for i in range(layer_num):
# linear weight operation
if layer_list[i].gettype() == "Linear":
weight_list.append(Optimizer.Node(Optimizer.WeightIni.init_linear_weight(layer_list[i].getinputdim(), layer_list[i].getoutputdim()),"weight"))
elif layer_list[i].gettype() == "BN":
dim = layer_list[i-1].getoutputdim()
gamma, beta = Optimizer.WeightIni.init_BN_weight(dim)
weight_list.append(Optimizer.Node(gamma,"weight"))
weight_list.append(Optimizer.Node(beta,"weight"))
layer_list[i].input_dim = dim
layer_list[i].output_dim = dim
# kernel parse operation
elif layer_list[i].gettype() == "Conv2D":
weight_list.append(Optimizer.Node(Optimizer.WeightIni.init_conv2D_kernel(layer_list[i].getkernelsize()),"weight"))
else:
return NameError
# check if you need BN init
if layer_list[i].getBN():
dim = layer_list[i].getoutputdim()
gamma, beta = Optimizer.WeightIni.init_BN_weight(dim)
weight_list.append(Optimizer.Node(gamma,"weight"))
weight_list.append(Optimizer.Node(beta,"weight"))
return weight_list
@staticmethod
def forword(passer, weight_list, layer_list):
layer_num = len(layer_list)
passer_list = [Optimizer.Node(passer, "data")]
# Every layer not necessarily has only one weight, like BN has 2 weights in a single layer
weight_count = 0
for i in range(layer_num):
if layer_list[i].gettype() =='Linear':
passer = passer@weight_list[weight_count].getdata()
# append binary tree after inner product of weight and previous layer
node = Optimizer.Node(passer,"@")
node.left = passer_list[-1]
node.right = weight_list[weight_count]
passer_list.append(node)
weight_count += 1
if layer_list[i].getBN():
node_cache = [passer, np.var(passer,axis = 0), np.mean(passer, axis=0 )]
passer = (passer - np.mean(passer,axis=0))/np.sqrt(np.var(passer,axis=0))
node = Optimizer.Node(passer,"normalization")
node.cache = node_cache
node.left = passer_list[-1]
passer_list.append(node)
node = Optimizer.Node(passer,"*scalar")
node.left = passer_list[-1]
node.right = weight_list[weight_count]
passer_list.append(node)
passer = passer + weight_list[weight_count+1].getdata()
node = Optimizer.Node(passer,"+scalar")
node.left = passer_list[-1]
node.right = weight_list[weight_count+1]
passer_list.append(node)
weight_count += 2
passer = layer_list[i].getact(passer)
#append binary tree after activation function
node = Optimizer.Node(passer,layer_list[i].getactname())
node.left = passer_list[-1]
passer_list.append(node)
# elif layer_list[j].gettype() == "Conv2D":
else: raise NameError
return passer_list
@staticmethod
def backpropagation(node):
epsilon = 1e-8
if node.getleft() is not None:
if node.gettype() == "@":
node.getleft().back = node.getback()@node.getright().getdata().T
node.getright().back = node.getleft().getdata()[email protected]()
elif node.gettype() == "sigmoid":
node.getleft().back = np.multiply(node.getback(),np.multiply(NN.ActivationFunc.sigmoid(node.getback()),
1-NN.ActivationFunc.sigmoid(node.getback())))
elif node.gettype() == "ReLU":
back = copy.deepcopy(node.getback())
back[back<=0] = 0
node.getleft().back = back
elif node.gettype() == "LeakyReLU":
back = copy.deepcopy(node.getback())
back[back<0] = 0.01*back[back<0]
node.getleft().back = back
elif node.gettype() == "tanh":
node.getleft().back = np.multiply((np.ones(node.getback().shape)-NN.ActivationFunc.tanh(node.getback())**2),
node.getback())
elif node.gettype() == "+":
node.getleft().back = node.getback()
node.getright().back = node.getback()
elif node.gettype() == "-":
node.getleft().back = node.getback()
node.getright().back = -node.getback()
elif node.gettype() == "+scalar":
node.getleft().back = node.getback()
node.getright().back = np.sum(node.getback(),axis=0)
elif node.gettype() == "*scalar":
node.getleft().back = node.getright().getdata() * node.getback()
node.getright().back = np.sum(node.getleft().getdata().T,axis=0)@node.getback()
elif node.gettype() == "none":
node.getleft().back = node.getback()
elif node.gettype() == "normalization":
# cache = [x, sigma_beta^2, mu_beta]
# dx = 1/N / std * (N * dx_norm -
# dx_norm.sum(axis=0) -
# x_norm * (dx_norm * x_norm).sum(axis=0))
x = node.cache[0]
sigma2 = node.cache[1]
mu = node.cache[2]
dl_dx_hat = node.getback()
dl_dsigma2 = np.sum(dl_dx_hat,axis=0) * (x-mu) * -0.5*(sigma2+epsilon)**-3/2
dl_dmu = np.sum(dl_dx_hat,axis=0) * -1/np.sqrt(sigma2+epsilon) + dl_dsigma2 * np.sum(-2*(x-mu),axis= 0)/x.shape[0]
dl_dx = dl_dx_hat * 1/np.sqrt(sigma2+epsilon) + dl_dsigma2*2*(x-mu)/x.shape[0] + dl_dmu /x.shape[0]
node.getleft().back = dl_dx
Optimizer.backpropagation(node.getleft())
else:
return
def lrdecay(self, iter):
"""
Learning rate decay function. Given iteration, modify learning rate
:param iter: int, iteration count
"""
self.lr = 1 / (1 + self.decay_rate * iter) * self.lr
def GD(self, root: Node, weight_list):
"""
Gradient descent, do the back propagation and update weight list
:param root: Node, the root of passer binary tree
:param weight_list: list, weight list
:return: list, updated weight list
"""
Optimizer.backpropagation(root)
gradient_list = []
for node in weight_list:
node.data = node.data - self.lr * node.back
gradient_list.append(node.back)
return weight_list, gradient_list
def SGD(self, weight_list, passer_list):
# we resume mini-batch equals 1 each time
"""
Stochastic gradient descent. It takes weight list and passer list as inputs, it will
:param weight_list:
:param passer_list:
:return:
"""
def init_random_node(node, random_num_list, mini_weight_list):
node.data = node.data[random_num_list,:]
node.back = None
if node.getright() is not None:
mini_weight_list.append(node.getright())
if node.getleft() is not None:
init_random_node(node.getleft(), random_num_list, mini_weight_list)
else: return
# obs = observation number = output layer's dim 0
num_obs = self.nn.dataset.gettrainset().getX().shape[0]
mini_passer_list = copy.deepcopy(passer_list)
root = mini_passer_list[-1]
gradient_list = []
# randomly pick observations from original obs
random_num_list = np.random.randint(0, num_obs, num_obs)
# initial random node
mini_weight_list = []
init_random_node(root, random_num_list, mini_weight_list)
# back propagation
root.back = 2 * (- self.nn.dataset.gettrainset().gety()[random_num_list] + root.getdata()[random_num_list])
Optimizer.backpropagation(root)
i = 0
# update weight list
for weight in weight_list:
weight.data = weight.data - self.lr * mini_weight_list[-i-1].back
gradient_list.append(mini_weight_list[-i-1].back)
i = i + 1
return weight_list, gradient_list
def momentumgd(self, root: Node, weight_list, beta = 0.2):
"""
:param root: Node, the root of passer binary tree
:param weight_list: list, weight list
:param beta: momentum conservation rate
:return: list, updated weight list
"""
Optimizer.backpropagation(root)
gradient_list = []
for node in weight_list:
if node.getmomentum() is None:
node.momentum = (1 - beta) * node.getback()
else:
node.momentum = beta * node.getmomentum() + (1 - beta) * node.getback()
node.data = node.getdata() - self.lr * (1 - beta) * node.getback()
gradient_list.append(node.back)
return weight_list, gradient_list
def RMSprop(self, root: Node, weight_list, beta = 0.2, eps =1e-10):
Optimizer.backpropagation(root)
gradient_list = []
for node in weight_list:
if node.getmomentum() is None:
node.momentum = (1 - beta) * node.getback() ** 2
else:
node.momentum = beta * node.getmomentum() + (1 - beta) * node.getback() ** 2
node.data = node.getdata() - self.lr * node.getback() / (np.sqrt(node.getmomentum()) + eps)
gradient_list.append(node.back)
return weight_list, gradient_list
def Adam(self, root: Node, weight_list, beta_mom = 0.2, beta_rms = 0.2, eps = 1e-10):
"""
Adam optimizer
:param root:
:param weight_list:
:param beta_mom:
:param beta_rms:
:param eps:
:return:
"""
Optimizer.backpropagation(root)
gradient_list = []
for node in weight_list:
if node.getmomentum() is None:
node.momentum = [(1 - beta_mom) * node.getback(), (1 - beta_rms) * node.getback() ** 2]
else:
node.momentum[0] = (beta_mom * node.getmomentum()[0] + (1 - beta_mom) * node.getback()) / (1 - beta_mom)
node.momentum[1] = (beta_rms * node.getmomentum()[1] + (1 - beta_rms) * node.getback() ** 2 ) / (1 - beta_rms)
node.data = node.getdata() - self.lr * node.getmomentum()[0] / (np.sqrt(node.getmomentum()[1])+eps)
gradient_list.append(node.back)
return weight_list, gradient_list
def train(self):
"""
train process, it will first initial weight, loss, gradient and passer list, then, optimize weights by given optimizer.
In the end, calculate loss and step to the next epoch.
It will finally stock all the weight, loss, gradient and passer during the training process
"""
layer_list = self.nn.getlayers()
# initial weight, loss and gradient list
self.weight_list = [[] for i in range(self.epoch+1)]
self.weight_list[0] = Optimizer.WeightIni.initial_weight_list(layer_list)
self.loss_list = np.zeros(self.epoch)
self.gradient_list = [[] for i in range(self.epoch)]
self.passer_list = [[] for i in range(self.epoch)]
# for GD and SGD, they use full dataset, so need only read X and y once
if self.optimizer =="GD" or self.optimizer == "SGD":
X = self.nn.dataset.gettrainset().getX()
X = Optimizer.Node(X, "data")
for i in range(self.epoch):
# forward propagation
self.passer_list[i] = Optimizer.forword(X.getdata(), self.weight_list[i],layer_list)
root = self.passer_list[i][-1]
# calculate loss by using: loss 2 * (-self.nn.dataset.gettrainset().gety() + root.getdata())
loss_func = self.loss_function(self.nn.dataset.gettrainset().gety(), root.getdata())
self.loss_list[i] = loss_func.loss()
root.back = loss_func.diff()
# upgrade gradient by selected optimizer
if self.optimizer =="GD":
self.weight_list[i+1], self.gradient_list[i] = Optimizer.GD(self, root, self.weight_list[i])
elif self.optimizer =="SGD":
self.weight_list[i+1], self.gradient_list[i] = Optimizer.SGD(self, self.weight_list[i], self.passer_list[i])
# mini batch type gradient descent
else:
for i in range(self.epoch):
start_time = time.time()
# get mini batch
minisets = self.nn.dataset.gettrainset().getminiset()
epoch_weight_list = [copy.deepcopy(self.weight_list[i])]
epoch_loss_list = np.zeros(len(minisets))
# GD for every mini batch
for j in range(len(minisets)):
X_bar = minisets[j]
self.passer_list[i].append(Optimizer.forword(X_bar.getX(), epoch_weight_list[j], layer_list))
root = self.passer_list[i][j][-1]
loss_func = self.loss_function(X_bar.gety(), root.getdata())
epoch_loss_list[j] = loss_func.loss()
root.back = loss_func.diff()
root.momentum = root.getback()
if self.optimizer == "minibatchgd":
weight, gradient = Optimizer.GD(self, root, epoch_weight_list[j])
elif self.optimizer == "momentumgd":
weight, gradient = Optimizer.momentumgd(self, root, epoch_weight_list[j])
elif self.optimizer == "RMSprop":
weight, gradient = Optimizer.RMSprop(self, root, epoch_weight_list[j])
elif self.optimizer == "Adam":
weight, gradient = Optimizer.Adam(self, root, epoch_weight_list[j])
else: raise NameError
epoch_weight_list.append(weight)
self.weight_list[i+1]= epoch_weight_list[-1]
self.gradient_list[i] = gradient
self.loss_list[i] = sum(epoch_loss_list)/len(epoch_loss_list)
# learnign rate decay
self.lrdecay(i)
# every epoch shuffle the dataset
self.nn.dataset.distribute()
if (i + 1) % 1 ==0:
used_time = time.time() - start_time
print("epoch " + str(i + 1) + ', Training time: %.4f' % used_time + ', Training loss: %.6f' % self.loss_list[i])
def test(self):
"""
Use trained weight on testset for the evaluation of the model
:return: model prediction and loss on the testset
"""
weight = self.weight_list[-1]
layer_list = self.nn.getlayers()
testset = self.nn.dataset.gettestset()
passer = testset.getX()
passer_list = self.forword(passer,weight,layer_list)
predicted = passer_list[-1].getdata()
loss = self.loss_function.loss(testset.gety(), predicted)
return predicted, loss
def predict(self, X):
"""
Use trained weight on X and output prediction
:param X: ndarray, feature data wish to be predicted
:return: model's prediction by using trained data
"""
passer = X
weight = self.weight_list[-1]
passer_list = self.forword(passer, weight, self.nn.getlayers())
return passer_list
class Visual:
def __init__(self, optim):
self.optim = optim
def plotloss(self):
"""
:return: plot loss flow during the training
"""
plt.style.use('seaborn-whitegrid')
fig = plt.figure()
ax = plt.axes()
ax.plot(self.optim.loss_list, label = 'loss')
ax.legend(loc='upper right')
ax.set_ylabel('Loss during the training')
def plotgradientnorm(self):
plt.style.use('seaborn-whitegrid')
fig, axs = plt.subplots(len(self.optim.getgradientlist()[0]))
for i in range(len(self.optim.getgradientlist()[0])):
gradient_norm_list = []
for j in range(len(self.optim.getgradientlist())):
gradient_norm_list.append(np.linalg.norm(self.optim.getgradientlist()[j][i]))
axs[i].plot(gradient_norm_list, label = 'norm 2')
axs[i].legend(loc='upper right')
axs[i].set_ylabel('W' + str(i) +" norm")
# total observation number
n = 300
# x1, x2 are generated by two
x1 = np.random.uniform(0,1,n)
x2 = np.random.uniform(0,1,n)
const = np.ones(n)
eps = np.random.normal(0,.05,n)
b = 1.5
theta1 = 2
theta2 = 5
Theta = np.array([b, theta1, theta2])
y = np.array(b * const+ theta1 * x1 + theta2 * x2 + eps)
y=np.reshape(y,(-1,1))
X = np.array([const,x1,x2]).T
layer_list = [NN.Layer('Linear',3,100,'LeakyReLU'),NN.Layer('Linear',100,3,'LeakyReLU'),
NN.Layer('Linear',3,1,'none')]
dataset = Dataset(X, y)
nn = NN(dataset)
nn.addlayers(layer_list)
loss_func = Optimizer.LossFunc.Quadratic
optim = Optimizer(nn,"SGD",loss_func, epoch = 10000, lr=1e-6)
optim.train()
visual = Visual(optim)
visual.plotloss()
visual.plotgradientnorm()
# total observation number
n = 10000
# x1, x2 are generated by two
x1 = np.random.uniform(0,1,n)
x2 = np.random.uniform(0,1,n)
const = np.ones(n)
eps = np.random.normal(0,.05,n)
b = 1.5
theta1 = 2
theta2 = 5
Theta = np.array([b, theta1, theta2])
y = np.array(b * const+ theta1 * x1 + theta2 * x2 + eps)
y=np.reshape(y,(-1,1))
X = np.array([const,x1,x2]).T
layer_list = [NN.Layer('Linear',3,10,'sigmoid',BN=True), NN.Layer('Linear',10,100,'sigmoid',BN=True),
NN.Layer('Linear',100,10,'sigmoid',BN=True),NN.Layer('Linear',10,3,'none') ]
dataset = Dataset(X, y, mini_batch= 64)
nn = NN(dataset)
nn.addlayers(layer_list)
loss_func = Optimizer.LossFunc.Quadratic
optim = Optimizer(nn,"Adam", loss_func, epoch = 10, lr=1e-2, decay_rate=0.01)
optim.train()
visual = Visual(optim)
visual.plotloss()
visual.plotgradientnorm()
```
| github_jupyter |
```
import tushare as ts
import sina_data
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
from datetime import datetime, timedelta
from dateutil.parser import parse
import time
import common_util
import os
def get_time(date=False, utc=False, msl=3):
if date:
time_fmt = "%Y-%m-%d %H:%M:%S.%f"
else:
time_fmt = "%H:%M:%S.%f"
if utc:
return datetime.utcnow().strftime(time_fmt)[:(msl-6)]
else:
return datetime.now().strftime(time_fmt)[:(msl-6)]
def print_info(status="I"):
return "\033[0;33;1m[{} {}]\033[0m".format(status, get_time())
def judgement(df, change_rate=0.01, buy1_rate=0.03, buy1_volume=1e5):
float_share = df['float_share'].to_numpy().astype(np.int)
open = df['今日开盘价'].to_numpy().astype(np.float)
pre_close = df['昨日收盘价'].to_numpy().astype(np.float)
limit_up = limit_up_price(pre_close)
price = df['当前价'].to_numpy().astype(np.float)
high = df['今日最高价'].to_numpy().astype(np.float)
low = df['今日最低价'].to_numpy().astype(np.float)
volume = df['成交股票数'].to_numpy().astype(np.int)
buy_1v = df['买一量'].to_numpy().astype(np.int)
judge_list = [
low < limit_up,
price < limit_up,
volume < float_share * change_rate,
buy_1v < float_share * buy1_rate,
buy_1v < buy1_volume
]
return judge_list
# 基于前一交易日收盘价的涨停价计算
def limit_up_price(pre_close):
return np.around(pre_close * 1.1, decimals=2)
# 日K数据判断是否开板
def is_sold(code, start_date):
print(code)
try:
time.sleep(1)
pro = ts.pro_api('ba73b3943bdd57c2ff05991f7556ef417f457ac453355972ff5d01ce')
start_date = (parse(str(start_date))+timedelta(1)).strftime('%Y%m%d')
end_date = datetime.now().strftime('%Y%m%d')
daily_k = pro.daily(ts_code=code, start_date=start_date, end_date=end_date)
if len(daily_k) > 0:
daily_k['flag'] = daily_k.apply(
lambda x: x['high'] == x['low'] and x['open'] == x['close'] and x['high'] == x['low'],
axis=1
)
flag = daily_k['flag'].sum()
result = True
for each in daily_k['flag'].tolist():
result = result and each
return result
else:
return True
except Exception as e:
print('再次请求ts数据')
time.sleep(1)
a = is_sold(code, start_date)
return a
# 获取流通股本
def get_float_share(code):
print(code)
try:
time.sleep(1)
pro = ts.pro_api('ba73b3943bdd57c2ff05991f7556ef417f457ac453355972ff5d01ce')
# target_date = datetime.now().strftime('%Y%m%d')
target_data = []
delta = 0
count = 1
while len(target_data) == 0:
target_date = datetime.now() + timedelta(delta)
target_data = pro.daily_basic(
ts_code=code, trade_date=target_date.strftime('%Y%m%d'), fields='free_share'
)
delta = delta - 1
time.sleep(0.5)
count = count + 1
if count > 3:
return 1000000
return target_data.values[0][0] * 10000
except Exception as e:
time.sleep(1)
get_float_share(code)
print('再次请求ts数据.....')
# 新股筛选
# 获取股票列表
pro = ts.pro_api('ba73b3943bdd57c2ff05991f7556ef417f457ac453355972ff5d01ce')
basic_data = pro.stock_basic()
print('股票筛选')
# basic_data.to_excel(r'C:\Users\duanp\Desktop\test\stock_basic.xlsx')
# basic_data = pd.read_excel(r'C:\Users\duanp\Desktop\test\stock_basic.xlsx')
# 筛选上市日期为近一月的股票
start_date = datetime.now() + timedelta(-30)
end_date = datetime.now() + timedelta(1)
basic_data['list_date'] = basic_data['list_date'].apply(lambda x: parse(str(x)))
basic_data = basic_data[basic_data['list_date'] > start_date]
basic_data = basic_data[basic_data['list_date'] < end_date]
# 剔除科创板股票
basic_data = basic_data[basic_data['market'] != '科创板']
# 筛选未开板的股票
basic_data['target_flag'] = basic_data.apply(lambda x: is_sold(x['ts_code'], x['list_date']), axis=1)
# basic_data = basic_data[basic_data['target_flag']]
print('补充流通股本数据')
# 补充流通股本信息
basic_data['float_share'] = basic_data.apply(lambda x: get_float_share(x['ts_code']), axis=1)
basic_data['float_share'] = basic_data['float_share'].fillna('100000')
print('预警股票如下:')
print(basic_data)
change_rate = 0.01
buy1_rate = 0.03
buy1_volume = 1e5
tick_list = [
'股票代码',
'今日开盘价',
'昨日收盘价',
'当前价',
'今日最高价',
'今日最低价',
'成交股票数',
'买一量'
]
flag_dict = {
"low_flag": "当日曾开板!",
"price_flag": "已经开板!",
"volume_top_flag": "换手率超过 {:.0%}!".format(change_rate),
"buy1_percent_flag": "买一量不足总流通市值的 {:.0%}!".format(buy1_rate),
"buy1_volume_flag": "买一量不足 {} 股!".format(buy1_volume),
}
flag_list = list(flag_dict.keys())
flag_len = len(flag_list)
basic_data['target_code'] = basic_data['ts_code'].apply(lambda x: common_util.get_format_code(x, 'num'))
basic_data['ts_code'].to_list()
tick_data = sina_data.get_tick_data(basic_data['symbol'].to_list())
tick_data['股票代码'] = tick_data['股票代码'].apply(lambda x: common_util.get_format_code(x, 'wind'))
tick_data = tick_data[tick_list]
temp_data = basic_data.merge(tick_data, left_on='ts_code', right_on='股票代码')
judge_list = judgement(temp_data, change_rate, buy1_rate, buy1_volume)
judge_list
alert_dict = dict()
count = 0
for idx in range(flag_len):
temp_data[flag_list[idx]] = judge_list[idx]
alert_dict[flag_list[idx]] = temp_data[temp_data[flag_list[idx]]]["name"].tolist()
if len(alert_dict[flag_list[idx]]) > 0:
print(print_info("W"), end=" ")
print(flag_dict[flag_list[idx]])
print(",".join(alert_dict[flag_list[idx]]))
else:
count += 1
idx=1
temp_data[flag_list[idx]] = judge_list[idx]
alert_dict[flag_list[idx]] = temp_data[temp_data[flag_list[idx]]]
alert_dict
```
| github_jupyter |
```
%matplotlib inline
%pylab inline
pylab.rcParams['figure.figsize'] = (10, 6)
import numpy as np
from numpy.lib import stride_tricks
import cv2
from matplotlib.colors import hsv_to_rgb
import matplotlib.pyplot as plt
import numpy as np
np.set_printoptions(precision=3)
class PatchMatch(object):
def __init__(self, a, b, patch_size):
assert a.shape == b.shape, "Dimensions were unequal for patch-matching input"
self.A = a
self.B = b
self.patch_size = patch_size
self.nnf = np.zeros((2, self.A.shape[0], self.A.shape[1])).astype(np.int)
self.nnd = np.zeros((self.A.shape[0], self.A.shape[1]))
self.initialise_nnf()
def initialise_nnf(self):
self.nnf[0] = np.random.randint(self.B.shape[0], size=(self.A.shape[0], self.A.shape[1]))
self.nnf[1] = np.random.randint(self.B.shape[1], size=(self.A.shape[0], self.A.shape[1]))
self.nnf = self.nnf.transpose((1, 2 ,0))
for i in range(self.A.shape[0]):
for j in range(self.A.shape[1]):
pos = self.nnf[i,j]
self.nnd[i,j] = self.cal_dist(i, j, pos[0], pos[1])
def cal_dist(self, ai ,aj, bi, bj):
dx0 = dy0 = self.patch_size//2
dx1 = dy1 = self.patch_size//2 + 1
dx0 = min(ai, bi, dx0)
dx1 = min(self.A.shape[0]-ai, self.B.shape[0]-bi, dx1)
dy0 = min(aj, bj, dy0)
dy1 = min(self.A.shape[1]-aj, self.B.shape[1]-bj, dy1)
return np.sum((self.A[ai-dx0:ai+dx1, aj-dy0:aj+dy1]-self.B[bi-dx0:bi+dx1, bj-dy0:bj+dy1])**2) / (dx1+dx0) / (dy1+dy0)
def reconstruct(self):
ans = np.zeros_like(self.A)
for i in range(self.A.shape[0]):
for j in range(self.A.shape[1]):
pos = self.nnf[i,j]
ans[i,j] = self.B[pos[0], pos[1]]
return ans
def reconstruct_img_voting(self, patch_size=3,arr_v=None):
if patch_size is None:
patch_size = self.patch_size
b_prime = np.zeros_like(self.A,dtype=np.uint8)
for i in range(self.A.shape[0]): #traverse down a
for j in range(self.A.shape[1]): #traverse across a
dx0 = dy0 = patch_size//2
dx1 = dy1 = patch_size//2 + 1
dx0 = min(i,dx0)
dx1 = min(self.A.shape[0]-i, dx1)
dy0 = min(j, dy0)
dy1 = min(self.A.shape[1]-j, dy1)
votes = self.nnf[i-dx0:i+dx1, j-dy0:j+dy1]
b_patch = np.zeros(shape=(votes.shape[0],votes.shape[1],self.A.shape[2]))
for p_i in range(votes.shape[0]):
for p_j in range(votes.shape[1]):
b_patch[p_i, p_j] = self.B[votes[p_i,p_j][0] , votes[p_i,p_j][1]]
averaged_patch = np.average(b_patch,axis=(0,1))
b_prime[i, j] = averaged_patch[:]
plt.imshow(b_prime[:,:,::-1])
plt.show()
def visualize_nnf(self):
nnf = self.nnf
nnd = self.nnd
def angle_between_alt(p1, p2):
ang1 = np.arctan2(*p1[::-1])
ang2 = np.arctan2(*p2[::-1])
return np.rad2deg((ang1 - ang2) % (2 * np.pi))
def norm_dist(arr):
return (arr)/(arr.max())
img = np.zeros((nnf.shape[0], nnf.shape[1], 3),dtype=np.uint8)
for i in range(1, nnf.shape[0]):
for j in range(1, nnf.shape[1]):
angle = angle_between_alt([j, i], [nnf[i, j][0], nnf[i, j][1]])
img[i, j, :] = np.array([angle, nnd[i,j], 250])
img = hsv_to_rgb(norm_dist(img/255))
plt.imshow(img)
plt.show()
def propagate(self):
compare_value = -1
for i in range(self.A.shape[0]):
for j in range(self.A.shape[1]):
x,y = self.nnf[i,j]
bestx, besty, bestd = x, y, self.nnd[i,j]
compare_value *=-1
if (i + compare_value >= 0 and compare_value == -1) or (i + compare_value < self.A.shape[0] and compare_value == 1) :
rx, ry = self.nnf[i+compare_value, j][0] , self.nnf[i+compare_value, j][1]
if rx < self.B.shape[0]:
val = self.cal_dist(i, j, rx, ry)
if val < bestd:
bestx, besty, bestd = rx, ry, val
if (j+compare_value >= 0 and compare_value == -1)or (j + compare_value < self.A.shape[1] and compare_value == 1) :
rx, ry = self.nnf[i, j+compare_value][0], self.nnf[i, j+compare_value][1]
if ry < self.B.shape[1]:
val = self.cal_dist(i, j, rx, ry)
if val < bestd:
bestx, besty, bestd = rx, ry, val
rand_d = min(self.B.shape[0]//2, self.B.shape[1]//2)
while rand_d > 0:
try:
xmin = max(bestx - rand_d, 0)
xmax = min(bestx + rand_d, self.B.shape[0])
ymin = max(besty - rand_d, 0)
ymax = min(besty + rand_d, self.B.shape[1])
#print(xmin, xmax)
rx = np.random.randint(xmin, xmax)
ry = np.random.randint(ymin, ymax)
val = self.cal_dist(i, j, rx, ry)
if val < bestd:
bestx, besty, bestd = rx, ry, val
except:
print(rand_d)
print(xmin, xmax)
print(ymin, ymax)
print(bestx, besty)
print(self.B.shape)
rand_d = rand_d // 2
self.nnf[i, j] = [bestx, besty]
self.nnd[i, j] = bestd
print("Done")
x = cv2.imread("./blue.jpg")
y = cv2.imread("./yellow.jpg")
x = cv2.resize(x,(200,200))
y = cv2.resize(y,(200,200))
pm = PatchMatch(x,y, 3)
pm.visualize_nnf()
def do():
pm.propagate()
pm.reconstruct_img_voting(patch_size=3)
# pm.propagate()
# pm.reconstruct_img_voting(patch_size=3)
# pm.propagate()
# pm.reconstruct_img_voting(patch_size=3)
# pm.propagate()
# pm.reconstruct_img_voting(patch_size=3)
do()
pm.visualize_nnf()
do()
plt.figure(1)
plt.subplot(131)
plt.axis('off')
plt.imshow(x[:,:,::-1])
plt.subplot(132)
plt.axis('off')
plt.imshow(y[:,:,::-1])
plt.subplot(133)
plt.axis('off')
plt.imshow(pm.reconstruct()[:,:,::-1])
plt.show()
import os
import sys
# add the 'src' directory as one where we can import modules
src_dir = os.path.join(os.getcwd(), os.pardir)
sys.path.append(src_dir)
os.path.join(os.getcwd(), os.pardir)
from src.PatchMatch import PatchMatchSimple
pm = PatchMatchSimple(x,y,patch_size=3)
for i in range(15):
pm.propagate()
pm.reconstruct_img_voting(patch_size=3)
pm.visualize_nnf()
```
| github_jupyter |
```
# -*- coding: utf-8 -*-
# เรียกใช้งานโมดูล
file_name="data"
import codecs
from tqdm import tqdm
from pythainlp.tokenize import word_tokenize
#import deepcut
from pythainlp.tag import pos_tag
from nltk.tokenize import RegexpTokenizer
import glob
import nltk
import re
# thai cut
thaicut="newmm"
from sklearn_crfsuite import scorers,metrics
from sklearn.metrics import make_scorer
from sklearn.model_selection import cross_validate,train_test_split
import sklearn_crfsuite
from pythainlp.corpus.common import thai_stopwords
stopwords = list(thai_stopwords())
#จัดการประโยคซ้ำ
data_not=[]
def Unique(p):
text=re.sub("<[^>]*>","",p)
text=re.sub("\[(.*?)\]","",text)
text=re.sub("\[\/(.*?)\]","",text)
if text not in data_not:
data_not.append(text)
return True
else:
return False
# เตรียมตัวตัด tag ด้วย re
pattern = r'\[(.*?)\](.*?)\[\/(.*?)\]'
tokenizer = RegexpTokenizer(pattern) # ใช้ nltk.tokenize.RegexpTokenizer เพื่อตัด [TIME]8.00[/TIME] ให้เป็น ('TIME','ไง','TIME')
# จัดการกับ tag ที่ไม่ได้ tag
def toolner_to_tag(text):
text=text.strip().replace("FACILITY","LOCATION").replace("[AGO]","").replace("[/AGO]","").replace("[T]","").replace("[/T]","")
text=re.sub("<[^>]*>","",text)
text=re.sub("(\[\/(.*?)\])","\\1***",text)#.replace('(\[(.*?)\])','***\\1')# text.replace('>','>***') # ตัดการกับพวกไม่มี tag word
text=re.sub("(\[\w+\])","***\\1",text)
text2=[]
for i in text.split('***'):
if "[" in i:
text2.append(i)
else:
text2.append("[word]"+i+"[/word]")
text="".join(text2)#re.sub("[word][/word]","","".join(text2))
return text.replace("[word][/word]","")
# แปลง text ให้เป็น conll2002
def text2conll2002(text,pos=True):
"""
ใช้แปลงข้อความให้กลายเป็น conll2002
"""
text=toolner_to_tag(text)
text=text.replace("''",'"')
text=text.replace("’",'"').replace("‘",'"')#.replace('"',"")
tag=tokenizer.tokenize(text)
j=0
conll2002=""
for tagopen,text,tagclose in tag:
word_cut=word_tokenize(text,engine=thaicut) # ใช้ตัวตัดคำ newmm
i=0
txt5=""
while i<len(word_cut):
if word_cut[i]=="''" or word_cut[i]=='"':pass
elif i==0 and tagopen!='word':
txt5+=word_cut[i]
txt5+='\t'+'B-'+tagopen
elif tagopen!='word':
txt5+=word_cut[i]
txt5+='\t'+'I-'+tagopen
else:
txt5+=word_cut[i]
txt5+='\t'+'O'
txt5+='\n'
#j+=1
i+=1
conll2002+=txt5
if pos==False:
return conll2002
return postag(conll2002)
# ใช้สำหรับกำกับ pos tag เพื่อใช้กับ NER
# print(text2conll2002(t,pos=False))
def postag(text):
listtxt=[i for i in text.split('\n') if i!='']
list_word=[]
for data in listtxt:
list_word.append(data.split('\t')[0])
#print(text)
list_word=pos_tag(list_word,engine="perceptron", corpus="orchid_ud")
text=""
i=0
for data in listtxt:
text+=data.split('\t')[0]+'\t'+list_word[i][1]+'\t'+data.split('\t')[1]+'\n'
i+=1
return text
# เขียนไฟล์ข้อมูล conll2002
def write_conll2002(file_name,data):
"""
ใช้สำหรับเขียนไฟล์
"""
with codecs.open(file_name, "w", "utf-8-sig") as temp:
temp.write(data)
return True
# อ่านข้อมูลจากไฟล์
def get_data(fileopen):
"""
สำหรับใช้อ่านทั้งหมดทั้งในไฟล์ทีละรรทัดออกมาเป็น list
"""
with codecs.open(fileopen, 'r',encoding='utf-8-sig') as f:
lines = f.read().splitlines()
return [a for a in tqdm(lines) if Unique(a)] # เอาไม่ซ้ำกัน
def alldata(lists):
text=""
for data in lists:
text+=text2conll2002(data)
text+='\n'
return text
def alldata_list(lists):
data_all=[]
for data in lists:
data_num=[]
try:
txt=text2conll2002(data,pos=True).split('\n')
for d in txt:
tt=d.split('\t')
if d!="":
if len(tt)==3:
data_num.append((tt[0],tt[1],tt[2]))
else:
data_num.append((tt[0],tt[1]))
#print(data_num)
data_all.append(data_num)
except:
print(data)
#print(data_all)
return data_all
def alldata_list_str(lists):
string=""
for data in lists:
string1=""
for j in data:
string1+=j[0]+" "+j[1]+" "+j[2]+"\n"
string1+="\n"
string+=string1
return string
def get_data_tag(listd):
list_all=[]
c=[]
for i in listd:
if i !='':
c.append((i.split("\t")[0],i.split("\t")[1],i.split("\t")[2]))
else:
list_all.append(c)
c=[]
return list_all
def getall(lista):
ll=[]
for i in tqdm(lista):
o=True
for j in ll:
if re.sub("\[(.*?)\]","",i)==re.sub("\[(.*?)\]","",j):
o=False
break
if o==True:
ll.append(i)
return ll
data1=getall(get_data(file_name+".txt"))
print(len(data1))
'''
'''
#del datatofile[0]
datatofile=alldata_list(data1)
tt=[]
#datatofile.reverse()
import random
#random.shuffle(datatofile)
print(len(datatofile))
#training_samples = datatofile[:int(len(datatofile) * 0.8)]
#test_samples = datatofile[int(len(datatofile) * 0.8):]
'''training_samples = datatofile[:2822]
test_samples = datatofile[2822:]'''
#print(test_samples[0])
#tag=TrainChunker(training_samples,test_samples) # Train
#run(training_samples,test_samples)
#import dill
#with open('train.data', 'rb') as file:
# datatofile = dill.load(file)
with open(file_name+"-pos.conll","w") as f:
i=0
while i<len(datatofile):
for j in datatofile[i]:
f.write(j[0]+"\t"+j[1]+"\t"+j[2]+"\n")
if i+1<len(datatofile):
f.write("\n")
i+=1
with open(file_name+".conll","w") as f:
i=0
while i<len(datatofile):
for j in datatofile[i]:
f.write(j[0]+"\t"+j[2]+"\n")
if i+1<len(datatofile):
f.write("\n")
i+=1
def isThai(chr):
cVal = ord(chr)
if(cVal >= 3584 and cVal <= 3711):
return True
return False
def isThaiWord(word):
t=True
for i in word:
l=isThai(i)
if l!=True and i!='.':
t=False
break
return t
def is_stopword(word):
return word in stopwords
def is_s(word):
if word == " " or word =="\t" or word=="":
return True
else:
return False
def lennum(word,num):
if len(word)==num:
return True
return False
def doc2features(doc, i):
word = doc[i][0]
postag = doc[i][1]
# Features from current word
features={
'word.word': word,
'word.stopword': is_stopword(word),
'word.isthai':isThaiWord(word),
'word.isspace':word.isspace(),
'postag':postag,
'word.isdigit()': word.isdigit()
}
if word.isdigit() and len(word)==5:
features['word.islen5']=True
if i > 0:
prevword = doc[i-1][0]
postag1 = doc[i-1][1]
features['word.prevword'] = prevword
features['word.previsspace']=prevword.isspace()
features['word.previsthai']=isThaiWord(prevword)
features['word.prevstopword']=is_stopword(prevword)
features['word.prepostag'] = postag1
features['word.prevwordisdigit'] = prevword.isdigit()
else:
features['BOS'] = True # Special "Beginning of Sequence" tag
# Features from next word
if i < len(doc)-1:
nextword = doc[i+1][0]
postag1 = doc[i+1][1]
features['word.nextword'] = nextword
features['word.nextisspace']=nextword.isspace()
features['word.nextpostag'] = postag1
features['word.nextisthai']=isThaiWord(nextword)
features['word.nextstopword']=is_stopword(nextword)
features['word.nextwordisdigit'] = nextword.isdigit()
else:
features['EOS'] = True # Special "End of Sequence" tag
return features
def extract_features(doc):
return [doc2features(doc, i) for i in range(len(doc))]
def get_labels(doc):
return [tag for (token,postag,tag) in doc]
X_data = [extract_features(doc) for doc in tqdm(datatofile)]
y_data = [get_labels(doc) for doc in tqdm(datatofile)]
X, X_test, y, y_test = train_test_split(X_data, y_data, test_size=0.2)
crf = sklearn_crfsuite.CRF(
algorithm='lbfgs',
c1=0.1,
c2=0.1,
max_iterations=500,
all_possible_transitions=True,
model_filename=file_name+"-pos.model0"
)
crf.fit(X, y);
labels = list(crf.classes_)
labels.remove('O')
y_pred = crf.predict(X_test)
e=metrics.flat_f1_score(y_test, y_pred,
average='weighted', labels=labels)
print(e)
sorted_labels = sorted(
labels,
key=lambda name: (name[1:], name[0])
)
print(metrics.flat_classification_report(
y_test, y_pred, labels=sorted_labels, digits=3
))
#del X_data[0]
#del y_data[0]
!export PYTHONIOENCODING=utf-8
import sklearn_crfsuite
crf2 = sklearn_crfsuite.CRF(
algorithm='lbfgs',
c1=0.1,
c2=0.1,
max_iterations=500,
all_possible_transitions=True,
model_filename=file_name+".model"
)
crf2.fit(X_data, y_data);
import dill
with open("train.data", "wb") as dill_file:
dill.dump(datatofile, dill_file)
# cross_validate
"""
import dill
with open("datatrain.data", "wb") as dill_file:
dill.dump(datatofile, dill_file)
f1_scorer = make_scorer(metrics.flat_f1_score, average='macro')
scores = cross_validate(crf, X, y, scoring=f1_scorer, cv=5)
# save data
print(scores)
"""
```
| github_jupyter |
# Introduction
This notebook can be used to both train a discriminator on the AG news dataset and steering text generation in the direction of each of the four classes of this dataset, namely world, sports, business and sci/tech.
My code uses and builds on a text generation plug-and-play model developed by the Uber AI research team, which can be found here: https://github.com/uber-research/PPLM.
I had a lot of problems setting up the code provided by the original paper, since the package versions is old and has a lot of incompatability issues. I spent loads of times trying to set up pip and/or anaconda environments to run their code, but there was always an issue.
Therefore, I developed this in Google Colab, which seems to be the only place where I can run their code without problems. **I strongly recommend you running this in Google Colab as well**. Thus, my code is kind of hard to use exactly because the original PPLM code is hard to use. I forked the PPLM repo and removed lots of unecessary stuff, only keeping the parts I'm using in this notebook. Also, I added my newly trained discriminator model.
By running this entire notebook cell for cell, you both train the discriminator and performs the generation experiment. However, since I've already trained this very discriminator, you can skip those cells. You can also skip the cells corresponding to saving models and results to disk. I've marked the "mandatory" cells with the comment "# MUST BE RUN" for this purpose.
## Main functionality
This notebook essentially just runs my experiment setup using the newly trained discriminator to steer text generation in the direction of the discriminator classes text.
The main function is named *text_generation*, which can be used to generate a user-chosen amount of samples using either an unperturbed model or perturbed model. In the latter case, the user might choose which class he/she wished to steer text generation towards. I should also say that it's not quite new functionality, it's based on some of the PPLM code modified to suit my experiment.
## Termology used throughout:
- Model setting: using a general language model (GPT-2) together with the discriminator fixed on optimizing for one specific class.
- Perturbed and unperturbed: This is essentially whether a discriminator has been used in the text generation. For instance, unperturbated text is "clean", meaning unsteered, while perturbated text is steered in a class direction.
# Setup: import the code base from github, and install requirements
```
# MUST BE RUN
!git clone https://github.com/eskilhamre/PPLM.git
# MUST BE RUN
import os
os.chdir('PPLM')
# MUST BE RUN
!pip install -r requirements.txt
```
# Train a discriminator on AG news dataset
## First, download the general lanaguage model used to train the discriminator
```
from transformers.modeling_gpt2 import GPT2LMHeadModel
# This downloads GPT-2 Medium, it takes a little while
_ = GPT2LMHeadModel.from_pretrained("gpt2-medium")
```
## Import the dataset
The data can be found at: https://www.kaggle.com/amananandrai/ag-news-classification-dataset/version/2?select=train.csv
The PPLM interface requires the data to be a tsv file containing the entire dataset, where the first column is the labels and seconds column the text. Thus, we have to prepare the dataset for this.
First, download the dataset following the link above, and upload both files in the set below.
```
import pandas as pd
from google.colab import files
import torch
torch.cuda.is_available()
uploaded = files.upload()
data_fp = "./ag-news-data.tsv" # where we want to store our prepared dataset
def prepare_dataset(text_index,
label_index,
label_names=None
):
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
all_data = pd.concat([train, test])
all_data = all_data.iloc[:, [label_index, text_index]]
if label_names:
labels_map = {i+1: label_name for i, label_name in enumerate(label_names)} # here assuming labels are numerated 1,...,n, which is the case for AG news
all_data.iloc[:, 0] = all_data.iloc[:, 0].map(labels_map) # exchange label numbers by their name
return all_data
idx2class = ["world", "sports", "business", "sci/tech"]
data = prepare_dataset(2, 0, idx2class)
data.to_csv(data_fp, sep='\t', index=False, header=False)
from run_pplm_discrim_train import train_discriminator
# ensure reproducible discriminator
torch.manual_seed(444)
np.random.seed(444)
discriminator, disc_info = train_discriminator(
dataset="generic",
dataset_fp=data_fp,
pretrained_model="gpt2-medium",
epochs=8,
learning_rate=0.0001,
batch_size=128,
log_interval=10,
save_model=True,
cached=False,
no_cuda=False,
output_fp='models/',
idx2class=idx2class
)
```
We achieve about 90% accuracy on unseen data, which is pretty good in my opinion. I haven't studied the training accuracy (so I can't say the following for sure), but I don't think we're neither underfitting or overfitting here. This is good stuff!
Also, the validation/test accuracy seems to stagnate on ~90%, so more epochs would probably be in no use.
## Training the discriminator is done, let's download it
```
classifier_name = "models/news_classifierhead.pt"
torch.save(discriminator.get_classifier().state_dict(), "models/news_classifierhead.pt")
files.download(classifier_name)
```
At this point, I put the newly generated model in the discrim_models/ folder, and updated my Github code to include this model. I went back to the beginning of the notebook and recloned the repo.
# Scoring the generated samples
When doing manual comparison between text generated from different model settings, I'm only interested in comparing only the best sample for each model setting. The idea is to generate lots of samples using the same setting, and picking the best one based on some type of scoring.
What do I mean by best samples? I'm automating this evaluation as means of scoring and ranking the sentences in a similar way as described in the PPLM paper;
- fluency is measured by the general language model likelihood p(sentence). In scoring, I utilize the fact that the lower the language model loss(sentence), the higher the p(sentence). I use GPT-1 for this, as in the PPLM paper (in the paper however, they use GPT-1 to calculate perplexity, and as I understand it this should correspond to loss.)
- diversity of words is measured by the mean of the (length normalized) Dist-1, Dist-2 and Dist-3 score, (the PPLM paper was inspired by the way they use this metric in this paper: https://arxiv.org/pdf/1510.03055.pdf)
```
# MUST BE RUN
from transformers.modeling_gpt2 import GPT2LMHeadModel
from transformers import GPT2Tokenizer, OpenAIGPTLMHeadModel, OpenAIGPTTokenizer
from nltk import ngrams
import numpy as np
```
### Instantiate models used for scoring samples
```
# MUST BE RUN
device = "cuda" if torch.cuda.is_available() else "cpu"
# tokenizer and language model used for calculating fluency / "perplexity"
gpt1_tokenizer = OpenAIGPTTokenizer.from_pretrained("openai-gpt")
gpt1_model = OpenAIGPTLMHeadModel.from_pretrained("openai-gpt")
gpt1_model.eval()
gpt1_model.to(device)
device
# MUST BE RUN
##############
# This is to be used on all generated sentences (to be aggregated wrt. model setting), not used for selection
##############
def lm_score(sentence):
"""
Calculates the language model total loss of the sentence.
Code heavily inspired from: https://github.com/huggingface/transformers/issues/1009
The total loss is equivalent to
- [ log P(x1 | <|endoftext|>) + log P(x2 | x1, <|endoftext|>) + ... ]
which means it corresponds to perplexity, and can be used as such in comparisons.
"""
tokens = gpt1_tokenizer.encode(sentence)
input_ids = torch.tensor(tokens).unsqueeze(0)
input_ids = input_ids.to(device)
with torch.no_grad():
outputs = gpt1_model(input_ids, labels=input_ids)
loss, logits = outputs[:2]
return loss.item() # * len(tokens) don't multiply with length, this would prefer shorter sentences
###############
# This is used for selecting the best sample when model setting and prefix is fixed
###############
def dist_n_score(sentence, n):
"""Calculates the number of distinct n-grams in the sentence, normalized by the sentence length"""
if len(sentence.split()) < n:
raise ValueError("Cannot find ngram of sentence with less than n words")
sentence = sentence.lower().strip()
dist_n_grams = set()
for n_gram in ngrams(sentence.split(), n):
dist_n_grams.add(n_gram)
return len(dist_n_grams) / len(sentence.split())
def dist_score(sentence):
"""
Calculcates the dist-1, dist-2 and dist-3 score of the sentence, as well as their mean
"""
sentence = sentence.lower().strip()
sentence = sentence.replace(".", "").replace(",", "").replace("\n", "")
dist_scores = [dist_n_score(sentence, n) for n in range(1, 4)]
dist_1, dist_2, dist_3 = dist_scores
return np.mean(dist_scores), dist_1, dist_2, dist_3
sentences =['there is a book on the desk', 'there is a plane on the desk', 'there is a book in the desk', "desk desk desk desk cat cat"]
print([lm_score(s) for s in sentences])
print([dist_score(s)[0] for s in sentences])
```
We can see that the most sensible of the four sentences receives lowest language model score (thus higher probability). Also, we can see that the non-sensible sentence receives both bad language model and dist-score.
# Text generation
```
# MUST BE RUN
from run_pplm import run_pplm_example, generate_text_pplm, get_classifier, PPLM_DISCRIM
# MUST BE RUN
def text_generation(
model,
tokenizer,
discrim="news",
class_label="sports",
prefix_text="Last summer",
perturb=False,
num_samples=3,
device="cuda",
length=150,
stepsize=0.04,
num_iterations=10,
window_length=0, # 0 corresponds to entire sequence
gamma=1.0,
gm_scale=0.95,
kl_scale=0.01,
verbosity_level=1 # REGULAR
):
"""
Used to generate a user-specified number of samples, with optional use of the discriminator
to perturbate the generated samples in the direction of it's gradient.
This is a modified version of the PPML text generation function to suit my experiment.
Only supports generating text using discriminator models (BoW models not supported)
The default hyper parameters chosen here are the same as in the PPLM Colab demo, since
this seems to work great for discriminators.
Returns a list of generated text samples and their corresponding attribute model losses
"""
# we pass the discriminator even if we want unpertubated text, since it's used for attribute scoring
discrim_model, class_id = get_classifier(
discrim,
class_label,
device
)
# encode prefix text
tokenized_cond_text = tokenizer.encode(
tokenizer.bos_token + prefix_text,
add_special_tokens=False
)
gen_text_samples = []
discrim_losses = []
if device == 'cuda':
torch.cuda.empty_cache()
for i in range(num_samples):
gen_tok_text, discrim_loss, _ = generate_text_pplm(
model=model,
tokenizer=tokenizer,
context=tokenized_cond_text,
device=device,
perturb=perturb,
classifier=discrim_model,
class_label=class_id,
loss_type=PPLM_DISCRIM, # BoW not supported as of now
length=length,
stepsize=stepsize,
sample=True,
num_iterations=num_iterations,
horizon_length=1,
window_length=window_length,
gamma=gamma,
gm_scale=gm_scale,
kl_scale=kl_scale,
verbosity_level=verbosity_level
)
gen_text = tokenizer.decode(gen_tok_text[0][1:]) # decode generated text
gen_text_samples.append(gen_text)
discrim_losses.append(discrim_loss.item()) #.data.cpu().numpy())
if device == "cuda":
torch.cuda.empty_cache()
return gen_text_samples, discrim_losses
def select_best(gen_text_samples, discrim_losses):
"""
Given the outout from the text_generation function, filters away 3/4 of the
generated samples based on mean dist-score, and rank the remaining 1/4 based
on discriminator losses.
Returns the best sample based smallest discriminator loss (the one maximizing
the attribute, according to the discriminator)
"""
if len(gen_text_samples) < 4:
raise ValueError("Cannot filter away 3/4 of less than 4 samples")
n_keep = 1 * len(gen_text_samples) // 4 # number of samples to keep
# filter out the 3/4 samples with lowest mean dist-score
mean_dists = [dist_score(sample)[0] for sample in gen_text_samples]
idx_to_keep = np.argpartition(mean_dists, -n_keep)[-n_keep:] # indices of samples with highest mean dist score
samples = np.array([gen_text_samples, discrim_losses, mean_dists]).T
filtered_samples = samples[idx_to_keep]
# fetch best sample among the remaining ones
best_idx = np.argmin(filtered_samples[:, 1]) # index of sample with minimal discrim loss
best_sample, smallest_loss, mean_dist = filtered_samples[best_idx]
return best_sample, smallest_loss, mean_dist
```
## Import the base model used to sample from
```
# MUST BE RUN
pretrained_model = "gpt2-medium"
model = GPT2LMHeadModel.from_pretrained(
pretrained_model,
output_hidden_states=True
)
model.to(device)
model.eval()
# Freeze GPT-2 weigths
for param in model.parameters():
param.requires_grad = False
tokenizer = GPT2Tokenizer.from_pretrained(pretrained_model)
```
## Sample from all combinations of model setting and prefix sentences
First, let's create some data structures to gather relevant information from the sampling process.
```
# MUST BE RUN
# most relevant hyper params wrt. speed
generated_len = 120
num_samples = 12
prefixes = [
"Last week",
"The potato",
"Breaking news:",
"In the last year",
"The president of the country",
]
model_settings = ["world", "sports", "business", "sci/tech"] # the classes of the discriminator
# MUST BE RUN
# data structures of generated results
gen_samples = {model_setting: [] for model_setting in ["unpert"] + model_settings.copy()} # contains all generated samples
comparisons = {model_setting: {prefix: dict() for prefix in prefixes} for model_setting in model_settings} # contains the best samples for each model setting and prefix combo
```
The cell below runs the *entire* sampling process, it took ~5 hours to run on Googles Compute Engine backend using their GPUs.
Here I decided that generate unperturbed text for each model setting. This might seem silly and redundant, since the unperturbed text is not affected by this choice.
And while that is partly true, I did this to be able to calculate the discriminator losses of the generated text, so that I can select the "best" sample wrt. to the classes (even though it's best by chance). I thought this is only fair: the perturbed model gets many chances to generate a "good" sample (in the eyes of the discriminator), so the unperturbed model should also have this.
Also, I didn't find a easy way of using the discriminator to just score the text sample wrt. a class right of the bat. This is partly due to the fact that discriminator is actually trained on the transformer output.
```
# MUST BE RUN
# since we're sampling, set seed for reproducibility
torch.manual_seed(444)
np.random.seed(444)
n_combinations = len(prefixes) * len(model_settings)
i = 1
for prefix_sentence in prefixes:
for j, model_setting in enumerate(model_settings):
print(f"\n\nRun {i:3d}/{n_combinations:3d} : optimizing for class: {model_setting}, with prefix: {prefix_sentence}\n")
unpert_text_samples, unpert_discrim_losses = text_generation(
model,
tokenizer,
device=device,
length=generated_len,
num_samples=num_samples,
prefix_text=prefix_sentence,
discrim="news",
class_label=model_setting,
perturb=False
)
pert_text_samples, pert_discrim_losses = text_generation(
model,
tokenizer,
device=device,
length=generated_len,
num_samples=num_samples,
prefix_text=prefix_sentence,
discrim="news",
class_label=model_setting,
perturb=True
)
# store generated samples
if j == 0:
gen_samples["unpert"].extend(unpert_text_samples) # only store unpertubated generation once per prefix
gen_samples[model_setting].extend(pert_text_samples)
# save the best sample, it's discriminator loss and mean dist-score for both the perturbated and unperturbated samples
comparisons[model_setting][prefix_sentence]["unpert"] = list(select_best(unpert_text_samples, unpert_discrim_losses))
comparisons[model_setting][prefix_sentence]["pert"] = list(select_best(pert_text_samples, pert_discrim_losses))
i += 1
```
## Generation analysis
First, let's download the generated samples.
```
import json
with open("all-samples.json", "w") as fp:
json.dump(gen_samples, fp)
files.download("all-samples.json")
with open("comparisons.json", "w") as fp:
json.dump(comparisons, fp)
files.download("comparisons.json"")
```
## Let's extract the metrics from the generated samples
In the code below, for each model setting, I calculate the perplexity score and dist-1, dist-2, and dist-3 scores for all samples. I then accumulate the mean and standard deviations of the scores wrt. to each model setting, to study how well each model setting actually performed in the experiment above.
```
# MUST BE RUN
metrics_means_dict = {}
metrics_stds_dict = {}
for model_setting, samples in gen_samples.items():
perplexities = [lm_score(sample) for sample in samples]
dist_scores = [dist_score(sample)[1:] for sample in samples] # stored as (mean_dist_score, dist-1, dist-2, dist-3), ignore mean
all_metrics = np.c_[np.array(perplexities), np.array(dist_scores)]
metrics_means_dict[model_setting] = np.mean(all_metrics, axis=0)
metrics_stds_dict[model_setting] = np.std(all_metrics, axis=0)
# structure the statistics neatly dataframes
metrics_means_df = pd.DataFrame(data=metrics_means_dict, index=["perplexity", "dist-1", "dist-2", "dist-3"])
metrics_means_df = pd.DataFrame(data=metrics_means_dict, index=["perplexity", "dist-1", "dist-2", "dist-3"])
# save the extracted statistics as csv files
metrics_means_df.to_csv("metrics-means.csv")
metrics_std_df.to_csv("metrics-std.csv")
files.download("metrics-means.csv")
files.download("metrics-std.csv)
```
## Let's see the best examples for each model setting and prefix
```
# MUST BE RUN
for model_setting, prefix_dict in comparisons.items():
print(f"Model setting: {model_setting}\n")
for prefix_sentence in prefix_dict.keys():
unpert_sample, unpert_loss, unpert_mean_dist = prefix_dict[prefix_sentence]["unpert"]
pert_sample, pert_loss, pert_mean_dist = prefix_dict[prefix_sentence]["pert"]
print(f"Prefix is: {prefix_sentence}\n")
print(f"Unperturbated:\nSample: {unpert_sample}\nDiscrim loss: {unpert_loss:2.2f} | Mean dist-n score: {unpert_mean_dist:2.1f}\n")
print(f" Perturbated:\nSample: {pert_sample}\nDiscrim loss: {pert_loss:2.2f} | Mean dist-n score: {pert_mean_dist:2.1f}")
print("\n\n")
```
| github_jupyter |
```
%run ../Python_files/util_data_storage_and_load.py
%run ../Python_files/load_dicts.py
%run ../Python_files/util.py
import numpy as np
from numpy.linalg import inv
# load link flow data
import json
with open('../temp_files/link_day_minute_Apr_dict_JSON_adjusted.json', 'r') as json_file:
link_day_minute_Apr_dict_JSON = json.load(json_file)
# week_day_Apr_list = [2, 3, 4, 5, 6, 9, 10, 11, 12, 13, 16, 17, 18, 19, 20, 23, 24, 25, 26, 27, 30]
# testing set 1
week_day_Apr_list_1 = [20, 23, 24, 25, 26, 27, 30]
# testing set 2
week_day_Apr_list_2 = [11, 12, 13, 16, 17, 18, 19]
# testing set 3
week_day_Apr_list_3 = [2, 3, 4, 5, 6, 9, 10]
link_flow_testing_set_Apr_MD_1 = []
for link_idx in range(24):
for day in week_day_Apr_list_1:
key = 'link_' + str(link_idx) + '_' + str(day)
link_flow_testing_set_Apr_MD_1.append(link_day_minute_Apr_dict_JSON[key] ['MD_flow'])
link_flow_testing_set_Apr_MD_2 = []
for link_idx in range(24):
for day in week_day_Apr_list_2:
key = 'link_' + str(link_idx) + '_' + str(day)
link_flow_testing_set_Apr_MD_2.append(link_day_minute_Apr_dict_JSON[key] ['MD_flow'])
link_flow_testing_set_Apr_MD_3 = []
for link_idx in range(24):
for day in week_day_Apr_list_3:
key = 'link_' + str(link_idx) + '_' + str(day)
link_flow_testing_set_Apr_MD_3.append(link_day_minute_Apr_dict_JSON[key] ['MD_flow'])
testing_set_1 = np.matrix(link_flow_testing_set_Apr_MD_1)
testing_set_1 = np.matrix.reshape(testing_set_1, 24, 7)
testing_set_1 = np.nan_to_num(testing_set_1)
y = np.array(np.transpose(testing_set_1))
y = y[np.all(y != 0, axis=1)]
testing_set_1 = np.transpose(y)
testing_set_1 = np.matrix(testing_set_1)
testing_set_2 = np.matrix(link_flow_testing_set_Apr_MD_2)
testing_set_2 = np.matrix.reshape(testing_set_2, 24, 7)
testing_set_2 = np.nan_to_num(testing_set_2)
y = np.array(np.transpose(testing_set_2))
y = y[np.all(y != 0, axis=1)]
testing_set_2 = np.transpose(y)
testing_set_2 = np.matrix(testing_set_2)
testing_set_3 = np.matrix(link_flow_testing_set_Apr_MD_3)
testing_set_3 = np.matrix.reshape(testing_set_3, 24, 7)
testing_set_3 = np.nan_to_num(testing_set_3)
y = np.array(np.transpose(testing_set_3))
y = y[np.all(y != 0, axis=1)]
testing_set_3 = np.transpose(y)
testing_set_3 = np.matrix(testing_set_3)
np.size(testing_set_2, 0), np.size(testing_set_3, 1)
testing_set_3[:,:1]
# write testing sets to file
zdump([testing_set_1, testing_set_2, testing_set_3], '../temp_files/testing_sets_Apr_MD.pkz')
```
| github_jupyter |
<a href="https://colab.research.google.com/github/sapinspys/DS-Unit-2-Regression-Classification/blob/master/DS7_Sprint_Challenge_5_Regression_Classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
_Lambda School Data Science, Unit 2_
# Regression & Classification Sprint Challenge
To demonstrate mastery on your Sprint Challenge, do all the required, numbered instructions in this notebook.
To earn a score of "3", also do all the stretch goals.
You are permitted and encouraged to do as much data exploration as you want.
### Part 1, Classification
- 1.1. Begin with baselines for classification
- 1.2. Do train/test split. Arrange data into X features matrix and y target vector
- 1.3. Use scikit-learn to fit a logistic regression model
- 1.4. Report classification metric: accuracy
### Part 2, Regression
- 2.1. Begin with baselines for regression
- 2.2. Do train/validate/test split.
- 2.3. Arrange data into X features matrix and y target vector
- 2.4. Do one-hot encoding
- 2.5. Use scikit-learn to fit a linear regression (or ridge regression) model
- 2.6. Report validation MAE and $R^2$
### Stretch Goals, Regression
- Make visualizations to explore relationships between features and target
- Try at least 3 feature combinations. You may select features manually, or automatically
- Report validation MAE and $R^2$ for each feature combination you try
- Report test MAE and $R^2$ for your final model
- Print or plot the coefficients for the features in your model
```
# If you're in Colab...
import sys
in_colab = 'google.colab' in sys.modules
if in_colab:
!pip install category_encoders==2.0.0
!pip install pandas-profiling==2.3.0
!pip install plotly==4.1.1
```
# Part 1, Classification: Predict Blood Donations 🚑
Our dataset is from a mobile blood donation vehicle in Taiwan. The Blood Transfusion Service Center drives to different universities and collects blood as part of a blood drive.
The goal is to predict whether the donor made a donation in March 2007, using information about each donor's history.
Good data-driven systems for tracking and predicting donations and supply needs can improve the entire supply chain, making sure that more patients get the blood transfusions they need.
```
import pandas as pd
donors = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/blood-transfusion/transfusion.data')
assert donors.shape == (748,5)
donors = donors.rename(columns={
'Recency (months)': 'months_since_last_donation',
'Frequency (times)': 'number_of_donations',
'Monetary (c.c. blood)': 'total_volume_donated',
'Time (months)': 'months_since_first_donation',
'whether he/she donated blood in March 2007': 'made_donation_in_march_2007'
})
donors.head()
```
## 1.1. Begin with baselines
What accuracy score would you get here with a "majority class baseline"?
(You don't need to split the data into train and test sets yet. You can answer this question either with a scikit-learn function or with a pandas function.)
```
y_train = donors.made_donation_in_march_2007
y_train.value_counts(normalize=True)
# We can cross-check this using scikit-learn
majority_class = y_train.mode()[0]
majority_class
y_pred = [majority_class] * len(y_train)
len(y_pred)
from sklearn.metrics import accuracy_score
accuracy_score(y_train, y_pred)
```
## 1.2. Do train/test split. Arrange data into X features matrix and y target vector
Do these steps in either order.
Split randomly. Use scikit-learn's train/test split function. Include 75% of the data in the train set, and hold out 25% for the test set.
```
train_features = donors[donors.columns.difference(['made_donation_in_march_2007'])]
print(train_features.shape)
train_features.head()
train_labels = donors['made_donation_in_march_2007']
print(train_labels.shape)
train_labels.head()
from sklearn.model_selection import train_test_split
X_train = train_features
y_train = train_labels
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, train_size=0.75, test_size=0.25,
stratify=y_train
)
X_train.shape, X_val.shape, y_train.shape, y_val.shape
X_train.isnull().sum()
train_labels.isnull().sum()
```
## 1.3. Use scikit-learn to fit a logistic regression model
You may use any number of features
```
# No categorical features, only numerical, no need for OHE
from sklearn.linear_model import LogisticRegression
# Right now we include all numerical features
# If we want to split into less features:
# X_train_subset = X_train[features]
# X_val_subset = X_val[features]
model = LogisticRegression(
solver='lbfgs', multi_class='auto', max_iter=1000, n_jobs=-1) # Optimized from class
model.fit(X_train, y_train)
```
## 1.4. Report classification metric: accuracy
What is your model's accuracy on the test set?
Don't worry if your model doesn't beat the mean baseline. That's okay!
_"The combination of some data and an aching desire for an answer does not ensure that a reasonable answer can be extracted from a given body of data."_ —[John Tukey](https://en.wikiquote.org/wiki/John_Tukey)
```
print('Validation Accuracy', model.score(X_val, y_val))
```
# Part 2, Regression: Predict home prices in Ames, Iowa 🏠
You'll use historical housing data. There's a data dictionary at the bottom of the notebook.
Run this code cell to load the dataset:
```
import pandas as pd
URL = 'https://drive.google.com/uc?export=download&id=1522WlEW6HFss36roD_Cd9nybqSuiVcCK'
homes = pd.read_csv(URL)
assert homes.shape == (2904, 47)
homes.head()
```
## 2.1. Begin with baselines
What is the Mean Absolute Error and R^2 score for a mean baseline?
```
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
import numpy as np
y_train = homes['SalePrice']
y_pred_train = [y_train.mean()] * len(y_train)
print('Mean Baseline:')
print('Train Mean Absolute Error:', mean_absolute_error(y_train, y_pred_train))
print('Train R^2 Score:', r2_score(y_train, y_pred_train))
# 0% indicates that the model explains none of the variability of the response data around its mean.
```
## 2.2. Do train/test split
Train on houses sold in the years 2006 - 2008. (1,920 rows)
Validate on house sold in 2009. (644 rows)
Test on houses sold in 2010. (340 rows)
```
train = homes[(homes.Yr_Sold >= 2006) & (homes.Yr_Sold <= 2008)]
print(train.shape)
val = homes[homes.Yr_Sold == 2009]
print(val.shape)
test = homes[homes.Yr_Sold == 2010]
print(test.shape)
```
## 2.3. Arrange data into X features matrix and y target vector
Select at least one numeric feature and at least one categorical feature.
Otherwise, you many choose whichever features and however many you want.
```
homes.isnull().sum()
target = 'SalePrice'
numeric_features = train[train.columns.difference(['SalePrice'])].select_dtypes(include='number').columns.tolist()
cardinality = train.select_dtypes(exclude='number').nunique()
low_cardinality_features = cardinality[cardinality <= 10].index.tolist()
features = numeric_features + low_cardinality_features
features
```
## 2.4. Do one-hot encoding
Encode your categorical feature(s).
```
X_train = train[features]
y_train = train[target]
X_val = val[features]
y_val = val[target]
X_test = test[features]
y_test = test[target]
import category_encoders as ce
from sklearn.preprocessing import StandardScaler
X_train_subset = X_train[features]
X_val_subset = X_val[features]
X_test_subset = X_test[features]
encoder = ce.OneHotEncoder(use_cat_names=True)
X_train_encoded = encoder.fit_transform(X_train_subset)
X_val_encoded = encoder.transform(X_val_subset)
X_test_encoded = encoder.transform(X_test_subset)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train_encoded)
X_val_scaled = scaler.transform(X_val_encoded)
X_test_scaled = scaler.fit_transform(X_test_encoded)
print(X_train_scaled.shape, X_val_scaled.shape, X_test_scaled.shape)
```
## 2.5. Use scikit-learn to fit a linear regression (or ridge regression) model
Fit your model.
```
# STRETCH GOAL: Try at least 3 feature combinations. You may select features manually, or automatically
# STRETCH GOAL: Report validation MAE and R2 for each feature combination you try
from sklearn.linear_model import RidgeCV
from sklearn.feature_selection import f_regression, SelectKBest
for k in range(1, len(X_train_encoded.columns)+1):
print(f'{k} features')
selector = SelectKBest(score_func=f_regression, k=k)
X_train_selected = selector.fit_transform(X_train_scaled, y_train)
X_test_selected = selector.transform(X_test_scaled)
model = RidgeCV()
model.fit(X_train_selected, y_train)
y_pred = model.predict(X_test_selected)
mae = mean_absolute_error(y_test, y_pred)
print(f'Test MAE: ${mean_absolute_error(y_test, y_pred):,.0f}')
print(f'Test R2: {r2_score(y_test, y_pred):,.3f} \n')
```
## 2.6. Report validation MAE and $R^2$
What is your model's Mean Absolute Error and $R^2$ score on the validation set?
```
# STRETCH GOAL: Report test MAE and $R^2$ for your final model
selector = SelectKBest(score_func=f_regression, k=157)
X_train_selected = selector.fit_transform(X_train_scaled, y_train)
X_val_selected = selector.transform(X_val_scaled)
model = RidgeCV()
model.fit(X_train_selected, y_train)
y_pred_val = model.predict(X_val_selected)
print('Mean Baseline:')
print('Val Mean Absolute Error:', mean_absolute_error(y_val, y_pred_val))
print('Val R^2 Score:', r2_score(y_val, y_pred_val))
# STRETCH GOAL: Print or plot the coefficients for the features in your model
coefficients = pd.Series(model.coef_, X_train_encoded.columns)
plt.figure(figsize=(10,30))
coefficients.sort_values().plot.barh(color='blue');
```
# Stretch Goals, Regression
- Make visualizations to explore relationships between features and target
- Try at least 3 feature combinations. You may select features manually, or automatically
- Report validation MAE and $R^2$ for each feature combination you try
- Report test MAE and $R^2$ for your final model
- Print or plot the coefficients for the features in your model
```
#STRETCH GOAL: Make visualizations to explore relationships between features and target
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
for col in sorted(low_cardinality_features):
sns.catplot(x=col, y='SalePrice', data=train, kind='bar', color='grey')
plt.xticks(rotation=45)
plt.show()
```
# Data Dictionary
Here's a description of the data fields:
```
1st_Flr_SF: First Floor square feet
Bedroom_AbvGr: Bedrooms above grade (does NOT include basement bedrooms)
Bldg_Type: Type of dwelling
1Fam Single-family Detached
2FmCon Two-family Conversion; originally built as one-family dwelling
Duplx Duplex
TwnhsE Townhouse End Unit
TwnhsI Townhouse Inside Unit
Bsmt_Half_Bath: Basement half bathrooms
Bsmt_Full_Bath: Basement full bathrooms
Central_Air: Central air conditioning
N No
Y Yes
Condition_1: Proximity to various conditions
Artery Adjacent to arterial street
Feedr Adjacent to feeder street
Norm Normal
RRNn Within 200' of North-South Railroad
RRAn Adjacent to North-South Railroad
PosN Near positive off-site feature--park, greenbelt, etc.
PosA Adjacent to postive off-site feature
RRNe Within 200' of East-West Railroad
RRAe Adjacent to East-West Railroad
Condition_2: Proximity to various conditions (if more than one is present)
Artery Adjacent to arterial street
Feedr Adjacent to feeder street
Norm Normal
RRNn Within 200' of North-South Railroad
RRAn Adjacent to North-South Railroad
PosN Near positive off-site feature--park, greenbelt, etc.
PosA Adjacent to postive off-site feature
RRNe Within 200' of East-West Railroad
RRAe Adjacent to East-West Railroad
Electrical: Electrical system
SBrkr Standard Circuit Breakers & Romex
FuseA Fuse Box over 60 AMP and all Romex wiring (Average)
FuseF 60 AMP Fuse Box and mostly Romex wiring (Fair)
FuseP 60 AMP Fuse Box and mostly knob & tube wiring (poor)
Mix Mixed
Exter_Cond: Evaluates the present condition of the material on the exterior
Ex Excellent
Gd Good
TA Average/Typical
Fa Fair
Po Poor
Exter_Qual: Evaluates the quality of the material on the exterior
Ex Excellent
Gd Good
TA Average/Typical
Fa Fair
Po Poor
Exterior_1st: Exterior covering on house
AsbShng Asbestos Shingles
AsphShn Asphalt Shingles
BrkComm Brick Common
BrkFace Brick Face
CBlock Cinder Block
CemntBd Cement Board
HdBoard Hard Board
ImStucc Imitation Stucco
MetalSd Metal Siding
Other Other
Plywood Plywood
PreCast PreCast
Stone Stone
Stucco Stucco
VinylSd Vinyl Siding
Wd Sdng Wood Siding
WdShing Wood Shingles
Exterior_2nd: Exterior covering on house (if more than one material)
AsbShng Asbestos Shingles
AsphShn Asphalt Shingles
BrkComm Brick Common
BrkFace Brick Face
CBlock Cinder Block
CemntBd Cement Board
HdBoard Hard Board
ImStucc Imitation Stucco
MetalSd Metal Siding
Other Other
Plywood Plywood
PreCast PreCast
Stone Stone
Stucco Stucco
VinylSd Vinyl Siding
Wd Sdng Wood Siding
WdShing Wood Shingles
Foundation: Type of foundation
BrkTil Brick & Tile
CBlock Cinder Block
PConc Poured Contrete
Slab Slab
Stone Stone
Wood Wood
Full_Bath: Full bathrooms above grade
Functional: Home functionality (Assume typical unless deductions are warranted)
Typ Typical Functionality
Min1 Minor Deductions 1
Min2 Minor Deductions 2
Mod Moderate Deductions
Maj1 Major Deductions 1
Maj2 Major Deductions 2
Sev Severely Damaged
Sal Salvage only
Gr_Liv_Area: Above grade (ground) living area square feet
Half_Bath: Half baths above grade
Heating: Type of heating
Floor Floor Furnace
GasA Gas forced warm air furnace
GasW Gas hot water or steam heat
Grav Gravity furnace
OthW Hot water or steam heat other than gas
Wall Wall furnace
Heating_QC: Heating quality and condition
Ex Excellent
Gd Good
TA Average/Typical
Fa Fair
Po Poor
House_Style: Style of dwelling
1Story One story
1.5Fin One and one-half story: 2nd level finished
1.5Unf One and one-half story: 2nd level unfinished
2Story Two story
2.5Fin Two and one-half story: 2nd level finished
2.5Unf Two and one-half story: 2nd level unfinished
SFoyer Split Foyer
SLvl Split Level
Kitchen_AbvGr: Kitchens above grade
Kitchen_Qual: Kitchen quality
Ex Excellent
Gd Good
TA Typical/Average
Fa Fair
Po Poor
LandContour: Flatness of the property
Lvl Near Flat/Level
Bnk Banked - Quick and significant rise from street grade to building
HLS Hillside - Significant slope from side to side
Low Depression
Land_Slope: Slope of property
Gtl Gentle slope
Mod Moderate Slope
Sev Severe Slope
Lot_Area: Lot size in square feet
Lot_Config: Lot configuration
Inside Inside lot
Corner Corner lot
CulDSac Cul-de-sac
FR2 Frontage on 2 sides of property
FR3 Frontage on 3 sides of property
Lot_Shape: General shape of property
Reg Regular
IR1 Slightly irregular
IR2 Moderately Irregular
IR3 Irregular
MS_SubClass: Identifies the type of dwelling involved in the sale.
20 1-STORY 1946 & NEWER ALL STYLES
30 1-STORY 1945 & OLDER
40 1-STORY W/FINISHED ATTIC ALL AGES
45 1-1/2 STORY - UNFINISHED ALL AGES
50 1-1/2 STORY FINISHED ALL AGES
60 2-STORY 1946 & NEWER
70 2-STORY 1945 & OLDER
75 2-1/2 STORY ALL AGES
80 SPLIT OR MULTI-LEVEL
85 SPLIT FOYER
90 DUPLEX - ALL STYLES AND AGES
120 1-STORY PUD (Planned Unit Development) - 1946 & NEWER
150 1-1/2 STORY PUD - ALL AGES
160 2-STORY PUD - 1946 & NEWER
180 PUD - MULTILEVEL - INCL SPLIT LEV/FOYER
190 2 FAMILY CONVERSION - ALL STYLES AND AGES
MS_Zoning: Identifies the general zoning classification of the sale.
A Agriculture
C Commercial
FV Floating Village Residential
I Industrial
RH Residential High Density
RL Residential Low Density
RP Residential Low Density Park
RM Residential Medium Density
Mas_Vnr_Type: Masonry veneer type
BrkCmn Brick Common
BrkFace Brick Face
CBlock Cinder Block
None None
Stone Stone
Mo_Sold: Month Sold (MM)
Neighborhood: Physical locations within Ames city limits
Blmngtn Bloomington Heights
Blueste Bluestem
BrDale Briardale
BrkSide Brookside
ClearCr Clear Creek
CollgCr College Creek
Crawfor Crawford
Edwards Edwards
Gilbert Gilbert
IDOTRR Iowa DOT and Rail Road
MeadowV Meadow Village
Mitchel Mitchell
Names North Ames
NoRidge Northridge
NPkVill Northpark Villa
NridgHt Northridge Heights
NWAmes Northwest Ames
OldTown Old Town
SWISU South & West of Iowa State University
Sawyer Sawyer
SawyerW Sawyer West
Somerst Somerset
StoneBr Stone Brook
Timber Timberland
Veenker Veenker
Overall_Cond: Rates the overall condition of the house
10 Very Excellent
9 Excellent
8 Very Good
7 Good
6 Above Average
5 Average
4 Below Average
3 Fair
2 Poor
1 Very Poor
Overall_Qual: Rates the overall material and finish of the house
10 Very Excellent
9 Excellent
8 Very Good
7 Good
6 Above Average
5 Average
4 Below Average
3 Fair
2 Poor
1 Very Poor
Paved_Drive: Paved driveway
Y Paved
P Partial Pavement
N Dirt/Gravel
Roof_Matl: Roof material
ClyTile Clay or Tile
CompShg Standard (Composite) Shingle
Membran Membrane
Metal Metal
Roll Roll
Tar&Grv Gravel & Tar
WdShake Wood Shakes
WdShngl Wood Shingles
Roof_Style: Type of roof
Flat Flat
Gable Gable
Gambrel Gabrel (Barn)
Hip Hip
Mansard Mansard
Shed Shed
SalePrice: the sales price for each house
Sale_Condition: Condition of sale
Normal Normal Sale
Abnorml Abnormal Sale - trade, foreclosure, short sale
AdjLand Adjoining Land Purchase
Alloca Allocation - two linked properties with separate deeds, typically condo with a garage unit
Family Sale between family members
Partial Home was not completed when last assessed (associated with New Homes)
Sale_Type: Type of sale
WD Warranty Deed - Conventional
CWD Warranty Deed - Cash
VWD Warranty Deed - VA Loan
New Home just constructed and sold
COD Court Officer Deed/Estate
Con Contract 15% Down payment regular terms
ConLw Contract Low Down payment and low interest
ConLI Contract Low Interest
ConLD Contract Low Down
Oth Other
Street: Type of road access to property
Grvl Gravel
Pave Paved
TotRms_AbvGrd: Total rooms above grade (does not include bathrooms)
Utilities: Type of utilities available
AllPub All public Utilities (E,G,W,& S)
NoSewr Electricity, Gas, and Water (Septic Tank)
NoSeWa Electricity and Gas Only
ELO Electricity only
Year_Built: Original construction date
Year_Remod/Add: Remodel date (same as construction date if no remodeling or additions)
Yr_Sold: Year Sold (YYYY)
```
| github_jupyter |
```
import cv2
import numpy as np
import matplotlib.pyplot as plt
import glob
import pandas as pd
import os
def imshow(img):
img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
plt.imshow(img)
def get_lane_mask(sample,lane_idx):
points_lane = []
h_max = np.max(data['h_samples'][sample])
h_min = np.min(data['h_samples'][sample])
x_idx = data['lanes'][sample][lane_idx]
y_idx = data['h_samples'][sample]
for x,y in zip(x_idx,y_idx):
offset = (y-h_min)/20
# print(offset)
if x>-100:
points_lane.append([x-offset/2,y])
x_idx_=x_idx.copy()
y_idx_=y_idx.copy()
x_idx_.reverse()
y_idx_.reverse()
for x,y in zip(x_idx_,y_idx_):
offset = (y-h_min)/20
# print(offset)
if x>-100:
points_lane.append([x+offset/2,y])
return points_lane
def create_lane_mask(img_raw,sample):
colors = [[255,0,0],[0,255,0],[0,0,255],[0,255,255]]
laneMask = np.zeros(img_raw.shape, dtype=np.uint8)
for lane_idx in range(len(data.lanes[sample])):
points_lane = get_lane_mask(sample,lane_idx)
if len(points_lane)>0:
pts = np.array(points_lane, np.int32)
pts = pts.reshape((-1,1,2))
laneMask = cv2.fillPoly(laneMask,[pts],colors[lane_idx])
colors = [[255,0,0],[0,255,0],[0,0,255],[0,255,255]]
# create grey-scale label image
label = np.zeros((720,1280),dtype = np.uint8)
for i in range(len(colors)):
label[np.where((laneMask == colors[i]).all(axis = 2))] = i+1
else: continue
return(img_raw, label)
data = pd.read_json(os.path.join(data_dir, 'label_data.json'), lines=True)
data.info()
print(len(data.raw_file))
data
print(len(data.raw_file))
for i in range(len(data.raw_file)):
img_path = data.raw_file[i]
img_path = os.path.join(data_dir,img_path)
print('Reading from: ', img_path)
path_list = img_path.split('/')[:-1]
mask_path_dir = os.path.join(*path_list)
img_raw = cv2.imread(img_path)
img_, mask = create_lane_mask(img_raw,i)
"""
fig = plt.figure(figsize=(15,20))
plt.subplot(211)
imshow(img_raw)
plt.subplot(212)
print(mask.shape)
plt.imshow(mask)
"""
mask_path_dir = mask_path_dir.replace('clips', 'masks')
print('Saving to: ', mask_path_dir)
try:
os.makedirs(mask_path_dir)
except:
pass
for i in range(1, 21):
cv2.imwrite(os.path.join( mask_path_dir, f'{i}.tiff'), mask)
# i = i+1
cv2.imwrite('/Users/srinivas/Projects/Lane_Detection/datasets/LaneDetection/train/masks/0313-1/300/1.tiff', mask)
mask_img = cv2.imread('20.tiff', cv2.IMREAD_GRAYSCALE)
mask_img.shape
plt.imshow(mask_img)
print(np.unique(mask_img))
print(np.unique(mask))
```
| github_jupyter |
# Navigation
---
In this notebook, you will learn how to use the Unity ML-Agents environment for the first project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893).
### 1. Start the Environment
We begin by importing some necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
```
from unityagents import UnityEnvironment
import numpy as np
from collections import deque
import torch
import matplotlib.pyplot as plt
%matplotlib inline
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Banana.app"`
- **Windows** (x86): `"path/to/Banana_Windows_x86/Banana.exe"`
- **Windows** (x86_64): `"path/to/Banana_Windows_x86_64/Banana.exe"`
- **Linux** (x86): `"path/to/Banana_Linux/Banana.x86"`
- **Linux** (x86_64): `"path/to/Banana_Linux/Banana.x86_64"`
- **Linux** (x86, headless): `"path/to/Banana_Linux_NoVis/Banana.x86"`
- **Linux** (x86_64, headless): `"path/to/Banana_Linux_NoVis/Banana.x86_64"`
For instance, if you are using a Mac, then you downloaded `Banana.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Banana.app")
```
```
env = UnityEnvironment(file_name="Banana.app")
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
The simulation contains a single agent that navigates a large environment. At each time step, it has four actions at its disposal:
- `0` - walk forward
- `1` - walk backward
- `2` - turn left
- `3` - turn right
The state space has `37` dimensions and contains the agent's velocity, along with ray-based perception of objects around agent's forward direction. A reward of `+1` is provided for collecting a yellow banana, and a reward of `-1` is provided for collecting a blue banana.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents in the environment
print('Number of agents:', len(env_info.agents))
# number of actions
action_size = brain.vector_action_space_size
print('Number of actions:', action_size)
# examine the state space
state = env_info.vector_observations[0]
print('States look like:', state)
state_size = len(state)
print('States have length:', state_size)
```
### 3. Take Random Actions in the Environment
In the next code cell, you will learn how to use the Python API to control the agent and receive feedback from the environment.
Once this cell is executed, you will watch the agent's performance, if it selects an action (uniformly) at random with each time step. A window should pop up that allows you to observe the agent, as it moves through the environment.
Of course, as part of the project, you'll have to change the code so that the agent is able to use its experience to gradually choose better actions when interacting with the environment!
```
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
state = env_info.vector_observations[0] # get the current state
score = 0 # initialize the score
while True:
action = np.random.randint(action_size) # select an action
env_info = env.step(action)[brain_name] # send the action to the environment
next_state = env_info.vector_observations[0] # get the next state
reward = env_info.rewards[0] # get the reward
done = env_info.local_done[0] # see if episode has finished
score += reward # update the score
state = next_state # roll over the state to next time step
if done: # exit loop if episode finished
break
print("Score: {}".format(score))
```
When finished, you can close the environment.
```
#env.close()
```
### 4. It's Your Turn!
Now it's your turn to train your own agent to solve the environment! When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
```python
env_info = env.reset(train_mode=True)[brain_name]
```
### Training using DQN based off the previous assignments
```
from dqn_agent import Agent
agent = Agent(state_size=37, action_size=4, seed=42)
def dqn(n_episodes=2000, max_t=1000, eps_start=1.0, eps_end=0.01, eps_decay=0.99):
"""Deep Q-Learning.
Params
======
n_episodes (int): maximum number of training episodes
max_t (int): maximum number of timesteps per episode
eps_start (float): starting value of epsilon, for epsilon-greedy action selection
eps_end (float): minimum value of epsilon
eps_decay (float): multiplicative factor (per episode) for decreasing epsilon
"""
scores = [] # list containing scores from each episode
scores_window = deque(maxlen=100) # last 100 scores
eps = eps_start # initialize epsilon
for i_episode in range(1, n_episodes+1):
env_info = env.reset(train_mode=True)[brain_name]
state = env_info.vector_observations[0]
score = 0
for t in range(max_t):
action = agent.act(state, eps)
env_info = env.step(action)[brain_name]
next_state = env_info.vector_observations[0]
reward = env_info.rewards[0]
done = env_info.local_done[0]
agent.step(state, action, reward, next_state, done)
state = next_state
score += reward
if done:
break
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
eps = max(eps_end, eps_decay*eps) # decrease epsilon
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)), end="")
if i_episode % 100 == 0:
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_window)))
if np.mean(scores_window)>=13.0:
print('\nEnvironment solved in {:d} episodes!\tAverage Score: {:.2f}'.format(i_episode-100, np.mean(scores_window)))
torch.save(agent.qnetwork_local.state_dict(), 'checkpoint_311220201515.pth')
break
return scores
scores = dqn()
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
# closes the environment
env.close()
```
| github_jupyter |
# Data Download - *read description before running*
Term project for ESS 490/590
Grad: Erik Fredrickson
Undergrad: Ashika Capirala
*This notebook demonstrates how the open access datasets can be downloaded, but these data are provided at significantly higher temporal resolution than needed for the purposes of our study, so for the sake of this project we recommend that the user use the provided reduced data, which will save significant time, computing power, and disc space.*
```
# Imports
import obspy
import obspy.clients.fdsn.client as fdsn
from obspy import UTCDateTime
```
## APG pressures and temperatures
Get bottom temperature and bottom pressure from IRIS (https://www.iris.edu/hq/; https://doi.org/10.7914/SN/XO_2018)
<img src="AACSE.png" width="600">
<center>Alaska Amphibious Community Seismic Experiment</center>
```
# Pull pressure and temperature data from IRIS
network = 'XO'
staNames = ['LA21', 'LA34', 'LA33', 'LA23', 'LA25', 'LA22', 'LA28', 'LA39', 'LA32', 'LA30', 'LT07', 'LT06', \
'LT13', 'LT03', 'LT11', 'LT04', 'LT01', 'LT20', 'LT14', 'LT16', 'LT10', 'LT12']
staCodes = 'LA21,LA34,LA33,LA23,LA25,LA22,LA28,LA39,LA32,LA30,LT07,LT06,LT13,LT03,LT11,LT04,LT01,LT20,LT14,LT16,LT10,LT12'
chaNames = ['HDH', 'HKO']
chaCodes='HDH,HKO'
Tstart = UTCDateTime(2018, 06, 01)
Tend = UTCDateTime(2019, 06, 20)
fdsn_client = fdsn.Client('IRIS')
# DO NOT RUN AS WRITTEN -- way too much data, so we'll need to make a loop to parse it by station and by day
Dtmp = fdsn_client.get_waveforms(network=network, station=staCodes, location='--', channel=chaCodes, starttime=Tstart, \
endtime=Tend, attach_response=False)
```
## Satellite altimetry
Get altimetry data from Copernicus Marine (https://marine.copernicus.eu/; https://resources.marine.copernicus.eu/?option=com_csw&view=details&product_id=SEALEVEL_GLO_PHY_CLIMATE_L4_REP_OBSERVATIONS_008_057)
<img src="jason-2-altimeter.jpg" width="600">
<center>Jason-2 Satellite</center>
```
# installer to handle data download
!pip install motuclient --upgrade
# Get desired data (would need to change directory, user, and password fields)
!python -m motuclient --motu https://my.cmems-du.eu/motu-web/Motu --service-id \
SEALEVEL_GLO_PHY_CLIMATE_L4_REP_OBSERVATIONS_008_057-TDS --product-id \
dataset-duacs-rep-global-merged-twosat-phy-l4 --longitude-min 198 \
--longitude-max 210 --latitude-min 53 --latitude-max 60 \
--date-min "2018-06-01 00:00:00" --date-max "2019-06-20 23:59:59" \
--variable adt --variable err --variable sla --variable ugos --variable ugosa \
--variable vgos --variable vgosa --out-dir <OUTPUT_DIRECTORY> --out-name \
<OUTPUT_FILENAME> --user <USERNAME> --pwd <PASSWORD>
```
## Oceanographic model
Model data not currently publicly available :(
Load from netcdf
## Eddy catalog
Labeled dataset hosted by AVISO. Requires registration, but free for academics (https://www.aviso.altimetry.fr/en/home.html; https://doi.org/10.24400/527896/a01-2021.001)
Full code is available on GitHub! (https://github.com/AntSimi/py-eddy-tracker)
<img src="eddy_field.jpg" width="600">
<center>https://doi.org/10.1175/JTECH-D-14-00019.1</center>
| github_jupyter |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, ReLU, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.losses import categorical_crossentropy
from keras.optimizers import Adam
from keras.preprocessing.image import ImageDataGenerator
from keras import backend as K
%matplotlib inline
# load data
train_df = pd.read_csv('data/train.csv')
test_df = pd.read_csv('data/test.csv')
train_df.head(3)
test_df.head(3)
# Convert data to numpy arrays
img_rows, img_cols = 28, 28
num_classes = train_df['label'].nunique()
# Split train + val data
X = train_df.drop(columns=['label']).values
y = train_df['label'].values
# one-hot encode the labels
y = keras.utils.to_categorical(y, num_classes)
if K.image_data_format() == 'channels_first':
X = X.reshape(-1, 1, img_rows, img_cols)
X_test = test_df.values.reshape(-1, 1, img_rows, img_cols)
input_shape = (1, img_rows, img_cols)
else:
X = X.reshape(-1, img_rows, img_cols, 1)
X_test = test_df.values.reshape(-1, img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)
# normalize data
X = X.astype('float32')
X_test = X_test.astype('float32')
X /= 255
X_test /= 255
# Split train + val data
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.33, random_state=42)
# train array shape
X_train.shape, y_train.shape
# val array shape
X_val.shape, y_val.shape
# plot first image to check if it is in the correct format
plt.imshow(X_train[0,:,:, 0])
# create model
def get_model():
model = Sequential()
model.add(Conv2D(filters=32,
kernel_size=(3,3),
activation="relu",
input_shape=input_shape))
model.add(Conv2D(filters=64,
kernel_size=(3,3),
activation="relu"))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Conv2D(filters=128,
kernel_size=(3,3),
activation="relu"))
model.add(MaxPooling2D(pool_size=(2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.compile(loss=categorical_crossentropy,
optimizer=Adam(),
metrics=['accuracy'])
return model
# Model summary
model = get_model()
model.summary()
# Setup train data transformer
train_datagen = ImageDataGenerator(featurewise_center=True,
featurewise_std_normalization=True,
width_shift_range=0.2,
height_shift_range=0.2,
horizontal_flip=True)
train_datagen.fit(X_train)
# Setup validation data transformer
val_datagen = ImageDataGenerator(featurewise_center=True,
featurewise_std_normalization=True,
horizontal_flip=False)
val_datagen.fit(X_train)
batch_size = 128
epochs = 10
model_gen = get_model()
model_gen.fit_generator(train_datagen.flow(X_train, y_train, batch_size=batch_size),
steps_per_epoch=len(X_train) / batch_size,
epochs=epochs,
shuffle=True,
validation_data=val_datagen.flow(X_val, y_val, batch_size=batch_size),
validation_steps=len(X_val) / batch_size,
verbose=1)
score = model_gen.evaluate_generator(val_datagen.flow(X_val, y_val, batch_size=batch_size),
steps=len(X_val) / batch_size,
verbose=1)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
batch_size = 128
epochs = 10
model.fit(X_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=1,
validation_data=(X_val, y_val))
score = model.evaluate(X_val, y_val, batch_size=256, verbose=1)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# train model on the full train data
batch_size = 128
epochs = 10
model_final = get_model()
model_final.fit(X, y,
batch_size=batch_size,
epochs=epochs,
verbose=1)
# create submission predictions
predictions = model_final.predict(X_test, batch_size=256, verbose=1)
# save predictions
out_df = pd.DataFrame({"ImageId": list(range(1, len(predictions) + 1)),
"Label": np.argmax(predictions, axis=1)})
out_df.to_csv('keras_submission.csv', index=False)
```
| github_jupyter |
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# tf.dataを使って画像をロードする
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/load_data/images"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ja/tutorials/load_data/images.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ja/tutorials/load_data/images.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
Note: これらのドキュメントは私たちTensorFlowコミュニティが翻訳したものです。コミュニティによる 翻訳は**ベストエフォート**であるため、この翻訳が正確であることや[英語の公式ドキュメント](https://www.tensorflow.org/?hl=en)の 最新の状態を反映したものであることを保証することはできません。 この翻訳の品質を向上させるためのご意見をお持ちの方は、GitHubリポジトリ[tensorflow/docs](https://github.com/tensorflow/docs)にプルリクエストをお送りください。 コミュニティによる翻訳やレビューに参加していただける方は、 [[email protected] メーリングリスト](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ja)にご連絡ください。
このチュートリアルでは、'tf.data' を使って画像データセットをロードする簡単な例を示します。
このチュートリアルで使用するデータセットは、クラスごとに別々のディレクトリに別れた形で配布されています。
## 設定
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# Colab only
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
AUTOTUNE = tf.data.experimental.AUTOTUNE
```
## データセットのダウンロードと検査
### 画像の取得
訓練を始める前に、ネットワークに認識すべき新しいクラスを教えるために画像のセットが必要です。最初に使うためのクリエイティブ・コモンズでライセンスされた花の画像のアーカイブを作成してあります。
```
import pathlib
data_root_orig = tf.keras.utils.get_file(origin='https://storage.googleapis.com/download.tensorflow.org/example_images/flower_photos.tgz',
fname='flower_photos', untar=True)
data_root = pathlib.Path(data_root_orig)
print(data_root)
```
218MB をダウンロードすると、花の画像のコピーが使えるようになっているはずです。
```
for item in data_root.iterdir():
print(item)
import random
all_image_paths = list(data_root.glob('*/*'))
all_image_paths = [str(path) for path in all_image_paths]
random.shuffle(all_image_paths)
image_count = len(all_image_paths)
image_count
all_image_paths[:10]
```
### 画像の検査
扱っている画像について知るために、画像のいくつかを見てみましょう。
```
import os
attributions = (data_root/"LICENSE.txt").open(encoding='utf-8').readlines()[4:]
attributions = [line.split(' CC-BY') for line in attributions]
attributions = dict(attributions)
import IPython.display as display
def caption_image(image_path):
image_rel = pathlib.Path(image_path).relative_to(data_root)
return "Image (CC BY 2.0) " + ' - '.join(attributions[str(image_rel)].split(' - ')[:-1])
for n in range(3):
image_path = random.choice(all_image_paths)
display.display(display.Image(image_path))
print(caption_image(image_path))
print()
```
### 各画像のラベルの決定
ラベルを一覧してみます。
```
label_names = sorted(item.name for item in data_root.glob('*/') if item.is_dir())
label_names
```
ラベルにインデックスを割り当てます。
```
label_to_index = dict((name, index) for index,name in enumerate(label_names))
label_to_index
```
ファイルとラベルのインデックスの一覧を作成します。
```
all_image_labels = [label_to_index[pathlib.Path(path).parent.name]
for path in all_image_paths]
print("First 10 labels indices: ", all_image_labels[:10])
```
### 画像の読み込みと整形
TensorFlow には画像を読み込んで処理するために必要なツールが備わっています。
```
img_path = all_image_paths[0]
img_path
```
以下は生のデータです。
```
img_raw = tf.io.read_file(img_path)
print(repr(img_raw)[:100]+"...")
```
画像のテンソルにデコードします。
```
img_tensor = tf.image.decode_image(img_raw)
print(img_tensor.shape)
print(img_tensor.dtype)
```
モデルに合わせてリサイズします。
```
img_final = tf.image.resize(img_tensor, [192, 192])
img_final = img_final/255.0
print(img_final.shape)
print(img_final.numpy().min())
print(img_final.numpy().max())
```
このあと使用するために、簡単な関数にまとめます。
```
def preprocess_image(image):
image = tf.image.decode_jpeg(image, channels=3)
image = tf.image.resize(image, [192, 192])
image /= 255.0 # normalize to [0,1] range
return image
def load_and_preprocess_image(path):
image = tf.io.read_file(path)
return preprocess_image(image)
import matplotlib.pyplot as plt
image_path = all_image_paths[0]
label = all_image_labels[0]
plt.imshow(load_and_preprocess_image(img_path))
plt.grid(False)
plt.xlabel(caption_image(img_path))
plt.title(label_names[label].title())
print()
```
## `tf.data.Dataset`の構築
### 画像のデータセット
`tf.data.Dataset` を構築するもっとも簡単な方法は、`from_tensor_slices` メソッドを使うことです。
文字列の配列をスライスすると、文字列のデータセットが出来上がります。
```
path_ds = tf.data.Dataset.from_tensor_slices(all_image_paths)
```
`shapes` と `types` は、データセット中のそれぞれのアイテムの内容を示しています。この場合には、バイナリ文字列のスカラーのセットです。
```
print(path_ds)
```
`preprocess_image` をファイルパスのデータセットにマップすることで、画像を実行時にロードし整形する新しいデータセットを作成します。
```
image_ds = path_ds.map(load_and_preprocess_image, num_parallel_calls=AUTOTUNE)
import matplotlib.pyplot as plt
plt.figure(figsize=(8,8))
for n,image in enumerate(image_ds.take(4)):
plt.subplot(2,2,n+1)
plt.imshow(image)
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.xlabel(caption_image(all_image_paths[n]))
plt.show()
```
### `(image, label)`のペアのデータセット
おなじ `from_tensor_slices` メソッドを使ってラベルのデータセットを作ることができます。
```
label_ds = tf.data.Dataset.from_tensor_slices(tf.cast(all_image_labels, tf.int64))
for label in label_ds.take(10):
print(label_names[label.numpy()])
```
これらのデータセットはおなじ順番なので、zip することで `(image, label)` というペアのデータセットができます。
```
image_label_ds = tf.data.Dataset.zip((image_ds, label_ds))
```
新しいデータセットの `shapes` と `types` は、それぞれのフィールドを示すシェイプと型のタプルです。
```
print(image_label_ds)
```
注: `all_image_labels` や `all_image_paths` のような配列がある場合、 `tf.data.dataset.Dataset.zip` メソッドの代わりとなるのは、配列のペアをスライスすることです。
```
ds = tf.data.Dataset.from_tensor_slices((all_image_paths, all_image_labels))
# The tuples are unpacked into the positional arguments of the mapped function
# タプルは展開され、マップ関数の位置引数に割り当てられます
def load_and_preprocess_from_path_label(path, label):
return load_and_preprocess_image(path), label
image_label_ds = ds.map(load_and_preprocess_from_path_label)
image_label_ds
```
### 基本的な訓練手法
このデータセットを使ってモデルの訓練を行うには、データが
* よくシャッフルされ
* バッチ化され
* 限りなく繰り返され
* バッチが出来るだけ早く利用できる
ことが必要です。
これらの特性は `tf.data` APIを使えば簡単に付け加えることができます。
```
BATCH_SIZE = 32
# シャッフルバッファのサイズをデータセットとおなじに設定することで、データが完全にシャッフルされる
# ようにできます。
ds = image_label_ds.shuffle(buffer_size=image_count)
ds = ds.repeat()
ds = ds.batch(BATCH_SIZE)
# `prefetch`を使うことで、モデルの訓練中にバックグラウンドでデータセットがバッチを取得できます。
ds = ds.prefetch(buffer_size=AUTOTUNE)
ds
```
注意すべきことがいくつかあります。
1. 順番が重要です。
* `.repeat` の前に `.shuffle` すると、エポックの境界を越えて要素がシャッフルされます。(ほかの要素がすべて出現する前に2回出現する要素があるかもしれません)
* `.batch` の後に `.shuffle` すると、バッチの順番がシャッフルされますが、要素がバッチを越えてシャッフルされることはありません。
1. 完全なシャッフルのため、 `buffer_size` をデータセットとおなじサイズに設定しています。データセットのサイズ未満の場合、値が大きいほど良くランダム化されますが、より多くのメモリーを使用します。
1. シャッフルバッファがいっぱいになってから要素が取り出されます。そのため、大きな `buffer_size` が `Dataset` を使い始める際の遅延の原因になります。
1. シャッフルされたデータセットは、シャッフルバッファが完全に空になるまでデータセットが終わりであることを伝えません。 `.repeat` によって `Dataset` が再起動されると、シャッフルバッファが一杯になるまでもう一つの待ち時間が発生します。
最後の問題は、 `tf.data.Dataset.apply` メソッドを、融合された `tf.data.experimental.shuffle_and_repeat` 関数と組み合わせることで対処できます。
```
ds = image_label_ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds = ds.batch(BATCH_SIZE)
ds = ds.prefetch(buffer_size=AUTOTUNE)
ds
```
### データセットをモデルにつなぐ
`tf.keras.applications`からMobileNet v2のコピーを取得します。
これを簡単な転移学習のサンプルに使用します。
MobileNetの重みを訓練不可に設定します。
```
mobile_net = tf.keras.applications.MobileNetV2(input_shape=(192, 192, 3), include_top=False)
mobile_net.trainable=False
```
このモデルは、入力が `[-1,1]` の範囲に正規化されていることを想定しています。
```
help(keras_applications.mobilenet_v2.preprocess_input)
```
<pre>
...
This function applies the "Inception" preprocessing which converts
the RGB values from [0, 255] to [-1, 1]
...
</pre>
このため、データをMobileNetモデルに渡す前に、入力を`[0,1]`の範囲から`[-1,1]`の範囲に変換する必要があります。
```
def change_range(image,label):
return 2*image-1, label
keras_ds = ds.map(change_range)
```
MobileNetは画像ごとに `6x6` の特徴量の空間を返します。
バッチを1つ渡してみましょう。
```
# シャッフルバッファがいっぱいになるまで、データセットは何秒かかかります。
image_batch, label_batch = next(iter(keras_ds))
feature_map_batch = mobile_net(image_batch)
print(feature_map_batch.shape)
```
MobileNet をラップしたモデルを作り、出力層である `tf.keras.layers.Dense` の前に、`tf.keras.layers.GlobalAveragePooling2D` で空間の軸にそって平均値を求めます。
```
model = tf.keras.Sequential([
mobile_net,
tf.keras.layers.GlobalAveragePooling2D(),
tf.keras.layers.Dense(len(label_names))])
```
期待したとおりの形状の出力が得られます。
```
logit_batch = model(image_batch).numpy()
print("min logit:", logit_batch.min())
print("max logit:", logit_batch.max())
print()
print("Shape:", logit_batch.shape)
```
訓練手法を記述するためにモデルをコンパイルします。
```
model.compile(optimizer=tf.keras.optimizers.Adam(),
loss='sparse_categorical_crossentropy',
metrics=["accuracy"])
```
訓練可能な変数は2つ、全結合層の `weights` と `bias` です。
```
len(model.trainable_variables)
model.summary()
```
モデルを訓練します。
普通は、エポックごとの本当のステップ数を指定しますが、ここではデモの目的なので3ステップだけとします。
```
steps_per_epoch=tf.math.ceil(len(all_image_paths)/BATCH_SIZE).numpy()
steps_per_epoch
model.fit(ds, epochs=1, steps_per_epoch=3)
```
## 性能
注:このセクションでは性能の向上に役立ちそうな簡単なトリックをいくつか紹介します。詳しくは、[Input Pipeline Performance](https://www.tensorflow.org/guide/performance/datasets) を参照してください。
上記の単純なパイプラインは、エポックごとにそれぞれのファイルを一つずつ読み込みます。これは、CPU を使ったローカルでの訓練では問題になりませんが、GPU を使った訓練では十分ではなく、いかなる分散訓練でも使うべきではありません。
調査のため、まず、データセットの性能をチェックする簡単な関数を定義します。
```
import time
default_timeit_steps = 2*steps_per_epoch+1
def timeit(ds, steps=default_timeit_steps):
overall_start = time.time()
# Fetch a single batch to prime the pipeline (fill the shuffle buffer),
# before starting the timer
it = iter(ds.take(steps+1))
next(it)
start = time.time()
for i,(images,labels) in enumerate(it):
if i%10 == 0:
print('.',end='')
print()
end = time.time()
duration = end-start
print("{} batches: {} s".format(steps, duration))
print("{:0.5f} Images/s".format(BATCH_SIZE*steps/duration))
print("Total time: {}s".format(end-overall_start))
```
現在のデータセットの性能は次のとおりです。
```
ds = image_label_ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds = ds.batch(BATCH_SIZE).prefetch(buffer_size=AUTOTUNE)
ds
timeit(ds)
```
### キャッシュ
`tf.data.Dataset.cache` を使うと、エポックを越えて計算結果を簡単にキャッシュできます。特に、データがメモリに収まるときには効果的です。
ここでは、画像が前処理(デコードとリサイズ)された後でキャッシュされます。
```
ds = image_label_ds.cache()
ds = ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds = ds.batch(BATCH_SIZE).prefetch(buffer_size=AUTOTUNE)
ds
timeit(ds)
```
メモリキャッシュを使う際の欠点のひとつは、実行の都度キャッシュを再構築しなければならないことです。このため、データセットがスタートするたびにおなじだけ起動のための遅延が発生します。
```
timeit(ds)
```
データがメモリに収まらない場合には、キャッシュファイルを使用します。
```
ds = image_label_ds.cache(filename='./cache.tf-data')
ds = ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds = ds.batch(BATCH_SIZE).prefetch(1)
ds
timeit(ds)
```
キャッシュファイルには、キャッシュを再構築することなくデータセットを再起動できるという利点もあります。2回めがどれほど早いか見てみましょう。
```
timeit(ds)
```
### TFRecord ファイル
#### 生の画像データ
TFRecord ファイルは、バイナリの大きなオブジェクトのシーケンスを保存するための単純なフォーマットです。複数のサンプルをおなじファイルに詰め込むことで、TensorFlow は複数のサンプルを一度に読み込むことができます。これは、特に GCS のようなリモートストレージサービスを使用する際の性能にとって重要です。
最初に、生の画像データから TFRecord ファイルを構築します。
```
image_ds = tf.data.Dataset.from_tensor_slices(all_image_paths).map(tf.io.read_file)
tfrec = tf.data.experimental.TFRecordWriter('images.tfrec')
tfrec.write(image_ds)
```
次に、TFRecord ファイルを読み込み、以前定義した `preprocess_image` 関数を使って画像のデコード/リフォーマットを行うデータセットを構築します。
```
image_ds = tf.data.TFRecordDataset('images.tfrec').map(preprocess_image)
```
これを、前に定義済みのラベルデータセットと zip し、期待どおりの `(image,label)` のペアを得ます。
```
ds = tf.data.Dataset.zip((image_ds, label_ds))
ds = ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds=ds.batch(BATCH_SIZE).prefetch(AUTOTUNE)
ds
timeit(ds)
```
これは、`cache` バージョンよりも低速です。前処理をキャッシュしていないからです。
#### シリアライズしたテンソル
前処理を TFRecord ファイルに保存するには、前やったように前処理した画像のデータセットを作ります。
```
paths_ds = tf.data.Dataset.from_tensor_slices(all_image_paths)
image_ds = paths_ds.map(load_and_preprocess_image)
image_ds
```
`.jpeg` 文字列のデータセットではなく、これはテンソルのデータセットです。
これを TFRecord ファイルにシリアライズするには、まず、テンソルのデータセットを文字列のデータセットに変換します。
```
ds = image_ds.map(tf.io.serialize_tensor)
ds
tfrec = tf.data.experimental.TFRecordWriter('images.tfrec')
tfrec.write(ds)
```
前処理をキャッシュしたことにより、データは TFRecord ファイルから非常に効率的にロードできます。テンソルを使用する前にデシリアライズすることを忘れないでください。
```
ds = tf.data.TFRecordDataset('images.tfrec')
def parse(x):
result = tf.io.parse_tensor(x, out_type=tf.float32)
result = tf.reshape(result, [192, 192, 3])
return result
ds = ds.map(parse, num_parallel_calls=AUTOTUNE)
ds
```
次にラベルを追加し、以前とおなじような標準的な処理を適用します。
```
ds = tf.data.Dataset.zip((ds, label_ds))
ds = ds.apply(
tf.data.experimental.shuffle_and_repeat(buffer_size=image_count))
ds=ds.batch(BATCH_SIZE).prefetch(AUTOTUNE)
ds
timeit(ds)
```
| github_jupyter |
# Character level language model - Dinosaurus Island
Welcome to Dinosaurus Island! 65 million years ago, dinosaurs existed, and in this assignment they are back. You are in charge of a special task. Leading biology researchers are creating new breeds of dinosaurs and bringing them to life on earth, and your job is to give names to these dinosaurs. If a dinosaur does not like its name, it might go berserk, so choose wisely!
<table>
<td>
<img src="images/dino.jpg" style="width:250;height:300px;">
</td>
</table>
Luckily you have learned some deep learning and you will use it to save the day. Your assistant has collected a list of all the dinosaur names they could find, and compiled them into this [dataset](dinos.txt). (Feel free to take a look by clicking the previous link.) To create new dinosaur names, you will build a character level language model to generate new names. Your algorithm will learn the different name patterns, and randomly generate new names. Hopefully this algorithm will keep you and your team safe from the dinosaurs' wrath!
By completing this assignment you will learn:
- How to store text data for processing using an RNN
- How to synthesize data, by sampling predictions at each time step and passing it to the next RNN-cell unit
- How to build a character-level text generation recurrent neural network
- Why clipping the gradients is important
We will begin by loading in some functions that we have provided for you in `rnn_utils`. Specifically, you have access to functions such as `rnn_forward` and `rnn_backward` which are equivalent to those you've implemented in the previous assignment.
## <font color='darkblue'>Updates</font>
#### If you were working on the notebook before this update...
* The current notebook is version "3a".
* You can find your original work saved in the notebook with the previous version name ("v3")
* To view the file directory, go to the menu "File->Open", and this will open a new tab that shows the file directory.
#### List of updates
* Sort and print `chars` list of characters.
* Import and use pretty print
* `clip`:
- Additional details on why we need to use the "out" parameter.
- Modified for loop to have students fill in the correct items to loop through.
- Added a test case to check for hard-coding error.
* `sample`
- additional hints added to steps 1,2,3,4.
- "Using 2D arrays instead of 1D arrays".
- explanation of numpy.ravel().
- fixed expected output.
- clarified comments in the code.
* "training the model"
- Replaced the sample code with explanations for how to set the index, X and Y (for a better learning experience).
* Spelling, grammar and wording corrections.
```
import numpy as np
from utils import *
import random
import pprint
```
## 1 - Problem Statement
### 1.1 - Dataset and Preprocessing
Run the following cell to read the dataset of dinosaur names, create a list of unique characters (such as a-z), and compute the dataset and vocabulary size.
```
data = open('dinos.txt', 'r').read()
data= data.lower()
chars = list(set(data))
data_size, vocab_size = len(data), len(chars)
print('There are %d total characters and %d unique characters in your data.' % (data_size, vocab_size))
```
* The characters are a-z (26 characters) plus the "\n" (or newline character).
* In this assignment, the newline character "\n" plays a role similar to the `<EOS>` (or "End of sentence") token we had discussed in lecture.
- Here, "\n" indicates the end of the dinosaur name rather than the end of a sentence.
* `char_to_ix`: In the cell below, we create a python dictionary (i.e., a hash table) to map each character to an index from 0-26.
* `ix_to_char`: We also create a second python dictionary that maps each index back to the corresponding character.
- This will help you figure out what index corresponds to what character in the probability distribution output of the softmax layer.
```
chars = sorted(chars)
print(chars)
char_to_ix = { ch:i for i,ch in enumerate(chars) }
ix_to_char = { i:ch for i,ch in enumerate(chars) }
pp = pprint.PrettyPrinter(indent=4)
pp.pprint(ix_to_char)
```
### 1.2 - Overview of the model
Your model will have the following structure:
- Initialize parameters
- Run the optimization loop
- Forward propagation to compute the loss function
- Backward propagation to compute the gradients with respect to the loss function
- Clip the gradients to avoid exploding gradients
- Using the gradients, update your parameters with the gradient descent update rule.
- Return the learned parameters
<img src="images/rnn.png" style="width:450;height:300px;">
<caption><center> **Figure 1**: Recurrent Neural Network, similar to what you had built in the previous notebook "Building a Recurrent Neural Network - Step by Step". </center></caption>
* At each time-step, the RNN tries to predict what is the next character given the previous characters.
* The dataset $\mathbf{X} = (x^{\langle 1 \rangle}, x^{\langle 2 \rangle}, ..., x^{\langle T_x \rangle})$ is a list of characters in the training set.
* $\mathbf{Y} = (y^{\langle 1 \rangle}, y^{\langle 2 \rangle}, ..., y^{\langle T_x \rangle})$ is the same list of characters but shifted one character forward.
* At every time-step $t$, $y^{\langle t \rangle} = x^{\langle t+1 \rangle}$. The prediction at time $t$ is the same as the input at time $t + 1$.
## 2 - Building blocks of the model
In this part, you will build two important blocks of the overall model:
- Gradient clipping: to avoid exploding gradients
- Sampling: a technique used to generate characters
You will then apply these two functions to build the model.
### 2.1 - Clipping the gradients in the optimization loop
In this section you will implement the `clip` function that you will call inside of your optimization loop.
#### Exploding gradients
* When gradients are very large, they're called "exploding gradients."
* Exploding gradients make the training process more difficult, because the updates may be so large that they "overshoot" the optimal values during back propagation.
Recall that your overall loop structure usually consists of:
* forward pass,
* cost computation,
* backward pass,
* parameter update.
Before updating the parameters, you will perform gradient clipping to make sure that your gradients are not "exploding."
#### gradient clipping
In the exercise below, you will implement a function `clip` that takes in a dictionary of gradients and returns a clipped version of gradients if needed.
* There are different ways to clip gradients.
* We will use a simple element-wise clipping procedure, in which every element of the gradient vector is clipped to lie between some range [-N, N].
* For example, if the N=10
- The range is [-10, 10]
- If any component of the gradient vector is greater than 10, it is set to 10.
- If any component of the gradient vector is less than -10, it is set to -10.
- If any components are between -10 and 10, they keep their original values.
<img src="images/clip.png" style="width:400;height:150px;">
<caption><center> **Figure 2**: Visualization of gradient descent with and without gradient clipping, in a case where the network is running into "exploding gradient" problems. </center></caption>
**Exercise**:
Implement the function below to return the clipped gradients of your dictionary `gradients`.
* Your function takes in a maximum threshold and returns the clipped versions of the gradients.
* You can check out [numpy.clip](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.clip.html).
- You will need to use the argument "`out = ...`".
- Using the "`out`" parameter allows you to update a variable "in-place".
- If you don't use "`out`" argument, the clipped variable is stored in the variable "gradient" but does not update the gradient variables `dWax`, `dWaa`, `dWya`, `db`, `dby`.
```
### GRADED FUNCTION: clip
def clip(gradients, maxValue):
'''
Clips the gradients' values between minimum and maximum.
Arguments:
gradients -- a dictionary containing the gradients "dWaa", "dWax", "dWya", "db", "dby"
maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue
Returns:
gradients -- a dictionary with the clipped gradients.
'''
dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients['dby']
### START CODE HERE ###
# clip to mitigate exploding gradients, loop over [dWax, dWaa, dWya, db, dby]. (≈2 lines)
for gradient in [dWaa, dWax, dWya, db, dby]:
np.clip(gradient,a_min=-maxValue,a_max=maxValue,out=gradient)
### END CODE HERE ###
gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}
return gradients
# Test with a maxvalue of 10
maxValue = 10
np.random.seed(3)
dWax = np.random.randn(5,3)*10
dWaa = np.random.randn(5,5)*10
dWya = np.random.randn(2,5)*10
db = np.random.randn(5,1)*10
dby = np.random.randn(2,1)*10
gradients = {"dWax": dWax, "dWaa": dWaa, "dWya": dWya, "db": db, "dby": dby}
gradients = clip(gradients, maxValue)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
```
** Expected output:**
```Python
gradients["dWaa"][1][2] = 10.0
gradients["dWax"][3][1] = -10.0
gradients["dWya"][1][2] = 0.29713815361
gradients["db"][4] = [ 10.]
gradients["dby"][1] = [ 8.45833407]
```
```
# Test with a maxValue of 5
maxValue = 5
np.random.seed(3)
dWax = np.random.randn(5,3)*10
dWaa = np.random.randn(5,5)*10
dWya = np.random.randn(2,5)*10
db = np.random.randn(5,1)*10
dby = np.random.randn(2,1)*10
gradients = {"dWax": dWax, "dWaa": dWaa, "dWya": dWya, "db": db, "dby": dby}
gradients = clip(gradients, maxValue)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
```
** Expected Output: **
```Python
gradients["dWaa"][1][2] = 5.0
gradients["dWax"][3][1] = -5.0
gradients["dWya"][1][2] = 0.29713815361
gradients["db"][4] = [ 5.]
gradients["dby"][1] = [ 5.]
```
### 2.2 - Sampling
Now assume that your model is trained. You would like to generate new text (characters). The process of generation is explained in the picture below:
<img src="images/dinos3.png" style="width:500;height:300px;">
<caption><center> **Figure 3**: In this picture, we assume the model is already trained. We pass in $x^{\langle 1\rangle} = \vec{0}$ at the first time step, and have the network sample one character at a time. </center></caption>
**Exercise**: Implement the `sample` function below to sample characters. You need to carry out 4 steps:
- **Step 1**: Input the "dummy" vector of zeros $x^{\langle 1 \rangle} = \vec{0}$.
- This is the default input before we've generated any characters.
We also set $a^{\langle 0 \rangle} = \vec{0}$
- **Step 2**: Run one step of forward propagation to get $a^{\langle 1 \rangle}$ and $\hat{y}^{\langle 1 \rangle}$. Here are the equations:
hidden state:
$$ a^{\langle t+1 \rangle} = \tanh(W_{ax} x^{\langle t+1 \rangle } + W_{aa} a^{\langle t \rangle } + b)\tag{1}$$
activation:
$$ z^{\langle t + 1 \rangle } = W_{ya} a^{\langle t + 1 \rangle } + b_y \tag{2}$$
prediction:
$$ \hat{y}^{\langle t+1 \rangle } = softmax(z^{\langle t + 1 \rangle })\tag{3}$$
- Details about $\hat{y}^{\langle t+1 \rangle }$:
- Note that $\hat{y}^{\langle t+1 \rangle }$ is a (softmax) probability vector (its entries are between 0 and 1 and sum to 1).
- $\hat{y}^{\langle t+1 \rangle}_i$ represents the probability that the character indexed by "i" is the next character.
- We have provided a `softmax()` function that you can use.
#### Additional Hints
- $x^{\langle 1 \rangle}$ is `x` in the code. When creating the one-hot vector, make a numpy array of zeros, with the number of rows equal to the number of unique characters, and the number of columns equal to one. It's a 2D and not a 1D array.
- $a^{\langle 0 \rangle}$ is `a_prev` in the code. It is a numpy array of zeros, where the number of rows is $n_{a}$, and number of columns is 1. It is a 2D array as well. $n_{a}$ is retrieved by getting the number of columns in $W_{aa}$ (the numbers need to match in order for the matrix multiplication $W_{aa}a^{\langle t \rangle}$ to work.
- [numpy.dot](https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html)
- [numpy.tanh](https://docs.scipy.org/doc/numpy/reference/generated/numpy.tanh.html)
#### Using 2D arrays instead of 1D arrays
* You may be wondering why we emphasize that $x^{\langle 1 \rangle}$ and $a^{\langle 0 \rangle}$ are 2D arrays and not 1D vectors.
* For matrix multiplication in numpy, if we multiply a 2D matrix with a 1D vector, we end up with with a 1D array.
* This becomes a problem when we add two arrays where we expected them to have the same shape.
* When two arrays with a different number of dimensions are added together, Python "broadcasts" one across the other.
* Here is some sample code that shows the difference between using a 1D and 2D array.
```
import numpy as np
matrix1 = np.array([[1,1],[2,2],[3,3]]) # (3,2)
matrix2 = np.array([[0],[0],[0]]) # (3,1)
vector1D = np.array([1,1]) # (2,)
vector2D = np.array([[1],[1]]) # (2,1)
print("matrix1 \n", matrix1,"\n")
print("matrix2 \n", matrix2,"\n")
print("vector1D \n", vector1D,"\n")
print("vector2D \n", vector2D)
print("Multiply 2D and 1D arrays: result is a 1D array\n",
np.dot(matrix1,vector1D))
print("Multiply 2D and 2D arrays: result is a 2D array\n",
np.dot(matrix1,vector2D))
print("Adding (3 x 1) vector to a (3 x 1) vector is a (3 x 1) vector\n",
"This is what we want here!\n",
np.dot(matrix1,vector2D) + matrix2)
print("Adding a (3,) vector to a (3 x 1) vector\n",
"broadcasts the 1D array across the second dimension\n",
"Not what we want here!\n",
np.dot(matrix1,vector1D) + matrix2
)
```
- **Step 3**: Sampling:
- Now that we have $y^{\langle t+1 \rangle}$, we want to select the next letter in the dinosaur name. If we select the most probable, the model will always generate the same result given a starting letter.
- To make the results more interesting, we will use np.random.choice to select a next letter that is likely, but not always the same.
- Sampling is the selection of a value from a group of values, where each value has a probability of being picked.
- Sampling allows us to generate random sequences of values.
- Pick the next character's index according to the probability distribution specified by $\hat{y}^{\langle t+1 \rangle }$.
- This means that if $\hat{y}^{\langle t+1 \rangle }_i = 0.16$, you will pick the index "i" with 16% probability.
- You can use [np.random.choice](https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.random.choice.html).
Example of how to use `np.random.choice()`:
```python
np.random.seed(0)
probs = np.array([0.1, 0.0, 0.7, 0.2])
idx = np.random.choice([0, 1, 2, 3] p = probs)
```
- This means that you will pick the index (`idx`) according to the distribution:
$P(index = 0) = 0.1, P(index = 1) = 0.0, P(index = 2) = 0.7, P(index = 3) = 0.2$.
- Note that the value that's set to `p` should be set to a 1D vector.
- Also notice that $\hat{y}^{\langle t+1 \rangle}$, which is `y` in the code, is a 2D array.
##### Additional Hints
- [range](https://docs.python.org/3/library/functions.html#func-range)
- [numpy.ravel](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ravel.html) takes a multi-dimensional array and returns its contents inside of a 1D vector.
```Python
arr = np.array([[1,2],[3,4]])
print("arr")
print(arr)
print("arr.ravel()")
print(arr.ravel())
```
Output:
```Python
arr
[[1 2]
[3 4]]
arr.ravel()
[1 2 3 4]
```
- Note that `append` is an "in-place" operation. In other words, don't do this:
```Python
fun_hobbies = fun_hobbies.append('learning') ## Doesn't give you what you want
```
- **Step 4**: Update to $x^{\langle t \rangle }$
- The last step to implement in `sample()` is to update the variable `x`, which currently stores $x^{\langle t \rangle }$, with the value of $x^{\langle t + 1 \rangle }$.
- You will represent $x^{\langle t + 1 \rangle }$ by creating a one-hot vector corresponding to the character that you have chosen as your prediction.
- You will then forward propagate $x^{\langle t + 1 \rangle }$ in Step 1 and keep repeating the process until you get a "\n" character, indicating that you have reached the end of the dinosaur name.
##### Additional Hints
- In order to reset `x` before setting it to the new one-hot vector, you'll want to set all the values to zero.
- You can either create a new numpy array: [numpy.zeros](https://docs.scipy.org/doc/numpy/reference/generated/numpy.zeros.html)
- Or fill all values with a single number: [numpy.ndarray.fill](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.fill.html)
```
# GRADED FUNCTION: sample
def sample(parameters, char_to_ix, seed):
"""
Sample a sequence of characters according to a sequence of probability distributions output of the RNN
Arguments:
parameters -- python dictionary containing the parameters Waa, Wax, Wya, by, and b.
char_to_ix -- python dictionary mapping each character to an index.
seed -- used for grading purposes. Do not worry about it.
Returns:
indices -- a list of length n containing the indices of the sampled characters.
"""
# Retrieve parameters and relevant shapes from "parameters" dictionary
Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
vocab_size = by.shape[0]
n_a = Waa.shape[1]
### START CODE HERE ###
# Step 1: Create the a zero vector x that can be used as the one-hot vector
# representing the first character (initializing the sequence generation). (≈1 line)
x = np.zeros((vocab_size,1))
# Step 1': Initialize a_prev as zeros (≈1 line)
a_prev = np.zeros((n_a,1))
# Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate (≈1 line)
indices = []
# idx is the index of the one-hot vector x that is set to 1
# All other positions in x are zero.
# We will initialize idx to -1
idx = -1
# Loop over time-steps t. At each time-step:
# sample a character from a probability distribution
# and append its index (`idx`) to the list "indices".
# We'll stop if we reach 50 characters
# (which should be very unlikely with a well trained model).
# Setting the maximum number of characters helps with debugging and prevents infinite loops.
counter = 0
newline_character = char_to_ix['\n']
while (idx != newline_character and counter != 50):
# Step 2: Forward propagate x using the equations (1), (2) and (3)
a = np.tanh(np.dot(Wax,x)+np.dot(Waa,a_prev)+b)
z = np.dot(Wya,a)+by
y = softmax(z)
# for grading purposes
np.random.seed(counter+seed)
# Step 3: Sample the index of a character within the vocabulary from the probability distribution y
# (see additional hints above)
idx = np.random.choice(list(range(0,vocab_size)),p=y.ravel())
# Append the index to "indices"
indices.append(idx)
# Step 4: Overwrite the input x with one that corresponds to the sampled index `idx`.
# (see additional hints above)
x = np.zeros((vocab_size,1))
x[idx] = 1
# Update "a_prev" to be "a"
a_prev = a
# for grading purposes
seed += 1
counter +=1
### END CODE HERE ###
if (counter == 50):
indices.append(char_to_ix['\n'])
return indices
np.random.seed(2)
_, n_a = 20, 100
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
indices = sample(parameters, char_to_ix, 0)
print("Sampling:")
print("list of sampled indices:\n", indices)
print("size indices:\n", len(indices))
print("list of sampled characters:\n", [ix_to_char[i] for i in indices])
```
** Expected output:**
```Python
Sampling:
list of sampled indices:
[12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 17, 24, 12, 13, 24, 0]
list of sampled characters:
['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'q', 'x', 'l', 'm', 'x', '\n']
```
* Please note that over time, if there are updates to the back-end of the Coursera platform (that may update the version of numpy), the actual list of sampled indices and sampled characters may change.
* If you follow the instructions given above and get an output without errors, it's possible the routine is correct even if your output doesn't match the expected output. Submit your assignment to the grader to verify its correctness.
## 3 - Building the language model
It is time to build the character-level language model for text generation.
### 3.1 - Gradient descent
* In this section you will implement a function performing one step of stochastic gradient descent (with clipped gradients).
* You will go through the training examples one at a time, so the optimization algorithm will be stochastic gradient descent.
As a reminder, here are the steps of a common optimization loop for an RNN:
- Forward propagate through the RNN to compute the loss
- Backward propagate through time to compute the gradients of the loss with respect to the parameters
- Clip the gradients
- Update the parameters using gradient descent
**Exercise**: Implement the optimization process (one step of stochastic gradient descent).
The following functions are provided:
```python
def rnn_forward(X, Y, a_prev, parameters):
""" Performs the forward propagation through the RNN and computes the cross-entropy loss.
It returns the loss' value as well as a "cache" storing values to be used in backpropagation."""
....
return loss, cache
def rnn_backward(X, Y, parameters, cache):
""" Performs the backward propagation through time to compute the gradients of the loss with respect
to the parameters. It returns also all the hidden states."""
...
return gradients, a
def update_parameters(parameters, gradients, learning_rate):
""" Updates parameters using the Gradient Descent Update Rule."""
...
return parameters
```
Recall that you previously implemented the `clip` function:
```Python
def clip(gradients, maxValue)
"""Clips the gradients' values between minimum and maximum."""
...
return gradients
```
#### parameters
* Note that the weights and biases inside the `parameters` dictionary are being updated by the optimization, even though `parameters` is not one of the returned values of the `optimize` function. The `parameters` dictionary is passed by reference into the function, so changes to this dictionary are making changes to the `parameters` dictionary even when accessed outside of the function.
* Python dictionaries and lists are "pass by reference", which means that if you pass a dictionary into a function and modify the dictionary within the function, this changes that same dictionary (it's not a copy of the dictionary).
```
# GRADED FUNCTION: optimize
def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):
"""
Execute one step of the optimization to train the model.
Arguments:
X -- list of integers, where each integer is a number that maps to a character in the vocabulary.
Y -- list of integers, exactly the same as X but shifted one index to the left.
a_prev -- previous hidden state.
parameters -- python dictionary containing:
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
b -- Bias, numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
learning_rate -- learning rate for the model.
Returns:
loss -- value of the loss function (cross-entropy)
gradients -- python dictionary containing:
dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
db -- Gradients of bias vector, of shape (n_a, 1)
dby -- Gradients of output bias vector, of shape (n_y, 1)
a[len(X)-1] -- the last hidden state, of shape (n_a, 1)
"""
### START CODE HERE ###
# Forward propagate through time (≈1 line)
loss, cache = rnn_forward(X, Y, a_prev, parameters)
# Backpropagate through time (≈1 line)
gradients, a = rnn_backward(X, Y, parameters, cache)
# Clip your gradients between -5 (min) and 5 (max) (≈1 line)
gradients = clip(gradients, 5)
# Update parameters (≈1 line)
parameters = update_parameters(parameters, gradients, learning_rate)
### END CODE HERE ###
return loss, gradients, a[len(X)-1]
np.random.seed(1)
vocab_size, n_a = 27, 100
a_prev = np.random.randn(n_a, 1)
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
X = [12,3,5,11,22,3]
Y = [4,14,11,22,25, 26]
loss, gradients, a_last = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)
print("Loss =", loss)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("np.argmax(gradients[\"dWax\"]) =", np.argmax(gradients["dWax"]))
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
print("a_last[4] =", a_last[4])
```
** Expected output:**
```Python
Loss = 126.503975722
gradients["dWaa"][1][2] = 0.194709315347
np.argmax(gradients["dWax"]) = 93
gradients["dWya"][1][2] = -0.007773876032
gradients["db"][4] = [-0.06809825]
gradients["dby"][1] = [ 0.01538192]
a_last[4] = [-1.]
```
### 3.2 - Training the model
* Given the dataset of dinosaur names, we use each line of the dataset (one name) as one training example.
* Every 100 steps of stochastic gradient descent, you will sample 10 randomly chosen names to see how the algorithm is doing.
* Remember to shuffle the dataset, so that stochastic gradient descent visits the examples in random order.
**Exercise**: Follow the instructions and implement `model()`. When `examples[index]` contains one dinosaur name (string), to create an example (X, Y), you can use this:
##### Set the index `idx` into the list of examples
* Using the for-loop, walk through the shuffled list of dinosaur names in the list "examples".
* If there are 100 examples, and the for-loop increments the index to 100 onwards, think of how you would make the index cycle back to 0, so that we can continue feeding the examples into the model when j is 100, 101, etc.
* Hint: 101 divided by 100 is zero with a remainder of 1.
* `%` is the modulus operator in python.
##### Extract a single example from the list of examples
* `single_example`: use the `idx` index that you set previously to get one word from the list of examples.
##### Convert a string into a list of characters: `single_example_chars`
* `single_example_chars`: A string is a list of characters.
* You can use a list comprehension (recommended over for-loops) to generate a list of characters.
```Python
str = 'I love learning'
list_of_chars = [c for c in str]
print(list_of_chars)
```
```
['I', ' ', 'l', 'o', 'v', 'e', ' ', 'l', 'e', 'a', 'r', 'n', 'i', 'n', 'g']
```
##### Convert list of characters to a list of integers: `single_example_ix`
* Create a list that contains the index numbers associated with each character.
* Use the dictionary `char_to_ix`
* You can combine this with the list comprehension that is used to get a list of characters from a string.
* This is a separate line of code below, to help learners clarify each step in the function.
##### Create the list of input characters: `X`
* `rnn_forward` uses the `None` value as a flag to set the input vector as a zero-vector.
* Prepend the `None` value in front of the list of input characters.
* There is more than one way to prepend a value to a list. One way is to add two lists together: `['a'] + ['b']`
##### Get the integer representation of the newline character `ix_newline`
* `ix_newline`: The newline character signals the end of the dinosaur name.
- get the integer representation of the newline character `'\n'`.
- Use `char_to_ix`
##### Set the list of labels (integer representation of the characters): `Y`
* The goal is to train the RNN to predict the next letter in the name, so the labels are the list of characters that are one time step ahead of the characters in the input `X`.
- For example, `Y[0]` contains the same value as `X[1]`
* The RNN should predict a newline at the last letter so add ix_newline to the end of the labels.
- Append the integer representation of the newline character to the end of `Y`.
- Note that `append` is an in-place operation.
- It might be easier for you to add two lists together.
```
# GRADED FUNCTION: model
def model(data, ix_to_char, char_to_ix, num_iterations = 35000, n_a = 50, dino_names = 7, vocab_size = 27):
"""
Trains the model and generates dinosaur names.
Arguments:
data -- text corpus
ix_to_char -- dictionary that maps the index to a character
char_to_ix -- dictionary that maps a character to an index
num_iterations -- number of iterations to train the model for
n_a -- number of units of the RNN cell
dino_names -- number of dinosaur names you want to sample at each iteration.
vocab_size -- number of unique characters found in the text (size of the vocabulary)
Returns:
parameters -- learned parameters
"""
# Retrieve n_x and n_y from vocab_size
n_x, n_y = vocab_size, vocab_size
# Initialize parameters
parameters = initialize_parameters(n_a, n_x, n_y)
# Initialize loss (this is required because we want to smooth our loss)
loss = get_initial_loss(vocab_size, dino_names)
# Build list of all dinosaur names (training examples).
with open("dinos.txt") as f:
examples = f.readlines()
examples = [x.lower().strip() for x in examples]
# Shuffle list of all dinosaur names
np.random.seed(0)
np.random.shuffle(examples)
# Initialize the hidden state of your LSTM
a_prev = np.zeros((n_a, 1))
# Optimization loop
for j in range(num_iterations):
### START CODE HERE ###
# Set the index `idx` (see instructions above)
idx = j%len(examples)
# Set the input X (see instructions above)
single_example = examples[idx]
single_example_chars = [c for c in single_example]
single_example_ix = [char_to_ix[c] for c in single_example_chars]
X = [None]+single_example_ix
# Set the labels Y (see instructions above)
ix_newline = char_to_ix["\n"]
Y = X[1:]+[ix_newline]
# Perform one optimization step: Forward-prop -> Backward-prop -> Clip -> Update parameters
# Choose a learning rate of 0.01
curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters, learning_rate = 0.01)
### END CODE HERE ###
# Use a latency trick to keep the loss smooth. It happens here to accelerate the training.
loss = smooth(loss, curr_loss)
# Every 2000 Iteration, generate "n" characters thanks to sample() to check if the model is learning properly
if j % 2000 == 0:
print('Iteration: %d, Loss: %f' % (j, loss) + '\n')
# The number of dinosaur names to print
seed = 0
for name in range(dino_names):
# Sample indices and print them
sampled_indices = sample(parameters, char_to_ix, seed)
print_sample(sampled_indices, ix_to_char)
seed += 1 # To get the same result (for grading purposes), increment the seed by one.
print('\n')
return parameters
```
Run the following cell, you should observe your model outputting random-looking characters at the first iteration. After a few thousand iterations, your model should learn to generate reasonable-looking names.
```
parameters = model(data, ix_to_char, char_to_ix)
```
** Expected Output**
The output of your model may look different, but it will look something like this:
```Python
Iteration: 34000, Loss: 22.447230
Onyxipaledisons
Kiabaeropa
Lussiamang
Pacaeptabalsaurus
Xosalong
Eiacoteg
Troia
```
## Conclusion
You can see that your algorithm has started to generate plausible dinosaur names towards the end of the training. At first, it was generating random characters, but towards the end you could see dinosaur names with cool endings. Feel free to run the algorithm even longer and play with hyperparameters to see if you can get even better results. Our implementation generated some really cool names like `maconucon`, `marloralus` and `macingsersaurus`. Your model hopefully also learned that dinosaur names tend to end in `saurus`, `don`, `aura`, `tor`, etc.
If your model generates some non-cool names, don't blame the model entirely--not all actual dinosaur names sound cool. (For example, `dromaeosauroides` is an actual dinosaur name and is in the training set.) But this model should give you a set of candidates from which you can pick the coolest!
This assignment had used a relatively small dataset, so that you could train an RNN quickly on a CPU. Training a model of the english language requires a much bigger dataset, and usually needs much more computation, and could run for many hours on GPUs. We ran our dinosaur name for quite some time, and so far our favorite name is the great, undefeatable, and fierce: Mangosaurus!
<img src="images/mangosaurus.jpeg" style="width:250;height:300px;">
## 4 - Writing like Shakespeare
The rest of this notebook is optional and is not graded, but we hope you'll do it anyway since it's quite fun and informative.
A similar (but more complicated) task is to generate Shakespeare poems. Instead of learning from a dataset of Dinosaur names you can use a collection of Shakespearian poems. Using LSTM cells, you can learn longer term dependencies that span many characters in the text--e.g., where a character appearing somewhere a sequence can influence what should be a different character much much later in the sequence. These long term dependencies were less important with dinosaur names, since the names were quite short.
<img src="images/shakespeare.jpg" style="width:500;height:400px;">
<caption><center> Let's become poets! </center></caption>
We have implemented a Shakespeare poem generator with Keras. Run the following cell to load the required packages and models. This may take a few minutes.
```
from __future__ import print_function
from keras.callbacks import LambdaCallback
from keras.models import Model, load_model, Sequential
from keras.layers import Dense, Activation, Dropout, Input, Masking
from keras.layers import LSTM
from keras.utils.data_utils import get_file
from keras.preprocessing.sequence import pad_sequences
from shakespeare_utils import *
import sys
import io
```
To save you some time, we have already trained a model for ~1000 epochs on a collection of Shakespearian poems called [*"The Sonnets"*](shakespeare.txt).
Let's train the model for one more epoch. When it finishes training for an epoch---this will also take a few minutes---you can run `generate_output`, which will prompt asking you for an input (`<`40 characters). The poem will start with your sentence, and our RNN-Shakespeare will complete the rest of the poem for you! For example, try "Forsooth this maketh no sense " (don't enter the quotation marks). Depending on whether you include the space at the end, your results might also differ--try it both ways, and try other inputs as well.
```
print_callback = LambdaCallback(on_epoch_end=on_epoch_end)
model.fit(x, y, batch_size=128, epochs=1, callbacks=[print_callback])
# Run this cell to try with different inputs without having to re-train the model
generate_output()
```
The RNN-Shakespeare model is very similar to the one you have built for dinosaur names. The only major differences are:
- LSTMs instead of the basic RNN to capture longer-range dependencies
- The model is a deeper, stacked LSTM model (2 layer)
- Using Keras instead of python to simplify the code
If you want to learn more, you can also check out the Keras Team's text generation implementation on GitHub: https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py.
Congratulations on finishing this notebook!
**References**:
- This exercise took inspiration from Andrej Karpathy's implementation: https://gist.github.com/karpathy/d4dee566867f8291f086. To learn more about text generation, also check out Karpathy's [blog post](http://karpathy.github.io/2015/05/21/rnn-effectiveness/).
- For the Shakespearian poem generator, our implementation was based on the implementation of an LSTM text generator by the Keras team: https://github.com/keras-team/keras/blob/master/examples/lstm_text_generation.py
| github_jupyter |
```
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
import argparse
net = cv.dnn.readNetFromTensorflow("graph_opt.pb")
inWidth = 368
inHeight = 368
thr = 0.2
BODY_PARTS = { "Nose": 0, "Neck": 1, "RShoulder": 2, "RElbow": 3, "RWrist": 4,
"LShoulder": 5, "LElbow": 6, "LWrist": 7, "RHip": 8, "RKnee": 9,
"RAnkle": 10, "LHip": 11, "LKnee": 12, "LAnkle": 13, "REye": 14,
"LEye": 15, "REar": 16, "LEar": 17, "Background": 18 }
POSE_PAIRS = [ ["Neck", "RShoulder"], ["Neck", "LShoulder"], ["RShoulder", "RElbow"],
["RElbow", "RWrist"], ["LShoulder", "LElbow"], ["LElbow", "LWrist"],
["Neck", "RHip"], ["RHip", "RKnee"], ["RKnee", "RAnkle"], ["Neck", "LHip"],
["LHip", "LKnee"], ["LKnee", "LAnkle"], ["Neck", "Nose"], ["Nose", "REye"],
["REye", "REar"], ["Nose", "LEye"], ["LEye", "LEar"] ]
img = cv.imread("image.jpg")
plt.imshow(img)
plt.imshow(cv.cvtColor(img,cv.COLOR_BGR2RGB))
def pose_estiamtion(frame):
frameWidth = frame.shape[1]
frameHeight = frame.shape[0]
net.setInput(cv.dnn.blobFromImage(frame, 1.0, (inWidth, inHeight), (127.5, 127.5, 127.5), swapRB=True, crop=False))
out = net.forward()
out = out[:, :19, :, :] # MobileNet output [1, 57, -1, -1], we only need the first 19 elements
assert(len(BODY_PARTS) == out.shape[1])
points = []
for i in range(len(BODY_PARTS)):
# Slice heatmap of corresponging body's part.
heatMap = out[0, i, :, :]
# Originally, we try to find all the local maximums. To simplify a sample
# we just find a global one. However only a single pose at the same time
# could be detected this way.
_, conf, _, point = cv.minMaxLoc(heatMap)
x = (frameWidth * point[0]) / out.shape[3]
y = (frameHeight * point[1]) / out.shape[2]
# Add a point if it's confidence is higher than threshold.
points.append((int(x), int(y)) if conf > thr else None)
for pair in POSE_PAIRS:
partFrom = pair[0]
partTo = pair[1]
assert(partFrom in BODY_PARTS)
assert(partTo in BODY_PARTS)
idFrom = BODY_PARTS[partFrom]
idTo = BODY_PARTS[partTo]
if points[idFrom] and points[idTo]:
cv.line(frame, points[idFrom], points[idTo], (0, 255, 0), 3)
cv.ellipse(frame, points[idFrom], (3, 3), 0, 0, 360, (0, 0, 255), cv.FILLED)
cv.ellipse(frame, points[idTo], (3, 3), 0, 0, 360, (0, 0, 255), cv.FILLED)
t, _ = net.getPerfProfile()
freq = cv.getTickFrequency() / 1000
cv.putText(frame, '%.2fms' % (t / freq), (10, 20), cv.FONT_HERSHEY_SIMPLEX, 0.5, (0, 0, 0))
return frame
estimated_image = pose_estiamtion(img)
plt.imshow(cv.cvtColor(estimated_image,cv.COLOR_BGR2RGB))
cap = cv.VideoCapture(1)
cap.set(cv.CAP_PROP_FPS,10)
cap.set(3,800)
cap.set(4,800)
if not cap.isOpened():
cap = cv.VideoCapture(0)
if not cap.isOpened():
raise IOError("Cannot open the Webcame")
while cv.waitKey(1) < 0 :
hasFrame, frame = cap.read()
if not hasFrame:
cv.waitKey()
break
frameWidth = frame.shape[1]
frameHeight = frame.shape[0]
net.setInput(cv.dnn.blobFromImage(frame, 1.0, (inWidth, inHeight), (127.5, 127.5, 127.5), swapRB=True, crop=False))
out = net.forward()
out = out[:, :19, :, :] # MobileNet output [1, 57, -1, -1], we only need the first 19 elements
assert(len(BODY_PARTS) == out.shape[1])
points = []
for i in range(len(BODY_PARTS)):
# Slice heatmap of corresponging body's part.
heatMap = out[0, i, :, :]
# Originally, we try to find all the local maximums. To simplify a sample
# we just find a global one. However only a single pose at the same time
# could be detected this way.
_, conf, _, point = cv.minMaxLoc(heatMap)
x = (frameWidth * point[0]) / out.shape[3]
y = (frameHeight * point[1]) / out.shape[2]
# Add a point if it's confidence is higher than threshold.
points.append((int(x), int(y)) if conf > thr else None)
for pair in POSE_PAIRS:
partFrom = pair[0]
partTo = pair[1]
assert(partFrom in BODY_PARTS)
assert(partTo in BODY_PARTS)
idFrom = BODY_PARTS[partFrom]
idTo = BODY_PARTS[partTo]
if points[idFrom] and points[idTo]:
cv.line(frame, points[idFrom], points[idTo], (0, 255, 0), 3)
cv.ellipse(frame, points[idFrom], (3, 3), 0, 0, 360, (0, 0, 255), cv.FILLED)
cv.ellipse(frame, points[idTo], (3, 3), 0, 0, 360, (0, 0, 255), cv.FILLED)
t, _ = net.getPerfProfile()
freq = cv.getTickFrequency() / 1000
cv.putText(frame, '%.2fms' % (t / freq), (10, 20), cv.FONT_HERSHEY_SIMPLEX, 0.5, (0, 0, 0))
cv.imshow('Pose Estimtion Tutorial',frame)
```
| github_jupyter |
## Moodle Database: Educational Data Log Analysis
The Moodle LMS is a free and open-source learning management system written in PHP and distributed under the GNU General Public License. It is used for blended learning, distance education, flipped classroom and other e-learning projects in schools, universities, workplaces and other sectors. With customizable management features, it is used to create private websites with online courses for educators and trainers to achieve learning goals. Moodle allows for extending and tailoring learning environments using community-sourced plugins .
In this notebokk we are going to explore the 10 Academy Moodle logs stored in the database together with many other relevant tables.
# Table of content
1. Installing the required libraries
2. Importing the required libraries
3. Moodle database understanding
4. Data Extraction Transformation and Loading (ETL)
### Installing the necessary libraries
```
#!pip install ipython-sql
#!pip install sqlalchemy
#!pip install psycopg2
```
### Importing necessary libraries
```
import pandas as pd
import numpy as np
from sqlalchemy import create_engine
import psycopg2
import logging
from IPython.display import display
#allowing connection to the database
%load_ext sql
#ipython-sql
%sql postgresql://bessy:Streetdance53@localhost/moodle
#sqlalchemy
engine = create_engine('postgresql://bessy:Streetdance53@localhost/moodle')
```
### Moodle database Understanding.
Now, let's have a glance of how some of the tables look like.We will consider the following tables;
`mdl_logstore_standard_log`,
`mdl_context`,
`mdl_user`,
`mdl_course`,
`mdl_modules `,
`mdl_course_modules`,
`mdl_course_modules_completion`,
`mdl_grade_items`,
`mdl_grade_grades`,
`mdl_grade_categories`,
`mdl_grade_items_history`,
`mdl_grade_grades_history`,
`mdl_grade_categories_history`,
`mdl_forum`,
`mdl_forum_discussions`,
`mdl_forum_posts`.
`Table:mdl_logstore_standard_log`
```
%%sql
SELECT *FROM mdl_logstore_standard_log LIMIT 3;
```
`Table: mdl_context`
```
%%sql
SELECT * FROM mdl_context LIMIT 3;
```
`mdl_course`
```
%%sql
SELECT * FROM mdl_course LIMIT 3;
```
`mdl_user`
```
%%sql
SELECT * FROM mdl_user LIMIT 3;
```
`mdl_modules`
```
%%sql
SELECT * FROM mdl_modules LIMIT 3;
```
`mdl_course_modules`
```
%%sql
SELECT * FROM mdl_course_modules LIMIT 3;
```
`mdl_course_modules_completion`
```
%%sql
SELECT * FROM mdl_course_modules_completion LIMIT 3
```
`mdl_grade_grades`
```
%%sql
SELECT * FROM mdl_grade_grades LIMIT 3
```
### Number of tables in the database;
```
%%sql
SELECT COUNT(*) FROM information_schema.tables
```
### Number of records in the following tables;
```
mit = ['mdl_logstore_standard_log', 'mdl_context', 'mdl_user', 'mdl_course', 'mdl_modules' , 'mdl_course_modules', 'mdl_course_modules_completion',
'mdl_grade_items', 'mdl_grade_grades', 'mdl_grade_categories', 'mdl_grade_items_history', 'mdl_grade_grades_history',
'mdl_grade_categories_history', 'mdl_forum', 'mdl_forum_discussions', 'mdl_forum_posts']
# fetches and returns number of records of a given table in a moodle database
def table_count(table):
count = %sql SELECT COUNT(*) as {table}_count from {table}
return count
for table in mit:
display(table_count(table))
```
### Number of quiz submission by time
```
%%sql
select date_part('hour', timestamp with time zone 'epoch' + timefinish * interval '1 second') as hour, count(1)
from mdl_quiz_attempts qa
where qa.preview = 0 and qa.timefinish <> 0
group by date_part('hour', timestamp with time zone 'epoch' + timefinish * interval '1 second')
order by hour
%%sql
SELECT COUNT(id), EXTRACT(HOUR FROM to_timestamp(timecreated)) FROM mdl_logstore_standard_log WHERE action ='submitted' AND component='mod_quiz'
group by EXTRACT(HOUR FROM to_timestamp(timecreated));
```
## Monthly usage time of learners who have confirmed and are not deleted
```
%%sql
select extract(month from to_timestamp(mdl_stats_user_monthly.timeend)) as calendar_month,
count(distinct mdl_stats_user_monthly.userid) as total_users
from mdl_stats_user_monthly
inner join mdl_role_assignments on mdl_stats_user_monthly.userid = mdl_role_assignments.userid
inner join mdl_context on mdl_role_assignments.contextid = mdl_context.id
where mdl_stats_user_monthly.stattype = 'activity'
and mdl_stats_user_monthly.courseid <>1
group by extract(month from to_timestamp(mdl_stats_user_monthly.timeend))
order by extract(month from to_timestamp(mdl_stats_user_monthly.timeend))
%%sql
SELECT COUNT(lastaccess - firstaccess) AS usagetime, EXTRACT (MONTH FROM to_timestamp(firstaccess)) AS month
FROM mdl_user WHERE confirmed = 1 AND deleted = 0 GROUP BY EXTRACT (MONTH FROM to_timestamp(firstaccess))
```
## Count of log events per user
```
actions = ['loggedin', 'viewed', 'started', 'submitted', 'uploaded', 'updated', 'searched',
'answered', 'attempted', 'abandoned']
# fetch and return count of log events of an action per user
def event_count(action):
count = %sql SELECT userid, COUNT(action) AS {action}_count FROM mdl_logstore_standard_log WHERE action='{action}' GROUP BY userid limit 5
return count
for action in actions:
display(event_count(action))
```
### python class to pull
* Overall grade of learners
* Number of forum posts
```
class PullGrade():
def __init__(self):
pass
def open_db(self, **kwargs):
# extract args, if they are not provided assign a default value
user = kwargs.get('user', 'briodev')
password = kwargs.get('password', '14ConnectPsq')
db = kwargs.get('db', 'moodle')
# make a connection to PostgreSQL
# use exception to show error message if failed to connect
try:
params = dict(user=user,
password=password,
host="127.0.0.1",
port = "5432",
database = db)
proot = 'postgresql://{user}@{host}:5432/{database}'.format(**params)
logging.info('Connecting to the PostgreSQL database... using sqlalchemy engine')
engine = create_engine(proot)
except (Exception, psycopg2.Error) as error:
logging.error(r"Error while connecting to PostgreSQL {error}")
return engine
# fetch and return number of forum posts
def forum_posts(self):
count = %sql SELECT COUNT(*) from mdl_forum_posts
return count
# fetch and return overall grade of learners
def overall_grade(self):
overall = %sql SELECT userid, round(SUM(finalgrade)/count(*), 2) as overall_grade from mdl_grade_grades WHERE finalgrade is not null group by userid LIMIT 10
return overall
db = PullGrade()
db.open_db()
#Forum_posts
db.forum_posts()
#Overall grade.
db.overall_grade()
```
### Data Extraction Transformation and Loading (ETL)
```
#reading the mdl_logstore_standard_log
log_df = pd.read_sql("select * from mdl_logstore_standard_log", engine)
def top_x(df, percent):
total_len = df.shape[0]
top = int((total_len * percent)/100)
return df.iloc[:top,]
```
### Login count
```
log_df_logged_in = log_df[log_df.action == 'loggedin'][['userid', 'action']]
login_by_user = log_df_logged_in.groupby('userid').count().sort_values('action', ascending=False)
login_by_user.columns = ["login_count"]
top_x(login_by_user, 1)
```
### Activity count
```
activity_log = log_df[['userid', 'action']]
activity_log_by_user = activity_log.groupby('userid').count().sort_values('action', ascending=False)
activity_log_by_user.columns = ['activity_count']
top_x(activity_log_by_user, 1)
log_in_out = log_df[(log_df.action == "loggedin") | (log_df.action == "loggedout")]
user_id = log_df.userid.unique()
d_times = {}
for user in user_id:
log_user = log_df[log_df.userid == user].sort_values('timecreated')
d_time = 0
isLoggedIn = 0
loggedIn_timecreated = 0
for i in range(len(log_user)):
row = log_user.iloc[i,]
row_next = log_user.iloc[i+1,] if i+1 < len(log_user) else row
if(row.action == "loggedin"):
isLoggedIn = 1
loggedIn_timecreated = row.timecreated
if( (i+1 == len(log_user)) | ( (row_next.action == "loggedin") & (isLoggedIn == 1) ) ):
d_time += row.timecreated - loggedIn_timecreated
isLoggedIn = 0
d_times[user] = d_time
dedication_time_df = pd.DataFrame({'userid':list(d_times.keys()),
'dedication_time':list(d_times.values())})
dedication_time_df
top_x(dedication_time_df.sort_values('dedication_time', ascending=False), 35)
```
### References
* https://docs.moodle.org/39/en/Custom_SQL_queries_report
* https://docs.moodle.org/39/en/ad-hoc_contributed_reports
* https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.331.667&rep=rep1&type=pdf
* http://informatics.ue-varna.bg/conference19/Conf.proceedings_Informatics-50.years%20177-187.pdf
| github_jupyter |
# Format DataFrame
```
import pandas as pd
from sklearn.datasets import make_regression
data = make_regression(n_samples=600, n_features=50, noise=0.1, random_state=42)
train_df = pd.DataFrame(data[0], columns=["x_{}".format(_) for _ in range(data[0].shape[1])])
train_df["target"] = data[1]
print(train_df.shape)
train_df.head()
```
# Set Up Environment
```
from hyperparameter_hunter import Environment, CVExperiment
from sklearn.metrics import explained_variance_score
env = Environment(
train_dataset=train_df,
results_path="HyperparameterHunterAssets",
metrics=dict(evs=explained_variance_score),
cv_type="KFold",
cv_params=dict(n_splits=3, shuffle=True, random_state=1337),
runs=2,
)
```
Now that HyperparameterHunter has an active `Environment`, we can do two things:
# 1. Perform Experiments
*Note: If this is your first HyperparameterHunter example, the CatBoost classification example may be a better starting point.*
In this Experiment, we're also going to use `model_extra_params` to provide arguments to `CatBoostRegressor`'s `fit` method, just like we would if we weren't using HyperparameterHunter.
We'll be using the `verbose` argument to print evaluations of our `CatBoostRegressor` every 50 iterations, and we'll also be using the dataset sentinels offered by `Environment`. You can read more about the exciting thing you can do with the `Environment` sentinels in the documentation and in the example dedicated to them. For now, though, we'll be using them to provide each fold's `env.validation_input`, and `env.validation_target` to `CatBoostRegressor.fit` via its `eval_set` argument.
You could also easily add `CatBoostRegressor.fit`'s `early_stopping_rounds` argument to `model_extra_params["fit"]` to use early stopping, but doing so here with only `iterations=100` doesn't make much sense.
```
from catboost import CatBoostRegressor
experiment = CVExperiment(
model_initializer=CatBoostRegressor,
model_init_params=dict(
iterations=100,
learning_rate=0.05,
depth=5,
bootstrap_type="Bayesian",
save_snapshot=False,
allow_writing_files=False,
),
model_extra_params=dict(
fit=dict(
verbose=50,
eval_set=[(env.validation_input, env.validation_target)],
),
),
)
```
Notice above that CatBoost printed scores for our `eval_set` every 50 iterations just like we said in `model_extra_params["fit"]`; although, it made our results rather difficult to read, so we'll switch back to `verbose=False` during optimization.
# 2. Hyperparameter Optimization
Notice below that `optimizer` still recognizes the results of `experiment` as valid learning material even though their `verbose` values differ. This is because it knows that `verbose` has no effect on actual results.
```
from hyperparameter_hunter import DummyOptPro, Real, Integer, Categorical
optimizer = DummyOptPro(iterations=10, random_state=777)
optimizer.forge_experiment(
model_initializer=CatBoostRegressor,
model_init_params=dict(
iterations=100,
learning_rate=Real(0.001, 0.2),
depth=Integer(3, 7),
bootstrap_type=Categorical(["Bayesian", "Bernoulli"]),
save_snapshot=False,
allow_writing_files=False,
),
model_extra_params=dict(
fit=dict(
verbose=False,
eval_set=[(env.validation_input, env.validation_target)],
),
),
)
optimizer.go()
```
| github_jupyter |
# Durables vs Non Durables At Low And High Frequencies
```
!pip install numpy
!pip install matplotlib
!pip install pandas
!pip install pandas_datareader
!pip install datetime
!pip install seaborn
# Some initial setup
from matplotlib import pyplot as plt
import numpy as np
plt.style.use('seaborn-darkgrid')
import pandas as pd
import pandas_datareader.data as web
import datetime
import seaborn as sns
# Import Quarterly data from Fred using Data Reader
start = datetime.datetime(1947, 1, 1) #beginning of series
start1 = datetime.datetime(1956, 10, 1) #beginning of series
end = datetime.datetime(2018, 4, 1) #end of series
PCDG = web.DataReader('PCDG', 'fred', start, end) #loads your durable goods quarterly series data
PCND= web.DataReader('PCND', 'fred', start, end) #Loads your non durable goods quarterly series data
PCDG1 = web.DataReader('PCDG', 'fred', start1, end) #loads your durable goods quarterly series data, helps in having time series of identical length
PCND1= web.DataReader('PCND', 'fred', start1, end) #Loads your non durable goods quarterly series data, , helps in having time series of identical length
# Constructing PCDG and PCND growth series ()
z1=PCDG.pct_change(periods=40)# 10*4
z2=PCND.pct_change(periods=40)#10*4
z3=PCDG1.pct_change(periods=1)#
z4=PCND1.pct_change(periods=1)#
s1=z1*100 #(In percentage terms)
s2=z2*100 #(In percentage terms)
s3=z3*100 #(In percentage terms)
s4=z4*100 #(In percentage terms)
# Plotting the growth rates
plt.figure(figsize=((14,8))) # set the plot size
plt.title('Durables vs Non Durables Growth 10 year vs Quarterly')
plt.xlabel('Year')
plt.ylabel(' Growth (Percentage Terms)')
plt.plot(s1,label="PCDG 10 year growth")
plt.plot(s2,label="PCND 10 year growth")
plt.plot(s3,label="PCDG quarterly growth")
plt.plot(s4,label="PCND quarterly growth")
plt.legend()
plt.show()
# Drops the missing NAN observations
a1=s1.dropna()#Drops the missing values from s1 series
a2=s2.dropna()#Drops the missing values from s2 series
a3=s3.dropna()#Drops the missing values from s3 series
a4=s4.dropna()#Drops the missing values from s4 series
# concatate (merge) the two series
c1=pd.concat([a1, a2], axis=1)
c2=pd.concat([a3, a4], axis=1)
#Pairwise Plotting for the 10 year growth series
sns.pairplot(c1)
plt.suptitle('10 Year Growth Rates')
plt.show()
#Pairwise Plotting for the quarterly growth series
sns.pairplot(c2)
plt.suptitle('1 Quarter Growth Rates')
plt.show()
```
For each frequency [quarterly|10-year] each moment of time would correspond to a single point (x=nondurables growth, y=durables growth). Such a plot shows that at the 10 year frequency, there is a very strong relationship between the two growth rates, and at the 1 quarter frequency, much much less.
| github_jupyter |
[source](../../api/alibi_detect.od.isolationforest.rst)
# Isolation Forest
## Overview
[Isolation forests](https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icdm08b.pdf) (IF) are tree based models specifically used for outlier detection. The IF isolates observations by randomly selecting a feature and then randomly selecting a split value between the maximum and minimum values of the selected feature. The number of splittings required to isolate a sample is equivalent to the path length from the root node to the terminating node. This path length, averaged over a forest of random trees, is a measure of normality and is used to define an anomaly score. Outliers can typically be isolated quicker, leading to shorter paths. The algorithm is suitable for low to medium dimensional tabular data.
## Usage
### Initialize
Parameters:
* `threshold`: threshold value for the outlier score above which the instance is flagged as an outlier.
* `n_estimators`: number of base estimators in the ensemble. Defaults to 100.
* `max_samples`: number of samples to draw from the training data to train each base estimator. If *int*, draw `max_samples` samples. If *float*, draw `max_samples` *times number of features* samples. If *'auto'*, `max_samples` = min(256, number of samples).
* `max_features`: number of features to draw from the training data to train each base estimator. If *int*, draw `max_features` features. If float, draw `max_features` *times number of features* features.
* `bootstrap`: whether to fit individual trees on random subsets of the training data, sampled with replacement.
* `n_jobs`: number of jobs to run in parallel for `fit` and `predict`.
* `data_type`: can specify data type added to metadata. E.g. *'tabular'* or *'image'*.
Initialized outlier detector example:
```python
from alibi_detect.od import IForest
od = IForest(
threshold=0.,
n_estimators=100
)
```
### Fit
We then need to train the outlier detector. The following parameters can be specified:
* `X`: training batch as a numpy array.
* `sample_weight`: array with shape *(batch size,)* used to assign different weights to each instance during training. Defaults to *None*.
```python
od.fit(
X_train
)
```
It is often hard to find a good threshold value. If we have a batch of normal and outlier data and we know approximately the percentage of normal data in the batch, we can infer a suitable threshold:
```python
od.infer_threshold(
X,
threshold_perc=95
)
```
### Detect
We detect outliers by simply calling `predict` on a batch of instances `X` to compute the instance level outlier scores. We can also return the instance level outlier score by setting `return_instance_score` to True.
The prediction takes the form of a dictionary with `meta` and `data` keys. `meta` contains the detector's metadata while `data` is also a dictionary which contains the actual predictions stored in the following keys:
* `is_outlier`: boolean whether instances are above the threshold and therefore outlier instances. The array is of shape *(batch size,)*.
* `instance_score`: contains instance level scores if `return_instance_score` equals True.
```python
preds = od.predict(
X,
return_instance_score=True
)
```
## Examples
### Tabular
[Outlier detection on KDD Cup 99](../../examples/od_if_kddcup.nblink)
| github_jupyter |
```
from google.colab import drive
drive.mount('/content/drive')
import warnings
warnings.filterwarnings('ignore')
# !pip install tensorflow_text
!pip install transformers emoji
# !pip install ktrain
from transformers import AutoTokenizer
import pandas as pd
dataset = pd.read_excel("/content/drive/MyDrive/English Category Transformer Model/en_category_model_data.xlsx")
dataset = dataset.sample(frac=1, axis=1).sample(frac=1).reset_index(drop=True)
dataset = dataset[['p_message','Category']]
dataset.head()
dataset.groupby('Category').size()
def to_int_sentiment(label):
if label == "business":
return 0
elif label == "education":
return 1
elif label == 'entertainment':
return 2
elif label == 'fashion':
return 3
elif label == 'food':
return 4
elif label == 'health':
return 5
elif label == 'politics':
return 6
elif label == 'sports':
return 7
elif label == 'technology':
return 8
elif label == 'telecom':
return 9
elif label == 'tourism':
return 10
elif label == 'transport':
return 11
elif label == 'weather':
return 12
dataset['Category'] = dataset.Category.apply(to_int_sentiment)
dataset = dataset.dropna()
dataset['Category'] = dataset.Category.apply(int)
dataset.head()
from preprocessing import CleaningText
en_text_clean = CleaningText()
dataset['p_message'] = dataset['p_message'].apply(str)
dataset['p_message'] = dataset['p_message'].apply(en_text_clean.text_preprocessing)
dataset.head()
dataset.groupby('Category').size()
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
import torch
from transformers import TrainingArguments, Trainer
from transformers import BertTokenizer, BertForSequenceClassification
from transformers import EarlyStoppingCallback
# Read data
# dataset = pd.read_excel("/content/drive/MyDrive/ar_general_sentiment_data.xlsx")
# dataset = dataset[['text','Sentiment']]
# Define pretrained tokenizer and model
model_name = "prajjwal1/bert-small"
tokenizer = BertTokenizer.from_pretrained(model_name)
model = BertForSequenceClassification.from_pretrained(model_name, num_labels=13)
# ----- 1. Preprocess data -----#
# Preprocess data
X = list(dataset["p_message"])
y = list(dataset["Category"])
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
X_train_tokenized = tokenizer(X_train, padding=True, truncation=True, max_length=512)
X_val_tokenized = tokenizer(X_val, padding=True, truncation=True, max_length=512)
# Create torch dataset
class Dataset(torch.utils.data.Dataset):
def __init__(self, encodings, labels=None):
self.encodings = encodings
self.labels = labels
def __getitem__(self, idx):
item = {key: torch.tensor(val[idx]) for key, val in self.encodings.items()}
if self.labels:
item["labels"] = torch.tensor(self.labels[idx])
return item
def __len__(self):
return len(self.encodings["input_ids"])
train_dataset = Dataset(X_train_tokenized, y_train)
val_dataset = Dataset(X_val_tokenized, y_val)
# ----- 2. Fine-tune pretrained model -----#
# Define Trainer parameters
def compute_metrics(p):
pred, labels = p
pred = np.argmax(pred, axis=1)
accuracy = accuracy_score(y_true=labels, y_pred=pred)
recall = recall_score(y_true=labels, y_pred=pred,average='micro')
precision = precision_score(y_true=labels, y_pred=pred,average='micro')
f1 = f1_score(y_true=labels, y_pred=pred,average='micro')
return {"accuracy": accuracy, "precision": precision, "recall": recall, "f1": f1}
# Define Trainer
args = TrainingArguments(
output_dir="output",
evaluation_strategy="steps",
eval_steps=500,
per_device_train_batch_size=8,
per_device_eval_batch_size=8,
num_train_epochs=5,
seed=0,
load_best_model_at_end=True,
)
trainer = Trainer(
model=model,
args=args,
train_dataset=train_dataset,
eval_dataset=val_dataset,
compute_metrics=compute_metrics,
# callbacks=[EarlyStoppingCallback(early_stopping_patience=3)],
)
# Train pre-trained model
trainer.train()
model_path = "/content/drive/MyDrive/English Category Transformer Model/en_category_model"
trainer.save_model(model_path)
X_test_tokenized = tokenizer(X_val, padding=True, truncation=True, max_length=512)
# Create torch dataset
test_dataset = Dataset(X_test_tokenized)
# Load trained model
# model_path = "sentiment_model"
model = BertForSequenceClassification.from_pretrained(model_path, num_labels=13)
# Define test trainer
test_trainer = Trainer(model)
# Make prediction
raw_pred, _, _ = test_trainer.predict(test_dataset)
# Preprocess raw predictions
y_pred = np.argmax(raw_pred, axis=1)
y_pred
from sklearn.metrics import classification_report, confusion_matrix
class_names = ["0","1","2","3","4","5","6","7","8","9","10","11","12"]
print(classification_report(y_val, y_pred, target_names=class_names))
print(confusion_matrix(y_val, y_pred))
df = pd.DataFrame(X_val,columns =['p_message'])
df.head()
df['prediction'] = y_pred
df.head()
df.groupby('prediction').size()
from transformers import BertTokenizer, BertForSequenceClassification
from transformers import EarlyStoppingCallback
from transformers import AutoTokenizer
from preprocessing import CleaningText
model_name = "prajjwal1/bert-small"
model_path = "en_category"
```
| github_jupyter |
# Self-Driving Car Engineer Nanodegree
## Project: **Finding Lane Lines on the Road**
***
In this project, you will use the tools you learned about in the lesson to identify lane lines on the road. You can develop your pipeline on a series of individual images, and later apply the result to a video stream (really just a series of images). Check out the video clip "raw-lines-example.mp4" (also contained in this repository) to see what the output should look like after using the helper functions below.
Once you have a result that looks roughly like "raw-lines-example.mp4", you'll need to get creative and try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4". Ultimately, you would like to draw just one line for the left side of the lane, and one for the right.
In addition to implementing code, there is a brief writeup to complete. The writeup should be completed in a separate file, which can be either a markdown file or a pdf document. There is a [write up template](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) that can be used to guide the writing process. Completing both the code in the Ipython notebook and the writeup template will cover all of the [rubric points](https://review.udacity.com/#!/rubrics/322/view) for this project.
---
Let's have a look at our first image called 'test_images/solidWhiteRight.jpg'. Run the 2 cells below (hit Shift-Enter or the "play" button above) to display the image.
**Note: If, at any point, you encounter frozen display windows or other confounding issues, you can always start again with a clean slate by going to the "Kernel" menu above and selecting "Restart & Clear Output".**
---
**The tools you have are color selection, region of interest selection, grayscaling, Gaussian smoothing, Canny Edge Detection and Hough Tranform line detection. You are also free to explore and try other techniques that were not presented in the lesson. Your goal is piece together a pipeline to detect the line segments in the image, then average/extrapolate them and draw them onto the image for display (as below). Once you have a working pipeline, try it out on the video stream below.**
---
<figure>
<img src="examples/line-segments-example.jpg" width="380" alt="Combined Image" />
<figcaption>
<p></p>
<p style="text-align: center;"> Your output should look something like this (above) after detecting line segments using the helper functions below </p>
</figcaption>
</figure>
<p></p>
<figure>
<img src="examples/laneLines_thirdPass.jpg" width="380" alt="Combined Image" />
<figcaption>
<p></p>
<p style="text-align: center;"> Your goal is to connect/average/extrapolate line segments to get output like this</p>
</figcaption>
</figure>
**Run the cell below to import some packages. If you get an `import error` for a package you've already installed, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**
## Import Packages
```
#importing some useful packages
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import cv2
%matplotlib inline
```
## Read in an Image
```
#reading in an image
image = mpimg.imread('test_images/solidWhiteRight.jpg')
#printing out some stats and plotting
print('This image is:', type(image), 'with dimensions:', image.shape)
plt.imshow(image) # if you wanted to show a single color channel image called 'gray', for example, call as plt.imshow(gray, cmap='gray')
```
## Ideas for Lane Detection Pipeline
**Some OpenCV functions (beyond those introduced in the lesson) that might be useful for this project are:**
`cv2.inRange()` for color selection
`cv2.fillPoly()` for regions selection
`cv2.line()` to draw lines on an image given endpoints
`cv2.addWeighted()` to coadd / overlay two images
`cv2.cvtColor()` to grayscale or change color
`cv2.imwrite()` to output images to file
`cv2.bitwise_and()` to apply a mask to an image
**Check out the OpenCV documentation to learn about these and discover even more awesome functionality!**
## Helper Functions
Below are some helper functions to help get you started. They should look familiar from the lesson!
```
import math
def grayscale(img):
"""Applies the Grayscale transform
This will return an image with only one color channel
but NOTE: to see the returned image as grayscale
(assuming your grayscaled image is called 'gray')
you should call plt.imshow(gray, cmap='gray')"""
return cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
# Or use BGR2GRAY if you read an image with cv2.imread()
# return cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
def canny(img, low_threshold, high_threshold):
"""Applies the Canny transform"""
return cv2.Canny(img, low_threshold, high_threshold)
def gaussian_blur(img, kernel_size):
"""Applies a Gaussian Noise kernel"""
return cv2.GaussianBlur(img, (kernel_size, kernel_size), 0)
def region_of_interest(img, vertices):
"""
Applies an image mask.
Only keeps the region of the image defined by the polygon
formed from `vertices`. The rest of the image is set to black.
`vertices` should be a numpy array of integer points.
"""
#defining a blank mask to start with
mask = np.zeros_like(img)
#defining a 3 channel or 1 channel color to fill the mask with depending on the input image
if len(img.shape) > 2:
channel_count = img.shape[2] # i.e. 3 or 4 depending on your image
ignore_mask_color = (255,) * channel_count
else:
ignore_mask_color = 255
#filling pixels inside the polygon defined by "vertices" with the fill color
cv2.fillPoly(mask, vertices, ignore_mask_color)
#returning the image only where mask pixels are nonzero
masked_image = cv2.bitwise_and(img, mask)
return masked_image
# def draw_lines(img, lines, color=[255, 0, 0], thickness=10):
# """
# NOTE: this is the function you might want to use as a starting point once you want to
# average/extrapolate the line segments you detect to map out the full
# extent of the lane (going from the result shown in raw-lines-example.mp4
# to that shown in P1_example.mp4).
# Think about things like separating line segments by their
# slope ((y2-y1)/(x2-x1)) to decide which segments are part of the left
# line vs. the right line. Then, you can average the position of each of
# the lines and extrapolate to the top and bottom of the lane.
# This function draws `lines` with `color` and `thickness`.
# Lines are drawn on the image inplace (mutates the image).
# If you want to make the lines semi-transparent, think about combining
# this function with the weighted_img() function below
# """
# for line in lines:
# for x1,y1,x2,y2 in line:
# cv2.line(img, (x1, y1), (x2, y2), color, thickness)
def hough_lines(img, rho, theta, threshold, min_line_len, max_line_gap):
"""
`img` should be the output of a Canny transform.
Returns an image with hough lines drawn.
"""
lines = cv2.HoughLinesP(img, rho, theta, threshold, np.array([]), minLineLength=min_line_len, maxLineGap=max_line_gap)
line_img = np.zeros((img.shape[0], img.shape[1], 3), dtype=np.uint8)
draw_lines(line_img, lines)
return line_img
# Python 3 has support for cool math symbols.
def weighted_img(img, initial_img, α=0.8, β=1., γ=0.):
"""
`img` is the output of the hough_lines(), An image with lines drawn on it.
Should be a blank image (all black) with lines drawn on it.
`initial_img` should be the image before any processing.
The result image is computed as follows:
initial_img * α + img * β + γ
NOTE: initial_img and img must be the same shape!
"""
return cv2.addWeighted(initial_img, α, img, β, γ)
```
New draw_lines function to extrapolate the line<br/>
Here fraction of shape of image i.e **fraction*img.shape[0]** is taken to make it work with optoional problem as its image has different dimensions.
```
def draw_lines(img, lines, color=[255, 0, 0], thickness=10):
left_slope = 0
right_slope = 0
x_left = 0
y_left = 0
x_right = 0
y_right = 0
count_left = 0 # count of left linesegments for average calculation
count_right = 0 # count of right linesegments for average calculation
for line in lines:
for x1,y1,x2,y2 in line:
slope = (y2-y1)/(x2-x1)
# slope boundary is taken almost tan(30) as from camera point of view it has slope arount the same
if slope>0.5: #Left lane
# Adding all values of slope and average positions of a line
left_slope += slope
x_left += (x1+x2)/2
y_left += (y1+y2)/2
count_left += 1
elif slope<-0.5: # right lane
# Adding all values of slope and average positions of a line
right_slope += slope
x_right += (x1+x2)/2
y_right += (y1+y2)/2
count_right += 1
# Left lane - averaging all slopes, x co-ordinates and y co-ordinates
if count_left>0: # if left lane has been detected
avg_left_slope = left_slope/count_left
avg_left_x = x_left/count_left
avg_left_y = y_left/count_left
# Calculate bottom x and top x assuming fixed positions for corresponding y
# It has been calculated based on slope formula y = mx+c then x = (y-c)/m
bottom_x_left = int(((int(img.shape[0])-avg_left_y)/avg_left_slope) + avg_left_x)
top_x_left = int(((int(0.60*img.shape[0])-avg_left_y)/avg_left_slope)+ avg_left_x)
else: # If Left lane is not detected - best guess positions of bottom x and top x
bottom_x_left = int(0.21*img.shape[1])
top_x_left = int(0.43*img.shape[1])
# Draw a line
cv2.line(img, (top_x_left, int(0.60*img.shape[0])), (bottom_x_left, int(img.shape[0])), color, thickness)
#Right lane - Average across all slope and intercepts
if count_right>0: # If right lane is detected
avg_right_slope = right_slope/count_right
avg_right_x = x_right/count_right
avg_right_y = y_right/count_right
# Calculate bottom x and top x assuming fixed positions for corresponding y
# It has been calculated based on slope formula y = mx+c then x = (y-c)/m
bottom_x_right = int(((int(img.shape[0])-avg_right_y)/avg_right_slope) + avg_right_x)
top_x_right = int(((int(0.60*img.shape[0])-avg_right_y)/avg_right_slope)+ avg_right_x)
else: # If right lane is not detected - best guess positions of bottom x and top x
bottom_x_right = int(0.89*img.shape[1])
top_x_right = int(0.53*img.shape[1])
# Draw a line
cv2.line(img, (top_x_right, int(0.60*img.shape[0])), (bottom_x_right, int(img.shape[0])), color, thickness)
```
## Test Images
Build your pipeline to work on the images in the directory "test_images"
**You should make sure your pipeline works well on these images before you try the videos.**
```
import os
os.listdir("test_images/")
image_file = ['test_images/whiteCarLaneSwitch.jpg','test_images/solidWhiteCurve.jpg', 'test_images/solidWhiteRight.jpg', 'test_images/solidYellowCurve.jpg', 'test_images/solidYellowCurve2.jpg', 'test_images/solidYellowLeft.jpg']
```
## Build a Lane Finding Pipeline
Build the pipeline and run your solution on all test_images. Make copies into the `test_images_output` directory, and you can use the images in your writeup report.
Try tuning the various parameters, especially the low and high Canny thresholds as well as the Hough lines parameters.
```
# TODO: Build your pipeline that will draw lane lines on the test_images
# then save them to the test_images_output directory.
def lane_finding_pipeline(img, vertices):
# image = mpimg.imread(img)
gray = grayscale(img)
kernel_size = 5
blur_gray = gaussian_blur(gray, kernel_size)
low_threshold = 50
high_threshold = 150
edges = canny(blur_gray, low_threshold, high_threshold)
masked_edges = region_of_interest(edges, vertices)
rho = 1 # distance resolution in pixels of the Hough grid
theta = np.pi/180 # angular resolution in radians of the Hough grid
threshold = 10 # minimum number of votes (intersections in Hough grid cell)
min_line_len = 60 #minimum number of pixels making up a line
max_line_gap = 30 # maximum gap in pixels between connectable line segments
final = hough_lines(masked_edges, rho, theta, threshold, min_line_len, max_line_gap)
# color_edges = np.dstack((edges, edges, edges))
final_image = weighted_img(final, img)
return final_image
img = mpimg.imread(image_file[0])
vertices = np.array([[(150,img.shape[0]),(450, 323), (500, 323), (img.shape[1],img.shape[0])]], dtype=np.int32)
cv2.imwrite('test_images_output/whiteCarLaneSwitch.png', cv2.cvtColor(lane_finding_pipeline(img, vertices), cv2.COLOR_BGR2RGB))
plt.imshow(lane_finding_pipeline(img, vertices))
img = mpimg.imread(image_file[1])
vertices = np.array([[(150,img.shape[0]),(450, 323), (500, 323), (img.shape[1],img.shape[0])]], dtype=np.int32)
cv2.imwrite('test_images_output/solidWhiteCurve.png', cv2.cvtColor(lane_finding_pipeline(img, vertices), cv2.COLOR_BGR2RGB))
plt.imshow(lane_finding_pipeline(img, vertices))
img = mpimg.imread(image_file[2])
vertices = np.array([[(150,img.shape[0]),(450, 323), (500, 323), (img.shape[1],img.shape[0])]], dtype=np.int32)
cv2.imwrite('test_images_output/solidWhiteRight.png', cv2.cvtColor(lane_finding_pipeline(img, vertices), cv2.COLOR_BGR2RGB))
plt.imshow(lane_finding_pipeline(img, vertices))
img = mpimg.imread(image_file[3])
vertices = np.array([[(150,img.shape[0]),(450, 323), (500, 323), (img.shape[1],img.shape[0])]], dtype=np.int32)
cv2.imwrite('test_images_output/solidYellowCurve.png', cv2.cvtColor(lane_finding_pipeline(img, vertices), cv2.COLOR_BGR2RGB))
plt.imshow(lane_finding_pipeline(img, vertices))
img = mpimg.imread(image_file[4])
vertices = np.array([[(150,img.shape[0]),(450, 323), (500, 323), (img.shape[1],img.shape[0])]], dtype=np.int32)
cv2.imwrite('test_images_output/solidYellowCurve2.png', cv2.cvtColor(lane_finding_pipeline(img, vertices), cv2.COLOR_BGR2RGB))
plt.imshow(lane_finding_pipeline(img, vertices))
img = mpimg.imread(image_file[5])
vertices = np.array([[(150,img.shape[0]),(450, 305), (500, 305), (img.shape[1],img.shape[0])]], dtype=np.int32)
cv2.imwrite('test_images_output/solidYellowLeft.png', cv2.cvtColor(lane_finding_pipeline(img, vertices), cv2.COLOR_BGR2RGB))
plt.imshow(lane_finding_pipeline(img, vertices))
```
## Test on Videos
You know what's cooler than drawing lanes over images? Drawing lanes over video!
We can test our solution on two provided videos:
`solidWhiteRight.mp4`
`solidYellowLeft.mp4`
**Note: if you get an import error when you run the next cell, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**
**If you get an error that looks like this:**
```
NeedDownloadError: Need ffmpeg exe.
You can download it by calling:
imageio.plugins.ffmpeg.download()
```
**Follow the instructions in the error message and check out [this forum post](https://discussions.udacity.com/t/project-error-of-test-on-videos/274082) for more troubleshooting tips across operating systems.**
```
# Import everything needed to edit/save/watch video clips
from moviepy.editor import VideoFileClip
from IPython.display import HTML
def process_image(image):
# NOTE: The output you return should be a color image (3 channel) for processing video below
# TODO: put your pipeline here,
# you should return the final output (image where lines are drawn on lanes)
gray = grayscale(image)
kernel_size = 5
blur_gray = gaussian_blur(gray, kernel_size)
low_threshold = 50
high_threshold = 150
edges = canny(blur_gray, low_threshold, high_threshold)
vertices = np.array([[(150,image.shape[0]),(445, 320), (500, 320), (image.shape[1],image.shape[0])]], dtype=np.int32)
masked_edges = region_of_interest(edges, vertices)
rho = 1 # distance resolution in pixels of the Hough grid
theta = np.pi/180 # angular resolution in radians of the Hough grid
threshold = 10 # minimum number of votes (intersections in Hough grid cell)
min_line_len = 60 #minimum number of pixels making up a line
max_line_gap = 30 # maximum gap in pixels between connectable line segments
final = hough_lines(masked_edges, rho, theta, threshold, min_line_len, max_line_gap)
# color_edges = np.dstack((edges, edges, edges))
result = weighted_img(final, image)
# plt.imshow(result)
return result
```
Let's try the one with the solid white lane on the right first ...
```
white_output = 'test_videos_output/solidWhiteRight.mp4'
## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video
## To do so add .subclip(start_second,end_second) to the end of the line below
## Where start_second and end_second are integer values representing the start and end of the subclip
## You may also uncomment the following line for a subclip of the first 5 seconds
##clip1 = VideoFileClip("test_videos/solidWhiteRight.mp4").subclip(0,5)
clip1 = VideoFileClip("test_videos/solidWhiteRight.mp4")
white_clip = clip1.fl_image(process_image) #NOTE: this function expects color images!!
%time white_clip.write_videofile(white_output, audio=False)
```
Play the video inline, or if you prefer find the video in your filesystem (should be in the same directory) and play it in your video player of choice.
```
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(white_output))
```
## Improve the draw_lines() function
**At this point, if you were successful with making the pipeline and tuning parameters, you probably have the Hough line segments drawn onto the road, but what about identifying the full extent of the lane and marking it clearly as in the example video (P1_example.mp4)? Think about defining a line to run the full length of the visible lane based on the line segments you identified with the Hough Transform. As mentioned previously, try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4".**
**Go back and modify your draw_lines function accordingly and try re-running your pipeline. The new output should draw a single, solid line over the left lane line and a single, solid line over the right lane line. The lines should start from the bottom of the image and extend out to the top of the region of interest.**
Now for the one with the solid yellow lane on the left. This one's more tricky!
```
yellow_output = 'test_videos_output/solidYellowLeft.mp4'
## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video
## To do so add .subclip(start_second,end_second) to the end of the line below
## Where start_second and end_second are integer values representing the start and end of the subclip
## You may also uncomment the following line for a subclip of the first 5 seconds
##clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4').subclip(0,5)
clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4')
yellow_clip = clip2.fl_image(process_image)
%time yellow_clip.write_videofile(yellow_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(yellow_output))
```
## Writeup and Submission
If you're satisfied with your video outputs, it's time to make the report writeup in a pdf or markdown file. Once you have this Ipython notebook ready along with the writeup, it's time to submit for review! Here is a [link](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) to the writeup template file.
## Optional Challenge
Try your lane finding pipeline on the video below. Does it still work? Can you figure out a way to make it more robust? If you're up for the challenge, modify your pipeline so it works with this video and submit it along with the rest of your project!
```
def process_image_1(image):
# NOTE: The output you return should be a color image (3 channel) for processing video below
# TODO: put your pipeline here,
# you should return the final output (image where lines are drawn on lanes)
gray = grayscale(image)
kernel_size = 5
blur_gray = gaussian_blur(gray, kernel_size)
low_threshold = 50
high_threshold = 150
edges = canny(blur_gray, low_threshold, high_threshold)
# vertices = np.array([[(220,690),(550, 450), (740, 450), (1150,690), (1000, 650),(750, 500),(600, 500),(400, 650),(700, 550)]], dtype=np.int32)
vertices = np.array([[(220,690),(550, 450), (740, 450), (1150,690)]], dtype=np.int32)
masked_edges = region_of_interest(edges, vertices)
rho = 1 # distance resolution in pixels of the Hough grid
theta = np.pi/180 # angular resolution in radians of the Hough grid
threshold = 10 # minimum number of votes (intersections in Hough grid cell)
min_line_len = 20 #minimum number of pixels making up a line
max_line_gap = 7 # maximum gap in pixels between connectable line segments
final = hough_lines(masked_edges, rho, theta, threshold, min_line_len, max_line_gap)
# color_edges = np.dstack((edges, edges, edges))
result = weighted_img(final, image)
# plt.imshow(image)
return result
challenge_output = 'test_videos_output/challenge.mp4'
## To speed up the testing process you may want to try your pipeline on a shorter subclip of the video
## To do so add .subclip(start_second,end_second) to the end of the line below
## Where start_second and end_second are integer values representing the start and end of the subclip
## You may also uncomment the following line for a subclip of the first 5 seconds
##clip3 = VideoFileClip('test_videos/challenge.mp4').subclip(0,5)
clip3 = VideoFileClip('test_videos/challenge.mp4')
challenge_clip = clip3.fl_image(process_image_1)
%time challenge_clip.write_videofile(challenge_output, audio=False)
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(challenge_output))
```
| github_jupyter |
# Classification models using python and scikit-learn
There are many users of online trading platforms and these companies would like to run analytics on and predict churn based on user activity on the platform. Keeping customers happy so they do not move their investments elsewhere is key to maintaining profitability.
In this notebook, we'll use scikit-learn to predict classes. scikit-learn provides implementations of many classification algorithms. In here, we have chosen the random forest classification algorithm to walk through all the different steps.
<a id="top"></a>
## Table of Contents
1. [Load libraries](#load_libraries)
2. [Data exploration](#explore_data)
3. [Prepare data for building classification model](#prepare_data)
4. [Split data into train and test sets](#split_data)
5. [Helper methods for graph generation](#helper_methods)
6. [Prepare Random Forest classification model](#prepare_model)
7. [Train Random Forest classification model](#train_model)
8. [Test Random Forest classification model](#test_model)
9. [Evaluate Random Forest classification model](#evaluate_model)
10.[Build K-Nearest classification model](#model_knn)
11. [Comparative study of both classification algorithms](#compare_classification)
### Quick set of instructions to work through the notebook
If you are new to Notebooks, here's a quick overview of how to work in this environment.
1. The notebook has 2 types of cells - markdown (text) such as this and code such as the one below.
2. Each cell with code can be executed independently or together (see options under the Cell menu). When working in this notebook, we will be running one cell at a time.
3. To run the cell, position cursor in the code cell and click the Run (arrow) icon. The cell is running when you see the * next to it. Some cells have printable output.
4. Work through this notebook by reading the instructions and executing code cell by cell. Some cells will require modifications before you run them.
<a id="load_libraries"></a>
## 1. Load libraries
[Top](#top)
Install python modules
NOTE! Some pip installs require a kernel restart.
The shell command pip install is used to install Python modules. Some installs require a kernel restart to complete. To avoid confusing errors, run the following cell once and then use the Kernel menu to restart the kernel before proceeding.
```
!pip install pandas==0.24.2
!pip install --user pandas_ml==0.6.1
#downgrade matplotlib to bypass issue with confusion matrix being chopped out
!pip install matplotlib==3.1.0
!pip install --user scikit-learn==0.21.3
!pip install -q scikit-plot
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer, make_column_transformer
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
import pandas as pd, numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.colors as mcolors
import matplotlib.patches as mpatches
import scikitplot as skplt
```
<a id="explore_data"></a>
## 2. Data exploration
[Top](#top)
In this tutorial, we use a data set that contains information about customers of an online trading platform to classify whether a given customer’s probability of churn will be high, medium, or low. This provides a good example to learn how a classification model is built from start to end.
```
df_churn_pd = pd.read_csv("https://raw.githubusercontent.com/IBM/ml-learning-path-assets/master/data/mergedcustomers_missing_values_GENDER.csv")
df_churn_pd.head()
```
We use numpy and matplotlib to get some statistics and visualize data.
print("The dataset contains columns of the following data types : \n" +str(df_churn_pd.dtypes))
Notice below that Gender has three missing values. This will be handled in one of the preprocessing steps that is to follow.
```
print("The dataset contains following number of records for each of the columns : \n" +str(df_churn_pd.count()))
```
If we are not satisfied with the representational data, now is the time to get more data to be used for training and testing.
```
print( "Each category within the churnrisk column has the following count : ")
print(df_churn_pd.groupby(['CHURNRISK']).size())
#bar chart to show split of data
index = ['High','Medium','Low']
churn_plot = df_churn_pd['CHURNRISK'].value_counts(sort=True, ascending=False).plot(kind='bar',
figsize=(4,4),title="Total number for occurences of churn risk "
+ str(df_churn_pd['CHURNRISK'].count()), color=['#BB6B5A','#8CCB9B','#E5E88B'])
churn_plot.set_xlabel("Churn Risk")
churn_plot.set_ylabel("Frequency")
```
<a id="prepare_data"></a>
## 3. Data preparation
[Top](#top)
Data preparation is a very important step in machine learning model building. This is because the model can perform well only when the data it is trained on is good and well prepared. Hence, this step consumes the bulk of a data scientist's time spent building models.
During this process, we identify categorical columns in the dataset. Categories need to be indexed, which means the string labels are converted to label indices. These label indices are encoded using One-hot encoding to a binary vector with at most a single value indicating the presence of a specific feature value from among the set of all feature values. This encoding allows algorithms which expect continuous features to use categorical features.
```
#remove columns that are not required
df_churn_pd = df_churn_pd.drop(['ID'], axis=1)
df_churn_pd.head()
```
### [Preprocessing Data](https://scikit-learn.org/stable/modules/preprocessing.html)
Scikit-learn provides a method to fill empty values with something that would be applicable in its context. We used the <i><b> SimpleImputer <b></i> class that is provided by Sklearn and filled the missing values with the most frequent value in the column.
### [One Hot Encoder](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html)
```
# Defining the categorical columns
categoricalColumns = ['GENDER', 'STATUS', 'HOMEOWNER']
print("Categorical columns : " )
print(categoricalColumns)
impute_categorical = SimpleImputer(strategy="most_frequent")
onehot_categorical = OneHotEncoder(handle_unknown='ignore')
categorical_transformer = Pipeline(steps=[('impute',impute_categorical),('onehot',onehot_categorical)])
```
The numerical columns from the data set are identified, and StandardScaler is applied to each of the columns. This way, each value is subtracted with the mean of its column and divided by its standard deviation.<br>
### [Standard Scaler](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html)
```
# Defining the numerical columns
numericalColumns = df_churn_pd.select_dtypes(include=[np.float,np.int]).columns
print("Numerical columns : " )
print(numericalColumns)
scaler_numerical = StandardScaler()
numerical_transformer = Pipeline(steps=[('scale',scaler_numerical)])
```
The preprocessing techniques that are applied must be customized for each of the columns. Sklearn provides a library called the [ColumnTransformer](https://scikit-learn.org/stable/modules/generated/sklearn.compose.ColumnTransformer.html?highlight=columntransformer#sklearn.compose.ColumnTransformer), which allows a sequence of these techniques to be applied to selective columns using a pipeline.
Only the specified columns in transformers are transformed and combined in the output, and the non-specified columns are dropped. By specifying remainder='passthrough', all remaining columns that were not specified in transformers will be automatically passed through
```
preprocessorForCategoricalColumns = ColumnTransformer(transformers=[('cat', categorical_transformer,
categoricalColumns)],
remainder="passthrough")
preprocessorForAllColumns = ColumnTransformer(transformers=[('cat', categorical_transformer, categoricalColumns),
('num',numerical_transformer,numericalColumns)],
remainder="passthrough")
```
Machine learning algorithms cannot use simple text. We must convert the data from text to a number. Therefore, for each string that is a class we assign a label that is a number. For example, in the customer churn data set, the CHURNRISK output label is classified as high, medium, or low and is assigned labels 0, 1, or 2. We use the [LabelEncoder](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelEncoder.html?highlight=labelencoder#sklearn.preprocessing.LabelEncoder) class provided by Sklearn for this.
```
# prepare data frame for splitting data into train and test datasets
features = []
features = df_churn_pd.drop(['CHURNRISK'], axis=1)
label_churn = pd.DataFrame(df_churn_pd, columns = ['CHURNRISK'])
label_encoder = LabelEncoder()
label = df_churn_pd['CHURNRISK']
label = label_encoder.fit_transform(label)
print("Encoded value of Churnrisk after applying label encoder : " + str(label))
```
### These are some of the popular preprocessing steps that are applied on the data sets. Look at [Data Processing in detail](https://developer.ibm.com/articles/data-preprocessing-in-detail/) for more information
```
area = 75
x = df_churn_pd['ESTINCOME']
y = df_churn_pd['DAYSSINCELASTTRADE']
z = df_churn_pd['TOTALDOLLARVALUETRADED']
pop_a = mpatches.Patch(color='#BB6B5A', label='High')
pop_b = mpatches.Patch(color='#E5E88B', label='Medium')
pop_c = mpatches.Patch(color='#8CCB9B', label='Low')
def colormap(risk_list):
cols=[]
for l in risk_list:
if l==0:
cols.append('#BB6B5A')
elif l==2:
cols.append('#E5E88B')
elif l==1:
cols.append('#8CCB9B')
return cols
fig = plt.figure(figsize=(12,6))
fig.suptitle('2D and 3D view of churnrisk data')
# First subplot
ax = fig.add_subplot(1, 2,1)
ax.scatter(x, y, alpha=0.8, c=colormap(label), s= area)
ax.set_ylabel('DAYS SINCE LAST TRADE')
ax.set_xlabel('ESTIMATED INCOME')
plt.legend(handles=[pop_a,pop_b,pop_c])
# Second subplot
ax = fig.add_subplot(1,2,2, projection='3d')
ax.scatter(z, x, y, c=colormap(label), marker='o')
ax.set_xlabel('TOTAL DOLLAR VALUE TRADED')
ax.set_ylabel('ESTIMATED INCOME')
ax.set_zlabel('DAYS SINCE LAST TRADE')
plt.legend(handles=[pop_a,pop_b,pop_c])
plt.show()
```
<a id="split_data"></a>
## 4. Split data into test and train
[Top](#top)
Scikit-learn provides in built API to split the original dataset into train and test datasets. random_state is set to a number to be able to reproduce the same data split combination through multiple runs.
[Split arrays or matrices into random train and test subsets](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html)
```
X_train, X_test, y_train, y_test = train_test_split(features,label , random_state=0)
print("Dimensions of datasets that will be used for training : Input features"+str(X_train.shape)+
" Output label" + str(y_train.shape))
print("Dimensions of datasets that will be used for testing : Input features"+str(X_test.shape)+
" Output label" + str(y_test.shape))
```
<a id="helper_methods"></a>
## 5. Helper methods for graph generation
[Top](#top)
```
def colormap(risk_list):
cols=[]
for l in risk_list:
if l==0:
cols.append('#BB6B5A')
elif l==2:
cols.append('#E5E88B')
elif l==1:
cols.append('#8CCB9B')
return cols
def two_d_compare(y_test,y_pred,model_name):
#y_pred = label_encoder.fit_transform(y_pred)
#y_test = label_encoder.fit_transform(y_test)
area = (12 * np.random.rand(40))**2
plt.subplots(ncols=2, figsize=(10,4))
plt.suptitle('Actual vs Predicted data : ' +model_name + '. Accuracy : %.2f' % accuracy_score(y_test, y_pred))
plt.subplot(121)
plt.scatter(X_test['ESTINCOME'], X_test['DAYSSINCELASTTRADE'], alpha=0.8, c=colormap(y_test))
plt.title('Actual')
plt.legend(handles=[pop_a,pop_b,pop_c])
plt.subplot(122)
plt.scatter(X_test['ESTINCOME'], X_test['DAYSSINCELASTTRADE'],alpha=0.8, c=colormap(y_pred))
plt.title('Predicted')
plt.legend(handles=[pop_a,pop_b,pop_c])
plt.show()
x = X_test['TOTALDOLLARVALUETRADED']
y = X_test['ESTINCOME']
z = X_test['DAYSSINCELASTTRADE']
pop_a = mpatches.Patch(color='#BB6B5A', label='High')
pop_b = mpatches.Patch(color='#E5E88B', label='Medium')
pop_c = mpatches.Patch(color='#8CCB9B', label='Low')
def three_d_compare(y_test,y_pred,model_name):
fig = plt.figure(figsize=(12,10))
fig.suptitle('Actual vs Predicted (3D) data : ' +model_name + '. Accuracy : %.2f' % accuracy_score(y_test, y_pred))
ax = fig.add_subplot(121, projection='3d')
ax.scatter(x, y, z, c=colormap(y_test), marker='o')
ax.set_xlabel('TOTAL DOLLAR VALUE TRADED')
ax.set_ylabel('ESTIMATED INCOME')
ax.set_zlabel('DAYS SINCE LAST TRADE')
plt.legend(handles=[pop_a,pop_b,pop_c])
plt.title('Actual')
ax = fig.add_subplot(122, projection='3d')
ax.scatter(x, y, z, c=colormap(y_pred), marker='o')
ax.set_xlabel('TOTAL DOLLAR VALUE TRADED')
ax.set_ylabel('ESTIMATED INCOME')
ax.set_zlabel('DAYS SINCE LAST TRADE')
plt.legend(handles=[pop_a,pop_b,pop_c])
plt.title('Predicted')
plt.show()
def model_metrics(y_test,y_pred):
print("Decoded values of Churnrisk after applying inverse of label encoder : " + str(np.unique(y_pred)))
skplt.metrics.plot_confusion_matrix(y_test,y_pred,text_fontsize="small",cmap='Greens',figsize=(6,4))
plt.show()
print("The classification report for the model : \n\n"+ classification_report(y_test, y_pred))
```
<a id="prepare_model"></a>
## 6. Prepare Random Forest classification model
[Top](#top)
We instantiate a decision-tree based classification algorithm, namely, RandomForestClassifier. Next we define a pipeline to chain together the various transformers and estimators defined during the data preparation step before.
Scikit-learn provides APIs that make it easier to combine multiple algorithms into a single pipeline.
We fit the pipeline to training data and apply the trained model to transform test data and generate churn risk class prediction.
[Understanding Random Forest Classifier](https://towardsdatascience.com/understanding-random-forest-58381e0602d2)
```
from sklearn.ensemble import RandomForestClassifier
model_name = "Random Forest Classifier"
randomForestClassifier = RandomForestClassifier(n_estimators=100, max_depth=2,random_state=0)
```
Pipelines are a convenient way of designing your data processing in a machine learning flow. The following code example shows how pipelines are set up using sklearn.
Read more [Here](https://scikit-learn.org/stable/modules/classes.html?highlight=pipeline#module-sklearn.pipeline)
```
rfc_model = Pipeline(steps=[('preprocessorAll',preprocessorForAllColumns),('classifier', randomForestClassifier)])
```
<a id="train_model"></a>
## 7. Train Random Forest classification model
[Top](#top)
```
# Build models
rfc_model.fit(X_train,y_train)
```
<a id="test_model"></a>
## 8. Test Random Forest classification model
[Top](#top)
```
y_pred_rfc = rfc_model.predict(X_test)
```
<a id="evaluate_model"></a>
## 9. Evaluate Random Forest classification model
[Top](#top)
### Model results
In a supervised classification problem such as churn risk classification, we have a true output and a model-generated predicted output for each data point. For this reason, the results for each data point can be assigned to one of four categories:
1. True Positive (TP) - label is positive and prediction is also positive
2. True Negative (TN) - label is negative and prediction is also negative
3. False Positive (FP) - label is negative but prediction is positive
4. False Negative (FN) - label is positive but prediction is negative
These four numbers are the building blocks for most classifier evaluation metrics. A fundamental point when considering classifier evaluation is that pure accuracy (i.e. was the prediction correct or incorrect) is not generally a good metric. The reason for this is because a dataset may be highly unbalanced. For example, if a model is designed to predict fraud from a dataset where 95% of the data points are not fraud and 5% of the data points are fraud, then a naive classifier that predicts not fraud, regardless of input, will be 95% accurate. For this reason, metrics like precision and recall are typically used because they take into account the type of error. In most applications there is some desired balance between precision and recall, which can be captured by combining the two into a single metric, called the F-measure.
```
two_d_compare(y_test,y_pred_rfc,model_name)
#three_d_compare(y_test,y_pred_rfc,model_name)
```
### Confusion matrix
In the graph below we have printed a confusion matrix and a self-explanotary classification report.
The confusion matrix shows that, 42 mediums were wrongly predicted as high, 2 mediums were wrongly predicted as low and 52 mediums were accurately predicted as mediums.
```
y_test = label_encoder.inverse_transform(y_test)
y_pred_rfc = label_encoder.inverse_transform(y_pred_rfc)
model_metrics(y_test,y_pred_rfc)
```
[Precision Recall Fscore support](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.precision_recall_fscore_support.html)
[Understanding the Confusion Matrix](https://towardsdatascience.com/confusion-matrix-for-your-multi-class-machine-learning-model-ff9aa3bf7826)
### Comparative study
In the bar chart below, we have compared the random forest classification algorithm output classes against the actual values.
```
uniqueValues, occurCount = np.unique(y_test, return_counts=True)
frequency_actual = (occurCount[0],occurCount[2],occurCount[1])
uniqueValues, occurCount = np.unique(y_pred_rfc, return_counts=True)
frequency_predicted_rfc = (occurCount[0],occurCount[2],occurCount[1])
n_groups = 3
fig, ax = plt.subplots(figsize=(10,5))
index = np.arange(n_groups)
bar_width = 0.1
opacity = 0.8
rects1 = plt.bar(index, frequency_actual, bar_width,
alpha=opacity,
color='g',
label='Actual')
rects6 = plt.bar(index + bar_width, frequency_predicted_rfc, bar_width,
alpha=opacity,
color='purple',
label='Random Forest - Predicted')
plt.xlabel('Churn Risk')
plt.ylabel('Frequency')
plt.title('Actual vs Predicted frequency.')
plt.xticks(index + bar_width, ('High', 'Medium', 'Low'))
plt.legend()
plt.tight_layout()
plt.show()
```
<a id="model_knn"></a>
## 10. Build K-Nearest classification model
[Top](#top)
K number of nearest points around the data point to be predicted are taken into consideration. These K points at this time, already belong to a class. The data point under consideration, is said to belong to the class with which most number of points from these k points belong to.
```
from sklearn.neighbors import KNeighborsClassifier
model_name = "K-Nearest Neighbor Classifier"
knnClassifier = KNeighborsClassifier(n_neighbors = 5, metric='minkowski', p=2)
knn_model = Pipeline(steps=[('preprocessorAll',preprocessorForAllColumns),('classifier', knnClassifier)])
knn_model.fit(X_train,y_train)
y_pred_knn = knn_model.predict(X_test)
y_test = label_encoder.transform(y_test)
two_d_compare(y_test,y_pred_knn,model_name)
y_test = label_encoder.inverse_transform(y_test)
y_pred_knn = label_encoder.inverse_transform(y_pred_knn)
model_metrics(y_test,y_pred_knn)
```
<a id="compare_classification"></a>
## 11. Comparative study of both classification algorithms.
[Top](#top)
```
uniqueValues, occurCount = np.unique(y_test, return_counts=True)
frequency_actual = (occurCount[0],occurCount[2],occurCount[1])
uniqueValues, occurCount = np.unique(y_pred_rfc, return_counts=True)
frequency_predicted_rfc = (occurCount[0],occurCount[2],occurCount[1])
uniqueValues, occurCount = np.unique(y_pred_knn, return_counts=True)
frequency_predicted_knn = (occurCount[0],occurCount[2],occurCount[1])
n_groups = 3
fig, ax = plt.subplots(figsize=(10,5))
index = np.arange(n_groups)
bar_width = 0.1
opacity = 0.8
rects1 = plt.bar(index, frequency_actual, bar_width,
alpha=opacity,
color='g',
label='Actual')
rects6 = plt.bar(index + bar_width*2, frequency_predicted_rfc, bar_width,
alpha=opacity,
color='purple',
label='Random Forest - Predicted')
rects4 = plt.bar(index + bar_width*4, frequency_predicted_knn, bar_width,
alpha=opacity,
color='b',
label='K-Nearest Neighbor - Predicted')
plt.xlabel('Churn Risk')
plt.ylabel('Frequency')
plt.title('Actual vs Predicted frequency.')
plt.xticks(index + bar_width, ('High', 'Medium', 'Low'))
plt.legend()
plt.tight_layout()
plt.show()
```
Until evaluation provides satisfactory scores, you would repeat the data preprocessing through evaluating steps by tuning what are called the hyperparameters.
[Choosing the right estimator](https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html)
### For a comparative study of some of the current most popular algorithms Please refer to this [tutorial](https://developer.ibm.com/tutorials/learn-classification-algorithms-using-python-and-scikit-learn/)
<p><font size=-1 color=gray>
© Copyright 2019 IBM Corp. All Rights Reserved.
<p>
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file
except in compliance with the License. You may obtain a copy of the License at
https://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the
License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either
express or implied. See the License for the specific language governing permissions and
limitations under the License.
</font></p>
| github_jupyter |
```
from bs4 import BeautifulSoup as bs
from splinter import Browser
import pandas as pd
with Browser("chrome") as browser:
# Visit URL
url = "https://mars.nasa.gov/news/"
browser.visit(url)
browser.fill('search', 'splinter - python acceptance testing for web applications')
# Find and click the 'search' button
button = browser.find_by_css('input.search_submit')
print(button[0])
# Interact with elements
button[0].click()
if browser.is_text_present('There are no items matching these criteria.'):
print("Yes, the official website was found!")
else:
print("No, it wasn't found... We need to improve our SEO techniques")
#Scrape the [NASA Mars News Site](https://mars.nasa.gov/news/) and collect the latest News Title and Paragraph Text. Assign the text to variables that you can reference later.
#```python
# Example:
news_title = "NASA's Next Mars Mission to Investigate Interior of Red Planet"
news_p = "Preparation of NASA's next spacecraft to Mars, InSight, has ramped up this summer, on course for launch next May from Vandenberg Air Force Base in central California -- the first interplanetary launch in history from America's West Coast."
with Browser("chrome") as browser:
url = "https://mars.nasa.gov/news/"
browser.visit(url)
html = bs(browser.html, 'html.parser')
body = html.body
# body.strippedtext
# print(body.a)
print(body.find_all("div", class_='content_title')[1].getText())
# titles = body.find_all("div", class_='content_title')
# first = titles[1].getText()
# print(first)
# Use splinter to navigate the site and find the image url for the current Featured Mars Image and
#assign the url string to a variable called `featured_image_url`.
# * Make sure to find the image url to the full size `.jpg` image.
# * Make sure to save a complete url string for this image.
# ```python
# # Example:
# featured_image_url = 'https://www.jpl.nasa.gov/spaceimages/images/largesize/PIA16225_hires.jpg'
base_url = "https://www.jpl.nasa.gov"
search_url = '/spaceimages/?search=&category=Mars'
url = base_url + search_url
featured_image_url = None
with Browser("chrome") as browser:
browser.visit(url)
image = browser.find_by_id('full_image')[0]
featured_image_url = base_url + image['data-fancybox-href']
print(featured_image_url)
#Visit the Mars Weather twitter account [here](https://twitter.com/marswxreport?lang=en) and
#scrape the latest Mars weather tweet from the page. Save the tweet text for the weather
#report as a variable called `mars_weather`.
#Note: Be sure you are not signed in to twitter, or scraping may become more difficult.**
import time
with Browser("chrome") as browser:
url_weather = "https://twitter.com/marswxreport?lang=en"
browser.visit(url_weather)
html_weather = browser.html
time.sleep(5)
soup = bs(html_weather, "html.parser")
main = soup.main
temp = main.find_all('section', attrs={"aria-labelledby": "accessible-list-0"})
elements = soup.find_all("section", class_="css-1dbjc4n")
for e in elements:
print(e)
print(temp.text)
print(temp[0])
# url= "https://astrogeology.usgs.gov/search/results?q=hemisphere+enhanced&k1=target&v1=Mars"
# with Browser("chrome") as browser:
# browser.visit(url)
# html = browser.html
# soup = bs(html, 'html.parser')
# xpath = "//div[@class='description']//a[@class='itemLink product-item']/h3"
# results = browser.find_by_xpath(xpath)
# hemisphere_image_urls = []
# for i in range(4):
# html = browser.html
# soup = bs(html, 'html.parser')
# # find the new Splinter elements
# results = browser.find_by_xpath(xpath)
# # save name of the hemisphere
# header = results[i].html
# # go to hemisphere details page
# details_link = results[i]
# details_link.click()
# html = browser.html
# soup = bs(html, 'html.parser')
# # Save the image url
# hemisphere_image_urls.append({"title": header, "image_url": soup.find("div", class_="downloads").a["href"]})
# # Go back to the original page
# browser.back()
# print(hemisphere_image_urls)
#Visit the Mars Facts webpage [here](https://space-facts.com/mars/) and use Pandas to scrape the table
#containing facts about the planet including Diameter, Mass, etc.
url = "https://space-facts.com/mars/"
data = pd.read_html(url)
df = data[0]
df.columns = ['Description', 'Value']
df.set_index('Description', inplace=True)
mars_html_table = df.to_html()
print(df)
#Use Pandas to convert the data to a HTML table string.
# * Visit the USGS Astrogeology site [here](https://astrogeology.usgs.gov/search/results?q=hemisphere+enhanced&k1=target&v1=Mars)
# to obtain high resolution images for each of Mar's hemispheres.
# * You will need to click each of the links to the hemispheres in order to find
# the image url to the full resolution image.
# * Save both the image url string for the full resolution hemisphere image, and
# the Hemisphere title containing the hemisphere name. Use a Python dictionary to store
#the data using the keys `img_url` and `title`.
# * Append the dictionary with the image url string and the hemisphere title to a list.
# This list will contain one dictionary for each hemisphere.
# ```python
# # Example:
# hemisphere_image_urls = [
# {"title": "Valles Marineris Hemisphere", "img_url": "..."},
# {"title": "Cerberus Hemisphere", "img_url": "..."},
# {"title": "Schiaparelli Hemisphere", "img_url": "..."},
# {"title": "Syrtis Major Hemisphere", "img_url": "..."},
# ]
# ```
url= "https://astrogeology.usgs.gov/search/results?q=hemisphere+enhanced&k1=target&v1=Mars"
with Browser("chrome") as browser:
browser.visit(url)
html = browser.html
soup = bs(html, 'html.parser')
xpath = "//div[@class='description']//a[@class='itemLink product-item']/h3"
results = browser.find_by_xpath(xpath)
hemisphere_image_urls = []
for i in range(4):
html = browser.html
soup = bs(html, 'html.parser')
# find the new Splinter elements
results = browser.find_by_xpath(xpath)
# save name of the hemisphere
header = results[i].html
# go to hemisphere details page
details_link = results[i]
details_link.click()
html = browser.html
soup = bs(html, 'html.parser')
# Save the image url
hemisphere_image_urls.append({"title": header, "image_url": soup.find("div", class_="downloads").a["href"]})
# Go back to the original page
browser.back()
print(hemisphere_image_urls)
#to make it prettier
for i in hemisphere_image_urls: print(i)
```
| github_jupyter |
<small><small><i>
Introduction to Python - available from https://gitlab.erc.monash.edu.au/andrease/Python4Maths.git
The original version was written by Rajath Kumar and is available at https://github.com/rajathkumarmp/Python-Lectures.
The notes have been updated for Python 3 and amended for use in Monash University mathematics courses by [Andreas Ernst](http://users.monash.edu.au/~andreas)
</small></small></i>
# Python-Lectures
## Introduction
Python is a modern, robust, high level programming language. It is very easy to pick up even if you are completely new to programming.
Python, similar to other languages like matlab or R, is interpreted hence runs slowly compared to C++, Fortran or Java. However writing programs in Python is very quick. Python has a very large collection of libraries for everything from scientific computing to web services. It caters for object oriented and functional programming with module system that allows large and complex applications to be developed in Python.
These lectures are using jupyter notebooks which mix Python code with documentation. The python notebooks can be run on a webserver or stand-alone on a computer.
To give an indication of what Python code looks like, here is a simple bit of code that defines a set $N=\{1,3,4,5,7\}$ and calculates the sum of the squared elements of this set: $$\sum_{i\in N} i^2=100$$
```
N={1,3,4,5,7,8}
print('The sum of ∑_i∈N i*i =',sum( i**2 for i in N ) )
```
## Contents
This course is broken up into a number of notebooks (chapters).
* [00](00.ipynb) This introduction with additional information below on how to get started in running python
* [01](01.ipynb) Basic data types and operations (numbers, strings)
* [02](02.ipynb) String manipulation
* [03](03.ipynb) Data structures: Lists and Tuples
* [04](04.ipynb) Data structures (continued): dictionaries
* [05](05.ipynb) Control statements: if, for, while, try statements
* [06](06.ipynb) Functions
* [07](07.ipynb) Classes and basic object oriented programming
* [08](08.ipynb) Scipy: libraries for arrays (matrices) and plotting
* [09](09.ipynb) Mixed Integer Linear Programming using the mymip library.
* [10](10.ipynb) Networks and graphs under python - a very brief introduction
* [11](11.ipynb) Using the numba library for fast numerical computing.
This is a tutorial style introduction to Python. For a quick reminder / summary of Python syntax the following [Quick Reference Card](http://www.cs.put.poznan.pl/csobaniec/software/python/py-qrc.html) may be useful. A longer and more detailed tutorial style introduction to python is available from the python site at: https://docs.python.org/3/tutorial/
## Installation
### Loging into the web server
The easiest way to run this and other notebooks for staff and students at Monash University is to log into the Jupyter server at [https://sci-web17-v01.ocio.monash.edu.au/hub](https://sci-web17-v01.ocio.monash.edu.au/hub). The steps for running notebooks are:
* Log in using your monash email address. The first time you log in an empty account will automatically be set up for you.
* Press the start button (if prompted by the system)
* Use the menu of the jupyter system to upload a .ipynb python notebook file or to start a new notebook.
### Installing
Python runs on windows, linux, mac and other environments. There are many python distributions available. However the recommended way to install python under Microsoft Windows or Linux is to use the Anaconda distribution available at [https://www.continuum.io/downloads](https://www.continuum.io/downloads). Make sure to get the Python *3.6* version, not 2.7. This distribution comes with the [SciPy](https://www.scipy.org/) collection of scientific python tools as well as the iron python notebook. For developing python code without notebooks consider using [spyder](https://github.com/spyder-ide/spyder) (also included with Anaconda)
To open a notebook with anaconda installed, from the terminal run:
ipython notebook
Note that for the Monash University optimisation course additional modules relating to the commercial optimisation library [CPLEX](http://www-01.ibm.com/software/commerce/optimization/cplex-optimizer/index.html) and possibly [Gurobi](http://www.gurobi.com/) will be used. These libraries are not available as part of any standard distribution but are available under academic licence. Cplex is included on the [Monash server](https://sci-web17-v01.ocio.monash.edu.au/hub).
## How to learn from this resource?
Download all the notebooks from Moodle or https://gitlab.erc.monash.edu.au/andrease/Python4Maths.git
Upload them to the monash server and lauch them or launch ipython notebook from the folder which contains the notebooks. Open each one of them
Cell > All Output > Clear
This will clear all the outputs and now you can understand each statement and learn interactively.
## License
This work is licensed under the Creative Commons Attribution 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by/3.0/
| github_jupyter |
# Overfitting demo
## Create a dataset based on a true sinusoidal relationship
Let's look at a synthetic dataset consisting of 30 points drawn from the sinusoid $y = \sin(4x)$:
```
import graphlab
import math
import random
import numpy
from matplotlib import pyplot as plt
%matplotlib inline
```
Create random values for x in interval [0,1)
```
random.seed(98103)
n = 30
x = graphlab.SArray([random.random() for i in range(n)]).sort()
```
Compute y
```
y = x.apply(lambda x: math.sin(4*x))
```
Add random Gaussian noise to y
```
random.seed(1)
e = graphlab.SArray([random.gauss(0,1.0/3.0) for i in range(n)])
y = y + e
```
### Put data into an SFrame to manipulate later
```
data = graphlab.SFrame({'X1':x,'Y':y})
data
```
### Create a function to plot the data, since we'll do it many times
```
def plot_data(data):
plt.plot(data['X1'],data['Y'],'k.')
plt.xlabel('x')
plt.ylabel('y')
plot_data(data)
```
## Define some useful polynomial regression functions
Define a function to create our features for a polynomial regression model of any degree:
```
def polynomial_features(data, deg):
data_copy=data.copy()
for i in range(1,deg):
data_copy['X'+str(i+1)]=data_copy['X'+str(i)]*data_copy['X1']
return data_copy
```
Define a function to fit a polynomial linear regression model of degree "deg" to the data in "data":
```
def polynomial_regression(data, deg):
model = graphlab.linear_regression.create(polynomial_features(data,deg),
target='Y', l2_penalty=0.,l1_penalty=0.,
validation_set=None,verbose=False)
return model
```
Define function to plot data and predictions made, since we are going to use it many times.
```
def plot_poly_predictions(data, model):
plot_data(data)
# Get the degree of the polynomial
deg = len(model.coefficients['value'])-1
# Create 200 points in the x axis and compute the predicted value for each point
x_pred = graphlab.SFrame({'X1':[i/200.0 for i in range(200)]})
y_pred = model.predict(polynomial_features(x_pred,deg))
# plot predictions
plt.plot(x_pred['X1'], y_pred, 'g-', label='degree ' + str(deg) + ' fit')
plt.legend(loc='upper left')
plt.axis([0,1,-1.5,2])
```
Create a function that prints the polynomial coefficients in a pretty way :)
```
def print_coefficients(model):
# Get the degree of the polynomial
deg = len(model.coefficients['value'])-1
# Get learned parameters as a list
w = list(model.coefficients['value'])
# Numpy has a nifty function to print out polynomials in a pretty way
# (We'll use it, but it needs the parameters in the reverse order)
print 'Learned polynomial for degree ' + str(deg) + ':'
w.reverse()
print numpy.poly1d(w)
```
## Fit a degree-2 polynomial
Fit our degree-2 polynomial to the data generated above:
```
model = polynomial_regression(data, deg=2)
```
Inspect learned parameters
```
print_coefficients(model)
```
Form and plot our predictions along a grid of x values:
```
plot_poly_predictions(data,model)
```
## Fit a degree-4 polynomial
```
model = polynomial_regression(data, deg=4)
print_coefficients(model)
plot_poly_predictions(data,model)
```
## Fit a degree-16 polynomial
```
model = polynomial_regression(data, deg=16)
print_coefficients(model)
```
###Woah!!!! Those coefficients are *crazy*! On the order of 10^6.
```
plot_poly_predictions(data,model)
```
### Above: Fit looks pretty wild, too. Here's a clear example of how overfitting is associated with very large magnitude estimated coefficients.
#
#
#
#
# Ridge Regression
Ridge regression aims to avoid overfitting by adding a cost to the RSS term of standard least squares that depends on the 2-norm of the coefficients $\|w\|$. The result is penalizing fits with large coefficients. The strength of this penalty, and thus the fit vs. model complexity balance, is controled by a parameter lambda (here called "L2_penalty").
Define our function to solve the ridge objective for a polynomial regression model of any degree:
```
def polynomial_ridge_regression(data, deg, l2_penalty):
model = graphlab.linear_regression.create(polynomial_features(data,deg),
target='Y', l2_penalty=l2_penalty,
validation_set=None,verbose=False)
return model
```
## Perform a ridge fit of a degree-16 polynomial using a *very* small penalty strength
```
model = polynomial_ridge_regression(data, deg=16, l2_penalty=1e-25)
print_coefficients(model)
plot_poly_predictions(data,model)
```
## Perform a ridge fit of a degree-16 polynomial using a very large penalty strength
```
model = polynomial_ridge_regression(data, deg=16, l2_penalty=100)
print_coefficients(model)
plot_poly_predictions(data,model)
```
## Let's look at fits for a sequence of increasing lambda values
```
for l2_penalty in [1e-25, 1e-10, 1e-6, 1e-3, 1e2]:
model = polynomial_ridge_regression(data, deg=16, l2_penalty=l2_penalty)
print 'lambda = %.2e' % l2_penalty
print_coefficients(model)
print '\n'
plt.figure()
plot_poly_predictions(data,model)
plt.title('Ridge, lambda = %.2e' % l2_penalty)
data
```
## Perform a ridge fit of a degree-16 polynomial using a "good" penalty strength
We will learn about cross validation later in this course as a way to select a good value of the tuning parameter (penalty strength) lambda. Here, we consider "leave one out" (LOO) cross validation, which one can show approximates average mean square error (MSE). As a result, choosing lambda to minimize the LOO error is equivalent to choosing lambda to minimize an approximation to average MSE.
```
# LOO cross validation -- return the average MSE
def loo(data, deg, l2_penalty_values):
# Create polynomial features
data = polynomial_features(data, deg)
# Create as many folds for cross validatation as number of data points
num_folds = len(data)
folds = graphlab.cross_validation.KFold(data,num_folds)
# for each value of l2_penalty, fit a model for each fold and compute average MSE
l2_penalty_mse = []
min_mse = None
best_l2_penalty = None
for l2_penalty in l2_penalty_values:
next_mse = 0.0
for train_set, validation_set in folds:
# train model
model = graphlab.linear_regression.create(train_set,target='Y',
l2_penalty=l2_penalty,
validation_set=None,verbose=False)
# predict on validation set
y_test_predicted = model.predict(validation_set)
# compute squared error
next_mse += ((y_test_predicted-validation_set['Y'])**2).sum()
# save squared error in list of MSE for each l2_penalty
next_mse = next_mse/num_folds
l2_penalty_mse.append(next_mse)
if min_mse is None or next_mse < min_mse:
min_mse = next_mse
best_l2_penalty = l2_penalty
return l2_penalty_mse,best_l2_penalty
```
Run LOO cross validation for "num" values of lambda, on a log scale
```
l2_penalty_values = numpy.logspace(-4, 10, num=10)
l2_penalty_mse,best_l2_penalty = loo(data, 16, l2_penalty_values)
```
Plot results of estimating LOO for each value of lambda
```
plt.plot(l2_penalty_values,l2_penalty_mse,'k-')
plt.xlabel('$\ell_2$ penalty')
plt.ylabel('LOO cross validation error')
plt.xscale('log')
plt.yscale('log')
```
Find the value of lambda, $\lambda_{\mathrm{CV}}$, that minimizes the LOO cross validation error, and plot resulting fit
```
best_l2_penalty
model = polynomial_ridge_regression(data, deg=16, l2_penalty=best_l2_penalty)
print_coefficients(model)
plot_poly_predictions(data,model)
```
#
#
#
#
# Lasso Regression
Lasso regression jointly shrinks coefficients to avoid overfitting, and implicitly performs feature selection by setting some coefficients exactly to 0 for sufficiently large penalty strength lambda (here called "L1_penalty"). In particular, lasso takes the RSS term of standard least squares and adds a 1-norm cost of the coefficients $\|w\|$.
Define our function to solve the lasso objective for a polynomial regression model of any degree:
```
def polynomial_lasso_regression(data, deg, l1_penalty):
model = graphlab.linear_regression.create(polynomial_features(data,deg),
target='Y', l2_penalty=0.,
l1_penalty=l1_penalty,
validation_set=None,
solver='fista', verbose=False,
max_iterations=3000, convergence_threshold=1e-10)
return model
```
## Explore the lasso solution as a function of a few different penalty strengths
We refer to lambda in the lasso case below as "l1_penalty"
```
for l1_penalty in [0.0001, 0.01, 0.1, 10]:
model = polynomial_lasso_regression(data, deg=16, l1_penalty=l1_penalty)
print 'l1_penalty = %e' % l1_penalty
print 'number of nonzeros = %d' % (model.coefficients['value']).nnz()
print_coefficients(model)
print '\n'
plt.figure()
plot_poly_predictions(data,model)
plt.title('LASSO, lambda = %.2e, # nonzeros = %d' % (l1_penalty, (model.coefficients['value']).nnz()))
```
Above: We see that as lambda increases, we get sparser and sparser solutions. However, even for our non-sparse case for lambda=0.0001, the fit of our high-order polynomial is not too wild. This is because, like in ridge, coefficients included in the lasso solution are shrunk relative to those of the least squares (unregularized) solution. This leads to better behavior even without sparsity. Of course, as lambda goes to 0, the amount of this shrinkage decreases and the lasso solution approaches the (wild) least squares solution.
| github_jupyter |
# Gridworld

The Gridworld environment (inspired from Sutton and Barto, Reinforcement Learning: an Introduction) is represented in figure. The environment is a finite MDP in which states are represented by grid cells. The available actions are 4: left, right, up, down. Actions move the current state in the action direction and the associated reward is 0 for all actions. Exceptions are:
- Border cells: if the action brings the agent outside of the grid the agent state does not change and the agent receives a reward of -1.
- Good cells: $G_1$ and $G_2$ are special cells. For these cells each action brings the agent in state $G_1$' and $G_2$' respectively. The associated reward is +10 for going outside state $G_1$ and +5 for going outside state $G_2$.
- Bad cells: $B_1$ and $B_2$ are bad cells. For these cells the associated reward is -1 for all actions.
The goal of the activity is to calculate and represent visually the state values for the random policy, in which the agent selects each action with equal probability (1/4) in all states. The discount factor is assumed to be equal to 0.9.
## Solution
Imports:
```
from enum import Enum, auto
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg
from typing import Tuple
```
Visualization function:
```
# helper function
def vis_matrix(M, cmap=plt.cm.Blues):
fig, ax = plt.subplots()
ax.matshow(M, cmap=cmap)
for i in range(M.shape[0]):
for j in range(M.shape[1]):
c = M[j, i]
ax.text(i, j, "%.2f" % c, va="center", ha="center")
# Define the actions
class Action(Enum):
UP = auto()
DOWN = auto()
LEFT = auto()
RIGHT = auto()
# Agent Policy, random
class Policy:
def __init__(self):
self._possible_actions = [action for action in Action]
self._action_probs = {
a: 1 / len(self._possible_actions) for a in self._possible_actions
}
def __call__(self, state: Tuple[int, int], action: Action) -> float:
"""
Returns the action probability
"""
assert action in self._possible_actions
# state is unused for this policy
return self._action_probs[action]
class Environment:
def __init__(self):
self.grid_width = 5
self.grid_height = 5
self._good_state1 = (0, 1)
self._good_state2 = (0, 3)
self._to_state1 = (4, 2)
self._to_state2 = (2, 3)
self._bad_state1 = (1, 1)
self._bad_state2 = (4, 4)
self._bad_states = [self._bad_state1, self._bad_state2]
self._good_states = [self._good_state1, self._good_state2]
self._to_states = [self._to_state1, self._to_state2]
self._good_rewards = [10, 5]
def step(self, state, action):
i, j = state
for good_state, reward, to_state in zip(
self._good_states, self._good_rewards, self._to_states
):
if (i, j) == good_state:
return (to_state, reward)
reward = 0
if state in self._bad_states:
reward = -1
if action == Action.LEFT:
j_next = max(j - 1, 0)
i_next = i
if j - 1 < 0:
reward = -1
elif action == Action.RIGHT:
j_next = min(j + 1, self.grid_width - 1)
i_next = i
if j + 1 > self.grid_width - 1:
reward = -1
elif action == Action.UP:
j_next = j
i_next = max(i - 1, 0)
if i - 1 < 0:
reward = -1
elif action == Action.DOWN:
j_next = j
i_next = min(i + 1, self.grid_height - 1)
if i + 1 > self.grid_height - 1:
reward = -1
else:
raise ValueError("Invalid action")
return ((i_next, j_next), reward)
```
Probability and reward matrix:
```
pi = Policy()
env = Environment()
# setup probability matrix and reward matrix
P = np.zeros((env.grid_width * env.grid_height, env.grid_width * env.grid_height))
R = np.zeros_like(P)
possible_actions = [action for action in Action]
# Loop for all states and fill up P and R
for i in range(env.grid_height):
for j in range(env.grid_width):
state = (i, j)
# loop for all action and setup P and R
for action in possible_actions:
next_state, reward = env.step(state, action)
(i_next, j_next) = next_state
P[i * env.grid_width + j, i_next * env.grid_width + j_next] += pi(
state, action
)
# the reward depends only on the starting state and the final state
R[i * env.grid_width + j, i_next * env.grid_width + j_next] = reward
# check the correctness
assert((np.sum(P, axis=1) == 1).all())
# expected reward for each state
R_expected = np.sum(P * R, axis=1, keepdims=True)
# reshape the state values in a matrix
R_square = R_expected.reshape((env.grid_height,env.grid_width))
# Visualize
vis_matrix(R_square, cmap=plt.cm.Reds)
```
The previous figure is a color representation of the expected reward associated to each state considering the current policy. Notice the expected reward of bad states is exactly equal to -1. The expected reward of good states is exactly equal to 10 and 5 respectively.
```
# define the discount factor
gamma = 0.9
# Now it is possible to solve the Bellman Equation
A = np.eye(env.grid_width*env.grid_height) - gamma * P
B = R_expected
# solve using scipy linalg
V = linalg.solve(A, B)
# reshape the state values in a matrix
V_square = V.reshape((env.grid_height,env.grid_width))
# visualize results
vis_matrix(V_square, cmap=plt.cm.Reds)
```
Notice that the value of good states is less than the expected reward from those states. This is because landing states have an expected reward that is negative or because landing states are close to states for which the reward is negative. You can notice that the state with higher value is state $G_1$, followed by state $G_2$. It is also interesting to notice the high value of state in position (1, 2), being close to good states.
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.